Chapter 16 Circumference Of Circle
Wbbse Class 9 Maths Chapter 16 Definitions:
1. Circle: When a curved line rotates around a point keeping a fixed distance, then the figure formed by its rotation is called a circle.
2. Circumference: The curved line which forms the circle is called the circumference.
3. Centre of a circle: The point inside a circle from which the distance between any point on the circumference is equal, is called the center of the circle.
4. Radius: The distance between the center and the circumference is called the radius.
5. Diameter: The straight line passing through the center which touches the circumference on both sides is called the diameter.
6. Arc: A part of the circumference is called arc.
7. Chord: The straight line joining any two points on the circumference is called a chord. The longest chord is the diameter.
8. Cyclic Quadrilateral: The quadrilateral whose vertices lie on the circumference of a circle is called a cyclic quadrilateral.
9. Segment: A figure formed by an arc and a chord of a circle is called a segment.
Read and Learn More WBBSE Solutions For Class 9 Maths
Wbbse Class 9 Maths Chapter 16 Memorable Facts:
1. Infinite number of circles can be drawn from a point.
2. Infinite number of circles can be drawn from two points.
3. Only one circle can be drawn from three non-collinear points.
4. It is not possible to draw a circle from more than three points. If it is, then those points are called the same circle points.
5. There are an infinite number of diameters in a circle and all diameters are equal in length.
6. There are an infinite number of radii in a circle and all radii are equal in length.”
7. The part of a circle that is enclosed on one side by diameter and on the other by circumference is called a semi-circle.
8. Angle in a semi-circle is a right angle.
9. The greatest chord of a circle is its diameter.
10. All angles of the same segment of a circle are equal.
Wbbse Class 9 Maths Chapter 16 Formulae:
1. Circumference of a circle = 2πr=πd units
2. Perimeter of a semicircle = (x+2) units
3. Circumference of a semi-circle = πr units

Wbbse Class 9 Maths Chapter 16 Circumference Of Circle Solutions
Chapter 16 Circumference Of Circle Exercise 16
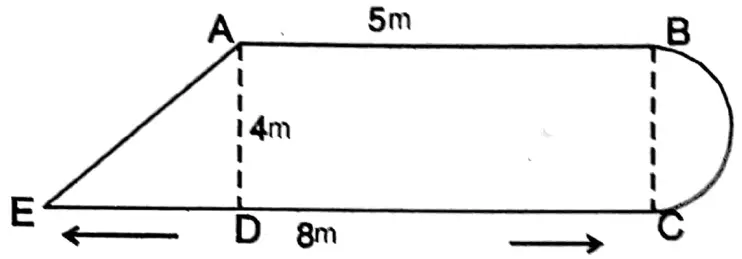
Question1. Let us calculate the perimeter of each of the following Images
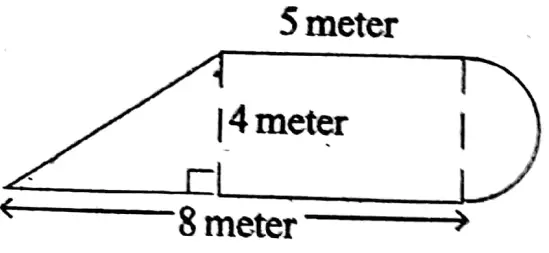
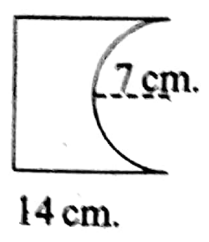
Wbbse Class 9 Circumference Of Circle Exercise Solutions
Solution: DE = (CE-CD) = (8-5) m = 31m
In right-angled ΔADE
\(\begin{aligned}& A E=\sqrt{A D^2+D E^2} \\
& =\sqrt{(4)^2+(3)^2} \mathrm{~m} \\
& =\sqrt{16+9} \mathrm{~m} \\
& =\sqrt{25} \mathrm{~m} \\
& =5 \mathrm{~m}
\end{aligned}\)
The perimeter of the semi-circle = πr2
\(\begin{aligned}& =\frac{22}{7} \times \frac{4}{2} \mathrm{~m} \\
& =\frac{44}{7} \mathrm{~m} \\
& =6 \frac{2}{7} \mathrm{~m}
\end{aligned}\)
∴ Perimeter of 1st Image = (5+5+8+\(6 \frac{2}{7}\))m = \(24 \frac{2}{7}\) m
2. Perimeter of a semi-circle = πr
= \(\frac{22}{7} \times 7\) cm = 22 cm
∴ Perimeter of 2nd Image = (14+14 +14 +22) cm = 64 cm.
Class 9 Wbbse Maths Circumference Of Circle Solved Problems
Question 2. Let us calculate how long the wire will be taken to make a circular ring of radius 35 meters.
Solution: Circular ring of radius = 35 m
∴ Circumference = 2πr
= \(2 \times \frac{22}{7} \times 35 \mathrm{~m}\)= 220 m
∴ 220 m is the required length of the wire.
Wbbse Class 9 Maths Chapter 16 Question 3.
The radius of a wheel of a train is 35 meters. If It makes 450 revolutions per minute, let us calculate the velocity of the train per hour.
Solution: The radius of the wheel of the train is = 0.35 m.
∴ Circumference of wheel = 2πr
= \(2 \times \frac{22}{7} \times \frac{35}{100} \mathrm{~m}\) = 2.2 m
∵ The wheel of the train moves in 1 minute = 450 revolution
∴ The wheel moves in 60 minutes = 60 x 450 revolutions.
∴ Wheel moves in 1 hr = 27000 revolution
∵ Wheel moves in 1 revolution = 2.2 m
∴ Wheel moves in 27000 revolution = 27000 × 2.2 m = 59400 m = 59.4 km
∴ Speed = 59.4 km/hr.
Wbbse Class 9 Maths Chapter 16 Circumference Of Circle Notes
Question 4. The radius of the circular field of the village Amadpur is 280 meters. Chaltall wants to go around the field by walking with a speed 5.5 km/hour, let us calculate how long time will be taken by Chaltall to complete one revolution.
Solution:
Given
The radius of the circular field of the village Amadpur is 280 meters. Chaltall wants to go around the field by walking with a speed 5.5 km/hour
Radius of a circular field = 280 m.
∴ Circumference = 2πr = \(2 \times \frac{22}{7} \times \frac{35}{100} \mathrm{~m}\) = 1760 m
5.5 km 5.5 x 1000 m = 5500 m
1 hr = 60 minute = 60 x 60 sec = 3600 sec
∵ Chaitali goes 5500 m in 3600 sec
∴ She goes 1 m in \(\frac{3600}{5500}\) sec
∴ She goes 1760 m in \(\frac{3600}{5500} \times 1760\) sec
∴ She goes 1760 m in 1152 sec = 19 minutes 12 sec.
Wbbse Class 9 Maths Chapter 16 Question 5.
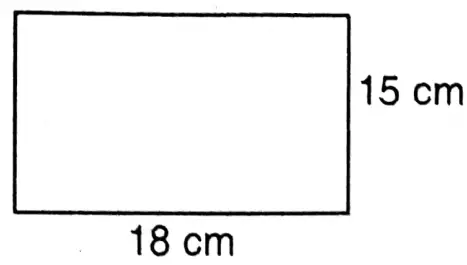
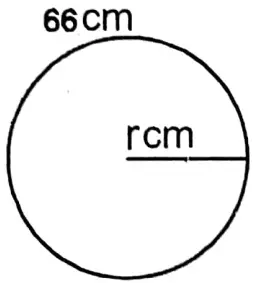
Tathagata bent a copper wire in the form of a rectangle whose length is 18 cm and breadth is 15 cm. I made a circle by bending this copper wire. Let us calculate the length of the radius of the circular copper wire.
Solution:
Given
Tathagata bent a copper wire in the form of a rectangle whose length is 18 cm and breadth is 15 cm. I made a circle by bending this copper wire.
Perimeter of the rectangle = 2(18+15) cm = 66 cm
If the wire is bent in form of a circle, its circumference is 66 cm.
Let the radius of the circle be r cm.
∴ Circumference of the circle = 2πr cm
\(\begin{aligned}& =2 \times \frac{22}{7} r \mathrm{~cm} \\
& =\frac{44 r}{7} \mathrm{~cm}
\end{aligned}\)
As for questions,
\(
\frac{44 r}{7}=66
or, r=\frac{66 \times 7}{44}
or, r=\frac{21}{2}=10.5\)
∴ Radius = 10.5 cm.
West Bengal Board Class 9 Circumference Of Circle Chapter Solutions
Question 6. The perimeter of a semi-circular field is 108 meters. Let us calculate the diameter of the field.
Solution:
Given
The perimeter of a semi-circular field is 108 meters.
Let the radius of the semi-circular field be r m.
∴ Perimeter of semi-circle = (πr+2r) m
\(\begin{aligned}& =r(\pi+2) m \\
& =r\left(\frac{22}{7}+2\right) m \\
& =r\left(\frac{22+14}{7}\right) m \\
& =\frac{36 r}{7} m
\end{aligned}\)
As for question,
\(\frac{36 r}{7}=108
or, r=\frac{108 \times 7}{36}\)
or, r = 21
∴ Diameter of the field = 2r m = 2 × 21 m = 42 m
Question 7. The difference between the circumference and the diameter of a wheel is 75 cm, let us calculate the length of the radius of this wheel.
Solution:
Given
The difference between the circumference and the diameter of a wheel is 75 cm,
Let the radius of the wheel be r cm.
∴ Circumference of the wheel 2πr cm
Diameter of the wheel = 2r cm
∴ Difference between the circumference and diameter = (2πr-2г) cm
\(\begin{aligned}& =2 r(\pi-1) \mathrm{cm} \\
& =2 r\left(\frac{22}{7}-1\right) \mathrm{cm} \\
& =2 r\left(\frac{22-7}{7}\right) \mathrm{cm} \\
& =2 r \times \frac{15}{7} \mathrm{~cm}
\end{aligned}\)
As for question,
\(2 r \times \frac{15}{7}=75
or, r=\frac{7-\times 7}{2 \times 15}
or, r=\frac{35}{2}\)
or, r = 17.5
∴ Radius = 17.5 cm.
Wbbse Class 9 Circumference Of Circle Important Questions
Question 8. In a race, Puja and Jakir start to compete from the same point and same time on a circular track of a length of diameter 56 meter. When Puja finishes the race at the competition by 10 revolutions, Jakir is one revolution behind. Let us calculate how many meters is the length of the race and by how many meters Puja beats Jakir.
Solution:
Given
In a race, Puja and Jakir start to compete from the same point and same time on a circular track of a length of diameter 56 meter. When Puja finishes the race at the competition by 10 revolutions, Jakir is one revolution behind.
Radius of track = \(\frac{56}{2} \mathrm{~m}\) = 28 m
∴ Circumference = 2πr = \(2 \times \frac{22}{7} \times 28 \mathrm{~m}\) = 176 m
∴ Length of the race = 10 x 176 m = 1760 m
& Puja beats Jakir by 176 m.
Ganit Prakash Class 9 Solutions Question 9.
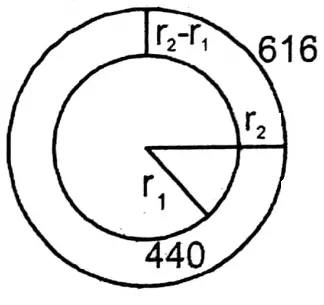
The perimeter of the borewell of our village is 440 cm. There is an equally wide stone parapet around this borewell. If the perimeter of the borewell with parapet is 616 cm, let us write by calculating how much is the width of the stone parapet.
Solution:
Given
The perimeter of the borewell of our village is 440 cm. There is an equally wide stone parapet around this borewell. If the perimeter of the borewell with parapet is 616 cm,
Let the radius of the (borewell) be r1 cm and the radius including the stone parapet be r2 cm.
∴ Circumference of the borewell = 2πr1 cm
∴ 2πr1 = 440 ……(1)
∴ Circumference of the borewell including the stone parapet = 2πr2 cm
∴ 2πr2 =616 ……(2)
Subtracting (1) from (2),
2πr2-2πr1 = 616-440
or, 2π(r2-r1) =176
or, r_2-r_1=\frac{176 \times 7}{2 \times 22}\)
or, r2 -r1 = 28
∴ Width of stone parapet is 28 cm.
Wbbse Class 9 Maths Circumference Of Circle Chapter 16
Question 10. Niyamat chacha of the village attaches the motor’s wheel with a machine’s wheel with a belt. The length of diameter of the motor wheel is 14 cm and the machine wheel is 94.5 cm. If the motor’s wheel revolves 27 times in a second then let us calculate how many times the machine’s wheel will revolve in an hour.
Solution:
Given
Niyamat chacha of the village attaches the motor’s wheel with a machine’s wheel with a belt. The length of diameter of the motor wheel is 14 cm and the machine wheel is 94.5 cm. If the motor’s wheel revolves 27 times in a secon
Radius of the wheel of motor (r) = \(\frac{14}{2}\) = 7cm
∴ Circumference of motor’s wheel = 2πr
= \(2 \times \frac{22}{7} \times 7 \mathrm{~cm}\) = 44cm
∴ In 1 revolution motor wheel moves 44 cm.
∵ In 27 revolutions it moves = 44 x 27 cm
∴ In 1 hour it moves = 3600 x 27 x 44 cm
Radius of the motor wheel = \(\frac{94.5}{2} \mathrm{~cm}\) = 47.25 cm
Circumference of the motor wheel = 2πr
= \(2 \times \frac{22}{7} \times \frac{4725}{100} \mathrm{~cm}\) = 297 cm
∴ The motor wheel can traverse a 297 cm distance in 1 revolution.
∴ The motor wheel can traverse 1 cm distance in \(\frac{1}{297}\) revolution
∴ The motor wheel can traverse a 3600×27 x 44 cm distance in \(\frac{1 \times 3600 \times 27 \times 44}{297}\) revolution.
∴ The motor wheel can traverse 3600 x 27 x 44 cm distance in 14400 revolution.
∴ In an hour the motor wheel will revolve 14400 times.
Question 11. The lengths of hour’s hand and minute’s hand are 8.4 cm and 14 cm respectively of our club clock. Let us calculate how much distance will be covered by each hand in a day.
Hints: Hour’s hand goes in 12 hours = \(2 \times \frac{22}{7} \times 8.4 \mathrm{~cm}\)
Minute’s hand goes in one hours = \(2 \times \frac{22}{7} \times 14 \mathrm{~cm}\)
Solution:
Given
The lengths of hour’s hand and minute’s hand are 8.4 cm and 14 cm respectively of our club clock.
Radius of hour hand (r) = 8.4 cm.
∴Hour’s hand will traverse distance in 12 hours = \(2 \times \frac{22}{7} \times 8.4 \mathrm{~cm}[/latex = 52.8 cm
∴ Hour’s hand will traverse distance in 1 hours = [latex]\frac{52.8}{12} \mathrm{~cm}\)
∴ Hour hand will move in a day (= 24 hours) twice = \(\frac{52.8}{12} \times 24 \mathrm{~cm}\)
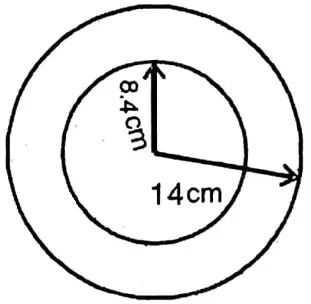
∵ Circumference = \(2 \times \frac{22}{7} \times 14 \mathrm{~cm}\) = 88 cm.
∴ The minute hand will moves in a day (= 24 here) 24 x 88 cm = 2112 cm.
∴ In a day the hour’s hand and minute’s hand will move 105.6 cm and 2112 cm respectively.
Question 12. The ratio of diameters of two circles which are drawn by me and my friend Mihir is □:□ It was found by calculating that the ratio of perimeters of two circles is □:□
Solution: If the ratio of diameter = x:y of two circles then the ratio of their perimeter (circumference) is also x:y.
Ganit Prakash Class 9 Solutions Question 13.
The time that Rahim takes to cover up by running a circular field is 40 seconds less when he goes from one end to another end diametrically. The velocity of Rahim is 90 meters per minute. Let us calculate the length of the diameter of the field.
Solution:
Given
The time that Rahim takes to cover up by running a circular field is 40 seconds less when he goes from one end to another end diametrically. The velocity of Rahim is 90 meters per minute.
Let the radius of the circular field be r m.
∴ Circumference of the circular field = 2πr m.
Diameter of the circular field = 2r m.
∵ Rahim can travel a 1m distance in \(\frac{60}{90}\)
∴ Rahim can travel 2πr m distance in \(\frac{2}{3} \times 2 \pi r \text { sec }\)
∴ Rahim can travel 2 r m distance in \(\frac{2}{3} \times 2 r\)
By the problem,
\(\frac{2}{3} \times 2 \pi r-\frac{2}{3} \times 2 r=40
or, \frac{2}{3} \times 2 r(\pi-1)=40
or, \frac{2}{3} \times 2 r\left(\frac{22}{7}-1\right)=40\)
\(or, \frac{2}{3} \times 2 r\left(\frac{22-7}{7}\right)=40
or, \frac{2}{3} \times 2 r \times \frac{15}{7}=40
or, r=\frac{40 \times 7 \times 3}{2 \times 2 \times 15}\)
or, r = 14
∴ Diameter of the field = 2r m = 2 x 14 m = 28 m.
Question 14. The ratio of perimeters of two circles is 2 : 3 and the difference of their length of radii is 2 cm. Let us calculate the lengths of diameters of the two circles.
Solution:
Given
The ratio of perimeters of two circles is 2 : 3 and the difference of their length of radii is 2 cm.
The radius of the smaller circle = r cm
∴ Radius of the larger circle = (r + 2) cm
∴ Radius of the smaller circle circle = 2πr cm and circumference of the larger circle = 2π(r+2) cm
B.T.P.,
2πг: 2π(г+2)=2:3
or, \frac{r}{r+2}=\frac{2}{3}\)
or, 3r = 2r+4
or, 3r – 2r=4
or, r = 4
∴ Diameter of the first circle = 2r cm
= 2 x 4 cm = 8 cm.
∴ Diameter of the second circle = 2(r + 2) cm
= 2(4+2) cm = 12 cm.
Ganit Prakash Class 9 Solutions Question 15.
The four maximum-sized circular plates are cut out of a brass plate of square size. Having an area of 196 sq. cm; let us calculate the circumference of each circular plate.
Solution:
Given
The four maximum-sized circular plates are cut out of a brass plate of square size. Having an area of 196 sq. cm
The area of the square plate is 196 sq. cm
∴ Length of each side = √196 cm = 14.cm
Diameter of each circle = \(=\frac{14}{2} \mathrm{~cm}\) = 7 cm
∴ The radius of the maximum-sized circular plate cut out of a square plate of side 7 cm will be 7 cm.
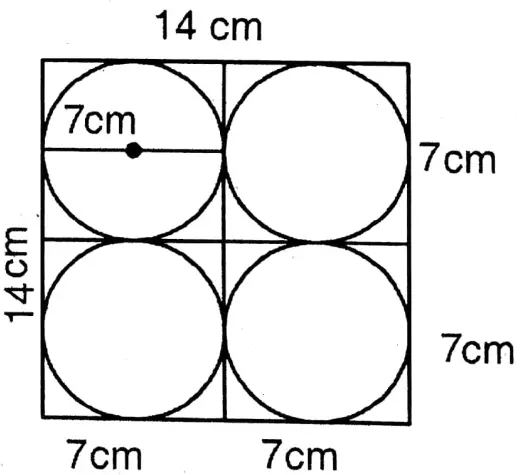
∴ Radius of each circular plate (r) = latex]\frac{7}{\dot{2}} \mathrm{~cm}[/latex]
∴ Circumference of each circular plate p = 2πr cm
= \(2 \times \frac{22}{7} \times \frac{7}{2} \mathrm{~cm}\) = 22 cm
Question 16. The time that Nashifer takes to cover up a circular field from one end to other end is 45 seconds less when he goes diametrically. Let us calculate the length of the diameter of this field.
Solution:
Given
The time that Nashifer takes to cover up a circular field from one end to other end is 45 seconds less when he goes diametrically.
Let the radius of the circular field r m
∴ Semi-circumference of the circular field = r m
Diameter of the circular field = 2r m
∴ Nashifer covers up 80 m distance in 60 sec
∴ Nashifer covers up 1 m distance in \(\frac{60}{80} \mathrm{sec}\)
∴ Nashifer covers up r m distance in \(\frac{3}{4} \times \pi r \sec\)
∴ Nashifer covers up 2r m distance in \(\frac{3}{4} \times 2 r\)
B.T.P.,
\(\frac{3}{4} \times \pi r-\frac{3}{4} \times 2 r=45
or, \frac{3}{4} r(\pi-2)=45\) \(\text { or, } \frac{3}{4} r\left(\frac{22}{7}-2\right)=45\) \(\text { or, } \frac{3}{4} r\left(\frac{22-14}{7}\right)=45\) \(\text { or, , } \frac{3}{4} r \times \frac{8}{7}=45\) \(\text { or, } r=\frac{45 \times 7 \times 4}{8 \times 3}\) \(\text { or, } r=\frac{105}{2}\)
Diameter of the field = 2r m
\(\begin{aligned}& =2 \times \frac{105}{2} \mathrm{~m} \\
& =105 \mathrm{~m}
\end{aligned}\)
Ganit Prakash Class 9 Solutions Question 17.
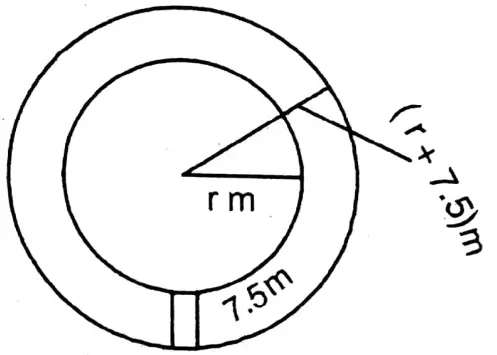
Mohim takes 46 seconds and 44 seconds respectively to go around along the outer and the inner edges of a circular path with 7 meters 5 dcm width by a cycle. Let us calculate the diameter of the circle along the inner edge of the path.
Solution:
Given
Mohim takes 46 seconds and 44 seconds respectively to go around along the outer and the inner edges of a circular path with 7 meters 5 dcm width by a cycle.
Let the inner radius of the circular path = r m
Width of the path = 7 m 5 dcm = 7.5 m
∴ The other radius of the circular path = (r+7.5) m
∴ Inner circumference = 2πr m
And other circumference = 2(r+7.5) m
To cover up 2π(r+7.5) m distance it takes 46 seconds
∴ To cover up 1 m distance it takes \(\frac{46}{2 \pi(r+7.5)} \text { seconds }\)
∴ To cover up 2πr m distance it takes \(\frac{46 \times 2 \pi r}{2 \pi(r+7.5)} \text { seconds }\)
B.T.P..
\(\begin{aligned}
& \frac{46 \times 2 \pi r}{2 \pi(r+7.5)}=44 \\
& \text { or, } \frac{46 r}{r+7.5}=44
\end{aligned}\)
or, 46r = 44r + 330
or, 46r- 44r330
or, 2r=330
∴ Diameter of the circle along the inner edge of the path = is 330 m. Ans.
Class 9 Ganit Prakash Solutions
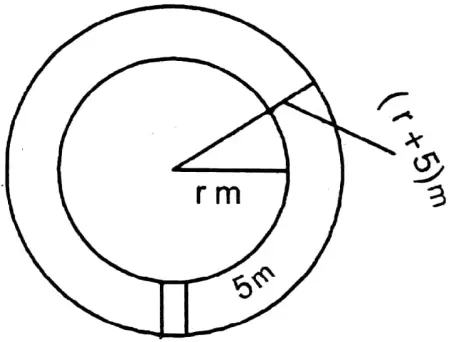
Question 18. The ratio of time taken by a cyclist to go around the outer and inner circumference of a circular path is 20: 19; if the path is 15 meters wide, let us calculate the length of the diameter of the inner circle.
Solution:
Given
The ratio of time taken by a cyclist to go around the outer and inner circumference of a circular path is 20: 19; if the path is 15 meters wide,
Width of the path = 5 m.
Let the inner radius of a circular path be r m and
the speed of the cycle is v m/second.
∴ The outer radius of the circular path = (r + 5) m
∴ The inner and outer circumferences of the path is 2r m and 2π(r+5) m respectively.
∴ Cycle covers up v m distance in 1 sec
∴ Cycle covers up 1 m distance in \(\frac{1}{v} \sec\)
∴ Cycle covers up 2πr m distance in \(\frac{2 \pi r}{v} \sec\)
∴ Cycle covers up, 2π(r+5) m distance in \(\frac{2 \pi(r+5)}{v} \sec\)
B. T. P.,
\(\frac{2 \pi\left(r+5\right)}{v}: \frac{2 \pi r}{v}=20: 19\) \(\text { or, } \frac{\frac{2 \pi(r+5)}{v}}{\frac{2 \pi r}{v}}=\frac{20}{19}\) \(\text { or, } \frac{2 \pi(r+5)}{v} \times \frac{v}{2 \pi r}=\frac{20}{19}\) \(\text { or, } \frac{r+5}{r}=\frac{20}{19}\)or, 20r = 19r+ 95
or, 20r – 19r = 95
or, r = 95
∴Length of the inner diameter of the path = 2r m
= 2 x 95 m 190 m.
Wbbse 9th Class Maths Circumference Of Circle Step By Step Solutions
Class 9 Maths Chapter 16 Circumference Of Circle Multiple Choice Questions
1. The ratio of the velocity of the hour’s hand and minute’s hand at a clock is
1. 1: 12
2. 12:1
3. 1:24
4. 24: 1
Solution: Let the radius of the clock be r unit.
∴ Circumference of the clock = 2πr unit.
∵ The hour’s hand in 12 hours covers up 2πr unit distance.
∴ The hour’s hand in 1 hours covers up \(\frac{2 \pi r}{12}\)
∵ The minute’s hand in 1 hour covers up 2πr unit distance.
∴ Rotio of the velocity of hour’s hand and minute’s hand = \(\frac{2 \pi r}{12}: 2 \pi r\)
\(\begin{aligned}& =\frac{1}{12}: 1 \\
& =\frac{1}{12} \times 12: 1 \times 12 \\
& =1: 12
\end{aligned}\)
∴ 1. 1: 12
Class 9 Ganit Prakash Solutions
2. Soma takes \(\frac{\pi x}{100}\) minutes to go one complete round of a circular path. Soma will take how much time for going around the park diametrically?
1. \(\frac{x}{200}\) minute
2. \(\frac{x}{100}\) minute
3. \(\frac{\pi}{100}\) minute
4. \(\frac{\pi}{200}\) minute
Solution: Let the radius of the circular park be r m.
∴ Circumference of the circular park = 2πr m and
Diameter of the circular park = 2r m
∴ Soma will take to cover up 2πr m distance \(\frac{\pi x}{100}\) minute
∴ Soma will take to cover up 1 m distance \(\frac{\pi \mathrm{x}}{100.2 \pi \mathrm{r}}\) minute
∴ Soma will take to cover up 2r m distance \(\frac{\pi x .2 r}{100.2 \pi r}\) minute
∴ Soma will take to cover up 2r m distance \(\frac{x}{100}\) minut
∴ Soma will take time for going round the park diametrically \(\frac{x}{100}\) minute
∴ 2. \(\frac{x}{100}\) minute
3. A circle is inscribed by a square. The length of a side of the square is 10 cm. The length of diameter of the circle is
1. 10 cm
2. 5 cm
3. 20 cm
4. 10√2 cm
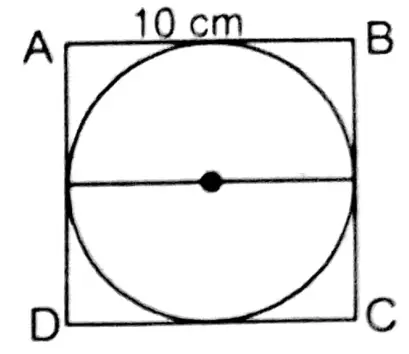
Solution: Let ABCD is a square in which
AB = BC= CD = DA = 10 cm
∵ A circle is inscribed by the square.
∴ Length of the diameter of the circle Length of each side of the square
∴ 1. 10 cm
Class 9 Ganit Prakash Solutions
4. The minute’s hand of a clock is 7 cm. How much length does the minute’s hand move in 15 minutes?
1. 5√2 cm
2. 10√2 cm
3. 5 cm
4. 10 cm
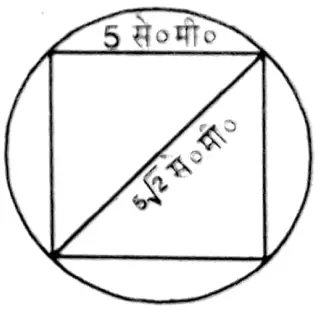
Solution: Length of each side of the square 5 cm.
∴ Length of diagonal of the square = √2x side
= √2×5 cm =5√2 cm
∵ A square is inscribed in a circle.
∴ Diameter of the circle = 5√2 cm
Solution: 1. 5√2 cm
Wbbse Class 9 Maths Circumference And Area Of Circle Formulas With Examples
5. A circular ring is 5 cm wide. The difference between the outer and inner radii is
1. 5 cm
2. 2.5 cm
3. 10 cm
4. none of these.
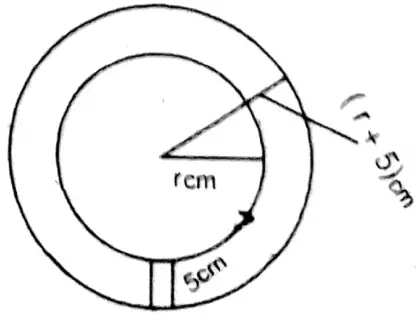
Solution: Width of the circular ring = 5 cm.
Let the inner radius of the circular ring be r cm.
∴ The outer radius of the ring = (r+ 5) cm.
∴ Difference between outer and inner radius of the ring = {(r+5)-r} cm = (r+5-r) cm = 5 cm
Answer: 1. 5 cm
Class 9 Maths Chapter 16 Circumference Of Circle Short Answer Type Questions
1. Perimeter of a semi-circle is 36 cm. What is the length of the diameter?
Solution: Let the radius of the semi-circle be r cm.
∴ Perimeter of the semi-circle = (r+2r) cm
Diameter of the semi-circle = 2r cm.
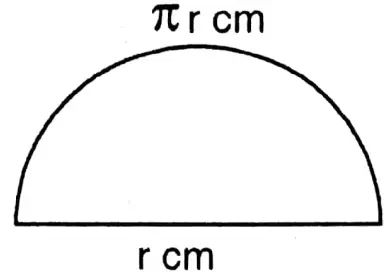
B. T. P., πг+2r=36
or, r(x+2)=36
or, r=\frac{36 \times 7}{36}\)
or, r = 7
∴ Length of the diameter of the semi-circle = 2r cm = 2 x 7 cm = 14 cm.
Class 9 Ganit Prakash Solutions
2. The length of the minute’s hand is 7 cm. How much length will a minute’s hand go to rotate 90°?
Solution: Length of the minute’s hand of the watch = 7 cm
∴ Circumference of the clock = 2πr
\(2 \times \frac{22}{7} \times 7 \mathrm{~cm}\) = 44 cm
∵ To rotate 360° degrees the minute’s hand will cover 44 cm distance.
∴ To rotate 1° degrees the minute’s hand will cover \(\frac{44}{360} \mathrm{~cm}\) distance
∴ To rotate 90° degrees the minute’s hand will cover \(\frac{44}{360} \times 90\) distance.
∴ To rotate 90° degrees the minute’s hand will cover \(\frac{44}{360} \times 90\) cm distance.
Wbbse Class 9 Ex 16
3. What is the ratio of radii of the inscribed and circumscribed circles of a square?
Solution: Let each side of the square = a unit.
∴ Diameter of the inner circle = a unit.
∴ Radius of the inner circle = \(\frac{a}{2}\) unit.
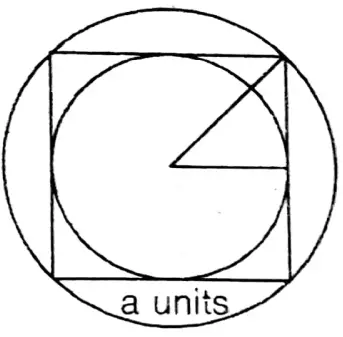
Diameter of the circumcircle = Length of the diagonal of the square = √2a unit.
∴ Radices of the circumcircle = \(\frac{\sqrt{2} a}{2} \text { unit. }\)
∴ Ratio of radii of inscribed circle and circumscribed circle = \(=\frac{a}{2}: \frac{\sqrt{2} a}{2}=1: \sqrt{2}\)
Class 9 Wbbse Circumference Of Circle Chapter 16 Solved Exercises
4. The minute’s hand of a clock is 7 cm. How much longer does the minute’s hand move in 15 minutes?
Solution: Radius of the circle = 7 cm.
∴ Circumference of the clock = 2πr
= \(2 \times \frac{22}{7} \times 7 \mathrm{~cm}=44 \mathrm{~cm}\)
∴ The minute hand moves in 60 minutes = 44 cm.
∴ It will move in 15 minute =\(\frac{44}{60}\)
∴ The minute’s hand in 15 minutes will cover = \(\frac{44}{60} \times 15 \mathrm{~cm}\) = 11 cm.
Wbbse Class 9 Ex 16
5. What is the ratio of the side of a square and the perimeter of a circle when the length of the diameter of the circle is equal to the length of the side of the square?
Solution: Let the radius of the circle = r cm.
∴ One side of the square = 2r unit.
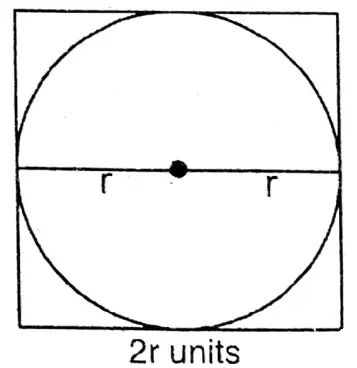
∴ Circumference 2πr cm.
∴ Length of one side of the square = 2r cm
= 4 × side
= 4 x 2r cm = 8r cm.
∴ Ratio of the side of the square & the circumference
= 2πг: 8r
= π: 4
& =\frac{22}{7}: 4 \\
& =\frac{22}{7} \times 7: 4 \times 7=22: 28
\end{aligned}\)
∴ 11:14
