Chapter 17 Theorems On Concurrence Exercise 17
Question 1. The bisectors of ∠B and ∠C of ABC intersect each other at point I. Let us prove that \(\angle B I C=90^{\circ}+\frac{\angle B A C}{2}\)
Solution:
Given
The bisectors of ∠B and ∠C of ABC intersect each other at point I.
∵ Bl and Cl respectively are the bisectors of ∠ABC and ∠ACB.
∴ ∠IBC = \(\frac{1}{2}\) ∠ABC and ∠ICB = \(\frac{1}{2}\) ∠ACB
In ΔBIC, ∠BIC+∠IBC + ∠ICB = 180°
or, ∠BIC+ \(\frac{1}{2}\) ∠ABC + \(\frac{1}{2}\) ∠ACB=180°
or, ∠BIC+ \(\frac{1}{2}\) + (∠ABC + ∠ACB) = 180°
or, ∠BIC + \(\frac{1}{2}\) (∠ABC+∠ACB+ ∠BAC) = 180° + \(\frac{1}{2}\) ∠BAC
Adding \(\frac{1}{2}\) ∠BAC on both sides)
or, ∠BIC+ \(\frac{1}{2}\) x 180° = 180° + \(\frac{1}{2}\) ∠BAC
or, ∠BIC = 90° + \(\frac{\angle B A C}{2}\) Proved
Read and Learn More WBBSE Solutions For Class 9 Maths
Question 2. If the lengths of the three medians of a triangle are equal, let us prove that the triangle is an equilateral triangle.
Solution:
Given
If the lengths of the three medians of a triangle are equal
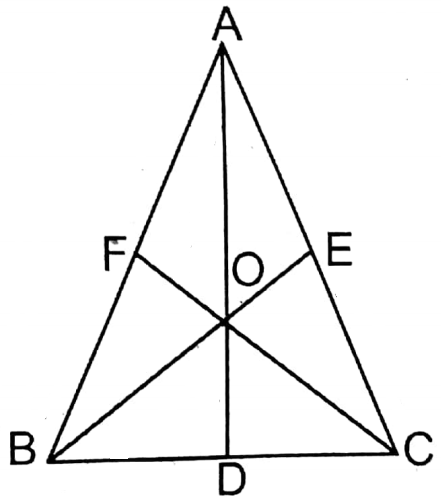
Let ABC is a triangle whose three medians AD, BE and CF cut each other at O and AD = BE = CF.
To prove ABC is an equilateral triangle
Wbbse Class 9 Maths Chapter 17 Theorems On Concurrence Solutions
Proof: Centroid divides the median in the ratio of 2: 1.
∴ AO = \(\frac{2}{3}\), BO = \(\frac{2}{3}\) BE and CO = \(\frac{2}{3}\) CF
∵ AD = BE = CF (∵ Lengths of 3 medians of a triangle are equal.)
∴ \(\frac{2}{3}\) AD = \(\frac{2}{3}\) BE = \(\frac{2}{3}\) CF
∴ AO = BO=CO
∴ AD – AO = BE – BO = CF-CO
or, OD = OE = OF
In ΔAOF and ΔCOD,
OF = OD, AO = CO
∠AOF = VOA ∠COD
∴ ΔAOF ≅ ΔCOD (S-A-S congruency)
∴ AF = CD
or, 2AF 2CD
∴ AB = BC ……(1)
Similarly, from ABOD and AAOE, it can be proved that AE = BD.
or, 2AE = 2BD
∴ AC = BC ….(2)
∴ In ΔABC AB = BC = CA
∴ ΔABC is an equilateral triangle. Proved

Wbbse Class 9 Theorems On Concurrence Exercise Solutions
Question 3. Let us prove that in an equilateral triangle, circumcentre, incentre, centroid, and orthocentre will coincide.
Solution:
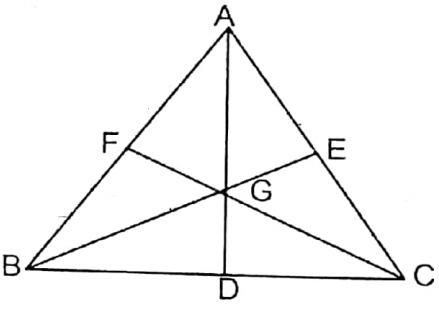
ABC is an equilateral triangle.
To prove cireum center, incentre, other center & centroid will coincide.
Proof: From A, B & C perpendiculars are drawn on BC, CA & AB. The perpendiculars AD, BE & CF meet at G
In ΔABD and ΔACD,
1. AB = AC
2. ∠ABD = ∠ACD
3. ∠ADB = ∠ADC
∴ ΔABD ≅ ΔACD
∴ ∠BAD = ∠CAD
∴ AD, ∠BAC is the bisector of ∠BAC. Similarly, BE & CF are the bisectors of ∠ABC & ∠ACB respectively. G is the centroid of the triangle. BD
∴ AD is the median
Similarly, BE & CF are two medians.
∴ G is the centroid.
Three medians are perpendicular on respective sides. C is the circumcentre of the triangle. (Proved)
Question 4. AD, BE and CF are three medians of a triangle ABC. Let us prove that the centroid of ABC and DEF are the same point.
Solution:
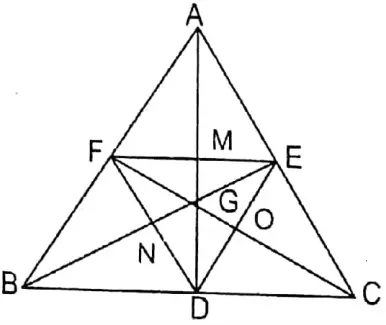
Given
AD, BE and CF are three medians of a triangle ABC.
To prove the centroid of ΔABC and ΔDEF are the same point.
Proof: Three medians AD, BE & CF meet at G.
∴ G is the centroid of ΔABC
In ΕABC, F & E are the midpoints of AB & AC respectively.
∴ EF II BC, i.e., EF II BD.
Similarly, DE II BF
∴ BDEF is a parallelogram.
Its diagonals BE & DF intersect each other at N.
∴ N is the mid-point of DF.
Similarly, in parallelogram AFDE, M is the midpoint of EF. The two medians EN & DM meet each other at G.
∴ G is the centroid of ADEF.
∴The centroid of ΔABC & ΔDEF is the same point.
Class 9 Wbbse Maths Theorems On Concurrence Solved Problems
Question 5. Let us prove that the two medians of a triangle are together greater than the third median.
Solution:
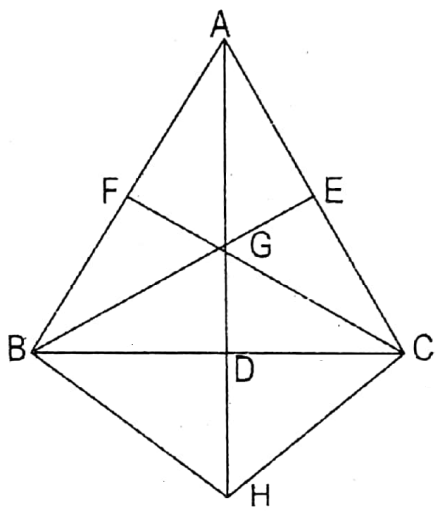
In ΔABC, AD, BE & CF are the medians
To prove, BE+ CF > AD
Produce AD to H such that GD = DH
B, H and C, H are joined.
Proof: In □BHCG, BD = CD (∵ AD is median)
GD = DH (By construction)
BC & GH bisect each other at D.
∴ BHCG is a parallelogram.
∴ BH = CG
Now, ΔBGH in BG + BH > GH
or, BG+CG > 2GD ( ∵ BH = CG and GD = DH)
or, \(\frac{2}{3}\) BE +\(\frac{2}{3}\) CF > 2. \(\frac{1}{3}\) AD
or, \(\frac{2}{3}\) BE+ \(\frac{2}{3}\) CF > \(\frac{2}{3}\) AD
or, BE+ CF > AD Proved
Question 6. AD, BE and CF are the three medians of ΔABC. Let us prove that
1. 4(AD + BE + CF) > 3(AB+ BC + CA);
2. 3(AB+ BC + CA) > 2(AD + BE + CF).
Solution: In triangle ABC, 3 medians AD, BE and CF cut each other at G. Prove that
1. 4(AD+ BE + CF) > 3(AB + BC + CA);
2. 3(AB+ BC + CA) > 2(AD + BE + CF)
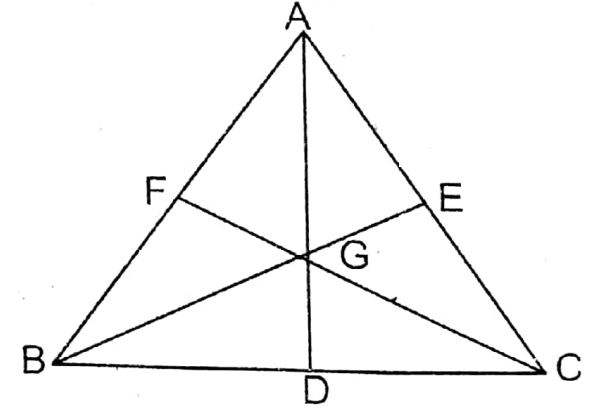
Wbbse Class 9 Maths Chapter 17 Theorems On Concurrence Notes
Proof: ∵Medians of a triangle cut each other in a ratio-2: of 1 at the centroid.
∴ AG = \(\frac{2}{3}\) AD, BG = \(\frac{2}{3}\) BE & CG = \(\frac{2}{3}\) CF
In ΔABG, AG + BG > AB
In ΔBCG, BG + CG > BC
In ΔACG, AG + CG > CA
∴ 2 (AG + BG+CG) > AB + BC + CA
or, \(2\left(\frac{2}{3} A D+\frac{2}{3} B E+\frac{2}{3} C F\right)>A B+B C+C A\)
or, \(\frac{4}{3}\)(AD+BE+CF) > AB + BC + CA
or, 4(AD + BE + CF) > 3 (AB+ BC + CA)
2. In ΔABD, AB + BD > AD
or, AB + \(\frac{1}{2}\) BC > AD ( ∵ D, is the midpoint of BC)
In ΔBCE, BC + CE > BE
or, BC+ \(\frac{1}{2}\) CA> BE ( ∵ E, is the midpoint of CA)
In ΔCAF, CA + AF > CF
or, CA + \(\frac{1}{2}\) AB > CF (∵ F is the midpoint of AB)
∴ AB + \(\frac{1}{2}\) BC+BC+ \(\frac{1}{2}\) CA + CA + \(\frac{1}{2}\) AB > AD+ BE + CF
or, \(\frac{3}{2}\) (AB+BC+ CA)> (AD + BE+CF)
or, 3(AB+ BC + CA) > 2(AD + BE + CF)
Question 7. Three medians AD, BE and CF of ΔABC intersect each other at point G. If the area of AABC is 36 sq cm, let us calculate
1. Area of ΔAGB;
2. Area of ΔCGE;
3. Area of quadrilateral ΔDGF.
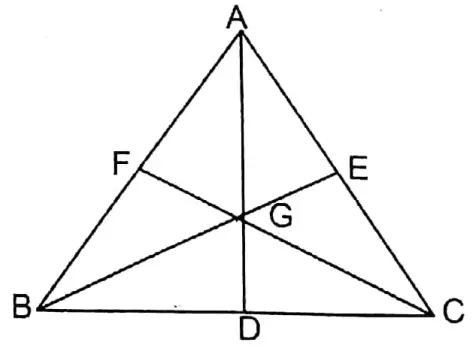
Solution:
Given
Three medians AD, BE and CF of ΔABC intersect each other at point G. If the area of AABC is 36 sq cm
AD is the median of ΔABC
∴ ΔABD = ΔACD
∴ ΔGBD = ΔGCD [GD is the median of AGBC]
ΔABD- ΔGBD = ΔACD- ΔGCD
∴ ΔAGB = ΔAGC
Similarly,
ΔAGB = ΔBGC
∴ ΔAGB = ΔBGC = ΔAGC = \(\frac{1}{3}\) (ΔAGB+ΔBGC + ΔAGC)
= \(\frac{1}{3}\) ΔABC
∴ ΔAGB = \(\frac{1}{3}\) x 36 sq. cm = 12 sq. cm
2. ΔCGE = \(\frac{1}{2}\) ΔAGC
= \(\frac{1}{2}\).\(\frac{1}{3}\) ΔABC
= \(\frac{1}{6}\)ΔΑΒC
= \(\frac{1}{6}\) x 36 sq. cm = 6 cm
3. Area of quadrilateral BDGF
= \(\frac{1}{6}\) x area of ΔABC + \(\frac{1}{6}\) x area of ΔABC
= \(\frac{1}{3}\) x 36 sq. cm + \(\frac{1}{6}\) x 36 sq. cm
= (3+5) sq. cm = 12 sq. cm
West Bengal Board Class 9 Theorems On Concurrence Chapter Solutions
Question 8. AD, BE and CF are the medians of ΔABC. If \(\frac{2}{3}\) AD = BC, then let us prove that the angle between two medians is 90°.
Solution:
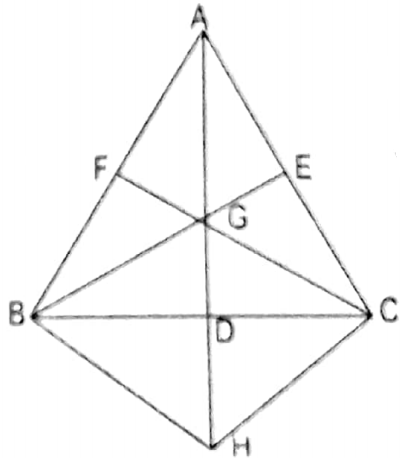
Given
AD, BE and CF are the medians of ΔABC. If \(\frac{2}{3}\) AD = BC
Produce GD to point H, such that GD = DH. As G is the centroid of ΓABC,
∴ AG: GD = 2:1
∴ GD = \(\frac{1}{3}\) AD = DH (∵ GD = DH)
∴ GD = GD + DH
= \(\frac{1}{3}\) AD + \(\frac{1}{3}\) AD
= AD \(\frac{2}{3}\) = BC (given)
∵ AD is the median.
∴ BD = DC & GD = DH
∴ In quadrilateral BHCG, diagonals bisect each other at D.
∴ BHCG is a parallelagram.
∵ The other diagonals bisect equally ∴BC= GH
∴ BHCG is a rectangle.
∴ ∠BGC = 90° = ∠EGF
Question 9. P and Q are the mid-points of sides BC and CD respectively of a parallelogram ABCD; the diagonals AP and AQ cut BD at the points K and L. Let us prove that, BK = KL = LD.
Solution:
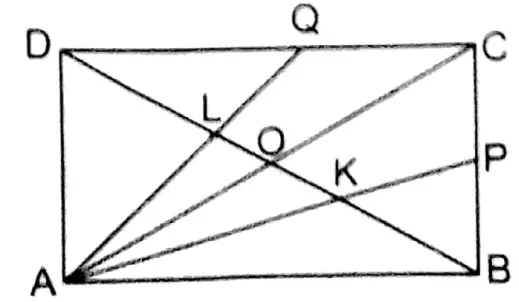
Given
P and Q are the mid-points of sides BC and CD respectively of a parallelogram ABCD; the diagonals AP and AQ cut BD at the points K and L.
Diagonal AC bisects BD at O.
Two medians of AADC, DO & AQ intersect at L.
∴ DL: LO = 2:1
∴ DL = \(\frac{2}{3}\) DO and LO = \(\frac{1}{3}\) DO
KO = \(\frac{1}{3}\) BO = \(\frac{1}{3}\) DO and BK = \(\frac{2}{3}\) BO = \(\frac{2}{3}\) DO
KL = LO+KO = \(\frac{1}{3}\) DO + \(\frac{1}{3}\) DO
= \(\frac{\mathrm{DO}+\mathrm{DO}}{3}=\frac{2}{3} \mathrm{DC}\)
∴ BK = KL = LD = \(\frac{2}{3}\) DO Proved
Wbbse Class 9 Theorems On Concurrence Important Questions
Question 10. Multiple choice questions
1. O is the circumcentre of ABC; if ∠BOC = 80°, the measure of ∠BAC is
1. 40°
2. 160°
3. 130°
4. 110°
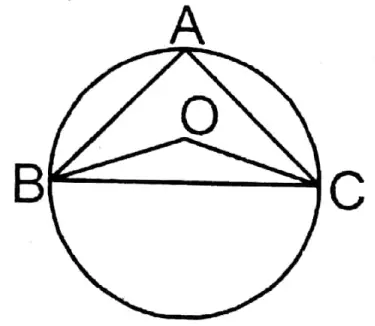
Solution: ∠BOC = 2 ∠BAC
∴ ∠BAC = \(\frac{1}{2}\) ∠BOC
= \(\frac{1}{2}\) × 80° = 40°
Solution: 1. 40°
2. O is the orthocentre of ABC; if ∠BAC = 40°, the measure of ∠BOC is
1. 80°
2. 140°
3. 110°
4. 40°
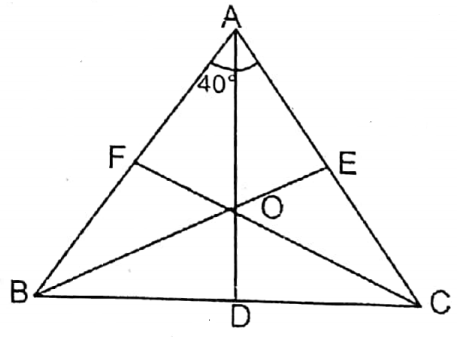
Solution: Let in ΔABC AD, BE and CF on sides BC, CA, and AB are perpendicular; the orthocentre is O.
In □AFOE,
∠FOE = 360°-(∠OFA + ∠OEA + ∠FAE)
= 360° (90° + 90° + 40°) = 360° – 220° = 140°
∴ ∠BOC = VOA ∠FOE = 140°
∴ 2. 140°
Wbbse Class 9 Maths Theorems On Concurrence Chapter 17
3. O is the orthocentre of ABC; if ∠BAC 40° then
1. 80°
2. 110°
3. 140°
4. 40°
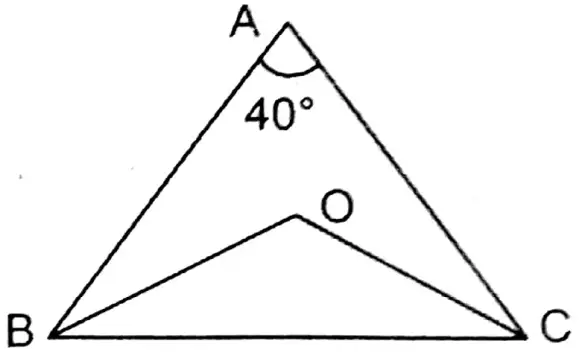
Solution: ΔABC
∠A+∠B+∠C = 180°
or, 40°+ ∠B+∠C = 180°
or, ∠B+∠C= 180° – 40° = 140°
In ΔBOC,
∠BOC+∠OBC+∠OCB = 180°
or, ∠BOC + \(\frac{1}{2}\) ∠B+ \(\frac{1}{2}\) ∠C=180°
or, ∠BOC + \(\frac{1}{2}\)(∠B + ∠C) = 180°
or, ∠BOC+ \(\frac{1}{2}\) x 140° = 180°
or, ∠BOC+70° = 180°
or, ∠BOC = 180° – 70° = 110°
∴ 2.110°
4. G is the centroid of triangle ABC; if the area of GBC is 20 sq cm, then the area of ABC is
1. 24 sq. cm
2. 6 sq. cm
3. 36 sq. cm
4. none of them
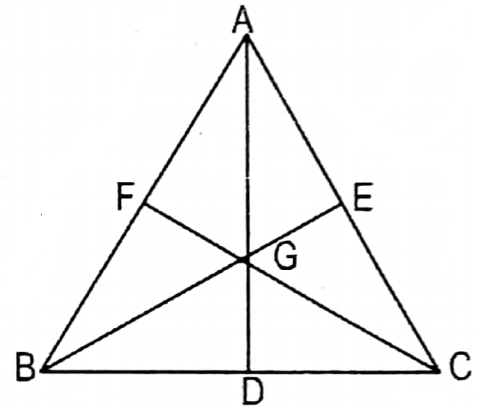
Solution: In a triangle, ABC G is the centroid.
∴ ΔAGB = ΔGBC = ΔCGA
∴ \(\frac{1}{3}\) ΔABC = ΔGBC
or, ΔABC = 12 sq. cm
or, ΔABC = 3 x 12 sq. cm 36 sq. cm
∴ 3. 36 sq. cm
Wbbse 9th Class Maths Theorems On Concurrence Step By Step Solutions
5. If the length of the circumradius of a right-angled triangle is 5 cm, then the length of its hypotenuse is
1. 2.5 cm
2. 5 cm
3. 10 cm
4. none of this
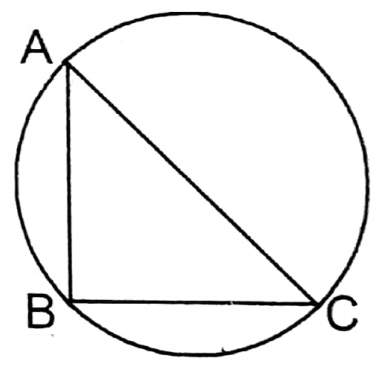
Solution: In a right-angled triangle, the circumcentre lies at the mid-point of the hypotenuse.
∵ Length of circumradius = 5 cm
∴ Lengths of hypotenuse 2 x 5 cm = 10 cm.
∴ 3. 10 cm
Question 11. Short answer type questions:
1. If the lengths of the sides of a triangle are 6 cm, 8 cm, and 10 cm, then let us write where the circumcentre of this triangle lies.
Solution: ∵ (10)2 = (6)2 + (8)2
∴ The triangle whose three sides are 6 cm, 8 cm, and 10 cm is a right-angled triangle. And we know that the circumcentre is at the midpoint of the hypotenuse.
∴ Circumcentre lies at the midpoint of the side of 10 cm.
2. AD is the median and G is the centroid of an equilateral triangle. If the length of side is 3√3 cm, then let us write the length of AG.
Solution: ∵ Median of an equilateral triangle = Height of the triangle
∴ AD = \(\frac{\sqrt{3}}{2}\) x side 3√3 = \(\frac{9}{2}\)
∴ AG = \(\frac{2}{3}\) AD= \(\frac{2}{3}\) x \(\frac{9}{2}\) cm = 3 cm.
3. Let us write how many points are equidistant from the sides of a triangle.
Solution: One point is equidistance from the sides of the triangle.
Wbbse Class 9 Maths Concurrence Of Medians, Altitudes, And Angle Bisectors Explained
4. DEF is a pedal triangle of an equilateral triangle ABC. Let us write the measure of ∠FDA.
Solution: The triangle formed by the foot of perpendiculars from the vertices to the opposite sides in a triangle is called Pedal Triangle.
‘O’ is the orthocentre of ΔABC.
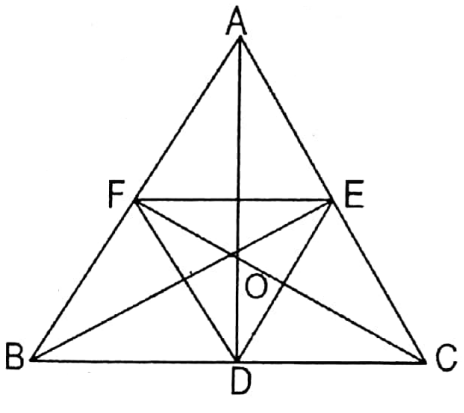
D, E, and F are the foot of perpendiculars of AD, BE & CF.
The triangle joining the points D, E, and F is a pedal triangle.
Δ DEF is a pedal triangle.
∵ ΔABC is an equilateral triangle.
∴ DA is the bisector of ∠FDE
∴ ∠FDA = \(\frac{1}{2}\) x 60° = 30°
Class 9 Wbbse Theorems On Concurrence Chapter 17 Solved Exercises
5. ABC is an isosceles triangle in which ∠ABC = ∠ACB and median AD = BC. If AB = √2 cm, let us write the length of the circumradius of this triangle.
Solution: ABC is an isosceles triangle whose ∠ABC = ∠ACB.
∴ AB AC = √2 cm
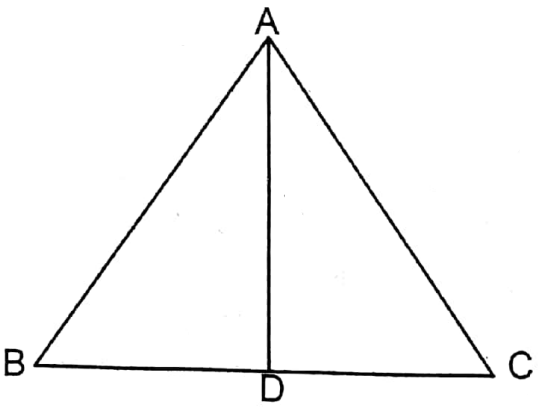
∵ AD is median
∴BD = CD
∵ AD = \(\frac{1}{2}\) BC
∴ BD = CD = AD
The height of an isosceles triangle is the median of that triangle.
∴ AD ⊥ BC
∴ In rt. angled ΔADB,
AD2+ BD2 = AB2
or, AD2 + AD2 = (√2)2 [∵ BD = AD]
or, 2 AD2=2
or, AD2 = \(\frac{2}{2}\) = 1
or, AD = √1
or, AD = 1
∴ Circumradius of the triangle = 1 cm.
