WBBSE Solutions For Class 9 Maths Chapter 19 Coordinate Geometry Internal And external Division Of A Straight Line Segment

Chapter 19 Coordinate Geometry Internal And external Division Of A Straight Line Segment Exercise 19

Important Formulae :

1. Distance of (x, y) from the origin = \(\sqrt{x^2+y^2}\) units.

2. Distance between 2 points P(x₁,y₁) and Q(x₂,y₂)

= \(\overline{\mathrm{PQ}}=\sqrt{\left(\mathrm{x}_1-\mathrm{x}_2\right)^2+\left(\mathrm{y}_1-\mathrm{y}_2\right)^2} \text { units. }\)

3. If two points A(x₁,y₁) and B(x₂,y₂) are internally divided by point P(x, y) in ratio mn, then the co-ordinates of P are

P = \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)

4. If two points A(x₁,y₁) and B(x₂,y₂) are externally divided by point P(x, y) in ratio mn, then the co-ordinates of P are

P = \(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\)

Question 1. Find the co-ordinate of the point which divides the line segment joining two points in the given ratio for the following:

Read and Learn More WBBSE Solutions For Class 9 Maths

1. (6, -14) and (-8, 10) in the ratio 3 4 internally

Solution: The coordinates of the point

\(\begin{aligned}
& =\left\{\frac{3 \times(-8)+4 \times 6}{3+4}, \frac{3 \times 10+4(-14)}{3+4}\right\} \\
& =\left(\frac{-24+24}{7}, \frac{30-56}{7}\right) \\
& =\left(0, \frac{-26}{7}\right)
\end{aligned}\)

Wbbse Class 9 Maths Chapter 19 Coordinate Geometry Solutions

∴ \(\left(0, \frac{-26}{7}\right)\)

2. (5, 3) and (-7, -2) in the ratio 2 3 internally

Solution: The coordinates of the point

\(\begin{aligned}
& =\left\{\frac{2 \times(-7)+3 \times 5}{2+3}, \frac{2(-2)+3 \times 3}{2+3}\right\} \\
& =\left(\frac{-14+15}{5}, \frac{-4+9}{5}\right) \\
& =\left(\frac{1}{5}, 1\right)
\end{aligned}\)

 

∴ \(\left(\frac{1}{5}, 1\right)\)

3. (-1, 2) and (4, -5) in the ratio 3: 2 externally

Solution: The coordinates of the point

\(\begin{aligned}
& =\left\{\frac{3 \times 4-2 \times(-1)}{3-2}, \frac{3(-5)-2 \times 2}{3-2}\right\} \\
& =\left(\frac{12+2}{1}, \frac{-15-4}{1}\right) \\
& =(14,-19)
\end{aligned}\)

= (14,-19)

∴ (14,-19)

Wbbse Class 9 Maths Coordinate Geometry Section Formula And Examples

4. (3, 2) and (6, 5) in the ratio externally

Solution: The coordinates of the point

=\(\left\{\frac{2 \times 6-1 \times 3}{2-1}, \frac{2 \times 5-1 \times 2}{2-1}\right\}\)

= \(\left(\frac{12-3}{1}, \frac{10-2}{1}\right)\)

= (9,8)

∴ (9,8)

Question 2. Find the co-ordinates of the mid-point of the line segment joining two points for the following:

1. (5, 4) and (3,-4)

Solution: The co-ordinates of the mid-point of the join of (5, 4) and (3,-4)

\(\begin{aligned}
& =\left(\frac{5+3}{2}, \frac{4-4}{2}\right) \\
& =\left(\frac{8}{2}, 0\right)
\end{aligned}\)

= (4, 0)

∴ (4, 0)

2. (6, 0) and (0, 7)

Solution: The co-ordinates of the midpoint of the join of (6,0) and (0,7)

\(\begin{aligned}
& =\left(\frac{6+0}{2}, \frac{0+7}{2}\right) \\
& =\left(3, \frac{7}{2}\right)
\end{aligned}\)

Wbbse Class 9 Coordinate Geometry Internal And External Division Solutions

Question 3. Let us calculate the ratio in which point (1, 3) divides the line segment joining points (4, 6) and (3, 5).

Solution: Let the required ratio = m:n.

∴ \(1=\frac{m \times 3+n \times 4}{m+n}\)

or, m+n=3m + 4n.
or, m-3m = 4n-n
or, -2m=3n

or, \(\frac{m}{n}=\frac{-3}{2}\)

or, m: n= (-3):2

Question 4. Let us calculate in what ratio is the line segment joining the points (7, 3) and (-9, 6) divided by the y-axis.

Solution: Here the abscissa of the point P = x

∴ Point P point abscissa of (x co-ordinate) = \(\frac{m \times(-9)+n \times 7}{m+n}\)

∴ Point P point is situated on y-axis.  ∴x=0.

∴ \(\frac{-9 m+7 n}{m+n}=0\)

or, -9m+7n = 0
or, -9m=-7n
or, 9m = 7n

or, \(\frac{m}{n}=\frac{7}{9}\)

∴ m:n = 7:9

Class 9 Wbbse Coordinate Geometry Chapter 19 Solved Exercises

Question 5. Prove that when the points A(7, 3), B(9, 6), C(10, 12) and D(8, 9) are joined in the order mentioned then they will form a parallelogram.

Solution: Mid-point of the diagonal AC is E.

\(\begin{aligned}
& =\left(\frac{7+10}{2}, \frac{3+12}{2}\right) \\
& =\left(\frac{17}{2}, \frac{15}{2}\right)
\end{aligned}\)

& the mid-point of the diagonal BD is F = \(\left(\frac{9+8}{2}, \frac{6+9}{2}\right)\)

= \(=\left(\frac{17}{2}, \frac{15}{2}\right)\)

Diagonals of the quadrilateral, AC & BD intersect each other at

= \(=\left(\frac{17}{2}, \frac{15}{2}\right)\)

∴ ABCD is a parallelogram. Proved

Class 9 Wbbse Maths Coordinate Geometry Straight Line Segment Solved Problems

Question 6. If the points (3, 2), (6, 3), (x, y) and (6, 5) when joined in the order mentioned and form a parallelogram, then let us calculate the point (x, y).

Solution:

Given

If the points (3, 2), (6, 3), (x, y) and (6, 5) when joined in the order mentioned and form a parallelogram,

Let A(3,2), B(6,3), C(x,y) & D(6,5) be the four points of the parallelogram ABCD. E and F are the mid-points of the diagonals AC & BD.

∴ E is the mid-point of AC.

∴ Co-ordinate of E= \(\left(\frac{3+x}{2}, \frac{2+y}{2}\right)\)

∵ F is the mid-point of BD.

∴ Co-ordinates of F = \(\left(\frac{6+6}{2}, \frac{3+5}{2}\right)\) = (6,4)

∴ ABCD is a parallelogram.

∴ AC and BD will bisect each other, i.e., E and F will be the same point.

∴ \(\frac{3+x}{2}=6\)

or, 3+ x = 12
or, x = 12-3=9

\(\frac{2+y}{2}=4\)

or, 2+ y = 8
or, y=8-2=6

∴ The required point is (9,6).

Question 7. If ((x₁,y₁), (x₂,y₂), (x₃,y₃)  and (x₄,y₄) points are joined in order to form a parallelogram, then prove that x₁ +x₃ = x₂ +x₄ and y₁ + y₃ = y₂+y₄

Solution:

Given

If ((x₁,y₁), (x₂,y₂), (x₃,y₃)  and (x₄,y₄) points are joined in order to form a parallelogram

Let A((x₁,y₁), B(x₂,y₂), C(x₃,y₃) & D(x₄,y₄) are the four points of the parallelogram ABCD.

∴ E is the mid-point of AC.

Co-ordinates of E = \(\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\right)\)

F is the mid-point of BD.

Co-ordinates of F = \(\left(\frac{\mathrm{x}_2+\mathrm{x}_4}{2}, \frac{\mathrm{y}_2+\mathrm{y}_4}{2}\right)\)

∵ ABCD is a parallelogram.
Diagonals AC & BD intersect at a point if E & F are the same points.

∴ \(\frac{x_1+x_3}{2}=\frac{x_2+x_4}{2} \text { or, } x_1+x_3=x_2+x_4\)

& \(\frac{y_1+y_3}{2}=\frac{y_2+y_4}{2} \text { or, } y_1+y_3=y_2+y_4\)

Wbbse Class 9 Maths Chapter 19 Coordinate Geometry Notes

Question 8. The coordinates of vertices A, B, and C of a triangle ABC are (-1, 3), (1, -1) and (5, 1) respectively, let us calculate the length of the median AD.

Solution:

 

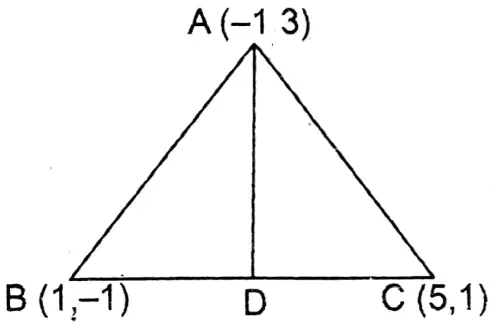
Given

The coordinates of vertices A, B, and C of a triangle ABC are (-1, 3), (1, -1) and (5, 1) respectively

Let D is the mid-point of BC.

Co-ordinates of D = \(\left(\frac{1+5}{2}=\frac{-1+1}{2}\right)\) = (3,0)

∴ Length of median AD = \(\sqrt{(-1-3)^2+(3-0)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(-4)^2+(3)^2} \text { unit } \\
& =\sqrt{16+9} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)

 

Question 9. The coordinates of the vertices of the triangle are (2, 4), (6, -2) and (-4, 2) respectively. Let us find the length of three medians of a triangle.

Solution:

 

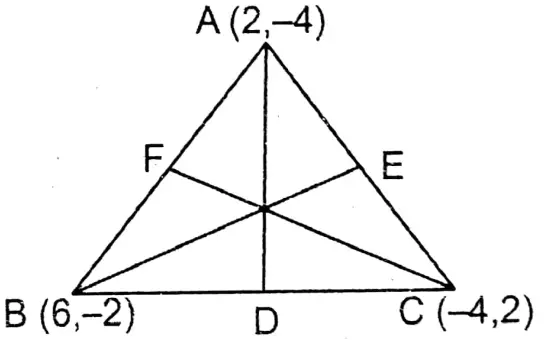
Given

The coordinates of the vertices of the triangle are (2, 4), (6, -2) and (-4, 2) respectively.

Let D, E, & F be the mid-points of BC, CA & AB respectively.

∴ Now co-ordinates of

D= \(\begin{aligned}
& D=\left(\frac{6-4}{2}=\frac{-2+2}{2}\right) \\
& =(1,0)
\end{aligned}\)

Co-ordinates of E = \(\left(\frac{2-4}{2}=\frac{-4+2}{2}\right)\) = (-1,-1)

Co-ordinates of F = \(\left(\frac{2+6}{2}=\frac{-4-2}{2}\right)\) = (4,-3)

∴ Length of median BE = \(\sqrt{(2-1)^2+(-4-0)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(1)^2+(-4)^2} \\
& =\sqrt{1+16} \text { unit } \\
& =\sqrt{17} \text { unit }
\end{aligned}\)

Length of median BE = \(\sqrt{(6+1)^2+(-2+1)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(7)^2+(-1)^2} \\
& =\sqrt{50} \text { unit } \\
& =5 \sqrt{2} \text { unit }
\end{aligned}\)

Length of median CF = \(\sqrt{(-4-4)^2+(2+3)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(-8)^2+(5)^2} \text { unit } \\
& =\sqrt{64+25} \text { unit } \\
& =\sqrt{89} \text { unit }
\end{aligned}\)

West Bengal Board Class 9 Coordinate Geometry Internal External Division Solutions

Question 10. The coordinates of the midpoints of sides of a triangle are (4, 3), (-2, 7) and (0, 11). Let us calculate the coordinates of its vertices.

Solution:

Given

The coordinates of the midpoints of sides of a triangle are (4, 3), (-2, 7) and (0, 11).

Let A (x₁,y₁) B (x₂,y₂) & C(x₃,y₃) are three vertices of the ΔABC
& P(4, 3); Q (-2, 7) & R (0, 11) are the three mid-points of the AB, BC & CA respectively.

 

 

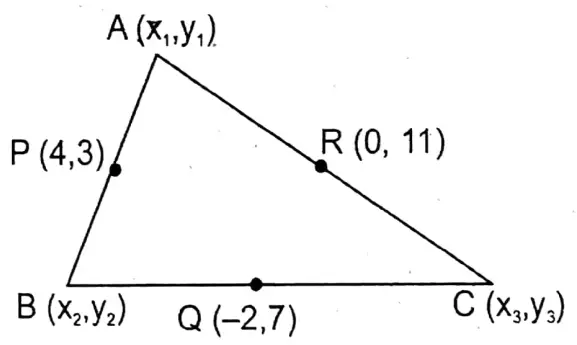
\(\frac{x_1+x_2}{2}=4, \text { or, } x_1+x_2=8\) ….(1)

\(\frac{y_1+y_2}{2}=3, \text { or, } y_1+y_2=6\) …(2)

\(\frac{x_2+x_3}{2}=-2, \text { or, } x_2+x_3=-4\) ….(3)

\(\frac{y_2+y_3}{2}=7, \text { or, } y_2+y_3=14\) ….(4)

\(\frac{x_3+x_1}{2}=0, \text { or, } x_3+x_1=0\) ….(5)

\(\frac{y_3+y_1}{2}=11, \text { or, } y_3+y_1=22\) …(6)

Adding (1), (3) & (5), we get 2(x₁+ x₂+x₃)= 4

or, x₁+ x₂+x₃ = 4/2

or, x₁+ x₂+x₃ = 2 ….(7)

(6) – (1) => x₃ =-6
(6) – (3) => x₁= 6
(6) – (5) => x = 2

Again, by adding (2), (4) & (5), we get
2(y₁+ y₂+y₃)= 42

∴ y₁+ y₂+y₃ = 21 …… (8)
(8) – (2) => y₃= 15
(8) – (4) => y₁ = 7
(8) – (4) => y₂ = -1

∴ The coordinates of the vertices of the triangle are (6, 7) (2, -1), and (-6, 15).

Question 11. Multiple choice questions

1. The mid-point of line segment joining two points (1, 2m), and (-1 + 2m, 21 – 2m) is

1. (1, m)
2. (1, -m)
3. (m, -1)
4. (m, 1)

Solution; Mid-point

= \(\left(\frac{1-1+2 m}{2}, \frac{2 m+21-2 m}{2}\right)\) = (m, 1)

∴ 4. (m + 1)

Wbbse Class 9 Coordinate Geometry Internal And External Division Important Questions

2. The abscissa at point P which divides the line segment joining two points A(1, 5) and B(-4, 7) internally in the ratio 2:3 is

1. -1
2. 11
3. 1
4. -11

Solution:

Co-ordinates of P = \(\left(\frac{2 \times(-4)+3 \times 1}{2+3}, \frac{2 \times 7+3 \times 5}{2+3}\right)\)

= \(\left(-1, \frac{29}{5}\right)\)

∴ The abscissa is -1.

∴ – 1

3. The coordinates of the end points of a diameter of a circle are (7, 9) and (-1,-3). The coordinates of the centre of the circle is

1. (3, 3)
2. (4, 6)
3. (3, -3)
4. (4, -6)

Solution: Co-ordinates of the centre
\(=\left(\frac{7-1}{2}, \frac{9-3}{2}\right)\)

= (3, 3)

∴ (3, 3)

4. A point which divides the line segment joining two points (2,-5) and (-3,-2) externally in the ratio 4: 3. The ordinate of the point is

1. -18
2. -7
3. 18
4. 7

Solution: The coordinates of the point

=\(\left(\frac{4 \times(-3)-3 \times 2}{4-3}, \frac{4 \times(-2)-3 \times(-5)}{4-3}\right)\)

= (-18, 7)
∴ The ordinate of the point is 7.

4. 7

5. If the points P(1, 2), Q(4, 6), R(5, 7) and S(x, y) are the vertices of a parallelogram PQRS, then

1. x = 2, y = 4
2. x = 3, y=4
3. x = 2, y = 3
4. x = 2, y = 5

Solution: The mid-point of the diagonal PR is

= \(\left(\frac{1+5}{2}, \frac{2+7}{2}\right)=\left(3, \frac{9}{2}\right)\)

= \(\left(3, \frac{9}{2}\right)\)

The mid-point of the diagonal QS = \(\left(\frac{4+x}{2}, \frac{6+y}{2}\right)\)

∴ As mid-points PR & QS are the same point.

∴ \(\frac{4+x}{2}=3\)

or, 4+ x = 6
or, x = 2

or, \(\frac{6+y}{2}=\frac{9}{2}\)

or, 12+2y= 18
or, 2y= 18-12

or, y = 6/2=3

∴ 3. x = 2, y = 3

Question 12. Short answer type questions:

1. C is the centre of a circle and AB is its diameter; the coordinates of A and C are (6, -7) and (5, -2). Let us calculate the coordinates of B.

Solution:

Given

C is the centre of a circle and AB is its diameter; the coordinates of A and C are (6, -7) and (5, -2).

Let the co-ordinate of B = (x, y)

∴ The mid-point of AB = \(\left(\frac{6+x}{2}, \frac{-7+y}{2}\right)\)

∴As centre is the mid-point of the diameter.

∴ \(\frac{6+x}{2}=5[\latex]

or, 6+x=10
or, x = 4

and [latex]\frac{-7+y}{2}=-2\)

or, – 7+ y = -4
or, y = -4+7
or, y = 3

∴ The coordinates of B = (4,3).

Wbbse Class 9 Maths Coordinate Geometry Chapter 19

2. The points P and Q lie on 1st and 3rd quadrants respectively. The distance of the two points from the x-axis and y-axis is 6 units and 4 units respectively. Let us write the coordinates of the mid-point of line segment PQ.

Solution:

Given

The points P and Q lie on 1st and 3rd quadrants respectively. The distance of the two points from the x-axis and y-axis is 6 units and 4 units respectively.

As P lies in 1st quadrant
∴ The abscissa & the ordinate both are positive.
∴ The coordinates of P = (4, 6).

Again, Q lies in the 3rd quadrant.
∴ The abscissa & the ordinate both are negative.

∴ The coordinates of Q = (-4, -6).

∴ The mid point of PQ is = \(\left(\frac{4-4}{2}, \frac{6-6}{2}\right)=(0,0) .\)

= (0, 0).

3. points A and B lie in the 2nd and 4th quadrants respectively and the distance of each point from x-axis and y-axis are 8 units and 6 units respectively. Let us write the coordinate of the mid-point of line segment AB.

Solution:

Given

points A and B lie in the 2nd and 4th quadrants respectively and the distance of each point from x-axis and y-axis are 8 units and 6 units respectively.

As lies in the 2nd quadrant.
∴ The abscissa is negative, but the ordinate is positive.
∴ The coordinates of A = (-6, 8).

Again, B lies in the 4th quadrant.
∴ The abscissa is positive, but the ordinate is negative.

∴ The coordinates of B = (6, -8).

∴ The mid-point of A and B is \(\left(\frac{-6+6}{2}, \frac{8-8}{2}\right)=(0,0)\)

= (0, 0).

4. The point Plies on the segment AB and AP = PB; the coordinates of A and B are (3,-4) and (-5, 2) respectively. Let us write the coordinates of point P.

Solution:

Given

The point Plies on the segment AB and AP = PB; the coordinates of A and B are (3,-4) and (-5, 2) respectively.

As P lies on AB and AP = PB
∴ P is the mid-point of AB.

∴ The co-ordinates of P = \(\left(\frac{3-5}{2}, \frac{-4+2}{2}\right)\) =(-1,-1).

Wbbse 9th Class Maths Coordinate Geometry Internal And External Division Step By Step Solutions

5. The sides of rectangle ABCD are parallel to the coordinate axes. The coordinates of B and D are (7, 3) and (2, 6). Let us write the coordinates of A and C and the mid-point of diagonal AC.

Solution:

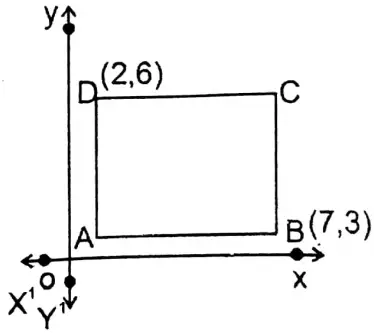
Given

The sides of rectangle ABCD are parallel to the coordinate axes. The coordinates of B and D are (7, 3) and (2, 6).

ABCD is a rectangle, AB II x-axis & AD II y-axis.
∴The coordinates of A = (2, 3).
∴ The coordinates of C

∴ The midpoint of AC = \(\left(\frac{2+7}{2}, \frac{3+6}{2}\right)=\left(\frac{9}{2}, \frac{9}{2}\right)\)