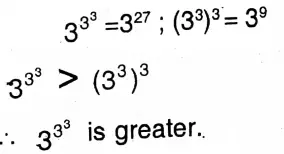Ganit Prabha Class 9 Solutions Chapter 2 Laws Of Indices
Important Formula:
1. xm.xn = xm+n
2. \(x^m \div x^n=\frac{x^m}{x^n}=x^{m-n}\)
3. (xm)n = xmn
4. (xy)m = xmym
5. \(\left(\frac{x}{y}\right)^m=\frac{x^m}{y^m}\)
6. \(\frac{1}{x^{-m}}=x^m\)
7. x0=1
8. \(x^{-1}=\frac{1}{x}\)
9. \(x^{-n}=\frac{1}{x^n}\)
10. xm=Yn ,n ≠ 0 ⇒ x= y when x and y positive
11. xm=Yn ⇒ m = n when x>n and x ≠1
12. xm = y ∴ \(x=y^{\frac{1}{m}}\)
Read and Learn More WBBSE Solutions For Class 9 Maths
Class 9 Math Solution West Bengal Board Chapter 2 Laws Of Indices: Exercise 2.1
Question 1. Let us find out the values of the following:
1. \((\sqrt[5]{8})^{\frac{5}{2}} \times\left(16^{\frac{-3}{2}}\right)\)
Solution:
Given
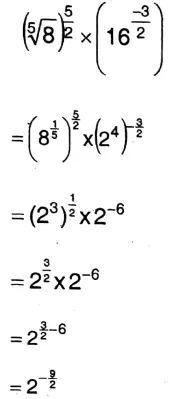

Wbbse Class 9 Maths Chapter 2 Laws Of Indices Solutions
2. \(\left\{(125)^{-2} \times(16)^{\frac{-3}{2}}\right\}^{\frac{-1}{6}}\)
Solution:
Given
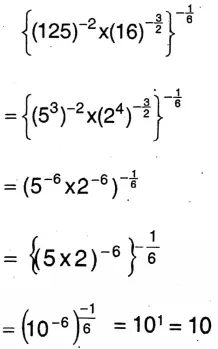
WBBSE Class 9 Math Book Solution
3. \(4^{\frac{1}{3}} \times\left[2^{\frac{1}{3}} \times 3^{\frac{1}{2}}\right] \div 9^{\frac{1}{4}}\)
Solution: \(4^{\frac{1}{3}} \times\left[2^{\frac{1}{3}} \times 3^{\frac{1}{2}}\right] \div 9^{\frac{1}{4}}\)
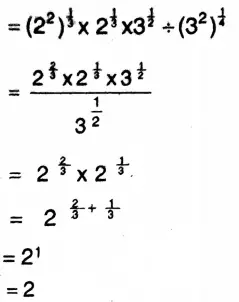
Wbbse Class 9 Laws Of Indices Exercise Solutions
Question 2. Let us simplify:
1. \(\left(8 a^3 \div 27 x^{-3}\right)^{\frac{2}{3}} \times\left(64 a^3 \div 27 x^{-3}\right)^{-2}\)
Solution:
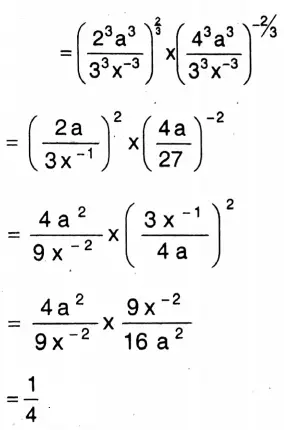
WBBSE Class 9 Math Book Solution
2. \(\left\{\left(x^{-5}\right)^{\frac{2}{3}}\right\}^{\frac{-3}{10}}\)
Solution:
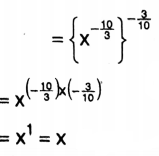
3. \(\left[\left\{\left(2^{-1}\right)^{-1}\right\}^{-1}\right]^{-1}\)
Solution:
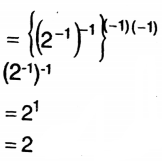
WB Board Class 9 Math Solution
4. \(\sqrt[3]{a^{-2}} \cdot b \times \sqrt[3]{b^{-2}} \cdot c \times \sqrt[3]{c^{-2}} \cdot a\)
Solution:
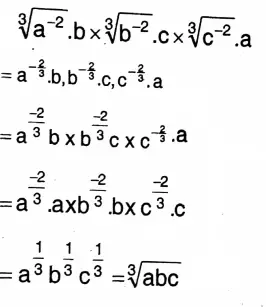
Class 9 Wbbse Maths Laws Of Indices Solved Problems
5. \(\left(\frac{4^{m+\frac{1}{4}} \times \sqrt{2.2^m}}{2 \cdot \sqrt{2^{-m}}}\right)^{\frac{1}{m}}\)
Solution:
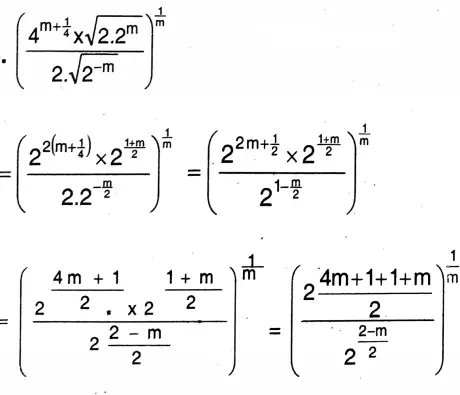
West Bengal Class 9 Maths Solutions
\(\left(2^{\frac{5 m+2-2+m}{2}}\right)^{\frac{1}{m}}\)
\(=\left(2^{\frac{6 m}{2}}\right)^{\frac{1}{m}}=2^3=8\)
6. \(9^{-3} \times \frac{16^{\frac{1}{4}}}{6^{-2}} \times\left(\frac{1}{27}\right)^{-\frac{4}{3}}\)
Solution:
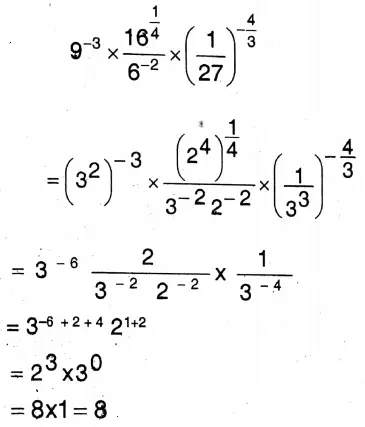
West Bengal Class 9 Maths Solutions
7. \(\left(\frac{x^a}{x^b}\right)^{a^2+a b+b^2} \times\left(\frac{x^b}{x^c}\right)^{b^2+b c+c^2} \times\left(\frac{x^c}{x^a}\right)^{c^2+c a+a^2}\)
Solution:
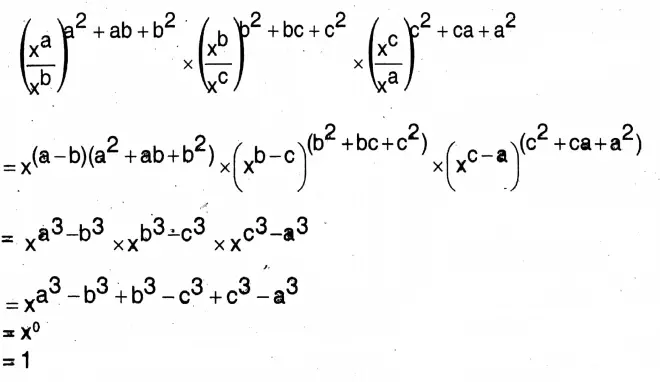
Wbbse Class 9 Maths Chapter 2 Laws Of Indices Notes
Question 3. Let us arrange in ascending order:
1. \(5^{\frac{1}{2}}, 10^{\frac{1}{4}}, 6^{\frac{1}{3}}\)
Solution:
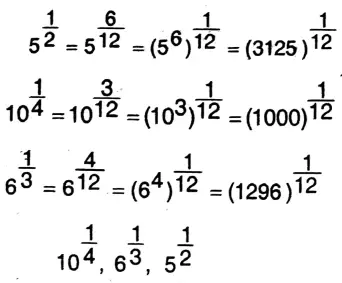
Class 9 Math Solution West Bengal Board
2. \(3^{\frac{1}{3}}, 2^{\frac{1}{2}}, 8^{\frac{1}{4}}\)
Solution:
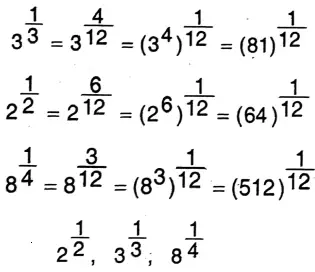
3. \(2^{60}, 3^{48}, 4^{36}, 5^{24}\)
Solution:
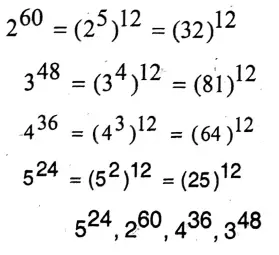
Class 9 Math Solution West Bengal Board
Question 4. Let us prove:
1. \(\left(\frac{a^q}{a^r}\right)^p \times\left(\frac{a^r}{a^p}\right)^q \times\left(\frac{a^p}{a^q}\right)^r=1\)
Solution: L.H.S\(\left(\frac{a^q}{a^r}\right)^p \times\left(\frac{a^r}{a^p}\right)^q \times\left(\frac{a^p}{a^q}\right)^r\)
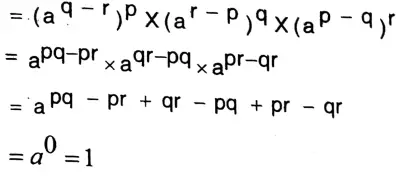
Ganit Prabha Class 9 Solutions
= R.H.S Proved.
2. \(\left(\frac{x^m}{x^n}\right)^{m+n} \times\left(\frac{x^n}{x^1}\right)^{n+1} \times\left(\frac{x^1}{x^m}\right)^{1+m}\)
Solution:
L.H.S = \(=\left(\frac{x^m}{x^n}\right)^{m+n} \times\left(\frac{x^n}{x^{\prime}}\right)^{n+1} \times\left(\frac{x^{\prime}}{x^m}\right)^{l+m}\)
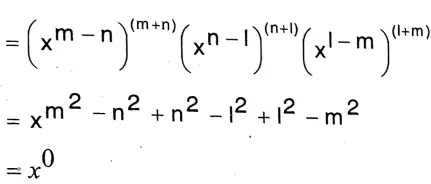
= 1 = R.H.S Proved.
3. \(\left(\frac{\mathbf{x}^m}{\mathbf{x}^n}\right)^{m+n-1} \times\left(\frac{\mathbf{x}^n}{\mathbf{x}^1}\right)^{n+1-m} \times\left(\frac{\mathbf{x}^{\prime}}{\mathbf{x}^m}\right)^{1+m-n}=1\)
Solution: L.H.S \(=\left(\frac{x^m}{x^n}\right)^{m+n-1} \times\left(\frac{x^n}{x^{\prime}}\right)^{n+1-m} \times\left(\frac{x^{\prime}}{x^m}\right)^{1+m-n}\)
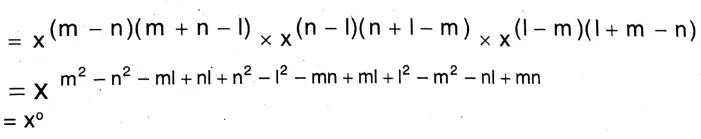
=1= R.H.S Proved.
West Bengal Board Class 9 Laws Of Indices Chapter Solutions
4. \(\left(a^{\frac{1}{x-y}}\right)^{\frac{1}{x-z}} \times\left(a^{\frac{1}{y-z}}\right)^{\frac{1}{y-x}} \times\left(a^{\frac{1}{z-x}}\right)^{\frac{1}{z-y}}=1\)
Solution: L.H.S \(=\left(a^{\frac{1}{x-y}}\right)^{\frac{1}{x-z}} \times\left(a^{\frac{1}{y-x}}\right)^{\frac{1}{y-x}} \times\left(a^{\frac{1}{z-x}}\right)^{\frac{1}{z-y}}\)
\(=a \frac{1}{(x-y)(x-z)}+\frac{1}{(y-z)(y-x)}+\frac{1}{(z-x)(z-y)}\)
Ganit Prabha Class 9 Solutions
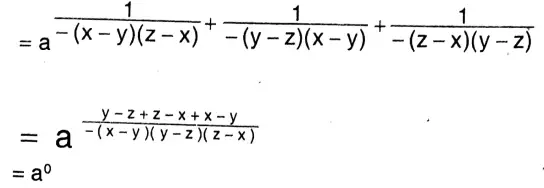
Question 5. If x+z=2y and b2=ac, then let us show that a y-z b z-x cx-y = 1.
Solution:
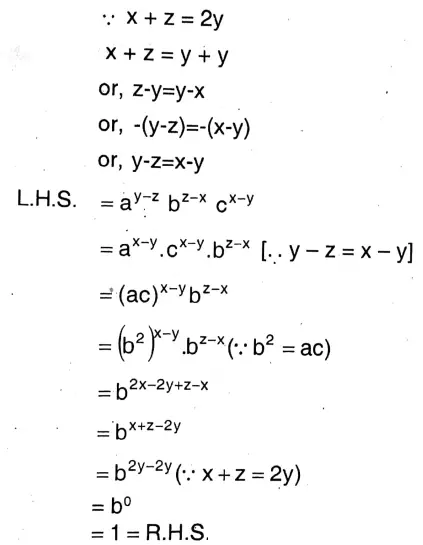
Wbbse Class 9 Laws Of Indices Important Questions
Question 6. If a = xyp-1, b = xyq-1 ,and c = xyr-1, then let us show that a q-r b r-p cp-q=1.
Solution: L.H.S. a q-r b r-p cp-q
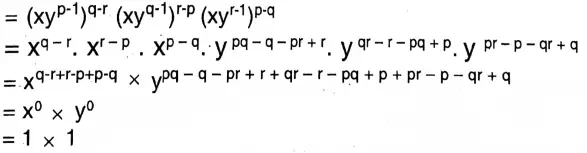
=1 R.H.S Proved.
Question 7. If \(x^{\frac{1}{a}}=y^{\frac{1}{b}}=z^{\frac{1}{c}}\) and =xyz=1, then let us show that a+b+c =0.
Solution: \(x^{\frac{1}{a}}=y^{\frac{1}{b}}=z^{\frac{1}{c}}\)=k(let)
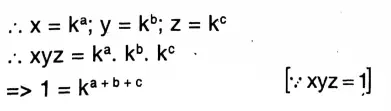
or, a q-r b r-p cp-q=1 ka+b+c= ko [ k0=1]
or, a+b+c=0 Proved.
Question 8. If ax = by = cz and abc = 1 then let us show that xy+yz+zx=0.
Solution:
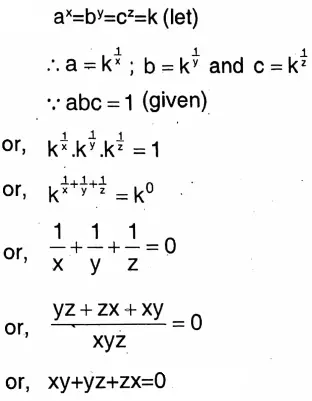
Question 9. Let us solve:
1. 49x=73
Solution: 49x=73
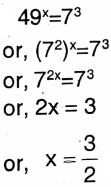
2. 2x+2+2x-1=9
Solution: 2x+2+2x-1=9
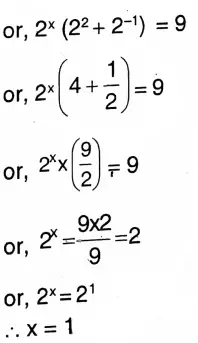
Ganit Prabha Class 9 Solutions
3. 2x+1+ 2x+2= 48
Solution: 2x+1+ 2x+2= 48
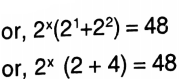
or, 2^x=8=2^3\)
∴x = 3
Wbbse Class 9 Maths Laws Of Indices Chapter 2
4. \(2^{4 x} \cdot 4^{3 x-1}=\frac{4^{2 x}}{2^{3 x}}\)
Solution:
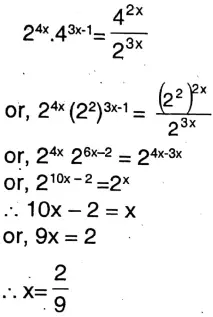
5. 9Χ81x = 272-x
Solution:
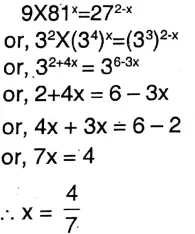
Ganit Prabha Class 9 Solutions
6. 25x+4 + 29 = 210
Solution: 25x+4 + 29 = 210
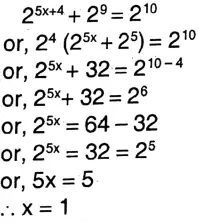
Class 9 Math Solution WBBSE
7. 62x+4=33x 2x+8
Solution:
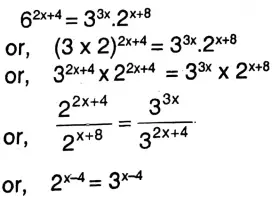
\(\text { or, }\left(\frac{2}{3}\right)^{x-4}=\left(\frac{2}{3}\right)^0\)
or, x-4=0
∴ x = 4
Wbbse Class 9 Maths Laws Of Indices Rules And Examples
Question 10.
1. The value of (0.243)0.2 x (10)0.6 is
(1)0.3
(2)3
(3)0.9
(4)9
Solution: (0.243)0.2 x (10)0.6
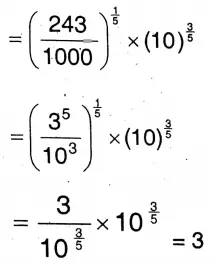
∴ (2)3
2. The value of \(2^{\frac{1}{2}} \times 2^{-\frac{1}{2}} \times(16)^{\frac{1}{2}}\) is
(1) 1
(2) 2
(3) 4
(4)1/2
Solution:\(2^{\frac{1}{2}} \times 2^{-\frac{1}{2}} \times(16)^{\frac{1}{2}}\)
Class 9 Math Solution WBBSE
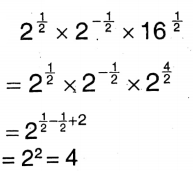
∴(3) 4
Class 9 Wbbse Laws Of Indices Chapter 2 Solved Exercises
3. If 4x=83, then the value of x is
(1)3/2
(2)9/2
(3)3
(4)9
Solution: 4x=83
or, 22x=29
∴ x=9/2
∴ (2)9/2
4. If 20-x= 1/7 then the value of (20)2x is
(1) 1/49
(2)7
(3)49
(4)1
Solution: 20-x= 1/7
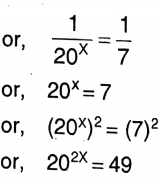
∴ (3)49
5. If 4 x 5x = 500 then the value of xx is
(1) 8
(2)1
(3)64
(4)27
Solution: 4 x 5x = 500
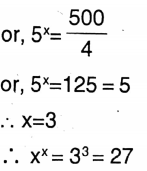
∴ (4)27
Wbbse 9th Class Maths Laws Of Indices Step By Step Solutions
Question 11. Short answer type questions:
1. If (27)x = (81)y, then let us write the ratio x: y.
Solution: (27)x = (81)y
or, 33x=34y
or, 3x=4y
or, \(\frac{x}{y}=\frac{4}{3}\)
= x:y 4:3
2. If (55+0.01)2– (55-0.01)2=5x, then let us calculate the value of x and write it.
Solution: (55+0.01)2– (55-0.01)2=5x
or, 4 x 55x 0.01= 5x
or,\(4 \cdot 5^5 \cdot \frac{1}{100}=5^x\)
or, \(5^5 \times \frac{1}{25}=5^x\)
Class 9 Math Solution WBBSE
or, 53 =5x
∴ x = 3 .
3. If 3 x 27x=9x+4, then let us calculate the value of x and write it.
Solution: 3 x 27x=9x+4
or, 3 x (33)=(32)x+4
or, 3 x 33x=32x+8
or, 31+ 3x = 32x+8
or,3x-2x=8-1
∴ x = 7
4. Let us find out the value of \(\sqrt[3]{\left(\frac{1}{64}\right)^{\frac{1}{2}}}\)and write it.
Solution:
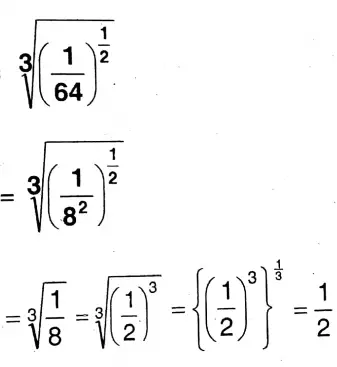
5. Let us write explaining the greater value between \(3^{3^3} \text { and }\left(3^3\right)^3\)with reason.
Solution: