Chapter 21 Logarithm Exercise 21
Important Formulae:
1. If \(a^x=M\) (a and M are two natural nos. and a > 0, a ≠ 1 and M > 0) then x is a real number, called the base, and with respect to a, M is called logarithm and is written in form x = logaM. It is read as ‘s is the logarithm of M to the base a’.
2. If \(a^x=M\) then x = logaM and conversely, if x = logaM then \(a^x=M\)
3. logaMN = logaM+logaN
4. logaMNP = logaM+logaN + logaP
5. \(\log _a \frac{M}{N}=\log _a M-\log _a N\)
6. \(\log _a M^C=C \log _a M\)
7. logaM = logaM x logab
8. \(\log _a^1=0\)
9. \(\log _a^a=0\)
10. \(a^{\log _a M}=M\)
11. \(\log _a^b \times \log _b a=1\)
12. \(\log _b a=\frac{1}{\log _a b}\)
13. \(\log _b M=\frac{\log _a M}{\log _a b}\)
14. \(\log _a\left(M_1 M_2 M_3 \ldots . . M_n\right)
=\log _a M_1+\log _a M_2+\log _a M_3 \ldots . \log _a M_n\)
[n = is a positive whole number]
15. If \(\log _a M=\log _a N \text { then } M=N\)
Read and Learn More WBBSE Solutions For Class 9 Maths
Question 1. Let us evaluate :
1. \(\log _{2 \sqrt{3}} 1728\)
Solution: Let, x = \(\log _{2 \sqrt{3}} 1728\)
∴ By definition, we get (2√3)x = 1728
\(or, (2 \sqrt{3})^x=2^6 \times 3^3or, (2 \sqrt{3})^x=2^6 \times(\sqrt{3})^6
or, (2 \sqrt{3})^x=(2 \sqrt{3})^6\)
∴ X = 6
∴ The value of \(\log _{2 \sqrt{3}} 1728\) is 6.
2. \(\log _{0.01} 0.000001\)
Solution: Let x = \(\log _{0.01} 0.000001\)
∴ By definition, we get (0.01)x= 0.000001
or, (0.01)x= (0.01)3
∴ X = 3
∴ The value of \(\log _{0.01} 0.000001\) is 3.

Wbbse Class 9 Maths Chapter 21 Logarithm Solutions
3. \(x=\log _{\sqrt{6}} 216\)
Solution: Let \(x=\log _{\sqrt{6}} 216\)
∴ By definition, we get (√6)x =216
or, (√6)x =(6)3
or, (√6)x= (√6)6
∴ X = 6
∴ The value of \(x=\log _{\sqrt{6}} 216\) is 6.
4. \(\log _4\left(\frac{1}{64}\right)\)
Solution: Let x = \(\log _4\left(\frac{1}{64}\right)\)
\(therefore(4)^x=\frac{1}{64}or, (4)^x=\frac{1}{4^3}
or, (4)^x=(4)^{-3}\)
∴ X=-3
∴ The value of \(\log _4\left(\frac{1}{64}\right)\) is -3.

Wbbse Class 9 Logarithm Exercise Solutions
Question 2. Let us evaluate:
1. Let us write by calculating, and find its base when the logarithm of 625 is 4.
Solution: Let base be x.
& therefore \log _x 625=4 \\
& therefore x^4=625
\end{aligned}
or, x^4=5^4
therefore x=5
\)
∴ The required base is 5.
2. Let us write by calculating, and find its base if the logarithm of 5832 is 6. Solve: Let log, 5832 = 6
Solution: Let logx 58326
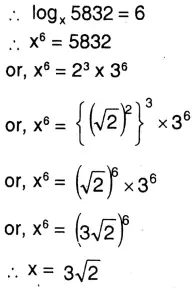
∴ Required base is \( x=3 \sqrt{2}\)
Question 3. Let us evaluate:
1. If \(1+\log _{10} a=2 \log _{10} b\) then express a in terms of b.
Solution: \(1+\log _{10} a=2 \log _{10} b\)
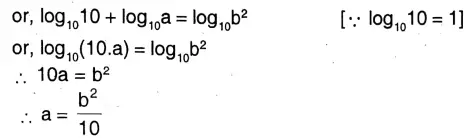
Class 9 Wbbse Maths Logarithm Solved Problems
2. \(3+\log _{10} x=2 \log _{10} y\) then express x in terms of y.
Solution: \(3+\log _{10} x=2 \log _{10} y\)
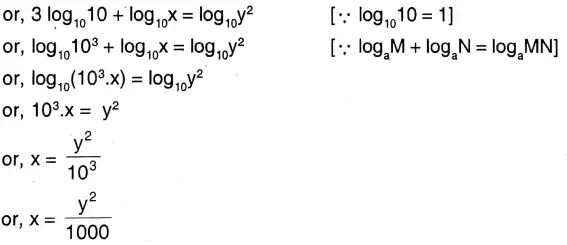
Question 4. Let us evaluate:
1. \(\log _2\left[\log _2\left\{\log _3\left(\log _3 27^3\right)\right\}\right]\)
Solution: \(\log _2\left[\log _2\left\{\log _3\left(\log _3 27^3\right)\right\}\right]\)

2. \(\frac{\log \sqrt{27}+\log 8-\log \sqrt{1000}}{\log 1.2}\)
Solution: \(\frac{\log \sqrt{27}+\log 8-\log \sqrt{1000}}{\log 1.2}\)
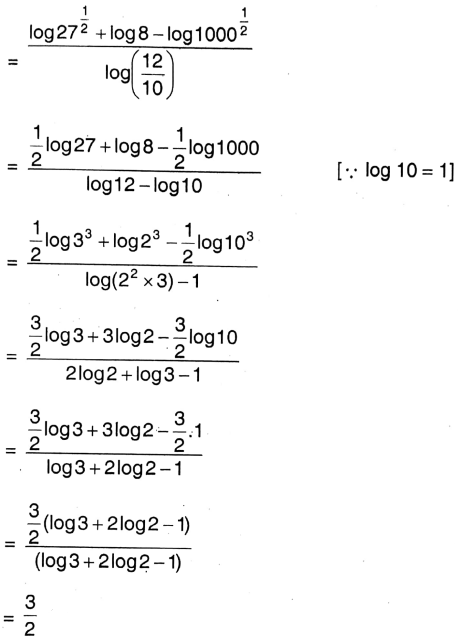
Wbbse Class 9 Maths Chapter 21 Logarithm Notes
3. \(\log _3 4 \times \log _4 5 \times \log _5 6 \times \log _6 7 \times \log _7 3\)
Solution: \(\log _3 4 \times \log _4 5 \times \log _5 6 \times \log _6 7 \times \log _7 3\)

4. \(\log _{10} \frac{384}{5}+\log _{10} \frac{81}{32}+3 \log _{10} \frac{5}{3}+\log _{10} \frac{1}{9}\)
Solution: \(\log _{10} \frac{384}{5}+\log _{10} \frac{81}{32}+3 \log _{10} \frac{5}{3}+\log _{10} \frac{1}{9}\)
\(=\log _{10} 384-\log _{10} 5+\log _{10} 81-\log _{10} 32+3 \log _{10} 5-3 \log _{10} 3+\log _{10} 1-\log _{10} 9\)\(=\log _{10}\left(3 \times 2^7\right)-\log _{10} 5+\log _{10} 3^4-\log _{10} 2^5+3 \log 5-3 \log 3+0-\log _{10} 3^2\)
\(=\log _{10} 3+\log _{10} 2^7-\log _{10} 5+4 \log _{10} 3-5 \log _{10} 2+3 \log 5-3 \log 3-2 \log _{10} 3\)
\(=5 \log _{10} 3-5 \log _{10} 3+7 \log _{10} 2-5 \log _{10} 2+2 \log _{10} 5\)
\(\begin{aligned}
& =2 \log _{10} 2+2 \log _{10} 5 \\
& =2 \log _{10}(2 \times 5) \\
& =2 \log _{10} 10 \\
& =2 \times 1 \\
& =2 \text { Ans. }
\end{aligned}\)
West Bengal Board Class 9 Logarithm Chapter Solutions
Question 5. Let us prove:
1. \(\log \frac{75}{16}-2 \log \frac{5}{9}+\log \frac{32}{243}=\log 2\)
Solution: L.H.S
= \(=\log \frac{75}{16}-2 \log \frac{5}{9}+\log \frac{32}{243}\)

= R.H.S proved.
2. \(\log _{10} 15\left(1+\log _{15} 30\right)+\frac{1}{2} \log _{10} 16\left(1+\log _4 7\right)-\log _{10} 6\left(\log _6 3+1+\log _6 7\right)=2\)
Solution:

3. \(\log _2 \log _2 \log _4 256+2 \log _{\sqrt{2}} 2=5\)
Solution:
\(\begin{aligned}& \text { L.H.S. }=\log _2 \log _2 \log _4 256+2 \log _{\sqrt{2}} 2 \\
& =\log _2 \log _2 \log _4 4^4+2 \log _{\sqrt{2}}(\sqrt{2})^2
\end{aligned}\)
\(\log _2 \log _2 4 \log _4 4+2 \times 2 \log _{\sqrt{2}}(\sqrt{2})\)
\(\log _2 \log _2 4 \log _4 4+4\)
\(\begin{aligned}
& =\log _2 \log _2 4+4 \\
& =\log _2 \log _2 2^2+4 \\
& =\log _2 2 \log _2 2+4 \\
& =\log _2 2+4
\end{aligned}\)
= 1 + 4 = 5 R.H.s Proved
\(\begin{aligned}
&\begin{aligned}
& {\left[because \log _{\sqrt{2}} \sqrt{2}=1\right]} \\
& {\left[because \log _4 4=1\right]}
\end{aligned}\\
&\left[because \log _2 2=1\right]
\end{aligned}\)
Wbbse Class 9 Logarithm Important Questions
4. \(\log _{x^2} x \times \log _{y^2} y \times \log _{z^2} z=\frac{1}{8}\)
Solution:
L.H.S.= \(\log _{x^2} x \times \log _{y^2} y \times \log _{z^2} z\)
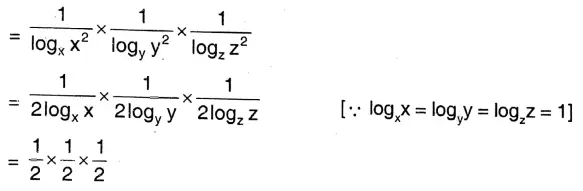
\(\frac{1}{8}\) = R.H.S. Proved
5. \(\log _{b^3} a \times \log _{c^3} b \times \log _{a^3} c=\frac{1}{27}\)
Solution:
L.H.S = \(\log _{b^3} a \times \log _{c^3} b \times \log _{a^3} c\)
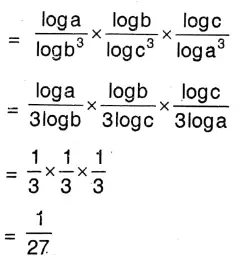
= R.H.S (Proved)
6. \(\frac{1}{\log _{x y}(x y z)}+\frac{1}{\log _{y z}(x y z)}+\frac{1}{\log _{z x}(x y z)}=2\)
L.H.S.= \(\frac{1}{\log _{x y}(x y z)}+\frac{1}{\log _{y z}(x y z)}+\frac{1}{\log _{z x}(x y z)}\)
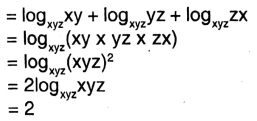
= R.H.S (Proved)
7. \(\log \frac{a^2}{b c}+\log \frac{b^2}{c a}+\log \frac{c^2}{a b}=0\)
Solution:
L.H.S = \(\log \frac{a^2}{b c}+\log \frac{b^2}{c a}+\log \frac{c^2}{a b}\)
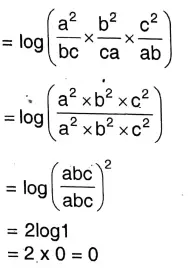
R.H.S Proved
Wbbse Class 9 Maths Logarithm Chapter 21
8. \(x^{\log y-\log z} \times y^{\log z-\log x} \times z^{\log x-\log y}=1\)
Solution:
\(\text { Let } P=x^{\log y-\log z} \times y^{\log z-\log x} \times z^{\log x-\log y}=1\)Taking log on both sides
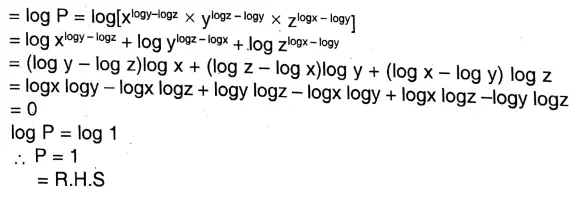
Question 6. Let us prove
1. If \(\log \frac{x+y}{5}=\frac{1}{2}(\log x+\log y)\), then let us show that \(\frac{x}{y}+\frac{y}{x}=23\)
Solution:
Given
\(\log \frac{x+y}{5}=\frac{1}{2}(\log x+\log y)\)
⇒ \(\log \frac{x+y}{5}=\frac{1}{2}(\log x+\log y)\)
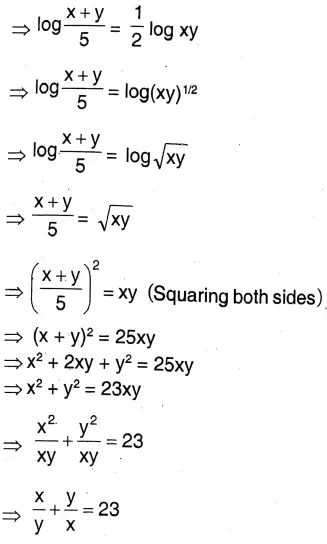
Wbbse 9th Class Maths Logarithm Step By Step Solutions
2. If \(a^4+b^4=14 a^2 b^2\) then let us show that xyz = 1.
Solution:
Given
\(a^4+b^4=14 a^2 b^2\)
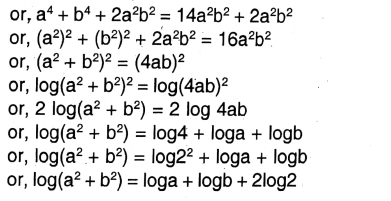
Question 7. If \(\frac{\log x}{y-z}=\frac{\log y}{z-x}=\frac{\log z}{x-y}\) then let us show that xyz = 1.
Solution: \(\frac{\log x}{y-z}=\frac{\log y}{z-x}=\frac{\log z}{x-y}\) = k
∴ \(\frac{\log x}{y-z}=k \Rightarrow \log x=k(y-z)\) …….(1)
∴ \(\frac{\log y}{z-x}=k \Rightarrow \log y=k(z-x)\) ….(2)
∴ \(\frac{\log z}{x-y}=k \Rightarrow \log z=k(x-y)\) …(3)
Adding equations (1), (2) and (3) we get
logx+logy + logz = k(y-z) + k(z-x) + k(x-y)
log(xyz) = k(y-Z+Z-x+x-y)
log(xyz) = k.0 = 0
∴ log(xyz) log1
∴ xyz= 1 Proved
Question 8. If, \(\frac{\log x}{b-c}=\frac{\log y}{c-a}=\frac{\log z}{a-b}\) then let us show that:
1. \(x^{b+c} \cdot y^{c+a} \cdot z^{a+b}=1\)
2. \(x^{b^2+b c+c^2} \cdot y^{c^2+c a^2+a^2} \cdot z^{a^2+a b+b^2}=1\)
Solution:
\(\frac{\log x}{b-c}=\frac{\log y}{c-a}=\frac{\log z}{a-b}=k\)
logx = k(b-c)
logy = k (c-a)
logz= k ( a – b)
1. \([\log \left(x^{b+c} \cdot y^{c+a} \cdot z^{a+b}\right)=\log x^{b+c}+\log y^{c+a}+\log z^{a+b}\)
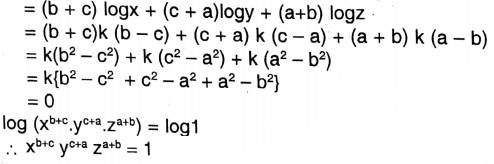
2. \(\log \left(x^{b^2+b c+c^2} \cdot y^{c^2+c a^2+a^2} \cdot z^{a^2+a b+b^2}\right)\)
= \(\log \dot{x}^{b^2+b c+c^2}+y^{c^2+c a^2+a^2}+z^{a^2+a b+b^2}\)
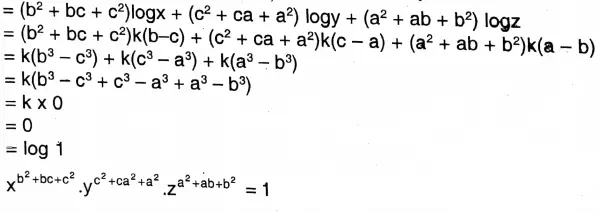
Question 9. If a3-x.b5x = a5+x.b3x, then let us show that \(\)
Solution:
Given
a3-x.b5x = a5+x.b3x
\(or, \frac{b^{5 x}}{b^{3 x}}=\frac{a^{5+x}}{a^{3-x}}or, b^{5 x-3 x}=a^{(5+x)-(3-x)}
or, b^{5 x-3 x}=a^{5+x-3+x}
or, b^{2 x}=a^{2+2 x}
or, b^{2 x}=a^2 \cdot a^{2 x}\) \(\begin{aligned}
& \text { or, } \frac{b^{2 x}}{a^{2 x}}=a^2 \\
& \left(\frac{b}{a}\right)^{2 x}=a^2 \\
& \log \left(\frac{b}{a}\right)^{2 x}=\log a^2 \\
& 2 x \log \left(\frac{b}{a}\right)=2 \log a \\
& x \log \frac{b}{a}=\log a
\end{aligned}\)
Wbbse Class 9 Maths Logarithm Laws And Examples
Question 10. Let us evalute:
1. \(\log _8\left[\log _2\left\{\log _3\left(4^x+17\right)\right\}\right]=\frac{1}{3}\)
Solution:
Given
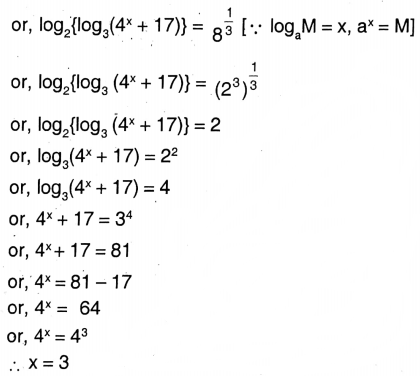
2. \(\log _8 x+\log _4 x+\log _2 x=11\)
Solution: \(\log _8 x+\log _4 x+\log _2 x=11\)
\(\text { or, } \frac{1}{\log _x 8}+\frac{1}{\log _x 4}+\frac{1}{\log _x 2}=11\)\(\text { or, } \frac{1}{\log _x 2^3}+\frac{1}{\log _x 2^2}+\frac{1}{\log _x 2}=11\)
\(\text { or, } \frac{1}{3 \log _x 2}+\frac{1}{2 \log _x 2}+\frac{1}{\log _x 2}=11\)
\(\text { or, } \frac{1}{\log _x 2}\left(\frac{1}{3}+\frac{1}{2}+1\right)=11\)
\(\text { or, } \frac{1}{\log _x 2}\left(\frac{2+3+6}{6}\right)=11\)
\(\text { or, } \frac{1}{\log _x 2}\left(\frac{11}{6}\right)=11\)
\(\text { or, } \frac{1}{\log _x 2}=11 \times \frac{6}{11}\)
\(\text { or, } \frac{1}{\log _x 2}=6\)
\(or, \log _2 x=6
or, x=2^6
or, x=64 \)
Question 11. Let us show that the value of \(\log _{10} 2\) lies between \(\frac{1}{4} \text { and } \frac{1}{3}\)
Solution: Let \(\log _{10} 2=x\)
10x = 2

Question 12. Multiple choice questions
1. If \(\log _{\sqrt{x}} 0.25=4\) then the value of x will be
1. 0.5
2. 0.25
3. 4
4. 16
Solution: \(\log _{\sqrt{x}} 0.25=4\)
\(therefore(\sqrt{x})^4=0.25or, \left\{(\sqrt{x})^2\right\}^2=0.25
or, \mathrm{x}^2=0.25
or, x=\sqrt{0.25}
or, x=0.5\)
∴ 1. 0.5
2. If log10(7x-5)= 2, then the value of x will be
1. 10
2. 12
3. 15
4. 18
Solution: log10(7x-5)=2
\(or, 10^2=7 x-5or, (7 x-5)=100
or, 7 x=105
or, x=15\)
3. If log23 = a, then the value of log827 is
1. 3a
2. \(\frac{1}{a}\)
3. 2a
4. a
Solution: log23 = a
\(\begin{aligned}& \log _8 27=\log _8 3^3 \\
& =3 \log _8 3 \\
& =3 \times \frac{1}{\log _3 8} \\
& =3 \times \frac{1}{\log _3 2^3} \\
& =3 \times \frac{1}{3 \log _3 2} \\
& =\log _2 3
\end{aligned}\)
log827 = a
∴ 4. a
Class 9 Wbbse Logarithm Chapter 21 Solved Exercises
4. If \(\log _{\sqrt{2}} x=a\), then the value of \(\log _{2 \sqrt{2}} x\) is
1. \(\frac{a}{3}\)
2. a
3. 2a
4. 3a
Solution: \(\log _{\sqrt{2}} x=a\)
∴ \(\begin{aligned}
therefore & \log _{2 \sqrt{2}} x=\frac{1}{\log _x 2 \sqrt{2}} \\
& =\frac{1}{\log _x\left\{(\sqrt{2})^2 \cdot \sqrt{2}\right\}} \\
& =\frac{1}{\log _x(\sqrt{2})^3} \\
& =\frac{1}{3 \log _x \sqrt{2}} \\
& =\frac{1}{3} \log _{\sqrt{2}} x \\
& =\frac{a}{3} \\
therefore & \log _{2 \sqrt{2}} x=\frac{a}{3}
\end{aligned}\)
∴ 1. \(\frac{a}{3}\)
5. If \(\log _x \frac{1}{3}=-\frac{1}{3}\) then the value of x is
1. 27
2. 9
3. 3
4. \(\frac{1}{27}\)
Solution: \(\log _x \frac{1}{3}=-\frac{1}{3}\)
\(or, \log _x 3^{-1}=-\frac{1}{3}\) \( or, -\log _x 3=-\frac{1}{3}\) \( or, \log _x 3=\frac{1}{3}\) \( or, x^{\frac{1}{3}=3}\) \( or, \left(x^{\frac{1}{3}}\right)^3=3^3\)X = 27
∴ 1. 27
Question13. Short answer type questions:
1. Let us calculate the value of \(\log _4 \log _4 \log _4 256\)
Solution: \(\log _4 \log _4 \log _4 256\)
=\(\log _4 \log _4 \log _4 4^4\)
\(\begin{aligned}& =\log _4 \log _4 4 \log _4 4 \\
& =\log _4 \log _4 4 \\
& =\log _4 1
\end{aligned}\)
∴\(\log _4 \log _4 \log _4 256\) = 0
2. Let us calculate the value of \(\log \frac{a^n}{b^n}+\log \frac{b^n}{c^n}+\log \frac{c^n}{a^n}\)
Solution: \(\log \frac{a^n}{b^n}+\log \frac{b^n}{c^n}+\log \frac{c^n}{a^n}\)
\(\begin{aligned}& =\log \left(\frac{a}{b}\right)^n+\log \left(\frac{b}{c}\right)^n+\log \left(\frac{c}{a}\right)^n \\
& =n \log \frac{a}{b}+n \log \frac{b}{c}+n \log \frac{c}{a} \\
& =n(\log a-\log b)+n(\log b-\log c)+n(\log c-\log a) \\
& =n(\log a-\log b+\log b-\log c+\log c-\log a) \\
& =n .0 \\
& =0
\end{aligned}\)
3. Let us show that \(a^{\log _a x}=x .\)
Solution: Let loga = x
\(\begin{aligned}& a^u=x \\
& a^{\log _a x}=x
\end{aligned}\)
\(\left[because \mathrm{u}=\log _{\mathrm{a}} \mathrm{x}\right]\)
4. If \(\log _e 2 \cdot \log _x 25=\log _{10} 16 \cdot \log _9 10 \) then let us calculate the value of x.
Solution: \(\log _e 2 \cdot \log _x 25=\log _{10} 16 \cdot \log _9 10 \)

