Class IX Maths Solutions WBBSE Chapter 4 Co-ordinate Geometry: Distance Formula Let Us Work Out
Question 1. I measure the length of the straight line joining the following pairs of points
1. (18, 0); (8, 0)
Solution: Let P and Q be two points whose coordinates are (18,0) and (8,0). Points P and Q are situated in the positive direction of the x-axis.
∴ \(\overline{\mathrm{PQ}}=(\overline{\mathrm{OP}}-\overline{\mathrm{OQ}})\) = (18 – 8) unit = 10 units.
Read and Learn More WBBSE Solutions For Class 9 Maths
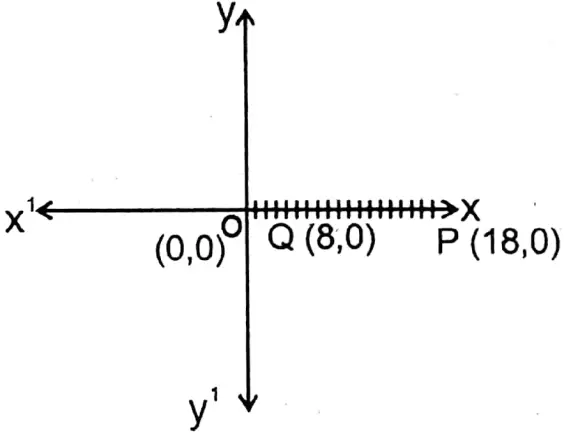
∴ The length of the straight line \(\overline{\mathrm{PQ}}\) = 10 units.
∴ Length of the line segment by joining two points is 10 units.

Wbbse Class 9 Maths Chapter 4 Coordinate Geometry Distance Formula Solutions
2. (0, 15); (0, 4)
Soltion: Let P and Q are two points whose coordinates are (0, 15) and (0, 4). P and Q are situated in the positive direction of the y-axis.
∴ \(\overline{\mathrm{OP}}\) =15 unit
∴ \(\overline{\mathrm{OQ}}\)= 4 unit
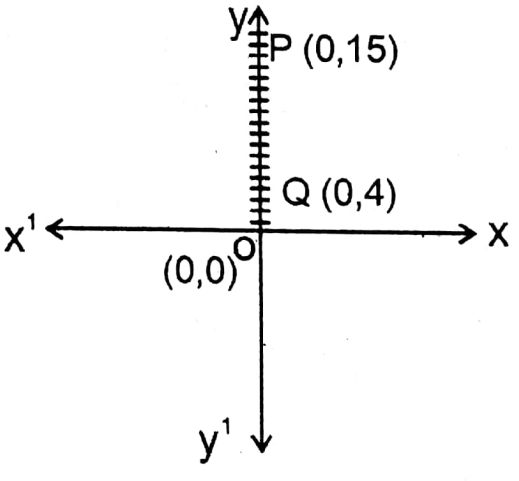
∴ \(\overline{\mathrm{PQ}}=(\overline{\mathrm{OP}}-\overline{\mathrm{OQ}}))\) = (15 – 4) units = 11 units.
∴ The length of the straight line PQ is 11 units.
∴ The length of the line segment formed by joining the two points is 11 units.
3. (-7, 0) (-2, 0)
Solution: Let P and Q are two points whose coordinates are (-7, 0) and (-2, 0). Points P and Q are situated in the negative direction of the x-axis.
∴ \(\overline{\mathrm{OP}}\) = 7 units
∴\(\overline{\mathrm{OQ}}\)= 2 units
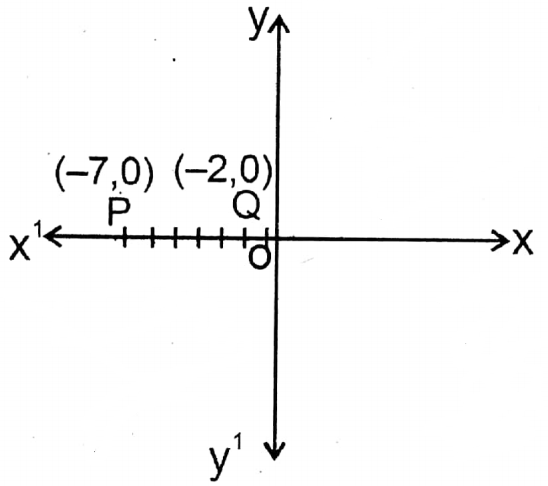
Wbbse Class 9 Coordinate Geometry Distance Formula Exercise Solutions
∴ \(\overline{\mathrm{PQ}}=\overline{\mathrm{QP}}=\overline{\mathrm{OP}}-\overline{\mathrm{OQ}}\) = (7-2) units = 5 units
∴ Length of straight line PQ is 5 units.
∴ The length of the straight line formed by joining the two points is 5 units.
Class 9 Mathematics West Bengal Board
4. (0, -10) (0, -3)
Solution: Let P and Q are two points whose coordinates are: (0, -10) and (0, -3).
∴ \(\overline{\mathrm{OP}}\) = 10 units
∴ \(\overline{\mathrm{OQ}}OQ\) = 3 units
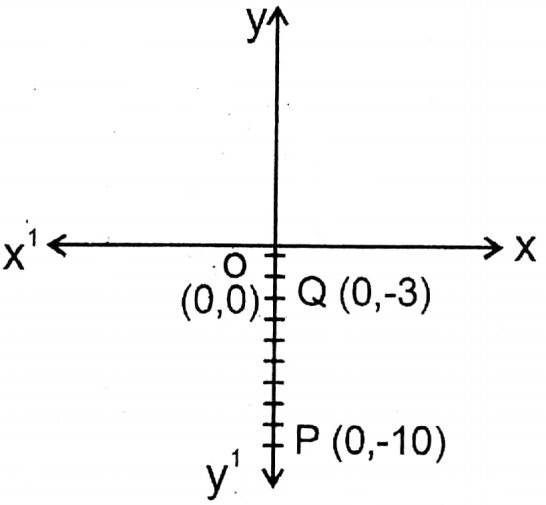
\(\overline{\dot{\mathrm{PQ}}}=\overline{\mathrm{QP}}=\overline{\mathrm{OP}}-\overline{\mathrm{OQ}}\) = (10 – 3) units = 7 units.
∴ Length of straight line PQ is 7 units.
∴ The length of the line segment formed by joining the two points is 7 units.
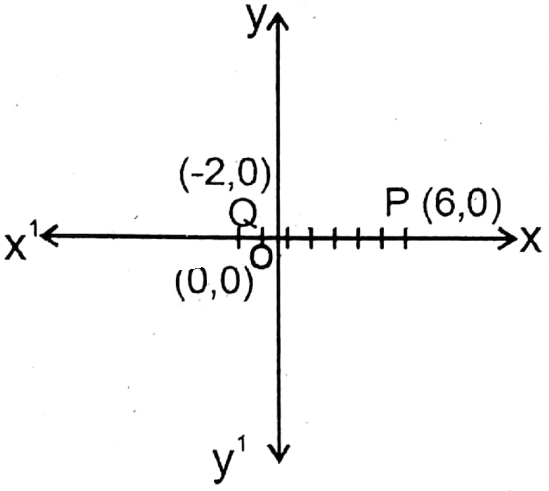
5. (6, 0) (-2, 0)
Solution: Let P and Q are two points whose coordinates are: (6, 0) and (-2, 0). Point P is situated in the positive direction and point Q is situated in the negative direction of x-axis.
∴ \(\overline{\mathrm{OP}}\) = 6 units
∴ \(\overline{\mathrm{OQ}}\) = 2 units
Class 9 Wbbse Maths Distance Formula Solved Problems
\(\overline{\mathrm{PQ}}=\overline{\mathrm{QP}}=(\overline{\mathrm{OP}}+\overline{\mathrm{OQ}})\) = (6 + 2) units = 8 units.
∴ Length of straight line PQ is 8 units.
∴ The length of the line segment formed by joining the two points is 8 units.
Class 9 Mathematics West Bengal Board
6. (0,-5) (0, 9)
Solution: Let P and Q are two points whose co-ordinates are: (0, -5) and (0, 9). Point P is situated in the negative direction and point Q is situated in the positive direction of y-axis.
∴ \(\overline{\mathrm{OP}}\) = 5 units
∴ \(\overline{\mathrm{OQ}}OQ\)=9 units
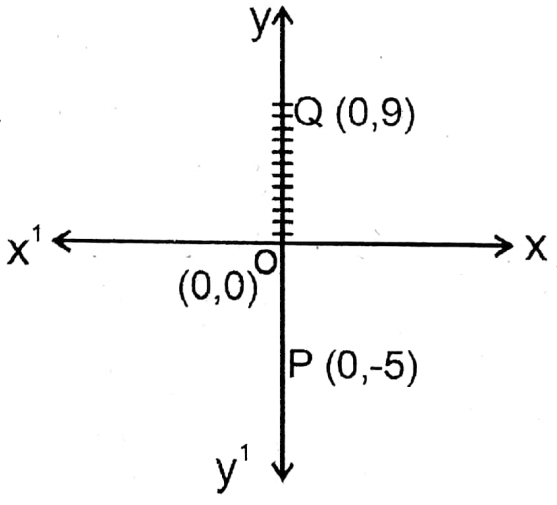
∴ \(\overline{\mathrm{PQ}}=\overline{\mathrm{QP}}=(\overline{\mathrm{OP}}+\overline{\mathrm{OQ}})\) = (5+9) units = 14 units.
∴ Length of the straight line PQ is 14 units.
∴ The length of the line segment formed by joining the two points is 14 units.
7. (5, 0): (0, 10)
Solution: Let P and Q are two points whose coordinates are (5, 0) and (0, 10)
∴OP = 5 units
OQ = 10 units
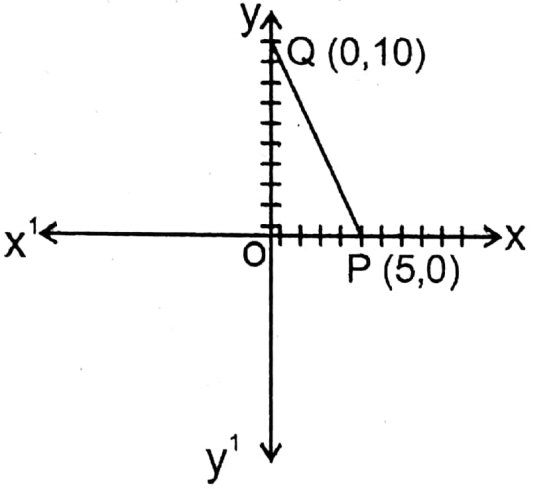
In right angled ΔPOQ from Pythagoras’ theorem,
PQ2 = OP2 + OQ2
or, PQ2 = (5)2 + (10)2 sq.units
or, PQ2 = 25+ 100 sq.units
or, PQ2 = 125 sq.units
∴ PQ= √125 units = 5√5 units
∴ Distance between points P and Q is 5√5 units.
∴ The length of the line segment formed by joining the two points is 5√5 units.
Wbbse Class 9 Maths Chapter 4 Distance Formula Notes
8. (3,0): (0, 4)
Solution: Let P and Q be two points whose co-ordinates are (3, 0) and (0, 4).
∴ OP = 3 units
OQ = 4 units
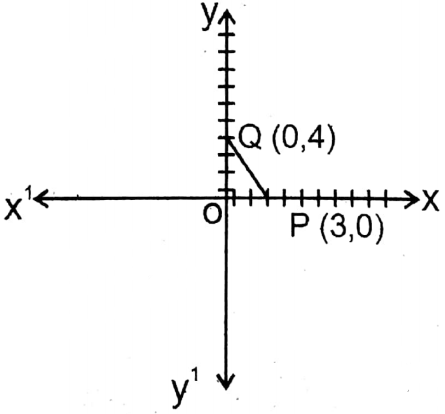
In right-angled APOQ we get by Pythagoras’ theorem,
PQ2 = OP2+OQ2
or, PQ2 = (3)2 + (4)2 sq.units
or, PQ2 = 9 + 16 sq.units
or, PQ2 = 25 sq.units
∴ PQ= √25 units = 5 units
∴ Distance between points P and Q is 5 units.
Length of the straight line formed by joining the two points is 5 units.
Class 9 Maths WB Board
9. (4,3); (2, 1)
Solution: Let A and B are two points whose co-ordinates are (2, 1) and (4, 3).
In Image, OM = 2 units and AM = 1 units.
ON 4 units and BN = 3 units.
∴ AP = MN = ON-OM = (4-2) units = 2 units
Again, BP= BN-PN = (3-1) units = 2 units
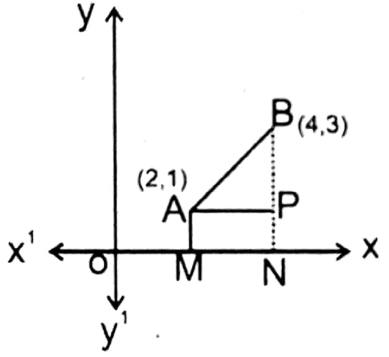
In right angled Δ APB we get by Pythagoras’ theorem,
AB2 = AP2 + BP2
or, AB2 = (2)2 + (2)2 sq.units
or, AB2 = 4+4 sq.units
or, AB2 = 8 sq.units
∴ AB = √8 units = 2√2 units
∴ Distance between the points A and B, i.e., length of the straight line formed by lining the two points is 2√2 units.
Class 9 Maths WB Board
10. (-2,-2) (2, 2)
Solution: Let A and B are two points whose co-ordinates are (-2, -2) and (2, 2).
∴ A point lies in third quadrant. B lies in first quadrant. From points A and B on axis respectively AP and BQ perpendiculars are drawn which cut x-axis at points p and Q respectively.
∴ OP 2 units and OQ = 2 units.
BQ 2 units and AP 2 units
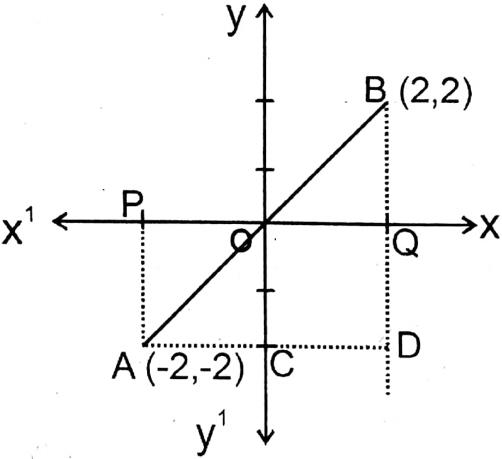
From point A on extended-BQ a perpendicular is drawn which cuts extended BQ at point D.
∴ AD = PQ = OP + OQ
(2+2) units = 4 units
BD = BQ + QD = BQ + PA (2+2) units = 4 units
In right angled AADB we get by Pythagoras’ theorem, AB2
AD2+ BD2
or, AB2 = (4)2+(4)2 sq.units
or, AB2 = 16+ 16 sq.units
or, AB2 = 32 sq.units
∴ AB = √32 units = 4√√2 units
∴ Length of the straight line AB is 4√2 units, i.e., the length of the straight line formed by joining the two points is 4√2 units.
West Bengal Board Class 9 Coordinate Geometry Distance Formula Solutions
Class 9 Mathematics West Bengal Board Chapter 4 Co-ordinate Geometry: Distance Formula Exercise 4.1
Question 1. Let us calculate the distances of the following points from the origin
Here, distance formula = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)unit.
1. (7, -24)
Solution: The distance of the point (7,-24) from the origin is
D & =\sqrt{(7-0)^2+(-24-0)^2} \text { unit } \\
& =\sqrt{49+576} \text { unit } \\
& =\sqrt{625} \text { unit } \\
& =25 \text { unit }
\end{aligned}\)
2. (3,-4)
Solution:The distance of the point (3, 4) from the origin (0,0) is
D & =\sqrt{(3-0)^2+(-4-0)^2} \text { unit } \\
& =\sqrt{9+16} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)
Maths WBBSE Class 10 Solutions
3. (a+b, a-b)
Solution: The distance of the point (a+b, a-b) from the origin (0,0) is
\(\begin{aligned}& D=\sqrt{(a+b-0)^2+(a-b-0)^2} \text { unit } \\
& =\sqrt{(a+b)^2+(a-b)^2} \text { unit } \\
& =\sqrt{2\left(a^2+b^2\right)} \text { unit }
\end{aligned}\)
Question 2. Let us calculate the distances between the pairs of points given below:
1. (5, 7) and (8, 3)
Solution: The distance between (5, 7) and (8, 3) is
& =\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \text { unit } \\
& D=\sqrt{(5-8)^2+(7-3)^2} \text { unit } \\
& =\sqrt{-3^2+4^2} \text { unit } \\
& =\sqrt{9+16} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)
Maths WBBSE Class 10 Solutions
2. (7,0) and (2,-12)
Solution: Distance between (7, 0) and (2,-12) is
\(\begin{aligned}& =\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \text { unit } \\
& D=\sqrt{(5-8)^2+(7-3)^2} \text { unit } \\
& =\sqrt{-3^2+4^2} \text { unit } \\
& =\sqrt{9+16} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)
Wbbse Class 9 Distance Formula Important Questions
3. \(\left(-\frac{3}{2}, 0\right)\) and (0, -2)
Solution: Distance between \(\left(-\frac{3}{2}, 0\right)\) and (0, -2)
\(=\sqrt{\left(\frac{-3}{2}-0\right)^2+(0+2)^2} \text { unit }\)
\(\begin{aligned}
& =\sqrt{\frac{9}{4}+4} \text { unit } \\
& =\sqrt{\frac{9+16}{4}} \text { unit } \\
& =\sqrt{\frac{25}{4}} \text { unit } \\
& =\frac{5}{2} \text { unit } \\
& =2.5 \text { unit }
\end{aligned}\)
Maths WBBSE Class 10 Solutions
4. (3, 6) and (-2, -6)
Solution: Distance between (3, 6) and (-2, -6) is
\(\begin{aligned}& D=\sqrt{(3+2)^2+(6+6)^2} \text { unit } \\
& =\sqrt{25+144} \text { unit } \\
& =\sqrt{169} \text { unit } \\
& =13 \text { unit }
\end{aligned}\)
5. (1,-3) and (8,3)
Solution: Distance between (1,-3) and (8,3) is
& =\sqrt{(1-8)^2+(-3-3)^2} \text { unit } \\
& =\sqrt{7^2+6^2} \text { unit } \\
& =\sqrt{49+36} \text { unit } \\
& =\sqrt{85} \text { unit }
\end{aligned}\)
Maths WBBSE Class 10 Solutions
6. (5,7) and (8,3)
Solution: The distance between the points (5, 7) and (8, 3) is
\(\begin{aligned}D & =\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2} \text { unit } \\
& =\sqrt{(5-8)^2+(7-3)^2} \text { unit } \\
& =\sqrt{3^2+4^2} \text { unit } \\
& =\sqrt{9+16} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)
Question 3. Let us prove that the point (-2, -11) is equidistant from the two points (3,7) and (4,6).
Solution: The distance (D1) between the points (-2, -11) and (-3, 7) is
\(\begin{aligned}& =\sqrt{(-2+3)^2+(-11-7)^2} \text { unit } \\
& =\sqrt{1^2+(-18)^2} \text { unit } \\
& =\sqrt{1+324} \text { unit } \\
& =\sqrt{325} \text { unit }
\end{aligned}\)
Maths WBBSE Class 10 Solutions
And the distance (D) between the points (-2, -11) and (4, 6) is
\(\begin{aligned}& =\sqrt{(-2-4)^2+(-11-6)^2} \text { unit } \\
& =\sqrt{(-6)^2+(-17)^2} \text { unit } \\
& =\sqrt{36+289} \text { unit } \\
& =\sqrt{325} \text { unit }
\end{aligned}\)
Here, D1 = D2
∴ The point (-2, -11) is equidistant to the two points (-3, 7) and (4, 6). Proved
Question 4. By calculation let us show that the points (7, 9), (3, -7), and C (-3, 3) are the vertices of a right-angled triangle.
Solution: Let the points be A = (7, 9), B = (3, -7), and C = (-3, 3).
\(\begin{aligned}
\text { Distance } A B & =\sqrt{(7-3)^2+(9+7)^2} \text { unit } \\
& =\sqrt{16+256} \text { unit } \\
& =\sqrt{272} \text { unit }
\end{aligned}\)
WBBSE Solution Class 10 Maths
\(\begin{aligned}\text { Distance } B C & =\sqrt{(3+3)^2+(-7-3)^2} \text { unit } \\
& =\sqrt{36+100} \text { unit } \\
& =\sqrt{136} \text { unit }
\end{aligned}\)
\(\begin{aligned}
\text { Distance } A C & =\sqrt{(7+3)^2+(9-3)^2} \text { unit } \\
& =\sqrt{100+36} \text { unit } \\
& =\sqrt{136} \text { unit }
\end{aligned}\)
WBBSE Solution Class 10 Maths
Here, BC2+ CA2 = 136+ 136 = 272 & AB2 = 272
∴ BC2+ CA2= AB2
Δ ABC is a right angled triangle, right angle being at ∠C.
Question 5. Let us prove that in both of the following cases, the three points are the vertices of an isosceles triangle:
- (1, 4), (4, 1), and (8, 8)
Solution: Let A = (1,4); B = (4,1) & C = (8,8)
\text { Distance } A B & =\sqrt{(1-4)^2+(4-1)^2} \text { unit } \\
& =\sqrt{9+9} \text { unit } \\
& =\sqrt{18} \text { unit }
\end{aligned}\)
\(\begin{aligned}
\text { Distance AC } & =\sqrt{(1-8)^2+(4-8)^2} \text { unit } \\
& =\sqrt{49+16} \text { unit } \\
& =\sqrt{65} \text { unit }
\end{aligned}\)
WBBSE Solution Class 10 Maths
\(\begin{aligned}\text { Distance } B C & =\sqrt{(4-8)^2+(1-8)^2} \text { unit } \\
& =\sqrt{16+49} \text { unit }
\end{aligned}\)
∴ In ΔABC AC= BC
∴ ABC is an isosceles triangle. Proved
Wbbse Class 9 Maths Distance Formula Chapter 4
2. (-2,-2), (2, 2) and (4,-4)
Solution:Let P= (-2,-2), Q=2, 2) and R = (4,-4)
\text { Distance } P Q & =\sqrt{(-2-2)^2+(-2-2)^2} \text { unit } \\
& =\sqrt{4^2+4^2} \text { unit } \\
& =\sqrt{16+16} \text { unit } \\
& =\sqrt{32} \text { unit }
\end{aligned}\)
\(\begin{aligned}
\text { Distance } Q R & =\sqrt{(2-4)^2+(2+4)^2} \text { unit } \\
& =\sqrt{(2)^2+(6)^2} \text { unit } \\
& =\sqrt{4+36} \text { unit } \\
& =\sqrt{40} \text { unit }
\end{aligned}\)
\(\begin{aligned}
\text { Distance PR } & =\sqrt{(-2-4)^2+(-2+4)^2} \text { unit } \\
& =\sqrt{(-6)^2+(2)^2} \text { unit } \\
& =\sqrt{36+4} \text { unit } \\
& =\sqrt{40} \text { unit }
\end{aligned}\)
WBBSE Solution Class 10 Maths
∴ In triangle PQR, QR = PR= √40
∴ ΔPQR is an isosceles triangle. Proved
Question 6. Let us prove that the three points A (3, 3), B (8,-2), and C (-2,-2) are the vertices of a right-angled triangle. Let us calculate the length of the hypotenuse of ΔABC.
Solution:
Given, A (3,3); B = (8,-2); C = (-2,-2)
AB2 = (38)2 + (3 + 2)2 = 52 +52 = 25+ 25 = 50
AC2 = (3 + 2)2 + (3 + 2)2 = 52 +52 = 25+ 25 =50
BC2 = (8+ 2)2 + (-2 + 2)2 = 102 +0 =100+ 0 = 100
∴ AB2+ AC2 = 50+50 = 100∴ Δ ABC is right angled triangle and Hypotenuse BC= √100 = 10 units.
Question 7. Let us show by calculation that the points (2, 1), (0, 0), (-1, 2), and (1, 3) are the angular points of a square.
Solution: A = (2, 1), B = (0, 0), C (-1, 2), and D = (1, 3).
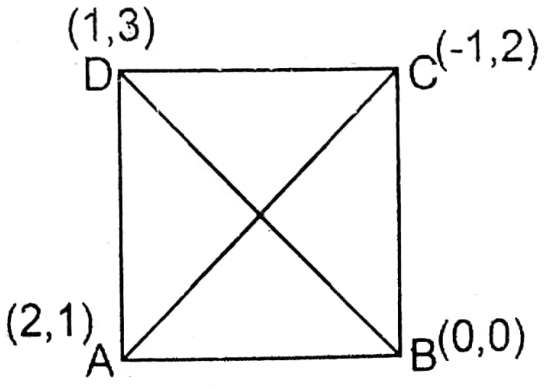
\(Distance A B=\sqrt{(2-0)^2+(1-0)^2} units =\sqrt{4+1} units =\sqrt{5} units\)
\(Distance B C=\sqrt{(0+1)^2+(0-2)^2} units =\sqrt{1+4} units =\sqrt{5} units\)
Class 10 Math Solution WBBSE Chapter 4
\(\begin{aligned}\text { Distance CD } & =\sqrt{(-1-1)^2+(2-3)^2} \text { units } \\
& =\sqrt{4+1} \text { units } \\
& =\sqrt{5} \text { units }
\end{aligned}\)
\(\begin{aligned}
\text { Distance DA } & =\sqrt{(1-2)^2+(3-1)^2} \text { units } \\
& =\sqrt{1+4} \text { units } \\
& =\sqrt{5} \text { units }
\end{aligned}\)
\(Again, Diagonal A C=\sqrt{(2+1)^2+(1-2)^2} units =\sqrt{9+1} units =\sqrt{10} units\)
Class 10 Math Solution WBBSE Chapter 4
\(\begin{aligned}\text { and Diagonal BD } & =\sqrt{(0-1)^2+(0-3)^2} \text { units } \\
& =\sqrt{1+9} \text { units } \\
& =\sqrt{10} \text { units }
\end{aligned}\)
∴ In the quadrilateral ABCD all the sides are equal and diagonals AC = BD.
∴ ABCD is a square. Proved
Question 8. Let us calculate and see that for what value of y, the distance between the two points (2,y) and (10, -9) will be 10 units.
Solution:
Given
Distance of the points (2, y) from the point (10, -9)= 10 units.
∴ \(\begin{aligned}
& \sqrt{(2-10)^2+(y+9)^2}=10 \text { (given) } \\
& \sqrt{(-8)^2+(y+9)^2}=10
\end{aligned}\)
Class 10 Math Solution WBBSE Chapter 4
or, 64 +(y+9)2= 100 (Squaring both sides)
or, (y+9) = 100 -64 =36
∴ y+9 = ±6
(1) y+9=6
y=6-9=-3 and
(2) y+9=-6
∴ y-6-9=-15
Question 9. Let us find a point on x-axis which is equidistant from the two points (3,5) and (1,3).
Hints the required point on x-axis is (x,0) = (x-3)2 + (0-5)2 = (x-1)2 + (0-3)2
Solution:
Given
Two points (3,5) and (1,3)
Let the point on the x-axis is (x, 0).
∴ Distance of the point (3, 5) from the point (x,0) is
\(\begin{aligned}& =\sqrt{(x-3)^2+(0-5)^2} \text { unit } \\
& =\sqrt{(x-3)^2+5^2} \text { unit }
\end{aligned}\)
Class 10 Math Solution WBBSE Chapter 4
and the distance of the point (1,3) from the point (x, 0) is
\(\begin{aligned}& =\sqrt{(x-1)^2+(0-3)^2} \text { unit } \\
& =\sqrt{(x-1)^2+3^2} \text { unit }
\end{aligned}\)
According to the condition, \(\sqrt{(x-3)^2+25}=\sqrt{(x-1)^2+9}\)
or,(x -3)2 + 25 = (x -1 )2 +9
or, (3 – x)2 – (1 – x) 2 = 9 – 25
or, (3-x+1-x) (3-x-1+x)=-16
or, (4-2x) x 2 = -16
or, 2(2 – x) x2 = -16
or, 2 – x = -4
or, 2 + 4 = x
∴ X = 6
∴ The required point is (6,0).
Class 10 Math Solution WBBSE Chapter 4
Question 10. Let us write by calculation whether the three points O(0, 0), A(4, 3), and B (8, 6) are collinear.
Hints: If OA + AB = OB, then they are collinear.
Solution:
Given
O(0, 0), A(4, 3), and B (8, 6)
\(\begin{aligned}
\text { Diștance } & O A=\sqrt{(0-4)^2+(0-3)^2} \text { unit } \\
= & \sqrt{16+9} \text { unit } \\
= & \sqrt{25} \text { unit } \\
= & 5 \text { unit }
\end{aligned}\)
\(\begin{aligned}
\text { Distance } O B & =\sqrt{(0-8)^2+(0-6)^2} \text { unit } \\
& =\sqrt{64+36} \text { unit } \\
& =\sqrt{100} \text { unit } \\
& =10 \text { unit }
\end{aligned}\)
Wbbse 9th Class Maths Coordinate Geometry Distance Formula Step By Step Solutions
\(\begin{aligned}\text { Distance } A B & =\sqrt{(4-8)^2+(3-6)^2} \cdot \text { unit } \\
& =\sqrt{16+9} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)
Here OA+ AB OB, hence they are collinear.
Question 11. Let us show that the three points (2,2), (-2,-2), and (-2√3,2√3) vertices of an equilateral triangle.
Solution: Let A (2,2); B (-2,-2) and C (-2√3, 2√3).
Distance A B & =\sqrt{(2+2)^2+(2+2)^2} \text { unit } \\
& =\sqrt{16+16} \text { unit } \\
& =\sqrt{32} \text { unit }
\end{aligned}\)
\(\text { Distance } B C=\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2} \text { unit }\)
\(\begin{aligned}
& =\sqrt{(2 \sqrt{3}-2)^2+(2+2 \sqrt{3})^2} \text { unit } \\
& =\sqrt{2\left\{(2)^2+(2 \sqrt{3})^2\right\}} \text { unit } \\
& =\sqrt{2(4+12)} \text { unit } \\
& =\sqrt{32} \text { unit }
\end{aligned}\)
\(\text { Distance } B C=\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2} \text { unit }\) \(\begin{aligned}
& =\sqrt{(2 \sqrt{3}-2)^2+(2+2 \sqrt{3})^2 \text { unit }} \\
& =\sqrt{2\left\{(2)^2+(2 \sqrt{3})^2\right\}} \text { unit } \\
& =\sqrt{2(4+12)} \text { unit } \\
& =\sqrt{32} \text { unit }
\end{aligned}\)
∴ AB = BC = CA
∴ A, B, & C are the vertices of an equilateral triangle.
Wbbse Class 9 Maths Coordinate Geometry Distance Formula Derivation And Examples
Question 12. Let us show that the points (-7, 2), (19, 8), (15, -6), and (-11, -12) form a parallelogram when they are joined orderly.
Solution: Let A = (-7,2); B = (19,8); C = (15,-6); D = (-11, -12).
\(The length of A B=\sqrt{(-7-19)^2+(2-8)^2} unit
\begin{aligned}
& =\sqrt{(-26)^2+(-6)^2} \text { unit } \\
& =\sqrt{676+36} \text { unit } \\
& =\sqrt{712} \text { unit }
\end{aligned}
\)
\(\begin{aligned}
\text { Length of } B C & =\sqrt{(19-15)^2+(8+6)^2} \text { unit } \\
& =\sqrt{(4)^2+(14)^2} \text { unit } \\
& =\sqrt{16+196} \text { unit } \\
& =\sqrt{212} \text { unit }
\end{aligned}\)
\(\begin{aligned}
\text { Length of } C D & =\sqrt{(15+11)^2+(-6+12)^2} \text { unit } \\
& =\sqrt{(26)^2+(6)^2} \text { unit } \\
& =\sqrt{26^2+6^2} \text { unit } \\
& =\sqrt{676+36} \text { unit }
& = \sqrt{712} \text { unit }
\end{aligned}\)
\(\begin{aligned}
\text { Length of } D A & =\sqrt{(-11+7)^2+(-12-2)^2} \text { unit } \\
& =\sqrt{(-4)^2+(14)^2} \text { unit } \\
& =\sqrt{4^2+14^2} \text { unit } \\
& =\sqrt{16+196} \text { unit } \\
& =\sqrt{212} \text { unit }
\end{aligned}\)
\(Length of Diagonal A C=\sqrt{(-7-15)^2+(2+6)^2} unit
\begin{aligned}
& =\sqrt{(-22)^2+8^2} \text { unit } \\
& =\sqrt{22^2+8^2} \text { unit } \\
& =\sqrt{484+64} \text { unit }
\end{aligned}\)
Class 9 Maths WB Board
\(\begin{aligned}\text { Length of Diagonal } B D & =\sqrt{(19+11)^2+(8+12)^2}=\sqrt{(30)^2+(20)^2} \\
& =\sqrt{900+400} \text { unit } \\
& =\sqrt{1300} \text { unit }
\end{aligned}\)
In the quadrilateral ABCD, ABCD and BC = DA [opposite sides are equations]
Diagonal AC ≠ Diagonal BD
∴ ABCD is a parallelogram.
Question 13. Let us show that the points (2,-2), (8, 4), (5, 7), and (-1, 1) are the vertices of a rectangle.
Solution: Let P = (2,-2), Q = (8,4); R = (5,7) and S = (-1,1)
To prove the PQRS is a rectangle.

Here, Diagonal PR = Diagonal QS.
∴ In quadrilateral PQRS, opposite sides are equal, and diagonal PR diagonal
∴ PQRS is a rectangle.
Question 14. Let us show that the points (2,5), (5,9), (9,12), and (6,8) form a rhombus when they are joined orderly.
Solution: Let the points A (2, 5); B (5, 9), C (9, 12), and D (6, 8).
\(\text { Here, } \begin{aligned}
A B= & \sqrt{(2-5)^2+(5-9)^2} \text { unit } \\
& =\sqrt{9+16} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)
Class 9 Maths WB Board
\(\begin{aligned}& B C=\sqrt{(5-9)^2+(9-12)^2} \text { unit } \\
&=\sqrt{16+9} \text { unit } \\
&=\sqrt{25} \text { unit } \\
&=5 \text { unit }
\end{aligned}\)
\(\begin{aligned}
& C D=\sqrt{(9-6)^2+(12-8)^2} \text { unit } \\
& =\sqrt{9+16} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit } \\
&
\end{aligned}\)
\(\begin{aligned}
& D A=\sqrt{(6-2)^2+(8-5)^2} \\
&=\sqrt{16+9} \text { unit } \\
&=\sqrt{25} \text { unit } \\
&=5 \text { unit }
\end{aligned}\)
∴ AB BC CD = DA
\(Again, Diagonal A C=\sqrt{(2-9)^2+(5-12)^2} unit\begin{aligned}
& =\sqrt{49+49} \text { unit } \\
& =\sqrt{98} \text { unit }
\end{aligned}
\)
\(\begin{aligned}
\text { Diagonal BD } & =\sqrt{(5-6)^2+(9-8)^2} \text { unit } \\
& =\sqrt{1+1} \text { unit } \\
& =\sqrt{2} \text { unit }
\end{aligned}\)
∴ Diagonals are not equal.
∴ In quadrilateral ABCD, all the sides are equal but the diagonals are not equal.
∴ ABCD is a rhombus.
Class 9 Wbbse Distance Formula Chapter 4 Solved Exercises
Chapter 4 Co-ordinate Geometry Distance Formula Multiple Choice Questions
1. The distance between the two points (a + b, c-d) and (a-b, c + d) is
(1)\(2 \sqrt{a^2+c^2}\)
(2)\(2 \sqrt{b^2+d^2}\)
(3)\(\sqrt{a^2+c^2}\)
(4)\(\sqrt{b^2+d^2}\)
Solution: The distance between (a + b, c-d) and (a-b, c + d)
\(\begin{aligned}& =\sqrt{(a+b-a+b)^2+(c-d-c-d)^2} \text { unit } \\
& =\sqrt{(2 b)^2+(-2 d)^2} \text { unit } \\
& =\sqrt{4 b^2+4 d^2} \text { unit } \\
& =2 \sqrt{b^2+d^2} \text { unit }
\end{aligned}\)
∴(2)\(2 \sqrt{b^2+d^2}\)
2. If the distance between the two points (x, -7) and (3, -3) is 5 units, then the values of x are
(1)0 or 6
(2)2 or 3
(3)5 or 1
(4)-6 or 0
Solution: The distance between (x, -7) and (3,-3)
\(=\sqrt{(x-3)^2+(-7+3)^2} \text { unit }\) \(=\sqrt{(x-3)^2+16} \text { unit }\)
By the problem, \(\sqrt{(x-3)^2+16}=5\)
or, (x-3)2+16= (5)2 (Squaring both sides)
or, (x-3)2=25-16
or, (x-3)2 = 9
or, x-3 = ± 3
or, x = 3+3 or x = 3-3
or, x = 6 or x = 0
∴ (1)0 or 6
3. If the distance of the point (x, 4) from the origin is 5 units, then the values of x are
(1)±4
(2)±5
(3)±3
(4)None of these
Solution: The distance of the point (x, 4) from (0,0)
\(\begin{aligned}& =\sqrt{\mathrm{x}^2+4^2} \text { unit } \\
& =\sqrt{\mathrm{x}^2+16} \text { unit }
\end{aligned}\)
By the problem, \(\sqrt{x^2+16}=5\)
or, x2+16= (5)2 (Squaring both sides)
or, x2+16=25
or, x2 = 25-16
or, x2= 9
or, x = +3
∴ (3)±3
4. The triangle formed by the points (3, 0), (-3, 0), and (0,3) is
(1)Equilateral
(2)Isosceles
(3)Scalene
(4)Isosceles right-angled.
Solution: Let the co-ordinates of A, B & C be (3,0) (3,0); & (0,3) respectively.
\(\text { Here, } A B=\sqrt{(2-5)^2+(5-9)^2} \text { unit }\) \(=\sqrt{9+16} \text { unit }\) \(=\sqrt{25} \text { unit }\) \(=5 \text { unit }\)\(\begin{aligned}
& =\sqrt{9+9} \text { unit } \\
& =\sqrt{18} \text { unit } \\
& =3 \sqrt{2} \text { unit }
\end{aligned}\)
\(\text { Length of } B C=\sqrt{(-3-0)^2+(0-3)^2} \text { unit }
& =\sqrt{9+9} \text { unit } \\
& =\sqrt{18} \text { unit } \\
& =3 \sqrt{2}\text { unit }
\end{aligned}\)
\(\begin{aligned}
A C & =\sqrt{(3-0)^2+(0-3)^2} \text { unit } \\
& =\sqrt{9+9} \text { unit } \\
& =\sqrt{18} \text { unit } \\
& =3 \sqrt{2} \text { unit }
\end{aligned}\)
∴ \(B C^2+A C^2=(\sqrt{18})^2+(\sqrt{18})^2\) = 18+ 18 = 36 = 62 = AB2
∴AC = BC and AB2 = BC2 + AC2
∴ The ΔABC formed by the points (3,0), (-3,0) & (0,3) is an isosceles right-angled triangle.
∴(4)Isosceles right-angled.
5. The co-ordinates of the centre of a circle are (0,0) and the co-ordinates of a point on the circumference are (3,4); the length of the radius of the circle is
(1)5 units
(2)4 units
(3)3 units
(4)None of these.
Solution: Distance between the points (0, 0) and (3, 4) is
\(\begin{aligned}& =\sqrt{(0-3)^2+(0-4)^2} \text { units } \\
& =\sqrt{9+16} \text { units } \\
& =\sqrt{25} \text { units } \\
& =5 \text { units }
\end{aligned}\)
∴ (1)5 units
Question 16. Short answer type questions:
1. Let us write the value of y if the distance of the point (-4, y) from the origin is 5 units.
Solution:
\sqrt{16+\mathrm{y}^2}=5 \text { (given) }
\)
or, 16 + y2 = 25
∴ y2 = 9
∴ y =±3
2. Let us write the co-ordinates of a point on y-axis which is equidistant from the two points (2,3) and (-1,2).
Solution: Let the point on y-axis is (0,b).
\(\begin{aligned}& =\sqrt{(2-0)^2+(3-b)^2} \\
& =\sqrt{(-1-0)^2+(2-b)^2} \\
& =4+(3-6)^2 \\
& =1+(2-b)^2
\end{aligned}\)
∴ b = 4
∴ The point is (0,4).
