Class IX Maths Solutions WBBSE Chapter 5 Linear Simultaneous Equations Exercise 5.2
Question 1. Let us draw the graph of the following equations and write whether they are solvable or not and if they are solvable, let us write that particular solution or solutions if they have an infinite number of solutions:
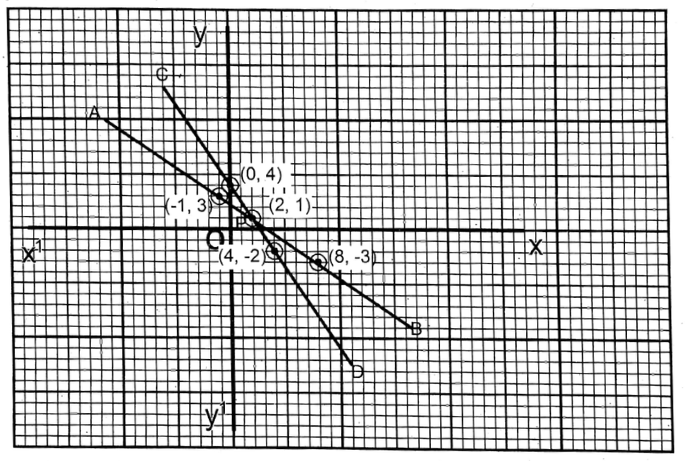
1. 2x + 3y-7=0, 3x+2y-8=0
Solution:
Given
2x+3y-7=0 ….(1)
3x+2y-8=0….(2)
From equation ….(1)
2x + 3y-7=0
or, \(x=\frac{7-3 y}{2}\)
Read and Learn More WBBSE Solutions For Class 9 Maths
| x | 2 | 8 | -1 |
| y | 1 | -3 | 3 |
From equation ……(2)
3x + 3y-7=0
or, \(x=\frac{8-2 y}{3}\)
| x | 2 | 0 | 4 |
| y | 1 | 4 | -2 |
∴ The equations are solvable.
∴ x = 2;
y =1
Class IX Maths Solutions WBBSE
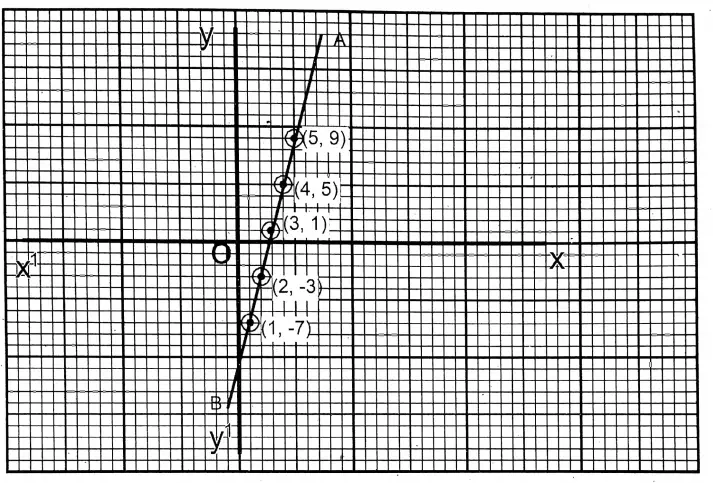
2. 4x-y=11, -8x+2y=-22
Solution:
Given
4x – y = 11 ….(1)
⇒ \(x=\frac{2 y+22}{8}\)
| x | 4 | 3 | 2 |
| y | 5 | 1 | -3 |
– 8x + 2y = -22 ….(2)
⇒ \(x=\frac{2 y+22}{8}\)
| x | 3 | 5 | 1 |
| y | 1 | 9 | -7 |
Here, \(\frac{4}{-8}=\frac{-1}{2}=\frac{11}{-22}\)
∴ The equations are solvable and have an infinite number of solutions, i.e., x = 2, y = -3; x = 3, y=1; and x = 4, y = 5.
Class IX Maths Solutions WBBSE
3. 7x + 3y = 42,
Solution: \(x=\frac{42-3 y}{7}\)
| x | 6 | 3 | 9 |
| y | 0 | 7 | -7 |
21x+9y=42
\(x=\frac{42-9 y}{21}\)
| x | 2 | -1 | 5 |
| y | 0 | 7 | -7 |
Class 9 Math Chapter 5 WBBSE
Here = \(\frac{7}{21}=\frac{3}{9} \neq \frac{42}{42}\)
∴ There two equations are inconsistent, i.e., they are unsolvable.
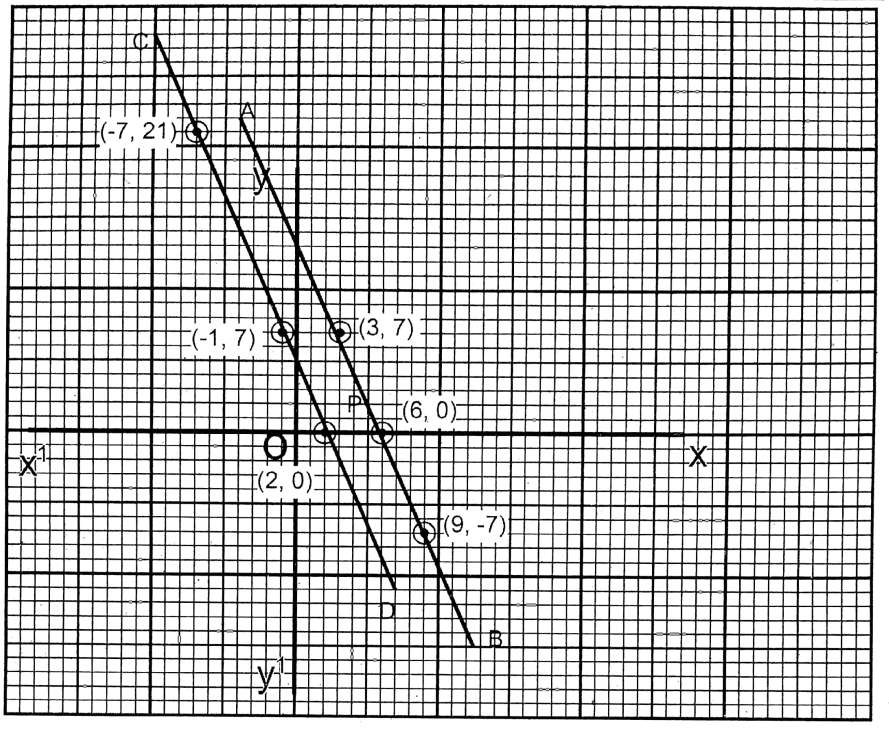
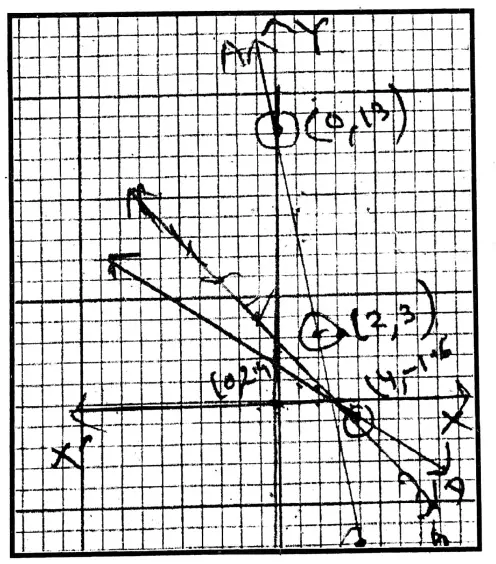
4. 5x + y = 13, 5x +5y = 12
Solution:
Given
5x + y = 13 ….(1)
\(y=\frac{13-5 x}{1}\)Class 9 Math Chapter 5 WBBSE
→AB
| x | 2 | 0 | 4 |
| y | 3 | 13 | -7 |
5x+5y= 12 ……(2)
⇒ \(y=\frac{12-5 x}{5}\)
→ CD
| x | 4 | 0 | \(\frac{53}{20}\) |
| y | -1.6 | 2.4 | \(\frac{-1}{4}\) |
The equations are solvable.
∴ x = \(\frac{53}{20}\)
y = \(\frac{-1}{4}\)
Question 2. By comparing the coefficients of the same variables and constants of the following pairs of equations, let us write whether the pair of equations is solvable or not and check them by drawing the graphs of the equations.
1. x+5y=7, x+5y=20
Solution:
Given
x+5y=7, x+5y=20
x + 5y = 7 …(1)
∴ x=7-5y
Class 9 Math Chapter 5 WBBSE
→AB
| x | 2 | -8 | 7 |
| y | 1 | 3 | 0 |
x+5y=20 ….(2)
→CD
| x | 0 | 10 | -10 |
| y | 4 | 2 | 6 |
Here, \(\frac{1}{1}=\frac{5}{5} \neq \frac{7}{20}\)
∴ There two equations are in consistent, i.e., they are unsolvable.
2. 2x + y = 8, y=8-2x
Solution:
Given
2x + y = 8, y=8-2x
2x + y = 8 ….(1)
→AB
| x | 2 | 0 | -1 | 4 |
| y | 4 | 8 | 10 | 0 |
-3x+2y=-5 ……(2)
\(y=\frac{3 x-5}{2}\)Class 9 Maths WB Board
→CD
| x | 1 | 3 | -1 |
| y | -1 | 2 | -4 |
\(\frac{2}{-3} \neq \frac{1}{2} \neq \frac{8}{-5}\)
∴ The two equations are solvable. x=3, y=2
3. 5x + 8y = 14, 15x + 24y = 42
Solution: 5x+8y = 14 …(1)
⇒ \(y=\frac{14-5 x}{8}\)
| x | -2 | 6 | 2 |
| y | 3 | -2 | 5 |
15x + 24y = 42 ….(2)
⇒ \(y=\frac{42-15 x}{24}\)
→PQ
| x | 2 | -2 |
| y | 5 | 3 |
\(\frac{5}{15}=\frac{8}{24}=\frac{14}{42}\)
Class 9 Maths WB Board
∴ The two equations are solvable and have an infinite number of solutions.
4. 3x+2y= 6, 12x + 8y = 24
Solution: 3x+2y=6…(1)
⇒ \(y=\frac{6-3 x}{2}\)
| x | 0 | -2 | 6 |
| y | 3 | 6 | -6 |
12x + 8y = 24 …(2)
⇒ \(y=\frac{24-12 x}{8}\)
| x | 0 | -2 | 6 |
| y | 3 | 6 | -6 |
\(\frac{3}{12}=\frac{2}{8}=\frac{6}{24}\)
Class 9 Maths WB Board
∴ The two equations are solvable and have infinite number of solutions.
Question 3. Let us determine the relations of ratios of the same variable and constants of the following pairs of equations and write whether the graphs of the equations will be parallel or intersecting or overlapping.
1. 5x + 3y = 11, 2x – 7y = – 12
Solution: 5x+3y= 11 ….(1)
2x-7y=-12 …(2)
∴ The graphs of the equations will be intersecting.
2. 6x – 8y = 2, 3x-4y = 1
Solution: 6x-8y = 2 …(1)
3x-4y = 1 ….(2)
Here, = \(\frac{6}{3}=\frac{-8}{-4}=\frac{2}{1}\)
∴The graphs of the equations are one straight lines, i.e., they are coincident.
3. 8x-7y = 0, 8x – 7y = 56
Solution: 8x-7y=0 ….(1)
8x – 7y = 56 …(2)
∴ The graphs of the equations are parallel.
4. 4x-3y= 6, 4y – 5x = -7
Solution: 4x-3y=6 ….(1)
– 5x + 4y = -7 …(2)
Here \(\frac{4}{-5} \neq \frac{-3}{4} \neq \frac{6}{-7}\)
∴ The graphs of two equations will intersect each other.
Class 9 Mathematics West Bengal Board
Question 4. Let us solve the following pairs of equations by drawing graphs which are solvable and write 3 solutions which have infinite number of solutions.
1. 4x + 3y = 20, 8x +6y= 40
Solution: 4x + 3y = 20 …(1)
8x + 6y= 40 …(2)
From equation…….(1)
4x + 3y = 20
⇒ \(y=\frac{20-3 y}{4}\)
| x | -1 | 2 | 5 |
| y | 8 | 4 | 0 |
From equation …(2)
8x+6y= 40
⇒ \(x=\frac{40-6 y}{8}\)
There two equations are solvable, has infinite of solvitions, i.e., (1) x = 5, y = 0;
(2) x=-1, y = 8 (3) x = 2, y = 4.
2. 4x + 3y = 20, 12x + 9y=20
Solution: 4x+3y=20 ….(1)
⇒ \(y=\frac{20-4 x}{3}\)
| x | -1 | 2 | 5 |
| y | 8 | 4 | 0 |
12x + 9y=20 ….(2)
⇒ \(y=\frac{20-12 x}{9}\)
Here, \(\frac{4}{12}=\frac{3}{9} \neq \frac{20}{20}\)
∴ These two equations have no general solutions; they are parallel straight lines.
Class 9 Mathematics West Bengal Board
3. 4x + 3y = 20, \(\frac{3 x}{4}-\frac{y}{8}=1\)
Solution: 4x+3y=20 ….(1)
\(\frac{3 x}{4}-\frac{y}{8}=1\) ….(2)
4x = 20-3y (1)
or, \(x=\frac{20-3 y}{4}\)
→CD
| x | 5 | 2 | 8 |
| y | 0 | 4 | -4 |
\(\frac{3 x}{4}-\frac{y}{8}=1\) ….(2)
or, \(x=\frac{4}{3}\left(1+\frac{y}{8}\right)\)
→ PQ
| x | 4 | 1.5 | 2 |
| y | 16 | 1 | 4 |
Here, \(\frac{4}{3 / 4}=\frac{3}{-1 / 8}=\frac{20}{1}\)
∴ The two equations are solvable.
4. p-q=3, \(\frac{p}{3}+\frac{q}{2}=6\)
Solution: p-q=3 …(1)
\(\frac{p}{3}+\frac{q}{2}=6\) ….(2)
p=3+q …(1)
→AB
| p | 3 | 0 | -6 |
| q | 0 | -3 | 3 |
Class 9 Mathematics West Bengal Board
\(\frac{p}{3}+\frac{q}{2}=6\) …(2)
⇒ \(p=3\left(6-\frac{q}{2}\right)\)
→ CD
| p | 15 | 18 | 12 |
| q | 2 | 0 | 4 |
Here, \(\frac{1}{1 / 3} \neq \frac{-1}{1 / 2} \neq \frac{3}{6}\)
5. p − q = 3, \(\frac{p}{5}-\frac{q}{5}=3\)
Solution: p-q=3
⇒p=3+q …(1)
→PQ
| p | 4 | 3 | 1 |
| q | 1 | 0 | -2 |
\(\frac{p}{5}+\frac{q}{5}=3\)
⇒ \(p=5\left(3+\frac{q}{5}\right)\) …(2)
→RS
| p | 20 | 5 | 10 |
| q | 5 | -10 | -5 |
Here, \(\frac{1}{1 / 5}=\frac{-1}{-1 / 5} \neq \frac{3}{3}\)
∴ The two equations have no solutions, they are parallel straight lines.
99
6. p-q=3, 8p-8q = 5
Solution: p-q=3 ⇒ p=3+q …(1)
| p | 3 | 0 | 5 |
| q | 0 | -3 | 2 |
Class 9 Mathematics West Bengal Board
8p-8q= 5
⇒ \(p=\frac{5+8 q}{8}\)
∴ The two equations have no solutions, they are parallel straight lines.
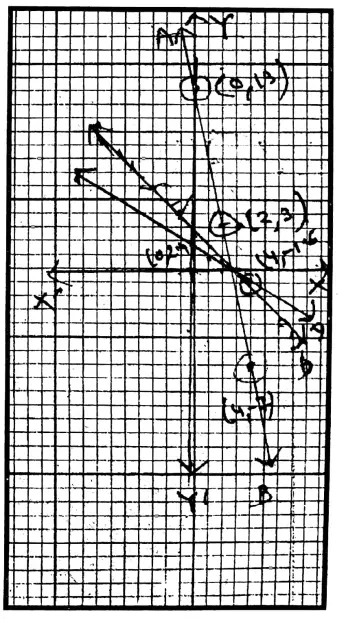
Question 5. Tathagata has written a linear equation in two variables x + y = 5. I write another linear equation in two variables, so that, the graphs of two equations will be
1. Parallel to each other,
2. Intersecting,
3. Overlapping.
Solution: x + y = 5
1. Equation of parallel straight line is 5x + 5y = 20
2. Equation of intersecting straight line is 2x+5y = 16
3. Equation of overlapping straight line is 2x + 2y = 10