Class IX Maths Solutions WBBSE Chapter 9 Transversal And Mid Point Theorem Exercise 9
Question 1. In the triangle ABC, D is the midpoint of the side BC. From point D, the parallel straight lines CA and BA intersect the sides BA and CA at points E and F respectively, Let us prove that, \(E F=\frac{1}{2} B C\)
Solution:
Given
In ΔABC the midpoint of side D is BC. From point D, CA and BA parallel to CA and BA are drawn which intersect BA at point E and CA at point F.
Prove that \(E F=\frac{1}{2} B C\)
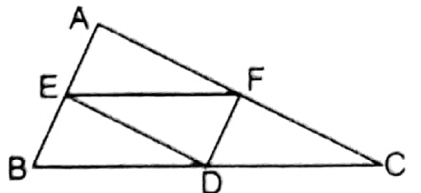
Proof: DF II BA (Given) and D are the midpoint of BC
∴ Point F is the midpoint of side AC.
Similarly, DE II CA and point D is the midpoint of BC.
∴ point E is the midpoint of AB
Read and Learn More WBBSE Solutions For Class 9 Maths
Now E and F points respectively are mid points of AB and AC sides ΔABC.
∴ \(E F=\frac{1}{2} B C\)
Wbbse Class 9 Maths Chapter 9 Transversal And Midpoint Theorem Solutions
Question 2. D and E lie on AB and AC respectively of the triangle ABC such that \(A D=\frac{1}{4} A B\) and \(A E=\frac{1}{4} A C\). Let us prove that DE II BC and \(D E=\frac{1}{4} B C\)
Solution:
Given
In ΔABCD and F lie on sides AB and AC respectively such that \(A D=\frac{1}{4} A B\) and \(A E=\frac{1}{4} A C\).
Prove that DE II BC and \(D E=\frac{1}{4} B C\)
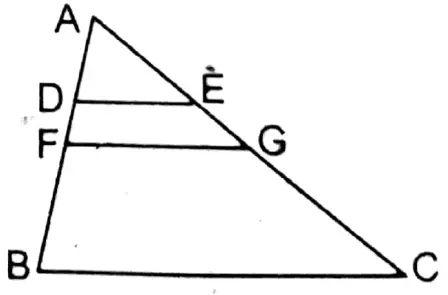
Construction: Midpoints of sides F AB and AC, G and are joined.
Proof: In ΔABC the midpoints of sides AB and AC are F and G.
∴ FG II BC and \(F G=\frac{1}{2} B C\)
∴ F is the and midpoint of AB \(A D=\frac{1}{4} A B\)

Class IX Maths Solutions WBBSE
∴ D is the midpoint of AF.
Similarly, E is the midpoint of AG.
So, in ΔAFG the midpoints of sides AF and AG are respectively D and E
∴ DE II FG and FG II BC.
∴ DE II BC.
Again, \(D E=\frac{1}{2} F G=\frac{1}{2} \times \frac{1}{2} B C=\frac{1}{4} B C\)
Question 3. In the triangle PQR, the midpoints of the sides QR and QP are X and Z respectively. The side QP is extended upto the point S so that PS = ZP. SX intersects the side PR at the point Y. Let us prove that PY = \(P Y=\frac{1}{4} P R\)
Solution:
Given
In ΔPQR the midpoints of sides QR and PQ are X and Z. Side QP is extended up to points S so that PS = ZP. SX, at Y, intersects the side PR.
Prove that PY = \(P Y=\frac{1}{4} P R\)
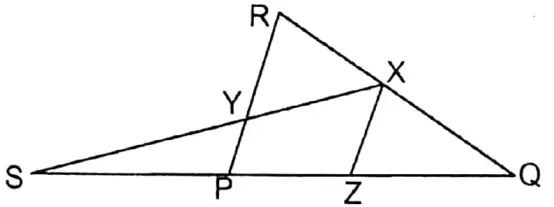
Construction: X, and Y are joined.
Proof: Of QP and QR the midpoints are Z and X.
∴ ZX II PR and \(Z X=\frac{1}{2} P R\)
Now, in ΔSZX the midpoint SZ is and P and PY II XZ.
∴ Y is the midpoint of SX.
∴ \(P Y=\frac{1}{2} Z X\) \(\left[because \mathrm{ZX}=\frac{1}{2} \mathrm{PR}\right]\)
or, \(P Y=\frac{1}{2} \times \frac{1}{2} P R\)
or, \(P Y=\frac{1}{4} P R\)
Class IX Maths Solutions WBBSE
Question 4. Let us prove that the quadrilateral formed by joining mid-points of the consecutive sides of a parallelogram is a parallelogram.
Solution: Let in the quadrilateral of ABCD the midpoints sides AB, BC, CD, and DA are P, Q, R, and S respectively joining. PQ, QR, RS and SP we get PQRS quadrilateral.
Prove that PQRS is a parallelogram.
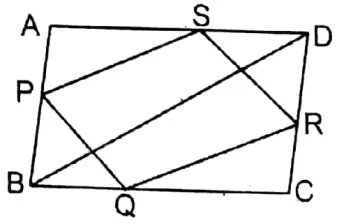
Construction: diagonal BD is drawn.
Proof: In ΔABD the midpoints of sides AB and AD are P and S respectively.
∴ PS II BD and \(P S=\frac{1}{2} B D\)
Similarly, in ΔCBD the midpoints of sides CB and CD are Q and R respectively.
∴ QR II BD and \(\mathrm{QR}=\frac{1}{2} \mathrm{BD}\)
∴ PS = QR
Now, in quadrilateral PQRS, PS II QR and PS = QR. So, PQRS is a parallelogram.
Wbbse Class 9 Transversal And Midpoint Theorem Exercise Solutions
Question 5. Let us prove that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangular figure is not a square figure but a rhombus.
Solution: Let ABCD is a rectangle whose midpoints of sides AB, BC, CD, and DA are P, Q, R, and S respectively P, Q; Q, R; R, S; and S, P are joined.
Prove that PQRS is a rhombus, not a square.
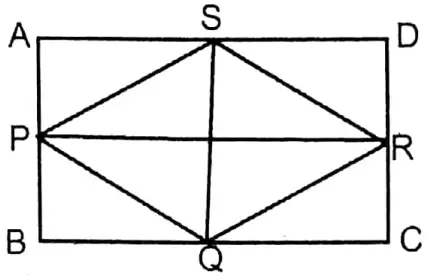
Construction: P, R, and S, Q are joined.
Proof: In ΔAPS and ΔPBQ,
AP = BP, AS BQ [By construction]
∠PAS ≅ ∠PBQ [Both are right angles]
∴ ΔPAS ≅ ΔPBQ (S-A-S congruency)
∴ PS = PQ
Similarly, in ΔPBQ and ΔRCQ, PQ = QR
In ΔQRC and ΔRCD, QR = RS
In ΔRSD and ΔAPS, RS = PS
∴ PQ = QR RS = SP
Now, in quadrilateral PQRS, PQ = QR = RS = SP
But PR > SQ.
∴ The four sides of quadrilateral PQRS are equal but the diagonals are not. So is a rhombus but not a square.
Class IX Maths Solutions WBBSE
Question 6. Let us prove that the quadrilateral formed by joining the mid-points of consecutive sides of a square is a square.
Solution: Let the midpoints of sides AB, BC, CD, and DA of the square ABCD be P, Q, R & S respectively. P, Q; Q, R; R, S, and S, P are joined.
Prove that PQRS is a square.
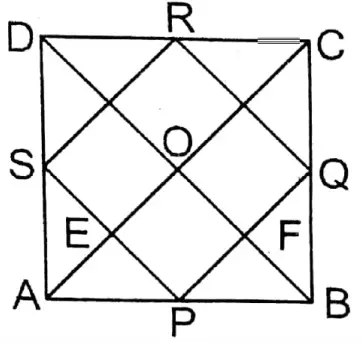
Class 9 Wbbse Maths Transversal And Midpoint Theorem Solved Problems
Construction: Diagonals AC and BD are joined which intersect each other at O. In □PQRS, PQ cuts diagonal BD at point F and PS cuts diagonal AC at point E.
Proof: In ΔADC the midpoint of AD is S and the midpoint DC is R.
∴ SR II AC and \(S R=\frac{1}{2} A C\) ….(1)
Similarly, in ΔABC, PQ II AC and \(P Q=\frac{1}{2} A C\) …(2)
∴ PQ II SR and PQ = SR.
∴ PQRS is a parallelogram.
Class 9 Mathematics West Bengal Board
∴ In ΔABD the midpoints of sides AB and AD are P and S respectively.
∴ \(P S=\frac{1}{2} B D\). But ACBD.
∴ \(P Q=\frac{1}{2} A C=\frac{1}{2} B D=P S\)
∴ In Parallelogram PQRS the length of adjacent sides are equal.
∴PQRS is a rhombus.
∴ PE II FO and PF II EO.
∴ ∠EOF= 90°
∴ ∠EPF = 90°
∴ PQRS is a square.
Question 7. Let us prove that the quadrilateral formed by joining the mid-points of a rhombus is a rectangle.
Solution: Let in rhombus ABCD the midpoints of sides AB, BC, CD, and DA are E, F, G, and H respectively. E, F; F, G; G, H, and H, E are joined.
Prove that EFGH is a rectangle.
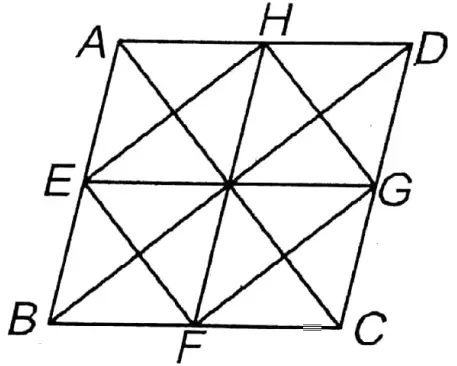
Construction: B, D; A, C; E, G and H, F are joined.
Proof: In ΔABD the midpoints of sides AB and AD are E and H respectively.
∴ EH II BD and \(\mathrm{EH}=\frac{1}{2} \mathrm{BD}\)
Class 9 Mathematics West Bengal Board
Similarly, in ΔBCD the midpoints of sides BC and CD are F and G respectively.∴ FG II BD and FG = 1BD
∴ EH II FG and \(\)
∴ EFGH is a parallelogram.
Now, in □ABFH, AH II BF and AH = BF
∴ ABFH is a parallelogram.
∴ AB = HF
Similarly, ADGE is a parallelogram.
∴ AD = EG
But AB = AD ( ABCD is a rhombus)
∴ FH = EG
∴ Diagonals of the parallelogram EFGH are equal in length.
∴ EFGH is a rectangle.
Question 8. In the triangle ABC, the mid-points of AB and AC are D and E respectively; the mid-points of CD and BD are P and Q respectively. Let us prove that BE and PQ bisect each other.
Solution:
Given
In ΔABC the midpoints of sides AB and AC are D and E respectively and P & Q are the midpoints of CD and BD respectively.
Prove that BE and PQ bisect each other.
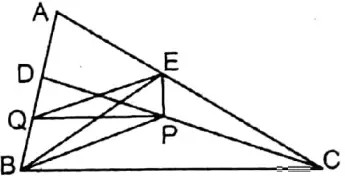
Construction: B, P; P, E; E, Q and P, Q bisect each other.
Proof: In ΔACD the midpoints of sides AC and CD are E and P respectively.
∴ PE II AD and \(\mathrm{PE}=\frac{1}{2} \mathrm{AD}\)
Again, AD = BD and \(B Q=\frac{1}{2} B D\)
(∵ D is the midpoint of AB and Q the midpoint of BD)
∴ \(P E=\frac{1}{2} A D=\frac{1}{2} B D=B Q\)
In □BPEQ, PE II BQ and PE = BQ
∴ BPEQ is a parallelogram whose diagonals are BE and PQ.
∴ BE and PQ bisect each other.
Class 9 Mathematics West Bengal Board
Question 9. In the triangle ABC, AD is perpendicular on the bisector of ZABC. From point D, a straight line DE parallel to side BC is drawn which intersects side AC at point E. Let us prove that AE = EC.
Solution:
Given
In triangle ABC on the bisector of ZABC AD is perpendicular. From point D parallel to BC of parallel straight line DE is drawn which intersects AC side at point E.
Prove that AE = EC.
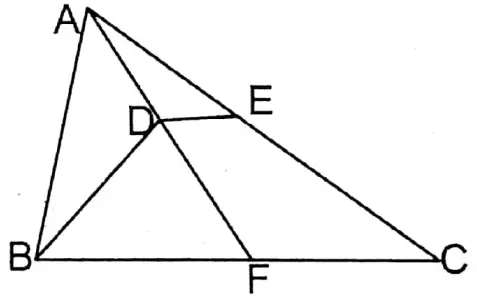
Construction: AD is extended forwards which at intersects BC point F.
Proof: In ΔABD and ΔBDF,
∠BDA = ∠BDF (∵ AD ⊥ BD)
∠ABD = ∠FBD (∵ ∠ZABC is the bisector of BD) and BD is a common side.
∴ ΔABD ≅ ΔBDF (A-A-S Congrency)
∴ AD DF, that is D is the midpoint of AF
In ΔAFC of AF D is the midpoint and DE II FC.
∴ E is the midpoint of AC
∴ AE = EC
Wbbse Class 9 Maths Chapter 9 Transversal And Midpoint Theorem Notes
Question 10. In the triangle ABC, AD is a median. From points B and C, two straight lines BR and CT, parallel to AD are drawn, which meet extended BA and CA at points T and R respectively. Let us prove that \(\frac{1}{A D}=\frac{1}{R B}+\frac{1}{T C}\)
Solution:
Given
In a triangle, ABC AD is the median. from points BC and parallel to AD straight lines BR and CT are drawn which intersect extended BA and CA at points T and R.
Prove that = \(\frac{1}{A D}=\frac{1}{R B}+\frac{1}{T C}\)
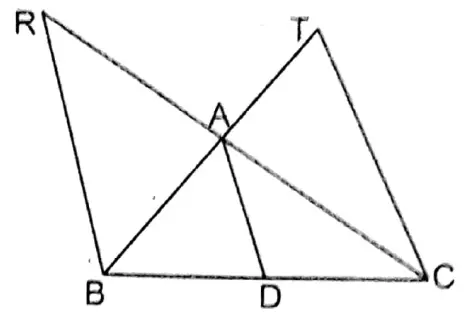
Proof: In AD is the median
∴ D, is the midpoint of BC
In ΔBCT the midpoint of BC is D and DA II CT
∴ A is the midpoint of BT
∴ AD II CT and \(\mathrm{AD}=\frac{1}{2} \mathrm{TC}\)
∴ TC= 2AD
Now, in ΔBCR the mid point of BC is D and DA II BR
∴ A is the midpoint of RC
Class 9 Maths WB Board
∴ AD II RB and \(A D=\frac{1}{2} R B\)
∴ RB = 2AD
\(\frac{1}{\mathrm{RB}}+\frac{1}{T C}=\frac{1}{2 A D}+\frac{1}{2 A D}=\frac{2}{2 A D}=\frac{1}{A D}\) \(\frac{1}{A D}=\frac{1}{R B}+\frac{1}{T C}\)
Question 11. In the trapezium ABCD, AB II DC and AB > DC; the mid-points of two diagonals AC and BD are E and F respectively. Let us prove that \(E F=\frac{1}{2}(A B-D C)\)
Solution:
Given
In trapezium ABCD AB II DC and AB > DC; E and F are the midpoints of AC and BD diagonals respectively.
Prove that \(E F=\frac{1}{2}(A B-D C)\)
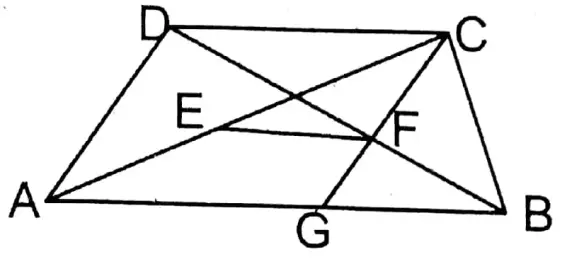
Construction: E, and F are joined. CF is extended forwards which intersect AB at point G point.
Proof: In ΔCFD and ΔBFG,
∠CDF = alternate ∠FBG (∴ DC II AB and BD is transversal)
∠CFD = VOA ∠BFG and DF = BF (∵ F is the midpoint of BD).
∴ ΔCFD ≅ ΔBFG (A -A – S congruency)
∴ DC = GB and CF = FG
Now, in ΔACG the midpoints of sides AC and CG are E and F respectively
∴ EF II AG and \(E F=\frac{1}{2} A G\)
∴ \(E F=\frac{1}{2} A G=\frac{1}{2}(A B-G B)\)
∴ \(=\frac{1}{2}(A B-D C)(because G B=D C)\)
West Bengal Board Class 9 Transversal And Midpoint Theorem Solutions
12. C is the mid-point of the line segment AB and PQ is any straight line. The minimum distances of the line PQ from points A, B, and C are AR, BS, and CT respectively; let us prove that AR + BS = 2CT.
Solution:
Given
The midpoint of st. line AB is C and PQ is any st. line. from points A, B, and C the minimum distance of straight line PQ are respectively AR, BS, and CT.
Prove that AR + BS = 2CT
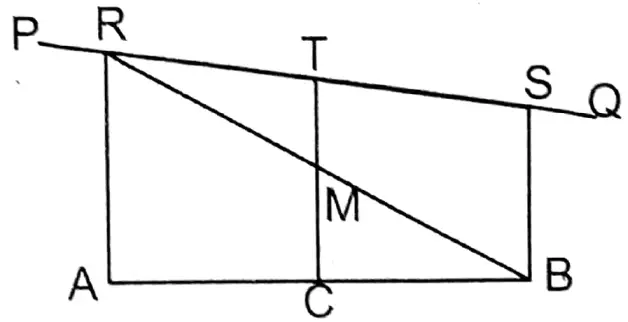
Proof: ∵AR, BS, and CT are perpendicular on PQ
∴AR II BS II CT
In ΔABR of side AB, the midpoint is C and CM II AR
∴ M, BR is the midpoint
Again, in ΔBRS of BR is the midpoint M and MT II BS
∴ T, RS is the midpoint of
∴ RT=TS
In ΔABR we get, \(C M=\frac{1}{2} A R\)
∴ AR = 2CM
Again, in ΔBRS we get \(M T=\frac{1}{2} B S\)
Or, BS = 2MT
∴ AR+ BS 2CM + 2MT = 2(CM + MT) = 2CT Proved
Class 9 Math Solution WBBSE
Question 13. In a triangle ABC, D is the mid-point of the side BC; through point A, PQ is any straight line. The perpendiculars from the points B, C, and D on PQ are BL, CM, and DN respectively; let us prove that, DL = DM.
Solution:
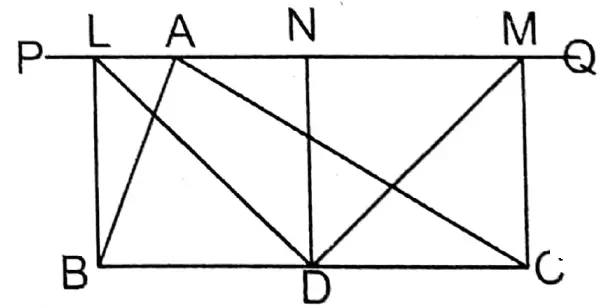
Given
In a triangle ABC, D is the mid-point of the side BC; through point A, PQ is any straight line. The perpendiculars from the points B, C, and D on PQ are BL, CM, and DN respectively
Construction: D, Land D, and M are joined.
Proof: On a straight line PQ BL, CM, and DN are perpendicular.
∴ BL II DN II CM
∵ BD = DC ( ∵D, is the midpoint of BC)
∴ LN = NM
In ΔDLN and ΔDMN, LN = NM Proved
∠DNL = ∠DNM and DN is a common side. (∵ DN ⊥ PQ)
∴ ΔDLN ≅ ΔDMN (S-A-S Congruency)
∴ DL = DM
Ganit Prakash Class 9 Solutions
Question 14. ABCD is a square figure. The two diagonals AC and BD intersect each other at point O. The bisector of ∠BAC intersects BO at the point P and BC at point Q. Let us prove that \(O P=\frac{1}{2} C Q\)
Solution:
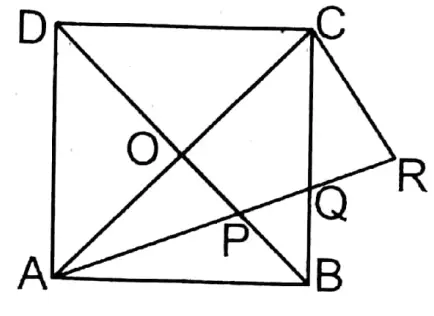
Given
ABCD is a square figure. The two diagonals AC and BD intersect each other at point O. The bisector of ∠BAC intersects BO at the point P and BC at point Q.
Construction from point C parallel to OP an st. line CR is drawn which cuts extended AQ at point R.
Proof: In ΔACR midpoint AC the is O and OP II CR.
\(O P=\frac{1}{2} C R\)∴ ∠AOP = 90° ( ∵The diagonals of a square bisect each other at right angles.) and ∠AOP = ∠ACR = 90° (corresponding angles).
In ΔACR and ΔABQ,
∠ACR = ∠ABQ ( ∵ Each angle is a right angle)
∠CAR = ∠BAQ ( ∵ ∠BAC is the bisector of AQ)
Remaining ∠ARC= remaining ∠AQB
But ∠AQB VOA ∠CQR
∠CRQ = ∠CQR ( Each is equal to ∠AQB)
∴ CR = CQ
Ganit Prakash Class 9 Solutions
Question 15. Multiple Choice Question
1. In the triangle PQR, ∠PQR = 90° and PR = 10 cm. If S is the midpoint of PR, then the length of QS is
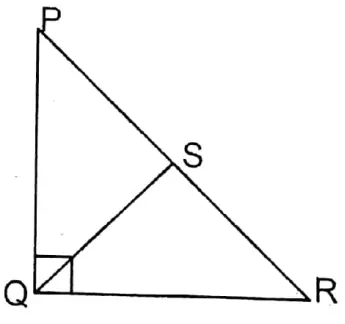
(1)4 cm
(2)5 cm
(3)6 cm
(4)3 cm
Solution: PR= 10 cm
We know that in a right-angled triangle the straight line from the vertex of the right angle to the midpoint of the hypotenuse is equal to half of the hypotenuse.
∴ \(\begin{aligned}
& Q S=\frac{1}{2} P R \\
& =\frac{1}{2} \times 10 \mathrm{~cm}
\end{aligned}\) = 5
∴ (2)5 cm.
Wbbse Class 9 Transversal And Midpoint Theorem Important Questions
2. In the trapezium ABCD, AB II DC and AB = 7 cm and DC = 5 cm. The mid-points of AD and BC are E and F respectively, the length of EF is
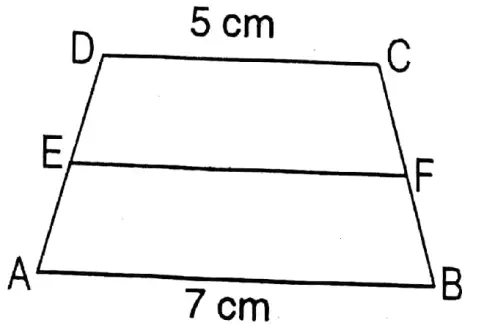
(1)5 cm
(2)6 cm
(3)7 cm
(4)12 cm
Solution: EF =1/2(AB+DC)
\(\begin{aligned}& =\frac{1}{2}(7+5) \mathrm{cm} \\
& =\frac{1}{2} \times 12 \mathrm{~cm}=6 \mathrm{~cm}
\end{aligned}\)
Ganit Prakash Class 9 Solutions
∴ 2. 6cm
3. In the triangle ABC, E is the mid-point of the median AD; the extended BE intersects AC at the point F. If AC = 10.5 cm then the length of AF is
(1)3 cm
(2)3.5 cm
(3)2.5 cm
(4)5 cm
Solution: In triangle ABC the midpoint of median AD is E. The extended part of BE AC cuts at F. From point D parallel to BF a straight line is drawn which cuts AC at G point.
\(\begin{aligned}& A F=\frac{1}{3} A C=\frac{1}{3} \times 10.5 \mathrm{~cm} \\
& =3.5 \mathrm{~cm}
\end{aligned}\)
∴(2) 3.5 cm
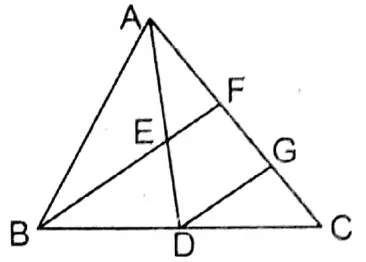
4. In the triangle ABC, the mid-points of BC, CA, and AB are D, E, and F respectively; 3E and DF intersect at the point X and CF and DE intersect at the point Y, the length of XY is equal to
(1)1/2 BC
(2)1/4 BC
(3)1/3 BC
(4)1/8 BC
Solution: E and F are joined.
∴ \(\mathrm{FE}=\frac{1}{2} \mathrm{BC}\) and FE II BC, i.e., FE II BD
∴ ED II AB, i.e., ED II FB
∴ FEDB is a parallelologram.
∴ Diagonals of a paralelogram bisect each other.
∴ BE and DF bisect each other at point X.
∴ X is the midpoint of FD
∴ Y, is the midpoint of the ED
∴ (2)1/4 BC
Ganit Prakash Class 9 Solutions
5. In the parallelogram ABCD, E is the mid-point of the side BC; DE and extended AB meet at point F. The length of AF is equal to
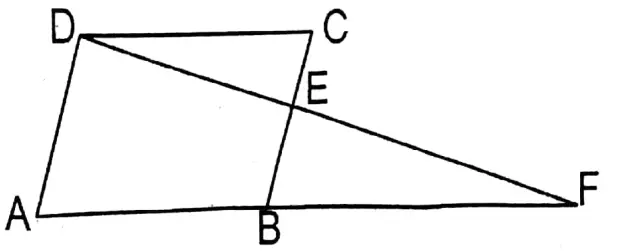
(1) 3/2 AB
(2)2AB
(3)3AB
(4)5/4 AB
Solution: ΔDEC and ΔBEF
CE = BE ( ∵E, is the midpoint of BC)
∠CED = VOA ∠BEF and ∠DCE = alternate ∠EBF
∴ΔDEC ≅ ΔBEF (A-A-S congruency)
∴ DC = BF
∴ AF = AB+ BF =AB+ DC ( ∵BF = DC)
= AB+ AB (∵DC = AB)
= 2AB
∴ (2)2AB
Question 16. Short answer type questions
1. In the triangle ABC, AD and BE are two medians, and DF parallel to BE, meets AC at point F. If the length of the side AC is 8 cm, then let us write the length of the side CF.
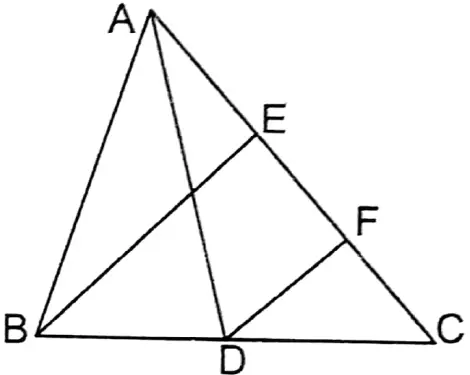
Solution:
Given
In ΔABC, AD, and BE are medians.
∴ D and E are the midpoints of BC and AC respectively.
∴ \(C E=\frac{1}{2} A C\)
In ΔBCE the midpoint of BC is D and DF II BE.
∴ F, is the midpoint of CE
& therefore C F=\frac{1}{2} C E=\frac{1}{2} \times \frac{1}{2} A C \\
& =\frac{1}{4} \times 8 \mathrm{~cm}=2 \mathrm{~cm}
\end{aligned}\)
Wbbse Class 9 Maths Transversal And Midpoint Theorem Chapter 9
2. In the triangle ABC, the mid-points of BC, CA, and AB are P, Q, and R respectively; if AC = 21 cm, BC= 29 cm, and AB = 30 cm, then let us write the perimeter of the quadrilateral ARPQ.
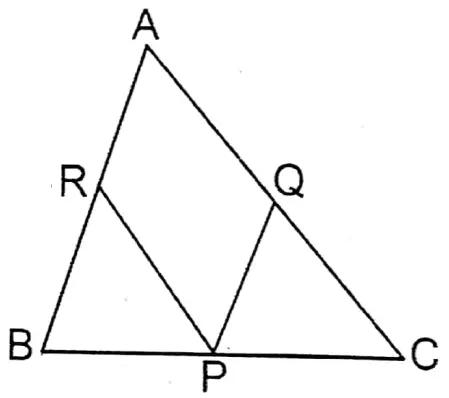
Solution:
Given
In the triangle ABC, the mid-points of BC, CA, and AB are P, Q, and R respectively; if AC = 21 cm, BC= 29 cm, and AB = 30 cm
Q, is the midpoint of AC
∴ \(A Q=\frac{1}{2} A C=\frac{1}{2} \times 21 \mathrm{~cm}\) = 10.5 cm
∵ R is the midpoint of AB
∴ \(A R=\frac{1}{2} A B=\frac{1}{2} \cdot 30 \mathrm{~cm}\)= 15 cm
In ΔABC the midpoints of sides BC and AB are P and R respectively.
\(P R=\frac{1}{2} A C=\frac{1}{2} \times 21 \mathrm{~cm}=10.5 \mathrm{~cm}\)Similarly,\(P Q=\frac{1}{2} A B=\frac{1}{2} \times 30 \mathrm{~cm}=15 \mathrm{~cm}\)
Perimeter of quadrilateral ARPQ = AQ + PQ+ PR + AR=(10.5+15+ 10.5+15) cm = 51 cm
Wbbse Class 9 Maths Proofs Of Transversal And Midpoint Theorem With Examples
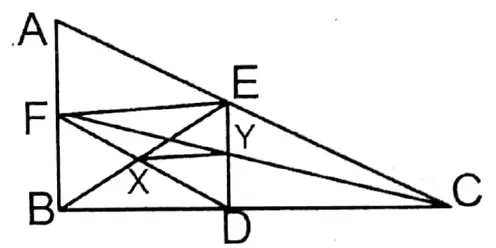
3. In the triangle ABC, D is any point on the side AC. The mid-points of AB, BC, AD, and DC are P, Q, X, Y respectively. If PX = 5 cm, then let us write the length of the side QY.
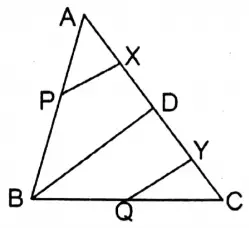
Solution:
Given
In the triangle ABC, D is any point on the side AC. The mid-points of AB, BC, AD, and DC are P, Q, X, Y respectively. If PX = 5 cm
B, and D are joined.
In ΔABD the midpoints of AB are ads are P and X respectively.
∴ BD = 2PX = 2 x 5 cm = 10 cm
In ΔBCD the midpoints of BC and CD are Q and Y respectively.
\(Q Y=\frac{1}{2} B D=\frac{1}{2} \times 10 \mathrm{~cm}=5 \mathrm{~cm}\)
4. In the triangle ABC, the medians BE and CF intersect at point G. The mid-points of BG and CG are P and Q respectively. If PQ is 3 cm, then let us write the length of BC.
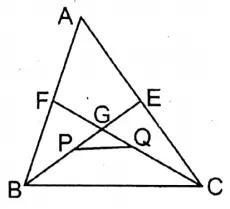
Solution:
Given
In the triangle ABC, the medians BE and CF intersect at point G. The mid-points of BG and CG are P and Q respectively. If PQ is 3 cm,
In ΔGBC the midpoints of BG and CG are P and Q respectively.
\(P Q=\frac{1}{2} B C\)∴ BC= 2PQ = 2 x 3 cm = 6 cm
Wbbse 9th Class Maths Transversal And Midpoint Theorem Step By Step Solutions
5. In the triangle ABC, the mid-points of BC, CA, and AB are D, E, and F respectively; FE intersects AD at the point O. If AD = 6 cm, let us write the length of AO.
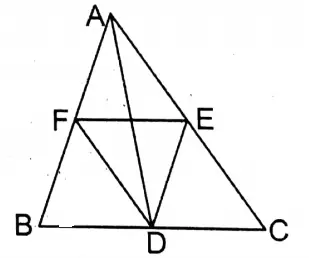
Solution:
Given
In the triangle ABC, the mid-points of BC, CA, and AB are D, E, and F respectively; FE intersects AD at the point O. If AD = 6 cm
D, E, and DF are joined.
In □AEDF, AF II ED, and FD II AE.
∴ AEDF is a parallelogram.
∵ Diagonals of a parallelogram bisect each other.
∴ AO = OD
∴O, is the midpoint of AD
∴ \(A O=\frac{1}{2} A D=\frac{1}{2} \times 6 \mathrm{~cm}=3 \mathrm{~cm}\)
