supriyag

Verification Of The Relation Between The Angles And The Sides Of A Triangle

Today Tania, Kuntal, Tulika and I have decided that we will try to make different types of shapes like triangles with different colored straws and pins.

I formed by three straws-

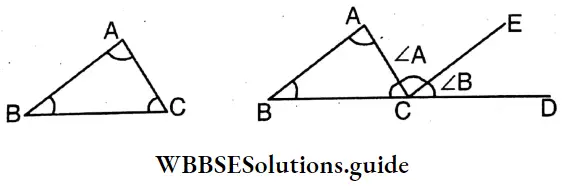
The shape ABC is like a triangle. It has three sides AB,BC and three angles  and CA and three angles ∠BAC, ∠ABC and ∠ACB

l also formed a shape of a triangle like Tutika –

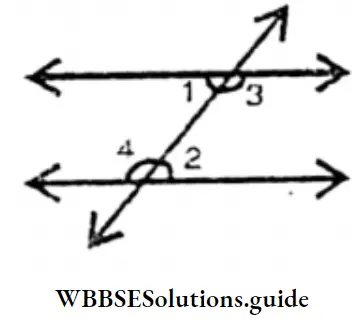
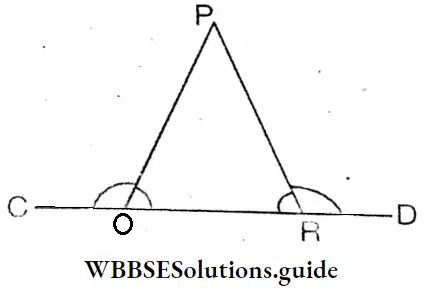
The exterior angle of ΔUVW is ∠UWX (∠UWX/∠UWV). In ΔUVW the interior opposite angles of the exterior angle ∠UWX are ∠UVW and ∠VUW

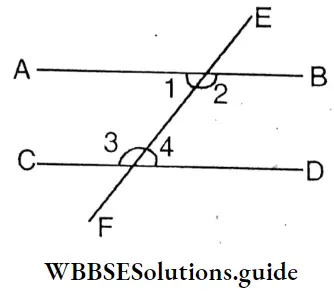
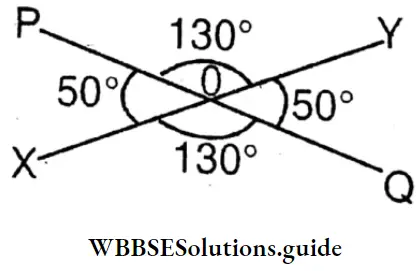
In figure1 the exterior angle is ∠ACD = 140 degree. So interior opposite angle ∠ABC = 50 degree and ∠BAC = 90 degree.

Now I will find the relation between the exterior angle and the interior opposite angle.

Read and Learn More WBBSE Solutions For Class 8 Maths

It is seen by measuring by a protractor, ∠ABC + ∠BAC= 140 degree = ∠ACD (approx).

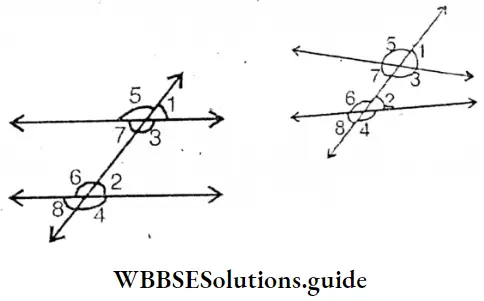
My brother wrote by measuring three angles of each triangle by a protractor. In ΔABC the exterior angles are 90°, 50° and 40°; ∠ABC=50 degree, ∠BCA=40 degree, and ∠CAB=90 degree.

It is seen that ∠ABC + ∠BCA + ∠CAB =180 degree.

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

“WBBSE Class 8 Maths Chapter 16 solutions, Verification of the Relation Between the Angles and the Sides of a Triangle”

It is seen by measuring with a protractor, the sum of measurement of three angles of each triangle in figure 2 and 3 is 180 degree

4 Let’s cut off two angles ∠A and ∠B from another triangle and paste those two angles on the exterior angles of the first triangle as shown in the figure below :

It is seen that the exterior angle ∠ACD = ∠A + ∠B = ∠BAC + ∠ABC

Theorem : We try to identify which postulates are required in the construction of the theorem. We also write which postulates are required for this theorem.

Tania drew triangle PUT and produced the side UT to R for this one exterior angle (∠PTR; and two interior opposite angles ∠PUT and  produced. Let’s prove logically step-by-step that ∠PTR= ∠PUT + ∠UPT.

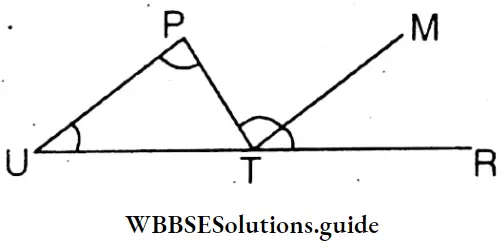
Given : PUT is a triangle whose side UT is extended to R. As a result an exterior angle ∠PTR and two opposite interior angles ∠PUT and ∠UPT are formed.

We have to prove that ∠PTR = ∠PUT + ∠UPT.

Construction : In ΔPUT from T parallel to UP a straight line TM is drawn.

Proof: UP//TM and UR is a transversal.

∴ ∠MTR = Corresponding ∠PUT

Again : UP//TM and PT is a transversal.

∴ ∠PTM = Alternate ∠UPT

∴ ∠MTR + ∠PTM = ∠PUT + ∠UPT

∴ ∠PTR = ∠PUT + ∠UPT Proved

The Sides Of A Triangle Exercise

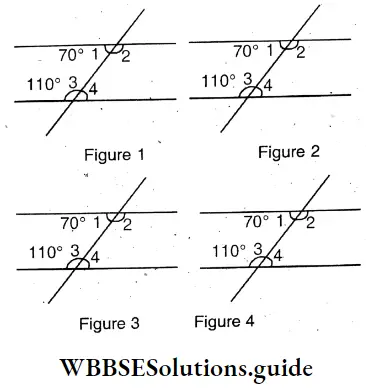
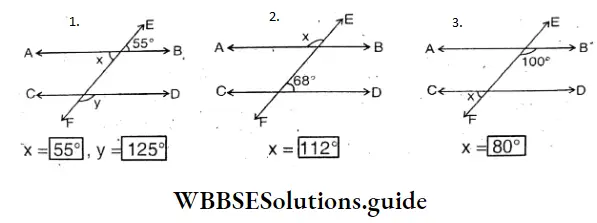
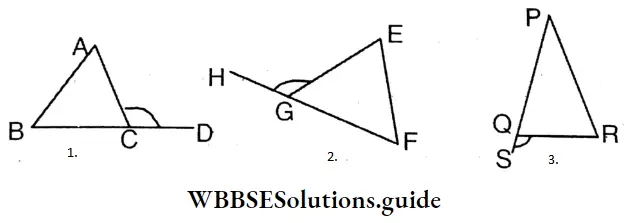
Question 1. Let’s calculate and write the measurement of each of the exterior angles x° in each of the following triangles –

Solution:

The measurement of each of the exterior angles x° in each of the following triangles are

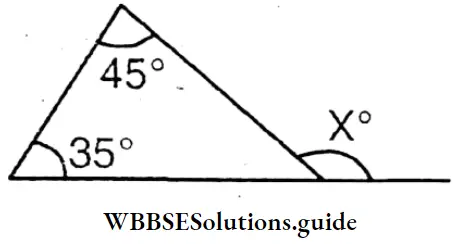
∠X = 35°+45°= 80°

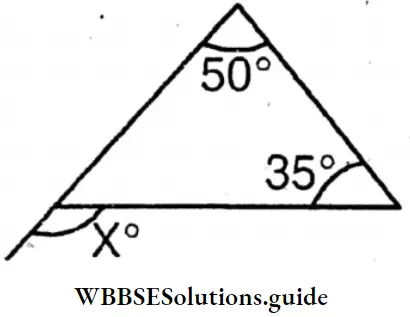
∠X = 50°+35°= 85°

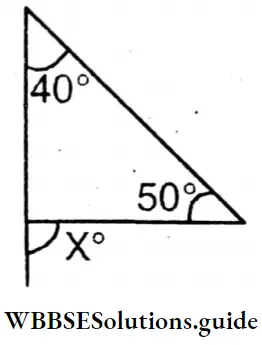
∠X = 50°+40°= 90°

“Class 8 WBBSE Maths Chapter 16 solutions, Relation Between Angles and Sides of a Triangle study material”

Question 2. Let’s write the relation between the exterior angle ∠PRS and the interior opposite angles –

Solution:

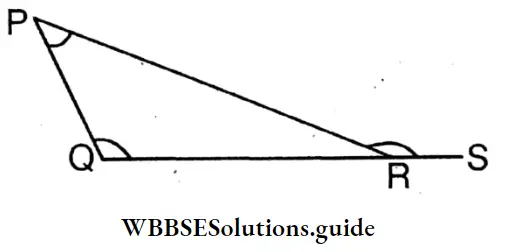
∠PRS = ∠PQR + ∠QPR

Pallabi and Kuntal drew some triangles of different shapes.

In is seen by measuring by a protractor that in ΔABC ∠BAC = 85 degree ∠ABC =60 degree and ∠ACB =35 degree. Again ∠BAC + ∠ABC + ∠ACB =180 degrees.

Kuntal measured with a protractor that in ΔACT ∠CAT = 145 degree ∠ACT = 20 degree and ∠CTA =15 degree. Again ∠ACT + ∠QAT + ∠CTA = 180 degree.

Pallabi measured and saw in ΔAMN that the sum of measurement of the three angles is =180 degrees.

The Sides Of A Triangle Exercise

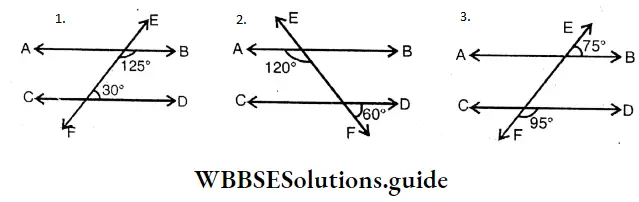
I will find the value of missing angles from the triangles below.

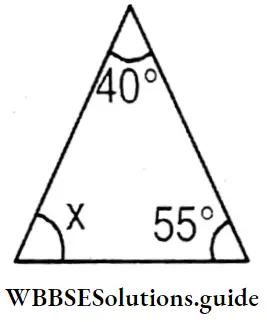
x = 180° – (40° + 55°)

= 180° – 95° = 85°

x = 85°

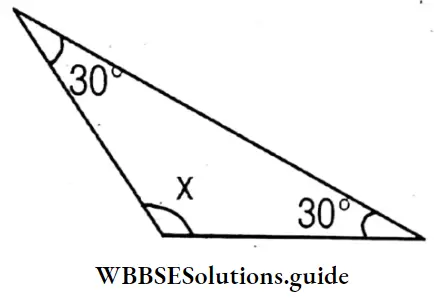
x = 180° – (30°+30°)

= 180° – 60° = 120°

x = 120°

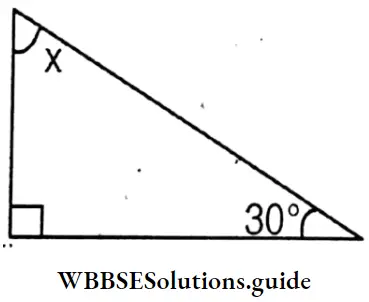
x = 180° – (30°+90°)

= 180° – 120° = 60°

x = 60°

The Sides Of A Triangle Exercise 16.3

Question 1. Find the value of ∠x in each of the following regions :

Solution:

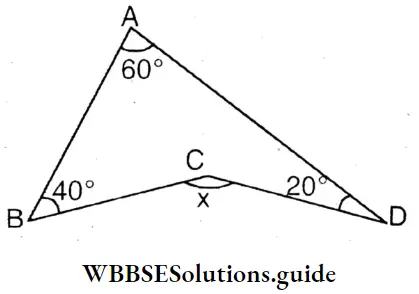
x = 60° + 40° + 20° =120

x =120

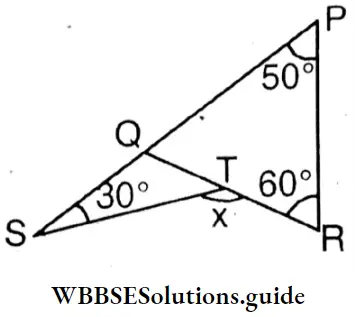
∠PQR = 180° – (50° + 60°) = 180° – 110° = 70

∴ ∠SQT = 180° -70° = 110°

∴ x = ∠SQT+ ∠QST =110° + 30°= 140°

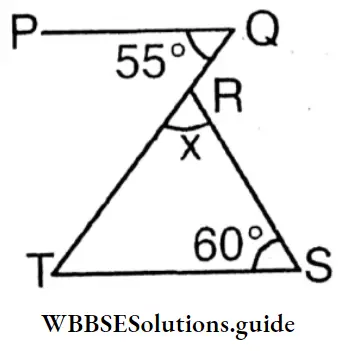
x = 180°-( ∠S+ ∠T) = 180° – (60°+55°) = 180°-115°= 65°

The value of ∠x = 65°

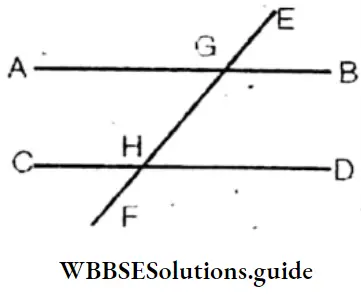
Question 2. From the figure beside find the value of the angles of ΔEHG.

Solution: 

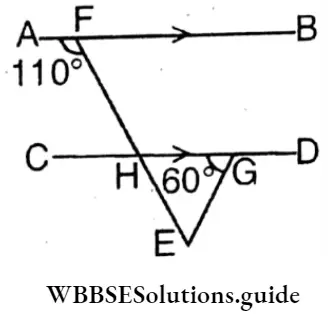
∠AFH = Corresponding ∠CHE = 110° (∵ AB//CD and EF is a transveral).

ΔEHG∠EHG = 180°- 110° = 70°

HGE = 60° (Given) and HEG = 180° – (70°+60°)

= 180° – 130° = 50°

The value of the angles of ΔEHG = 50°

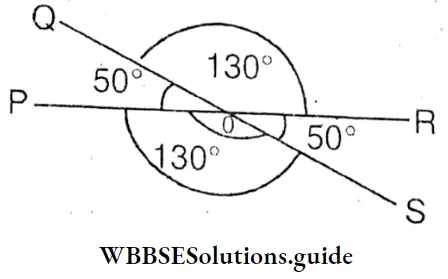
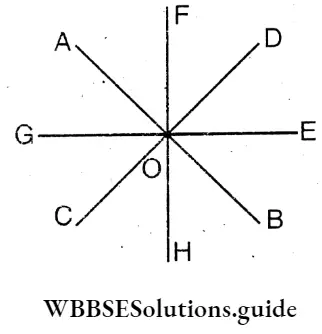
Question 3. From the figure beside find the value of ∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F.

Solution:

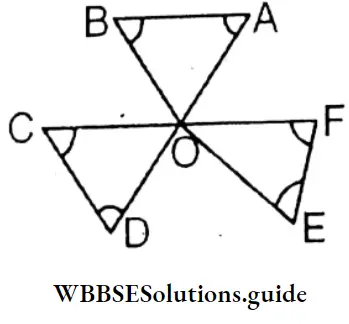
In ΔAOB ∠A+∠B+∠AOB=180° (1)

In ΔCOD ∠C+ ∠D+ ∠COD = 180° (2)

In ΔEOF ∠E + ∠F + ∠EOF-180° (3)

Adding (1), (2) and (3)

∠A + ∠B + ∠C + ∠D +∠E + ∠F + ∠AOB + ∠COD + ∠EOF = 540°

∵ ∠AOB = ∠DOE (∵ Vertically opposite angles)

∠COD = ∠AOF (∵ Vertically opposite angles)

and ∠EOF = ∠BOC (∵Vertically opposite angles)

∵ ∠AOB + ∠DOE + ∠COD + ∠AOF + ∠EOF + ∠BOC = 360°

∵ ∠AOB + ∠COD + ∠EOF = \(\frac{1}{2}\) × 360°= 180°

∵ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 540° – 180° = 360°

The value of ∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F = 360°

Question 4. If AB = AC then find the value of ∠ABC,∠ACB +∠ACD = 180°

Solution:

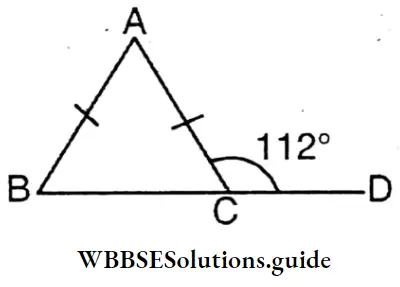
∠ACB +∠ACD = 180°

∴ ∠ACB + 112° = 180°

∴ ∠ACB =180° – 112° = 68°

∵ AB = AC

∴ ∠ACB = ∠ABC = 68°

∠BAC = 180° – (68° + 68°) = 180° – 136° = 44°

∴ ∠ABC = 68°,∠ACB = 68°, ∠BAC = 44°

The value of ∠ABC,∠ACB +∠ACD = 180°

Question 5. If AB = AC then find the value of ∠ABC and ∠ACB.

Solution:

In ΔABC ∠BAC = 80°

∠ABC + ∠ACB = 180° – 80° = 100°

∵ AB = AC

∴ ∠ABC = ∠ACB =\(\frac{100^{\circ}}{2}\) 50°

∴ ∠ABC = 50°, ∠ACB = 50°

Question 6. If AB = AC then find the value of ∠ACB and ∠BAC.

Solution:

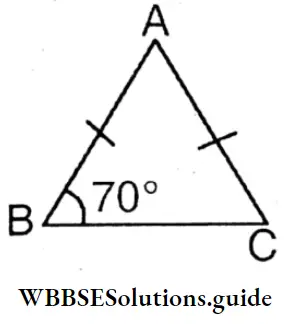
In ΔABC ∠ABC = 70c

∵ AB = AC

∠ABC = ∠ACB = 70°

∠BAC = 180° – (70° + 70°) = 180° – 140° = 40°

∴ ∠ACB = 70° and ∠BAC = 40°

“WBBSE Class 8 Maths Chapter 16, Verification of Angles and Sides of a Triangle solved examples”

Question 7. If AB = BC and ∠BAC + ∠ACB =50°; then find the value of the angles of ΔABC.

Solution:

∵ ∠BAC + ∠ACB = 50°

∵ AB = BC

∠BAC = ∠ACB = \(\frac{50^{\circ}}{2}\) = 25°

∴ ∠ABC = 180°-50°= 130°

If ΔABC ∠ABC = 130°, ∠BAC = 25°, ∠ACB = 25°

Question 9. If we produce the side BC on both sides, the two exterior angles are fomed. Let’s prove that the sum of the measurement of these two exterior angles is more than 2 right angles.

Solution:

Given: In ΔABC side BC is extended on both sides.

We have to prove that the sum of the exterior angles is more than 2 right angles, i.e., ∠ABD + ∠ACE > two right angles.

Proof : According to the relation between the exterior angle and the interior opposite angles, ∠ABD = ∠BAC + ∠ACB and ∠ACE = ∠BAC + ∠ABC

∴ ∠ABD + ∠ACE = ∠BAC + ∠ACB + ∠BAC + ∠ABC

∠ABD + ∠ACE = ∠BAC + ∠ACB + ∠ABC + ∠BAC

∠ABD + ∠ACE = 2 right angles + ∠BAC

(∵ The sum of all three angles of a triangle is equal to two right angles.)

∴ ∠ABD + ∠ACE > two right angles.

Question 9. Two straight lines parallel to sides BC and BA respectively through two vertices A and C of A ABC meet at D. Let’s prove that ∠ABC = ∠ADC.

Solution:

Given: Two straight lines parallel to sides BC and BA respectively through two vertices A and C of A ABC are drawn, which meet at D.

We have to prove that ∠ABC = ∠ADC.

Proof: In ΔABC and ΔADC

∠BAC = Alternate ∠ACD (∴ BA//CD and AC is a transversal)

∠ACB = Alternate. ZCAD (∴ BC//AD and AC is a transversal)

and AC is a common side.

∴ ΔABC = ΔADC(A-A-S)

∴ ∠ABC = ∠ADC Proved.

Question 10 .In ΔABC the internal bisectors of ∠ACB and ∠ACB angles meet at O. Let’s prove that ∠BOC = 90°-\(\frac{1}{2}\) ∠BAC.

Solution:

Given: In A ABC the internal bisectors of angles ∠ABC and ∠ACB meet at O.

Let’s prove that ∠BOC = ∠90° +\(-\frac{1}{2}\) ∠BAC.

Proof: In A ABC

∠A + ∠B + ∠C = 180°

∴ \(\frac{1}{2}\) ∠A + \(\frac{1}{2}\) ∠B + \(\frac{1}{2}\) ∠C × 180° = 90°

∴ \(\frac{1}{2}\) ∠B + \(\frac{1}{2}\) ∠C = 90° – \(\frac{1}{2}\) ∠A

Now, in ΔBOC

= \(\frac{1}{2}\) ∠B+ \(\frac{1}{2}\) ∠C + ∠BOC = 180°

∴  ∠BOC = 180° – (\(\frac{1}{2}\) ∠B+ \(\frac{1}{2}\) ∠C)

∴ ∠BOC=180°-(90°-\(\frac{1}{2}\) ∠A)

∴ ∠BOC = 180° – 90° + \(\frac{1}{2}\) ∠A = 90° + \(\frac{1}{2}\) ∠A Proved

Question 11. In A ABC the external bisectors of ∠ABC and ∠ABC meet at O. Let’s prove that ∠BOC = 90° \(-\frac{1}{2}\) ∠BAC.

Solution:

Given

In ΔABC the external bisectors of ∠ABC and ∠ACB meet at O.

We have to prove that ∠BOC = 90° – \(\frac{1}{2}\)∠BAC.

Proof: ∵ ∠ABC + ∠OBC + ∠OBP = 180°

or, ∠ABC + ∠OBC + ∠OBC = 180° (∵ ∠OBC = ∠OBP)

or, ∠ABC + 2 ∠OBC = 180°

or, 2 ∠OBC = 180°- ∠ABC

or, ∠OBC = 90° –\(\frac{1}{2}\) ∠ABC

Similarly, ∠OCB = 90°-\(\frac{1}{2}\) ∠ACB

Now, in ΔBOC,

∠OBC + ∠OCB + ∠BOC = 180°

or, 90° – \(\frac{1}{2}\) ∠ABC + 90° – \(\frac{1}{2}\) ∠ACB + ∠BOC = 180°

or, 180° – \(\frac{1}{2}\) (∠ABC + ∠ACB) + ∠BOC = 180°

or, ∠BOC = \(\frac{1}{2}\) (∠ABC + ∠ACB)

or, ∠BOC = \(\frac{1}{2}\)(180°- ∠BAC) (∵ ∠A+ ∠B + ∠C = 180°)

∴ ∠B + ∠C = 180° -∠A

or, ∠BOC = 90°\(\frac{1}{2}\) ∠BAC Proved.

Question 12. One base angle of the isosceles triangle ABC is twice of the vertical angle. Let’s write the measurement of the three angles of the triangle.

Solution:

Given

One base angle of the isosceles triangle ABC is twice of the vertical angle.

Let ABC is a triangle where AB = AC and ∠B = 2 ∠A

∵ In ΔABC, AB = AC

∴ ∠B= ∠C

Let ∠A = X

∴ ∠B= ∠C = 2X

Proof: In ΔABC,

∠A + ∠B + ∠C = 180°

or, X + 2X + 2X = 180°

or, 5X = 180°

or X = \(\frac{180^{\circ}}{5}\)

or, X = 36°

∴ ∠A = X = 36°

∴ ∠B = ∠C = 2 x 36° = 72°

∴ The angles of the triangle are 36°, 72°, 72°

Question 13. In ΔABC, ∠BAC = 90° and ∠BCA = 30°. Let’s prove that AB: \(\frac{1}{2}\) BC.

Solution:

Given

In ΔABC, ∠BAC = 90° and ∠BCA = 30

Let’s prove that AB = \(\frac{1}{2}\) BC.

Proof: In A ABC

∠ABC = 180° – (90° + 30°) = 180° – 120° = 60°

∵ ∠C= 30° and ∠B= 60° ,

∴ ∠B = 2∠C

∵ The opposite side is proportional to the angles of a triangle. The opposite side of ZC is AB and the opposite side of ∠B is AC.

∵ The opposite side of the largest angle is the largest and that of the smallest angle is the smallest. Here the value of ∠B is double than that of ∠C.

∴ AB = \(\frac{1}{2}\) AC Proved.

Question 14. In ΔXYZ, ∠XYZ = 90° and XY=XZ. Let’s prove that ∠YXZ = 60°

Solution:

Given : ∠XYZ = 90° and XY = XZ

Here ∠Y is the largest.

∴ XZ is the largest side

∴ XY≠XZ The question is fallacious.

“WBBSE Class 8 Verification of Relation Between Angles and Sides of a Triangle solutions, Maths Chapter 16”

Question 15. Let’s prove that the measurement of-each angle of an equilateral triangle is 60°.

Solution:

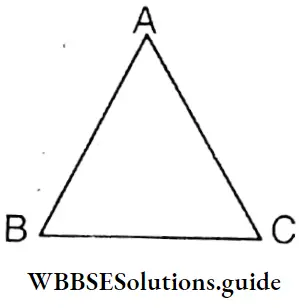
Let ABC is a triangle where AB = BC = AC.

Let’s prove that ∠A = ∠B = ∠C = 60°.

Proof : The sides of a triangle are proportional to the angles.

∵ AB = BC = AC

∴ ∠A = ∠B = ∠C

∵ The sum of the three angles of a triangle is 180°.

∴ ∠A + ∠B + ∠C = 180°

or, ∠A + ∠A + ∠A = 180°

or, 3∠A = 180°

or, ∠A =\(\frac{180^{\circ}}{3}\) = 60°

∴ ∠A = ∠B = ∠C = 60° Proved.

Question 16. The bisector of ∠BAC of ΔABC and the straight line through the mid point D of the side AC and parallel to the side AB meet at a point E, outside BC. Let’s prove that ∠AEC = 1 right angle.

Solution:

Given

The bisector of ∠BAC of ΔABC and the straight line through the mid point D of the side AC and parallel to the side AB meet at a point E, outside BC.

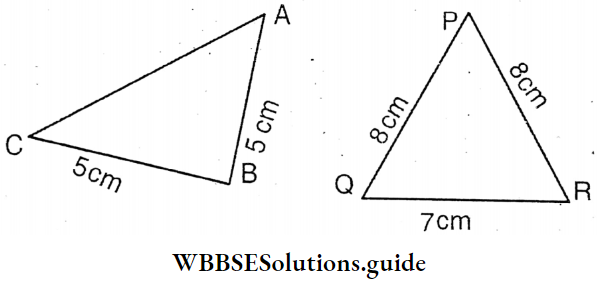
Diptarka and Puja have made different triangles of different shapes and colours. Any two sides of these triangles are unequal. They formed-

I measure the length of each side of each triangle and let’s compare which side is smaller and which one is greater.

Measuring we see, in ΔABC, the length of AC > the length of AB.

In ΔPQR, the length of PR > the length of QR.

In ΔXYZ, the length of XZ > the length of XY

Now, let’s measure each angle triangle with a protractor and compare.

Measuring we see, in ΔABC ∠ACB [>] ∠ACB [ Put</> ]

In ΔPQR, ∠PQR [>] ∠QPR [ Put</> ]

In ΔXYZ, ∠XYZ > ∠YZX ∠YXZ /∠YZX Put ]

But it is seen that in ΔABC, AC is opposite to the side ∠ABC, and AB is opposite to the side ∠ACB.

Again, in ΔPQR, the opposite angle to the side PR is ∠PQR and the opposite angle to the side QR is ∠QPR

And, in ΔXYZ, the opposite angle to the side XZ is ∠XYZ and the opposite angle to the side XY is ∠XYZ

“Class 8 WBBSE Maths Chapter 16, Verification of Angles and Sides easy explanation”

Measuring with a protractor I got the measurement of the angle opposite to the greater side of each triangle than the angle opposite to the smaller side is greater [greater/smaller]. Pallabi and Sirap drew some triangles whose two sides are unequal.

Measuring the sides of the triangle with a scale and the angles of the triangle with a protractor we see that the measurement of the angle opposite to the greater side is greater (smaller/greater) than the measurement of the angle opposite to the smaller side .

The Sides Of A Triangle Exercise

Question 1. Let’s measure the length of the sides of the following triangles and let’s compare the angles :

Solution:

1. ∠P>∠R(∠R/∠Q)
2. ∠X>∠Z(∠Y/∠Z)
3. ∠C>∠B(∠A/∠B)

Pallabi and Siraj drew some triangles, each of whose two angles are unequal.

Now I measure the angles with a protractor and let’s compare the angles of each triangles.

Measuring I see, in ΔMAN, ∠AMN > ∠MAN [</>Put]

In ΔPAN, ∠PAN > ∠PNA [∠PNA / ∠APN Put ]

In ΔFAN, ZFNA < FAN [ ∠FAN / ZAFN Put ]

Let’s measure each side of each triangle with a scale and let’s compare the length of the sides.

Measuring I see, in ΔMAN, MN < AN [ >/< Put ]

In ΔPAN, PN > PA [ PA / AN Put ]

In ΔFAN, AN < FN [ FA / FN Put ]

But it is seen that in ΔMAN the opposite side of ∠AMN is AN

and the opposite side of ∠MAN is MN

In ΔPAN the opposite side of ∠PAN is PN

and the opposite side of ∠PNA is AP

In ΔFAN the opposite side of ∠FNA is FA

and the opposite side of ∠FAN is FN

I got by measuring with a scale and a protractor that in each triangle the length of the side opposite is to greater side than the length of the side opposite |greater| (greater/smaller).

The Sides Of A Triangle Exercise

Question 1. Let’s observe the angles of the following triangles and let’s compare the length of the sides which one is smaller and which one is greater:

Solution:

Side BC > side AB [Put >/<]

Side YZ > side XY [Put XZ/XY]

Side PR > side PQ [Put up side]

The Sides Of A Triangle Exercise 16.6

Question 1. In figure ∠QPR > ∠PQR. Let’s write the relation between PR and QR.

Solution:

Given ∠QPP > ∠PQR

The opposite side of ∠QPR is QR and the opposite side of ∠PQR is PR.

∵  The side of the largest angle of a triangle is greater than that of the smallest angle.

∴ QR>PR

Question 2. In ΔABC, AC>AB. D is any point on the side AC such that ∠AOB = ∠ABD. Prove that ∠ABC > ∠ACB.

Solution:

Given

In ΔABC, AC > AB; D is any point on the side AC such that ∠ADB = ∠ABD.

Prove that ∠ABC > ∠ACB.

Proof : ∠ADB = ∠DBC + ∠BCD (∵ The exterior angle of A BCD is ZADB)

or, ∠ABD = ∠DBC + ∠BCD (∵ ∠ADB = ∠ABD)

or, ∠ABD = ∠DBC + ∠ACB (∵ ∠BCD and ∠ACB are the same angle)

Again, ∠ABC = ∠ABD + ∠ACB

Question 3. In triangle ABC, AD is perpendicular to BC, and AD, BC, AC > AB. Let’s prove that :

Solution:

1. ZCAD > ZBAD
2. DC > BD.

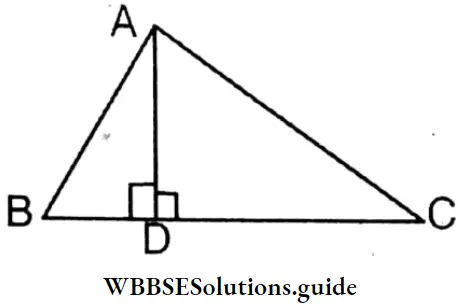
Given

In ΔABC, AD is perpendicular to BC and AC > AB.

Prove that: 1. ∠CAD > ∠BAD; 2.  DC > BD.

Proof: In Δ ∠ABC ∠BAC + ∠ABC + ∠ACB = 180°

In ΔADC ∠DAC + ∠ADC +∠ACD = 180°

or, ∠DAC + 90° + ∠ACD = 180° [∵ AD⊥C]

or, ∠DAC + ∠ACD = 180° – 90° = 90°

In ΔABD ∠BAD + ∠ABD + ∠ADB = 180°

or, ∠BAD + ∠ABD + 90° = 180° [∵ AD⊥C]

or, ∠BAD + ∠ABD = 180° – 90° = 90°

∴  ∠BAD +∠ABD = ∠DAC + ∠ACD = 90°

∵ AC > AB

∴  ∠B > ∠C

∴ ∠CAD > ∠BAD

(1) (Proved)

∴ In ΔABD ∠D= 90° and ∠A + ∠B = 90°, ∠B> ∠A

∴ AD > BD

Similarly in ΔADC, DC > AD

∴ DC > AD > BD

∴ BD > BD (ii) (Proved)

“WBBSE Class 8 Maths Chapter 16 solutions, Verification of Relation Between Angles and Sides PDF”

Question 4. In figure AB < OB and CD > OD. Let’s prove that ∠BAO > ∠OCD.

Solution:

Given

AB < OB and CD > OD

Prove that ∠BAO > ∠OCD

Proof : ∵ CD > OD

∴  ∠COD >∠OCD

and ∠COD = ∠BOA (Vertically opposite angles)

Again, AB < ∠OB

∠BOA < ∠BAO

or, ∠COD < ∠BAO (∵ ∠BOA = ∠COD)

In triangle OCD, ∠COD > ∠OCD (∵ CD > OD)

and ∠BAO > ∠COD –

∴ ∠BAO > ∠OCD (Proved)

Simplification Of Algebraic Expressions

Sumita has a 20 meter long red ribbon. Santanu and I have made some cards. We have decided that we will cover the four sides of the cards by the red ribbon.

If Sumita has a 4x²meter long red ribbon and Santanu and I took ax meter and 2xb meter respectively from Sumita’s ribbon, then let’s calculate how much portion we took from Sumita’s ribbon.

1 took \(\frac{2 x b}{4 x^2}\) Part = \(\frac{b}{2 x}\)2 Par

I have seen that \(\frac{2 x b}{4 x^2}\) and \(\frac{b}{2 x}\) are same. What are these called?

Santanu took \(\frac{a x}{4 x^2}\) part = \(\frac{a}{4 x}\) part.

“WBBSE Class 8 Maths Chapter 15 solutions, Simplification of Algebraic Expressions”

We took, \(\frac{b}{2 x}\) part + \(\frac{a}{4 x}\) part.

= \(\left(\frac{b}{2 x}+\frac{a}{4 x}\right)\) part = \(\left(\frac{2 b+a}{4 x}\right)\) part of the total ribbon. Let’s simplify the algebraic expression.

Question 1. \(\frac{1}{(b-c)(c-a)}+\frac{1}{(c-a)(a-b)}+\frac{1}{(a-b)(b-c)}\)

Solution:

Given

\(\frac{1}{(b-c)(c-a)}+\frac{1}{(c-a)(a-b)}+\frac{1}{(a-b)(b-c)}\)

First we see the L.C.M. of (b-c) (c-a), (c-a) (a-b) and (a-b) (b-c) (b-c) (c-a), (c-a) (a-b) and (a-b) (b-c) = (a-b) (b-c) (c-a)

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

= \(\frac{1}{(b-c)(c-a)}+\frac{1}{(c-a)(a-b)}+\frac{1}{(a-b)(b-c)}\)

= \(\frac{a-b}{(a-b)(b-c)(c-a)}+\frac{b-c}{(a-b)(b-c)(c-a)}+\frac{c-a}{(a-b)(b-c)(c-a)}\)

(a-b)(b-c)(c-a)÷(b-c)(c-a)=(a-b)

(a-b)(b-c)(c-a)÷(c-a)(a-b)=(b-c)

(a-b)(b-c)(c-a)÷(a-b)(b-c)=(c-a)

= \(\frac{a-b+b-c+b-a}{(a-b)(b-c)(c-a)}=\frac{0}{(a-b)(b-c)(c-a)}=0\)

\(\frac{1}{(b-c)(c-a)}+\frac{1}{(c-a)(a-b)}+\frac{1}{(a-b)(b-c)}\) = 0

Read and Learn More WBBSE Solutions For Class 8 Maths

Question 2. Let the length of the ribbon is 8a²x²meter. I took 2ax meter ribbon.

Solution:

Given

The length of the ribbon is 8a²x²meter. I took 2ax meter ribbon

I took \(\frac{2 a x}{8 a^2 x^2}\) part = \(\frac{1}{4 a x}\) part

∴ The reduced from of \(\frac{2 a x}{8 a^2 x^2}\) is \(\frac{1}{4 a x}\)

Question 3. Let’s express \(\frac{(a+1)}{a+2} \times \frac{a^2-a-2}{a^2+a}\) in reduced form-

Solution:

Given

\(\frac{(a+1)}{a+2} \times \frac{a^2-a-2}{a^2+a}\)

= \(\frac{a+1}{a+2} \times \frac{a^2-a-2}{a^2+\bar{a}}=\frac{a+1}{a+2} x\)

= \(=\frac{(a-2) \times(a+1)}{a(a+1)}\)

= \(\frac{(a+1)(a-2)}{a(a+2)}\)

\(\frac{(a+1)}{a+2} \times \frac{a^2-a-2}{a^2+a}\) = \(\frac{(a+1)(a-2)}{a(a+2)}\)

Algebraic Expressions Exercise

Question 1. Let’s express \(\frac{a(a+b)}{(a-b)} \times \frac{(a-b)}{b(a+b)} \times \frac{a}{b}\) in reduced form.

Solution:

Given

\(\frac{a(a+b)}{(a-b)} \times \frac{(a-b)}{b(a+b)} \times \frac{a}{b}\)

= \(\frac{a(a+b)}{a-b} \times \frac{a-b}{b(a+b)} \times \frac{a}{b}\)

= \(\frac{a^2(a+b)(a-b)}{b^2(a-b)(a+b)}=\frac{a^2}{b^2}\)

\(\frac{a(a+b)}{(a-b)} \times \frac{(a-b)}{b(a+b)} \times \frac{a}{b}\) = \(\frac{a^2(a+b)(a-b)}{b^2(a-b)(a+b)}=\frac{a^2}{b^2}\)

“Class 8 WBBSE Maths Chapter 15 solutions, Simplification of Algebraic Expressions study material”

Question 2. Let’s express \(\frac{x^2+x-2}{x^2-2 x-8} \div \frac{x^2-x-6}{x^2-3 x-4}\) in reduced form.

Solution:

Given

\(\frac{x^2+x-2}{x^2-2 x-8} \div \frac{x^2-x-6}{x^2-3 x-4}\)

= \(\frac{x^2+x-2}{x^2-2 x-8} \div \frac{x^2-x-6}{x^2-3 x-4}=\frac{x^2+x-2}{x^2-2 x-8} \times \frac{x^2-3 x-4}{x^2-x-6}\)

= \(\frac{x^2+2 x-x-2}{x^2-4 x+2 x-8} \times \frac{x^2-4 x+x-4}{x^2-3 x+2 x-6}\)

= \( \frac{x(x+2)-1(x+2)}{x(x-4)+2(x-4)} \times \frac{x(x-4)+1(x-4)}{x(x-3)+2(x-3)}\)

= \(\frac{(x+2)(x-1)}{(x-4)(x+2)} \times \frac{(x-4)(x+1)}{(x-3)(x+2)}\)

= \(\frac{(x+2)(x-1)(x-4)(x+1)}{(x-4)(x+2)(x-3)(x+2)}\)

[In numerator and in denominator [x+2×x-4] is the common factor, so dividing numerator and denominator by (x+2) (x-4) we get the reduced form.]

= \(\frac{(x+2)(x-1)(x-4)(x+1)}{(x-4)(x+2)(x-3)(x+2)}\)

= \(\frac{(x-1)(x+1)}{(x-3)(x+2)}\)

\(\frac{x^2+x-2}{x^2-2 x-8} \div \frac{x^2-x-6}{x^2-3 x-4}\) = \(\frac{(x-1)(x+1)}{(x-3)(x+2)}\)

Question 3. Let’s express \(\frac{p^2-q^2}{x-y} \div \frac{p+q}{x^2-y^2}\) in reduced form and let’s write the common factor of the numerator and the denominator.

Solution:

Given

\(\frac{p^2-q^2}{x-y} \div \frac{p+q}{x^2-y^2}\)

= \(\frac{p^2-q^2}{x-y} \div \frac{p+q}{x^2-y^2}\)

= \(\frac{p^2-q^2}{x-y} \div \frac{x^2-y^2}{p+q}\)

= \(\frac{(p+q)(p-q)}{(x-y)} \times \frac{(x-y)(x+y)}{p+q}\)

\(\frac{p^2-q^2}{x-y} \div \frac{p+q}{x^2-y^2}\) = (p-q)(x+y)

The common factor of the numerator and the denominator is (p-q)(x+y)

Algebraic Expressions Exercise

Let’s express the algebraic expressions given below in reduced form:

1. \(\frac{a^2 \times c^2}{c^2 \times d^2} \div \frac{b c}{a d}\)

Solution:

Given

= \(\frac{a^2 \times c^2}{c^2 \times d^2}\)

= \(\frac{a^3}{b c d}\)

\(\frac{a^2 \times c^2}{c^2 \times d^2} \div \frac{b c}{a d}\) = \(\frac{a^3}{b c d}\)

2. \(\frac{x^2 y-x y^2}{x^2-x y}\)

Solution:

Given

= \(\frac{x^2 y-x y^2}{x+y}\)

= \(\frac{x y(x-y)}{x(x-y)}\)

= y

\(\frac{x^2 y-x y^2}{x^2-x y}\) = y

“WBBSE Class 8 Maths Chapter 15, Simplification of Algebraic Expressions solved examples”

3. \(\frac{p^2-q^2}{x^2-x y} \div \frac{p-q}{x^2-y^2}\)

Solution:

Given

= \(\frac{p^2-q^2}{x^2-x y} \div \frac{p-q}{x^2-y^2}\)

= \(\frac{(p+q)(p-q)}{(x+y)} \times \frac{(x+y)(x-y)}{(p-q)}\)

= (p+q)(x-y)

\(\frac{p^2-q^2}{x^2-x y} \div \frac{p-q}{x^2-y^2}\) = (p+q)(x-y)

Solution:

Algebraic Expressions Exercise

Question 1. Let’s see the relations below and find which one is true and which one is false :

1. \(\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}\)

Solution:

L.H.S = \(\)

= \(\frac{a+b}{c}\)

= R.H.S

∴ True

2. \(\frac{a}{x+y}=\frac{a}{x}+\frac{a}{y}\)

Solution:

L.H.S = \(\frac{a}{x+y}\)

R.H.S = \(\frac{a}{x}+\frac{a}{y}=\frac{a y+a x}{x y}\)

L.H.S≠R.H.S

∴ False

3. \(\frac{x-y}{a-b}=\frac{y-x}{b-a}\)

Solution:

= \(\frac{x-y}{a-b}\)

= \(\frac{-(x-y)}{-(a-b)}\)

= \(\frac{x-y}{a-b}\)

∵ L.H.S=R.H.S

∴ True

“WBBSE Class 8 Simplification of Algebraic Expressions solutions, Maths Chapter 15”

4.  \(\frac{1}{x}+\frac{1}{y}=\frac{1}{x+y}\)

Solution:

L.H.S = \(\frac{1}{x}+\frac{1}{y}\)

= \(\frac{y+x}{x y}\)

R.H.S = \(\frac{1}{x+y}\)

∵ L.H.S≠R.H.S

∴ False

Question 2. Let’s express the following algebraic fractions in reduced form:

Solution:

1. \(\frac{63 a^3 b^4}{77 b^5}\)

Solution:

= \(\frac{63 a^3 b^4}{77 b^5}\)

= \(\frac{63 a^3 b^4}{77 b^4}{\prime\cdot b}\)

= \(\frac{9 a^3}{11 b}\)

\(\frac{63 a^3 b^4}{77 b^5}\) = \(\frac{9 a^3}{11 b}\)

2. \(\frac{18 a^4 b^5 c^2}{21 a^7 b^2}\)

Solution:

= \(\frac{18 a^4 b^5 c^2}{77 a^7 b^2}\)

= \(\frac{18 \times a^4 \times b^2 \times b^3 \times c^2}{21 \times a^4 \times a^3 \times b^2}\)

= \(\frac{6 b^3 c^2}{7 a^3}\)

\(\frac{18 a^4 b^5 c^2}{21 a^7 b^2}\) = \(\frac{6 b^3 c^2}{7 a^3}\)

3. \(\frac{x^2-3 x+2}{x^2-1}\)

Solution:

= \(\frac{x^2-3 x+2}{x^2-1}\)

= \(\frac{x^2-2 x-x+2}{(x)^2-(1)^2}\)

= \(\frac{x(x-2)-1(x-2)}{(x+1)(x-1)}\)

= \(\frac{(x-2)(x-1)}{(x+1)(x-1)}\)

= \( \frac{x-2}{x+1}\)

\(\frac{x^2-3 x+2}{x^2-1}\) = \( \frac{x-2}{x+1}\)

4.  \(\frac{a+1}{a-2} \times \frac{a^2-a-2}{a^2+a}\)

Solution:

= \(\frac{a+1}{a-2} \times \frac{a^2-a-2}{a^2+a}\)

= \(\frac{a+1}{a-2} \times \frac{a^2-2 a+a-2}{a(a+1)}\)

= \( \frac{(a+1)}{(a-2)} \times \frac{a(a-2)+1(a-2)}{a(a+1)}\)

= \(\frac{(a+1)}{(a-2)} \times \frac{(a-2)(a+1)}{a(a+1)}\)

= \(\frac{a+1}{a}\)

\(\frac{a+1}{a-2} \times \frac{a^2-a-2}{a^2+a}\) = \(\frac{a+1}{a}\)

5.  \(\frac{p^3+q^3}{p^2-q^2} \div \frac{p+q}{p-q}\)

Solution:

= \(\frac{p^3+q^3}{p^2-q^2} \div \frac{p+q}{p-q}\)

= \(\frac{(p+q)\left(p^2-p q+q^2\right)}{(p+q)(p-q)} \times \frac{(p-q)}{(p+q)}\)

= \(\frac{p^2-p q+q^2}{p+q}\)

\(\frac{p^3+q^3}{p^2-q^2} \div \frac{p+q}{p-q}\) = \(\frac{p^2-p q+q^2}{p+q}\)

6.  \(\frac{x^2-x-6}{x^2+4 x-5} \times \frac{x^2+6 x+5}{x^2-4 x+3}\)

Solution:

= \(\frac{x^2-x-6}{x^2+4 x-5} \times \frac{x^2+6 x+5}{x^2-4 x+3}\)

= \(\frac{x^2-3 x+2 x-6}{x^2+5 x-x-5} \times \frac{x^2+5 x+x+5}{x^2-3 x-x+3}\)

= \(\frac{x(x-3)+2(x-3)}{x(x+5)-1(x+5)} \times \frac{x(x+5)+1(x+5)}{x(x-3)-1(x-3)}\)

= \(\frac{(x-3)(x+2)}{(x+5)(x-1)} \times \frac{(x+5)(x+1)}{(x-3)(x-1)}\)

= \(\frac{(x+2)(x+1)}{(x-1)(x-1)}\)

\(\frac{x^2-x-6}{x^2+4 x-5} \times \frac{x^2+6 x+5}{x^2-4 x+3}\) = \(\frac{(x+2)(x+1)}{(x-1)(x-1)}\)

“Class 8 WBBSE Maths Chapter 15, Simplification of Algebraic Expressions easy explanation”

7. \(\frac{a^2-a b+b^2}{a^2+a b} \div \frac{a^2+b^3}{a^2-b^2}\)

Solution:

= \(\frac{a^2-a b+b^2}{a^2+a b} \div \frac{a^2+b^3}{a^2-b^2}\)

= \(\frac{a^2-a b+b^2}{a(a+b)} \div \frac{(a+b)\left(a-a b+b^2\right)}{(a+b)(a-b)}\)

= \(\frac{\left(a^2-a b+b^2\right)}{a(a+b)} \times \frac{(a+b)(a-b)}{(a+b)\left(a^2-a b+b^2\right)}\)

= \(\frac{a-b}{a}(a+b)

= [latex]\frac{a-b}{a^2+a b}\)

\(\frac{a^2-a b+b^2}{a^2+a b} \div \frac{a^2+b^3}{a^2-b^2}\) = \(\frac{a-b}{a^2+a b}\)

Question 3. Let’s simplify the following algebraic expressions:

Solution:

= \(\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}\)

= \(\frac{1}{a b}+\frac{1}{b c}+\frac{1}{c a}\)

= \(\frac{c+a+b}{a b c}\)

= \(\frac{a+b+c}{a b c}\)

2. \(\frac{a-b-c}{a}+\frac{a+b+c}{a}\)|

Solution:

= \(\frac{a-b-c}{a}+\frac{a+b+c}{a}\)

= \(\frac{a-\not b-\not c+a+\not b+\not c}{a}\)

= \(\frac{2 a}{a}\)

= 2

\(\frac{a-b-c}{a}+\frac{a+b+c}{a}\)| = 2

3. \(\frac{x^2+a^2}{a b}+\frac{x-a}{a x}-\frac{x^3}{b}\)

Solution:

= \(\frac{x^2+a^2}{a b}+\frac{x-a}{a x}-\frac{x^3}{b}\)

= \(\frac{x\left(x^2+a^2\right)+b(x-a)-a x^4}{a b x}\)

= \(\frac{x^3+a^2 x+b x-a b-a x^4}{a b x}\)

\(\frac{x^2+a^2}{a b}+\frac{x-a}{a x}-\frac{x^3}{b}\) = \(\frac{x^3+a^2 x+b x-a b-a x^4}{a b x}\)

4. \(\frac{2 a^2 b}{3 b^2 c} \times \frac{c^4}{3 a^3} \div \frac{4 b c^3}{9 a^2}\)

Solution:

= \(\frac{2 a^2 b}{3 b^2 c} \times \frac{c^4}{3 a^3} \div \frac{4 b c^3}{9 a^2}\)

= \(\frac{2 a^2 b}{3 b^2 c} \times \frac{c^4}{3 a^3} \times \frac{9 a^2}{4 b c^3}\)

= \(\frac{a}{2 b^2}\)

\(\frac{2 a^2 b}{3 b^2 c} \times \frac{c^4}{3 a^3} \div \frac{4 b c^3}{9 a^2}\) = \(\frac{a}{2 b^2}\)

“WBBSE Class 8 Maths Chapter 15 solutions, Simplification of Algebraic Expressions PDF”

5. \(\frac{1}{x^2-3 x+2}+\frac{1}{x^2-5 x+6}+\frac{1}{x^2-4 x+3}\)

Solution:

= \(\frac{1}{x^2-3 x+2}+\frac{1}{x^2-5 x+6}+\frac{1}{x^2-4 x+3}\)

= \(\frac{1}{x^2-2 x-x+2}+\frac{1}{x^2-3 x-2 x+6}+\frac{1}{x^2-3 x-x+3}\)

= \(\frac{1}{x(x-2)-1(x-2)}+\frac{1}{x(x-3)-2(x-3)}+\frac{1}{x(x-3)-1(x-3)}\)

= \(\frac{1}{(x-2)(x-1)}+\frac{1}{(x-3)(x-2)}+\frac{1}{(x-3)(x-1)}\)

= \(\frac{x-3+x-1+x-2}{(x-1)(x-2)(x-3)}\)

= \(\frac{3 x-6}{(x-1)(x-2)(x-3)}\)

= \(\frac{3(x-2)}{(x-1)(x-2)(x-3)}\)

= \(\frac{3}{(x-1)(x-3)}\)

=\(\frac{3}{x^2-4 x+3}\)

\(\frac{1}{x^2-3 x+2}+\frac{1}{x^2-5 x+6}+\frac{1}{x^2-4 x+3}\) =\(\frac{3}{x^2-4 x+3}\)

“WBBSE Maths Class 8 Simplification of Algebraic Expressions, Chapter 15 key concepts”
“WBBSE Class 8 Maths Chapter 15, Simplification of Algebraic Expressions summary”

6. \(\frac{1}{x-1}+\frac{1}{x+1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\)

Solution:

= \(\frac{1}{x-1}+\frac{1}{x+1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\)

= \(\frac{x+1+x-1}{(x-1)(x+1)}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\)

= \(\frac{2 x}{x^2-1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\)

= \(\frac{2 x\left(x^2+1\right)+2 x\left(x^2-1\right)}{\left(x^2 1\right)\left(x^2+1\right)}+\frac{4 x^3}{x^4+1}\)

= \(\frac{2 x^3+2 x+2 x^3-2 x}{x^4-1}+\frac{4 x^3}{x^4+1}\)

= \(\frac{4 x^3}{x^4+1}+\frac{4 x^3}{x^4-1}\)

= \(\frac{4 x^3\left(x^4+1\right)+4 x^3\left(x^4-1\right)}{\left(x^4 1\right)\left(x^4+1\right)}\)

= \(\frac{4 x^7+4 x^2+4 x^7-4 x^8}{x^8-1}\)

= \(\frac{8 x^7}{x^8-1}\)

\(\frac{1}{x-1}+\frac{1}{x+1}+\frac{2 x}{x^2+1}+\frac{4 x^3}{x^4+1}\) = \(\frac{8 x^7}{x^8-1}\)

7.  \(\frac{b^2-5 b}{3 b-4 a} \times \frac{9 b^2-16 a^2}{b^2-25} \div \frac{3 b^2+4 a b}{a b+5 a}\)

Solution:

= \(\frac{b^2-5 b}{3 b-4 a} \times \frac{9 b^2-16 a^2}{b^2-25} \div \frac{3 b^2+4 a b}{a b+5 a}\)

= \(\frac{b(b-5)}{3 b-4 a} \times \frac{(3 b)^2-(4 a)^2}{(b)^2-(5)^2} \div \frac{b(3 b+4 a)}{a(b+5)}\)

= \(\frac{b(b-5)}{(3 b-4 a)} \times \frac{(3 b+4 a)(3 b-4 a)}{(b+5)(b-5)} \times \frac{a(b+5)}{b(3 b+4 a)}\)

= a

\(\frac{b^2-5 b}{3 b-4 a} \times \frac{9 b^2-16 a^2}{b^2-25} \div \frac{3 b^2+4 a b}{a b+5 a}\) = a

“WBBSE Class 8 Chapter 15 Maths, Simplification of Algebraic Expressions step-by-step solutions”

8.  \(\frac{b+c}{(a-b)(a-c)}+\frac{c+a}{(b-a)(b-c)}+\frac{a+b}{(c-a)(c-b)}\)

Solution:

= \(\frac{b+c}{(a-b)(a-c)}+\frac{c+a}{(b-a)(b-c)}+\frac{a+b}{(c-a)(c-b)}\)

= \(\frac{b+c}{-(a-b)(c-a)}+\frac{c+a}{-(a-b)(b-c)}+\frac{a+b \cdot}{-(c-a)(b-c)}\)

= \( -\left\{\frac{b+c}{(a-b)(c-a)}+\frac{c+a}{(a-b)(b-c)}+\frac{a+b}{(c-a)(b-c)}\right\}\)

= \(-\left\{\frac{(b+c)(b-c)+(c+a)(c-a)+(a+b)(a-b)}{(a-b)(b-c)(c-a)}\right\}\)

= \(-\left\{\frac{b^2-e^2+e^2-a^2+a^2-b^2}{(a-b)(b-c)(c-a)}\right\}\)

= \(\frac{0}{(a-b)(b-c)(c-a)}=0\)

\(\frac{b+c}{(a-b)(a-c)}+\frac{c+a}{(b-a)(b-c)}+\frac{a+b}{(c-a)(c-b)}\) = 0

9. \(\frac{b+c-a}{(a-b)(a-c)}+\frac{c+a-b}{(b-c)(b-a)}+\frac{a+b-c}{(c-a)(c-b)}\)

Solution:

= \(\frac{b+c-a}{(a-b)(a-c)}+\frac{c+a-b}{(b-c)(b-a)}+\frac{a+b-c}{(c-a)(c-b)}\)

= \(\frac{b+c-a}{-(a-b)(c-a)}+\frac{c+a-b}{-(b-c)(a-b)}+\frac{a+b-c}{-(c-a)(b-c)}\)

= \(-\left\{\frac{b+c-a}{(a-b)(c-a)}+\frac{c+a-b}{(b-c)(a-b)}+\frac{a+b-c}{(c-a)(b-c)}\right\} \)

= \(-\left\{\frac{(b-c)(b+c-a)+(c-a)(c+a-b)+(a-b)(a+b-c)}{(a-b)(b-c)(c-a)}\right\}\)

= \(-\left\{\frac{b^2+b c-a b-b c-c^2+a c+c^2+a c-b c-a c-a^2+a b+a^2+a b-a c-a b-b^2+b c}{(a-b)(b-c)(c-a)}\right\}\)

= \(-\frac{0}{(a-b)(b-c)(c-a)}=0\)

\(\frac{b+c-a}{(a-b)(a-c)}+\frac{c+a-b}{(b-c)(b-a)}+\frac{a+b-c}{(c-a)(c-b)}\)= 0

“Class 8 Maths Simplification of Algebraic Expressions solutions, WBBSE syllabus”

10.  \(\frac{\frac{a^2}{x-a}+\frac{b^2}{x-b}+\frac{c^2}{x-c}+a+b+c}{\frac{a}{x-a}+\frac{b}{x-b}+\frac{c}{x-c}}\)

Solution:

= \(\frac{\frac{a^2}{x-a}+\frac{b^2}{x-b}+\frac{c^2}{x-c}+a+b+c}{\frac{a}{x-a}+\frac{b}{x-b}+\frac{c}{x-c}}\)

= \(\frac{\frac{a^2+a x-a^2}{x-a}+\frac{b^2+b x-b^2}{x-b}+\frac{c^2+c x-c^2}{x-c}}{\frac{a}{x-a}+\frac{b}{x-b}+\frac{c}{x-c}}\)

= \(\frac{\frac{a x}{x-a}+\frac{b x}{x-b}+\frac{c x}{x-c}}{\frac{a}{x-a}+\frac{b}{x-b}+\frac{c}{x-c}}\)

= \(=\frac{x\left(\frac{a}{x-a}+\frac{b}{x-b}+\frac{c}{x-c}\right)}{\left(\frac{a}{x-a}+\frac{b}{x-b}+\frac{c}{x-c}\right)}=x\)

\(\frac{\frac{a^2}{x-a}+\frac{b^2}{x-b}+\frac{c^2}{x-c}+a+b+c}{\frac{a}{x-a}+\frac{b}{x-b}+\frac{c}{x-c}}\)=x

11.  \(\left(\frac{a^2+b^2}{a^2-b^2}-\frac{a^2-b^2}{a^2+b^2}\right) \div\left(\frac{a+b}{a-b}-\frac{a-b}{a+b}\right) \times\left(\frac{a}{b}+\frac{b}{a}\right)\)

Solution:

= \(\left(\frac{a^2+b^2}{a^2-b^2}-\frac{a^2-b^2}{a^2+b^2}\right) \div\left(\frac{a+b}{a-b}-\frac{a-b}{a+b}\right) \times\left(\frac{a}{b}+\frac{b}{a}\right)\)

= \(\left\{\frac{\left(a^2+b^2\right)^2-\left(a^2-b^2\right)^2}{\left(a^2+b^2\right)\left(a^2-b^2\right)}\right\} \div\left\{\frac{(a+b)^2-(a-b)^2}{(a+b)(a-b)}\right\} \times\left(\frac{a^2+b^2}{a b}\right)\)

= \(\frac{a^4+2 a^2 b^2+b^4-\left(a^4-2 a^2 b^2+b^4\right)}{\left(a^2+b^2\right)(a+b)(a-b)} \div \frac{a^2+2 a b+b^2-\left(a^2-2 a b+b^2\right)}{(a+b)(a-b)} \times \frac{\left(a^2+b^2\right)}{a b}\)

= \(\frac{a^4+2 a^2 b^2+b^4-a^4+2 a^2 b^2+b^4}{\left(a^2+b^2\right)(a+b)(a-b)} \div \frac{a^2+2 a b+b^2-a^2+2 a b-b^2}{(a+b)(a-b)} \times \frac{\left(a^2+b^2\right)}{a b}\)

= \(=\frac{4 a^2 b^2}{\left(a^2+b^2\right)(a+b)(a-b)} \times \frac{(a+b)(a-b)}{4 a b} \times \frac{\left(a^2+b^2\right)}{a b}\)

= \(\frac{4 a^2 b^2}{4 a^2 b^2}\)

= 1

\(\left(\frac{a^2+b^2}{a^2-b^2}-\frac{a^2-b^2}{a^2+b^2}\right) \div\left(\frac{a+b}{a-b}-\frac{a-b}{a+b}\right) \times\left(\frac{a}{b}+\frac{b}{a}\right)\)=1

“WBBSE Class 8 Maths Chapter 15, Simplification of Algebraic Expressions important questions”

12.  \(\frac{y^2+y z+z^2}{(x-y)(x-z)}+\frac{z^2+z x+x^2}{(y-z)(y-x)}+\frac{x^2+x y+y^2}{(z-x)(z-y)}\)

Solution:

= \(\frac{y^2+y z+z^2}{(x-y)(x-z)}+\frac{z^2+z x+x^2}{(y-z)(y-x)}+\frac{x^2+x y+y^2}{(z-x)(z-y)}\)

= \(\frac{y^2+y z+z^2}{(x-y)(x-z)}+\frac{z^2+z x+x^2}{(y-z)(y-x)}+\frac{x^2+x y+y^2}{(z-x)(z-y)}\)

= \(-\left\{\frac{y^2+y z+z^2}{(x-y)(z-x)}+\frac{z^2+z x+x^2}{(y-z)(x-y)}+\frac{x^2+x y+y^2}{(z-x)(y-z)}\right\}\)

= \(-\left\{\frac{(y-z)\left(y^2+y z+z^2\right)+(z-x)\left(z^2+z x+x^2\right)+(x-y)\left(x^2+x y+y^2\right)}{(x-y)(y-z)(z-x)}\right\}\)

= \(\frac{y^3-z^3+z^3-x^3+x^3-y^3}{(x-)(y-z)(z-x)}\)

= \(-\frac{0}{(x-y)(y-z)(z-x)}\)

= 0

\(\frac{y^2+y z+z^2}{(x-y)(x-z)}+\frac{z^2+z x+x^2}{(y-z)(y-x)}+\frac{x^2+x y+y^2}{(z-x)(z-y)}\) = 0

Factorization Of Algebraic Expressions

Today at school we have made rectangles and squares of different sizes using coloured cardboard.

Papia and Tathagaiha stuck those figures on a long thick chart paper and wrote the algebraic expressions for their area below the corresponding figures.

We all have planned to find out the length of each side of a rectangle or a square by fractions of each algebraic expression.

Question 1. On the school blackboard, I resolve \(49 x^2+70 x y+25 y^2\)

Solution:

\(49 x^2+70 x y+25 y^2=7 x^2+2 x 7 x \times 5 y+5 y^2\)

= \((7 x+5 y)^2\)

I got \(49 x^2+70 x y+25 y^2=(9 x+5 y) x(9 x+5 y)\)

The length of each side of the square = 7x + 5y unit.

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

“WBBSE Class 8 Maths Chapter 13 solutions, Factorisation of Algebraic Expressions”

Question 2. It is seen on the factorization of \(\left(81 a^2-72 a b+16 b^2\right)\)

The length of each side of the square = 9a – 4b

Read and Learn More WBBSE Solutions For Class 8 Maths

Question 3. Rehana factorized \(\left(64 m^2-121 n^2\right)\)

Solution:

She got, \(\left(64 m^2-121 n^2\right)\) = (8m + 11 n) x (8m – 11 n)

The length of the rectangle = 8m + 11n units and the length of the other side is units (8m – 11n).

Question 4. But Shiraz factorized [/latex]\left(125 a^3+8 b^3\right)[/latex]

Solution:

Given

\(125 a^3+8 b^3=5 a^3+2 b^3\)

= \((5 a+2 b)\left\{(5 a)^2-(5 a) \times(2 b)+4 b^2\right\}\)

[/latex]\left(125 a^3+8 b^3\right)[/latex] = (5a + 2b) (25a² – 10ab + 4b²)[/latex][/latex]

Question 5. Utpal factorized \(\left(27 x^3-343 y^3\right)\)

Solution:

Given

\(27 x^3-343 y^3=3 x^3-7 y^3\)

\(\left(27 x^3-343 y^3\right)\) = \((3 x-7 y)\left(9 x^2+21 x y+49 y^2\right)\)

I factorize \(\left(x^2+7 x+12\right)\) but how shall I write down \(\left(x^2+7 x+12\right)\) as the product of two algebraic expressions?

Question 6. At first, let us write all known identities that help to factorize:

Solution:

\((a+b)^2=a^2+2 a b+b^2\) ………………………….. (1)

\((a-b)^2=a 2-2 a b+b^2\)  ……………………………(2)

\(a^2-b^2=(a+b) \times(a-b)\)  ………………………… (3)

\(a^3+b^3=(a+b) \times\left(a^2-a b+b^2\right)\)  ………………….(4)

\(a^3-b^3=(a-b) \times\left(a^2+a b+b^2\right)\) …………………(5)

\(x^2+(a+b) x+a b=(x+a)(x+b)\)  ………………….(6)

Question 7. I try to factorize the algebraic expression \(\left(x^2+7 x-18\right)\) with the help of identity no. 4

Solution:

\(x^2+7 x-18\)

There a + b = 7 and a × b = -18

-18 = 1 x(-18)=(-1 )x(18)=(-2)x9=2x(-9)=(-3)x6=3x(-6) and 7=9+(-2)

∴ Here a = 9 and b = -2

∴ I get from the identity no. 4

\(x^2+7 x-18=(x+9)\{x+(-2)\}\)

= (x+9)(x-2)

I get by factorizing

\(x^2+7 x-18=x^2+(9-2) x-18\)

= \(x^2+9 x-2 x-18\)

= x (x+9)-2 (x+9) = (x+9)(x-2)

Question 8. Let’s try to factorize \(\left(a^2-11 a+30\right) \text { and }\left(m^2-4 m-12\right) \cdot a^2-11 a+30\)

Solution:

30= 1×30=2×15=3×10=5×6

30=5×6, 11=5+6

1. \(m^2-4 m-12\)

Solution:

-12=(-1)×12= 1×(-12) = (-2)×6

= 2×(-6)= 3×(-4)= -3×4

-12 =(-2)×6, 4 =6+(-2)

2. \(a^2-11 a+30\)

Solution:

= \(a^2-(5+6) a+30\)

= \(a^2-5 a-6 a+30\)

= a (a-5)-6(a-5)

= (a-5)(a-6)

\(a^2-11 a+30\) = (a-5)(a-6)

3. \(m^2-4 m-12\)

Solution:

= \(m^2-(6-2) m-12\)

= \(m^2-6 m+2 m-12\)

= m(m-6) +2(m-6)

= (m-6)(m+2)

∴ We will find out two numbers a and b to resolve the binomial expression \(x^2+p x+q\)(the highest power of the variable in the algebraic expression is 2) into factors so that

a+b = p and a x b =q

∴ In that case the algebraic expression will be

\(x^2+(a+b) x+a b\)

=\(x^2+a x+b x+a b\)

= x (x+a) + b (x+a)

= (x+a) (x+b)

= (m-6)(m+2) = (x+a) (x+b)

“Class 8 WBBSE Maths Chapter 13 solutions, Factorisation study material”

Question 9. I try to resolve \(\left(x^2-x-20\right) \text { and }\left(b^2-10 b+16\right)\). 

1. \(x^2-x-20\)

Solution:

-20 =5×(-4)

and 1= 5-4

2. \(b^2-10 b+16\)

Solution:

16= 8 × 2

and 10 = 8 + 2

3. \(x^2-x-20\)

Solution:

= \(x^2-(5-4) x-20\)

= \(x^2-5 x+4 x-20\)

= x(x-5)+4(x-5)

= (x-5)(x+4)

\(x^2-x-20\) = (x-5)(x+4)

4. \(b^2-10 b+16\)

Solution:

= \(b^2-(8+2) b+16\)

= \(b^2-8 b-2 b+16\)

= b(b-8)-2(b-8)

= (b-8)(b-2)

\(b^2-10 b+16\) = (b-8)(b-2)

“WBBSE Class 8 Maths Chapter 13, Factorisation of Algebraic Expressions solved examples”

Question 11. We factorize (x²+ 20xy – 96y2) and (1-5x-36×2). Each term of (x²+20xy-96y²) has variable. At first eliminate the variable from the last term.

Solution:

Given

\(x^2+20 x y-96 y^2\)

= \(\left\{\frac{x^2}{y^2}+\frac{20 x y}{y^2}-\frac{96 y^2}{y^2}\right\} x y^2\)

= \(\left\{\left(\frac{x}{y}\right)^2+20\left(\frac{x}{y}\right)-96\right\} x y^2\)

= \(\left(a^2+20 a-96\right) y\)       [Let \(\frac{x}{y}\) = a]   

= \(\left(a^2+24 a-4 a-96\right) y^2\)     [96=24×4 and 20=24-4]                                                           

= \(\{a(a+24)-4(a+24)\} y^2\)

= \((a+24)(a-4) y^2\)

= \(\left(\frac{x}{y}+24\right)\left(\frac{x}{y}-4\right) y^2\) [Puting a=\(\frac{x}{y}\)

= \(\left(\frac{x+24 y}{y}\right)\left(\frac{x-4 y}{y}\right) y^2\)

= \(\frac{(x+24 y)(x-4 y)}{y^2} y^2\)

= (x + 24y) (x-4y)

Alternative method

= \(x^2+20 x y-96 y^2\)

= \(x^2+(24 y-4 y) x-24 y \times 4 y\)

= \(x^2+24 x y-4 x y-24 y \times 4 y\)

= x (x + 24y) – 4y (x + 24y)

= x + 24y × x- 4y

Question 12. We try to factorize \(\left(1-5 x-36 x^2\right)\).

Solution:

Given

\(\left(1-5 x-36 x^2\right)\).

= \(1-5 x-36 x^2\)

= \(1-(9-4) \times(-9) \times 4 x^2\)

= \(1-9 x+4 x-9 \times 4 \times x^2\)

= 1 (1-9x) + 4x(1-9x)

= (1-9x)(1+4x)

\(\left(1-5 x-36 x^2\right)\) = (1-9x)(1+4x)

Question 13. I try to factorize (x-1) (x+3) (x-2)(x-6) +96.
Solution:

Given

(x-1) (x+3) (x-2)(x-6) +96.

But how will we factorize and with the help of which identity

x-1, x+3, x-2 and x-6? Let’s find the sum of the coefficients of two terms containing x only will be the product of two pair of expression among the four expressions

– 1-2 = – 3 and + 3 – 6= – 3

Then, the coefficient of x is the product (x-1)(x-2) is -3 and that of (x+3)(x-6) is (-3).

Then, (x-1)(x+3)(x-2)(x-6)+96

= (x-1 )(x+3)(x-2)(x-6) + 96

= \(\left(x^2-x-2 x+2\right)\left(x^2+3 x-6 x-18\right)+96\)

= \(\left(x^2-3 x+2\right)\left(x^2-3 x-18\right)+96\)

= (a+2) (a-18) + 96

= \(a^2-2 a-18 a-36+96\)

= \(a^2-16 a+60\)

= \(a^2-(10+6) a+60\)

= \(a^2-10 a-6 a+60\)

= a (a=10) -6 (a=10)

= (a-10) (a-6)

= \(\left(x^2-3 x-10\right)\left(x^2-3 x-6\right)\) [Let a=x²-3x]

= \(\left(x^2-5 x+2 x-10\right)\left(x^2-3 x-6\right)\)

= \(\{x(x-5)+2(x-5)\}\left(x^2-3 x-6\right)\)

= \((x-5)(x+2)\left(x^2-3 x-6\right)\)

(x-1) (x+3) (x-2)(x-6) +96 = \((x-5)(x+2)\left(x^2-3 x-6\right)\)

Question 14. Let’s factorize the algebraic expression \(x^2+3 x-(p+5)(p+2)\).

Solution:

Given

\(x^2+3 x-(p+5)(p+2)\) \(x^2+3 x-(p+5)(p+2)\)

= \(x^2+\{(p+5)-(p+2)\} x-(p+5)(p+2)\)

= \(x^2+(p+5) x-(p+2) x-(p+5)(p+2)\)

= x (x+p+5) – (p+2) (x+p+5)

= (x+p+5) (x-p-2)

\(x^2+3 x-(p+5)(p+2)\) = (x+p+5) (x-p-2)

Algebraic Expressions Exercise

Question 1. Comparing the following algebraic expressions with the identity \(x^2+(p+q) x+p q=(x+p)(x+q)\), let’s write the values of p and q and factorize them.

Algebraic expression:

Given

\(x^2+(p+q) x+p q=(x+p)(x+q)\)

= \(x^2-8 x+15\)

= \(x^2-40 x-129\)

= \(m^2+19 m+60\)

= \(x^2-x-6\)

= \((a+b)^2-4(a+b)-12\)

= \((x-y)^2-x+y-2\)

Values of p & q:

p= -5, q= -3

p=3, q=-43

p=15, q=4

p=-3, q=2

p=-6, q=2

p=-2, q=1

Resolve into factors: 

= (x-5) (x-3)

= (x+3) (x-43)

= (m+15) (m+4)

= (x-3) (x+2)

= (a+b-6) (a+b+2)

= (x-y-2) (x-y+1)

“WBBSE Class 8 Factorisation of Algebraic Expressions solutions, Maths Chapter 13”

Question 2. Let’s resolve into factors :

1. \((a+b)^2-5 a-5 b+6\)

= \((a+b)^2-5 a-5 b+6\)

= \((a+b)^2-5(a-b)+6\)

Let a + b = x

∴ \(x^2-5 x+6\)

= \(x^2-(3+2) x+6\)

= \(x^2-3 x-2 x+6\)

= x(x-3)-2 (x-3)

= (x-3) (x-2)

Putting the value of x (a+b-3) (a+b-2),

2. \(\left(x^2-2 x\right)^2+5\left(x^2-2 x\right)-36\)

Solution:

\(\left(x^2-2 x\right)^2+5\left(x^2-2 x\right)-36\)

Let \(x^2-2 x=a\)

∴ \(a^2+5 a-36\)

= \(a^2+(9-4) a-36\)

= \(a^2+9 a-4 a-36\)

= a (a+9) – 4 (a+9)

= (a+9) (a-4)

Putting the value of a, (x² – 2x +9) (x² – 2x – 4)[/latex][/latex]

3. (p²-3q²)²-16(p²-3q²) + 63[/latex][/latex]

Solution:

(p²-3q²)²-16(p²-3q²) + 63[/latex][/latex]

Let x p² – 3q² = x[/latex][/latex]

∴ x2-16x + 63[/latex][/latex]

= x² – (9+7) x + 63[/latex][/latex]

= x² – 9x – 7x + 63[/latex][/latex]

= x (x-9) -7 (x-9)

= (x-9) (x-7)

Putting the value of x, (p² – 3q²-9)(p²-3q²-7)[/latex][/latex]

4. a⁴+4a²-5[/latex][/latex]

Solution:

a⁴+4a⁴-5[/latex][/latex]

= a⁴+ (5-1) a²-5[/latex][/latex]

= a⁴ + 5a2-a²-5[/latex][/latex]

= a² (a²+5) – 1 (a²+5)[/latex][/latex]

= (a²+5) (a²-1) = (a²+5) (a+1) (a-1)[/latex][/latex]

a⁴+4a²-5[/latex][/latex] = (a²+5) (a²-1) = (a²+5) (a+1) (a-1)[/latex][/latex]

5. \(x^2 y^2+23 x y-420\)

Solution:

\(x^2 y^2+23 x y-420\)

= \(x^2 y^2+(35-12) x y-420\)

= \(x^2 y^2+35 x y-12 x y-420\)

= xy (xy + 35) -12 (xy + 35)

= (xy + 35) (xy -12)

\(x^2 y^2+23 x y-420\) = (xy + 35) (xy -12)

6. \(x^4-7 x^2+12\)

Solution:

= \(x^4-7 x^2+12\)

= \(x^4-(4+3) x^2+12\)

= \(x^4-4 x^2-3 x^2+12\)

= \(x^2\left(x^2-4\right)-3\left(x^2-4\right)\)

= \(\left(x^2-4\right)\left(x^2-3\right)\)

= \((x+2)(x-2)\left(x^2-3\right)\)

\(x^4-7 x^2+12\) = \((x+2)(x-2)\left(x^2-3\right)\)

7. \(a^2+a b-12 b^2\)

Solution:

\(a^2+a b-12 b^2\)

= \(a^2+(4-3) a b-12 b^2\)

= \(a^2+4 a b-3 a b-12 b^2\)

= a(a+4b) -3b (a+4b)

= (a+4b) (a-3b)

\(a^2+a b-12 b^2\) = (a+4b) (a-3b)

8. \(p^2+31 p q+108 q^2\)

Solution:

\(p^2+31 p q+108 q^2\)

= \(p^2+(27+4) p q+108 q^2\)

= \(p^2+27 p q+4 p q+108 q^2\)

= p (p+27q) + 4q (p+27q)

= (p+27q) (p+4q)

\(p^2+31 p q+108 q^2\) = (p+27q) (p+4q)

9. \(a^6+3 a^3 b^3-40 b^6\)

Solution:

\(a^6+3 a^3 b^3-40 b^6\)

= \(a^6+(8-5) a^3 b^3-40 b^6\)

= \(a^6+8 a^3 b^3-5 a^3 b^3-40 b^6\)

= \(a^3\left(a^3+8 b^3\right)-5 b^3\left(a^3+8 b^3\right)\)

= \(\left(a^3+8 b^3\right)\left(a^3-5 b^3\right)\)

= \(\left\{(a)^3+(2 b)^3\right\}\left(a^3-5 b^3\right)\)

= \((a+2 b)\left(a^2-2 a b+4 b^2\right)\left(a^3-5 b^3\right)\)

\(a^6+3 a^3 b^3-40 b^6\) = \((a+2 b)\left(a^2-2 a b+4 b^2\right)\left(a^3-5 b^3\right)\)

10. (x+1) (x+3) (x-4) (x-6) + 24 .

Solution:

(x+1) (x+3) (x-4) (x-6) + 24

= (x+1) (x-4) (x+3) (x-6) + 24

= \(\left(x^2-3 x-4\right)\left(x^2-3 x-18\right)+24\)

Let \(x^2-3 x=a\)

∴ (a-4) (a-18) + 24

= \(a^2-22 a+72+24\)

= \(a^2-22 a+96\)

= \(a^2-(16+6) a+96\)

= \(a^2-16 a-6 a+96\)

= a (a-16) -6 (a-16)

= (a-16) (a-6)

(x+1) (x+3) (x-4) (x-6) + 24 = (a-16) (a-6)

Putting the value of a, \(\left(x^2-3 x-16\right)\left(x^2-3 x-6\right)\)

“Class 8 WBBSE Maths Chapter 13, Factorisation easy explanation”

11. \((x+1)(x+9)(x+5)^2+63\)

Solution:

\((x+1)(x+9)(x+5)^2+63\)

= \(\left(x^2+10 x+9\right)\left(x^2+10 x+25\right)+36\)

Let \(x^2+10 x=a\)

∴  (a+9) (a+25) + 63

= \(a^2+34 a+225+63\)

= \(a^2+34 a+288\)

= \(a^2+(18+16) a+288\)

= \(a^2+18 a+16 a+288\)

= a (a+18 + 16(a+18)

= (a+18) (a+16)

Putting the value of a, \(\left(x^2+10 x+18\right)\left(x^2+10 x+16\right)\)

= \(\left(x^2+10 x+18\right)\left\{\left(x^2+(8+2) x+16\right\}\right.\)

= \(\left(x^2+10 x+18\right)(x 2+8 x+2 x+16)\)

= \(\left(x^2+10 x+18\right)\{x(x+8)+2(x+8)\}\)

= \(\left(x^2+10 x+18\right)(x+8)(x+2)\)

= \((x+2)(x+8)\left(x^2+10 x+18\right)\)

12. x(x+3) (x+6) (x+9) + 56

Solution:

= x(x+3) (x+6) (x+9) + 56

= x(x+9) (x+3) (x+6) + 56

= \(\left(x^2+9 x\right)\left(x^2+9 x+18\right)+56\)

∴ Let \(x^2+9 x=a\)

= a (a+18) + 56

= \(a^2+18 a+56\)

= \(a^2+(14+4) a+56\)

= \(a^2+14 a+4 a+56\)

= a(a+14) +4 (a+14)

= (a+14) (a+4)

Putting the value of a,

\(\left(x^2+9 x+14\right)\left(x^2+9 x+4\right)\)

= \(\left(x^2+7 x+2 x+14\right)\left(x^2+9 x+4\right)\)

= \(\{x(x+7)+2(x+7)\}\left(x^2+9 x+4\right)\)

= \((x+7)(x+2)\left(x^2+9 x+4\right)\)

13. \(x^2-2 a x+(a+b)(a-b)\)

Solution:

\(x^2-2 a x+(a+b)(a-b)\)

= \(x^2-2 a x+a^2-b^2\)

= \((x-a)^2-(b)^2\)

= (x-a+b) (x-a-b)

\(x^2-2 a x+(a+b)(a-b)\) = (x-a+b) (x-a-b)

14. \(x^2-b x-(a+3 b)(a+2 b)\)

Solution:

\(x^2-\{(a+3 b)-(a+2 b)\} x-(a+3 b)(a+2 b)\)

= \(x^2-(a+3 b) x+(a+2 b) x-(a+3 b)(a+2 b)\)

= x(x-a-3b) + (a + 2b) (x-a-3b)

= (x-a-3b) (x+a+2b)

\(x^2-b x-(a+3 b)(a+2 b)\) = (x-a-3b) (x+a+2b)

15. \((a+b)^2-5 a-5 b+6\)

Solution:

\((a+b)^2-5 a-5 b+6\)

= \((a+b)^2-5(a+b)+6\)

Let a + b = x

∴ \(x^2-5 x+6\)

= \(x^2-(3+2) x+6\)

= \(x^2-3 x-2 x+6\)

= x (x-3) – 2 (x-3)

= (x-3) (x-2)

Putting the value of x, (a+b-3) (a+b-2)

\((a+b)^2-5 a-5 b+6\) = (a+b-3) (a+b-2)

16. \(x^2+4 a b x-\left(a^2-b^2\right)^2\)

Solution:

\(x^2+4 a b x-\left(a^2-b^2\right)^2\)

= \(x^2+4 a b x-\{(a+b)(a-b)\}^2\)

= \(x^2+4 a b x-(a+b) 2(a-b)^2\)

= \(x^2+\left\{(a+b)^2-(a-b)^2\right\} x-(a+b)^2(a-b)^2\)

= \(x^2+(a+b)^2 x-(a-b) 2 x-(a+b)^2(a-b)^2\)

= \(x\left\{x+(a+b)^2\right\}-(a-b)^2\left\{x+(a+b)^2\right\}\)

= \(\left\{x+(a+b)^2\right\}\left\{x-(a-b)^2\right\}\)

= \(\left(x+a^2+2 a b+b^2\right)\left(x-a^2+2 a b-b^2\right)\)

\(x^2+4 a b x-\left(a^2-b^2\right)^2\) = \(\left(x+a^2+2 a b+b^2\right)\left(x-a^2+2 a b-b^2\right)\)

17. x² – \(\left(a+\frac{1}{a}\right)\)x + 1

Solution:

= \(x^2-a x-\frac{x}{a}+\frac{a}{a}\)

= \(x(x-a)-\frac{1}{a}(x-a)=(x-a)\left(x-\frac{1}{a}\right)\)

x² – \(\left(a+\frac{1}{a}\right)\)x + 1 = \(x(x-a)-\frac{1}{a}(x-a)=(x-a)\left(x-\frac{1}{a}\right)\)

18. \(x^6 y^6-9 x^3 y^3+8\)

Solution:

\(x^6 y^6-9 x^3 y^3+8\)

= \(x^6 y^6-(8+1) x^3 y^3+8\)

= \(x^6 y^6-8 x^3 y^3-x^3 y^3+8\)

= \(x^3 y^3\left(x^3 y^3-8\right)-1\left(x^3 y^3-8\right)\)

= \(\left(x^3 y^3-8\right)\left(x^3 y^3-1\right)\)

“WBBSE Class 8 Maths Chapter 13 solutions, Factorisation of Algebraic Expressions PDF”

= \(\left\{(x y)^3-(2)^3\left\{(x y)^3-(1)^3\right\}\right.\)

= \((x y-2)\left(x^2 y^2+2 x y+4\right)(x y-1)\left(x^2 y^2+x y+1\right)\)

\(x^6 y^6-9 x^3 y^3+8\) = \((x y-2)\left(x^2 y^2+2 x y+4\right)(x y-1)\left(x^2 y^2+x y+1\right)\)

Question 19. \(3 x^2+14 x+18\)

Solution:

= \(\frac{9 x^2+42 x+24}{3}\)

= \(\frac{(3 x)^2+14 \times 3 x+24}{3}\)

= \(\frac{y^2+14 y+24}{3}\) [Let 3x=y]

= \(\frac{y^2+12 y+2 y+24}{3}\)

= \( \frac{y(y+12)+2(y+12)}{3}\)

= \(\frac{(y+12)(y+2)}{3}\)

= \(\frac{(y+12)(y+2)}{3}\)

= \(\frac{(3 x+12)(3 x+2)}{3}\)            [Putting y=3x,we get]

= \(\frac{3(x+4)(3 x+2)}{3}\)

= (x+4)(3x+2)

Alternatively we write,

\(3 x^2+14 x+8\)

We find two numbers a and b such that a+b = 14 and a × b = 3 × 8 = 24

= 12×2 and 14= 12+2

= \(3 x^2+14 x+8\)

= \(3 x^2+(12+2) x+8\)

= \(3 x^2+12 x+2 x+8\)

= 3x (x+4) +2 (x+4)

= (x+4) (3x+2)

\(3 x^2+14 x+18\) = (x+4) (3x+2)

Question 20. Lets resolve \(6 x^2-x-15\) into factors and let’s write what are the possible lengths of the side (in units) of the yellow rectangular board.
Solution:

\(6 x^2-x-15\)

∴ -90 =10×(-9) and -1 = 10+(-9)

= \(6 x^2-x-15\)

= \(6 x^2-(10-9) x-15\)

= \(6 x^2-10 x+9 x-15\)

= 2x (3x-5)+3(3x-5)

= (3x-5) (2x + 3)

Question 21. Let’s express 2 algebraic expressions \(x^2+13 x-48 \text { and } 6 y^2-y-15\) as the difference between two squares. Now let’s try to resolve into factors with the help of the identity \(a^2-b^2=(a+b)(a+b)\).

Solution:

= \(x^2+13 x-48\)

= \( x^2+2 \cdot x \cdot \frac{13}{2}+\left(\frac{13}{2}\right)^2-\left(\frac{13}{2}\right)^2-48\)

= \(\left(x+\frac{13}{2}\right)^2-\frac{169}{4}-48\)

= \(\left(x+\frac{13}{2}\right)^2-\left(\frac{169}{4}+48\right)\)

= \( \left(x+\frac{13}{2}\right)^2-\frac{169+192}{4}\)

= \(\left(x+\frac{13}{2}\right)^2-\frac{361}{4}\)

= \(\left(x+\frac{13}{2}\right)^2-\left(\frac{19}{4}\right)^2\)

= \(\left(x+\frac{13}{2}+\frac{19}{2}\right)\left(x+\frac{13}{2}-\frac{19}{2}\right)\)

= \(\left(x+\frac{13+19}{2}\right)\left(x+\frac{13-19}{2}\right)\)

= (x+16) (x-3)

Factorize \(\left(x^2+13 x-48\right)\) by middle-term factor method.

\(x^2+13 x-48\)

= \(x^2+16 x-3 x-48\)

= x (x+16) -3 (x+16)

= (x+16) (x-3)

“WBBSE Class 8 Maths Chapter 13, Factorisation important questions”

Algebraic Expressions Exercise 13.2

Question 1. Let’s resolve into factors \(\left(a^2-a-72\right) \text { and }\left(2 x^2-x-1\right)\) by expressing the algebraic expressions as the difference of two squares.
Solution:

Given

\(\left(a^2-a-72\right) \text { and }\left(2 x^2-x-1\right)\) 

\(a^2-a-72\)

= \(a^2-(9-8) a-72\)

= \(a^2-9 a+8 a-72\)

= a (a-9) +8 (a-9)

= (a-9) (a+8)

\(2 x^2-x-1\)

= \(2 x^2-(2-1) x-1\)

= \(2 x^2-2 x+x-1\)

= 2x (x-1) +1 (x-1)

= (x-1) (2x+1)

Question 2.  Let’s resolve into factors —

1. \(2 a^2+5 a+2\)

Solution:

\(2 a^2+5 a+2\)

= \(2 a^2+(4+1) a+2\)

= \(2 a^2+4 a+a+2\)

= 2a (a+2) +1 (a+2)

= (a+2) (2a+1).

\(2 a^2+5 a+2\) = (a+2) (2a+1).

2. \(3 x^2+14 x+8\)

Solution:

\(3 x^2+14 x+8\)

= \(3 x^2+(12+2) x+8\)

= \(3 x^2+12 x+2 x+8\)

= 3x (x+4) +2 (x+4)

= (x+4) (3x+2)

\(3 x^2+14 x+8\) = (x+4) (3x+2)

3. \(2 m^2+7 m+6\)

Solution:

\(2 m^2+7 m+6\)

= \(2 m^2+(4+3) m+6\)

= \(2 m^2+4 m+3 m+6\)

= 2m (m+2) +3 (m+2)

= (m+2) (2m+3)

\(2 m^2+7 m+6\) = (m+2) (2m+3)

4. \(6 x^2-x-15\)

Solution:

\(6 x^2-x-15\)

= \(6 x^2-(10-9) x-15\)

= \(6 x^2-10 x+9 x-15\)

= 2x (3x – 5) +3 (3x – 5)

= (3x – 5) (2x + 3)

\(6 x^2-x-15\) = (3x – 5) (2x + 3)

5. \(9 r^2+r-8\)

Solution:

\(9 r^2+r-8\)

= \(9 r^2+(9-8) r-8\)

= \(9 r^2+9 r-8 r-8\)

= 9r (r+1) -8 (r+1)

= (r+1) (9r-8)

\(9 r^2+r-8\) = (r+1) (9r-8)

6. \(6 m^2-11 m n-10 n^2\)

Solution:

\(6 m^2-11 m n-10 n^2\)

= \(6 m^2-(15-4) m n-10 n^2\)

= \(6 m^2-15 m n+4 m n-10 n^2\)

= 3m (2m-5n) +2n (2m-5n)

= (2m-5n) (3m+2n)

\(6 m^2-11 m n-10 n^2\) = (2m-5n) (3m+2n)

7. \(7 x^2+48 x y-7 y^2\)

Solution:

\(7 x^2+48 x y-7 y^2\)

= \(7 x^2+(49-1) x y-7 y^2\)

= \(7 x^2+49 x y-x y-7 y^2\)

= 7x (x+7y)-y(x+7y)

= (x+7-y) (7x-y)

\(7 x^2+48 x y-7 y^2\) = (x+7-y) (7x-y)

8. \(12+x-6 x^2\)

Solution:

\(12+x-6 x^2\)

= \(12+(9-8) x-6 x^2\)

= \(12+9 x-8 x-6 x^2\)

= 3 (4+3x) – 2x (4+3x)

= (4+3x) (3-2x)

\(12+x-6 x^2\) = (4+3x) (3-2x)

9. \(6+5 a-6 a^2\)

Solution:

\(6+5 a-6 a^2\)

= \(6+(9-4) a-6 a^2\)

= \(6+9 a-4 a-6 a^2\)

= 3 (2+3a)-2a (2+3a)

= (2+3a) (3-2a)

\(6+5 a-6 a^2\) = (2+3a) (3-2a)

10. \(6 x^2-13 x+6\)

Solution:

\(6 x^2-13 x+6\)

= \(6 x^2-(9+4) x+6\)

= 3x (2x-3) -2 (2x-3)

= (2x-3) (3x-2)

\(6 x^2-13 x+6\) = (2x-3) (3x-2)

11. \(99 a^2-202 a b+99 b^2\)

Solution:

\(99 a^2-202 a b+99 b^2\)

= \(99 a^2-(121+81) a b+99 b^2\)

= \(99 a^2-121 a b-81 a b+99 b^2\)

= 11 a (9a-11 b)-9b(9a-11 b)

= (9a-11b) (11a-9b)

\(99 a^2-202 a b+99 b^2\) = (9a-11b) (11a-9b)

“Class 8 Maths Factorisation solutions, WBBSE syllabus”

12. \(2 a^6-13 a^3-24\)

Solution:

\(2 a^6-13 a^3-24\)

= \(2 a^6-(16-3) a^3-24\)

= \(2 a^6-16 a 3+3 a^3-24\)

= \(2 a 3\left(a^3-8\right)+3\left(a^3-8\right)\)

= \(\left(a^3-8\right)\left(2 a^3+3\right)\)

= \(\left\{(a)^3-(2) 3\right\}\left(2 a^3+3\right)\)

= \((a-2)\left(a^2+2 a+4\right)\left(2 a^3+3\right)\)

\(2 a^6-13 a^3-24\)= \((a-2)\left(a^2+2 a+4\right)\left(2 a^3+3\right)\)

13. \(8 a^4+2 a^2-45\)

Solution:

\(8 a^4+2 a^2-45\)

= \(8 a^4+(20-18) a^2-45\)

= \(8 a^4+20 a^2-18 a^2-45\)

= \(4 a^2\left(2 a^2+5\right)-9\left(2 a^2+5\right)\)

= \(\left(2 a^2+5\right)(4 a 2-9)\)

= \(\left(2 \mathrm{a}^2+5\right)\left\{(2 \mathrm{a})^2-(3)^2\right\}\)

= \(\left(2 a^2+5\right)(2 a+3)(2 a-3)\)

\(8 a^4+2 a^2-45\) = \(\left(2 a^2+5\right)(2 a+3)(2 a-3)\)

14. \(6(x-y)^2-x+y-15\)

Solution:

[/latex]6(x-y)^2-x+y-15[/latex]

= \(6(x-y)^2-(x-y)-15\)

Let x-y=a

∴ \(6 a^2-a-15\)

= \(6 a^2-(10-9) a-15\)

= \(6 a^2-10 a+9 a-15\)

= 2a (3a – 5) + 3 (3a – 5)

= (3a – 5) (2a + 3)

Putting the value of a, (3x-3y-5) (2x-2y+3)

\(6(x-y)^2-x+y-15\) = (3x-3y-5) (2x-2y+3)

15. \(3(a+b)^2-2 a-2 b-8\)

Solution.

\(3(a+b)^2-2 a-2 b-8\)

= \(3(a+b)^2-2(a+b)-8\)

Let a + b = x

∴ \(3 x^2-2 x-8\)

= \(3 x^2-(6-4) x-8\)

= \(3 x^2-6 x+4 x-8\)

= 3x (x-2) +4 (x-2)

= (x-2) (3x+4)

Putting the value of x, (a+b-2) (3a+3b+4)

\(3(a+b)^2-2 a-2 b-8\) = (a+b-2) (3a+3b+4)

16. \(6(a+b)^2+5\left(a^2-b^2\right)-6(a-b)^2\)

Solution:

\(6(a+b)^2+5\left(a^2-b^2\right)-6(a-b)^2\)

= \(6(a+b)^2+5(a+b)(a-b)-6(a-b)^2\)

Let a+b=x and a-b=y

∴ \(6 x^2+5 x y-6 y^2\)

= \(6 x^2+(9-4) x y-6 y^2\)

= \(6 x^2+9 x y-4 x y-6 y^2\)

= 3x (2x+3y) -2y (2x+3y)

= (2x+3y) (3x-2y)

Putting the values x and y, (2a+2b+3a-3b) (3a+3b-2a+2b) = (5a-b) (a+5b)

\(6(a+b)^2+5\left(a^2-b^2\right)-6(a-b)^2\)= (5a-b) (a+5b)

Question 3. Let’s resolve the following algebraic expressions into factors by expressing them as the difference of two squares.

1. \(x^2-2 x-3\)

Solution:

\(x^2-2 x-3\)

= \(x^2-2 x+1-4\)

= \((x)^2-2 \times 1+(1) 2-(2)^2\)

= \((x-1)^2-(2)^2\)

= (x-1+2) (x-1-2)

= (x+1) (X-3)

\(x^2-2 x-3\) = (x+1) (X-3)

2. \(x^2+5 x+6\)

Solution:

\(x^2+5 x+6\)

= \((x)^2+2 \cdot x \cdot \frac{5}{2}+\left(\frac{5}{2}\right)^2+6-\left(\frac{5}{2}\right)^2 \)

= \(\left(x+\frac{5}{2}\right)^2+6-\frac{25}{4}\)

= \(\left(x+\frac{5}{2}\right)^2+\frac{24-25}{4}\)

= \(\left(x+\frac{5}{2}\right)^2-\frac{1}{4}\)

= \(\left(x+\frac{5}{2}\right)^2-\left(\frac{1}{2}\right)^2\)

= \( \left(x+\frac{5}{2}+\frac{1}{2}\right)\left(x+\frac{5}{2}-\frac{1}{2}\right)\)

= (x+3) (x+2)

\(x^2+5 x+6\) = (x+3) (x+2)

“WBBSE Class 8 Chapter 13 Maths, Factorisation of Algebraic Expressions step-by-step solutions”

3. \(3 x^2-7 x-6\)

Solution:

\(3 x^2-7 x-6\)

= \(3\left(x^2-\frac{7}{3} x-2\right)\)

= \( \left\{(x)^2-2 \cdot x \cdot \frac{7}{6}+\left(\frac{7}{6}\right)^2-\left(\frac{7}{6}\right)^2-2\right\}\)

= \(3\left\{\left(x-\frac{7}{6}\right)^2-\left(\frac{49}{36}+\frac{2}{1}\right)\right\}\)

\(=3\left\{\left(x-\frac{7}{6}\right)^2-\frac{121}{36}\right\}\) \(=3\left\{\left(x-\frac{7}{6}\right)^2-\left(\frac{11}{6}\right)^2\right\}
\)

= \(3\left(x-\frac{7}{6}+\frac{11}{6}\right)\left(x-\frac{7}{6}-\frac{11}{6}\right) \)

= \(3\left(x+\frac{4}{6}\right)(x-3)\)

= (3x+2) (x-3)

\(3 x^2-7 x-6\) = (3x+2) (x-3)

4. \(3 a^2-2 a-5\)

Solution:

= \(3\left(a^2-\frac{2}{3} a-\frac{5}{3}\right)\)

= \(3\left\{(a)^2-2 \cdot a \cdot \frac{1}{3}+\left(\frac{1}{3}\right)^2-\left(\frac{1}{3}\right)^2-\frac{5}{3}\right\}\)

= \(3\left\{\left(a-\frac{1}{3}\right)^2-\frac{1}{9}-\frac{5}{3}\right\}\)

= \(3\left\{\left(a-\frac{1}{3}\right)^2-\left(\frac{1+15}{9}\right)\right\}\)

= \(3\left\{\left(a-\frac{1}{3}\right)^2-\frac{16}{9}\right\}\)

= \(3\left\{\left(a-\frac{1}{3}\right)^2-\left(\frac{4}{3}\right)^2\right\}\)

= \(3\left(a-\frac{1}{3}+\frac{4}{3}\right)\left(a-\frac{1}{3}-\frac{4}{3}\right)\)

= \(3(a+1)\left(a-\frac{5}{3}\right)\)

= (a+1) (3a-5)

\(3 a^2-2 a-5\) = (a+1) (3a-5)

Question 4. Let’s resolve into factors

1. \(a x^2+\left(a^2+1\right) x+a\)

Solution:

\(a x^2+\left(a^2+1\right) x+a\)

= \(a x^2+a^2 x+x+a\)

= ax (x + a) + 1 (x + a)

= (x + a) (ax + 1)

\(a x^2+\left(a^2+1\right) x+a\) = (x + a) (ax + 1)

2. \(x^2+2 a x+(a+b)(a-b)\)

Solution:

\(x^2+2 a x+(a+b)(a-b)\)

= \(x^2+2 a x+a^2-b^2\)

= \((x+a)^2-(b)^2\)

= (x + a + b) (x + a – b)

\(x^2+2 a x+(a+b)(a-b)\) = (x + a + b) (x + a – b)

3. \(a x^2-\left(a^2+1\right) x+a\)

\(a x^2-\left(a^2+1\right) x+a\)

= \(a x^2-a^2 x-x+a\)

= ax (x – a) -1 (x – a)

= (x – a) (ax – 1)

\(a x^2-\left(a^2+1\right) x+a\) = (x – a) (ax – 1)

4. \(a x^2+\left(a^2-1\right) x-a\)

Solution:

\(a x^2+\left(a^2-1\right) x-a\)

= \(a x^2+a^2 x-x-a\)

= ax (x + a) – 1 (x + a)

= (x + a) (ax – 1)

\(a x^2+\left(a^2-1\right) x-a\) = (x + a) (ax – 1)

5. \(a x^2-\left(a^2-2\right) x-2 a\)

Solution:

\(a x^2-\left(a^2-2\right) x-2 a\)

= \(a x^2-a^2 x+2 x-2 a\)

= ax (x – a) + 2 (x – a)

= (x – a) (ax + 2)

\(a x^2-\left(a^2-2\right) x-2 a\) = (x – a) (ax + 2)

“WBBSE Maths Class 8 Factorisation of Algebraic Expressions, Chapter 13 key concepts”

6. \(a^2+1-\frac{6}{a^2}\)

Solution:

= \(a^2+1-\frac{6}{a^2}\)

= \(a^2+3-2-\frac{6}{a^2}\)

= \(a\left(a+\frac{3}{a}\right)-\frac{2}{a}\left(a+\frac{3}{a}\right)\)

= \(\left(a+\frac{3}{a}\right)\left(a-\frac{2}{a}\right)\)

\(a^2+1-\frac{6}{a^2}\) = \(\left(a+\frac{3}{a}\right)\left(a-\frac{2}{a}\right)\)

H.C.F And L.C.M Of Algebraic Expressions

We had some coloured ribbons of different lengths. We had a green ribbon of length 32 metre and a yekkow ribbon of length 104 metre and a yellow ribbon of length 56 metre.

We have decided that we cut off the gretedt length of same side from the ribbons in such away that no portion of the ribbon is left cut.

Question 1. Let us calculate what will be the G.C.D of 32,104,56

Solution.

Given

32,104,56

G.C.D of 32, 104, 56

32=2×2×2×2×2

104=2×2×2×13

56= 2×2×2×7

∴ G.C.D of 32,104,and56 2×2×2×8

∴ The greatest length of ribbon we have to cut is metre, i.e., we factorise the three numbers into prime factors and consider the highest common factor, G.C.D of the three numbers.

Question 2. If we had a green ribbon of length 2a²b metre, a yellow ribbon of length 4ab²metre and a blue ribbon of length 6a²b², let’s calculate the greatest length of the same size we have cut from the ribbons in such a way that no portion of the ribbon is left.

How will I get the G.C.D of 2a²b,4ab² and 6a2b²?

Solution.

Given

If we had a green ribbon of length 2a²b metre, a yellow ribbon of length 4ab²metre and a blue ribbon of length 6a²b²

G.C.D of 2a²b,4ab² and 6a2b²

At first we resolve 2a²b,4ab2 and 6a²b² into prime factors.

2a²b= 2×a×a×b

4ab²= 2×2×a×b×b

6a²b²= 3×2×a×a×b×b

Alternately, G.C.D of 2,4 and 6=2 Lowest power of a is a, the lowest power of is bis b in the expressions 2a2b,4ab² and 6a²b².

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

“WBBSE Class 8 Maths Chapter 14 solutions, H.C.F and L.C.M of Algebraic Expressions”

∴ The required G.C.D = 2a¹b¹=2ab

∴ G.C.D of 2a²,4ab² and 6a²b² is 2ab

Read and Learn More WBBSE Solutions For Class 8 Maths

Question 3. Let’s find the G.C.D of 6x²yz3,10x³y³z³ and 8x2yz⁴.

Solution:

Given

6x²yz³,10x³y³z³ and 8x²yz⁴.

At first we factorize 6x²yz³, 10x3y3z³and 8x²yz⁴into prime factors.

6x²yza = 3×2×x×x×y×z×z×z

10x3y³z³ = 5×2×x×x×x×y×y×y×z×z×z

8x²yz4 = 2×2×2×x×x×y×z×z×z×z

∴ G.C.D of 6x²yz³, 10x3y3z³and 8x2yz⁴ is = 2x²z³

Alternately, G.C.D of 6,10 and 8 is = 2

In 6x²yz³, 10x3y3z³and 8x2yz⁴ the lowest power of x is 2, the lowest power of y is 1 and the lowest power of z is 3;

∴ G.C.D of 6x²yz³, 10x3y3z³and 8x2yz⁴ is = 2x²z³

Question 4. Let’s find the G.C.D of (x³ + 2×2) and (x³+11×2+18x).

Solution.

Given,

First expression, x³+2x² =x²(x + 2)

Second expression, x³ + 11 x² + 18x = x (x² + 11 x + 18).

= x (x² + 9x + 2x + 18) = x (x+9) (x+2)

∴ Required G.C.D is = x (x+2)

Algebraic Expressions Exercise

Question 1. Let’s find the G.C.D of the algebraic expressions x (x²-9), x²-x-12

Solution:

Given algebraic expressions x (x²-9), x²-x-12

First expression = x (x²-9)

= x {(x)²-(3)²}

First expression = x (x+3) (x-3)

Second expression = x² – x – 12

= x²-(4-3) x – 12

= x² – 4x + 3x – 12

= x (x-4) +3 (x-4)

Second expression = (x-4) (x+3)

Required G.C.D is = (x+3)

“Class 8 WBBSE Maths Chapter 14 solutions, H.C.F and L.C.M study material”

Question 2. However; if we stich 4xy²z decimeter red ribbon, 6yz²x decimeter blue ribbon, and 10zx²y decimeter green ribbon on the curtain step by step then let’s calculate the least amount of curtain is required to stich the ribbons completely.

Solution:

Given

If we stich 4xy²z decimeter red ribbon, 6yz²x decimeter blue ribbon, and 10zx²y decimeter green ribbon on the curtain step by step

Let’s try to find the L.C.M of 4xy²z, 6yz²z and 10zx²y.

Let’s factorize 4xy²z, 6yz²x and 10zx²y.

4xy²Z = 2×2× x ×y ×y ×z

6yz²x = 3×2× x × y × z ×z

10zx²y=5×2×x×x×y×z

∴ The common factor of 4xy²z, 6yz²x and 10zx²y is 2xyz, and other factors are 2,3,5,x,y,z.

∴ L.C.M. of 4xy²z, 6yz²x and 10zx²y is 2xyz×2×3×5×x×y×z = 60x²y²z²

In 4xy²z, 6yz²x and 10zx²y the highest power of x is 2, the highest power of y is 2 and the highest power of z is 2.

∴ L.C.M. of 4xy²z, 6yz²x and 10zx²y = 60x²y²z²

Algebraic Expressions Exercise

Question 1. Let’s find the L.C.M of 2(x-4) and (x²-3x+2). And Let’s find the G.C.D L.C.M of and (x³-8), (x²+3x-10) and (x³+2x²+8x).

Solution:

Given expressions (x³-8), (x²+3x-10) and (x³+2x²+8x)

First expression, x³-8

= x³-(2)³

First expression= (x-2) (x²+2x+4)

Second expression, x²+3x-10

= x²+5x-2x-10

= x(x+5)-2 (x+5)

= (x+5) (x-2)

Second expression= x(x²+2x-8)

Third expression, x³+2x²-8x

= x (x²+2x-8)

= x {x²+4x-2x-8}

= x {x(x+4)-2 (x+4)}

Third expression= x(x+4) x (x-2)

Required G.C.D. = x – 2

Required L.C.M. = x(x-2)(x²+2x+4)(x-5)(x+4)

Algebraic Expressions Exercise

Question 1. Let’s find the G.C.D and the L.C.M of (y³-8), (y³-4y²+4y) and (y²+y-6).

Solution:

Given (y³-8), (y³-4y²+4y) and (y²+y-6).

First expression, y³-8

= (y)³-(2)³

First expression= (y-2)(y²+2y+4)

Second expression, y³-4y²+4y

= y (y²-4y+4)

= y{(y)²-2.y.2 + (2)²}

Second expression= y (y-2)² = y (y-2) (y-2)

Third expression, y²+y-6

= y²+(3-2) y-6

= y²+3y-2y-6

= y(y+3)-2 (y+3)

Third expression= (y+3) (y-2)

Required G.C.D. = (y-2)

Required L.C.M = y(y+3)(y-2)²(y²+2y+4)

“WBBSE Class 8 Maths Chapter 14, H.C.F and L.C.M of Algebraic Expressions solved examples”

Algebraic Expressions Exercise

Question 1. Let’s find the G.C.D of the following algebraic expressions :

1. 4a²b², 20ab²

Solution:

Given 4a²b², 20ab²

4a²b² = 2×2×a×a×b×b

20ab² =2×2×5×a×b×b

Required G.C.D. = 2×2×a×b×b

G.C.D= 4ab²

G.C.D = 4ab²

2. 5p²q²,10p²q², 25p4q³

Solution:

Given 5p²q², 10p²q², 25p4q³

5p²q²= 5×p×p×q×q

10p²q² = 2×5×p×p×q×q

25p4q³= 5×5×p×p×p×p×q×q×q

Required G.C.D. = 5×p×p×q×q = 5p²q²

G.C.D. = 5p²q²

3. 7y³z6, 21 y²,14z²

Solution:

Given 7y³z6, 21 y²,14z²

7y³z6= 7×y×y×y×z×z×z×z×z×z

21y² =3×7×y×y

14z² = 2×7 × z × z

Required G.C.D. = 7

4. 3a²b²c, 12a²b4c², 9a⁵b⁴

Solution:

Given 3a²b²c, 12a²b4c², 9a⁵b⁴

3a²b²c= 3×a×a×b×b×c .

12a²b4c²= 2×2×3×a×a×b×b×b×b×c×c

9a⁵b⁴= 3×3×a×a×a×a×a×b×b×b×b

Required G.C.D. = 3a²b²

“WBBSE Class 8 H.C.F and L.C.M of Algebraic Expressions solutions, Maths Chapter 14”

Question 2. Let’s find the L.C.M. of the following expressions :

1. 2x²y³,10x³y

Solution:

Given 2x²y³, 10x³y

2x²y³= 2×X×x×y×y×y

10x³y= 2×5×X×X×X×y

2. 7p²q3, 35p³q, 42pq⁴

Solution:

Given 7p²q³, 35p³q, 42pq⁴

7p²q³ = 7 x p x p x q x q x q

35p³q = 5×7×p×p×p×q

42pq⁴= 2×3×7×p×q×q×q×q

Required L.C.M. = 2×3×5×7×p³q³

Required L.C.M.  = 210 p³q⁴

3. 5a⁵b, 15ab²c, 25a²b²c²

Solution:

Given 5a⁵b, 15ab²c, 25a²b²c²

5a⁵b = 5 × a × a × a × a × a × b

15ab²c = 3×5×a×b×b×c

25a²b² c²= 5×5×a×a×b×b×c×c

Required L.C.M. = 75a5b²c²

4. 11a²bc², 33a²b²c, 55a²bc²

Solution:

Given 11 a²bc², 33a²b²c, 55a²bc²

11 a²bc² = 11×a×a×b×c×c

33a²b²c = 3×11×a×a×b×b×c

55a²bc²= 5×11×a×a×b×c×c

Required L.C.M. =165a²b²c²

“Class 8 WBBSE Maths Chapter 14, H.C.F and L.C.M easy explanation”

Question 3. Let’s find G.C.D of the following algebraic expressions :

1. 5x (x+y), x³-xy²

Solution:

Given 5x (x+y), x³-xy²

First expression, = 5x (x+y)

Second expression, x³-xy²

= x (x²-y²) .

= x (x+y) (x-y)

Required G.C.D. = x (x+y)

2. x³-3x²y, x²-9y²

Solution:

Given x³-3x²y, x²-9y²

First expression, x³-3x²y

= x²(x-3y)

Second expression, x²-9y²

=(x)²-(3y)²

= (x+3y) (x-3y)

Required G.C.D. = (x-3y)

3. 2ax(a-x)², 4a2x (a-x)³

Solution:

Given 2ax(a-x)², 4a2x (a-x)³

First expression, 2ax(a-x)²

=2ax (a-x) (a-x)

Second expression, 4a²x (a-x)³

= 2×2×a×a×x (a-x) (a-x) (a-x)

Required G.C.D. = 2ax (a-x)²

4. x²-1, x²-2x+1, x³+x²-2x

Solution:

Given x²-1, x²-2x+1, x³+x²-2x

First expression, x²-1

= (x)²-(1)²

= (x+1) (x-1)

Second expression, x²-2x+1

= (x)²-2.x.1 + (1)²

= (x-1)²

= (x-1) (x-1)

Third expression, x³+x²-2x

= x(x²+x-2)

= x (x²+ 2x – x-2)

= x {x(x +2) -1 (x+2)}

= x (x+2) (x-1)

Required G.C.D. = (x-1)

5. a²-1, a³-1, a²+a-2

Solution:

Given a²-1, a³-1, a²+a-2

First expression, a²-1

= (a)²-(1)

= (a+1) (a-1)

Second expression, a³-1

= (a)³– (1 )³

= (a-1) (a²+a-2)

Third expression, a²+a-2

= a²+(2-1) a-2

= a²+2a-a-2

= a (a+2) -1 (a+2)

= (a+2) (a-1)

Required G.C.D. = (a-1)

6. x²+3x+2, x²+4x+3, x²+5x+6

Solution:

Given x²+3x+2, x²+4x+3, x²+5x+6

First expression, x²+3x+2

= x²+(2+1)x+2

= x²+2x+x+2

= x (x+2)+1 (x+2)

= (x+2) (x+1)

Second expression, x²+4x+3

= x² + (3+1)x + 3

= x² + 3x + x + 3

= x (x+3) +1 (x+3)

= (x+3) (x+1)

Third expression, x²+5x+6

= x² + (3+2) x+6

= x²+3x+2x+6

= x(x+3) + 2 (x+3)

= (x+3) (x+2)

Required G.C.D. = 1

“WBBSE Class 8 Maths Chapter 14 solutions, H.C.F and L.C.M of Algebraic Expressions PDF”

7. x²+xy, xz + yz, x²+ 2xy+y²

Solution:

Given x²+xy, xz + yz, x²+ 2xy+y²

First expression, x²+xy

= x (x+y)

Second expression, xz + yz

= z (x+y)

Third expression, x²+ 2xy+y²

= (x+y)²

= (x+y) (x+y)

Required G.C.D. = (x+y)

8. 8 (x²-4), 12 (x³+8), 36 (x²-3x-10)

Solution:

Given 8 (x²-4), 12 (x³+8), 36 (x²-3x-10)

First expression, 8 (x2-4)

= 8{(x)²-(2)²}

= 2×2×2 (x+2) (x-2)

Second expression, 12 (x³+8)

= 12{(x)³+(2)³}.

= 2x2x³ (x+2) (x²-2x+4)

Third expression, 36 (x²-3x-10)

= 36 {x²-(5-2) x-10}

= 36 (x²-5x+2x-10)

= 36 {x (x-5) +2 (x-5)}

= 2×2×3×3 (x-5) (x+2)

Required G.C.D. = 4(x+2)

9. a²-b²-c²+2bc, b²-c²-a²+2ac, c²-a²-b²+2ab

Solution:

Given a²-b²-c²+2bc, b²-c²-a²+2ac, c²-a²-b²+2ab

First expression, a²-b²-c²+2bc

= a²-(b²-2bc + c²)

= (a)²– (b-c)²

= (a+b-c) (a-b+c)

Second expression, b²-c²-a²+2ac

= b²– (a²-2ac+c²)

= (b)² – (a-c)²

= (b+a-c) (b-a+c)

= (a+b-c) (b-a+c)

Third expression, c²-a²-b²+2ab

= c²-(a²-2ab+b²)

= (c)² – (a-b)² = (c+a-b) (c-a+b)

= (a-b+c) (c-a+b)

Required G.C.D. = 1

10. x³-16x, 2x³+9×2+4x, 2x³+x2-28x

Solution:

Given x³-16x, 2x³+9x²+4x, 2x³+x²-28x

First expression, x³-16x

= x (x²-16)

= x {(x)²– (4)²}

x (x+4) (x-4)

= x (2x²+8x+x+4)

= x {2x (x+4) +1 (x+4)}

= x (x+4) (2x +1)

Third expression, 2x³+x²-28x = x (2x²+x-28)

= x (2x² + 8x – 7x – 28)

= x {2x (x + 4) – 7 (x + 4)}

= x (x + 4) (2x – 7)

Required G.C.D. = x (x + 4)

11. 4x²-1, 8x³-1, 4x²-4x+1

Solution:

Given 4x²-1,8x³-1,4x²-4x+1

First expression, 4x²-1

= (2x)²– (1)²

= (2x +1) (2x-1)

Second expression, 8x³-1

= (2x)³ – (1)³

= (2x-1) {(2x)²+2x.1 + (1)²}

= (2x-1) (4×2+2x+1)

“WBBSE Class 8 Maths Chapter 14, H.C.F and L.C.M important questions”

Third expression, 4x²-4x+1

= (2x)²– 2.2x.1 + (1)²

= (2x-1)²= (2x-1) (2x-1)

Required G.C.D. = (2x-1)

12. x³-3x²-10x, x³+6x²+8x, x⁴-5x³-14x²

Solution:

Given x³-3x²-10x, x³+6x²+8x, x⁴-5x³-14x²

First expression, x³-3x²-10x

= x (x²-3x-10)

= x {x²– (5-2) x -10}

= x (x²-5x+2x-10)

= x {x (x-5) +2 (x-5)}

= x (x-5) (x+2)

= x (x+4) (x+2)

Third expression, x⁴-5×3-14x²

= x² (x²-5x-14)

= x² (x²-7x+2x-14)

= x²{x (x-7)+2(x-7)}

= x.x(x-7)(x+2)

Required G.C.D. = x(x+2)

13. 6x²-13xa+6a²2, 6x²+11xa-10a², 6x²+2xa-4a²

Solution:

Given 6x²-13xa+6a², 6x²+11xa-10a², 6x²+2xa-4a²

First expression, 6x²-13xa+6a²

= 6x² – (9+4) xa + 6a²

= 6x² – 9ax – 4ax + 6a²

= 3x (2x-3a)-2a(2x-3a)

= (2x – 3a) (3x – 2a)

Second expression, 6x²+11xa-10a²

=6x²+(15-4) xa -10a²

= 6x²+ 15ax-4ax-10a²

= 3x (2x+5a) -2a (2x+5a)

= (2x+5a) (3x-2a)

Third expression, 6x²+2xa-4a²

= 2 (3x²+xa-2a²)

= 2 (3x²+3ax-2ax-2a²)

= 2 (3x (x+a) -2a (x+a)}

= 2 (x+a) (3x-2a)

Required G.C.D. = (3x – 2a)

Question 4. Let’s find the L.C.M of the following algebraic expressions :

1. p²-q², (p+q)²

Solution:

Given p²-q², (p+q)²

First expression, p²-q²

= (p+q) (p-q)

Second expression, (p+q)²

= (p+q) (p+q)

Required L.C.M. .= (p+q)² (p-q)

2. (x²y²-x²), (xy²-2xy+x)

Solution:

Given (x²y²-x²), (xy²-2xy+x)

First expression, (x²y²-x²)

= x²(y²-1)

= x²(y+1) (y-1)

Second expression, (xy²-2xy+x)

= x(y²-2y+1)

= x (y-1 )²

= X (y-1) (y-1)

Required L.C.M. = x² (y-1)² (y+1)

“Class 8 Maths H.C.F and L.C.M solutions, WBBSE syllabus”

3. (p+q) (p+r), (q+r) (r+p), (r+p) (p+q)

Solution:

Given (p+q) (p+r), (q+r) (r+p), (r+p) (p+q)

Required L.C.M. = (p+q) (q+r) (r+p)

4. ab⁴-8ab, a²b⁴+8a²b, ab⁴-4ab²

Solution:

Given ab⁴-8ab, a²b⁴+8a²b, ab⁴4-4ab²

First expression, ab⁴-8ab

= ab(b³-8)

= ab {(b)³-(2)³}

= ab (b-2) {(b)²+b² + (2)²}

= ab (b-2) (b²+2b+4)

Second expression, a²b⁴+8a²b

= a²b (b³+8)

= a²b {(b)³+(2)³}

= a²b (b+2) {(b)²-b.2. + (2)²}

= a²b (b+2) (b²-2b+4)

Third expression, ab⁴-4ab²–

= ab²(b2-4)

= ab² {(b)2 – (2)²}

= ab² (b+2) (b-2)

Required L.C.M. = a²b² (b-2) (b+2) (b²+ 2b+4) (b²– 2b+4)

5. x⁴+x²y²+y⁴, x³y+y⁴, (x²-xy)³

Solution:

Given x⁴+x²y²+y⁴, x³+y⁴, (x²-xy)³

First expression, x⁴+x²y²+y⁴

= (x²)² + 2.x².y²+ (y²)² – x²y²

= (x²+y²)² – (xy)²

= (x²+y²+xy) (x²+y²-xy)

= (x²+xy+y²) (x²-xy+y²)

Second expression, x³y+y⁴ = y (x³+y³)

= y (x+y) (x²-xy+y²)

Third expression, (x²-xy)³

= {x (x-y)}³

= x³ (x-y)³ .

Required L.C.M. = x³y (x+y) (x-y)³ (x²+ xy + y²) (x²-xy+y²)

6. p² + 2p, 2p⁴+3p³-2p², 2p³-3p²-14p.

Solution:

Given p² + 2p, 2p⁴+3p³-2p², 2p³-3p²-14p

First expression, p²+ 2p

p²+ 2p = P (P+2)

Second expression, 2p⁴+3p³-2p²

= p² (2p²+3p-2)

= p² (2p²+4p-p-2)

= p² (2p (p+2) -1 (p+2)}

2p⁴+3p³-2p² = p² (p+2) (2p-1)

Third expression, 2p³-3p²-14p

= p (2p²-3p-14)

= P (2.P²– (7-4) p-14}

= p (2p²-7p+4p-14)

= P (P (2p-7) +2 (2p-7)}

2p³-3p²-14p = P (2p-7) (p+2)

Required L.C.M. = p² (p+2) (2p-1) (2p-7)

7. x²-y²+z²-2xz, x²-y²-z²+2yz, xy+zx+y²-z²

Solution:

Given x²-y²+z²-2xz, x²-y²-z²+2yz, xy+zx+y²-z²

First expression, x²-y²+z²-2xz

= x²-2xz+z²-y²

= (x-z)²– (y)²

= (x-z+y) (x-z-y)

x²-y²+z²-2xz = (x+y-z) (x-y-z) .

Second expression, x²-y²-z²+2yz

=x² – (y²-2yz+z²)

= (x)² – (y-z)²

x²-y²-z²+2yz = (x+y-z) (x-y+z)

Third expression, xy+zx+y²-z²

= x (y+z) + (y+z) (y-z)

xy+zx+y²-z² = (y+z) (x+y-z)

Required LC.M. = (y+z) (x+y-z) (x-y+z) (x-y-z)

7. x²-xy-2y², 2x²-5xy+2y², 2x²+xy-y²

Solution:

Given x²-xy-2y²,2x²-5xy+2y²,2x²+xy-y²

First expression, x²-xy-2y²

= x²-(2-1 )xy-2y²

= x²-2xy + xy – 2y²

= x (x-2y) + y (x-2y)

x²-xy-2y² = (x-2y) (x+y)

Second expression, 2x²-5xy+2y²

= 2x²-(4+1) xy + 2y²

= 2x² – 4xy – xy + 2y²

= 2x (x-2y) -y (x-2y)

2x²-5xy+2y²= (x-2y) (2x-y)

Third expression, 2x²+xy-y²

= 2x²+(2-1) xy -y²

= 2x²+2xy-xy-y²

= 2x (x+y) – y (x+y)

2x²+xy-y² = (x+y) (2x-y)

Required L.C.M. = (x+y) (x-2y) (2x-y)

“WBBSE Class 8 Chapter 14 Maths, H.C.F and L.C.M of Algebraic Expressions step-by-step solutions”

8. 3x²-15x+18, 2x²+2x-24, 4x²+36x+80

Solution:

3x²-15x+18, 2x²+2x-24, 4x²+36x+80

First expression, 3x²-15x+18

= 3(x²-5x+6)

= 3 (x²-(3+2) x+6)

= 3 (x²-3x-2x+6)

= 3 (x (x-3) -2 (x-3)}

= 3 (x-3) (x-2)

= 2 {x (x+4) -3 (x+4)}

3x²-15x+18 = 2 (x+4) (x-3)

Third expression, 4x²+36x+80

= 4 (x²+9x+20)

= 4 {x² + (5+4) x+20}

= 4 (x²+5x+4x+20)

= 4{x (x+5) +4 (x+5)}

4x²+36x+80 = 2x² (x+5 (x+4) .

Required L.C.M. =2×2×3 (x-2) (x-3) (x+4) (x+5)

= 12 (x-2) (x-3) (x+4) (x+5)

L.C.M. = 12 (x-2) (x-3) (x+4) (x+5)

9. (a²+2a)², 2a³+3a³-2a, 2a⁴-3a³-14a²

Solution:

Given (a²+2a)2, 2a³+3a³-2a, 2a⁴-3a³-14a²

First expression, (a²+2a)²

= {a(a+2)}²

= a² (a+2)²

(a²+2a)² = a.a (a+2) (a+2)

Second expression, 2a³+3a³-2a

= a (2a²+3a-2)

= a {2a²+(4-1) a-2}

= a (2a²+4a-a-2)

= a {2a (a+2) -1 (a+2)

2a³+3a³-2a = a (a+2) (2a-1)

Third expression, 2a⁴-3a³-14a²

= a² (2a²-3a-14)

= a²{2a²-(7-4) a-14}

= a² (2a²-7a+4a-14)

= a² {a (2a-7) +2 (2a-7)}

2a⁴-3a³-14a² = a.a (2a-7) (a+2)

Required L.C.M. = a² (a+2)² (2a-1) (2a-7)

10. 3a²-5ab-12b², a⁵-27a²b³, 9a²+24ab+16b²

Solution:

Given 3a²-5ab-12b², a⁵-27a²b³, 9a²+24ab+16b²

First expression, 3a²-5ab-12b²

= 3a²-(9-4)ab-12b²

= 3a²-9ab+4ab-12b²

= 3a (a-3b) + 4b (a-3b)

3a²-5ab-12b² = (a-3b) (3a+4b)

Second expression, a⁵-27a2b³

= a² (a³-27b³)

= a² {(a)³-(3b)³}

= a² (a-3b) {(a)²+a.3b+(3b)²}

a⁵-27a2b³ = a² (a-3b) (a²+3ab+9b²)

Third expression, 9a²+24ab+16b²

= (3a)²+2.3a.4b + (4b)²

9a²+24ab+16b² = (3a+4b)²= (3a+4b) (3a+4b)

Required L.C.M. = a² (a-3b) (3a+4b)²(a²+3ab+9b²)

Question 5. Let’s find the G.C.D and the L.C.M of the following expressions :

1. x³-8, x²+3x-10, x³+2x²-8x

Solution:

Given x³-8, x²+3x-10, x³+2x²-8x

First expression, x³-8

= (x)³ – (2)³

x³-8 = (x-2) (x²+2x+4)

Second expression, x²+3x-10

= x²+(5-2) x-10

= x² + 5x- 2x-10

= x (x+5) -2 (x+5)

x²+3x-10 = (x+5) (x-2)

Third expression, x³+2x²-8x

= x (x²+2x-8)

= x {x²+(4-2)x-8}

= x (x²+4x-2x-8)

= x (x(x+4)-2(x+4)}

x³+2x²-8x = x (x+4) (x-2)

Required G.C.D. = (x-2)

Required L.C.M. = x (x-2) (x+4) (x+5) (x2+2x+4)

2. 3y²-15y+18, 2y²+2y-24, 4y²+36y+80

Solution:

Given 3y²-15y+18, 2y²+2y-24, 4y²+36y+80

First expression, 3y²-15y+18

= 3 (y²-5y+6)

= 3 (y²-3y-2y+6)

= 3 {y (y-3) -2 (y-3)}

3y²-15y+18 = 3 (y-3) (y-2)

Second expression, 2y²+2y-24 = 2(y²+y-12)

= 2 (y²+4y-3y-12)

= 2 {y (y+4) -3 (y+4)}

2y²+2y-24 = 2 (y+4) (y-3)

Third expression, 4y²+36y+80

= 4 (y²+9y+20)

= 4 (y²+5y+4y+20)

= 4 {y (y+5) +4 (y+5)}

4y²+36y+80 = 2x² (y+5) (y+4)

Required G.C.D. = 1

Required L.C.M. = 12 (y-2) (y-3) (y+4) (y+5)

3. a³-4a²+4a, a²+a-6, a³-8

Solution:

Given a³-4a²+4a, a²+a-6, a³-8

First expression, a³-4a²+4a = a (a²-4a+4)

= a {(a)²-2.a.2 + (2)²}

a³-4a²+4a = a (a-2)² = a (a-2) (a-2)

Second expression, a²+a-6

= a² + 3a – 2a – 6

= a (a+3) -2 (a+3)

a²+a-6 = (a+3) (a-2)

Third expression, a³-8 = (a)³-(2)³

= (a-2) {(a)² + a.2 + (2)²}

a³-8 = (a-2) (a²+2a+4)

Required G.C.D. = (a-2)

Required L.C.M. = a(a-2)²(a+3) (a²+2a+4)

“WBBSE Maths Class 8 H.C.F and L.C.M of Algebraic Expressions, Chapter 14 key concepts”

4. a²+b²-c²+2ab, c²+a²-b²+2ca, b²+c²-a²+2bc

Solution:

Given a²+b²-c²+2ab, c²+a²-b²+2ca, b²+c²-a²+2bc

First expression, a²+b²-c²+2ab

= a²+2ab+b²-c²

= (a+b)²-(c)² = (a+b+c) (a+b-c)

Second expression, c²+a²-b²+2ca

= a²+2ca+c²-b²

= (a+c)²-(b)²

= (a+c+b) (a+c-b)

c²+a²-b²+2ca = (a+b+c) (a-b+c)

Third expression, b²+c²-a²+2bc

= b²+2bc+c²-a²

= (b+c)²-(a)²

= (b+c+a) (b+c-a)

b²+c²-a²+2bc = (a+b+c) (b+c-a)

Required G.C.D. = (a+b+c)

Required L.C.M. = (a+b+c) (a-b+c) (a+b-c) (b+c-a)

5. x³-4x, 4(x²-5x+6), (x²-4x+4)

Solution:

Given x³-4x, 4(x²-5x+6), (x²-4x+4)

First expression, x³-4x

= x (x²-4)

First expression= x {(x)²-(2)²}

x³-4x= x (x+2) (x-2)

Second expression, 4(x²-5x+6)

= 4 {x²– (3+2) x+6}

= 4 (x²-3x-2x+6)

Second expression= 4 {x (x-3) -2 (x-3)}

4(x²-5x+6)= 2x² (x-3) (x-2) .

Third expression, (x²-4x+4)

= (x)²-2.x.2 + (2)²

Third expression= (x-2)²

(x²-4x+4) = (x-2) (x-2)

Required G.C.D. = (x-2)

Required L.C.M. = 4x (x+2) (x-2) (x-3)

Mixture

The ratio of Assam tea and Darjeeling tea in casket number 1 is 5: 2

The ratio of Assam tea and Darjeeling tea in casket number 2 is 2: 1

Have we got a new variety of tea after blending various qualities of tea in different ratios?

What can be termed such blending?

Solution:

Such blending

Such blending is called mixture.

The proportional part of Assam tea in the blended tea of casket number 1 is

= \(\frac{5}{5+2}=\frac{5}{7}\)

The proportional part of Darjeeling tea in the blended tea of casket number 1 is

= \(\frac{2}{7}\)

“WBBSE Class 8 Maths Chapter 12 solutions, Mixture”

The proportional part of Assam tea in the blended tea of casket number 2 is

= \(\frac{2}{2+1}=\frac{2}{3}\)

The proportional part of Darjeeling tea in the blended tea of casket number 2 is

= \(\frac{1}{3}\)

Read and Learn More WBBSE Solutions For Class 8 Maths

Question 1. Let’s calculate the quantities of Assam tea and Darjeeling tea out of 21 kg of blended tea in casket number 1.

Solution:

The quantity of Assam tea out of 21 kg blended tea in casket  number 1

= \(21 \mathrm{~kg} \times \frac{\mathrm{5}}{7}\) =15 kg

And the quantity of Darjeeling tea is = \(21 \mathrm{~kg} \times \frac{\mathrm{2}}{7}\) = 6 kg

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

Question 2. Let’s calculate the quantities of Assam tea and Darjeeling tea out of 21 kg of blended tea is casket number 2.

Solution:

The quantity of Assam tea out of 21 kg of blended tea of casket number 2 is

= \(21 \times \frac{2}{3} \mathrm{~kg}\) = 14 kg

And the quantity of Darjeeling tea is

= \(21 \times \frac{1}{3} \mathrm{~kg}\) = 7 kg

Question 3. Let’s work out the quantities of the ratio of Assam tea and Darjeeling tea if an additional 7 kg of Assam tea is mixed with 25 kg of blended tea in casket number 3.

Solution:

The quantity of Assam tea in casket number 3 is = 15 kg

And the quantity of Darjeeling tea is =10 kg

Total quantity of Assam tea after mixing 7 kg of that of the same

= 15 kg + 7 kg = 22 kg

Total quantity of Assam tea after mixing 7 kg of that of the same = 22 kg

Question 4. Let’s calculate what quantity of Darjeeling tea needs to be mixed with the blending casket number. 2 so that ratio of Darjeeling tea and Assam tea will be 7: 4 in the new blend.

Solution:

Let x kg Darjeeling tea will be mixed.

∴ If x kg Darjeeling tea is mixed, quantity of Darjeeling tea is = (7 + x) kg.

In the new mixture Assam tea : Darjeeling tea = 14 : (7 + x)

B.T.P.,

= \(\frac{14}{7+x}=\frac{7}{4}\)

or, 49 + 7x = 56

or, 7x = 56 – 49

or,7x=7

or, x= 7/7

or, x= 1

If we mix 1 kg Darjeeling tea in casket number 2, the ratio of the quantities of Assam tea and Darjeeling tea in the new mixture will be 7:4

“Class 8 WBBSE Maths Chapter 12 solutions, Mixture study material”

Question 5. I prepared two types of beverage in my house. The ratios of measurement of syrup and water in the 2 types of beverage are 2 : 7 and 1: 5 respectively. Let’s calculate the ratio of measurement of syrup and water if 27 liters of the first beverage is mixed with 18 liters of the second.

Solution:

Given

I prepared two types of beverage in my house. The ratios of measurement of syrup and water in the 2 types of beverage are 2 : 7 and 1: 5 respectively.

The proportional part of the quantity of syrup in the 1st beverage is

= \(\frac{2}{2+7}=\frac{2}{9}\)

And the proportional part of the quantity of water is = \(\frac{7}{9}\)

The quantity of syrup in the first beverage is = \(\frac{2}{9} \times 27\)= 6

And the quantity of water is = \(\frac{7}{9} \times 27\) =21

The proportional part of the quantity of syrup of the second beverage is

= \(\frac{1}{6}\)

And the proportional part of water is = \(\frac{5}{6}\)

∴ The quantity of syrup in 181 of beverage of the second type is = 3 And the quantity of water is = 15

∴ The quantity of syrup in the new beverage is = 6 I + 3 I = 9

And the quantity of water is = 21 1 + 15 1 = 36

∴ In the new beverage the quantity of syrup : quantity of water is = 9 : 36 = 1 : 4.

Question 6. Let’s try to calculate in what ratio of the measurements of two beverage needs to be mixed so that the ratio of syrup and water will be 5 : 21.

Solution:

Let x I of first beverage is mixed with y I of second beverage.

∴ The quantity of syrup in x I of 1st beverage is = \(\frac{2}{9} \times X=\frac{2 x}{9}\)

And the quantity of water is = \(\frac{7}{9} \times x\)

= \(\frac{2 x}{9}\)

The quantity of syrup in y I of 2nd beverage is = \(\frac{1}{6} \times y\)

= \(\frac{y}{6}\)

And the quantity of water is = \(\frac{5}{6} \times y\)

= \(\frac{5y}{6}\)

∴ The quantity of syrup in the new mixture is = \(\frac{2 x}{9} 1+\frac{y}{6}\)

= \(\left(\frac{2 x}{9}+\frac{y}{6}\right)\)

And the quantity of water is = \(\frac{7 x}{9} 1+\frac{5 y}{6}\)

= \(\left(\frac{7 x}{9}+\frac{5 y}{6}\right)\)

B.T.P.,

= \(\frac{\frac{2 x}{9}+\frac{y}{6}}{\frac{7 x}{9}+\frac{5 y}{6}}=\frac{5}{21}\)

or, \(21\left(\frac{2 x}{9}+\frac{y}{6}\right)=5\left(\frac{5 y}{6}+\frac{7 x}{9}\right)\)

or, \(21\left(\frac{4 x+3 y}{18}\right)=5\left(\frac{14 x+15 y}{18}\right)\)

or, 21 (4x + 3y) = 5(14x + 15y)

or, 84x + 63y = 70x + 75y

or, 84x – 70x = 75y – 63y

or, 14x = 12y

or, \(\frac{x}{y}=\frac{12}{14}=\frac{6}{7}\)

∴ x : y=6 : 7

∴ If the two beverages are mixed up in the ratio of measures of 6 : 7, then the ratio of measures of syrup and water in the new beverage will be 5 : 21.

Question 8. My brother has prepared a beverage in a jug with syrup and water in a ratio of measurement of 3 : 1. Let’s work out what part of the drink should be removed and replaced by water so that the volume of syrup and water becomes equal.

Solution:

Given

My brother has prepared a beverage in a jug with syrup and water in a ratio of measurement of 3 : 1.

Let in the jug there is x units beverage. Of this y units beverage is taken out and the same quantity of water is mixed.

Quantity of syrup in x units beverage

= \(\frac{3}{4} \times x\) units = \(\frac{3 x}{4}\) units

And the quantity of water is = \(\frac{x}{4}\) units

The quantity of syrup in y units beverage

= \(\frac{3}{4} \times y\) units

= \(\frac{3 y}{4}\)

And the quantity of water is = \(\frac{y}{4}\) units

If y units are taken out from x units beverage,

syrup in the remaining beverage = \(\left(\frac{3 x}{4}-\frac{3 y}{4}\right)\) units

and the quantity of water is = \(\left(\frac{x}{4}-\frac{y}{4}\right)\)

Again, y units of water is added.

∴ Now quantity of water is = \(\left(\frac{x}{4}-\frac{y}{4}+y\right)\)

B.T.P,

= \(\frac{\frac{x}{4}-\frac{y}{4}+y}{\frac{3 x}{4}-\frac{3 y}{4}}=\frac{2}{1}\)

or, \(\frac{x}{4}-\frac{y}{4}+y=\frac{6 x}{4}-\frac{6 y}{4}\)

or, \(\frac{x}{4}-\frac{6 x}{4}=\frac{y}{4}-y-\frac{6 y}{4}\)

or, \(\frac{x-6 x}{4}=\frac{y-4 y-6 y}{4}\)

or, \(-\frac{5 x}{4}=-\frac{9 y}{4}\)

or, 5x = 9y

or, = \(y=\frac{5 x}{9}\)

∴ Total \(\frac{5}{9}\) part of the beverage will be removed and a 9 replaced by water with same quantity so that ratio becomes 2:1

Mixture Exercise

Question 1. The ratio of measurements of water and dettol in 36 liters of water is 5 : 1. Let’s work out what volume of water should be added to the mixture so that the ratio of measurements of water and dettol becomes 3:1.

Solution:

Given

The ratio of measurements of water and dettol in 36 liters of water is 5 : 1.

Ratio of water and dettol is = 5:1

Proportional part of water in the mixture

= \(\frac{5}{5+1}=\frac{5}{6}\)

Proportional part of dettol in the mixture

= \(\frac{1}{5+1}=\frac{1}{6}\)

∴ Quantity of water in 36 liters of the mixture

= \(\frac{5}{6} \times 36\)

= 30

∴ Quantity of dettol in 36 liters of the mixture

= \(\frac{1}{6} \times 36\)

= 6

Let after adding x liters dettol in the mixture, the ratio of quantities of dettol and water will be 3 : 1.

∴ Total quantity of dettol after adding x liters of dettol = (6 + x) I. The ratio of water and dettol in the new mixture = 30 : 6 + x.

B.T.P.

= \(\frac{30}{6+x}=\frac{3}{1}\)

or, 18+3x=30

or, 3x=30-18

or, \(x=\frac{12}{3}\)

or, x = 4

4 liters dettol should be added into the mixture.

“WBBSE Class 8 Maths Chapter 12, Mixture solved examples”

Question 2. In a certain type of brass the ratio of measurements of Copper and Zinc is 5 : 2. Let’s work out what will be the ratio of Copper and Zinc in 25 kg of such brass if 4 kg of Copper is added to it.

Solution:

Given

In a certain type of brass the ratio of measurements of Copper and Zinc is 5 : 2.

Ratio of Copper and Zinc in the Brass = 5 : 2

Proportional part of Copper in the Brass

= \(\frac{5}{5+2}=\frac{5}{7}\)

Proportional part of Zinc in the Brass

= \(\frac{2}{5+2}=\frac{2}{7}\)

Quantity of Copper in 28 kg Brass

= \(\frac{5}{7} \times 28\) kg

= 20 kg

Quantity of Zinc in 28 kg Brass

= \(\frac{2}{7} \times 28\) kg

= 8kg

After adding 4 kg Copper, total quantity of Copper = (20 + 4) kg

= 24 kg

The ratio of Copper and Zinc in the new Brass = 24:8

= 3:1

Question 3. Brijan babu has made phenyl water solution of 60 liters in which the ratio of measurements of phenyl and water is 2 : 23. Let’s workout how much phenyl should be added to this solution so that the ratio of measurements of phenyl and water becomes 9 : 46.

Solution:

Given

Brijan babu has made phenyl water solution of 60 liters in which the ratio of measurements of phenyl and water is 2 : 23.

Ratio of phenyl and water in the mixture = 2 : 23

Proportional part of water in the mixture = \(\frac{2}{2+23}=\frac{2}{25}\)

Proportional part of phenyl in the mixture = \(\frac{23}{2+23}=\frac{23}{25}\)

The quantity of phenyl in 60 liters of the mixture

= \(\frac{2}{25} \times 60\)

= \(\frac{24}{5} I=4.8 I\)

Quantity of phenyl in 60 liters of the mixture

= \(\frac{23}{25} \times 60\)

= \(\frac{276}{5}\)

= 55.2

Let by adding x liters phenyl in the mixture, the ratio of water and phenyl will become 9 : 46.

∴ After adding x liters phenyl, the total quantity of phenyl = (4.8 + x)

Ratio of phenyl and water in the new mixture = (4.8 + x) : 55.2

B.T.P.,

(4.8 + x) : 55.2 = 9:46 .

or, \(\frac{4.8+x}{55.2}=\frac{9}{46}\)

or, 220.8 + 46x = 496.8

or, 46x = 496.8 – 220.8

or, 46x = 276.0

or, \(x=\frac{276}{46}\)

or, x = 6

After adding 6 liters phenyl in the mixture the ratio of water and phenyl will become 9 : 46.

Question 4. Amina bibi has prepared masonry mixture with sand and cement in a ratio of measurement 7 r 1. But after the brick work it is seen that 72 kg of mixture remains. She has added more cement with this mixture and the ratio of measurement of sand to cement becomes 6 :1. Let’s work out the total quantity of cement she has mixed.

Solution:

Given

Amina bibi has prepared masonry mixture with sand and cement in a ratio of measurement 7 r 1. But after the brick work it is seen that 72 kg of mixture remains. She has added more cement with this mixture and the ratio of measurement of sand to cement becomes 6 :1.

Ratio of sand and cement in the mixture =7:1

Proportional part of sand in the mixture

= \(\frac{7}{7+1}=\frac{7}{8}\)

Proportional part of cement in the mixture

= \(\frac{1}{7+1}=\frac{1}{8}\)

Quantity of sand in 72 kg mixture

= \(\frac{7}{8} \times 72\) kg = 63 kg

Quantity of cement in 72 kg mixture

= \(\frac{1}{8} \times 72\) kg = 9 kg

Let after adding x kg cement in the mixture the ratio of sand ant cement will be 6 : 1.

∴ Total quantity of cement after adding x kg cement = (9+x) kg

Ratio of sand and cement in the new mixture = 63 : (9 + x)

B.T.P.

= \(\frac{63}{9+x}=\frac{6}{1}\)

or, 54 + 6x = 63

or, 6x = 63 – 54

or, 6x = 9

or, x = \(\frac{9}{6}\)

or, x = 1.5

∴ 1.5 kg cement was added.

“WBBSE Class 8 Mixture solutions, Maths Chapter 12”

Question 5. The ratio of measurements of Copper, Zinc and Nickel ir German silver is 4 : 3 : 2 respectively. Let’s work out what weight (in kgs) of Zinc should be added to 54 kg of German silver, sc that the ratio of measurements becomes 6:5:3.

Solution:

Given

The ratio of Copper, zinc and Nickel in the German silver is =4:3:2

Quantity of Copper in 54 kg mixture

= \(\frac{4}{9} \times54\) kg

= 24 kg 1 6

Quantity of Zinc in 54 kg mixture

= \(\frac{3}{9} \times54\) kg

= 18 kg

Quantity of Nickel in 54 kg mixture

= \(\frac{2}{9} \times54\) kg

=12 kg

Ratio of Copper, Zinc and Nickel in the new German silver = 6:5:3

Proportional part of Copper in the new German silver = \(\frac{6}{14}\)

Proportional part of Zinc in the new German silver = \(\frac{5}{14}\)

Proportional part of Nickel in the new German silver = \(\frac{3}{14}\)

∴ In the new German silver the quantity of copper will be 24 kg but by adding Zinc the quantity of mixture will increase.

In mathematical language the problem is –

Here the proportion is direct.

∴ Total quantity of new German silver

= \(24 \times \frac{14}{6}\)

= 56 kg

∴ Zinc will be added = (56 – 54) kg

=2 kg

∴ 2kg Zinc should be added.

Question 6. In two different kinds of washing powder the ratios of measurement of soda and soap powder are 2 : 3 and 4 : 5. Let’s work out the part of the soap powder in the new washing powder which is prepared by mixing 10 kg of first soap powder with 18 kg of second soap powder.

Solution:

Given

In two different kinds of washing powder the ratios of measurement of soda and soap powder are 2 : 3 and 4 : 5.

In the first washing powder the ratio of soda arid soap powder = 2:3.

Proportional part of first washing powder in the soda

= \(\frac{2}{2+3}=\frac{2}{5}\)

Proportional part of soap powder in the first washing powder

= \(\frac{3}{2+3}=\frac{3}{5}\)

Quantity of powder in 10 kg of the 1st washing powder

= \(\frac{3}{5} ×10\) kg

= 6 kg

Ratio of soda and soap powder in the second washing powder = 4:5

Proportional part of soap powder in the 2 nd washing powder

= \(\frac{5}{4+5}=\frac{5}{9}\)

Quantity of soap powder in 18 kg of the 2nd washing powder

= \(\frac{5}{9} \times 18\)kg

= 10kg

Total quantity of soap powder by mixing both types of washing powder

= (6+10) kg = 16 kg

And the total quantity of washing power = (10 + 18) kg = 28 kg

Soap powder in new washing powder

= \(\frac{16}{28}\) part = \(\frac{4}{7}\) part

In new washing powder \(\frac{4}{7}\) part is soap powder.

Question 7. Two similar vessels contain \(\frac{1}{3}\) and  \(\frac{1}{4}\)parts fruit juice. I filled water in the remaining empty part of these vessels and poured the juice mixed with water of the two vessels into another big vessel. Let’s work out the ratio of measurement of fruit and water in the new vessel.

Solution:

Given

Two similar vessels contain \(\frac{1}{3}\) and  \(\frac{1}{4}\)parts fruit juice. I filled water in the remaining empty part of these vessels and poured the juice mixed with water of the two vessels into another big vessel.

Fruit juice in 1st vessel = \(\frac{1}{3}\) part

∴ Water in 1st vessel = \(\left(1-\frac{1}{3}\right)\) part

= \(\frac{2}{3}\)

Fruit juice in 2nd vessel = \(\frac{1}{4}\) part

Water in 2nd vessel

= \(\left(1-\frac{1}{4}\right) \text { part }=\frac{3}{4} \text { part }\)

Total quantity of fruit juice in new vessel

= \(\left(\frac{1}{3}+\frac{1}{4}\right)\) part

=\(\frac{4+3}{12} \text { part }=\frac{7}{12} \text { part }\) part

Total quantity of fruit juice in new vessel

= \(\left(\frac{2}{3}+\frac{3}{4}\right)\) part

= \(\frac{8+9}{12}\) part

= \(\frac{17}{12}\) part

The ratio of quantities of fruit juice and water in new vessel

= \(\frac{7}{12}: \frac{17}{12}\)

= 7 : 17

The ratio of quantities of fruit juice and water in new vessel = 7 : 17

Question 8. Reshmi Khatiin has filled 3 similar glasses of equal size with beverage. The ratios of measurements of water and syrup in these glasses are respectively 3 : 1, 5 : 3 and 9 : 7. I poured the beverage of these three glasses into a big vessel. Let’s workout the ratio of measurements of water and syrup in the new vessel.

Solution:

Given

Reshmi Khatiin has filled 3 similar glasses of equal size with beverage. The ratios of measurements of water and syrup in these glasses are respectively 3 : 1, 5 : 3 and 9 : 7. I poured the beverage of these three glasses into a big vessel.

Ratio of water and syrup in 1st glass = 3:1

Proportional part of water = \(\frac{3}{3+1}=\frac{3}{4}\)

And proportional part of syrup = \(\frac{1}{3+1}=\frac{1}{4}\)

Ratio of water and syrup in second glass = 5:3

Proportional part of water = \(\frac{5}{5+3}=\frac{5}{8}\)

Proportional part of syrup = \(\frac{3}{5+3}=\frac{3}{8}\)

Ratio of water and syrup in third glass = 9:7

“Class 8 WBBSE Maths Chapter 12, Mixture easy explanation”

Proportional part of water = \(\frac{9}{9+7}=\frac{9}{16}\)

Proportional part of syrup = \(\frac{7}{9+7}=\frac{7}{16}\)

The beverages of all three glasses are poured into a big vessel.

∴ Water in the big vessel

= \(\left(\frac{3}{4}+\frac{5}{8}+\frac{9}{16}\right) \text { part }\)

= \(\frac{12+10+9}{16} \text { part }\)

= \(\frac{13}{16} \text { part }\)

Syrup in the big vessel

= \(\left(\frac{1}{4}+\frac{3}{8}+\frac{7}{16}\right) \text { part }\)

= \(\frac{4+6+7}{16} \text { part }\)

= \(\frac{17}{16} \text { part }\)

Ratio of syrup and water in the new vessel

= \(\frac{31}{16}: \frac{17}{16}\)

= 31 : 17

Ratio of syrup and water in the new vessel = 31 : 17

Question 9. Two different types of brass contain Copper and Zinc in the ratios of measurement respectively 8 : 3 and 15:7. Let’s workout in what ratio of measurement of Copper and Zinc will be if these two types of brass are mixed together in the ratio of measurement 5:2.

Solution:

Given

Two different types of brass contain Copper and Zinc in the ratios of measurement respectively 8 : 3 and 15:7.

Let 5 x kg of first kind of brass is mixed with 2 x kg of second kind of brass. The ratio of Copper and Zinc in first brass =8:3.

Sum of ratio = 8 + 3 = 11

Quantity of Copper in 5 x kg of first brass

= \(\frac{8}{11} \times 5 x=\frac{40 x}{11}\) kg

Quantity of Zinc in 5 x kg of the first brass

= \(\frac{3}{11} \times 5 x=\frac{15 x}{11} \mathrm{~kg}\) kg

Ratio of copper and Zinc in the second brass = 15:7

Sum of ratio = 15 + 7 = 22

Quantity of Copper in 2 x kg of the second brass

= \(\frac{15}{22}\) 2x kg

= \(\frac{15 x}{11} \cdot \mathrm{kg}\)

Quantity of Copper in 2 x kg of the second brass

= \(\frac{7}{22}\) 2x kg

= \(\frac{7 x}{11} \mathrm{~kg}\) kg

Total quantity of Copper in the new brass

= \(\left(\frac{40 x}{11}+\frac{15 x}{11}\right)\) kg

= \(\left(\frac{40 x+15 x}{11}\right)\) kg

= \(\frac{55 x}{11} \mathrm{~kg}=5 x\) kg

Total quantity of Zinc in the new brass

= \(\left(\frac{15 x}{11}+\frac{7 x}{11}\right)\) kg

= \(\left(\frac{15 x+7 x}{11}\right)\) kg

= \(\frac{22 x}{11} \mathrm{~kg}=2 \mathrm{x}\) kg

So, the ratio of Copper and Zinc in the new brass = 5x : 2x

= 5:2

The ratio of Copper and Zinc in the new brass = 5:2

“Class 8 Maths Mixture solutions, WBBSE syllabus”

Question 10. Two different types of stainless steel contain chromium and steel in the ratio of measurement respectively 2:11 and 5 : 21. Let’s workout in what proportion these two types of steel should be mixed so that the ratio of measurement of chromium and steel becomes 7 : 32.

Solution:

Given

Two different types of stainless steel contain chromium and steel in the ratio of measurement respectively 2:11 and 5 : 21.

Let by adding x kg of first stainless steel with y kg of second stainless steel the ratio of chromium and steel in the new stainless steel will be

Ratio of chromium and steel in the first stainless steel = 2:11

Proportional part of chromium = \(\frac{2}{2+11}=\frac{2}{13}\)

Proportional part of steel = \(\frac{11}{2+11}=\frac{11}{13}\)

Chromium in x kg of first stainless steel =\(\frac{2 x}{13}\) kg

Steel in x kg of first stainless steel = \(\frac{11 x}{13}\) kg

Ratio of chromium and steel in the second stainless steel = 5:21

Proportional part of chromium = \(\frac{5}{5+21}=\frac{5}{26}\)

Proportional part of steel = \(\frac{21}{5+21}=\frac{21}{26}\)

Chromium in y kg of second stainless steel

=\(\frac{5}{26} \times y \mathrm{~kg}=\frac{5 y}{26} \mathrm{~kg}\)

Total quantity of chromium in new stainless steel

= \(\left(\frac{2 x}{13}+\frac{5 y}{26}\right)\) kg

= \(\frac{4 x+5 y}{26}\) kg

Total quantity of steel in new stainless steel

= \(\left(\frac{11 x}{13}+\frac{21 y}{26}\right)\) kg

= \(\frac{22 x+21 y}{26}\) kg

B.T.P.,

= \(\frac{4 x+5 y}{26}: \frac{22 x+21 y}{26}\) = 7:32

or, (4x + 5y) : (22x + 21y) = 7:32

or, \(\frac{4 x+5 y}{22 x+21 y}=\frac{7}{32}\) = 7:32

or, 154x + 147y = 128x + 160y

or, 154x – 128x = 160y – 147y

or, 26x = 13y

or, \(\frac{x}{y}=\frac{13}{20}\)

or, \(\frac{x}{y}=\frac{1}{2}\)

or, x : y = 1 : 2

If both types of stainless steel are mixed in the ratio 1 : 2, the ratio of chromium and steel in the new stainless steel will be 7 : 32.

Question 11. In a vessel of beverage the ratio of measurement of syrup and water is 5 : 2. Let’s work out what part of the drink should be removed and replaced by water so that the volumes of syrup and water become equal.

Solution:

Given

In a vessel of beverage the ratio of measurement of syrup and water is 5 : 2.

Ratio of water and syrup in the beverage = 5:2

Proportional part of syrup = \(\frac{5}{5+2}=\frac{5}{7}\)

Proportional part of water = \(\frac{2}{5+2}=\frac{2}{7}\)

Let x part of the beverage is taken out and is replaced by the same quantity of water so that the ratio of syrup and water will be equal.

Syrup in x part of the beverage

= \(\frac{5}{7} \times x\) part = \(\frac{5 x}{7}\) part

Water in x part of the beverage

= \(\frac{2}{7} \times x\) part = \(\frac{2 x}{7}\) part

Syrup in remaining part of the beverage

= \(\left(\frac{5}{7}-\frac{5 x}{7}\right)\) part

= \(\frac{5-5 x}{7}\) part

Water in syrup = \(\left(\frac{2}{7}-\frac{2 x}{7}+x\right)\) part

= \(\frac{2-2 x+7 x}{7}\) part

= \(\frac{2+5 x}{7}\) part

B.T.P.,

= \(\frac{2+5 x}{7}=\frac{5-5 x}{7}\)

of, 2 + 5x = 5 – 5x

or, 5x + 5x = 5 – 2

or, 10x = 3

or, \(x=\frac{3}{10}\)

If \(\frac{3}{10}\) part of this beverage is taken out and replaced by the same quantity of water then the ratio syrup and water will be equal.

Question 12. Let’s see the table below write in mathematical language and try to find out the answer.

Solution:

Question 13. There are 3 kinds of liquids in a beverage of 700 liters. The ratio of measurements of the first and second liquid is 2 : 3 and the ratio of measurements of the second and the third liquid is 4:3. Let’s work out the ratio in which the first and second liquid should be mixed so that the ratio of measurement of the three liquid^ may become 6 : 5 : 3 in the same beverage.

Solution:

Given

There are 3 kinds of liquids in a beverage of 700 liters. The ratio of measurements of the first and second liquid is 2 : 3 and the ratio of measurements of the second and the third liquid is 4:3.

Ratio of first and second liquids in the mixture = 2:3

= 2×4 : 3×4 = 8 : 12

∴ Ratio of first second and third liquids in the mixture = 8 : 12 : 15

Total mixture = 700 I

∴ Amount of 1st liquid in the mixture = \(\frac{8}{35} \times 700\) = 160

Amount of 2nd liquid in the mixture = \(\frac{12}{35} \times 700\) = 240

Amount of 3rd liquid in the mixture = \(\frac{15}{35} \times 700\) = 300

Ratio of first second and third liquids in the new mixture =6 : 5 : 3

= 6×100 : 5×100 : 3×100

= 600 : 500 : 300

∴ Amount of first liquid to be taken = (600 – 160) = 440

Amount of second liquid to be taken = (500 – 240) = 260

440 of first and 260 of second mixture should be mixed.

Question 14. In a certain quantity of syrup the ratio of measurements of water and the rest part of the syrup is 89 : 11. Let’s workout what quantity of water should be added in 22 liters of the syrup so that the ratio of measurement of syrup and the rest part of the liquid becomes 90 : 10.

Solution:

Given

In a certain quantity of syrup the ratio of measurements of water and the rest part of the syrup is 89 : 11.

Ratio of water and the rest part of the syrup = 89 : 11

Proportional part of water in the syrup

= \(\frac{89}{89+11}=\frac{89}{100}\)

Proportional part of rest of the syrup in the syrup

= \(\frac{11}{89+11}=\frac{11}{100}\)

∴ Quantity of water in 22 liters of the syrup

= \(\frac{89}{100} \times 22\)

“WBBSE Class 8 Maths Chapter 12, Mixture important questions”

= \(\frac{979}{50}\)

Quantity of rest of syrup in 22 liters of the syrup

= \(\frac{11}{100} \times 22\)

= \(\frac{121}{50}\)

Let by adding x liters syrup the ratio of water and the rest part is 9:1

B.T.P.,

= \(\left(\frac{979}{50}+x\right): \frac{121}{50}=90: 10\)

or, \(\left(\frac{979+50 x}{50}\right): \frac{121}{50}=90: 10\)

or, (979+50x) : (121 = 9 : 1

or, \(\frac{979+50 x}{121}=\frac{9}{1}\)

or, 979+50x = 1089

or, 50x =  1089-979

or, 50x = 110

or, x = \(\frac{110}{50}\)

or, x = \(\frac{11}{5}\)

or, x = 2.2

In 22 liters of this syrup, by adding 2.2 liters water, the ratio of water and the rest part of syrup becomes 90 : 10.

Question 15. The ratio of the volumes of three bottles is 5 : 3 : 2. These three bottles are filled will the solution of phenyl and water. The ratios of measurement of phenyl and water in three bottles each are 2 : 3, 1 : 2 and 1 : 3 respectively. \(\frac{1}{3}\)part of the first bottle,\(\frac{1}{2}\) part of the second bottle and \(\frac{2}{3}\) part of the third bottle are mixed together now. Let’s work out the ratio of phenyl and water in the new solution.

Solution:

Given

The ratio of the volumes of three bottles is 5 : 3 : 2. These three bottles are filled will the solution of phenyl and water. The ratios of measurement of phenyl and water in three bottles each are 2 : 3, 1 : 2 and 1 : 3 respectively. \(\frac{1}{3}\)part of the first bottle,\(\frac{1}{2}\) part of the second bottle and \(\frac{2}{3}\) part of the third bottle are mixed together now.

Let the volumes of the three bottles are respectively : 5x I, 3x I and 2x I

Ratio of water and phenyl in the first bottle =2 : 3

Sum of ratio =2 + 3 = 5

∴ Amount of phenyl in the bottle first

=\(\frac{2}{5} \times 5 x \times \frac{1}{3} \quad I=\frac{2 x}{3}\)

Amount of water in the first bottle

= \(\frac{3}{5} \times 5 \times \times \frac{1}{3} I=\times I\)

Amount of phenyl and water in the second bottle = 1:2

Sum of ratio = 1+2 = 3

Amount of phenyl in the second bottle

= \(\frac{1}{3} \times 3 \times \times \frac{1}{2} \mid=\frac{x}{2}\)

Amount of water in the second bottle

= \(\frac{2}{3} \times 3 \times \times \frac{1}{2} \quad I=x I\)

Ratio of water and phenyl in the third bottle = 1:3

Sum of ratio = 1+3+4

Amount of phenyl in the third bottle

= \(\frac{1}{4} \times 2 x \times \frac{2}{3} \quad \mid=\frac{x}{3}\)

Amount of water in the third bottle

“WBBSE Class 8 Maths Chapter 12 solutions, Mixture PDF”

= \(\frac{3}{4} \times 2 x \times \frac{2}{3} 1=x\)

Ratio of phenyl and water in the new mixture

= \(\left(\frac{2 x}{3}+\frac{x}{2}+\frac{2 x}{3}\right):(x+x+x)\)

= \(\frac{4 x+3 x+2 x}{6}: 3 x\)

= \(\frac{9 x}{6}: 3 x\)

= \(\frac{9}{6}: 3\)

= \(\frac{9}{6} \times 6: 3 \times 6=9: 18\)

= 1 : 2

The ratio of phenyl and water in the new solution = 1 : 2

Percentage

Today we will go to the fair at Khadinan village. My sister and I will go there with our elder brother. There is Rs. 75 with my elder brother, Rs. 50 with me and Rs. 35 with my sister.

Question 1.  Let’s calculate in percentage the amount which my elder brother has more than me.

Solution:

My brother has more than me Rs. 75 – Rs. 50 = Rs. 25

The excess amount he has in percentage is =\(\frac{25}{50}\) x100 = Rs. 50

My brother has 50% more amount than me. In other language,

On Rs. 50, Rs. 25 is more

On Rs.1, Rs. \(\frac{25}{50}\) is more 50

On Rs. 100, Rs.\(\frac{25}{50}\) x 100 = Rs. 50 is more.

My brother has 50% more amount than me.

“WBBSE Class 8 Maths Chapter 11 solutions, Percentage”

Question 2. Let’s calculate in percentage the amount which I have less than my elder brother.

Solution:

My elder brother’s money in comparison with me, I have less Rs. 25

For Rs. 1, I have less amount of Rs. \(\frac{25}{75}\)

For Rs. 100, I have less amount of Rs. \(\frac{25}{75} \times 100=\text { Rs. } 33 \frac{1}{3}\)

I have \(33 \frac{1}{3} \%\) less amount than my elder brother.

The sum total of amount we have = Rs. (75+50+35) = Rs. 160

Read and Learn More WBBSE Solutions For Class 8 Maths

My elder brother calculated that we spent 10% of the amount at the time of going to the fair.

Let’s work out the sum we spent at the time of going to the fair.

= \(10 \%=\frac{.10}{100} \text { part }=\frac{1}{10} \text { part }\)

∴ Of the total amount the part was spent at the time of going to the fair.

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

So, of Rs. 160, 10% = Rs. \(\left(160 \times \frac{10}{100}\right)\) = Rs. 16

∴ Rs. 16 was spent at the time of going to the fair.

I came across Sunit at the fair.

Four of us rode on a merry-go-round. We spent Rs. 40 for this ride.

Question 3. Let’s work out the amount we spent for riding on the merry-go-round.

Solution:

Out of Rs. 160, we spent Rs. 40

Out of Rs. 1 the amount spent Rs. \(\frac{40}{160}\)

Out of 100 the amount spent Rs. \(\frac{40}{160} \times 100=\text { Rs. } 25\)

∴ Of the total amount 25% was spent on the ride of merry-go-round.

We have decided to spend 35% of the total amount for fooding.

“Class 8 WBBSE Maths Chapter 11 solutions, Percentage study material”

Question 4. Let’s calculate the sum for this purpose.

Solution:

Out of Rs.160, I spent 35% = Rs.\(\left(160 \times \frac{35}{100}\right)\) = Rs. 56

∴ We shall spend Rs. 56 in the fair for our food.

I spent Rs. 24 to buy glass bangles in the fair.

Question 5. Let’s calculate in percentage the amount I spent for purchasing glass bangles in the fair.

Solution:

Out of Rs. 160, I spent to purchase glass bangles Rs, 24

Out of Rs. 1,1 spent to purchase glass bangles Rs. \(\frac{24}{160}\)

Out of Rs. 100, I spent to purchase glass bangles Rs. =\(\frac{24}{160} \times 100\)= Rs. 15

∴ Out of the total amount I spent for glass bangles =15%

Question 6.  I painted in red 15% of the bamboo and \(\frac{1}{5}\) part in green.

Solution:

∴ Of the total length I painted \(\frac{15}{100}\) part = \(\frac{3}{20}\) part in red, but how much percent of total length is painted in yellow, let’s calculate.

Question 7.  If the bamboo is 2 m long and of which 38 cm is coloured with yellow then what is the percentage of yellow in relation to the whole length of the bamboo?

Solution:

Given

If the bamboo is 2 m long and of which 38 cm is coloured with yellow

Length of bamboo = 2 m = 200 cm.

∵ Of 200 cm long bamboo yellow coloured is 38.

∴ Of 1 cm long bamboo yellow coloured is \(\frac{38}{200}\)

∴ Of 100 cm long bamboo yellow coloured is \(\frac{38}{200} \times 100 \mathrm{~cm}=19\)

∴ Of the total length of the bamboo,19% is yellow coloured.

“WBBSE Class 8 Maths Chapter 11, Percentage solved examples”

Question 8.  A train will go to Budwan from Howrah station. The distance of cord line between Burdwan and Howrah is 85 km. But .the distance in the main line is 5% more than in the cord line. Let’s calculate the distance between Howrah and Burdwan in the main line by the method of proportion.

Solution:

Given

A train will go to Budwan from Howrah station. The distance of cord line between Burdwan and Howrah is 85 km. But .the distance in the main line is 5% more than in the cord line.

That distance is 5% more through main line.

That means, if the distance in cord line is 100 km then in the main line it is 5 km more.

So the distance through main line is (100 + 5) km = 105 km.

In mathematical language the problem is –

If the distance between Howrah and Burdwan is more / less in the cord line, in the main line it is inversely or less. Both those distances are Directly (directly/inversely) related.

So, 100:85::105:?

The distance in mainline is = \(\frac{85 \times 105}{100}\)

Let’s work out by unitary method.

If the distance in the cord line is 100 km then in the main line is 105 km.

If the distance in the cord line is 1 km then in the main line it is

= \(\frac{105}{100} \mathrm{~km}.\)

If the distance in the cord line is 85 km then in the main line it is will be

= \(85 \times \frac{105}{100}\) km. = 89.25km

Question 9. Niyamat uncle of Faridpur has used high – yielding paddy seed in his field. For this, the cost of production of paddy has increased by 35% but the cost of cultivation has increased by 35%. Let’s workout the present profit of Niyamat uncle in comparison with the previous return of Rs. 1220 by investing Rs. 450 in the same field.

Solution:

Given

Niyamat uncle of Faridpur has used high – yielding paddy seed in his field. For this, the cost of production of paddy has increased by 35% but the cost of cultivation has increased by 35%.

Let’s work out the increase in the cost of cultivation after using light- yielding paddy seeds by the rule of three.

In mathematical language the problem is –

For using high – yielding paddy seeds the expense earlier and the expense at present are there in the Directly (directly / inverse) relation.

∴ For using high-yielding paddy seed the present is

=  Rs. 135 × \(\frac{450}{100}\) = Rs.607.50

Let’s work out by unitary method.

Before the use of high-yielding seed

If Rs.100 was the expense, now it is Rs.135

If Re. 1 was the expense,now it is Rs. \(\frac{135}{100}\)

If Rs. 450 was the expense, now it is Rs.\(\frac{135×450}{100}\) = Rs. 607.50

Question 10. Let’s workout by the rule of three the production of paddy after using high-yielding seeds.

Solution:

The production of paddy increased by 30%, i.e., if the production of paddy was Rs. 100, it is now Rs. (100 + 30) = Rs 130.

In mathematical language the problem is –

The production before the use of high-yielding paddy is with the production after that use Direct (direct / inverse) related.

As the production of paddy in earlier has increased (i.e., from Rs. 100 to Rs. 1220)

So, the production of paddy will now Increase (increase/decrease).

Due to the use of high-yielding seed the production will be

= Rs. \(130 \times \frac{1220}{100}=\text { Rs. } 1586\)

Let’s work out by unitary method.

Before the use of high-yielding seed :

If the production was Rs.100, it is now Rs. 130.

If the production was Rs. 1, it is Rs. \(\frac{130}{100}\)

If the production was Rs. 1220, it is now \(\frac{130 \times 1220}{100}\)

Before the use of high-yielding seeds Niyamat uncle got an income of Rs. 1220- Rs. 450 = Rs. 770

Now the income is = Rs. (1586 – 607.50 ) = Rs. 978.50

More income is = Rs. ( 978.50 – 770 ) = Rs. 208.50

“WBBSE Class 8 Percentage solutions, Maths Chapter 11”

To reach a certain distance earlier the speed needs to increase (increase/decrease)

The speed is in increased (direct / inverse) relation with the time to reach a certain distance.

Let’s work out by the rule of three to reach in 100-20 = 80 seconds the speed of the vehicle will be 125 (unit / second).

Let’s work out by unitary method.

To reach in 100 seconds the speed of the vehicle will be 100 unit /second.

To reach in 1 second the speed of the vehicle will be 100 x 100 unit/second.

To reach in 80 seconds the speed of the vehicle will be \( \frac{100 \times 100}{80}\)unit/second.

= 125 unit/second

∴ To reduce the time of going to station from house by 20% the speed of the vehicle will be increased by –

(125 unit / second – 100 unit / second ) = 25 unit/ second So the speed needs to be increased by 25%.

Let’s work out how much the speed of my vehicle will have to be increased if I want to reduce time by 10% for the same distance.

Let by going from home to station at 100 unit/second speed 100 seconds time is taken.

In mathematical language, the problem is –

Speed is increased to cover same distance in less time, i.e., time and speed are inversely related.

∴ To reach in 90 seconds the speed of car will be = \(\frac{100 \times 100}{90}\) unit/second = 111.11 unit/second

∴  Increase in the speed of car = (111.11 – 100) unit/second

=11.11 unit/second

2. 12% of Rs. 215

Solution:

Given Rs. 215 x 12%

= Rs. \(\frac{215 \times 12}{100}\)

= Rs. \(\frac{129}{5}\)

= Rs. 25.80

Rs. 215 x 12% = Rs. 25.80

3. 110% of 37.8 meters

Solution:

Given 110% of 37.8 meters

= \(\frac{37.8 \times 110}{100} \mathrm{~m}\)

= 41.58m

110% of 37.8 meters = 41.58m

4. 200% of 480 gm

Solution:

Given 200% of 480 gm

= \(\frac{480 \times 200}{100} \mathrm{gm}\)

= 960 gm.

200% of 480 gm = 960 gm.

Question 4. (1)How much is Rs. 2.25 of Rs. 5?

Solution:

Given Rs.2.24 of Rs.5

= \(\frac{2.25}{5} \times 100 \%\)

= 45%

Rs.2.24 of Rs.5 = 45%

“Class 8 WBBSE Maths Chapter 11, Percentage easy explanation”

2. How much is 85 gm of 17 gm?

Solution:

Given 85 gm of 17 gm

= \(\frac{85}{17 \times 1000} \times 100 \%\)

= 0.1%

85 gm of 17 gm = 0.1%

3. How much is 2 kg 250 gm of 0.72 quintal?

Solution:

Given 250 gm of 0.72 quintal

2 kg 250 gm = 2250 gm

0.72 quintal = .72 x 100 x 1000 gm.

= 72000 gm.

∴ \(\frac{2250}{72000} \times 100 \%\)

= \(3 \frac{1}{8} \%=3.125 \%\)

250 gm of 0.72 quintal = \(3 \frac{1}{8} \%=3.125 \%\)

Question 5. Let’s fill up the table below:

Solution:

Question 6. The ratio of hydrogen and oxygen in water is 2:1. Let’s workout the percentage of hydrogen and oxygen in water.

Solution:

Given

Ratio of hydrogen and oxygen in water = 2:1

Sum of ratio = 2 + 1 =3

Hydrogen in water = \(\frac{2}{3}\) part

= \(\frac{2}{3} \times 100 \%\)

= \(66 \frac{2}{3} \%\)

Oxygen in water = \(\frac{1}{3}\) part

= \(\frac{1}{3} \times 100 \%\)

= \(33 \frac{1}{3} \%\)

Of the quantity of water, hydrogen is \(66 \frac{2}{3} \%\) and oxygen is \(33 \frac{1}{3} \%\).

Question 7. 1500 bottles were produced in a factory at Hridaypur. New 1695 bottles are produced there. Let’s workout the percentage increase in production in that factory.

Solution:

Given

1500 bottles were produced in a factory at Hridaypur. New 1695 bottles are produced there.

Bottles were produced in a factory = 1500

New bottles are produced = 1695

Increase in production = (1695 – 4500) = 195

% increase in production = \(\frac{195}{1500} \times 100 \%\) = 13%

The production has increased by 13%.

Question 8. The quantity of Nitrogen, Oxygen and Carbon dioxide in air is 75.6%, 23.04%, and 1.36%. Let’s work out the quantity of each in 25 liters of air.

Solution:

Given

The quantity of Nitrogen, Oxygen, and Carbon dioxide in air is 75.6%, 23.04%, and 1.36%.

In 25 I air nitrogen is = 25 I x 75.6 %

= \(\frac{25 \times 756}{100 \times 10}\)

= 18.9 liters

In 25 I air oxygen is = 25 I x 23.04%

= \(\frac{25 \times 23.04}{100}\)

= 5.76 liters

In 25 I air carbon dioxide is = 251x 1.36%

= \(\frac{25 \times 1.36}{100}\)

= 0.34 I

∴ In 25 I air nitrogen is 18.9 I, oxygen is 5.6 I, and carbondioxide is 0.34.

Question 9. Trisha has bought a book from the book stall of Milan dada. He gave her discounts of 10% and 5% respectively. Let’s work out how much Trisha paid to Milan dada if the M.R.P of the book was Rs. 200.

Solution:

Given

Trisha has bought a book from the book stall of Milan dada. He gave her discounts of 10% and 5% respectively.

Price of book = Rs. 200

First discount = Rs. 200 x 10%

= Rs. \(\frac{200 \times 10}{100}\)

= Rs. 20

Price of book after giving first discount = Rs.(200-20)

= 180

Second discount = Rs. 180×5

= Rs. \(\frac{180 \times 5}{100}\)

= Rs. 9

Price of book after giving second discount = Rs. (180-9)

= 171

Trisha gave Milan Dada Rs. 171.

“WBBSE Class 8 Maths Chapter 11 solutions, Percentage PDF”

Question 10. The length of each arm of a rectangle was increased by 10%. Let’s work out the percentage of increase in area by the rule of three.

Solution:

Given

The length of each arm of a rectangle was increased by 10%.

Let the length of each side of rectangle is 100 units.

∴ Area of the rectangle = (100)2sq.units.

= 10,000sq.units.

Increase in each side of the rectangle = 10%of100

= \(\frac{100 \times 10}{100} \text { units. }\)

= 10 units

∴ After increase, length of each side of the rectangle = (100+10) units

= 110units.

∴ Area of rectangle = (110)2 units

= 12100 units

Increase in area = (12100-10000)

= 2100 units.

% Increase in area of rectangle = \(\frac{2100 \times 100}{10000}\)

= 21%

The area of that rectangle increased by 21%.

There is a direct relation.

Percentage increase in area of rectangle = \(2100 \times \frac{100}{10000}=21 \%\)

Question 11. We get 15% discount if electricity bill is paid in time. My aunt got a rebate of Rs. 54 by paying the bill in time. Let’s v/ork out the total amount of the bill.

Solution:

Given

We get 15% discount if electricity bill is paid in time. My aunt got a rebate of Rs. 54 by paying the bill in time.

Let the bill was Rs. x.

Discount = 15% X. Rs. x

= Rs. \(\frac{X \times 15}{100}\) = Rs. \(\frac{3 x}{20}\)

B.T.P.,

= \(\frac{3 x}{20}=54\)

or x = \(\frac{54 \times 20}{3}\)

or, x = 360

∴ The electricity bill was of Rs. 360.

“WBBSE Class 8 Maths Chapter 11, Percentage important questions”

Question 12. The price of sugar has increased by 20%. Let’s work out the percentage of sugar if the monthly expenses of sugar remained same.

Solution:

Given

The price of sugar has increased by 20%.

Let in Rs. 100r 100 kg sugar is bought and its price is Rs. 100. Increase in the price of sugar = 20% of Rs. 100.

= Rs. \(\frac{100 \times 20}{100}\)

= Rs. 20

∴ After increase new price of 100 kg sugar

= Rs. (100 + 20) = Rs. 120

∴ After increase, in Rs. 120, 100 kg sugar will be bought.

∴ After increase, in Rs. 1, \(\frac{100}{120}\) kg sugar will be bought.

∴ After increase, in Rs. 100, \(\frac{100}{120} \times 100\) kg sugar will be bought.

∴ After increase, in Rs. 100, \(\frac{250}{3}\) kg sugar will be bought.

∴ Decrease in sugar consumption \(=\left(100-\frac{250}{3}\right) \mathrm{kg} .\)

= \(\frac{50}{3} \mathrm{~kg}\)

∴ % decrease in sugar consumption = \(\frac{50 \times 100}{3 \times 100}\)

= \(16 \frac{2}{3} \%\)

∴ If the monthly expenses of sugar remains same, its consumption is to be decreased by 16

= \(16 \frac{2}{3} \%\)

“Class 8 Maths Percentage solutions, WBBSE syllabus”

Question 13. When water freezes into ice, it increases in volume by 10%. Let’s workout in percentage how much it will decrease in volume if the ice melts into water.

Solution:

Given

When water freezes an increase of 10% occurs in volume. If 100 cube units be the volume of ice = (100 + 10) cube units = 110 cubic units

In mathematical language the problem is –

Relation will be – Directly proportional.

∴ Volume of water ( ?) = \(100 \times \frac{100}{110}=\frac{1000}{11}=90 \frac{10}{11}\)

∴ Decrease in volume due to melting = \(\left(100-90 \frac{10}{11}\right)=9 \frac{1}{11} \%\)

∴ There will be \(9 \frac{1}{11} \%\) decrease in volume.

Question14. Due to use of high-yielding seed Utpal babu has got 55% production hike in paddy cultivation. But for this the cost of cultivation has increased by 40%. Previously a yield of Rs. 3000 was produced by investing Rs. 1200. Let’s work out whether his income will be increased or decreased after using high-yielding seeds.

Solution:

Given

Due to use of high-yielding seed Utpal babu has got 55% production hike in paddy cultivation. But for this the cost of cultivation has increased by 40%. Previously a yield of Rs. 3000 was produced by investing Rs. 1200.

Earlier cost in paddy farming = Rs. 1200

Earlier price of yield = Rs. 3000

Increase in cost = 40% of Rs. 1200

= Rs. \(\frac{1200 \times 40}{100}\)

= Rs. 480

New cost after using high-yielding seed = Rs. (1200 + 480)

= Rs. 1680

Increase in yield = 55% of Rs. 3000

= Rs. \(\frac{3000 \times 55}{100}\)

= Rs. 1650

New, the price of yield is = Rs. (3000 + 1650)

= Rs. 4650

Earlier income = Rs. (3000 – 1200)

= Rs. 1800

New income = Rs. (4650 – 1680) = Rs. 2970

Increase in income = Rs. (2970- 1800) = Rs. 1170

∴ Income increased by Rs. 1170

“WBBSE Class 8 Chapter 11 Maths, Percentage step-by-step solutions”

Question 15. In a legislative election 80% voters cast their votes and the winning candidate got 65% of the cast votesi Let’s workout the percentage of total voters who supported him.

Solution:

Given

In a legislative election 80% voters cast their votes and the winning candidate got 65% of the cast votes

Let the total number of voters are 100.

∴ Votes cast = 80% of 100

= \(\frac{100 \times 80}{100}=80\)

Votes got by winning candidate = 65% of 80

= \(\frac{80 \times 65}{110}=52\)

∴ The winning candidate got 52% of the total votes cast.

Question 16. This year the students of Waianda H.S. school have passed 85% in Hindi, 70% in maths and 65% in both subjects A+ scoring. If the number of students are 120 then let’s work out how many students :

Solution:

1. Who got A+ in both subjects
2. Who got A+ only in maths
3. Who got A+ only in Hindi
4. Who got A+ in no subject

Number of students = 120

1. In both subjects got A+

Solution:

= 65% of 120

= \(\frac{120 \times 65}{100}\) = 78 Students

2. Students who got A+ in Maths Only

Solution:

= 70% of 120

= \(\frac{120 \times 70}{100}\) = 84 Students

Who got A+ only in Maths are = (84 – 78) = 6

3. Got A+ in Hindi only

Solution:

Students who got A+ in Hindi = 85% of 120

= \(\frac{120 \times 85}{100}\)

Who got A+ only in Hindi are = (102 – 78) = 24

4. Did not get A+ in both subjects

Solution:

= 120 – (78 + 6 + 24)

= 120-108=12

“WBBSE Maths Class 8 Percentage, Chapter 11 key concepts”

Question 17. The income of Amina bibi was increased by 20% and later decreased by 20%. Let’s workout the total percentage change of her income.

Solution:

Given

The income of Amina bibi was increased by 20% and later decreased by 20%.

Let the original income was Rs. 100.

1st increased = 20% of Rs. 100

= Rs. \(\frac{100 \times 20}{100}\)

= Rs. 20

Income after 1st increase = Rs. (100 + 20)

= Rs. 120

Then decrease = 20% of Rs. 120

= Rs. \(\frac{120 \times 20}{100}\)

= Rs. 24

Income after decrease = Rs. (120 – 24)

= Rs. 96

Decrease in her income = Rs. (100 – 96) = Rs. 4

% decrease in her income = \(\frac{4 \times 100}{100}\)= 4%.

The original income of Amina bibi has decreased by 4%.

“WBBSE Class 8 Maths Chapter 11, Percentage summary”

Question 18. The length of a rectangle is increased by 15% and the breadth is reduced by 15%. Let’s work out the percentage increase or decrease of area.

Solution:

Given

The length of a rectangle is increased by 15% and the breadth is reduced by 15%.

Let the length of rectangle is x units & breadth is y units.

∴ Area of the rectangle = L x B

= x×y sq. units

= xy sq. units

Length of rectangle after 15% increase

= x+xX15%

= \(x+\frac{x \times 15}{100}\)

= \(\frac{23 x}{20}\) units

Breadth of rectangle after 15% decrease = y-y×15%

= \(y-\frac{y \times 15}{100}\)

= \(\frac{17y}{20}\) units

∴ New area of the rectangle = \(\frac{23 x}{20} \times \frac{17 y}{20}\) sq.units

= \(\frac{391 x y}{400}\) sq.units

∴ Decreases in the area of the rectangle = xy – \(\frac{391 x y}{400}\) sq.units

= \(\frac{400 x y-391 x y}{400}\) sq.units

= \(\frac{9 x y}{400}\) sq.units

∴ % decrease in the area of the rectangle = \(\frac{9 x y \times 100}{400 ×x y}=2 \frac{1}{4} \%\)

∴ The area of the rectangle decreased by \(2 \frac{1}{4} \%\).

Question 19. The length, breadth and height of a room are 15 m, 10m and 5 m. If the length, breadth and height are increased by 10 % each then work out the increase of the area of the 4 walls of the room.

Solution:

Given

The length, breadth and height of a room are 15 m, 10m and 5 m. If the length, breadth and height are increased by 10 %

Area of the 4 walls of the room = 2 (15 + 10) x 5 sq.m = 250 sq.m

After 10% increase, length of the room = \(\frac{110}{100} \times 15 \mathrm{~m}=\frac{33}{2} \mathrm{~m}\)

After 10% increase, breadth of the room =\(\frac{110}{100} \times 10\) =11 m

After 10% increase, hight of the room = \(\frac{110}{100} \times 5 \mathrm{~m}\) = \(\frac{11}{2}\) m

After 10% increase, the area of the 4 walls of the room = \(2\left(\frac{33}{2}+11\right) \times \frac{11}{2}\) sq.m

= \(2\left(\frac{33+22}{2}\right) \times \frac{11}{2}\) sq.m

= \(\frac{605}{2}\) sq.m

Increase in the area of the 4 walls of the room

= \(\left(\frac{605}{2}-250\right)\)

= \(\left(\frac{605-500}{2}\right) \mathrm{sq} \cdot \mathrm{m}=\frac{105}{2} \mathrm{sq} \cdot \mathrm{m}\)

Percentage increase in the area of the 4 walls of the room = = \(\frac{105 \times 100}{2 \times 250}\) = 21%

There will be 21 % increase in the area of the 4 walls of the room.

Question 20. In annual sports 20% of the students took part in 100 m race 15% of the students in 200 m sprint and 10% of the students took part in the long jump event. 5% of the students took part in these three events. Let’s work out the number of students who did not take part in any of the events if the total number of the students were 780.

Solution:

Given

In annual sports 20% of the students took part in 100 m race 15% of the students in 200 m sprint and 10% of the students took part in the long jump event. 5% of the students took part in these three events.

Total number of students = 780

Number of students taking part in 100 m race = 20% of 780

= \(\frac{780 \times 20}{100}\)

= 156

Number of students taking part in 200 m race = 15% of 780

= \(\frac{780 \times 15}{100}\)

= 117

Number of students taking part in long jump race = 10% of 780

= \(\frac{780 \times 150}{100}\)

= 78

Number of students taking part in all three games = 5% of 780

= \(\frac{780 \times 5}{100}\)

= 39

Number of students taking part only in 100 m race = (156- 39) = 117

Number of students taking part only in 200 m race = (117- 39) = 78

Number of students taking part only in long jump = (78 – 39) = 39

Number of students who did not take part in any of the three games

= 780-(39+ 117 + 78 + 39)

= 780-273 = 507

The number of students who did not take part in any of the three games = 507

Rule Of Three

Question 1. I have bought a dozen of exercise books from the Banerjee book stall of our locality for Rs. 90 only. Let’s calculate the price of such exercise book by the Rule of three.

Solution:

Given

I have bought a dozen of exercise books from the Banerjee book stall of our locality for Rs. 90 only.

In mathematical language the problem is

No. of exercise books (pcs.) Price of exercise books in Rs.

1 dozen = 12 90

8                  ?

The relation is: If the number of exercise books increases Increase price will increase. If the number of exercise books decreases price Will Decrease decrease.

∴ 12 : 8 :: 90:?

Or, cost of exercise books ( ?) = Rs. 90×8/12

∴ Cost of 8 books = Rs 60

We got, Second quantity variable value =

Question 2. If Rs.1772 is needed for making 7 ploughs, how much will be needed for making 12 ploughs? (apply the rule of three)

Solution:

Given

Rs.1772 is needed for making 7 ploughs

To make more number of ploughs much much less money will be needed.

Number of ploughs and their making costs are Directly (directly/inversely) proportional.

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

“WBBSE Class 8 Maths Chapter 10 solutions, Rule of Three”

Question 3. 24 people had food provision for 20 days. Let’s work out using the method of Rule of Three how long the remaining food will last for 40 people.

Solution:

Given

24 people had food provision for 20 days.

With the same quantity of food the more number of people will cover will cover (much/less) days.

So the number of people and number of days are inversely (direct / inversely) proportional.

Read and Learn More WBBSE Solutions For Class 8 Maths

Rule Of Three Exercise 10.1

Question 1. Today my father has bought 15 kg of rice for Rs. 390. Let’s work out using the Rule of Three method how much he would require if he would have bought the same quality of 17 kg of rice.

Solution:

Given

Today my father has bought 15 kg of rice for Rs. 390.

In mathematical language, the problem is –

Relation will be – If quantity of rice increases the price of rice will increase; so the quantity and price of rice will be directly proportional.

∴ 15: 17:: 390:?

or, \(\frac{15}{17}=\frac{390}{?}\)

∴ Value (?) = \(\frac{17 \times 390}{15}\)

= Rs. 442

∴ Price of 17 kg rice will be 442.

“Class 8 WBBSE Maths Chapter 10 solutions, Rule of Three study material”

Question 2. Venkat uncle will make 4 shirts of same size with 20 meters of cloth. Let’s work out using the rule of three method how many meters of cloth Venkat uncle will have to purchase for making 12 such shirts.

Solution:

Given

Venkat uncle will make 4 shirts of same size with 20 meters of cloth.

In mathematical language, the problem is –

Relation will be – If the number of shirts increases, the quantity of cloth will increase, so they will be directly proportional.

4 : 12 :: 20:?

or, \(\frac{4}{12}=\frac{20}{?}\)

or, Quantity of cloth (?) =\(\frac{12 \times 20}{4}\)= 60 meter

∴ In making 12 shirts 60 meter cloth will be needed.

60 meters of cloth Venkat uncle will have to purchase for making 12 such shirts.

“WBBSE Class 8 Maths Chapter 10, Rule of Three solved examples”

Question 3. It took 15 days for 30 labourers to dig a pond at Bakultala village. Let’s work out using the rule of three method in how many days 25 heads of labourers could have completed the said work.
Solution:

Given

It took 15 days for 30 labourers to dig a pond at Bakultala village.

In mathematical language the problem is –

Relation will be – If the number of days increases, the number of people will decrease, so they will be inversely proportional.

30: 25 :?:15

or, \(\frac{30}{25}=\frac{?}{15}\)

∴ Time(?)= \(\frac{30}{25}\) ×15 = 18 days.

∴ 25 men will require 18 days.

In 18 days 25 heads of labourers could have completed the said work

Question 4. My aunt reached my maternal uncle’s house in five hours by driving the car at a speed of 40 kmph. Let’s work out using the rule of three method how long it would have taken if she would drive the car at a speed of 50 kmph.

Solution:

Given

My aunt reached my maternal uncle’s house in five hours by driving the car at a speed of 40 kmph.

In mathematical language the problem is – Speed of Car (kmph) Time (in hours)

Relation will be – If speed of car increases, time will decrease, so they are inversely proportional.

∴ 40 : 50 : 5

or, \(\frac{40}{50}=\frac{?}{5}\)

or. Time (?) = \(\frac{40}{50} \times 5=4\)

∴ 50 kmph speed will require 4 hours time.

Question 5. There was a stock of food grains for 9 days to cater the needs of 4000 people in a shelter camp in Mongalpur village. After 3 days 1000 people left the camp for another place. Let’s work out for how many days the rest of people will consume.

Solution:

Given

There was a stock of food grains for 9 days to cater the needs of 4000 people in a shelter camp in Mongalpur village. After 3 days 1000 people left the camp for another place.

Stock of food grains for 9 days to cater = 4000

After 3 days people left the camp = 1000

3 days later number of remaining people (4000 – 1000) = 3000

Remaining food grains for = (9-3) days = 6 days

In mathematical language the problem is –

Relation will be – If number of people decreases the foodgrains will last longer, so they are inversely proportional.

4000 : 3000 : : ? : 6

or, \(\frac{4000}{3000}=\frac{?}{6}\)

or, Time ( ?) = \(\frac{4000}{3000} \times 6=8\)

Remaining people will consume the food for 8 days.

“WBBSE Class 8 Rule of Three solutions, Maths Chapter 10”

Question 6. 42 labourers of a farm at Nasirpur village can cultivate the entire land of the farm in 24 days. But suddenly 6 labourers became ill during the period of cultivation. Let’s work out using the rule of three method how many days it will take to cultivate the entire land of the farm by the rest of the labourers.

Solution:

Given

42 labourers of a farm at Nasirpur village can cultivate the entire land of the farm in 24 days. But suddenly 6 labourers became ill during the period of cultivation.

Labourers of a farm at Nasirpur village = 42

Suddenly labourers became ill during the period of cultivation = 6

Members becoming ill, remaining left = (42 – 6) = 36 In mathematical language the problem is-

Relation will be – if number of members decreases then the number of days will increase. So they are inversely proportional.

∴ 42 : 36 : 24

or, \(\frac{42}{36}=\frac{?}{24}\)

or, Time ( ?) = \(\frac{24 \times 42}{36}\) x 42 = 28 days

Rest of the labourers will require to cultivate 28 days.

“Class 8 WBBSE Maths Chapter 10, Rule of Three easy explanation”

Question 7. It take 27 days to make 1000 spare parts by 16 numbers of machines. Let’s work out using the rule of three method how many days it will take to make the same number of spare parts if additional two machines are installed.

Solution:

Given

It take 27 days to make 1000 spare parts by 16 numbers of machines.

2 machines are installed, new number = 16 + 2 =18

In mathematical language, the problem is –

Relation will be – If number of machines increases, number of days will decrease, so they are inversely proportional.

16 : 18 :: ? : 27

or, \(\frac{16}{18}=\frac{?}{27}\)

or, Time ( ?) = \(\frac{16}{18}\) x 27 = 24

18 machines will require 24 days to produce same number of spare parts in 24 days.

Question 8. See the relations below, express them in mathematical language, and solve by using rule of three.

Solution:

If prices are of Rs. 112.50 then what will be the value of 12 pens?

Relation will be – If number of pens increases, its price will increase, so they are directly proportional.

∴ 25 : 12 :: 112.5: ?

or, \(\frac{25}{12}=\frac{112.5}{?}\)

∴  Value ( ?) = \(\frac{12 \times 112.5}{25}\)

= 54

∴ 12 pens will value Rs. 54.

A car with velocity 9 kmph, in a given time, can cover 112.5 km distance.

The same car will cover how much distance in the same time with speed 12 kmph? .

Relation will be – If velocity increases, distance will-increase, so they are directly proportional.

∴ 9:12:: 112.5 : ?

or, \(\frac{9}{12}=\frac{112.5}{?}\)

or, Distance ( ?) = \(\frac{12 \times 112.5}{9}\)

or, Distance ( ?) = \(\frac{12 \times 1125}{9 \times 10}\)

= 150

That car with speed 12 kmph in the given time will cover 150 km distance.

6 pumps in a given time can irrigate 31.2 Bigha land, 13 pumps in the same time will cultivate how much ?

Relation will be – If number of pumps increases, measure of land will increase, so they are directly proportional.

∴ 6 : 13: : 31.2:?

or, \(\frac{6}{13}=\frac{31.2}{?}\)

or, Measure of land ( ?) = \(\frac{13 \times 31.2}{6}\)

= \(\frac{13 \times 312}{6 \times 10}\)

= \(\frac{13 \times 52}{10}\)

= 67.6 Bighas.

13 pumps in the same time will cultivate 67.6 bighas land.

If each student eats 306 gm grains, total grains required for 425 students = 306 x 425 gm = 130050 gm If in a school for 425 students 130050 gm grain is required then if students are 458 how much grain will be required?

Relation will be – If number of students increases, amount of grain

will increase, so they are directly proportional.

∴ 425 : 458 :: 130050 : ?

or, \(\frac{425}{458}=\frac{130050}{?}\)

or, Measure of grain ( ?) = \(\frac{458 \times 130050}{425}\)

= \(\frac{458 \times 5222}{17}\) gm.

“WBBSE Class 8 Maths Chapter 10 solutions, Rule of Three PDF”

Question 9. The walls and boundary walls of Bapan’s house are to be built. So, masons are working for building the wall. Let’s work out using the Rule of Three method how many days it will take for 10 masons tp build 320 sq.m, of walls if 5 masons can build 120 sq m. of walls in 4 days.

Solution:

Given

The walls and boundary walls of Bapan’s house are to be built. So, masons are working for building the wall. L

In mathematical language the problem is –

There are three items :

1. No. of masons
2. Time,
3. Quantity of work

Let’s find the relation in two steps.

First step – During the same work if the number of masons increases then the time will decrease (much / less) and if number of masons decreases time will much (much / less). The number of masons and time are inversely (inversely/directly) proportional.

∴ ?:4:: 5: 10

Required time = \(4 \times \frac{5}{10}\)

Required time = 2 days ‘ Second step – If the number of masons is constant, the time will be needed for doing more work much (More / less) amount of work is less, time is needed will cover (More / less). So number of masons and amount of work are Directly (directly / Inversely) proportional.

So, 7:2:: 320 : 128

Required time = \(2 \times \frac{320}{128}\) days = 5 days – 64

So we get putting two steps together-

∴ Required time = \(4 \times \frac{5}{10} \times \frac{320}{128}\) days = 5 days 32

Question 10. Milkman Mahesh of Rashedpur fed 4 bundles of straw to 8 cows for 15 days. Let’s work out using the rule of three method how many bundles of straw will have to be stored to feed 10 cows for 72 days during raing season.

Solution:

Given

Milkman Mahesh of Rashedpur fed 4 bundles of straw to 8 cows for 15 days.

In mathematical language, the problem is –

Let’s find the relation.

First step- If the number of cows increases, the quantity of straw will Increase (increase / decrease) and if the number of cows decreases, straw will be will cover (More / less).

Second step – If the number of cows remains constant then the quantity of straw will Increase (increase / decrease) and if time decreases, quantity of straw less (more/less).

∴  With time quantity of straw is Direct (inversely / directly)

The required amount required of straw = \(4 \times \frac{10}{8} \times \frac{72}{15}\) = 24 bundles.

Rule Of Three Exercise Exercise

Question 1. The work for construction of the village road will be started. It has been decided that 14 people will work 4 hours daily for 15 days to complete the total work. Let’s work out using the rule of three method how long it will take to complete the work by 24 people working 7 hours daily.

Solution:

Given

The work for construction of the village road will be started. It has been decided that 14 people will work 4 hours daily for 15 days to complete the total work.

In mathematical language the problem is –

Relation will be – If number of people and daily hours of work increase, days will decrease, so they are inversely proportional.

∴ Required days ( ?) = \(15 \times \frac{14 \times 4}{24 \times 7}\)=5

24 people do daily 7 hours work then the work will be is completed in 5 days.

Question 2. In a book of 105 pages written by Subhash uncle there are average 25 lines in each page and there are average 8 words in each line. Let’s work out using the rule of three method how many pages will be there in the book if there are 30 lines in each page having 10 words in each line.

Solution:

Given

In a book of 105 pages written by Subhash uncle there are average 25 lines in each page and there are average 8 words in each line.

In mathematical language the problem is –

Relation will be – If number of words and number of lines increase, number of pages will decrease, so they are inversely proportional.

∴ Number of pages = 105×\(\frac{8 \times 25}{10 \times 30}\)

= 70

There will be 70 pages.

“WBBSE Class 8 Maths Chapter 10, Rule of Three important questions”

Question 3. 540 bighas of land of an agricultural farm are to be cultivated in 14 days. 120 bighas of land was cultivated in first 4 days by 5 tractors of equal strength. Let’s work out using rule of three method how many tractors are required to complete the cultivation in time.

Solution:

Given

540 bighas of land of an agricultural farm are to be cultivated in 14 days. 120 bighas of land was cultivated in first 4 days by 5 tractors of equal strength.

540 bighas of land of an agricultural farm are to be cultivated = 14 days

120 bighas of land was cultivated = 4 days

After 4 days cultivating land,

Remaining days = (14 – 4) = 10

Remaining land = (540 -120) = 420 bighas

Relation will be – If number of days increases, and days also, number of tractors will decrease.

∴ Number of tractors (?) = \(5 \times \frac{420}{120} \times \frac{4}{10}\)

= 7

Number of more tractors = (7-5) = 2

For cultivating land an additional of 2 tractors are required.

Question 4. 30 heads of people repair 3/7 part of a road of a village in 15 days. Let’s work out using the method of rule of three how many days it will take to repair the rest of the road if additional 10 heads of people join.

Solution:

Given

30 heads of people repair 3/7 part of a road of a village in 15 days.

Remaining Work  \(=\left(1-\frac{3}{7}\right)=\frac{4}{7}\) Part

Number of people = (30+10) = 40 In mathematical language the problem is-

Relation will be – If number of people and part of work decrease, days will increase.

∴ Required days ( ?) = \(15 \times \frac{30 \times 4 \times 7}{40 \times 7 \times 3}=15\)

To repair the remaining road 15 days are required.

Question 5. A pump of 5 HP can lift 36000 L of water in 8 hrs. Let’s work out using rule of three method how long it will take to lift 63000 L water by a 7 HP pump.

Solution:

Given

A pump of 5 HP can lift 36000 L of water in 8 hrs.

In mathematical language the problem is –

Relation will be – If HP increases time will decrease. If quantity of water increases time will increase.

∴ Required time = \(8 \times \frac{5}{7} \times \frac{63000}{36000}\)

= 10 hours

10 hours time is required.

“Class 8 Maths Rule of Three solutions, WBBSE syllabus”

Question 6. There are two motors of 5 HP and 3 HP in a factory. The 5 HP motor requires 20 units of electricity in 8 hrs. Let’s work out using the rule of three how many units will be required if the 3 HP motor works for 10 hours.

Solution:

Given

There are two motors of 5 HP and 3 HP in a factory. The 5 HP motor requires 20 units of electricity in 8 hrs.

In mathematical language the problem is –

Relation will be – If HP and time increase, electricity will increase

∴ Required electricity ( ?) = \(20 \times \frac{3}{5} \times \frac{10}{8}\) units

= 15 units

∴ If 3 HP motor 10 hours use requires 15 units of electricity.

Question 7. In a loom at Gopalnagar 14 weavers can weave 210 sarees in 12 days. The workshop got an order to supply 300 sarees within 10 days during the pujas. Let’s work out using the rule of three how many extra weavers have to be employed to complete the work in time.

Solution:

Given

In a loom at Gopalnagar 14 weavers can weave 210 sarees in 12 days. The workshop got an order to supply 300 sarees within 10 days during the pujas.

In mathematical language the problem is-

The relation will be – If days increase, weavers will decrease and if number of sarees increase, weavers will increase.

∴ Number of weavers = \(14 \times \frac{12}{10} \times \frac{300}{210}\)

= 24

Number of more weavers = (24- 14) = 10

To complete the work in time 10 more weavers are required.

“WBBSE Class 8 Chapter 10 Maths, Rule of Three step-by-step solutions”

Question 8. A company has got the work of unloading goods from a ship in 10 days. 280 people have been employed for this purpose. After 3 days it is seen that 1/4th of the work has been completed. Let’s work out using the rule of three method how many people are to be engaged to complete the work in time.

Solution:

Given

A company has got the work of unloading goods from a ship in 10 days. 280 people have been employed for this purpose. After 3 days it is seen that 1/4th of the work has been completed.

3 days later remaining work = \(\left(1-\frac{1}{4}\right) \frac{3}{4}\) = part

Remaining Time = (10 – 3) = 7 days

In mathematical language, the problem is –

Relation will be – If work increases number of people will increase. If days increase number of people will decrease.

∴ Number of people = \(280 \times \frac{3}{4} \times \frac{4}{1} \times \frac{3}{7}\) = 360

Number of more people = (360 – 280) = 80

To complete the work in time 80 more people are required.

Question 9. A power loom is 2 \(\frac{1}{4}\) times powerful than a hand loom. 12 hand looms weave 1080 m of length of cloth is 18 days. Let’s work out by the rule of three how many powerlooms would be required to weave 2700 m length of cloth in 15 days.

Solution:

Given

A power loom is 2 \(\frac{1}{4}\) times powerful than a hand loom. 12 hand looms weave 1080 m of length of cloth is 18 days.

In mathematical language the problem is –

Relation will be – If length of cloth increases number of powerlooms increases and if days decrease, number of powerlooms will increase.

∴ Number of landlooms (?) = 12 × \(\frac{27000}{1080} \times \frac{18}{15}\)

= 36

∵ \(frac{9}{4}\)handlooms1 production = 1 Powerlooms’ production

∴ 1 handlooms’ production = \(\frac{4}{9}\) Powerlooms’ production

∴ 36 handlooms’ production = \(\frac{4}{9} \times 36\) Powerlooms’ production

= 16 Powerlooms’ production

To complete 2700 m long clpth in 15 days, 16 powerlooms are required.

Question 10. 2400 bighag of land of a cooperative society can be cultivated by 25 farmers in 36 days. It was seen that half of the land of the society could be cultivated in 30 days after purchasing a tractor. Let’s work out the power of a tractor equivalent to the number of farmers using the rule of three.

Solution:

Given

2400 bighag of land of a cooperative society can be cultivated by 25 farmers in 36 days. It was seen that half of the land of the society could be cultivated in 30 days after purchasing a tractor.

In mathematical language the problem is –

Relation will be – It area of land increases, number of farmers will increase. If number of farmers decrease, days wiH increase.

∴ Number of farmers = \(25 \times \frac{1200}{2400} \times \frac{36}{30}\)= 15

∴ A tractor’s power is equal to 15 farmers.

Question 11. A ship takes 25 days to Sail from Kolkata to Cochin. The ship started With 36 sailors for each of which 850 gm of food was alloted. But the ship rescued 15 sailors from another sinking-ship after 13 days of journey and the ship reached Cochin in 10 days increasing the speed. Let’s work out using the method of the rule of three what will be the quantity of food of each sailor will require to reach cochin safely if entire storage of food could be consumed by this time.

Solution:

Given

A ship takes 25 days to Sail from Kolkata to Cochin. The ship started With 36 sailors for each of which 850 gm of food was alloted. But the ship rescued 15 sailors from another sinking-ship after 13 days of journey and the ship reached Cochin in 10 days increasing the speed.

13 days later:

Number of sailors =36+15

= 51

Food for remaining days = (25-13)

= 12 days

In mathematical language, the problem is –

Relation will be – If number of sailors and days increase, food stock will decrease.

∴ Food stock (?) = \(850 \times \frac{36}{51} \times \frac{12}{10}\)

Every sailor will comsume 720 gm per day.

Question 12. 36 people of a certain village construct 120 m of road by 8 people working 6 hours daily. Another 6 people are involved in this work and the duration of work of each day is increased by 2 hours. Find the length of road to be constructed in 3 days.

Solution:

Given

36 people of a certain village construct 120 m of road by 8 people working 6 hours daily. Another 6 people are involved in this work and the duration of work of each day is increased by 2 hours.

In mathematical language, the problem is –

Relation will be – If number of people increases, work will increase. If hours increase, work will increase. If days increase, work will increase.

Length of road (?) = \(120 \times \frac{42}{36} \times \frac{8}{6} \times \frac{9}{8}\)

= 210

Now, in 9 days 210 m long road can be constructed.

Question 13. 250 people can excavate a pond of size 15m long, 35 m wide and 5.2 m deep in 18 days by working 10 hours daily. Let’s work out using the rule of three method how many days it will take-for 300 people to excavate a pond of size 65 m long, 40 m wide and 5.6 m deep by working 8 hours daily.

Solution:

Given

250 people can excavate a pond of size 15m long, 35 m wide and 5.2 m deep in 18 days by working 10 hours daily.

In mathematical language, the problem is –

Number of people Volume of pond Work per day Days (L x B x H) time (hours)

Relation will be – If number of people increases, days will decrease. If volume of pond increases, days will increase.

∴ Required days (?) = \(18 \times \frac{250}{300} \times \frac{65 \times 40 \times 5.6}{50 \times 35 \times 5.2} \times \frac{10}{8}\)

= 30

∴ 30 days are required.

“WBBSE Maths Class 8 Rule of Three, Chapter 10 key concepts”

Question 14. Let’s make mathematical problems with the help of given relations and find out their solutions by rule of three.

Solution:

If 5 famers can cultivate 18 bigha land in 15 days then 10 farmers will cultivate how many bighas land in 10 days?

Relation will be – If number of farmers and days increase, quantity of land will increase.

∴ Quantity of land (?) = \(18 \times \frac{10}{5} \times \frac{10}{15}\) = 24 Bigha

∴ 24 Bighas land can be cultivated by 10 farmers in 10 days.

Properties Of Parallel Lines And Transversal

The transversal is PQ [AB/PQ] but there is transversal.

My sister Sahali formed a transversal as in the picture shown below by fixing bits of cardboard with the help of nails.

As a result of it, many angles have been formed. She has named some of the angles. Measuring with a protractor I have seen∠1=∠3 again ∠2=∠4; they are VOA angles.

Again,∠5=vercically opposite ∠7and ∠6 vertically opposite Angle = angle ∠8

4 pairs of corresponding angles are (∠l and ∠5), ( ∠2 and ∠6]),(∠4 and ∠8), and (∠3 and∠7])

It is seen by measuring with a protractor ∠1 =110° and ∠5 = 110°

“WBBSE Class 8 Maths Chapter 8 solutions, Properties of Parallel Lines and Transversal”

[ Let’s draw parallel lines and their transversals and write by measuring corresponding angles ]

Read and Learn More WBBSE Solutions For Class 8 Maths

∴∠1 = ∠5

and ∠2=70° and ∠6=70°

∴∠2 = ∠6

[ Let’s write and measure ]

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

Pritam, Sonali, Seemanta, and Meher, them, drew a pair of parallel lines and transversal in their respective exercise book. By measuring the corresponding angles by the protractor they say the measurement of each angle is the same. [Let’s draw and write]

 

AB and CD are two parallel straight lines. A transversal EF is drawn which cuts both transversals, at M and N points respectively.

Here four pairs of corresponding angles are the following :

∠1 and ∠5, ∠2and ∠6, ∠4 and ∠8, ∠3and ∠7

∠1 = 120° and ∠5= 120°  ∴ ∠1 =∠5

∠2 = 60°and ∠6=60°  ∴ ∠2=z6

∠4 = 60° and ∠8= 60°  ∴ ∠4 = ∠8

∠3 = 120° and ∠7= 60°  ∴ ∠3=∠7

Two pairs of alternate angles on the blackboard are (∠4 and ∠6), (∠3 and ∠5)

It is seen by measuring with a protractor, ∠4 = 70° and ∠6 = 70°,

“Class 8 WBBSE Maths Chapter 8 solutions, Parallel Lines and Transversal study material”

[ Let’s draw parallel lines and their transversals and write the measurement of alternate angles by measuring with a protractor]

∴ ∠4=∠6

and ∠3=70° and ∠5=70°

∴ ∠3≠∠5 [=/≠put]

Four of our friends have drawn two parallel lines and their transversal in their exercise books. Two pairs of alternate angles have been named and measuring with a protractor, it is seen that the measurements of alternate angles are equal.

[Let’s draw and examine]

Two parallel lines AB and CD and transversal EF are drawn, which result in a pair of alternate angles ∠1 and ∠4 and ∠2 and ∠3, formed.

∠1 = 75°, ∠4= 75°

∴ ∠1 = ∠4

∠3 = 115°, ∠2= 115°

∴ ∠2 = ∠3

If a straight line intersects two parallel lines then the interior angles opposite to the transversal form a pair of alternate angles.

“WBBSE Class 8 Maths Chapter 8, Properties of Parallel Lines and Transversal solved examples”

Measurement of each pair of these angles is [ equal/ unequal]. (∠3and ∠6) (and ∠4 and ∠5) It is seen by measuring with a protractor,

∠3= 110° and ∠6 = 70° and

∠4= 70° and ∠5 = 110°

It seen that ∠3+∠6=180° and ∠4+∠5=180°

∠1 and ∠3 and ∠2 and ∠4

In figure 1, ∠1=70°,∠3=110º

∠2=110°,∠4=70°

∴ ∠1+∠3=180° and ∠2+∠4=180°

In figure 2, ∠1+∠3=180° and ∠2+∠4=180°

In figure 3,  ∠1 + ∠3 = 180° and ∠2 + ∠ 4 = 180°

In figure 4, ∠1 + ∠3 = 180° and ∠2 +∠4 = 180°

If a straight line intersects two parallel lines then the sum of measurement of two interior angles in the same side of the transversal is 2 right angles. Nipa drew many pairs of the parallel lines and nonparallel lines. I draw transversal of each pair. Consequently, corresponding angles, alternate angles, and interior angles in the same side of transversal have been formed.

1. ∠1 = ∠2
2. ∠1≠ ∠2
3. ∠1 ≠∠2(=/≠)
4. ∠1 ≠2(=/≠)
5. ∠1 =∠2 (=/≠)
6. ∠1 + ∠2= 120° degree
7. ∠1 +∠2=180° degree’
8. ∠1 +∠2 = 210° degree

I have drawn a few more. Let’s see what I have. got.

Let’s verify by placing two interior angles ∠3 and ∠6 in the same side of the transversal whether ∠3 + ∠6 = [180°] is true or not.

Let’s write in the table below as we get by activity-

Now I have drawn two straight lines on my exercise book and their transversal. I have measured alternate angles with a protractor.

It is seen when the measurement of the alternate angles are equal then the straight fines are parallel.

 [parallel/nonparallel [let’s write & verify],

I draw two straight lines and a transversal on the exercise book. Let’s measure the corresponding angles are equal then two straight lines are parallel (Parallel/unparallel)

If a straight line intersects a pair of straight lines and the measurement of one pair of corresponding angles is equal then the two straight lines are parallel to each other.

Priya has drawn a pair of straight lines and their transversal on the blackboard. Consequently, many interior angles have been formed.

“WBBSE Class 8 Parallel Lines and Transversal solutions, Maths Chapter 8”

I will see by measuring with a protractor whether the interior angles on the same side of the transversal are supplementary with one another, i.e., the sum of the interior angles of the same side of the transversal is 2 right angles.

Measuring we get ∠1 + ∠2 = 80° Measuring we get ∠1 + ∠2= 120

It is seen by using a scale that AB and CD are parallel [ Parallel/ unparallel ]

In the second figure AB and CD are unparallel [ Parallel/unparallel ]

Properties Of Parallel Lines And Transversal Exercise

Question 1. Chandra takes ruled paper. She draws a transversal between two lines. As a result, 4 corresponding angles, two pairs of alternate angles, and two pairs of interior angles are formed. Let’s find out and number them. Verify by measuring with a protractor:

Solution:

Given

Chandra takes ruled paper. She draws a transversal between two lines. As a result, 4 corresponding angles, two pairs of alternate angles, and two pairs of interior angles are formed.

Corresponding angles are equal in measure;

Alternate angles are equal in measure; and,

The interior angles on the same side of a traversal are supplementary.

AB and CD are two parallel lines and EF is a transversal. 4 pairs of corresponding angles are: ∠1 and ∠2, ∠3 and ∠4, ∠5 and ∠7, ∠6 and ∠8

2 pairs of alternate angles are :

∠3and ∠7, ∠6and ∠2

2 pairs of interior angles are :

∠3 and ∠2, ∠6 and ∠7

1. ∠1 = 110° and ∠2 = 110°  ∴ ∠1 = ∠2

∠1 =70°and ∠7 = 70°  ∴ ∠5= ∠7

∠3 = 70° and ∠4 = 70°  ∴ ∠3= Z4

∠6 = 110°and ∠8 = 110° ∴  ∠6- ∠8

2. ∠3 = 70° and ∠7 = 70°  ∴ ∠3= ∠7

∠6 = 110°and ∠2 = 110° ∠6 = ∠2

3. ∠3 = 70°and ∠2 = 110°.∠3 + ∠2 = 180°

∴ Supplementary to each other.

∠6 = 110° and ∠7 = 70°  ∴ ∠6+∠7=180°

Question 2. Let’s see and write from the figure beside which are corresponding angles, which are alternate angles and which are the interior angles in the same of the transversal.

Solution:

Corresponding → ∠1 and ∠5, ∠2and∠6

∠4and ∠8, ∠3and ∠7

Alternate →  ∠4 and ∠6,∠3and ∠5

Interior angles in the same side of the transversal ∠4 and ∠5, ∠3 and ∠6 are supplementary to each other.

“Class 8 WBBSE Maths Chapter 8, Properties of Parallel Lines easy explanation”

Question 3. If AB||CD then let’s write the measurement of the angles given below :

Solution:

Given

AB||CD

The measurement of the angles given below

Question 4. In the figure beside if XY||PQ, write the measurement of 7 angles.

Solution:

Given

XY||PQ

The measurement of 7 angles are given below

∠1=130°, ∠2=50°, ∠3=130°, ∠4=130°, ∠5=50°, ∠6=130°, ∠7=50°

Question 5. Examining the measurement of the angles given below let’s conclude logically that AB & CD are parallel.

Solution:

1. In figure 1 the sum of interior angles in same side of transversal isn’t 180°, so AB and CD are not parallel.
2. In figure EF stands on sraight line AB. Measurement of adjacent angle is 60°. Corresponding angle of this angle is 60°. So AB and CD are parallel.
3. The measurement of corresponding angles is unequal. So AB and CD aren’t parallel.

Question 6. In figure AB||CD and ∠EGB = 50°; find the measure of ∠AGE, ∠AGH, ∠BGH.∠GHC, ∠GHD, ∠CHF and ∠DHF.

Solution:

Given

In figure AB||CD and ∠EGB = 50°

∠AGE = 130°, ∠AGH = 50°, ∠BGH = 130°, ∠GHC = 130°, ∠GHD = 50°, ∠CHF = 50°, ∠DHF = 130°

Question 7.

From figure AB||CD; find the measure of ∠PQR.

Solution:

 

AB and CD are parallel and PQ and QR intersect at Q. From point Q parallel to AB a straight line QM is drawn.

∴ QM||AB and QM||CD

∠APQ = alternate ∠PQM = 30°

∠CRQ = alternate ∠RQM = 40°

∠PQR = ∠PQM + ∠RQM = 30° + 40° = 70°

Question 8.

“WBBSE Class 8 Maths Chapter 8 solutions, Parallel Lines and Transversal PDF”

From the figure PQ||RS, ∠BPQ = 40°; ∠BPR=155° and ∠CRS = 70°. Find the value of the angles of A APR.

Solution:

Given

From the figure PQ||RS, ∠BPQ = 40°; ∠BPR=155° and ∠CRS = 70°.

∠BPQ = 40°, ∠BPR = 155°

∴ ∠QPR = ∠BPR – ∠BPQ = 155°-40° = 115°

∴ PQ//RS  ∴ ∠QPR + ∠PRS = 180°

∴ ∠PRS = 180° -∠QPR = 180° – 115° = 65°

In Δ APR ∠APR = 180° – ∠BPR = 180° – 155° = 25°

∠ARP = 180° – (∠CRS + ∠PRS)

= 180° – (70°+65°)

= 180° – 135° ,

= 45°

∠ARP = 45°

∴ ∠APR = 180° – (25° + 45°)

∠APR = 180° – 70°= 110°

∠APR = 110°

Question 9. In midst of two parallel lines AB and CD is a point O. OP and OQ respectively are perpendicular to parallel lines AB and CD. Prove that P,0,Q all are concurrent.

Solution:

Given

In midst of two parallel lines AB and CD is a point O. OP and OQ respectively are perpendicular to parallel lines AB and CD.

∴ OP⊥ AB

∴ ∠OPB = 90°

∴ On point P sum of the adjacent angles is = 90° + ∠1 = 180°

∴ ∠1 = 180°- 90° = 90°

∴ Both external sides lie on a same straight line.

Again, OQ⊥CD

∴ ∠OQD = 90°

∴ On point Q the sum of adjacent angles is

= 90° + ∠2 = 180°.

∠2 = 180° – 90° = 90°

∴ Both external sides lie on a same straight line.

∴ P, O, Q all three are concurrent.

“WBBSE Class 8 Maths Chapter 8, Properties of Parallel Lines and Transversal important questions”

Question 10. The diagonal AC of two angles is parallel to each other. Let’s prove either these angles are equal in measurement or they are supplementary.

Solution:

Given

The diagonal AC of two angles is parallel to each other.

∴ AB||DE and BC a transversal.

∴ ∠ABC= ∠BDE (Alternate angles)

Again BC||EF and DE is a transversal.

∠BDE=∠DEF(Alternate angles).

∴ ∠ABC = ∠DEF Proved

Question 11. The diagonal AC of the parallelogram ABCD bisects ∠BAD. Let’s prove that the diagonal AC also bisects ∠BCD.

Solution:

Given

The diagonal AC of the parallelogram ABCD bisects ∠BAD.

In the parallelogram, ABCD AB||DC and AC is a transversal.

∴ ∠BAC = alternate ∠ACD

and ∠DAC = alternate ∠ACB

AC is the bisector of ∠BAD

∴ ∠BAC = ∠DAC

∴ ∠ACD = ∠ACB

∴ AC diagonal also bisects ∠BCD

Question 12. Let’s prove that if one angle of a parallelogram is a right angle, then all other angles of the parallelogram are also right angles.

Solution:

Let ABCD is a parallelogram whose ∠ABC=1 right angle.

“Class 8 Maths Properties of Parallel Lines and Transversal solutions, WBBSE syllabus”

We have to prove that ABCD is a parallelogram whose each angle is a right angle.

Proof : ∵ ABCD is a parallelogram.

∴ ∠ABC = ∠ADC

∴ ∠ABC = 1 right angle ∠ADC = 1 right angle

∴ AB||DC and BC is a transversal.

∴ ∠ABC + ∠BCD = 2 right angles

or, 1 right angles + ∠BCD = 2 right angles

or, ∠BCD = 1 right angle

∴ ∠BAD = ∠BCD = 1 right angle

∴ In parallelogram ABCD each angle is a right angle.

Relation Between Two Sides Of A Triangle And Their Opposite Angles

Subina has formed many colourful pieces of cardboard. Now she is trying to make a simple closed figure with three colourful pieces of cardboard and nails.

She makes –

Measurements of opposite angles equal [ equal/unequal ]

“WBBSE Class 8 Maths Chapter 9, Relation Between Two Sides of a Triangle and Their Opposite Angles solved examples”

Tapan drew a triangle MAT in which MA=MT. Let’s prove logically and step by step that ΔMAT ∠MAT= ∠MTA

Given: MAT is a triangle where MA = MT. Prove that ∠MAT = ∠MTA.

Construction: In A MAT MX the bisector of ZAMT, is drawn which cuts AT at X.

Proof: ΔMAX and ΔMXT

MA = MT .

∠AMX = ∠TMX [ MX is the bisector of ∠AMT] MX is common to both.

∴ΔMAX = ΔMXT(S-A-S)

∴∠MAX = ∠MTX, i.e., ∠MAT = ∠MTA Proved

“WBBSE Class 8 Maths Chapter 9 solutions, Triangle sides and opposite angles PDF”

Read and Learn More WBBSE Solutions For Class 8 Maths

Now we draw such triangles where measurement of two angles are equal. Let’s find the length of sides of these triangles by scale.

Let measure by scale,

In ΔABC AB=1.5cm, BC=1.5cm, and CA=2.1cm

ΔPQR PQ=1.7cm, QR=1.7cm and RS= 1.7cm

ΔXYZ XY=2cm,YZ=2cm and ZX=3.5cm

It is seen that the length of the sides are equal] [equal/unequal]

Relation Between Two Sides Of A Triangle  Exercise

Question 1. Let’s see the isoceles triangles below and let’s write without measuring which angles are equal in measurement in each triangle.

Solution:

In ΔABC ∠BAC = ∠BCA = 70°

In ∠ABC is drawn BD which cuts AC at D.

ΔABD and ΔBCD

∠ABD = ∠CBD = 20° [∵ BD in bisector of Z BAC ]

∠BAD = ∠BCD (Given)

And BD is common.

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

∴ ΔABD ≅ ΔBCD (A-A-S)

∴ AB = BC

In ΔPQR , ∠QOR = Z PRQ = 45°

∴ PQ = QR

In ΔXYZ ∠YXZ = ∠YZX = 35°

∴ XY = YZ

“WBBSE Class 8 Maths Chapter 9 solutions, Relation Between Two Sides of a Triangle and Their Opposite Angles”

Question 2. Let’s see the isoceles triangles below and let’s write without measuring which angles are equal in measurement in each triangle.

Solution:

The angles are equal in measurement in each triangle are

In ΔABC AB = BC = 5 cm.

∴∠ACB = ∠BAC

In ΔPQR PQ = PR = 8 cm.

∴∠PRQ = ∠PQR

“WBBSE Class 8 Triangle sides and opposite angles solutions, Maths Chapter 9”

Question 3. Line segments AB and CD intersect each other at O. Let’s prove that AC and BD are parallel. Let’s write what kind of quadrilateral is ABCD.

Solution:

Given

Line segments AB and CD intersect each other at O.

AB and CD are straight lines which bisect each other at O, i.e.,

AO = OB and CO = OD.

Prove that AC and BD straight lines are parallel to each other.

Proof: In ΔAOD and ΔBOC

AO = OB and CO = OD

And ∠AOD = Vertically Opposite Angle ∠BOC

∴ ΔAOB ≅ ΔBOC (S-A-S)

∴ AD = BC

Now, In ΔAOC and ΔBOD

AO = OB and CO = OD

and AOC = Vertically Opposite Angie ∠BOD

∴ ΔAOC = ΔBOD

∴ AC = BD

The lengths of opposite sides of □ ABCD are equal and the lengths of both diagonals are equal.

ABCD is a rectangle and AC = BD. Proved

“Class 8 WBBSE Maths Chapter 9 solutions, Triangle sides and opposite angles study material”

Question 4. E and F are two points on two straight lines AB and CD respectively. O is the mid point of line segment EF; we draw a straight line passing through O which intersects AB and CD at P and Q respectively. Let’s prove that O bisects the line segment PQ.

Solution:

Given

E and F are two points on two straight lines AB and CD respectively. O is the mid point of line segment EF; we draw a straight line passing through O which intersects AB and CD at P and Q respectively.

AB//CD and O is the midpoint of, EF i.e., OE = OF Prove that PO = OQ.

Proof: In ΔEOP and ΔQOF

∠EOP = Vertically Opposite Angle ∠FOQ

OE = OF

and ∠PEO = alternate ∠OFQ (∵ AB//CD and EF is a transversal)

∴ ΔEOP ≅ ΔQOF (A – A – S)

∴ PO = OQ, i.e., PQ straight line is bisected at O.

Question 5. If we produce the base of an isoceles triangle in both sides then two exterior angles are formed. Let’s prove that they are equal in measurement.

Solution:

Given

If we produce the base of an isoceles triangle in both sides then two exterior angles are formed.

ABC is an isoceles triangle where AB = AC. Base of isosceles ΔABC base, BC is extended to BD and CE on both sides.

∠ABD = ∠ACE

In ΔABC, AB = AC

∴ ∠ABC = ∠ACB

∵ AB stands on CD straight line

∴ ∠ABC + ∠ABD = 180°

∴ Similarly, ∠ACB + ∠ACE = 180°

∴ ∠ABC + ∠ABD = ∠ACB + ∠ACE

∵ ∠ABC = ∠ACB

∴ ∠ABD = ∠ACE Proved.

“Class 8 WBBSE Maths Chapter 9, Relation Between Two Sides and Angles easy explanation”

Question 6. Let’s prove that the lengths of the medians are equal in an equilateral triangle.

Solution:

Let ABC is an equilateral triangle whose medians are AD, BE, and CF. Prove that AD = BE = CF.

∵ AB = AC (∵ ABC is an equilateral triangle)

∴  1/2AB=1/2AC

∴ BF = CE

In ΔBCF and ΔBCE,

BF = CE (Proved)

∠FBC = ∠BCE (∵ ABC is an equilateral triangle Each angle is 60°.) and BC is common.

∴ ΔBCF ≅ ΔBCE (S-A-S)

∴ BE = CF

Similarly, it can be proved that AD = BE.

∴ AD = BE = CF. Proved

Concept Of Vertically Opposite Angles

It is seen that two pieces of ribbons on the card of Motiur are in one way while the two pieces of ribbons on the card of Annesha are in another way. However, the ribbons in the two cards intersect each other and form several angles. Let’s find the relation between them.

Measuring by protractor we see that in the first card ∠1 = 90 degree ∠2 = 90 degree ∠3 = 90 degree ∠4 = 90 degree

∠1= ∠2= ∠3= ∠4= 90 degree

Class 8 General Science	Class 8 Maths
Class 8 History	Class 8 Science LAQs
Class 8 Geography	Class 8 Science SAQs
Class 8 Maths	Class 8 Geography
Class 8 History MCQs	Class 8 History

“WBBSE Class 8 Maths Chapter 7 solutions, Concept of Vertically Opposite Angles”

Measuring by protractor we see that in the ∠1 = 120 degree ∠2 = 60 degree ∠3 = 120 degree ∠4 = 60 degree

Also, we see by measuring by protractor ∠1 =∠3 =120 degree ∠ 2 = ∠4 = 60 degree

Read and Learn More WBBSE Solutions For Class 8 Maths

Theorem: If two straight lines intersect each other then the measurements of vertically opposite angles are equal.

(Given): AB and CD intersect at O. As a result two pairs of vertically opposite angles ∠AOD, ∠BOG, and ∠AOC, ∠BOD are formed.

∠AOD = ∠BOC and ∠AOC = ∠BOD

Proof :

∠AOD + ∠AOC = 180° [As CD stands on OA, therefore the sum of the measurement of angles is 180°]

∠AOC + ∠BOC = 180° [As AB stands on OC, therefore the sum of measurement of adjacent angles is 180°

∠AOD + ∠AOC = ∠AOC + ∠BOC Hence, ∠AOD = ∠BOC ( Subtracting ∠AOC from both sides). Again, we can write-

BOC + BOD = 180° [As AB stands on CD, therefore the sum of measurement of adjacent angles is 2 right angles.]

Concept Of Vertically Opposite Angles Exercise

Question 1.  Two straight lines PQ and RS intersect at O and some vertically opposite angles are formed, let’s draw and write the names.

Given

Two straight lines PQ and RS intersect at O and some vertically opposite angles are formed

1. Let’s try to find the measurement of the angles from the figure below.

Solution:

1. ∠1=35°
2. ∠2=145°
3. ∠3=35°
4. ∠4=145°

2. 

1. ∠TOS=20°
2. ∠ROQ=60°
3. ∠POT=40°
4. ∠ROP=120°
5. ∠QOS=120°

Question 3. Tirtha drew two straight lines PQ and XY intersecting at O. Let’s measure the vertically opposite angles by a protractor.

Solution:

Given

Tirtha drew two straight lines PQ and XY intersecting at O.

∠POX = opposite ∠YOQ = 50c

or, ∠POY = opposite ∠QOX= 130°

Question 4. Let’s try to find the answer to the questions given below, studying the figure beside.

Solution:

1. ∠AOM and ∠MOD are complementary angles
2. ∠AOC and ∠BOC are complementary angles
3. ∠AOC and ∠BOD are complementary angles

Question 5. If two straight lines intersect each other then the measurement of vertically opposite angles are equal; prove it logically.

Solution:

Given

If two straight lines intersect each other then the measurement of vertically opposite angles is equal

AB and CD are straight lines intersecting at O. As a result two pairs of vertically opposite angles are formed- ∠AOD, ∠BOC, and ∠AOC and ∠BOD. Prove that ∠AOD=∠BOC and ∠AOC= ZBOD.

Proof: Straight-line CD stands on OA

∴ ∠AOD + ∠AOC = 180°

Again, AB stands on a straight line OC.

∠AOC + ∠BOC = 180°

∴ ∠AOD + ∠AOC = ∠AOC + ∠BOC

Hence, ∠A0D= ∠B0C( ZSubtracting AOC from both sides) Similarly, it can be proved that ∠AOC =∠BOD.

Question 6. Find the value of ∠BOD, ∠BOC, and ∠AOC

Solution:

∴ OD stands on a straight line AB

∠AOD + ∠BOD = 180° .

or, 120° + ∠BOD = 180°

or, ∠BOD = 180° – 120° = 60°

∠QOR and ∠POR

∠BOC = Vertically Opposite Angle ∠AOD = 120°

∠AOC = Vertically Opposite Angle ∠BOD = 60°

“Class 8 WBBSE Maths Chapter 7 solutions, Vertically Opposite Angles explained”

Question 7. The sum of ∠POR and ∠QOS is 110°, find the value of ∠POS, ∠QOS,

Solution:

Given

The sum of ∠POR and ∠QOS is 110°

The sum of ∠POR and ∠QOS is 110°.

∠POR = VOA ∠QOS = \(\frac{110^{\circ}}{2}\) =55°

∠POS = 180° – 55° = 125°

∠QOR = VOA ∠POS = 125°

Question 8. OP, OQ, OR, and OS are concurrent. OP and OR are on the same straight line. P and R point are situated on opposite sides of O. ∠POQ = Z ROS and ∠POQ = ∠QOR. If ∠POQ = 50° then find the measurement of ∠QOR, ∠ROS, and ∠POS.

Solution:

Given

OP, OQ, OR, and OS are concurrent. OP and OR are on the same straight line. P and R point are situated on opposite sides of O. ∠POQ = Z ROS and ∠POQ = ∠QOR. If ∠POQ = 50°

∠POQ + ∠QOR = 180°

or, 50° + ∠QOR = 180°

or, ∠QOR = 180° – 50° – 130°

∠ROS = VOA ∠POQ = 50°

∠POS = VOA ∠QOR = 130°

Question 9. Four rays meet at a point in such a way that the measurement of opposite angles is equal. Let’s prove that two straight lines are formed by those four rays.

Solution:

Given

Four rays meet at a point in such a way that the measurement of opposite angles are equal.

Let OA, OB, OC, and OD four rays meet at the O point, as a result of which ∠AOB = Vertically Opposite Angle ∠COD and ∠AOD = Vertically Opposite Angle ∠BOC. We have to prove OA, OC and BO, OD lie on the same straight line.

“WBBSE Class 8 Maths Chapter 7, Concept of Vertically Opposite Angles solved examples”

Proof : ∠AOB + ∠AOD = ∠COD + ∠BOC

= 1/2 (∠AOB + ∠AOD + ∠COD + ∠BOC)

= \(\frac{1}{2}\)x360°

= 180°

∴  ∠AOB and ∠AOD are two adjacent angles whose sum of measurements is equal to two right angles.

∴ Their external sides OB and OD lie on the same straight line.

Similarly, it can be proved that OA and OC lie on the same straight line.

Question 10. Let’s prove that the internal and external bisectors of an angle are perpendicular to each other.

Solution:

Let the external  ∠BOC be ∠AOC OD be the internal bisector of ∠BOC and OE be the bisector of ∠AOC.

We have to prove that ∠COD + ∠COE = 1 right angle.

Proof: OC stands on a straight line AB ∠BOC + ∠AOC = 2 right angles 2 ∠COD + 2 ∠COE = 2 right angles or, ∠COD+ ∠COE = 1 right angle or, ∠EOD = 1 right angle So, OD and OE are perpendicular to each other.

∴ The internal and external bisectors of an angle are perpendicular to each other.

“WBBSE Class 8 Vertically Opposite Angles solutions, Maths Chapter 7”

Question 11. If two straight lines intersect each other then four angles are formed. Let’s prove that the sum of measures of the four angles is four right angles.

Solution:

Given

If two straight lines intersect each other then four angles are formed.

Straight lines AB and CD intersect at O

Prove that ∠AOD + ∠DOB + ∠BOC + ∠COA = 4 right angles.

Proof: OD stands on a straight line AB

∠AOD + ∠DOB = 2 right angles

Again, AB straight line stands on OC

∴ ∠BOC + ∠COA = 2 right angles

∠AOD + ∠DBO + ∠BOC + ∠COA = 4 right angles

“Class 8 WBBSE Maths Chapter 7, Vertically Opposite Angles easy explanation”

Question 12. In triangle PQR, Z PQR = z PRQ. If we extend QR on both sides then two exterior angles are formed. Let’s prove that the measurement of external angles are formed. Let’s prove that the bisectors of these angles are two perpendicular straight lines.

Solution:

Given

In triangle PQR, Z PQR = z PRQ. If we extend QR on both sides then two exterior angles are formed.

In triangle PQR ∠PQR = ∠PRQ. On both sides of QR, C, and D are extended. We have to prove that ∠PQC = ∠PRD.

Proof: PQ stands on CD straight line ∠PQC + ∠PQR = 180°

Hence, straight-line PR stands on the straight-line CD.

∴ ∠PRQ + ∠PRD = 180°

∴ ∠PQC + ∠PQR = ∠PRQ + ∠PRD

∴ ∠PQR – ∠PRQ (Given)

∠PQC = ∠PRD Proved

“WBBSE Class 8 Maths Chapter 7 solutions, Vertically Opposite Angles PDF”

Question 13. Two straight lines intersect each other at a point and thus four angles are formed. Let’s prove that the bisectors of these angles are two perpendicular straight lines.

Solution:

Given

Two straight lines intersect each other at a point and thus four angles are formed.

Let two straight lines AB and CD intersect at O. AOD, ∠DOB, ∠BOC, and ∠AOC are formed. Again let OF, OE, OH, and OG are respectively the external bisectors of ∠AOD, ∠DOB, ∠BOC, and ∠AOC. We have to prove that OE⊥LOF, OG⊥LOH, OF⊥ LOG, and OH⊥OE

“WBBSE Class 8 Maths Chapter 7, Vertically Opposite Angles important questions”

Proof:  OD stands on a straight line AB

∠AOD + ∠BOD = 2 right angles

or, \(\frac{1}{2} \angle \mathrm{AOD}+\frac{1}{2} \angle \mathrm{BOD}=\frac{1}{2} \times 2\) right angles

or, ∠DOF + ∠DOE = 1 right angle

or, ∠EOF = 1 right angle

∴ OE ⊥OF

Similarly, it can proved that OG⊥LOH, OF ⊥OG, and OH⊥OE Proved.