Class 11 Chemistry

Hydrogen

Hydrogen Is The Lightest And The Simplest Atom Known In The Family Of Chemical Elements.

It Was Discovered By The English Chemist Henry Cavendish In 1766. Although On Earth Hydrogen In Combined Form Is The Ninth Most Abundant Element, It Is The Most Abundant Element In The Universe.

Some Of The Planets Appear To Have Significant Amounts Of It Including The Atmospheres Of Jupiter, Saturn And Uranus.

Collected By Gravitational Forces In Stars, Hydrogen Is Converted Into Helium By Nuclear Fusion.

This Process Leads To The Release Of Enormous Energy, Which Is Supplied To Stars Including The Sun.

Being a light gas, hydrogen continually escapes into space and is, therefore, found in low concentration in the Earth’s atmosphere. In 1781, Cavendish confirmed that water was produced by the burning of hydrogen.

This led the French chemist Antoine Lavoisier to coin the name ‘hydrogen’ (Greek: maker of water). The two heavier isotopes of hydrogen—deuterium and tritium—were discovered in 1931 and 1935, respectively.

The nuclear fusion of each of these isotopes occurs at a very high temperature and gives an enormous amount of energy. The hydrogen bomb makes use of this phenomenon.

Hydrogen Position In The Periodic Table

The atomic mass of hydrogen is 1.0079 u and the atomic number is 1. It has the simplest electronic configuration (Is¹), resembling those of alkali metals, which have one electron in their outermost orbits.

Alkali metals tend to lose the outermost electron and form univalent positive ions. Hydrogen can also lose an electron to form H+.

Therefore, hydrogen can be placed above alkali metals in Group 1 of the periodic table.

On the other hand, a closer look at the electronic configuration of hydrogen shows that it has one electron less than helium (Is²), a noble gas, and resembles halogens (F, Cl, Br, I), which too have one electron less in their outermost shells than their nearest noble gases.

Halogens gain an electron to form univalent negative ions. H- ions are rarely formed, and a hydrogen atom gains an electron from highly electropositive metals only.

On the basis of its unique properties, hydrogen can be placed either in Group 1 (along with the alkali metals) or in Group 17 (along with halogens).

Conventionally, hydrogen is said to be the first member of Group 1 of the periodic table. According to many, however, hydrogen should be treated as a group in itself.

In the present form of the periodic table hydrogen along with helium is placed in the first period.

Hydrogen shows similarities in chemical behaviour with alkali metals as well as halogens. However, it also differs from them in many ways.

Let us now compare hydrogen with alkali metals and halogens in greater detail.

Hydrogen Comparison With Alkali Metals Similarities

1. Electronic configuration As already stated, the hydrogen atom has one electron in its only s orbital, and alkali metals have only one electron in their outermost orbital.

• H Is¹
• Li 1S²2S¹
• Na lS²2s²2p3s¹

2. Electropositive character Hydrogen as well as alkali metals are electropositive.

They lose one electron to form the corresponding ion. Alkali metals are more electropositive than hydrogen. The hydrogen ion exists only in a discharge tube but not in solution.

In an aqueous solution, H+ combines with water and is represented as H+ (aq). For example, when hydrogen chloride is dissolved in water, it produces hydronium ions (H3O+).

The electropositive nature of hydrogen and alkali metals is also reflected by the fact that during the electrolysis of their salts, both are liberated at the cathode.

⇒ \(2 \mathrm{NaCl} \stackrel{\text { electrolyals }}{\longrightarrow} \frac{\text { At cathode }}{2 \mathrm{Na}}+\frac{\text { At anode }}{\mathrm{Cl}_2}\)

⇒ \(2 \mathrm{HCl} \stackrel{\text { electrolygis }}{\longrightarrow} \mathrm{H}_2+\mathrm{Cl}_2\)

3. Reducing nature Like alkali metals, hydrogen acts as a strong reducing agent.

⇒ \(\begin{aligned}
2 \mathrm{H}_2+\mathrm{O}_2 & \longrightarrow 2 \mathrm{H}_2 \mathrm{O} \\
2 \mathrm{Na}+2 \mathrm{H}_2 \mathrm{O} & \longrightarrow 2 \mathrm{NaOH}+\mathrm{H}_2
\end{aligned}\)

4. Oxidation state Alkali metals as well as hydrogen show an oxidation state of +1 in their compounds, e.g., hydrogen chloride (H+C1-) and sodium chloride (Na+Cl-).

Hydrogen also shows an oxidation state of 1 in hydrides.

5. Combination with nonmetals Hydrogen and alkali metals readily form compounds with nonmetals like oxygen, sulphur and halogens.

Differences

1. Ionisation enthalpy The ionisation enthalpy of hydrogen (1312 kJ Mol^-1) is much higher than the ionisation enthalpies of alkali metals, e.g., Li =520 kJ Mol^-1 and Cs = 375.6 kJ Mol^-1. This implies that hydrogen has less tendency to form positive ions than alkali metals do.
2. Halides Hydrogen halides and alkali-metal halides differ in character. For instance, HC1 is a covalent compound and NaCl is ionic; HC1 is gaseous and NaCl is a solid at room temperature.
3. Nonmetallic character Hydrogen is a nonmetal whereas all the Group1 elements are metals.
4. Atomicity The hydrogen molecule exists as H₂, i.e., it is diatomic. In contrast, alkali metals are monoatomic. Atomic hydrogen exists only at high temperatures.
5. Oxides Alkali-metal oxides, e.g., Li;0 and K20, are basic while the oxide of hydrogen—HzO—is neutral.
6. Ionic size H+ ions (~ L5 x 10_3pm) are much smaller than alkali-metal ions (50-220 pm).

Hydrogen Comparison With Halogens Similarities

1. Electronic configuration Halogens have seven electrons in their outermost shells, one electron less than the stable configuration of the nearest noble gas. Having one electron in its outermost shell, hydrogen is one electron short of the stable configuration of the corresponding noble gas (helium)
   • H(ls¹)
   • F(ls² 2s² 2p5)
   • Cl(ls² 2s²2ph 3s² 3p5)
   • Hc(ls²)
   • Ne(ls² 2s² 2pf )
   • Ar(ls² 2s² 2p6 3s² 3p6)
2. Atomicity Hydrogen as well as halogens exist as diatomic molecules (H₂, CI₂, F₂, llr₂, etc.),
3. Nonmetallic character Hydrogen as well as halogens arc nonmetals.
4. Formation of covalent compounds Hydrogen as well as halogens combine with nonmetals like carbon, and nitrogen and metalloids like germanium to form covalent compounds.
5. Ionisation enthalpy The ionisation enthalpies of hydrogen (1312 kJ Mol^-1) and halogens are comparable. Chlorine, for instance, has an ionisation enthalpy of 1255 kJ Mol^-1.
6. Electronegative nature Halogens readily gain one electron to form a halide ion. Hydrogen gains one electron to form a hydride ion (H-) only with a few extremely electropositive metals, e.g., LiH and CaH₂.

Differences

1. Nature of Oxides The oxide of hydrogen (HzO) is neutral, whereas some oxides of halogens, e.g., HI03, are acidic.
2. Absence of unshared electrons The hydrogen molecule has no unshared pairs of electrons while halogen molecules have six such pairs.

Degree of electronegativity Hydrogen is less electronegative than halogens. This is borne out by the fact that halogens form compounds with several metals while hydrogen docs so with very few highly electropositive metals such as sodium, lithium and calcium.

⇒ \(\mathrm{H}: \mathrm{H} \quad \text { : } \ddot{\mathrm{F}}-\ddot{\mathrm{F}}:\)

Hydrogen Occurrence

Hydrogen constitutes about 92% of the universe. However, its abundance in the earth’s atmosphere is very low. This is because the earth’s gravitational field is not strong enough to hold such a light element.

Some H₂, however, is found in volcanic gases. It occurs in water, organic compounds, fossil fuels (like coal, petroleum and natural gas), clay, ammonia and acids.

All animal and vegetable matter also contains hydrogen. In fact, hydrogen forms more compounds than any other element.

Although it is often said that there are more known compounds of carbon than of any other element, the fact is that almost all carbon compounds contain hydrogen.

Hydrogen Multiple-Choice Questions

Question 1. At 925 K, palladium adsorb

1. 50 volumes of hydrogen
2. 100 volumes of hydrogen
3. 800 volumes of hydrogen
4. 1000 volumes of hydrogen

Answer: 3. 800 volumes of hydrogen

Question 2. Interstitial hydrides are obtained using

1. Elements Of The D Block
2. Actinide elements of the f block
3. lanthanide elements in the f block
4. Ca⁺⁺, Na⁺ and K⁺

Answer: 1. Elements Of The D Block

Question 3. In the reaction the product obtained is

1. Nascent Hydrogen
2. Atomic hydrogen
3. Ortho hydrogen
4. Para hydrogen

Answer: 2. Atomic hydrogen

Question 4. Which of the following reactions is explosive in sunlight?

1. \(\mathrm{N}_2+3 \mathrm{H}_2 \longrightarrow 2 \mathrm{NH}_3\)
2. \(\mathrm{S}+\mathrm{O}_2 \longrightarrow \mathrm{SO}_2\)
3. \(\mathrm{H}_2+\mathrm{Cl}_2 \longrightarrow 2 \mathrm{HCl}\)
4. \(\mathrm{Na}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{NaOH}+\mathrm{H}_2[latex]\)

Answer: 3. \(\mathrm{H}_2+\mathrm{Cl}_2 \longrightarrow 2 \mathrm{HCl}\)

Question 5. Deionised water can be obtained by

1. Distillation
2. The Calgon Process
3. The Permutit Process
4. The ion-exchange method

Answer: 1. Distillation

Question 6. In which of the following reactions does hydrogen form compounds by gaining electrons?

1. \(2 \mathrm{Na}+\mathrm{H}_2 \longrightarrow 2 \mathrm{NaH}\)
2. \(\mathrm{CuO}+\mathrm{H}_2 \longrightarrow \mathrm{Cu}+\mathrm{H}_2 \mathrm{O}\)
3. \(\mathrm{H}_2+\mathrm{Cl}_2 \stackrel{\text { darkness }}{\longrightarrow} 2 \mathrm{H}-\mathrm{Cl}\)
4. \(\mathrm{H}_2+\mathrm{F}_2 \underset{\text { light }}{\stackrel{\text { diffused }}{\longrightarrow}} 2 \mathrm{H}-\mathrm{F}\)

Answer: 1. \(2 \mathrm{Na}+\mathrm{H}_2 \longrightarrow 2 \mathrm{NaH}\)

Question 7. Hydrogen gas does not reduce heat

1. A1₂O₃
2. CuO
3. SnO₂
4. Fe₂O₃

Answer: 4. Fe₂O₃

Question 8. Which of the following is used as a moderator in nuclear reactions?

1. Heavy water
2. Hard water
3. Deionised water
4. Soft water

Answer: 1. Heavy water

Question 9. In H₂O₂ the O—O—H bond angle is

1. 94.8º
2. 106º
3. 109º 28′
4. 111º

Answer: 1. 94.8º

Question 10. Which of the following metals does not liberate hydrogen by reacting with dilute HC1?

1. Cu
2. Fe
3. Zn
4. Mg

Answer: 1. Cu

Question 11. The decomposition of H₂O₂ is prevented by

1. Urea
2. Acetanilide
3. Oxalic Acid
4. KOH

Answer: 1. Urea

Question 12. Usually, hydrogen combines with other elements by

1. Gaining an electron
2. Sharing an electron
3. Losing an electron
4. None of these

Answer: 2. Sharing an electron

Question 13. The permanent hardness of water is not removed by boiling because

1. It is caused due to the bicarbonates of calcium and magnesium
2. It is caused due to the sulphates of calcium and magnesium
3. It cannot drive away SO^2-₄
4. It cannot drive away CO₂

Answer: 2. It is caused due to the sulphates of calcium and magnesium

Question 14. H₂O₂ has a higher boiling point than water because it

1. Is More Dense Than Water
2. Has A Higher Dielectric Constant Than That Of Water
3. Is More Hydrogen Bonded Than Is Water
4. None Of These

Answer: 3. Is More Hydrogen Bonded Than Is Water

Question 15. Which of the following statement(s) is/are correct?

1. Both hydrogen and halogens have the tendency to accept electrons.
2. Hydrogen and halogens form hydrides and halide ions respectively with equal ease.
3. Both hydrogen and halogens combine with nonmetals to form covalent compounds.
4. Both hydrogen and halogens are very reactive.

Answer: 3. Both hydrogen and halogens combine with nonmetals to form covalent compounds.

Question 16. The exhausted permit is generally regenerated by percolating through it a solution of

1. Polyphosphates
2. Calcium Chloride
3. Aluminium Oxide
4. Polyphosphates

Answer: 3. Aluminium Oxide

Question 17. Hydrogen(c) sodium is chloride-commercially prepared from 4

1. Water Gas
2. Natural Gas
3. Coal Gas
4. Producer Gas

Answer: 1. Water Gas

Question 18. The oxide that gives hydrogen peroxide on treatment with a dilute acid is

1. PbO₂
2. MnO₂
3. BaO₂
4. TiO₂

Answer: 3. BaO₂

Question 19. The aggregates of water molecules, in the liquid state, are held due to

1. Intermolecular hydrogen bonds
2. Van der waals forces
3. Intramolecular hydrogen bonds
4. Intermolecular hydrogen bonds
5. Covalent bonds

Answer: 1. Intermolecular hydrogen bonds

Question 20. Which among the following is an electron-deficient covalent hydride?

1. CH₄
2. NH₃
3. B₂H₆
4.  H₂O

Answer: 3. B₂H₆

Hydrogen Peroxide Preparation

In the laboratory, hydrogen peroxide is prepared by the following methods.

1. From sodium peroxide Calculated quantities of sodium peroxide are added in small portions to ice-cold dilute sulphuric acid (20%)

⇒ \(\mathrm{Na}_2 \mathrm{O}_2+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{Na}_2 \mathrm{SO}_4+\mathrm{H}_2 \mathrm{O}_2\)

On cooling, most of the sodium sulphate separates out as Na₂SO4- 10H₂O and is filtered. By this process, a 30 per cent solution of hydrogen peroxide containing a bit of sodium sulphate is obtained.

2. From barium peroxide The reaction of hydrated barium peroxide with dilute sulphuric add gives hydrogen peroxide and barium sulphate, which is insoluble is filtered off. The method was first used to prepare hydrogen peroxide in 1818 by Thenard.

⇒ \(3 \mathrm{BaO}_2+2 \mathrm{H}_3 \mathrm{PO}_4 \longrightarrow \mathrm{Ba}_3\left(\mathrm{PO}_4\right)_2+3 \mathrm{H}_2 \mathrm{O}_2\)
Barium peroxide Phosphoric Acid Barium Phosphate

By electrolysis, This method used earlier involves the electrolysis of an equimolar mixture of sulphuric acid and r ammonium sulphate using a platinum anode and a graphite cathode.

⇒ \(\mathrm{H}_2 \mathrm{SO}_4 \rightleftharpoons \mathrm{H}^{+}+\mathrm{HSO}_4^{-}\)

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

⇒ \(\underset{{\text { anmonium } \\ \text { sulphiate }}}{\left(\mathrm{NH}_4\right)_2 \mathrm{SO}_4}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \underset{{\text { amrmonium hydrogen } \\ \text { sulphate }}}{2 \mathrm{NH}_4 \mathrm{HSO}_4}\)

⇒ \(\mathrm{NH}_4 \mathrm{HSO}_4 \longrightarrow \mathrm{NH}_4^{+}+\mathrm{HSO}_4^{-}\)

⇒ \(2 \mathrm{HSO}_4^{-} \longrightarrow \mathrm{H}_2 \mathrm{~S}_2 \mathrm{O}_8+2 \mathrm{e}^{-} \text {(at anode) }\)

⇒ \(\mathrm{NH}_4 \mathrm{HSO}_4 \longrightarrow \mathrm{NH}_4^{+}+\mathrm{HSO}_4^{-}\)

The solution, on hydrolysis, produces hydrogen peroxide.

⇒ \(\mathrm{H}_2 \mathrm{~S}_2 \mathrm{O}_8+\mathrm{H}_2 \mathrm{O} \longrightarrow \underset{{\text { perowomono- } \\ \text { sulphuric acid }}}{\mathrm{H}_2 \mathrm{SO}_5}+\mathrm{H}_2 \mathrm{SO}_4\)

⇒ \(\mathrm{H}_2 \mathrm{SO}_5+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{H}_2 \mathrm{SO}_4+\mathrm{H}_2 \mathrm{O}_2\)

By the oxidation of 2-ethyl anthraquinol Hydrogen peroxide is nowadays produced on a commercial scale by a cyclic process.

In this method, 2-ethyl anthraquinol is oxidised by air to the corresponding quinone and hydrogen peroxide at a moderate temperature.

The anthraquinone is reduced back to anthraquinone with hydrogen using platinum, palladium or Raney nickel as a catalyst. The cycle is repeated.

The hydrogen peroxide formed is extracted with water and the aqueous solution (containing 1-2% H₂O₂) is concentrated under reduced pressure. It is sold as a 30 per cent (by weight) solution which has a pH of about 4.0. It is stored in plastic or wax-coated glass vessels.

The coating is done to prevent the decomposition of hydrogen peroxide on account of the traces of alkali present in glass, which catalyse the decomposition. Small amounts of urea or sodium stannate are added as stabilisers, to prevent the breakdown of H₂O₂ into water and oxygen.

For further concentration, the solution is cooled to about 263 K when crystals enriched in H₂O₂ separate out. The process of fractional crystallisation is repeated to obtain 100 per cent H₂O₂.

Hydrogen Peroxide Physical properties

Hydrogen peroxide is a colourless, odourless, syrupy liquid. It has a bluish tinge and is soluble in water, ether and alcohol in all proportions.

It is a liquid in which molecules are highly associated with each other due to the presence of intramolecular hydrogen bonds.

In fact, it is more hydrogen-bonded than water and has a boiling point of 423.2 K and a melting point of 273.6 K. Also, it has a dipole moment of 2.1 D, a little more than that of water (1.84 D).

Hydrogen Peroxide Chemical properties

Hydrogen peroxide is unstable and its rate of decomposition depends on temperature and concentration.

It V behaves as an oxidising as well as a reducing agent in both acidic and alkaline media. The oxidation state of oxygen in hydrogen peroxide is -1, compared to zero in O₂ and -2 in H₂O.

Therefore, hydrogen peroxide can be oxidised to or reduced to H₂O. H₂O₂ is a powerful oxidising agent.

1. Oxidation in an acidic medium: It oxidises acidified solutions of ferrous salts, iodides, sulphides and ferrocyanides to ferric salts, iodine, sulphates and ferricyanides respectively.

⇒ \(2 \mathrm{FeSO}_4+\mathrm{H}_2 \mathrm{SO}_4+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{Fe}_2\left(\mathrm{SO}_4\right)_3+2 \mathrm{H}_2 \mathrm{O}\)

⇒ \(2 \mathrm{KI}+\mathrm{H}_2 \mathrm{SO}_4+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{K}_2 \mathrm{SO}_4+\mathrm{I}_2+2 \mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{PbS}+4 \mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{PbSO}_4+4 \mathrm{H}_2 \mathrm{O}\)

⇒ \(\underset{{\text { potassium } \\ \text { ferrocyanide }}}{2 \mathrm{~K}_4\left[\mathrm{Fe}(\mathrm{CN})_6\right]+\mathrm{H}_2 \mathrm{SO}_4}+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \underset{{\text { potassium } \\ \text { ferricyanide }}}{2 \mathrm{~K}_3\left[\mathrm{Fe}(\mathrm{CN})_6\right]+\mathrm{K}_2 \mathrm{SO}_4}+2 \mathrm{H}_2 \mathrm{O}\)

Hydrogen peroxide oxidises sulphites, nitrites and arsenites to sulphates, nitrates and arsenates respectively.

⇒ \(\underset{\text { sodium sulphite }}{\mathrm{Na}_2 \mathrm{SO}_3}+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \underset{\text { sodium sulphate }}{\mathrm{Na}_2 \mathrm{SO}_4}+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{KNO}_2+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{KNO}_3+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{Na}_3 \mathrm{AsO}_3+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{Na}_3 \mathrm{AsO}_4+\mathrm{H}_2 \mathrm{O}\)

2. Oxidation in an alkaline medium: Hydrogen peroxide oxidises chromium salts to chromates and manganese salts to manganese dioxide.

⇒ \(\mathrm{Cr}_2\left(\mathrm{SO}_4\right)_3+3 \mathrm{H}_2 \mathrm{O}_2+10 \mathrm{NaOH} \longrightarrow 2 \mathrm{Na}_2 \mathrm{CrO}_4+3 \mathrm{Na}_2 \mathrm{SO}_4+8 \mathrm{H}_2 \mathrm{O}\)

⇒ \(\underset{{\text { manganese } \\ \text { sulphate }}}{\mathrm{MnSO}_4}+\mathrm{H}_2 \mathrm{O}_2+2 \mathrm{NaOH} \longrightarrow \mathrm{Na}_2 \mathrm{SO}_4+\underset{{\text { manganese } \\ \text { dioxide }}}{\mathrm{MnO}_2}+2 \mathrm{H}_2 \mathrm{O}\)

3. Reducing action in an acidic medium: The following reactions depict the reducing action of H₂O₂ in an acidic medium.

⇒ \(\mathrm{H}_2 \mathrm{O}_2+\mathrm{Cl}_2 \longrightarrow 2 \mathrm{HCl}+\mathrm{O}_2\)

4. It reduces acidified potassium permanganate (pink) to manganese sulphate (colourless)

⇒ \(2 \mathrm{KMnO}_4+3 \mathrm{H}_2 \mathrm{SO}_4+5 \mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{K}_2 \mathrm{SO}_4+2 \mathrm{MnSO}_4+8 \mathrm{H}_2 \mathrm{O}+5 \mathrm{O}_2\)

It reduces the acidified potassium dichromate solution (yellow) to chromic sulphate (green).

⇒ \(\mathrm{K}_2 \mathrm{Cr}_2 \mathrm{O}_7+4 \mathrm{H}_2 \mathrm{SO}_4+3 \mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{K}_2 \mathrm{SO}_4+\mathrm{Cr}_2\left(\mathrm{SO}_4\right)_3+7 \mathrm{H}_2 \mathrm{O}+3 \mathrm{O}_2\)

It reduces silver oxide to silver with the liberation of oxygen gas, and lead dioxide to lead monoxide.

⇒ \(\mathrm{Ag}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow 2 \mathrm{Ag}+\mathrm{H}_2 \mathrm{O}+\mathrm{O}_2\)

⇒ \(\mathrm{PbO}_2+\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{PbO}+\mathrm{H}_2 \mathrm{O}+\mathrm{O}_2\)

5. Manganese dioxide is reduced to manganous sulphate.

⇒ \(\underset{{\text { Manganese } \\ \text { dioxide }}}{\mathrm{MnO}_2}+\mathrm{H}_2 \mathrm{O}_2+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \underset{{\text { Manganous } \\ \text { sulphite (pink) }}}{\mathrm{MnSO}_4}+2 \mathrm{H}_2 \mathrm{O}+\mathrm{O}_2\)

4. Reducing action in an alkaline medium reduces an alkaline solution of potassium ferrocyanide to potassium ferrocyanide.

⇒ \(\underset{\text { ferricyanide }}{2 \mathrm{Fe}(\mathrm{CN})_6{ }^{3-}}+\mathrm{H}_2 \mathrm{O}_2+2 \mathrm{OH}^{-} \longrightarrow \underset{\text { ferrocyanide }}{2 \mathrm{Fe}(\mathrm{CN})_6{ }^{4-}}+2 \mathrm{H}_2 \mathrm{O}+\mathrm{O}_2\)

It reduces ferric salts to ferrous salts.

⇒ \(\underset{\text { ferric ion }}{2 \mathrm{Fe}^{3+}}+\mathrm{H}_2 \mathrm{O}_2+2 \mathrm{OH}^{-} \longrightarrow \underset{\text { ferrous ion }}{2 \mathrm{Fe}^{2+}}+2 \mathrm{H}_2 \mathrm{O}+\underset{\text { dioxygen }}{\mathrm{O}_2}\)

Reaction with ozone Hydrogen peroxide reduces ozone to oxygen.

⇒ \(\mathrm{H}_2 \mathrm{O}_2+\mathrm{O}_3 \longrightarrow 2 \mathrm{O}_2+\mathrm{H}_2 \mathrm{O}\)

Bleaching action Hydrogen peroxide is used to bleach delicate articles like ivory, feathers, silk, etc. The bleaching action is due to the following reaction.

⇒ \(\mathrm{H}_2 \mathrm{O}_2 \longrightarrow \mathrm{H}_2 \mathrm{O}+\mathrm{O}\)

The nascent oxygen obtained on the decomposition of hydrogen peroxide oxidises the colouring matter of the article to be bleached. When this happens the article loses colour, i.e., it gets bleached.

Hydrogen Peroxide Uses

1. Hydrogen peroxide is used as an antiseptic and germicide for washing wounds. It is also employed in mouthwashes.
2.  H₂O₂ is used as an oxidant for rocket fuel and as a propellant for submarines and torpedoes.
3. It is employed in the manufacture of many inorganic and organic compounds like sodium peroxoborate [Na2B2(02)2(0H)4 -6 H₂O₂ and epoxides. Sodium peroxoborate is used in washing powder. Organic peroxides are used to initiate addition polymerisation reactions (FVC, polyurethane and epoxy resins).
4. It is used in organic synthesis for the conversion of an aldehydic group (—CHO) into a hydroxyl group (—OH). The oxidation is carried out in an alkaline medium.
5. It is employed as an oxidising agent in the laboratory.
6. In the textile industry, it is used as what is known as an antichlor. This means that it helps remove excess chlorine after bleaching.

Structure Of Hydrogen Peroxide

The hydrogen peroxide molecule is nonplanar. The two oxygen atoms are linked to each other by a covalent bond, known as a peroxide bond in this case.

Also, each oxygen atom is linked to a hydrogen atom by covalent bonds. The two O—H bonds are in different planes.

The angle between the two planes is 111.5° in the gaseous phase. Because of hydrogen bonding in the crystalline state, however, this angle becomes 90.2° in the crystalline state.

Water

An essential constituent of all animal and vegetable matter, water is the most abundant substance on earth.

It occurs as a colourless liquid at room temperature and is present as water vapour in the air which condenses at low temperatures to form mist, rain, hail or snow, depending on the atmospheric conditions.

Water on the earth’s surface in the form of oceans, rivers, etc., covers about three-quarters of the earth’s crust.

Of the total amount of water on the earth, oceans and other saline water bodies constitute 97.3%.

Most of the freshwater, amounting to about 2.7%, is not readily accessible since it occurs in the form of frozen lakes, glaciers, etc. Water available for human use is far less than 1% of the total water on the earth.

Water – Physical Properties

Water is a colourless, odourless and tasteless liquid. Pure water is neutral to litmus and is a bad conductor of electricity.

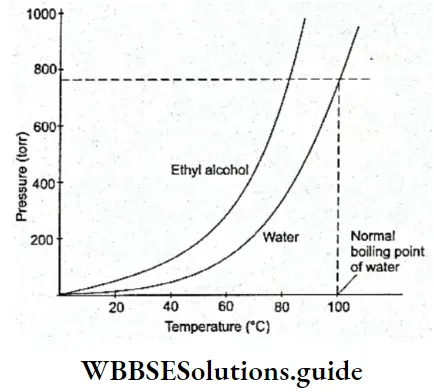
Its b.p. is 373 K at ATM pressure. It has a maximum density (1 g cm^-3) of 277 K. Due to the presence of hydrogen bonding, water has a high boiling point, enthalpy of fusion (6.01 kJ Mol^-1) and enthalpy of vaporisation (40.66 kJ Mol^-1).

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

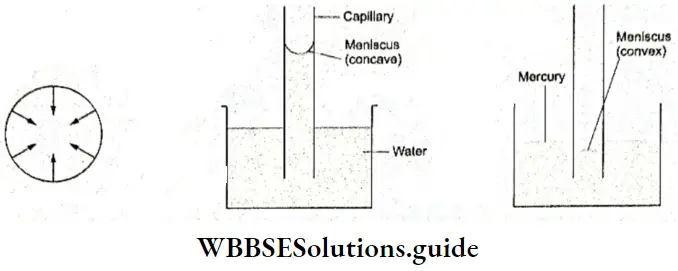
Water has a high specific heat, thermal conductivity and surface tension (compared to most of the other liquids). These properties are responsible for its vital role in the biosphere.

The moderation of the climate and body temperature regulation is due to the high enthalpy of vaporisation and high heat capacity of water. It is polar in nature and an excellent solvent for many other polar and ionic substances.

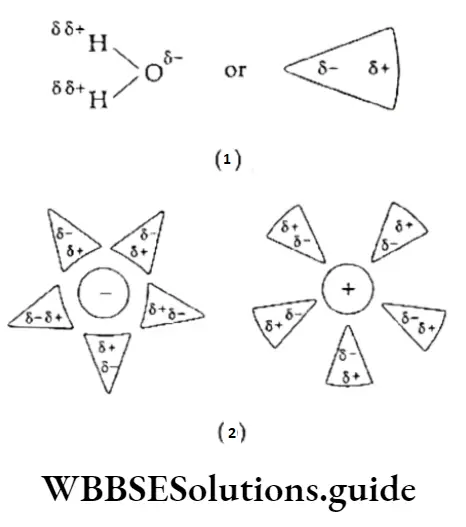
Why is the water molecule polar? The difference in the electronegativity of oxygen and hydrogen in the water molecule makes the covalent bond polar. Thus, the molecule behaves as a tiny dipole.

The slight charges on the water molecules are attracted to the charges on ions.

When an ionic solid is placed in water, the ions from its surface are pulled into the solution.

Since water has the capacity to dissolve most of the inorganic substances, it is regarded as a universal solvent.

A few organic substances such as urea, alcohol, sugar, etc., also dissolve in water. This is due to the presence of intermolecular hydrogen bonding in the molecules of the solute and water.

Water Chemical Properties

1. Dissociation of water Being stable, the water molecule does not dissociate into its constituent elements even at high temperatures. However, pure water has a small electrical conductivity. It dissociates as

⇒ \(\mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) hydronium ion\)

From this reaction, it is clear that water acts as an acid as well as a base. In other words, it is amphoteric. The following reactions illustrate the nature of water.

⇒ \(\begin{aligned}
&\mathrm{H}_2 \mathrm{O}+\mathrm{HCl} \longrightarrow \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{Cl}^{-}\\
&\underset{\text { did }}{\mathrm{H}_2 \mathrm{O}}+\underset{\text { base }}{\mathrm{NH}_3} \longrightarrow \underset{\text { acid }}{\mathrm{NH}_4^{+}}+\underset{\text { base }}{\mathrm{OH}^{-}}
\end{aligned}\)

The self-ionisation of water has significance in acid-base chemistry.

2. Reactions with metals Alkali metals like Na and K react with cold water.

⇒ \(2 \mathrm{Na}+2 \mathrm{H}_2 \mathrm{O}(\text { cold }) \longrightarrow 2 \mathrm{NaOH}+\mathrm{H}_2\)

However, alkaline earth metals, e.g., Mg, react with hot water.

⇒ \(\mathrm{Mg}+\mathrm{H}_2 \mathrm{O} \text { (warm) } \longrightarrow \mathrm{MgO}+\mathrm{H}_2\)

Thus, water is easily reduced by highly electropositive metals.

Reactions with nonmetals Fluorine reacts with cold water to form hydrogen fluoride and liberates oxygen. Thus, water is oxidised and fluorine is reduced

⇒ \(2 \mathrm{~F}_2+2 \mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{H}_2 \mathrm{~F}_2+\mathrm{O}_2\)

Chlorine forms hydrochloric acid and hypochloric acid upon reacting with water. Bromine is less reactive with water and iodine does not react at all.

⇒ \(\mathrm{Cl}_2+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{HCl}+\mathrm{HOCl}\)

⇒ \(\mathrm{Br}_2+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{HBr}+\mathrm{HOBr}\)

However, in the presence of sunlight, water reacts only with chlorine (among the halogens) forming hydrochloric acid and liberating oxygen.

⇒ \(2 \mathrm{Cl}_2+2 \mathrm{H}_2 \mathrm{O} \stackrel{\text { sunlight }}{\longrightarrow} 4 \mathrm{HCl}+\mathrm{O}_2\)

Carbon decomposes steam, liberating hydrogen. Thus, water is reduced to hydrogen and carbon is oxidised to carbon monoxide.

⇒ \(\mathrm{C}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{CO}+\mathrm{H}_2\)

Reactions with oxides Metallic oxides react with water to form leases. For example,

⇒ \(\mathrm{Na}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{NaOH}\)

Reactions with oxides Metallic oxides react with water to form leases. For example

⇒ \(\mathrm{Na}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{NaOH}\)

However, nonmetallic oxides react with water to form acids

⇒ \(\begin{aligned}
& \mathrm{SO}_2+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{H}_2 \mathrm{SO}_3 \\
& \mathrm{SO}_3+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{H}_2 \mathrm{SO}_4
\end{aligned}\)

Hydrolysis of compounds Water hydrolyses many compounds like hydrides, nitrides and carbides, liberating hydrogen, ammonia and acetylene respectively.

⇒ \(\mathrm{CaH}_2+2 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Ca}(\mathrm{OH})_2+\underset{\text { ditydrogen }}{2 \mathrm{H}_2}\)

⇒ \(\mathrm{AlN}+3 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Al}(\mathrm{OH})_3+\mathrm{NH}_3\)

⇒ \(\mathrm{Mg}_3 \mathrm{~N}_2+6 \mathrm{H}_2 \mathrm{O} \longrightarrow 3 \mathrm{Mg}(\mathrm{OH})_2+2 \mathrm{NH}_3\)

⇒ \(\mathrm{CaC}_2+2 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Ca}(\mathrm{OH})_2+\underset{\text { acetylene }}{\mathrm{C}_2 \mathrm{H}_2}\)

Water also hydrolyses compounds, forming acids.

⇒ \(\mathrm{PBr}_3+3 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{H}_3 \mathrm{PO}_3+3 \mathrm{HBr}\)

Water as a catalyst In many reactions, water acts as an effective catalyst. Perfectly dry gases fail to react and a trace of moisture promotes the reaction.

For example, hydrogen and chlorine do not react in the dry state but do so in the presence of moisture.

Hydrates Water forms compounds with some metal salts called hydrates, of which there are three types.

Complex compounds are formed when water molecules combine with metal ions through coordinate bonds, e.g.,

⇒ \(\left[\mathrm{Ni}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{2+},\left[\mathrm{Li}\left(\mathrm{H}_2 \mathrm{O}\right)_5\right]^{+} \text {and }\left[\mathrm{Cr}\left(\mathrm{H}_2 \mathrm{O}\right)_6\right]^{3+}\)

Compounds in which water molecules are hydrogen bonded to certain oxygen-containing anions, e.g., CuSO₄5H₂O  with four water molecules coordinated to the central Cu²⁺ ion through the lone pairs on the oxygen atoms while the fifth water molecule is hydrogen bonded to a sulphate group Compounds in which water molecules may occupy interstitial sites in crystal lattices, e.g., BaCl₂ 2H₂O

Structure Of The Water Molecule And Its Aggregates

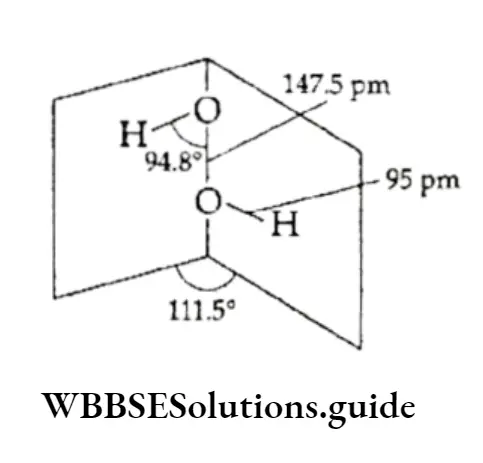
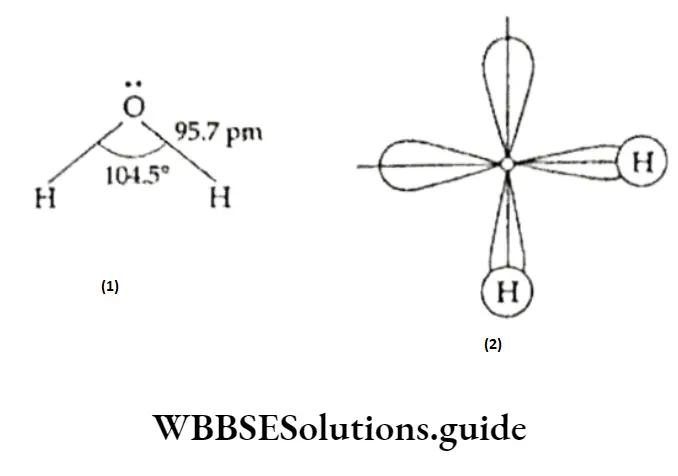
In a tire water molecule, oxygen is the central atom and has six valence electrons. Two of the valence electrons of oxygen form covalent bonds with two hydrogen atoms, thus completing the octet.

The other two pairs of valence electrons of oxygen are nonbonding. Thus, in the water molecule, there are two bond pairs and two lone pairs, and their interactions with each other reduce the bond angle.

Thus, in the gaseous form, the water molecule has an O —H bond length of 95.7 pm and an HOH bond angle of 104.5°.

As already stated, due to the high electronegativity of oxygen, the water molecule is highly polar.

The partial negative charge on the oxygen atom in a water molecule attracts a hydrogen atom (which has a partial positive charge) of another water molecule.

Also, the partial positive charge on a hydrogen atom attracts the partial negative charge on the oxygen atom of still another molecule of water.

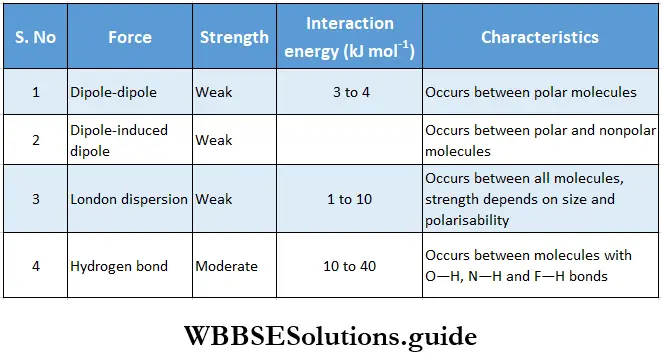
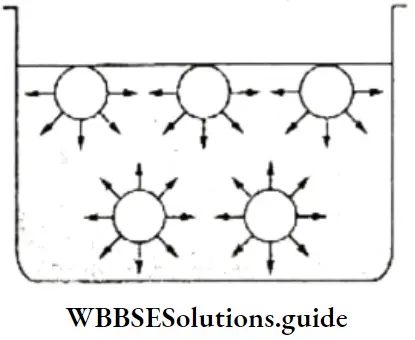
Thus, in the liquid state, the water molecules are held together by hydrogen bonds resulting from a weak electrostatic attraction. The hydrogen bonding in water can be shown as follows.

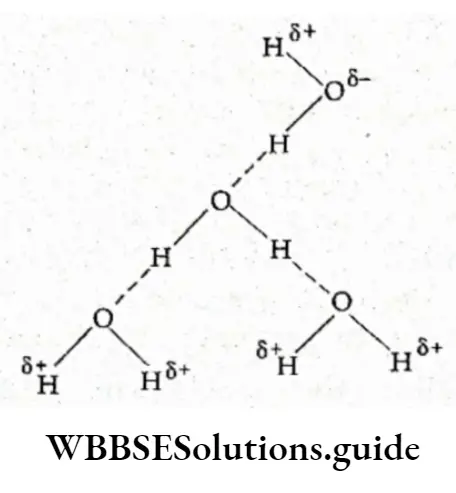
Water is a liquid at room temperature due to hydrogen bonding between the molecules. One after the other the molecules are held together by the hydrogen bonds, to form an aggregate of molecules.

There may be several aggregates of varying numbers of water molecules in liquid water. Since hydrogen bonds are very weak (bond enthalpy is about 10 kJ Mol^-1), the water molecules break away from one aggregate to join another in liquid water and maintain a dynamic equilibrium.

Like water, many other polar molecules, e.g., HF and NH₃, form intermolecular hydrogen bonds. The water molecules are joined together in a three-dimensional network in which each oxygen atom is bonded to three hydrogen atoms by one hydrogen bond and by two normal covalent bonds in a tetrahedral configuration. This is, however, not the case in molecules like HF and NH₃.

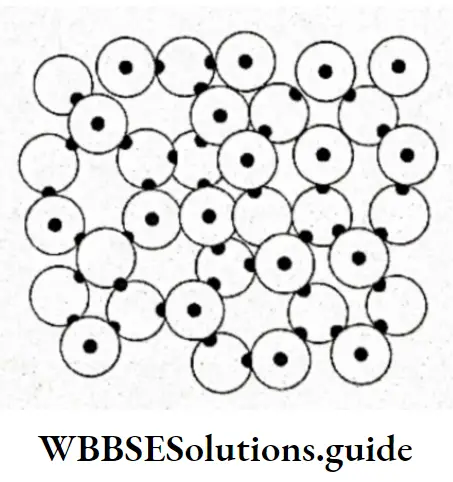
The Structure Of Ice

Ice can exist in nine different crystalline forms. These structures depend on the conditions of temperature and pressure in which water is frozen to make the ice.

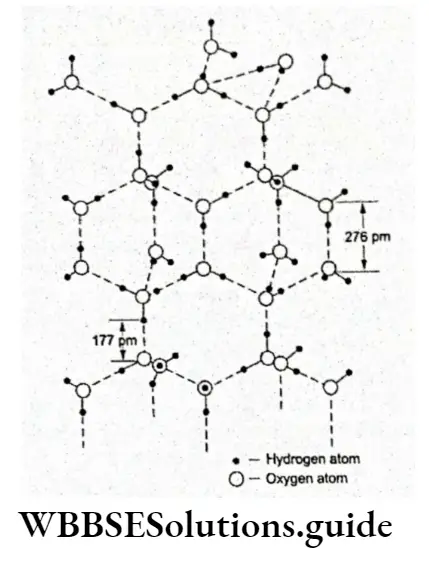
In normal hexagonal ice, each oxygen is tetrahedrally surrounded by four other oxygen atoms, there being a hydrogen atom between each pair of oxygen atoms.

Each 2hydrogen atom is covalently bonded to one oxygen atom and linked to another oxygen atom by a hydrogen bond.

Such an arrangement leads to packing with comparatively large open spaces.

Therefore, the density of ice is less than that of liquid water and so ice floats on water.

However, when ice melts, some of the hydrogen bonds are broken and the water molecules become more closely packed.

The result is an increase in density above the melting point (273 K) of ice. Floating blocks of ice prevent or delay the freezing of underlying water, enabling aquatic life to survive in the colder regions of the earth.

Heavy Water

Normal water has one part of heavy water in 6,000 parts of it. molecule of heavy water contains two atoms of heavy hydrogen (deuterium) combined with one oxygen atom. Represented by the formula D20, it is also called deuterium oxide.

Heavy water Preparation

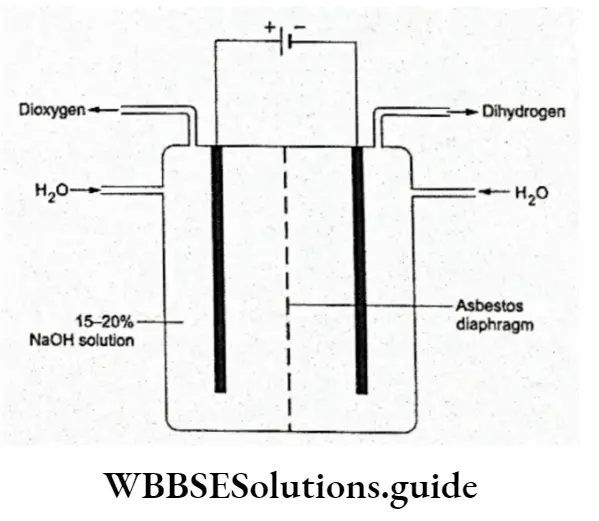
Heavy water is prepared by the exhaustive electrolysis of natural water containing an alkali. Electrolysis is continued in stages till the electrolyte is reduced to one-sixth of the original volume.

The alkali present is neutralised partially by passing carbon dioxide gas through the electrolyte. The solution is then distilled, and the distillate contains about 0.5% DzO.

Distillation is repeated and 99% D₂O is obtained after the seventh stage. This is possible because natural water dissociates about three to four times as much as heavy water does.

The equilibrium constant for the dissociation of H₂O is10 x10’14 while that for D₂O is 3.0 x10-15.

Protonium bonds are broken more readily than deuterium bonds. Thus, when water is electrolysed, H₂ is liberated much faster than D2 and the remaining water gets enriched in D₂O.

Water and DzO can also be separated to an extent by fractional distillation, using a fractionating column about 13 metres long. The lighter fraction (H₂O) distils first leaving behind a residue richer in D₂O

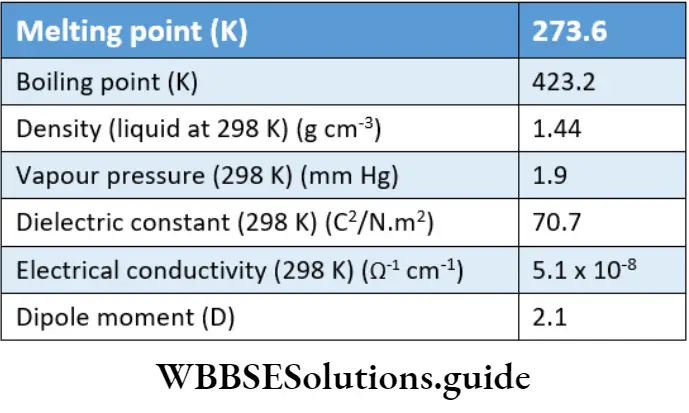
Heavy water  Properties

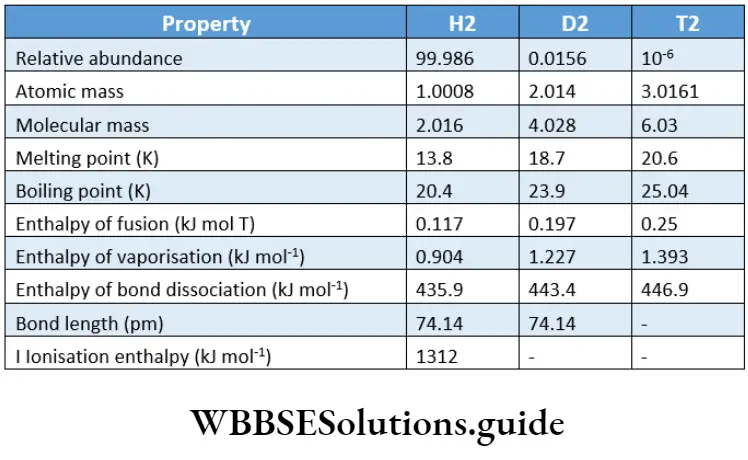
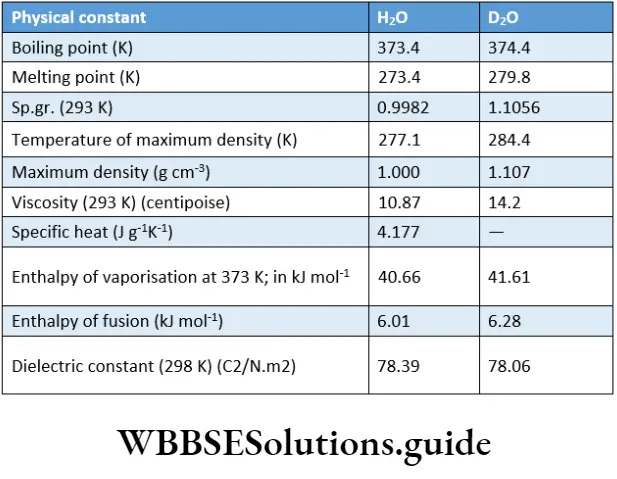
Like normal water, heavy water is a colourless, odourless and tasteless liquid. Almost all the physical constants for heavy water are higher than those for normal water.

This is because of the higher molecular mass of heavy water, and also owing to the strong van der Waals forces between its molecules. A few physical constants of normal water and heavy water are compared.

However, the surface tension of D₂O (67.8) is lower than that of ordinary water. Also, the refractive index of heavy water (1.3284) is lower than that of normal water (1.333) at 293 K.

The solubility of salts like barium chloride and sodium chloride is less in normal water than in heavy water. Heavy water is harmful to living organisms. For instance, it hinders plant growth.

D₂O and H₂O differ very little in chemical behaviour, a rare example being that the reaction rate of D₂O reactions is slightly less than that of H₂O reactions. One significant property of D₂O is that it participates in ‘exchange’ reactions.

For example, D₂ reacts with H₂ at high temperatures to form FID. Exchange reactions also occur with NH₃ and CH4, the products being NH₂D, NHD₂, ND3, and CH₃D and CD₄. D₂O can also be used directly to prepare deuterium compounds through such reactions. For example,

⇒ \(\begin{aligned}
& \mathrm{NaOH}+\mathrm{D}_2 \mathrm{O} \longrightarrow \mathrm{NaOD}+\mathrm{HDO} \\
& \mathrm{NH}_4 \mathrm{Cl}+\mathrm{D}_2 \mathrm{O} \longrightarrow \mathrm{NH}_3 \mathrm{DCl}+\mathrm{HDO}
\end{aligned}\)

In such reactions, deuterium is exchanged for hydrogen in the formation of compounds. Some of these, e.g., NaOD and D₂SO₄, are useful in the study of reaction mechanisms, e.g., those of esterification or hydrolysis.

Heavy water Uses

D20 is used to detect the presence of acidic hydrogen. For example, upon reacting with D20, a carboxylic acid (R—COOH) gives the exchanged product (R—COOD) and a phenolic compound (R—OH) gives R—OD.

The presence of D in the exchanged product can be ascertained by the use of spectroscopic techniques (particularly nuclear magnetic resonance).

However, a discussion of these techniques is beyond the scope of this book. Heavy water is used in nuclear reactors as a moderator.

In other words, it slows down the fast-moving neutrons in nuclear reactors so that nuclear fission may take place in a controlled way. When heavy water is made to react with sodium, deuterium is formed. This reaction is used in the production of deuterium.

Hard and Soft Water

Water containing soluble salts of calcium and magnesium (viz., chlorides, bicarbonates and sulphates) is called hard water. Such water does not readily form a lather with soap.

In contrast, soft water, which does not contain calcium or magnesium ions, lathers readily with soap. Soap is the sodium salt of a higher fatty acid, e.g., sodium stearate.

The sodium salt is soluble in water but the corresponding calcium and magnesium salts are not.

When added to hard water (which contains calcium and magnesium ions), soap is precipitated as insoluble salts of calcium and magnesium (scum). Therefore, no lather is formed till all these ions are removed

⇒ \(2 \mathrm{C}_{17} \mathrm{H}_{35} \mathrm{COONa}+\mathrm{CaCl}_2 \longrightarrow 2 \mathrm{NaCl}+\left(\mathrm{C}_{17} \mathrm{H}_{35} \mathrm{COO}\right)_2 \mathrm{Ca}\)
Sodium stearate (In hard water) Calcium Stearate (white ppt)
(soap)

If a sample of hard water can be rendered soft by boiling, it is said to have temporary hardness.

Temporary hardness is due to the presence of bicarbonates of calcium and magnesium. If a sample of hard water cannot be made soft by boiling, it is said to have permanent hardness.

Permanent hardness is due to the presence of chlorides and sulphates of calcium and magnesium.

Water Softening

Removal of hardness is called softening. Depending on the type of hardness, water can be softened by suitable processes. Temporary hardness can be removed by the following methods.

1. By boiling As already stated, temporary hardness is due to the presence of bicarbonates of calcium and magnesium.

When hard water is boiled, the bicarbonates decompose to form insoluble carbonates, which can be removed by filtration.

⇒ \(\begin{aligned}
& \mathrm{Ca}\left(\mathrm{HCO}_3\right)_2 \stackrel{\text { heat }}{\longrightarrow} \mathrm{CaCO}_3(\downarrow)+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2(\uparrow) \\
& \mathrm{Mg}\left(\mathrm{HCO}_3\right)_2 \stackrel{\text { heat }}{\longrightarrow} \mathrm{MgCO}_3(\downarrow)+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2(\uparrow)
\end{aligned}\)

By the Clark process By adding a calculated quantity of slaked lime to a sample of hard water, the soluble bicarbonates are converted into insoluble carbonates, which are removed by filtration.

⇒ \(\mathrm{Ca}\left(\mathrm{HCO}_3\right)_2+\mathrm{Ca}(\mathrm{OH})_2 \longrightarrow 2 \mathrm{CaCO}_3(\downarrow)+2 \mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{Mg}\left(\mathrm{HCO}_3\right)_2+\mathrm{Ca}(\mathrm{OH})_2 \longrightarrow \mathrm{MgCO}_3(\downarrow)+\mathrm{CaCO}_3(\downarrow)+2 \mathrm{H}_2 \mathrm{O}\)

In the above process, an excess of calcium hydroxide (slaked lime) must not be used, since it causes permanent hardness.

Permanent hardness may be removed by the following methods.

1. By adding washing soda The addition of washing soda (sodium carbonate) removes temporary as well as permanent hardness from samples of hard water by the precipitation of carbonates of calcium and magnesium from their chlorides and sulphates.

⇒ \(\mathrm{CaCl}_2+\mathrm{Na}_2 \mathrm{CO}_3 \longrightarrow \mathrm{CaCO}_3 \downarrow+2 \mathrm{NaCl}\)

⇒ \(\mathrm{MgCl}_2+\mathrm{Na}_2 \mathrm{CO}_3 \longrightarrow \mathrm{MgCO}_3 \downarrow+2 \mathrm{NaCl}\)

⇒ \(\mathrm{MgSO}_4+\mathrm{Na}_2 \mathrm{CO}_3 \longrightarrow \mathrm{MgCO}_3 \downarrow+\mathrm{Na}_2 \mathrm{SO}_4\)

By the pennutit process In this process, the ions responsible for the hardness of water (e.g., Ca++, Mg++) are 4 exchanged for sodium ions by using certain complex salts called ion-exchange resins.

These complex salts are also known as zeolites. They can be either naturally occurring or artificially synthesised. The name permit is used for * these zeolites.

A typical zeolite, e.g., sodium aluminium orthosilicate (Na2Al2Si208) is obtained by fusing together sodium carbonate (Na₂CO₃), alumina (A1₂O₃) and silica (SiO₃)

When hard water is passed through a zeolite, the calcium and magnesium ions are absorbed (exchanged) by the zeolite, and an equivalent amount of sodium ions passes into the water.

⇒ \(\mathrm{Na}_2 \mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8+\mathrm{Ca}^{2+} \longrightarrow \mathrm{Ca}\left(\mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8\right)+2 \mathrm{Na}^{+}\)

⇒ \(\mathrm{Na}_2 \mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8+\mathrm{Mg}^{2+} \longrightarrow \mathrm{Mg}\left(\mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8\right)+2 \mathrm{Na}^{+}\)

⇒ \(\mathrm{Na}_2 \mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8+\mathrm{Mg}^{2+} \longrightarrow \mathrm{Mg}\left(\mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8\right)+2 \mathrm{Na}^{+}\)

When all the sodium ions are exchanged for the calcium and magnesium ions, no further removal of hardness is possible.

Therefore, the used zeolite is treated with a sodium chloride solution (10%) so that all the calcium and 4 magnesium ions in the used zeolite are replaced by sodium ions. The zeolite is thus regenerated.

⇒ \(\mathrm{Ca}\left(\mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8\right)+2 \mathrm{NaCl} \longrightarrow \mathrm{Na}_2\left(\mathrm{Al}_2 \mathrm{Si}_2 \mathrm{O}_8\right)+\mathrm{CaCl}_2\)

The regenerated peanut is reused to soften water.

3. By the Calgon process In this process, calcium and magnesium ions, which are responsible for the hardness of water, are made ineffective by treatment with sodium hexametaphosphate [Na2Na4(P03)6 or Na6P6Ol8], which is known by the trade name Calgon.

The calcium and magnesium ions present in hard water combine with Calgon to form a soluble complex of calcium and magnesium salts. The following reactions take place in this process.

⇒ \(2 \mathrm{CaCl}_2+\mathrm{Na}_2 \mathrm{Na}_4\left(\mathrm{PO}_3\right)_6 \longrightarrow \mathrm{Na}_2 \mathrm{Ca}_2\left(\mathrm{PO}_3\right)_6+4 \mathrm{NaCl}\)

⇒ \(2 \mathrm{MgSO}_4+\mathrm{Na}_2 \mathrm{Na}_4\left(\mathrm{PO}_3\right)_6 \longrightarrow \mathrm{Na}_2 \mathrm{Mg}_2\left(\mathrm{PO}_3\right)_6+2 \mathrm{Na}_2 \mathrm{SO}_4\)

Once the calcium and magnesium ions go into the solution, the water readily forms a lather with soap.

The water softened by this procedure can be used only for washing purposes, and for raising steam in boilers. However, it is not fit for drinking.

4. By synthetic resins Water used in chemical laboratories and industries should be devoid of minerals (cation impurities and anion impurities).

Such water is called deionised or demineralised water and is as good as distilled water. Certain synthetic organic exchangers, also called ion-exchange resins, remove all types of cations and anions from water.

Such resins are preferable to zeolites since the latter remove only calcium and magnesium ions. There are two types of ion-exchange resins.

Cation-exchange resins: These resins have acidic groups like —COOH (carboxylic) or —SOaOH (sulphonic) attached to a large hydrocarbon molecule.

Thus, the molecules are represented as R—COOH or R—SO₃OH. Such resins can exchange ions with all cations present in water and are, therefore, called cation-exchange resins.

Anion-exchange resins: These have basic groups like —OH, usually in the form of substituted ammonium hydroxides and are represented as R—NH₃OH, R being a large hydrocarbon molecule.

These resins can exchange OH- ions with all anions present in water and are, therefore, called anion-exchange resins.

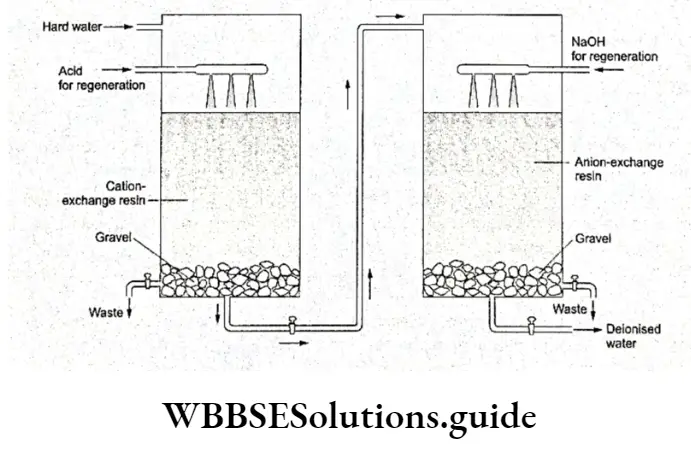
To obtain deionised water, hard water is passed through a tank packed with a cation-exchange resin supported over gravel.

The water thus obtained is passed through a second tank, which is packed with an anion-exchange resin supported on gravel.

By this treatment, all cations (Ca²⁺, Mg²⁺, etc.) are exchanged with H⁺ in the first tank and all anions (like C^1-, SO^2-) are exchanged with O^H- in the second tank.

The water now obtained is devoid of any cations or anions which were originally present. The reactions involved are as follows.

⇒ \(\mathrm{R}-\mathrm{COOH}+\mathrm{CaCl}_2 \longrightarrow(\mathrm{RCOO})_2 \mathrm{Ca}+2 \mathrm{H}^{+}+2 \mathrm{Cl}^{-}\)
cation-exchange resin orMgClj from water or(RCOO)2Mg exhausted resin

⇒ \(\mathrm{R}-\mathrm{NH}_3 \mathrm{OH}+\mathrm{Cl}^{-} \longrightarrow \mathrm{R}-\mathrm{NH}_3 \mathrm{Cl}+\mathrm{OH}^{-}\)
Anion exchange Resin Or SO2-4 or R—NH₃SO₄ exhausted resin

The exhausted resins can be regenerated from the first tank by treatment with moderately concentrated HC1 or H₂SO₄, and those from the second tank by treatment with an NaOH solution.

⇒ \((\mathrm{RCOO})_2 \mathrm{Ca}+2 \mathrm{HCl} \longrightarrow \mathrm{RCOOH}+\mathrm{Ca}^{2+}+2 \mathrm{Cl}^{-}\)

⇒ \(\mathrm{RNH}_3 \mathrm{Cl}+\mathrm{NaOH} \longrightarrow \mathrm{RNH}_3 \mathrm{OH}+\mathrm{Na}^{+}+\mathrm{Cl}^{-}\)

Thus, the cation exchange and the anion exchange resins can be used over and over again.

Alternatively, a ‘mixed bed’, i.e., a single column made of two different ion exchange resins, may be used.

Purification of Water for Drinking

Pure water is required for drinking purposes. The suspended impurities have to be removed, and the bacteria present destroyed before water can be used for drinking.

The water to be purified is taken in a large tank and treated with the requisite quantity of aluminium sulphate.

This treatment coagulates the impurities, which settle down along with bacteria and other suspended particles.

The water is then filtered through sand filters. The sand filters consist of a top layer of fine sand (1-1.25 m thick), a middle layer of coarse sand (0.3-0.5 m thick) and a bottom layer of graded sand (0.5-1 m thick).

Through this process, all the coagulated and suspended impurities along with most of the bacteria are removed.

The filtered water thus obtained is treated with liquid chlorine in big tanks. This kills the bacteria in the water.

Chlorinated Water is Fit for Drinking.

Some households use water filters. An ordinary water filter is fitted with porous tubes made of unglazed porcelain.

Such a filter, though, has to be cleaned frequently. Some water purifiers are also fitted with mercury vapour lamps. The ultraviolet light from the lamps destroys the bacteria in impure water.

River water is purified by the natural process of aeration. The oxygen present in the air is absorbed in water and oxidises the organic matter.

The shortage of drinking water has become an acute problem. Therefore, attempts are being made to convert seawater into drinking water on a large scale.

Some methods which can be used for this purpose are as follows.

Distillation Sea water is distilled by using solar heaters. However, only limited quantities of seawater can be purified using this method.

Reverse osmosis In this process, seawater is passed through a semipermeable membrane under an applied pressure that is greater than normal osmotic pressure. The semipermeable membrane only permits the solvent to pass through leaving the solute behind.

Filtration Special membranes are used to filter water. This allows water to pass through, leaving behind dissolved salts.

Hydrogen Economy

As you are aware, the reserves of fossil fuels are limited. Therefore, attempts are being made to use alternate materials as sources of energy. One such material is dihydrogen.

Because of the wide use of hydrogen in the processing industries and for the hydrogenation of various oils and fats in the food industry, hydrogen has become much better understood during the past several decades.

However, it was only after the late 1960s that hydrogen could be thought of as a major energy source.

However, to date, it has been used only to a limited extent due to its non-availability in the free state of nature. Also, putting pure hydrogen vehicles on the road would create another major problem—the safe storage of hydrogen.

Thus, to use hydrogen as a major fuel two problems need to be overcome—those related to production and safe storage. Though water is a potential source of dihydrogen, its use for the production of hydrogen is limited due to the cost involved in electrolysis.

The hydrogen economy involves the transportation and storage of energy in the liquid or gaseous form of hydrogen.

Compressing the gas needs energy and compressed hydrogen contains far less energy than the same volume of gasoline.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

The hydrogen economy aims to solve the problems associated with the transfer of energy in the form of hydrogen. One solution is the storage of hydrogen in a solid, sodium borohydride.

This compound is made from borax. After releasing hydrogen, sodium borohydride gives back borax, which can be recycled.

One more technology already in use involves the — production of large quantities of hydrogen using electricity and the storage of hydrogen in insulated — cryogenic tanks. This is used in space programs.

Once the storage problem is solved, hydrogen stations and pipelines have to develop. Small quantities of hydrogen can be stored using some metal alloys like Ti—TiH₂ and Mg—MgH₂.

The present concept of a hydrogen fuel economy involves a primary energy source such as a nuclear reactor, a geothermal source or a solar-powered source with hydrogen being produced as a portable energy carrier.

Thermal energy would be used to generate electricity that would then be used to electrolyse water for the production of hydrogen and oxygen.

The hydrogen would be distributed by pipelines to distant points of use with storage provided underground in gaseous or liquid form.

Hydrogen Advantages

Using hydrogen as a fuel eliminates major problems created by using fossil fuels. The advantages include:

1. Elimination of pollutants like NO₂, CO, CO₂ and SO₂. The only by-product is water.
2. If hydrogen is produced from the electrolysis of water then no greenhouse gases are added to the environment.
3. Hydrogen can release more energy than petrol and other fuels like methane and butane.
4. Hydrogen can be produced anywhere with electricity and water. There has been a major breakthrough in fuel-cell technology and fuel cells for regeneration of electric power are a success commercially.
5. A fuel cell is a device that converts the chemical energy of a fuel directly into electricity. In batteries, the electrodes are the source of the active ingredients, in fuel cells the gas or liquid fuel (often hydrogen) is supplied continuously to one electrode and oxygen or air to the other from an external source. So as long as the fuel and the oxidant are supplied, the fuel cell will continue to function.
6. The hydrogen economy will also help nations which depend on the Middle East for its oil reserves.

Active Forms Of Hydrogen

You already know that the diatomic hydrogen molecule is almost inert due to its high bond enthalpy. However, under appropriate conditions, hydrogen exists in two active forms.

Nascent Hydrogen

It is a reactive form of hydrogen produced in situ, which means it is generated and used in the reaction mixture itself.

Some elements and compounds which do not readily react with ordinary molecular hydrogen can be easily reduced by nascent hydrogen.

For example, when a current of ordinary molecular hydrogen is passed through acidified potassium permanganate there is no reaction.

However, if a piece of granulated zinc is added to the solution, the latter loses its pink colour.

This is due to the reduction of potassium permanganate by nascent hydrogen, which is produced by the action of the acid on zinc.

⇒ \(\underset{\text { pink }}{2 \mathrm{KMnO}_4}+3 \mathrm{H}_2 \mathrm{SO}_4+\underset{\substack{\text { nascent } \\ \text { hydrogen }}}{10 \mathrm{H}} \longrightarrow \underset{\text { colourless }}{\mathrm{K}_2 \mathrm{SO}_4}+2 \mathrm{MnSO}_4+8 \mathrm{H}_2 \mathrm{O}\)

Studies have revealed that nascent hydrogen is probably the hydrogen molecule in the excited state, which is used up before it returns to the ground state.

Atomic Hydrogen

Atomic hydrogen is the hydrogen obtained by passing the ordinary molecular hydrogen through an electric arc at low pressure.

On coming in contact with the surface of a metal, atomic hydrogen forms molecular hydrogen with the liberation of a large amount of heat.

The heat produced is so much that the temperature rises to about 4200 K. This reaction is made use of in the atomic hydrogen torch, used for welding metals.

Hydrides

Binary compounds of elements with hydrogen are known as hydrides. The kind of hydride an element forms depends on its electronegativity. Hydrides can be of the following types.

1. Ionic, or saltlike
2. Covalent, or molecular
3. Metallic, or interstitial

Ionic (Saltlike) Hydrides

Most of the alkali and alkaline earth metals form nonvolatile ionic, or saltlike hydrides. The hydrides of alkali metals have rock-salt structures.

The thermal stability of the hydrides decreases as the size of the metal cation increases from Li⁺ to Cs⁺ (as lattice energy decreases with an increase in size).

Ca, Sr and Ba form ionic hydrides at high temperatures. The order of stability of these hydrides is CaH₂ > SrH₂ > BaH₂.

Ionic hydrides are solids with high melting points. However, hydrides of beryllium (BeHz) and magnesium (MgH₂) have covalent polymeric structures.

In the molten or fused state, they can be electrolysed, giving hydrogen to the anode. This confirms the presence of H- ions.

Ionic hydrides react explosively with water to liberate dihydrogen gas.

⇒ \(\mathrm{LiH}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{LiOH}+\mathrm{H}_2\)

They are powerful reducing agents as illustrated by the following examples.

⇒ \(\begin{gathered}
\mathrm{NaH}+2 \mathrm{CO} \longrightarrow \mathrm{HCOONa}+\mathrm{C} \\
2 \mathrm{CaH}_2+\mathrm{PbSO}_4 \longrightarrow \mathrm{PbS}+2 \mathrm{Ca}(\mathrm{OH})_2
\end{gathered}\)

Complex metal hydrides like LiAlH4 and NaBH4, which are extensively used as reducing agents in inorganic { as well as organic synthesis, can be obtained from NaH and LiH.

⇒ \(\begin{gathered}
4 \mathrm{LiH}+\mathrm{AlCl}_3 \longrightarrow \mathrm{LiAlH}_4+3 \mathrm{LiCl} \\
4 \mathrm{NaH}+\mathrm{B}\left(\mathrm{OCH}_3\right)_3 \longrightarrow \mathrm{NaBH}_4+3 \mathrm{NaOCH}_3
\end{gathered}\)

Covalent (molecular) Hydrides

They are hydrides of p-block elements and have the formula XH„ or XH8_„ where n is the group in the periodic table to which X belongs.

The molecules of these hydrides are held together only by weak van der Waals forces and are thus usually volatile.

They are obtained as follows.

1. Reaction of dihydrogen with certain nonmetals under appropriate conditions.

⇒ \(3 \mathrm{H}_2+\mathrm{N}_2 \underset{\mathrm{Fe}_2 \mathrm{O}_3}{\stackrel{700 \mathrm{~K}, 200 \mathrm{~atm}}{\longrightarrow}} 2 \mathrm{NH}_3 \text { (Haber process) }\)

⇒ \(\mathrm{H}_2+\mathrm{Cl}_2 \longrightarrow 2 \mathrm{HCl}\)

The method is used to prepare pure hydrogen chloride.

2. Reaction of a halide with LiAlH₄ in a dry solvent

⇒ \(\mathrm{SiCl}_4+\mathrm{LiAlH}_4 \longrightarrow \mathrm{SiH}_4+\mathrm{AlCl}_3+\mathrm{LiCl}\)

⇒ \(4 \mathrm{BCl}_3+3 \mathrm{LiAlH}_4 \longrightarrow 2 \mathrm{~B}_2 \mathrm{H}_6+3 \mathrm{AlCl}_3+3 \mathrm{LiCl}\)

The names of the covalent, or molecular, hydrides are derived from the name of the element and the suffix ane. For instance, phosphane for PH₃, oxidane for H₂O and azane for NH₃.

However, common names like phosphine, water and ammonia are retained and used more often than their systematic names.

Covalent, or molecular, hydrides can be electron-deficient (e.g., diborane, B₂H₆), electron-precise (e.g., methane, CH₄) and electron-rich (e.g., ammonia, NH₃). All elements of Group 13 form electron-deficient hydrides whereas those of Group 15-17 form electron-rich hydrides.

The electron-rich hydrides have lone pair(s) of electrons. Owing to the presence of lone pairs in the electronegative atoms, these hydrides usually form hydrogen bonds.

The presence of hydrogen bonding in compounds like water, ammonia and hydrogen fluoride leads to a change in their physical properties.

Metallic (Nonstoichiometric) Hydrides

Such hydrides are obtained by the reaction of dihydrogen with many elements in the d block, and the lanthanides and actinides.

However, the elements in the middle of the d block do not form hydrides—this part of the block is referred to as the hydride gap.

The elements of Groups 7, 8 and 9 do not form hydrides and only chromium from Group 6 forms a hydride.

Metallic hydrides are generally prepared by heating the corresponding metal along with hydrogen.

However, at higher temperatures, the hydrides decompose, and this phenomenon can be used to prepare very pure hydrogen.

When finely powdered metallic hydrides are heated, finely divided metals are obtained, and they can be used as catalysts in various reactions.

Metallic hydrides were originally called interstitial hydrides because it was thought that hydrogen occupied varying numbers of interstitial positions in the metal lattice, causing distortion.

However recent experimental findings reveal that except for a few hydrides (e.g., that of Ni), the other hydrides have a lattice different from that of the parent metal.

Unlike ionic hydrides, these are nonstoichiometric compounds. (Nonstoichiometric compounds are those chemical compounds in which the elements do not combine in simple ratios.) For example, LaHi8₇, YbH 255, TiHlg ,ZrHJ₁₉, VH₁₆, NbHO₇ and PdHO₇

Isotopes

Hydrogen has three isotopes—protium, deuterium and tritium—of mass number 1, 2 and 3 respectively.

The natural abundance of these isotopes is in the ratio 1: 1.56 x 10″2:1 x 10″16. As you will learn later, the properties of the different isotopes of hydrogen are significantly different. Thus, giving them different names is justified.

This is not the case with the isotopes of other elements, e.g., C-12 and C-14, N-14 and N-15.

Proliant (11H) has one proton in the nucleus and one electron in the extranuclear part. Highly stable and nonradioactive, it constitutes approximately 99.986% of hydrogen gas.

Deuterium (21H) has one proton and one neutron in the nucleus, and one electron in the extranuclear part.

Like hydrogen, it is stable and nonradioactive. Represented as D, it is called heavy hydrogen. It is present to the extent of approximately 0.014% of hydrogen gas.

Tritium (31H) has one proton and two neutrons in the nucleus, and one electron in the extranuclear part. In contrast to protium and deuterium, it is unstable and radioactive.

Tritium emits low-energy p-particles (t1/2= 1Z26 years). It occurs in traces in hydrogen gas (approximately one in 1017 parts). Tritium is also represented as.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

The isotopes of an element have the same electronic configuration and so exhibit similar chemical behaviour. However, a chemical reaction may occur at different rates for each isotope.

Due to their different masses, their physical properties are different. Since deuterium is heavier than protium, reactions involving deuterium are slower than those involving protium.

Due to the same reason the boiling point of deuterium is higher than that of protium. The physical and atomic properties of the isotopes of hydrogen.

Dihydrogen Preparation

Dihydrogen (H₂), the stable form of elemental hydrogen, is prepared by the following methods.

From reactions between metals and acids Metals above hydrogen in the electrochemical series react with dilute acids to produce hydrogen.

Sodium and potassium are much too reactive. However, zinc and magnesium react moderately enough.

⇒ \(\begin{aligned}
& \mathrm{Mg}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{MgSO}_4+\mathrm{H}_2 \\
& \mathrm{Mg}+\underset{\text { d }}{2 \mathrm{HCl}} \longrightarrow \mathrm{MgCl}_2+\mathrm{H}_2 \\
& \mathrm{Zn}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{ZnSO}_4+\mathrm{H}_2 \\
&
\end{aligned}\)

The last of these reactions, i.e., the one involving granulated zinc and dilute H₂SO₄, is used to produce hydrogen in the laboratory. The use of concentrated H₂SO₄ in the reaction evolves SO₂ gas rather than hydrogen.

⇒ \(\mathrm{Zn}+2 \mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{ZnSO}_4+2 \mathrm{H}_2 \mathrm{O}+\mathrm{SO}_2\)

Also, magnesium and manganese react with dilute HN03 to produce hydrogen.

⇒ \(\mathrm{Mg}+2 \mathrm{HNO}_3 \longrightarrow \mathrm{Mg}\left(\mathrm{NO}_3\right)_2+\mathrm{H}_2\)

From reactions between metals and strong alkalis Metals like aluminium, zinc, lead and powdered silicon react with hot solutions of strong alkalis like NaOH and KOH to evolve hydrogen.

⇒ \(\begin{aligned}
2 \mathrm{Al}+2 \mathrm{NaOH}+2 \mathrm{H}_2 \mathrm{O} & \longrightarrow 2 \mathrm{NaAlO}_2+3 \mathrm{H}_2 \\
\mathrm{Zn}+2 \mathrm{NaOH} & \longrightarrow \mathrm{Na}_2 \mathrm{ZnO}_2+\mathrm{H}_2 \\
\mathrm{Si}+2 \mathrm{NaOH}+\mathrm{H}_2 \mathrm{O} & \longrightarrow \mathrm{Na}_2 \mathrm{SiO}_3+2 \mathrm{H}_2
\end{aligned}\)

The reaction of an alkali with aluminium is also used in the laboratory preparation of hydrogen. From reactions between metal hydrides and water Hydrides of metals react with water to produce hydrogen.

⇒ \(\begin{gathered}
\mathrm{CaH}_2+2 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Ca}(\mathrm{OH})_2+2 \mathrm{H}_2 \\
\mathrm{NaH}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{NaOH}+\mathrm{H}_2
\end{gathered}\)

Hydrogen is manufactured on a large scale by the following methods. By the electrolysis of water Pure dihydrogen (99.9% pure) may be prepared by the electrolysis of water in the presence of a small amount of sulphur using an iron cathode and a nickel anode.

⇒ \(2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\text { electrolysis }}{\longrightarrow} 2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g})
(acidic or basic)\)

The reaction is represented as

⇒ \(\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}^{+}+\mathrm{OH}^{-}\)

⇒  \(\text { At anode } \quad 4 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g})+4 \mathrm{e}^{-}\)

⇒ \(\text { At cathode } \quad 4 \mathrm{H}^{+}(\mathrm{aq})+4 \mathrm{e}^{-} \rightarrow 2 \mathrm{H}_2(\mathrm{~g})\)

The two compartments housing the anode and cathode are separated by an asbestos diaphragm so that the gases evolved in both compartments do not mix. However, this method is generally expensive and is commercially viable only where electricity is cheap.

By passing steam over red-hot coke (Bosch process) When steam is passed over red-hot coke, a mixture of equal volumes of carbon monoxide and dihydrogen is obtained. This mixture is known as water gas.

⇒ \(\mathrm{C}(\mathrm{s})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \longrightarrow \mathrm{CO}(\mathrm{g})+\mathrm{H}_2(\mathrm{~g})\)

The carbon monoxide is difficult to remove. Therefore, the gas mixture, mixed with steam, is passed over an F0jO3 catalyst (and a Cr203 promoter) at 673 K, when carbon monoxide is oxidised to carbon dioxide. The carbon dioxide is removed by dissolving the mixture in cold water under pressure.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{CO}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \stackrel{\mathrm{Fe}_2 \mathrm{O}_3 / \mathrm{Cr}_2 \mathrm{O},}{\underset{673 \mathrm{~K}}{\longrightarrow}} \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2(\mathrm{~g})\)

From natural gas, Natural gas contains hydrogen (20%), methane (70%) and some other hydrocarbons.

When natural gas along with steam is passed over a nickel catalyst at 1270 K, a mixture of carbon monoxide, carbon dioxide and dihydrogen is obtained. The mixture of gases is cooled to 770 K and passed over catalysts (Fe/Cu) to convert carbon monoxide into carbon dioxide.

⇒ \(\begin{gathered}
\mathrm{CH}_4+\mathrm{H}_2 \mathrm{O} \stackrel{\mathrm{Ni}, 1270 \mathrm{~K}}{\longrightarrow} \mathrm{CO}+3 \mathrm{H}_2 \\
\mathrm{CH}_4+2 \mathrm{H}_2 \mathrm{O} \stackrel{\mathrm{Ni}, 1270 \mathrm{~K}}{\longrightarrow} \mathrm{CO}_2+4 \mathrm{H}_2 \\
\mathrm{CO}+\mathrm{H}_2 \mathrm{O} \stackrel{\mathrm{Fe} / \mathrm{Cu}}{\underset{70 \mathrm{~K}}{\longrightarrow}} \mathrm{CO}_2+\mathrm{H}_2
\end{gathered}\)

The carbon dioxide is then removed by passing the mixture of gases through a potassium carbonate solution.

⇒ \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{K}_2 \mathrm{CO}_3(\mathrm{l})+\mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{KHCO}_3\)

Instead of using natural gas, one can use methane obtained by the cracking of hydrocarbons to produce dihydrogen. The mixture of hydrogen and carbon monoxide obtained by steam reforming of natural gas is called ‘syngas’.

To produce hydrogen, syngas are further processed using a water gas shift reactor to convert carbon monoxide to carbon dioxide and increase the amount of hydrogen, which is eventually separated. Partial oxidation of coal is also one of the clean methods of producing syngas.

This process is known as coal gasification. Rather than burning coal directly, gasification breaks down coal, which is exposed to steam and controlled amounts of oxygen, into a mixture that mainly contains carbon monoxide and hydrogen.

The environmental benefit from the process is that the syngas obtained is virtually free of oxides of nitrogen. Nowadays attempts are being made to build gasifiers which are capable of processing municipal waste to produce syngas.

As a by-product in the manufacture of sodium hydroxide Sodium hydroxide is manufactured by the electrolysis of an aqueous solution of sodium chloride. Hydrogen is obtained as a by-product in this process.

Dihydrogen  Physical Properties

Dihydrogen is a colourless, odourless and tasteless gas. It is the lightest gas (density 0.0899 g cm-3) known. Highly inflammable, it should be handled with care.

It is practically insoluble in water and neutral towards litmus. An interesting property of hydrogen is its adsorption or occlusion by certain metals like platinum or palladium. Adsorption is the process of soaking up only on the surface.

(This should not be confused with absorption, in which soaking takes place through the entire mass.)

It is found that one volume of platinum black adsorbs 100 volumes of hydrogen at 925 K, while palladium adsorbs about 500-800 volumes of hydrogen at this temperature.

This property is made use of in the purification of hydrogen since only pure hydrogen is adsorbed by these metals. The adsorbed hydrogen is released when the metals are heated in a vacuum.

Dihydrogen  Chemical Properties

In spite of its high bond energy (435.9 kJ mol-1), dihydrogen reacts with almost all elements under appropriate conditions, except noble gases. Some reactions of dihydrogen are given below.

1. Dihydrogen is quite stable and can be broken up into its constituent atoms only when heated to above 2000 K.

⇒ \(\mathrm{H}_2 \stackrel{2000 \mathrm{~K}}{\longrightarrow} 2 \mathrm{H}\)

Due to the high H—H bond enthalpy, dihydrogen is almost inert at room temperature. Therefore, the use of heterogenous catalysis and high temperatures in chemical reactions involving hydrogen can be attributed to the strength of that H—H bond.

2. Dihydrogen is combustible and inflammable. In fact, it bums in the air to form water, and a large amount of heat is liberated.

⇒ \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ; \quad \Delta H=-485 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

This reaction is utilised in the oxy-hydrogen flame.

3. Reactions with metals Dihydrogen combines with alkali metals (Na, K, Li, etc.) and alkaline earth metals, e.g., Ca, to form hydrides.

⇒ \(2 \mathrm{Na}+\mathrm{H}_2 \stackrel{573 \mathrm{~K}}{\longrightarrow} 2 \mathrm{NaH}\)

⇒ \(\mathrm{Ca}+\mathrm{H}_2 \stackrel{573 \mathrm{~K}}{\longrightarrow} \mathrm{CaH}_2\)

Metal hydrides are extremely reactive and have many applications in organic reactions. Hydrides like CaH₂ and LiAlH4 are used for drying solvents, and LiAlH4 is also used to reduce groups like —CHO (aldehydes), C=C, etc. With transition metals like platinum, nickel and cobalt, hydrogen forms what are known as interstitial hydrides.

That is, they occupy the interstitial spaces in the crystal lattices of the metals. The hydrides have been further described later in the chapter.

4. Reactions with nonmetals Under appropriate conditions, dihydrogen reacts with most nonmetals like dioxygen, halogens, dinitrogen, sulphur and carbon. Hydrogen reacts with halogens.

The reaction with fluorine is violent and that with chlorine is explosive in sunlight.

The reaction with bromine occurs at a high temperature. A direct combination of hydrogen with chlorine is used to prepare hydrogen chloride.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{F}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{HF}(\mathrm{g})\)

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \stackrel{\text { sunlight }}{\longrightarrow} 2 \mathrm{HCl}(\mathrm{g})\)

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Br}_2(\mathrm{~g}) \stackrel{670 \mathrm{~K}}{\longrightarrow} 2 \mathrm{HBr}(\mathrm{g})\)

The reaction of hydrogen with nitrogen produces ammonia. This is used in the manufacture of ammonia by the Haber process.

⇒ \(3 \mathrm{H}_2(\mathrm{~g})+\mathrm{N}_2(\mathrm{~g}) \stackrel{\mathrm{Fe} / \mathrm{Mo}, 200 \mathrm{~atm}}{\underset{673 \mathrm{~K}}{\rightleftharpoons}} 2 \mathrm{NH}_3(\mathrm{~g})\)

Hydrogen reacts with sulphur and carbon at high temperatures to yield hydrogen sulphide, methane and ethyne. The reactions also form the basis of the manufacture of these compounds.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{S}(\mathrm{s}) \stackrel{710 \mathrm{~K}}{\longrightarrow} \mathrm{H}_2 \mathrm{~S}(\mathrm{~g})\)

⇒ \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{C}(\mathrm{s}) \stackrel{1275 \mathrm{~K}}{\longrightarrow} \mathrm{CH}_4(\mathrm{~g})\)

⇒ \(\mathrm{H}_2+2 \mathrm{C}(\mathrm{s}) \stackrel{\text { electric art }}{\longrightarrow} \mathrm{C}_2 \mathrm{H}_2(\mathrm{~g})\)

5. Reaction with metallic oxides Dihydrogen reduces the metallic oxides of some less electropositive metals (less active than iron) to the corresponding metals at high temperatures

⇒ \(\mathrm{H}_2+\mathrm{ZnO} \stackrel{\text { heat }}{\longrightarrow} \mathrm{Zn}+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{PbO}+\mathrm{H}_2 \stackrel{\text { heat }}{\longrightarrow} \mathrm{Pb}+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{CuO}+\mathrm{H}_2 \stackrel{\text { heat }}{\longrightarrow} \mathrm{Cu}+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{Ag}_2 \mathrm{O}+\mathrm{H}_2 \stackrel{\text { heat }}{\longrightarrow} 2 \mathrm{Ag}+\mathrm{H}_2 \mathrm{O}\)

6. Reaction with carbon monoxide Dihydrogen reacts with carbon monoxide in the presence of heated metal oxides at 573 K and 200 atm to form methyl alcohol.

⇒ \(\mathrm{CO}+2 \mathrm{H}_2 \underset{573 \mathrm{~K}, 200 \mathrm{~atm}}{\stackrel{\mathrm{ZnO}+\mathrm{Cr}_2 \mathrm{O}_3}{\longrightarrow}} \mathrm{CH}_3 \mathrm{OH}\)

The above reaction is used in the manufacture of methyl alcohol.

Dihydrogen  Uses

Dihydrogen has the following uses.

Being the lightest gas, it is used for filling balloons. However, since it is inflammable, hydrogen is mixed with another light gas—helium—for this purpose.

It helps extract iron, tungsten and molybdenum from their oxide ores.

The catalytic hydrogenation of organic compounds is an industrial process for the manufacture of aldehydes alcohols and other products. For example, the hydroformylation (reaction in the presence of H₂ and CO is known as hydroformylation) of olefins gives aldehydes, which can further be reduced to give alcohols.

⇒ \(\underset{\text { olefin }}{\mathrm{RCH}}=\mathrm{CH}_2+\mathrm{H}_2+\mathrm{CO} \stackrel{\text { catalyst }}{\longrightarrow} \underset{\text { RCH }}{\mathrm{RCH}_2 \mathrm{CH}_2 \mathrm{CHO}}\)

⇒ \(\mathrm{RCH}_2 \mathrm{CH}_2 \mathrm{CHO}+\mathrm{H}_2 \stackrel{\text { catalyst }}{\longrightarrow} \mathrm{RCH}_2 \mathrm{CH}_2 \mathrm{CH}_2 \mathrm{OH}\)

Hydrogen is also employed for the hydrogenation of vegetable oils (like cottonseed, coconut and groundnut oilskin the presence of a nickel catalyst to convert them into solid fats like vanaspati, which are used as cooking mediums. They are produced on a large scale in our country by the hydrogenation process.

Vegetable oils ⇒ \(\stackrel{\mathrm{H}_2 / \mathrm{Ni}, 473 \mathrm{~K}}{\longrightarrow}\)solid fats (hydrogenated edible oils)

The vegetable oils are unsaturated (since they contain double bonds in their molecules). When dihydrogen is passed through the oils at 473 K in the presence of a catalyst, solid fats are produced.

As we already know, hydrogen is used in the manufacture of ammonia (Haber’s process), methyl alcohol, hydrogen fluoride, hydrogen chloride, hydrogen bromide, acetylene and metal hydrides.

The oxy-hydrogen torch is used for welding and cutting iron and other metals. The temperature of the flame is approximately 2270-2710 K. The atomic-hydrogen torch gives a temperature of 3770-4270 K and is used for welding.

It is used as a rocket fuel, in combination with oxygen and fluorine.

States Of Matter

That matter exists in three physical states—solid, liquid and gaseous—is something you know from everyday experience. You must also be aware of the fact that a particular substance can exist as a solid, a liquid, or a gas, depending upon the temperature and pressure, example, water can exist in all three states.

In fact almost all substances can exist in the three states if the conditions of pressure and temperature are appropriate. Also, every pure substance can exist in the three states simultaneously (the three states are said to be in equilibrium) at a characteristic temperature and pressure called the triple point, about which you will learn later.

Generally speaking, we call a substance a solid if its melting point is above room temperature, a liquid if its melting point is below room temperature and boiling point is above room temperature, and a gas if its boiling point is below room temperature. This is under atmospheric pressure.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

• Certain other differences in the properties or behaviour of solids, liquids and gases are obvious from common observation. A solid, for example, has a definite shape and volume. It cannot be compressed easily and generally has a high density.
• A liquid has a definite volume but not a definite shape—it takes on the shape of the vessel it is poured into. It can be compressed more easily than a solid and generally has a lower density than a solid. A gas has neither a definite shape, nor a definite volume. It is highly compressible and has the least density among the three, i.e., solid, liquid and gas.
• Tire differences in these macroscopic or bulk properties of the three states of matter are due to the different arrangements of the constituent particles in the different states.
• In solids, the constituent particles are packed closely and are held together by a strong force of attraction between the particles. In liquids, the distance between the particles is greater and this force is weaker.
• In gases, the particles are far apart and this force is negligible. The particles in a solid are not really free to move. They possess only vibratory motion. The particles in a liquid enjoy greater freedom of movement. The particles constituting a gas have the greatest freedom of movement.

Intermolecular Forces

Intermolecular forces are responsible for the bulk properties of matter such as melting point and boiling point. The word bulk indicates a collection of atoms, molecules or ions. Intermolecular forces are those which exist between molecules as against intramolecular forces which hold the atoms together.

• In order to understand the difference between the two types of forces, let us take the example of water whose chemical formula is H₂O. There are two O—H bonds in the molecule and the energy required to break the two bonds is high; it is 930 kJ per mole of water.
• However, if we want to evaporate water, it requires only 41 kJ per mole of water. Generally, intermolecular forces are weaker than intramolecular forces.What are the forces that hold together the molecules in the different states of matter?
  What are the physical laws that govern the formation of a particular state of matter?
  Let us now study the types of forces existing between the particles of a matter that make it acquire a particular state.
  The particles may be molecules, atoms or ions.

van der Waals forces: Dipole-dipole forces, dipole-induced dipole and dispersion forces make up van der Waals forces, called so after the Dutch physicist Johannes van der Waals. These occur between molecules (intermolecular forces) or atoms (interatomic forces).

Dipole-dipole forces Neutral but polar molecules experience dipole forces as a result of electrical interactions among dipoles on neighbouring molecules. There is partial positive (δ+) or partial negative (δ-) charge associated with the two ends of the dipoles in a molecule.

• The molecules in a sample could be oriented in various ways and so the forces could be attractive (when unlike charges are close together) or repulsive (when like charges are close together) between the dipoles of neighbouring molecules.
• The overall effect is the average of all such forces. The potential energy is lower for the attractive orientation and so this predominates. The net potential energy will, therefore, be an average of the different orientations.
• It increases as the distance between the interacting dipoles decreases. The potential energy of interaction is proportional to 1/r⁶ where r is the distance between the dipoles (molecules). It also varies inversely as a function of temperature.

The strength of the given dipole-dipole interaction depends on the sizes of the dipole moments involved. The more polar the substance, the greater is the strength of its dipole-dipole interaction. This is reflected in the boiling point values for different substances. Substances with higher dipole moments tend to have higher boiling points.

Dipole-induced dipole forces Let us first understand what an induced dipole is. A molecule having a permanent dipole moment (polar molecule) can induce a dipole in another molecule by deforming its electronic cloud. The latter molecule, thus, gets an induced dipole.

• This induced dipole interacts with the dipole of the other molecule and the forces involved are called dipole-induced dipole forces. The strength of the interaction depends on the dipole moment of the polar molecule and the polarisability (the ease with which the electron cloud can get deformed) of the second molecule.
• The potential energy of interaction is directly proportional to these two factors. It also varies as 1/r⁶ as in the case of dipole-dipole forces.

London dispersion forces Intermolecular forces not only exist between charged and polar particles but also among nonpolar molecules. These are called London dispersion forces after Fritz London, who first explained them. In fact, all atoms and molecules experience London dispersion forces which result from the motion of electrons.

• Let us consider the example of a nonpolar molecule Br₂. It has a zero dipole moment averaged over time but at any point of time, the electrons may be more towards one end than the other resulting in a short-lived dipole. This dipole may induce temporary dipoles in neighbouring molecules resulting in attractive forces between the molecule with the permanent dipole and the neighbouring molecule.
• These forces are weak and the energy of interaction is small, in the range of 1-10 kJ mol^-1. The exact magnitude of the energy depends on the polarisability of the molecule. Smaller atoms or molecules are less polarisable as compared to larger ones and the dispersion forces are also loss. This can be easily understood by taking halogens as examples. F₂ and Cl₂ are gases at room temperature, Br₂ is a liquid and I₂ is a solid.

The intermolecular force of attraction increases in the order: F₂ <Cl₂; <Br₂, <I₂.

The increase in force of attraction with the increase in the size of atoms involved can be explained by London’s theory, In a larger atom, the valence electrons are, on an average, farther from the nuclei than those in a smaller atom.

• Also, they are loss tightly held and can more easily form the temporary dipoles that cause the attraction between molecules. Dispersion forces usually increase with molar mass because such molecules have more electrons and dispersion forces increase in strength with the number of electrons. Another factor which is important in determining the magnitude of the dispersion forces is its shape.
• Shapes which have larger molecular surface area allow greater contact between molecules and give rise to higher dispersion forces than do compact molecules. For instance, the boiling point of u-pentane is 309.4 K while that of neopentane or 2,2-dimethyl propane is 282.7 K though both of them have the same molecular formula.
• Tire reason behind this behaviour is that in n-pentane there is a possibility of greater contact between molecules because of its spread-out structure. Hence, this leads to stronger intermolecular dispersion forces and, therefore, a higher boiling point.
• The potential energy associated with London dispersion forces is again inversely proportional to the sixth power of the distance between tire molecules.

Hydrogen bonding: As already explained in Chapter 4, a hydrogen bond is formed whenever a hydrogen atom is bonded to one or more electronegative atoms (fluorine, oxygen or nitrogen). The large electronegativity difference between the atoms leads to a highly polar covalent bond with a partial positive charge on the hydrogen atom and a partial negative charge obviously on the electronegative atom.

• Tire electrostatic attraction between the partially positive H atom in one molecule and the partially negative atom in another molecule gives rise to a strong dipole-dipole attraction—the hydrogen bond. Hydrogen bonds are weaker than ordinary covalent bonds but stronger than other dipole-dipole attractions and London dispersion forces.
• Hydrogen bonds have a pronounced effect on the properties of condensed phases—solid and liquids.

Generally, the energy required to overcome the intramolecular forces decreases with a decrease in molar mass. The amount of heat required to evaporate 1 mole of the hydrides in a particular group generally decreases with decrease In molar mass but H₂O, HF and NH₃ exhibit exceptionally high values. This is because more energy is required to overcome H-bonding in these three cases.

Thermal Energy: Thermal energy (i.e., heat energy) is the kinetic energy associated with the random motion of atoms and molecules. The greater the amount of thermal energy in a sample, the more vigorous is the motion of atoms and molecules. This is called thermal motion. Thermal energy is directly proportional to temperature.

• If we increase the amount of thermal energy in a sample of matter, then either the temperature of the matter increases or the substance melts or evaporates with no change in temperature. If we decrease the thermal energy, then either the temperature decreases or the substance condenses or freezes with no change in temperature. The change in thermal energy of a substance can be observed by observing the change in temperature or state of that substance.
• Thus, the state of a matter depends on its intermolecular forces and thermal energy. An increase in the thermal energy of a solid or liquid helps to overcome the attractive forces between the particles and the substance melts (or evaporates). Similarly, if the thermal energy is decreased the intermolecular forces play a greater role than thermal motion and a liquid (or gas) is transformed to a solid (or liquid). Now we will learn about the laws which govern the behaviour of matter in different states and thus know more about the states of matter.

Measurement Of Properties Of Gases

Let us begin our study of the states of matter with gases and liquids. The behaviour of gases is studied in terms of their mass, volume, temperature and pressure and the relationship between these properties. So, we must know how these properties are measured before we examine the behaviour of gases.

Mass: The mass of a gas can be determined by weighing a container filled with the gas and then subtracting the weight of the empty container from this weight. The number of moles or the amount of the gas can be determined from the following equation.

n = m/M,

where n = number of moles,

m = mass of gas, and

M = molar mass of gas.

The number of molecules present in a particular mass of a gas can be determined by multiplying the number of moles (in that mass of the gas) by the Avogadro constant, 6.022 x 10²³ mol^-1.

Volume: The volume of a substance is the space occupied by it. A gas occupies the entire space available to it, so the volume of a gas is the same as the volume of the container it occupies. The SI unit of volume is m³, but usually volume is expressed in litres (L) or millilitres (mL).

1 m³ = 10³ dm³ = 10⁶ cm³

1 mL = 1 cm³

1 L = 1000 cm³ = 1 dm³

Pressure: Pressure is force per unit area. A gas confined in a container exerts uniform pressure on the walls of the container in all directions. The pressure of the gas is the outward force exerted by the gas per unit area on the walls of the container. The pressure exerted by the gases of the atmosphere on the surface of the earth is known as atmospheric pressure.

Barometer A (mercury) barometer is a simple device used to measure atmospheric pressure. It consists of a long glass tube (longer than 76 cm) filled with mercury, which is closed at one end and inverted (the open end) into an open vessel containing mercury. The level of mercury in the tube drops until the downward pressure exerted by the column of mercury (in the tube) on the mercury in the vessel is exactly balanced by the atmospheric pressure, which acts on the open surface of the mercury in the vessel. Normally, the height of the mercury in the tube is 76 cm. It increases or decreases as the atmospheric pressure increases or decreases.

Atmospheric pressure The atmospheric pressure can be calculated from the pressure exerted by the column of mercury. Let the height of the column of mercury be h cm and its area of cross section be A cm². Then the pressure exerted by the column of mercury can be calculated as follows.

Pressure (p) = \(\frac{\text { force }}{\text { area }}=\frac{\text { mass } \times \text { acceleration }}{\text { cross-sectional area }}\)

= \(\frac{m \times g}{A}\)

where m = mass of mercury column and

g = acceleration due to gravity.

Let V be the volume of mercury in the tube and d its density.

Then p = \(\frac{V \times d \times g}{A}=\frac{A \times h \times d \times g}{A}\) = hdg (V =A x h)

Knowing the density of mercury (1.35951 x 10⁴ kg m^-3 at 0°C) and the acceleration due to gravity (9.8065 m s^-2), it is possible to calculate the pressure exerted by the column of mercury 76 cm in height.

p = \((0.760 \mathrm{~m})\left(1.35951 \times 10^4 \frac{\mathrm{kg}}{\mathrm{m}^3}\right)\left(9.8065 \frac{\mathrm{m}}{\mathrm{s}^2}\right)=101,325 \mathrm{~kg} \mathrm{~m}^{-1} \mathrm{~s}^{-2}\) = 101, 325 N m^-2

Thus the measurement of the atmospheric pressure does not depend upon the area of cross section of the glass tube of the barometer.

The SI unit of pressure is pascal (Pa), which is defined as the pressure exerted when a force of 1 N acts on an area of 1 m².

1 Pa = 1 N m².

As calculated above, 1 atm = 101,325 N m^-2 = 101,325 Pa = 101.325 kPa.

The unit pascal is too small for gases and generally we express the pressure of the gas in terms of bar. The standard atmospheric pressure is 1 bar.

1 bar = 10⁵ Pa = 100 kPa.

Pascal and bar are related to the older unit of measurement, atm, as

1 atm = 1.01325 bar = 1.01325 x 10² kPa

or 1 bar = 0.987 atm.

One atmosphere may approximately be taken to be equal to 10² kPa or 10⁵ Pa.

1 atm is also referred to as 760 torr. The ‘torr’ is still used as a unit of pressure in some laboratories.

Manometer A manometer is used to measure the pressure of a gas. It consists of a U-tube partially filled with mercury. One of the limbs of the tube is longer than the other. The longer limb is open, while the shorter limb with its horizontal arm is connected to a closed vessel containing the gas whose pressure is to be measured.

The mercury in the open limb is exposed to atmospheric pressure, while the mercury in the shorter tube is subjected to the pressure of the gas. The difference in the level of the mercury in the two limbs can be used to determine the pressure of the gas.

1. If the level of mercury is equal in both limbs, the pressure of the gas is equal to the atmospheric pressure.
2. If the level is higher in the open tube, the pressure of the gas is higher than the atmospheric pressure (that is why the mercury gets pushed into the longer limb). Then the pressure of the gas can be determined as follows. Gas pressure (p_g) = atmospheric pressure (p_atm) + difference in mercury levels in two columns (h)
3. If the level of mercury is higher in the shorter tube, it means the pressure exerted by the gas is less than the atmospheric pressure. In this case, the pressure of the gas is determined as follows.

Gas pressure (p_g) = atmospheric pressure (p_atm) – difference in mercury levels in two columns (h)

The kind of manometer we have just discussed is called an open-end manometer. In some manometers, the longer limb is closed and the space above mercury on the closed end-side is completely evacuated. They are called closed-end manometers and are used only for gases at pressures less than the atmospheric pressure.

Temperature: The temperature of a gas, like that of other substances, is measured with the help of a thermometer. A thermometer, as you must already know, uses the fact that most substances expand on heating. The substance most commonly used in thermometers is mercury. Three scales are used for the measurement of temperature.

Celsius scale The Celsius (centigrade) scale, named after the Swedish astronomer, Anders Celsius, takes the freezing point of water as 0°C and the boiling point (both points at normal atmospheric pressure) of water as 100°C. The scale is divided into 100 equal parts. Meteorologists use this scale.

Fahrenheit scale The Fahrenheit scale, named after the German physicist, Daniel Fahrenheit, takes the freezing point of water as 32°F and the boiling point of water as 212°F. The scale is divided into 180 equal parts. Clinical thermometers use this scale.

Kelvin scale The Kelvin scale, named after the British physicist, Lord Kelvin, was the result of the study of gases. You will read more about this scale later in this chapter, kelvin is the SI unit of temperature and degrees are not used while expressing temperatures on this scale. For instance, 0°C – 273.15 K, not 273.15°K. The size of the degree on a Kelvin scale is the same as on the Celsius scale. Thus, on the Kelvin scale, water freezes at 273.15 K and boils at 373.15 K at 1 bar pressure.

We can measure the amount, pressure, volume and temperature of a gas in a sealed container. The observed relationships between these four interdependent variables are expressed in the form of gas laws. These laws are the quantitative relationships between any two of these variables when the other two are kept constant.

States Of Matter Multiple Choice Questions

Question 1. At the same temperature and pressure, which of the following gases will have the highest kinetic energy per mole?

1. Hydrogen
2. Oxygen
3. Methane
4. Same in all cases

Answer: 4. Same in all cases

Question 2. The mass of 5.6 L of a gas at stp is 11 g. The gas may be

1. PH₃
2. CoCl₂
3. NO
4. N₂O

Answer: 4. N₂O

Question 3. Equal weights of ethane and hydrogen are mixed in an empty container at 25°C. The fraction of the total pressure exerted by hydrogen is

1. 1/4
2. 1/2
3. 15/16
4. 1/16

Answer: 4. 1/16

Question 4. If you take 5.0 g of each of the following gases at 87°C and 750 mm Hg pressure, which will have the least volume?

1. HF
2. HCl
3. HBr
4. HI

Answer: 2. HCl

Question 5. The density of neon will be the highest at

1. stp
2. 0°C, 2 atm
3. 273°C, 1 atm
4. 273°C, 2 atm

Answer: 2. 0°C, 2 atm

Question 6. The temperature below which a gas does not obey the ideal gas law is called the

1. Critical temperature
2. Inversion temperature
3. Boyle temperature
4. Reduced temperature

Answer: 3. Boyle temperature

Question 7. 1.0 g of H₂ is heated from 300 K to 600 K in a dosed flask of volume 5 L. Which of the following statements is not correct?

1. The tire pressure of the gas increases.
2. The rate of collisions increases.
3. The number of moles increases.
4. The energy of the gaseous molecules increases.

Answer: 3. The number of moles increases.

Question 8. At constant temperature, for a given mass of an ideal gas,

1. The ratio of pressure and volume remains constant
2. The pressure remains constant
3. The volume remains constant
4. The product of pressure and volume remains constant

Answer: 4. The product of pressure and volume remains constant

Question 9. The compressibility factor for an ideal gas is

1. 1.5
2. 1.0
3. 2.0
4. ∞

Answer: 3. 2.0

Question 10. The molecular weights of O₂ and SO₂ are 32 and 64 respectively. If 1 L of O₂ at 15°C and 750 mm Hg contains N molecules, the number of molecules in 2 L of SO₂ under the same conditions of temperature and pressure will be

1. 2N
2. N
3. 2N
4. 4N

Answer: 3. 2N

Question 11. Two separate bulbs contain gas A and gas B. The density of gas A is twice that of B. The molecular mass of A is 12 that of B. If the temperature is constant, the ratio of the pressures of A and B is

1. 1:1
2. 1: 2
3. 4 :1
4. 2:1

Answer: 3. 4 :1

 

Liquids

Liquids, like gases, have no definite shape, but they do have a definite volume. One can, under ordinary conditions of temperature and pressure, assume that the volume of gaseous particles (atoms or molecules) is negligible compared to the volume of a gas.

• But one cannot do so in the case of a liquid. Nor can one ignore the intermolecular force which holds together the molecules of a liquid quite strongly (as one can in the case of a gas). It is because this attraction is quite strong so liquids have a definite volume.
• However, this attraction is not as strong as the attraction between the molecules of a solid, which is why liquids, unlike solids, do not have a definite shape. The molecules of a liquid do not occupy fixed positions as do the molecules of a solid. They exhibit translatory motion unlike the molecules of a solid. A liquid possesses the fluidity of a gas and the incompressibility of a solid. The liquid state is intermediate between the state of disorder in a gas and the state of order in a solid.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

The properties of a liquid can be explained in terms of the kinetic molecular theory which makes the following assumptions.

1. The molecules of a liquid are relatively closer together than the molecules of a gas.
2. The intermolecular force holding the molecules of a liquid together is appreciable.
3. The molecules of a liquid are in a constant state of random motion.
4. The average kinetic energy of the molecules of a liquid is directly proportional to its absolute temperature.

Properties of Liquids

Shape: Liquids do not have a definite shape. They take on the shape of the vessel they are placed in. This is because the molecules of a liquid have so much freedom that they flow readily and take up the shape of the container due to the continuous breaking and making of weak van der Waals bonds between the neighbouring molecules.

Volume: When you fill a container (closed) with a gas, the gas molecules spread out to occupy the whole container because they are free to move into whatever space is available. Liquid molecules, on the other hand, are held together by a relatively strong force of attraction, which does not allow them to move about quite so freely. This is why a liquid has a definite volume which does not change with the vessel it is placed in.

Density: The fact that liquid molecules are held much closer together than the molecules of a gas explains why liquids have a much greater density than gases under similar conditions. For instance, the density of water at 100°C and 1 atm pressure is about 1600 times the density of water vapour at the same temperature and pressure. The density of a liquid decreases or the liquid expands when temperature increases. This can be explained by the fact that the average kinetic energy of the molecules increases with temperature and they are able to overcome the intermolecular force to a small extent.

Compressibility: The much stronger attractive force between liquid molecules holds them close together than gaseous molecules. In fact, the intermolecular space in liquids is very little and this makes liquids far less compressible than gases under similar conditions.

Evaporation: The change of state of a liquid into a vapour at a temperature below the boiling point of the liquid is called evaporation. It is a surface phenomenon, that is to say the process occurs at the surface of a liquid. During evaporation, the molecules at the surface of a liquid manage to overcome the intermolecular force which binds them to the rest of the molecules, and escape into the space above the liquid. How does this happen? The molecules of a liquid are in a constant state of motion and their average kinetic energy is directly proportional to the absolute temperature of the liquid.

• However, just as in a gas, all the molecules of a liquid do not have the same energy. The energy distribution depends on the temperature of the liquid. At any temperature, a certain fraction of the molecules have enough energy to overcome the attractive force exerted on them by neighbouring molecules.
• The molecules at the surface of a liquid are attracted only by the molecules below them, while the molecules in the bulk of the liquid are attracted by molecules all around them. Surface molecules, thus, need less energy to overcome intermolecular attraction and it is easier for them to escape. The molecules which escape are the more energetic ones and the molecules that are left behind in the liquid are the less energetic ones.
• In other words, the molecules left behind have a lower average kinetic energy, which means that the temperature of the liquid falls due to evaporation. Of the molecules left behind, a certain energetic fraction will continue to change to the vapour phase, until all the liquid evaporates, provided the liquid is placed in an open vessel.

Rate of evaporation It is true that evaporation is a property of liquids but all liquids do not evaporate at the same rate. The rate of evaporation depends on many factors. The nature of the liquid is one of these factors.

• It should be obvious to you by now that the weaker the intermolecular force in a Liquid, the easier it will be for its molecules to escape into the vapour phase. Volatility is a term used to describe the readiness of a liquid to evaporate. The weaker the intermolecular force, the more volatile is the liquid, i.e., the more readily it evaporates. For instance, alcohol is more volatile than water.
• The rate of evaporation of a particular liquid depends on temperature. The higher the temperature, the greater will be the fraction of molecules which are energetic enough to escape from the surface, so the higher will be the rate of evaporation.
• Since evaporation is a surface phenomenon, it stands to reason that increasing the surface area of a liquid will increase the rate of evaporation. That is why we spread out our clothes to dry.
• Blowing a current of air across the surface of a liquid increases the rate of evaporation. The current of air carries away the molecules that have already escaped from the liquid and prevents them from returning to the liquid state.

Enthalpy of Vaporisation: The molecules of a liquid need energy to overcome the intermolecular force binding them to the liquid and escape into the vapour phase.

• The amount of heat required to evaporate 1 mole of a given liquid at a constant temperature is called the enthalpy of vaporisation. Obviously, the enthalpy of vaporisation of a liquid depends on its intermolecular force.
• The greater the intermolecular force, the greater will be the enthalpy of vaporisation. Water has a relatively high enthalpy of vaporisation because of the presence of strong hydrogen bonds between its molecules. The molar enthalpy of vaporisation of water at 25°C is 44.01 kJ mol^-1.

Vapour Pressure: When a liquid is placed in an open vessel, it evaporates slowly until all the liquid has changed into the vapour state. What happens when a liquid is placed in a closed vessel? If a liquid is placed in a closed vessel with some free space above the liquid, and the vessel is connected to a manometer, as shown in Figure, it initially evaporates and the level of the liquid falls. However, there comes a time when the level of the liquid becomes constant and so does the mercury level in the manometer.

• As explained earlier (in the section on evaporation), initially, the more energetic liquid molecules overcome the intermolecular force and escape from the surface of the liquid.
• These molecules accumulate in the space above the liquid since they cannot escape from the vessel and the pressure exerted by the vapour increases (raising the level of the mercury in the manometer).
• The vapour molecules are also in a state of random motion and their energy distribution follows the Maxwell-Boltzmann pattern.

As these molecules collide with each other, the walls of the container and the surface of the liquid, of them have low enough kinetic energy to be recaptured by the liquid molecules. Thus begins the process of condensation of the vapour molecules.

• The processes of evaporation and condensation proceed simultaneously. The rate of condensation increases as the number of vapour molecules in the space above the liquid increases.
• Ultimately a stage is reached when condensation takes place at the same rate as evaporation and the system (liquid and vapour) is said to be in a state of dynamic equilibrium.
• In this state, the level of the liquid in the vessel becomes constant, as do the number of molecules in the vapour state and the pressure exerted by them, which is indicated by the manometer.
• This pressure, or the pressure exerted by the vapour of a liquid in equilibrium with it, is called the equilibrium vapour pressure or the vapour pressure of the liquid.

The vapour pressure of a liquid rises with temperature because a greater number of molecules acquire the minimum kinetic energy to escape from the liquid phase.

Every liquid has a characteristic vapour pressure at a particular temperature. The higher the intermolecular force in a liquid, the less volatile it is, and the lower is the vapour pressure at a particular temperature.

Boiling Point: Boiling is similar to evaporation. However, there are certain differences between the two processes. Evaporation occurs spontaneously at all temperatures, while boiling takes place at a particular temperature at which the vapour pressure of a liquid becomes equal to the atmospheric pressure. There are some other differences between boiling and evaporation, but we will come to those later.

• What happens when a liquid boils? Suppose a liquid is heated gradually. The average energy of its molecules rises and more molecules have the energy to escape from its surface, i.e., the rate of vaporisation increases, as does the vapour pressure of the liquid. Then there comes a temperature (boiling point) when the vapour pressure of the liquid becomes equal to the atmospheric pressure.
• At this point, the bubbles of vapour formed inside the liquid become energetic enough to rise through the bulk of the liquid and escape from the surface.
• Before this temperature, when the vapour pressure is still lower than the atmospheric pressure, the bubbles of vapour formed inside the liquid remain trapped inside and evaporation takes place only from the surface of the liquid.

The temperature at which bubbles of vapour rise freely to the surface and the liquid starts to boil is the boiling point of the liquid.

• The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to the atmospheric pressure. Then obviously, the boiling point will depend on pressure. The boiling point of a liquid at 1 atm pressure is called its normal boiling point.
• The water has a vapour pressure equal to 1 atmosphere at 373.15 K which is the normal boiling point of water. If the pressure is higher, the boiling point rises and if it is lower, the boiling point falls. This is why water boils at a lower temperature in the hills (where atmospheric pressure is lower) than in the plains.
• A liquid may be made to boil at a higher or lower temperature than its normal boiling point by increasing or reducing the pressure. Liquids which decompose at their normal boiling point are made to boil under low pressure.
• Liquids in which tire intermolecular force is strong are less volatile and boil at a higher temperature.

Surface Tension: The molecules of a liquid are held together by the intermolecular force of attraction. However, all the molecules are not subjected to the same kind of attraction. The molecules below the surface of a liquid are attracted equally on all sides by other molecules which surround them, so there is no net force acting on them. The molecules at the surface, however, are attracted only by the molecules beside and below them.

• Thus, there is a net downward force of attraction acting on them, which tends to pull them into the liquid and to reduce the surface area to the minimum possible.
• Another way of looking at this is that the molecules at the surface are in a state of higher energy (since they experience a net downward force) than the molecules below the surface.
• Every system tends to a state of minimum energy’, so a liquid tends to have the minimum surface area possible. Whichever way you look at it, the downward force on the surface molecules tends to make the surface of a liquid behave like a stretched membrane.
• This property of the surface of a liquid to contract and behave as if it were in a state of tension is called surface tension. The formation of water droplets on a glossy surface is due to surface tension.
• Now that you know that a liquid surface tends to contract and behave like a stretched membrane, it should be easy enough to understand that work would need to be done to extend the surface of a liquid. Thus, surface tension is defined as the work (energy) required to expand the surface of a liquid by unit area. It is expressed in J m’. This is also referred to as surface energy.

Surface tension = \(\frac{\text { work }}{\text { change in area }}\)

Surface tension can also be defined as the force acting at right angles to the surface along unit length of the surface. The SI unit is N m^-1.

The greater the intermolecular force, the greater is the surface tension. You should be able to reason this out for yourself. It should also be easy to understand that if temperature increases, so will the energy of the molecules and their ability to break free of intermolecular attraction and consequently, surface tension will decrease.

Capillary Action When one end of a capillary tube is dipped into water, the water rises to a certain height. In fact, most liquids rise in capillary tubes. Different liquids rise to different heights depending on their surface tension. This phenomenon can be used to measure the surface tension of a liquid.

• You have read about the intermolecular force of attraction in a liquid. Now, when a liquid comes into contact with, say, a glass tube, there is a force of attraction between the liquid molecules and the glass molecules. The attractive force between molecules of the same substance is referred to as cohesive force and that between molecules of different substances is called adhesive force.
• In the case of glass and water, the adhesive force is stronger than the cohesive force, which tends to make water spread over glass (or wet it)2. When a capillary tube comes into contact with water, water tends to spread into it, forming a concave surface. This increases the surface area, and water rises in the capillary to reduce the total surface area. This continues till the adhesive force is balanced by die weight of water in the tube. The greater the surface tension, the higher is the rise in the capillary.
• One can find many examples of capillary action in everyday life. To mention only a few, oil rises in the wick of a stove due to capillary action and water rises in the stem of a plant due to capillary action.

Shape of Liquid Meniscus The surface of a liquid in a tube is curved. This curved surface is called a meniscus. Liquids which wet glass, like water, have a concave meniscus. You will learn more about this in your physics lessons.

For the moment, think of it this way that the stronger adhesive force pulls the surface of the water towards the glass, or makes the water stick to the glass, so the surface curves upwards. In the case of mercury, the cohesive force is stronger, so mercury draws away from glass and has a convex meniscus in a glass tube.

Shape of Liquid Drop You may have noticed that drops of water are spherical. Liquid drops are spherical due to surface tension. You have already learnt that a liquid tends to have the minimum surface area possible. For a given volume, a sphere has the minimum surface area, so a drop of liquid is spherical.

Dissolved Substances The surface tension of a liquid changes if some substance is dissolved in it. For example, soaps and detergents lower the surface tension of water. This enhances its ‘spreading property’. Synthetic detergents are often added to toilet creams and medicinal jellies so that they spread more evenly.

Viscosity: It is true that all liquids flow, but they do not flow at the same rate. Water, for instance, flows much more rapidly than honey. The readiness with which a liquid flows is governed by a property known as viscosity. The resistance offered by a liquid to flow is called viscosity. This resistance is a frictional effect due to the passage of one layer of liquid over another, and arises due to intermolecular force. The stronger the intermolecular force, the greater is the resistance to flow, i.e., the greater is the viscosity of the liquid.

• Let us examine the motion of a liquid flowing through a pipe. It is not as though the entire liquid moves along at the same velocity.
• Different layers of the liquid slide past each other at different velocities because of the resistance offered by one layer to another. The layer in contact with the pipe is almost stationary and the central layer moves the fastest. Thus, the velocities of the layers increase with distance from the fixed surface.

When the flow of the liquid becomes steady, there will be a constant difference in the velocity between two different layers. Consider the three consecutive layers shown in Figure. The velocity in the lowest layer is v – dυ, that in the middle layer is ν, and that in the top layer is v + dν. The force required to maintain the flow, in the three layers considered above, is directly proportional to the area of contact and velocity gradient, i.e.

⇒ \(f \propto A \quad (area)\)

⇒ \(f \propto \frac{d v}{d x} \quad\) (velocity gradient)

or, \(f=\eta A \frac{d v}{d x}\) (the two layers are separated by the distance dx ).

Here n is the coefficient of viscosity and is defined as the force required to maintain unit difference in velocity between two parallel layers of a liquid 1 cm apart. If all the variables are expressed in cgs units, the units of q turn out to be dyn s cm^-2. The quantity 1 dyn s cm^-2 is called 1 poise after Poiseuille, who did pioneering work in the field of fluid mechanics. In the SI system, the unit is Pa s, i.e., N s m^-2 or kg m^-1s^-1.

1 poise = 1/10 Pa s

Since viscosity depends on the intermolecular force, it should be obvious that viscosity decreases with rise in temperature.

Example 1. A gas occupies 2 L at 0°C and 1 atm pressure. What will be the change in temperature if the pressure is adjusted to 2.5 atm after the gas is transferred to a container of volume 1 L?
Solution:

Initial conditions

p₁ = 1atm

V₁ = 2L

T₁ = 0°C = 273 K

Final conditions

p₂ =2.5 atm

V₂ = 1L

T₂ =?

By the gas equation, \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\).

∴ \(\quad T_2=\frac{p_2 V_2 T_1}{p_1 V_1}=\frac{2.5 \times 1 \times 273}{1 \times 2}=341.25 \mathrm{~K}\)

∴ change in temperature = 34125 -273 = 68.25°C

Example 2. A sealed tube which can withstand a pressure of 3 atm is filled with air at 37 °C and 760 mmHg pressure. Find the temperature above which it will burst.
Solution:

Given,

V₁ = V mL

V₂ = V mL

p₁ = 760 mmHg = 1 atm

p₂ = 3 atm

T₁ = 37°C = 37 + 273 = 310K

T₂ = ?

According to the gas equation

⇒ \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\)

⇒ \(T_2 =\frac{p_2 V_2 T_1}{p_1 V_1}=\frac{3 \times V \times 310}{1 \times V}=930 \mathrm{~K}\) .

Therefore, the temperature above which the tube will burst = 930 – 273 = 657°C.

Example 3. A sample of a gas occupies a volume of 100 L at 4 atm and 20 °C. What will be its temperature when it is placed in an evacuated container of volume 175 L? The pressure of the gas in the container is one-third the initial pressure.
Solution:

Given, V₁ = 100 L V₂ = 175 L

p1 = 4 atm

p₂ = 1/3 x 4 = 4/3 atm

T₁ =20°C = 20 + 273 = 293K T2=?

Applying the gas equation

⇒ \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\)

⇒ \(T_2=\frac{p_2 V_2 T_1}{v_1 V_1}=\frac{4 / 3 \times 175 \times 293}{100 \times 4}=170.9 \mathrm{~K}\)

= 170.9- 273 =- 102.1 °C.

Example 4. The weight of 350 mL o/a diatomic gas at 0°C and 2 bar is 1.0 g. Calculate the weight of one atom in grams.
Solution:

Given,

p = 2 bar, V = 350 mL = 0.35L,T=0°C = 273 K

According to the equation

pV = nRT,

n = \(\frac{p V}{R T}\)

= \(\frac{2 \times 0.35}{0.08314 \times 273} \quad\left(because \quad R=0.08314 \mathrm{Lbar} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\right)\) = 0.031 mol

Weight of 0.031 mol of the gas =1 g.

Therefore, weight of1 mol of the gas = \(\frac{1}{0.031}\) = 32.2 g.

Since 1 mol contains 6.022 x 10²³ molecules, the weight of 6.022 x 10²³ molecules is 32.2 g.

Therefore, weight of one molecule = \(\frac{32.2}{6.022 \times 10^{23}}\) = 5.35 x 10^-23 g.

Since the gas is diatomic, one molecule has two atoms.

Therefore, the weight of one atom of the gas

= \(\frac{5.35 \times 10^{-23}}{2}=2.67 \times 10^{-23}\)

Example 5. How many moles of oxygen will there be in a 400 cm³ sample of the gas at a pressure of 760 mmHg and a temperature of 27°C? (R = 8.31 kPa dm³ K^-1 mol^-1)
Solution:

Given R = 8.31 kPa dm3 K^-1 mol^-1

V = 400 cm³ = 400/100 = 0.4 dm³ (1000 cm³ = 1 dm³ or 1 cm³ = 1/1000 dm³)

p = 760 mmHg = 101.3 kPa

T = 27°C = 27 + 273 = 300 K

According to the ideal gas equation,

pV = nRT.

∴ n = \(\frac{p V}{R T}=\frac{1013 \times 0.4}{8.31 \times 300}\) = 0.0162 mol.

Example 6. Calculate the number of nitrogen molecules present in a 1-L flask at a pressure of 7.6×10^-10 temperature of 10 °C (R = 0.082 L atm K^-1 mol^-1).
Solution:

Given V =1L

T =10°C = 10 + 273 = 283 K

p = \(7.6 \times 10^{-10} \mathrm{mmHg}=\frac{7.6 \times 10^{-10}}{760}=10^{-12} \mathrm{~atm}\)

According to the ideal gas equation pV = nRT.

∴ n = \(\frac{p V}{R T}=\frac{10^{-12} \times 1}{0.082 \times 283}=4.3 \times 10^{-14} \mathrm{~mol}\)

Number of molecules in1 mol of a gas = 6.022 x 10²³.

∴ number of nitrogen molecules in 4.3 x10^-14 mol = 4.3 x 10¹⁴ x 6.022 x 10²³ = 25.89 x 10⁹.

Example 7. 3.7 g of a gas at 25°C occupies the same volume as 0.184 g of H₂ at 17°C and at the same pressure. What is the molar mass of the gas?
Solution:

According to the ideal gas equation pV = nRT.

Number of moles (n) = n/M

∴ V = \(\frac{m}{M} \frac{R T}{p}\)

The volume and pressure of the two gases are the same.

⇒ \(\frac{m_1}{M_1} R T_1=\frac{m_2}{M_2} R T_2\)

where m₁ and m₁ are the masses of the given gas and hydrogen respectively and M₁ and M₂ are the molar masses of the given gas and hydrogen respectively.

Substituting the values of the known variables,

⇒ \(\frac{3.7}{M_1} \times R \times 298=\frac{0.184}{2} \times R \times 290\)

∴ \(\quad M_1=\frac{3.7 \times 298 \times 2}{0.184 \times 290}=4133 \mathrm{~g}\).
\end{aligned}

Example 8. Hydrogen gas is produced by passing steam over hot magnesium according to the following equation.

⇒ \(\mathrm{Mg}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{MgO}+\mathrm{H}_2\)

Calculate the volume of H₂ liberated by passing steam over 30 g of magnesium at 77°C and 1 atm.
Solution:

⇒ \(\underset{24 \mathrm{~g}}{\mathrm{Mg}}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{MgO}+\underset{224 \mathrm{~L}}{\mathrm{H}_2}\)

24 g of Mg produces 22.4 L of hydrogen at1 atm and 0°C.

∴ 30 g of Mg will produce = \(\frac{22.4 \times 30}{24}\) = 28L of H₂.

Let us find the volume of H₂ at 77°C and 1 atm.

p₁ =1 atm

V₁=28L

T₁ = 273 K

p₂ =latm

V₂ = ?

T₂ =77°C = 273 + 77 = 350 K

∴ \(V_2=\frac{p_1 V_1 T_2}{p_2 T_1}=\frac{1 \times 28 \times 350}{1 \times 273}=35.89 \mathrm{~L}\)

Example 9. How many litres of oxygen at 57°C and 2 bar is required to bum completely 2.5 g of butane (C₄H₁₀)?
Solution:

The equation for the reaction is \(\mathrm{C}_4 \mathrm{H}_{10}+\frac{13}{2} \mathrm{O}_2 \longrightarrow 4 \mathrm{CO}_2+5 \mathrm{H}_2 \mathrm{O}\)

⇒ \(58 \mathrm{~g} \quad \frac{13}{2} \times 22.7 \mathrm{~L}\)

At stp 58 g of butane requires 13/2 x 22.7 L of O₂.

∴ 2.5 g of butane would require = \(\frac{13}{2} \times \frac{22.7 \times 2.5}{58}\) = 6.36 L of O₂.

At stp

p₁ = 1 bar

V₁ = 6.36L

T₁ = 273K

At given conditions

p₂ = 2 bar

V₂ = ?

T₂ = 57°C = 57 + 273 = 330K

By the gas equation,

∴ \(V_2=\frac{p_1 V_1 T_2}{p_2 T_1}=\frac{1 \times 6.36 \times 330}{2 \times 273}=3.84 \mathrm{~L}\)

Example 10. 6.022 x 10²³ oxygen molecules are present at -13°C in a 1500 mL vessel. What is the pressure of the gas (R = 0.08314 L bar K^-1 mol^-1)?
Solution:

6.022 x 10²³ molecules = 1 mol.

Given

n = 1 mol

V = 1500 mL = 1.5 L

p = ?

T = -13°C = 273 -13 = 260 K

R = 0.08314 L bar K^-1 mol^-1.

Applying the ideal gas equation,

p = \(\frac{n R T}{V}=\frac{1 \times 0.08314 \times 260}{1.5}=14.4 \mathrm{bar}\).

Example 11. A gas of molar mass 84.5 g enclosed in a flask at 27°C, has a pressure of 2 atm. Calculate the density of the gas (R = 0.082 L atm K^-1 mol^-1).
Solution:

Given

Molar mass (M) = 84.5 g mol^-1

T = 27°C = 27 + 273 = 300 K.

Pressure = 2 atm

R = 0.082 L atm K^-1 mol^-1.

According to the ideal gas equation, pV = nRT = m/M RT.

∴ \(\frac{m}{V}=\rho=\frac{p M}{R T}=\frac{2 \times 84.5}{0.082 \times 300}=6.86 \mathrm{~g} \mathrm{~L}^{-1} \text {. }\)

Example 12. The density of a certain mass of gas is 0.326 g L^-1 at 2TC and 190 mm pressure. What is its density at 57°C?
Solution:

∴ \(operatorname{Density}(\rho)=\frac{\text { mass }(M)}{\text { volume }(V)}\)

∴ \(\quad \rho \propto \frac{1}{V}\) when M is constant.

According to Charles’s law,

V ∝ T.

∴ \(\rho \propto \frac{1}{T}\)

⇒\(\rho T=\text { constant } \Rightarrow \rho_1 T_1=\rho_2 T_2\).

Given,

⇒ \(\rho_1 =0.326 \mathrm{~g} / \mathrm{L} \quad T_1=27^{\circ} \mathrm{C}=27+273=300 \mathrm{~K}\)

⇒ \(T_2 =57^{\circ} \mathrm{C}=57+273=330 \mathrm{~K} . \)

⇒ \(\quad \rho_2=\frac{0.326 \times 300}{330}=0.296 \mathrm{~g} \mathrm{~L}^{-1}\).

Example 13. At 25°C, the air contains mostly nitrogen (79%) and oxygen (21%). How much faster do the nitrogen molecules move than the molecules of oxygen?
Solution:

⇒ \(\frac{u_{\mathrm{N}_2}}{u_{\mathrm{O}_2}}=\sqrt{\frac{M_{\mathrm{O}_2}}{M_{\mathrm{N}_2}}}=\sqrt{\frac{32}{28}}=1.07\)

The ratio of \(u_{\mathrm{N}_2} \text { to } u_{\mathrm{O}_2}\) is 1.07 (107%) indicating that the nitrogen molecules move 7% faster than oxygen molecules do.

Example 14. Calculate the height of the column of mercury in a mercury barometer. The diameter of the barometer is 5 mn% the pressure exerted is the atmospheric pressure i.e., 1.013 x10⁵ Pa and the density of mercury is 13.58 g cm^-3.
Solution:

Since p = hpg, where h is the height of the mercury column, p is the density of mercury and g is the acceleration due to gravity,

h = \(\frac{p}{p g}\)

First, let us express p in SI units.

⇒ \(\rho=13.58 \mathrm{~g} \mathrm{~cm}^{-3}=\frac{13.58}{1000} \times 10^6 \mathrm{~kg} \mathrm{~m}^{-3}\)

= \(13.58 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3} . \)

h = \(\frac{1013 \times 10^5}{13.58 \times 10^3 \times 9.81}\) = 0.76 m = 760 mmHg

Avogadro’s Hypothesis

You have already learnt that Avogadro had proposed the hypothesis that equal volumes of all gases contain an equal number of molecules under the same conditions of pressure and temperature. This means the volume of a gas is directly proportional to the number of molecules (N) at a given temperature and pressure.

V ∝ N at constant temperature and pressure. You also know that 1 mol of any gas at stp contains 6.022 x 10²³ molecules, which means that the number of molecules and the number of moles are related as follows.

Number of moles (n) = \(\frac{\text { number of molecules }(N)}{\text { Avogadro constant }\left(N_{\mathrm{A}}\right)}\)

Thus, Avogadro’s hypothesis can be expressed in terms of the number of moles rather than the number of molecules. Equal volumes of all gases contain the same number of moles under the same conditions of pressure and temperature, or volume is directly proportional to the number of moles at constant temperature and pressure.

V ∝ n at constant temperature and pressure

or V = a constant x n, where n is the amount or number of moles of a substance.

• The above observation was generalised by Amedeo Avogadro in the year 1811 as follows. All gases containing an equal number of moles occupy the same volume at the same temperature and pressure. This means that all the gases with the same value of n, at the same temperature and pressure, will have exactly the same value of V. It also follows that 1 mol of any gas occupies the same volume at the same temperature and pressure.
• This volume is known as molar volume (V_m) of the gas. Experiments show that the volume of 1 mol of any gas at standard temperature and pressure (stp) is 22.7109 L. Standard temperature refers to 0°C or 273.15 K and standard pressure to 1 bar. (According to the earlier convention stp referred to the same temperature, CTQ, but 1 atm pressure, and the molar volume was 22.4 L.) Accordingly the molar volume of any gas under these conditions is 22.7 L.

The total volume of n moles of a gas is V = nV_m.

Ideal Gas Equation

You have learnt that provided the pressure is constant, the volume of a gas is directly proportional to its Kelvin temperature. You have also leamt that the volume of a gas varies inversely with the pressure applied on it, provided the temperature is constant. And then that the volume of a gas is proportional to the number of moles at constant pressure and temperature. Is there a way in which we can sum up these three relations into one? Let us consider a particular amount of gas occupying volume V₁ at pressure p₁ and temperature T₁ What volume will it occupy at some other pressure p₂ and temperature T₂? Since the laws we have considered so far do not consider situations in which both the pressure and temperature change, let us take one step at a time. Let the temperature remain constant in the first step and the pressure change from p₁ to p₂ and let the volume change from V₁ to V_x, i.e.,

⇒ \(p_1 V_1 \stackrel{T_1 \text { constant }}{\longrightarrow} p_2 V_x\)

Then, according to Boyle’s law (p₁ V₁ = p₂V₂),

⇒ \(V_x=p_1 V_1 / p_2\) …..(1)

Now let the pressure remain constant at p₂ and let the temperature change from T₁ to T₂ and the volume change from V₁ to V₂, i.e.,

⇒ \(V_x T_1 \stackrel{p_2 \text { constant }}{\longrightarrow} V_2 T_2\)

Then according to Charles’s law \(\left(V_x / T_1=V_2 / T_2\right)\) ……(2)

From equations (1) and (2),

∴ \(p_1 V_1 / p_2=V_2 T_1 / T_2 \quad \text { or } \quad \frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2} \text {. }\)

This is a very useful equation for calculating the value of one of the variables if the other five arc known. It A implies that for a particular amount of gas, the ratio of the product of pressure and volume to the absolute temperature is constant

pV/T = constant, say K. ……. (3)

This constant K depends upon the mass or quantity of the gas we are considering. How do we make Equation (3)independent of the quantity of the gas? According to Avogadro’s hypothesis, the volume of a gas at constant temperature and pressure is directly proportional to the number of moles. In that case K in Equation (3) must also be proportional to the number of moles.

K = nR n = number of moles

⇒ pV/T = nR, where R is a constant independent of the amount of gas.

or pV = nRT.

This equation is called the ideal gas equation. The word ideal is used because it describes the behaviour of an ideal gas. In reality, no gas is ideal but you will read about that later in this chapter. The constant R is independent of the quantity of the gas and is the same for all gases. It is called the universal gas constant and has the value of pV/T for 1 mol of a gas.

The ideal gas equation may be alternatively derived by combining the four measurable variables of a gas as follows:

V ∝ n(p,T are constant) — Avogadro’s law

V ∝ r (n, p are constant) — Charles’s law

V ∝ yp («, T are constant) — Boyle’s law

Combining the above three equation,

⇒ \(V \propto \frac{n T}{p} \quad \text { or } \quad p V \propto n T \quad \text { or } \quad p V=n R T \text {. }\)

The ideal gas equation can be used to find the molar mass and density of a gas. We can express the ideal gas equation in terms of molar mass as follows.

⇒ \(p V=\frac{m}{M} R T{\left[n=\frac{m}{M}=\frac{\text { mass of gas }}{\text { molar mass of gas }}\right]}\)

⇒ \(p=\frac{m}{V} \frac{R T}{M}{\left[\frac{m}{V}=\rho \text {, density }\right]}\)

⇒ \(p=\rho \frac{R T}{M}\)

⇒ \(M=\rho \frac{R T}{n}\)

Universal gas constant: What exactly does the gas constant signify? To understand its nature, let us analyse the different quantities in the ideal gas equation.

pV = nRT

∴ \(R=\frac{p V}{n T}=\frac{\frac{\text { force }}{\text { area }} \times \text { volume }}{n \times \text { temperature }}=\frac{\frac{\text { force }}{\text { length }}{ }^2 \times \text { length }^3}{n \times \text { temperature }^3}\)

= \(\frac{\text { force } \times \text { length }}{n \times \text { temperature }}\)

Force multiplied by length has the dimensions of work or energy. Therefore, R lias the dimensions of (let us say R represents) work done or energy per degree per mole.

Depending upon the units used to express work (or energy), R may have different numerical values. The values of R can be calculated using the gas equation once the values of the pressure, volume and temperature are known.

1. In cgs units

Since p = hpg,

density of Hg = 13.6 g cm^-3, g = 981 cm s^-2

p = 76 cmHg = (76 x 13.6 x 981) dynes cm^-2

V = 22400 mL

T = 273.15 K

n = 1 mol

∴ R = \(\frac{p V}{n T}=\frac{76 \times 13.6 \times 981 \times 22400}{1 \times 273}=8.314 \times 10^7 \mathrm{erg} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\).

2. In SI units

p = 1 bar or 10⁵Pa = 10⁵ Nm^-2

V = 22.7 x 10^-3 m³

T = 273.15K

∴ R = \(\frac{1 \mathrm{~atm} \times 22.4 \mathrm{~L}}{1 \mathrm{~mol} \times 273.15 \mathrm{~K}}=0.0821 \mathrm{~L} \mathrm{~atm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\)

3. If p i taken as 1 atm and V as 22.4 L

R = \(=\frac{1 \mathrm{~atm} \times 22.4 \mathrm{~L}}{1 \mathrm{~mol} \times 273.15 \mathrm{~K}}=0.0821 \mathrm{~L} \mathrm{~atm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\)

4. If p is taken as 1 bar and T as 273 K (stp conditions)

We know that the volume occupied by 1 mol of any gas is 22.7109 L.

∴ R = \(\frac{(22.7109 \mathrm{~L})(1 \mathrm{bar})}{(273.15 \mathrm{~K})(1 \mathrm{~mol})}=0.08314 \mathrm{~L} \text { bar } \mathrm{K}^{-1} \mathrm{~mol}^{-1} .\)

Note that the value differs from the value in SI units only in the place of decimal point.

Example 1. 40 mL of oxygen was collected at 10°C and 1 bar pressure. Calculate its volume at 273 K and 1.013 bar.
Solution:

p₁ = 1 bar

p₂ = 1.013 bar

V₁ = 40mL

V₂ = ?

T₁ = 10C = 283K

T₂ = 273 K

According to the gas equation

⇒ \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\)

∴ \(\quad\frac{1 \times 40}{283}=\frac{1013 \times V_2}{273}\)

∴ \(\quad V_2=\frac{1 \times 40 \times 273}{283 \times 1013}=38.07 \mathrm{~mL}\).

Example 2. Calculate the number of moles of hydrogen contained in 20° L of the gas at 27°C and 70 cmHg pressure. Given that R = 0.0821 L atm K^-1 mol^-1.
Solution:

Given R = 0.0821 L atm K^-1 mol^-1

V = 20L

p = 70 cm = 70/76 atm

T = 27°C = 300 K

Using the ideal gas equation pV = nRT,

n = \(\frac{p V}{R T}=\frac{(70 / 76)(20)}{(0.0821)(300)}=0.747\)

Example 3. A gas has a density of 1.2504 kg m^-3 at 0°C and a pressure lx 10⁵Pa. Calculate its molar mass (given R = 8.314 J K^-1 mol^-1).
Solution:

⇒ \(p V_m=p \cdot \frac{M}{d}=R T\)

or \(M=\frac{d R T}{p}\)

= \(\frac{1.2504 \times 8.314 \times 273.15}{10 \times 10^5} \quad\left(1 \mathrm{~Pa}=1 \mathrm{Nm}^{-2}\right)\)

Deviation from Ideal Gas Behaviour

A gas which obeys the equation pV = nRT under all conditions of temperature and pressure is called an ideal gas. In reality no gas does this. Deviations from the ideal gas behaviour occur as the temperature becomes low and pressure becomes high. In other words, real gases obey the ideal gas equation at low pressure and high temperature. All gases condense at higher pressures and sufficiently low temperature.

That real gases deviate from the ideal gas behaviour is known to us. But, how much is the deviation and on what factors does it depend? Let us plot a graph of pressure against volume for ideal and real gases as shown in Figure. The curve shows the deviation of the behaviour of a real gas from ideal gas behaviour but we cannot determine the quantity of deviation from it.

Let us introduce a quantity Z in tire ideal gas equation to account for the deviation of real gas behaviour from ideal gas behaviour. Then

⇒ \(p V=Z n R T \quad \text { or } \quad Z=\frac{p V}{n R T} \quad \text { or } \quad Z=\frac{p V_m}{R T} \quad\left(V_m\right. \text { is the molar volume of the gas), }\)

where Z = 1 for an ideal gas, i.e., \(p V_m / R T=1 \text { or } p V_m=R T\) for ideal gases. The quantity Z is called the compressibility factor. It is not equal to 1 in case of real gases, i.e., \(p V_m \neq R T\) for real gases. It can be negative or positive. The deviation of Z from 1 determines the deviation of a gas from ideal behaviour.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

When Z < 1, a gas is said to show negative deviation. This means the gas is more compressible than the ideal gas. When Z > 1, a gas is said to show positive deviation, which implies that it is less compressible than the ideal gas. Gases are more compressible due to the predominance of attractive forces and less compressible due to strong repulsive forces among their molecules.

Nature of gas One of the factors on which deviation from ideal behaviour depends is the nature of the gas. Different gases show different extents of deviation at the same temperature and pressure. For example (at 300 K), CO2 and N₂ are more compressible at low pressure (negative deviation) and less compressible at high pressure. But hydrogen shows positive deviation for all pressures. At intermediate pressures the CO₂ curve shows a greater dip (larger negative deviation) indicating that it can be liquefied with greater ease.

Effect of pressure At very low pressure Z approaches unity for all gases and they exhibit nearly ideal behaviour. For pressures between 1-10 bar Z is close to 1 and the ideal gas equation can be applied to real gases. At high pressures all gases have Z> 1 as repulsive forces arc predominant.

Effect of temperature The deviation from ideal behaviour decreases as temperature increases. For every gas, there is a temperature at which the value of Z is close to unity for a fairly large range of pressure.

This temperature is known as Boyle temperature or Boyle point.

Remember that the larger the deviation from ideal gas behaviour, the more easily can a gas be liquefied.

For the same number of moles of a real gas and an ideal gas, we may write \(p V_{\text {real }}=Z n R T\) ….(1)

and \(p V_{\text {ideal }}=n R T\)…. (2)

Substituting for nRT from equation (2) in Equation (i), we get

⇒ \(p V_{\text {real }}=Z p V_{\text {ideal }}\)

or \(\mathrm{Z}=V_{\text {real }} / V_{\text {ideal }} \text {. }\)

From this equation it can be inferred that the compressibility factor of a gas is simply the ratio of its actual volume to the volume it would have occupied had it behaved ideally.

Causes of deviation from ideal behaviour: Real gases follow the ideal gas equation only at low pressure and high temperature. Why do they deviate from ideal behaviour otherwise? There must surely be something wrong with the assumptions made in the kinetic theory (when experimental observations do not tally with the predictions of a theory, there has to be something wrong with the assumptions made while formulating the theory). Two of the important assumptions made were that

1. The volume of the molecules is negligible compared to the volume of the gas and
2. The intermolecular force is negligible.

• It is true that at low pressure and high temperature, or even under normal conditions of temperature and pressure, the volume of the molecules of a gas is a very small fraction of the volume of the gas.
• If we consider the molecules of a gas to be of radius 2.0 x 10^-10 m the volume of the molecules is only 0.1% of the volume of the gas at room temperature and 1 bar pressure. But what happens when pressure increases or temperature falls? The total volume of the gas decreases, while the volume of the molecules remains unchanged. Under such conditions, the volume of the molecules is no longer a negligible fraction of the total volume of the gas.
• The second assumption that intermolecular forces are negligible cannot really hold under all conditions of temperature and pressure. Consider the fact that gases can be condensed into liquids. Surely this would not have been possible had the molecules of gases really been totally independent of each other.
• At high pressure or low temperature, the volume of a gas decreases and the same number of molecules are crowded in less space, so the attraction between them becomes appreciable and can no longer be neglected.
• The number of collisions with the walls of the container decreases due to intermolecular interaction. This results in lower values of pressure than would have been the case in the absence of intermolecular interaction. It has been determined that if oxygen gas behaved ideally, it would have exerted a pressure of 1.003 bar at 0°C.

van der Waals equation: The ideal gas equation was modified to describe the behaviour of real gases by J D van der Waals, a Dutch physicist. He introduced two correction terms to account for the volume of the molecules and the attraction between them.

Volume correction If the molecules of a gas occupy an appreciable volume then the actual volume available for their movement inside a container is less than the observed volume of the container, say V. Let us suppose that the volume of 1 mol of molecules is v and that there are n moles of molecules in a container of volume V. Then the space available for the molecules to move about should be V- nν.

Actually, the effective volume of molecules in motion is calculated to be four times their real volume. If the molecules are assumed to be spheres having radius r, then volume of one molecule of the gas is \(4 / 3 \pi r^3\). Therefore, effective volume would be 4 x \(4 / 3 \pi r^3\)(for one molecule). Thus, the effective volume of 1 mol of molecules is 4u and that of n moles of molecules is 4nv. Suppose we let b = 4z>.

Then corrected volume = V – b, when V contains 1 mol of molecules.

And corrected volume = V -nb, when V contains n moles of molecules.

This quantity b is known as the excluded volume or co-volume. It depends on the nature of the real gas and its units are L mol^-1.

Pressure correction The intermolecular attraction does not allow the molecules to move as freely as they would had they been completely independent of each other. The pressure exerted by a gas is due to the collisions of its molecules with the walls of the vessel. If the molecules hitting the walls are being pulled back by other molecules, the collisions will naturally be less vigorous than if the molecules had been completely independent. In other words, a real gas exerts less pressure than the ideal gas because of the force of attraction between its molecules, or the observed pressure is less than the ideal pressure. Let us call the ideal pressure p, and the observed pressure p. The relation between them turns out to be

∴ \(p_i=p+\frac{a n^2}{V^2}\)

where n is the number of moles, V is the volume of the gas, and A is a constant which depends on the nature of the gas or the force of attraction between the molecules. The units of a are atm L² mol^-2.

If we substitute the corrected values of volume and pressure in the ideal gas equation, we get the equation of state for real gases.

⇒ \(\left(p+\frac{a n^2}{V^2}\right)(V-n b)=n R T\) for n moles

or \(\left(p+\frac{a}{V_m^2}\right)\left(V_m-b\right)=R T\) for 1 mol,

where \(V_{\mathrm{m}}=\) molar volume.

The term \(\left(\frac{a}{V_m^2}\right)\) is also called the internal pressure of the gas.

The equation of state for real gases is also known as the van der Waals equation and a and b are called van der Waals constants, which are different for different gases. p, V and T are the observed values of pressure, volume and temperature of a gas.

Significance of van der Waals constants The constant a is the measure of the intermolecular forces between the molecules of a gas. The greater the value of a, the greater is the intermolecular force of attraction. The constant b is a measure of the effective size of the molecules of a gas. When the molecular size is the predominant factor influencing the behaviour of a gas, Z > 1 the gas shows positive deviation from ideal behaviour. On the other hand, when the effect of intermolecular attraction predominates, Z < 1 and the gas shows negative deviation from ideal behaviour.

The molecules of hydrogen and helium are very small, so the intermolecular force in these gases is negligible. This is why the molecular size factor predominates and Z is always greater than unity.

Example 1. Calculate the pressure exerted by 2 mol of ammonia gas at 27°C in a flask whose volume is 0.9 L. Given that a = 4.17 atm L² mol^-2, b = 0.0371 L mol^-1, R = 0.082 L atm K^-1 mol^-1.
Solution:

According to the van der Waals equation

⇒ \(\left(p+\frac{a n^2}{V^2}\right)(V-n b)=n R T\)

∴ \(\quad p=\frac{n R T}{V-n b}-\frac{a n^2}{V^2}\)

= \(\frac{2 \times 0.082 \times 300}{0.9-2 \times 0.0371}-\frac{4.17 \times(2)^2}{(0.9)^2}\) = 39.0 atm.

Example 2. 1 mol of CO₂ occupies 0.35 L at 300 K and 60 atm pressure. Determine the compressibility factor of the gas.
Solution:

∴ \(Z=\frac{p V}{n R T}=\frac{60 \times 0.35}{1 \times 0.082 \times 300}=0.8536\)

Liquefaction of gases and critical point: Gases can be liquefied by the increase of pressure and decrease of temperature. If we consider the microscopic properties of a gas, then high pressure brings the molecules of a gas close together to allow attractive forces to operate and cause condensation. In case of decrease of temperature, the kinetic energy of molecules decreases. As a result the slow moving molecules come closer to one another and ultimately the gas changes into the liquid state.

• Thomas Andrew in 1863 discovered the essential condition for liquefaction. He studied the pressure-volume relation of CO₂ at different temperatures. Figure shows the isotherms of carbon dioxide gas obtained by plotting data collected by Andrew. (An isotherm is a curve obtained at constant temperature conditions.) The isotherm obtained at a relatively high temperture, say 50°C, is close to that for an ideal gas.
• This shows that at this temperature CO₂ follows Boyle’s law rather closely. Now consider an isotherm at low temperature, say 13°C. The deviation from the expected theoretical curve is much more pronounced here.

• The isotherm PQRS, consists of three parts PQ, QR and RS. Let us see what happens when a gas is compressed at this temperature. As the pressure is increased, the behaviour of the gas follows the curve PQ which is roughly in accordance with Boyle’s law, i.e., the volume of the gas decreases. When the point Q is reached, the gas liquefies partially exhibiting considerable change in volume.
• Attempts to increase the pressure result in a sudden decrease in volume with no change in pressure, along QR. Finally, at R all the gas liquefies. Once the complete liquefaction has occurred even the application of a large pressure results only in a very little change in volume of the liquid as liquids are relatively incompressible.

Andrew observed that CO₂ could be liquefied below 31.1°C but not at and above this temperature. This is called the critical temperature, T_c. At temperatures below T_c, p-V isotherms contain a flat portion in the middle corresponding to liquid-vapour equilibrium (Andrew called the gas a vapour below Tc when it was in equilibrium with the liquid).

• What if we try to compress the gas along the isotherm at T_c? Starting at A an increase in pressure results in a decrease in volume. At point C, the surface separating the two phases, viz vapour and liquid does not appear.
• This is called the critical point. At this point, the densities of both the liquid and the vapour phase are the same so that they cannot be distinguished. Therefore, further increase in pressure does not result in liquefaction.
• The region below the dashed line in shows the liquid-vapour region where the two phases are in equilibrium. Any gas can be liquefied by applying pressure only if its isotherm passes through this region and this happens only below the critical temperature.
• The pressure at the critical point is called critical pressure (P_c) and the corresponding volume occupied by one mole of the gas is called critical volume (V_c).

The observations of Andrew regarding CO₂ are generally valid for all other gases. The value of critical temperature, pressure and volume may vary but the nature of isotherms at different temperatures is almost the same.

Those gases whose critical temperatures lie below room temperature, such as nitrogen and oxygen cannot be liquefied by pressure alone without cooling. Generally gases below their critical temperatures are called vapours. Critical constants for some gases are given in Table.

Kinetic Molecular Theory Of Gases

The gas laws that we have studied so far, such as Boyle’s law, Charles’s law and Dalton’s law, describe the relationships between the macroscopic properties of gases, and their behaviour as observed in experiments. They tell us how gases behave, but not why they behave the way they do. Experiments are a vital aspect of science because they tell us how nature behaves.

• But science has another aspect. The scientist is curious to know why or what makes nature behave in a particular way. To answer the whys of science, scientists construct theories or models. Often, a theory is built around an inspired guess. Such theories make certain assumptions and attempt to explain the behaviour of nature observed in experiments. If the predictions made by a theory fit experimental observations, the theory is accepted.
• The kinetic molecular theory of gases was developed to explain the (observed) behaviour of gases. J C Maxwell (British physicist), L E Boltzmann (Austrian physicist), R J E Clausius (German physicist) and James Joule (British physicist) were some of the scientists who contributed to build this theory. The model we will consider was an improvement of an earlier model of gases put forward by a Swiss mathematician called Bernoulli.

Assumptions of kinetic theory The kinetic theory is based on the microscopic model of a gas. It makes certain assumptions about the particles (atoms or molecules) that constitute gases.

1. The particles (molecules) that constitute a gas are so small and so far apart that the actual volume of these particles is negligible compared to the volume occupied by the gas. The fact that gases are highly compressible seems to support this assumption. When a gas is compressed, the spaces between its molecules (or atoms) become lesser.

2. The molecules of a gas are so far apart that the force of attraction between them is negligible and they are completely independent of each other. Gases are known to expand and occupy all the space available. This justifies the assumption that the attractive force between the molecules is negligible.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

3. The molecules of a gas are in a state of constant motion. They move in straight lines but in any random direction. In doing so they collide with each other and against the walls of the container. The pressure exerted by a gas is a result of these collisions. When a molecule collides with another molecule or with a wall of the container, its path changes. It still moves in a straight line but in another direction.

Molecules are too small to be observed even through sophisticated microscopes, so it is not possible to verify whether they really are in a state of constant motion. However, it is possible to observe the movement of particles (much larger than molecules) caused by collisions with molecules. You may have noticed that the dust particles caught in a beam of a sunlight entering a darkened room seem to be moving in zig-zag lines. The dust particles cannot be moving on their own. The movement must be caused by collisions with randomly moving air molecules.

4. The collisions between molecules are elastic, i.e., there is no net loss of kinetic energy during such a collision. There may be transfer of energy from one molecule to another, however. Therefore, the momenta of the molecules are conserved. Had the collisions between molecules been inelastic, there would be some loss of energy during each collision and the molecules would ultimately stop moving and the temperature and pressure would become zero.

5. The molecules of a gas do not all move with the same speed, so they have different kinetic energies. However, the average kinetic energy of the molecules is directly proportional to the absolute temperature of the gas. The assumption that at any instant different molecules have different speeds is valid in view of molecular collisions. Suppose we imagine an instant when they all have the same speed.

The very next instant, their speeds will become different due to intermolecular collisions. As for the second part of this assumption—when the temperature of a gas increases, so does its pressure. This means that the number of collisions with the walls of the vessel increases or that the molecules start moving faster and their average kinetic energy increases. When the temperature of a gas falls, on the other hand, the average kinetic energy of the molecules decreases (they slow down). This is borne out by the fact that if a gas is cooled enough it becomes a liquid.

For example Atomic and molecular sizes are typically of the order of a few angstroms. Assuming that an N₂ molecule is spherical in shape with radius (r) = 2 x 10^-8 cm, calculate

1. The volume of a single N₂ molecule, and
2. The percentage of empty space in one mole of N₂ gas at stp.

Solution:

1. The volume of a sphere = 4/3πr³, where r is the radius.

The volume of one N₂ molecule = 4/3 x 22/7 x (2 x 10^-8)³ cm³ = 3.35x 10^-23 cm³.

2. To calculate the empty space, first calculate the total volume of the Avogadro number of N₂ molecules.

Volume of 6.022 x 10²³ N₂ molecules = 3.35 x 10^-23 x 6.022 x 10²³ = 20.2 cm³.

The volume occupied by 1 mol of the gas at stp = 22.7 L or 22700 cm³.

Empty space = 22700 -20.2 = 22679.8 cm³.

Percentage of empty space = \(\frac{\text { empty volume }}{\text { available volume }} \times 100\)

= \(\frac{22679.8 \times 100}{22700}=99.9\).

This calculation shows that particles of a gas occupy only a tiny fraction of the total gaseous volume.

Maxwell-Boitzmann distribution of velocities: You have just read that at any given temperature, the molecules of a gas have different speeds and that the speeds and direction of motion of the molecules change constantly. You have also read that the average speed, or average kinetic energy of the molecules, depends on the temperature.

• Maxwell and Boltzmann showed (independently) that though it is not possible to know the individual speeds of the molecules, and though these speeds are constantly changing, the distribution of speeds (of the molecules) is constant at a particular temperature.
• This means that at a particular temperature, a certain fraction of the molecules will have a certain speed. These two scientists predicted the shape of the distribution curve of molecular speeds at a given temperature and the distribution is called the Maxwell-Boitzmann distribution. Some important features of this distribution are as follows.

1. A small fraction of the molecules have very high or very low speeds. We come across this kind of distribution quite often in our everyday lives. Suppose we consider the marks obtained by students (out of 100) in a particular examination. There would be very few students with marks between 95% and 100% and between 0% and 5%. If we were to plot the number of students versus the number of marks, we would get a curve similar to the ones shown in Figure. The maximum number of students would get marks corresponding to the maximum in the curve.

2. The fraction of molecules possessing greater and greater speeds (than the lowest) keeps increasing until the
maximum of the curve is reached and then it keeps falling. The maximum fraction of molecules have the speed corresponding to the peak of the curve. This speed is called the most probable speed (or velocity), ump.

3. When temperature increases, the most probable speed increases. The entire distribution shifts to the right as shown by the dotted curve. The area under the curve remains the same as the total number of molecules remains the same. Just the fraction of molecules with higher speeds increases.

Molecular speed: By now, we know that all molecules do not move with the same speed and that it is in fact not possible to determine the individual speeds. From the Maxwell-Boitzmann distribution, however, it is possible to find the speed of the maximum fraction of molecules at a particular temperature for a particular gas. This speed is called the most probable speed and is given by the relation

⇒ \(\alpha=\sqrt{\frac{2 R T}{M}}\), ….. (1)

where R is the gas constant, T is the temperature and M is the molar mass of the gas.

From Equation (1) it is clear that the speed of a gas molecule also depends on its mass.

Another speed often used in calculations is the root mean square speed (u_rms). It is the square root of the mean of the squares of the speeds of the molecules.

∴ \(u_{\mathrm{ms}}=\sqrt{u^2}=\sqrt{\frac{u_1^2+u_2^2+u_3^2+\ldots}{n}}\),

where u₁, u₂, u₃,… are the speeds of individual molecules and n is the number of molecules.

The root mean square speed is given by the following expression.

⇒ \(u_{\text {mas }}=\sqrt{\frac{3 R T}{M}} \text { or } u_{\text {rus }}=\sqrt{\frac{3 p V}{M}} \text {. }\) …..(2)

Yet another speed that is commonly used is the average speed. It is the simple average of the individual speeds of the molecules.

⇒ \(\bar{u}=\frac{u_1+u_2+u_3+\ldots}{n}\)

The average speed is given by \(\bar{u}=\sqrt{\frac{8 R T}{\pi M}}\) ….(3)

Comparing Equations (1), (2) and (3)

∴ \(\bar{u}=0.921 u_{\mathrm{rms}}, \quad \alpha=0.816 u_{\mathrm{mms}}\)

∴ \(\quad \alpha: \bar{u}: u_{\mathrm{mms}}=1: 1128: 1.224\)

Gas equation in terms of u_rms: The kinetic theory of gases leads to an equation, the mathematical derivation of which is beyond the scope of this book. However, it is useful to know this equation, which yields an expression relating the average kinetic energy of molecules with the absolute temperature. All the gas laws can be deduced from this equation given here. It is called the kinetic gas equation.

⇒ \(p V=\frac{1}{3} m N \overline{u^2}\) ……(1)

where m = mass of one molecule of gas,

N = number of molecules,

⇒ \(\overline{u^2}\) = mean square speed,

p = pressure exerted by the gas, and

V = volume of the gas.

We will use this relationship and gas laws to derive a relationship between average translational kinetic energy of a molecule and the temperature of the gas.

The average kinetic energy of a molecule \(E_k=\frac{1}{2} m \overline{u^2}\) at a temperature T.

We also know that pV = RT …..(2) for 1 mole of a gas.

For one mole of the gas, Equation (1) becomes \(p V=\frac{1}{3} N_{\mathrm{A}} m \overline{u^2},\) ….(3)

where N_A = Avogadro number (because one mole contains the Avogadro number of molecules).

Comparing Equations (2) and (3), \(\frac{1}{3} N_{\mathrm{A}} m \overline{u^2}=R T\) …..(4)

Dividing both sides by 2, we get

⇒ \(\frac{1}{3} N_{\mathrm{A}} \times \frac{1}{2} m \overline{u^2}=\frac{1}{2} R T\)

⇒ \(\frac{1}{2} m \overline{u^2}=\frac{3}{2} \frac{R T}{N_{\mathrm{A}}} \text {. }\)

⇒ \(E_k=\frac{3}{2} \cdot \frac{R}{N_A} \cdot T\)

= \(\frac{3}{2} k T \text {, }\) …..(5)

where k = Boltzmann constant = \(\frac{R}{N_{\mathrm{A}}}\)

R is the gas constant for one molecule. Equation (4) can be modified as \(\frac{1}{3} N_{\mathrm{A}} m \overline{u^2}=R T\)

= \(\frac{1}{3} M \overline{u^2}=R T\)

or, \(\quad \frac{1}{2} M \overline{u^2}=\frac{3}{2} R T\)

\(\quad \frac{1}{2} M \overline{u^2}\) is the average kinetic energy of 1 mol of the gas molecules.

⇒ \(\underset{\text { (for 1 mol) }}{E_k}=\frac{3}{2} R T\) ….(6)

From Equations (5) and (6) we can see that the average kinetic energy of the gas molecules is proportional to the absolute temperature.

Explanation of gas laws on the basis of the kinetic theory: Boyle’s law According to the kinetic theory, the pressure exerted by a gas depends on the number of collisions between its molecules and the walls of the vessel it is contained in. The number of collisions depends on the number of molecules and on their average speed. For a given mass of a gas at a constant temperature, the number of molecules and the average speed will remain the same.

Now, if the volume of the container is reduced (at constant temperature), the same number of molecules moving at the same average speed will have less space in which to move. Hence, they will collide more often with the walls, which means that the pressure will increase. If the volume is increased, the molecules will have more space, collisions will decrease and so will pressure. This is in accordance with Boyle’s law, according to which the pressure exerted by the gas is inversely proportional to the volume. This can be readily observed from the kinetic gas equation also.

We know that pV = \(\frac{1}{3} m N \overline{u^2}\)

or, \(p=\frac{1}{3} \cdot \frac{1}{V} \cdot m N \overline{u^2}\)

or, \(p \propto \frac{1}{V}\).

Charles’s law According to the kinetic theory, the average kinetic energy (also the speed) of the molecules of a gas is directly proportional to its absolute temperature. When the temperature of a given mass of gas is raised, the average energy of molecules increases and they collide more often and harder with the walls of the container.

This naturally causes the pressure to increase. If the pressure is to remain constant (as in Charles’s law), the volume must increase, so that the number of collisions per unit area of the walls decreases enough to compensate for the fact that the collisions are more vigorous at a higher temperature. Therefore, higher the temperature, the larger is the volume. In other words, volume is directly proportional to the absolute temperature.

You can easily deduce what happens when the temperature decreases. V ∝ T