Class 11 Chemistry

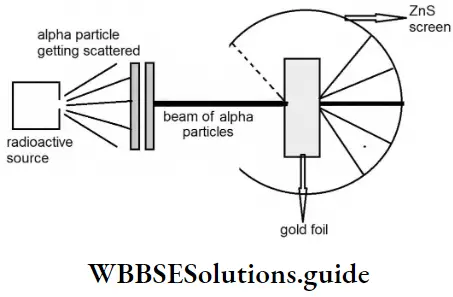
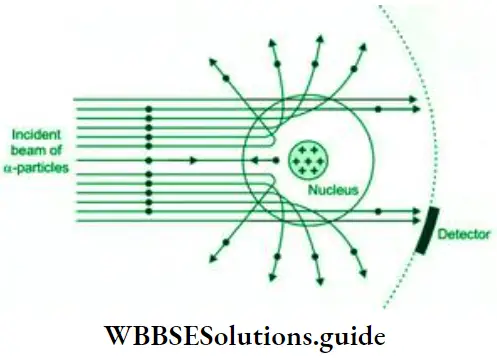
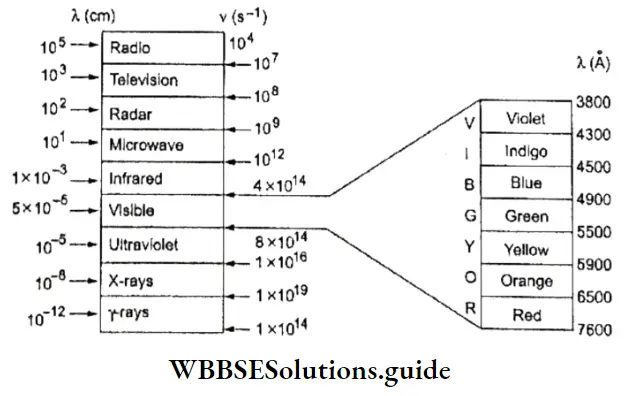
Heisenberg’s Uncertainty Principle

All moving particles follow well-defined paths and the path may be determined if we know the position and velocity of the particle at different instances of time. In 1927, Heisenberg stated that since matter has a dual nature it is impossible to determine simultaneously both the velocity and the position of a moving object with absolute precision (remember that we are talking about the microscopic world).

‘This, in essence, is Heisenberg’s uncertainty principle. To put it more formally, it is not possible to determine simultaneously the position and momentum of a small moving particle, such as an electron, with absolute accuracy. Mathematically, this may be expressed as follows.

∴ \(\Delta x \times \Delta p_x \geq \frac{h}{4 \pi} \quad \text { or } \quad \Delta x \times m \Delta v_x \geq \frac{h}{4 \pi}\)

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

where, Δx = uncertainty in determination of position,

Δp_x = uncertainty in the determination of momentum,

Δv_x = uncertainty in the determination of velocity, and

m = mass of particle.

This mathematical expression means \(\Delta x \propto \frac{1}{\Delta p_x}\), which implies that the greater the precision in the determination of the momentum of a particle, the lesser will be the precision in defining its position, and vice versa. Heisenberg was awarded the Nobel Prize in Physics in 1932.

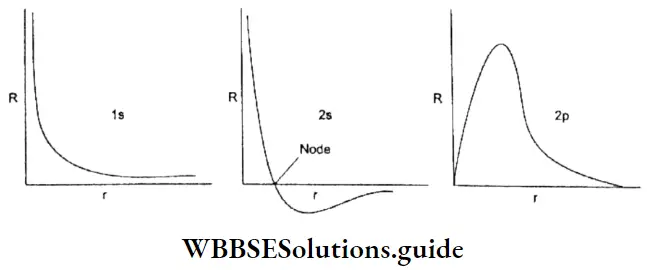
It should be made clear that uncertainty is due to the disturbance caused by the microscopic particle or an electron while measuring its dimensions. To observe an electron we need to illuminate it with some electromagnetic radiation, which will make protons strike the electrons and change their velocity.

Example 1. The uncertainty in the momentum of a particle is 6 x 10^-2 kg m s^-1. Calculate the uncertainty in its position.
Solution:

According to the uncertainty principle,

⇒ \(\Delta x \times \Delta p_x \geq \frac{h}{4 \pi}\)

or \(\Delta x=\frac{h}{4 \pi \Delta p_x}\).

∴ \(\quad \Delta x =\frac{h}{4 \pi \Delta p_x}=\frac{6.62 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{4 \times 3.14 \times 6 \times 10^{-2} \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1}}\)

= \(8.76 \times 10^{-34} \mathrm{~m}\).

Example 2. An electron has a velocity of 300 m s^-1 that is accurate to 0.01%. With what accuracy can one locate the position of this electron (mass of electron = 9.1 x 10^-31 kg)?
Solution:

Velocity = 300 ms^-1.

Uncertainty in velocity = 0.01% of 300

= \(\frac{0.01}{100}\) x 300 = 3 x 10^-2 ms^-1.

According to the uncertainty principle,

⇒ \(\Delta x m \Delta v_x=\frac{h}{4 \pi}\)

∴ \(\quad \Delta x=\frac{h}{4 \pi m \Delta v_x}=\frac{6.62 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{4 \times 3.14 \times 9.1 \times 10^{-31} \mathrm{~kg} \times 3 \times 10^{-2} \mathrm{~m} \mathrm{~s}^{-1}}\)

The uncertainty in position and velocity is negligible for macroscopic objects. If it is applied to an object of mass 1 g, i.e., 10^-3 kg then

⇒ \(\Delta v_x \Delta x=\frac{h}{4 \pi m}=\frac{6.62 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{4 \times 3.14 \times 10^{-3} \mathrm{~kg}}=5 \times 10^{-32} \mathrm{~m}^2 \mathrm{~s}^{-1}\)

This value is extremely small and therefore insignificant.

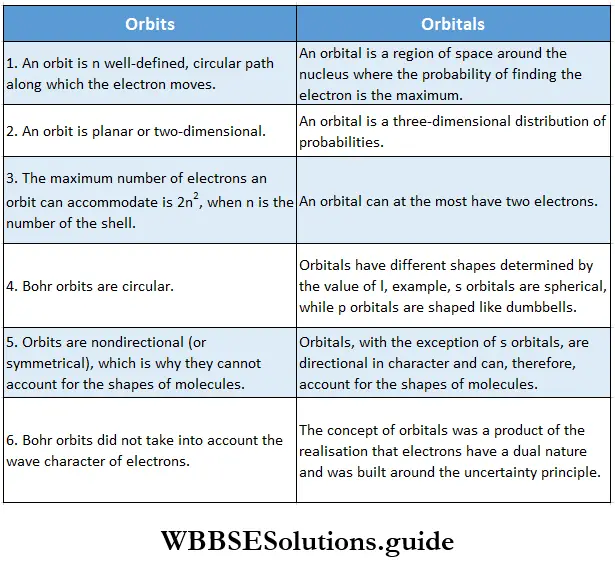
Why Bohr’s model failed: If one accepts Heisenberg’s uncertainty principle, one must reject Bohr’s model of the atom. Since it is impossible to determine accurately the position and the momentum of an electron at the same time, it is quite futile to talk about determining its orbit.

• Talking about fixed orbits of electrons, as Bohr did, implies that it is possible to know, with some precision, both the position and the velocity of an electron at the same time. Clearly, this violates the uncertainty principle, and it should become clear to you why Bohr’s model was not extended further.
• To describe the structure of the atom, what was needed was a concept that took into account the wave-particle duality of matter and at the same time was consistent with the Heisenberg uncertainty principle.

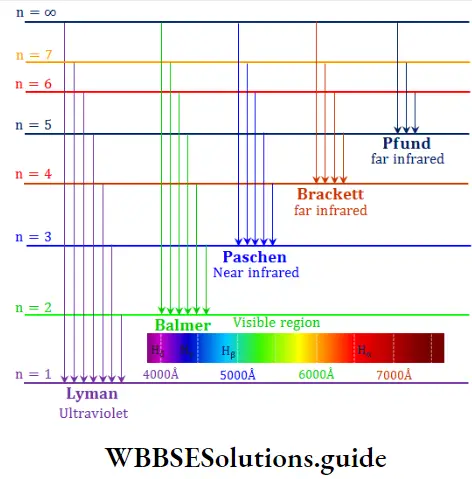
Energy Sequence Of Orbitals

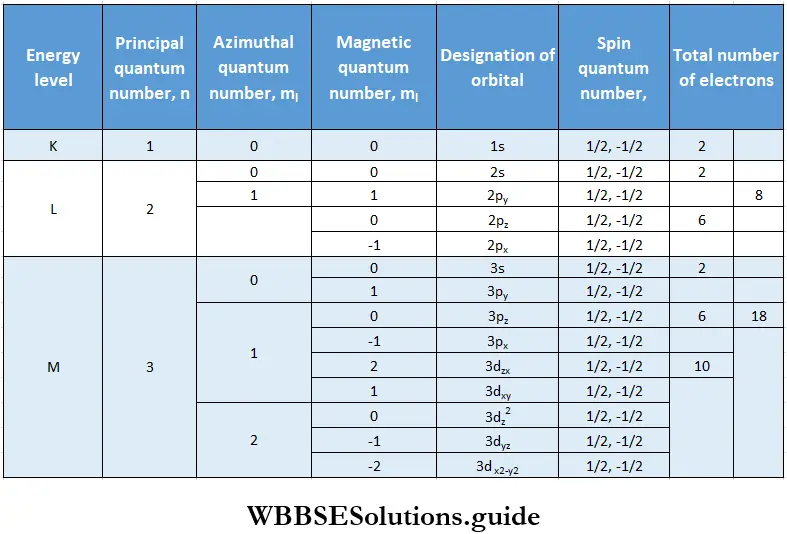
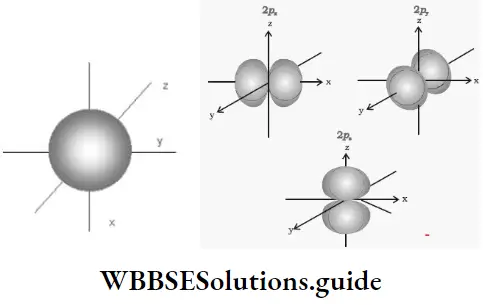
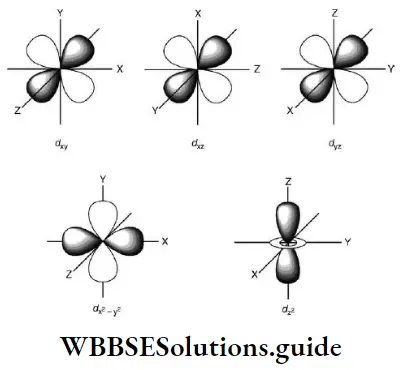
The hydrogen atom has only one electron. In a single-electron system (for example, H, He⁺ and Li²⁺), all the orbitals of a given principal shell have the same energy. For instance, the 2s and 2p orbitals have the same energy. The energy of an orbital in such an atom depends only on n and is independent of l.

In multi-electron atoms, the picture is different because of the presence of other electrons in the atom. The energy of an electron depends not only on its principal quantum number but also on its azimuthal quantum I number.

• The stability of an electron in the atom is the net result of attraction between the electron and the nucleus and repulsion between the electron and the other electrons present in the atom. It is not possible to calculate exactly the energies of the orbitals in such an atom, but it is possible to get an idea about these energy levels from spectral data.
• In general, subshells of the same principal shell have different energies and a subshell with a higher value of l has higher energy. For instance, the energy of the 2p shell (1 = 1) is higher than that of the 2s (l = 0) shell.
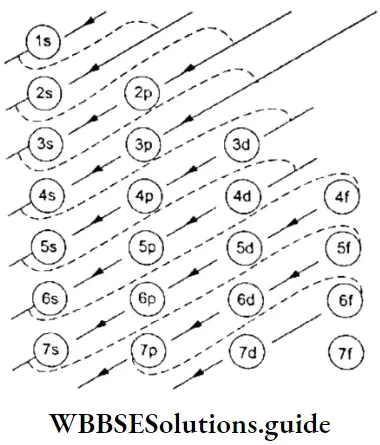
• Some subshells of a lower energy level (principal shell) may have higher energies than some subshells of a higher energy level (principal shell). The energies of the various subshells are in the following order.

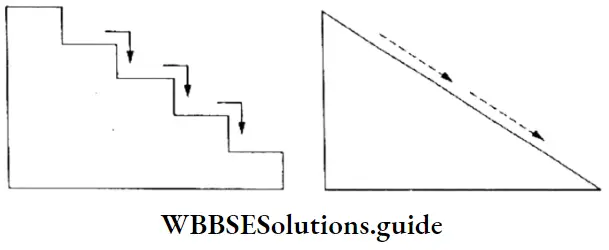
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p …

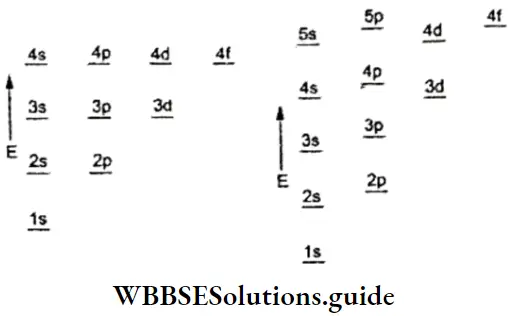
The energy of an orbital depends upon the nuclear charge, the principal quantum number, and the presence of other electrons in the lower energy levels.

• In relative energies of the various orbitals in an atom is called hydrogenlike atoms, there is only one electron and the on energy level diagram. attractive force of the nucleus on the single electron is always constant, thus the energy of any orbital occupied by this solitary electron at any instant is given by the principal quantum number.
• In a multi-electron atom the situation is different because an increase in the number of electrons is also accompanied with increase in nuclear charge. As the nuclear charge increases, the orbitals are somewhat contracted. The electrons in the lower-lying orbitals tend to reduce the effect of the nuclear charge on the electrons present in the higher-energy orbitals.
• This is referred to as screening effect or shielding effect. The electrons present in lower-lying orbitals act as a “screen” so that the outer electrons “see” only part of the nuclear charge. Thus the nuclear charge felt by the outer electrons is less than the actual nuclear charge. The reduced charge felt by the outer electrons is called the effective nuclear charge (Zeff).

∴ Zeff =Z-S

where Z = actual nuclear charge and S =shielding constant.

1. In neutral atoms, a subshell with a lower value of n + l has lower energy. For example, the 4s(n +1 – 4 + 0 = 4) orbital has lower energy than the3d orbital (n + l =3 + 2 = 5).
2. If two subshells have the same value of n + l, the subshell with the lower value of n has lower energy. For instance, 4p(n + l =3 + 2 =5)  and 3d(n +Z =3 + 2=5) orbitals have the same value of n + 1, but 3d (5) has lower energy than 4p.
3. The energies of the orbitals in the same subshell of two different „ atoms are not the same. They decrease with the increase in atomic number (Zeff). For example, the energy of the 2s orbital of the hydrogen atom is greater than the energy of the 2s orbital of the lithium atom.

Electronic Configuration

The distribution of electrons in the different orbitals of an atom is known as the electronic configuration of the atom. An atom in its lowest energy state is said to be in the ground state. This is the most stable state of the atom. The orbitals in the ground state are filled according to the following rules.

Aufbau principle Aufbau, in German, means building up. This rule of “building up” the atom or filling the orbitals in the ground state says that the orbitals arefilled in order of increasing energies, or that electrons occupy the lowest energy orbital available, subject to the Pauli principle.

Pauli exclusion principle You have already read that according to this rule, two electrons of an atom cannot have the same set of (all four) quantum numbers.

Hund rule Also referred to as the Hund rule of maximum multiplicity, this rule deals with the filling of orbitals of the same subshell (degenerate orbitals). According to this rule, pairing of electrons in the orbitals of a particular subshell (p, d, or f) does not take place until all the orbitals of the subshell are singly occupied.

• Also, the singly occupied orbitals must have electrons with parallel spins. This is because it is energetically preferable to have single electrons in different orbitals than to have a pair of electrons in a particular orbital (two electrons in the same orbital experience more repulsion).
• As for the second part of the rule, when two electrons occupy two different orbitals, energy is lower if their spins are parallel. For example, the electronic configuration of 6C is \({ }_6 \mathrm{C} \text { is } 1 \mathrm{~s}^2 2 \mathrm{~s}^2 2 \mathrm{p}_x^1 2 \mathrm{p}_y^1\), rather than \(1 \mathrm{~s}^2 2 \mathrm{~s}^2 2 \mathrm{p}_x^2\). (This is a way of representing the electronic configuration of atoms—you will learn about it in the next section.)

Representation of electronic configuration: There are two ways of representing the electronic configuration of an atom. Of these, the first is the one used most often because the second one is rather cumbersome.

1. The electron population of an orbital is represented symbolically as nl^x, where n stands for tire principal quantum number, l for the subshell or orbital, and x for tire number of electrons present in the orbital. For example, if two electrons are present in the s subshell of the first principal shell, it would be represented as 1s² in this notation.

2. In the second method of representing the electronic configuration of an atom, squares or circles stand for orbitals and electrons are represented by arrows within the squares or circles. For instance, 1s² would be represented as ↓↑

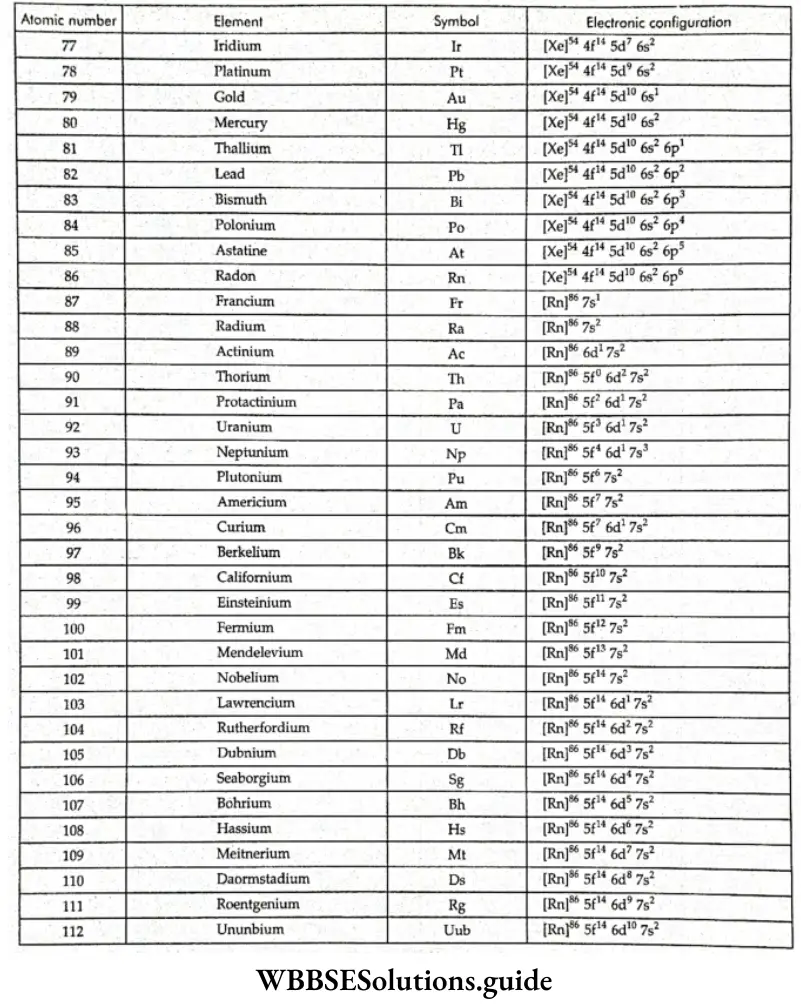
The electronic configurations of some elements are represented below.

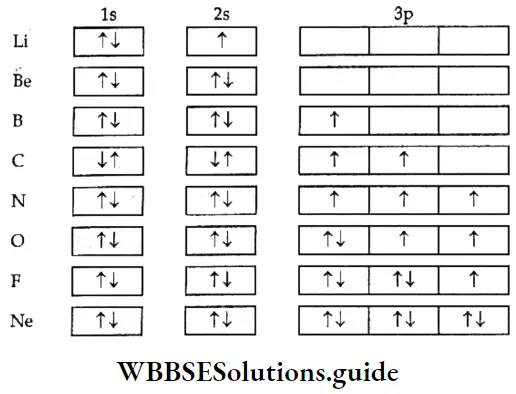
• The electronic configurations of the elements sodium (\(1 s^2 2 s^2 2 p^6 3 s^1 \text { or }[\mathrm{Ne}]\)) to argon (\(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6\) or \(\left.[\mathrm{Ne}] 3 s^2 3 p^6\right)\)) follow the same pattern as the elements horn lithium to neon except that the 3s and 3p orbitals begin to get filled.
• In potassium and calcium, the 4s orbitals, being lower in energy than the 3d orbitals, get occupied. Tire 3d orbitals (being lower in energy than the 4p orbitals) are filled from scandium (atomic number 21) to zinc (30).

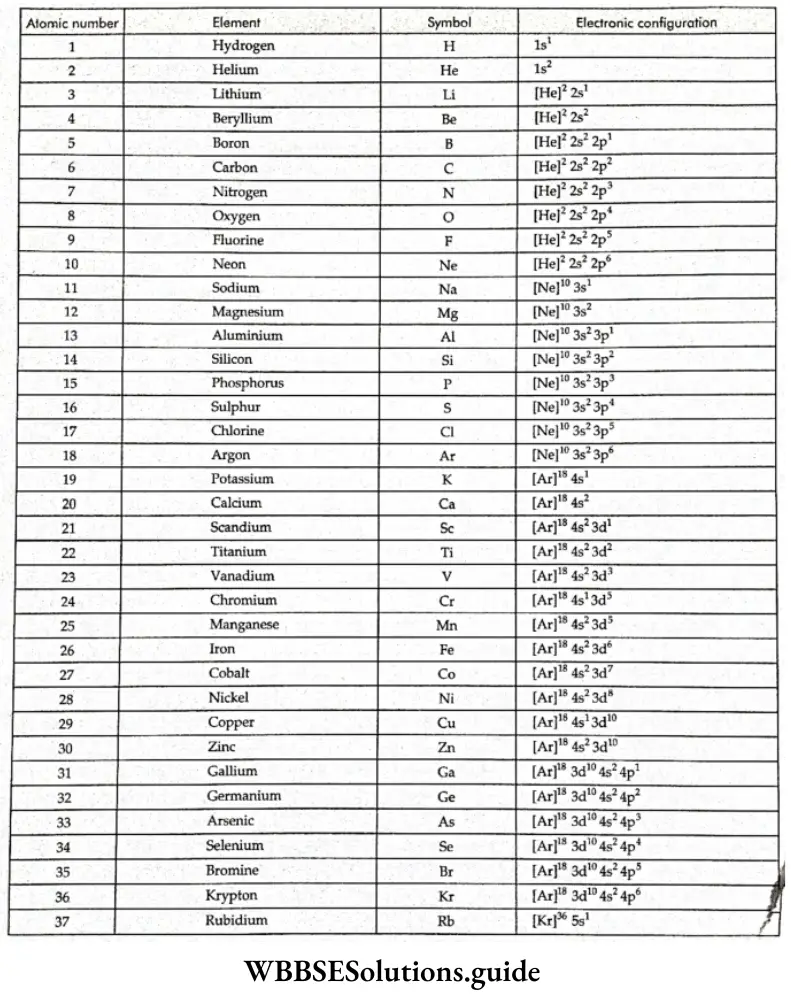
Note: The superscripts on the noble-gas atoms should not be confused with mass numbers. They are the numbers of electrons in the atoms of the noble gases.

• Chromium and copper have five and ten electrons in the 3d orbitals rather than four and nine, as their positions would have indicated. This is because half-filled and completely filled orbitals are more stable. In order to acquire this stability, one of the 4s electrons goes into the 3d orbitals.
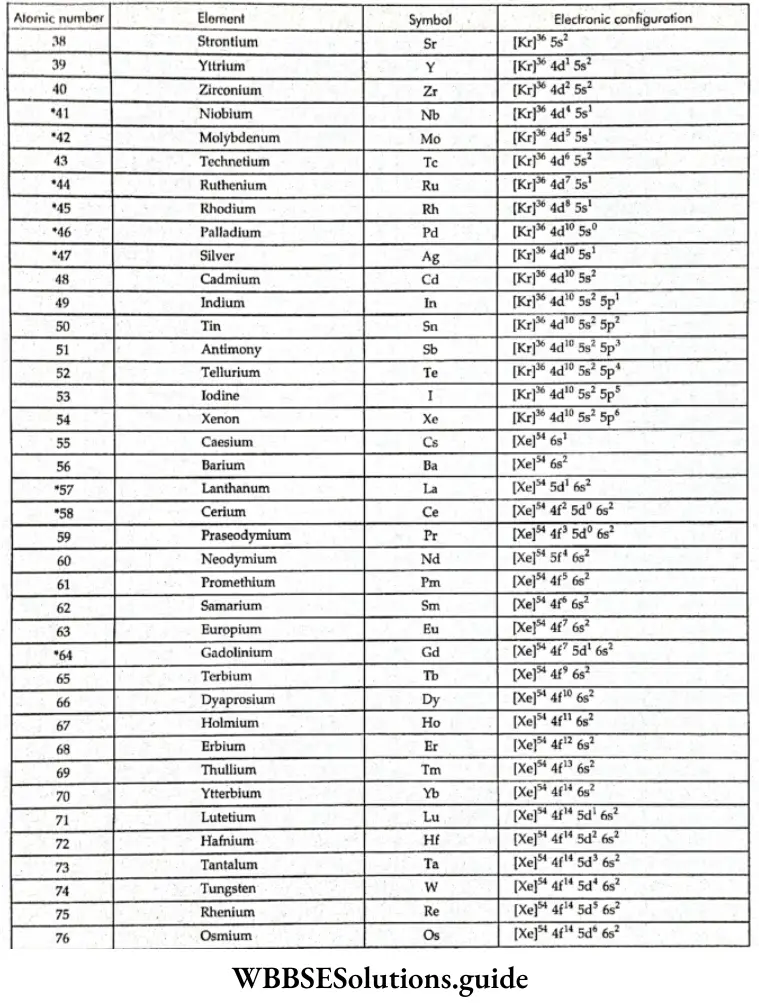
• With the saturation of the 3d orbitals, the 4p orbitals get filled from gallium (Ga) to krypton (Kr). In the next 18 elements, from rubidium (Rb) to xenon (Xe), the pattern of filling of the 5s, 4d, and 5p orbitals is similar to that of the 4s, 3d and 4p orbitals. The 6s orbital gets filled in cesium (Cs) and barium.
• The 44 and 5d orbitals get filled from lanthanum to mercury. The 6p, 7s, 5f, and 6d orbitals get filled (in that order) after this. The elements after uranium are all short-lived and produced artificially.
• It is important to remember that orbitals are not like boxes into which electrons are filled. When we talk about electrons filling orbitals we mean that they have a particular distribution corresponding to a particular level of energy.
• Electrons always try to have the distributions with the lowest energy possible and orbitals merely determine the shape, size, and orientation of the electron distribution.

Stability of half-filled and completely filled orbitals: While discussing the configurations of chromium and copper it was mentioned that half-filled and completely filled orbitals are more stable (than those that are almost half-filled or almost full). There are two reasons for this stability.

Symmetry Orbitals which are half-filled or completely filled have a more symmetrical distribution of electrons. Consequently, they have lower energy and greater stability.

Exchange energy Electrons in degenerate orbitals (orbitals of the same energy) can exchange positions with other electrons with the same spin. In die process they gain exchange energy. The greater the possibility of exchange, tire more stable is the configuration. The exchange energy (or stabilisation energy) can be calculated from the formula given below.

∴ Exchange energy = \(\frac{n !}{2 \times(n-2) !}\)

where n is the number of electrons with parallel spin.

Let us consider the case of chromium.

Expected configuration [Ar] 4s²3d⁴

Actual configuration [Ar]4s¹ 3d⁵

Exchange energy for expected configuration =\(\frac{n !}{2 \times(n-2) !}=\frac{4 !}{2 \times 3 !}=\frac{4 \times 3 \times 2 \times 1}{2 \times 3 \times 2 \times 1}\) = 2 units

Exchange energy for actual configuration = \(\frac{n !}{2 \times(n-2) !}=\frac{6 !}{2 \times 4 !}=\frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 4 \times 3 \times 2 \times 1}\) = 15 units

Thus, the actual configuration has more exchange or stabilisation energy and is more stable.

Electronic configuration of ions: Follow the steps given below to obtain the electronic configuration of an ion.

1. Write the electronic configuration of the atom in the ground state.
2. Rearrange the subshells in increasing order of the values of n and l
3. Remove electrons from the outermost subshell.

Example: Write the electronic configurations of Fe²⁺ and Fe³⁺.

⇒ \({ }_{26} \mathrm{Fe}=[\mathrm{Ar}] 4 \mathrm{~s}^2 3 \mathrm{~d}^6\) (ground state electronic configuration rearranged according to increasing n and l of Fe)

⇒ \(\mathrm{Fe}^{2+}=[\mathrm{Ar}] 3 \mathrm{~d}^6\) on removing two electrons from valence shell

⇒ \(\mathrm{Fe}^{3+}=[\mathrm{Ar}] 3 \mathrm{~d}^5\) on removing two electrons from the 4s subshell and one from the 3d subshell

 

Quantum Mechanical Model of the Atom

Quantum mechanics is the branch of science which takes into account the dual character of matter. Classical mechanics failed to describe the motion of microscopic particles like electrons, and when quantum mechanics is applied to macroscopic objects (with insignificant wavelike properties), the results are the same as those derived from classical mechanics.

Since the conceptual viewpoint of quantum mechanics is built around the uncertainty principle (which states that the exact position and exact velocity of a particle cannot be simultaneously specified), it resorts to a probabilistic description. Before we move on further to explain the quantum mechanical model you must understand clearly what probability means and what the Schrodinger equation is.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

Quantum Mechanical Model Of The Atom Probability

What do you do when you cannot be certain about the outcome of an event (such as a match), or about whether something will happen at all (example, whether it will rain on a particular afternoon)? You talk about the chances of a particular result or the chances of something happening. You try to study the various factors and make a prediction. You may place the chances (or probability) of something happening at 50%.

• Suppose you say that the chances of your school winning a match against a rival school is 50%. All you mean is that the two teams are equally likely to win in a particular match. And that if they happen to play 10 matches, it is most likely or most probable that your school will win five and the other school will win five. But you cannot really predict with any precision.
• It could happen that the other school wins seven matches, while your school wins only three. The probability of something happening is the likelihood of something happening. Even if the probability of a particular happening is very high, it doesn’t mean that in reality, just the opposite thing will not happen. Probabilistic estimates are the only way to describe a situation or an event that cannot be described or predicted with certainty.

Quantum Mechanical Model Of The Atom Schrodinger Equation

The Schrodinger equation forms the fundamental equation of quantum mechanics in the same manner as Newton equations in classical mechanics. The equation takes into account the dual character (wave-particle) of the electron. The equation is quite complex, you will leam about it in detail in your higher classes.

For a system whose energy does not change with time, the equation is written as \(H \psi=E \psi\) where H is a mathematical operator called the Hamiltonian operator, \(\psi\) is the amplitude of the wave associated with the electron, and E is the total energy of the electron. The values of £ represent the quantised values of energy that an electron in the atom possesses.

Important features of the quantum mechanical model of the atom

1. The electrons in an atom can have only quantised values of energy.
2. The Schrodinger equation gives the possible energy states the electron can occupy and the corresponding wave function \(\psi\). The wave function is obtained by solving the wave equation.
3. Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously (Heisenberg’s uncertainty principle). Thus, the path of an electron in an atom can never be determined. Instead, we can talk about a probability of finding the electron in a specific region.
4. The term atomic orbital is used for an electron wave function \(\psi\). Since.many wave functions are possible for an electron, there are many atomic orbitals in an atom. An electron has a definite energy in each atomic orbital, which also corresponds to the specific wave function. The information about the motion of an electron in an atom is given by its orbital wave function \(\psi\), which is determined by solving the Schrondinger wave equation.
5. The probability of finding the electron at a point within an atom is proportional to the square of the wave function, i.e., \(|\psi|^2\) at that point. \(|\psi|^2\) is known as probability density. It is always positive.
6. If we determine the values of \(|\psi|^2\) at different points in an atom, the region around the nucleus where the electron will most probably be found can be predicted.

You may find the quantum description difficult and complicated to understand. This is because microscopic objects do not behave in the way the macroscopic or large objects do, In our everyday lives, we come across examples of only macroscopic (and not microscopic or subatomic objects) in motion.

The quantum mechanical study of a system is done to describe the electron’s behaviour in that system. It helps to relate microscopic behaviour to macroscopic characteristics. In other words, the electronic wave functions account for the electronic structure of the atom, the periodicity of atomic properties, the nature of chemical bonds in molecules, and shape and geometry of molecules.

Quantum Mechanical Model Of The Atomic Orbitals

The quantum mechanical model of the atom is built around the uncertainty principle, which implies that we cannot know the orbit (or trajectory) of an electron with certainty. We can only talk in terms of the probability of finding an electron in a particular region of space around the nucleus.

• Here is another difference between Bohr’s model and the quantum mechanical model. The Bohr orbits were two-dimensional or planar, whereas in the quantum mechanical model, the probability of finding an electron in a region around the nucleus is not confined to one plane.
• In the quantum mechanical model of the atom we are concerned with the probability of finding an electron at different points in the space around the nucleus at any instant of time. There are certain regions around the nucleus where the probability of finding an electron is high and there are regions where the probability of finding an electron is low.
• However, the probability of finding an electron jn any region (at any instant of time), no matter how far away from the nucleus, is never zero. Similarly, the probability of finding an electron in any region is never 100%.

The concept of an orbital in the quantum mechanical model is a little difficult.to grasp. As already stated the probabilities of finding an electron in different regions can be obtained by solving the Schrodinger wave equation which is beyond the scope of this book. And an atomic orbital is conceptually a probability distribution around the nucleus.

• For the sake of simplicity, one could say that an orbital is that region of space around the nucleus where the probability of finding an electron (of a particular energy) is the maximum. [The region of space around the nucleus where the probability of finding the electron is the minimum is called a node.].
• Remember that we are not talking about a concrete boundary. There is no real line marking an orbital. We are just talking about an arbitrary boundary enclosing a region where the probability of finding an electron (which has a certain energy) is the maximum, for the sake of convenience.

This does not mean that the probability of finding an electron outside this boundary is zero. Also, orbitals are not definite paths of an electron, the way orbits are.

• Each orbital is associated with a definite amount of energy and the transition in energy from one orbital to another is discontinuous. In other words energy is quantised. Now you should be able to appreciate how quantisation of energy in Bohr’s model was a big step in the right direction.
• Another way of trying to visualise an orbital is in terms of an electron cloud. If one took a picture of one hydrogen atom, the picture would show the position of the electron in the atom at that particular instant of time. Then suppose one took many such pictures at different instants of time and superimposed them over each other.
• In this method of representing an orbital, the probability of finding an electron in a particular region of space is directly proportional to the density of dots (electron cloud) in that region. As shown in the figure, most of the dots are concentrated in a certain region and this is where the electron can be found most of the time.
• A sphere drawn to enclose most of the dots can be thought of as an orbital. It is not possible to draw a sphere to include all the dots because the boundary of such a sphere would have to be at infinity.

Quantum Numbers

The solution of Schrodinger equation for the hydrogen atom, which is the simplest atom with only one electron, gives a large number of permissible orbitals (each associated with a definite amount of energy).

In fact, theoretically, an infinite number of orbitals are permissible for the electron in the hydrogen atom. These orbitals differ from each other in size, shape, and orientation. The size of an orbital determines how far from the nucleus the electron is most likely to be (most of the time).

• The smaller the size of the orbital, the greater is the chance of finding the electron near the nucleus. The shape and orientation of an orbital determine the direction along which the electron cloud is denser or along which the probability of finding the electron is greater.
• The parameters that define an orbital (shape, size, and orientation) are expressed in terms of the principal (n), azimuthal (f), and magnetic (m_l) quantum numbers which arise as a natural consequence in the solution of the Schrodinger equation.
• An additional quantum number called the spin (m_s) quantum number is required to define completely the state of an electron in a particular orbital. It was a little different to apply the Schrodinger equation on multi-electron atoms. This difficulty arose as a consequence of increased nuclear charge which resulted in a contraction of the orbitals. Unlike those of the hydrogen orbitals, the energies of the orbitals of multi-electron atoms depend on the principal (n) and azimuthal (l) quantum numbers.

Principal Quantum Number (n)

1. The principal quantum number n is a positive integer with value 1,2,3,— It determines the size of the orbital or electron cloud. In other words, it tells us what the average distance of the electron from the nucleus is. Orbitals with the same principal quantum number belong to the same shell. These shells are called K(n = 1), L (n = 2), M(n = 3), N(n = 4), etc.

2. It is also define the energy of an electron in a particular orbital. Each orbital is associated with a definite amount of energy is given by

⇒ \(E_n=-\frac{2 \pi^2 Z^2 e^4 m k^2}{n^2 h^2}\)

This expression is similar to the one obtained for Bohr orbits. Obviously, E changes with n. Energy increases as n increases, or as the electron moves farther from the nucleus.

3. The principal quantum number also determines the maximum number of electrons that can be accommodated in a shell, which is 2n². Thus, when n = 2 the maximum number of electrons is 2; when n = 2, the maximum number of electrons is 8, and so on. There is, however, an upper limit to the number of electrons that a shell (orbital) can accommodate. No shell has more than 32 electrons.

Azimuthal Quantum Number (l)

 

1. This is also called the orbital angular momentum or subsidiary quantum number because it determines the angular momentum of an electron in a particular orbital. If l is the azimuthal quantum number of an electron, its angular momentum works out to \((h / 2 \pi) \sqrt{l(l+1)}\). The magnitude of the angular momentum changes discontinuously from one orbital to another, or the angular momentum can have only certain discrete values.

2. Each shell consists of one or more subshells, the number of subshells equals the value of n. The number of each subshell is the azimuthal quantum number, 1. The values that l may have for a given n are 0 and all positive integers up to n -1. Thus, for example, when n = 1, l can have only one value, i.e., 0; when n-2, l can be 0 or 1; when n = 3, l can be 0,1, or 2, and so on.

• Just as n denotes the shell an orbital (or an electron) belongs to, l stands for the subshell. The subshells are named s, p, d, and f. The letters s, p, d, and f originally were spectroscopic designations given to certain line spectra that correspond to atomic structure, s stood for sharp series, p for principal, d for diffuse, and f for fundamental series respectively. Now for higher values of n, say 5, l can attain values of 0,1,2, 3, and 4.
• The orbital for l = 4 is called g orbital. For higher l values the orbitals are named alphabetically (if onwards). However, these orbitals are too high in energy and not filled for known elements. The first shell has only one subshell designated Is (when n = 1, l = 0), the second shell has two (2s and 2p), the third shell has three (3s, 3p, 3d) and the fourth shell has four (4s, 4p, 4d, 4f) and so on. The maximum number of permissible subshells any shell has is four.

3. The value of 1 also determines the shape of an orbital. Different orbitals have different shapes. The s subshell (l = 0) is spherical, the p subshell (l = 1) is shaped like a dumbbell, the d subshell is shaped like double dumbbells and the f subshell has a rather complex shape.

4. The energy of a subshell depends on the value of l. The energies of subshells of the same principal shell increase as l increases in the following order.

s<p<d<f

This explains the fine lines (fine structure) observed in the hydrogen spectrum which Bohr’s model could not explain.

Magnetic Quantum Number (m_l)

1. This is called the magnetic quantum number because it determines the behaviour of an electron under the influence of an external magnetic field. A revolving electron, possessing an angular momentum, has its own small magnetic field. When such an electron is placed in an external magnetic field, its own field gets oriented in a particular way, depending on the magnetic quantum number of the electron. Another way of saying this is that the magnetic quantum number determines the energies or the orientations of the orbitals of electrons in an external magnetic field.

2. The magnetic quantum number determines the number of orientations of orbitals permitted in each subshell. The values that ml can have for a given l range from +l through 0 to -l, meaning that it can have 2l+1 values. If l = 1, for instance, the values of m} can be + 1,0 and -1.

3. The magnetic quantum number determinen the number of orientations possible in cacti subshcll or the number of orbitals that can be present in a subshell. Those orbitals have the same energy under normal circumstances, but not under the influence of an external magnetic field. This explains why spectral lines split into a number of fine lines when the source emitting the spectrum is placed in a magnetic field (Zeeman effect).

Spin Quantum Number (m_s)

1. The spin quantum number was introduced by George Uhlenbeck and Samuel Goudsmit in 1925 to account for the spinning motion of an electron in Bohr’s model. The electron was thought to spin around its axis much the same way as planets do. The spin quantum number (associated with Bohr’s model) could be +1/2 or -1/2 depending on whether the electron rotated clockwise or anticlockwise about its axis.

An electron in the quantum mechanical model also has a spin quantum number but it is not associated with the direction of axial rotation. It is a characteristic of the electron which determines its magnetic behaviour. The two possible values of the spin quantum number, called up-spin and down-spin, are symbolically represented as ↑ and ↓. The values of the spin quantum number are independent of the values of the other three quantum numbers.

2. The spin quantum number is connected with the magnetic properties of the atom or the element. There is a simple explanation for this. An electron, as we have just discussed, is like a small magnet with a magnetic field of its own and a definite magnetic moment. (You will read more about this later.)

• Magnetic moment is a vector quantity and if an orbital contains two electrons, their magnetic moments are directed in opposite directions. (You will read in the next section that an orbital can have at most two electrons and they must have opposite spins.) The resultant of the oppositely directed magnetic moments is zero.
• Thus, if all the orbitals of an atom are completely filled, the net magnetic moment of the atom is zero. The magnetic properties of a substance depend on the magnetic moments of its atoms and molecules. If the net magnetic moment of the atoms of a substance is zero, the substance is diamagnetic If, on the other hand, the atoms of a substance contain half-filled orbitals, the net magnetic moment of the atoms is not zero and the substance is paramagnetic**.

The Pauli Exclusion Principle

By now you know that an electron in an orbital is defined by four quantum numbers, much as you are recognised by your name and address. However, two people from two different families can have the same name, but not the same address. Similarly, two electrons in an atom cannot have the same set of quantum numbers. This principle was first put forward by the Austrian-Swiss physicist Wolfgang Pauli, who was awarded the Nobel Prize in Physics in 1945. According to the principle, “No two electrons in an atom can have the same values for all the four quantum numbers,” because if one electron in an atom has a particular set of quantum numbers, all other electrons are excluded from having the same set of quantum numbers.

• This rule implies that an orbital can at the most have two electrons and the two electrons must have different spin quantum numbers. This is because electrons belonging to the same orbital must have the same values of n, l, and m_l, so the only quantum number that can be different is m_s, which can have only two values, which means that an orbital can have only two electrons in order not to violate Pauli’s rule.
• Take the 2s orbital, for example. All the electrons in this orbital have n = 2, l = 0, and m_t = 0. The only variation possible is in the value of ms, so the 2s orbital can only accommodate two electrons, one with an up-spin (↑) and one with a down-spin (↓). Pauli’s rule makes it possible to calculate the maximum number of electrons that a subshell can accommodate.

Now that you have a clear idea of orbitals in the quantum mechanical model of the atom, it would be worthwhile to enumerate the differences between the Bohr orbits and quantum mechanical orbitals.

Example 1. An electron is in 4d orbital. What are the possible values of n, l, m_s, and ms for the electron.
Solution:

Since the orbital is 4d, n = 4 and l = 2.

m_l can have values from -l to +l.

∴ m_s =-2, -1,0,1,2.

m_s = ±1/2(for each m_l value).

Example 2. Which of the following sets of quantum numbers is are not permitted?

1. n=3, 1 = 3, m,=-2, m_s = -1/2
2. it =4, 1=3, mi = -3, m_s = 1/2
3. n =2, 1 = 0, m, =0, m_s =0
4. n=0, 1 = 0, mI =0, m_s = -1/2
5. n= 6, 1 = 4, m,=-2, m_s = +1/2

Solution:

1. Not permitted as l can take values from 0 to n – 1. l cannot be equal to n.
2. Permitted.
3. Not permitted as ms cannot be 0. It can be ± 1/2
4. Not permitted as n cannot be 0.
5. Permitted.

Example 3. Which of these orbitals are not possible? Give reasons to your answer. 1p, 2d, 3s, 4f, 3f
Solution:

lp is not possible as for n = 1, l = 0, therefore we can have only an s orbital.

2d is not possible because for n = 2, l = 0 and 1 and the corresponding orbitals are 2s and 2p.

3f is not possible because for n =3,1 = 0,1,2 and the permitted orbitals are 3s, 3p, 3d.

Example 4. Using s,p,d, and f notations, describe the orbital with the following quantum numbers:

1. n = 2, l =0
2. n =3,1 =2
3. n =4,1 =3
4. n=5,l = 4.

Solution:

1. 2s
2. 3d
3. 4f and
4. 5g

Shapes of orbitals: The orbitals of an atom have characteristic shapes. Imagine an electron in motion around the nucleus. The solutions of the Schrodinger equation for this electron cannot predict its exact location at any instant but it can give the probability of finding the electron in a certain location. The probability distribution for an electron in the Is orbital could be likened to the holes in a rifle target of a good shooter.

• The probability would be high (many holes) near the centre and decrease (fewer holes) as the distance from the centre (target) increases. Likewise, an electron is found, at any instant, with a higher probability closer to the nucleus than at a distance farther away. One way of representing this is as shown in Figure.
• This plot of probability versus distance takes into account two dimensions.
• An atomic orbital is that three-dimensional region in space where the probability of finding the electron is maximum. The shape of an orbital is defined as the surface enclosing 90% of the probability of finding the electron.

As stated earlier the square of the wave function, i.e., \(|\psi|^2\) at a point in an atom is a measure of the probability density at that point. The probability density \(|\psi|^2\) is not uniform in an atom. It never becomes zero. To find out the shape of an atomic orbital, we draw the shapes based on the values of \(|\psi|^2\) in an atom.

• These most probable regions of finding electrons represent shapes of the orbitals and are called boundary surface diagrams. We cannot draw a boundary surface diagram in which the probability of finding an electron is 100% as \(|\psi|^2\) is never zero at any finite distance from the nucleus. In other words, it is not possible to draw a boundary surface diagram of a rigid size in which the probability of finding the electron is 100%.

Probability distribution curves: The plot of probability, i.e., \(|\psi|^2\) versus distance from the nucleus is called a probability distribution curve. Different orbitals are characterised by different probability distribution curves. The plot of the total probability density gives a boundary surface diagram and it indicates the shape of an orbital.

The wave function \(|\psi|^2\) of an electron can be divided into the radial part (dependent on the quantum numbers— n,l) and the angular part (dependent on the quantum numbers—l,m_l) so that

⇒ \(\Psi=\underset{\text { radial angular }}{R} \underset{ }{\Phi}\)

Thus the wave function is split into two parts—radial and angular—which are solved separately.

Plots of radial wave function (R): The plots of R against r for 1s, 2s, and 2p orbitals are shown.

In all the cases R > 0 as r → ∞. In the 2s radial function, there is a node (region of zero probability). In general, ns orbitals have (n -1) nodes and tip orbitals have (n – 2) nodes. At a node, the sign of R changes.

Plot of radial probability density (R²) As you can see in Figure, for s orbitals the maximum electron density is close to the nucleus whereas for p orbital the electron density at the nucleus is zero.

Plot of radial probability function: The plot of R² against r gives the probability density of finding an electron at a distance r from the nucleus.

Atoms are considered to be spherical in shape. Let us consider the space around the nucleus to be divided into a large number of thin concentric spherical shells of thickness dr. Consider one of these shells with inner radius r.

The volume of such a shell is given by

dV = \(\frac{4}{3} \pi(r+d r)^3-\frac{4}{3} \pi r^3\)

Neglecting very small terms like dr² and dr³, dV = 4πr²dr

The probability of finding an electron within this small radial shell is called the radial probability density function and is equal to 4πr²R². A plot of the radial probability density function against the distance is called the radial probability distribution curve and gives the probability of finding an electron at a distance r from the nucleus.

Interpretation of radial probability distribution curve: 1s orbital The probability of finding an electron at the nucleus is zero. This is significant as plots of R and R² against r indicate that the maximum probability of finding an electron is at the nucleus, which is not true.

• The probability increases up to a point and then decreases. The maximum in the curve corresponds to the distance at which the probability of finding an electron is the maximum. This is called the radius of maximum probability.
• The curve indicates that the maximum probability of finding the electron of an atom is at the radius of maximum probability but does not rule out the fact that the electron may be at any other distance. This is in sharp contrast to the Bohr model in which the electron is restricted to a particular distance from the nucleus.

2s and 2p orbitals The curve for the 2s orbital has two maxima and a lldde (region of zero probability) between the two maxima, lire distance of maximum probability for a 2p electron is slightly less than that for a 2s electron.

• But the additional maximum in tire 2s curve is very significant. It indicates that a 2s electron in contrast to a 2p electron spends some time nearer the nucleus. It has greater penetration power and is more tightly held than a 2p electron. Hence a 2s electron is more stable and has lower energy than a 2p electron.
• As stated earlier the total wave function is made up of both radial and angular functions. It is difficult to picture angular functions but easier to visualise the probability density function. This can be done by representing the probability density by the density of shading Irt a diagram. A simpler method is to show only the boundary surface, the solid shape that contains about 90 pet cent t)f the electron probability.

Boundary surfaces: For an s orbital, l = 0, so m₁ = 0. This means that this orbital can have only one orientation about the nucleus; this will be possible only if the s orbital has the shape of a sphere.

The sphere is called the boundary surface, of the orbital. The s orbitals of higher energy levels are also spherical, but they have spherical shells within them where the probability is zero. These regions are called nodal surfaces or nodes or radial nodes. The 2s orbital has one node and the 3s orbital has two nodes. In general the 11s orbital has (n -1) nodes. The size and energy of the s orbitals increase with the value of n, i.e… Is < 2s < 3s ….

• We hope the question “How does an electron move from one probable region (orbital) to another when it is not allowed to be at the node (zero probability)?” is not bothering you. If it is, focus on the wavelike nature of the electron. In fact, nodes are an intrinsic property of waves.
• Apart from s orbitals, all other types of orbitals (l ≠ 0) have complicated boundary surfaces. The probability plots for a p orbital show three double-lobed or dumbbell-shaped orbitals oriented along each of the three mutually perpendicular axes.
• The two lobes in each orbital are separated by a nodal plane. There is zero probability density for electrons at this plane. Since the plane cuts through the nucleus, the probability of finding an electron at the nucleus is zero.

For p orbital, l = 1 and m_l = -1, 0, +1, Consequently there are three orientations for the p orbitals. The size and energy of p orbital increases with n. Also as n increases, the p orbitals become bigger (as in the case of s orbitals) and show a complex radial nodal structure.

• Generally speaking, the np orbital has (n- 2) radial nodes. For the same value of u, the three p orbitals have the same energy. Such orbitals, with the same energy, are called degenerate orbitals. When an external magnetic or electric field is applied these three orbitals get oriented differently and are no longer degenerate, (This explains the Zeeman effect.)
• Starting with the third principal energy level, one can have d orbitals. For d orbitals, l = 2 and m_l = -2,-1,0,1- 1, + 2, Thus there are five degenerate d orbitals whose shapes are shown in Figure.
• The d_xy, d_xz, and d_yz orbitals are alike except for the plane of their orientation and point between the two Cartesian axes. The \(\mathrm{d}_{x^2-y^2}\)orbital is like the d_xy orbital except that it is rotated through 45° around the z axis and consists of a doughnut-scaped ring and dumbbell-shaped lobes.
• The \(\mathrm{d}_{z^2}\) orbital is symmetrical around the z axis. The probability density function of np and nd orbitals is zero at certain planes depending on the orientation of the orbital. The p and d orbitals are not spherically symmetrical. For the p7 orbital, there is no probability of finding the electron in the xy plane and this is a nodal plane. This is called an angular node and the number of angular nodes is given by l. Thus the p orbital has one angular node and the d orbital has two.

Atomic Structure Multiple Choice Questions

Question 1. Which energy level would allow the hydrogen atom to absorb a photon but not to emit a photon?

1. 2s
2. 2p
3. 1s
4. 3d

Answer: 3. 1s

Question 2. The value of the azimuthal quantum number for all the electrons present in 4d orbitals is

1. 2
2. 3
3. 4
4. 1

Answer: 1. 2

Question 3. Which of the following transitions in the hydrogen atom would require the largest amount of energy?

1. From n =1 to n = 2
2. From n =∞  to n = 1
3. From n = 2 to n = 3
4. From n = 3 to n = 5

Answer: 1. From n =1 to n = 2

Question 4. The maximum number of 3d electrons with the spin quantum number -1/2 is

1. 5
2. 7
3. 10
4. 1

Answer: 1. 5

Question 5. The number of electrons present in -1/2 is

1. 12
2. 17
3. 7
4. 10

Answer: 4. 10

Question 6. Which of the following configurations is not possible?

1. 3p⁶
2. 2s¹
3. 3f⁷
4. 4d⁵

Answer: 3. 3f⁷

Question 7. The number of unpaired electrons in Fe³⁺ (Z = 26) is

1. 2
2. 3
3. 4
4. 5

Answer: 4. 5

Question 8. Which of the following radiations is associated with the highest energy?

1. λ =  300 pm
2. λ = 30 nm
3. v = 3 x 10² s^-1
4. v = 3 x 10¹⁰ s^-1

Answer: 1.  λ =  300 pm

Atomic Structure Multiple Choice

Question 9. Krypton (₃₆Kr) has the electronic configuration [Ar] 4s² 3d¹⁰ 4p⁶. The 37th electron will go into which of the following subshells?

1. 4f
2. 4d
3. 3p
4. 5s

Answer: 4. 5s

Question 10. The set of quantum numbers not applicable to an electron in an atom is

1. n = 1, l = 1, m = 1, s = +1/2
2. n = 1, l = 0, m = 0, s = -1/2
3. n = 1, l = 0, m = 0, s = +1/2
4. n = 2, l = 0, m = 0, s = 1/2

Answer: 1. n = 1, l = 1, m = 1, s = +1/2

Question 11. Which of the following represents a noble gas configuration?

1. \(1 s^2 2 s^2 2 p^6 3 s^2\)
2. \(1 s^2 2 s^2 2 p^6 3 s^1\)
3. \(1 s^2 2 s^2 2 p^6\)
4. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 4 s^2\)

Answer: 3. \(1 s^2 2 s^2 2 p^6\)

Question 12. The maximum wavelength of light that can excite an electron from the energy level n = 1 to the level n = 3 in atomic hydrogen is

1. 1 nm
2. 102 nm
3. 487 nm
4. 10^-7 nm

Answer: 2. 102 nm

Question 13. The wave number of the first line in the Balmer series of hydrogen is 15,200 cm^-1. What would be the wave number of the first line in the Balmer series of the Be³⁺ ion?

1. 2.4 x 10⁵ cm^-1
2. 24.3 x 10⁵ cm^-1
3. 6.08 x 10⁵ cm^-1
4. 24.3 x 10⁴ cm^-1

Answer: 1. 2.4 x 10⁵ cm^-1, 4. 24.3 x 10⁴ cm^-1

Question 14. The electronic configuration of an element is 1s² 2s² 2p⁴. The number of impaired electrons is

1. 1
2. 2
3. 3
4. 4

Answer: 2. 2

Question 15. Which is the correct electronic configuration of Sc (Z = 21)?

1. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 4 s^2 3 d^1\)
2. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^3\)
3. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 4 s^1 3 d^2\)
4. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^3 3 d^5 4 s^1\)

Answer: 1. \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 4 s^2 3 d^1\)

Question 16. The total number of electrons in a 2p orbital is

1. 3
2. 6
3. 4
4. 8

Answer: 2. 6

Question 17. Which of these has the configuration of a hydrogen atom?

1. He^–
2. He²⁺
3. Li⁺
4. Li²⁺

Answer: 4. Li⁺

Question 18. If the radius of the first Bohr orbit is a₀, then the radius of the third Bohr orbit will be

1. 3a0
2. 1/3 a₀
3. 9a₀
4. 1/3a₀

Answer: 3. 9a₀

Atomic Structure Multiple Choice

Question 19. The spectrum of He will be similar to that of

1. H
2. Li
3. Li²⁺
4. Li⁺

Answer: 4. Li⁺

Question 20. The maximum number of electrons in an orbit of n = 4, l= 3 is

1. 2
2. 4
3. 10
4. 6

Answer: 3. 10

Question 21. Which of these has maximum number of unpaired electrons?

1. Mn²⁺
2. Fe
3. Cu⁺
4. Zn

Answer: 1. Mn²⁺

Question 22. In which orbital diagram (given below) is both Pauli exclusion principle and Hund rule violated?

Answer: 2

Question 23. The ratio of the energy of a photon of λ = 100 pm to that of one of λ =  200 pm is

1. 2
2. 1/2
3. 4
4. 1/4

Answer: 1. 2

Question 24. The correct set of quantum numbers for the unpaired electron in a sodium atom is

1. n = 3, 1 = 0, m_l = 0, m_s = +1/2
2. n = 3, l = 1, m_l = 0, m_s = -1/2
3. n = 2, l = 0, m_l = 0, m_s = -1/2
4. n = 3, l=0, m_l = 1, m_s = -1/2

Answer: 1. n = 3, 1 = 0, m_l = 0, m_s = +1/2

Question 25. The energy of the first excited state of the hydrogen atom is -3.2 eV. The kinetic energy of the same orbit will be

1. -6.4eV
2. +3.2 eV
3. +1.6 eV
4. +64 eV

Answer: 2. +3.2 eV

 

Bohr’s Model Of The Atom

It was Niels Bohr, a Danish physicist, who found a way to solve the problem created by Rutherford’s model. He did not reject the nuclear model since it tallied with a-scattering experimental results.

• He tried to modify the model to account for the fact that in reality, the revolving electrons do not continuously emit radiation. He toyed with the idea that there must be some special orbits along which an electron can revolve without emitting radiation though it is constantly accelerating (i.e., changing direction).
• It is not necessary or possible (at this stage) to go into the details of how he worked out his model, but it is necessary to know its salient features. It was another of those marvellous ideas that have, from time to time, given science a big push forward.
• In fact, this was a golden era, with Planck’s quanta of energy, Einstein’s photoelectrons, Bohr’s atomic model, and other brilliant contributions that you will learn about later. For the moment, let us go back to Bohr’s model proposed in 1913, in which the electrons revolved around the nucleus according to the following rules.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

1. Electrons move around the nucleus only along certain select circular orbits, associated with definite energies. They do not revolve around any arbitrary orbit. These select orbits are also referred to as energy shells or energy levels. The shells are numbered 1, 2, 3,…, or called K, L, M,… Bohr’s model, thus, utilised the concept of quantization of energy—a concept introduced by Planck and used by Einstein to explain photo electricity.

• Simply put, the quantisation of a physical quantity (like energy) means that it can have only certain specific values, it cannot vary continuously to have any arbitrary value. If it changes, it can do so only discontinuously to take on particular values.
• When you go to the market to buy bananas, for example, you can buy 6, or 12, or some whole number of bananas. You cannot buy 3.25 or 5.16 bananas. In a way, the number of bananas you can buy is quantised. If this is not clear to you, consider the example illustrated in Figure.

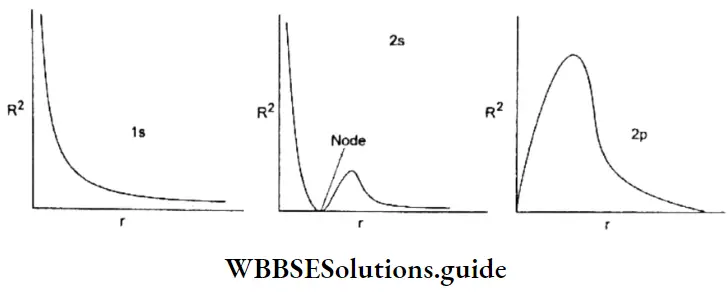
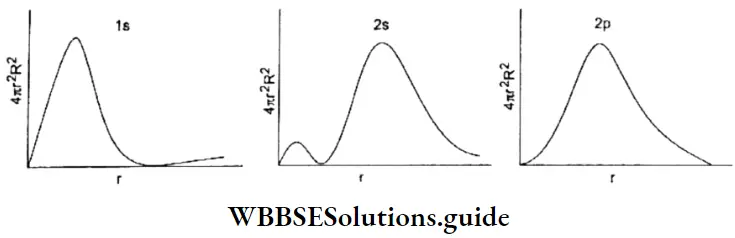
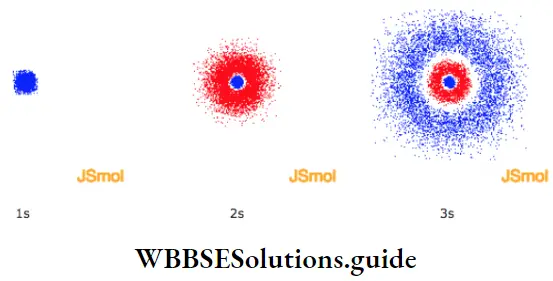
2. As long as an electron revolves in a particular orbit or shell, it neither absorbs, nor emits energy. In other words, the energy of an electron is constant in a particular orbit. This is why an orbit is referred to as a stationary state. It is a stationary state in terms of energy.

3. The orbits an electron is permitted to move in are not only defined in terms of energy but also angular momentum. If an electron moves in a circular orbit, it will naturally have some angular momentum. Just as it can move along only select orbits associated with definite energies, it can only have specific angular momentums. The angular momentum of an electron can only be whole number multiples of h/2π, where h is the Planck constant.

Limitations Of Bohr’s Atomic Model

• Angular momentum \(\left(m_{\mathrm{e}} v r\right)=n \frac{h}{2 \pi}\), where m_e is the mass of the electron, v is its linear velocity, r is the radius of the circular path around the nucleus in which the electron is moving and n = 1,2,3…..
• Thus, just as the energy of an electron is quantised, its angular momentum to is quantised. In other words, the energy and position of an electron in an atom are quantised.

4. When energy is supplied by some external source to an electron (moving in a particular stationary orbit) it may jump to a higher energy level (orbit) by absorbing a definite amount of energy. The amount of energy absorbed by the electron is equal to the difference in the energies of the higher energy level and its original (ground state) energy level.

ΔE = E₂ – E₁

where, ΔE = energy absorbed,

E₂ = energy of higher level, and

E₁ = energy of original or ground state.

• When an electron jumps to a higher energy level by absorbing a particular amount (quantum) of energy, il becomes unstable. It stays at the higher energy level only for a short while before returning to its ground state or original energy level.
• It does so by radiating the amount (photon, quantum) of energy it hac absorbed to become excited, or to jump to the higher level. An electron docs not always jump back to the ground state by radiating the energy it had absorbed in one packet. It may radiate the energy in smaller packets, or in several steps. The amount of energy it may radiate in one step, however, is quantised.

Success of Bohr’s model: Bohr was awarded the Nobel prize in Physics in 1922. His model was a major breakthrough in understanding the atomic structure. It could explain several things that Rutherford’s model could not account for.

1. It could explain why an electron does not emit radiation continuously though it is in a constant state of acceleration. In other words, it could account for the stability of the atom, which Rutherford’s model could not. (Remember, according to Bohr, an electron does not lose energy as long as it revolves in a particular stationary orbit.)

Limitations Of Bohr’s Atomic Model

2. Bohr’s theory could be used to calculate the energy of an electron in a particular orbit of the hydrogen atom (it was not valid for atoms with more than one electron, but we will come to that later). The details of the mathematical derivation are not required here, but it can be shown that the energy of an electron in the nth orbit of the hydrogen atom works out to

\(E_n=-\frac{2 \pi^2 m e^4}{n^2 h^2}\)

where m = mass of electron,

e = charge on electron,

n = number of orbits,

h = Planck constant.

Substituting the values of m,e, and h, the equation works out to be

⇒ \(E_n=-\frac{218 \times 10^{-18} \times \mathrm{Z}^2}{n^2} \mathrm{~J}\)

or, \(E_n=-\frac{1312 \times \mathrm{Z}^2}{n^2} \mathrm{~kJ} \mathrm{~mol}^{-1}\)

This formula can be used for the hydrogen atom and hydrogenlike ions, i.e., ions which have only one electron, for example, He⁺, Li^2+, and Be³⁺. For He²⁺,

⇒ \(E_n=-\frac{4 \times 1312}{n^2} \mathrm{~kJ} \mathrm{~mol}^{-1}\)

You may wonder why the expression for the energy of an electron in the nth orbit carries a negative sign.

Limitations Of Bohr’s Model Class 11

• This is because it is assumed that when the electron is at an infinite distance from the nucleus (i.e., when the atom is ionised and there is no force of attraction between the electron and the nucleus) its energy is zero. As the electron approaches the nucleus and enters its field of attraction, it loses energy and the atom becomes more stable.
• This is why the energy of an electron in the nth orbit is negative. By the same logic, the closer the electron gets to the nucleus, the more negative its energy becomes, or an electron in the n +1 energy level has more energy than an electron in the nth level because the nth level is closer to the nucleus than the n +1 level. The electron in the n =1 orbit has the lowest possible energy as it is closest to the positive charge of the nucleus.

Another way of looking at it is that if we wish to ionise hydrogen atoms, i.e., take the electrons from the ground state (n = 1) to infinity, we will have to supply + 1312 kJ mol ^-1 of energy (in this case Z =1 and n =1).

Bohr radius The radius of stationary orbitals can be calculated from the expression: \(r_n=0.529 AA\left(n^2\right)\) where n =1,2,3,….

The radius of the first stationary state is called the Bohr radius, which Is \(0.529\left(1^2\right) AA=0.529 AA\) = 52.9 pm (\(1 AA=10^{-10} \mathrm{~m}\)).

The radius of the second orbit is \(0.529\left(2^2\right) AA=2.12 AA=212 \mathrm{pm}\).

As n increases r_n also increases due to the increasing distance between nucleus and the orbit. For atoms like the hydrogen atom (containing one electron), the expression for radius of the orbit is given by

⇒ \(r_n=\frac{0.529 AA\left(n^2\right)}{Z}\)

where Z is the atomic number. Thus, with the increase of Z the radius becomes smaller, which means that the electron will be tightly bound to the nucleus.

3. Bohr’s model could also explain the line spectrum of hydrogen. According to his theory, an electron in the ground state (lowest possible energy level) does not emit radiation. It can, however, absorb a definite amount of energy from an external source and jump to a higher energy level, when it is said to be excited.

The electron cannot remain in an excited state for long. It returns to the ground state by emitting the energy it had absorbed in the form of radiation. The frequency of the radiation emitted by the electron depends upon the difference between the energies of the two energy levels.

⇒ \(E_2-E_1=h v\)

∴ v = \(\frac{E_2-E_1}{h}\).

If E₂ is the energy of the electron in the n = n₂ orbit and E₂ that in the n = n₁ orbit then

⇒ \(v=\frac{E_{n_2}-E_{n_1}}{h}\)

⇒ \(E_{n_2}=\frac{\left(-2.18 \times 10^{-18}\right)}{n_2^2} \mathrm{~J}\)

and \(E_{n_1}=\frac{\left(-2.18 \times 10^{-18}\right)}{n_1^2} \mathrm{~J}\).

Substituting the values in the equation v = (E2- E1)/h, we get

Limitations Of Bohr’s Model Class 11

⇒ \(\mathrm{v}=\left(\frac{\left(2.18 \times 10^{-18}\right.}{6.626 \times 10^{-34}}\right)\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{s}^{-1} \quad\left(because h=6.626 \times 10^{-34} \mathrm{Js}\right)\)

⇒ \(\mathrm{v}=\left(3.29 \times 10^{15}\right)\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{s}^{-1}\).

In terms of wave number (v), we have

⇒ \(\overline{\mathrm{v}}=\frac{\mathrm{v}}{c}=\frac{3.29 \times 10^{15} \mathrm{~s}^{-1}}{3 \times 10^{10} \mathrm{~cm} \mathrm{~s}^{-1}}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

⇒ \(\overline{\mathrm{v}}=109,677\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{cm}^{-1}\).

Since an electron can only have certain definite energies, the energy difference between these energy levels can also only have definite values. Consequently, the frequencies of the radiations an electron emits while jumping from a higher energy level to a lower energy level will also have certain definite values. This explains why the hydrogen spectrum consists of discrete lines and is not a continuous spectrum.

4. Bohr’s model thus can explain the line spectrum of hydrogen, but how does it account for the fact that the hydrogen spectrum has so many lines and that too, in different regions of the electromagnetic spectrum? What actually happens is that when energy is supplied to hydrogen gas the electrons of all the atoms do not absorb the same amount of energy.

• Different electrons absorb different quanta of energy to jump to different energy levels. An electron in the first shell (K) may jump to the second shell (L), or the third shell (M), and so on. When these excited electrons return to the ground state they may do so in one step (from M to K) or in more than one step (from M to L and then from L to K).
• Obviously, the frequency of the radiation emitted by an excited electron depends on the kind of jump or transition it makes. This accounts for the various lines in the hydrogen spectrum.

The lines in the Lyman series correspond to transitions from higher energy levels to the first energy level. Similarly, the Balmer, Paschen, Brackett, and Pfund series correspond to transitions (from higher levels) to the second, third, fourth, and fifth energy levels respectively.

Example 1. According to Bohr’s model what would be the wavelength of radiation emitted by an electron in a hydrogen atom making a transition from the fourth energy level to the first energy level?
Solution:

Energy of electron in nth orbit (E_n) = \(-\frac{1312}{n^2} \mathrm{~kJ} \mathrm{~mol}^{-1}\).

∴ energy of electron in fourth orbit(E₁) = \(-\frac{1312}{1^2} \mathrm{~kJ} \mathrm{~mol}^{-1}\)

And energy of electron in fourth orbit (E₄) = \(-\frac{1312}{4^2} \mathrm{~kJ} \mathrm{~mol}^{-1}\)

∴ \(\quad \Delta E=E_4-E_1=-1312\left(\frac{1}{4^2}-\frac{1}{1^2}\right)\)

= \(1230 \mathrm{~kJ} \mathrm{~mol}^{-1} \text {. }\)

∴ \(\Delta E \text { per atom }=\frac{1230 \mathrm{~kJ} \mathrm{~mol}^{-1}}{\text { the Avogadro constant }}=\frac{1230 \mathrm{~kJ} \mathrm{~mol}^{-1}}{6.022 \times 10^{23} \mathrm{~mol}^{-1}}\)

Limitations Of Bohr’s Model Class 11

= \(2.04 \times 10^{-21} \mathrm{~kJ}=2.04 \times 10^{-18} \mathrm{~J} \text {. }\)

∴ \(\Delta E=h v=h \frac{c}{\lambda}\)

∴ \(\quad \lambda=\frac{h c}{\Delta E}=\frac{6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times 3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{2.04 \times 10^{-18} \mathrm{~J}}=9.7 \times 10^{-8} \mathrm{~m}\)

or, \(\lambda=97 \mathrm{~nm} \text {. }\)

Example 2. The ionisation energy of the hydrogen atom is 13.6 eV. What will be the ionisation energy of the Li²⁺ ion?
Solution:

The ionisation energy or the energy required to remove an electron from its ground state to infinity is

∴ ionisation energy of \(\mathrm{Li}^{2+}=\frac{Z^2 E_{\mathrm{H}}}{n^2}\)

= \(\frac{(3)^2 \times 13.6}{1^2}=1224 \mathrm{eV}\)

where Z = atomic number of Li,

Eh = ionisation energy of hydrogen, and

n = number of orbit = 1.

Limitations of Bohr’s model: Bohr’s model of the atom was a great leap forward, but it by no means provided the complete picture, as scientists soon reliased. It ws very succesful in explaining the spectrum and ionisation energy of the hydrogen atom, but even with several refinements, it could not account for the spectra of atoms with more than one electron.

• Nor could it explain how molecules are formed and why they have particular shapes. Its predictions about orbital radii and velocities were also not supported by experimental results.
• A Dutch physicist, Pieter Zeeman, found that if a source emitting line spectrum is placed in a magnetic field, the spectral lines split up into finer lines. A similar thing happens when the source is placed in an electric field.
• This was discovered by the German physicist Johannes Stark. The splitting up of spectral lines in a magnetic field is called Zeeman effect and the splitting up of the lines in an electric field is called Stark effect. Neither of these could be accounted for by Bohr’s model. Let us summarise the difficulties Bohr’s model ran into.

1. It could not account for the spectra of multi-electron atoms. Besides, the development of more sophisticated spectroscopes made it evident that each line in the hydrogen spectrum is made up of a number of fine lines (called fine structure), Bohr’s model could not account for this either.
2. Bohr’s model could not explain the shapes of molecules or how they were formed.
3. It could not explain the Zeeman effect and the Stark effect.
4. The predictions made about atomic radii, velocities, etc., were not borne out by experiments.

Despite its drawbacks, Bohr’s model made a major contribution—it showed that quantum restrictions had to be applied to understand the structure of the atom.

Application Of Bohr’s Atomic Model

Dual Nature Of Matter

Inspired by the dual nature of light (a concept introduced by Planck and Einstein), a French physicist, Prince Louis de Broglie, made a bold suggestion in 1924. He said that matter in general, and electrons in particular, may also have a dual nature. To be more precise all material particles in motion have a dual behavior. This was another of those flashes of insight that we have already discussed. Louis de Broglie’s hypothesis came about a decade after Bohr’s model of the atom and almost two decades after it was established by Einstein in 1905 that light has a dual nature.

An expression for the wavelength (λ) of the wave associated with a particle of mass (m), moving with a velocity (v) was deduced by the Broglie and it is now generally known as the de Broglie equation.

∴ \(\lambda=\frac{h}{p}=\frac{h}{m v}\)

where p = momentum of particle, and

h = the Planck constant.

This relationship implies that the wavelength of a particle in motion is inversely proportional to its momentum. It will interest you to know that most of these brilliant ideas received recognition in the form of Nobel prizes, de Broglie received the Nobel prize in 1929.

Application Of Bohr’s Atomic Model

Example 1. Calculate the wavelength of a body of mass 1 mg moving with a velocity of 100 m s^-1.
Solution:

Applying the de Broglie equation

∴ \(\lambda=\frac{h}{m v},\)

∴ \(\lambda=\frac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{1 \times 10^{-6} \mathrm{~kg} \times 100 \mathrm{~m} \mathrm{~s}^{-1}}=6.626 \times 10^{-30} \mathrm{~m}\).

Example 2. A moving electron has 5 x 10^-25 J Of kinetic energy. What is its de broglie wavelength (mass of electron = 9.1 x 10^-31 kg).
Solution:

Mass of electron = 9.1 x 10^-31 kg

Kinetic energy = \(\frac{1}{2} m v^2=5 \times 10^{-25} \mathrm{~J}\)

∴ \(\quad v =\sqrt{\frac{2 \times \mathrm{KE}}{m}}\)= \(=\sqrt{\frac{2 \times 5 \times 10^{25}J}{9.1 \times 10^{-31} \mathrm{~kg}}}\)

= \(1.048 \times 10^3 \mathrm{~m} \mathrm{~s}^{-1}\)

∴ \(\quad \lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^2 \mathrm{~s}^{-1}}{9.1 \times 10^{-31} \mathrm{~kg} \times 1048 \times 10^3 \mathrm{~m} \mathrm{~s}^{-1}}\)

= \(6.94 \times 10^{-7} \mathrm{~m}\).

Example 3. A and D are two particles in motion. The momentum B is half that of A. Find the wavelength associated with B if the wavelength associated with A is 4 x 10^-8 m.
Solution:

⇒ \(\lambda_{\mathrm{A}}=\frac{h}{p_{\mathrm{A}}} \text { and } \lambda_{\mathrm{B}}=\frac{h}{p_{\mathrm{B}}}\)

where X is the wavelength, p the momentum (p = nw) and h is Planck constant.

Now, \(p_{\mathrm{B}}=\frac{1}{2} p_{\mathrm{A}} \text { (given) }\)

∴ \(\lambda_{\mathrm{B}}=\frac{2 h}{p_{\mathrm{A}}}\)

∴ \(\frac{\lambda_{\mathrm{A}}}{\lambda_{\mathrm{B}}}=\frac{h}{p_{\mathrm{A}}} \times \frac{p_{\mathrm{A}}}{2 h}=\frac{1}{2}\)

∴ \(\lambda_{\mathrm{B}}=2 \lambda_{\mathrm{A}}=8 \times 10^{-8} \mathrm{~m}\)

The idea put forward by de Broglie had to be tested. The best way to test the wave nature of electrons was to see if they exhibited diffraction, a property that only waves have.

• It was shown experimentally that electrons do exhibit diffraction and the wavelength of electron waves measured from diffraction patterns tallied with de Broglie’s prediction.
• Tire most important application of the de Broglie equation is in the construction of the electron microscope which is based on the wavelike behaviour of electrons. In this context, we must recall that an ordinary (light) microscope uses the wavelike nature of light.
• You may wonder why it took scientists so long to discover the wave nature of matter. The answer is that in the macroscopic world (the world we are concerned with in everyday life), objects have very large masses and the wavelengths associated with such objects are very small.

They are too small to be of any significance while describing normal motion or motion in the macroscopic world. Even the wavelengths associated with electrons are too small to be of any significance while considering interactions of electrons with large objects like the oil drop in Millikan’s experiment.

• Thus, Newtonian laws, which deal with only the particle nature of matter, could so successfully describe phenomena in the macroscopic world. This is exactly why Bohr’s model could not fully account for atomic phenomena (because it ignored the wave nature of matter which becomes significant while describing atomic and subatomic events).
• The new way of looking at matter (that it has both particle and wave nature) meant that a new kind of mechanics would have to be developed, to take into account its dual nature.
• This is precisely what happened. Wemer Heisenberg, a German physicist, and Erwin Schrodinger, an Austrian physicist, formulated the theory of quantum mechanics, at the same time, but independently. Others who contributed in a major way are Paul Dirac, a British mathematician and physicist, Wolfgang Pauli, an Austrian-born Swiss physicist, and Max Bom, a German-bom British physicist.
• Quantum, mechanics is valid for events in the macroscopic world as well as the atomic and subatomic world. In the case of macroscopic phenomena its equations reduce to those used in Newtonian mechanics. Before we consider the quantum mechanical model of the atom, it would be worthwhile to know a little about what is called the Heisenberg uncertainty principle because, conceptually, this is what the whole of quantum mechanics revolves around.

Rutherford’s Scattering Experiment

Ernest Rutherford, a physicist from New Zealand, decided to test the validity of Thomson’s model by bombarding a tin gold foil with a-particles. The idea was that the incident charged particles would be deflected by the charged particles in the gold atoms and that the amount of deflection would indicate how exactly the charged particles are distributed in the atom.

The thickness of the gold foil used by Rutherford was 4 x 10^-5 cm. A circular screen coated with ZnS was placed around the foil to detect the deflected a-particles. The tiny flashes made by the a-particles on the screen coated with ZnS would make them detectable. Rutherford made the following observations.

1. Most of the α-particles passed right through the foil without being deflected.
2. A small fraction of the a-particles were deflected by small angles.
3. Just a few particles (about 1 in 20,000) were deflected by very large angles or reflected right back.

Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

The last observation was something totally unexpected and paved the way for a new picture of the atom. Rutherford came to the following conclusions from his observations.

1. Since most of the α-particles passed undeflected through the gold foil, the charge inside the gold atoms could not be evenly distributed. There had to be large empty spaces inside the atom. In fact, most of the space inside the atom must be empty.
2. Thomson’s model of evenly distributed positive charge could not explain the violent deflection of the α-particles which were reflected right back. It would need a far more concentrated positive charge to produce such an impact. The fact that only 1 in 20,000 α-particles encountered such a repulsive force also pointed in the direction of a concentration of the positive charge in a small portion of the gold atom.

Rutherford’s Model Of The Atom

The conclusions drawn from the scattering experiment prompted Rutherford to put forward a nuclear model of the atom. The salient features of his model are as follows.

1. Most of the mass and all the positive charge of an atom is concentrated in a very small region (radius of the order of 10^-13cm). Rutherford called this region the nucleus of the atom. You can imagine the difference in size of the nucleus and the atom if the radius of the atom is of the order of 10^-8 cm.
2. The nucleus is surrounded by electrons with negligible mass which revolve around it at very high speeds, just as the planets revolve around the sun.
3. The total negative charge on the electrons of an atom is equal to the total positive charge on the nucleus, making the atom as a whole electrically neutral. The positive charge of the nucleus is due to protons present in it.
4. Most of the space inside the atom is empty.

Rutherford received the Nobel prize for his work in Chemistry in 1908.

Discovery Of The Neutron

Rutherford’s experiment provided a method of determining the positive charge on the nucleus of an atom. By counting the number of a-particles scattered in different directions, it was possible to count the positive charge on the nucleus.

• It was observed that the charge on the nucleus of an atom is always an integral multiple of the charge on an electron. This integral value was called the atomic number (Z) of an atom and was supposed to be equal to the number of positive particles or protons in the nucleus. Obviously, for the atom to be electrically neutral, there had to be Z electrons revolving around the nucleus.
• The next difficulty was accounting for the mass of the atom. The number of protons and electrons determined by the a-particle-scattering experiment could not account for the mass of the atom. Sir James Chadwick, a British physicist, solved this problem by discovering the neutron in 1932.
• He found that highly penetrating rays consisting of electrically neutral particles were produced when a thin foil of beryllium was bombarded with fast-moving a-particles. These neutral particles turned out to have the same mass (1.675 x 10^-24 g) as the proton and were called neutrons.

Atomic Number And Mass Number

Rutherford’s experiment had provided a means of determining the positive charge on the nucleus of an atom. A British physicist called H G J Moseley devised a finer method of determining the positive charge on the nucleus by determining the wavelength of the X-rays emitted by an element. The number of positive charges on the nucleus of an atom was designated the atomic number, Z, as mentioned earlier.

• Chadwick’s discovery was actually a confirmation of what scientists had been hypothesising when they found that the number of protons and electrons in the atom could not account for its mass. In fact, electrons are so light that they hardly contribute anything to the atomic mass.
• Most of the mass of the atom is due to the protons and neutrons in the nucleus, which are together called nucleons. The total number of nucleons in an atom is called its mass number, A. Hence, the mass number of an element = number of protons + number of neutrons. The mass number and atomic number of an element X is indicated as \({ }_Z^A X\). In the case of carbon, it would be indicated as \({ }_6^12 C\).

Isotopes Atoms of the same element have the same number of protons (atomic number), but may not have the same number of neutrons. Atoms of such elements which have the same number of protons but different numbers of neutrons are called isotopes.

• Hydrogen, for instance, has three isotopes—\({ }_1^1 H\) (protium), \({ }_1^2 H\) (deuterium), and \({ }_1^3 H\) (tritium). In the case of hydrogen, the three isotopes have different names, but this is not the case with other elements. Some of the other examples are \({ }_17^35 Cl\) and  \({ }_17^37 Cl\).
• It is important to mention here that the isotopes behave nearly the same chemically. This is because the chemical properties of an atom (or element) depend on the number of electrons that actually participate in bond formation. The number of electrons in an atom are determined by the number of protons and not neutrons.

Isobars Atoms of different elements sometimes have the same mass number. Obviously, they have different atomic numbers and different chemical properties, example, \({ }_{19}^{40} \mathrm{~K} \text { and }{ }_{20}^{40} \mathrm{Ca}\). Isotopes differ in the number of neutrons, whereas isobars differ both in the number of protons and neutrons.

Isotones When atoms of different elements have the same number of neutrons, they are called isolones. For instance, \({ }_7^{15} \mathrm{~N} \text { and }{ }_8^{16} \mathrm{O}\) are isotones. Another example is \({ }_11^{23} \mathrm{~Na} \text { and }{ }_12^{24} \mathrm{Mg}\).

Example 1. Calculate the number of electrons which will together weigh 3 g.
Solution:

Mass of1 electron = 9.11 x10^-31 kg

or, 9.11 x10^-31 kg is mass of 1 electron.

∴ 3 g or 3 x10^-3 kg is mass of \(\frac{1}{9.11 \times 10^{-31} \mathrm{~kg}} \times 3 \times 10^{-3} \mathrm{~kg}\) = 3.294 x10²⁷electrons.

Example 2. Calculate the mass and charge of 2 moles ofelectrons.
Solution:

1 mole contains 6.022 x 10²³ electrons.

Mass of 1 electron = 9.11 x10^-31 kg.

Mass of 2 moles of electrons = (9.11 x 10³¹) kg x 2 x 6.022 x10²³ = 10.972 x10^-7=1.0972 x10^-6 kg.

Charge on one electron =1602 x10^-19 coulombs.

∴ charge on 2 moles of electrons =1602 x10^-19 coulomb x 2 x 6.022 x 10²³ =1930 x 10⁵ coulombs.

Example 3. Find the number and mass of neutrons in 32 mg of O₂ at stp (mass of a neutron =1675 x 10^-27 kg).
Solution:

1 mole of O₂ =16 g = (6.022 x10²³) x (8 + 8) neutrons = 9.6352 x10²⁴ neutrons.

Now, 16 g of O₂ =1 mole.

∴ 32 g of O₂ = 2 moles

or, 32 mg of O₂ = 0.002 moles

Number of neutrons in 32 mg of O₂ = 9.6352 x 10²⁴ x 2 x10^-3 =19270 x 10²².

Mass of 1 neutron =1675 x 10^-27 kg.

∴ mass of 19270 x 10²² neutrons =19270 x 10²² x1675 x 10^-27 = 3.228 x 10^-5 kg.

Electromagnetic Waves

The Rutherford model of the atom explained the results of the a-partide-scattering experiment very successfully, so it was accepted for a while. But when sdentists tried to find explanations for the arrangement of electrons in the atom, the stability of the atom, and in particular, atomic spectra (characteristic light emitted by an atom) in terms of the Rutherford model, they failed completely. The theory did not match experimental observations.

To understand how the Rutherford model failed, we must first know something about atomic spectra, or rather about the nature of electromagnetic waves. Light is just a kind of electromagnetic radiation, as you may already know.

Electromagnetic Wave theory: Newton and his contemporaries thought of light as a stream of particles/ called corpuscles of light. Newton’s corpuscular theory of light could explain certain phenomena, like reflection and refraction but not others, like interference and diffraction. It was, therefore, discarded and the wave theory of light replaced it. According to the wave theory, light, or rather electromagnetic radiation, is propagated in the form of waves, and waves are characterized by wavelength (λ—Greek letter lambda) and frequency (ν—Greek letter nu). The speed of propagation is given by

∴ c = vX.

This speed is constant for all electromagnetic radiation (in vacuum) and is equal to 3.00 x 10⁸ ms^-1. You will learn more about the wave theory later. For the moment it will suffice to remember the following points.

1. In 1856, James Clark Maxwell, a British physicist, first showed that light is a form of electromagnetic radiation. And, in addition to light (visible form of radiation), there are other forms of electromagnetic radiation like heat and ultraviolet radiation.
2. Electromagnetic radiation comprises electric and magnetic fields oscillating at right angles to each other.
3. In any electromagnetic radiation, the direction of propagation, direction of the electric field, and the direction of the magnetic field are at right angles to each other.
4. Electromagnetic radiation does not need a material medium for propagation. The speed of propagation of electromagnetic radiation through vacuum is constant (c). Different forms of radiation differ only in their frequency and wavelength, since the speed of propagation (c), which is the product of the frequency and wavelength, is constant. wave are mutually perpendicular.

Electromagnetic Characteristics of a Wave: You have just read that any electromagnetic radiation travels with a particular speed in vacuum, and that what distinguishes one form of radiation from another is its characteristic wavelength and frequency. What exactly are the wavelength and frequency of a wave?

1. Wavelength Is the distance travelled by the wave in one cycle, or the distance between neighboring crests or troughs of the wave. It is generally measured in Angstrom units (A) or nanometres (nm). 1 A = 10^-10 m; 1 nm = 10^-9 m.

2. Frequency The frequency of n radiation can be defined as the number of waves which pass through a particular point In one second, It is measured in hertz (Hz) or cycles per second (cps).

∴ 1cps = 1 Hz

One cycle is said to be completed when a wave consisting of a crest and a trough passes through a point.

3. Wave number The wave number may be defined as the number of wavelengths per centimeter and is equal to the inverse of the wavelength expressed in centimetres. It is denoted by \(\bar{v}\)(nu bar) and its unit is cm^-1 (centimeter inverse).

∴ \(\bar{v}=\frac{1}{\lambda} \mathrm{cm}^{-1}\)

4. Amplitude It is the height of the crest or the depth of the trough of a wave. It is generally denoted by a. The amplitude of the wave determines the intensity of radiation, which is the energy per unit volume of the wave.

Example 1. A radio station broadcasts on a frequency of 1.360 kHz. Calculate the wavelength of the radiation emitted by the transmitter of the station.
Solution:

Frequency (v) = 1360 kHz = 1.360 x 10³ Hz.

Velocity (c) = 3 x 10⁸ m s^-1

∴ wavelength (λ) = \(\frac{c}{v}=\frac{3 \times 10^8}{1360 \times 10^3}=219.3 \mathrm{~m}\)= 219.3 m.

Example 2. The wavelength of the light emitted by a source in a laboratory is 700 nm. Calculate its frequency.
Solution:

Wavelength (λ) = 700 nm = 7 x 10^-7 m.

Velocity (c) = 3 x 10⁸ m s^-1

∴ frequency (v) = \(\frac{c}{\lambda}=\frac{3 \times 10^8}{7 \times 10^{-7}}=4.28 \times 10^{14} \mathrm{~s}^{-1}\).

Electromagnetic Failure of Wave Theory: The wave theory of light could not provide the complete picture of the nature of light. Two major phenomena that the wave theory could not explain are photoelectric emission and black-body radiation.

Electromagnetic Black-body radiation You may have noticed that objects change colour when they are heated. The element of a heater, for example, is red first, then orange, and then yellowish, which means that the kind of light (frequency of radiation) an object emits depends on its temperature.

Actually, a hot body emits a whole range of radiations, and what varies with its temperature is the intensity of these radiations. A particular radiation (say red) is most intense at a particular temperature.

• The intensities of the various radiations emitted by a hot body depend on its temperature. A body which emits and absorbs all radiations is called a black body. The intensities of radiations of different wavelengths emitted by a black body at different temperatures were obtained experimentally. These observations could not be explained by the wave theory of light.
• Photoelectric effect Another phenomenon which the wave theory could not explain is the photoelectric effect. When a beam of monochromatic light (light of a single wavelength) falls on a clear metallic surface in vacuum, the metal emits electrons.

• This is called the photoelectric effect and the electrons emitted by the metal are called photoelectrons. It was observed that the energy of the photoelectrons increases with the frequency of the light falling on the metal. Also if the frequency of the incident light falls below a certain critical value or threshold frequency, the emission of electrons stops.
• This threshold frequency is different for different metals. Light of frequency less than the threshold frequency cannot eject electrons no matter how long it falls on the surface or how high is its intensity.
• Also, the intensity of the incident radiation has no impact on the energy of the photoelectrons emitted although the number of electrons ejected does depend on the intensity of incident light.
• The wave theory of light could not explain why the energy of the photoelectrons should remain unaffected when the intensity of the incident radiation increases, nor why it should increase when the frequency of the radiation increases. According to the wave theory the energy carried by a radiation depends on its intensity (amplitude) and not on its frequency.

Electromagnetic Planck’s theory: Max Planck, a German physicist, proposed a theory that could explain black-body radiation. He showed that the radiation emitted by such a body and the way it changed with temperature (energy distribution as a function of temperature) could be explained if one assumed that radiant energy (energy of a radiation) is emitted and absorbed in the form of packets. You will read about Planck’s theory in detail later. Just the salient features of this theory will suffice for the present discussion.

1. Radiant energy is not emitted or absorbed continuously but discontinuously, in the form of small packets called quanta. Each wave packet or quantum is associated with a definite amount of energy. The term photon is often used while referring to a packet of energy in the case of light.

2. The amount of energy associated with a quantum of radiation is proportional to the frequency of the radiation.

∴ E ∝ v

or E = hv or E = \(h \frac{c}{\lambda},\)

where h is the Planck constant and is equal to 6.626 x 10^-34 J s.

3. A body can emit or absorb energy only in integral multiples of hv, i.e., hv, 2hv,3hv, etc. It cannot emit or absorb fractional values of hv.

Planck’s theory explained the distribution of intensity of radiation from a black body as a function of frequency at different temperatures. However, the theory could not explain why energies should be quantised in this manner.

Example 1. Calculate the energy of one photon of ultraviolet light of wavelength 100 nm.
Solution:

Wavelength, λ = 100 nm.

∴ frequency \(\mathrm{v}=\frac{c}{\lambda}=\frac{3 \times 10^8 \mathrm{~ms}^{-1}}{100 \times 10^{-9} \mathrm{~m}}=3 \times 10^{15} \mathrm{~s}^{-1}\)

Energy of photon, E = hv = 6.626×10^-34 x 3 x 10¹⁵ = 1.987 x 10^-18 J

Example 2. How many photons of light of wavelength 4000 pm would provide 1 J of energy?
Solution:

Energy of photon (E) = hv = h c/λ

∴ E =\(\frac{6.626 \times 10^{-4} \mathrm{~J} \mathrm{~s} \times 3 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{4000 \times 10^{-12} \mathrm{~m}}=4.9695 \times 10^{-17} \mathrm{~J}\)

∴ 4.9695 x 10^-17 J is provided by 1 photon.

∴ 1 J will be provided by \(\frac{1 \mathrm{~J}}{4.9695 \times 10^{-17} \mathrm{~J}}=2.012 \times 10^{16}\) photons.

Einstein’s explanation for the photoelectric effect: In 1905, Albert Einstein showed that if one extended Planck’s theory (which talked only about absorption and emission) to the propagation of radiation, one could explain the phenomenon of photoelectricity quite easily. According to the quantum theory (Planck’s theory) of radiation, the energy of a photon is proportional to its frequency. Obviously, then the energy of photoelectrons emitted by a metal surface increases with the frequency of the light falling upon it. How?

• To understand this clearly, let us take into account the threshold frequency once again. As stated earlier, each metal has its characteristic minimum frequency below which it does not show photoelectric effect.
• This minimum frequency or threshold frequency is represented as v₀. If we take the example of potassium, the photoelectric effect is observed in the case of yellow light and not red light. This means that when yellow light falls on the surface of potassium, electrons are emitted. The threshold frequency (v₀) for potassium is 5 x 10¹⁴ Hz. The frequencies of red light and yellow light are 4.4-4.6 x 10¹⁴ Hz and 5.1-5.2 x 10¹⁴ Hz respectively. If the striking photon has a frequency greater than the threshold frequency, photoelectric effect occurs.
• When a photon strikes a metal with frequency v and energy hv, some of its energy is used up to eject the electron from the metal atom. This energy is equal to the minimum energy required to eject the electron i.e., hv0 (also called work function W). The remaining energy of the striking photon is transformed into the kinetic energy of the photoelectron. The kinetic energy is equal to \(\frac{1}{2} m_{\mathrm{e}} v^2\) where m_e is the mass of the photoelectron and v is its velocity. Since the total energy is conserved, we can state that

hv – hv₀ = kinetic energy of the electron = \(\frac{1}{2} m_{\mathrm{e}} v^2\)

or, \(h v=\frac{1}{2} m_{\mathrm{e}} v^2+W_0\)

If hv increases (frequency increases), so will \(m_{\mathrm{e}} v^2 / 2\), which is the energy of the photoelectron. Also, an increase in the intensity of the incident radiation means an increase in the number of photons striking the metallic surface. An increase in the number of photons would naturally lead to an increase in the number of photoelectrons produced.

• Planck and Einstein showed that light has a particle or corpuscular nature which explains the photoelectric effect satisfactorily. On the other hand, the phenomena of diffraction and interference definitely show that it has a wave nature.
• The complete picture of the nature of light, thus, includes both its wave and particle nature and it is said that light exhibits a dual character.

Example 1. The threshold frequency v₀ for a metal is 8.0 x 10^-15 s^-1. Calculate the kinetic energy of the electron which is ejected when radiation of frequency v = 2.0 x 10¹⁶ s^-1 hits the metal.
Solution:

KE of an electron = \(\frac{1}{2}\)mv² = hv – hv₀ where hv₀ = work function of the metal.

Now, KE = h(v – v₀)

= \(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}\left(2.0 \times 10^{16} \mathrm{~s}^{-1}-8.0 \times 10^{15} \mathrm{~s}^{-1}\right)\)

= \(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times(20-8) 10^{15} \mathrm{~s}^{-1}\)

= \(6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s} \times 12 \times 10^{15} \mathrm{~s}^{-1}\)

= \(79.512 \times 10^{-19} \mathrm{~J}=7.9 \times 10^{-18} \mathrm{~J}\).

Example 2. A photon of wavelength 4x 10⁷ m strikes a metal whose work function is 4.0 x 10^-19 J. Calculate the velocity of the ejected electron (mass of electron =9 x 10^-31 kg).
Solution:

KE = hv – hv₀

hv = energy of the photon and hv₀ = work function.

Now v = \(\frac{c}{\lambda}=\frac{3 \times 10^8}{4 \times 10^{-7}}=7.5 \times 10^{14} \mathrm{~s}^{-1}\).

∴ hv = 6.626 x 10^-34 J s x 7.5 x 10¹⁴ s^-1 = 494 x 10^-19 J.

KE = (4.9 x 10^-19 – 4.0 x 10^-19 J)

= 0.9 x 10^-19 or 9 x 10^-20 J.

⇒ \(/frca{1}{2}\)mv² =9 x 10^-20 J.

∴ \(v^2=\frac{2 \times 9 \times 10^{-20}}{9 \times 10^{-31}}=2 \times 10^{11}=20 \times 10^{10}\)

∴ \(v=\sqrt{20 \times 10^{10}}=4.5 \times 10^5 \mathrm{~m} \mathrm{~s}^{-1}\)

Atomic Spectra

You have already studied that when a beam of ordinary white light is passed through a prism, it gets refracted and splits into a series of coloured bands called spectrum (VIBGYOR), the seven constituent colours. This kind of spectrum is called a continuous spectrum. In a continuous spectrum the different bands of colours merge into each other.

• The spectrum ranges from violet at 750 x 10¹⁴ Hz to red at 4 x 10¹⁴ Hz. What actually happens is that when the beam of light passes through the prism, it gets deviated and the angle of deviation is directly proportional to the frequency of radiation. Remember that visible light is just a small portion of the electomagnetic radiation.
• When electromagnetic radiation interacts with matter, i.e., when energy is supplied to an element either by heating or by some other method like passing an electric discharge, its atoms get excited and emit electromagnetic radiations of definite frequencies on returning to their lower stable energy states.

• This set of radiations of particular frequencies is called the emission spectrum of the element. It is also called the atomic spectrum because the radiations are emitted as a result of energy changes in the atom. The characteristic radiations (of particular frequencies) absorbed by the excited atoms of an element constitute its absorption spectrum.
• Two German physicists, Gustav Robert Kirchhoff and Robert Wilhelm Bunsen, started studying the emission spectra of elements around 1860. Spectra arc analysed with the help of an instrument called spectroscope. In its simplest form a spectroscope is a hollow tube with a lens to produce a parallel beam of light which passes through a prism.
• The spectra produced by the excited atoms of elements, unlike the one produced by white light when passed through a prism, are discontinuous. They generally consist of a few bright lines separated by dark bands. That is why atomic spectra are also called line specif a livery element has its characteristic line spectrum. Thus, atomic spectra are called fingerprints of atoms and are used to identify elements. In fact, the study of atomic spectra stalked in the context of chemical analysis, and elements like rubidium, cesium, thallium, indium, gallium, and scandium were discovered this way.

Spectrum of hydrogen: In order to study the emission spectrum of hydrogen, the gas is taken in a gas-discharge tube at low pressure, and an electric discharge is passed through it. The H₂ molecules dissociate into energetically excited hydrogen atoms.

• The radiations emitted by the excited atoms of the gas are passed through a prism and the radiation coming out of the prism is brought to a focus on n photographic film, This is known as spectroscopy. The spectrum obtained this way consists of n large number of sharp lines separated by dark bands. Only the lines in the visible and ultraviolet regions can be obtained this way. The lines in the infrared region require other methods of detection.
• The emission spectrum of hydrogen has several groups of lines which are divided into different series, named after their discoverers.

J J Balmer, a Swiss mathematician, studied the spectrum of hydrogen in the visible region and showed that the wave numbers of the spectral lines obey the following formula, known as the Balmer formula.

⇒ \(\bar{v}=\frac{1}{\lambda}=109,677\left(\frac{1}{2^2}-\frac{1}{n^2}\right) \mathrm{cm}^{-1}\)

where n is an integer greater than 2.

Later, J R Rydberg, a Swedish physicist, came up with a more general formula that can be applied to all the series in the hydrogen spectrum.

⇒ \(\overline{\mathrm{v}}=109,677\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{cm}^{-1}\)

where n₁ and n₂ are integers, such that n₂>n₁

The value 109,677 cm^-1 is called the Rydberg constant (R) for hydrogen.

Example 1. Calculate the wavelength of the light emitted by a hydrogen atom, given that n₁ = 1 and n₂ = 4.
Solution:

According to the Rydberg formula,

⇒ \(\frac{1}{\lambda}=\bar{v}\left(\mathrm{~cm}^{-1}\right)=109,677\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{cm}^{-1}\)

Given n₁ = 1, n₂ =4.

∴ \(\quad \bar{v}=109,677\left(\frac{1}{1^2}-\frac{1}{4^2}\right)\)

= \(109,677 \times \frac{15}{16}=102,822 \mathrm{~cm}^{-1}\)

∴ \(\quad \lambda=\frac{1}{\bar{v}}=\frac{1}{102,822}=9.7 \times 10^{-6} \mathrm{~cm}\).

Example 2. Calculate the frequency and the wavelength of the radiation emitted than an electron in the hydrogen atom jumps from the second to the first orbital?
Solution:

According to Rydberg formula

⇒ \(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

But R = 109,677cm^-1,n₂ =2 and n₁ =1

⇒ \(\bar{v}=109,677\left(\frac{1}{1^2}-\frac{1}{2^2}\right) \mathrm{cm}^{-1}\)

= \(109,677 \times \frac{3}{4} \mathrm{~cm}^{-1}=82257.75 \mathrm{~cm}^{-1}\)

⇒ \(\lambda=\frac{1}{\bar{v}}=\frac{1}{82257.75} \mathrm{~cm}=121.56 \times 10^{-7} \mathrm{~cm}\) = 121 x 10^-9 cm

Failure Of Rutherford’s Model

Rutherford’s nuclear model of the atom resembled the solar system, with a heavy, positively charged nucleus around which the much lighter electrons were supposed to revolve. Also, the coulomb force (F =q₁q₂/r² )which is proportional to the product of the charges and inversely proportional to the square of the distance between them, is mathematically similar to the gravitational force (Gm₁m₂/r²) between a planet and the sun.

It was natural, therefore, for scientists to think that the motion of electrons around the nucleus should be similar to the motion of planets around the sun. Applying the Newtonian theory to the solar system, it had been shown earlier that planets move in definite orbits around the sun.

• However, a problem arose when this concept was applied to the atom. If electrons were to move around the nucleus in well-defined orbits, they would have to be in a constant state of acceleration (even a body moving with constant speed in an orbit is accelerating because it is changing direction continuously).
• This would lead to an impossible situation according to Maxwell’s electromagnetic theory, which says that when charged particles are accelerated they emit electromagnetic radiation.
• If an electron moving around the nucleus were to emit radiation constantly, it would slow down because the energy of the radiation emitted by the electron would come from the motion of the electron. Thus, the orbit of the electron would keep shrinking and the electron would follow a path resembling a spiral and ultimately fall into the nucleus.

This would lead to the collapse of the atom (such a thing does not happen in the case of planets because they are uncharged bodies). Rutherford’s model of the atom could not explain its stability in terms of Newtonian mechanics and Maxwell’s electromagnetic theory.

• Nor could it explain the line spectra associated with atoms. According to Maxwell’s theory, the frequency of radiation emitted by a charged body is equal to its frequency of revolution.
• So, the frequency of the radiation emitted by Rutherford’s electron, following Newtonian mechanics and Maxwell’s theory, would change continuously as its orbit and, consequently, its frequency of revolution would change. This would lead to atomic spectra being continuous, rather than discrete (line spectra), as observed experimentally.
• Thus, Rutherford’s model, with its concentration of positive charge in the nucleus, could explain the scattering experiment, but its planetary electrons could neither account for the stability of the atom, nor for the line spectra exhibited by excited atoms. It says nothing about how the electrons are distributed around the nucleus and what are the energies of these electrons.