Class 6 Maths

Class 6 WBBSE Math Solutions Chapter 25 Fun With Numbers Exercise 25

Question 1. Let’s observe the interesting numbers.
Solution:

Let’s observe the interesting numbers

11 x 11 = 121

11 x 11 x 11 = 1331

11 x 11 x 11 x11 = 14641

11 x 11 x 11 x 11 x 11 = 161051

Other interesting numbers

10 x 1 = 10; 1+0=1

11 x 1 = 11; 1+1=2

12 x 1 = 12; 1+2=3

13 x 1 = 13; 1+3=4

14 x 1 = 14; 1+4=5

15 x 1 = 15; 1+5=6

16 x 1 = 16; 1+6=7

17 x 1 = 17; 1+7=8

18 x 1 = 18; 1+8=9

19 x 1 = 19; 1+9=10

Read and Learn More WBBSE Solutions For Class 6 Maths

An interesting arrangement of the square and square root of natural number.

1 =1 =1²

1 + 3 = 4 = 2²

1 + 3 + 5 = 9 = 3²

1 + 3 + 5 + 7 = 16 = 4²

1 + 3 + 5 + 7 + 9 = 25 = 5²

1 + 3 + 5 + 7 + 9 + 11 = 36 = 6²

1 + 3 + 5 + 7 + 9 + 11 + 13 = 49 = 7²

Class 6 WBBSE Math Solutions

Question 2. By arranging the buttons, let’s understand the relation between square and square root of natural numbers.
Solution:

By arranging the buttons, let’s understand the relation between square and square root of natural numbers.

Class 6 Math Solutions WBBSE Chapter 25 Fun With Numbers Exercise 25.1

Question 1. With four 4 ‘4s’, let us make numbers from 1 to 18.
Solution:

1. \(\frac{4+4}{4+4}=\frac{8}{8}=1\)

2. \(\frac{4}{4}+\frac{4}{4}=1+1=2\)

3. \(\frac{4+4+4}{4}=\frac{12}{4}=3\)

4. \(\frac{4-4}{4}+4=0+4=4\)

5. \(\frac{4+4 \times 4}{4}=-\frac{4+16}{4}=\frac{20}{4}=5\)

6. \(4+\frac{4+4}{4}=4+2=6\)

7. \(4+4-\frac{4}{4}=8-1=7\)

8. \(4+\frac{4 \times 4}{4:}=4+4=8\)

9. \(4+4+\frac{4}{4}=8+1=9\)

10. \(\frac{44-4}{4}=\frac{40}{4}=10\)

11. \(\frac{4}{4}+\frac{4}{4}=\frac{4 \times 10}{4}+1=11\)

12. \(\frac{44+4}{4}=\frac{48}{4}=12\)

13. \(\frac{44}{4}+\sqrt{4}=11+2=13\)

14. \(4(4-4)-4=14 \cdot 4-4=14\)

15. \(4 \times 4-\frac{4}{4}=16-1=15\)

16. \(4+4+4+4=16\)

17. \(4 \times 4+\frac{4}{4}=16+1=17\)

18. \(44 x \cdot 4+\cdot 4=17 \cdot 6+\cdot 4=18\)

Question 2. With five ‘9s’, let me make 1000.
Solution:

⇒ \(999+\frac{9}{9}=999+1000\)

Question 3. Let’s solve puzzles with Roman letters:

1. If 9 is taken from 6,10 is taken from 9,50 is taken from 40, we get 6 – let’s try now it can be made possible.
Solution:

If 9 is taken from 6 i.e., VI-IX = 0,

10 is taken from 9 i.e., IX – X = 1

50 is taken 40 i.e., XL – L = 2

∴ We get, with three match sticks I made VI.

2. By just shifting one match stick, let us get our answer correct.
Solution: As there are three sticks on both sides.

WBBSE Class 6 Maths Solutions

Question 4. There are 5 apples in a basket. Let’s divide them among 5 girls in such a way that each gets 1 apple but one apple remains in the basket.
Solution: If 4 girls get I apple each while the fifth girl gets the basket in the remaining apple still in it.

Question 5. Azim has 3 match sticks. He asked me to write 4 with those 3 match sticks. Let me try to do.
Solution: Azim has 3 match sticks I write 4 with 3 match sticks IV.

Question 6. I have 3 match sticks. I took 2 more sticks to write 8.
Solution: I have 3 match sticks. I took 2 more sticks.

Total number of sticks = 3 + 2 + 5

I write – VIII.

Question 7. I have 7 match sticks and 6 buttons. I arranged the 7 match sticks on a table in a form given below.
Solution:

If I start from 1, the next one will be 3.

I start with 2, the next one will be 4.

I start at 5, the next one will be 7.

I start from 6, and the next one will be 1.

The button I have placed already.

So, next can not start from button 6.

Question 8. Few other fun with match sticks:

1. With 6 match sticks I made 1/7 as
Solution:

With 5 match sticks I made \(\frac{1}{3} \text { as } \frac{1}{\text { III }}\)

WBBSE Class 6 Maths Solutions

2. Let’s make 2 fractions whose value is 1/3.
Solution:

With 6 match sticks I made \(\frac{2}{6} \text { as } \frac{11}{V 1}\)

Question 9. I have 12 match sticks. I shall make a puzzle with these 12 match sticks and try to solve them. With these 12 sticks, 4 squares (and a big square) have been found.

1. First removing 2 sticks, 2 different-sized squares are made.
Solution:

One small and one big squares.

2. By shifting 3 sticks, let’s try to get 3 equal-sized squares.
Solution:

Three equal-sized squares

3. Again, by changing side of 4 sticks, 3 equal-sized squares can be formed
Solution:

Three equal-sized squares.

4. Just by moving 2 sticks, let’s try to get 7 different-sized squares. (In this case 2 sticks may be placed diagonally.)
Solution:

Seven different-sized squares.

WBBSE Math Solutions Class 6

5. I moving 4 sticks, let’s try to make 10 small and big squares (but in this case 2 sticks can be put diagonally).
Solution:

10 small and big squares.

Question 10. We know 2 + 2 = 2 x 2 i.e., two 2’s added and two 2’s multiplied gives the same value.

1. For 3 natural numbers _____, _____, and _____, it is found that their sum is equal to their product. i.e., ____ + ______ + _______ = ______ x _______ x ________
Solution: 1 + 2 + 3 = 1 x 2 x 3

2. Let us find 4 natural numbers, whose sum and product are the same. i.e., ____ + ____ + ______+ ____ + ______ + _____ + _______ + _____
Solution: 1+1+2+4=1x1x2x4

3. Is it possible to have 5 natural numbers where this relation holds good ? (find myself) Yes, I can make the sum and product of 5 natural numbers are equal, one example is: 1+1+1+2+5=1x1x1x2x5

Let us try to find other numbers _____ + _____ + _____ + _____ + ______ = ______ x _______ x _______ x ________ x ________

Solution: 1 + 1 + 1 + 3 + 3 = 1 x 1 x 1 x 3 x 3

Question 11.

1 x 1 = 1

11 x 11 = 121

111 x 111 = 12321

1111 x 1111 = 1234321

_______ x _____ = ________

_________ x ______ = _______

Solution:

1 x 1 = 1

11 x 11 = 121

111 x 111 = 12321

1111 X 1111 = 1234321

11111 X 11111 = 123454321

111111 X 111111 = 12345654321

 

Class 6 Math Solutions WBBSE Chapter 27 Equivalence Of Fraction Decimal Fraction Percentage And Ratio Exercise 27

Question 1. Today we have cut off different geometric-shaped pieces of paper. Preetam took circular and rectangular pieces. He then divided these circular and rectangular pieces into equal parts and colored different parts.
Solution:

Now, let’s write without looking at the illustration:

Read and Learn More WBBSE Solutions For Class 6 Maths

Class 6 Math Solutions WBBSE Chapter 26 Open Shapes Of Regular Solids Exercise 26

Question 1. I opened a cube-shaped paper box.

Which of the following shapes shall I get?

Solution: 3

Question 2. I opened a cuboid-shaped paper box.

Read and Learn More WBBSE Solutions For Class 6 Maths

Which of the following shapes shall I get?

Solution: 1

Question 3. A paper-made tetrahedron is opened.

Let’s find which shape we will get.

Class 6 WBBSE Math Solutions

Solution: 2

Question 4. Now I opened this soild.

Let’s find the shape.

Solution: 1

Question 5. I opened this solid.

Which shape will it be?

Solution: 3

WBBSE Math Solutions Class 6

Question 6. Let’s open the solid

Let us find the shape.

Solution: 3

Question 7. This solid is opened.

The shape will be

Solution: 4

 

Class 6 Math Solutions WBBSE Chapter 24 Solids From Different Sides Perspective Exercise 24

Question 1. I have many plastic cubes. By putting them together different solid shapes can be formed. Let me find out how these shapes will look when viewed from front, side, and 1rom top. Let us write in the blank space how these solids will look [from side/from top].

Solution:

Read and Learn More WBBSE Solutions For Class 6 Maths

Class 6 Math Solutions WBBSE Chapter 23 Symmetry Exercise 23

In the pictures given below, let us find the pictures which are not symmetrical and let’s colour them, and the pictures which are symmetrical, let’s mark the line/lines of symmetry.
Solution:

Question 1. A graph paper with square cells, taking the straight line AB as a line of symmetry, let us complete the symmetrical pictures.
Solution:

Question 2. Let me draw 5 symmetrical pictures I have seen.
Solution:

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 3. In the figure given, taking AB and CD as the lines of symmetry, let us draw a symmetrical picture.
Solution:

Question 4. In the pictures on the graph paper given below, let’s draw the line/lines of symmetry and note down the number of lines of symmetry that are possible for each figure.

Class 6 Math Solutions WBBSE
Solution:

Question 5. Using graph paper let’s draw.

1. A triangle having 1 line of symmetry.
Solution:

2. A triangle having no line of symmetry.
Solution:

3. A triangle having 3 lines of symmetry.
Solution:

Class 6 Math Solutions WBBSE

4. A quadrilateral having 4 lines of symmetry.
Solution:

5. A quadrilateral has 2 lines of symmetry.
Solution:

6. A quadrilateral having just 1 line of symmetry.
Solution:

7. A quadrilateral which does not have a line of symmetry.
Solution:

Question 6. Let’s draw in the exercise book and mention the number of line of symmetry.
Solution:

Question 7. Let’s draw the reflection on the mirror.
Solution:

Class 6 Math Solutions WBBSE

Question 8. Let’s draw the lines of symmetry for the following pictures.
Solution:

Class 6 WBBSE Math Solutions Chapter 22 Drawing Of Different Geometrical Figures Exercise 22

Question 1. In the following figures, let’s identify which two straight lines have intersected at right angles.
Solution:

In the figures (2) and (3), the two straight lines intersected at right angles.

Question 2. Let’s fill in the blanks:

1. At 3’o clock the arms of the clock will be at _____
Solution: A 3’o clock the arms of the clock will be at [right angles].

2. The straight lamp post on the road is at _______ to the ground.
Solution: The straight lamp post on the road is at [right angles] to the ground.

Question 3. Let me write two such things which are at right angles to each other.
Solution: Walls and the floor of a room are at right angles to each other.

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 4. Let us draw a line segment AB of length 4 cm; a point O is taken on the line segment AB, such that AO = 1 cm and OB = 3 cm. Now, at O, let’s draw a perpendicular AB at O.
Solution:

Question 5. A line segment PQ of length 4 cm is drawn. A point O is taken on the segment PQ. With the help of scale and pencil, compass, let’s draw perpendicular OM on PQ at O.

Class 6 WBBSE Math Solutions
Solution:

Draw a line segment PQ of 4 cm. Take a point O on PQ. Now, a perpendicular OR is drawn on PQ at O.

Question 6. A line segment XY of length 5 cm is drawn. A point P is taken outside the line segment XY. With a set square, let’s draw a perpendicular PL, on line segment XY from the point P.
Solution:

A line segment XY of length 5 cm is drawn. A point is taken outside the line segment XY.

Now, with the help of a scale and a set square, I draw a perpendicular PL on the line segment XY from the point P.

Class 6 WBBSE Math Solutions

Question 7. A line segment AB of length 8 cm is taken. A point P is taken on the line segment AB, so that AP = 3 cm, and BP = 5 cm, let’s draw a perpendicular PL on the line segment AB, at point P with the help of scale and pencil and a compass.
Solution:

Draw a straight line AB of 8 cm. A point P is taken on AB, such that AP – 3 cm and PB = 5 cm.

Now, a perpendicular PL is drawn on AB at P with scale pencil and a compass.

Question 8. A line segment AB of length 6 cm is drawn. Let’s take a point K outside this line segment. With the help of scale and compass, let’s draw a perpendicular KL on the line segment AB.
Solution:

A straight line AB of length 6 cm is taken. A point K is taken outside AB. Now, with centre K, an arc is drawn which cuts AB at P and Q.

Now, with centre P and Q, two arcs with radii more than of 1/2 of PQ are drawn, which cut each other at R. Join KR which cuts AB at L. KL is the required perpendicular on AB.

Class 6 WBBSE Math Solutions

Question 9. Let’s draw a triangle ABC with the help of scale and pencil. From the three vertices A, B and C of the triangle, perpendiculars AP, BQ and CR are drawn on the sides BC, AC and AB respectively. Let’s see from the figure, if the line segments AP, BQ and CR are concurrent, i.e., they intersect at a point.
Solution:

A triangle ABC is drawn. From three vertices A, B and C of the triangle ABC, three perpendiculars AP, BQ and CR are drawn. The three perpendiculars AP, BQ and CR meet at O, i.e., perpendiculars are concurrent.

Class 6 Maths Solutions WBBSE

Question 10. With the help of a set square, let us draw a right-angled triangle ABC such that ABC = ∠90°. From point B, let’s draw a perpendicular on the hypotenuse AC. Let’s also find if the perpendiculars from A, B and C on the opposite sides meet at point. If so, name the point.
Solution:

ABC is a right-angled triangle, ABC = ∠90°. A perpendicular BD is drawn on AC. AB is perpendicular on BC from point A and BC is particular on AB from point C.

These three perpendiculars meet at B.

Question 11. At a fixed point on a straight line ___ perpendicular can be drawn.
Solution: At a fixed point on a straight line one perpendicular can be drawn.

Question 12. From a fixed point outside a straight line _____ (one/more than one) perpendicular can be drawn to that straight line.
Solution: From a fixed point outside a straight line one perpendicular can be drawn to the straight line.

Class 6 Maths Solutions WBBSE

Question 13. Let’s draw a line segment AB, let’s take any two points P and Q on the line segment. Let’s draw two perpendiculars PM and QN at P and Q on the line segment AB; let’s find if line segments PM and QN are parallel or intersecting.
Solution:

Let P and Q are the two points on the line segment AB. Two perpendiculars r PM and QN are drawn on AB at P and Q. Here PM and QN are two parallel lines.

Question 14. Let’s draw a line segment of length 4 cm; taking this length as radius a circle is drawn. Let the centre of the circle be named O. A chord AB which is not a diameter is drawn. From O a perpendicular OM is drawn on the chord AB. Let’s measure the line segments AM and BM with a scale and write the conclusion derived.
Solution:

O is the centre of the circle of radius 4 cm (OC).

AB is a chord. A perpendicular OM is drawn from the centre O. AB is bisected at M.

AB = 6.6 cm; AM = BM = 3.3 cm.

Class 6 Maths Solutions WBBSE Chapter 22 Drawing Of Different Geometrical Figures Exercise 22.1

I drew a line segment XY with scale and pencil on my exercise book. I Now we shall draw the perpendicular bisector of line segment XY with the help of scale, pencil and pencil compass.
Solution:

A line segment XY is drawn with a scale and pencil. Now, with centres X and Y, two arcs with the same radius are drawn on both sides of XY.

The arcs intersect each other at C and D. Join C and, D which cuts XY at P.

∴ XP = PY = 4 cm.

Question 1. If taken a radius, less than half the length of the line segment XY and try to draw an arc with centres X and Y, on both sides, what shall I find?
Solution: Now, with centres X and Y, we draw two arcs with a radius less than half the length of line segment XY on both sides.

Question 2. Again, if I draw arcs with centers X and Y and radius equal to the length 1 more than half the length of the line segment, what shall I observe?
Solution:

Again, with centres X and Y, we draw two more arcs with a radius half of the length of line segment XY.

The two arcs cut the previous arcs at QR and MN.

WBBSE Math Solutions Class 6 Chapter 22 Drawing Of Different Geometrical Figures Exercise 22.2

Question 1. Let’s draw a line segment AB of length 5 cm with scale and pencil. By folding the paper, let us find the perpendicular bisector of the line segment AB. Then, we actually measure the two bisected parts with scale.
Solution:

1. Let’s take a thick paper. It is folded at any end and then unfolded. The line formed by the fold is marked with a pencil.

2. On this, two points A and B are taken. Now the paper is again folded in such a way that points A and B coincide. Again, on this fold mark a line segment. CD is drawn and we get the mid point of the line segment AB. That D is the midpoint of the line segment AB and the line segment CD is perpendicular at D on line segment AB.

Hence, the line segment CD is perpendicular to the line segment AB at its midpoint. Line segment CD is called the Perpendicular Bisector of the line segment AB.

The perpendicular bisector of a line segment divides it into two equal parts.

WBBSE Math Solutions Class 6

Question 2. Let’s draw a line segment of length 8 cm with scale and pencil. Then let’s draw a perpendicular bisector of this line segment and each part measured.
Solution:

Let AB is a line segment of 8 cm. Now with centres A and B two arcs with radii more than 1/2 of AB are drawn on both sides of AB. They intersect each other at C and D. Join C, D which cuts AB at P.

AP = PB = 4 cm.

Question 3. Let’s draw a line segment PQ of length 6 cm with scale and pencil, now, taking line segment PQ as diameter, let’s draw a circle.
Solution:

Let PQ is a line segment of length 6 cm. It is bisected at O. Now, with centre O and radius PO a circle is drawn.

WBBSE Math Solutions Class 6

Question 4. With the help of scale and pencil, a line segment AB of length 8 cm is drawn. Let’s divide the line segment AB into four equal parts and measure each part.
Solution:

1. First we bisect the line segment AB into equal parts such that AR = RB.
2. Again, we bisect the line segment AR and RB into two equal parts such that AE = ER and RF = FB. Hence, the segment AB is divided four equal parts.

∴ AE = EF = RF = FB = 2 cm.

WBBSE Math Solutions Class 6

Question 5. Let’s draw two circles whose diameters are 5 cm and 7 cm respectively.
Solution:

AB and PQ are two line segments of lengths 5 cm and 7 cm respectively. Line segment AB is bisected at C and line segment PQ is bisected at R.

Now, with centres C and R two circles are drawn with radii of 2.5 cm and 3.5 cm respectively.

Question 6. Masum drew a triangle ABC. Then with the help of scale and pencil, compass, she bisected the sides BC, AC and AB perpendicularly. She verified that the three perpendicular bisectors are concurrent. When found concurrent, she named it O. Now with centre O and radius equal to the line segment AO, she drew a circle.
Solution:

ABC is a triangle, the sides BC, CD and DA are bisected at D, E, and F. These 3 bisectors meet at O. Now, with centre O and radius OA, a circle is drawn which passes through B and C. Point O is called circumcentre of the triangle ABC.

WBBSE Class 6 Maths Solutions Chapter 22 Drawing Of Different Geometrical Figures Exercise 22.3

Question 1. Let us draw the following angles with the help of protractor: 30°, 42°, 105°, 67°, 88°, 120°, 205°, 282°.
Solution:

Question 2. When a clock shows the following time, the angles formed by their arms are to be drawn with a protractor on the exercise book.

1. 3 p.m.
Solution: At 3 p.m.: The angle formed by the arms is 90°.

2. 5 a.m.
Solution: At 5 p.m.: The angle formed by the arms is 150°.

3. 10a.m
Solution: At 10 a.m.: The angle formed by the arms is 60°.

4. 4 p.m.
Solution: At 4 p.m.: The angle formed by the arms is 120°.

WBBSE Class 6 Maths Solutions

Question 3. Let’s draw the following angles with the help of set square and bisect them with a scale, pencil and compass.

1. 30°
Solution:

∠ABC = 30°

PB is the bisector ∠ABC.

2. 45°
Solution:

∠PQR = 45°

QC is the bisector ∠PQR.

3. 60°
Solution:

∠MBN = 60

BR is the bisector of ∠MBN.

4. 90°
Solution:

∠XYZ = 90°

YP is the bisector of ∠XYZ.

5. 105°
Solution:

∠ABC = V ABR + VRBC = 60° + 45° = 105°

∠BK is the bisector of ∠ABC.

WBBSE Class 6 Maths Solutions

Question 4. Without using a protractor let us draw an angle of 45° with a scale, pencil, compass.
Solution:

1st BAC = 90° is drawn

Now, ∠BAC is bisected, ∠BAD = 45°, and ∠CAD = 45°.

Question 5. Let’s draw an angle of 120° with the help of a protractor, then divide it into 4 equal parts with the help of scale, pencil and compass.
Solution:

With the protractor 1st ∠PQR = 120° is drawn. Now, 1st bisect the ∠PQR into two equal parts.

QK is the bisector of ∠PQR. The two equal angles are ∠PQK and ∠KQR, each equal to 60°.

Again, bisect two angles ∠PQK and ∠KQR.

∴ 4 equal parts of ∠PQR are ∠PQM = ∠MQK = ∠KQN = ∠NQR = 30°.

WBBSE Class 6 Maths Solutions

Question 6. Let’s draw a triangle ABC with the help of a scale and pencil. Then the three angles of the triangle are bisected. Let’s find if the bisectors of the angles are concurrent.
Solution:

Let ABC is a triangle. Its 3 angles are ∠BAC, ∠ABC and ∠ACB. Now, with the help of a compass and scale these angles are bisected.

AD, BE and CF are the three bisectors of the angles respectively. The bisectors of the angles meet at O. The point ‘O’ is called the in centre of the triangle.

Question 7. Let’s draw any angle ∠PQR using a scale, pencil and compass. Z PQR is bisected and the bisector of ∠RQP is produced up to point X. Again with scale, pencil and compass, ∠PQS is bisected by QY. What angle do QX and QY line segments make with each other? — Let us measure by protractor.
Solution:

Angle PQR is drawn using scale. Now, with help of compass ∠PQR is bisected. ∠PQR = 70°

QS is the bisector of ∠PQR.

∴ ∠RQS = ∠SQP = 35°.

Again, ∠PQS is bisected by QY with a compass.

∴ ∠SQY= ∠YQP = 17.5°.

∴ ∠XQY= ∠YQP = 17.5°.

Class 6 Math WBBSE Solutions

Question 8. Let’s draw a line segment PQ. At points P and Q of PQ, two perpendiculars PR and QS are drawn with scale, pencil and compass, ∠QPR and ∠PQS are bisected using scale, pencil and compass. The triangle so formed — its angles are measured and their values are written.
Solution:

PQ is a line segment. At P and Q two perpendiculars RP and SQ are drawn with the help of scale and compass.

∴ ∠RPQ = ∠SQP = 90°.

Again, ∠RPQ and ∠SQP are bisected with the help of scale and compass. The bisectors meet each other at A. Therefore, ΔAPQ is formed.

Now, ∠APQ = 1/2 of 90° = 45°

and ∠AQP = 1/2 of 90° = 45°

∴ ∠PAQ = 180°- (45° + 45) = 180°- 90° = 90°.

Class 6 Math Solutions WBBSE Chapter 20 Geometrical Concept Of Circle Exercise

Question 1. From the figure, let us answer the following :

1. O is the _____ of the circle.
Solution: O is the centre of the circle

2. Line segment OQ is the ____ of the circle.
Solution: radius of the circle.

3. Line segment PQ is the ______ of circle.
Solution: diameter of circle.

4. Line segment OP is the _______ of circle.
Solution: Line segment OP is radius of circle.

5. Line segment MN is ______ of the circle.
Solution: Line segment MN is a chord of the circle.

Read and Learn More WBBSE Solutions For Class 6 Maths

6. The points M and N have divided the circle into two _______ parts.
Solution: The points M and N have divided the circle into two arcs.

7. The area bounded by arc SR and radii SO and RO is called ______
Solution: The area bounded by the arc SR and radii SO and RO is called sector.

8. The diameter PQ has divided the circle into two equal parts which are called _____
Solution: The diameter PQ has divided the circle into two equal parts which are called semi-circles.

Class 6 Math Solutions WBBSE

Question 2. Let us write (✓) for the correct statement and (X) for the wrong one.

1. All diameters of a circle are chords. [✓]
2. All chords of a circle are its diameter. [X]
3. The length of the diameter of a circle is twice the length of its radius. [✓]
4. Sector of a circle is part of its circular area. [✓]
5. Arc of a circle is part of the circle. [✓]
6. Centre of the circle is a fixed point in the circle. [✓]
7. Two diameters always intersect each of them. [✓]

Question 3. With the help of a compass and a pencil, a circle of radius 3 cm is drawn. Let’s name its centre, radius, diameter, chord, and arc.
Solution:

1. Centre O
2. Radius OP
3. Diameter AB
4. Chord MN
5. Arc PRB

Question 4. In this figure, let us colour the major segment yellow and minor segment green.

Solution:

1. Major segment — yellow portion
2. Minor segment — green portion

Class 6 Math Solutions WBBSE

Question 5. The radii of two circles are 2 cm and 4 cm respectively. Let’s write the lengths of their diameter without measuring.
Solution:

Radius of 1st circle = 2 cm.

Diameter of 1st circle = 2×2 cm. = 4 cm.

Radius of 2nd circle = 4 cm.

Diameter of 2nd circle = 2 x 4cm. = 8 cm.

Question 6. If the length of the greatest chord of a circle is 10 cm, let’s write what will be the length of its radius.
Solution:

Length of the greatest chord of a circle = 100 cm.

∴ Diameter of the circle = 10 cm.

∴ Radius of the circle = 10/2 cm = 5 cm.

Class 6 Math Solutions WBBSE Chapter 19 Measurement Of Time Exercise 19

Question 1. Given below is the time chart of Priya on a holiday. Let’s try to get few information.
Solution:

On that day, Priya woke up: at 6.00 a.m

Priya studied at: 9.00 a.m

Priya gossips with friends at: 11.00 a.m

She had lunch at: 1.00 a.m

After lunch at: 4.00 p.m

On that day Priya went to bed: at 10.00 p.m

Question 2. Today I left my house at 10:20 a.m. for school. Returned home at 4:45 p.m. Let’s calculate how long I was out of home.
Solution:

I was out of home = 4:45 p.m – 10:20 am = 6 hrs 25 min

Question 3. Yesterday Deba went to bed at 10: 25 p.m. But today he woke up at 6:10 a.m. Let’s find out how long he slept.
Solution:

Deba slept = 6:10 a.m – 10: 25 p.m = 7 hrs 45 mins

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 4. Today I am going to Puri with my family. The train will leave from Howrah station at 22:35 hours, we will reach Howrah station at 20:44 hrs. Let’s calculate how long we have to wait at the station.
Solution:

We have to wait at the station = 22:35 hours – 20:44 hours

= 1 hour 51 mins Hrs min

⇒ \(\begin{array}{lc}
\text { Hrs } & \text { min } \\
22 & 35 \\
20 & 44 \\
\hline 1 & 51 \\
\hline
\end{array}\)

Class 6 Math Solutions WBBSE

Question 5. Today I have a history examination. Exam started at 11: 30 a.m. The teacher’s digital wristwatch is showing 13:15. Let me find out how long I had already written the examination. If the exam is to end at 2:30 p.m., how long shall I be able to write the examination, when the exam will be over, let me find out what will the digital watch of the teacher read.
Solution:

I had already written the examination = 13:15 – 11:30 am = 1 hr 45 min.

I shalf be able to write the examination = 2:30 p.m. -13:15 = 1 hr 15 min.

The time of digital watch of the teacher = 13:15 + 1 hr 15 min = 14:30.

Question 6. To reach father’s office from home, it takes 2 hrs 27 min but while returning home, it takes 2 hrs 51 min. Let me find out how long it takes in total to go to my father’s office and back.
Solution:

The time to go to father’s office and back

= 2 hrs 27 mins + 2 hrs 57 mins

= 5 hrs 24 mins.

⇒ \(\begin{array}{lll}
\text { Hrs } & \min & \\
2 & 27 & \\
2 & 57 & \\
5 & 24 &
\end{array}\)

⇒ \(\begin{array}{rcc}
7 . \mathrm{hr} & \min & \mathrm{sec} \\
8 & 32 & 41 \\
+18 & 42 & 25 \\
& 74 & 66 \\
\hline \mathrm{hrs} & \min & \mathrm{sec} \\
\hline
\end{array}\)

Solution:

1. \(\begin{array}{rrr}
\mathrm{hr} & \mathrm{min} & \mathrm{sec} \\
8 & 32 & 41 \\
+18& 42 & 25 \\
26 & 74 & 66 \\
\hline 27 \mathrm{hrs} & 15 \mathrm{~min} & 6 \mathrm{sec} \\
\hline
\end{array}\)

2. \(\begin{array}{ccc}
\text { 2 hr } & \text { min } & \text { sec } \\
\text { (8) } & 60+11 & 60+37 \\
9 & 12 & 37 \\
-3 & 38 & 41 \\
\hline 5 \mathrm{hr} & 33 \mathrm{~min} & 56 \mathrm{sec} \\
\hline
\end{array}\)

Class 6 Math Solutions WBBSE

Question 8. Let’s add and subtract

1. (4 hr 33 min 20 sec) + (9 hr 52 min 25 sec)
Solution:

⇒ \(\begin{array}{ccc}
\text { Hrs } & \text { Mins } & \text { Sec } \\
4 & 33 & 20 \\
+9 & 52 & 25 \\
13 & 85 & 45 \\
\hline=14 \mathrm{Hrs} & 25 \mathrm{~min} & 45 \mathrm{sec} . \\
\hline
\end{array}\)

2. (6 hr 42 min 2 sec) – (2 hr 55 min 42 sec)
Solution:

⇒ \(\begin{array}{ccc}
\text { Hrs } & \text { Min } & \text { Sec } \\
5 & 60+41 & 60+2 \\
6 & 42 & 2 \\
-2 & 55 & 42 \\
\hline 3 & 46 & 20
\end{array}\)

= 3 hrs 46 min 20 Sec

3. (18 hr 19 min 15 sec) + (9 hr 55 min 48 sec)
Solution:

⇒ \(\begin{array}{rcc}
\text { Hrs } & \text { Min } & \text { Sec } \\
18 & 19 & 15 \\
9 & 55 & 48 \\
\hline 27 & 74 & 63 \\
\hline
\end{array}\)

= 28 hrs 15 min 3 sec

4. (23 hr 7 min) – (19 hr 29 min 18 sec)
Solution:

⇒ \(\begin{array}{ccc}
\text { Hrs } & \min& \text { Sec } \\
22 & 60+6 & 60+0 \\
23 & 7 & 00 \\
9 & 55 & 48 \\
\hline 13 & 11 & 12 \\
\hline
\end{array}\)

= 13 hrs 11 min 12 Sec.

Class 6 WBBSE Math Solutions Chapter 19 Measurement Of Time Exercise 19.1

Question 1. Debubabu built a new house. He will paint the two windows of his house. Each window has two panes. If he takes 2 hr 15 min to paint 1 window pane, let’s find how long he will take to colour 2 windows.
Solution:

Time required to paint 1 window pane = 2 hrs 15 m

∴ Time required to paint 2 window panes = 2 hr 15 min x 2 = 4 hrs 30 min

Question 2. In 11 hrs 36 min, Phani Da can make 4 exactly similar clay statues. Let’s find out how long he will take to make one such statue. He takes equal time to make each statue.
Solution:

Time required to make 4 clay statues = 11 hrs 36 min

∴ Time required to make 1 clay statue = 11 hr 36 min ± 4

= 2 hrs 54 mins.

Question 3.

1. 3 hrs 26 min x 4 = How many hours and minutes?
Solution:

3 hrs 26 min x 4

= 12 hr 104 min = 13 hrs 44 min

2. 7 hrs 13 min x 12 = How many hours and minutes?
Solution:

7 hrs 13 min x 12

= 84 hrs 156 min = 86 hr. 36 min

Class 6 WBBSE Math Solutions

3. 3 hrs 27 min ÷ 9 = How many minutes and seconds?
Solution:

4. 15 hrs ÷ 12 = How many hrs and mins?
Solution:

5. 6 hrs 18 sec ÷ 9 = How many min, sec?
Solution:

6. 5 hrs10 min 4 sec ÷ 4 = How many hours, min, sec?
Solution:

Class 6 WBBSE Math Solutions

7. 2 hrs 32 min 41 sec÷ 3 = How many hours, min, secs?
Solution:

2 hr 32 min 4 sec x 3

2 hr 32 min 4 sec x 3

6 hr 96 min 12 sec

= 7 hr 36 min 12 sec

Class 6 Maths Solutions WBBSE Chapter 19 Measurement Of Time Exercise 19.1

Question 1. 1st February of 2010 was Monday. Let’s calculate 1st March 2010 and 1st April 2010 will be which days.
Solution:

1 st February 2010 was monday and February has 28 days.

∴ 1st March 2010 was Monday and March has 31 days.

∴ 3 days after Monday is Thursday.

∴ 1st April 2010 is Thursday.

Question 2. 01/02/2012 was Wednesday, then let’s calculate which days were the following dates: 01/03/2012, 01/04/2012, 01/05/2015,04/06/2012
Solution:

1st February of 2012 was Wednesday and February 2012 had 29 days.

∴ 1 day after Wednesday is Thursday.

∴ . 1st March 2012 was Thursday.

March has 31 days.

3 days after Thursday is Sunday.

∴ 1st April 2012 was Sunday.

April has 30 days.

2 days after Sunday is Tuesday.

∴ 1st May 2012 was Tuesday.

May has 31 days, 6 days after Tuesday is Monday.

4th June 2012 is Monday.

Class 6 Maths Solutions WBBSE

Question 3. 1st January of 1996 was Sunday. Let us calulate which day 1st January of 1997 will be.
Solution:

1st January 1996 was Monday.

Since 1996 was a leap year so 1996 had 366 days.

2 days after Monday is Wednesday.

∴ 1st January 1997 was Wednesday.

Question 4. 1st March of 2004 was Monday, which day will be 1st April of 2005.
Solution:

1st March 2004 was Monday 2005 year had 365 days.

1 day after Monday is Tuesday.

1st March 2005 was Tuesday

1st March 2005 had 31 days.

3days after Tuesday is Friday.

∴ 1st April 2005 was Friday.

Question 5. 1st June of 2008 was Tuesday. Let’s calculate which day was 1st June of 2006.
Solution:

1st June 2008 was Sunday. 2008 was a leap year.

So, 2008 had 366 days.

2006 and 2007 had 365 days.

4days before Sunday is Thursday.

1st June 2006 was Thursday.

Class 6 Maths Solutions WBBSE

Question 6. Independence day of 2013 is Thursday, let’s find which day will be Independence day of 2016.
Solution:

Independence day of 2013, 15th August 2013 was Thursday.

2013 had 365 days and 2016 is a leap year.

So 2016 has 366 days.

4 days after Thursday is Monday.

∴  Independence day of 2016 will be Monday.

Question 7. From the calendar of 2013 let us write which day of the week are the following and without looking into calender, let’s find which days of the week these days were in the year 2011 — Children’s day, Teachers’ day, Gandhi birthday, Republic day, Netaji Jayanti, World environment day (5th of June).
Solution:

1. Children’s Day (14th November)

14th November 2013 was Thursday.

2014 had 365 days and 2012 had 366 days.

3 days before Thursday is Monday.

2. Teachers’ day (5th September)

5th September of 2013 was Thursday.

2011 had 365 days and 2012 had 366 days.

3 days before Thursday is Monday.

∴ Teachers’ day – 5th September 2011 was Monday.

WBBSE Math Solutions Class 6

3. Gandhi birthday – 2nd October.

2nd October 2013 was Wednesday.

2011 had 365 days and 2012 had 366 days.

3 days before Wednesday Sunday.

∴ Gandhi birthday (2nd October) 2011 was Sunday.

4. Republic day (26th January)

26th January of 2013 was Saturday.

2011 had 365 days and 2012 had 366 days.

3 days before Saturday is Wednesday.

∴ Republic day (26th January, 2011) was Wednesday.

5. Netaji Jayanti (23rd January)

23rd January 2013 was Wednesday.

2011 had 365 days and 2012 had 366 days.

3 days before Wednesday is Sunday.

∴ Netaji Jayanti (23rd January) 2011 was Sunday.

6. World Environment Day (5th June)

5th June 2013 was Wednesday.

2011 had 365 days and 2012 had 366 days.

3 days before Wednesday is Sunday.

World Environment Day 5th June, 2011 was Sunday.

WBBSE Math Solutions Class 6

Question 8.

1. Let’s write the leap years between 1895 to 1915.
2. Let’s write the leap years between 2010 to 2030.

Solution:

1. Leap years between 1895 to 1915 = 1896; 1900; 1904,1908, and 1912.
2. Leap years between 2010 to 2030 = 2012, 2016, 2020, 2024, and 2028.

Question 9. I stayed for 4 years in a house at College Ghat Road, from 2010 to 2013. Let’s calculate for how many days I stayed in that house.
Solution:

In 2010 – Number of days = 365 In 2011 — Number of days = 365

In 2012 — Number of days = 366 In 2013 — Number of days = 365 Total days in 4 years = 365 + 365 = 366 + 365 = 1461

Question 10. My birthday is on 15th December. In 2013, my birthday was on Sunday. Which day of the week will my birthday be in the years 2014, 2015 and 2016?
Solution:

My birthday is on 15th December 2013, which was Sunday. In 2014 had 365 days

1 day after Sunday is Monday.

∴ 15th December 2014 was Monday.

In 2015 had 365 days.

∴ 1 days after Monday is Tuesday.

∴ 15th December, 2015 is Tuesday.

2016 is of 366 days.

∴ 2 days after Tuesday is Thursday.

∴ 15th December 2016 will be Thursday.

Question 11. After independence, how many leap years have passed till 2014?
Solution:

Independence day was 15th August 1947.

The leap years that have passed till 2014 are 1948,1952,1956,1960,1964,1968 1972,1976,1980,1984,1988,1992 1996, 2000, 2004,2008 and 2012.

WBBSE Class 6 Maths Solutions Chapter 19 Measurement Of Time Exercise 19.2

Question 1. My date of birth is 19 -11 -1975, i.e., 19th November 1975. Let us find my
Solution:

⇒ \(\begin{array}{lll}
\text { Years } & \text { Months } & \text { Days } \\
& 12+9 & 30+10 \\
2010 & 10 & 10 \\
-1975 & 11 & 19 \\
\hline 24 & 10 & 21 \\
\hline
\end{array}\)

= 24 years 10 months 21 days.

Question 2. The construction of our main road began in summer on 6/6/2010. It took 1 yr 3 months 18 days to finish the work. Let’s calculate to find on which date the road construction work was completed.
Solution:

⇒ \(\begin{array}{ccc}
\text { Years } & \text { Months } & \text { Days } \\
2010 & 06 & 06 \\
+\quad 1 & 03 & 18 \\
\hline 2011 & 09 & 24 \\
\hline
\end{array}\)

The date of road construction work was completed on 24/09/ 2011.

Question 3. My present age is 11 yrs 7 months 10 days. Let me calculate after how many years I shall be eligible to cast my vote.
Solution:

⇒ \(\begin{array}{cll}
\text { Years } & \text { Months } & \text { Days } \\
17 & 12+0 & 30 \\
(-) 11 & 07 & 10 \\
\hline 6 & 08 & 20 \\
\hline
\end{array}\)

= 6 yrs 04 months 20 days.

WBBSE Class 6 Maths Solutions

Question 4. The age of my father is 52 years 8 months 20 days. My uncle is 3 years 10 months 26 days older than my father. Let me find the age of my uncle.
Solution:

⇒ \(\begin{array}{ccl}
\text { Years } & \text { Months } & \text { Days } \\
52 & 8 & 20 \\
+3 & 10 & 26 \\
\hline 56 & 7 & 16 \\
\hline
\end{array}\)

= Age of my uncle = 56 years 7 months 16 days.

Question 5. Let us find values

1. \(\begin{array}{rcc}
\text { Year } & \text { Months } & \text { Days } \\
9 & 10 & 27 \\
+\quad 5 & 8 & 21 \\
\hline 14 & 18 & 48 \\
\hline
\end{array}\)

Solution: 15 years 7 months 18 days.

2. \(\begin{array}{ccc}
\text { Year } & \text { Month } & \text { Days } \\
29 & 11 & 19 \\
5 & 9 & 25 \\
+6 & 3 & 13 \\
\hline 40 & 23 & 57 \\
\hline
\end{array}\)

Solution: 42 years 0 months 27 days

3. \(\begin{array}{ccl}
\text { Year } & \text { Month } & \text { Days } \\
& 12+3 & 30 \\
11 & 3 & \mathrm{x} \\
-6 & 10 & 28 \\
\hline 5 & 5 & 02 \\
\hline
\end{array}\)

Solution: 5 years 5 months 2 days.

4. \(\begin{array}{|c|c|c|}
\hline \text { Year } & \begin{array}{c}
\text { Month } \\
12+6
\end{array} & \begin{array}{l}
\text { Days } \\
30+19
\end{array} \\
\hline 11 & 6 & 19 \\
\hline-6 & 10 & 21 \\
\hline 5 & 8 & 28 \\
\hline
\end{array}\)

Solution: 5 years 8 months 28 days.

Class 6 Math WBBSE Solutions

Question 6. (1) 8 yrs 8 months 28 days + 11 yrs 8 months 18 days = How many yr, months and days?
Solution:

⇒ \(\begin{array}{rcl}
\text { Years } & \text { Months } & \text { Days } \\
8 & 8 & 28 \\
+11 & 8 & 18 \\
\hline 19 & 16 & 46 \\
\hline
\end{array}\)

= 20 yrs 5 months 16 days.

2. 20 yrs 11 months and days? -10 yrs 8 months 23 days = How many yr, month
Solution:

⇒\(\begin{array}{ccc}
\text { Years } & \text { Months } & \begin{array}{c}
\text { days } \\
30+0
\end{array} \\
20 & 11 & 0 \\
10 & 89 & 23 . \\
\hline 10 & 2 & 7 \\
\hline
\end{array}\)

= 10 years 2 months 7 days

3. 8 yrs 7 months 21 days x 9 = How many yr, month and days?
Solution:

= 77 yrs.9 months 9 days.

Question 7. My age is □ yrs □ months □ days. The age of my friend is □ yrs □ months □ days. What is the sum of our age and who is older than the two and by how much? Let us find out.
Solution:

My age is 15 years 11 months 26 days. The age of my friend is 14 yrs 9 months 20 days.

⇒ \(\text { Sum }=\begin{array}{ccc}
\text { Year } & \text { Month } & \text { Days } \\
15 & 11 & 26 . \\
14 & 9 & 20 \\
\hline 29 & 20 & 46 \\
\hline
\end{array}\)

= 30 yrs 9 months 16 days.

I am older than my friends.

Difference

⇒ \(\begin{array}{lll}
\text { Years } & \text { Month } & \text { Days } \\
15 & 11 & 26 \\
14 & 9 & 20 \\
\hline 1 & 2 & 6 \\
\hline
\end{array}\)

= 1 yr 2 months 6 days.

Class 6 Math WBBSE Solutions

Question 8. My date of birth is □. Today my age is □ yrs □ months □ days.
Solution:

My date of birth is 04.10-2001

Today my age is — (19-11 -2014)

⇒ \(\begin{array}{rll}
\text { Year } & \text { Month } & \text { Days } \\
2014 & 11 & 19 \\
-2001 & 10 & 04 \\
\hline 13 & 1 & 15 \\
\hline
\end{array}\)

Today my age is 13yrs 1month 15days

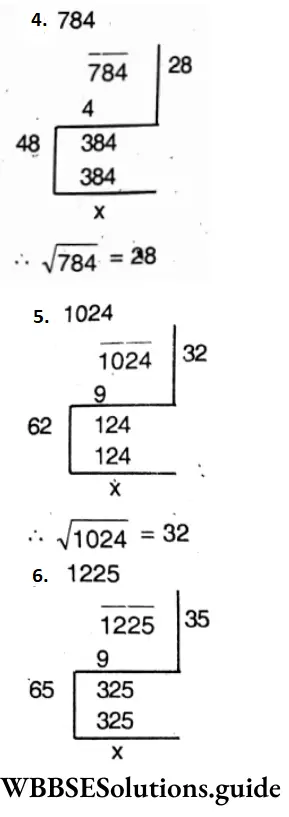
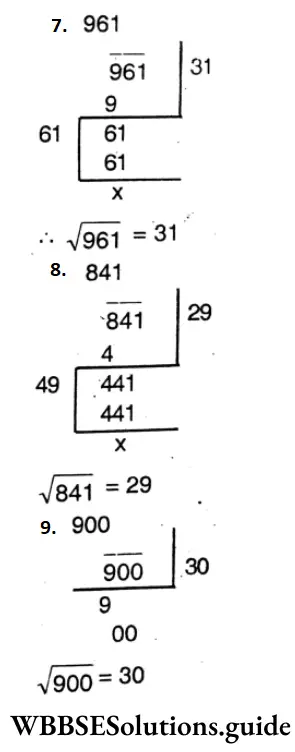
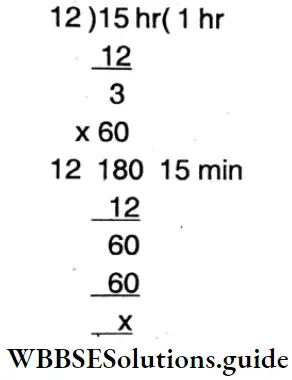Class 6 Math Solutions WBBSE Chapter 21 Fundamental Concept Of Ratio And Proportion

We take lengths of our pen caps and lengths of pens without cap and try to take their ratio and write them in a table like below.

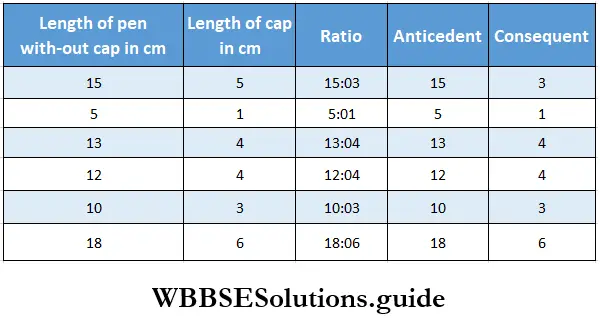
Let us see the picture count the number ratio in its lowest form and write the ratio.

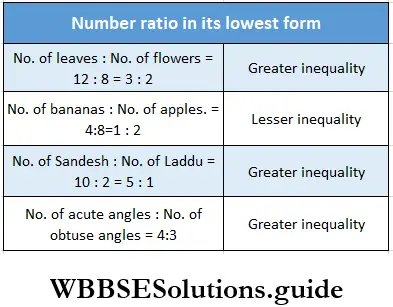
Class 6 WBBSE Math Solutions Chapter 21 Fundamental Concept Of Ratio And Proportion Exercise 21

Question 1. I have taken measurement of the floor of my living room. I see that the rectangular floor is of 8 m length and 5 m in breadth. Let’s find the ratio of its length to its breadth. Let’s also write if the ratio is ratio of greater or lesser inequality.

Read and Learn More WBBSE Solutions For Class 6 Maths
Solution:

Length of the floor = 8 m.

Breadth of the floor = 5 m.

∴ Ratio of length and breadth = 8:5

It is a ratio of greater inequality.

Question 2. Sabita is making garlands of chinarose and marigold, if she made 12 garlands of chinarose and 15 of marigold, then let’s find what is the ratio of the number of garlands of chinarose and marigold. Let’s also write if the ratio is a ratio of greater or lesser inequality.
Solution:

Number of garlands of china rose = 12 and

Number of garlands of marigold = 15

∴ Ratio of garlands of qhinarose and marigold = 12:15 = 4:5

It is a ratio of lesser inequality.

Question 3. The ratio of my age to Sutapa’s age is 5: 6. If my age is 10 years, let’s find the age of Sutapa.
Solution:

The ratio of my age to Sutapa’s age = 5:6

or, \(\frac{\text { My age }}{\text { Sutapa’s age }}=\frac{5}{6}\)

or, \(\frac{10 \text { years }}{\text { Sutapa’s age }}=\frac{5}{6}\)

∴ 5 x Sutapa’s age = 6 x 10 years 6×10

∴ Sutapa’s age = \(\frac{6 \times 10}{5}\)  years = 12 years.

Class 6 WBBSE Math Solutions

Question 4. My mother gave sweets to me and Raju. Me and Raju ate sweets in the ratio of 1:3. Let’s find how many sweets my mother gave us [Let’s try any 4 values].

⇒ \(\frac{\text { No. of sweets I ate }}{\text { No. of sweets Raju ate }}=\frac{1}{3}=\frac{2}{6}\) i.e., mother gave (2 + 6) = 8 sweets also she can give (1 + 3) = 4 sweets

Solution:

\(\frac{\text { No. of sweets I ate }}{\text { No. of sweets Raju ate }}=\frac{1}{3}=\frac{2}{6}\) = \(\frac{3}{9}=\frac{4}{12}\)

In 1st case, mother gave us = 1 +3 = 4 sweets

In 2nd case, mother gave us = 2 + 6 = 8 sweets

In 3rd case, mother gave us = 3 + 9 = 12 sweets

In 4th case, mother gave us = 4 +12 = 16 sweets

Question 5. Today 10 of us have come to the park to play. If the ratio of number of girls and boys is 2:3 in our group, let’s find how many girls and boys have come to play.
Solution:

Total number of students = 10

Ratio of number of girls and boys = 2:3

∴ Number of girl students = 2/5 parts

∴ Number of boy students = 3/5 parts

Number of girl students = 2/5 x 10 = 4

Number of boy students = 3/5 x 10 = 6

Question 6. Father bought 4 pairs of bananas from market. If brother and sister ate those bananas in the ratio of 1 : 3, let’s find how many bananas each of them ate.
Solution:

Total number of bananas = 4 pairs = 4 x 2 = 8

Ratio of bananas brother and sister ate = 1:3

∴ Number of bananas brother ate = \(\frac{1}{1+3} \times 8=\frac{1}{4} \times 8=2\)

Number of bananas sister ate = \(\frac{3}{1+3} \times 8=\frac{3}{4} \times 8=6\)

Class 6 Maths Solutions WBBSE Chapter 21 Fundamental Concept Of Ratio And Proportion Exercise 21.1

Question 1. Let’s find if the following numbers are in proportion or not:

1. 13, 52,30,120
Solution:

1st term x 4th term = 13 x 120 = 1560

2nd term x 3rd term = 52 x 30 = 1560

∴ 13: 52 :: 30:120 (In proportion)

2. 22,11,72, 36
Solution:

1 st term x 4th term = 22 x 36 = 792

2nd term x 3rd term = 11 x 72 = 792

∴ 22: 11:: 72: 36 (In proportion)

3. 45, 27,15, 25
Solution: 45,27, 15,25

1st term x 4th term = 45 x 25 = 1125

2nd term x 3rd term = 27 x 15 = 405

∴ 1st term x 4th term  2nd term x 3rd term

∴ 45, 27,15, 25 are not in proportion.

Class 6 Maths Solutions WBBSE

4. 18, 20, 27, 30
Solution:

1st term x 4th term = 18 x 30 = 540

2nd term x 3rd term = 20 x 27 = 540

∴ 18: 20:: 27: 30 (In proportion)

5. 11,22, 36, 72
Solution:

1st term x 4th term = 11 x 72 = 792

2nd term x 3rd term = 22 x 36 = 792 (In proportion) .

Question 2. Let’s write if the folowing relations are True/False.

1. 4.5 litre: 13.5 litre:: 4 kg: 12 kg
Solution:

4.5 litre: 13.5 litre:: 4kg: 12 kg

4.5: 13.5:: 4: 12

1st term x 4th term = 4.5 x 12 = 54

2nd term x 3rd term = 13.4 x 4 = 54

∴ The relation is True.

Class 6 Maths Solutions WBBSE

2. 12 km: 8 km:: 61 km:: 40 km
Solution:

12 km: 8 km:: 60 km: 40 km

or, 12: 8:: 60: 40

1st term x 4th term = 12 x 40 = 480

2nd term x 3rd term = 8 x 60 = 480

∴ The relation is True.

3. 20 men: 45 men:: 180 rupee: 270 rupee
Solution:

20 men: 45 men:: 180 rupees: 270 rupees

∴ 1 st term x 4th term = 20 x 270 = 5400

2nd term x 3rd term = 45 x 180 = 8100

∴ 20:45 ≠ 180:270

∴ The relation is False.

4. 15m: 9m :: 35m: 21m.
Solution:

15m: 9 m :: 35 m: 21 m

or 15:9:: 35:21

1st term x 4th term = 15 x 21 = 315

2nd term x 3rd term = 9 x 35 = 315

∴ The relation is True.

WBBSE Math Solutions Class 6 Chapter 21 Fundamental Concept Of Ratio And Proportion Exercise 21.2

Question 1. Let’s find if the following numbers are in proportion or not. If they are in proportion, let’s write all the possible proportions with them.

1. 3,15, 4, 20
Solution:

1st case: 3, 15, 4, 20

1st term x 4th term = 3 x 20 = 60

2nd term x 3rd term = 15 x 4 = 60

∴ 3: 15:: 4.20

2nd case: 3, 4,15, 20

1st term x 4th term = 3 x 20 = 60

2nd term x 3rd term = 4 x 15 = 60

∴ 3:4:: 15: 20

3rd case: 15, 3, 20, 4

1st term x 4th term = 15 x 4 = 60

2nd term x 3rd term = 3 x 20 = 60

∴  15: 3:: 20: 4

4th case: 15, 20, 3, 4

1st term x 4th term = 15×4 = 60

2nd term x 3rd term = 20 x 3 = 60

∴ 15: 20:: 3: 4

WBBSE Math Solutions Class 6

2. 6,18,7, 21
Solution:

1st case: 6,18, 7, 21

1st term x 4th term = 6×21 = 126

2nd term x 3rd term = 18 x 7 = 126

∴ 6:18:: 7: 21

2nd case: 6, 7,18, 21

1st term x 4th term = 6 x 21 =126

2nd term x 3rd term = 7 x 18 = 126

∴ 6: 7:: 18: 21

3rd case: 18, 6, 21: 7

1st term x 4th term = 18 x 7 = 126

2nd term x 3rd term = 6 x 21 =126

∴ 18: 6:: 21: 7

4th case: 18, 21,6, 7

1st term x 4th term = 18 x 7 = 126

2nd term x 3rd term = 21 x 6 = 126

∴ 18: 21:: 6: 7

WBBSE Math Solutions Class 6

3. 5, 15, 7, 21
Solution:

1st case: 5,15, 7, 21

1st term x 4th term = 5 x 21 =105

2nd term x 3rd term = 15×7 = 105

∴ 5: 15:: 7: 21

2nd case: 15, 5, 21,7

1st term x 4th term = 15 x 7 = 105

2nd term x 3rd term = 5×21 =105

∴ 15: 5 :: 21: 7

3rd case: 5, 7, 15, 21

1st term x 4th term = 5 x 21 = 105

2nd term x 3rd term = 7 x 15 = 105

∴ 5:7:: 15: 21

4th case: 15, 21,5, 7

1st term x 4th term = 15 x 7 = 105

2nd term x 3rd term = 21 x 5 = 105

∴ 15:21:: 5: 7

4. 7, 21,4, 12
Solution:

1st case: 7, 21, 4,12

1st term x 4th term = 7 x 12 = 84

2nd term x 3rd term =21 x 4 = 84

∴ 7:21:: 4: 12

2nd Case: 21, 7,12, 4

1st x 4th term = 21 x 4 = 84

2nd term 3rd term = 7 x 12 = 84

∴ 21: 7:: 12: 4

3rd case: 7, 4, 21, 12

1st term x 4th term = 7 x 12 = 84

2nd term x 3rd term = 4×21 =84

∴  7:4:: 21: 12

4th case 21,12, 7, 4

1st term x 4th term = 21 x 4 = 84

2nd term x 3rd term = 12 x 7 = 84

∴ 21: 12:: 7: 4

WBBSE Class 6 Maths Solutions

5. 3,15,10,50
Solution:

1st case: 3, 15,10, 50

1st term x 4th term = 3 x 50 = 150

2nd term x 3rd term = 15 x 10 = 150

∴ 3: 15:: 10:50

2nd case: 15, 3, 50,10

1st term x 4th term = 15 x 10 = 150

2nd term x 3rd term = 3 x 50 = 150

∴ 15:3 :: 50:15

3rd case: 3, 10,15, 50

1st term x 4th term = 3 x 50 = 150

2nd term x 3rd term = 10×15=150

∴ 3: 10:: 15: 50

4th case: 15, 50, 3,10

1st term x 4th term = 15 x 10 = 150

2nd term x 3rd term = 50 x 3 = 150

∴ 15: 50:: 3: 10

6. 2, 6, 7, 21.
Solution:

1st case: 2, 6, 7, 21

1 st term x 4th term = 2 x 21 = 42

2nd term x 3rd term = 6 x 7 = 42

∴ 2:6:: 7: 21

WBBSE Class 6 Maths Solutions

2nd case: 6, 2, 21,7

1 st term x 4th term = 6 x 7 = 42

2nd term x 3rd term = 2 x 21 =42

∴ 6: 2:: 21: 7

3rd case: 2, 7, 6, 21

1st term x 4th term = 2 x 21 = 42

2nd term x 3rd term = 7 x 6 = 42

∴ 2: 7:: 6: 21

4th case: 6, 21,2, 7

1st term x 4th term = 6 x 7 = 42

2nd term x 3rd term = 21 x 2 = 42

∴ 6: 21:: 2: 7

Question 2. Let’s take 4 positive whole numbers:

1. 4,6,8,12
Solution:

1st case: 4, 6, 8, 12

1st term x 4th term = 4 x 12 = 48

2nd term x 3rd term = 6 x 8 = 48

∴ 4: 6:: 8: 12

2nd case: 6, 4,12, 8

1st term x 4th term = 6 x 8 = 48

2nd term x 3rd term = 4 x 12 = 48

∴ 6:4 :: 12:8

3rd case: 6,12, 4, 8

1st term x 4th term = 6 x 8 = 48

2nd term x 3rd term = 12 x 4 = 48

∴ 6:12 :: 4:8

4th case: 12, 6, 8, 4

1st term x 4th term = 12 x 4 = 48

2nd term x 3rd term = 6 x 8 = 48

∴12: 6:: 8:4

WBBSE Class 6 Maths Solutions

Question 3.

1. 3.5, 7, 2, 4
Solution: 3.5, 7, 2, 4

1st case: 3.5, 7, 2, 4

1st term x 4th term = 3.5 x 4 = 14

2nd term x 3rd term = 7×2 = 14

∴ 3.5: 7:: 2: 4

2nd case: 7, 3.5, 4, 2

1st term x 4th term = 7×2 = 14

2nd term x 3rd term = 3.5 x 4 = 14

∴ 7: 3.5:: 4:2

3rd case: 3.5, 2, 7, 4

1st term x 4th term = 3.5 x 4 = 14

2nd term x 3rd term = 2×7 = 14

∴ 3.5: 2:: 7: 4

4th case: 7,4, 3.5, 2

1st term x 4th term = 7×2 = 14

2nd term x 3rd term = 4 x 3.5 = 15

∴ 7: 4:: 3.5:2

2. 1.5, 4.5, 2.5; 7.5
Solution: 1.5, 4.5, 2.5, 7.5

1st case: 1.5, 4.5, 2.5, 7.5

1st term x 4th term = 1.5 x 7.5 = 11.25

2nd term x 3rd term = 4.5 x 2.5 = 11.25

∴ 1.5: 4.5:: 2.5: 7.5

2nd case: 4.5, 7.5,1.5, 2.5

1st term x 4th term = 4.5 x 2.5 = 11.25

2nd term x 3rd term = 7.5 x 1.5 = 11.25

∴ 4.5: 7.5:: 1.5:2.5

WBBSE Class 6 Maths Solutions

3rd case: 1.5, 2.5, 4.5, 7.5

1st term x 4th term = 1.5 x 7.5 = 11.25

2nd term x 3rd term = 2.5 x 4.5 = 11.25

∴1.5: 2.5:: 4.5 4.5: 4.5

4th case: 4.5,1.5, 7.5, 2.5

1st term x 4th term = 4.5 x 2.5 = 11.25

2nd term x 3rd term = 1.5 x 7.5 = 11.25

∴ 4.5: 1.5:: 7.5:2.5

3. 0.35,1.05, 0.09, 0.27
Solution: 0.35,1.05, 0.09, 0.27

1st case: 0.35,1.05,0.09, 0.27

1st term x 4th term = 0.35 x 0.27 = 0.0945

2nd term x 3rd term = 1.05 x 0.09 = 0.0945

∴ 0.35:1.05 :: 0.09:0.27

2nd case: 1.05, 0.35, 0.27, 0.09

1st term x 4th term = 1.05 x 0.09 = 0.0945

2nd term x 3rd term = 0.35 x 0.27 = 0.0945

∴ 1.05: 0.35:: 0.27: 0.09

3rd case: 0.35,1.05,0.09, 0.27

1st term x 4th term = 0.35 x 0.27 = 0.0945

2nd term x 3rd term = 1.05 x 0.09 = 0.0945

∴ 0.35:1.05 :: 0.09:0.27

WBBSE Class 6 Maths Solutions

4th case: 1.05,0.27,0.35, 0.09

1st term x 4th term = 1.05 x 0.09 = 0.0945;

2nd term x 3rd term = 0.27 x 0.35 = 0.0945

∴ 1.05: 0.27 ::0.35:0.09

4. Let’s take 4 positive decimal numbers:
Solution:

1st case: 2.4,4.8,7.5,15

Here, 1st term x 4th term = 2.4 x 15 = 36

2nd term x 3rd term F 4.8 x 7.5 = 36

= 2.4: 4.8:: 7.5:15

2nd case: 4.8, 2.4,15, 7.5

Here, 1 st term x 4th term = 4.8 x 7.5 = 36

2nd term x 3rd term = 2.4 x 15 = 36

∴ 4.8: 2.4:: 15:7.5

3rd case: 15, 7.5, 4.8, 2.4

Here, 1 st term x 4th term = 15 x 2.4 = 36

2nd term x 3rd term = 7.5 x 4.8 = 36

∴ 15:7.5:: 4.8 : 2.4

4th case: 2.4, 7.5, 4.8,15

Here, 1 st term x 4th term = 2.4 x 15 = 36

2nd term x 3rd term = 7.5 x 4.8 = 36

∴ 2.4: 7.5:: 4.8:15

Question 4.

1. \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{6}\)
Solution:

1st case: \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{6}\)

1st term x 4th term = \(\frac{1}{2} \times \frac{1}{6}=\frac{1}{12}\)

2nd term x 3rd term = \(\frac{1}{3} \times \frac{1}{4}=\frac{1}{12}\)

∴ \(\frac{1}{2}: \frac{1}{3}:: \frac{1}{4}: \frac{1}{6}\)

2nd case: \(\frac{1}{3}, \frac{1}{2}, \frac{1}{6}, \frac{1}{4}\)

1st term x 4th term = \(\frac{1}{3} \times \frac{1}{4}=\frac{1}{12}\)

2nd term x 3 rd term = \(\frac{1}{2} \times \frac{1}{6}=\frac{1}{12}\)

∴ \(\frac{1}{3}: \frac{1}{2}:: \frac{1}{6}: \frac{1}{4}\)

Class 6 Math WBBSE Solutions

3rd case: \(\frac{1}{2}, \frac{1}{4}, \frac{1}{3}, \frac{1}{6}\)

1st term x 4th term = \(\frac{1}{2} \times \frac{1}{6}=\frac{1}{12}\)

2nd term x 3rd term = \(\frac{1}{4} \times \frac{1}{3}=\frac{1}{12}\)

∴ \(\frac{1}{2}: \frac{1}{4}:: \frac{1}{3}: \frac{1}{6}\)

4th case: \(\frac{1}{3}, \frac{1}{6}, \frac{1}{2}, \frac{1}{4}\)

1st term x 4th term = \(\frac{1}{3} \times \frac{1}{4} \times=\frac{1}{12}\)

2nd term x 3rd term = \(\frac{1}{6} \times \frac{1}{2}=\frac{1}{12}\)

∴ \(\frac{1}{3}: \frac{1}{6}:: \frac{1}{2}: \frac{1}{4}\)

2. \(\frac{1}{5}, \frac{1}{10}, \frac{1}{16}, \frac{1}{32}\)

1st case: \(\frac{1}{5}, \frac{1}{10}, \frac{1}{16}, \frac{1}{32}\)

1st term  x 4th term = \(\frac{1}{5} \times \frac{1}{32}=\frac{1}{160}\)

2nd term x 3rd term = \(\frac{1}{10} \times \frac{1}{16}=\frac{1}{160}\)

∴ \(\frac{1}{5}: \frac{1}{10}:: \frac{1}{16}: \frac{1}{32}\)

2nd case: \(\frac{1}{10}, \frac{1}{5}, \frac{1}{32}, \frac{1}{16}\)

1st term x 4th term = \(\frac{1}{10} \times \frac{1}{16}=\frac{1}{160}\)

2nd term x 3rd term = \(\frac{1}{5} \times \frac{1}{32}=\frac{1}{160}\)

∴ \(\frac{1}{10}: \frac{1}{5}:: \frac{1}{32}: \frac{1}{16}\)

3rd case: \(\frac{1}{5}, \frac{1}{16}, \frac{1}{10}, \frac{1}{32}\)

1st term x 4th term = \(\frac{1}{5} \times \frac{1}{32}=\frac{1}{160}\)

2nd term x 3rd term = \(\frac{1}{16} \times \frac{1}{10}=\frac{1}{160}\)

∴ \(\frac{1}{5}: \frac{1}{16}:: \frac{1}{10}: \frac{1}{32}\)

Class 6 Math WBBSE Solutions

4th case: \(\frac{1}{10}, \frac{1}{32}, \frac{1}{5}, \frac{1}{16}\)

1st term x 4th term = \(\frac{1}{10} \times \frac{1}{16}=\frac{1}{160}\)

2nd term x 3rd term = \(\frac{1}{32} \times \frac{1}{5}=\frac{1}{160}\)

∴ \(\frac{1}{10}: \frac{1}{32}:: \frac{1}{5}: \frac{1}{16}\)

3. \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{18}\)

1st case: \(\frac{1}{3}, \frac{1}{6}, \frac{1}{9}, \frac{1}{18}\)

1st term x 4th term = \(\frac{1}{3} \times \frac{1}{18}=\frac{1}{54}\)

2nd term x 3rd term = \(\frac{1}{6} \times \frac{1}{9}=\frac{1}{54}\)

∴ \(\frac{1}{3}: \frac{1}{6}:: \frac{1}{9}: \frac{1}{18}\)

2nd case: \(\frac{1}{6}, \frac{1}{3}, \frac{1}{18}, \frac{1}{9}\)

1st term x 4th term = \(\frac{1}{6} \times \frac{1}{9}=\frac{1}{54}\)

2nd term x 3rd term = \(\frac{1}{3} \times \frac{1}{18}=\frac{1}{54}\)

∴ \(\frac{1}{6}: \frac{1}{3}:: \frac{1}{18}: \frac{1}{9}\)

3rd case: \(\frac{1}{3}, \frac{1}{9}, \frac{1}{6}, \frac{1}{18}\)

1st term x 4th term = \(\frac{1}{3} \times \frac{1}{18}=\frac{1}{54}\)

2nd term x 3rd term = \(\frac{1}{9} \times \frac{1}{6}=\frac{1}{54}\)

∴ \(\frac{1}{3}: \frac{1}{9}:: \frac{1}{6}: \frac{1}{18}\)

4th case: \(\frac{1}{6}, \frac{1}{18}, \frac{1}{3}, \frac{1}{9}\)

1st term x 4th term = \(\frac{1}{6} \times \frac{1}{9}=\frac{1}{54}\)

2nd term x 3rd term = \(\frac{1}{18} \times \frac{1}{3}=\frac{1}{54}\)

∴ \(\frac{1}{6}: \frac{1}{18}:: \frac{1}{3}: \frac{1}{9}\)

4. \(\frac{1}{8}, \frac{1}{24}, \frac{1}{5}, \frac{1}{15}\)
Solution:

1st case: \(\frac{1}{8}, \frac{1}{24}, \frac{1}{5}, \frac{1}{15}\)

1st term x 4th term = \(\frac{1}{8} \times \frac{1}{15}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{24} \times \frac{1}{5}=\frac{1}{120}\)

2nd case: \(\frac{1}{24}, \frac{1}{8}, \frac{1}{15}, \frac{1}{5}\)

1st term x 4th term = \(\frac{1}{24} \times \frac{1}{5}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{8} \times \frac{1}{15}=\frac{1}{120}\)

∴ \(\frac{1}{24}: \frac{1}{8}:: \frac{1}{15}: \frac{1}{5}\)

3rd case: \(\frac{1}{8}, \frac{1}{5}, \frac{1}{24}, \frac{1}{15}\)

1st term x 4th term = \(\frac{1}{8} \times \frac{1}{15}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{5} \times \frac{1}{24}=\frac{1}{120}\)

∴ \(\frac{1}{8}: \frac{1}{5}:: \frac{1}{24}: \frac{1}{15}\)

4th case: \(\frac{1}{24}, \frac{1}{15}, \frac{1}{8}, \frac{1}{5}\)

1st term x 4th term = \(\frac{1}{24} \times \frac{1}{5}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{15} \times \frac{1}{8}=\frac{1}{120}\)

∴ \(\frac{1}{24}: \frac{1}{15}:: \frac{1}{8}: \frac{1}{5}\)

5. \(\frac{1}{3}, \frac{1}{5}, \frac{1}{4}, \frac{3}{10}\)
Solution:

1st case: \(\frac{1}{3}, \frac{1}{5}, \frac{1}{4}, \frac{3}{10}\)

1st term x 4th term = \(\frac{1}{3} \times \frac{3}{10}=\frac{1}{20}\)

2nd term x 3rd term = \(\frac{1}{5} \times \frac{1}{4}=\frac{1}{20}\)

∴ \(\frac{1}{3}: \frac{1}{5} \neq \frac{1}{4}: \frac{3}{10}\)

∴ \(\frac{1}{3} \times \frac{1}{4}=\frac{1}{20}\)

4th case: \(\frac{1}{6}, \frac{1}{18}, \frac{1}{3}, \frac{1}{9}\)

1st term x 4th term = \(\frac{1}{6} \times \frac{1}{9}=\frac{1}{54}\)

2nd term x 3rd term = \(\frac{1}{18} \times \frac{1}{3}=\frac{1}{54}\)

∴ \(\frac{1}{6}: \frac{1}{18}:: \frac{1}{3}: \frac{1}{9}\)

Class 6 Math WBBSE Solutions

6. \(\frac{1}{8}, \frac{1}{24}, \frac{1}{5}, \frac{1}{15}\)

1st case: \(\frac{1}{8}, \frac{1}{24}, \frac{1}{5}, \frac{1}{15}\)

1st term x 4th term = \(\frac{1}{8} \times \frac{1}{15}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{24} \times \frac{1}{5}=\frac{1}{120}\)

2nd case: \(\frac{1}{24}, \frac{1}{8}, \frac{1}{15}, \frac{1}{5}\)

1st term x 4th term = \(\frac{1}{24} \times \frac{1}{5}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{8} \times \frac{1}{15}=\frac{1}{120}\)

∴ \(\frac{1}{24}: \frac{1}{8}:: \frac{1}{15}: \frac{1}{5}\)

3rd case: \(\frac{1}{8}, \frac{1}{5}, \frac{1}{24}, \frac{1}{15}\)

1st term x 4th term = \(\frac{1}{8} \times \frac{1}{15}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{5} \times \frac{1}{24}=\frac{1}{120}\)

∴ \(\frac{1}{8}: \frac{1}{5}:: \frac{1}{24}: \frac{1}{15}\)

4th case: \(\frac{1}{24}\), \(\frac{1}{15}\), \(\frac{1}{8}\), \(\frac{1}{5}\)

1st term x 4th term = \(\frac{1}{24} \times \frac{1}{5}=\frac{1}{120}\)

2nd term x 3rd term = \(\frac{1}{15} \times \frac{1}{8}=\frac{1}{120}\)

∴ \(\frac{1}{24}: \frac{1}{15}:: \frac{1}{8}: \frac{1}{5}\)

7. \(\frac{1}{3}, \frac{1}{5}, \frac{1}{4}, \frac{3}{10}\)

1st case: \(\frac{1}{3}, \frac{1}{5}, \frac{1}{4}, \frac{3}{10}\)

1st term x 4th term = \(\frac{1}{3} \times \frac{3}{10}=\frac{1}{20}\)

2nd term x 3rd term = \(\frac{1}{5} \times \frac{1}{4}=\frac{1}{20}\)

∴ \(\frac{1}{3}: \frac{1}{5} \neq \frac{1}{4}: \frac{3}{10}\)

∴ \(\frac{1}{3} \times \frac{1}{4}=\frac{1}{20}\)

2nd case: \(\frac{1}{3}, \frac{1}{5}, \frac{3}{10}, \frac{1}{4}\)

= \(\frac{1}{5} \times \frac{3}{10}=\frac{3}{50}\)

∴ \(\frac{1}{3}: \frac{1}{5} \neq \frac{3}{10}: \frac{1}{4}\)

Again, \(\frac{1}{3} \times \frac{1}{4}=\frac{1}{12}, \frac{1}{5} \times \frac{3}{10}=\frac{3}{50}\)

∴ \(\frac{1}{3}, \frac{1}{5}, \frac{1}{4}, \frac{3}{10}\) are not in proportion.

8. \(\frac{8}{3}, 8, \frac{5}{3}, 8\)

1st case: \(\frac{8}{3} \times 8=\frac{64}{3}, 8 \times \frac{5}{3}=\frac{40}{3}\)

2nd case: \(\frac{8}{3} \times \frac{5}{3}=\frac{40}{.3}, 8 \times 8=64\)

∴ \(\frac{8}{3}, 8, \frac{5}{3}, 8\) are not in proportion.

Class 6 Math WBBSE Solutions Chapter 21 Fundamental Concept Of Ratio And Proportion Exercise 21.3

Question 1. Which of the following cases can be represented in ratio? Let’s write.

1. My friend Jatita’s weight and her height.
Solution: My friend Jatita’s weight and her height are not possible.

2. In this month, number of days I went to school and number of days my friend Jahir went to school.
Solution: In this month, the number of days I went to school and number of days my friend Jahir went to school — Possible.

3. The money I had and the money I spent.
Solution: The money I had and the money I spent — Possible.

4. Litres of water in my water bottle and temperature of water.
Solution: Litres of water in my water bottle and temperature of water — Not possible.

5. How long I played today and how long my brother played.
Solution: How long I play today and how long my brother played — Possible.

Question 2. Let’s express the following quantities in ratio and identify the ratio of greater inequality and the ratio of lesser inequality.

1. 10 kg, 15 kg.
Solution: 10 kg: 15 kg

= 10:15

= 2:3

(Ratio of lesser inequality).

2. 27 things and 18 things
Solution: 27 things: 18 things

= 27:18 = 3:2

(Ratio of greater inequality).

3. Rs. 30 and Rs. 22.50
Solution: Rs. 30: Rs. 22.50

= 30: 22.5

= 6 : 4.5 = 4:3

(Ratio of greater inequality).

4. 4.9 litre and 8.4 litre
Solution: 4.9 litre: 8.4 litre

= 4.9: 84

= 49 : 84

= 7:12

(Ratio of lesser inequality).

5. 52 m and 78 m
Solution: 52 m: 78 m = 52: 78

=4:6

= 2:3

(Ratio of lesser inequality).

6. 1 hr 24 mins and 6 hrs 18 min
Solution: 1 hr 24 min: 6 hr 18 min

= (60 + 24) min : (360 + 10) min = 84 min : 378 m

= 12:54

= 2:9

(Ratio of lesser inequality).

Question 3. A bamboo stick is 2 m long. 0.75 m of it is coloured red and rest part is colored white.
Solution:

Length of the bamboo stick = 2 m.

Portion of red colour = 0.75 m.

∴ Portion of white colour = (2 – 0.75) m = 1.25 m.

1. Let us find the ratio between the total length of bamboo and the portion painted red.
Solution: Length of bamboo: Length of red portion

= 2 : 0.75 = 2 : 75/100

= 2 : 3/4 = 8 : 3

2. Let’s find the ratio between the total length of bamboo and the portion painted white.
Solution: Length of bamboo: Length of white portion

= 2: 1.25 = 2: 125/100

= 2 : 5/4 = 8.5

3. Let’s find the ratio between the part coloured red and that coloured white.
Solution: Length of red portion: Length of white portion = 0.75:1.25

= 75:125

= 3:5

Class 6 Math Solutions WBBSE

Question 4. The ratio of length and breadth of my room is 7: 5. Let’s write 4 possible perimeters of the room in the above ratio.
Solution: Length: Breadth = 7:5

∴ \(\frac{\text { Length }}{\text { Breadth }}=\frac{7}{5}=\frac{14}{10}=\frac{28}{20}=\frac{56}{40}\)

1. Perimeter = 2(7 + 5) = 2 x 12 = 24 units
2. Perimeter = 2(14 + 10)= 2 x 24 = 48 units
3. Perimeter = 2(28 + 20) = 2 x 48 = 96 units
4. Perimeter = 2(56 + 40) = 2 x 96 = 192 units.

Question 5. I have 26 stamps. Myself and Mita shall divide the stamps in the ratio of 8: 5. Let’s find how many stamps each of us will have.
Solution:

Total number of stamps = 26

∴ \(\frac{\text { No. of Stamps of me }}{\text { No. of Stamps of Mita }}=\frac{8}{5}=8: 5\)

No. of Stamps of mine = 8/13 x 26 = 16

No. of stamps of Mita = 5/13 x 26 = 10

Question 6. The ratio of my textbooks and story books is 4:3. If number of textbooks are 28, let’s find the number of story books and a total number of books.
Solution:

The ratio of my textbooks and story books = 4:3

Total number of textbooks = 28.

∴ \(\frac{\text { No. of my text books }}{\text { No. of story books }}=\frac{4}{3}\)

or, \(\frac{28}{\text { No. of story books }}=\frac{4}{3}\)

4 x No. of story books = 3 x 28

No. of story books = \(\frac{3 \times 28}{4}\) = 21.

∴ Total number of books = No. of text books + No. of storybooks

= 28 + 21 = 49

Question 7. In a particular type of jewellery the ratio of gold and silver is 4: 7. In such type of jewelry ornament, how many milligrams of gold has been mixed with 357 milligrams of silver, it is to be calculated.
Solution:

Ratio of Gold and Silver = 4:7

∴ \(\frac{\text { Gold }}{\text { Silver }}=\frac{4}{7}\)

⇒ \(\frac{\text { Weight of Gold }}{\text { Weight of Silver }}=\frac{4}{7}\)

⇒ \(\frac{\text { Weight of Gold }}{357 \mathrm{mg}}=\frac{4}{7}\)

7 x weight of Gold = \(4 \times 357 \mathrm{mg}\)

Weight of Gold = \(\frac{4 \times 357}{7} \mathrm{mg} . \)

∴ Weight of Gold = 204 mg

Question 8. Let’s write the ratio of the three angles of an equilateral triangle.
Solution:

Each angle of an equilateral triangle = 60°

∴ 1st angle : 2nd angle : 3rd angle = 60°: 60°: 60°

= 1:1:1.

Class 6 Math Solutions WBBSE

Question 9. Let’s write the ratio of the angles of a right-angled isosceles triangle.
Solution:

The three angles of the right-angled isosceles triangle are 90°, 45°, and 45°.

∴ 1st angle : 2nd angle : 3rd angle = 90° : 45°, 45°

= 2:1:1 .

Question 10. Let me divide Rs. 210 among Fatema and Sakira in the ratio of 3:4. Let me find how much each would get.
Solution:

Total Amount = Rs. 210.

Amount of Fatema: Amount of Sakira = 3:4

∴ Amount of money Fatema received

Amount of money Sakira received = Rs. (210 – 90) = Rs. 120.

Question 11. Mohit bought 6 bananas for Rs. 18 from a vendor and Raju bought 2 dozen of bananas for Rs. 72 from another vendor. Let’s express in ratio to find who paid more for bananas.
Solution:

Mohit bought 6 bananas for Rs. 18.

∴ Mohit bought 1 banana for Rs. 18/6 = Rs. 3.

Raju bought 2 dozen (24) bananas for Rs. 72.

∴ Raju bought 1 banana for Rs. 72/24 = Rs. 3.

∴ Ratio of prices = 3:3 = 1 :1 (Equal amount)

Question 12. The distances of Ayesha and Kamal’s house from our school are 1 km and 600 m respectively. Today Ayesha and Kamal came to school in 20 min and 12 min respectively. Let’s find, expressed in ratios, if they reached school at the same time or one of them has reached earlier.
Solution:

Distance of Ayesha’s house from school: Distance of Kamal’s house from school

= 1 km : 600 m

= 1000 m: 600 m = 5:3

Again, time taken by Ayesha: time taken by Kamal = 20 min: 12 min

= 5:3

∴ Their speeds are equal.

Question 13. Let’s find which of the following ratios are equal ratios

1. 3:3 and 5:5
Solution: = 1: 1 and 1: 1

∴ Equal ratio

2. 20 : 24 and 25 : 30
Solution: 20: 24 and 25: 30

= 5: 6 and 5: 6.

∴ Equal ratio.

3. 1: 9 and 9:18
Solution: 1:9 and 9: 18

= 1: 9 and 1: 2

∴ Not equal ratio

4. 28 : 21 and 20:15
Solution: 28:21 and 20:15

= 4 : 3 and 4 : 3

∴ Equal ratio

5. 1.4: 0.6 and 6.3 : 2.7
Solution: 1.4 : 0.6 and 6.3 : 2.7

= 14 : 6 and 63 : 27

= 7 : 3 and 7 : 3

∴ Equal ratio

6. 52 : 39 and 44 : 33
Solution: 52: 39 and 44: 33

= 4 : 3 and 4 : 3

∴ Equal ratio

Question 14. Let’s verify which of the following numbers are in proportion:

1. 9, 7, 36, 28
Solution: 9, 7, 36, 28

1st term x 4th term = 9 x 28 = 252

2nd term x 3rd term = 7 x 36 = 252

∴ 9, 7, 36, and 28 are in proportion.

2. 12, 30,14, 70
Solution: 12, 30, 14, 70

1st term 4th term = 1 2 x 70 = 840

2nd term x 3rd term = 30 x 1 4 = 420

∴ 12, 30, 14, 70 are not in proportion.

3. 24, 6, 108, 27
Solution: 24, 6, 108, 27

1st term x 4th term = 24 x 27 = 648

2nd term x 3rd term = 6 x 1 08 = 648

∴ 24, 6, 108, 27 are in proportion.

4. \(\frac{1}{2}, 1, \frac{3}{5}, 1 \frac{1}{5}\)
Solution: \(\frac{1}{2}, 1, \frac{3}{5}, 1 \frac{1}{5}\)

= \(\frac{1}{2}, 1, \frac{3}{5}, \frac{6}{5}\)

1st term x 4th term = \(\frac{1}{2} \times \frac{6}{5}=\frac{3}{5}\)

2nd term x 3rd term = \(1 \times \frac{3}{5}=\frac{3}{5}\)

∴ \(\frac{1}{2}, 1, \frac{3}{5}, 1 \frac{1}{5}\) are in proportion.

5. 72, 45, 70, 25
Solution: 72, 45, 70, 25

1st term x 4th term = 72 x 25 = 1800

2nd term x 3rd term = 45 x 70 = 31 50

∴ 72, 45, 70, 25 are not in proportion

6. _______ Let’s take + positive whole numbers.
Solution: 7, 8, 35, 40

1 st term x 4th term = 7 x 40 = 280

2nd term x 3rd term = 8 x 35 = 280

∴ 7, 8, 35, 40 are in proportion.

Class 6 Math Solutions WBBSE

Question 15. Let’s first try to find, if the following numbers are in proportion, let’s find all other possible proportions for each of them.

1. 60, 2,10,12
Solution: 60, 2,10,12

Case 1: Here, 1st term x 4th term = 60 x 12 = 720

2nd term x 3rd term = 2 x 10 = 20

∴ 60: 2 ≠10: 12

Case 2: 60, 12, 10,2

Here, 1st term x 4th term = 60 x 2 = 120

2nd term x 3rd term = 12 x 10 = 120

∴ 60: 12 :: 10: 2

Case 3: 60, 12,12, 2

Here, 1 st term x 4th term = 60 x 2 = 120

2nd term x 3rd term = 10 x 12 = 120

∴ 60 : 10 :: 12 : 2

Case 4: 10,2,60, 12

Here, 1 st term x 4th term = 10 x 12 = 120

2nd term x 3rd term = 2 x 60 = 120

∴ 10: 2:: 60: 12

2. 4,10, 6,15
Solution: 4,10, 6,15

Case 1: 4, 10, 6,15

Here, 1 st term x 4th term = 4 x 15 = 60

2nd term x 3rd term = 6 x 10 = 60

∴ 4 : 10 :: 6: 15

Case 2: 4, 6,10, 15

Here, 1 st term x 4th term = 4 x 15 = 60

2nd term x 3rd term = 6 x 10 = 60

∴ 4 : 6:: 10 : 15

Case 3: 60, 10, 12,2

Here, 1st term x 4th term = 10 x 6

60 2nd term x 3rd term = 4 x 15 = 60

∴ 10 : 4:: 15 : 6

Case 4: 10, 15, 4,6

Here, 1st term x 4th term = 10 x6 = 60

2nd term x 3rd term = 15 x 4 = 60

∴ 10: 15:: 4: 6

3. 8, 9, 24, 2
Solution: 8, 9, 24, 2

Case 1: 8, 24, 2, 9

Here, 1 st term X 4th term = 8 x 9 = 72

2nd term x 3rd term = 24 x 2 = 48

∴ 8: 24 ≠ 2: 9

Case 2: 8, 9, 2, 24

Here, 1st term x 4th term = 8 x 24 = 192

2nd term x 3rd term = 9×2 = 18

∴ 8: 9 ≠ 2: 24

Case 3: 8, 24, 9, 2

Here, 1st term x 4th term = 8×2 = 16

2nd term x 3rd term = 24 x 9 = 216

∴ 8 : 24 ≠ 9:2

∴ 8, 9, 24, 2 are not in proportion

4. 3, 5,15, 25
Solution: 3, 5, 15, 25

Case 1: 5, 3, 25, 15

Here, 1 st term x 4th term = 5 x 15 = 75

2nd term x 3rd term = 3 x 25 = 75

∴ 5 : 3:: 25 :15

Case 2: 5, 25, 3, 15

Here, 1 st term x 4th term = 5 x 15 = 75

2nd term x 3rd term = 25 x 3 = 75

∴ 5: 25 :: 3:15

Case 3: 25, 5, 15, 3

Here, 1st term x 4th term = 25 x 3 = 75

2nd term x 3rd term = 5×15 = 15

∴ 10: 4:: 15:6

Case 4: 25,15, 5, 3

Here, 1st term x 4th term = 25 x 3 = 75

2nd term x 3rd term = 15 x 5 = 75

∴ 25 : 15 :: 5 : 3

5. 45, 5,75,5

Solution: 45, 5, 75: 5

Here, 45 x 5 = 225 75 X 5 = 375

∴ 45:5 ≠ 75.5

Again, 45 x 75 5 x 5 = 25

∴ 45 : 5 ≠ 5: 75

∴ 45, 5, 75, and 5 are not in proportion.

6. 24, 4, 36, 6
Solution: 24, 4, 36, 6

Case 1: 24, 4, 36, 6

Here, 1 st term x 4th term = 24 x 6 = 144

2nd term x 3rd term = 4 x 36 = 144

∴ 24 : 4:: 36 : 6

Case 2: 24, 36, 4, 6

Here, 1st term x 4th term = 24 x 6 = 144

2nd term x 3rd term = 36 x 4 = 144

∴ 24 : 36 :: 4: 6

Case 3: 4, 24, 6, 36

Here,. 1 st term x 4th term = 4 x 36 = 144

2nd term x 3rd term = 24 x 6 = 144

∴ 4: 24 6: 36

Case 4: 4, 6, 24, 36

Here, 1 st term x 4th term = 4 x 36 = 144

2nd term x 3rd term = 6 x 24 = 144

∴ 4:6:: 24 : 36

Class 6 Math Solutions WBBSE

Question 16. The height of my friend Priya is 160 cm and the height of her mother is 170 cm. Again, Priya’s weight is 40 kg and her mother’s weight is 42.5 kg. Let’s find if their weights are in proportion to their heights.
Solution:

Height of Priya = 160 m.

Height of Priya’s mother = 170 m.

∴  Ratio of their heights = 160 m: 170 m.

= 16:17

Again, weight of Priya = 40 kg.

Weight of Priya’s mother = 42.5 kg.

∴ Ratio of their weights = 40 kg: 42.5 kg.

= 40: 425/10

= 16:17

∴ Their weights are in proportion to their heights.

 

Class 6 Math Solutions WBBSE Chapter 18 Square Root Exercise 18

Question 1. 441 oranges were picked from Nisar’s fruit garden. Oranges are to be kept in a basket. Each basket will contain as many oranges as there are a number of baskets. Let’s calculate to find the number of baskets.
Solution:

Total number of oranges = 441

No. of baskets = \(\sqrt{441}=\sqrt{21 \times 21}=21\)

Question 2. Today morning I arranged the books in the almirah of my room. In each shelf, I arranged books equal to the number of shelves of the almirah. But 5 books remained out of the almirah. If total number of books are 86, let’s find the number of shelves of the almirah.
Solution:

Total number of books = 86.

But 5 books remained out of the almirah.

∴ Total number of books in the aimirah = 86 – 5 = 81.

∴ Number of shelves of the aimirah = \(\sqrt{81}=\sqrt{9 \times 9}=9\)

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 3. In the playground, we decided to arrange ourselves and stand in a square form. After some have formed this square, it’s found that 4 friends are staying apart. If they join the square, it will not remain square anymore. 40 students are present today in our class. Let’s calculate in this arrangement how many students are there in each row.
Solution:

Number of students present today = 40.

To make a square form 4 students will be excess.

∴ Number of students required to make a square form = 40 – 4 = 36.

∴ Number of students is each row = \(\sqrt{36}=\sqrt{6 \times 6}=6\)

Class 6 Math Solutions WBBSE

Question 4. In the Sukanta Memorial Library of our locality, the members contributed as many rupees as there are members. If the total collection is Rs. 729 let’s find the number of members of the library.
Solution:

Total collections from the members = Rs. 729

As each members contribute as many rupees as there are members.

∴ Number of members = \(\sqrt{729}=\sqrt{3 \times 3 \times 3 \times 3 \times 3 \times 3}\)

Question 5. To dig a pond in Raghunathpur village, the number of people employed worked for as many numbers of days as there were number of people working, and got as payment Rs. 12375.
Solution:

Number of people working and get as payment Rs 12375.

If each, gets daily wage of Rs. 55.

Number of people joined the work  =\(\sqrt{\frac{12375}{55}}=\sqrt{225}=\sqrt{15 \times 15}=15\)

Class 6 Math Solutions WBBSE

Question 6. If each gets a daily wage of Rs. 55 then let’s find how many pepole joined the work.
Solution:

The total money collected = Rs. 4096.

As each member paid an amount 4 times the number of members.

∴ Number of members went for the trip

= \(\frac{\sqrt{4096}}{4}=\sqrt{1024}=\sqrt{4 \times 4 \times 4 \times 4 \times 2 \times 2}\)

= 4x4x2 = 32

Question 7. Today is Children’s Day. Few of us distributed toffee and biscuits among the other students of the school. But 800 toffees were left. So each took twice the number of toffees as we are in number. Let’s calculate among how many of us those 800 toffees were divided.
Solution:

Each took twice the number of toffees as we are in number.

800 toffee were left.

∴ Number of children = \(\sqrt{\frac{800}{2}}=\sqrt{400}=\sqrt{20 \times 20}=20\)

Question 8. Safikul uncle of Atla village brought 780 saplings of papaya tree. He decided to plant them in as many rows as there are number of plants in each row. But by trying to do, he fell short of 4 saplings. In how many rows did Rafikul’s uncle decide to plant the saplings, let’s find. Solution:

The number of saplings of the papaya tree = 780 He fell short of 4 saplings.

∴ Total number of saplings required = 780 + 4 = 784

∴ Number of rows = \(\sqrt{784}=\sqrt{4 \times 4 \times 7 \times 7}\) = 4 x 7 = 28.

Class 6 Math Solutions WBBSE

Question 9. I made a square cardboard box which has many square cells. Each row has many cells as there are a number of rows. My brother kept one 5 rupee, one two rupee, and a one rupee coin in each cell. If total money kept is Rs. 1152, then let’s find how many cells there are in each row of may cardboard box.
Solution:

The total money kept is Rs. 1152.

My brother kept one 5 rupee, a two rupee and a one rupee coin in each cell.

∴ Number of cells = \(\sqrt{\frac{1152}{5+2+1}}=\sqrt{\frac{1152}{8}}\)

= \(\sqrt{144}=\sqrt{12 \times 12}=12\)

Question 10. Let’s find the value of the following

1. Square of 7 = ____
Solution: Square of 7 = 7 x 7 = 49

2. Square root of 121 = _______
Solution: Square root of 121 = √121

= \(\sqrt{11 \times 11}=11\)

3. 9² = _______
Solution: 92 = 9 x 9 = 81

4. √100 = ______
Solution: \(\sqrt{100}=\sqrt{10 \times 10}=10\)

5. √49 = _________
Solution: \(\sqrt{49}=\sqrt{7 \times 7}=7\)

6. √144 = ______
Solution: \(\sqrt{144}=\sqrt{12 \times 12}=12\)

7. \(\sqrt{3^2 \times 2^2}\) = ________
Solution: \(\sqrt{3^2 \times 2^2}=\sqrt{9 \times 4}\)

= \(\sqrt{36}=\sqrt{6 \times 6}=6\)

8. \(\sqrt{5 \times 7 \times 5 \times 7}\) = ________
Solution: \(\sqrt{5 \times 7 \times 5 \times 7}=\sqrt{5^2 \times 7^2}\) = 5 x 7 = 35

9. \(\sqrt{13 \times 13}\) = _____
Solution: \(\sqrt{13 \times 13}\) = 13

Class 6 WBBSE Math Solutions

Question 11. Let’s find the square root of the following by finding factors

1. 169
Solution: \(\sqrt{169}=\sqrt{13 \times 13}=13\)

2. 225
Solution: \(\sqrt{225}=\sqrt{15 \times 15}=15\)

3. 4² + 3²
Solution: \(\sqrt{4^2+3^2}=\sqrt{16+9}\)

= \(\sqrt{25}=\sqrt{5 \times 5}=5\)

4. √144
Solution: \(\sqrt{144}=\sqrt{12 \times 12}=12\)

5. 576
Solution: \(\sqrt{576}=\sqrt{4 \times 4 \times 6 \times 6}\) = 4 x 6 = 24

6. 15² + 20²
Solution: \(\sqrt{15^2+20^2}=\sqrt{225+400}\)

= \(\sqrt{625}=\sqrt{5 \times 5 \times 5 \times 5}\)

= \(5 \times 5=25\)

7. 900
Solution: \(\sqrt{900}=\sqrt{3 \times 3 \times 10 \times 10}\)

Class 6 WBBSE Math Solutions Chapter 18 Square Root Exercise 18.1

Question 1. Let’s find if 108, 64,162, 81 are square numbers or not let us find the smallest whole number other than ‘0’ with which these should be multiplied or divided to give a square number.

1. 108
Solution:

108 = 2x2x3x3x3

∴ 108 is not a square number.

If 3 is multiplied or divided with 108, it will be a square number.

∴ 108 x 3 = 324, a square number or, 108 ÷ 3 = 36, a square number

2. √64
Solution:

= \(\sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2}\)

=2x2x2=8

∴ 64 is a square number.

3. 162
Solution:

∴162 = 3x3x3x3x2

∴ 162 is not a square number.

If 2 is multiplied or divided with 162, it will be a square number.

∴ 162 x 2 = 324 = 18 x 18, a square number,

or, 162 ÷ 2 = 81 = 9 x 9, a square number.

4. √81
Solution:

= \(\sqrt{3 \times 3 \times 3 \times 3}\) =3×3 = 9

∴ 81 is a square number.

Class 6 Maths Solutions WBBSE Chapter 18 Square Root Exercise 18.2

Question 1. Apart from 0, by which least whole number the following numbers must be divided to get square numbers

1. 845
2. 450
3. 18 x 6
4. 25 x 35

1. 845
Solution:

845 = 13x13x5

Hence, it is not a square number.

If we divide the number by 5, we will get a square number.

∴ The required number is 5.

2. 450
Solution:

∴ 450 = 5x5x3x3x2

Hence, it is not a square number, if we divide the number by 2, it will be a square number.

∴ The required number is 2.

Class 6 Maths Solutions WBBSE

3. 18×6
Solution:

= (3 x 3 x 2) x (2 x 3)

=3x3x2x2x3

Hence, it is not a square number, if we divide the number by 3, it will be a square number.

∴ The required number is 3.

4. 25 x 35 = (5 x 5) x (5 x 7)
Solution:

Hence, it is not a square number, if we divide the number by 35 (5 x 7), it will be a square number.

∴ The required number = 35.

Question 2. By which least whole number apart from 0, the following numbers should be multiplied to give a square number:

1. 432
Solution:

=2x2x3x7x7x3

Hence, 588 is not a square number, if we multiply 3 with it, it will be a square number.

∴ The required number is 3.

Class 6 Maths Solutions WBBSE

2. 588
Solution:

= 2x2x3x7x7x3

Hence 588 is not a square number, if we multiply 3 with it, it will be a square number.

∴ The required number is 3

3. 25×20
Solution:

= 5x5x2x2x5

Hence, it is not a square number, if we multiply 5 with it, it will be a square number.

∴ The required number is 5.

4. 24x 28
Solution:

=2x2x2x3x2x2x7

Hence, it is not a square number, if we multiply 2x3x7 with it, it will be a square number.

∴ The required number is 2 x 3 x 7 = 42.

WBBSE Math Solutions Class 6 Chapter 18 Square Root Exercise 18.3

Question 1. Let’s work out to find the least square number other than 0, which is divisible by 12,16, 20, and 24.
Solution:

∴ L.C.M.of 12, 16, 20 and 24 = 2x2x2x2x3x5 = 240

Hence, 240 is not a least square number

If we multiplied 240 by 3 x 5, then it will be the least square number.

∴ The required least square number.

= 240 x 3 x 5 = 3600.

WBBSE Math Solutions Class 6

Question 2. The product of two positive whole numbers is 98 and the greater one is twice the smaller number. Let’s find the two numbers.
Solution:

Greater number = 2x smaller number

Greater number x smaller number = 98

or, (2 x smaller number) x smaller number = 98

or, 2 x (smaller number)² = 98

∴ (Smaller number)² = 98/2 = 49

∴ Smaller number = √49 =7

∴ Greater number = 2 x smaller number = 2×7 = 14

∴ The required numbers are 7 and 14.

Question 3. Let’s find which least square number has factor 17.
Solution: The least square number which has a factor =17×17 = 289

Question 4. Let’s find the least square number other than 0 which is divisible by 10,15,20 and 30. Also, let’s write the next square number which will be divisible by these numbers.
Solution:

∴ L.C.M. = 2x2x3x5 = 60

It is not a square number. If we multiplily by 3 x 5, we will get a square number.

∴ Least square number = 60 x 3 x5 = 900.

∴ The next square number = 900 x 4 = 3600.

WBBSE Math Solutions Class 6

Question 5. Let’s analyse the given numbers and place them in their respective columns-20, 27, 50, 75, 100, 108,144, 169,180, 256
Solution:

20 = 2 x 2 x 5 – it is not a square number

27 = 3 x 3 x 3 – it is not a square number

50 = 5 x 5 x 2 – it is not a square number

75 = 5 x 5 x 3 – it is not a square number

100 = 2 x 2 x 5 x 5 – it is a square number

108 = 6 x6 x 3 – it is not a square number

144 = 2 x 2 x 6 x 6 – it is a square number

169 = 13 x 13 – it is a square number

180 = 2 x 2 x 3 x 3 x 5 – it is not a square number

256 = 4 x 4 x 4 x 4 – it is a square number

Question 6. This year on Netaji’s birthday, the students present in Physical Education class were made to stand in rows of 18,24,27, at different points of time, to march past At one point of time we formed a solid square. Let us find the least number of students present in school on that day.
Solution: L.C.M of 18, 24, 27

= 2 x 2 x 2 x 3 x 3 x 3

= 216

It is not a square number, if we multiply 2×3 with it, it will be a square number.

∴ Least number of students = 216x2x3 = 1296

WBBSE Math Solutions Class 6

Question 7. The product of two positive numbers is 147. The greater number is 3 times the smaller number. Let’s find the numbers.
Solution:

Greater number = 3 x smaller number .

Greater number x smaller number = 147

or, 3 x smaller number x smaller number = 147

or, (Smaller number)² = 147/3 = 49

∴ Smaller number = √49 = 7

Greater number = 3×7 = 21.

Question 8. Arrange the following in ascending order of their value:

⇒ \((\sqrt{36}+\sqrt{25}),(\sqrt{49}+\sqrt{9}) ;(\sqrt{25}+\sqrt{100}),(\sqrt{4}+\sqrt{16})\)

Solution:

⇒ \((\sqrt{36}+\sqrt{25})\)

= 6 + 5 = 11

⇒ \((\sqrt{49}+\sqrt{9})\)

= 7 + 3 = 10

⇒ \((\sqrt{25}+\sqrt{100})\)

= 5 + 10 = 125

⇒ \(\sqrt{4}+\sqrt{16}\)

= 2 + 4 = 6

In ascending order

6 ∠ 10 ∠ 11 ∠ 15

i.e., \(\sqrt{4}+\sqrt{16} ; \sqrt{49}+\sqrt{9} ; \sqrt{36}+\sqrt{25} ; \sqrt{25}+\sqrt{100}\)

WBBSE Class 6 Maths Solutions

Question 9. Of three positive numbers, the product of first and second is 24 second and third is 48 and that of first and third is 32. Let’s find the three numbers.
Solution:

1st number x 2nd number = 24

2nd number x 3rd number = 48

1st number x 3rd number = 32

(1st number x 2nd number) x (1st number x 3rd number)/ (2nd number x 3rd number)

∴ (1st number)² = 16

∴ 1st number = √16 = 4

Again, 1st number x 2nd number = 24

or, 4 x 2nd number = 24

∴ 2nd number = 24/4 = 6

Again, 2nd number x 3rd number = 48

6 x 3rd number = 48

∴ 3rd number = 48/6 = 8

∴ Required numbers are 4, 6, and 8.

Question 10. On Republic Day, our Physical Education teacher made all students stand in rows having 12,15, and 20 students, at different points of time, for march past. At one point of time, the students were arranged in solid square. Let’s find out at least how many students were present in school on that day.
Solution:

L.C.M. of 12, 15 and 20

= 2 x 2 x 3 x 5

But 60 is not a square number, if we multiply 3 and 5 with it, it will be square number.

∴ The required number = 60 x 3 x 5 = 900.

WBBSE Class 6 Maths Solutions Chapter 18 Square Root Exercise 18.4

Question 1. Let’s find the square number nearest to 1000.
Solution:

∴ 1000 – 39 = 961 is a square number.

∴ √961 = 31

Next square number is (32)² = 1024

1024- 1000 = 24 ∠ 39

∴ Square number nearest to 1 000 is 1024.

Question 2. Let’s find the least number that will be subtracted from 9585 to give a square number.
Solution:

∴ The required number is 176.

Question 3. Let’s find what least number must be added to 5320 to make it a perfect square.
Solution:

Next square number is (73)² = 5329.

∴ The required number that is to be added to 5320 to make a square number is 5329-5320 = 9.

Class 6 Math WBBSE Solutions

Question 4. Let’s find the least square number other than 0, which is divisible by 15, 25, 35, 45.
Solution:

L.C.M.of 15,25, 35 and 45

= 3x5x5x7x3 = 1575.

It is not a square number, if we multiply 7 with it, it will be a square number.

∴ The required least square number = 1575 x 7 = 11025.

Question 5. Let’s find the least square number of 4 digits which are divisible by 8, 15, 20, and 25.
Solution:

L.C.M. of 8, 15, 20 and 25

= 2 x 2 x 5 x 2 x 3 x 5 = 600

If we multiply 600 by 2 and 3 then we get a square number.

∴ The least-square number of 4 digits = 600 x 6 = 3600.

Question 6. Let’s find the least square number of 4 digits.
Solution:

The least 4 digit number is 1000.

1000- 39 = 961 is a square number.

√961 =31

Next square number = (32)² = 1 024.

∴ Least square number of 4 digits = 1 024.

Class 6 Math WBBSE Solutions

Question 7. Let’s find the greatest square number of 4 digits.
Solution:

The greatest number of 4 digits = 9999.

The greatest square number of 4 digits = 9999 -198 = 9801.

Question 8. Let us find the square root of the following by the method of division:
Solution:

Question 9. Without finding square root, let us find the possible digits in unit’s place and number of digits in the square root number:

1. 784
Solution:

Possible digits in unit’s place = 2, 4

∴ Number of digits in the square root number = 2

Class 6 Math WBBSE Solutions

2. 3676
Solution:

Possible digits in 4 unit’s place = 6

∴ Number of digits in the square root number = 2

3. 160000
Solution:

Possible digits in unit’s place = 0

Number of digits in the square root number = 3

4. 1225
Solution:

Possible digits in unit’s place = 5

∴ Number of digits in the square root number = 2

5. 2401
Solution:

Possible digits in unit’s place = 1,9

∴ Number of digits in the square root number = 2

6. 10201
Solution:

Possible digits in unit’s place =,1,9.

∴ Number of digits in the square root number = 3

Question 10. Let’s find two square numbers nearest to 5000.
Solution: 5000

Nearest to 5000 = (70)² and (71)²

= 4900 and 5041

Question 11. The product of two numbers is 1576 and their quotient is 9/7, let’s find the numbers.
Solution:

1st number x 2nd number = 1575

and \(\frac{1 \text { st number }}{2 \text { nd number }}=\frac{9}{7}\)

∴ \((1 \text { st number } \times 2 \text { nd number }) \times \frac{1st number }{2nd num ber}=1575 \times \frac{9}{7}\)

∴ (1st number)² = 225 x

1st number = \(\sqrt{225 \times 9}\) = 15 x 3 = 45

∴ 2nd number = 1575 ÷ 45 = 35

∴ The numbers are 45, 35.

Question 12. Let us find what digit will be placed in * of 202*, so that it becomes a square number.
Solution: 202 *

1 st if we put 1, then 2021 is not a square number.

2nd if we put 2, then 2022 is not a square number.

3rd if we put 3, then 2023 is not a square number.

4th, if we put 4, then 2024 is not a square number.

5th if we put 5, then 2025 is a square number.

∴ The required digit is 5.