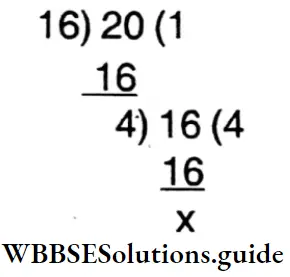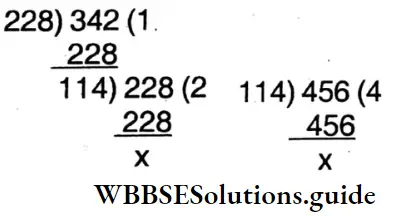Class 6 Maths

Class 6 Math Solutions WBBSE Chapter 17 Geometrical Concepts Based On Different Instruments Of Geometry Box Exercise 17

Question 1. I myself drew a quadrilateral and a triangle with the help of scale. I also measured their sides with the scale.
Solution:

ABCD is a quadrilateral whose AB = 7 cm, BC = 1.8 cm, CD = 5 cm. and DA = 4 cm.

PQR is a triangle whose PQ = 4.5 cm, QR = 6 cm, and RP = 5.4 cm.

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 2. I have drawn two line segments of length 2.8 cm, and 5.3 cm, and named them.
Solution:

MN is a line segment whose length = 2.8 cm and EF is another line segment whose length = 5.3 cm.

Class 6 WBBSE Math Solutions Chapter 17 Geometrical Concepts Based On Different Instruments Of Geometry Box Exercise 17.1

Question 1. Let’s draw a line segment of length 4.5 cm with scale and divider.
Solution:

PR is a line segment whose length is 4.5 cm.

Question 2. From a straight line let’s mark out a length – XY equal to 6 cm.
Solution:

Question 3. Using scale and divider, let’s draw two line segments of length 6 cm and 5.7 cm, and name them.
Solution:

Question 4. Using scale and divider let us draw two line segments AB and CD of lengths 3.6 cm and 2.2 cm.
Solution:

Class 6 WBBSE Math Solutions

Question 5. On a straight line, let’s draw a line segment XY which is the sum of the line segments AB and CD marked with a divider separately on the line. On another straight line, the segments AB and CD are separately marked in a way with a divider such that the line segment EF is the difference of the line segments AB and CD.
Solution:

Question 6. Using scale and compass and taking two separate points as centres let is draw two circles having radii of lengths 3.2 cm and 2.9 cm
Solution:

Class 6 WBBSE Math Solutions

Question 7. Let’s measure and write the values of the angles given below with a protractor. Let’s identify the angles as acute angle or right angle obtuse angle straight angle or reflex angle and arrange them in the increasing order of their values.
Solution:

1. ∠ACB = 40°; (Acute angle)
2. ∠CDE = 180° (Straight angle)
3. ∠JLK = 120° (Obtuse angle)
4. ∠PQR = 30° (Acute angle)

Reflex Z PQR = 360°-30° = 330°

1. ∠IJH = 120° (Obtuse angle)
2. ∠FEG = 90° (Right angle)
3. ∠YXZ = 30° (Acute angle)
4. ∠XYZ = 140° (Obtuse angle)

Class 6 WBBSE Math Solutions

Question 8. Let’s write the sides and the vertex for each of the following angles.
Solution:

1. Arms: \(\overrightarrow{\mathrm{OA}}\); \(\overrightarrow{\mathrm{OB}}\)

Sides: \(\overrightarrow{\mathrm{OA}} ; \overrightarrow{\mathrm{OB}}\)

Vertex: O

Class 6 Math Solutions WBBSE

2. Arms: \(\overrightarrow{\mathrm{OC}}, \overrightarrow{\mathrm{OD}}\)

Sides: \(\overrightarrow{O C}, \overrightarrow{O D}\)

Vertex: O

3. Arms: \(\overrightarrow{X Y}, \overrightarrow{Y Z}\)

Sides: \(\overrightarrow{X Y}, \overrightarrow{Y Z}\)

Vertex: Q

4. Arms: \(\overrightarrow{P Q}, \overrightarrow{Q R}\)

Class 6 Math Solutions WBBSE

Sides: \(\overrightarrow{\mathrm{PQ}}, \overrightarrow{\mathrm{QR}}\)

Vertex: Y

Question 9. Let us draw the following angles with a protractor. Let’s name the angle and write their sides and vertex. Also mention the type of the angles – 38°, 75°, 90°, 145°, 180°, 200°, 270°.
Solution:

1. ∠ABC =38°(Acute angle)

Sides: \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}\)

Vertex: B

Class 6 Math Solutions WBBSE

2. ∠PQR = 75°(Acute angle)

Sides: \(\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}\)

Vertex: Q

3. ∠DEF = 90°(Rigth angle)

Sides: \(\overline{\mathrm{DE}}, \overline{\mathrm{EF}}\)

Vertex: E

4. ∠MNR = 145°(Obtuse angle)

Sides: \(\overline{\mathrm{MN}}, \overline{\mathrm{NR}}\)

Vertex: N

WBBSE Class 6 Maths Solutions

5. ∠COD = 180°(Strigth angle)

Sides: \(\overline{\mathrm{CO}} ; \overline{\mathrm{OD}}\)

Vertex: O

6. ∠IJK = 200°, (Reflex angle)

Sides: \(\overline{\mathrm{IJ}}, \overline{\mathrm{JK}}\)

WBBSE Class 6 Maths Solutions

Vertex: J

7. ∠APC = 270°(Reflex angle)

Sides: \(\overline{\mathrm{AP}}, \overline{\mathrm{PC}}\)

Vertex: P

Question 10. Let Do It
Solution:

∠BAD = 30°; ∠CAD = 60° and ∠BAC = 90°

∠BAD + ∠CAD = ∠BAC

Again, ∠BAC-∠BAD =∠DAC

∠ADC + ∠ADB = 180° = ∠BDC

∠BDC – ∠ADB = ∠ADC = 90°

1. ∠EAG + ∠GAF = 90°;
2. ∠FAE – ∠FAG = 40°
3. ∠ADC+ ∠ADB = 180°;
4. 180°-∠ADC = 60°
5. ∠SPR + ∠RPQ = ∠SPQ
6. ∠SPQ – ∠SPR = ∠RPQ

Class 6 Math WBBSE Solutions Chapter 17 Geometrical Concepts Based On Different Instruments Of Geometry Box Exercise 17.2

Question 1. Using the outer and inner scales of the protractor, let’s draw the following angles

1. 54°
Solution: Angle POQ = 54°

2. 67°
Solution: ∠CDE = 67°

3. 85°
Solution: ∠ABC = 85

4. 95°
Solution: ∠MNK = 95°

5. 120°
Solution: ∠RPK = 120°

Class 6 Math WBBSE Solutions

Question 2. Let’s draw 187°, 235°, 310° and 325° angles using protractor:
Solution: 187°

Reflex ∠ABC = 187°

Reflex ∠PQR = 235°

Class 6 Math WBBSE Solutions

Reflex ∠MKL = 310

Reflex ∠CDE = 325°

Question 3. Let’s observe the figure and comprehend and write:

1. Let’s measure angle number 1, name the angle, type of angle. [Measure with protractor]
2. Let angle number 2 be measured with a protractor, name the angle, and write the type of angle.
3. The measures of angles 1 and 2 are added and the angle formed.

Solution:

1. ∠1 =40° (Acute angle)

∠BOC= 40°

2. ∠2 = 50° (Acute angle)

∠AOB = 50°

3. ∠1 + ∠2 = 40° + 50° = 90° (Right angle)

∠AOC = 90°

Class 6 Maths Solutions WBBSE

Question 4. In the figure, let’s take angle number 1 = ∠AOB; angle number 2 = ∠BOC; angle number 3 = ∠COD

1. Let’s measure angle number 1 with a protractor and note its value.
2. Let’s measure angle number 2 with a protractor and note its value.
3. Let’s measure angle number 3 with a protractor and note its value.
4. By adding angle number 1 and angle number 2, we get an angle, name that angle from the figure. ‘
5. By adding angle number 2 and angle number 3, the angle that is formed is named from the figure.
6. The angle formed by adding angle number 1, number 2, and number 3 is named from the figure and let’s express it as the sum of three angles.

Solution:

1. ∠1 = ∠AOB = 60°
2. ∠2 = ∠BOC = 90°
3. ∠3 =∠COD = 30°
4. ∠1 + ∠2 = ∠AOB + ∠BOC = 60° + 90° = 150°
5. ∠2+ ∠3 = ∠BOC + ∠COD.= 90° + 30° = 120°
6. ∠1 + ∠2 + ∠3 = ∠AOB+ ∠BOC+ ∠COD= 60° + 90° + 30° = 180°

Question 5. Let’s answer from the figure:

1. Let’s name one acute angle: ∠AOB
2. Let’s name one obtuse angle:∠BOD
3. Let’s name one right angle: ∠COD
4. Let’s name one straight angle: ∠AOD
5. Let’s name a reflex angle: ∠AOE
6. ∠AOB + ∠BOC =∠AOC
7. ∠BOC + ∠COD = ∠BOD
8. ∠AOC – ∠BOC = ∠AOB
9. ∠BOD – ∠BOC = ∠COD

Class 6 Maths Solutions WBBSE Chapter 17 Geometrical Concepts Based On Different Instruments Of Geometry Box Exercise 17.3

Question 1. Lengths of the sides of triangles are given. Let’s identify the types, of triangles according to angles:

1. 18 cm 18 cm 10 cm;
2. 5.2 cm, 5.2 cm, 5.2 cm;
3. 8 cm, 2 cm, 9 cm

Solution:

1. 18 cm, 18 cm, 10 cm: Here the lengths of two sides of a triangle are equal, then it is an isosodes, triangle.

2. 5.2 cm, 5.2 cm, 5.2 cm: Here the lengths of three sides of a triangle are equal, then it is an equilateral triangle.

3. 8 cm, 8 cm, 9 cm: Here the lengths of the three sides of a triangle are not equal, then it is a scalene triangle.

Question 2. The measures of the three angles of the triangles are given below. Let’s identify the types according to angles:

1. 90°, 45°, 45°
2. 90°, 30°, 60°
3. 75°, 70°, 35°
4. 60°, 60°, 60″
5. 120°, 30°, 60°

Solution:

1. 90°, 45°, 45°: Here one angle of a triangle is 90° and the other two angles are equal. So it is a right-angled isosceles triangle.

2. 90°, 30°, 60°: Here one angle is 90°; so, it is a right-angled triangle.

3. 75°, 70°, 35°: Here three angles of a triangle are not equal so it is a scalono trianglo.

4. 60°, 60°, 60°: Here three angles of a triangle are equal; so, it is an equilateral triangle.

5. 120°, 30°, 60°: Here one angle is 120°, greater than 90°- it is an obtuse angle. So tho triangle is an obtuse, angled triangle.

Question 3. A, B, and C are non-collinear points. Let’s join A, B; B, C, and C, A, and try to find answers of the following.

1. Let’s identify the geometric figure formed by joining the line segments.
2. Let’s write the angle opposite to side BC.
3. Let’s write the angle opposite to side AC.
4. Let’s write the side opposite to ∠BAC.
5. Let’s write the side opposite to ∠ACB.

Solution:

1. It is a triangle.
2. ∠BAC
3. ∠ABC
4. Side BC
5. Side AB

Class 6 Maths Solutions WBBSE

Question 4. Let’s find if the statements given below are correct or not
Solution:

1. Hypotenuse is the smallest side of a right-angled triangle.(x)
2. One angle of a right-angled triangle is 90°. (√)
3. There are at least two acute angles in a triangle. (√)
4. Each equilateral triangle is called an isosceles triangle. (√)
5. The sum of three angles of a triangle is 360°. (X)
6. The right-angled triangle can never be an equilateral triangle.(√)
7. The right-angled triangle can not be an isosceles triangle. (X)

Question 5. Let’s try to draw 120°, 135°, 150° angles using set squares.
Solution:

∠ABC = 90° + 45° = 135°

To draw 120°

∠ABC = 90°+ 60° = 150°

To draw 150°

∠ABC = 90°+ 60° = 150°

WBBSE Math Solutions Class 6 Question 6. Let’s write the observations in a tabular form.
Solution:

Question 7. Let’s write a logical statement for the set of words given below.

1. Square, Rectangle, Parallelogram — are all quadrilateral.
Solution: Square, rectangle, parallelogram — all have 4 sides, so they are quadrilateral.

2. A rectangle is a special type of parallelogram.
Solution: A rectangle is a special type of parallelogram as opposite sides of the rectangle are equal and parallel.

3. Parallelogram is a special trapezium.
Solution: Parallelogram is a special type of trapezium as the its two sides are parallel.

4. Rhombus is a special type of parallelogram.
Solution: Rhombus is a special type of parallelogram as its opposite sides are equal and parallel.

Question 8. Let’s mark (√) and (X) the incorrect and correct statements respectively given below:

1. A rectangular figure has all the sides equal. (X)
2. Each angle of a square is a right angle. (√)
3. Opposite sides of a parallelogram are parallel. (√)
4. For any trapezium, all its sides are equal. (X)
5. None of the angles of a rhombus are right angles. (√)

 

Class 6 Math Solutions WBBSE Chapter 16 Concept Of Directed Numbers And Number Line  Exercise 16

Question 1. Let us draw a number line put the following numbers on the line and name them.

1. Name + 5;- 2, + 3;- 6, + 2,- 5 respectively as A, B, C, D, E, and F.
Solution: + 5;-2; + 3;-6; + 2;-5,

name as A, B, C, D, E, F respectively.

2. Let’s measure how many units E is from B.
Solution: Measure of E from B is units.

3. How many units is A from B towards right?
Solution: Measure of A from B towards the right is 7 units.

4. How many units is D from E towards left?
Solution: Measure of D from E towards the left is 8 units.

5. How many units is D from F towards left ?
Solution: Measure of D from F towards left is 1 unit.

Read and Learn More WBBSE Solutions For Class 6 Maths

6. What is the relation between the numbers which are at A and F?
Solution: Relation between the numbers which are at A and F – Mutually opposite numbers.

7. What are the absolute values of the numbers of B and E?
Solution: Absotute values of the numbers of B and E = 2.

Class 6 Math Solutions WBBSE

Question 2. What do the following mean?

1. Profit of -10 rupees
Solution: Profit of -10 rupees = Loss of Rs. 10.

2. -15 m above
Solution: -15 m above = 15 m down

3. -36 g less
Solution: -36 gm less = 36 gm more.

4. -18 meter towards East
Solution: -18 meter towards East = 18 meter toward West.

5. Saved -23 rupees
Solution: Saved -23 rupees = Spent Rs. 23.

6. -5 km towards South.
Solution: -5 km towards south = 5 km towards North.

Question 3. Let’s write the absolute values of the following numbers

1. -12
2. + 13
3. – 22
4. – 61
5. + 17

Solution: Absolute value of the following

1. -12 → 12
2. +13 → 13
3. -22 → 22
4. -61 → 61
5. +17 → 17

Class 6 Math Solutions WBBSE

Question 4. Let’s find the opposite of the following:

1. Spent Rs.-10
Solution: Spent Rs. -10 Rs. 10 saved

2. Climbed up -15 m.
Solution: Climbed up -15m 15m going up

3. Profit of 81
Solution: Profit of 81 :- Loss of Rs. – 81

4. move – 35m down
Solution: move – 35 m down: and 35 m up

5. – 24 kg increase in weight.
Solution: – 24 kg increase in weight = 24 kg weight decreased

6. 28 m towards the right
Solution: 28 m towards right = 28 m towards right

7. 9 kg decrease of weight.
Solution: 9 kg decrease of weight = 9 kg decrease of weight.

Question 5. Using a number line, put < or > in the blank spaces.

Class 6 Math Solutions WBBSE

1. 0 ______ 5
Solution: 0 < 5

2. 0 ________ -6
Solution: 0 > -6

3. 6 ________ -6
Solution: 6 > -6

4. – 8
Solution: -8 > -10

5. -1 ______ -11
Solution: -1 > -11

6. ______ 15
Solution: 11 < 15

7. —10 _____ 12
Solution: -10 < 2

8. -100 _____ -50
Solution: -100 < -50

Question 6. (1) Let’s write 4 negative whole numbers less than -12.
Solution: —15; —18; — 20; – 25;

(2) Let’s write 4 negative whole numbers greater than – 8.
Solution: -6; -4; -3; -1

Class 6 WBBSE Math Solutions Chapter 16 Concept Of Directed Numbers And Number Line  Exercise 16.1

Question 1. Let us add on a number line

1. (+7) – (+2)
Solution: (+7) – (+2)

∴ (+7) + (+2) = +9.

2. (+2)- (-4)
Solution: (+2)- (-4)

∴ (+2) + (—4) = -2

3. (+6) + (-11)
Solution: (+6) + (-11)

∴ (+6) + (-11) = -5

Class 6 WBBSE Math Solutions

4. (-5), (-7)
Solution: (-5), (-7)

∴ (-5), (-7) = -12

5. (+8) + (-8)
Solution: (+ 8), (-8)

∴ (+8) + (-8) = 0

6. (+7), (-7)
Solution: (+7), (-7)

∴ (+ 7) + (-7) = 0

7. (+9), (-17)
Solution: (+9), (-17)

∴ + 9 +(-17)=-8.

Class 6 Maths Solutions WBBSE

8. (-11), (-9)
Solution: (-11), (-9)

∴ (-11) +(-9) = -20

Question 2. Let’s add the following

1. (+9) + (+2)
Solution:

(+9) + (+2) = + 11

2. (+11) – (+ 5)
Solution: (+11) +(+5) = +16

3. (+27) + (-11)
Solution: (+27)+ (-11) = +16

4. (-25) + (+6)
Solution: (-25) + (+6) = -19;

5. (-5) + (+9)
Solution: (—5) + (+9) = +4

6. (+13)+ (-13)
Solution: (+13) + (-13) = 0

Question 3. Let us simplify

1. (+13) + (+12) + (-10)
Solution: (+13) + (+12) + (-10) = +25 – 10 = (+15)

2. (+31) + (+13) + (-16)
Solution: (+31)+ (+13)+ (-16)

= +44 + (-16)

= 44 – 16 = (+28)

Class 6 Maths Solutions WBBSE

3. (+25) + (-16) + (+ 2)
Solution: (+25) +(-16) +(+2)

= (+9) + (+2)

= (+11)

4. (-11) + (+18) + (-16)
Solution: (-11)+ (+18)+ (-16)

= (+7)+ (-16)

= (-9)

Question 4. Let’s add the following

1. (-2), (-10), (+21)
Solution: (-2)+ (-10)+ (+21)

= (-12) + (+21)

= (+9)

2. (-18), (-7), (-2)
Solution: (-18) + (-7) + (-2)

=(-25)+ (-2)

= (-27)

Class 6 Maths Solutions WBBSE

3. (+10), (-8), (-10)
Solution: (+10) + (-8) + (-10)

= (+2) + (-10)

= (-8)

4. (-8), (-10), (+2)
Solution: (-8) + (-10) + (+2)

= (-18) + (+2)

= (-16)

5. (-19),(-9),(+5)
Solution: (-19) + (-9) + (+5)

= (-28) + (+5)

= (-23)

6. (+20), (-9), (-6)
Solution: (+ 20) + (-9) + (-6)

= (+11) + (-6)

= (+5)

7. (-14), (-12), (+ 21)
Solution: (-14) + (-12) + (+21)

= (-26) + (+21)

= (-5)

8. (-13), (+7), (-2)
Solution: (-13) + (+7) + (-2)

= (-6) + (-2)

= (-8)

9. (+15), (-9), (-5)
Solution: (+15) + (-9) + (-6)

= (+6) + (-6)

= 0

WBBSE Math Solutions Class 6 Chapter 16 Concept Of Directed Numbers And Number Line  Exercise 16.2

Question 1. Let’s do it

1. (- 6) – (+2) = _____
Solution: (-6) – (+2)

= -6-2 = —8

2. (-12) — (+12) = ______
Solution: (-12) – (+12)

= -12-12 = -24

3. (+11)-(+3) = ______
Solution: (+11)-(+3)

= 11-3 = +8

4. (-7) – (+8) = _____
Solution: (-7) – (+8)

= -7-8 = -15

5. (+20) – (-7) = ______
Solution: (+20) – (-7)

= 20 + 7 = 27

6. (-18)-(-8) = _________
Solution: (-18)-(-8)

= -18 + 8

= -10

7. (- 9) – (-9) = _______
Solution: (- 9) – (- 9)

= -9+9

= 0

WBBSE Math Solutions Class 6

8. (+ 13)- (-7) = ________
Solution: (+ 13)-(-7)

= 13 + 7 = 20

Question 2. Let’s complete the table given below

Solution:

Question 3. Let us mark (√) for the correct statement and (x) for wrong statement:

1. There are definite numbers of positive whole numbers.
Solution: There are definite numbers of positive whole numbers. [√]

2. 5.3 is a natural number.
Solution: 5.3 is a natural number. [X]

3. – 2.1 is a negative whole number.
Solution: -2.1 is a negative whole number. [x]

4. There is no existence of biggest whole number.
Solution: There is no existence of biggest whole number. [√]

WBBSE Math Solutions Class 6

Question 4. 1. (+14) — (+16)
Solution: (+14)-(+16)

= (+14)+ (-16)

= 14-16 = – 2

2. (+25) – (+21)
Solution: (+ 25)-(+21)

= (+ 25) + (-21)

= 25-21 = 4

3. (+ 34) – (-19)
Solution: (+ 34) – (-19)

= (+34)+ (+19)

= 34 + 19

= +53

4. (-15)-(-27)
Solution: (-15)-(-27)

=(-15)+(+27)

= -15 + 27

= +12

5. (-25) -(+13)
Solution: (-25) -(+13)

= (-25) + (-13)

= -25-13

= -38

6. (-16)-(-10)
Solution: (-16)-(-10)

= (-16)+ (+10)

= -16 + 10

= – 6

7. (+ 31) — (— 12)
Solution: (+31)-(-12)

= (+31)+ (+12)

= +31+12 = +43

8. (—31) — (—45)
Solution: (-31)-(-45)

= (-31)+ (+45)

= – 31 + 45 = +14

9. (-21)-(+21)
Solution: (-21)-(+21)

= (-21)+ (-21)

= -21-21

= -42

WBBSE Math Solutions Class 6

Question 5. Let’s put >, < or = in respective blank spaces:

1. (+13) + (- 8) _______ (+3) – (-2)
Solution: L.H.S. = (+13) + (-8)

= 13-8 = 5

R.H.S. = (+ 3) – (-2)

= 3 + 2 = 5

∴ (+13) + (-8) [ = ] (+3) – (-2)

2. (-12)-(-10) _______ (-9) +(+3)
Solution: L.H.S. = (-12)-(-10)

= -12 + 10 = – 2

R.H.S. = (-9) + (+3)

= -9 + 3

= -6

∴ (-12) – (-10) [ > ] (-9) + (+3)

3. (+35) – (-5) _____ (- 24) – (-64)
Solution: L.H.S. = (+ 35) – (-5)

= 35 + 5 = 40

R.H.S. = (-24)-(-64)

= – 24 + 64 = 40

∴ (+35) – ( -5) [ = ] (-24) – (-64)

Class 6 Math WBBSE Solutions

4. (-18) – (+6) ______ (-18) – (-6)
Solution: L.H.S. = (-18) – (+6)

= -18-6 = -24

R.H.S. = (-18) -(-6)

= -18 + 6 = -12

∴ (-18) (+ 6) [ < ] (—18) — (—6)

5. (-45) – (-52) _______ (-52) – (-45)
Solution: L.H.S. = (-45) – (-52)

= -45 + 52 = + 7

R.H.S. = (-52)-(- 45)

= – 52 + 45 = —7

∴ (-45) – (—52) [ > ] (-52) – (-45)

6. (+25) -(-19) _______ (-25) -(+19)
Solution: L.H.S. = (+25)-(-19)

= +25 + 19 = + 44

R.H.S. = (-25)-(+19)

= -25-19 = -44

∴ (+25) — (—19) [ > ] (—25) – (+19)

Question 6. Let’s put number in blank spaces:

1. (-3) + ________ = 0
Solution: (—3) + [+3] = 0

2. (+16) + ________ = 0
Solution: (+16) + [-16] = 0

3. (-9) + _______ = (-15)
Solution: (-9) + [-6] = – 15

4. _____ + (-7) = (-10)
Solution: [-3] +(-7) = (-10)

Question 7. Let’s simplify:

1. (-5) + (opposite number of -7) – (-5)
Solution: (-5) + (+7) + (5)

= + 7

2. 12 – (-3) + (opposite number of +6)
Solution: 12 + 3 + (-6)

= 15-6 = 9

3. 15 – (+4) + (opposite number of +9)
Solution: 15 – 4 + (-9)

= 15-4-9 = 15-13 = 2

4. (opposite number of +20) – (opposite number of -7) – (-8)
Solution: (-20) – (+7) + 8

= -20 – 7 + 8 = – 27 + 8

= -19

Question 8. Let’s find what must be added to the first to get the second:

1. -7,-12
Solution: -12-(-7)

= -12 + 7 = – 5

2. 24, – 32
Solution: -32 – (+24)

= – 32 – 24

= -56

3. -17,12
Solution: 12-(-17)

= 12+17

= 29

Class 6 Math WBBSE Solutions

4. 16, 0
Solution: 0 – (+ 16)

= 0-16

= -16

5. 25,-42
Solution: -42 – (+25)

= -42 -25 = -67

Question 9. Let’s find what must be added to the first to get the second:

1. (+7), (+2)
Solution: (+2) – (+7)

= 2-7 = -5

.2. (+7), (-2)
Solution: (-2)-(+7)

= -2-7 = —9

3. (-7), (+2)
Solution: (+2)-(-7)

= 2 + 7 = 9

4. (-7), (-2)
Solution: (-2)-(-7)

= -2 + 7

= + 5

Question 10. Let’s verify the commutative property of addition for the following:

1. (+5), (+3)
Solution: (+5) + (+3) = +8,

Again, (+3) + (+5) = +8 (+5) + (+3) = (+3) + (+5)

2. (+ 5), (-3)
Solution: (+5) + (-3) = +2,

Again, (-3) + (+5) = + 2 (+5) + (-3) = (-3) + (+5)

3. (-5), (+3)
Solution: (-5) + (+3) = -2,

Again, (+3) + (-5) = – 2 (-5) + (+3) = (+3) + (-5)

4. (-5), (-3)
Solution:

(-5) + (-3) = -8,

Again (-3) + (-5) = -8

(-5) + (-3) = (-3) + (-5)

Question 11. Let’s verify the associative property of addition for the following:

1. (+5), (+3), (+2)
Solution: (+5), (+3), (+2)

= {(+5) + (+3)} + (+2)

= (+8) + (+2)

= (+10)

and, = (+5) + {(+3) + (+2)}

= +5 + 5 = (+10)

{(+5) + (+3)} + (+2)

= (+5) + {(+3) + (+2)}

2. (+5), (-3), (+2)
Solution: (+5), (-3), (+2)

= {(+5) + (-3)) + (+2)

= (+2) + (+2) = (+4)

and, (+5) + {(-3) + (+2)}

= (+5) + (-1) = (+4)

= {(+ 5) + (-3)} + (+2)

= (+5) + {(-3) + (+2)}

Class 6 Math WBBSE Solutions

3. (-5), (-3), (+2)
Solution: (-5), (-3), (+2)

{(-5) + (-3)} + (+2)

= (-8) + (+2) = -6 and, (—5) + {(—3) + (+2)}

= (—5) + (—1) = -6

{(-5) + (-3)} + (+2)

= -5 + {(-3) + (+2)}

4. (—5), (—3), (-2)
Solution: (-5), (-3), (-2)

{(- 5) + (-3)} + (-2)

= (-8) + (-2) = (-10)

and, (-5) + {(-3) + (-2)}

= (- 5) + (- 5) = (-10)

{(-5) + (-3)} + (-2)

= (-5) + {(-3) + (-2)}

 

Class 6 Math Solutions WBBSE Chapter 15 Determination Of Area And Perimeter Exercise 15

Let’s us draw, observe and write what I know

Question 1. I found my brother’s first geometric shape model is a triangle.
Solution:

Its perimeter is = _____ cm + _______ cm + ______ cm = 3 x 12 cm

To put a border around this geometric model, we need 36 cm of colored paper.

Solution:

Perimeter of the 1 st figure = 12 cm + 12 cm + 12 cm = 36 cm

Question 2. Let me find the perimeter of the second geometric figure. The perimeter of the second geometric figure = _____ cm + ________ cm + _________ cm + _________ cm = _______ cm. I shall need ______ cm of colored paper to put a border on it.

Solutions:

Perimeter of the 2nd figure

= 20 cm + 22 cm + 22 cm + 18 cm = 82 cm

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 3. The perimeter of the third geometric shape is = ________ cm + _______ cm + _____ cm + ______ cm + ________ cm + _____ cm = ________ cm

Solution:

Perimeter of the 3rd figure = 6 cm + 6 cm + 6 cm + 6 cm + 6 cm + 6 cm = 36 cm

Class 6 Math Solutions WBBSE

Question 4. Perimeter of the fourth geometric figure. = _____ cm + _____ cm + ______ cm + ______ cm + ______ cm + _______ cm + _______ cm + ______ cm + = _____ cm

Solution:

Perimeter of the 4th figure

= 5 cm + 13 cm + 30 cm + 13 cm + 5 cm + 7 cm + 20 cm + 7 cm

= 100 cm

Question 5. Perimeter of fifth geometric figure = _____ cm. + _______ cm + _____ cm + ________ cm + ______ cm + _________ cm + _______ cm + _______ cm = _____ cm

Solution:

Perimeter of the 5th figure

= 16 cm + 4 cm + 6 cm + 10 cm + 4 cm + 10 cm + 6 cm + 4 cm = 60 cm

WBBSE Math Solutions Class 6

Question 6. Let’s find the perimeter of the sixth geometric figure.

Solution:

Perimeter of the 6th figure

= 4 cm + 9 cm + 11 cm + 9 cm + 4 cm + 22 cm + 4 cm + 9 cm + 11 cm + 9 cm + 4 cm + 22 cm = 118 cm.

Hands-on trial: Now, we shall join points on graph paper to form different geometric figures and try to find the space occupied by these figures.

We pasted the graph paper on a cardboard. We formed different geometric figures on it by joining points and let’s try to find the area enclosed by them.

Example: Let’s fill up the data and let’s measure the area:
Solution:

 

Class 6 Math Solutions WBBSE Chapter 14 Concept Of Line Segment Ray And Point

Let’s us draw, observe, and write what I know

My friends and me draw pictures, observe and identify the things we know, let’s note down

Example 1. Figure (1) is the picture of a ____.
Answer:

Figure (1) is a picture of a cottage or house.

Example 2. In the picture of the house we can find many ___ [Straight lines or Angular points]
Answer:

In the picture of the house we can find many Angular points.

Read and Learn More WBBSE Solutions For Class 6 Maths

Example 3. Let’s mention the four angular points — ______, ____, _____, ______ and mark them with ‘O’ in the picture.
Answer:

The four angular points are A, B, C, and D.

Example 4. Again, we find several ____[Ray/Line segment] in the picture of the house. From Figure (1) let us find and name 4 of the line segments ____, ___, _____, and _____
Answer:

Again, we find several line segments in the picture of the house. From Figure (1) 4 names of the line segments are AB, BC, CD, and GD.

Example 5. We find the line segments DE and DC are intersecting at ______.
Answer:

We find the line segments DE and DC intersect at D.

Class 6 Math Solutions WBBSE

Example 6. Again, in Figure (1) ______ and ____ line segments have intersected at E.
Answer:

Again, in Figure (1) DE and EF line segments have intersected at E

Example 7. But, we see the 2 line segments DE, CF, and the line segments DC and _____ are on the same plane but they will never intersect each other, no matter how far they be produced on either side.
Answer:

But, we see the 2 line segments DE, CF, and the line segments DC and EF are on the same plane but they will never intersect each other, no matter how far they be produced on either side.

Example 8. The line segments DE and DC are on the same plane and intersect each other at ____, hence these lines are called _____(Intersecting/Parallel).
Answer:

The line segments DE and DC are on the same plane and are intersecting each other at D, hence these lines are called Intersecting.

Example 9. The line segments DE and CF are on the same plane but will never meet, no matter how far they be produced. Hence, these line segments are (Intersecting/Parallel).
Answer:

The line segments DE and CF are on the same plane but will never meet, no metter how far they are produced. Flence these line segments are parallel.

Class 6 WBBSE Math Solutions Chapter 14 Concept Of Line Segment Ray And Point Exercise 14

Question 1. From the picture (2), let’s identify 4 angular points and name them _______, _________, ________, ______
Solution:

From the picture (2), let’s identify 4 angular points and name them I, J, K, L.

Question 2. Let’s identify and write the four line segments which are named in the picture (2) _______, ______ and ______
Solution:

Let’s identify and write the four line segments which are named in the picture (2) SP, PQ, QR, and SR.

Question 3. From picture (2), let’s identify two pairs of intersecting line segments on a plane and find the points at which they intersect.
Solution:

1. SP, PQ are two pairs of intersecting line segments at P as intersecting point.
2. SP, SR are two pairs of intersecting line segments at S as an intersecting point.
3. SR, QR are two pairs of intersecting line segments at R as an intersecting point.
4. QR, PQ are two pairs of intersecting line segments at Q as an intersecting point.

Question 4. In picture (2), let’s find two pairs of parallel line segments on a plane which are already named in the figure.
Solution:

PQ || SR and SP || QR are two pairs of parallel line segments on a plane.

Question 5. From the picture (3) — let’s identify and write 3 intersecting points and 4 line segments already named in the picture.
Solution:

3 intersecting points: M, N, O.

4 line segments: MN; NO; OP and PM.

Class 6 Maths Solutions WBBSE Chapter 14 Concept Of Line Segment Ray And Point 14.1

Question 1. Let’s draw 6 concurrent straight lines and name them.
Solution:

The 6 concurrent straight lines are \(\overrightarrow{A B}, \overrightarrow{C D}, \overrightarrow{E F}, \overrightarrow{G H}, \overrightarrow{I J}, \ \overrightarrow{K L}\)

Question 2. 5 non-collinear points are to be drawn and find how many straight lines can be drawn through them.
Solution:

A, B, D, and E, are 5 non-collinear points

Through the point A, we can draw 4 straight lines.

Through the point B, we can draw 3 straight lines.

Through the point C, we can draw 2 straight lines.

Through the point D, we can draw 1 straight line

Question 3. Let’s draw 5 points which are collinear.
Solution:

The points A, B, C, D, and E are 5 collinear points.

WBBSE Math Solutions Class 6 Chapter 14 Concept Of Line Segment Ray And Point 14.2

Question 1. Let’s identify the points of intersection in the following figures and note them down.

Solution:

1. D, E, and F are the points of intersection.
2. P, Q, R, S, and T are the points of intersection.
3. A, B, C, and D are the points of intersection.
4. K, L, M, N, and O are the points of intersection.

Question 2. In the figures given below, let’s identify line segments and rays and note them down.

Solution:

1. Line segments = \(\overline{X Y}, \overline{X Z}\)

Rays = \(\overrightarrow{X Y}, \overrightarrow{X Z}\)

2. Line segments = \(\overline{\mathrm{AD}}, \overline{\mathrm{AB}}, \overline{\mathrm{BC}}\)

Rays = \(\overrightarrow{A D}, \overrightarrow{B C}\)

3. Line segments = \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CD}}, \overline{\mathrm{DE}}\)

Rays = \(\overrightarrow{B A}, \overrightarrow{D E}\)

4. Line segments = \(\overline{\mathrm{AB}}, \overline{\mathrm{CD}}\)

Rays = \(\overrightarrow{O B}, \overrightarrow{O C}\)

Question 3.

1. What are these three points X, Y, and Z called?
2. How many line segments are formed with these three points?

Solution:

The points X, Y, and Z are called collinear points.

Three line segments are formed with these points.

WBBSE Math Solutions Class 6

Question 4. From the figure:

1. Let’s find and write three pairs of parallel lines.
2. Let us find and write three pairs of intersecting lines.
3. Let us find and write six-line segments.

Solution:

1. \((\stackrel{\leftrightarrow}{A B}, \overleftrightarrow{C D}),(\overleftrightarrow{C D}, \overleftrightarrow{E F}),(\stackrel{\leftrightarrow}{A B}, \overleftrightarrow{E F})\)

2. \((\stackrel{\leftrightarrow}{\mathrm{PQ}}, \stackrel{\leftrightarrow}{\mathrm{MN}}) ;(\stackrel{\leftrightarrow}{\mathrm{PQ}}, \overleftrightarrow{\mathrm{G}-1}) \&(\stackrel{\leftrightarrow}{\mathrm{MN}}, \stackrel{\leftrightarrow}{\mathrm{RS}})\)

3. \((\overline{\mathrm{PB}}, \overline{\mathrm{AC}}, \overline{\mathrm{CE}}, \overline{\mathrm{BD}}, \overline{\mathrm{DF}}, \& \overline{\mathrm{AB}})\)

Question 5. From the figure:

1. Let’s find the points of intersection.
2. Let’s write all sets of collinear points separately.
3. Let’s write the line segments separately.
4. Let’s write the line segments that are concurrent.

Solution:

1. A, F, B, D, C, E and 0.
2. (A, F, B); (A, O, D), (A, E, C); (B, D, C); (C, 0, F), (B, O, E).
3. AB, BC, CA, AF, FB, AB, AD, OD, BO, BE, OE, CO, CF, OF, AE EC BD DC
4. AD, BE and CF.

Question 6. Let us put (√) for correct and (x) for wrong answers

1. On the line segment \(\overrightarrow{\mathrm{YW}}\), Z and W are coliinear.

2. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{WV}}\) are the same rays.

3. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{ZX}}\) are same rays.

4. On the ray \(\overrightarrow{\mathrm{YX}}\), Z is a point.

WBBSE Math Solutions Class 6

Solution:

1. On the line segment \(\overrightarrow{\mathrm{YW}}\), Y, Z and W are coliinear. (√)

2. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{WC}}\), \(\overrightarrow{\mathrm{WV}}\) WV are the same rays- (√)

3. \(\overrightarrow{\mathrm{ZV}}\) and \(\overrightarrow{\mathrm{ZX}}\) are the same raYs- (X)

4. On the ray \(\overrightarrow{\mathrm{YX}}\), Z is a point. (X)

Question 7. Let’s try and find the answers

1. How many straight lines can be drawn through one fixed point?
Solution: Infinite

2. How many straight lines can be drawn through two fixed points?
Solution: One

3. How many line segments can be drawn through three non-collinear points?
Solution: Three

4. How many endpoints are there in a line segment \(\overline{\mathrm{AB}}\)?
Solution: A, B

5. How many endpoints are there in ray \(\overrightarrow{\mathrm{AB}}\)?
Solution: A, B

6. Straight line, line segment, and ray — of these three which one has a fixed length?
Solution: Line segment

7. Are the rays \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{BA}}\) same?
Solution: Not Same

8. Are the line segments \(\overrightarrow{\mathrm{AB}}\) and \(\overrightarrow{\mathrm{BA}}\) equal? In what way are they equal?
Solution: Yes

9. What is the maximum number of points at which two line segments can meet?
Solution: One

WBBSE Math Solutions Class 6

10. Let’s find the maximum number of points at which three non-concurrent lins can intersect.
Solution: Three

Question 8. Let’s draw ourselves

1. \(\overline{\mathrm{PQ}}\) and \(\overline{\mathrm{RS}}\) are two line segments interseceting at O.

2. Using scale, let us draw \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) and \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) as two Parallel lines

3. Let’s draw a ray \(\overrightarrow{\mathrm{MN}}\) on which S is a point.

4. Let’s draw two line segments AC and DC meeting at C.

Solution:

1. PQ and RS are two line segments interecting at O.
2. AB and CD are two parallel line segments.
3. MN is a ray on which S is a point.
4. AC and CD are two line segments meeting at C.

Question 9. From the figure given below, let’s measure the lengths with scale and fill in the blank spaces accordingly.

1. \(\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}\)=____ \(\mathrm{cm} \cdot=\overline{\mathrm{PR}}\)

2. \(\overline{\mathrm{QR}}+\overline{\mathrm{RS}}\) = _____ \(\mathrm{cm}\) = _____

3. \(\overline{\mathrm{PS}}\) = ____ + \(\overline{\mathrm{QR}}\) + _____

4. \(\overline{\mathrm{PR}}-\overline{\mathrm{QR}}\) = _______ cm = _______

5. PR – PQ = ______ cm

6. QS – QR = _______ cm.

7. QS – RS = ______ cm.

Solution:

1. \(\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}=(3+3) \mathrm{cm} \cdot=\overline{\mathrm{PR}}=6 \mathrm{~cm}\)

2. \(\overline{\mathrm{QR}}+\overline{\mathrm{RS}}=(3+3) \mathrm{cm} .=\overline{\mathrm{QS}}=6 \mathrm{~cm}\)

3. \(\overline{\mathrm{PS}}=\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}+\overline{\mathrm{RS}}\)

4. \(\overline{\mathrm{PR}}-\overline{\mathrm{QR}}=3 \mathrm{~cm} .=\overline{\mathrm{PQ}}\)

5. \(\mathrm{PR}-\mathrm{PQ}=(6-3) \mathrm{cm}=3 \mathrm{~cm}\)

6. \(\mathrm{QS}-\mathrm{QR}=(6-3) \mathrm{cm}=3 \mathrm{~cm}\)

7. \(\mathrm{QS}-\mathrm{RS}=(6-3) \mathrm{cm}=3 \mathrm{~cm}\)

Class 6 Math Solutions WBBSE Chapter 13 Data Handling And Analysis Exercise 13

Example: Like every year, this year the Physical Education teacher of our school took measurements (in cm) of the height of the students of class 6 who would be taking part in school sports. The data obtained is given below

The shortest height = 120 and the tallest height = 127.

Question 1. In a class test of 15 marks, I prepare a list showing marks obtained by 20 students. Let’s write down these marks by giving tally marks and prepare a frequency distribution chart. 9, 8, 6, 10, 2, 1,15, 12, 8, 6, 9, 2, 8, 5, 9, 10, 5, 9, 10, 8
Solution:

Frequency Distribution Table

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 2. In Jahanara’s school classes were held for 22 days only this month. The number of students attending classes on these 22 days are given below. 30, 28, 34,29,25,30,28,26,29,30, 22,25,26,29, 30, 31,21,27, 25,13, 32, 28. Using the above raw data, let’s prepare a frequency distribution chart with tally marks.

Class 6 Math Solutions WBBSE
Solution:

Frequency distribution table

Question 3. Given below is the data showing what fruits my 20 friends like to have. Let me draw a bar graph based on this data.
Solution:

Question 4. I prepared a raw data showing the number of students present in the class for 6 days of this week. From this raw data, I prepare a list using tally marks. Let’s write down from the list the day of week on which least number of students are present.
Solution:

I prepare a raw data showing number of students present in the class for 6 days of the week.

Class 6 Math Solutions WBBSE

Frequency distribution table

Question 5. I write down the weight (kg) of 30 students of class VI of Soham’s school. 32, 32, 37, 34, 37, 35, 35, 36,37, 39, 40, 36, 37, 36, 33,31,32,36, 37,38, 40, 34, 36, 34, 35, 33, 34, 35, 32, 35 Using the above raw data, let’s prepare a frequency distribution chart.
Solution:

Weight (kg) of 30 students of class 32, 32, 37, 34, 37, 35, 35, 36, 37, 39, 40, 36, 37, 36, 33, 31,32, 36, 37, 38, 40, 34, 36, 34, 35, 33, 34, 35, 32, 35

Frequency Distribution Table

Class 6 Math Solutions WBBSE

Question 6. From a survey conducted on 150 students of our school, it is seen how many students like to study a special subject. The raw data from the survey is given below
Solution:

Question 7. Ram da has a shop selling bags in Haidar Para. Ram da himself makes the bags. I prepare a list of bags sold from the shop this week.

Let take a scale of my choice and draw a bar diagram.
Solution:

Question 8. I have prepared a bar diagram showing the number of students appearing at the Madhymik Examination each year during the five years.

1. I have prepared a set of questions from the bar diagram and let’s answer the questions.
2. Let us see in which year a maximum number of students have sat for the exam.
3. Let us see in which year least number of students have sat for the exam.
4. Let see how many more students have appeared for the examination in 2011 than in 2010.
5. In 2010, let us see how many less students have appeared for the exam than in 2009.
6. Let’s see how many total students have sat for examination between 2008 and 2010.

Class 6 WBBSE Math Solutions

Solution:

1. 2012
2. 2010
3. 120-100 = 20
4. 100-90 = 10
5. 110 + 100 + 90

 

Class 6 Math Solutions WBBSE Chapter 11 Geometrical Concepts Related To Regular Solids Exercise 11

Question 1. Let’s place a tetrahedron and place the face of a hemisphere on an exercise book and mark the boundary with a pencil. Let’s observe the shapes and write these names.
Solution:

Question 2. Let me try and find a solid which has only one surface.
Solution:

Name of solid: Football (sphere)

Surface: Curved surface

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 3. Let me write the name of such a soild that has one curved surface and two plane surfaces.
Solution:

Name of solid: Glass(cylinder)

Surface: One curved surface and two plane surfaces

Class 6 WBBSE Math Solutions

Question 4. Let me draw such a solid which has one curved and one plane surface.
Solution:

Name of solid: Cone

Surface: One plane and one curved surface

Question 5. With 6 plane surfaces, let me make a solid figure and write my observations for the solid made.
Solution:

Name of solid: Box (cuboid)

Surface: Six-plane surface

Class 6 WBBSE Math Solutions Chapter 11 Geometrical Concepts Related To Regular Solids Exercise 11.1

Question 1. Fill in the blank spaces given in the chart below

Solution:

Question 2. Let us identify the solids and write their names: Pyramid, Tetrahedron, Cube, Cuboid

Solution:

Question 3. Let us choose the right option

1. Which of these is not cuboid?

1. Brick
2. Dice
3. Book
4. Bottle

Answer: 4. Bottle

2. Which of these is of cylindrical shape?

1. Eraser
2. Duster
3. Milk powder can
4. Ball

Answer: 3. Milk powder can

WBBSE Math Solutions Class 6

3. A solid having one surface is

1. Dice
2. Pencil
3. Exercise Book
4. Ball

Answer: 4. Ball

4. Observing the figures find out which one will not make a cube

Answer: 2.

 

 

Class 6 Math Solutions WBBSE Chapter 10 Recurring Decimal Numbers Exercise 10

Question 1. Identify which is a Terminating and Non-terminating decimal number

⇒ \(\frac{1}{3}, \frac{7}{9}, \frac{1}{6}, \frac{7}{11}, \frac{11}{12}, \frac{15}{37}, \frac{2}{15}, \frac{49}{63}, \frac{11}{37}, \frac{12}{70}, \frac{1}{2}, \frac{9}{45}, 11 \frac{10}{12}, \frac{6}{13}\)

Solution:

Read and Learn More WBBSE Solutions For Class 6 Maths

These are non-terminating decimals

These are non-terminating decimals

These are terminating decimals

Question 2. Identify which is Mixed recurring and pure recurring decimal number.

⇒ \(\frac{5}{6}, \frac{34}{510}, \frac{1}{15} \frac{52}{41}, \frac{15}{13}, \frac{4}{7}, \frac{6}{7}, \frac{8}{9}, \frac{5}{11}, \frac{7}{11}, \frac{3}{13}, \frac{4}{15}, \frac{13}{15}\)

Class 6 Math Solutions WBBSE

Solution:

These are mixed recurring decimals

These are mixed recurring decimals

Class 6 Math Solutions WBBSE

These are mixed recurring decimals

Question 3. Let’s directly convert the following pure recurring decimal numbers to corresponding fractions:

1. \(0 . \dot{3}\)
Solution:

= \(\frac{3}{9}\)

2. \(0 . \dot{8}\) = ______
Solution:

= \(\frac{8}{9}\)

3. \(0 . \ddot{1} \dot{8}\) = _______
Solution:

= \(\frac{18}{99} = \frac{2}{11}\)

4. \(0 . \dot{2} \dot{7}\) = _______
Solution:

= \(\frac{27}{99}=\frac{3}{11}\)

5. \(0 . \dot{1} 6 \dot{2}\) _____
Solution:

= \(\frac{162}{999}=\frac{18}{111}\)

6. \(0 . \dot{2} 9 \dot{7}\) = ______
Solution:

= \(\frac{297}{999}=\frac{33}{111}\)

7. \(0 . \dot{5} 64 \dot{3}\) = ________
Solution:

= \(\frac{5643}{9999}=\frac{627}{1111}\)

Question 4. Let’s express the following pure recurring decimal numbers in fractions

⇒ \(0 . \dot{5}, 0 . \ddot{4} \dot{5}, 0 . \ddot{5} \dot{3}, 0 . \ddot{1}, \quad 0 . \dot{5} \dot{1}\)

Solution:

⇒ \(0 . \dot{5}=\frac{5}{9} ; \quad 0 . \dot{4} \dot{5}=\frac{45}{99}=\frac{5}{11} ; \quad 0 . \dot{5} \dot{3}=\frac{53}{99}\)

⇒ \(0 . \ddot{12}=\frac{12}{99}=\frac{4}{33} ; \quad 0 . \dot{5} 1 \dot{2}=\frac{512}{999}\)

Class 6 Maths Solutions WBBSE

Question 5. Convert the following mixed recurring decimal numbers into fractions:

1. \(0.2 \dot{7}\)
Solution:

= \(\frac{27-2}{90}\)=\(\frac{25}{90}\) = \(\frac{5}{18}\)

2. \(0.08 \ddot{1}\)
Solution:

= \(\frac{81}{990}=\frac{9}{110}\)

3. \(2.8 \dot{2}\)
Solution:

= \(\frac{282-28}{90}=\frac{254}{90}\)

= \(\frac{127}{45}\)

4. \(0.2 \ddot{7} \dot{2}\)
Solution:

= \(\frac{272-2}{990}=\frac{270}{990} =\frac{3}{11}\)

5. \(3.4 \ddot{3} \dot{2}\)
Solution:

= \(\frac{3432-34}{990}=\frac{3398}{990} =\frac{1699}{495}\) .

Class 6 Maths Solutions WBBSE Chapter 10 Recurring Decimal Numbers Exercise 10.1

Question 1. By actual division let us find if the quotients are terminating decimal numbers or recurring decimal numbers

1. A 7 m long ribbon is divided into 8 equal pieces, let’s find the length of each piece.
Solution:

7m long ribbon is divided into 8 equal pieces.

∴ Length of each piece = \(\frac{7}{8}\) m.

= 0.875 m (T erminating)

2. Let’s find the weight of each packet of sugar when 11 kg sugar is divided equally in 12 packets.
Solution:

11 kg sugar is divided in 12 packets.

∴ Each packet contains \(\frac{11}{12}\)kg.

= 0.9166 kg

= 0.916 kg (Recurring)

3. Let’s calculate the amount of water each bottle can hold when 12 litres water is poured into 7 equal-sized bottles.
Solution:

The amount of water in each bottle = \(\frac{12}{7}\) litre.

= 1.7142857

= 1.71428 5 litre (Recurring)

WBBSE Math Solutions Class 6

4. If 15 trees are planted along the side of a 24 m long road including its two ends, let’s find the distance between two consecutive trees.
Solution:

The distance between two consecutive trees

= \(\frac{24}{15}\) m= \(\frac{8}{5}\) m = 1.6 m. (Terminating)

Question 2. Express the following fractions in decimal fractions and identify the terminating and recurring decimal numbers:
Solution:

Question 3. Let’s identify the pure and mixed recurring decimal numbers and convert them to fractions:

WBBSE Math Solutions Class 6

1. \(0 . \dot{5} \dot{4}\)
Solution:

= \(\frac{54}{99}=\frac{6}{11}\)

2. \(0 . \ddot{3} \dot{9}\)
Solution:

= \(\frac{39}{99}=\frac{13}{33}\)

3. \(0.0 \dot{2} \dot{4}\)
Solution:

= \(\frac{24}{990}=\frac{4}{165}\)

4. \(0 . \dot{6} \dot{9}\)
Solution:

= \(\frac{69}{99}=\frac{23}{33}\)

5. \(0 . \dot{9} \dot{3}\)
Solution:

= \(\frac{93}{99}=\frac{31}{33}\)

6. \(0.0 \ddot{8} \ddot{1}\)
Solution:

= \(\frac{81}{990}=\frac{9}{110}\)

7. \(0.27 \dot{2}\)
Solution:

= \(\frac{272-27}{900}=\frac{245}{900}\)

= \(\frac{49}{180}\)

WBBSE Math Solutions Class 6

8. \(0 . \dot{5} 1 \dot{3}\)
Solution:

= \(\frac{513}{999}=\frac{19}{37}\)

9. \(0 . \dot{14} \dot{4}\)
Solution:

= \(\frac{144}{999}\)

10. \(3: 4 \ddot{3} \dot{2}\)
Solution:

= \(\frac{3432-34}{990}=\frac{3398}{990}\)

= \(\frac{1699}{495}=3 \frac{214}{495}\)

11. \(7.0 \ddot{2} \dot{8}\)
Solution:

= \(\frac{7028-70}{990}=\frac{6958}{990}\)

= \(\frac{3479}{495}=7 \frac{14}{495}\)

12. \(0 . \dot{3} 7 \dot{5}\)
Solution:

= \(\frac{375}{999}\)=\(\frac{125}{333}\)

13. \(0 . \dot{29} \dot{1}\)
Solution:

= \(\frac{291}{999}=\frac{97}{333}\)

14. \(3 . \dot{200}\)
Solution:

= \(\frac{3205-3}{999}\)=\(\frac{3202}{999}\)

15. 0.375
Solution:

= \(\frac{375}{999}=\frac{125}{333}\)

16. \(0 . \dot{29 \dot{1}}\)
Solution:

= \(\frac{291}{999}=\frac{97}{333}\)

WBBSE Math Solutions Class 6

17. \(3 . \dot{20} \dot{5}\)
Solution:

= \(\frac{3205-3}{999}=\frac{3202}{999}\)

= \(3 \frac{205}{999}\)

18. \(0 . \dot{0} 12 \dot{1}\)
Solution:

= \(\frac{121}{9999}=\frac{11}{909}\)

Pure: 1, 2, 4, 5, 8, 9, 12, 13, 14, 15

Mixed: 3, 6, 7, 10, 11

Question 4. Let’s arrange the following in ascending order:

1. \(0 . \dot{3}, 0 . \dot{1}, 0 . \dot{1}\)
Solution:

⇒ \(0 . \dot{3}=0.333\)

⇒ \(0 . \dot{16}=0.166\)

⇒ \(0 . \dot{1}=0.111\)

In ascending order: 0.111 ; 0.166; 0.333

i.e., \(0 . \dot{1}, 0 . \dot{1}, 0 . \dot{3}\).

2. \(0 . \dot{6} \dot{3} ; \frac{3}{4}, \frac{5}{6}\)
Solution:

⇒ \(0 . \ddot{6} \dot{3}=0.6363\)

⇒ \(\frac{5}{6}=0.8333\)

⇒ \(\frac{3}{4}=0.7500\)

In ascending order: 0.6363; 0.7500; 0.8333

i.e., \(0 . \dot{6} 3 ; \frac{5}{6}, \frac{3}{4}\)

3. \(0.5 \dot{3} ; \frac{2}{25} ; \frac{16}{75}\)

⇒ \(0.5 \dot{3}=0.533\)

⇒ \(\frac{2}{25}=0.80\)

⇒ \(\frac{16}{75}=0.213\)

In ascending order: 0.080; 0.213,0.533

i.e., \(\frac{2}{25}, \frac{16}{75}, 0.5 \dot{3}\)

4. \(0.91 \dot{6}, \frac{1}{121} ; \frac{3}{44}\)

⇒ \(0.916=0.916000\)

⇒ \(\frac{1}{121}\)=0.008264

⇒ \(\frac{3}{44}=0.068181\)

In ascending order: 0.008264; 0.068181; 0.916000

i.e., \(\frac{1}{121} ; \frac{3}{44} ; 0.916\)

Class 6 Math Solutions WBBSE Chapter 12 HCF And LCM Of Three Numbers Exercise 12

Question 1. Let’s find the greatest number which will divide both 564 and 630 to keep the remainder 3 in both cases.
Solution:

564 – 3 = 561

and 630-3 = 627

∴ The greatest number is the H.C.F. of 561 and 627.

∴ H.C.F. = 3 x 11 =33

Question 2. Let’s find the greatest number which divides 78,182 and 195 and keeps number remainder.
Solution: 78; 182; 195

∴ Required H.C.F = 13

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 3. Mill bought few exercise books for Rs. 80.50 p. Her brother bought few more for Rs. 57.50 paise. Let’s find the maximum price of an exercise book and total number of exercise books bought.

Class 6 Math Solutions WBBSE
Solution:

Rs. 80.50 = 8050 p

Rs. 57.50 = 5750 p

∴ H.C.F. =  5x 10 x 23 = 1150

∴ Maximum price of an exercise book = 1150 p.

Total Amount = (8050 + 5750) p = 13800 p.

∴ Number of exercise books = 13800/1150 = 12

Class 6 WBBSE Math Solutions Chapter 12 HCF And LCM Of Three Numbers Exercise 12.1

Question 1. Four bells ring at an interval of 45 min, 1 hour, 1 hr 15 min, and 1 hr 30 m. Let’s find bells ringing together at 12, when will these ring together again? Also, let’s find out how many times the bells will separately ring during these hours.
Solution:

Class 6 Math Solutions WBBSE

45 min = 45 mins

1 hour = 60 mins

1 hr 15 mins = 75 mins

1 hr 30 mins = 90 mins

L.C.M. of 45,60,75, 90

∴ Required L.C.M =2x3x5x3x2x5 = 900 mins = 15hrs.

The bells ring together at 12 room, then again the bells will ring together at 12 noon + 15 hrs. = 3 A.M.

Number of times 1st bell rings separately = 900 ÷ 45 = 20

Number of times 2nd bell rings separately = 900 ÷ 60 = 15

Number of times 3rd bell rings separately = 900 ÷ 75 = 12

Number of times 3rd bell rings separately = 900 ÷ 90 = 10

Class 6 WBBSE Math Solutions

Question 2. Let’s work to find the least number of four digits which will be divisible by 12,15, 20, and 35.
Solution:

L.C.M. of 12,15, 20 and 35

= 2x2x3x5x7 = 420

Least number of 4 digits, divisible by 12,15, 20, and 35 is = 420 x 3 = 1260.

Question 3. Let’s work out to find the greatest number of five digits which when divided by 16, 24, 30 and 36 will leave a remainder 10 in each case.
Solution:

L.C.M. of 16, 24, 30 and 36

= 2x2x3x2x5x3x1 = 720

Greatest number of five digits = 99999

Class 6 WBBSE Math Solutions

∴ The required number = (99999 – 639) + 10

= 99360 + 10 = 99370.

WBBSE Math Solutions Class 6 Chapter 12 HCF And LCM Of Three Numbers Exercise 12.2

Question 1. There are three small tanks of capacity 35 liters, 56 liters, and 84 liters. Let’s find what will be the biggest capacity of a container that will measure the oil of the 3 tanks in exact whole numbers.
Solution:

To find the biggest capacity of a container we have to find the H.C.F. of 35 litres, 56 litres, and 84 litres

∴ The biggest capacity of the container = 7 litres.

Question 2. The length and breadth of our school hall are 2000 cm and 1600 cm respectively. Let s find the length of the longest tape which can measure both length and breadth in exact whole numbers.
Solution:

WBBSE Math Solutions Class 6

To find the longest tape to measure 2000 cm and 1600 cm we have to find the H.C.F. of 2000 and 1600 cm.

2000 cm = 20 m.

1600 cm = 16 m.

∴ Length of the tape = 4 m.

Question 3. There is a stock of 1071 dhotis, 595 sarees, and 357 dresses. Let us calculate the maximum number of families among which these can be distributed equally. How many of these things will each family receive?
Solution:

Number of dhotis = 1071

Number of sarees = 595

Number of dresses = 357

WBBSE Math Solutions Class 6

Now find H.C.F. of 1071,595,357 357,595, 357

Number of Dhotis = \(\frac{1071}{119}=9\)

Number of Sarees = \(\frac{595}{119}=5\)

Number of Dresses = \(\frac{357}{119}=3\)

∴ Maximum number of families = 119.

Question 4. The perimeter of the front wheel of an engine is 1 m 4 dcm and the perimeter of its hind wheel is two and a half times more than the front wheel. Let’s find the least distance covered by the wheels when they will simultaneously take an exact number of complete revolutions.
Solution:

The perimeter of the front wheel = 1 m 4 dcm = 14 dcm

and the perimeter of its hind wheel = 14 x 2\(\frac{1}{2}\)

= 14 x \(\frac{5}{2}\) dcm.

= 35 dcm.

Now, H.C.F. of 14 dcm and 35 dcm = 7 dcm.

∴ Least distance covered by the wheels = 7 dcm.

WBBSE Class 6 Maths Solutions

Question 5. Let’s find the H.C.F. of the following numbers,

1. 24, 36, 54
2. 24, 30, 40, 48
3. 296, 703, 814
4. 160,165, 305
5. 165,264,286
6. 906,1510,1057

Solution:

1. 24, 30, 40, 48
Solution:

∴ H.C.F. = 2×3 = 6

2. 24, 30, 40, 48
Solution:

H.C.F. of 24, 30,40, 48

24 = 2 x 2 x 2 x 3.

30 = 2 x 3 x 5

40 = 2 x 2 x 2 x 5

48 = 2 x 2 x 2 x 2 x 3

∴ H.C.F. = 2

WBBSE Class 6 Maths Solutions

3. 296,703,814
Solution:

H.C.F. of 296, 703, 814

∴ Required H.C.F. = 37

4. 160,165, 305
Solution:

H.C.F. of 160, 165, 305

∴ H.C.F. = 5

WBBSE Class 6 Maths Solutions

5. 165, 264, 286
Solution:

H.C.F. of 165, 264, 286

∴ H.C.F. = 11

6. 906, 1510, 1057
Solution:

H.C.F. of 906, 1510, 1057

∴ Required H.C.F. = 151

Question 6. Let’s find the greatest number which divides 306,810 and 2214 and keeps the number remainder.
Solution:

Class 6 Math WBBSE Solutions

To find the required greatest number we have to find the H.C.F. of 306, 810, and 2214.

∴ H.C.F. = 18.

∴ The required number = 18.

Question 7. The traffic signal lights at three different crossings of a road change at every 16 seconds, 28 sec, and 40 sec respectively. If the signal lights changed together at 8 a.m in the morning, let’s find when the three signal lights will change together again.
Solution:

L.C.M. of 16 sec, 28 sec, and 40 sec

∴ L.C.M = 2x2x2x2x7x5 = 560 sec = 9 mins 20 sec.

The three signal lights will change together 9 min 20 sec after 8 am, i.e., 8 hr 9 min 20 sec.

Question 8. There are three sticks in our house of lengths 45 cm, 50 cm, and 75 cm. Let’s find the least length of a tape which can be completely measured by each stick.
Solution:

To find the required length of the tape we have to find the LC.M. of 45,50, and 75.

Class 6 Math WBBSE Solutions

L.C.M. = 5x5x 3x3x2 = 450

∴ The least length of the tape = 450 cm.

Question 9. Let’s find the least number which is divisible by 15,20,24 and 32.
Solution:

The least number is the L.C.M. of 15, 20, 24, and 32.

∴ L.C.M. = 2x2x2x3x5x4 = 480

Question 10. Let’s find the L.C.M. of the following:

1. 36, 60, 72
2. 24, 36, 45, 60
3. 105,119,289
4. 144,180, 348
5. 110,165, 330
6. 204, 408, 306

Solution:

Class 6 Math WBBSE Solutions

1. 36, 60,72
Solution:

L.C.M. of 36, 60, 72

∴ L.C.M. = 2x2x3 x 3x5x2 = 360

2. 24, 36, 45, 60
Solution:

L.C.M. of 24, 36, 45, 60

∴ L.C.M. = 2x2x3x3x5x2 = 360

3. 105,119,289
Solution:

Class 6 Math WBBSE Solutions

L.C.M. of 105,119, 289

∴ L.C.M. = 7x 17 15 x 17 = 30345

4. 144,180, 348
Solution:

L.C.M of 144,180, 348

∴ L.C.M. = 2x2x3x3x4x5x29 = 20880

5. 110, 165, 330
Solution:

L.C.M Of 110, 165, 330

L.C.M = 2x2x3x3x4x5x29 = 20880

6. 204, 408, 306
Solution:

WBBSE Class 6 Maths Solutions

L.C.M of 204, 408, 306

L.C.M = 2x2x3x17x2x3 = 1224

Question 11. Let’s find the H.C.F. and the L.C.M. of the following.

1. 6 Rs. 50 paise, 5 Rs. 20 paise and 7 Rs. 80 paise.
Solution:

Rs. 6, 50p = 650p

Rs. 5, 20p = 520p

Rs. 7, 80p = 780p

H.C.F.

H.C.F. = 130p = Rs. 1 30p

L.C.M.

L.C.M. = 2x2x3x5x10x13 = 7800p = Rs. 78.

2. 2 m 28 cm, 3 m 42 cm, 4 m 56 cm.
Solution:

WBBSE Class 6 Maths Solutions

2 m 28 cm. = 228 cm.

3 m 42 cm = 342 cm.

56 cm = 456 cm.

H.C.F

H.C.M. = 114 cm

= 1 m 14 cm

L.C.M

L.C.M = 2 x 2 x 2 x 3 x 3 x 1 9 = 1 368 cm

= 13 m 68 cm

3. 3 I 600 ml, 4 I 800 ml, 6 I.
Solution:

3 litre 600 ml = 3600 ml

4 litre 800 ml = 4800 ml

6 litre = 6000 ml

WBBSE Class 6 Maths Solutions

H.C.F

H.C.F. = 1200 ml.

= 1 litre 200 ml

L.C.M

L.C.M. = 2 x 2 x 3 x 3 x 3 x 4 x 5 x 100 = 72000 ml.

= 72 litre,

4. 6 hours 4 min 30 sec, 2 hours 42 min.
Solution:

6 hr, 4 min 30 sec – (6 x 3600 + 4 x 60 + 30) secting

= 21600 + 240 + 30 sec = 21870 sec

2 hr 42 min = (2 x 60 + 42) = 162 min

= 162 x 60 sec

WBBSE Class 6 Maths Solutions

H.C.F

H.C.F.= 9720 sec

L.C.M

L.C.M = 9 x 9 x 3 x 4 x 9 x 10

= 87480 sec

= 1458 min

= 24 hr 18 min

WBBSE Class 6 Maths Solutions

Question 12. From the pairs of numbers given below, let’s find if the product of two numbers is equal to the product of their H.C.F and L.C.M

1. 87,145
Solution:

147 = 5×29

L.C.M = 3 x 5 x 29 = 435

∴ Product of the two numbers = 87 x 145 = 12615

Product of their H.C.F. x L.C.M. = 29 x 435 = 12615

∴ Product of the two numbers = Product of their H.C.F. x L.C.M.

2. 60, 75
Solution:

60 = 2x2x3x5

75 = 3 x 5 x 5

H.C.F = 3×5 = 15

L.C.M = 2x2x3x5x5 = 300

Product of the two numbers = 60 x 75 = 4500

Product of their H.C.F. x L.C.M. = 15 x 300 = 4500

∴ Product of the two numbers = Product of their H.C.F. x L.C.M.

3. 42, 63
Solution:

42 = 2 x 3 x 7

63 = 3x3x7

∴ H.C.F. = 3×7 = 21

L.C.M. = 2x3x3x7 = 126

Product of the two numbers = 42 x 63 = 2646

Class 6 WBBSE Math Solutions

Product of their H.C.F. and L.C.M. = 21 x 126 = 2646

Product of the two numbers = Product of their H.C.F. and L.C.M.

4. 186, 403
Solution:

186 = 2x3x31

403= 13×31

H.C.F. = 31

L.C.M. = 2x3x13x31 =2418

Product of the two numbers = 186 x 403 = 74958

Product of their H.C.F. and L.C.M. = 74958

∴ Product of the two numbers = Product of their H.C.F. and L.C.M.

Question 13. The L.C.M. and H.C.F. of the two numbers are 2175 and 145 respectively. If one number is 725, let’s find the other number.
Solution:

L.C.M. = 2175

H.C.F. = 145

∴ Product of the two numbers = Product of L.C.M. and H.C.F. = 2175 x 145

One number = 725

∴ Other number = \(\frac{2175 \times 145}{725}=435\)

Question 14. Let’s find the H.C.F. of 145 and 232. Using H.C.F. let us find L.C.M.
Solution:

145 = 5×29

232 = 2 x 2 x 2 x 29

∴ H.C.F. = 29

∴ H.C.F. x L.C.M. = Product of two numbers

∴ 29 x L.C.M. = 145×232

∴ L.C.M = \(\frac{145 \times 232}{29}=1160\)

∴ L.C.M. = 1160

Class 6 WBBSE Math Solutions

Question 15. Let’s find the L.C.M of 144 and 384. Using L.C.M let’s find their H.C.F.
Solution:

144 = 2x2x2x2x3x3

384 = 2x2x2x2x2x2x2x3

∴ L.C.M = 2x2x2x2x2x2x2x3x3 = 1152

H.C.F x L.C.M = Product of two numbers

∴ H.C.F x 1152 = 144×384

HCF = \(\frac{144 \times 384}{1152}=48\) = 48

∴ H.C.F = 48

Question 16. Find the least number that must be subtracted from 5834, so that the result is divisible by 20, 28, 32, and 35.
Solution:

L.C.M. = 2x2x5x7x8 = 1120

∴ The required least number = 234

Class 6 WBBSE Math Solutions

Question 17. Let’s find the greatest number which divides 2300 and 3500 to leave the remaining 32 and 56 respectively.
Solution:

The required number is the H.C.F. of (2300 – 32) = 2268 and (3500 – 56) = 3444

H.C.F. = 84

∴ Required greatest number = 84

Question 18. Let’s find the greatest number that divides 650, 775 and 1250 to keep equal remainder in all cases.
Solution:

H.C.F. = 25

∴ Required greatest number = 25

Question 19. The sum of two numbers is 384 and their H.C.F. is 48, what may be the 2 possible numbers?
Solution:

8 = 1+7……..(1)

= 2 + 6 …….(2)

= 3 + 5 …….(3)

= 4 + 4 …….(4)

In 1st case, the numbers are (48 x 1) and (48 x 7) = 48, 336.

In 2nd case, the numbers are (48 x 2) and (48 x 6) = 96, 288.

But it is not possible as the H.C.F of 96 and 288 is 96.

In 3rd case, the numbers are (48 x 3) and (48 x 5) = 144, 240.

In 4th case, the numbers are (48 x 4) and (48 x 4) = 192, 192.

But it is not possible as the H.C.F of 192 and 192 is 192.

.-. Required numbers are (48, 336) and (144,240).

Question 20. The H.C.F. and L.C.M. of two numbers are 12 and 720. Let’s try to find how many pairs are possible and what may be those numbers.
Solution:

The factors of 12 are 1,2, 3, 4, 6, and 12.

Case 1 12×1= 12; 720-1 =720

H.C.F. =12, L.C.M. = 720

∴ (12, 720) is possible.

Case 2 12×2 = 24; 720 + 2 = 360

H.C.F. = 24, L.C.M. = 360

∴ (24,360) is not possible.

Case 3 12×3 = 36; 720 + 3 = 240

H.C.F. = 12, L.C.M. = 720,

∴ (36, 240) is possible.

Case 4 12 x 4 = 48; 720 + 4 = 180

∴ (48, 180) is possible.

H.C.F. = 48, L.C.M. = 720

Case 5 12×6 = 72; 720 + 6=120

H.C.F. =24, L.C.F. = 360

∴ (72,120) is not possible.

Case 6 12×12= 14; 720 + 2 = 60

H.C.F. = 12 L.C.M. = 60

∴ (60, 144) is possible.

∴ 4 pairs are (12, 720); (36,240); (48,180), and (60, 144)

Question 21. Let us find the least number from which if 4000 is subtracted, the result will be divisible by 7,11, and 13.
Solution:

L.C.M. of 7, 11 and 13 = 7×11 x 13 = 1001

∴ Required number = 4000 + 1001 = 5001

Question 22. Let’s find two pairs of numbers between 50 and 100, whose H.C.F. is 16.
Solution:

16 x 3 = 48

16×4 = 64

16×5 = 80

16×6 = 96

16×7 = 112

As the numbers are in between 50 and 100.

∴ The numbers are, (64, 80) and (80, 96).

Question 23. Let us find a number that is divisible by 28, 33, 42, and 77 and t nearest to 98765.
Solution:

L.C.M. of 28, 33, 42, and 77

L.C.M. = 2 x 3 x 7 x 11 x 2 = 924

∴ The required number = 107 x 924 = 98868.

Question 24. Let us find the least number divisible by 13 such that when the number is divided by 8,12,16 and 20, it leaves 1 as the remainder of all the cases.
Solution:

L.C.M of 8, 12, 16 and 20

If it leaves 1 as the remainder the number is 240 + 1 = 241 which is not possible as 241 is not divisible by 13.

Again, the L.C.M is 240 x 2 = 480 and 480 + 1 = 481, it is divisible by 13.

∴ The required number = 481.

 

Class 6 Math Solutions WBBSE Chapter 9 Percentage Exercise 9

Question 1. Let’s convert the following percentages into proper fractions:

1. 10%
Solution:

= \(\frac{10}{100}=\frac{1}{10}\)

2. 70%
Solution:

= \(\frac{70}{100}=\frac{7}{10}\)

3. 15%
Solution:

= \(\frac{15}{100}=\frac{3}{20}\)

4. 257 %
Solution:

= \(\frac{257}{100}\)

5. \(33 \frac{1}{3} \%\)
Solution:

= \(\frac{100}{3} \times \frac{1}{100}=\frac{1}{3}\)

Question 2. Let’s convert the following percentages into proper fractions:

Read and Learn More WBBSE Solutions For Class 6 Maths

1. 61%
Solution:

= \(\frac{61}{100}=0.61\)

2. 3%
Solution:

= \(\frac{3}{100}=0.03\)

Class 6 Math Solutions WBBSE

3. 105%
Solution:

= \(\frac{105}{100}=1.05\)

4. 1.26%
Solution:

= \(\frac{126}{100 \times 100}=0.0126\)

5. 0.07%
Solution: 

= \(\frac{7}{100} \times \frac{1}{100}\)

= \(\frac{7}{10000}=0.0007\)

Question 3. Let us express the following in percentages and arrange them in ascending order

1. \(\frac{1}{2}, \frac{1}{4}, \frac{3}{5}\)
Solution:

⇒ \(\frac{1}{2}=\frac{1}{2} \times 100 \%=50 \%\)

⇒ \(\frac{1}{4}=\frac{1}{4} \times 100 \%=25 \%\)

⇒ \(\frac{3}{5}=\frac{3}{5} \times 100 \%=60 \%\)

Ascending order: 25%; 50% ; 60%

∴ \(\frac{1}{4}, \frac{1}{2}, \frac{3}{5}\)

2. \(\frac{2}{5} ; \frac{13}{25} ; \frac{7}{10}\)
Solution:

⇒ \(\frac{2}{5}=\frac{2}{5} \times 100 \%\) = 40%

⇒ \(\frac{13}{25}=\frac{13}{25} \times 100 \%\) = 52%

⇒ \(\frac{7}{10}=\frac{7}{10} \times 100 \%\)= 70

Ascending order: 40% ; 52% ; 70%

Class 6 Math Solutions WBBSE

i.e., \(\frac{2}{5} ; \frac{13}{25} ; \frac{7}{10}\)

3. \(1 \frac{2}{5}, 1 \frac{1}{2}, 1 \frac{9}{10}\)
Solution:

⇒ \(1 \frac{2}{5}\)

= \(\frac{7}{5}=\frac{7}{5} \times 100 \%\) =140%

⇒ 1 \(\frac{1}{2}\)

= \(\frac{3}{2}=\frac{3}{2} \times 100 \%\) =150%

⇒ 1 \(\frac{9}{10}\)

= \(\frac{19}{10}=\frac{19}{10} \times 100 \%\) =190%

Ascending order: 140% ; 150% ; 190%

i.e., \(\frac{7}{5} ; \frac{3}{2} ; \frac{19}{10}\)

i.e., \(1 \frac{2}{5}, 1 \frac{1}{2}, 1 \frac{9}{10}\)

Class 6 Math Solutions WBBSE

4. 0.02,0.15,0.6
Solution:

0.02 = \(\frac{2}{100} \times 100 \%=2 \%\)

0.15 = \(\frac{15}{100} \times 100 \%=15 \%\)

0.6 = \(\frac{6}{10} \times 100 \%=60 \%\)

Ascending order: 2%; 15%; 60%

i.e., 0.02; 0.15; 0.6

Question 4. 1. If 3 out of 5 candies were taken, let’s find the percentage of candies taken.
Solution:

3 out of 5 candies are taken.

∴ Percentage of candies taken = \(\frac{3}{5}\) x 20% = 60%.

2. If 6 out of 24 berries are rotten. Let’s find the percentage of berries that have rotten.
Solution:

6 out of 24 berries are rotten.

∴ Percentage of rotten berries = \(\frac{6}{24}\) x 100% =25%.

WBBSE Math Solutions Class 6

3. Today 7 students of our class are absent. There are 35 students in our class. Let us find the percentage of students present today in our class.
Solution:

7 students out of 35 students are absent.

∴ 35 -7 = 28 students are present.

∴ Percentage of present students = \(\frac{28}{35}\) x100% = 80%.

4. A bamboo is of length 55 m. 11 m of it is under muddy water. Let’s find what percentage of the bamboo is above the muddy water.
Solution:

Total length of bamboo = 55 m.

Under muddy water = 11 m.

Length of bamboo above muddy water = (55-11)m = 44m.

Percentage of the bamboo above the muddy water

= \(\frac{44}{55}\) 100% = 80 %

WBBSE Math Solutions Class 6

Question 5. There are 2100 story books in our local library. If 30% more storybooks are bought, what will be the total number of storybooks in the library now also find out the additional number of storybooks bought.
Solution:

Total number of story books in our library = 2100.

30% of 2100 story books = \(\frac{30}{100}\) x 2100 = 630.

∴ Total number of books now = 2100 + 630 = 2730.

Question 6. It’s raining heavily since morning. Hence only 20% of students were present in Alam’s school. Let’s find how many students were actually present in school if the total number of students in Alam’s school is 1230.
Solution:

Total number of students in Alam’s school = 1230.

Number of students present today = 20% of 1230

= \(\frac{20}{100}\) X 1230 = 246.

Question 7. 10. Today I shall prepare orange juice, ‘sherbet’ (drink) myself. For preparing 300 ml of ‘sherbet’ I added 18% orange juice to it. Let’s find how many milliliters of orange juice I added to the ‘sherbet’.
Solution:

Quantity of sherbet = 300 ml.

Orange juice added = 18% of 300ml

= \(\frac{18}{100}\) x 300 ml = 54 ml.

WBBSE Math Solutions Class 6

Question 8. Shobhan used organic fertilizer this year in his land This increased the production of paddy by 25% than last year. If last year’s production of paddy is 12 quintals, let’s find the production of oaddv this year.
Solution:

Last year production of paddy = 12 Quintals.

This year production increased by 25%

= \(\frac{25}{100}\) x 12 Quintals = 3 Quintals.

∴ Total production = (12 + 3) Quintals = 15 Quintals.

Question 9. In Rasulpur village, the population has increased by 12% than the previous year. Till last year, the population of the village was 775. Let’s find the present population of the village.
Answer:

Till last year, the population of the village was 775.

The population increased by 12%

= 12/100 x 775 = 993

∴ Present population of the village = 775 + 93 = 868.

Question 10. 80 students appeared for the Madhyamik Examination this year from our school. If 65% of students have passed, let us find how many students have actually passed.
Answer:

Number of students appeared for the Madhyamik Examination this year = 80.

Percentage of passed = 65%.

∴ Number of students passed = \(\frac{65}{100}\) x 80 = 52.

Class 6 WBBSE Math Solutions

Question 11. A certain alloy contains 70% popper and rest zinc. In 20 kg of such alloy let’s find how many kg of zinc is required.
Solution:

Total weight of alloy = 20 kg.

Percentage of copper present = 70%

= \(\frac{70}{100}\) X 20 kg = 14 kg.

∴ Quantity of zinc required = 20 – 14 = 6 kg.

Question 12. Due to the rise in the price of sugar we decided to reduce the consumption of sugar by 4%. Presently, we consume 625 gm of sugar every day. Let’s find how many grams the consumption of sugar is reduced and also the amount of sugar consumed each day now.
Solution:

At present we consume sugar every day = 625 gm.

Consumption of sugar reduced by 4% = \(\frac{4}{100}\) x 625 = 25gm

∴ Amount of sugar consumption today = 625gm – 252gm = 600gm

Question 13. Anilbabu pays 22% of his salary for house rent. If he pays Rs. 1870 per month for rent, let’s find his monthly salary.
Solution:

Monthly rent
22
1870

Monthly salary
100
?

When Rs. 22 is the rent, monthly salary = Rs. 100.

When Rs. 1 is the rent, monthly salary = Rs. \(\frac{100}{22}\)

When Rs. 1870 is the rent, monthly salary = Rs. \(\frac{100}{22}\) x 1870 = Rs. 8500.

Class 6 WBBSE Math Solutions

Question 14. Yasina Khatoon cultivates jute in 55% of her agricultural land. If she cultivates jute in 11 bighas of land, let’s find her total agricultural land.
Solution:

If Yasina cultivated 55 bighas of land, she had 100 bighas of agricultural land.

Cultivated land
55
11

Total agricultural land
100
?

If 55 bighas of cultivated land, total agricultural land = 100 bighas.

If 11 bighas of cultivated land, total agricultural land = 100 bighas = \(\frac{100}{55}\) x 11 bighas = 20 bighas.

Question 15. Out of total monthly expenses of our family, Rs. 4750 is spent on food and 5900 for all other expenses. If expenses on food is increased by 10% and other expenses is decreased by 16%, then let’s calculate whether the total monthly expenses will increase or decrease.
Solution:

Expenses for food = Rs. 4750

and other expenses = Rs. 5900

Expenses for food increased by 10%

= Rs. 4750 x \(\frac{10}{100}\)

= Rs. 475

Now expenses for food = Rs. 4750 + Rs. 475 = Rs. 5225

Expenses for other decreased by 16%

= Rs. 5900 x \(\frac{16}{100}\) = Rs. 944

Now other expenses = Rs. 5900 – Rs. 944 = Rs. 4956

Previously total expenses were = Rs. 4750 + Rs. 5900 = Rs. 10650

Presently total expenses are = Rs. (5225 + 4956) = Rs. 10181

Expenses Decrease in = Rs. (10650 -10181) = Rs. 469

Class 6 WBBSE Math Solutions

Question 16. The present population of the city is 26250. If the population increases at the rate of 4% every year, then let’s find what will the population of the city be next year. Also, let’s find what the population will be after two years.
Solution:

The present population of a city = 26250.

Population increases by 4%

= \( x 26250 = 1050.

∴ The population of the city in 1st year = 26250 + 1050 = 27300.

Next year population again increased by 4%

= [latex]\frac{4}{100}\) x 27300 = 1092

∴ The population of the city in 2nd year = 27300 + 1092 = 28392.

WBBSE Class 6 Maths Solution for Question 17. During harvesting the price of paddy was Rs. 1080 per quintal. In monsoon the price increased by 15%, let’s find out how much more the farmer who sold 12 quintals of paddy earlier could have earned, had he sold the same amount during monsoon.
Solution:

During harvesting, the price of paddy per quintal was Rs. 1080.

In monsoon, the price increased by 15%

= \(\) x Rs. 1080

= Rs. 162.

∴ During monsoon, he sold paddy at

= Rs. (1080 + 162) per quintal.

= Rs. 1242 per quintal

During monsoon, he will earn by selling 12 quintals

= Rs. 162×12

= Rs. 1944 more.

Class 6 Math Solutions WBBSE Chapter 6 Multiplication And Division Of A Fraction By Whole Number And By Fraction Exercise 6

Question 1. Hands-on trial Four circular pieces of paper of equal size are taken. Half a portion of the circles are colored. Let us see what we can do with colored half positions.
Solution:

4 x \(\frac{1}{2}\) → \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) = 2

Hence, 4 x \(\frac{1}{2}\) = \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) + \(\frac{1}{2}\) = \(\frac{1+1+1+1}{2}\) = \(\frac{4}{2}\) = 2

Or, 4x\(\frac{1}{2}\) = \(\frac{1\times1}{2}\) = 2

Read and Learn More WBBSE Solutions For Class 6 Maths

Again, let us take four circular pieces of paper of equal size. \(\frac{3}{4}\) part of it are coloured. Let us find what is the sum total of coloured portions.

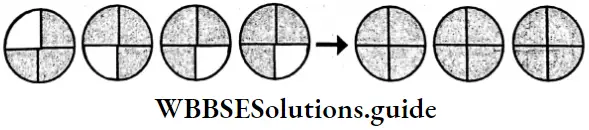
4 x \(\frac{3}{4}\) = \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) + \(\frac{3}{4}\) = 3

4 x \(\frac{3}{4}\) = \(\frac{3+3+3+3}{4}=\) = 3 or 4 x \(\frac{3}{4}\) = \(\frac{4 \times 3}{4}\) = 3

Class 6 Math Solutions WBBSE

Question 2. If 8 equal pieces \(\frac{1}{2}\) of 12 equal pieces of \(\frac{3}{4}\) meter and 16 equal pieces of \(\frac{3}{8}\) meter of ribbon are needed, let us find what length of ribbon will be required in all.
Solution:

8 pieces of \(\frac{1}{2}\) meter = 8 x \(\frac{1}{2}\)m = \(\frac{8 \times 1}{2}\) = \(\frac{8}{2}\) = 4 m.

12 pieces of \(\frac{3}{4}\) metre = 12 x \(\frac{3}{4}\) m = \(\frac{16 \times 3}{4}\) = 6 m.

Total length of ribbon required = 4m + 9m + 6m = 19m.

Question 3. (1)

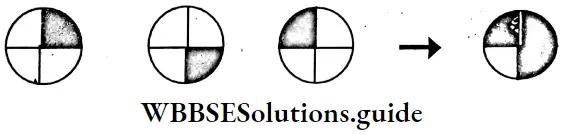
Solution: That is 3 x \(\frac{1}{4}\) = \(\frac{3}{4}\)

(2)

Solution: 3 x \(\frac{2}{5}\) = \(\frac{6}{5}\) = 1 + \(\frac{1}{5}\)

(3) Let us color and deduce
Solution:

1 + \(\frac{1}{2}\) = 1\(\frac{1}{2}\) = \(\frac{3}{2}\)

Class 6 Math Solutions WBBSE

(4) Similarly, colour twice and let us bring together the colored position to conclude
Solution:

⇒ \(\frac{3}{2}\) + \(\frac{3}{2}\) = 3

Hence, 2 x \(\frac{3}{2}\) = 3.

(5 + \(\frac{2}{5}\)) = 5\(\frac{2}{5}\) = \(\frac{27}{5}\)

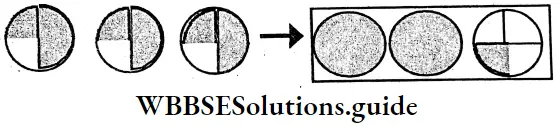
(5) Let us draw three similar pictures and let us find the total color portions.
Solution:

1. 1 + \(\frac{2}{5}\) = 1\(\frac{2}{5}\) = \(\frac{7}{5}\)

2. 1 + \(\frac{3}{5}\) = \(\frac{8}{5}\)

3. 1 + \(\frac{4}{5}\) = \(\frac{9}{5}\)

Class 6 WBBSE Math Solutions

3 x \(\frac{7}{5}\) = \(\frac{7 \times 3}{5}\) = \(\frac{21}{5}\) = 4\(\frac{1}{5}\)

7 x \(\frac{3}{5}\) = 4 + \(\frac{1}{5}\)

Let us calculate and color accordingly

(6) 3 x \(\frac{3}{4}\) = \(\frac{3 \times 3}{4}\) = \(\frac{9}{4}\) = 2\(\frac{1}{4}\)
Solution:

(7) 2 x \(\frac{7}{6}\) = \(\frac{2 \times 7}{6}\) = \(\frac{14}{6}\) = \(\frac{7}{3}\) = 2\(\frac{1}{3}\)
Solution:

Class 6 WBBSE Math Solutions Chapter 6 Multiplication And Division Of A Fraction By Whole Number And By Fraction Exercise 6.1

Question 1. Sraboni had Rs. 100. She spent \(\frac{1}{2}\) of her money at a bookshop and \(\frac{1}{4}\) of her money at a grocery shop. Let us find how much money she paid at the book shop and at the grocery and how much money is left with her.
Solution:

At book shop, Sraboni paid \(\frac{1}{2}\) part of Rs. 100

= Rs. 100 x \(\frac{1}{2}\) = Rs. \(\frac{100 \times 1}{2}\) = Rs. \(\frac{100}{2}\) = Rs. 50

At the grocery, she paid \(\frac{1}{4}\) part of Rs. 100

= Rs. 100 x \(\frac{1}{4}\) = Rs. \(\frac{100 \times 1}{4}\) = Rs. \(\frac{100}{4}\) = Rs. 25.

Hence, Sraboni is left with Rs. 100 – (Rs. 50 + Rs. 25)

= Rs. 100 – Rs. 75 = Rs. 25

Question 2. In our art class, we were asked to draw a scenery. Samir took \(\frac{2}{5}\) part of 1 hr, Mita took \(\frac{5}{12}\) part of 1 hr, Ajij did it in \(\frac{1}{2}\) part of 1 hr and Sabbar finished it in \(\frac{7}{12}\) part of 1 hr. Let us calculate how much time each of them took to draw the scenery and also who took maximum time to finish the work and who took minimum time.
Solution:

∴ 1 hr = 60 min.

Samir finished his drawing in \(\frac{2}{5}\) part of 1 hr.

i.e., \(\frac{2}{5}\) of 60 min = 60 min x \(\frac{2}{5}\) = \(\frac{60 \times 2}{5}\) min = 24 min.

Mita finished her drawing in \(\frac{5}{12}\) of 1 hr, i.e., \(\frac{5}{12}\) of 60 min

= 60 min x \(\frac{5}{12}\) = \(\frac{60 \times 5}{12}\) min = 25 min.

Similarly, Ajij finished his drawing in \(\frac{1}{2}\) part of 1 hr = 30 min

Sabbar look \(\frac{7}{12}\) part of 1 hr = 60 min x \(\frac{7}{12}\) = 35 min.

Hence, to draw the same scenery Samir took minimum time and Sabbar took maximum time.

Class 6 WBBSE Math Solutions

Question 3. For a school picnic, Rehena paid \(\frac{5}{6}\) part of Rs. 30 and Javed paid \(\frac{5}{9}\) part of Rs. 45. Let us find who paid more.
Solution:

Rehana paid \(\frac{5}{6}\) part of Rs. 30 = Rs. 25 and Javed paid \(\frac{5}{9}\) part of 45 =
Rs. 25.

Hence, Rahana and Javed both paid Rs. 25.

Question 4. Let us express \(\frac{5}{8}\) part of Rs. 2 in rupees and paise.
Solution:

Rs. 2 = 200 paise

Hence, \(\frac{5}{8}\) part of Rs. 2 = \(\frac{5}{8}\) part of 200 paise

= 200 x \(\frac{5}{8}\) paisa = 125 paise = Re 1 and 25 paise.

Question 5. Let us multiply

1. 120 x \(\frac{3}{5}\)
Solution:  24 x 3 = 72

2. 2 x 215 x \(\frac{3}{5}\)
Solution: 2 x 43 x 3 = 258

3. 500 x \(\frac{17}{25}\)
Solution: 20 x 17 = 340

4. 169 x \(\frac{4}{13}\)
Solution: 13 x 4 = 52

Question 6. Lets do it

WBBSE Math Solutions Class 6

1. \(\frac{3}{4}\) of 1 year = ____ month
Solution: \(\frac{3}{4}\) of 1 year = \(\frac{3}{4}\) x 12 months = 3 x 3 = 9 months

2. \(\frac{3}{4}\) of Rs. 5 = ____ paise
Solution: \(\frac{3}{4}\) of Rs. 5 = \(\frac{3}{4}\) x 500 paise = 3 x 125 = 375 paise

3. \(\frac{3}{5}\) of 60 apples = _______ apples
Solution: \(\frac{3}{5}\) of 60 apples = 3 x 12 apples = 36 apples

4. \(\frac{3}{20}\) of 40 litre = ___ litre
Solution: \(\frac{3}{20}\) of 40 litre = 3 x 2 = 6 litre

Let Us Measure Land

Question 7. Rahim uncle planted flowering plants in half portion of his rectangular field. The length and breadth of the field are 50 metre and 40 metre respectively.
Solution:

Area of Rahim uncle’s field = (50 x 40) sq.m = 2000 sq.m.

\(\frac{1}{2}\) portion of 2000 sq.m, of field = \(\frac{1}{2}\) x 2000 sq.m = 2000 sq.m.

Hence, he planted flowering plants in 1000 sq.m, of field.

But in half a portion of his flower garden, Rahim uncle planted marigold. Therefore, marigold is planted in \(\frac{1}{2}\) part of 1000 sq.m

= 1000 x \(\frac{1}{2}\) sq.m = 500 sq.m.

Total land = 2000 sq.m.

Hence, 500 sq.m = \(\frac{500}{2000}\) part of 2000 sq.m. = \(\frac{1}{4}\) part.

i. e., he has planted marigolds in \(\frac{1}{4}\) part of his land. He planted marigolds or half of half portion of his land

= \(\frac{1}{2}\) of \(\frac{1}{2}\) portion of land = \(\frac{1}{2}\) x \(\frac{1}{2}\) = \(\frac{1}{4}\) part.

WBBSE Math Solutions Class 6 Chapter 6 Multiplication And Division Of A Fraction By Whole Number And By Fraction Exercise 6.2

Question 1. Rohit can walk 1\(\frac{1}{2}\) km in 1 hr. Let us find how far he can walk in 6\(\frac{1}{2}\) hrs. [1\(\frac{1}{2}\) km= \(\frac{3}{2}\) km; 6\(\frac{1}{2}\) hrs = \(\frac{3}{2}\) hrs]
Solution:

Rohit can walk in 1 hr 1\(\frac{1}{2}\) km = \(\frac{3}{2}\) km.

∴ Rohit can walk in 6\(\frac{1}{2}\) hr = \(\frac{13}{2}\) hr = \(\frac{3}{2}\) x \(\frac{13}{2}\) = \(\frac{39}{4}\) km = 9\(\frac{3}{4}\) km

Question 2. Rafikul’s uncle built a house on \(\frac{3}{5}\) of \(\frac{4}{7}\) part of his land and the rest of the land is left for cultivation. Let us find out on what part of land he built his house.
Solution:

Rafikul’s uncle built a house on \(\frac{3}{5}\) of \(\frac{4}{7}\) part of his land.

Part of the land he built his house on = \(\frac{3}{5}\) x \(\frac{4}{7}\) = \(\frac{12}{35}\) Part

Question 3. Let us multiply the following:

1. \(\frac{2}{3}\) x \(\frac{5}{6}\)
Solution: 5/9

2. \(\frac{7}{8}\) x \(\frac{3}{10}\)
Solution: 21/80

WBBSE Class 6 Maths Solutions

3. 19\(\frac{3}{4}\) x \(\frac{1}{7}\)
Solution:

= \(\frac{79}{4} \times \frac{1}{7}=\frac{79}{28}\)

= \(2 \frac{23}{28}\)

4. \(\frac{16}{5}\) x \(\frac{4}{7}\)
Solution: \(\frac{432}{35}\) = 12\(\frac{12}{35}\)

Question 4. The product of two proper fractions is always a ____ (proper Aim- proper) fraction.
Solution: The product of two proper fractions is always a proper fraction.

Example: \(\frac{3}{7} \times \frac{5}{5}=\frac{6}{35}\)

Question 5. The product of two improper fractions is always a/an ______ (proper/improper) fraction.
Solution: The product of two improper fractions is always an improper fraction.

Example: \(\frac{8}{3} \times \frac{11}{5}=\frac{88}{15}\)

WBBSE Class 6 Maths Solutions Chapter 6 Multiplication And Division Of A Fraction By Whole Number And By Fraction Exercise 6.3

Question 1. Few friends have come at Ayesha’s House. Ayesha brought 6 apples. Each friend ate 1— apple and no apples were left. Let’s find out how many friends of Ayesha ate apples.
Solution:

Number of apples = 6.

Each friend ate 1\(\frac{1}{2}\) apples = \(\frac{3}{2}\) apples.

∴ Number of friends = 6 ÷ \(\frac{3}{2}\)= 6 x \(\frac{2}{3}\) = 4

Question 2. There are 9 boiled eggs if each wants to have 1\(\frac{1}{2}\) eggs, let’s find how many can eat eggs.
Solution:

Total number of eggs = 9

Each want to have = 1\(\frac{1}{2}\) = \(\frac{3}{2}\) eggs

Number of persons =9÷ \(\frac{3}{2}\) = 9x\(\frac{2}{3}\)=6

WBBSE Class 6 Maths Solutions

Question 3. There are 5 packets of biscuits. If each person eats \(\frac{1}{4}\) part of a packet of biscuit, let’s find how many persons can eat the biscuits.
Solution:

Number of packs of biscuits = 5

Each person eats \(\frac{1}{4}\) part of a packet.

∴ Number of persons = 5 x \(\frac{4}{1}\) = 20

Question 4. Let’s find the values of the following

1. 4 ÷ \(\frac{1}{3}\)
Solution: 4×3 = 12

2. 3 ÷ \(\frac{1}{6}\)
Solution: 3×6 = 18

3. 8 ÷ \(\frac{1}{5}\)
Solution: 8X5 = 40

4. 5 ÷ \(\frac{1}{4}\)
Solution: 5×4 = 20

5. 6 ÷ \(\frac{1}{2}\)
Solution: 6×2 = 12

6. 15 ÷ \(\frac{5}{7}\)
Solution: 15x\(\frac{7}{5}\) = 21

7. 20 ÷ \(\frac{4}{5}\)
Solution: 20 x \(\frac{5}{4}\) = 25

8. 9 ÷ 1\(\frac{2}{25}\)
Solution: 9 \(\frac{27}{25}\)

= 9 ÷ \(\frac{27}{25}\)

= 9 x \(\frac{25}{27}\) = \(\frac{25}{3}\) = 8\(\frac{1}{3}\)

9. 7 ÷ 2\(\frac{3}{16}\)
Solution: 7 ÷ \(\frac{35}{16}\)

= 7 x \(\frac{16}{35}\) = 7x\(\frac{16}{5}\) = 3\(\frac{1}{5}\)

10. 4 ÷ 2\(\frac{10}{13}\)
Solution: 4 ÷ \(\frac{36}{13}\)

= \(4 \times \frac{13}{36}=\frac{13}{9}=1 \frac{4}{9}\)

WBBSE Class 6 Maths Solutions

11. 11 ÷ \(\frac{55}{18}\)
Solution: 11 x \(\frac{18}{55}\)

= \(\frac{18}{5}\) = 3\(\frac{3}{5}\)

12. 18 ÷ \(\frac{3}{5}\)
Solution: 18 x \(\frac{5}{3}\) = 6 x 5 = 30

Chapter 6 Multiplication And Division Of A Fraction By Whole Number And By Fraction Exercise 6.4

Question 1. Let’s find the values of the following:

1. \(\frac{7}{8} \div \frac{21}{5}\)
Solution:

= \(\frac{7}{8} \times \frac{5}{21}=\frac{5}{24}\)

2. \(\frac{3}{28} \div \frac{9}{7}\)
Solution:

= \(\frac{3}{28} \times \frac{7}{9}=\frac{1}{12}\)

3. \(5 \frac{2}{3} \div \frac{1}{6}\)
Solution:

= \(\frac{17}{3} \times \frac{6}{1}=34\)

4. ______ ÷ __________
Solution:

= \(\frac{4}{7} \div \frac{12}{21}=\frac{4}{7} \times \frac{21}{12}=1\)

WBBSE Class 6 Maths Solutions

Question 2. 1. Let’s do mentally

(1) How much is \(\frac{1}{2}\) of Rs. 10?
Solution: \(\frac{1}{2}\) of Rs. 10 = Rs. 5.

(2) How much is \(\frac{1}{5}\) part of Rs. 25?
Solution: \(\frac{1}{5}\) of Rs. 25 = Rs. \(\frac{1}{5}\) x 25 = Rs. 5.

(3) \(\frac{1}{3}\) of how much is Rs. 4?
Solution: Let \(\frac{1}{3}\) of Rs. x = 4

∴ x = Rs. 4 x 3 = Rs. 12.

(4) \(\frac{1}{4}\)part of what time is 65 min?
Solution: Let \(\frac{1}{3}\) of x min = 65

∴ x = 65 x 6 = 390 min.

(5) I have taken \(\frac{1}{3}\) part of mangoes from Mala’s basket of mangoes. If I have taken 7 mangoes, how many mangoes Mala had in her basket, let’s find.
Solution: \(\frac{1}{3}\) part of mangoes from Mala’s basket = 7.

∴ Total number of mangoes of Mala’s basket = 7÷\(\frac{1}{3}\) = 7 x 3 = 21

(6)

Solution:

Total circles = 7; \(\frac{2}{7}\) part of 7 circles = 2.

Total triangles = 10; \(\frac{3}{5}\) part of 10 triangles = 6.

Total quadrilaterals = 7; \(\frac{1}{7}\) part of 7 quadrilaterals = 1.

(7) Today father has brought 10 I of drinking water from a nearby tubewell. Mother used \(\frac{1}{5}\) part of water for cooking and \(\frac{1}{4}\) part of remaining water was used for drinking purpose. Let us find how many liters of water is left.
Solution:

Class 6 Maths Solutions WBBSE

Quantity of drinking water = 10 litres

Mother used water for cooking = \(\frac{1}{5}\) x 10 litres = 2 litres

Remaining water = (10-2) litre = 8 litres

Used for drinking water = \(\frac{1}{4}\) x 8 liters = litres

Remaining water = (8- 2) litres = 6 litres

Question 3. Let’s find the value of:

1. \(3 \times \frac{6}{11}\)
Solution:

= \(\frac{18}{11}=1 \frac{7}{11}\)

2. \(11 \times \frac{2}{3}\)
Solution:

= \(\frac{22}{3}=7\frac{1}{3}\)

3. \(\frac{7}{3} \times 2 \frac{3}{2}\)
Solution:

= \(\frac{7}{3} \times \frac{7}{2}=\frac{49}{6}=8 \frac{1}{6}\)

4. \(\frac{3}{8} \times \frac{6}{4}\)
Solution:

= \(\frac{3 \times 6}{8 \times 4}=\frac{9}{16}\)

5. \(\frac{6}{49} \times \frac{7}{3}\)
Solution:

= \(\frac{6 \times 7}{49 \times 3}=\frac{2}{7}\)

6. \(\frac{15}{28} \times 2 \frac{1}{3}\)
Solution:

= \(\frac{15}{28} \times \frac{7}{3}=\frac{5}{4}\)

7. \(4 \frac{8}{13} \times 7 \frac{4}{5}\)
Solution:

= \(\frac{60}{13} \times \frac{39}{5}=36\)

Question 4. A bucket holds \(\frac{1}{2}\) liter of water. Let us calculate how much water 7 such buckets can hold.
Solution:

A bucket holds = \(\frac{1}{2}\) litre water

∴ 7 such buckets contain = 7 x \(\frac{1}{2}\) litres = \(\frac{7}{2}\) = 3.5 litres water.

Class 6 Maths Solutions WBBSE

Question 5. After retirement, Akhilbabu donated \(\frac{1}{4}\) part of his property to the local library, \(\frac{1}{6}\) part of the remaining property was given to his wife and rest was divided equally among his two sons. Let us calculate to find what part of his property was given to his wife and each of two sons.
Solution:

Akhilbabu donated = \(\frac{1}{4}\) part to local library.

Remaining part = 1 – \(\frac{1}{4}\) = \(\frac{4-1}{4}\) = \(\frac{3}{4}\) part.

Wife received = \(\frac{1}{6}\) x \(\frac{3}{4}\) = \(\frac{1}{8}\) part.

Remaining part= \(\frac{3}{4}\) – \(\frac{1}{8}\) = \(\frac{3 \times 2 -1}{8}\) = \(\frac{5}{8}\)

∴ Two sons will get = \(\frac{5}{8}\) part.

Each son received = \(\frac{1}{2}\) X \(\frac{5}{8}\) = \(\frac{5}{16}\) part.

Question 6. From \(\frac{1}{2}\) part of Rs. 150, how much is to be taken away so that only Rs. 30 is left?
Solution:

⇒ \(\frac{1}{2}\) part of Rs. 150 = 150 x \(\frac{1}{2}\) = Rs. 75

Remaining money = Rs. 30.

We will take = Rs. 75 — Rs. 30 = Rs. 45

Question 7. Let us find the value when 3 times of \(\frac{6}{7}\) is added to 2\(\frac{6}{7}\)
Solution:

= 3 times of \(\frac{6}{7}\) + \(\frac{20}{7}\)

= 3 X \(\frac{6}{7}\) + \(\frac{20}{7}\)= \(\frac{38}{7}\)

=5\(\frac{1}{7}\)

Question 8. In the first year the cultural program of the town had 1400 spectators. Next year the number increased by \(\frac{7}{10}\) parts let’s find the total number of next year.
Solution:

Number of spectators = 1400.

Next year spectators increased by \(\frac{7}{10}\)

i.e., \(\frac{7}{10}\) x 1400 = 980

Total number of spectators in next year = 1400 + 980 = 2380

Class 6 Maths Solutions WBBSE

Question 9. Let’s find the reciprocals of the following fractions and mark the reciprocals by ‘O’ sign which are proper fractions:
Solution:

1. Reciprocal of \(\frac{7}{5}=\frac{5}{7}\)

2. Reciprocal of \(\frac{1}{3}\) = 3

3. Reciprocal of \(\frac{5}{8}=\frac{8}{5}\)

4. Reciprocal of \(\frac{9}{7}=\frac{7}{9}\)

5. Reciprocal of \(\frac{12}{5}=\frac{5}{12}\)

6. Reciprocal of \(\frac{5}{8}=\frac{8}{5}\)

7. Reciprocal of \(\frac{1}{8}=\frac{8}{1}\)

Question 10. Which number has reciprocal as itself?
Solution: The number which has reciprocal as itself = 1.

Question 11. Sita gives me \(\frac{2}{3}\) part of the total number of stamps she has. If she gives me 18 stamps, let us find how many stamps Sita has.
Solution:

2/3 part of total number of stamps = 18.

∴ Total number of stamps of Sita = 18 \(\frac{2}{3}\) = 18 x \(\frac{3}{2}\) = 27.

Question 12. Rajia gave \(\frac{2}{5}\) part of her money to Debnath and \(\frac{3}{10}\) part of money to Sunita. If she has Rs. 180 left, let us find how much money Rajia had at the begining.
Solution:

Rajia gave \(\frac{2}{5}\) part and \(\frac{3}{10}\) part of her money to Debnath and Sunita respectively.

∴ She gave \(\frac{2}{5}+\frac{3}{10}=\frac{4+3}{10}=\frac{7}{10}\) part of money.

Remaining part of her money = \(1-\frac{7}{10}=\frac{10-7}{10}=\frac{3}{10}\)

According to problem, \(\frac{3}{10}\) part of money = Rs. 180

∴ Total amount of money she had = Rs. 180 x \(\frac{10}{3}\) = Rs. 600.

Question 13. Let’s find the values

1. \(15 \div \frac{5}{3}\)
Solution:

= \(15 \times \frac{3}{5}=9\)

2. \(14 \div \frac{7}{2}\)
Solution:

= \(14 \times \frac{2}{7}=4\)

3. \(\frac{6}{13} \div 3\)
Solution:

= \(\frac{6}{13} \times \frac{1}{3}=\frac{2}{13}\)

4. \(\frac{12}{19} \div 6\)
Solution:

= \(\frac{12}{19} \times \frac{1}{6}=\frac{2}{19}\)

5. \(5 \frac{1}{5} \div \frac{13}{2}\)
Solution:

= \(5 \frac{1}{5} \div \frac{13}{2}=\frac{26}{5} \times \frac{2}{13}=\frac{4}{5}\).

Class 6 Maths Solutions WBBSE

6. \(2 \frac{2}{5} \div 1 \frac{1}{5}\)
Solution:

= \(2 \frac{2}{5} \div 1 \frac{1}{5}=\frac{12}{5} \div \frac{6}{5}=\frac{12}{5} \times \frac{5}{6}=2\)

7. \(4 \frac{3}{7} \div 3 \frac{2}{7}\)
Solution:

= \(\frac{31}{7} \div \frac{23}{7}=\frac{31}{7} \times \frac{7}{23}=\frac{31}{23}=1 \frac{8}{23}\).

Question 14. Let’s mark ‘√’ for the correct answer

1. How many \(\frac{1}{16}\) are there in \(\frac{3}{4}\)?

1. 64
2. 12
3. 4
4. 3

Solution:

Required no. = \(\frac{3}{4}\) ÷ \(\frac{1}{16}\)

= \(\frac{3}{4}\) x \(\frac{16}{1}\)

∴ 2. 12.

2. \(\frac{3}{4}\) part of a ribbon is 56 m. Let’s calculate the original length of the ribbon.

1. 43 m
2. 64 m
3. 63 m
4. 72 m

Solution: Original length of the ribbon

= 56 m x \(\frac{8}{7}\) = 64 m

∴ 2. 64 m

3. Reciprocal of 5\(\frac{6}{7}\) will be

1. 5\(\frac{3}{4}\)
2. \(\frac{41}{7}\)
3. \(\frac{7}{41}\)
4. \(\frac{7}{56}\)

Solution: Reciprocal of 5\(\frac{6}{7}\), i.e., \(\frac{41}{7}\)= \(\frac{7}{41}\)

∴ 3. \(\frac{7}{41}\)

Question 15. From 16\(\frac{2}{3}\)m long ribbon, \(\frac{3}{8}\) part is cut off. If it is further divided into 5 equal pieces, let’s find the length of each pieces.
Solution:

Length of the ribbon = \(16 \frac{2}{3}=\frac{50}{3}\) m

⇒ \(\frac{3}{8} \text { part }=\frac{50}{3} \times \frac{3}{8}=\frac{50}{8} \mathrm{~m}=\frac{25}{4} \mathrm{~m}\)

∴ Length of each piece = \(\frac{25}{4} \div 5=\frac{25}{4} \times \frac{1}{5}=\frac{5}{4} m .=1 \frac{1}{4} m\)

Question 16. Father bought 12\(\frac{7}{10}\) m of cloth for window curtains. But there was already 5\(\frac{3}{5}\)m of cloth for curtains at home. 4\(\frac{5}{6}\) m of cloth is required to make curtains for each of 3 windows. What length of cloth will remain?
Solution:

Length of cloth

= \(12 \frac{7}{10} \mathrm{~m}+5 \frac{3}{5} \mathrm{~m}\)

= \(\frac{127}{10}+\frac{28}{5}\)

= \(\frac{127+56}{10} \mathrm{~m}\)

= \(\frac{183}{10} \mathrm{~m} .\)

Cloth required to make one curtain = \(4 \frac{5}{6} m=\frac{29}{6} m\)

∴ To make 3 curtains cloth required = \(\frac{29}{6} \times 3 \mathrm{~m}=\frac{29}{2} \mathrm{~m}\)

Remaining cloth = \(\frac{183}{10} m-\frac{29}{2} m\)

= \(\frac{183-145}{10} m=\frac{38}{10}m\)

= \(\frac{19}{5}m=3\frac{4}{5}m\)

Question 17. My grandmother prepared some pickle. She removed \(\frac{4}{7}\) part of the pickle in a glass jar for future use. Rest she divided among 6 of us. Let’s find how much each of us will get.
Solution:

Grandmother removed \(\frac{4}{7}\) part of the pickle.

Remaining part = \(1-\frac{4}{7}=\frac{7-4}{7}=\frac{3}{7} \text { part. }\)

∴ \(\frac{3}{7}\) part was divided among 6 of us.

∴ Each of us will get = \(\frac{3}{7} \div 6=\frac{3}{7} \times \frac{1}{6}=\frac{1}{14} \text { part. }\)

Question 18. Mehboob and his group have decided that in 33 days they would repair 24\(\frac{11}{15}\) km of road. They repaired \(\frac{11}{15}\) km of road each day for 25 days. If they are to finish the work in due time, at what rate they would work for the remaining days?
Solution:

They repaired in each day = \(\frac{11}{15}\) km.

∴ They repaired in 25 days = \(\frac{11}{15}\) x 25 = \(\frac{55}{3}\) km

∴ Remaining work = 24\(\frac{11}{15}\) – \(\frac{55}{3}\) = \(\frac{371}{15}\) – \(\frac{55}{3}\) = \(\frac{371-275}{15}=\frac{96}{15} \mathrm{~km}\)km.

Remaining days = 33 – 25 = 8.

∴ In 8 days they have to repair \(\frac{35}{5}\) km.

∴ In 1 day they will repair \(\frac{32}{5} \times \frac{1}{8}=\frac{4}{5} \mathrm{~km}\)

Multiplication For Class 6

Question 19. 5 is added to —\(\frac{3}{7}\) and the sum is multiplied by 4\(\frac{2}{3}\) Now, the  product is divided by 4\(\frac{4}{9}\) and the quotient is subtracted from 8\(\frac{2}{5}\). Let’s find the number after subtraction.
Solution:

⇒ \(5+\frac{3}{7}=\frac{35+3}{7}=\frac{38}{7}\)

The sum is multiplied by \(4 \frac{2}{3}\).

∴ \(\frac{38}{7} \times 4 \frac{2}{3}=\frac{38}{7} \times \frac{14}{3}=\frac{76}{3}\)

Then the product is divided by 4\(\frac{4}{9}\)

i.e., \(\frac{76}{3} \div 4 \frac{4}{9}=\frac{76}{3} \div \frac{40}{9}=\frac{76}{3} \times \frac{9}{40}=\frac{57}{10}\)

The quotient is subracted from 8\(\frac{2}{5}\).

i.e., \(8 \frac{2}{5}-\frac{57}{10}=\frac{42}{5}-\frac{57}{10}=\frac{84-57}{10}\)

= \(\frac{27}{10}=2 \frac{7}{10}\)

∴ Required No. = \(2 \frac{7}{10}\)

Multiplication For Class 6

Question 20. Let us simplify

1. \(\frac{1}{5}+\frac{2}{3}-\frac{1}{2}\)
Solution:

= \(\frac{6+20-15}{30}=\frac{26-15}{30}=\frac{11}{30}\)

2. \(\frac{1}{5}+\frac{1}{2}\)–\(\frac{2}{15}-\frac{1}{6}\)
Solution:

= \(\frac{6+15-4-5}{30}=\frac{26-9}{30}=\frac{12}{30}=\frac{2}{5}\)

3. \(\frac{7}{12}+5 \frac{2}{9}+\frac{11}{18}-2 \frac{5}{12}\)
Solution:

= \(\frac{7}{12}+\frac{47}{9}+\frac{11}{18}-\frac{29}{12} \)

= \(\frac{21+188+22-87}{36}\)

= \(\frac{231-87}{36}\)

= \(\frac{144}{36}\) = 4

4. \(3 \frac{1}{2}+\frac{7}{6} \times \frac{3}{8}-\frac{5}{24}\)
Solution:

= \(\frac{7}{2}+\frac{7}{16}-\frac{5}{24}\)

= \(\frac{168+21-10}{48}=\frac{189-10}{48}=\frac{179}{48}=3 \frac{35}{48}\)

5. \(\frac{3}{8} \div \frac{2}{3}\) of \(\frac{1}{9}\) of \(\frac{1}{16}\)
Solution:

= \(\frac{3}{8} \div \frac{2}{3} \times \frac{1}{9} \times \frac{1}{16}\)

= \(\frac{3}{8} \div \frac{1}{3 \times 9 \times 8}=\frac{3}{8} \times \frac{3 \times 9 \times 8}{1}=81\)

6. \(6 \frac{2}{5}+3 \frac{1}{3}+\frac{1}{2}-\frac{7}{10}\)
Solution:

= \(\frac{192+100+15-21}{30}=\frac{307-21}{30}=\frac{286}{30}=9 \frac{8}{15}\)

Division For Class 6

7. \(\left\{\frac{11}{16} \div\left(\frac{5}{6}+\frac{2}{3}\right)\right\}-\frac{1}{3}\)
Solution:

= \(\left(\frac{11}{16} \div \frac{9}{6}\right)-\frac{1}{3}=\left(\frac{11}{16} \times \frac{6}{9}\right)-\frac{1}{3}\)

= \(\frac{11}{24}-\frac{1}{3}=\frac{11-8}{24}=\frac{3}{24}=\frac{1}{8}\)

8. \(4 \frac{2}{3} \div \frac{2}{3}-\frac{3}{8}\)
Solution:

= \(\frac{14}{3} \times \frac{3}{2}-\frac{3}{8}\)

= \(\frac{7}{1}-\frac{3}{8}=\frac{56-3}{8}=\frac{53}{8}=6 \frac{5}{8}\)

9. \(\left(2 \frac{3}{4}+3 \frac{1}{2} \div 2 \frac{1}{7}\right) \div 13 \frac{1}{4}\)
Solution:

= \(\left(\frac{11}{4}+\frac{7}{2} \div \frac{15}{7}\right) \div \frac{53}{4}\)

= \(\left(\frac{11}{4}+\frac{49}{30}\right) \div \frac{53}{4}\)

= \(\frac{165+98}{60} \times \frac{4}{53}=\frac{263}{60} \times \frac{4}{53}=\frac{263}{795}\)

10. \(1-\left[\frac{1}{2} \div\left\{2-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\right\}\right]\)
Solution:

= \(1-\left[\frac{1}{2} \div\left\{2-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{6}\right)\right\}\right]\)

= \(1-\left[\frac{1}{2} \div\left\{2-\frac{1}{2}\left(\frac{3-2+1}{6}\right)\right\}\right]\)

= \(1-\left[\frac{1}{2} \div\left\{2-\frac{1}{2} \times \frac{2}{6}\right\}\right]\)

= \(1-\left[\frac{1}{2} \div\left\{2-\frac{1}{6}\right\}\right]\)

= \(1-\left[\frac{1}{2} \div\left\{\frac{12-1}{6}\right\}\right]\)

= \(1-1-\left[\frac{1}{2} \div \frac{11}{6}\right]=1-\left[\frac{1}{2} \times \frac{6}{11}\right]=1-\frac{3}{11}=\frac{11-3}{11}=\frac{8}{11}\)

Division For Class 6

11. \(2-\frac{1}{10} \times \frac{1}{3} \div \frac{4}{25} \div \frac{1}{8}\)
Solution:

= \(2-\frac{1}{10} \times \frac{1}{3} \times \frac{25}{4} \times \frac{8}{1}\)

= \(2-\frac{5}{3}=\frac{6-5}{3}=\frac{1}{3}\)

12. \(\frac{1}{2}\left[3 \frac{1}{2} \div 2 \frac{1}{3}\left\{1 \frac{1}{4} \div\left(2+3 \frac{2}{3}\right)\right\}\right]\)
Solution:

= \(\frac{3}{2}\left[\frac{7}{2} \div \frac{7}{3}\left\{\frac{5}{4} \div \frac{17}{3}\right\}\right]\)

= \(\frac{3}{2}\left[\frac{7}{2} \div \frac{7 \times 5}{17 \times 4}\right]\)

= \(\frac{3}{2}\left[\frac{7}{2} \times \frac{17 \times 4}{7 \times 5}\right]\)

= \(\frac{3}{2} \times \frac{17 \times 2}{5}=\frac{51}{5}=10 \frac{1}{5}\)

13. \(\left(1 \frac{1}{13} \times 2 \frac{3}{5}\right) \div\left(7 \frac{1}{2} \times 3 \frac{1}{10}\right) \div \frac{28}{279}\)
Solution:

= \(\left(\frac{14}{13} \times \frac{13}{5}\right) \div\left(\frac{15}{2} \times \frac{31}{10}\right) \div \frac{28}{279}\)

= \(\frac{14}{5} \div \frac{93}{4} \div \frac{28}{279} \)

= \(\frac{14}{5} \times \frac{4}{93} \times \frac{279}{28}\)

= \(\frac{6}{5}=1 \frac{1}{5}\)

Division For Class 6

Question 21. (1) In the figure given below, let \(\frac{2}{3}\) be multiplied by the fractions
at the angular portion and the product be written in the blank circles outside.

(2) Let \(\frac{2}{3}\) be multiplied by the fractions in horizontal and vertical circles and let the product be placed in the corresponding blank circles outside.

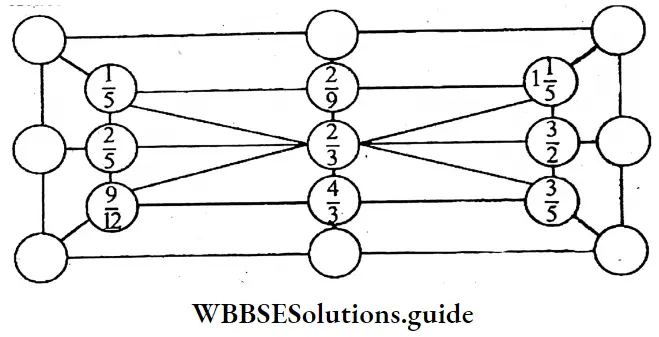
Solution:

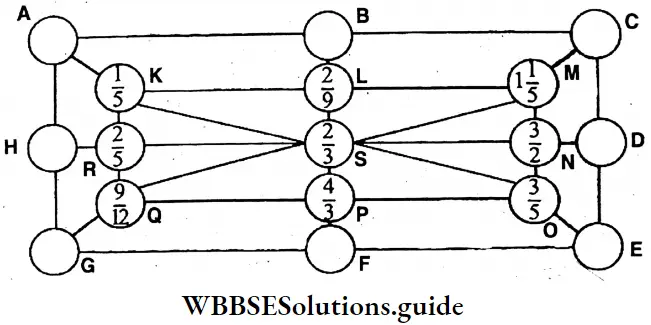
(s) is multiplied by the fraction of the angular points we get the following results (K, M, O, P).

1. sxk= \(\frac{2}{3} x \frac{1}{5}=\frac{2}{15}\)…. (A)

2. sxM = \(\frac{2}{3} \times 1 \frac{1}{5}=\frac{2}{3} \times \frac{6}{5}=\frac{4}{5}\)….(C)

3. sxO = \(\frac{2}{3} \times \frac{3}{5}=\frac{2}{3}\)…….(E)

4. sxQ = \(\frac{2}{3} \times \frac{9}{12}=\frac{1}{2}\)…..(G)

Division For Class 6

Again, \(\frac{2}{3}\) (s) is divided by the fractions of the horizontal & vertical mid¬points (R, N, and L, P) we get.

1. \(S \div R=\frac{2}{3} \div \frac{2}{5}=\frac{2}{3} \times \frac{5}{2}=\frac{5}{3}\) …..(H)

2. \(\mathrm{S} \div \mathrm{N}=\frac{2}{3} \div \frac{3}{2}=\frac{2}{3} \times \frac{2}{3}=\frac{4}{9}\)……(D)

3. \(\mathrm{S} \div \mathrm{L}=\frac{2}{3} \div \frac{2}{9}=\frac{2}{3} \times \frac{9}{2}\)….(B)

4. \(S \div P=\frac{2}{3} \div \frac{4}{3}=\frac{2}{3} \times \frac{3}{4}=\frac{1}{2}\)….(F)