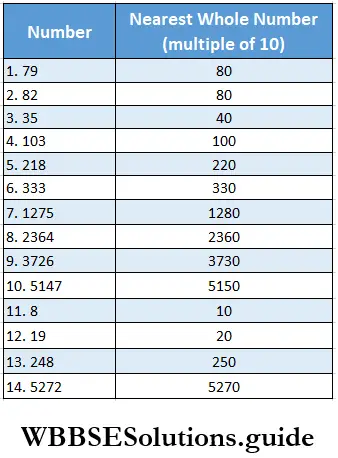
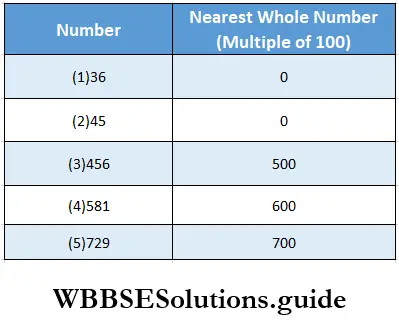
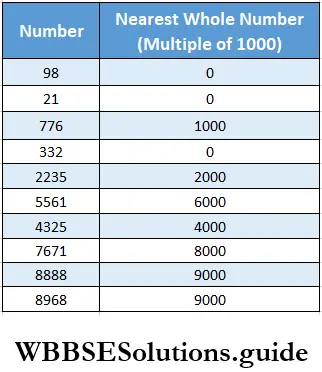
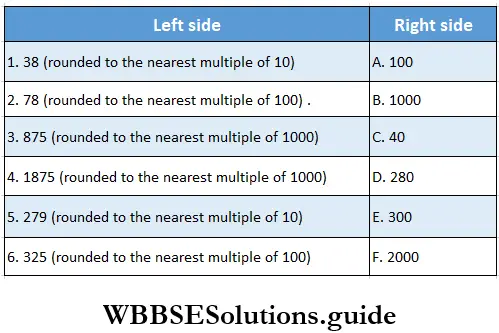
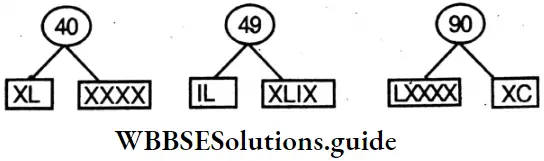
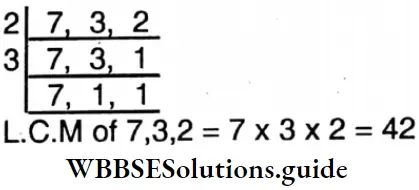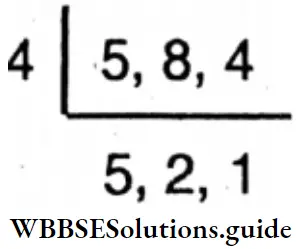Class 6 Maths

Class 6 Math WBBSE Solutions Chapter 7 Multiplication And Division Of Decimal Fraction By Whole Number And Decimal Fraction Exercise 7

Question 1. Let’s draw and find the product of 0.4 x 0.7 and 0.2 x 0.8 by taking a square of white paper.
Solution:

1. 0.4 x 0.7

2. 0.2 x 0.8

1. 0.4 x 0.7

Read and Learn More WBBSE Solutions For Class 6 Maths

2. 0.2 x 0.8

Question 2. The side of a square is 5.2 cm. Let’s find its perimeter and area.
Solution:

The side of a square = 5.2 cm.

1. Perimeter of the square = 4 x one side

= 4 x 5.2 cm

= 20. 8 cm

2. Area of the square = side x side

= 5.2 cm x 5.2 cm

= \(\frac{52}{10} \times \frac{52}{10} \mathrm{sq} \cdot \mathrm{cm}\)

= \(\frac{2704}{100} \mathrm{sq} . \mathrm{cm}\)

= 27.04 sq. cm.

Class 6 Math WBBSE Solutions

Question 3. Let’s find the values of the following:

1. 6.2 x 3.1
Solution:

= \(\frac{62}{10} \times \frac{31}{10}=\frac{1922}{100}\)

= 19.22

2. 11.3 x 2.5
Solution:

= \(\frac{113}{10} \times \frac{25}{10}=\frac{2825}{100}\)

= 282.5

3. 11.25 x 7.3
Solution:

= \(\frac{1125}{100} \times \frac{73}{10}=\frac{82125}{1000}\)

= 82.125

4. 0.03 x 0.3
Solution:

= \(\frac{3}{100} \times \frac{3}{10}=\frac{9}{1000}\)

= 0.009

5. 0.04 x 0.04.
Solution:

= \(\frac{4}{100} \times \frac{4}{100}=\frac{16}{10000}\)

= 0.0016

= 19

Class 6 Math Solutions WBBSE Multiplication And Division Of Decimal Fraction By Whole Number And Decimal Fraction Exercise 7.1

Question 1. On a white square paper let’s draw 10×10 small squares. By using different colours let’s find the value of 0.5 x 0.9, 0.2 x 0.8.
Solution:

1. 0.5 x 0.9

2. 0.2 x 0.8

Question 2. Mithu wants to buy 4 exercise books. If an exercise book costs Rs. 12.75, let’s find how much money Mithu will need.
Solution:

Price of each exercise book = Rs. 12.75.

∴ Price of 4 exercise books = Rs. 12.75 x 4 = Rs. 51.

∴ Mithu will need = Rs. 51.

Class 6 Math Solutions WBBSE

Question 3. Rajinabibi built a house in 0.35 part of her land. She cultivated flowers in 0.2 part of the remaining land. Let’s find in what part of her land she cultivated flowers.
Solution:

Rajinabibi built a house in 0.35 part of her land.

Remaining land = 1 – 0.35 = 0.65 part.

She cultivated flowers on 0.2 part of the remaining land

= \(0.2 \times 0.65=\frac{2}{10} \times \frac{65}{100}=\frac{13}{100}=0.13 \mathrm{part}\)

Question 4. 1 have Rs. 150. With 0.3 part of my money, I bought exercise books and with 0.4 part I bought a storybook. Let me find out what amount of money is left with me.
Solution:

I have Rs. 150.

I bought an exercise book with 0.3 part and bought a story book with 0.4 part.

∴ Total expenditure (0.3 + 0.4) = 0.7 part

= Rs. 150 x 0.7

= Rs. 150 x \(\frac{7}{10}\) = Rs. 105

∴ Remaining amount = Rs. (150 – 105) = Rs. 45.

Class 6 Math Solutions WBBSE

Question 5. Today we shall travel a distance of 94.5 km. If 0.078 liter of petrol is used per kilometer, let’s calculate the total amount of petrol required.
Solution:

To travel 1 km petrol required 0.078 litre.

∴ To travel 94.5 km petrol required = 0.078 x 94.5 litre = 7.37 litre.

Question 6. Alisha’s brother took 1.4 hours to reach Shibpur Launch pier (ghat) from his house in a cycle. If the speed of his cycle is 11.5 km per hour, then let us calculate the distance of Shibpur Launch pier from Alisha’s house.
Solution:

Speed of the cycle is 11.5 km per hour, i.e., in 1 hour he goes 11.5 km.

∴ In 1.4 hour he goes 1.4 x 11.5 km = 16.1 km.

∴ Required distance = 16.1 km.

Question 7. My mother asked me to buy 2.5 kg of pulse. The cost of 1 kg of pulse is Rs. 62.50. Let me calculate how much money I must carry to the shop.
Solution:

The cost of 1 kg of pulse is Rs. 62.50.

∴ The cost of 2.5 kg of pulse = Rs. 62.50 x 2.5.

∴ I must carry to the shop Rs. 156.25 = Rs. 156.25.

Class 6 Math Solutions WBBSE

Question 8. The perimeter of an equilateral triangle is 10.4 cm. Let’s find the length of the side of the equilateral triangle in decimal fractions.
Solution:

The perimeter of an equilateral triangle = 14.4 cm.

∴ Length of each side of this triangle = \(\frac{14.4}{3}\) cm = 4.8 cm.

Question 9. Let’s multiply

1. 0.7 x 0.9
Solution: = 0.63

2. 0.6 x 0.5
Solution: = 0.30

3. 0.02 x 0.2
Solution: = 0.004,

4. 0.67 x 0.39
Solution:

= \(\frac{67}{100} \times \frac{39}{100}=\frac{2613}{10000}=0.2613\)

5. 0.52 x 0.43
Solution:

= \(\frac{52}{100} \times \frac{43}{100}=\frac{2236}{10000}\) = 0.2236

6. 0.07 x 0.97
Solution:

= \(\frac{7}{100} \times \frac{97}{100}=\frac{679}{10000}\) = 0.0679

WBBSE Math Solutions Class 6

7. 6.23 x 2.51
Solution:

= \(\frac{623}{100} \times \frac{251}{100}=\frac{156373}{10000}\) = 15.6373

8. 5.77 x 2.93
Solution:

= \(\frac{577}{100} \times \frac{293}{100}=\frac{169061}{10000}\) = 16.

9. 8.23 x 0.3
Solution:

= \(\frac{823}{100} \times \frac{3}{10}=\frac{2469}{1000}\) = 2.469

10. 82.03 x 0.06
Solution:

= \(\frac{8203}{100} \times \frac{6}{100}=\frac{49218}{10000}\) = 4.9218

11. 85.29 x 3.92
Solution:

= \(\frac{8529}{100} \times \frac{392}{100}=\frac{3343368}{10000}\) = 334.3368

12. 72.2 x 2.65
Solution:

= \(\frac{722}{10} \times \frac{265}{100}=\frac{191330}{1000}\) =191.33

WBBSE Math Solutions Class 6

13. 72.04 x 0.05
Solution:

= \(\frac{7204}{100} \times \frac{5}{100}=\frac{36020}{10000}\)

= 3.602

14. 72.156 x 12.16
Solution:

= \(\frac{72156}{1000} \times \frac{1216}{100}\)=\(\frac{87741696}{100000}\)

= 877.41696

15. 0.6 x 0.3 x 0.2
Solution:

= \(\frac{6}{10} \times \frac{3}{10} \times \frac{2}{10}=\frac{36}{1000}\)

= 0.036

16. 0.2 x 0.06 x .03
Solution:

= \(\frac{2}{10} \times \frac{6}{100} \times \frac{3}{100}=\frac{36}{100000}\)

= 0.00036

17. 2. 14 x 0.4 x 0.9
Solution:

= \(\frac{214}{100} \times \frac{4}{10} \times \frac{9}{10}=\frac{7704}{10000}\)

= 0.7704

WBBSE Math Solutions Class 6

18. 1.21 x0.5 x 5.2
Solution:

= \(\frac{121}{100} \times \frac{5}{10} \times \frac{52}{10}=\frac{31460}{10000}\)

= 3.146

19. 3.06 x 100
Solution:

= \(\frac{306}{100} \times 100\)

= 306

20. 7.92 x 1000
Solution:

= \(\frac{792}{100} \times 1000\)

= 7920

Question 10. Arrange the following in descending order (bigger to smaller) of their values:

1. 0.5 x 0.3, 0.5, 0.3
Solution:

= 0.15; 0.5; 0.3

WBBSE Math Solutions Class 6

In descending order = 0.5; 0.3; 0.5 x 0.3

2. 0.6 x 0.7, 0.6, 0.7
Solution:

= 0.42 ; 0.6; 0.7

In descending order = 0.7; 0.6 x 3; 0.6 x 0.7

3. 0.9 x 0.2, 0.9, 0.2
Solution:

= 0.18; 0.9; 0.2

In descending order = 0.9; 0.2 ; 0.9 x 0.2

4. 0.4 x 0.8, 0.4, 0.8
Solution:

= 0.32; 0.4; 0.8

In descending order = 0.8; 0.4; 0.4 x 0.8

5. 1.2 X 1.5,1.2,1.5
Solution:

= 1.8; 1.2; 1.5

In descending order = 1.2 x 1.5; 1.5; 1.2

6. 2.3 x 2.4, 2.3, 2.4
Solution:

= 5.52; 2.3; 2.4

In descending order = 2.3 x 2.4; 2.4; 2.3

7. 6.7 x 7.2, 6.7, 7.2
Solution:

= 48.24; 6.7; 7.2

In descending order = 6.7 x 7.2 ; 7.2 ; 6.7

8. 8.2 x 1.9, 8.2,1.9
Solution:

= 15.58; 8.2; 1.9

In descending order = 8.2 x 1.9; 8.2; 1.9

Question 11. Let’s find values in decimal numbers

1. 0.625÷ 5
Solution:

⇒ \(\frac{625}{1000} \times \frac{1}{5}=\frac{125}{1000}=0.125\)

2. \(0.627 \div 3\)
Solution:

⇒ \(\frac{627}{1000} \times \frac{1}{3}=\frac{209}{1000}\)

= 0.209

Class 6 WBBSE Math Solutions

3. \(0.343 \div 7\)
Solution:

⇒ \(\frac{343}{1000} \times \frac{1}{7}\)=\(\frac{49}{1000}\)

= 0.049

4. \(651.2 \div 4\)
Solution:

⇒ \(\frac{6512}{10} \times \frac{1}{4}=\frac{1628}{10}\).

= 162.8

5. \(7 \div 3.5\)
Solution:

⇒ \(7 \div \frac{35}{10}=\frac{7 \times 10}{35}=\frac{70}{35}\)

= 2

6. \(18 \div 0.2\)
Solution:

⇒ \(18 \div \frac{2}{10}=\frac{18 \times 10}{2}\)

= 90

7. \(28.8 \div 1.2\)
Solution:

⇒ \(\frac{288}{10} \div \frac{12}{10}\)

= \(\frac{288}{10} \times \frac{10}{12}\)

= 24

8. \(11.7 \div 1.3\)
Solution:

⇒ \(\frac{117}{10} \times \frac{10}{13}\)

= 9

Class 6 WBBSE Math Solutions

9. \(1.35 \div 1.5\)
Solution:

⇒ \(\frac{135}{100} \div \frac{15}{10}\)

= \(\frac{135}{100} \times \frac{10}{15}\)

= \(\frac{9}{10}\)

= 0.9

10. \(0.65 \div 0.5\)
Solution:

⇒ \(\frac{65}{100} \div \frac{5}{10}\)

= \(\frac{65}{100} \times \frac{10}{5}\)

= \(\frac{13}{10}\)

= 1.3

11. \(0.07 \div 0.5\)
Solution:

⇒ \(\frac{7}{100} \div \frac{5}{10}\)

= \(\frac{7}{100} \times \frac{10}{5}\)

= \(\frac{14}{100}\)

= 0.14

Class 6 WBBSE Math Solutions

Question 12. Let’s make a story and then work out:

1. 2.50 x 5 + 3.25 x 6
Solution:

= 12.50 +19.50 = 32

2. 3.75 x 8 – 2.50 x 3
Solution:

Find the difference of prices of 8 pens (each cost Rs. 3.75) and 3 pencils (each cost Rs. 2.50)

= Rs. 3.75 x 8 – Rs. 2.50 x 3

= Rs. (30 – 7.50) = Rs. 22.50

3. 22.50 x 3.50
Solution:

If the cost price of 1 kg rice is Rs. 22.50, then the cost price of 3.50 kg rice

= Rs. 22.50 x 3.50 = Rs. 78.75

4. 13.75 x 2 + 12.50 x 3
Solution:

The total cost price color boxes (the price of each Rs. 13.75) and 3 pencils (price of each Rs. 12.50)

Rs. 13.75 x 2 + Rs. 12.50 x 3

= Rs. 27.50 + Rs. 37.50 = Rs. 65.

Question 13. Let’s find the values of the following simplification:

1. 13.28 – 4.07 + 2.7 x 0.02
Solution:

13.28-4.07 + 0.054 = 13.334-4.07

= 9.264

2. {45.85 – (6.29 + 15.06)} ÷ 5
Solution:

{45.85 -21.35} ÷ 5

= 24.5-5

= 4.9

Class 6 WBBSE Math Solutions

3. (7.8 – 7.8 x 0.2) ÷ 1.2
Solution:

= (7.8-1.56) ÷ 1.2

= 6.24 ÷ 1.2

= 5.2

4. 0.35 x 0.35 + 0.15 x 0.15 + 2 x 0.35 x 0.15
Solution:

0.1225 + 0.0225 + 0.105

= 0.25

5. {(4 – 2.07) x 2.5} -1.93
Solution:

= (1.93 x 2.5) -1.93

= 4.825 – 1.93

= 2.5

Class 6 Math WBBSE Solutions Chapter 2 Concept Of Seven And Eight Digit Numbers

Example: Population of Howrah District 48,41,638 Population of Kolkata District 44, 86, 679 Population of Howrah District
Solution:

48 lac 41 thousand 6 hundred thirty-eight

Population of Kolkata District

Forty-four lac eighty-six thousand six hundred seventy-nine

Population of Purulia District 29,27, 975

Population of Jalpaiguri District 38,69,675

Read and Learn More WBBSE Solutions For Class 6 Maths

Population of Purulia District

29 lac 27 thousand 9 hundred seventy-five

Population of Jalpaiguri District,

38 lac 69 thousand 9 hundred seventy-five

Let’s write a seven-digit number and expand it.

Using each digit only once, let us write four numbers of seven digits and then write the numbers in words.

Question 1. With the help of sticks and colored balls, a number of children who took the Polio Vaccine in four districts are shown below.
Solution:

28,22,000 (approx) children in North 24-Parganas

26,10,500 (approx.) children in South 24 – Parganas.

24,12,300 (approx.) children in Kolkata

Class 6 Math WBBSE Solutions

22,34,200 (approx.) children in Kolkata

Total number of children from Kolkata and Howrah who were given the Polio Vaccine.

Total number of children from 24 – Parganas, North, South, Kolkata, and Howrah, who all got Polio Vaccine.

Class 6 Math WBBSE Solutions

In Ten Lac stick, more than 10 balls can not be placed. Hence another strict or ‘place’ is needed. The name of this stick or ‘Place’ is “Crore”(c). Instead of 10 orange balls, I take 1□ ball.

Let us put balls in respective sticks and write the number:

1. One crore eleven lac six hundred five
2. Five crore two lac eigth thousand sixty-nine

Question 4. In the morning, people of our locality are very busy. They have queued up before our school to cast a vote. I could not do so, because my age is less than 18 years. I later came to know the results of the election.
Solution:

Party A got 46, 87, 905 votes

Party B got 44, 50, 896

Party C got 42, 95, 739 votes

The total number of votes parties have got is 13, 4, 34, 540 votes

Total number of voters are 135, 07, 375 in this locality

Total number of voters 135,07, 375

Votes that are cast 134,34, 540

Votes that are not cast or canceled = 72,835

Let us find which party won the election and by how many votes.

Class 6 Math WBBSE Solutions

Out of 46, 87, 905; 44, 50, 896, and 42, 95, 739, 46, 87, 905 is the greatest number.

Hence, Party A won the elections.

Let us find how many votes Party A got more than Party B.

Party A got 46, 87, 905 Party B got 44, 50, 896 Party A won by 2, 37, 009

WBBSE Class 6 Maths Solutions Chapter 2 Concept Of Seven And Eight Digit Numbers Exercise 2

Question 1. 30439872 ÷ 516
Solution:

⇒ \(\text { 516) } 30439872(58992 \\
2580 \\
4639 \\
\underline{4128} \\
5118 \\
\frac{4644}{4747} \\
\frac{4644}{1032} \\
\frac{1032}{\mathrm{x}}\)

Answer: 58992

Question 2. ▭ x 32=75285600
Solution: Required number =75285600 ÷ 32

⇒ \(\text { 32) } 75285600 \text { ( } 2352675 \\
\frac{64}{112} \\
\frac{96}{168} \\
\frac{160}{85} \\
\frac{64}{216} \\
\frac{192}{240} \\
\frac{224}{160} \\
\frac{160}{x}\)

Answer: 2352675

Question 3. 9128088 ÷ 388=
Solution:

⇒ \(\begin{aligned}
& 388) 9128088(23526 \\
& \frac{776}{1368} \\
& \frac{1164}{2040} \\
& \frac{1940}{1008} \\
& \frac{776}{2328} \\
& \frac{2328}{x}
\end{aligned}\)

Answer: 23526

Question 4. ▭ ÷ 297=65833
Solution: Required number = 65833 x 297

⇒ \(\begin{array}{r}
& 65833 \\
& 297 \\
& 460831 \\
& 592497 x \\
& 131666 x x \\
& \hline 19552401
\end{array}\)

WBBSE Class 6 Maths Solutions

Question 5. 30,08,00000 ÷ ▭=2,00000
Solution:

Required number =300800000 ÷ 200000 =1504

⇒ \(\begin{aligned}
& 200000) 300800000(1504 \\
& \frac{200000}{1008000} \\
& \frac{1000000}{800000} \\
& \frac{800000}{x}
\end{aligned}\)

Question 6. 752 x ▭ =3556208
Solution:

Required number =3556208 ÷ 752 =4729

⇒ \(\begin{aligned}
& \text { 752) } 3556208(4729 \\
& \frac{3008}{5482} \\
& \frac{5264}{2180} \\
& \frac{1504}{6768} \\
& \frac{6768}{x}
\end{aligned}\)

Class 6 Maths Solutions WBBSE Chapter 2 Concept Of Seven And Eight Digit Numbers Exercise 2.1

Question 1. Let us write in words

1. 782005
Solution: Seven lacs eighty-two thousand five

2. 4207029
Solution: Forty-two lacs seven thousand twenty-nine.

3. 30030030
Solution: Three crores thirty thousand thirty

4. 50505005
Solution: Five crores five lacs five thousand five

WBBSE Class 6 Maths Solutions

5. 42034047
Solution: Four crores twenty lacs thirty-four thousand forty-seven

Question 2. Let’s write these numbers using numerals

1. Seventy-eight lac eight hundred eight
Solution: 7800808

2. Ninety-three lac forty-four thousand six hundred five
Solution: 9344605

3. Three crore three lac three thousand three hundred three
Solution: 30303303

4. Thirty-three crore thirty-three lac thirty-three thousand thirty-three.
Solution: 333333033

5. Seventy-seven crore seven thousand seven
Solution: 770007007

Question 3. Let’s match the two sides

Solution: 1. D, 2. C, 3. A, 4. E, 5. B

Question 4. Let us write by choosing the correct answer

1. Twenty lac ten thousand eight

1. 2001008
2. 2010008
3. 2100008

Solution: 2. 2010008

WBBSE Class 6 Maths Solutions

2. One crore eleven lac eight thousand forty-one 

1. 11018041
2. 11010841
3. 11108041

Solution: 3. 11108041

3. Two crore three lac sixty thousand five hundred twenty-six

1. 20360526
2. 20365026
3. 20360562

Solution: 1. 20360526

Question 5. Let us write the expanded from of the following numbers

1. 4627593
Solution: 4000000 + 600000 + 20000 + 7000 + 500 + 90 + 3

2. 2213101
Solution: 2000000 + 200000 + 10000 + 3000 + 100 + 1

3. 9999999
Solution: 9000000 + 900000 + 90000 + 9000 + 900 + 90+9

4. 7007007
Solution: 7000000 + 7000 + 7

5. 2406739
Solution: 2000000 + 400000 + 6000 + 700 + 30 + 9.

Question 6. In the number 37452129, let us find the difference between the place values of the digit ‘2’.
Solution:

In the number 37452129,

Place values of 2 are 2000 and 20.

∴ The difference between 2000 and 20 is (2000-20) = 1980.

Question 7. In the number 27946138, let us find the difference between the place value and the actual value of ‘9′
Solution:

In the number 27946138, the place value of 9 is 900000.

∴ The difference between 900000 and 9 is (900000 – 9) = 899991.

Question 8. Let’s form greatest and least numbers of 8 digits with the digits given below:

1. 3, 5, 7, 9, 2, 6, 5, 6
Solution:

Greatest number = 9 7 6 6 5 5 3 2

Least number = 2 3 5 5 6 6 7 9

2. 6, 4, 8, 5,1,2, 0, 3
Solution:

Greatest number — 8 6 5 4 3 2 1 0

Least number- 1 0 2 3 4 5 6 8

3. 7, 3, 2,1, 9, 5, 6, 0
Solution:

Greatest number – 9 7 6 5 3 2 1 0

Least number – 1 0 2 3 5 6 7 9

4. 8, 9, 2, 4, 7, 3, 2, 1
Solution:

Greatest number – 9 8 7 4 3 2 2 1

Least number – 1 2 2 3 4 7 8 9

Class 6 Math Solutions WBBSE

Question 9. Let us write the following numbers in ascending (increasing) order:

1. 7525762,7525662,7526762,7525652
Solution: 7525652 < 7525662 < 7525762 < 7526762

2. 8705321,8702358, 8707341,8703741
Solution: 8705321 <8703741 <8705321 <8707341

3. 518896,872300, 27562, 300252
Solution: 27562 < 300252 < 518896 < 872300.

Question 10. Let us write the following numbers in descending (decreasing) order:

1. 4503210,4503201,4503120, 4502210
Solution: 4503210 > 4503201 > 4503120 > 4502210

2. 301516,8640051,302560, 6352289
Solution: 8640051 > 6352289 > 302560 >301516

3. 5102080, 5108200, 5100280, 5182000
Solution: 5182000 > 5108200 > 5102080 > 5100280

Question 11. The sum of two numbers is 82945195. If one number is 69100278, let us find the other number.
Solution: Other number = 82945195 – 69100278 = 13844917

Question 12. The difference between two numbers is 28351036. If one number is 30529179, let us find the other number.
Solution: Other number = 30529179 + 28351036 = 58880215

Question 13. From a factory in Bakultala, last year there was an income of Rs. 7521200. This year there is an additional earning of Rs. 3250325. Let us find the total earning in two years.
Solution:

The total earning in two years

= Rs. 7521200 + Rs. 3250325

= Rs. 10771525

Class 6 Math Solutions WBBSE

Question 14. The product of the numbers is 15050490. If one number is 5, let us find the other number.
Solution: Other number = 15050490 ÷ 5 = 3010098.

Question 15. By selling certain property Samirbabu got Rs. 35629850. He gave Rs. 1006200 to his wife and divided Rs. 13050000 among his three children. Rent of the money he donated for constructing a village school. Let us find
Solution:

1. Each child got = 13050000 ÷ 3 = 4350000

2. He donated for the school

= Rs. 35629850 – (1006200 + 13050000)

= Rs. (35629850-23112000)

= Rs. 12517850

Question 16. The population of a city is two crore ninety-eight lac seventy-two thousand six hundred. Of them 12500500 are men and 8872435 are women. Let us calculate the number of children.
Solution:

Total population = 29872600

⇒ \(\begin{array}{ll}
\text { Number of men } & =12500500 \\
\text { Number of women } & \equiv 8872435 \\
\hline \text { Total number of men and women } & \equiv 21372935
\end{array}\)

∴ Number of children = 29872600 – 21372935 = 8499665

Question 17. Let us find what least number must be added to 234567 so that it is divisible by 835.
Solution:

⇒ \(\begin{aligned}
& 835) 234567(280 \\
& \frac{1670}{6756} \\
& \frac{6680}{767}
\end{aligned}\)

∴ Required number = 835 – 767 = 68

Question 18. An organization bought two paintings of an artist for Rs. 900000 and Rs. 2000000 and two more paintings of another artist for Rs. 30,21636 and Rs. 1761084. Let us find how much has been spent on paintings by the organization.
Solution:

Total price of 4 paintings

= Rs. 900000 + Rs. 2000000 + Rs. 3021636 + Rs. 1761084

= Rs. 7682720

∴ Organisation spent on paintings = Rs. 7682720

Class 6 Math Solutions WBBSE

Question 19. The area of a country is 3287263 sq. km. It has 754740 sq. km of forest area and 2503000 sq. km area is river basin. Let us find the area of the remaining land leaving forest and river basin areas.
Solution:

Total area of the country = 3287263 sq. km.

Area of forest = 754740 sq. km.

and area of river basin = 2503000 sq. km.

Total area of forest = 3257740 sq. km.

and river basin

Remaining Land = (3287263 – 3257740) sq. km = 29523 Sqkm.

 

Class 6 Math Solutions WBBSE Chapter 3 Logical Approximation Of Number

Example 1. Let us find the nearest whole number which is a multiple of 10, by the following numbers.

1. 79
2. 82
3. 35
4. 103
5. 218
6. 333
7. 1275
8. 2364
9. 3726
10. 5147

Solution: Nearest whole number = 80

Example 2. Let us find the nearest whole number which is a multiple of 100, for the following numbers

1. 36
2. 45
3. 456
4. 581
5. 729

Solution:

Read and Learn More WBBSE Solutions For Class 6 Maths

Example 3. Let us find the nearest whole numbers to the following numbers which will be multiples of 1000.

1. 98
2. 21
3. 776
4. 332
5. 2235
6. 5561
7. 4325
8. 7671
9. 8888
10. 8968

Solution:

Class 6 Math Solutions WBBSE

Example 4. Convert the following numbers to their nearest whole numbers which are multiples of 10,100 and 1000 and calculate.

1. 28 + 71
2. 316 + 45
3. 728 – 156
4. 489 – 36

Solution:

1. 28 + 71

Nearest multiple of 10 = 30 + 70

Nearest multiple of 100 = 0 + 100

Nearest multiple of 1000 = 0 + 0

2. 316 + 45

Nearest multiple of 10 = 320 + 50 = 370

Nearest multiple of 100 = 300 + 0 = 300

Nearest multiple of 1000 = 0 + 0 =0 Ans

3. 728 – 156

Nearest multiple of 10 = 730 – 160 = 570

Nearest multiple of 100 = 700 – 200 = 500

Nearest multiple of 1000 = 1000 – 0 =1000

4. 489 – 36

Nearest multiple of 10 = 490- 40 = 450

Nearest multiple of 100 =500-0 =500

Nearest multiple of 1000 =0 -0 =0

 

Class 6 WBBSE Math Solutions Chapter 3 Logical Approximation Of Number Exercise 3

Question 1. Let us convert the following numbers to their nearest whole number which are multiples of 10:

1. 12
2. 347
3. 1324
4. 5968

Solution:

Nearest Whole Number (Multiples of 10)

1. 12: 10
2. 347: 350
3. 1324: 1320
4. 5968: 5970

Question 2. Let us convert the following numbers to the nearest whole number which are multiples of 100:

1. 621
2. 483
3. 6521
4. 2178

Solution:

Nearest Whole Number (Multiples of 10)

1. 621: 600
2. 483: 500
3. 6521: 6500
4. 2178: 2200

Question 3. Let us convert the following numbers to their nearest whole numbers which are multiples of 1000:

1. 346
2. 827
3. 6719
4. 8394

Solution:

Nearest Whole Number (Multiples of 10)

1. 346: 0
2. 827: 1000
3. 6719: 7000
4. 8394: 8000

Class 6 WBBSE Math Solutions

Question 4. Let us change the following numbers to their nearest whole numbers which are multiples of 10 and calculate.

1. 37 + 54
Solution: For the nearest multiple of 10, 40 + 50 = 90

2. 73 – 78
Solution: For the nearest multiple of 10, 70 – 50 = 20

3. 24 + 59
Solution: For the nearest multiple of 10, 20 + 60 = 80

4. 97 – 38
Solution: For the nearest multiple of 10,100 – 40 = 60

5. 76 – 29
Solution: For the nearest multiple of 10, 80 – 30 = 50

6. 66 + 73
Solution: For the nearest multiple of 10, 70 + 70 = 140

7. 251 + 175
Solution: For the nearest multiple of 10, 250 + 180 = 430

8. 462 – 271
Solution: For the nearest multiple of 10, 460 – 270 = 190

Question 5. Let us change the following numbers to their nearest whole numbers which are multiples of 100 and calculate:

1. 426+ 589
Solution: For the nearest multiple of 100, 400 + 600 = 1000

2. 356+ 435
Solution: For the nearest multiple of 100, 400 + 400 = 800

3. 678 -125
Solution: For the nearest multiple of 100, 700 -100 = 600

4. 1248 + 4329
Solution: For the nearest multiple of 100,1200 + 4300 = 5500

5. 170 + 895
Solution: For the nearest multiple of 100,200 + 900 = 1100

Class 6 WBBSE Math Solutions

6. 947 + 448
Solution: For the nearest multiple of 100, 900 + 400 = 1300

7. 5612 + 2095
Solution: For the nearest multiple of 100, 5600 + 2100 = 7700

8. 4258 – 2436
Solution: For the nearest multiple of 100, 4300 – 2400 = 1900

Question 6. Let us change the following numbers 1o their nearest whole nunv bers which are multiples of 1000 and calculate.

1. 2836 + 7466
Solution: For the nearest multiple of thousand, 3000 + 7000 = 10,000

2. 3076 + 5731
Solution: For the nearest multiple of thousand, 3000 + 6000 = 9000

3. 7767 + 3685
Solution: For the nearest multiple of thousand, 8000 + 4000 = 12000

4. 8005 + 7483
Solution: For the nearest multiple of thousand, 8000 + 7000 = 15000

5. 1375 + 6307
Solution: For the nearest multiple of thousand, 1000 + 6000 = 7000

Class 6 WBBSE Math Solutions

6. 8643 + 5285
Solution: For the nearest multiple of thousand, 9000 + 5000 = 14000

Question 7. Match left side with right side:

Solution: 1. C, 2. A, 3. B, 4. F, 5. D, 6. E

WBBSE Class 6 Maths Solutions Chapter 4 Roman Numbers And Numbers Upto Hundred Exercise 4

Question 1. Let us write the following numbers in Roman numerals:

1. 7
2. 9
3. 14
4. 25
5. 36
6. 54
7. 65
8. 89
9. 90
10. 98

Solution:

1. 7 – VII
2. 9 – IX
3. 14 – XIV
4. 25 – XXV
5. 36 – XXXVI
6. 54 – LIV
7. 65 – LXV
8. 89 – LXXXIX
9. 90 – XC
10. 98 – XCVIII

Question 2. Let us write the following Roman numbers in Hindu-Arabic numbers:

1. IX, VIII, VII, IV, VI
2. XXX, XXXIX, XL, XLIX, XU
3. LV, LIX, LX, XC, XCV
4. XXVI, XI, XXXVI, XLV, LXXV

Read and Learn More WBBSE Solutions For Class 6 Maths

Solution:

1. IX – 9; VIII – 8, VII – 7, IV – 4, VI – 6
2. XXX – 30; XXXIX – 39; XL – 40; XLIX – 49; XLI – 41 .
3. LV – 55; LIX – 59; LX – 60; XC – 90; XCV – 95
4. XXVI – 26; XI – 11; XXXVI – 36; XIV – 45; LXXV -75

Question 3. Let’s choose the right answer.

Solution: 40 – XL; 49 – XLIX; 90 – XC

Class 6 WBBSE Math Solutions

Question 4. Let us put <, = or > signs in the boxes given below.

1. 5 □ IV
2. XIV □ 14
3. XIX □ XXI
4. LXXVI □ LXXIV

Solution:

1. 5 [>] IV;
2. XIV [=];
3. XIX
4. XXI
5. LXXVI [>] LXXIV

 

Class 6 Math Solutions WBBSE Chapter 5 Concept Of Algebraic Variables

Example:  To make 15 such triangles, let us find the number of match sticks required without actually forming the triangles.

Solution:

Total number of match sticks = 3 x Number of triangles.

If there are triangles, No. of match sticks required = 3n.

WBBSE Class 6 Maths Solutions Chapter 5 Concept Of Algebraic Variables Exercise 5.1

Question 1. Let us find the perimeter of the triangle in terms of x, y, and z.
Solution:

The perimeter of the triangle = x cm + ycm + z cm = (x+y+z) cm.

Read and Learn More WBBSE Solutions For Class 6 Maths

Question 2. Let me form the letters V, Z, E, D………with match sticks, as given below, and try to form a relation to find the total number of match sticks required for any of these figures.
Solution:

1.

Total number of match sticks = 2x

2.

Total number of match sticks = 3x

3.

Total number of match sticks = 4x

4.

Total number = 4x Where x = Number of sticks in V, Z, E, D.

Question 3. I am 4 years younger than my brother. If my brother’s age is x years, let me write my age in terms of my brother’s age.
Solution:

My brother’s age = x years

I am 4 years younger than my brother.

∴  My age = (x – 4) years.

Class 6 Maths Solutions WBBSE

Question 4. Rafika Begum and Aajma Khatoon are making garlands. Aajma Khatoon made 6 garlands more than Rafika Begum. Let us form a relation to find the number of garlands Aajma Khatoon made.
Solution:

Let Rafika Begum made x garlands.

Aajma Khatoon made 6 garlands more than Rafika Begum.

∴ Aajma Khatoon made (x + 6) garlands.

Question 5. In our shop, there are many oil pastel color boxes. Each box has 12 pastel colours. Without counting, let us form a relation to find how many pastel colors are there in the shop.
Solution:

Let there are x number of colour boxes.

Each box contains 12 pastel colors.

∴ Number of total pastel colours in the shop = 12 x.

Question 6. Today at a program of our school we seated ourselves in many rows. In each row there are 15 students. Let us form a relation to find the total number of students seated in the program of our school.
Solution:

Let there are x number of rows in the school. In each row there are 15 students.

∴ Total number of students = 15x.

Question 7. Sitting beside a pond, Partha and Tirtha, both were trying to catch fish. Partha caught 5 fishes more than Tirtha. Let us express the number of fishes caught by Partha in terms of the number of fishes caught by Tirtha.
Solution:

Let Tirtha caught x number of fishes. Partha caught 5 fishes more than Tirtha.

∴ Partha caught (x – 5) fishes.

Class 6 Maths Solutions WBBSE

Question 8. Mita and Maya are making paper boats. Mita made 2 boats less than Maya. Let us form a relation to find the number of boats made by Mita.
Solution:

Let Maya made x number of boats. Mita made 2 boats less than Maya.

∴ Mita made (x – 2) boats.

Question 9. Father bought several packets of sweets. If each packet contains 5 sweets, let us form a relation to find the total number of sweets bought by the father.
Solution:

Let father buy x packets of sweets. Each packet contains 5 sweets.

∴ Total number of sweets father bought = 5x.

Question 9. Grandmother prepared coconut sweets today. She gave my brother 2 more sweets than she gave me and my sister 3 less. Let us form a relationship to find how many sweets my brother and sister got in terms of the unknown number of sweets I got.
Solution:

Let I get x number of sweets.

My brother got (x + 2) sweets.

My sister got (x – 3) sweets.

Question 10. In the expressions given below, let us identify the variables and constants:

1. x + 2
Solution: x + 2 —  variable x Constant 2

2. 5
Solution: 5 – Constant 5

3. y – 6
Solution: y-6 – variable y Constant6

4. 2p + 8
Solution: 2p + 8 – variable p –  Constant 2, 8

5. -4
Solution: – 4 – Constant 4

6. 5 (3x – 2) + 5
Solution: 5 (3x-2)+5 – variable x – Constant 5, 3, – 2

7. 10-2p
Solution: 10p-2 – variable p – Constant 10,-2

8. 15z
Solution: 15z – variable z – Constant 15

9. x + 2y
Solution: x + 2y – variable x,y – Constant 2

Class 6 Maths Solutions WBBSE

Question 11. Let us express in language the following expressions:

1. y + 6
Solution: Sum of y and 6

2. a-2
Solution: Difference of a and 2

3. 5y
Solution: 5 times of y or y is multiplied by 5

4. a/9
Solution: a is divided by 9

5. 3x
Solution: 3 times of x or x is multiplied by 3

6. 5x+2
Solution: Sum of 2 and 5 times of x

7. a+b
Solution: Sum of a and b

8. 6x-4
Solution: Difference of 6 times of x and 4

9. x>5
Solution: x is greater than 5

10. x≥7
Solution: x is greater than or equal to 7

11. y ≯  10
Solution: y is not greater than  0

12. y≤10
Solution: y is less than or equal to 10

13. x ≮  7
Solution: x is not less than 7

14. x<9
Solution: x is less than 9

15. x≥12
Solution: x is greater than or equal to 12

16. x≥5
Solution: x is not greater than 5

Forming expressions with signs and symbols

Solution:

Chapter 5 Concept Of Algebraic Variables Exercise 5.2

Question 1. Let us write in language the following expressions.

1. 10a
Solution: Ten times of a or a is multiplied by 10

2. a + c
Solution: Sum of a and c

3. x – y
Solution: Difference of x and y

4. 9x + 2
Solution: Sum of 9 times of x and 2

5. x + y + z
Solution: Sum of x, y and z

6. 3 x – 7
Solution: Seven less than three times of x

7. p/3-4
Solution: Four less than one-third of p

8. x > 6
Solution: x is greater than 6

9. p ≯  9
Solution: p is not greater than 9

Question 2. Let us form the algebraic expressions of the following with signs and symbols

1. Sum of a and 7
Solution: a + 7

2. Subtract 9 from y
Solution: y – 9

3. Multiply a by 3
Solution: 3a

4. x is greater than 13
Solution: x>13

5. y is not equal to 5
Solution: y ≠ 5

6. x is divided by 8
Solution: x/8

7. Sum of ten times p and 7
Solution: 10p + 7

8. 8 is subtracted from 3 times x
Solution: 3x – 8

9. Sum of x and y
Solution: x + y

10. Product of x and y
Solution: x X y

11. k is less than y
Solution: k < y

12. b is not less than 8
Solution: b ≮  8

Question 3. Let us find the difference between the following sets of algebraic expressions:

1. x+5, x-5, 5x
2. 2p+3, 2p-3, 3p+2, 3p-2

Solution:

1. x+5 → Sum of x and 5

x- 5 → 5 is subtracted from x

5x → 5 times of x

2. 2p + 3 → Sum of twice p and 3

2p – 3  → 3 less than twice of p

3p + 2 → Sum of times of p and 2

3p – 2 → 2 less than 3 times of p

3. Let us prepare four different algebraic expressions with the variable x and constant 6. Let us write in a statement the expressions formed and find the difference amongst them :
Solution:

Four algebraic expressions x + 6; x – 6, 6x + 2 ; 6x – 2

x + 6 → Sum of x and 6

x – 6 > Difference of x and 6

6x + 2 > Sum of six times of x and 2

6x – 2 > Difference of six times of x and 2

4. Let us prepare four different algebraic expressions with the variable x and two different constants 9 and
Solution:

Four different algebraic expressions with variable x and two different constants 9 and 11.

9X + 11 → Sum of nine times of x and 11

11X —9 → Difference of 11 times x and 9

9x X 11 → Product of 11 and nine times of x

9 ÷ 11x → Nine divided by 11 times of x

5. With two variables and one constant, let us prepare four different expressions and find the difference among them
Solution:

Four different algebra expression with two variables and one constant. 2x + y + 1, 2x + 1 – y, 2y + x + 1,  2y + 1 – x

2x + y + 1 → Sum of twice x and y and 1

2x + 1 – y → y is subtracted from the sum of twice x and 1

2y + x + 1 → Sum of twice y and x and 1

2y + 1 – x → x is subtracted from the sum of twice y and 1.

Problem 4. Let us match the two sides

Solution: 1. B, 2. C, 3. D, 4. E, 5. A

Question 5. Let us read and fill in the gaps

1. Present age of Mukti is x years, 4 years later her age will be years.
Solution:

Present age of Mukti is x years, 4 years later her age will be [x + 4] years.

2. Present age of Firoz is y years; 7 years ago his age was years.
Solution:

Present age of Firoz is y years; 7 years ago his age was [y- 7] years.

3. In Kumud’s garden there are x number of saplings of marigold. But in Shahida’s garden, there are three times more saplings than Kumud’s garden. There are saplings in Shahid’s garden.
Solution:

In Kumud’s garden there are x number of saplings of marigolds. But in Shahida’s garden there are three times more saplings than Kumud’s garden. There are [3x] saplings in Shahida’s garden.

4. Funds were collected for repairing the roads of Durganagar. Habib paid Rs. x but Muskan paid Rs. 10 more than twice the money Habib paid. Muskan paid Rs .
Solution:

Funds were collected for repairing the roads of Durganagar. Habib paid Rs. x but Muskan paid Rs. 10 more than twice the money Habib paid. Muskan paid Rs. [2x + 10].

5. The height of David is 3 cm less than Aminur. If height of Aminur is ‘x’ cm, height of David is cm.
Solution:

Height of Devid is 3 cm less than Aminur. If the height of Aminur is ‘x’ cm, height of David is [x- 3] cm.

Problem 6. Let us prepare stories which will satisfy the following expressions

1. Rs. (x + 18)
Solution:

Price of my exercise book is Rs. x. Price of Mihir’s exercise book is Rs.18 more than mine. Hence, price of Mihir’s exercise book is Rs. (x + 18).

2.(y — 21) cm.
Solution:

Length of my classroom is y cm, but the length of another room is 21 cm less than my classroom. So the length Of the other room is (y – 21) cm.

3. 5x years
Solution:

My sister’s age is x years and I am 5 times older than her.

∴ My age is 5x years.

4. p/4
Solution:

A man bought p cakes, his 4 boys, each boy got p/4.

5. (2x + 3) metres
Solution:

The length of a room is x m but the length of another room is 3 m more than the twice of the 1st room.

∴ The length of 2nd room is (2x + 3) metres.

6. (3 x – 5) hours
Solution: A boy took x hours to do all the sums of an exercise but his friend took 5 hours less than thrice of the time taken by the 1 st boy.

So, the 2nd boy took (3x – 5) hours to do the sums.

Class 6 Math Solutions WBBSE Fraction

Question 1. Let us find the value of (40 ÷ 5) ÷ 4 (5 – 3) If there is no ‘sign’ after a number, it means multiplication
Solution:

(40 ÷ 5) ÷ 4 (5 – 3)

= 8 ÷ 4 of 2

= 8 + 8

= 1

Question 2. Let me find the values of {25 – (4 ÷ 9)} ÷ 3 and 25 – 4 + 9 ÷ 3
Solution:

{25 – (4 + 9)} ÷ 3

= {25-13}÷3

= 12÷3

= 4

and

Read and Learn More WBBSE Solutions For Class 6 Maths

25 – 4 + 9÷3

= 25-4 + 3

= 28-4

= 24

Class 6 Maths Solutions WBBSE

Question 3. Shall we get same values for (16 – 4) (5 – 3) and 16 – 4(5 -3).
Solution:

(16 – 4) (5 – 3)

= 12×2

= 24 and

16-4(5-3)

= 16 – 4 of 2

= 16-8

= 8

Question 4. Let me find the values for 10 – 3 – 5 and 20 ÷ 5 ÷ 2.
Solution:

10 – 3 – 5

= 7 – 5

= 2 and

20 ÷ 5 ÷ 2

= 4 ÷ 2 = 2

Class 6 Maths Solutions WBBSE Fraction Exercise 1.1

Question 1. Verify, if the values are same for all these cases

1. 20 + 8 ÷ (4 – 2)
Solution:

20 + 8 ÷ (4 – 2)

= 20 + 8 ÷ 2

= 20 + 4

= 24

2. (20 + 8) ÷ (4 – 2)
Solution:

(20 + 8) ÷ (4 – 2)

= (20 + 8) ÷ 2

= 28 ÷ 2

= 14

3. (20-8)(4-2)
Solution:

(20 – 8) (4 – 2)

= 12 x 2

= 24

4. 20 – 8 (4 – 2)
Solution:

20 – 8 (4 – 2)

= 20 – 8(2)

= 20 – 16 =4

5. (20 + 8) ÷ 4 – 2
Solution:

(20 + 8) ÷ 4 – 2

= 28 ÷ 4 – 2

=7 – 2 = 5

Class 6 Maths Solutions WBBSE

Question 2. Let us form similar simplification sums with numbers 12, 6, 3 and 1 and then find their values:

1. 12 + 6 ÷ (3 -1)
Solution:

= 12 + 6 ÷2

=12 + 3

= 15

2. (12 + 6) ÷ (3 -1)
Solution:

= 18 ÷ 2

= 9

3. (12-6) (3-1)
Solution:

= 6 x 2

= 15

4. 12 – 6(3 – 1)
Solution:

= 12 – 6 x 2 =12-12 = 0

5. (12 + 6) ÷ 3-1
Solution:

= 18 ÷ 3-1

= 6-1 = 5

Class 6 WBBSE Math Solutions

Question 3. Let us find the value of simplification sums:

1. \(256 \div \overline{16 \div 2} \div \overline{18 \div 9} \times 2\)
Solution:

⇒ \(256 \div \overline{16 \div 2} \div \overline{18 \div 9} \times 2\)

= 256 ÷ 8 ÷ 2 x 2

= 32 ÷ 2 x 2

= 16 x 2

= 32

2. (72 ÷ 8 x 9)- (72 ÷ 8 of 9)
Solution:

(72 ÷ 5- 8 x 9) – (72 ÷ 5- 8 of 9)

= (9 x 9) – (72 ÷ 72)

= 81-1

= 80

3. 76-4 -[6 + {19-(48- \(\overline{57-17}\)))]
Solution:

76-4 -[6 + {19-(48- \(\overline{57-17}\)))]

= 76- 4 [6+ {19 – (48 – 40)}]

= 76 – 4 – [6+{19 – 8}]

= 76-4-[6+11]

= 76-4-17 = 72-17 = 55

4. {25 x 16 ÷ (60 ÷15) – 4 x (77 – 62)} ÷ (20 x 6 ÷ 3)
Solution:

{25 x 16 ÷ (60 ÷15) – 4 x (77 – 62)} ÷ (20 x 6 ÷ 3)

= {25 x 16 ÷ 4 – 4 x 15} ÷ (120 ÷ 3)

= {25 x 4 – 60} ÷ 40

= {100 – 60} ÷ 40

= 40 ÷ 40

= 1

5. [16 ÷ {42 – 38 + 2}] 12 ÷ (24 ÷ 6) x 2 + 4
Solution:

[16 ÷ {42 – 38 + 2}] 12 ÷ (24 ÷ 6) x 2 + 4

= [16 ÷ {42 – 40}] 12 ÷ 4 x 2 + 4

= [16 ÷ 2] 12 ÷ 4 x 2 + 4

= 8 of 12 ÷ 4 x 2 + 4

= 96 ÷ 4 x 2 + 4

= 24 x 2 + 4

= 48 + 4

= 52

Class 6 WBBSE Math Solutions

6. 4 x [24-{110- \(\overline{11+3}\) x4) ÷ 9}] ÷ 2 of 9
Solution:

4 x [24-{110- \(\overline{11+3}\) x 4) ÷ 9}] ÷ 2 of 9

= 4 x [24 – {110-14×4) ÷ 9}] ÷18.

= 4 x [24 – {(110-56) ÷ 9}] ÷18.

= 4 x [24 – {54 ÷ 9}] ÷18 = 4 x [24 – 6] ÷18

= 4 x 18 ÷ 18

= 4 x 1

= 4

7. 200 ÷ [88-{(12×13)-3(40-9)}]
Solution:

200 ÷ [88 -{(12×13)- 3(40 – 9)}]

= 200 ÷ [88-{156-3×31}]

= 200 ÷ [88-{156-93}]

= 200 ÷ [88 – 63]

= 200 ÷ 25

= 8

8. (987- \(\overline{43+25}\))-10[5 + {(999 ÷ \(\overline{9×3}\)+(\(\overline{8×9}\) ÷ 6)4}]
Solution:

(987- \(\overline{43+25}\))-10[5 + {(999 ÷ \(\overline{9×3}\)+(\(\overline{8×9}\) ÷ 6)4}]

= (987 – 68) – 10 [5 + {999 ÷ 27 + (72 ÷ 6)4}]

= 919 -10 [5 + {37+12 of 4}]

= 919-10 [5+ {37+ 48}]

= 919-10 [5+ 85]

= 919-10 x 90

= 919 – 900

= 19

Class 6 WBBSE Math Solutions

Question 4. Let us form a story for the following simplification and then solve:

1. You bring 12 eggs from the market, but 2 eggs are rotten. Now you divide the rest of the eggs between 2 of your friends. Find how many eggs each will get.
Solution:

(12-2) ÷ 2

=10 ÷2 = 5

∴ Each will get 5 eggs.

2. You have 90 rupees, you spent Rs. 48 on books. Again, your father gives you Rs. 21. With this total money you buy 7 pens of equal price. What is the price of each pen?
Solution:

(90-48+ 21) ÷ 7

= (42 + 21) ÷ 7

= 63 ÷ 7

= 9

∴ Price of each pen = Rs. 9.

Question 4. Let us express in mathematical language and solve:

Rajdeep’s father sold 125 guavas from their guava orchard at Rs. 2 each to Baruipur market. With the money, he bought 2 pens for Rs. 5 each and 2 exercise books for Rs. 20 each and divided the remaining money among two brothers and sisters to buy sweets. Let us find out how much money Rajdeep got for sweets.
Solution:

The total amount of money Rajdeep’s father received by selling 125 guavas at Rs. 2 each = 125 x Rs. 2 = Rs. 250

Now, he bought 2 pens for Rs. 5 each = Rs. 5×2 = Rs. 10 and he bought 2 exercise books for 20 each = Rs. 20 x 2 = Rs 40

∴  Total amount he spent = Rs. 10 + Rs. 40 = Rs. 50

Rest amount = Rs. 250 -(40 + 10) = 200

Each will get = Rs. 200 ÷ 2 = Rs. 100.

∴ In mathematical language,

[125 x 2-{(5×2)+ (20×2)}] ÷ 2

= [250-{10+ 40}] ÷ 2

= [250-50] ÷ 2

= 200 ÷ 2

= 100

WBBSE Math Solutions Class 6 Fraction Excercise 1.2

Question 1. 6 multiples of 5 which do not not contain ‘O’.
Solution: 5,15,25, 35, 45,55.

Question 2. Let us find 3 multiples of 7 which are greater than 50.
Solution: 56, 63, 70.

Question 3. Let us think and find 2-digit numbers which are multiples of 4.
Solution: 12,16,20,24,28,32,36,40.

Question 4. Let’s find three numbers which are the factors of 4.
Solution: 1,2, 4.

Question 5. Let’s find two numbers whose L.C.M. is 12 and their sum is 10.
Solution: The required numbers are 4 and 6as4 + 6 = 10 and L.C.M of 4 and 6 = 12.

Question 6. What are the prime factors of 14?
Solution: Prime factors of 14: 2, 7.

Question 7. What is the least prime number?
Solution: The least prime number is 2.

Question 8. Which number is neither prime nor composite?
Solution: 1

Question 9.

1. 42 is a multiple of which of the following numbers?

1. 7
2. 13
3. 5
4. 6

Solution: 42 is a multiple of

1. 7,

4. 6.

2. Which of the following numbers has 11 as a factor?

1. 101
2. 111
3. 121
4. 112

Solution: 3. 121.

WBBSE Math Solutions Class 6

Question 10. Which of the following pairs of numbers are mutually prime?

1. 5, 7
2. 10, 21
3. 10, 15
4. 16, 15.

Solution: 1. 5, 7

Question 11. Let us find two pairs of composite numbers which are mutually prime.
Solution: (4,15) and (4,9).

Question 12.

1. Let’s write H.C.F. of mutually prime numbers,
2. Let’s write L.C.M. of mutually prime numbers.

Solution:

Let the two prime numbers are 15 and 16.

1. H.C.F of 15 and 16 is 1.
2. L.C.M of 1 5 and 1 6 is (15 x 16) = 24.

Question 13. Finding prime factors and let’s find H.C.F. of the following

1. 22,44;
2. 54, 72;
3. 27,64;
4. 36,30;
5. 28, 35, 49;
6. 30, 72, 96;
7. 20, 40, 80.

Solution:

1. 22 = 2 x 1 1 x 1; 44 = 2 x 2 x 1 1 x 1

∴ H.C.F. = 2×11 x 1 =22

2. 54 = 2 x 3 x 3 x 3 x 1; 72 = 2x2x2x3x3x1

∴ H.C.F. = 2 x 3 x 3x 1 =18

3. 27 = 3 x 3 x 3 x 1; 64=2x2x2x2x2x2x1

∴ H.C.F =1

4. 36 = 2 x 2 x 3 x 3 x 1; 30 = 2x3x5x1

∴ H.C.F. = 2x3x1 =6

5. 28 = 2x2x7x1; 35 = 5 x 7 x 1; 49 = 7x7x1

∴ H.C.F. = 7×1=7

6. 30 = 2 x 3 x 5 x 1; 72 = 2x2x2x3x3x1; 96=2x2x2x2x2x3x1

∴ H.C.F =2x3x1=6

7. 20 = 2 x 2 x 5 x 1; 40 = 2x2x2x5x1; 80=2x2x2x2x5x1

∴ H.C.F = 2x2x5x1=20

WBBSE Math Solutions Class 6

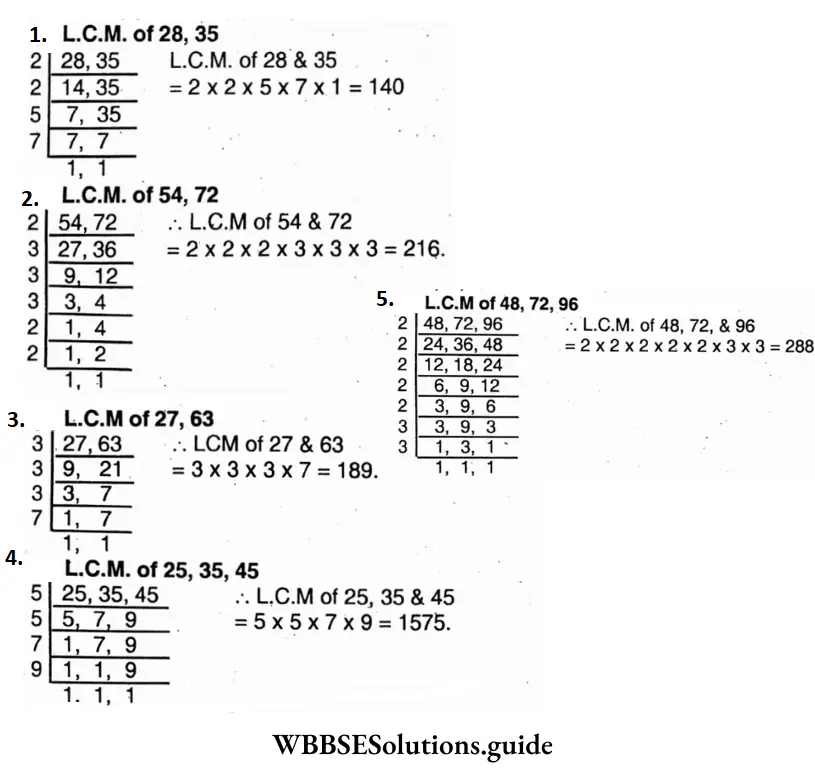
Question 14. Let’s find L.C.M. of the following by division method

1. 28, 35;
2. 54, 72;
3. 27, 63;
4. 25, 35, 45;
5. 48, 72, 96.

Solution:

Question 15. Let’s find L.C.M. of the following by finding their prime factors

1. 25, 80;
2. 36, 39;
3. 32, 56;
4. 36, 48 and 72;
5. 25, 35 and 45;
6. 32,
7. 40 and 84.

Solution:

1. 25 = 5 x 5 x 1; 80=2x2x2x2x5x1

∴ L.C.M of 25, 35 & 45

2. 6 = 2 x 2 x 3 x 3 x 1; 39 = 3 x 13 x 1

∴ L.C.M. of 36 and 39 =2x2x3x3x13 = 468.

3. 32 = 2x2x2x2x2x1; 56 = 2x2x2x7

∴ L.C.M. of 32 and 56 =2x2x2x 2x2x7 = 224

4. 36 = 2 x 2 x 3 x 3 x 1; 48=2x2x2x2x3x1; 72 = 2x2x2x3x3x1

∴ L.C.M of 36, 48 and 72 = 2x2x2x2x3x3 = 144

5. 25 = 5 x 5 x 1; 35 = 5 x 7 x 1; 45 = 3x3x5x1

∴ L.C.M. of 25,35 and 45 = 3x3x5x5x7=1575

6. 32 = 2x2x2x2x2x1; 40 = 2 x 2 x 2 x 5 x 1; 84 = 2x2x3x7x1

∴ L.C.M. of 32, 40 and 84 =2x2x2x2x2x3x5x1 = 3360

WBBSE Math Solutions Class 6

Question 16. Let’s find which pairs of numbers are mutually prime 

1. 47, 23;
2. 25, 9;
3. 49,35;
4. 36, 54.

Solution:

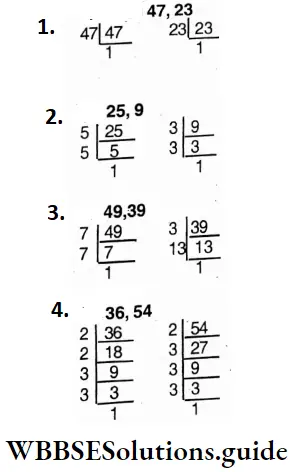
1. 47 = 47×1; 23 = 23 x 1

There are no common factors between 47 and 23.

∴ They are mutually prime.

2. 25 = 5 x 5 x 1; 9 = 3 x 3 x1

There are no common factors between 25 and 9.

∴ They are mutually prime.

3. 49 = 7 x 7 x 1; 39 = 3x13x1

There are no common factors between 49 and 39.

∴ They are mutually prime.

4. 36 = 2 x 2 x 3 x 3 x 1; 54 = 2x3x3x3x1

There are three common factors (2,3,3).

∴ 36  and 54 are not mutually prime.

Question 18. Let’s find H.C.F, and L.C.M. of the following numbers by short division method:

1. 33 and 132,
2. 90 and 144,
3. 32, 40 and 72,
4. 28, 49, 70

Solution:

Question 19. Let’s find the least number which is divisible by 18, 24 and 42.
Solution:

First we have to find the L.C.M. of the least numbers.

L.C.M. = 2x2x2x3x3x7 = 504

∴ The required L.C.M = 504

Question 20. Let’s find the greatest number which when divided 45 and 60 does not leave any remainders.
Solution:

To find the greatest number we have to find the H.C.F. of 45 and 60.

∴ The required greatest number 15

Question 21. Let’s find the product of two numbers whose L.C.M. and H.C.F are 252 and 6 respectively.
Solution:

Product of two numbers = L.C.M. x H.C.F. = 252 x 6 = 1512

Question 22. If the H.C.F. and L.C.M. of two numbers are 8 and 280 and one of the numbers is 56, let’s find the other number.
Solution:

Product of two numbers = L.C.M. x H.C.F.

One number = \(\frac{\text { L.C.M } \times \text { H.C.F }}{\text { other number }}=\frac{280 \times 8}{56}=40\)

Question 23. Let’s write two numbers whose H.C.F. is 1.
Solution:

H.C.F. of two prime numbers is one. Similarly the H.C.F. of one prime number and one another number is one.

Question 24. Let’s find the maximum number of people among whom 48 rasogollas and 64 sandeshes are to be distributed in equal numbers.
Solution:

To find the number of people we have to find the H.C.F of 48 and 64.

H.C.F = 16

∴ The required number of people = 16.

WBBSE Math Solutions Class 6

Question 25. Bibhash and his friends decided to form a drama group of either 8 or 10 people. Let’s find the minimum number of people who will be able to form both types of groups.
Solution:

To find the number of people, we have to find the L.C.M. of 8 and 10.

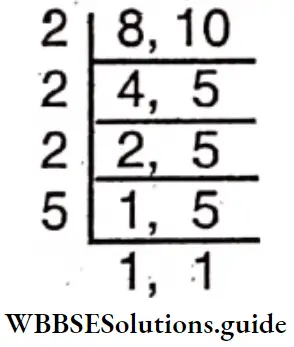
L.C.M. =2x2x2x5 = 40

∴ The required number of people is 40

Question 26. Panchayat has sent flower saplings to the students of class 6 of Jodunath Vidya Mandir for their school garden. It was found that if the saplings can be put in rows of 20, 24 and 30, then the number of sap lings in each row will be equal. Let’s find the minimum number of saplings that Panchayat sent to school.
Solution:

To find the minimum number of saplings, we have to find the L.C.M. of 20, 24 and 30.

L.C.M. of 20, 24, 30

L.C.M. = 2x2x2x3x5=120

∴ The minimum required of flower saplings = 120

Question 27. The perimeter of the front wheel and rear wheel of an engine are 14 dcm and 35 dcm respectively. Let’s find the minimum distance the engine can cover before both wheels take complete revolutions together.
Solution:

To find the minimum distance we have to find the L.C.M of 14 and 25

∴ L.C.M = 2x5x7 = 70.

∴ The required minimum distance = 70 dcm.

Question 28. For each of the following cases, let’s write two numbers whose:

1. H.C.F. is 7,
2. L.C.M. is 12,
3. H.C.F. is (put 1 digit number),
4. L.C.M. is (Put 1 digit number.)

Solution:

1. The required numbers are 7 and 14 as H.C.F. of 7 and 14 is 7.
2. The required numbers are 3 and 12 as L.C.M of 3 and 12 is 12.
3. The required numbers are 4 and 8. H.C.F. = 4
4. The required numbers are 3 and 6. L.C.M. = 6

Fraction Exercise 1.3

Question 1. I took a white rectangular piece of paper. I divided it horizontally into 3 equal parts and coloured. In the colours of our national flag, find the proportion of each colour.
Solution: Portion of saffron colour = 1/3 part

Portion of white colour = 1/3 part

Portion of green colour = 1/3 part

Question 2. Seema took a paper, same as mine, but coloured it different. Let’s find how and what portion she coloured.
Solution:

Portion of saffron colour = 2/3 part

1/2 part is coloured.

Let’s colour 1/4 part

Portion of green colour = 1/3 part

3/5 part is coloured

3/4 part is coloured

2/5 is coloured

1/6 is coloured

2/6 is coloured

4/10 is coloured

1/2 is coloured

Question 3. Let me find what part of the mangoes I disposed of.

1/3 part of the number of mangoes collected are rotten.

In the picture 1/3 part of mangoes are circled with red —>

It is found, rotten mangoes are 1/3 part = 4 mangoes.

From picture it is found 2/3 part of mangoes are fish.

∴ 2/3 part of total number of mangoes = 8 mangoes.

Hence, from picture it is found, that 4 mangoes are rotten and 8 mangoes are fresh.

WBBSE Math Solutions Class 6

Question 4. Let’s find out from my picture in which parts the different fruits are present.
Solution:

In the picture, out of the 4 equal parts of the fruits, the apples are 1/4 part.

That is, in the picture number of apples are 1/4 part of the total number of furits.

In the picture, mango is 3 part of 4 equal parts.

That is, in the picture mango is 3/4 part of the total number of fruits.

In the picture aside, red flowers are 2 part of 3 equal parts of flowers.

Thus, 10/15 part of flowers are red flowers.

White flowers are 1 part of 3 equal parts of flowers.

Thus, 5/15 part of flowers are white flowers.

∴ 2/5 parts = 2 parts out of 5 equal parts = 4 balls.

∴ 1/4 parts = 1 part out of 4 equal parts = 2 coins.

Question 5. I Painted ted one of the window panes and a part of the other pane. Let me find, how much has been painted.
Solution:

Coloured → \(\left(2+\frac{1}{2}\right)=2 \frac{1}{2}=\frac{2 \times 2+1}{2}=\frac{5}{2}\)

Coloured → \(\left(2+\frac{1}{6}\right)=2 \frac{1}{6}=\frac{2 \times 6+1}{6}=\frac{13}{6}\)

Question 6. Let’s find four equivalent fractions for each of the fractions 2/3 and 5/9
Solution:

Four equivalent fractions of 2/3 are

1. 4/6 [Multiply numerator and denominator by 2]
2. 6/9 [Multiply numerator and denominator by 3]
3. 8/12 [Multiply numerator and denominator by 4]
4. 10/15 [Multiply numerator & denominator by 5]

Four equivalent fractions of 5/9 are

1. 10/18 [Multiply numerator and denominator by 2]
2. 15/27 [Multiply numerator and denominator by 3]
3. 20/36 [Multiply numerator and denominator by 4]
4. 25/45 [Multiply numerator and denominator by 5]

WBBSE Class 6 Maths Solutions Fraction Exercise 1.4

Question 1. Let us write in blank boxes:
Solution:

1. 7/10 part is coloured.
2. 5/6 part is not coloured.
3. 2/5 part is coloured.

Question 2. Let us write in blank boxes:

1. When we say half bread, what part of the whole bread we see?
Solution:

When we say half bread, what part of the whole bread we see 1-1/2 = 1/2 part.

2. I have a big chocolate. Dividing it into 8 pieces, I gave 3 pieces to my sister, 2 pieces to my brother and rest I ate myself. Let’s find what parts of chocolate we individually ate.
Solution:

My sister got 2/8 part of the chocolate.

My brother got 2/8 part = 1/4 part

∴ Remaining part = \(\left[1-\left(\frac{3}{8}+\frac{1}{4}\right)\right]\)

= \(\left[1-\left(\frac{3+2}{8}\right)\right]\)

= \(\left[1-\frac{5}{8}\right]=\frac{8-5}{8}=\frac{3}{8} \text { part }\)

∴ Part of chocolate I received = 3/8 part.

3. Let us write all numbers from 1 to 10. Out of these numbers what fraction are the prime numbers?
Solution:

The prime numbers between 1 to 10 are 2,3,5, and 7.

Total number=4 Fractional part of the prime number = 4/10 = 2/5 part.

WBBSE Class 6 Maths Solutions

4. There are few oranges in a basket. After giving half of the oranges to my grandfather, 2 oranges are left. Let’s find how many oranges were there in the basket.
Solution:

Number of oranges = \(2 \div \frac{1}{2}=2 \times \frac{2}{1}\) = 4

5. In two glasses of equal size equal amount of lemon drink was prepared. One glass contains 1/5 part of sugar and the other contains 2/7 part of sugar. Let’s find without taking the drinks, which glass of lemon drink tastes sweeter.
Solution:

∴ \(\frac{2}{7}\) part of sugar glass of lemon drink testes sweeter.

6. \(\frac{5}{7}\) part of school gate has been painted. Let’s find out which part is still to be painted.
Solution:

⇒ \(\frac{5}{7}\) part of school gate has been painted.

Rest part of the gate which is still to be painted = \(\text { 1. }-\frac{5}{7}=\frac{7-5}{7}=\frac{2}{7} \text { part }\)

7. I have Rs. 20.1 spent Rs. 5. Let’s find what part I spent and what part is left with me.
Solution:

Total amount = Rs. 20.

I spent Rs. 5 = \(\frac{5}{20}\) = \(\frac{1}{4}\) part.

Remaianing part = \(\left(1-\frac{1}{4}\right) \text { part }=\left(\frac{4-1}{4}\right) \text { part }=\frac{3}{4} \text { part. }\)

8. Rajia has 36 berries. She will give me — part of her berries. Let me find out how many berries she will give me.
Solution:

Rajia has 36 berries.

She will give me = \(\frac{2}{3}\) of 36 berries = (2 x 12) = 24 berries.

Question 4. Let us mark proper fraction by ; improper fraction by and mixed fraction by Δ
Solution:

Let us mark

1. Proper fraction
2. Imoroper fraction
3. Mixed fraction Δ

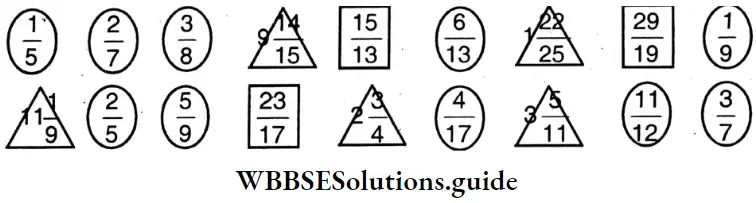
Proper fraction: \(\frac{1}{5}, \frac{2}{7}, \frac{3}{8}, \frac{6}{13}, \frac{1}{9}, \frac{2}{5}, \frac{5}{9}, \frac{4}{17}, \frac{11}{12}, \frac{3}{7}\)

Improper fraction: \(\frac{15}{13}, \frac{29}{19}, \frac{23}{17}\)

⇒ \(9 \frac{14}{15}, 1 \frac{22}{25}, 11 \frac{1}{9}, 2 \frac{3}{4}, 3 \frac{5}{11}\)

Mixed fraction: \(9 \frac{14}{15}, 1 \frac{22}{25}, 11 \frac{1}{9}, 2 \frac{3}{4}, 3 \frac{5}{11}\)

WBBSE Class 6 Maths Solutions

Question 5. Let us write three equivalent fractions for each of the following

1. \(\frac{1}{5}\)
2. \(\frac{2}{5}\)
3. \(1 \frac{1}{3}\)
4. \(6 \frac{1}{6}\)
5. \(3 \frac{4}{5}\)

Solution:

1. \(\frac{1}{5}\)

1st equivalent fraction of \(\frac{1}{5}=\frac{2}{10}\)

2nd equivalent fraction of \(\frac{1}{5}=\frac{3}{15}\)

3rd equivalent fraction of \(\frac{1}{5}=\frac{4}{20}\)

2. \(\frac{2}{5}\)

1st equivalent fraction of \(\frac{2}{5}=\frac{4}{10}\)

2nd equivalent fraction of \(\frac{2}{5}=\frac{6}{15}\)

3rd equivalent fraction of \(\frac{2}{5}=\frac{8}{20}\)

3. 1\(\frac{1}{3}=\frac{4}{3}\)

1st equivalent fraction of \(\frac{4}{3}=\frac{8}{6}\)

2nd equivalent fraction of \(\frac{4}{3}=\frac{12}{9}\)

3rd equivalent fraction of \(\frac{4}{3}=\frac{16}{12}\)

4. 6\(\frac{1}{6}=\frac{37}{6}\)

1st equivalent fraction of \(\frac{37}{6}=\frac{74}{12}\)

2nd equivalent fraction of \(\frac{37}{6}=\frac{111}{18}\)

3rd equivalent fraction of \(\frac{37}{6}=\frac{148}{24}\)

5. 3\(\frac{4}{5}=\frac{19}{5}\)

1st equivalent fraction of \(\frac{19}{5}=\frac{38}{10}\)

2nd equivalent fraction of \(\frac{19}{5}=\frac{57}{15}\)

3rd equivalent fraction of \(\frac{19}{5}=\frac{76}{20}\)

Question 6. Let us express the following in their lowest form:

1. \(\frac{28}{49}\)
2. \(\frac{54}{81}\)
3. \(\frac{72}{108}\)
4. \(\frac{243}{405}\)
5. \(\frac{165}{180}\)

Solution:

1. \(\frac{28}{49}=\frac{4}{7}\)

2. \(\frac{54}{81}=\frac{18}{27}=\frac{2}{3}\)

3. \(\frac{72}{108}=\frac{2}{3}\)

4. \(\frac{243}{405}=\frac{3}{5}\)

5. \(\frac{165}{180}=\frac{11}{12}\)

WBBSE Class 6 Maths Solutions

Question 7. Let us arrange the following fractions from smaller to bigger in ascending order

1. \(\frac{7}{2}, \frac{4}{4}, \frac{7}{5}\)
Solution:

L.C.M. of 2,4,5=20

⇒ \(\frac{7}{2}=\frac{7 \times 10}{2 \times 10}=\frac{70}{20}\)

⇒ \(\frac{7}{4}=\frac{7 \times 5}{4 \times 5}=\frac{35}{20}\)

⇒ \(\frac{7}{5}=\frac{7 \times 4}{5 \times 4}=\frac{28}{20}\)

∴ \(\frac{28}{20}<\frac{35}{20}<\frac{70}{20}\)

i.e., \(\frac{7}{5}<\frac{7}{4}<\frac{7}{2}\)

2. \(5 \frac{3}{4}, 5 \frac{5}{9}, 5 \frac{8}{12}\)
Solution:

⇒ \(5 \frac{3}{4}, 5 \frac{5}{9}, 5 \frac{8}{12}\)

or, \(\frac{23}{4}, \frac{50}{9}, \frac{68}{12}\)

L.C.M of 4,9 and 12=36

⇒ \(\frac{23}{4}=\frac{23 \times 9}{4 \times 9}=\frac{207}{36}\)

⇒ \(\frac{50}{9}=\frac{50 \times 4}{9 \times 4}=\frac{200}{36}\)

⇒ \(\frac{68}{12}=\frac{68 \times 3}{12 \times 3}=\frac{204}{36}\)

⇒ \(\frac{200}{36}<\frac{204}{36}<\frac{207}{36}\)

or, \(\frac{200}{36}<\frac{204}{36}<\frac{207}{36}\)

or, \(\frac{50}{9}<\frac{68}{12}<\frac{23}{4}\)

∴ \(5 \frac{5}{9}<5 \frac{8}{12}<5 \frac{3}{4}\)

3. \(1 \frac{1}{5}, 1 \frac{1}{7}, 1 \frac{1}{8}\)
Solution:

⇒ \(1 \frac{1}{5}, 1 \frac{1}{7}, 1 \frac{1}{8}\)

or, \(\frac{6}{5}, \frac{8}{7}, \frac{9}{8}\)

L.C.M. of 5, 7, 8 = 280

⇒ \(\frac{6}{5}=\frac{6 \times 56}{5 \times 56}=\frac{336}{280}\)

⇒ \(\frac{8}{7}=\frac{8 \times 40}{7 \times 40}=\frac{320}{280}\)

⇒ \(\frac{9}{8}=\frac{9 \times 35}{8 \times 35}=\frac{315}{280}\)

∴ \(\frac{315}{280}<\frac{320}{280}<\frac{336}{280}\)

i.e., \(\frac{9}{8}<\frac{8}{7}<\frac{6}{5}\)

⇒ \(1 \frac{1}{8}<1 \frac{1}{7}<1 \frac{1}{5}\)

Class 6 Math WBBSE Solutions

4. \(\frac{1}{3}, \frac{4}{5}, \frac{7}{15}\).
Solution:

L.C.M of 3,5 and 15=15

⇒ \(\frac{1}{3}=\frac{1 \times 5}{3 \times 5}=\frac{5}{15}\)

⇒ \(\frac{4}{5}=\frac{4 \times 3}{5 \times 3}=\frac{12}{15}\)

⇒ \(\frac{7}{15}=\frac{7 \times 1}{15 \times 1}=\frac{7}{15}\)

∴ \(\frac{5}{15}<\frac{7}{15}<\frac{12}{15}\)

i.e., \(\frac{1}{3}<\frac{7}{15}<\frac{4}{5}\)

5. \(\frac{5}{7}, \frac{3}{4}, \frac{1}{4}\)
Solution:

L.C.M. of 7,4 and 4=28

⇒ \(\frac{5}{7}=\frac{5 \times 4}{7 \times 4}=\frac{20}{28}\)

⇒ \(\frac{3}{4}=\frac{3 \times 7}{4 \times 7}=\frac{21}{28}\)

⇒ \(\frac{1}{4}=\frac{1 \times 7}{4 \times 7}=\frac{7}{28}\)

∴ \(\frac{7}{28}<\frac{20}{28}<\frac{21}{28}\)

∴ \(\frac{1}{4}<\frac{5}{7}<\frac{3}{4}\)

6. \(3 \frac{1}{2}, 7 \frac{5}{9}, 7 \frac{1}{5}\)
Solution:

⇒ \(3 \frac{1}{2}, 7 \frac{5}{9}, 7 \frac{1}{5}\)

⇒ \(\frac{7}{2}, \frac{68}{9}, \frac{36}{5}\)

L.C.M. of 2,9 and 5=90

⇒ \(\frac{7}{2}=\frac{7 \times 45}{2 \times 45}=\frac{315}{90}\)

⇒ \(\frac{68}{9}=\frac{68 \times 10}{9 \times 10}=\frac{680}{90}\)

⇒ \(\frac{36}{5}=\frac{36 \times 18}{5 \times 18}=\frac{648}{90}\)

⇒ \(\frac{315}{90}<\frac{648}{90}<\frac{680}{90}\)

or, \(\frac{7}{2}<\frac{36}{5}<\frac{68}{9}\)

∴ \(3 \frac{1}{2}<7 \frac{1}{5}<7 \frac{5}{9}\)

Class 6 Math WBBSE Solutions

7. \(\frac{1}{8}, \frac{7}{10}, \frac{3}{5}\)
Solution:

L.C.M. of 8,10 and 5=40

⇒ \(\frac{1}{8}=\frac{1 \times 5}{8 \times 5}=\frac{5}{40}\)

⇒ \(\frac{7}{10}=\frac{7 \times 4}{10 \times 4}=\frac{28}{40}\)

⇒ \(\frac{3}{5}=\frac{3 \times 8}{5 \times 8}=\frac{24}{40}\)

⇒ \(\frac{5}{40}<\frac{24}{40}<\frac{28}{40}\)

∴ \(\frac{1}{8}<\frac{3}{5}<\frac{7}{10}\)

8. \(3 \frac{1}{2}, 3 \frac{5}{9}, 3 \frac{1}{5}\)
Solution:

⇒ \(3 \frac{1}{2}, 3 \frac{5}{9}, 3 \frac{1}{5}\)

or, \(\frac{7}{2}, \frac{32}{9}, \frac{16}{5}\)

L.C.M. of 2,9 and 5=90

⇒ \(\frac{7}{2}=\frac{7 \times 45}{2 \times 45}=\frac{315}{90}\)

⇒ \(\frac{32}{9}=\frac{32 \times 10}{9 \times 10}=\frac{320}{90}\)

⇒ \(\frac{16}{5}=\frac{16 \times 18}{5 \times 18}=\frac{288}{90}\)

⇒ \(\frac{288}{90}<\frac{315}{90}<\frac{320}{90}\)

or, \(\frac{16}{5}<\frac{7}{2}<\frac{32}{9}\)

∴ \(3 \frac{1}{5}<3 \frac{1}{2}<3 \frac{5}{9}\)

Question 8. Let us find the values of the following

1. \(\frac{2}{7}+\frac{2}{3}+1 \frac{1}{2}\)
Solution:

= \(\frac{2}{7}+\frac{2}{3}+\frac{3}{2}\)

= \(\frac{2 \times 6+2 \times 14+3 \times 21}{42}\)

= \(\frac{12+28+63}{42}=\frac{103}{42}\)

= \(2 \frac{19}{42}\)

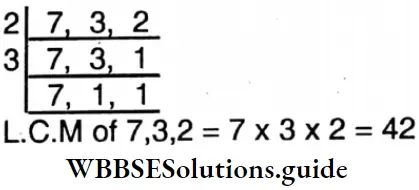
2. \(1 \frac{2}{5}-\frac{3}{8}+\frac{1}{4}\)
Solution:

L.C.M Of 5, 8 and 4

= \(\frac{7}{5}-\frac{3}{8}+\frac{1}{4}\)

= \(\frac{7 \times 8-3 \times 5+1 \times 10}{40}\)

= \(\frac{56-15+10}{40}\)

= \(\frac{51}{40}\)=1 \(\frac{11}{40}\)

Class 6 Math WBBSE Solutions

 

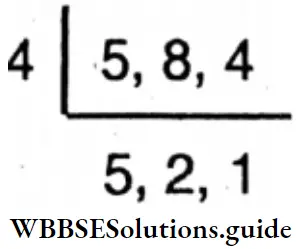
3. \(\frac{2}{5}+\frac{3}{8}-\frac{1}{4}\)
Solution: 

L.C.M Of 5, 8 and 4

= \(\frac{2 \times 8+3 \times 5-1 \times 10}{40}\)

= \(\frac{16+15-10}{40}=\frac{21}{40}\)

4. \(7-3 \frac{1}{8}-2 \frac{1}{3}\)
Solution:

L.C.M of 1, 8 and 3 = 24

= \(\frac{7}{1}-\frac{25}{8}-\frac{7}{3}\)

= \(\frac{24 \times 7-25 \times 3-7 \times 8}{24}\)

= \(\frac{168-75-56}{24}\)

= \(\frac{37}{24}=1 \frac{13}{24}\)

5. \(\frac{4}{5}+\frac{5}{8}-1 \frac{1}{3}\)
Solution: 

L.C.M of 5, 8 and 3

= \(\frac{4}{5}+\frac{5}{8}-\frac{4}{3}\)

= \(\frac{4 \times 24+5 \times 15-4 \times 40}{120}\)

= \(\frac{96+75-160}{120}\)

= \(\frac{171-160}{120}\)

= \(\frac{11}{120}\)

L.C.M = 2x2x2x3x5 =120

Class 6 Math WBBSE Solutions

6. \(1 \frac{3}{10}+1 \frac{4}{5}-1 \frac{1}{4}\)
Solution: 

L.C.M of 10, 5 and 4

= \(\frac{13}{10}+\frac{9}{5}-\frac{5}{4}\)

= \(\frac{13 \times 2+9 \times 4-5 \times 5}{20}\)

L.C.M = 2 x2 x 5 = 20

= \(\frac{26+36-25}{20}\)

= \(\frac{37}{20}=1 \frac{17}{20}\)

7. \(2 \frac{5}{6}-1 \frac{8}{9}+1 \frac{3}{4}\)
Solution: 

L.C.M of 6, 9, 4

= \(\frac{17}{6}-\frac{17}{9}+\frac{7}{4}\)

= \(\frac{17 \times 6-17 \times 4+7 \times 9}{36}\)

= \(\frac{102-68+63}{36}\) L.C.M = 2 x 2x 3x 3 = 36

= \(\frac{97}{36}=2 \frac{25}{36}\)

8. \(4 \frac{1}{7}\)+2 \(\frac{2}{5}-5\)
Solution: 

L.C.M of 7, 5 and 1

= \(\frac{29}{7}+\frac{12}{5}-\frac{5}{1}\) = 7 x 5x 1 = 35

= \(\frac{29 \times 5+12 \times 7-5 \times 35}{35}\)

= \(\frac{145+84-175}{35}\)

= \(\frac{54}{35}\)

= \(1 \frac{19}{35}\)

Question 9. Let us work out

1. During tiffin hours of school \(\frac{1}{4}\) part of drinking water of a tank was used. Another \(\frac{1}{3}\) part of water was used when school got over. Let’s find what part of water is still left in the tank.
Solution:

Let total amount of water = 1 part

Water used = \(\left(\frac{1}{4}+\frac{1}{3}\right) \text { part }=\frac{3+4}{12}=\frac{7}{12} \text { part }\)

∴ Remaining water = \(1-\frac{7}{12}=\frac{12-7}{12}=\frac{5}{12}\) part of the thank.

2. Today, I took a piece of cake for tiffin. My two friends Ayush ar Sabana respectively ate \(\frac{1}{3}\) part and \(\frac{2}{5}\) part of the cake. I ate the remaining part. Let me find who ate the most part of cake.
Solution:

Let total part of cake = 1

Ayush and Sabana ate = \(\frac{1}{3}+\frac{2}{5}\)

= \(\frac{5+6}{15}=\frac{11}{15}\)

Remaining part = \(1-\frac{11}{15}=\frac{15-11}{15}=\frac{4}{15}\) part

Now Ayush, Sabana and I get \(\frac{1}{3}, \frac{2}{5} and \frac{4}{15}\) parts of the cake respectively.

⇒ \(\frac{1}{3}=\frac{1 \times 5}{3 \times 5}=\frac{5}{15}\)

⇒ \(\frac{2}{5}=\frac{2 \times 3}{5 \times 3}=\frac{6}{15}\)

⇒ \(\frac{4}{15}=\frac{4 \times 1}{15 \times 1}=\frac{4}{15}\)

∴ \(\frac{2}{5}\) is the greatest part.

Sabana ate most part of the cake.

Class 6 Math WBBSE Solutions

3. Out of 25 bighas of land Ratanbabu cultivated jute in 16 bigha But, out of 15 bighas of land, Ushadebi cultivated jute in 8 bighas. Let work out to find in what part of their land Ratanbabu and Ushade cultivated jute and who cultivated jute more.
Solution:

Ratanbabu cultivated jute in \(\frac{16}{25}\) part of his land. Ushadebi cultivated jute in \(\frac{8}{15}\) part of her land.

⇒ \(\frac{16}{25}=\frac{16 \times 3}{25 \times 3}=\frac{48}{75}\) L.C.M. of 25 and15

⇒ \(\frac{8}{15}=\frac{8 \times 5}{15 \times 5}=\frac{40}{75}\)

⇒ \(\begin{array}{ccc}
3 & 25, & 15 \\
5 & 25, & 5 \\
5 & 5, & 1 \\
& 1, & 1
\end{array}\)

∴ L.C.M. = 3x5x5 = 75

∴ Ratanbabu cultivated jute more.

4. I have a 15-metre long white ribbon. I cut off \(\frac{1}{3}\) part from it. What part of ribbon is left? Let’s find the length of the remaining part of the ribbon.
Solution:

Total length of white ribbon = 15 metres.

I take = \(\frac{1}{3}\) x 15 m = 5 metre.

Remaining part = \(1-\frac{1}{3}=\frac{3-1}{3}=\frac{2}{3}\) part

And the length of the remaining part of the ribbon = (15 – 5) m = 10 metres.

Class 6 Math Solutions WBBSE Decimal Fractions

We decided to decorate the front portion of the dais of our village club with some coloured tiles of equal size. 2 red tiles were given by me, 3 yellow tiles by Reba, 4 green tiles by Samsur and 1 white tile by Tina.

We all gathered before the dais with a total of 10 tiles.

Out of 10 tiles I gave 2 tiles → \(\frac{2}{10}\) part = 0.2 part = .2

Out of 10 tiles, Reba gave 3 tiles → \(\frac{3}{10}\) part = 0.3 part = .3

Out of 10 tiles, Samsur gave 4 tiles →\(\frac{4}{10}\)part = 0.4 part = .4

Tena give 1 tile → \(\frac{1}{10}\) part = 0.1 part = .1

Hence, \(\begin{array}{cc}
\text { Decimal } & \text { Tenths }\left(\frac{1}{10}\right) \\
\text { number } & \\
0.2 & 2 \\
0.3 & 3 \\
0.4 & 4 \\
0.1 & 1
\end{array}\)

Now, few tiles on floor of the room of our club are broken. We need to replace them.

First, we do arrange for 100 tiles.

I shall give 12 tiles out of those 100 tiles.

I shall give \(\frac{12}{100}\) part = 0.12 part or point one two parts. .

Rohit will give 38 tiles. Thus, he will give \(\frac{38}{100}\)part = 0.38 part.

Mira will give \(\frac{34}{100}\) part = 0.34 part.

Class 6 Math Solutions WBBSE Fraction Exercise 1.5

Question 1. Let us express the coloured portion in terms of decimal fraction

Solution:

1. \(\frac{3}{10}\) part = 0.3

2. \(\frac{36}{100}\) part = 0.36

3. \(\frac{60}{100}\) = 0.6

4. \(\frac{16}{100}\) part = 0.6

5. \(\frac{27}{100}\) part 0.27

Question 2.

1. Let us colour 0.15 part green and 0.53 part yellow. Find total coloured part.

Solution:

0.15 part green and 0.53 part yellow.

∴ Total coloured part = 0.15 + 0.53 = 0.68.

2. Let us colour 0.33 part blue first and 0.15 part red. Find the total uncoloured parts.

Class 6 Math  WBBSE Solution:

0.33 part blue and 0.1 5 part red

∴ Total coloured part = 0.33 + 0.1 5 = 0.48

Total uncoloured part = 1-0.48 = 0.52

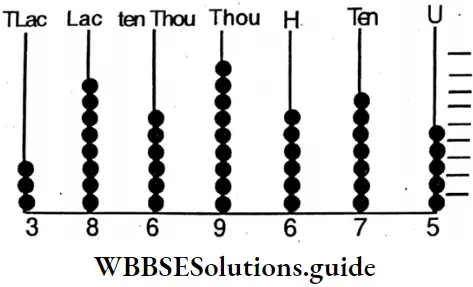
Question 3. Let’s prepare a place value table for the following numbers and write the numbers in words.

1. 27.9
Solution:

=27+ \(\frac{9}{10}\)= Twenty seven point nine

= Two tens seven unit and nine tenth

2. 1.28
Solution:

= \(1+\frac{2}{10}+\frac{8}{100}\)

= one point two eight = one unit and two-tenth eight hundredths.

3.65.134
Solution:

65.134 = \(60+5+\frac{1}{10}+\frac{3}{100}+\frac{4}{1000}\)= Sixty five point one three four

= Six tens five units one tenth three hundredth four thousandths.

4. 42.009
Solution:

42.009+40+2+\(\frac{9}{1000}\)= Forty two point zero zero nine

= Four tens two units nine thousandths.

Class 6 Math Solutions WBBSE

5. 38.205
Solution:

= \(30+8+\frac{2}{10}+\frac{5}{1000}\)

= Thirty-eight point two zero five

= Three tens eight units and two-tenth five thousandths.

6. 4003.08
Solution:

4003.08 = Four thousand three point zero eight

= Four thousand three units eight hundedths.

7. 712.5
Solution:

712.5 = 700+10+2+\(\frac{5}{10}\)

= Seven hunderd twelve point five

= Seven hundred one tenth two units five tenths

8. 45.06
Solution:

45.06 = 40+5+\(\frac{6}{100}\)

= Forty-five point zero six

= Four tens five units six hundredths.

Question 4. Let’s convert the following decimal numbers to fractions:

1. 0.3,
2. 0.21,
3. 0.039,
4. 5.4,
5. 102.035.

Solution:

1. 0.3 = \(\frac{3}{10}\)
2. 0.21 = \(\frac{21}{100}\)
3. 0.039 = \(\frac{39}{1000}\)
4. 5.4 = \(\frac{54}{10}\) = \(\frac{27}{5}\)
5. 102.035 = \(\frac{102035}{1000}\) = \(\frac{20407}{200}\) = 102\(\frac{7}{200}\)

Question 5. Let’s arrange the following in increasing order (ascending order):

1. 0.534, 0.52, 5.34, 0.513
Solution: In ascending order 0. 513, 0.52; 0.534, 5.34

2. 0.536, 0.335, 0.3354, 0.52
Solution: In ascending order 0.335; 0.3354; 0.52; 0.536

3. 2.0, 2.005, 20.05, 2.5
Solution: In ascending order 2.0; 2.005; 2.5; 20.05

Question 6. Let’s arrange the following in decreasing order (descending order):

1. 13.3,11.3,1.33,2.31
Solution: In descending order 13.3,11.3, 2.31,1.33

2. 3.007, 3.07, 37.30, 7.13
Solution: In descending order 37.30; 7.13, 3.07, 3.007

3. 0.88, 0.45, 8.45, 0.8217
Solution: In descending order 8.45, 0.88, 0.8217, 0.45

Question 7.

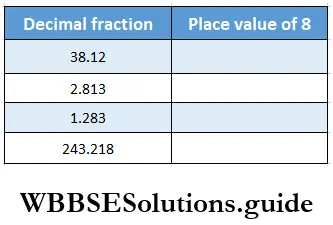
Solution:

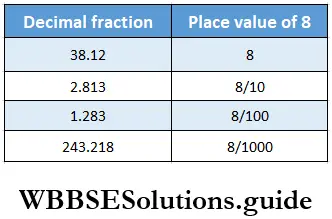
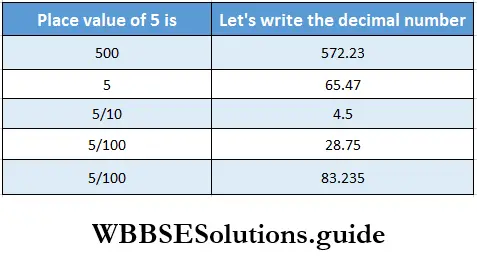
Question 8.

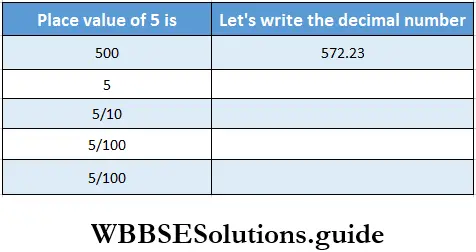
Solution:

Question 9. Let’s put >, = or < in the boxes given below.

1. 5.0 □ 0.5
Solution: 5.0>0.5

2. 72.1 □ 72.10
Solution: 72.1 =72.10

3. 68.5 □ 68.52
Solution: 68.5 < 68.52

4. 72.93 □ 729.3
Solution: 72.93 <729.3

5. 42.6 □ 42.600
Solution: 42.6 = 42.600

6. 2.33 □ 3.22
Solution: 42.6 = 42.600

7. 924 □ 924.0
Solution: 924 = 924.00

8. □ □ □ (Let us write own decimal numbers)
Solution: 84.67 > 72.67

Question 10. Let’s express the following in decimal numbers:

1. Six tenths
Solution: \(\frac{6}{10}\) = 0.6

2. Nine hundredths
Solution: \(\frac{9}{100}\) = 0.09

3. Two thousandths
Solution: \(\frac{2}{1000}\) = 0.02

4. Two hundred three point four-five
Solution: 203.45

5. Four thousand two units five thousandths
Solution: 4002.005

6. Six hundred twenty-nine point zero five
Solution: 629.005

7. 2 + \(\frac{3}{10}\)
Solution: 2 +0.3 = 2.3

8. 10+7+\(\frac{8}{1000}\)
Solution: 17.008

Question 11. I had Rs. 5. I bought a pen for Rs. 3.50. Let’s find out how much money is left.
Solution: Remaining money = Rs. 5 – Rs. 3.50 = Rs. 1.50.

Question 12. What must be added to 2.75 to get 3?
Solution: Required number = 3 – 2.75 = 0.25.

Question 13. From a string of length 12.5 cm, Mira cuts off 8.5 cm. Let’s find, what portion of the string is left?
Solution: Remaining portion = 12.5 cm – 8.5 cm = 4 cm.

Question 14. The length of my exercise book is □ cm and its breadth is □ cm. Let me find the perimeter of my exercise book.
Solution: Let the length of the exercise book = 18 cm and the breadth of the exercise book = 12 cm.

∴ Perimeter = 2 x (length + breadth)

= 2 x (18 cm + 12 cm) = 2 x 30 cm = 60 cm.

Question 15. For an occasion at our house, father bought rice for Rs. 200, pulses for Rs. 125.50 and vegetables for Rs. 242.50. Let’s calculate the total amount of money spent by father.
Solution: Total amount of money spent = Rs. (200 + 125.50 + 242.50) = Rs. 568.

Question 16. In a long-jump competition, Sahil jumped 182.88 cm and Munna jumped 179.25 cm of length. Let’s find how much more did Sahil jump.
Solution: Sahil jumped more than Munna

= 182.88 cm – 179.25 cm = 3.63 cm.

Question 17. What must be added to 2.172 to get 5?
Solution: Required number = 5-2.172 = 2.828.

Question 18. 2.647 is subtracted from 4.15. How much is to be added to the result to get 10?
Solution: Subtraction of 2.647 from 4.15 = 4.150-2.647=1.503.

∴ Required number = 10 -1.503 = 8.497.

Question 19. Let’s find the values of the following

1. 0.07 + 0.09
Solution: 0.07 + 0.09 = 0.16

⇒ \(\begin{aligned}
& 0.07 \\
& +0.09 \\
& \hline 0.16 \\
& \hline
\end{aligned}\)

2. 4.11 + 1.6
Solution: 4.11 +1.6 = 5.71

⇒ \(\begin{array}{r}
4.11 \\
+1.6 \\
\hline 5.71 \\
\hline
\end{array}\)

3. 312.61 + 276.72
Solution: 589.33

⇒ \(\begin{aligned}
& 312.61 \\
& \underline{276.72} \\
& \underline{589.33} \\
& \hline
\end{aligned}\)

4. 5 – 0.555
Solution: 4.445

5. 27.56 + 14.69
Solution: 42.25

⇒ \(\begin{aligned}
& 27.56 \\
& 14.69 \\
& \hline 42.25 \\
& \hline
\end{aligned}\)

6. 4.3 + 3 – 6.4
Solution: 7.3 – 6.4 = 0.9

= 11.3-6.4 = 0.0

7. 3.36 – 4.62 + 2.18
Solution: 3.36 + 2.18- 4.62

= 5.54 – 4.62 = 0.92

8. 2.67 – 3.727 + 4.2.
Solution: 6.870 – 3.727 = 3.143

Fraction Exercise 1.6

Question 1. Let us try to place the following angles under right heading: 12°, 22.5°, 180°, 179°, 100°,39°,90°,69°,910
Solution:

Actute angles: 12°, 22.5°, 39°, 69°

Obtuse angles: 179°, 100°, 91°

Right angles: 90°

Straight angles: 180°

Question 2. Straight angle = 2 x □, hence straight angle is twice a right angle.
Solution:

Straight angle = 180° = 2 x 90° = 2 x right angle.

Question 3. Let’s find with which set of the lengths of line segments, triangles can be drawn:

1. 2 cm, 3 cm, 4 cm,
Solution:

Sum of 2 smaller sides = 2 cm + 3 cm = 5 cm is greater than the 3rd side (4 cm).

∴ Triangle can be drawn.

2. 4 cm, 3 cm, 7 cm
Solution:

Here sum of 2 smaller sides = 4 cm + 3cm = 7 cm is equal to the 3rd side (7 cm).

∴ Triangle can not be drawn.

3. 1 cm, 3 cm, 2 cm
Solution:

Here sum of 2 smaller sides = 1 cm + 2 cm= 3 cm is equal to the 3rd side (3 cm).

∴ Triangle can not be drawn.

4. □ cm, □ cm, □ cm.
Solution:

6 cm, 8 cm, 10 cm (let)

Here sum of 2 smaller sides = 6 cm + 8 cm = 14 cm is greater than the 3rd side (10 cm).

∴ Triangle can be drawn.

Question 4. Let us define actute angled and obtuse angled triangles.
Solution:

Acute angled triangle: A triangle whose three angles are acute, i.e., less than 90° is called an acute angled triangle.

Obtuse angled triangle: A triangle whose one angle is obtuse, i.e., greater than 90° but less than 180° is called obtuse angled triangle.

Question 5. Let’s measure the perimeter of the square in the figure.
Solution:

Side = 4 cm

Perimeter = 4 x side

= 4 x 4 cm

= 16 cm

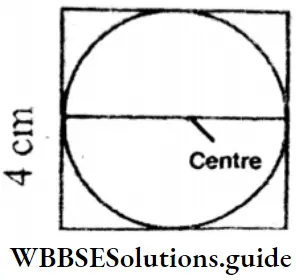
Question 6. The diameter of circle in the figure = □ cm. Radius = □□□ cm = □ cm.
Solution:

Diameter = 4 cm

Radius = 4 ÷ 2 cm = 2 cm.

Fraction Exercise 1.7

Question 1. To construct an embankment on a certain part of river Ichhamati, 40 labourers are required to work for 35 days. If the work has to be finished in 28 days, let us find how many labourers will be needed.
Solution:

To finish the work:

⇒ \(\begin{array}{ll}
\text { No. of days } & \text { No. of Labourers } \\
35 & 40 \\
28 & x \text { (let) }
\end{array}\)

Number of days is inversely proportional to number of labourers.

∴ \(\frac{40}{x}\) = \(\frac{28}{35}\)

∴ 28 x = 40 x 35

X = \(\frac{40 \times 35}{28}\) = 50

∴ Number of labourers = 50

OR

To construct an embarkment.

To construct an embarkment in 35 days, number of labourers required 40

To construct an embarkment in 1 day number of labourers required is 40×35

To construct an embarkment in 28 days number of labourers required \(\frac{40 \times 35}{28}\) = 50

∴ Number of labourers required = 50

Question 2. Rajeeb, Debangana, Masum and Tajmira can do 150 sums in 6 days. Let us find in how many days Rajeeb and Tajmira will finish 250 sums if each of them does equal number of sums everyday.
Solution:

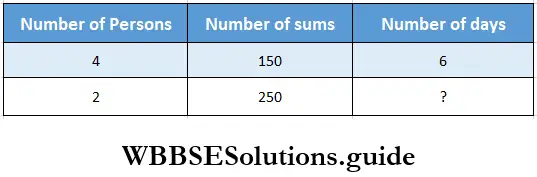
4 persons can do 150 sums in 6 days.

1 person can do 150 sums in 6 x 4 days

1 persons can do 1 sum in \(\frac{6 \times 4}{150}\) days

2 persons can do 1 sum in \(\frac{6 \times 4}{150 \times 2}\) days.

2 persons can do 250 sums in \(\frac{6 \times 4 \times 250}{150 \times 2}\) = 20 days.

∴ Number of days required = 20.

Question 3. Two labourers can polish 1/3 of a door in 1 day. Let us find how many labourers are needed to polish 2/3 of a door in 2 days.
Solution:

In 1 day \(\frac{1}{3}\) part of the door is polished by 2 labourers.

In 1 day full part of the door is polished by 2 x 3 labourers.

In 2 days full part of the door is polished by \(\frac{2 \times 3}{2}\) labourers.

In 2 days \(\frac{2}{3}\) part of the door is polished by \(\frac{2 \times 3}{2} \times \frac{2}{3}\) labourers = 2 labourers.

∴ Number of labourers required = 2

Question 4. For a mid-day meal of 500 students, 175 kg of rice is required for a week. After 75 kg of rice has been used, let us find how long remaining rice will last for 400 students.
Solution:

500 students can eat 175 kg rice in 7 days.

1 student can eat 175 kg rice in 7 x 500 days.

1 student can eat 1 kg rice in \(\frac{7 \times 500}{175}\) days.

400 student can eat 1 kg rice \(\frac{7 \times 500}{400 \times 175}\) days

400 student can eat 100 kg rice in \(\frac{7 \times 500 \times 400}{400 \times 175}\) =5 days.

∴ Number of days required = 5.

Question 5. 4 tractors are required to cultivate 360 bighas of land in 20 days. Let us find how many tractors are needed to cultivate 1800 bighas of land in 10 days.
Solution:

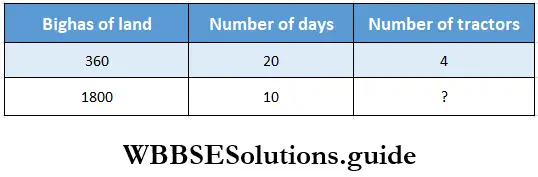
360 bighas of land are cultivated in 20 days by 4 tractors.

1 bigha of land are cultivated in 1 days by \(\frac{4}{360}\) tractors.

1 bigha of land are cultivated in 1 day by \(\frac{4 \times 20}{360}\) tractors.

180 bighas of land are cultivated in 1 day by \(\frac{4 \times 20 \times 1800}{360}\)

1800 bighas of land are cultivated in 10 days by \(\frac{4 \times 20 \times 1800}{360 \times 10}\)=40 tractors.

∴ Number of tractors required is 40.

Question 6. In a fair, if 12 generators work for 6 hours a day, then 7 litres of deposited oil is required. If generators run for 4 hours a day for 9 days, then let us find how many generators can run with that remaining amount of oil.
Solution:

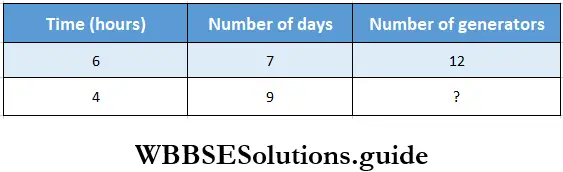
For 6 hours a day in 7 days oil deposited for 12 generators.

For 6 hours a day in 1 day oil deposited for 12×7 generators.

For 1 hour a day in 1 day oil deposited for 12 x 7 x 6 generators.

For 4 hours a days in 1-day oil deposited for \(\frac{12 \times 7 \times 6}{4}\) generators.

For 4 hours a day in 9 days oil deposited for \(\frac{12 \times 7 \times 6}{9 \times 4}\) =14 generators.

∴ 14 generators can run with that remaining amount of oil.

Question 7. 15 Vans can carry 75 quintals of vegetables in 40 mins. Let us find out how long will 20 vans take to carry 100 quintals of vegetables.
Solution:

15 vans can carry 75 quintals of vegetables in 40 minutes.

1 van can carry 75 quintals of vegetables in 40 x 15 minutes.

1 van can carry 100 quintals of vegetables in \(\frac{40 \times 15}{75}\)minutes.

20 vans can carry 100 quintals of vegetables in \(\frac{40 \times 15 \times 100}{20 \times 75}\) minutes

∴ Time required = 20 minutes.

Question 8. 150 kg of wheat is stored for 20 hostel boys. But 30 kg wheat was wasted and 5 boys went home. With the remaining amount of wheat, let us find for how long the remaining boys be fed.
Solution:

150 kg of wheat is stored for 20 boys for 30 days.

150 kg of wheat is stored for 1 boy for 30 x 20 days.

1 kg of wheat is stored for 1 boy for \(\frac{30 \times 20}{150}\) days.

120 kg of wheat is stored for 1 boy for \(\frac{30 \times 20 \times 120}{150}\) days.

120 kg of wheat is stored for 15 boys for \(\frac{30 \times 20 \times 120}{15 \times 150}\) =32 days.

• Chapter 1 Fraction
• Chapter 2 Concepts of Seven & Eight Digit Numbers
• Chapter 3 Logical Approximation of Numbers
• Chapter 4 Roman Numbers Upto Hundred
• Chapter 5 Concepts of Algebraic Variables
• Chapter 6 Multiplication & Division of a Fraction By a Whole Number and By a Fraction
• Chapter 7 Multiplication and Division of Decimal Fractions With Whole Numbers and Decimal Fractions
• Chapter 8 Metric System
• Chapter 9 Percentage
• Chapter 10  Recurring Decimal Numbers
• Chapter 11 Geometrical Concepts Related To a Regular Solides
• Chapter 12 LCM and HCF of 3 Numbers
• Chapter 13 Data Handling and Analysis
• Chapter 14 Concept of Line, Line Segment, Ray & Point
• Chapter 15 Determination of Area and Perimeter
• Chapter 16 Concept of Directed Numbers and Number Line
• Chapter 17 Geometrical Concepts Based on Different Instruments of Geometry Box
• Chapter 18 Square Root
• Chapter 19 Measurement of Time
• Chapter 20 Geometrical Concept of Circle
• Chapter 21 Fundamental Concept of Ration & Proportion
• Chapter 22 Drawing of Different Geometrical Figures
• Chapter 23 Summetry
• Chapter 24 Solids From Different Sides (Perspective)
• Chapter 25 Fun With Numbers
• Chapter 26 Open Shapes of Regular Solids
• Chapter 27 Equivalence of Fractions, Decimal Fractions, Percentage and Ratio