Class 9 Mathematics

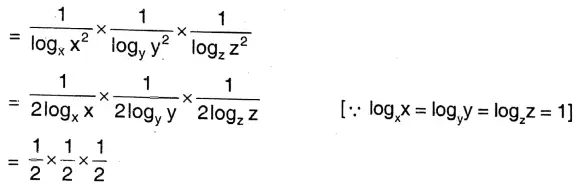
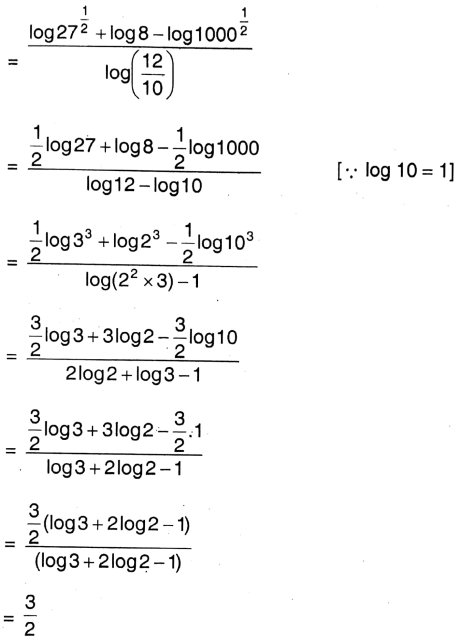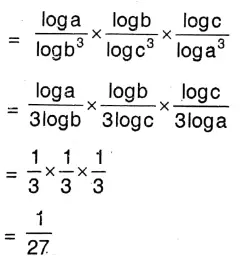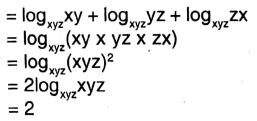Class IX Maths Solutions WBBSE Chapter 5 Linear Simultaneous Equations Exercise 5.7

Question 1. My friend Rita has bought 5 pens and 3 pencils at Rs. 34 from the bookshop nearby our school. But Sumita has bought 7 pens and 6 pencils at Rs. 53 at the same rate and from the same shop. I write by calculating the price of each pen and pencil by framing simultaneous equations.

Solution:

Given

My friend Rita has bought 5 pens and 3 pencils at Rs. 34 from the bookshop nearby our school. But Sumita has bought 7 pens and 6 pencils at Rs. 53 at the same rate and from the same shop.

Let the price of one pen is Rs. x & the price of one pencil is Rs. y.

According to 1st condition,
5x + 3y = 34…(1)

According to 2nd condition,
7x+6y=53…(2)

Multiplying equation (1) by 2 & equation (1) by 1

10x+6y = 68 ….(3)

Ading eq(3)+(2)

Read and Learn More WBBSE Solutions For Class 9 Maths

\(
\begin{aligned}
& 10 x+6 y=68 \\
& 7 x+6 y=53
\end{aligned}
\)

Class IX Maths Solutions WBBSE

Adding, 3 x=15

Or, \( x=\frac{15}{3} \)

or, x =5

Putting the value of x in equation (1),
5 x 5+3y=34
or, 25+3y=34
or, 3y=34-25
or, 3y=9

or, y= \( y=\frac{9}{3} \)

or, y = 3

∴ Price of one pen Rs. 5 and one pencil = Rs. 3.

Question 2. The weights of my friend Ayesha and Refique altogether are 85 kg. The half \( \frac{4}{9} \) of weight of Ayesha is equal to the th of weight of Rafique. Let us calculate and write the weights of them separately by forming simultaneous equations.

Solution:

Given

The weights of my friend Ayesha and Refique altogether are 85 kg. The half \( \frac{4}{9} \) of weight of Ayesha is equal to the th of weight of Rafique.

Let the weight of Ayesha = x kg and the

weight of Refique = y kg.

According to 1st condition,
x+y= 85….(1)

According to 2nd condition,

\( \frac{x}{2}=\frac{4 y}{9} \) ….(2)

or, 9x = 8y
or, 9x – 8y = 0…. (3)

Multiplying equation (1) by 8,
8x+8y = 680…. (4)

Adding eq(4)+(3)

8x+8y = 680
8x+8y = 680

We get, 17x= 680

or, \( x=\frac{680}{17} \)

or, x = 40

Putting the value of x in equation (1),

40+ y = 85

or, y = 85-40

or, y = 45

Weight of Ayesha = 40 kg & weight of Refique = 45 kg.

Class IX Maths Solutions WBBSE

Question 3. My uncle’s present age is twice of my sister’s age. 10 years ago, my uncle’s age was thrice of my sister’s age. Let me calculate and write their present age separately by forming simultaneous equations.

Solution:

Given

My uncle’s present age is twice of my sister’s age. 10 years ago, my uncle’s age was thrice of my sister’s age.

Let the pesent age of uncle = x years

and the present age of sister = y years

10 years ago, uncle’s age = (x-10) years &

10 years ago, sister’s age (y-10) years

According to 1st condition,

x = 2y

or, x-2y= 0…. (1)

According to 2nd condition,

(x-10)=3(y-10)

or, x-10=3y-30

or, x-3y=30+ 10

or, x-3y=-20…. (2)

Adding eq (2) + (1) we get

\(\begin{aligned}
& x-3 y=-20 \\
& x-2 y=0  \\
& \begin{array}{l}
(-) \quad(+) \quad(-)
\end{array} \\
& \text { Adding, }-y=-20
\end{aligned}\)

Class IX Maths Solutions WBBSE

or, y = 20

Putting the value of x in equation (1),

X- 2×20=0

or, x = 40

Present age of my uncle is 40 years and of my sister is 20 years.

Question 4. Debkumarkaku of our village draws Rs. 590 through a cheque from the bank. If he receives 70 notes in a total of the notes of Rs. 10 and Rs. 5, then let us calculate and write the number of notes of Rs. 10 and Rs. 5.

Solution:

Given

Debkumarkaku of our village draws Rs. 590 through a cheque from the bank. If he receives 70 notes in a total of the notes of Rs. 10 and Rs. 5,

Let the number of Rs. 10 notes = x

and the number of Rs. 5 notes = y.

According to 1st condition,

x + y = 70. ….(1)

According to 2nd condition,

5x + 10y=590….(2)

Multiplying equation (1) by 10,

10x + 10y=700.….(3)

Adding, eq(3) + eq(2)

\(
\begin{aligned}
& 10 x+10 y=700 \\
& 5 x+10 y=590 \\
& (-) \quad (-) \quad(-)
\end{aligned}\)

Class 9 Mathematics West Bengal Board

\(Adding, \quad 5 x=110 \)

 

Or, \( x=\frac{11}{5} \)

or, x = 22

Putting the value of x in equation (1)

22 + y = 70

or, y = 70-22 or, y = 48

∴ Number of Rs. 10 notes = 48

& Number of Rs. 5 notes = 22

Question 5. I write a proper fraction in our school blackboard whose denominator is greater than its numerator by 5 and when 3 is added to both the numerator and denominator it becomes 3/4. Let us form the simultaneous equations and by solving write the proper fraction on the blackboard.

Solution:

Given

I write a proper fraction in our school blackboard whose denominator is greater than its numerator by 5 and when 3 is added to both the numerator and denominator it becomes 3/4.

Let the fraction be \( \frac{x}{y} \) where the numerator is x and denominator is y and x < y.

According to 1st condition,

y = x + 5….(1)

According to 2nd condition,

\( \frac{x+3}{y+3}=\frac{3}{4} \) …(2)

Class 9 Mathematics West Bengal Board

or, \( \frac{x+3}{x+5+3}=\frac{3}{4}(because y=x+5) \)

or, \( \frac{x+3}{x+8}=\frac{3}{4} \)

or, 4x+12= 3x + 24

or, 4x-3x=24-12

or, x = 12

Putting the value of x in equation (1)

y=12+5

or, y = 17

Required fraction = \( \frac{12}{17} \)

Question 6. Maria has written two numbers in her exercise copy such that the addition of 21 with the first number gives twice of the second number. A gain, addition of 12 with the second number gives twice of the first number. Let us calculate and write the two numbers Maria has written.

Solution:

Given

Maria has written two numbers in her exercise copy such that the addition of 21 with the first number gives twice of the second number. A gain, addition of 12 with the second number gives twice of the first number.

The two numbers are x &y.

According to 1st condition,

x +21= 2y.  …(1)

According to 2nd condition,

or, x = y + 12 …(2)

From equation (1) x=2y-21   …(3)

From equation (2) x = \( \frac{y+12}{2} \)

Comparing two values of x from equations (3) & (4),

2y-21= \( \frac{y+12}{2} \)

or, 4y-42 = y+12

or, 4y -y 12+42

or, 3y = 54

or, y = \( \frac{54}{3} \)

or, y = 18

Putting the value of x in equation (4)

\( x=\frac{18+12}{2} \)

Class 9 Mathematics West Bengal Board

Or, \( x=\frac{30}{2} \)

or, x = 15

1st number is 15 & 2nd number is 18.

Question 7. Both of Lalima and Romen clean their garden. If Lalima works for 4 days and Romen works for 3 days, then \( \frac{2}{3} \) part of the work is completed. Again, if Lalima works for 3 days and Romen works for 6 days, then \( \frac{11}{12} \) part of the work is completed. Let us form the simultaneous equations and write the number of days required to complete the work separately by Lalima and Romen by calculating the solution.

Solution:

Given

Both of Lalima and Romen clean their garden. If Lalima works for 4 days and Romen works for 3 days, then \( \frac{2}{3} \) part of the work is completed. Again, if Lalima works for 3 days and Romen works for 6 days, then \( \frac{11}{12} \) part of the work is completed.

Let Lalima can do the whole (I) work in x days

and Romen can do the whole work in y days.

According to 1st condition,

\( \frac{4}{x}+\frac{3}{y}=\frac{2}{3} \) …(1)

According to 2nd condition,

\( \frac{3}{x}+\frac{6}{y}=\frac{11}{12} \) ….(2)

 

Multiplying equation (1) by 2,

\( \frac{8}{x}+\frac{6}{y}=\frac{4}{3} \) …(3)

Class 9 Mathematics West Bengal Board

Adding eq(3)+eq(2)

\( \begin{aligned}
& \frac{8}{x}+\frac{6}{y}=\frac{4}{3} \\
& \frac{3}{x}+\frac{6}{y}=\frac{11}{12} \\
& (-)(-)(-)
\end{aligned} \)

 

We get, \( \frac{8}{x}-\frac{3}{x}=\frac{4}{3}-\frac{11}{12} \)

 

\( or, \frac{8-3}{x}=\frac{16-11}{12}
or, \frac{5}{x}=\frac{5}{12}
or, \frac{1}{x}=\frac{1}{12} \)

or, x = 12

Putting the value of x in equation (1)

 

\(\frac{4}{12}+\frac{3}{y}=\frac{2}{3}
or, \frac{1}{3}+\frac{3}{y}=\frac{2}{3}
or, \frac{3}{y}=\frac{2}{3}-\frac{1}{3}
or, \frac{3}{y}=\frac{2-1}{3}
or, \frac{3}{y}=\frac{1}{3}\)

Class 9 Maths WB Board

or, y =9

∴Lalima can do the work in 12 days and Romen can do the work in 9 days.

Question 8. My mother has prepared two types of sherbet. There is 5 kg sugar in 100 litre sherbat of the first type and 8 kg sugar in 100 litre sherbat of the second type. By mixing these two types, I will prepare 150 litre sherbet which contains \( 9 \frac{2}{3} \) kg sugar. Forming simultaneous equations let us calculate how much quantity of the two types of sherbat will be mixed to prepare 150 litre sherbat.

Solution:

Given

My mother has prepared two types of sherbet. There is 5 kg sugar in 100 litre sherbat of the first type and 8 kg sugar in 100 litre sherbat of the second type. By mixing these two types, I will prepare 150 litre sherbet which contains \( 9 \frac{2}{3} \) kg sugar.

Let the quantity of 1st type of sherbet = x liter & the quantity of 2nd type of sherbat = y litre.

According to 1st condition,

x + y = 150 …(1)

According to 2nd condition,

\(\frac{5 x}{100}+\frac{8 y}{100}=9 \frac{2}{3} \)

 

Or, \( \frac{5 x+8 y}{100}=\frac{29}{3} \)

or, 15x + 24y= 2900 …(2)

Multiplying both sides of equation (1) by 15,

15x+15y = 2250 ….(3)

Adding eq(3) + eq(2)

\( \begin{aligned}
& 15 x+15 y=2250 \\
& 15 x+24 y=2900 \\
& (-) \quad(-) \quad(-)
& -9 y=-650
\end{aligned} \)

Class 9 Maths WB Board

We get, -9y = -650

Or, \( y=\frac{-650}{-9} \)

Or, \( y=72 \frac{2}{9} \text { litre } \)

Putting the value x in equation (1)

\( x+\frac{650}{9}=150 \)

 

Or, \( \text { or, } x=150-\frac{650}{9} \)

Or, \( x=\frac{1350-650}{9} \)

Or, \( x=\frac{700}{9} \)

Or, \( x=77 \frac{7}{9} \) litre.

Question 9. Last year Akhilbabu and Chhandadebi were the candidates in Bakultala Gram-Panchayat election. Akhilbabu defeated Chhandadebi by 75 votes. If 20% of the voters who have casted Ahkilbabu would have casted to Chhandadebi, then Chhandadebi could be won by 19 votes. By forming simultaneous equations let us solve and find out how many votes each of them had got.

Solution:

Given

Last year Akhilbabu and Chhandadebi were the candidates in Bakultala Gram-Panchayat election. Akhilbabu defeated Chhandadebi by 75 votes. If 20% of the voters who have casted Ahkilbabu would have casted to Chhandadebi, then Chhandadebi could be won by 19 votes.

Let Akhilbabu got x votes & Chhandadevi got y votes.

20% of Akhilbabu’s vote = \( \frac{x \times 20}{100}=\frac{x}{5} \)

According to 1st condition,

x – y = 75 ….(1)

According to 2nd condition,

\(
\left(y+\frac{x}{5}\right)-\left(x-\frac{x}{5}\right)=19
or, \quad y+\frac{x}{5}-x+\frac{x}{5}=19
or, \quad \frac{5 y+x-5 x+x}{5}=19 \)

 

or, -3x+5y=95  …(2)
3x – 3y = 225 …(3)

Adding eq(3) +eq(2)

\( \begin{array}{r}
3 x-3 y=225 \\
-3 x+5 y=95 \\
\quad 2 y=320
\end{array}\)

Class 9 Maths WB Board

Or, \( y=\frac{320}{2} \)

Or, y = 160

Putting the value y in equation (1)

X-160=75
or, x = 75+ 160
or, x = 235

Akhilbabu got 235 votes & Chhandadevi got 160 votes.

Question10. If the length is increased by 2 m and breadth is increased by 3m, then the area of rectangular floor of Rafique is increased by 75 sq.m. But if the length is reduced by 2 m and breadth is increased by 3 m, the area is increased by 15 sq.m. By forming simultaneous linear equations, let us determine the length and breadth of the floor.

Solution:

Given

If the length is increased by 2 m and breadth is increased by 3m, then the area of rectangular floor of Rafique is increased by 75 sq.m. But if the length is reduced by 2 m and breadth is increased by 3 m, the area is increased by 15 sq.m. By forming simultaneous linear equations

Let the length = xm &
breadth = y m
Area = xy sq. m

According to 1st condition,
(x+2) (y+3)= xy + 75

Or, xy + 3x + 2y + 6-xy = 75
or, 3x + 2y = 75-6

or, 3x + 2y = 69 …(1)

According to 2nd condition,
(x-2) (y+3)=xy + 15

Or, xy+3x-2y-6-xy=15
Or, 3x-2y = 15+6

Or, 3x-2y=21 …(2)

Adding eq(2) + (1)

\(\begin{gathered}
3 x-2 y=21 \\
3 x+2 y=69 \\
\hline , 6 x=90
\end{gathered} \)

Class 9 Maths WB Board

Or, \( x=\frac{90}{6} \)

Or, x = 15

Putting the value y in equation (1)

3 x 15+ 2y = 69
or, 45+2y=69
or, 2y=69-45
or, 2y = 24

or, \( y=\frac{24}{2} \)

or, y = 12

Length of the floor = 15 m

Breadth of the floor = 12 m

Question 11. My friend Meri told Ishan, give me \( \frac{1}{3} \) of your money, then I shall have Rs. 200. Ishan told Meri, give me half of your money, I shall have Rs. 200. Forming simultaneous equations let us calculate how much money each of them possesses.

Solution:

Given

My friend Meri told Ishan, give me \( \frac{1}{3} \) of your money, then I shall have Rs. 200. Ishan told Meri, give me half of your money, I shall have Rs. 200.

Let Meri has Rs. x & Inhan has Rs. y.

According to 1st condition,

\( x+\frac{y}{3}=200 \)

 

Or,\( \frac{3x+y}{3}=200 \)

Or, 3x+y =600 …(1)

According to 2nd condition,

\( \frac{x}{2}+y=200 \)

Or,\( \frac{x+2 y}{2}=200 \)

Or, x+2y=400 …(2)

Multiplying equation (1) by 2,

6x + 2y = 1200 ….(3)

Adding eq(3)+(2)

\( \begin{array}{cc}
6 x+2 y= & 1200 \\
x+2 y= & 400 \\
(-) \quad(-) & (-)
\end{array} \)

Maths WBBSE Class 9 Solutions

We get, 5x = 800

Or, \( x=\frac{800}{5} \)

or, x = 160

Putting the value y in equation (1)

160+ 2y = 400
or, 2y= 400-160
or, 2y = 240

or, \( y=\frac{240}{2} \)

or, y = 120

∴ Meri has Rs 160 & Ishan has Rs. 120.

Question 12. Today my elder brother and some of his friends will go to a fair. So, grandfather divided some money equally among them. We are observing that if the number of friends is less by 2, then each of them would get Rs. 18. Again, if the number of friends is more by 3, then each of them would get Rs. 12. Let us calculate and write the number of persons went to the fair and how much money grandfather divided among them in total.

Solution:

Given

Today my elder brother and some of his friends will go to a fair. So, grandfather divided some money equally among them. We are observing that if the number of friends is less by 2, then each of them would get Rs. 18. Again, if the number of friends is more by 3, then each of them would get Rs. 12

Let grandfather gives Rs x & number of friends is

According to 1st condition,

\( \frac{x}{y-2}=18 \)

 

Or, x = 18(y-2)   …..(1)

According to 2nd condition,

\( \frac{x}{y+3}=12 \)  …(2)

Maths WBBSE Class 9 Solutions

Comparing the values of x in equation (1) & equation (2),

18(y – 2) = 12 (y+3)
or, 18y – 36 = 12y +36
or, 18y – 12y= 36+36
or, 6y=72

or, \( y=\frac{72}{6} \)

or, y = 12

Putting the value y in equation (2)

x = 12 (12+3)
or, x = 12 x 15
or, x = 180

No. of rupees = Rs 180. No. of friends = 15.

Question 13. In my elder brother’s bag there are Rs. 350 with the coins of Rs. 1 and 50 paise together. My sister has put out \( \frac{1}{3} \) part of 50 paise coins from the bag and in its place she has put into the bag equal number of coins of Rs. 1 and now the total amount of money in the bag is Rs. 400. Let us calculate and write the original number of coins of Rs. 1 and 50 paise kept at first separately in my brother’s bag.

Solution:

Given

In my elder brother’s bag there are Rs. 350 with the coins of Rs. 1 and 50 paise together. My sister has put out \( \frac{1}{3} \) part of 50 paise coins from the bag and in its place she has put into the bag equal number of coins of Rs. 1 and now the total amount of money in the bag is Rs. 400.

Let no. of Re. 1 coin = x; no. of 50p coin = y.

According to 1st condition,

\(x+\frac{y}{2}=350
or, \quad \frac{2 x+y}{2}=350 \)

 

or, 2x + y = 700 …(1)

According to 2nd condition,

\( \left(y-\frac{y}{3}\right) \times \frac{1}{2}+\left(x+\frac{y}{3}\right) \times 1=400 \)

Maths WBBSE Class 9 Solutions

Or, \( \frac{y}{2}-\frac{y}{6}+x+\frac{y}{3}=400 \)

Or, \( \frac{3 y-y+6 x+2 y}{6}=400 \)

Or,6x + 4y = 2400

or, 3x + 2y = 1200 …(2)

Multiplying equation (1) by 2,

4x + 2y = 1400 …(3)

\( \begin{aligned}
& 4 x+2 y=1400 \\
& 3 x+2 y=1200 \\
& (-) \quad(-) \quad(-)
\end{aligned} \)

 

Putting the value of x in equation (1) x = 200

Putting the value y in equation (2)

2 x 200 + y = 700
or, y = 700 – 400
or, y = 300

No. of Re. 1 coin 200 & 50p coin = 300.

Question 14. Today, we will go to my maternal uncle’s house, so a motor car sets out from our house towards my maternal uncle’s house at a uniform speed. If the speed of the car would be increased by 9 km/hr then the time required to cover this path would be less by 3 hours. Again, if the speed would be decreased by 6 km hr, then 3 hours more time would be required to cover this path. Let us calculate and write the distance between our house and my maternal uncle’s house and the speed of the car.

Solution:

Given

Today, we will go to my maternal uncle’s house, so a motor car sets out from our house towards my maternal uncle’s house at a uniform speed. If the speed of the car would be increased by 9 km/hr then the time required to cover this path would be less by 3 hours. Again, if the speed would be decreased by 6 km hr, then 3 hours more time would be required to cover this path.

Let the distance =  x km & speed of car = y km/hr.

According to 1st condition,

\( \frac{x}{y+9}=\frac{x}{y}-3 \)  ….(1)

According to 2nd condition,

\( \frac{x}{y-6}=\frac{x}{y}+3 \) ….(2)

Maths WBBSE Class 9 Solutions

From equation (2) \( \frac{x}{y+9}-\frac{x}{y}= 3\)

Or, \( x\left(\frac{1}{y+9}-\frac{1}{y}\right)=-3 \)

Or, \( x\left(\frac{y-y-9}{y(y+9)}\right)=-3 \)

Or, \( \frac{-9 x}{y(y+9)}=-3 \)

or, \( \frac{3 x}{y(y+9)}=1 \)

Or, \( x=\frac{y(y+9)}{3} \) …(3)

From equation (1) \( \frac{x}{y-6}-\frac{x}{y}=3 \)

Or, \( x\left(\frac{1}{y-6}-\frac{1}{y}\right)=3 \)

Or, \( x\left(\frac{y-y+6}{y(y-6)}\right)=3 \)

or, \( \frac{6 x}{y(y-6)}=3 \)

Or, \( \frac{2 x}{y(y-6)}=1 \)

Or, \( x=\frac{y(y-6)}{2} \) ….(4)

Comparing the values of x from equations (3) & (4),

\( \frac{y(y+9)}{3}=\frac{y(y-6)}{2} \)

 

Or, \( \frac{y+9}{3}=\frac{y-6}{2} \)

or, 3y 18 2y + 18
or, 3y-2y= 18+ 18
or, y = 36

Putting the value y in equation (3)

Or, \( x=\frac{36(36+9)}{3} \)

or, x = 12 x 45

or, x = 540

∴ Distance = 540 km & speed of the car = 36 km/hr.

Question 15. Mohit will write such a two digit number that 4 times of the sum total of he two digits will be 3 more of the number; and if the digits are reversed, the number will be increased by 18. Let us calculate the number which Mohit would write.

Solution:

Given

Mohit will write such a two digit number that 4 times of the sum total of he two digits will be 3 more of the number; and if the digits are reversed, the number will be increased by 18.

Let two digit no. = 10x + y.

According to 1st condition,

10x + y = 4(x + y) +3
or, 10x + y -4x-4y = 3
or,6x-3y=3

or,2x – y = 1 …(1)

According to 2nd condition,

10y + x = 10x + y + 18
Or, 10y+x-10x-y=18
Or, – 9x+9y= 18
Or, -9(x – y)- 18

Or, \( x-y=\frac{18}{-9} \)

X – y= -2 …(2)

Adding eq(2)+(1)

\(\begin{aligned}
& x-y=-2 \\
& 2 x-y=1 \\
& (-)(+)(-)
\end{aligned} \)

Maths WBBSE Class 9 Solutions

We get, -x = -3
Or, x =3

Putting the value y in equation (1)

2 x 3-y=1
or,-y = 1-6

or, – y = -5
or, y = 5

Required Number
= 10x + 3
= 10 x 3 +5
= 30+ 5
= 35

Question 16. I shall write a two digit number, the sum of two digits of which is 14 and if 29 is subtracted from the number, the two digits will be equal. Let us form simultaneous equations and by solving them let us see what will be the two digit number.

Solution:

Given

I shall write a two digit number, the sum of two digits of which is 14 and if 29 is subtracted from the number, the two digits will be equal.

Let the two digit number be 10x + y whose tenths digit is x and units digit y.

According to 1st condition,
x + y = 14 …(1)

After subtracting 29 from the number we get, the new number is = 10x + y – 29

or, 10x+y30+1

or, 10x-30+ y + 1

or, 10(x-3)+(y+1)

According to 2nd condition,

or, x-3= y + 1

or, x-y=1+3

or, x-y= 4 …(2)

Adding eq (2) + (1)

 

\(\begin{array}{r}
x-y=4 \\
x+y=14 \\
\hline  2 x=18
\end{array} \)

 

Or, \(x=\frac{18}{2}\)

Or, x =9

Putting the value y in equation (1)

9+y=14
or, y = 14-9

or, y=5

Required Number

= 10x + y
= 10 x 9 +5
= 90 + 5
= 95

Class 9 Maths WB Board

Question 17. Rahamat chacha covers 30 miles in 6 hours in downstream and returns the same distance in 10 hours in upstream by his boat. Let us calculate and write the speed of Rahamat chacha’s both in still water and the speed of the stream too.

Solution:

Given

Rahamat chacha covers 30 miles in 6 hours in downstream and returns the same distance in 10 hours in upstream by his boat.

Let speed of boat = x mile / hr speed of stream = y mile/hr.

∴ Speed of boat in downstream = (x + y) mile/hr

∴ Speed of boat in upstream = (x − y) mile/hr

According to 1st condition,
6(x + y) = 30

Or, \( x+y=\frac{30}{6} \)

Or, x + y = 5 …(1)

According to 2nd condition,
10(x-y) = 30

Or, \( x-y=\frac{30}{10} \)

Or, x – y = 3 ….(2)

Adding eq(2) + eq(1)

\(\begin{aligned}
& x-y=3 \\
& {x+y}=5 \\
& \hline 9,2 x=8
\end{aligned}\)

 

Or, \( x=\frac{8}{2} \)

Or, x = 4

Putting the value y in equation (1)

4+y=5
or, y 5-4
or, y = 1

Speed of boat = 4 mile/hr

Speed of stream = 1 mile/hr.

Question 18. Leaving Howrah station after 1 hour a train is late by 1 hour for special \( \frac{3}{5} \) reason and then running with th of its initial speed it reaches its destination after 3 hours. If the special reason would be 50 km, away from its first place, then Ithe train would reach its destination 1 hour 20 minutes before its previous time. Let us calculate the distance that the train had covered and the original speed of the train.

Solution:

Given

Leaving Howrah station after 1 hour a train is late by 1 hour for special \( \frac{3}{5} \) reason and then running with th of its initial speed it reaches its destination after 3 hours. If the special reason would be 50 km, away from its first place, then Ithe train would reach its destination 1 hour 20 minutes before its previous time.

Let speed of the train be x km/hr & the time = y hr.

Distance = speed x time= x x y km = xy km

According to 1st condition,

\( \frac{x y-x}{\frac{3 x}{5}}+1+1=y+3 \) …(1)

 

According to 2nd condition,

\(\frac{x+50}{x}+1+\frac{x y-(x+50)}{\frac{3 x}{5}}=y+3-\frac{4}{3}\) …(2)

 

From equation (1) \(\frac{x y-x}{\frac{3 x}{5}}+1+1=y+3\)

\(or,\frac{5(x y-x)}{3 x}+2=y+3
or, \frac{5(y-1)}{3}+2=y+3 \)

 

or, 5y-5+6=3y+9
or, 5y-3y=9+5-6
or, 2y = 8

or, \( y=\frac{8}{2} \)
or, y = 4

Putting the value y in equation (2)

Or, \( \frac{x+50}{x}+1+\frac{x \times 4-x-50}{\frac{3 x}{5}}=4+3-\frac{4}{3} \)

or, \( \frac{x+50}{x}+\frac{5(4 x-x-50)}{3 x}=7-\frac{4}{3}-1 \)

or, \( \frac{3 x+150+15 x-250}{3 x}=\frac{14}{3} \)

or, \( 18 x-100=\frac{14}{3} \times 3 x \)

or, 18x-100 = 14x

or, 18x-14x= 100

or, 4x = 100

or, \( =\frac{100}{4}\)

or, x = 25 of the train 25 km/hr

Distance = 25 x 4 km = 100 km

Class 9 Maths WB Board

Question 19. Mousumi divides a two digit number with the sum of its digits and gets quotient as 6 and remainder as 6. But if she divides the number interchanging the digits with the sum of its digits, she will get quotient as 4 and remainder as 9. Let us determine the number that Mousumi has taken by forming simultaneous equations.

Solution:

Given

Mousumi divides a two digit number with the sum of its digits and gets quotient as 6 and remainder as 6. But if she divides the number interchanging the digits with the sum of its digits, she will get quotient as 4 and remainder as 9.

Let the two digit number = 10x + y.

According to 1st condition,

10x+y=6(x + y) +6

or, 10x+y=6x+6y+ 6

or, 10x+y-6x-6y= 6

or, 4x-5y = 6 …(1)

According to 2nd condition,

10y + x = 4(x + y) +9

Or, 10y+x-4x-4y=9

or, -3x+6y=9

or,-3(x-2)= 9

or, \( x-2 y=\frac{9}{-3} \)

or, x-2y= 3

or, x = 2y-3

Putting the value y in equation (1)

4(2y3)5y=6

or, 8y 12-5y=6

or, 3y=6+12

or, \( y=\frac{18}{3}\)

or, y =  6

Putting the value y in equation (2)

x=2×6-3

or, x = 12-3

or, x = 9

Required Number

=10x + y

=10 x 9 +6

= 90 +6

= 96

Question 20. When Faridabibi put oranges in some boxes, she observed that if she would put 20 oranges more in each box, then 3 boxes less would be required. But if she would put 5 oranges less in each box, 1 more box would be required. Forming simultaneous equations, let us calculate how many boxes and oranges Faridabibi had.

Solution:

Given

When Faridabibi put oranges in some boxes, she observed that if she would put 20 oranges more in each box, then 3 boxes less would be required. But if she would put 5 oranges less in each box, 1 more box would be required.

Let the number of boxes = y & no of oranges in each box = x.

No of oranges = xy

According to 1st condition,

(x+20) (y-3)=xy

Or, xy-3x+20y-60-xy = 0

or,-3x+20y=60  ….(1)

According to 2nd condition,

(x-5) (y+1)=xy

or, xy+x-5y-5-xy = 0

or, x-5y=5 …(2)

Multiplying the equation (2) by 3

3 x-15 y=15 …(3)

Adding eq(3) + (1)

3 x-15 y=15
-3 x+20 y=60

we get, 5y = 75

Or, \( y=\frac{75}{5} \)

Or,  y = 15

Putting the value y in equation (2)

X-5 x 15 = 5

or, x = 5 + 75

or, x = 80

No. of oranges = 80 x 15 = 1200

No. of boxes = 15

Question 21. Short answer type questions

 1. If x = 3t and \( y=\frac{2 t}{3}-1 \) then find for what value of t, x = 3y.

Solution:  x = 3y

or, \( 3 t=3\left(\frac{2 t}{3}-1\right) \)

or, \( t=\frac{2 t-3}{3} \)

or, 3t = 2t 3

or, 3t-2t=-3

or, t=-3

t=-3 when x = 3y

2. For what value of k, the two equations 2x+5y= 8 and 2x-ky-3 will have no solutions?

Solution:  2x+5y=8, 2x-ky = 3

\( \frac{2}{2}=\frac{5}{-k}\left[therefore \frac{a_1}{a_2}=\frac{b_i}{b_2} \neq \frac{c_1}{c_2}\right] \)

Maths WBBSE Class 9 Solutions

Or, \( \frac{1}{1}=\frac{5}{-k} \)

or, – k = 5

k = -5

3. If x, y are real numbers and (x-5)² + (x-y)² = 0, then what are the values of x and y?

 Solution: (x-5)² + (x − y)² = 0

Now, x-5= 0 and x – y = 0

x = 5 and x = y

x=y=5

x=5, y=5

4. If x² + y²-2x+4y=-5, then what are the values of x and y?

 Solution: x²+ y²-2x + 4y = -5

or, x²+y²-2x+4y+5=0

or, x² – 2x + 1+ y²+4y+4=0

or, (x-1)²+(y+2)²=0

Now, x-1= 0 and y + 2 = 0

x= 1 and y=-2

x=1,y=-2

5. For what value of r, the two equations rx-3y-1 = 0 and (4-r) x – y + 1 = 0 would have no solution?

Solution:

\( \begin{aligned}
&\frac{r}{4-r}=\frac{-3}{-1}\\
&\left(because \frac{a_1}{a_2}=\frac{D_1}{b_2} \neq \frac{c_1}{c_2}\right)
\end{aligned} \)

 

Or, \( \frac{r}{4-r}=\frac{3}{1} \)

or, r = 12-3r

or, r+ 3r = 12

or, 4r = 12

or, \( r=\frac{12}{4} \)

or, r = 3

If r = 3 the equations. have no solution.

6.  Let us write the equation a₁x+b₁y+c₁ = 0 in the form of y = mx + c where m & c are constants.

Solution: a₁x+b₁y+c₁ = 0

Or, b₁y=-a₁x-c₁

 or, \( y=-\frac{a_1}{b_1} x-\frac{c_1}{b_1} \)

or, y = mx + c

where  \( \frac{-a_1}{b_1} \text { and } c=\frac{-c_1}{b_1} \)

7. For what value of k, the two equations kx – 21y+ 15 = 0 and 8x – 7y = O have only one solution?

Solution: If \( \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \) the equations will be solvable and have only one solution.

\( \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \)

 

Or, \( \frac{k}{8} \neq \frac{-21}{-7} \)

Or, k≠24

8. For what values of a and b, the two equations 5x+8y = 7 and (a+b)x+(a – b)y = (2a+b+1) have infinite number of solutions ?

 Solution: If \( \frac{a_1}{b_1}=\frac{b_1}{b_2}=\frac{c_1}{c_2} \text { and } c_1 \neq 0, c_2 \neq 0 \) then the equations will have infinite number of solutions.

From the condition \( \frac{a_1}{a_2}=\frac{b_1}{b_2} \text { we get, } \frac{5}{a+b}=\frac{8}{a-b} \)

Or, 8a+ 8b = 5a-5b

Or, 8a-5b =-5b-8b

Or, 3a = -13b

\( a=\frac{-13 b}{3} \) …(1)

Maths WBBSE Class 9 Solutions

Again, from the relation \( \frac{b_1}{b_2}=\frac{c_1}{c_2} \text { we get, } \frac{8}{a-b}=\frac{7}{2 a+b+1} \)

Or, 16a + 8b+ 8 = 7a -7b

or, 16a-7a+8b+7b+8=0

or, 9a+15b+8=0

or, \( 9\left(\frac{-13 b}{3}\right)+15 b+8=0 \quad\left(because a=\frac{-13 b}{3}\right) \)

or,- 39b + 15b+8=0

or, -24b=-8

\( \begin{aligned}
& b=\frac{-8}{-24} \\
& b=\frac{1}{3}
\end{aligned} \)

 

Putting the value of b in equation

or,  \( a=\frac{-13}{3} \cdot \frac{1}{3} \)

or, \( a=\frac{-13}{9} \)

∴ Required value, \( a=\frac{-13}{9}, b=\frac{1}{3} \)

Question 22. Multiple choice questions

1. The two equations 4x + 3y = 7 and 7x-3y = 4 have

1. Only one solution
2. Infinite number of solutions
3. No solution
4. None of them

Solution: If \( \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \) then two equations have only one solutions

Here, \( \frac{3}{6}=\frac{6}{12}=\frac{15}{30} \)

∴ 2. Infinite number of solutions

2. The two equations 3x+6y= 15 and 6x + 12y = 30 have

1. Only one solution
2. Infinite number of solutions.
3. No solution
4. None of them

∴ 2. Infinite number of solutions.

3. The two equations 4x + 4y = 20 and 5x+5y = 30 have

1. Only one solution
2. Infinite number of solutions.
3. No solution
4. None of them

Solution: If \( \frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2} \& \quad c_1 \neq 0, c_2 \neq 0 \) then the equations have infinite

4x + 4y = 20 or, x+ y = 5

5x+5y= 30 or, x + y = 6

\( \frac{1}{1}=\frac{1}{1} \neq \frac{5}{6} \)

Class 9 Maths WB Board

∴ 3. No solution

4. Which one of the following equations has the solution (1, 1)?

1. 2x + 3y = 9
2. 6x + 2y = 9
3. 3x + 2y = 5
4. 4x+6y= 8

Solution:

1. 2x + 3y = 2×1+3×1=5
2. 6x + 2y = 6×1+2×1=8
3. 3x+2y= 3×1+2×1 = 5
4. 4x+6y=4×1+6×1 = 10

∴ 3. 3x + 2y = 5

5. The two equations 4x + 3y = 25 and 5x-2y= 14 have the solutions.

1. x = 4, y = 3
2. x = 3, y=4
3. x = 3, y=3
4. x = 4, y = -3

Solution:

4x + 3y = 25 …(1)
5x-2y= 14 …(2)

Multiplying equation (1) by 2 & equation (2) by 3,

Adding,

\(\begin{aligned}
& 8 x+6 y=50 \\
& 15 x-6 y=42 \\
& \hline 23 x=92
\end{aligned} \)

 

Or, \( x=\frac{92}{23}=4 \)

Putting the value x in equation (1)

4×4 + 3y = 25

or, 3y=25-16

or, 3y=9

or, \( x=\frac{92}{23}=4 \)

6. The solutions of the equation x + y = 7 are

1. (1, 6), (3,-4)
2. (1, -6), (4, 3)
3. (1, 6), (4, 3)
4. (-1, 6), (-4, 3)

Solution: (1,6), (4,3) satisfy the equation

3. ( 1, 6), (4, 3)

 

 

Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.3

Question 1. Ratul draws a parallelogram with a length of base 5 cm and a height 4 cm. Let us calculate the area of the parallelogram drawn by Ratul.

Solution:

Given

Ratul draws a parallelogram with a length of base 5 cm and a height 4 cm.

Area of parallelogram = base x height
= 5 x 4 sq. cm
= 20 sq. cm

Question 2. The base of a parallelogram is twice its height. If the area of shape of a parallelogram is 98 sq. cm, then let us calculate the length and height of the parallelogram.

Solution:

Given

The base of a parallelogram is twice its height. If the area of shape of a parallelogram is 98 sq. cm

Let the height of a parallelogram = x cm.
∴ Base of the parallelogram = 2x cm.

∴ Area of parallelogram = base x height
= 2x.x sq. cm
= 2x² sq. cm

Read and Learn More WBBSE Solutions For Class 9 Maths

According to the problem, 2x² = 98

or, x² = 98
or, x² = 49
or, x = √49
or, x = 7

∴ Height of the parallelogram = 7 cm.
∴ Base of the parallelogram = 2 x 7 cm = 14 cm.

Question 3. There is a shape of parallelogram land beside our house, with lengths of adjacent sides of which are 15 meters and 13 meters. If the length of one diagonal is 14 meters, then let us calculate the area of shape of parallelogram land.

Solution:

Given

There is a shape of parallelogram land beside our house, with lengths of adjacent sides of which are 15 meters and 13 meters. If the length of one diagonal is 14 meters,

Let ABCD is a parallelogram whose = AB = DC = 15 m
AD = BC = 13 m
Diagonal BD = 14 meter

Semi-perimeter ΔABD (s) = \(\frac{13+14+15}{2} m\)

= \(\frac{42}{2}\) m = 21 m

Area of ΔABD = \(\sqrt{21(21-13)(21-14)(21-15)} \text { sq. cm }\)

= \(\sqrt{21 \times 8 \times 7 \times 6} \text { sq. cm }\)

= \(\sqrt{3 \times 7 \times 2 \times 2 \times 2 \times 7 \times 2 \times 3} \text { sq. cm }\)

= 2 × 2 × 3 × 7 sq. cm
= 84 sq. cm

∴ The diagonal divides the parallelogram in two equal triangles.

∴ Area of parallelogram □ABCD = 2xΔABD
= 2 × 84 sq. m
= 168 sq. m

Question 4. Pritha drew a parallelogram, adjacent sides of which are 25 cm and 15 cm, and length of one diagonal is 20 cm. Let us write by calculating the height of the parallelogram which is drawn on the side of 25 cm.

Solution:

Given

Pritha drew a parallelogram, adjacent sides of which are 25 cm and 15 cm, and length of one diagonal is 20 cm.

Let ABCD is a parallelogram whose = AB = DC = 25 cm
AD = BC= 15 cm

and diagonal = AC = 20 cm

Semi-perimeter of ΔABC (s) = \(\frac{25+15+20}{2} \mathrm{~cm}\)

= \(\frac{60}{2} \mathrm{~cm}=30 \mathrm{~cm}\)

∴ Area of ΔABC = \(\sqrt{30(30-25)(30-15)(30-20)} \text { sq.cm }\)

= \(\sqrt{30 \times 5 \times 15 \times 10} \text { sq.cm }\)

= \(\sqrt{2 \times 3 \times 5 \times 5 \times 3 \times 5 \times 2 \times 5} \text { sq.cm }\)

=2x 3 x 5 x 5 sq.cm =150 sq.cm

∴ Area of □ABCD = 2x ΔABC
= 2 × 150 sq.cm
= 300 sq.cm

Length of the perpendicular drawn from D on AB = H cm

∴ Area of parallelogram □ABCD = base x height = 25 x h sq.cm

According to the problem, 25h=300

or, h = \(\frac{300}{25}\)

or, h = 12

∴ Height of the parallelogram drawn on the side of length 25 cm from the opposite vertex = 12 cm.

Question 5. The lengths of two adjacent sides are 15 cm and 12 cm of a parallelogram; the distance between two smaller sides is 7.5 cm. Let us calculate the distance between the two sides.

Solution:

Given

The lengths of two adjacent sides are 15 cm and 12 cm of a parallelogram; the distance between two smaller sides is 7.5 cm.

Let ABCD is a parallelogram whose larger side AB = DC = 15 cm and smaller side BC = AD = 12 cm.

Distance between two smaller sides = 7.5 cm and let the distance between two bigger sides = h cm.

Area of parallelogram □ABCD base x height
= 12 x 7.5 sq. cm
= 90 sq.cm

Again, area of the parallelogram ABCD base x height
= AB × h
= 15 x h sq. cm
= 15h sq. cm

According to the problem,15h = 90

or, h= \(\frac{90}{15}\) = 6

∴ Distance between two longer sides = 6 cm.

Question 6. If the measure of two diagonals of a rhombus are 15 meters and 20 meters, then let us write by calculating its perimeter, area, and height.

Solution:

 

Let ABCD is a rhombus whose diagonals AC & BD intersect at O & AC = 15 m and BD = 20 m.

∴ We know the diagonals of a rhombus bisect each other perpendicularly.

∴ AO = OC = \(\frac{15}{2}\)

and BO = OD= \(\frac{20}{2}\) m = 10 m

In right angled ΔBOC,

BC = \(\sqrt{O B^2+O C^2}\)

= \(\sqrt{\left(\frac{15}{2}\right)^2+(10)^2}\)

= \(\sqrt{\frac{225}{4}+100}\)

= \(\sqrt{\frac{225+400}{4}}\)

= \(\sqrt{\frac{625}{4}}\)

= \(\frac{25}{2} \mathrm{~m}\)

∴ Perimeter of the Rhombus = 4 x side

= \(4 \times \frac{25}{2}\)m

= 50 m

Area of rhombus = \(\frac{1}{2}\) x product of the diagonals

= \(\frac{1}{2}\) x 15 × 20 sq.m = 150 sq.m

Base x height = Area of the rhombus

∴ \(\frac{25}{2}\)x height = 150

or, height = \(\frac{150 \times 2}{25}\) m = 12 m.

Question 7. If the perimeter of a rhombus is 440 meters and the distance between two parallel sides is 22 meters, let us write by calculating the area of the rhombus.

Solution: Perimeter of rhombus = 440 m

∴ Length of each side of the rhombus = \(\frac{440}{4}\) m = 110m

Area of rhombus = base x height
= 110 x 22 sq.m
= 2420 sq.m

Question 8. If perimeter of the rhombus is 20 cm and the length of its diagonal is 6 cm, then let us write by calculating the area of the rhombus.

Solution: Perimeter of rhombus = 20 cm.

∴ Length of one side of the rhombus = \(\frac{440}{4}\) cm = 5 cm.

Length of the diagonal = 6 cm & diagonals AC & BD intersect each other at O.

∴ OA = \(\frac{6}{2}\) cm = 3 cm and AB = 5 cm

In right-angled ΔAOB

OA²+ OB² = AB²
or, (3)²+ OB²= (5)²
or, OB² = 25-9
or, OB²= 16
or, OB = √16 =4

∴ 2nd diagonal of the rhombus = BD = 2 x OB = 2 x 4 cm = 8 cm.

∴ Area of the rhombus = \(\frac{1}{2}\) x product of the diagonals

= \(\frac{1}{2}\) x 6 x 8 sq.cm = 24 sq.cm.

Question 9. The area of field shaped in trapezium is 1400 sq. dcm. If the perpendicular distance between two parallel sides are 20 dcm and the length of two parallel sides is in the ratio 3: 4, then let us write by calculating the lengths of two sides.

Solution:

Given

The area of field shaped in trapezium is 1400 sq. dcm. If the perpendicular distance between two parallel sides are 20 dcm and the length of two parallel sides is in the ratio 3: 4

Let the lengths of the parallel sides of the trapezium be 3x dm & 4x dm.

Area of the trapezium = \(\frac{1}{2}\) x (3x+4x) x 20 sq.dcm = 70x sq.dcm

According to the problem, 70x = 1400

or, x = \(\frac{1400}{70}\) = 20

∴ Length of 1st side = 3 x 20 dm = 60 dm
& length of 2nd side = 4 x 20 dm = 80 dm.

Question 10. Let us write by calculating the area of a regular hexagon field whose length of sides is 8 cm.

[Hints: If we draw diagonals, we get equal six equilateral triangles]

Solution:

 

By joining the diagonals of a regular hexagon six equilateral triangles are formed.

∴ Area of the regular hexagon = 6 x Area of six equilateral triangles

= 6 x \(\frac{\sqrt{3}}{4}\) x (8)² sq. cm

=6 x \(\frac{\sqrt{3}}{4}\) x 64 sq. cm

= 96√3 sq. cm

Question 11. In a quadrilateral ABCD, AB = 5 meters, BC = 12 meters, CD = 14 meters, DA = 15 meters, and ∠ABC = 90°, let us write by calculating the area of the quadrilateral shape of the field.

Solution:

 

In quadrilateral ABCD, AB = 5 m, BC = 1 m, CD = 14 m, DA = 15 m and ∠ABC = 90°
AC is the diagonal.

In a right-angled triangle ΔABC,

AC²= AB² + BC²
or, AC² = (5)² + (12)²
or, AC² = 25+144

or, AC²= 169
or, AC = √169
or, AC = 13

Area of right-angled triangle ΔABC = \(\frac{1}{2}\) X AB X BC

= \(\frac{1}{2}\)  x 5×12 sq.cm = 30 sq. cms

Semi-perimeter of ΔACD (s) = \(\frac{13+14+15}{2}\)

= \(\frac{42}{2}\) m = 21 m

Area of ΔACD = \(\sqrt{s(s-a)(s-b)(s-c)}\)

= \(\sqrt{21(21-13)(21-14)(21-15)} \text { sq.m }\)

= \(\sqrt{21 \times 8 \times 7 \times 6} \text { sq.m }\)

= \(\sqrt{3 \times 7 \times 2 \times 2 \times 2 \times 7 \times 2 \times 3} \text { sq.m }\)

= 2 x 2 x 3 x 7 sq.m
= 84 sq.m

Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
= 30 sq.m +84 sq.m
= 114 sq.m

Question 12. Sahin draws a trapezium ABCD whose length of diagonal BD is 11 cm and draws two perpendiculars whose lengths are 5 cm and 11 cm respectively from points A and C on the diagonal BD. Let us write by calculating the area of ABCD of the trapezium.

Solution:

Given

Sahin draws a trapezium ABCD whose length of diagonal BD is 11 cm and draws two perpendiculars whose lengths are 5 cm and 11 cm respectively from points A and C on the diagonal BD.

ABCD is a trapezium on the diagonal BD, AE & CF are the perpendiculars drawn from A & C respectively, AE = 5 cm & CF = 11 cm.

Area of trapezium ABCD = area of ΔABD + area of ΔBCD

= \(\frac{1}{2}\) x BD X AE+ \(\frac{1}{2}\) x BD X CF

= \(\frac{1}{2}\) x BD(AE+CF)

= \(\frac{1}{2}\) x 11(5+11) sq.cm

= \(\frac{1}{2}\)x11x16 sq.cm = 88 sq.cm.

Question 13. ABCDE is a pentagon whose side BC is parallel to diagonal AD, EP is perpendicular on BC, and EP intersects AD at the point Q. BC= 7 cm, AD = 13 cm, PE = 9 cm, and if PQ=\(\frac{4}{9}\) PE, let us write by calculating the area of ABCD: pentagon.

Solution:

 

In pentagon ABCDE, BC II AD & EP ⊥ BC and EP cuts AD at Q. BC= 7 cm, AD 13 cm, PE = 9 cm

PQ = \(\frac{4}{9}\) PE = \(\frac{4}{9}\) X 9 cm = 4 cm

EQ=PE-PQ (9-4) cm = 5 cm

Area of ΔAED = \(\frac{1}{2}\) x ADXEQ

= \(\frac{1}{2}\)x13x5 sq.cm

= \(\frac{65}{2}\)sq.cm = 32.5 sq.cm

Area of trapezium ABCD = \(\frac{1}{2}\) (AD+BC) x PQ

= \(\frac{1}{2}\) (13+7)x4 sq.cm = 40 sq.cm

Area of pentagon ABCDE = Area ΔAED + Area of trapezium ΔBCD
=(32.5+40) sq.cm
= 72.5 sq.cm.

Question 14. The length of a rhombus is equal to the length of a square and the length of a diagonal of the square is 40√2 cm. If the lengths of diagonals of a rhombus are in the ratio 3: 4, then let us write by calculating the area of a field in the shape of the rhombus.

Solution:

 

Length of the diagonal of square = 40√2 cm.

∴ Length of one side of the square = \(\frac{40 \sqrt{2}}{\sqrt{2}}\) cm = 40 cm.

∴ Length of one side of the rhombus = 40 cm.

Diagonals AC & BD of the rhombus ABCD bisect each other at O; and AC = 3x cm and BD = 4x cm & AB = 40 cm.

∴ AO = OC= \(\frac{3 x}{2}\)cm

BO = OD = \(\frac{4x}{2}\) cm = 2x cm

In the right-angled triangle ΔAOB, AO²+ BO² = AB²

or, \(\left(\frac{3 x}{2}\right)^2\) + (2x)² = (40)²

or,\(\frac{9 x^2}{4}+4 x^2=1600\)

or, \(\frac{9 x^2+16 x^2}{4}=1600\)

or, 25x²= 6400

or, \(x^2=\frac{6400}{25}\)

or, x² = 256
or, x= √256 = 16

∴ Length of one diagonal of the rhombus = 3 x 16 cm = 48 cm
& the length of the 2nd diagonal = 4 x 16 cm = 64 cm.

∴ Area of the rhombus = \(\frac{1}{2}\) x product of the diagonals

= \(\frac{1}{2}\) x 48 x 64 sq.cm
= 1536 sq.cm.

Question 15. In a trapezium, the length of each slant side is 10 cm and the length of the parallel sides are 5 cm and 7 cm respectively. Let us write by calculating the area of the field in the shape of the trapezium and its diagonal.

Solution:

 

Let ABCD is an isosceles trapezium whose each slant side: AD = BC = 10 cm, CD = 5 cm, and AB = 17 cm. DF and CF are the perpendiculars drawn on AB from D and C.

∴ DC EF = 5 cm

ΔAED and ΔCFB are congruent triangles.
∴ AE = FB = 6 cm

In right-angled ΔAED,
DE²= AD² – AE²
or, DE²= 100-36
or, DE² = 64
or, DE = √64 = 8

∴ Area of trapezium ABCD = \(\frac{1}{2}\)(5+17)x8 sq.cm

= \(\frac{1}{2}\) x 22 x 8 sq.cm = 88 sq.cm

Join A, C

In right-angled ΔAFC,
AC²= AF²+ CF²
or, AC²= (11)² + (8)²
or, AC² =121 +64
or, AC²= 185
or, AC = √185

The diagonal of the trapezium is √185 cm & its area is 88 sq. cm.

Question 16. The lengths of the parallel sides of a trapezium are 19 cm and 9 cm and the length of the slant sides are 8 cm and 6 cm. Let us calculate the area of the field in the shape of a trapezium.

Solution:

 

Let the length of the slant sides AD & BC of the trapezium are 6 cm & 8 cm respectively and the lengths of AB & CD be 19 cm & 9 cm respectively.
DE and CF are the perpendiculars on AB from D & C respectively.

Let DE = CF = h cm

In right-angled ΔAED, \(A E=\sqrt{A D^2-D E^2}\)

\(\begin{aligned}
& \sqrt{(6)^2-h^2} \\
& \sqrt{36-h^2}
\end{aligned}\)

In right-angled ΕCFB, FB = \(\sqrt{B C^2-C F^2}\)

\(\begin{aligned}
& \sqrt{(8)^2-h^2} \\
& \sqrt{64-h^2}
\end{aligned}\)

∴ AE+ EF + FB = 19

∴ \(\sqrt{36-h^2}\) +9+\(\sqrt{64-h^2}\)= 19

or, \(\sqrt{36-h^2}\)=19-9-\(\sqrt{64-h^2}\)

or, \(\sqrt{36-h^2}\)=10-\(\sqrt{64-h^2}\)]

or, \(\left(\sqrt{36-h^2}\right)^2=\left(10-\sqrt{64-h^2}\right)^2\) (squaring both sides)

or, 36-h² = 100+ 64-h²-20\(\sqrt{64-h^2}\)

or, 20\(\sqrt{64-h^2}\) = 164-36+ h² – h²

or, 20\(\sqrt{64-h^2}\) = 128

or, \(\sqrt{64-h^2}=\frac{128}{20}\)

or, \(\sqrt{64-h^2}\) = 6.4

or, \(\left(\sqrt{64-h^2}\right)^2=(6.4)^2\)

(squaring both sides)

or, 64 – h² = 40.96
or, -h² = 40.96-64
or, -h² = -23.04
or, h²=23.04

or, h= \(\sqrt{23.04}\) = 4.8

∴ Height of the trapezium = 4.8 cm

∴ Area of the trapezium = \(\frac{1}{2}\) (19+9) x 4.8 sq.cm

= \(\frac{1}{2}\) x 28 x 4.8 sq.cm
= 67.2 sq.cm.

Question 17. Multiple choice question

1. The height of a parallelogram is \(\frac{1}{3}\)th of its base. If the area of the field is 192 sq. cm in the shape of a parallelogram, the height is

1. 4 cm
2. 8 cm
3. 16 cm.
4. 24 cm

Solution: Let the base of a parallelogram = x cm

∴ Height of the parallelogram = \(\frac{x}{3}\) cm

∴ Area of the parallelogram = base x height

= X. \(\frac{x}{3}\)  sq.cm

= \(\frac{x^2}{3}\) sq. cm

According to the problem, \(\frac{x^2}{3}\)= 192

or, x² = 576
or, x= √576 = 24

∴ Height of the parallelogram = \(\frac{24}{3}\) = 8cm

∴ 2. 8 cm

2.  If the length of one side of a rhombus is 6 cm and one angle is 60°, then the area of field in the shape of a rhombus is

1. 9√3 sq. cm
2. 18/3 sq. cm
3. 36√3 sq. cm
4. 6√3 sq. cm

 

 

Solution: Let ABCD is a rhombus whose side AB = 6 cm and ∠BAD = 60°.

In ΔABD,
AB = AD (all the sides of the rhombus are equal)

∴ ∠ADB = ∠ABD = 60°
∴ ΔABD is an equilateral triangle whose each side = 6 cm.

∴ Area of ΔABD= \(\frac{\sqrt{3}}{4} \times(6)^2\) sq.cm

= \(\frac{\sqrt{3}}{4}\) x 36 sq.cm = 9√3 sq. cm

Similarly, area of ΔBCD = 9√3 sq.cm

∴ Area of rhombus = Area ΔABD + Area ΕBCD

= (9/3+9√3) sq.cm
=18√3 sq.cm

∴ 2. 18√3 sq. cm

3. The length of one diagonal of a rhombus is thrice of its the other diagonal. If the area of the field in the shape of a rhombus is 96 sq. cm, then the length of the longer diagonal is

1. 4 cm
2. 12 cm
3. 16 cm
4. 24 cm

Solution: Let one diagonal of rhombus = x cm
∴ Length of 2nd diagonal = 3x cm.

∴ Area of rhombus = \(\frac{1}{2}\).x.3x sq.cm

= \(\frac{3 x^2}{2}\) cm

According to the problem,

\(\frac{3 x^2}{2}\) = 96

or, \(x^2=\frac{96 \times 2}{3}\)

or, x² = 64
or, x = √64 = 8

∴ Length of the longer diagonal = 3 x 8 cm = 24 cm.

∴ 4. 24 cm

4. A rhombus and a square are on the same base. If the area of the square is x2 sq. unit and the area of the field in the shape of a rhombus is y sq. unit. then

1.  y > x
2. y < x²
3. y = x²
4. y = 2x²

 

 

Solution: The lengths of the base of a rhombus and a square are the same.

∴ Area of the square is greater than the area of the rhombus as the height of the square is greater than the height of the rhombus.

∴ x² > y

∴ 2.  y < x

5. Area of a field in the shape of the trapezium is 162 sq. cm and the height is 6 cm. If the length of one side is 23 cm, then the length of the other side is

1. 29 cm
2. 31 cm
3. 32 cm
4. 33 cm

Solution: Let the other side of the parallelogram = x cm

∴ Area of trapezium = \(\frac{1}{2}\) (23+x) x6 sq.cm
= 3(23+x) sq.cm

According to the problem, 3(23+x) = 162

or, 23 + x = \(\frac{162}{3}\)

or, 23+ x = 54
or, x = 54-23
or, x = 31

∴ Length of 2nd side of the trapezium = 31 cm.

∴ 2. 31 cm

Question 18. Short answer type questions

1. Area of the field in the shape of parallelogram ABCD is 96 sq. cm, length of diagonal BD is 12 cm. What is the perpendicular length drawn on diagonal BD from point A?

Solution:

 

Let AE is the perpendicular from A on the diagonal BD of the parallelogram ABCD.

∴ Diagonal bisects the parallelogram in two equal triangles.

∴ Area of ΔABD= \(\frac{1}{2}\) x Area of the parallelogram ABCD

or, \(\frac{1}{2}\) x BDX AE = \(\frac{1}{2}\) x 96 sq.cm

or, \(\frac{1}{2}\) x 12 x AE= 48 sq.cm

or, AE = \(\frac{48}{6}\) = 8cm

∴ Perpendicular length from A on the diagonal BD = 8 cm.

2. Length of the height of the rhombus is 14 cm and the length of the side is 5 cm. What is the area of the field in the shape of a rhombus?

Solution:

 

Let ABCD is a parallelogram whose AB = DC = 5 cm and BC = AD = 3 cm. Distance between two greater sides AB & DC= 2 cm.

∴ Area of parallelogram □ =base x height
= 5 x 2 sq. cm
= 10.sq.cm

Let the distance between AD & BC of the parallelogram = h cm.

∴ Area of parallelogram □ABCD base x height
= BC x h
= 3 × h sq. cm

According to the problem,
3h = 10

or, h= \(\frac{10}{3:}=3 \frac{1}{3}\)

The distance between two smaller sides = \(3 \frac{1}{3}\)

3. Length of the height of the rhombus is 14 cm and the length of each side is 5 cm. What is the area of the field in the shape of a rhombus?

Solution: Area of Rhombus = base x height
= 5 x 14 sq. cm
= 70 sq. cm

4. Any adjacent parallel sides of a trapezium make an angle 45° and the length of its slant side is 62 cm, what is the distance between its two parallel sides?

Solve: Let ABCD is an isoceles trapezium whose : AD = BC= 62 cm and ∠DAB = 45°.
DE is the perpendicular from D on AB.

∴ ∠AED = 90°
∴ ∠ADE 180°-(90°+45°) = 45°

In ΔADE ∠DAE = ∠ADE
∴ AE = DE = h (let)

In right-angled ΔAED
AE²+ DE² = AD²
or, h² + h² = (62)²
or, 2h² = 62 × 62

or, \(h^2=\frac{62 \times 62}{2}\)\

or, h²= 31 x 62
or, h= √31×62
or, h = √31x31x2
or, h= 31√2

∴ Distance between the parallel sides = 31√2 cm.

5. In parallelogram ABCD, AB = 4 cm, BC = 6 cm, and ∠ABC = 30°, find the area of the field in the shape of parallelogram ABCD.

Solution:

 

In parallelogram, ABCD, AB = 4 cm, BC = 6 cm and ∠ABC = 30°.

AO is the perpendicular from A on BC, AO produced such that AO = OP.

In ΔAOB and ABOP, AO = OP (By construction)
and BO is common and ∠AOB = ∠POB ( each = 90°)

∴ ΔAOB≅ΔBOP (S-A-S condition)

∴ AB = BP & ZABO ZPBO = 30°
In ΔABP ∠ABP = ∠BAP = ∠BPA = 60°

∴ΔABP is an equilateral triangle.
∴AP AB = 4 cm

∴ \(A O=\frac{1}{2} A P=\frac{1}{2} A B=\frac{1}{2} \times 4 \mathrm{~cm}=2 \mathrm{~cm}\)

Area of ABCD parallelogram = Base x Height
= BC × AO
= 6 x 2 sq.cm
= 12 sq.cm

 

 

Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.2

Question 1. Let us write by calculating the area of the following regions:

Solution:

 

1. In the Image it is an equilateral triangle whose each side = 10 cm.

∴ Area of ΔABC = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)

\(\begin{aligned}
& =\frac{\sqrt{3}}{4} \times(10)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{1} \times 100 \text { sq.cm }=25 \sqrt{3} \text { sq.cm }
\end{aligned}\)

Read and Learn More WBBSE Solutions For Class 9 Maths

 

 

 

2. In the 2nd image it is an isosceles triangle whose equal sides are 10 cm each and the base = 8 cm.

∴ Area of ΔABC = \(=\frac{1}{2} \cdot 8 \sqrt{(10)^2-\frac{(8)^2}{4}} \text { sq.cm }\)

\(\begin{aligned}
& =4 \sqrt{100-16} \text { sq.cm } \\
& =4 \sqrt{84} \text { sq.cm } \\
& =4 \sqrt{2 \times 2 \times 21} \text { sq.cm } \\
& =4.2 \sqrt{21} \text { sq.cm } \\
& =8 \sqrt{21} \text { sq.cm. }
\end{aligned}\)

 

 

 

3. In the 3rd image in ABCD, ∠ADC= ∠BCD = 90°
∴ AD II BC
∴ ABCD is a trapezium.

∴ Area of ABCD =  \(\frac{1}{2}\) (4+5)x3 sq.cm

=\( \frac{1}{2}\) x27 sq.cm
= 13.5 sq.cm.

 

 

4. In the 4th image ABCD is a trapezium.

∴ Area of ABCD = \(\frac{1}{2}\)(40+15)×9 sq.cm

= \(\frac{1}{2}\) x55x9 sq.cm

= \(\frac{495}{2}\)

= 247.5 sq. cm.

 

 

5. In 5th image ABCD is a rectangle whose length = 38 cm & diagonal (AC)= 42 cm.

In ΔADC, AD = \(\sqrt{A C^2-C D^2}\)

\(\begin{aligned}
& =\sqrt{(42)^2-(38)^2} \mathrm{~cm} \\
& =\sqrt{(42+38)(42-38)} \mathrm{cm} \\
& =\sqrt{80 \times 4} \mathrm{~cm} \\
& =8 \sqrt{5} \mathrm{~cm} .
\end{aligned}\)

 

∴ Area of ABCD = ABX AD
= 38×8√5 sq.cm
=304√5 sq.cm.

Question 2. The perimeter of any equilateral triangle is 48 cm. Let us write by calculating its area.

Solution:

Given

The perimeter of any equilateral triangle is 48 cm.

Length of each side of the equilateral triangle = \(\frac{48}{3} \cdot \mathrm{cm}=16 \mathrm{~cm}\)

Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)

\(\begin{aligned}
& =\frac{\sqrt{3}}{4} \times(16)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 256 \text { sq.cm } \\
& =64 \sqrt{3} \text { sq.cm }
\end{aligned}\)

 

Question 3. If the height of an equilateral triangle ABC is 5√3 cm, let us write by calculating the area of this triangle.

Solution:

Given

If the height of an equilateral triangle ABC is 5√3 cm

Height of an equilateral triangle = \(\frac{\sqrt{3}}{2} \times \text { side }\)

∴ Each side of an equilateral triangle = \(\frac{2}{\sqrt{3}} \times \text { height }\)

= \(\frac{2}{\sqrt{3}} \times 5 \sqrt{3} \mathrm{~cm}=10 \mathrm{~cm}\)

∴ Perimeter of the equilateral triangle = 3 x 10 cm 30 cm

Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { angle })^2\)

\(\begin{aligned}
& =\frac{\sqrt{3}}{4} \times(10)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 100 \text { sq.cm } \\
& =25 \sqrt{3} \text { sq.cm. }
\end{aligned}\)

 

Question 4. If each equal side of an isosceles triangle ABC is 10 cm and length of base is 4 cm, let us write by calculating the area of ΔABC.

Solution:

Given

If each equal side of an isosceles triangle ABC is 10 cm and length of base is 4 cm

Area ΔABC = \(\frac{1}{2} \cdot 4 \cdot \sqrt{(10)^2-\frac{(4)^2}{4}} \text { sq.cm }\)

\(\begin{aligned}
& =2 \sqrt{100-4} \text { sq.cm } \\
& =2 \sqrt{96} \text { sq.cm } \\
& =2 \sqrt{4 \times 4 \times 6} \text { sq.cm } \\
& =8 \sqrt{6} \text { sq.cm. }
\end{aligned}\)

 

Question 5. If length of base of any isosceles triangle is 12 cm and length of each equal side is 10 cm, let us write by calculating the area of that isosceles triangle.

Solution:

Given

If length of base of any isosceles triangle is 12 cm and length of each equal side is 10 cm

Area of the isosceles triangle = \(\frac{1}{2} \cdot 12 \sqrt{(10)^2-\frac{(12)^2}{4}} \text { sq. cm }\)

\(\begin{aligned}
& =6 \cdot \sqrt{100-36} \text { sq. } \mathrm{cm} \\
& =6 \cdot \sqrt{64} \text { sq. } \mathrm{cm} \\
& =6 \times 8 \text { sq. } \mathrm{cm}=48 \mathrm{sq} . \mathrm{cm}
\end{aligned}\)

 

Question 6. The perimeter of any isosceles triangle is 544 cm and the length of each equal side is \(\frac{5}{6}\) th of length of base. Let us write by calculating the area of this triangle.

Solution:

Given

The perimeter of any isosceles triangle is 544 cm and the length of each equal side is \(\frac{5}{6}\) th of length of base.

Let the base of an isosceles triangle = x cm.

∴ Length of each equal side of the isosceles triangle = \(\frac{5 x}{6}\) cm

∴ Perimeter of the triangle = \(\left(x+\frac{5 x}{6}+\frac{5 x}{6}\right) \mathrm{cm}\)

\(\begin{aligned}
& =\frac{6 x+5 x+5 x}{6} \mathrm{~cm} \\
& =\frac{16 x}{6} \mathrm{~cm}=\frac{8 x}{3} \mathrm{~cm}
\end{aligned}\)

 

According to the problem, \(\frac{8 x}{3}=544\)

or, \(x=\frac{544 \times 3}{8}=204\)

∴ Length of the base of the isosceles triangle = 204 cm.

Length of each equal side of the triangle= \(\frac{5}{6}\) x 204 cm = 170 cm.

∴ Area of the isosceles triangle = \(\frac{1}{2} \times 204 \sqrt{(170)^2-\frac{(204)^2}{4}} \text { sq.cm }\)

\(\begin{aligned}
& =102 \sqrt{(170)^2-(102)^2} \text { sq. cm } \\
& =102 \sqrt{(170+102)(170-102)} \text { sq. cm } \\
& =102 \sqrt{272 \times 68} \text { sq. cm } \\
& =102 \sqrt{4 \times 68 \times 38} \text { sq. cm }
\end{aligned}\)

 

= 102 x 2 x 68 sq. cm
= 13872 sq. cm.

Question 7. If the length of hypotenuse of an isosceles right-angled triangle is 12√2 cm, let us write by calculating the area of this triangle.

Solution:

Given

If the length of hypotenuse of an isosceles right-angled triangle is 12√2 cm,

Let each equal side of the right angled isosecles triangle = x cm.

Length of the hypotenuse of the triangle = \(\begin{aligned}
& \sqrt{x^2+x^2} \mathrm{~cm} \\
& \sqrt{2 x^2} \mathrm{~cm} \\
& x \sqrt{2} \mathrm{~cm}
\end{aligned}\)

According to the problem,

\(
x \sqrt{2}=12 \sqrt{2}
or, x=\frac{12 \sqrt{2}}{\sqrt{2}}
or, x=12 \)

 

∴Length of each equal side of the right-angled isosecles triangle = 12 cm.

∴ Area of the triangle = \(\frac{1}{2}\) x 12×12 sq. cm = 72 sq. cm.

Question 8. Pritha drew a parallelogram of which lengths of two diagonals are 6 cm and 8 cm and each angle between two diagonals is 90°. Let us write the length of sides of the parallelogram and what type of parallelogram it is.

Solution:

Given

Pritha drew a parallelogram of which lengths of two diagonals are 6 cm and 8 cm and each angle between two diagonals is 90°.

Let the diagonals AC & BD of the parallelogram ABCD intersect each other at O.
And AC = 8 cm; BD = 6 cm

According to the problem,
∠AOB = ∠BOC = ∠COD = ∠AOD = 90°

We know if the diagonals of a parallelogram bisect each other at right angles, it will be a rhombus.

∴ ABCD is a rhombus.

\(\begin{aligned}
& therefore O C=\frac{1}{2} A C=\frac{1}{2} \times 8 \mathrm{~cm}=4 \mathrm{~cm} \\
& \& O D=\frac{1}{2} B D=\frac{1}{2} \times 6 \mathrm{~cm}=3 \mathrm{~cm}
\end{aligned}\)

 

In right angled ΔCOD,
CD² = OC²+ OD²
or, CD²=(4)²+ (3)²

or, CD²= 16+9
or, CD² = 25

or, CD = √25=5

Each side of the rhombus is equal.
∴ AB = BC = CD = DA = 5 cm
∴ Parallelogram ABCD is a rhombus.

Question 9. The ratio of the lengths of sides of a triangular park of our village is 2:3: 4; perimeter of park is 216 meters.

1. Let us write by calculating the area of the park.
2. Let us write by calculating how long is to be walked from oppositevertex of the longest side to that side straightly.

Solution:

Given

The ratio of the lengths of sides of a triangular park of our village is 2:3: 4

Let the sides of a triangular park are = 2x m 3x m, & 4x m
∴ Perimeter of the park = (2x + 3x + 4x) m = 9x m

According to the problem,
9x = 216

or, x = \(\frac{216}{9}\) = 24

∴ One side of the park = 2 x 24 m = 48 m
∴ 2nd side of the park = 3 x 24 m = 72 m
∴ 3rd side ut the park = 4 x 24 m = 96 m

Semi-perimeter of the park = \(\frac{216}{2} \mathrm{~m}\) = 108 m

1. Area of the park = \(\sqrt{108(108-48)(108-72)(108-96)} \text { sq.m }\)

\(\begin{aligned}
& =\sqrt{108 \times 60 \times 36 \times 12} \text { sq.m } \\
& =\sqrt{3 \times 36 \times 3 \times 4 \times 5 \times 36 \times 3 \times 4} \text { sq.m } \\
& =3 \times 36 \times 4 \sqrt{3 \times 5} \text { sq.m } \\
& =432 \sqrt{15} \text { sq.m }
\end{aligned}\)

 

2. Perpendicular distance from the opposite vertex to the biggest side

\(\begin{aligned}
& =\frac{2 \times \text { Area of the park }}{\text { Length of the longest side }} \\
& =\frac{2 \times 432 \sqrt{15}}{96} \mathrm{~m} \\
& =9 \sqrt{15} \mathrm{~m}
\end{aligned}\)

 

∴ Distance to be walked from the opposite vertex to the longest side straightly
= 9√15 m.

Question 10. The length of three sides of a triangular field of village of Paholampur are 26 meter, 25 meter and 30 meter.

1. Let us write by calculating what will be the cost of planting grass in the triangular field at the rate of Rs. 5 per sq. meter.
2. Let us write by calculating how much cost will be incurred for fencing around three sides at the rate of Rs. 18 per meter leaving a space 5 meter for constructing entrance gate of that triangular field.

Solution: Semi-perimeter of the triangular field = \(\frac{26+28+30}{2} m\)

=\(\frac{84}{2} m\)

= 42 m

Area of the field =

\(\begin{aligned}
& =\sqrt{42(42-26)(42-28)(42-30)} \text { sq.m } \\
& \sqrt{42 \times 16 \times 14 \times 12} \text { sq.m } \\
& \sqrt{3 \times 14 \times 16 \times 14 \times 4 \times 3} \text { sq.m } \\
& 3 \times 14 \times 4 \times 2 \text { sq.m }=336 \text { sq.m }
\end{aligned}\)

 

1. Cost of planting grass in the field at the rate of Rs. 5 per sq.m Rs. 336 x 5 = Rs. 1680.
2. Perimeter of the field (26+28+30) m = 84 m

∴ Length of the fence = (84-5) m = 79 m
∴ Cost of fencing the garden, leaving 5 m for entrance gate at the rate of Rs. 18 per m. = Rs. 79 x 18 = Rs. 1422.

Question 11. Shakil draws an equilateral triangle PQR. I draw three perpendiculars from a point inside of that equilateral triangle on three sides, lengths of which are 10 cm, 12 cm and 8 cm. Let us write by calculating the area of the triangle.

Solution:

Given

Shakil draws an equilateral triangle PQR. I draw three perpendiculars from a point inside of that equilateral triangle on three sides, lengths of which are 10 cm, 12 cm and 8 cm.

Let each side of the equilateral triangle = a cm. OA, OB & OC are the perpendiculars drawn from O to the sides PQ, QR & RD respectively.

∴ OA = 10 m, OB = 12 m OC = 8 m

ΔPQR= ΔPOQ+ΔQOR+ΔPOR

\(or, \frac{\sqrt{3}}{4} a^2=\frac{1}{2} \times a \times 10+\frac{1}{2} \times a \times 12+\frac{1}{2} \times a \times 8\)

or, \(\frac{\sqrt{3}}{4} a^2=5 a+6 a+4 a\)

or, \(\frac{\sqrt{3}}{4} a^2=15 a\)

or, \(\frac{\sqrt{3}}{4} a=15\)

\(or, a=\frac{60}{\sqrt{3}}
or, a=\frac{60 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}=\frac{60 \sqrt{3}}{3}=20 \sqrt{3}\)

 

∴ Length of each side of the equilateral triangle = 20√3 m

∴ Area of equilateral triangle ΔPOR = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)

\(\begin{aligned}
& =\frac{\sqrt{3}}{4} \times(20 \sqrt{3})^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 20 \sqrt{3} \times 20 \sqrt{3} \text { sq.cm } \\
& =300 \sqrt{3} \text { sq.cm. }
\end{aligned}\)

 

Question 12. The length of each equal side of an isosceles triangle is 20 m and the angle included between them is 45°. Let us write by calculating the area of the triangle.

Solution:

Given

The length of each equal side of an isosceles triangle is 20 m and the angle included between them is 45°.

Let ABC is an equilateral triangle whose AB = AC = 20 cm & ∠A = 45°.
Draw the perpendicular CD on AB.

In ΔABC, AB is the base & CD is perpendicular.
∠ACD = 45°
∴ AD = CD

In the right-angled triangle ΔADC,
AD²+CD² =AC²
or, CD²+ CD² = (20)²

or, 2CD² =400

or, \(C D^2=\frac{400}{2}=200\)

or, \(C D=\sqrt{200}=10 \sqrt{2} \mathrm{~cm}\)

∴ Area of the triangle = \(\frac{1}{2} \times A B \times C D\)

\(\begin{aligned}
& =\frac{1}{2} \times 20 \times 10 \sqrt{2} \text { sq.cm } \\
& =100 \sqrt{2} \text { sq.cm. }
\end{aligned}\)

 

Question 13. The length of each equal side of an isosceles triangle is 20 cm, and the angle included between them is 30°. Let us write by calculating the area of the triangle.

Solution:

Given

The length of each equal side of an isosceles triangle is 20 cm, and the angle included between them is 30°.

Let ABC is an isosceles triangle whose AB = AC = 20 cm and ∠BAC = 30°. CD is the perpendicular on AB.
∴∠ACD = 60°

In right-angled ΔACD,
∠ACD = 2∠DAC

∴ \(C D=\frac{1}{2} A C=\frac{1}{2} \times 20 \mathrm{~cm}=10 \mathrm{~cm}\)

∴ Area of ΔABC = \(\frac{1}{2} \times A B \times C D\)

= \(\frac{1}{2} \times 20 \times 10 \text { sq.cm }\)

= 100sq.cm

Question 14. If the perimeter of an isosceles right-angled triangle is (√2+1)cm. Let us write by calculating the length of the hypotenuse and area of the triangle.

Solution: Let the length of the isosceles right angled triangle, length of equal side = a cm.

∴ Length of the hypotenuse = \(\sqrt{\mathrm{a}^2+\mathrm{a}^2} \mathrm{~cm}\)

\(\begin{aligned}
& =\sqrt{2 \mathrm{a}^2} \mathrm{~cm} \\
& =\sqrt{2} \mathrm{a} \mathrm{cm}
\end{aligned}\)

 

∴ Perimeter of the triangle = (a+a+ √2 a) cm
= (2a + √2 a) cm

According to the problem, 2a+√2a = √2+1

or, \(a=\frac{\sqrt{2}+1}{2+\sqrt{2}}=\frac{(\sqrt{2}+1)}{\sqrt{2}(\sqrt{2}+1)}=\frac{1}{\sqrt{2}}\)

∴ Length of the hypotenuse = √2 a cm

= \(\sqrt{2} \times \frac{1}{\sqrt{2}} \mathrm{~cm}\)
= 1 cm

Area of the triangle = \(\frac{1}{2} \times a \times a\)

\(\begin{aligned}
& =\frac{1}{2} \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}} \text { sq.cm } \\
& =\frac{1}{4} \text { sq.cm }
\end{aligned}\)

= 0.25 sq.cm.

Question 15. Maria cycling at a speed of 18 km per hour covers the perimeter of an equilateral triangular field in 10 minutes. Let us write by calculating the time required for Maria to go directly to the mid-point of the side of the field starting from its opposite vertex. (√3≈ 1.732)

Solution:

Given

Maria cycling at a speed of 18 km per hour covers the perimeter of an equilateral triangular field in 10 minutes.

Speed = 18 km/hr

Time 10 minutes = \(\frac{10}{60} \mathrm{hr}=\frac{1}{6} \mathrm{hr}\)

∴ Distance = speed x time = \(\)

= \(18 \times \frac{1}{6} \mathrm{~km}\) = 3 km

∴ Perimeter of triangular field = 3 km

∴ Length of each side of the field = \(\frac{3}{3} \mathrm{~km}\) = 1km

Height of the triangular field = \(\frac{\sqrt{3}}{2} \times(\text { side })\)

\(\begin{aligned}
& =\frac{\sqrt{3}}{2} \times 1 \mathrm{~km} \\
& =\frac{\sqrt{3}}{2} \mathrm{~km}
\end{aligned}\)

 

∴ Time required to go from the vertex to the mid-point of the opposite side

\(\begin{aligned}
& =\frac{\sqrt{3}}{2} \div 18 \mathrm{hr} \\
& =\frac{\sqrt{3}}{2} \times \frac{1}{18} \times 60 \text { minutes } \\
& =\frac{5 \sqrt{3}}{3} \text { minutes } \\
& =\frac{5 \times 1.732}{3} \text { minutes } \\
& =\frac{8.66}{3} \text { minutes }
\end{aligned}\)

 

= 2.89 minutes (approx)

Question 16. If the length of each side of an equilateral triangle is increased by 1 meter, then its area will be increased by √3 sq. meter. Let us write by calculating the length of a side of the equilateral triangle.

Solution:

Given

If the length of each side of an equilateral triangle is increased by 1 meter, then its area will be increased by √3 sq. meter.

Let each side of an equilateral side = a m.

∴ Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} a^2 \text { sq.m. }\)

It the length is increased by 1 m then new length = (a + 1) m.

∴ New area of the triangle = \(\frac{\sqrt{3}}{4}(a+1)^2 \text { sq.m }\)

According to the problem,

\(
\frac{\sqrt{3}}{4}(a+1)^2=\frac{\sqrt{3}}{4} a^2+\sqrt{3}
or, \frac{\sqrt{3}}{4}(a+1)^2-\frac{\sqrt{3}}{4} a^2=\sqrt{3}\)

 

\(or, \frac{\sqrt{3}}{4}\left\{(a+1)^2-a^2\right\}=\sqrt{3}
or, \frac{\sqrt{3}}{4}\left(a^2+2 a+1-a^2\right)=\sqrt{3}\)

 

\(or, \frac{\sqrt{3}}{4}(2 a+1)=\sqrt{3}
or, 2 a+1=\sqrt{3} \times \frac{4}{\sqrt{3}}\)

 

or, 2a+1=4
or, 2a =4-1
or, 2a = 3

or, \(a=\frac{3}{2}\)

or, a = 1.5

∴ Each side of the equilateral triangle = 1.5 m.

Question 17. The area of an isosceles triangle and area of the square are in the ratio √3:2. If the length of the diagonal of the square is 60 cm, let us write by calculating the perimeter of the isosceles triangle.

Solution:

Given

The area of an isosceles triangle and area of the square are in the ratio √3:2. If the length of the diagonal of the square is 60 cm

Let each side of an equilateral triangle is a cm & each side of a square = x cm.

Length of the diagonal = \(\sqrt{\mathrm{x}^2+\mathrm{x}^2} \mathrm{~cm}\)

= \(=\sqrt{2 x^2} \mathrm{~cm}=x \sqrt{2} \mathrm{~cm}\)

According to the problem, x√2 = 60

or, x = \(\frac{60}{\sqrt{2}}=\frac{60 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}=\frac{60 \sqrt{2}}{2}\)

or, x = 30√√2

Again, according to the problem,

\(=\frac{\text { Area of the equilateral triangular }}{\text { Area of the square }}=\frac{\sqrt{3}}{2}\)

 

\(or, \frac{\frac{\sqrt{3}}{4} a^2}{x^2}=\frac{\sqrt{3}}{2}\)

 

\(or, \frac{\sqrt{3} a^2}{4 x^2}=\frac{\sqrt{3}}{2}\)

or, a = √2.30√2 = 60

Length of each side of the equilateral triangle = 60 cm.
∴ And the perimeter of the triangle = 3 x 60 cm = 180 cm.

Question 18. Length of the hypotenuse and perimeter of a right-angled triangle is 13 cm and 30 cm. Let us write by calculating the area of a triangle.

Solution: Let the length of the sides containing the right angle of a right-angled triangle are a cm & b cm respectively.

∴ Length of the diagonal = \(\sqrt{a^2+b^2}\) and perimeter of the triangle

= \(a+b+\sqrt{a^2+b^2} \cdot c m\)

According to the 1st condition,

\(\begin{aligned}
& \sqrt{a^2+b^2}=13 \\
& \text { or, }\left(\sqrt{a^2+b^2}\right)^2=(13)^2
\end{aligned}\)

(squaring both sides)

or, a²+b²  = 169 ….(1)

According to the 2nd condition,

a+b+ \(\sqrt{a^2+b^2}\) = 30

or, a+b+13=30
or, a+b=30-13
or, a + b = 17

(squaring both sides)

or, (a + b)²= (17)²
or, a²+ b²+2ab = 289

or, 169 +2ab = 289 (a²+ b² = 169)

or, 2ab 289-169
or, 2ab = 120

or, \(a b=\frac{120}{2}\)

or, ab = 60

∴ Area of the right-angled triagle = \(\frac{1}{2} a b\)

= \(\frac{1}{2}\).60 sq.cm

= 30 sq. cm.

Question 19. The lengths of the sides containing the right angle are 12 cm and 5 cm. Let us write by calculating the length of the perpendicular drawn from the vertex of right angle on the hypotenuse.

Solution: Length of the hypotenuse of the right-angled triangle = \(\sqrt{(12)^2+(5)^2} \mathrm{~cm}\)

\(\begin{aligned}
& =\sqrt{144+25} \mathrm{~cm} \\
& =\sqrt{169} \mathrm{~cm} \\
& =13 \mathrm{~cm}
\end{aligned}\)

 

Area of the right-angled triangle = \(\frac{1}{2}\)x12×5 = 30 sq.cm

∴ Length of the perpendicular drawn from the vertex of the right angle on the Hypotenuse

= \(\frac{2 x \text { Area of the triangular }}{\text { Length of the hypotenuse }}\)

\(\begin{aligned}
& =\frac{2 \times 30}{13} \mathrm{~cm} \\
& =\frac{60}{13} \mathrm{~cm}
\end{aligned}\)

 

= 4.615 cm (Approx).

Question 20. The largest square is cut out from a right-angled triangular region with lengths of 3 cm, 4cm, and 5 cm respectively in such a way that one vertex of the square lies on the hypotenuse of the triangle. Let us write by calculating the length of a side of the square.

Solution:

 

Let ABC is a right-angled triangle whose AB = 3 cm, BC= 4 cm, and length of the hypotenuse AC = 5 cm, and length of each side of the largest square which is cut from the triangle = a cm.

∴ AF (3-a) cm, CD = (4-a) cm

Area of ΔABC = \(\frac{1}{2}\) x ABxBC

= \(\frac{1}{2}\) x 3x 4 sq.cm

= 6 sq.cm

Area of ΔAFE= \(\frac{1}{2}\) × AF XFE

= \(\frac{1}{2}\) × (3 -a) xa sq.cm

Area of ΔCDE = \(\frac{1}{2}\)x CDx DE

= \(\frac{1}{2}\)  x (4-a) x a sq.cm

Area of the square BDEF = ΔABC – (ΔAFE + ΔCDE)

or, \(a^2=6-\left\{\frac{1}{2}(3-a) \times a+\frac{1}{2}(4-a) \times a\right\}\)

or, \(a^2=6-\left(\frac{3 a-a^2+4 a-a^2}{2}\right)\)

or, \(a^2=6-\left(\frac{7 a-2 a^2}{2}\right)\)

or, 2a² =  12-7a+2a²
or, 2a²-2a²+7a= 12
or, 7a = 12

\(or, a=\frac{12}{7}
or, a=1 \frac{5}{7}\)

Length of each side of the square= \(1 \frac{5}{7}\)

Question 21. Multiple choice questions

1. If each side of an equilateral triangle is 4 cm, the measure of height is

1. 4√3 cm
2. 16√3 cm
3. 8√3 cm
4. 2√3 cm

Solution: Height of equilateral triangle = \(\frac{\sqrt{3}}{2} \times(\text { side })\)

= \(\frac{\sqrt{3}}{2} \times 4 \mathrm{~cm}\)

= 2√3 cm

∴ 4. 2√3 cm

2. An isosceles right-angled triangle of which the length of each side of equal two sides is a unit. The perimeter of the triangle is

1. (1+ √2)a unit
2. (2+ √2)a unit
3. 3a unit
4.(3+2√2)a unit

Solution: Length of the hypotenuse of the right-angled isosceles triangle

\(\begin{aligned}
& =\sqrt{a^2+a^2} \text { unit } \\
& =\sqrt{2 a^2} \text { unit }=\sqrt{2} \text { a unit }
\end{aligned}\)

 

= √2 a unit

∴ Perimeter of the triangle = a+a+√2 a unit
= 2a+√2 a unit
= (2+ √2)a unit

∴ 2.  (2+√√2)a unit

3. If the area, perimeter, and height of an isosceles triangle are a, s, and h, then the value of \(\frac{2 a}{s h}\) is

1. 1

2. \(\frac{1}{2}\)

3. \(\frac{1}{3}\)

4. \(\frac{1}{4}\)

Solution: Let each side of an equilateral triangle = x unit.

Area of the equilateral triangle = (a) = \(\frac{\sqrt{3}}{4} x^2 \text { unit. }\)

The perimeter of the equilateral triangle (s) = 3x unit.

Height of the equilateral triangle =(h) = \(\frac{\sqrt{3}}{4} \times \text { unit. }\)

∴ \(\frac{2 a}{s h}=\frac{2 \cdot \frac{\sqrt{3}}{4} x^2}{3 x \cdot \frac{\sqrt{3}}{2} x}\)

or, \(\frac{2 a}{s h}=\frac{2 \sqrt{3}}{4} \times \frac{2}{3 \sqrt{3}}=\frac{1}{3}\)

∴ 3. \(\frac{1}{3}\)

4. The length of each equal side of an isosceles triangle is 5 cm and the length of base is 6 cm. The area of the triangle is

1. 18 sq. cm
2. 12 sq. cm.
3. 15 sq. cm
4. 30 sq. cm.

Solution: Area of the isosceles = \(\frac{1}{2} \times 6 \times \sqrt{(5)^2-\frac{(6)^2}{4}} \text { sq. cm. }\)

\(\begin{aligned}
& =3 \sqrt{25-\frac{36}{4}} \text { sq. } \mathrm{cm} . \\
& =3 \sqrt{25-9} \text { sq. } \mathrm{cm} . \\
& =3 \times \sqrt{16} \text { sq. } \mathrm{cm} . \\
& =3 \times 4 \text { sq. } \mathrm{cm} . \\
& =12 \text { sq. } \mathrm{cm} .
\end{aligned}\)

 

∴ 2. 12 sq. cm

5. D is such a point on AC of triangle ABC so the AD; DC = 3 : 2. If the area of triangle ABC is 40 sq. cm, the area of triangle BDC is

1. 16 sq. cm.
2. 24 sq. cm
3. 30 sq. cm.
4. 36 sq. cm

 

 

Solution: AD : DC = 3 : 2

or, \(\frac{A D}{D C}=\frac{3}{2}\)

or, \(\frac{\mathrm{AD}}{\mathrm{DC}}+1=\frac{3}{2}+1\)

or, \(\frac{A D+D C}{D C}=\frac{3+2}{2}\)

or, \(\frac{A C}{D C}=\frac{5}{2}\)

or, \(\frac{\triangle \mathrm{ABC}}{\triangle \mathrm{BDC}}=\frac{5}{2}\)

or, \(\frac{40 \text { sq. cm }}{\Delta \mathrm{BDC}}=\frac{5}{2}\)

or, area of = ΔBDC = \(\frac{80 \text { sq. cm }}{5}\)

∴ 1. 16 sq.cm

6. The difference of length of each side of a triangle from its semi- perimeter are 8 cm, 7 cm, and 5 cm respectively. The area of the triangle is

1. 20√7 sq. cm.
2. 10√14 sq. cm.
3. 20√14 sq. cm.
4. 140 sq. cm.

Solution: Let the length of 3 sides of the triangle be a cm, b cm & c cm.
∴ Perimeter of the triangle (2s) = a+b+c

According of the problem, sa 8, s-b7, s-c=5
∴ s-a+s-b+s-c=8+7+5
or, 3s (a+b+c) 20
or, 3s 2s 20
or, s = 20

∴ Area of the triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\)

\(\begin{aligned}
& =\sqrt{20 \times 8 \times 7 \times 5} \text { sq.cm. } \\
& =\sqrt{4 \times 5 \times 4 \times 2 \times 7 \times 5} \text { sq. cm. } \\
& =4 \times 5 \sqrt{2 \times 7} \text { sq. cm. } \\
& =20 \sqrt{14} \text { sq. cm. }
\end{aligned}\)

 

∴ 3. 20√14 sq. cm.

Question 22. Short answer type questions

1. The numerical values of area and height of an equilateral triangle are equal. What is the length of a side of the triangle ?

Solution: Let each side of an equilateral triangle = a unit.

∴ Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} a^2 \text { sq. cm. }\)

∴ Height of the equilateral triangle \(\frac{\sqrt{3}}{2} a \text { sq. cm. }\)

According of the problem,

\(
\frac{\sqrt{3}}{4} a^2=\frac{\sqrt{3}}{2} a
or, \frac{a}{2}=1
or, a=2\)

∴ Length of each side of the equilateral triangle = 2 unit.

2. If length of each side of an equilateral triangle is doubled, what percent of area will be increased of this triangle?

Solution: Let the 3 sides of a triangle are a unit, b unit, and c unit.

∴ Semi-perimeter of the triangle (s) = \(\frac{a+b+c}{2}\)

∴Area of the triangle (Δ) = \(\sqrt{s(s-a)(s-b)(s-c)}\)

If each side of the triangle be doubled,

Perimeter = 2a + 2b + 2c
= 2(a + b + c)
2(a+b+c)

∴ Semi-perimeter = \(\frac{2(a+b+c)}{2}\)

= a+b+c
= 2s

∴ Area of the new triangle = \(\sqrt{2 s(2 s-2 a)(2 s-2 b)(2 s-2 c)} \text { sq. cm }\)

\(\begin{aligned}
& \sqrt{2 s \cdot 2(s-a) \cdot 2(s-b) \cdot 2(s-c)} \text { sq. } \mathrm{cm} \\
& 4 \sqrt{s(s-a)(s-b)(s-c)} \text { sq. cm }
\end{aligned}\)

 

= 4Δ

∴ Percentage of increased area = \(\frac{4 \Delta-\Delta}{\Delta} \times 100 \%=300 \%\)

3. If the length of each side of an equilateral triangle is trippled, what percent of area will be increased of this triangle ?

Solution: Let the 3 sides of a triangle are a unit, b unit & c unit.

∴ Area of triangle = (Δ) = \(\sqrt{s(s-a)(s-b)(s-c)} \text { sq. } \mathrm{cm}\)

If each side of the triangle be trippled = \(\sqrt{3 s .3(s-a) 3(s-b) 3(s-c)} \text { sq. } \mathrm{cm}\)

New area = 9Δ

∴ Percentage of increased area = \(\frac{9 \Delta-\Delta}{\Delta} \times 100 \%=800 \%\)

4. The lengths of sides of a right-angled triangle are (x-2) cm, x cm and (x+2) cm. How much is the length of hypotenuse ?

Solution: As the hypotenuse of an right angle triangle is the biggest side,
∴ Length of the hypotenuse = (x+2) cm

According to Pythagoras’ theorem,

(x + 2)²= (x)² +(x-2)²
or, x² + 4x + 4 = x² + x² – 4x + 4
or, x²-8x=0

or, x(x-8)=0
or, x = 0 and x-8=0

If x-8=0 or x = 8 , x = 0, 8
but x ≠ 0
X = 8

∴ Length of the hypotenuse = (8 + 2) cm = 10 cm.

5. A square is drawn on the height of a equilateral triangle. What is the ratio of areas of triangle and square?

Solution: Let the each side of an equilateral triangle = a unit.

∴ Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} a^2\)

Height of the equilateral triangle = \(\frac{\sqrt{3}}{2} \text { a unit. }\)

∴ Area of the square drawn on the height of the triangle = \(\left(\frac{\sqrt{3}}{2} a\right)^2 \text { sq.unit }\)

= \(\frac{3 a^2}{4} \text { sq.unit }\)

∴ Ratio of area of the triangle & the area of square= \(\frac{\sqrt{3}}{4} a^2: \frac{3 a^2}{4}\)= √3:3
= √3:√3.√3 =1:√3

 

 

Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15.1

Question 1. I see the house of Kamal and let us find the answer :

1. Let us write by calculating the area of Kamal’s garden.
2. Let us write by calculating how much cost is required to repair the floor of Kamal’s verandah.
3. Kamal wants to cover the floors of his reading room with tiles. Let us write by calculating how many tiles will be required to cover his floor of reading room with size of tiles 25 cm. x 25 cm.

Solution:

 

 

1. Area of Kamal’s garden = 20 x 20 sq.m = 400 sq.m
2. Area of verandah = 10 x 5 sq.m = 50 sq.m
Cost for repairing the floor of verandah = Rs. 50 x 30= Rs. 1500

3. Length of the reading room = 6 m = 600 cm
Breadth of the reading room = 5 m = 500 cm

Area of the reading room = 600 x 500 sq.cm
Area of each tile = 25 x 25 sq.cm

Read and Learn More WBBSE Solutions For Class 9 Maths

∴ No. of tiles = \(\frac{600 \times 500}{25 \times 25}=480\)

Question 2. Let us see the following pictures and calculate the area of its colored part.

Solution:

 

1. Length = 12 m
Breadth = 8 m

∴ Area = 12 x 8 sq.m = 96 sq.m

Length of the square except the colored part =  (12 – 3) m = 9 m
Width of the square except the colored part = (8 – 3) m = 5 m

∴ Area of the square except coloured part = 9 x 5 sq.m = 45 sq.m
∴ Area of the colored part = (96-45) sq.m = 51 sq.m

 

 

2. Area of the coloured part = (26 x 3 + 14 x 3-3 x 3) sq.m = (78+ 429) sq.m
= (1209) sq.m = 111 sq.m

 

 

3. Length of the coloured part = (16+2 x 4) m = 24 m
Width of the coloured part = (9+ 2 × 4) m = 17 m

∴ Area of the rectangle including the colored part = (24 x 17) sq.m = 408 sq.m

Length of the rectangle excluding the colored part = 16 mWidth of the rectangle excluding the colored part = 9 m
Area of the rectangle excluding the colored part 16 x 9 m = 144 sq.m

∴ Area of the coloured part = (408-144) sq.m = 264 sq.m

 

 

4. Area of the rectangle including the colored part = 28 x 20 sq.m = 560 sq.m
Area of the rectangle excluding the colored part = (28-2x 3) (20-2x 3) sq.m = 22 x 14 sq.m = 308 sq.m
∴ Area of the colored part of the rectangle = (560-308) sq.m = 252 sq.m

 

 

5. Area of the colored part of the rectangle = {120×3+90×3+90×3-(3×3)-(3×3)} sq.m
= (360+270 +270-9-9) sq.m
= (900-18) sq.m = 882 sq.m

Question 3. The length and breadth of the rectangular field of Birati Mahajati Sangha are in the ratio 4: 3. The path of 336 meters is covered by walking once round the field. Let us write by calculating the area of the field.

Solution:

Given

The length and breadth of the rectangular field of Birati Mahajati Sangha are in the ratio 4: 3. The path of 336 meters is covered by walking once round the field.

Let the length & the breadth of the rectangular are 4x m & 3x m respectively.

∴ Perimeter of the rectangular field = 2x(Length + Breadth)
= 2(4x+3x) m = 14x m

According to the problem, 14x = 336

or, \(x=\frac{336}{14}\) = 24

∴ Length of the field = 4 x 24 m = 96 m
∴Breadth of the field= 3 x 24 m = 72 m

∴  Area of the field = Length x Breadth
= 96 × 72 sq.m
= 6912 sq.m

Question 4. The cost of farming a square land of Samar at the rate of Rs. 3.50 per sq. meter is Rs. 1,400. Let us calculate how much cost will be for fencing Samar’s land around its four sides with same height at the rate of Rs. 8.50 per meter.

Solution:

Given

The cost of farming a square land of Samar at the rate of Rs. 3.50 per sq. meter is Rs. 1,400.

Cost of farming a square at the rate of Rs. 3.50 per sq.m is Rs. 1400.

∴ Area of the square = \(\frac{1400}{3.50} \text { sq.m }\)

= \(\frac{1400 \times 100}{350} \text { sq.m }=400 \mathrm{sq} \cdot \mathrm{m}\)

∴ Length of each side of the square = √400 m = 20 m
Perimeter of the square = 4 x 20 m = 80 m.

∴ The cost for fencing the four sides of the square at the rate of Rs. 8.50 per meter 80 x Rs. 8.50 = Rs. 680.

Question 5. The area of the rectangular land of Suhas is 500 sq. meters. If the length of the land is decreased by 3 meters and the breadth is increased by 2 meters, then the land formed is a square. Let us write by calculating the length and breadth of the land of Suhas.

Solution:

Given

The area of the rectangular land of Suhas is 500 sq. meters. If the length of the land is decreased by 3 meters and the breadth is increased by 2 meters, then the land formed is a square.

Let the length of rectangular land = x m

∴ Breadth of the rectangular fland = \(\frac{500}{x} \mathrm{~m}\)

New length of the land = (x-3) m

& the new breadth of the land = \(\left(\frac{500}{x}+2\right) m\)

∵ Then the length will be equal to breadth.

∴ \(x-3=\frac{500}{x}+2\)

or, \(x-\frac{500}{x}=2+3\)

or, \(\frac{x^2-500}{x}=5\)

or, x²-500 = 5x
or, x² -5x-500 = 0

or, x² – (25-20)x-500 = 0
or, x² -25x+20x-500 = 0

or, x(x-25)+20(x-25) = 0
or, (x-25)(x+20)=0

or, x+20=0
∴ X=-20

Length will never be negative.
∴ Length of the land is 25 m.

Breadth of the land = \(\frac{500}{25}\) m = 20 m.

Question 6. Each side of a square land of our village is 300 meters. We shall fence that square land by 3 dcm wide wall with the same height around its four sides. Let us see how much will it cost for the wall at the rate of Rs. 5,000 per 100 sq. nicer.

Solution:

Given

Each side of a square land of our village is 300 meters. We shall fence that square land by 3 dcm wide wall with the same height around its four sides.

Each side of the square = 300 m

Width of the wall = 3 dcm = \(\frac{3}{10}\) m = 0.3 m

Area of the land with wall =  (300)² sq.m

Area of the land without wall = (300-2x.3)² sq.m (299.4)² sq.m

Area of the wall = {(300)²– (299.4)²)} sq.m
= (300+299.4) (300-299.4) sq.m = 599.4 x 0.6 sq.m = 359.64 sq.m

∴ Cost of making 100 sq.m wall = Rs. 5000

∴ Cost of making 1 sq.m wall = \(\frac{5000}{100}\)

∴ Cost of making 359.64 sq.m wall = Rs. \(\frac{5000}{100}\) x 359.64 = Rs. 17982. 100

Question 7. The length and breadth of the rectangular garden of Rehana are 14 meters and 12 mars. If the cost of constructing an equally wide path inside the garden is Rs. 1,380 at the rate of Rs. 20 per sq. meter, then let us write by calculating how wide is the path.

Solution:

Given

The length and breadth of the rectangular garden of Rehana are 14 meters and 12 mars. If the cost of constructing an equally wide path inside the garden is Rs. 1,380 at the rate of Rs. 20 per sq. meter,

Length of the rectangle = 14m
The breadth of the rectangle = 12 m

Area of the garden including the path = 14 x 12 sq.m = 168 sq.m
Let the width of the path = x m

∴ Length of the garden without path = (14-2x)
Breadth of the garden without path = (12 -2x) m

Area of the garden without the path = (14-2x) (12-2x) sq.m

∵ Cost of constructing the path at the rate of Rs. 20 per sq.m = Rs. 138

∵ Area of the path = \(\frac{1380}{20}\) sq.m = 69 sq.m

According to the problem, 168- (14-2x) (12-2x) = 69

or, 168 (168-28x-24x+4x²) = 69
or, 168 (168-52x + 4x²) = 69
or, 168-168+52x-4x²-69=0.

or, – 4x²+52x-69 = 0
or, 4x²-52x + 69 = 0

or, 4x²-46x-6x+69 = 0
or, 2x(2×23)-3(2x-23) = 0
or, (2x-23) (2x-3)= 0

∴ Either (2x-23) or (2x-3) will be zero.

If 2x-23=0

∴ \(x=\frac{23}{2}\)

If 2x-3=0

∴ = \(\frac{3}{2}\)

Breadth of the path = 11.5 m

Length of garden without path = (14-2×11.5) m
= (14-23) m = -9m

∵ Length cannot be negative
∴ Breadth of the path = 1.5 m.

Question 8. If the length of a rectangular garden with area 1200 sq. cm is 40 cm. then let us write by calculating the area of square field which is drawn on its diagonal.

Solution: Area of the rectangular garden = 1200 sq.cm
Length of rectangular garden = 40 cm

∴ Width of the rectangular garden = Area/Length

= \(\frac{1200}{40} \mathrm{~cm}=30 \mathrm{~cm}\)

Diagonal of the rectangular garden = \(\sqrt{(\text { length })^2+(\text { width })^2}\)

\(\begin{aligned}
& =\sqrt{(40)^2+(30)^2} \mathrm{~cm} \\
& =\sqrt{1600+900} \mathrm{~cm} \\
& =\sqrt{2500} \mathrm{~cm} \\
& =50 \mathrm{~cm}
\end{aligned}\)

Each side of the square drawn on the diagonal of the rectangular garden = 50 cm.

∴ Area of the square =(50)² sq.cm = 2500 sq.cm.

Question 9. The length, breadth, and height of a hall are 4 meters, 6 meters, and 4 meters. There are three doors and four windows in the room. The measurement of each door is 1.5 meters x 1 meter and each window is 1.2 meters x 1 meter. How much will it cost for covering four walls by colored paper at the rate of Rs. 70 per square meter?

Solution:

Given

The length, breadth, and height of a hall are 4 meters, 6 meters, and 4 meters. There are three doors and four windows in the room. The measurement of each door is 1.5 meters x 1 meter and each window is 1.2 meters x 1 meter.

Area of the 4 walls of a room = 2x( L + B) xh
= 2(4+6) x 4 sq.m = 80 sq.m

Area of 3 doors and 4 windows
=(3x 1.5 x 14 x 1.2 x 1) sq.m
= (4.5+ 4.8) sq.m
= 9.3 sq.m

Area of the walls excluding the areas
= (80-9.3) sq.m
= 70.7 sq.m

Cost of covering colored papers on the walls at the rate of Rs. 70 per sq.m Rs. 70 x 70.7 = Rs. 4949.

Question 10. The area of four walls of a room is 42 sq. meters and area of the floor is 12 sq. meters. Let us write by calculating the height of the room if the length of the room is 4 meter.

Solution:

Given

The area of four walls of a room is 42 sq. meters and area of the floor is 12 sq. meters.

Area of floor of the room = 12 sq.m
Length of the room = 4 m

∴ Breadth of the room = \(\frac{12}{4}\) m = 3m

Let the height of the room = x m.

∴ Area of 4 walls of the room
= 2(4+3) x x sq.m = 14x sq.m

According to the problem, 14x = 42

or, x = \(\frac{42}{14}\)

∴ Height of the room = 3 m

Question 11. Sujata will draw a rectangular picture on paper with area of 84 sq. cm. The difference between the length and breadth of the paper is 5 cm. Let us calculate the perimeter of paper of Sujata.

Solution:

Given

Sujata will draw a rectangular picture on paper with area of 84 sq. cm. The difference between the length and breadth of the paper is 5 cm.

Length of the paper = x cm
∴ Breadth of the paper = (x-5) cm

∴Area of the paper = LXB
= x(x-5) sq.cm
=  x² – 5x sq.cm

According to the problem,
 x² – 5x = 84
or,  x²  -5x-84 = 0
or,  x²  – 12x+7x-84 = 0

or, x(x-12)+7(x-12)=0
or, (x-12) (x+7)=0

Either (x-12) or (x+7) will be equal to zero.

If x-12=0
∴ x = 12

or, If x+7=0
∴ X=-7

∵ Length of paper will not be zero.
∴ Length of the room = 12 cm

Breadth of the room = (12-5) cm = 7 cm

Perimeter of the paper = 2(L+B)
= 2(12+7) cm
= 2 x 19 cm
= 38 cm.

Question 12. There is a 2.5-meter wide path around the square garden of Shiraj’s. The area of path is 165 sq meters. Let us calculate the area of the garden and the length of diagonal. (√2-1.414)

Solution:

Given

There is a 2.5-meter wide path around the square garden of Shiraj’s. The area of path is 165 sq meters.

Let each side of the square garden = x m.
∴ Area of the garden = x² sq.m

Length of side with the path = (x + 2 x 2.5) m = (x+5) m
Area of the garden with the path = (x+5)² sq.m

∴ Area of the path = {(x+5)²-x²} sq.m

According to the problem, (x+5)² – x² = 165
or, x²+10x + 25-x2 = 165
or, 10x 165-25
or, 10x = 140

or, x = \(\frac{140}{10}\) = 14

∴ Length of each side of the square = 14 m
∴ Area of the garden = (14)² sq.m 196 sq.m

Length of the diagonal = √2×14 m
= 1.414 x 14 m
= 19.796 m.

Question 13. Let us write by calculating how much length of wall in meter is required for walling outside round the square field, whereas the length of diagonal of the square land is 20√2 meter. Let us write by calculating how much cost will be incurred for planting grass at the rate of Rs. 20 per sq. meter.

Solution: Length of the diagonal of the square field = 20√2 m

Length of one side of the square field = \(\frac{\text { Diagnal }}{\sqrt{2}}=\frac{20 \sqrt{2}}{\sqrt{2}} \mathrm{~m}=20 \mathrm{~m}\)

Perimeter of the field = 4 x 20 m= 80m

Area of the field = (20)² sq.m
=400sq.m
= Rs.400x 20 = Rs. 8000

Question 14. We shall fence our rectangular garden diagonally. The length and breadth of the rectangular garden are 12 meters and 7 meters. Let us calculate the length of the fence.

Solution:

Given

We shall fence our rectangular garden diagonally. The length and breadth of the rectangular garden are 12 meters and 7 meters.

Length of the diagonal of the garden

\(\begin{aligned}
& =\sqrt{(\text { length })^2+(\text { breadth })^2} \\
& =\sqrt{(12)^2+(7)^2} \mathrm{~m} \\
& =\sqrt{144+49} \mathrm{~m} \\
& =\sqrt{193} \mathrm{~m}
\end{aligned}\)

 

∴ Length of fence = √193 m

or, Perimeter of the triangle formed by the diagonal of the rectangle
=(12+7+√193) m = (19+ √193) m

Question 15. The big hall of house of Mousumi is in the form of a rectangle, of which length and breadth are in the ratio 9: 5 and the perimeter is 140 meters. Mousmi wants to cover the floor of her hall with rectangular tiles of dimensions 25 cm x 20 cm. The rate of each 100 tiles is Rs. 500. Let us calculate the cost for covering the floor with tiles.

Solution:

Given

The big hall of house of Mousumi is in the form of a rectangle, of which length and breadth are in the ratio 9: 5 and the perimeter is 140 meters. Mousmi wants to cover the floor of her hall with rectangular tiles of dimensions 25 cm x 20 cm. The rate of each 100 tiles is Rs. 500.

Let the length & breadth of the floor are 9x m and 5x m respectively.
∴ Perimeter = 2(L+B)
= 2(9x+5x) m
= 2 x 14x m = 28x m

According to the problem, 28x=140

or, x = \(x=\frac{140}{28}\)

∴ Length of the hall = 9x 5 m = 45 m
= 45 x 100 cm = 4500 cm

Breadth of the hall = 5 x 5 m = 25 m
= 25 x 100 cm 2500 cm

Area of the hall = 4500 x 2500 sq.cm

Area of each tile = 25 cm x 20 cm

∴ Number of tiles = 4500 x 2500 25×20 = 22500

∴ Cost of 100 tiles = Rs. 500

∴ Cost of 1 tile = Rs. \(\frac{500}{100}\) = Rs. 5

∴ Cost of 22500 tiles = Rs. 22500 x 5 = Rs. 112500
∴ Cost for covering the floor with tiles = Rs. 112500.

Question 16. The cost of carpeting a big hall of length 18 meters is Rs. 2160. If the breadth of the floor would be 4 meters less, then the cost would have been Rs. 1,620. Let us calculate the perimeter and area of the hall.

Solution:

Given

The cost of carpeting a big hall of length 18 meters is Rs. 2160. If the breadth of the floor would be 4 meters less, then the cost would have been Rs. 1,620.

If the breadth is 4 m less, cost will decrease = Rs. (2160-1620) = Rs. 540

∴ If the breadth is 1 m less, cost will decrease = Rs. \(\frac{540}{4}\) = Rs. 135

∵ Cost of 1 m carpet is Rs. 135, i.e., Rs. 135 is the cost of 1 m carpet.

∴ Re. 1 is cost of \(\frac{1}{135}\) m carpet.

∴ Rs. 2160 is the cost of \(\frac{1}{135} \times 2160\) m carpet.

∴ Rs. 2160 is the cost of 6 m carpet.

∵ The breadth of the room = 16 m
∵ Length of the room = 18 m

∴ Area of the hall = 18 x 16 sq.m = 288 sq.m.

Question 17. The length of the diagonal of a rectangular land is 15 meter and the difference of length and breadth is 3 meters. Let us calculate the perimeter and area.

Solution:

Given

The length of the diagonal of a rectangular land is 15 meter and the difference of length and breadth is 3 meters.

Let the breadth of the rectangular land = xm
∴ Length of the land = (x + 3) m

∴ Length of the diagonal of the land = \(\sqrt{(x+3)^2+(x)^2} m\)

\(\begin{aligned}
& =\sqrt{x^2+6 x+9+x^2} m \\
& =\sqrt{2 x^2+6 x+9} \mathrm{~m}
\end{aligned}\)

 

According to the problem,

\(\begin{aligned}
& \sqrt{2 x^2+6 x+9}=15 \\
& \text { or, }\left(\sqrt{2 x^2+6 x+9}\right)^2=(15)^2
\end{aligned}\)

 

or, 2x²+6x+9=225
or, 2x²+6x+9-225 = 0

or, 2x²+6x-216=0
or, 2(x²+3x-108) = 0

or,x²+3x-108 = 0
or,x² + 12x-9x-108=0

or, x(x+12)-9(x+12)=0.
or, (x+12) (x-9)=0

Either, x+12= 0 or x-9=0

If x + 12 = 0
∴  X=-12

or, If x-9=0
∴ X=9

As the breadth will not be negative,
∴ Breadth of the rectangular land = 9m
∴ Length of the rectangular land = (9+3) m = 12 m

Perimeter of the land = 2(L + B)
= 2(12+9) m = 42 m

Area of the land = L x B
= 12 x 9 sq.m = 108 sq.m.

Question 18. Let us calculate what is the longest size of the square tile that can be used for paving the rectangular courtyard with measurement of 385 meter x 60 meter and also find the number of tiles.

Solution: As the tiles are square shaped
∴ Length of the side of the square tiles is the H.C.F of 385 m & 60m = 5 m.

∴ For paving the rectangular courtyard with square tiles whose maximum size is 5 m. sq. Area of each tiles =(5)² sq.m = 25 sq.m

∴ Number of tiles = \(\frac{385 \times 60}{25}\) = 924

Question 19. Multiple choice questions

1. The length of diagonal of square is 12√2 cm. The area of the square is

1. 288 sq. cm.
2. 144  m²
3. 72  m²
4. 18  m²

Solution: Diagonal of the square= 12√2 cm

∴ Area of the square = \(=\frac{1}{2} \times(12 \sqrt{2})^2 \text { sq.cm }\)

= \(\frac{1}{2} \times 144 \times 2 \text { sq.cm }\)

= 144 sq. cm

∴ 2. 144 sq. cm

2. If the area of square is A₁ sq. units and the area of the square drawn on the diagonal of the square is A₂ sq. unit, then the ratio of A₁ : A₂ is

1. 1:2
2. 2:1
3.1:4
4. 4:1

Solution: Let the length of one side of the square = x unit
∴ Area of the square = (A₁) = x² sq.unit

Length of the diagonal = √2x unit

∴Area of the square drawn on the diagonal of the square = ( A₂) = (√2x)² sq.unit = 2 x²sq.unit

∴ A₁: A₂ = x²: 2×2

∴ 1. 1:2

3. If a rectangular place of which length and breadth are 6 meter and 4 meter, is desired to pave it with 2 cm square tiles, then the number of tiles is required are

1. 1200
2. 2400
3. 600
4. 1800

Solution: Length of rectangular land = 6 m x 10 d.cm = 60 d.cm
Breadth of the rectangular land = 4 m x 10 d.cm = 40 d.cm

∴ Area of the rectangular land = 60 × 40 sq d.cm
Area of one tile =(2)² sq d.cm = 4 sq d.cm

∴ Number of tiles  \(=\frac{\text { Area of the rectangular land }}{\text { Area of each tile }}\)

= \(\frac{60 \times 40}{4}=600\)

∴ 3. 600

4. If a square and a rectangle have the same perimeter and their areas are S and R respectively then

1.  S = R
2. S>R
3. S<R
4. None of these

Solution: Between the square & a rectangle of same perimeter, area of the square is greater than the area of the rectangle.

∴ 2. S> R

5. If the length of the diagonal of a rectangle is 10 cm and area is 62.5 sq. cm, then the sum of their length and breadth is

1. 12 cm.
2. 15 cm
3. 20 cm
4.  25 cm

Solution:

Given

If the length of the diagonal of a rectangle is 10 cm and area is 62.5 sq. cm

Let the length and breadth of a rectangle are x cm & y cm respectively.

∴ Length of the diagonal of the rectangle = \(\sqrt{x^2+y^2} \mathrm{~cm}\) cm

∴ Area of the rectangle = xy sq. cm

According to 1st condition, \(\sqrt{x^2+y^2}=10\)

or, \(\left(\sqrt{x^2+y^2}\right)^2=(10)^2\) (Squaring both sides)

or, x² + y²= 100 …(1)

According to 2nd condition,
xy = 62.5

∴ 2xy=2x 62.5 (multiplying both sides by 2)
or, 2xy = 125 …(2)

Adding (1) & (2),

x² + y²+ 2xy = 100 + 125
or, (x + y)² = 225

or, x+y= √√225
or, x + y = 15

∴ Sum of the length and breadth of the rectangle = 15 cm.

∴ 2. 15 cm.

Question 20. Short answer type questions

1.  If the length of square is increased by 10%, then what percent of area of the square will be increased?

Solution:

Given

If the length of square is increased by 10%,

Let each side of the square = x unit

∴ Area of the square =  x² sq.unit.

Increasing 10% of each side of the square = x 10% = \(\frac{x \times 10}{100} \text { unit }=\frac{x}{10} \text { unit }\)

∴ New length of each side of the square = \(\left(x+\frac{x}{10}\right) \text { unit }=\frac{11 x}{10} \text { unit }\)

Area of new square= \(\left(\frac{11 x}{10}\right)^2 \text { sq.unit }=\frac{121 x^2}{100} \text { sq.unit }\)

Increase in area = \(\left(\frac{121 x^2}{100}-x^2\right) \text { sq.unit }\)

 \(\begin{aligned}
& =\frac{121 x^2-100 x^2}{100} \text { sq.unit } \\
& =\frac{21 x^2}{100} \text { sq.unit }
\end{aligned}\)

 

Percentage increase in area = \(\frac{21 x^2}{100} \times \frac{100}{x^2}=21 \%\)

2. If the length is increased by 10% and the breadth is decreased by 10% of a rectangle, then what percent of area will be increased or decreased?

Solution:

Given

If the length is increased by 10% and the breadth is decreased by 10% of a rectangle

Let the length & breadth of a rectangle are x unit & y unit respectively.

∴ Area of the rectangle = xy sq.unit

Length is increased by 10% = x + 10% of x.

= \(\left(x+\frac{10 x}{100}\right) \text { unit }=\frac{11 x}{10} \text { unit }\)

Breadth is decreased by 10% = \(\left(y-\frac{10 y}{100}\right) \text { unit }=\frac{9 y}{10} \text { unit }\)

∴ New area of this rectangle = \(\frac{11 x}{10} \times \frac{9 x}{10} \text { sq.unit }\)

∴ Decrease in area = \(\left(x y-\frac{99 x y}{100}\right) \text { sq.unit }\)

= \(\frac{x y}{100} \text { sq.unit }\)

∴ Percentage decrease in area = \(\frac{x y}{100} \times \frac{100}{x y}=1 \%\)

3. The length of a rectangle is 5 cm. The length of the perpendicular on the breadth of the rectangle from an intersecting point between two diagonals is 2 cm. What are the length and breadth?

Solution:

 

Given

The length of a rectangle is 5 cm. The length of the perpendicular on the breadth of the rectangle from an intersecting point between two diagonals is 2 cm.

Let diagonals AC & BD of the rectangle ABCD intersect at O. OP is the perpendicular drawn from O on AD; OP = 2 cm.

∴ Length of the rectangle = (AB) = 2 × OP = 2x 2 cm 4 cm

ΔABC is a right-angled triangle whose ∠B is a right angle ( ABCD is a rectangle) From the Pythagoras theorem,

AC² = AB² + BC²

or, (5)² = (4)² + BC²

or, 25 -16 BC²

or, 9 = BC² 

or, BC² = 9

or, BC = +3

As the breadth is not negative,
∴BC = 3 cm

∴ Breadth of the rectangle = 3 cm.

4. If the length of the perpendicular from the intersecting point between two diagonals on any side of square is 2√2 cm, then what is the length of each diagonal or square?

Solution:

Given

If the length of the perpendicular from the intersecting point between two diagonals on any side of square is 2√2 cm,

Let the diagonals AC & BD of the square ABCD intersect at P. PQ is the perpendicular from P on AB.

∴ PQ = 2√2 cm

∴ Length of each side of square = 2×2√2 cm = 4√2 cm

∴ Length of each diagonal of square = √2 × side = √2×4√2 cm = 8 cm.

5. The perimeter of a rectangle is 34 cm and its area is 60 sq. cm. What is the length of each diagonal?

Solution: Let the length and breadth of a rectangular are x cm & y cm respectively.

∴ Perimeter of the rectangle = 2(x + y) cm

& Area of the rectangle = xy sq.cm

According to 1st,condition, 2(x+y)=34

or, x + y = \(\frac{34}{2}\)

or, x + y = 17.

According to 2nd condition, xy = 60

From equation (1), x + y = 17 …(2)

or, (x + y)²=(17)² (Squaring both sides)

or, (x-y)² + 4xy = 289

or, (x-y)²+4 x 60 = 289

or, (x-y)²+240 = 289

or, (x-y)² = 289-240

or, (x-y)² = 49

or, x – y = √49

or, x – y = 7 …(2)

Adding (1) & (2),

2x = 24

or, \(x=\frac{24}{2}=12\)

Putting the value of x in equation (1),

12+y=17

or, y = 17-12=5

Length of the rectangle 12 cm & breadth = 5 cm

Length of the diagonal of the rectangle = \(\sqrt{(12)^2+(5)^2} \mathrm{~cm}\) 

\(\begin{aligned}
& =\sqrt{144+25} \mathrm{~cm} \\
& =\sqrt{169} \mathrm{~cm} \\
& =13 \mathrm{~cm}
\end{aligned}\) 

 

 

Chapter 15 Area And Perimeter Of Triangle And Quadrilateral

Definitions:

1. Rectangle: The region bounded by 4 sides, whose opposite sides are equal and parallel and each angle is equal to 90° is called a rectangle. ABCD is a rectangle.

 

Read and Learn More WBBSE Solutions For Class 9 Maths

2. Square: The region bounded by 4 sides, whose all sides are equal and each angle is a right angle (90°), is called a square. ABCD is a square

 

 

Important Formulae :

Rectangle

1. Perimeter of Rectangle = 2 (Length + Breadth) units.

2. Length of Rectangle = \(\left(\frac{\text { Perimeter }}{2}-\text { Breadth }\right)\) units.

3. Breadth of Rectangle = \(\left(\frac{\text { Perimeter }}{2}-\text { Lenght }\right)\) units.

4. Area of Rectangle = Length x Breadth sq.units

5. Length of Rectangle = \(\frac{\text { Area }}{\text { Breadth }}\) units

6. Breadth of Rectangle = \(\frac{\text { Area }}{\text { Length }}\) units

7. Length of diagonal of a rectangle = \(\sqrt{(\text { Length })^2+(\text { Breadth })^2}\)

Square

1. Perimeter of a square = 4 x side units

2. Length of a side of a square \(=\frac{\text { Perimeter }}{4}\) units

3. Area of a square = (side)² sq.units

4. Length of one side of a square = \(\sqrt{\text { Area }}\)units

5. Length of diagonal of a square = √2 × side units

6. Length of a side of a square= \(\frac{\text { Diagonal }}{\sqrt{2}}\)

7. Area of a square= \(\frac{(\text { Diagonal })^2}{2}\)

Triangle

1. Perimeter of a triangle = (a + b + c) units where a, b, and c are the lengths of the sides of the triangle.

2. Semi-perimeter of a triangle = (s) = \(\frac{a+b+c}{2}\) units

3. Area of a triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\) sq.units

4. Area of a triangle = \(\frac{1}{2}\) x base x height sq.units

5. Height of an equilateral triangle = \(\frac{\sqrt{3}}{2}\) x side units

6. Area of an equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { side })^2 \text { sq.units }\)

7. Height of an isosceles triangle = \(\sqrt{b^2-\frac{a^2}{4}}\) where ‘b’ is the length of equal side ‘a’ is the length of base.

8. Area of an isosceles triangle = \(\frac{1}{2} \cdot a \cdot \sqrt{b^2-\frac{a^2}{4}} \text { sq.units }\)

9. Height of a right-angled triangle = \(\sqrt{(\text { perpendicular })^2+\text { (base) }^2}\)

10. Area of a right-angled trangle = \(\frac{1}{2}\) x base x Perpendicular sq.units 2

= \(\frac{1}{2}\)  Χ Product of the sides forming the right-angle

11. Length of the perpendicular drawn on a side of a triangle

= Area of triangle / Length of the side on which perpendicular is drawn

Formulae relating to room

1. Area of floor of a room = Length x Breadth sq.units

2. Area of roof of a room = Area of floor Length x Breadth sq.units

3. Area of four walls of a room 2 (Length + Breadth) x Height sq.units

Area of path formed around a rectangular or a square region

1. If the path is outside:

1. Area of path = Area of the region including path – Area of the region
2.  Length including path Length of region + 2 x Breadth of path
3. Breadth including path = Breadth of region + 2x Breadth of path

2. If the path is inside:

1. Area of path = Area of rectangle or square – Area of rectangle or square
2. Length of rectangle or square excluding path = Length of rectangle or square 2 x Width of path
3. Breadth of rectangle or square excluding path = Breadth of rectangle or square 2 x Breadth of path

 

Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15

 

Question 1. 

 

 

Solution: Perimeter (10+12+13+14.8+ 16.2) cm = 66 cm

Question 2. 

 

 

Solution: Perimeter (7+ 19.4+21+ 10) cm = 57.4 cm

Question 3.

 

 

Solution: Perimeter (12+3+5.6+19) cm 39.6 cm

Question 4.

 

 

Solution: Perimeter (9+15+ 6+19+8+6) cm = 63 cm

Question 5.

 

 

 
Solution: Perimeter (12+9+16+26) cm = 63 cm

Question 6. If in a square land, the length of the diagonal is 20√2 meters, let us write by calculating how much length in meters is required for fencing a wall surrounding it.

Solution: The length of the diagonal of the square land is 20√2 m.

∴ Length of each side of the square land = \(\frac{20 \sqrt{2}}{\sqrt{2}}\) m = 20 m.

∴ The perimeter of square land = 4 x 20 m = 80 m.
∴ Length of the wall for fencing the surrounding of square 80 meters.

Question 7. The rectangular land of Pritam has a 5-meter wide path all around it on the outside. The length and width of the rectangular land are 2.5 dkm and 1.7 dkm respectively. Let us write by calculating how much cost will be required for fencing around the other side of path at the rate of Rs. 18 per meter.

Solution:

Given

The rectangular land of Pritam has a 5-meter wide path all around it on the outside. The length and width of the rectangular land are 2.5 dkm and 1.7 dkm respectively.

Length of rectangle = 2.5 dkm
= 2.5 x 10 m = 25 m

Width of the rectangle = 1.7 dkm
= 1.7 x 10 m = 17 m

Width of the path = 5 meter
Length of the land with the path = (25 + 2 x 5) m = 35 m
Width of the land with the path = (17+2×5) m = 27 m
The perimeter of the land including the path = 2(35+27) m = 2 x 62 m = 124 m

Total cost for fencing around the outer side of the path at the rate of Rs. 18 per meter = Rs. 18 x 124 Rs. 2,232.

Question 8. Let us see the card below, find the perimeter and let us write by calculating what will be the length of one side of an equilateral triangle with the same perimeter.

Solution: perimeter of the 1st card = 2(18+12)cm = 2 X 30cm = 60cm

∴The perimeter of the equilateral triangle = 60 cm.
∴ Length of one side of the equilateral triangle (60÷ 3) cm = 20 cm

Perimeter of the 2nd card = 4 x 9 cm = 36 cm

∴ Perimeter of the equilateral triangle = 36 cm
∴ Length of one side of the equilateral triangle (36÷ 3) cm = 12 cm

Perimeter of the 3rd card = (15+ 7+ 8+ 9) cm = 39 cm

∴ Perimeter of the equilateral triangle = 39 cm
∴ Length of one side of the equilateral triangle = (39÷ 3) cm = 13 cm

Perimeter of the 4th card (21+ 12+21 +12) cm = 66 cm

∴ Perimeter of the equilateral triangle = 66 cm
∴ Length of one side of the equilateral triangle = (66 ÷ 3) cm = 22 cm

Perimeter of the 5th card (12+5+13) cm = 30 cm

∴ Perimeter of the equilateral triangle = 30 cm
∴ Length of one side of the equilateral triangle (30÷ 3) cm = 10 cm

Perimeter of the 6th card (14+ 14+17) cm = 45 cm

∴ Perimeter of the equilateral triangle = 45 cm
Length of one side of the equilateral triangle (45÷ 3) cm = 15 cm

Question 9. Look at the figures below and let us write by calculating their area.

Solution:

 

 

1. First image is a right-angled triangle whose base is 5 cm and its hypotenuse is 13 cm.

∴ Height of the triangle

= \(\begin{aligned}
& \sqrt{(\text { Hypotenuse })^2-(\text { base })^2} \\
& =\sqrt{(13)^2-(5)^2} \mathrm{~cm} \\
& =\sqrt{169-25} \mathrm{~cm} \\
& =\sqrt{144} \mathrm{~cm} \\
& =12 \mathrm{~cm}
\end{aligned}\)

∴ Area of the right angle = \(\frac{1}{2}\) x 5 x 12 sq.cm = 30 sq.cm

 

 

2. It is an equilateral triangle, whose each side = 6 cm.

Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)

\(\begin{aligned}
& =\frac{\sqrt{3}}{4} \times(6)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 36 \text { sq.cm } \\
& =9 \sqrt{3} \text { sq.cm }
\end{aligned}\)

 

 

 

3. It is an isosceles triangle whose base is 8 cm and length of each equal side = 6cm

Area of the isoceles triangle = \(=\frac{1}{2} \times 8 \sqrt{(6)^2-\frac{(8)^2}{4}} \text { sq.cm }\)

\(\begin{aligned}
& =4 \sqrt{36-\frac{64}{4}} \text { sq.cm } \\
& =4 \sqrt{36-16} \text { sq.cm } \\
& =4 \sqrt{20} \text { sq.cm } \\
& =4 \sqrt{2 \times 2 \times 5} \text { sq.cm } \\
& =8 \sqrt{5} \text { sq.cm }
\end{aligned}\)

 

 

 

4. Fourth figure is a rectangle whose length & breadth are 14 cm & 10 cm respectively.

Area of the rectangle = Length x Breadth
= 14 x 10 sq. cm
= 140 sq. cm

Question 9. In a lake of the Botanical Garden the tip of lotus was seen 2 cm above the surface of water. Being forced by the wind, it gradually advanced and submerged at a distance of 15 cm from the previous position. Let us write by calculating the depth of the water.

Solution:

Given

In a lake of the Botanical Garden the tip of lotus was seen 2 cm above the surface of water. Being forced by the wind, it gradually advanced and submerged at a distance of 15 cm from the previous position.

Let part of the lotus lies in water and AB part lies above BC water and the water surface is BD.
∵ AC = AD = (x + 2) cm

In right-angled ΔABD, AD² = AB²+ BD²

or, (x+2)=(x)2 + (15)2
or, x2 + 4x + 4 = x2 + 225 or, x2 + 4x-x2 = 225-4
or, 4x = 221

or, \(x=\frac{221}{4}=55.25\)

Depth of the water = 55.25 cm.

Question 10. The length of the hypotenuse of an isosceles right-angled triangle is 12√2 cm. Let us write by calculating what will be the area of that field.

Solution:

Given

The length of the hypotenuse of an isosceles right-angled triangle is 12√2 cm

Let ABC is an isosceles right-angled triangle whose ∠ABC = 90° & AB = BC= x cm.

AC² = AB² + BC²
or, AC² = x² + x²

or, AC = \(2 \sqrt{x^2}\)

or, AC = √2x

According to the problem,

\(
\sqrt{2} x=12 \sqrt{2}
or, x=\frac{12 \sqrt{2}}{\sqrt{2}}=12\)

∴ AB = BC= 12 cm

∴ Area of the triangle = \(\frac{1}{2}\) x 12×12 sq.cm = 72 sq.cm.

Question 11. The lengths of three sides of our triangular park are 65 m, 70 m, and 75 m. Let us write by calculating the length of the perpendicular drawn from the opposite vertex on the longest side.

Solution:

Given

The lengths of three sides of our triangular park are 65 m, 70 m, and 75 m.

Semi-perimeter of the triangle = \(\frac{65+70+75}{2} m=\frac{210}{2} m=105 m\)

∴ Area of the triangular park \(\sqrt{s(s-a)(s-b)(s-c)}\)

\(\begin{aligned}
& =\sqrt{105(105-65)(105-70)(105-75)} \text { sq.m } \\
& =\sqrt{105 \times 40 \times 35 \times 30} \text { sq.m } \\
& =\sqrt{3 \times 5 \times 7 \times 2 \times 2 \times 2 \times 5 \times 5 \times 7 \times 2 \times 3 \times 5} \text { sq.m }
\end{aligned}\)

= 2 × 2 × 3 × 5 x 5 x 7 sq.m
= 2100 sq.m

Perpendicular distance from the opposite vertex to the longest side

\(\begin{aligned}
& =\frac{2 \times \text { Area of the park }}{\text { Length of the longest side }} \\
& =\frac{2 \times 2100}{75} \mathrm{~m}=56 \mathrm{~m} .
\end{aligned} \)

= 56 m.

Question 12. The ratio of heights of two triangles which are drawn by Suja and I is 3:4 and the ratio of their area is 4: 3. Let us write by calculating what will be the ratio of two bases.

Solution:

Given

The ratio of heights of two triangles which are drawn by Suja and I is 3:4 and the ratio of their area is 4: 3.

Let the heights of the two triangles are 3x unit & 4x unit & their bases are a unit & b unit respectively.

Ratio of the areas of the two triangles = \(\frac{1}{2} \cdot a \cdot 3 x: \frac{1}{2} \cdot b \cdot 4 x=3 a x: 4 b x\)

According to the problem, 3ax: 4bx. = 4:3

\(
\frac{3 a x}{4 b x}=\frac{4}{3}
or, \frac{3 a}{4 b}=\frac{4}{3}
or, \frac{a}{b}=\frac{16}{9}\)

or, a: b=16:9

∴ The ratio of the bases of the two triangles = 16 9.

 

 

• Chapter 1 Real Numbers
• Chapter 2 Laws of Indices
• Chapter 3 Graph
• Chapter 4 Co-ordinate Geometry: Distance Formula
• Chapter 5 Linear Simultaneous Equations
  • Linear Simultaneous Equations Exercise 5.1
  • Linear Simultaneous Equations Exercise 5.2
  • Linear Simultaneous Equations Exercise 5.3
  • Linear Simultaneous Equations Exercise 5.4
  • Linear Simultaneous Equations Exercise 5.5
  • Linear Simultaneous Equations Exercise 5.6
  • Linear Simultaneous Equations Exercise 5.7
• Chapter 6 Properties of Parallelogram
• Chapter 7 Polynomial
• Chapter 8 Factorisation
• Chapter 9 Transversal & Mid-Point Theorem
• Chapter 10 Profit & Loss
• Chapter 11 Statistics
• Chapter 12 Theorems On Area
• Chapter 13 Construction
• Chapter 14 Construction
• Chapter 15 Area & Perimeter of Triangle & Quadrilateral
  • Area And Perimeter Of Triangle And Quadrilateral Exercise 15.1
  • Area And Perimeter Of Triangle And Quadrilateral Exercise 15.2
  • Area And Perimeter Of Triangle And Quadrilateral Exercise 15.3
• Chapter 16 Circumference of Circle
• Chapter 17 Theorems on Concurrence
• Chapter 18 Area of Circle
• Chapter 19 Co-Ordinate Geometry: Internal and External
• Chapter 20 Logarithm
• Chapter 21 Set Theory

Chapter 19 Coordinate Geometry Internal And external Division Of A Straight Line Segment Exercise 19

Important Formulae :

1. Distance of (x, y) from the origin = \(\sqrt{x^2+y^2}\) units.

2. Distance between 2 points P(x₁,y₁) and Q(x₂,y₂)

= \(\overline{\mathrm{PQ}}=\sqrt{\left(\mathrm{x}_1-\mathrm{x}_2\right)^2+\left(\mathrm{y}_1-\mathrm{y}_2\right)^2} \text { units. }\)

3. If two points A(x₁,y₁) and B(x₂,y₂) are internally divided by point P(x, y) in ratio mn, then the co-ordinates of P are

P = \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)

4. If two points A(x₁,y₁) and B(x₂,y₂) are externally divided by point P(x, y) in ratio mn, then the co-ordinates of P are

P = \(\left(\frac{m x_2-n x_1}{m-n}, \frac{m y_2-n y_1}{m-n}\right)\)

Question 1. Find the co-ordinate of the point which divides the line segment joining two points in the given ratio for the following:

Read and Learn More WBBSE Solutions For Class 9 Maths

1. (6, -14) and (-8, 10) in the ratio 3 4 internally

Solution: The coordinates of the point

\(\begin{aligned}
& =\left\{\frac{3 \times(-8)+4 \times 6}{3+4}, \frac{3 \times 10+4(-14)}{3+4}\right\} \\
& =\left(\frac{-24+24}{7}, \frac{30-56}{7}\right) \\
& =\left(0, \frac{-26}{7}\right)
\end{aligned}\)

 

∴ \(\left(0, \frac{-26}{7}\right)\)

2. (5, 3) and (-7, -2) in the ratio 2 3 internally

Solution: The coordinates of the point

\(\begin{aligned}
& =\left\{\frac{2 \times(-7)+3 \times 5}{2+3}, \frac{2(-2)+3 \times 3}{2+3}\right\} \\
& =\left(\frac{-14+15}{5}, \frac{-4+9}{5}\right) \\
& =\left(\frac{1}{5}, 1\right)
\end{aligned}\)

 

∴ \(\left(\frac{1}{5}, 1\right)\)

3. (-1, 2) and (4, -5) in the ratio 3: 2 externally

Solution: The coordinates of the point

\(\begin{aligned}
& =\left\{\frac{3 \times 4-2 \times(-1)}{3-2}, \frac{3(-5)-2 \times 2}{3-2}\right\} \\
& =\left(\frac{12+2}{1}, \frac{-15-4}{1}\right) \\
& =(14,-19)
\end{aligned}\)

= (14,-19)

∴ (14,-19)

4. (3, 2) and (6, 5) in the ratio externally

Solution: The coordinates of the point

=\(\left\{\frac{2 \times 6-1 \times 3}{2-1}, \frac{2 \times 5-1 \times 2}{2-1}\right\}\)

= \(\left(\frac{12-3}{1}, \frac{10-2}{1}\right)\)

= (9,8)

∴ (9,8)

Question 2. Find the co-ordinates of the mid-point of the line segment joining two points for the following:

1. (5, 4) and (3,-4)

Solution: The co-ordinates of the mid-point of the join of (5, 4) and (3,-4)

\(\begin{aligned}
& =\left(\frac{5+3}{2}, \frac{4-4}{2}\right) \\
& =\left(\frac{8}{2}, 0\right)
\end{aligned}\)

= (4, 0)

∴ (4, 0)

2. (6, 0) and (0, 7)

Solution: The co-ordinates of the midpoint of the join of (6,0) and (0,7)

\(\begin{aligned}
& =\left(\frac{6+0}{2}, \frac{0+7}{2}\right) \\
& =\left(3, \frac{7}{2}\right)
\end{aligned}\)

Question 3. Let us calculate the ratio in which point (1, 3) divides the line segment joining points (4, 6) and (3, 5).

Solution: Let the required ratio = m:n.

∴ \(1=\frac{m \times 3+n \times 4}{m+n}\)

or, m+n=3m + 4n.
or, m-3m = 4n-n
or, -2m=3n

or, \(\frac{m}{n}=\frac{-3}{2}\)

or, m: n= (-3):2

Question 4. Let us calculate in what ratio is the line segment joining the points (7, 3) and (-9, 6) divided by the y-axis.

Solution: Here the abscissa of the point P = x

∴ Point P point abscissa of (x co-ordinate) = \(\frac{m \times(-9)+n \times 7}{m+n}\)

∴ Point P point is situated on y-axis.  ∴x=0.

∴ \(\frac{-9 m+7 n}{m+n}=0\)

or, -9m+7n = 0
or, -9m=-7n
or, 9m = 7n

or, \(\frac{m}{n}=\frac{7}{9}\)

∴ m:n = 7:9

Question 5. Prove that when the points A(7, 3), B(9, 6), C(10, 12) and D(8, 9) are joined in the order mentioned then they will form a parallelogram.

Solution: Mid-point of the diagonal AC is E.

\(\begin{aligned}
& =\left(\frac{7+10}{2}, \frac{3+12}{2}\right) \\
& =\left(\frac{17}{2}, \frac{15}{2}\right)
\end{aligned}\)

& the mid-point of the diagonal BD is F = \(\left(\frac{9+8}{2}, \frac{6+9}{2}\right)\)

= \(=\left(\frac{17}{2}, \frac{15}{2}\right)\)

Diagonals of the quadrilateral, AC & BD intersect each other at

= \(=\left(\frac{17}{2}, \frac{15}{2}\right)\)

∴ ABCD is a parallelogram. Proved

Question 6. If the points (3, 2), (6, 3), (x, y) and (6, 5) when joined in the order mentioned and form a parallelogram, then let us calculate the point (x, y).

Solution:

Given

If the points (3, 2), (6, 3), (x, y) and (6, 5) when joined in the order mentioned and form a parallelogram,

Let A(3,2), B(6,3), C(x,y) & D(6,5) be the four points of the parallelogram ABCD. E and F are the mid-points of the diagonals AC & BD.

∴ E is the mid-point of AC.

∴ Co-ordinate of E= \(\left(\frac{3+x}{2}, \frac{2+y}{2}\right)\)

∵ F is the mid-point of BD.

∴ Co-ordinates of F = \(\left(\frac{6+6}{2}, \frac{3+5}{2}\right)\) = (6,4)

∴ ABCD is a parallelogram.

∴ AC and BD will bisect each other, i.e., E and F will be the same point.

∴ \(\frac{3+x}{2}=6\)

or, 3+ x = 12
or, x = 12-3=9

\(\frac{2+y}{2}=4\)

or, 2+ y = 8
or, y=8-2=6

∴ The required point is (9,6).

Question 7. If ((x₁,y₁), (x₂,y₂), (x₃,y₃)  and (x₄,y₄) points are joined in order to form a parallelogram, then prove that x₁ +x₃ = x₂ +x₄ and y₁ + y₃ = y₂+y₄

Solution:

Given

If ((x₁,y₁), (x₂,y₂), (x₃,y₃)  and (x₄,y₄) points are joined in order to form a parallelogram

Let A((x₁,y₁), B(x₂,y₂), C(x₃,y₃) & D(x₄,y₄) are the four points of the parallelogram ABCD.

∴ E is the mid-point of AC.

Co-ordinates of E = \(\left(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\right)\)

F is the mid-point of BD.

Co-ordinates of F = \(\left(\frac{\mathrm{x}_2+\mathrm{x}_4}{2}, \frac{\mathrm{y}_2+\mathrm{y}_4}{2}\right)\)

∵ ABCD is a parallelogram.
Diagonals AC & BD intersect at a point if E & F are the same points.

∴ \(\frac{x_1+x_3}{2}=\frac{x_2+x_4}{2} \text { or, } x_1+x_3=x_2+x_4\)

& \(\frac{y_1+y_3}{2}=\frac{y_2+y_4}{2} \text { or, } y_1+y_3=y_2+y_4\)

Question 8. The coordinates of vertices A, B, and C of a triangle ABC are (-1, 3), (1, -1) and (5, 1) respectively, let us calculate the length of the median AD.

Solution:

 

Given

The coordinates of vertices A, B, and C of a triangle ABC are (-1, 3), (1, -1) and (5, 1) respectively

Let D is the mid-point of BC.

Co-ordinates of D = \(\left(\frac{1+5}{2}=\frac{-1+1}{2}\right)\) = (3,0)

∴ Length of median AD = \(\sqrt{(-1-3)^2+(3-0)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(-4)^2+(3)^2} \text { unit } \\
& =\sqrt{16+9} \text { unit } \\
& =\sqrt{25} \text { unit } \\
& =5 \text { unit }
\end{aligned}\)

 

Question 9. The coordinates of the vertices of the triangle are (2, 4), (6, -2) and (-4, 2) respectively. Let us find the length of three medians of a triangle.

Solution:

 

Given

The coordinates of the vertices of the triangle are (2, 4), (6, -2) and (-4, 2) respectively.

Let D, E, & F be the mid-points of BC, CA & AB respectively.

∴ Now co-ordinates of

D= \(\begin{aligned}
& D=\left(\frac{6-4}{2}=\frac{-2+2}{2}\right) \\
& =(1,0)
\end{aligned}\)

Co-ordinates of E = \(\left(\frac{2-4}{2}=\frac{-4+2}{2}\right)\) = (-1,-1)

Co-ordinates of F = \(\left(\frac{2+6}{2}=\frac{-4-2}{2}\right)\) = (4,-3)

∴ Length of median BE = \(\sqrt{(2-1)^2+(-4-0)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(1)^2+(-4)^2} \\
& =\sqrt{1+16} \text { unit } \\
& =\sqrt{17} \text { unit }
\end{aligned}\)

Length of median BE = \(\sqrt{(6+1)^2+(-2+1)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(7)^2+(-1)^2} \\
& =\sqrt{50} \text { unit } \\
& =5 \sqrt{2} \text { unit }
\end{aligned}\)

Length of median CF = \(\sqrt{(-4-4)^2+(2+3)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(-8)^2+(5)^2} \text { unit } \\
& =\sqrt{64+25} \text { unit } \\
& =\sqrt{89} \text { unit }
\end{aligned}\)

Question 10. The coordinates of the midpoints of sides of a triangle are (4, 3), (-2, 7) and (0, 11). Let us calculate the coordinates of its vertices.

Solution:

Given

The coordinates of the midpoints of sides of a triangle are (4, 3), (-2, 7) and (0, 11).

Let A (x₁,y₁) B (x₂,y₂) & C(x₃,y₃) are three vertices of the ΔABC
& P(4, 3); Q (-2, 7) & R (0, 11) are the three mid-points of the AB, BC & CA respectively.

 

 

\(\frac{x_1+x_2}{2}=4, \text { or, } x_1+x_2=8\) ….(1)

\(\frac{y_1+y_2}{2}=3, \text { or, } y_1+y_2=6\) …(2)

\(\frac{x_2+x_3}{2}=-2, \text { or, } x_2+x_3=-4\) ….(3)

\(\frac{y_2+y_3}{2}=7, \text { or, } y_2+y_3=14\) ….(4)

\(\frac{x_3+x_1}{2}=0, \text { or, } x_3+x_1=0\) ….(5)

\(\frac{y_3+y_1}{2}=11, \text { or, } y_3+y_1=22\) …(6)

Adding (1), (3) & (5), we get 2(x₁+ x₂+x₃)= 4

or, x₁+ x₂+x₃ = 4/2

or, x₁+ x₂+x₃ = 2 ….(7)

(6) – (1) => x₃ =-6
(6) – (3) => x₁= 6
(6) – (5) => x = 2

Again, by adding (2), (4) & (5), we get
2(y₁+ y₂+y₃)= 42

∴ y₁+ y₂+y₃ = 21 …… (8)
(8) – (2) => y₃= 15
(8) – (4) => y₁ = 7
(8) – (4) => y₂ = -1

∴ The coordinates of the vertices of the triangle are (6, 7) (2, -1), and (-6, 15).

Question 11. Multiple choice questions

1. The mid-point of line segment joining two points (1, 2m), and (-1 + 2m, 21 – 2m) is

1. (1, m)
2. (1, -m)
3. (m, -1)
4. (m, 1)

Solution; Mid-point

= \(\left(\frac{1-1+2 m}{2}, \frac{2 m+21-2 m}{2}\right)\) = (m, 1)

∴ 4. (m + 1)

2. The abscissa at point P which divides the line segment joining two points A(1, 5) and B(-4, 7) internally in the ratio 2:3 is

1. -1
2. 11
3. 1
4. -11

Solution:

Co-ordinates of P = \(\left(\frac{2 \times(-4)+3 \times 1}{2+3}, \frac{2 \times 7+3 \times 5}{2+3}\right)\)

= \(\left(-1, \frac{29}{5}\right)\)

∴ The abscissa is -1.

∴ – 1

3. The coordinates of the end points of a diameter of a circle are (7, 9) and (-1,-3). The coordinates of the centre of the circle is

1. (3, 3)
2. (4, 6)
3. (3, -3)
4. (4, -6)

Solution: Co-ordinates of the centre
\(=\left(\frac{7-1}{2}, \frac{9-3}{2}\right)\)

= (3, 3)

∴ (3, 3)

4. A point which divides the line segment joining two points (2,-5) and (-3,-2) externally in the ratio 4: 3. The ordinate of the point is

1. -18
2. -7
3. 18
4. 7

Solution: The coordinates of the point

=\(\left(\frac{4 \times(-3)-3 \times 2}{4-3}, \frac{4 \times(-2)-3 \times(-5)}{4-3}\right)\)

= (-18, 7)
∴ The ordinate of the point is 7.

4. 7

5. If the points P(1, 2), Q(4, 6), R(5, 7) and S(x, y) are the vertices of a parallelogram PQRS, then

1. x = 2, y = 4
2. x = 3, y=4
3. x = 2, y = 3
4. x = 2, y = 5

Solution: The mid-point of the diagonal PR is

= \(\left(\frac{1+5}{2}, \frac{2+7}{2}\right)=\left(3, \frac{9}{2}\right)\)

= \(\left(3, \frac{9}{2}\right)\)

The mid-point of the diagonal QS = \(\left(\frac{4+x}{2}, \frac{6+y}{2}\right)\)

∴ As mid-points PR & QS are the same point.

∴ \(\frac{4+x}{2}=3\)

or, 4+ x = 6
or, x = 2

or, \(\frac{6+y}{2}=\frac{9}{2}\)

or, 12+2y= 18
or, 2y= 18-12

or, y = 6/2=3

∴ 3. x = 2, y = 3

Question 12. Short answer type questions:

1. C is the centre of a circle and AB is its diameter; the coordinates of A and C are (6, -7) and (5, -2). Let us calculate the coordinates of B.

Solution:

Given

C is the centre of a circle and AB is its diameter; the coordinates of A and C are (6, -7) and (5, -2).

Let the co-ordinate of B = (x, y)

∴ The mid-point of AB = \(\left(\frac{6+x}{2}, \frac{-7+y}{2}\right)\)

∴As centre is the mid-point of the diameter.

∴ \(\frac{6+x}{2}=5[\latex]

or, 6+x=10
or, x = 4

and [latex]\frac{-7+y}{2}=-2\)

or, – 7+ y = -4
or, y = -4+7
or, y = 3

∴ The coordinates of B = (4,3).

2. The points P and Q lie on 1st and 3rd quadrants respectively. The distance of the two points from the x-axis and y-axis is 6 units and 4 units respectively. Let us write the coordinates of the mid-point of line segment PQ.

Solution:

Given

The points P and Q lie on 1st and 3rd quadrants respectively. The distance of the two points from the x-axis and y-axis is 6 units and 4 units respectively.

As P lies in 1st quadrant
∴ The abscissa & the ordinate both are positive.
∴ The coordinates of P = (4, 6).

Again, Q lies in the 3rd quadrant.
∴ The abscissa & the ordinate both are negative.

∴ The coordinates of Q = (-4, -6).

∴ The mid point of PQ is = \(\left(\frac{4-4}{2}, \frac{6-6}{2}\right)=(0,0) .\)

= (0, 0).

3. points A and B lie in the 2nd and 4th quadrants respectively and the distance of each point from x-axis and y-axis are 8 units and 6 units respectively. Let us write the coordinate of the mid-point of line segment AB.

Solution:

Given

points A and B lie in the 2nd and 4th quadrants respectively and the distance of each point from x-axis and y-axis are 8 units and 6 units respectively.

As lies in the 2nd quadrant.
∴ The abscissa is negative, but the ordinate is positive.
∴ The coordinates of A = (-6, 8).

Again, B lies in the 4th quadrant.
∴ The abscissa is positive, but the ordinate is negative.

∴ The coordinates of B = (6, -8).

∴ The mid-point of A and B is \(\left(\frac{-6+6}{2}, \frac{8-8}{2}\right)=(0,0)\)

= (0, 0).

4. The point Plies on the segment AB and AP = PB; the coordinates of A and B are (3,-4) and (-5, 2) respectively. Let us write the coordinates of point P.

Solution:

Given

The point Plies on the segment AB and AP = PB; the coordinates of A and B are (3,-4) and (-5, 2) respectively.

As P lies on AB and AP = PB
∴ P is the mid-point of AB.

∴ The co-ordinates of P = \(\left(\frac{3-5}{2}, \frac{-4+2}{2}\right)\) =(-1,-1).

5. The sides of rectangle ABCD are parallel to the coordinate axes. The coordinates of B and D are (7, 3) and (2, 6). Let us write the coordinates of A and C and the mid-point of diagonal AC.

Solution:

Given

The sides of rectangle ABCD are parallel to the coordinate axes. The coordinates of B and D are (7, 3) and (2, 6).

ABCD is a rectangle, AB II x-axis & AD II y-axis.
∴The coordinates of A = (2, 3).
∴ The coordinates of C

∴ The midpoint of AC = \(\left(\frac{2+7}{2}, \frac{3+6}{2}\right)=\left(\frac{9}{2}, \frac{9}{2}\right)\)

 

 

Chapter 20 Coordinate Geometry Area Of Triangular Region Exercise 20

Important Formulae :

1. Co-ordinates of the mid-point of A(x₁,y₁) and B(x₂,y₂) = \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

2. In ΔABC, if the coordinates of the vertices are: A(x₁,y₁), B(x₂,y₂), and C(x₃,y₃) then the co-ordinates of its centroid are:

= \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)\)

3. In ΔABC if the coordinates of the vertices are: A(x₁,y₁), B(x₂,y₂), and C(x₃,y₃) then the area of the triangle ABC will be

= \(\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]\)

4. Three points will be collinear if the area of the triangle formed by them is zero. (v) Area of the quadrilateral formed by the points (x₁,y₁), (x₂,y₂),(x₃,y₃), and (x₄,y₄)

\(\frac{1}{2}\left[\left(x_1 y_2+x_2 y_3+x_3 y_4+x_4 y_1\right)-\left(y_1 x_2+y_2 x_3+y_3 x_4+y_4 x_1\right)\right] \text { sq.units. }\)

Question 1. Find the area of a triangular region with the vertices given below:

Read and Learn More WBBSE Solutions For Class 9 Maths

1. (2,-2), (4, 2), and (-1, 3)

Solution: (2,-2), (4, 2), and (-1,3)

\(\begin{aligned}
& =\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\} \\
& =\frac{1}{2}\{2(2-3)+4(3+2)-1(-2-2)\} \text { sq. unit } \\
& =\frac{1}{2}(-2+20+4) \text { sq. unit } \\
& =\frac{1}{2} \times 22 \text { sq. unit } \\
& =11 \text { sq. unit }
\end{aligned}\)

2. (8, 9) (2, 6) and (9, 2)

Solution: (8, 9) (2, 6) and (9, 2)

\(\begin{aligned}
& =\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\} \\
& =\frac{1}{2}\{8(6-2)+2(2-9)+9(9-6)\} \text { sq. unit } \\
& =\frac{1}{2}(32-14+27) \text { sq. unit } \\
& =\frac{45}{2} \text { sq. unit } \\
& =22 \frac{1}{2} \text { sq. unit }
\end{aligned}\)

3. (1, 2), (3, 0) and origin (0,0)

Solution: (1, 2), (3, 0) and origin (0,0)

\(\begin{aligned}
& =\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\} \\
& =\frac{1}{2}\{1(0-0)+3(0-2)+0(2-0)\} \text { sq. unit } \\
& =\frac{1}{2}(-6) \text { sq. unit } \\
& =-3 \text { sq. unit }
\end{aligned}\)

Question 2. Prove that the points (3,-2), (-5, 4), and (-1, 1) are collinear.

Solution: Here the area of the triangle with vertices (3,-2), (-5, 4), and (-1, 1)

\(\begin{aligned}
& =\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\} \\
& =\frac{1}{2}\{3(4-1)-5(1+2)-1(-2-4)\} \text { sq. unit } \\
& =\frac{1}{2}(9-15+6) \text { sq. unit } \\
& =\frac{1}{2} \times 0 \text { sq. unit }=0
\end{aligned}\)

∴ The points are collinear.
∴ (3,-2), (-5, 4), and (-1, 1) are collinear points.

Question 3. Let us write by calculating for what value of K, the points (1, -1), (2, -1), and (K, -1) lie on the same straight line.

Solution: (1,-1), (2, -1), and (K, -1)

\(\begin{aligned}
& =\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\} \\
& =\frac{1}{2}\{1(-1+1)+2(-1+1)+K(-1+1)\} \text { sq. unit }=0 \text { sq. unit }
\end{aligned}\)

∴For any real value of K, the points are collinear.

Question 4. Let us prove that the line joining two points (1, 2) and (-2, -4) passes through the origin.

Solution: The coordinate of the origin is (0, 0).

∴ Area of the triangle formed by the points (1, 2), (-2, -4), and (0, 0) as vertices

\(\begin{aligned}
& =\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\} \\
& =\frac{1}{2}\{1(-4-0)-2(0-2)+0(2+4)\} \text { sq. unit } \\
& =\frac{1}{2}(-4+4+0) \text { sq. unit } \\
& =0
\end{aligned}\)

∴ The three points are collinear.

Question 5. Let us prove that the mid-point of the line segment joining two points (2, 1) and (6, 5) lies on the line joining two points (-4, -5) and (9, 8).

Solution: The mid-point of the line joining (2, 1) and (6, 5) is

= \(=\left(\frac{2+6}{2}, \frac{1+5}{2}\right)=(4,3)\)

∴ Now area of the triangle formed by (4, 3), (-4,-5), and (9,8)

\(\begin{aligned}
& =\frac{1}{2}\{4(-5-8)+(-4)(8-3)+9(3+5)\} \text { sq. unit } \\
& =\frac{1}{2}(-52-20+72) \text { sq. unit } \\
& =\frac{1}{2}(72-72) \text { sq. unit } \\
& =\frac{1}{2} \times 0=0
\end{aligned}\)

∴ The three points are collinear.
∴ The mid-point of the line joining (2, 1) & (6, 5) lies on the line joining two points (-4, -5) & (9,8).

Question 6. Let us find the area of the quadrilateral region formed by the line joining four given points each.

1. (1, 1), (3, 4), (5, -2), and (4, -7)

Solution:

Given

The four points are (1, 1), (3, 4), (5, -2), and (4, -7)

\(\begin{aligned}
& =\frac{1}{2}\left\{\left(x_1 y_2+x_2 y_3+x_3 y_4+x_4 y_1\right)-\left(y_1 x_2+y_2 x_3+y_3 x_4+y_4 x_1\right)\right\} \\
& =\frac{1}{2}[\{1.4+3(-2)+5(-7)+4.1\}-\{1.3+4.5+(-2) \cdot 4+(-7) .1\}] \\
& =\frac{1}{2}\{(4-6-35+4)-(3+20-8-7)\} \text { sq. unit } \\
& =\frac{1}{2}\{(8-41)-(23-15)\} \text { sq. unit } \\
& =\frac{1}{2}(-33-8) \text { sq. unit } \\
& =\frac{1}{2}(-41) \text { sq. unit } \\
& =\frac{41}{2} \text { sq. unit } \\
& =20 \frac{1}{2} \text { sq. unit }
\end{aligned}\)

2. (1, 4), (-2, 1), (2, 3), (3, 3)

Solution:

Given

The four points are = (1, 4), (-2, 1), (2, -3), and (3, 3)

=\(\begin{aligned}
& \left.=\frac{1}{2}\left\{x_1 y_2+x_2 y_3+x_3 y_4+x_4 y_i\right)-\left(y_1 x_2+y_2 x_3+y_3 x_4+y_4 x_1\right)\right\} \\
& =\frac{1}{2}\{(1+6+6+12)-(-8+2-9+3)\} \text { sq. unit } \\
& =\frac{1}{2}\{25-(-12)\} \text { sq. unit } \\
& =\frac{1}{2}(25+12) \text { sq. unit } \\
& =\frac{37}{2} \text { sq. unit } \\
& =18.5 \text { sq. unit }
\end{aligned}\)

Question 7. The coordinates of three points A, B, and C are (3, 4) (-4, 3), and (8, -6) respectively. Let us find the area of the triangle and the perpendicular length drawn from point A on BC.

Solution:

Given

The coordinates of three points A, B, and C are (3, 4) (-4, 3), and (8, -6) respectively.

Area of the triangle ABC

\(=\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\} \text { sq. unit }\) \(\begin{aligned}
& =\frac{1}{2}\{3(3+6)-4(-6-4)+8(4-3)\} \text { sq. unit } \\
& =\frac{1}{2}(27+40+8) \text { sq. unit } \\
& =\frac{75}{2} \text { sq. unit } \\
& =37.5 \text { sq. unit }
\end{aligned}\)

Length of BC = \(\sqrt{(-4-8)^2+(3+6)^2} \text { unit }\)

\(\begin{aligned}
& =\sqrt{(-12)^2+(9)^2} \text { unit } \\
& =\sqrt{144+81} \text { unit } \\
& =\sqrt{225} \text { unit } \\
& =15 \text { unit }
\end{aligned}\)

∵ Area of ΔABC \(\frac{1}{2}\) x base x height

= \(\frac{1}{2}\) x BC x height

= \(\frac{1}{2}\) x 15x height

= \(\frac{75}{2}\)

Height of the triangle = \(\frac{75 \times 2}{2 \times 15}\) = 5 unit

Question 8. In triangle ABC, the coordinates of A are (2, 5) and the centroid of a triangle is (-2,1), let us find the coordinates of the mid-point of BC.

Solution:

 

Given

In triangle ABC, the coordinates of A are (2, 5) and the centroid of a triangle is (-2,1),

In ABC the coordinates of vertex A are (2, 5).
Co-ordinates of the centroid of AABC = G (-2, 1) & the co-ordinate of A = (2,5).

∵ We know the centroid intersects the median at G in the ratio 2: 1.

\(therefore \frac{2 \times x+1 \times 2}{2+1}=-2\)

or, \(\frac{2 x+2}{3}=-2\)

or, 2x+2 = -6
or, 2x = -6-2
or, 2x = -8

or, \(x=\frac{-8}{2}=-4\)

and \(\frac{2 \times y+1 \times 5}{2+1}=1\)

or, 2y+5=3
or, 2y=3-5
or, 2y=-2

or, \(y=\frac{-2}{2}=-1\)

∴ The coordinate of the mid-point of BC= (-4, -1).

Question 9. The coordinates of vertices of a triangle are (4, -3), (-5, 2), and (x, y); let us find the values of x and y if the centroid of a triangle is at the origin.

Solution:

Given

The coordinates of vertices of a triangle are (4, -3), (-5, 2), and (x, y);

We know the coordinates of the centroid

\(\begin{aligned}
& =\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right) \\
& =\left(\frac{4-5+x}{3}, \frac{-3+2+y}{3}\right) \\
& =\left(\frac{-1+x}{3}, \frac{-1+y}{3}\right)
\end{aligned}\)

 

∵ The centroid of the triangle is the origin.
∴ The coordinate of the centroid is (0,0).

∴ \(\frac{-1+x}{3}=0\)

or, -1+x=0
or, x = 1

and \(\frac{-1+y}{3}=0\)

or, – 1+ y = 0
or, y = 1

∴ x=1,y=1

Question 10. The vertices at AABC are A(-1,5), B(3,1) and C(5,7). D, E, and F are the midpoints of BC, CA, and AB respectively. Let us find the area of the triangular region ΔDEF and prove that ΔABC=4ΔDEF.

Solution:

 

Given

The vertices at AABC are A(-1,5), B(3,1) and C(5,7). D, E, and F are the midpoints of BC, CA, and AB respectively.

As D, E & F are the mid-points of BC, CA & AB respectively.

∴ Co-ordinates of D = \(\left(\frac{3+5}{2}, \frac{1+7}{2}\right)=(4,4)\)

Co-ordinates of E = \(=\left(\frac{5-1}{2}, \frac{7+5}{2}\right)=(2,6)\)

Co-ordinates of F = \(\left(\frac{-1+3}{2}, \frac{5+1}{2}\right)=(1,3)\)

Area of ΔABC = \(\frac{1}{2}\left\{x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right\}\)

\(\begin{aligned}
& =\frac{1}{2}\{(-1)(1-7)+3(7-5)+5(5-1)\} \text { sq. unit } \\
& =\frac{1}{2}\{(-1) \times(-6)+3 \times 2+5 \times 4\} \text { sq. unit } \\
& ==\frac{1}{2}(6+6+20) \text { sq. unit } \\
& =\frac{1}{2} \times 32 \text { sq. unit } \\
& =16 \text { sq. unit }
\end{aligned}\)

 

Area of ΔDEF = \(\frac{1}{2}\{4(6-3)+2(3-4)+1(4-6)\} \text { sq. unit }\)

\(\begin{aligned}
& =\frac{1}{2}\{4 \times 3+2(-1)+1(-2)\} \text { sq. unit } \\
& =\frac{1}{2}(12-2-2) \text { sq. unit } \\
& =\frac{1}{2} \times 8 \text { sq. unit } \\
& =4 \text { sq. unit }
\end{aligned}\)

 

Area of ΔABC = 16 sq. unit
Area of 4ΔDEF = 4 x 4 sq. unit
= 16 sq. unit

∴ ΔABC = 4ΔDEF

Question 11. Multiple choice question

1. The area of the triangular region formed by the three points (0, 4), (0, 0) and (-6, 0) is

1.  24 sq. unit
2. 12 sq. unit
3. 6 sq. unit
4. 8 sq. unit

Solution: (0.4), (0,0), and (-6, 0)

= \(\frac{1}{2}\) {(0(0-0)+0(0-4)+(-6)(-4-0)} sq. unit

= \(\frac{1}{2}\) (0+0+24) sq. unit

= 12 sq. unit

∴ 2. 12 sq. unit

2. The coordinates of the centroid of a triangle formed by the three points (7,-5), (-2, 5), and (4, 6) are

1. (3,-2)
2. (2, 3)
3. (3, 2)
4. (2,-3)

Solution: (7,-5), (-2, 5), and (4, 6)

\(\begin{aligned}
& =\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right) \\
& =\left(\frac{7-2+4}{3}, \frac{-5+5+6}{3}\right)
\end{aligned}\)

 

= (3,2)

∴ 3. (3,2)

3. If ABC is a right-angled triangle whose ZABC 90°, co-ordinates of A and C are (0,4) and (3,0) respectively, then the area of triangle ABC is

1. 12 sq. unit
2. 6 sq. unit
3. 24 sq. unit
4. 8 sq. unit

 

 

Solution: In ABC ∠ABC = 90°

Co-ordinates of A = (0, 4)
Co-ordinates of B = (3,0)
Co-ordinates of C = (0, 0)

∴ \(\overline{\mathrm{AB}}\) = 4 unit

and \(\overline{\mathrm{BC}}\) = 3 unit

∴ Area of ΔABC = \(\frac{1}{2} \times \overline{\mathrm{BC}} \times \overline{\mathrm{AB}}\)

= \(\frac{1}{2}\) Χ 3 Χ 4 sq.unit = 6 sq.unit

4. If (0, 0), (4,-3), and (x, y) are collinear then

1. x = 8, y = -6
2. x = 8, y = 6
3. x = 4, y = -6
4. x = -8, y = -6

Solution: The area of the triangle formed by (0, 0), (4, -3), and (x, y) is zero.

∴ 0(-3- y) + 4 (y-0) + x (0 + 3) = 0
or, 3x + 4y = 0 ….(1)

Now, of the options given, putting in equation (i) only x = 8 and y = 6 satisfies the equation.
Because 3 x 8+4(-6)=24-24=0

∴ 1. x = 8, y = -6

5. If in triangle ABC, the co-ordinates of vertex A are (7, -4) and the centroid of the triangle (1,2), the the co-ordinates of mid-point of BC are

1. (-2,-5)
2. (-2,5)
3. (2,-5)
4. (5,-2)

 

 

Solution: D is the midpoint BC, let the coordinate of D be (x, y).
∴ G (1, 2) cuts median AD in the ratio 2:1

∴ \(\frac{2 \times x+1 \times 7}{2+1}=1\)

or, 2x+7=3
or, 2x = -4
or, 2x = -2

and \(\frac{2 \times y+1(-4)}{2+1}=2\)

or, 2y-4=6
or, 2y = 6+4

or, 2y= 10.
or, y = 5

∴ Co-ordinates of the midpoint of BC = (-2,5)

∴ 2. (-2, 5)

Question 12. Short answer type questions:

1. The coordinates of midpoints of the sides of a triangle ABC are (0,1), (1,1), and (1,0); let us find the coordinates of its centroid.

Solution:

Given

The coordinates of midpoints of the sides of a triangle ABC are (0,1), (1,1), and (1,0);

Let the co-ordinates of A= (x₁,y₁)
Co-ordinates of B = (x₂,y₂)
Co-ordinates of C = (x₃,y₃)

∴ The mid-point of AB = \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

∴ \(\frac{x_1+x_2}{2}=0\) or, x₁+ x₂ = 0

and \(\frac{y_1+y_2}{2}\) or, y₁ + y₂ =0

The mid-point of BC = \(\left(\frac{\mathrm{x}_2+\mathrm{x}_3}{2}, \frac{\mathrm{y}_2+\mathrm{y}_3}{2}\right)\)

∴ \(\frac{x_2+x_3}{2}=1\) or, x₂+x₃=2

and \(\frac{y_2+y_3}{2}=1\) or, y₂+y₁ = 2

Again, the mid-point of CA = \(\left(\frac{x_3+\dot{x}_1}{2}, \frac{y_3+y_1}{2}\right)\)

∴ \(\frac{x_3+x_1}{2}=1\) or, x₃ +x₁ = 2

and \(\frac{y_3+y_1}{2}=0\) or, y₃+ y₁ =0

Adding (1), (3), and (5),

x₁ + x₂ + x₂ + x₃ + x₃ + x₁ = 0 + 2 + 2

or, 2x₁ + 2x₂ +2x₃ = 4

or, 2(x₁ + x₂+x₃)= 4

or, x₁ + x₂+x₃ \(\frac{4}{2}\) = 2

Again, adding (2), (4), and (6),

\(2 y_1+2 y_2+2 y_3=4\)

 

or, \(2\left(x_1+x_2+x_3\right)=4\)

or, \(y_1+y_2+y_3=\frac{4}{2}\)

or, \(y_1+y_2+y_3=2\)

Co-ordinates of the centroid of ΔABC =

\(=\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)=\left(\frac{2}{3}, \frac{2}{3}\right)\)

∵ \(\left[x_1+x_2+x_3=2 \text { and } y_1+y_2+y_3=2\right]\)

3. The coordinates of the centroid of a triangle are (6,9) and the two vertices are (15,0) and (0, 10); let us find the coordinates of the third vertex.

Solution:

Given

The coordinates of the centroid of a triangle are (6,9) and the two vertices are (15,0) and (0, 10);

Let the coordinates of the 3rd vertex of the triangle be (x, y).

Co-ordinates of the centroid

\(\begin{aligned}
& =\left(\frac{15+0+x}{3}, \frac{0+10+y}{3}\right) \\
& =\left(\frac{15+x}{3}, \frac{10+y}{3}\right)
\end{aligned}\)

 

By the problem,

\(\frac{15+x}{3}=6 \text { and } \frac{10+y}{3}=9\)

or, 15+ x = 18
or, x = 18-15
or, x = 3

or, 10+ y = 27
or, y = 27-10
or, y = 17

∴ The co-ordinate of the third vertex of the triangle is (3, 17)

3. If the three points (a, 0), (0, b), and (1, 1) are collinear then let us show that \(\frac{1}{a}+\frac{1}{b}\) = 1

Solution:

Given

If the three points (a, 0), (0, b), and (1, 1) are collinear

Area of the triangle formed by (a, 0), (0, b), and (1, 1) = 0

∴ \(\frac{1}{2}{a(b-1)+0(1-0)+1(0-b)}\)= 0

or, ab-a-b=0
or, – a – b = – ab
or, a + b = – ab

\(or, \frac{a}{a b}+\frac{b}{a b}=\frac{a b}{a b}
or, \frac{1}{b}+\frac{1}{a}=1\) \(\frac{1}{a}+\frac{1}{b}=1\)

 

4. Let us calculate the area of the triangular region formed by the three points (1, 4), (1, 2), and (-4, 1).

Solution: The area of the triangle formed by three points (1, 4), (-1, 2), and (-4, 1)

= \(\frac{1}{2}\) {1(2 − 1) + (− 1)(1 − 4) + (−4) (4 – 2)} sq. unit ((2-1)+(-1)(1-4)+(-4)(4-2)}

= \(\frac{1}{2}\) (1+3-8) sq. unit

= \(\frac{1}{2}\) (-4) sq. unit

= \(\frac{1}{2}\) Χ 4 sq. unit = 2 sq. unit

5. Let us write the coordinates of the centroid of a triangle formed by the three points (x-y. y-z), (-x, -y), and (y, z).

Solution: Co-ordinates of the centroid of the triangle formed by (x-y, y-z), (-x, -y), and (y, z)3

\(\begin{aligned}
& =\left(\frac{x-y-x+y}{3}, \frac{y-z-y+z}{3}\right) \\
& =\left(\frac{0}{3}, \frac{0}{3}\right) \\
& =(0,0) .
\end{aligned}\)

 

 

 

Chapter 21 Logarithm Exercise 21

Important Formulae:

1. If \(a^x=M\) (a and M are two natural nos. and a > 0, a ≠ 1 and M > 0) then x is a real number, called the base, and with respect to a, M is called logarithm and is written in form x = log_aM. It is read as ‘s is the logarithm of M to the base a’.

2. If  \(a^x=M\) then x = log_aM and conversely, if x = log_aM then \(a^x=M\)

3. log_aMN = log_aM+log_aN
4. log_aMNP = log_aM+log_aN + log_aP

5. \(\log _a \frac{M}{N}=\log _a M-\log _a N\)

6. \(\log _a M^C=C \log _a M\)

7. log_aM = log_aM x log_ab

8. \(\log _a^1=0\)

9. \(\log _a^a=0\)

10. \(a^{\log _a M}=M\)

11. \(\log _a^b \times \log _b a=1\)

12. \(\log _b a=\frac{1}{\log _a b}\)

13. \(\log _b M=\frac{\log _a M}{\log _a b}\)

14. \(\log _a\left(M_1 M_2 M_3 \ldots . . M_n\right)
=\log _a M_1+\log _a M_2+\log _a M_3 \ldots . \log _a M_n\)

[n = is a positive whole number]

15. If \(\log _a M=\log _a N \text { then } M=N\)

Read and Learn More WBBSE Solutions For Class 9 Maths

Question 1. Let us evaluate :

1. \(\log _{2 \sqrt{3}} 1728\)

Solution: Let, x = \(\log _{2 \sqrt{3}} 1728\)

∴ By definition, we get (2√3)^x = 1728

\(or, (2 \sqrt{3})^x=2^6 \times 3^3
or, (2 \sqrt{3})^x=2^6 \times(\sqrt{3})^6
or, (2 \sqrt{3})^x=(2 \sqrt{3})^6\)

 

∴ X = 6
∴ The value of \(\log _{2 \sqrt{3}} 1728\) is 6.

2. \(\log _{0.01} 0.000001\)

Solution: Let x = \(\log _{0.01} 0.000001\)

∴ By definition, we get (0.01)^x= 0.000001

or, (0.01)^x= (0.01)³
∴ X = 3

∴ The value of \(\log _{0.01} 0.000001\) is 3.

3. \(x=\log _{\sqrt{6}} 216\)

Solution: Let \(x=\log _{\sqrt{6}} 216\)

∴ By definition, we get (√6)^x =216

or, (√6)^x =(6)³
or, (√6)^x=  (√6)⁶

∴ X = 6
∴ The value of \(x=\log _{\sqrt{6}} 216\) is 6.

4. \(\log _4\left(\frac{1}{64}\right)\)

Solution: Let x = \(\log _4\left(\frac{1}{64}\right)\)

\(therefore(4)^x=\frac{1}{64}
or, (4)^x=\frac{1}{4^3}
or, (4)^x=(4)^{-3}\)

∴ X=-3
∴ The value of \(\log _4\left(\frac{1}{64}\right)\) is -3.

 

Question 2. Let us evaluate:

1. Let us write by calculating, and find its base when the logarithm of 625 is 4.

Solution: Let base be x.

\(\begin{aligned}
& therefore    \log _x 625=4 \\
& therefore    x^4=625
\end{aligned}
or, x^4=5^4
therefore     x=5
\)

 

∴ The required base is 5.

2. Let us write by calculating, and find its base if the logarithm of 5832 is 6. Solve: Let log, 5832 = 6

Solution: Let log_x 58326

∴ Required base is \( x=3 \sqrt{2}\)

Question 3. Let us evaluate:

1. If \(1+\log _{10} a=2 \log _{10} b\) then express a in terms of b.

Solution: \(1+\log _{10} a=2 \log _{10} b\)

 

2. \(3+\log _{10} x=2 \log _{10} y\) then express x in terms of y.

Solution: \(3+\log _{10} x=2 \log _{10} y\)

Question 4. Let us evaluate:

1. \(\log _2\left[\log _2\left\{\log _3\left(\log _3 27^3\right)\right\}\right]\)

Solution: \(\log _2\left[\log _2\left\{\log _3\left(\log _3 27^3\right)\right\}\right]\)

 

2. \(\frac{\log \sqrt{27}+\log 8-\log \sqrt{1000}}{\log 1.2}\)

Solution: \(\frac{\log \sqrt{27}+\log 8-\log \sqrt{1000}}{\log 1.2}\)

 

3. \(\log _3 4 \times \log _4 5 \times \log _5 6 \times \log _6 7 \times \log _7 3\)

Solution: \(\log _3 4 \times \log _4 5 \times \log _5 6 \times \log _6 7 \times \log _7 3\)

 

4. \(\log _{10} \frac{384}{5}+\log _{10} \frac{81}{32}+3 \log _{10} \frac{5}{3}+\log _{10} \frac{1}{9}\)

Solution: \(\log _{10} \frac{384}{5}+\log _{10} \frac{81}{32}+3 \log _{10} \frac{5}{3}+\log _{10} \frac{1}{9}\)

\(=\log _{10} 384-\log _{10} 5+\log _{10} 81-\log _{10} 32+3 \log _{10} 5-3 \log _{10} 3+\log _{10} 1-\log _{10} 9\)

 

\(=\log _{10}\left(3 \times 2^7\right)-\log _{10} 5+\log _{10} 3^4-\log _{10} 2^5+3 \log 5-3 \log 3+0-\log _{10} 3^2\)

 

\(=\log _{10} 3+\log _{10} 2^7-\log _{10} 5+4 \log _{10} 3-5 \log _{10} 2+3 \log 5-3 \log 3-2 \log _{10} 3\)

 

\(=5 \log _{10} 3-5 \log _{10} 3+7 \log _{10} 2-5 \log _{10} 2+2 \log _{10} 5\)

 

\(\begin{aligned}
& =2 \log _{10} 2+2 \log _{10} 5 \\
& =2 \log _{10}(2 \times 5) \\
& =2 \log _{10} 10 \\
& =2 \times 1 \\
& =2 \text { Ans. }
\end{aligned}\)

 

Question 5. Let us prove:

1. \(\log \frac{75}{16}-2 \log \frac{5}{9}+\log \frac{32}{243}=\log 2\)

Solution: L.H.S

= \(=\log \frac{75}{16}-2 \log \frac{5}{9}+\log \frac{32}{243}\)

= R.H.S proved.

2. \(\log _{10} 15\left(1+\log _{15} 30\right)+\frac{1}{2} \log _{10} 16\left(1+\log _4 7\right)-\log _{10} 6\left(\log _6 3+1+\log _6 7\right)=2\)

Solution:

 

3. \(\log _2 \log _2 \log _4 256+2 \log _{\sqrt{2}} 2=5\)

Solution:

\(\begin{aligned}
& \text { L.H.S. }=\log _2 \log _2 \log _4 256+2 \log _{\sqrt{2}} 2 \\
& =\log _2 \log _2 \log _4 4^4+2 \log _{\sqrt{2}}(\sqrt{2})^2
\end{aligned}\)

 

\(\log _2 \log _2 4 \log _4 4+2 \times 2 \log _{\sqrt{2}}(\sqrt{2})\)

 

\(\log _2 \log _2 4 \log _4 4+4\)

 

\(\begin{aligned}
& =\log _2 \log _2 4+4 \\
& =\log _2 \log _2 2^2+4 \\
& =\log _2 2 \log _2 2+4 \\
& =\log _2 2+4
\end{aligned}\)

 

= 1 + 4 = 5 R.H.s Proved

 

\(\begin{aligned}
&\begin{aligned}
& {\left[because \log _{\sqrt{2}} \sqrt{2}=1\right]} \\
& {\left[because \log _4 4=1\right]}
\end{aligned}\\
&\left[because \log _2 2=1\right]
\end{aligned}\)

 

4. \(\log _{x^2} x \times \log _{y^2} y \times \log _{z^2} z=\frac{1}{8}\)

Solution:
L.H.S.= \(\log _{x^2} x \times \log _{y^2} y \times \log _{z^2} z\)

\(\frac{1}{8}\) = R.H.S. Proved

5. \(\log _{b^3} a \times \log _{c^3} b \times \log _{a^3} c=\frac{1}{27}\)

Solution:

L.H.S = \(\log _{b^3} a \times \log _{c^3} b \times \log _{a^3} c\)

= R.H.S (Proved)

6. \(\frac{1}{\log _{x y}(x y z)}+\frac{1}{\log _{y z}(x y z)}+\frac{1}{\log _{z x}(x y z)}=2\)

L.H.S.= \(\frac{1}{\log _{x y}(x y z)}+\frac{1}{\log _{y z}(x y z)}+\frac{1}{\log _{z x}(x y z)}\)

= R.H.S (Proved)

7. \(\log \frac{a^2}{b c}+\log \frac{b^2}{c a}+\log \frac{c^2}{a b}=0\)

Solution:

L.H.S = \(\log \frac{a^2}{b c}+\log \frac{b^2}{c a}+\log \frac{c^2}{a b}\)

R.H.S Proved

8. \(x^{\log y-\log z} \times y^{\log z-\log x} \times z^{\log x-\log y}=1\)

Solution:

\(\text { Let } P=x^{\log y-\log z} \times y^{\log z-\log x} \times z^{\log x-\log y}=1\)

Taking log on both sides

 

Question 6. Let us prove

1. If \(\log \frac{x+y}{5}=\frac{1}{2}(\log x+\log y)\), then let us show that \(\frac{x}{y}+\frac{y}{x}=23\)

Solution:

Given

\(\log \frac{x+y}{5}=\frac{1}{2}(\log x+\log y)\)

 

⇒ \(\log \frac{x+y}{5}=\frac{1}{2}(\log x+\log y)\)

 

 

2. If \(a^4+b^4=14 a^2 b^2\) then let us show that xyz = 1.

Solution: 

Given

\(a^4+b^4=14 a^2 b^2\)

 

Question 7. If \(\frac{\log x}{y-z}=\frac{\log y}{z-x}=\frac{\log z}{x-y}\) then let us show that xyz = 1.

Solution: \(\frac{\log x}{y-z}=\frac{\log y}{z-x}=\frac{\log z}{x-y}\) = k

∴ \(\frac{\log x}{y-z}=k \Rightarrow \log x=k(y-z)\) …….(1)

∴ \(\frac{\log y}{z-x}=k \Rightarrow \log y=k(z-x)\) ….(2)

∴ \(\frac{\log z}{x-y}=k \Rightarrow \log z=k(x-y)\) …(3)

Adding equations (1), (2) and (3) we get

logx+logy + logz = k(y-z) + k(z-x) + k(x-y)
log(xyz) = k(y-Z+Z-x+x-y)
log(xyz) = k.0 = 0

∴ log(xyz) log1
∴ xyz= 1 Proved

Question 8. If, \(\frac{\log x}{b-c}=\frac{\log y}{c-a}=\frac{\log z}{a-b}\)  then let us show that:

1. \(x^{b+c} \cdot y^{c+a} \cdot z^{a+b}=1\)

2. \(x^{b^2+b c+c^2} \cdot y^{c^2+c a^2+a^2} \cdot z^{a^2+a b+b^2}=1\)

Solution:

\(\frac{\log x}{b-c}=\frac{\log y}{c-a}=\frac{\log z}{a-b}=k\)

 

logx = k(b-c)
logy = k (c-a)
logz= k ( a – b)

1. \([\log \left(x^{b+c} \cdot y^{c+a} \cdot z^{a+b}\right)=\log x^{b+c}+\log y^{c+a}+\log z^{a+b}\)

 

2. \(\log \left(x^{b^2+b c+c^2} \cdot y^{c^2+c a^2+a^2} \cdot z^{a^2+a b+b^2}\right)\)

= \(\log \dot{x}^{b^2+b c+c^2}+y^{c^2+c a^2+a^2}+z^{a^2+a b+b^2}\)

 

 

Question 9. If a^3-x.b^5x = a^5+x.b^3x, then let us show that \(\)

Solution:

Given

a^3-x.b^5x = a^5+x.b^3x

\(or, \frac{b^{5 x}}{b^{3 x}}=\frac{a^{5+x}}{a^{3-x}}
or, b^{5 x-3 x}=a^{(5+x)-(3-x)}
or, b^{5 x-3 x}=a^{5+x-3+x}
or, b^{2 x}=a^{2+2 x}
or, b^{2 x}=a^2 \cdot a^{2 x}\) \(\begin{aligned}
& \text { or, } \frac{b^{2 x}}{a^{2 x}}=a^2 \\
& \left(\frac{b}{a}\right)^{2 x}=a^2 \\
& \log \left(\frac{b}{a}\right)^{2 x}=\log a^2 \\
& 2 x \log \left(\frac{b}{a}\right)=2 \log a \\
& x \log \frac{b}{a}=\log a
\end{aligned}\)

 

Question 10. Let us evalute:

1. \(\log _8\left[\log _2\left\{\log _3\left(4^x+17\right)\right\}\right]=\frac{1}{3}\)

Solution:

Given

 

2. \(\log _8 x+\log _4 x+\log _2 x=11\)

Solution: \(\log _8 x+\log _4 x+\log _2 x=11\)

\(\text { or, } \frac{1}{\log _x 8}+\frac{1}{\log _x 4}+\frac{1}{\log _x 2}=11\)

 

\(\text { or, } \frac{1}{\log _x 2^3}+\frac{1}{\log _x 2^2}+\frac{1}{\log _x 2}=11\)

 

\(\text { or, } \frac{1}{3 \log _x 2}+\frac{1}{2 \log _x 2}+\frac{1}{\log _x 2}=11\)

 

\(\text { or, } \frac{1}{\log _x 2}\left(\frac{1}{3}+\frac{1}{2}+1\right)=11\)

 

\(\text { or, } \frac{1}{\log _x 2}\left(\frac{2+3+6}{6}\right)=11\)

 

\(\text { or, } \frac{1}{\log _x 2}\left(\frac{11}{6}\right)=11\)

 

\(\text { or, } \frac{1}{\log _x 2}=11 \times \frac{6}{11}\)

 

\(\text { or, } \frac{1}{\log _x 2}=6\)

 

\(or, \log _2 x=6
or, x=2^6
or, x=64 \)

 

Question 11. Let us show that the value of \(\log _{10} 2\) lies between \(\frac{1}{4} \text { and } \frac{1}{3}\)

Solution: Let \(\log _{10} 2=x\)

10^x = 2

Question 12. Multiple choice questions

1. If \(\log _{\sqrt{x}} 0.25=4\) then the value of x will be

1. 0.5
2. 0.25
3. 4
4. 16

Solution: \(\log _{\sqrt{x}} 0.25=4\)

\(therefore(\sqrt{x})^4=0.25
or, \left\{(\sqrt{x})^2\right\}^2=0.25
or, \mathrm{x}^2=0.25
or, x=\sqrt{0.25}
or, x=0.5\)

∴ 1. 0.5

2. If log₁₀(7x-5)= 2, then the value of x will be

1. 10
2. 12
3. 15
4. 18

Solution: log₁₀(7x-5)=2

\(or, 10^2=7 x-5
or, (7 x-5)=100
or, 7 x=105
or, x=15\)

3. If  log₂3 = a, then the value of log₈27 is

1. 3a
2. \(\frac{1}{a}\)
3. 2a
4. a

Solution: log₂3 = a

\(\begin{aligned}
& \log _8 27=\log _8 3^3 \\
& =3 \log _8 3 \\
& =3 \times \frac{1}{\log _3 8} \\
& =3 \times \frac{1}{\log _3 2^3} \\
& =3 \times \frac{1}{3 \log _3 2} \\
& =\log _2 3
\end{aligned}\)

 

log₈27 = a

∴ 4. a

4. If \(\log _{\sqrt{2}} x=a\), then the value of \(\log _{2 \sqrt{2}} x\) is

1. \(\frac{a}{3}\)
2. a
3. 2a
4. 3a

Solution: \(\log _{\sqrt{2}} x=a\)

∴ \(\begin{aligned}
therefore  & \log _{2 \sqrt{2}} x=\frac{1}{\log _x 2 \sqrt{2}} \\
& =\frac{1}{\log _x\left\{(\sqrt{2})^2 \cdot \sqrt{2}\right\}} \\
& =\frac{1}{\log _x(\sqrt{2})^3} \\
& =\frac{1}{3 \log _x \sqrt{2}} \\
& =\frac{1}{3} \log _{\sqrt{2}} x \\
& =\frac{a}{3} \\
therefore  & \log _{2 \sqrt{2}} x=\frac{a}{3}
\end{aligned}\)

∴ 1. \(\frac{a}{3}\)

5. If \(\log _x \frac{1}{3}=-\frac{1}{3}\) then the value of x is

1. 27
2. 9
3. 3
4. \(\frac{1}{27}\)

Solution: \(\log _x \frac{1}{3}=-\frac{1}{3}\)

\(or, \log _x 3^{-1}=-\frac{1}{3}\) \( or, -\log _x 3=-\frac{1}{3}\) \( or, \log _x 3=\frac{1}{3}\) \( or, x^{\frac{1}{3}=3}\) \( or, \left(x^{\frac{1}{3}}\right)^3=3^3\)

X = 27

∴ 1. 27

Question13. Short answer type questions:

1. Let us calculate the value of \(\log _4 \log _4 \log _4 256\)

Solution: \(\log _4 \log _4 \log _4 256\)

=\(\log _4 \log _4 \log _4 4^4\)

\(\begin{aligned}
& =\log _4 \log _4 4 \log _4 4 \\
& =\log _4 \log _4 4 \\
& =\log _4 1
\end{aligned}\)

 

∴\(\log _4 \log _4 \log _4 256\) = 0

2. Let us calculate the value of \(\log \frac{a^n}{b^n}+\log \frac{b^n}{c^n}+\log \frac{c^n}{a^n}\)

Solution: \(\log \frac{a^n}{b^n}+\log \frac{b^n}{c^n}+\log \frac{c^n}{a^n}\)

\(\begin{aligned}
& =\log \left(\frac{a}{b}\right)^n+\log \left(\frac{b}{c}\right)^n+\log \left(\frac{c}{a}\right)^n \\
& =n \log \frac{a}{b}+n \log \frac{b}{c}+n \log \frac{c}{a} \\
& =n(\log a-\log b)+n(\log b-\log c)+n(\log c-\log a) \\
& =n(\log a-\log b+\log b-\log c+\log c-\log a) \\
& =n .0 \\
& =0
\end{aligned}\)

 

3. Let us show that \(a^{\log _a x}=x .\)

Solution: Let  log_a = x

\(\begin{aligned}
& a^u=x \\
& a^{\log _a x}=x
\end{aligned}\)

 

\(\left[because \mathrm{u}=\log _{\mathrm{a}} \mathrm{x}\right]\)

 

4. If \(\log _e 2 \cdot \log _x 25=\log _{10} 16 \cdot \log _9 10 \) then let us calculate the value of x. 

Solution: \(\log _e 2 \cdot \log _x 25=\log _{10} 16 \cdot \log _9 10 \)

 

 

Class IX Maths Solutions WBBSE Chapter 5 Linear Simultaneous Equations Exercise 5.2

Question 1. Let us draw the graph of the following equations and write whether they are solvable or not and if they are solvable, let us write that particular solution or solutions if they have an infinite number of solutions:

1. 2x + 3y-7=0, 3x+2y-8=0

Solution:

Given

2x+3y-7=0 ….(1)
3x+2y-8=0….(2)

From equation ….(1)
2x + 3y-7=0

or, \(x=\frac{7-3 y}{2}\)

Read and Learn More WBBSE Solutions For Class 9 Maths

x	2	8	-1
y	1	-3	3

From equation ……(2)
3x + 3y-7=0

or, \(x=\frac{8-2 y}{3}\)

x	2	0	4
y	1	4	-2

 

∴ The equations are solvable.
∴ x = 2;
y =1

 

Class IX Maths Solutions WBBSE

2. 4x-y=11, -8x+2y=-22

Solution:

Given

4x – y = 11 ….(1)

⇒ \(x=\frac{2 y+22}{8}\)

x	4	3	2
y	5	1	-3

 

– 8x + 2y = -22 ….(2)

⇒ \(x=\frac{2 y+22}{8}\)

x	3	5	1
y	1	9	-7

 

Here, \(\frac{4}{-8}=\frac{-1}{2}=\frac{11}{-22}\)

∴ The equations are solvable and have an infinite number of solutions, i.e., x = 2, y = -3; x = 3, y=1; and x = 4, y = 5.

 

Class IX Maths Solutions WBBSE

3. 7x + 3y = 42,

Solution: \(x=\frac{42-3 y}{7}\)

x	6	3	9
y	0	7	-7

 

21x+9y=42

\(x=\frac{42-9 y}{21}\)

 

x	2	-1	5
y	0	7	-7

 

Class 9 Math Chapter 5 WBBSE

Here = \(\frac{7}{21}=\frac{3}{9} \neq \frac{42}{42}\)

∴ There two equations are inconsistent, i.e., they are unsolvable.

 

 

4. 5x + y = 13, 5x +5y = 12

Solution:

Given

5x + y = 13 ….(1)

\(y=\frac{13-5 x}{1}\)

Class 9 Math Chapter 5 WBBSE

→AB

x	2	0	4
y	3	13	-7

 

5x+5y= 12 ……(2)

⇒ \(y=\frac{12-5 x}{5}\)

→ CD

x	4	0	\(\frac{53}{20}\)
y	-1.6	2.4	\(\frac{-1}{4}\)

 

The equations are solvable.

∴ x = \(\frac{53}{20}\)

y = \(\frac{-1}{4}\)

 

Question 2. By comparing the coefficients of the same variables and constants of the following pairs of equations, let us write whether the pair of equations is solvable or not and check them by drawing the graphs of the equations.

1. x+5y=7, x+5y=20

Solution:

Given

x+5y=7, x+5y=20

x + 5y = 7 …(1)

∴ x=7-5y

Class 9 Math Chapter 5 WBBSE

→AB

x	2	-8	7
y	1	3	0

x+5y=20  ….(2)

→CD

x	0	10	-10
y	4	2	6

Here, \(\frac{1}{1}=\frac{5}{5} \neq \frac{7}{20}\)

∴ There two equations are in consistent, i.e., they are unsolvable.

2. 2x + y = 8, y=8-2x

Solution:

Given

2x + y = 8, y=8-2x

2x + y = 8 ….(1)

→AB

x	2	0	-1	4
y	4	8	10	0

-3x+2y=-5 ……(2)

\(y=\frac{3 x-5}{2}\)

Class 9 Maths WB Board

→CD

x	1	3	-1
y	-1	2	-4

 

\(\frac{2}{-3} \neq \frac{1}{2} \neq \frac{8}{-5}\)

∴ The two equations are solvable. x=3, y=2

3. 5x + 8y = 14, 15x + 24y = 42

Solution: 5x+8y = 14  …(1)

⇒ \(y=\frac{14-5 x}{8}\)

x	-2	6	2
y	3	-2	5

15x + 24y = 42  ….(2)

⇒ \(y=\frac{42-15 x}{24}\)

→PQ

x	2	-2
y	5	3

 

\(\frac{5}{15}=\frac{8}{24}=\frac{14}{42}\)

Class 9 Maths WB Board

∴ The two equations are solvable and have an infinite number of solutions.

4. 3x+2y= 6, 12x + 8y = 24

Solution: 3x+2y=6…(1)

⇒ \(y=\frac{6-3 x}{2}\)

x	0	-2	6
y	3	6	-6

 

12x + 8y = 24  …(2)

⇒ \(y=\frac{24-12 x}{8}\)

x	0	-2	6
y	3	6	-6

 

\(\frac{3}{12}=\frac{2}{8}=\frac{6}{24}\)

Class 9 Maths WB Board

∴ The two equations are solvable and have infinite number of solutions.

Question 3. Let us determine the relations of ratios of the same variable and constants of the following pairs of equations and write whether the graphs of the equations will be parallel or intersecting or overlapping.

1. 5x + 3y = 11, 2x – 7y = – 12

Solution: 5x+3y= 11  ….(1)
2x-7y=-12 …(2)

\(\frac{5}{2} \neq \frac{3}{-7} \neq \frac{11}{-12}\)

∴ The graphs of the equations will be intersecting.

2. 6x – 8y = 2, 3x-4y = 1

Solution: 6x-8y = 2  …(1)
3x-4y = 1 ….(2)

Here, = \(\frac{6}{3}=\frac{-8}{-4}=\frac{2}{1}\)

∴The graphs of the equations are one straight lines, i.e., they are coincident.

3. 8x-7y = 0, 8x – 7y = 56

Solution: 8x-7y=0 ….(1)
8x – 7y = 56 …(2)

\(\frac{8}{8}=\frac{-7}{7} \neq \frac{0}{56}\)

∴ The graphs of the equations are parallel.

4. 4x-3y= 6, 4y – 5x = -7

Solution: 4x-3y=6 ….(1)
– 5x + 4y = -7 …(2)

Here \(\frac{4}{-5} \neq \frac{-3}{4} \neq \frac{6}{-7}\)

∴ The graphs of two equations will intersect each other.

Class 9 Mathematics West Bengal Board

Question 4. Let us solve the following pairs of equations by drawing graphs which are solvable and write 3 solutions which have infinite number of solutions.

1. 4x + 3y = 20, 8x +6y= 40

Solution: 4x + 3y = 20 …(1)
8x + 6y= 40 …(2)

From equation…….(1)
4x + 3y = 20

⇒ \(y=\frac{20-3 y}{4}\)

x	-1	2	5
y	8	4	0

From equation  …(2)
8x+6y= 40

⇒ \(x=\frac{40-6 y}{8}\)

There two equations are solvable, has infinite of solvitions, i.e., (1) x = 5, y = 0;
(2) x=-1, y = 8 (3) x = 2, y = 4.

 

 

2. 4x + 3y = 20, 12x + 9y=20

Solution: 4x+3y=20 ….(1)

⇒ \(y=\frac{20-4 x}{3}\)

x	-1	2	5
y	8	4	0

 

12x + 9y=20 ….(2)

⇒ \(y=\frac{20-12 x}{9}\)

Here, \(\frac{4}{12}=\frac{3}{9} \neq \frac{20}{20}\)

∴ These two equations have no general solutions; they are parallel straight lines.

Class 9 Mathematics West Bengal Board

3. 4x + 3y = 20, \(\frac{3 x}{4}-\frac{y}{8}=1\)

Solution: 4x+3y=20   ….(1)

\(\frac{3 x}{4}-\frac{y}{8}=1\)  ….(2)

4x = 20-3y (1)

or, \(x=\frac{20-3 y}{4}\)

→CD

x	5	2	8
y	0	4	-4

 

\(\frac{3 x}{4}-\frac{y}{8}=1\)  ….(2)

or, \(x=\frac{4}{3}\left(1+\frac{y}{8}\right)\)

→ PQ

x	4	1.5	2
y	16	1	4

 

Here, \(\frac{4}{3 / 4}=\frac{3}{-1 / 8}=\frac{20}{1}\)

∴ The two equations are solvable.

4. p-q=3, \(\frac{p}{3}+\frac{q}{2}=6\)

Solution: p-q=3 …(1)

\(\frac{p}{3}+\frac{q}{2}=6\) ….(2)

 

p=3+q …(1)

→AB

p	3	0	-6
q	0	-3	3

 

Class 9 Mathematics West Bengal Board

\(\frac{p}{3}+\frac{q}{2}=6\)  …(2)

⇒ \(p=3\left(6-\frac{q}{2}\right)\)

→ CD

p	15	18	12
q	2	0	4

Here, \(\frac{1}{1 / 3} \neq \frac{-1}{1 / 2} \neq \frac{3}{6}\)

 

 

5. p − q = 3, \(\frac{p}{5}-\frac{q}{5}=3\)

Solution: p-q=3
⇒p=3+q   …(1)

→PQ

p	4	3	1
q	1	0	-2

 

 

\(\frac{p}{5}+\frac{q}{5}=3\)

 

⇒ \(p=5\left(3+\frac{q}{5}\right)\) …(2)

 

→RS

p	20	5	10
q	5	-10	-5

 

Here, \(\frac{1}{1 / 5}=\frac{-1}{-1 / 5} \neq \frac{3}{3}\)

∴ The two equations have no solutions, they are parallel straight lines.
99

6. p-q=3, 8p-8q = 5

Solution: p-q=3 ⇒ p=3+q …(1)

p	3	0	5
q	0	-3	2

 

Class 9 Mathematics West Bengal Board

8p-8q= 5

⇒ \(p=\frac{5+8 q}{8}\)

∴ The two equations have no solutions, they are parallel straight lines.

Question 5. Tathagata has written a linear equation in two variables x + y = 5. I write another linear equation in two variables, so that, the graphs of two equations will be
1. Parallel to each other,
2. Intersecting,
3. Overlapping.

Solution: x + y = 5
1. Equation of parallel straight line is 5x + 5y = 20
2. Equation of intersecting straight line is 2x+5y = 16
3. Equation of overlapping straight line is 2x + 2y = 10