Class 9 Mathematics

Class 9 Mathematics West Bengal Board Chapter 3 Graph

The graph is used to locate a point on a plane. From a point on a plane, two mutually perpendicular straight lines are drawn, which are called axes. Let from O point two mutually perpendicular straight lines XOX’ and YOY’ are drawn. O point is called (Origin) XOX’ and YOY! are called X axis Y axis XOX’ and YOY’ divide the plane in four parts.

These four parts are called (Quadrant). From the origin toward OX the value of X is positive and toward OX’ the value of X is negative. Similarly from the origin toward OY the value of Y is positive and toward OY’ the value of Y is negative.

Read and Learn More WBBSE Solutions For Class 9 Maths

Memorable Facts:

1. The equation of the x-axis is y = 0
2. The equation of the y-axis is x = 0
3. Equation of a straight line parallel to x-axis y = c where c is a constant
4. Equation of a straight line parallel to the y-axis: x = c where c is a constant
5. Coordinates of the origin are (0,0))
6. The equation of a graph passing through origin is of the form ax + by = 0
7. Distance from the origin O (0,0) to point P (x, y) is = \(\sqrt{\left(x_1\right)^2+\left(y_1\right)^2}\)
8. The ordinary equation of a straight line is ax+by+c=0
9. The equation \(\frac{x}{a}+\frac{y}{b}=1\) cuts the x-axis in the direction from origin a dist. ‘a’ and y-axis in the positive direction at a distance ‘s’.
10. The equation \(\frac{x}{a}+\frac{y}{b}=1\)forms a triangle with the co-ordinate axes whose area is 1/2 ab square units.

 

Class 9 Maths WB Board Chapter 3 Graph Exercise 3.1

 

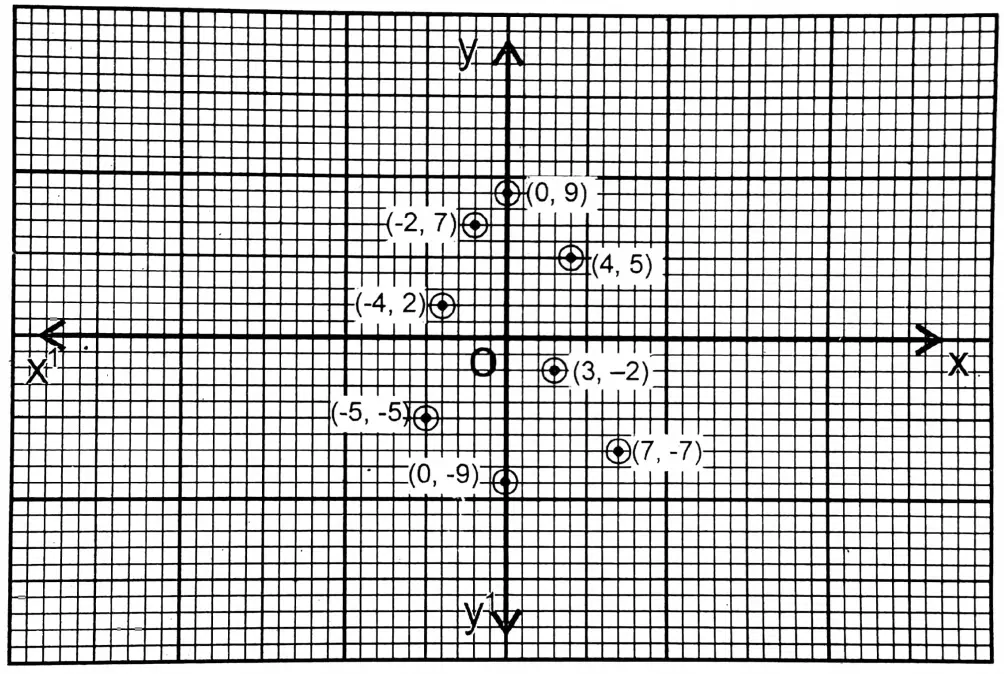
Question 1. I plot the following points on graph paper and write which points lie above and below the x-axis.
(3,-2), (-4, 2), (4, 5), (-5,-5), (-2, 7), (7, -7), (0, 9), (0, -9)

Solution: The points above the x-axis are (-4, 2), (-2, 7), (0, 9), and (4, 5) The points below the x-axis are (-5,-5), (0, -9), (3,-2), (7, -7)

 

 

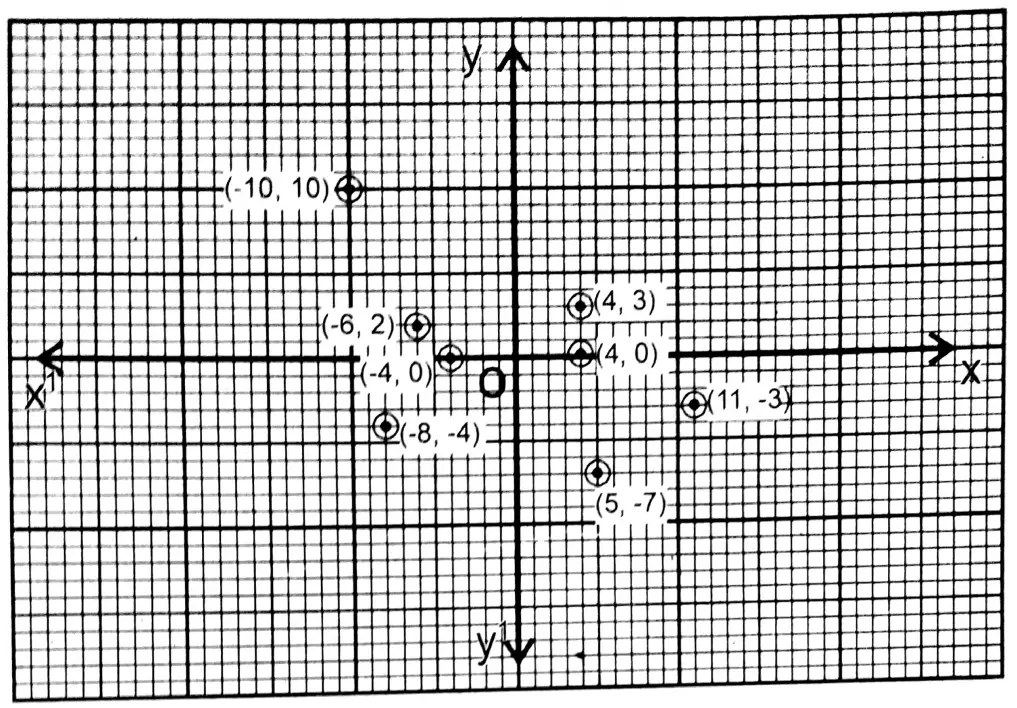
Question 2. I plot the following points on graph paper and write which points lie on the right and left sides of the y-axis.
(5, -7), (-10, 10), (-8, -4), (4, 3), (-6, 2), (11, -3), (4, 0), (-4, 0).

Solution:The points lying on the left side of the y-axis are (-10, 10), (-6, 2), (-4, 0) (-8, -4)
The points lying on the right side of the y-axis are (4, 3), (4, 0) (11,-3) (5,-7)

 

 

 

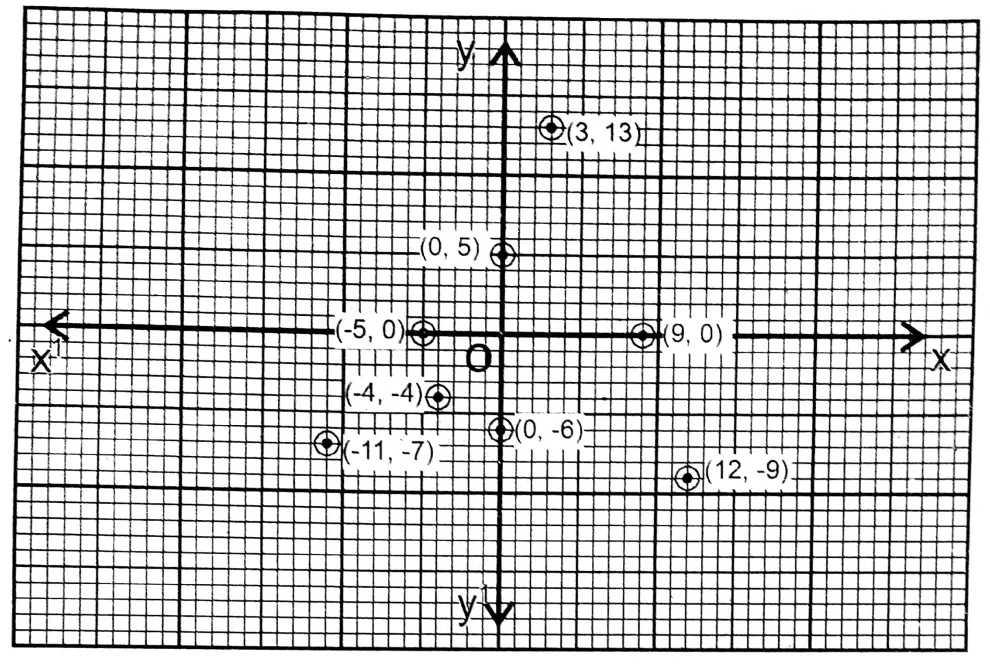
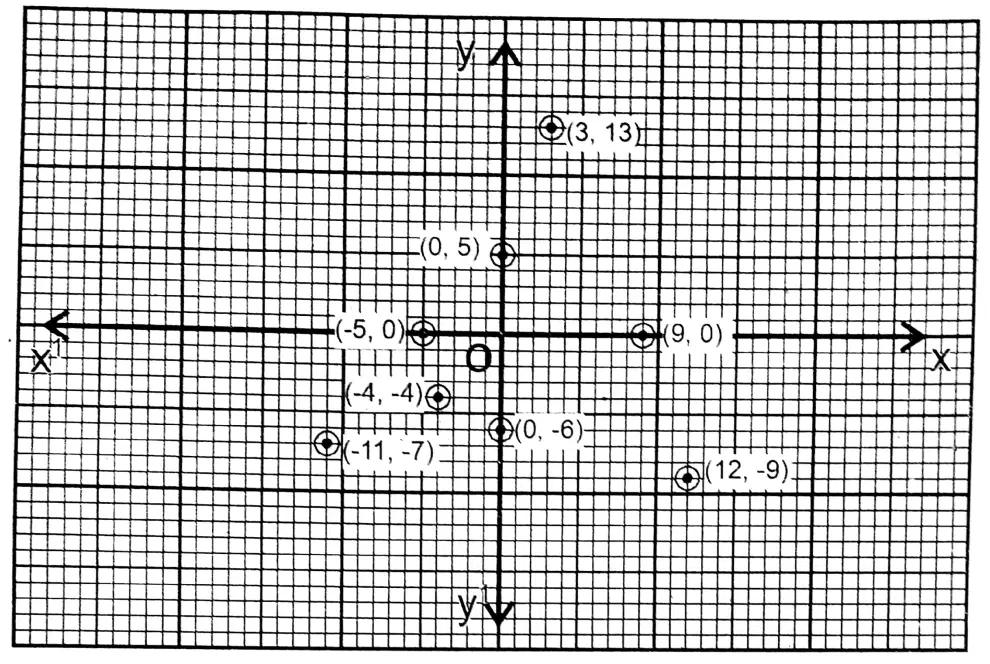
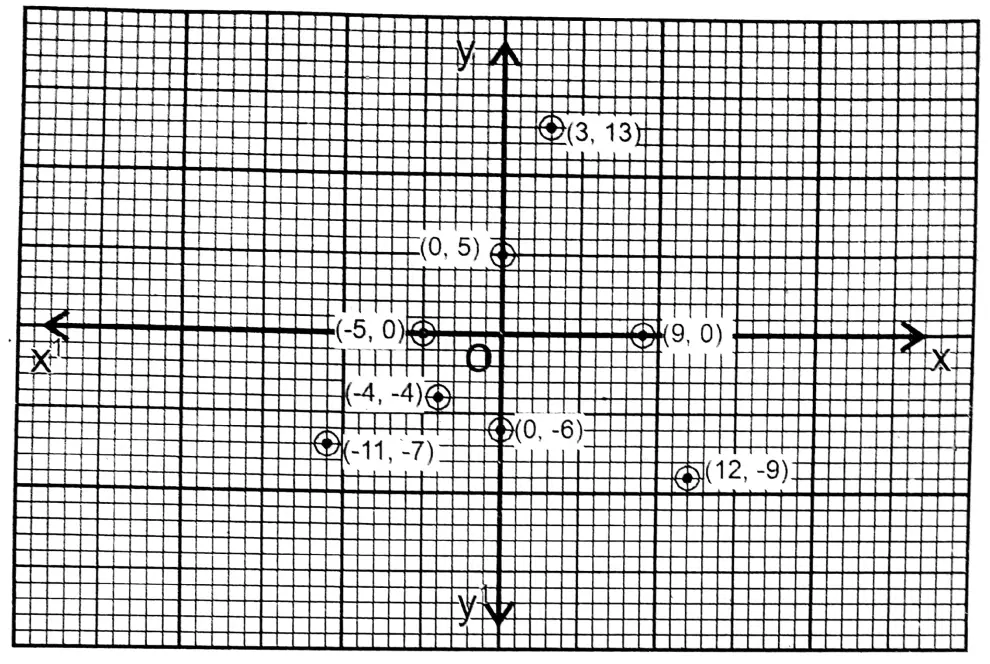
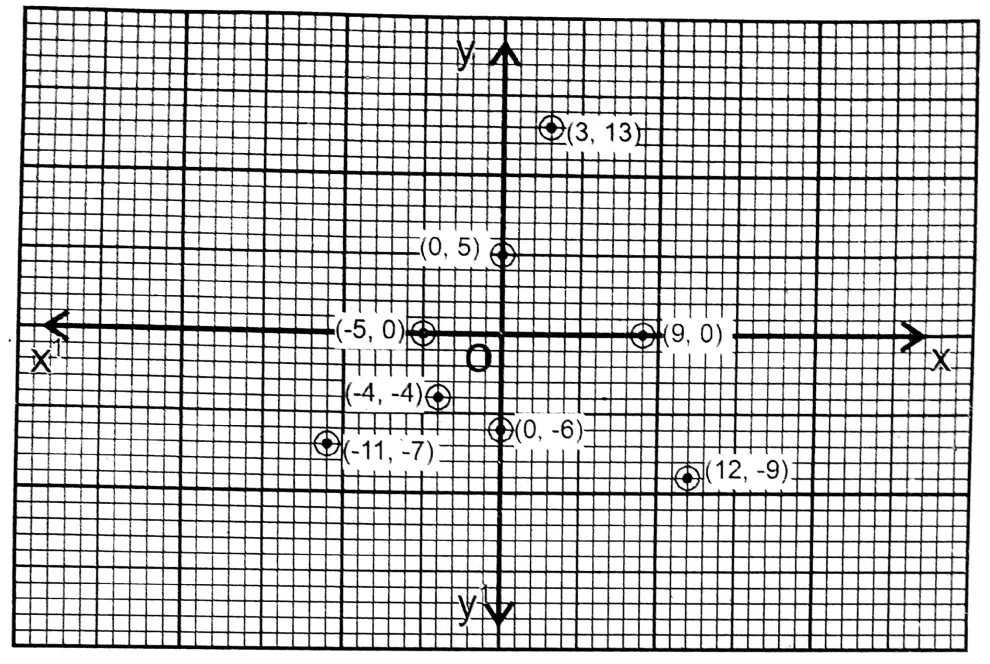
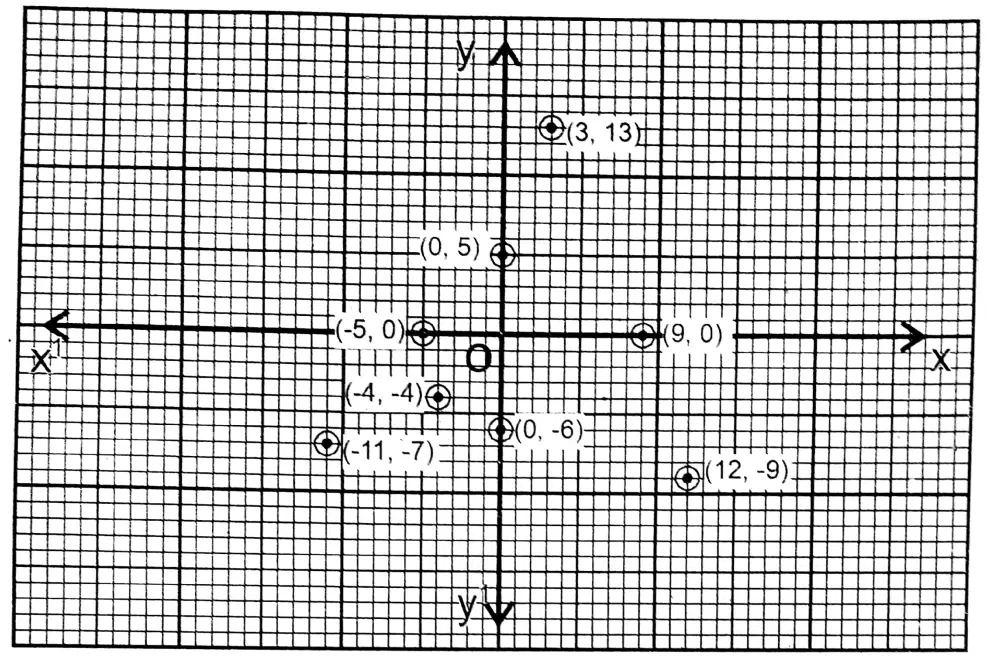
Class IX Maths Solutions WBBSE Question 3. I plot the following points on graph paper and write their positions (in which quadrant or on which axis and in which direction).
(-11, -7), (0, 5), (9, 0), (-4, -4), (12, -9), (3, 13), (0, -6), (-5, 0)

Solution: (-11, -7) and (-4, -4) points are in the 3rd quadrant.
Point (0, 5) is in the positive direction of the y-axis
Point (9, 0) is in the positive direction of the x-axis Point (12, -9) is in the first quadrant
Point (3, 13) is in the first quadrant
Point (0,-6) is in the negative direction of the y-axis Point (-5, 0) is in the negative direction of the x-axis.

 

 

Question 4. Let us write the coordinates of any four points lying on the x-axis.

Solution: Four points lying on the x-axis are:(-7, 0) (-4, 0), (5, 0), and (8, 0).

 

 

Class IX Maths Solutions WBBSE Question 5. Let us write the coordinates of any four points lying on the y-axis.

Solution: Four points lying on the y-axis are: (0, 8); (0, 2); (0, -6), and (0, -10).

 

 

Question 6. Let us write the coordinates of any four points lying in each quadrant.

Solution: 1st Quadrant:- (3,2); (5,7); (8,3); (12,6)
2nd Quadrant:- (-2,6), (-7,8); (-9,3); (-10,6)
3rd Quadrant :- (-3,-5); (-6, -7); (-4,-2); (-8,-3)
4th Quadrant (4,-2); (8,-6); (+3,-5); (6,-7)

 

 

 

Question 7. The distances of a point from x-axis and y-axis are 5 units and 7 units respectively. Let us write the coordinates of the point.

Solution: The co-ordinates of the point are (7,5).

 

 

WBBSE Class 9 Math Chapter 3 Graph Exercise 3.2

 

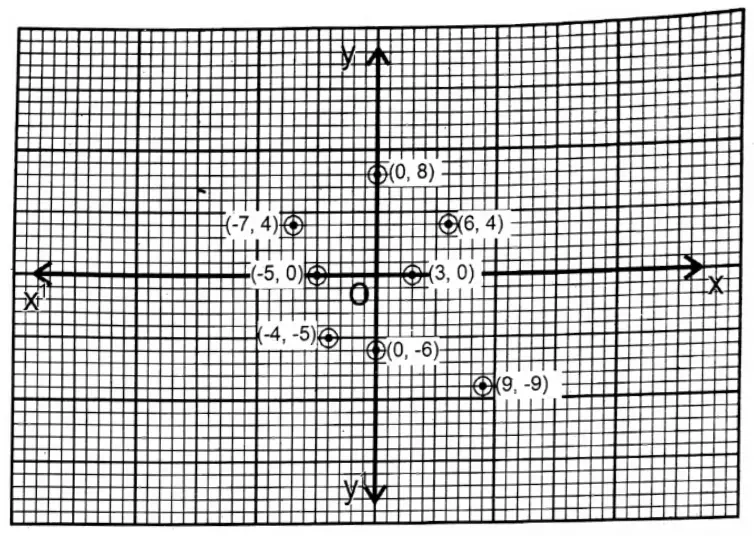
Question 1. Let us plot the following points on graph paper and write their positions (on the axes or in quadrants).

1. (3, 0)
2. (0,8)
3. (-5, 0)
4. (0, -6)
5.  (6, 4)
6. (-7, 4)
7. (9, -9)
8. (-4,-5)

Solution:

1. (3, 0) on the x-axis (positive direction)
2. (0, 8) on the y-axis (positive direction)
3. (-5, 0) on the x-axis (negative direction)
4. (0,-6) on the y-axis (negative direction)
5. (6, 4) lies in 1st Quadrant
6. (-7, 4) lies in 2nd Quadrant
7. (9,-9) lies in 4th Quadrant
8.  (-4,-5) lies in 3rd Quadrant

WBBSE Class 9 Math Chapter 3.2

 

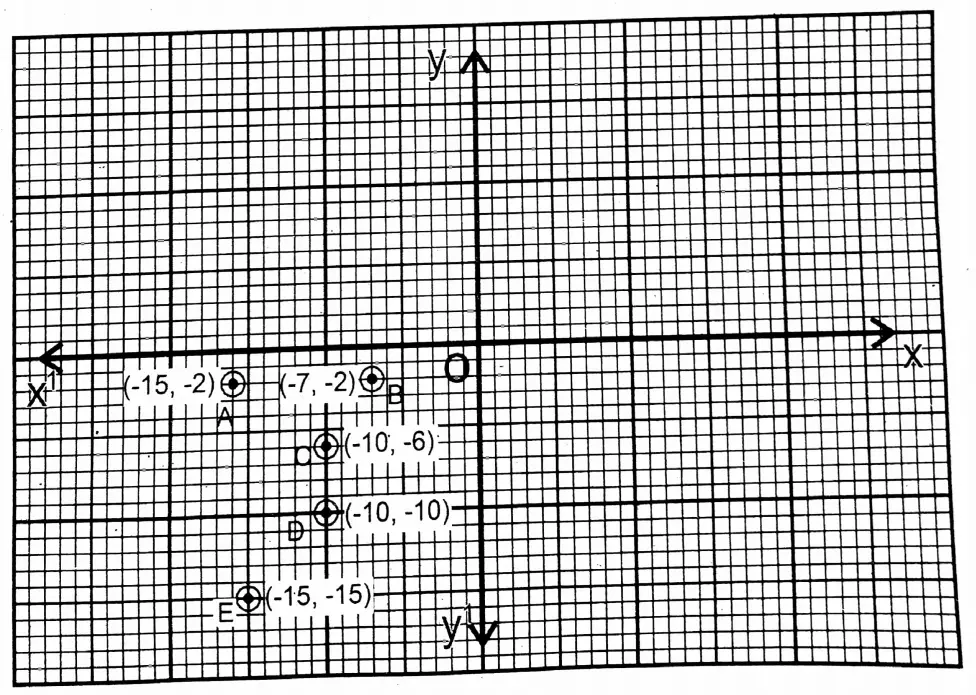
Question 2. On the graph paper, let us draw XOX’ & YOY’, the two perpendicular axes, and plot any 5 points lying in the 3rd quadrant.

Solution: 5 points on the 3rd quadrant are:-

1. (-15, -2);
2. (-7, -2);
3. (-10, -6);
4.  (-10, -10);
5. (-15, -15).

Question 3. Let us express the following statements into simultaneous linear equations:

(1) The total price of 3 exercise copies and 2 pens is Rs. 55 and the total price of 4 exercise copies and 3 pens is Rs. 75.

Solution: 3x+2y=55
4x + 3y = 75
Here x = price of each exercise copy and y = price of each pen.

(2) The sum of two numbers is 80 and thrice of the difference of those two num- bers is 20 more than the larger number.

Solution: x + y = 80
3(x-y) -x = 20
Here x is the larger number and y is the smaller number.

WBBSE Class 9 Math Chapter 3.2

(3) When 2 is added to the numerator and denominator of a fraction, its value will be 7/9, and when 3 is subtracted from both the numerator and denominator, its value will be

Solution:

\(\begin{aligned}
& \frac{x+2}{y+2}=\frac{7}{9} \\
& \frac{x-3}{y-3}=\frac{1}{2}
\end{aligned}\)

Here \(\frac{x}{y}\) is the fraction.

(4)The tenth’s place digit is twice of the units place digit of a two-digit number. If the digits interchange their places, the resultant number will be 27 less than the original number.

Solution:x = 2y (10x + y) (10y – x) = 27
Here x = The digit in tenth place
y= The digit in the unit’s place & (10x + y) is the number

Question 4. Let us express the following statements into linear equations in two variables and draw the graph of the equations.

1. At present, the age of Sujata’s father is more than the age of Sujata by 26 years. [Let us suppose Sujata’s father’s age is x years and Sujata’s age is y years.]
2. The sum of the two numbers is 15.
3. If the numerator and denominator of a fraction are increased by 2, the Trection will be \(\frac{7}{9}\)
4. The perimeter of our rectangular yard is 80 m.
5. Of the two numbers, 5 times of the larger number equals to 8 times of the smaller one.

Class 9 Math Chapter 3 WBBSE

Solution:

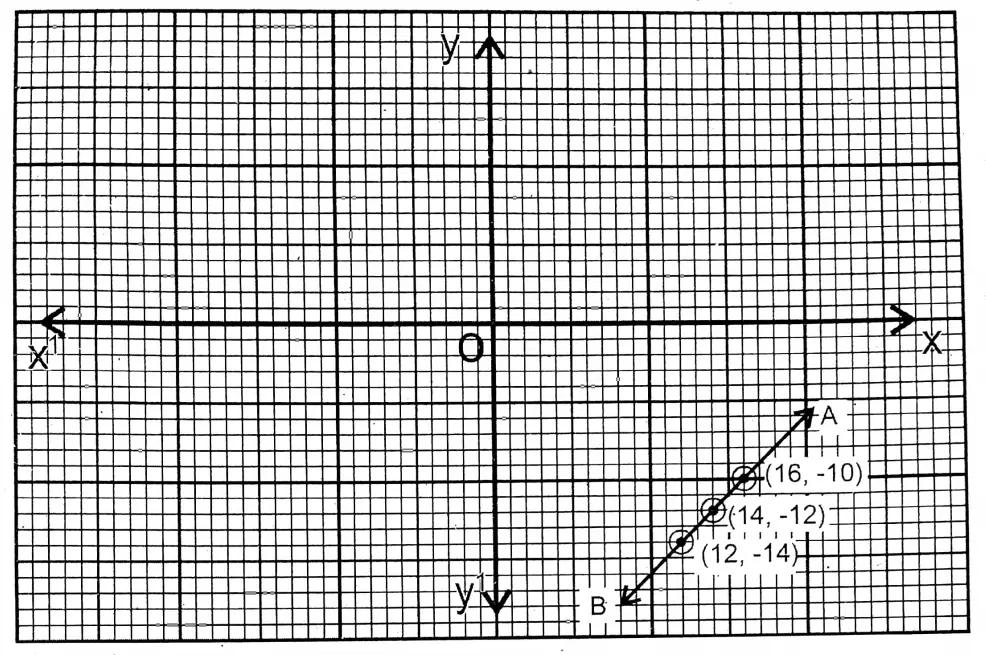
1. Let Sujata’s father’s age = x years and Sujata’s age = y years.
As for questions,
x – y = 26
x = 26+ y

x	10	16	8	14	12
y	-16	-10	-18	-12	-14

 

In the graph paper, AB is the graph of equation x – y = 26.

 

 

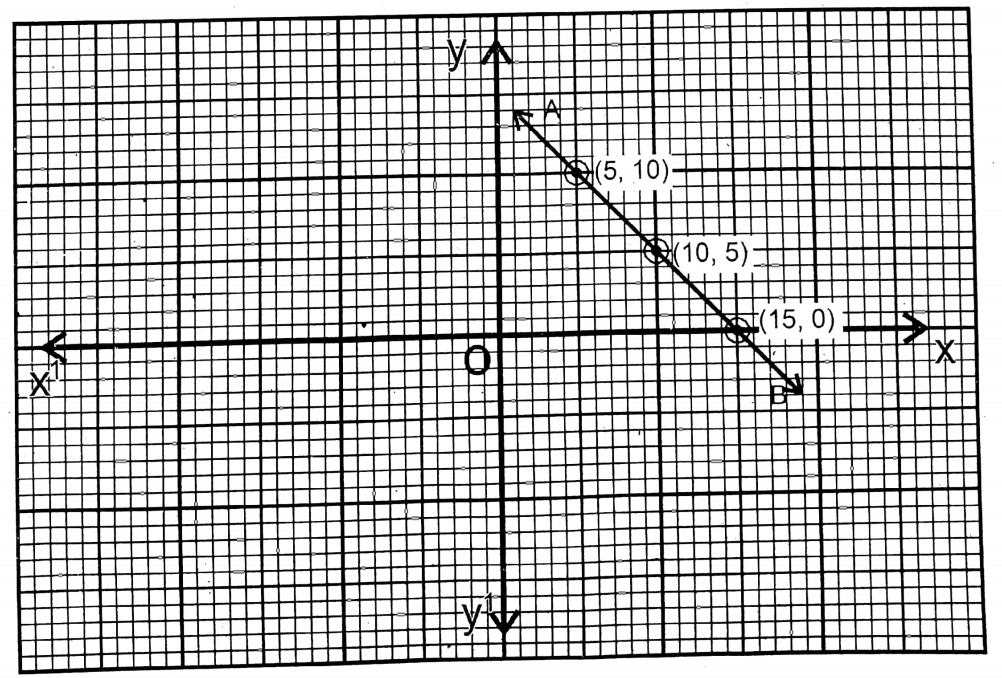
2. Let one number is x & the other number is y.
x + y = 15….(1)
or, x = 15-yx=15-y

x = 15-y	7	10	5
y	8	5	10

 

AB is the graph of the equation x+y=15

Class 9 Math Chapter 3 WBBSE

 

 

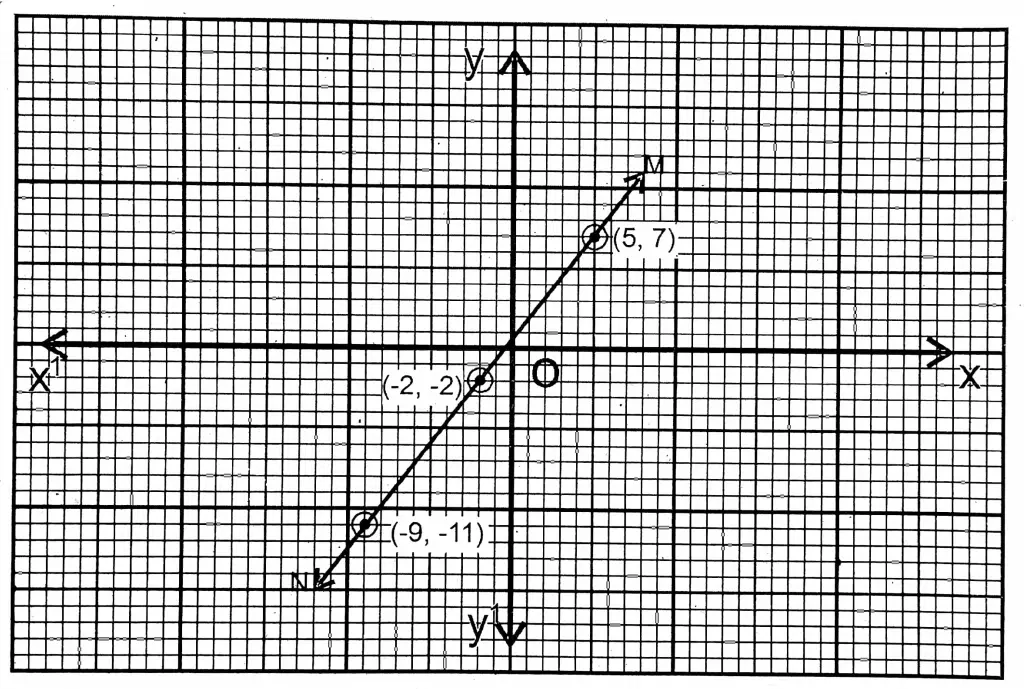
3. Let the fraction be \(\frac{x}{y}\) whose numerator is x and denominator is y.
or, 9x+18=7y+ 14
or, \(y=\frac{9 x+4}{7}\)

x	5	-2	12	-9
y = \(\frac{9 x+4}{7}\)	7	-2	16	-11

 

Here MN is the graph of the equation \(\frac{x+2}{y+2}=\frac{7}{9}\)

 

Class 9 Maths WB Board

4. Length = x m
Breadth = y m
2(x + y) = 80
y = 40- x

x	20	30	10
y =40-x	20	10	30

Here AB is the graph of this equation.

 

 

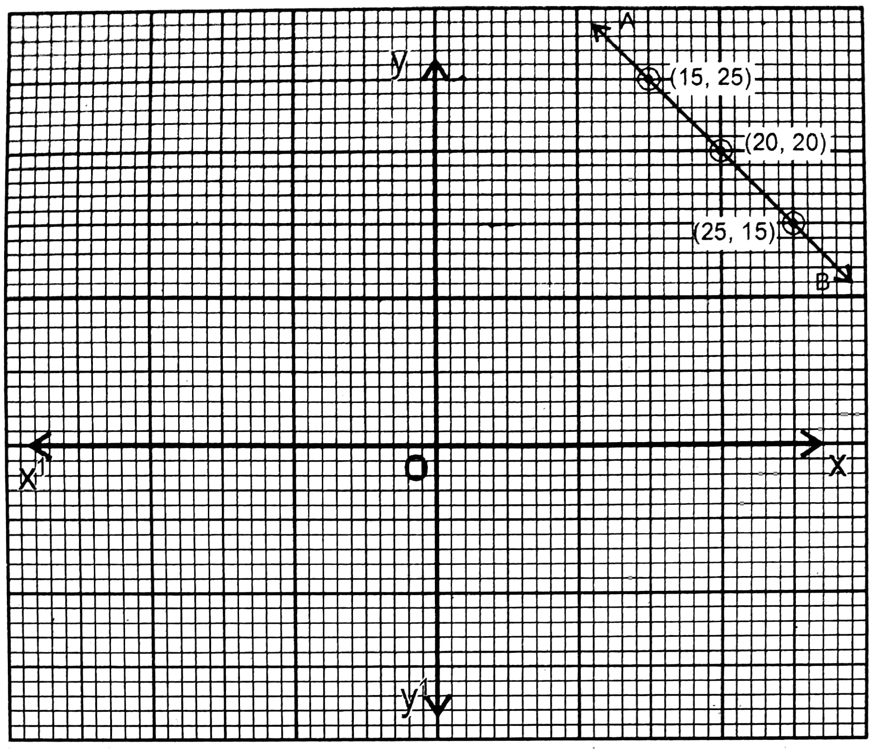
5. Larger no. = x
Smaller no.=y
5x = 8y or, \(x=\frac{8 y}{5}\)

x =8y/5	8	16	-16
y	5	10	-10

Here AB is the graph of the equation 5x = 8y.

 

 

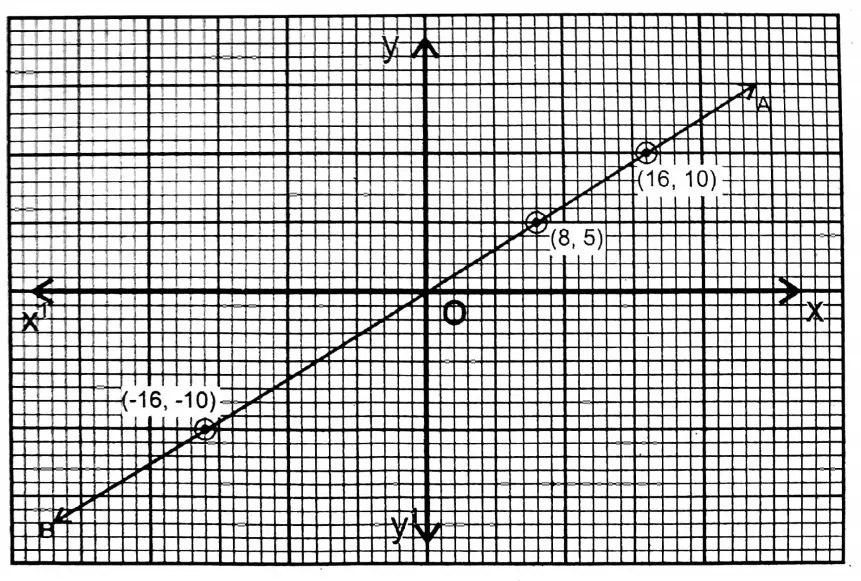
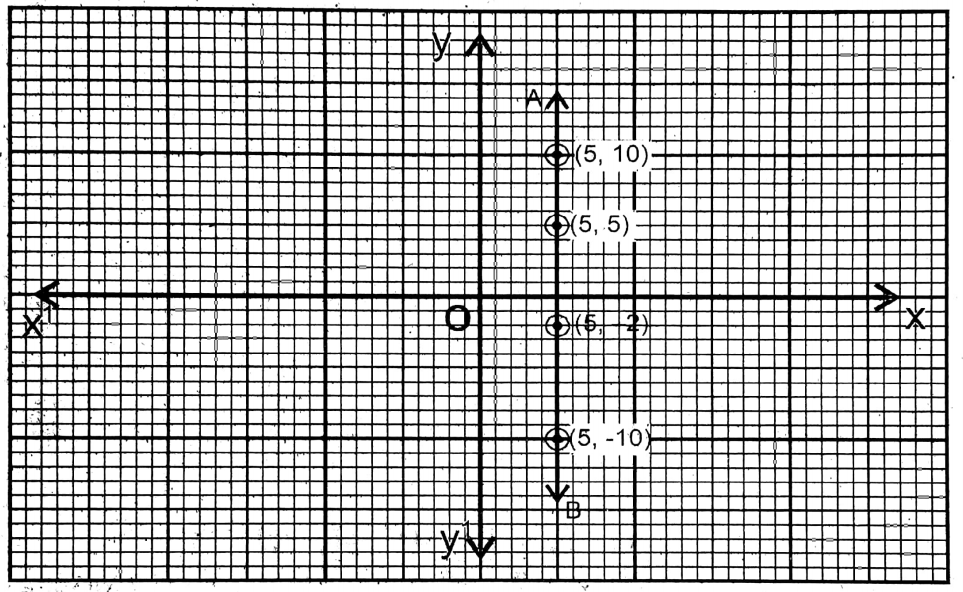
Question 5. Let us draw the graph of the following equations :

1. x = 5

Solution:For any value of y, the value of x will be 5.

∴ From the equation x = 5

x	5	5	5	5
y	-2	10	-10	5

 

On a graph paper the two perpendicular axes XOX’ & YOY’ are drawn and the points (5,-2), (5,10), and (5,3) (5,5) are plotted and joined. The straight line AB is the graph of the given equation.

 

Class 9 Maths WB Board

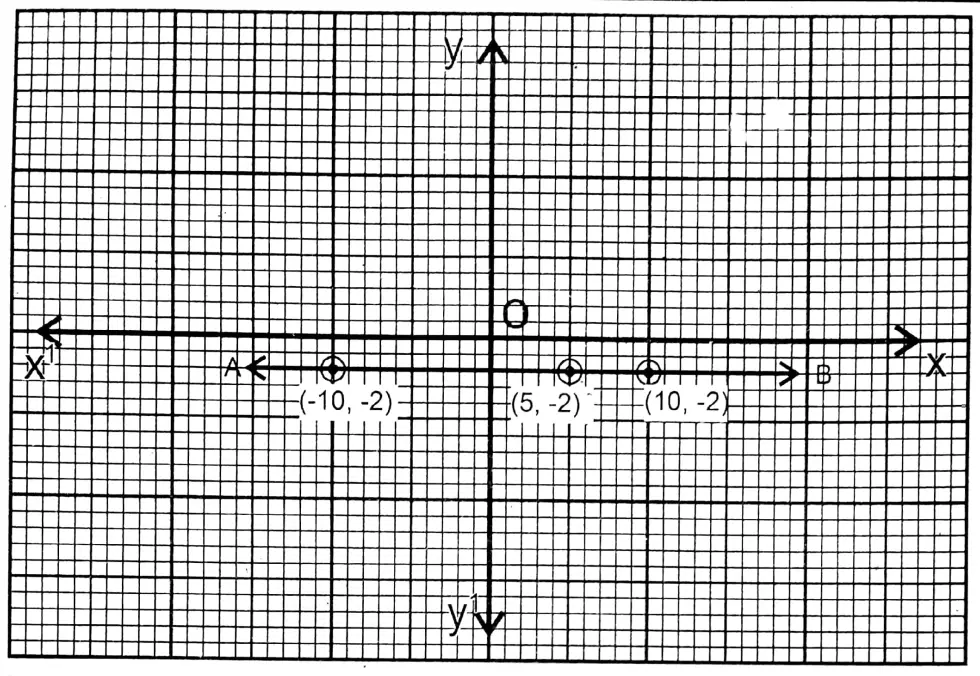
2. y+2=0

Solution: y +20 ie y = -2
∴For any value of x, the value of y will be (-2).
∴ y +2=0, i.e., y = -2
For any value of x, the value of y will be (-2)

x	-10	10	5
y	-2	-2	-2

 

On a graph paper, the two perpendicular axes XOX’ and YOY’ are drawn and the points (-10, -2), (10,-2), and (5,-2) are plotted and joined. The straight line AB is the graph of the given equation.

 

 

3. x = 3-4y

Solution:x=3-4y

x = 3- 4y	-13	11	3
y	0	2	0

 

The points are (3,0), (11,-2) & (-13, -4) and AB is the graph of this equation.

 

 

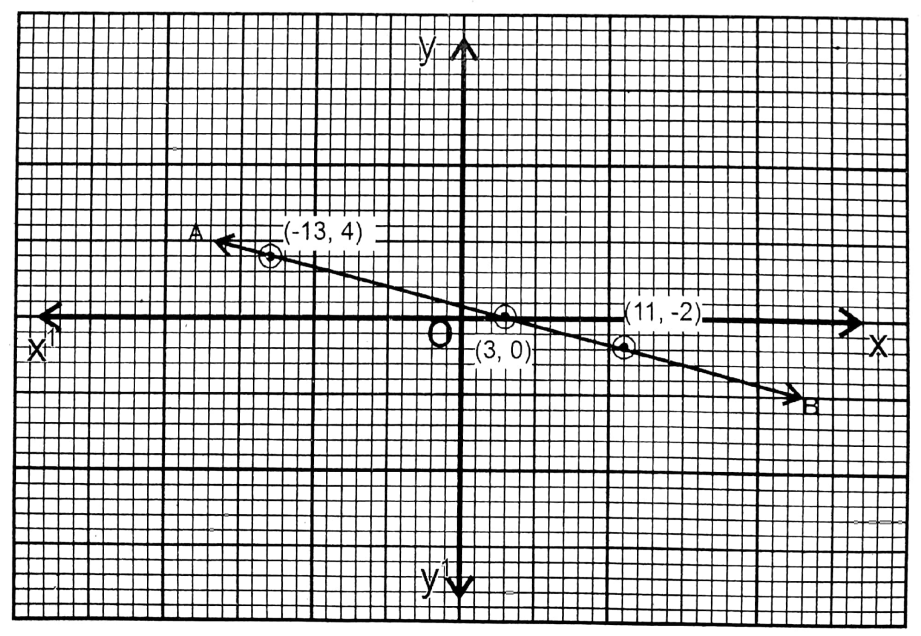
4. 3x7y = 21

Solution: 3x-7y=21 = 3x=21+ 7y

∴ \(x=\frac{21+7 y}{3}\)

 

x =\(\frac{21+7 y}{3}\)	7	0	14
y	0	-3	3

 

The points are (7,0), (0-3), (14, 3). MN is the graph of this equation.

 

 

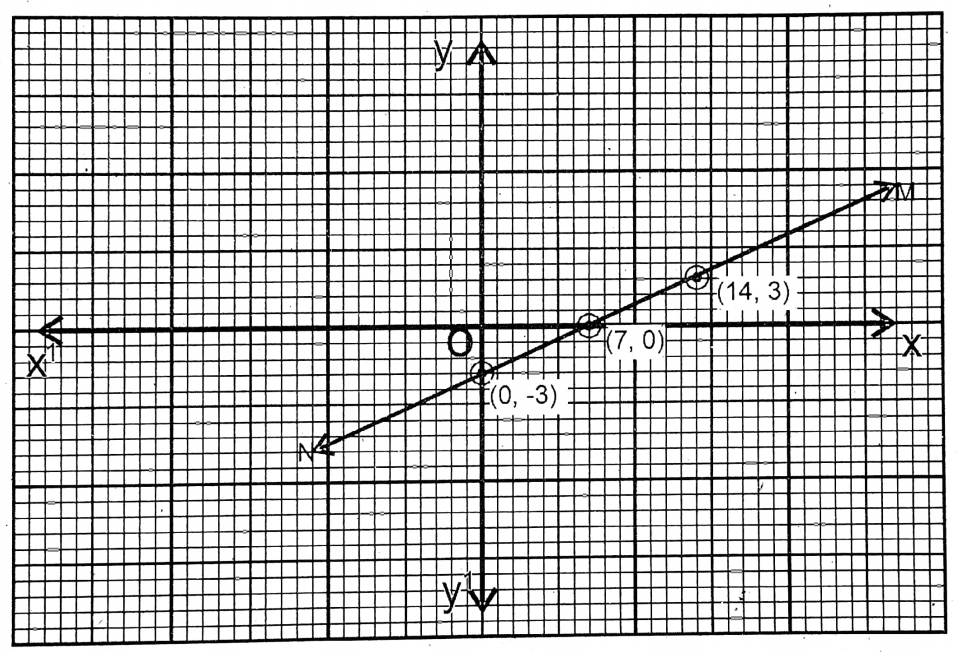
5. 5x-3y=8

Solution: 5x-3y=8
or, 5x = 8+ 3y

x =\(\frac{8+3 y}{5}\)	1	4	-2
y	-1	4	-6

 

The points are (1,-1); (4,4) & (7,9). EF is the graph of this equation.

 

 

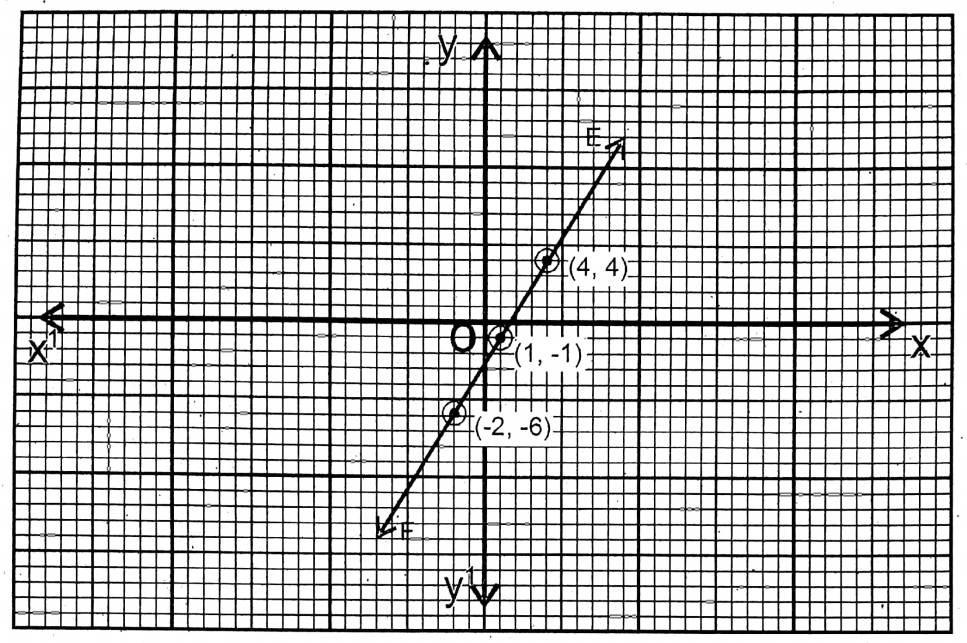
6. 2x + 3y = 11

Solution: 2x+3y= 11
or, 2x 11-3y

x	1	-2	4
y = \(\frac{11-2 x}{3}\)	3	5	1

 

The points are (1,3); (-2,5) & (4,1). KL is the graph of this equation.

 

 

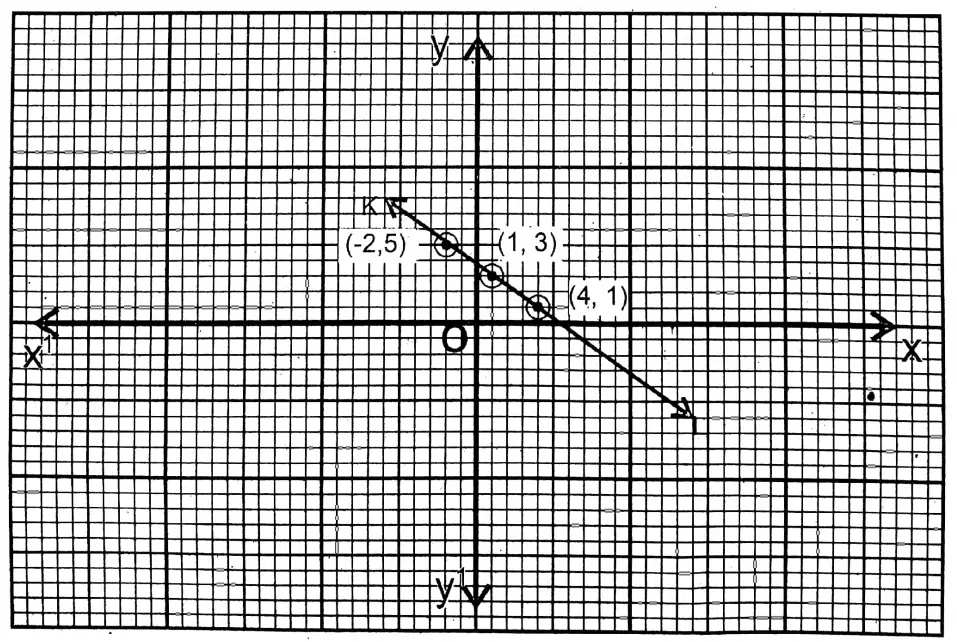
7. \(\frac{x}{3}+\frac{y}{4}=0\)

Solution:\(\frac{x}{3}+\frac{y}{4}=0\)

 

x = \(3 x\left(\frac{-y}{4}\right)\)	-3	6	4
y	4	-8	8

 

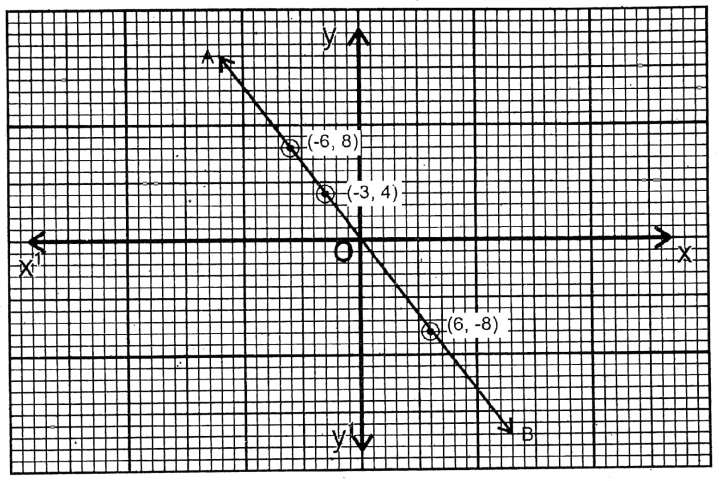
The points are (-6, 8); (-3,4); (6,-8). AB is the graph of the equation.

 

 

8. 6x-7y= 12

Solution: 6x-7y= 12

x = \(\frac{12+7 y}{6}\)	2	-5	16	9
y	0	-6	12	6

 

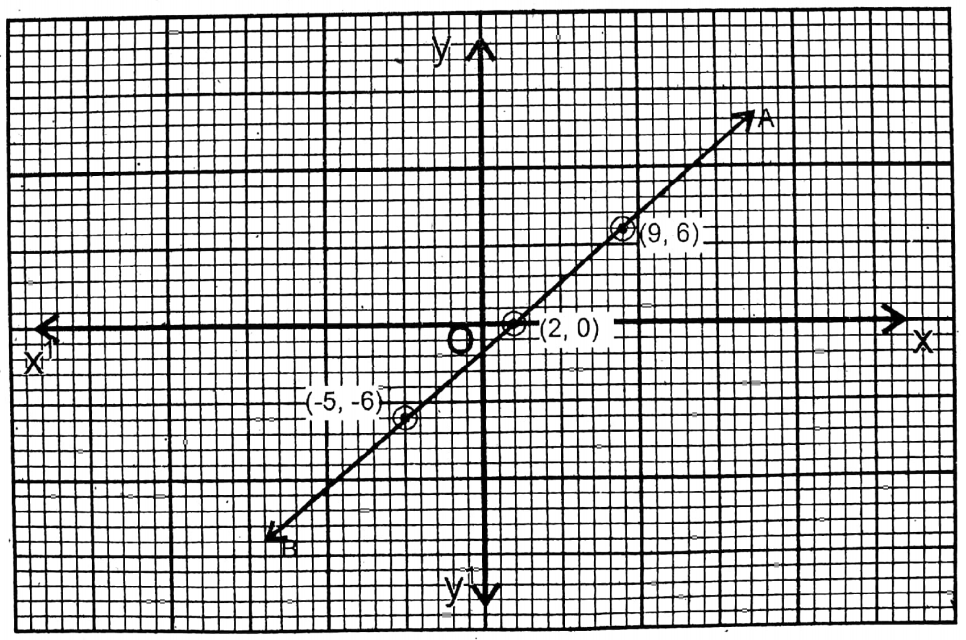
The points are (2,0); (-5, -6); (16,12) & (9, 6). AB is the graph of this equation.

 

 

9. x + y -10=0

Solution: x+y-10=0

x	0	5	15
y =10-x	10	5	5

 

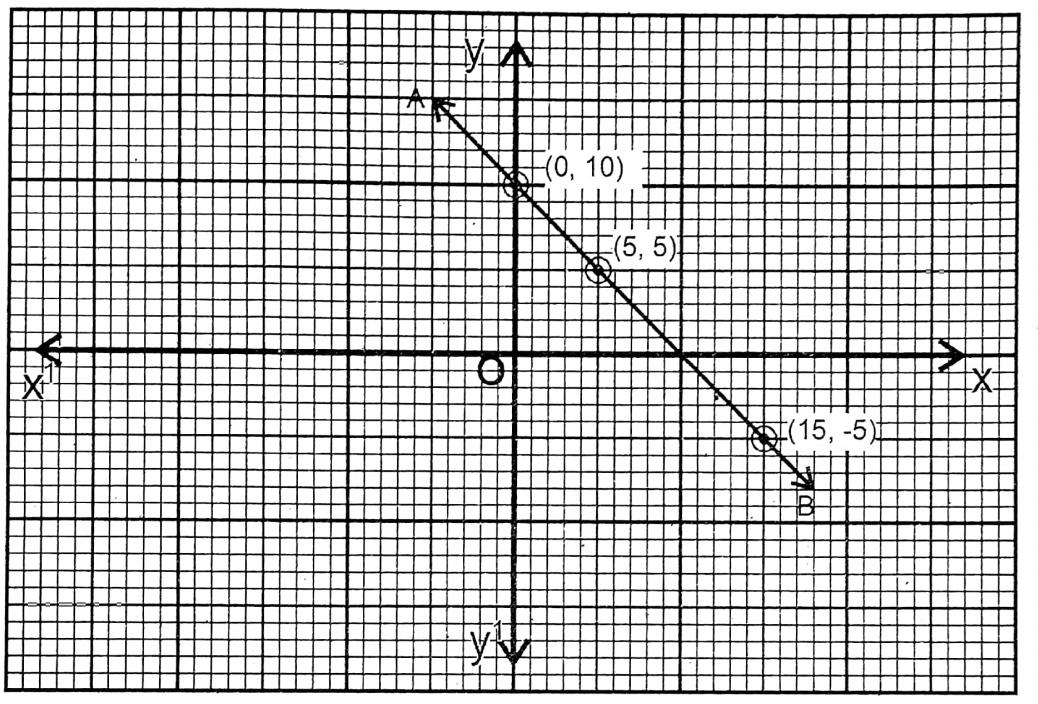
The points are (0,10); (15, -5), & (5,5) & AB is the graph of this equation.

 

 

10. y = 5x − 3

Solution: y=5x-3

x	2	0	-2
y = 5x-3	7	-3	-13

 

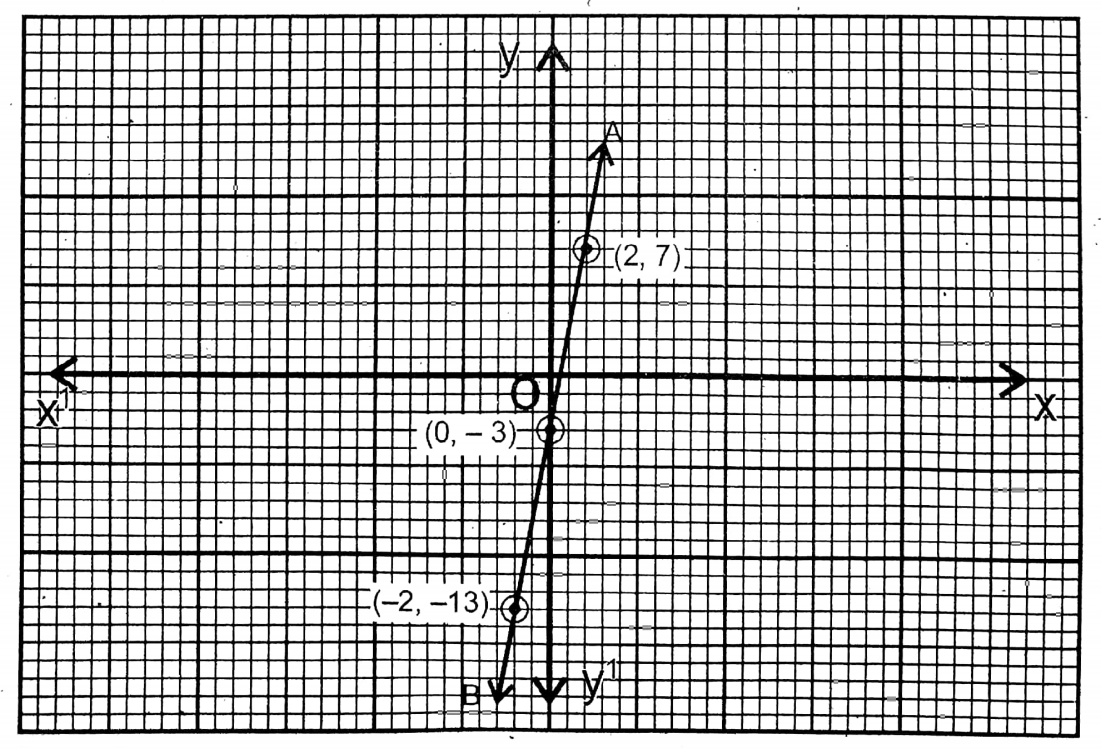
The points are (2,7); (0,-3); (-2, -13), and AB is the graph of this equation.

 

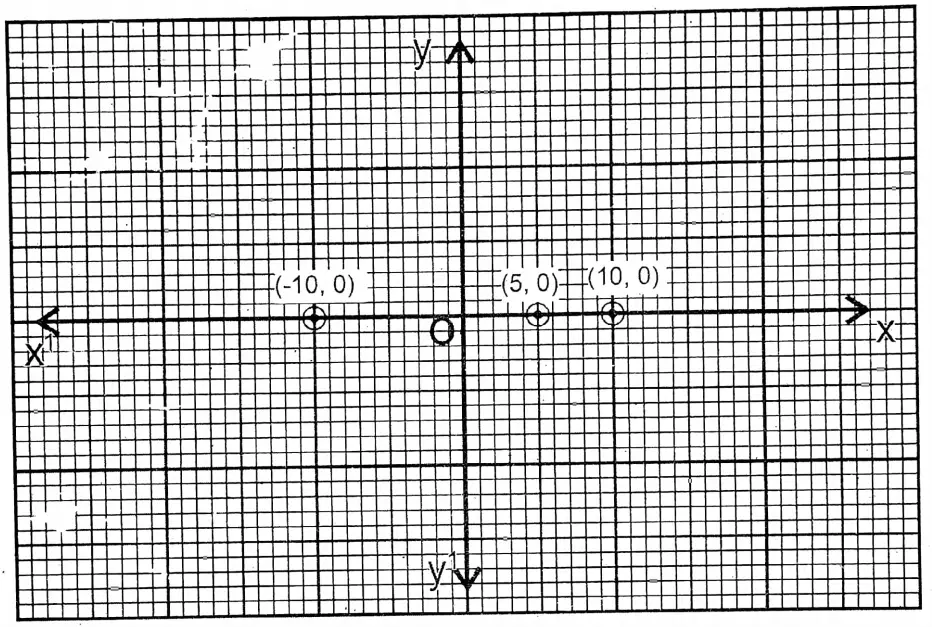
11. y = 0.

Solution:y = 0

x	-10	10	5
y	0	0	0

 

Here for any value x, the value of y will be ‘0’.

On a graph paper, two perpendicular axes XOX’ and YOY’ are drawn, and the points (-10,0); (10,0), and (5,0) are plotted and joined. The straight line PQ is the graph of the given equation (i.e., the x-axis).

 

 

Question 6. Let us express the following statements into simultaneous linear equations and solve them graphically.

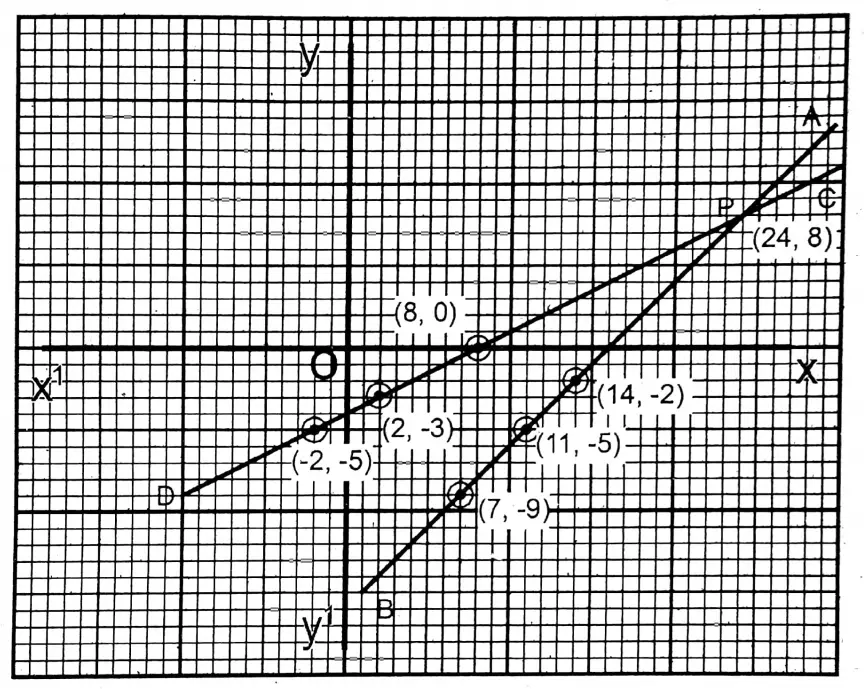
1. At present Rajat’s maternal uncle is 16 years older than Rajat. 8 years later, his maternal uncle’s age will be 2 times of his age. Let us calculate the present age of Rajat and that of his maternal uncle graphically.

Solution: Let at present Rajat’s maternal uncle’s age is x years & Rajat’s age is y years. x – y = 16…….(1)

x = y +16	7	11	14
y	-9	-5	-2

 

x+8=2(y +8)……(2)
or, x-2y= 8

x = 8 + 2y	8	2	-2
y	0	-3	-5

 

On graph paper, I drew XOX’ and YOY’ perpendicular to each other as the x-axis and y-axis respectively. Taking the side of the smallest square on graph paper as 1 unit the points (7,-9), (11, -5) & (14,-2) are plotted, joined, and extended to both sides.

The straight \(\overleftrightarrow{\mathrm{AB}}\) has been obtained. Similarly, the points (8,0), (2,-3) & (-2,- 5) are plotted and joined and the straight line \(\overleftrightarrow{C D}\) has been obtained.

\(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{C D}\) intersect each other at P. The coordinates of P are (24,8). Hence, from the graph x = 24 and y = 8.

∴ The present age of Rajat’s maternal uncle age is 24 years and the present age of Rajat is 8 years.

 

 

 

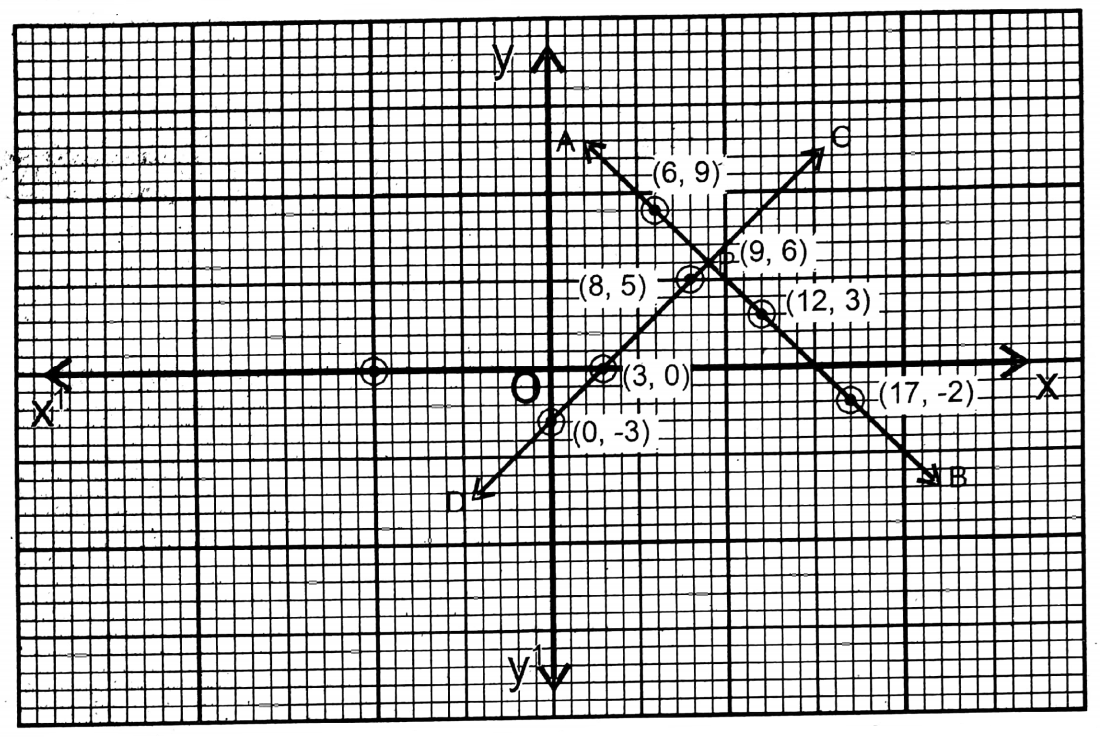
2. The sum of two numbers is 15 and their difference is 3. Let us write the numbers by solving them graphically.

Solution: Let one number be x and the other number be y.
From the 1st condition, x + y = 15 …..(1)
From the 2nd condition, x-y=3 …..(2)

From equation…..(1)

x	6	7	12
y	9	8	3

 

From equation….. (2)

x	3	0	8	12
y	0	-3	5	9

 

Plotting the points (6,9), (17,-2) & (12,3) and (4,1), (3,0) and (0,-3) on the graph paper and joining them respectively, the two straight lines PQ & RS are obtained. The two straight lines AB and CD intersect at P. (9,6)
∴ The 1st number (x) = 9
∴ The 2nd number (y) = 6

 

 

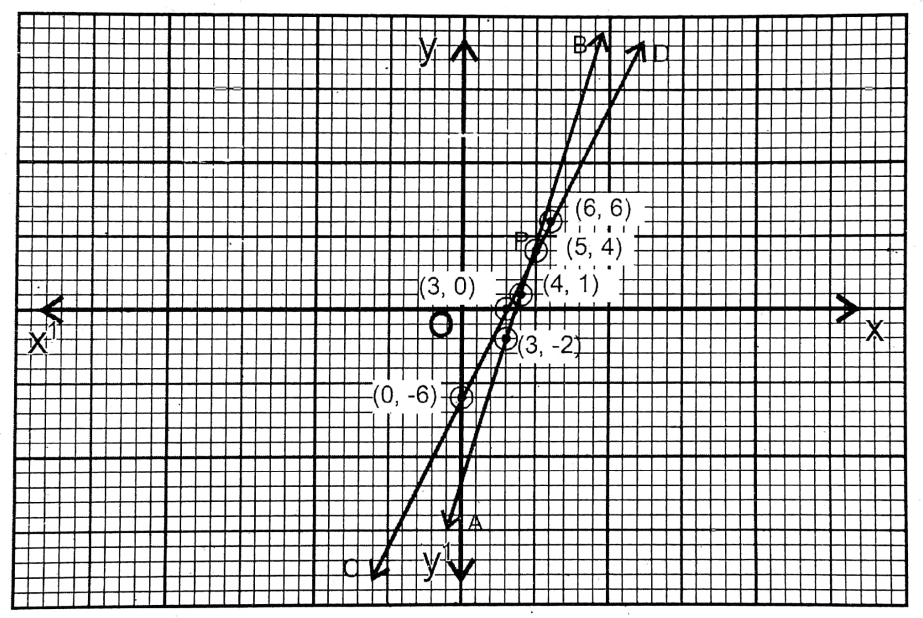
3. If 3 is subtracted from the numerator and 2 is added to the denominator, the fraction will be \(\frac{1}{3}\), and if 4 is subtracted from the numerator and 2 is subtracted from the denominator, the fraction will be \(\frac{1}{2}\). Let us construct the equation of from the denominator, the fraction will be a statement, and write the fraction by solving graphically.

Solution: Let the fraction = \(\frac{x}{y}\)

From the 1st condition, \(\frac{x-3}{y+2}=\frac{1}{3}\)  …….(1)

or, 3x-9= 2y + 2
or, 3x-2y= 11

From the 2nd condition, \(\frac{x-4}{y-2}=\frac{1}{2}\)  …..(2)

or, 2x-8=y-2
or, 2x – y = 6

From equation …….(1)

x	4	5	3
y = 3x-11	1	4	-2

 

\(\overleftrightarrow{\mathrm{AB}}\) is the graph of this equation.

 

From equation………(2)

x	3	0	6
y = 2x-6	0	-6	6

 

\(\overleftrightarrow{C D}\) is the graph of this equation.

 

Taking the side of the smallest square on the graph paper as 1 unit in both the equations, \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{C D}\) intersect at P(5,4).
∴ x = 5, y = 4

∴ The fraction is \(\frac{5}{4}\)

 

 

4. The perimeter of Rohit’s rectangular garden is 60 m. If the length of the garden is increased by 2 m and the breadth is decreased by 2 m, the area of the garden is decreased by 24 sq.m. Let us write the length and breadth of the garden by solving graphically.

Answer: Let the length and breadth of the garden be x and y m respectively. From the 1st condition, 2(x+y)= 60
or, x + y = 30. ….(1)
∴ x = 30-y

\(\overleftrightarrow{\mathrm{AB}}\) is the graph of this equation.

 

x	20	15	18
y	10	15	12

 

From the 2nd condition, (x + 2) (y2) = xy-24
or, xy + 2y – 2x-4=xy-24
or, -2x+2y=-24+4 =2(x – y) = 20 = x – y = 10

x	5	15	10
y	-5	5	0

 

\(\overleftrightarrow{C D}\) is the graph of this equation. AB & CD intersect each other at P (20,10), i.e., x = 20; y = 10.

 

∴ Length 20 m & Breadth = 10 m.

 

 

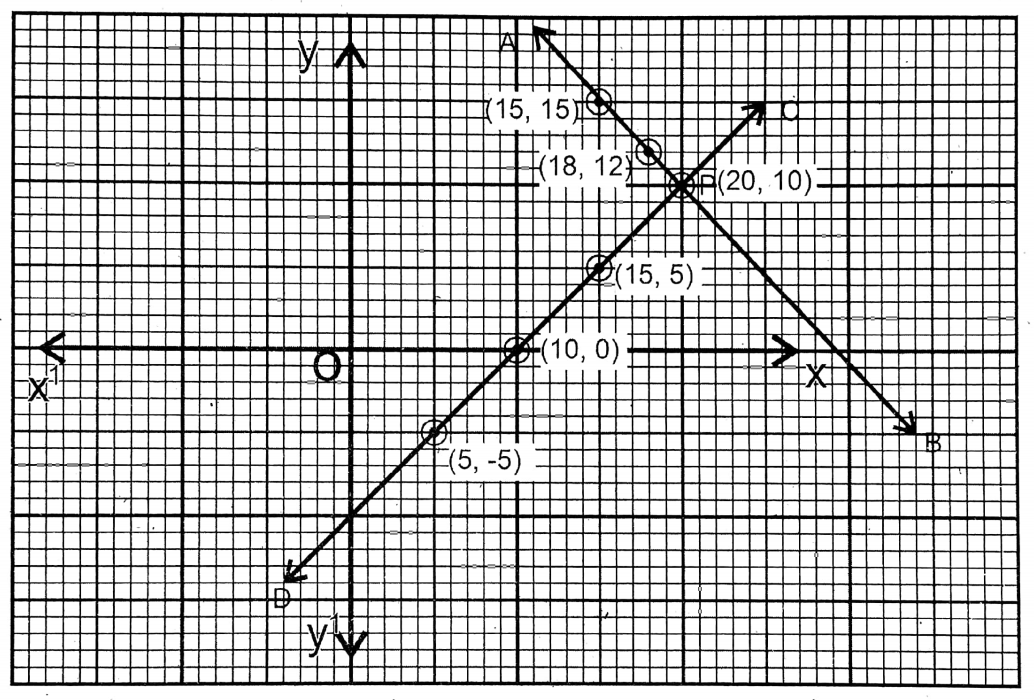
5. A boat covers 64 km in 16 hrs. while traveling downstream and it covers 24 km in 8 hrs. while traveling upstream. Let us write the speed of the boat in still water and the speed of the stream by solving graphically.

Solution: Let the speed of the boat is still water = x km/hr and the speed of the stream = y km/hr.
From 1st condition, 16(x + y) = 64
∴ x + y = 4……….. (1)

From 2nd condition, 8(x − y) = 24
∴ x -y = 3….. (2)

From equation no …….(1)
= x +y = 4

x	10	4	-6
y	-6	0	10

 

From equation no….(2)
or, x-y=3

x	3	0	10
y	0	-3	7

 

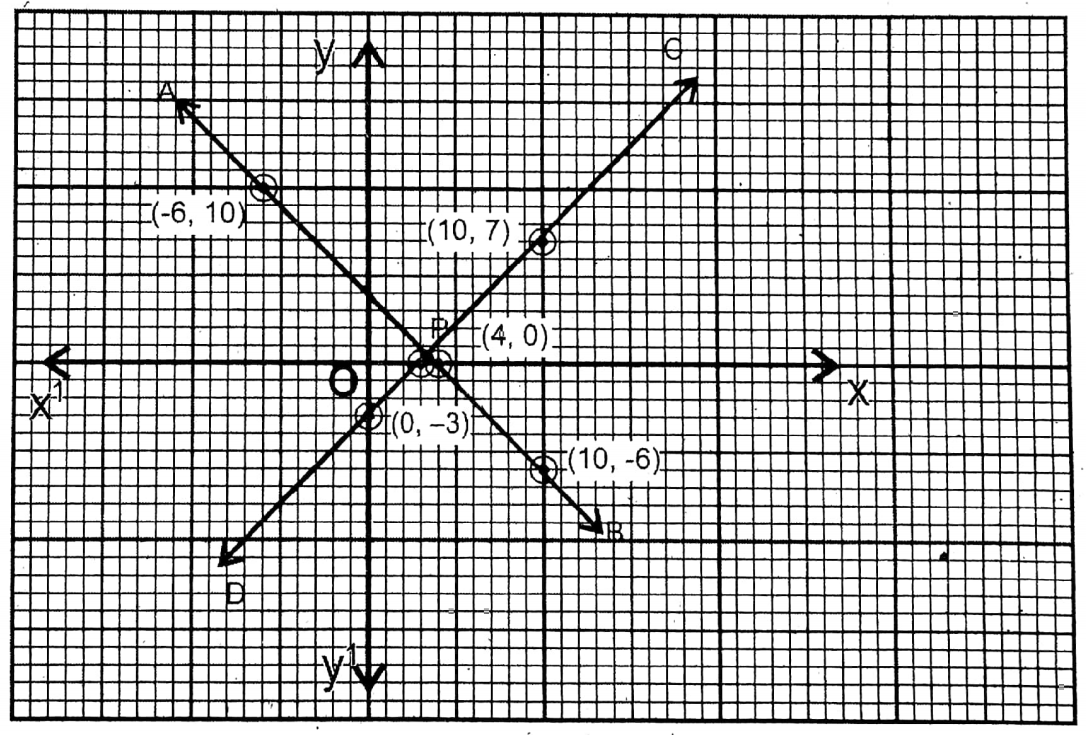
On the graph paper XOX’ and YOY’ are drawn, perpendicular to each other as x- axis and Y-axis respectively. Taking the side of the small square on graph paper as 1 unit the points (10,-6), (4,0), and (-6,10) are plotted and joined and extended to both sides, and the straight line \(\overleftrightarrow{\mathrm{AB}}\) is obtained.

similarly, the points (3,0); (0,-3), and (10,7) are plotted and joined, the straight line \(\overleftrightarrow{C D}\) is obtained \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{C D}\) intersect each other at P \(\left(\frac{7}{2}, \frac{1}{2}\right)\).

∴ \(x=\frac{7}{2}, y=\frac{1}{2}\)

 

∴ The speed of the boat = \(\frac{7}{2}\) 3.5 km/hr and the speed of the stream= \(\frac{1}{2}\) = .5 km/hr.
[in each case, take the side of the smallest square on the graph paper as 1 unit.]

 

 

 

Question 7. Let us draw the graph of the following simultaneous linear equations and determine the coordinates of their point of intersection.

1. x = 0 and 2x + 3y = 15

Solution: x = 0… (1)

x	0	0	0
y	5	10	-10

 

2x + 3y = 15…..(2)

x	0	3	-3
y =\(\frac{15-2 x}{3}\)	5	3	7

 

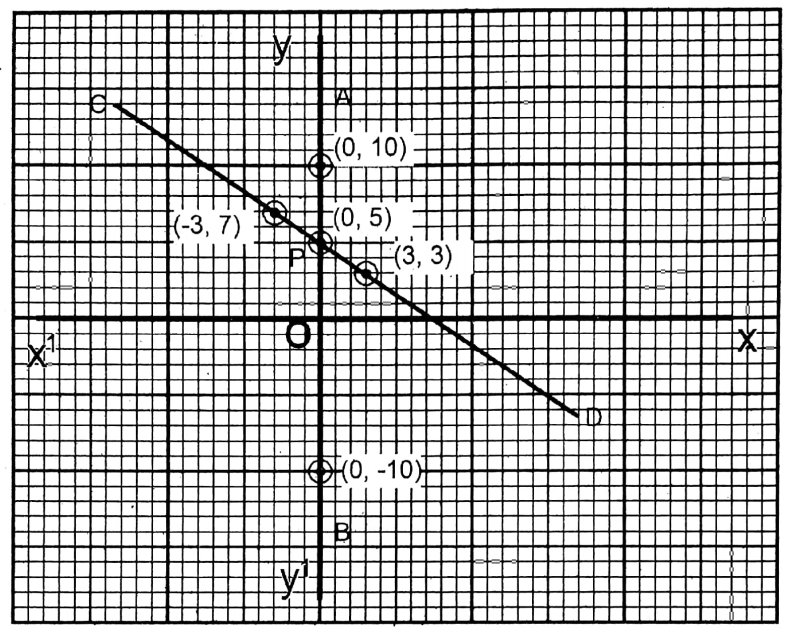
On the graph paper, take two axes, XOX’ & YOY’ perpendicular to each other as the x-axis and y-axis respectively. The points (0,5) (0,10) (0,-10) and (0,5), (3,3) & (-3,7) are plotted. The two straight lines interest each other at P (0,5).
∴ x = 0; y = 5

 

 

 

2. y = 5 and 2x + 3y = 11.

Solution: y = 5 and 2x + 3y = 11
∴ y = 5…(1)

2x + 3y ….(2)

x	4	1	-2
y =\(\frac{11-2 x}{3}\)	1	3	5

 

 

 

 

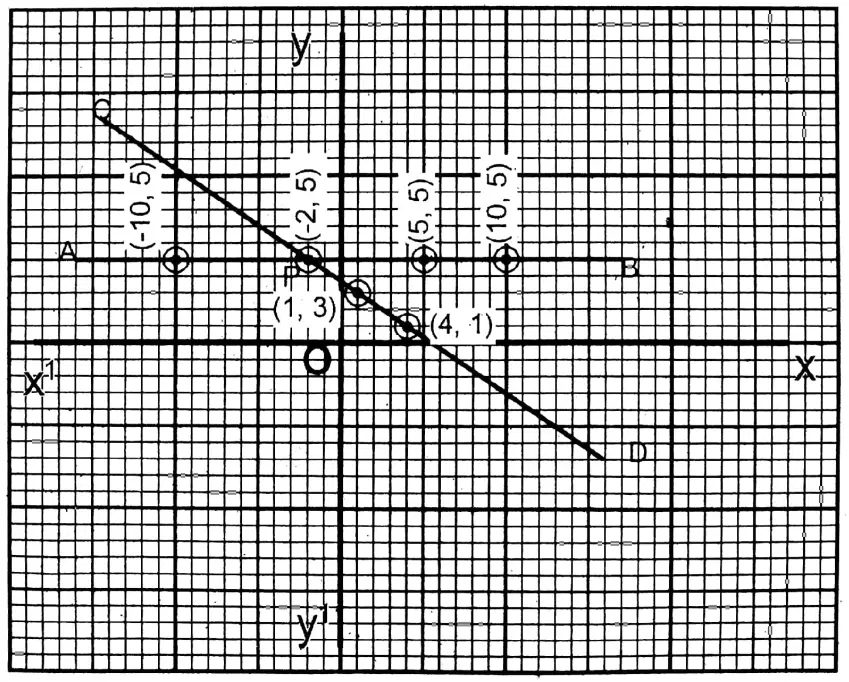
From the graph, after plotting the points (-5,5), (0,5), (2,5) & (1,3), (7,-1) (-8,9), two straight lines are drawn. They intersect each other at (-2,5).
∴ x=-2, y = 5

3. x + y = 12 and x – y = 2

Solution: x+y= 12 …..(1)

x	3	7	15
y	9	5	-3

 

x-y=2…(2)

x	2	-3	10
y	0	-5	8

 

 

 

 

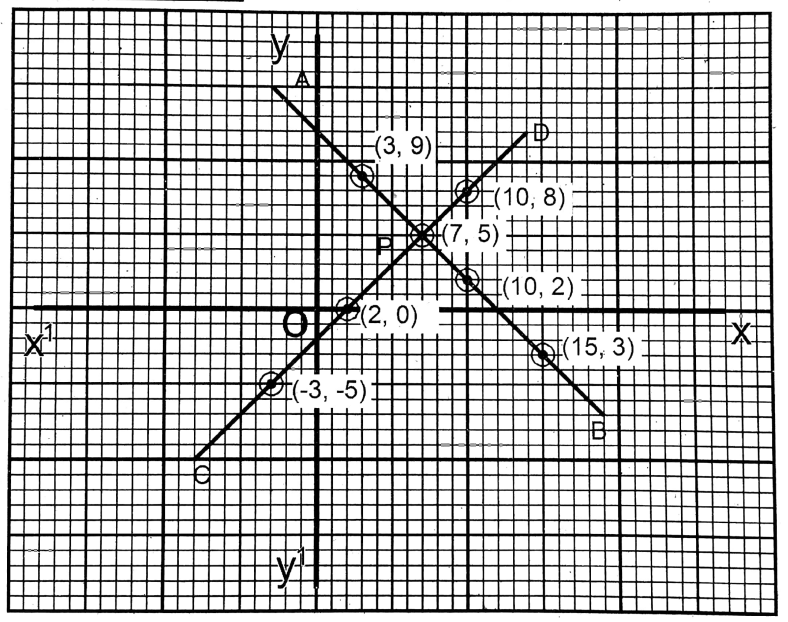
The two straight lines obtained from these two equations intersect each other at P (7,5).
∴ x=7;y=5

4. 3x-5y = 16 and 2x-9y=5

Solution: 3x5y= 16…..(1)

x	2	-3	7
y =\(\frac{3 x-16}{5}\)	-2	-5	1

 

2x-9y=5….(2)

x =\(\frac{5+9 y}{2}\)	-2	7	-11
y	-1	1	-3

 

 

 

 

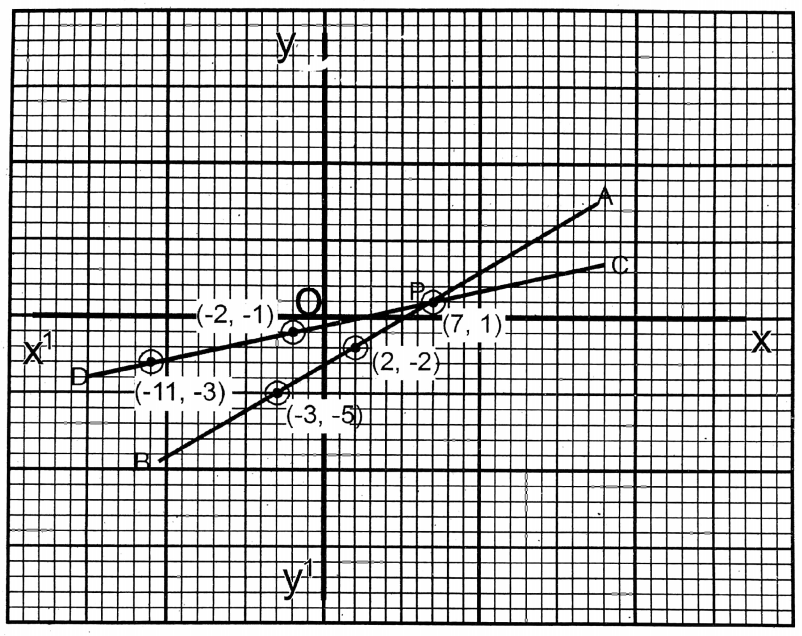
The two straight lines AB & CD obtained from these two equations intersect each other at P (7, 1).
∴ x = 7; y = 1

Question 8. Let us solve the following equations graphically:

1. 4x – y = 3; 2x + 3y = 5

Solution: 4x – y = 3 …… (1)

x =\(\frac{3+y}{4}\)	2	1	0
y	5	1	3

 

2x + 3y = 5…..(2)

x =\(\frac{5-3 y}{2}\)	1	-2	-5
y	1	3	5

 

 

 

 

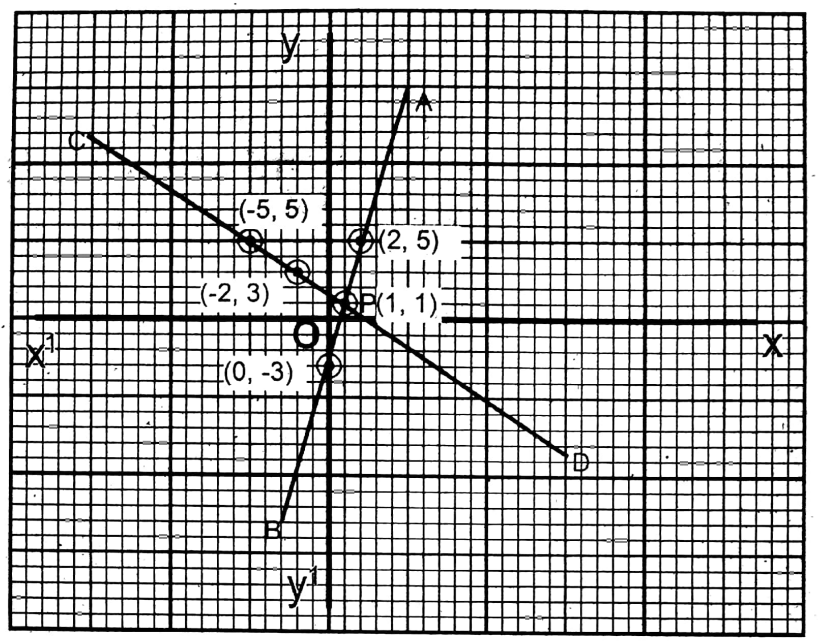
From the graph after plotting the points (2,5); (1,1); (0, -3) and (-2,3), (-5,5), (1,1), two straight lines are drawn. They intersect each other at P (1,1).
∴ x = 1; y = 1

2. 3x – y = 5; 4x + 3y = 11

Solution: 3x-y=5…….. (1)
4x + 3y = 11……… (2)

x	0	3	4
y = 3x-5	-5	4	7

 

x	-1	5	-2
y =\(\frac{11-4 x}{3}\)	5	-3	1

 

 

 

 

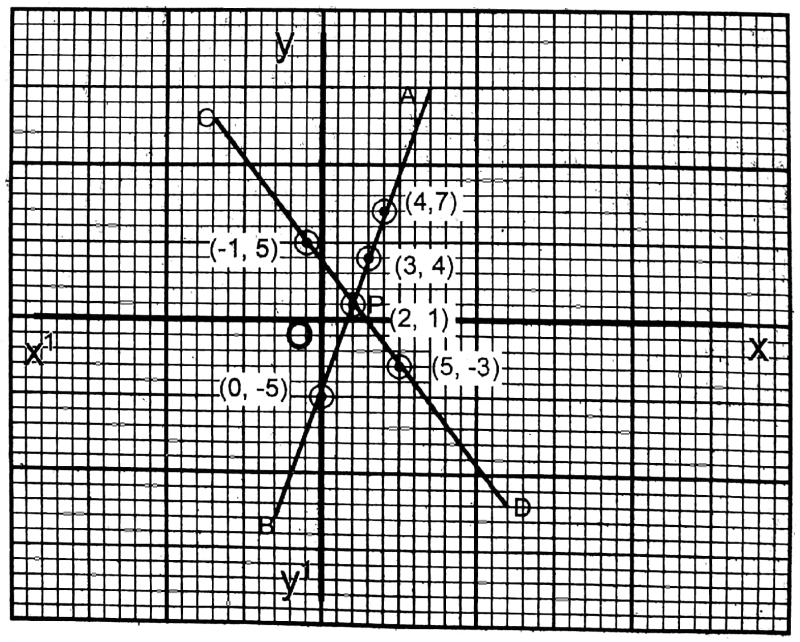
The two straight lines intersect each other at P (2, 1).
∴ x = 2, y =1

3. 3x-2y= 1; 2x – y = 3

Solution: 3x-2y= 1……… (1)

x =\(\frac{1+2 y}{3}\)	1	3	-3
y	1	4	-5

 

2x – y = 3…(2)

x =\(\frac{3-y}{2}\)	5	0	3
y	7	-3	3

 

 

 

 

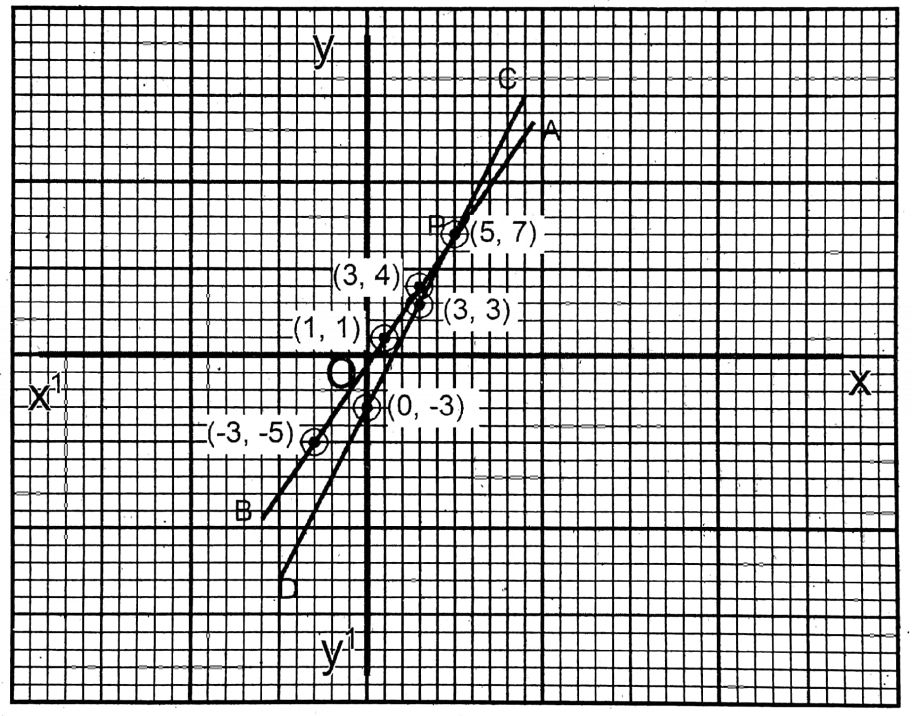
The two straight lines intersect each other at P (5, 7).
∴ x = 5; y = 7

4. 2x + 3y = 12; 2x = 3y

Solution: 2x + 3y = 12 ….(1)

x	0	-3	6
y =\(\frac{12-2 x}{3}\)	4	6	0

 

2x = 3y…..(2)

x	-6	9	3
y =\(\frac{2 x}{3}\)	-4	6	2

 

 

 

 

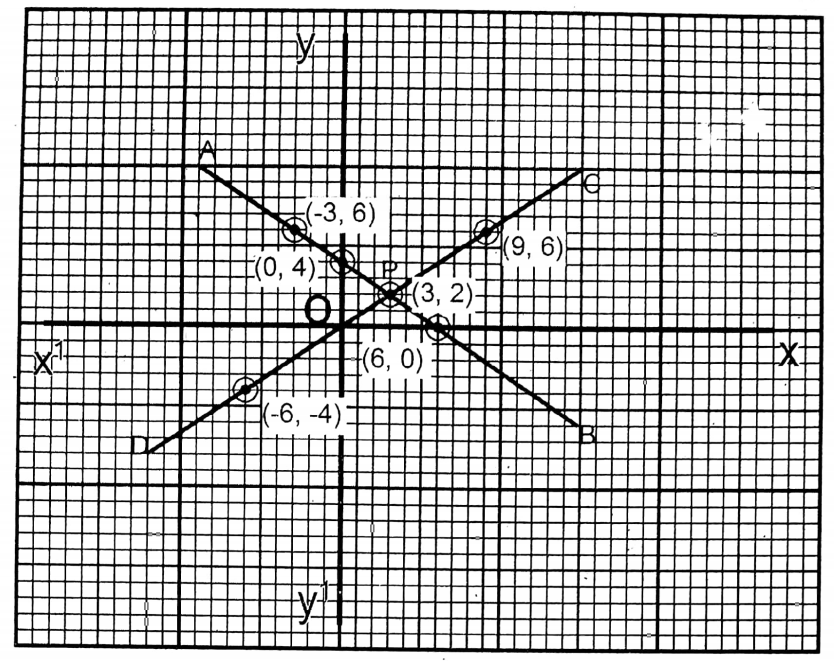
The two straight lines intersect each other at P(3, 2).
∴ x=3, y=2

5. 5x-2y= 1; 3x+5y= 13

Solution: 5x-2y= 1…..(1)

x =\(\frac{1+2 y}{5}\)	3	-1	1
y	7	-3	2

 

3x+5y= 13….(2)

x =\(\frac{13-5 y}{3}\)	6	-4	1
y	-1	5	2

 

 

 

 

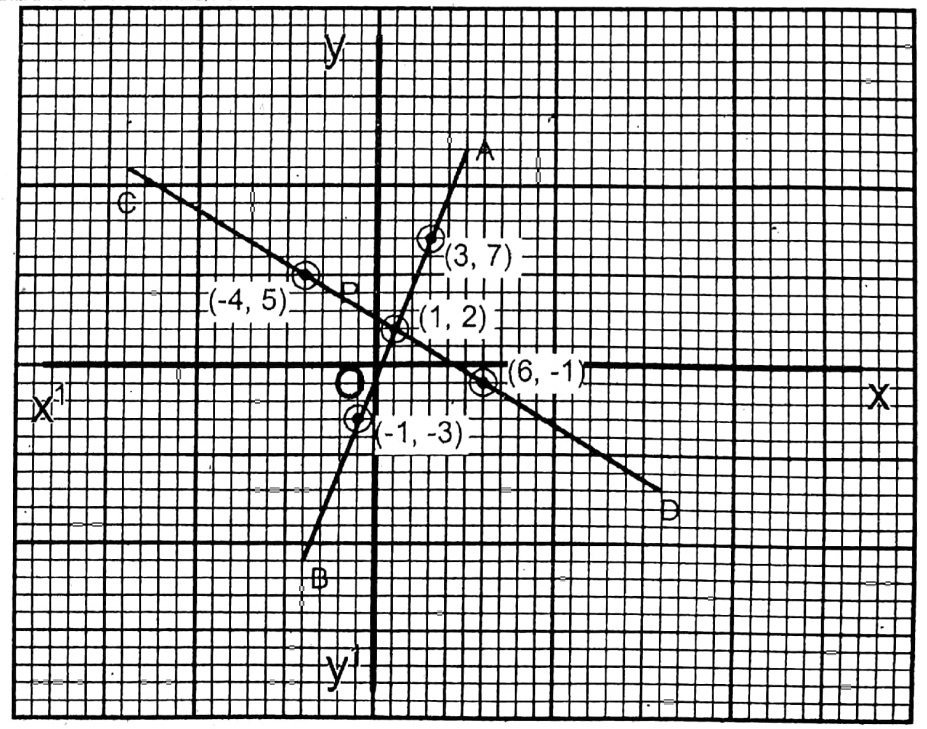
The two straight lines PQ and RS are obtained from two given equations after plotting the points (3,7), (-3,-8), (1,2) and (6,-1), (-4,5) (1,2) and they intersect at N (1,2).
∴ x = 1, y = 2

Question 9. Let us determine the solution of the given equations graphically: 3x+2y= 12, 12 = 9x-2y

Solution: 3x+2y= 12 …… (1)

x =\(\frac{12-2 y}{3}\)	4	0	6
y	0	6	-3

 

9x-2y= 12…(2)

x =\(\frac{12+2 y}{9}\)	0	2	4
y	-6	3	12

 

 

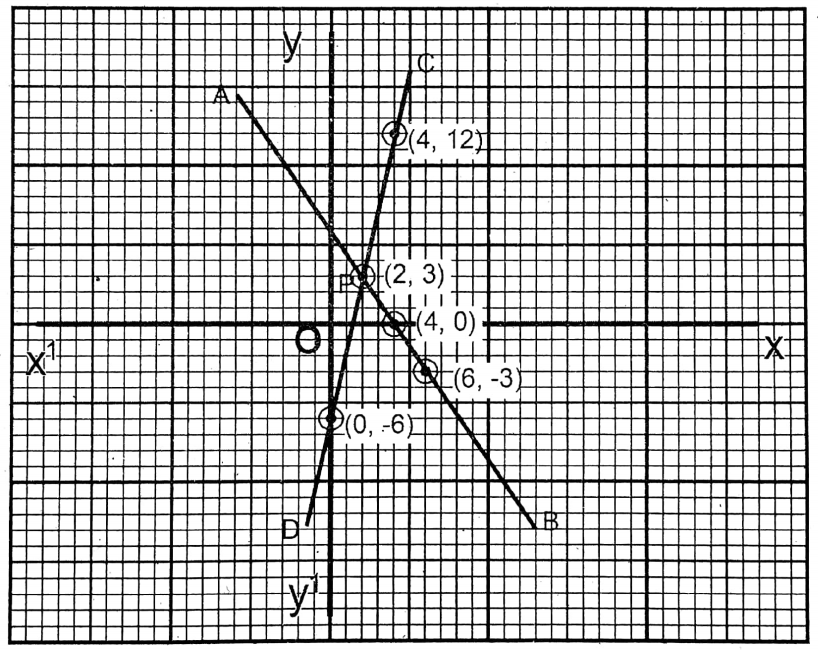
On the graph paper XOX’ & YOY’ are drawn perpendicular to each other as the x-axis and y-axis respectively. Taking the side of the smallest square on graph paper as 1 unit the points (4,0), (2,3), (6,-3) are plotted, joined, and extended to both sides; the straight line \(\overleftrightarrow{\mathrm{AB}}\) is obtained.

Similarly, the points (0,-6), (2,3), and (4,12) are plotted and joined; the straight line \(\overleftrightarrow{C D}\) is obtained. \(\overleftrightarrow{\mathrm{AB}}\) and \(\overleftrightarrow{C D}\) intersect each other at P (2,3).
∴x=2, y = 3

Question 10. Let us draw the graph of the equation \(\frac{x}{3}+\frac{y}{4}=2\) and calculate the area 3 4 of the triangle formed by the graph and the axes and write the area.

Solution:

\(\frac{x}{3}+\frac{y}{4}=2\)

or, 4x + 3y = 24

x	6	9	3
y	0	-4	4

 

 

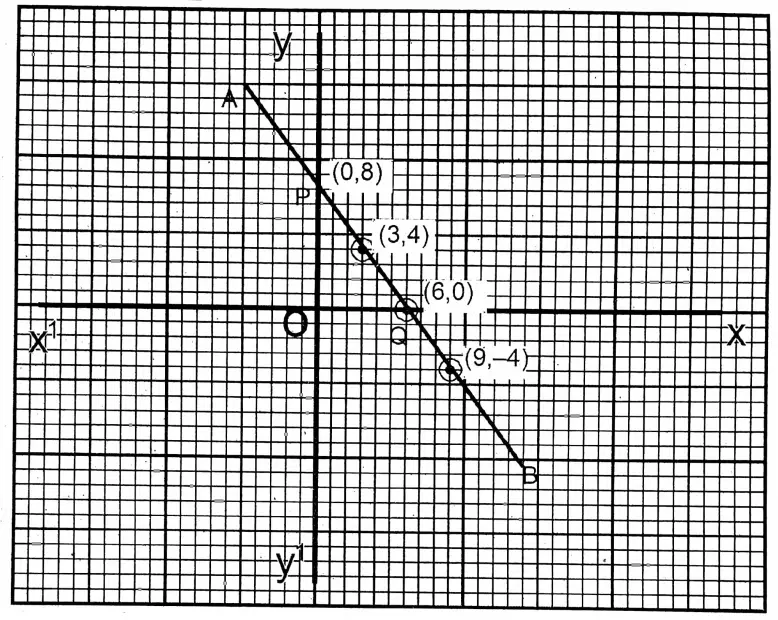
We take the side of the smallest square on the graph paper as one (1) unit. The points (6, 0), (9,-4), (3, 4) are plotted and joined, and extended to both sides; the straight line \(\overleftrightarrow{\mathrm{PQ}}\) is obtained. The straight line \(\overleftrightarrow{\mathrm{AB}}\) cuts the x-axis and y-axis at P and Q respectively. The coordinates of Q are (6,0) and the coordinates of P are (0,8).

∴ POQ is the triangle formed by the straight line PQ and the axes.

∴ Area of ΔPOQ

\(\frac{1}{2}\) Χ OP Χ OQ = \(\frac{1}{2}\) Χ 6 Χ8 = 24 units.

Question 11. Let us draw the graph of the three equations x = 4, y = 3, and 3x + 4y = 12 and determine the area of the triangle formed by the graph.

Solution: x = 4…………(1)

x	4	4	4
y	-10	10	5

 

y = 3…………(2)

x	10	4	6
y	3	3	3

 

3x + 4y = 12…..(3)

x	0	4	8
y =\(\frac{12-3 x}{4}\)	3	0	-3

 

 

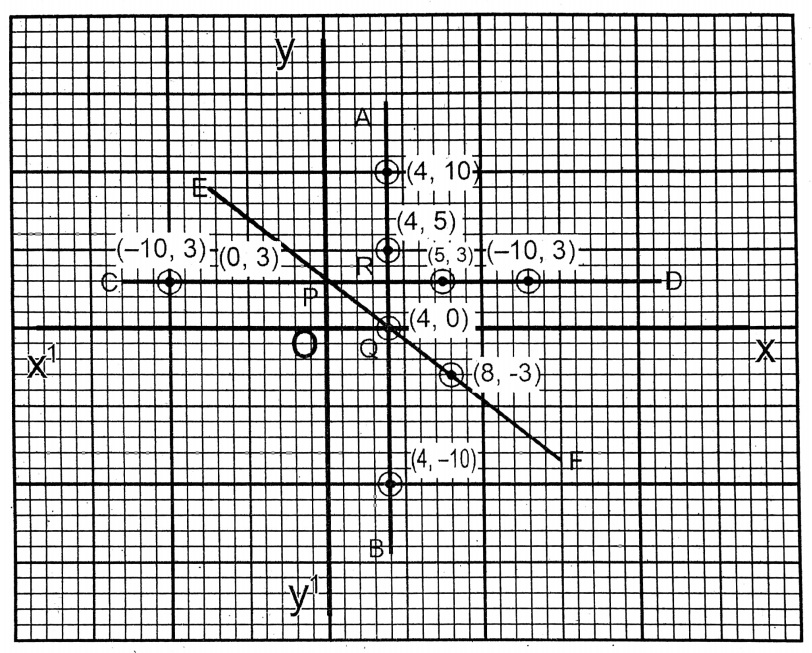
On the graph paper, taking the side of the smallest square as one (1) unit, the points (4,-10), (4,0) (4,5); (10,3), (4,3), (-10,3) and (0,3), (4,0), (8,-3) are plotted; and three straight lines are obtained (AB, CD, EF) and the triangle thus formed is (POQ).

∴ The area of ΔPOQ= \(\frac{1}{2}\) Χ OP Χ OQ = \(\frac{1}{2}\) Χ 3 x 46 square units.

Question 12. Let us draw the graph of the equation \(y=\frac{x+2}{3}\) From the graph let’s determine the value of y when x = -2 and the value of x when y = 3.

Solution: \(y=\frac{x+2}{3}\)

 

x	4	7	-5
y	2	3	-1

 

 

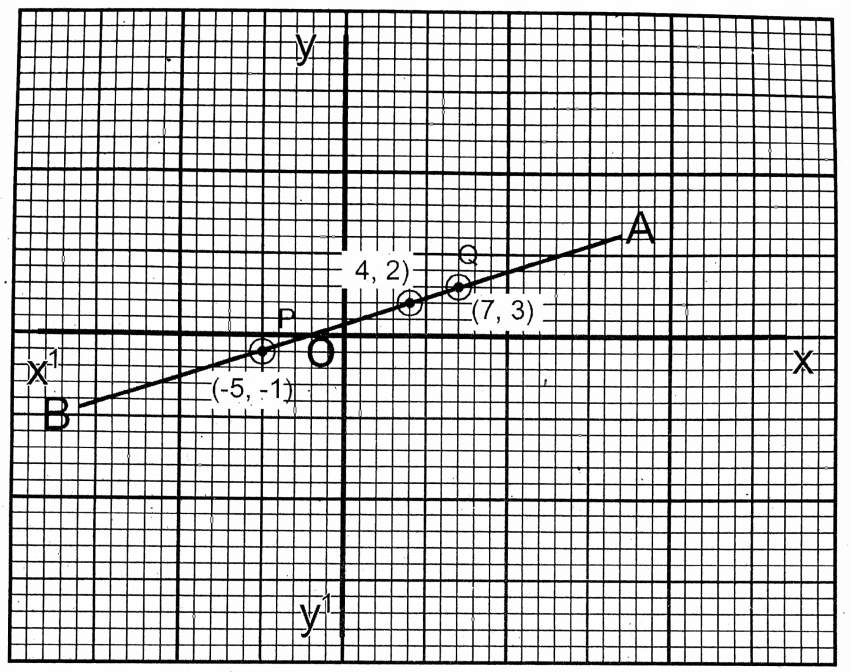
On the graph paper, we take the side of the smallest square as one (1) unit. The points (4,2), (7,3) and (-5,-1) are plotted and joined. The straight line AB is obtained. Now from the graph, when x = -2, the value of y = 0 (P), and when y = 3, the value of x = 7 (Q).

Question 13. Let us solve graphically: \(\frac{3 x-1}{2}=\frac{2 x+6}{3}\)

Solution: Let \(y=\frac{3 x-1}{2}\) …..(1)

x	3	7	-5
y	4	10	-8

 

and \(y=\frac{2 x+6}{3}\) …..(2)

x	0	3	-3
y	2	4	0

 

 

 

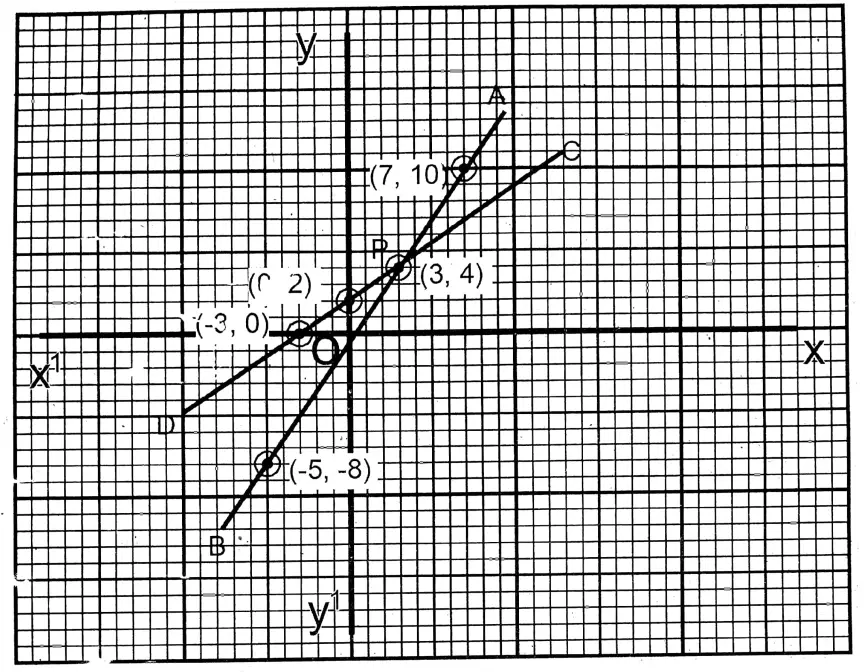
On the graph paper, taking the side of the smallest square as one (1) unit, the points (5,8), (-1,-2) and (1,1) and (6,6), (-6,-2) and (-3,2) are plotted and joining them we get \(\overleftrightarrow{A B}[latex] and [latex]\overleftrightarrow{C D}\) respectively. The two straight lines \(\overleftrightarrow{A B}[latex] and [latex]\overleftrightarrow{C D}\) intersect at P (3, 4).

Question 14. Multiple Choice Questions

1)The graph of equation 2x + 3 = 0 is
(1)Parallel to the x-axis
(2)Parallel to the y-axis
(3)Not parallel to any axis
(4)Passing through the origin

Solution: (1)Parallel to the x-axis

2)The graph of the equation ay + b = 0 (a and b are constants and a + 0, b + 0) is
(1)Parallel to the x-axis
(2)Parallel to the y-axis
(3)Not parallel to any axis
(4)passing through origin

Solution: (1) parallel to the x-axis

3) The graph of equation 2x + 3y = 0 is
(1)Parallel to x-axis
(2)Parallel to y-axis
(3)Passing through origin
(4)Passing through (2, 0)

Solution: (3)Passing through origin

4)The graph of the equation cx + d = 0 (c & d are constants and c≠0) will be y-axis, when
(1)d = -c
(2)d = c
(3)d = 0
(4)d = 1

Solution: (3)d = 0

5)The graph of the equation ay + b = 0 (a & b are constants and a ≠0) will be x-axis, when
(1)b = a
(2)b = -a
(3)b = 2
(4)b = 0

Solution: (4) b=0

Question 15. Short answer type questions:

(1)Let us write the coordinates of the point of intersection of the graph of equation 2x + 3y = 12 and the x-axis.

Solution: Equation of the x-axis is y = 0.
∴ And the 1st equation is 2x + 3y = 12 = 2x + 3(0) = 12
∴ x = 6
∴ The point of intersection is (6,0).

(2)Let us write the co-ordinates of the point of intersection of the graph of the equation 2x-3y= 12 and the y-axis.

Solution: Equation of the y-axis is x = 0
∴ And the 1st equation is 2x-3y = 12 =2×0-3y=12
∴ y=-4
∴ The point of intersection is (0,-4).

(3) Let us write the area of the triangle formed by the graph of the equation 3x + 4y = 12 and the co-ordinate axes.

Solution: The given is 3x + 4y = 12 => \(\frac{x}{4}+\frac{y}{3}=10\)

∴ Area of the triangle = x

x	6	0	9
y	0	-4	2

 

(4)Let us write the distances of the point (6, -8) from x-axis and y-axis.

Solution: The distance of the point (6,-8) from x-axis is 8 and the distance of the point (6, -8) from y-axis is 6.

(5) Let us write the angle derived from the equation x = y in the positive direction of x-axis.
Solution: The graph of the equation x=y is a straight line passing through the origin (0,0). The straight line makes an angle of 45° with the positive direction of x-axis.