WBCHSE Class 11 Chemistry Notes On Charle’s Law Definition And Formula
Charles Law:
Two Frenchmen, Gay-Lussac, and Jacques Charles, independently studied the thermal expansion of the gases, i.e., the variation of tire volume of a gas with the temperature at a constant pressure.
They observed that, at constant pressure, the gas expands when heated and contracts when cooled. Both of them arrived at the same conclusion, which is known after their names as Gay-Lussac’s and Charles’s law more commonly as Charles’s law. It is stated as follows:
At constant pressure, the tire volume of a fixed amount of gas is proportional to the temperature.
“Class 11 Chemistry, WBCHSE syllabus, Charles’s law, with solved examples”
V ∝ T
or V/T = k at constant n and p,
where k is a constant, n is the number of moles of the gas, and p is the pressure.
Read and Learn More WBCHSE For Class11 Basic Chemistry Notes

Absolute Zero: Charles’s law raises an interesting question. If the volume of a gas decreases with a decrease in temperature, will it become zero at any temperature? If so, at what temperature?
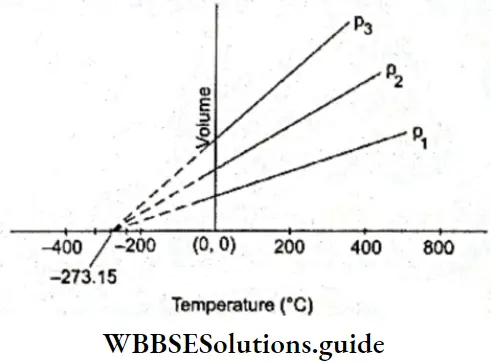
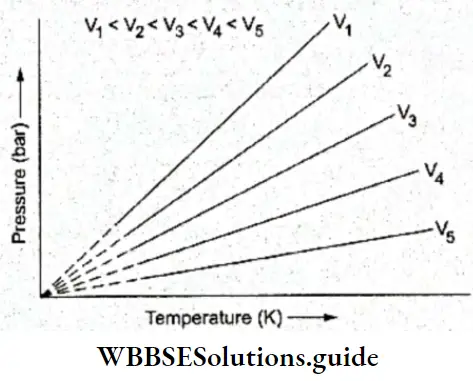
We could try to grasp this concept graphically as well. According to Charles’s law, the volume of a gas is a linear function of its temperature. Thus, a plot of the volume of a given amount of a gas (at constant pressure) against its temperature would be a straight line somewhat like those shown.
| Class 11 Biology | Class 11 Chemistry |
| Class 11 Chemistry | Class 11 Physics |
| Class 11 Biology MCQs | Class 11 Physics MCQs |
| Class 11 Biology | Class 11 Physics Notes |
“WBCHSE Class 11 Chemistry, Charles’s law, definition, formula, and derivation”
Slopes of lines obtained at different pressures are different. If these straight lines were to be extrapolated, as shown in the figure, they would touch the x-axis at -273.15°C, the temperature at which the volume would become zero.
For a particular value of temperature t and a fixed volume of gas V0 at CTC, the following relation holds:
Vt = V0 (1+ αt)
where Vt is the volume at temperature t and α is the cubic expansion coefficient. The value of α is 1/273.15
The volume of the gas at t°C may, therefore, be written as \(V_t=V_0\left(1+\frac{t}{273.15}\right)\)
“Charles’s law, derivation, explanation, and applications, for WBCHSE Class 11 students”
It may be seen from this expression that the volume changes by 1/273.15 of V0 for every degree change in temperature Charles’s law can thus be formally stated as follows. The volume of a given amount of a gas at constant pressure increases (or decreases) by a constant fraction O273.15) volume at 0°C for each degree rise (or fall) in temperature.
The volume at -273.15°C is \(V_{-273.15}=V_0\left(1-\frac{273.15}{273.15}\right)=0\)
Thus, a direct implication of Charles’s law is that the volume of a gas becomes zero at -273.15 °C. Since one cannot have negative volumes, -273.15 °C should be the lowest possible temperature.
“Charles’s law, WBCHSE Class 11, chemistry notes, and step-by-step derivation”
This is why -273.15°C, the hypothetical temperature at which the volume of a gas should become zero, is referred to as the absolute zero of temperature. We use the word hypothetical because, in reality, all gases liquefy before this temperature is reached. This temperature exists only in theory—no one has managed to reach the absolute zero of temperature.
Charle’s Law In Real-Life Applications For WBCHSE Class 11 Chemistry
Absolute Scale Of Temperature: Based on the above observations Lord Kelvin suggested the adoption of a new scale for the scientific measurement of temperature. The zero of this scale is at -273.15°C. This is taken as 0 K (not 0°K). It is now used by scientists the world over and is called the Kelvin scale. Temperatures expressed on the Kelvin scale and the Celsius scale are related as follows.
TK = (t + 273.15)° C ≈ (t + 273)° C
Accepting the absolute scale of temperature for scientific measurements was not just an arbitrary choice. It can be justified by concepts you will learn about later in thermodynamics. The absolute scale or the kelvin scale is also called the thermodynamic scale.
Also, many relations, such as the one between volume and temperature defined by Charles’s law, assume a simpler form if you use this scale. Let us try to express Charles’s law in terms of temperature on the Kelvin scale.
“WBCHSE Class 11 Chemistry, Charles’s law, explanation, and real-life applications”
⇒ \(V_t=V_0\left(1+\frac{t}{273}\right)=V_0\left(\frac{273+t}{273}\right)\)
where V0 = volume at 0°C and
Vt = volume at t°C.
But 273 + t = T, the temperature on the Kelvin scale which has -273.15°C as its zero.
Thus \(V_t=\frac{V_0}{273} T\)
On the Kelvin scale, 273 is the temperature corresponding to V0 (t = 0°C) and can be denoted as T0. We can write the above equation as
⇒ \(\frac{V_t}{V_0}=\frac{T}{T_0}\)
or \(\frac{V}{T}\) = constant if T is the temperature on the Kelvin scale.
Thus, Charles’s law can be expressed as follows. The volume of a given mass of gas is directly proportional to its temperature on the Kelvin scale at a constant pressure. The following equation is convenient (for numerical problems)
⇒ \(\frac{V_1}{T_1}=\frac{V_2}{T_2} \quad(n, p \text { are constant })\)
Remember that temperature is always expressed in kelvin while dealing with pressure and volume in the case of gases.
Application of Charles’s Law:
According to Charles’s law the volume of a gas increases as its temperature rises. In other words, hot air is less dense than cold air, so if one fills a balloon with hot air and lets it go, it rises. In the early part of the twentieth century, hot-air balloons were used for meteorological observations.
“Charles’s law, definition, mathematical formula, derivation, and practical uses”
Ballooning also became a sport. In the 1930s hydrogen balloons became more popular and were even used as a means of public transport (called airships). An accident, that caused a German airship to catch fire, brought an end to the use of airships for transport, but hot-air balloons and hydrogen balloons continued to be used for meteorological purposes and ballooning is still a sport. Charles was the first person to use hydrogen to inflate balloons.
Class 11 WBCHSE Chemistry Charle’s Law Formula And Derivation
Example 1. A certain mass of gas occupies a volume of 1 L at 2 7°C. Calculate the temperature at which the gas will occupy 500 cm3 if the pressure remains constant.
Solution:
Given
A certain mass of gas occupies a volume of 1 L at 2 7°C.
V1 = 1L = 1000 cm3 V2 = 500 cm3
T1 = 27°C = 300K T2 = ?
According to Charle’s law,
⇒ \(\frac{V_1}{T_1}=\frac{V_2}{T_2}\)
∴ \(T_2=\frac{V_2 \times T_1}{V_1}=\frac{500 \times 300}{1000}=150 \mathrm{~K}\) = (150 – 273)°C = -123°C.
Example 2. Suppose you want to increase the volume of 500 cm3 of gas by 25% while keeping the pressure constant. To what temperature would you have to heat the gas if its initial temperature is 25°C?
Solution:
Given
Suppose you want to increase the volume of 500 cm3 of gas by 25% while keeping the pressure constant.
V1 = 500 cm3
V2 = 500 + 25% of 500 = 500 + 125 = 625 cm
T1 = 25° C = 298 K T2 = ?
According to Charle’s law
⇒ \(\frac{V_1}{T_1}=\frac{V_2}{T_2}\)
∴ \(\quad T_2=\frac{V_2 \times T_1}{V_1}=\frac{625 \times 298}{500}=372.5 \mathrm{~K}\)
= \((372.5-273)^{\circ} \mathrm{C}=99.5^{\circ}\mathrm{C}\)
“WBCHSE Class 11, chemistry notes, on Charles’s law, volume-temperature relationship”
Pressure-temperature relationship
The mathematical relationship between pressure and temperature was given by Gay-Lussac. It states that when the temperature of a fixed amount of a gas is changed keeping the volume constant, the pressure of the gas changes and is directly proportional to the temperature. As in the case of volume the pressure increases (or decreases) by 1/273 of its value at 0°C for each one-degree rise (or fall) in temperature. Thus,
p ∝ T (n, V are constant)
or, \(\frac{p}{T}=\text { constant }\)
or \(\frac{p_1}{T_1}=\frac{p_2}{T_2}\).