WBCHSE Class 11 Chemistry Chemical Combination Notes
Laws Of Chemical Combination:
The laws of chemical combination are the outcome of the dedicated work of Lavoisier. Son of a wealthy French lawyer, Lavoisier graduated in law but was far more fascinated by chemistry and spent his life studying chemical phenomena.
He was perhaps the first chemist to realise how important quantitative measurements are to the study of chemical processes. Unfortunately, he was guillotined (beheaded) during the French Revolution.
It was Lavoisier who showed that weighing substances before and after a chemical change could be an important tool in understanding chemical phenomena.
Through careful weighing, he proved that mercury combines with the oxygen present in air to form a red solid, mercuric oxide, which when heated strongly gives the same amount of mercury as was used to prepare the mercuric oxide originally.
“WBCHSE Class 11 Chemistry, chemical combination, overview, laws, and examples”
⇒ \(2 \mathrm{Hg}+\mathrm{O}_2 \longrightarrow 2 \mathrm{HgO}\)
⇒ \(2 \mathrm{HgO} \stackrel{\text { heat }}{\longrightarrow} 2 \mathrm{Hg}+\mathrm{O}_2\)
Read and Learn More WBCHSE For Class11 Basic Chemistry Notes
This proved that mercuric oxide is not an element, but a compound. Lavoisier’s studies revealed the nature of combustion and proved that air consists of oxygen, which supports combustion, and nitrogen, which does not.
Out of the work of Lavoisier and other scientists after him arose a few experimental laws on how elements combine to form compounds. These laws were based entirely on observations related to the weight-weight, weight-volume, and volume-volume relationships between reacting substances and the products formed. These laws are listed below.
| Class 11 Biology | Class 11 Chemistry |
| Class 11 Chemistry | Class 11 Physics |
| Class 11 Biology MCQs | Class 11 Physics MCQs |
| Class 11 Biology | Class 11 Physics Notes |
- Law of conservation of mass (Lavoisier, 1774)
- Law of constant compositions (Proust, 1799)
- Law of reciprocal proportions (Richter, 1792)
- Law of multiple proportions (Dalton, 1803)
- Gay-Lussac’s law of combining volumes (Gay-Lussac, 1808)
1. Law of conservation of mass: This law states that in a chemical change, the total mass of the products is equal to the total mass of the reactants. In other words, matter can neither be created nor destroyed. Landolt, a chemist, experimented to verify this law. The experiment has come to be known as Landolt’s experiment.
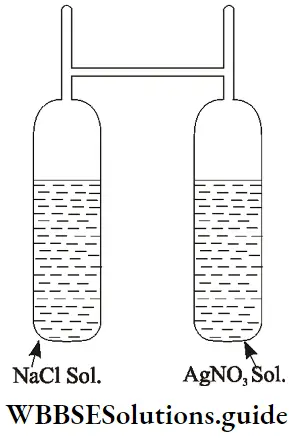
He took a solution of sodium chloride (NaCl) and a solution of silver nitrate (AgNO3) in the two limbs of an H-shaped tube (called Landolt’s tube), sealed the tube and weighed it. Then he allowed the two solutions to mix and react by shaking the tube. After the AgNO3 and NaCl solutions had reacted to form a white precipitate of AgCl he weighed the tube again.
⇒ \(\mathrm{AgNO}_3(\mathrm{aq})+\mathrm{NaCl}(\mathrm{aq}) \longrightarrow \mathrm{AgCl}(\mathrm{s})+\mathrm{NaNO}_3(\mathrm{aq})\)
“Chemical combination, WBCHSE Class 11, chemistry notes, and key concepts”
He found that the weight of the tube and its contents after the reaction was the same as its weight before the reaction. This proved Lavoisier’s law of conservation of mass or indestructibility of matter.
Example: When 4.48 g of KClO3 is heated, 1.73 g of oxygen is produced and the residue of KCI left behind weighs 2.75 g. Show that these observations illustrate the law of conservation of mass.
Solution:
Given
When 4.48 g of KClO3 is heated, 1.73 g of oxygen is produced and the residue of KCI left behind weighs 2.75 g.
The chemical equation is
⇒ \(\underset{4.48 \mathrm{~g}}{2 \mathrm{KClO}_3} \stackrel{\text { heat }}{\longrightarrow} \underset{2.75 \mathrm{~g}}{2 \mathrm{KCl}}+\underset{1.73 \mathrm{~g}}{3 \mathrm{O}_2}\)
The total mass of the products (2.75 + 1.73 = 4.48 g) formed is equal to the mass of the reactant (4.48 g).
This proves that the law of conservation of mass holds good for this reaction.
The discovery of nuclear reactions and radioactive disintegration has changed this view of the indestructibility of matter. The change in mass in such reactions is very significant. The mass that seems to be lost is actually converted into energy by Einstein’s equation, E = mc2,
∴ where m is the mass in kilograms, E is the energy in joules, and c is the velocity of light (3 x 108 ms-1).
“WBCHSE Class 11, chemistry notes, on chemical combination, and fundamental laws”
Because of such reactions, the law of conservation of mass has now been modified and is known as the law of conservation of mass-energy. According to the modified law, mass and energy are interconvertible and the sum of the mass and energy of the system remains constant.
You may wonder why there is no decrease in the mass of the reactants in a chemical reaction in which heat is liberated, or why there is no gain in mass in reactions in which heat is absorbed.
The truth is that the gain or loss in mass in such (chemical) reactions is too small to be detected by ordinary methods of chemical analysis. If, for example, the energy produced (heat liberated) in a reaction is of the order of 9 x 107 kJ, the corresponding loss in mass is only 0.001 g. This is why the law of conservation of mass holds good for all chemical reactions.
2. Law of constant composition: This law, postulated by Joseph Louis Proust (1799), a French chemist, states that a sample of a pure chemical compound always consists of the same elements combined in the same definite proportion by mass. For example, carbon dioxide will always contain only carbon and oxygen combined in the ratio of 3: 8 by mass, no matter what its source.
- Similarly, pure water, obtained from any source, will always contain hydrogen and oxygen combined in the ratio of 1: 8 by mass. This may sound very obvious to you now, but when Proust came up with this conclusion, after painstaking observations, it was a breakthrough in chemistry. The law of constant composition is also called the law of definite proportions.
- The law of constant composition is not valid if the same compound is obtained from isotopes of an element since the mass of each isotope is different. For example, two samples of sodium chloride obtained from two isotopes of chlorine (Cl35 and Cl37) have different compositions. The ratio of the masses of the elements in the two samples would be 23:35 and 23:37 respectively.
Example: A sample of copper nitrate was obtained by dissolving 1.58 g of copper in nitric acid. This sample of copper nitrate yielded on ignition 1.97 g of copper oxide. In another experiment, 1.02 g of copper was dissolved in nitric acid and precipitated as copper hydroxide by adding sodium hydroxide to the solution. The sample of copper hydroxide (after being washed and dried) produced 1.26 g of copper oxide when it was ignited. Show that the results of the tivo experiments illustrate the law of constant composition.
Solution:
Given:
A sample of copper nitrate was obtained by dissolving 1.58 g of copper in nitric acid. This sample of copper nitrate yielded on ignition 1.97 g of copper oxide.
In another experiment, 1.02 g of copper was dissolved in nitric acid and precipitated as copper hydroxide by adding sodium hydroxide to the solution.
The sample of copper hydroxide (after being washed and dried) produced 1.26 g of copper oxide when it was ignited.
In the first experiment, 100 g of copper oxide contained \(\frac{1.58}{1.97}\) x 100 = 80.1g of copper.
In the second experiment, 100 g copper oxide contained \(\frac{1.02}{1.28}\) x 100 = 79.9 g of copper.
The percentage of copper in the two samples of copper oxide is nearly the same, so the results illustrate the law of constant composition.
“Chemical combination, laws of chemical combination, and examples, WBCHSE syllabus”
3. Law of multiple proportions: John Dalton, a British chemist and physicist, formulated this law in 1803. In essence, this law states that there is a simple relationship between the masses of elements which combine to form different compounds.
- A more precise way to say this is, that when two elements A and B combine to form two or more compounds (for example, AB, A2B, AB2), the different masses of one of the elements (say A) that combine with a fixed mass of the other (say B) (or vice versa) are in a simple ratio. For example, nitrogen and oxygen combine to form 5 oxides, viz., nitrous oxide (N2O), nitric oxide (NO), nitrogen trioxide (N2O3), nitrogen tetraoxide (N2O4) and nitrogen pentoxide (N2O5). Calculations show that the masses of oxygen which combine with a fixed mass of nitrogen to form these oxides are in the simple ratio 1:2:3 :4: 5.
- Similarly, if two pure samples of cuprous oxide (Cu2O) and cupric oxide (CuO) are heated strongly in two crucibles, while a current of hydrogen is passed over them, it can be shown that the weights of copper combined with the same weight of oxygen in the two samples are in the ratio 2:1. The weights of copper are obtained by first weighing the empty crucibles, then the crucibles with the samples of Cu2O and CuO and finally, the crucibles after they have been heated strongly in a current of hydrogen.
⇒ \(\mathrm{CuO}+\mathrm{H}_2 \stackrel{\text { heat }}{\longrightarrow} \mathrm{Cu}+\mathrm{H}_2 \mathrm{O}\)
⇒ \(\mathrm{Cu}_2 \mathrm{O}+\mathrm{H}_2 \stackrel{\text { heat }}{\longrightarrow} 2 \mathrm{Cu}+\mathrm{H}_2 \mathrm{O}\)
Importance Of Chemical Combination In Chemistry WBCHSE
Example: Three oxides of nitrogen contained 63.6%, 46.7%, and 30.4% nitrogen respectively. Show that these figures illustrate the law of multiple proportions.
Solution:
Given
Three oxides of nitrogen contained 63.6%, 46.7%, and 30.4% nitrogen respectively.
The first oxide of nitrogen contains 63.6% N
⇒ 63.6 g of N reacts with (100 – 63.6) g of O = 36.4 g of O.
∴ 1 g of N will react with \(\frac{36.4}{63.6}\) g of O = 0.57 g of O.
The second oxide of nitrogen contains 46.7% N
⇒ 46.7 g of N reacts with (100 – 46.7) g of O = 53.3 g of O.
∴ 1 g of N will react with \(\frac{53.3}{46.7}\) g of O = 1.14 g of O.
The third oxide of nitrogen contains 30.4% N
⇒ 30.4 g of N reacts with (100 – 30.4) g of O = 69.6 g of O.
∴ 1 g of N will react with \(\frac{69.6}{30.4}\) g of O = 2.26 g of O.
This means the ratio of the masses of oxygen which combine with 1 g of nitrogen is 0.57:1.14:2.26, i.e., 1:2:4. This is obviously by the law of multiple proportions.
“WBCHSE Class 11 Chemistry, laws of chemical combination, and their significance”
4. Law of reciprocal proportions: This law, postulated by Richter in 1792, also deals with the relationship between the masses of elements that combine.
According to Richter, when two elements (say A and B) combine separately with the same weight of a third element (say C), the ratio in which they do so is the same or some simple multiple of the ratio in which they (A and B) combine.
- Take sulphur, oxygen, and hydrogen, for example. Sulphur and oxygen combine with hydrogen to form hydrogen sulphide (H2S) and water (H2O) respectively. They also combine to form sulfur dioxide (SO2). According to this law, the ratio of the weights of S and O which combine with the same weight of H will either be the same or a simple multiple of the ratio in which S and O combine.
- This can be easily verified. In H2S, two parts by weight of hydrogen combine with 32 parts by weight of sulphur. In H2O, two parts by weight of hydrogen combine with 16 parts by weight of oxygen. Therefore, the ratio of the weights of S and O which combine separately with a fixed weight (2 parts) of hydrogen is 32:16 or 2 :1. And the ratio of S and O in SO2 is 32: 32, or 1 :1. The two ratios are related to each other as (2/1): (1/1)/ or 2 :1. Which means that the first ratio is a simple multiple of the second.
Example: Methane contains 75% carbon and 25% hydrogen, carbon dioxide contains 27.27% carbon and 72.73% oxygen and water contains 11.10% hydrogen and 88.96% oxygen. Can you use these to prove the law of reciprocal proportions?
Solution:
Given
Methane contains 75% carbon and 25% hydrogen, carbon dioxide contains 27.27% carbon and 72.73% oxygen and water contains 11.10% hydrogen and 88.96% oxygen.
In methane, 1 g of H combines with \(\frac{75}{25}\) g of C = 3 g of C.
In water, 1 g of H combines with \(\frac{88.96}{11.10}\) g of O = 8 g of O.
∴ the ratio of weights of C and O which combine with 1 g of H = 3:8 = 1: 2.66.
In the CO2 ratio of the weights of C and O = 27.27: 72.73 = 1: 2.68.
∴ The two ratios are nearly the same, which proves the law of reciprocal proportions.
“Laws of chemical combination, conservation of mass, definite proportions, and multiple proportions, WBCHSE notes”
5. Gay-Lussac’s law of gaseous volumes: While studying reactions between gases, Joseph Louis Gay-Lussac, a French chemist and physicist, found that there is a simple relationship between the volumes of gaseous reactants and products.
Gay-Lussac’s law of combining volumes (as his law is called) states that under similar conditions of temperature and pressure, gases react with each other in volumes which bear a simple ratio to one another and the volumes of the products (if those too are gases). It can be shown experimentally, for example, that 1 volume of hydrogen reacts with 1 volume of chlorine to produce 2 volumes of hydrogen chloride.
⇒ \(\underset{\text { 1 volume }}{\mathrm{H}_2}+\underset{\text { 1 volume }}{\mathrm{Cl}_2} \longrightarrow \underset{2 \text { volumes }}{2 \mathrm{HCl}}\)
The ratio between the volumes of the reactants and the product in this reaction is 1:1:2, which is a simple ratio.

Berzelius Hypothesis
Dalton’s theory could not explain Gay-Lussac’s law of combining volumes, which made Dalton doubt Gay-Lussac’s observations. A Swedish scientist, Jons Jacob Berzelius, convinced of the correctness of Gay-Lussac’s observations, put forward a hypothesis to reconcile Dalton’s theory with Gay-Lussac’s experimental law.
Berzelius stated that equal volumes of all gases under the same conditions of temperature and pressure contain the same number of atoms.
However, this hypothesis seemed to have a drawback. Let us apply it to the formation of hydrochloric acid gas from hydrogen and chlorine to see what the drawback was. It can be shown experimentally that one volume of hydrogen combines with one volume of chlorine to form two volumes of hydrochloric acid gas.
“Chemical combination, theoretical explanation, experimental evidence, and applications, WBCHSE syllabus”
⇒ \(\underset{1 \mathrm{vol}}{\text { Hydrogen }}+\underset{1 \mathrm{vol}}{\text { Chlorine }} \longrightarrow \underset{2 \mathrm{vol}}{\text { Hydrogen chloride gas }}\)
Let one volume of a gas contain n atoms. Then
⇒ \(\text { Hydrogen }+ \text { Chlorine } \longrightarrow \text { Hydrogen chloride gas }\)
⇒ \(\begin{array}{lll}
n \text { atoms } & \text { atoms } & 2 \text { ri compound atoms } \\
1 \text { atom } & 1 \text { atom } & 2 \text { compound atoms } \\
\frac{1}{2} \text { atom } & \frac{1}{2} \text { atom } & 1 \text { compound atom }
\end{array}\)
The Berzelius hypothesis would imply that one compound atom of HC1 is formed by the combination of half an atom each of hydrogen and chlorine. However, the possibility that atoms may undergo division during a chemical reaction is against Dalton’s theory. This is why this hypothesis could not be accepted.
Avogadro’s Hypothesis
In 1811, an Italian physicist and lawyer, Amedeo Avogadro, finally resolved the problem that Berzelius had been unable to resolve. This was another flash of insight, a seemingly simple idea possible only for a great mind to conceive of.
- Avogadro suggested that matter consists of two kinds of particles—atoms and molecules. An atom is the smallest particle of an element which participates in chemical reactions, but it may or may not have independent existence.
- A molecule, according to Avogadro, is the smallest particle of an element or compound which is capable of independent existence. Based on this view of the smallest particles of matter, Avogadro put forward a hypothesis which was a modification of the one proposed by Berzelius. He said that equal volumes of all gases under the same conditions of temperature and pressure contain the same number of molecules. This hypothesis has been found to hold for all gaseous reactions.
Let us apply Avogadro’s hypothesis to the reaction we considered in the previous section.
⇒ \(\begin{gathered}
\text { Hydrogen } \\
1 \mathrm{vol}
\end{gathered}+\underset{1 \mathrm{vol}}{\text { Chlorine }} \longrightarrow \underset{2 \mathrm{vol}}{\text { Hydrogen chloride }}\)
Let us assume that 1 volume of a gas contains n molecules.
\(\text { Hydrogen }+ \text { Chlorine } \longrightarrow \text { Hydrogen chloride }\)⇒ \(\begin{array}{lll}
n \text { molecules } & n \text { molecules } & 2 n \text { molecules } \\
\frac{1}{2} \text { molecule } & \frac{1}{2} \text { molecule } & 1 \text { molecule }
\end{array}\)
“WBCHSE Class 11, chemistry notes, on chemical combination, Gay-Lussac’s law, and Avogadro’s law”
This implies that one molecule of hydrogen chloride contains half a molecule of hydrogen and half a molecule of chlorine. A molecule is the smallest particle of an element (or compound) which is capable of independent existence and may contain two or more atoms, so according to Avogadro’s hypothesis the existence of half a molecule is possible. In the case of hydrogen and chlorine half a molecule contains one atom, as both are diatomic molecules. Therefore, a half-molecule will contain at least one atom, which is in agreement with Dalton’s atomic theory.
Atomicity of gases: The number of atoms present in one molecule of a gas is known as its atomicity. We know now that the number of hydrogen atoms in a hydrogen molecule is two, the number of oxygen atoms in an oxygen molecule is two and the number of oxygen atoms in a molecule of ozone is three, so the atomicity of hydrogen is two, the atomicity of oxygen is two, and that of ozone is three.
Avogadro’s hypothesis can be used to find the atomicity of a gas. Consider hydrogen. Two volumes of hydrogen combine with 1 volume of oxygen to form 2 volumes of water vapour.
⇒ \(\underset{2 \text { vol }}{\text { Hydrogen }}+\underset{1 \text { vol }}{\text { Oxygen }} \rightarrow \underset{2 \text { vol }}{\text { Water vapour }}\)
Class 11 WBCHSE Chemistry Chemical Combination
Assuming that 1 volume of a gas contains n molecules
\(\text { Hydrogen }+ \text { Oxygen } \longrightarrow \text { Water vapour }\)⇒ \(\begin{array}{lll}
2 n \text { molecules } & n \text { molecules } & 2 n \text { molecules } \\
1 \text { molecule } & \frac{1}{2} \text { molecule } & 1 \text { molecule }
\end{array}\)
Thus, 1 molecule of water contains 1/2 molecule of oxygen. It has been found experimentally that 1 molecule of water contains 1 atom of oxygen.
Hence 1/2 molecule of oxygen = 1 atom of oxygen.
or 1 molecule of oxygen = 2 atoms of oxygen.
∴ the atomicity of oxygen = 2.
