Chemical Equation
Chemical Equation:
A chemical reaction can be represented by a chemical equation in which the reactants and products are represented by their molecular formulae. In other words, a chemical equation is a symbolic representation of a chemical change.
Essential of chemical equation
1. A chemical equation should represent a true chemical change. For example, the following equation represents a true chemical change.
⇒ \(2 \mathrm{NaCl}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{Na}_2 \mathrm{SO}_4+2 \mathrm{HCl}\)
On the other hand, silver and hydrogen do not react to form silver hydride, so the equation given below is not a chemical equation since it does not represent a true chemical reaction.
⇒ \(2 \mathrm{Ag}+\mathrm{H}_2 \longrightarrow 2 \mathrm{AgH}\)
2. A chemical equation must be balanced, i.e., the number of atoms of each element on both sides of the equation must be the same. This follows from the law of conservation of mass.
| Class 11 Biology | Class 11 Chemistry |
| Class 11 Chemistry | Class 11 Physics |
| Class 11 Biology MCQs | Class 11 Physics MCQs |
| Class 11 Biology | Class 11 Physics Notes |
“WBCHSE Class 11 Chemistry, Chemical Equation, definition, components, and examples”
3. It should be molecular, i.e., every species involved in the reaction must be represented in its molecular form. The equation \(\mathrm{Zn}+2 \mathrm{HCl} \longrightarrow \mathrm{ZnCl}_2+2 \mathrm{H}\), for example, represents a true chemical change and is balanced, but it is still not a complete equation since hydrogen has not been expressed in its molecular form. The correct representation would be
⇒ \(\mathrm{Zn}+2 \mathrm{HCl} \longrightarrow \mathrm{ZnCl}_2+\mathrm{H}_2\)
Read and Learn More WBCHSE For Class11 Basic Chemistry Notes
Significance of a chemical equation: A chemical equation conveys a lot of information about the reaction, both qualitative and quantitative.
- It gives the names of the reactants and products taking part in the chemical reaction.
- It indicates the relative number of moles of the reactants and the products.
- It shows the relative masses of the reactants and products.
- It indicates the relative volumes of gaseous reactants and products.
Consider the information provided by the following equation.
⇒ \(\underset{\frac{40+12+3 \times 16}{100}}{\mathrm{CaCO}_3}+\underset{\frac{2(1+35.5)}{73}}{2 \mathrm{HCl}} \rightarrow \underset{\frac{40+2 \times 35.5}{111}}{\mathrm{CaCl}_2}+\underset{\frac{2 \times 1+16}{18}}{\mathrm{H}_2 \mathrm{O}}+\underset{\frac{12+2 \times 16}{44}}{\mathrm{CO}_2}\)
- It shows that calcium carbonate reacts with hydrochloric acid to produce calcium chloride, carbon dioxide, and water.
- It also shows that one molecule (one mole) of calcium carbonate reacts with two molecules (two moles) of hydrochloric acid to produce one molecule (one mole) each of calcium chloride, carbon dioxide, and water.
- It indicates that 100 parts by weight of calcium carbonate reacts with 73 parts by weight of hydrochloric acid to give 111 parts by weight of calcium chloride, 44 parts by weight of carbon dioxide, and 18 parts by weight of water.
A chemical equation does provide a lot of valuable information about a chemical reaction, but it has a number of limitations. We can overcome these limitations by using certain appropriate additional symbols in the chemical equations.
To begin with, the state of reactants and products can be indicated by (s) for solid, (l) for a liquid, (g) for gas, and (aq) for an aqueous solution. The arrow pointing upwards (↑) indicates the evolution of a gas whereas that pointing downward (↓) signifies precipitation.
⇒ \(\mathrm{AgNO}_3(\mathrm{aq})+\mathrm{NaCl}(\mathrm{aq}) \longrightarrow \mathrm{AgCl}(\mathrm{s}) \downarrow+\mathrm{NaNO}_3(\mathrm{aq})\)
The conditions (temperature, pressure, and catalyst) can be indicated on the arrow. The heat changes accompanying a chemical reaction can be indicated by change in enthalpy AH.
⇒ \(\mathrm{N}_3(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \underset{\text { Fe(anlyst) }}{\stackrel{773 \mathrm{~K}, 350 \mathrm{~atm}}{\longrightarrow}} 2 \mathrm{NH}_3(\mathrm{~g})\)
⇒ \(\mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ; \Delta H^{\oplus}=-890.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
“Chemical Equation, WBCHSE Class 11, chemistry notes, and key concepts”
The superscript Θ denotes standard conditions of temperature and pressure.
The reversible nature of a reaction is indicated by a double-head arrow,
∴ \(2 \mathrm{SO}_2+\mathrm{O}_2 \rightleftharpoons 2 \mathrm{SO}_3\)
Balancing chemical equation: According to the law of conservation of mass a chemical equation must be balanced, Le., the number of atoms of a particular kind on one side of the equation must he equal to the number of atoms of the same kind on the other side of the equation. Consider, for example, the reaction between hydrogen and oxygen to form water.
∴ H2 +O2 → H2O
Writing the equation, as shown above, is not correct because the oxygen atoms on the two sides of the equation are not balanced. An equation of this kind is called skeleton equation. To balance an equation, use suitable coefficients such that the number of atoms of each species is the same on both sides of the equation. You can use one of the following methods to do this.
- Trial and error method
- Partial equation method
1. Trial and error method This method needs skill and practice. One has to keep trying until the equation is balanced. You can proceed in the following manner.
- Write the skeleton equation, using symbols and formulae of the reactants and products.
- Change elementary gases (like hydrogen, oxygen and nitrogen), if present, to their atomic states.
- Start balancing the equation by selecting the formula containing the maximum number of atoms and balance the number of atoms of each of its constituents on both sides of the equation by multiplying with suitable numbers. Then proceed to balance the other atoms, if they are not balanced already.
- Alternatively, first balance the atoms of the element which appear the least number of times on both sides of the equation. Then proceed to balance the other atoms.
- Once the equation is balanced, change the elementary’ gases to their molecular form and multiply the other atoms by two.
Example: When steam is passed over iron, the products formed are magnetic oxide of iron (Fe3O4) and hydrogen. Write a balanced equation for the reaction.
Solution:
Given
When steam is passed over iron, the products formed are magnetic oxide of iron (Fe3O4) and hydrogen.
Let us write the skeleton equation first.
⇒ \(\mathrm{Fe}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Fe}_3 \mathrm{O}_4+\mathrm{H}_2\)
Changing the elementary gas (hydrogen) to its atomic form:
⇒ \(\mathrm{Fe}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Fe}_3 \mathrm{O}_4+\mathrm{H}\)
“WBCHSE Class 11, chemistry notes, on Chemical Equation, balancing, and significance”
Fe3O4 has the largest number of atoms, so it should be balanced first. Let us start by multiplying Fe by 3 and H2O by 4 on the left of the equation. This gives us 4 molecules of H2O which contain 8 atoms of H on the left side. To balance hydrogen atoms on both sides, let us multiply H by 8 on the right side. The equation now becomes
⇒ \(3 \mathrm{Fe}+4 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Fe}_3 \mathrm{O}_4+8 \mathrm{H}\)
The last step is to convert hydrogen to its molecular form and writing the balanced equation as shown below.
⇒ \(3 \mathrm{Fe}+4 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Fe}_3 \mathrm{O}_4+4 \mathrm{H}_2\)
This method is rather tedious and also difficult to use when the same element is repeated in a number of compounds in an equation. This method does not povide any information about the mechanism or pathway of a reaction either.
Partial equation method This method involves a number of steps which provide an insight into the mechanism of the reaction. The reaction is broken up into several steps and each step is represented by a partial equation.
These equations are individually balanced by the trial and error method. If necessary, the partial equations are multiplied by suitable integers in order to cancel the intermediate products which do not occur in the final equation. The partial equations are then added to obtain the final balanced equation.
Example: Zinc reacts with dilute nitric acid to produce zinc nitrate, nitrous oxide and water. Write the balanced equation for this reaction.
Solution:
Given
Zinc reacts with dilute nitric acid to produce zinc nitrate, nitrous oxide and water.
The skeleton equation for the reaction is given below.
⇒ \(\mathrm{Zn}+\mathrm{HNO}_3 \longrightarrow \mathrm{Zn}\left(\mathrm{NO}_3\right)_2+\mathrm{N}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O}\)
The partial equations for the possible steps in the reaction are as follows
⇒ \(\mathrm{Zn}+\mathrm{HNO}_3 \longrightarrow \mathrm{Zn}\left(\mathrm{NO}_3\right)_2+\mathrm{H}\)
⇒ \(\mathrm{HNO}_3+\mathrm{H} \longrightarrow \mathrm{N}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O}\)
“Chemical Equation, definition, types, and components, WBCHSE syllabus”
Balancing the partial equations by the trial and error method
⇒ \(\begin{gathered}
{\left[\mathrm{Zn}+2 \mathrm{HNO}_3 \longrightarrow \mathrm{Zn}\left(\mathrm{NO}_3\right)_2+2 \mathrm{H}\right] \times 4} \\
2 \mathrm{HNO}_3+8 \mathrm{H} \longrightarrow \mathrm{N}_2 \mathrm{O}+5 \mathrm{H}_2 \mathrm{O} \\
\hline 4 \mathrm{Zn}+10 \mathrm{HNO}_3 \longrightarrow 4 \mathrm{Zn}\left(\mathrm{NO}_3\right)_2+\mathrm{N}_2 \mathrm{O}+5 \mathrm{H}_2 \mathrm{O}
\end{gathered}\)
Stoichiometric calculations: A balanced chemical equation provides information about the quantitative relations between the various reactants and products or the mass and volume relations between them. This aspect of an equation, or the relative proportions in which the reactants react and the products are formed, is called stoichiometry (from the Greek word meaning ‘to measure an element’).
The quantitative information provided by an equation can be used to make the following calculations.
- If the mass of one of the reactants or products is given, the mass of another reactant or product can be calculated.
- If the mass or volume of one of the reactants or products is given, the mass or volume of another reactant or product can be calculated.
- If the volume of one of the reactants or products is given, the volume of another reactant or product can be calculated.
While doing any such calculation, proceed step by step. First, write the balanced chemical equation. Then, write the number of moles, gram-atomic, or gram-molecular masses of the reactants and the products. If one of the reactants or products is gas, write its volume at stp instead of the number of moles, gram-atomic, or gram molecular mass.
Example: Methane bums in oxygen to form carbon dioxide and water, raising the amount of oxygen required to bum 4.0 g of methane. The balanced chemical equation for the reaction is \(\mathrm{CH}_4+2 \mathrm{O}_2 \rightarrow \mathrm{CO}_2+2 \mathrm{H}_2 \mathrm{O}\).
Solution:
⇒ \(\underset{1 \mathrm{~mol}}{\mathrm{CH}_4}+\underset{2 \mathrm{~mol}}{2 \mathrm{O}_2} \longrightarrow \underset{1 \mathrm{~mol}}{\mathrm{CO}_2}+\underset{2 \mathrm{~mol}}{2 \mathrm{H}_2 \mathrm{O}}\)
⇒ \(\underset{16 \mathrm{~g}}{12+4} \underset{164 \mathrm{~g}}{2 \times 32}\)
16 g of methane needs 64 g of oxygen for complete burning.
∴ 4 g of methane will need 64/16 x 4 = 16 g of oxygen for complete burning.
Limiting reagent: A chemical reaction always takes place in the molar ratio given by the balanced chemical equation. If the reactants are present in this ratio, they will be consumed completely. But what if they are not? Then the reaction will stop as soon as one of the reactants is used up completely.
Suppose A and B react in the molar ratio 1 : 2 and that the amounts of the reactants taken in an experiment are in the ratio 2 : 2. Then the reaction will stop as soon as the reactant B is completely used up and half the amount of A will be left unused. In such cases B is called the Untiling reagent, because the amount of B present determines when the reaction will stop, or rather, the amount of the product formed. One could define the limiting reagent as the reactant which is completely consumed during a reaction. This aspect is also important in stoichiometric calculations. The following solved example will make it clear.
Example: How much water can be obtained from 2.00 g of hydrogen and 2.00 g of oxygen by the reaction \(2 \mathrm{H}_2+\mathrm{O}_2 \rightarrow 2 \mathrm{H}_2 \mathrm{O}\)? Which is the limiting reagent in this case? Calculate the amount of the other reactant that will be left behind.
Solution:
2.00 g of H2 = \(\frac{2.00}{2.00}\) = 1 mole of hydrogen.
2.0 g O2 = \(\frac{2.00}{32.00}\) = 0.062 moles of oxygen.
From the equation, 1 mol of oxygen reacts with 2 mol of hydrogen to form 2 mol of water. Therefore, 0. 062 mol of oxygen will react with 2 x 0.062 = 0.124 mol of hydrogen to form 0.124 mol of water.
∴ Hydrogen used up = 0.124 mol
∴ hydrogen left = 1 – 0.124 = 0.876 mol.
∴ Mass of hydrogen left = 0.876 x 2 = 1.752 g
Mass of water formed = 0.124 x 18 = 2.132 g
The limiting reagent is obviously oxygen since all of it is consumed.
Reactions in solution: A solution is a homogeneous mixture of at least two non reacting substances. The component present in the smaller amount is called the solute, while the other component is called the solvent.
“WBCHSE Class 11 Chemistry, components of a chemical equation, reactants, and products”
The relative amounts of solvent and solute present in a solution is expressed in terms of concentration. The concentration is usually expressed in terms of mass percent, mole fraction, molality, or molarity.
Mass percent It is the grams of solute in 100 g of the solution and is obtained by the following relation:
∴ Mass percentage = \(\frac{\text { mass of solute }}{\text { mass of solution }} \times 100\)

Example 1. A solution is prepared by adding 5 g of cane sugar in 20 g of water. Calculate the mass per cent of the solute.
Solution:
Given
A solution is prepared by adding 5 g of cane sugar in 20 g of water.
Mass percent of solute = \(\frac{\text { mass of cane sugar }}{\text { mass of solution }} \times 100 \)
= \(\frac{5 \mathrm{~g}}{5 \mathrm{~g} \text { of cane sugar }+20 \mathrm{~g} \text { water }} \times 100 \)
= \(\frac{5 \mathrm{~g}}{25 \mathrm{~g}} \times 100=20 \% \).
Mole fraction The mole fraction (x) of any component in a solution is given by the number of moles of the component divided by the total number of moles making up the solution (including the solvent). For example, if nA moles of substance A is dissolved in nB moles of substance B then the mole fraction of A(xa) and that of B (xb), respectively, are
⇒ \(x_{\mathrm{A}}=\frac{n_{\mathrm{A}}}{n_{\mathrm{A}}+n_{\mathrm{B}}} \text { and } x_{\mathrm{B}}=\frac{n_{\mathrm{B}}}{n_{\mathrm{A}}+n_{\mathrm{B}}} \text {. }\)
Note that a mole fraction has no units (it is a ratio) and has a value between 0 and 1 (since xa + xb = 1). Except in a few situations, mole fractions are not often used for liquid solutions but for calculations involving gaseous mixtures.
Example 2. 58,5 g of sodium chloride is dissolved in 180 g of water. Calculate the mole fraction of sodium chloride in the solution.
Solution:
Given
58,5 g of sodium chloride is dissolved in 180 g of water.
58.5 g of sodium chloride = 1 mol.
∴ 180 gof H2O = 10 moL
Mole fraction of NaCl = \(=\frac{\text { number of moles of } \mathrm{NaCl}}{\text { total number of moles of solution }}\)
= \(\frac{1}{1+10}=\frac{1}{11}=0.090\)
Molality It is defined as the number of moles of solute present in 1 kg of the solvent and is denoted by m.
Molality (m) = \(\frac{\text { number of moles of solute }}{\text { mass of solvent in } \mathrm{kg}} \text {. }\)
Molarity The molarity of a solution is the number of moles of the solute per litre of the solution. The unit of molarity js mol L-1. A more common unit is mol dm-3.
“Chemical Equation, law of conservation of mass, and balancing techniques, WBCHSE notes”
⇒ \(\text { Molarity }(M)=\frac{\text { number of moles of solute }}{\text { volume of solution in litres }(V)}\)
⇒ \(\text { Number of moles }=\frac{\text { weight of solute }(W)}{\text { molecular weight }(M) \text { of solute }}\)
∴ \(\text { Molarity }=\frac{\text { weight of solute }}{\text { molecular weight of solute }} \times \frac{1000}{\text { volume of solution in } \mathrm{mL}}\)
⇒ \( M=\frac{W}{M} \times \frac{1000}{\mathrm{~V}(\mathrm{~mL})}\)
If some more solvent is added to a solution, it becomes more dilute, but the number of moles present in if does not change. Suppose the molarity of a solution is M1 and its volume is V1. Thus the number of moles of solute present in it is M1, V1. Now suppose this solution is diluted to volume V2 and the molarity of the diluted solution is M2. Then the number of moles present in the dilute solution, i.e., M2V2, must be the same as the number of moles in the original solution.
∴ M1V1=M2V2.
This equation is called the molarity equation. The molarity of a solution depends upon temperature because volume is temperature-dependent,
Example 3. Find the molality 0.02M NaCl solution.
Solution:
Since M = 0.02 mol L-1,
0. 02 moles of NaCl are presept ip 1 L of water.
In case of water, for dilute solutions:
1000 mL = 1000 g (since the density of water Is 1 g mL-1)
So the mass of the solvent (HO) is 1000 g = 1 kg
Molality(m) = \(\frac{\text { no. of moles of solute }}{\text { mass of solvent in } \mathrm{kg}}\)
= \(\frac{0.02 \mathrm{~mol}}{1 \mathrm{~kg}}=0.02 \mathrm{~mol} \mathrm{~kg}^{-1}\)
Example 4. A solution sodium hydroxide is prepared by dissolving 20.0 g of sodium hydroxide (NaOH) in distilled water to give 250mL of a solution. Calculate the molarity of the sodium hydroxide solution.
Solution:
Given
A solution sodium hydroxide is prepared by dissolving 20.0 g of sodium hydroxide (NaOH) in distilled water to give 250mL of a solution.
Molar mass of NaOH = \(\frac{20.0 \mathrm{~g}}{40.0 \mathrm{~g} \mathrm{~mol}^{-1}}=0.50 \mathrm{~mol}\)
Volume of solution = 250 mL = 0.25 L.
Molarity = \(\frac{0.50 \mathrm{~mol}}{0.25 \mathrm{~L}}\) = 2.0 molL = 2.0 M.
Example 5. 250 cm3 of a solution of oxalic acid contains 1,26 g of axqlic acid. Calculate its molarity.
Solution:
Given
250 cm3 of a solution of oxalic acid contains 1,26 g of axqlic acid.
Weight of solute = 1.26 g.
Volume of solution = 250 cm3 = 250 mL.
Molecular weight of oxalic acid [(COOH)2-2H2O] = 126.
M = \(\frac{1.26}{126} \times \frac{1000}{250}\) = 0.04 M
Example 6.
- When 4.2 g of NaHCO3 was added to a sample of acetic acid (CH3COOH) weighing 10.0 g, 2.2 g of CO2 was produced and the residue left weighed 12.0 g. Show that these observations are in agreement with the law of conservation of mass.
- In another experiment, 6.3 g of NaHCO3 Teas was added to 15.0 g of acetic acid. The residue weighed 18.0 g. Find the mass of CO2 released in the reaction.
Solution:
1. The given reaction can be represented by the following chemical equation.
⇒ \(\mathrm{NaHCO}_3+\mathrm{CH}_3 \mathrm{COOH} \longrightarrow \mathrm{CH}_3 \mathrm{COONa}+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2\)
Sum of the masses of the reactants = 4.2 + 10.0 = 14.2g.
Sum of the masses of the products = 12 + 2.2 = 14.2 g.
Thus, sum of the masses of the reactants is the same as that of the products. This is in accordance with the law of conservation or mass.
2. According to the law of conservation of mass, the mass of the reactants must be the same as the mass of the products.
⇒ \(\mathrm{NaHCO}_3+\mathrm{CH}_3 \mathrm{COOH} \longrightarrow \underbrace{\mathrm{CH}_3 \mathrm{COONa}+\mathrm{H}_2 \mathrm{O}}+\mathrm{CO}_2 \uparrow\)
Mass of NaHCO3 = 6.3 g. (given)
Mass of CH3COOH = 15.0 g.
Mass of CH3COONa + H2O = 18 g,
∴ Mass of CO2 = (15.0 + 6.3) -18 = 3.3 g.
Example 7. Phosphorus trichloride contains 22.55% of phosphorus, phosphine contains 91.18% phosphorus, while HCl contains 97.26% of chlorine. Shore that this data illustrates the law of reciprocal proportions.
Solution:
Given
Phosphorus trichloride contains 22.55% of phosphorus, phosphine contains 91.18% phosphorus, while HCl contains 97.26% of chlorine.
In PCI2, weight of phosphorus = 22.55 g and weight of chlorine = 100 – 22.55 = 77.45 g,
i.e., 22.55 g of P combines with 77.45 g Cl.
∴ 1 g of P will combine with \(\frac{77.45}{22.55}\) = 3.43 g of Cl.
In PH3, weight of phosphorus = 91.18 g.
and weight of hydrogen = 100 – 9118 = 8.82 g,
i.e., 91.18 g of P combines with 8.82 g of hydrogen.
∴ 1 g of P combines with \(\frac{8.82}{91.18}\) = 0.096 g of H.
In HCl, the weight of chlorine = 97.26 g.
and weight of hydrogen = 100 – 97.26 = 2.74 g,
i.e. 2.74 g of hydrogen combines with 97.26 g of chlorine.
∴ 1 g of hydrogen combines with \(\frac{97.26}{2.74}\) = 35.49 g of chlorine.
The ratio of the weights of H and Cl which combine with a fixed weight of P (1 g) = 0.096 : 3.43 = 1:35.7.
The ratio of the weights of H and Cl which combine directly with each other = 2.74:97.26 = 1:35.49.
Thus, the two ratios are the same, in accordance with the law of reciprocal proportions.
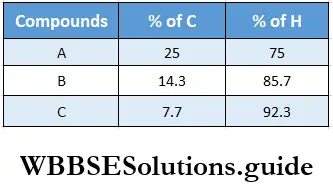
Example 8. Carbon combines with hydrogen to form three compounds A, B, and C. The percentages of hydrogen in A, B, and C are 25,14.3, and 7.7 respectively. Which law of chemical combination does this example illustrate?
Solution:
Given
Carbon combines with hydrogen to form three compounds A, B, and C. The percentages of hydrogen in A, B, and C are 25,14.3, and 7.7 respectively.
In compound A, 25 parts of carbon combine with 75 parts of hydrogen.
∴ 1 part of carbon combines with \(\frac{75}{25}\) = 3 parts of H.
In compound B, 14.3 parts of carbon combine with 85.7 parts of hydrogen.
∴ 1 part of carbon combines with \(\frac{85.7}{14.3}\) = 6 parts of hydrogen.
In compound C, 7.7 parts of carbon combine with 92.3 parts of hydrogen.
∴ 1 part of carbon combines with \(\frac{92.3}{7.7}\) = 12 parts of hydrogen.
This example illustrates the law of multiple proportions because the weights of hydrogen that combine with a fixed weight of carbon bear a simple whole-number ratio to one another, viz., 3:6:12, or 1: 2:4.
Example 9. When 5.625 g of the higher oxide of a metal was heated it produced 5.325 g of the lower oxide. The sample of the lower oxide, on reductions yielded 5.025 g of the metal. Show that this illustrates the law of multiple proportions.
Solution:
Given
When 5.625 g of the higher oxide of a metal was heated it produced 5.325 g of the lower oxide. The sample of the lower oxide, on reductions yielded 5.025 g of the metal.
Weight of lower oxide = 5.325 g.
Weight of higher oxide = 5.625 g.
Weight of oxygen in lower oxide = 5.325 – 5.025 = 0.300 g.
Weight of oxygen in higher oxide = 5.625 – 5.025 = 0.600 g (because the weight of the metal is the same in both the oxides).
Therefore, the ratio of the weight of oxygen that combines with a fixed weight of the metal in the two oxides = 0.300: 0.600 = 1:2.
This is a simple whole-number ratio, so the experiment illustrates the law of multiple proportions.
Example 10. Iron reacts zvith steam to produce iron oxide (Fe3O4). Calculate the zveight of iron zuhich will be converted into its oxide (Fe3O4) by 9 g of steam.
Solution:
Given
Iron reacts zvith steam to produce iron oxide (Fe3O4).
The balanced chemical equation is 3 \(\mathrm{Fe}+4 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{Fe}_3 \mathrm{O}_4+4 \mathrm{H}_2\)
(4 x 18) g of steam reacts with (3 x 56) g of iron
or 72 g of steam reacts with 168 g of iron.
∴ 9 g of steam will react with \(\frac{168}{72}\) x 9 = 21 g of iron.
Thus 9 g of steam can convert 21 g of iron into its oxide.
“WBCHSE Class 11, chemistry notes, on Chemical Equations, stoichiometry, and reaction types”
Example 11. How much potassium chlorate ivould be required to produce 1.12 L of oxygen at stp?
Solution:
The balanced chemical equation for the reaction is
⇒ \(\underset{2(39+35.5+3 \times 16) \mathrm{g} / \mathrm{L}}{2 \mathrm{KClO}_3} \longrightarrow 2 \mathrm{KCl}+\underset{3 \times 227}{3 \mathrm{O}_2}\)
From the equation, 22.7 x 3 L of oxygen is produced by 2(39 + 35.5 + 3 x 16)g of KCIO3
∴ 1.12 L of oxygen can be obtained from \(\frac{245}{68.1}\) x 1.12 = 4.03 g of KCIO3.
The required amount of KCIO3 is 4.03 g.
Example 12. How much hydrochloric acid (HCl) is produced by 0.8 g of hydrogen and an excess of chlorine?
Solution:
The balanced chemical equation for the reaction is
∴ \(\mathrm{H}_2+\mathrm{Cl}_2 \longrightarrow 2 \mathrm{HCl}\)
From the equation, 2 g of hydrogen will yield 2(1 + 35.5) = 73 g of HC1.
∴ 0. 8 g of hydrogen will yield \(\frac{73}{2}\) x 0.8 = 29.2 g of HCl.
The amount of HCl produced is 29.2 g.
Example 13. 2 g of an impure sample of magnesium sulfate was dissolved in water and treated with an excess of barium chloride. The weight of the dry precipitate of BaSO4 produced was 3.0 g. Calculate the percentage purity of the sample.
Solution:
Given
2 g of an impure sample of magnesium sulfate was dissolved in water and treated with an excess of barium chloride. The weight of the dry precipitate of BaSO4 produced was 3.0 g.
The chemical equation for tlie reaction is
⇒ \(\mathrm{MgSO}_4+\mathrm{BaCl}_2 \longrightarrow \mathrm{BaSO}_4+\mathrm{MgCl}_2\)
From the equation, (137 + 32 + 4 x 16) g of BaSO4 is obtained from (24 + 32 + 4 x 16) g of MgSO4 or 233 g of BaSO4 is obtained from 120 g of MgSO4.
∴ 3.0 g of BaSO4, will be obtained from \(\frac{120}{233}\) x 3.0 = 1.54 g of MgSO4.
This means that 2 g of the impure sample of MgSO4 contains 1.54 g of pure MgSO4.
∴ 100 g of the impure sample will contain \(\frac{154}{2}\) x 100 = 77.0 g of pure MgSO4.
Therefore, the percentage purity of MgSO4 is 77.0.
Example 14. What is the volume of oxygen that will be required to burn 1L of methane completely? How much carbon dioxide will be produced in the process?
Solution:
The chemical equation for the reaction is
⇒ \(\mathrm{CaCO}_3+2 \mathrm{HCl} \longrightarrow \mathrm{CaCl}_2+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2\)
According to the equation, 2 mol of CH4 combines with 3 mol of O2 to produce 2 mol of CO2 and 2 mol of water vapour
or 2 volumes of CH4 combine with 3 volumes of O2 to produce 2 volumes of CO2 and 2 volumes of water vapour
or 2 L of CH4 combine with 3 L of O2 to produce 2 L of CO2 and 2 L of water vapor,
i. e., 2 L of CH4 require 3 L of O2.
∴ 1L of CH4 requires — = 15 L of oxygen.
Also 2 L of CH4 yield 2 L of CO2
∴ 1 L of CH4 yields 2/2 = 1L of CO2.
Example 15. What is the volume of carbon dioxide measured at stp that would be obtained by the action of dilute hydrochloric acid on 15.0 g of calcium carbonate?
Solution:
The chemical equation representing the reaction is
⇒ \(\mathrm{CaCO}_3+2 \mathrm{HCl} \longrightarrow \mathrm{CaCl}_2+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2\)
From the equation (40 +12 + 3 x 16) g = 100 g of CaCO3 reacts with HCl to produce 22.7 L of CO2 at stp.
∴ 15 g of CaCO3 will produce \(\frac{22.7}{100}\) x 15 L = 3.41 L of CO2 at stp.
Example 16. How much oxygen will be required at stp for the complete combustion of 300 cm3, of acetylene? How much CO2 will be produced in the process?
Solution:
The chemical equation for the reaction is
⇒ \(2 \mathrm{C}_2 \mathrm{H}_2+5 \mathrm{O}_2 \longrightarrow 4 \mathrm{CO}_2+2 \mathrm{H}_2 \mathrm{O}\)
From the equation, 2 volumes of C2H2 bum in 5 volumes of qxygen to produce 4 volumes of CO2, and 2 volumes of water vapour.
Using Gay-Lussac’s law of gaseous volumes, 300 cm3 of acetylene would require 5/2 x 300 = 750 cm3 of oxygen at stp for complete combustion.
Also, 2 volumes of acetylene produce 4 volumes of CO2 at stp.
∴ 300 cm3 of acetylene will produce \(\frac{4}{2}\) x 300 = 600 cm3 of CO2 at stp.
Example 17. How much hydrogen will be liberated if 6.5 g of Zn is added to 1 L of a hydrochloric acid solution containing 3.65 g of HCl per litre? Which reactant will be left behind when the reaction stops? How much of it will be left behind?
Solution:
Number of moles of Zil taken = \(\frac{6.5}{65}\) = 0.L
Number of moles of HCl in solution = \(\frac{3.65}{36.5}\) = 0.1
The equation for the reaction is
⇒ \(\mathrm{Zn}+2 \mathrm{HCl} \longrightarrow \mathrm{ZnCl}_2+\mathrm{H}_2\)
According to the equation, 1 mol of Zn reacts with 2 mol of HCl to produce 1 mol of H2.
⇒ 0.1 mol of Zn Would require 0.2 mol Of HCl.
But the solution contains 0.1 mol of HCl.
“Chemical Equations, exothermic and endothermic reactions, and their importance, WBCHSE syllabus”
Therefore, the limiting reagent is HCl. The reaction will stop when all the HCl is used up. Number of moles of H2 liberated = 0.05.
∴ mass of H2 liberated = 0.05 x 2 = 0.10 g.
∴ Number of moles of Zn used up = 0.05.
The number of moles of Zn left = 0.1 – 0.05 = 0.05.
∴ mass of Zn left = 0.05 x 65 = 3.25 g.
Example 18. Determine the number of moles of barium phosphate produced when 0.2 mol of sodium phosphate is treated with 0.1 mol of barium nitrate if the reaction proceeds according to the following equation.
⇒ \(2 \mathrm{Na}_3 \mathrm{PO}_4+3 \mathrm{Ba}\left(\mathrm{NO}_3\right)_2 \longrightarrow \mathrm{Ba}_3\left(\mathrm{PO}_4\right)_2+6 \mathrm{NaNO}_3\)
Solution:
According to the equation, 2 mol of Na3PO4 reacts with 3 mol of Ba(NO3)2 to produce 1 mol of Ba3(PO4)2.
Therefore, 0.1 mol of Ba(NO3)2 will react with \(\frac{2}{3}\) x 0.1 = 0.066 mol of Na3PO4. Thus, barium nitrate is the limiting reagent.
0.1 mol of Ba(NO3)2 will produce \(\frac{1}{3}\) x 0.1 = 0.033 mol of Ba3(PO4)2.
Example 19. Find the number of moles o/KMn04 required to oxidise 1.35 g of oxalic acid completely in an acidic medium. How much 0.05-M KMnO4 will be required for the above oxidation? The reaction takes place according to the following equation.
⇒ \(2 \mathrm{KMnO}_4+3 \mathrm{H}_2 \mathrm{SO}_4+5 \mathrm{H}_2 \mathrm{C}_2 \mathrm{O}_4 \longrightarrow \mathrm{K}_2 \mathrm{SO}_4+2 \mathrm{MnSO}_4+10 \mathrm{CO}_2+8 \mathrm{H}_2 \mathrm{O}\)
Solution:
Molecular mass of oxalic acid = 2×1 + 2×12 + 4×16 = 90.0 u.
∴ number of moles of oxalic acid in 1.35 g of it = \(\frac{135}{90}\) = 0.015.
According to the equation given, 5 mol of oxalic acid is oxidised by 2 mol of KMnO4.
∴0.015 mol of oxalic acid will require \(\frac{2 \times 0.015}{5}\) = 0.006 rnol of KMnO4.
It is given that 0.05 mol of KMnO4 is present in 1000 cm of the solution.
∴ 0.06 mol KMnO4 will be contained in \(\frac{1000}{0.05}\) x 0.006 = 120 cm3 of the solution.
So the required volume of the 0.05-M KMnO4 solution = 120 cm3
Example 20. 100 cm3 of a solution of NaOH contains 2.0 g of NaOH. Calculate its molarity.
Solution:
Given
100 cm3 of a solution of NaOH contains 2.0 g of NaOH.
Weight of solute = 2.0 g.
Volume of solution = 100 cm3 = 0.1 L.
Molecular weight of NaOH = 23 + 16 + 1 = 40.
∴ Molarity = \(\frac{\text { weight of solute }}{\text { molecular weight }} \times \frac{1000}{\text { volume }\left(\mathrm{cm}^3\right)}\)
= \(\frac{2}{40} \times \frac{1000}{100}=0.5 \mathrm{M}\) .
Example 21. Calculate the amount of NaOH required to prepare 250 cm3 of a 0.1 M NaOH solution.
Solution:
Weight of solute = molarity x molecular weight x volume (L)
= 0.1 x 40 x \(\frac{250}{1000}\) = 1 g.
Example 22. How many grams 0f BaSO4 will beformed when 500 cm3 of a 0.250-M Na2SO4 solution is added to an aqueous solution of 15.00 g o/BaCl2?
Solution:
The balanced equation for the given reaction is
⇒ \(\mathrm{BaCl}_2+\mathrm{Na}_2 \mathrm{SO}_4 \longrightarrow 2 \mathrm{NaCl}+\mathrm{BaSO}_4\)
According to the equation,1 mol of BaCl2 reacts with 1 mol of N2SO4 to form 1 mol of BaSO4.
Number of moles of BaCl2 =\(\frac{\text { weight of } \mathrm{BaCl}_2}{\text { molecular weight of } \mathrm{BaCl}_2}=\frac{15}{208.4}=0.072\)
“Chemical Equations, WBCHSE Class 11, real-world applications, and importance in chemistry”
Number of moles of Na2SO4 = molarity x volume (L) = 0.250 x \(\frac{500}{1000}\) = 0.125
Thus the limiting reagent is BaCl2.
0.072 mol of BaCl2 will react with 0.072 mol of Na2SO4 to yield 0.072 mole of BaSO4.
∴ mass of BaSO4 = 0.072 x 233.4 =16.80 g.
Example 23. Commercially available concentrated sulphuric acid is 98% by mass. Its density is 1.84 g cm-3.
- Calculate the molarity of the solution.
- What is the volume of concentrated H2SO4 that will be required to prepare 2 L of a 5-M sulphuric acid solution?
Solution:
1. The concentration of the given solution can be determined by two methods.
Density of solution = 1.84 g cm3.
∴ weight of 1000 cm3 of solution =184 x 1000 =1840 g.
Concentration of solution = 98% by mass
i.e., 100 g of solution contains = 98 g of H2SO4.
∴ 1840 g of solution contains =\(\frac{98 \times 1840}{100}\) g of H2SO4
“WBCHSE Class 11 Chemistry, Chemical Equation, solved examples, and step-by-step explanations”
Molarity = \(\frac{\text { weight of solute }}{\text { molecular weight }} \times \frac{1}{\text { volume in litre }}\)
= \(\frac{98 \times 1840}{98 \times 100}=18.4\)
Alternative method
Volume = \(\frac{\text { mass }}{\text { density }}\)
Volume 100 g of the solution = \(\frac{\text { mass percentage }}{\text { molecular weight }} \times \frac{1000}{\text { volume }\left(\mathrm{cm}^3\right)}\)
= \(\frac{98}{98} \times \frac{1000}{54.3}=18.4 \mathrm{M}\)
2. M1V = M2V2
M1 = 18.4 M; V1 = ?
M2 = 5 M; V2 = 20 L66
∴ \(V_1=\frac{M_2 V_2}{M_1}=\frac{5 \times 20}{18.4}=5.43 \mathrm{~L}\)
The volume of the concentrated H2SO4 required is 5.43 L
