NEET Physics System Of Particles And Rotational Motion Notes

System Of Particles And Rotational Motion

Angular displacement is given by

⇒ \(\theta=\frac{\text { length of the arc }}{\text { radius }}=\frac{s}{r} \text { radian }\)

Average angular velocity

⇒ \(\bar{\omega}=\frac{\theta_2-\theta_1}{t_2-t_1}=\frac{\Delta \theta}{\Delta t} \mathrm{rads}^{-1}\)

Instantaneous angular velocity

⇒ \(\omega=\frac{d \theta}{d t} \mathrm{rads}^{-1}\)

⇒ \(\omega=2 \pi f=\left(\frac{2 \pi}{T}\right)\)

Angular acceleration

Average angular acceleration

⇒ \(\bar{\alpha}=\frac{\omega_2-\omega_1}{t_2-t_1}=\frac{\Delta \omega}{\Delta t} \mathrm{rads}^{-2}\)

Read And Learn More: NEET Physics Notes

Instantaneous Angular Acceleration

⇒ \(\alpha=\frac{d \omega}{d t}=\frac{d^2 \theta}{d t^2} \mathrm{rads}^{-2}\)

NEET Physics System of Particles and Rotational Motion Notes

Relation between linear velocity and angular velocity

⇒ \(v=\omega r=2 \pi f r=\frac{2 \pi r}{T}\)

⇒ \(\vec{v}=\vec{\omega} \times \vec{r}\)

Relation between linear acceleration and angular acceleration

⇒ \(a=\frac{d v}{d t}=r \frac{d \omega}{d t}=r \alpha\)

Tangential acceleration

⇒ \(\vec{a}_i=\vec{\alpha} \times \vec{r}\)

Radial acceleration

⇒ \(\vec{a}_r=\vec{\omega} \times \vec{v}\)

Resultant acceleration

⇒ \(\vec{a}=\vec{a}_t+\vec{a}_r\)

NEET Physics Rotational Motion Important Formulas

The center of mass of a body is an imaginary point at which the entire mass of the body is considered to be concentrated.

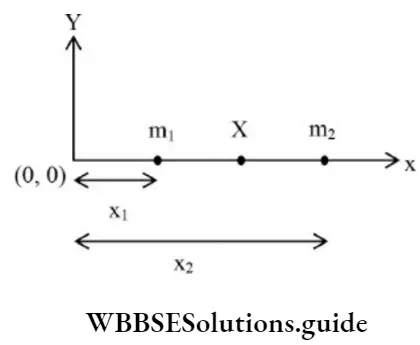
If m₁ and m₂ are situated at a distance of x₁ and x₂ w.r.to origin then their center of mass is given by,

⇒ \(\mathrm{x}=\frac{\mathrm{m}_1 \mathrm{x}_1+\mathrm{m}_2 \mathrm{x}_2}{\mathrm{~m}_1+\mathrm{m}_2}\)

if m₁=m₂=m, then

⇒ \(\mathrm{X}=\frac{\mathrm{x}_1+\mathrm{x}_2}{2}\)

Suppose we have three particles, then

Best Short Notes for System of Particles and Rotational Motion NEET

⇒ \(\mathrm{X}=\frac{\mathrm{m}_1 \mathrm{x}_1+\mathrm{m}_2 \mathrm{x}_2+\mathrm{m}_3 \mathrm{x}_3}{\mathrm{~m}_1+\mathrm{m}_2+\mathrm{m}_3}\)

⇒ \(\mathrm{Y}=\frac{\mathrm{m}_1 \mathrm{y}_1+\mathrm{m}_2 \mathrm{y}_2+\mathrm{m}_3 \mathrm{y}_3}{\mathrm{~m}_1+\mathrm{m}_2+\mathrm{m}_3}\)

If m₁ = m₂ = m₃= m, then

⇒\(\mathrm{X}=\frac{\mathrm{x}_1+\mathrm{x}_2+\mathrm{x}_3}{3} \text { and } \mathrm{Y}=\frac{\mathrm{y}_1+\mathrm{y}_2+\mathrm{y}_3}{3}\)

Then, for three particles of equal mass center of mass coincides with the centroid of the triangle formed by the particles.

Conservation Of Momentum For System Of Particles

The total momentum of a system of particles is equal to the product of the total mass of the system and the velocity of its center of mass.

Note: External force is required to change the position of the center of mass.

The moment of force is called torque.

If a force F acts on a particle at a point P whose position for the origin ‘O’ is defined as the vector product,

⇒ \(\vec{\tau}=\vec{r} \times \vec{F}\)

⇒ \(\tau=\mathrm{rF} \sin \theta\)

Torque is a measure of the turning effect of a force.

System of Particles and Rotational Motion NEET Important Questions and Answers

Moment of linear momentum is called angular momentum.

The angular momentum \(\vec{\ell}\) of the particle w.r.to the origin ‘O’ is,

⇒ \(\vec{\ell}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}\)

⇒ \(\mathrm{rp} \sin \theta\)

The rate of change of angular momentum is equal to torque.

⇒ \(\text { i.e., } \frac{\mathrm{d} \vec{\ell}}{\mathrm{dt}}=\overrightarrow{\boldsymbol{\tau}}\)

This is the rotational analog of the equation,

⇒ \(\frac{\mathrm{d} \overrightarrow{\mathrm{p}}}{\mathrm{dt}}=\overrightarrow{\mathrm{F}}\)

NEET Physics Rotational Motion MCQs with Solutions

Conditions for Mechanical Equilibrium of a Rigid Body

The vector sum of all the forces acting on a rigid body should be zero. i.e.,

⇒ \(\text { i.e., } \overrightarrow{\mathrm{F}}_1+\overrightarrow{\mathrm{F}}_2+\ldots .+\overrightarrow{\mathrm{F}}_{\mathrm{n}}=0\)

(This is the condition for translation equilibrium)

The vector sum of all the torques acting on a rigid body is zero. i.e.,

⇒ \(\text { i.e., } \vec{\tau}_1+\vec{\tau}_2+\ldots+\vec{\tau}_n=0\)

(This is the condition for rotational equilibrium)

Principle of Moments

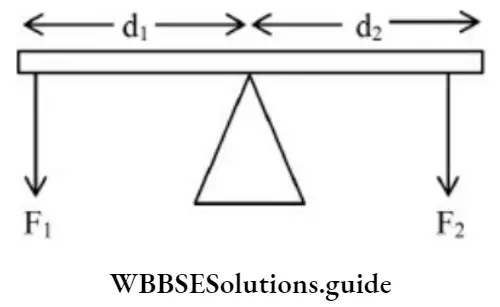
For translational equilibrium of lever

⇒ \(\mathrm{R}-\mathrm{F}_1-\mathrm{F}_2=0 \text {, }\)

where R is the reaction of the support at the fulcrum. For rotational equilibrium

d₁F₁ – d₂F₂ = 0

or, d₁F₁= d₂F₂

System Of Particles

Where F₁ is the load, d₁ is the load arm, F₂ is effort and d₂ is effort arm.
The ratio \(\frac{F_1}{F_2}\) is called mechanical advantage (M.A.)

⇒ \(\text { M.A. }=\frac{F_1}{F_2}=\frac{d_2}{d_1}\)

NEET Study Material for Rotational Motion Chapter

The moment of inertia of a rigid body is given by,

⇒\(\mathrm{I}=\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{m}_{\mathrm{i}} \cdot \mathrm{r}_{\mathrm{i}}^2\)

Moment of inertia of is also  given by,

I = MK²

Where k is called the radius of gyration.

The radius of gyration is the distance from the axis of a mass point whose mass is equal to the mass of the whole body and whose moment of inertia is equal to the moment of inertia of the body about its axis.

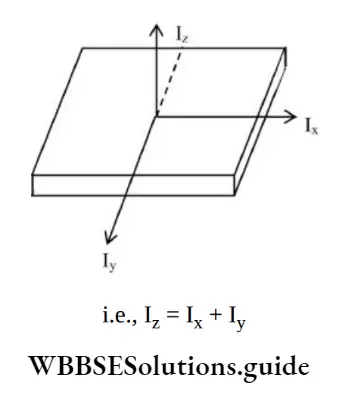
Theorem of Perpendicular Axes

The moment of inertia of a planar body about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.

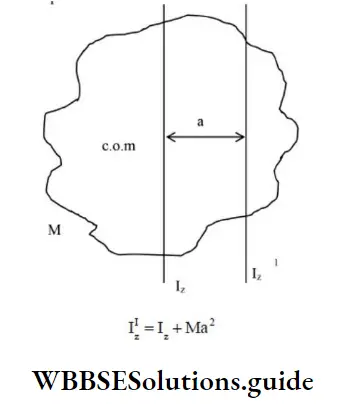
Theorem of Parallel Axes

The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its center of mass and the product of its mass (M) and the square of the distance (a) between two parallel axes.

Kinematic equations for rotational motion

⇒ \(\omega=\omega_0+\alpha t\)

⇒ \(\theta=\omega_0 t+\frac{1}{2} \alpha t^2\)

⇒ \(\omega^2=\omega_0^2+2 \alpha \theta\)

Where Q0 is the initial angular velocity, Q is the final angular velocity, a is the angular acceleration, 0 is the angular displacement, and ‘t’ is time.

Rotational Motion Class 11 NCERT NEET

According to the law of conservation of angular momentum

\(\mathrm{L}=\mathrm{I} \omega=\text { constant }\)

“If the net external torque on the system is zero, the angular momentum is conserved”. The kinetic energy of rolling motion is given by,

⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{I} \omega^2+\frac{1}{2} \mathrm{mv}_{\mathrm{cm}}^2\)

⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{~m} v_{\mathrm{cm}}^2\left(1+\frac{\mathrm{K}^2}{\mathrm{R}^2}\right)\)

where v_cm is the velocity of the center of mass.

The moment of inertia of some objects

Ring: I = MR² (about axis)

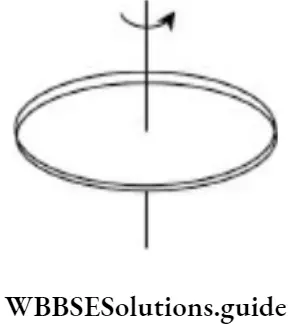
I = MR²/2 (about diameter)

I = 2 MR² (tangential to ring, parallel to the axis)

Where R is the radius and M is the mass of the ring.

Disc: \(I=\frac{1}{2} M R^2 \text { (axis) }\)

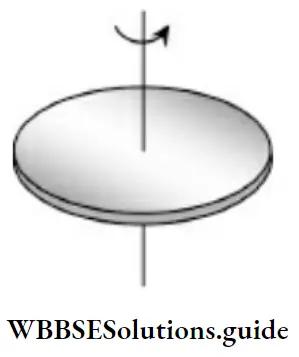
I = 1/4 MR² (diameter)

I = 3/2 MR² (tangential to the rim, parallel to the axis)

Cylinder:

About axis I = 1/2 MR²

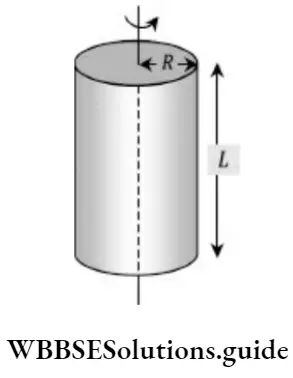
Center of Mass and Torque NEET Notes

Perpendicular the length and passing through C.M.

⇒ \(I=\frac{M L^2}{12}+\frac{M R^2}{4}\)

Thin rod:

⇒ \(I_{\text {dia }}=\frac{2}{3} M R^2\)

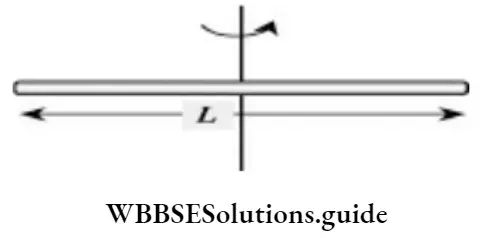
⇒ \(I=\frac{1}{3} M \amalg^2 \text { (aboutoneend) }\)

Hollow sphere:

⇒ \(I_{\text {dia }}=\frac{2}{3} M R^2\)

⇒ \(I_{\text {tarmgential }}=\frac{5}{3} M R^2\)

Solid sphere:

⇒ \(I_{\text {dia }}=\frac{2}{5} M R^2\)

⇒ \(I_{\text {tangential }}=\frac{7}{5} M R^2\)

Rectangular plate:

⇒ \(I_c=\frac{M\left(L^2+B^2\right)}{12}\)

Where L and B are the length and breadth of the plate respectively.

Motion on An Inclined Plane

1. For translational motion (without rotation)

⇒ \(\frac{1}{2} m v^2=m g h, \text { velocity } v=\sqrt{2 g h}=\sqrt{2 g s \sin \theta}\)

⇒ \(\text { Acceleration } a=g \sin \theta \text {, time } t=\left(\frac{2 s}{g \sin \theta}\right)^{1 / 2}\)

2. For rolling motion (translational + rotational)

⇒ \(\frac{1}{2} m v^2\left(1+\frac{K^2}{R^2}\right)=m g h\)

⇒ \(\text { velocity } v=\left[\frac{2 g s \sin \theta}{\left(1+\frac{K^2}{R^2}\right)}\right]^{1 / 2}=\left[\frac{2 g h}{\left(1+\frac{K^2}{R^2}\right)}\right]^{7^2}\)

⇒ \(\text { Acceleration } f=\frac{g \sin \theta}{\left(1+\frac{K^2}{R^2}\right)}\)

⇒ \(\text { Time } t=\sqrt{\frac{2 s}{a}}=\left[\frac{2 s\left(1+\frac{K^2}{R^2}\right)}{g \sin \theta}\right]^{1 / 2}\)