Vector
- A scalar is a physical quantity that has only magnitude but no direction.
- Example: Distance, Speed, Temperature, energy, Mass, etc.
- A vector is a physical quantity that has both magnitude and direction.
- Examples: displacement, velocity, acceleration, weight, force, electric field, etc.
Vectors Classification
(1) Null vector: A vector with zero magnitude and an arbitrary direction is called a null vector.
i.e. \(\vec{A}+(-\vec{A})=\overrightarrow{0}\)
⇒ \(\vec{A}-\vec{A}=\overrightarrow{0} \text { and }|\overrightarrow{0}|\)
= 0
Since the magnitude of a null vector is zero, its direction cannot be specified.
Read And Learn More: NEET Physics Notes
Properties Of Null Vector
1. \(\vec{A} \times 0=\overrightarrow{0}\)
2. \(\vec{A}+\overrightarrow{0}=\vec{A}\)
3. \(\lambda \overrightarrow{0}=\overrightarrow{0}\)
- Negative of a vector: A vector is said to be the negative of another vector if their magnitudes are equal but directions are opposite.
- Equal vectors: Two vectors are considered equal if they have the same magnitude and direction.
- Unequal vectors: Two vectors are said to be unequal if they have different magnitudes different directions or both.
- Parallel vectors: Two vectors are said to be parallel if they have the same direction. Their magnitude may or may not be equal. “All equal vectors are parallel but the converse may not be true. ”
- Antiparallel vectors: Two vectors are said to be anti-parallel if they point in opposite directions. Their magnitudes may or may not be equal.
- Collinear vectors: Two or more vectors, which are in the same line are known as collinear vectors. A real-life example of collinear vectors is seen in a tug-of-war game. the individual forces applied by the players on the rope represent collinear vectors.
- Coplanar vectors: Those vectors, that lie in the same plane, are called coplanar vectors.
- Orthogonal vectors: If two or three vectors are perpendicular to each other, they are known as orthogonal vectors. The best example for orthogonal vectors is the Cartesian coordinate axes.
- Unit vector: A vector having a magnitude equal to unity but having a specific direction is called a unit vector. To convert any vector into a unit vector, we divide the vector by its magnitude. Generally, a unit vector is represented by an alphabet in lowercase with a cap on it.
- Co-initial vectors: Vectors that have a common initial point are known as co-initial vectors.
NEET Physics Vector notes
If a is \(\vec{a}\) vector then its unit vector in the direction of \(\vec{a}\) is written as, a (read as a cap’ or ‘a hat’)
∴ \(\hat{a}=\frac{\vec{a}}{|\vec{a}|}\)
Unit vector \(\hat{a}=\frac{a}{|\vec{a}|}\)
It is a dimensionless quantity.

Multiplication Of A Vector By A Real Number
Multiplying a vector with a positive number X gives a vector whose magnitude is changed by the factor λ but the direction is the same as that of \(\vec{A}\).
For example, if A is multiplied by 2, the resultant vector 2\(\vec{A}\) is in the same direction as \(\vec{A}\).
Triangle law of vector addition
If two vectors \(\vec{a}\) and \(\vec{b}\) are represented by two sides of a triangle in head-to-tail form, the closing side of the triangle taken from the tail of the first to the head of the second represents their vector sum.
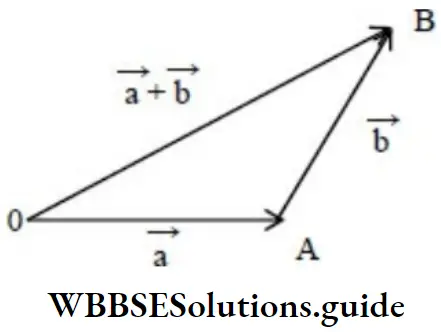
From the figure, \(\vec{OA}\) + \(\vec{AB}= \) – \(\vec{OB}\)
\(\vec{OB}\)= \(\vec{a}\) +\(\vec{b}\)
Vector addition and subtraction NEET questions
Note:
1. Vector addition is commutative
i.e., \(\vec{A}+\vec{B}=\vec{B}+\vec{A}\)
2. Vector addition is associative
⇒ \((\vec{A}+\vec{B})+\vec{C}=\vec{A}+(\vec{B}+\vec{C})\)
Subtraction of vectors can be defined in terms of the addition of vectors:
We can define the difference between two vectors A and B as follows
⇒ \(\vec{A}-\vec{B}=\vec{A}+(-\vec{B})\)
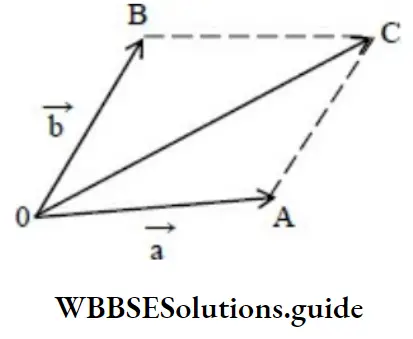
Parallelogram Law Of Vector Addition
If two vectors are represented by two adjacent sides of a parallelogram, then the diagonal of the parallelogram drawn from the common initial point represents their vector sum.
In the below \(\vec{a} \text { and } \vec{b}\) is drawn with a common initial point and a parallelogram is constructed using these two vectors as adjacent sides of a parallelogram. The diagonal \(\overrightarrow{O C}\) originating from the common initial point is the vector sum \(\vec{a}+\vec{b}\)
Important vector formulas for NEET Physics
Resolution of a vector
The process of splitting a vector into two or more vectors in such a way that their combined effect is the same as that of the given vector.
“The components of a vector in two or three mutually perpendicular directions are called rectangular components”.
Unit vectors along the X, Y, and Z axes of a rectangular coordinate system are denoted by \(\hat{i}, \hat{j}\) and \(\hat{k}\) respectively. Since these are unit vectors we have,
⇒ \(|\hat{i}|=|\hat{j}|=|\hat{k}|\)
= 1
These unit vectors are perpendicular to each other.
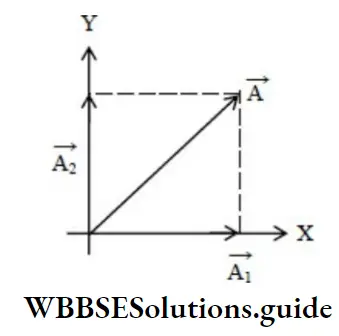
Consider a vector \(\vec{A}\) in the XY plane.
Scalar and vector quantities NEET
We draw lines from the head of \(\vec{A}\) perpendicular to the coordinate axes and we get \(\vec{A}_1 \& \vec{A}_2\) such that,
⇒ \(\overrightarrow{A_1}+\overrightarrow{A_2}=\vec{A}\)
⇒ \(\vec{A}=A_x \hat{i}+A_y \hat{j}\)
If A and θ are known Ax and Ay can be obtained using
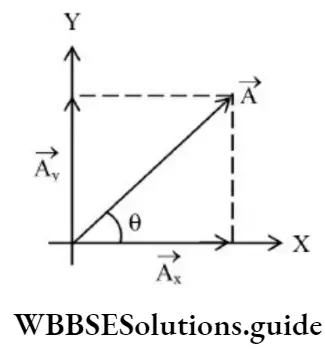
Ax = A cos θ and Ay = A sin θ
If Ax and Ay are given A and θ can be obtained as follows:
⇒ \(A_x^2+A_y^2=A^2 \cos ^2 \theta+A^2 \sin ^2 \theta\)
⇒ \(A_x^2+A_y^2=A^2\left(\cos ^2 \theta+\sin ^2 \theta\right)\)
A= \(\sqrt{A_x^2+A_y^2}\)
Because Cos2 θ + Sin2θ =1 and
tan θ \(=\frac{A_y}{A_x}\)
θ = tan-1\(\frac{A_y}{A_x}\)
The same procedure can be used to resolve a general vector A into three components along the X, Y, and Z axes in 3-D.
Ax = Acos α. Ay = A cos β & Az = A cos δ
⇒ \(A_x^2+A_y^2+A_z^2A^2=A^2 \cos ^2 \alpha+A^2 \cos ^2 \beta+A^2 \cos ^2 \delta\)
= \(A^2\left(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \delta\right)\)
⇒ \(A_x^2+A_y^2+A_z^2=A^2\)
i.e. A= \(\sqrt{A_x^2+A_y^2+A_z^2}\)
Tricks to solve vector problems for NEET
Vector Addition Analytical Method
⇒ If \(\vec{A}=A_x \hat{i}+A_y \hat{j}\) and \(\vec{B}=B_x \hat{i}+B_y \hat{j}\) are given vectors. Let R be their resultant.
⇒ \(\vec{R}=\vec{A}+\vec{B}=\left(A_x \hat{i}+A_y \hat{j}\right)+\left(B_x \hat{i}+B_y \hat{j}\right)\)
⇒ \(\vec{R}=\left(A_x+B_x\right) \hat{i}+\left(A_y+B_y\right) \hat{j}\)
⇒ \(\vec{R}=R_x \hat{i}+R_y \hat{j}\) where,
⇒ \(R_x=A_x+B_x\) and \(R_y=A_y+B_y\)
In 3-D:
Vector resolution and components NEET
⇒ \(\vec{A}=A_x \hat{i}+A_y \hat{j}+A_z \hat{k}, \vec{B}=B_x \hat{i}+B_y \hat{j}+B_z \hat{k}\)
⇒ \(\vec{R}=\vec{A}+\vec{B}=R_x \hat{i}+R_y \hat{j}+R_z \hat{k}\)
Where, \(R_x=A_x+B_x, R_y=A_y+B_y, R_z=A_z+B_z\)
Magnitude and direction of the resultant of two vectors A and B in terms of their magnitudes and the angle 9 between them.
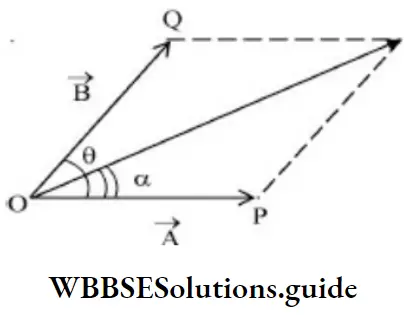
Dot product and cross product NEET questions
Let OP and OQ represent the two vectors A and B making an angle θ
Using the parallelogram law of vector addition,
⇒ \(\vec{R}=\vec{A}+\vec{B}\)
⇒ \(R^2=A^2+B^2+2 A B \cos \theta\) (Law of cosines)
⇒ \(R=\sqrt{A^2+B^2+2 A B \cos \theta}\) (This equation gives the magnitude of resultant)
⇒ \(\frac{R}{\sin \theta}=\frac{A}{\sin \beta}=\frac{B}{\sin \alpha}\) (Law of sines )
⇒ \(\tan \alpha=\frac{B \sin \theta}{A+B \cos \theta}\) (This equation gives the direction)
Dot Product (scalar product) of Two Vectors
⇒ \(\vec{a} \cdot \vec{b}=a b \cos \theta\)
Where, \(a=|\vec{a}|, b=|\vec{b}|\) and θ is the angle between \(\vec{a}\) and \(\vec{b}\)
If \(\vec{a} \cdot \vec{b}\) = 0 then \(\vec{a}\) and \(\vec{b}\) are perpendicular to each other
If θ = 0. then \(\vec{a} \cdot \vec{b}\) = ab
⇒ \(\vec{a} \cdot \vec{a}=a^2\)
⇒ \(\hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1 \text { and } \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0\)
The angle between two vectors \(\vec{a}\) and \(\vec{a}\) is given by,
\(\cos \theta=\frac{\vec{a} \cdot \vec{b}}{a b}\)= Or
θ = \(\cos ^{-1}\left(\frac{\vec{a} \cdot \vec{b}}{a b}\right)\)
Scalar product is commutative i.e.,\(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)
Projection of a vector a on the other vector \(\vec{a}\) on the vector \(\vec{a}\) is given by, \(\frac{\vec{a} \cdot \vec{b}}{b}\)
If α,β, and γ are the direction angles of the vector \(\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\) then its direction cosines are given by,
⇒ \(\cos \alpha=\frac{a_1}{a}, \cos \beta=\frac{a_2}{a} \text { and } \cos \gamma=\frac{a_3}{a}\)
Cross Product (vector product) Of Two Vectors
\(\vec{a} \times b=a b \sin \theta \hat{n}\) = ab sin \(\hat{n}\)
Where \(\hat{n}\) is a unit vector perpendicular to both \(\vec{a} and \vec{b}\) and \(\hat{n}\)\(\vec{a} and \vec{b}\) such that and h form a right-handed system.
⇒ If \(\vec{a} \times \vec{b}\) = 0 then \(\vec{a}\) and \(\vec{a}\)are parallel to each other.
⇒ If \(\theta=\frac{\pi}{2}\) , then \(\vec{a} \times \vec{b}=a b\)
Vector and projectile motion NEET
⇒ \(\hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{0}\)
⇒ \(\hat{i} \times \hat{j}=\hat{k}, \quad \hat{j} \times \hat{k}=\hat{i}, \quad \hat{k} \times \hat{i}=\hat{j}\)
⇒ \(\hat{j} \times \hat{i}=-\hat{k}, \quad \hat{k} \times \hat{j}=-\hat{i}, \quad \hat{i} \times \hat{k}=-\hat{j}\)
Vector Product Is Not Commutative
i.e., \(\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\)
But, \(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)
⇒ If \(\) and b represent the adjacent sides of a triangle then its area is given by
Area = \(\frac{1}{2}|\vec{a} \times \vec{b}|\)
⇒ If \(\vec{a}\) and \(\vec{b}\) represent the adjacent sides of a parallelogram, then its area is given by
Area = \(|\vec{a} \times \vec{b}|\)
⇒ If \(\vec{a}=a_x \hat{i}+a_y \hat{j}+a_z \hat{k}\) and \(\vec{b}=b_x \hat{i}+b_y \hat{j}+b_z \hat{k}\) then,
\(\vec{a} \times \vec{b}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\a_1 & a_2 & a_3 \\b_1 & b_2 & b_3\end{array}\right|\)