Work Energy And Power
Work is said to be done if there is a displacement in the direction of applied force.
Work done is the dot product of force and displacement.
W = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{x}}\)
W = Fx cosθ
Work is zero, if F = 0, x = 0 or cosθ = 0 (θ= 90°)
NEET Physics Work Energy and Power notes
Example:
- Work done by gravitational force of earth on its satellite is zero. (Since angle between gravitational force and instantaneous displacement is 900)
- Work done by force of tension of string on the bob of simple pendulum is zero. (Since angle between tension in the string and instantaneous displacement of the bob is 900)
- When a charged particle is moving in a uniform magnetic field in a circular path, work done by magnetic field is zero. (Since angle between magnetic force and instantaneous displacement of the charged particle is 900)
Read And Learn More: NEET Physics Notes
Potential Energy
Energy possessed by a body due to its position or configuration.
Example:
1. If a body is raised to a height ‘h’ from the ground, then its potential energy is given by,
U = mgh
2. P.E. of a spring is given by,
U= \(\frac{1}{2} \mathrm{kx}^2\)
Where k is spring constant and x is elongation/extension.
F=\(-\frac{\mathrm{dU}}{\mathrm{dx}}\)
Where U is potential energy.

Important formulas of Work Energy and Power for NEET
When the system is in equilibrium
\(\frac{\mathrm{dU}}{\mathrm{dx}}\)=0
Relation between kinetic energy and linear momentum
The kinetic energy of a body of mass ‘m’ and moving with velocity ‘v’ is given by
⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{mv}^2\)
⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{mv}^2 \times \frac{\mathrm{m}}{\mathrm{m}}=\frac{\mathrm{m}^2 \mathrm{v}^2}{2 \mathrm{~m}}=\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)
⇒ \(\mathrm{K}=\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)
⇒ \(\mathrm{P}=\sqrt{2 \mathrm{mK}}\)
Conservation of mechanical energy NEET questions
Conservative Force
A force is said to be conservative if work done by the force is independent of path. Or A force is said to be conservative if work done by the force depends only on initial and final position. Or A force is said to be conservative if work done by the force in a cyclic process is zero.
Work-Energy Theorem
If the forces acting on a body are conservative then change in kinetic energy of the body is equal to work done by the net force.
ΔK = W
Kf – Ki = W
Work Energy theorem NEET questions
Work Done By Variable Force
Constant force is rare in nature.
When there is variable force area under force versus displacement graph has to be calculated by the method of calculus.
⇒ \(\mathrm{W}=\int_{\mathrm{x}_1}^{\mathrm{x}} \overrightarrow{\mathrm{F}} \cdot \overline{\mathrm{dx}}\)
(Work done is the definite integral of force over displacement).
Area under F versus x graph gives work done.
Power
The rate at which work is done is called power.
⇒ \(P=\frac{W}{t}\)
⇒ \(P=\frac{\vec{F} \cdot \vec{x}}{t}\)
⇒ \(\mathrm{P}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}}\)
(i.e., power is the dot product of force and velocity)
Motion Of A Body In A Vertical Circle
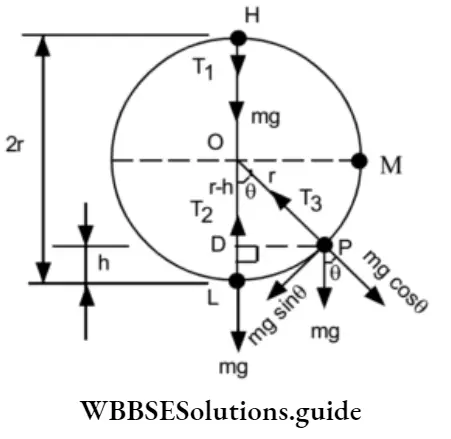
Power and efficiency NEET Physics notes
If the body moving in a vertical plane has to complete a vertical circle, at the highest point,
⇒ \(\frac{m v_H^2}{r}=m g\)
So the minimum condition is
⇒ \(\frac{m v_H^2}{r}=m g\)
⇒ \(\mathrm{T}_{\mathrm{H}}=\frac{\mathrm{mv_{ \textrm {H } } ^ { 2 }}}{\mathrm{r}}-\mathrm{mg}\) ____________ (1)
⇒ \(\mathrm{T}_{\mathrm{A}}=\mathrm{T}_{\mathrm{B}}=\frac{\mathrm{mv_{ \textrm {A } } ^ { 2 }}}{\mathrm{r}}=\frac{\mathrm{mv_{B } ^ { 2 }}}{\mathrm{r}}\) (∵VA=VB)________________(2)
⇒ \(\mathrm{T}_{\mathrm{L}}=\frac{\mathrm{mv_{ \textrm {L } } ^ { 2 }}}{\mathrm{r}}+\mathrm{mg}\)____________(3)
In general, the tension at any point P is given by,
⇒ \(\mathrm{T}_{\mathrm{P}}=\frac{\mathrm{mv_{ \textrm {p } } ^ { 2 }}}{\mathrm{r}}+\mathrm{mg} \cos \theta\)
w.k.t., (TH)min= 0
⇒ (∵ at minimum condition \(\frac{\mathrm{mv}_{\mathrm{H}}^2}{\mathrm{r}}=\mathrm{mg}\))
∴(1) ⇒ \(0=\frac{m v_H^2}{r}-m g\)
⇒ \(\frac{m v_{\mathrm{H}}^2}{\mathrm{r}}=\mathrm{mg}\)
⇒ \(\mathrm{v}_{\mathrm{H}}=\sqrt{\mathrm{gr}}\)
Therefore the minimum velocity to be given at H so that the body completes a vertical circle is \(\sqrt{\mathrm{gr}}\)
Now, using law of conservation of mechanical energy we will calculate the minimum velocity to be given at L in order to complete a vertical circle.
KH + UH = KL + UL
⇒ \(\frac{1}{2} m v_{\mathrm{H}}^2+m g(2 r)=\frac{1}{2} m v_{\mathrm{L}}^2+0\)
⇒ \(\frac{1}{2}(\mathrm{gr})+2 \mathrm{gr}=\frac{1}{2} \mathrm{v}_{\mathrm{L}}^2\)
⇒ ∵ \(\mathrm{v}_{\mathrm{H}}=\sqrt{\mathrm{gr}}\)
⇒ \(g r+4 g r=v_L^2\)
⇒ \(\mathrm{v}_{\mathrm{L}}=\sqrt{5 \mathrm{gr}}\)
Similarly, it can be shown that,
⇒ \(\mathrm{v}_{\mathrm{A}}=\sqrt{3 \mathrm{gr}}\)
∴ \(T_A=\frac{m v_A^2}{r}=\frac{m(3 g r)}{r}\)
⇒ \(\mathrm{T}_{\mathrm{A}}=3 \mathrm{mg}\)
⇒ \(\mathrm{T}_{\mathrm{L}}=\frac{\mathrm{mv_{ \textrm {L } } ^ { 2 }}}{\mathrm{r}}+\mathrm{mg}=\frac{\mathrm{m}}{\mathrm{r}} 5 \mathrm{gr}+\mathrm{mg}\)
⇒ \(\mathrm{T}_{\mathrm{L}}=6 \mathrm{mg} .\)
⇒ \(\left(T_H\right)_{\min }=0\)
⇒ \(\left(T_A\right)_{\min }=\left(T_B\right)_{\min }=3 \mathrm{mg}\)
⇒ \(\left(\mathrm{T}_{\mathrm{L}}\right)_{\mathrm{mg}}=6 \mathrm{mg}\)
⇒ \(\left(\mathrm{V}_{\mathrm{H}}\right)_{\min }=\sqrt{\mathrm{gr}}\)
⇒ \(\left(\mathrm{V}_{\mathrm{A}}\right)_{\min }=\left(\mathrm{V}_{\mathrm{B}}\right)_{\min }=\sqrt{3 \mathrm{gr}}\)
⇒ \(\left(\mathrm{V}_{\mathrm{L}}\right)_{\min }=\sqrt{5 \mathrm{gr}}\)
⇒ \(T_L-T_H=6 m g\)
Always,
Workdone in pulling a uniform chain on a frictionless table
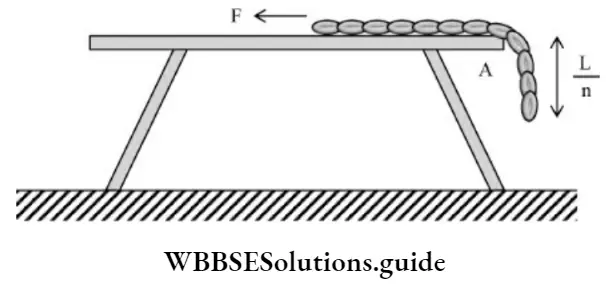
Let mass of chain be M and length L.
Workdone in pulling the hanging portion is given by,
⇒ \(\mathrm{W}=\left(\frac{\mathrm{M}}{\mathrm{n}}\right) \mathrm{g}\left(\frac{\mathrm{L}}{2 \mathrm{n}}\right)^2\)
⇒ \(\mathrm{W}=\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)
( centre of mass of hanging portion is a point A it is a distance of from the top).
Velocity of the chain when it just leaves the frictionless table
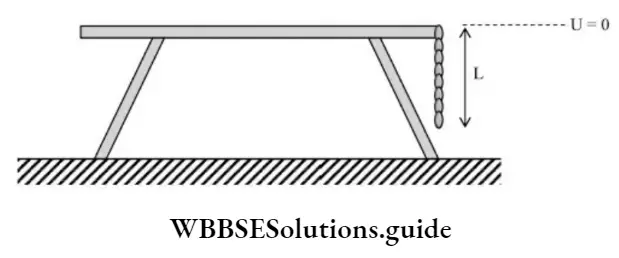
Kinetic and potential energy NEET problems
P.E. when \(\frac{\mathrm{L}}{\mathrm{n}}\) portion is hanging is given by,
⇒ \(\mathrm{U}_{\mathrm{i}}=-\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)
P.E. when the chain just leaves the table surface is,
⇒ \(\mathrm{U}_{\mathrm{f}}=-\frac{\mathrm{MgL}}{2}\)
w.k.t., K.E. gain = P.E. loss
⇒ \(\frac{1}{2} \mathrm{mv}^2=-\frac{\mathrm{MgL}}{2 \mathrm{n}^2}-\left[-\frac{\mathrm{MgL}}{2}\right]\)
⇒ \(\frac{1}{2} \mathrm{mv}^2=\frac{\mathrm{MgL}}{2}-\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)
⇒ \(\mathrm{v}^2=\mathrm{gL}-\frac{\mathrm{gL}}{\mathrm{n}^2}\)
⇒ \(\mathrm{v}^2=\mathrm{gL}\left(1-\frac{1}{\mathrm{n}^2}\right)\)
⇒ \(\mathrm{v}=\sqrt{\mathrm{gL}\left(1-\frac{1}{\mathrm{n}^2}\right)}\)
Collison
A body is said to undergo collision if there is an abrupt change in its velocity.
The collision is said to be perfectly elastic if there is no kinetic energy loss.
The collision is said to be inelastic if there is a kinetic energy loss during collision.
The collision is said to be perfectly inelastic if bodies undergoing collision move together with common velocity after collision.
Expression of K.E. loss in the case of perfectly inelastic collision in 1-D:
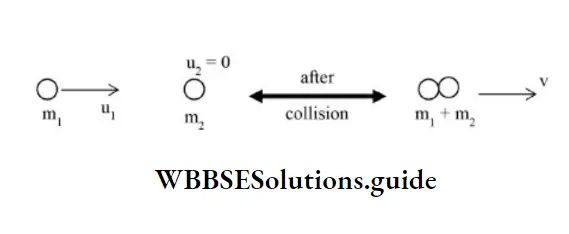
ΔK=\(\frac{1}{2} \frac{m_1 m_2}{m_1+m_2} u_1^2\)
Expression for final velocities when two bodies undergoing elastic collision in 1-D
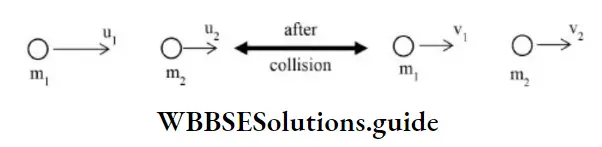
Work done by variable force NEET questions
⇒ \(v_1=\left(\frac{m_1-m_2}{m_1+m_2}\right) u_1+\frac{2 m_2 u_2}{m_1+m_2}\)
⇒ \(v_2=\left(\frac{m_2-m_1}{m_1+m_2}\right) u_2+\frac{2 m_1 u_1}{m_1+m_2}\)
If u2 = 0, then
⇒ \(v_1=\frac{\left(m_1-m_2\right)}{m_1+m_2} u_1\)
⇒ \(v_2=\frac{2 m_1 u_1}{m_1+m_2}\)
Case 1. If mx = m2, then vx = 0 & V2 = %
Case 2. If mx >> m2, then vx = ux & V2 = 2ux
Case3. If mx << m2, then vx = -ux & V2 = 0
Coefficient of Restitution (e)
⇒ \(\mathrm{e}=\frac{\mathrm{v}_2-\mathrm{v}_1}{\mathrm{u}_1-\mathrm{u}_2}=\frac{\text { Relative velocity of separation }}{\text { Relative velocity of appraoch }}\)
For perfectly elastic collision, e = 1
For perfectly inelastic collision, e = 0
For all other collisions, 0 < e < 1
If a ball is dropped from a height ‘h’,
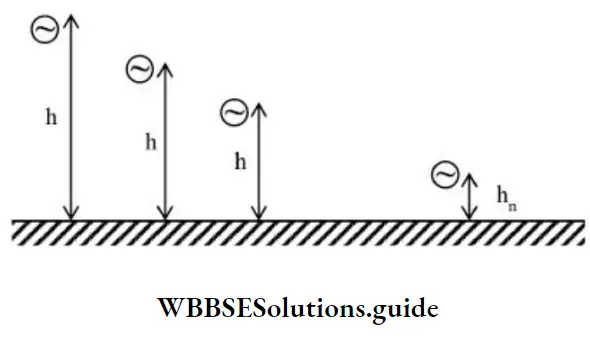
Maximum height attained by the ball decreases progressively due to K.E. loss. After 1 collision the height attained is h1
∴ e = \(=\frac{\sqrt{2 g h_1}}{\sqrt{2 g h}}=\sqrt{\frac{h_1}{h}}\)
⇒ \(\mathrm{e}^2=\frac{\mathrm{h}_1}{\mathrm{~h}}\)
⇒ \(\mathbf{h}_{\mathrm{l}}=\mathrm{he}^{2 \times 1}\)
After 2 collisions,
⇒ \(\mathrm{e}=\frac{\sqrt{2 \mathrm{gh}_2}}{\sqrt{2 \mathrm{gh}_1}}=\sqrt{\frac{\mathrm{h}_2}{\mathrm{~h}_1}}\)
⇒ \(\mathrm{e}^2=\frac{\mathrm{h}_2}{\mathrm{~h}_1}=\frac{\mathrm{h}_2}{\mathrm{he}^2}\)
∴ \(h_2=h^4 \Rightarrow h_2=h e^{2 \times 2}\)
∴ After ‘n’ collisions.
⇒ \(h_n=h e^{2 n}\)
Collision in 2D
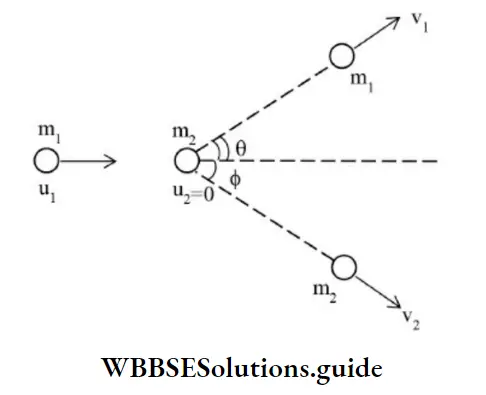
According to the law of conservation of linear momentum,
m1u1=m1v1cosθ+m2v2cosΦ
