WBCHSE Class 11 Properties Of Liquids Notes
Liquids:
Liquids, like gases, have no definite shape, but they do have a definite volume. One can, under ordinary conditions of temperature and pressure, assume that the volume of gaseous particles (atoms or molecules) is negligible compared to the volume of a gas.
- But one cannot do so in the case of a liquid. N or can one ignore the intermolecular force which holds together the molecules of a liquid quite strongly (as one can in the case of a gas)? It is because this attraction is quite strong so liquids have a definite volume.
- However, this attraction is not as strong as the attraction between the molecules of a solid, which is why liquids, unlike solids, do not have a definite shape.
- The molecules of a liquid do not occupy fixed positions as do the molecules of a solid. They exhibit translatory motion, unlike the molecules of a solid.
- A liquid possesses the fluidity of a gas and the incompressibility of a solid. The liquid state is intermediate between the state of disorder in a gas and the state of order in a solid.
“Properties of liquids, WBCHSE Class 11, chemistry notes, and explanations”
Read and Learn More WBCHSE For Class 11 Basic Chemistry Notes

The properties of a liquid can be explained in terms of the kinetic molecular theory which makes the following assumptions.
- The molecules of a liquid are relatively closer together than the molecules of a gas.
- The intermolecular force holding the molecules of a liquid together is appreciable.
- The molecules of a liquid are in a constant state of random motion.
- The average kinetic energy of the molecules of a liquid is directly proportional to its absolute temperature.
Properties of Liquids
Shape: Liquids do not have a definite shape. They take on the shape of the vessel they are placed in. This is because the molecules of a liquid have so much freedom that they flow readily and take up the shape of the container due to the continuous breaking and making of weak van der Waals bonds between the neighbouring molecules.
| Class 11 Biology | Class 11 Chemistry |
| Class 11 Chemistry | Class 11 Physics |
| Class 11 Biology MCQs | Class 11 Physics MCQs |
| Class 11 Biology | Class 11 Physics Notes |
Volume: When you fill a container (closed) with a gas, the gas molecules spread out to occupy the whole container because they are free to move into whatever space is available. Liquid molecules, on the other hand, are held together by a relatively strong force of attraction, which does not allow them to move about quite so freely. This is why a liquid has a definite volume which does not change with the vessel it is placed in.
Density: The fact that liquid molecules are held much closer together than the molecules of a gas explains why liquids have a much greater density than gases under similar conditions. For instance, the density of water at 100°C and 1 atm pressure is about 1600 times the density of water vapour at the same temperature and pressure.
“WBCHSE Class 11, chemistry notes, on properties of liquids, and intermolecular forces”
The density of a liquid decreases or the liquid expands when temperature increases. This can be explained by the fact that the average kinetic energy of the molecules increases with temperature and they can overcome the intermolecular force to a small extent.
Compressibility: The much stronger attractive force between liquid molecules holds them closer together than gaseous molecules. The intermolecular space in liquids is very little and this makes liquids far less compressible than gases under similar conditions.
Evaporation: The change of state of a liquid into a vapour at a temperature below the boiling point of the liquid is called evaporation. It is a surface phenomenon, that is to say, the process occurs at the surface of a liquid.
During evaporation, the molecules at the surface of a liquid manage to overcome the intermolecular force which binds them to the rest of the molecules and escape into the space above the liquid. How does this happen? The molecules of a liquid are in a constant state of motion and their average kinetic energy is directly proportional to the absolute temperature of the liquid.
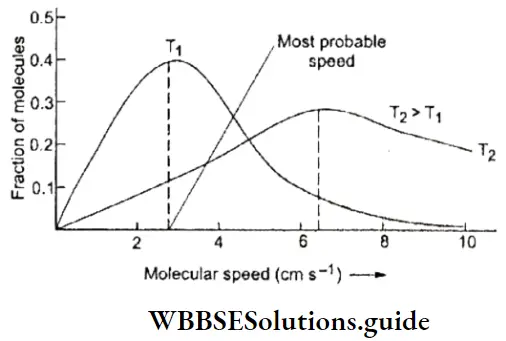
- However, just as in a gas, all the molecules of a liquid do not have the same energy. The energy distribution depends on the temperature of the liquid. At any temperature, a certain fraction of the molecules have enough energy to overcome the attractive force exerted on them by neighbouring molecules.
- The molecules at the surface of a liquid are attracted only by the molecules below them, while the molecules in the bulk of the liquid are attracted by molecules all around them. Surface molecules, thus, need less energy to overcome intermolecular attraction and it is easier for them to escape. The molecules which escape are the more energetic ones and the molecules that are left behind in the liquid are the less energetic ones.
- In other words, the molecules left behind have a lower average kinetic energy, which means that the temperature of the liquid falls due to evaporation. Of the molecules left behind, a certain energetic fraction will continue to change to the vapour phase, until all the liquid evaporates, provided the liquid is placed in an open vessel.
Liquid Properties WBCHSE Class 11
Rate of evaporation evaporation is indeed a property of liquids but all liquids do not evaporate at the same rate. The rate of evaporation depends on many factors. The nature of the liquid is one of these factors.
- It should be obvious to you by now that the weaker the intermolecular force in a Liquid, the easier it will be for its molecules to escape into the vapour phase. Volatility is a term used to describe the readiness of a liquid to evaporate. The weaker the intermolecular force, the more volatile the liquid, i.e., the more readily it evaporates. For instance, alcohol is more volatile than water.
- The rate of evaporation of a particular liquid depends on temperature. The higher the temperature, the greater the fraction of molecules which are energetic enough to escape from the surface, so the higher will be the rate of evaporation.
- Since evaporation is a surface phenomenon, it stands to reason that increasing the surface area of a liquid will increase the rate of evaporation. That is why we spread out our clothes to dry.
- Blowing a current of air across the surface of a liquid increases the rate of evaporation. The current of air carries away the molecules that have already escaped from the liquid and prevents them from returning to the liquid state.
Enthalpy of Vaporisation: The molecules of a liquid need energy to overcome the intermolecular force binding them to the liquid and escape into the vapour phase.
“Liquids, physical and chemical properties, WBCHSE Class 11, chemistry notes”
- The amount of heat required to evaporate 1 mole of a given liquid at a constant temperature is called the enthalpy of vaporisation. The enthalpy of vaporisation of a liquid depends on its intermolecular force.
- The greater the intermolecular force, the greater will be the enthalpy of vaporisation. Water has a relatively high enthalpy of vaporisation because of the presence of strong hydrogen bonds between its molecules. The molar enthalpy of vaporisation of water at 25°C is 44.01 kJ mol-1.
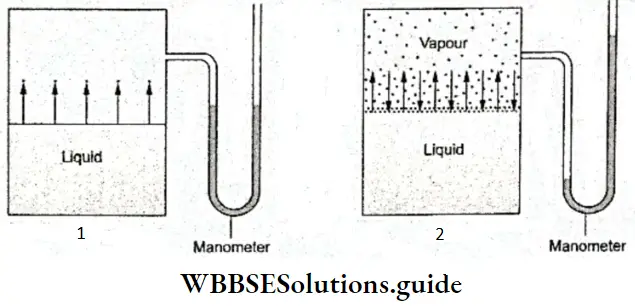
Vapour Pressure: When a liquid is placed in an open vessel, it evaporates slowly until all the liquid has changed into the vapour state. What happens when a liquid is placed in a closed vessel? If a liquid is placed in a closed vessel with some free space above the liquid, and the vessel is connected to a manometer, as shown in Figure, it initially evaporates and the level of the liquid falls. However, there comes a time when the level of the liquid becomes constant and so does the mercury level in the manometer.
- As explained earlier (in the section on evaporation), initially, the more energetic liquid molecules overcome the intermolecular force and escape from the surface of the liquid.
- These molecules accumulate in the space above the liquid since they cannot escape from the vessel and the pressure exerted by the vapour increases (raising the level of the mercury in the manometer).
- The vapour molecules are also in a state of random motion and their energy distribution follows the Maxwell-Boltzmann pattern.
As these molecules collide with each other, the walls of the container and the surface of the liquid, of them have low enough kinetic energy to be recaptured by the liquid molecules. Thus begins the process of condensation of the vapour molecules.
“WBCHSE Chemistry, Class 11, properties of liquids, viscosity, and surface tension”
- The processes of evaporation and condensation proceed simultaneously. The rate of condensation increases as the number of vapour molecules in the space above the liquid increases.
- Ultimately a stage is reached when condensation takes place at the same rate as evaporation and the system (liquid and vapour) is said to be in a state of dynamic equilibrium.
- In this state, the level of the liquid in the vessel becomes constant, as do the number of molecules in the vapour state and the pressure exerted by them, which is indicated by the manometer.
- This pressure, or the pressure exerted by the vapour of a liquid in equilibrium with it, is called the equilibrium vapour pressure or the vapour pressure of the liquid.
The vapour pressure of a liquid rises with temperature because a greater number of molecules acquire the minimum kinetic energy to escape from the liquid phase.
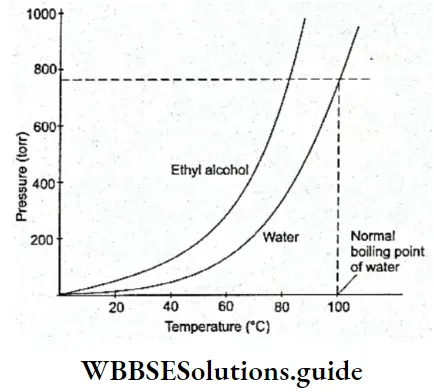
Every liquid has a characteristic vapour pressure at a particular temperature. The higher the intermolecular force in a liquid, the less volatile it is, and the lower the vapour pressure at a particular temperature.
Boiling Point: Boiling is similar to evaporation. However, there are certain differences between the two processes. Evaporation occurs spontaneously at all temperatures while boiling takes place at a particular temperature at which the vapour pressure of a liquid becomes equal to the atmospheric pressure. There are some other differences between boiling and evaporation, but we will come to those later.
Class 11 Chemistry Liquid Properties WBCHSE
- What happens when a liquid boils? Suppose a liquid is heated gradually. The average energy of its molecules rises and more molecules have the energy to escape from its surface, i.e., the rate of vaporisation increases, as does the vapour pressure of the liquid. Then there comes a temperature (boiling point) when the vapour pressure of the liquid becomes equal to the atmospheric pressure.
- At this point, the bubbles of vapour formed inside the liquid become energetic enough to rise through the bulk of the liquid and escape from the surface.
- Before this temperature, when the vapour pressure is still lower than the atmospheric pressure, the bubbles of vapour formed inside the liquid remain trapped inside and evaporation takes place only from the surface of the liquid.
The temperature at which bubbles of vapour rise freely to the surface and the liquid starts to boil is the boiling point of the liquid.
- The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to the atmospheric pressure. Then obviously, the boiling point will depend on pressure. The boiling point of a liquid at 1 atm pressure is called its normal boiling point.
- The water has a vapour pressure equal to 1 atmosphere at 373.15 K which is the normal boiling point of water. If the pressure is higher, the boiling point rises and if it is lower, the boiling point falls. This is why water boils at a lower temperature in the hills (where atmospheric pressure is lower) than in the plains.
- A liquid may be made to boil at a higher or lower temperature than its normal boiling point by increasing or reducing the pressure. Liquids which decompose at their normal boiling point are made to boil under low pressure.
- Liquids in which tyre intermolecular force is strong are less volatile and boil at a higher temperature.
“Properties of liquids, boiling point, vapor pressure, and density, WBCHSE Class 11”
Surface Tension Of A Liquid: The molecules of a liquid are held together by the intermolecular force of attraction. However, all the molecules are not subjected to the same kind of attraction. The molecules below the surface of a liquid are attracted equally on all sides by other molecules which surround them, so there is no net force acting on them. The molecules at the surface, however, are attracted only by the molecules beside and below them.
- Thus, there is a net downward force of attraction acting on them, which tends to pull them into the liquid and reduce the surface area to the minimum possible.
- Another way of looking at this is that the molecules at the surface are in a state of higher energy (since they experience a net downward force) than the molecules below the surface.
- Every system tends to a state of minimum energy, so a liquid tends to have the minimum surface area possible. Whichever way you look at it, the downward force on the surface molecules tends to make the surface of a liquid behave like a stretched membrane.
- This property of the surface of a liquid to contract and behave as if it were in a state of tension is called surface tension. The formation of water droplets on a glossy surface is due to surface tension.
- Now that you know that a liquid surface tends to contract and behave like a stretched membrane, it should be easy enough to understand that work would need to be done to extend the surface of a liquid. Thus, surface tension is defined as the work (energy) required to expand the surface of a liquid by unit area. It is expressed in J m’. This is also referred to as surface energy.
Surface tension = \(\frac{\text { work }}{\text { change in area }}\)
Surface tension can also be defined as the force acting at right angles to the surface along the unit length of the surface. The SI unit is N m-1.
The greater the intermolecular force, the greater the surface tension. You should be able to reason this out for yourself. It should also be easy to understand that if the temperature increases, so will the energy of the molecules and their ability to break free of intermolecular attraction and consequently, surface tension will decrease.
Liquid Properties And Applications WBCHSE Class 11
Capillary Action When one end of a capillary tube is dipped into water, the water rises to a certain height. Most liquids rise in capillary tubes. Different liquids rise to different heights depending on their surface tension. This phenomenon can be used to measure the surface tension of a liquid.
- You have read about the intermolecular force of attraction in a liquid. Now, when a liquid comes into contact with, say, a glass tube, there is a force of attraction between the liquid molecules and the glass molecules. The attractive force between molecules of the same substance is referred to as cohesive force and that between molecules of different substances is called adhesive force.
- In the case of glass and water, the adhesive force is stronger than the cohesive force, which tends to make water spread over glass (or wet it)2.
- When a capillary tube comes into contact with water, water tends to spread into it, forming a concave surface. This increases the surface area, and water rises in the capillary to reduce the total surface area. This continues till the adhesive force is balanced by the die weight of water in the tube. The greater the surface tension, the higher the rise in the capillary.
- One can find many examples of capillary action in everyday life. To mention only a few, oil rises in the wick of a stove due to capillary action and water rises in the stem of a plant due to capillary action.
Shape of Liquid Meniscus The surface of a liquid in a tube is curved. This curved surface is called a meniscus. Liquids with wet glass, like water, have a concave meniscus. You will learn more about this in your physics lessons.
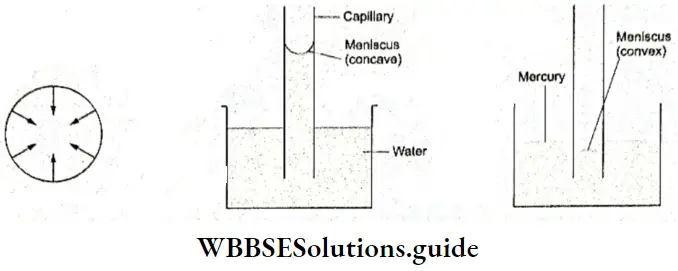
For the moment, think of it this way the stronger adhesive force pulls the surface of the water towards the glass or makes the water stick to the glass, so the surface curves upwards. In the case of mercury, the cohesive force is stronger, so mercury draws away from glass and has a convex meniscus in a glass tube.
Shape of Liquid Drop You may have noticed that drops of water are spherical. Liquid drops are spherical due to surface tension. You have already learnt that a liquid tends to have the minimum surface area possible. For a given volume, a sphere has the minimum surface area, so a drop of liquid is spherical.
Dissolved Substances The surface tension of a liquid changes if some substance is dissolved in it. For example, soaps and detergents lower the surface tension of water. This enhances its ‘spreading property’. Synthetic detergents are often added to toilet creams and medicinal jellies so that they spread more evenly.
Viscosity: All liquids indeed flow, but they do not flow at the same rate. Water, for instance, flows much more rapidly than honey. The readiness with which a liquid flows is governed by a property known as viscosity. The resistance offered by a liquid to flow is called viscosity. This resistance is a frictional effect due to the passage of one layer of liquid over another and arises due to intermolecular force. The stronger the intermolecular force, the greater the resistance to flow, i.e., the greater the viscosity of the liquid.
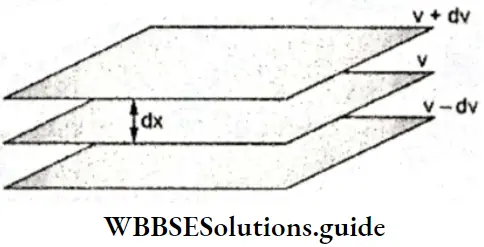
- Let us examine the motion of a liquid flowing through a pipe. It is not as though the entire liquid moves along at the same velocity.
- Different layers of the liquid slide past each other at different velocities because of the resistance offered by one layer to another. The layer in contact with the pipe is almost stationary and the central layer moves the fastest. Thus, the velocities of the layers increase with distance from the fixed surface.
When the flow of the liquid becomes steady, there will be a constant difference in the velocity between two different layers. Consider the three consecutive layers shown in Figure. The velocity in the lowest layer is v – dυ, that in the middle layer is ν, and that in the top layer is v + dν. The force required to maintain the flow, in the three layers considered above, is directly proportional to the area of contact and velocity gradient, i.e.
⇒ \(f \propto A \quad (area)\)
⇒ \(f \propto \frac{d v}{d x} \quad\) (velocity gradient)
or, \(f=\eta A \frac{d v}{d x}\) (the two layers are separated by the distance dx ).
Here n is the coefficient of viscosity and is defined as the force required to maintain the unit difference in velocity between two parallel layers of a liquid 1 cm apart. If all the variables are expressed in cgs units, the units of q turn out to be dyn s cm-2. The quantity 1 dyn s cm-2 is called 1 poise after Poiseuille, who did pioneering work in the field of fluid mechanics. In the SI system, the unit is Pa s, i.e., N s m-2 or kg m-1s-1.
1 poise = 1/10 Pa s
“WBCHSE Class 11, chemistry notes, on liquid state, compressibility, and fluidity”
Since viscosity depends on the intermolecular force, it should be obvious that viscosity decreases with rise in temperature.
Example 1. A gas occupies 2 L at 0°C and 1 atm pressure. What will be the change in temperature if the pressure is adjusted to 2.5 atm after the gas is transferred to a container of volume 1 L?
Solution:
Given
A gas occupies 2 L at 0°C and 1 atm pressure.
Initial conditions
p1 = 1atm
V1 = 2L
T1 = 0°C = 273 K
Final conditions
p2 =2.5 atm
V2 = 1L
T2 =?
By the gas equation, \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\).
∴ \(\quad T_2=\frac{p_2 V_2 T_1}{p_1 V_1}=\frac{2.5 \times 1 \times 273}{1 \times 2}=341.25 \mathrm{~K}\)
∴ change in temperature = 34125 -273 = 68.25°C
Properties Of Liquids In Chemistry WBCHSE
Example 2. A sealed tube which can withstand a pressure of 3 atm is filled with air at 37 °C and 760 mmHg pressure. Find the temperature above which it will burst.
Solution:
Given,
A sealed tube which can withstand a pressure of 3 atm is filled with air at 37 °C and 760 mmHg pressure.
V1 = V mL
V2 = V mL
p1 = 760 mmHg = 1 atm
p2 = 3 atm
T1 = 37°C = 37 + 273 = 310K
T2 = ?
According to the gas equation
⇒ \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\)
⇒ \(T_2 =\frac{p_2 V_2 T_1}{p_1 V_1}=\frac{3 \times V \times 310}{1 \times V}=930 \mathrm{~K}\) .
Therefore, the temperature above which the tube will burst = 930 – 273 = 657°C.
Example 3. A sample of a gas occupies a volume of 100 L at 4 atm and 20 °C. What will be its temperature when it is placed in an evacuated container of volume 175 L? The pressure of the gas in the container is one-third the initial pressure.
Solution:
Given,
A sample of a gas occupies a volume of 100 L at 4 atm and 20 °C.
V1 = 100 L V2 = 175 L
p1 = 4 atm
p2 = 1/3 x 4 = 4/3 atm
T1 =20°C = 20 + 273 = 293K T2=?
Applying the gas equation
⇒ \(\frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2}\)
⇒ \(T_2=\frac{p_2 V_2 T_1}{v_1 V_1}=\frac{4 / 3 \times 175 \times 293}{100 \times 4}=170.9 \mathrm{~K}\)
= 170.9- 273 =- 102.1 °C.
Example 4. The weight of 350 mL o/a diatomic gas at 0°C and 2 bar is 1.0 g. Calculate the weight of one atom in grams.
Solution:
Given,
The weight of 350 mL o/a diatomic gas at 0°C and 2 bar is 1.0 g.
p = 2 bar, V = 350 mL = 0.35L,T=0°C = 273 K
According to the equation
pV = nRT,
n = \(\frac{p V}{R T}\)
= \(\frac{2 \times 0.35}{0.08314 \times 273} \quad\left(because \quad R=0.08314 \mathrm{Lbar} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\right)\) = 0.031 mol
Weight of 0.031 mol of the gas =1 g.
Therefore, weight of1 mol of the gas = \(\frac{1}{0.031}\) = 32.2 g.
Since 1 mol contains 6.022 x 1023 molecules, the weight of 6.022 x 1023 molecules is 32.2 g.
Therefore, weight of one molecule = \(\frac{32.2}{6.022 \times 10^{23}}\) = 5.35 x 10-23g.
Since the gas is diatomic, one molecule has two atoms.
Therefore, the weight of one atom of the gas
= \(\frac{5.35 \times 10^{-23}}{2}=2.67 \times 10^{-23}\)
Example 5. How many moles of oxygen will there be in a 400 cm3 sample of the gas at a pressure of 760 mmHg and a temperature of 27°C? (R = 8.31 kPa dm3 K-1 mol-1)
Solution:
Given R = 8.31 kPa dm3 K-1 mol-1
V = 400 cm3 = 400/100 = 0.4 dm3 (1000 cm3 = 1 dm3 or 1 cm3 = 1/1000 dm3)
p = 760 mmHg = 101.3 kPa
T = 27°C = 27 + 273 = 300 K
According to the ideal gas equation,
pV = nRT.
∴ n = \(\frac{p V}{R T}=\frac{1013 \times 0.4}{8.31 \times 300}\) = 0.0162 mol.
Example 6. Calculate the number of nitrogen molecules present in a 1-L flask at a pressure of 7.6×10-10 temperature of 10 °C (R = 0.082 L atm K-1 mol-1).
Solution:
Given V =1L
T =10°C = 10 + 273 = 283 K
p = \(7.6 \times 10^{-10} \mathrm{mmHg}=\frac{7.6 \times 10^{-10}}{760}=10^{-12} \mathrm{~atm}\)
According to the ideal gas equation pV = nRT.
∴ n = \(\frac{p V}{R T}=\frac{10^{-12} \times 1}{0.082 \times 283}=4.3 \times 10^{-14} \mathrm{~mol}\)
Several molecules in 1 mol of a gas = 6.022 x 1023.
∴ number of nitrogen molecules in 4.3 x10-14 mol = 4.3 x 1014 x 6.022 x 1023 = 25.89 x 109.
Example 7. 3.7 g of gas at 25°C occupies the same volume as 0.184 g of H2 at 17°C and at the same pressure. What is the molar mass of the gas?
Solution:
Given
3.7 g of gas at 25°C occupies the same volume as 0.184 g of H2 at 17°C and at the same pressure.
According to the ideal gas equation pV = nRT.
Number of moles (n) = n/M
∴ V = \(\frac{m}{M} \frac{R T}{p}\)
The volume and pressure of the two gases are the same.
⇒ \(\frac{m_1}{M_1} R T_1=\frac{m_2}{M_2} R T_2\)
where m1 and m1 are the masses of the given gas and hydrogen respectively and M1 and M2 are the molar masses of the given gas and hydrogen respectively.
Substituting the values of the known variables,
⇒ \(\frac{3.7}{M_1} \times R \times 298=\frac{0.184}{2} \times R \times 290\)
∴ \(\quad M_1=\frac{3.7 \times 298 \times 2}{0.184 \times 290}=4133 \mathrm{~g}\).
\end{aligned}
Example 8. Hydrogen gas is produced by passing steam over hot magnesium according to the following equation.
⇒ \(\mathrm{Mg}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{MgO}+\mathrm{H}_2\)
“Properties of liquids, capillary action, cohesion, adhesion, WBCHSE Chemistry notes”
Calculate the volume of H2 liberated by passing steam over 30 g of magnesium at 77°C and 1 atm.
Solution:
⇒ \(\underset{24 \mathrm{~g}}{\mathrm{Mg}}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{MgO}+\underset{224 \mathrm{~L}}{\mathrm{H}_2}\)
24 g of Mg produces 22.4 L of hydrogen at1 atm and 0°C.
∴ 30 g of Mg will produce = \(\frac{22.4 \times 30}{24}\) = 28L of H2.
Let us find the volume of H2 at 77°C and 1 atm.
p1 =1 atm
V1=28L
T1 = 273 K
p2 =latm
V2 = ?
T2 =77°C = 273 + 77 = 350 K
∴ \(V_2=\frac{p_1 V_1 T_2}{p_2 T_1}=\frac{1 \times 28 \times 350}{1 \times 273}=35.89 \mathrm{~L}\)
Example 9. How many litres of oxygen at 57°C and 2 bar is required to bum completely 2.5 g of butane (C4H10)?
Solution:
The equation for the reaction is \(\mathrm{C}_4 \mathrm{H}_{10}+\frac{13}{2} \mathrm{O}_2 \longrightarrow 4 \mathrm{CO}_2+5 \mathrm{H}_2 \mathrm{O}\)
⇒ \(58 \mathrm{~g} \quad \frac{13}{2} \times 22.7 \mathrm{~L}\)
At step, 58 g of butane requires 13/2 x 22.7 L of O2.
∴ 2.5 g of butane would require = \(\frac{13}{2} \times \frac{22.7 \times 2.5}{58}\) = 6.36 L of O2.
At step
p1 = 1 bar
V1 = 6.36L
T1 = 273K
At given conditions
p2 = 2 bar
V2 = ?
T2 = 57°C = 57 + 273 = 330K
By the gas equation,
∴ \(V_2=\frac{p_1 V_1 T_2}{p_2 T_1}=\frac{1 \times 6.36 \times 330}{2 \times 273}=3.84 \mathrm{~L}\)
Example 10. 6.022 x 1023 oxygen molecules are present at -13°C in a 1500 mL vessel. What is the pressure of the gas (R = 0.08314 L bar K-1 mol-1)?
Solution:
6.022 x 1023 molecules = 1 mol.
Given
6.022 x 1023 oxygen molecules are present at -13°C in a 1500 mL vessel.
n = 1 mol
V = 1500 mL = 1.5 L
p = ?
T = -13°C = 273 -13 = 260 K
R = 0.08314 L bar K-1 mol-1.
Applying the ideal gas equation,
p = \(\frac{n R T}{V}=\frac{1 \times 0.08314 \times 260}{1.5}=14.4 \mathrm{bar}\).
Liquid Properties And Applications WBCHSE Class 11
Example 11. A gas of molar mass 84.5 g enclosed in a flask at 27°C, has a pressure of 2 atm. Calculate the density of the gas (R = 0.082 L atm K-1 mol-1).
Solution:
Given
A gas of molar mass 84.5 g enclosed in a flask at 27°C, has a pressure of 2 atm.
Molar mass (M) = 84.5 g mol-1
T = 27°C = 27 + 273 = 300 K.
Pressure = 2 atm
R = 0.082 L atm K-1 mol-1.
According to the ideal gas equation, pV = NRT = m/M RT.
∴ \(\frac{m}{V}=\rho=\frac{p M}{R T}=\frac{2 \times 84.5}{0.082 \times 300}=6.86 \mathrm{~g} \mathrm{~L}^{-1} \text {. }\)
“Properties of liquids, WBCHSE Class 11, solved examples, and real-world applications”
Example 12. The density of a certain mass of gas is 0.326 g L-1 at 2TC and 190 mm pressure. What is its density at 57°C?
Solution:
Given
The density of a certain mass of gas is 0.326 g L-1 at 2TC and 190 mm pressure.
∴ \(operatorname{Density}(\rho)=\frac{\text { mass }(M)}{\text { volume }(V)}\)
∴ \(\quad \rho \propto \frac{1}{V}\) when M is constant.
According to Charles’s law,
V ∝ T.
∴ \(\rho \propto \frac{1}{T}\)
⇒\(\rho T=\text { constant } \Rightarrow \rho_1 T_1=\rho_2 T_2\).
Given,
⇒ \(\rho_1 =0.326 \mathrm{~g} / \mathrm{L} \quad T_1=27^{\circ} \mathrm{C}=27+273=300 \mathrm{~K}\)
⇒ \(T_2 =57^{\circ} \mathrm{C}=57+273=330 \mathrm{~K} . \)
⇒ \(\quad \rho_2=\frac{0.326 \times 300}{330}=0.296 \mathrm{~g} \mathrm{~L}^{-1}\).
Example 13. At 25°C, the air contains mostly nitrogen (79%) and oxygen (21%). How much faster do the nitrogen molecules move than the molecules of oxygen?
Solution:
Given
At 25°C, the air contains mostly nitrogen (79%) and oxygen (21%).
⇒ \(\frac{u_{\mathrm{N}_2}}{u_{\mathrm{O}_2}}=\sqrt{\frac{M_{\mathrm{O}_2}}{M_{\mathrm{N}_2}}}=\sqrt{\frac{32}{28}}=1.07\)
The ratio of \(u_{\mathrm{N}_2} \text { to } u_{\mathrm{O}_2}\) is 1.07 (107%) indicating that the nitrogen molecules move 7% faster than oxygen molecules do.
“WBCHSE Class 11 Chemistry, liquid properties, phase transitions, and key formulas”
Example 14. Calculate the height of the column of mercury in a mercury barometer. The diameter of the barometer is 5 mn% the pressure exerted is the atmospheric pressure i.e., 1.013 x105 Pa and the density of mercury is 13.58 g cm-3.
Solution:
Given
The diameter of the barometer is 5 mn% the pressure exerted is the atmospheric pressure i.e., 1.013 x105 Pa and the density of mercury is 13.58 g cm-3
Since p = hpg, where h is the height of the mercury column, p is the density of mercury and g is the acceleration due to gravity,
h = \(\frac{p}{p g}\)
First, let us express p in SI units.
⇒ \(\rho=13.58 \mathrm{~g} \mathrm{~cm}^{-3}=\frac{13.58}{1000} \times 10^6 \mathrm{~kg} \mathrm{~m}^{-3}\)
= \(13.58 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3} . \)
h = \(\frac{1013 \times 10^5}{13.58 \times 10^3 \times 9.81}\) = 0.76 m = 760 mmHg
