WBCHSE Class 11 Chemistry Chapter 1 Notes On Basic Concepts
Chemistry is the study of the materials that make up the universe. It deals with the composition, structure, properties, and interaction of substances.
The universe is made up of a large variety of materials. Chemists determine how chemical transformations occur among these substances.
Chemistry finds application in diverse areas. For instance, chemical fertilizers have helped increase crop yield to a large extent.
“WBCHSE Class 11 Chemistry, Some Basic Concepts of Chemistry, notes, and key concepts”
Chemical industries also manufacture acids, alkalis, salts, drugs, dyes, soaps, detergents, alloys, polymers, etc.
- Chemistry has provided many life-saving drugs. Cisplatin and Taxol are very effective in cancer therapy, and AZT (Azidothymidine) is used to treat AIDS victims.
- In recent years chemistry has given us many new materials with specific magnetic, electric, and optical properties. These types of materials include conducting polymers, superconducting ceramics, and optical fibers.
- Environmentally hazardous refrigerants like CFCs (chlorofluorocarbons), which are responsible for the depletion of the ozone layer, have been replaced by alternatives.
- Like the study of all other sciences, the study of chemistry is based on the careful observation of various phenomena (like a reaction between substances) under controlled conditions.
- In other words, experiments form the foundation of chemistry. The observations made during an experiment may be qualitative or quantitative. Quantitative observations involve the measurement of one or more quantities and are discussed later in the chapter.
Read and Learn More WBCHSE For Class11 Basic Chemistry Notes
Classification Of Matter
We are often struck by the diversity of the things that surround us. The diversity of plant and animal life, the diversity of climate, and the diversity of geographical features. And yet, what is perhaps more wonderful is that all that surrounds us, in fact, everything in the entire universe, of which our surroundings comprise an infinitesimal part, is made of two things—matter and energy. Energy is something that we cannot hold in our hands or feel directly.

- We can experience its effects like when we feel the warmth of sunlight on our bodies.
- Matter, on the other hand, is something we can feel and see directly. Expressed more formally, matter is anything that occupies space, has mass, offers resistance, and can be perceived directly by our senses.
- Matter can be classified according to its physical state or according to its chemical composition. Physically, matter can exist in three states, viz., solid, liquid, and gaseous.
| Class 11 Biology | Class 11 Chemistry |
| Class 11 Chemistry | Class 11 Physics |
| Class 11 Biology MCQs | Class 11 Physics MCQs |
| Class 11 Biology | Class 11 Physics Notes |
Chemical classification of matter: Based on chemical composition, matter can be broadly divided into pure substances and mixtures. Pure substances can be of two types, viz., elements and compounds, while mixtures can be homogeneous or heterogeneous.
An element can be a metal, a nonmetal, or a metalloid, while a compound can be either inorganic or organic. The following chart should make you more familiar with this classification of matter.
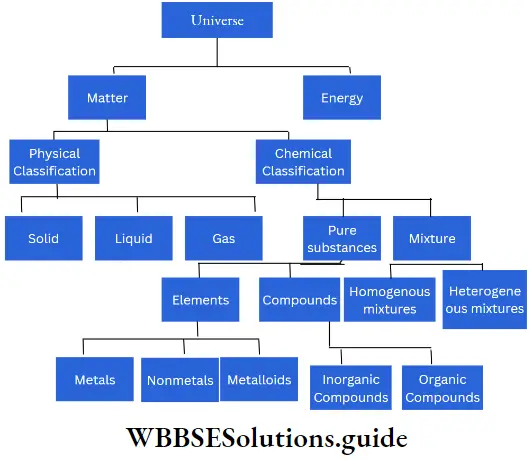
Elements, Compounds And Mixtures
The substances that we see around us are either elements (like gold), compounds (like sugar), or mixtures (like air). Molecules are the units of matter. They may be made up of two or more atoms of the same element or different elements combined in a definite ratio (compounds).
A mixture is a combination of elements, compounds, or element(s) and compound(s) in any ratio. Elements and compounds are pure substances that have a particular set of properties. Early chemists found it very difficult to distinguish an element from a compound.
It was Lavoisier who made a breakthrough and showed how elements can be distinguished from compounds.
“Some Basic Concepts of Chemistry, WBCHSE Class 11, chemistry notes, and explanations”
1. Elements: An element is the simplest form of a pure substance, which can neither be decomposed into nor built from simpler substances by ordinary physical or chemical methods. This definition of an element arose out of Lavoisier’s work, about which you will learn later in this chapter.
- Of course, there were difficulties related to defining an element this way. Until a substance could be disintegrated into simpler substances, it was considered to be an element, and when someone showed that it could be broken up, it was no longer considered to be an element. For example, water was considered to be an element until Sir Humphrey Davy showed that it could be decomposed by passing an electric current through it.
- A more exact definition of an element came up after the discovery of radioactivity, which showed that elements can be broken up and also that they can be synthesized from simpler substances. The modern definition, thus, is that an element is a pure substance that contains only one kind of atom. Mono-, di- or polyatomic molecules with the same kinds of atoms constitute elements, for example, He, O2, N2, and S8.
- We know of 111 elements so far. Only 90 of these occur in nature and just 20 elements make up 99% of the Earth’s crust. Some of the most abundant elements on the Earth’s crust are oxygen, silicon, aluminum, iron, carbon, calcium, sodium, and potassium. An element can be a metal, a nonmetal, or a metalloid.
Metals except for mercury, metals are generally solid at room temperature. They are malleable (can be beaten into thin sheets) and ductile (can be drawn into wires), and are good conductors of heat and electricity. Most metals have a high tensile strength and are lustrous. About 75-80 percent of the known elements are metals, gold, silver, copper, iron, and aluminum being some of the common ones.
Nonmetals These elements are poor conductors of electricity and heat. They are generally brittle (if solid), and without luster except iodine which shows a metallic luster. Carbon, sulfur, hydrogen, oxygen, and nitrogen are some common nonmetals
Chemical Reactions And Equations Class 11 WBCHSE Chemistry Notes
Metalloids These elements have some properties of metals and some of nonmetals. Some common examples of metalloids are silicon, arsenic, antimony, and selenium.
2. Compounds: A compound is a pure substance that is formed by the union of two or more elements in a definite proportion by mass and which can be decomposed into its constituent elements by suitable chemical methods. The composition of a compound is always the same regardless of the source from which it is obtained or the method by which it is produced.
- For example, water obtained from different sources (for example seas, lakes, rivers, or wells) is always made of hydrogen and oxygen chemically combined in the ratio of 1: 8 by mass.
- A compound is homogeneous (uniform throughout) and has fixed properties. For example, sodium chloride is a compound of sodium and chlorine and has a fixed melting point, density, and solubility in water.
- The properties of a compound are completely different from those of its constituent elements. For example, hydrogen and oxygen are gases at room temperature, also hydrogen is combustible and oxygen is a supporter of combustion.
- These two gases combine to form water, which is liquid at room temperature and is used to extinguish fire.
The basic differences between elements and compounds are listed in Table, while some compounds and the ratios of their constituents are mentioned in Table.
Differences between elements and compounds

Some compounds and their constituents
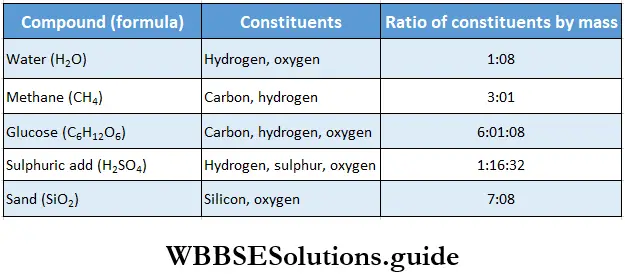
Compounds can be of two types, inorganic and organic.
Inorganic compounds These compounds are derived from nonliving sources like rocks and minerals. Common salt, washing soda, and lime are some inorganic compounds we use in everyday life.
Organic compounds These compounds are derived from living sources like plants and animals, or their remains buried under the earth (for example, petroleum). All organic compounds, like carbohydrates, fats, oils, waxes, and proteins contain carbon.
3. Mixtures: Mixtures, like compounds, contain more than one element, but the constituents of a mixture are not present in any particular ratio. Also, the components of a mixture do not lose their identity, so the properties of a mixture are not completely different from those of its constituents.
For example, when we dissolve sugar in water, it still tastes sweet. The components of a mixture do not combine chemically. They can be separated by some physical means. Mixtures can be homogeneous or heterogeneous.
“WBCHSE Class 11, chemistry notes, on Some Basic Concepts of Chemistry, and fundamental principles”
Homogeneous mixtures A mixture that has the same composition throughout is called a homogeneous mixture. Air is a homogeneous mixture of CO2, O2, N2, etc. A solution of sugar in water, natural gas, and alloys, like brass, bronze, and steel, are all homogeneous mixtures. Homogeneous mixtures can be solids, liquids, or gaseous.
Such mixtures are also called solutions. The components of a homogeneous mixture cannot be distinguished even under a microscope.
Heterogeneous mixtures Such mixtures do not have the same composition throughout. In other words, the components of a heterogeneous mixture are not distributed evenly. These components (called phases) can be distinguished with the naked eye, for example, a mixture of sand and sugar, a mixture of salt and pepper, or clay and water.
Some mixtures look homogeneous to the naked eye but are heterogeneous, for example, milk. Seen under a microscope, milk looks like a clear liquid in which droplets of the fat arc suspended.
Differences between mixtures and compounds
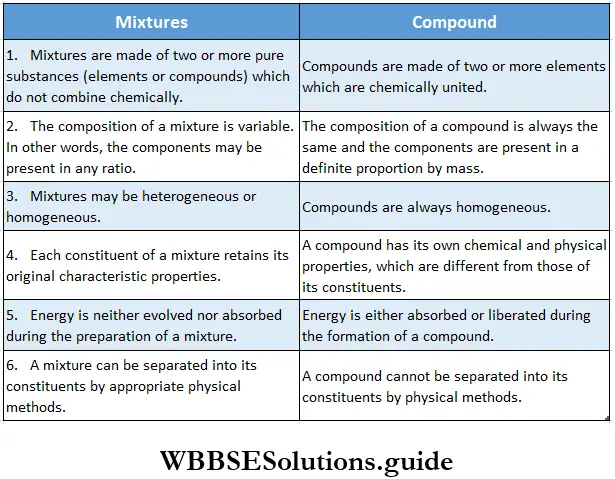
Some of the characteristics of mixtures mentioned in Table do not apply to homogeneous mixtures like bronze. Bronze is an alloy (a solution in the solid state) of copper and zinc in a definite proportion (3:2).
The properties of bronze are different from those of copper or zinc. Besides, bronze cannot be separated into copper and zinc by ordinary physical methods. And yet, bronze is a mixture and not a compound because the constituents do not combine chemically.
Properties of Matter: The characteristics of matter are called properties of matter. Such characteristics may include solubility, melting point, odour and chemical behaviour. Properties of matter can be classified as physical or chemical depending on whether the property involves a change in the chemical make-up of a substance.
- The physical properties are those characteristics that do not involve a chemical reaction. Examples are colour, odour, boiling point, solubility and electrical conductivity. The chemical properties, in contrast, describe the chemical reactions a substance will undergo. For example, sodium reacts violently with water to form sodium hydroxide solution and hydrogen gas. This is a chemical property of sodium.
- Properties can also be classified as either intensive or extensive depending on whether their values change with the size/amount of the sample. Properties like melting point and boiling point are intensive—they do not change with the change in amount of a substance. As you know, the boiling point of 1 g or 1 kg water is the same—373 K. Length and volume are extensive properties. The length and volume of an ice cube are certainly much smaller than those of an iceberg.
Measurements
When any quantity has to be measured, it is compared with a fixed standard, known as the unit of measurement. As an illustration, if we say that the height of a person is 150 centimeters (usually written as cm), it means that this height is 150 times the unit of measurement, which in this case is 1 cm.
The height is measured using a scale with centimeter and millimeter markings. Thus the result of any measurement has two parts—a number (150) and a unit (cm). One does not make sense without the other.
- Different types of units have been used for the measurement of physical quantities around the world. Even in the first half of the twentieth century people used different units to measure the same physical quantity. For example, weight was measured in pounds and ounces, and seers; distance was measured in feet and yards, and furlongs and miles.
- The units used varied according to the profession, too. For example, jewellers used tolas and raties to measure weight. The use of different units to measure the same physical quantity was confusing and caused complications. Besides, these systems of units were rather cumbersome. For example, 1 stone = 14 pounds j and 1 pound —16 ounces.
- To get around these difficulties, the French Academy of Science devised the metric system in 1791. In this simple system, the different units of a physical quantity are related to each other by powers of 10, and these powers are indicated by prefixes used with the unit for the particular physical quantity. The unit of length, for example, is k the metre. The kilometer, a larger unit, is 103 meters, while the centimeter, a smaller unit, is 10-2 metre. Soon, scientists across the world adopted the metric system, and today, the whole world uses it.
“Some Basic Concepts of Chemistry, definitions, laws, and chemical calculations, WBCHSE syllabus”
The Measurement International System of Units (SI): Though almost the whole world was using the metric system by the middle of the twentieth century, scientists noticed that different metric units were being used for the same physical quantity.
- In 1960, the General Conference of Weights and Measures adopted a set of units to be used by scientists all over the world to measure six basic physical quantities.
- Mole, as a unit of amount of substance, was added in the year 1971. This system, known as the International System of Units, is popularly referred to as the SI units (after the French Sysfeme International d’ Unites).
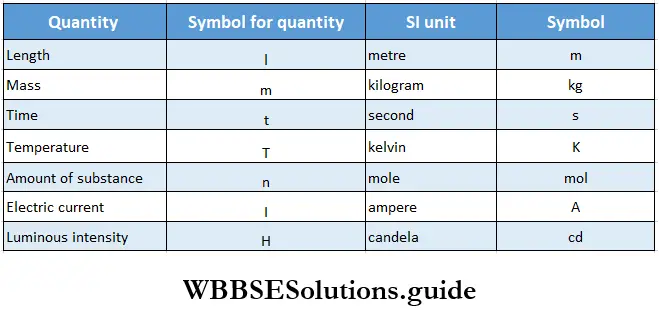
The seven basic units from which all other units are derived are given in Table Some derived units are listed in Table, while the standard prefixes used to reduce or enlarge the basic units are mentioned in Table.
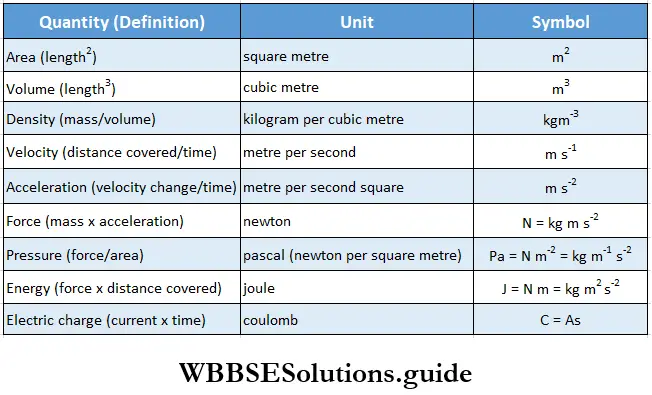
Measuring quantities: Some of the quantities which are often used in experimentation in chemistry at this level have been discussed below.
Mass The mass of a substance is the quantity of matter possessed by it.
- Though the SI unit of mass is the kilogram, it is too large to be used for many purposes in a chemical laboratory. The milligram (1 mg = 0.001 g = 10-6 kg) and the microgram (1 μg = 0.001 mg = 10-6 g = 10-9 kg), are more commonly used in the laboratory.
- Mass is measured during chemical transformations. To measure with high accuracy, one needs an analytical balance. The standard kilogram is defined as the mass of a cylindrical bar of a platinum-sodium alloy stored in a vault in a suburb of Paris. Here it is worthwhile to mention that mnss is a physical property measuring the amount of matter in a substance whereas weight is the measure of the pull of gravity on that object by the Earth (or any other celestial body).
- Volume It is a derived quantity, defined as the amount of space occupied by an object. The volume is measured in ST units in cubic metres (m3). But for convenience, measurements in chemistry are usually made in cubic decimetres (1 dm3 = 0.001 m3) and cubic centimetres (1 cm3 = 0.001dm3 = 10-6 m3). The litre is a common unit of volume in everyday life (1L = 1000 mL = 1000 cm3 = 1 dm3). In the laboratory, mostly a graduated cylinder, a volumetric flask, a burette, and pipette are used for measuring volumes of liquids.
- Density It is an intensive physical property of a substance and relates the mass of an object to its volume. The density of a substance is its mass per unit volume. The SI-derived unit of density is kg m-3, which is too large to measure densities such as that of water (1.00 g cm-3). Chemists often use smaller units—g cm-3 for solids and g/mL for liquids.
- The densities of substances change with change in temperature (since volume of a substance varies with temperature). Therefore, it is better to specify the temperature while stating the density of a substance. Temperature The three common scales to measure temperature are °C (degree Celsius), °F (degree Fahrenheit) and K (kelvin).
The temperature on the Celsius and the Fahrenheit scales are related to each other as:
∴ C =5(F-32)/9.
The magnitude of the kelvin is equal to that of the degree Celsius but the two are related as:
∴ K=°C + 273.15.
Practically speaking, the lowest temperature permitted in nature is -273.15 °C (0 K). This temperature is known as absolute zero.
Chemists measure time as it helps to know how long it takes for a chemical process or reaction to occur. Some reactions like the formation of fossil fuels take millions of years. On the other hand, when hydrochloric add is added to a solution of silver nitrate, silver chloride is precipitated in a fraction of a second.
WBCHSE Chemistry Notes On Laws Of Chemical Combination
Measurement Dimensional analysis: All derived quantities, like area, volume, density, and speed, can be derived from the seven basic quantities. The units of the derived quantities can be obtained from the seven basic units, as shown in Table.
For example, if the side of a square is expressed in meters (m), the area is expressed in square meters (m2). Similarly, if the distance covered is expressed in meters and the time taken in seconds, the velocity is expressed in m s-1.
- Quite often it becomes necessary to convert one set of units into another. This can be done quite simply by dimensional analysis. The dimensions of a derived quantity are the powers to which the basic quantities have to be raised in a product defining the quantity.
- Dimensional analysis involves calculations based on the fact that if two quantities have to be equated, they must have the same dimensions or the same units. Some calculations involving the dimensions of physical quantities follow.
Measurement Conversion of one unit into another
1. Suppose you want to convert 10 minutes into seconds.
First, find the unit conversion factor.
1 min = 60 s.
∴ 1 = \(\frac{60 \mathrm{~s}}{1 \mathrm{~min}}\)
Thus, 60 s/1 min is the conversion factor. Note that the quantities are dimensionless since time is divided by time on the right-hand side.
Let us convert 10 minutes into seconds.
10 min = 10 min x \(\frac{60 \mathrm{~s}}{1 \mathrm{~min}}\) = 600 s. ….(1)
Dimensionally both sides of Equation (1) are the same. Also, multiplying 10 minutes by (60 s/1 min) does not change its value, since (60 s/1 min) is equal to unity. A great advantage of using this method is that any mistake made in writing the conversion factor can be spotted easily.
In Equation (1) the unit minutes in the numerator and denominator of the right-hand side cancel, leaving behind the unit seconds. This would not have been so if the wrong conversion factor had been used and the mistake would have been noticed immediately. For example, if 1 min/60 s had been used as the conversion factor
“WBCHSE Class 11 Chemistry, atomic mass, molecular mass, and mole concept, in basic chemistry”
10 min = 10 min \(\frac{1 \mathrm{~min}}{60 \mathrm{~s}}=\frac{1 \mathrm{~min}^2}{6 \mathrm{~s}}\)
2. Similarly, to convert 170 pounds (lb) into kilograms (kg), first find the unit conversion factor.
1 kg = 2205 lb.
∴ 1 = \(\frac{2.205 \mathrm{lb}}{1 \mathrm{~kg}}=\frac{1 \mathrm{~kg}}{2.205 \mathrm{lb}}\)
Mass(kg) = 170 lb x \(\frac{1 \mathrm{~kg}}{2.205 \mathrm{Ib}}\) = 77.09 kg ……..(2)
If the wrong conversion factor had been used, the units on the two sides of Equation would not have been the same.
Measurement Validity of an equation: Dimensional analysis is also used to check the validity of an equation. If the dimensions on both sides of the equation do not match, the equation cannot be correct. Let us take an example.
∴ E = mc2 …….(3)
Using SI units, E is in joules, m in kg and c in m s-1. Let us see if the units on both sides of Equation (3) match.
J = kg (ms-1)2 or
or, Nm = kg m2 s-2
or kg m2 s-2 = kg m2 s-2.
Uncertainty in measurement: You can be very certain about the measurement of a quantity when it involves the counting of objects. For example, when you count the number of chairs in your class you can be certain about the exactness of your answer. You can also be sure that if someone else were to count the number of chairs, one would get the same result.
However, can you be as certain about the result you get when you measure your friend’s height with a measuring tape? You may read it as 150.1 cm and another friend may measure it as 150.3 cm. At the most you and your friend can conclude that his height is greater than 150 cm and less than 151 cm.
- There is always a certain amount of uncertainty in such measurements. This uncertainty arises not because the height of your friend (or any other measured quantity) is uncertain, but because of the way the measuring instrument is calibrated (accuracy of the scale) and because two people may record the same reading differently (human error).
- The accuracy of a measurement thus, depends on the accuracy of the measuring instrument and the skill of the person making the measurement. The difference between the two kinds of measurements that we have just considered (counting chairs and measuring a person’s height) is that in one case, we used a discrete variable and in the other we used a continuous variable.
- This means that while the number of chairs in your class can be 30 or 31 but not between 30 and 31 (discrete value), the height of your friend can be anything between 150 cm and 151 cm (continuous variable).
Measurement Precision and accuracy: If you repeat a particular measurement, you may not obtain precisely the same result (experimental error). Precision refers to the closeness of a set of values obtained from two or more measurements of the same quantity.
Accuracy, on the other hand, refers to the closeness of a single measurement to its true value. For example, three students A, B, and C separately determine the weight of the same person which is actually 50.45 kg. The results obtained are given below. (The measurements are made in kilograms.)
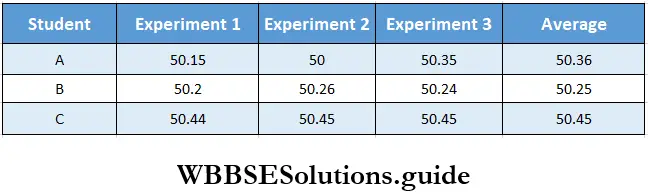
The values obtained by student A differ widely from one another and the average value is incorrect. Thus the data is neither precise nor accurate. The values determined by student 13 are more precise as they deviate little from one another. The average weight is still not accurate. The data obtained by student C arc both precise and accurate.
Measurement Significant figures: How does one express the uncertainty about the accuracy of a measurement while writing the result of an observation? The convention is to include all the digits which are certain and the last digit that is uncertain while writing the result of a measurement.
- The total number of digits is called the number of significant figures. It represents the accuracy and precision with which a quantity has been measured. Remember that the number of significant figures is the number of digits in the result, including the last digit which is uncertain.
- Suppose the length of a piece of wood is reported by three students as 123 cm, 123.0 cm, and 123.00 cm. Thu results may seem equivalent to you but the scientific significance of the three results is very different. The number of significant figures in the three results is 3, 4, and 5 respectively.
- In other words, in the first case (123 cm), the digits 1 and 2 are certain but not 3—it is only the best estimate. This generally means that the actual value lies between 122 and 124 or that the length is 123 ± 1 cm. When the result of a measurement is expressed in this fashion, it implies that the measurement has been made with a crude scale.
- The second result has four significant numbers, which means that the length lies between 122.9 cm and 123.1 cm. In other words, in this case, the third digit is also certain, so obviously, the scale used for this measurement (123.0 cm) is more precise than the one used for the first measurement.
- The last result shows that the length lies between 122.99 cm and 123.01 cm (5 significant figures) and implies that the scale used is the most precise of the three.
- While reporting the result of a measurement, one must be very careful about indicating the precision with which the measurement has been made. To write more significant figures than the scale of measurement allows would be wrong while writing fewer significant figures than the situation allows for would be holding back information that could be useful. It would be useful to remember the following rules in this context.
- All digits are significant except zeros at the beginning of a number. For example, 132 cm, 0.132 cm, and 0. 0132 cm have three significant figures each. Zeros to the left of the first nonzero digit are not significant, even if such zeros follow the decimal point.
- Zeros to the right of the decimal point are significant. Thus, 151 g, 151.0 g, and 151.00 g have 3, 4, and 5 significant figures respectively.
The following examples should help you understand these rules better.
- 678 has 3 significant figures
- 0. 42 has 2 significant figures
- 40.5 has 3 significant figures
- 2004 has 4 significant figures
- 0. 02 has one significant figure
- 0. 0022 has two significant figures
- 2.20 has three significant figures
- 0. 0200 has three significant figures
In numbers that do not contain a decimal point, trailing zeros may or may not be significant. In case of a very large number of significant figures, for instance, the value of n (n = 3.1415926) one may choose the number of digits according to the calculation. In other words, all the numeral values involved in a calculation should be so expressed that they have almost the same number of significant figures.
Measurement Calculations involving significant figures: Several calculations may have to be made in the course of an experiment and these calculations may involve the addition, subtraction, multiplication or division of different measured quantities. The measurement of all the quantities (used to arrive at the final result of the experiment) may not be made with the same precision.
The precision of the final result depends on the precision of the least accurate of the measurements. In other words, the final result cannot be more precise than the least precise of the quantities involved in the calculations. Remembering a couple of rules will be helpful while making calculations involving quantities of different precisions.
“Some Basic Concepts of Chemistry, laws of chemical combination, and stoichiometry, WBCHSE notes”
Rule 1: In additions or subtractions the final result should be reported to the same number of decimal places as that of the term with the least number of decimal places. The number of significant figures of the different numbers have no role to play.
Example 1. The three numbers to be added have 3,1 and 2 decimal places respectively, while the significant figures in the three numbers are 4,2 and 3 respectively.
Solution:
Given
The three numbers to be added have 3,1 and 2 decimal places respectively, while the significant figures in the three numbers are 4,2 and 3 respectively.
⇒ \(\begin{aligned}
2.512 \\
2.2 \\
5.23 \\
\hline 9.942
\end{aligned}\)
∴ Actual sum 9.942
∴ Reported sum 9.9
The reported sum is 9.9 because the term with the least number of decimal places is 2.2, which has only one decimal place.
Example 2. Each number has three decimal places, so the answer is to be reported up to three decimal places. The significant figures in each of the terms is 4 but the result has 5 significant figures.
Solution:
Given
Each number has three decimal places, so the answer is to be reported up to three decimal places. The significant figures in each of the terms is 4 but the result has 5 significant figures.
⇒ \(\begin{array}{r}
6.612 \\
5.234 \\
2.020 \\
\hline 13.866
\end{array}\)
∴ Actual sum 13.866
∴ Reported sum 13.866
Example 3. The first number has 2 decimal places and the second has 4 decimal places, so the answer is reported up to 2 decimal places.
Solution:
Given
The first number has 2 decimal places and the second has 4 decimal places, so the answer is reported up to 2 decimal places
⇒ \(\begin{array}{r}
19.26 \\
(-)11.02534 \\
\hline 8.23466
\end{array}\)
∴ Actual difference 8.23466
∴ Reported difference 8.23
“WBCHSE Class 11, chemistry notes, on empirical and molecular formulas, and chemical reactions”
Rule 2: In multiplications and divisions, the result is reported to the same number of significant figures as the least precise term or the term with the least number of significant figures.
Example 1: The first term has 5 significant figures, while the second term has 3 significant figures, so the result can have only 3 significant figures.
Solution:
⇒ \(\begin{aligned}
41.012 \\
\times 1.21 \\
\hline 49.62452
\end{aligned}\)
∴ Actual product 49.62452
∴ Reported product 49.6
Example 2: In this division, 0.41 has 2 significant figures, while 15-724 has 5 significant figures. The result can have only two significant figures.
Solution:
⇒ \(\begin{aligned}
& 15.724 \\
& +0.41 \\
& \hline 0.0260747
\end{aligned}\)
∴ Actual result 0.0260747
∴ Reported result 0.026
Rule 3: If one of the term is in an expression is an exact number, the result should have the same number of significant figures as the least precise term other than the exact number. The presence of exact numberfs) in an expression atfect the number of significant figures that should be included in the answer because an exact number is supposed to have an infinite number of significant figures.
Example 1: All the terms other than the two exact numbers have 3 significant figures. So the answer should also have 3 significant figures.
Solution:
⇒ \(\frac{4.23 \times 0.141 \times 3}{0.0214 \times 2}\)
∴ Actual result 41.8058
∴ Reported reult 41.8
- Rounding off As seen in the above examples, the final result often has more figures than die number of significant figures in the least precise quantity involved in the calculations. lVhile reporting the result, only the significant figures are retained. The others are dropped. This procedure is called rounding off. The convention followed while rounding off a number can be summarised as follow’s.
- If the digit which follows the last digit to be reported is less than 5, the last digit is left unchanged and all the digits to its right are dropped. If, however, the digit following the last digit is equal to or more than 5, the last significant figure is increased by one. Thus 1.234,1277 and 12252 become 122,13 and 13 respectively, if the fire result is to be reported up to the first decimal place.
- While solving a problem remember to take up all significant digits used in calculations and round off only the final result to the desirable number of significant digits.
Scientific (exponential notation): Consider the quantity 10600 g. Written as such, it implies that there are 5 significant figures. Suppose the measurement was made in such a way that the number is precise to only 3 significant figures? Writing the result as 10600 g would then not be correct because it would not indicate the precision of the measurement To remove such ambiguity, results are expressed in the scientific notation.
Thus, 10600 g may be expressed in one of the following ways, depending on the precision of the measurement
1.06 x 104 g (3 significant figures)
1.060 x 104 g (4 significant figures)
1.0600 x 104 g (5 significant figures)
- You are familiar with the Avogadro number, which is 6.022 x 1023. If you write it in the ordinary way and not in terms of 10 raised to a power, it will be 602,213,700 000 000 000 000 000. It is difficult to write such numbers in an ordinary way and errors may creep in while doing so. The scientific or exponential notation is a better way to represent such numbers.
- In scientific notation, all numbers, large or small, are expressed as a number between 1.000 and 9.999 multiplied or divided by 10 an appropriate number of times. For example, the number 2484.32 may be expressed as 2.48432 x 10 x 10 x 10 or 24832 x 103. Here 3 is the power or exponent, to which 10 is raised. In general in scientific notation a number is represented as N x 10n,
- where N is a number between 1.000 and 9.999 and n is a number (not necessarily a single digit) called exponent. To express a number smaller than 1.000 in scientific notation, the decimal point is moved to the right until there is only one nonzero digit before the decimal point.
- The number is then divided by 10 an appropriate number of times. For example, to express 0.00032481 in scientific notation, we move the decimal point to the right. The number is divided 4 times by 10, as the decimal has shifted four places. In this example, the exponent n = -4.
- Take another example of a number larger than 9.999. To express it in scientific notation the decimal point is moved to the left until there is only one nonzero digit before the decimal point. Suppose the number is 14872.5. When this number is expressed in scientific notation, the decimal point is moved to the left and the number thus obtained is multiplied by 10.
⇒ 00032481 = \(\frac{3.2481}{10 \times 10 \times 10 \times 10}\) =3.2481 x 10-4
⇒ 14872.5 = \(1.48725 \times 10 \times 10 \times 10 \times 10=1.48725 \times 10^4\)
∴ The exponent n = 4.
To subtract or add numbers in scientific notation the exponent n or power of 10 should be the same in all the numbers. If the exponent is not the same, it has to be made the same by shifting the decimal place in any of the numbers before adding or subtracting. For example, suppose we have to add 6.426 x 103 and 2.045 x 104. We can transform 6.426 x 103 to 0.6426 x 104 and then add,
∴ 2.045 x 104 + 0.6426 x 104 = (2.045 + 0.6426) x 104 = 2.6876 x 104.
To multiply two numbers in scientific notation, we make use of the relation, (10)x x(10)y =10(x+y).
In this case, the exponent need not be the same. For example, (2.0456 x 104) (4.132 x 10-7) = 8.452 x 10[4+(-7)] = 8.452 x 10-3.
To divide two numbers in scientific notation, we make use of the relation
∴ \(\frac{10^x}{10^y}=10^{x-y}\)
The exponent need not be the same here too. For example,
∴ \(\frac{2.45 \times 10^{14}}{9.24 \times 10^{24}}=\frac{2.45}{9.24} \times 10^{14-24}=0.265 \times 10^{-10}\)
In scientific notation, the number is expressed as 2.65 x 10-11. In similar example,
“Basic concepts of chemistry, significant figures, unit conversions, and molarity, WBCHSE syllabus”
∴ \(\frac{4.65 \times 10^{-4}}{2.92 \times 10^{-10}}=\frac{4.65}{2.92} \times 10^{[-4-(-10)]}=1.59 \times 10^{(-4+10)}=1.59 \times 10^6\)
Historical Approach To The Particulate Nature Of Matter
The concept that matter is made up of tiny bits of material—particles—originated in Greek natural philosophy. The Greek philosopher Democritus in the fifth century BC proposed the “particulate nature of matter” He believed that matter is composed of indivisible particles called atoms (from the Greek atoms, meaning indivisible).
However, now we know that atom is divisible into smaller subatomic particles like protons, neutrons, and electrons. Nevertheless, the word “atom” as indivisible still makes sense as once split, an atom loses its identity. Also, it is the smallest particle of an element that takes part in a chemical combination.
- The atomic theory of Democritus was not appreciated for many years. Aristotle’s theory that matter is composed of four elements—air, wind, fire, and water—was widely accepted. However, after a series of experiments in more recent times, the particulate nature of matter was established.
- The French chemist Antoine Laurent Lavoisier, in the late 1700s, discovered that during a chemical reaction, the components involved change in terms of appearance and form only, and the total mass remained the same. In other words, the total mass of the reactants is equal to that of the products (law of conservation of mass).
- This prompted him to conclude that some basic part of the components which was not visible, did not change. Later, in 1800, scientists working on chemical reactions found that something ruled the behaviour of matter that even their microscopes could not perceive.
- The law of conservation of mass helped establish the law of constant composition or the law of definite proportions. These laws were a result of Joseph Proust’s extension of Lavoisier’s work.
- In 1803, John Dalton proposed the atomic theory of matter on the basis of the laws of chemical combination and other related chemical observations. The theory stated that all matter is made of indivisible and indestructible ultimate particles called atoms. Thus the start of the nineteenth century brought back Democritus’ view to the forefront of science.
Percentage Composition And Molecular Formula
To study a chemical compound, mainly its chemical properties, it is essential to know its chemical formula. The chemical formula of a compound can be determined by analyzing the compound for the amount of elements (moles) in a given mass of the compound. The result may also be expressed in percentage composition.
The mass percentage composition of a compound is defined as the number of grams of different elements present in 100 g of the compound. The mass percentage of an element may be calculated by dividing the mass of the element in one mole of the compound by the molar mass of the compound and multiplying the result by 100.
Let us consider CO2.1 mol of carbon dioxide will always contain 1 mol of carbon and 2 mol of oxygen atoms.
The molar mass of CO2 is 12 + (2 x 16) = 44.0 g.
Now 44.0 g of CO2 contains 12.0 g of C and 32.0 g of O.
Mass percentage of C in CO2 = \(\frac{\text { mass of } \mathrm{C} \text { in } 1 \mathrm{~mole} \mathrm{CO}_2}{\text { molar mass of } \mathrm{CO}_2} \times 100\)
= \(\frac{12.0 \mathrm{~g}}{44.0 \mathrm{~g}} \times 100=27.27\)
Similarly, we may calculate the mass percentage of O in 1 mole of CO2.
Mass percentage of O in CO2 = \(\frac{32.0 \mathrm{~g}}{44.0 \mathrm{~g}}\) x 100 = 72.73.
The molecular composition of a compound can be expressed in any of the following ways.
- A chemical formula giving the number of atoms of each type per molecule, i.e., CO2.
- The number of moles of each element per mole of a compound.
- The mass of each element per 100 g of a compound.
We may conclude that if the formula of a compound is known we can determine its percentage composition and vice versa.
Empirical Formula And Molecular Formula
Tire empirical formula of a compound represents the simplest whole-number ratio of the atoms of the various elements present in a molecule. For example, the empirical formula of benzene is CH.
This indicates that carbon and hydrogen are present in benzene in a the ratio 1 :1, The empirical formula of ethanoic acid is CH2O which means that that a molecule of ethanoic acid contains carbon, hydrogen, and oxygen atoms in the ratio 1:2:1
The molecular formula of a compound, on the other hand, shows the actual number of atoms of the various elements present in one molecule of the compound. For example, the molecular formula of benzene is C6H6, which means that one molecule of benzene contains 6 atoms of carbon and 6 atoms of hydrogen.
“WBCHSE Class 11 Chemistry, chemical reactions, balancing equations, and their importance”
Similarly, the molecular formula of ethanoic acid is C2H4O2, which indicates that 1 molecule of ethanoic acid contains 2 atoms of carbon, 4 atoms of hydrogen, and 2 atoms of oxygen.
The molecular formula of a compound is a simple whole-number multiple of its empirical formula. This can be expressed mathematically as follows.
Molecular formula = n x empirical formula
∴ where n is an integer. The value of n can be determined from the relation
∴n = \(\frac{\text { molecular mass }}{\text { empirical formula mass }}\)
For example, the molecular mass of glucose (C6H12O6) is 180 and its empirical formula (CH2O) mass is 30.
∴ n = \(\frac{180}{30}\)
When the value of n = 1, the empirical formula and molecular formula are the same.
Determination of empirical formula: The empirical formula of a compound can be determined from the percentage of the different elements present in it and their atomic masses. Such calculations involve the following steps.
- Divide the percentage of each element by its atomic mass. This will tell you the relative number of moles of the elements present in a molecule of the compound.
- Divide the quotients obtained by the smallest in value to get a simple ratio of moles of various elements present.
- If the results obtained in step 2 are not whole numbers, raise the values to the nearest whole numbers or multiply all of them by a suitable integer to obtain whole numbers.
- Write the symbols of the elements side by side and insert the corresponding numerical values you have obtained in step 3 at the lower right-hand comer of each symbol. This is the empirical formula of the compound.
Determination of molecular formula: The determination of the molecular formula of a compound involves the following steps.
- Determine the empirical formula as described above.
- Find the empirical formula mass by adding the atomic masses of the atoms in the empirical formula.
- Divide the molecular mass of the compound (determined by a suitable method) by the empirical formula mass to obtain n.
- Multiply the empirical formula by n to obtain the molecular formula.
Example 1. The percentages of carbon and hydrogen in an organic compound are 92.5 and 7.5. Determine the molecular formula of the compound if its molecular mass is 78.
Solution:
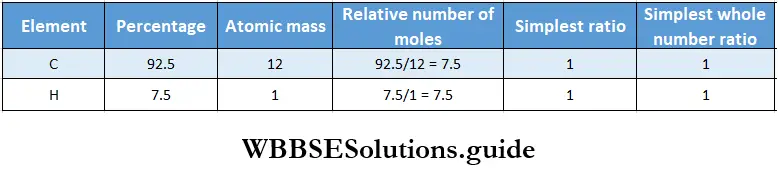
Given
The percentages of carbon and hydrogen in an organic compound are 92.5 and 7.5.
Thus the empirical formula of the compound is CH.
Therefore, its empirical formula mass = 12×1 + 1×1 = 13
Given that its molecular mass is 78.
∴ n = \(\frac{\text { molecular mass }}{\text { empirical formula mass }}=\frac{78}{13}=6\)
Therefore, the molecular formula of the compound is 6 x (CH) = C2H6.
Example 2. Calculate the molecular formula of a compound on the basis of the following data.
- 4.24 mg of an organic compound yielded 8.45 mg of CO2 and 3.46 mg of H2O on combustion.
- The moleadar mass of the compound is 88 g.
Solution :
1. Calculate the percentage of carbon in the compound as follows.
44 mg of CO2 contains 12 mg of C.
Therefore, 8.45 mg of CO2 contains 12/44 x 8.45 mg of carbon.
∴ percentage of carbon =\(\frac{\text { weight of carbon }}{\text { weight of compound }}\) x 100
= \(\frac{12}{44}\) x \(\frac{8.45}{4.24}\) x 100 = 543.
2. Calculate the percentage of hydrogen in the compound as follows.
18 mg of H2O contains 2 mg of hydrogen.
Therefore, 3.46 mg of H2O contains 2/18 x 3.46 mg of hydrogen.
“Some Basic Concepts of Chemistry, WBCHSE Class 11, solved numerical problems, and real-world applications”
∴ percentage of hydrogen = \(=\frac{\text { weight of hydrogen }}{\text { weight of compound }}\) x 100
= \(\frac{2}{18}\) x \(\frac{3.46}{4.24}\) x 100 = 9.0
3. Percentage of oxygen = 100 – (54.3 + 9.0) = 36.7.
4. Determine the empirical formula as usual.
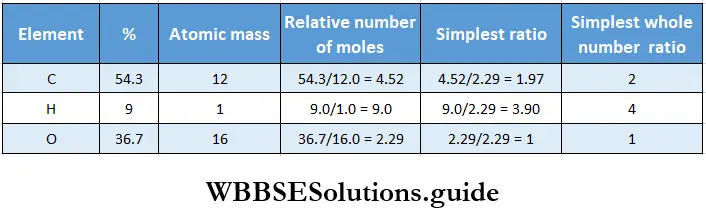
Thus the empirical formula of the compound is C2H4O.
∴ empirical formula mass = 2 x 12 + 4 x 1 +16 = 44 g.
Given that the molecular mass of the compound is 88 g.
∴ n = \(\frac{88}{44}\)= 2.
∴ molecular formula = 2(C2H4O) = C4H8O2.
