Valence Bond Theory Of Coordination Compounds Notes

Valence bond theory (VBT)

This theory was proposed by Linus Pauling in 1931 and is closely related to the concept of hybridisation.

What Is A Valence Bond Theory ?

The main postulates of Valence Bond theory are as follows.

1. The central metal ion makes a number of vacant orbitals (equal to the coordination number of the metal) available to accept electron pairs from the ligands.
2. Appropriate combinations of s, p and d orbitals hybridise to give equivalent orbitals having specific spatial orientations making for a definite geometry.
   • The common hybridisations we come across in coordination compounds are sp³ (tetrahedral), dsp² (square planar), sp³d (trigonal bipyramidal or square pyramidal) and d₂sp³ (octahedral).
3.  Each ligand has at least one orbital containing a lone pair of electrons.
4. The vacant hybrid orbitals of the metal overlap with the filled orbitals (with the lone pair of electrons) of the ligand to form a coordinate bond. Let us now study how VBT is applied to coordination compounds with coordination numbers 6 and 4

Coordination number 6

1. [Fe(CN)₆]^3- ion

Iron (Z = 2₆) has the outer electronic configuration of 3d⁶ 4s². In this compound, iron is in the +3 oxidation state, so the outer electronic configuration is 3d5.

Since Fe(3) has a 3d5 configuration, it is implied that the d orbitals are singly filled (Hund’s rule), i.e., they are five impaired electrons. But it was experimentally found that the complex has one unpaired electro! This is explained by the presence of the ligand (CN^–), the d electrons get paired up.

Now out of the fr degenerate d orbitals two contain a pair of electrons each, while one contains a single electron. The other two are vacant and accept electron pairs from ligands.

The six empty orbitals of the metal (two 3d, one and three 4p) hybridise forming d2₂p³ orbitals, which accept a pair of electrons from each CN^– ion.

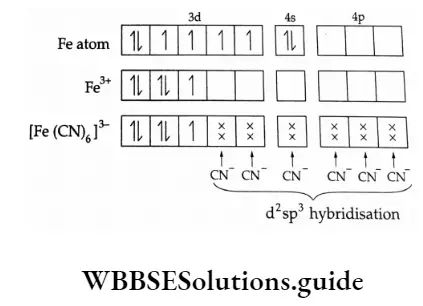
The molecule has octahedral geometry and is paramagnetic due to the presence of one unpaired electrical

Valence Bond Theory Examples

Note: CN^– is referred to as a strong-field ligand and induces pairing of the d electrons of the metal. Another example of a strong-field ligand is NH₃. The terms strong-field and weak-field originate from spectroscopy and crystal field effects, which are beyond the scope of this book.

2. [Fe(H₂O)6]³⁺ ion

Iron in this compound is in the +3 oxidation state. The compound is paramagnetic with five unpaired electrons. The d electrons remain unpaired and the metal makes available one 4s orbital, three 4p orbitals and two 4d orbitals (total 6) to form an octahedral complex.

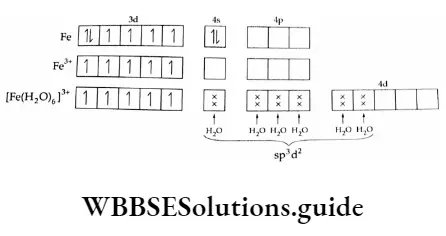
Note: H₂O and F are weak-field ligands and do not induce pairing of the d electrons of the metal.

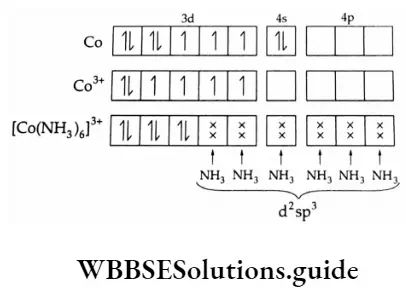
3. [CO(NH₃)₆]³⁺ ion

The outer electronic configuration of cobalt is 3d⁷4s² and in this compound, its oxidation state is +3. Ammonia is a strong-field ligand and induces pairing of 3d electrons giving a diamagnetic octahedral complex.

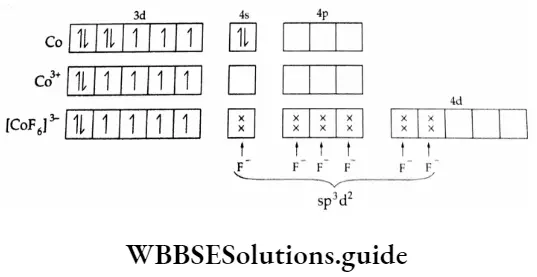
4. [CoF₆]^3- ion

This octahedral complex of Co³⁺ is paramagnetic having four unpaired electrons. The 3d electrons are not paired up as F^– is a weak-field ligand; thus the central metal utilises 4d orbitals for bond formation.

Valence Bond Theory Examples

From the above examples, it should be clear that in octahedral complexes, the central metal may (n- 1)d or nd orbitals for bond formation. When a complex is formed by using (n- 1)d orbitals (when a strong-field ligand coordinates) it is called an inner orbital complex and when a complex is formed by using ud orbitals, it is called an outer orbital complex.

An outer orbital complex has a greater number of unpaired electrons than an inner orbital complex—consequently the former is called a high-spin comp ex and the latter, a low-spin complex.

Coordination number 4

1. [Ni(CN)₄]^2- .

The outer electronic configuration of nickel is 3d⁸ 4s². CN^– is a strong-field ligand and causes the pairing of the 3d electrons leaving a vacant 3d orbital. The complex is therefore diamagnetic, has a dsp² hybridisation and is square planar.

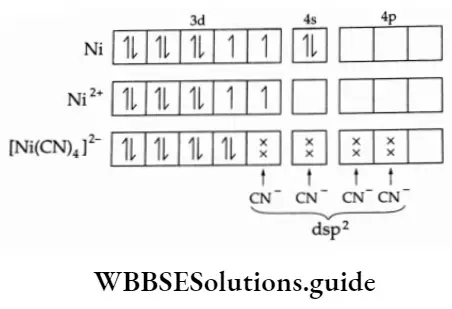
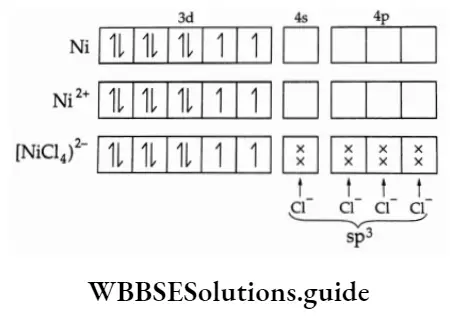
2. [NiCl₄]^2-

The complex is paramagnetic and tetrahedral. The d electrons are not paired up as Cl is a weakfield ligand.

Valence Bond Theory Examples

Limitations of VB theory or Valence Bond Theory Of Coordination Compounds Limitations

The valence bond theory is able to explain the structure and magnetic properties of a large number of coordination compounds.

However,Valence Bond Theory Of Coordination Compounds has the following limitations.

1. It cannot explain the colour and spectra of complexes.
2. The theory gives a rough idea about the magnetic behaviour of a complex from a knowledge of the number of unpaired electrons but does not explain the variation of magnetic moment with temperature.
3. It does not give an idea about the kinetic stability of a complex.
4. One cannot distinguish between a strong-field ligand and a weak-field ligand using this theory.

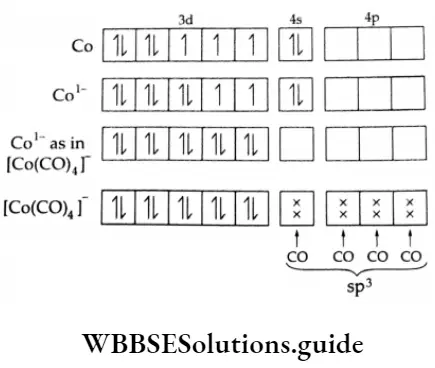
Example Applying Vbt to predict the shape and magnetic behaviour of [Co(CO)₄]^–.
Solution

Carbon monoxide is a neutral ligand and the oxidation state of cobalt is -1. The outer electronic configuration of Co is 3d^-74s². CO is a strong-field ligand that induces the pairing of 3d electrons and forces the 4s electron into the 3d orbital. Thus, the complex is sp³ hybridised, i.e., tetrahedral in shape and diamagnetic.

Example Applying VBT predicts the number of unpaired electrons in the following complexes.

1. [Fe(CN)₆]^4-
2. [FeF₆]^3-
3. [Pt(CN)₄]^2-
4. [PtCI₄ ]^2-

Solution

1. 0
2. 5
3.  0
4. 2