Properties Of Parallel Lines And Transversal
The transvarsal in figure no. 1 is PQ [AB/PQ] but there is transversal in Figure 2.
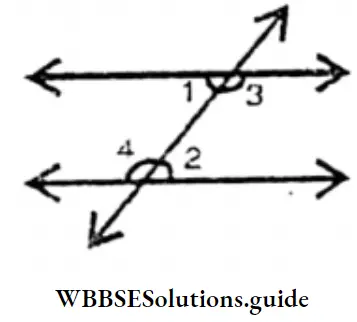
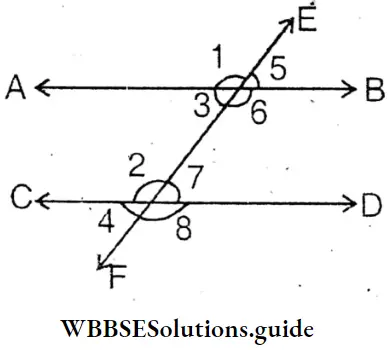
My sister Sahali formed transversal as the picture shown below by fixing bits of cardboard with the help of nails.
As a result of it, many angles have been formed. She has named some of the angles. Measuring with a protractor I have seen∠1=∠3 again ∠2=∠4; they are VOA angle.

Again,∠5=vercically opposite ∠7and ∠6 vertically opposite Angle = angle ∠8
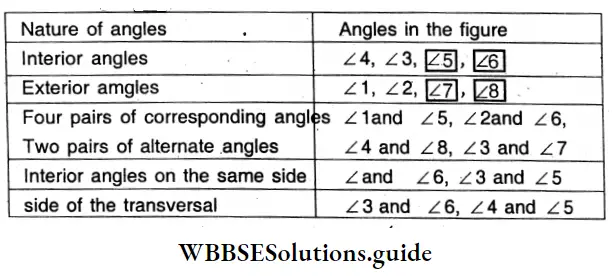
4 pairs of corresponding angles are (∠l and ∠5), ( ∠2 and ∠6]),(∠4 and ∠8), and (∠3 and∠7])
It is seen by measuring with a protractor ∠1 =110° and ∠5 = 110°
[ Let’s draw parallel lines and their transversals and write by measuring corresponding angles ]
Read and Learn More WBBSE Solutions For Class 8 Maths
∴∠1 = ∠5
and ∠2=70° and ∠6=70°
∴∠2 = ∠6
[ Let’s write and measure ]
Pritam, Sonaii, Seemanta, and Meher, each of them drew a pair of parallel lines and transversal in their respective exercise book. By measuring the corresponding angles by the protractor they say the measurement of each angle is same. [Let’s draw and write]
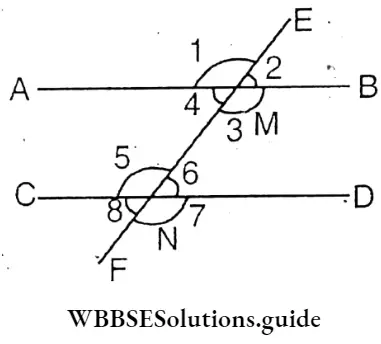
AB and CD are two parallel straight lines. A transversal EF is drawn which cuts both transversals, at M and N points respectively.
Here four pairs of corresponding angles are the following :
∠1 and ∠5, ∠2and ∠6, ∠4 and ∠8, ∠3and ∠7
∠1 = 120° and ∠5= 120° ∴ ∠1 =∠5
∠2 = 60°and ∠6=60° ∴ ∠2=z6
∠4 = 60° and ∠8= 60° ∴ ∠4 = ∠8
∠3 = 120° and ∠7= 60° ∴ ∠3=∠7
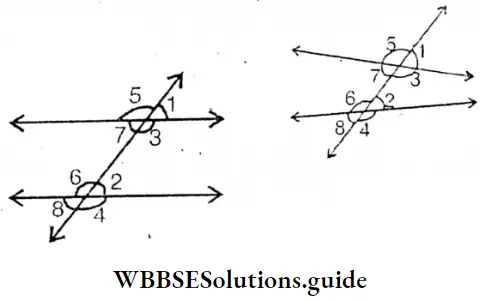
Two pairs of alternate angles on the blackboard are (∠4 and ∠6), (∠3 and ∠5)
It is seen by measuring with a protractor, ∠4 = 70° and ∠6 = 70°,
[ Let’s draw parallel lines and their transversals and write the measurement of alternate angles by measuring with a protractor]
∴ ∠4=∠6
and ∠3=70° and ∠5=70°
∴ ∠3≠∠5 [=/≠put]
Four of our friends have drawn two parallel lines and their transversal in their exercise books. Two pairs of alternate angles have been named and measuring with a protractor, it is seen that the measurements of alternate angles are equal.
[Let’s draw and examine]
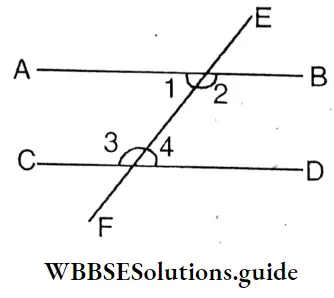
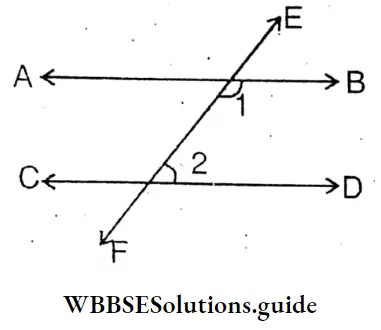
Two parallel lines AB and CD and transversal EF are drawn, which result in a pair of alternate angles ∠1 and ∠4 and ∠2 and ∠3, formed.
∠1 = 75°, ∠4= 75°
∴ ∠1 = ∠4
∠3 = 115°, ∠2= 115°
∴ ∠2 = ∠3
If a straight line intersects two parallel lines then the interior angles opposite to the transversal form a pair of alternate angles.
Measurement of each pair of these angles are [ equal/ unequal]. (∠3and ∠6) (and ∠4 and ∠5) It is seen by measuring with a protractor,
∠3= 110° and ∠6 = 70° and
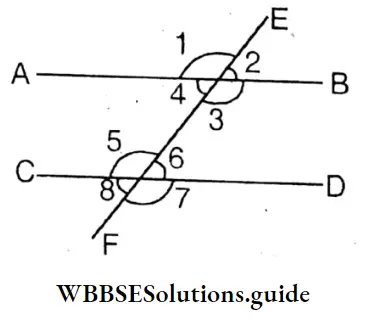
∠4= 70° and ∠5 = 110°
It seen that ∠3+∠6=180° and ∠4+∠5=180°
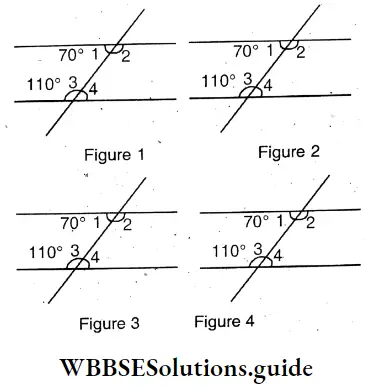
∠1 and ∠3 and ∠2 and ∠4
In figure 1, ∠1=70°,∠3=110º
∠2=110°,∠4=70°
∴ ∠1+∠3=180° and ∠2+∠4=180°
In figure 2, ∠1+∠3=180° and ∠2+∠4=180°
In figure 3, ∠1 + ∠3 = 180° and ∠2 + ∠ 4 = 180°
In figure 4, ∠1 + ∠3 = 180° and ∠2 +∠4 = 180°
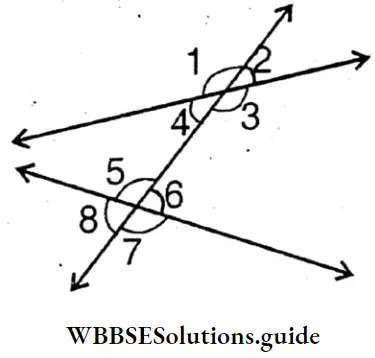
If a straight line intersects two parallel lines then the sum of measurement of two interior angles in the same side of the transversal is 2 right angles. Nipa drew many pairs of the parallel lines and nonparallel lines. I draw transversal of each pair. Consequently, corresponding angles, alternate angles, and interior angles in the same side of transversal have been formed.
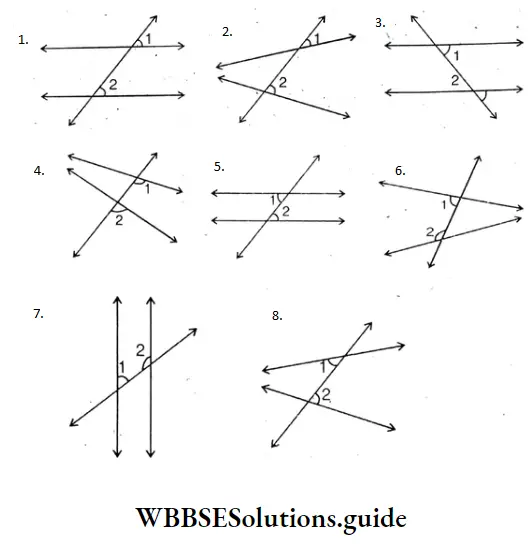
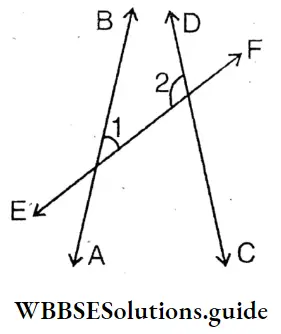
- ∠1 = ∠2
- ∠1≠ ∠2
- ∠1 ≠∠2(=/≠)
- ∠1 ≠2(=/≠)
- ∠1 =∠2 (=/≠)
- ∠1 + ∠2= 120° degree
- ∠1 +∠2=180° degree’
- ∠1 +∠2 = 210° degree
I have drawn a few more. Let’s see what I have. got.
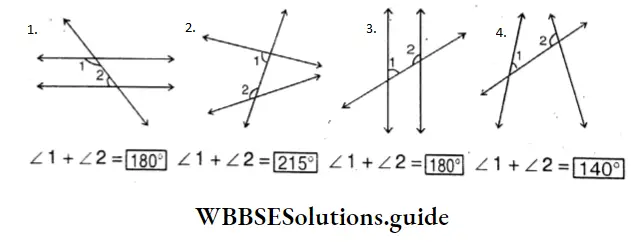
Let’s verify by placing two interior angles ∠3 and ∠6 in the same side of the transversal whether ∠3 + ∠6 = [180°] is true or not.
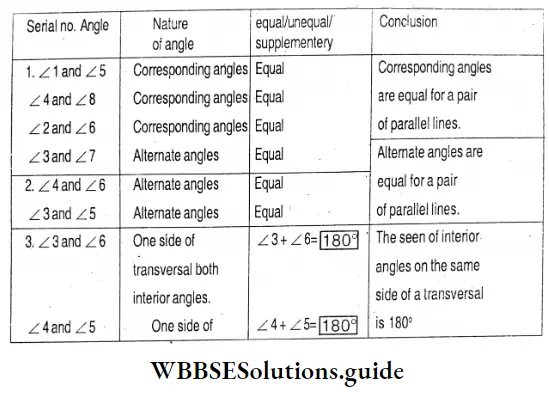
Let’s write in the table below as we get by activity-
Now I have drawn two straight lines on my exercise book and their transversal. I have measured alternate angles with a protractor.
It is seen when the measurement of the alternate angles are equal then the straight fines are parallel.
[parallel/nonparallel [let’s write & verify],
I draw two straight lines and a transversal on the exercise book. Let’s measure the corresponding angles are equal then two straight lines are parallel (Parallel/unparallel)
If a straight line intersects a pair of straight lines and the measurement of one pair of corresponding angles is equal then the two straight lines are parallel to each other. Priya has drawn a pair of straight lines and their transversal on the blackboard. Consequently, many interior angles have been formed.
I will see by measuring with a protractor whether the interior angles on the same side of the transversal are supplementary with one another, i.e., the sum of the interior angles of the same side of the transversal is 2 right angles.
Measuring we get ∠1 + ∠2 = 80° Measuring we get ∠1 + ∠2= 120
It is seen by using a scale that AB and CD are parallel [ Parallel/ unparallel ]
In the second figure AB and CD are unparallel [ Parallel/unparallel ]
Properties Of Parallel Lines And Transversal Exercise 8.1
Question 1. Chandra takes ruled paper. She draws a transversal between two lines. As a result, 4 corresponding angles, two pairs of alternate angles, and two pairs of interior angles are formed. Let’s find out and number them. Verify by measuring with a protractor:
Solution:
Corresponding angles are equal in measure;
Alternate angles are equal in measure; and,
The interior angles on the same side of a traversal are supplementary.
AB and CD are two parallel lines and EF is a transversal. 4 pairs of corresponding angles are: ∠1 and ∠2, ∠3 and ∠4, ∠5 and ∠7, ∠6 and ∠8
2 pairs of alternate angles are :
∠3and ∠7, ∠6and ∠2
2 pairs of interior angles are :
∠3 and ∠2, ∠6 and ∠7
1. ∠1 = 110° and ∠2 = 110° ∴ ∠1 = ∠2
∠1 =70°and ∠7 = 70° ∴ ∠5= ∠7
∠3 = 70° and ∠4 = 70° ∴ ∠3= Z4
∠6 = 110°and ∠8 = 110° ∴ ∠6- ∠8
2. ∠3 = 70° and ∠7 = 70° ∴ ∠3= ∠7
∠6 = 110°and ∠2 = 110° ∠6 = ∠2
3. ∠3 = 70°and ∠2 = 110°.∠3 + ∠2 = 180°
∴ Supplementary to each other.
∠6 = 110° and ∠7 = 70° ∴ ∠6+∠7=180°
Question 2. Let’s see and write from the figure beside which are corresponding angles, which are alternate angles and which are the interior angles in the same of the transversal.
Solution:
Corresponding → ∠1 and ∠5, ∠2and∠6
∠4and ∠8, ∠3and ∠7
Alternate → ∠4 and ∠6,∠3and ∠5
Interior angles in the same side of the transversal ∠4 and ∠5, ∠3 and ∠6 are supplementary to each other.
Question 3. If AB||CD then let’s write the measurement of the angles given below :
Solution:
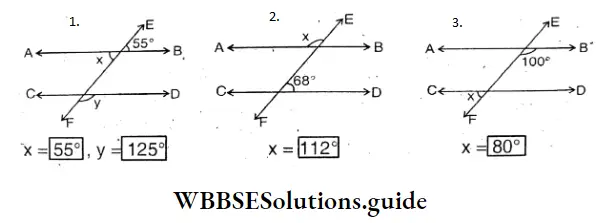
Question 4. In the figure beside if XY||PQ, write the measurement of 7 angles.
Solution:
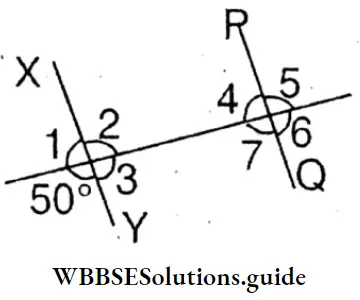
∠1=130°, ∠2=50°, ∠3=130°, ∠4=130°, ∠5=50°, ∠6=130°, ∠7=50°
Question 5. Examining the measurement of the angles given below let’s conclude logically that AB & CD are parallel.
Solution:
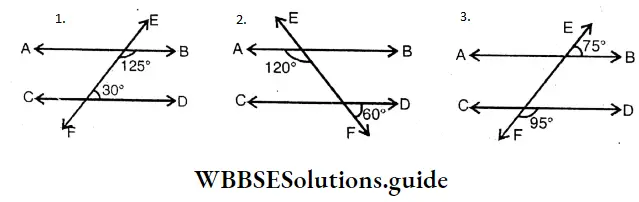
- In figure 1 the sum of interior angles in same side of transversal isn’t 180°, so AB and CD are not parallel.
- In figure EF stands on sraight line AB. Measurement of adjacent angle is 60°. Corresponding angle of this angle is 60°. So AB and CD are parallel.
- The measurement of corresponding angles is unequal. So AB and CD aren’t parallel.
Question 6. In figure AB||CD and ∠EGB = 50°; find the measure of ∠AGE, ∠AGH, ∠BGH.∠GHC, ∠GHD, ∠CHF and ∠DHF.
Solution:
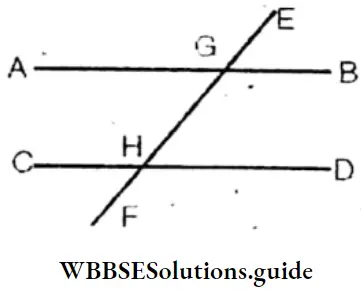
∠AGE = 130°, ∠AGH = 50°, ∠BGH = 130°, ∠GHC = 130°, ∠GHD = 50°, ∠CHF = 50°, ∠DHF = 130°
Question 7.
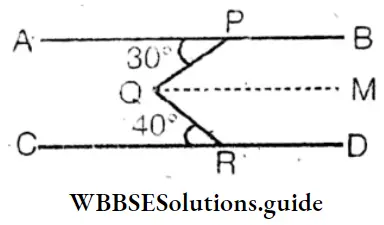
From figure AB||CD; find the measure of ∠PQR.
Solution:
AB and CD are parallel and PQ and QR intersect at Q. From point Q parallel to AB a straight line QM is drawn.
∴ QM||AB and QM||CD
∠APQ = alternate ∠PQM = 30°
∠CRQ = alternate ∠RQM = 40°
∠PQR = ∠PQM + ∠RQM = 30° + 40° = 70°
Question 8.
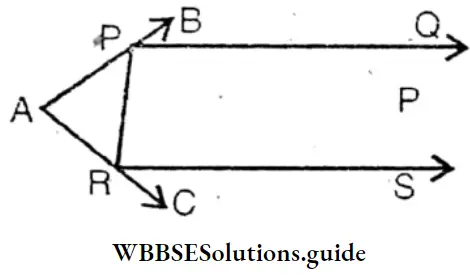
From the figure PQ||RS, ∠BPQ = 40°; ∠BPR=155° and ∠CRS = 70°. Find the value of the angles of A APR.
Solution:
∠BPQ = 40°, ∠BPR = 155°
∴ ∠QPR = ∠BPR – ∠BPQ = 155°-40° = 115°
∴ PQ//RS ∴ ∠QPR + ∠PRS = 180°
∴ ∠PRS = 180° -∠QPR = 180° – 115° = 65°
In Δ APR ∠APR = 180° – ∠BPR = 180° – 155° = 25°
∠ARP = 180° – (∠CRS + ∠PRS)
= 180° – (70°+65°)
= 180° – 135° ,
= 45°
∴ ∠APR = 180° – (25° + 45°)
= 180° – 70°= 110°
Question 9. In midst of two parallel lines AB and CD is a point O. OP and OQ respectively are perpendicular to parallel lines AB and CD. Prove that P,0,Q all are concurrent.
Solution:
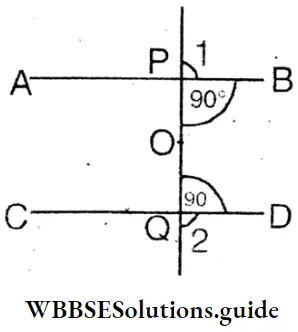
∴ OP⊥ AB
∴ ∠OPB = 90°
∴ On point P sum of the adjacent angles is = 90° + ∠1 = 180°
∴ ∠1 = 180°- 90° = 90°
∴ Both external sides lie on a same straight line.
Again, OQ⊥CD
∴ ∠OQD = 90°
∴ On point Q the sum of adjacent angles is
= 90° + ∠2 = 180°.
∠2 = 180° – 90° = 90°
∴ Both external sides lie on a same straight line.
∴ P, O, Q all three are concurrent.
Question 10. The diagonal AC of two angles is parallel to each other. Let’s prove either these angles are equal in measurement or they are supplementary.
Solution:
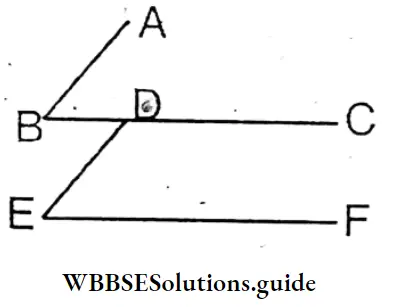
∴ AB||DE and BC a transversal.
∴ ∠ABC= ∠BDE (Alternate angles)
Again BC||EF and DE is a transversal.
∠BDE=∠DEF(Alternate angles).
∴ ∠ABC = ∠DEF Proved
Question 11. The diagonal AC of the parallelogram ABCD bisects ∠BAD. Let’s prove that the diagonal AC also bisects ∠BCD.
Solution:
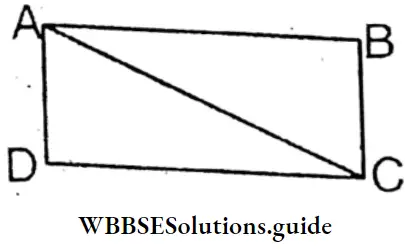
In the parallelogram, ABCD AB||DC and AC is a transversal.
∴ ∠BAC = alternate ∠ACD
and ∠DAC = alternate ∠ACB
AC is the bisector of ∠BAD
∴ ∠BAC = ∠DAC
∴ ∠ACD = ∠ACB
∴ AC diagonal also bisects ∠BCD
Question 12. Let’s prove that if one angle of a parallelogram is right angle, then all other angles of the parallelogram are also right angles.
Solution:
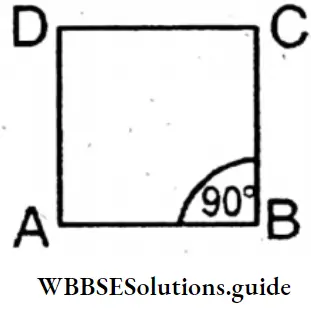
Let ABCD is a parallelogram whose ∠ABC=1 right angle.
We have to prove that ABCD is a parallelogram whose each angle is a right angle.
Proof : ∵ ABCD is a parallelogram.
∴ ∠ABC = ∠ADC
∴ ∠ABC = 1 right angle ∠ADC = 1 right angle
∴ AB||DC and BC is a transversal.
∴ ∠ABC + ∠BCD = 2 right angles
or, 1 right angles + ∠BCD = 2 right angles
or, ∠BCD = 1 right angle
∴ ∠BAD = ∠BCD = 1 right angle
∴ In parallelogram ABCD each angle is a right angle.

