WBBSE Class 7 Math Solution Algebra Chapter 7 Formation Of Equation And Solutions Exercise 7 Solved Problems
1. Variable, constant, and ‘equal to’ signs are used to express the problem in the language of Mathematics. This method is called the framing of the equation.
2. The value of the variable used in the equation is called an unknown number.
3. The specific value of an unknown number for which the two sides of the sign are equal is the root or the solution of the equation.
4. The method of finding the value of the unknown number is called solving the equation.
Example: 3x – 5 = 7 [x is variable]
⇒ 3x = 5 +7
⇒ 3x = 12
⇒ \(x=\frac{12}{3}=4\)
Here 4 is the root of the equation 3x – 5 = 7.
Again, (x-2)2 = x2 – 4x + 4 is true for any value of the variable.
Let, x = 3, (x-2)2 = (3-2)2= (1)2 = 1
⇒ x2 – 4x + 4 = (3)2 – 4 x 3+4=1
It is true for x = 3
⇒ x=-5, (x-2)2 = (-5-2)2 = (-7)2 = 49
⇒ x2-4x+4= (-5)2– 4 (-5)+ 4 = 25 +20 + 4 = 49
It is also true for x = – 5 so it is identified.
Read and Learn More WBBSE Solutions for Class 7 Maths
⇒ If both sides of the equation become equal for any value of the unknown quantity then this is called an identity.
⇒ An equation containing only one unknown quantity is known as a simple equation. Solving an equation is the process of finding its root.
Method of solving linear equations in one variable.
1. Simplify both sides of an equation and collect the like terms.
2. Multiply both sides by an appropriate factor (L. C. M of fractions) to remove fractions (if any).
3. Keep all the variable terms on LHS and the constant terms on the RHS following the rules of transposition.
[Any term may be brought from one side of the equation to the other by simply changing its sign. This is called transposition.]
4. Simplify both sides.
5. Divide both sides by the coefficient of the variable. The resulting coefficient of the variable becomes 1.
6. Thus the solution or root of the equation is obtained.
“WBBSE Class 7 Maths Algebra Chapter 7 solutions step-by-step”
Question 1. Choose the correct answer
1. If \(\frac{x}{2}-\frac{5}{6}=1 \frac{2}{3}\) then the root of the equation is
1. 2
2. 3
3. 5
4. 6
Solution:
Given
If \(\frac{x}{2}-\frac{5}{6}=1 \frac{2}{3}\)
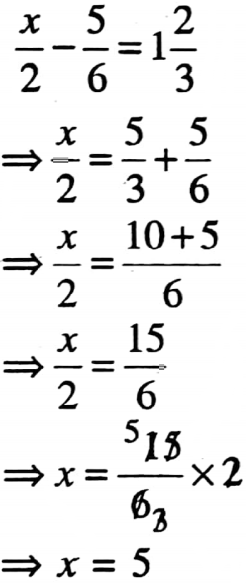
The root of the equation is 5.
So the correct answer is 3. 5
2. If \(\frac{x}{2}-\frac{2}{5}=\frac{x}{3}+\frac{1}{4}\) then value of x is
1. \(1 \frac{9}{10}\)
2. \(2 \frac{9}{10}\)
3. \(3 \frac{9}{10}\)
4. \(4 \frac{9}{10}\)
Solution:
Given
If \(\frac{x}{2}-\frac{2}{5}=\frac{x}{3}+\frac{1}{4}\)
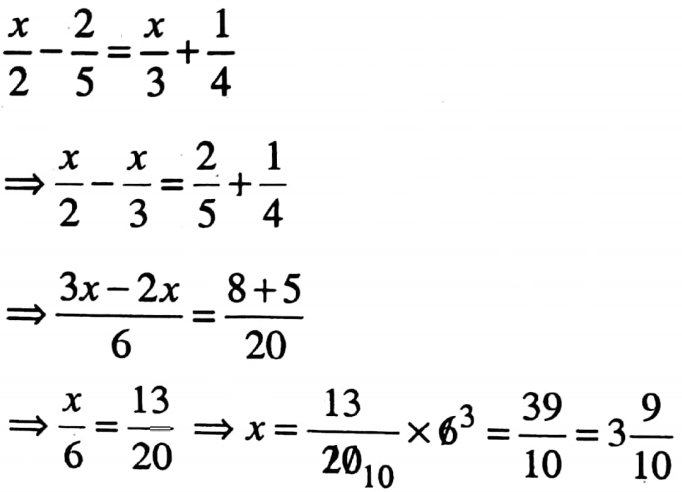
So the correct answer is 3. \(3 \frac{9}{10}\)
3. If the sum of \(\frac{1}{5}\)th and \(\frac{1}{7}\) th of a number is 144, then the number is
1. 288
2. 420
3. 1008
4. 720
Solution:
Given
If sum of \(\frac{1}{5}\)th and \(\frac{1}{7}\) th of a number is 144
Let the required number be x.
According to question, \(\frac{x}{5}\) + \(\frac{x}{7}\)=144
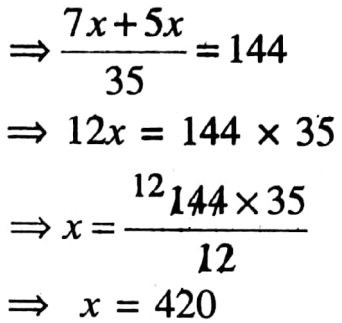
The number is 420
So the correct answer is 2. 420
Question 2. Write ‘true’ or ‘false’
1. For x= \(\frac{2}{3}\) the expressions (3 + 2x) and (1-x) are equal.
Solution 3 + 2x = 1 − x
⇒ 2x + x = 1-3
⇒ 3x= -2
⇒x=\(-\frac{2}{3}\)
The statement is false.
“West Bengal Board Class 7 Algebra Chapter 7 Formation of Equations solved problems”
2. The root of equation 6 (7-3x) + 12x = 0 is 7.
Solution:
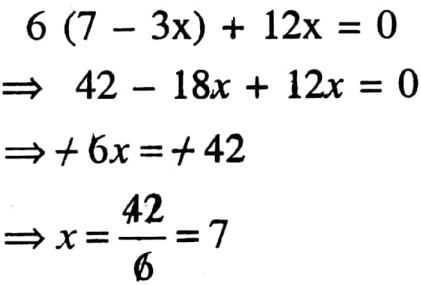
The statement is true.
Wbbse Class 7 Maths Solutions
3. 2x-3= \(\frac{3}{10}\)(5x-2), then the value of x is \(\frac{24}{5}\)
Solution: 2x-3=\(\frac{3}{10}\) (5x-2)
⇒ 20x – 30=15x – 6
⇒ 20x – 5x = 30 -6
⇒ 5x = 24
⇒ x = \(\frac{24}{5}\)
The statement is true.
Question 3. Fill in the blanks
1. If \(\frac{2x}{3}\) = \(\frac{3x}{8}\) + \(\frac{7}{12}\) then the value of x = _____
Solution:
Given
If \(\frac{2x}{3}\) = \(\frac{3x}{8}\) + \(\frac{7}{12}\)
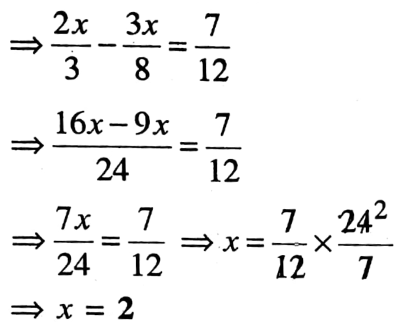
The value of x =2
2. When x = ____, then \(\frac{ax+b}{3}\) and \(\frac{cx+d}{2}\) are equal.
Solution: \(\frac{ax+b}{3}\) = \(\frac{cx+d}{2}\)
⇒ 2ax + 2b = 3cx + 3d
⇒ 2ax – 3cx =3d – 2b
⇒ x(2a – 3c) = 3d – 2b
⇒ x = \(\frac{3d-2b}{2a-3c}\)
“WBBSE Class 7 Maths Chapter 7 Algebra equation formation exercise solutions”
3. If the measurement of the three angles of a triangle is x°, 2x, and 3x°, then the triangle is a ________ triangle.
Solution:
Given
The measurement of the three angles of a triangle are x°, 2x, and 3x°
The sum of the measurement of the angles of a triangle is 180°
So x°+ 2x° + 3x° = 180°
⇒ 6x° = 180°
⇒x° = \(\frac{180°}{6}\) = 30°
⇒ 3x° = 3 x 30° = 90°
=2x° = 2 x 30° 60°
The triangle is right-angled.
Question 4. Solve the following equations
1. \(\frac{x}{6}\) + \(\frac{3x-1}{12}\) + \(\frac{x-5}{18}\) = 4
2. 0.5x + \(\frac{x}{3}\) = 0.25+7
3. \(\frac{ax}{b}\) – \(\frac{bx}{a}\) =a2 -b2
4. \(\frac{1}{6}\) (x−6) + \(\frac{1}{3}\) (x – 3)= \(\frac{1}{4}\) (x-4) + \(\frac{1}{5}\) (x-5)
5. \(\frac{3x+1}{16}\) + \(\frac{2x-1}{7}\) = \(\frac{x+3}{8}\) + \(\frac{3x-1}{14}\)
6. \(\frac{x-a}{b}\) + \(\frac{x-b}{4}\) + \(\frac{x-3a-3b}{a+b}\)=0
Solution:
1. \(\frac{x}{6}\) + \(\frac{3x-1}{12}\) + \(\frac{x-5}{18}\) = 4
⇒ \(\frac{6x+9x-3+2x-10}{36}\) =4
⇒ \(\frac{17x-13}{36}\) = 4
⇒ 17x-13= 144
⇒ 17x= 144 + 13
⇒ 17x = 157
⇒ x = \(\frac{157}{17}\) = 9 \(\frac{4}{17}\)

2. 0.5x + \(\frac{x}{3}\) = 0.25 + 7
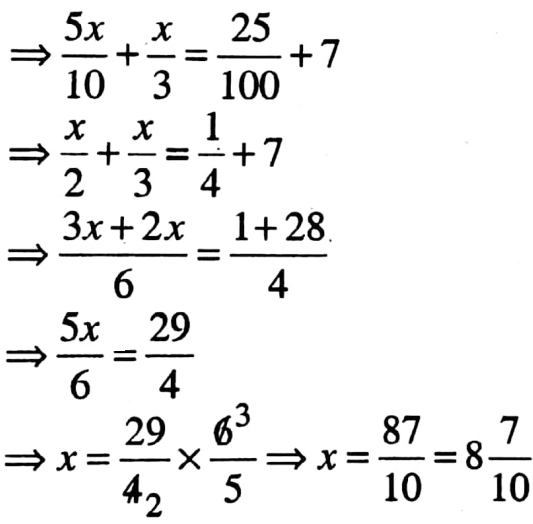
3. \(\frac{ax}{b}\) – \(\frac{bx}{a}\) =a2 -b2
Wbbse Class 7 Maths Solutions
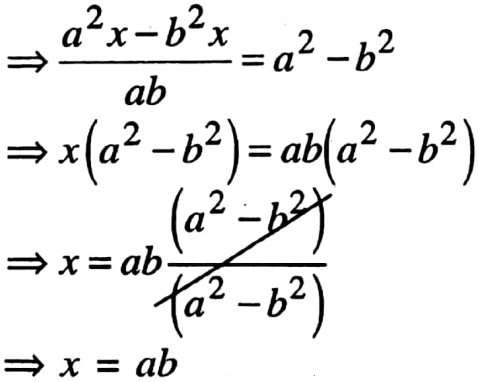
4. \(\frac{1}{6}\) (x−6) + \(\frac{1}{3}\) (x – 3)= \(\frac{1}{4}\) (x-4) + \(\frac{1}{5}\) (x-5)
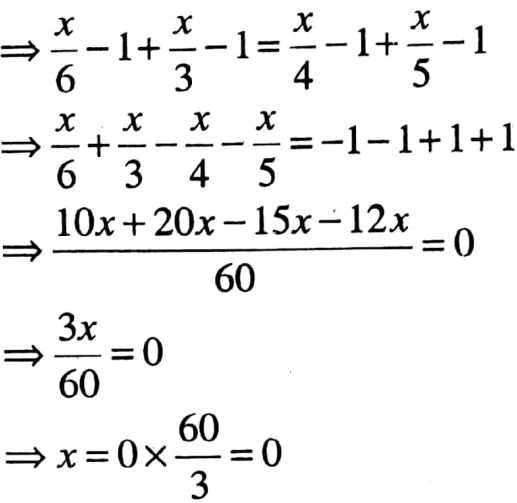
5. \(\frac{3x+1}{16}\) + \(\frac{2x-1}{7}\) = \(\frac{x+3}{8}\) + \(\frac{3x-1}{14}\)
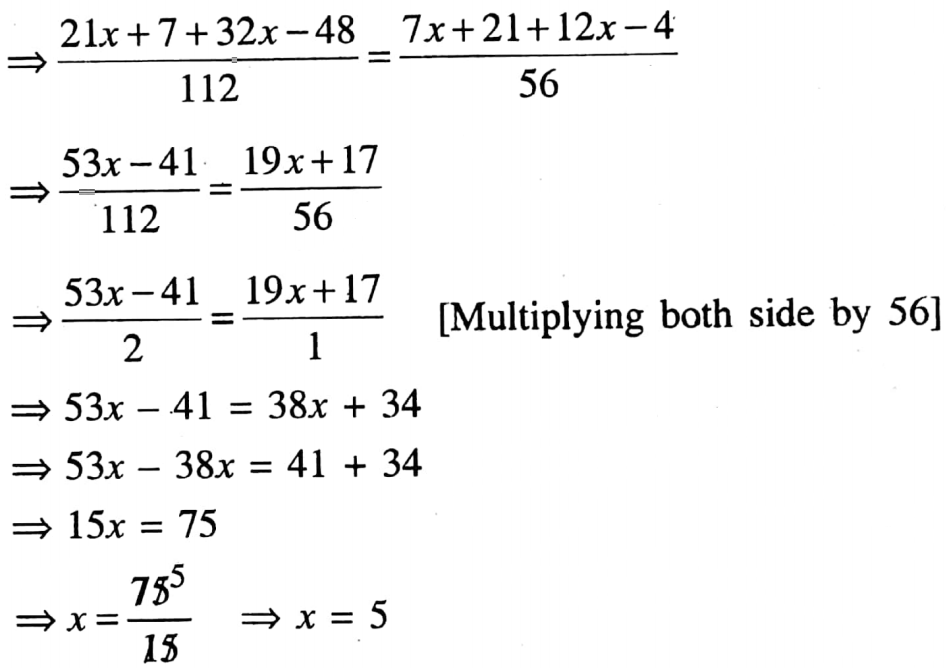
6. \(\frac{x-a}{b}\) + \(\frac{x-b}{4}\) + \(\frac{x-3a-3b}{a+b}\)=0
Wbbse Class 7 Maths Solutions
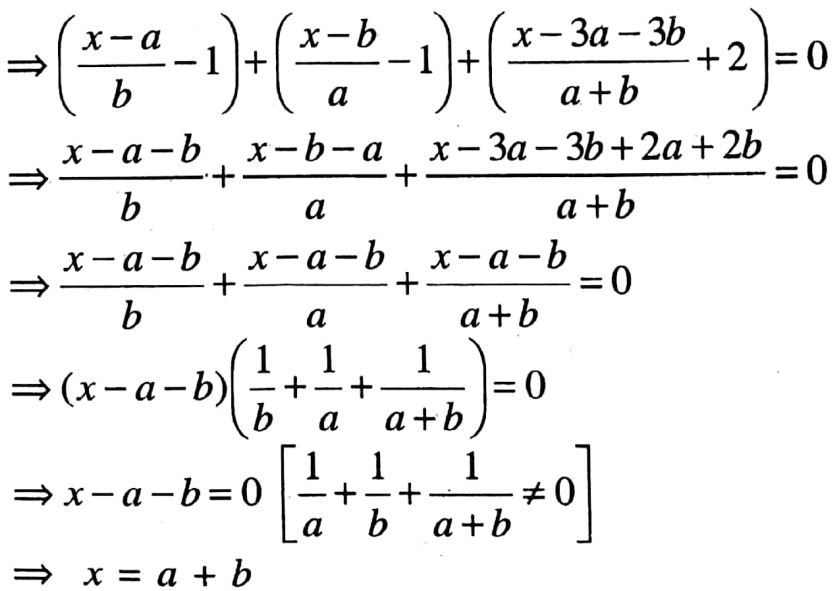
“How to solve WBBSE Class 7 Maths Algebra Chapter 7 equations”
Question 5. Frame and solve the equations
1. In the fruit shop there are \(\frac{1}{3}\) part apples, \(\frac{2}{7}\) part is oranges, and the remaining 160 are pears. Find out the total number of fruits.
Solution:
Given
In the fruit shop there are \(\frac{1}{3}\) part apples, \(\frac{2}{7}\) part is oranges, and the remaining 160 are pears.
Let the total number of fruits be x [x > 0]
∴ Number of apples is \(\frac{x}{3}\)
The number of oranges is \(\frac{2x}{7}\)
Remaining 160 are pears.
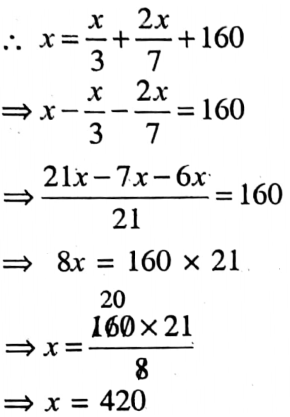
∴ Total number of fruits is 420.
2. The ratio of the length and breadth of a rectangle is 5: 2 and its perimeter is 140 cm. Find the area of the rectangle.
Solution:
Given
⇒ The ratio of the length and breadth of a rectangle is 5: 2 and its perimeter is 140 cm.
⇒ Let x be a common factor of the ratio where x > 0.
∴ Length of the rectangle is 5x cm and breadth is 2x cm.
⇒ The perimeter is 2(5x + 2x) cm = 14x cm.
⇒According to given condition, 14x= 140
⇒ x= \(\frac{140}{14}\) = 10
∴ Length is (10 x 5) cm or 50 cm and breadth is (10 x 2) cm or 20 cm.
∴ Area of the rectangle is (50 x 20) sq. cm = 1000 sq. cm.
“WBBSE Maths Class 7 Chapter 7 Formation of Equations and Solutions exercise answers”
3. Arun babu borrows some money to build his house. He returned ₹ 2000 more than \(\frac{1}{3}\)rd of the money he borrowed. However, he still has to repay amount of money he borrowed. However he still has to repay ₹ 21000. Find the amount of money he borrowed
Solution:
Given
⇒Arun babu borrows some money to build his house. He returned ₹ 2000 more than \(\frac{1}{3}\)rd of the money he borrowed.
⇒ Let the amount of money Arun babu borrowed be ₹ x
⇒ He returned ₹ ( \(\frac{x}{3}\) + 2000)
⇒However he still has to reply ₹ 21000.
⇒ According to given condition, x=( \(\frac{x}{3}\) + 2000 + 21000) + \(\frac{x}{3}\) + 2000
⇒ x- \(\frac{x}{3}\) – \(\frac{x}{3}\) = 25000
⇒ \(\frac{3x-x-x}{3}\) = 75000
∴ The amount of money he borrowed ₹ 75000.
4. The sum of the ages of A and B is 54 years. 2 years ago \(\frac{2}{3}\)rds A’s age was greater than \(\frac{3}{4}\)ths the present age of B by 12 years. What are their present ages?
Solution:
Given
⇒ The sum of the ages of A and B is 54 years. 2 years ago \(\frac{2}{3}\)rds A’s age was greater than \(\frac{3}{4}\)ths the present age of B by 12 years.
⇒ Let present age of A is x years.
∴ Present age of B is (54 – x) years.
2 years ago A’s age was (x – 2) years.
⇒ According to given condition, \(\frac{2}{3}\)(x-2) =\(\frac{3}{4}\)(54-x)+12
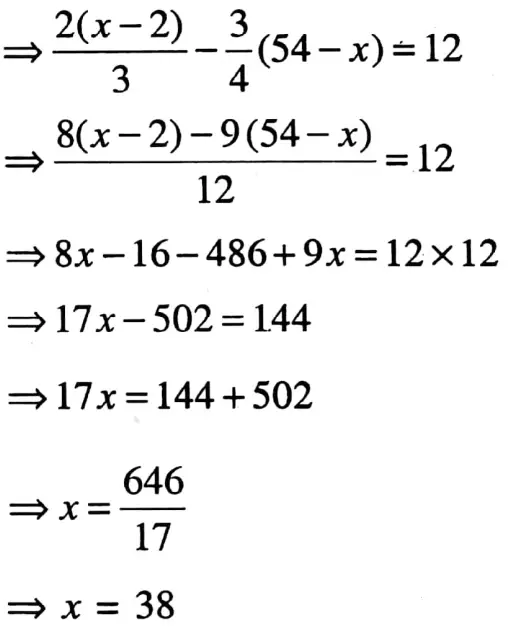
The present age of A is 38 years and that of B is (5438) years or 16 years.
“West Bengal Board Class 7 Maths Algebra Chapter 7 questions and answers”
5. In a two digit number the digit in the unit’s place is 2 more than the digit in ten’s place. If the sum of the digits is 12 then find the number.
Solution:
Given
In a two digit number the digit in the unit’s place is 2 more than the digit in ten’s place. If the sum of the digits is 12
Let the digit in ten’s place be x
∴ The digit in unit place is (x + 2)
∴ The number is (10x+x+2)= (11x+2)
According to question, x + x + 2 = 12
⇒ 2x= 12-2 = 10
⇒x=\(\frac{10}{2}\) =5
∴ The required number is 11 x 5 + 2 = 57
6. A train traveled over a certain distance in a certain time at the rate of 30 km/hr. If the speed had been 25 km/hr, he would have taken 36 minutes more to cover the same distance. Find the distance.
Solution:
Given
⇒ A train traveled over a certain distance in a certain time at the rate of 30 km/hr. If the speed had been 25 km/hr, he would have taken 36 minutes more to cover the same distance.
⇒ Let the required distance is x km.
⇒ The time taken to cover the distance x km at 30 km/hr is \(\frac{x}{30}\)
⇒ The time taken to cover the distance x km at 25 km/hr is \(\frac{x}{25}\)
⇒ According to condition \(\frac{x}{25}\) – \(\frac{x}{30}\) = \(\frac{36}{60}\)
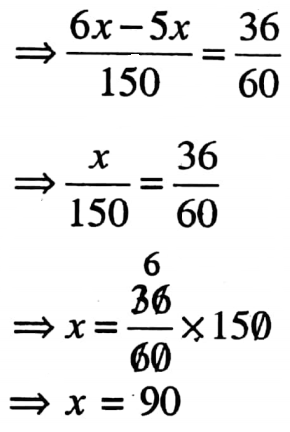
The required distance is 90 km
“WBBSE Class 7 Algebra Chapter 7 Formation of Equations important questions”
7. The difference between the numerator and denominator of a fraction is 5. If 2 is added to both the numerator and denominator, the fraction would become \(\frac{2}{3}\) Find 3′ the fraction.
Solution:
Given
⇒ The difference between the numerator and denominator of a fraction is 5. If 2 is added to both the numerator and denominator, the fraction would become \(\frac{2}{3}\)
⇒ Let the numerator of the fraction is x.
∴ Denominator is (x + 5). So the fraction is \(\frac{x}{x+5}\)
According to question \(\frac{x+2}{x+5+2}\) = \(\frac{2}{3}\)
⇒ \(\frac{x+2}{x+7}\) = \(\frac{2}{3}\)
⇒ 3x+6= 2x + 14
⇒ 3x – 2x = 14-6
⇒x= 8
∴ The fraction is \(\frac{8}{8+5}\) = \(\frac{8}{13}\)
