Class 7 Math Solution WBBSE Arithmetic Chapter 1 Revision Of Old Lesson Exercise 1 Solved Problems
Question 1. Simplify
1. \(3 \frac{1}{2}+2 \frac{3}{4}+3 \frac{4}{5} \text { of } 1 \frac{2}{3}\)
2. 0.125+0.2 of 0.5 x 2.5
Given \(3 \frac{1}{2}+2 \frac{3}{4}+3 \frac{4}{5} \text { of } 1 \frac{2}{3}\)
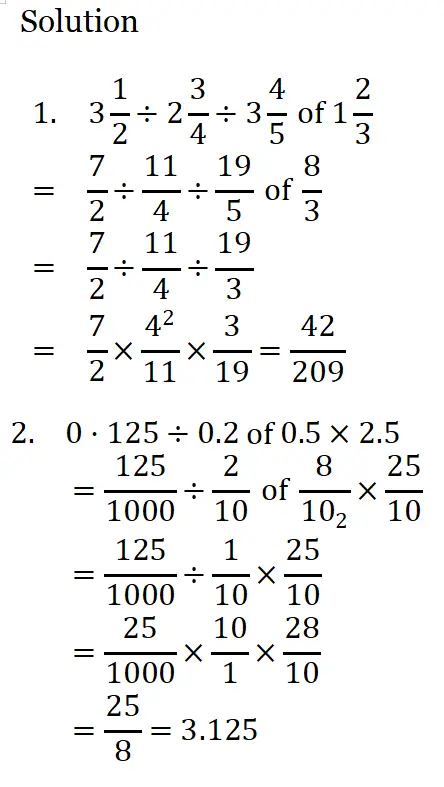
Question 2: The cost of \(\frac{5}{7}\) part of a property is 2825. Find the cost of \(\frac{2}{7}\) part of the property.
Solution:
Given
\(\frac{5}{7}\) part of the property costs ₹ 2825
1 part of the property costs ₹ \(\left(2825 \times \frac{7}{5}\right)\)
∴ \(\frac{2}{7}\) part of the property cost ₹ \(\left(2825 \times \frac{7}{8} \times \frac{2}{7}\right)\)
“WBBSE Class 7 Maths Arithmetic Chapter 1 revision of old lesson solutions”
Read and Learn More WBBSE Solutions for Class 7 Maths
Question 3. 20 men decided to complete the repairing work of a house in 30 days. But after 6 days 8 men fell sick. Find how many days they will take to complete the work.
Solution:
Given
⇒ 20 men decided to complete the repairing work of a house in 30 days. But after 6 days 8 men fell sick.
⇒ In Mathematical language, the problem is:
⇒ Men (by heads) 20
⇒ 20- 8 = 12
⇒ Time (in days)
⇒ 30-6=24
?
⇒ Number of days and the number of persons are in inverse proportion.
⇒ For a particular work, if the number of persons decreases, several days required increases.
⇒ 20 men can do the work in 24 days
⇒ 1 man can do the work in (24 x 20) days
⇒ 12 men can do the work in \(\frac{24 \times 20}{12}\) days = 40 days
⇒ Hence, to complete the work (40+ 6) days or 46 days are required.

Question 4. Find \(12 \frac{1}{2} \%\) of 4 is equal to how much paise.
Solution:
Given
\(12 \frac{1}{2} \%\) of ₹ 4
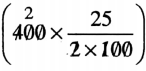
= 50 paise.
\(12 \frac{1}{2} \%\) of 4 = 50 paise.
Question 5. Find the square root of the following:
1. 108241
2. 186624
Solution:
Given 108241
1.
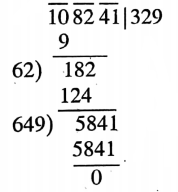
2.
Given 186624

“WBBSE solutions for Class 7 Maths arithmetic chapter 1 exercise 1”
Question 6 Find the least positive whole number that must be subtracted from 9545 so that the resultant number is a perfect square.
Solution :
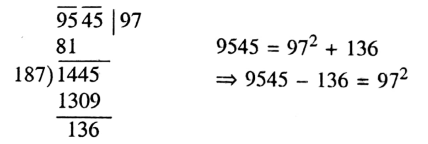
⇒ So the least number is 136, which must be subtracted from 9545 so that the resultant number is a perfect square.
Question 7. Simplify
1. \(\frac{2 \cdot 46-2 \cdot \dot{3} \dot{0}}{0 \cdot 3+0 \cdot 12 \dot{7}}+\frac{4 \frac{1}{3}}{19}\)
2. \(\frac{0 \cdot 007 \dot{4} \times 0 \cdot 135}{0 \cdot 00 \dot{8} \times 0 \cdot 09}+\frac{3 \frac{1}{2} \div 2 \frac{1}{2} \times 1 \frac{1}{2}}{3 \frac{1}{2} \div 2 \frac{1}{2} \text { of } 1 \frac{1}{2}} \times \frac{5}{18}\)
Solution:
Given \(\frac{2 \cdot 46-2 \cdot \dot{3} \dot{0}}{0 \cdot 3+0 \cdot 12 \dot{7}}+\frac{4 \frac{1}{3}}{19}\)
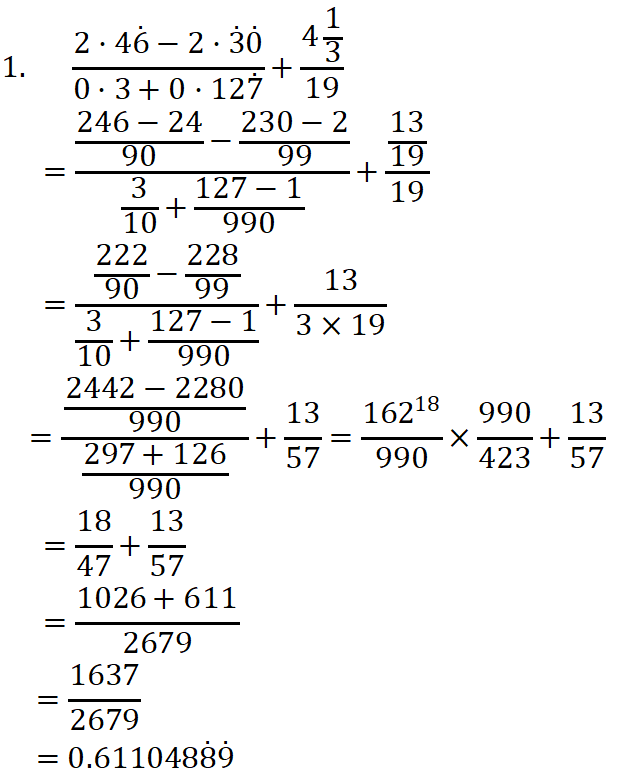
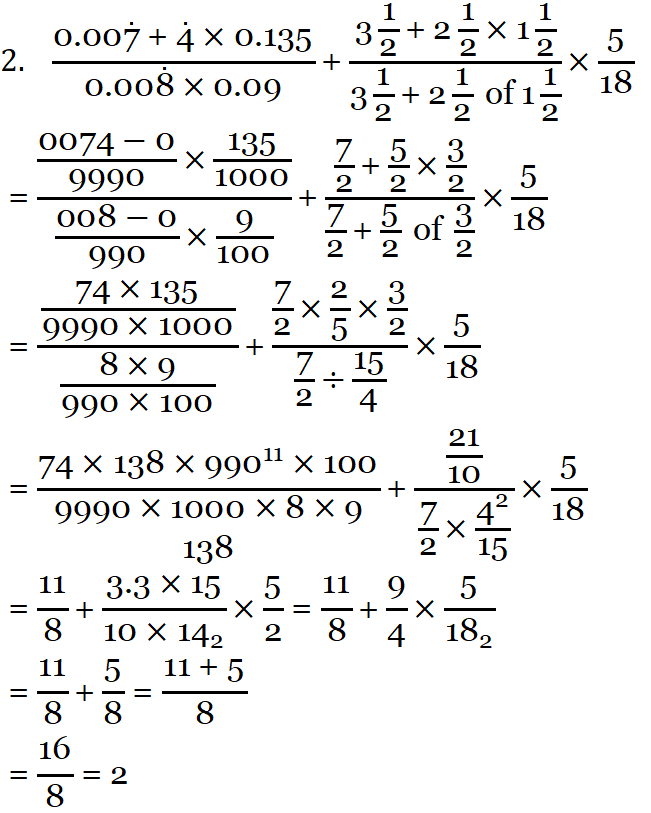
“Class 7 Maths WBBSE Chapter 1 revision of old lesson solved problems”
Question 8: There are three positive whole numbers, the product of first and second number is 48, a product of second and third numbers is 40 and that of the first and third is 30. Find the three numbers.
Solution:
Given
⇒ There are three positive whole numbers, the product of first and second number is 48, a product of second and third numbers is 40 and that of the first and third is 30.
⇒ Let 1st number is x, 2nd number is y and the Third number is z.
⇒ According to question, x x y = 48
y x z = 40
⇒ and x x z = 30
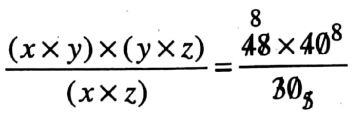
⇒ y2 = 64
⇒ y = √64=8
⇒ x x y = 48
∴ \(x=\frac{48}{y}=\frac{48}{8}=6\)
y x z = 40
8 x z = 40
⇒ \(z=\frac{40}{8}=5\)
∴ 1st, 2nd, and third numbers are 6, 8, and 5 respectively.
Wbbse Class 7 Maths Solutions
Question 9 Calculate what is the biggest whole square number of 4 digits which will be divisible by 12, 18, and 30.
Solution: The least number which is divisible by 12, 18, and 30 is the L. C. M. of 12, 18, and 30.
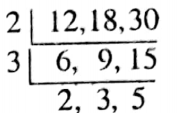
L. C. M. of 12, 18, and 30 is 2 x 3 x 2 x 3 x 5
= 22 x 32 x 5 = 180
The number 180 is not a perfect square.
∴ Square number which is divided by 12, 18, and 30 is (180 x 5) or 900.
But 900 is not a 4 digit number.
∴ 900 is to be multiplied by the square numbers 4, 9, 16, 25… to get 4 digits square number which will be divisible by 12, 18, and 30.
⇒ 900 x 4 = 3600 → 4 digit square number
⇒ 900 × 9 = 8100 → 4 digit square number
⇒ 900 x 16 =14400 → 5 digit square number.
Hence the greatest square number of 4 digit which is divisible by 12, 18, 30 is 8100.
“Step-by-step solutions for arithmetic revision Class 7 WBBSE”
Question 10 Out of total monthly expenses of our family, 4750 is spent on food and 5900 for all other expenses. If expenses on food is increased by 10% and other expenses are decreased by 16%, then calculate whether the total monthly expenses will increase or decrease.
Solution:
Given
⇒ Out of total monthly expenses of our family, 4750 is spent on food and 5900 for all other expenses. If expenses on food is increased by 10% and other expenses are decreased by 16%,
⇒ Monthly expenses is ₹ 4750
⇒ Other expenses is ₹ 5900
⇒ Total expenses is ₹ (4750+ 5900) = ₹ 10,650
⇒ Monthly expenses is increased by 10%.
⇒ Now monthly expenses is ₹
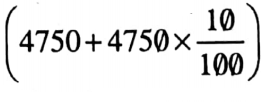
= ₹ (4750+ 475)
= ₹ 5225
⇒ Other expenses is decreased by 16%.
⇒ Now other expenses is ₹
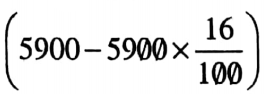
= ₹ (5900 -944)
= ₹ 4956
⇒ Now total expenses is ₹(5225 + 4956)
= ₹ 10,181
⇒ Now total expenses will decreased by ₹ (10,650-10,181) or ₹469
Class 7 Math Solution WBBSE Simplifications Exercise 1
Question 1. \(\frac{1}{2}\) part of Re. 1
Solution:
⇒ \(\frac{1}{2}\)100 Paisa
= 50 Paisa
\(\frac{1}{2}\) part of Re. 1 = 50 Paisa
Question 2. \(\frac{1}{4}\) th part of 1 year
Solution:
⇒ \(\frac{1}{4}\) th × 12 months
=3 months
\(\frac{1}{4}\) th part of 1 year =3 months
“WBBSE Class 7 Maths Chapter 1 important questions and answers”
Question 3.\(\frac{5}{8}\) th part of Rs. 4
Solution:
⇒ 250 Paisa = Rs. 2.50 Paisa
\(\frac{5}{8}\) th part of Rs. 4 = Rs. 2.50 Paisa
Question 4. \(\frac{1}{5}\) th part of 2kg
Solution:
⇒ \(\frac{1}{5}\) th × 2000g
= 400g
\(\frac{1}{5}\) th part of 2kg = 400g
Problem 5. \(\frac{1}{5}\) th part of 5 I 2d I
Solution:
5 I 2d I = 2 I 6d I
\(\frac{1}{5}\) th part of 5 I 2d I = 2 I 6d I
Question 6. Required number
Solution:
⇒ (35-20) × 3
= 45
Question 7. Required number
Solution:
⇒ 3-2 × \(\frac{5}{7}\)
= 3- × \(\frac{10}{7}\)
= \(\frac{21-10}{7}\)
= \(\frac{11}{7}\)
= 1\(\frac{4}{7}\)
Question 8. Required number \(\frac{4-7}{5}\)
Solution:
⇒ \(\frac{4-7}{5}\)
= \(\frac{28}{5}\)
= 5\(\frac{3}{5}\)
\(\frac{4-7}{5}\) = 5\(\frac{3}{5}\)
Question 9. Least Number
Solution:
1. \(\frac{2}{3}\)= \(\frac{2 \times 5}{15}\)= \(\frac{10}{15}\)
2. \(\frac{4}{5}\)= \(\frac{4 \times 3}{15}\)= \(\frac{12}{15}\)
3. \(\frac{2}{3}\) x \(\frac{4}{5}\) = \(\frac{8}{15}\)
∴ Least Value = \(\frac{2}{3}\) x \(\frac{4}{5}\)
Question 10. Greatest Number
Solution:
1. \(\frac{5}{2}\)= \(\frac{5 \times 3}{2 \times 3}\) = \(\frac{15}{6}\)
2. \(\frac{7}{3}\)= \(\frac{7 \times 2}{3 \times 2}\)= \(\frac{14}{6}\)
3. \(\frac{5}{2}\) x \(\frac{7}{3}\) = \(\frac{35}{36}\)
∴ Greast number = \(\frac{5}{2}\) x \(\frac{7}{3}\)
Question 11. The sum of 4 times a number and half of its is 1 \(\frac{2}{3}\). Let us find the number.
Solution:
Given
⇒ The sum of 4 times a number and half of its is 1 \(\frac{2}{3}\).
⇒ According to the problem. 4x + \(\frac{x}{2}\) = 1 \(\frac{2}{3}\)
Or,\(\frac{8 x+x}{2}\) = \(\frac{5}{3}\)
x = \(\frac{5}{3}\)× \(\frac{2}{9}\) Or, \(\frac{9x}{2}\)× \(\frac{5}{3}\)
= \(\frac{10}{27}\)
⇒ The required number = \(\frac{10}{27}\)
Question 12. The fraction ( \(\frac{1}{2}\) – \(\frac{1}{3}\)) is……. times.
Solution:
Given
⇒ The fraction ( \(\frac{1}{2}\) – \(\frac{1}{3}\))
\(\frac{1}{2}\) – \(\frac{1}{3}\) = \(\frac{3-2}{6}\)
= \(\frac{1}{6}\)
And
\(\frac{1}{2}\) + \(\frac{1}{3}\) = \(\frac{3+2}{6}\)
= \(\frac{5}{6}\)
⇒ Now we have to find how many times \(\frac{1}{6}\) contains in \(\frac{5}{6}\)
∴ The required number = \(\frac{5}{6}\) ÷\(\frac{1}{6}\)
= \(\frac{5}{6}\) ×\(\frac{1}{6}\)
= 5 times
Exercise 1.1
Question 1. Sitara Begam had 60 guavas in her fruit shop. She sold part of the number of guavas she had, let’s calculate how many guavas are left with her.
Solution :
Given
⇒ Sitara Begum had 60 guavas.
⇒ She sold \(\frac{1}{4}\)th part of number of guavas
= \(\frac{1}{4}\)× 60 = 15 guavas.
∴ Now, Remaining guavas = 60 – 15 = 45
45 guavas are left with her.
Question 2. Mother gave me \(\frac{5}{6}\)th part of Rs. 60 and my elder brother \(\frac{7}{9}\)th part of Rs. 45. Letts find, to whom mother gave more money.
Solution:
Given
⇒ Mother gave me \(\frac{5}{6}\)th part of Rs. 60 and my elder brother \(\frac{7}{9}\)th part of Rs. 45.
⇒ I received \(\frac{5}{6}\)th part of Rs. 60
= Rs.\(\frac{5}{60}\) × 60 = Rs.50
⇒ My elder brother received \(\frac{7}{9}\) th part of Rs. 45
= Rs. \(\frac{7}{9}\)×45
= Rs.35
My mother gave me = Rs. (50 – 35) = Rs. 15 more money
Question 3. Ganeshbabu did \(\frac{3}{14}\),\(\frac{4}{7}\) ,\(\frac{1}{21}\) and — parts of a work in three days respectively, let’s find what part of the did in three days and what part of work is left to be completed.
Solution:
Given
⇒ Ganeshbabu did \(\frac{3}{14}\),\(\frac{4}{7}\) ,\(\frac{1}{21}\) and — parts of a work in three days respectively
⇒ Let the whole work = 1
⇒ Ganeshbabu did in 3 days (\(\frac{3}{14}\)+\(\frac{4}{7}\)+\(\frac{1}{21}\) )
= \(\left(\frac{9+24+2}{42}\right)=\frac{35}{42}\)
= \(\frac{5}{6}\)th part work
⇒ Remaining = \(\left(1-\frac{5}{6}\right)=\frac{6-5}{6}\)
= \(\frac{1}{6}\) part of work is left to be completed
Question 4. \(\frac{1}{3}\)rd part of the length of bamboo is colored red and — part of It is colored green and the remaining 14m length is colored yellow. Let’s find the length of the bamboo.
Solution:
Given
\(\frac{1}{3}\)rd part of the length of bamboo is colored red and — part of It is colored green and the remaining 14m length is colored yellow.
⇒ Let the length of a bamboo = 1
⇒ Red coloured part of a bamboo = \(\frac{1}{3}\)rd part
⇒ Green coloured part of the bamboo = \(\frac{1}{5}\)th
⇒ Total coloured part of the bamboo (\(\frac{1}{3}\)+\(\frac{1}{3}\)) = \(\frac{5+3}{15}\)
= \(\frac{8}{15}\) th part
⇒ Remaining part = (\(\left(1-\frac{8}{15}\right)=\frac{5-8}{15}\))
= \(\frac{7}{15}\)th part
⇒ According to the problem, \(\frac{7}{15}\)th part = 14m.
∴ Length of the bamboo = 14x— m = 30m.
“Solved examples of arithmetic revision WBBSE Class 7 Maths”
Question 5. If the price of one exercise book is Rs. 6.50, let’s find the price of 15 such exercise books.
Solution:
Given
⇒ Price of one exercise book = Rs. 6 -50
∴ Price of 15 exercise books =. Rs. 6 -50×15 = Rs. 97-50
Class Vii Math Solution WBBSE
Question 6. There are 12 packets of sugar in a box. The weight of each packet is 2.84 kg. If the total weight <3f box along with packets is 36 kg. Let’s calculate the weight of the box.
Solution:
Given
⇒ There are 12 packets of sugar in a box. The weight of each packet is 2.84 kg. If the total weight <3f box along with packets is 36 kg.
⇒ Weight of one packet of Sugar = 2 -84kg
∴ Weight of 12 packets of Sugar = 2 . 84 x 12kg = 34 .08 kg
⇒ Weight of the box and 12 packets of sugar = 36 kg & the weight of 12 packets of sugar = 34 .08 kg
⇒ Weight of the box = (36 -34 .08) kg = 1.92 kg.

Question 7. If the cost of 0.75 part of a bag of rice is Rs. 1800, let’s find the cost of 0.15 part of it.
Solution:
Given
⇒ Cost of 0.75 parts of a bag of rice = Rs. 1800
⇒ Cost of 0.15 part of a bag of rice = Rs. \(\frac{1800}{0.75}\) × 0.15
= Rs. \(\frac{1800}{0.75}\)
= Rs. 360.
⇒ The cost of 0.15 part of it. = Rs. 360.
Question 8. Anitadi gave \(\frac{7}{8}\) part of her land to her brother and the remaining part of the land she divided equally among her three sons. Let’s draw a picture to show the part of land each son has got.
Solution:
Given
⇒ Anitadi gave \(\frac{7}{8}\) part of her land to her brother and the remaining part of the land she divided equally among her three sons.
⇒ Let the total land of Anitadi = 1
⇒ She gave half of \(\frac{7}{8}\) th part of land to her brothers = \(\frac{1}{2}\) \(\frac{7}{8}\) \(\frac{7}{16}\)
⇒ Remaining part of land = 1- (1-\(\frac{7}{16}\)) th = \(\frac{16-7}{16}\)=
= \(\frac{9}{16}\)th
⇒ She divided \(\frac{9}{16}\) part of land to her 3 sons
⇒ Each son will get \(\frac{9}{16}\)×\(\frac{1}{3}\)
= \(\frac{3}{16}\) th
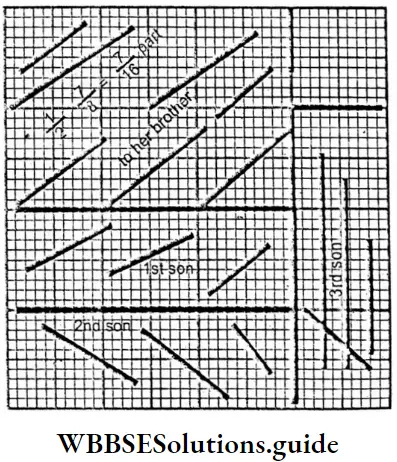
Question 9. Let’s simplify :
1. \(\frac{13}{25}\) × 1\(\frac{7}{8}\)
Solution:
\(\frac{13}{25}\) × 1\(\frac{7}{8}\) = \(\frac{13}{25}\) × \(\frac{15}{8}\)
= \(\frac{39}{40}\)
\(\frac{13}{25}\) × 1\(\frac{7}{8}\) = \(\frac{39}{40}\)
2. 2\(\frac{5}{8}\) × 2\(\frac{2}{21}\)
Solution:
= \(\frac{21}{8}\) × \(\frac{44}{21}\)
= 5 \(\frac{1}{2}\)
2\(\frac{5}{8}\) × 2\(\frac{2}{21}\) = 5 \(\frac{1}{2}\)
3. 10\(\frac{3}{10}\)x 6\(\frac{4}{3}\)x\(\frac{4}{11}\)
Solution:
= \(\frac{103}{10}\) × \(\frac{22}{3}\) × \(\frac{4}{11}\)
= \(\frac{412}{15}\)
= 27\(\frac{7}{15}\)
10\(\frac{3}{10}\)x 6\(\frac{4}{3}\)x\(\frac{4}{11}\) = 27\(\frac{7}{15}\)
4. 0 . 025 x 0 . 02
Solution:
⇒ 0 . 025 x 0 . 02 = 0 . 00050 = 0 . 0005
⇒ 0 . 025 x 0 . 02 = 0 . 0005
5. 0 07 x 0.2 x 0-5
Solution:
⇒ 0 07×0-2 x 0-5 =0 014 x 0.5
= 0.0070
= 0.007
0 07 x 0.2 x 0-5 = 0.007
6. 0.029 x 2.5 x 0.002
Solution:
⇒ 6. 0.029 x 2.5 x 0.002 =0.0725 x 0 .002
= 0.000145
0.029 x 2.5 x 0.002 = 0.000145
Class VII Math Solution WBBSE Question 10. Let’s simplify :
1. 3\(\frac{3}{4}\) ÷ 2\(\frac{1}{2}\)
Solution:
3\(\frac{3}{4}\) ÷ 2\(\frac{1}{2}\)= \(\frac{15}{4}\)÷ \(\frac{5}{2}\)
=\(\frac{5}{2}\) x \(\frac{5}{2}\)
= \(\frac{3}{2}\)
= 1 \(\frac{1}{2}\)
3\(\frac{3}{4}\) ÷ 2\(\frac{1}{2}\) = 1 \(\frac{1}{2}\)
2. \(\frac{50}{51}\)÷ 15
Solution:
\(\frac{50}{51}\)÷ 15= \(\frac{50}{51}\) x \(\frac{1}{15}\)
= \(\frac{10}{153}\)
\(\frac{50}{51}\)÷ 15 = \(\frac{10}{153}\)
3. 1÷ \(\frac{5}{6}\)
Solution:
1÷ \(\frac{5}{6}\)= 1 × \(\frac{6}{5}\)
= \(\frac{6}{5}\)
= 1 \(\frac{1}{5}\)
1÷ \(\frac{5}{6}\) = 1 \(\frac{1}{5}\)
4. \(\frac{156}{121}\)÷\(\frac{13}{22}\)
Solution:
\(\frac{156}{121}\)÷\(\frac{13}{22}\)= \(\frac{156}{121}\) × \(\frac{22}{13}\)
= \(\frac{24}{11}\) =
= 2\(\frac{2}{11}\)
\(\frac{156}{121}\)÷\(\frac{13}{22}\) = 2\(\frac{2}{11}\)
5. 1 \(\frac{1}{2}\)÷ \(\frac{4}{9}\) ÷13 \(\frac{1}{2}\)
Solution:
1 \(\frac{1}{2}\)÷ \(\frac{4}{9}\) ÷13 \(\frac{1}{2}\)= \(\frac{3}{2}\)÷\(\frac{4}{9}\)÷\(\frac{27}{2}\)
= \(\frac{3}{2}\) x \(\frac{9}{4}\) x \(\frac{2}{27}\)
= \(\frac{1}{4}\)
1 \(\frac{1}{2}\)÷ \(\frac{4}{9}\) ÷13 \(\frac{1}{2}\) = \(\frac{1}{4}\)
6. \(\frac{9}{10}\)÷\(\frac{3}{8}\)×\(\frac{2}{5}\)
Solution:
\(\frac{9}{10}\)÷\(\frac{3}{8}\)×\(\frac{2}{5}\)= \(\frac{9}{10}\)×\(\frac{8}{3}\)×\(\frac{2}{5}\)
= \(\frac{24}{25}\)
\(\frac{9}{10}\)÷\(\frac{3}{8}\)×\(\frac{2}{5}\) = \(\frac{24}{25}\)
7. 2 \(\frac{1}{3}\)÷ 1 \(\frac{1}{6}\)÷2\(\frac{1}{4}\)
Solution:
2 \(\frac{1}{3}\)÷ 1 \(\frac{1}{6}\)÷2\(\frac{1}{4}\) = \(\frac{7}{3}\) ÷\(\frac{7}{6}\)÷ \(\frac{9}{4}\)
= \(\frac{7}{3}\) x \(\frac{6}{7}\) x \(\frac{4}{9}\)
=\(\frac{8}{9}\)
2 \(\frac{1}{3}\)÷ 1 \(\frac{1}{6}\)÷2\(\frac{1}{4}\) =\(\frac{8}{9}\)
8. 20 ÷7\(\frac{1}{4}\) × \(\frac{3}{5}\)
Solution:
20 ÷7\(\frac{1}{4}\) × \(\frac{3}{5}\) = 20 \(\frac{4}{29}\) x \(\frac{3}{5}\)
= 1\(\frac{19}{29}\)
20 ÷7\(\frac{1}{4}\) × \(\frac{3}{5}\) = 1\(\frac{19}{29}\)
9. 3. 15 ÷ 2.5
Solution:
3. 15 ÷ 2.5= \(\frac{3.15}{2.5}\)
= 1.26
15 ÷ 2.5= 20\(\frac{3.15}{2.5}\)
3. 15 ÷ 2.5 = 20\(\frac{3.15}{2.5}\)
10. 35.4 ÷0-03 x 0.06
Solution:
35.4 ÷0-03 x 0.06 =1180 x 0 06 = 70.8
35.4 ÷0-03 x 0.06 = 70.8
11. 2.5 x 6 ÷0.5
Solution:
2.5 x 6 ÷0.5 =15 ÷0.5
= 30
2.5 x 6 ÷0.5 = 30
Question 11. Let’s see the picture and multiply and color
Solution:
1. \(\frac{1}{6}\) × 3 = \(\frac{1}{2}\)
2. \(\frac{2}{12}\) × 3 = \(\frac{6}{12}\)
= \(\frac{1}{2}\)
3. \(\frac{2}{7}\) × 3 = \(\frac{6}{7}\)
WB Class 7 Math Solution Simplifications Exercise 1.2
Question 1. A wheel turns 55 times to cover a distance of 77m. Let’s calculate, how many revolutions the wheel will take to cover a distance of 98m.
Solution :
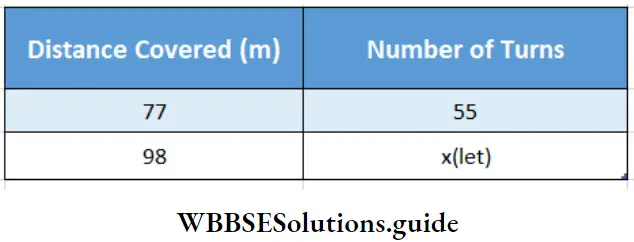
Given
⇒ A wheel turns 55 times to cover a distance of 77m.
⇒ Here distance covered & No. of turns are in direct proportion
∴ \(\frac{77}{98}\) = \(\frac{55}{x}\)
⇒ 77 x = 98 × 55
⇒ 77x = \(\frac{98 \times 55}{77}\)
= 70
∴ No of turns 70 times revolution the wheel will take to cover the distance.
Question 2. Diptarka learns swimming once a week. Let’s calculate how many days he goes for swimming in 364 days.
Solution :
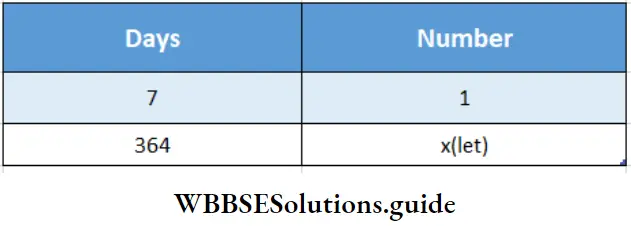
Given
Diptarka learns swimming once a week.
∴ \(\frac{7}{364}=\frac{1}{x}\)
⇒ 7x= 364
x = \(\frac{364}{7}\)
∴ x = 52 days
∴ Number odf days = 52 , he goes for swimming
Question 3. Kavita needs 120 sheets of paper. There are 24 sheets in each bundle. Let’s find out how many bundles of paper Kavita would buy.
Solution:
Given
Kavita needs 120 sheets of paper. There are 24 sheets in each bundle.
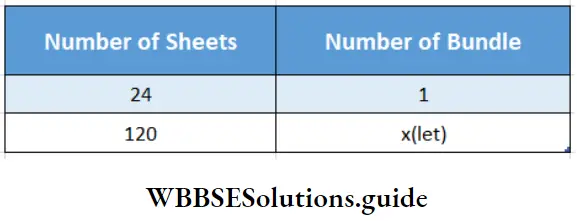
Here number of sheets & no. of bundles are in direct proportion
∴ \(\frac{24}{120}=\frac{1}{x}\)
⇒ 24x = 120
∴ x = \(\frac{120}{24}\)
x = 5
∴ No. of bundles = 5
∴ Kavita would buy 5 bundles of paper
Question 4. If. the cost of a dozen eggs is Rs. 48. Let’s find the cost of 32 eggs.
Solution :
Given
⇒ The Cost price of 12 eggs (1 dozen) = Rs. 48
⇒ The Cost price of 1 egg = Rs. \(\frac{48}{12}\)
⇒ The cost price of 32 eggs = Rs.\(\frac{48}{12}\) x 32= Rs. 128.
⇒ the Cost price of 32 eggs = Rs. 128.
Question 5. Working 5 hours a day, work can be completed in 30 days. Let’s find, out how long it would take to complete the work, working 6 hours a day.
Solutions :
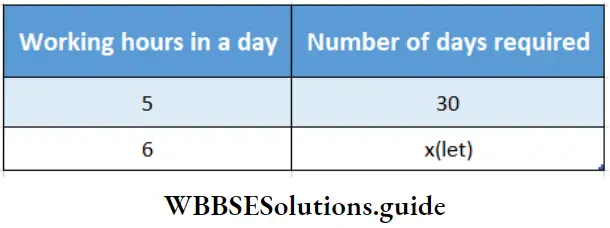
Given
⇒ Working 5 hours a day, work can be completed in 30 days.
⇒ Here working hours & no. of days required are in inverse proportion
∴ \(\frac{5}{6}=\frac{x}{30}\)
⇒ 6x = 5 x 30
x = \(\frac{5 \times 30}{6}\)
∴ x= 25 days
Or by the unitary method:
⇒ Working 5 hours a day, time required 30 days
⇒ Working 1 hour a day, time required 30 × 5 days
⇒ Working 6 hours a day, the time required \(\frac{30 \times 5}{6}\) = 25 days.
Question 6. The cost of \(\frac{5}{7}\) part of a property is Rs. 2825. Let’s find the cost of \(\frac{5}{7}\) part of the property.
Solutions :
Given
⇒ Cost of \(\frac{5}{7}\) the part of a property = Rs. 2825
⇒ Cost of whole (1) property = Rs. 2825 × \(\frac{7}{5}\)
∴ Cost of \(\frac{2}{7}\)th part of property = Rs. 2825 x \(\frac{7}{5}\) × \(\frac{2}{7}\)
= Rs . 565 × 2
= Rs. 1130
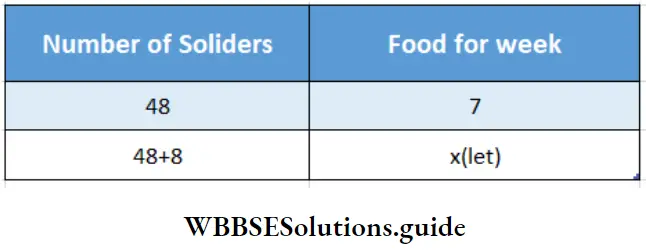
WB Class 7 Math Solution Question 7. There were stored food of 48 soldiers for 7 weeks in a camp. If 8 more soldiers join the camp, let’s find for how many weeks it will be sufficient With the same food.
Solution :
Given
⇒ There were stored food of 48 soldiers for 7 weeks in a camp. If 8 more soldiers join the camp
⇒ Here No. of soldiers & no. of week for food are in inverse proportion.
∴ \(\frac{48}{56}=\frac{x}{7}\)
∴ 56 x = 48 x 7
⇒ x= \(\frac{48 \times 7}{56}\)
= 6 weeks.
It will be sufficient with the same food for 6 weeks.
Question 8. In a ship, there was stored food for 50 sailors for 16 days. After 10 days 10 more sailors joined them. Let’s find, out how many days the remaining food would last.
Solution :
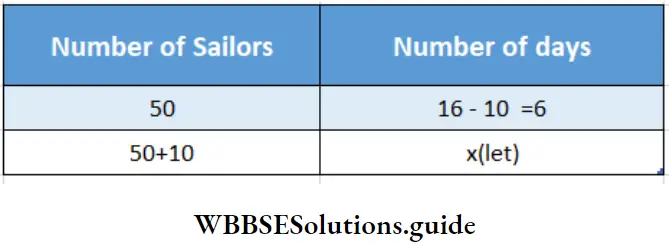
Given
⇒ In a ship, there was stored food for 50 sailors for 16 days. After 10 days 10 more sailors joined them.
⇒ Here ho. of Sailors & no. of days for food are in inverse ratio.
∴ \(\frac{50}{60}=\frac{x}{6}\)
∴x × 60 = 50 × 6
⇒ x = \(\frac{50 \times 6}{60}\)
⇒ x = 5 days.
The remaining food would last for 5 days
Question 9. 20 men decided to complete the repairing work, of a house in 30 days. But after 6 days 8 men fell sick. Let’s find, how long they will take to complete the work.
Solution :
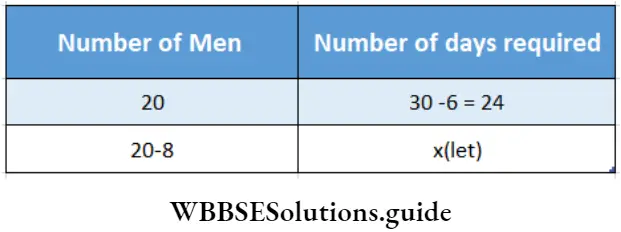
Given
⇒ 20 men decided to complete the repairing work, of a house in 30 days. But after 6 days 8 men fell sick.
⇒ Here no. of men & no. of days required are in inverse proportion.
⇒ \(\frac{20}{12}=\frac{x}{24}\)
⇒ 12x = 20 × 24
⇒ x = \(\frac{20 \times 24}{12}\)
⇒ x = 40 days
∴ They will take to complete the work = 40 + 6 = 46 days.
“Best guide for Class 7 Maths WBBSE arithmetic revision problems”
Question 10. 25 farmers take 12 days to plough 15 bighas of land. Then, let’s find, out how many bighas of land can be plowed by 30 farmers in 16 days.
Solution :
Given
⇒ 25 farmers take 12 days to plow 15 bighas of land.
⇒ 1 farmer takes 12 days to plough \(\frac{15}{25}\)bighas of land.
⇒ 1 farmer takes 1 day to plough \(\frac{15}{25 \times 12}\) bighas
⇒ 30 farmers takes 16 days to plough \(\frac{15 \times 30 \times 16}{25 \times 12}\) bighas
= 24 bighas of land (Ans.)
WB Class 7 Math Solution Simplifications Exercise 1.3
Question 1. Let’s find \(12 \frac{1}{2} \%\)of Rs. 2 is equal to how much paise.
Solution:
⇒ \(12 \frac{1}{2} \%\) of rs. 2 = \(\frac{25}{2} \%\) of 200P
= \(\frac{25}{2}\)× \(\frac{1}{100}\) × 200P
= 25 P
\(12 \frac{1}{2} \%\)of Rs. 2 = 25 P
1. Let’s find out how much grams is 30% of 840 grams.
Solution:
⇒ 30% of 840 gm
= \(\frac{30}{100}\) x 840 = 252 gm.
⇒ 30% of 840 gm = 252 gm.
2. Let’s find how much 8% of Rs. 25.
Solution:
8% of Rs. 25 = \(\frac{8}{100}\) × Rs. 25
= Rs. 2.
8% of Rs. 25 = Rs. 2.
3. Lets find what percent is 55 grms of 5 kg.
Solution:
⇒ 5 kg = 500 gm
⇒ Let x% of 5000 gm = 55 gm
∴ \(\frac{x}{100} \times 5000\) = 55
∴ x= \(\frac{55}{50}\)
⇒ x = 1 \(\frac{1}{10}\)
55 grms of 5 kg. = 1 \(\frac{1}{10}\)
4. Let’s find out what percent is Rs. 1.25 of Rs. 5.
Solution :
Let x% of Rs. 5 = Rs. 1-25
⇒ \(\frac{x}{100}\) = 1\(\frac{1}{10}\)
= \(\frac{1 \cdot 25 \times 100}{5}\)
= \(\frac{125}{5}\)
= 25%
1.25 of Rs. 5 = 25%
5. Let’s find what percent is 16 L. of 1000 L.
Solution:
⇒ Required percentage = \(\frac{16 \times 100}{1000}\)
= 1.6%
⇒ 16 L. of 1000 L = 1.6%
Question 2. \(\frac{1}{5}\)th part of house has been painted. What percent of the house is still to be painted, let’s find out.
Solution:
⇒ \(\frac{1}{5}\) The part of the house has been painted.
⇒ Remaining part = 1- \(\frac{1}{5}\) th part
= \(\frac{4}{5}\) th × part
= \(\frac{4}{5}\)100%
= 80%
⇒ 80% of the house is still to be painted.
Question 3. In Noorjahan’s class 30% of the students are girls. There are 60 students in the class. Let’s calculate to find number of boys in Noorjahan’s class.
Solution :
Given
⇒ In Noorjahan’s class 30% of the students are girls. There are 60 students in the class.
⇒ Total no. of student = 60
∴ No. of girls = 30% of 60
= \(\frac{30}{60}\) x 60
∴ No. of boys = 60 – 1 8 = 42
∴ There are 42 boys in Noorjahan’s class.
Question 4. In 120 kg of mixed fertilizer, the amount of urea and potash are 60% and 40% respectively. Let’s find and write, how many kgs of fertilizers of each type are present in the mixed fertilizer.
Solution:
Given
⇒ In 120 kg of mixed fertilizer, the amount of urea and potash are 60% and 40% respectively.
⇒ Total weight of mixed fertilizer = 120 kg.
= 18
⇒ Weight of urea = 60% = \(\frac{60}{100} \) x 120 = 72 kg
⇒ Weight of Potash = 40% = \(\frac{60}{100} \) x 120 = 48 kg
Question 5. The cost of my school exercise book was Rs. 10. Now l buy the same exercise book for Rs. 12. Let’s calculate the percentage increase in the price of the exercise book.
Solution:
Given
⇒ The cost of my school exercise book was Rs. 10. Now l buy the same exercise book for Rs. 12.
⇒ The present price of an exercise book – Rs. 12
⇒ The previous price of an exercise book – Rs. 10
⇒ Price increased = Rs. (12 – 10) = Rs. 2
⇒ Increased percentage = \(\frac{2}{10}\) × 100
= 20
∴ 20% increase in the price of the exercise book.
Question 6. The bus fare from Sumitra’s house to school was Rs. 4. Now to travel the same distance she has to pay Rs. 6. Let’s find the percentage rise in bus fare.
Solution :
Given
⇒ The bus fare from Sumitra’s house to school was Rs. 4. Now to travel the same distance she has to pay Rs. 6.
⇒ Present bus fare = Rs. 6
⇒ Previous bus fare = Rs. 4
⇒ Bus fare increased = Rs. (6 – 4) = Rs. 2
⇒ Percentage of increased fare = \(\frac{2}{4}\) × 100 = 50
∴ 50% rise in bust fare.
Question 7. Due to the increase in the price of sugar, the amount of sugar bought for Rs. 125 is now bought for Rs. 150. Let us calculate the percentage rise in the price of sugar at present.
Solution:
Given
⇒ Due to the increase in the price of sugar, the amount of sugar bought for Rs. 125 is now bought for Rs. 150.
⇒ The present price of the same quantity of sugar= Rs. 150
⇒ The previous price of the same quantity of sugar= Rs. 125
Rise of sugar price = Rs. (150 – 125)
= Rs. 25
∴ Percentage rise in the price of sugar \(\frac{25}{125}\) x100 = 20
Question 8. Rojina worked out 90 sums in 1 day. Shefali did 65 sums at the same time. Let’s find what percentage of sums Rojina did more than Shefali. Let’s find the percentage of sums Shefali did less than Rojina during that period of time.
Solution:
Given
⇒ Rojina worked out 90 sums in 1 day. Shefali did 65 sums at the same time. Let’s find what percentage of sums Rojina did more than Shefali.
⇒ Rojina work (90 – 65) = 25 more sums
⇒ Then Shefali during that period of time.
∴ Percentage of Sums Rojina did more than Shefali = \(\frac{25}{65}\) x100%
= \(\frac{500}{13}\)%
= 38\(\frac{6}{13}\)100%
∴ Percentage of sum Shefali did less than Rojina = \(\frac{25}{90}\) x100%
\(\frac{250}{9}\) 100%
= 27 \(\frac{7}{9}\) x100%
Question 9. Suhasbabu spends 66\(\frac{2}{3}\)% of his monthly income. If he spends Rs. 3250 per month, then what is his monthly income? Let’s calculate.
Solution:
Given
⇒ Suhasbabu spends 66\(\frac{2}{3}\)% of his monthly income. If he spends Rs. 3250 per month,
⇒ Let monthly income of suhashbabu = Rs. 100
His monthly expenditure = 66\(\frac{2}{3}\)%
= \(\frac{200}{3}\)%
= Rs.\(\frac{200}{3}\)x\(\frac{1}{100}\) x 100
= Rs \(\frac{200}{3}\)
⇒ When expenditure Rs. \(\frac{200}{3}\) Total income = \(\frac{100}{200 / 3}\)
= \(\frac{3 \times 100}{200}\)
= \(\frac{3}{2}\)
⇒ When expenditure = Re.1, Total Income = 3250 × \(\frac{3}{2}\)
= Rs. 4875
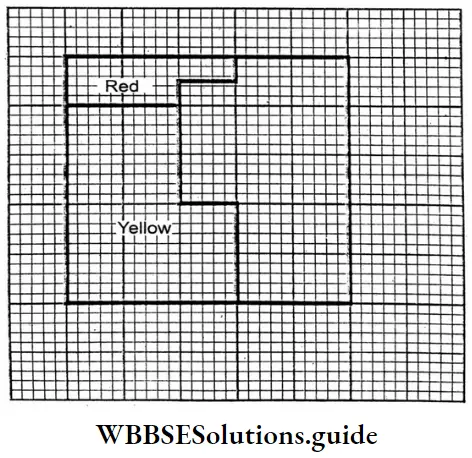
Question 10. Let’s color 10% of the squares red and 40% of the squares yellow in the squared figure given below.
Solution:
1. In New edition:

⇒ Total number of square 5 x 4 = 20
⇒ Red portion = 10%. = \(\frac{10}{100}\) x 20 = 2
⇒ Yellow portion = 40 % = \(\frac{40}{100}\)x 20 = 8
2. In old edition:
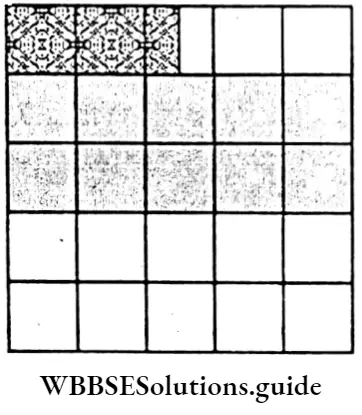
⇒ Total number of square = 5 x 5 = 25
⇒ Red portion 1 0% = \(\frac{10}{100}\) x 25 = 2.5
⇒ Yellow portion = 40% = \(\frac{40}{100}\) x 25 = 10
WBBSE Class 7 Math Solution Simplifications Exercise 1.4
Question 1.
1. (+ 6) + (+ 3)
Solution:
(+ 6) + (+ 3)= 9
2. (+ 3) + (+ 6)
Solution:
(+ 3) + (+ 6) = 9
3. (+ 2) + (- 2)
Solution:
(+ 2) + (- 2) = 0
4. (- 4) + (+4)
Solution:
(- 4) + (+4)= 0
5. (+ 3) + (- 6)
Solution:
(+ 3) + (- 6) = -3
6. (+ 6) – (- 9)
Solution:
(+ 6) – (- 9) = 15
7. (- 6) + (- 3)
Solution:
(- 6) + (- 3) = – 9
8. (- 6) + (- 5)
Solution:
(- 6) + (- 5) = -11
Question 2. Let’s verify the following using a number line.
1. (+ 2) + {(+ 3) + (+ 5)) = {(+ 2) + (+ 3)} + (+ 5)
Solution:
⇒ (+ 2) + {(+ 3) + (+ 5)) = {(+ 2) + (+ 3)} + (+ 5)
⇒ L.H.S. = {(+ 2) + (+) 3 + (+5)} = + 2 + 3 + 5 = 10
⇒ R.H.S. = {(+ 2) + (+ 3)) + (+ 5) = 2 + 3 + 5 = 10
⇒ L.H.S. = R.H.S.
“Understanding arithmetic concepts from previous lessons Class 7 WBBSE”
2. (- 8) + {(- 2) + (+ 6)} = {(- 8) + (- 2)} + (+ 6)
Solution:
⇒ (- 8) + {(- 2) + (+ 6)} = {(- 8) + (- 2)} + (+ 6)
⇒ L.H.S = (- 8) + {(- 2) + (+ 6)} = (- 8) + (+ 4) = – 8 + 4 = – 4
⇒ R.H.S ={(- 8) + (- 2)} + (+ 6) = (-10) + (+ 6) = – 10 + 6 = – 4
⇒ L.H.S = R.H.S
3. (+ 2) – {(+ 3) – (- 5)} ≠ {(+ 2) – (+ 3)) -(- 5)
Solution:
⇒ (+ 2) – {(+ 3) – (- 5)} * {(+ 2) – (+ 3)) -(- 5)
⇒ L.H.S = (+ 2) – {(+ 3) – (- 5)} = + 2 – {3 + 5}= 2 – 8 + 5 = – 6
⇒ R.H.S = {(+ 2) – (+ 3)} – (- 5)}= {+ 2 – 3} – (- 5) = -1+5 = 4
⇒ L.H.S ≠ R.H.S .
4. (-8) – {(-2) – (+6)} ≠{(-8) – (-2)) – (+6)
Solution:
⇒ (-8) – {(-2) – (+6)} ≠{(-8) – (-2)) – (+6)
⇒ L.H.S = (-8) – {(-2) – (+6)} = – 8 – (-2 -6} = -8 – (-8)= -8+8 = 0
⇒ R.H.S = {(-8) – (-2)} – (+6) = {-8+2} – (+6) = -6-6 = -12
⇒ LHS ≠ R.H.S.
Class 7 Math Solution WBBSE Simplifications Exercise 1.5
Question 1. Let’s measure the perimeters of the following figures
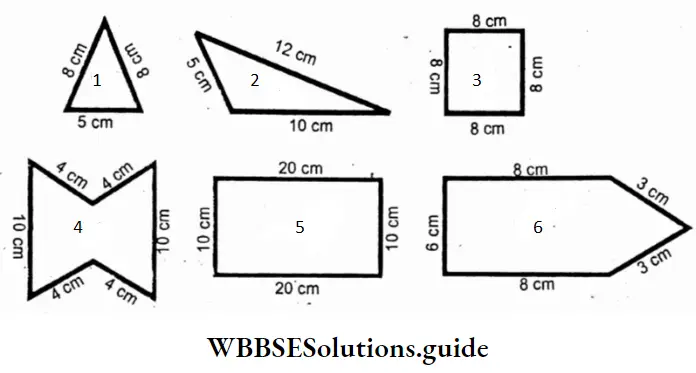
To find perimeters :
Perimeter = Sum of the length of the boundary.
- Perimeter = (8+8+5) cm = 21 cm
- Perimeter = (12+10+5) cm = 27 cm
- Perimeter = Sum of 4 sides = (8+8+8+8) cm = 32 cm
- Perimeter = Sum of 6 sides = (10+4+4+10+4+4) cm = 36 cm
- Perimeter = Sum of 4 sides = (10+20+10+20) cm = 60 cm
- Perimeter =. Sum of 5 sides = (6+8+3+3+8) cm = 28 cm
Question 2. Let’s find, how much areas the figures given below have occupied (1 small square = 1 square cm) m:
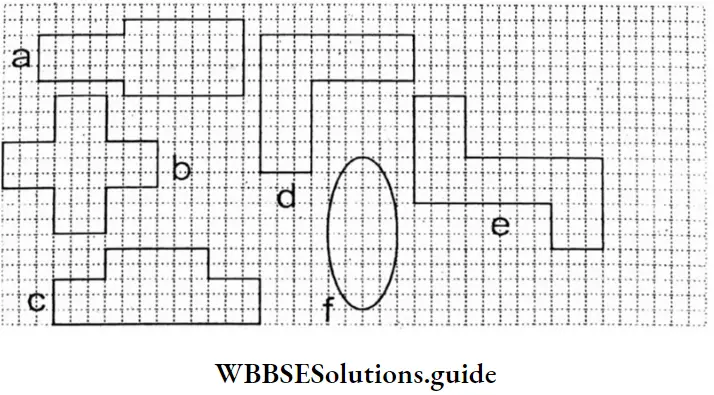
1. No. of small squares = 50
∴ Area of the figure = 50 x 1 sq.cm = 50 sq.cm.
2. No. of small square = 48
∴ Area of the figure = 48 x 1 sq.cm = 48 sq.cm.
3. No. of small square = 48
∴ Area of the figure = 48 x 1 sq.cm = 48 sq.cm
4. No. of small squares = 42
∴ Area of the figure = 42 x 1 sq.cm = 42 sq.cm
5. No. of small square = 51
∴ Area of the figure = 51 x 1 sq.cm = 51 sq.cm
6. No. of small square = 30 (appx.)
∴ Area of the figure = 30 x 1 sq.cm = 30 sq.cm (appx.)
Class 7 Math Solution WBBSE
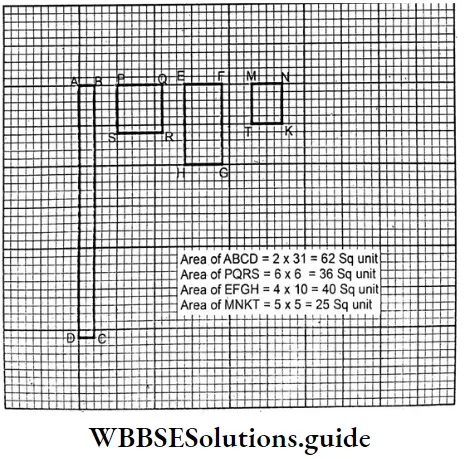
Question 3. Prepare a graph paper and draw such figures on it so that they occupy 25 square units, 40 square units, 36 square units, and 62 square units respectively.
Question 4. Let us measure the length of the sides of the squares drawn on the graph paper and find their areas. [ taking 1 small square = 1 sq.cm]
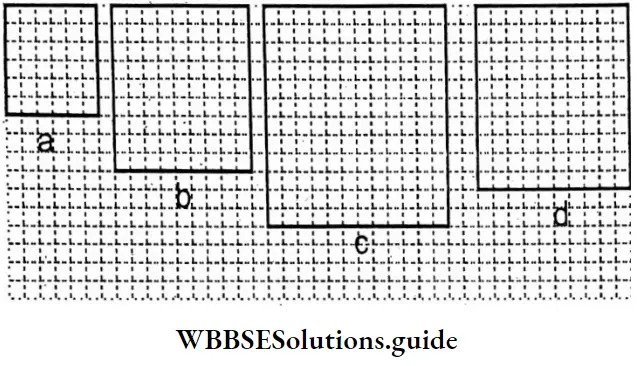
1. Length of the square = 5cm
∴ Area of the square = 5cm x 5cm = 25 sq.cm.
2. Length of the square = 8cm
∴ Area of the square = 8cm x 8cm = 64 sq.cm.
3. Length of the square = 1 1 cm
∴ Area of the square = 1 1cm x 1 1cm = 121 sq.cm.
4. Length of the square = 9cm
∴ Area of the square = 9cm x 9cm = 81 sq.cm.
Question 5. Let’s find the square root ‘of the following :
1. 5 2 x 82
Solution :
=\(\sqrt{5^2 \times 8^2}\)
= 5 × 8 = 40
The square root of 5 2 x 82 = 40
2. 4225
Solution :
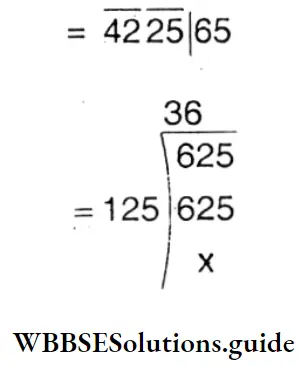
The square root of 4225 = 65
3. 10609
Solution:
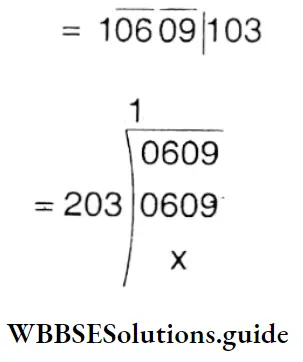
The square root of 10609 = 103
4. 108241
Solution :
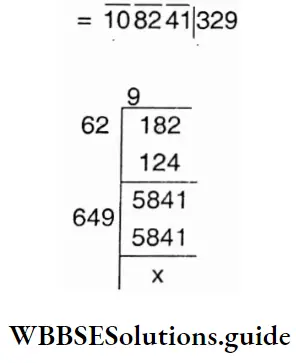
The square root of 108241 is 329
5. 186624
Solution:

The square root of 186624 = 432 (Ans.)
6. \(\sqrt{(24)^2+(10)^2}\)
⇒ \(\sqrt{576+100}\)
⇒ \(\sqrt{676}\)
⇒ \(\sqrt{26 \times 26}\)
= 26
\(\sqrt{(24)^2+(10)^2}\) = 26
Question 6. Let us find square numbers nearest to 3000 so that it is (a) greater than 3000 and (b) less than 3000.
Solution:
Set us to find the square root of 3000
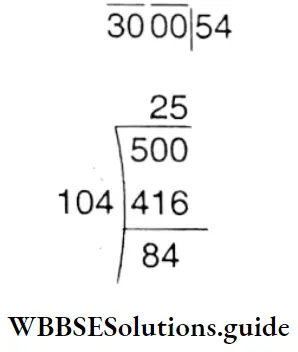
Next number of 54 = 55
(55)2 = 3025
1. The required square number nearest to 3000 but greater than 3000 is- 3025.
2. The required square number nearest to 3000 but less than 3000 is 3000 – 84 = 2916.
⇒ 3000 – 84 = 2916.
“How to solve arithmetic problems Class 7 WBBSE Maths Exercise 1”
Question 7. Let us find the least positive whole number that must be subtracted from 9545 so that the resultant number is a perfect square.
Solution:
First, find the square root of 9545.
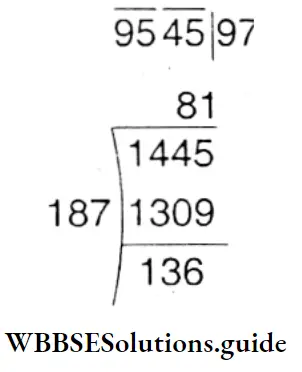
∴ Required number = 136
Question 8. Let us find the least positive whole number that must be added to 5050 to make it a perfect square.
Solution: First find the square root of 5050
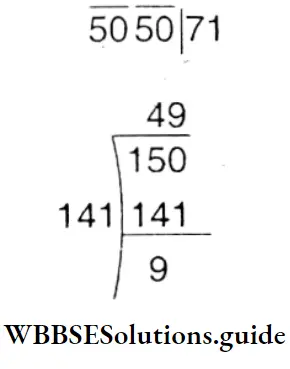
Now the next number of 71 is 72 . . (72)2 = 5184
Required number = 5184 – 5050 = 134 (Ans.)
Question 9. In a guava ochard at Baruipur, there are 1764 guava trees. The number of guava trees is equal to number of guava trees in each row. Let us find the number of guava trees in each row.
Solution:
Given
In a guava ochard at Baruipur, there are 1764 guava trees. The number of guava trees is equal to number of guava trees in each row.
The number of guavas in each row is = \(\sqrt{1764}\) = 42
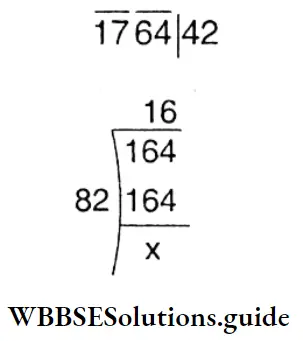
Question 10. A box in which homeopathy medicines are kept has compartments for 1225 bottles. These compartments are arranged in such a way that each row has as many compartments as there are a number of rows. Let’s find, how many rows are there in the box.
Solution :
Given
A box in which homeopathy medicines are kept has compartments for 1225 bottles. These compartments are arranged in such a way that each row has as many compartments as there are a number of rows.
No. of bottles = 1225
∴ No. of rows = \(\sqrt{1225}\)
= 35
Question 11. There are 3 positive whole numbers, the product of the first and second numbers is 24, a product of the second and third numbers is 48 and that of first and third is 32; let’s calculate to find the three numbers.
Solution:
Given
There are 3 positive whole numbers, the product of the first and second numbers is 24, a product of the second and third numbers is 48 and that of first and third is 32;
1st No. x 2nd No. = 24
2nd No. x 3rd No. = 48
1st NO. x 3rd No. = 32
∴ \(\frac{(1 \mathrm{stNo} \times 2 \text { ndNo. }) \times(1 \mathrm{stNo} \times 3 \mathrm{rdNo})}{2 \mathrm{ndNo} \times 3 \mathrm{rdNo}}=\frac{24 \times 32}{48}\)
∴ (1stNo.)2 = \(\sqrt{16}\)
= 4
⇒ Again, 1st No. x 2nd No. = 24 & the 1st No. = 4
∴ 2nd No. = \(\frac{24}{4}\)= 6
⇒ Again, 2nd No. x 3rd No. = 48
& the 2nd No.
= 6 (Ans.)
∴ 3rd No. = \(\frac{48}{6}\) = 8
“WBBSE Class 7 Maths revision of old lesson step-by-step solutions”
Class Vii Math Solution WBBSE Question 12. In Shivaji club, each member subscribed an amount five times the number of members of the club. The total subscription is RS. 515205. Let’s find the number of members of the club.
Solution:
Given
In Shivaji club, each member subscribed an amount five times the number of members of the club. The total subscription is RS. 515205.
Set the number of members = x
∴ Each member subscribe = Rs. 5x
According to the problem
5x . x = 515205
Or 5x = 515205
x2 = \(\frac{515205}{5}\)
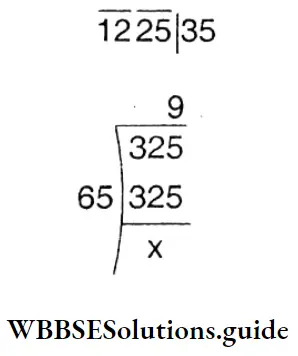
= 103041
x= \(\sqrt{103041}\) = 321
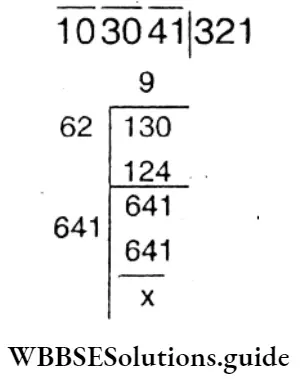
∴ Number of member = 321.
Question 13. The owner of an orange orchard in Darjeeling plucked 1080 oranges. He got some baskets ad tried to put as many number of oranges in each basket as there were baskets but fell short of 9 oranges. Let’s calculate the number of baskets he had got.
Solution:
Given
⇒ The owner of an orange orchard in Darjeeling plucked 1080 oranges. He got some baskets ad tried to put as many number of oranges in each basket as there were baskets but fell short of 9 oranges.
⇒ No. of oranges = 1080
⇒ Set No. of baskets = x
According to the problem
 –
–
He had got 33 numbers of baskets.
Question 14. For cleaning and purification of a pond in Bakultala, local panchayat appointed few men. The men worked as many days as there were number of men appointed and got a total amount of Rs. 12375. If each one got Rs. 55/day, then let’s find how many men worked.
Solution:
Given
For cleaning and purification of a pond in Bakultala, local panchayat appointed few men. The men worked as many days as there were number of men appointed and got a total amount of Rs. 12375. If each one got Rs. 55/day,
⇒ Total amount = Rs. 12375
⇒ Each man receives = Rs. 55 / day
⇒ Let the number of men = x
⇒ According to the problem x x x Rs.55 = Rs. 12375
⇒ x2 = \(\frac{\text { Rs. } 12375}{\text { Rs.55 }}\)
= 225
∴ No. of men = \(\sqrt{225}\) = 15 worked.
“WBBSE Class 7 Maths Chapter 1 worksheet with solved problems”
Question 15. Let’s calculate what is the biggest whole number of 4 digits which will be divisible by 12, 18, and 30.
⇒ L.C.M of 12, 18, 30 = 180
⇒ Biggest whole number of 4 digits = 9999
⇒ Now 180 = 2 x 2 x 3 x 3 x 5
∴180 is not a perfect of square number.
⇒ If we multiply 5, with it will be a perfect square.
∴ 180 x 5 = 900, but it is of 3 digits
∴ 900 x 4 = 3600 it is 4 digits but not biggest
⇒ 900 x 9 = 8100 it is the biggest 4 digits number
⇒ 900 x 16 = 14400 it is 5 digits number
∴ Required the biggest whole number = 8100 of 4 digits.
Question 16. Let’s find the least whole number of five digits which is divisible by 8, 15, 20, and 25.
Solution :
Least whole number of digits = 1000
To find L.C.M of 8, 15, 20, 25

∴ L.C.M = 2 x 2 x 2 x 5 x 5 x 2 x 3 = 600
But 600 is not a perfect square number, if we multiply 2 & 3 = 6 by 600 it will be a perfect square number = 600 x 2 x 3 = 3600, but it is not 5 digit number.
∴ 3600 x 1 = 3600 → It is a 4-digit number
3600 x 4 = 14400 → It is a 5 -digits number
3600 x 9 = 32400 → It is also 5 – digits number but not the least
∴ Required least whole number of five digits = 14400.
Class 7 Math Solution WBBSE Simplifications Exercise – 1.6
Question 1. Let us draw a line segment \(\overline{P Q}\) of length 9 cm. Let us bisect the line segment \(\overline{P Q}\) with the help of a compass and measure each part.
Solution:
To bisect a line segment \(\overline{P Q}\) of length 9 cm
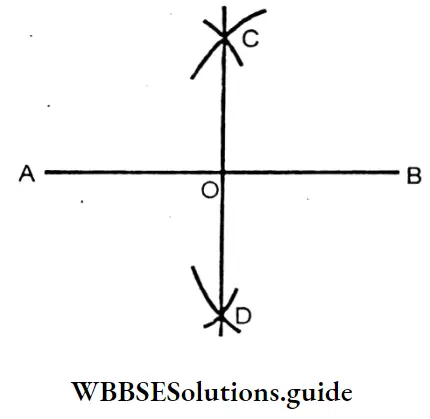
1. Let us draw a line segment of length 9 cm ( \(\overline{P Q}\) ) with the help of a scale.
2. Let us put the pin of the compass at P and with a radius more than half of the length of \(\overline{P Q}\) two arcs are drawn on either side of the line segment \(\overline{P Q}\).
3. Again putting the pin of the compass at Q and with same radius two arcs are drawn on either side of the line segment \(\overline{P Q}\) .
“Basic arithmetic operations and formulas Class 7 WBBSE solutions”
4. The two arcs interest at C & D respectively C D joined with a scale to get the midpoint O of the line segment \(\overline{P Q}\).
5. PO = OQ = 4. 5 cm.
Question 2. Let us draw a line segment of length 12cm with a scale and let’s measure its parts and verify, that they are equal.
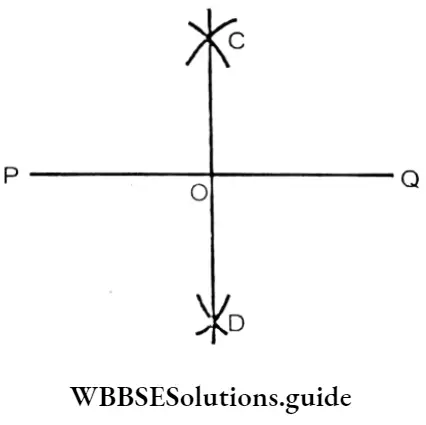
Solution: AB is a line segment of 12cm. It is bisected at o into two
equal parts (as before)
∴ AO = OB = 6cm
Question 3. Let us draw an angle of 720 with a protractor. Let us bisect the angle with a compass. Let’s measure its each part with a protractor to verify if the angle has been bisected.
Solution: To bisect an angle of 72°
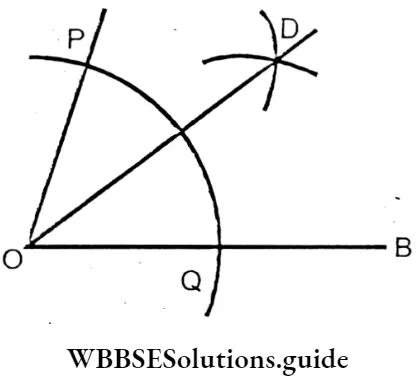
∠AOB is an angle of 72°. We have to bisect it with center O, draw
an arcs PQ, which cut AO at P & OB at Q.
Now, with center P & Q draw two arcs of same radius which cut each other D. Join DO. DO is the bisect of AOB
∴ ∠AOD = ∠BOD = 36°
Question 4. On the line segment AB, let us draw a perpendicular BC at the point B with a compass. Let’s then bisect the ∴ ABC with a compass.
Solution :
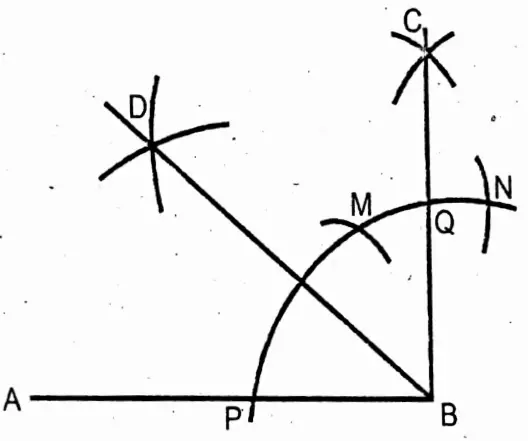
AB is a line segment. At B, we have to draw a. perpendicular on AB
Now, with centre B draw an arc that cuts AB & BC at P & Q respectively. Now with centre P, draw two more areas that cuts the previous arc at M & N.
Then with centre M & N and with the same radius draw two arcs, which cut each other at C. BC is perpendicular on AB. ∠ABC = 90°
Now, bisect ∠ABC with a compass as a previous way. BD is the bisector of ∠ABC
∴ ∠ABD = ∠CBD = 45°
Question 5. Let us draw a perpendicular from an external point P on the line segment latex]\overline{M N}[/latex] or \(\overline{M N}\) produced.
Solution:
To draw a perpendicular from an external point P on the line segment \(\overline{M N}\).
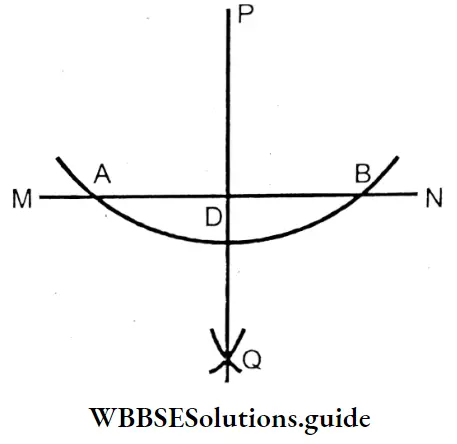
With the center at P, draw an arc that cuts \(\overline{M N}\)at A & B respectively.
Now, with center A & B draw two arcs of equal radius, which cut each
other at Q. Join PQ, which cuts M N at D.
∴ PD is the perpendicular from P (External point) on
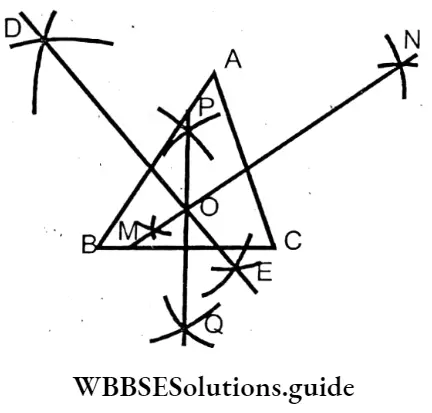
Question 6. Let us draw a triangle ABC with a scale and pencil. Now, with the help of a compass, let us bisect each of the three angles of the triangle and find if the angle bisectors are concurrent.
Solution:
To draw the angle bisectors of a (triangle).
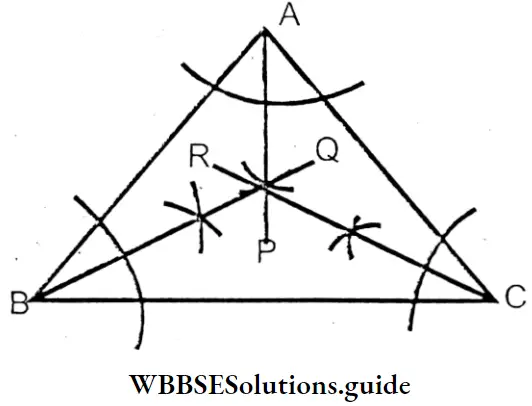
ABC is a triangle. We have drawn three angle bisectors AP, BQ & CR of the three angles ∠A, ∠B & ∠C of the triangle. These three bisectors meet at a point O, which is called the ‘in-center’ of the triangle.
Question 7. With the help of a protractor let us draw two angles 80° and 100° respectively. Now, with the help of a compass let us construct. two more angles equal to 80° and 100° Let’s write the types of angles so drawn.
Solution:
To draw an angle with a protractor & then draw an angle equal to that angle with a compass.
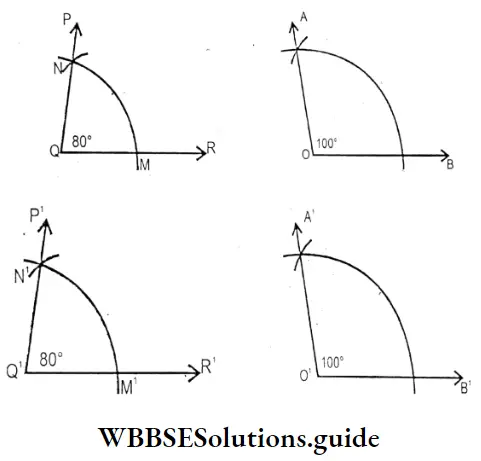
First, we draw two angles ∠PQR = 80° & ∠AOB = 100c with the help of a protractor.
Now we have to draw two angles equal to those angles with the help of a compass.
Take a line Q¹R¹. NOW with centre Q¹, draw an area with radium QM, which cuts Q¹R¹ at M¹. Now with center draw an area with a radius equal to MN, which cuts the previous are at. Join Q¹N¹ & produce to π
P¹ Q¹ R¹ = ∠PQR = 80° (Acoute angle)
Similarly we can draw ∠A¹O¹B¹ = ∠AOB = 100c (obtuse angle)
“Tips and tricks to solve arithmetic problems Class 7 WBBSE”
Question 8. Let us draw a triangle ABC with a scale and pencil. Let’s bisect the three sides with a compass. Let’s find if the side bisectors are concurrent.
Solution:
To draw a triangle ABC. Next, we have to bisect the three sides of the triangle with a compass.
First, we bisect the three sides of AB, BC, & CA of the A ABC . DE, PQ & MN are the three bisectors of the sides AB, BC & CA respectively.
These three bisectors meet at O. Three bisectors are concurrent (i.e. meet at a point). The point (O) is called circum centre. i.e if we draw a circle with center O and radius OA, the circle will pass through the vertexes of the triangle.
Simplifications Exercise 1.6
Question 1. The figure that will be formed if two 450 -450 -900 set squares are put together is.
Solution: Square.
Question 2. The figure that will be formed when two 30°-60°-90° -nurses are placed in a way is shown in the figure.
Solution:Parallelogram
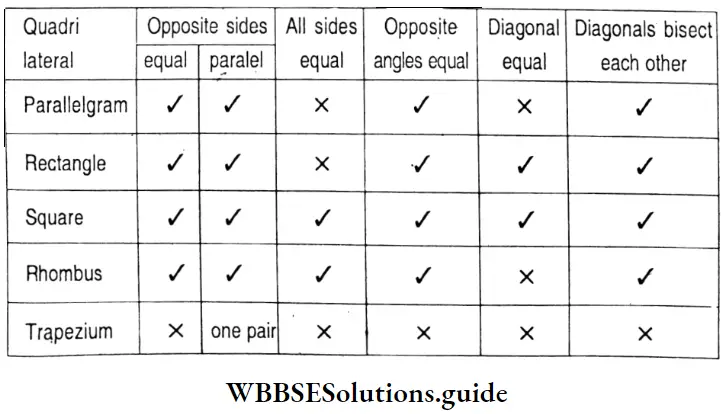
Question 3. Let’s- find if the following statements are true or false.
1. All the angles of a square are right angles.
Solution:True.
2. The sides of any rectangular figures are equal.
Solution:False.
3. Four sides of a rhombus are equal.
Solution:True.
4. Opposite sides of any parallelogram are equal.
Answer: True
5. The sides of any trapezium are equal.
Answer: False.
6. The diagonals of any rectangular figure are equal.
Solution:True.
Question 5. Let’s give reasons for the following statements :
1. A square, a rectangular and a parallelogram are all quadrilaterals.
Solution:All are rectilinear figures with four sides.
“WBBSE Class 7 Maths Chapter 1 complete guide with solved exercises”
2. All rectangles are parallelograms.
Solution:As opposite sides are equal and parallel. ,
3. All squares are rectangles.
Solution: Opposite sides are equal & each angle is 90°.
4. All parallelograms are trapeziums.
Solution: Opposite sides are parallel.
5. AIl rhombuses are parallelograms.
Solution:Opposite sides are equal and parallel.
6. Let’s fill up the table given below :
Solution: