Class 7 Math Solution WBBSE Arithmetic Chapter 5 Square Root Of Fractions Exercise 5 Solved Problems
1. Square root of a fraction = \(\sqrt{\frac{\text { Numerator }}{\text { Denominator }}}\)
Example: \(\sqrt{1\frac{9}{16}}=\sqrt{\frac{25}{16}}=\frac{\sqrt{25}}{\sqrt{16}}=\frac{5}{4}=1 \frac{1}{4}\)
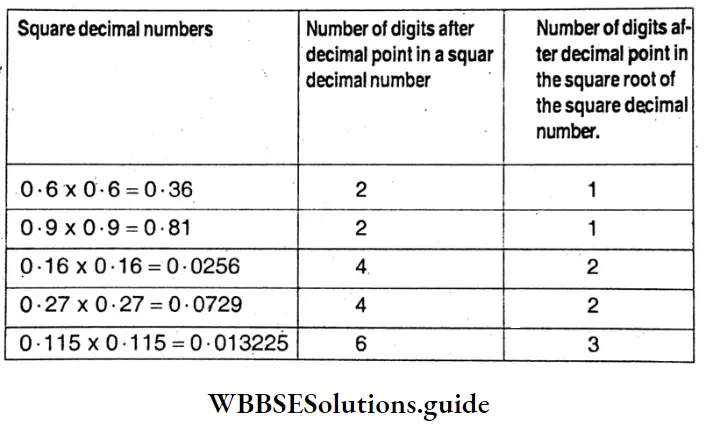
2. Perfect square decimal number: A decimal number whose square root is a finite decimal number is termed a perfect square decimal number.
Example: 0.8 x 0.8 (0.8)2 = 0.64
Hence 0.64 is a perfect square decimal number and 0-8 is a square root.
[The perfect square of any decimal number should contain an even number of digits offer the decimal point]
3. To find the square root of the perfect square decimal number by factorization. Method
Read and Learn More WBBSE Solutions for Class 7 Maths
Method 1
By converting decimal numbers to its fraction.
Example: \(\sqrt{1 \cdot 44}=\sqrt{\frac{144}{100}}=\frac{\sqrt{144}}{\sqrt{100}}\)
= \(\frac{\sqrt{2 \times 2 \times 2 \times 2 \times 3 \times 3}}{\sqrt{2 \times 2 \times 5 \times 5}}\)
= \(\frac{\sqrt{2^2 \times 2^2 \times 3^2}}{\sqrt{2^2 \times 5^2}}=\frac{2 \times 2 \times 3}{2 \times 5}\)
= \(12\) = 1.2
∴ Square root of 1-44 is 1.2
Wbbse Class 7 Maths Solutions
Method 2
We will consider the decimal number as whole number (by removing the decimal sign)
Example: Find the square root of 1.96
The whole number without the decimal point in 1.96 is 196.
\(\sqrt{196}=\sqrt{2 \times 2 \times 7 \times 7}\)
= \(\sqrt{2^2 \times 7^2}\)
=2×7 14
Since in the square decimal number, there are 2 digits after the decimal point.
So, in the square root of 1.96, there will be 1 digit to the right after the decimal point.
∴ \(\) = 1.4
The rule for putting decimal points:
| Number of digits after the decimal point in the square decimal | Number of decimal digits in the square root |
| 2 | 1 |
| 4 | 2 |
| 6 | 3 |
| 8 | 4 |
4. To find the square root of a perfect square decimal number by the method of division.
To find a square root there must be an even number of digits after the decimal point. Hence from the extreme right of the decimal point, pairs of digits are marked by an arrow sign as done on the right-hand side (if can not be paired ‘O’ is to be put to the extreme right of the decimal point)
Then we proceed by the same method as is done for finding the square root of a whole number by division.
Example: Find the values of \(\sqrt{2 \cdot 4025}\)
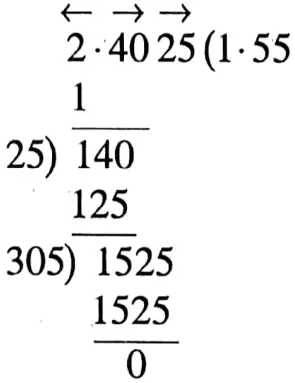
∴ Square root of 2.4025 is 1.55
Class 7 Math Solution WBBSE 5. To find out the square root of numbers that are not perfect squares by the method of divisions and find their approximate values up to 3 decimal places.
[In case of division if a decimal comes we take down one ‘0’ every time after the decimal, but for finding square root by division, 2 zeros are taken down after the decimal]
Example: Find the approximate value, of √5 up to 3 decimal places.
Question 1. Choose the correct answer
1. The area of a square root of \(1 \frac{496}{729}\) is
1. \(2 \frac{11}{27}\)
2. \(\frac{27}{65}\)
3. \(1 \frac{11}{27}\)
4. \(3 \frac{11}{27}\)
Solution:
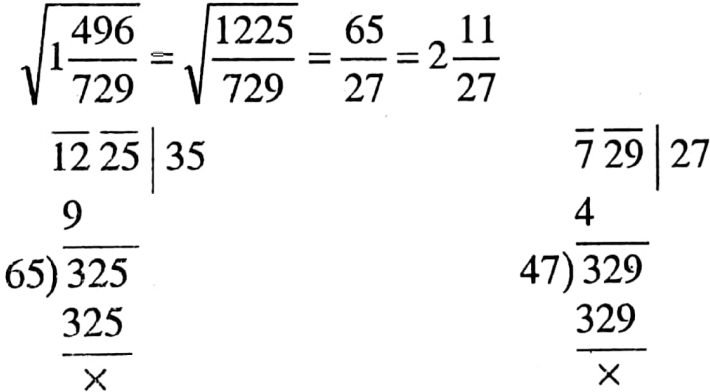
So the correct answer is 1. \(2 \frac{11}{27}\)
Wbbse Class 7 Maths Solutions
2. The least positive integer which will divide the fraction \(\frac{245}{64}\) to make perfect fraction is
1. 2
2. 3
3. 7
4. 5
Solution:
\(\frac{245}{64}=\frac{5 \times 7 \times 7}{2 \times 2 \times 2 \times 2 \times 2 \times 2}=\frac{7^2 \times 5}{2^2 \times 2^2 \times 2^2}\)
So \(\frac{245}{64}\) is to be divided by the least positive integer 5 so as to make it a perfect square fraction.
So the correct answer is 4. 5
Question 2. True or false
1. The square root of 0.0256 is 0.016
Solution: √0.0256=0.16
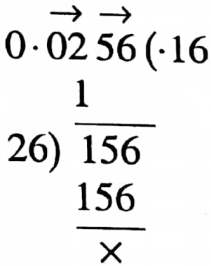
The statement is false.
2. The value of
\(\left(\sqrt{\frac{16}{25}}+\sqrt{\frac{36}{49}}\right) \sqrt{\frac{9}{16}}-\sqrt{\frac{9}{16}} \times \sqrt{\frac{16}{25}} \text { is } \frac{9}{14}\)
Solution:
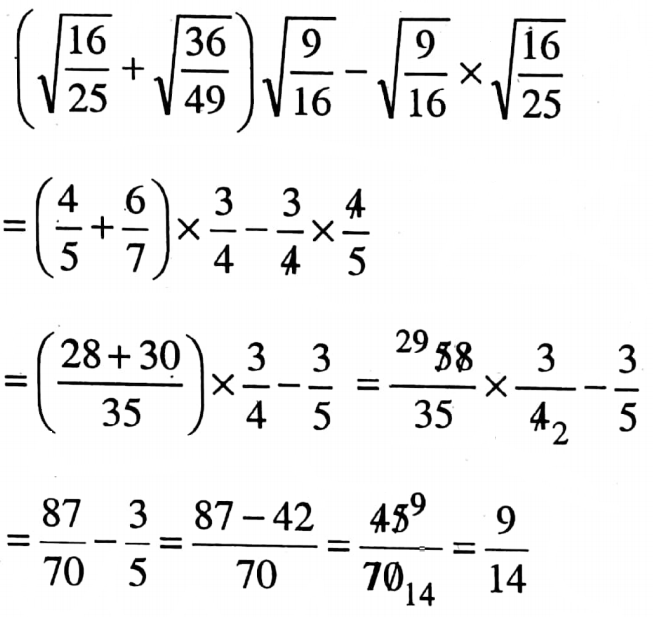
The statement is true.
Wbbse Class 7 Maths Solutions
Question 3. Fill up the blanks
1. The value of \(\sqrt{240 \cdot 25}+\sqrt{2 \cdot 4025}+\sqrt{0 \cdot 024025}\) is_____
Solution: \(\sqrt{240 \cdot 25}+\sqrt{2 \cdot 4025}+\sqrt{0 \cdot 024025}\)
= 15.5+1.55+0.155 = 17.205
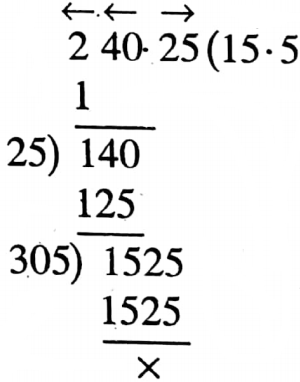
Question 4. The product of two positive numbers is \(\frac{6}{5}\) and their quotient is \(\frac{32}{15}\) Find the numbers.
Solution: Let the two positive numbers are x and y respectively.
According to the question, x x y= \(\frac{6}{5}\) and \(\frac{x}{y}=\frac{32}{15}\)
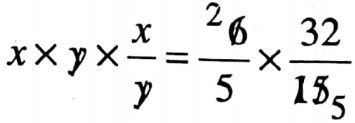
⇒ \(x^2=\frac{64}{25}\)
= \(x=\sqrt{\frac{64}{25}}=\frac{8}{5}\)
x x y = \(\frac{6}{5}\)
\(\frac{8}{5}\) x y = \(\frac{6}{5}\)
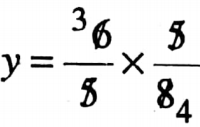
= \(\frac{3}{4}\)
∴ The two number are \(\frac{8}{5}\) and \(\frac{3}{4}\)
Question 5. Arrange the following in the descending order of their magnitude.
\(\sqrt{\frac{4}{25}}, \sqrt{\frac{9}{16}}, \sqrt{\frac{16}{49}}, \sqrt{\frac{1}{36}}\)
Solution: \(\sqrt{\frac{4}{25}}=\frac{2}{5}=\frac{2 \times 84}{5 \times 84}=\frac{168}{420}\)
\(\sqrt{\frac{9}{16}}=\frac{3}{4}=\frac{3 \times 105}{4 \times 105}=\frac{315}{420}\)
\(\sqrt{\frac{16}{49}}=\frac{4}{7}=\frac{4 \times 60}{7 \times 60}=\frac{240}{420}\)
\(\sqrt{\frac{1}{36}}=\frac{1}{6}=\frac{1 \times 70}{6 \times 70}=\frac{70}{420}\)
∴ \(\frac{315}{420}>\frac{240}{420}>\frac{168}{420}>\frac{70}{420}\)
⇒ \(\sqrt{\frac{9}{16}}>\sqrt{\frac{16}{49}}>\sqrt{\frac{4}{25}}>\sqrt{\frac{1}{36}}\)
Wbbse Class 7 Maths Solutions
Question 6. Find which decimal number is to be added to 0.75; So that the square root of the sum will be 2.
Solution: The required number is 22 -0.75 = 4 – 0.75 = 3.25
Question 7. The area of a square is 213-16 sq. cm. Find its perimeter.
Solution: The area of a square is 213-16 sq. cm
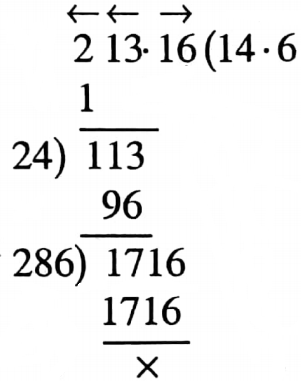
∴ The length of each side = √213.16 cm = 14.6 cm
∴ The perimeter is (14.6 x 4) cm = 58.4 cm
Question 8. Find the approximate value √15 up to 3 decimal places.
Solution:
∴ √15 = 3. 873
Wbbse Class 7 Maths Solutions
Question 9. Find the least decimal number that must be subtracted from 0.000679 to make it a square decimal number.
Solution:
As (0·026)2 = 0.000676
∴ The least decimal number (0.0006790-0.00676) or 0.000003 be subtracted from 0-000679 to make it a square decimal number.
Question 10. Find the values of \(\sqrt{2-(0 \cdot 01)^2}\) upto 3 decimal places.
Solution: \(\sqrt{2-(0 \cdot 01)^2}\)= \(\sqrt{2-(0 \cdot 0001)}\)
= \(\sqrt{1.9999}\)
≈1.414
Wbbse Class 7 Maths Solutions
Question 11. A room is one and a half as long as its breadth and the area of its floor is \(98 \frac{37}{54}\) sq. m. Find its perimeter.
Solution: Let the breadth of the room is x m.
Length is \(\left(1 \frac{1}{2} \times x\right)\) m or, \(\frac{3 x}{2}\) m
Area = \(\left(\frac{3 x}{2} \times x\right)\) sq.m.= \(\frac{3 x^2}{2}\) sq.m.
According to question \(\left(\frac{3 x}{2} \times x\right)\) = \(98 \frac{37}{54}\)
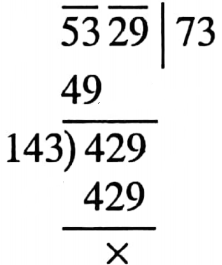
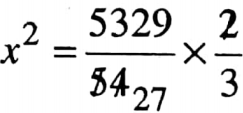
⇒ \(x=\sqrt{\frac{5329}{81}}\)
⇒ \(x=\frac{73}{9}\)
Breadth of room is \(\frac{73}{9}\) m and length is
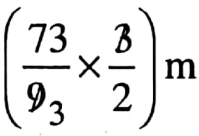
= \(\frac{73}{6}\)
Perimeter = 2\(\left(\frac{73}{9}+\frac{73}{6}\right)\) m
=2 x \(\left(\frac{146+219}{18}\right)\) m
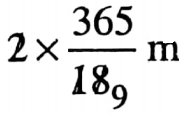
= \(\frac{365}{9} \mathrm{~m}=40 \frac{5}{9} \mathrm{~m}\)
Class VII Math Solution WBBSE Square Root Of Fractions
Square Root Of Fractions Exercise 5.1
Question 1. Let’s find the square of the following fractions.
1. \(\frac{4}{5}\)
Solution:
Square of (\(\frac{4}{5}\))²
= \(\frac{4}{5}\)
= \(\frac{16}{25}\)
2. \(\frac{6}{7}\)
Solution :
Square of \(\frac{6}{7}\)
= (\(\frac{6}{7}\))²
= \(\frac{36}{49}\)
3. \(\frac{8}{10}\)
Solution:
Square of \(\frac{8}{10}\)
= (\(\frac{4}{5}\))²
= \(\frac{16}{25}\)
4. \(\frac{11}{12}\)
Solution:
Square of \(\frac{11}{12}\)
= (\(\frac{11}{12}\))²
= \(\frac{11 \times 11}{12 \times 12}\)
= \(\frac{121}{144}\)
Question 2. Let’s find the square root of the following
1. \(\frac{16}{25}\)
Solution:
⇒ \(\sqrt{\frac{16}{25}}=\sqrt{\frac{4 \times 4}{5 \times 5}}\)
= \(\sqrt{\frac{4^2}{5^2}}\)
= \(\frac{4}{5}\)
2.\(\frac{9}{64}\)
Solution:
⇒ \(\sqrt{\frac{9}{64}}=\sqrt{\frac{3 \times 3}{8 \times 8}}\)
= \(\sqrt{\frac{3^2}{8^2}}\)
= \(\frac{3}{8}\)
3. \(\frac{36}{121}\)
Solution:
⇒ \(\sqrt{\frac{36}{121}}=\sqrt{\frac{6 \times 6}{11 \times 11}}\)
= \(\sqrt{\frac{6^2}{11^2}}\)
= \(\frac{6}{11}\)
4. \(\frac{144}{169}\)
Solution:
⇒ \(\sqrt{\frac{144}{169}}=\sqrt{\frac{12 \times 12}{13 \times 13}}\)
= \(\sqrt{\frac{12^2}{13^2}}\)
= \(\frac{12}{13}\)
5. \(\frac{225}{289}\)
Solution:
⇒ \(\sqrt{\frac{225}{289}}=\sqrt{\frac{15 \times 15}{17 \times 17}}\)
= \(\sqrt{\frac{15^2}{17^2}}\)
= \(\frac{15}{17}\)
Class VII Math Solution WBBSE Square Root Of Fractions Exercise 5.2
Question 1. Let’s find the least positive integer which will multiply the given fractions to make them perfect square fractions.
1. \(\frac{64}{147}\)
Solution:
⇒ \(\frac{64}{147}=\frac{8^2}{7^2 \times 3}\)
∴ \(\frac{64}{147}\) Is not perfect square fraction
To make if a perfect square, we have to multiply 3 with
∴ \(\frac{64}{147}\) × 3
= \(\frac{64}{49}\)
= \(\frac{8^2}{7^2}\)
∴ \(\frac{64}{49}\) will be a perfect square fraction.
∴ The required number is 3
2. \(\frac{25}{162}\)
Solution:
⇒ \(\frac{25}{162}\)
= \(\frac{5 \times 5}{9 \times 9 \times 2}\)
∴ \(\frac{5^2}{9^2 \times 2}\) is not perfect square fraction.
To make \(\frac{25}{162}\) a perfect square fraction we have to multiply by 2. i.e
= \(\frac{25}{162}\) × 2 = \(\frac{25}{81}\)
= \(\frac{5^2}{9^2}\), It Will be a Perfect square fraction.
∴ The required number is 2
3. \(\frac{100}{128}\)
Solution:
⇒ \(\frac{100}{128}\) = \(\frac{25}{32}\)
= \(\frac{5^2}{4^2 \times 2}\) which is not perfect square fraction
To make \(\frac{25}{32}\) a perfect square fraction we have to multiply it by 2
i.e \(\frac{25}{32}\) × 2
= \(\frac{25}{16}\)
= \(\frac{5^2}{4^2}\)
∴ The required number is 2
4. \(\frac{81}{288}\)
Solution:
⇒ \(\frac{81}{288}\) = \(\frac{9}{32}\)
= \(\frac{3^2}{4^2 \times 2}\) which is not a perfect of square fraction
To make it a perfect square fraction, we have to multiply it by 2
i.e \(\frac{9}{32}\) × 2
⇒ \(\frac{9}{16}\)
= \(\frac{3^2}{4^2}\)
∴ The required number is 2
Question 2. Let’s find the least positive integer which will divide the given fraction to make the perfect square fraction.
1. \(\frac{450}{625}\)
Solution :
⇒ \(\frac{450}{625}\)
= \(\frac{18}{5}\)
= \(\frac{3^2 \times 2}{5^2}\) Which is not a perfect square fraction.
To make it a perfect square fraction, we have to divide it by 2.
⇒ \(\frac{450}{625}\) × \(\frac{1}{2}\)
= \(\frac{225}{625}\)
= \(\frac{9}{25}\)
= \(\frac{3^2}{5^2}\), which is a perfect square fracation.
The required number is 2.
2. \(\frac{320}{121}\)
Solution:
⇒ \(\frac{320}{121}\) x \(\frac{8^2 \times 5}{5^2}\)
To make it a perfect square fraction, we have to divide it by 5.
⇒ \(\frac{320}{625}\) × \(\frac{1}{5}\)
⇒ \(\frac{64}{121}\)
= \(\frac{8^2}{11^2}\), Which is perfect square fraction.
∴ The required number is 5.
3. \(\frac{245}{64}\)
Solution:
⇒ \(\frac{245}{64}\) = \(\frac{49 \times 5}{64}\)
= \(\frac{7^2 \times 5}{8^2}\), Which is not a perfect square fraction
To make it a perfect square fraction we have to divide it with 5
⇒ \(\frac{245}{64} \times \frac{1}{5}\)
= \(\frac{49}{64}\)
= \(\frac{7^2}{8^2}\) , which is the Perfect square fraction.
∴ The required number is 5.
4. \(\frac{243}{14}\)
Solution:
⇒ \(\frac{243}{144}\)= \(\frac{27}{16}\)
= \(\frac{3^2 \times 3}{4^2}\) , Which is not a Perfect square fraction.
To make it a perfect square fraction we have to divide it by 3
∴ \(\frac{3^2 \times 3}{4^2} \times \frac{1}{3}\)
= \(\frac{3^2}{4^2}\), Which is a perfect square fraction..
∴ The required number is 3.
Class VII Math Solution WBBSE Square Root Of Fractions Exercise 5.3
Question 1. The area of a square is \(\frac{1089}{625}\) sq.cm. Let’s find the length of its side.
Solution :
The area of a square = \(\frac{1089}{625}\) sq.cm.
Length of its side = \(\sqrt{\frac{1089}{625}}\)
= \(\sqrt{\frac{3 \times 3 \times 11 \times 11}{25 \times 25}}\) cm
= \(\frac{3 \times 11}{25}\) cm.
= \(\frac{33}{25}\) cm.
Question 2. Let us find the square root of the following fractions
1. 3\(\frac{22}{49}\)
Solution:
⇒ 3 \(\frac{22}{49}\) = \(\frac{169}{49}\)
= \(\frac{13 \times 13}{7 \times 7}\)
= \(\frac{13^2}{7^2}\)
⇒ \(\sqrt{3 \frac{22}{49}}=\sqrt{\frac{13^2}{7^2}}\)
= \(\frac{13}{7}\)
= \(1 \frac{6}{7}\)
2. \(\frac{375}{1215}\)
Solution:
⇒ \(\frac{375}{1215}\)
= \(\frac{25}{81}\)
= \(\frac{5^2}{9^2}\)
⇒ \(\sqrt{\frac{375}{1215}}=\sqrt{\frac{5^2}{9^2}}\)
= \(\frac{5}{9}\)
3. 6 \(\frac{433}{676}\)
Solution:
⇒ \(\frac{433}{676}\)
= \(\sqrt{\frac{4489}{676}}=\sqrt{\frac{67^2}{26^2}}\)
= \(\frac{67}{26}\)
= \(2 \frac{15}{26}\)
4. 1\(\frac{496}{729}\)
Solution:
⇒ \(1 \frac{496}{729}=\frac{1225}{729}\)
= \(\frac{5 \times 5 \times 7 \times 7}{3 \times 3 \times 3 \times 3 \times 3 \times 3}\)
= \(\frac{5^2 \times 7^2}{3^2 \times 3^2 \times 3^2}\)
= \(\sqrt{1 \frac{496}{729}}=\sqrt{\frac{5^2 \times 7^2}{3^2 \times 3^2 \times 3^2}}\)
= \(\frac{5 \times 7}{3 \times 3 \times 3}\)
= \(\frac{35}{27}\)
5. \(\frac{324}{576}\)
Solution:
⇒ \(\frac{324}{576}\)
= \(\frac{9}{16}\)
= \(\frac{3^2}{4^2}\)
The required square = \(\sqrt{\frac{3^2}{4^2}}\)= \(\frac{3}{4}\)
Question 3. With what should the square root of \(\frac{121}{169}\)be multiplied to give 1, let’s find.
Solution :
⇒ \(\sqrt{\frac{121}{169}}=\sqrt{\frac{11^2}{13^2}}\)
= \(\frac{11}{13}\)
= \(\frac{11}{13}\) × 1
∴ The required number = 1 × \(\frac{13}{11}\)
= \(\frac{13}{11}\)
Question 4. Two positive numbers are such that one is twice the other. The product of these two numbers is 1 \(\frac{17}{32}\), let’s find the numbers
The product of two number = 1\(\frac{17}{32}\)
As one is twice the other
∴ Square of 1st number \(\frac{49}{32}\) × \(\frac{1}{2}\)
= \(\frac{49}{64}\)
= \(\frac{7^2}{8^2}\)
∴ 1st number = \(\sqrt{\frac{7^2}{8^2}}=\frac{7}{8}\)
∴ 2nd number = 2 × \(\frac{7}{8}\) = \(\frac{7}{8}\)
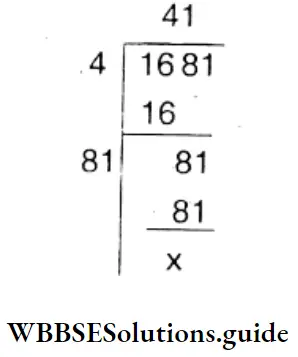
Question 5. Let’s find a fraction, which when multiplied by itself gives \(6 \frac{145}{256}=\frac{1681}{256}\)
Solution :
⇒ \(6 \frac{145}{256}=\frac{1681}{256}\)
= \(\frac{41^2}{16^2}\)
The required no. = \(\sqrt{\frac{1681}{256}}\)
= \(\sqrt{\frac{41^2}{16^2}}=\frac{41}{16}\)
Question 6. By which fraction should \(\frac{49}{91}\) be multiplied, so that the square root of the product is 1 Let’s find.
Solution :
⇒ \(\frac{49}{91}\)× _________ = 1²
∴ The required number = 1 × \(\frac{91}{49}\)
= 1\(\frac{42}{49}\)
= 1 \(\frac{6}{7}\)
Question 7. Let’s find, by which fraction should \(\frac{35}{42}\) be multiplied so that the square root of the product is 2.
Solution :
⇒ \(\frac{35}{42}\)× _________ = 2²
∴ The required number = \(\frac{4 \times 42}{35}\)
= \(\frac{24}{5}\)
= 4 \(\frac{4}{5}\)
WBBSE Class 7 Math Solution Question 8. Let’s find the least positive integer which when multiplied — makes it a perfect square.
Solution :
⇒ \(\frac{9}{50}=\frac{3^2}{5^2 \times 2}\) is not a Perfect Square
If we multiply 2 with it, it will be \(\frac{3^2}{5^2 \times 2} \times 2=\frac{3^2}{5^2}\)= a perfect
∴ The required number = 2.
Question 9. The product of two positive numbers is \(\frac{14}{15}\) and their quotient is \(\frac{14}{15}\), let’s find the numbers.
Solution :
Let one number = x & the other number = y
∴ x × y = \(\frac{14}{15} \& \frac{x}{y}=\frac{35}{24}\)
∴ (x+y) × = \(\frac{x}{y}=\frac{14}{15} \times \frac{35}{24}\)
= \(\frac{49}{36}=\frac{7^2}{6^2}\)
x = \(\left(\frac{7}{6}\right)^2\)
And y = \(\frac{14}{15} \times \frac{6}{7}\)
= \(\frac{4}{5}\)
One number = \(\frac{7}{6}\) & the other number = \(\frac{4}{5}\)
Question 10. The product of two positive numbers is \(\frac{16}{50}\) and their quotient is \(\frac{1}{2}\) let’s find the numbers.
Solution :
Let one number be x & the other number is y.
∴ x × y = \(\frac{16}{50}\) × \(\frac{x}{y}\)
= \(\frac{1}{2}\)
∴ (x × y) × (\(\frac{x}{y}\)) = \(\frac{16}{50} \times \frac{1}{2}\)
= \(\frac{4}{25}\)
= \(\frac{2^2}{5^2}\)
(x)² = \(\left(\frac{2}{5}\right)^2\)
∴ x = \(\frac{2}{5}\)
∴ y = \(\frac{16}{50}\) × \(\frac{5}{2}\)
= \(\frac{4}{5}\)
= One number = \(\frac{2}{5}\) and other number \(\frac{4}{5}\)
Question 11. \(\sqrt{\sqrt{\frac{9}{64}}+\sqrt{\frac{25}{64}}}\) let’sfinditsvalue
Solution:
⇒ \(\sqrt{\sqrt{\frac{9}{64}}+\sqrt{\frac{25}{64}}}=\sqrt{\sqrt{\frac{3^2}{8^2}}+\sqrt{\frac{5^2}{8^2}}}\)
= \(\sqrt{\frac{3}{8}+\frac{5}{8}}\)
= \(\sqrt{\frac{3+5}{8}}\)
= \(\sqrt{\frac{8}{8}}\)
=\(\sqrt{1}\)
= 1
Question 12. \(\sqrt{\frac{1}{4}}+\sqrt{\frac{1}{9}}-\sqrt{\frac{1}{16}}-\sqrt{\frac{1}{25}}\) let s find the value
Solution:
⇒ \(\sqrt{\frac{1}{4}}+\sqrt{\frac{1}{9}}-\sqrt{\frac{1}{16}}-\sqrt{\frac{1}{25}}c\)
= \(\sqrt{\frac{1^2}{2^2}}+\sqrt{\frac{1^2}{3^2}}-\sqrt{\frac{1^2}{4^2}}-\sqrt{\frac{1^2}{5^2}}\)
= \(\frac{1}{2}+\frac{1}{3}-\frac{1}{4}-\frac{1}{5}\)
= \(\frac{30+20-15-12}{60}\)
= \(\frac{50-27}{60}\)
= \(\frac{23}{60}\)
WBBSE Class 7 Math Solution Question 13. Arrange the following in the descending order of their magnitude
\(\)
Solution:
⇒ \(\sqrt{\frac{1}{16}}, \sqrt{\frac{1}{25}}, \sqrt{\frac{1}{36}}, \sqrt{\frac{1}{49}}\)
⇒ \(\sqrt{\frac{1}{16}}=\sqrt{\frac{1^2}{4^2}}=\frac{1}{4}\)
⇒ \(\sqrt{\frac{1}{25}}=\sqrt{\frac{1^2}{5^2}} \quad=\frac{1}{5}\)
⇒ \(\sqrt{\frac{1}{36}}=\sqrt{\frac{1^2}{6^2}} \quad=\frac{1}{6}\)
⇒ \(\sqrt{\frac{1}{49}}=\sqrt{\frac{1^2}{7^2}}, \quad=\frac{1}{7}\)
⇒ \(\frac{1}{4}>\frac{1}{5}>\frac{1}{6}>\frac{1}{7}\)
∴ \(\frac{1}{16}>\frac{1}{25}>\frac{1}{36}>\frac{1}{49}\)
Question 14. Let’s find, by what magnitude is \((\sqrt{25}+\sqrt{81})\) more than \((\sqrt{16}+\sqrt{36})\)
Solution:
⇒ \((\sqrt{25}+\sqrt{81})\) – \((\sqrt{16}+\sqrt{36})\)
= (5 + 9) -(4 + 6) = 14 -10
= 4
Question 15. Let’s find the square roots of the following fractions
1. \(3 \frac{22}{49}\)
Solution:
⇒ \(\sqrt{3 \frac{22}{49}}\)
= \(\sqrt{\frac{169}{49}}=\sqrt{\frac{13^2}{7^2}}\)
= \(\frac{13}{7}\)
= 1 \(\frac{6}{7}\)
2. \(7 \frac{57}{256}\)
Solution:
⇒ \(\sqrt{7 \frac{57}{256}}\)
= \(\sqrt{\frac{1849}{256}}=\sqrt{\frac{43^2}{16^2}}\)
= \(\frac{43}{16}\)
= 2 \(\frac{11}{16}\)
3. \(\frac{1089}{2025}\)
Solution:
⇒ \(\sqrt{\frac{1089}{2025}}\)
= \(\sqrt{\frac{33^2}{45^2}}\)
= \(\frac{33}{45}\)
= \(\frac{11}{15}\)
4. \(3 \frac{814}{1225}\)
Solution:
⇒ \(\sqrt{3 \frac{814}{1225}}\)
= \(\sqrt{\frac{4489}{1225}}=\sqrt{\frac{67^2}{35^2}}\)
= \(\frac{67}{35}\)
= 1 \(\frac{32}{35}\)
We found that in perfect square decimal numbers, there are even numbers of digits after the decimal point
WBBSE Class 7 Math Solution Square Root Of Fractions Exercise 5.4
Question 1. Let’s find the value of the square of the following decimal numbers
1. 0.7
Solution :
0.7 × 0.7 = 0.49
(0.7)² = 0.49
2. 0 .16
Solution :
= 0.16 × 0.16 = 0.0256
(0.16)² = 0 . 0256
3. 0. 08
Solution :
= 0 . 08 × 0 . 08 = 0. 0064
(0. 08) = 0 .0064
4. 0.25
Solution :
0 . 25 × 0 . 25 = 0 . 0625
(0-25)² = 0. 0625
Question 2. By counting the number of digits after the decimal point, let’s identify the square decimal numbers from the following decimal numbers
1. 22.5
Solution:
= 22.5 – Here one digit after the decimal point, so it is not a square decimal number.
2. 1.44
Solution :
1 .44 – Here after the decimal point there is two digits, so it is a square decimal number.
3. 62.5.
Solution:
62.5 – Here after the decimal point there i§ one digit, so it is not a square decimal number.
4. 12.1
Solution:
12.1 – Here after the decimal point there is one digit, so it is not a square decimal number.
Question 3. Let’s find the square root of the following decimal numbers.
1. 4. 41
Solution:
⇒ \(\sqrt{4 \cdot 41}=\sqrt{\frac{441}{100}}\)
= \(\sqrt{\frac{7 \times 7 \times 3 \times 3}{10 \times 10}}\)
= \(\sqrt{\frac{7^2 \times 3^2}{10^2}}\)
= \(\frac{7 \times 3}{10}\)
= \(\frac{21}{10}\)
= 2.1
2. 4. 41
Solution:
⇒ \(\sqrt{2 \cdot 25}=\sqrt{\frac{225}{100}}\)
= \(\sqrt{\frac{5 \times 5 \times 3 \times 3}{10 \times 10}}\)
= \(\sqrt{\frac{5^2 \times 3^2}{10^2}}\)
= \(\frac{5 \times 3}{10}\)
= \(\frac{15}{10}\)
= 0.16
3. 0.0484
Solution:
⇒ \(\sqrt{0 \cdot 0.0484}=\sqrt{\frac{484}{10000}}\)
= \(\sqrt{\frac{2 \times 2 \times 11 \times 11}{100 \times 100}}\)
= \(\sqrt{\frac{2^2 \times 11^2}{100^2}}\)
= \(\frac{2 \times 11}{100}\)
= \(\frac{22}{100}\)
= 0.22
WBBSE Class 7 Math Solution Square Root Of Fractions Exercise 5.5
Question 1. Let’s find the square roots of the following decimal numbers by the method of division.
1. 0.000256
Solution :
⇒ \(\sqrt{0.000256}\)
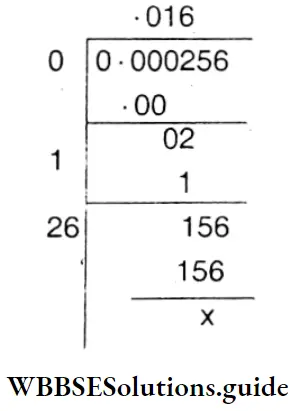
∴ \(\sqrt{0.000256}\) = 0.016
2. 0. 045369
Solution :
⇒ \(\sqrt{0. 045369}\)
∴ \(\sqrt{0. 045369}\)= 0.213
3.1.0609
Solution :
⇒ \(\sqrt{1.0609}\)
∴ \(\sqrt{1.0609}\) = 1.03
4. 75.609
Solution :
⇒ \(\sqrt{75.609}\)
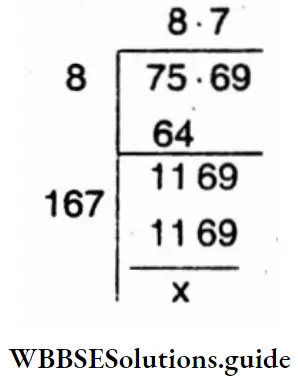
∴ \(\sqrt{75.609}\)
Question 2. The area of a square is 32.49 sq. cm. Let’s find the length of one side of the square.
Solution :
The area of a square = 32.49 sq. cm.
∴ The length of one side of the square = \(\sqrt{32.49}\) cm
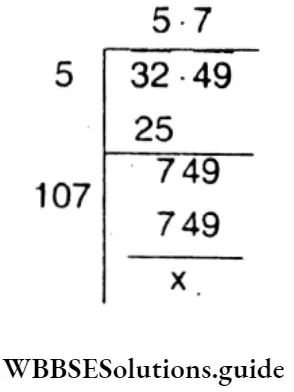
= 5.7m
Question 3. Let’s find the length of one side of a square whose area is equal to the sum of the areas of rectangles of areas 2.1214 sq. cm, and 2.9411 sq. cm.
Solution :
The area of the square = (2.1214 + 2.9411) sq. cm.
= 5.0625 sq. cm.
∴ The length of one side of the square =
= 2.25
Question 4. Let’s calculate what must be added to 0.28 so that the square root of the sum is 1.
Solution :
Square of 1 = 1
∴ The required number = 1 – 0.28 = 0.72
Question 5. Let’s find the square root of the product of 0.162 and 0.2
Solution:
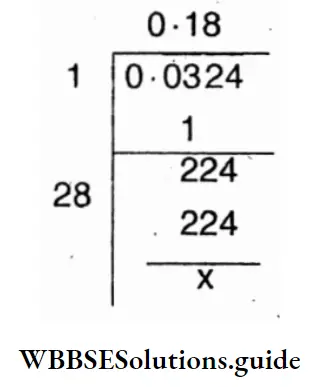
= 0.18
Question 6. Let’s calculate the value of \(\sqrt{240.25}+\sqrt{2.4025}+\sqrt{0.024025}\)
Solution:
⇒ \(\sqrt{240.25}+\sqrt{2.4025}+\sqrt{0.024025}\)
15.5 + 1. 55 + 0.155 =17.205
Question 7. Of the two squares of areas 1.4641 sq.m, and 1.0609 sq.m, Let’s Find which one has a bigger side and by how much it is big.
Solution:
Area of the 1st square = 1 .4641 sq.m.
Area of the 2nd square = 1 .0609 sq.m.
∴ Each, side of the 1st square = \(\sqrt{1.4641}\)
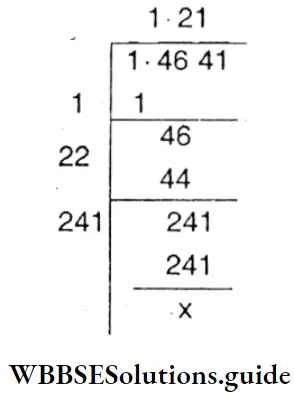
= 1.21
The each side of the 2nd square = \(\sqrt{1.0609}\)
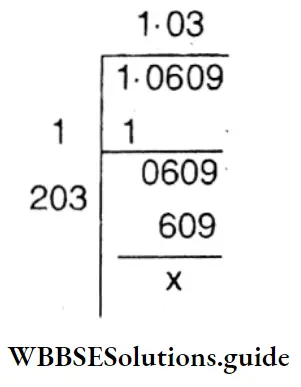
∴ Side of 1st square is bigger than the 2nd square by (1.21 – 1 . 03 ) m = 0 . 18 m
WB Class 7 Math Solution Question 8. The sum of the squares of 0.4 and 0.3 is the squares of which number, let’s find.
Solution :
(0.4)² + (0.3)² = 0.16 + 0.09 = 0.25
The required number = \(\sqrt{0.25}\)
= \(\sqrt{\frac{25}{100}}\)
= \(\frac{5}{10}\)
= 0.5
Question 9. Let’s find the square root of the following by the method of division.
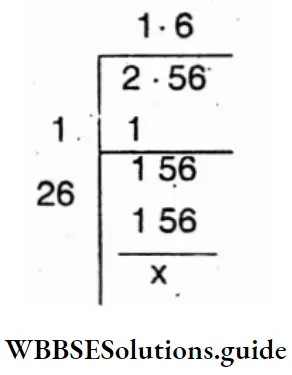
1. 2.56
Solution :
⇒ \(\sqrt{0.25}\)
2. 4.84
Solution :
⇒ \(\sqrt{4.84}\)
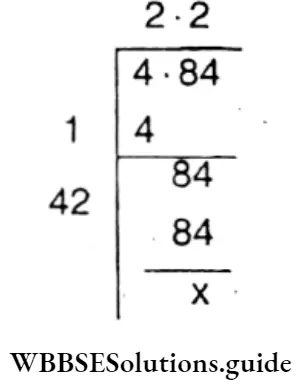
= 2.2
3. 5.76
Solution :
⇒ \(\sqrt{5.76}\)
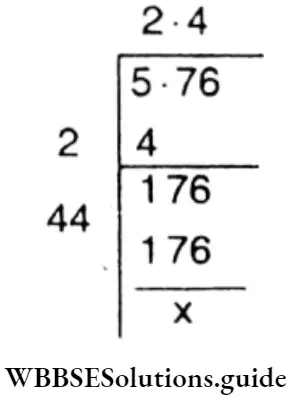
= 2.4
4. 6.76
Solution :
⇒ \(\sqrt{6.76}\)
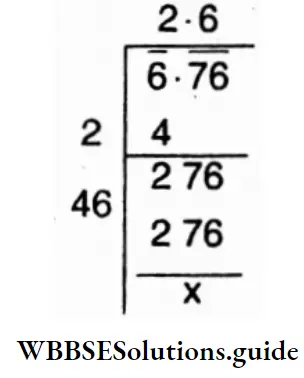
= 2.6
5. 0.045369
Solution :
⇒ \(\sqrt{0.045369}\)
= 0.213
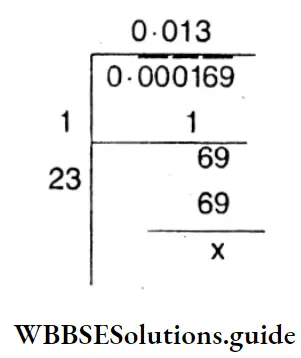
6. 0.000169
Solution :
⇒ \(\sqrt{0.000169}\)
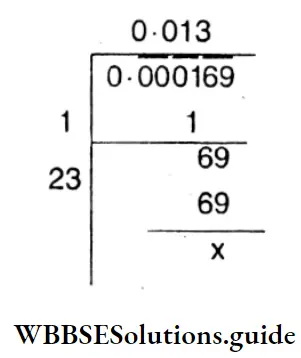
= 0.013
7. 76.195441
Solution :
⇒ \(\sqrt{76.195441}\)
= 8.729
8. 170.485249
Solution :
⇒ \(\sqrt{76.195441}\)
= 13.0.57
9. 5505.64
Solution :
⇒ \(\sqrt{5505.64}\)
= 74.2
WB Class 7 Math Solution Question 10. Let’s find the decimal number which when multiplied by itself gives the product as 1.1025.
Solution :
The required number \(\sqrt{1.1025}\)
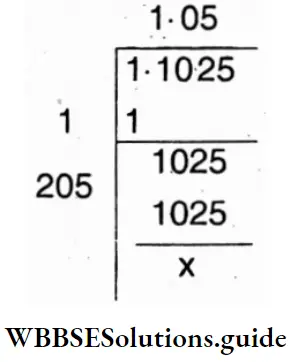
= 1.05
Question 11. Let’s find, which decimal number is to be added to 0.75 so that square root of the sum will be 2.
Solution :
Square of 2 = 2² = 4
∴ The required number = 4 – 0.75 = 3.25
11. Let’s find, which decimal number is to be subracted from 48.09 so that the square root of the result is 5.7.
Solution :
Square of 5.7 = (5.7)² = 32.49
The required number = 48.09 – 32.49
=15.6
Question 12. Let’s find the least decimal number that must be subtracted from 0.000328 to make it a square decimal number (up to 6 decimal place
Solution :
⇒ \(\sqrt{0.000328}\)
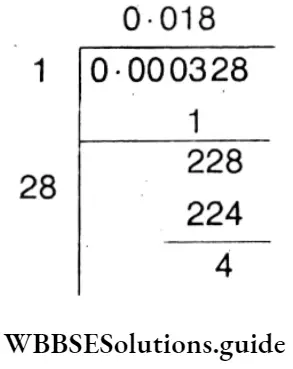
If we subtract 0.000004 from 0.000328
It will be = 0.000324 = (0.01 8)²
The required number = 0.000004
Question 13. Let’s find the approximate value of the following
1. \(\sqrt{6}\) (upto 2 decimal places)
Solution:
⇒ \(\sqrt{6}\)
= 2.45
2. \(\sqrt{8}\) (upto 2 decimal places)
Solution:
⇒ \(\sqrt{8}\)
= 2.828
= 2.83 (upto 2 decimal places)
3. \(\sqrt{11}\) (upto 3 decimal places)
Solution:
⇒ \(\sqrt{11}\)
= 3.3166
= 3.317 (up to 3 decimal places)
4. \(\sqrt{12}\) (upto 3 decimal places)
Solution:
⇒ \(\sqrt{11}\)
= 3.4641
= 3.464 (up to 3 decimal places)
Question 14. Let’s find the approximate value of 7T5 upto 2 – places of decimal. Let’s then square this approximate value to find how big or less it is from 15.
Solution :
= 3.872
= 3.87 (up to 2 decimal places)
Now (3.87)² = 14.9761
Difference
= 15.9761
= 0.0231
