WBBSE Solutions For Class 8 Maths Chapter 10 Rule Of Three

Rule Of Three

Question 1. I have bought a dozen of exercise books from the Banerjee book stall of our locality for Rs. 90 only. Let’s calculate the price of such exercise book by the Rule of three.
Solution:

In mathematical language the problem is

No. of exercise books (pcs.) Price of exercise books in Rs.

1 dozen = 12 90

8                  ?

The relation is: If the number of exercise books increases Increase price will increase. If the number of exercise books decreases price Will Decrease decrease.

∴ 12 : 8:: 90:?

Or, cost of exercise books ( ?) = Rs. 90×8/12

∴ Cost of 8 books = Rs 60

We got, Second quantity variable value =

Question 2. If Rs. 1772 is needed for making 7 ploughs, how much will be needed for making 12 ploughs? (apply the rule of three)
Solution:

To make more number of ploughs much much less money will be needed.

Number of ploughs and their making costs are Directly (directly/inversely) proportional.

Question 3. 24 people had food provision for 20 days. Let’s work out using the method of Rule of Three how long the remaining food will last for 40 people.
Solution:

With the same quantity of food the more number of people will cover will cover (much/less) days.

So the number of people and number of days are inversely (direct / inversely) proportional.

Read and Learn More WBBSE Solutions For Class 8 Maths

Rule Of Three Exercise 10.1

Question 1. Today my father has bought 15 kg of rice for Rs. 390. Let’s work out using the Rule of Three method how much he would require if he would have bought the same quality of 17 kg of rice.
Solution:

In mathematical language, the problem is –

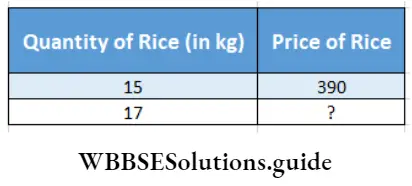
Relation will be – If quantity of rice increases the price of rice will increase; so the quantity and price of rice will be directly proportional.

∴ 15: 17:: 390:?

or, \(\frac{15}{17}=\frac{390}{?}\)

∴ Value (?) = \(\frac{17 \times 390}{15}\)

= Rs. 442

∴ Price of 17 kg rice will be 442.

Question 2. Venkat uncle will make 4 shirts of same size with 20 meters of cloth. Let’s work out using the rule of three method how many meters of cloth Venkat uncle will have to purchase for making 12 such shirts.
Solution:

In mathematical language, the problem is –

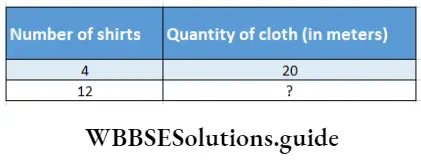
Relation will be – If the number of shirts increases, the quantity of cloth will increase, so they will be directly proportional.

4 : 12:: 20:?

or, \(\frac{4}{12}=\frac{20}{?}\)

or, Quantity of cloth (?) =\(\frac{12 \times 20}{4}\)= 60 meter

∴ In making 12 shirts 60 meter cloth will be needed.

Question 3. It took 15 days for 30 labourers to dig a pond at Bakultala village. Let’s work out using the rule of three method in how many days 25 heads of labourers could have completed the said work.
Solution:

In mathematical language the problem is –

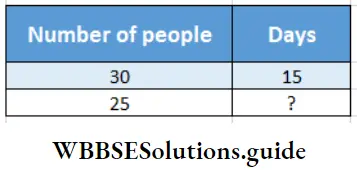
Relation will be – If the number of days increases, the number of people will decrease, so they will be inversely proportional.

30: 25 :?:15

or, \(\frac{30}{25}=\frac{?}{15}\)

∴ Time(?)= \(\frac{30}{25}\) ×15 = 18 days.

∴ 25 men will require 18 days.

Question 4. My aunt reached my maternal uncle’s house in five hours by driving the car at a speed of 40 kmph. Let’s work out using the rule of three method how long it would have taken if she would drive the car at a speed of 50 kmph.
Solution:

In mathematical language the problem is – Speed of Car (kmph) Time (in hours)

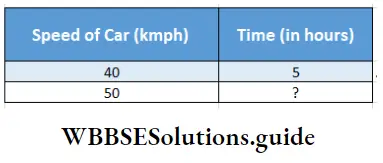
Relation will be – If speed of car increases, time will decrease, so they are inversely proportional.

∴ 40 : 50 : 5

or, \(\frac{40}{50}=\frac{?}{5}\)

or. Time (?) = \(\frac{40}{50} \times 5=4\)

∴ 50 kmph speed will require 4 hours time.

Question 5. There was a stock of food grains for 9 days to cater the needs of 4000 people in a shelter camp in Mongalpur village. After 3 days 1000 people left the camp for another place. Let’s work out for how many days the rest of people will consume.
Solution:

3 days later number of remaining people (4000 – 1000) = 3000

Remaining food grains for = (9-3) days = 6 days

In mathmatical language the problem is –

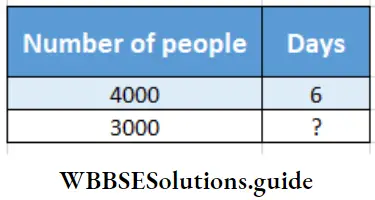
Relation will be – If number of people decreases the foodgrains will last longer, so they are inversely proportional.

4000 : 3000 : : ? : 6

or, \(\frac{4000}{3000}=\frac{?}{6}\)

or, Time ( ?) = \(\frac{4000}{3000} \times 6=8\)

Remaining people will consume the food for 8 days.

Question 6. 42 labourers of a farm at Nasirpur village can cultivate the entire land of the farm in 24 days. But suddenly 6 labourers became ill during the period of cultivation. Let’s work out using the rule of three method how many days it will take to cultivate the entire land of the farm by the rest of the labourers.
Solution:

Members becoming ill, remaining left = (42 – 6) = 36 In mathematical language the problem is-

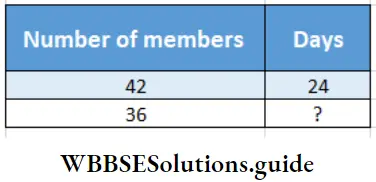
Relation will be – if number of members decreases then the number of days will increase. So they are inversely proportional.

∴ 42 : 36 : 24

or, \(\frac{42}{36}=\frac{?}{24}\)

or, Time ( ?) = \(\frac{24 \times 42}{36}\) x 42 = 28 days

Rest of the labourers will require to cultivate 28 days.

Question 7. It take 27 days to make 1000 spare parts by 16 numbers of machines. Let’s work out using the rule of three method how many days it will take to make the same number of spare parts if additional two machines are installed.
Solution:

2 machines are installed, new number = 16 + 2 =18

In mathematical language, the problem is –

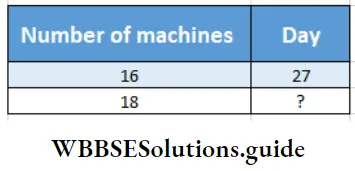
Relation will be – If number of machines increases, number of days will decrease, so they are inversely propotional.

16 : 18 :: ? : 27

or, \(\frac{16}{18}=\frac{?}{27}\)

or, Time ( ?) = \(\frac{16}{18}\) x 27 = 24

18 machines will require 24 days to produce same number of spare parts in 24 days.

Question 8. See the relations below, express them in mathematical language, and solve by using rule of three.
Solution:

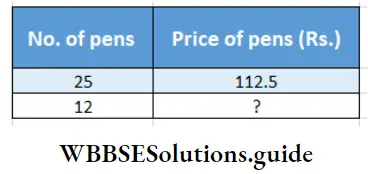
If prices are of Rs. 112.50 then what will be the value of 12 pens?

Relation will be – If number of pens increases, its price will increase, so they are directly proportional.

∴ 25 : 12 :: 112.5: ?

or, \(\frac{25}{12}=\frac{112.5}{?}\)

∴  Value ( ?) = \(\frac{12 \times 112.5}{25}\)

= 54

∴ 12 pens will value Rs. 54.

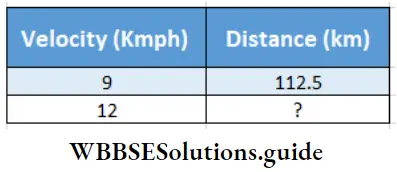
A car with velocity 9 kmph, in a given time, can cover 112.5 km distance.

The same car will cover how much distance in the same time with speed 12 kmph? .

Relation will be – If velocity increases, distance will-increase, so they are directly proportional.

∴ 9:12:: 112.5 : ?

or, \(\frac{9}{12}=\frac{112.5}{?}\)

or, Distance ( ?) = \(\frac{12 \times 112.5}{9}\)

or, Distance ( ?) = \(\frac{12 \times 1125}{9 \times 10}\)

= 150

That car with speed 12 kmph in the given time will cover 150 km distance.

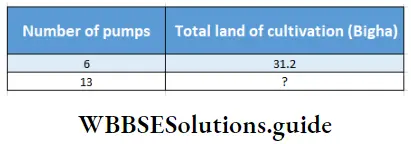
6 pumps in a given time can irrigate 31.2 Bigha land, 13 pumps in the same time will cultivate how much ?
Relation will be – If number of pumps increases, measure of land
will increase, so they are directly proportional.

∴ 6 : 13: : 31.2:?

or, \(\frac{6}{13}=\frac{31.2}{?}\)

or, Measure of land ( ?) = \(\frac{13 \times 31.2}{6}\)

= \(\frac{13 \times 312}{6 \times 10}\)

= \(\frac{13 \times 52}{10}\)

= 67.6 Bighas.

13 pumps in the same time will cultivate 67.6 bighas land.

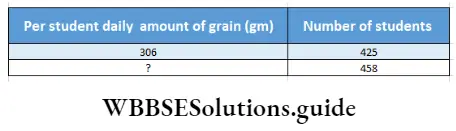
If each student eats 306 gm grains, total grains required for 425 students = 306 x 425 gm = 130050 gm If in a school for 425 students 130050 gm grain is required then if students are 458 how much grain will be required?

Relation will be – If number of students increases, amount of grain

will increase, so they are directly proportional.

∴ 425 : 458 :: 130050 : ?

or, \(\frac{425}{458}=\frac{130050}{?}\)

or, Measure of grain ( ?) = \(\frac{458 \times 130050}{425}\)

= \(\frac{458 \times 5222}{17}\) gm.

Question 9. The walls and boundary walls of Bapan’s house are to be built. So, masons are working for building the wall. Let’s work out using the Rule of Three method how many days it will take for 10 masons tp build 320 sq.m, of walls if 5 masons can build 120 sq m. of walls in 4 days.
Solution:

In mathematical language the problem is –

There are three items :

1. No. of masons
2. Time,
3. Quantity of work

Let’s find the relation in two steps.

First step – During the same work if the number of masons increases then the time will decrease (much / less) and if number of masons decreases time will much (much / less). The number of masons and time are inversely (inversely/directly) proportional.

∴ ?:4:: 5: 10

Required time = \(4 \times \frac{5}{10}\)

Required time = 2 days ‘ Second step – If the number of masons is constant, the time will be needed for doing more work much (More / less) amount of work is less, time is needed will cover (More / less). So number of masons and amount of work are Directly (directly / Inversely) proportional.

So, 7:2:: 320 : 128

Required time = \(2 \times \frac{320}{128}\) days = 5 days – 64

So we get putting two steps together-

∴ Required time = \(4 \times \frac{5}{10} \times \frac{320}{128}\) days = 5 days 32

Question 10. Milkman Mahesh of Rashedpur fed 4 bundles of straw to 8 cows for 15 days. Let’s work out using the rule of three method how many bundles of straw will have to be stored to feed 10 cows for 72 days during raing season.
Solution:

In mathematical language, the problem is –

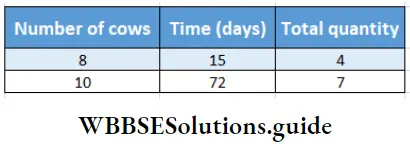
Let’s find the relation.

First step- If the number of cows increases, the quantity of straw will Increase (increase / decrease) and if the number of cows decreases, straw will be will cover (More / less).

Second step – If the number of cows remains constant then the quantity of straw will Increase (increase / decrease) and if time decreases, quantity of straw less (more/less).

∴  With time quantity of straw is Direct (inversely / directly)

The required amount required of straw = \(4 \times \frac{10}{8} \times \frac{72}{15}\) = 24 bundles.

Rule Of Three Exercise Exercise 10.2

Question 1. The work for construction of the village road will be started. It has been decided that 14 people will work 4 hours daily for 15 days to complete the total work. Let’s work out using the rule of three method how long it will take to complete the work by 24 people working 7 hours daily.
Solution:

In mathematical language the problem is –

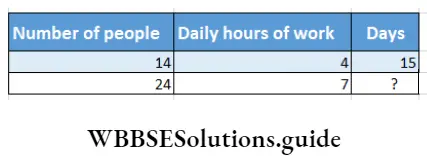
Relation will be – If number of people and daily hours of work increase, days will decrease, so they are inversely proportional.

∴ Required days ( ?) = \(15 \times \frac{14 \times 4}{24 \times 7}\)=5

24 people do daily 7 hours work then the work will be is completed in 5 days.

Question 2. In a book of 105 pages written by Subhash uncle there are average 25 lines in each page and there are average 8 words in each line. Let’s work out using the rule of three method how many pages will be there in the book if there are 30 lines in each page having 10 words in each line.
Solution:

In mathematical language the problem is –

Relation will be – If number of words and number of lines increase, number of pages will decrease, so they are inversely proportional.

∴ Number of pages = 105×\(\frac{8 \times 25}{10 \times 30}\)

= 70

There will be 70 pages.

Question 3. 540 bighas of land of an agricultural farm are to be cultivated in 14 days. 120 bighas of land was cultivated in first 4 days by 5 tractors of equal strength. Let’s work out using rule of three method how many tractors are required to complete the cultivation in time.
Solution:

After 4 days cultivating land,

Remaining days = (14 – 4) = 10

Remaining land = (540 -120) = 420 bighas

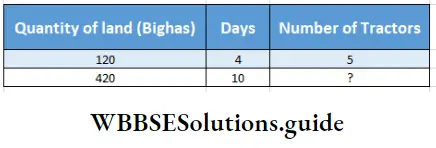
Relation will be – If number of days increases, and days also, number of tractors will decrease.

∴ Number of tractors (?) = \(5 \times \frac{420}{120} \times \frac{4}{10}\)

= 7

Number of more tractors = (7-5) = 2

For cultivating land an additional of 2 tractors are required.

Question 4. 30 heads of people repair 3/7 part of a road of a village in 15 days. Let’s work out using the method of rule of three how many days it will take to repair the rest of the road if additional 10 heads of people join.
Solution:

Remaining Work  \(=\left(1-\frac{3}{7}\right)=\frac{4}{7}\) Part

Number of people = (30+10) = 40 In mathematical language the problem is-

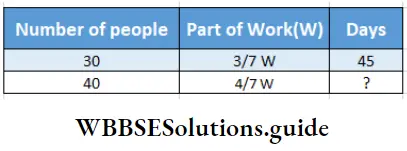
Relation will be – If number of people and part of work decrease, days will increase.

∴ Required days ( ?) = \(15 \times \frac{30 \times 4 \times 7}{40 \times 7 \times 3}=15\)

To repair the remaining road 15 days are required.

Question 5. A pump of 5 HP can lift 36000 L of water in 8 hrs. Let’s work out using rule of three method how long it will take to lift 63000 L water by a 7 HP pump.
Solution:

In mathematical language the problem is –

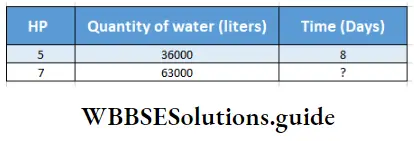
Relation will be – If HP increases time will decrease. If quantity of water increases time will increase.

∴ Required time = \(8 \times \frac{5}{7} \times \frac{63000}{36000}\)

= 10 hours

10 hours time is required.

Question 6. There are two motors of 5 HP and 3 HP in a factory. The 5 HP motor requires 20 units of electricity in 8 hrs. Let’s work out using the rule of three how many units will be required if the 3 HP motor works for 10 hours.
Solution:

In mathematical language the problem is –

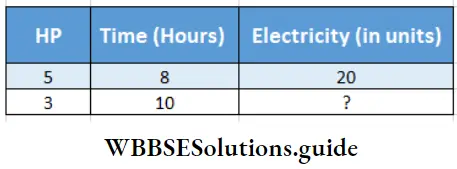
Relation will be – If HP and time increase, electricity will increase

∴ Required electricity ( ?) = \(20 \times \frac{3}{5} \times \frac{10}{8}\) units

= 15 units

∴ If 3 HP motor 10 hours use requires 15 units of electricity.

Question 7. In a loom at Gopalnagar 14 weavers can weave 210 sarees in 12 days. The workshop got an order to supply 300 sarees within 10 days during the pujas. Let’s work out using the rule of three how many extra weavers have to be employed to complete the work in time.
Solution:

In mathematical language the problem is-

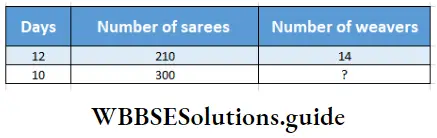
The relation will be – If days increase, weavers will decrease and if number of sarees increase, weavers will increase.

∴ Number of weavers = \(14 \times \frac{12}{10} \times \frac{300}{210}\)

= 24

Number of more weavers = (24- 14) = 10

To complete the work in time 10 more weavers are required.

Question 8. A company has got the work of unloading goods from a ship in 10 days. 280 people have been employed for this purpose. After 3 days it is seen that 1/4th of the work has been completed. Let’s work out using the rule of three method how many people are to be engaged to complete the work in time.
Solution:

3 days later remaining work = \(\left(1-\frac{1}{4}\right) \frac{3}{4}\) = part

Remaining Time = (10 – 3) = 7 days

In mathematical language, the problem is –

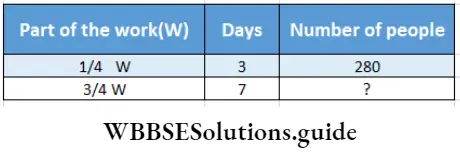
Relation will be – If work increases number of people will increase. If days increase number of people will decrease.

∴ Number of people = \(280 \times \frac{3}{4} \times \frac{4}{1} \times \frac{3}{7}\) = 360

Number of more people = (360 – 280) = 80

To complete the work in time 80 more people are required.

Question 9. A power loom is 2 \(\frac{1}{4}\)times powerful than a hand loom. 12 hand looms weave 1080 m of length of cloth is 18 days. Let’s work out by the rule of three how many powerlooms would be required to weave 2700 m length of cloth in 15 days.
Solution:

In mathematical language the problem is –

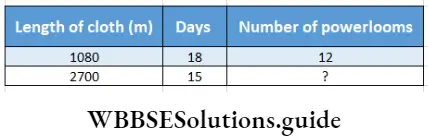
Relation will be – If length of cloth increases number of powerlooms increases and if days decrease, number of powerlooms will increase.

∴ Number of landlooms (?) = 12 × \(\frac{27000}{1080} \times \frac{18}{15}\)

= 36

∵ \(frac{9}{4}\)handlooms1 production = 1 Powerlooms’ production

∴ 1 handlooms’ production = \(\frac{4}{9}\) Powerlooms’ production

∴ 36 handlooms’ production = \(\frac{4}{9} \times 36\) Powerlooms’ production

= 16 Powerlooms’ production

To complete 2700 m long clpth in 15 days, 16 powerlooms are required.

Question 10. 2400 bighag of land of a cooperative society can be cultivated by 25 farmers in 36 days. It was seen that half of the land of the society could be cultivated in 30 days after purchasing a tractor. Let’s work out the power of a tractor equivalent to the number of farmers using the rule of three.
Solution:

In mathematical language the problem is –

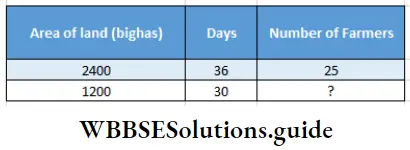
Relation will be – It area of land increases, number of farmers will increase. If number of farmers decrease, days wiH increase.

∴ Number of farmers = \(25 \times \frac{1200}{2400} \times \frac{36}{30}\)= 15

∴ A tractor’s power is equal to 15 farmers.

Question 11. A ship takes 25 days to Sail from Kolkata to Cochin. The ship started With 36 sailors for each of which 850 gm of food was alloted. But the ship rescued 15 sailors from another sinking-ship after 13 days of journey and the ship reached Cochin in 10 days increasing the speed. Let’s work out using the method of the rule of three what will be the quantity of food of each sailor will require to reach cochin safely if entire storage of food could be consumed by this time.
Solution:

13 days later:

Number of sailors =36+15

= 51

Food for remaining days = (25-13)

= 12 days

In mathematical language, the problem is –

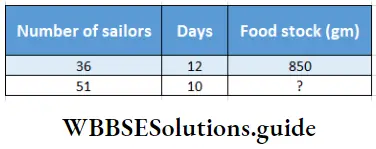
Relation will be – If number of sailors and days increase, food stock will decrease.

∴ Food stock (?) = \(850 \times \frac{36}{51} \times \frac{12}{10}\)

Every sailor will comsume 720 gm per day.

Question 12. 36 people of a certain village construct 120 m of road by 8 people working 6 hours daily. Another 6 people are involved in this work and the duration of work of each day is increased by 2 hours. Find the length of road to be constructed in 3 days.
Solution:

In mathematical language, the problem is –

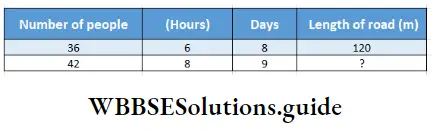
Relation will be – If number of people increases, work will increase. If hours increase, work will increase. If days increase, work will increase.

Length of road (?) = \(120 \times \frac{42}{36} \times \frac{8}{6} \times \frac{9}{8}\)

= 210

Now, in 9 days 210 m long road can be constructed.

Question 13. 250 people can excavate a pond of size 15m long, 35 m wide and 5.2 m deep in 18 days by working 10 hours daily. Let’s work out using the rule of three method how many days it will take-for 300 people to excavate a pond of size 65 m long, 40 m wide and 5.6 m deep by working 8 hours daily.
Solution:

In mathematical language, the problem is –

Number of people Volume of pond Work per day Days (L x B x H) time (hours)

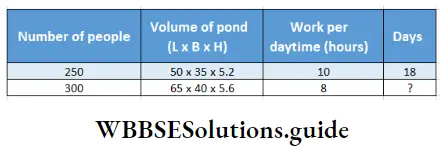
Relation will be – If number of people increases, days will decrease. If volume of pond increases, days will increase.

∴ Required days (?) = \(18 \times \frac{250}{300} \times \frac{65 \times 40 \times 5.6}{50 \times 35 \times 5.2} \times \frac{10}{8}\)

= 30

∴ 30 days are required.

Question 14. Let’s make mathematical problems with the help of given relations and find out their solutions by rule of three.
Solution:

If 5 famers can cultivate 18 bigha land in 15 days then 10 farmers will cultivate how many bighas land in 10 days?

Relation will be – If number of farmers and days increase, quantity of land will increase.

∴ Quantity of land (?) = \(18 \times \frac{10}{5} \times \frac{10}{15}\) = 24 Bigha

∴ 24 Bighas land can be cultivated by 10 farmers in 10 days.