Mixture
Ratio of Assam tea and Darjeeling tea in casket number 1 is 5: 2
Ratio of Assam tea and Darjeeling tea in casket number 2 is 2: 1
Have we got a new variety of tea after blending various qualities of tea in different ratios?
What can be termed such blending?
Solution:
Such blending is called mixture.
The proportional part of Assam tea in the blended tea of casket number 1 is
= \(\frac{5}{5+2}=\frac{5}{7}\)
The proportional part of Darjeeling tea in the blended tea of casket number 1 is
= \(\frac{2}{7}\)
The proportional part of Assam tea in the blended tea of casket number 2 is
= \(\frac{2}{2+1}=\frac{2}{3}\)
The proportional part of Darjeeling tea in the blended tea of casket number 2 is
= \(\frac{1}{3}\)
Read and Learn More WBBSE Solutions For Class 8 Maths
Question 1. Let’s calculate the quantities of Assam tea and Darjeeling tea out of 21 kg of blended tea in casket number 1.
Solution:
The quantity of Assam tea out of 21 kg blended tea in casket number 1
= \(21 \mathrm{~kg} \times \frac{\mathrm{5}}{7}\) =15 kg
And the quantity of Darjeeling tea is = \(21 \mathrm{~kg} \times \frac{\mathrm{2}}{7}\) = 6 kg
Question 2. Let’s calculate the quantities of Assam tea and Darjeeling tea out of 21 kg of blended tea is casket number 2.
Solution:
The quantity of Assam tea out of 21 kg of blended tea of casket number 2 is
= \(21 \times \frac{2}{3} \mathrm{~kg}\) = 14 kg
And the quantity of Darjeeling tea is
= \(21 \times \frac{1}{3} \mathrm{~kg}\) = 7 kg
Question 3. Let’s work out the quantities of the ratio of Assam tea and Darjeeling tea if additional 7 kg of Assam tea is mixed with 25 kg of blended tea in casket number 3.
Solution:
The quantity of Assam tea in casket number 3 is = 15 kg
And the quantity of Darjeeling tea is =10 kg
Total quantity of Assam tea after mixing 7 kg of that of the same
= 15 kg + 7 kg = 22 kg
Total quantity of Assam tea after mixing 7 kg of that of the same = 22 kg
Question 4. Let’s calculate what quantity of Darjeeling tea needs to be mixed with the blending casket number. 2 so that ratio of Darjeeling tea and Assam tea will be 7: 4 in the new blend.
Solution:
Let x kg Darjeeling tea will be mixed.
∴ If x kg Darjeeling tea is mixed, quantity of Darjeeling tea is = (7 + x) kg.
In the new mixture Assam tea : Darjeeling tea = 14 : (7 + x)
B.T.P.,
= \(\frac{14}{7+x}=\frac{7}{4}\)
or, 49 + 7x = 56
or, 7x = 56 – 49
or,7x=7
or, x= 7/7
or, x= 1
If we mix 1 kg Darjeeling tea in casket number 2, the ratio of the quantities of Assam tea and Darjeeling tea in the new mixture will be 7:4
Question 5. I prepared two types of beverage in my house. The ratios of measurement of syrup and water in the 2 types of beverage are 2 : 7 and 1: 5 respectively. Let’s calculate the ratio of measurement of syrup and water if 27 liters of the first beverage is mixed with 18 liters of the second.
Solution:
Given
I prepared two types of beverage in my house. The ratios of measurement of syrup and water in the 2 types of beverage are 2 : 7 and 1: 5 respectively.
The proportional part of the quantity of syrup in the 1st beverage is
= \(\frac{2}{2+7}=\frac{2}{9}\)
And the proportional part of the quantity of water is = \(\frac{7}{9}\)
The quantity of syrup in the first beverage is = \(\frac{2}{9} \times 27\)= 6
And the quantity of water is = \(\frac{7}{9} \times 27\) =21
The proportional part of the quantity of syrup of the second beverage is
= \(\frac{1}{6}\)
And the proportional part of water is = \(\frac{5}{6}\)
∴ The quantity of syrup in 181 of beverage of the second type is = 3 And the quantity of water is = 15
∴ The quantity of syrup in the new beverage is = 6 I + 3 I = 9
And the quantity of water is = 21 1 + 15 1 = 36
∴ In the new beverage the quantity of syrup : quantity of water is = 9 : 36 = 1 : 4.
Question 6. Let’s try to calculate in what ratio of the measurements of two beverage needs to be mixed so that the ratio of syrup and water will be 5 : 21.
Solution:
Let x I of first beverage is mixed with y I of second beverage.
∴ The quantity of syrup in x I of 1st beverage is = \(\frac{2}{9} \times X=\frac{2 x}{9}\)
And the quantity of water is = \(\frac{7}{9} \times x\)
= \(\frac{2 x}{9}\)
The quantity of syrup in y I of 2nd beverage is = \(\frac{1}{6} \times y\)
= \(\frac{y}{6}\)
And the quantity of water is = \(\frac{5}{6} \times y\)
= \(\frac{5y}{6}\)
∴ The quantity of syrup in the new mixture is = \(\frac{2 x}{9} 1+\frac{y}{6}\)
= \(\left(\frac{2 x}{9}+\frac{y}{6}\right)\)
And the quantity of water is = \(\frac{7 x}{9} 1+\frac{5 y}{6}\)
= \(\left(\frac{7 x}{9}+\frac{5 y}{6}\right)\)
B.T.P.,
= \(\frac{\frac{2 x}{9}+\frac{y}{6}}{\frac{7 x}{9}+\frac{5 y}{6}}=\frac{5}{21}\)
or, \(21\left(\frac{2 x}{9}+\frac{y}{6}\right)=5\left(\frac{5 y}{6}+\frac{7 x}{9}\right)\)
or, \(21\left(\frac{4 x+3 y}{18}\right)=5\left(\frac{14 x+15 y}{18}\right)\)
or, 21 (4x + 3y) = 5(14x + 15y)
or, 84x + 63y = 70x + 75y
or, 84x – 70x = 75y – 63y
or, 14x = 12y
or, \(\frac{x}{y}=\frac{12}{14}=\frac{6}{7}\)
∴ x : y=6 : 7
∴ If the two beverages are mixed up in the ratio of measures of 6 : 7, then the ratio of measures of syrup and water in the new beverage will be 5 : 21.
Question 8. My brother has prepared a beverage in a jug with syrup and water in a ratio of measurement of 3 : 1. Let’s work out what part of the drink should be removed and replaced by water so that the volume of syrup and water becomes equal.
Solution:
Given
My brother has prepared a beverage in a jug with syrup and water in a ratio of measurement of 3 : 1.
Let in the jug there is x units beverage. Of this y units beverage is taken out and the same quantity of water is mixed.
Quantity of syrup in x units beverage
= \(\frac{3}{4} \times x\) units = \(\frac{3 x}{4}\) units
And the quantity of water is = \(\frac{x}{4}\) units
The quantity of syrup in y units beverage
= \(\frac{3}{4} \times y\) units
= \(\frac{3 y}{4}\)
And the quantity of water is = \(\frac{y}{4}\) units
If y units are taken out from x units beverage,
syrup in the remaining beverage = \(\left(\frac{3 x}{4}-\frac{3 y}{4}\right)\) units
and the quantity of water is = \(\left(\frac{x}{4}-\frac{y}{4}\right)\)
Again, y units of water is added.
∴ Now quantity of water is = \(\left(\frac{x}{4}-\frac{y}{4}+y\right)\)
B.T.P,
= \(\frac{\frac{x}{4}-\frac{y}{4}+y}{\frac{3 x}{4}-\frac{3 y}{4}}=\frac{2}{1}\)
or, \(\frac{x}{4}-\frac{y}{4}+y=\frac{6 x}{4}-\frac{6 y}{4}\)
or, \(\frac{x}{4}-\frac{6 x}{4}=\frac{y}{4}-y-\frac{6 y}{4}\)
or, \(\frac{x-6 x}{4}=\frac{y-4 y-6 y}{4}\)
or, \(-\frac{5 x}{4}=-\frac{9 y}{4}\)
or, 5x = 9y
or, = \(y=\frac{5 x}{9}\)
∴ Total \(\frac{5}{9}\) part of the beverage will be removed and a 9 replaced by water with same quantity so that ratio becomes 2:1
Mixture Exercise
Question 1. The ratio of measurements of water and dettol in 36 liters of water is 5 : 1. Let’s work out what volume of water should be added to the mixture so that the ratio of measurements of water and dettol becomes 3:1.
Solution:
Given
The ratio of measurements of water and dettol in 36 liters of water is 5 : 1.
Ratio of water and dettol is = 5:1
Proportional part of water in the mixture
= \(\frac{5}{5+1}=\frac{5}{6}\)
Proportional part of dettol in the mixture
= \(\frac{1}{5+1}=\frac{1}{6}\)
∴ Quantity of water in 36 liters of the mixture
= \(\frac{5}{6} \times 36\)
= 30
∴ Quantity of dettol in 36 liters of the mixture
= \(\frac{1}{6} \times 36\)
= 6
Let after adding x liters dettol in the mixture, the ratio of quantities of dettol and water will be 3 : 1.
∴ Total quantity of dettol after adding x liters of dettol = (6 + x) I. The ratio of water and dettol in the new mixture = 30 : 6 + x.
B.T.P.
= \(\frac{30}{6+x}=\frac{3}{1}\)
or, 18+3x=30
or, 3x=30-18
or, \(x=\frac{12}{3}\)
or, x = 4
4 liters dettol should be added into the mixture.
Question 2. In a certain type of brass the ratio of measurements of Copper and Zinc is 5 : 2. Let’s work out what will be the ratio of Copper and Zinc in 25 kg of such brass if 4 kg of Copper is added to it.
Solution:
Given
In a certain type of brass the ratio of measurements of Copper and Zinc is 5 : 2.
Ratio of Copper and Zinc in the Brass = 5 : 2
Proportional part of Copper in the Brass
= \(\frac{5}{5+2}=\frac{5}{7}\)
Proportional part of Zinc in the Brass
= \(\frac{2}{5+2}=\frac{2}{7}\)
Quantity of Copper in 28 kg Brass
= \(\frac{5}{7} \times 28\) kg
= 20 kg
Quantity of Zinc in 28 kg Brass
= \(\frac{2}{7} \times 28\) kg
= 8kg
After adding 4 kg Copper, total quantity of Copper = (20 + 4) kg
= 24 kg
The ratio of Copper and Zinc in the new Brass = 24:8
= 3:1
Question 3. Brijan babu has made phenyl water solution of 60 liters in which the ratio of measurements of phenyl and water is 2 : 23. Let’s workout how much phenyl should be added to this solution so that the ratio of measurements of phenyl and water becomes 9 : 46.
Solution:
Given
Brijan babu has made phenyl water solution of 60 liters in which the ratio of measurements of phenyl and water is 2 : 23.
Ratio of phenyl and water in the mixture = 2 : 23
Proportional part of water in the mixture = \(\frac{2}{2+23}=\frac{2}{25}\)
Proportional part of phenyl in the mixture = \(\frac{23}{2+23}=\frac{23}{25}\)
The quantity of phenyl in 60 liters of the mixture
= \(\frac{2}{25} \times 60\)
= \(\frac{24}{5} I=4.8 I\)
Quantity of phenyl in 60 liters of the mixture
= \(\frac{23}{25} \times 60\)
= \(\frac{276}{5}\)
= 55.2
Let by adding x liters phenyl in the mixture, the ratio of water and phenyl will become 9 : 46.
∴ After adding x liters phenyl, the total quantity of phenyl = (4.8 + x)
Ratio of phenyl and water in the new mixture = (4.8 + x) : 55.2
B.T.P.,
(4.8 + x) : 55.2 = 9:46 .
or, \(\frac{4.8+x}{55.2}=\frac{9}{46}\)
or, 220.8 + 46x = 496.8
or, 46x = 496.8 – 220.8
or, 46x = 276.0
or, \(x=\frac{276}{46}\)
or, x = 6
After adding 6 liters phenyl in the mixture the ratio of water and phenyl will become 9 : 46.
Question 4. Amina bibi has prepared masonry mixture with sand and cement in a ratio of measurement 7 r 1. But after the brick work it is seen that 72 kg of mixture remains. She has added more cement with this mixture and the ratio of measurement of sand to cement becomes 6 :1. Let’s work out the total quantity of cement she has mixed.
Solution:
Given
Amina bibi has prepared masonry mixture with sand and cement in a ratio of measurement 7 r 1. But after the brick work it is seen that 72 kg of mixture remains. She has added more cement with this mixture and the ratio of measurement of sand to cement becomes 6 :1.
Ratio of sand and cement in the mixture =7:1
Proportional part of sand in the mixture
= \(\frac{7}{7+1}=\frac{7}{8}\)
Proportional part of cement in the mixture
= \(\frac{1}{7+1}=\frac{1}{8}\)
Quantity of sand in 72 kg mixture
= \(\frac{7}{8} \times 72\) kg = 63 kg
Quantity of cement in 72 kg mixture
= \(\frac{1}{8} \times 72\) kg = 9 kg
Let after adding x kg cement in the mixture the ratio of sand ant cement will be 6 : 1.
∴ Total quantity of cement after adding x kg cement = (9+x) kg
Ratio of sand and cement in the new mixture = 63 : (9 + x)
B.T.P.
= \(\frac{63}{9+x}=\frac{6}{1}\)
or, 54 + 6x = 63
or, 6x = 63 – 54
or, 6x = 9
or, x = \(\frac{9}{6}\)
or, x = 1.5
∴ 1.5 kg cement was added.
Question 5. The ratio of measurements of Copper, Zinc and Nickel ir German silver is 4 : 3 : 2 respectively. Let’s work out what weight (in kgs) of Zinc should be added to 54 kg of German silver, sc that the ratio of measurements becomes 6:5:3.
Solution:
Given
The ratio of Copper, zinc and Nickel in the German silver is =4:3:2
Quantity of Copper in 54 kg mixture
= \(\frac{4}{9} \times54\) kg
= 24 kg 1 6
Quantity of Zinc in 54 kg mixture
= \(\frac{3}{9} \times54\) kg
= 18 kg
Quantity of Nickel in 54 kg mixture
= \(\frac{2}{9} \times54\) kg
=12 kg
Ratio of Copper, Zinc and Nickel in the new German silver = 6:5:3
Proportional part of Copper in the new German silver = \(\frac{6}{14}\)
Proportional part of Zinc in the new German silver = \(\frac{5}{14}\)
Proportional part of Nickel in the new German silver = \(\frac{3}{14}\)
∴ In the new German silver the quantity of copper will be 24 kg but by adding Zinc the quantity of mixture will increase.
In mathematical language the problem is –
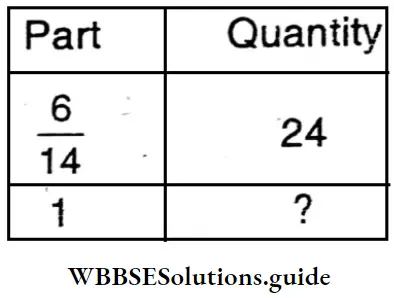
Here the proportion is direct.
∴ Total quantity of new German silver
= \(24 \times \frac{14}{6}\)
= 56 kg
∴ Zinc will be added = (56 – 54) kg
=2 kg
∴ 2kg Zinc should be added.
Question 6. In two different kinds of washing powder the ratios of measurement of soda and soap powder are 2 : 3 and 4 : 5. Let’s work out the part of the soap powder in the new washing powder which is prepared by mixing 10 kg of first soap powder with 18 kg of second soap powder.
Solution:
Given
In two different kinds of washing powder the ratios of measurement of soda and soap powder are 2 : 3 and 4 : 5.
In the first washing powder the ratio of soda arid soap powder = 2:3.
Proportional part of first washing powder in the soda
= \(\frac{2}{2+3}=\frac{2}{5}\)
Proportional part of soap powder in the first washing powder
= \(\frac{3}{2+3}=\frac{3}{5}\)
Quantity of powder in 10 kg of the 1st washing powder
= \(\frac{3}{5} ×10\) kg
= 6 kg
Ratio of soda and soap powder in the second washing powder = 4:5
Proportional part of soap powder in the 2 nd washing powder
= \(\frac{5}{4+5}=\frac{5}{9}\)
Quantity of soap powder in 18 kg of the 2nd washing powder
= \(\frac{5}{9} \times 18\)kg
= 10kg
Total quantity of soap powder by mixing both types of washing powder
= (6+10) kg = 16 kg
And the total quantity of washing power = (10 + 18) kg = 28 kg
Soap powder in new washing powder
= \(\frac{16}{28}\) part = \(\frac{4}{7}\) part
In new washing powder \(\frac{4}{7}\) part is soap powder.
Question 7. Two similar vessels contain \(\frac{1}{3}\) and \(\frac{1}{4}\)parts fruit juice. I filled water in the remaining empty part of these vessels and poured the juice mixed with water of the two vessels into another big vessel. Let’s work out the ratio of measurement of fruit and water in the new vessel.
Solution:
Given
Two similar vessels contain \(\frac{1}{3}\) and \(\frac{1}{4}\)parts fruit juice. I filled water in the remaining empty part of these vessels and poured the juice mixed with water of the two vessels into another big vessel.
Fruit juice in 1st vessel = \(\frac{1}{3}\) part
∴ Water in 1st vessel = \(\left(1-\frac{1}{3}\right)\) part
= \(\frac{2}{3}\)
Fruit juice in 2nd vessel = \(\frac{1}{4}\) part
Water in 2nd vessel
= \(\left(1-\frac{1}{4}\right) \text { part }=\frac{3}{4} \text { part }\)
Total quantity of fruit juice in new vessel
= \(\left(\frac{1}{3}+\frac{1}{4}\right)\) part
=\(\frac{4+3}{12} \text { part }=\frac{7}{12} \text { part }\) part
Total quantity of fruit juice in new vessel
= \(\left(\frac{2}{3}+\frac{3}{4}\right)\) part
= \(\frac{8+9}{12}\) part
= \(\frac{17}{12}\) part
The ratio of quantities of fruit juice and water in new vessel
= \(\frac{7}{12}: \frac{17}{12}\)
= 7 : 17
The ratio of quantities of fruit juice and water in new vessel = 7 : 17
Question 8. Reshmi Khatiin has filled 3 similar glasses of equal size with beverage. The ratios of measurements of water and syrup in these glasses are respectively 3 : 1, 5 : 3 and 9 : 7. I poured the beverage of these three glasses into a big vessel. Let’s workout the ratio of measurements of water and syrup in the new vessel.
Solution:
Given
Reshmi Khatiin has filled 3 similar glasses of equal size with beverage. The ratios of measurements of water and syrup in these glasses are respectively 3 : 1, 5 : 3 and 9 : 7. I poured the beverage of these three glasses into a big vessel.
Ratio of water and syrup in 1st glass = 3:1
Proportional part of water = \(\frac{3}{3+1}=\frac{3}{4}\)
And proportional part of syrup = \(\frac{1}{3+1}=\frac{1}{4}\)
Ratio of water and syrup in second glass = 5:3
Proportional part of water = \(\frac{5}{5+3}=\frac{5}{8}\)
Proportional part of syrup = \(\frac{3}{5+3}=\frac{3}{8}\)
Ratio of water and syrup in third glass = 9:7
Proportional part of water = \(\frac{9}{9+7}=\frac{9}{16}\)
Proportional part of syrup = \(\frac{7}{9+7}=\frac{7}{16}\)
The beverages of all three glasses are poured into a big vessel.
∴ Water in the big vessel
= \(\left(\frac{3}{4}+\frac{5}{8}+\frac{9}{16}\right) \text { part }\)
= \(\frac{12+10+9}{16} \text { part }\)
= \(\frac{13}{16} \text { part }\)
Syrup in the big vessel
= \(\left(\frac{1}{4}+\frac{3}{8}+\frac{7}{16}\right) \text { part }\)
= \(\frac{4+6+7}{16} \text { part }\)
= \(\frac{17}{16} \text { part }\)
Ratio of syrup and water in the new vessel
= \(\frac{31}{16}: \frac{17}{16}\)
= 31 : 17
Ratio of syrup and water in the new vessel = 31 : 17
Question 9. Two different types of brass contain Copper and Zinc in the ratios of measurement respectively 8 : 3 and 15:7. Let’s workout in what ratio of measurement of Copper and Zinc will be if these two types of brass are mixed together in the ratio of measurement 5:2.
Solution:
Given
Two different types of brass contain Copper and Zinc in the ratios of measurement respectively 8 : 3 and 15:7.
Let 5 x kg of first kind of brass is mixed with 2 x kg of second kind of brass. The ratio of Copper and Zinc in first brass =8:3.
Sum of ratio = 8 + 3 = 11
Quantity of Copper in 5 x kg of first brass
= \(\frac{8}{11} \times 5 x=\frac{40 x}{11}\) kg
Quantity of Zinc in 5 x kg of the first brass
= \(\frac{3}{11} \times 5 x=\frac{15 x}{11} \mathrm{~kg}\) kg
Ratio of copper and Zinc in the second brass = 15:7
Sum of ratio = 15 + 7 = 22
Quantity of Copper in 2 x kg of the second brass
= \(\frac{15}{22}\) 2x kg
= \(\frac{15 x}{11} \cdot \mathrm{kg}\)
Quantity of Copper in 2 x kg of the second brass
= \(\frac{7}{22}\) 2x kg
= \(\frac{7 x}{11} \mathrm{~kg}\) kg
Total quantity of Copper in the new brass
= \(\left(\frac{40 x}{11}+\frac{15 x}{11}\right)\) kg
= \(\left(\frac{40 x+15 x}{11}\right)\) kg
= \(\frac{55 x}{11} \mathrm{~kg}=5 x\) kg
Total quantity of Zinc in the new brass
= \(\left(\frac{15 x}{11}+\frac{7 x}{11}\right)\) kg
= \(\left(\frac{15 x+7 x}{11}\right)\) kg
= \(\frac{22 x}{11} \mathrm{~kg}=2 \mathrm{x}\) kg
So, the ratio of Copper and Zinc in the new brass = 5x : 2x
= 5:2
The ratio of Copper and Zinc in the new brass = 5:2
Question 10. Two different types of stainless steel contain chromium and steel in the ratio of measurement respectively 2:11 and 5 : 21. Let’s workout in what proportion these two types of steel should be mixed so that the ratio of measurement of chromium and steel becomes 7 : 32.
Solution:
Given
Two different types of stainless steel contain chromium and steel in the ratio of measurement respectively 2:11 and 5 : 21.
Let by adding x kg of first stainless steel with y kg of second stainless steel the ratio of chromium and steel in the new stainless steel will be
Ratio of chromium and steel in the first stainless steel = 2:11
Proportional part of chromium = \(\frac{2}{2+11}=\frac{2}{13}\)
Proportional part of steel = \(\frac{11}{2+11}=\frac{11}{13}\)
Chromium in x kg of first stainless steel =\(\frac{2 x}{13}\) kg
Steel in x kg of first stainless steel = \(\frac{11 x}{13}\) kg
Ratio of chromium and steel in the second stainless steel = 5:21
Proportional part of chromium = \(\frac{5}{5+21}=\frac{5}{26}\)
Proportional part of steel = \(\frac{21}{5+21}=\frac{21}{26}\)
Chromium in y kg of second stainless steel
=\(\frac{5}{26} \times y \mathrm{~kg}=\frac{5 y}{26} \mathrm{~kg}\)
Total quantity of chromium in new stainless steel
= \(\left(\frac{2 x}{13}+\frac{5 y}{26}\right)\) kg
= \(\frac{4 x+5 y}{26}\) kg
Total quantity of steel in new stainless steel
= \(\left(\frac{11 x}{13}+\frac{21 y}{26}\right)\) kg
= \(\frac{22 x+21 y}{26}\) kg
B.T.P.,
= \(\frac{4 x+5 y}{26}: \frac{22 x+21 y}{26}\) = 7:32
or, (4x + 5y) : (22x + 21y) = 7:32
or, \(\frac{4 x+5 y}{22 x+21 y}=\frac{7}{32}\) = 7:32
or, 154x + 147y = 128x + 160y
or, 154x – 128x = 160y – 147y
or, 26x = 13y
or, \(\frac{x}{y}=\frac{13}{20}\)
or, \(\frac{x}{y}=\frac{1}{2}\)
or, x : y = 1 : 2
If both types of stainless steel are mixed in the ratio 1 : 2, the ratio of chromium and steel in the new stainless steel will be 7 : 32.
Question 11. In a vessel of beverage the ratio of measurement of syrup and water is 5 : 2. Let’s work out what part of the drink should be removed and replaced by water so that the volumes of syrup and water become equal.
Solution:
Given
In a vessel of beverage the ratio of measurement of syrup and water is 5 : 2.
Ratio of water and syrup in the beverage = 5:2
Proportional part of syrup = \(\frac{5}{5+2}=\frac{5}{7}\)
Proportional part of water = \(\frac{2}{5+2}=\frac{2}{7}\)
Let x part of the beverage is taken out and is replaced by the same quantity of water so that the ratio of syrup and water will be equal.
Syrup in x part of the beverage
= \(\frac{5}{7} \times x\) part = \(\frac{5 x}{7}\) part
Water in x part of the beverage
= \(\frac{2}{7} \times x\) part = \(\frac{2 x}{7}\) part
Syrup in remaining part of the beverage
= \(\left(\frac{5}{7}-\frac{5 x}{7}\right)\) part
= \(\frac{5-5 x}{7}\) part
Water in syrup = \(\left(\frac{2}{7}-\frac{2 x}{7}+x\right)\) part
= \(\frac{2-2 x+7 x}{7}\) part
= \(\frac{2+5 x}{7}\) part
B.T.P.,
= \(\frac{2+5 x}{7}=\frac{5-5 x}{7}\)
of, 2 + 5x = 5 – 5x
or, 5x + 5x = 5 – 2
or, 10x = 3
or, \(x=\frac{3}{10}\)
If \(\frac{3}{10}\) part of this beverage is taken out and replaced by the same quantity of water then the ratio syrup and water will be equal.
Question 12. Let’s see the table below write in mathematical language and try to find out the answer.
Solution:
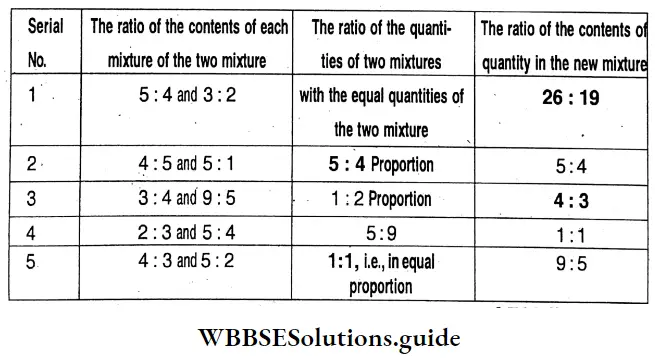
Question 13. There are 3 kinds of liquids in a beverage of 700 liters. The ratio of measurements of the first and second liquid is 2 : 3 and the ratio of measurements of the second and the third liquid is 4:3. Let’s work out the ratio in which the first and second liquid should be mixed so that the ratio of measurement of the three liquid^ may become 6 : 5 : 3 in the same beverage.
Solution:
Given
There are 3 kinds of liquids in a beverage of 700 liters. The ratio of measurements of the first and second liquid is 2 : 3 and the ratio of measurements of the second and the third liquid is 4:3.
Ratio of first and second liquids in the mixture = 2:3
= 2×4 : 3×4 = 8 : 12
∴ Ratio of first second and third liquids in the mixture = 8 : 12 : 15
Total mixture = 700 I
∴ Amount of 1st liquid in the mixture = \(\frac{8}{35} \times 700\) = 160
Amount of 2nd liquid in the mixture = \(\frac{12}{35} \times 700\) = 240
Amount of 3rd liquid in the mixture = \(\frac{15}{35} \times 700\) = 300
Ratio of first second and third liquids in the new mixture =6 : 5 : 3
= 6×100 : 5×100 : 3×100
= 600 : 500 : 300
∴ Amount of first liquid to be taken = (600 – 160) = 440
Amount of second liquid to be taken = (500 – 240) = 260
440 of first and 260 of second mixture should be mixed.
Question 14. In a certain quantity of syrup the ratio of measurements of water and the rest part of the syrup is 89 : 11. Let’s workout what quantity of water should be added in 22 liters of the syrup so that the ratio of measurement of syrup and the rest part of the liquid becomes 90 : 10.
Solution:
Given
In a certain quantity of syrup the ratio of measurements of water and the rest part of the syrup is 89 : 11.
Ratio of water and the rest part of the syrup = 89 : 11
Proportional part of water in the syrup
= \(\frac{89}{89+11}=\frac{89}{100}\)
Proportional part of rest of the syrup in the syrup
= \(\frac{11}{89+11}=\frac{11}{100}\)
∴ Quantity of water in 22 liters of the syrup
= \(\frac{89}{100} \times 22\)
= \(\frac{979}{50}\)
Quantity of rest of syrup in 22 liters of the syrup
= \(\frac{11}{100} \times 22\)
= \(\frac{121}{50}\)
Let by adding x liters syrup the ratio of water and the rest part is 9:1
B.T.P.,
= \(\left(\frac{979}{50}+x\right): \frac{121}{50}=90: 10\)
or, \(\left(\frac{979+50 x}{50}\right): \frac{121}{50}=90: 10\)
or, (979+50x) : (121 = 9 : 1
or, \(\frac{979+50 x}{121}=\frac{9}{1}\)
or, 979+50x = 1089
or, 50x = 1089-979
or, 50x = 110
or, x = \(\frac{110}{50}\)
or, x = \(\frac{11}{5}\)
or, x = 2.2
In 22 liters of this syrup, by adding 2.2 liters water, the ratio of water and the rest part of syrup becomes 90 : 10.
Question 15. The ratio of the volumes of three bottles is 5 : 3 : 2. These three bottles are filled will the solution of phenyl and water. The ratios of measurement of phenyl and water in three bottles each are 2 : 3, 1 : 2 and 1 : 3 respectively. \(\frac{1}{3}\)part of the first bottle,\(\frac{1}{2}\) part of the second bottle and \(\frac{2}{3}\) part of the third bottle are mixed together now. Let’s work out the ratio of phenyl and water in the new solution.
Solution:
Given
The ratio of the volumes of three bottles is 5 : 3 : 2. These three bottles are filled will the solution of phenyl and water. The ratios of measurement of phenyl and water in three bottles each are 2 : 3, 1 : 2 and 1 : 3 respectively. \(\frac{1}{3}\)part of the first bottle,\(\frac{1}{2}\) part of the second bottle and \(\frac{2}{3}\) part of the third bottle are mixed together now.
Let the volumes of the three bottles are respectively : 5x I, 3x I and 2x I
Ratio of water and phenyl in the first bottle =2 : 3
Sum of ratio =2 + 3 = 5
∴ Amount of phenyl in the bottle first
=\(\frac{2}{5} \times 5 x \times \frac{1}{3} \quad I=\frac{2 x}{3}\)
Amount of water in the first bottle
= \(\frac{3}{5} \times 5 \times \times \frac{1}{3} I=\times I\)
Amount of phenyl and water in the second bottle = 1:2
Sum of ratio = 1+2 = 3
Amount of phenyl in the second bottle
= \(\frac{1}{3} \times 3 \times \times \frac{1}{2} \mid=\frac{x}{2}\)
Amount of water in the second bottle
= \(\frac{2}{3} \times 3 \times \times \frac{1}{2} \quad I=x I\)
Ratio of water and phenyl in the third bottle = 1:3
Sum of ratio = 1+3+4
Amount of phenyl in the third bottle
= \(\frac{1}{4} \times 2 x \times \frac{2}{3} \quad \mid=\frac{x}{3}\)
Amount of water in the third bottle
= \(\frac{3}{4} \times 2 x \times \frac{2}{3} 1=x\)
Ratio of phenyl and water in the new mixture
= \(\left(\frac{2 x}{3}+\frac{x}{2}+\frac{2 x}{3}\right):(x+x+x)\)
= \(\frac{4 x+3 x+2 x}{6}: 3 x\)
= \(\frac{9 x}{6}: 3 x\)
= \(\frac{9}{6}: 3\)
= \(\frac{9}{6} \times 6: 3 \times 6=9: 18\)
= 1 : 2
The ratio of phenyl and water in the new solution = 1 : 2

