Time And Work
There are 18 looms in Mansur’s factory in Shantipur. But last week 3 looms were closed. So Last week only 165 dhotis and sarees were weaved. This week all the looms are running.
Question 1. Let’s calculate in a proportional method how many dhotis and sarees will be weaved this week in Mansur’s factory.
Solution:
Given
There are 18 looms in Mansur’s factory in Shantipur. But last week 3 looms were closed. So Last week only 165 dhotis and sarees were weaved. This week all the looms are running.
The problem in mathematical language is
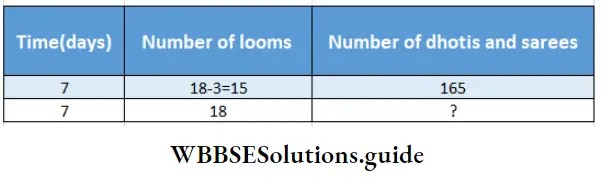
If the time is constant and the number of looms increases or decrease, then the number of dhotis and sarees will Increase or Decrease (increase/decrease).
∴ There is a direct proportion between the number of looms and the number of dhotis and sarees.
∴ The direct proportion is –
15 : 18:: 165:? (Required number of dhotis and sarees)
∴ The required number of dhotis and sarees is = \(\frac{165 \times 18}{15}\) = 198.
So in this week, all looms being run, 198 dhotis and sarees will be made.
Read and Learn More WBBSE Solutions For Class 8 Maths
Question 2. If all the looms run, calculate in how many days 594 dhotis and sarees will be made.
Solution:
In mathematical language, the problem is –
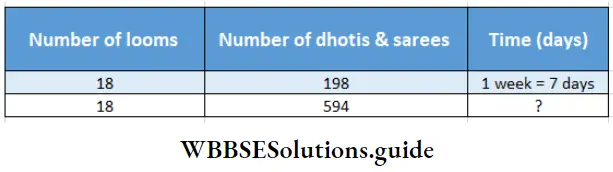
The number of looms being constant, as the number of dhoti-sarees increases/decreases, the required time will Increase or Decrease (increase / decrease)
∴ The direct proportion is –
198 : 594:: 7:?
∴ Required time = \(\frac{594 \times 18}{198}\) days = 21 days
| Class 8 General Science | Class 8 Maths |
| Class 8 History | Class 8 Science LAQs |
| Class 8 Geography | Class 8 Science SAQs |
| Class 8 Maths | Class 8 Geography |
| Class 8 History MCQs | Class 8 History |
“WBBSE Class 8 Maths Chapter 17 solutions, Time and Work”
Question 3. If all the looms, i.e., 18 looms would run, 594 dhotis and sarees can be woven in 21 days. Let’s calculate how many looms will run to weave 594 dhotis and sarees in 14 days.
Solution:
Given
If all the looms, i.e., 18 looms would run, 594 dhotis and sarees can be woven in 21 days.
In mathematical language the problem is
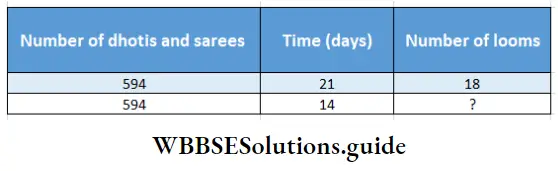
If the number of dhotis and sarees is constant then the number of looms will Increase (increase/decrease) with the increase of time and the number of looms will Decrease (increase / decrease) with the decrease of time.
The number of looms and time are inversely proportional.
The inverse proportion is –
21 : 14:: ? (required number of looms) : 18 ∴ 14 : 21:: 18 : ? (required number of looms)
∴ Required number of looms = \(\frac{21\times18}{14}\) = 27
∴ In 21 days, to weave 594 dhotis and sarees 27 looms, i.e., (27 – 18) = 9 more looms will run.
So we see that there is a relation between time and work in Monsur’s loom. Let’s write the relation between the required time, the amount of work, and the number of workers is the chart given below.

Question 4. In a village of Niamatpur 15 men can cultivate 10 bighas of land in a week. Let’s calculate how many men can cultivate 18 bighas of land in a week.
Solution:
Given
In a village of Niamatpur 15 men can cultivate 10 bighas of land in a week.
In mathematical language the problem is –

As work increases or decreases, the number of workers will, time being constant, Increase or Decrease (increase/decrease).
The amount of work and the number of workers are in Direct (direct / inverse) relation.
Let’s calculate in the proportional method.
So, 10 : 18 :: 15 : ? (required number of workers)
∴ Required number of people = \(\frac{15 \times 18}{10}\) = 27 people
∴ 27 workers can cultivate 18 bighas of land in a week.
Let’s do the above problem by unitary method.
“Class 8 WBBSE Maths Chapter 17 solutions, Time and Work study material”
Question 5. 250 volunteers of Bakultala gram panchayat have constructed half of a dam in 24 days. Let’s calculate how many men will be needed to construct the rest half part in 20 days.
Solution:
Given
250 volunteers of Bakultala gram panchayat have constructed half of a dam in 24 days.
The problem in mathematical language is –
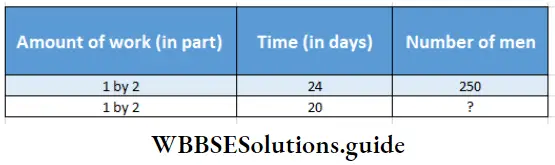
Keeping work constant, with an increase or decrease of time, the number of workers will respectively d] or CH (increase/decrease).
∴ The time and the number of workers are in (direct/inverse) relation.
∴ The inverse proportion is
24 : 20 :: ? (the required number of workers) : 250
∴ 20 : 24 :: 250 : ? (the required number of workers) .
∴ The required number of workers = \(\frac{250 \times 24}{20}\)
So, additional workers 300-250 = 50 need to be absorbed in the team of workers. Let’s calculate this problem by unitary method.
Time And Work Exercise 17.1
Question 1. In Aman’s factory 216 parts of machine are made in 3 days. Let’s calculate how many parts of machine will be made in 7 days.
Solution:
Given
In Aman’s factory 216 parts of machine are made in 3 days.
In mathematical language the problem is –
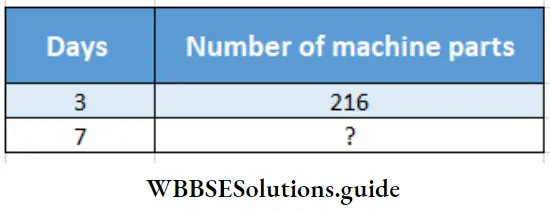
If number of days increases or decreases, number of machine parts will increase or decrease.
∴ Days and number of machine parts are in direct proportion.
∴ 3 : 7 :: 216 : ?
or, \(\frac{3}{7}=\frac{216}{?}\)
or, Required number of parts = \(\frac{7 \times 216}{3}\) = 504
Question 2. In loom factory at Atpur 12 looms can weave 380 sarees. During the puja season for doing more work 3 looms have been established. Let’s make a proportion and calculate how many sarees can be woven in this month.
Solution:
Given
In loom factory at Atpur 12 looms can weave 380 sarees. During the puja season for doing more work 3 looms have been established.
In mathematical language the problem is –
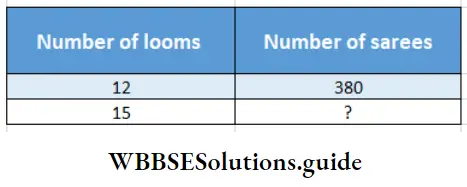
If number of looms increases, number of sarees will increase.
∴ Number of looms and number of sarees are in direct proportion.
∴ 12 : 15 :: 380 : ?
or, Required number of sarees = \(\frac{15 \times 380}{12}\)
Question 3. Let’s make the story of mathematics and find out the relation seeing the above chart.
Solution:
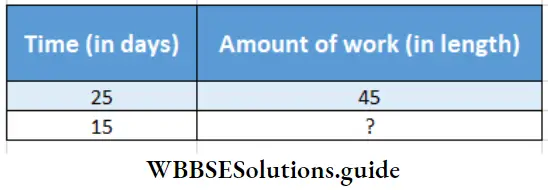
In a factory a given number of looms can weave 45 m cloth in 25 days, in 15 days the same number of looms will weave how much cloth?
Relation : If number of days increases, length of cloth will increase.
∴ Days and length of cloth are in direct proportion.
∴ 25 : 15 :: 45 : ?
or, Length of cloth woven in 15 days =\(\frac{15 \times 45}{25}\) = 27 m
Question 4. We can see after 15 days of digging a canal of 1200 metre length, 3/4 parts of the canal have been dug. Let’s calculate how many days are needed to dig the rest of the part.
Solution:
Given
We can see after 15 days of digging a canal of 1200 metre length, 3/4 parts of the canal have been dug.
Length of the canal dug in 15 days
Length of remaining part of canal = (1200 – 900) = 300 m
In mathematical language the problem is –
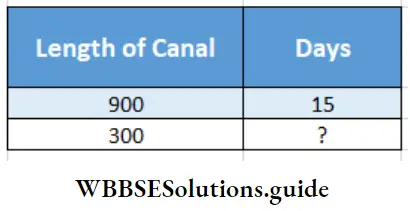
Relation : If length of canal increases, days will increase.
∴ Length of canal and days are in direct relation.
∴ 900 : 300 :: 15 : ?
or, \(\frac{900}{300}=\frac{15}{?}\)
∴ Required days = \(\frac{300 \times 15}{900}\)
Question 5. 3 tractors can plough 18 bighas in a day. By rule of three method let’s calculate how many bighas can be ploughed in a day.
Solution:
Given
3 tractors can plough 18 bighas in a day.
In mathemetical language the problem is –
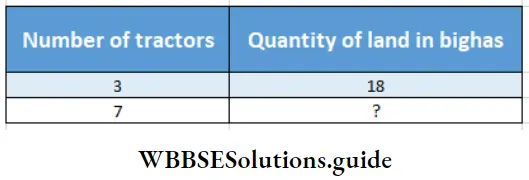
Relation : If number of tractors increases, quantity of land will increase.
∴ Number of tractors and quantity of land are in direct proportion.
or, Required quantity of land = g Bighas = 42 Bighas
Question 6. In Kusum’s factory 35 men can cast 10 ton iron parts in a week. The owner has got an order of casting 14 ton iron parts in a week. Let’s find out the proportion and calculate how many new men will be needed.
Solution.
Given
In Kusum’s factory 35 men can cast 10 ton iron parts in a week. The owner has got an order of casting 14 ton iron parts in a week.
In mathematical language the problem is –
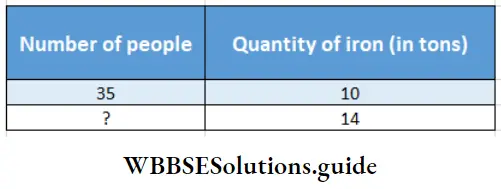
Relation : If quantity of iron increases, number of people will increase.
∴ Quantity of land and number of people are in direct proportion.
∴ \(\frac{10}{14}=\frac{35}{?}\)
or, Required number of people = \(\frac{14 \times 35}{10}\) = 49
Number of extra people = (49 – 35) = 14
So 14 more men will be appointed.
Question 7. Let’s make the story in mathematical language and find out the relation seeing the above chart.
Solution:

If 9 people make 6 cycles every day then 72 people will make how many cycles?
Relation : If the number of people increases, amount of work will increase.
∴ Number of people and number of cycles are in direct proportion.
∴ 9 : 72 :: 6 : ?
or, \(\frac{9}{72}=\frac{6}{?}\)
or, Required number of cycles = \(\frac{72 \times 6}{9}\) = 48
Question 8. A pond will be dug in our locality. 24 men need 12 days to cut that pond. Let’s find out the proportion and find relation how many men will be needed to dig that pond in 8 days.
Solution:
Given
A pond will be dug in our locality. 24 men need 12 days to cut that pond.
In mathematical language the problem is –
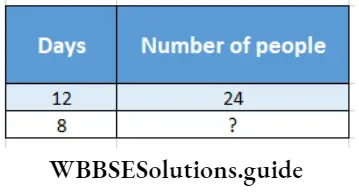
Relation : If days decrease, number of people will increase.
∴ Days and number of people are in inverse proportion.
∴ \(\frac{12}{8}=\frac{?}{24}\)
∴ Required number of men = \(\frac{12 \times 24}{8}\) = 36
To dig that pond in 8 days, more men will be needed.
Question 9. 5 members in a bulb manufacturing co-operative factory can make 10000 bulbs in 12 days. Based on a sudden order, 10000 bulbs have to be made in 9 days. Let’s calculate how many extra members will be appointed to supply the bulbs according to the agreement.
Solution:
Given
5 members in a bulb manufacturing co-operative factory can make 10000 bulbs in 12 days. Based on a sudden order, 10000 bulbs have to be made in 9 days.
In mathematical language the problem is –
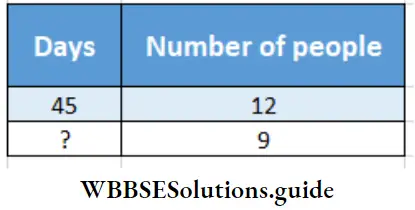
Relation : If days decrease, number of people will increase.
∴ Days and number of people are in inverse proportion.
∴ \(\frac{12}{9}=\frac{?}{45}\)
∴ Required number of people = \(\frac{12 \times 45}{9}\) = 60
More number of members = (60-45) = 15. To complete the work in time, 15 more members will be appointed.
“WBBSE Class 8 Maths Chapter 17, Time and Work solved examples”
Question 10. 250 men need 18 days to dig a pond of 50 metre length and 35 metre breath. Let’s calculate how many days will be needed by 300 men to dig a pond of 70 metre length and 40 metre breadth of the same depth.
Solution:
Given
250 men need 18 days to dig a pond of 50 metre length and 35 metre breath.
Relation : If days decrease, number of people will increase.
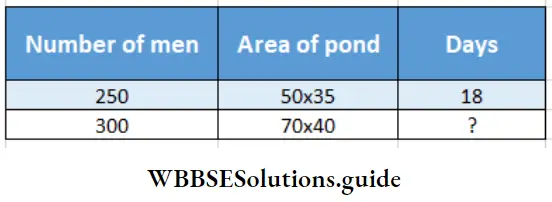
Relation : If number of men increases, days will decrease and if area of pond increases, days will increase. So number of people and days are in inverse proportion and area of pond and days are in direct proportion.
∴ Required number of days To dig this kind of pond of length 70 m and breadth 40 m it will take 300 people days.
Question 11. Anawarabibi and Mihir uncle started to plaster three rooms of same size. But Harun. chacha, Anawarabibi and Mihir uncle finished the work in 10 days, 12 days and 15 days respectively. If the three members worked together in one room, the work would finish in less time. How will we calculate the number of days for plastering 1 room where three men work together?
Solution:
Given
Anawarabibi and Mihir uncle started to plaster three rooms of same size. But Harun. chacha, Anawarabibi and Mihir uncle finished the work in 10 days, 12 days and 15 days respectively. If the three members worked together in one room, the work would finish in less time.
Let’s see how many parts of the work was done by every one in a day.
Haran chacha plasters 1 room in 10 days.
Haran chacha plasters \(\frac{1}{10}\) part of the total work in 1 day.
Anawarabibi plasters 1 room in 12 days.
Anawarabibi plasters \(\frac{1}{12}\) part of the total work in 1 day.
Mihir uncle plasters 1 room in 15 days.
Mihir uncle plasters \(\frac{1}{15}\) part of the total work in* 1 day.
∴ Three men together plaster part of a room in 1 day
= \(\frac{1}{10}\) part + \(\frac{1}{10}\) part + \(\frac{1}{10}\) part
= \(\frac{6+5+4}{60}\) part
= \(\frac{15}{60}\) part
= \(\frac{1}{4}\) part
∴ Three of them together do \(\frac{1}{4}\) part of the total work in a day.
∴ The total work, i.e., 1 part is done in 1 ÷ \(\frac{1}{4}\) = 4 days.
∴ If three of them work, together, then they can complete the work in 4 days.
Question 12. Let’s calculate the number of days Mihlr uncle takes to complete the remaining \(\frac{1}{5}\) part of the work.
Solution:
Given
\(\frac{1}{5}\)Mihir uncle does 1 part in 15 days.
Mihir uncle does \(\frac{1}{5}\) part in = \(15 \times \frac{1}{5}\) =3 days.
∴ Mihir uncle .alone completes the rest of the work in 3 days.
∴ If the work goes on such way, the required time to complete the work is = 2+2+4=7 days.
Question 13. Let’s calculate the part of the total work done by each of the if the work would go on such way.
Solution:
Harunchacha did the \(\left(\frac{1}{10} \times 2\right)\) part = \(\frac{1}{5}\) part of the total work.
Anawarabibi did the \(\left(\frac{1}{12} \times 4\right)\) part = \(\frac{1}{3}\) part of the total work.
Mihir uncle did the \(\left(\frac{1}{15} \times 7\right)\) part = \(\frac{7}{15}\) part of the total work. 15
Question 14. Bulu and Tathagata can do a work separately in 20 days and 30 days respectively. After working 7 days together both of them left away. Then Tatai came and completed the rest of the work alone in 10 days. Let’s make proportion and calculate how many days Tatai will take to complete the work alone.
Solution:
Given
Bulu and Tathagata can do a work separately in 20 days and 30 days respectively. After working 7 days together both of them left away. Then Tatai came and completed the rest of the work alone in 10 days.
Let’s calculate the remaining part of the total work after 7 days when Bulu and Tathagata left.
Bulu alone does \(\frac{1}{20}\) part in 1 day.
Tathagata alone does \(\frac{1}{30}\) part in 1 day.
∴ Together they do \(\left(\frac{1}{20}+\frac{1}{30}\right)\) part in 1 day.
= \(\frac{3+2}{60} \text { part }=\frac{5}{60} \text { part }=\frac{1}{12} \text { part }\)
∴ Bulu and Tathagata do =\(\frac{1}{12}\) part × 7 = \(\frac{7}{12}\) part in 7 days.
∴ After 7 days when Bulu and Tathagata left the remaining work is
= \(\left(1-\frac{7}{12}\right) \text { part }=\frac{5}{12} \text { part }\)
Tatai does the remaining \(\frac{5}{12}\) part in 10 days.
∴ The problem in mathematical language is
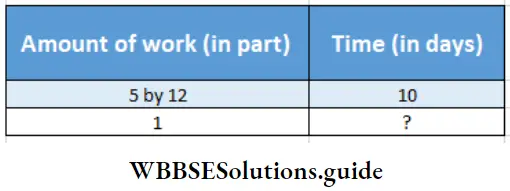
If the amount of work increases or decreases, the required time will (increase/decrease) Increase or Decrease.
∴ The amount of work and time are in Direct (direct/inverse)proportion.
The direct proportion is
= \(\frac{5}{12}\) : 1 : 10 : ?
∴ Required time days = \(\frac{10 \times 1}{\frac{5}{12}}\) days= \(10 \times \frac{12}{5}\) = 24 days
∴ Tatai alone will do the work in 24 days.
“WBBSE Class 8 Time and Work solutions, Maths Chapter 17”
Question 15. An empty tank is filled up with two pipes separately in 12 minutes and 15 minutes respctively. Let’s calculate the time required to fill up the half full tank while two pipes are opened together.
Solution:
Given
An empty tank is filled up with two pipes separately in 12 minutes and 15 minutes respctively.
It takes 1 minute to fill up \(\frac{1}{12}\) part of the empty tank by the first pipe.
By the second pipe it takes 1 minute to fill up \(\frac{5}{12}\) part of the empty tank.
∴ If the two pipes are opened together, it takes 1 minute to fill up the \(\left(\frac{1}{12}+\frac{1}{15}\right)\) part
= \(\frac{5+4}{60} \text { part }\)
= \(\frac{9}{60} \text { part }=\frac{3}{20} \text { part }\)
Half of the tank is full.
∴ Two pipes together will fill \(\left(1-\frac{1}{2}\right)\) part = \(\frac{1}{2}\) part of the tank.
Two pipes together fill \(\frac{3}{20}\) part of the tank in 1 minute.
Two pipes together fill 1 part in 1× \(\frac{20}{3}\) minute.
Two pipes together fill \(\frac{1}{2}\) part in \(1 \times \frac{20}{3} \times \frac{1}{2}\) minute
= \(\frac{10}{3}\) minute = \(3 \frac{1}{3}\) minute
= 3 minute 20 seconds.
Let’s calculate using proportion. ,
∴ The problem in mathematical language is –
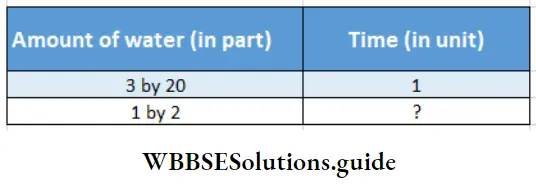
The amount of water and time are in Direct (direct/inverse) proportion.
∴ Using direct proportion, we get –
= \(\frac{3}{20}: \frac{1}{2}:: 1: ? \)(Required time) –
∴ Required time = \(1 \times \frac{1}{2} \times \frac{20}{3}\)
= \(\frac{10}{3}\) minutes = 3 minutes 20 seconds.
The time required to fill up the half full tank while two pipes are opened together = 3 minutes 20 seconds.
Time And Work Exercise 17.2
Question 1. Priya and Debu individually complete a work in 10 hours and 12 hours respectively. If they do the work together, let’s calculate in how many hours they will complete the work.
Solution:
Given
Priya and Debu individually complete a work in 10 hours and 12 hours respectively.
Priya can do \(\frac{1}{10}\) part of the in 1 hour. Debu cah do \(\frac{1}{12}\) part in 1 hour.
∴ Both can do \(\frac{11}{60}\) part of the work in 1 hour.
Both can do 1 part work in \(1 \div \frac{11}{60}\) hours.
= \(\frac{60}{11}\)
= \(5 \frac{5}{11}\)
If they work for \(5 \frac{5}{11}\) hours, the work will be completed.
Question 2. My elder brother, my elder sister and me together will paint our windows. My elder brother, my elder sister and me can complete the work separately in 12, 4 & 6 days respectively. If we do the work together then let’s calculate’ and write how many days we will take to complete the work.
Solution:
Given
My elder brother, my elder sister and me together will paint our windows. My elder brother, my elder sister and me can complete the work separately in 12, 4 & 6 days respectively.
My sister can do \(\frac{1}{12}\) part in 1 day.
My brother can do \(\frac{1}{4}\) part in 1 day. I can do \(\frac{1}{6}\) part in 1 day.
Three of us can do \(\left(\frac{1}{12}+\frac{1}{4}+\frac{1}{6}\right)\) part = \(\frac{1+3+2}{12}\) part in 1 day.
= \(\frac{6}{12} \text { part }\)
= \(\frac{1}{2} \text { part }\)
∵ Three of us can do \(\frac{1}{2}\) part in 1 day.
∴ Three of us can do 1 part in \(1 \div \frac{1}{2}\) days = 2 days.
If the three of us work together, then in 2 days we will complete the work.
Question 3. Abani and Anawar complete a work separately in 20 and 25 days respectively. After 10 days of their working together, they both left; then Sukhen came and completed the remaining work in 3 days. If Sukhen alone would do the work, let’s calculate how many days he would take to complete the work.
Solution:
Given
Abani and Anawar complete a work separately in 20 and 25 days respectively. After 10 days of their working together, they both left; then Sukhen came and completed the remaining work in 3 days.
Abani works \(\frac{1}{20}\) part in 1 day. Anawar works \(\frac{1}{25}\) part in 1 day.
Both of them together can do \(\left(\frac{1}{20}+\frac{1}{25}\right)\) part in 1 day
= \(\frac{5+4}{100} \text { part }\)
= \(\frac{9}{100} \text { part }\)
∴ Both of them together can do in 10 days = \(10 \times \frac{9}{100} \text { part }\)
= \(\frac{9}{10} \text { part }\)
Remaining work = \(\left(1-\frac{9}{10}\right) \text { part }\)
Remaining work = \(\frac{10-9}{10} \text { part }=\frac{1}{10} \text { part }\)
Remaining work = Sukhen does \(\frac{1}{10}\)part in 3 days.
∴ Sukhen does 1 part in 3 x 10 days.
∴ Sukhen does 1 part in 30 days. If Sukhen works alone, then he will complete the work in 30 days.
Question 4. There are two pipes for taking water from the municipality water tank. The tank can be made empty in 4 hours by the two pipes separately. If both the pipes remain opened, let’s calculate when the full tank will be empty.
Solution:
Given
There are two pipes for taking water from the municipality water tank. The tank can be made empty in 4 hours by the two pipes separately. If both the pipes remain opened
Both pipes will together empty
Both pipes can empty part in 1 hour.
= \(\left(\frac{1}{4}+\frac{1}{4}\right) \text { part }\)
= \(\frac{1+1}{4} \text { part }\)
= \(\frac{2}{4} \text { part }\)
= \(\frac{1}{2} \text { part }\)
∵ Both pipes can empty \(\frac{1}{2}\)part in 1 hour.
∴ Both pipes can empty 1 part in 2 hours. If both pipes are opened then in 2 hours the full tank will be empty.
“Class 8 WBBSE Maths Chapter 17, Time and Work easy explanation”
Question 5. In our tank there are 3 pipes. With these three pipes separately the tank can be filled up in 18, 21 and 24 hours respectively
1. If the 3 pipes remain open together, let’s make proportion and calculate when the tank will be filled up with water.
Solution:
Given
In our tank there are 3 pipes. With these three pipes separately the tank can be filled up in 18, 21 and 24 hours respectively
If the three pipes remain open then in 1 hour the tank will fill up
= \(\left(\frac{1}{18}+\frac{1}{21}+\frac{1}{24}\right)\) part
= \(\frac{28+24+21}{504}\) part
= \(\frac{73}{504}\) part
In mathematical language the problem is
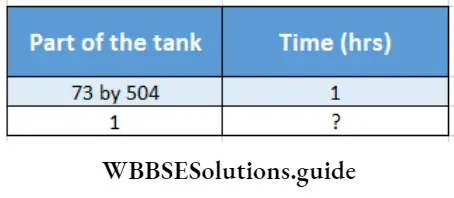
If part of the tank increases, time will increase.
∴ Here is direct proportion.
∴ \(\frac{\frac{73}{504}}{1}=\frac{1}{?}\)
or, \(\frac{73}{504}=\frac{1}{?}\) hrs.
∴ Required time = \(\frac{504}{73}\) hrs.
= \(6 \frac{66}{73}\) hrs.
If the three pipes remain open then in \(6 \frac{66}{73}\) hours the tank will be filled up.
2. If the first two pipes would remain open, let’s calculate the time required to fill up the tank with water.
Solution:
First two pipes will fill in 1 hour \(\left(\frac{1}{18}+\frac{1}{21}\right)\)
= \(\frac{7+6}{126}\)
= \(\frac{13}{126}\)
First two pipes fill up \(\frac{13}{126}\) part in 1 hour.
∴ First two pipes will fill 1 part in \(1 \div \frac{13}{126}\) hours
= \(\frac{126}{13}\) hours
= \(9 \frac{9}{13}\) hours
If first two pipes remain open, tank will require \(9 \frac{9}{13}\) hours to fill up.
Question 6. Rehana’s tank can be filled up in 30 minutes for by the municipality water supply pipe, opening all the taps, three hours. The can work for 4 hours with the water of the full tank. In one day the water supply pipe remains open for 25 minute. Let’s calculate how long they will work with that water.
Solution:
Given
Rehana’s tank can be filled up in 30 minutes for by the municipality water supply pipe, opening all the taps, three hours. The can work for 4 hours with the water of the full tank. In one day the water supply pipe remains open for 25 minute.
∵ Municipality pipe fills up 1 part in 30 minutes.
∴ Municipality pipe fills up \(\frac{1}{30}\) part in 1 minutes.
∴ Municipality pipe fills up \(\frac{25}{30}\) part in 25 minutes.
∴ Municipality pipe fills up \(\frac{5}{6}\) part in 25 minutes.
In mathematical language the problem is –
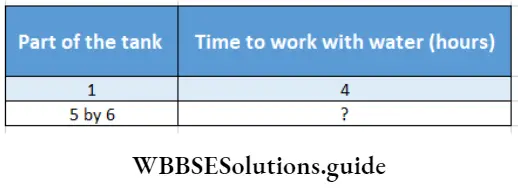
If part of tank decreases, time will decrease.
∴ Here is direct proportion.
∴ \(\frac{1}{\frac{5}{6}}=\frac{4}{?}\)
or, \(\frac{6}{5}=\frac{4}{?}\)
∴ Required time = \(\frac{4 \times 5}{6}\) hours
= \(\frac{10}{3}\) hours
= \(3 \frac{1}{3}\) hours
With that water they can work for \(3 \frac{1}{3}\) hours.
Question 7. Ruma and Rohit can complete a work in 20 days. Rohit and Sobha can complete that work in 15 days. Let’s calculate in how many days they will complete the work together.
Solution:
Given
Ruma and Rohit can do \(\frac{1}{20}\) part in 1 day. Rohit and Sobha can do in 1 day. Ruma and Sobha can do \(\frac{1}{15}\) part in 1 day. Ruma and Sobha can do \(\frac{1}{20}\) part in 1 day.
∴ 2 × (Ruma + Rohit + Sobha) can do \(\left(\frac{1}{20}+\frac{1}{15}+\frac{1}{20}\right)\) part in 1 day part
= \(\frac{3+4+3}{60}\) part
= \(\frac{10}{60}\) part
= \(\frac{1}{6}\) part
∴ Ruma + Rohit + Sobha can do \(\frac{1}{2 \times 6}\) part in 1 day
= \(\frac{1}{12}\)
∵ Three of then can do \(\frac{1}{12}\) part in 1 day.
∴ All three together can complete the work in 12 day.
∴ Ruma can do \(\left(\frac{1}{12}-\frac{1}{15}\right)\) part in 1 day
= \(\frac{5-4}{60} \text { part }\)
= \(\frac{1}{60} \text { part }\)
Ruma can do \(\frac{1}{60} \text { part }\) part in 1 day.
∴ Ruma can complete the work alone in 60 days.
Ruma can do \(\left(\frac{1}{12}-\frac{1}{20}\right)\) part in 1 day
= \(\frac{5-3}{60}\) part
= \(\frac{2}{6}\) part
= \(\frac{1}{30}\) part
Rohit can do \(\frac{1}{30}\) part in 1 day.
∴ Rohit can complete the work alone in 30 days.
Sobha can do in 1 day \(\left(\frac{1}{12}-\frac{1}{20}\right)\) part
= \(\frac{5-3}{60}\)
= \(\frac{2}{6} \)
=\(\frac{1}{30} \)
Sobha can complete \(\frac{1}{30}\) part in 1 day.
∴ Sobha can do the work alone in 30 days.
Question 8. Alok, Kalam and Joseph individually can complete a work in 10, 12 and 15 days respectively. They started doing the work together. After 3 days Kalam had to go. Let’s make proportion and calculate in how many days Alok and Joseph will complete the remaining work.
Solution:
Given
Alok, Kalam and Joseph individually can complete a work in 10, 12 and 15 days respectively. They started doing the work together. After 3 days Kalam had to go.
Alok can do \(\frac{1}{10}\) part in 1 day.
Kalam can do \(\frac{1}{12}\) part in 1 day.
Joseph can do \(\frac{1}{15}\) part in 1 day.
All three together can do \(\left(\frac{1}{10}+\frac{1}{12}+\frac{1}{15}\right)\)
= \(\frac{6+5+4}{60}\)
= \(\frac{15}{60}\) part
= \(\frac{1}{4}\) part
All three together can do 3 × \(\frac{1}{4}\) part =\(\frac{3}{4}\) part in 3 days.
Remaining work \(\left(1-\frac{3}{4}\right)\) part
= \(\frac{4-3}{4}\) part = \(\frac{1}{4}\)
Alok and Joseph can do together \(\left(\frac{1}{10}+\frac{1}{15}\right)\) part in 1 day
= \(\frac{3+2}{30}\) part
= \(\frac{5}{30}\) part
= \(\frac{1}{6}\) part
Alok and Joseph can together work \(\frac{1}{6}\) part in 1 day.
∴ Alok and Joseph can together work 1 part in 6 days.
∴ Alok and Joseph can together work \(\frac{1}{4}\) part in \(\frac{1}{6}\)×6 days
= \(\frac{3}{2}\) days
= \(1 \frac{1}{2}\) days
Alok and Joseph will complete the remaining work in \(1 \frac{1}{2}\)days.
Question 9. Mary and David can do a work individually in 10 days and 15 days respectively. At first Mary alone worked for 4 days, then David alone worked for 5 days and left. Maria came and completed the remaining work in 4 days. If Mary, David and Maria would work together, let’s calculate in how many days they woild complete the work.
Solution:
Given
Mary and David can do a work individually in 10 days and 15 days respectively. At first Mary alone worked for 4 days, then David alone worked for 5 days and left. Maria came and completed the remaining work in 4 days.
Mary can do \(\frac{1}{10}\) part in 1 day.
∴ Mary can do \(\frac{4}{10}\) part = \(\frac{2}{5}\) part in 4 days.
David alone can do \(\frac{1}{15}\) part in 1 day.
∴ David alone can do \(\frac{5}{15}\) part = \(\frac{1}{3}\) part in 5 days.
Both can do \(\left(\frac{2}{5}+\frac{1}{3}\right)\) part of the total work
= \(\frac{6+5}{15}\) part
= \(\frac{11}{15}\) part
Remaining work = \(\left(1-\frac{11}{15}\right)\)
= \(\frac{15-11}{15}\) part
= \(\frac{4}{15}\) part
Maria can do \(\frac{4}{15}\) part in 4 days.
∴ Maria can do \(\frac{4}{4 \times 15}\) part = \(\frac{1}{15}\) part in 1 day.
Mary, David and Maria together can do \(\left(\frac{1}{10}+\frac{1}{15}+\frac{1}{15}\right)\) part in 1 day.
= \(\frac{3+2+2}{30}\) part
= \(\frac{7}{30}\) part
All three can do \(\frac{7}{30}\) part of the work in 1 day.
∴ All three can do 1part of the work in \(\frac{30}{7}\) days.
∴ All three can complete the work in \(4 \frac{2}{7}\) days.
If Mary, David and Maria do the work together, then in \(4 \frac{2}{7}\) days it will be completed.
Question 10. A municipality made a tank for water preservation and added pumps with it. The pumps separately can fill the empty tank in 16, 20 & 30 hours respectively. Today when the 3 pumps started together at 7 am, \(\frac{1}{3}\) part of the tank was filled with water. After 1 hour 36 minutes the first pump, and after 2 more hours, the third pump were stopped.
Solution:
Given
A municipality made a tank for water preservation and added pumps with it. The pumps separately can fill the empty tank in 16, 20 & 30 hours respectively. Today when the 3 pumps started together at 7 am, \(\frac{1}{3}\) part of the tank was filled with water. After 1 hour 36 minutes the first pump, and after 2 more hours, the third pump were stopped.
First pump can fill \(\frac{1}{16}\) part in 1 hour.
Second pump can fill \(\frac{17}{20}\) part in 1 hour.
Third pump can fill \(\frac{1}{30}\) part in 1 hour.
All three pumps can fill
= \(\left(\frac{1}{16}+\frac{1}{20}+\frac{1}{30}\right)\) part in 1 hour
= \(\frac{15+12+8}{240}\) part
= \(\frac{35}{240}\) part
= \(\frac{7}{48}\) part
1 hour 36 minutes = 96 minutes
∵ All three pumps fill = \(\frac{7}{48}\) part in 60 minutes.
∴ All three pumps fill \(\frac{7 \times 96}{48 \times 60}\) part in 96 minutes.
= \(\frac{7}{30}\)
Second and third pump fill = \(\left(\frac{1}{20}+\frac{1}{30}\right)\) part in 1 hour.
= \(\frac{3+2}{60}\) part
= \(\frac{5}{60}\) part
= \(\frac{1}{12}\) part
∴ Second and third pump fill = \(2 \times \frac{1}{12}\) part part in 2 hours.
= \(\frac{1}{6}\) part
Now, the filled part of the tank = \(\left(\frac{1}{3}+\frac{1}{30}+\frac{1}{6}\right)\) part
= \(\frac{10+7+5}{30}\) part
= \(\frac{22}{30}\) part
= \(\frac{11}{15}\) part
Remaining to be filled = \(\left(1-\frac{11}{15}\right)\) part
= \(\frac{15-11}{15}\) part
= \(\frac{4}{15}\) part
First pump fills 1 part in 20 hours.
∴ Second pump will fill
= \(\frac{4}{15}\) part in
= \(\frac{4}{15} \times 20\) hours
= \(\frac{16}{3}\) hours
= 5 hours 20 minutes
1. Let’s calculate when the tank was totally filled up.
Solution:
Time required to fill the tank fully
= 1 hour 36 minutes + 2 hours + 5 hours 20 minutes
= 8 hours 56 minutes
Morning 7 am + 8 hours 56 minutes = Evening 3 hours 56 minutes
The tank will be filled completely at 3 o’clock 56 minutes.
2. Let’s calculate how much of the tank the second pump filled up.
Solution:
Time of second pump
= 1 hours 36 minutes + 2 hours + 5 hours 20 minutes
= 8 hours 56 minutes
= (8 x 60 + 56) minutes (480 + 56) minutes
= 536 minutes
Second pump can fill up = \(\frac{1}{20}\) part in 60 minutes.
∴ Second pump can fill up = \(\frac{1}{20 \times 60}\) part in 1 minutes.
∴ Second pump can fill up = \(\frac{1 \times 536}{20 \times 60}\) part in 536 minutes.
∴ Second pump can fill up = \(\frac{67}{150}\) part in 536 minutes.
Second pump filled up = \(\frac{67}{150}\) part of the tank.
“WBBSE Class 8 Maths Chapter 17 solutions, Time and Work PDF”
3. When the third pump is stopped, let’s calculate how much of the tank was filled with water.
Solution:
When third pump was was stopped, \(\frac{4}{15}\) part was empty.
∴ Filled up part = \(\left(1-\frac{4}{15}\right)\)
= \(\frac{15-4}{15}\)
= \(\frac{11}{15}\)
When the third pump was stopped, \(\frac{11}{15}\) part of the tank was filled with water.
Question 11. My friend Rina can do garden work alone in 4 hours. I can do that work alone in 9 hours. But if we together do that work, let’s calculate how much time will be needed with number.
Solution:
Given
My friend Rina can do garden work alone in 4 hours. I can do that work alone in 9 hours.
Rina can do \(\frac{1}{4}\) part of the work in 1 hour.
I can do\(\frac{1}{3}\) part of the work in 1 hour.
Both can do together
= \(\left(\frac{1}{4}+\frac{4}{15}\right)\) part of the work in 1 hour
= \(\frac{3+4}{12}\) part
= \(\frac{7}{12}\) part
Both can do \(\frac{7}{12}\) part of the work in 1 hour.
∴ Both can do the work in \(\frac{12}{7}\) hours
= \(1 \frac{5}{7}\) hours.
Both can do the work in = \(1 \frac{5}{7}\) hours.
