Geometrical Proofs
Mitali gave me two sticks of length 3 cm and 5 cm respectively.
I took a stick of length 2 cm and attached it with sticks given by Mitali and we got a figure like the given figure beside.
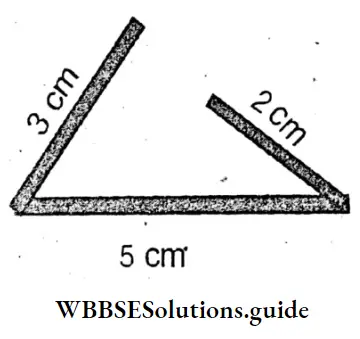
But it is seen that we are not able to form a triangle. Here it is seen – that 3 cm + 2 cm [I] 5 cm (put =/</> ). Jasmin replaced the stick of length 2 cm by a stick of length 3 cm and she tried to form a figure like a triangle and she is able to make the figure.
Here it is seen that 3 cm + 3 cm > 5 cm ( put =/</>)
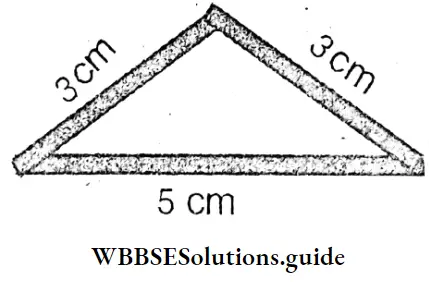
Sneha made a figure Triangle with three sticks 3 cm, 5 cm and 4 cm respectively.
Here it is seen that 4 cm + 3 cm g] 5 cm ( put =/</>).
“WBBSE Class 8 Maths Chapter 22 solutions, Construction of Parallel Lines”
I am able to form a shape like a triangle with two sides of lengths 3 cm, 5 cm and a third stick of length 6 cm or 7 cm, i.e., it is seen that the figures like triangles are formed with the sticks of length (3 cm,6 cm & 5 cm) and (3 cm, 7 cm & 5 cm).
Read and Learn More WBBSE Solutions For Class 8 Maths
Sneha, by placing the shapes like this triangle on the exercise book, she got some triangles, of which the sum of length of third sides Big (big / small).
| Class 8 General Science | Class 8 Maths |
| Class 8 History | Class 8 Science LAQs |
| Class 8 Geography | Class 8 Science SAQs |
| Class 8 Maths | Class 8 Geography |
| Class 8 History MCQs | Class 8 History |
Now Sucheta tried to make a shape like a triangle with the sticks of lengths 9 cm, 3 cm, and 5 cm and she got –
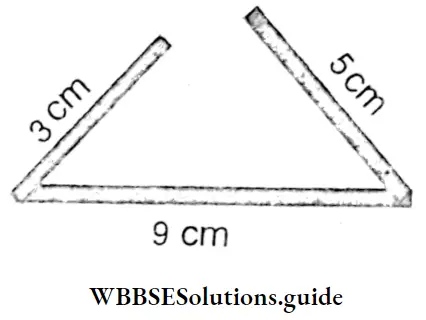
Here the sum of lengths of any two sides is not greater than the length of the third side.
We got,
1. The length of the sticks which makes a figure like a triangle with the sticks of length 5 cm and 3 cm is Big (less / more) than 5 cm – 3 cm = 2 cm and then small (less/more) (5 + 3) cm = 8 cm
2. The sum of the length of any two sides of a triangle is then the length of the third side Big (less/more)
Now Anik gave two sticks of length 2 cm and 4 cm.
“Class 8 WBBSE Maths Chapter 22 solutions, Construction of Parallel Lines study material”
Now let’s try to make a figure like a triangle with sticks of different lengths and let’s see what I get.
It is seen that
1. It is possible to construct a figure like a triangle with the (4-2) cm = 2 cm Big (less/more) long stick and (4 + 2) cm = 6 cm small (less/more) long stick 2 cm and 4 cm long sticks.
2. Again it is also seen that the sum of the lengths of any two sides is Big (less/more) than the length of the third side.

Geometrical Proofs Exercise
Question 1. Let’s see what the length of the sticks can make a figure like a triangle with the sticks of length 4 cm and 6 cm.
Solution:
It is possible to make a triangle with sticks of length greater than (6-4) cm = 2 cm and less than less than (6+4) cm = 10, i.e., from 3 to 9 cm triangle can be made with sticks of any length.
Question 2. If the length of two sides of triangle are 3 cm and 6 cm then let’s find the length of the third side that will lie between which two numbers. Let’s write the relation between the sum of the lengths of any two sticks with the length of the third stick.
Solution:
Given
If the length of two sides of triangle are 3 cm and 6 cm then let’s find the length of the third side that will lie between which two numbers.
(6-3) cm = 3 cm greater than
∴ The length of the third side can be 4 cm or 5 cm.
Aminur has drawn some triangles on the exercise books. He said let’s try to find the relation between the length of each side of these triangles.
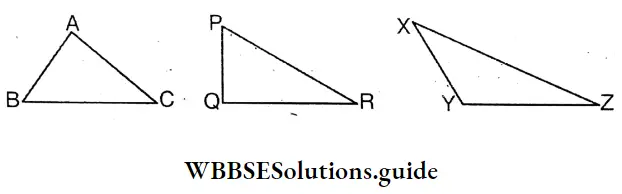
AB = 2.6 cm, BC = 4.6 cm, CA = 3.4 cm
AB+BC > CA [Put >/<]
BC+CA > BC [Put >/<]
CA+AB > [put >/>]
Similarly measuring the length of the sides of ΔPQR & ΔXYZ, it is seen that the sum of the lengths of two sides is Big than the length of third side.
Question 3. Megha has drawn PQR triangle. I will prove with the help of facts that PQ + QR > PR ; OR + RP > PQ and RP + PQ > QR.
Solution:
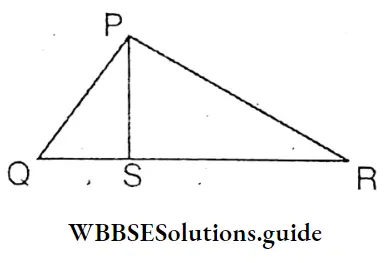
Given : Let the greatest side of PQR triangle is QR.
We have to prove that RP + PQ > QR.
Construction : From P, the highest point of ΔPQR, PS a perpendicular is drawn on OR which cuts, QR at S i.e., PS ⊥ QR.
Proof : In ΔPSR ∠PSR=1 right angle (Constructed)
∴ ∠PSR is a right angle and ∠SPR is an acute angle.
∴ ∠PSR> ∠SPR
So, PR > SR …………. (1)
In ΔPSQ < PSQ = 1 right angle (∵ PS⊥QR)
∴ ∠PSQ right angle and ∠QPS acute angle ∠
∴ PSQ>∠QPS
So : PQ > QS …………… (2)
by adding equations (1) and (2)
PR + PQ > SR + QS
or, PR + PQ > QR Proved
“WBBSE Class 8 Maths Chapter 22, Construction of Parallel Lines solved examples”
Geometrical Proofs Exercise
Question 1. Let’s prove logically step by step that the difference of the lengths of any two sides of triangle is less than the length of the third side.
Solution:
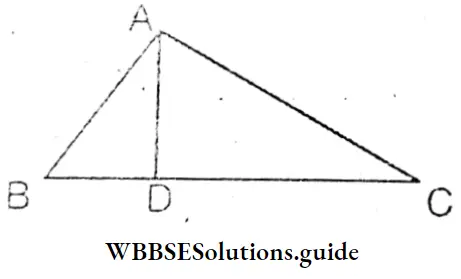
Let the greatest side of ΔABC is BC.
We have to prove that AB-AC<BC.
Construction : From A, the highest point of ΔABC, AD a perpendicular is drawn on BC which cuts BC at D, i.e., AD ⊥ BC
Proof : In ΔABD ∠ADB=1 right angle (∵ AD ⊥ BC)
∴ ∠ADB > ∠BAD
∴ AB > BD ………………..(1)
In ΔADC ∠ADC=1 right angle
∴ ∠ADC is a right angle and ∠DAC is an acute angle.
∴ ∠ADC > ∠DAC
∴ AC > DC ………………(2)
(1) — (2) AB – AC < BD + DC
or, AB – AC < BC Proved
Question 2. Let’s observe the lengths of the following sides and let’s write in which cases it is possible to draw a triangle –
1. (3 cm, 6 cm and 8 cm)
Solution:
Given
3 cm + 6 cm > 8 cm
∴ It is possible to construct a triangle.
2. (8 cm, 6 cm and 15 cm)
Solution:
Given
8 cm + 6 cm < 15 cm
∴ It is not possible to construct a triangle.
3. (2.7 cm, 6.1 cm and 8.8 cm) .
Solution:
Given
2.7 cm + 6.1 cm – 8.8 cm
∴ It is possible to construct a triangle.
4. (2.5 cm, 8 cm and 6 cm) .
Solution:
Given
2.5 cm + 6 cm > 8 cm
∴ It is possible to construct a triangle.
Geometrical Proofs Exercise
Question 1. D is any, point on the side BC of A ABC. Let’s prove that AB + BC + CA > 2AD.
Solution:
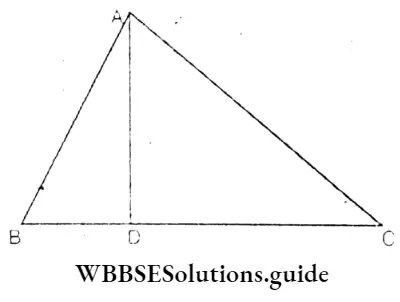
Given
In A ABC, D is a point on BC.
Prove that AB + BC + CA > 2AD
Construction : A straight line AD is drawn.
Proof : In ΔABD,
AB + BD > AD …………(1)
(∴ The sum of two sides of a triangle is greater than the third side.)
Again, In ΔADC,
DC + AC > AD …………….(2)
by . adding equations (1) and (2) .
AB + BD + DC + AC > AD + AD
or, AB + BC + AC > 2AD Proved
Question 2. O is any point inside ΔABC. Let’s prove that:
- AB + AC > OB + OC
- AB + BC + AC > OA + OB + OC
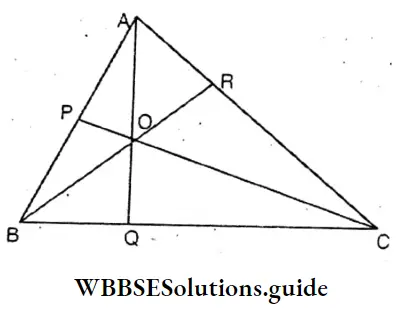
Construction : AO is extended which cuts BC at Q. Similarly BO and CO are extended which cut AC and AB at points R and P respectively.
Proof : In ΔABQ, AB + AQ > BQ >
or, AB + AQ > OB + OQ ………….(1)
In A COQ, OQ + CQ > OC ………..(2)
By adding equations (1) and (2)
AB + AQ + OQ + CQ > OB > OB + OQ + OC
or, AB + (AQ + CQ) > OB + OC
or, AB + AC > OB + OC ……………(3)
∵ BC > OA ………………………(4)
By adding equations (3) and (4)
AB + AC + BC > OB + OC + OA Proved
Question 3. Let’s prove that the perimeter of a triangle is more than the sum of lengths of the medians.
Solution:
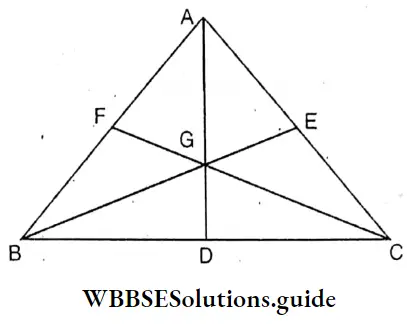
Let the three medians of A ABC are AD, BE and CF.
We have to prove that AB + BC + CA > AD + BE + CF.
Proof : ∵ BA + AC > 2AD …………….(1)
BC + AC > 2CF …………………..(2)
and AB + BC > 2BE ………………….(3)
By adding (1), (2) and (3)
AB + AC + BC + AC + AB +BC > 2AD + 2CF + 2BE
or, 2(AB + BC + AC) > 2 (AD + CF + BE)
or, AB + BC + AC > AD + BE + CF Proved
Question 4. P is any point inside A ABC. Let’s prove that,
- AB + BP > AB
- AB + BC + AC < 2 (AP + BP + CP)
Solution:
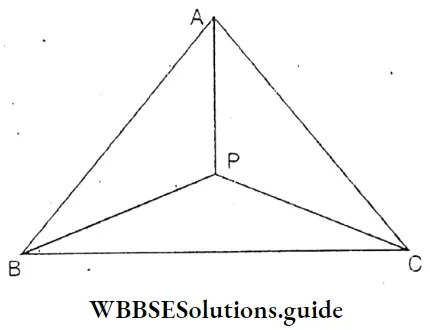
Given
In ΔABC, P is any point. Prove that (1) AP + BP > AB (2) AB + BC + AC < 2 (AP + BC + CP)
Construction: A, P ; B, P and C, P are joined.
Proof: In A ABP
(1) AP + BP > AB (∵ The sum of any two sides of a triangle is greater than the third side.)
In A ABP, AB<AP + BP……………………….. (1)
In A BPC, BC < BP + PC………………. (2)
and in A APC, AC < AP + PC …………….. (3)
by adding (1), (2) and (3)
AB + BC + AC < 2AP + 2BP + 2PC
or, AB + BC + AC < 2 (AP + BP + PC) (2) Proved
“WBBSE Class 8 Construction of Parallel Lines solutions, Maths Chapter 22”
Question 6. Let’s prove that the sum of lengths of two diagonals is greater than the sum of the lengths of any two opposite sides of a quadrilateral.
Solution:
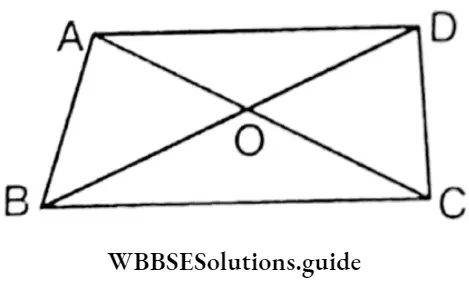
Let ABCD is a quadrilateral whose two diagonals are AC and BD. Let’s prove that AC + BD > AD + BC.
Proof : In AOD, OA + OD > AD …………..(1)
In BOC, OB + OC > BC ………….(2)
by adding (1) and (2)
OA + OD + OB + OC > AD + BC or, (OA + OC) + (OB + OD) > AD + BC
or, AC + BD > AD + BC Proved
Question 7. Let’s prove that the sum of lengths of two diagonals of a quadrilateral is more tham the semi-perimeter of the quadrilateral.
Solution:
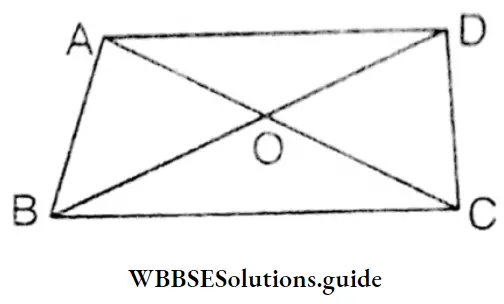
Let ABCD is a quadrilateral whose two diagonals AC and BD cut each other at 0.
Proof: In AOD, AO + OD > AD ………………… (1)
In AOB, AO + OB > AB ………………… (2)
In BOC, OB + OC > BC ………………… (3)
In COD, OC + OD > CD ………………… (4)
by adding (1), (2), (3) and (4)
AO + OD + AO + OB + OB + OC + OC + OD > AD + AB + BC + CD
or, 2A0 + 20C + 20D + 20B > AB + BC + CD + AD
or, 2 (A0 + OC) + 2(0D + OB) > AB + BC + CD + AD
or, 2AC + 2BD > AB + BC + CD + AD
or, 2 (AC + BD) > AB + BC + CD + AD
or, AC + BD > (AB + BC + CD + AD) Proved
Question 8. From a point inside a quadrilateral (not on any diagonal) we join the vertices of the quadrilateral. Let’s prove that the sum of lengths of these line segments is greater than the sum of lengths of the diagonals. Now let’s see for which position of the point inside the quadrilateral the sum of lengths of the line segment obtained by the vertices of the quadrilateral with that point will be the smallest.
Solution:
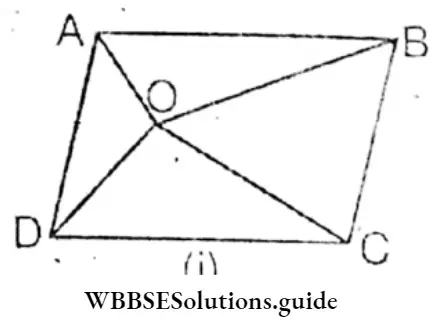
Given
From a point inside a quadrilateral (not on any diagonal) we join the vertices of the quadrilateral.
Let inside ABCD quadrilateral 0 is any point and AC and BD are the two diagonals.
Let’s prove that: OA + OB + OC + OB > AC + BD
Construction : O, A; O, B; C; and O, D
Proof: From figure (1) In ΔAOC, OA + OC > AC ……………….(1)
and in ΔBOD, OB + OD > BD ……………….(2),
From (1) + (2), OA + OC + OB + OD > AC + BD (Proved)
From figure (2) In ΔAOB, AO + OB > AB ………………….(1)
(The sum of lengths of any two sides of a triangle is greater than length of the third side.)
In A AOC, BO + OC > BC ……………….. (2) (For the above reason)
In A GOD, OC + OD > CD ………………. (3) (For the above reason)
In A ODA, OD + OA > AD ……………………. (4) (For the above reason)
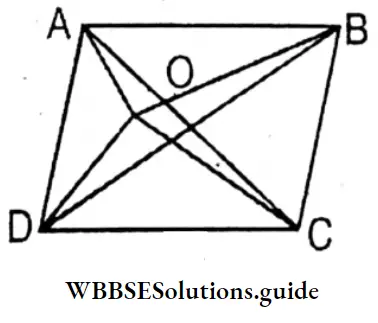
Now, from A + B + C + D
AO+OB+BO+OC+OC+OD+OD+OA>AB+BC+AD
or, 2A0+20C+20B+20D>AB+BC+CD+CA
or, AO+OG+OB+OD> \(\frac{1}{2}\) (AB+BC+GD+GA)………….(A)
From figure (3) In ΔAOD, AO + OD > AD ……………(1)
In ΔAOB, AO + OB > AB ………..(2)
In ΔBOC, OB + OC > BC ………………(3)
In ΔCOD, OC + OD > CD ……………. (4)
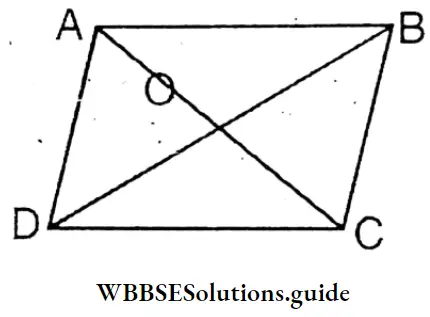
by adding (1+2+3+4)
AO+OD+AO+OB+OB+OC+OC+OD>AD+AB+BC+CD
or, 2AC + 20C + 20D+20B>AD+AB+BC+CD
or, 2(AO+OC)+2(OD+OB)>AD+AB+BC+CD
or, 2AC =2BD>AD+AB+BC+CD
or, AC+BD> (AB+BC+CD+AD)
AC+BD> (AB+BC+CD+AD) ………………….(B)
From (A) and (B)
AC + BD < OA + OB + OC + OD
So we see that if the point inside the quadrilateral is the point of intersection of two diagonals then the sum of lengths of line segments obtained by vertices of quadrilateral with that point will be the smallest.
Salema and Bibhas have made-
I drew these figures on a thick art paper and named them. I measured the interior angles b>Ca protractor and got :
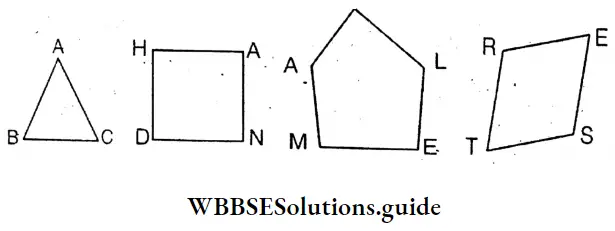
Measuring by protractor, we see, In ΔABC ∠ABC = 60 degree ∠ABC = 60 degree and ∠ACB= 60 degree
By measuring angles of quadilateral HAND we see ∠AHD = 90 degree ∠HAN = 90 degree ∠AND = 90 degree ∠HDN = 90 degree
By measuring angles of pentagon CAMEL we see ∠ACL = 90 degree ∠CLE = 110 degree ∠LEM =100 degree ∠EMA = 90 degree and ∠MAC = 140 degree
By measuring angles of quadrilateral REST we see
∠ERT = 100 degree ∠RES = 80 degree ∠EST = 110 degree and ∠RTS = 70 degree
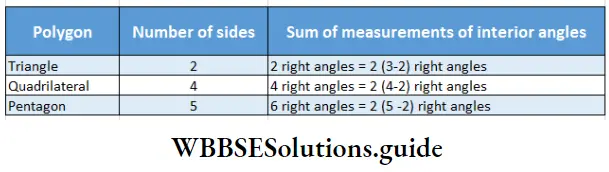
Now I add the measurement of the interior angles of each polygon and then let’s try to find a general formula.
Sum of the measurement of the interior angles of ΔABC = ∠BAC + ∠ABC +∠ACB = 180 degree = 2 right angles
“Class 8 WBBSE Maths Chapter 22, Construction of Parallel Lines easy explanation”
Sum of the measurement of the interior angles of HAND = ∠AHD + ∠HAN + ∠AND + ∠BAC = 360 degree = 4 right angles
Sum of the interior angles of CAMEL = ∠ACL + ∠CAM + ∠AME + ∠MEL + ∠ELC = 540 degree = 6 right angles
Sum of the interior angles of REST = ∠ERS + ∠RES + ∠EST + ∠RTS = 360° degree= 4 right angles
Let’s try to find out the relation between the interior angles and the number of sides of a polygon.
Question 9. The number of sides of a regular polygon is 18. Let’s find the measurement of each interior angle and each exterior angle.
Solution:
Given
The number of sides of a regular polygon is 18.
Sum of measurements of 18 interior angles of the polygon is = 2 (18-2) × 90°
= 2 × 16 × 90°= 2880°
∴ Measure of each interior angle is = 2880° -18 = 160°
Sum of measurements of all exterior angles is = 360°
∴ Measurement of each exterior angle is = 360, 18=20°
Alternatively, measurement of 1 interior angle + 1 measurement of exterior angle = 180°
∴ Measurement of 1 exterior angle = 360° 18 = 20°
Measurement of 1 interior angle = 180° – 20° = 160°
Question 10. Measurement of each exterior angle of a regular polygon is 144°. Let’s find the number of sides of the polygon.
Solution:
Given
Measurement of each exterior angle of a regular polygon is 144°.
Measurement of 1 interior angle + measurement of 1 exterior angle = 180
∴ Measurement of 1 exterior angle = 180°
-144° = 36°
∴ Number of sides of the regular polygon = 360° ÷ 360° = 10
Geometrical Proofs Exercise
Question 1. Let’s prove logically the sum of four interior angles of a quadrilateral is 360°.
Solution:
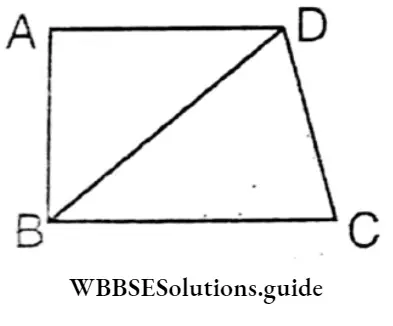
Let ABCD is a quadrilateral.
Let’s prove that ∠A + ∠B + ∠C + ∠D = 360°
Construction : Diagonal BD is drawn.
Proof : In ΔABD, ∠A + ∠ABD + ∠ADB = 180°
(∵ Sum of all angles of a triangle is 180°)
Again, In ΔBCD ZBDC + ZCBD + ZC = 180°
ΔABD+ ABCD= ∠A+ ∠ABD+ ∠ADB+ ∠BDC+ ∠CBD+ ∠C= ∠A+ ∠B+ ∠C+ ∠D
∴ ΔABD + ABCD = ∠A+∠B+∠C+∠D = 180°+180°
∴ ABCD =∠A+ ∠B+ ∠C+ ∠D= 360° Proved
Question 2. Let’s write by calculation the sum of the measurements of eight interior angles of an octagon.
Solution:
Sum of measurements of the interior angles of an octagon = 2 (8-2) × 90°
Sum = 2 (8-2) × 90°
= 2 × 6 × 90°
= 10802°
The sum of the measurements of eight interior angles of an octagon = 10802°
Question 3. Let’s write the measurement of each interior and enterior angle of a regular polygon with 10 sides.
Solution:
Sum of measurements of 10 interior angles of a decagon = 2 (10-2) × 90° .
= 2 × 8 × 90° = 1440°
∴ Measurement of each interior angle = 1440° ÷ 10 = 144°
Measurement of each exterior angle = \(\frac{360^{\circ}}{10}\)= 36°
“WBBSE Class 8 Maths Chapter 20, Geometrical Proofs solved examples”
Question 4. Let’s write by calculation the number of sides of a regular polygon where measurement of each angle is 120°.
Solution:
Each interior angle of the polygon = 120°
∴ Measurement of each exterior angle of the polygon = 180° – 120°
Number of sides of the regular polygon = \(\frac{360^{\circ}}{10}\) = 6
Geometrical Proofs Exercise
Question 1. Let’s write the sum of the interior angles of the following polygons:
- Pentagon
- Hexagon
- Heptagon
- Octagon
- Decagon
- A polygon with 12 sides.
1. Pentagon
Solution:
Sum of measurements of the interior angles of a pentagon
= 2 (5-2) × 90°
= 2 × 3 × 90° = 540°
pentagon = 540°
2. Hexagon
Solution:
Sum of measurements of the interior angles of a hexagon
= 2(6-2) × 90°
= 2 × 4 × 90°
= 720°
Hexagon = 720°
3. Heptagon
Solution:
Sum of measurements of the interior angles of a heptagon = 2
(7-2) × 90°
= 900°
Heptagon = 900°
4. Octagon
Solution:
Sum of measurements of the interior angles of an octagon
= 2 (8-2) × 90°
= 2 × 6 × 90° = 1080°
Octagon = 1080°
5. Decagon
Solution:
Sum of measurements of the interior angles of a decagon = 2
(10-2) × 90°
= 2×8×90°
= 1440°
Decagon = 1440°
6. Polygon with 12 sides
Solution:
Sum of measurements of the interior angles of a polygon with 12 sides
= 2 (12-2) × 90°
= 1800°
Polygon with 12 sides = 1800°
Question 2. Three angles of a quadrilateral are 104.5°, 65° and 72.5°; find the measurement of the fourth angle.
Solution:
Given
Three angles of a quadrilateral are 104.5°, 65° and 72.5°
Sum of measurements of three angles of a quadrilateral.
= 104.5° + 65° + 72.5°
= 242°
Sum of measurements of all four angles of a quadrilateral = 360°
∴ Measurements of the 4th angle of the quadrilateral = 360° – 242°
= 118°
Question 3. Four angles of a pentagon are respectively 65°, 89°, 132° and 116°. Let’s write the measurement of the fifth angle.
Solution:
Given
Four angles of a pentagon are respectively 65°, 89°, 132° and 116°.
Sum of 4 angles of a pentagon = 65° + 89° + 132° + 116° = 402°
Sum of all the interior angles of a pentagon = 2 (5- 2) × 90° .
= 2×3×90° =540°
Measurement of the 5th angle of the pentagon = 540°-402° = 138°
Question 4. Let’s write whether the measurement of 3 angles of a convex v quadrilateral being 68°, 70° and 75° is possible or not.
Solution:
Sum of 3 angles of a quadrilateral = 68° + 70° + 75° = 213°
∵ Sum of 4 angles of a quadrilateral = 360°
∵ 213° < 360°
∴ The three angles of a convex quadrilateral can be respectively 68°, 70° and 75°
Question 5. Let’s write whether the five angles of a convex hexagon 120°, 70°, 95°, 78° and 160° is possible or not.
Solution:
Sum of 5 angles of a hexagon = 120°+70°+95°+78°+160° = 523°
Sum of six angles of a hexagon = 2 (6-2) × 90°
= 2 × 4 × 90°
= 720°
∵ Measure of the 6th angle of a hexagon = 720° – 523° = 197°
∵ 197° > 180°, which is impossible.
∴ The five angles of a convex hexagon can’t be respectively 120°,
70°, 95°, 78° and 160°.
“WBBSE Class 8 Maths Chapter 22 solutions, Construction of Parallel Lines PDF”
Question 6. Let’s write the measurement of each interior and exterior angle of the following polygons :
1. Pentagon
Solution:
Sum of measurements of the interior angles of a pentagon
= 2 (5-2) × 90°
= 2 × 3 × 90°
= 540°
∴ Measurement of each interior angle of a regular pentagon
= 54° ÷ 5
= 108°
Interior angle + Exterior angle = 180°
Measurement of each interior angle of a reguiar pentagon= 180°
108° =72°
2. Hexagon
Solution:
Sum of measurements of the interior angles of a hexagon = 2 (6-2) × 90°
= 2 × 4 × 90°
= 720°
∴ Measurement of each interior angle of an regular hexagon = 720°÷6 = 120°
∴ Measurement of each exterior angle of a regular hexagon = 180° -120° = 60°
3. Octagon
Solution:
Sum of measurements of the interior angles of an Octagon
= 2 (8-2) x 90° = 2 × 6 × 90° = 1080°
∴ Measurement of each interior angle = 1080° + 8 = 135°
∴ Measurement of each exterior angle of the octagon = 180° – 135° = 45°
4. Polygon with 9 sides
Solution:
Sum of the interior angles of a polygon with 9 sides = 2 (9-2) × 90° = 1260° .
∴ Measurement of each interior angle of a polygon with 9 sides = 1260°-9= 140° –
∴ Measurement of each exterior angle of a polygon with 9 sides = 180°-120° = 40°
5. Decagon
Solution:
Sum of measurements of the interior angles of a Decagon
= 2 (10-2) x 90° = 2 × 8 × 90° = 1440°
∴ Measurement of each interior angle of a polygon with 10 sides = 1440° – 10 = 144°
∴ Measurement of each exterior angle of a regular polygon with 10 sides
= 180°-144° = 36°
6. Polygon with 18 sides
Solution:
Sum of measurements of the interior angles of a regular polygon with 18 sides.
= 2 (18-2) × 90°
= 2 × 16 × 90°
= 2880°
∴ Measurement of each interior angle of a polygon with 18 sides = 2880° ÷ 18 = 160°
∴ Measurement of each exterior angle of a polygon with 18 sides = 180°-160°=20°
Question 7. Let’s find whether the following measurements are possible or not for an exterior angle of a regular polygon – (write yes /no):
- 6°
- 10°
- 13°
- 18°
- 35°
1. 6°
Solution:
The measurement of each exterior angle of a regular polygon can be 6°
2. 10°
Solution:
The measurement of each exterior angle of a regular polygon can be 10°.
3. 13°
Solution:
The measurement of each exterior angle of a regular polygon can be .13°.
4. 18°
Solution:
The measurement of each exterior angle of a regular polygon can be 18°.
5. 35°
Solution:
The measurement of each exterior angle of a regular polygon can be 35°.
“WBBSE Class 8 Maths Chapter 22, Construction of Parallel Lines important questions”
Question 8. Let’s find whether the following measurement of each interior angle is possible or not for a regular polygon
Solution:
- 80°
- 100°
- 120°
- 144°
- 155°
- 160°
1. 80°
Solution:
The measurement of each interior angle of a regular polygon can be 80° .
2. 100°
Solution:
The measurement of each interior angle of a regular polygon can be 100°.
3. 120°
Solution:
The measurement of each interior angle of a regular polygon can be 120°.
4. 144°
Solution:
The measurement of each interior angle of a regular polygon can be 144°.
5. 155°
Solution:
The measurement of each interior angle of a regular polygon can be 155°.
6. 160°
Solution:
The measurement of each interior angle of a regular polygon can be 160°.
Question 9. Each exterior angle of a regular polygon is 60°. What is the number of sides of it?
Solution:
Given
Each exterior angle of a regular polygon is 60°.
The measurement of each exterior angle of a regular polygon can be = 60°
∴ Number of sides of the regular polygon = \(\frac{360^{\circ}}{60^{\circ}}\)= 6
Question 10. Each interior angle of a regular polygon is 135°. What is the number of sides of that polygon?
Solution:
Given
Each interior angle of a regular polygon is 135°.
The measurement of each interior angle of a regular polygon can be = 135°
∴ The measurement of each exterior angle of a regular polygon can be = 180° – 135° = 45°
∴ Number of sides of the regular polygon = \(\frac{360^{\circ}}{45^{\circ}}\)= 8
Question 11. The ratio of measurements of an interior angle and an exterior angle of a polygon is 3:2. Let’s write the number of sides of the polygon.
Solution:
Given
Ratio of measurements of each interior and exterior angles of a regular polygon = 3:2
Sum of ratio = 3 + 2 = 5
∴ Measurement of exterior angle = \(\frac{2}{5}\) × 180° = 72°
∴ Number of sides of the regular polygon = \(\frac{360^{\circ}}{72^{\circ}}\) = 5
Question 12. The sum of measurements of all exterior angles of a polygon is 18000°. Let’s write the number of sides of the polygon.
Solution:
Given
The sum of measurements of all exterior angles of a polygon is 18000°.
Let the number of sides’ of the polygon = n
Sum of measurements of all the interior angles of the polygon = 2 (n-2) × 9
B.T.P.,
2 (n-2) × 90° = 1800°
or’ \(n-2=\frac{1800^{\circ}}{2 \times 90^{\circ}}\)
or, n – 2 = 10
or, n -2 = 10 + 2 = 12
∴ Number of sides of the polygon = 12
Question 13. Measurement of each of 5 interior angles is 172° and the measurement of each of the other interior angles of a polygon is 160°. Let’s write number of sides of the polygon.
Solution:
Given
Measurement of each of 5 interior angles is 172° and the measurement of each of the other interior angles of a polygon is 160°.
Let the number of sides of the polygon be n.
∴ Sum of measurements of the interior anqles of the polyqon = 2 (n-2) × 90°
Total of five interior angles ofthe polygon = 5 × 172° = 860°
∴ Measurements of the remaining interior angles = (n- 5) × 160°
2(n-2)×90° = 860°-(n-5)×160°
or, 2(n-2)×90°-(n-5)×160°= 860°
or, 20°{9(n-2)-8(n-5)} = 860°
or, 9x-18-8n+40 = 43
or, n = 43+18-40
or, n = 21
∴ n = 21
∴ Number of sides of polygon = 21
“Class 8 Maths Construction of Parallel Lines solutions, WBBSE syllabus”
Question 14. ABODE is a regular pentagon. Let’s prove the AABC is an isosceles triangle, BE and CD are two parallel line segments.
Solution:
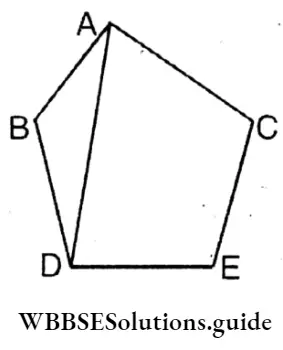
Given : ABODE is a regular pentagon.
We have to prove that :
1. ABC is an isoceles triangle and
2. BE//CD.
Proof : In ΔABC
AB = BC (∵ABCDE is a regular pentagon)
∴ ΔABC is an isoceles triangle.
Question 15. ABCDEF is a regular hexagon. The bisector of ∠BAF interects DE at X. Let’s write the measurement of ∠AXD.
Solution:
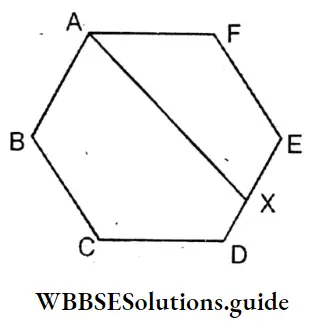
Given
∴ ABCDEF is a regular hexagon.
∴ Measurement of each of its interior angles
= \(\frac{2(6-2) \times 90^{\circ}}{6}\) = \(\frac{2 \times 4 \times 90^{\circ}}{6}=120^{\circ}\)
∴ ∠B= ∠C= ∠D = 120°
∴ ∠B + ∠C + ∠D = 3 x 120° = 360°
∠BAX = \(\frac{120^{\circ}}{2^{\circ}}\) = 60° (∵ ∠A is the bisector of AX.)
∵ ABCDX is a pentagon
∴ Sum of measurements of the interior angles of ABCDX = 2(5-2) × 906 = 2 × 3 × 90° = 540°
Sum of measurements of the 4 angles of ABCDX = 360° + 60° = 420°
∴ Pentagon AXD = 540° – 420° = 120°
Manasi constructs some triangles with some sticks like the figure beside. The bases of these triangles are in a same straight line and have same vertex.
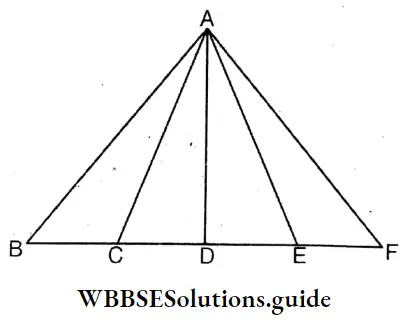
Question 17. Let’s try to measure the lengths of the sides of the triangle, i.e., the lengths of the sides only from the measurement of the angles of the triangle.
Solution:
It is seen that in ΔABC, ∠ACB is an obtuse angle.
∴ ABC is an acute angle (obtuse angle/acute angle)
We know that the opposite side of greater angle is than the opposite side of smaller angle Big (less/more), i.e, AB > AC [ Put >/<]
Again, measuring by protractor we see, side AD is perpendicular to FC, i.e, AD⊥FC
∴ ∠ADB = 90°
∴ In ΔADC,∠ACD acute angle (is an obtuse/acute angle), i.e, AC>AD [Put >/< ]
∴ It is seen the relation between sides, AC, AD and AB is AD < AC < AB.
Geometrical Proofs Exercise
Question 1. Two persons, one of them is coming along south direction to reach to east-west road and the other person is coming along the south-east direction, starting from the same place. Let’s calculate which person reaches first to the road.
Solution:
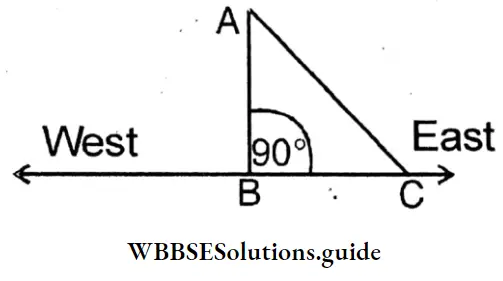
Given
Two persons, one of them is coming along south direction to reach to east-west road and the other person is coming along the south-east direction, starting from the same place.
Let BC is an east-west straight line.
Both persons started journey together from point A to C. First person traversed in the southern direction distance AB, while the second traversed BC distance in the eastern direction.
Second person traversed AC distance in south-east.
Distance covered by the first person = AB + BC
Distance covered by the second person = AC
∵ AB + BC > AC (∵ The sum of measurements of two sides of a triangle is greater than that of its third side.)
∴ The second person reached first.
Question 2. In a quadrilateral ABCD, AB=AD and BC = DC; and DP is the smallest distance drawn from D on AC. Let’s prove that B5 P and D are collinear.
Solution:
Given : In quadrilateral ABCD, AB = AD and BC = DC, the shortest distance from point D to side AC is DP.
Let’s prove that three points B, P, D are collinear.
Construction : DB is extended B to point forwards.
Proof: ∵ DP is at the shortest distance from AC.
∴ DP ⊥ AC
∴ ∠APD = 90° and ∠DPC = 90°
∴ APB = 90° (∵ the Vertically Opposite Angle of ∠DPC is ∠APB)
∴ APD + APB = 90° = 180°
∴ BPD = 180°
“WBBSE Class 8 Chapter 22 Maths, Construction of Parallel Lines step-by-step solutions”
Question 3. AD is a median of the triangle ABC. The smallest distance of AD from B and C are BP and CQ respectively. Let’s prove that BP = CQ.
Solution:
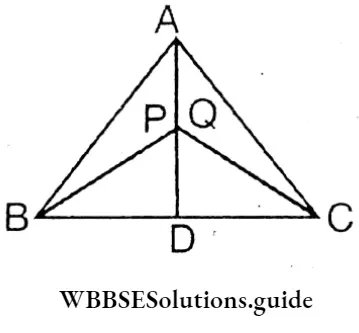
Given: ABC is the median of AD. The shortest distance of AD From points B and C is BP and CQ.
∴ BP ⊥ AD and CQ ⊥ AD
∴ ∠BPD = ∠CQD = 90°
In equiangular ΔBPD and equiangular ΔCQD, angle BD = angle DC (∵ AD is the median ∴ BD = DC)
And PD is a common side.
∴ ΔBPD = ΔCQD (R-H-S congruency)
∴ BP = CQ Proved
