WBBSE Solutions For Class 8 Maths Chapter 21 Construction Of Triangles

by

Construction Of Triangles

If I draw a triangle, lengths of whose two sides are 5 cm and 4 cm and the measurement of the angle opposite to the side of length 4 cm is 45°, then let’s see what type of triangle I shall get.

It is seen that it is not possible to draw any triangle with these conditions.

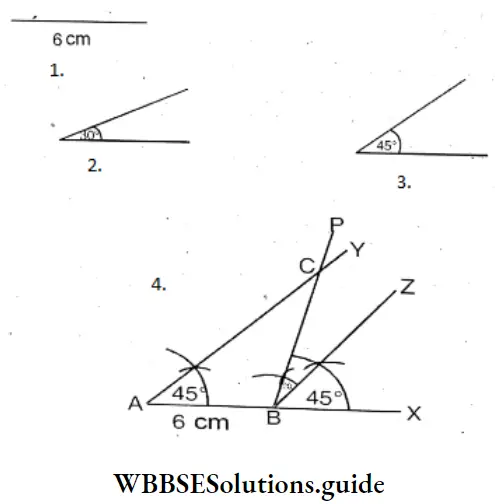
WBBSE Solutions Class 8 Chapter 21 Construction Of Triangles Measurement Of The Angles

  1. Firstly, 30° arid 45° are drawn and a straight line 6 cm long is drawn.
  2. Now straight line AX is drawn and from it 6 cm long is cut off.
  3. On points A and B of straight line AB, two angles equal to 45° ∠YAB and ∠ZBX are drawn respectively.
  4. Now on point B equal to 30° is drawn AY straight line on the same side of BZ ZPBZ. PB and AY cut each other at C point

In ΔABC = 6 cm

Read and Learn More WBBSE Solutions For Class 8 Maths

∠CAB = 45 and ∠ACB = 30°

Proof : ∠XBZ = ∠XAY (By construction)

∴ ∠BZ//AY (∵ Corresponding angles)

∴ ∠ZBP = Alternate angle ∠BCA

∵ ∠ZBP = 30°

∴∠BCA = 30°

∴ In ΔABC ∠CAB = 45°, ∠ACB = 30°

and the opposite side of 30° is AB = 6 cm

Construction Of Triangles Exercise 21.1

Question 1. If I draw a triangle of whose 2 sides are 5 cm and 4 cm and the measurement of the angle opposite to the side of length 4 cm is 45°, then let’s see what type of triangle I shall get. It is seen that it isn’t possible to draw any triangle with these conditions.

Solution:

Given

If I draw a triangle of whose 2 sides are 5 cm and 4 cm and the measurement of the angle opposite to the side of length 4 cm is 45°

  1. With the help of scale two 5 cm long straight lines are drawn.
  2. With the help of scale a ray AX is drawn. On the ray off. Taking AX at point A an angle of 45° ∠XAY is drawn.
  3. From the ray AX a straight line AB equal to 5 cm is cut off. Taking B as centre, taking as radius equal to the straight line 4 cm, an arc is drawn which cuts ray AX at point C. B, C are joined. A ABC is drawn whose AB = 5 cm, ∠BAC = 45° and BC = 4 cm and the angle opposite to the side BC ∠BAC = 45°.

WBBSE Solutions Class 8 Chapter 21 Construction Of Triangles Measurement Of The Angle Opposite To The Side Of Length

Question 2. But why is it so ? Sometimes we are getting one triangle, sometimes two triangles and sometimes no triangle. It is seen that the perpendicular distance from B on AX line segment is BM = cm = I say.

Solution:

WBBSE Solutions Class 8 Chapter 21 Construction Of Triangles Perpendicular Distance From B On AX Line Segment

We see that perpendicular distance AX from point B to the straight line

BM = 3.6 cm l = let

a = 5cm

b = 4cm

We see that, if b > a then | 1 | triangle can be drawn.

If l < b < a then 2 triangles can be drawn.

If b = a then 1 triangle can be drawn.

If b < l then no triangle can be drawn.

If b, = l then 1  triangle can be drawn.

If a = b, i.e., try to form a triangle whose two sides a = 5 cm, b = 5 cm and opposite angle to the 5 cm long side is ∠x= 100°

Question 3. Let’s see whether such a triangle can be drawn.

Solution:

WBBSE Solutions Class 8 Chapter 21 Construction Of Triangles Perpendicular Distance From B On AX Line Segment 2

straight line AC is drawn and on point A equal to angle 100°, ∠BAC is drawn.

From AD side 5 cm long AB is cut off. Now taking B as centre 5 cm straight line equal to taking as radius, on a point on AC an arc is drawn then it is seen thatit cuts at only on one point of AC, A. So it is not possible to draw a triangle.

Question 4.  if a < b, i.e., try to form a triangle whose two sides a = 5 cm, b = 4 cm and opposite angle of 4 cm long side is x = 100°. Let’s see if such a triangle can be drawn.

Solution:

WBBSE Solutions Class 8 Chapter 21 Construction Of Triangles Opposite Angle Of 4 cm Long Side

Given

if a < b, i.e., try to form a triangle whose two sides a = 5 cm, b = 4 cm and opposite angle of 4 cm long side is x = 100°.

A straight line AC is drawn and on point A equal to angle 100°, ∠BAC is drawn. From AD side 5 cm long AB is cut off.

Now taking point B as centre and taking as radius length equal to 4 cm straight line AC cut an arc on any point of then it is seen that the AC arc doesn’t cut at any point.

So it is not possible to construct a triangle.

Construction Of Triangles Exercise 21.2

Question 1. Let’s draw a triangle whose two sides are 6 cm and 7 cm and the measurement of the angle opposite to the side of length 7 cm is 60°. Let’s write what will be the measurement of the sides to form a triangle.

Solution:

WBBSE Solutions Class 8 Chapter 21 Construction Of Triangles Measurement Of The Sides To Form A Triangle

Measurement of the sides to form the triangle

A straight line AX is drawn and on point A equal to angle 60°, ∠DAX is drawn. From side AD, AB is cut equal to 6 cm long. Taking B as centre and equal to 7 cm long taking as radius point AX is cut at C. B, C are joined. ABC is the required triangle.

From point B to AC, if the length of the side be more than the length of the perpendicular drawn then two triangles will be formed.

Question 2. Let’s construct a triangle whose lengths of two sides are 6 cm and 9 cm and the measurement of the angle opposite to the side of length 9 cm is 105°. Let’s write for what length of sides we will not be able to construct two triangles.

Solution:

WBBSE Solutions Class 8 Chapter 21 Construction Of Triangles Measurement Of The Angle Opposite

A straight line AX is drawn and at AX on point A equal to angle 105°, ∠DAX is drawn. From side AD AB is cut equal to 6 cm long. Taking B as centre equal to 9 cm length taking as radius AX is cut at point C. B , C are joined. ABC is the required triangle.

Leave a Comment