Chapter 15 Area And Perimeter Of Triangle And Quadrilateral
Definitions:
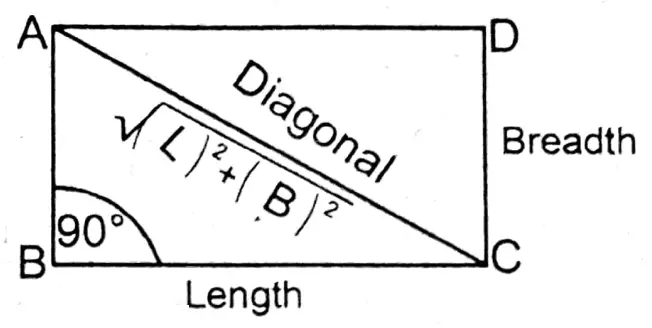
1. Rectangle: The region bounded by 4 sides, whose opposite sides are equal and parallel and each angle is equal to 90° is called a rectangle. ABCD is a rectangle.
Read and Learn More WBBSE Solutions For Class 9 Maths
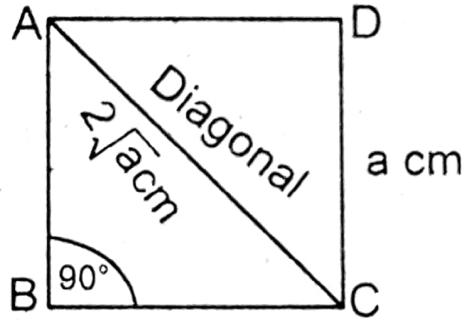
2. Square: The region bounded by 4 sides, whose all sides are equal and each angle is a right angle (90°), is called a square. ABCD is a square
Wbbse Class 9 Maths Chapter 15 Area And Perimeter Solutions
Important Formulae :
Rectangle
1. Perimeter of Rectangle = 2 (Length + Breadth) units.
2. Length of Rectangle = \(\left(\frac{\text { Perimeter }}{2}-\text { Breadth }\right)\) units.
3. Breadth of Rectangle = \(\left(\frac{\text { Perimeter }}{2}-\text { Lenght }\right)\) units.
4. Area of Rectangle = Length x Breadth sq.units
5. Length of Rectangle = \(\frac{\text { Area }}{\text { Breadth }}\) units
6. Breadth of Rectangle = \(\frac{\text { Area }}{\text { Length }}\) units
7. Length of diagonal of a rectangle = \(\sqrt{(\text { Length })^2+(\text { Breadth })^2}\)

Wbbse Class 9 Area And Perimeter Of Triangle And Quadrilateral Exercise 15 Solutions
Square
1. Perimeter of a square = 4 x side units
2. Length of a side of a square \(=\frac{\text { Perimeter }}{4}\) units
3. Area of a square = (side)2 sq.units
4. Length of one side of a square = \(\sqrt{\text { Area }}\)units
5. Length of diagonal of a square = √2 × side units
6. Length of a side of a square= \(\frac{\text { Diagonal }}{\sqrt{2}}\)
7. Area of a square= \(\frac{(\text { Diagonal })^2}{2}\)
Triangle
1. Perimeter of a triangle = (a + b + c) units where a, b, and c are the lengths of the sides of the triangle.
2. Semi-perimeter of a triangle = (s) = \(\frac{a+b+c}{2}\) units
3. Area of a triangle = \(\sqrt{s(s-a)(s-b)(s-c)}\) sq.units
4. Area of a triangle = \(\frac{1}{2}\) x base x height sq.units
5. Height of an equilateral triangle = \(\frac{\sqrt{3}}{2}\) x side units
6. Area of an equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { side })^2 \text { sq.units }\)
7. Height of an isosceles triangle = \(\sqrt{b^2-\frac{a^2}{4}}\) where ‘b’ is the length of equal side ‘a’ is the length of base.
8. Area of an isosceles triangle = \(\frac{1}{2} \cdot a \cdot \sqrt{b^2-\frac{a^2}{4}} \text { sq.units }\)
9. Height of a right-angled triangle = \(\sqrt{(\text { perpendicular })^2+\text { (base) }^2}\)
10. Area of a right-angled trangle = \(\frac{1}{2}\) x base x Perpendicular sq.units 2
= \(\frac{1}{2}\) Χ Product of the sides forming the right-angle
11. Length of the perpendicular drawn on a side of a triangle
= Area of triangle / Length of the side on which perpendicular is drawn
Formulae relating to room
1. Area of floor of a room = Length x Breadth sq.units
2. Area of roof of a room = Area of floor Length x Breadth sq.units
3. Area of four walls of a room 2 (Length + Breadth) x Height sq.units
Area of path formed around a rectangular or a square region
1. If the path is outside:
1. Area of path = Area of the region including path – Area of the region
2. Length including path Length of region + 2 x Breadth of path
3. Breadth including path = Breadth of region + 2x Breadth of path
2. If the path is inside:
1. Area of path = Area of rectangle or square – Area of rectangle or square
2. Length of rectangle or square excluding path = Length of rectangle or square 2 x Width of path
3. Breadth of rectangle or square excluding path = Breadth of rectangle or square 2 x Breadth of path
Class 9 Wbbse Maths Area And Perimeter Of Triangle And Quadrilateral Solved Problems
Chapter 15 Area And Perimeter Of Triangle And Quadrilateral Exercise 15
Question 1.
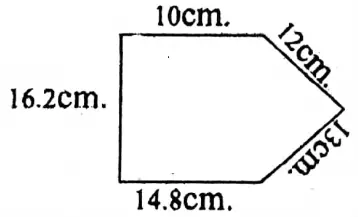
Solution: Perimeter (10+12+13+14.8+ 16.2) cm = 66 cm
Question 2.
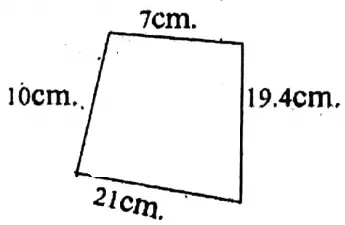
Solution: Perimeter (7+ 19.4+21+ 10) cm = 57.4 cm
Question 3.
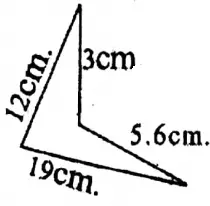
Solution: Perimeter (12+3+5.6+19) cm 39.6 cm
Question 4.
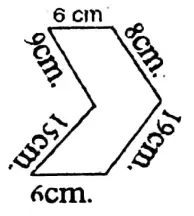
Wbbse Class 9 Maths Chapter 15 Area And Perimeter Notes
Solution: Perimeter (9+15+ 6+19+8+6) cm = 63 cm
Question 5.
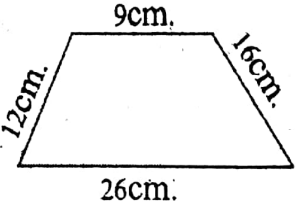
Solution: Perimeter (12+9+16+26) cm = 63 cm
Question 6. If in a square land, the length of the diagonal is 20√2 meters, let us write by calculating how much length in meters is required for fencing a wall surrounding it.
Solution: The length of the diagonal of the square land is 20√2 m.
∴ Length of each side of the square land = \(\frac{20 \sqrt{2}}{\sqrt{2}}\) m = 20 m.
∴ The perimeter of square land = 4 x 20 m = 80 m.
∴ Length of the wall for fencing the surrounding of square 80 meters.
West Bengal Board Class 9 Area And Perimeter Chapter Solutions
Question 7. The rectangular land of Pritam has a 5-meter wide path all around it on the outside. The length and width of the rectangular land are 2.5 dkm and 1.7 dkm respectively. Let us write by calculating how much cost will be required for fencing around the other side of path at the rate of Rs. 18 per meter.
Solution:
Given
The rectangular land of Pritam has a 5-meter wide path all around it on the outside. The length and width of the rectangular land are 2.5 dkm and 1.7 dkm respectively.
Length of rectangle = 2.5 dkm
= 2.5 x 10 m = 25 m
Width of the rectangle = 1.7 dkm
= 1.7 x 10 m = 17 m
Width of the path = 5 meter
Length of the land with the path = (25 + 2 x 5) m = 35 m
Width of the land with the path = (17+2×5) m = 27 m
The perimeter of the land including the path = 2(35+27) m = 2 x 62 m = 124 m
Total cost for fencing around the outer side of the path at the rate of Rs. 18 per meter = Rs. 18 x 124 Rs. 2,232.
Question 8. Let us see the card below, find the perimeter and let us write by calculating what will be the length of one side of an equilateral triangle with the same perimeter.
Solution: perimeter of the 1st card = 2(18+12)cm = 2 X 30cm = 60cm
∴The perimeter of the equilateral triangle = 60 cm.
∴ Length of one side of the equilateral triangle (60÷ 3) cm = 20 cm
Perimeter of the 2nd card = 4 x 9 cm = 36 cm
∴ Perimeter of the equilateral triangle = 36 cm
∴ Length of one side of the equilateral triangle (36÷ 3) cm = 12 cm
Perimeter of the 3rd card = (15+ 7+ 8+ 9) cm = 39 cm
∴ Perimeter of the equilateral triangle = 39 cm
∴ Length of one side of the equilateral triangle = (39÷ 3) cm = 13 cm
Perimeter of the 4th card (21+ 12+21 +12) cm = 66 cm
∴ Perimeter of the equilateral triangle = 66 cm
∴ Length of one side of the equilateral triangle = (66 ÷ 3) cm = 22 cm
Perimeter of the 5th card (12+5+13) cm = 30 cm
∴ Perimeter of the equilateral triangle = 30 cm
∴ Length of one side of the equilateral triangle (30÷ 3) cm = 10 cm
Perimeter of the 6th card (14+ 14+17) cm = 45 cm
∴ Perimeter of the equilateral triangle = 45 cm
Length of one side of the equilateral triangle (45÷ 3) cm = 15 cm
Wbbse Class 9 Area And Perimeter Of Triangle And Quadrilateral Important Questions
Question 9. Look at the figures below and let us write by calculating their area.
Solution:
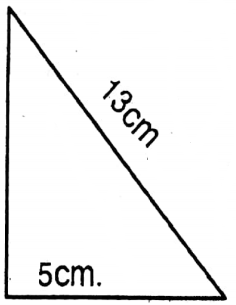
1. First image is a right-angled triangle whose base is 5 cm and its hypotenuse is 13 cm.
∴ Height of the triangle
= \(\begin{aligned}
& \sqrt{(\text { Hypotenuse })^2-(\text { base })^2} \\
& =\sqrt{(13)^2-(5)^2} \mathrm{~cm} \\
& =\sqrt{169-25} \mathrm{~cm} \\
& =\sqrt{144} \mathrm{~cm} \\
& =12 \mathrm{~cm}
\end{aligned}\)
∴ Area of the right angle = \(\frac{1}{2}\) x 5 x 12 sq.cm = 30 sq.cm
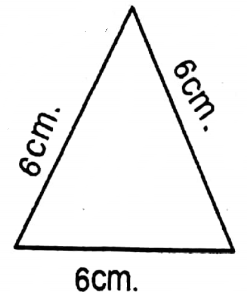
2. It is an equilateral triangle, whose each side = 6 cm.
Area of the equilateral triangle = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)
\(\begin{aligned}& =\frac{\sqrt{3}}{4} \times(6)^2 \text { sq.cm } \\
& =\frac{\sqrt{3}}{4} \times 36 \text { sq.cm } \\
& =9 \sqrt{3} \text { sq.cm }
\end{aligned}\)
Wbbse Class 9 Maths Area And Perimeter Exercise 15
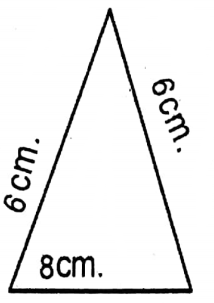
3. It is an isosceles triangle whose base is 8 cm and length of each equal side = 6cm
Area of the isoceles triangle = \(=\frac{1}{2} \times 8 \sqrt{(6)^2-\frac{(8)^2}{4}} \text { sq.cm }\)
\(\begin{aligned}& =4 \sqrt{36-\frac{64}{4}} \text { sq.cm } \\
& =4 \sqrt{36-16} \text { sq.cm } \\
& =4 \sqrt{20} \text { sq.cm } \\
& =4 \sqrt{2 \times 2 \times 5} \text { sq.cm } \\
& =8 \sqrt{5} \text { sq.cm }
\end{aligned}\)
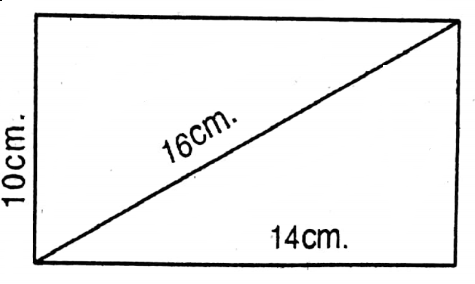
4. Fourth figure is a rectangle whose length & breadth are 14 cm & 10 cm respectively.
Area of the rectangle = Length x Breadth
= 14 x 10 sq. cm
= 140 sq. cm
Wbbse 9th Class Maths Area And Perimeter Step By Step Solutions
Question 9. In a lake of the Botanical Garden the tip of lotus was seen 2 cm above the surface of water. Being forced by the wind, it gradually advanced and submerged at a distance of 15 cm from the previous position. Let us write by calculating the depth of the water.
Solution:
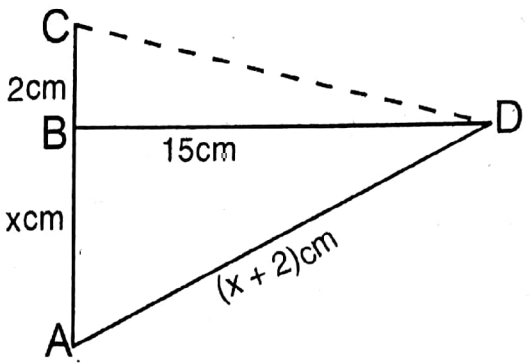
Given
In a lake of the Botanical Garden the tip of lotus was seen 2 cm above the surface of water. Being forced by the wind, it gradually advanced and submerged at a distance of 15 cm from the previous position.
Let part of the lotus lies in water and AB part lies above BC water and the water surface is BD.
∵ AC = AD = (x + 2) cm
In right-angled ΔABD, AD2 = AB2+ BD2
or, (x+2)=(x)2 + (15)2
or, x2 + 4x + 4 = x2 + 225 or, x2 + 4x-x2 = 225-4
or, 4x = 221
or, \(x=\frac{221}{4}=55.25\)
Depth of the water = 55.25 cm.
Question 10. The length of the hypotenuse of an isosceles right-angled triangle is 12√2 cm. Let us write by calculating what will be the area of that field.
Solution:
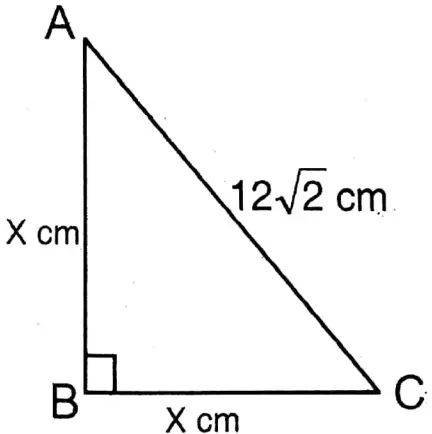
Given
The length of the hypotenuse of an isosceles right-angled triangle is 12√2 cm
Let ABC is an isosceles right-angled triangle whose ∠ABC = 90° & AB = BC= x cm.
AC2 = AB2 + BC2
or, AC2 = x2 + x2
or, AC = \(2 \sqrt{x^2}\)
or, AC = √2x
According to the problem,
\(\sqrt{2} x=12 \sqrt{2}
or, x=\frac{12 \sqrt{2}}{\sqrt{2}}=12\)
∴ AB = BC= 12 cm
∴ Area of the triangle = \(\frac{1}{2}\) x 12×12 sq.cm = 72 sq.cm.
Wbbse Class 9 Maths Area And Perimeter Formulas With Examples
Question 11. The lengths of three sides of our triangular park are 65 m, 70 m, and 75 m. Let us write by calculating the length of the perpendicular drawn from the opposite vertex on the longest side.
Solution:
Given
The lengths of three sides of our triangular park are 65 m, 70 m, and 75 m.
Semi-perimeter of the triangle = \(\frac{65+70+75}{2} m=\frac{210}{2} m=105 m\)
∴ Area of the triangular park \(\sqrt{s(s-a)(s-b)(s-c)}\)
\(\begin{aligned}& =\sqrt{105(105-65)(105-70)(105-75)} \text { sq.m } \\
& =\sqrt{105 \times 40 \times 35 \times 30} \text { sq.m } \\
& =\sqrt{3 \times 5 \times 7 \times 2 \times 2 \times 2 \times 5 \times 5 \times 7 \times 2 \times 3 \times 5} \text { sq.m }
\end{aligned}\)
= 2 × 2 × 3 × 5 x 5 x 7 sq.m
= 2100 sq.m
Perpendicular distance from the opposite vertex to the longest side
\(\begin{aligned}& =\frac{2 \times \text { Area of the park }}{\text { Length of the longest side }} \\
& =\frac{2 \times 2100}{75} \mathrm{~m}=56 \mathrm{~m} .
\end{aligned} \)
= 56 m.
Question 12. The ratio of heights of two triangles which are drawn by Suja and I is 3:4 and the ratio of their area is 4: 3. Let us write by calculating what will be the ratio of two bases.
Solution:
Given
The ratio of heights of two triangles which are drawn by Suja and I is 3:4 and the ratio of their area is 4: 3.
Let the heights of the two triangles are 3x unit & 4x unit & their bases are a unit & b unit respectively.
Ratio of the areas of the two triangles = \(\frac{1}{2} \cdot a \cdot 3 x: \frac{1}{2} \cdot b \cdot 4 x=3 a x: 4 b x\)
According to the problem, 3ax: 4bx. = 4:3
\(\frac{3 a x}{4 b x}=\frac{4}{3}
or, \frac{3 a}{4 b}=\frac{4}{3}
or, \frac{a}{b}=\frac{16}{9}\)
or, a: b=16:9
∴ The ratio of the bases of the two triangles = 16 9.
