WBBSE Solutions For Class 9 Physical Science And Environment Chapter 1 Measurement

Physical Science Class 9 WBBSE Chapter 1 Measurement Very Short Answer Type

Question 1. What do you mean by mass?
Answer:

Mass: The mass of a body is the quantity of matter contained in it.

Question 2. What is the function of ordinary scale?
Answer:

Function of ordinary scale: We generally use an ordinary scale for the measurement of length.

Question 3. What is solar day?
Answer:

Solar Day: The interval of time between two consecutive apparent transits of the sun across the meridian at any place is called a solar day.

Read and Learn all WBBSE Solutions for Class 9 Physical Science And Environment

Question 4. What is the definition of second in the SI system?
Answer:

Definition of a second in SI system: The time taken for 9, 192, 631, and 770 vibrations of a radioactive atom CS133 in a standard magnetic field is called one second.

Question 5. What do you mean by volume?
Answer:

Volume: It is defined to be the space occupied by a substance. Solids have three dimensions, i.e., length, breadth, and height.

Wbbse Class 9 Physical Science Solutions

Question 6. What is liter?
Answer:

Litre: A volume of 1 kg of pure water at 4°C or 277 K is called a liter.

Question 7. What is spring balance?
Answer:

Spring balance: With the help of this instrument, the weight of a body can be measured.

Question 8. Is the density of a material dependent on its mass or volume?
Answer:

The density of a substance is independent of its mass or volume.

Question 9. In which unit is the wavelength of X-rays measured?
Answer:

The wavelength of x-rays is measured in angstrom (A) unit.

Question 10. The yellow light of sodium has a wavelength of 589 nanometres. Express it in meters and Angstrom.
Answer:

589 nanometre = 0.000000589 metre = 0.0000000589 Angstrom.

Question 11. Give an example of a physical quantity that has no unit. Write the dimension of velocity.
Answer:

A physical quantity that ‘has no unit is the Mechanical Advantage of a machine. The dimension of velocity is \(\mathrm{LT}^{-1} .\)

Question 12. Name two quantities having the same unit.
Answer:

Velocity and speed have the same unit, e.g. m/s in the SI system.

Question 13.1 A=__cm,1 micron =___ cm. [Fill in the blanks]
Answer:

⇒ \(10^{-8}\), \(10^{-4}\)

Question 14. What is the unit of measuring the distance between the stars?
Answer:

Light year is the unit used for measuring the distance between the stars.

Question 15. Which physical quantity is normally measured with a common balance?
Answer:

Mass is normally measured with a common balance.

Question 16. Name the suitable units that should be chosen to measure

(1) Distance between two cities
(2) Mass of a small grain
(3) Distance between two stars
(4) Atomic radius
(5) Volume of water contained in an overhead tank. (Each part of the question carries )
Answer:

(1) Kilometre
(2) Milligram
(3) Light year
(4) Fermi
(5) Kilolitre.

Question 17. Why is the temperature 4°C mentioned in defining the density of water in the CGS system?
Answer:

Because at 4°C, water has maximum density, which is 1g/cc.

Wbbse Class 9 Physical Science Solutions

Question 18. What is the necessity of measurement of a physical quantity?
Answer:

Measurement of a physical quantity gives a clear idea about the largeness or smallness of the quantity. Simple eye estimation does not give any exact magnitude of the physical quantity, so measurement of a physical quantity is very important.

Question 19. Define light year.
Answer:

A light year is the distance traveled by light in one year at the rate of 3 x \(10^8\) meters per second.

Question 20. Name a scalar quantity which is the product of two vector quantities.
Answer:

The scalar quantity is work which is the product of two vector quantities force and displacement in the direction of force.

Question 21. Name a physical quantity that has both magnitude and direction but it is not a vector quantity.
Answer:

The quantity is electric current.

Question 22. Name a physical quantity that has a unit but not a dimension.
Answer:

Plane geometric angle.

Question 23. What is a cubic foot?
Answer:

It is the volume of a cube on the edge of one foot.

Question 24. What is the relation between a cubic foot and a gallon?
Answer:

One cubic foot = 6.25 gallons.

Wbbse Class 9 Physical Science Solutions

Question 25. What is the physical quantity?
Answer:

Physical Quantity: A physical quantity is any measurable quantity of an object or an event.

Example: mass, length, time, weight, density, etc.

Question 26. Define scalar quantity.
Answer:

Scalar quantity: The quantity which has only magnitude but no direction is called a scalar quantity.

Question 27. Define vector quantity.
Answer:

Vector Quantity: The quantity which has both magnitude and direction is called a vector quantity

Wbbse Physical Science And Environment Class 9 Solutions

Question 28. What is the unit?
Answer:

Unit: In measuring any physical quantity, some convenient and definite quantity of it is taken as the standard and in terms of this standard the physical quantity is measured. This standard is called a unit.

Question 29. Mention one importance of units.
Answer:

Importance of units: Measurement of any physical quantity without a unit is meaningless because we cannot have any idea about a physical quantity with its magnitude only.

Question 30. What is fundamental unit?
Answer:

Fundamental Unit: The units of physical quantities which are independent of each other and from which other units can be derived are called fundamental units.

Question 31. What is a derived unit?
Answer:

Derived unit: The units of physical quantity which are derived with the help of one or more than one fundamental unit are called derived units.

Example: The unit of area is obtained by using the unit of length twice. Similarly, units of speed, force, work, etc. are all derived units.

Question 32. What is accuracy?
Answer:

Accuracy: The closeness of the measured value to the true value of the physical quantity. is known as the accuracy of measurement.

Wbbse Physical Science And Environment Class 9 Solutions

Question 33. What is precision?
Answer:

Precision: It means the extent or limit to which the measurement of a physical quantity is done

Physical Science Class 9 WBBSE Chapter 1 Measurement 2 Marks Questions And Answers:

Question 1. Is every physical quantity a unit?
Answer:

No, some physical quantities are measured by the ratio of two identical quantities, e.g. atomic weight, specific heat, specific gravity, etc. These physical quantities have no units, they are pure numbers.

Question 2. What are the characteristics of fundamental units?
Answer:

Characteristics of fundamental units :

(1) They do not depend on each other.
(2) They can form the units of other physical quantities.
(3) They are only three in number.

Question 3. What are the types of different systems of units? y
Answer:

Different systems of units: At present two different systems of units are used in science throughout the world.

(1) CGS or Metric system.
(2) SI or international systems of units (1960).

Question 4. What is the CGS system?
Answer:

CGS or French or Metric system: This system originated in France but now it is used in scientific measurements and is widely used throughout the world including India. From the initial letters of the words centimeter, gram, and second, this system is called the CGS system. This is a decimal system.

Question 5. What is the SI system of units?
Answer:

SI or International System of Units: In 1960, an international system of units of measurement known as the SI system was recommended by the General Conference on Weights and Measures to have a consistent system of units and to simplify communications among scientists.

Question 6. Define meter.
Answer:

Metre: The distance between the two marks made on a platinum-iridium (90: 10) bar maintained at 0°C temperature preserved at the International Bureau of Weights and Measures at Sevres near Paris, is considered as one meter (symbol: m).

Question 7. What is the modern concept of meter?
Answer:

Modern concept of meter (October 1983): The distance traveled by light in;1/3x \(10^8\)sec in vacuum is called 1 meter.

Wbbse Physical Science And Environment Class 9 Solutions

Question 8. What do you mean by mass?
Answer:

Mass: The mass of a body is the quantity of matter contained in it.

Question 9. State the bigger units of mass.
Answer:

Bigger units of mass:

(1) Quintal (= 100 kg)
(2) Metric ton or tonne (= 1000 kg = 10 Quintal)
(3) CSL (= 1.4 x mass of the sun).

Question 10. State the smaller units of mass.
Answer:

Smaller units of mass :

(1) a.m.u. (= 1:6603 x \(10^{-24}\)g)
(2) 1 carat = 200 mg

Question 11. What is density? State its CGS and SI units.
Answer:

Density: The density of the material of a body is the quantity of its mass per unit volume.

Unit of density in CGS system: g \(\mathrm{cm}^{-3}\)

Unit of density in SI system: kg \(\mathrm{m}^{-3}\)

Wbbse Physical Science And Environment Class 9 Solutions

Question 12. What do you mean by solar day?
Answer:

Mean solar day: The length of the solar day varies from day to day owing to various reasons and the mean value of the actual solar days averaged over a full year is called the mean solar day.

Question 13. What are the advantages of the metric system?
Answer:

Advantages of the metric system:

(1) In the metric system, multiples and sub-multiples of the units of length and mass are always ten times the preceding ones.

(2) In the metric system, units of length, mass, and volume are related by the same relation.

(3) In the metric system, the same prefixes (such as milli, centi, deci, etc.) are used in the units of length and mass.

Question 14. Define dimension.
Answer:

Definition of dimension: Dimensions of a derived unit are the powers to which the fundamental units of mass, length, and time must be raised to represent that unit.

Wbbse Physical Science And Environment Class 9 Solutions

Question 15. Define dimensional expression.
Answer:

Definition of dimensional expression: Dimensional expression is a product or quotient of the symbols of fundamental physical quantities involved in a derived physical quantity raised to appropriate powers.

Example: Dimensional expression of force : \(\left[\mathrm{MLT}^{-2}\right]\)

Question 16. State physical quantities without dimension.
Answer:

Physical quantities without dimension: A physical quantity is expressed as a ratio between two physical quantities of the same unit, it becomes a number only, which will not have dimension.

Example: Mechanical advantage of a machine, specific gravity, refractive index, etc. are dimensionless. Again, angle, although has a unit (radian), it has no dimension.

Question 17. How can you measure the length of a curved line?
Answer:

Measurement of the length of a curved line: If the length of a curved line is to be measured with the help of a scale, we make use of a thread and place it along the curved line and measure the length of the straightened thread with the help of a scale.

Question 18. Why are scales made usually with wood or plastic?
Answer:

Scabies are made usually with wood or plastic: In making an ordinary scale wood or plastic is usually used instead of metal because, with the change in atmospheric temperature, metal scales change in length.

A metal scale gives correct readings only at a temperature at which it has been graduated. At any other temperature, it would give incorrect measurements. But in the case of wood or plastic, these changes are negligible. So the scales are made usually with wood or plastic.

Question 19. What is common balance?
Answer:

Common balance: In the laboratory, we measure the mass of a body with a common balance. The weighing balance used in our daily lives is a simple version of this common balance.

Question 20. What is the working principle of measurement of mass?
Answer:

Working principle of measurement of mass: We find the mass of a body by comparing its mass with some standard weights. Generally, the measurable object is kept on the left pan of the balance and the standard weights are placed on the right pan. When the balance beam is horizontal, then.

Mass of the objective= Mass of the standard weights

Question 21. What is the working principle of the measurement of weight?
Answer:

Working principle of the measurement of weight: The spring balance should be kept vertical and the pointer should coincide with the ‘0’ mark of the scale. When a weight is suspended from the hook, the spring elongates, elongation being proportional to the weight.

So, the pointer attached to the spring moves over the graduated scale. By noting its position against the scale, we can directly measure the weight of a body.

Question 22. What is a measuring cylinder?
Answer:

Measuring cylinder: The instrument by which the volume of a liquid is measured is known as measuring cylinder.

Question 23. What points should be noted during measuring the volume of a liquid
Answer:

Points to be noted while measuring the volume of a liquid

(1) The volume of a liquid cannot be measured by measuring a cylinder that reacts with glass.

(2) The volume of a liquid cannot be measured by a cylinder which is very volatile.

Question 24. How can you measure the density of an irregularly shaped body by using a common balance and measuring cylinder?
Answer:

Density: The density of a substance is defined as mass per unit volume of the substance.

If M is the mass of the substance, V is the volume, then the density D is given by D = M/V…..(1)

The mass of the irregularly shaped body is determined by a common balance and volume is measured by a measuring cylinder. From equation (1) density of the body can be determined.

Wbbse Physical Science Class 9 Chapter 1

Question 25. How will you determine the volume of a solid by a measuring cylinder?
Answer:

Determination of the volume of a solid by a measuring cylinder: To find the volume of the solid, some liquid in which the solid sinks but does not dissolve is taken in a dry measuring cylinder. The reading of the upper meniscus of the liquid in the cylinder is noted, let it be \(\left(V_1\right)\) ml.

The solid substance tied with a waxed thread is now slowly immersed in the liquid. Let the reading of the upper meniscus of the liquid in a measuring cylinder be\(\left(V_2\right)\)ml. So, the volume of the given solid is \(\left(V_2-V_1\right)\)ml.

Question 26. What is measurement?
Answer:

Measurement: Measurement is the determination of the size or magnitude of something. , The comparison of an unknown quantity with some standard quantity of the same type is known as measurement.

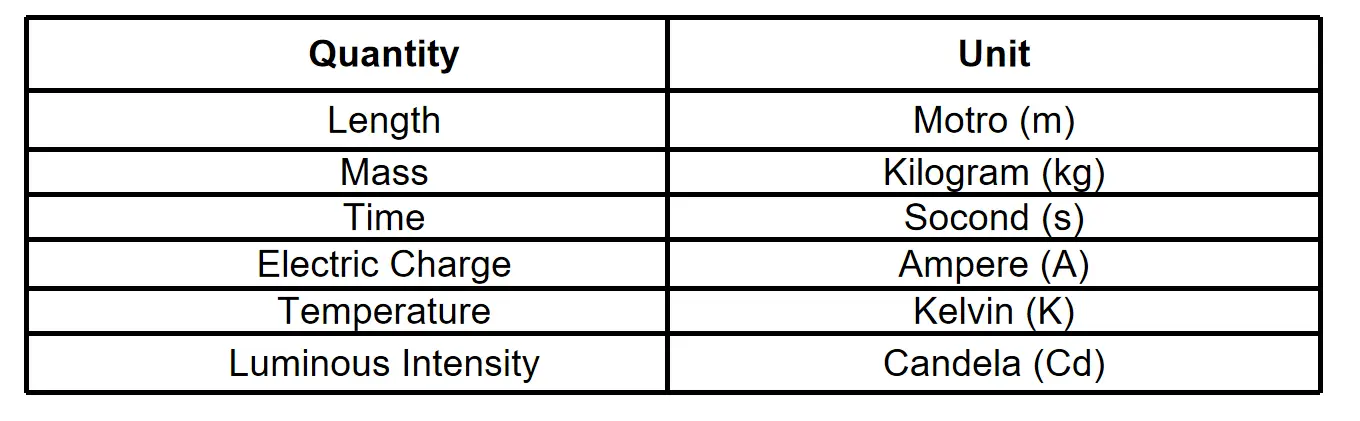
Question 27. What are the basic units to measure the physical quantities?
Answer:

The basic units are shown in the following table.

Question 28. Define Astronomical Unit.
Answer:

Astronomical unit (AU): It is the mean distance between the sun and the earth. It is used in measuring astronomical distances.

AU = 1.5 x \(10^{13}\) m

Question 29. Why is temperature mentioned in the unit of length but not in the unit of mass?
Answer:

The length is measured by a scale made of metals, plastic, wood gataparcha, etc. The length of these substances varies with temperature difference. So in determining the unit of length, temperature is to be specified to get the exact length. On the other hand, mass is an intrinsic property of matter, it does not vary with the change of temperature. So, it is not necessary to specify the temperature.

Wbbse Physical Science Class 9 Chapter 1

Question 30. If the mass and volume of a piece of iron be 760 g and 100 cm, then what would be its density?
Answer:

Density of iron = mass of iron/volume of iron

= \(\frac{760 \mathrm{~g}}{100 \mathrm{~cm}^3}\)=7.6g/\(\mathrm{cm}^3\)

Question 31. State two rules for writing the S.I. units.
Answer:

The following guidelines are followed while writing the units of physical quantities.

(1) The symbol for a unit that is not named in honor of any scientist is written in small letters.

Example: The symbol! for meter is ‘m’.

(2) The symbol for a unit that is named in honor of any scientist is written with an initial capital letter.

Example: The symbol for a unit of force (newton) is N.

Question 32. When is a common balance called defective?
Answer:
A defective common balance: A common balance is called defective if

(1) the arms of the balance are of unequal length.

(2) the scale pans are of unequal weight.

(3) the center of gravity is not exactly below the fulcrum of the balance when the beam is horizontal.

Question 33. Why are the masses of weights in a weight box taken in the ratio of 5: 2 : 2: 1?
Answer:

The masses of the standard weights in a weight box in gm are 100g, 50g, 20g, 20, 10g, 5g, 2g, 2g, and 1 gm and in milligrams are 500, 200, 200, 100, 50,20, 20 and, 10, i.e in the ratio of 5 : 2: 2: This is because, with this ratio of the masses, the mass of any body within 211.11 gm can be measured with a common balance without the need of any larger weight.

For example, if the mass of a body is 56.86 gm., its mass can be measured by placing standard weights of (50 + 5 + 1) gm and (500 + 200 + 100 + 50 + 10) mg in the right-hand pan of the balance.

Question 34. How will you measure the volume of tea in a teacup?
Answer:

The volume of tea in a teacup can be conveniently measured with the help of a narrow measuring cylinder whose volume is graduated in centimeters and decimals of centimeters.

The total amount of tea is poured inside the cylinder and the reading of the upper level of tea in the cylinder gives the volume of tea.

Question 35. If the bus fare per mile is changed into per kilometer, find whether a Passenger pays more or less than the actual fare if he travels a distance of 10 miles and pays at the rate of a kilometer.
Answer:

As the rate of fare is equal both in the mile and kilometer and 10 miles being equal to 10 x 1.60 km = 16 km, the Passenger will pay more if he pays at the rate of kilometer.

Question 36. In a ration shop, one metric ton of rice is sold per week. How many kilograms of rice are sold per week?
Answer:

1 metric ton = 1000 kilograms.

So, 1000 kilograms of rice are sold per week.

Wbbse Physical Science Class 9 Chapter 1

Question 37. Which is greater in length a table of 2 meters in length or a table of 2 yards in length? Give a reason for your answer.
Answer:

1 (one) metre = 39.37 inches
2 metres     = 39.37 x 2 inches
                     = 39.37 x 2/12 x 3 yards
                     = 2.186 yards.
As 2 meters = 2.186 yards, hence a table of the length of 2 meters is greater than a table of the length of 2 yards.

Question 38. Which is cheaper—rice at Rs. 2 per kg or rice at Rs. 1 per pound?
Answer:

1 (one) kg = 2.2056 Ibs.

Therefore, the cost of 2.2046 Ibs of rice at the rate of Rs. one per pound = Rs. 2.204. Again, the cost of 1 kg of rice at a rate of Rs. 2.00 per kg = Rs. 2.00. Hence, rice of 2 rupees per kg is cheaper than that of one rupee per pound.

Question 39. Which one will be profitable to you—kerosene costing rupees forty per gallon or kerosene costing ten rupees per liter? Give a reason for your answer.
Answer:

We know,

1 gallon = 4.536 litres.

Now if a gallon of kerosene is purchased at the rate of liter, it costs rupees 45.36 (Rs.4.536 x 10), but if it is purchased at a gallon rate, it costs rupees forty only. Hence, it is profitable to purchase at a gallon rate.

Question 40. What is the mass of 100\(\mathrm{cm}^3\)? of a liquid whose density is 1.2 gm/cc?
Answer:

We know, density = mass/volume
or, Mass = volume x density.
Hence, volume = 100 cubic centimeters.
Density = 1.2 gm/c.c.
Mass = 100 x 1.2 = 120 gm.

Question 41. The mass and volume of a piece of iron are 510 gm and 60 c.c. respectively. What is the density of the iron piece? Express the value also in S.I. unit.
Answer:

Solin. Density (d) =\(\frac{\text { mass }(M)}{\text { volume }(V)}\)=\(\frac{510 \mathrm{~g}}{60 \mathrm{v} \cdot \mathrm{c}}\)=8.5/c.c

Density of iron in S.I. unit = 8.5\(\times 10^3 \mathrm{~kg} / \mathrm{m}^3\)

Question 42. How is the volume of a regularly shaped body determined?
Answer:

To find the volume of a regularly shaped body its dimensions such as length, breadth, height, radius, etc. are measured.

Then use the following relations:

Volume of cuboid = length x breadth x height

Volume of a cube =\((\text { side })^3\)

Volume of sphere =\( \frac{4}{3} \pi \text { (radius) }^3\)

Question 43. Is light year a fundamental unit or a derived unit? Arrange in descending order of magnitude—angstrom, femtometre, micron, nanometre.
Answer:

A light year is a fundamental unit since it denotes length. Arranged in descending order: micron, nanometer, angstrom, femtometre.

Question 44. Why does one not express his age in seconds?
Answer:

A person does not express his age in seconds because, with such a small unit of time, the number expressing his age will be very large which does not give one a clear idea about the age.

Wbbse Physical Science Class 9 Chapter 1

Moreover, in calculating age in seconds and then expressing it with a large number, some more seconds will pass off which do not come into the calculation. Thus, the correct age of one cannot be expressed in seconds.

Question 45. Is the density of a material dependent on its mass or volume?
Answer:

The density of a substance is independent of its mass or volume. If the mass of a substance is increased or decreased, its volume correspondingly increases or decreases proportionately and vice versa, so density, the ratio of mass to volume, remains unchanged.

Question 46. What precautions should be taken while determining the volume and density of a solid body with the help of a common balance?
Answer:

To find the volume and thus density of a body, the following points should be kept in mind :

(1) The body must sink completely in the liquid taken in the measuring cylinder.

(2) The body must not react chemically with the liquid and also it must not dissolve in the liquid.

(3) While dipping the body in the liquid taken in the measuring cylinder, it should be done carefully so that no liquid splashes out of the cylinder.

Question 47. The mass of a proton is 1.67 x 10 Kg. How many protons would be required to make 1 kg?
Answer: Number of protons = \(\frac{1 \mathrm{~kg}}{1.67 \times 10^{-27} \mathrm{~kg}}    =\frac{10^{27}}{1.67} \)

=\(6 \times 10^{27}\) approx.

Question 48. Light of a certain color is composed of a train of waves each of 0.3048 microns long. How many of these are there in a meter?
Answer:

Number of waves    =\(\frac{1 \mathrm{~m}}{0.3048 \times 10^{-6} \mathrm{~m}}\)=\(\frac{1 \times 10^6}{0.3048}\)

=\(33 \times 10^5\) approx.

Wbbse Physical Science Class 9 Chapter 1

Question 49. Mankind has existed for about 10° years, whereas the universe is about 10 years old. if the age of the universe is taken to be one day, for how many seconds has mankind existed?
Answer:

⇒ \(10^{10}\) years is taken as equivalent to 24×60×60 s.

so, yrs is equivalent to \(\frac{24 \times 60 \times 60 \times 10^6}{10^{10}}\)s.

⇒\(\frac{24 \times 9}{25} s\)

∴ \(8.64 \mathrm{~s}\)

Question 50. What are the characteristics of fundamental units?
Answer:

Characteristics of fundamental units:

(1) They do not depend on each other.
(2) They can form the units of other physical quantities.
(3) They. are only three in number.

Question 51. What is the working principle of measurement of weight?
Answer:

Working principle of measurement of weight: The spring balance should be kept vertical and the pointer should coincide with the ‘0’ mark of the scale. When a weight is suspended from the hook, the spring elongates, elongation being proportional to the weight.

So, the pointer attached to the spring moves over the graduated scale. By noting its position against the scale, we can directly measure the weight of a body.

Wbbse Class 10 Physical Science 

Question 52. Why is the unit of area not called a fundamental unit?
Answer:

The area is the product of two lengths (length and breadth) whose unit is a fundamental unit. So unit of area has been obtained by multiplying the two fundamental units.

Question 53. Which will be of greater density—a kilogram of iron or a kilogram of cotton? Give a reason for your answer.
Answer:

If the volume of a kilogram of cotton is larger than that of a kilogram of iron, the density of cotton will be less than that of iron.

Question 54. How can a physical quantity be classified? :
Answer:

A physical quantity can be classified into two broad categories:

(1) Scalar quantity
(2) Vector quantity.

Question 55. Express a light year in a megametre.
Answer:

Light year is the distance traveled by light in one year at the speed of 3 x \(10^8\) VMS.
One megametre = \(10^6\) m.
Distance traveled by light in one year (865 days) in megametre (Mm)
\(\frac{3 \times 10^8 \times 60 \times 60 \times 24 \times 365}{10^6}\)Mm=9.4608×\(10^9\)  Mm

Question 56. Arrange in ascending order of magnitude; 1 micron, 1 angstrom, 1 fermi, 1 millimeter, 1 nanometre.
Answer:

1 micron     = \(10^{-6}\)m
1 angstrom = \(10^{-10}\)m
1 fermi (or femtometre)= \(10^{-15}\)m
1  millimetre = \(10^{-3}\)m
1 nanometer = \(10^{-9}\)m.

The required ascending order is 1 fermi, 1 angstrom, 1 nanometre, 1 micron, 1 millimeter.

Question 57. Light of a certain color is composed of a train of waves, each of wavelength 6355 angstrom. How many such waves are present in an inch or 2.54 centimeters?
Answer:

1 angstrom = \(10^{-8}\)mcm

∴ 6355 angstrom.= 6355 x \(10^{-8}\)cm. Since, 1 inch = 2.54, cm.

∴  The required number of waves=\(\frac{2.54}{6355 \times 10^{-8}}\)=\(40 \times 10^3\)

Question 58. In the CGS system density of water is 1 g/cc. Find the density of water in SI.
Answer:

Density of water =1 g/cc=1g/1\(\mathrm{cm}^3\)
=\(\frac{1 g}{(1 \mathrm{~cm})^3}\)=\(\frac{\frac{1}{1000} \mathrm{~kg}}{\left(\frac{1}{100} \mathrm{~m}\right)^3}\)=\(\left(\frac{1}{1000} \times \frac{1000000}{1}\right) \mathrm{kg} / \mathrm{m}^3\)

=\(1000 \mathrm{~kg} / \mathrm{m}^3\)

 Therefore,Density of water in the SI system is \(1000 \mathrm{~kg} / \mathrm{m}^3\)

Wbbse Class 10 Physical Science 

Question 59. In a faulty balance, the lengths of the left and right arms are respectively 11 cm and 10.5 cm. The apparent mass of a body determined by the balance is found to be 22 g; find the true mass of the body.
Answer:

The standard mass of 22 g is kept in the right pan. So, from the principle of balance, mass on the left pan x length of left arm = mass on the tight pan x length of right arm, or m X 11 = 22x 10.5
m=\(\frac{22 \times 10.5}{11}\)=21

So, the true mass is 21 g.

Question 60. The mass of an empty bucket of 10 I Capacity is 1 kg. Find its mass when it is completely filled with a liquid of density 800 \(\mathrm{kg} / \mathrm{m}^3\)
Answer:

1 =I \(\mathrm{dm}^3\)=8kg;

Mass of 10 I of the given liquid=\(\frac{800 \mathrm{~kg}}{(10 \mathrm{dm})^3}\times 10 \mathrm{dm}^3\)

So, the mass of the bucket with the liquid (8+1) or 9 kg.

Question 61. The dimension of a physical quantity is given as [M][L]?(T}2. Name the quantity. What is its SI unit? Give reasons for your answer.
Answer:

\([\mathrm{M}][\mathrm{L}]^2[T]^{-2}\)=M\(\left[\frac{\mathrm{L}}{\mathrm{T}}\right]^2 \)  = mass x velocity?.

=2x½× mass ×velocity? = 2 x kinetic energy. So, the given quantity is twice the kinetic energy. The SI unit of K.E. is Joule, for a unit of kinetic energy is the same as the unit of work.

Question 62. Deduce the dimension of power.
Answer:

Dimension of power

Power=\(\frac{\text { work }}{\text { time }}\)=\(\frac{\text { force } \times \text { distance }}{\text { time }}\)=force x velocity

=mass x acceleration \(\times \frac{\text { distance }}{\text { time }}\)

=Mx Lx \(\mathrm{T}^{-2} \times  \mathrm{LT}^{-1}\)=\(\mathrm{ML}^2 \mathrm{~T}^{-3}\)

Question 63. Find the value of 1 unified atomic mass unit (a.m.u.) in kg.
Answer:

1 a.m.u=\(\frac{1}{12} \text { of a } C_{12} \text { isotope. }\)

\(1 \mathrm{ml}^{12} \mathrm{C}\)=\(12 \mathrm{~g}^{12} \mathrm{C}\)

\(\text { i.e., } \mathrm{N}_{\mathrm{A}} \text { number of }{ }^{12} \mathrm{C}\)=12g\(\left[N_A=\text { Avogadro number }\right]\)

Therefore, 1 a.m.u =\(\frac{1}{12} \times \frac{1}{N_A} \times 12 g\)=\(\frac{1}{N_A} g\)=\(\frac{1}{1000 N_A} \mathrm{~kg}\)=\(1.66 \times 10^{-27} \mathrm{~kg}\)

Question 64. Calculate the angle of (a) 1° (degree) (b) 1° (minute of arc or arc minute) (c) 1” (second of arc or arc second) in radians
Answer:

360°=2π rad, 1°=60′, 1′=60″.

(1)360°=2π rad=
∴ 1°=\(\frac{2 \pi}{360} \times \mathrm{rad}\)=\(1.745 \times 10^{-2}\)rad

(2) 1°=60°=\(1.745 \times 10^{-2}\)rad
∴ 1′=\(\frac{1.745}{60} \times 10^{-2} \mathrm{rad} \simeq 2.91 \times\)rad

(3) 1′=60″=2.91\(2.91 \times 10^{-4}\)rad
∴ 1″=\(\frac{2.91}{60} \times 10^{-4}\)rad=\(4.85 \times 10^{-6}\)rad

Question 65. Express the numbers in exponential notation :
(a) 563
(b) 0.0012
(c) 43,900,000
(d) 0.0000007190
Answer:

(a) 5.63 x \(10^2\)
(b) 1.20 x \(10^{-3}\)
(c) 4.39 x \(10^7\)
(d) 7.19 x \(10^{-7}\)

Question 66. How many protons would be required to make 1 kg? m, = 1.67 107 kg.
Answer:

Number of protons(n)× \(m_p\) =1 kg
∴n=\(\frac{1}{1.67 \times 10^{-27}}\) =\(5.99 \times 10^{26}\)

Question 67.
(1) How many millimeters (mm) are there in a kilometer (km)?
(2) How much larger is a millisecond (ms) than a nanosecond (ns)?
(3) A microwatt (UW) is what fraction of a kilowatt (kW)?
(4) A gigaparsec (GPsc) is how many kiloparsecs (kpsc)?
(5) What fraction of a kilovolt (kV) is a millivolt (mV)?
Answer:

(a) \(10^6\)
(b)\(10^6\)
(c)\(10^{-9}\)
(d) \(10^6\)
(e) \(10^6\)

Question 68. If 325 sheets of paper make a stack 2.54 cm high, what is the thickness of a sheet of a single paper?
Answer:

The thickness of a single sheet of paper \(=\frac{2.54 \mathrm{~cm}}{325}\)=\(7.8 \times 10^{-3}\)cm.

Question 69. There are 120 small divisions on a stopwatch dial. What is the least count of the watch?
Answer:

1 Complete rotation =60 s
i.e., 120 division =60 s
∴ divisions= \(\frac{60}{120}\) =0.5 s
∴Lest count=0.5 s.

Wbbse Class 10 Physical Science 

Question 70. The length of an object was measured to be 30 cm by a linear scale of least count 0.1 cm. What is the % error?
Answer:

 % error=\(\frac{\text { least count }}{\text { measured value }} \times 100\)=\(\frac{0.1}{30} \times 100\)=0.33 \%

Question 71. A piece of iron has a volume of 500 mi and a mass is 4kg. Find the density of the object.
Answer:

Density =\(\frac{\text { mass }}{\text { volume }}\)=\(\frac{4 \mathrm{~kg}}{500 \mathrm{ml}}\)\(=\frac{4000 \mathrm{~g}}{500 \mathrm{ml}}\)=\(8 \mathrm{~g} / \mathrm{mL}\)

Question 72. 100 g of water is added to a 100 cc solution of sugar of density 1.5 g/cc. What is the density of the new mixture?
Answer:

Mass of sugar = density x volume = 1.5 g/cc x 100 cc = 150 g.
Assume 100 g water = 100 cc water (density of water = 1 g/cc).
∴ Total volume = 100 + 100 = 200 cc, mass of solution = 150 g + 100 g = 250 g.
∴ Density \(=\frac{250 \mathrm{~g}}{200 \mathrm{cc}}\)=1.25g/cc

Question 73. Find the dimension of force.
Answer:

Force = mass x acceleration =\(\text { mass } \times \frac{\text { change in velocity }}{\text { time }}\)

\(=\frac{\text { mass } \times(\text { final velocity }-\text { initial velocity )}}{\text { time }}\)

\(=\frac{m \times \frac{L}{T}}{T}\)=\(\frac{M L}{T^2}\)=\(\left[M L^2 T^{-3}\right]\)

Question 74. Power [P] is the rate of doing work. Find the dimensional equation of power.
Answer:

power\(=\frac{\text { work }}{\text { time }}\)\(=\frac{\text { force } \times \text { displacement }}{\text { time }}\)

\([P]=\frac{\left[M L T^{-2}\right] \times[l]}{[T]}\)=\(\left[\mathrm{MLT}^{-2}\right]\)

Question 75. Specific gravity is the ratio of two densities. Show that it has no dimension.
Answer:

Specific gravity of a substance \(=\frac{\text { Density of the substance }}{\text { Density of water at } 4^{\circ} \mathrm{C}}\)

\(=\frac{M L^{-3} T^0}{M L^{-3} T^0}\)=\(\left[M^0 L^0 T^0\right]\)

So, Specific gravity is dimensionless.

Wbbse Class 10 Physical Science 

Question 76. Kinetic energy is given by amv’ and potential energy by mgh. Show that both of them have the same dimensions.
Answer:

Kinetic energy \(=\frac{1}{2} m v^2\)=\((M) \times\left(L T^{-1}\right)^2\)\(=\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]\)

Potential energy = mgh =(M)\(×\left(\mathrm{LT}^{-1}\right)^2\)=\(\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]\)
So, kinetic and potential energies have the same dimensions.

WBBSE Class 9 Physical Science Solutions Chapter 1 Measurement 3 Marks Questions And Answers:

Question 1. State different smaller units of length in the SI system.
Answer:

Smaller units of length in the SI system :

(1) Femtometre or Fermi (\(=10^{-15}\) m) (fm)

(2) Picometre ( \(=10^{-12}\) m) (pm)

(3) X-ray unit (  \(=10^{-13}\) m) (Xu)

(4) Angstrom ([late]=10^{-10}[/latex] m) (A)

(5) Nanometre (\(=10^{-9}\) m) (nm)

(6) Micrometre or micron (\(=10^{-6}\) m)

(7) Centimetre (\(=10^{-2}\) m) (cm)

(8) Decimetre ( \(=10^{-1}\) m) (dm)

Wbbse Class 10 Physical Science 

Question 2. What are the bigger units of length?
Answer:

Bigger units of length:

(1) Astronomical unit (AU): The average distance between the earth and the sun.

1 AU = 14.95 X \(=10^8\) km

(2) Light year: The distance that a light wave travels in the year in a vacuum.

1 light year = 9.46 x \(=10^{12}\) km

(3) Parsec: The biggest unit for the measurement of distance. 1 parsec = 3-26 light

years = 30.84 x \(=10^{12}\) km.

Question 3. What are the requisites of a good balance?
Answer:

Requisites of a good balance :

(1) The balance must be true, i-e., the balance beam should be horizontal with no loads or with equal loads on the pans.

(2) The balance must be sensitive.

(3) The balance must be stable, i.e., the balance beam must come quickly to its equilibrium position once it is displaced.

(4) The balance must be rigid, i.e., all the parts of the balance must be strongly built.

Wbbse Class 10 Physical Science 

Question  4. What is a sensitive balance? What are the conditions to be a sensitive balance?
Answer:

Sensitive balance: A balance is said to be sensitive when even for slight differences in weights on the two pans the beam should be tilted from its horizontal position.

Conditions for a balance to be sensitive :

(1) The balance beam should be light with long arms.
(2) The center of gravity of the beam should be near the fulcrum.

Question  5. What is the concept of measurement?
Answer:

Measurement

Measurements are an integral part of the human race, without them, there would be no trade, no statistics.

Scales are used to measure. One would know a simple ruler or tape could be used to measure small distances. The current system of small units has three standard units meter, kilogram, and second. These three units form the MKS system or the metric system. A meter is a unit of length, currently defined as the distance light travels within 1/299782458th of a second.

A kilogram is a unit of mass. While it was previously defined as a specific volume of water (e.g. 1 liter or a 10 cm? cube), its current definition is based on a prototype platinum-iridium cylinder.

A second is a unit of time. Originally defined as the amount of time the earth needs to make 1/86400 of a rotation, it is now defined as 9192631770 oscillations of a Cesium-133 atom. The bigger units of measurement are astronomical units (AU).

Question  6. Define scalar quantities and vector quantities. Give examples.
Answer:

Scalar quantities: The physical quantities which have only magnitude but no direction are called scalar quantities.

Examples: mass, distance, time, volume, speed, work, energy, power, density, electric current, etc.

Vector quantities: The physical quantities which have magnitude, as well as direction, are called vector quantities.

Examples: displacement, velocity, acceleration, momentum, force, weight, electric field, magnetic field, etc.

Question  7. What do you mean by the unit of a physical quantity? All physical quantities do not have units, explain it.
Answer:

The known standard constant quantity which is used for comparison of a physical quantity is said to be a unit.

For example, the length of an iron rod is 5 meters. It means the unit of length is meter (m) and this unit is contained 5 times the length of that iron rod. Hence,

Physical quantity = numerical value x unit.

All physical quantities do not have units. Those physical quantities which are expressed as the ratio of the same quantities do not have units.

For example, atomic weight of elements, specific gravity, and refractive index.

Question  8. What observations should be taken for the choice of a unit?
Answer :

The selection of a unit to measure a physical quantity should have the following properties :

(1) The unit chosen should be of convenient size.

(2) The unit should be well-defined.

(3) The unit should not change with space, time, and temperature.

(4) It should be reproducible.

Question  9. Define fundamental and derived units. Give examples.
Answer:

Fundamental units: The unit that is independent of any other unit or which can neither be changed nor be related to any other unit is called a fundamental unit.

Examples: Units of length, mass, time, temperature, current, luminous, intensity, etc. are fundamental units.

Derived units: The units which depend on the fundamental units or which can be expressed in terms of the fundamental units are called derived units.

Example: The units of velocity, acceleration, energy, force, momentum, etc. are the derived units.

The velocity of a moving body is obtained by dividing the distance traveled by the body by the time taken. When distance is expressed in the unit of length as centimeters and time in seconds, then

a unit of velocity = unit of length/unit of time = cm/second = cm/sec.

Question  10. Define the C.G.S. system and S.I. system of measurement of units.
Answer:

C.G.S system: In this system, the unit of length is centimeter (cm), a unit of mass is gram (g) and the unit of time is second (s).

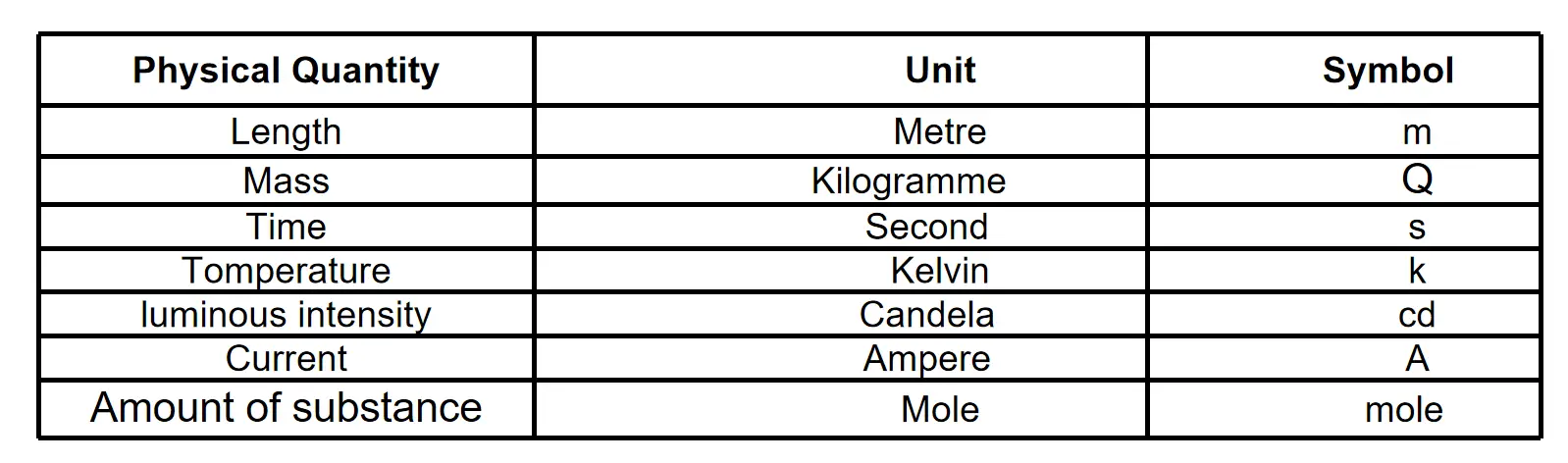
S.I. System: In this system units of seven physical quantities have been considered as fundamental units.

In the S.1. system following are considered as the fundamental units :

Question  11. Define the S.I. units of length, mass, and time.
Answer:

The unit of length is meter (m), the mass is kilogram (kg) and that of time is second (s). They are defined as

Metre (m): A meter is defined as 1,553,164.1 times the wavelength of the red line in the spectrum of cadmium.

Kilogram (kg): A kilogram is the mass of a cylindrical piece of platinum-iridium alloy kept at the International Bureau of Weights and Measures at Sevres near Paris.

Second (s): A second is defined as. 1/86400 is the part of a mean solar day.

Question  12. Explain the reason for using different smaller and larger units for measuring a particular quantity.
Answer:

To measure a particular quantity we use both smaller units and larger units as per requirement. For example, to measure the length of a room, we use meter (m), to measure the distance between two cities we use kilometer (km) units.

For the measurement of the distance of a star from the earth, the commonly used unit is light year because a kilometer is considered a very small unit in this case. To measure the length of a very small quantity we consider smaller units of length as centimeters, millimeters, microns, etc.

For example, to measure the thickness (or diameter) of a wire, we use centimeters or millimeters. In this case unit taken as meter is absurd. If the thickness of a paper measured in millimeters (mm) is 1 mm, then expressed in meters is 0.001 m, which looks odd.

Question  13. What do you mean by the dimension of a physical quantity?
Answer:

Dimension of a physical quantity

Generally, the dimension of a physical quantity represents the powers to which the fundamental unit (or units) has to be raised to obtain the derived unit of the physical quantity.

The dimensions of length, mass, and time are expressed as L, M, and T respectively. Dimensions generally represent the nature of the units only. They do not indicate the magnitude of the units.

For example, the volume of a cube L’ units

\begin{equation}
\text { Dimension of density of a cube }=\frac{\text { Dimension of mass of a body }}{\text { Dimension of volume of a body }}
\end{equation}

\begin{equation}
=\frac{M}{L^3}=M L^{-3}
\end{equation}
Dimension of force = dimension of mass x acceleration.

Question  14. State the different measuring devices to measure the different physical quantities.
Answer:

To measure the different physical quantities, the commonly used measuring devices are the following :

(1) Ordinary scale (or meter scale): Used to measure the length of an object.

(2) Common balance:  Used to measure the mass of a body.

(3) Spring balance:  Used to measure the weight of a body.

(4) Measuring cylinder:  Used to measure the volume of a liquid. It is also used to measure the volume of a solid by displacement method.

(5) Clock:  Used for measuring time.

(6) Stopwatch: Used for measuring a time interval between two events such as race, sports, etc.

Question  15. What is ordinary scale? Describe the method of measuring length with the help of an ordinary scale.
Answer:

Ordinary scale

An ordinary scale is a measuring device used to measure the length of an object. Ordinary scale is generally made up of wood, metal, or plastic. It is graduated in centimeters and millimeters. 1 centimeter is divided into 10 equal parts, each part is 1 millimeter.

To measure the length of a line say AB, we place the scale in such a way that it remains perpendicular to the line AB. Now note the readings of the starting point A and the end point B from the scale. Then,

Length of line AB = Reading of end B – Reading of end A. Let the starting point, A of the line AB at 2 cm, coincide with the scale. If the endpoint, B of the line does not coincide exactly with the graduation of the scale, the reading has to be taken by the eye approximation method. While taking the reading eye should be placed

directly above point B. In the figure given below the correct position of the eye should be at E. If we place our eye sideways, say\(E_1 \text { or } E_2\) then it leads to an error called parallax error. S

Let the end B coincides with the scale at 6.5 cm. Therefore, the length of the line AB = 6.5 cm- 2cm = 4.5 cm.

Question  16. What is density? State its units. How is the density of an irregular body insoluble in water measured?
Answer:

Density: The density of a substance is defined as its mass per unit volume. Density is a scalar quantity and is represented by the letter d. If the mass of a body is M gm, and the volume of the body is V cubic cm, then

d = M/V. Its C.G.S. unit is gm per \(\mathrm{cm}^3\), SI unit is kg/\(m^3\)

To find the density of an irregular body, first find the mass of the body by common balance. Now find the volume of the body insoluble in water by measuring the cylinder. By dividing the mass of the body by volume, we get the density of the body.

Question  17. What is a common balance? How will you measure the mass of a body with the help of a common balance? 
Answer:

Common balance: Common balance is an instrument used to measure the mass of a body. By common balance, we find the mass of a body by comparing its mass with some known standard weights.

Generally, we put the body on the left pan of the balance whose mass is to be determined, and the standard weights are placed on the right pan. When the beam of the balance becomes horizontal (or the pointer rests at zero scale) then the mass of the body is equal to the standard weight.

The different parts of a common balance are shown in the figure given below :

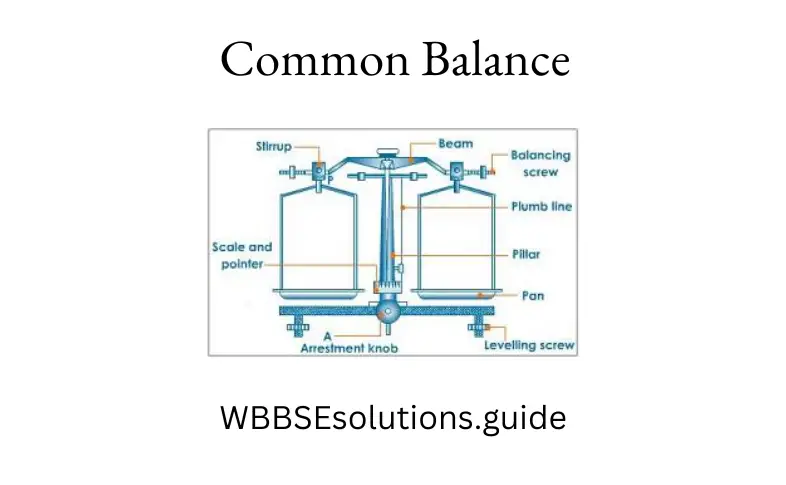
Different parts of common balance:

1- plumb line
2 – levelling screws
3- arrester
4- pans
5- beam
6- adjusting nuts
7-pointer
8- scale

A horizontal rigid beam is placed on a vertical pillar. Two scale pans (marked 4 in figure) of the same mass are suspended on the two ends of the beam supported by two strips placed on knife edges at the two ends.

The centre of the beam is kept on the fulcrum which is also attached with a pointer and a plumb line. The pointer moves over a scale fixed on the pillar when the pillar is raised with the help of a knob. The correct weight is known with the help of the pointer and the scale.

To adjust the balance, it is first leveled by leveling screws (marked 2 in the above figure). The horizontal beam is also adjusted by the two adjusted nuts (marked 6 in the figure).

Question  18. What is the volume of a body? How will you measure the volume of a given liquid by measuring devices?
Answer:

Volume of a body

The space occupied by a body is called its volume. The volume of a liquid in the laboratory is measured by the following measuring devices:

(1) Measuring cylinder
(2) Measuring flasks
(3) Burette
(4) Pipette

A measuring cylinder is commonly used to measure the volume of liquids. It is a glass cylinder of uniform radius. The outer wall is graduated in cubic centimeters and millimeters from the bottom upwards. It is available in different sizes.

Before measuring the volume of a ‘liquid through a measuring cylinder, it is cleaned and kept fixed vertically. The liquid whose volume has to be measured is poured into it and the reading of the upper layer of the liquid is noted. This reading is the volume of the given liquid.

Question  19. What is a spring balance? How will you measure the weight of a body with the help of the spring balance?
Answer:

Spring balance

Spring balance is a type of balance used to measure the weight of a body. It consists of a spring kept in a metal tube. It is partially exposed in front of the metal tube. The Graduate upper end of the spring is rigidly fixed. The lower end of the engram spring is attached to a metal rod.

One hook is attached with a Pointer to the lower end of the metal rod. The body whose weight is to be determined is hanged from this hook. A pointer attached to Spring spring moves on a graduated scale (usually in grams or kilograms). The position of the pointer indicates the weight of the body.

Question  20. Describe a method to find the volume of an irregular solid heavier than and insoluble in water, with the help of a measuring cylinder.
Answer:

To find the volume of an irregularly shaped solid body, we take a graduated cylinder. Fill the cylinder partly with water. Note the reading of the lower level of water, say x, c.c. Now tie the given solid with a thin string and lower it gently into the cylinder so that the solid is completely immersed in water.

The level of water rises again. Note the new reading of the raised water level (say, \(x_2\) C.C.). Since the body displaces water equal to its volume, the volume of the solid = second reading first reading. Thus, the volume of solid \(=\left(x_2-x_1\right)\)cubic centimeters.

Question  21. How will you measure time?
Answer:

Time is measured by a wall clock, wristwatch, and table clock. To measure a fraction of time, the stopwatch is used.

Clock :
In our day-to-day life, time is measured by a pendulum clock, whose functioning is based on the oscillation of a pendulum. In this type of clock, a metal rod is suspended from a rigid support. A heavy metal ball is suspended from the end of the rod. The time taken by the metal ball in one oscillation is regulated as 1 second.

It consists of a circular dial which is divided into 60 equal divisions. Each division represents 1 minute. It is further divided into 12 equal parts, where each part represents 1 hour. Hours are marked from 1 to 12. In this clock, the long arm is the arm of minute and the short arm is the arm of hour.

Spring is wound up with the help of a key in an old type of clock and by a battery in digital clocks or battery-operated clocks. The potential energy stored in the spring is converted to kinetic energy and it rotates the arms of the clock.

Stopwatch:

A stopwatch is used to measure the time interval between two events. it consists of a circular dial which is divided into 60 equal divisions. Each division represents 1 second. A long light needle called the second’s hand, pivoted at the center, rotates over the circular scale.

A big circular dial also contains a small circular dial to read the time in minutes. The smaller dial graduated in 30 or 60 divisions and the small needle called the minute’s hand rotates over the scale. When the second’s hand completes one rotation, the minute’s hand moves through one division or 1 minute.

A knob is provided at the top of the frame for winding the watch. By pressing the knob in succession, the watch can be started and stopped and both the needles can be brought to the starting point for further use.

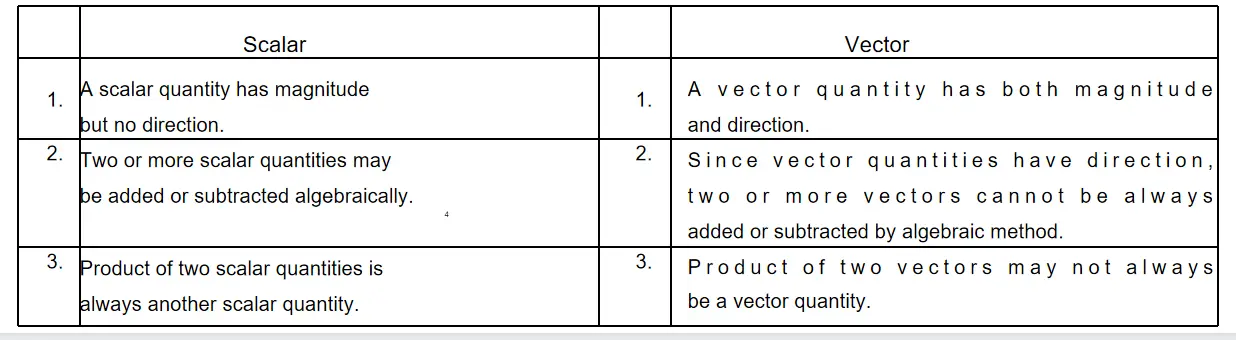
Question  22. Distinguish between scalar and vector quantities mentioning three points of difference.
Answer:

Difference between scalar and vector quantities

Question  23. How can you measure (1) the thickness of a page of a book, (2) the diameter of a piece of hair or thread, and (3) the length of a segment of a zigzag line, with the help of a ruler?
Answer:

(1) To determine the thickness of a page of a book :

The thickness of about, say, 25 pages of the book together is measured with a ruler. Dividing this thickness by the number of pages chosen, the thickness of a page is calculated.

The same procedure is followed for different numbers of pages at different sections of the book. The average of these gives the required thickness of a page found out.

(2) To find the diameter of a fine thread or a hair :

For this, a long piece of thread or hair is taken. The piece is then coiled over the millimeter marks on the scale. The coiling should be such that each turn remains in close contact to its adjacent one.

Thus the added diameters of the segments of thread in all the turns cover a few millimetres of the scale which is noted. New dividing the length on the scale by the number of turns, the diameter of the thread or hair is determined.

(3) To measure the length of a curved or a zigzag line:

A piece of thread is taken help of. A required portion of the thread is very carefully laid over the given line. Now, the length of the straightened part of the thread that was used just to cover up the given line is measured with the help of a ruler, which gives the length of the given line.

Question 24. How can you determine the density of a liquid using a common balance and a measuring cylinder?
Answer:

A clean and dry measuring cylinder is placed on the left pan of a good common balance and it is counterpoised with the mass m, gram, say. Now, some quantity of the given liquid is poured cautiously inside the measuring cylinder upto a certain level and the level is noted avoiding parallax error; let it be V cc.

Now mass of the cylinder with the liquid in it is also determined and let it be m, gram. So, the mass of the liquid taken in the measuring cylinder is (m, – m,) gram.

∴ Density of the liquid \(=\frac{\text { mass }}{\text { volume }}\)=\(\frac{\left(m_2-m_1\right) \text { gram }}{V c c}\)

\(=\frac{m_2-m_1}{V} \mathrm{~g} / \mathrm{cc}\)

Question  25. State three differences between common balance and spring balance.
Answer:

The three differences are :

(1) Common balance measures the mass of a body, and spring balance measures the weight of a body

(2) Common balance will show the same value of the mass of a body at different parts of the earth; spring balance will show different weights of a body at different parts of the earth

(3) In a common balance, several standard masses have to be placed in steps on one scale pan to counterpoise with the mass of a given body placed on another scale pan. It is a time-consuming process. But in a spring balance, the weight of the given body can be known instantaneously.

Question  26. How can you measure the exact mass of a solid by a common balance with unequal arm length? 
Answer:

Suppose the length of the left and right arm of the balance are |, and |, respectively. Now, keeping the solid with a mass of m gram at the right-hand pan it is counterpoised with a mass of w, gram at the left-hand pan.

Now,\(w_1 \times I_1\)=\(m \times I_2\)

\(\text { or, } \frac{l_1}{l_2}\)=\(\frac{m}{w_1}\)…………(1)

Again, the solid of mass is kept at the left-hand pan, and let us suppose it is counterpoised with a load of mass w, at the right-hand pan.

So,\(m \times I_1\)=\(w_2 \times I_2\)

\(\text { or, } \frac{I_1}{I_2}\)=\(\frac{w_2}{m}\)………….(2)

Now, from (1) and (2), we get

\(\frac{m}{w_1}\)=\(\frac{w_2}{m}\)

\(\text { or, } m_2\)=\(w_1 w_2\)

\(\text { or, } m\)=\(\sqrt{w_1 w_2}\)

Therefore, the correct mass \(=\sqrt{\text { Product of counterpoising   loads}}\)

Physical Science And Environment Class 9

Question  27. The mass of a piece of gold in the air is 193. g. In a measuring cylinder, there is 50 cm? of water. When the piece of gold is immersed in water in the measuring cylinder, the reading of the volume of water is found to be 60 cm. What is the density of gold?
Answer:

Given

The mass of a piece of gold in the air is 193. g. In a measuring cylinder, there is 50 cm? of water. When the piece of gold is immersed in water in the measuring cylinder, the reading of the volume of water is found to be 60 cm.

From the problem we get,

Volume of the piece of gold \(=(60-50) \mathrm{cm}^3\) \(=10 \mathrm{~cm}^3(\mathrm{~N})\)

We know, density \(=\frac{\text { mass }}{\text { volume }}\)

So, density of gold \(=\frac{\text { mass of gold }}{\text { volume of gold }}\)
\(=\frac{193 \mathrm{~g}}{10 \mathrm{~cm}^3}=19.3 \mathrm{~g} / \mathrm{cm}^3\)

Question  28. The volume of a can is 100 ml and it weighs 20g. It is then filled fully by a liquid and weighs 180 g. Find the density of the liquid.
Answer:

Given

The volume of the liquid (v) = 100 ml

Mass of the liquid (M) = (180 – 20) g = 160g

So, density of the liquid \(=\frac{\text { mass of the liquid }}{\text { volume of the liquid }}\)
\(=\frac{160 \mathrm{~g}}{100 \mathrm{~cm}^3}\)=\(1.6 \mathrm{~g} / \mathrm{cm}^3\)

Question  29. The density of a liquid is 1°2 g/\(\mathrm{cm}^3\). What will be the mass of 100 \(\mathrm{cm}^3\) of the liquid?
Answer:

Volume of the liquid \(=100 \mathrm{~cm}^3\)

Density of the liquid \(=1^{\prime} 2 \mathrm{~g} / \mathrm{cm}^3\)

We know the mass of liquid  = volume of the liquid x density of the liquid

= (100×1.2)g= 120g.

Question  30. The density of silver in a CGS unit is 10°5 g/cm®. What will be the density of silver in SI unit?
Answer:

From the problem we get,

Density of silver in CGS unit \(=10^{\circ} 5 \mathrm{~g} / \mathrm{cm}^3\)

So, the density of silver in SI unit

\(=10^{\circ} 5 \times 1000 \mathrm{~kg} / \mathrm{m}^3\) \(=10500 \mathrm{~kg} / \mathrm{m}^3\)

Question  31. The radius of a solid sphere is 10 cm. The density of its matter is 8 g/\(\mathrm{cm}^3\). What is the mass of the sphere ?.
Answer: We know,

Volume of a sphere V \(=\frac{4}{3} \pi r^3(r=\text { radius of the sphere) }\)

V\(=\frac{4}{3} \times \frac{22}{7} \times(10)^3 \mathrm{~cm}^3\)          r=10cm

Density of its matter \(=8 \mathrm{~g} / \mathrm{cm}^3\)

So, mass of sphere = volume x density

\(=\frac{4}{3} \times \frac{22}{7} \times(10)^3 \times 8 \mathrm{~g}\)=33.51 kg.

Question  32. The mass of a piece of solid substance is 20-52 g. When the piece is immersed in water its mass becomes 12-48 g. What will be its volume and density?
Answer:

Mass of displaced water by the body = (20.52 – 12.48) g = 8.04 g.

Volume of displaced water \(=\frac{8.04}{1 \mathrm{~g} / \mathrm{cc}}\)

So, the volume of the solid substance =  8.04 c.c.

Question  33. Define liter and gallon and find the relation between them.
Answer:

Liter and gallon

Litre is the space occupied by the mass of one kilogram of water at 4°C. The volume of 1 liter may also be considered as the space of a cube of length, breadth, and height 10 cm each, occupied by a gas or a liquid.

Thus, 1 litre = 1.0 cm x 10 cm x 10 cm \(=1000 \mathrm{~cm}^3\)

1 litre = 1000 cubic centimeters.

Gallon is the volume of 10 pounds of water at 62°F

1 gallon = 4,536 litres.

Question  34. State the limitation of an ordinary scale for the measurement of length. Why should the zero mark of the scale not be used while measuring length by a meter scale?
Answer:

Limitation of an ordinary scale :

A meter scale can measure length correctly only up to 1 mm (or 0.1 cm), which is the least count of a meter scale. For more accurate measurement, a vernier scale is to be used. Besides, an ordinary meter scale is not useful for the measurement of the diameter of rods, wire, spheres, internal and external diameters of hollow cylinders, etc.

For these, an instrument called a slide caliper is to be used. For measurement of the diameter of very thin objects like hair, or thread, an instrument called a screw gauge is usually used Measurement should be made from the graduation mark other than the ‘0’ mark at one end of the scale to avoid error due to wear and tear of this end.

Question  35. How would you measure the volume of an irregular solid that can not be introduced into a measuring cylinder given to you?
Answer:

If the measuring cylinder is not wide enough for the solid to enter into it, the value of the solid can be measured with the help of an overflow jar which consists of an iron vessel provided with a spout.

The jar is filled with water up to the point of overflowing. The given measuring cylinder is placed under the spout of the overflow jar. The solid is carefully and slowly lowered into the overflow jar.

The solid displaces its volume of water and this water flows out from the spout into the measuring cylinder. The volume of water collected in the measuring cylinder is recorded. This is also the volume of the given solid.

Physical Science And Environment Class 9

Question  36. What will be the mass of 454 liters of water?
Answer:

Mass = volume x density

Density of water = 1 gm/cc.

Now, 1 gm \(=\frac{1}{1000} \mathrm{~kg} .\)=\(10^{-3} \mathrm{~kg}\)

454 litres = 454 x \(10^{3} \)c.c.

A mass of 454 liters of water

= 454 x \(10^{3} \) x1gm

= 454 x \(10^{3} \) x\(10^{-3}

= 454 kg.

Question  37. The length, breadth, and height of a water reservoir are 2 m, 1m, and 1m respectively. How many liters of water it can hold?
Answer:

The volume of the water reservoir = length x breadth x height

=2m x 1m x 1m

=2 x 10dm x 1 x 10dmx 1 x 10dm

= 2000 cubic decimetre

So the volume of water in the reservoir

= 2x [latex]10^{3} \) cubic decimetre

=2x \(10^{3} \) litre

(∴ cubic decimetre = 1000 cubic centimetre = 1 litre)

Question  38. What are the bigger units of length?
Answer:

The bigger units of length are kilometer (km), light year, and Astronomical Unit (A.U.).

1 Kilometre (km) = 1000 m (or\(10^{3} \) m)

A light year is the distance traveled by light in a vacuum in one year.

1 Light year = Speed of light x 1 year

= 3 x \(10^{8} \) m/s x 1 year

=3 x \(10^{8} \) m/s (865 x 24×60 60)s =9.46 x \(10^{12} \) km

Astronomical Unit (AU) is the mean distance of Earth from the sun.

1 A.U. = 1.496 x\(10^{11} \) metre.

Question  39. What are the smaller units of length?
Answer:

The S.I. unit of length is 1 meter. Its smaller units are centimeters (cm), millimeters (mm), micro, and nanometer (nm)

1 Metre =100cm or, 1cm\(=1 / 100 \mathrm{~m}\)

1 Metre = 1,000 mm_ or, 1 mm \(=1 / 1000 \mathrm{~m}\)

1 Metre = 10,00,000 micron or, 1 Micron =\(10^{-5} \)m

1 Nanometre=\(10^{-9} \)m.

Question  40. What is the utility of a unit? Do all physical quantities have units?
Answer:

Utility of a unit: Measurement of a physical quantity is just a process of comparing it with a well-defined standard quantity which is of similar nature to that of the quantity to be measured. This standard quantity, known as a unit, is chosen before measuring a physical quantity.

Now, with a preconception about the magnitude of the chosen unit, a comparison of a certain quantity with it gives a clear idea about the measured quantity. Hence, without

A unit, any measurement is meaningless:
There are some physical quantities, each of which is expressed by a ratio of similar physical quantities, so they have no units.

Examples: Mechanical advantage of a machine, solubility, refractive index, atomic weight, etc.

Question  41. What are the advantages of the metric system?
Answer:

Advantages of the metric system:

(1) In the metric system, multiples and sub-multiples of the units of length and mass are always ten times the preceding ones.

(2) In the metric system, units of length, mass, and volume are related by the same relation.

(3) In the metric system, the same prefixes (such as milli, centi, deci, etc.) are used in the units of length and mass. 2

Question  42. What precautions should be taken while determining the volume and density of a solid body with the help of a common balance?
Answer:

Precautions :

(1) The body must sink completely in the liquid taken in the measuring cylinder.

(2) The body must not react chemically with the liquid and also it must not dissolve in the liquid.

(3) While dipping the body in the liquid taken in the measuring cylinder, it should be done carefully so that no liquid splashes out.

Question  43. State the relationship between
(1) Inch and centimetre
(2) Kilometre and mile
(3) Kilogram and pound
(4) Pound and gram.
Answer:

(1) One Inch = 2.54 Centimetre
(2) One Kilometre = 0.6213 Mile
(3) One Kilogram = 2.2046 Pounds (Ibs.)
(4) One Pound = 453.56 grams.

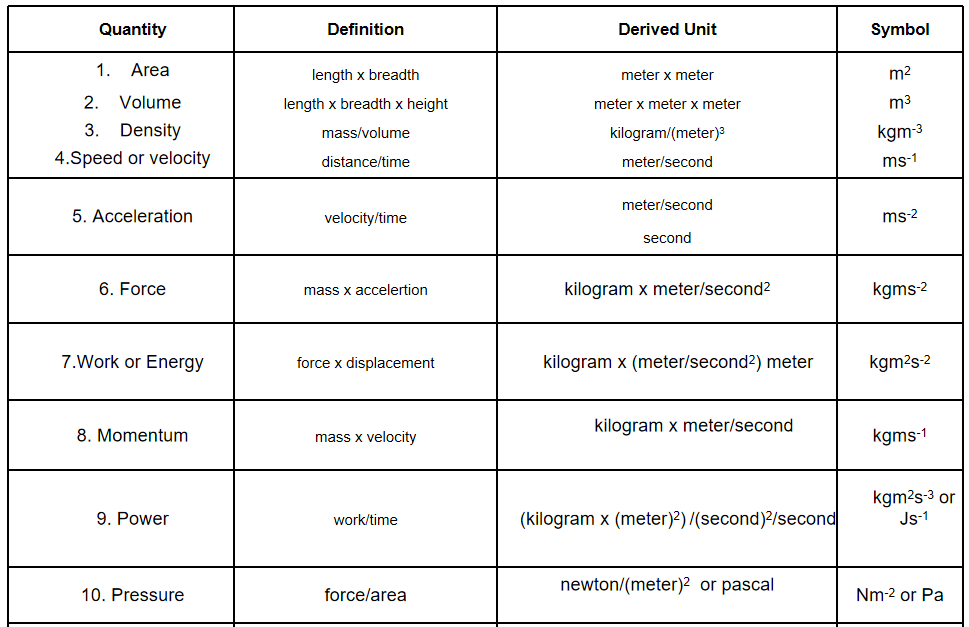
Question  44. Define the units of the following physical quantities using the fundamental units : area, volume, density, velocity, acceleration, force, work, momentum, power and pressure.
Answer:

Question  45. State the applications of dimensional analysis.
Answer:

Applications of dimensional analysis :

(1) Addition or subtraction can be done with only those physical quantities which have the same dimensions. ‘

Total energy \(=\text { kinetic energy }\left(\frac{1}{2} m v^2\right)\)+Potential energy

Each of energy terms-has the same dimension =\(\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]\)

(2) Identical dimensions can be canceled in the numerator and the denominator.

Acceleration :\(\frac{\text { Velocity }}{\text { Time }}\)=\(\frac{\left.\mid M^0 L T^{-2}\right]}{[T]}\)=\(\left[M 2 L T^{-2}\right]\)

Pressure :\(\frac{\text { Force }}{\text { Area }}\)=\(\frac{\left[\mathrm{MLT}^{-2}\right]}{\left[\mathrm{L}^2\right]}\)=\(\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\)

(3) Every correct formula or equation must have the same dimension on both sides of the equation.

Question  46. State the utility of dimensional analysis.
Answer:

Dimensional analysis helps us in deducting certain relations among different physical quantities.

It is of much help in checking the derivation, accuracy, and dimensional consistency of mathematical expressions.

Examples: Deducing a relation

The period of oscillation (T) of a simple pendulum depends on its length (1), mass (m), and g.

Let, T\(=k l^a g^b m^c ; k\)= dimensionless quantity; a, b, c = exponents

\(\left[L^0 M^0 T^1\right]\)=\([L]^a\left[L T^{-2}\right]^b\left[M^c\right]^c\)\(L^{a+b} \cdot T^{-2 b} \cdot M^c\)
On equating the dimensions on both sides, we have
a+b=0,-2b=1,c=0, or b=-½,va=-b=½,c=0

T\(=k l^a g^b m^c ; k\)=\(\left.k\right|^{\frac{1}{2}} g^{\frac{1}{2}} \cdot m^0\)=\(k \sqrt{\frac{1}{g}}\)

Actually, k is observed to be 2π 

T=\(2π \sqrt{\frac{1}{g}}\)

Examples: Dimensional Consistency :

Check whether the equation\(\frac{1}{2} m v^2\)  = mg is dimensionally correct or not.

L.H.S.:  \([M]\left[L T^{-1}\right]^2\)=\(\left[M L^2 T^{-2}\right]\),     R.H.S: \([\mathrm{M}]\left[\mathrm{LT}^{-2}\right][\mathrm{L}]\) =\(   \left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]\)
L.H.S. = R.H.S., the equation is dimensionally correct.

Physical Science And Environment Class 9

Question  47. Write a note on the different types of errors in measuring physical quantities.
Answer:

Errors :

Least count, Range, Absolute, Relative, and Percentage: Measurement errors, which are, in general, of two types :

(1) Systematic error
(2) Random error.

Systematic error is of three types :

(1) Instrumental error,
(2) Experimental error and
(3) personal error.

They can be minimized or eliminated by improving techniques or experimental procedures, opting for a better instrument, and removing personal error by more careful measurement. unpredictable fluctThe type (b) is irregular and random.

They may arise due to random mutations in experimental conditions. Temperature variation, mechanical vibration, and voltage fluctuation are the possible reasons.

Least count error :

The smallest value that can be measured by an instrument is called its least count. All the readings are. good only upto this value. The least count error is the error associated with the resolution of the instrument. It belongs to the random error category but within a limited size.

A meter scale has the least count of 1 mm or 0.1 cm, and a Vernier caliper has the least count of 0.01 cm. We can improve the least count error by selecting an instrument of higher precision or by repeating the observations several times and then taking the mean or average value.

Absolute and relative error :

Let us consider n number of measurements giving values, \(m_1, m_2, \ldots m_k \ldots m\), and the true value is \(m_{\text {true }}\)

Then mean value \(m_{\text {mean }}\) \(=\left(m_1+m_2 \ldots+m_k+\ldots+m_n\right) / n\)\(=\sum_i m_i / n\)

Absolute error\(\left|\Delta m_k\right|=m_k-m_{\text {mean }}\),k=1,2,………n

Mean absolute error,\(\Delta m_{\text {mean }}\)=\(\sum_k\left|\Delta m_k\right| / n\)

The range of a single measurement \(=m_{\text {mean }} \pm \Delta m_{\text {mean }} \text { i.e. }\)\(=m_{\text {mean }} \pm \Delta m_{\text {mean }}\)
or,\(m_{\text {mean }}-\Delta m_{\text {mean }} \leq m \leq m_{\text {mean }}+\Delta m_{\text {mean }}\)

i.e., any measurement of the physical quantity m is likely to lie between \(\left(m_{\text {mean }}+\Delta m_{\text {mean }}\right)\) and (\(\left(m_{\text {mean }}-\Delta m_{\text {mean }}\right)\)

Relative error =\(=\Delta m_{\text {mean }} / m_{\text {mean }}\)

Percentage error = Relative error 100% \(=\frac{\Delta \mathrm{m}_{\text {mean }}}{\mathrm{m}_{\text {mean }}} \times 100\)

Note that | Δm | is always positive but Δm may be both (+) ve.

WBBSE Class 9 Physical Science Solutions

48. In 5 successive measurements, the values of the period of oscillation of a simple pendulum are obtained as T, = 2.63, T, = 2.56, T, = 2.42, T, = 2.71 and T, = 2.80 (ins). Demonstrate the different errors and range of measurement.
Answer:

\(T_{\text {mean }}=\sum_i T_i / 5\)=(2.63+2.56+2.42+2.71+2.80)/5

\(=\frac{13.12}{5}\) =2.624 s[Mean value of T]

\(\left|\Delta T_i\right|\)=|2.63-2.62|,|2.56-2.62|,|2.42-2.62|,|2.71-2.62|,|2.80-2.62|

=0.01,0.06,0.20,0.09,and,0.18,(s)[absolute errors]

\(\mathrm{T}_{\text {mean }}=\sum_i\left|\Delta \mathrm{T}_{\mathrm{i}}\right| / 5\)=(0.0+0.06+0.20+0.09+0.18)/5=0.54/5

= 0.11 s [mean absolute error]

Range of measurement : \(T_{\text {mean }} \pm \Delta T_{\text {mean }}\)=2.62±0.11s

Relative error \(=\Delta T_{\text {mean }} / T_{\text {mean }}=\frac{0.11}{2.62} \times 100\)=4%

The least count (or the minimum value), the maximum value measurable, and the relative error of a few simple instruments are listed in the following table.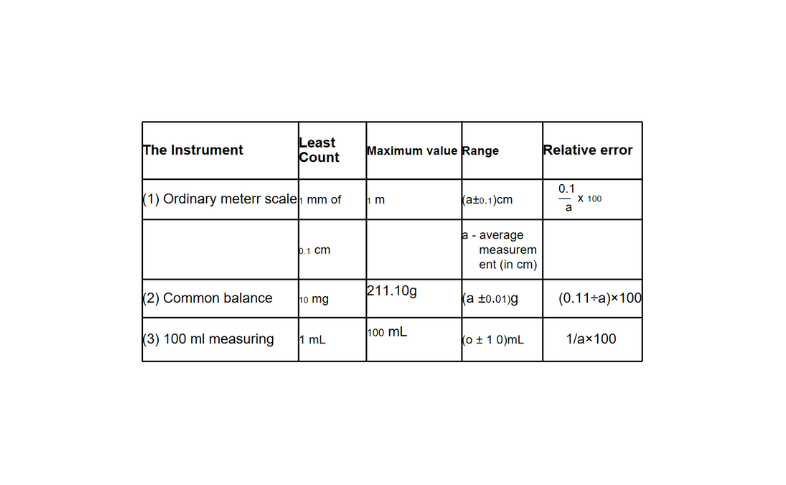 Question  49. State the characteristics. of the units of measurement.
Answer:

Characteristics of the units of measurement :

(1) The unit should be well-defined.

(2) The unit should be of considerable size.

(3) The unit should be easily reproducible.

(4) The unit should be imperishable. ‘

(5) The unit should be constant with respect to time or with physical conditions like pressure, temperature, etc.

Question  50. State the different types of variables and constants based on dimensions.
Answer:

Different types of variables and constants :

(1) Dimensional constants :

The quantities which have dimensions but which are of constant value are called dimensional constants.

Example: Gravitational constant, Planck’s constant.

(2) Dimensionless constants :

The constant quantities having no dimensions are called dimensionless constants.

Example: Pure Numbers 1, 2, 3 … 1, π (= 2.718).

(3) Dimensional variables :

The quantities which have dimensions but do not have any fixed value are called dimensional variables.

Example: Volume, Velocity, Force, etc.

(4) Dimensionless variables :

The quantities which have neither dimensions nor any constant value are called dimensionless variables.

Example: Angle, Specific Gravity, Strain, etc.

Question  51. State the limitations of dimensional analysis.
Answer:

Limitations of dimensional analysis :

(1) This method fails to determine the dimensionless constants in the formula.

(2) If a physical quantity depends on more than three factors having dimensions, the formula cannot be determined.

(3) This method cannot be used to derive a relation involving trigonometric or exponential or log functions.

(4) This method fails to derive an exact form of a relation when it consists of more than one part on any one side.

(5) It gives no information regarding whether a physical quantity is scalar or vector.

(6) Even when dimensions are given, the physical quantity may not be unique, as many physical quantities have the same dimensions.

Question  52. Mention some points to be noted while writing SI units.
Answer:

The following points may be noted while writing SI units :

(1) Punctuation marks like full stops, commas, etc. are not written after the symbols of the units. (e.g. we should write cm and not cm.).

(2) The symbols of the units are always used in singular form (i.e., we write 1m, 5 m, etc., and not 5 ms).

(3) The name of a unit is never written in the initial capital letter, even if it is named after some person. (e.g. we write ampere, joule, Newton, etc. and not as Ampere, Joule, Newton, etc.).

(4) If a unit is named after a person, its symbol is written in capital letters but the symbols of other units are not written in capital letters (e.g., we write newton (N), joule (J), metre (m), kilogram (kg), etc.).

(5) When temperature is expresed in kelvin scale, (°) degree sign is not used, i.e., we write 300 K and not 300°K.

(6) Units like metre per-second, etc. are written as m/s or \(\mathrm{ms}^{-1}\)

Question  53. Describe how time is measured by clocks and stopwatch.
Answer:

Clocks and Stop Watch : Time is measured by a clock and small time interval is measured by stopwatch. They are described below

The Pendulum clock : In this clock a simple pendulum is used. At a particular place, a pendulum of a given length takes a fixed time to complete one oscillation, i.e., starting from one extreme position and coming back to that position. This time is called the time period of the pendulum clock.

With the help of a coiled spring a gear (a toothed wheel) is rotated. A second pendulum regulates the speed of this gear being connected with it. Due to this regulated rotation of the gear, the hands of the clock being attached with it turn over a graduated circular dial and indicates the time. The spring requires to be wound after regular interval.

 

The Stop watch : This watch resembles a pocket watch in appearance. On pressing a knob the watch starts and it stops when the knob is pressed for the second time. From the positions of the hands the time interval is obtained. This watch can measure a time interval of one-tenth of a second accurately. The watch is used in sports, scientific work, etc. for measuring time.Question  54. Define the units of area, volume, density and temperature scales in different systems.
Answer:

Units of Area, Volume, Density, and Temperature scales :

(1) The units of area: of a surface in CGS, MKS or SI systems are correspondingly square centimeters (\(\mathrm{cm}^2\), square meter \(\left(m^2\right)\)

(2) Units of volume: of a solid body in CGS, MKS or SI systems are cubic centimeters (cc) and cubic meter (\(\left(m^3\right)\)) respectively.

For measuring volume of a liquid, the units usually used are litres or gallons.

Smaller units of litre are decilitres, millilitres of a cubic centimeter (cc).

10 decilitres = 1 litre; 1000 millitres (ml) = 1 litre or 1000 cubic centimetre (cc) = 1 litre.

(3) Units of density : Density of the material of a body is defined us the quantity of its

Mass per unit volume. Thus ,density \(=\frac{\text { mass }}{\text { volume }}\)

So, the unit of density in CGS is gm/cc or gm \(\left(m^{-3}\right)\), that in MKS or SI is kg/\(\left(m^3\right)\) or Kg \(\left(m^{-3}\right)\). Density of a substance is not dependent on its mass or volume.

If the mass of a substance is increased or decreased, its volume correspondingly increases or decreases proportionately and vice versa, so density, the ratio of mass of volume, remains unchanged, provided temperature remains constant.

For this reason, density of a solid golden bar and that of a solid golden ball is same, although the said bar andthe ball may have different masses, and hence, corresponding different volumes.

(4) Temperature scales : In CGS system, temperature is measured in Celsius scale. A temperature in Celsius scale is written with °C at the end of a number that indicates the magnitude of the temperature. In SI system the temperature scale used is known as Kelvin or Absolute scale. To write any temperature in this scale the degree sign is not written. For example, 300K but not 300°K.

Question  55. Define Ampere, Candela and Mole.
Answer:

Definition of Ampere, Candela, Mole : These three are considered as fundamental physical quantities in SI.

(1) Ampere : Symbol :A. It is the constant current which, flowing in two straight parallel infinite conductors of negligible cross-section placed one metre apart-in vacuum, produces 2 X \(10^{-7} \mathrm{Nm}^{-1}\) force between the conductors. The force is attractive or repulsive accordingly as the currents in the conductors are in same or opposite directions.

(2) Candela: Symbol: Cd. It is the radiant intensity of \(\frac{1}{683}\)watt per steradian (unit of solid angle) in a given direction sent by a source that emits monochromatic radiations of frequency 540 x 1012 Hz.

(3) Mole: Symbol: mole. Mole is a counting unit for chemists and it is the number 6.023

A mole stands for Avogadro’s number of items.
1 mole of atoms                 =  6.023   \(10^{23}\) atoms
1 mole H Molecules           =  6.023   \(10^{23}\) H Molecules
1 mole\(\mathrm{CO}_2\) Molecules       = 6.023  \(10^{23}\)\(\mathrm{CO}_2\) Molecules
1 mole  eletrons                 =  6.023   \(10^{23}\) eletrons
1 mole  rupees                   =  6.023    \(10^{23}\) rupees .

Question  56. How can we measure the area of an irregularly shaped lamina?
Answer:

Measurement of an irregularly shaped lamina : Take a graph paper of 1 m\(m^2\) or \(\frac{1}{100}\) area of each of its small squares. Place the irregular lamina on the graph paper and draw its outline.

Now count the number of complete number of squares inside the outline drawn. In the counting process, the number of squares more than half part of which are within the outline is also added. Let the total number of squares counted as stated above be x. So, the area of the lamina is x m\(\)m^2[/latex

WBBSE Solutions for Class 9 Physical Science And Environment

• Chapter 1 Measurement
• Chapter 2 Force And Motion
• Chapter 3 Matter: Structure And Properties
• Chapter 4 Matter: Atomic Structure; Physical & Chemical Properties of Matter
  • 4.1 Atomic Structure
  • 4.2 Concept Of Mole
  • 4.3 Solution
  • 4.4 Acids, Bases & Salts
  • 4.5 Separation Of Components Of Mixtures
  • 4.6 Water
• Chapter 5. Energy In Action: Work, Power & Energy
• Chapter 6 Heat
• Chapter 7 Sound