Chapter 2 Forces And Motion Very Short Answer Type:
Question 1. Give an example of motion when there is no change of speed but there is only a change in direction.
Answer:
A runner running with uniform speed across a circular track will have to change his direction of motion at every instant of his journey.
Question 2. A body goes around the sun with constant speed in a circular orbit. Is the motion uniform or accelerated?
Answer:
Though the body moves with uniform speed, the direction of its velocity changes continuously. Hence, the motion is accelerated.
Speed And Velocity Difference Class 9
Question Question 3. Give an example where acceleration is produced due to change in the direction of velocity although the magnitude of the velocity remains unchanged.
Answer:
The revolution of earth around the sun is an accelerated motion though its velocity is uniform.
Read and Learn all WBBSE Solutions for Class 9 Physical Science And Environment
Question 4. What is meant by “motion in one direction”?
Answer:
When a body moves in a straight line, its motion is said to be in one direction (one dimension) only.
Question 5. What do you mean by the distance between two locations?
Answer:
Distance is the total path traveled from one location to another. It is a scalar quantity.

WBBSE Class 9 forces and motion solutions
Question 6. What is a reference frame?
Answer:
To locate the position of a body concerning the reference body or observer, a system of coordinates fixed on the observer or reference body is constructed and it is known as a reference frame.
Question 7. What is a body?
Answer:
Body: A natural object possessing mass, weight, and volume is called a body.
Question 8. What is a particle?
Answer:
Particle: It is a hypothetical minute object having mass and existence. So it is called point mass, it has only translatory motion, i.e., motion along a line. It has no volume, so it has no rotational motion about its own axis or center.
Speed And Velocity Difference Class 9
Question 9. What is a rigid body?
Answer:
Rigid body: Theoretically, a rigid body is one, such that under no circumstances an external applied force, however large may it be, can increase or decrease the distance between two of its constituents parts.
Question 10. What is the role of frame of reference?
Answer:
To determine relative motion or position of a body we compare the state of motion or position of it with respect to a fixed frame of reference. Without a frame of reference we cannot understand or measure the quantity of motion or distance of position of body from another body.
Question 11. What is rest?
Answer:
Rest: A body is said to be at rest if it always remains at a fixed or unchanged position from a frame of reference. : Or more simply, a body is said to be at rest if it does not change its position with time from a fixed neighboring object.
Question 12. What is motion?
Answer:
Motion: A body is in motion if its position from a fixed neighboring obj ect or reference point changes with respect to time.
Question 13. What is vibratory motion?
Answer:
Vibratory motion: Repetition of the to-and-fro motion of a body about a mean position in a horizontal plane or a vertical plane is called vibratory motion. Oscillation of a tuning fork is a vibratory motion.
Question 14. What is periodic motion?
Answer:
Periodic motion: A motion which repeats at regular intervals of time is called periodic motion.
Example: When the earth moves around the sun once in 365 days, itis a periodic motion.
Speed And Velocity Difference Class 9
Question 15. What is average speed?
Answer:
If an object traverses different distances in equal time intervals, its speed is said to be non-uniform. For a body moving with non-uniform speed, its average speed is calculated by dividing the total distance covered with the total time required to cover the distance.
What Is Uniform Velocity Class 9
Question 16. What is uniform velocity?
Answer:
Uniform velocity of an object occurs if it traverses equal distances in equal inter- vals of time in a given direction.
Question 17. What is non-uniform velocity?
Answer:
Non-uniform velocity: A body is said to move with non-uniform velocity if it covers unequal distances in a certain direction in equal time intervals or if it changes its direction of motion at different points on its path, even covering equal distances in equal time intervals.
Question 18. What is acceleration?
Answer:
Acceleration: Increase or decrease of velocity per unit time is the acceleration of a body. It is also defined as the rate of change of velocity with time.
∴\(\frac{\text { unit of displacement }}{\text { unit of time }} \times \frac{1}{\text { unit of time }} \)
Forces and motion WBBSE Class 9 solutions with answers
Question 19. What is the principle of physical independence of force?
Answer:
The principle of physical independence of a force states that if a body is under simultaneous action of a number of forces, each force independently changes velocity or thus, the momentum of the body in its own direction, any other member of tne applied forces cannot influence it.
Question 20. Define inertia
Answer:
Inertia of a material body is its intrinsic property due to which the body tends to preserve its state of rest or uniform motion in a straight line.
What Is Uniform Velocity Class 9
Question 21. A motor car moving with uniform velocity goes 60 km in 3 hours. Find the velocity of the car.
Answer:
Velocity of the car\(=\frac{\text { displacement }}{\text { time }}\)
⇒ \(=\frac{60 \mathrm{~km}}{3 \mathrm{hrs}}\)
= 20 km/hr from north to south.
Question 22. A man is running at a velocity of 5 m/s. How far will the man goin15s?
Answer:
Distance moved = velocity x time = 5 m/s x 15s = 75 m.
Question 23. A body starts from rest with uniform Osacecly of 2 m/\(s^2\) What will be its velocity after 10 s ?
Answer:
Given, u = 0; t= 10s; f =2 m/s
Then, v=u+ft=0+2×10=20 mis.
Question 24. Same force acting on two bodies of masses 5g and 2g produces an acceleration of 2 cm/\(s^2\) in the former. What is the acceleration of the second body?
Answer:
Mass of the first body = 5 g
Acceleration produced in it = 2 cm/\(s^2\)
there fore Applied force = mass x acceleration = 5 x 2 = 10 dyne.
∴ Same force, i.e., a force of 10 dyne acts also on the second body of mass 2 g.
So, acceleration produced in it \(=\frac{\text { force }}{\text { mass }}\) =\( \frac{10}{2}\) = 5 cm/\(s^2\)
Question 25. A body initially at rest starts moving with an acceleration of 20 cm/s\(s^2\) After what time would its velocity be 2 m/s ?
Answer:
Given, a = 20 cm/\(s^2\) u = 0; v = 2 m/s = 200 cm/s.
Now, v=u+at or, 200=0+2x t
∴ Required time=\( \frac{200}{20}\) = 10s.
Question 26. Calculate the amount of force required to produce an acceleration of 4 m/\(s^2\) in a body of mass 0.8 kg.
Answer:
Given mass (m) = 0.8 kg, acceleration (a) = 4 m/\(s^2\)
Hence, force, F = ma = 0.8 kg x 4 m/\(s^2\) = 3.2 N.
Question 27. Find the acceleration produced by a force of 20 N acting ona body of mass 5 kg.
Answer:
Given mass (m) = 5 kg, force (F) = 20 N,
acceleration (a) =?
∴F=ma
∴ a \(=\frac{\text { force }}{\text { mass }}\)
=\( \frac{20N}{5Kg}\)
=4m/\(s^2\)
Chapter 2 Forces And Motion 2 Marks Questions And Answers:
Question 1. When is a body said to be at rest?
Answer:
If the position of a body is not changing with time with respect to a given frame of rest, motionless, immobile, stationary or to have constant position.
Question 2. What do you mean by the statement that there is nothing at absolute rest?
Answer:
“There is nothing at absolute rest”
In reality, there is nothing at absolute rest. For example, earth’s gravitation constantly pulls objects towards its surface, while earth is one of the objects the sun constantly pulls towards itself, causing it to orbit the sun: the sun, in turn, orbits the center of the Milky Way; and so on.
Wbbse Class 9 Physical Science What is scalar
Question 3. When is a body said to be in motion?
Answer:
Motion is a change in the position of an object with respect to time. Motion is typically described in terms of displacement, distance (scalar), velocity, acceleration, time and speed. Attaching a frame of reference to an observer and measuring the change in position of the body relative to that frame, we observe motion of a body.
Question 4. What is absolute motion?
Answer:
Absolute motion
When there is no absolute frame of reference, absolute motion cannot be determined. Thus, everything in the universe can be considered to be moving. More generally, notion is a concept that applies to objects, bodies and matter particles, to radiation, radiaion fields and radiation particles, and to space, its curvature and space-time.
Question 5. Define Displacement.
Answer:
Displacement
Displacement is the distance between two locations measured along the shortest path connecting them, in specified location. It is a vector quantity. The SI unit of distance and displacement is meter (m).
Wbbse Physical Science And Environment Class 9 Solutions
Question 6. Define Speed.
Answer:
Speed
Speed is the distance travelled per unit time or the rate of change of distance. Speed = total distance traveled / time taken.
Question 7. Define Velocity.
Answer:
Velocity
Velocity is the speed in a given direction or the rate of change of displacement. Average velocity = displacement/ time taken.
Question 8. Define Acceleration and Deceleration.
Answer:
Acceleration and Deceleration
Acceleration is the rate of change of velocity.
Acceleration = change of velocity/time taken, where change of velocity = final velocity (v) – initial velocity (u)
Hence, Acceleration = (final velocity – initial velocity) / time taken =(v-u)/t
Negative Acceleration is called Deceleration.
Question 9. State Newton’s first law of motion.
Answer:
Newton’s first law of motion: An object either remains at rest or continues to move at a constant velocity unless acted upon by an external force. Newton’s first law is often referred to as the law of inertia.
Question 10. State Newton’s second law of motion.
Answer:
Newton’s second law of motion: The vector sum of the external forces F on an object is equal to the mass m of that object multiplied by the acceleration vector a of the object. F=mxa
Question 11. State Newton’s third law of motion.
Answer:
Newton’s third law of motion: When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
WBBSE Class 9 Physical Science forces and motion notes
Question 12. State some applications of Newton’s first law of motion.
Answer:
Applications of Newton’s first law of motion
A person in motion stays in motion with the same speed and in the same direction unless acted upon by the unbalanced force of a seat belt. Seat belts are used to provide safety for passengers whose motion is governed by Newton’s laws. The seat belt provides the unbalanced force that brings you from a state of motion to a state of rest.
Question 13. State some applications of Newton’s second law of motion.
Answer:
Applications of Newton’s second law of motion
A car speeding down the road at a constant speed hits the brakes (unbalanced force), so the car slows down (negative acceleration).
Question 14. State some applications of Newton’s third law of motion.
Answer:
Applications of Newton’s third law of motion
When a model rocket is ignited, there is a force from the engine that thrusts downward (all that cool fire & smoke). In response, the model rocket accelerates up.
Question 15. What is Friction?
Answer:
Friction
Friction is a force that opposes motion between two surfaces that are in contact with each other. The amount of friction depends on two things: the type of surface and how hard they press against each other. When we consider “how hard” two surfaces are pressing against each other, we are really talking about the force of contact between the surfaces.
There are three types of friction; they are sliding friction, rolling friction etc. fluid friction.
Question 16. Define Momentum.
Answer:
Momentum
Momentum is defined as the mass multiplied by the velocity: p= m x v.
Since the momentum depends on the velocity, it is also a vector quantity. The units for momentum are [kg.m/s].
Question 17. Define Impulse.
Answer:
Impulse
The force multiplied by the time has a special name, the impulse. The impulse i is the change in the momentum. Impulse is a vector quantity and is equivalent to a Newton [N], the units of impulse are [N.s].
Impulse is the force multiplied by time the force acts on an object.
I=F×t
Question 18. What is Conservation of Momentum?
Answer:
Conservation of Momentum
Conservation is an important principle in physics that allows us to determine That happens in collisions or explosions. Ifa body A of mass \(\mathrm{m}_1\)and velocity\(\mathrm{v}_1\) collides another body B of mass \(\mathrm{m}_2\) and velocity \(\mathrm{v}_2\) moving in the same direction.
If A exerts a force F to the right on B for a time t, then by Newton’s third law, body B will exert an equal and opposite force to the left on A also for atime t but to the left. Thus, the bodies receive equal but opposite impulses “Ft”. The changes of momentum must be equal and opposite.
Therefore, the total momentum change Is zero. In other words, the total momentum of A and B together remains constant.
Question 19. What do you mean by physical independence of a force?
Answer:
Physical independence of a force
Physical independence of a force states that if a body is under simultaneous action of a number of forces, each force independently changes or thus the momentum of the body in its original direction, any other member of the applied force the single existence of it.
Question 20. Argue against the single existence of a force.
Answer:
When one body exerts a force on the other, the force is called action, the second body also offers at the same time an equal force on the first body on the opposite direction and this force is called reaction. Now, since every force of action is associated with an opposite force of reaction, no force can exist singly in nature, that is, in nature forces always appear in pairs.
Question 21. What is thrust?
Answer:
Thrust
When the weight of a body acts on another body, the force the first body offers is called thrust. This is the action, the second body simultaneously exerts an equal and opposite force on the first, this is the reaction.
When a book rests on the table, its weight on the table is a thrust which is the action, the tabletop also exerts an upward force on the book as the reaction. Push is also a kind of thrust. If the leaf of a door or a window is pushed (action) by hand, the leaf also exerts equal and opposite force on the Hepa as reaction.
Question 22. What are ‘pull’ and ‘tension’?
Answer:
‘Pull’ and ‘tension’
If some weight is attached to the lower end of a wire Supported from a beam, the weight tries to elongate the wire downward, which is the pull; it is the action. The wire also at the same time pulls the weight upward, which |is called the tension and this force of tension is the reaction.
 Question 23. What are ‘attraction’ and ‘repulsion’?
Question 23. What are ‘attraction’ and ‘repulsion’?
Answer:
‘Attraction’ and ‘repulsion’
Two bodies may attract or repel each other when they are in contact or without contact. The mutual forces of ‘attraction’ and ‘reaction’ in opposite directions between the earth and a body on or near it, the force acting between two unlike magnetic poles or two unlike electric charges of opposite kind form action-reaction pairs when they are in contact or away from each other within a limit. The forces of repulsion between a pair of similar magnetic poles or electric charges also form action-reaction pairs.
Question 24. Why is retardation called negative acceleration?
Answer:
Retardation is called negative acceleration as its magnitude is same as that of acceleration but its direction is opposite to that of acceleration.
Question 25. Can a body have velocity in one direction and acceleration in the opposite direction? Give an example.
Answer:
When a stone is thrown vertically upwards, the velocity is in upward direction while it is subjected to an acceleration due to gravity in vertically downward direction.
Question 26. Is it possible for a body to have average speed with average velocity of zero? Explain with an example.
Answer:
Yes, a body can have average speed with an average velocity of zero. When a body moves in a circle, the displacement after one complete rotation is zero. So its average velocity is zero. But it covers a certain distance in a certain interval of time. So its speed is not zero.
Question 27. Two particles are moving at the same constant speed of 50 meters per minute. Which one of them has a constant velocity if Gils moves in a straight line while the other in a circle? Explain your answer.
Answer:
The particle moving in a straight line has constant velocity because both the direction and magnitude of its speed remain unchanged. The direction of motion of the particle moving in a circle constantly changes. So its velocity also changes.
Question 28. What is a rigid body?
Answer:
Rigid body: A rigid body is one such that under no circumstances an externally applied force, however large it may be, can increase or decrease the separation between two of its constituent parts. ;
Wbbse Physical Science And Environment Class 9 Solutions
Question 29. What is a frame of reference and what is its necessity?
Answer:
The frame of reference is any nearby or distant fixed object from which the distance and position of a body are observed as time elapses. Frame of reference is necessary since the state of rest or motion of a body can be observed or measured with respect to it.
Question 30. Explain that the state of rest and state of motion are relative terms.
Answer:
The state of rest and state of motion of a body are relative rather than absolute terms. An object may be in motion with regard to another object but may be in rest with respect to a third object.
For example, suppose you are travelling in a train and you pass a person standing alongside the tracks. The person standing along the tracks will see you and everyone else on the train as being in motion. But the person sitting next to you on the train will be at rest with respect to you.
Question 31. Can a body be called at absolute rest? Explain the statement.
Answer:
Nobody is present in the universe which is said to be in absolute rest. All the bodies in the universe are in the state of motion. When we speak of bodies to be at rest o. in motion, we speak of their apprent state of rest or apparent state of motion.
When we compare the position of a tree with a running train, we say that the tree is in rest. But the tree is situated on earth and the Earth is always in a state of motion.
Question 32. What is relative velocity? Give a practical example.
Answer:
Relative velocity: As in this universe all the points with respect to which motion is studied are also in motion, the motion is termed as relative motion and the corresponding velocity is known as relative velocity. Relative velocity of a body ‘B’ with respect to a body ‘A’ when both are in motion, is the velocity with which ‘B’ appears to move towards or away from ‘A’.
Example: Let us consider a flat train moving on earth on a straight track with velocity\(\mathrm{V}_{\mathrm{TE}}\) (velocity of train with respect to earth). Let us consider again a car moving on a roac parallel to the train in the same direction with a velocity \(\mathrm{V}_{\mathrm{CE}}\) (velocity of car w.r.t earth).
Now the relative velocity of the train w.r.t to the car will be \((\mathrm{V}_{\mathrm{TE}}+ \mathrm{V}_{\mathrm{CE}}\)). If the car moves in the opposite direction, the relative velocity will be \((\mathrm{V}_{\mathrm{TE}}+ \mathrm{V}_{\mathrm{CE}}\)).
Question 33. State the conditions under which a train will appear to be at rest to a person sitting in a nearby train.
Answer:
To a person sitting in a train, another train will appear to be at rest when the following three criteria are fulfilled :
(1) The two trains are moving parallel to each other
(2) The two trains are moving in the same direction
(3) The two trains are moving with the same velocity.
In other words, if the relative velocity of the trains relative to the person is always the same, the train will appear to be at rest.
Question 34. Why do both mass and velocity of a body pertain to its momentum?
Answer:
The momentum of a moving body is its quantity of motion. When two bodies of unequal masses move with same velocity, momentum or quantity of motion of the body of large mass is greater than that of the body of smaller mass. Thus momentum depends on mass of a moving body.
Again, of two bodies of equal mass moving with unequal velocities. momentum of the body moving with larger velocity is more than that of the body moving with smaller velocity. So, momentum also depends on velocity. Hence, momentum of a body depends on both its mass and velocity. Infact, momentum = mass x velocity.
Question 35. What is meant by.a unit force? Why is an absolute unit of force ‘absolute’?
Answer:
Unit force
A unit force means the quantity of force that when acts on a body of unit mass produce unit acceleration. Absolute units are so called because they are universally valid without admitting any exception, they are complete and independent of restrictions like altitude, position, etc.
Question 36. What can you say regarding the acceleration of a body having a constant kinetic energy?
Answer:
The kinetic energy of a body \(=\frac{1}{2} m v^2\),where ‘m’ is the mass and ‘v’ is its velocity. Now
If Kinetic energy, i.e., \(=\frac{1}{2} m v^2\) is constant, then the velocity ‘v’ is constant. Again, if velocity Is constant, there is no acceleration.
Wbbse Physical Science And Environment Class 9 Solutions
Question 37. Deduce Newton’s first law of motion from the second law.
Answer:
Newton’s first law of motion from the second law
From the relation, force = mass x acceleration (or retardation), if the applied force is zero, i.e., in absence of any external force, acceleration or retardation is zero, since mass cannot be zero.
Now, that acceleration or retardation is zero means, either the body is at rest or it is in uniform motion; thus, in absence of an external force, a body is either at rest or in uniform motion, this is Newton’s first law of motion.
Important questions on forces and motion WBBSE Class 9
Question 38. How can a body have uniform speed but variable velocity? Is the converse possible?
Answer:
While a body moves along a circular path or a curved path, its direction of motion at an instant, at any point on its route is along the tangent at that point; obviously, the direction of motion of the body changes from point to point.
So, even if the body covers equal distances in equal intervals of time, i.e., it possesses uniform speed, its velocity is non-uniform due to change of direction of motion.
Thus a body may move with uniform speed but its velocity may be non-uniform. But the converse is not true. A body moving with uniform velocity covers equal distances in equal time, so its speed is uniform.
Question 39. Is it possible for a body to have acceleration without velocity? Explain with an example.
Answer:
Yes, it is possible for a body to have acceleration without velocity. We consider the instance of a continuously swinging body like the swinging bob of a pendulum. At the extreme end of the path described, on either side of the mean position, the bob stops momentarily and at that moment it has no velocity but has acceleration directed towards the mean position.
Question 40. The velocity of a body changes from 14 cm/s to 12 cm/s. How can we conclude that a force is acting on it? Is it helping or opposing the motion?
Answer:
Since the velocity of the body gradually decreases, an external force must be acting on it, because Newton’s first law of motion says that an external force only can change the motion of a body. Since, the motion of the body gradually decreases, the force opposes the motion of the body.
Question 51. Why is it that a freely falling body is in weightless condition?
Answer:
We can feel our body weight because of a reaction force. Due to gravity, the weight of one’s body acts downward on the ground where he stands, this is the action. The ground exerts an equal upward force on his body, that is the reaction.
Due to this reaction force we can feel the weight of our body. A freely falling body has no other body on which it can exert its weight, so no reaction force acts on it. Hence, the body is in a weightless condition.
Question 52. To catch a flying cricket ball why does a fielder draw back his hands along with the ball?
Answer:
While the fielder goes for the catch, he puts his palms against the motion of the cricket ball, so the ball strikes his palms as an action. Due to reaction from the palms, the ball moves away in the opposite direction and tends to spill before the fielder clutches it.
The fielder draws back his hands at the moment of holding the ball, allowing it to move a bit more in its direction of motion so that its velocity decreases. If the ball strikes the palms of the fielder with less velocity, the reaction force due to which the ball rebounds also lessens. The fielder gets enough time to grasp the ball that rebounds now a bit slowly.
Wbbse Physical Science And Environment Class 9 Solutions
Question 53. Why is it more painful to drop on a concrete surface than on a sandy bed?
Answer:
A person when drops on a concrete surface, which is a continuous body, the thrust exerted by him is the action. The concrete surface exerts equal and opposite reaction force on the person’s feet that causes appreciable pain. But, if the person drops on a sandy bed.
Which is a discontinuous body, major part of the exerted force transmits down inside the sand layers. This force gradually weakens, for, it is utilised to compress the sand layers which have some entrapped air pockets. The reaction of the remaining force on the surface of sand does not produce any painful force on the person’s feet.
Question 54. Is the motion of a body from rest to rest uniform motion? Give reason.
Answer:
The motion of a body from rest to rest is an instance of non-uniform motion. While a body initially at rest begins to move, and after moving through some distance again comes to rest, its motion cannot be uniform. As it starts moving from rest, its velocity (or speed) gradually increases and then its velocity gradually decreases before coming to rest.
Question 55. Two identical lorries move with same velocity—one of them is loaded and the other is not, which of the two may be stopped with less effort ? Why?
Answer:
The quantity of motion of a body depends on both the mass and the velocity of the body. Here, the loaded lorry has larger quantity of motion due to greater mass than the unloaded lorry. So, the unloaded lorry of less quantity of motion can be stopped with less effort.
Question 56. Why is it easier to accelerate a moving vehicle by push than one at rest?
Answer:
When the car or a roller is at rest, to set it into motion, a large force is necessary to overcome the inertia of rest of its large mass and also to overcome its frictional force with the ground. On the other hand, when it is already in motion, since it itself tries to maintain its forward motion due to inertia of motion and also has overcome opposing frictional force, a smaller effort can accelerate it.
Question 57. Why does an electric fan continue its motion for some time even after the switch is off?
Answer:
By switching off, the supply of electricity to the motor of the fan is stopped, so the motor no longer works, but due to inertia of motion the blades of the fan continue to move for some time. Finally, the blades stop due to opposing frictional forces of air, ball bearings, etc.
Question 58. Will a boat move when air from an electric fan situated in it strikes the sails?
Answer: T
he electric fan on the boat and the sails constitute a single system. So, the force to blow of air from the fan is not an external force, that is why the boat will not move.
Wbbse Physical Science And Environment Class 9 Solutions
Question 59. Distinguish between rotation and circular motion.
Answer:
Difference between rotation and circular motion :
(1 ) When a body moves along a circular path about a point as center, then the motion of that body. is called circular motion. But the rotation is the characteristic motion of a rigid body in which each constituent particle on it undergoes such circular motion in which the centers of all the circles lie on a single straight line perpendicular to the plane of each circular path.
(2) Circular motion is the motion of a point along a circular path but rotation is the change of orientation of an extended object without suffering change in position. For example, orbital motion of the Earth and other planets around the sun is circular motion but daily rotation of the Earth about its own axis is a rotational motion.
Question 60. Define displacement. Is it vector or scalar?
Answer:
Displacement: The change of position of a moving body in a particular direction is called the displacement of the body and is measured by the linear distance between its initial and final positions. Thus displacement has both magnitude and direction. So displacement is a vector quantity.
Question 61. Define speed. It is vector or scalar?
Answer:
Speed: The rate of change of position of a body with respect to time is known as its speed. In other words, the distance traversed by a body in unit time is its speed. In the case of speed we have not mentioned about any direction. Thus, speed has only magnitude but no direction. So speed is a scalar quantity.
Wbbse Class 9 Difference Between Speed And Velocity
Question 62. State two differences between speed and velocity.
Answer:
Differences between speed and velocity

Question 63. Define balanced forces.
Answer:
Definition of balanced forces: When two forces are of equal magnitude but acting in opposite directions on an object simultaneously, the object continues to be in its state of rest or of uniform motion in a straight line. Such forces acting on the body are said to form a system of balanced forces.
Question 64. Define unbalanced forces.
Answer:
Definition of unbalanced forces: When two forces of unequal magnitudes act in opposite directions on an object simultaneously, then the object moves in the direction of the larger force. Such forces acting on the body are said to form a system of unbalanced forces.
Question 65. State Newton’s first law of motion and define force from it.
Answer:
Statement of Newton’s first law of motion: Everybody continues in its state of rest or of uniform motion in a straight line unless it is acted on by some unbalanced force to change that state.
Definition of Force: From Newton’s first law of motion we get the definition of force. Force is that, which acting on a body, changes or tends to change the state of rest or uniform motion of the body in a straight line.
Wbbse Physical Science Class 9
Question 66. When a running bus stops suddenly, the passengers inside it lean forward. Why?
Answer:
When a running bus stops suddenly, a passenger sitting inside it leans forward. Here also as soon as the bus stops, the lower portion of the body of the passenger being in contact with the bust stops immediately. But the the upper: portion wants to maintain its motion due to inertia of motion and hence leans forward.
Again, when a bus suddenly starts, a passenger sitting in it leans backward. As soon as the bus starts, the lower portion of the body begins to move along with it. But upper portion of the body due to inertia of rest tends to continue in that state and thus leans backward.
Question 67. State Newton’s second law of motion and hence define the unit of force in CGS system.
Answer:
Newton’s second law of motion gives the relationship: between the force applied or the body and the acceleration produced in the body. When an unbalanced force acts on a body then the applied force is proportional to the acceleration produced in it.
Wbbse Physical Science Class 9
Question 68. Why do we have to make a great effort to hold a hose pipe to throw a stream of water through it?
Answer:
Water flowing through a hose pipe: We have to make a great effort to hold a hose pipe to throw a stream of water through it. The stream of water coming out through the hose pipe in the forward direction with great speed exerts a large force on the hose pipe in the backward direction. Thus we have to make great effort to hold the hose pipe strongly to keep it at rest.
Question 69. The moving blades of an electric fan do not stop as soon as the switch is off. Why?
Answer:
The moving blades of an electric fan do not stop as soon as the switch is off.
Explanation: By switching off the supply of electricity to the motor of the fan is stopped, so the motor no longer works, but due to inertia of motion the blades of the fan continue to move for some time.
Question 70. Why should a person slightly lean back before alighting from a moving vehicle?
Answer:
Before alighting from a moving vehicle, bus or tram, one should slightly lean back.
Reason: As long as the person remains inside the moving vehicle, his whole body moves with the speed of the vehicle. As soon as he descends on ground his feet suddenly come to stop but the upper part of his body still possesses forward speed due to inertia of motion. If he has no support to grab he stumbles on ground.
But if he leans back a bit beforehand, it makes up the short span he moves through forward when he descends and ultimately he remains erect. This practice saves one from stumbling down when he unwisely alights from a moving vehicle.
Question 71. Deduce Newton’s second law of motion from his first law.
Answer:
Newton’s first law of motion from the second law: From the relation, force = mass x acceleration (or retardation), if the applied force be zero, i.e., in absence of any external force, acceleration or retardation is zero, since mass cannot be zero.
Now, acceleration or retardation is zero means either the body is at rest or it is in uniform motion; thus, in absence of an external force, a body is either at rest or in uniform motion, that is Newton’s first law of motion.
Wbbse Class 9 Physical Science Chapter 2 Question Answer
Question 72. The velocity of a train in a particular direction increases from 30 km/hr to 60 km/ hr in 1 minute. If the train be moving with uniform acceleration, what is its acceleration?
Answer:
Given
The velocity of a train in a particular direction increases from 30 km/hr to 60 km/ hr in 1 minute. If the train be moving with uniform acceleration,
Initial velocity of the train = 30 km/hr.
Final velocity of the train = 60 km/hr.
Time required = 1 minute\(=\frac{1}{60}\) hr.
Change in velocity = 60 — 30 = 30 km/hr.
∴acceleration \(=\frac{\text { change in velocity }}{\text { time }}\)=\(\frac{30 \mathrm{~km} / \mathrm{hr}}{1 / 60 \mathrm{hr}}\)
= 1800 km/hr)\(^2\).
WBBSE Class 9 solved exercises on forces and motion
Question 73. A train starting from rest attains a velocity of 72 km\(\mathrm{h}^{-1}\)in 5 minutes. Assuming that the acceleration is uniform, find
(1) the acceleration and
(2) the distance travelled by the train for attaining this velocity.
Answer:
Given,u=0,v=72km\(\mathrm{h}^{-1}\)
⇒ \(=\frac{72 \times 1000}{60 \times 60} \mathrm{~ms}^{-1}\)
⇒ \(=20 \mathrm{~ms}^{-1}\)
t=5 min= 300s.
(1)Fromv=u+at 0r, a\(=\frac{v-u}{t}\)=\(\frac{20-0}{300}\)=\(\frac{1}{15} \mathrm{~ms}^{-2}\)
(2) Again,\(v^2\)=\(u^2+2 a s\) or, s \(=\frac{v^2-u^2}{2 a}\)=\(\frac{20^2-0^2}{2 \times \frac{1}{15}}\)=3000m=3km.
Question 74. A force of 1000 kg-wt is applied on a body. Express this force in dyne and Newton.
Answer:
1000 kg-wt = 1000 x 9.81 newton = 9810 N
Again, 1N \(=10^5\) dyne
therefore 9810 N = 9810 x \(10^5\) dyne = 9.81 \(10^5\) dyne.
Question 75. When a force acts on a body of mass 10 g initially at rest, it acquires a velocity of 15 cm/s in 5 seconds. Find the acceleration and final momentum of the body and the magnitude of the force.
Answer:
Final velocity c = 15 cm/s; mass of the body = 10 g. therefore Final momentum of the body = mass x speed = 10 x 15 = 150 g-cm/s
Again,acceleration a\(=\frac{v-u}{t}\)=\(\frac{15-0}{5}\)=3cm/\(s^2\) and force = mass x acceleration = 10 x 3 = 30 dyne.
Wbbse Class 9 Physical Science Chapter 2 Question Answer
Question 76. The initial velocity of a body of mass 20 g is 10 cm/s and after 5 s its velocity becomes 40 cm/s. Find the magnitude of the force acting on the body.
Answer:
Given, mass of the body m = 20 g; initial velocity u = 10 cm/s
final velocity v = 40 cm/s; time t = 5 s.
Now, v=u+at
or,acceleration a\(=\frac{v-u}{t}\)=\(\frac{40-10}{5}\)=\(\frac{30}{5}\)=6 cm/\(s^2\)
∴ Required force = m.a = 20 x 6 = 120 dyne.
Question 77. A body of mass 147 g at rest is subjected to a force of 15 g-wt. What is the acceleration of the body ? What will be the velocity of the body after 2s?
Answer:
Given, m = 147g; u=0
p= 15 g-wt = 15 x 980 dyne
∴acceleration a\( =\frac{p}{m}\)=\(\frac{15 \times 980}{147}\) =100cm/\(s^2\)
Again, v=u+at=0+ 100 x 2=200cm/s=2 m/s.
Question 78. A bullet of mass 100 g is fired from a gun of mass 20 kg with a velocity of 100. m\(s^{-2}\). Calculate the velocity of recoil of the gun.
Answer:
Given mass of the bullet, \(\left(m_1\right)\)= 100 g = 0.1 kg
velocity of the bullet, v = 100\(s^{-1}\); mass of the gun, \(\left(m_2\right)\) = 20 kg.
Let the recoil velocity of the gun = V.
Initial momentum of the gun-bullet system\(=\left(m_1+m_2\right)\)x 0 =0.
Final momentum of the system\(=m_1 v+m_2 v\) 0.1 x 100 + 20x V=10+ 20V.
Applying the law of conservation of momentum,
10+20 V=0 V=-0.5\(s^{-1}\)
The -ve sign indicates that the gun moves backward.
Wbbse Class 9 Physical Science Chapter 2 Question Answer
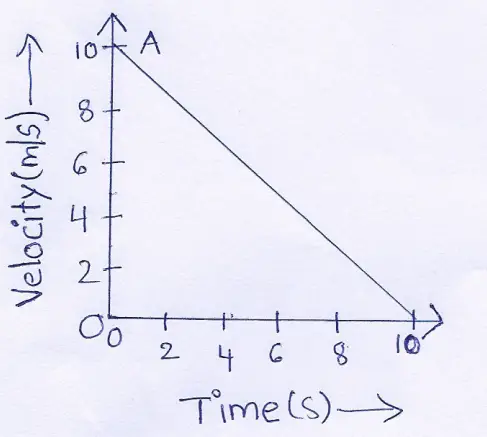
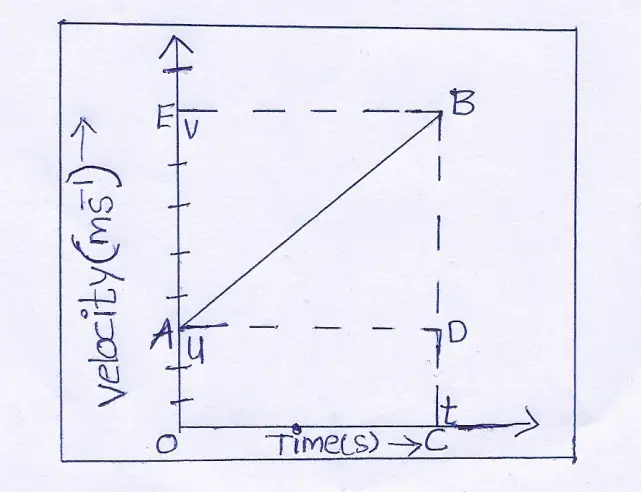
Question 79. Velocity-time graph for a body moving with retardation is shown. Calculate the
(1) retardation and (2) displacement of the body.
Answer:
(1) Here, retatdation \(=\frac{\text { Decrease in velocity }}{\text { time taken }}\)
⇒ \(=\frac{(10-0) \mathrm{m} / \mathrm{s}}{(10-0) \mathrm{s}}\)=\(\frac{10}{10} \mathrm{~m} / \mathrm{s}^2\)=2m/\(s^2\)
(2) Displacement = Area of velocity-time graph 3 5
= Area of ΔAOB B
=½×OB×OA=(½×10×10)m=50\(m^2\).
Question 80. Calculate the force required to impart to a car a velocity of 40 m/s in 10 seconds starting from rest. The mass of the car is 1500 kg.
Answer:
Here, mass (m) = 1500 kg,
Initial velocity (u) = 0, Final velocity (v) = 40 m/s, Time taken (t)= 10s.
∴Force required, F=ma
⇒ \(=m\left(\frac{v-u}{t}\right)\)=\(1500\left(\frac{40-0}{10}\right) N\)\(=\left(1500 \times \frac{40}{10}\right) \mathrm{N}\)=6000N.
Wbbse Class 9 Physical Science Chapter 2 Question Answer
Question 81. A cricket ball of mass 200 g moving with a speed of 30 m/sis brought to rest by a player in 0.03 seconds. Find
(1) The change in the momentum of the ball and
(2) The average force applied by the player.
Answer:
Here, mass (m) = 200g = 0.2 kg, Initial velocity (u) = 30 m/s,
Final velocity (v) = 0, Time taken (t) = 0.03 s.
(1) Change in momentum = (mv — mu) = 0.2 (0 — 30) =— 6 kg m/s.
(2) Average force applied, F = Rate of change of momentum
⇒ \(=\frac{\text { change of momentum }}{\text { time }}\)
⇒ \(=\frac{6}{0.03} \frac{\mathrm{kg} \mathrm{m} / \mathrm{s}}{\mathrm{s}}\)=200N.
Question 82. A force of 4 kg-wt acts on a body of mass 9.8 kg. Calculate the acceleration. [Take g = 9.8 m/\(s^2\) ]
Answer:
4 kg-wt = 4 kg. x 9.8 m/\(s^2\) = 39.2 N.
Now, force = mass x acceleration, ∴ 39.2 N = 9.8 kg x acceleration
∴ acceleration \(=\frac{39.2 \mathrm{~N}}{9.8 \mathrm{~kg}}=\)=4m/\(s^2\)
Question 83. Two bodies A and B are of equal mass and are at rest. A is acted upon with 1. kg-wt force and B with 1N. Will the acceleration generated in them be equal? force
Answer:
Using the relation, acceleration \(=\frac{\text { force }}{\text { mass }}\),Acceleration of A
⇒ \(=\frac{1 \mathrm{~kg} \mathrm{wt}}{\mathrm{m}}\)=\(\frac{9.8 \mathrm{~N}}{\mathrm{~m}}\),where ‘m’ is the mass of A or B.
acceleration of B \(\frac{1\mathrm{~N}}{\mathrm{~m}}\). ∴acceleration of A is 9.8 times more than that of
Question 84. A constant force of 30 dyne acts on a body, initially at rest, for 4 seconds and then ceases to act. The body moves 48 cm in the next 8 seconds. What is the mass of the body?
Answer:
On withdrawal of the force, the body moves with a constant velocity with which it covers 48 cm in 8 s.
∴Velocity acquired by the body after 4 seconds \(=\frac{48 \mathrm{~cm}}{8 \mathrm{~s}}\) = 6 cm/s.
Now, acceleration\(=\frac{\text { Change of velocity }}{\text { time }}\)\(=\frac{(6-0) \mathrm{cm} / \mathrm{s}}{4}\)
(∴ initial velocity = 0) = 1.5 cm/\(\mathbf{s}^2\)
From the relation, force = mass x acceleration,
30 dyne = mass x 1.4 cm/\(s^2\)
∴ mass \(=\frac{30 \mathrm{dyn}}{1.5 \mathrm{~cm} / \mathrm{s}^2}\)=20 g.
Wbbse Class 9 Physical Science Chapter 2 Question Answer
Question 85. A cricket ball of mass 100 g moves with a velocity 20 m/s. A batsman stops the ball in 0.05 seconds. Find the force applied.
Answer:
Retardation \(=\frac{(0-20) \mathrm{m} / \mathrm{s}}{0.05 \mathrm{~s}}\)=\(400 \mathrm{~m} / \mathrm{s}^2\)
Mass of the ball \(=\frac{100}{1000} \mathrm{~kg}\)=o.1 kg.
Hence, force applied on the ball = 0.1 kg x 400 m/\(s^2\) = 40 N.
Question 86. A force acting on a body of mass 10 kg changes the velocity of the body from 5m/s to 10 m/s in 5 seconds. Find the value of the force in dyne and Newton.
Answer:
10 kg = 10,000g, 5 m/s = 500 cm/s, 10 m/s = 1000 cm/s.
Now, acceleration=\(\frac{(1000-500) \mathrm{cm} / \mathrm{s}}{5 \mathrm{~s}}\)=100 cm/\(s^2\)
So, the applied force = 10,000 g x 100 cm/\(s^2\) \(=10^6\) dyne = 10 N.
Question 87. What is straight linear motion?
Answer:
Straight linear motion: If any particle moves along any straight line and any particle of the body travels the same distance at same speed, then the motion is called straight linear motion. :
Question 88. What is curvilinear motion?
Answer:
Curvilinear motion: If any particle does not move in a definite direction but moves in a curvilinear way and changes its direction in that way, then the motion is called curvilinear motion.
Question 89. What is circular motion?
Answer:
Circular motion: If any particle moves around a particular point or axis, then this motion is called circular motion.
Question 90. What is mixed motion?
Answer:
Mixed motion: If any motion is a combined form of linear motion and circular motion, then that motion is called mixed motion.
Wbbse Physical Science And Environment Class 9 Solutions
Question 91. What is inertial frame of reference?
Answer:
Inertial frame of reference: A frame of reference which is either at rest or moving with uniform velocity is called an inertial frame of reference. In this frame of reference Newton’s first law of motion is valid.
Wbbse Physical Science And Environment Class 9 Solutions
Question 92. What is non-inertial frame of reference?
Answer:
Non-inertial frame of reference: A frame of reference which is accelerated is called non-inertial frame of reference. In this frame of reference Newton’s first law of motion is not valid.
Question 93. What is one-dimensional motion?
Answer:
One dimensional motion: If the motion of a particle be along a straight line, the motion is one-dimensional.
Example :
(1) A train moving along a straight track.
(2) A body falling freely under gravity.
Question 94. What is two dimensional motion?
Answer:
Two dimenstional motion: If the motion of a particle be in a plane, i.e., when two of the three coordinates are required to specify the position of the particle in motion, the motion is called two-dimensional.
Example :
(1) The earth revolving around the sun.
(2) An insect crawling on the floor.
Wbbse Physical Science And Environment Class 9 Solutions
Question 95. What is three dimensional motion?
Answer:
Three dimensional motion: If the motion of a particle be in space, i.e., when all the three coordinates are required to specify the position of the particle in motion, then the motion is called three-dimensional.
Example :
(1) A flying bird.
(2) A flying aeroplane.
(3) A flying kite.
WBBSE Class 9 Physical Science Newton’s laws solutions
Question 96. State the units of displacement in CGS and SI systems.
Answer:
Units of displacement :
(1) CGS: cm
(2) SI: m.
Question 97. State two characteristics of displacement.
Answer:
The characteristics of displacement are:
(1) Displacement has the unit of length.
(2) The displacement may be positive, negative, or zero.
Question 98. State two differences between displacement and distance.
Answer:
Difference between displacement and distance :

Question 99. State two characteristics of speed.
Answer:
Characteristics of speed :
(1) Speed does not give any idea about the direction of motion.
(2) Speed can be positive, but never negative or zero.
Wbbse Physical Science And Environment Class 9 Solutions
Question 100. State the units of speed in CGS and SI systems.
Answer:
Units of speed :
(1) CGS : cm/\(s^{-1}\)
(2) SI: m\(s^{-1}\).
Question 101. What is average speed?
Answer:
Average speed: When a body is moving with variable speed, the constant speed with which the body covers the same distance in a given time as it does while moving with variable speed during the given time, is called average speed.
Average speed \(=v_{a v} \)= \(\frac{\text { total dis tance covered }}{\text { total time taken }} \)
If a body moves distances \(\mathrm{S}_1, \mathrm{~S}_2, \mathrm{~S}_3\)……..etc. in times \(\mathrm{t}_1, \mathrm{~t}_2, \mathrm{~t}_3\) ………etc. respectively, then
Average speed \(=v_{a v} \)\(=\frac{S_1+S_2+S_3+\ldots \ldots}{t_1+t_2+t_3+\ldots \ldots}\)
Question 102. State two characteristics of velocity.
Answer:
Characteristics of velocity :
(1) The velocity can be positive, negative or zero.
(2) Velocity has both magnitude and direction, and hence, it is a vector quantity.
Wbbse Physical Science And Environment Class 9 Solutions
Question 103. State the units of velocity in CGS and SI systems.
Answer:
Units of velocity (same as speed) :
(1) CGS : cm/\(s^{-1}\)
(2) SI: m/\(s^{-1}\).
Question 104. What is average velocity ?
Answer:
Average Velocity: When a body is moving with variable velocity, the average velocity is the value of that constant velocity at which the same body could have under- gone the same displacement in the same interval of time as the body has actually gone.
Average velocity \(=\frac{\text { Total displacement }}{\text { Total time }}\)
Question 105. State two characteristics of acceleration.
Answer:
Characteristics of acceleration :
(1) When the velocity is increasing, the acceleration is called positive and
(2) when it is decreasing, it is called negative or retardation or deceleration.
Question 106. State the units of acceleration in CGS and SI systems
Answer:
Units of acceleration :
(1) CGS : cm/\(s^{-2}\)
(2) SI: m\(s^{-2}\)
Question 107. What is average acceleration?
Answer:
Average acceleration: When a body is moving with variable acceleration, then the defined as the ratio of total change in velocity of the body to the total time taken.
Wbbse Physical Science And Environment Class 9 Solutions
Question 108. State two characteristics of retardation.
Answer:
Characteristics of retardation :
(1) Retardation is opposite to acceleration and thus it is considered as negative acceleration.
(2) Retardation has both magnitude and direction, and hence it is vector quantity.
Question 109. What is uniform retardation?
Answer:
Uniform retardation: The retardation of a moving body is a said to be uniform if its velocity changes by equal amounts in equal intervals of time, however small the intervals may be.
Question 110. What is non-uniform retardation ?
Answer:
Non-uniform retardation: The retardation of a moving body is said to be variable if it does not have equal changes in velocity in equal intervals of time.
Chapter 2 Forces And Motion 3 Marks Questions And Answers:
Question 1. State the different types of motion
Answer:
The different types of motion are :
(1)Simple harmonic motion.
(2)Anharmonic motion
(3)Periodic motion
(4)Rectilinear motion — motion that follows a straight linear path, and whose displacement is exactly the same as its trajectory
(5) Reciprocal motion (e.g. vibration)
(6) Random motion (e.g. vibration)
(7) Brownian motion (i.e., the random movement of particles)
(8)Circular motion (e.g. the orbits of planets)
(9)Rotary motion – a motion about a fixed point. (e.g. Ferris wheel).
(10)Curvilinear motion – It is defined as the motion along a curved path that may be planar or in three dimensions.
(11)Rotational motion – (as of the wheel of a bicycle)
(12)Oscillation
(13)Combination (or simultaneous) motions – Combination of two or more above-listed motions
(14)Projectile motion – uniform horizontal motion + vertical accelerated motion.
Question 2. What are Balanced and Unbalanced Forces?
Answer:
Balanced and Unbalanced Forces
A force is defined as a push or a pull and more than one force can and usually does act on an object at the same time. Every force has a certain strength or magnitude. Forces also have direction.
The net force on an object is the sum (in both magnitude and direction) of all the forces acting on it. If the net force is zero, the forces are balanced. Balanced forces produce a change in motion of an object.
When the net force is greater than zero, the forces acting on the object are not balanced. Unbalanced forces cause an object at rest to move and an object in motion to change speed and/or direction.
Question 3. How is measurment of force obtained from the second law of motion?
Answer:
Measurement of force: From the second law of motion, measurement of force is possible. Say, a body of mass ‘m’ moves uniformly in a certain direction with the velocity ‘u’ and after ‘t’ seconds, due to the application of an external force F, in the same direction, its final velocity becomes ‘v’.
∴ the initial momentum of the body = mu
final momentum of the body = mv
So, change of momentum after ‘t’ seconds = mv – mu
∴ Change of momentum after 1 second \(=\frac{m v-m u}{t}\)\(=\frac{m(v-u)}{t}\)
i.e., rate of change of momentum \(=\frac{ v- u}{t}\)
=ma(∴\(=\frac{ v- u}{t}\)=acceleration,a)
Now, according to Newton’s second law of motion,
∴F α ma or F = k ma where k is a constant.
Now, the force that acting on a body of unit mass produces unit acceleration in the body is called unit force.
So, when m = 1 and a= 1 then F = 1; hence, the relation F = kmf changes to 1 = k.1.1. So, k = 1. Therefore F = ma, i.e., Force = mass x acceleration.
Question 4. Establish the relation between absolute and gravitational units of force.
Answer:
Relation between gravitational and absolute units of force :
The CGS absolute unit of force 1dyne = 1 g x 1 cm/s?, the CGS gravitational unit of force
1 gram weight = 1 gram x g (acceleration due to gravity)= 1 gram x 981 m/\(s^{2}\)
= (1 gram x 1 cm/\(s^{2}\)) x 981
= 1 dyne x 981
= 981 dynes
= g dynes.
Hence, 1 gram weight = g dynes. This is the relation between gravitational unit (1 gram weight) and absolute unit of force (1 dyne).
Also, the MKS absolute unit of force = 1 kg x 1 m/\(s^{2}\)? and the MKS gravitational unit of
force = 1 kg x g (g = acceleration due to gravity) = 1 kg x 9.81 m/\(s^{2}\)?
= (1kg x 1m/\(s^{2}\)?) x 9.81 = 1N x 9.81 = 9.81 N = g Newton.
Hence, in general, it can be written as
Gravitational unit of force = Absolute unit of force x g.
Wbbse Physical Science And Environment Class 9 Solutions
Question 5. How does a horse cart move forward, though the force with which the horse pulls the cart is equal and opposite to the force with which the cart pulls the horse?
Answer:
It may be noticed that just at the moment of start, the horse bends its head and body to exert a force on ground in an inclined way with its legs [The same thing does a rickshaw-puller; athletes also do so at the start of a race.]. The ground also exerts an equal and opposite reaction force on the horse in an inclined direction.

This reaction may be resolved in the vertical and the horizontal directions. The vertical component reduces the weight of the horse and the horizontal component helps the horse and the cart to move forward. If the horizontal component can exceed the frictional force between the ground and wheels of the cart, then the whole system, horse and cart, moves forward.
Question 6. Taking force (F) length (L) and time (T) as fundamental quantities, express (1) density, (2) pressure, and (3) momentum.
Answer:
Acceleration \(=\frac{L}{T^2}\) mass \(=\frac{\text { force }}{\text { acceleration }}\)=\(\frac{F}{L}\)=\(\frac{F T^2}{L}\)
∴(1)\(\frac{\text { force }}{\text { acceleration } \times L^3}\)=\(\frac{F T^2}{L^4}\)
(2)\(\frac{F}{L^2}\)
(3)\(\frac{\mathrm{FT}^2}{\mathrm{~L}} \times \frac{\mathrm{L}}{\mathrm{T}}\)=\(\mathrm{FT} \text {. }\)
Question 7. Define translation. Classify it.
Answer:
Translation
If the different particles constituting a body travel in a definite direction so that the line joining any two points of it remains parallel to itself, then the motion of the body is called translation. Translational motion, again, is divided into two kinds:
(1) Rectilinear motion: When the translational motion of a body takes place along a straight line, it is called Rectilinear motion. (e.g. motion of a freely falling body under gravity).
 (2) Curvilinear motion: When the translational motion of a body takes place along a curved path, it is called curvilinear motion. (e.g. motion of a seat of vertical merry-go-round).
(2) Curvilinear motion: When the translational motion of a body takes place along a curved path, it is called curvilinear motion. (e.g. motion of a seat of vertical merry-go-round).
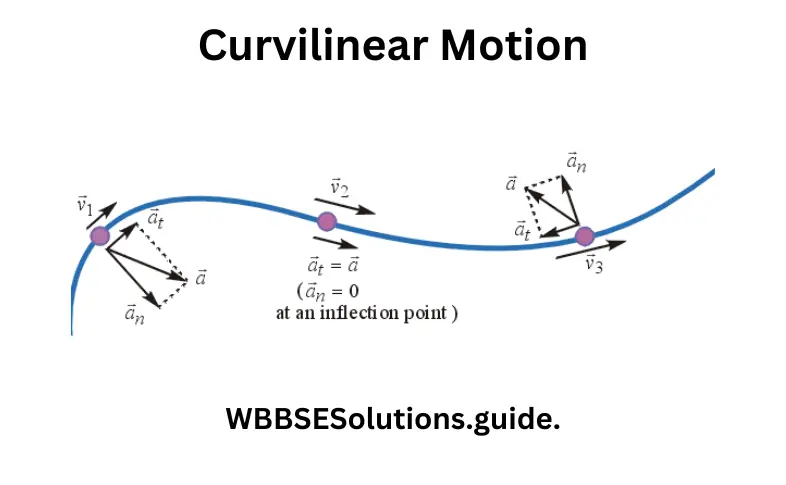
Laws of motion and inertia Class 9 WBBSE notes
Question 8. Wrtie a short note on circular motion.
Answer:
Circular motion: If a body moves along a circular path around a fixed point or about a fixed axis, then the motion of the body is called circular motion. Examples include the Supvllingsametion motion of the earth about the sun, the motion of a satellite around the earth, the motion of an electron around the nucleus of an atom, a stone tied at one end of a string and revolving along a circular path, etc.
In translation a body moves along a straight line while in circular motion a body moves along a circular path etc.. is around a fixed point. The direction of motion does not Cha Rotational change in case of translation but the direction of motion axis changes continuously in circular motion.
Moreover, in ’ translation, if a body moves with constant speed, it has i. no acceleration; but in circular motion, a body, even if travels with uniform speed possesses acceleration.
Again, motion may occur in one dimension, in two dimensions, and also in three dimensions. When a body moves along a straight line it is known as one-dimensional motion. Motion of a freely falling body under gravity, oscillatory motion of a body motion.
If a body moves along a curved path in a plane, then its motion is known as two-dimensional motion. Motion of an ant crawling on a globe, revolution of a planet around the sun, etc. are examples of two-dimensional motion.
Again, when a body moves in space, then its motion is known as three-dimensional motion. This kind of motion is the most general type of motion. Its examples are a bee flying in air or a kite flying on a windy day, etc.
 Question 9. Write a short note on rotational motion
Question 9. Write a short note on rotational motion
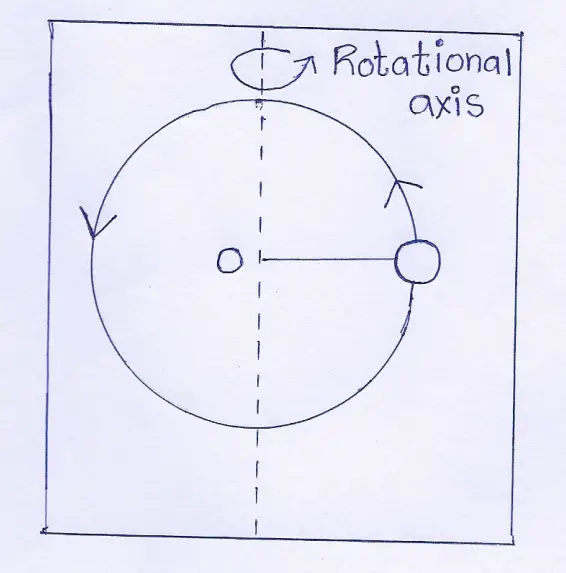
Answer:
Rotational motion: To describe rotational motion, the concepts adopted in circular motion are not sufficient; because in rotational motion change of orientation rather than position of an extended object is to be considered. An extended body is made up of a continuous distribution of particles of fixed masses with an external force.
Let us consider three constituent particles P, Q, and R of an extended rigid body and for a pure rotation of this extended body; each and every particle undergoes circular motion and centers of such motion for those particles lie on the same straight line or axis, known as axis of rotation.
Axis of rotation for an extended rigid body may pass through the body or it may lie outside the body.
Wbbse Physical Science And Environment Class 9 Solutions
Now, for an extended rigid body three kinds of rotation are possible, viz. orbital motion, spin motion and precessional motion. When a body is rotated around a distant axis of rotation then the motion of the body is called orbital motion.
Example: Motion of different planets around the sun.
When an extended rigid body rotates around its axis of symmetry then the motion of the body is called spin motion. Motion of a spinning top, daily rotation of the Earth about its axis passing through its two poles are examples of spin motion. Again, the spin axis of a rotating rigid body wobbles around another fixed axis to describe a cone.
Then that kind of motion is called precessional motion. At the last stage of a spinning top just before it comes to stop, the motion is such that the axis of the top rotates like a cone around a definite vertical axis. It is an example of precessional motion.
Question 10. Distinguish between translation and rotation
Answer:
We get the following differences between translation and rotation :
(1) In pure translation, the body travels along a straight line but in pure rotation, a body describes circular motion in a plane.
(2) In a pure translation, the direction of motion of the body remains fixed whereas in pure rotation axis of rotation remains fixed.
(3) In a pure translation, the displacement of all the particles constituting a rigid body occurs in the same direction and in pure rotation, the orientation of a rigid body changes but the relative distance between the constituent particles remains unaltered.
Wbbse Class 9 Physical Science Distance And Displacement
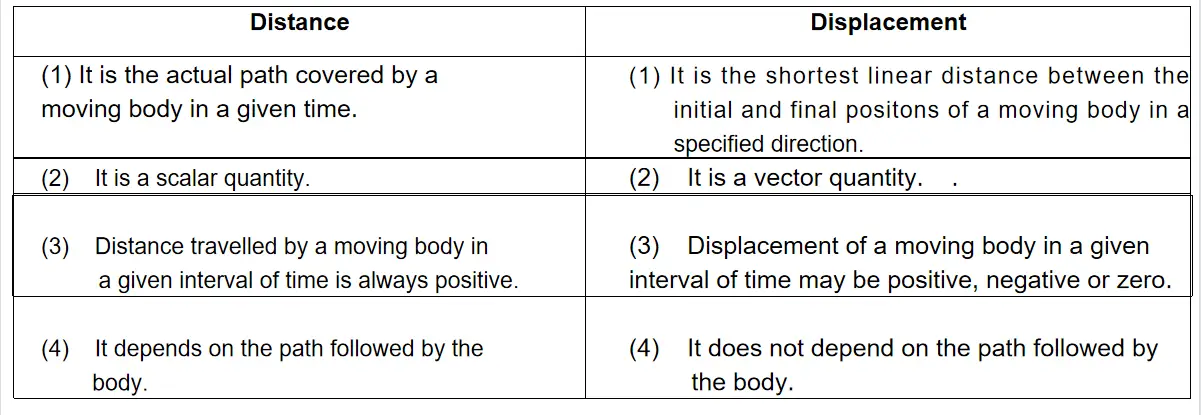
Question 11. Distinguish between distance and displacement.
Answer:
Difference between distance and displacement :
12. State and explain the meaning of resolution of forces.
Answer:
Resolution of forces: Resolution of force means splitting up of a force into two components. When a force is resloved into mutually perpendicular components then those components are called rectangular components of the force.Resolution of a force is utilised in towing of a boat by a simple rope. If a boat is pulled
Along the direction \(\overrightarrow{O C}\)with the help of a rope then with OC as diagonal and a parallelogram
OACB is drawn, then according to parallelogram law of vectors, the vector \(\overrightarrow{O C}\) can be resolved into two mutually perpendicular components \(\overrightarrow{O A}\)and \(\overrightarrow{O B}\).
The component \(\overrightarrow{O B}\) being normal to the river tries the boat to move across the river but its effect is cancelled by the rudder and as a result, the boat moves in the direction of the component\(\overrightarrow{O A}\)

Question 13. Write a short note on balanced and effective forces.
Answer:
Effective force and balanced force : If the resultant of a number of forces acting on a body is not zero, then the forces are called unbalanced forces. The net force acting on the body under the influence of a number of unbalanced forces is called the effective force. If the rider of a bicycle stops pedalling it then it will slow down. This is because. when the
Rider stops pedaling, the force of friction acting between the tires of the bicycle and the road opposes the motion of the bicycle.
An effective force has to be applied on the bicycle to keep it in motion. When the bicycle is moving with some non-uniform velocity, then the net force or unbalanced force acting on the bicycle becomes equal to the force applied by the rider while pedaling the bicycle minus force of friction between the tires and the road.
Unbalanced forces:
(1) may increase the speed,
(2) may decrease the speed or
(3) may
change the direction of motion of a body. This means that unbalanced forces or an effective force can produce acceleration in a body. Here, effective force is the cause and acceleration (change of motion) is the effect. On the other hand, if the resultant of all the forces acting on a body is zero, the forces are called balanced force.
Question 14. State and explain the concept of inertial mass.
Answer:
Concept of inertial mass: Newton’s second law of motion leads us to the concept of inertia and the concept of inertial mass.
According to Newton’s second law of motion, we know that for a given body, the acceleration is directly proportional to the net force applied.
Thus, force,\(\overrightarrow{F}\)α acceleration \(\overrightarrow{a}\)Or, \(\overrightarrow{F}\) = m.\(\overrightarrow{a}\), where m is a constant of proportionality,.called mass of the body.
Let an equal amount of force \(\overrightarrow{F}\)be applied separately on two bodies of different masses \(\mathrm{m}_1\) and\(\mathrm{m}_2\) (\(\mathrm{m}_1\), > \(\mathrm{m}_2\))
and if the accelerations produced in the two bodies are \(\overrightarrow{a_1}\) and a\(\overrightarrow{a_2}\) respectively, then according to the relation \(\overrightarrow{F}\)=m. \(\overrightarrow{a}\) we get,
⇒ \(\overrightarrow{F}\)=\(\mathrm{m}_1\) \(\overrightarrow{a_1}\)=\(\mathrm{m}_2\)\(\overrightarrow{a_2}\)
∴\(\frac{\overrightarrow{a_1}}{\overrightarrow{a_2}}=\frac{m_2}{m_1}\)
∴(\(\mathrm{m}_1\), > \(\mathrm{m}_2\))
∴\(\overrightarrow{a_1}\) › a\(\overrightarrow{a_2}\)
Hence, acceleration produced in the heavier body is less than that in the lighter body. Hence, mass of a body may be considered as the measure of the opposition for the produced in it. It leads to give us the concept of ‘intertial mass’.
Question 15. Is Newton’s second law of motion consistent with his first law?
Answer:
Consistency of Newton’s second law of motion with the first law of motion: According to Newton’s second law of motion, \(\overrightarrow{F}\) = (\(\overrightarrow{m}_a\) where F is the force applied on a body, m is the mass of the body and a is the acceleration produced in the body.
Now, in absence of any external force Bing on the body, i.e., when \(\overrightarrow{F}\) =0, \(\overrightarrow{m}_a\) =0.
∴ m can not be zero ,so \(\overrightarrow{a}\) =0.
Now, acceleration (1) of the body zero indicates that if the body is initially at rest, it will remain at rest and if it is in motion, then it will continue its motion with the same velocity which is nothing but Newton’s first law of motion. Therefore, Newton’s second law of motion is consistent with the first law.
Question 16. Write a short note on contact forces.
Answer:
Contact forces: The forces which exist because of actual contact between the sources and the body are called contact forces.
Different types of contact forces are
(1) Normal reaction: When a body appliés a force on another, the latter body also exerts a reactionary force which acts normal to its surface and this is known as normal reaction. For example when a book is placed on a table, the table exerts normal reaction on the book against its weight in the upward direction.
(2) Elastic force: It is the force exerted by.a deformed elastic body by virtue of its elasticity. Force exerted by a compressed string is an example of elastic force.
(3) Tension: The force that comes into play in a suspension string is called tension.
(4) Frictional force: Force that acts tangentially to the two surfaces due to the interlocking of undulations present on the surfaces is called frictional force. Force of friction exerted between the tyre of a car and the road surface is an example of such force.
(5) Air resistance: When the motion of a body takes place through air then the retarding force which comes into play is called air resistance. This force is exerted on an aeroplane when it flies through air at high speeds.
Wbbse Physical Science And Environment Class 9 Solutions
Question 17. Write a short note on non-contact forces
Answer:
Non-contact forces: The forces which exist without any physical contact between the bodies but are due to some intrinsic characteristics of the bodies, are called non-contact forces.
Some non-contact forces are:
(1) Gravitational force: The force of attraction acting between. any two bodies in the universe due to gravitational attraction between them.
Example: force of attraction acting on a body nearer to the Earth by virtue of which the body falls downwards towards the center of the earth.
(2) Electrical force: The force of attraction or repulsion acting between two unlike or like charges is called electrical force. Force of attraction acting between the nucleus of an atom and its orbiting electrons is an example of such kind of force.
(3) Magnetic force: The force that comes into play between two bodies due to their magnetic behavior is called magnetic force. Force of attraction acting between two unlike
Question 18. What are the four basic forces in nature?
Answer:
Basic forces in nature : There are four basic forces in nature. These are:
(1) Gravitational force: It is always attractive, mass-dependent but change independent force which obeys inverse-square law; gravitational is a long-range, the weakest and conservative central force. :
(2) The weak force: It is a short range but 10% times stronger than the gravitational force. In the process of β-decay, this force plays an important role and it explains the interaction between leptons, mesons and baryons.
(3) The strong force : It is a very short Tange, attractive, charge-independent but spin-dependent force; gravitational force is about 100 times stronger than electromotive force and is operative in between different nucleons inside a nucleus.
(4) Electromagnetic forces: It is a long-range, mass-independent, attractive or repulsive force that obeys the inverse-square law; electromagnetic force is a central force and is about 10*5 times stronger than the weak force. It is also a conservative force.
Question 19. Write a short note on the principle of conservation of linear momentum.
Answer:
Principle of conservation of linear momentum
The principle of conservation of linear momentum states that — “If no net external unbalanced force acts on the system of isolated bodies then the total linear momentum of the system in a given direction remains constant.”
According to Newton’s second law of motion, the time rate of change of linear momentum is equal to the applied force.
Thus,\(\vec{F}\)=\(\frac{\Delta \vec{p}}{\Delta t}\)
If the system is isolated, then \(\vec{F}\) =0
∴\(\frac{\Delta \vec{p}}{\Delta t}\)=0
∴\(\vec{P}\)=Constant.
Collisions of two bodies moving in same straight line: Let us consider an isolated system consisting of two bodies of masses m, and m, respectively. Let the two bodies be moving along a straight line in the same direction with velocities \(\overrightarrow{u_1}\) and \(\overrightarrow{u_2}\) ( \(\overrightarrow{u_1}\)>\(\overrightarrow{u_2}\))respectively.
The two bodies will collide after some time and let their final velocities after collision be \(\overrightarrow{v_1}\) and \(\overrightarrow{v_2}\) respectively.
Prior to collision, total linear momentum of the system\(=m_1 \overrightarrow{u_1}+m_2 \overrightarrow{u_2}\)
After collision takes place, total linear momentum of the system \(=m_1 \overrightarrow{v_1}+m_2 \overrightarrow{v_2}\)
Now, at the time of collision the first body of mass \(m_2\), exerts of force \(\vec{F}\)on the second body of mass \(m_2\) , and the second body also exerts an equal but opposite reactionary force ( \(\vec{-F}\) ) on the first body.
Now, according to Newton’s second law of motion, force acting on the body of mass \(m_2\) is
⇒ \(\vec{F}\)= Rate of change of momentum of the body of mass \(m_2\)
⇒ \(=m_2\left(\frac{\overrightarrow{v_2}-\overrightarrow{u_2}}{t}\right)\)……………..(1) (t=time during which collision occurs)
Again, force acting on the body of mass \(m_2\) is pars}
⇒ \(\vec{-F}\)= Rate of change of mementum of the body of mass\(\overrightarrow{m_1}\)
⇒ \(=m_1\left(\frac{\overrightarrow{v_1}-\overrightarrow{u_1}}{t}\right)\)………………(2)
From equation (1)and (2), we get
⇒ \(=m_2\left(\frac{\overrightarrow{v_2}-\overrightarrow{u_2}}{t}\right)\)–\(=m_1\left(\frac{\overrightarrow{v_1}-\overrightarrow{u_1}}{t}\right)\)
or,\(m_2 \vec{v}_2-m_2 \vec{u}_2=-m_1 \vec{v}_1+m_1 \vec{u}_1\)
or,\(m_2 \vec{v}_2+m_1 \vec{v}_1=m_2 \vec{u}_2+m_1 \vec{u}_1\)
∴\(m_1 \vec{u}_1+m_2 \vec{u}_2=-m_1 \vec{v}_1+m_2 \vec{v}_2\)
i.e., total momentum of the system before collision is equal to total momentum of the system after collision this is the law of conservation of linear momentum.
Wbbse Physical Science And Environment Class 9 Solutions
Question 20. Derive the equations of motion by graphical method.
Answer:
Equations of motion by graphical method : An object moving along a straight line with initial velocity u and uniform acceleration a can be related to its velocity v and distance s covered in a certain time interval t by the following equations :
(1) v=u+at
(2) s = ut + ½a\(t^2\)
(3) \(v^2\)=\(u^2+2 a s\)
These equations are called equations of motion and can be derived from the velocity-time graph.
(1) Derivation of v = u + at: The velocity-time graph of an object moving under uniform acceleration a and initial velocity u is shown in Fig. It is seen from the graph, the initial velocity is u at A which increases to v at B in time t. If BC and BE be the perpendiculars drawn from B on time and velocity axes respectively, then u = OA, v = BC and t = OC.
So, BD = BC − CD = change in velocity in time interval t.
If AD be drawn parallel to OC, then from the graph,
BC = BD + DC=BD+OA
or, v=BD+u
or, BD=v-u
Now, acceleration, a \(=\frac{\text { change in velocity }}{\text { time }}\)=\(\frac{\mathrm{BD}}{\mathrm{AD}}\)=\(\frac{\mathrm{BD}}{\mathrm{OC}}\)
Putting OC=t, \(a \)= \(\frac{B D}{t}\) or, BD = at=v-u
∴ V=u+at
(2) Derivation of s = ut + ½a\(t^2[\): Let the object moves a distance s in time t under uniform acceleration a. The distance traveled by the object is given by area OABC enclosed under the velocity-time graph A
So, distance traveled,
s = area OABC
= area of rectangle OADC + area of the AABD
= OA x OC + ½ (AD x BD) =u t+ ½(t xat)
∴ s=ut+ ½at.
(3) Derivation of \(v^2\)=\(u^2+2 a s\): Let the object travels a distance s in time t under uniform acceleration a. It is seen from the.
s = area of trapezium OABC \(=\frac{(O A+B C) \times O C}{2}\)=\(\frac{(u+v) t}{2}\)
Further, from the relation v = u + at, we have t \(=\frac{v-u}{a} .\)
so,s\(=\frac{(v+u)(v-u)}{2 a}\)
V \(=u^2+2 a s\).
Best study material for forces and motion WBBSE Class 9
Question 21. Show the displacement-time graphs of an object moving with uniform velocity and uniform acceleration.
Answer:
Displacement-Time graphs: The displacement of an object moving with uniform velocity along a straight path. The hypothetical time-displacement data of a particle are
Show in the following table.
Time (t) (second) 0 10 20 30 40
Displacement (s) (meter) 0 9 19 28 38
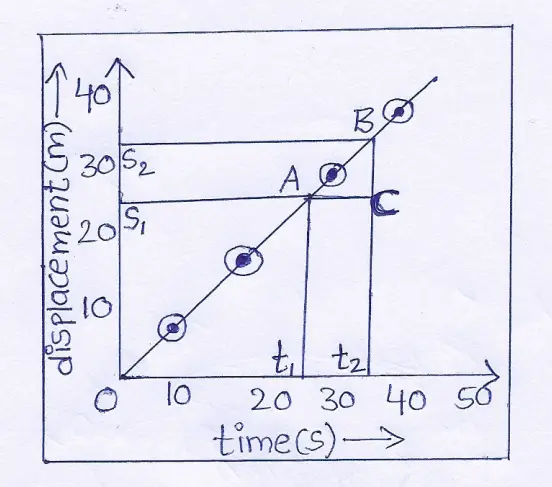
The displacement-time graph is shown in fig. 1. It is a straight-line graph passing through origin. From the graph it is seen that in time interval AC \(=\left(t_2-t_1\right)\) the corresponding displacement BC is equal to (\(\left(s_2-s_1\right)\)) =s.
Thus, v \(=\frac{s_2-s_1}{t_2-t_1}\)=\(\frac{s}{t}\)
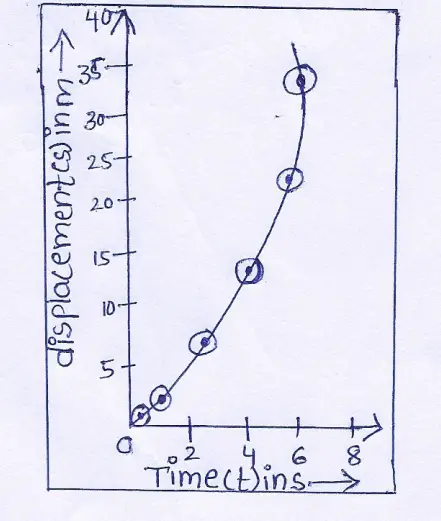
Again when the object is moving with uniform acceleration along a straight path, let the corresponding data are shown in the following table.
Time (t) in s 0 1 2 3 4 5 6
Displacement in m 0 1 4 9 16 22 36
The displacement-time graph is shown in the
Question 22. Write a short note on the parallelogram law of forces.
Answer:
The parallelogram law of forces: If simultaneously two forces act on a particle, the forces being represented in magnitude and direction by two adjacent sides of a resulting force, represented in magnitude and direction by the diagonal of the parallelogram passing through the same point.
If P and Q be two forces acting at an acute angle θ with each other, and be represented in magnitude and direction by R.
The two adjacent sides of a parallelogram, Q then their resultant force R is given in magnitude and direction by the diagonal of the parallelogram.
And if α be angle, the resultant R makes with the force P, then its value can be determined by measuring this angle.
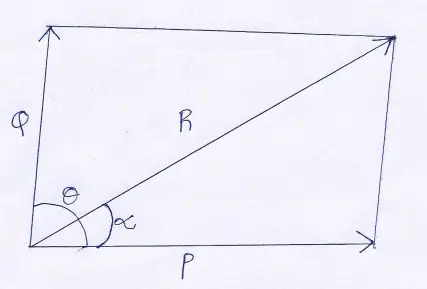
In our daily life we find applications of this law. Two applications are given as below :
(1) A boat pulled by two tugs in two different directions, then the boat does not move in either of these two directions, but moves along direction which is the diagonal of the parallelogram formed by two tugs as the sides of the parallelogram.
(2) If a man walks across the floor of a compartment of a train moving along a straight railway line, then the resultant velocity of the man can be found by the diagonal of the rectangle so formed.
Wbbse Physical Science And Environment Class 9 Solutions
Question 23. Give some examples of action and reaction forces.
Answer:
The following examples explain the action and reaction forces:
(1) When we sit on a chair, their is a downward gravitational force on us (i.e., our weight) which acts on the chair. This.is action. The chair also applies an equal reaction force on us in the opposite (i.e., upward) direction.
Because of these two equal and opposite forces acting on us we keep steady and do not fall to the ground. It is to be noted that equilibrium is restored not between the action and reaction forces but between our weight and the reaction of the chair, both acting on our bodies.
(2) While flying, a bird applies a force on the air by its wings. The air also exerts an equal and opposite reaction force to this action force of the wings which helps the bird to fly floating on the air. For this reason birds cannot fly in vacuum.
(3) Consider two magnets separated by a distance. When opposite poles of the magnets face each other, they attract each other and similar poles are facing each other they repel. Of the two magnets, weaker or lighter one is drawn or repelied from the other.
Here both the magnets attract or repel each other with some force but the lighter one moves towards or away from the heavier one. If we hold one of them hard on the table, the other would move towards or away, when the force of attraction or repulsion between the magnets are sufficient to pull each other.
(4) The Earth orbits around the sun. The only force that acts on the Earth by the sun is the gravitational force exerted by the sun on the earth, which provides the centripetal force required by the earth for its revolution.
Now where is the corresponding reaction force? The answer is the gravitational attractive force of the Earth on the sun. It is known that these gravitational forces are equal in magnitude and opposite in sign. Thus it is seen that action and reaction forces are equal and opposite to each other.
(5) Let us take two spring balances whose hooks be connected to each other. Holding them firmly, they are drawn in the opposite directions. The readings of the spring balances are found to be always the same.
Now, if one of the balances is fixed to a firm support like wall and the other is pulled with a certain force, it will be found that each of the spring balances shows same reading. Thus it proves conclusively that action and reaction forces are equal and opposite.
WBBSE Class 9 Physical Science friction and motion solutions
Question 24. What are the ways in which a force may be exerted?
Answer:
There are four different ways in which a force may be exerted. These are :
(1) Pull: It is usually applied along some length of a substance.
Example: the force is applied along a string, a chain, etc. and the string is said to be in a state of tension.
The pull substance like a rod. A rope tied to the ceiling through a hook. When pull the rope from the lower end, a force is exerted on the hook. The hook, in turn, exerts a reaction through the rope.
A pull is thus exerted along the length of a substance. Thus the effect of the pair of action and reaction forces exerted through a material medium is to bring the two interacting bodies together orto prevent them from separating.
(2) Push: When a man presses a wall with his hands, he applies a force on the wall, which in turn, applies a reaction on the man. As a result, the man and the wall tend to separate from each other.
So, by push it is meant a pair of action and reaction between two bodies which tries to keep the bodies apart from each other. A push distributed over an area is often called thrust and can be applied through rigid bodies only and not by flexible bodies. :
(3) Attraction and repulsion: When a pair of actions between two bodies separated by a distance tries to bring them together, attraction between them is said to exist and when it tends to keep apart, repulsion between them occurs.
Gravitational, magnetic, electrical forces are examples of this type of force. These forces exist always. It does not matter whether there is the presence of a material medium between them or not, though the magnitude of the forces may depend upon them.
(4) Friction: When a body tends to slide over another, the second body exerts a reaction on the first acting opposite to the direction of motion and trying to prevent the motion is called friction.
Wbbse Physical Science And Environment Class 9 Solutions
Question 25. “Rest and motion are relative”. Explain.
Answer:
Rest and motion are relative: A body seems to be at rest with respect to one neighboring fixed object but the same body may appear to be in motion with respect to some other fixed neighbouring object. So, rest and motion are relative terms.
Examples :
(1) In a moving train, a passenger finds his co-passengers at rest, but to an observer standing outside the train the same passengers appear to be in motion.
(2) A person standing on a road finds a car moving away from him. So, the car is in motion with respect to him. Now, if another car near it moves with the same speed and direction, thento a person in the second car, the first car seems to be at rest. In fact, every object in the universe is in motion with respect to one or the other object.
Example: A passenger in a moving train finds trees, buildings, etc. in motion, but. those things appear to be at rest to a person standing somewhere outside the train. ~ Thus, absolute rest and absolute motion are meaningless terms.
Question 26. Write a short note on displacement.
Answer:
Displacement: When an object changes its position as time passes on, the distance measured in the direction from its initial to final position along a straight line is known as its displacement.
Displacement is a vector quantity, it is directed from the initial position of a body to its final position. The measurement of displacement of a body solely depends upon its initial and final positions, not on the paths followed by it in reaching the final position from its initial position.

As in the adjacent figure, an object moves from its initial position A to its final position B. It may do this in two ways.
It may either follow the path ACDEB or the path AOB, but in each instant the displacement is the straight line AB that joins the initial position C, D, E in the latter case and at O in the former case. A
lso the distances of ACDEB, and AOB are of different magnitudes but displacement AB is same in both some cases. One thing is common to both. It is that both distance and displacement denote some length of path covered by a moving body.
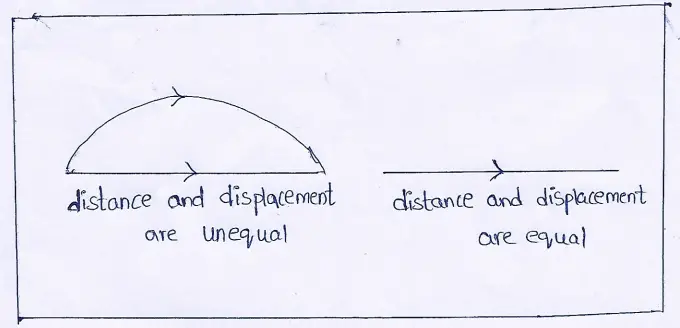
But measurement of displacement is always directed from the initial position of a body to its final position. If the initial position of a moving body coincides with the final position occupied by it after moving through some length of path, the displacement of the body is zero.
Thus a body while moving along a circular or a curved path, if returns to its starting position, its displacement and the distance covered are different in magnitude but if it travels along a straight line, both the distance and displacement are equal in magnitude.
Wbbse Physical Science And Environment Class 9 Solutions
Question 27. Write a short note on inertia of rest.
Answer:
Inertia of rest: It is that property of a body by virtue of which the body tends to remain at rest and itself does not change its state.
Definition: Inertia of rest is the inherent property of a material body by virtue of which it continues in its state of rest until and unless no external unbalanced force compels it to move.
Example: A book kept on a table remains at rest as long as it is not disturbed by any externally applied force.
For disturbing from its state of rest, it can be raised or displaced.to other positions only by the application of a force by way of pulling up or pushing through Of course, the body at rest will not respond to an external force of any magnitude, the force to which the body responds, depends on the mass of the body; greater the mass of the body, greater external force is required.
A smaller force can disturb the rest condition of a body of a smaller mass. Another definition of the inertia of rest may also be derived : it is the ability of a body to stistain its initial state of rest. This property of sustaining ability of a body depends on its mass.
For example, a blackboard duster lying at rest on a table can be easily set into motion by pushing it gently with a finger, but such a small force cannot move a table of larger mass. From this we can infer that the ability of a body to sustain its initial state of rest or motion increases with increase of its mass.
But it is true that the force exerted on the table with finger brings forth a tendency of its motion, for, if the magnitude of the force is increased, the table starts moving. Thus, the ability of a body to sustain its intial state of rest or motion is limited.
Examples of inertia of rest :
(1) To remove dusts from a blanket or a cloth it is struck by a stick or jerked vigorously. When struck by a stick or jerked suddenly, fibres of the article are just made to move away, but the dust particles, due to their inertia of rest, remain at their initial positions and they fall off in absence of any support.
(2) A person sitting or standing in a bus at rest leans backward as the bus starts suddenly. While the bus is at rest, the person’s body in contact with it also remains at rest. As soon as the bus starts, the lower part of the person’s body in contact of the bus moves forward but his upper part tends to remain in the former position due to inertia of rest, the result is nothing but leaning back.
Question 28. Write a short note on the inertia of motion.
Answer:
Inertia of motion: Definition: The tendency of a moving body to maintain its uniform motion in a straight line in absence of any effective external force is called inertia of motion.
Another meaning is that a body moving uniformly tries to defy the effect of an external. force acting on it. The ‘effect’ of the force here refers to the disturbing actions over the uniformity of motion of the body.
But this ability is limited upto certain magnitudes of the said force. A body of large mass can maintain this property upto a large value of this force while a smaller mass yields to a much smaller force.
Example :
A person runs or walks uniformly along a road. His uniform motion may be changed simply by pushing or pulling him with hand, but a similar force cannot affect the uniform motion of a running locomotive engine that possesses a huge mass. But, a vigorous pull or push executed with the help of another engine can definitely change its uniform motion of it.
An external force changes the uniformity of motion of a body in either of these ways — if the force is directed in the direction of initial motion of the body, velocity of it increases.If it is in opposite direction, velocity decreases and if it is tangential to the body, the direction of motion changes.
Also, everywhere the inertia of a body and an external force acting on it are in opposition to each other. Thus it is also true that inertia of rest or inertia of motion of a body is a measure of its ability of sustaining its state of rest or uniform motion.
Wbbse Physical Science And Environment Class 9 Solutions
Question 29. “Mass is a measure of inertia.” Explain.
Answer:
Mass is a measure of Inertia: This means, both types of inertia (of rest and of motion) are large for a body of large mass and they are small for a body of small mass. That is, greater the mass, greater is the ability of a body to sustain its initial state of rest or motion even under the effects of an external force and smaller the mass, smaller is its ability to do so.
Thus, a small force of push offered with hand can easily displace a book at rest. But to displace a large chunk of rock, a force of enormous magnitude is necessary. Here, the book of small mass has a large inertia of rest, soa very large force can move it.
Similarly, a small force can change the motion of a cyclist but a very large force is necessary to do so in case of a moving truck, for the inertia of motion of the truck of large mass is greater than that of the cyclist of smaller mass.
Question 30. State and explain Newton’s third law of motion.
Answer:
Third law of motion: To every action there is an equal and opposite reaction. Discussions on the third law of motion: If someone pushes with his hand a fixed massive body, like a wall or a tabletop, he feels pain on his fist; if he offers blow gently or violently he will feel the effect accordingly.
This means whenever a body applies a force on another, the second body also returns a force of the same magnitude on the former.
For application of force, always two different bodies or two different parts of a single body are necessary. When one body exerts a force on the other, the force is called the action, the second body also offers at the same time an equal force on the first body in the opposite direction and this force is called reaction.
Due to this fact Newton’s third law of motion Says, action and reaction are equal in magnitude but opposite in direction.
Since every force of action is associated with an opposite force of reaction, no force can exist singly in nature, that is, in nature forces always appear in pairs.
Any force acting at some point in an inclined direction may be considered to consist of two parts or two components in two suitable directions such that the result of the combined effect of the components on the point is exactly same as that of the initial force. So the components are equivalent to the single force.
Question 31. What are the characteristics of displacement’?
Answer:
Displacement has the following characteristics :
(1) Displacement has the unit of length.
(2) The displacement may be positive, negative or zero.
(3) The magnitude of the displacement of a moving particle between two points gives the shortest distance between them.
(4) From the displacement of a moving particle between two points we do not get any idea about the path followed by the moving particle.
(5) The displacement of a moving particle between two points has a unique value.
(6) The actual distance traveled by the moving particle may be greater than or equal to the magnitude of the displacement. ;
(7) Altering the origin of the coordinate axis has no effect on displacement.
(8) As a particle cannot be at two different positions at the same time, so displacement is a single-valued function of time.
(9) The displacement changes if its direction be changed.
Wbbse Class 9 Difference Between Speed And Velocity
Question 32. Distinguish between speed and velocity.
Answer:
Difference between Speed and Velocity :
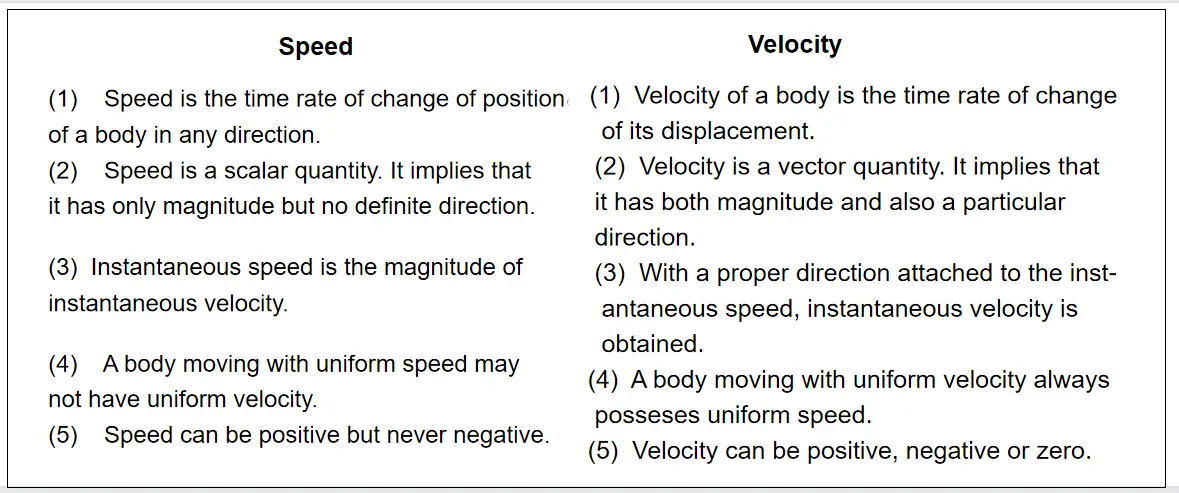
Question 33. Write a short note on velocity-time graphs.
Answer:
Velocity-time graphs: Velocity-time graphs under different conditions are shown in the to In velocity-time graph for a particle moving with uniform velocity is shown.
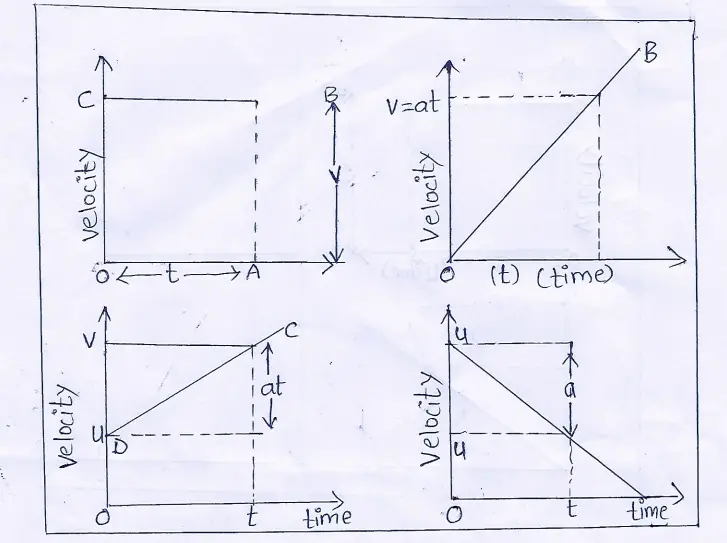
As the velocity V. is uniform, so the plot of the velocity against time would be a straight line parallel to the time axis. The distance moved in time t is equal to it, which is seen from the graph as the area of the rectangle OABC. Thus the distance traveled by a particle in uniform motion is given by the area under the velocity-time graph.
In, the velocity-time graph for a particle moving in a straight line with uniform acceleration and starting with initial velocity u = 0 is shown. All these conditions being same, motion starting with initial velocity u is shown in .
In both cases, velocity-time curves are straight lines. In each case the constant slope of the straight line gives the uniform accleration.
In the velocity-time graph for a particle moving with uniform retardation in a straight line is shown. The curve is again a straight line but the slope is negative. In all the cases, the distance moved by the particle is given by the area under the velocity-time graph.
Question 34. How is a graph plotted?
Answer:
Plotting a graph: A graph is plotted to display the relationship between two quantities. Generally, one of the two quantities changes independently and the other quantity depends on it.
(1) Choosing the axes: Draw two perpendicular lines crossing each other at a point. Each line represents one of the two quantities to be plotted. Generally, a horizontal line from left to right is drawn to represent the independent quantity and a perpendicular line is drawn to represent the dependent quantity. These lines are called the x-axis and the y- axis, or the horizontal axis and the vertical axis respectively.
(2) Choosing the scale: The size of the paper on which a graph is drawn is limited. On the available length of the axes, values are marked at equal distances. This is done in such a way that all the values of the quantity represented on the axis can be accommodated in the available length.
(3) Plotting the points: Each set of values of the two quantities. is represented by a point on the graph.
(4) Joining the points: Once all the points corresponding to the available sets of values of the quantities are plotted, they are joined by a smooth curve to get the graph.
Question 35. Write a short note on impulse.
Answer:
Impulse: The total effect of a force is called impulse and is measured by the product of the force and the time for which the force acts on the body.
Impulsive force: Impulsive force is a force of very large magnitude but of extremely short duration, which acting on a body, produces a finite change of its momentum, displacement of the body during the action of the force being negligible.
The effect of the force is measured by its impulse.
Example of impulsive force: A player lowers his hands while catching a cricket ball. In doing so he increases the time of catch to reduce the momentum of the ball to zero. We know,
Impulse = force x time = change in linear momentum.
So, to produce a particular change in linear momentum, if one takes longer time, then the force required would be less. Thus in catching a cricket ball, the player increases the time of catch by lowering his hands and thereby decreases the force and smaller reaction occurs on the hands.
Question 36. How does the value of ‘g’ vary from place to place?
Answer:
The value of ‘g’ varies from place to place :
(1)Both as we go up from earth’s surface or go down inside below the surface of the earth, The value of acceleration due to gravity decreases.
(2) At the center of the earth the sete of acceleration due to gravity is found to be zero.
(3) Moreover, acceleration due to gravity changes due to earth’s spin about its axis also. Standard value of acceleration due to gravity is taken at 45° latitude sea level.
(4) Again, on the surface of earth it is maximum at the poles. Because, due to orange shape of the earth, the distance of the poles is shorter than that of the equator from the center of the earth.
Question 37. An object of mass 20 kg is accelerated uniformly from a velocity of 36 km\(h^{-1}\)“ to 54 km\(h^{-1}\)” in 20 s. Calculate
(1) the initial momentum of the body
(2) final momentum of the body and
(3) the force acting on the body.
Answer:
m = 20 kg; initial velocity, u = 36 km\(h^{-1}\) = 36 x 18 =10m\(s^{-1}\)
final velocity, v = 54 km\(h^{-1}\)\(=54 \times \frac{5}{18}\) =15 m\(s^{-1}\); time, t= 25s
(1) Initial momentum of the body, \(\mathrm{p}_1\) = mu = 20 x 10 = 200 kg m\(s^{-1}\)
(2) Final momentum of the body, \(\mathrm{p}_2\) = mv = 20 x 15 = 300 kgm\(s^{-1}\)
(3) Force \(=\frac{\text { change in momentum }}{\text { time taken }}\)=\(\frac{p_2-p_1}{t}\)\(=\frac{300-200}{25}\)=4N.
Question 38. A revolver of mass 500 g fires a bullet of mass 10 g with a speed of 100 ms. Find
(1) momentum of the bullet
(2) the initial momentum of the revolver and bullet as a system and
(3) recoil velocity of the revolver.
Answer:
Given, mass of the revolver, \(\mathrm{m}_1\) = 500 g = 0.5 kg.
mass of the bullet, \(\mathrm{m}_2\) = 10g = 0.01 kg
initial velocity of (revolver + bullet) system, u = 0
final velocity of bullet, v = 100 m\(s^{-1}\)
Let the recoil velocity of the revolver be V m\(s^{-1}\)
(1) momentum of the bullet = \(\mathrm{m}_2\)v = 0.01 x 100= 1 kgm\(s^{-1}\)
(2) initial momentum of (revolver + bullet) = (\(\mathrm{m}_1+ \mathrm{m}_2\))u= 0
(3) momentum of the revolver after firing = \(\mathrm{m}_1\)v = 0.5 x V kgm\(s^{-1}\)
momentum of (revolver + bullet) after firing = initial momentum of (revolver + bullet)
or,0.5v+1=0 or, V= -2m\(s^{-1}\)
∴ recoil velocity of the revolver = 2 m\(s^{-1}\).
39. Velocity-time graph for a body is shown. Find its (1) A acceleration, (2) velocity and (3) distance covered in 20
Answer:
(1) Acceleration \(=\frac{\text { Change in velocity }}{\text { Time }}\)=\(\frac{0}{t}\)=0
(2) Velocity of the body = 15 m/s (from the graph).
(3) Distance covered in 20 seconds
= Area under v — t graph.
= OA x AB = (20 x 15) m = 300 m.
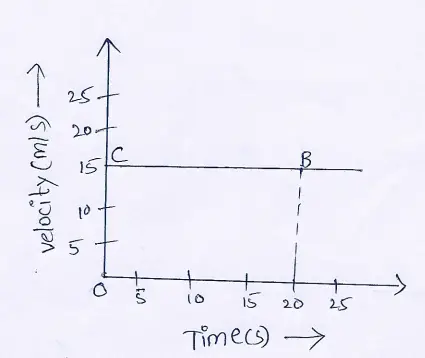
Question 40. Velocity-time graph for the motion of a particle is shown:
(1) Which part of the graph indicates accelerated motion? Calculate the acceleration
(2) Which part of the graph shows retarded motion?
(3) Calculate the distance traversed by the body in the first 20 seconds of its journey.
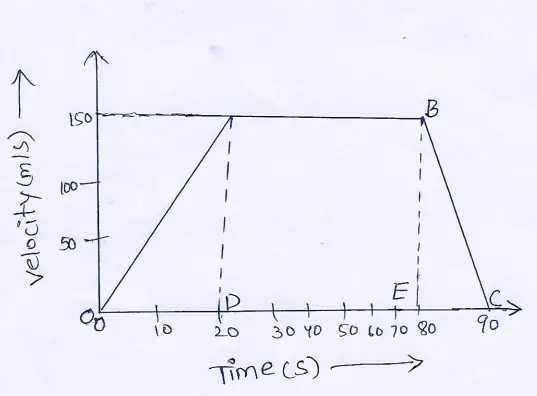
Answer:
(1) In the graph OA part indicates accelerated motion as velocity goes on increasing from O to A.
Acceleration (a) \(=\frac{v-u}{t}\)=\(\frac{150-0}{20}\)=7.5m/\(s^{2}\).
(2) The part BC of the graph indicates retarded motion as velocity goes on decreasing from B to C.
Retardation(-a)\(=\frac{v-u}{t}\)=\(\frac{0-150}{10}\)=-15m/\(s^{2}\).
(3) Distance traveled by the body in the first 4 s of its journey Area under OA part of the graph = Area of OAD
=½×OD×AD=½×4×4=8cm.
Question 41. The driver of a train A travelling at a speed of 54 km/h applies brakes and retards the train uniformly.
The train stops in 5 seconds. Another train B is travelling on the parallel track with a speed of 36 km/h. His driver applies the brakes and the train retards uniformly. The train B stops in 10 seconds. Draw speed-time graphs for both the trains on the same graph and calculate the F 2 distance travelled by each train after the brakes were Ot>34567 8910 applied.
 Answer:
Answer:
In case of train A:
Initial velocity (u) = 54 km/h\(=\left(54 \times \frac{5}{18}\right)\)m/s = 15 m/s
Final velocity (v) = 0, time (t) =5s
Velocity-time graph for a is shown by straight line EF
∴ Distance travelled by A = Area of ΔEOF
=½×OF×OE=(½×5×15)m=3.75m.
In case of train B :
Initial velocity (u) = 36 km/h =\(=\left(36 \times \frac{5}{18}\right)\)m/s =10m/s
Final velocity (v) = 0
Time taken (t) = 10s
Velocity-time graph for (B) is shown by the straight line CD.
Distance traveled by B = Area of ΔCOD
= ½×OD×OC=(½×10×10)m=50m.
Question 42. For a moving object distance-time graph is shown beside. From the graph,
(1) Find the speed of the object during first 4 s of its motion.
(2) State how long it was stationary.
(3) State whether this situation is real or not.
 Answer:
Answer:
(1) Speed of the object during first 4s
= slope of OP part of the graph Time (s}
⇒ \(=\frac{P S}{O S}\)=\(\frac{75 m}{4 s}\)=18.75m/s.
(2) From 4 seconds to 14 seconds, distance does not change with time and hence it remains stationary for (14−4) = 10 seconds.
(3) This situation is impractical because the distance traversed can not be decreased with time. Moreover, time can not go backward as is shown by QR part of the graph. Hence it is not a real situation.
Question 43. Velocity-time graph for a moving body is shown.
(1) What is the initial velocity?
(2) What is the velocity of the body at the point C?
(3) Find the acceleration of the body between A and B.
(4) Find the acceleration acting on the body between B and C.
Answer:
(1) Initial velocity of the body = 20 m/s.
(2) Velocity of the body at the point C = 40 m/s.
(3) Acceleration between A and B
⇒ \(=\frac{v-u}{t}\)\(=\frac{(40-20) m / s}{3 s}\)=\(\frac{20}{3} \mathrm{~m} / \mathrm{s}^2\)
=6.67m/\({s}^2\)(approx).
(4) Acceleration between B and C\(=\frac{(v-u)}{t}\) =\(\frac{0}{t}\)
(∴ No change in velocity occurs between B and C) = 0
44. A force of 5 N gives a mass m, an acceleration of 8 m/s? and a mass m, an acceleration of 24 m/s. What acceleration would it give if both the masses are tied together?
Answer:
In the first case: force (F) = 5 N, mass (m) =\(\mathrm{m}_1\) acceleration (a) = 8 m/\({s}^2\)
∴F=ma ∴ 5=\(\mathrm{m}_1\) 8 or,m=\(\frac{5}{8}\) kg
∴ The mass \(\mathrm{m}_1\) is \(\frac{5}{8}\) kg.
In the second case: Force (F) = 5 N, mass (m) =\(\mathrm{m}_2\), acceleration (a) = 24 m\({s}^2\)
∴F=ma ∴5=\(\mathrm{m}_2\) x 24 ∴\({m}^2\) =\(\frac{5}{24}\) kg
∴The mass\(\mathrm{m}_2\) is\(\frac{5}{24}\)kg.
In the third case: mass (m) = \(\mathrm{m}_1\) +\(\mathrm{m}_2\)=\(\left(\frac{5}{8}+\frac{5}{24}\right) \mathrm{kg}\)=\(\frac{20}{24} \mathrm{~kg}\)=\(\frac{5}{6} \mathrm{~kg}\)
Force (F) =5N
Acceleration (a) =?
∴F=ma ∴5\(=\frac{5}{6}\)a ∴ a=5×\(\frac{6}{5}\)=6m/\({s}^2\)
∴Hence, the required acceleration is 6 m/\({s}^2\).
Question 45. From the given velocity-time graph, answer the following :
(1) What type of motion does OA represent?
(2) What type of motion does AB represent?
(3) Find the acceleration of the body. ‘ Y
(4) Find the distance traveled by the body from O to C.
Answer:
(1) The graph is a straight line having upward slope, it represents uniform acceleration.
(2) Since it is a straight line parallel to time axis, it represents uniform speed.
(3) We know acceleration is the slope of the time-velocity graph. So, \(\frac{A D}{O D}\)=\(\frac{10 m}{5 s}\) = 2 m/s.
(4) Distance is the area enclosed between velocity time graph and time axis = area of
trapezium OABC = ½ (AB + OC) x BE = ½{(25−5) + 30) x 10 m/s = 250 m.
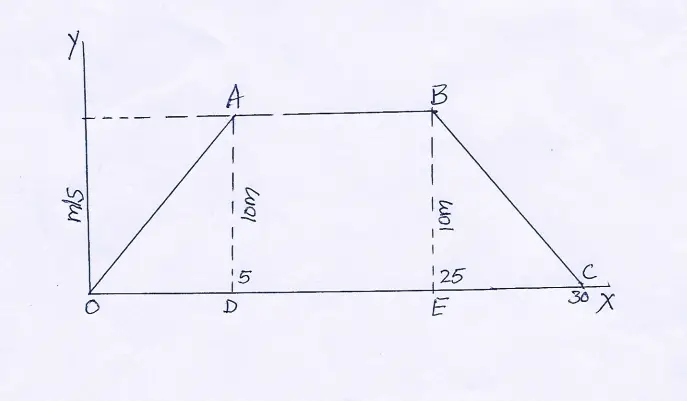
Question 46. From the given velocity-time graph of a body :
(1) Calculate the distance traveled by it in 4 s.
(2) Calculate the distance traveled by it in 8 s.
Answer:
(1) We know that the area between ~ velocity time graph and time axis gives the distance traveled by the body. The distance traveled in 4 sec is the area of
triangle OAC = ½ x OC x AC= ½ x4s x 10 m/s = 20m.
The distance traveled in 4 s is 20 m. Time per second
(2) Distance traveled in 8 s is given by the area of the trapezium OABD.
Area of trapezium OABD = ½ (AB + OD) x BD
Now, AB = CD = OD-OC=8-4=4s
BD = 10 m/s. OD = 8s.
Area of trapezium OABD = ½(4 + 8) x 10 =60m.
Thus, distance traveled in 8 s = 60 m.
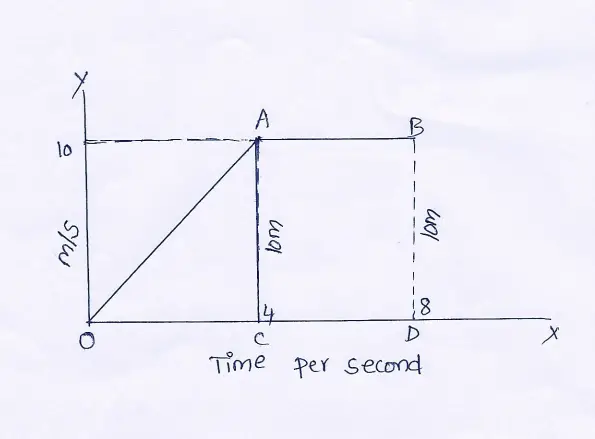
Question 47. A particle moves in a straight line with a retardation of 10 m/s\(s^2\) If its initial velocity is 50 m/s, when would it stop?
Answer:
(1) The deceleration is 10 m/ \(s^2\)means that in each second velocity of the particle diminishes by 10 m. So, at this rate, the time in which its initial velocity diminishes.
To zero, then it stops. Hence, the required time \(=\frac{50 \mathrm{~m} / \mathrm{s}}{10 \mathrm{~m} / \mathrm{s}^2}\)=5s.
(2) By using the formula, v = u + at, where symbols are of usual significance, when the particle stops, its final velocity, v = 0, and ‘a’ should be (-ve) for deceleration.
∴V=u-at or, 0=50−10.t or, 10t=50 ∴ t=5.
So, the required time is 5 seconds.
Question 48. Equal forces act on two masses ‘m’ and ‘2m’. If the acceleration acquired by ‘m’ be ‘f’, what is the acceleration acquired by 2 m?
Answer:
From the relation, force = mass x acceleration, the force acting on the mass‘m’ is mf.
Now the same force mf acts on the mass 2 m, and since, acceleration \(=\frac{\text { force }}{\text { mass }}\),
acceleration of the second body \(=\frac{m f}{2 m} \)= \(\frac{f}{2}\).
Otherwise: since, acceleration α\(\frac{1}{\text { mass }}\) , if the mass of one body is double the other, for the same force, the acceleration of the former body is half that of the latter and it is \(\frac{f}{2}\).
WBBSE Solutions for Class 9 Physical Science And Environment
- Chapter 1 Measurement
- Chapter 2 Force And Motion
- Chapter 3 Matter: Structure And Properties
- Chapter 4 Matter: Atomic Structure; Physical & Chemical Properties of Matter
- Chapter 5. Energy In Action: Work, Power & Energy
- Chapter 6 Heat
- Chapter 7 Sound
