WBBSE Solutions For Class 9 Physical Science And Environment Chapter 3 Matter: Structure And Properties

Chapter 3 Matter: Structure And Properties Very Short Answer Type:

Question 1. What is the unit of density in the SI system?
Answer: The unit of density in the SI system is: kg\(m^{-3}\).

Question 2. What is the unit of specific gravity in the CGS system?
Answer: The unit of specific gravity in the CGS system is: gc\(m^{-3}\).

Question 3. What is fluid?
Answer: The word fluid comes from the Latin word ‘fluere’ meaning ‘to flow’.

Question 4. Is pressure a scalar quantity?
Answer: No, pressure is not a scalar quantity. It is a vector quantity.

Read and Learn all WBBSE Solutions for Class 9 Physical Science And Environment

Question 5. Give the dimensional formula of pressure.
Answer: The dimensional formula of pressure is : \(\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\).

Question 6. What is the relation between the density and the specific gravity of a substance?
Answer: The relation is ey of substance = specific gravity of the substance x density of water at 4°C.

Question 7. What is buoyancy?
Answer: The upward thrust that any fluid exerts upon a body partly or wholly submerged in it is called its buoyancy.

Question 8. Does buoyancy depend on the depth of the liquid in which a body is immersed?
Answer: The buoyancy does not depend on the depth of the liquid in which the body is immersed.

Question 9. Is there any gas in the Torricellian space?
Answer: The space above the mercury level in the tube contains practically nothing but a negligible amount of mercury vapor and is known as the Torricellian vacuum.

Question 10. Will the siphon work if there is a hole at any point in the longer arm above the surface of the liquid in the vessel in which the shorter arm is placed?
Answer: When a hole is made at any point in the longer arm above the surface of the liquid in the vessel in which the shorter arm is placed, the siphon will not work.

Question 11. Is surface tension a vector quantity?
Answer: Surface tension is a scalar quantity as it has no specific direction.

Question 12. What is the unit of surface energy?
Answer: The unit of surface energy is Joule.

Question 13. What is capillarity?
Answer: The phenomenon of rise or fall of liquid in a capillary tube is called capillarity.

Question 14. Define ‘angle of contact’.
Answer: The angle at which the tangent to the liquid surface at the point of contact makes with the solid surface inside the liquid is called the angle of contact.

Question 15. What happens to the surface tension of a liquid when an impurity is mixed in it?
Answer: The presence of impurities in the liquid surface or dissolved in it considerably affect the force of surface tension and surface tension depends on the degree of contamination.

Question 16. How can the rough sea be calmed?
Answer: The rough sea can be calmed by pouring oil on seawater.

Question 17. In a streamlined flow, what is the velocity of the liquid in contact with the containing vessel?
Answer: Zero.

Question 18. What is terminal velocity?
Answer: Terminal velocity of a body is the constant maximum velocity acquired by a body while falling through a viscous fluid.

Question 19. Can two streamlines cross each other?
Answer: No. Two streamlines cannot cross each other.

Question 20. What is the terminal velocity of a body in a freely falling system?
Answer: Terminal velocity of a body in a freely falling system is zero.

Question 21. What is the acceleration of a body falling through a viscous fluid after terminal velocity is reached?
Answer: Zero.

Question 22. The velocity of water in a river is less on the bank and large in the middle. Explain.
Answer: The velocity of water in contact with solid banks is zero and it increases as we go towards the middle of the river.

Question 23. The velocity of fall of a man jumping with a parachute first increases and then becomes constant. Why?
Answer: It is because of the fact the man attains terminal velocity.

Question 24. What is the SI unit of coefficient of viscosity?
Answer: The SI unit of coefficient of viscosity is Decapoise (Ns\(m^{-2}\)).

Question 25. What is critical velocity?
Answer:

Critical velocity: It is the velocity of flow of a liquid up to which its flow is streamlined and above which its flow becomes turbulent.

Question 26. Does viscosity come into play if there is relative motion of the liquid layers?
Answer: Yes, it depends on the relative velocity of the two layers.

Question 27. Does viscosity depend on the area of the layers in contact?
Answer: Viscosity depends on the area of the liquid layers.

Question 28. What do you mean by an ideal fluid?
Answer: An ideal fluid has zero viscosity and zero compressibility.

Question 29. Is viscosity a vector?
Answer: No, viscosity is a scalar quantity.

Question 30. Write down the dimensional formula for the coefficient of viscosity.
Answer: The dimensional formula for the coefficient of viscosity is : \(\left[\mathrm{ML}^{-1} \mathrm{~T}^{-1}\right]\)

Question 31. How does the viscosity of a liquid change with change in temperature?
Answer: The viscosity of liquid increases with a decrease in temperature and vice-versa.

Question 32. How does the viscosity of a gas change with change in temperature?
Answer: The viscosity of a gas increases with increase in temperature and vice-versa.

Question 33. What is the value Reynold  number for streamline flow?
Answer: NR < 2000.

Question 34. Why does an air bubble in a liquid rise up?
Answer: As terminal velocity of the air bubble is negative.

Question 35. Is Bernoulli’s theorem valid for viscous liquid?
Answer: No.

Question 36. Water and castor oil are taken in two different flasks and shaken Violently and kept on a table. Which liquid will come to rest earlier?
Answer: Castor oil having higher viscosity will come to rest earlier.

Question 37. Between friction force and viscous force, which one depends on velocity?
Answer: Viscous force depends on velocity, but friction force is independent of velocity.

Question 38. The hotter liquid flows faster than a colder one. Why? 
Answer: The coefficient of viscosity of ligule decreases with rise in temperature and so liquid flows faster.

Wbbse Class 9 Physical Science Solutions

Question 39. What are the properties of a liquid satisfying Bernoulli’s theorem?
Answer: The liquid must be an ideal one.

Question 40. What are the dimensions of stress and strain?
Answer: Stress = \(\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\) and strain = \(\left[\mathrm{M}^{0}{L}^{0} \mathrm{~T}^{0}\right]\).

Question 41. What is more elastic — water or air?
Answer: Water.

Question 42. Why are springs made of steel and not of copper?
Answer: Because the modulus of elasticity of steel is more than that of copper.

Question 43. What is the value of modulus of rigidity for a liquid ?
Answer: Zero.

Question 44. What is the value of Young’s modulus for an incompressible liquid ?
Answer: Zero.

Question 45. What is the unit of Poisson’s ratio?
Answer: Poisson’s ratio is a pure number and thus it has no unit.

Question 46. What is the value of bulk modulus for an incompressible liquid ?
Answer: Infinite.

Question 47. What is more elastic — steel or rubber?
Answer: Steel.

Question 48. What is more fundamental stress or strain?
Answer: Strain, as stress is developed only when a body is strained.

Question 49. Is Poisson’s ratio an elastic modulus?
Answer: No. Poisson’s ratio is unitless while elastic modulus has unit N\(m^{-2}\).

Wbbse Class 9 Physical Science Solutions

Question 50. Is there any truly rigid body?
Answer: No.

Question 51. If the barometer reading at a place be 74.5 cm, find the pressure per square centimeter.
Answer:

Here, h = 74.5 cm, d = 13.6 g/c\(m^{3}\)

Hence the pressure, p = hdg = 74.5 x 13.6 x 980 = 992936 dyn/c\(m^{2}\).

Question 52. Atmospheric pressure at a place is 750 mm. Find the pressure at the place. [Given, density of mercury = 13.6 g/cc and g = 980 cm/\(m^{2}\).
Answer:

p = hdg = 75 x 13.6 x 980 = 0.9995 x 106 dyn/c\(m^{2}\).

Question 53. Find the pressure at a depth of 5 m below the surface of a lake. (Density of water = 1000 kg \(m^{-3}\)).
Answer:

Pressure = hpg

=5 x 1000 x 9.8 = 4.9 x \({10}^{4}\) N\(m^{-2}\).

Wbbse Class 9 Physical Science Solutions

Question 54. What is hydrostatics?
Answer:

Hydrostatics: The branch of physics that deals with fluid at rest is called hydrostatics.

Question 55. What is hydrodynamics ?
Answer:

Hydrodynamics: The branch which deals with fluid in motion is called hydrody- namics.

Question 56. What is density?
Answer:

Density: The density of a substance is its mass per unit volume.

Question 57. What is specific gravity?
Answer:

Specific gravity: Specific gravity of a substance is the ratio of the density of the substance to the density of water at 4°C.

Question 58. What is relative density?
Answer:
Relative density: The specific gravity being ratio of two densities, it is also called relative density.

Question 59. What is hydrostatic pressure?
Answer:

Hydrostatic pressure: The normal force exerted by a fluid at rest per unit area of the surface in contact with it is called the pressure of the fluid or hydrostatic pressure.

Wbbse Class 9 Physical Science Solutions

Question 60. What is thrust ?
Answer:

Thrust: The total normal force exerted by a fluid at rest on a surface in contact with it is called thrust.

Question 61. What are the units of pressure?
Answer:

Unit of pressure :

(1) CGS : Dyne c\(m^{-2}\)
(2) SI: N\(m^{-2}\) or pascal (Pa).

WBBSE class 9 physical science chapter 3 question answer

Question 62. Write the dimensional formula of pressure.
Answer:

Dimension of pressure : \(\left[\mathrm{ML}^{-1} \mathrm{~T}^{-2}\right]\)

Question 63. What are the units of thrust?
Answer:

Units of Thrust :

(1) CGS: Dyne
(2) SI: Newton (N).

Question 64. What are the units of surface tension?
Answer:

Units of surface tension :

(1) CGS: Dyne c \(m^{-1}\)
(2) Sl: N \(m^{-1}\).

Question 65. What is the dimensional formula of surface tension?
Answer:

Dimensional formula of surface tension : \(\left[\mathrm{MT}^{-2}\right]\)

Question 66. What is decompose?
Answer:

Decapoise: If 1-newton tangential force is required to maintain a velocity gradient of 1 m \(s^{-1}\)/m between two layers each of area 1 \(m^{2}\), it is called 1 decapoise.

Question 67. What is poise?
Answer:

Poise: If 1 dyne tangential force is required to maintain a velocity gradient of 1 cm \(s^{-1}\)/cm. between two layers each of area 1 c \(m^{2}\), it is called 1 poise

WBBSE class 9 physical science chapter 3 question answer

Question 68. Write the mathematical expression of terminal velocity.
Answer:

The expression of terminal velocity : v\(=\frac{2 r^2(\alpha-d) g}{9 \eta}\)

(Consider a small sphere of radius r and density d falling under gravity in a viscous fluid of density α and coefficient of viscosity η and terminal velocity is r)

Question 69. What is Reynold’s number?
Answer:

Reynold’s number (R): It is the ratio of the inertial force per unit area to viscous force per unit area for a flowing fluid.

Question 70. What is the perfectly inelastic body?
Answer:

Perfectly inelastic body: A body is said to be perfectly inelastic or plastic when it does not regain its original configuration at all on the removal of deforming force, however small it may be.

Question 71. What is tensible stress?
Answer:

Tensible stress: If there be an increase in length or extension of a body in the direction of the applied force, the stress developed is called tensile stress.

Question 72. What is compression stress?
Answer:

Compression stress: When the deforming force acts tangentially to the surface of a body to produce a change in the shape of the body, then the stress developed in the body is called tangential stress.

Chapter 3 Matter: Structure And Properties 2 Marks Questions And Answers:

Question 1. What is air pressure?
Answer:

Air pressure

Air has weight. Air pressure is the weight of the column of air above a horizontal surface of a unit area (e.g. one square meter). The column of air extends to the top of the atmosphere. As we go up and reach a higher altitude, the pressure is lower because the column of air is reduced.

Question 2. How is air pressure measured?
Answer:

Mercury barometers and aneroid barometers are commonly used to measure air pressure. The height of the mercury column will vary according to the air pressure. The higher the air pressure, the greater will be the height of the mercury column. By measuring the height of the column, the air pressure at the base of the column can be determined.

Question 3. What is an aneroid barometer?
Answer:

Aneroid barometer

An aneroid barometer consists of a disk-shaped capsule made of a thin metal membrane. The capsule is partially evacuated of air. Changes in atmospheric pressure change the size of the capsule, which in turn, moves an ink pointer.

In this way, pressure changes are recorded continuously as the pointer moves over a rotating drum. Nowadays, digital barometer is commonly used because it is portable and accurate. An electrical capacitor it is used to measure the change in air pressure.

WBBSE class 9 physical science chapter 3 question answer

Question 4. What is the unit of pressure?
Answer:

Unit of pressure

Pascal (Pa) is the international standard unit for pressure. The meteorological community uses hectopascal (hPa) as the unit of pressure.

Question 5. How do we compare the pressure measured at different locations?
Answer:

To compare pressure readings taken at different locations, it is convenient to convert them to a common level, e.g. the sea level. The conversion takes into account a number of factors that affect the weight of air (e.g. temperature, gravity of the earth).

Question 6. What is pressure in liquids?
Answer:

Pressure in liquids

Liquid has its own weight, this causes pressure on the wall of the container in which liquid is held; it also causes pressure on any object immersed in the liquid.

Question 7. How is the pressure of liquids measured?
Answer:

Pressure in liquids is due to the weight of the liquid acting on the surface of any object in the liquid.

Formula: Pressure caused by liquid, P=h.d.g

P = Pressure
h = Depth
d = Density of liquid
g = Gravitational Field Strength.

Question 8. What are the characteristics of pressure in liquid?
Answer:

Characteristics of pressure in liquid

(1) Pressure acts in all directions.
(2) Pressure acting on a liquid at rest will be transmitted equally in all directions.
(3) The pressure in a liquid increases with depth.
(4) Pressure in a liquid depends only on its vertical distance from the surface of the liquid.

WBBSE class 9 physical science chapter 3 question answer

Question 9. What does Archimedes’ principle state?
Answer:

The principle states that : “A body immersed in a liquid forces weight by an amount equal to the weight of the liquid displaced.”

Archimedes’ principle also states that  “When a body is immersed in a liquid, an upward thrust, equal to the weight of the liquid displaced, acts on it.” Thus, when a solid is fully immersed in a liquid, it loses weight which is equal to the weight of the liquid it displaces.

Question 10. What does the law of floatation state? 
Answer:

Law of floatation state

A body will float if the weight of the body is equal to the weight of the liquid displaced. If the weight of the immersed body is more than the weight of the water displaced, the body will sink.

Question 11. Define the density of a substance.
Answer:

Density of a substance

The density of a substance is its mass per unit volume:

Density = Mass /Volume.

Wbbse Physical Science And Environment Class 9 Solutions

Question 12. Define relative density or specific gravity.
Answer:

Relative density or specific gravity

The “relative density” or “specific gravity” of a substance is defined as the ratio of its density to the density of water at 4 degrees Celsius.

Relative density = Density of substance ÷ Density of water at 4°C.

Question 13. What is surface tension?
Answer:

Surface tension

Surface tension is a property of liquids that arises from unbalanced molecular cohesive forces at or near a surface. At an air-water interface, the surface tension results from the greater attraction of water molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion). The net effect is an inward force at its surface that causes water to behave as if its surface were covered with a stretched elastic membrane.

Because of the relatively high attraction of water molecules for each other, water has a high surface tension. Surface tension arises from the strong interactions between water molecules, called hydrogen bonding. It is this strong interaction which also manifests itself in the other unusual properties of water such as its high boiling point.

Question 14. Why is a meniscus the curve in the upper surface of a liquid close to the surface of the container? 
Answer:

The meniscus is the curve in the upper surface of a liquid close to the surface of the container or another object. It is caused by surface tension. It can be either convex or concave, depending on the liquid and the surface.

Question 15. Explain the formation of a meniscus in the upper surface of a liquid.
Answer:

A concave meniscus occurs when the particles of the liquid are more strongly attracted to the container than to each other, causing the liquid to climb the walls of the container. This occurs b

etween water and glass.

A convex meniscus occurs when the particles in the liquid have a stronger attraction to each other than to the material of the container. Convex menisci. occur, for example, between mercury and glass in barometers.

Question 16. State the factors affecting the surface tension: of a liquid.
Answer:

(1) Presence of impurities in the liquid surface or dissolved in it.
(2) Surface tension is dependent on temperature.

Question 17. What is viscosity?
Answer:

Viscosity

The viscosity of a fluid is a measure of its resistance to gradual deformation by shear stress or tensile stress. For liquids, it corresponds to the informal concept of “thickness”. For example, honey has a much higher viscosity than water.

Viscosity is a property arising from collisions between neighboring particles in a fluid that are moving at different velocities. When the fluid is forced through a tube, the particles that comprise the fluid generally move more quickly near the tube’s axis and more slowly near its walls.

Wbbse Physical Science And Environment Class 9 Solutions

Question 18. Explain the Laminar Flow.
Answer:

Laminar Flow

The resistance to flow in a liquid can be characterized in terms of the viscosity of the fluid if the flow is smooth. In the case of a moving plate in a liquid, it is found that there is a layer or lamina that moves with the plate, and a layer, which is essentially stationary if it is next to a stationary plate.

There is a gradient of velocity as you move from the stationary to the moving plate, and the liquid tends to move in layers with successively higher speed. This is called laminar flow, or sometimes, “streamlined” flow. Viscous resistance to flow can be modeled for laminar flow, but if the lamina breaks up into turbulence, it is very difficult to characterize the fluid flow.

Question 19. What is Dynamic (shear) viscosity?
Answer:

Dynamic (shear) viscosity

The dynamic (shear) viscosity of a fluid expresses its resistance to shearing flows, where adjacent layers move parallel to each other with different speeds. It can be defined through the idealized situation known as a Couette flow, where a layer of fluid is trapped between two horizontal plates, one fixed and one moving horizontally at constant speed u.

Question 20. What is Kinematic viscosity?
Answer:

Kinematic viscosity

The kinematic viscosity (also called “momentum diffusivity”) is the ratio of the dynamic viscosity “μ” to the density of the fluid “μ”. It is usually denoted by the Greek letter nu (μ).

Question 21. What is Bulk viscosity?
Answer:

Bulk viscosity

When a compressible fluid is compressed or expanded evenly, without shear, it may still exhibit a form of internal friction that resists its flow. These forces are related to the rate of compression or expansion by a factor “μ”; called the volume viscosity, bulk viscosity or second viscosity.

Question 22. What is a Viscometer?
Answer:

Viscometer

Viscosity is measured with various types of viscometers and rheometers. A rheometer is used for those fluids that cannot be defined by a single value of viscosity and, therefore, require more parameters to be set and measured than is the case for a viscometer. One of the most common instruments for measuring kinematic viscosity is the glass capillary viscometer.

Wbbse Physical Science And Environment Class 9 Solutions

Question 23. Explain the rate of flow. of a liquid.
Answer:

Rate of flow. of a liquid

The common application of laminar flow would be in the smooth flow of a viscous liquid through a tube or pipe. In that case, the velocity of the flow varies from zero at the walls to a maximum along the centerline of the vessel. Dividing the flow into thin cylindrical elements and applying the viscous force to them, we can calculate the flow profile of the laminar flow in a tube.

Question 24. Define Bernoulli’s Theorem.
Answer:

Bernoulli’s Theorem

Bernoulli’s Theorem states that for the streamlined flow of an ideal liquid, the total energy (i.e., the sum of pressure energy, potential energy, and kinetic energy) per unit mass remains constant at every cross-section throughout the liquid flow.

Question 25. What is elasticity?
Answer:

Elasticity

Elasticity is the property of an object or material that causes it to be restored to its original shape after distortion. It is said to be more elastic if it restores itself more precisely to its original configuration.

Question 26. Give an example of an elastic object.
Answer:

Example of an elastic object

A spring is an example of an elastic object when stretched, it exerts a restoring force that tends to bring it back to its original length. This restoring force is generally proportional to the amount of stretch, as described by Hooke’s Law. For wires or columns, the elasticity is generally described in terms of the amount of deformation (strain) resulting from a given stress.

Question 27. Define stress and strain.
Answer:

Stress and strain

Normal stress on a body causes a change in length or volume and tangential stress produces a change in the shape of the body. The ratio of change produced in the dimensions of a body by a system of forces or couples, in equilibrium, to its original dimensions is called strain.

Strain = Change in Dimension / Original Dimension.

Question 28. What are the units of strain?
Answer:

Units of strain

As strain is a ratio, it has no units and dimensions.

Question 29. What is Hooke’s law?
Answer:

Hooke’s law

Hooke’s law gives a relationship between stress and strain. According to Hooke’s law, within the elastic limit, the strain produced in a body is directly proportional to the stress produced.

Or stress /strain = a constant.

Question 30. What is the Modulus of Elasticity?
Answer:

Modulus of Elasticity

Stress/Strain a constant, known as the Modulus of Elasticity. Its unit is N\(m^2\).

Corresponding to the three types of strain, there are three moduli of elasticity :
1. Young’s modulus, corresponding to longitudinal strain;
2. Bulk modulus, corresponding to volume strain; and,
3. Rigidity modulus, corresponding to shearing strain.

Question 31. Calculate the pressure at the bottom of a pond of depth 10 m. Given that density of water = 1000 kg/\(m^3\) and acceleration due to gravity at that place = 9.8 m/\(s^2\).
Answer:

Here, depth of the pond (h) = 10 m, density of water (d) = 1000 kg/\(m^3\)

acceleration due to gravity (g) = 9.8 m/\(s^2\)

∴  Pressure at the bottom of the pond (P) = hdg = 10 x 1000 x 9.8 = 98000 N/\(m^2\).

∴  Required pressure at the bottom of the pond = 98000 N/\(m^2\).

Question 32. Calculate the depth of water in a cistern that is filled with water of density 1000 kg/\(m^3\) and pressure at any point on its bottom is 9800 N/\(m^2\). Take g = 9.8 m/\(s^2\)
Answer:

Here, pressure at the bottom (P) = 98000 N/\({m}^{2}\); density of water (d) = 1000 kg/\(m^3\) acceleration due to gravity (g) = 9.8 m/\(s^2\).

∴ P=hdg    ∴h\(=\frac{P}{d g}\)=\(\frac{9800}{1000 \times 9.8}\)=1m.

∴Depth of water in the cistern = 1 m.

Wbbse Class 9 Physical Science And Environment Solutions

Question 33. The mass of 4 m of iron is 31200 kg. Calculate the density of iron in SI unit.
Answer:

Given

The mass of 4 m of iron is 31200 kg.

Density \(=\frac{\text { Mass }}{\text { Volume }}\)     (Here, mass = 31200 kg, volume = 4 \(m^3\))

⇒ \(=\frac{31200}{4}\) kg/ \(m^3\) =7800 kg/\(m^3\)

∴ Density of iron = 7800 kg/\(m^3\).

Question 34. A body of mass 100 g has a volume of 40 cc. Determine the density of the material of the body. If the density of water is 1 g/cc, then state whether the body will sink or float in water.
Answer:

Given

A body of mass 100 g has a volume of 40 cc.

Here, mass = 100 g, volume = 40 cc.

∴ Density for the material of the body\(=\frac{\text { Mass }}{\text { Volume }}\) \(=\frac{100}{40}\)g/cc=2.5g/cc

Since the density of the body (2.5 g/cc) is greater than the density of water (1 g/cc), the body will sink in water.

Question 35. The relative density of gold is 19.3. If the density of water be \({10}^{3}\)Kg/\({m}^{3}\)‘, calculate the density of silver in SI unit.
Answer:

Given

The relative density of gold is 19.3. If the density of water be \({10}^{3}\)Kg/\({m}^{3}\)‘,

Relative density of a substance \(=\frac{\text {Density of the substanc }}{\text { Density of water }}\)

19.3\(=\frac{\text { Density of the gold }}{10^3 \mathrm{~kg} / \mathrm{m}^3}\).

∴Density of gold =19.3 × \({10}^{3}\)Kg/\({m}^{3}\)

Question 36. When a tensile force of 60 N is applied to a metal wire of length 50 m and area of cross-section \({10}^{-6}\) \({m}^{2}\), elongation of the wire is 4 x 10\({m}^{-3}\). Calculate :
(1) stress and
(2) strain.
Answer:

Hence, force (F) = 60 N, area of cross-section (A) = \({10}^{-6}\) \({m}^{2}\)

The original length of the wire (1) = 5 m,

Expansion in length (Δl) = 4 x\({10}^{-3}\) m.

(1) Stress \(=\frac{F}{A}\)= \(\frac{60}{10^{-6}} \mathrm{~N} / \mathrm{m}^2\)

\(=6 \times 107 \mathrm{~N} / \mathrm{m}^2\)

(2) Strain \(=\frac{\Delta l}{I}\)

=\(\frac{4 \times 10^{-3}}{5}\)

=0.8 \(10^{-3}\)=\(8 \times 10^{-4}\)

Wbbse Class 9 Physical Science And Environment Solutions

Question 37. If the strain be 1% of 0.1, find the change in length of a wire 5 m long. If the cross-section is 1 mm? and load 19 kg-wt, what is the ratio of stress to strain? Change in length
Answer:

Strain\(=\frac{\text { Change in length }}{\text { Original length }}\)

∴ Change in length = Strain x original length\(=\left(\frac{1}{100} \times 0.1 \times 5\right)\)=5×\(10^{-3}\) m=5mm.

Now, stress =\(\frac{\text { Load }(F)}{\text { Area of cross }-\sec \text { tion }(A)}\)\(=\frac{10 \times 9.8 \mathrm{~N}}{1 \times 10^{-6} \mathrm{~m}^2}\)=9.8 ×\(10^7 \mathrm{~N} / \mathrm{m}^2\).

⇒ \(\frac{\text { Stress }}{\text { Strain }}\)=\(\frac{9.8 \times 10^7}{\frac{1}{100} \times 0.1} \mathrm{~N} / \mathrm{m}^2\)=N/\({m}^2\)=9.8×1010 N\({m}^2\).

Question 38. A solid body weighs 50 N. It is immersed in water and the weight of it in water is 45 ar the relative density of the solid.
Answer:

Weight of the body in air (\(W_1\)) = 50 N.

Weight of the body in water (\(W_2\)) = 45 N.

Loss of weight of the body in water=50N-45N=5N

Therefore, R.D. of the body \(=\frac{W_1}{W_1-W_2}\)=\(\frac{50 N}{5 N}=\)=10.

Question 39. A block of 36 cc ice floats on water. What volume of it remains above water surface?
Answer:

It is known that nearly 1/12 part of the volume of an ice block remains above water when it floats on water.

Here, the total volume of the ice block is 36 cc.

∴1/12 of 36 cc = 3 cc.

So, 3 cc of ice remains above the water surface.

Wbbse Class 9 Physical Science And Environment Solutions

Question 40. The weight of a body in air is 33 g-wt and when immersed in a liquid of density 0.75 g/cc, it weighs 24 g-wt. Determine the volume and density of the body.
Answer:

Given

The weight of a body in air is 33 g-wt and when immersed in a liquid of density 0.75 g/cc, it weighs 24 g-wt.

Apparent loss of weight of the body when immersed in the liquid

= (33 — 24) g-wt, or 9 g-wt, so, the mass of the liquid displaced by the body is 9 g.

Now, volume of the body = volume of the displaced liquid = 9 g/0.75 g/cc = 12 cc.

Density of the body = mass/volume = 33 g/12 cc = 2.75 g/cc. (sin¢e, 33 g-wt has the mass 33 g).

Question 41. Gold has a density of 19.3 g/cc. An ornament weighs 5.80 g in air and 5.25 g in water. Is the ornament made of pure gold?
Answer:

Given

Gold has a density of 19.3 g/cc. An ornament weighs 5.80 g in air and 5.25 g in water.

From Archimedes’ principle, the volume of the ornament = (5.80 − 5.25) cc = 0.55 cc. Now, considering the density of pure gold as 19.3 g/cc, the weight of the ornament in air = (19.3 x 0.55) g-wt = 10.615 g-wt. But as indicated in the problem, the weight of the ornament in the air is 5.80 g-wt. Hence, the ornament is not made of pure gold.

Question 42. 20 kg weight is suspended from a wire 600.5 cm long and 1 m\(m^2\)cross section. When the weight is removed, the length of the wire decreases by 0.5 cm. Find Young’s modulus of the wire.
Answer:

Given

20 kg weight is suspended from a wire 600.5 cm long and 1 m\(m^2\)cross section. When the weight is removed, the length of the wire decreases by 0.5 cm.

We. know if the initial length of a wire is L the change of its length is x, weight suspended from the wire is mg, then longitudinal strain = x/L and longitudinal stress  = mg/π\(r^2\);

Therefore, Young’s modulus, Y \(=\frac{\text { Longitudinal stress }}{\text { Longitudinal strain }}\)\(\frac{m g / \pi r^2}{x / L}\)=\(\frac{m g L}{\pi r^2 x}\).

In the problem, mass m is 20 x 1000 g and acceleration due to gravity is g = 980 cm/\(\sec ^2\)

Initial length L= 600.5 − 0.5 = 600 cm, change of length x = 0.5 cm. π\(r^2\)= 1 m\(m^2\)

=0.01c\(m^2\)

therefore, Y\(=\frac{20 \times 1000 \times 980 \times 600}{0.01 \times 0.5}\)=2.35×\(10^{12} \mathrm{dyn} / \mathrm{cm}^2\).

Wbbse Class 9 Physical Science And Environment Solutions

Question 43. 2.2 kg weight is suspended from a wire 10 m long and a cross-section area 2mm. If the strain be 0.001%, find the elongation of the wire.
Answer:

Given

2.2 kg weight is suspended from a wire 10 m long and a cross-section area 2mm. If the strain be 0.001%,

The length of the wire is 1000 cm if the increase in length of the wire is x cm, then percentage strain \(\frac{x}{1000} \times 100\)= 0.001 (according to the problem).

Therefore, x = 0.001 x 10 = 0.01 cm.

Cross-section of the wire = 2 m\({m}^{2}\) = 0.02 c\({m}^{2}\), 1 kg weight = 1000 x 980 d

Hence, stress \(=\frac{1000 \times 980}{0.02}\)=\(\frac{98 \times 10^4}{2 \times 10^{-2}}\)=48×106 dyne/c\({m}^{2}\).

Question 44. 8 kg weight is suspended from a wire of length 2 m and diameter 0.5 mm. If the length of the wire increases by 2.88 mm, find Young’s modulus of the wire.
Answer:

Given

8 kg weight is suspended from a wire of length 2 m and diameter 0.5 mm. If the length of the wire increases by 2.88 mm

Here, the length of the wire L = 200 cm, the radius of the wire (r) = 0.25 mm = 0.025 cm.

Therefore, the cross-section area of the wire = π\({r}^{2}\) = π x\((0.025)^2\); increase in length, x = 0.228 cm, weight (mg) = 8 x 1000 x 980 dyne.

Therefore, Young’s. modulus \(=\frac{\text { Stress }}{\text { Strain }}\)

= \(\frac{\mathrm{mg} / \pi r^2}{\mathrm{x} / \mathrm{L}}\)

⇒ \(=\frac{m g L}{\pi r^2 x}\)

⇒ \(=\frac{8 \times 1000 \times 980 \times 200}{\pi \times(0.025)^2 \times 0.288}\)

⇒ \(=2.773 \times 10^{12} \mathrm{dyn} / \mathrm{cm}^2\).

Wbbse Class 9 Physical Science And Environment Solutions

Question 45. A cylindrical vessel of diameter 28 cm contains a liquid up to a height of 20 cm. Find the pressure and thrust on the bottom of the vessel. (Given density of the liquid = 0.9 g\({m}^{-3}\)).
Answer:

Given, diameter of the vessel = 28 cm; radius, r \(=\frac{28}{2}\) = 14cm

Height of the liquid in the vessel = 20cm

Area of the bottoms of the vessel =π\(r^2\)=π×\({14}^{2}\)=616c\({m}^{2}\)

Density of the liquid, ρ= 0.9 g c\({m}^{-3}\)

Pressure = hρg = 20 x 0.9 x 980 =17840 dynes/\({m}^{-2}\)

Thrust = Pressure x area = 17640 x 616 = 10866240 dyne.

Question 46. A body having a volume of  \(50 \mathrm{~cm}^3\) weighs 0.5 kg In air. Find its density.
Answer:

Given, volume of the body = 50c[latex]{m}^{3}[/latex]=50×\({10}^{-6}\)\({m}^{3}\)

Mass of the body =0.5kg.

Density of the body \(=\frac{\text { mass }}{\text { volume }}\)\(=\frac{0.5}{50 \times 10^{-6}}\)=104 Kg\({m}^{-3}\).

Question 47. The density of water is 1000 kg \({m}^{-3}\). if the density of gold be 19320 kgm\({m}^{-3}\), find the relative density of the gold. 
Answer:

Given, density of water = 1000 kg\({m}^{-3}\).

Density of gold = 19320 kg\({m}^{-3}\).

∴ Relative density of gold \(=\frac{\text { density of gold }}{\text { density of water }}\)

⇒ \(=\frac{19320}{1000}\)=19.32.

Question 48. The relative density of silver is 10.5. Find the density of silver.
Answer:

Given, the relative density of silver = 10.5

Now, relative density of silver \(=\frac{\text { density of gold }}{\text { density of water }}\)

∴ density of silver = relative of silver x density. of water

= 10.5 x 1000 = 10500 kg\({m}^{-3}\).

Question 49. A metallic wire of length 60 cm when stretched along length by a normal force becomes 61 cm. Find the longitudinal strain.
Answer:

Given, the original length of the wire, l= 60cm.

The final length of the wire, l’= 61 cm.

Increase in length, Δl = l− l’=61 = 60 = 1 cm.

Longitudinal strain \(=\frac{\Delta l}{1}\)=\(\frac{1}{60}\)=0.017.

Question 50. A metallic wire of radius 0.1 cm and length 2 m is extended by a weight of 2.5 kg. Find the normal stress set up.
Answer:

Given external deforming force, F = 2.6 kg wt = 2.5 x 9.8 N.

Radius of the wire, r=0.1cm=0.1×\({10}^{-2}\)

Area of cross-section of the wire =π\({r}^{2}\)\(=\pi(10-3)^2 \mathrm{~m}^2\).

∴ Normal stress \(=\frac{\text { external decor ming force }}{\text { area }}\)

∴ \(=\frac{2.5 \times 9.8}{\pi\left(10^{-3}\right)^2}\)=\(7.8106 \mathrm{Nm}^{-2}\).

Question 51. The ratio of radii of two Wires of the same material is 2: 1. If these wires are stretched by equal force, find the ratio of the stresses produced in them.
Answer:

Given,\(r_1: r_2\)=2:1;\(F_1: F_2\)=F

stress(S)\(=\frac{\text { force }}{\text { area }}\)\(=\frac{F}{\pi r^2}\) or, sα\(\frac{1}{r^2}\)

∴\(\frac{s_1}{s_2}\)=\(\frac{r_2^2}{r_1^2}\)\(=\left(\frac{1}{2}\right)^2=\frac{1}{4}\).

Question 52. A force on 1000 N causes an increase of 0.1% in the length of a wire of area of cross-section\(10^{-6} \mathrm{~m}^2\), Calculate the Young’s modulus of the material of: ‘the wire.
Answer:

Given, F = 1000 N; a =\({10}^{-6}\)

⇒ \({m}^{2}\)

⇒ \(\frac{\Delta l}{I}\)=0.1%\(=\frac{1}{1000}\)=\(10^{-3}\)

Y\(=\frac{\mathrm{F} / \mathrm{a}}{\Delta \mathrm{l} / \mathrm{l}}\)=\(\frac{1000}{10^{26} \times 10^{-3}}\)\(=10^{12} \mathrm{Nm}^{-2}\)

Question 53. A water-filled cone of height 50 cm and the base area 20 cm? is placed on a table with the base on the table. What is the thrust offered by the water on the table?
Answer:

Thrust = Pressure x area = hdg x A

∴Thrust

= 50 x 1 x 980 x 20, h = 50cm

= 9.8 x 105 dyne, d = 1 gc\({m}^{-3}\)

= 9.8N, g = 980cm/\({s}^{-2}\)

A = 20 c\({m}^{2}\)                                    

Question 54. The pressure of air in a soap bubble of 0.7 cm diameter is 8 mm of water above the atmospheric pressure. Calculate the surface tension of the soap solution.
Answer:

The excess of pressure inside a soap bubble is given by

P\(=\frac{4 T}{r}\) , P=8mm=0.8cm, r=0.7cm/2=0.35cm

∴T\(=\frac{\mathrm{Pr}}{4}\)

∴ \(=\frac{0.8 \times 980 \times 0.35}{4}\)

=68.6 dyne c\(m^{-1}\).

Question 55. The surface tension of water is 0.072 N\({m}^{-1}\) Calculate the excess pressure inside a water drop of diameter 1.2 mm.
Answer:

P\(=\frac{2 T}{r}\)=\(\frac{4 T}{d}\),  R=0.72N\({m}^{-1}\)

⇒ \(=\frac{4 \times 0.072}{1.2 \times 10^{-3}}\)

d=1.2 mm=1.2×\({10}^{-3}\)

⇒ \(=240 \mathrm{Nm}^{-2}\)

Question 56. One end of an iron wire of length 250 cm of diameter 1 mm is rigidly fixed with a beam and a weight of 8 kg is placed at the other end. Calculate the elongation of the wire. (Y of iron\(=20 \times 10^{11} \text { dyne } \mathrm{cm}^{-2}\),=9.8 m \({s}^{-2}\)).
Answer:

l\(=\frac{F L}{A}\)

L=250cm=2.5m

or,l\(=\frac{8 \times 9.8 \times 2.5}{\pi / 4\left(10^{-3}\right)^2 \times 2 \times 10^{11}}\)

=0.125×\({10}^{-2}\)m

d =1mm=\({10}^{-3}\)m

W=8kg-wt

=20 1011 dyne c\({m}^{-2}\) =2.01011N\({m}^{-2}\)

g = 9.8 m \({s}{-2}\)

l  = ?

Question 57. What is Pascal’s law?
Answer:

Pascal’s Law: The pressure applied at any place to an enclosed fluid at rest is transmitted with undiminished magnitude to every portion of the fluid and acts normally to the surface in contact with the fluid.

Question 58. What are the conditions for Archimedes’ principle and buoyancy?
Answer:

Conditions for Archimedes’s principle and buoyancy :

(1) As Archimedes’ principle involves the weight of a body, so the principle does not hold when the body is in weightless condition like the state of free fall of the body in an artificial satellite moving in a circular orbit. ‘
(2) The buoyancy does not depend on the depth of the liquid to which the body is immersed or on the immersed volume of the body and the density of the displaced liquid at a particular place.

Question 59. What is S.T.P.?
Answer:

Standard or Normal temperature and pressure: The standard or normal atmospheric pressure is defined as the pressure exerted by a column of mercury 76 cm high at 0°C at 45° latitude and mean sea level.

Question 60. State any two conditions for working of a. siphon.
Answer:

Conditions for the working of a siphon are :

(1) At first the whole tube must be filled with liquid.
(2) The end of the longer tube must be below the level of the liquid in the other vessel.

Question 61. What is: surface energy?
Answer:

Surface energy: It is the amount of work done against the force of surface tension in forming the liquid surface of a given area at a constant temperature.

Question 62. What is the angle of contact?
Answer:

The angle of contact: The angle at which the tangent to the liquid surface at the point of contact makes with the solid surface inside the liquid is called the angle of contact.

Question 63. State two factors on which the value of the angle of contact depends.
Answer:

The value of angle of contact :

(1) Depends on the nature of the liquid and the solid in contact.
(2) Depends on the medium above the free surface of the liquid.

Question 64. State two applications of surface tension.
Answer:

Applications of surface tension :

(1) The surface tension of soap solution is low, and thus it is used for washing. Hot soap solution is still better as surface tension decreases with rise in temperature.

(2) Surface tensions of lubricating oils and paints are kept low so that they can spread easily.

Question 65. State the units of co-efficient of viscosity in CGS and SI systems.
Answer:

Units of co-efficient of viscosity :

(1) CGS: Poise
(2) SI: Pascal-second (PaS) or decompose.

Question 66. State two factors on which terminal velocity depends.
Answer:

(1) The terminal velocity of a sphere varies directly as the square of its radius of it.
(2) The terminal velocity of a sphere is inversely proportional to the coefficient of viscosity.

Question 67. State two factors affecting viscosity.
Answer:

(1) The viscosity of a liquid decreases with an increase in temperature.
(2) The viscosity of all gases increases with increase in temperature.

Question 68. What is streamlined flow?
Answer:

Streamline Flow: The streamlined or orderly flow of a fluid is that flow in which every particle of the fluid follows exactly the path of its preceding particle and has the same velocity in magnitude and direction as that of its preceding particle while crossing that point.

Question 69. What is Turbulent flow?
Answer:

Turbulent Flow: When a fluid moves with a velocity greater than its critical velocity, the motion of the particles of the fluid becomes disorderly or irregular and such a flow is called turbulent flow. :

Question 70. What is the significance of Reynold’s number?
Answer:

Significance of Reynold’s number (R) :

(1) R < 2000, the flow of a liquid is streamline or laminar.
(2) R > 3000, the flow of a liquid is turbulent.
(3) 2000 < R < 3000, the flow is streamline or turbulent.

Question 71. What is pressure energy?
Answer:

Pressure energy: The energy possessed by a liquid by virtue of its pressure and is measured by work done in pushing the liquid in the vessel against the pressure without imparting any velocity to it is called the pressure energy of the liquid.

Question 72. State any application of Bernoulli’s theorem. 
Answer:

(1) Atomiser or sprayer: It is based on Bernoulli’s principle. It is used for spraying liquids like perfumes, etc.

Question 73. State two limitations of Bernoulli’s theorem.
Answer:

(1) It is assumed that the velocity of every particle of a liquid passing through any particular cross-section of the tube is uniform. But actually, particles of the liquid in the central layer have maximum velocity and those closer to the tubewell have minimum velocity. Thus, the mean velocity of the particles should be taken.

(2) The liquid in motion experiences a viscous drag, which should be considered.

Question 74. What is a perfectly rigid body?
Answer:

Perfectly rigid body: A body is said to be perfectly rigid when no relative displacement between its parts occurs under the action of a deforming force, however large it may be.

Question 75. What is normal stress?
Answer:

Normal stress: When the deforming force acts normally over an area of a body, then the internal restoring force set up per unit area of cross-section is called normal stress.

Question 76. What is tangential stress?
Answer:

Tangential stress: When the deforming force acts tangentially to the surface of a body to produce a change in the shape of the body, then the stress developed in the body is called tangential stress.

Question 77. A floating body loses it weight explains.
Answer:

Explanation: The weight of a floating body is equal to the weight of the liquid displaced by it. These two forces act in opposite directions along the vertical line. Thus these forces balance each other and apparently, the floating body loses weight.

Question 78. Does siphon work on the surface of the moon? Explain.
Answer:

Explanation: There being no atmosphere on the moon, there is no atmospheric pressure. So, the siphon does not work on the moon.

Question 79. Explain whether the rate of flow of a liquid through a siphon will change if the atmospheric pressure changes.
Answer:

Explanation: No. The rate of flow of a liquid through a siphon depends on the differences of pressures of liquid columns in its two limbs and not on the barometric pressure.

Question 80. Can you siphon out water from a leaking boat to the river?
Answer:

Explanation: No, the boat is floating on the river, and water leaks into the boat from the river. Thus water inside the boat would be always on the same level as that of the river outside. So, it is not possible to siphon out water in this case.

Question 81. Why should a field be plowed before sowing?
Answer:

Explanation: This is done to break the tiny capillaries through which water rises and finally evaporates. The plowing of the field helps the soil to retain moisture.

Question 82. Explain why oil rises in the wick of a lamp.
Answer:

Explanation: The pores in the wick serve the purpose of a number of line capillaries. The oil rises due to capillary action.

Question 83. What is elastic fatigue?
Answer: The property of an elastic body by virtue of which its behavior becomes less elastic under the action of repeated alternating deforming forces is called elastic fatigue.

Question 84. How will the reading of a mercury barometer, placed inside a lift, change if the lift starts moving downwards with a given acceleration? Give reasons for your answer.
Answer:

Reason: Let the left descend with acceleration f. The effective acceleration with which it descends will be (g − f). Thus, the weight of the mercury column in the barometer decreases. But atmospheric pressure remains the same, the height of the mercury column in the barometer would be more.

Question 85. Will the rate of flow change in a siphon if water is replaced by mercury?
Answer:

No, the rate of flow of liquid in a siphon does not depend on the density of the liquid.

Question 86. Can you use water in a barometer?
Answer:

The height of the water barometer would be about 10 m, which is not practicable. Further, water sticks to glass, and water is to be colored.

Question 87. Why does not water wet a glass rod coated with wax?
Answer:

Because the force of adhesion between water and wax is less than the force of cohesion between water molecules.

Question 88. Water is coming out of a hole made on the wall of a freshwater tank. If the size of the hole is increased,
(1) will the velocity of the efflux of water change?
(2) will the volume of water coming out per second change?
Answer:

(1) Velocity of efflux remains unaltered, as it depends only on the depth of the hole below the fresh surface of the water,
(2) Volume changes, as the volume of the liquid flowing per second depends upon the area of the cross-section of the hole.

Question 89. Explain why still water runs deep.
Answer:

Explanation: From the equation of continuity, we have, av = constant.

The speed of still water is very small so the area would be large. Thus still water becomes deep.

Question 90. Why does the velocity increase when water flowing in a broader pipe enters into a narrower pipe?
Answer:

From the equation of continuity, we have av = constant. So, when water enters into a narrower pipe flowing from a broader pipe, then the area of the cross-section decreases, and thus the velocity of flow increases.

Question 91. Why does not mercury wet glass?
Answer:

The cohesive force between mercury molecules is greater than the adhesive force between mercury and glass.

Question 92. Why does hot soup taste better than cold soup?
Answer:

Soap bubbles burst when the pressure inside them becomes more than outside atmospheric pressure. So, soap bubbles burst after some time.

Question 93. The diameter of a ball is twice that of another ball. What will be the ratio of their terminal velocities in water?
Answer:

We know that the terminal velocity is directly proportional to the square of the radius of the ball, i.e., the terminal velocity o (radius of the ball).

∴ The ratio of their terminal velocities will be 4: 1.

Question 94. Small air bubbles rise slower than the bigger on through a liquid, why?
Answer:

The terminal velocity of the bubble is proportional to the square of the radius of the bubble. So, smaller air bubbles having smaller radii would have low values of terminal velocities and. rise at a slower rate.

Question 95. Why do clouds float in the sky?
Answer:

The tiny drops of water present in clouds have negligibly small terminal velocities. So, clouds float in the sky.

Question 96. Why should the lubricant oils be of high viscosity?
Answer:

Lubricants are used to decrease dry friction between different parts of the machines. The lubricants with high viscosity would stick to the machine parts and would not come out during the movements of the machine parts.

Question 97. Why is viscosity called internal friction?
Answer: There is a backward drag on each of the upper layers of a flowing liquid by the lower layer. So, viscosity acts like friction from within and thus it is called internal friction.

Question 98. What is the elastic limit?
Answer:

Elastic limit: It is the upper limit of deforming force up to which the body regains its original shape or size completely or the removal of deforming force and beyond which, on increasing the deforming force, the body loses its property of elasticity and gets permanently deformed.

Question 99. How will the weight of a body be affected when it falls with its terminal velocity through a viscous medium?
Answer:

When a body falls through a viscous medium with its terminal velocity, it moves with constant velocity. So, no resultant force is acting on the body, as pull due to gravity is balanced by viscous drag and buoyancy of the medium. Hence the effective weight of the body becomes zero.

Question 100. The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up but tends to narrow down when held vertically down. Why?
Answer:

As the stream falls, its speed v increases, and consequently its area of cross-section, a will decrease; according to the equation of continuity, av = constant, and hence the stream becomes narrow. When the stream goes up, its speed decreases, so its area of cross-section increases, and hence it becomes broader and spreads out like a fountain.

Question 101. It is advised not stand near a running train. Why?
Answer:

When a fast-moving train passes on a rail, the velocity of streams of air between the rail and the man standing near the rail will be larger than the velocity of air streams on the other side of the man away from the rail.

Following Bernoulli’s theorem, the pressure of air will be low in between the man and the rail and high on the other side of the man. Thus the man may be pushed towards the rail and may meet with an accident.

Question 102. ‘The Poisson’s ratio depends only on the nature of the material and not at all on the stress applied within elastic limit’ explains.
Answer:

Poisson’s ratio\(=\frac{\text { lateral strain }}{\text { longitudinal strain }}\) which does not involve stress within the elastic limit and depends only on the nature of the material.

Question 103. Why are small liquid drops spherical in shape, while big drops are flat?
Answer:

A liquid drop attains a spherical shape to have minimum surface area and hence minimum potential energy state. In a small liquid drop the force due to surface tension is large compared to the force due to the weight of the drop or gravitational pull and the drop attains a spherical shape. But as the size of the drop increases, its weight also increases, which pulls the drop downwards and it becomes flat.

Question 104. Water rises in a capillary tube whereas mercury falls in the same tube. Explain.
Answer:

Explanation: The cohesive force between mercury molecules is much larger than the force of adhesion between mercury and glass, while the force of adhesion between water and glass is much more than the force of cohesion between water molecules.

Question 105. Two soap bubbles of unequal sizes are blown at the ends of a capillary tube. Which one will grow at the cost of the other?
Answer:

Excess of pressure p is inversely proportional to the radius r of the soap bubble,i.e., p inside a small bubble will be more than that inside the large bubble. So, the big bubble will grow at the cost of the smaller one.

Question 106. Oil spreads over the surface of the water while it does not do so on the oil surface. Explain.
Answer:

Explanation: The surface tension of oil is less than the surface tension of water. So on spreading oil on the surface of water, it spreads in all directions due to the higher force of surface tension of water.

Question 107. Why does? surface tension varies with temperature?
Answer:

With the increase of temperature, the force of cohesion of the liquid molecules decreases. So surface tension decreases with the increase of temperature.

Question 108. Why do two mercury drops form one drop when brought in contact?
Answer:

Explanation: Liquids tend to attain a minimum surface area state due to surface tension. When two drops come in contact, they form a single drop for decreasing surface area.

Question 109. Explain how a spider walks easily on the surface of water.
Answer:

Explanation: The free surface of water behaves as a stretched membrane due to surface tension. This membrané is depressed due to the weight of the spider. The vertical component of the surface tension balances the weight of the spider and hence it is able to walk on the water surface.

Question 110. A needle may float on clean water but sink in water having detergent. Explain.
Answer:

Explanation: The free surface of water acts like a stretched membrane due to surface tension and a needle can float on it. But on adding some detergent, the surface tension of water decreases and the tension in the membrane is weakened and it can no longer hold the weight of the needle. ?

Question 111. Small pieces of camphor dance when placed on the surface of water. Why?
Answer:

The surface tension of water decreases when camphor dissolves in it. Due to its irregular shape, the camphor dissolves unevenly on different sides. So, unbalanced surface tension forces act on the camphor, and hence the piece of camphor moves randomly in different directions.

Question 112. The velocity of water in a river is less on the bank and larger in the middle; why?
Answer:

Explanation: The water in the river flows in the form of streams. The forces of adhesion is less on the streams in the middle of the river than near the bank. So, the velocity of streams near the bank is minimum and maximum in the middle of the river.

Chapter 3 Matter: Structure And Properties 3 Marks Questions And Answers

Question 1. What happens when a metallic block is immersed in a liquid?
Answer:

When a metallic block is immersed in water (or any other liquid), four vertical forces act upon the block below the surface of water. These forces can be grouped into two types of forces.

Downward forces:
(1) The weight of the block.
(2) The downward thrust due to the pressure of the liquid on the upper surface of the block.

Upward forces :
(1) The tension of the spring which measures the apparent weight.
(2) The upward thrust due to the liquid present below the lower surface of the block. This upward thrust is known as Buoyancy.

Question 2. What happens to the weight of a body when immersed in water?
Answer: T

he more a body is immersed in water, the more the weight of the body decreases. The weight of the body is least when it is completely immersed in water. This means that loss in weight of the body increases as it is completely immersed in water. When a body is partly or completely immersed in water (or any other liquid), then Loss in weight of the body

= Weight of water (liquid) displaced by the body

= Buoyant forcé or upthrust exerted by water (any liquid) on the body.

Question 3. Explain the effects of surface tension.
Answer:
Several effects of surface tension can be seen with ordinary water:

(1) Beading of rain water on a waxy surface, such as a leaf. Water adheres weakly to wax and strongly to itself, so water clusters into drops.

(2) Formation of drops occurs when a mass of liquid is stretched. The animation shows water adhering to the faucet gaining mass until it is stretched to a point where the surface tension can no longer keep the drop bonded to the faucet.

(3) Floatation of objects denser than water occurs when the object is non-wettable and
its weight is small enough to be borne by the forces arising from surface tension.

(4) Separation of oil and water (in this case, water, and liquid wax) is caused by a tension in the surface between dissimilar liquids. This type of surface tension is called “interface tension”.

Question 4. Explain the types of Strain.
Answer: Strain is of three types depending upon the change produced in a body and the stress applied.

The three types of strain are :
1. Longitudinal Strain,
2. Volume Strain and
3. Shearing Strain.

Longitudinal Strain: It is the ratio of the change in the length of a body to the original length of the body. If L is the original length of a wire or a rod and the final length of the wire or the rod is L+ΔL under the action of normal stress, the change in length is ΔL.

Longitudinal. Strains = Change in length/ Original length = ΔL/L

Volume Strain: It is the ratio of the change in volume of a body to its original volume. if V is the original volume of a body and V+ΔV is the volume of the body under the action of normal stress, the change in volume is ΔV.

Volume Strains Change in volume/ Original volume= ΔV/V

Shearing Strain: It is the angle through which a face originally perpendicular to the fixed face is tuned. (or) 4 is the ratio of the displacement of a layer to its distance from the fixed layer.

Question 5. Explain the effect of
(1) Density,
(2) Temperature,
(3) Pressure on the viscosity of liquids and gases.
Answer:

(1) With the increase in density, the viscosity of liquid increases, while for gases, it decreases.

(2) With the increase in temperature, the viscosity of a liquid decreases, while that of gases increases.

(3) With the increase in pressure, the viscosity of liquids except water increases and that of water decreases. In the case of gases, viscosity is practically independent of pressure.

Question 6. Write a short note on the siphon and its application.
Answer:

Siphon and its application: Siphon is an arrangement used to transfer liquid from one vessel to the other without disturbing the liquid. Its action depends on atmospheric pressure. A siphon, in its simplest form, consists of an inverted U-tube, completely filled with liquid and its shorter arm dips into the liquid to be transferred, while the longer arm is put in the vessel of lower level with respect to the liquid to be transferred.

The action of siphon : Let us take two points A and B inside the liquid on the same horizontal plane.

Now, pressure at the point A, \(\left(P_A\right)\)

= Atmospheric pressure − pressure of the liquid column AC =\(P_0-h_1\) dg and d = density of the liquid

Again, pressure at the point B, \(\left(P_B\right)\)= Atmospheric pressure − pressure of the liquid column BD \(=P_0-h_2\)

As \(h_1<h_2\)  ∴\(h_1 d g<h_2 d g\)

∴\(\left(P_0-h_1 d g\right)>\left(P_0-h_2 d g\right)\) or,\(P_A>P_B\)

Hence, liquid will flow from A to B and it flows continuously until \(\mathrm{h}_1\)=\(\mathrm{h}_2\)   siphon does not work in vacuum and for the working of siphon, the height,\(\mathrm{h}_1\) should not be greater than the barometric height for the liquid used.

Application : A siphon is used to transfer liquid from one vessel to the other easily without disturbing the whole volume of the liquid.:It is also used in automatic flushes fitted in lavatories.

Question 7. What are the factors affecting the surface tension of a liquid?
Answer:

The surface tension of a liquid depends on. the following factors :

(1) Temperature: The surface tension of a liquid usually decreases with an increase in the temperature of the liquid. Beyond a certain characteristic temperature of a liquid, called critical temperature, the surface tension of the liquid vanishes.

(2) Presence of dissolved substances in a liquid : The surface tension a liquid is affected by the presence of dissolved substances. in a liquid, its surface tension changes. Presence of dissolved inorganic substances in a liquid surface tension of the liquid increases but due to the Riesenes of dissolved organic substances in a liquid, its surface tension decreases.

(3) Presence, of impurity : Due to presence. of impurity surface tension of a liquid usually decreases. For example, due to the presence of oil, grease, etc. in water, the surface tension of contaminated water decreases.

(4) Nature of the medium in contact with the liquid: The surface tension of the liquid depends on the nature of the medium in contact with the liquid. For example, the surface tension of water in contact with dry air is more than the surface tension of water in contact with moist air.

(5) Electrification of the surface of a liquid: Usually surface tension of a liquid decreases the surface of that liquid is electrified.

Question 8. State and explain Bernoulli’s theorem.
Answer:

For the streamlined flow of a non-viscous and incompressible ideal fluid, the sum of the pressure energy, kinetic energy, and potential energy per unit mass of the fluid is always constant. This is known as Bernoulli’s theorem.

Mathematically\(\frac{P}{\rho}+\frac{1}{2} v^2+\)+gh=Constant

(Where \(\frac{P}{\rho}\) is the pressure energy per unit mass; oY is the kinetic energy per unit mass \(\frac{1}{2} v^2\)is the potential energy per unit mass]

If the pressure of the fluid be P, then work done by the fluid pressure

W = Force displacement = PA. x = P.V [A = area, V = volume]

∴pressure energy per unit mass\(=\frac{W}{m}\)=\(\frac{P V}{m}\)=\(\frac{P}{\frac{m}{V}}\)=\(\frac{P}{\rho}\)

∴(\(\rho=\frac{m}{\rho}\) = density of the fluid)

Kinetic energy per unit mass\(=\frac{\frac{1}{2} m v^2}{m}\)  [v = velocity of the fluid]\(=\frac{1}{2} v^2\)

Potential energy per unit mass \(=\frac{P . E}{\text { mass }}\)=\(\frac{m g h}{m}\) (where the symbols have their usual meanings)

So, Bernoulli’s theorem states that the total energy of a small amount of an ideal liquid flowing without friction from one point to the other, in a streamlined flow, remains constant. It should be noted here that while obtaining Bernoulli’s equation, the force of viscosity of the fluid that comes into play has not been accounted for. In this equation loss of energy due to heat is also not considered.

Question 9. Write a short note on Hooke’s law.
Answer:

Hooke’s law: English physicist Robert Hooke studied the relation between elongation produced in an elastic wire and the tension in it. He formulated a law in 1676, known as Hooke’s law of elasticity. It is stated that within the elastic limit, stress is directly proportional to strain.

Mathematically, stress cc strain (within elastic limit) = constant this constant is known as modulus of elasticity which depends mainly upon the nature of the material of the body.

Question 10. What are the characteristics of liquid pressure? 
Answer:

(1) The liquid at rest exerts equal pressure at a point inside the liquid in all directions.

(2) The liquid at rest exerts equal pressure at all points at the same horizontal level in the liquid.

(3) The liquid pressure is independent of the shape of the liquid surface or the area of the liquid surface but depends upon the height of the liquid column.

(4) Total pressure at a depth ‘h below the liquid surface is equal to (p + hdg), where ‘p’ is the atmospheric pressure and is the density of the liquid.

(5) Average pressure on the side walls of a container having liquid of density D up to a height; h’ is ½ hdg.

(6) The liquid pressure is a scalar quantity.

(7) The thrust exerted by a liquid on the walls of the vessel in contact with the liquid acts normally to the surface of the vessel.

(8) The free surface of a liquid at rest is horizontal.

(9) The liquid always finds its own level.

(10) The gauge pressure at a point in a liquid is the difference between total pressure at that point and atmospheric pressure.

11. What are the conditions for the floatation of a body?
Answer:

Conditions for floatation of a body :

(1) When the weight of the body (w) is greater than the weight of the liquid displaced (w), then the body sinks, i.e., w > w.

(2) When the weight of the body (w) is equal to the weight of the liquid displaced (w), then the body floats completely immersed anywhere within the liquid, i.e., w = w’.

(3) When the weight of the body is less than the weight of the liquid displaced, then the body floats partly immersed on the surface of the liquid, j.e., w < wi.

Question 12. What are the conditions for the working of a siphon?
Answer:

Conditions for the working of a siphon are :

(1) At first the whole tube must be filled with liquid.

(2) The end of the longer tube must be below the level of the liquid in the other vessel.

(3) The height h must be less than the height of the corresponding liquid barometer, otherwise, the atmospheric pressure will not be able to raise the liquid to the top of the tube.

(4) The siphon will not work in a vacuum due to the absence of atmospheric pressure.

Question 13. State some applications of surface tension.
Answer:

Applications of surface tension :

(1) Surface tension of soap solution is low, and thus it is used for washing. Hot soap solution is still better as surface tension decreases with rise in temperature.

(2) Surface tension of lubricating oils and paints is kept low so that they can spread easily.

(3) The surface tensions of antiseptics are kept low so that they can spread quickly.

(4) Oil spreads over the surface of water because the surface tension of oil is less than that of water.

(5) Rough sea can be calmed by pouring oil on seawater.

(6) In soldering, flux is added to reduce the surface tension of molten tin, so that it can spread.

Question 14. What are the factors on which terminal velocity depends?
Answer:

Terminal velocity depends upon :

(1) The terminal velocity of a sphere varies directly as the square of the radius of it.

(2) The terminal velocity of a sphere is inversely proportional to the coefficient of viscosity.

(3) If the density of the material of the sphere be less than the density of the fluid, then the sphere would move upwards to attain terminal velocity.

Question 15. What are the factors on which viscosity depends?
Answer:

Variation of viscosity:

(1) The viscosity of a liquid decreases with an increase in temperature.

(2) The viscosity of all gases increases with increase in temperature.

(3) With the increase in pressure, the viscosity of liquids increases, but the viscosity of water decreases.

(4) With the increase in pressure, the viscosity of gases remains unchanged.

Question 16. What are the types of energy a liquid possesses in motion?
Answer:

Energy of a liquid in motion: A liquid in motion possesses three types of energy. These are :

(1) Pressure energy : The energy possessed by a liquid by virtue of its pressure and is measured by the work done in pushing the liquid in the vessel against the pressure without imparting any velocity to it is called the pressure energy of the liquid.

(2) Potential energy: The energy possessed by a liquid by virtue of its height or position above the surface of the earth or any reference level taken as zero level is called the potential energy of the liquid.

(3) Kinetic energy: The energy possessed by a liquid by virtue of its. motion or velocity is called the kinetic energy of the liquid.

Question 17. State some applications of Bernoulli’s theorem.
Answer:

Applications of Bernoulli’s theorem :

(1) Atomiser or sprayer: It is based on Bernoulli’s principle. It is used for spraying liquids like perfumes, etc.

(2) Blowing off the roofs during storms: During storms or cyclones, sometimes, the roofs of a hut are found to blow off without causing any damage to the side walls of the house.

(3) Motion on two parallel boats: The boats sailing in the same direction parallel to each other, a small distance apart, are found to come closer to each other.

(4) Shape of an airplane wing: The shape of an airplane’s wings, i.e., aerofoil is made in such a way that its upper surface is curved more than its lower surface.

(5) Spinning of a ball (Magnus effect): A cricket ball is thrown straight without any spin. The streamlines of air passing are seen evenly passing above and below the ball and the ball continues to move along the original straight direction. But if the ball is released with a spin, the streamlines of air in the same direction as the direction of spinning of the ball, while these are oppositely directed.

Question 18. State the limitations of Bernoulli’s theorem.
Answer:

Limitations of Bernoullis’s theorem :

(1) It is assumed that the velocity of every particle of the liquid passing through any particular cross-section of the tube is uniform. But actually, particles of liquid in the central layer have maximum velocity and those closer to the tubewell have minimum velocity. Thus, the mean velocity of the particles should be taken.

(2) The liquid in motion experiences a viscous drag, which should be considered.

(3) It is assumed here that there is no loss of energy when liquid is in motion. But there is always some loss of energy as some kinetic energy is lost as heat.

(4) When the liquid is flowing on a curved path, the energy due to centrifugal force should be considered.

Question 19. Classify physical bodies on the basis of elastic property.
Answer:

Types of bodies according to elastic property :

(1) Perfectly rigid body: A body is said to be perfectly rigid when no relative displacement between its parts occurs under the action of a deforming force, however large it may be.

(2) Perfectly elastic body: A body is said to be perfectly elastic when it regains its original configuration immediately and completely after the removal of the deforming force, however large it may be.

(3) Perfectly inelastic body: A body is said to be perfectly inelastic or plastic when it does not regain its original configuration at all on the removal of deforming force, however small it may be.

(4) Partly elastic body: A body is said to be partly elastic when after the removal of the deforming force, it regains only partly its original configuration.

Question 20. Classify the modulus of elasticity.
Answer:

Types of modulus of elasticity :

(1) Young’s modulus of elasticity: It is the ratio of the longitudinal stress to the longitudinal strain within the elastic limit.

(2) Bulk Modulus of Elasticity: Bulk modulus of elasticity is the volume stress (normal stress) to the volume strain within the elastic limit. ape

(3) Modulus of rigidity: Modulus of rigidity or shear modulus of a material fs the ratio of the shearing stress to the shearing strain within the elastic limit.

Question 21. Write a short note on the elastic property of a material.
Answer:

Elastic property of Material: A stress-strain curve for a wire of elastic material is shown in the figure below. From the figure it is found that OA y portion of the curve is a straight line, i.e., stress is linearly related to strain. Hence, the material obeys Haoke’s law. This is the c region of perfect elasticity and ‘A’ represents the elastic limit of the material.

 

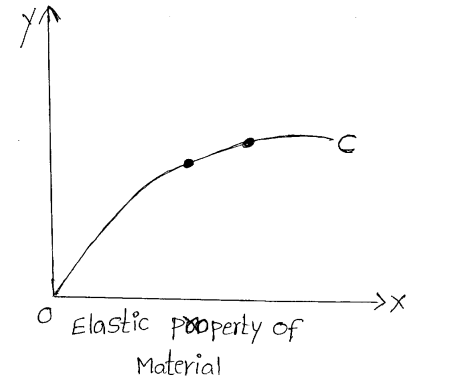
When the stress on the wire is increased beyond ‘A’, ie., of elastic limit. Hooke’s law is no longer capable of explaining the =O elastic behavior. On removal of stress, the wire does not regain the Elastic property of its original length completely and the wire is said to have acquired a material permanent set. The wire behaves like a plastic body.

If the process of stretching continues further, a stage is reached when the wire is found to undergo a relatively large strain with almost no increase of stress. This occurs at point ‘B’ called yield point. Beyond this point, metals are called ductile.

Further, an increase in stress ultimately results in the breaking of the wire, and the corresponding point ‘C’ on the curve is called the breaking point. Breaking stress is the maximum stress that can be applied to a material before it ruptures. If a solid breaks soon after crossing the elastic limit, it is called brittle.

Question 22. Mathematically express the flow of a liquid.
Answer:

Flow’ of liquid: Let us consider a non-viscous liquid in streamlined flow through a tube AB of varying cross-section. Let \(a_1\) and \(a_2\) are the areas of a cross-section of the tube at A and B and\(v_1\) and \(v_2\) are the velocities of the flow of liquid at A and B respectively.

Also, let \(ρ_1\) and (be the densities of the liquid at A and \(ρ_2\). Thus volume of liquid entering per second at A =\(a_1\)\(v_1\) , and mass ot this liquid =\(a_1\)\(v_1\) \(ρ_1\).

Similarly, volume of the liquid leaving per second at B =\(a_2\)\(v_2\) and its mass = \(a_2\)\(v_2\) \(ρ_2\).

If the flow is steady and there is no loss of liquid, then \(a_1\)\(v_1\) \(ρ_1\). = \(a_2\)\(v_2\) \(ρ_2\).

As the liquid is incompressible, then \(a_1\)\(v_1\)=\(a_2\) \(v_2\) Or, av = constant.\(ρ_1\)=\(ρ_2\)
This is known as the equation of continuity. Thus, the larger the area of the cross-section, the smaller will be the velocity of liquid flow and vice-versa. Again, the rate of flow of liquid = av = constant.

Thus in a streamlined flow of a non-viscous liquid through a tube the rate of flow of liquid is constant. It is found that the stream of water coming out has different velocities at different places, consider two points A and B separated by a vertical distance h, having cross-sectional areas\(a_1\) and\(a_2\) respectively. Let the velocities of the stream of water at A and B be \(v_1\) and \(a_1\) respectively. Now we have,

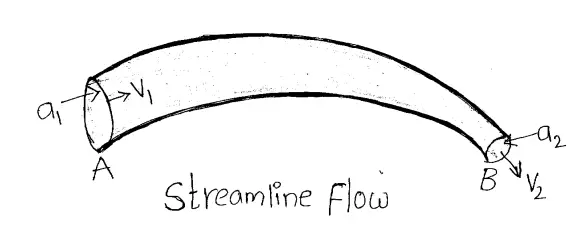
⇒ \(v_2^2\)=\(v_1^2+2 g h\)

i.e.,\(v_1\) >\(v_2\)

Now, from\(a_1\)\(v_1\)=\(a_2\)\(v_2\)we have

⇒ \(a_1\)>\(a_1\)

So, the jet of following water becomes narrower as it goes down. For the same reason, deep water runs slow.

Question 23. Mention some applications of elasticity in daily life.
Answer:

Elasticity in daily life: In our daily lives, most of the materials we use undergo different types of stress. So, in designing a structure, proper consideration is given to possible stresses.

Some of the examples are :

(1) The parts of the machine are designed in such a way that they are not subjected to stress beyond the elastic limit.

(2) In cranes, used for lifting heavy loads, thick and strong metallic ropes are used and the thickness of these ropes is determined by the elastic limit of the material of the rope.

(3) The bridges are so designed that they do not bend much or break under their own weight or of the heavy load of traffic.

(4) Electric poles are made hollow instead of solid ones as hollow shafts are stronger than solid ones.

(5) Maximum height of a mountain on the earth can be estimated from the elastic behavior of the earth.

Question 24. How do materials behave beyond elastic limits?
Answer:

The behavior of materials beyond the elastic limit: When a wire is stressed beyond the elastic limit of the material of the wire, Hooke’s law is no longer applicable to account for the elastic behavior of the material. The wire does not regain its original shape completely even after the removal of stress and the wire acquires a permanent set. The solid behaves like a plastic body.

(1) Ductility: The materials that show a light plastic range beyond the elastic limit are called ductile materials. Now a wire of the material is found to undergo a relatively large strain with practically no increase of stress. At this stage, wires can be drawn from the rods of metals. This property of the materials is called ductility. Examples of ductile materials are copper, silver, iron, aluminum, etc:

(2) Brittleness: The solids which break soon after crossing the elastic limit, are called brittle and the property is called brittleness. Examples include glass, cast iron, etc.

(3) Malleability: If a solid is subjected to compression, instead of tension, then also the body acquires a permanent set beyond a certain stage. This is the elastic limit for compression. Beyond this limit, the body behaves like a plastic body and the material of the body is called malleable. These materials can be hammered or rolled into sheets.

Question 25. Derive the expression of pressure of a liquid at a point.
Answer:

Pressure of a liquid at a point: As shown in the diagram, a vessel contains some liquid of density d. P is a point within the liquid. Around P area A is considered. This area A is considered as the base of an imaginary cylinder whose height ‘h’ extends up to the surface of the liquid.

So, the weight of the liquid is contained. in this imaginary cylinder is the thrust on the area a. Volume of the liquid contained in the imaginary cylinder = Ah. Mass of the liquid in the imaginary cylinder = Ahd (∴mass = volume x density).

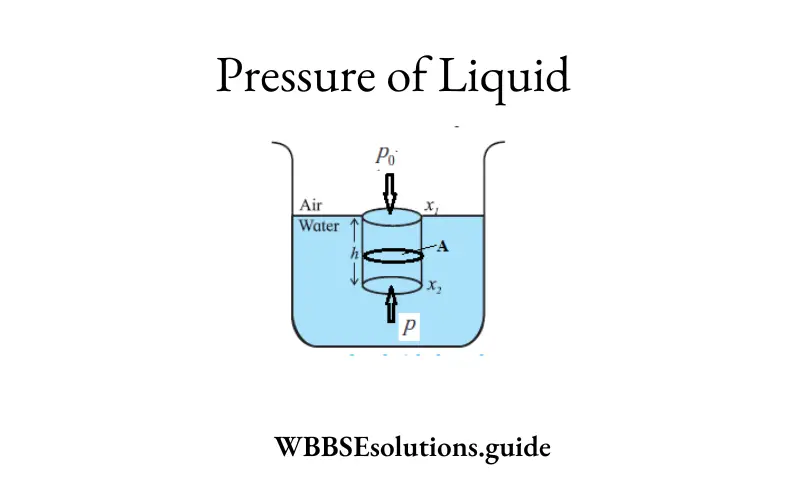
∴ Weight of the liquid in the imaginary cylinder = Ahdg (g is acceleration due to gravity). Thus, the thrust on the area A = Ahdg

And pressure P \(=\frac{\text { Thrust }}{\text { Area }}\)=\(\frac{\text { Ahdg }}{A}\)=hdg.

Hence, pressure at a point inside a liquid = depth of the point x density of the liquid x acceleration due to gravity. ‘ Thus it can be concluded that pressure at a point in a liquid thus increases with depth.

Question 26. Experimentally prove that liquid has a lateral pressure which increases with depth.
Answer:

Experiment: A long jar with three outlets A, B, and C along its length is taken. The three outlets are closed with corks or with molten wax. The jar is now filled with water or with any other liquid. The three openings are then opened simultaneously. Liquid flows out through the holes in jets. other vessels also. Although the vessels have different shapes

Observation: Of the three liquid jets, the range of the middle one is the longest on the horizontal plane that passes through the base of the cylinder. The liquid jets exert a pushing force on finger tips with which the liquid flow is put to stop.

Now, it can be noted that the force increases appreciably from the upper outlet A to the lower ones; it is maximum at the lowermost outlet C.
Inference: Liquid has lateral pressure which increases with depth.

Question 27. Demonstrate the principle liquid finds its own level.
Answer:

Water finds its own level: It means that different segments of water or any other liquid in unequal levels attain the same horizontal level when the segments are brought in an interconnected state.

A demonstration: As shown in the adjacent diagram, A, B, C, D, and E are a few glass vessels, the shapes and each other at their bases. Now, some water, preferably colored, is poured in any of the vessels.

It will be seen that the liquid flows into And volumes and contains unequal in quantities of water, yet, the height of water in each is the same. Also, the water surface in each vessel is horizontal.

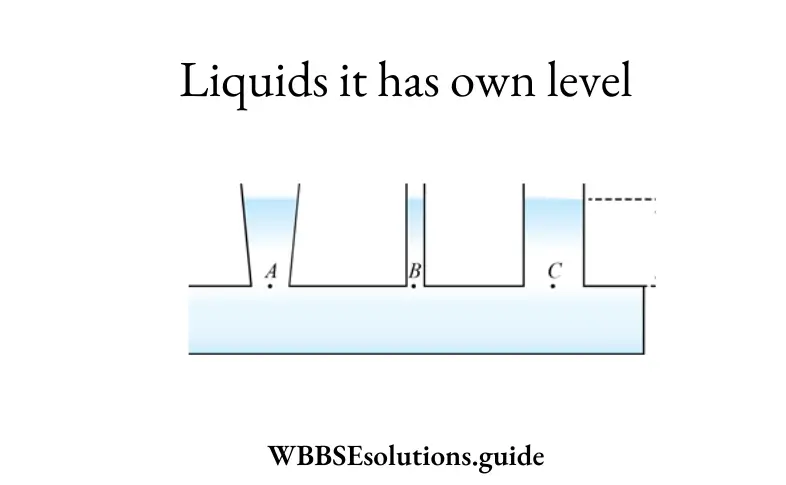
Question 28. State two applications of the principle that liquid finds its own level.
Answer:

(1) Water supply in the city: The important property of a liquid is that it finds its own level helps the water supply in cities. Here, drinking water is raised with a pump to the main reservoir placed at such a great height that taps, tanks, etc. in domestic and public uses at different parts of the city are much below it.
Thus, a large difference of levels is maintained between the water in the main reservoir and that in any domestic water tank. Since liquid flows from higher level to lower level, water from the main reservoir flows to domestic taps and reservoirs.

(2) Artesian well: An artesian well is named after the province of Artois in France. Various types of rocks exist below the earth’s surface. One type of these is generally made of sand, clay, gravel, etc. and so water can sip through it. This rock is known as permeable rock. Another type of rock made of slate and stone is known as impermeable rock.

Water cannot percolate through it. Due to atmospheric pressure as well the heavy weight of impermeable rocks above, the water in the permeable rock is under high pressure. But water cannot flow up or down, because impermeable rock layers are present above and below the permeable rock.

Now, if a vertical tunnel is drilled to reach nearly the bottom of the permeable rock, water gushes out. This rush of water occurs because liquid finds its own level.

Question 29. Write a short note on the barometer.
Answer:

In the laboratory, occasionally, information about atmospheric pressure becomes necessary for different experiments. A barometer is an instrument used to measure atmospheric pressure at a place.

The principle of the barometer is dependent on Pascal’s law. The law states that if pressure is exerted within a confined liquid, the; iL liquid transmits that pressure within itself in all directions in Gas: Soe unchanged magnitude, and the transmitted pressure acts normally at each point on the walls of the container.
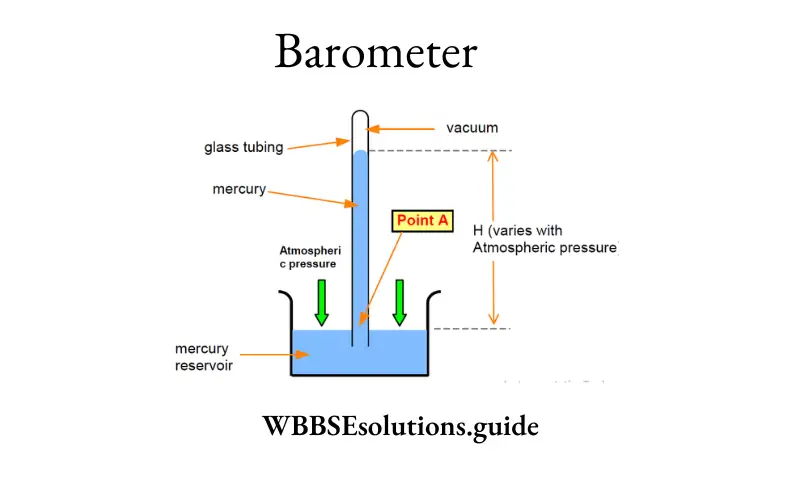Uses of barometer :

(1) It is normally used to measure atmospheric pressure at a place.

(2) It is known that atmospheric pressure changes by about 2.5 cm for a change of altitude of 275 m. With this relation, the altitude of some places may be determined. For this purpose, a modified form of the barometer, known as an Aneroid barometer is used. This instrument is used in airplanes. Reservoir

(3) It is used for forecasting weather.

Question 30. How is buoyancy measured?
Answer:

Take a spring balance and a block of wood. Also, take a beaker containing some water. First, the body is weighed in air with the help of a spring balance. The reading in the balance is noted. Now weigh the body with about half a portion of the body being immersed in water. Reading in the balance is noted.

Now weigh the body with the spring balance, the body is fully immersed in water. The reading in the balance is noted. It is seen that the weight of the body decreases as a greater portion of it is immersed in water.

Thus, buoyancy a body depends on the volume of it immersed in water. The greater part of the body immersed in water, the less is the weight.

Question 31. The base area of a bottle is 5 c\({m}^{2}\)? and the depth of water in that bottle when it is completely filled is 30 cm. If the density of water be 1 g/cc then calculate the pressure and the thrust exerted by water at the bottom of the bottle. (Given g = 980 cm/\({s}^{2}\)),
Answer:

Here, depth of water (h) = 30 cm

density of water (d) = 1 g/cc

acceleration due to gravity (g) = 980 cm/\({s}^{2}\).

area of the base (A) = 5 c\({m}^{2}\)

∴The pressure of water at the bottom of the bottle,

P = hdg = 30 x 1 x 980 = 29400 dyne/c\({m}^{2}\)

Thrust exerted at the bottom = Pressure x Area = (29400 x 5) dyne = 147000 dyne.

∴Pressure at the bottom = 29400 dyne/c\({m}^{2}\)

and thrust at the bottom = 147000 dyne.

Question 32. The volume of a solid body of mass 490 g is 175 cc. Calculate
(1) The density of the solid body,
(2) Mass of water displaced by the solid body when fully immersed,
(3) Relative density of the solid. State whether the body will float or sink in water.
Answer:
Solution: (1) Density of the solid body\(=\frac{\text { Mass }}{\text { Volume }}\)=\(\frac{490}{175}\) =2.8/cc

(2) Here, the solid body will displace its own volume of water when fully immersed. So, the volume of displaced water is 175 cc, As the density of water is 1g/cc, so the mass of water displaced by the body = volume x density = (175 x 1)g = 175 g.

(3) Relative density of this solid\(=\frac{\text { Density of Solid }}{\text { Density of Water }}\)=\(\frac{2.8 \mathrm{~g} / \mathrm{c} . c \text { : }}{1 \mathrm{~g} / \mathrm{c} . \mathrm{c} .}\)=2.8.

As the relative density of the material of the solid (2.8) is greater than that of water (1); so the solid body will sink in water.

Question 33. Relative densities of two substances P and Q are 3.5 and 0.8 respectively. Find the densities of P and Q. Also find whether they will float or sink in water (Given that density of water = 1000 kg/\({m}^{3}\)).
Answer:

Relative density of P = 3.5

∴\(\frac{\text { Density of } P}{\text { Density of water }}\)=3.5

∴ Density of P = 3.5 x density of water = (3.5 x 1000) kg/\({m}^{3}\) = 3500 kg/\({m}^{3}\) .

Similarly, density of Q = 0.8 x density of water = (0.8 x 1000) kg/\({m}^{3}\) = 800 kg/\({m}^{3}\) .

Since the density of P is greater than that of water, the substance P will sink in water.

Again, the density of Q is less than that of water, so the substance Q will float in water.

Question 34. A wire 30 m long and 2 m\({m}^{2}\)? The cross-section is stretched by 0.49 cm when a load of 5 kg is hung from its free end. Find
(1) longitudinal stress,
(2) longitudinal strain and
(3) Young’s modulus for the material of the wire.
Answer:

Here, the original length of the wire (l) = 30 m.

Area of its cross-section (A) = 2 m.\({m}^{2}\) = 2 x  \({10}^{-6}\) \({m}^{2}\) .

Elongation in length (Δl) = 0.49 cm = 4.9 x \({m}^{-3}\) m.

Load applied (F) = 5 kg-wt = (5 x 9.8) N.

(1) Longitudinal stress \(\left(\frac{F}{A}\right)\)=\(\frac{5 \times 9.8}{2 \times 10^{-6}}\)=\(2.45 \times 10^7 \mathrm{~N} / \mathrm{m}^{2}\)

(2) Longitudinal strain \(\left(\frac{\Delta l}{1}\right)\)=\(\frac{4.9 \times 10^{-3}}{30}\)=1.5×\(10^{11} \mathrm{~N} / \mathrm{m}^2\)

(3) Young’s modulus (Y) \(=\frac{\frac{F}{A}}{\frac{\Delta I}{1}}\)=\(\frac{2.45 \times 10^7}{1.63 \times 10^{-4}}\)
=1.5×\(10^{11} \mathrm{~N} / \mathrm{m}^2\)

Question 35. A steel rod has a radius of 1 cm and a length of 1 m. A 100 KN force stretches it along its length. Calculate the
(1) Stress,
(2) Elongation and
(3) Percentage strain on the rod. Given that Young’s modulus of elasticity for the steel rod = 2 x \({10}^{11}\) N/\({m}^{2}\)
Answer:

Here, the area of the cross-section of the rod (A) =π\(\left(10^{-2}\right)^2 \mathrm{~m}^2\)\(10^{-4}\)π=\({m}^{2}\).

Initial length (l) = 1m

Force applied (F) = 100 kN =\({10}^{5}\)N

Young’s modulus (Y) = 2 x\({10}^{11}\)N/\({m}^{2}\).

(1) Stress \(=\frac{F}{A}\)=\(\frac{10^5}{10^{-4} \pi}\)=3.18×\(10^8 \mathrm{~N} / \mathrm{m}^2\)

(2) Elongation =Δl\(=\frac{F \cdot L}{A Y}\)=\(\frac{10^5 \times 1}{10^{-4} \pi \times 2 \times 10^{11}}\) =1.59×\({10}^{-3}\)

(3) Percentage strain \(=\frac{\Delta l}{1} \times 100 \%\)\(=\frac{1.59 \times 10^{-3}}{1} \times 100 \%\)=1.59×\({10}^{-3}\)×100%=0.159%.

Question 36. The volume of a solid of mass 700 g is 350 cc. Find the density of the solid, the weight of water displaced by it, and R.D. of the body.
Answer:

Mass of the body = 700 g.

The volume of the body = 350 cc

Therefore, density of the solid\(=\frac{700 \mathrm{~g}}{350 \mathrm{cc}}\) = 2 g/cc.

The body displaces water equal to its own volume. The volume of the body is 350 cc, so the body displaces 350 cc of water. The weight of 350 cc water is 350 gram-weight. Hence, the weight of water displaced by the body is 350 grams.

So, R.D.\(=\frac{700 \text { gram weight }}{350 \text { gram weight }}\)=2.

Question 37. A body weighs 78 g-wt in air. It displaces 13 g-wt water when completely immersed in it.
(1) What is the apparent weight of the body?
(2) What is the buoyancy on the body?
(3) What is the volume of displaced water?
(4) What is the volume of the body?
Answer:

(1) Apparent wt. = wt. in air −wt. of displaced water. = (78− 13) g-wt = 65 g-wt.
(2) Buoyancy on the body = wt. of the water displaced by the body = 13 g-wt.
(3) The volume of displaced water is 13 cc, for, 1 g-wt water has 1 cc volume.
(4) Volume of the body = volume of the water displaced by it = 13 cc.

WBBSE Solutions for Class 9 Physical Science And Environment

• Chapter 1 Measurement
• Chapter 2 Force And Motion
• Chapter 3 Matter: Structure And Properties
• Chapter 4 Matter: Atomic Structure; Physical & Chemical Properties of Matter
  • 4.1 Atomic Structure
  • 4.2 Concept Of Mole
  • 4.3 Solution
  • 4.4 Acids, Bases & Salts
  • 4.5 Separation Of Components Of Mixtures
  • 4.6 Water
• Chapter 5. Energy In Action: Work, Power & Energy
• Chapter 6 Heat
• Chapter 7 Sound