Class 11 Chemistry

• Chapter 1 Some Basic Concepts of Chemistry Notes
  • Atomic Mass of Elements Notes
  • Chemical Combination Overview, Laws and Examples
  • Mole Concept- Formula, Explanations, Examples
  • Chemical Equation – Definition, Components and Examples
  • Some Basic Concepts Of Chemistry Multiple Choice Questions
  • Some Basic Concepts of Chemistry Notes
• Chapter 2 Atomic Structure Notes
  • Rutherford Atomic Model and Limitations
  • Bohr’s Atomic Model And Its Limitations
  • Atomic Structure Multiple Choice Questions
  • Quantum Mechanical Model of the Atom Notes
  • Heisenberg’s Uncertainty Principle Notes
  • Atomic Structure – Discovery of Subatomic Particles
• Chapter 3 Classification of Elements and Periodicity of Properties Notes
  • Periodic Properties of the Elements Notes
  • Periodic Properties Of Elements and Their Functions
• Chapter 4 Bonding and Molecular Structure Notes
  • Covalent Bond – Definition, Formation, Properties and Types
  • Shapes Of Molecules In Chemistry Notes
  • Valence Bond Theory
  • Hybridization – Definition, Types and Features
  • Polar Covalent Bond – Definition, Properties, Examples
  • Bonding And Molecular Structure Multiple Choice Questions
  • Bonding And Molecular Structure Notes
• Chapter 5 States of Matter Notes
  • Charle’s Law – Definition, Formula, Derivation, Application
  • Boyle’s Law – Definition, Equation and Examples
  • Kinetic Molecular Theory Of Gases Notes
  • Deviation from Ideal Gas Behaviour Notes
  • Ideal Gas law – Definition, Equation Notes
  • Properties of Liquids Notes
  • Intermolecular Forces – Definition and Types
• Chapter 6 Thermodynamics Notes
• Chapter 7 Equilibrium Notes
• Chapter 8 Redox Reactions Notes
• Chapter 9 Hydrogen Notes
• Chapter 10 The s-Block Elements Notes
• Chapter 11 The p-Block Elements Notes
  • Isotopes of Hydrogen Notes
  • Hydrogen Economy Notes
  • Properties Of Water: Physical And Chemical
  • Hydrogen Peroxide – Structure, Formula and Properties
  • MCQs On Hydrogen
• Chapter 12 Organic Chemistry-Some Basic Principles and Techniques Notes
• Chapter 13 Hydrocarbons Notes
• Chapter 14 Environmental Chemistry Notes

The S-Block Elements

You have already learnt that elements in the periodic table are arranged in order of increasing atomic number.

The long form of the periodic table is divided into four blocks—s, p, d and f—depending on the type of the orbitals (s, p, d or f) that are being filled with valence electrons.

The elements belonging to the s block can have one or a maximum of two s-electrons in their outermost shell.

The s-block of the periodic table comprises two groups—Group 1 and Group 2. The elements of Group 1 have the general ground state electronic configuration of ns¹ and are called alkali metals.

The elements of Group 2 have the general ground state electronic configuration of ns² and are called alkaline earth metals.

Elements in which the p orbitals are being filled with valence electrons fall in the p block.

This block constitutes Groups 13, 14, 15, 16, 17 and 18 with 1, 2, 3, 4, 5 and 6 electrons, respectively, in the p orbitals of the outermost shell, while the s orbitals are already filled.

General Characteristics of s-Block Elements

Some important characteristics of s-block elements are given below. A comparison with the p-block elements is also made, which will be helpful.

1. The s-block elements have the general outermost electronic configuration ns¹ (for alkali metals) or ns² (for alkaline earth metals). However, in the case of p-block elements the electronic configuration of the outermost shell is ns² np^1-6.
2. The s-block elements are metals and form ionic compounds with nonmetals whereas p-block elements are nonmetals and form predominantly covalent compounds with each other.
3. The s-block elements show only one oxidation state, which is equal to their group number.
4. Thus, alkali metals (Group 1) and alkaline earth metals (Group 2) show oxidation states of 1 and 2 respectively. On the other hand, most of the p-block elements show more than one positive as well as a negative oxidation state.
5. Diagonal relationship The first member of each group of the s-block and those of the other groups differ markedly from the rest of the members. Consider the elements of periods 2 and 3.

The first element of a group in the second period shows similarities with the second element of the neighbouring group on the right (diagonally opposite element). This is referred to as a diagonal relationship.

Thus, lithium resembles magnesium, beryllium resembles aluminium and boron resembles silicon.

This diagonal relationship is attributed to similarity in the size of the ions (e.g., Li+ =76 pm and Mg²⁺ =72 pm), and in the electropositive character and polarising power of the elements.

Alkali Metals (Group 1 Elements)

The elements of Group 1 are lithium (Li), sodium (Na), potassium (K), rubidium (Rb), caesium (Cs) and francium (Fr).

All these elements are metallic in nature and are known as alkali metals. The last element of this group, francium, is radioactive and has a very short half-life and so, very little is known about it. All the alkali metals are silvery-white, soft and light.

Occurrence

Alkali metals are very reactive and react with oxygen and water. Therefore, they do not occur in the free state.

However, they occur in the combined state in the form of salts like NaCl and KC1, which occur in large amounts in seawater.

Electronic Configuration

Alkali metals have only one electron (ns¹) in the s-orbital of their valence shell. The valence-shell electronic configuration of the alkali metals can be generalised as ns¹, where n = 2 to 7.

Atomic And Ionic Radii

The atoms of alkali metals have the largest size in their respective periods. The atomic radii increase as we go down the group (from Li to Cs) because there is a progressive addition of new energy shells.

This implies that the distance between the nucleus and the last shell increases and the valence electrons are farther from the nucleus. So the atomic radius increases with an increase in atomic number.

However, with the increase in atomic number the nuclear charge also increases. This tends to decrease the atomic radius by attracting the electron cloud inward with greater force.

However, the effective nuclear charge experienced by valence electrons is less than the actual nuclear charge because of the screening of the outermost electrons by the inner core of electrons.

For example, in the case of the sodium atom, the outermost 3s electron is screened by the inner Is and 2s electrons.

The alkali metals tend to lose their valence electrons and change to monovalent cations in order to achieve the noble-gas configuration.

So the radius of the positive ion is smaller than that of the parent atom. However, within the group, the ionic radius increases with an increase in atomic number.

This is accounted for by the addition of electron shells at every step as we go down the group.

Ionisation enthalpies

The first ionisation enthalpies of the elements of Group 1 are the lowest. This is because the valence electrons are loosely held, and can be easily lost by the atom to achieve the nearest noble-gas configuration.

The second ionisation enthalpies of alkali metals are very high. This is because it is difficult to remove an electron from a monovalent cation (formed by the removal of an electron from an atom of an alkali metal) having a noble-gas configuration.

Hydration Enthalpies

The standard enthalpy of hydration of an element is the energy released when 1 mol of gaseous ions of that element become hydrated (surrounded by water molecules) under standard conditions.

The higher the charge on the ions and the smaller their size, the more negative is the hydration enthalpy.

The hydration enthalpies of metal cations increase on moving down the group. Lithium has the most negative hydration enthalpy. ft Therefore, it mostly forms hydrated salts, e.g., LiCl₂H₂O.

Electropositive Character And Oxidation State

Elements that are electropositive tend to lose electrons and form positive ions. The alkali metals are typical electropositive elements.

The electropositive character increases from Li to Cs as the tendency to lose an electron increases on moving down the group.

While combining with other elements in a reaction, alkali metals have a strong tendency to lose the single valence electron to form a unipositive ion.

Thus, they show an oxidation state of +1 in their compounds and are strongly electropositive.

⇒ \(\mathrm{M} \rightarrow \mathrm{M}^{+}+\mathrm{e}^{-}\)

Melting And Boiling Points

The alkali metals have low melting and boiling points, which decrease down the group. This indicates weak inter¬ atomic bonding or metallic bonding.

In a metallic bond negatively charged electrons hold the positive ions together. The bonding is weak in alkali metals due to the presence of only a single valence electron for each atom. On moving down the group, atomic size increases, which progressively weakens intermolecular bonds.

Density

The densities of alkali metals are low and increase on moving down the group. However, potassium is an exception and is lighter than sodium.

The low density is attributed to the large atomic size. On moving down the group, atomic size as well as atomic mass increases.

However, the corresponding increase in atomic mass is not compensated by an increase in atomic volume. Thus, the density, which is the ratio of mass to volume, gradually increases.

Flame Colouration

All alkali metals impart a characteristic colour to a Bunsen flame.

When a sample of any metal salt is heated in a Bunsen burner (a laboratory gas burner) flame it imparts a characteristic colour to the flame.

The orbital electrons of the metal atoms absorb the heat energy supplied and get excited to higher energy states. When the excited electron loses the extra energy, it falls back to its ground state.

The extra energy lost is emitted in the form of radiation, which falls in the visible region, imparting a characteristic colouration to the flame.

Photoelectric effect

All alkali metals except lithium exhibit a photoelectric effect. Due to the low ionisation enthalpies of the metals, the metal surfaces emit electrons when exposed to visible light. Lithium has high ionisation enthalpy values and so does not exhibit a photoelectric effect.

Chemical properties

Alkali metals are very reactive. This is attributed to their low first ionisation enthalpies. We will now discuss some important chemical properties of alkali metals.

Reducing character

Alkali metals are good reducing agents. This is because they have a strong tendency to lose electrons and have large negative values of reduction potential. The reducing character increases from Na to Cs.

However, lithium, in spite of its highest ionisation enthalpy, is the strongest reducing agent among all alkali metals, as indicated by its reduction potential value (3.03 V).

The unusual behaviour of lithium is due to the exceptionally small size of the lithium atom and the high charge-to-radius ratio of the ion.

Being reducing agents, alkali metals react with compounds containing acidic hydrogen atoms (hydrogen atoms generally attached to oxygen or a triple bond are acidic and they can be replaced by metals), such as water, alcohol and acetylene, liberating hydrogen gas.

The standard electrode potential (Ee’)/ which measures the reducing power and is expressed as M+(aq)/M(s), represents the overall change as follows

⇒ \(\begin{aligned}
& \mathrm{M}(\mathrm{s}) \rightarrow \mathrm{M}(\mathrm{g}) \quad \text { (Sublimation enthalpy) } \\
& \mathrm{M}(\mathrm{g}) \rightarrow \mathrm{M}^{+}(\mathrm{g})+\mathrm{e}^{-} \quad \text { (Ionisation enthalpy) } \\
& \mathrm{M}^{+}(\mathrm{g})+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{M}^{+}(\mathrm{aq}) \quad \text { (Hydration enthalpy) } \\
&
\end{aligned}\)

The reactivity of alkali metals towards compounds containing acidic hydrogen increases from Li to Cs

⇒ \(\begin{aligned}
2 \mathrm{Li}+2 \mathrm{H}_2 \mathrm{O} & \rightarrow 2 \mathrm{LiOH}+\mathrm{H}_2 \\
2 \mathrm{Na}+2 \mathrm{C}_2 \mathrm{H}_5 \mathrm{OH} & \rightarrow \mathrm{C}_2 \mathrm{H}_5 \mathrm{ONa}+\mathrm{H}_2
\end{aligned}\)

⇒ \(2 \mathrm{Na}+\underset{\text { acetylene }}{\mathrm{HC}} \equiv \mathrm{CH} \rightarrow \underset{\text { sodium acetylide }}{\mathrm{HC}} \equiv \mathrm{C}-\mathrm{Na}+\mathrm{H}_2 acetylene sodium acetylide\)

Reaction With Oxygen

Alkali metals tarnish rapidly in dry air. Lithium forms a mixture of its oxide and nitride on the surface.

When burnt in air or oxygen, alkali metals form different types of oxides. For example, on a reaction with a limited quantity of oxygen, these metals form normal oxides (M₂O).

⇒ \(\begin{gathered}
2 \mathrm{M}+\frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{M}_2 \mathrm{O} \\
(\mathrm{M}=\mathrm{L}, \mathrm{Na}, \mathrm{K}, \mathrm{Kb}, \mathrm{Cs})
\end{gathered}\)

However, on being heated with an excess of air or oxygen, lithium forms the normal oxide or monoxide, sodium forms its peroxide (Na202) whereas potassium, rubidium and caesium form superoxides (MO₂).

⇒ \(2 \mathrm{Li}+\frac{1}{2} \mathrm{O}_2 \rightarrow \underset{\text { lithium oxide }}{\mathrm{Li}_2 \mathrm{O}}\)

⇒ \( 2 \mathrm{Na}+\mathrm{O}_2 \rightarrow \mathrm{Na}_2 \mathrm{O}_2 sodium peroxide\)

⇒ \(\mathrm{K}+\mathrm{O}_2 \rightarrow \quad \mathrm{KO}_2 potassium superoxide\)

Being the smallest in size, Li+ has a small, strong positive field around it. This implies that Li+ can stabilise only a small anion, O^2–. However, Na+, being larger in size has a weak positive field around it.

Therefore, it can stabilise a bigger peroxide ion, O²²⁺-, which has a weak negative field around it.

On the other hand, K+, Rb+, and Cs+ being still larger, stabilise the still bigger superoxide ion (O²⁺) to form superoxides.

The normal oxides and peroxides are colourless solids. However, superoxides are paramagnetic in nature (due to the presence of one impaired electron in the O^2–ion) and are yellow solids.

The oxides of alkali metals dissolve readily in water to form hydroxides. The reaction is exothermic.

⇒ \( \mathrm{M}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{MOH}+\text { heat } normal oxide \mathrm{Na}_2 \mathrm{O}_2+2 \mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{NaOH}+\mathrm{H}_2 \mathrm{O}_2+\text { heat } \)

These reactions show that the oxides of alkali metals are basic.

Reaction With Hydrogen

In general, alkali metals react with dihydrogen at about 673 K to give hydrides of the type MH. Lithium, however, reacts at 1073 K.

⇒ \(2 \mathrm{M}+\mathrm{H}_2 \rightarrow \underset{\text { metal hydride }}{2 \mathrm{MH}}\)

The reactivity of alkali metals with hydrogen decreases from Li to Cs. Also, the stability of the hydrides decreases from Li to Cs because, as the size of the alkali metal increases, the M—H bond becomes weak. The hydrides of alkali metals are strong reducing agents and are used in organic synthesis.

Reaction with halogens

Alkali metals react with halogens to form the corresponding halides, M+X

⇒ \(2 \mathrm{M}+\mathrm{X}_2 \rightarrow 2 \mathrm{MX}(\mathrm{X}=\mathrm{F}, \mathrm{Cl}, \mathrm{Br} \text { or } \mathrm{I})\)

The reactivity of alkali metals towards a particular halogen increase from Li to Cs. The reactivity of the halogens towards a particular alkali metal is of the order F2 >C12 > Br2 >I2.

Tire alkali metal halides (MX) are colourless, crystalline solids with high melting points. They can also be prepared conveniently from the corresponding oxide, hydroxide or carbonate by reaction with an aqueous hydrohalic acid (HX)

⇒ \(\begin{gathered}
\mathrm{Li}_2 \mathrm{O}+2 \mathrm{HCl} \rightarrow 2 \mathrm{LiCl}+\mathrm{H}_2 \mathrm{O} \\
\mathrm{Li}_2 \mathrm{CO}_3+2 \mathrm{HCl} \rightarrow 2 \mathrm{LiCl}+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2 \\
\mathrm{LiOH}+\mathrm{HCl} \rightarrow \mathrm{LiCl}+\mathrm{H}_2 \mathrm{O}
\end{gathered}\)

Alternatively, the nitrates of alkali metals can be decomposed on heating to give the corresponding oxide, which is then converted into a halide.

⇒ \(4 \mathrm{LiNO}_3 \rightarrow 2 \mathrm{Li}_2 \mathrm{O}+4 \mathrm{NO}_2+\mathrm{O}_2\)

Alkali metal halides are ionic compounds. However, Lil is slightly covalent due to polarisation (Li has the maximum polarising power as it is the smallest cation and the iodide ion can be polarised to the maximum extent as it is the largest anion).

Except for LiF, alkali metal halides are soluble in water. The insolubility of LiF is attributed to its high lattice enthalpy, as a result of the combination of the small anion (F-) and the small cation (Li+).

Melting and boiling points of alkali metal halides All the halides of alkali metals are colourless crystalline solids with high melting points because they contain ionic bonds. The melting and boiling points of these halides follow certain trends.

1. For the same alkali metal, the melting and boiling points decrease in the following order:

fluoride > chloride > bromide > iodide

This Can Be Explained On The Basis Of The Lattice Enthalpies Of These Halides. For The Same Alkali Metal Ion, The Lattice Enthalpies Decrease As The Size Of The Halide Ion Increases.

As The Lattice Enthalpies Decrease, The Energy Required To Break The Lattice (Melt The Solid) Decreases. Thus The Melting Points Of Sodium Halides Decrease From Naf To I.

2. For The Same Halide Ion, The Melting Point Of The Lithium Halide Is Lower Than That Of The Sodium Halide. Then There Is A Progressive Decrease In Melting Point From Na To Cs.

The low melting point of LiCl compared to that of NaCl, for example, is due to the fact that LiCl is covalent in nature, while NaCl is held together by ionic bonding.

The lattice enthalpy decreases from NaCl to CsCl as the size of the alkali metal ion increases. So the melting point decreases from NaCl to CsCl.

Reaction With Water

In reaction with water, alkali metals form hydroxides, liberating hydrogen gas.

⇒ \(\begin{aligned}
2 \mathrm{Na} & +2 \mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{NaOH}+\mathrm{H}_2 \\
2 \mathrm{~K}+2 \mathrm{H}_2 \mathrm{O} & \rightarrow 2 \mathrm{KOH}+\mathrm{H}_2
\end{aligned}\)

The reaction is so vigorous that the hydrogen evolved catches fire. The reaction becomes more violent on descending down the group. Therefore, alkali metals should be stored in an inert medium, usually kerosene oil.

Lithium is the only alkali metal which reacts gently with water. This is because it has the highest charge-to-radius ratio.

Owing to this it can polarise the water molecule more and with the highest hydration energy form a stronger metal-to-oxygen bond.

But its gentle behaviour towards water lies not in thermodynamics but in the kinetics of the reaction. Potassium, which liberates less energy, has a low melting point.

So it melts by the heat of the reaction, spreads and exposes a larger surface to the water, thus catching fire.

The hydroxides of the alkali metals are strongly basic and the strength of the base increases down the group.

On descending the group, the decrease in ionisation enthalpy results in weaker M —OH bonds from LiOH to C₂OH, and this accounts for the increase in the basic strength of the hydroxides. Alkali metal hydroxides in solution ionise easily to form M+ and OH ions due to the weak M—OH bond. This accounts for the strong basic nature of the hydroxides.

Reaction with oxoacids

Being electropositive in nature, alkali metals form oxo salts by reacting with oxoacids. For example, HOC₁, H₂CO₃ and HNO₃ react with alkali metals to give salts of oxoacids like MOCI, M₂CO₃ and MNO₃ respectively.

These salts are soluble in water and stable to heat. Li₂CO₃ is considerably less stable. Being strongly basic, Group 1 metals form solid bicarbonates.

Solutions of metals in liquid ammonia

All Group 1 metals and a few Group 2 metals dissolve in liquid ammonia, forming a deep blue solution. One reason why metals dissolve in liquid ammonia is ionisation.

⇒ \(\mathrm{M} \rightarrow \mathrm{M}^{+}+\mathrm{e}^{-}\)

The cations and electrons combine with ammonia to form ammoniated cations and ammoniated electrons respectively. The cations and electrons actually interact with the molecules of the solvent (ammonia). The overall reaction is

⇒ \(\mathrm{M}+(x+y) \mathrm{NH}_3 \rightarrow\left[\mathrm{M}\left(\mathrm{NH}_3\right)_x\right]^{+}+\left[\mathrm{e}\left(\mathrm{NH}_3\right)_y\right]^{-}
ammoniated cation ammoniated electron\)

The ammoniated electron is responsible for the blue colour of the solution. The solution absorbs energy corresponding to the red region of visible light and the ammoniated electrons get excited to higher energy levels.

When the electrons return to lower energy levels they transmit light which imparts a blue colour to the solution.

The solution is also conducting mainly due to the presence of solvated or ammoniated electrons. The solution fades on standing, slowly liberating hydrogen and forming a metal amide

⇒ \(\mathrm{M}^{+}+\mathrm{e}^{-}+\mathrm{NH}_3(\mathrm{l}) \rightarrow \mathrm{MNH}_2+\frac{1}{2} \mathrm{H}_2(\mathrm{~g})\)

The ammoniated electron is responsible for the blue colour of the solution. The solution absorbs energy corresponding to the red region of visible light and the ammoniated electrons get excited to higher energy levels.

When the electrons return to lower energy levels they transmit light which imparts a blue colour to the solution.

The solution is also conducting mainly due to the presence of solvated or ammoniated electrons. The solution fades on standing, slowly liberating hydrogen and forming a metal amide.

⇒ \(\mathrm{M}^{+}+\mathrm{e}^{-}+\mathrm{NH}_3(\mathrm{l}) \rightarrow \mathrm{MNH}_2+\frac{1}{2} \mathrm{H}_2(\mathrm{~g})\)

If the concentration of the solution is increased, the blue colour changes to copper-bronze with a metallic lustre.

This is because, with increased concentration, metal ion clusters are formed. The solutions of alkali metals in liquid ammonia act as powerful reducing agents and are used in organic reactions.

Solubility In Mercury

The alkali metals dissolve readily in mercury to form amalgams. The process is highly exothermic. The amalgams are also used as reducing agents in organic synthesis.

Anomalous Behaviour Of Lithium

The first element, lithium, of Group 1 differs from the other members of this group in many respects. The main reasons for the anomalous behaviour of lithium are as follows.

1. The exceptionally small size of the lithium atom and its ion.
2. The higher polarising power (charge to radius ratio) of Li+ is due to its smaller size
   and the covalent character of its compounds.
3. The high ionisation enthalpy and low electropositivity of lithium as compared to other alkali metals.
4. absence of vacant d-orbitals in its valence shell.

Some of the important properties in respect of which lithium differs from other members of the group are as follows.

1. Lithium is harder than the other alkali metals.
2. The melting point and boiling point of lithium are much higher than those of the other alkali metals.
3. Lithium is the least reactive as observed by its gentle behaviour towards water. In contrast/ the other alkali metals react violently with water.
4. In reaction ‘with oxygen, lithium forms only the monoxide (Li₂O) while other alkali metals form the peroxide (as in the case of sodium) or the superoxide (as in the case of potassium).
5. The ionic character of lithium salts is less pronounced than that of the salts of other alkali metals. This is because of the high polarising power of Li+. (The partial covalent character of ionic bonds. Due to its small size, Li+ has the maximum tendency to draw electrons towards itself from the negative ion in the salt molecule. This results in the distortion of the electronic cloud of the anion.
6. This distortion is known as polarisation. When the degree of polarization is large, the concentration of electrons increases between the two atoms. Therefore, the covalent character of the molecule increases.
7. Lithium is the only alkali metal that combines directly with the nitrogen of air to form the corresponding nitride.
   • \(6 \mathrm{Li}+\mathrm{N}_2 \rightarrow 2 \mathrm{Li}_3 \mathrm{~N}\)
8. The hydroxides, carbonates and nitrates of lithium decompose on heating to form lithium oxide. (Other alkali metal hydroxides and carbonates are stable and the nitrates decompose to give the corresponding nitrite.)
   • \(2 \mathrm{LiOH} \stackrel{\text { heat }}{\longrightarrow} \mathrm{Li}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O}\)
   • \(\mathrm{LiCO}_3 \stackrel{\text { heat }}{\longrightarrow} \mathrm{Li}_2 \mathrm{O}+\mathrm{CO}_2\)
   • \(4 \mathrm{LiNO}_3 \stackrel{\text { heat }}{\longrightarrow} 2 \mathrm{Li}_2 \mathrm{O}+4 \mathrm{NO}_2+\mathrm{O}_2\)
   • \(2 \mathrm{NaNO}_3 \longrightarrow 2 \mathrm{NaNO}_2+\mathrm{O}_2\)
9. The hydroxide of lithium (LiOH) is a weak base, whereas the hydroxides of other alkali metals are strong bases.
10. Due to their covalent nature, lithium halides (e.g., LiCl) are soluble in organic solvents, unlike the halides of other alkali metals. Also, LiCl is deliquescent and crystallises as LiCl.₂H₂0.
11. Due to its smaller size, the lithium-ion (Li⁺) is more strongly hydrated in an aqueous solution than other alkali metal ions.

Diagonal Relationship Of Lithium With Magnesium

As you know, the first element (Li) of Group 1 shows similarities in properties with the second element (Mg) of Group 2 (the diagonally opposite element).

This is referred to as a diagonal relationship.

Lithium resembles magnesium with respect to the following important properties.

1. Both lithium and magnesium are equally hard and light.
2. The similarities in lithium and magnesium are mainly due to their similar ionic size (Li+ =76 pm, Mg²⁺ = 72 pm). Both have nearly equal atomic radii, electronegativities and polarising powers.
3. The melting and boiling points of both lithium and magnesium are fairly high.
4. On heating in nitrogen both lithium and magnesium form nitrides, which are ionic compounds.
   • \(\begin{aligned}
     6 \mathrm{Li}+\mathrm{N}_2 & \rightarrow 2 \mathrm{Li}_3 \mathrm{~N} \\
     3 \mathrm{Mg}+\mathrm{N}_2 & \rightarrow \mathrm{Mg}_3 \mathrm{~N}_2
     \end{aligned}\)
5. The hydroxides, carbonates and nitrates of both lithium and magnesium decompose on heating to give the corresponding oxides. The chemical reactions of lithium compounds have been discussed in the previous section.
   • \(\mathrm{Mg}(\mathrm{OH})_2 \stackrel{\text { heat }}{\longrightarrow} \mathrm{MgO}+\mathrm{H}_2 \mathrm{O}\)
   • \(\mathrm{MgCO}_3 \stackrel{\text { heat }}{\longrightarrow} \mathrm{MgO}+\mathrm{CO}_2\)
   • \(2 \mathrm{Mg}\left(\mathrm{NO}_3\right)_2 \stackrel{\text { heat }}{\longrightarrow} 2 \mathrm{MgO}+4 \mathrm{NO}_2+\mathrm{O}_2\)
6. The hydroxides of both lithium and magnesium are weak bases.
7. The hydroxides, carbonates and fluorides of both lithium and magnesium are sparingly soluble in water.
8. The halides of lithium and magnesium are soluble in organic solvents (they are covalent compounds).
9. The chlorides of both lithium and magnesium are deliquescent and separate from aqueous solutions as hydrated salts (LiCl^2–2H₂O and MgCl₂-6H₂0).

Uses

Some of the important uses of alkali metals are as follows.

1. Lithium finds use in making useful alloys like the lithium-lead alloy used for making toughened bearings.
2. The lithium-magnesium alloy has high tensile strength and is used to manufacture aircraft components.
3. Lithium is also employed in the production of thermonuclear energy required for propelling rockets and guided missiles.
4. Sodium metal (molten) or its alloys with potassium are used as a coolant in nuclear reactors. The sodium-lead alloy is used for the preparation of lead tetraethyl [Pb(C2H5)4], which is used antiknock agent in petrol. However, its use has nowadays been discouraged as it causes environmental problems. Potassium chloride is used as a fertiliser and potassium hydroxide is used in the manufacture of soft soap.
5. Caesium finds use in the manufacture of photoelectric cells.

Compounds of Sodium

Sodium is the most abundant of the alkali metals. Being extremely reactive, it does not occur in the free state.

Sodium chloride (common salt) is the most common compound of sodium, but many others are also known. Sodium is commercially the most important metal of all alkali metals.

It is used in the manufacture of sodium carbonate, sodium hydroxide, sodium chloride and sodium bicarbonate, which are of great use in the chemical industry.

The process of manufacture, properties and uses of some of these compounds are as follows.

Sodium carbonate

It is also known as washing soda or soda ash. Soda ash is the white powder of sodium carbonate which aggregates on exposure to air due to the formation of monohydrates.

Na₂CO₃-H₂0 is a monohydrate and Na₂CO₃10H₂O is a decahydrate known as washing soda.

Since pre-historic times, it has been found to occur as natural deposits called trona (Na₂CO₃-NaHCO₃-2H₂O) in dried-up lake beds in Egypt. It is also mined in the USA and Kenya. The deposit of trona is converted into sodium carbonate by heating.

⇒ \(2\left(\mathrm{Na}_2 \mathrm{CO}_3 \cdot \mathrm{NaHCO}_3 \cdot 2 \mathrm{H}_2 \mathrm{O}\right) \stackrel{\text { heat }}{\longrightarrow} 3 \mathrm{Na}_2 \mathrm{CO}_3+\mathrm{CO}_2+5 \mathrm{H}_2 \mathrm{O}\)

The Solvay (or ammonia-soda) process

Sodium carbonate is manufactured by the Solvay or the ammonia-soda process. In this process, a purified concentrated solution of sodium chloride (brine) is saturated with ammonia gas.

The ammoniacal brine solution is then carbonated with carbon dioxide, forming sodium bicarbonate, which is insoluble in brine solution due to the common-ion effect and is filtered off.

The sodium bicarbonate on heating decomposes to give anhydrous sodium carbonate. We cannot prepare potassium carbonate by this process as the solubility of KHCO₃ is large in brine solution. The reactions taking place during the process are as follows.

⇒ \(\mathrm{NH}_3+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2 \rightarrow \mathrm{NH}_4 \mathrm{HCO}_3\)

⇒ \(\mathrm{NaCl}+\mathrm{NH}_4 \mathrm{HCO}_3 \rightarrow \mathrm{NaHCO}_3 \downarrow+\mathrm{NH}_4 \mathrm{Cl}\)

⇒ \(2 \mathrm{NaHCO}_3 \stackrel{\text { heat }}{\longrightarrow} \mathrm{Na}_2 \mathrm{CO}_3+\mathrm{CO}_2+\mathrm{H}_2 \mathrm{O}\)

Initially, the carbon dioxide required in the first step is generated by heating limestone.

⇒  \(\mathrm{CaCO}_3 \stackrel{\text { heat }}{\longrightarrow} \mathrm{CaO}+\mathrm{CO}_2\)

Subsequently, the CO₂ generated by heating sodium bicarbonate is used. The ammonia gas required for the reaction forming ammonium bicarbonate is obtained from CaO₂ (quicklime), which is shaken with water and then boiled with the ammonium chloride produced when sodium chloride reacts with ammonium bicarbonate.

The only raw materials used in the Solvay process are sodium chloride (common salt), limestone (to produce C02 initially) and ammonia. The by-product obtained in this process is calcium chloride, which is not of much use.

The plant used consists of an ammoniation tower (in which the brine solution is saturated with ammonia and a little carbon dioxide), a filter (in which the ammoniacal brine along with carbon dioxide is filtered), a carbonating tower (in which the ammoniacal liquor is carbonated), a vacuum filter (in which the sodium bicarbonate obtained is filtered) and the ammonia recovery tower (in which calcium hydroxide and ammonium chloride is heated to give ammonia gas).

The diagrammatic representation of the plant used for the Solvay process

Properties

Sodium carbonate is a white, crystalline substance and is obtained as a decahydrate (Na₂CO₃TOH₂O). On heating at 373 K, the decahydrate changes to the monohydrate. At a temperature above 373 K, the monohydrate becomes completely anhydrous.

⇒ [Latex]\mathrm{Na}_2 \mathrm{CO}_3 \cdot 10 \mathrm{H}_2 \mathrm{O} \stackrel{373 \mathrm{~K}}{\longrightarrow} \mathrm{Na}_2 \mathrm{CO}_3 \cdot \mathrm{H}_2 \mathrm{O}+9 \mathrm{H}_2 \mathrm{O}[/Latex]

⇒ [Latex]\mathrm{Na}_2 \mathrm{CO}_3 \cdot \mathrm{H}_2 \mathrm{O} \longrightarrow 3 / 3 \mathrm{~K} \longrightarrow \mathrm{Na}_2 \mathrm{CO}_3+\mathrm{H}_2 \mathrm{O}[/Latex]

The anhydrous sample absorbs moisture from the air and gives Na2C03-H20. It reacts with ads to give carbon dioxide with effervescence.

⇒ \(\mathrm{Na}_2 \mathrm{CO}_3+2 \mathrm{HCl} \rightarrow 2 \mathrm{NaCl}+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2\)

Sodium carbonate, when hydrolysed with water, forms an alkaline solution.

⇒ \(\mathrm{CO}_3{ }^{2-}+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{HCO}_3{ }^{-}+\mathrm{OH}^{-}\)

Sodium carbonate reacts with hot milk of lime to form sodium hydroxide.

⇒ \(\mathrm{Ca}(\mathrm{OH})_2+\mathrm{Na}_2 \mathrm{CO}_3 \rightarrow 2 \mathrm{NaOH}+\mathrm{CaCO}_3\)

Uses

1. Sodium carbonate is used in the manufacture of soap, detergents, paper, glass, phosphates and silicates.
2. It is also used in the manufacture of textiles, paints and dyes.
3. Sodium carbonate is employed for water softening, laundering and cleaning.
4. It is used in the laboratory as a reagent and as a primary standard in acid-base titrations. A mixture of sodium carbonate and potassium carbonate is used as a fusion mixture.

Sodium hydroxide

Sodium hydroxide, also known as caustic soda, is the most important alkali used iri the chemical industry.

It is manufactured by the electrolysis of a saturated solution of sodium chloride. In the past, it was also made by the causticising process, front sodium carbonate. This process is not in much use nowadays as other methods are cheaper.

⇒ \(\mathrm{Na}_2 \mathrm{CO}_3+\mathrm{Ca}(\mathrm{OH})_2 \rightarrow 2 \mathrm{NaOH}+\mathrm{CaCO}_3\)

Electrolysis of sodium chloride solution in a Castner-Kellner Cell

In this cell, a solution of sodium chloride (brine) is electrolysed. The mercury cathode is made to flow along the bottom of the cell. The brine also moves along the cathode and the sodium ions are reduced to form sodium metal.

⇒ \(At cathode:
\begin{aligned}
& \mathrm{Na}^{+}+\mathrm{e}^{-} \rightarrow \mathrm{Na} \\
& \mathrm{Na}+\mathrm{Hg} \rightarrow \underset{\text { sodium amalgam }}{\mathrm{Na}-\mathrm{Hg}}
\end{aligned} \)

The sodium metal formed dissolves in mercury to form an amalgam (a loose alloy), which is pumped to a different compartment (called the denuder).

In this compartment H20 trickles over lumps of graphite (here acting as an inert solid); this results in the reaction of water with the amalgam, producing an NaOH solution. The strength of the NaOH collected from this compartment is up to 50%.

⇒ \(\mathrm{Na} \text { (amalgam) }+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{NaOH}+\frac{1}{2} \mathrm{H}_2+\mathrm{Hg}\)

The mercury is recycled back to the electrolysis tank. Hydrogen and chlorine are the two by-products formed. Chlorine is liberated at the anode.

⇒At anode:\(\begin{aligned}
\mathrm{Cl}^{-} & \rightarrow \mathrm{Cl}+\mathrm{e}^{-} \\
\mathrm{Cl} & +\mathrm{Cl} \rightarrow \mathrm{Cl}_2
\end{aligned}\)

In the past, the anodes were made of graphite. However, due to traces of dioxygen produced in a side reaction, the graphite anode became pitted (holes were formed) because of the formation of C02.

Nowadays, in the Castner-Kellner cell, the anodes are made of steel coated with titanium. Titanium is very resistant to corrosion, so the problem of pitting is avoided. An additional advantage is that titanium lowers the electrical resistance.

Nowadays, a nafion membrane is also used in the cell to separate the anolyte and the catholyte. The nation is a 4 polymer of certain organic compounds.

Properties

Sodium hydroxide is a white, deliquescent solid and absorbs moisture from the air. It can even react with traces of carbon dioxide present in the air to form a solid hydrated carbonate.

⇒ \(2 \mathrm{NaOH}+\mathrm{CO}_2 \rightarrow \mathrm{Na}_2 \mathrm{CO}_3 \cdot \mathrm{H}_2 \mathrm{O}\)

It is soluble in water and forms a caustic alkali, which is one of the strongest bases known in an aqueous solution.

(Potassium hydroxide is another strong base.) Its solution is soapy to the touch and being basic in nature gives a pink colour with phenolphthalein. Some of the other properties of sodium hydroxide are as follows.

It reacts with acids to form salt and water.

⇒ \(\mathrm{NaOH}+\mathrm{HCl} \rightarrow \mathrm{NaCl}+\mathrm{H}_2 \mathrm{O}\)

It precipitates hydroxides of metals from metallic salt solutions.

⇒ \(\mathrm{Al}_2\left(\mathrm{SO}_4\right)_3+6 \mathrm{NaOH} \rightarrow 2 \mathrm{Al}(\mathrm{OH})_3+3 \mathrm{Na}_2 \mathrm{SO}_4\)

⇒ \(\underset{\text { ferric sulphate }}{\mathrm{Fe}_2\left(\mathrm{SO}_4\right)_3}+6 \mathrm{NaOH} \rightarrow \underset{\text { ferric hydroxide(red ppt) }}{2 \mathrm{Fe}(\mathrm{OH})_3}+3 \mathrm{Na}_2 \mathrm{SO}_4\)

⇒ \(\mathrm{Cr}_2\left(\mathrm{SO}_4\right)_3+6 \mathrm{NaOH} \rightarrow 2 \mathrm{Cr}(\mathrm{OH})_3+3 \mathrm{Na}_2 \mathrm{SO}_4\)

On being heated with ammonium salts, sodium hydroxide liberates ammonia.

⇒ \(\mathrm{NH}_4 \mathrm{Cl}+\mathrm{NaOH} \rightarrow \mathrm{NaCl}+\mathrm{NH}_3+\mathrm{H}_2 \mathrm{O}\)

On treatment with caustic soda, certain metals like aluminium, zinc, tin and silicon liberate hydrogen.

⇒ \(\mathrm{Zn}+2 \mathrm{NaOH} \rightarrow \mathrm{Na}_2 \mathrm{ZnO}_2+\mathrm{H}_2
sodium zincate\)

⇒ \(2 \mathrm{Al}+2 \mathrm{NaOH}+2 \mathrm{H}_2 \mathrm{O} \rightarrow \underset{\text { sodium aluminate }}{2 \mathrm{NaAlO}_2}+3 \mathrm{H}_2\)

⇒ \(\mathrm{Si}+2 \mathrm{NaOH}+\mathrm{H}_2 \mathrm{O} \rightarrow \underset{\text { sodium silicate }}{\mathrm{Na}_2 \mathrm{SiO}_3}+2 \mathrm{H}_2\)

Uses

1. Sodium hydroxide is used in the manufacture of soaps, paper, viscose rayon (artificial silk) and dyes.
2. It is used in the petroleum industry for refining crude oils. It is also used as a reagent in laboratories.
3. Sodium hydroxide is also employed in the extraction of metals like aluminium.
4. Its aqueous or alcoholic solution is used for carrying out organic reactions.

Sodium chloride

Sodium chloride (NaCl), also called common salt, is found most abundantly in seawater. It is also found in salt wells and in deposits of rock salt. In countries like India, it is obtained mainly by the evaporation of seawater.

Very pure sodium chloride is prepared by crystallisation of a clear, saturated NaCl solution.

It generally contains sodium sulphate (Na₂SO₄), calcium sulphate (CaSO₄), calcium chloride (CaCl₂) and magnesium chloride (MgCl₂) as impurities. Both CaCl₂ and MgCl₂, being deliquescent, absorb moisture from the atmosphere.

To obtain pure NaCl, the crude salt obtained is dissolved in water and then filtered. The insoluble impurities are removed and the filtrate is then saturated with HC₁ gas when pure crystalline sodium chloride separates out (due to the common-ion effect).

Properties

The melting point of sodium chloride is 801°C. It is soluble in water and glycerol, and slightly soluble in alcohol.

Uses

1. Sodium chloride is an essential constituent of our diet and is also used as a food preservative.
2. On being mixed with water, NaCl gives a mixture that has a freezing point about 10°C lower than that of pure water.
3. Sodium chloride mixed with ice (to achieve low temperatures) is used in the traditional method of making ice cream.
4. It is used in the manufacture of caustic soda, sodium peroxide, sodium carbonate and other sodium compounds.
5. NnCl is also employed in the manufacture of soap for salting out, and ion-exchange resins.

Sodium bicarbonate

It is commonly known as baking soda (NaHC03) and is obtained as the by-product of the ammonia-soda process (Solvay process) for the manufacture of sodium carbonate.

Ordinarily, sodium bicarbonate can be produced from sodium carbonate by passing carbon dioxide gas through its solution in water. Sodium bicarbonate, being sparingly soluble, precipitates out in the reaction.

⇒ \(\mathrm{Na}_2 \mathrm{CO}_3+\mathrm{CO}_2+\mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{NaHCO}_3\)

Properties

Sodium bicarbonate is a white crystalline substance. Its aqueous solution is alkaline in nature (gives a yellow colour with methyl orange and no colour with phenolphthalein). On heating, it decomposes to form sodium carbonate and carbon dioxide is released.

⇒ \(2 \mathrm{NaHCO}_3 \rightarrow \mathrm{Na}_2 \mathrm{CO}_3+\mathrm{CO}_2+\mathrm{H}_2\)

When used in baking powder the carbon dioxide gas released on heating leaves holes in cakes making them light and fluffy. NaHC03 reacts with adds with effervescence caused by to evolution of carbon dioxide.

⇒ \(\mathrm{NaHCO}_3+\mathrm{HCl} \rightarrow \mathrm{NaCl}+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2\)

Uses

1. It is used in medicine as an antacid. It is largely used in the treatment of acid spillage.
2. Sodium bicarbonate is also used in fire extinguishers. NaHC03 reacts with add to produce C02, which extinguishes fires.
3. It is also employed in the textiles, tanning, paper and ceramic industries.
4. The hydrogen carbonate ion (HCO^2–) has an important biological role as an intermediate between atmospheric CO₂/H₂CO₃ and the carbonate ion (CO^2–). For aquatic organisms, this is the most important and in some cases the only source of carbon.

Alkaline Earth Metals (Group 2 Elements)

The elements of Group 2 of the periodic table are beryllium (Be), magnesium (Mg), calcium (Ca), strontium (Sr), barium (Ba) and radium (Ra).

All these elements are metallic in nature and are commonly known as alkaline earth metals.

The oxides of the metals magnesium, calcium, barium and strontium were known before the corresponding metals and were named alkaline earths since they were found in the earth’s crust and alkaline in nature.

Subsequently, all the corresponding metals were called alkaline earth metals. These metals are silvery-white and lustrous. They are soft but harder than alkali metals. were

Occurrence

Magnesium is the sixth most abundant element in the earth’s crust whereas calcium is the fifth most. Magnesium salts occur in seawater to the extent of 0.13%.

Calcium occurs as sedimentary deposits of CaCO₃. Strontium and barium are much less abundant whereas beryllium is very rare. Radium, being radioactive, is extremely scarce.

Electronic Configuration

Alkaline earth metals have two electrons in the s orbital of their valence shell. Their general valence-shell electronic configuration is ns², where n = 2 to 7.

The electronic configuration of the individual members.

Alkaline earth metals exhibit similar physical and chemical properties. Beryllium, the first member of the group, differs from the rest of the members.

Let us now discuss the trend of variation in atomic and physical properties of the elements of Group 2. Group 2 elements show the same trend in properties as shown by the elements in Group 1.

Atomic And Ionic Radii

The atomic and ionic radii of elements of Group 2 increase from beryllium to radium because the addition of shells more than compensates for the increase in nuclear charge.

However, the atomic and ionic radii of alkaline earth metals are smaller than those of the corresponding alkali metals. This is because, in the same period, due to the extranuclear charge in the alkaline earth metal atom, the orbital electrons are drawn in.

Ionisation Enthalpy

The ionisation enthalpy of elements decreases within the group as the atomic number increases.

This is due to the increase in atomic size and in the magnitude of the screening effect caused by the electrons of the inner shells. Elements of Group 2 have higher values of first ionisation enthalpies than those of the corresponding elements of Group 1.

This is attributed to the smaller size and higher nuclear charge of alkaline earth metals due to which the electrons in their outermost shells are tightly held.

The values of the second ionisation enthalpies are higher than those of the first ionisation enthalpies in the case of alkaline earth metals since greater energy is required to pull out an electron from a positively charged ion than from a neutral atom.

However, the values of the second ionisation enthalpies of the alkaline earth metals are smaller than those of the corresponding alkali metals.

This is because the second electron is removed from a monovalent cation (in the case of an alkaline earth metal) when the atom has yet to acquire the stable noble-gas configuration.

Electropositive character and oxidation state

The electropositive character increases from beryllium to radium as the tendency of atoms to lose electrons increases.

However, alkaline earth metals are less electropositive than the corresponding alkali metals due to their high ionisation enthalpies.

The elements of Group 2 form bivalent cations and are in the bipositive (M2+) oxidation state, compared to the unipositive (M+) oxidation state of Group 1 elements.

Melting and boiling points

Alkaline earth metals have higher melting and boiling points than those of the corresponding alkali metals. This is because of the small atomic size and stronger metallic bonds due to the presence of two valence electrons in alkaline earth metals.

Density

The alkaline earth metals are denser than the corresponding alkali metals. The density decreases from beryllium to calcium and then increases from calcium to radium.

Flame colouration

Like alkali metals, alkaline earth metals also impart characteristic colours to a flame. Calcium, strontium and barium impart brick red, crimson and apple green colours respectively. The electrons absorb energy from the flame and get excited to higher energy levels.

When they drop back to the ground state, they emit this energy in the form of visible light.

Beryllium and magnesium do not give any flame colouration since their atoms are small in size and their electrons are strongly bound to the nucleus. They need a large amount of energy for excitation to higher energy levels and so much energy is not available in a Bunsen flame.

Photoelectric effect

Unlike alkali metals, alkaline earth metals do not exhibit a photoelectric effect. This is because their ionisation enthalpies are relatively high.

Hydration enthalpies

The hydration enthalpies of the cations of Group 2 elements are greater than those of the corresponding cations of Group 1 elements. This is due to the smaller size and increased charge on the cations formed by Group 2 elements.

The hydration enthalpies, decrease down the group as the size of the ions increases. Due to the high hydration enthalpies, the crystalline compounds of Group 2 elements contain more water of crystallisation than those of the corresponding Group 1 elements. For example, NaCl and KC₁ are anhydrous but MgCl^2–6H₂O, CaG^2–6H₂O and BaCl^2–2H₂O have water of crystallisation.

Chemical properties

Alkaline earth elements are less reactive than alkali metals. Some of the important chemical properties of Group 2 elements are discussed below.

Nature of compounds

Like alkali metals, alkaline earth metals predominantly form ionic compounds. However, their salts are less ionic than those of alkali metals.

The tendency of the elements to form ionic compounds increases down the group due to the decrease in ionisation enthalpies.

The first member of the group, beryllium, forms covalent compounds because of its small size and high ionisation enthalpy. Magnesium sometimes exhibits covalency. All other elements form ionic compounds.

Reducing character

Alkaline earth metals have a lower reducing power than alkali metals. This is due to the higher ionisation enthalpies of alkaline earth metals than those of the corresponding alkali metals.

Reaction with oxygen

All the alkaline earth metals bum in oxygen to form oxides MO, except Sr and Ba, which form dioxides or peroxides (MOz) in the presence of an excess of oxygen.

Beryllium is relatively unreactive and bums brilliantly in the powdered form above 873 K.

Magnesium bums with dazzling brilliance in the air to give magnesium oxide and combine with the nitrogen of the air to give magnesium nitride (Mg₃N₂)

⇒ \(\begin{aligned}
2 \mathrm{Be}+\mathrm{O}_2 & \rightarrow 2 \mathrm{BeO} \\
2 \mathrm{Mg}+\mathrm{O}_2 & \rightarrow 2 \mathrm{MgO} \\
2 \mathrm{Ca}+\mathrm{O}_2 & \rightarrow 2 \mathrm{CaO} \\
\mathrm{Sr}+\mathrm{O}_2 & \rightarrow \mathrm{SrO}_2 \\
\mathrm{Ba}+\mathrm{O}_2 & \rightarrow \mathrm{BaO}_2
\end{aligned}\)

The oxides of alkaline earth metals (except that of beryllium, which is covalent) are basic in nature. The reactivity with oxygen increases from beryllium to barium. The oxide of beryllium (BeO) is amphoteric since it reacts with acids as well as alkalis.

⇒ \(\mathrm{BeO}+2 \mathrm{HCl} \rightarrow \mathrm{BeCl}_2+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{BeO}+2 \mathrm{NaOH} \rightarrow \underset{\text { sodium beryllate }}{\mathrm{Na}_2 \mathrm{BeO}_2}+\mathrm{H}_2 \mathrm{O}\)

Reaction With Water

The reactions of alkaline earth metals with water are less vigorous than those of the corresponding alkali metals.

Beryllium does not react with water, and magnesium reacts with steam or boiling water.

\(\mathrm{Mg}+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{MgO}+\mathrm{H}_2\)

The elements Ca, Sr and Ba react with cold water, liberating hydrogen and forming metal hydroxides.

\(\mathrm{Ca}+2 \mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{Ca}(\mathrm{OH})_2+\mathrm{H}_2\)

Thus, the reactivity of water with alkaline earth metals increases as we move down the group.

The hydroxides of alkaline earth metals can also be obtained by dissolving their oxides (except BeO which is amphoteric) in water.

These hydroxides are strong bases. The hydroxides of alkaline earth metals are relatively less basic than those of the corresponding alkali metals.

This is because they have higher ionisation enthalpies and their ions are smaller in size and bipositive in character.

Consequently, the OH- ions are held more firmly by the M2+ ions and the M —OH bond does not break easily.

The basic character of the hydroxides increases from Be to Ba because of the decreasing ionisation enthalpy of the metal atoms.

⇒ \(\underset{\text { amphoteric }}{\mathrm{Be}(\mathrm{OH})_2}<\underset{\text { weak basc }}{\mathrm{Mg}(\mathrm{OH})_2}<\underset{\text { moderately strong hases }}{\mathrm{Ca}(\mathrm{OH})_2} \mathrm{Sr}(\mathrm{OH})_2<\underset{\text { strong base }}{\mathrm{Ba}(\mathrm{OH})_2}\)

These hydroxides are less soluble in water as compared to alkali metal hydroxides. However, they give strongly alkaline solutions because they readily form OH” ions in aqueous solutions. All these bases neutralise and are added to give salts and water.

⇒ \(\mathrm{M}(\mathrm{OH})_2+2 \mathrm{HCl} \rightarrow \mathrm{MCl}_2+2 \mathrm{H}_2 \mathrm{O}(\mathrm{M}=\mathrm{Mg}, \mathrm{Ca}, \mathrm{Sr}, \mathrm{Ba})\)

Ben-Ilium hydroxide, being amphoteric, reacts with alkalis as well to form the beryllate ion.

⇒ \(\mathrm{Be}(\mathrm{OH})_2+2 \mathrm{OH}^{-} \rightarrow\left[\mathrm{Be}(\mathrm{OH})_4\right]^{2-}beryllate ion\)

The solubility of the hydroxides in water increases with the increase in atomic number of the metal atom because of a decrease in lattice enthalpy with the increasing size of the metallic ion.

The hydroxides of beryllium and magnesium are almost insoluble, that of calcium is sparingly soluble while those of strontium and barium are increasingly more soluble.

The solubility of the hydroxides of alkaline earth metals depends on their lattice enthalpy and hydration enthalpy.

The lattice enthalpy of a crystal is the heat that would be released per mole if the ions (atoms/molecules) of the crystal were brought together from an infinite distance apart to form the lattice.

If the lattice enthalpy is higher, the ions are held more tightly in a crystal with the result that the solubility of the crystal in water is less.

The lattice enthalpy of the hydroxides of Group 2 elements decreases down the group due to the increase in the size of the cation.

Also, the greater the charge on the ion or the smaller the size of the ion, the greater the lattice enthalpy. If the hydration enthalpy of a salt is greater, the solubility of the salt in water is more.

The resultant of the lattice and the hydration enthalpies, Le., AÿH = A UlticeH – AhydH, becomes more as we move from Be(OH)2 to Ba(OH)2.

This accounts for the increase in solubility as we move down the group. Generally speaking, a hydroxide dissolves if its hydration enthalpy is more than its lattice enthalpy and vice versa.

The action of carbon dioxide on alkaline earth metal hydroxides On passing carbon dioxide gas through the solutions of alkaline earth metal hydroxides the corresponding carbonates are obtained.

⇒ \(\mathrm{M}(\mathrm{OH})_2+\mathrm{CO}_2 \rightarrow \mathrm{MCO}_3+\mathrm{H}_2 \mathrm{O}\)

The carbonates can also be obtained by the addition of sodium or ammonium carbonate to alkaline earth metal salts.

⇒ \(\mathrm{CaCl}_2+\mathrm{Na}_2 \mathrm{CO}_3 \rightarrow \mathrm{CaCO}_3+2 \mathrm{NaCl}\)

On being heated, the carbonates of alkaline earth metals decompose to give the corresponding oxides. The temperature of decomposition increases from beryllium to barium.

⇒ \(\mathrm{MCO}_3 \stackrel{\text { heat }}{\longrightarrow} \mathrm{MO}+\mathrm{CO}_2\)

The solubility of the carbonates of alkaline earth metals decreases in the group. This is due to a decrease in hydration enthalpy as the lattice enthalpy remains almost unchanged.

Reaction with hydrogen

On heating, alkaline earth metals, except beryllium, combine with hydrogen to form metal hydrides.

⇒ \(\mathrm{M}+\mathrm{H}_2 \stackrel{\text { neat }}{\longrightarrow} \mathrm{MH}_2\)

Beryllium hydride can, however, be prepared by the reduction of beryllium chloride with lithium aluminium hydride.

⇒ \(2 \mathrm{BeCl}_2+\mathrm{LiAlH}_4 \rightarrow 2 \mathrm{BeH}_2+\mathrm{LiCl}+\mathrm{AlCl}_3\)

Among all the hydrides of Group 2 elements calcium hydride finds uses in the preparation of dry solvents.

Salts of oxoacids —sulphates, nitrates and carbonates

The sulphates of alkaline earth metals are thermally stable. The solubility of the sulphates in water decreases down the group. Thus, BeS04 and MgS04 are readily soluble but CaS04 is sparingly soluble.

The rest are virtually insoluble. The higher solubilities of BeS04 and MgS04 are due to the high enthalpy of the solution of Be²⁺ and Mg²⁺ ions. The sulphates of Be, Mg and Ca have water of crystallisation, viz BeS04-4H20, Mg$04-7H20 and CaS04-2H20.

The nitrates of alkaline earth metals are prepared by dissolving their carbonates in dilute nitric acid. On heating, the nitrates decompose, forming oxides.

⇒ \(2 \mathrm{M}\left(\mathrm{NO}_3\right)_2 \stackrel{\text { heat }}{\longrightarrow} 2 \mathrm{MO}+4 \mathrm{NO}_2+\mathrm{O}_2\)

The carbonates of alkaline earth metals are insoluble in water. The metal carbonates are more stable to heat as we move down the group.

The carbonates decompose on heating to give carbon dioxide and the oxide. Beryllium carbonate is unstable and can be kept only in an atmosphere of C02.

Reaction with halogens

On heating with halogens, alkaline earth metals form the corresponding halides.

⇒ \(\mathrm{M}+\mathrm{X}_2 \rightarrow \mathrm{MX}_2\)

The halides can also be obtained by the action of halogen acids on metals, their oxides, hydroxides and carbonates. Beryllium halides cannot be prepared this way due to the formation of the hydrated ion,[Be(H20)4 ]2

⇒ \(\begin{gathered}
\mathrm{M}+2 \mathrm{HX} \rightarrow \mathrm{MX}_2+\mathrm{H}_2 \\
\mathrm{MO}+2 \mathrm{HX} \rightarrow \mathrm{MX}_2+\mathrm{H}_2 \mathrm{O} \\
\mathrm{M}(\mathrm{OH})_2+2 \mathrm{HX} \rightarrow \mathrm{MX}_2+2 \mathrm{H}_2 \mathrm{O} \\
\mathrm{MCO}_3+2 \mathrm{HX} \rightarrow \mathrm{MX}_2+\mathrm{CO}_2+\mathrm{H}_2 \mathrm{O}
\end{gathered}\)

Beryllium chloride is prepared from the oxide by heating with carbon and chlorine.

⇒ \(\mathrm{BeO}+\mathrm{C}+\mathrm{Cl}_2 \stackrel{870-1070 \mathrm{~K}}{=} \mathrm{BeCl}_2+\mathrm{CO}\)

General characteristics

The halides of alkaline earth metals (except those of beryllium) are ionic in nature; the ionic character increases as the size of the metal ion increases.

Beryllium chloride and fluoride, being covalent (due to the smaller size of Be2*), are soluble in organic solvents whereas the halides of other alkaline earth elements are insoluble. The fluorides of all alkaline earth metals except that of Be are almost insoluble in water. Beryllium fluoride is soluble because it has a high hydration energy. Also, the beryllium halides do not conduct electricity.

Beryllium chloride has low melting as compared to the halides of other alkaline earth metals.

The halides of alkaline earth metals (except those of beryllium) dissolve in water giving acidic solutions from which hydrates such as MgCl 2 -6H20, CaCl ^2–6H20 and BaCl ^2-2H20 crystallise out.

The tendency to form hydrated halides decreases with the increasing size of the metal ions structure of BeCl2 In the solid phase, BeCl 2 has the following polymeric chain structure.

However, in the vapour phase, it forms a chloro-bridged dimer, which dissociates into the linear triatomic monomer at high temperatures (approximately 1200 K).

Anomalous behaviour of beryllium

Beryllium is anomalous in many of its properties. It differs much more from the rest of the members of Group 2 than lithium does from the other elements of Group 1.

The main reasons for the anomalous behaviour of beryllium are the small size of the atom, high ionisation enthalpy and the absence of d orbitals in its valence shell. Beryllium differs from the rest of the members of its group in many of its properties, as listed below.

1. Beryllium is harder than the other elements of its group.
2. It has higher melting and boiling points.
3. It does not react with water even on heating, unlike the other members of the group.
4. It does not react with ads to liberate hydrogen, unlike the other members of the group.
5. Beryllium forms covalent compounds while the other members of Group 2 form ionic compounds.
6. Beryllium oxide is amphoteric whereas the oxides of other metals of Group 2 are basic.
7. Beryllium does not combine directly with hydrogen to form the hydride whereas other metals of this group form hydrides directly.
8. Beryllium carbide reacts with water to give methane. In contrast, the other alkaline earth metals give acetylene.

⇒ \(\mathrm{MgC}_2+2 \mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{Mg}(\mathrm{OH})_2+\mathrm{C}_2 \mathrm{H}_2\)

Diagonal Relationship Of Beryllium With Aluminium

Beryllium, the first element of Group 2, shows similarities in properties with aluminium, the second member of the next higher group, just as lithium shows a diagonal relationship with magnesium. Some of the properties in which beryllium resembles aluminium are as follows.

1. Both beryllium and aluminium ions have comparable ionic radius and charge-to-radius ratio.
2. Both form covalent compounds, which are soluble in organic solvents, e.g., BeCl2 and A1C13.
3. The oxides of both beryllium and aluminium, viz. BeO and Al203, are high-melting, hard solids. Also, the two oxides are amphoteric and they dissolve both in acids and alkalies. With excess alkalies the hydroxides of Be and A1 form beryllate and aluminate ions respectively.
4. Both beryllium and aluminium do not react readily with acids, due to the presence of an oxide on the surface of the metal.
5. In reaction with water, the carbides of both beryllium and aluminium liberate methane.

⇒ \(\begin{gathered}
\mathrm{Be}_2 \mathrm{C}+2 \mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{BeO}+\mathrm{CH}_4 \\
\mathrm{Al}_4 \mathrm{C}_3+6 \mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{Al}_2 \mathrm{O}_3+3 \mathrm{CH}_4
\end{gathered}\)

The chlorides of both metals have a bridged polymeric structure

Uses

Some of the important uses of alkaline earth metals are as follows.

1. Beryllium finds use in making alloys like copper-beryllium, which is used in the preparation of high strength springs.
2. Beryllium foil is also used in X-ray tubes to filter out visible light and allow only X-rays to pass through.
3. Magnesium is also used in the preparation of alloys. Duralumin—a magnesium-aluminium-copper alloy—is very light and durable and, therefore, used in the manufacture of aeroplanes and automobile parts. Magnalium, an alloy of aluminium and magnesium, is used for making beam balances.
4. Magnesium in the form of powder is used in incendiary bombs and signals and flash powders.
5. Calcium is used in the extraction of metals from their oxides.
6. Both calcium and barium are used to remove air from vacuum tubes because they can react with oxygen and nitrogen at elevated temperatures.
7. Radium, being radioactive, is used in radiotherapy in the treatment of cancer.

Compounds Of Calcium

Some of the commercially important compounds of calcium are calcium oxide, calcium hydroxide, calcium carbonate, calcium sulphate and cement. The process of manufacture, properties and uses of these compounds are discussed here.

Calcium oxide

Calcium oxide (CaO) is a white, amorphous solid with a high melting point—2845 K. It is commonly known as quicklime and is obtained commercially by heating limestone at 1273 K in specially designed lime kilns.

⇒ \(\mathrm{CaCO}_3 \stackrel{1273 \mathrm{~K}}{\rightleftharpoons} \mathrm{CaO}+\mathrm{CO}_2\)

The reaction is reversible. Maximum yields of calcium oxide are obtained if the carbon dioxide is allowed to escape from the kiln. Carbon dioxide escapes above 1100 K.

Properties

1. Quicklime readily absorbs moisture and carbon dioxide. Treatment of quicklime with water produces calcium hydroxide, Ca(OH)2. The reaction is highly exothermic and occurs with a hissing sound.

⇒ \(\mathrm{CaO}(\mathrm{s})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{Ca}(\mathrm{OH})_2(\mathrm{aq}) \quad \Delta H=-645 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Calcium hydroxide is also called slaked lime. Calcium oxide is usually obtained in the form of hard lumps.

The lump gets disintegrated by the addition of a limited amount of water, and slaked lime is formed. The process is known as slaking of lime. Quicklime, slaked with soda (aqueous sodium hydroxide) gives a solid, soda lime.

Soda lime is a mixture of sodium hydroxide (NaOH) and calcium hydroxide, Ca(OH)2. It is much easier to handle soda lime than NaOH, which is corrosive.

Calcium oxide reacts with carbon dioxide to give calcium carbonate (CaO + COz ->CaC03). Though calcium carbonate occurs in nature as limestone, marble, etc., pure CaC03 is obtained by this process

Calcium oxide is a basic oxide and reacts with acids to form salts.

⇒ \(\mathrm{CaO}+2 \mathrm{HCl} \rightarrow \mathrm{CaCl}_2+\mathrm{H}_2 \mathrm{O}\)

Calcium oxide combines with acidic oxides at a high temperature.

⇒ \(\begin{gathered}
\mathrm{CaO}+\mathrm{SiO}_2 \rightarrow \mathrm{CaSiO}_3 \\
6 \mathrm{CaO}+\mathrm{P}_4 \mathrm{O}_{10} \rightarrow 2 \mathrm{Ca}_3\left(\mathrm{PO}_4\right)_2
\end{gathered}\)

⇒ \(
\mathrm{CaO}+\mathrm{SO}_2 \rightarrow \mathrm{CaSO}_3
calcium sulphite\)

On heating with coke in an electric furnace at 2273-3273 K, calcium oxide forms calcium carbide.

⇒ \(\mathrm{CaO}+3 \mathrm{C} \stackrel{2273-3273 \mathrm{~K}}{\longrightarrow} \mathrm{CaC}_2+\mathrm{CO}\)

On heating with ammonium salts, calcium oxide liberates ammonia.

⇒ \(\mathrm{CaO}+2 \mathrm{NH}_4 \mathrm{Cl} \rightarrow \mathrm{CaCl}_2+2 \mathrm{NH}_3+\mathrm{H}_2 \mathrm{O}\)

Uses

1. Calcium oxide is used in the manufacture of bleaching powder, slaked lime, calcium carbide, cement, glass, mortar, etc.
2. It is employed in making glass.
3. It is used in steel-making to remove phosphates and silicates as slag.
4. It is used as the basic lining in furnaces.

Calcium hydroxide

Also known as slaked lime, it is obtained by the action of water on calcium oxide.

⇒ \(\mathrm{CaO}+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{Ca}(\mathrm{OH})_2\)

It can also be obtained by the action of caustic alkalis on a soluble calcium salt.

⇒ \(\mathrm{CaCl}_2+2 \mathrm{NaOH} \rightarrow \mathrm{Ca}(\mathrm{OH})_2+2 \mathrm{NaCl}\)

Properties

1. Calcium hydroxide is a white, amorphous solid and is sparingly soluble in water. The aqueous solution is known as limewater.
2. The suspension of calcium hydroxide in water is known as milk of lime. On heating above 700 K calcium hydroxide loses water to give calcium oxide (quicklime).
3. Carbon dioxide reacts with limewater to give a white precipitate of calcium carbonate. This is the reason why carbon dioxide turns limewater milky. Thus, limewater is used to detect the presence of carbon dioxide gas.

⇒ \(\mathrm{Ca}(\mathrm{OH})_2+\mathrm{CO}_2 \rightarrow \mathrm{CaCO}_3 \downarrow+\mathrm{H}_2 \mathrm{O}\)

However, if carbon dioxide is passed for a longer time, the milkiness disappears because the insoluble CaC03 gets converted into soluble calcium hydrogen carbonate, Ca(HC03 )

⇒ \(
\mathrm{CaCO}_3+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2 \rightarrow \mathrm{Ca}\left(\mathrm{HCO}_3\right)_2
soluble\)

Like C02, sulphur dioxide also reacts with limewater to give a white precipitate—of calcium sulphite.

⇒ \(\mathrm{Ca}(\mathrm{OH})_2+\mathrm{SO}_2 \rightarrow \mathrm{CaSO}_3 \downarrow+\mathrm{H}_2 \mathrm{O}\)

Chlorine reacts with milk of lime below 308 K to give bleaching powder.

⇒ \(
3 \mathrm{Ca}(\mathrm{OH})_2+2 \mathrm{Cl}_2 \stackrel{<308 \mathrm{~K}}{\longrightarrow} \mathrm{Ca}(\mathrm{OCl})_2 \cdot \mathrm{CaCl}_2 \cdot \mathrm{Ca}(\mathrm{OH})_2 \cdot 2 \mathrm{H}_2 \mathrm{O}
bleaching powder\)

Though the formula for bleaching powder is usually written as Ca (OCl2), it is really a mixture.

On heating with ammonium chloride, calcium hydroxide liberates ammonia and with acids, it forms salts.

⇒ \(\begin{gathered}
\mathrm{Ca}(\mathrm{OH})_2+2 \mathrm{NH}_4 \mathrm{Cl} \stackrel{\text { heat }}{\longrightarrow} \mathrm{CaCl}_2+2 \mathrm{NH}_3 \uparrow+2 \mathrm{H}_2 \mathrm{O} \\
\mathrm{Ca}(\mathrm{OH})_2+2 \mathrm{HCl} \longrightarrow \mathrm{CaCl}_2+2 \mathrm{H}_2 \mathrm{O}
\end{gathered}\)

Uses

1. Calcium hydroxide is used for whitewashing and construction purposes.
2. It is used for softening water. As you have already studied in Chapter 9, the temporary hardness of can be removed by adding slaked lime (the carbonates precipitate). This is called lime softening.
3. It is used in the manufacture of bleaching powder, caustic soda and glass.
4. Soda lime (a mixture of calcium hydroxide and caustic soda) is used in the decarboxylation of sodium salts of fatty acids.

⇒ \(\mathrm{CH}_3 \mathrm{COONa} \underset{\text { hest }}{\stackrel{\text { soda lime }}{\longrightarrow}} \mathrm{CH}_4 \uparrow+\mathrm{Na}_2 \mathrm{CO}_3\)

Plaster of Paris

Plaster of Paris is calcium sulphate hemihydrate, i.e., it has one molecule of water for every two calcium and two sulphate ions.

It is obtained by the controlled heating of gypsum at 393 K. If the heating is not controlled, the anhydrous salt is produced instead of the hemihydrate.

⇒ \(\begin{aligned}
& 2\left[\mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O}\right] \stackrel{\text { heat }}{\longrightarrow}\left(2 \mathrm{CaSO}_4\right) \cdot \mathrm{H}_2 \mathrm{O}+3 \mathrm{H}_2 \mathrm{O} \\
& \text { gypsum } \\
& \text { plaster of Paris } \\
& \text { (calcium sulphate } \\
& \text { hemilhydrate) } \\
&
\end{aligned}\)

Gypsum is a naturally occurring mineral. Calcium sulphate can be obtained by the reaction of any soluble calcium salt either with dilute sulphuric acid or with sodium sulphate and then used to prepare gypsum.

⇒ \(\begin{gathered}
\mathrm{CaCl}_2+\mathrm{H}_2 \mathrm{SO}_4 \rightarrow \mathrm{CaSO}_4+2 \mathrm{HCl} \\
\mathrm{CaCl}_2+\mathrm{Na}_2 \mathrm{SO}_4 \rightarrow \mathrm{CaSO}_4+2 \mathrm{NaCl}
\end{gathered}\)

Properties

1. Plaster of Paris is a white, powdery substance. A paste of plaster of Paris with one-third of its weight of water sets to a hard mass when allowed to stand for about fifteen minutes.

The setting into a hard mass occurs due to the interlocking of crystals of gypsum. This property is made use of in the setting of broken bones and involves the following two stages.

⇒ \(\underset{\text { plaster of Paris }}{\left(2 \mathrm{CaSO}_4\right) \cdot \mathrm{H}_2 \mathrm{O}} \underset{\text { setting }}{\stackrel{\mathrm{H}_2 \mathrm{O}}{\longrightarrow}} \underset{\substack{\text { gypsum } \\ \text { (orthorhombic crystals) }}}{\mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O}} \stackrel{\text { hardening }}{\longrightarrow} \underset{\substack{\text { gypsum } \\ \text { (monoclinic crystals) }}}{\mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O}}\)

The rate of setting of plaster of Paris is made faster by sodium chloride and slower by alum or borax. The air addition of alum to the plaster of Paris makes it set into a hard mass. This mixture is known as Keene’s cement.

On being heated above 475 K, plaster of Paris gives anhydrous calcium sulphate, commonly known as dead burnt plaster. It takes up water very slowly and does not set at all.

Uses

1. Plaster of Paris finds use in surgical bandages, dentistry and orthopaedic plaster for setting broken bones.
2. It is also used in making casts for toys and statues.
3. Plaster of Paris is also used in building materials.

Calcium carbonate

Calcium carbonate is a white solid that occurs naturally in two crystalline forms: calcite and aragonite.

These materials make up the bulk of such rocks as marble, limestone and chalk. Calcium carbonate can be prepared by passing a limited amount of carbon dioxide through slaked lime or by the addition of sodium carbonate to calcium chloride.

⇒ \(\begin{gathered}
\mathrm{Ca}(\mathrm{OH})_2+\mathrm{CO}_2 \rightarrow \mathrm{CaCO}_3+\mathrm{H}_2 \mathrm{O} \\
\mathrm{CaCl}_2+\mathrm{Na}_2 \mathrm{CO}_3 \rightarrow \mathrm{CaCO}_3+2 \mathrm{NaCl}
\end{gathered}\)

The use of excess carbon dioxide to prepare calcium carbonate results in the formation of calcium bicarbonate.

Properties

1. On heating, calcium carbonate decomposes and carbon dioxide is released

⇒ \(\mathrm{CaCO}_3 \stackrel{1200 \mathrm{~K}}{\longrightarrow} \mathrm{CaO}+\mathrm{CO}_2\)

2. It reacts with acids to liberate CO2

⇒ \(\begin{gathered}
\mathrm{CaCO}_3+2 \mathrm{HCl} \rightarrow \mathrm{CaCl}_2+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2 \\
\mathrm{CaCO}_3+\mathrm{H}_2 \mathrm{SO}_4 \rightarrow \mathrm{CaSO}_4+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2
\end{gathered}\)

Uses

1. Calcium carbonate is used as a building material in the form of marble.
2. It is employed in the manufacture of quicklime and also of sodium carbonate by the Solvay process.
3. With magnesium carbonate, calcium carbonate is used as a flux in the extraction of metals like iron.
4. Calcium carbonate is used in toothpaste, face powders, antacids, adhesives, paints and distempers.

Cement

Cement is one of the most important building materials. When mixed with water and allowed to stand, it sets to a very hard mass, which resembles Portland rock—a natural limestone in the Isle of Portland, England.

Hence, cement was given the name Portland cement in 1824 by Joseph Aspidin, a mason who lived in Leeds, England.

Composition of cement The composition of cement is given in terms of oxides. The average composition is:

• CaO 60-65%
• Fe203 2.5%
• Si02 22-25%
• MgO 2-3%
• A1203 6-8%

A lesser proportion of lime than that given above results in a decrease in the strength of the cement, while a higher proportion causes the cement to crack after setting.

Cement which sets slowly contains an excess of silica while quick-setting cement contains an excess of alumina.

At higher temperatures, the calcium oxide reacts with the aluminosilicates and silicates to form a mixture of various silicates and aluminates of calcium, chiefly tricalcium silicate (Ca3Si05), dicalcium silicate (Ca2Si04) and tricalcium aluminate (Ca3 A1206). Of these, tricalcium silicate is the most important constituent.

Manufacture

The most important raw materials needed for the manufacture of cement are limestone (which provides lime) and clay (which provides silica, along with oxides of aluminium, iron and magnesium). When clay and lime are strongly heated together in a rotatory kiln, they fuse and react to form cement clinker.

The following reactions take place.

⇒ \(\begin{aligned}
2 \mathrm{CaO}+\mathrm{SiO}_2 & \rightarrow 2 \mathrm{CaO} \cdot \mathrm{SiO}_2 \\
3 \mathrm{CaO}+\mathrm{SiO}_2 & \rightarrow 3 \mathrm{CaO} \cdot \mathrm{SiO}_2 \\
3 \mathrm{CaO}+\mathrm{Al}_2 \mathrm{O}_3 & \rightarrow 3 \mathrm{CaO} \cdot \mathrm{Al}_2 \mathrm{O}_3 \\
2 \mathrm{CaO}+\mathrm{Al}_2 \mathrm{O}_3 & \rightarrow 2 \mathrm{CaO} \cdot \mathrm{Al}_2 \mathrm{O}_3 \\
4 \mathrm{CaO}+\mathrm{Al}_2 \mathrm{O}_3+\mathrm{Fe}_2 \mathrm{O}_3 & \rightarrow 4 \mathrm{CaO} \cdot \mathrm{Al}_2 \mathrm{O}_3 \cdot \mathrm{Fe}_2 \mathrm{O}_3
\end{aligned}\)

The mixture (cement clinker) obtained is composed of silicates and aluminates. It is powdered and mixed with gypsum (1.5-2%) (CoS04-2H20) to slow down the process of setting. The final mixture is ground to a fine powder which is grey in colour and filled in airtight bags.

Setting Of Cement

When cement is to be used, it is mixed with water. The cement reacts with water to form a gelatinous mass (the reaction is exothermic), which slowly sets into a hard mass which has —Si—O—Si— and —Si—O—Al— chains.

The setting time depends on the final composition of the cement. Tricalcium silicate sets quickly, within 2-3 days.

Dicalcium silicate sets slowly and develops strength in 3-4 weeks. However, tricalcium aluminate sets instantaneously in the presence of water.

The demand for cement has increased considerably due to the increase in construction. Attempts are being made to find a substitute for cement. When mixed with cement, fly ash, a waste product of the steel industry, reduces the cost of cement without affecting its setting quality.

Uses

A mixture of cement and sand (in the ratio of 1:3) is mixed with water (the required amount) and is used as mortar for the construction and plastering of brick walls.

A mixture of cement, sand and gravel (in the ratio 1: 2: 4) is mixed with water (required amount) and is known as concrete, which is used as a building material.

Concrete used in conjunction with iron frameworks is known as reinforced cement concrete (RCC). It is used for the construction of roofs and pillars, and also for the construction of dams, bridges, etc.

High-alumina cement is obtained by fusing limestone and bauxite with small amounts of SiOz and Ti02 at 1750-1900 K in a rotary kiln.

It is more expensive than the usual Portland cement. However, it has the advantage that it is much quicker and acquires high strength in a short time (24 hours). It is used for making beams for bridges and buildings.

It can withstand temperatures up to 1800 K and is, therefore, used with refractory bricks in furnaces. An additional advantage of high-alumina cement is its resistance to seawater and dilute mineral acids.

Biological Role of Sodium, Potassium, Magnesium and Calcium

A number of elements play a very important role in biological systems. Of the 27 essential elements, 15 are metals.

The metals required in major quantities are Na, K, Mg and Ca. Minor quantities of Mn, Fe, Co, Cu, Zn and Mo, and trace amounts of V, Cr, Sn, Ni and Al are also required in biological systems.

Sodium and potassium ions balance the electrical charges associated with the negatively charged organic macromolecules in the cell. They also help to maintain the osmotic pressure inside the cell in order to keep it turgid and prevent its collapse.

Though sodium and potassium are similar in their chemical properties, their biological functions are quite different. Sodium ions are actively expelled from cells into the extracellular fluid whereas potassium ions are not.

In red blood cells, the ratio of potassium to sodium is 7:1 in human beings, rabbits, rats and horses, and 1:15 in cats and dogs. The difference in the amounts of each ion (Na⁺ and K⁺) in biological components is due to the quantitative difference in the ability of Na⁺ and K⁺ to penetrate cell membranes.

However, the different ratios of Na⁺ and K⁺ inside and outside the cell produce an electrical potential across the cell membrane; this is essential for the functioning of nerve and muscle cells. The movement of glucose into the cells is associated with Na ions. They enter the cell together.

The K+ ions inside the cell are essential for the metabolism of glucose, the synthesis of proteins and the activation of enzymes.

Thus, a sodium-potassium pump operates across the cell membranes, which is fuelled by the hydrolysis of ATP (adenosine triphosphate—the energy-currency molecule of living systems) to ADP (adenosine diphosphate).

Magnesium ions are concentrated inside animal cells and calcium ions are concentrated in the body fluids outside the cell, in the same way as K⁺ concentrates inside the cell and Na+ outside it.

Both Mg²⁺ and Ca²⁺ ions play a vital role in biological systems for the storage of energy. They are also essential for the transmission of impulses along nerve fibres. Magnesium is an important constituent of chlorophyll in green plants.

Calcium is an important constituent of bones and teeth. The amount of calcium in bones is nearly 30 grams at birth and builds up to about 1200 grams in an adult. Hence the individual daily amounts should reach 400 milligrams during the adolescent growth spurt.

Calcium ions are also important in blood clotting and are required to trigger the contraction of muscles and to maintain the regular beating of the heart.

The S-Block Elements Multiple Choice Questions

Question 1. The reducing characteristics of alkali metals follow the order:

1. Na < K < Rb < Cs < Li
2. Li < Cs < Rb < K < Na
3. K < Na < Eb < Li < Cs
4. Rb < Li < Cs < K < N a

Answer: 1. Na < K < Rb < Cs < Li

Question 2. What happens when CO₂ is passed into limewater?

1. The limewater becomes turbid due to the formation of calcium bicarbonate.
2. The limewater becomes turbid due to the formation of calcium carbonate.
3. The turbidity formed disappears on passing C02 for a long time.
4. There is no change.

Answer: 2. The limewater becomes turbid due to the formation of calcium carbonate

Question 3. Which of the following reacts slowly with water?

1. Na
2. Ca
3. Li
4. k

Answer: 3. Ca

Question 4. A salt imparts a brick-red colour to a flame. The salt can be one of

1. Na
2. Ca
3. Mg
4. Li

Answer: 2. Ca

Question 5. The chloride of a metal is soluble in an organic solvent. The chloride can be

1. CaCl₂
2. NaCl
3. MgCl₂
4. BeCl₂

Answer: 4. BeCl₂

Question 6. Alkali metals do not occur in nature because they

1. Have A Small Size
2. Are very reactive
3. Are Monovalent
4. Are Radioactive

Answer: 2. Are very reactive

Question 7. From among the following, name the metal, which and its salts will impart a characteristic blue colour to a Bunsen flame.

1. Na
2. K
3. Rb
4. Cs

Answer: 4. Cs

Question 8. Slaked lime reacts with chlorine to give

1. CaCl₂
2. CaO
3. CaOCl₂
4. None Of These

Answer: 3. CaOCl2

Question 9. Gypsum on heating to 393 K gives

1. CaSO₄-2H₂O
2. CaSO₄
3. CaSO₄.1/2 H₂O
4. None Of These

Answer: 3. CaSO₄.1/2 H₂O

Question 10. The by-product of the Solvay process is

1. CO₂
2. NH₃
3. CaCl₂
4. None Of These

Answer: 3. CaCl₂

Question 11. The thermal stability of alkaline earth metal carbonates decreases in the order

1. BaCO₃ > SrCO₃> MgCO₃> CaCO₃
2. BaCO₃> SrCO₃> CaCO₃> MgCO₃
3. MgCO₃> CaCO₃> SrCO₃> BaCO₃
4. CaCO₃> SrCO₃> MgCO₃> BaCO₃

Answer: 2. BaCO₃> SrCO₃> CaCO₃> MgCO₃

Question 12. The raw materials used in the manufacture of Na2C03 by the Solvay process are

1. Sodium Chloride, Limestone And Ammonia
2. Sodium chloride, limestone and carbon dioxide
3. Sodium chloride and carbon dioxide
4. Limestone and calcium chloride

Answer: 1. Sodium Chloride, Limestone And Ammonia

Question 13. Among the following, the correct order of increasing ionic character is

1. MgCl₂ < BeCI₂ < BaCl₂ < CaCl₂
2. BeCl₂ < MgCl₂ < CaCl₂ < BaCl₂
3. MgCl₂ < BaCl₂ < BeCl₂ < CaCl₂
4. BaCl₂ < CaCl₂ < BeCl₂ < MgCl₂

Answer: 2. BeCl₂ < MgCl₂ < CaCl₂ < BaCl₂

Question 14. In the context of alkali metals, which of the following increases with an increase in atomic number?

1. Solubility of sulphates
2. Solubility of hydroxides
3. Ionisation energy
4. Electronegativity

Answer: 2. Solubility of hydroxides

Question 15. A solution of sodium in liquid ammonia is blue. This blue colour is due to

1. Ammonia
2. Sodium metal
3. Solvated electrons
4. Sodium ion

Answer: 3. Solvated electrons

Question 16. Which of the following gives only the monoxide on heating in an excess of air?

1. Rb
2. K
3. Cs
4. Li

Answer: 4. Li

Question 17. The increasing order of the basic characters of MgO, SrO, Kfi) and Cs20 is

1. CS₂O < K₂O < SrO < MgO
2. MgO < SrO < K₂O < Cs₂0
3. SrO < MgO < CS₂O < K₂O
4. MgO < SrO < Cs₂O < K₂O

Answer: 2. MgO < SrO < K₂O < Cs₂0

Question 18. Which of the following is less stable thermally?

1. LiF
2. CsF
3. NaCl
4. RbF

Answer: 2. CsF

Question 19. Which of the following is most stable to heat?

1. MgCO₃
2. SrCO₃
3. CaCO₃
4. BaCO₃

Answer: 4. BaCO₃

Question 20. An electric potential is produced across the membrane of living cells by the different ratios of certain metal ions inside
and outside cells. The metal ions involved are

1. Ca2⁺ and Na⁺
2. K⁺ and Ba2⁺
3. Na⁺ and k⁺
4. Mg2⁺ and Ca2⁺

Answer: 3. Na⁺ and k⁺

Question 21. When beryllium hydroxide and aluminium hydroxide are dissolved in an excess of an alkali, the ions formed are

1. \(\left[\mathrm{Al}(\mathrm{OH})_4\right]^{-} \text {and }\left[\mathrm{Be}(\mathrm{OH})_4\right]^{-}\)
2. \(\left[\mathrm{Al}^{3+}, \mathrm{Be}^{2+}\right] \text { and } \mathrm{OH}^{-}\)
3. \(\left[\mathrm{Al}(\mathrm{OH})_4\right\}^{2-} \text { and }\left[\mathrm{Be}(\mathrm{OH})_4\right]^{-}\)
4. \(\left[\mathrm{Be}(\mathrm{OH})_4\right]^{2-} \text { and }\left[\mathrm{Al}(\mathrm{OH})_4\right]^{-}\)

Answer: 4. \(\left[\mathrm{Be}(\mathrm{OH})_4\right]^{2-} \text { and }\left[\mathrm{Al}(\mathrm{OH})_4\right]^{-}\)

Hydrocarbons

Hydrocarbons, or compounds which contain only carbon and hydrogen, are the simplest organic compounds, the main types being alkanes, alkenes, alkynes and arenes.

Hydrocarbons are mainly used as fuels for domestic and industrial purposes. Petroleum, kerosene, CNG, LPG, etc., are all mixtures of hydrocarbons.

All other families of organic compounds can be considered to be derived from hydrocarbons by replacing one or more hydrogen atoms with the appropriate functional group.

Hydrocarbons Classification

Hydrocarbons can be classified either on the basis of their structures or on the basis of whether they are saturated or unsaturated. Structurally, they can be of two types—acyclic and cyclic.

Acyclic Hydrocarbons

Hydrocarbons which have open chains of carbon atoms are called acyclic hydrocarbons.

These are also known as aliphatic hydrocarbons. The name aliphatic comes from the Greek word aliphos, meaning fat. Alkanes, alkenes and alkynes are acyclic hydrocarbons.

Alkanes are saturated and have only carbon-carbon single bonds. For example, ethane (CH₃CH₃), propane (CH₃CH₂CH₃) and butane (CH₃CH₂CH₂CH₃).

An alkene is an unsaturated hydrocarbon with at least one carbon-carbon double bond.

Some examples are ethene (CH₂=CH₂), propene (CH₃CH=CH₂) and but-2-ene (CH₃CH=CH—CH₃).

Like alkenes, alkynes too, are unsaturated hydrocarbons, but they have at least one carbon-carbon triple bond. Some examples are ethyne (CH=CH), propyne (CH₃C≡CH) and but-2-yne (CH₃C=CCH₃)

Cyclic Hydrocarbons

Hydrocarbons which contain closed chains or rings of carbon atoms are known as cyclic hydrocarbons. These can be of two types—alicyclic and aromatic.

Alicyclic hydrocarbons

They contain a ring of three or more carbon atoms. They resemble aliphatic hydrocarbons in their properties and are of three types, viz., cycloalkanes, cycloalkenes and cycloalkanes.

Cycloalkanes are saturated hydrocarbons in which all the carbon atoms are joined by single covalent bonds to form a ring. Cyclopropane, cyclobutane, cyclopentane and cyclohexane are a few examples.

Cycloalkenes Unsaturated, alicyclic hydrocarbons containing at least one carbon-carbon double bond are known/ as cycloalkenes.

Some examples of Cyclopropane, cyclobutane, cyclopentane and cyclohexane

Cycloalkynes Unsaturated alicyclic hydrocarbons containing one carbon-carbon triple bond are called cycloalkynes.

Some examples are Cyclopropane, cyclobutane, cyclopentane and cyclohexane are unstable since they are highly strained.

Aromatic Hydrocarbons

These are also called arenes. These compounds were obtained from natural resources like balsam and resins. They all had a pleasant odour and so, obtained their name from the Greek word aroma (a pleasing smell).

However, it was later found that not all aromatic compounds had a pleasant smell.

When subjected to various methods of treatment, the aromatic compounds finally produced benzene or its derivatives.

This led to the conclusion that aromatic compounds are hydrocarbons containing one or more benzene rings. These rings may be fused or isolated.

Arenes are also known as benzenoid compounds since their properties are similar to those of benzene. Some examples of aromatic hydrocarbons are as follows.

The classification discussed above may be represented as follows

As stated earlier, hydrocarbons can also be classified as

1. Saturated And
2. Unsaturated.

Saturated hydrocarbons contain only carbon-carbon single bonds and include alkanes and cycloalkanes.

Unsaturated hydrocarbons contain at least one carbon-carbon double or triple bond. Alkenes, alkynes and arenes fall in this class.

Of these, alkenes and alkynes can be either acyclic or cyclic, while arenes are cyclic.

Here it should be made clear that both aromatic and alicyclic compounds are closed-chain structures but their properties are totally different.

This can be attributed to the benzene-based structure of compounds which contains at least six carbon atoms.

Also, the percentage of carbon is higher in aromatic compounds than in the corresponding aliphatic and alicyclic hydrocarbons. For example,

Alkanes

If we examine the molecular formulae of alkanes which, we will see that the successive members of the family differ constantly by —CH₂.

In other words, if we replace one H atom in methane (CH₄) with CH₃, we get C₂H₆—the next higher member (ethane).

The alkanes, thus, form a homologous series with the general formula C_nH_2n+2, where n is the number of carbon atoms in the molecule.

A series of compounds in which each member differs from the next member by a constant number of carbon and hydrogen atoms is called a homologous series, and the members of the series are called homologues.

Hydrocarbons Conformations

For the sake of convenience, the structures of hydrocarbons are represented in two-dimensional forms or plane-structural formulae as shown below. But you are aware of the fact that most organic molecules have three-dimensional structures.

An important aspect of the three-dimensional shape of molecules is their conformations.

The above structural formulae do not show the spatial arrangement of atoms. This drawback can be overcome by representing the structures in their three-dimensional forms.

[These are discussed under conformations of alkanes. In hydrocarbons, the carbon-carbon single bond is a bond (formed by the overlapping of sp3 hybrid orbitals of carbon atoms) and has cylindrical symmetry.

This leads to the possibility of free rotation about the carbon-carbon single bond and hence, a large number of different spatial arrangements of atoms or groups of atoms attached to the carbon atoms.

These different spatial arrangements are called conformations. Thus, the large number of different arrangements of atoms in a molecule which result from the rotation of carbon-carbon single bonds are called conformers or rotational isomers.

Certain physical properties show that the rotation of carbon atoms around the C—C bond is not quite free. This is due to the difference in the energy of various arrangements. The rotation is hindered by an energy barrier which may vary from 1 to 20 kJ mol-1.

The difference in energy is caused due to the interaction between electron clouds of the carbon-hydrogen bonds. The repulsive interaction between electron clouds is referred to as torsional strain.

The energy required to rotate the molecule about the C—C bond is torsional energy. Torsional strain and torsional energy arise due to the steric hindrance that occurs whenever bulky portions of a molecule repel other molecules or other parts of the same molecule.

The angle of torsion is a dihedral angle between two planes. Actually, the dihedral angle is the one formed by the intersection of two planes. Conformational isomers or conformers are rapidly interconvertible and nonseparable.

X The energy for this interconversion or rotational motion is acquired from the collisions between the molecules and with the walls of the container.

Remember that no bonds are C broken or made during rotational motion or change of conformation, so there is only one compound. The phenomenon of conformation can be best understood by considering the case of ethane.

In the ethane molecule, the two carbon atoms are joined by a bond. If one of the carbon atoms (methyl group) is fixed and the other is rotated about the C —C bond, a large number of arrangements of the hydrogen atoms attached to one carbon atom with respect to the hydrogen atoms of the second carbon atom are possible.

Out of the several arrangements (conformations) possible, only the following two are important. Staggered conformation In this the hydrogen atoms bonded to the two carbon atoms arc staggered with respect to one another.

This implies that the hydrogen atoms of the two methyl groups are a maximum distance apart, making the repulsion between them the minimum possible. Therefore, the conformation is of the lowest potential energy for ethane.

Eclipsed conformation In this the hydrogen atoms bonded to one carbon atom are directly behind those connected to the other, leading to the maximum possible repulsion (maximum energy) between the sets of hydrogen atoms.

Of the two conformations, the staggered conformation is more stable because there is less repulsion between the hydrogen atoms.

All other possibilities between staggered and eclipsed forms are known as skew or gauche forms. Hence the order of stability is staggered > skew > eclipsed.

Conformers are mostly represented in one of two ways. One is called sawhorse projection and the other, is Newman projection.

Sawhorse projection In this method of projecting the three-dimensional structure on paper, the molecule is viewed from above.

The C —C bond is drawn diagonally. The carbon atom shown lower is the one in front and the one drawn above it and to the right represents the carbon atom at the back.

Newman projection Named after M. S. Newman, who first proposed this method of representing the three-dimensional structure on paper, this is easier to visualise than the one described before.

The projection is obtained by viewing the molecule along the C —C bond. The carbon atom closer to the viewer is represented by a circle. The other atom lies behind this and so cannot be seen.

Tire bonds between the first carbon atom and the hydrogen atoms attached to it are shown as equally spaced radial lines from the centre of the circle.

The bonds of the carbon atom which is at the back are shown as lines drawn from the circumference of the circle.

The energy difference between the staggered and eclipsed conformations is about 12.5 kJ mol-1.

This energy difference is not large enough to prevent rotation about the CT bond.

In fact, even at room temperature, the two conformations keep changing from one to the other and it is impossible to isolate either. The variation of energy with rotation about the C —C bond.

Isomerism

There can be only one way in which the carbon and hydrogen atoms combine in the first three members of the alkane homologous series.

But when the carbons and hydrogens in higher members combine, more than one structure can result.

For example, in butane (C₄H₁₀) the carbon atoms can be joined either in a continuous chain or in a branched chain.

Since the two butanes have the same molecular formula but different structures, they exhibit structural isomerism.

u-Butane has a continuous-chain structure and isobutane, has a branched-chain structure. Isomers which differ in the way their carbon chains are arranged are known as chain isomers.

Now consider the next homologue, pentane (C₅H₁₂). The carbon chain in this molecule can be arranged in three different ways.

As you can see, all three structures are chain isomers of pentane. We have already discussed the classification of carbon atoms as primary, secondary, tertiary and quaternary in a molecule. Can you identify the 1°, 2°, 3° and 4° carbon atoms in the above molecular structures?

Example An alkane with the molecular formula C8H18 can have the following structures. Identify which of them represents the same molecule and which is the isomer.

Solution:

Let us first write the IUPAC names for all three structures.

1. 2,4-Dimethylhexane
2. 2,4-Dimethylhexane
3. 2,5-Dimethylhexane

Thus, the IUPAC names suggest that structures represent the same molecule and are the isomers of and.

It is important to note that different isomers are different chemical compounds, and so they have different chemical and physical properties. For example, the b.p. of n-butane is 273 K whereas that of isobutane is 261 K.

We have already discussed the alkyl groups that are attached to carbon atoms in alkanes or other classes of compounds. These substituent alkyl groups have the general formula C_nH_2n+1.

Depending upon which carbon atom (of the alkyl group) is attached to the other group, the alkyl groups can be straight-chain or branched-chain. In other words, different types of alkyl groups result, depending upon which hydrogen is removed from the parent alkane.

For Example, there are four different kinds of butyl groups. Two (n-butyl and sec-butyl) are derived from the l straight-drain butane and two (isobutyl and ferf-butyl) are derived from the branched-chain butane.

The alkyl groups themselves are not stable compounds and are simply parts of molecules that help us name compounds.

The prefixes sec- and tert- refer to the kind of carbon (2° and 3° respectively) of the alkyl group which gets attached to the other group. We have already discussed the nomenclature of alkanes and other hydrocarbons.

The examples given in this chapter in the subsequent sections will help you to further understand the IUPAC 2 nomenclature.

Example Write the structure of 3-lsopropyl-2-methylhexane.
Solution:

1. Draw the carbon chain of the parent alkane (hexane) and number the carbon atoms.

⇒ \(\stackrel{1}{\mathrm{C}}-\stackrel{2}{\mathrm{C}}-\stackrel{3}{\mathrm{C}}-\stackrel{4}{\mathrm{C}}-\stackrel{5}{\mathrm{C}}-\stackrel{6}{\mathrm{C}}\)

2. Attach isopropyl at C-3 and a methyl group at C-2

3. Add the requisite number of hydrogen atoms to each carbon of the parent chain.

Thus, we get the correct structure of 3-isopropyl-2-methylhexane.

Example Draw the structural formula of the following compounds:

1. 3,3-Diethyl-5-isopropyl-4-methyl octane
2. 2,2,4-Trimethylpentane

Solution:

1. Draw the carbon chain of the parent alkane (octane) and number the carbon atoms in it

⇒ \(\underset{1}{\mathrm{C}}-\mathrm{C}_2-\mathrm{C}_3-\mathrm{C}_4-\mathrm{C}_5-\underset{6}{\mathrm{C}}-\underset{7}{\mathrm{C}}-{ }_8^{\mathrm{C}}\)

Attach two ethyl groups at C-3, one isopropyl at C-5 and one methyl group at C-4.

Add the requisite number of hydrogen atoms to each carbon of the parent chain.

This is the structure of 3,3-Diethyl-5-isopropyl-4-methyloctane.

In this case, the parent alkane is pentane with three substituent methyl groups attached.

Thus, the structure of the compound will be:

Preparation

The main source of alkanes is petroleum, together with the accompanying natural gas.

Natural gas, of course, contains low molecular weight (volatile) alkanes, i.e., 80 per cent of methane and 10 per cent of ethane, the remaining 10 per cent being a mixture of next higher homologues.

Crude petroleum, on the other hand, is a mixture of higher alkanes. Alkanes can be prepared by the following methods.

From Unsaturated Hydrocarbons

Alkanes are obtained by passing a mixture of unsaturated hydrocarbons (e.g., alkenes and alkynes) and hydrogen over a catalyst.

The catalyst is a finely divided metal, usually platinum, palladium or nickel.

A relatively higher temperature and pressure are required with nickel. The catalyst causes the addition of molecular hydrogen to the unsaturated bond.

⇒ \(\underset{\text { Ethene }}{\mathrm{CH}_2=\mathrm{CH}_2}+\mathrm{H}_2 \stackrel{\mathrm{Pt} / \mathrm{Pd} / \mathrm{Ni}}{\longrightarrow} \underset{\text { Ethane }}{\mathrm{CH}_3-\mathrm{CH}_3}\)

⇒ \(\underset{\text { Propene }}{\mathrm{CH}_3 \mathrm{CH}=\mathrm{CH}_2}+\mathrm{H}_2 \stackrel{\mathrm{Pt} / \mathrm{Pd} / \mathrm{Ni}}{\longrightarrow} \underset{\text { Propane }}{\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CH}_3}\)

⇒ \(\underset{\text { Propyne }}{\mathrm{CH}_3 \mathrm{C} \equiv \mathrm{CH}}+2 \mathrm{H}_2 \stackrel{\mathrm{Pt} / \mathrm{Pd} / \mathrm{Ni}}{\longrightarrow} \underset{\text { Propane }}{\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CH}_3}\)

From alkyl halides

Reduction of alkyl halides (except fluorides) with zinc and dilute acid (viz., hydrochloric acid) leads to the replacement of a halogen atom by a hydrogen atom.

Alkyl halides, on treatment with sodium metal in dry ether, give higher, symmetrical alkanes

⇒ \(\underset{\text { Bromomethane }}{\mathrm{CH}_3 \mathrm{Br}}+2 \mathrm{Na}+\mathrm{CH}_3 \mathrm{Br} \stackrel{\text { dryether }}{\longrightarrow} \underset{\text { Ethane }}{\mathrm{CH}_3-\mathrm{CH}_3+2 \mathrm{NaBr}}\)

This reaction is called the Wurtz reaction. If two different alkyl halides are used in this reaction (e.g., CH₃Br and C₂H₅Br), a mixture of alkanes (CH₃CH₃C₂H₅C₂H₅, CH₃C₂H₅) is obtained.

Decarboxylation of carboxylic acids

Sodium salts of carboxylic acids, on being heated strongly with soda lime (NaOH + CaO), give alkanes.

Since the carbon dioxide is removed, the corresponding alkane obtained has one carbon atom less than the carboxylate salt.

⇒ \(\underset{\text { Sodium acetate }}{\mathrm{CH}_3 \mathrm{COONa}}+\mathrm{NaOH} \underset{\text { heat }}{\stackrel{\mathrm{CaO}}{\longrightarrow}} \mathrm{CH}_4+\mathrm{Na}_2 \mathrm{CO}_3\)

Such a reaction in which carbon dioxide is eliminated from a carboxylic group is called decarboxylation.

Kolbe’s electrolytic method

This method involves the electrolysis of an aqueous solution of the sodium or potassium salt of a carboxylic acid.

A higher alkane containing an even number of carbon atoms is obtained.

⇒ \(\underset{\text { Sodium acrtate }}{2 \mathrm{CH}_3 \mathrm{COONa}}+2 \mathrm{H}_2 \mathrm{O} \stackrel{\text { dectrolysis }}{\longrightarrow} \mathrm{CH}_3 \mathrm{CH}_3+2 \mathrm{CO}_2+2 \mathrm{NaOH}+\mathrm{H}_2\)

The reaction proceeds as follows.

⇒ \(2 \mathrm{CH}_3 \mathrm{COO} \mathrm{Na}^{+} \stackrel{\text { electrolysis }}{\rightleftharpoons} 2 \mathrm{CH}_3-\stackrel{\mathrm{O}}{\rightleftharpoons}-\overline{\mathrm{O}}+2 \mathrm{Na}^{+}\)

At anode:

At cathode:

⇒ \(2 \mathrm{Na}^{+} \stackrel{+2 \mathrm{e}}{\longrightarrow} 2 \mathrm{Na} \stackrel{2 \mathrm{H}_2 \mathrm{O}}{\longrightarrow} 2 \mathrm{NaOH}+\mathrm{H}_2 \uparrow\)

Since the two free radicals produced as a result of the decarboxylation of the acetate radical combine to form alkanes, methane, which contains only one carbon atom, cannot be prepared by this method.

Physical Properties

Alkanes, being covalent in nature, are held together by weak van der Waals forces. The intermolecular forces are strong in the large molecules.

Thus, the first four members of the alkane homologous series are colourless gases, and the next thirteen members from C-5 to C-17 are colourless liquids. The higher members, from C-18 onwards, are waxy solids.

The alkane molecule is nonpolar or very weakly polar due to the very low electronegativity difference between carbon and the hydrogen atom.

Being nonpolar, alkanes are insoluble in water, which is polar. However, they are soluble in nonpolar solvents like carbon tetrachloride and benzene.

The boiling point of n-alkanes increases with an increase in molecular weight.

In the case of alkanes which exist in straight-chain as well as branched-chain forms, the branched-chain isomer has a lower boiling point than the corresponding straight-chain isomer.

Thus, n-butane has a higher boiling point than that of isobutane. The boiling point is still lower if the branching is more.

Thus, neopentane boils at a temperature lower than the boiling point of isopentane.

Why does the increase in branching of the carbon chain lead to the lowering of the boiling point of the alkane?

Because branching in a carbon chain reduces the surface area of the molecule and therefore brings down intermolecular attractive forces, resulting in a decrease in boiling point.

The melting points of alkanes also increase with the increase in molecular weight but the increase is not so regular.

This is because the intermolecular forces in a crystal depend not only on the size of the molecule but also on how it fits within a crystal lattice.

However, alkanes with an even number of carbon atoms have a higher melting point than those with an odd number of carbon atoms.

This is largely due to the better crystal lattice packing of the alkanes with an even number of carbon atoms.

Chemical Properties

Alkanes are inert in nature and do not undergo any chemical reactions under ordinary conditions with adds, alkalis, oxidising and reducing agents.

However, under certain conditions, alkanes undergo substitution reactions and some others like halogenation, combustion and isomerisation.

The nonreactivity of alkanes with ionic reagents can be attributed to the nonpolar nature of alkanes. We will now discuss some of the reactions of alkanes.

Halogenation

Alkanes react with halogens at 523-673 K or in the presence of sunlight to form halogen-substituted alkanes and hydrogen halide.

Reactions in which the hydrogen atoms of alkanes are substituted by other groups are known as substitution reactions.

The higher alkanes, apart from halogenation, also undergo nitration and sulphonation substitution reactions.

Methane reacts with chlorine to form chloromethane, which, on further reaction with chlorine, forms dichloromethane.

⇒ \(\mathrm{CH}_4+\mathrm{Cl}_2 \longrightarrow \underset{\text { Chloromethane }}{\mathrm{CH}_3 \mathrm{Cl}}+\mathrm{HCl}\)

⇒ \(\mathrm{CH}_3 \mathrm{Cl}+\mathrm{Cl}_2 \longrightarrow \underset{\text { Dichloromethane }}{\mathrm{CH}_2 \mathrm{Cl}_2}+\mathrm{HCl}\)

When the chlorination is continued further, trichloromethane (chloroform) and tetrachloromethane (carbon tetrachloride) are formed.

⇒ \(\mathrm{CH}_2 \mathrm{Cl}_2+\mathrm{Cl}_2 \longrightarrow \underset{{\text { Trichloromethane } \\ \text { (chloroform) }}}{\mathrm{CHCl}_3}+\mathrm{HCl}\)

⇒ \(\mathrm{CHCl}_3+\mathrm{Cl}_2 \longrightarrow \underset{{\text { Tetrachlomomethane } \\ \text { (earbon tetrachloride) }}}{\mathrm{CCl}_4}+\mathrm{HCl}\)

Thus, the chlorination of methane gives a mixture of products. The composition of the product mixture depends on the ratio in which the reactants (methane and chlorine) are used.

If chlorine is used in excess then the percentage of carbon tetrachloride obtained is more. The mixture obtained can be separated into its constituents by fractional distillation.

The chlorination of methane is an example of a chain reaction, a reaction that involves a series of steps. Each step in the chain reaction generates a reactive substance that brings about the next step.

The reactivity of bromine with alkanes is less than that of chlorine. Unlike chlorination and bromination of alkanes, the iodination of alkanes is a reversible process.

However, the reaction can be made to proceed in one direction in the presence of an oxidising agent, which decomposes the hydrogen iodide produced.

⇒ \(\mathrm{CH}_4+\mathrm{I}_2 \rightleftharpoons \mathrm{CH}_3 \mathrm{I}+\mathrm{HI}\)

⇒ \(5 \mathrm{HI}+\underset{\text { lodic acid }}{\mathrm{HIO}_3} \longrightarrow 3 \mathrm{I}_2+3 \mathrm{H}_2 \mathrm{O}\)

The fluorination of alkanes is explosive and even in the dark the reaction needs to be controlled by mixing the reactants in an inert solvent.

The reactivity of alkanes with halogens is of the order: F2 > Cl2 > Br2 > I2. The ease of abstraction of hydrogen atoms follows the sequence 3°> 2°> 1°> CH₃ —H.

Mechanism Let us discuss the mechanism of the chlorination of methane as an example.

The halogenation of other alkanes proceeds according to the same mechanism as that of methane.

The chlorination of methane is believed to proceed via a free-radical mechanism involving three steps—initiation, propagation and termination.

Initiation The reaction is initiated by the homolysis of the chlorine molecule to form free radicals. The Cl—Cl bond is weaker than the C —C and C—H bonds and breaks up easily in the presence of sunlight or heat.

Propagation The chlorine free radical attacks the C—H bond of the methane molecule to generate a methyl radical along with the formation of a molecule of hydrogen chloride.

The methyl free radical thus produced attacks the second molecule of chlorine to yield methyl chloride and another chlorine free radical.

Each of the two chain-propagation steps 1 and 2 consumes a reactive substance and generates another.

Termination Finally, when the chain reaction terminates, the reactive intermediates are not generated but consumed.

The two reactive intermediates like two chlorine radicals or two methyl radicals or one methyl and one chlorine radical combine.

⇒ \(\begin{aligned}
& \mathrm{Cl} \cdot+\mathrm{Cl} \cdot \longrightarrow \mathrm{Cl}_2 \\
& \mathrm{CH}_3+\mathrm{CH}_3+\mathrm{CH}_3 \mathrm{CH}_3 \\
& \mathrm{CH}_3+\mathrm{Cl} \cdot \longrightarrow \mathrm{CH}_3 \mathrm{Cl}
\end{aligned}\)

Oxidation

Combustion On being heated, alkanes completely oxidise in the presence of air or oxygen, producing C02, H2O and a large amount of heat.

⇒ \(\mathrm{CH}_4(\mathrm{~g})+(\text { excess }) 2 \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ; \Delta_c \mathrm{H}^{\ominus}=-890 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

The more the molecular weight of the alkane, the more is the heat produced on combustion. Alkanes (methane, ethane, propane, butane, etc.) are used as fuel, e.g., LPG.

In an insufficient amount of air, alkanes undergo incomplete combustion, producing carbon in a very finely divided state —carbon black.

Carbon black is used to make paints and printers’ ink. It is also used in the rubber industry to make tyres.

⇒ \(\mathrm{CH}_4(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{C}(\mathrm{s})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

Controlled oxidation The controlled oxidation, i.e., oxidation in a regulated supply of air at high temperature and pressure, under various conditions, of alkanes leads to different products. Some examples are as follows.

⇒ \(2 \mathrm{CH}_4+\mathrm{O}_2 \underset{\text { heat }}{\stackrel{\mathrm{Cu} .523 \mathrm{~K}, 1000 \mathrm{~atm}}{\longrightarrow}} \underset{\text { Methanol }}{2 \mathrm{CH}_3 \mathrm{OH}}\)

⇒ \(\mathrm{CH}_4+\mathrm{O}_2 \underset{\text { heat }}{\stackrel{\mathrm{Mo}_2 \mathrm{O}_3}{\longrightarrow}} \underset{\text { Methanal }}{\mathrm{HCHO}}+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\mathrm{CH}_3 \mathrm{CH}_3+3 \mathrm{O}_2 \stackrel{\left(\mathrm{CH}_3 \mathrm{COO}\right)_2 \mathrm{Mn}}{\longrightarrow} \underset{\text { heat }}{2} \underset{\text { Ethanoic adid }}{2 \mathrm{CH}_3 \mathrm{COOH}}+2 \mathrm{H}_2 \mathrm{O}\)

Normally, alkanes are resistant to strong oxidising agents but alkanes with a tertiary hydrogen atom can be oxidised to the corresponding alcohol by potassium permanganate.

⇒ \(\underset{\text { 2-Methylpropane }}{\left(\mathrm{CH}_3\right)_3 \mathrm{CH}}+[\mathrm{O}] \stackrel{\mathrm{KMnO}_4}{\longrightarrow} \underset{\text { 2-Methyl-propan-2-ol }}{\left(\mathrm{CH}_3\right)_3 \mathrm{COH}}\)

Isomerisation On heating in the presence of aluminium chloride and hydrogen chloride, normal alkanes get converted to their corresponding branched-chain isomers. For example,

The process is used to increase the branched-chain content of lower alkanes produced by cracking since branched-chain isomers in petrol are more valuable than n-alkanes.

Aromatisation Alkanes containing six to ten carbon atoms can be converted into benzene and its homologues at a high temperature in the presence of a catalyst.

The process is known as aromatisation and takes place through the simultaneous dehydrogenation and cyclisation of the alkane to give an aromatic compound containing a number of carbon atoms.

Reaction with steam Methane reacts with steam at 1273 K in the presence of nickel, which acts as a catalyst, to give carbon monoxide and dihydrogen. This mixture of carbon monoxide and hydrogen is known as water gas.

⇒ \(\mathrm{CH}_4+\mathrm{H}_2 \mathrm{O} \underset{\text { heat }}{\stackrel{\mathrm{Ni}}{\longrightarrow}} \mathrm{CO}+3 \mathrm{H}_2\)

This procedure is used for the industrial preparation of dihydrogen

Pyrolysis (Cracking)

When heated to high temperatures (773 K-873 K), alkanes decompose into smaller molecules.

This is known as cracking. The thermal decomposition of organic compounds is known as pyrolysis.

The products obtained from the cracking of alkanes depend on the structure of the alkane, pressure conditions and the catalyst present.

For example, dodecane, a constituent of kerosene oil, when heated to 973 K, in the presence of catalysts platinum palladium or nickel, gives a mixture of products (mainly heptane and pentene)

⇒ \(\underset{\text { Dodecane }}{\mathrm{C}_{12} \mathrm{H}_{26}} \underset{\mathrm{P} / \mathrm{Pd} / \mathrm{Ni}}{\stackrel{973 \mathrm{~K}}{\longrightarrow}} \mathrm{C}_7 \mathrm{H}_{16}+\mathrm{C}_5 \mathrm{H}_{10}+\text { other products }\)

Alkenes

Alkenes are unsaturated hydrocarbons with at least one carbon-carbon double bond. Their general formula is CnH2n. They are also called olefins (Greek: oil forming) since the lower members of this series produce oily products in reaction with halogens.

Structure Of Double Bond

The presence of the double bond in alkenes gives rise to certain special structural features which can be better understood if we consider the structure of the simplest alkene, ethene (ethylene).

Each carbon atom in ethene is sp² hybridised, which means that each carbon atom has three sp² orbitals lying in the same plane and inclined to one another at an angle of 120°, and an unhybridised 2p² orbital which is perpendicular to the plane of the sp² orbitals.

Two of the three sp² hybrid orbitals of each carbon atom overlap with the Is orbitals of two hydrogen atoms (forming C—H bonds).

The remaining sp² orbital of each carbon atom overlaps along the internuclear axis to form a (C —C) bond.

The unhybridised orbitals of the two carbon atoms (dash lines), which are perpendicular to the plane of the sp² orbitals, overlap sideways to form a π bond.

Thus, the C—C double bond consists of an o bond and an π bond. The n bond is weaker and makes alkenes reactive.

What makes TC a weaker bond? The n electrons are less involved in holding together the two carbon nuclei than the CT electrons are.

They form a cloud of π electrons above and below the plane of the atoms

During a reaction, these loosely held n electrons are particularly available to a reagent that is seeking electrons.

The electron-deficient reagents or compounds which are seeking a pair of electrons are called electrophilic reagents.

Electrophilic addition is the typical reaction of an alkene. The C —C bond length in ethene is 134 pm, which is less than that in ethane (154 pm). The C—C bond length in ethyne is still shorter (120 pm).

However the bond enthalpy of C=C (ethene) is greater (678 kJ mol-1) than that of C—C (ethane), which is 370 kJ mol-1.

Hence, the alkene molecule is more reactive than its corresponding alkane molecule, due to the presence of the double bond.

Example Calculate the number of it bonds in the following structures and write their IUPAC names

Solution:

1. The structure can be drawn as:

The IUPAC name is 2,5-Dimethylhex-2-ene.

2. The structure can be drawn as:

The IUPAC name of the structure is 7-Methyl-l,3,5-octatriene.

Isomerism

Alkenes normally show the following types of isomerism.

Position isomerism The first two members of the alkene series (viz., ethene, propene) do not show isomerism.

However, butene exhibits position isomerism as but-l-ene and but-2-ene. They differ in the position of the double bond.

⇒ \(\mathrm{H}_3 \mathrm{CCH}_2 \mathrm{CH}=\mathrm{CH}_2
But-1ene\)

⇒ \(\mathrm{H}_3 \mathrm{CCH}=\mathrm{CHCH}_3
But-2-ne\)

Chain isomerism Butene also shows chain isomerism as isobutene has a branched-chain structure and n-butene has a straight-chain structure

Geometrical isomerism Compounds which have the same structural formula, but in which atoms or groups have a different spatial arrangement about a double bond are called geometrical isomers and the phenomenon is known as geometrical isomerism.

Geometrical isomerism is exhibited by alkenes and their derivatives in which the double-bonded carbon atoms are linked to two different groups. In other words, all compounds containing a carbon-carbon double bond do not exhibit geometrical isomerism.

An alkene molecule exhibits geometrical isomerism only when the atoms or groups attached to each double-bonded carbon atom are different.

That is to say, geometrical isomerism is exhibited by molecules of the kind ABC=CAB or of the kind ABC=CDE but not of the kind AAC=CDE or of the kind ABC=CDD.

You have already studied the infinite number of conformational isomers which arise due to the rotation of carbon atoms connected through bonds in alkanes.

However, this is not the case in alkenes which have a double bond containing a cr bond and π bond. Rotation is possible in the case of a bond but not at all in that of a n bond.

The reason for this simply lies in the formation of π bonds. An π bond is formed by the overlap of two p orbitals.

The p orbitals lie perpendicular (above and below) to the plane of A orbitals(sp2 hybrid orbitals in this case) forming a CT bond.

Conversion of 1 into 2 is possible only when the molecule is twisted, which would definitely break the 71 bond. The n bond is formed by the sideways overlapping of p orbitals, the groups or atoms attached to the sp2 hybridised carbon atom cannot rotate about it.

Rotation is therefore possible by breaking the n bond, which would require energy of the order of 251 kJ mol-1.

This energy is not available at room temperature. Because of the energy barrier, there is hindered rotation about the double bond, which gives rise to geometric isomers.

Using a ball and stick model, geometrical isomers can be represented

Isomers in which similar atoms or groups lie on the same side of the double bond are called cis-isomers and those in which similar atoms or groups lie on opposite sides of the double bond are called trans-isomers.

The trans-isomers are usually more stable than the corresponding cis isomers. This will become clear if we consider cis- and trans-isomers with the formula ABC=CAB, in which A is the bulkier of the two groups A

And B (e.g., CH₃ —CH=CH—CH₃). In the cis-isomer, the two bulky A groups are very close to each other. The repulsion between the overlapping electron clouds of the A groups makes this isomer less stable than the trans isomer, in which the A groups are far apart.

There is no absolute method for determining whether a particular isomer is a cis- or trans-isomer.

However, the following characteristics are useful.

1. The cis-isomer is more polar than the trans-isomer. In other words, the cis-isomer has a greater dipole moment than the trans-isomer.

This will become clear if we consider the cis- and trans-isomers of 1,2-dichloroethene.

The trans-isomer has a small dipole moment. This is because the dipole moments of the two C—Cl bonds are opposed due to the symmetry of the molecule. The cis-isomer, being nonsymmetrical, has a larger dipole moment.

2. The cis-isomer has a lower melting point than the corresponding trans-isomer. For example, the m.p. of maleic acid, cis-HOOCCH=CHCOOH, is 130°C, while that of fumaric add trans-HOOCCH=CHCOOH, is 286º0.

3. The cis-isomer has a higher boiling point than the corresponding trans-isomer. For example, the b.p. of cis-2-butene is 4°C and that of trans-2-butene is 1ºC.

4. If the cis- and trans-isomers of an alkene have a COOH group then the cis compound forms an anhydride on heating while the trans compound does not. To give an example, this is how we distinguish between maleic acid and fumaric acid.

Example Draw cis and trans isomers of those which are capable of exhibiting cis-trans isomerism, of the following compounds.

1. Hex-l-ene
2. Hex-2-ene
3. Hex-3-ene

Solution: Hex-2-ene and Hex-3-ene will exhibit cis-trans isomerism.

Preparation

Alkenes are generally obtained from saturated compounds by the elimination of atoms or groups from the two adjacent carbon atoms.

Some common methods of preparation are discussed in the following.

Dehydration Of Alcohols

The elimination of a water molecule from a compound is called dehydration. On being heated with concentrated sulphuric acid or phosphoric acid, alcohols form the corresponding alkenes by the elimination of a water molecule.

This reaction is since the hydrogen attached to the p-carbon atom is removed. The carbon atom attached to the functional group is and the one next to it is p.

⇒ \(\underset{\text { Ethanol }}{\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{OH}} \underset{-43-453 \mathrm{~K}}{\stackrel{\operatorname{conc} \mathrm{H}_2 \mathrm{SO}_4}{\longrightarrow}} \underset{\text { Ethere }}{\mathrm{CH}_2}=\mathrm{CH}_2+\mathrm{H}_2 \mathrm{O}\)

⇒ \(\underset{\text { Propanol }}{\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CH}_2 \mathrm{OH}} \underset{43-453 \mathrm{~K}}{\stackrel{\text { Ponc } \mathrm{H}_2 \mathrm{SO}_4}{\longrightarrow}} \underset{\text { Prop-1 -ene }}{\mathrm{CH}_3 \mathrm{CH}}=\mathrm{CH}_2+\mathrm{H}_2 \mathrm{O}\)

The mechanism of the dehydration of alcohols by sulphuric arid is as follows.

The order of reactivity with respect to dehydration is 3° > 2° > 1°. Tertiary alcohols undergo rapid dehydration as they form the most stable carbocations (3°), which in turn form the most stable alkenes.

In the case of secondary or tertiary alcohols, the elimination of the water molecule gives rise to more than one alkene.

For example, but-2-ol on dehydration gives but-2-ene as the major product and but-l-ene as the minor product. As you can see, there are two p carbons in the structure of butane-2-ol.

The course of the reaction in such cases is determined by the Sayiezeff rule, according to which hydrogen is abstracted preferentially from the carbon atom attached to fewer hydrogen atoms.

Dehydrohalogenation of alkyl halides

The elimination of a molecule of hydrogen halide (H—X) from an alkyl halide in the presence of alcoholic potash forms an alkene.

This is dehydrohalogenation; it involves the elimination of one halogen atom and one hydrogen atom from the adjacent carbon atoms of a molecule of an alkyl halide.

This reaction is called p elimination. Ethyl bromide, on being heated with alcoholic potassium hydroxide, undergoes dehydrohalogenation.

⇒ \(\underset{\text { Ethyl bromide }}{\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{Br}} \stackrel{\text { KOH, } \mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}}{\longrightarrow} \underset{\text { Ethene }}{\mathrm{CH}_2}=\mathrm{CH}_2+\mathrm{KBr}+\mathrm{H}_2 \mathrm{O}\)

The mechanism of dehydrohalogenation of alkyl halides is shown below:

B’ is a base like C₂H₂O^–.

Depending on the structure of the starting alkyl halide, more than one product can be obtained in this case.

For example, 1-chlorobutane yields one product whereas 2-chlorobutane or sec-butyl chloride yields two products.

The ease of elimination of halogen atoms is of the order RF < RC1 < RBr < RI.

Dehalogenation of vicinal dihalides

Vicinal dihalides are those alkyl halides in which halogen atoms are present on adjacent carbon atoms. When treated with zinc, a vicinal dihalide gives an alkene.

Partial reduction of alkynes

On partial reduction with hydrogen in the presence of a catalyst (Lindlar’s catalyst), alkynes give alkenes.

A specially prepared palladium (palladised charcoal partially deactivated with poisons like quinoline) is Lindlar’s catalyst.

Unless the triple bond in the alkyne undergoing reduction is at the end of a chain, the probability of obtaining either cis- or a trans-alkene cannot be ruled out.

The choice of reducing agent decides the isomer which predominates. With Lindlar’s catalyst cis-alkenes are obtained. However, on reduction with sodium in liquid ammonia, alkynes form trans-alkenes.

Electrolysis of salts of carboxylic acids

Alkenes are obtained by the electrolysis of an aqueous solution of potassium salts of dicarboxylic acid.

Thus potassium succinate on electrolysis gives a carboxylate anion and a potassium cation. Carbon dioxide is released at the anode and hydrogen at the cathode.

At Anode: 

At Cathode: 

⇒ \(\begin{aligned}
& 2 \mathrm{~K}^{+}+2 \mathrm{e} \longrightarrow 2 \mathrm{~K} \\
& 2 \mathrm{~K}+2 \mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{KOH}+\mathrm{H}_2 \uparrow
\end{aligned}\)

Cracking or pyrolysis of alkanes.

On being heated to 773-873 K or in the presence of a catalyst to 498 K, higher alkanes yield alkenes.

Physical Properties

The physical properties of alkenes are similar to those of alkanes. The lower members of this class (up to C₄) are colourless gases, the higher members (C₆-C₁₈) are liquids and the rest are solids at room temperature.

They are less dense than water and insoluble in it but soluble in common organic solvents like benzene and chloroform.

The boiling points of alkenes, as is the case with alkanes, rise with the increase in the number of carbon atoms.

The boiling point increases by 20°C to 30°C for each carbon atom added to the molecule. Also, branching in an alkene lowers the boiling point.

Chemical properties

We know that the C=C double bond in alkenes consists of a bond and a n bond. Alkenes owe their reactivity to the weaker T₂ bonds. They usually undergo addition reactions, the most important being electrophilic and free radical additions.

As discussed earlier in the chapter, the addition of hydrogen to alkenes, in the presence of a catalyst, yields the corresponding alkanes.

Addition of halogens

Alkenes on treatment with halogens yield 1,2-halogenated alkanes (adduct). Alkenes react readily with chlorine and bromine at room temperature without any exposure to ultraviolet light.

The reaction is carried out in an inert solvent like carbon tetrachloride. The reaction of an alkene with bromine is used as a test for unsaturation.

A solution of bromine in carbon tetrachloride is red, which slowly decolourises as a colourless vicinal dihalide is formed.

The reaction is an example of electrophilic addition and involves two steps. In the first step, the electrophile (a positively charged species) adds to the carbon-carbon double bond, resulting in the formation of a carbocation intermediate.

The second step involves the addition of the nucleophile (a negatively charged species) to the positively charged carbon forming the adduct.

⇒ \(\stackrel{\oplus}{\mathrm{C}} \mathrm{H}_2-\mathrm{CH}_2-\mathrm{Br}+\mathrm{Br}^{\ominus} \longrightarrow \underset{\text { 1,2-Dibromoethane }}{\mathrm{CH}}-\mathrm{CH}_2-\mathrm{CH}_2-\mathrm{Br}\)

Addition of hydrogen halides

On reaction with hydrogen halides, alkenes give the corresponding alkyl halides.

In the case of symmetrical alkenes (like ethene), only one product is obtained

⇒ \(\mathrm{CH}_2=\mathrm{CH}_2+\mathrm{HBr} \longrightarrow \mathrm{CH}_3 \mathrm{CH}_2 \mathrm{Br}
Ethene   Ethyl bromide\)

However, in the case of unsymmetrical alkenes like propene, two products may be formed.

The above reaction shows that out of two possible products, only one product is formed.

Such reactions are called regiospecific reactions. The exclusive formation of one product can be explained by the Markovtiikov rule.

According to this rule (formulated by the Russian chemist Vladimir Markovnikov in 1870), a molecule of a hydrogen halide adds to an unsymmetrical alkene in such a way that the negative part of the reagent (X₆-) goes to that carbon atom of the alkene which is bonded to fewer hydrogen atoms. The Markovnikov rule was explained on the basis of the relative stability of carbocations.

Thus, in the above example, when hydrogen bromide is added to propene there is a possibility of formation of two carbocations — primary and secondary.

However, the secondary carbocation is more stable than the primary one. Therefore, the actual product formed is 2-bromopropane.

Sometimes, it has been seen that the addition of hydrogen bromide to unsymmetrical alkenes is in contradiction to the Markovnikov rule.

Kharasch and Mayo (1933) first observed and found the cause for such addition.

They observed the anti-Markovnikov addition of hydrogen bromide to propene in the presence of benzyl peroxide. This is also known as the Kharasch effect or peroxide effect.

You have already studied that peroxides are compounds with —O—O— linkage. Certain organic peroxides like benzoyl peroxide (C₆H₅COO)² are synthesised and used as reagents.

It is believed that the peroxide dissociates to give two alkoxy free radicals, which attack hydrogen bromide to form a bromine free radical.

The bromine free radical generated can add to any of the two carbon atoms of the double bond in an unsymmetrical alkene giving rise to either a primary or a secondary free radical.

The order of stability of free radicals is tertiary > secondary > primary. Therefore, in the presence of a peroxide the secondary free radical is predominantly formed and reacts with HBr to form an anti-Markovnikov product.

HC1 and HI give the normal Markovnikov addition products even in the presence of peroxides.

The chances of the homolytic cleavage of the H—Cl bond are lower than that of the H—Br bond because it is stronger than the H —Br bond.

The iodine free radical is easily formed since the H—I bond is weak (297 kJ mol-1) and combines with another iodine free radical to form an iodine molecule instead of the relatively unstable carbon-iodine bond.

Addition of sulphuric acid

An alkene reacts with cold concentrated sulphuric acid to form alkyl hydrogen sulphate, which on heating with water gives the corresponding alcohol. The method is used to manufacture ethyl alcohol.

In the case of unsymmetrical alkenes, the addition of sulphuric acid is consistent with the Markovnikov rule. Like the addition of alkyl halides, this reaction is also an example of electrophilic addition.

Addition of water

Water adds to the more reactive alkene only in the presence of an acid catalyst (H3P04) to form alcohols. The addition follows the Markovnikov rule.

Oxidation

Alkenes are more readily oxidised than alkanes are. This is due to the presence of a double bond, which is the site of attack. The nature of the oxidation products depends on the oxidising agent employed.

1. Hydroxylation On treatment with cold aqueous dilute potassium permanganate solution, a 1,2-dihydroxy compound (diol) is obtained. The reaction is known as hydroxylation of alkenes.

2. Oxidative cleavage of alkenes Oxidation by sodium periodate (NalO₄) in the presence of a permanganate solution yields a carboxylic add or a ketone. In the reactions that follow the double bond undergoes oxidative damage.

3. Ozonolysis When ozone gas is passed into a solution of an alkene in an inert solvent like carbon tetrachloride or chloroform at low temperatures, a cyclic unstable compound called ozonide is formed.

Ozonide is then treated with water or hydrogen in the presence of a reducing agent like zinc to give compounds containing the >C=0 group (carbonyl compounds), i.e., aldehydes and ketones.

The process of addition of ozone to an alkene-forming ozonide and then hydrolysis of the ozonide to form carbonyl compounds is called ozonolysis.

In this addition reaction, first, an unstable molozonide is formed, which rearranges spontaneously to form the ozonide. Some other examples of ozonolysis of alkenes are given below.

Ozonolysift is used for locating the position of the double bond in an alkene.

The carbon atoms in the carbonyl group of the two carbonyl compounds obtained after hydrolysis of ozonide are the ones bonded to each other by a double bond in the original alkene.

Polymerisation

A polymer is a substance with large molecules consisting of repeating units called monomers.

Polymers are formed by polymerisation, which is a chemical reaction in which the molecules join each other by addition or condensation (elimination of a small molecule, each time a molecule joins the other).

Some simple alkenes can also be converted into polymers. For example, ethylene (a monomer) polymerises on heating under pressure in the absence of air and the presence of a catalyst to give polyethene, a highly useful industrial polymer.

This polymer is formed by an addition reaction and is, therefore, called an addition polymer or chain-growth polymer. In the same way, propene polymerises into polypropene.

Nowadays, the excessive use of polythene and polypropylene has created environmental hazards, which is a matter of great concern.

Alkynes

Like alkenes, alkynes are also unsaturated hydrocarbons, but they contain a carbon-carbon triple bond (C=C).

The general formula of alkynes is C_nH_2n-2, which shows that they contain two hydrogen atoms less than the corresponding alkenes and four hydrogen atoms less than the corresponding alkanes.

Isomerism

Unlike alkenes, alkynes do not exhibit cis-trans isomerism since the molecules are linear. We normally encounter three types of isomerism in alkynes.

1. Chain isomerism: Alkynes exhibit chain isomerism. For example, Pent-l-yne is a straight-chain and 3-Methylbut-l-yne is a branched-chain isomer.

2. Position isomerism: This arises due to different positions of the triple bond.

⇒ \(\begin{gathered}
\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{C} \equiv \mathrm{CH} \\
\text { But-1-yne } \\
\text { (terminal) }
\end{gathered}\)

⇒ \(\mathrm{CH}_3 \mathrm{C} \equiv \mathrm{CCH}_3
But-2-yne (nonterminal)\)

3. Functional isomerism Alkynes exhibit functional isomerism with alkadienes. The tire functional group in But- 2-one is a triple bond whereas, in Buta-1,3-diene, it is a double bond.

⇒ \(\underset{\text { But-2-yne }}{\mathrm{CH}_3 \mathrm{C} \text { ant }} \mathrm{CCH}_3\)

⇒ \(\mathrm{CH}_2=\underset{\text { Buta-1,2-diene }}{\mathrm{CH}}-\mathrm{CH}=\mathrm{CH}_2\)

Structure Of Triple Bond

To understand the structure of a triple bond, let us consider acetylene, the first member with the simplest structure in the alkyne homologous series. Tire two carbon atoms in ethyne are sp hybridised.

That is to say, each carbon atom has two sp hybrid orbitals, which are collinear and two unhybridised orbitals (2p_yand 2p_z), which are perpendicular to each other and to the sp orbitals.

One sp hybrid orbital of one carbon atom overlaps with one sp orbital of the second carbon atom, forming a C—C CT bond. The other sp hybrid orbital of each carbon atom forms a bond with a hydrogen atom.

Since the two sp hybrid orbitals of the carbon atoms are collinear and overlapping of the orbitals takes place along the internuclear axis, the two carbon and the two hydrogen atoms lie along a straight line. In other words, the acetylene molecule is linear.

The two unhybridised orbitals of one carbon atom form two n bonds with the two unhybridised orbitals of the other carbon atom.

The orbital structure of acetylene is Thus, the carbon-carbon triple bond in acetylene consists of one strong bond and two weak n bonds.

The H —C—H bond angle is 180°, since die Hacetylene molecule is linear. Two n bonds formed together make a single cylindrical sheath about the line joining the two nuclei.

Preparation

From calcium carbide

Acetylene is manufactured by treating calcium carbide (CaC₂) with water.

⇒ \(\mathrm{CaC}_2+2 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{H}-\mathrm{C} \equiv \mathrm{C}-\mathrm{H}+\mathrm{Ca}(\mathrm{OH})_2\)

For this purpose, calcium carbide is obtained by heating a mixture of coke and limestone in an electric furnace.

⇒ \(\begin{gathered}
\mathrm{CaCO}_3 \stackrel{\text { heat }}{\longrightarrow} \mathrm{CaO}+\mathrm{CO}_2 \\
\mathrm{CaO}+3 \mathrm{C} \stackrel{2273-3273 \mathrm{~K}}{\longrightarrow} \mathrm{CaC}_2+\mathrm{CO}
\end{gathered}\)

Generally, there can be two processes for the synthesis of alkynes. One of them involves the formation of a triple bond by elimination reactions and the other involves the addition of alkyl groups to molecules containing a triple bond.

Dehydrohalogenation Of Dihalides

Alkynes can be prepared by the elimination of two molecules of hydrogen halides from a dihalide.

The dihalide may be geminal (in which both the halogen atoms are attached to the same carbon atom) or vicinal (in which the two halogen atoms are attached to adjacent carbon atoms).

1. Vicinal dihalides On treatment with suitable bases, vicinal dihalides undergo an elimination reaction whereby two molecules of hydrogen halide are eliminated from the adjacent carbon atoms to give an alkyne. A stronger base like sodamide is used for unreactive vinylic halides.

The dehydrohalogenation of dihalides is a useful method to obtain alkynes as dihalides can be readily obtained by the addition of halogens to the corresponding alkenes.

2. Geminal dihalides (1,1-dihalides) On treatment with a base, geminal dihalides also undergo dehydrohalogenation to give alkynes.

Dehalogenation of tetrahalides

Alkynes may also be obtained by the dehalogenation of tetrahalides.

Physical Properties

Alkynes resemble alkenes and alkanes in their physical properties. They are all colourless and odourless, with the exception of ethyne, which has a characteristic odour.

The first three members are gases, the next eight members are liquids and the higher members are solids at room temperature.

The melting points, boiling points and densities increase gradually with an increase in molecular weight and show the usual effects of chain branching.

Alkynes have slightly higher boiling points than the corresponding alkenes and alkanes.

They are weakly polar and dissolve readily in low-polarity solvents like ether, benzene and carbon tetrachloride. Alkynes are insoluble in water.

Chemical properties

The reactivity of alkynes is mainly due to the presence of two 7t bonds and their acidic nature.

The acidic nature of alkynes

Alkynes are acidic organic compounds but, unlike other acidic inorganic compounds, they do not turn blue litmus red or neutralise aqueous bases.

Yet, they are acidic because they have the tendency to lose hydrogen ions. A hydrogen atom can be released as a positive hydrogen ion by the breaking of a bond if it is bonded with an electronegative atom which can accommodate the bonded electron pair left behind.

If we consider the second period of the p block of the periodic table, the electronegativity of elements decreases as F > O > N > C.

From this order of electronegativity, we may conclude that HF is a strong acid, H₂O is a weak acid, NH₃ is still weaker and CH₄ is not considered an acid at all.

But in the case of a compound containing a triply bonded carbon atom, like acetylene, the relative acidity is of the order H₂O > HC=CH > NH₃.

It seems that the carbon atom in acetylene is a different element than the one in methane, CH₄ (single bond) and ethene (double bond).

Also, the alkynes, which contain hydrogen attached to triply bonded carbon atoms (known as terminal alkynes) show comparable acidity.

Why is the triple bond responsible for the acidity of alkynes? This can be explained on the basis of the hybridisation state of the carbon atom in the compound.

Electrons in the s orbital have lower energy than those in the p orbital. Since the s orbital is spherical the electrons in it are much closer to the nucleus than the electrons in the p orbital, which is lobed on either side of the nucleus.

Therefore, in the case of hybrid orbitals, more s character means more electronegativity and a more stable anion.

The sp hybrid orbital of the triply bonded carbon atom in ethyne has 50 per cent s character whereas it is 33.3 per cent in the sp² hybrid orbital of ethene and 25 per cent in the sp³ hybrid orbital of ethane.

Therefore, the electrons forming the C —H bond in ethyne are closer to carbon, making the carbon electronegative.

So, hydrogen has the tendency to leave as a positive ion, thereby showing acidity.

Acetylene and other terminal alkynes containing acidic hydrogen atoms can be converted into metal acetylides and metal alkynes on treatment with sodium and sodamide respectively in liquid ammonia.

The sodium derivatives obtained above on treatment with alkyl halides give alkynes. By this method, the lower alkynes can be converted to higher alkynes. Alkanes and alkenes do not undergo these reactions.

Acidic alkynes react with an ammoniacal solution of copper sulphate and an ammoniacal solution of silver nitrate (Tollen’s reagent) to give the corresponding copper and silver alkylides, which are red and white precipitates respectively.

The reaction can be used to distinguish between terminal and nonterminal alkynes and is used as a diagnostic test for the —C=CH group.

Addition Reactions

Like alkenes, alkynes undergo electrophilic addition reactions. However, with alkynes, the addition may occur once or twice depending on the number of molar equivalents of the reagents employed.

1. Addition of hydrogen (reduction) Alkynes can be reduced, first to alkenes and then to the corresponding alkanes in the presence of catalysts—finely divided platinum or palladium or nickel.

The above reaction can be stopped at the alkene stage by using Lindlar’s catalyst (Pd-BaSO₄ poisoned with quinoline)

\(\mathrm{HC} \equiv \mathrm{CH} \underset{\mathrm{Pd}-\mathrm{BuSO}_4}{\stackrel{\mathrm{H}_2}{\longrightarrow}} \mathrm{H}_2 \mathrm{C}=\mathrm{CH}_2\)

2. Addition of halogens Alkynes add one mole of bromine to give a dibromo and two moles of bromine to give a tetrabromo product.

A solution of bromine in carbon tetrachloride, which is red, gets decolourised in addition to an alkyne. This is used as a test to detect unsaturation.

Chlorine reacts in a similar fashion.

3. Addition of hydrogen halides Alkynes react with two moles of hydrogen bromide or hydrogen chloride to first form the corresponding haloalkene and finally geminal dihalide. Both the electrophilic addition reactions follow the Markovnikov rule.

The anti-Markovnikov addition of hydrogen bromide to alkynes takes place in the presence of peroxides. The reaction occurs through a free-radical mechanism.

\(\underset{\text { Propyne }}{\mathrm{CH}_3 \mathrm{C} \equiv \mathrm{CH}} \frac{\mathrm{HBr}}{\text { peroxide }}-\underset{\text { 1-Bromopropene }}{\mathrm{CH}_3 \mathrm{CH}=\mathrm{CHBr}}\)

4. Addition of water Alkynes, although immiscible with water, can be hydrated in the presence of mercuric sulphate dissolved in dilute sulphuric acid. The triple bond adds a molecule of water to form vinyl alcohol, an unstable product, which isomerises to an aldehyde or a ketone.

In the case of the substituted alkynes, the addition follows the Markovnikov rule and ketones are formed.

Oxidation Of Alkynes

When oxidised with an alkaline potassium permanganate solution, the acetylene or terminal alkyne molecule undergoes cleavage at the site of the triple bond to give carboxylic acids and carbon dioxide. But nonterminal alkynes give only carboxylic acids on oxidation.

⇒ \(\mathrm{R}-\mathrm{C} \equiv \mathrm{C}-\mathrm{H}+4[\mathrm{O}] \stackrel{\mathrm{KMnO}_4}{\longrightarrow} \mathrm{R}-\mathrm{COOH}+\mathrm{CO}_2\)

⇒ \(\mathrm{R}-\mathrm{C} \equiv \mathrm{C}-\mathrm{R}+4[\mathrm{O}] \stackrel{\mathrm{KMnO}_4}{\longrightarrow} \mathrm{R}-\mathrm{COOH}+\mathrm{RCOOH}\)

Thus, by identifying the products formed during oxidation by a potassium permanganate solution, it is possible to understand the structure of alkynes.

However, on treatment with ozone, alkynes form ozonides (their structure is different from the ozonides obtained in the case of alkenes), which on treatment with water yield carboxylic acids.

Polymerisation

Alkynes undergo polymerisation to form linear or cyclic polymers. Linear polymers are obtained in the presence of cuprous chloride and ammonium chloride, which, together, catalyse the reaction.

The linear polymer polyacetylene is a conductor of electricity and is used as an electrode in batteries.

When passed through a red hot tube, acetylene polymerises to form a cyclic product, benzene.

Aromatic Hydrocarbons

We already know that aromatic hydrocarbons, also known as arenes or benzenoid compounds, contain one or more benzene rings.

In fact, the scope of the term ‘aromatic’ is now not limited to benzenoid compounds, but also includes non-benzenoid compounds which do not have a carbon sextet and yet possess aromatic character. We will discuss aromaticity.

Isomerism

Position isomerism

Isomerism is not observed in the case of monosubstituted benzene compounds since all the six hydrogen atoms which may be substituted are equivalent.

Disubstituted and trisubstituted benzene compounds exhibit isomerism. Because substituents attached to the benzene ring have different relative positions. For example, dichlorobenzene can have the following three possible isomers.

Similarly, a trisubstituted benzene exhibits three isomers having different relative positions of the substituents.

Ring-chain isomerism

If two compounds have the same molecular formula but one has an open chain and the other a cyclic structure, they are called ring-chain isomers.

Structure Of Benzene

The number of hydrogen atoms in benzene (C6H6) is eight less than that in the corresponding saturated alkane, hexane (C6H14).

Benzene, therefore, should be expected to be an unsaturated compound. This expectation is supported by the fact that benzene adds three molecules of hydrogen in the presence of Raney nickel or platinum at 473-523 K when cyclohexane, C₆H₁₂, is formed.

⇒ \(\underset{\text { Bentene }}{\mathrm{C}_6 \mathrm{H}_6}+3 \mathrm{H}_2 \underset{473-523 \mathrm{~K}}{\stackrel{\text { RaneyNi }}{\longrightarrow}} \underset{\text { Cyclohecane }}{\mathrm{C}_6 \mathrm{H}_{12}}\)

The formation of benzene hexachloride (C₆H₆C₁₆) from benzene in the presence of sunlight is another reaction which proves the unsaturation of benzene.

On the other hand, certain reactions show that benzene unexpectedly behaves like a saturated compound. It undergoes substitution reactions and unlike alkenes and alkynes, it does not decolourise bromine in a solution of carbon tetrachloride. Instead, when treated with Br² in the presence of FeBr³, it forms monobromobenzene, which is a substitution product.

Also, like saturated compounds, benzene is resistant to oxidation. Unlike alkenes and alkynes, benzene does not undergo oxidation readily. Even with strong oxidising agents like chromic acid and potassium permanganate, benzene oxidises only very slowly to CO₂ and H₂O.

Kekule Structure

Until 1865 no scientist could come up with a satisfactory structure for benzene, though they knew its molecular formula.

Then Kekule, a German chemist, proposed that the six carbon atoms of benzene are joined to each other by alternate single and double bonds to form a six-membered ring and that each carbon atom is also bonded to a hydrogen atom.

Strangely enough, Kekuld got this insight into the structure of benzene in a dream. The structure he proposed was a major breakthrough in science, but it could not explain a few characteristics of benzene.

1. It could not explain, for example, why despite containing three double bonds, benzene is not easily oxidised by oxidising agents like KMnO₂ and why it undergoes substitution reactions.
2. If the Kekultf structure is valid, there should be two o-disubstituted products.
3. One with a single bond between the two chlorine atoms and the other with a double bond between the two chlorine atoms. However, in reality, there is only one o-dichlorobenzene.
4. Kekutd tried to account for this by proposing a dynamic equilibrium between the two structures. That is to say, the positions of the single and double bonds are not fixed but oscillate back and forth between the alternate positions.
5. According to Kekule, there should be two kinds of bonds in benzene and the C—C bond length should be greater than the C=C bond length.
6. However, X-ray diffraction studies show that benzene is a regular hexagon with an angle of 120° (all the bonds are alike) and that all the C —C bond lengths are equal (139 pm).
7. The C—C bond length in benzene lies between the single-bond length (154 pm) and the double-bond length (134 pm).
8. Thus, the Kekul6 structure could not explain the fact that the carbon-carbon bond lengths in benzene are equal, or account for the unusual stability of benzene. These were later explained on the basis of molecular orbitals and resonance.

Molecular Orbital Structure

According to the molecular orbital concept, each carbon atom in benzene is sp² hybridised, which means that each carbon atom has three sp² orbitals.

Of these orbitals, two ores are involved in forming a bond with two adjacent carbon atoms and the remaining orbital forms a CT bond with a hydrogen atom, meaning that there are six C—C o bonds and six C—H bonds which lie in one plane. This explains why the angle between any two adjacent a bond (C-C—C) is 120°

Each carbon atom in the molecule, being sp² hybridised, is left with an unhybridised p² orbital.

The six p. orbitals (with one electron each) are parallel to one another and perpendicular to the plane of the a-bonded ring of carbon atoms.

Each of these p orbitals overlaps with the p orbital of the adjacent carbon atom in equally good ways, forming three n bonds in all.

The electron cloud of one p² orbital spreads to the neighbouring p² orbitals equally well.

This type of participation of n electrons in more than one bond is called delocalisation of electrons.

All the six carbon atoms in benzene attract these delocalised electrons equally, thus leading to the formation of two n electron clouds—one above and the other below the plane of the carbon and hydrogen atom.

Due to this all the C—C bond lengths are equal, all the C—H bonds are equivalent and the dipole moment of the molecule is zero. All these factors contribute to the stability of benzene.

Resonance

The concept of resonance can also be used to explain the stability of benzene.

The real structure of benzene can be represented as a resonance hybrid of the two Kekule structures. Structures 1 and 2 are known as resonating or canonical structures.

The resonance structure of benzene explains the following observations.

1. The C—C bond length in benzene is 139 pm which lies between the C—C bond length (154 pm) and the C=C bond length (134 pm).
2. The existence of only one o-dichlorobenzene.
3. The stability of benzene or the fact that it behaves like a saturated hydrocarbon. Because of resonance, the n-electron charge in benzene gets distributed over a large area; in other words, it gets delocalised. This leads to a decrease in the energy of the resonance hybrid by about 50 kJ mol”1 as compared to that of the contributing structures. The difference in energy is called resonance energy.

Aromaticity

Despite being unsaturated, benzene resists addition and oxidation reactions. Thus, benzene shows characteristic stability. Earlier the term ‘aromatic character’ or ‘aromaticity’ was used to signify the characteristic chemical behaviour of benzene and its related compounds.

Robinson was the first to point out that the presence of alternate double and single bonds conferred aromaticity to the benzene ring. This was attributed to the delocalisation of the six n electrons over the planar carbon hexagon.

The modem theory of aromaticity was advanced by Eric Hiickel (1931). The basic concepts of this theory are as follows.

• The complete delocalisation of the n electrons in the ring system is necessary to make the system aromatic I in character.
• Ample or complete delocalisation of the n electrons is possible only if the ring is flat or coplanar so as to allow cyclic overlap of TC electrons. For example, benzene, which has a coplanar ring, is aromatic whereas 1,3,5,7-cyclooctatetraene, being nonplanar, lacks aromaticity.
• Hiickel’s rule or the (4n + 2) rule states that a planar, cyclic system should have n electrons to exhibit aromatic character. Here n is a natural number. Thus, in other words, to be aromatic, a molecule should have 6 7t(n =1), 10 n(n = 2) electrons and so on. Some examples of both aromatic and nonaromatic cyclic hydrocarbons are given below.

Preparation Of Benzene

Enormous quantities of aromatic compounds are obtained from coal and petroleum, petroleum being the chief source of benzene and toluene.

Still, larger quantities of aromatic hydrocarbons are synthesised from alkanes through the process of catalytic reforming. The process involves dehydrogenation, cyclisation and isomerisation.

As stated earlier in the chapter, acetylene (or ethyne) when passed through a heated tube polymerises to a small extent to benzene.

Recently, large-scale production of benzene from acetylene (from petroleum sources) has been achieved by using cobalt carbonyls and other metal complexes.

Decarboxylation of aromatic acids

On being heated with soda lime, sodium salts of benzoic acids give benzene.

By Reduction Of Phenol

When passed over heated zinc dust, phenol in vapour form is reduced to benzene.

Reduction of diazonium salts

Aryldiazonium salts, on reduction with hypophosphorous acid, yield the corresponding arene. The diazo group is replaced by H.

Physical Properties

Being nonpolar, aromatic hydrocarbons are insoluble in water but soluble in organic solvents. Benzene is a colourless liquid, b.p. 353 K. It freezes to a solid at 278.5 K.

It has a characteristic odour. It is highly inflammable and bums with a sooty flame. It is slightly soluble in water. Being toxic and carcinogenic in nature, its use as a solvent has been now prohibited in most advanced countries.

Chemical Properties

Arenes, the derivatives of benzene, do not undergo addition and oxidation reactions under normal conditions, though the benzene ring contains three double bonds. Benzene and its derivatives are characterised by electrophilic substitution reactions.

The stability of benzene has been attributed to resonance. It can also be explained by considering its enthalpies of hydrogenation and combustion, which are lower than expected.

The enthalpy of hydrogenation is the amount of energy that evolves when one mole of an unsaturated compound is hydrogenated. In most alkenes, this value is about 120 kJ mol _1 for each double bond.

On the basis of this value, one expects the enthalpy of hydrogenation for cyclohexatriene or benzene to be 120 x 3 = 360 kJ mol-1 whereas the actual value for benzene is only 208 kJ mol-1, which is 152 kJ mol-1 less than the expected value. This means that benzene is more stable than expected.

Similarly, the enthalpy of combustion of benzene is also lower than expected.

Electrophilic Substitution Reactions

The attacking reagent in the reaction is electron deficient, as the name electrophilic suggests, whereas the benzene ring serves as a source of electrons.

In the reaction, a hydrogen atom of the benzene ring is replaced by an active species, the electrophile (E⁺).

Depending upon the type of electrophile, electrophilic substitution reactions include nitration, halogenation, sulphonation, Friedel-Craft alkylation and acylation reactions.

1. Nitration of Benzene and its homologues, on reaction with a mixture of concentrated nitric acid and sulphuric acid, form nitrobenzene. In the mixture of the two acids, sulphuric acid serves as an acid and nitric acid as a base.

The mechanism of the reaction involves the generation of the electrophilic nitronium ion by protonation and its reaction with benzene to form a resonance-stabilised carbocation. The carbocation rapidly loses a proton to give nitrobenzene. The following steps exhibit the sequence of reactions.

2. Halogenation Arenes react with halogens (bromine or chlorine) in the presence of a Lewis add catalyst—ferric bromide, ferric chloride or aluminium chloride—to give aryl halides.

The mechanism of halogenation follows the same steps as that of nitration. The electrophile X+ is generated with the help of the Lewis acid.

⇒ \(\mathrm{Br}-\mathrm{Br}+\mathrm{FeBr}_3 \longrightarrow \underset{\text { Bromonium ion }}{\mathrm{Br}^{+}}+[\mathrm{FeBr}]_4^{-}\)

If an excess of the electrophilic reagent is used, all the hydrogen atoms can be replaced with the electrophile. For example, on treatment with an excess of anhydrous aluminium chloride in darkness, benzene gives hexachlorobenzene.

3. Sulphonation Benzene reacts with fuming sulphuric acid (H₂S₂O₇) to give benzene sulphonic acid. (Fuming sulphuric add is obtained by passing S03 through 98% H₂SO₄.) The electrophilic reagent in this reaction is the electron-deficient sulphur trioxide.

The mechanism of the reaction involves the generation of the electrophilic reagent SO₃, which attaches itself to the benzene ring to form the carbocation.

The intermediate carbocation formed rapidly loses a proton to give the anion of benzene sulphonic acid. The acid is strong and remains highly dissociated.

4. Friedel-Crafts reaction This electrophilic substitution reaction involves the introduction of an alkyl group in the benzene ring.

In the presence of a Lewis acid, which acts as a catalyst, an alkyl halide reacts with benzene. The products obtained are alkyl benzenes, which are not otherwise easily synthesised. The reaction is known as Friedel-Crafts alkylation.

The mechanism of the Friedel-Crafts reaction involves the following steps:

1. Generation of the electrophile (a carbocation in this case)

⇒ \(\mathrm{RCl}+\mathrm{AlCl}_3 \rightleftharpoons \mathrm{AlCl}_4^{-}+\mathrm{R}^{\oplus}\)

Elimination of a proton (H+)

In Friedel-Crafts alkylation, if in place of alkyl halides (RX), an acyl halide (e.g., acetyl chloride or benzoyl chloride) is used, the product obtained is the corresponding ketone. This reaction is known as Friedel-Crafts acylation.

Acetophenone (C₆H₅COCH₃) and benzophenone (C₆H₅COC₆H₅) can be prepared from acetyl chloride and benzoyl chloride respectively.

Addition Reactions

1. Addition reactions of hydrogen In the presence of finely divided platinum metal,
   benzene adds hydrogen to give cyclohexane.
2. Addition of halogens Benzene adds three molecules of chlorine or bromine under the influence of UV light to form the corresponding hexahalide. The chlorination of benzene gives benzene hexachloride, also called lindane, which has insecticidal properties.

Oxidation

Benzene bums with a sooty flame in oxygen, giving CO₂ and H₂O. A large amount of heat is liberated.

⇒ \(2 \mathrm{C}_6 \mathrm{H}_6+15 \mathrm{O}_2 \longrightarrow 12 \mathrm{CO}_2+6 \mathrm{H}_2 \mathrm{O} ; \quad \Delta H^{\Theta}=-6530 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Benzene can also be oxidised in presence of vanadium pentoxide catalyst at 773 K to give maleic acid and maleic anhydride.

Directive Influence Of Substituents In Monosubstituted Benzene

We have seen that benzene forms only one monosubstituted product. However, when the substituted benzene undergoes electrophilic attack, the group already present on the ring influences the rate of the reaction as well as the site of attack.

We, therefore, say that the substituent group affects the reactivity as well as orientation in electrophilic aromatic substitution reactions.

Depending on the reactivity or how readily the reaction occurs, the substituent groups can be divided into the following two classes.

1. Activating groups These groups cause the ring to be more reactive than benzene. For example, —CH₃ and —NH₂.
2. Deactivating groups These groups cause the ring to be less reactive than benzene. For example, —COOH and —NO₂.

According to orientation, the substituent groups can be divided into the following two classes.

1. Ortho-para directing The substituent groups that release electrons activate the benzene ring and direct the incoming groups to ortho and para positions. For example, —CH₃, —NH2 and —OH. In general, the activating groups are a-, and p-directing.

2. Meta directing The substituent groups that withdraw electrons deactivate the ring and direct the incoming groups to the meta position. For example, —NO₂, —CN and —COOH. In general, the deactivating groups are directed.

Halogens are exceptions—they are deactivating and still o-, p-directing.

Nitration Of Toluene

Toluene on nitration gives a mixture of all three isomers, o,p and m. The yield of o,p-nitrotoluenes is almost 96%, and a very small amount of the m-isomer (4%) is formed.

The example illustrates that the CH₃ group is o-, p-directing. As we have just said, the yield of o-, and p-isomers is much more than that of the m-isomer.

On the other hand, when benzene undergoes nitration, the yield is only 45- 50% which means it is less reactive than toluene.

The greater reactivity of toluene is also indicated by the fact that toluene can be nitrated under milder conditions i.e., lower temperature and lower concentration of HN03.

The alkyl group releases electrons into the ring, thus increasing the nucleophilicity of the ring and stabilising the intermediate carbocation.

To understand the reason behind the o-, p-directing nature of the alkyl group, let us observe the relative stabilities of the different carbocations formed by the electrophile attack at the o- p- and m-positions of toluene.

When the attack occurs at the ortho position, out of three canonical structures, the structure (1) is relatively stable because the positive charge is placed on the carbon atom immediately next to the alkyl group.

The canonical form (2) in case of the para attack, has a positive charge on the carbon atom adjacent to the alkyl group. There is no such equivalent structure formed by the attack at the meta position.

So the carbocations resulting from the attack at the ortho and para positions are more stable than the carbocations formed from the attack at the meta position. Thus, the alkyl groups are ortho- and para-directing. In the structures shown below, E denotes an electrophilic group.

The structures shown below depict the o- and p- p-directing nature of the —OH group in the case of a phenol. The stability of structures is due to the complete octet of electrons in every atom.

Nitration Of Nitrobenzene

Nitration of nitrobenzene gives the m-isomer in a large amount (93%).

Nitrobenzene undergoes nitration at the rate of only 10″4 times that of benzene. This shows that the NO₂ group is a strong deactivating group.

The nitro group is electron-withdrawing, and when present on an aromatic ring, tends to intensify the positive charge and destabilise the intermediate carbocation.

The destabilisation is more prominent in the intermediates arising from ortho and para attacks.

Thus, the meta attack is favoured. If we compare the resonance structures of carbocations formed by attacks at the ortho and para positions of nitrobenzene, the structures (1) and (2) are destabilised, because the positive charge is placed on the carbon atom next to the electron-withdrawing nitro group.

There is no such structure arising from the meta attack and so the meta attack is favoured.

Haloarenes

Halogens deactivate the ring through the inductive effect by direct substitution to the ortho and para positions.

Halogens, being more electronegative than carbon, withdraw (-1 effect) the electrons from the aromatic ring, leaving it less nucleophilic.

However, halogens have unshared electron pairs which can delocalise the electrons in the ring by extended n bonding. This is possible only when the attack occurs at the ortho and para positions.

The resonance structures (1) and (2) formed from ortho and para attacks have the halogens bonded directly to the carbon on which the positive charge is placed.

The halogen atom is able to effect a further delocalisation of positive charge by sharing one of its nonbonding electron pairs to give two resonance structures, (3) for ortho attack and (4) for para attack.

Halogens cannot exert their stabilising influence on the intermediate when the meta position is attacked. The result is that they deactivate the ring by one effect and direct substitution to ortho and para positions by another.

In general, except for the alkyl and phenyl substituents, all of the ortho-para directing groups have at least one pair of nonbonding electrons on the atom adjacent to the benzene ring.

On the basis of studies carried out with a large number of substituted benzene derivatives, the effect of substituents on electrophilic aromatic substitution.

Polynuclear Hydrocarbons

Polynuclear hydrocarbons are divided into two groups—one containing isolated rings and the other containing fused rings.

Biphenyl and diphenylmethane are examples of isolated rings. When two or more rings are fused together they are known as condensed polynuclear hydrocarbons, for example, naphthalene, anthracene, phenanthrene and pyrene.

Toxicity Of Polynuclear Hydrocarbons

Although many aromatic compounds are essential for life (e.g., vitamins, hormones, steroids, purines, pyrimidines), many others are quite toxic, and several benzenoid compounds, including benzene itself, are carcinogenic. Two other examples are benzo [a] pyrene and 7-methyl [a] anthracene.

Certain molecules from the environment become carcinogenic by activation through metabolic processes.

Two such examples are dibenzo (a, 1) pyrene, a polycyclic aromatic hydrocarbon, and aflatoxin BJ, a compound formed during the metabolism of certain fungi.

Some alkyl or alkyl derivatives of 3,4-benzphenanthrene (also called benzoic phenanthrene) have also been found to be carcinogenic. For instance, 2-methyl- 3,4-benzophenanthrene is mildly carcinogenic. People who work in industries dealing with such polynuclear aromatics are at a high risk of cancer. Also, prolonged exposure to coal tar leads to cancer. Though some hydrocarbons are toxic, many of them are useful too.

As already stated, hydrocarbons are used as fuels. In fact, as of now, they are one of the earth’s most important energy resources. For example, petroleum, LPG and CNG. Petroleum The word petroleum is derived from the Greek word ‘petra’ meaning ‘rock’ and ‘oleum’ meaning ‘oil’.

Petroleum is oily, viscous and usually dark. It is found deep below the earth’s crust, entrapped within rocks and below the surface of the oceans.

It is believed to have been formed from the dead remains of animals and trees which got buried deep inside the earth millions of years ago.

The absence of air, presence of moisture, high pressure and high temperature under the earth’s crust facilitates the conversion of dead remains to petroleum.

Petroleum is also formed from the decomposition of marine animals at the bottom of the sea.

In India, petroleum is obtained from the sea bed at Bombay High. It is found trapped in sedimentary rocks, in the oil centres situated at Assam and Gujarat. The crude oil is pumped out from the wells and is called black gold.

The composition of crude petroleum varies with its occurrence. However, they all contain alkanes (straight and branched-chain hydrocarbons from C1 to C40), cycloalkanes, naphthalenes and aromatic hydrocarbons. The low-boiling fractions of petroleum are composed of alkanes.

It is the composition of higher-boiling fractions which differs according to the source of petroleum Besides hydrocarbons, petroleum also contains compounds containing oxygen, nitrogen and sulphur.

LPG Liquefied petroleum gas (LPG) contains hydrocarbons like propane and butane and is obtained as a product from the refining of petroleum. The gas mixture is liquefied by compression and is used mostly as household cooking fuel. LPG is odourless, and small amounts of foul-smelling substances are added to detect any leakage.

It is also used in organic synthesis, especially of synthetic rubber. CNG (Compressed natural gas) Natural gas is a mixture of gases occurring in pockets below the earth’s surface along with petroleum. This mixture usually contains methane and ethane along with small amounts of higher hydrocarbon gases like propane and butane.

Like petroleum, it is believed to have been formed from the decomposition of organic matter trapped in layers of sedimentary rocks. CNG is widely used as a fuel. In India, it occurs in large amounts in Bombay High, the Gulf of Cambay and Ankleshwar in Gujarat.

Earlier, natural gas was considered a hazard in the petroleum industry, as it forms an explosive mixture with air. So it was ‘flared’, or burnt away. Natural gas is now recovered from the source through pipelines.

It is compressed and filled in cylinders for use. In India, CNG is used as a fuel for motor vehicles, buses, etc. The use of CNG, particularly in Delhi, has considerably reduced air pollution. Natural gas also serves as a starting material for making useful petrochemicals.

Hydrocarbons Multiple Choice Questions

Question 1. Which of the following statements is/are correct about methane?

1. The carbon atom is sp³ hybridised.
2. The H-C—H bond angle is109° 28′.
3. It has four bonds.
4. The carbon atom is sp² hybridised.

Answer: 1. The carbon atom is sp³ hybridised.

Question 2. How many 1°, 2°, 36 and 4° carbon atoms are present in 2,2,4-trimethylpentane?

1. Five 1°, one 2°, one 3°, one 4°
2. Four 1°, two 2°, two 3°, zero 4°
3. Four 1°, two 2°, one 3°, one 4°
4. Three 1°, two 2°, two 3°, one 4°

Answer: 1. Five 1°, one 2°, one 3°, one 4°

Question 3. How many a and it bonds are present in ethene?

1. 5ct, 2n
2. 5a, lit
3. 4a, 3it
4. 6a, zero it

Answer: 2. 5a, lit

Question 4. Which of the following statements is/are correct about acetylene?

1. It contains two and three bonds.
2. The H—C—C bond angle is 180°.
3. It contains two it and two bonds.
4. The molecule is nonlinear.

Answer: 1. It contains two and three o bonds.

Question 5. Which of the following statements is/are correct about benzene?

1. Each C atom in benzene is sp² hybridised.
2. All the C—C bond lengths are equal.
3. All the C—Co bonds and C—Ha bonds lie in the same plane.
4. Each C atom in benzene is sp³ hybridised.

Answer: 1. Each C atom in benzene is sp² hybridised.

Question 6. Which of the following is/are correct?

1. The eclipsed conformation of ethane is less stable than the staggered conformation.
2. The eclipsed conformation is more stable than the staggered conformation.
3. Both are equally stable.
4. Both the conformations can be separated.

Answer: 1. The eclipsed conformation of ethane is less stable than the staggered conformation.

Question 7. A compound on ozonolysis gives propanal and benzaldehyde. The compound can be

1. 1-Phenylbut-l-en
2. Pent-2-en
3. 2-Ethylbut-ene
4. None of the above

Answer: 1. 1-Phenylbut-l-en

Question 8. Propanal and Pentan-3-one are the products obtained by the ozonolysis of which of the following alkenes?

1. 3,4-Dimethylhept-3-ene
2. 1-Phenylbut-l-ene
3. 4-Ethylhex-3-ene
4. None Of The Above

Answer: 3. 4-Ethylhex-3-ene

Question 9. But-l-ene and but-2-ene are

1. Geometrical isomer
2. Chain isomers
3. Position isomers
4. Optical isomers

Answer: 2. Chain isomers

Question 10. How many structures can a compound with the molecular formula C₄H₈ have?

1. 1
2. 2
3. 3
4. 4

Answer: 3. 3

Question 11. Which of the following statements is/are true of geometrical isomers?

1. The frans-isomers of alkenes are more stable than the cis-isomers.
2. The cis-isomers of alkenes are more stable than the frans-isomers.
3. The c/s-isomer is more polar than the trans-isomer.
4. The frans-isomer is more polar than the cis-isomer.

Answer: 1. The frans-isomers of alkenes are more stable than the cis-isomers.

Question 12. Which of the following compounds will exhibit geometrical isomerism?

1. Hex-3-ene
2. 3-Ethylpent-2-ene
3. But-2-ene
4. 1,1,2-Tribromoethene

Answer: 1. Hex-3-ene

Question 13. An aqueous solution of a compound gives ethane on electrolysis. The compound can be

1. Sodium acetate
2. Sodium ethoxide
3. Sodium propanoate
4. None of these

Answer: 1. Sodium acetate

Question 14. Among the following, the most reactive compound in the context of electrophilic nitration is

1. Benzene
2. Toluene
3. Benzoic Add
4. Nitrobenzene

Answer: 2. Toluene

Question 15. In a reaction of QH5A, the major product is an m-isomer. So A is

1. -Cl
2. —COOH
3. —OH
4. All

Answer:  4. All

Question 16. Which of the following is aromatic in nature?

Answer: 3.

Question 17. The C—C bond distance is maximum in

1. Ethane
2. Ethyne
3. Benzene
4. All Are Equal

Answer: 1. Ethane

Question 18. The number of n electrons in naphthalene is

1. 3
2. 4
3. 5
4. 10

Answer: 4. 10

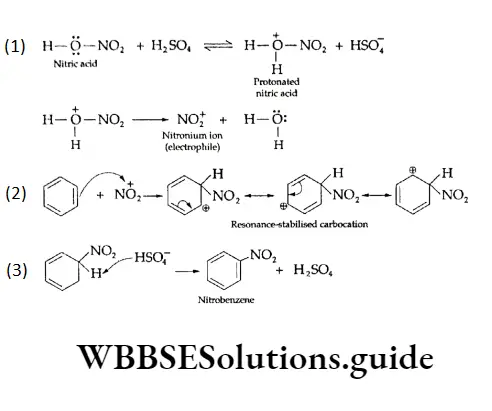
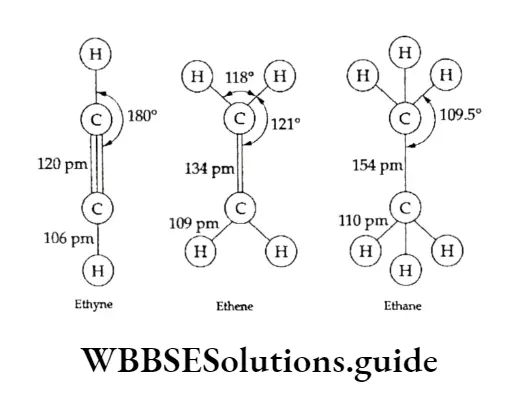
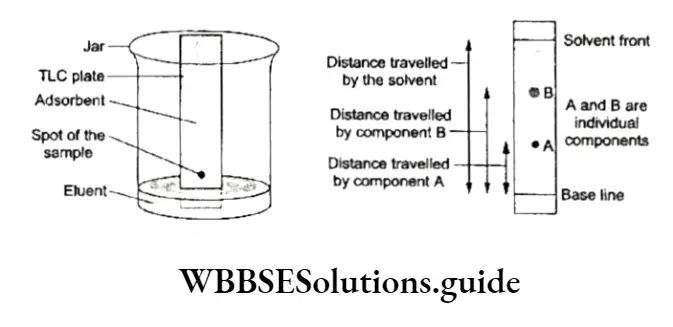
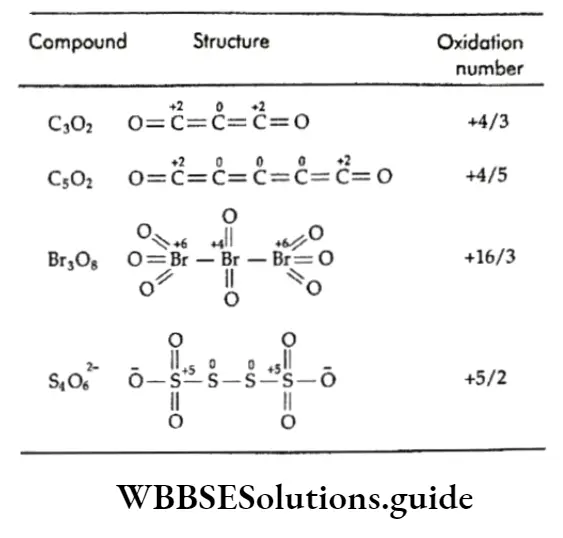
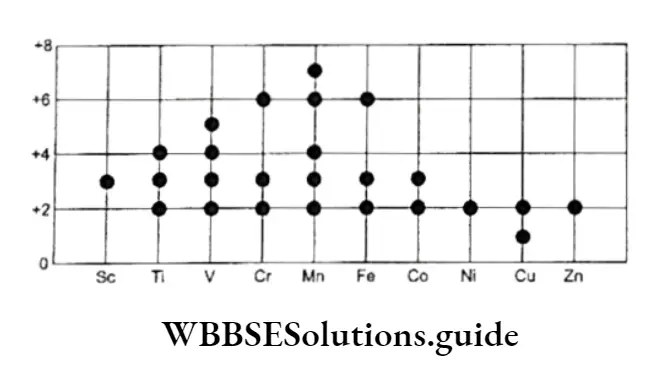
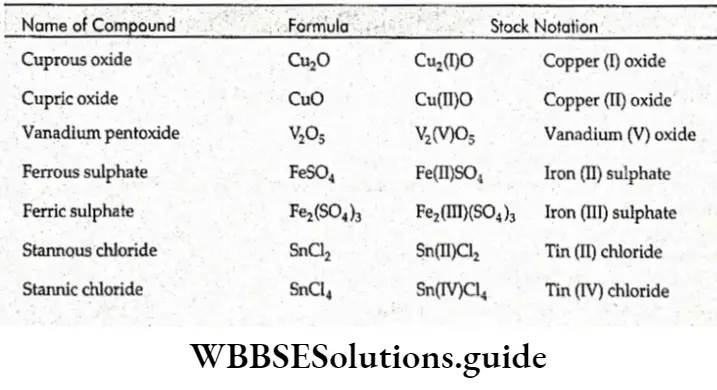
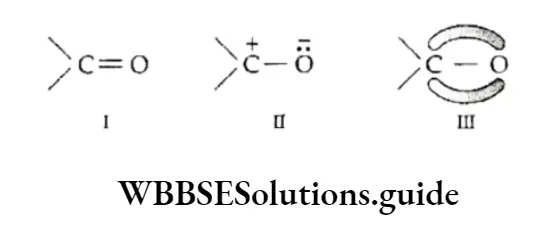Equilibrium

You have learnt about several aspects of a chemical reaction so far. You know, for example, that certain proportions of reactants react to form particular proportions of products and that these proportions are specified in a chemical equation. In the previous chapter, you learnt about the energy changes accompanying a chemical reaction. But there is one aspect of a chemical reaction that we have not considered at all.

Suppose we take reactants in exactly the required proportions (in the ratio of their respective number of moles in the balanced equation) and mix them together. Is it necessary that the reaction will proceed to completion? In other words, is it necessary that all of the reactants will be converted into products?

• We assume this in stoichiometric calculations (chemical arithmetic), but this is not always true. Quite often, a chemical reaction stops after a while and the resultant mixture contains reactants and products. It is said that the reaction has reached a state of chemical equilibrium.
• This state remains unchanged and the composition of the mixture remains the same, unless something forces a change. This something could be a change in temperature, pressure, or concentration of the reactants.
• It could even be a change in the concentration of the products, which could be achieved by removing the products (already formed) from the reaction site. These considerations, i.e., how to change the state of chemical equilibrium, are very important for industrial chemists. You can well imagine that the productivity of an industrial process may depend on these factors.
• When a reaction system reaches a chemical equilibrium, all the properties of the system, i.e., temperature, pressure, concentration of reactants and concentration of products, remain constant over time. What actually happens in such a system is that two opposing processes take place at the same time. Just as the reactants react to form the products, the products combine to produce the reactants.

And there comes a time when the forward process and the reverse process occur in such a way that the reaction seems to come to a standstill. At equilibrium, the rates at which the two opposing processes occur become equal.

• A double arrow (\(\rightleftharpoons\)) is used to denote an equilibrium, whereas a single arrow (-») is used to denote a reaction which proceeds to completion. The extent to which the chemical reactions proceed may be different. Some reactions proceed nearly to completion and only a negligible concentration of the reactants is left.
• There are reactions in which the concentrations of reactants and products are comparable at equilibrium. Lastly, there are a few reactions in which most of the reactants remain unchanged at equilibrium, i.e., small amounts of products are formed.
• Our discussion so far has been centred around chemical reactions, so you may be tempted to believe that a state of equilibrium can be reached only in chemical processes. But this is not true.
• A state of equilibrium may be reached in a physical process as well. When the forward process and the reverse process occur simultaneously at exactly the same rate, a state of equilibrium is reached.

Equilibrium In Physical Processes

You have already come across physical processes which reach a state of equilibrium. A liquid in equilibrium with its own vapour inside a closed vessel is a system in which the processes of evaporation and condensation proceed at the same rate. The examples of physical equilibrium are solid \(\rightleftharpoons\)liquid, liquid \(\rightleftharpoons\) gas, solid \(\rightleftharpoons\) solution and gas solution.

Solid-liquid equilibrium: If you drop a few ice cubes into a glass of water, all the ice changes into water after some time. This physical process or change proceeds in a particular direction until it is complete, i.e., until all the ice melts into water. Now suppose you pour a mixture of ice cubes and water at 273 K and normal atmospheric pressure into a perfectly insulated flask.

• The system, comprising the mixture of ice and water in the flask, will not exchange heat with the surroundings and a state of equilibrium will be reached, in which neither the temperature, the pressure, nor the composition of the mixture will change with time.
• It is not as though nothing will happen inside the flask, but there will be no way of telling that something is happening since there will be no outward indication.
• If you could become really small and enter the world of the molecules of water and ice, you would be able to see that what really happens is that molecules of ice go into the liquid state and molecules of water collide and stick to ice, constantly.

The two processes go on simultaneously and at the same rate. Consequently, neither the mass of ice nor the mass of water changes.

To put this in terms of change in free energy, when an ice-water system is in equilibrium at 273 K and at 1 atm pressure, ΔG = 0. For the process, ice \(\rightleftharpoons\) water

ΔG < 0 when T > 273 K, and

ΔG > 0 when T < 273 K.

• The system comprising ice and water at 1 atm pressure can be at equilibrium only at 273 K. The solid and liquid phases of any (pure) substance at 1 atm pressure can be in a state of equilibrium only at a particular temperature.
• This temperature at which the solid and liquid phases of a pure substance are at equilibrium at a pressure of 1 atm is called the normal melting point or the normal freezing point of the substance.

The same definition but at a pressure of 1 bar refers to standard freezing point of a substance. The equilibrium between the solid and liquid phases of a substance at its melting point is a dynamic equilibrium, in which the activity in one direction is balanced by the activity in the reverse direction. Let us recall the characteristics of a system in dynamic equilibrium.

1. The forward and reverse changes (processes) occur simultaneously and at the same rate, so that there is no change of mass of either side of the equilibrium.
2.  ΔG = 0

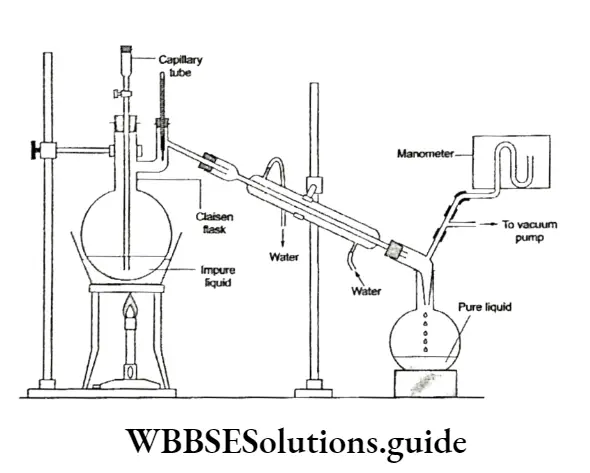
Liquid-vapour equilibrium: You have already come across this kind of equilibrium while studying vapour pressure. It can be demonstrated easily by performing a simple experiment. Take a small quantity of water at room temperature in a closed vessel connected to a manometer.

• Take care to see that the vessel has been evacuated first. To begin with, the level of mercury in both limbs of the manometer will be the ⇒ same. Then the level of mercury in the right limb of the manometer will rise slowly and the level of mercury in the left limb will fall.
• The level of water in the vessel falls gradually. There comes a time when the levels of mercury in tire two limbs become constant and so does the level of water in the vessel.

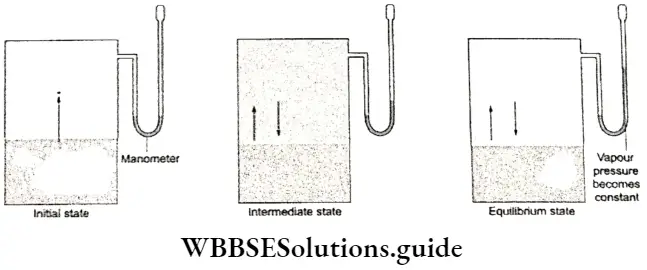
• Initially, there is no water vapour in the vessel and the level of mercury in both limbs is the same. As the water starts evaporating and more and more molecules escape into the gaseous phase, the pressure exerted by the water vapour increases, leading to a drop in the mercury level in the left limb and a rise in the right limb.
• But with the accumulation of vapour molecules in the vessel, the reverse process (condensation) starts. Some vapour molecules revert to the liquid phase. Condensation occurs at a lower rate than evaporation, to start with. But after a while, the two rates become equal and a state of equilibrium is established.

The pressure exerted by the vapour molecules becomes constant, as shown by the steady level of mercury in the manometer. The level of water in the vessel becomes constant because there is no net evaporation. The number of molecules entering the gas phase at any time is the same as the number of molecules entering the liquid phase.

∴ \(\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

The pressure exerted by the water vapour at equilibrium is called the equilibrium vapour pressure or simply the vapour pressure of water at the given temperature. In general, the pressure exerted by the vapour of a liquid in equilibrium with the liquid at a particular temperature is called the vapour pressure of the liquid at that temperature.

• Vapour pressure changes with temperature but is independent of the volume of the liquid. It does not depend on the volume of the container either.
• Different liquids have different vapour pressures at the same temperature and the liquid which has a higher vapour pressure is more volatile, or boils at a lower temperature. For instance, if the vapour pressure of liquid A is 3.2 kPa and that of another liquid B is 10.3 kPa at the same temperature, B is more volatile than A, or B has a lower boiling point than A.
• This should not be difficult to understand if you bear in mind that the vapour pressure of a liquid rises with temperature and that its boiling point is that temperature at which its vapour pressure becomes equal to the atmospheric pressure.
• Consider the two liquids A and B. The vapour pressure of B is higher than that of A at a particular temperature. As the temperature rises, the vapour pressures of both the liquids will rise.

Obviously, the vapour pressure of B will become equal to the atmospheric pressure at a temperature lower than that at which the vapour pressure of A will become equal to the atmospheric pressure. Consequently, the boiling point of B will be lower than that of A.

Solid-vapour equilibrium: In case of sublimable solids, the particles may escape occasionally into the vapour phase and establish vapour pressure.

• The particles which are at the surface of the solid and which have, at any point of time, higher average kinetic energy than the others, may escape into the vapour phase. If the solid is kept in a closed cylinder, particles are not able to escape and add to the vapour phase.
• Eventually, a point is reached when the particles from the vapour phase start returning to the solid phase. As in the case of liquid-vapour equilibrium initially, this reverse process is slow but after some time, an equilibrium is reached whereby rate of return of the particles to the solid phase becomes equal to the rate of escape.
• A dynamic equilibrium is thus established. The vapour pressure now corresponds to the equilibrium vapour pressure, which is characteristic of the solid.
• The tendency of the particles of the solid to escape depends on the intermolecular forces. Tire larger the intermolecular interaction, the less will be the vapour pressure of that solid.

Temperature also has a considerable effect on the vapour pressure of solids. The higher the temperature, the more energetic are the particles and the higher is the vapour pressure.

Iodine is a volatile solid. When solid iodine is placed in a closed vessel and the vessel is heated, the region above the solid becomes violet due to iodine vapours. The equilibrium is represented as \(\mathrm{I}_2 \text { (solid) } \rightleftharpoons \mathrm{I}_2 \text { (vapour). }\)

Another example is dry ice (solid CO₂); it sublimes directly from solid to gas at atmospheric pressure.

• So far we have been considering closed systems. Systems we encounter in our everyday lives are (generally) not closed. The atmosphere, into which water vapour from lakes and rivers and other water bodies escapes, is an open system.
• Though the rate of evaporation of a liquid at a particular temperature in an open system is the same as that in a closed system, equilibrium can never be reached in an open system.
• This is because the rate of condensation can never be equal to the rate of evaporation in an open system, in which the vapour molecules get dispersed in a large volume.
• The water molecules which escape into the atmosphere, for instance, do not remain confined to a small space, they, get dispersed by the wind.
• How much water vapour is there in the air (what we refer to as humidity) depends on several factors, such as the presence of water bodies in the area, the temperature and the velocity of the wind.
• At places close to the sea, especially when the wind velocity is not high, the accumulation of water vapour in the air leads to acute discomfort.

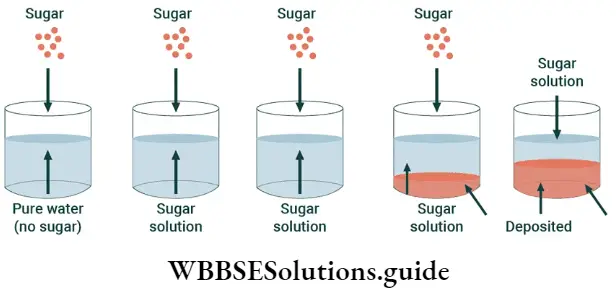
Solid-solution equilibrium: It is true that sugar dissolves in water. But you cannot dissolve an indefinite amount of sugar in a particular amount of water. You can, of course, dissolve more sugar in a particular amount of water if you heat the solution.

• This is what they do in sweet shops when they prepare sugar syrups. But when the syrup cools, crystals of sugar separate from the solution because when the solution (syrup) cools, the solubility of the solute (sugar) in the solvent (water) decreases.
• You may remember from your science courses in junior classes that a solution in which more solute cannot be dissolved is called a saturated solution.
• The amount of a solute that has to be dissolved in a certain amount of a solvent to prepare a saturated solution at a particular temperature is called the solubility of the solute in that solvent at that temperature.
• Solubility is usually expressed in terms of the number of grams of a solute that dissolves in 100 mL of the solvent.
• The solubility of a solid in a liquid depends on temperature, but we will come to that later. Pressure has hardly any effect on the solubility of a solid in a liquid.

What happens when a solution becomes saturated is that a dynamic equilibrium is established between the molecules of the solute in the solid state and the molecules of the solute in the solution.

Solute (in solution) \(\rightleftharpoons solute\) (solid)

• The process by which molecules of the solid solute go into solution is called dissolution. The reverse process by which molecules of the solute in the solution revert to the solid state is called precipitation.
• When a solute is added to a solvent, there are no molecules of the solute in the solvent to begin with. Slowly, as the solute dissolves in the solvent, the reverse process begins.

At first, the process of dissolution proceeds at a faster rate than the process of precipitation. Than there comes a point when the two processes proceed at the same rate. This happens when equilibrium is reached.

Rate of dissolution = rate of precipitation

It is not as though activity comes to a standstill in the solution, but the number of molecules of the solute going into the solution (in a certain time) becomes the same as the number of molecules returning to the solid state.

• This can be demonstrated with the help of an experiment. Prepare a saturated sugar solution in a beaker in such a way that some undissolved sugar remains at the bottom of the beaker.
• If you add some sugar-containing radioactive carbon to the solution, in a while the solution and the undissolved sugar contains sugar which has radioactive carbon.
• This shows that though the solution is saturated, the process of dissolution continues and that the rate of dissolution must be equal to the rate of precipitation, since the amount of sugar left undissolved remains the same.
• In other words, the experiment demonstrates the dynamic nature of the equilibrium reached.

Gas-solution equilibrium: You must have heard people referring to drinks like Pepsi or Mirinda as carbonated or aerated water.

• Well, strictly speaking, such drinks also contain sugar and other additives and it would be more correct to refer to soda as aerated water.
• Nonetheless, it is true that drinks like Pepsi, too, have carbon dioxide dissolved under pressure. It is this carbon dioxide which escapes with a hissing sound when a bottle of coke or soda is opened.
• The fizz that you enjoy in such drinks is also because of the dissolved carbon dioxide.
• Aerated drinks are manufactured by dissolving carbon dioxide in them at a high pressure. Unlike solids, the solubility of gases (in liquids) increases with pressure.

The effect of pressure on the solubility of a gas in a liquid is given by Henry’s law (William Henry was a British physician and chemist), which says that the mass of a gas dissolved in a given mass of a solvent at a particular temperature is proportional to the pressure of the gas above the solvent.

• The solubility of a gas in a liquid decreases as temperature increases. When an aerated drink is bottled there is a dynamic equilibrium between the gas molecules above the solution (tire drink) and the gas molecules in the solution.
• This equilibrium holds as long as the pressure is maintained. When the bottle is opened, the pressure above the solution falls and some of the dissolved gas escapes to reach a new equilibrium.
• If an aerated drink is left open to the air for some time, it turns ‘flat’ because most of the dissolved gas escapes as the pressure above the drink (solution) becomes equal to the atmospheric pressure.

Henry’s law can be expressed mathematically as follows.

∴ m∝ p or m = kp,

where m is the mass of the gas dissolved in the solution, p is the pressure of the gas above the solution and k is a constant of proportionality known as the Henry constant.

• Let us look at this another way. The mass of the gas dissolved in the solution will be related to the concentration of the gas in the solution.
• The pressure exerted by the gas above the solution will depend on the concentration of the gas above the solution. This gives us another way of expressing Henry’s law.
• Concentration of gas in solution x concentration of gas above solution

or \(\frac{\text { concentration of gas in solution }}{\text { concentration of gas in gaseous phase }}=\text { constant. }\)

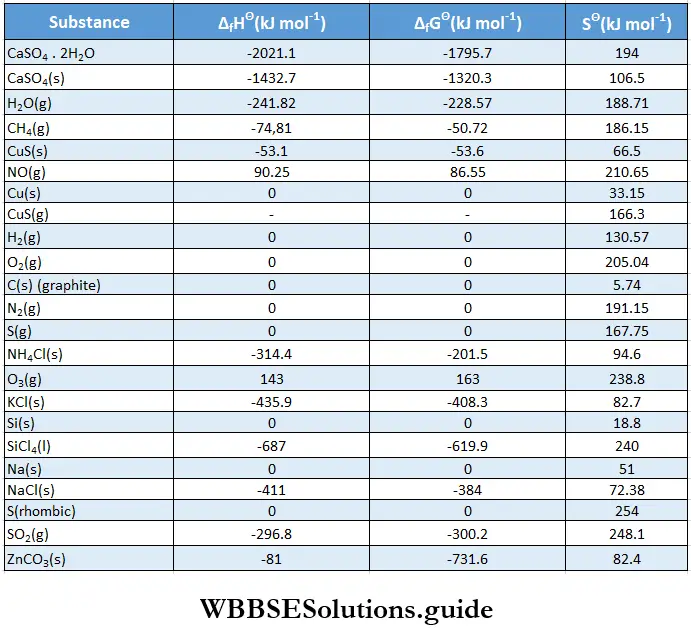
Example: Suppose 0.30 g of iodine is stirred in 100 mL of water at 288 K until equilibrium is reached. Hoiv much iodine would dissolve in the water, if the solubility of iodine in water at 288 K is 0.0011 mol L^-1 [Another way of expressing this is I₂ (aq) at equilibrium = 0.0011 mol L^-1 at 288 K]. Suppose another 100 mL of water is added to the solution after equilibrium is reached with 0.30 g of iodine and 100 mL of water. How much iodine would be left undissolved and what would be the concentration of iodine in the solution?
Solution:

The solubility of iodine (concentration at equilibrium) is given as 0.0011 mol L^-1 at 288 K.

This means at equilibrium mass of iodine dissolved in 1 L of water = 0.0011 x 254 ≅ 0.279 g s 0.28 g [molar mass of I₂ = 254 g]

∴ mass of iodine dissolved in 100 mL of water = 0.028 g.

If another 100 mL of water is added after equilibrium has been established, another 0.028 g of iodine would dissolve.

∴ mass of undissolved iodine – 0.30 – (0.028 x 2) = 0.30 – 0.056 = 0.244 g.

The concentration of iodine in the solution would simply be the solubility of iodine at equilibrium i. i.e., 0.28 gL^-1.

Characteristics of equilibrium in physical processes: We have discussed the attainment of an equilibrium state in relation to four different physical processes. They all have certain characteristics in common.

1. An equilibrium can be reached only in a dosed system, i.e., a system which neither gains matter from nor loses matter to the surroundings. For instance, in the case of a liquid—gas system, equilibrium is not reached if the vapour is allowed to escape from the vessel.
2. The equilibrium reached is dynamic in nature, i.e., there is a balance between two opposing processes occurring at the same rate.
3. At equilibrium, the measurable properties of the system become constant (under a given set of conditions). For instance, in the case of evaporation, the vapour pressure of the liquid is constant at a given temperature.
   • In solid-liquid equilibrium, the melting point (the temperature at which the two phases coexist provided no heat is exchanged) is constant for a particular pressure.
   • For the dissolution of a solid in a liquid, the solubility is constant at a given temperature. For the dissolution of a gas in a liquid, the concentration of the gas in the solution is constant for a particular pressure of the gas above the solution at a given temperature.
4. At equilibrium, the concentrations of substances in the liquid and gaseous phase bear a constant ratio at a particular temperature. For the dissolution of C02 in water, for example, \(\frac{\mathrm{CO}_2(\mathrm{aq})}{\mathrm{CO}_2(\mathrm{~g})}\) is constant at a given temperature. This constant is called the equilibrium constant and its magnitude indicates the extent to which the process proceeds before equilibrium is reached. For example, the greater the value of \(\frac{\mathrm{CO}_2(\mathrm{aq})}{\mathrm{CO}_2(\mathrm{~g})}\) greater is the extent to which CO₂ disiolves in water.

Equilibrium In Chemical Systems

We started this chapter with a discussion on whether a chemical reaction must always proceed to completion. There are some chemical reactions which proceed to completion, i.e., at equilibrium the concentration of the, reactants is negligible compared to the concentration of the products. (In reality, no reaction proceeds to completion in the true sense, but we need not concern ourselves with this now.) An example of this type of reaction is

⇒ \(\mathrm{BaCl}_2(\mathrm{aq})+\mathrm{Na}_2 \mathrm{SO}_4(\mathrm{aq}) \longrightarrow \mathrm{BaSO}_4(\mathrm{~s})+2 \mathrm{NaCl}(\mathrm{aq})\)

We could also call this reaction an irreversible reaction, since the reaction proceeds in one direction and the reverse process, i.e., the products reacting to form the reactants under the same conditions, does not take place. A few irreversible reactions are given below.

⇒ \(2 \mathrm{Na}+2 \mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{NaOH}+\mathrm{H}_2\)

⇒ \(\mathrm{AgNO}_3(\mathrm{aq})+\mathrm{NaCl}(\mathrm{aq}) \longrightarrow \mathrm{NaNO}_3(\mathrm{aq})+\mathrm{AgCl}(\mathrm{s})\)

⇒ \(2 \mathrm{Mg}(\mathrm{s})+\mathrm{O}_2(\mathrm{~s}) \longrightarrow 2 \mathrm{MgO}(\mathrm{s})\)

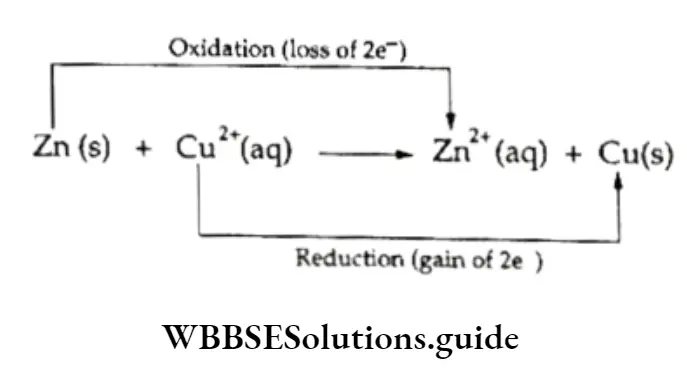
Let us now consider a reaction which is reversible, i.e., a reaction in which the reactants react to form products under certain conditions and the products combine to form the reactants under the same conditions.

For instance, iron reacts with steam to form hydrogen and iron oxide, and heated iron oxide reacts with hydrogen to produce iron and steam.

⇒ \(3 \mathrm{Fe}+4 \mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{Fe}_3 \mathrm{O}_4+4 \mathrm{H}_2\)

If a reversible reaction is carried out in such a way that one of the products escapes, the reaction becomes irreversible, or proceeds in only one direction.

• If, for instance, in the reaction between metallic iron and steam, the hydrogen formed is allowed to escape, the reverse reaction cannot take place and the process becomes virtually irreversible, or proceeds to completion.
• If, on the other hand, the reaction is carried out in a closed vessel, from which hydrogen cannot escape, both forward and backward reactions take place simultaneously and there comes a time when an equilibrium is established.
• At equilibrium, the reaction appears to have stopped, but what happens is that the forward and reverse reactions occur at the same rate.

For instance, when hydrogen and iodine are heated in a closed vessel at 717 K, they react to form hydrogen iodide. However, since the hydrogen iodide is not allowed to escape, the reverse reaction occurs. Hydrogen iodide decomposes to form hydrogen and iodine.

⇒ \(\underset{\text { colourless }}{\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g})} \rightleftharpoons \underset{\text { viclet }}{2 \mathrm{HI}(\mathrm{g})}\)

Initially, the reaction mixture is deep violet because of the presence of iodine.

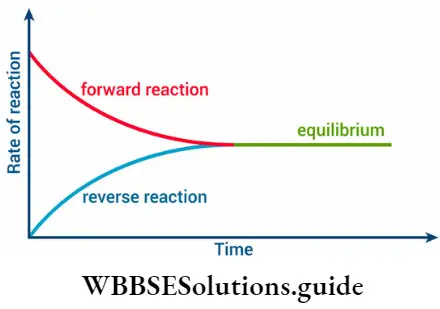
• The intensity of the colour decreases, as the reaction proceeds, and after a while, it becomes steady, indicating that an equilibrium has been reached.
• At equilibrium, it appears that the reaction has stopped, despite the presence of the reactants.
• But in reality, the rate at which hydrogen and iodine combine to form hydrogen iodide becomes equal to the rate at which hydrogen iodide decomposes.
• When we talk about the time it takes for the colour of the
  reaction mixture that we have just been discussing to become
  steady, we are talking about a finite time interval.
• However, to the naked eye, the change seems to be instantaneous. It is possible, though, to determine this time interval with modem instruments.
• It is also possible to establish the dynamic nature of the equilibrium using radioactive reagents.

Characteristics of chemical equilibrium

1. Consider a general reversible reaction \(\mathrm{A}+\mathrm{B} \rightleftharpoons \mathrm{C}+\mathrm{D}\)

• Initially, the concentrations of A and B are maximum and the concentrations of C and D are zero. As the reaction proceeds, the concentrations of A and B decrease and the concentrations of C and D increase.
• With this, the rate of the forward reaction starts decreasing, while the rate of the backward reaction starts increasing, until the two rates become equal, and equilibrium is reached.
• At this point the concentration of A and B, and C and D become constant.
• That the concentrations of the reactants and the products become constant at equilibrium can be demonstrated by connecting a manometer to a closed vessel containing CaCO₃.

If the vessel is heated, CaCO₃ decomposes to yield CaO and CO₂.

⇒ \(\mathrm{CaCO}_3(\mathrm{~s}) \rightleftharpoons \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})\)

To begin with, the pressure due to CO₂ keeps increasing. Then the level of mercury in the manometer becomes steady, indicating that the pressure has become constant. This shows that the concentration of CO₂ produced becomes constant (as those of CaCO₃ and CaO) at equilibrium.

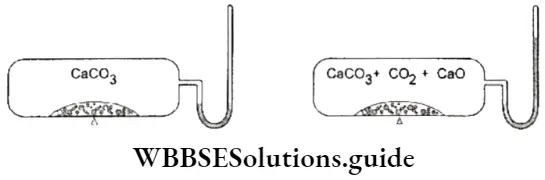
2. In the reaction that we have just considered, the pressure exerted by CO₂ becomes constant at equilibrium. In the reaction between hydrogen and iodine, the colour of the reaction mixture becomes constant.

In general, the observable properties of the system become constant at equilibrium. Actually, this follows from the fact that the concentrations of the reactants and products become constant at equilibrium.

3. A chemical equilibrium can be attained only in a closed system. This should be obvious. If the system is open, one or more of the products may escape, making the reverse reaction impossible.

4. The rates of the forward and backwards reactions become equal at equilibrium. We have discussed this point at length already.

If this were not so, the reaction between hydrogen and iodine, for instance, would not appear to come to a standstill, despite the presence of the reactants.

The dynamic nature of chemical equilibrium can be demonstrated in the synthesis of ammonia by the Haber process.

⇒ \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})\)

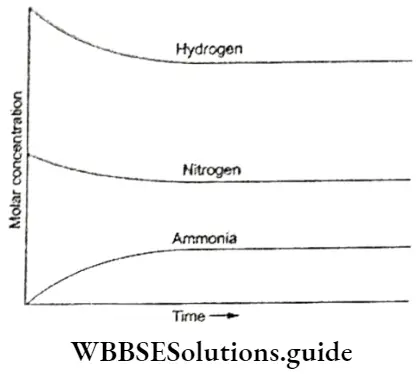
Known amounts of hydrogen and nitrogen are taken at high temperature and pressure, which react to form ammonia.

• The concentrations of all the three substances respectively are determined at regular intervals and a graph of the molar concentrations against time is plotted.
• The graph shows that initially the concentration of the reactants, i.c„ hydrogen and nitrogen decreases whereas that of the product ammonia increases.
• That equilibrium is reached is depicted in the graph when, after a certain time, the composition of the reaction mixture is constant.
• In order to prove the dynamic nature of equilibrium, the experiment is performed again in the same set of conditions except for the use of deuterium in place of hydrogen.
• The reaction mixture in this case, at equilibrium, has the same composition as that in the prior one except for the presence of deuterium in place of hydrogen (i.e., D₂, N₂ and ND₃).
• Once the equilibrium is attained in both cases, the two reaction mixtures are mixed together and left. After some time the concentration of ammonia in this new mixture is found to be the same as before.
• However, mass spectrometer analysis revealed that all forms containing hydrogen as well as deuterium are present—NH₃, NH₂D, NHD₂, ND₃, H₂, HD, D₂—in the reaction mixture.
• This is only possible when the bonds are continuously breaking and being made at equilibrium or the forward and reverse reactions are taking place.

Had the reaction stopped then there would have been no mixing of the isotopes. This proves that the equilibrium is dynamic in nature.

5. The equilibrium can be approached from either direction. For instance, in the case of \(\mathrm{Fe}_3 \mathrm{O}_4+4 \mathrm{H}_2 \rightleftharpoons 3 \mathrm{Fe}+4 \mathrm{H}_2 \mathrm{O}\), it would make no difference whether we started with iron oxide and hydrogen, or metallic iron and steam.

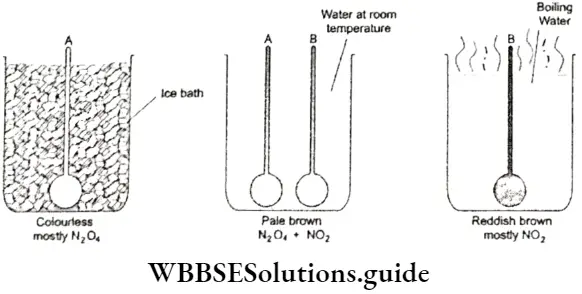
• The fact that equilibrium can be approached from either direction can be proved by performing a simple experiment. Dinitrogen tetroxide (N₂O₄) is a colourless gas and nitrogen dioxide (NO₂) is reddish brown in colour.
• Dinitrogen tetroxide decomposes almost completely to nitrogen dioxide at 373 K. N₂O₄ is stable at 273 K and exists almost entirely as pure N₂O₄, which is colourless.

⇒ \(\underset{\text { collourless }}{\mathrm{N}_2 \mathrm{O}_4(\mathrm{~g})} \rightleftharpoons \underset{\text { reddish brown }}{2 \mathrm{NO}_2(\mathrm{~g})}\)

If you take two identical flasks A and B, fill them with nitrogen dioxide and keep them at room temperature, both will actually contain a pale brown mixture of N₂O₄ and NO₂.

• Now place flask A in a bath maintained at 273 K and flask B in a vessel of boiling water. The gas in flask A will turn colourless, indicating that it is mostly N₂O₄, while the colour of the gas in flask B will deepen to reddish brown, showing that it is mostly NO₂.
• If you then transfer both the flasks to a bath maintained at room temperature (298 K), the gas in flask A will turn pale brown and the reddish brown colour of flask B will fade, until both appear the same colour.
• The fact that the gaseous mixtures in both flasks attain the same colour indicates that, at equilibrium, both flasks contain a mixture of N₂O₄ and NO₂ in the same proportion, which means that equilibrium can be approached from either direction.

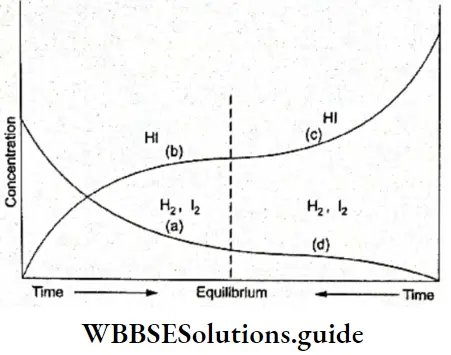
The fact is also demonstrated by Figure, which graphically represents the reaction \(\mathrm{H}_2+\mathrm{I}_2 \rightleftharpoons 2 \mathrm{HI}\) we have considered earlier in the chapter.

Whether we start the reaction from H₂ and I₂ or from HI, the composition of the reaction mixture at equilibrium is constant. The figure represents the forward and the backward reaction in the same graph.

• When we start the reaction with an equimolar mixture of H₂ and I₂, as you can see in Figure, the concentration of these two decreases (curve a) while that of HI increases (curve b). Both of them finally reach a stable concentration at equilibrium.
• When we move from right to left in the graph, we are actually starting with HI and its concentration decreases with time (curve c) while that of H₂ and I₂ increases (curve d), both of them stabilising at the equilibrium point.

6. You know that a catalyst increases the rate of a reaction. In the case of a reversible reaction, a catalyst increases the rates of the forward and reverse reactions to the same extent.

Hence it does not alter the state of equilibrium. That is to say, the concentrations of the reactants and products at equilibrium are the same with or without the catalyst. All that happens is that the state of equilibrium is attained faster.

7. To repeat what you already know, at equilibrium, ΔG = 0.

Law Of Mass Action

We have been discussing the fact that at equilibrium, the rates of the forward and reverse reactions become equal. But can one determine these rates? In 1863 two Norwegian chemists, C. M. Guldberg and P. Waage, came up with a law on the basis of experimental observations.

• This law, known as the law of mass action, relates the rate of chemical reaction with the concentrations of the reactants. It says that the rate at which a chemical reaction occurs at a given temperature is proportional to the product of the active masses of the reactants.
• You must remember that Guldberg and Waage came up with this law in connection with ideal gases and that the law is strictly correct only for ideal gases.

The active mass of a reactant is nothing but its molar concentration, or the number of moles dissolved per litre of the solution. For example, suppose a solution of HCl has x g of HCl dissolved in y L of solution. Then the concentration of the solution = \(\frac{x}{y} \mathrm{gL}^{-1}\)

= \(\frac{x}{36.5 \times y} \mathrm{~mol} \mathrm{~L}^{-1}\)(molar mass of HCl = 36.5)

Thus the active mass of the HCl solution, represented as [HCl], is x/36.5 y M, where M stands for molar concentration or mol L^-1.

Let us consider a reaction between two reactants A and B.

A + B → products

According to the law of mass action, the rate of reaction ∝ [A] [B] or rate = k[A][B],

where [A] and [B] are the concentrations of the reactants A and B respectively, and A is a proportionality constant, called the velocity constant or rate constant.

Now consider a reaction 3C + 4D → products

you could think of this reaction as C + C + C + D + D + D + D → products then rate = k[C][C][C][D][D][D][D] = k[C]³[D]⁴.

In general, for any reaction aA + bB → products

∴ rate of reaction = k[A]^a [B]^b.

Thus, the law of mass action can also be expressed as follows.

The rate of a reaction is proportional to the product of the concentrations of the reactants, each raised to the power equal to its coefficient (number of moles of the species) in the balanced chemical equation representing the reaction.

Law Of Chemical Equilibrium

This law follows from the law of mass action. Consider the following general reversible reaction.

aA + bB \(\rightleftharpoons\)cC + dD

If we apply the law of mass action to this reaction at equilibrium, rate of forward reaction = \(k[\mathrm{~A}]_{\mathrm{eq}}^a[\mathrm{~B}]_{\mathrm{eq}}^b\),

where k is the rate constant for the forward reaction and [A]_eq and [B]_eq are the molar concentrations of the reactants A and B at equilibrium.

Rate of reverse reaction = \(k^{\prime}[C]_{\mathrm{eq}}^c[\mathrm{D}]_{\mathrm{eq}}^d\),

where k’ is the rate constant for the reverse reaction and [C]_eq and [D]_eq are the molar concentrations of the products C and D at equilibrium.

At equilibrium, rate of forward reaction = rate of reverse reaction or \(k[\mathrm{~A}]_{\mathrm{eq}}^a[\mathrm{~B}]_{\mathrm{eq}}^b=k^{\prime}[\mathrm{C}]_{\mathrm{eq}}^c[\mathrm{D}]_{\mathrm{eq}}^d\)

or, \(\frac{k}{k^{\prime}}=\frac{[\mathrm{C}]_{\mathrm{eq}}^c[\mathrm{D}]_{\mathrm{eq}}^d}{[\mathrm{~A}]_{\mathrm{eq}}^a[\mathrm{~B}]_{\mathrm{eq}}^b}=K_c\)

Generally the subscript ‘eq’ is used to denote concentration at equilibrium. The subscript ‘c’ indicates that K_c is expressed in concentrations of mol L^-1.

K_c must be a constant at a given temperature since k and Ak’ are constants for a given temperature. Guldberg and Waage called it the equilibrium constant.

Thus, at equilibrium, the product of the molar concentrations of the reaction products, each raised to the power equal to its stoichiometric coefficient in the balanced chemical equation, divided by the product of the molar concentrations of the reactants, each raised to the power equal to its stoichiometric coefficient, is constant at a given temperature. This is referred to as the law of chemical equilibrium.

The equilibrium constant for the reaction \(4 \mathrm{NH}_3(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \text { is } K_{\mathrm{c}}=\frac{\left[\mathrm{NO}^4\left[\mathrm{H}_2 \mathrm{O}\right]^6\right.}{\left[\mathrm{NH}_3\right]^4\left[\mathrm{O}_2\right]^5}\)

The symbols used to denote phases in a chemical reaction are ignored while writing the expression for the equilibrium constant.

Reaction quotient: For any reversible reaction at any stage other than equilibrium, the ratio of the molar concentrations of the products to that of the reactants, where each concentration term is raised to the power equal to the stoichiometric coefficient of the substance concerned, is called the reaction quotient, Q.

It is symbolised as Q_c. while molar concentrations are considered and Q_p while partial pressures are considered for any reaction.

For a general reaction \(a\mathrm{~A}+b \mathrm{~B} \rightleftharpoons c \mathrm{C}+d \mathrm{D}\)

which is not at equilibrium  \(Q_c=\frac{[\mathrm{C}]^c[\mathrm{D}]^d}{[\mathrm{~A}]^a[\mathrm{~B}]^b}\).

1. If Q_c > K_c, the value of Q_c will tend to decrease to reach the value of K_c (towards equilibrium), and the reaction will proceed in the reverse direction.
2. If Q_c < K_c, it will tend to increase, and the reaction will proceed in the forward direction.
3. If Q_c = K_c, the reaction is at equilibrium.

So, if you know the relative concentrations of reactants and products at a particular stage of a reaction, you can predict the direction in which the reaction will proceed.

Also, if you know the initial concentrations of the reactants and the value of K_c, you can predict the composition of the reaction system at equilibrium.

Now consider the following reaction. \(\mathrm{CO}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2(\mathrm{~g})\)

Here \(Q_c=\frac{\left[\mathrm{CO}_2\right]\left[\mathrm{H}_2\right]}{[\mathrm{CO}]\left[\mathrm{H}_2 \mathrm{O}\right]}\) and Kc = 0.64 at 800°C. The initial conditions for a reaction can vary.

Here we have discussed three possibilities for the given reaction. The values taken are from different experiments. There is no need for you to memorise these values, the discussion will help you learn how to predict the direction of a reaction.

1. Only the reactants are present, say. [CO] = 0.0243 M and [H₂O] = 0.0243 M.

Since the concentration of products is zero, the reaction quotient Q_c = 0, i.e., Q_c < K_c.

The reaction thus proceeds in the forward direction till Qc reaches a value equal to K_c.

At equilibrium, the concentrations are [CO]_eq = 0.0135 M,[H₂O]_eq = 0.0135 M,[CO₂]_eq = 0.0108 M,[H₂]_eq = 0.0108 M.

∴ \(K_c=\frac{0.0108 \times 0.0108}{0.0135 \times 0.0135}=0.640\)

2. Only the products arc present, say. [CO₂] = 0.0468 M,[H₂] = 0.0468 M.

Q_c >K_c and hence the reaction proceeds in the reverse direction, forming CO and H₂O.

At equilibrium the concentrations are [CO]_eq = 0.0260 M,[H₂O]_eq = 0.0260 M,[CO₂]_eq = 0.0208 M,[H₂]_eq = 0.0208 M.

∴ \(K_2=\frac{(0.0208)(0.0208)}{(0.0260)(0.0260)}\)=0.640

3. The reactants and products are present in the following concentrations.

[CO]= 0.0094 M.[HO] =0.055 M,[CO₂] = 0.0005 M,[H₂]= 0.0046 M.

then, \(Q_c=\frac{(0.0006)(0.0046)}{(0.0094)(0.0065)}=0.044\)

As Q_c. <K_c, the reaction will proceeds in the forward direction and as expected, the concentrations at equilibrium are found to be [CO]_eq = 0.0074 M; [H₂O]_eq = 0.0035 M; [CO₂]_eq =0.0025 M and [H₂]_eq = 0.0066 M resulting in a K_c value of 0.64.

Types of equilibrium: A chemical equilibrium is called homogeneous if all the reactants and products are present in the same phase. Some examples of homogeneous equilibrium follow.

⇒ \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g})\rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})\)

⇒ \(\mathrm{CO}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2\)

⇒ \(\mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{aq}) \rightleftharpoons \mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

In a heterogeneous, chemical equilibrium, on the other hand, the reactants and products are not all in the same phases A few examples follow.

⇒ \(\mathrm{CaCO}_3(\mathrm{~s}) \rightleftharpoons \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})\)

⇒ \(\mathrm{C}(\mathrm{s})+\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{CO}(\mathrm{g})+\mathrm{H}_2(\mathrm{~g})\)

⇒ \(3 \mathrm{Fe}(\mathrm{s})+4 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightleftharpoons \mathrm{Fe}_3 \mathrm{O}_4(\mathrm{~s})+4 \mathrm{H}_2(\mathrm{~g})\)

∴ \(\mathrm{CrO}_4^{2-}(\mathrm{aq})+\mathrm{Pb}^{2+}(\mathrm{aq}) \rightleftharpoons \mathrm{PbCrO}_4(\mathrm{~s})\)

Gas-phase reactions: When all fee reactants and products of a reaction are gaseous, the reaction is called a gas-phase reaction and it is a case of homogeneous equilibrium.

In the case of such reactions, the equilibrium constant can be expressed either in terms of molar concentrations or partial pressures.

When expressed in terms of molar concentrations it is denoted by K_c and if it is expressed in terms of partial pressures, K_p is used. If A, B, X and Y are gases in the reaction the equilibrium constant can be expressed as follows.

⇒ \(a \mathrm{~A}+b \mathrm{~B} \rightleftharpoons x \mathrm{X}+y \mathrm{Y}\)

∴ \(K_p=\frac{\left(p_{\mathrm{X}}\right)^x\left(p_{\mathrm{Y}}\right)^y}{\left(p_{\mathrm{A}}\right)^a\left(p_{\mathrm{B}}\right)^{\mathrm{b}}}\)

In this expression, p_A, p_B, p_x and p_y are the partial pressures of A, B, X and Y, expressed in atmospheres or pascals.

At constant temperature, the pressure of a gas is proportional to its concentration.

In terms of concentrations, the equilibrium constant can be expressed as

∴ \(K_c=\frac{[X]^z[Y]^y}{[A]^a[B]^b} \quad \text { or } \quad \frac{\left(C_X\right)^x\left(C_Y\right)^y}{\left(C_A\right)^a\left(C_B\right)^b} \text {, }\)

where C_A, C_B, C_x and C_y are the molar concentrations of A, B, X and Y respectively.

If A, B, X and Y are ideal gases, pV = nRT

or \(p=\frac{n}{V} R T\)

or p =n/VRT = CRT [n/V = number of moles per litre or mol/dm³]

Then \(p_{\mathrm{A}}\)=\(\mathrm{C}_{\mathrm{A}} R T\) and \(p_{\mathrm{B}}\)=\(\mathrm{C}_{\mathrm{B}} R T\).

⇒ \(p_{\mathrm{X}}\)=\(C_{\mathrm{X}} R T\) and \(p_{\mathrm{Y}}\)=\(\mathrm{C}_{\mathrm{Y}} R T\).

∴ \(K_p=\frac{\left(C_X R T\right)^x\left(C_Y R T\right)^y}{\left(C_A R T\right)^a\left(C_B R T\right)^b}=\frac{\left(C_X\right)^x\left(C_Y\right)^y}{\left(C_{\mathrm{A}}\right)^a\left(C_B\right)^b} R T^{(x+y)-(a+b)}\).

But \(K_c=\frac{\left(C_X\right)^x\left(C_Y\right)^y}{\left(C_{\mathrm{A}}\right)^a\left(C_B\right)^b}\).

∴ \(K_p=K_c R T^{\Delta n}\),

where Δn = (x + y) – (a + b) = no. of moles of products – no. of moles of reactants in the balanced chemical equation.

Consider the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\) at equilibrium. If the equilibrium constant for the reaction is K_c then K_p would be K_p = K_cRT_Δn,

where Δn = no. of moles of HI- no. of moles of H₂ and I₂ = 2- 2 or 0.

Therefore, K_p =K_c for the reaction at equilibrium.

However, this is not always the case. Consider another example, \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})\) at equilibrium.

Here the number of moles of reactants is more than that of the product or Δn = 2 – 4 or -2.

Therefore, the equilibrium constant in terms of partial pressure Kp for the above reaction would be K_p = K_c(RT)^-2.

If the concentration is in mol L^-1 and p is in bar then R = 0.0831 L bar K^-1 mol^-1.

Nature of equilibrium constant

1. The equilibrium constant, as we have defined it so far, is the ratio of the product of the molar concentrations of the reaction products to that of the reactants, with each concentration term raised to the power equal to the stoichiometric coefficient of the substance in the balanced chemical equation. You may argue that if this is so, K should have units.

• Though the equilibrium constant was initially derived in terms of concentrations, strictly speaking, concentrations or partial pressures can be used only for ideal gases. However, nowadays, equilibrium constants are expressed in dimensionless quantities.
• This is possible only when the quantities (concentration and partial pressures) are measured with respect to a corresponding standard state.
• The standard state for a pure gas is taken to be 1 bar and for solute the standard state (C₀) is 1 molar solution. Thus a pressure of 4 bar in terms of standard state is 4, a number without a unit.
• Therefore the numerical value of the equilibrium constant depends on the standard state chosen and both K_p and K_c are dimensionless quantities.

2. The equilibrium constant has a definite value for a particular reaction at a given temperature. This value does not depend on the initial concentrations of the reactants.

If the reaction is reversed, the tire value of K becomes the inverse of the value of the forward process. For instance, suppose the value of the equilibrium constant for the combination of hydrogen and iodine at 720 K is K_c.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g}) ; \quad K_c=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]} \text {. }\)

Then the value of the equilibrium constant, say K’_c, for the decomposition of hydrogen iodide at the same temperature would be 1/K_c.

⇒ \(2 \mathrm{HI}(\mathrm{g}) \rightleftharpoons \mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) ; \quad K_c^{\prime}=\frac{1}{K_c}=\frac{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]}{[\mathrm{HI}]^2}\).

3. It is all very well to say that the value of the equilibrium constant remains the same for a particular reaction at a given temperature. But a reaction may be expressed in more ways than one. For instance, the reaction between hydrogen and iodine can be expressed in the following ways.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\)….(1)

⇒ \(\frac{1}{2} \mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{I}_2(\mathrm{~g}) \rightleftharpoons \mathrm{HI}(\mathrm{g})\)…(2)

⇒ \(n \mathrm{H}_2(\mathrm{~g})+n \mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 n \mathrm{HI}(\mathrm{g})\) …..(3)

If the equilibrium constant for (1) is \(K_c=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]}\)

then the equilibrium constant for (2) is \(K_c^{\prime}=\frac{[\mathrm{HI}]}{\left[\mathrm{H}_2\right]^{1 / 2}\left[\mathrm{I}_2\right]^{1 / 2}}=\sqrt{K_c} \text { or } K_c^{1 / 2}\)

and the equilibrium for  (3) is \(K_c^n=\frac{[\mathrm{HI}]^{2 n}}{\left[\mathrm{H}_2\right]^n\left[\mathrm{I}_2\right]^n}=K_c^n\).

Thus, the value of K_c depends on the coefficients of the reactants and products in the equation being considered.

4. If an equation is written in two steps and the values of the equilibrium constants for the two steps are K₁ and K₂ then the value of the equilibrium constant for the equation is the product of and K₂. For example, the reaction

⇒ \(\mathrm{N}_2+2 \mathrm{O}_2 \rightleftharpoons 2 \mathrm{NO}_2 ; \quad K_c=\left[\mathrm{NO}_2\right]^2 /\left[\mathrm{N}_2\right]\left[\mathrm{O}_2\right]^2\)

occurs in two steps.

⇒ \(\mathrm{N}_2+\mathrm{O}_2 \rightleftharpoons 2 \mathrm{NO} ; \quad K_1=\left[\mathrm{NO}^2 /\left[\mathrm{N}_2\right]\left[\mathrm{O}_2\right]\right.\)

⇒ \(2 \mathrm{NO}+\mathrm{O}_2 \rightleftharpoons 2 \mathrm{NO}_2 ; \quad K_2=\left[\mathrm{NO}_2\right]^2 /\left[\mathrm{NO}^2\left[\mathrm{O}_2\right]\right.\)

∴ \(K_1K_2=\frac{[\mathrm{NO}]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{O}_2\right]} \frac{\left[\mathrm{NO}_2\right]^2}{\left[\mathrm{NO}^2\left[\mathrm{O}_2\right]\right.}=\frac{\left[\mathrm{NO}_2\right]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{O}_2\right]^2}=K_c\)

5. The value of equilibrium constant does not change if a catalyst is present.

6. The magnitude of K_c helps to predict the extent to which the reactants will be converted into the products, or the equilibrium composition of the reaction system.

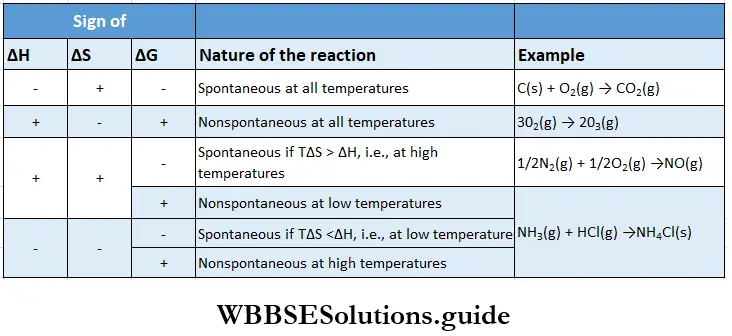
• As products appear in the numerator of the equilibrium constant expression, and reactants are in the denominator, a large value of K_c or K_p indicates that the ratio of products to reactants is very large.
• In other words, the reaction proceeds nearly to completion. A very low value of K_c indicates that the reaction cannot proceed much in the forward direction.

In other words the value of K_c tells us whether the particular reaction can actually take place. Let us consider an example.

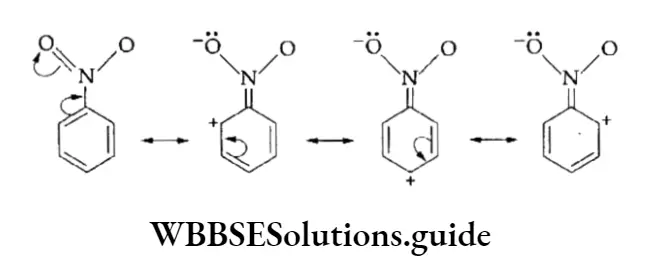
⇒ \(\mathrm{Fe}^{3+}(\mathrm{aq})+\mathrm{SCN}^{-}(\mathrm{aq}) \rightleftharpoons \mathrm{FeSCN}^{2+}(\mathrm{aq})\)

At 298 K, the equilibrium constant for the forward reaction is 138, which shows that the forward reaction is favoured or can occur. For the reverse reaction the equilibrium constant is 1/138, which shows that this reaction does not proceed much to the left.

Similarly, for the reaction, \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HCl} \text { at } 300 \mathrm{~K}\) the equilibrium constant is 4.0 x 10³¹. This shows that the reaction goes virtually to completion.

The equilibrium constant for the reverse reaction \(2 \mathrm{HCl}(\mathrm{g}) \rightleftharpoons \mathrm{H}_2(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \text { is } \frac{1}{4.0 \times 10^{31}}=25 \times 10^{-30}\) indicating that the reverse reaction is less favoured. While a large value of K_p or K_c favours the formation of products, a very small value favours the reverse reaction or the formation of reactants.

Consider the reaction \(\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g}) . \mathrm{K}_c \text { is } 4.8 \times 10^{-31}\) at 298 K for this reaction. Here, at equilibrium, the ratio of concentration of products to reactants is small, indicating that the reverse reaction is favoured.

Examples of reactions having intermediate values of equilibrium constants are

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g}) K_c=57 \text { at } 700 \mathrm{~K}\)

⇒ \(\text { and } \mathrm{N}_2 \mathrm{O}_4(\mathrm{~g})  \rightleftharpoons 2 \mathrm{NO}_2(\mathrm{~g}) K_c=4.64 \times 10^{-3} \text { at } 298 \mathrm{~K}\).

In both cases, there are appreciable amounts of reactants and products. This may be verified for the first reaction by substituting the concentrations of H₂ and I₂ (say 0.01 M) in the equilibrium constant expression

⇒ \(K_c=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]} \cdot\)

⇒ \({[\mathrm{HI}]^2 } =K_c \cdot\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]\)

∴ \({[\mathrm{HI}] } =\sqrt{K_c \cdot\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]}=\sqrt{57 \times 0.01 \times 0.01}=0.075 \mathrm{M}\).

It is worthwhile to mention here that the magnitude of an equilibrium constant of a reaction does not tell us anything about the rate of that reaction, i.e., how fast or how slowly the reaction will take place. It is quite possible that the equilibrium constant of a reaction may suggest completion but the rate is too low for all practical purposes.

We can make a generalisation about the extent to which a reaction proceeds based on the magnitude of K_c, as shown in Table.

Conventions regarding K

1. In the case of a homogeneous equilibrium involving products and reactants in the gaseous phase for example, \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\)

obtaining the expression for Kc or Kp is simple enough.

∴ \(K_{\mathrm{c}}=\frac{[\mathrm{HI}(\mathrm{g})]^2}{\left[\mathrm{H}_2(\mathrm{~g})\right]\left[\mathrm{I}_2(\mathrm{~g})\right]} \text { and } K_p=\frac{p_{\mathrm{HI}}^2}{p_{\mathrm{H}_2} p_{\mathrm{I}_2}} \text {. }\)

2. If one of the products or reactants involved in a heterogeneous equilibrium is a solid or a liquid its concentration is taken to be unity, by convention.

The molar concentration of a pure solid or liquid is coastant. In other words for any amount of substance ‘X’, [X(s)] and [X(l)] are constant. But [X(g)] and [X(aq)] will vary with the volume. Consider the following equilibrium.

⇒ \(\mathrm{CaCO}_3(\mathrm{~s}) \rightleftharpoons \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})\)

⇒ \(K_{\mathrm{c}}=\frac{[\mathrm{CaO}(\mathrm{s})]\left[\mathrm{CO}_2(\mathrm{~g})\right]}{\left[\mathrm{CaCO}_3(\mathrm{~s})\right]}=\frac{1 \times\left[\mathrm{CO}_2(\mathrm{~g})\right]}{1}=\left[\mathrm{CO}_2(\mathrm{~g})\right]\)

or \(K_p=p_{\mathrm{CO}_2}\)

This fits with the fact that the pressure of CO₂ becomes constant when equilibrium is reached in the decomposition of CaCO₃ in a closed vessel.

It has been found experimentally that the pressure of CO₂ is 2.5 x 10⁴ Pa when the reaction for the decomposition of CaCO₃ reaches equilibrium at 1073 K. Therefore the equilibrium constant at 1073 K for the above reaction is

⇒ \(K_p=p_{\mathrm{CO}_2}=\frac{2.5 \times 10^4 \mathrm{~Pa}}{10^5 \mathrm{~Pa}}\) = 0.25

(since 1 bar =10⁵ Pa and while calculating the value of K_p, pressure should be expressed in bar as the standard state of a substance is its pure state at exactly 1 bar.)

3. Consider an equilibrium in an aqueous medium.

⇒ \(\mathrm{NH}_3(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

In this case H₂O is the solvent and is present in a large quantity. Consequently, its concentration does not change much during the reaction and is taken to be constant (unity, by convention). In general, the concentration of a solvent is taken to be 1.

Thus, \(K_c=\frac{\left[\mathrm{NH}_4^{+}(\mathrm{aq})\right]\left[\mathrm{OH}^{-}(\mathrm{aq})\right]}{\left[\mathrm{NH}_3(\mathrm{aq})\right] \times 1}\).

4. In the light of what we have just discussed, let us reconsider the equilibrium between a liquid and its vapour in a closed system.

⇒ \(\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

⇒ \(K_c=\frac{\left[\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right]}{\left[\mathrm{H}_2 \mathrm{O}(\mathrm{l})\right]}=\left[\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right]\)

or \(K_p=p_{\mathrm{H}_2 \mathrm{O}}\).

Now do you see why the vapour pressure of a liquid is constant at a particular temperature and why it does not depend on the amount of liquid present.

5. Remember that in a chemical equilibrium the concentration of a liquid is taken as 1 only if the liquid is present as a solvent, or in a large quantity. Consider the following reaction.

⇒ \(\mathrm{CH}_3 \mathrm{COOH}(\mathrm{l})+\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{l}) \rightleftharpoons \mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5(\mathrm{l})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

Here \(K=\frac{\left[\mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5(\mathrm{l})\right]\left[\mathrm{H}_2 \mathrm{O}(\mathrm{l})\right]}{\left[\mathrm{CH}_3 \mathrm{COOH}(\mathrm{l})\right]\left[\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{l})\right]}\)

The concentration of H₂O cannot be taken as 1 in this case.

Example: A reaction between hydrogen and iodine to produce hydrogen iodide at 675 K is carried out in a closed flask of volume 4 L. At equilibrium, the reaction system contains 0.6 mol of hydrogen, 0.6 mol of iodine and 2.4 mol ofhydrogen iodide. Calculate the equilibrium constant.
Solution:

For the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\)

∴ \(K_{\mathrm{c}}=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]}\)

Given that,

[HI] = 2.4/4 = 0.6 mol L^-1.

[H₂] = 0.6/4 = 0.15 mol L^-1.

[I₂] = 0.6/4 = 0.15 mol L^-1.

Substituting these values in the expression for K_c, \(K_c=\frac{(0.6)^2}{0.15 \times 0.15}=16\)

The equilibrium constant, the reaction quotient and Gibbs energy: As already stated, the value of the equilibrium constant for a reaction does not depend on the rate of that reaction or vice versa.

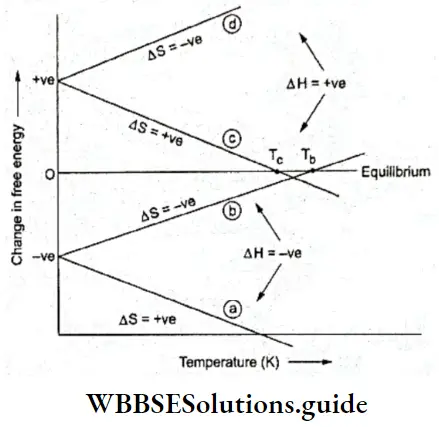
• However, it is directly related to the thermodynamics of the reaction and, in particular, to the change in free energy ΔG. You already know from the previous chapter that if ΔG is negative for a reaction then the reaction is spontaneous and should proceed in the forward direction.
• If, on the other hand, ΔG is positive, the reaction is considered nonspontaneous. Then the reverse reaction will have a negative ΔG value and will proceed, converting the products of the forward reaction into reactants.
• Either way, a reaction should proceed in the spontaneous direction until it achieves equilibrium. At this point, there is no free energy left to drive the reaction ΔG becomes zero and the reaction attains equilibrium.

This thermodynamic view of equilibrium is expressed mathematically as \(\Delta G=\Delta G^{\ominus}+R T\) ln Q

When equilibrium is achieved ΔG = 0, Q = K and this equation becomes \(\Delta G =\Delta G^{\ominus}+R T \ln K=0\)

or \(\Delta G^{\ominus} =-R T \ln K\).

Rearranging the above equation, we get

ln \(K=-\frac{\Delta G^{\ominus}}{R T}\)

or \(2.303 \log K =-\frac{\Delta G^{\ominus}}{R T}\)

or \(\log K =-\frac{\Delta G^{\ominus}}{2303 R T}\).

Taking antilog of both sides K = \(e^{-\Delta G^{\ominus} / R T}\)

or \(K=\mathrm{antilog}\left(-\frac{\Delta G^{\ominus}}{2.303 R T}\right)\)

This equation provides an interpretation of the spontaneity of a reaction.

If \(\Delta G^{\ominus}<0 \text { then } \frac{-\Delta G^{\ominus}}{R T}\) is positive, and \(e^{-\Delta C^{\ominus} / R T}>1 \text {, i.e., } K>1\). Such a reaction is spontaneous and proceeds in the forward direction so that the products are present predominantly.

Similarly, a nonspontaneous reaction is one for which \(\Delta G^\ominus>0\) and K < 1 Such a reaction proceeds in the forward direction to such a small extent that very small amounts of products are formed.

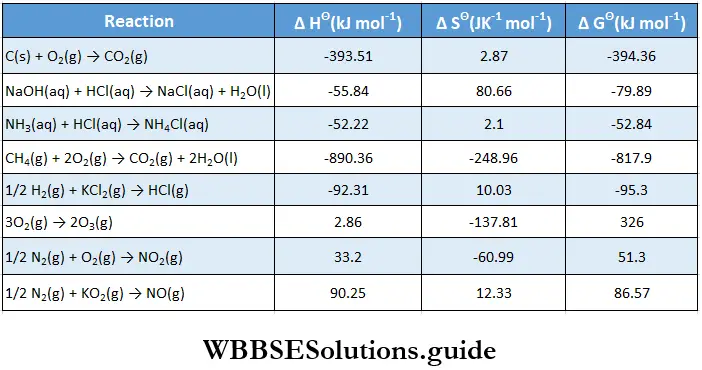
Example 1. Consider the reaction \(2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO}_3(\mathrm{~g})\). Amixture of SO₂, SO₃ and O₂ at equilibrium at 1000 K has [SO₂] = 3.8X10^-3 M, [SO₃] = 4.13X10^-3 M, and [O₂] = 4.3×10^-3 M. Calculate K_c and K_p of the reaction.
Solution:

⇒ \(K_c=\frac{\left[\mathrm{SO}_3\right]^2}{\left[\mathrm{SO}_2\right]^2\left[\mathrm{O}_2\right]}\)

Substituting the values in the expression, we get \(K_c=\frac{\left(4.13 \times 10^{-3}\right)^2}{\left(3.8 \times 10^{-3}\right)^2\left(4.3 \times 10^{-3}\right)}\)

(Note: The concentration must always be in ‘M’ or mol L^-1 for calculating Kc.]

⇒ K_c = 275.

To calculate K_p we must know Δn.

Δn = no. of moles of products- no. of moles of reactants. (considering only gaseous products and reactants)

Δn = 2- (2 + 1) = 2- 3 = -1

But K_p = K_c(RT)^Δn

= K_c(RT)^-1

= \(\frac{K_c}{R T}\)

∴ \(K_p=\frac{275}{(0.08312)(1000)}=3.3\). [While determining the value of K_p, pressure should be expressed in bar and the value of R must be in L bar K^-1 mol)^-1.]

Example 2. The concentration equilibrium constant, K_c for the reaction \(2 \mathrm{NO}_2 \rightleftharpoons \mathrm{N}_2 \mathrm{O}_4\) at 25° C is 216. Find the pressure equilibrium constant, K_p, of the reaction at the same temperature.
Solution:

K_p = K_c(RT)^Δn

Δn =1- 2 =-1

∴ K_p =K_c(RT)^-1

= \(\frac{K_c}{R T}\)

= \(\frac{216}{(0.08312) \times(298.15)}\).

K_p = 8.72. [R = 0.0312 L bar K^-1 mol^-1]

Example 3. The value of K_c for the production of phosgene, the reaction being \(\mathrm{CO}(\mathrm{g})+\mathrm{Cl}_2(\mathrm{~g}) \rightleftharpoons \mathrm{COCl}_2(\mathrm{~g})\), is 5 at 600 K. What are the equilibrium partial pressures ofthe gases if the initial pressures are as follows? \(p_{\mathrm{CO}}=0.265 \mathrm{bar}, p_{\mathrm{Cl}_2}=0.265 \mathrm{bar}, p_{\mathrm{COCl}_2}=0\).
Solution:

At first, K_p must be calculated from K_c.

K_p = K_c(RT)^Δn

Here, Δn =1- 2 = -1

∴ K_p = 5 x (0.08312 x 600)^-1 = 0.1

Let us now tabulate the partial pressures of all the gases. Suppose the partial pressure of COCl₂ at equilibrium is x bar.

Partial pressures:

⇒ \(\begin{array}{lccc}p_{\mathrm{CO}} p_{\mathrm{CO}_2} p_{\mathrm{COCl}_2} \\
\text { Initial } 0.265 \text { bar } 0.265 \text { bar }  0\end{array}\)

⇒ \(\begin{array}{lccc}
\text { Change } -x -x -x \\
\text { Equilibrium } 0.265-x 0.265-x x
\end{array}\)

∴ \(\dot{K}_p=0.1=\frac{p_{\mathrm{COC}_2}}{p_{\mathrm{CO} p_{\mathrm{Cl}_2}}}=\frac{x}{(0.265-x)^2}\)

0.1 = \(\frac{x}{\left(0.07-0.53 x+x^2\right)}\)

Rearranging, we get

0.1 x² – 0.053x + 0.007 = x

or 0.1 x² – 0.053x – x + 0.007 = 0

or 0.1 x² – 0.053 x + 0.007 = 0

or x = \(\frac{+1.053 \pm \sqrt{(1053)^2-4 \times 0.1 \times 0.007}}{2 \times 0.1}=\frac{1.053 \pm 1.0517}{0.2}=6.5 \times 10^{-3} \text { or } 10.52\)

x cannot be greater than 0.265 bar since even if all of CO and Cl₂ react, \(\mathrm{p}_{\mathrm{COCl}_2}\), cannot be more than 0.265 bar.

Choosing x to be 6.5 x 10^-3

at equilibrium, \(\mathrm{p}_{\mathrm{COCl}_2}\) =6.5 x 10^-3 bar

P_CO = 0-265 – 65 x 10^-3 = 0.2585 bar = pa

Example 4. The standard Gibbs free energy at 298 K for the reactions are given.

1. \(\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g}) \Delta \mathrm{G}^{\ominus}=173.2 \mathrm{~kJ}\)
2. \(2 \mathrm{NO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) [latex] \rightleftharpoons 2 \mathrm{NO}_2(\mathrm{~g}) \Delta \mathrm{G}^{\ominus}=-69.7 \mathrm{~kJ}\)

Calculate K_p at 298 K for the following reaction \(\mathrm{N}_2(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}_2(\mathrm{~g})\)

Solution:

First, we must find \(\Delta G^{\ominus}\), for the reaction of interest.

⇒ \(\begin{aligned}
\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g}) \quad \Delta \mathrm{G}^{\ominus}=173.2 \mathrm{~kJ} \\
2 \mathrm{NO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}_2(\mathrm{~g}) \quad \Delta G^{\ominus}=-69.7 \mathrm{~kJ} \\
\overline{\mathrm{N}_2(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}_2(\mathrm{~g}) \Delta G^{\ominus}=-173.2-69.7} \\
=0.103 .5 \mathrm{~kJ} \text {. } \\
\end{aligned}\)

Thus, \(\Delta G^{\ominus}\) for the reaction in question is the sum of \(\Delta G^{\ominus}\) for the other two reactions.

∴ \(\Delta G^{\ominus}\) = 103.5 kJ.

∴ \(K_p=e^{-\Delta G^{\ominus} / R T}\)

But \(\frac{-\Delta G^{\ominus}}{R T}=\frac{-103.5 \times 1000}{8.314 \times 298}=-4178\)

∴ \(\quad K_p=e^{-41.78}=7.16 \times 10^{-19}\).

Example 5. \(\Delta_f G^{\ominus}\) for ammonia gas is -16.5 kJ mol1 at 298 K. Find the equilibrium constant for the reaction \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightarrow 2 \mathrm{NH}_3(\mathrm{~g})\)
Solution:

2 mol of NH₃ is produced in the reaction but the \(\Delta_f G^{\ominus}\) value given is for only 1 mol. \(\Delta_f G^{\ominus}\) for the formation of 2 mol of NH₃ is equal to twice \(\Delta_f G^{\ominus}\)for 1 mol.

⇒ \(\Delta_f G^{\ominus}\) = 2 x -165 kJ = -33.0 kJ = -33,000 J.

Now, \(\frac{-\Delta_f G^{\ominus}}{R T}=\frac{33000}{8.314 \times 298}=13.32\)

∴ \(K_c=e^{-\Delta, G^4 / R T}=e^{+1332}=609,259.8=6.09 \times 10^5\).

Example 6. K_c for the hydrolysis of sucrose is 5.3 x 10¹² at 298 K. Find \(\Delta G^{\ominus}\) for the process sucrose + H₂O \(\rightleftharpoons\) glucose + fructose
Solution:

⇒ \(K_c=e^{-\Delta G^{\ominus} / R T}\)

ln \(K_c=-\Delta G^{\ominus} / R T\)

⇒ \(\Delta G^{\ominus}=-R T \ln K\)

= -8.314 x 298 x ln(53 x 10¹²) = -72,589.7 J.

∴ \(\Delta G^{\ominus}\)=-72.58 kJ.

Example 7. Consider the reaction \(\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})\). Kp =23.6 at 500K for the reaction. Calculate the equilibrium partial pressures of the reactants and products if the initial pressure of PCl₅ is 0.56 bar and those of PCl₃ and Cl₂ are zero. How will the concentration of PCl₅ and PCl₃ change if more Cl₂ is added once equilibrium is reached?
Solution:

Let us tabulate the partial pressure—initial, change and at equilibrium.

⇒ \(p_{\mathrm{PC}} p_{\mathrm{PC}_3} p_{\mathrm{C}_2}\)

⇒ \(\begin{array}{lccc}
\text { Initial } 0.56  0  0 \\
\text { Change } -x +x +x \\
\text { Equilibrium } 0.56-x  x  x
\end{array}\)

Putting these values in the expression for K_p,

⇒ \(K_p=\frac{p_{\mathrm{PCl}_3} p_{\mathrm{Cl}_2}}{p_{\mathrm{PCl}_5}}\)

23.6 = \(\frac{x \cdot x}{0.56-x}\)

Rearranging, we get 23.6(056- x)- x² = 0

or x²– 23.6(056 -x) = 0

or x² 23.6 x 056 + 23.6x = 0

or x²+23.6x- 13.2 = 0.

∴ x = \(\frac{-23.6 \pm \sqrt{(23.6)^2+4 \times 13.2}}{2}\)

= \(\frac{-23.6 \pm 24.69}{2}=0.547 \text { or }-24.14\)

Taking the positive root, x = 0547, we get

⇒ \(p_{\mathrm{PCl}_5}\) = 0.56 -0547 = 0.013 bar

⇒ \(p_{\mathrm{PCl}_3}\) = 0.547 bar

⇒ \(p_{\mathrm{Cl}_2}\) = 0547 bar,

On adding Cl₂ at equilibrium, the reaction will shift towards the left \(p_{\mathrm{PCl}_5}\) and will increase and \(p_{\mathrm{PCl}_3}\) will decrease.

Factors Affecting Equilibrium

In this section, we shall discuss what happens to a system at equilibrium when certain conditions are changed. We shall consider various changes, one by one.

• What happens to the equilibrium when the temperature is changed, for example? Or what happens when the concentration of either the reactants or the products is changed?
• In 1888, the French chemist Henri Louis Le Chatelier proposed a general law on the behaviour of a system in equilibrium.
• This law, called Le Chatelier’s principle, states that if a system at equilibrium is subjected to a change which displaces if from the equilibrium, a net reaction will occur in a direction that counteracts the change.
• This law is applicable to all physical and chemical equilibria. Let us now discuss in detail the various factors that can affect an equilibrium.

Change in concentration: Let us consider the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\) at equilibrium.

• If more of the reactant H₂ or I₂, or both, are added to the reaction system, the state of equilibrium will be disturbed and the tendency of the system would be to counteract this change so that equilibrium is established again.
• The only way this can happen is if more of the reactants react to form more of the products so that the ratio of the products of the concentrations the reaction products to that of the reactants, i.e., K, remains constant.
• Another way of saying this is, if the concentration of the reactants is increased, the equilibrium shifts in the forward direction, or the forward reaction is favoured.
• Applying Le Chatelier’s principle to a specific change (concentration), we may say, “When the concentration of any of the reactants or products in a reaction at equilibrium is changed, the composition of the equilibrium mixture changes so as to undo the effect of the concentration change.”

Let us study how equilibrium is re-established if we add H₂ at equilibrium. The concentration of H₂ increases and equilibrium is disturbed.

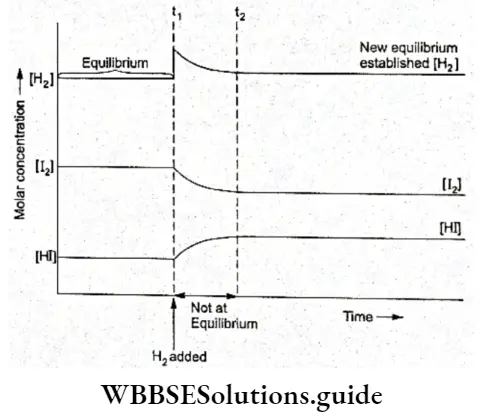
A new equilibrium will be set up in which the concentration of H₂ should be less than what it is after adding H₂. But the initial concentration of H₂ increases for the new equilibrium as shown in Figure.

• As you can see from the figure, till the time tx, the system is at equilibrium with the concentrations of H₂, I₂ and HI being given by the intercept of the three curves on the y-axis.
• At t₁, when some H₂ is added, its concentration increases as shown by the steep rise of the H₂ curve. The equilibrium is disturbed and the system responds to the change by forming more HI, thus decreasing the concentration of H₂ and I₂ than at time t₁. At t₂ a new equilibrium is established.

Let us consider the reaction quotient for this reaction \(Q_c=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]}\)

If hydrogen is added at equilibrium, the molar concentration of hydrogen increases and the equilibrium is disturbed. The denominator of the above equation increases and hence Q_c decreases or becomes less than K_c.

• Therefore, in order to make Q_c equal to K_c the numerator must increase or the denominator must decrease. This means more HI should be formed in order to counteract the disturbance in equilibrium.
• As a result more of H₂ and I₂ react to form more of HI to re-establish the equilibrium making the forward reaction more favourable.
• What if the concentration of hydrogen iodide is increased? Again there will be a tendency for the reaction system to counteract this change.
• This time, more hydrogen iodide will yield more hydrogen and iodine so that equilibrium is restored and K_c remains constant. That is to say, if the concentration of the products is increased, the equilibrium will shift in the reverse direction, or the reverse reaction will be favoured.

Changes in concentration (of either products or reactants) play an important role in the productivity of industrial processes. When ammonia is manufactured by the Haber process, for example, the equilibrium involved is the following.

⇒ \(3 \mathrm{H}_2(\mathrm{~g})+\mathrm{N}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})\)

The product, i.e., NH₃, is continuously removed from the site of the reaction. This disturbs the equilibrium and the system counteracts the change by producing more ammonia.

• Increasing the concentration of the reactants would have the same impact. But, obviously, the former is more economical.
• The large-scale production of CaO from CaCO₃ is another example: the constant removal of CO₂ from the lime kiln drives the reaction to completion.
• There are many applications of Le Chatelier’s principle in our everyday lives. For instance, on humid, cloudy days when there is hardly any breeze, we often dry clothes indoors, under the fan.
• When we do this, we are using Le Chatelier’s principle without knowing it. The water present in the clothes and the water vapour in the air in the vicinity of the clothes reach an equilibrium, which we disturb by turning on the fan.
• The artificial breeze (created by the fan) removes the water vapour from the immediate neighbourhood of the clothes and more water molecules from the clothes escape into the air to re-establish equilibrium.
• For the same reason, one feels more comfortable under the fan on a sultry day.
• A very vital life process depends on Le Chatelier’s principle. You know that haemoglobin (ITb) present in red blood corpuscles acts as a carrier of oxygen from the lungs to the tissues and as a carrier of carbon dioxide from the tissues to the lungs.

How does this happen? The blood that comes from the lungs and reaches the tissues has a high concentration of oxygen in comparison with the blood present in the tissues, where the partial pressure of oxygen is low.

This disturbs the equilibrium and in order to re-establish it, some of the oxyhaemoglobin (haemoglobin carrying oxygen) dissociates.

⇒ \(\mathrm{HbO}_2(\mathrm{~s}) \rightleftharpoons \mathrm{Hb}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g})\)

When the blood returns from the tissues to the lungs, more oxyhaemoglobin is formed.

• This happens because the concentration or partial pressure of oxygen in the lungs is high and to re-establish equilibrium, some of the haemoglobin in the blood returning from the tissues combines with oxygen to form oxyhaemoglobin.
• The removal of carbon dioxide from the tissues by haemoglobin happens in a similar manner.
• The partial pressure of carbon dioxide in the tissues is high, so some of it dissolves in the blood, which reaches the tissues from the lungs.

Carbon dioxide is released from the blood when it returns to the lungs, where the partial pressure of carbon dioxide is low.

⇒ \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_2 \mathrm{CO}_3(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{HCO}_3^{-}(\mathrm{aq})\)

The effect of concentration can also be demonstrated with the help of a simple experiment. You are familiar with the reaction

⇒ \(\underset{\text { yellow }}{\mathrm{Fe}^{3+}(\mathrm{aq})}+\underset{\text { colourless }}{\mathrm{SCN}^{-}(\mathrm{aq})} \rightleftharpoons \underset{\text { deep red }}{\mathrm{FeSCN}^{2+}(\mathrm{aq})}\)

⇒ \(K_c=\frac{\left[\mathrm{FeSCN}^{2+}(\mathrm{aq})\right]}{\left[\mathrm{Fe}^{3+}(\mathrm{aq})\right]\left[\mathrm{SCN}^{-}(\mathrm{aq})\right]}\)

If we take ferric nitrate solution and thiocyanate in a test tube in an appropriate proportion and shake, the colour changes from yellow to red due to the formation of FeSCN²⁺.

• This happens gradually and the colour does not change once equilibrium is attained. We can shift the equilibrium by adding or removing the reactant or product.
• If we add few more drops of thiocyanate solution in the test tube, Q_c becomes less than K_c. Therefore, the forward reaction is favoured and more FeSCN²⁺ is formed until Q_c = K_c and equilibrium is attained.
• At first, the intensity of the red colour decreases and then increases to deep red, at equilibrium.
• If on the other hand, we remove SCN^– by adding a reagent, say HgCl₂(aq) which forms a stable complex—[Hg(SCN)₄]^2-—the equilibrium shifts in the reverse direction so that the concentration of FeSCN²⁺( decreases because it dissociates to replenish SCN^–.
• A similar shift in the equilibrium will be observed if we add oxalic acid to the reaction mixture at equilibrium. Oxalic add reacts with Fe³⁺ to form a stable complex—[Fe(C₂O₄)₃]^3-.

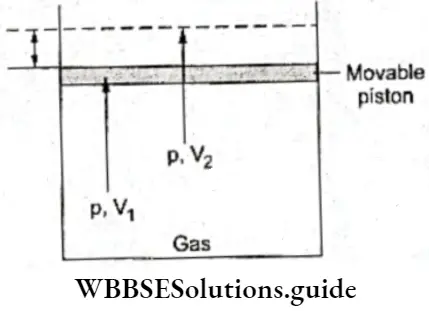
Change in pressure: If one of the reactants or products in a reaction system is in the gaseous phase, pressure becomes an important factor governing shifts in equilibrium. In the case of a gas, increase in partial pressure amounts to increase in concentration.

• Let us consider a heterogeneous system first. \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CO}_2(\mathrm{aq})\)
• In this case increasing the partial pressure of CO₂(g) would mean an increase in the number of moles of CO₂ per unit volume (concentration).
• According to Le Chatelier’s principle the system would try to counteract the change to re-establish equilibrium. The only way this is possible is if more CO₂ dissolves in water. This is why the solubility’ of gases increases with increase in pressure.
• Now consider a homogeneous system in which all the reactants and products are in the gaseous phase. The reaction could lead to an overall increase in the number of moles, if the number of moles of the products is more than that of the reactants.

It could lead to an overall decrease in the number of moles, if the number of moles of products is less than that of the reactants. There is a third possibility—there may be no net change in the number of moles. Let us consider these cases one by one.

1. The reaction involved in the manufacture of ammonia by the Haber process is as follows. \(3 \mathrm{H}_2(\mathrm{~g})+\mathrm{N}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g})\)

• This is obviously a case in which the forward reaction leads to a decrease in the number of moles.
• In such a case, if the total pressure is increased, say by decreasing the volume, the number of moles per unit volume increases and the system tries to nullify the change by decreasing the number of moles per unit volume (we already know that pV = constant and p ∝ moles of the gas).
• Since the forward reaction leads to a decrease in the number of moles, it is favoured and the equilibrium shifts in the forward direction.
• In short, increasing the pressure leads to an increase in the yield of the products. Obviously, if pressure is decreased, the reverse reaction will be favoured.

This can also be understood by considering reaction quotient. Let[H₂], [N₂] and [NH₃]be the molar concentrations at equilibrium in the reaction involved in the Haber process.

When the volume of the reaction mixture is halved the pressure as well as concentrations are doubled. Now, let us obtain the concentration quotient by replacing each value by its double.

⇒ \(Q_c=\frac{\left(2\left[\mathrm{NH}_3\right]\right)^2}{\left(2\left[\mathrm{H}_2\right]\right)^3\left(2\left[\mathrm{~N}_2\right]\right)}=\frac{1}{4} \frac{\left[\mathrm{NH}_3\right]}{\left[\mathrm{H}_2\right]\left[\mathrm{N}_2\right]}=\frac{K_c}{4}\)

As Q_c < K_c, the forward reaction is favoured.

2. Let us consider an equilibrium in which the forward reaction involves an increase in the number of moles.

⇒ \(\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})\)

Here an increase in pressure will favour the backward reaction, while a decrease in pressure will favour the forward reaction.

3. In certain reactions, for example, the ones which follow, the number of moles of the products is equal to that of the reactants.

⇒ \(\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})\)

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g})  \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\)

Changes in pressure have no impact on such reactions.

When we study the effect of change of pressure on a heterogenous system, the solid or liquid reactants or products are ignored because the volume (and concentration) of a solid or a liquid is nearly independent of pressure.

For instance, in the following reactions carbon and iodine are solids.

⇒ \(\mathrm{C}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{CO}(\mathrm{g})\)

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~s} \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\)

When the pressure on the reaction mixture is increased, the reverse reaction is favoured because the number of moles of the gases decreases in the reverse direction.

Change in temperature: Temperature affects the equilibrium constant K_c. The nature and extent of the change in K_c or K_p of a reaction due to the change in temperature depends on the enthalpy change of the reaction.

Suppose the forward reaction in a chemical equilibrium is exothermic then the reverse reaction will, naturally, be endothermic. Production of ammonia by the Haber process involves an exothermic reaction.

⇒ \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NH}_3(\mathrm{~g}) ; \Delta_r H^{\ominus}=-9238 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

• If such a reaction system attains equilibrium at a particular temperature and then heat is supplied to the system so that the temperature increases, the equilibrium gets disturbed.
• According to Le Chatelier’s principle, the system then tries to counteract the change in temperature and the only way it can do this is by absorbing heat.
• In other words, the equilibrium shifts to the left and the endothermic or reverse reaction is favoured.
• If, on the other hand, the temperature is decreased, the equilibrium shifts forward, favouring the forward or exothermic reaction, thus leading to high yield of ammonia.

In this context, refer to the experiment in Figure. NO₂ dimerises into N₂O₄ according to the following reaction.

⇒ \(2 \mathrm{NO}_2(\mathrm{~g}) \rightleftharpoons \mathrm{N}_2 \mathrm{O}_4(\mathrm{~g}) ; \Delta_r H^{\ominus}=-57.2 \mathrm{~kJ} \mathrm{~mol}^{-1} \text {. }\)

Here the formation of N₂O₄ is favoured at a low temperature (ice bath) whereas that of NO₂ is favoured at high temperature (hot water).

This reaction is exothermic. On increasing the temperature, in order to relieve the stress of added heat, the system will tend to absorb this heat and the reverse reaction will be favoured.

• Since NO₂ is brown and N₂O₄ is colourless, the effect of increasing temperature on this reaction may easily be seen.
• Decreasing the temperature, say by immersing the vessel containing a mixture of NO₂ and N₂O₄ in an ice bath, favours the forward reaction.
• When the dissolution of a solid in water (or any other solvent) is accompanied by the absorption (endothermic) or release (exothermic) of heat, its solubility changes with temperature.
• When NH₄Cl dissolves in water, for example, heat is absorbed. The solubility of NH₄Cl increases with temperature because an increase in temperature favours the endothermic process.
• CaCl₂, on the other hand, dissolves in water with the evolution of heat. The solubility of CaCl₂, thus, decreases with increase in temperature.

The solubility of NaCl is almost unaffected by changes in temperature because there is very little heat change during the dissolution of NaCl.

Effect of a catalyst: A catalyst merely changes the time taken to reach the state of equilibrium, it does not change the equilibrium constant. It lowers the activation energy of the forward and reverse reactions by the same amount.

• The activation energy is the energy barrier that has to be overcome for the reaction to proceed. If a reaction mixture is not at equilibrium, a catalyst accelerates the rate at which equilibrium is reached but it does not affect the composition of the equilibrium mixture.
• Hence it does not appear in the balanced chemical equation or in the equilibrium constant expression.
• It increases the rates of the forward and reverse reactions to the same extent. Nonetheless, the fact that a catalyst decreases the time taken to reach equilibrium is very important for many industrial processes.
• For instance, iron-molybdenum is used as a catalyst in the production of ammonia from nitrogen and hydrogen because at low temperature, the rate of the reaction is very slow and at high temperature, the reverse reaction is favoured.
• The optimum conditions of temperature and pressure for the synthesis of NH₃ using a catalyst are 400-500°C and 130-300 atm.

In the manufacture of sulphuric acid by the contact process, the conversion of SO₂ to SO₃ is very important.

⇒ \(2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO}_3(\mathrm{~g}) ; K_{\mathrm{c}}=1.7 \times 10^{26}\)

The magnitude of the equilibrium constant indicates that the reaction should reach completion.

However, the oxidation of SO₂ is very slow but in the presence of the catalyst V₂O₅ (vanadium pentoxide), the rate of the reaction increases. But if a reaction has a very low K_c, a catalyst would be of no help.

Effect of inert gas: While studying the effect of pressure, we have considered changes that result from a change in volume (as volume and pressure are inversely proportional).

• But what if we keep the volume constant and increase the pressure by adding an inert gas. The inert gas is added just to change the pressure—it does not take part in the reaction.
• We could also think of adding an inert gas at constant pressure. If an inert gas is added to a reaction system containing reactants and products in the gaseous phase at equilibrium, the effect it will have on the equilibrium will depend on whether it is added at constant volume or at constant pressure.
• If the equilibrium is readied at constant volume, i.e., in a closed vessel, the addition of the inert gas will not change the molar concentrations (or partial pressures) of the reactants and products. Consequently, the state of equilibrium will not be affected.

If an inert gas is added to a system at equilibrium at constant pressure, the volume will increase.

• An increase in volume will lead to a decrease in the molar concentrations (or partial pressures) of all the reactants and products.
• If the reaction is such that the number of moles of the reactants is the same as that of the products, a decrease in the molar concentrations of all the reactants and products will make no difference to the equilibrium constant since it is the ratio of the product of concentrations of the products to that of the reactants.
• (We came across a similar situation while studying the effect of a change in pressure on an equilibrium.) If, however, the number of moles of the reactants is not the same as that of the products, an increase in the total volume will disturb the equilibrium.

Suppose the number of moles of tire reactants is less than that of the products, as in the following equilibrium.

⇒ \(\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})\)

In such a case, a decrease in the molar concentrations (due to increase in total volume) of all the products and reactants will lead the system to counteract the change and the equilibrium will shift in the direction of increasing the number of moles, i.e., the forward direction.

• We can look at it in another way. At equilibrium \(K_{\mathrm{c}}=\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)
• If the concentrations of all the reactants and products decrease, the numerator will decrease more since there are two concentration terms in the numerator and Kc will decrease.
• For Kc to remain constant, the equilibrium will shift in the direction of an increase in the concentrations of products and decrease in the concentration of the reactants, i.e., in the forward direction.

Similarly, if a reaction is such that the number of moles of the reactants is more than that of the products, an increase in volume will push the equilibrium in the reverse direction.

⇒ \(2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO}_3(\mathrm{~g})\)

For example, for the reaction an increase in volume will favour the reverse reaction. In general, the addition of an inert gas at constant pressure (to a system at equilibrium) makes the equilibrium shift in the direction that increases the number of moles.

Ionic Equilibrium

When certain compounds like NaCl, KCl or NaOH are dissolved in water, the resultant solution is a good conductor of electricity. The solution of NaCl contains Na⁺ and Cl^– ions surrounded by water.

⇒ \(\mathrm{NaCl}(\mathrm{s}) \stackrel{\mathrm{H}_2 \mathrm{O}}{\longrightarrow} \mathrm{Na}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

⇒ \(\mathrm{KCl}(\mathrm{s}) \stackrel{\mathrm{H}_2 \mathrm{O}}{\longrightarrow} \mathrm{K}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

• The electrostatic attraction between the ion and water (ion-dipole interaction) results in the dissolution of such ionic compounds in water. The figure shows various interactions in the solution of KCI in water.
• When KCl is dissolved in water, the positive end of the polar water molecule (hydrogen) is attracted by negative chloride ions at the surface of the solid, similarly, the negative end of the water molecule (oxygen) is attracted by the positive potassium (K⁺) ions.
• The water molecules penetrate between K⁺ and Cl^– and surround them, thus reducing the strong interionic forces holding them together and allowing them to move as hydrated ions.
• This process is called ionisation, i.e., the process of breaking up of a compound into its ions in a solution.
• Though the exact definition of ionisation differs from that of dissociation, we have used both the terms to refer to the breaking up of an ionic substance into its constituent into ions for the sake of convenience.
• Michael Faraday in 1824 classified substances into electrolytes and nonelectrolytes. Nonelectrolytes do not conduct electricity.
• Electrical conductivity requires the existence of charged particles and in a solution of nonelectrolyte, the solute molecules retain their unbroken identity.

That is why though sucrose dissolves in water, it is not a conductor of electricity.

⇒ \(\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{~s}) \stackrel{\mathrm{H}_2 \mathrm{O}}{\longrightarrow} \mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{aq})\)

Not all electrolytes conduct electricity with equal ease. Faraday categorised electrolytes as strong and weak. For instance, sodium chloride is a strong electrolyte whereas acetic acid is weak electrolyte.

Ionisation: All electrolytes do not ionise to the same extent. The extent to which an electrolyte ionises is called its degree of dissociation.

• More accurately, the fraction of the total number of molecules of the electrolyte in the solution which dissociates into ions is called the degree of dissociation of the electrolyte.
• A truly ionic compound dissociates completely in solution. For example, if 1 mol of NaCl is dissolved in 1 L of water, the solution will contain 1 mol of Na⁺ and 1 mol of Cl^– ions.
• Compounds which dissociate completely in solution are called strong electrolytes.
• Polar covalent compounds may also produce ionic solutions or solutions which conduct electricity.
• Depending on the degree of ionisation or dissociation, such solutes are strong electrolytes or weak electrolytes.

H₂SO₄, for example, dissociates completely in solution and is a strong electrolyte. Equations for the ionisation of strong electrolytes are written with a single arrow.

⇒ \(\mathrm{HCl}(\mathrm{aq}) \longrightarrow \mathrm{H}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

⇒ \(\mathrm{NaOH}(\mathrm{aq}) \longrightarrow \mathrm{Na}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

Weak electrolytes, like NH₃ and CH₃COOH (acetic acid), on the other hand, do not dissociate completely. Their solutions arc weakly or partly ionised.

In such cases there is an equilibrium between the un-ionised molecules of the electrolyte and the ions in solution. Consequently, the ionisation of such an electrolyte is represented with a double arrow.

⇒ \(\mathrm{NH}_3(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

⇒ \(\mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})\)

• The degree of ionisation of weak electrolytes depends upon the nature of the electrolyte, temperature and dilution.
• We will not concern ourselves with the ionisation of strong electrolytes because such reactions proceed to completion and in this chapter we are examining reactions from the point of view of equilibrium.

Ionisation of weak electrolytes: An equilibrium between the (un-ionised) molecules of a weak electrolyte and its ions in solution is called an ionic equilibrium.

• If C is the concentration of an electrolyte in a solution, and a is the degree of dissociation, the number of moles of the electrolyte that dissociate is Cα.
• The degree of dissociation (α) of an electrolyte is the fraction of the total number of molecules of the electrolyte (in the solution) that ionise at equilibrium.
• For example, if the value of α = 0.5 or 1/2, it means that out of 1 mole of the electrolyte, 0.5 mol has ionised or there is 50% ionisation.
• So, if C is the concentration of the electrolyte, what is the concentration that is ionised? It is Cα.

Let us say that the concentration of some electrolyte XY in an aqueous solution is C and its degree of dissociation is a. At equilibrium, the ionisation of the electrolyte can be represented by

⇒ \(\mathrm{XY}(\mathrm{aq}) \rightleftharpoons \mathrm{X}^{+}(\mathrm{aq})+\mathrm{Y}^{-}(\mathrm{aq})\)

At equilibrium, the concentrations of X⁺ and Y^– must each be Cα. And the concentration of XY must be C -Cα = C(1 – α). (The concentration of X⁺ and Y^– are equal to the concentration of XY dissociated.)

Applying the law of chemical equilibrium

K = \(\frac{\left[\mathrm{X}^{+}(\mathrm{aq})\right]\left[\mathrm{Y}^{-}(\mathrm{aq})\right]}{[\mathrm{XY}(\mathrm{aq})]}\)

= \(\frac{(\mathrm{C} \alpha)(\mathrm{C} \alpha)}{C(1-\alpha)}=\frac{C \alpha^2}{1-\alpha}\).

For a weak electrolyte, a is so small compared to 1 that it can be neglected in approximate calculations. Then K = Cα²

or \(\quad \alpha^2=\frac{K}{C}\)

or \(\alpha=\sqrt{\frac{K}{C}}\)

⇒ \(\quad \alpha \propto \sqrt{\frac{1}{C}}\) (because K is a constant)

• Therefore, for a weak electrolyte, the degree of ionisation is inversely proportional to the square root of the molar concentration.
• This is known as Ostwald’s dilution law. As C approaches zero, or dilution approaches infinity, the degree of dissociation approaches unity.
• This means that the ionisation of a weak electrolyte will be more in a dilute solution than in a concentrated solution.

Example: Calculate the degree of dissociation of a 0.02-M solution of formic acid, given that K = 1.9 x 10^-4.
Solution:

The dissociation of formic acid in water can be represented as follows.

⇒ \(\mathrm{HCOOH}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{HCOO}^{-}\)

Let α be the degree of dissociation. Then the concentrations of the ionic species at equilibrium will be as follows:

[H₃O]⁺ = 0.02α

[HCOO]^– = 0.02α

[HCOOH] = 0.02 (1 – α) = 0.02, assuming a to be negligible compared to 1.

Now K = \(\frac{(0.02 \alpha)(0.02) \alpha}{0.02}=1.9 \times 10^{-4}\) (given)

or \(\alpha^2=\frac{1.9 \times 10^{-4}}{0.02}\)

or \(\alpha=\sqrt{95} \times 10^{-2}=9.75 \times 10^{-2}\).

The degree of dissociation of formic acid = 0.0097.

Acid Base Equilibrium

Acids and bases are also electrolytes. You are quite familiar with some properties of acids and bases. You know, for example, that adds turn blue litmus red and that bases (also called alkalis) turn red litmus blue.

You know that adds react with active metals like zinc and magnesium to liberate hydrogen. You know that acids are sour and corrosive and that bases are bitter and slippery. And you also know that adds and bases neutralise each other.

This is essentially the concept chemists had of acids and bases in the olden days. You could call this concept, based on certain properties of adds and bases, the dassical concept.

Arrhenius theory: In 1884, S A Arrhenius, a Swedish chemist, proposed a new definition of acids and bases. It was based on his general theory of ionisation of electrolytes, which basically said that an electrolyte, on dissolution in water, dissociated into positively and negatively charged ions.

Arrhenius defined an acid as a substance which produces hydrogen ions (H⁺) when mixed with water. Bases, according to Arrhenius, are substances which produce hydroxyl ions (OH^–) when mixed with water. And the neutralisation of adds and bases is a reaction between H⁺ and OH^– ions.

⇒ \(\mathrm{H}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq}) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

Strong acids like HCl, HNO₃ and H₂SO₄ dissociate completely when dissolved in water.

⇒ \(\mathrm{HCl} \stackrel{\text { water }}{\longrightarrow} \mathrm{H}^{+}+\mathrm{Cl}^{-}\)

⇒ \(\mathrm{HNO}_3 \stackrel{\text { water }}{\longrightarrow} \mathrm{H}^{+}+\mathrm{NO}_3\)

Weak acids like acetic acid, carbonic acid and phosphoric acid dissociate only to a small extent when dissolved in water.

⇒ \(\mathrm{CH}_3 \mathrm{COOH} \stackrel{\text { water }}{\rightleftharpoons} \mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{H}^{+}\)

⇒ \(\mathrm{H}_2 \mathrm{CO}_3 \stackrel{\text { water }}{\rightleftharpoons} 2 \mathrm{H}^{+}+\mathrm{CO}_3^{2-} \)

⇒ \(\mathrm{H}_3 \mathrm{PO}_4 \stackrel{\text { water }}{\rightleftharpoons}{=} 3 \mathrm{H}^{+}+\mathrm{PO}_4^{3-}\)

Bases like NaOH and KOH are strong bases because they dissociate completely.

⇒ \(\mathrm{NaOH} \stackrel{\text { water }}{\longrightarrow} \mathrm{Na}^{+}+\mathrm{OH}^{-}\)

⇒ \(\mathrm{KOH} \stackrel{\text { water }}{\longrightarrow} \mathrm{K}^{+}+\mathrm{OH}^{-}\)

Substances like NH₄OH, Ca(OH)₂ and Al(OH)₃ dissociate to a small extent and are called weak bases.

⇒ \(\mathrm{NH}_4 \mathrm{OH} \stackrel{\text { water }}{\rightleftharpoons} \mathrm{NH}_4^{+}+\mathrm{OH}^{-}\)

⇒ \(\mathrm{Ca}(\mathrm{OH})_2 \stackrel{\text { water }}{\rightleftharpoons} \mathrm{Ca}^{2+}+2 \mathrm{OH}^{-}\)

⇒ \(\mathrm{Al}(\mathrm{OH})_3 \stackrel{\text { water }}{\rightleftharpoons} \mathrm{Al}^{3+}+3 \mathrm{OH}^{-}\)

• According to Arrhenius, acids produce H⁺ ions and bases produce OH^– ions when dissolved in water.
• Actually, the H⁺ ion, formed by the loss of an electron from the hydrogen atom, is only an unshielded proton.
• This proton cannot exist independently since its charge density is very high.

In an aqueous solution, it binds itself with one of the two lone pairs available on the water molecule to form a hydronium ion (H₃O⁺).

⇒ \(\mathrm{H}^{+}+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{H}_3 \mathrm{O}^{+}\)

For the sake of convenience, the hydrated proton (hydronium ion) is represented as H⁺ (aq). In an aqueous solution, the H⁺ and OH^– ions exist as hydrated ions.

Limitations of Arrhenius’s theory This concept of acids and bases could explain neutralisation, salt hydrolysis and the strength of adds and bases, but it had a few drawbacks.

1. This theory cannot explain the basic nature of substances like NH₃, Na₂CO₃ and CaO, which do not possess a hydroxyl (OH^–) group. Nor cannot it explain the basic nature of CO₂, SO₂, SO₃, etc., which do not contain hydrogen.
2. Another limitation of this theory is its inability to explain reactions between acidic and basic substances in the absence of water. Two examples follow.

⇒ \(\mathrm{SO}_3(\mathrm{~g})+\mathrm{CaO}(\mathrm{s}) \longrightarrow \mathrm{CaSO}_4(\mathrm{~s})\)

⇒ \(\mathrm{NH}_3(\mathrm{~g})+\mathrm{HCl}(\mathrm{g}) \longrightarrow \mathrm{NH}_4 \mathrm{Cl}(\mathrm{s})\)

Bronsted-Lowry theory: In 1923, a Danish chemist, I N Bronsted, and a British chemist, T M Lowry, independently put forward a more general theory of acids and bases.

According to this theory, an acid is a proton donor and a base is a proton acceptor. This definition has some very interesting implications. To understand these, let us consider some examples.

⇒ \(\mathrm{HCl}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{Cl}^{-}\)

⇒ \(\mathrm{CH}_3 \mathrm{COOH}+\mathrm{H}_2 \mathrm{O}  \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{CH}_3 \mathrm{COO}^{-}\)

⇒ \(\mathrm{CO}_3^{2-}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{HCO}_3^{-}+\mathrm{OH}^{-}\)

⇒ \(\mathrm{NH}_3+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{OH}^{-}\)

⇒ \(\mathrm{NH}_4^{+}+\mathrm{H}_2 \mathrm{O}  \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{NH}_3\)

⇒ \(\mathrm{HCl}+\mathrm{NH}_3 \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{Cl}^{-}\)

Consider the first two reactions. HCl is an acid because it donates one proton to become Cl^– and H₂O is a base because it accepts a proton to become H₃O⁺.

• Similarly, in the second equation, CH₃COOH is an acid and H₂O is a base. Now consider the next two reactions. In these, water acts as an acid.
• It donates a proton to become OH^–. This means that the same substance can act as an acid or a base. Such substances which can act both as an acid and a base are called amphoteric.
• This definition of acids and bases does not restrict itself to neutral molecules. Even ions can act as acids or bases. For example, CO₃^2- in the third equation acts as a base by accepting a proton.

Nor is it necessary for an acid-base reaction to take place in an aqueous medium. For example, in the sixth equation HCI acts as an acid by donating a proton and NH₃ acts as a base by accepting a proton.

• The presence of the hydroxyl group (OH^–) is not necessary for a substance to act as a base. Similarly, a substance can act as an acid even if it does not contain hydrogen.
• For example, NH₃ acts as a base in the fourth reaction. All that is necessary for an acid-base reaction is that one substance should be able to donate a proton and the other should be able to accept the proton.
• A corollary is that a substance which acts as an acid in the presence of a proton-acceptor, will not act in the same way in the absence of a proton-acceptor.
• For example, though acetic acid acts as an acid in an aqueous solution (second equation), it does not do so in a benzene solution because benzene is not a proton-acceptor.

The Bronsted-Lowry concept of acids and bases has a very interesting consequence. When a substance acts as an acid it donates a proton. But on donating a proton, it becomes a base because it becomes capable of accepting a proton. Let us take the case of NH₃ and H₂O.

⇒ \(\mathrm{H}_2 \mathrm{O}+\mathrm{NH}_3 \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{OH}^{-}\)

Here water acts as an acid by donating a proton and becomes OH^–. Now OH^– can accept a proton, so it can act as a base.

• Similarly, NH₃ acts as a base by accepting a proton and becomes NH⁺₄, and NH⁺₄ has a proton to donate, so it is an acid.
• Now do you see how every acid turns into a base by donating a proton, and every base turns into an add by accepting a proton.
• The base formed when an acid donates a proton is called the conjugate base of the add and the acid formed when a base accepts a proton is called the conjugate acid of the base.

In the reaction between NH₃ and H₂O, OH^– is the conjugate base of H₂O and NH₄ is the conjugate acid of NH₃.

Thus, there are two acid-base pairs in the reaction and these are called conjugate acid-base pairs. A few examples will make this clearer.

⇒ \(\text { Acid } 1+\text { base } 2 \rightleftharpoons \text { acid } 2+\text { base } 1\)

⇒ \(\mathrm{HCl}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{Cl}^{-}\)

⇒ \(\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_3^{2-} \rightleftharpoons \mathrm{HCO}_3^{-}+\mathrm{OH}^{-}\)

⇒ \(\mathrm{HCO}_3^{-}+\mathrm{NH}_3 \rightleftharpoons \mathrm{NH}_4^{+}+\mathrm{CO}_3^{2-}\)

⇒ \(\mathrm{NH}_4^{+}+\mathrm{CH}_3 \mathrm{COO}^{-} \rightleftharpoons \mathrm{CH}_3 \mathrm{COOH}+\mathrm{NH}_3\)

• A strong add has a strong tendency to donate a proton but its conjugate base does not have an equally strong tendency to accept a proton.
• The conjugate base of a strong acid is weak and the conjugate base of a weak acid is strong. Also, if two acids are mixed, the weaker acid acts as a base.

⇒ \(\underset{\text { (perchloric acid) }}{\mathrm{HClO}_4}+\mathrm{H}_2 \mathrm{SO}_4 \rightleftharpoons \mathrm{H}_3 \mathrm{SO}_4^{+}+\mathrm{ClO}_4^{-}\)

In this reaction, H₂SO₄ acts as a base with respect to the stronger acid, HClO₄. Thus, H₂SO₄ is amphoteric or amphiprotic. Certain acids can lose two or three protons. They are called diprotic (H₂SO₄) or triprotic (H₃PO₄) adds.

Strengths of acids and bases: The strength of an acid or base depends upon its readiness to lose or gain a proton. Experimentally, the strength of an acid or base is measured by its ionisation constant or dissociation constant.

• A strong acid like HCl, HNO₃, H₂So₄, HBr, HI and HClO₄ dissociates almost completely in water. This means the molar concentration of H₃O⁺ ions in an aqueous solution of a strong acid is almost the same as that of the acid itself.
• But this is not the case for weak acids and we can compare the strengths of such acids if we know the dissociation constants at a particular temperature.
• The equilibrium constant for the dissociation of an acid is called its acid dissociation constant or acid ionisation constant and is denoted by K_a.
• Similarly, the base dissociation or base ionisation constant is K_b.

Consider a weak acid HA and suppose its dissociation equilibrium can be represented as follows.

⇒ \(\mathrm{HA}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{A}^{-}(\mathrm{aq})\)

At equilibrium, \(K_{\mathrm{a}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]\left[\mathrm{H}_2 \mathrm{O}\right]}\). Here [H₂O] = 1 as it is in a very large quantity and remains almost unchanged.

Suppose the initial concentration of HA is C mol L^-1 and its degree of dissociation is α. Then

⇒ \(K_{\mathrm{a}}=\frac{(C \alpha)^2}{C(1-\alpha)}=C \alpha^2\) (neglecting a in comparison with 1)

or \(\alpha =\sqrt{\frac{K_{\mathrm{a}}}{C}}\).

Thus, the degree of dissociation is inversely proportional to the square root of the concentration. Suppose we consider two acids of equimolar concentration (i.e., C is the same for both) and degrees of dissociation α₁ and α₂.

Then, \(\frac{\alpha_1}{\alpha_2}=\sqrt{\frac{K_{a_1}}{K_{a_2}}}\)

However, the degree of dissociation of an acid is a measure of its strength.

Therefore, \(\frac{\text { strength of acid }}{\text { strength of } \text { acid }_2}=\sqrt{\frac{K_{\mathrm{a}_1}}{K_{\mathrm{a}_2}}} \text {. }\)

• So, we may say that at a given temperature, the ionisation or dissociation constant of an add is the measure of
  its strength.
• As you already know, the equilibrium constant is a dimensionless quantity so Ka is also without any unit.
• Concentrations of all the speeds at ionisation equilibrium are measured with respect to the standard state concentration of 1 M.
• The larger the value of K_a, the stronger is the acid. Weak acids, however, show a great variation in their strengths. For instance, both formic add and hydrocyanic add are weak but their ionisation constants are very different.

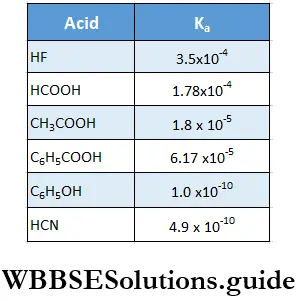
Example: The ionisation constants of formic acid (HCOOH) and hydrocyanic acid (HCN) are 1.77 x 10²⁴ and  4.9 x 10^-10 respectively. Compare their strengths.
Solution:

\(\frac{\text { Strength of formic acid }}{\text { Strength of hydrocyanic acid }}=\sqrt{\frac{K_{\mathrm{a}}(\mathrm{HCOOH})}{K_{\mathrm{a}}(\mathrm{HCN})}}=\sqrt{\frac{1.77 \times 10^{-4}}{4.9 \times 10^{-10}}}=601 \text {. }\)

Therefore, formic acid is 601 times stronger than hydrocyanic acid.

The relative strengths of bases can be determined in a similar manner. First, let us consider the equilibria involved in solutions of weak bases. If B is the base, the equilibrium may be represented as

⇒ \(\mathrm{B}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{BH}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

The equilibrium constant is K_b and is called base dissociation constant. The higher the value of K_b, the stronger is the base.

⇒ \(K_{\mathrm{b}}=\frac{\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{B}]}\)

If C is the molar concentration of a base and α is its degree of dissociation \(\alpha=\sqrt{\frac{K_b}{C}},\)

where K_b is the dissociation constant of the base.

If we take two bases b₁ and b₂ of equimolar concentrations and dissociation constants \(K_{b_1} \text { and } K_{b_2}\) then

∴ \(\frac{\text { strength of base }}{\text { strength of base }{ }_2}=\sqrt{\frac{K_{b_1}}{K_{b_2}}} \text {. }\)

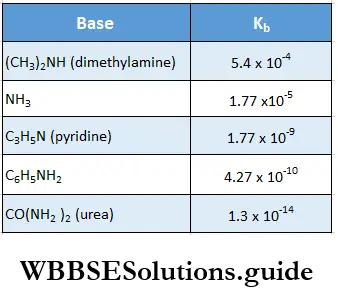
Relation between K_a and K_b We have seen that the strength of an acid (or a base) is expressed by its K_a (or K_b). For a conjugate acid-base pair, the two equilibrium constants are related in a simple manner.

Let us consider the case of the acid-base pair NH₄ and NH₃. The equilibrium for both acid and base may be represented as

⇒ \(\mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{NH}_3(\mathrm{aq})\)

∴ \(K_{\mathrm{a}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{NH}_3\right]}{\left[\mathrm{NH}_4^{+}\right]}=5.6 \times 10^{-10}\)

∴ \(\mathrm{NH}_3(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

∴ \(K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_4^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_3\right]}=1.8 \times 10^{-5}\).

On adding the two, we get the net reaction as \(2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

The sum of the two reactions is simply the dissociation of water, and its equilibrium constant,

⇒ \(K_{\mathrm{w}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_2 \mathrm{O}\right]^2}\)

or \(K_{\mathrm{w}}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.0 \times 10^{-14}\).

The equilibrium constant for the net reaction is equal to the product of the equilibrium constants for the individual reactions.

⇒ \(K_{\mathrm{a}} \times K_{\mathrm{b}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{NH}_3\right]}{\left[\mathrm{NH}_4^{+}\right]} \times \frac{\left[\mathrm{NH}_4^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_3\right]}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=K_w,\)

i. e., (5.6 x 10^-10) x (18 x 10^-5) = 10 x 10^-14. The ionic product of water (K_w) is discussed later in the chapter.

Whenever an equation can be written as a sum of two or more equations, the equilibrium constant for the net reaction is the product of the equilibrium constants of all the individual reactions.

Di- and polybasic acids and di- and polyacidic bases Polybasic or polyprotic acids are those which have more than one ionisable proton. For example, sulphuric acid has two and phosphoric acid has three ionisable protons. The ionisation reactions for a dibasic acid like H₂SO₄ can written as

⇒ \(\mathrm{H}_2 \mathrm{SO}_4(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{HSO}_4^{-}(\mathrm{aq}) \)

⇒ \(\mathrm{HSO}_4^{-}(\mathrm{aq}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{SO}_4^{2-}(\mathrm{aq})\)

The corresponding equilibrium constants for these reactions will be as follows.

⇒ \(K_{\mathrm{a}_1}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{HSO}_4^{-}\right]}{\left[\mathrm{H}_2 \mathrm{SO}_4\right]} \text { and } K_{\mathrm{a}_2}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{SO}_4^{2-}\right]}{\left[\mathrm{HSO}_4^{-}\right]} \text {. }\)

• As you can see, the dibasic acid H₂SO₄ has two ionisation constants. Similarly, tribasic acids like phosphoric acid will have three ionisation constants.
• Like polybasic acids, polyacidic bases also have the ionisation constants corresponding to the number of ionisation steps.
• For example, a diacidic base like ethylenediamine has two ionisation constants \(K_{b_1} \text { and } K_{b_2}\). Table gives some values of the ionisation constants of polyprotic acids.
• As you can seen in Table among all the ionisations in an individual polybasic acid the first ionisation constant is the largest followed by the second and then the third.
• This is because after the first ionisation, we are left with a negatively charged ion and it is difficult to remove a proton from a negative ion.

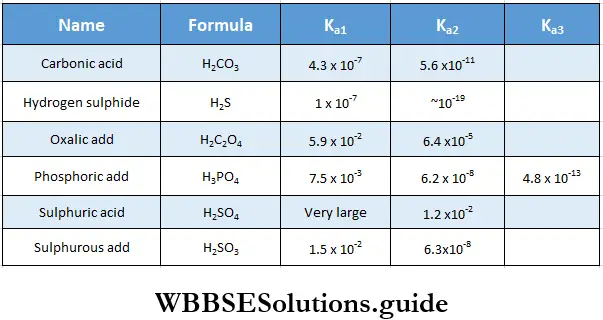
Factors affecting acid strength: We have already seen how to compare the strengths of two acids. But why is one acid stronger than the other? Put simply, the acid strength is determined by the strength and polarity of the H—A bond.

• The strength of the bond depends on the enthalpy change associated with the dissociation of the HA molecule into H and A.
• The polarity of the H—A bond depends on the electronegativity of A and the ease with which electron transfer can occur from H to A resulting in H⁺ and A^– ions. The weaker and more polar the HA bond, the stronger is the acid.
• Let us consider the acids of the halogen series HF, HCl, HBr and HI.
• The variation in polarity is not very significant while we move from HF to Til but there is a considerable difference in the bond strength, which is the deciding factor here.

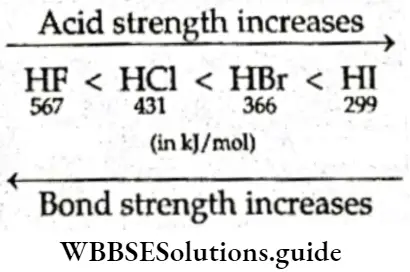
You already know that atomic size increases on moving down a group. Thus, the size increases from F to I and so the bond strength decreases, increasing the acidity from HF to HI.

• This trend is generally true of acids in the same group of the periodic table. When we go down the group from O to Te, the acid strength increases as H₂O<H₂S<H₂Se<H₂Te.
• For acids in the same row of the periodic table, the variation in bond strength is insignificant and the polarity of the bond is the deciding factor for acid strengths.
• Let us consider the hydrides of a few elements in the second period—CH₄, NH₃, H₂O and HF. As we move from C to F, electronegativity increases and hence the added strength also increases from CH₄ to HF.
• The electronegativities given are C, N, O and F respectively.

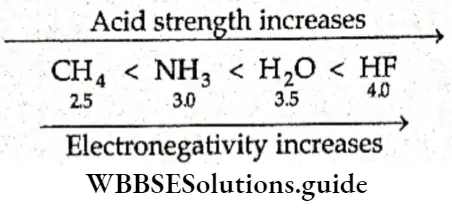
Oxoacids Oxoacids such as H₂SO₄, H₂CO₃ and HNO₃ have an O—H bond and the acid strength is dependent on the strength of this bond. Any factor that weakens the O—H bond or increases its polarity, increases the strength of the acid.

• In these acids, the nonmetallic atom is bonded on one side to the oxygen of O—H. The electronegativity of this atom and its oxidation number influences the acid strength.
• In the case of oxoacids containing the same number of O—H groups and the same number of O atoms, as the electronegativity of the nonmetallic atom increases, the acid strength increases.
• For example, consider HOCl, HOBr and HOI. The electronegativity decreases from Cl to I, and hence add strength increases from HOI to HOBr to HOCl.

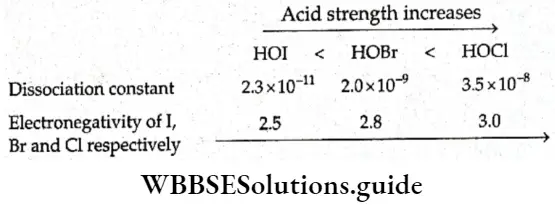
With the increase in the electronegativity of the nonmetallic atom attached to the O—H bond, the bonded electron cloud is pulled more towards the atom, thus weakening the O—H bond, which then tends to break easily.

If the oxoacids contain the same nonmetallic atom but different numbers of oxygen atoms, then as the oxidation number of the atom increases, the acid strength increases. For example, among the oxoacids of chlorine, the strength of the acids increases as

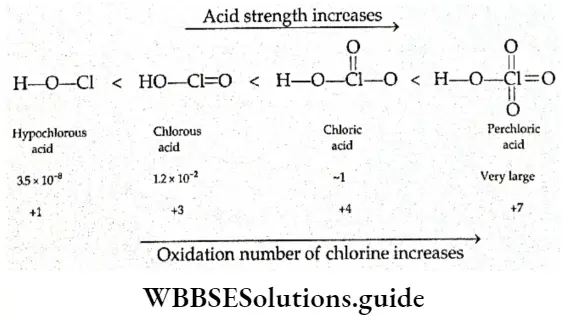
Common-Ion effect in the ionisation of acids and bases: You are already aware how acetic acid ionises in water. You also know how to calculate the degree of dissociation of this acid. The equilibriun involved is \(\mathrm{CH}_3 \mathrm{COOH}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{H}_3 \mathrm{O}^{+}\)

∴ \(K_{\mathrm{a}}=\frac{\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\left[\mathrm{CH}_3 \mathrm{COOH}\right]} .\)

If we add sodium acetate (the salt of the conjugate base of acetic acid) to the acetic acid solution, the hydrogen ion concentration changes (it decreases).

• This is because the addition of acetate ions causes an increase in the concentration of the products and the equilibrium shifts to the left-hand side, reducing the dissociation of acetic acid.
• This is according to Le Chatelier’s principle. This is called the common ion effect, which is simply the shift in equilibrium on the addition of a substance that provides more of an ion already involved in the equilibrium. Therefore, the concentration of H₃O⁺ decreases.

Suppose acetate ions of concentration 0.1 M are added a 0.1-M acetic acid solution. Then the initial concentrations of the acetate ion and acetic acid solution are both 0.1 M.

Let the concentration of the acetic acid dissociated be x. Then the concentrations of the species present can be given as follows:

⇒ \(\mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})\)

Initial conc. \( 0.1 0.1 \sim 0\)

Change \(-x +x +x\)

Equilibrium conc. \(0.1-x 0.1+x x\)

⇒ \(K_{\mathrm{a}}=18 \times 10^{-5}=\frac{\left[\mathrm{CH}_3 \mathrm{COO}^{-}\right]\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}{\left[\mathrm{CH}_3 \mathrm{COOH}\right]}\)

= \(\frac{(0.1+x)(x)}{0.1-x}\).

Since K_a is small for a very weak acid, x is small compared to 0.1 and we can make the approximation that 0.1 +x ≈ 0.1 ≈ 0.1-x.

∴ \(K_{\mathrm{a}}=18 \times 10^{-5}=\frac{x(0.1)}{0.1}=x\)

or x = [H₃O⁺] = 1.8 x 10^-5 M.

Example: Calculate the hydronium iott concentration of a 0.1-M solution of acetic acid, given K_a = 1.8 x 10^-5.
Solution:

⇒ \(\mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})\)

⇒ \(K_{\mathrm{a}}=\frac{\left[\mathrm{CH}_3 \mathrm{COO}^{-}\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\right.}{\left[\mathrm{CH}_3 \mathrm{COOH}\right]}\).

If x is the concentration of CH₃COOH that dissociates, then the concentrations for the various species in the solution are as follows.

⇒ \(\mathrm{CH}_3 \mathrm{COOH}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{H}_3 \mathrm{O}^{+}\)

Initial conc. \(0.1 0 0\)

Change \(-x +x +x\)

Equilibrium conc. \(0.1-x x x\)

Substituting the values at equilibrium in the expression for K_a,

⇒ \(K_{\mathrm{a}}=\frac{x \times x}{0.1-x}=\frac{x^2}{0.1-x}\)

This will result in a quadratic equation in x. However, it may be simplified by assuming that x << 0.1

Hence, \(K_{\mathrm{a}}=\frac{x^2}{0.1}\)

⇒ x² = 0.1 x K_a = 0.1 x 1.8 x 10^-5

x = 1.34 x 10^-3

∴ [H₃O⁺] = 1.34 x 10^-3

Limitations of Bronsted-Lowry theory The Bronsted-Lowry theory could explain many reactions which the Arrhenius theory could not. However, it still could not account for certain acid-base reactions which do not involve the transfer of a proton.

1. Reactions between acidic oxides like CO₂, SO₂ and SO₃ and basic oxides like CaO, BaO and MgO cannot be explained by the theory of proton transfer. Such reactions take place in the absence of a solvent.

⇒ \(\mathrm{CaO}+\mathrm{SO}_3 \longrightarrow \mathrm{CaSO}_4\)

⇒ \(\mathrm{MgO}+\mathrm{CO}_2 \longrightarrow \mathrm{MgCO}_3\)

2. The acidic behaviour of compounds like BF₃ and AlCl₃ cannot be explained by the Bronsted-Lowry theory.

Lewis theory: In 1923, G N Lewis, an American chemist, extended the concept of adds and bases further.

• According to the Lewis theory, an acid is a substance which can accept a pair of electrons and a base is a substance which can donate a pair of electrons.
• While this definition encompasses most add-base reactions, it has the drawback of being so general as to indude other types of reactions in its ambit.
• According to the Lewis theory, an acid-base reaction involves the donation of a pair of electrons by a base to an add, leading to the formation of a coordinate bond between them.

Lewis bases Lewis bases can be of two types,

1. Neutral molecules like H₂O, RNH₄, NH₃ and ROH, in which
   one atom has at least one unshared pair of electrons, can act as Lewis bases,
2. All negative ions (F^–, Cl^–, OH^–, CN^–, etc.) can behave as Lewis bases.

Lewis acids Species with vacant orbitals in the valence shell of one of the atoms can act as Lewis acids. Some examples of Lewis acids are as follows.

1. Simple cations like Ag⁺, Cu²⁺ and Fe³⁺ can accept a pair of electrons and act as Lewis acids.

2. Molecules which have an atom with an incomplete octet can behave as Lewis acids, for example, BF₃ and AlCl₃.

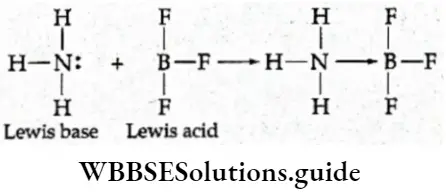
3. Molecules in which the central atom has vacant orbitals may acquire more than an octet of valence electrons, for example, SnCl₄, SiF₄ and PF₅, and can act as Lewis acids.

⇒ \(\underset{\substack{\text { Lewis acid } \\ \text { acid }}}{\mathrm{SiF}_4}+\underset{\text { Lewis base }}{2 \mathrm{~F}^{-}} \longrightarrow \mathrm{SiF}_6^{2-}\)

4. Molecules which have a multiple bond between two atoms of different electronegativities, for example, CO₂ and SO₂, also behave as Lewis acids.

In the CO₂ (O=C=O) molecule, carbon being less electronegative than oxygen, acquires a slight positive charge (because one n electron pair shifts more towards oxygen) and can, thus, accept a pair of electrons.

⇒ \(\underset{\substack{\text { Lewis } \\ \text { acid }}}{\mathrm{CO}_2}+\underset{\substack{\text { Lewis } \\ \text { base }}}{\mathrm{OH}^{-}} \longrightarrow \mathrm{HCO}_3^{-}\)

• While it is true that the definition of acids and bases proposed by Lewis is more general than the other definitions, it does not mean that it encompasses all acid-base reactions.
• There are substances, for instance, which are Bronsted acids but not Leivis acids. Bronsted acids like HCl and H₂SO₄ can donate a proton but are not capable of accepting a pair of electrons, so they are not Lewis acids.

However, all Bronsted bases are also Lewis bases because a species capable of donating an electron pair (Lewis base) also has the tendency to accept a proton (Bronsted base).

⇒ \(\mathrm{NH}_3+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{NH}_4^{+}+\mathrm{OH}^{-}\)

Here NH₃ is a Lewis base as well as n Bronsted base but H₂O is a Bronsted acid, but not a Lewis add.

Limitations of Lewis theory The Lewis theory of adds and bases can explain the acidic and basic nature of many substances which cannot be explained by either the Bronsted-Lowry theory or the Arrhenius theory. Still it is not a flawless theory.

1. This concept of adds and bases is so general that it labels all reactions leading to the formation of coordinate bonds as acid-base reactions.
2. It does not explain the addic behaviour of adds like HCl and H₂SO₃ which do not form coordinate bonds with bases.
3. The formation of coordination compounds is usually a slow process, so add-base reactions should be slow- according to the Lewis theory. But acid-base reactions are generally fast.
4. The Lewis theory cannot be used to ascertain the relative strengths of adds and bases.
5. The catalytic property of many adds is due to the H⁺(aq) ion. Since a Lewis add need not possess hydrogen, a Lewis acid need not have this property.

While dealing with acids and bases such as HCl, CH₃COOH, NaOH and NH₄OH in aqueous solutions, the Bronsted-LowTy concept is the most suitable and hence widely accepted.

Self Ionisation Of Water

So far we have considered water as a solvent and seen that it has both acidic and basic properties, i.e., it is amphoteric in nature. We will be using the Bronsted-Low’ry concept to understand the ionisation of water. In the presence of an add, it acts as a base while in the presence of a base, it acts as an acid.

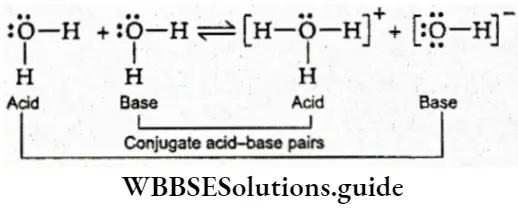
In pure water, one molecule of water can donate a proton to another molecule of water in a reaction in which water acts as acid and base simultaneously. There are always some H₃O⁺ and OH^– ions present in pure water.

or \(\mathrm{H}_2 \mathrm{O}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{OH}^{-}\)

This is referred to as dissociation self-ionisation or auto-ionisation of water and is characterised by the equilibrium constant,

or, \(K_{\mathrm{c}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_2 \mathrm{O}\right]\left[\mathrm{H}_2 \mathrm{O}\right]}\)

Multiplying the denominator of the above expression ([H₂O]²) by Kc (as H₂O is in excess and is essentially constant), we get K=[H₂O⁺][OH^–]

K_w is called the ionic product of water. It is a constant at a particular temperature. At 298 K its value is 1.0 x 10¹⁴ mol² L^-2. Such a small value of K_w indicates that the auto-ionisation of water does not occur to a large extent.

In fact, the reverse reaction, the formation of water by the reaction of H₃O⁺ and OH^– essentially goes to completion as its equilibrium constant is

⇒ \(\frac{1}{1 \times 10^{-14}}=1 \times 10^{14}\)(As stated earlier the units have been dropped.)

K_w increases with temperature because the degree of ionisation of water increases with temperature.

In pure water both H₃O⁺ and [OH^–] are equal.

⇒ \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]=\sqrt{1 \times 10^{-14}}=1 \times 10^{-7} \text { at } 298 \mathrm{~K} \text {. }\)

We can calculate the extent of dissociation of water molecules by finding the concentration of dissociated and undissociated water.

The concentration of dissociated water is simply the concentration of [H₃O⁺] or [OH^–]

Therefore concentration of dissociated water =1 x 10^-7 M at 298 K.

The molar concentration of pure water can be calculated from its density and volume.

Now, number of moles = \(\frac{\text { mass }}{\text { molar mass }}=\frac{D \times V}{\text { molar mass }}\) (since mass = density x volume)

Concentration of undissociated water =\(\left(\frac{1000 \mathrm{~g}}{\mathrm{~L}}\right)\left(\frac{1 \mathrm{~mol}}{18 \mathrm{~g}}\right)=55.4 \mathrm{~mol} \mathrm{~L}^{-1}\)

(The density of pure water is 1000 gL^-1 and its molar mass is 18.0 g mol^-1.)

Therefore degree of dissociation = \(\frac{\text { conc. of dissociated water }}{\text { conc. of undissociated water }}\)

= \(\frac{1 \times 10^{-7}}{55.4}=18 \times 10^{-9} \approx 2 \times 10^{-9} \text { or } \frac{2}{10^9} \text {. }\)

This means that out of 10⁹ molecules of water, two molecules are ionised.

Aqueous solutions of acids and bases: The concentrations of H₃O⁺ ions and OH^– ions are the same in pure water. When some acid or base is added to water, these concentrations do not remain equal, but the value of Kw remains the same (at a particular temperature).

• If some acid is added to water, the concentration of H₃O⁺ ions will increase.
• Then according to Le Chatelier’s principle, the system will try to counteract the change and the reverse reaction will be favoured, i.e., H₃O⁺ ions will combine with OH^– ions to form water molecules.
• In other words, the equilibrium will shift backwards, so that the value of Kw may remain the same.

At the new equilibrium, the concentration of OH^– ions will be less than the concentration of H₃O⁺ ions. The concentration of OH^– ions can be obtained from the following relation.

⇒ \(\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}\)

Similarly, the addition of a base will increase the concentration of OH^– ions and decrease the concentration of H₃O⁺ ions.

The concentration of H₃O⁺ ions in an aqueous solution of a base can be obtained from the following expression.

⇒ \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]} .\)

In pure water or neutral solutions [H₃O⁺] = [OH^–].

In acidic solutions [H₃O⁺]> [OH^–].

In basic solutions [H₃O⁺]<[OH^–].

According to Arrhenius, a strong acid or a strong base completely dissociates into hydrogen ions and the corresponding anions or hydroxyl ions and the corresponding cations (as the case may be).

Thus, a 0.1-M HCl solution will dissociate to give 0.1-M H⁺ ions and 0.1-M Cl^– ions.

Example: Calculate the hydronium ion and hydroxyl ion concentrations in

1. a 0.001-M HCl solution,
2. a 0.01-M HNO₃ solution,
3. a 0.01-M NaOH solution,
4. a 0.01-M Ba(OH)₂ solution,
5. a 0.1-M HCOOH which is 10% ionised and
6. a solution containing 3.65 x 10^-3 g of HCl per 100 mL.

Solution:

1. HCl is a strong acid which ionises completely in water, so[H₃O⁺] = 0.00 1 M = 1 x 10^-3 mol L^-1.

The equilibrium can be represented as follows.

⇒ \(\mathrm{HCl}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{Cl}^{-}\)

⇒ \(K_{\mathrm{w}}=\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\)

⇒ \({\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}=\frac{1 \times 10^{-14}}{10^{-3}}=1 \times 10^{-11} \mathrm{~mol} \mathrm{~L}^{-1}}\)

2. The equilibrium in this case can be represented as \(\mathrm{HNO}_3+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{NO}_3^{-}\)

Being a strong acid HN03 too dissociates completely and

⇒ \({\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{HNO}_3\right]=0.01 \mathrm{M}=1 \times 10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} . }\)

∴ \(\quad{\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_0 \mathrm{O}^{+}\right.}=\frac{1 \times 10^{-14}}{10^{-2}}=1 \times 10^{-12} \mathrm{~mol} \mathrm{~L}^{-1}.}\)

3. Since NaOH is a strong base it ionises completely in water.

∴ \(\quad\left[\mathrm{OH}^{-}\right]=[\mathrm{NaOH}]=0.01 \mathrm{M}=10^{-2} \mathrm{~mol} \mathrm{~L}^{-1}\)

∴ \(\quad\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1 \times 10^{-14}}{10^{-2}}=1 \times 10^{-12} \mathrm{~mol} \mathrm{~L}^{-1}\).

4. Since Ba(OH)₂ is completely ionised and its acidity is 2, i.e.,1 mol of Ba(OH)₂ gives 2 mol of OH^– ions,

⇒ \(\mathrm{Ba}(\mathrm{OH})_2 \longrightarrow \mathrm{Ba}^{2+}+2 \mathrm{OH}^{-}\)

⇒ \({\left[\mathrm{OH}^{-}\right]=2\left[\mathrm{Ba}(\mathrm{OH})_2\right]=2 \times 0.01=0.02 \mathrm{~mol} \mathrm{~L}^{-1} .}\)

∴ \({\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1 \times 10^{-14}}{2 \times 10^{-2}}=5 \times 10^{-13} \mathrm{~mol} \mathrm{~L}^{-1} .}\)

5. HCOOH is a weak acid whose degree of dissociation (α) is 10% (given).

⇒ \(\underset{\mathrm{C}(1-\alpha)}{\mathrm{HCOOH}}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \underset{\mathrm{C} \alpha}{\mathrm{H}_3 \mathrm{O}^{+}}+\underset{\mathrm{C} \alpha}{\mathrm{HCOO}^{-}}\)

⇒ \({\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\mathrm{C} \alpha=0.1 \times 0.1=0.01=10^{-2} \mathrm{~mol} \mathrm{~L}^{-1} .}\)

⇒ \({\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}=\frac{1 \times 10^{-14}}{10^{-2}}=10^{-12} \mathrm{~mol} \mathrm{~L}^{-1} .}\)

6. Molarity of a solution = no. of moles in1 L of solution.

The given solution contains 3.65 x 10^-3 g of HCl in 100 mL or 0.1 L.

∴ M = \(\frac{3.65 \times 10^{-3}}{36.5 \times 0.1}\) [mol. wt. of HCl = 36.5] = 1 x 10^-3

HCl is a strong acid.

∴ \({\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=[\mathrm{HCl}]=1 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1} .}\)

∴ \({\left[\mathrm{OH}^{-}\right]=\frac{1 \times 10^{-14}}{10^{-3}}=1 \times 10^{-11} \mathrm{~mol} \mathrm{~L}^{-1} .}\)

The pH scale: From our discussions on the ionisation of water so far, it must have become clear that K_w (ionic product) remains constant and that for a neutral solution [H₃O⁺] is equal to [OH^–], for an acidic solution [H₃O⁺] > [OH^–] and for a basic solution [H₃O⁺]< [OH^–].

• Surely then if we know the H₃O⁺ ion concentration in a solution we would have a fair idea about its relative acidic or basic character.
• The hydrogen ion concentration may vary from, say, 1 M in a strong acid to 10^-14 M in a strongly basic solution. Expressing H₃O⁺ ion concentrations in this fashion would be rather cumbersome.
• In 1909, P L Sorensen, a Danish chemist, proposed a more convenient way of expressing the
• H₃O⁺
• ion concentration in a solution. The scale proposed by Sorensen is called the pH (power of hydrogen) scale, which may be defined as

1. The magnitude of the negative power to which 10 must be raised to express the hydronium ion concentration; or
2. The negative logarithm (base 10) of the hydronium ion concentration in mol L^-1.

• Say the hydronium ion concentration in a solution is 10^-x Then its pH would be x, according to the first definition. This is simple enough and the first definition of pH seems to be apt.
• But what if the H₃O⁺ ion concentration in some solution is 1.5 x 10^-4 M? The first definition would not be so convenient.
• This is why the second definition is preferred. Actually, the second definition can be derived from the first.

Suppose [H₃O⁺] = 10^-x

Then log[H₃O⁺] = log 10^-x = -x log 10 = -x.

∴ x = pH = -log[H₃O⁺].

If you happen to know the pH of a solution, you could easily calculate the concentration of H₃O⁺ ions in it. [H₃O⁺]= antilog (-pH).

The hydroxyl ion concentration in a solution can be expressed in terms of pOH.

pOH = – log[OH^–].

For any solution at 298 K

K_w = [H₃O⁺][OH^–] = 10-14

∴ log[H₃O⁺] + log[OH^–] = logK_w = log 10-14 =-14

or -log[H₃O⁺]-log[OH^–] = -logK_w =14

or pH + pOH = pK_w =14.

For a neutral solution, [H₃O⁺] = [OH^–] = 10^-7.

∴ pH = -log 10^-7 =7.

This brings us to something very useful.

For an acidic solution, pH < 7.

For a basic solution, pH > 7.

For a neutral solution, pH = 7.

For practical purposes, the pH range is taken as 0 to 14, though theoretically, it may be possible to have H₃O⁺ ion concentrations of more than 10° M (i.e., 1 M) or less than 10^-14 M.

The table gives the pH values of some common substances in everyday life.

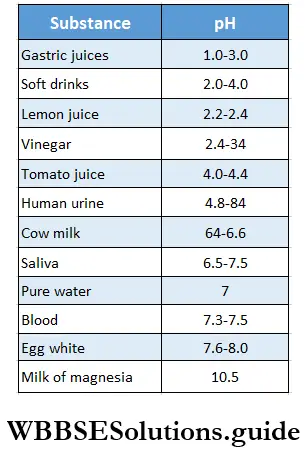
Example 1. Calculate the pH value of a solution of

1. 0.01-M HCl and
2. 0.01-M NaOH.

Solution:

1. \(\mathrm{HCl}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

Since HCl is completely ionised,

[H₃O⁺] = [HCl] = 0.01 M = 1 x 10^-2 mol L^-1.

pH = – log[H₃O⁺] = – log 1 x 10^-2 = – [-2] = 2.

2. \(\mathrm{NaOH}(\mathrm{aq}) \longrightarrow \mathrm{Na}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

NaOH is a strong base which ionises completely.

[OH^–] = [NaOH] = 0.01 M = 10^-2 mol L^-1.

∴ \(K_{\mathrm{w}}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]\)

∴  \(\quad {\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1 \times 10^{-14}}{1 \times 10^{-2}}=10^{-12} \mathrm{~mol} \mathrm{~L}^{-1} . }\)

∴ \(\quad \mathrm{pH}=-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log 10^{-12}=-[-12]=12\).

Example 2. 1000 mL of a solution contains 6.3 g of nitric acid. What is the pH of the solution if the acid is completely dissociated?
Solution:

The concentration of HNO₃ = 6.3 g L^-1.

Molecular weight of HNO₃ = 63.

∴ M = 6.3/6.3 = 0.1.

⇒ \(\mathrm{HNO}_3+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{NO}_3^{-}\)

Since the acid is completely dissociated

[H₃O⁺] = [HNO₃]=0.1M = 10^-1 M.

pH = – log[H₃O⁺] = – log 10^-1 = 1.

• The pH scale is very useful in getting an idea about the relative acidic (or basic) strengths of solutions. The higher the pH, the lower the concentration of hydronium ions in the solution.
• If the pH of a solution changes by one unit, there is a tenfold change in the molar concentration of that solution. Here it is important for you to know that pH is a measure of ‘hydrogen ion activity’.
• At the present level of learning, for the sake of simplicity, we have been using hydrogen ion concentration as a measure of pH since we are considering ideal (dilute) behavior of solutions.
• However, many solutions deviate from ideal behaviour with rise in concentration. To overcome this problem, we use the concept of activity.
• Activity is a physical quantity, a thermodynamic function that can be used in place of concentration. Now consider a concentrated solution, for example, 1 M HCl.

Let us use both its activity and molar concentration to determine its pH.

⇒ \(a_{\mathrm{H}_3 \mathrm{O}^{+}} \text {(activity) }=\gamma\left[\mathrm{H}_3 \mathrm{O}^{+} \right.\)., where y is the activity coefficient, a dimensionless quantity.

The activity being 0.81 the pH value of the solution turns out to be 0.092. On the other hand, if we use the concentration, pH = – log[1] = 0.

The ‘p’ in pH indicates (-log) so that px means -log(x). This is very useful in calculations involving exponential numbers so that it has been extended to other species. The most widely used are pK_w, pK_a, and pK_b.

PK_a = -logK_a; pK_b =-logK_b.

As you already know, for a conjugate acid-base pair, K_a x K_b = K_w.

Taking negative logarithm on both sides, (- log K_a) + (- log K_b ) = (- log K_w)

or PK_a+pK_b =pK_w.

Measuring pH The pH of a solution can be measured with the help of pH papers, indicators, or pH meters. While pH papers and indicators give an approximate pH value of the solution in question, pH meters give the exact value.

• An acid-base indicator is a substance that changes colour in a specific pH range of about 2 pH units. To determine the pH of a solution, a few drops of the indicator are added to the solution.
• To make the determination easier, nowadays a universal indicator is available, which is simply a mixture of several indicators, to make approximate measurements in the pH range 3-10.
• The color change on the addition of the indicator is noted and compared with a color chart to know the pH of the given solution.
• Nowadays, pH meters are available for commercial purposes. They measure pH with high precision.

A typical pH meter consists of a special measuring probe (a glass electrode) connected to an electronic meter that measures and displays the pH reading.

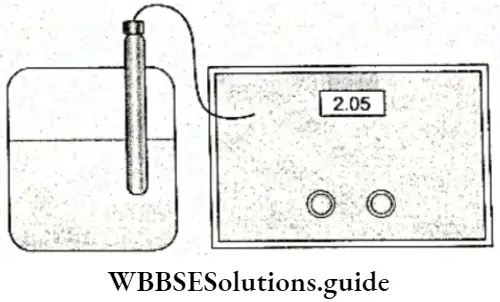
Hydrolysis Of Salts

The term hydrolysis refers to any reaction in which water is one of the reactants. Water, being an amphiprotic solvent, can act both as an acid or a base. When a salt is dissolved in water, it dissociates into its ions. If the salt is represented as MA, then we have

⇒ \(\mathrm{MA}(\mathrm{aq}) \longrightarrow \mathrm{M}^{+}(\mathrm{aq})+\mathrm{A}^{-}(\mathrm{aq})\)

Now, water may interact with the ions in two ways:

⇒ \(\underset{\text { acid }}{\mathrm{M}^{+}(\mathrm{aq})}+\underset{\text { base }}{2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})} \underset{\text { base }}{\mathrm{MOH}(\mathrm{aq})}+\underset{\text { adid }}{\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})}\) ….(1)

⇒ \(\underset{\text { base }}{\mathrm{A}^{-}(\mathrm{aq})}+\underset{\text { acid }}{\mathrm{H}_2 \mathrm{O}(\mathrm{l})} \underset{\text { add }}{\mathrm{HA}(\mathrm{aq})}+\underset{\text { base }}{\mathrm{OH}^{-}(\mathrm{aq})}\)…..(2)

As you can see in reaction (1), the base from which the cation is obtained is generated while in reaction (2), the acid from which the anion is obtained is generated. The salt MA is obtained by a neutralisation reaction between the base, MOH, and the acid, HA.

• A closer look at the reverse reactions shows that M⁺ is the conjugate acid of the base MOH while A^– is the conjugate base of the acid HA.
• On dissolving a particular salt in water, whether reaction (1) or (2) or both will occur and to what extent is dependent upon the strengths of the acid and the base from which the salt has been formed.
• The strength of an acid is inversely proportional to that of its conjugate form. If HA is a strong acid, its conjugate base, A^–, will be weak and hence reaction (2) will occur only insignificantly.
• Similarly, if the base MOH is strong, its conjugate acid M⁺ will be weak and reaction (1) will occur to a very small extent.
• If both M⁺ and A^– are obtained from a strong base and a strong acid respectively, hydrolysis occurs to a negligible extent or we may say that it does not occur at all. One such example is NaCl.
• Na⁺ is obtained from NaOH, a strong base, and Cl^– is obtained from HCl, a strong acid.
• A solution of NaCl will not show any hydrolysis and the species present in solution will be only Na⁺ (aq), Cl^–(aq), and H₂O. Hence the pH will be 7 and the solution is neutral.

When a salt dissociates into ions on dissolution in water, the ion which is the conjugate of a strong acid/base does not hydrolyse.

For example, sodium acetate, CH₃COONa (formed from a strong base and a weak acid), will dissociate in water as \(\mathrm{CH}_3 \mathrm{COONa}(\mathrm{aq}) \longrightarrow \mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{Na}^{+}(\mathrm{aq}).\)

Here CH₃COO^– is the conjugate base of the weak acid CH₃COOH. Therefore it will hydrolyse forming OH ions in the solution.

⇒ \(\mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)….(3)

However, Na⁺ will not hydrolyse as it is obtained from a strong base, NaOH. Therefore, the solution will be basic due to the hydrolysis reaction (3), in which hydroxyl ions are produced.

Similarly, NH₄Cl (formed from a strong acid and a weak base) dissociates as \(\mathrm{NH}_4 \mathrm{Cl}(\mathrm{aq}) \rightleftharpoons \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

In this case NH₄⁺ is the conjugate acid of the weak base NH₃ and hence undergoes hydrolysis as \(\underset{\text { acid }}{\mathrm{NH}_4^{+}(\mathrm{aq})}+\underset{\text { base }}{2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})} \rightleftharpoons \underset{\text { base }}{\mathrm{NH}_4 \mathrm{OH}(\mathrm{aq})}+\underset{\text { acid }}{\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})}\)…(4)

Cl^– will not undergo hydrolysis as it is obtained from HCl (strong acid). As a result, a solution of NH₄Cl will be acidic due to reaction (4), where H₃O⁺ is produced.

• Now let us see what happens when ammonium acetate, CH₃COONH₄, is dissolved in water.
• Since the salt is formed from the weak acid CH₃COOH and the weak base NH4OH, both the ions (CH₃COO^– and NH₄) formed will hydrolyse.
• Since both OH^– and H₃O⁺ are produced during hydrolysis, the pH of the solution will depend on the comparative strengths of the parent acid (K_a) and base (K_b) (from which the salt is formed).
• If K_a < K_b, the solution will be alkaline as then the conjugate base of the acid (A^–) is stronger and will hydrolyse more as compared to the conjugate acid of the base (M⁺).

If K_a >K_b, the solution will be acidic. However, if K_a = K_b, the solution will be neutral. It is interesting to note that the pH of such solutions is independent of the concentration of the salt and is given by

pH=7 + 1/2(pK_a-pK_b)

Example 1. The pH of a 0.1-M solution of aniline, a weak base, is 8.8. Find its pK_b.
Solution:

⇒ \(\underset{\text { anline }}(\mathrm{B})+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{BH}^{+}+\mathrm{OH}^{-}\)

Initial conc.(M) C 0 0

Change -x +x +x

Equilibrium cone. C-x x x

Since \(K_{\mathrm{b}}=\frac{\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{B}]}\),

∴ \(K_b=\frac{x^2}{C-x}\).

The pH of the solution = – log[H₃O⁺] = 8.8.

∴ [H₃O⁺] = antilog (-8.8) =16 x 10^-9 M.

Since we know that \(\left[\mathrm{OH}^{-}\right]=\frac{K_w}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]},\)

⇒ \(\left[\mathrm{OH}^{-}\right]=\frac{1 \times 10^{-14}}{16 \times 10^{-9}}=6.25 \times 10^{-6}=x\)

Substituting the values of x and C in the expression for K_b we get

∴\(K_{\mathrm{b}}=\frac{\left(6.25 \times 10^{-6}\right)^2}{0.1-6.25 \times 10^{-6}}\)

Since 6.25 x 10^-6 <<0.1, 0.1- 6.25 x 10^-6 = 0.1

∴ \(K_{\mathrm{b}}=\frac{\left(6.25 \times 10^{-6}\right)^2}{0.1}=3.9 \times 10^{-10}\).

pK_b =- log K_b =-log3.9 x 10^-10

pK_b =9.4

Example 2. The pK_a of hypobromous acid (HOBr) is 8.7. Calculate the pH of a 0.1-M solution of the acid.
Solution:

⇒ \(\mathrm{HA}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{A}^{-}\)

Equilibrium cone. (M) C- x x x

Since \(K_4=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}=\frac{x^2}{C-x}\),

pK_a =-log K_a =8.7.

K_a =antilog(-8.7) = 2 x 10^-9

Now substituting the value of K_a and C in the expression for K_a, we get

2 x 10^-9 = \(\frac{x^2}{0.1-x}\)

As K_a is small, 0.1 >> x.

∴ 2 x 10^-9 = \(\frac{x^2}{0.1}.\)

or x² =2×10^-9– x 0.1 = 2 x 10^-10

or x \(=\sqrt{2 \times 10^{-10}}=1.4 \times 10^{-5} \mathrm{M} .\)

This is the concentration of H₃O⁺ ions

[H₃O⁺]=x=1.4 X 10^-5 M.

pH =- log[H₃O⁺] = 4.8.

The pH of a 0.1-M solution of HOBr is 4.8.

Example 3. Calculate the degree of ionisation of 0.1-M acetic acid in the presence of 0.1-M HCl The pK_a of acetic acid is 4.74. Compare it with its ionisation in pure water.
Solution:

⇒ \(\mathrm{HAc}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{Ac}^{-}\)

⇒ \(K_{\mathrm{a}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{Ac}^{-}\right]}{[\mathrm{HAc}]}\)

or \(\mathrm{p} K_{\mathrm{a}}=-\log K_{\mathrm{a}}=4.74\)

or K_a = antilog(-4.74) =1.8 x 10^-5.

Let us first calculate α in pure water.

If the equilibrium concentration of [H₃O⁺] = Cα then that of Ac’ is also Cα and the concentration of acetic acid that remains undissociated is [HAc]= C(1 – α).

∴ \(K_4=\frac{(\mathrm{C} \alpha)(\mathrm{C} \alpha)}{C(1-\alpha)}\)

Since acetic add is a weak acid, α << 1

Hence \(K_{\mathrm{a}} \cong \frac{C^2 \alpha^2}{C}=C \alpha^2\)

or \(\alpha=\sqrt{\frac{K_a}{C}}=\sqrt{\frac{18 \times 10^{-5}}{0.1}}=0.013 .\)

Therefore the percentage dissociation is 1.3%. In the presence of 0.01-M HCl, the source of H₃O⁺ is acetic acid as well as hydrochloric acid. The equilibrium concentrations are as shown below.

⇒ \(\begin{array}{ll}
\mathrm{HAc}+\mathrm{H}_2 \mathrm{O} & \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{Ac}^{-} \\
\mathrm{C}(1-\alpha) & \mathrm{C} \alpha+0.01 \quad \mathrm{C} \alpha
\end{array}\)

Now, \(K_{\mathrm{a}}=\frac{(C \alpha+0.01)(C \alpha)}{C(1-\alpha)}\)

We may neglect α in comparison to 1.

∴ \(\quad K_a \cong \frac{C^2 \alpha^2+0.01 C \alpha}{C} \)

or \(K_a=C \alpha^2+0.01 \alpha\)

or \(C \alpha^2+0.01 \alpha-K_a=0\).

This is a quadratic equation and a can be calculated using the formula

x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

∴\(\quad \alpha =\frac{-0.01 \pm \sqrt{(0.01)^2+4 \times C \times K_a}}{2 C}\).

Substituting for K_a and C, we get

α = \(\frac{-0.01 \pm \sqrt{(0.01)^2+4 \times 0.1 \times 18 \times 10^{-5}}}{2 \times 0.1}=\frac{-0.01 \pm 0.0104}{0.2} .\)

Discarding the negative root, a = 2 x 10^-3 = 0.002

Percentage dissociation = 0.002 x 100 = 0.2%

This is far less than that in pure water. This shows that the equilibrium is affected in the presence of a common ion.

Buffer Solutions

Suppose you have a solution of a particular pH or a solution which has a certain concentration of H₃O⁺ ions. If you add even a small amount of add or base to this solution, its pH will change—it will decrease if you add an add and increase if you add a base.

Both in nature and in industries, it is necessary to have solutions whose pH values do not change with the addition of a small amount of an add or a base.

The pH value of an ordinary solution may change even if it comes in contact with air. It can absorb carbon dioxide from the air and become more addic, for example.

• A solution which can resist change in pH when a small amount of an acid or a base is added to it (or when it is diluted) is called a buffer solution. The ability of such a solution to resist change in pH is called buffer action.
• A buffer solution can be acidic. Such a solution contains a weak acid and its salt with a strong base in equimolar quantities (a weak acid and a salt formed from its conjugate base), example, a solution of acetic acid and sodium acetate, which acts as a buffer solution around pH 4.75.
• A basic buffer solution, on the other hand, contains equimolar quantities of a weak base and its salt with a strong acid (a weak base and a salt formed from its conjugate base), example, NH₄OH and NH₄Cl, which acts as a buffer around pH 9.25.
• A buffer solution may also contain a single substance, generally the salt of a weak acid and a weak base, example, ammonium acetate (CH₃COONH₄).
• In order to understand how a buffer solution maintains a constant pH value, let us consider a solution containing equimolar quantities of CH₃COOH (weak acid) and CH₃COONa (a salt of acetic acid with a strong base).

In an aqueous solution acetic acid will be weakly ionised and sodium acetate will be mostly dissociated.

⇒ \(\mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})\)

⇒ \(\mathrm{CH}_3 \mathrm{COONa}(\mathrm{aq}) \longrightarrow \mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})+\mathrm{Na}^{+}(\mathrm{aq})\)

The solution will contain a large concentration of Na⁺ and CH₃COO^– ions, a very small concentration of H₃O⁺ ions, and a large amount of undissociated acetic acid molecules.

If a few drops of an acid are added to this solution, the H₃O⁺ ions provided by the acid disturb the equilibrium (between ionised and un-ionised acid), and CH₃COO^– ions in the solution combine with the H₃O⁺ ions to counter the change.

⇒ \(\underset{\text { from buffer }}{\mathrm{CH}_3 \mathrm{COO}^{-}(\mathrm{aq})}+\underset{\text { from acid }}{\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})} \rightleftharpoons \mathrm{CH}_3 \mathrm{COOH}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

Thus, the H₃O⁺ ions provided by the acid are neutralised by CH₃COO ions from the buffer solution and there is no change in pH.

If a few drops of a base are added to the solution, the OH” ions from the base combine with the H₃O⁺ ions of the solution to form water.

⇒ \(\mathrm{OH}^{-}(\mathrm{aq})+\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq}) \longrightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

• This disturbs the equilibrium (by reducing the concentration of H₃O⁺ ions) and in accordance with Le Chatelier’s principle, more CH₃COOH molecules ionise, restoring the original concentration of H₃O⁺ ions or the pH.
• Blood is a natural buffer solution whose pH is about 7.4. The pH of sea water is also almost constant.
• Buffer solutions are required for electroplating and in the manufacture of photographic material and dyes, among many other industrial processes.
• The pH of culture media in biological laboratories also need to be resistant to change. The buffer solution of desired pH can be prepared by taking appropriate ratios of salt and acid or salt and base and by knowing the respective pKa and pKb values.
• An equation which is used to calculate the pH of a buffer solution is as follows.

pH = \(\mathrm{p} K_{\mathrm{a}}+\log \frac{[\text { salt }]}{\text { [acid] }}\) (for acidic buffer)

or pH = \(\mathrm{p} K_{\mathrm{a}}+\log \frac{[\text { base }]}{[\text { salt }]}\)
(for basic buffer)

This is called the Henderson-Hasselbalch equation. In the equation [acid], [base], and [salt] denote the concentrations of the acid, base, and salt respectively used to prepare the buffer solution.

Note that, in both the equations, pK_a appears and it may be calculated for the conjugate acid of the base by using the expression pK_a =pK_w -pK_b.

Example 1. Calculate the pH of an acetic acid-sodium acetate buffer in which the concentrations of the acid and salt are 0.5 M and 0.25 M respectively. K_a = 1.8x 10^-5 for acetic acid.
Solution:

Using the Henderson-Hasselbalch equation,

pH = \(\mathrm{pK}_{\mathrm{a}}+\log \frac{\text { [salt] }}{\text { [acid] }}\)

pH = \(-\log \left(18 \times 10^{-5}\right)+\log \frac{0.25}{0.5}\) = 4.74 – 0.3010 = 4.44.

Example 2. Find the pH of an ammonia-ammonium chloride buffer solution in which the concentrations are \(C_{\mathrm{NH}_3}\)=0.2M and \(C_{\mathrm{NH}_4^{+}}\)= 0.3 M. Given that K_a for NH₃ = 1. 76 x 10^-5.
Solution:

pK_a + pK_b=pK_w

or pK_a=pK_w-pK_b

pK_a = 14 – (- log 1.76 x 10^-5) = 14-4.75 = 9.25.

Using this value of pK_a in the equation

pH = \(\mathrm{p} K_{\mathrm{a}}+\log \frac{[\text { base] }}{[\text { salt }]}\)

pH = \(9.25+\log \frac{[0.2]}{[0.3]}\) = 9.25-0.18 = 9.07.

Example 3. Determine the pH of a buffer solution containing 0.03-M boric acid and 0.043-M sodium borate, given that pK_a for B(OH)₃ =9.00.
Solution:

pH = \(p K_{\mathrm{a}}+\log \frac{\text { [salt] }}{\text { [acid] }}\)

= \(9+\log \frac{0.04}{0.03}\) = 9 + 0.12 = 9.12.

Solubility Equilibria

The solubility of different salts in water or any other solvent varies to a large extent. For instance, calcium chloride is hygroscopic (absorbs water vapour from the atmosphere) in nature, and, on the other hand, lithium fluoride is almost insoluble.

There are certain factors which influence the solubility of salts in solvents. Common salt dissolves readily in water because the energies of coulmbic or ionic interaction between the two ions of a salt are overcome due to the high dielectric constant of water.

• Thus, in water Na⁺ and C- exist freely— the two do not attract each other. The dissolution of a salt in water has the effect of reducing the force between the ions, which then separate as a consequence.
• Ion solvation (solvation enthalpy—energy released in the process of solvation) also affects tire solubility of a salt in water or any other solvent. An ion is solvated when surrounded by several molecules of solvent.
• Solvation enthalpy is more for polar solvents and less for nonpolar solvents. Thus, salts do not dissolve in nonpolar solvents as the solvation enthalpy is not enough to overcome lattice enthalpy. Different salts exhibit different solubilities at different temperatures.
• Salts are divided into three categories based on solubility. Salts of solubility 0.1 M or greater are considered soluble.
• Salts of solubility between 0.1 M and 0.01 M are considered arc considered slightly soluble. And salts of solubility less than 0.01 M, though called insoluble, are actually sparingly soluble.
• A solid dissolves in a solvent until the solution and the solid are in equilibrium. The solution, at equilibrium, is saturated and its molar concentration is the molar solubility of the solid.

Solubility product: BaSO₄ and AgCl arc sparingly soluble in water. When such a sparingly soluble salt is mixed with water, a small
amount of it dissolves and makes the solution saturated.

• The rest of it remains undissolved and an equilibrium is set up between the undissolved salt and the salt ions in solution.
• At equilibrium, the rate of dissolution of ions from the undissolved solid is equal to the rate of precipitation of ions from the saturated solution.
• You may have noticed that we are talking about an equilibrium between the undissolved solid and the ions in solution, and not the molecules in solution.

This is because the small amount of the salt that dissolves gets completely dissociated into ions. The equilibrium can be represented as follows.

⇒ \(\underset{\text { or electrolyte }}Undissolved salt \rightleftharpoons ions in solution\)

Let us consider solid AgCl in contact with its saturated aqueous solution. The dissolution of the salt may be represented as

⇒ \(\mathrm{AgCl}(\mathrm{s}) \rightleftharpoons \mathrm{Ag}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

As in the other cases we have considered before, the equilibrium constant would be K= \(\frac{\left[\mathrm{Ag}^{+}\right]\left[\mathrm{Cl}^{-}\right]}{[\mathrm{AgCl}]}\)

The concentration of the undissolved salt is constant (it can be taken as 1) irrespective of the amount of the solid salt present. (This is true for any pure solid.)

Then K[AgCl] = [Ag⁺][C^–] =K_sp

This constant (K_sp) is called the solubility product. In general, if a sparingly soluble salt A_x B_y dissociates in water, the equilibrium thus set up can be represented as

⇒ \(\mathrm{A}_x \mathrm{~B}_y \rightleftharpoons x \mathrm{~A}^{y+}+y \mathrm{~B}^{x-}\).

The solubility product may be expressed as K_sp = [A^y+]^x[B^x-]^y

The solubility product of a sparingly soluble salt (or electrolyte) at a given temperature may be defined as the product of the molar concentrations of its ions in a saturated solution, with each concentration term raised to the power equal to the number of ions of that species produced by the dissociation of one molecule of the electrolyte.

A few examples will make this clear.

⇒ \(\mathrm{Ca}_3\left(\mathrm{PO}_4\right)_2: K_{\text {sp }}  =\left[\mathrm{Ca}^{2+}\right]^3\left[\mathrm{PO}_4^{3-}\right]^2\)

⇒ \(\mathrm{BaSO}_4: K_{\text {sp }} =\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{SO}_4^{2-}\right]\)

⇒ \(\mathrm{Mg}\left(\mathrm{OH}_2\right): K_{\text {sp }}=\left[\mathrm{Mg}^{2+}\right]\left[\mathrm{OH}^{-}\right]^2\)

⇒ \(\mathrm{Ag}_2 \mathrm{CrO}_4: K_{\text {sp }} =\left[\mathrm{Ag}^{+}\right]^2\left[\mathrm{CrO}_4^{2-}\right]\)

• It is worthwhile to mention here that ionic product (or Q_sp) is the product of the concentration of ions in any solution raised to their respective stoichiometries.
• It may have struck you that both solubility product and ionic products are products of the concentrations of ions in a solution (not considering the powers of the concentration terms for the moment).
• However, the ionic product has a more general application. It applies to both saturated and unsaturated solutions, while the solubility product applies only to saturated solutions.

1. The ionic product is the same as the solubility product in a saturated solution.
2. If the solubility product is greater than the ionic product, the solution is unsaturated.
3. The higher the value of the solubility product the greater is the solubility of a salt.
4. The ionic product cannot be greater than the solubility product. When it tends to exceed the value of the solubility product, precipitation (or combination of ions) starts.

If you know the solubility of a sparingly soluble salt at a particular temperature, you can easily calculate its solubility product.

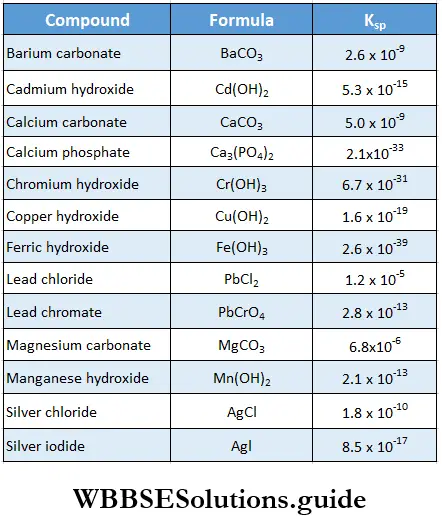
Example 1. Find the solubility product of AgCl at T°C if its solubility at this temperature is 1.08 x 10^-5 mol L^-1.
Solution:

⇒ \(\mathrm{AgCl}(\mathrm{s}) \rightleftharpoons \mathrm{Ag}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

It is given that the solubility of AgCl is 1.08×10^-5 mol L^-1. AgCl is a sparingly soluble salt and it dissociates completely.

That is to say, 1 mol of AgCl in solution dissociates completely to produce 1 mol of Ag⁺ and 1 mol of Cl^– ions.

Therefore, 1.08 x 10^-5 mol of AgCl will give 108 x 10^-5 mol of Ag⁺ and 1.08 x 10^-5 mol of Cl^– ions,

or [Ag⁺] = 1.08 x 10^-5 mol L^-1

and [Cl^–] = 1.08x 10^-5 mol L^-1

= (1.08 x 10^-5 )(1.08 x 10^-5) = 1.16 x 10^-10.

Example 2. The solubility of PbCl₂ at a particular temperature is 2.2 x 10^-2 mol L^-1. Find its solubility product at this temperature.
Solution:

⇒ \(\mathrm{PbCl}_2 \rightleftharpoons \mathrm{Pb}^{2+}+2 \mathrm{Cl}^{-}\)

PbCl₂ is a sparingly soluble salt, so it is completely ionised in solution.

In other words, 1 mol of PbCl₂ in solution will dissociate to produce 1 mol of Pb⁺ and 2 mol of Cl^– ions. It is given that the solubility of PbCl₂ is 2.2 x 10^-2 mol L^-1.

[Pb²⁺] = 2.2 x 10^-2 mol L^-1

and [Cl^–] = 2 x 2.2 x 10^-2 mol L^-1.

∴ K_sp =[Pb²⁺][Cl^–]² = [2.2 x 10^-2][2 x 2.2 x 10^-2]² =4.3×10^-5.

Calculation of solubility: The solubility of a salt is defined as grams of solute that can be dissolved in 100 mL of the solvent. The solubility of a sparingly soluble salt can be calculated if its solubility product is known.

• However, since K_sp is obtained considering the concentration in moles per litre (M), solubility is also obtained in moles per litre.
• This is called molar solubility—the amount of n salt that dissolves in a requisite amount of water to produce one litre of a saturated solution.
• The following examples illustrate the calculation of molar solubility from solubility product.

Example 1. The solubility product of Ag₂CrO₄ at 298 K is 4 x 10^-12. Find its solubility at this temperature.
Solution:

At equilibrium \(\mathrm{Ag}_2 \mathrm{CrO}_4 \rightleftharpoons 2 \mathrm{Ag}^{+}+\mathrm{CrO}_4^{2-}\)

Suppose the solubility of Ag₂CrO₄ is x mol L^-1

Then [Ag⁺]=2x and [CrO₄^2-] = x. (Ag₂CrO₄ forms 2 moles of Ag⁺ and one mole of CrO₄^2-)

∴ \(K_{\mathrm{sp}}=\left[\mathrm{Ag}^{+}\right]^2\left[\mathrm{CrO}_4^{2-}\right]=[2 x]^2[x]=4 x^3\)

Given that K_sp = 4 x 10^-12

or 4x³ =4 x 10^-12

∴ x = 1 x 10^-4

Therefore the solubility of Ag₂CrO₄ is 1 x 10^-4 mol L^-1.

Example 2. The solubility product of AgBr in water is 2.5 x 10^-13. Calculate its solubility in a 0.01-M NaBr solution.
Solution:

NaBr dissociates completely in solution.

∴ \(\left[\mathrm{Br}^{-}\right]=[\mathrm{NaBr}]_0=0.01 \mathrm{M}\) (The subscript ‘0’ denotes the initial concentration.)

Let the solubility of AgBr be x mol L^-1

Then [Ag⁺] = [Br^–] = x mol L^-1 (from the dissociation of AgBr)

∴ total[Br] = x + 0.01 M (x <<0.01 M; AgBr being sparingly soluble)^–

K_sp(AgBr) = [Ag⁺][B^–r] = x x 0.01

Given that K_sp(AgBr) = 2.5 x 10^-13

∴ x x 0.01 = 2.5 x 10^-13

or x = \(\frac{2.5 \times 10^{-13}}{0.01}=2.5 \times 10^{-11} \mathrm{~mol} \mathrm{~L}^{-1}\)

Factors affecting solubility: The principle that an equilibrium counteracts the change due to the addition of species to solutions is also applicable to solubility product constants.

Common-ion effect: The presence of a common ion can also affect the solubility equilibrium. Let us consider the dissolution of MgF₂ in water.

⇒ \(\mathrm{MgF}_2(\mathrm{~s}) \rightleftharpoons \mathrm{Mg}^{2+}(\mathrm{aq})+2 \mathrm{~F}^{-}(\mathrm{aq})\)

Let x be the solubility of MgF₂ in moles per litre. Then the concentrations of Mg²⁺ and F^– are as follows:

[Mg²⁺] = x mol L^-1 (as one mole of MgF₂ gives one mole of Mg²⁺ and 2 moles of F^–).

[F^–] = 2 xmol L^-1.

∴ K_sp =[Mg²⁺][F^–]² = x x(2x)² =4x³.

But the solubility product of MgF₂ is 7.4 x 10^-11

∴ 7.4 x 10^-11 = 4x³

or \(x^3=\frac{7.4 \times 10^{-11}}{4}=1.8 \times 10^{-11} \Rightarrow x=\sqrt[3]{1.8 \times 10^{-11}}=2.6 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1}\)

∴ \({\left[\mathrm{Mg}^{2+}\right]=2.6 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1} .}\)

Molar solubility = 2.6 x 10^-4 M.

∴ [F^–] = 2 x 2.6 x 10^-4 =5.2×10^-4M.

When NaF is added to a solution of MgF₂, F^– being the common ion, its concentration in solution increases.

In order to keep K_sp constant, [Mg²⁺] must become smaller, or in other words, MgF₂ is less soluble in an NaF solution than it is in pure water.

The presence of a common ion shifts the equilibrium to the left. This may be seen clearly from the following solved example.

Example: Calculate the molar solubility of MgF₂ in 0.05-M NaF at 298 K, given that K_spof MgF₂ is 7.4 x 10^-11.
Solution:

We have calculated the molar solubility of MgF₂ in pure water, which is 2.6×10^-4 M. Let us now calculate its solubility in NaF.

If we assume x to be the molar solubility of MgF₂ then one mole of MgF₂ gives 1 mol of Mg²⁺ ions and 2 moles of F^– ions.

Hence the concentrations of Mg²⁺ and F^– from MgF₂ alone are x and 2x respectively. There is another source of F^–, which is NaF. From 0.05 M of NaF, we get 0.05 M of F^– ions.

Equilibrium conc. \(\mathrm{MgF}_2(\mathrm{~s}) \rightleftharpoons \underset{x}{\mathrm{Mg}^{2+}(\mathrm{aq})}+\underset{2 x+0.05}{2 \mathrm{~F}^{-}(\mathrm{aq})}\)

Hence [F^–] = 2x+ 0.05 and [Mg²⁺] = x.

But K_sp =[Mg²⁺][F^–]² or 7.4 x 10^-11 = x x (2x + 0.05)²,

As K_sp is smqll 2x <<0.05.

Hence 7.4 x 10^-11 s x x (0.05)² or x = 7.4 x 10^-9 M.

The molar solubility of MgF₂ has decreased from 2.6 x 10^-4 M in pure water to 7.4 x 10^-9 M in the presence of NaF due to the common-ion effect.

pH of a solution: The solubility of salts of weak acids increases as the pH of the solution decreases or the acidity increases.

For example, the solubility of CaCO₃ increases with decreasing pH.

This is because the CO₃^2- ions react with H⁺ ions forming HCO₃^– ions react with H and thus are removed from the solution. As a result the reaction moves in the forward direction, dissolving more CaC03.

⇒ \(\begin{aligned}
\mathrm{CaCO}_3(\mathrm{~s}) \rightleftharpoons \mathrm{Ca}^{2+}(\mathrm{aq})+\mathrm{CO}_3^{2-}(\mathrm{aq}) \\
\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{CO}_3^{2-}(\mathrm{aq}) \rightleftharpoons \mathrm{HCO}_3^{-}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \\
\hline
\mathrm{CaCO}_3(\mathrm{~s})+\mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq}) \rightleftharpoons \mathrm{Ca}^{2+}(\mathrm{aq})+\mathrm{HCO}_3^{-}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \\
\hline
\end{aligned}\)

Salts containing anions such as \(\mathrm{PO}_4^{3-}, \mathrm{S}^{2-}, \mathrm{F}^{-} \text {and } \mathrm{CN}^{-}\) also behave in a similar fashion.

Predicting the precipitation of a salt: If the value of the ionic product exceeds that of the solubility product, precipitation of the excess ions occurs.

So, if you know the solubility product of a sparingly soluble salt, you will be able to predict whether or not mixing two solutions containing known concentrations of Us Ions will result in the precipitation of the salt.

Example 1. Predict whether precipitation will occur when equal volumes of a 0.02-M Na₂SO₄ solution and a 0.02-M BaC₂ solution are mixed.(K_sp of BaSO₄ = 1.5 x 10^-10)
Solution:

Let the volume of each solution = V mL

Total volume after mixing = 2V mL

Applying the relation \(\begin{aligned}
M_1 V_1=M_2 V_2 \\
0.02 \times V=M_2 \times 2 V
\end{aligned}\)

∴ after mixing [BaCl₂]₀ = 0.01 mol L^-1

Since BaCl₂, is completely ionised,

[Ba²⁺] =[BaCl₂]₀ = 0.01 mol L^-1

To determine the molarity of the Na₂SO₄ solution after mixing, we use the equation

M’₁V’₁(before mixing) = M’₂V’₂(after mixing)

∴ \(M_2^{\prime}=\frac{0.02 \times V}{2 V}=0.01\)

∴ after mixing[Na₂SO₄]₀ = 0.01 mol L^-1

Since Na₂SO₄is completely ionised,

[SO₄^2-] = [Na₂SO₄] = 0.01 mol L^-1

Ionic product of BaSO₄, LP. or Q_sp = [Ba²⁺][SO₄^2-] = 0.01 x 0.01 = 10^-4 mol L^-1

As Q_sp >  K_sp precipitation occurs.

Precipitation of soluble salts: The precipitation of soluble salts from their saturated solutions is called salting out This process is used to obtain pure sodium chloride from a saturated solution of impure sodium chloride.

• HCl gas is passed through a saturated solution of NaCL The addition of HCl (which ionises) increases the concentration of Cl^– ions.
• Consequently, the ink product exceeds the solubility product of NaCl and precipitation occurs. The salt which is precipitated is in the pure stale. The impurities remain in solution.
• Soap is salted out from its saturated solution by the addition of sodium chloride.
• Soaps are sodium salts of ratty acids. The addition of sodium chloride increases the concentration of Na⁺ ions in the solution, thus making the ionic product exceed the solubility product

Example 1. Calculate the solubility of BaSO₄ in pure water and in sea -water which contains 0.029-M SO₄^2- ions. [K_sp(BaSO₄) = 9.1x 10^-11n. ]
Solution:

⇒ \(\mathrm{BaSO}_4(\mathrm{~s}) \rightleftharpoons \mathrm{Ba}^{2+}(\mathrm{aq})+\mathrm{SO}_4^{2-}(\mathrm{aq})\)

Let x be the molar solubility of BaSO₄.

∴ \(\left[\mathrm{Ba}^{2-}\right]=x ;\left[\mathrm{SO}_4^{2-}\right]=x\)

⇒ [latexK_{\mathrm{sp}}=\left[\mathrm{Ba}^{2+}\right]\left[\mathrm{SO}_4^{2-}\right]=x^2 .[/latex]

But \(9.1 \times 10^{-11}=x^2 \text { or } x=\sqrt{9.1 \times 10^{-11}}=9.5 \times 10^{-6}\) .

Hence the solubility of BaSO₄ in pure water = 9.5 x 10^-6 M

In sea water, [SO₄^2-] = 0.029 M.

Total concentration of SO₄^2- = 0.029 + x’, where x’ is the solubility of BaSO₄ in sea water.

Now, K_sp = (x’)(0.029 + x’)

We may assume that x'<< 0.029 as K_sp is small.

∴ K_sp =(x’)(0.029)

∴or 9.1 x 10^-11 = 0.29x’

or x’ = 3.1x 10^-10

Therefore, the solubility of BaSO₄ in sea water is 3.1 x 10^-10 M. This is far less than that in pure water.

Example 2. A carbonated drink was saturated with CO₂ at 0°C and 5 atm pressure. What was the concentration of CO₂ in the bottled drink if the Henry constant for an aqueous solution of CO₂ at 0°C is 7.5 x 10^-2 mol L^-1 atm^-1?
Solution:

According to Henry’s law, C = kp,

where C is the concentration of a gas in a solution, p is the partial pressure of the gas and k is the Henry constant.

∴ concentration of CO₂ in the drink = kp = 7.5 x 10^-2 x5

=37.5 x 10^-2 =0.38 mol L^-1.

Example 3. Calculate the equilibrium constantfor a reaction given that the rate constantsfor thefonvard and reverse reactions are 2.48 x 10^-4 and 8.25 x10^-5 respectively.
Solution:

Equilibrium constant K = \(\frac{k}{k^{\prime}}\),

where k and k’ are the rate constants for the forward and the reverse reaction respectively.

∴ K = \(=\frac{2.48 \times 10^{-4}}{8.25 \times 10^{-5}}=3\)

Example 4. Two moles of PCl₅ was heated to 327°C in a closed vessel of volume 2 L. When equilibrium was established, 40% of the PCl₅ had dissociated into PCI₃ and Cl₂ Calculate the equilibrium constantfor the reaction.
Solution:

The dissociation of PCl₅ into PCI₃ and Cl₂ can be represented as follows.

⇒ \(\mathrm{PCl}_5 \rightleftharpoons \mathrm{PCl}_3+\mathrm{Cl}_2\)

Initial concentration of PCl₅ = 2 mol.

Percentage dissociation at equilibrium = 40%.

PCI₅ dissociated at equilibrium = 40% of 2 mol = 0.8 mol.

∴ amount of PCI₅ at equilibrium = 2- 0.8 =12 mol

and amount of PCI₃ and Cl₂ at equilibrium = 0.8 mol.

Since the volume of the vessel is 2 L, at equilibrium

⇒ \(\left[\mathrm{PCl}_5\right]=\frac{1.2}{2} \mathrm{~mol} \mathrm{~L}^{-1}\)

⇒ \(\left[\mathrm{PCl}_3\right]=\frac{0.8}{2} \mathrm{~mol} \mathrm{~L}^{-1}\).

⇒ \(\left[\mathrm{Cl}_2\right]=\frac{0.8}{2} \mathrm{~mol} \mathrm{~L}^{-1}\).

∴ K=\(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}=\frac{0.4 \times 0.4}{0.6}=0.267\).

Example 5. 0.1 mol of PCl₅ is heated in a 1-L flask at 250°C. Calculate the equilibrium concentrations of PCl₅, PCl₃ and Cl₂, if the equilibrium constant for the dissociation of PCl₅ is 0.0414.
Solution:

PCI₅ dissociates according to the following reaction.

∴ \(\mathrm{PCl}_5 \rightleftharpoons \mathrm{PCl}_3+\mathrm{Cl}_2\)

Suppose at equilibrium x mol of PCl₅ dissociates to form x mol of PCl₃ and x mol of Cl₂. Since the volume of the vessel is 1 L, at equilibrium,

⇒ [PCl₅] = 0.1 – x mol L^-1.

⇒ [PCl₃] = xmolL

⇒ [Cl₂] = x mol L^-1.

∴ K = \(\frac{\left[\mathrm{PCl}_3\right]\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}=\frac{x \times x}{0.1-x}\)

Given that K = 0.0414.

∴ 0.0414 = \(\frac{x^2}{0.1-x}\)

or x² +0.0414x-0.00414 = 0

This is a quadratic equation and x can be calculated using the formula

x =\(-\frac{b \pm \sqrt{b^2-4 a c}}{2 a}=\frac{-0.0414 \pm \sqrt{(0.0414)^2-4 \times 1 \times(-0.0414)}}{2 \times 1}\)

=\(\frac{-0.0414 \pm \sqrt{0.0017+0.1656}}{2}=\frac{-0.0414 \pm 0.135}{2}\) = 0.0882 and + 0.0468

The negative value of x is meaningless.

Thus, the concentrations of PCI₃, Cl₂ and PCl₅ at equilibrium are as follows.

[PCI₃] = [Cl₂] = x = 0.0468 mol LT^-1.

[PCI₅] = 0.1 – x = 0.0532 mol L^-1.

Example 6. The equilibrium constant for the reaction \(\mathrm{CH}_3 \mathrm{COOH}+\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH} \rightleftharpoons \mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5+\mathrm{H}_2 \mathrm{O}\) is 4.0 at 298 K. Calculate the weight of ethyl acetate that will be obtained when 120 g of acetic acid reacts with 92 g of alcohol.
Solution:

Weight of ethyl alcohol = 92 g.

Weight of acetic acid = 120 g.

Number of moles = \(\frac{\text { weight of substance }}{\text { molecular weight }} \text {. }\)

∴ number of moles of ethyl alcohol = 92/46 = 2

and number of moles of acetic acid = 120/60 = 2.

According to the chemical equation that represents the reaction, 1 mol each of the reactants produce 1 mol each of the products. Therefore, if x mol of each of the reactants reacted, x mol each of the products would be formed at equilibrium.

⇒ \(\mathrm{CH}_3 \mathrm{COOH}+\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH} \rightleftharpoons \mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5+\mathrm{H}_2 \mathrm{O}\)

Intial concentration \(\frac{2}{V} \frac{2}{V} \frac{0}{V} \frac{U}{V}\)

Conc. at equilibrium \(\frac{2-x}{V} \frac{2-x}{V} \frac{x}{V} \frac{x}{V}\)

Applying the law of equilibrium

K = \(\frac{\left[\mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5\right]\left[\mathrm{H}_2 \mathrm{O}\right]}{\left[\mathrm{CH}_3 \mathrm{COOH}\right]\left[\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}\right]}\)

= \(\frac{[x / V][x / V]}{\left[\frac{2-x}{V}\right]\left[\frac{2-x}{V}\right]}=\frac{x^2}{(2-x)^2}\).

Given that K = 4.

∴ 4 = \(\frac{x^2}{(2-x)^2}\)

or 2 = \(\frac{x}{2-x}\)

or 4-2x = x

or x = 4/3 =1.33 mol.

Hence the amoimt of ethyl acetate formed = 1.33 mol

=1.33 x molecular weight of ethyl acetate

=1.33 x 88 =117.04 g

Example 7. The equilibrium constant at 298 K for \(\mathrm{Cu}(\mathrm{s})+2 \mathrm{Ag}^{+}(\mathrm{aq}) \rightleftharpoons \mathrm{Cu}^{2+}(\mathrm{aq})+2 \mathrm{Ag}(\mathrm{s})\) is 4.0 x 10¹⁵. In a solution in which copper has displaced some silver ions, the concentration of Cu²⁺ ions is 16 x 10^-2 mol L^-1 and the concentration of Ag⁺ ions is 2.0 x 10^-9 mol L^-1. Is this system at equilibrium?
Solution:

Applying the law of chemical equilibrium, assuming that the system is at equilibrium,

⇒ \(K_{\mathrm{c}}=\frac{\left[\mathrm{Cu}^{2+}(\mathrm{aq})\right][\mathrm{Ag}(\mathrm{s})]^2}{\left[\mathrm{Ag}^{+}(\mathrm{aq})\right]^2[\mathrm{Cu}(\mathrm{s})]} .\)

By convention, concentration of a solid = 1.

∴\(K_{\mathrm{c}}=\frac{\left[\mathrm{Cu}^{2+}(\mathrm{aq})\right]}{\left[\mathrm{Ag}^{+}(\mathrm{aq})\right]^2}\)

Substituting the concentrations of Cu²⁺ and Ag⁺ ions

∴ \(K_c=\frac{1.6 \times 10^{-2}}{\left(2 \times 10^{-9}\right)^2}=4 \times 10^{15}\)

This is the value of K_c for the reaction in equilibrium. Hence the given system is in equilibrium.

Example 8. The equilibrium constant for the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\) is 50.5 at 718 K. Predict the direction in which the reaction will proceed to reach equilibrium at 718 K if we start with 2 x 10^-2 mol of HI,1.0 x 10^-2 mol of H₂ and 3.0 x 10^-2 mol of I₂ in a vessel of volume1 L

Solution:

Reaction quotient \(\left(\mathrm{Q}_c\right)=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right]\left[\mathrm{I}_2\right]}\)

If the reaction quotient is equal to K_c, the system is at equilibrium, and if it is less than Kc, the reaction will proceed in the forward direction to attain equilibrium.

Since the volume of the vessel is 1 L,

⇒ \(Q_c=\frac{\left[2 \times 10^{-2}\right]^2}{\left[1.0 \times 10^{-2}\right]\left[3.0 \times 10^{-2}\right]}=1.33\)

Since this is less than K_c, the reaction will proceed in the forward direction.

Example 9. 1 mol of ammonia was injected into a 1-L flask at a certain temperature. The equilibrium mixture was found to contain 0.3 mol of H₂. Calculate the concentrations of N₂ and NH₃ at equilibrium, and the equilibrium constant.
Solution:

The equilibrium can be represented as follows.

⇒ \(2 \mathrm{NH}_3 \rightleftharpoons \mathrm{N}_2+3 \mathrm{H}_2\)

The initial concentration of NH₃ =1 mol.

At equilibrium, 2 mol of ammonia produces 3 mol of hydrogen.

Therefore, 0.3 mol of H₂ will be obtained from 0.2 mol of NH₃.

Similarly, when 2 mol of NH₃ dissociates, 1 mol of N₂ is obtained.

Therefore, 0.2 mol of NH₃ will produce 0.1 mol of N₂.

Since the volume of the flask is1 L, at equilibrium,

[N₂] = 0.1 mol ^-1,

[H₂] = 0.3 mol L^-1,

[NH₃] =1-0.2 =0.8 mol L^-1.

∴ \(K_{\mathrm{c}}=\frac{\left[\mathrm{N}_2\right]\left[\mathrm{H}_2\right]^3}{\left[\mathrm{NH}_3\right]^2}=\frac{(0.1)(0.3)^3}{(0.8)^2}=0.004\)

Example 10. 1 mol of ammonium carbamate dissociates as shown below at 500 K. \(\mathrm{NH}_2 \cdot \mathrm{COONH}_4(\mathrm{~s}) \rightleftharpoons 2 \mathrm{NH}_3+\mathrm{CO}_2\) If the pressure exerted by the released gases is 3.0 bar, calculate the value of K_p.
Solution:

Applying the law of equilibrium,

⇒ \(K_p=\frac{p_{\mathrm{NH}_3}^2 p_{\mathrm{CO}_2}}{p_{\mathrm{NH}_2 \cdot \mathrm{COONH}_4(s)}}\)

By convention  \(p_{\mathrm{NH}_2 \mathrm{COONH}}\) =1 as it is a solid.

Given that the pressure exerted by the gases = 3 bar; this is the total pressure.

(To obtain the partial pressures, the total pressure must be multiplied by the mole fractions of the respective gases.)

∴ \(p_{\mathrm{NH}_3}=3 \times \frac{2}{3}=2 \mathrm{bar}\).

and \(p_{\mathrm{CO}_3}=3 \times \frac{1}{3}=1 \mathrm{bar}\).

∴ \(K_p=(2)^2(1)=4 bar.\)

Example 11. The dissociation constant of a weak acid HA is 1.6 x 10^-5 at 298 K. Calculate the H₃O⁺ ion concentration in a 0.01-M solution of the acid.
Solution:

The ionisation of the acid may be represented as

⇒ \(\mathrm{HA}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{A}^{-}(\mathrm{aq})\)

⇒ \(K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\) .

If the concentration of HA that dissociates is x, then the concentration of H₃O⁺ and A^– is also x.

Then the concentration of the undissociated acid is (0.01- x).

Since HA is a weak acid, its degree of dissociation is small and at equilibrium, x may be neglected in comparison to 0.1.

[HA] = (0.1 -x) = 0.1 mol L^-1

[H₃O⁺] =[A^–] = X

∴ \(\quad K_a=\frac{x^2}{0.1}\)

or \(x^2=K_a \times 0.1=16 \times 10^{-5} \times 0.1\)

or \(x=\sqrt{16 \times 10^{-5} \times 0.1}=126 \times 10^{-3}\).

∴ \(\quad\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{A}^{-}\right]=1.26 \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1}\).

Example 12. Calculate the degree of dissociation and the concentration of H₃O⁺ ions in a 0.1-M solution of formic acid, given that =2.1 x 10^-4 at 298 K.
Solution:

Formic acid dissociates in water according to the following equation.

⇒ \(\mathrm{HCOOH}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{HCOO}^{-}\)

The initial concentration of the acid is given as 0.1 mol L^-1

Let the degree of dissociation be α.

Then at equilibrium

[H₃O⁺] = α x 0.1 mol L^-1

[HCOO^–] =α x 0.1 mol L^-1

[HCOOH] = 0.1(1- α) mol ^-1

∴\(K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{HCOO}^{-}\right]}{[\mathrm{HCOOH}]}=\frac{(0.1 \alpha)(0.1 \alpha)}{0.1(1-\alpha)}\)

Since formic add is a weak acid, a is very small as compared to 1 and can be neglected in the denominator.

∴ \(K_a=\frac{(0.01 \alpha)^2}{0.1}=0.1 \times \alpha^2\)

Given that K_a = 2.1 x 10^-4.

or 2.1 x 10 = 0.1 x α²

or \(\frac{21 \times 10^{-4}}{0.1}=\alpha^2\)

or α² = 2.1 x 10^-3 = 21 x 10^-4

or α = 0.046

[H₃O⁺] = Cα = 0.1 x 0.046 = 4.6 x 10^-3 mol L^-1

Example 13. A solution of NaOH contains 4.0 g of the base per litre. Find the pH of the solution.
Solution:

Concentration of NaOH solution = 4 g L^-1; molecular weight of NaOH = 40.

∴ molarity of solution = 4/40 = 0.1

Since NaOH is completely dissociated, concentration of OH^– ions = 0.1 M = 10^-1 mol L^-1.

K_w=[H₃O⁺][OH^–]

or 1 x 10^-14 = [H₃O⁺][OH^–]

or \(\frac{1 \times 10^{-14}}{10^{-1}}=\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\)

or 1 x 10^-13 M = [H₃O⁺].

pH =- log[H₃O⁺] = -log 10^-13 = 13.

Example 14. Calculate the pH of a solution of a strong monobasic acid made by diluting 100 mL of a 0.01-M solution to 1 L
Solution:

M₁V₁ = M₂V₂

or 0.01 x100 = M₂ x 1000.

∴ \(M_2=\frac{0.01 \times 100}{1000}=10^{-3}\)

Assuming complete dissociation

[H₃O⁺] =10^-3. (it is a monobasic add, one mole of protons is released per mole of add.)

∴ pH =- log[H₃O⁺] =-[log10^-3] = 3.

Example 15. Calculate the pH of a

1. 0.02-M H₂SO₄ solution and
2. 0.01-M Ba(OH)₂ solution.

Solution:

1. The ionisation of H₂SO₄ can be represented by \(\mathrm{H}_2 \mathrm{SO}_4+2 \mathrm{H}_2 \mathrm{O} \longrightarrow 2 \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{SO}_4^{2-}\)

Being a strong acid, H₂SO₄ is completely ionised.

1 mol of H₂SO₄ dissodates to give 2 mol of H₃O⁺.

[H₃O⁺] =2 x 0.02 = 0.04 mol L^-1.

∴ pH = -log 0.04 =-log 4 x 10^-2 = -(-1.3980) =1.398.

2. Ba(OH)₂ dissodates completely.

1 mol of Ba(OH)₂ dissociates to give 2 mol of OH^–.

∴ [OH^–] = 2[Ba(OH)₂] =2 x 0.01 = 0.02 M.

K_w =[OH^–][H₃O⁺]

∴ \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{\mathrm{K}_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1 \times 10^{-14}}{0.02}=5 \times 10^{-13} \mathrm{M}\)

∴ pH =-log 5 x 10^-13 =-(-12. 3010) =12.301

Example 16. How many grams of NaOH must be dissolved in 1 L of a solution of the base so that the pH of the solution is 13?
Solution:

pH = -log[H₃O⁺]

[H₃O⁺] = -antilog pH = -antilog13 =1 x 10^-13 mol L^-1.

K_w =[H₃O⁺][OH^–].

∴ \(\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}=\frac{1 \times 10^{-14}}{1 \times 10^{-13}}=1 \times 10^{-1} \mathrm{~mol} \mathrm{~L}^{-1}\).

As NaOH is a strong electrolyte, [NaOH] =[OH^–] =1 x 10^-1 mol L^-1.

Amount of NaOH = number of moles x mol. wt. of NaOH =1 x10^-1 x 40 = 4 g.

Example 17. The dissociation constant of a weak acid HA is 1 x 10^-9. Find the pH of a 0.1-M solution of the acid.
Solution:

The dissociation of the acid in water may be represented as follows.

⇒ \(\mathrm{HA}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{A}^{-}\)

If x mol dissociates at equilibrium, [HA] = 0.1- x.

∴ \({\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{A}^{-1}\right]=x .}\)

∴ \(\mathrm{K}_{\mathrm{a}}=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}=\frac{x \times x}{0.1-x}\).

Since x is negligible compared to 1,

∴ \(K_{\mathrm{a}}=\frac{x^2}{0.1}\)

∴ x = \(\sqrt{\mathrm{K}_{\mathrm{a}} \times 0.1}=\sqrt{1 \times 10^{-9} \times 0.1}=10^{-5} \mathrm{~mol} \mathrm{~L}^{-1}\)

∴ \({\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=10^{-5} \mathrm{~mol} \mathrm{~L}^{-1} .}\)

∴ \(\mathrm{pH}=-\log \left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log 10^{-5}=5\) .

Example 18. Calculate, the[H₃O⁺] of a solution of a monobasic acid whose pH is 4.35.
Solution:

pH = -log[H₃O⁺]

∴ log[H₃O⁺] = -pH = -4.35.

[H₃O⁺ ] = antilog(-4.35).

Since mantissas are always positive in logarithmic tables, add -1 to the characteristic and +1 to mantissa in order to make the mantissa positive.

[H₃O⁺] = antilog[-4-1 + (-0.35 +1)] = antilog 5.65 = 4.467 x 10^-5

Equilibrium  Multiple Choice Questions

Question 1. Which of the following is a characteristic of a reversible reaction?

1. The number of moles of the reactants is equal to that of the products.
2. It can be influenced by a catalyst.
3. It can never proceed to completion.
4. None of the above

Answer: 3. It can never proceed to completion.

Question 2. A chemical reaction A ⇔ B is said to be in equilibrium when

1. A has been completely converted to b
2. The conversion of a to b is 50%
3. Only 10% of the conversion of a to b has taken place
4. The rate of conversion of a to b is just equal to that of b to a

Answer: 4. The rate of conversion of a to b is just equal to that of b to a

Question 3. The equilibrium constants of these reactions are related as

⇒ latex]2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO}_3(\mathrm{~g}) K_1[/latex]

⇒ \(2 \mathrm{SO}_3(\mathrm{~g}) \rightleftharpoons 2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) K_2\)

1. K₂ = K₁
2. \(K_2=K_1^2\)
3. \(K_2=\frac{1}{K_1^2}\)
4. \(K_2=\frac{1}{K_1}\)

Answer: 4. \(K_2=\frac{1}{K_1}\)

Question 4. In which of the following cases does the reaction proceed the fastest?

1. K =10²
2. K = 10^-2
3. K = 10
4. K = 1

Answer: 1. K =10²

Question 5. For the reaction \(\mathrm{PCl}_5(\mathrm{~g}) \rightleftharpoons \mathrm{PCl}_3(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g})\), the forward reaction at constant temperature is favoured by

1. The introduction of an inert gas at constant volume
2. The introduction of an inert gas at constant pressure
3. The introduction of Cl₂ at constant volume
4. An increase in pressure

Answer: 2. The introduction of an inert gas at constant pressure

Question 6. In the reaction \(2 \mathrm{~A}(\mathrm{~g})+\mathrm{B}(\mathrm{g}) \rightleftharpoons \mathrm{C}(\mathrm{g})+85 \mathrm{cal}\), which of the following conditions would give the best yield at equilibrium?

1. 500 atm, 100°C
2. 100 atm, 100°C
3. 500 atm, 500°C
4. 100 atm, 500°C

Answer: 1. 500 atm, 100°C

Question 7. Tire solubility of Agl in a solution of Nal is less than that in pure water because

1. Agl forms a complex with nal
2. Of the common-ion effect
3. The K_sp of AgI is less than that of nal
4. Of a decrease in temperature

Answer: 2. Of the common-ion effect

Question 8. Which of the following is not a Lewis acid?

1. BF₃
2. AlCl₃
3. BeCl₂
4. SnCl₄

Answer: 4. SnCl₄

Question 9. An acid solution of pH 6 is diluted a hundred times. The pH of the solution becomes

1. 6.95
2. 6
3. 4
4. 9

Answer: 1. 6.95

Question 10. If the solubility of a salt M₂X₃ is x mol L^-1, its solubility product is

1. x⁵
2. 76x²
3. 96x⁵
4. 108x²

Answer: 4. 108x²

Question 11. The solubility product of A₂B is 4 x 10^-9 mol L^-1 Its solubility is

1. 10^-3 M
2. 4^1/3 x 10^-3 M
3. 10^-4 M
4. 2 x 10^-5 M

Answer: 1. 10^-3 M

Question 12. Which of the following has the lowest value of K_sp at ordinary temperature?

1. Mg(OH)₂
2. Ba(OH)₂
3. Ca(OH)₂
4. Be(OH)₂

Answer: 4. Be(OH)₂

Question 13. Which of the following is the strongest Bronsted base?

1. ClO^–
2. ClO₂^–
3. ClO₃^–
4. ClO₄^–

Answer: 1. ClO^–

Question 14. The pH of a certain solution is 5.0. Just enough acid is added to decrease the pH to 2.0. The hydrogen ion concentration will

1. Increase 1000 times
2. Decrease 1000 times
3. Increase 100 times
4. Increase 10 times

Answer: 1. Increase 1000 times

Question 15. The K_sp of CaF₂ is 1.7 x 10^-10. The addition of what concentration of an equal volume of F^– ions to a solution containing 0.01-M Ca²⁺ ions will result in the precipitation of CaF₂?

1. 3.4×10^-8 M
2. 1.3×10^-4 M
3. 3.68 x 10^-4 M
4. 2.6×10^-4 M

Answer: 2. 1.3×10^-4 M

 

 

 

 

Organic Chemistry—Some Basic Principles And Techniques

The famous Swedish chemist, Berzelius, proposed in 1807 that chemicals should be divided into two separate groups—organic and inorganic.

It was believed that organic compounds were those that existed in or were created by living organisms by some ‘vital force’. And that inorganic compounds were simple and could be obtained from minerals.

However, this concept became outmoded when Wohler prepared urea, an organic compound, from an inorganic compound— ammonium cyanate.

The compound (urea) prepared was identical to the one found in urine.

This was followed by the synthesis and analysis of many more organic compounds. The modem definition of organic compounds states that such compounds are those that contain carbon.

However, carbon dioxide, carbon monoxide and carbon disulphide are considered to be inorganic compounds.

It is now well known that most organic compounds contain, apart from carbon and hydrogen, other elements like oxygen, nitrogen, sulphur, phosphorus and halogens.

In view of this, organic chemistry is now regarded as the chemistry of hydrocarbons (compounds containing carbon and hydrogen only) and their derivatives.

It is interesting to know that the total number of organic compounds is much more than that of the compounds of all other elements taken together.

What is so specific about carbon that it forms so many compounds? A unique property to form bonds with other carbon atoms.

This property is referred to as catenation. Owing to this characteristic property, carbon can form straight-chain compounds, branched-chain compounds and rings of different sizes.

Structure Of Organic Compounds

As you already know, carbon being tetravalent, methane has four covalent bonds, one each between a single carbon atom and each of the four hydrogen atoms.

You have already about hybridisation, i.e., the intermixing of atomic orbitals to form new orbitals.

In the case of methane, the three 2p orbitals of the carbon atom intermix with the 2s orbital to produce four sp³ hybrid orbitals which form four covalent bonds with the Is orbital of four hydrogen atoms.

The structure of ethene and ethyne molecules which have been discussed while we studied sp² and sp hybridisation respectively. To understand and predict the properties of organic compounds, it is important to know their molecular structures. sp²

The nature of orbitals depends on the type of hybridisation they have resulted from.

Nature of orbitals

In sp³ hybridisation, the four sp³ hybrid orbitals of carbon are formed by mixing one 2s and three 2p orbitals.

So each sp³ orbital has 25% s and 75% p character. The percentage changes in sp² hybridisation, to 33% s and 66% p character.

The sp hybridised carbon has orbitals with 50% s and 50% p character. With more s character the carbon atom becomes more electronegative in comparison to other carbon atoms (sp² and sp³ hybridised carbon atoms). This is because of the closeness of the s orbital to the nucleus.

Relative bond length and strength of hybrid orbitals

The bond length and the strength of the bonds formed by the combining of hybrid orbitals are influenced by the type of hybridisation in compounds. You know that hybridisation is a theoretical concept.

Therefore, the energy of hybrid orbitals is theoretically estimated. Let us see how bond length and strength are influenced by hybridisation considering the examples of ethane, ethene and ethyne.

The sp hybrid orbital of carbon in ethyne is shorter and stronger than the sp² hybrid orbital in ethene, owing to the 50% s character in ethyne, more than that in ethene.

The sp³ hybrid orbital of carbon in ethane forms longer and weaker bonds than those in ethene and ethyne. This can be attributed to less s character (25%) in the sp hybrid orbital. The distribution of hybrid orbitals in space leads to different bond angles.

The π Bond

A double bond exists between two carbon atoms in a molecule of ethene. Out of two, one is a bond (formed by the overlap of sp² hybrid orbitals, one each from each of the carbon atoms) and the other is it bond (formed by the overlap of the two 2p_z unhybridised orbitals of each carbon atom).

Similarly, the triple bond in a molecule of ethyne comprises one a bond and two n bonds. You have already studied the two types of bonds. Let us discuss some characteristic features of JI bonds.

The pi (it) bond is formed by the overlap of two 2p_z unhybridised orbitals. The overlapping (sidewise or lateral overlap) takes place in such a way that their axes remain parallel to each other and perpendicular to the internuclear axis.

The n bond is weaker than the bond. Due to lateral overlap, the electron charge cloud of the n bond is placed above and below the intermolecular axis.

This makes it easier for the reagent to attack n electrons than electrons. Acetylene, which has a triple bond between the carbon atoms, contains one a and two its bonds, and is, therefore, readily attacked by oxidising reagents.

Structural Representation Of An Organic Molecule

The structures of organic molecules can be represented in a number of ways. The simplest way of representing the structure of an organic compound is by representing a bond by a dash, viz., a single bond by a single dash (—), a double bond by two dashes (=) and a triple bond by three dashes (=).

The lone pair of electrons on atoms like oxygen, nitrogen and sulphur may or may not be shown. Some examples of such complete structural formulas are given below.

Organic molecules can also be represented by condensed structural formulae. In this type of representation, some or all of the covalent bonds in the molecule are omitted and the number of each of the identical atoms is indicated by a subscript.

⇒ \(\begin{array}{ccc}
\mathrm{CH}_3 \mathrm{CH}_3 & \mathrm{H}_2 \mathrm{C}=\mathrm{CH}_2 & \mathrm{HC} \equiv \mathrm{CH} \\
\text { or } & \text { or } & \text { or } \\
\mathrm{C}_2 \mathrm{H}_6 & \mathrm{C}_2 \mathrm{H}_4 & \mathrm{C}_2 \mathrm{H}_2 \\
\text { Ethane } & \text { Ethene } & \text { Ethyne }
\end{array}\)

Similarly, CH₃CH₂CH₂CH₂2CH₂CH₂CH₂CH₂CH₂COOH can be condensed to CH₃ (CH₂)₈COOH. In bond line representation only bonds or lines are used to represent a molecule, and carbon and hydrogen atoms are not shown.

The end of each line represents a carbon atom which is understood to be attached to the required number of hydrogen atoms necessary to satisfy the tetravalency of carbon.

The lines are drawn in a zig-zag fashion and represent carbon-carbon bonds. The atoms nitrogen, oxygen and chlorine are specifically written.

The terminals denote the methyl (—CH₃) group unless otherwise indicated. Thus CH₃CH₂CH₂CH₂CH₂CH₂CH₂CH₂CH₂COOH can be represented as

In the same way, the bond line formulas of 2-methyl butadiene and 1,3,5-hexatriene are written as follows

A compound containing one or more rings is called a cyclic compound and is represented by drawing the appropriate ring(s) without showing C and H atoms.

The comers of the ring represent C atoms and the sides I denote carbon-carbon bonds. Any functional group present is also shown in the structure.

The wedge-and-dash representation is used to represent the three-dimensional structure of a molecule.

By convention, a solid wedge indicates a bond projecting from the plane of paper towards the viewer and a dashed wedge shows a bond projecting inwards from the plane of the paper.

A normal line indicates the bond on the plane of the paper. The three-dimensional representation of methane is shown here.

Functional Groups

A functional group is an atom or n group of atoms responsible for the chemical behaviour of an organic compound. Structural features like double and triple bonds are also considered to be functional groups.

In an organic molecule, the functional group is the most reactive part whereas the remaining portion determines the physical properties of the compound. For example, amine).

If we attach the — NH₂ (amino) as a functional group In CH₃CH₂NH₂ (ethyl —NH2 group to some other alkyl radical like CH-,—(methyl) or I7 —(propyl), we would get the compounds CH₃ NH₂ and C₃H₇NH₂.

Compounds containing the same functional group undergo more or less similar reactions and are, therefore, said to belong to n family. There may be exceptions in the case of very large molecules or if more than one functional group is present.

Hie compounds we have just discussed belong to a family called amines. Some other functional groups which you may come across at the present level of learning.

Homologous Series

A family of organic compounds like alkanes and alcohols contains a characteristic functional group and forms what is known as a homologous series.

Each member of the series is known as a homologue. The members differ from each other in molecular formulae by a —CH₂ unit.

The first four members of the homologous series of the alcohol family are as follows.

⇒ \(\begin{array}{ll}
\mathrm{CH}_3 \mathrm{OH} & \text { Methyl alcohol } \\
\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{OH} & \text { Ethyl alcohol } \\
\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CH}_2 \mathrm{OH} & \text { Propyl alcohol } \\
\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{CH}_2 \mathrm{CH}_2 \mathrm{OH} & \text { Butyl alcohol }
\end{array}\)

Characteristics of a homologous series

1. A particular homologous series can be represented by a general formula. For example, in the case of alcohols, the general molecular formula is C_nH_2n+1OH. By putting the value of n as 1, 2, 3, 4,… where n is the number of carbon atoms in the molecule, we get the molecular formula of the corresponding homologues.
2. Any member of the homologous series differs from the next lower or higher by the unit CH₂(methylene group) or by 14 atomic mass units (12 + 2 x 1 = 14).
3. The different homologues of the series can be prepared by employing general methods of preparation.
4. The members of a homologous series show similar chemical properties.
5. The physical properties (such as density, melting point, and boiling point) of the successive members in a homologous series show a more or less regular gradation.

Nomenclature Of Organic Compounds

Hydrocarbons are compounds which contain only hydrogen and carbon. They are the simplest organic compounds.

Organic compounds bearing functional group(s) are derived from hydrocarbons by replacing one or more hydrogen atoms with the functional group.

As more and more carbon compounds were known it became necessary to introduce a system of nomenclature.

A formal system of nomenclature of organic compounds was introduced in 1931, known as the IUC system.

The system was further developed by the International Union of Pure and Applied Chemistry (IUPAC).

Before the IUPAC system of nomenclature was introduced, organic compounds were given common or trivial names. The names were based on the source of the compounds or some other specific features.

For example, acetic add can be obtained from vinegar and was, therefore, named after the Latin word for vinegar, aceluin. Some ants contain formic acid and the Latin word for ant isformica.

Urea was so named since it was first isolated from the urine of mammals. Methyl alcohol was called wood spirit since it could be obtained by the destructive distillation of wood.

Many of the common names are still used by chemists. Common names are useful when the other systematic names are very complicated.

The newly discovered allotrope of carbon (C₆₀) has been given the common name Buckminsterfullerene, after the architect Buckminster Fuller, whose designs are similar in structure to the C₆₀ cluster of carbon.

The IUPAC System Of Nomenclature

The IUPAC system is simple, and any chemist can deduce the structure of an organic compound if he or she knows its IUPAC name. In the IUPAC system of nomenclature, a chemical name has three parts: prefix, parent and suffix The parent name tells us how many carbon atoms are present in the principal chain.

The suffixes are of two types—primary and secondary, and both indicate the functional groups present in the compound.

The primary suffix is added to the root derived from the parent name indicating the nature of the bond between the carbon atoms. For example, the suffix one in ethyne shows the presence of a triple bond.

The secondary suffix is added after the primary suffix to indicate the functional group(s) present in the carbon chain. For example, the IUPAC name of alcohol—alkanol—has two suffixes an and ol.

Here an indicates a single C —C bond and ol indicates the class of the compound—alcohol.

Note While adding the secondary suffix to the primary suffix, the terminal e of the primary suffix is removed if the secondary suffix begins with a vowel but it is retained if the secondary suffix begins with a consonant.

The prefixes indicating substituents on the parent chain are also of two types—primary and secondary.

A primary prefix such as ‘cyclo’ is added before the root word to indicate the cyclic nature of the carbon skeleton. For example, cyclohexane.

In a polyfunctional compound the groups which are not considered the principal functional group in the IUPAC system of nomenclature, but regarded as substituents, are called secondary prefixes.

For example, halogens, alkoxy, alkyl, aryl and nitro groups. The secondary prefix comes before the primary prefix. For example,

To begin with, let us study the systemic IUPAC nomenclature of hydrocarbons. On the basis of their structure, hydrocarbons may be of three types—straight-chain, branched-chain and cyclic.

Alkanes

Primary prefix Secondary prefix Root word Primary suffix IUPAC name cydo Chloro hex ane Chlorocyclohexane The root word for alkanes from CH₄ to C₄H₁₀ are derived from trivial names.

However, the names of alkanes containing five or more carbon atoms are derived by adding prefixes such as pent (five), hex (six), hept (seven), oct (eight) and so on, indicating the number of carbon atoms in the molecule, with the suffix ane. The molecular formula and the IUPAC names of some straight-chain alkanes.

On removing one hydrogen atom from an alkane, a univalent alkyl group is formed. The individual alkyl group is named by replacing the suffix ane of the parent hydrocarbon with yl.

Branched-chain alkanes are named according to the following rules.

1. The longest continuous chain of carbon atoms is the parent chain. For example, the following compound is a hexane since the longest chain contains six carbon atoms.

The following compound is a heptane since the longest chain has seven carbon atoms.

In case a molecule contains two equally long carbon chains, the one attached to a greater number of side chains or substituents is selected. Correct longest chain: Parent chain of seven carbon atoms with one side chain and two substituents.

Incorrect longest chain: Parent chain of seven carbon atoms with only one side drain.

2. For the longest chain from one end to the other, the direction of numbering is chosen to give the lower number(s) to the substituent(s).

3. The location of the substituent groups is designated by using rule 2. The number indicating the position of the substituent should be prefixed to the name of the parent alkane.

The numbers are separated from the groups by hyphens. Note that the following common names are retained by IUPAC for unsubstituted hydrocarbons only.

Precisely speaking, isobutane is 2-methylpropane, isopentane is 2-methylbutane and neopentane is 2, 2-dimethylpropane.

Lowest sum rule: In case the parent chain has two or more side chains or substituents, the numbering must be done in such a way that the sum of the locants on the parent chain is the lowest possible.

4. When different substituents are present on the carbon chain, they are written in alphabetical order.

5. In case two substituents are present on the same carbon atom, the number indicating the position is written twice.

6. Identical substituents are indicated by using appropriate prefixes di, tri, tetra, etc. The numbers are separated by commas.

When two chains of equal length compete for selection as the parent chain, choose the chain with the greater number of substituents.

When two different substituents are in equivalent positions (from the two ends of the carbon chain), the groups are numbered in alphabetical order, while numbering the chain.

On removal of one hydrogen atom, both butane and isobutane give rise to two butyl groups.

The following examples illustrate the naming of compounds containing branched alkyl groups.

The prefixes iso, see, test and neo are approved by 1UPAC

Classification of carbon atoms

Being tetravalent, a carbon atom is attached to four other carbon or hydrogen atoms in hydrocarbons.

One carbon atom may be attached to one other carbon atom and three hydrogen atoms. Also, one carbon atom may be attached to three other carbon atoms and one hydrogen atom.

Depending upon these arrangements carbon atoms are classified into four types atom is attached to one other carbon—the primary atom.(1°), A secondary secondary carbon (2°), tertiary atom is(3°) attached to quaternary two other(4°). carbonA primary atoms, carbon and so on.

A hydrogen atom is also referred to as 1°, 2° or 3° depending on whether it is attached to a 1°, 2° or 3° carbon atom. In the following examples, 1°, 2°, 3° or 4° carbon atoms are shown.

Cycloalkanes

Cycloalkanes with only one ring are named by attaching the prefix ‘cydo’ to the names of the corresponding straight-chain alkanes. For example,

Substituted cycloalkanes are named applying the same rules as applied to branched-chain alkanes. If more than one substituent is present, its position is indicated by the appropriate number.

While naming the compound, the substituents are placed in alphabetical order. Also, the numbering is so done that the substituent(s) get the lowest possible number(s). The following examples illustrate the abovementioned points.

When a single ring is attached to a single chain with the same or a greater number of carbon atoms than in the ring, the compound is named as follows.

The carbon atom attached to the more-branched chain is assigned the lower number.

When the chain attached to the ring is longer than the ring, the ring becomes a substituent.

Alkenes

Alkenes are unsaturated hydrocarbons containing a double bond between two adjacent carbon atoms.

Ethene or ethylene is the first member of this homologous series. The rules for the IUPAC nomenclature of alkenes are similar in many respects to those of alkanes.

1. The longest carbon chain containing the double bond is chosen as the parent alkene. The suffix part of the corresponding alkane is changed into one. For example, the carbon chain with six carbon atoms and a double bond is hexene.

2. The numbering of the carbon chain is so done that the double bond has the lowest number. Designate the location of the double bond by writing the lower number as a prefix. The locant (number) is placed just before the functional group suffix.

3. The locations of the different substituents are indicated by the numbers of the carbon atoms to which they are attached. The lowest sum rule studied earlier in the case of alkanes also applies here.

4. Cycloalkenes are numbered in a way that gives the carbon atoms of the double bond the 1- and 2- positions and that also gives the substituent groups the lower numbers.

5. Compounds containing a double bond and an alcohol group are named by giving the alcohol carbon the lowest number.

The terminal e in the name of the alkene is dropped if it is followed by a suffix beginning with a, i,o, u or y. (The rule is the same for alkynes.)

6. The removal of the terminal hydrogen atom from ethene and propene gives the vinyl and the allyl group respectively. If a halogen atom is attached to these groups we obtain compounds with common names vinyl halide and allyl halide.

7. If two identical groups are on the same side of the double bond, the compound is designated as cis and if they are on opposite sides, it is designated as trans.

8. If there are two or three double bonds in a chain then the compound is called a diene or a triene respectively.

⇒ \(
\stackrel{1}{\mathrm{C}} \mathrm{H}_2=\stackrel{2}{\mathrm{C}} \mathrm{H}-\stackrel{3}{\mathrm{C}} \mathrm{H}=\stackrel{4}{\mathrm{C}} \mathrm{H}_2
Buta-1,3-diene\)

Alkynes

Alkynes are unsaturated hydrocarbons that contain a triple bond between two adjacent carbon atoms. The first member of the homologous series is acetylene or ethyne (HC=CH)

Alkynes are named in the same way as alkenes. The unbranched alkynes are named by replacing the suffix ane of the corresponding alkane with the suffix one. The first three members of the alkyne homologous scries ethyne, propyne and butyner.

The trivial name acetylene has been retained by the IUPAC system for HC=CH and is frequently used.

Where the double as well as the triple bond is present in the same molecule, the double bond is given the lowest number (order of priority of functional groups).

The locations of substituent groups of substituted alkynes are also indicated with the appropriate numbers. A hydroxyl (—OH) group is given priority over the triple bond while numbering the chain.

Here you should remember that the terminal e of meor yne is not dropped in case it is followed by di, tri or tetra.

Polyfunctional compounds

As stated earlier in the chapter, compounds containing the same functional group belong to a family. While naming the compound, the functional group is identified and the appropriate suffix is used.

The parent chain is so numbered that the carbon atom attached to the functional group gets the lowest possible number (as in the case of alkenes and alkynes).

But what if the compound has more than one functional group? In the case of polyfunctional compounds, one of the functional groups is chosen as the principal functional group according to the order of priority of functional groups.

The compound is named on the basis of that principal functional group and the remaining functional group(s) is named as substituents using appropriate prefixes.

The order of priority of some functional groups is COOH, —S03H, —COOR, —COG, —CONH2, —CN, =C—. —HC=0, —OH, -NH2, /C=CC

The alkyl (—R), phenyl (—C6H5), halogens (F, Cl, Br, I), nitro (—NOz), alkoxy (—OR), etc., are substituents and always prefixed.

Along with the different families of compounds, their respective prefixes and suffixes, Table 12.4 also contains examples of polyfunctional compounds and their IUPAC names.

Example Name the following compounds according to IUPAC rules

Solution:

1. The longest continuous chain is cyclic and of four carbon atoms. Hence the corresponding hydrocarbon is cyclobutane.
   1. Two functional groups (a double bond and an aldehyde) are present in the compound.
   2. According to the order of priority of functional groups, the aldehyde precedes the alkene.
   3. Hence the carbon attached to —CHO is numbered 1.
   4. Hence, the name of the compound is l-Formylcyclobut-2-ene.
2. The longest continuous chain (with two substituents) is of four carbon atoms, so the root word is but.
   1. Applying the lowest sum rule, the two substituents methyl (—CH3) are at carbons 2 and 3. The double bond is at position 1 of the carbon chain.
   2. Hence, the name of the compound is 2,3-Dimethyl-but-l-ene.

Aromatic Compounds

Benzene and substituted benzene compounds are the most important members of this class. Benzene contains six carbon atoms, numbered 1 to 6. The molecular formula of benzene is C6H6. It contains three double bonds.

The six hydrogen atoms in benzene are equivalent, each bonded to one carbon atom. Owing to this only one monosubstituted derivative is possible. But benzene can form three disubstituted derivatives with relative positions; 1,2;13 and 1,4.

The positions are indicated by trivial terms, ortho (o), meta (m) and para (p) respectively. While naming these derivatives according to IUPAC rules, we simply prefix the name of the substituent group to the word benzene.

Some derivatives of benzene have universally accepted, common names (written in brackets below) which have no resemblance to the names of the attached substituent.

Disubstituted or trisubstituted benzenes are named by numbering the positions of the substituents.

Dimethylbenzenes arc commonly called xylenes.

If different substituents are attached to the benzene ring then the following rules are observed.

1. The principal group or substituent of the base compound is assigned the number 1.
2. The numbering is so done that the substituents are located at the lowest numbers possible.
3. The substituents are written in alphabetical order.
4. In some cases, the common name of the die benzene derivative is considered the name of the parent compound.

Let us now look at a few categories of benzene derivatives.

The trivial names phenyl, benzyl, benzal and benzo have been accepted by IUPAC
Halogen derivatives.

Hydroxy derivatives

Amines

Ketones

Aromatic ethers

Aldehydes 

Carboxylic Acids 

Isomerism

When two or more compounds have the same molecular formula but differ in their physical and chemical properties, the phenomenon is called isomerism, and the compounds isomers (Greek, isos = equal; meros = parts).

Isomerism is of two types—structural isomerism and stereoisomerism.

Structural isomers are those which differ in the mode of linking of atoms whereas stereoisomers differ in the arrangement of atoms or groups in space. Stereoisomerism.

Structural isomerism is of different types, based on different functional groups, different carbon skeletons and different positions of the functional groups in the same carbon chain.

Chain isomerism This type of isomerism arises when the carbon skeletons of the isomers differ. For example, butane (C₄H₁₀) can have the following two structures.

In the same way the alcohol with the molecular formula, C₄H₉OH can be either n-butyl alcohol or is obutyl alcohol.

The alkene C₄H₈ can be either but -1-ene or isobutene.

Position isomerism When the isomers differ in the position of the substituent atom or group in the same carbon chain, the phenomenon is called position isomerism.

As you can see. the position of the —OH group is different in the same carbon chain of the isomers with the molecular formula C₃H₇OH.

Functional group isomerism When two or more compounds have the same molecular formula but different functional groups, they are called functional group isomers and the phenomenon is called functional group isomerism.

A compound with the molecular formula C₄H₁₀ can be an ether or an alcohol.

Similarly, C₃H₆₀ can be a ketone or an aldehyde.

C₂H₄0 can be an add or an ester.

Metamerism When the isomers differ in the alkyl groups attached to the same functional group, they are called metamers and the phenomenon is called metamerism.

An ether, C₄H₁₀, can be either methyl propyl ether or diethyl ether.

A ketone, C₅H₁₀, can have two metamers.

Tautomerism This is a type of isomerism in which the two isomers are in equilibrium. The most common land is keto-enol tautomerism.

In this form of tautomerism compound containing a —CH₂—CO— group (the keto form of the molecule) is in equilibrium with one containing the —CH=C(OH)— group (the enol).

This happens when a hydrogen atom migrates from a carbon atom to an oxygen atom bonded to an adjacent carbon.

Example What is the relationship between the following molecules and CH3CH(CH3)CH, CH3?

Solution:

1. The bond line formula for CH₃CH(CH₃ )CH₂CH₃ is which is the same as and Thus, all three molecules are the same.
2. Molecule
   • Is neopentane, i.e.,
3. Molecule is CH₃CH(CH₃)CH₂CH,CH₃ which is the next homologue of CH₃CH(CH₃)CH₂CH₃.

CH₃CH(CH₃)CH₂CH₃ and neopentane are chain isomers.

Reaction Mechanisms

Many reactions take place via intermediates, i.e., they are multi-step. When the products in a reaction are formed directly without any intermediate, the reaction is called a single-step reaction. In general, an organic reaction may be represented as follows.

⇒ \(\text { Substrate } \stackrel{\text { reagent }}{\longrightarrow} \text { [Intermediate] } \longrightarrow \text { Products }\)

The steps leading to the cleavage of bonds (covalent bonds in the substrate molecule) and the formation of new bonds in the products constitute the reaction mechanism.

A clear understanding of reaction mechanisms helps us identify patterns in complex organic reactions.

And recognising patterns helps us apply our knowledge about one reaction to many similar reactions.

The reaction mechanism of a complex organic reaction may depend on many factors such as the following.

1. The reactivity of the substrate molecule may be known by an understanding of the electron displacement effects caused due to the interaction of substrate and reagent molecules and the difference in electronegativities of the atoms in a molecule.
2. The nature of bond fission decides the type of the reaction intermediate formed. Carbocations, carbanions and free radicals are types of reaction intermediates.
3. The nature of the reagent, whether electrophilic or nucleophilic.
4. The type of reaction which occurs. Substitution, addition, elimination and rearrangement are some common types of organic reactions. You will study these reactions.

Let us now discuss these factors in greater detail.

Electron Displacement In A Molecule

Generally, unlike inorganic compounds, organic compounds do not react with each other on their own.

A reaction between organic compounds requires the presence of a reagent. Some examples of reagents are H2S04, HC1 and NaOH.

Although a substrate molecule is electrically neutral, it develops some polarity due to the difference in electronegativities of the atoms of the molecule or under the influence of an attacking reagent.

The polarity develops by the displacement of electrons in the substrate. This is referred to as the electron displacement effect.

We normally come across the following four types of such effects in organic molecules.

1. Inductive effect
2. Electromeric effect
3. Mesomeric effect
4. Hyperconjugation effect

Inductive effect When a covalent bond is formed between two dissimilar atoms, the shared electron pair will be displaced towards the atom which is more electronegative.

This causes the more electronegative atom to acquire a partial negative charge (5-) whereas a partial positive charge (8+) develops on the other atom.

For example, if we consider the covalent bond C—X, where X is more electronegative than carbon, then the bond is polarised so that C gains a partial positive charge (5+) and X gains a partial negative charge (8-).

Alternatively, in a covalent bond C—Y, where Y is less electronegative than C, the shared electron pair is displaced towards carbon, so that C attains a 8- charge and y attains a &+ charge.

The polarization induced in a substrate molecule is of a permanent nature.

Thus, an inductive effect involves the permanent shift of electrons towards the more electronegative element in a covalent bond.

When the electronegative group linked to a carbon atom withdraws electrons and gains an 8- charge it is said to be an electron-withdrawing group exerting a -I effect.

Some common electron-withdrawing groups (in decreasing order of -I effect) arc:

⇒ \(\mathrm{O}^{-}>\mathrm{CO}_2^{-}>\left(\mathrm{CH}_3\right)_3 \mathrm{C}>\left(\mathrm{CH}_3\right)_2 \mathrm{CH}>\mathrm{CH}_3 \mathrm{CH}_2>\mathrm{CH}_3\)

⇒ \(\mathrm{NO}_2>\mathrm{F}>\mathrm{COOH}>\mathrm{Cl}>\mathrm{Br}>\mathrm{I}>\mathrm{OH}\)

In contrast, if the substituent bonded to the carbon atom is electron donating (being less electronegative titan carbon) it acquires an 8+ charge and produces a +1 effect.

Some electron-donating groups in decreasing order of +1 effect are:

⇒ \(\mathrm{O}^{-}>\mathrm{CO}_2^{-}>\left(\mathrm{CH}_3\right)_3 \mathrm{C}>\left(\mathrm{CH}_3\right)_2 \mathrm{CH}>\mathrm{CH}_3 \mathrm{CH}_2>\mathrm{CH}_3\)

The inductive effect is transmitted along the chain of carbon atoms but the charge developed on all the carbon atoms in the chain decreases as the distance from the source increases.

In propyl chloride, the partial positive charge developed on C1 induces some positive charge on C2 and C3 gains still less positive charge.

The inductive effect is represented by an arrow pointing towards the electron-withdrawing atom or group, Electromeric effect When a reagent attacks a compound containing a multiple bond (double or a triple bond), n electrons are transferred completely from one atom to the other in the bond.

The atom that gains the electron pair becomes negatively charged and becomes positively charged. This is the electromagnetic effect.

The electromagnetic effect is temporary. The influence of an attacking reagent causes a polarisation in the substrate molecule.

As soon as the reagent is removed, the polarised molecule reverts to its original state.

The electromeric effect is represented by the symbol E and is said to be +E when the displacement of electrons is towards the atom to which the attacking reagent gets attached.

The effect is -E when the electrons are transferred to that atom to which the attacking reagent does not get attached. The curved arrow shows the displacement of the shared electron pair.

Mesomeric or resonance effect Like the inductive effect, the mesomeric effect also causes permanent polarisation in a molecule.

However, unlike the inductive effect which operates in molecules having single bonds (sigma bonds), the mesomeric or conjugative effect operates only in those molecules which have unsaturated conjugated systems.

A conjugated system in a molecule can be described as a double or triple bond separated by one single bond. In such molecules the delocalisation of some n.

orbital electrons occur between carbon atoms linked by a single bond. Consider the case of a carbonyl group. Its structural formulae I and II do not satisfactorily explain all its properties.

This led to the idea that it exists in a state which is some combination of two or more electronic structures. This is the resonance hybrid (HI) in which electrons are drawn partially towards oxygen.

The mesomeric effect is more pronounced if the carboxyl group is conjugated with an unsaturated system such as CH₃=CH—CH=CH—CH=0. The TI electrons of the C—O bond get displaced towards oxygen (which is more electronegative) giving rise to the resonance structures.

The resonance structure which has more dispersal of charge (negative charge on the more electronegative atom and positive charge on the more electropositive atom) is more stable.

As explained above, polarization in a molecule is transmitted via the n electrons. The mesomeric effect (denoted by M) can be +M or -M. A group of atoms causes a -M effect when the direction of displacement of electrons is towards it. Examples of groups that cause a -M effect are

The -M effect of the NO₂ group is shown as follows.

This effect can also be seen in a cyclic system with alternate single and double bonds, for example, nitrobenzene.

A group of atoms has a +M effect if the electron pair is displaced away from it. Some examples of electron-repelling groups are as follows.

These groups have one or more lone pairs of electrons which they furnish for conjugation with the attached unsaturated system. For example, the NH2 group, which has a lone pair of electrons, shows a +M effect.

This kind of electron transfer is called mesomeric or resonance effect. Recall that when the structure of a molecule can be represented by two or more conventional formulae, the phenomenon is known as resonance.

Hyperconjugation When an H—C bond is attached to an unsaturated n system (double or triple bond) which has an unshared p orbital, there is a conjugation.

In other words, the electrons of the H —C bond become less localised by entering into partial conjugation with the attached unsaturated system.

The interaction of and n electrons is made possible by the partial overlap of orbitals: sp³—s (C—H bond) with the empty p orbital of an adjacent positively charged carbon atom.

Hyperconjugation stabilises a molecule, for example, propene is more stable than expected.

Here the electrons of the C —H bond become partially delocalised through conjugation so that the hydrogen atoms are not free —only the ionic character of the C—H bond is increased. This is one way of looking at the hyperconjugative effect. Hyperconjugation may also be termed “no bond resonance”. It is a permanent effect.

Bond Fission

You already know from your previous classes that when a chemical reaction occurs the bonds in the reactant molecules are broken to form new ones in the products.

The whole mechanism of the reaction depends on the way these bonds are broken. The fission of a covalent bond can take place in two ways—homolytic and heterolytic.

The way in which the bond is broken depends more on the nature of the atoms constituting it and to some extent on the conditions prevailing during the reaction.

Bond fission leads to the formation of reaction intermediates, which are of transitory existence. Most organic reactions take place via the formation of reaction intermediates.

Being very reactive, reaction intermediates may or may not be isolated under normal conditions.

However, their structures have been established by indirect means either chemically or spectroscopically.

The most common reaction intermediates that we come across usually at the present level are carbocations, carbanions and free radicals.

Homolytic bond fission

When, during the fission of a bond, the separating atoms take away one electron each of the shared pair, the fission is symmetrical and called homolytic fission or homolysis.

Curved arrow notations are used to represent the shift of electrons. A single electron shift is represented by a half arrowhead (fish arrow).

The two fragments, which may be atoms or groups of atoms, obtained as a result of homolytic bond fission carry an unpaired electron each and are called free radicals.

These are highly reactive reaction intermediates and tend to pair up or react with other radicals or molecules to restore stability by being a part of the bonding pair.

Free radicals can be produced by photolysis or pyrolysis in which a bond is broken and ions are not formed.

For example, the cleavage of a chlorine or an alkyl halide molecule takes place in the presence of ultraviolet light or heat giving rise to two chlorine and one alkyl and one halide free radical respectively.

Alkyl free radicals can be classified as primary, secondary or tertiary, depending upon which hydrogen (1°, 2°, or 3°) is abstracted from the alkyl. Since the ease of abstraction of hydrogen atoms follows the sequence 3° > 2° > 1° > CH 4, the ease of formation (and stability) of free radicals follows the sequence:

Titus, the stability of alkyl free radicals increases from primary to tertiary. Organic reactions which have free radicals as intermediates are called free-radical or nonpolar reactions.

Heterolytic bond fission

In heterolytic cleavage, when the bond between two atoms breaks, both the electrons of the shared pair are taken over by one of the atoms.

Heterolytic cleavage is represented by a curved arrow that starts from the bonded pair of electrons and points at the atom which retains the shared pair of electrons.

Thus a heterolytic bond fission gives rise to one positive species, which lacks a pair of electrons in its valence shell and one negative species with a valence octet.

The more electronegative atom retains the shared pair of electrons. Heterolytic bond fission in organic molecules leads to the formation of either carbocations or carbanions.

In a carbocation, the carbon atom carries a positive charge, i.e., lacks a pair of electrons in its valence shell. In contrast, the carbanion, as the name suggests, is a negative group in which the carbon atom carries a negative charge, i.e., has an unshared pair of electrons.

The positively charged carbon atom with a sextet of electrons is sp² hybridised and it uses all its three hybridised orbitals to form bonds with other atoms. The remaining p_z orbital is empty and is perpendicular to the plane of the molecule.

The shape of a carbocation may be described as planar (trigonal coplanar) with a bond angle of 120°

Carbocations are also classified as primary (1°), secondary (2°) or tertiary (3°) depending on whether one, two or three carbon atoms respectively are attached to the carbon bearing the positive charge.

Since a carbocation has a positively charged (electron deficient) carbon, its relative stability is determined chiefly by how well it accommodates that charge.

Dispersal of the charge leads to the stability of the charged system. (This applies equally well to both positively and negatively charged systems.)

The greater the number of alkyl groups attached to a positively charged carbon atom, the greater the charge dispersion due to hyperconjugation lending to a greater stability of the carbocation.

In the hyperconjugative effect, electrons are provided by o bonds to the empty p orbital of the electron-deficient carbon. Thus, the order of stability of carbocations is

The arrows pointing towards the electron-deficient carbon indicate electron release from the alkyl groups. Benzyl and allyl carbocations, though primary in nature, are stable due to the resonance effect.

The greater the number of canonical structures for a carbocation, the more stable it is. In view of this, the order of stability of the carbocations is

⇒ \(\mathrm{C}_6 \mathrm{H}_5 \stackrel{\ominus}{\mathrm{C}} \mathrm{H}_2>\mathrm{CH}_2=\mathrm{CH}-\stackrel{\ominus}{\mathrm{C}} \mathrm{H}_2>\mathrm{CH}_3 \mathrm{CH}_2 \stackrel{\stackrel{\circ}{\mathrm{C}} \mathrm{H}_2}{ }\)

A carbanion is a species containing a carbon atom with one pair of unshared electrons and thus carrying a negative charge.

The carbanion is pyramidal and the central carbon atom is sp³ hybridised with the unshared or lone pair of electrons occupying one sp³ hybrid orbital.

The order of stability of carbanions is just the reverse of that in carbocations. This can be explained on the basis of the +1 (inductive) effect of the alkyl group.

Being electron-releasing, the alkyl group tends to increase the electron density on the negatively charged carbon atom, lowering its stability. Thus, the order of stability of carbanions is

Types Of Reagents

As already stated, generally an organic reaction proceeds when a reagent attacks a substrate molecule.

Under suitable reaction conditions and the influence of an attacking reagent, the substrate molecule undergoes bond fission to form reaction intermediates, which combine with the reagent to give the final product.

Attacking reagents may be of two types—electrophilic and nucleophilic, depending on the electron density at the attacking centre.

Electrophilic reagents

These are electron-loving species. Being electron-deficient, they attack the electron-rich centre in the substrate molecule—that specific atom in the substrate molecule which is electron-rich. Electrophiles (E+) include positively charged species and neutral molecules.

For example, H+, H30+ and carbocations (CH₃ ,RH₂C+). Neutral molecules like A1C1₃, BF₃ and SO₃ act as electrophiles as they are electron-deficient.

Molecules having polarisable functional groups like the carbonyl group (ÿC=0) and alkyl halides (halogen atom is polarised) also act as electrophiles.

In alkyl halides, due to the polarity of the C—X bond, a partial positive charge develops on the carbon atom, which becomes an electrophilic centre

Nucleophile reagents

These reagents are nucleus-loving and attack electron-deficient centres in the substrate molecule. Nucleophiles (Nu:) may be negatively charged ions or neutral molecules with a lone pair of electrons. For example, Cl~,OH_,CN+ and carbanions (R3C:).

Neutral molecules containing a lone pair of electrons such as H₂O, R₃N, NH₃, ROH and ROR act as nucleophiles.

As stated earlier, the mechanism of organic reactions, apart from the reactivity of the substrate, the nature of bond fission and reagents, also depends on the type of reaction that occurs.

You will come across different types of reactions while studying the preparation and properties of hydrocarbons.

Purification Of Organic Compounds

To study the structure and properties of an organic compound, it is essential to obtain the compound in its purest form.

An organic compound isolated from various sources contains many types of impurities.

Many methods are used to purify organic compounds. The choice of the purification method employed depends on the type of impurities present and the nature of the organic compound.

The common methods of purification are as follows.

1. Crystallisation
2. Distillation
3. Differential extraction
4. Sublimation
5. Chromatography

Crystallisation

Crystallisation is the process of the formation of a crystalline solid from a solution, generally by the evaporation of the solvent.

The process is most commonly used for the purification of solid organic compounds. The method is based on the difference in the solubilities of the compound and the impurities in a suitable solvent.

The choice of the solvent is very important. A solvent which dissolves less of the organic compound at room temperature and an appreciable quantity at a higher temperature is suitable for preparing the solution.

Also, the solvent should not dissolve the impurities and should not react with the compound. A hot saturated solution is filtered and then allowed to cool down slowly to room temperature when the compound separates in the form of crystals.

In case any coloured impurities are present in the organic compound, crystallisation is carried out by heating the hot saturated solution with a small amount of activated charcoal, which adsorbs the impurities.

Repeated crystallisation of a compound from a solvent to obtain the increasingly pure form is called recrystallisation.

It is generally done for the purification of compounds containing impurities of comparable solubilities. A mixture of two or more compounds can be separated by fractional crystallisation.

The method is based on the different solubilities of compounds in the same solvent. The less soluble compound separates out first while the more soluble one remains in the solution.

A mixture of benzoic acid and cane sugar can be separated by this method. Benzoic acid is less soluble in water than cane sugar.

Distillation

The process is used to separate liquids with appreciable differences in their boiling points. Also, a volatile liquid can be separated from nonvolatile impurities.

The process involves the conversion of the liquid into its vapours by heating followed by condensation of the vapours to obtain the pure liquid.

Distillation is of the following types:

1. Simple distillation
2. Fractional distillation
3. Distillation under reduced pressure, or vacuum distillation
4. Steam distillation

The choice of the distillation process depends on the nature of the liquids to be separated and the kind of impurities present in them.

Simple distillation

This method is used for the purification of liquids which boil without decomposition and contain nonvolatile impurities. The apparatus consists of a distillation flask with a side tube, connected to a Liebig condenser, through which water is passed.

The liquid to be purified is taken in the distillation flask. A few pieces of glass beads or unglazed porcelain are put in the flask.

This helps to avoid bumping (violent boiling of a liquid caused by super-heating) during distillation. For a liquid with a low boiling point, say 353-363 K, the flask is heated on a water bath and for a liquid with a high boiling point, say more than 373 K, an oil bath is used.

In place of the oil bath, the distillation flask can also be heated with a small flame over a wire gauze.

On heating, the liquid changes to vapours, which are passed through a condenser where they condense into liquid.

The pure distilled liquid is collected and the impurities are left behind in the distillation flask. The constant temperature at which most of the liquid distils is known as the boiling point of that liquid.

Fractional Distillation

Simple distillation cannot be used for the separation and purification of liquids with comparable boiling points. This is because both the liquids will be distilled simultaneously.

The separation of such liquid mixtures can be achieved by employing fractional distillation. This involves the use of a suitable fractionating column. Different types of fractionating columns can be used.

Basically, a fractionating column is a long tube filled with glass beads or a tube in which the walls have many inward-pointing indentations.

The fractionating column obstructs the passage of the vapours moving upwards and the liquid moving downwards. In fact, the indentations increase the cooling surface.

The fractionating column is fitted onto the mouth of a round bottom flask, which contains the liquid mixture.

When the flask is heated, the vapours of the more volatile liquid rise up in the fractionating column and the less volatile fraction condenses back into the flask (higher up the column, the temperature being lower).

As the vapour mixture rises up, it becomes rich in the low-boiling (volatile) component.

Thus, by the time the low-boiling vapours reach the top of the column, they become concentrated and pure. These vapours then pass through the condenser and pure liquid is collected.

After many successive distillations, the remaining liquid in the flask gets enriched in the high-boiling component.

Each successive condensation and vaporisation unit in the fractionating column is called a theoretical plate.

The temperature at the top of the fractionating column indicates the fraction being distilled.

Industrial applications of fractionating columns are in petroleum refineries, petrochemical plants and natural gas processing plants. This method is also used to separate the components of air.

Distillation under reduced pressure (vacuum distillation)

This method is used for the separation and purification of liquids which have high boiling points and those which decompose on heating. The distillation is carried out under reduced pressure.

The depression in the boiling point of the substance distilled means that the temperature is lower, which prevents the substance from decomposing. Low pressure can be achieved by using a vacuum pump.

The apparatus used in this method is more or less of the same type as that used in simple distillation except that instead of a round bottom flask, a two-necked flask, called the Claisenflask, is used.

In one of the necks, a capillary tube is fitted, which allows air bubbles to pass through (to prevent bumping) and in the second neck, a thermometer is fitted.

The pressure under which the liquid distils is measured with the help of a manometer.

A high-boiling liquid like glycerol (b.p. 563 K) can be easily separated from spent lye in the soap manufacturing process by this method.

Spent lye is a mixture of brine and glycerine, which is separated from crude soap during soap manufacturing. Another application of vacuum distillation is in the concentration of sugar cane juice.

Steam distillation

This method is used for the purification of those compounds which are volatile in steam, immiscible with water, and which contain nonvolatile impurities and possess a high vapour pressure.

In this process, the liquid to be purified is taken in a distillation flask and steam is continuously bubbled through it. The steam is generated using a steam generator.

The distillation flask is also heated so as to maintain the temperature at about 373 K. Initially, the steam heats the liquid but itself gets condensed.

But after some time, the mixture begins to boil. You already know that a liquid boils when its vapour pressure is equal to the atmospheric pressure.

In this case, water and the organic substance vaporise together and the total vapour pressure of the two becomes equal to the atmospheric pressure.

This implies that in steam distillation, the organic substance (being steam volatile) vapourises and gets distilled at a lower temperature than the boiling point, thus avoiding decomposition.

Thus, steam distillation serves the same purpose as distillation under reduced pressure.

The organic liquid is separated from water using a separating funnel. A mixture of water and aniline can be separated by this method. The process is also employed in the manufacture of essential oils.

Differential Extraction

This method is used to isolate or recover organic compounds (liquids or solids) present in an aqueous solution.

In this process, an aqueous solution of the organic compound is taken in a separating funnel, and mixed with a suitable organic solvent. The mixture is shaken.

The solubility of the organic compound should be higher in the organic solvent than in water. Also, the organic solvent should be immiscible with water.

Ether, benzene, chloroform, ethyl acetate, etc., are some of the common organic solvents used for this purpose.

When the contents are shaken thoroughly in the stoppered separating funnel, the organic phase dissolves the compound present in the aqueous phase.

The separating funnel is then allowed to stand for some time when the aqueous and the organic phase (solvent) separate as distinct layers. The two layers are extracted one after the other by opening the stop code, thus the phenomenon is known as differential extraction.

The process is repeated 2-3 times till all the organic compound originally dissolved in the aqueous layer is extracted with the organic solvent.

The organic compound is separated from the solvent by distillation. If the solubility of the organic compound is less in the solvent, then a large quantity of the solvent is used to extract a small quantity of the compound.

In that case, the same solvent is employed repeatedly. This technique is known as continuous extraction.

The method of differential extraction is useful for the isolation of nonvolatile compounds.

For example, benzoic add, which is soluble in water, can be extracted by the extraction of the aqueous solution using ether as the solvent.

Sublimation

On heating, some organic compounds change from the solid to the vapour state directly without passing through the intervening liquid state.

This process is called sublimation. Only those substances sublime whose vapour pressures equal the atmospheric pressure much before their melting points.

This process is useful for the purification of such solids which sublime on heating and contain nonvolatile impurities.

In this process, the impure solid is heated in a china dish which is covered with an inverted funnel.

A perforated filter paper is folded in the shape of the funnel and adjusted on the inner surface of the funnel. The stem of the funnel is plugged with cotton.

On heating, the substance volatilises and the vapours rise, solidify and get deposited on the inner, less hot surface of the inverted funnel. The non-volatile impurities are left in the china dish.

The perforations in the filter paper allow only the vapours to pass through it. The compounds which can be purified by sublimation are camphor, naphthalene and anthracene.

Chromatography

Chromatography is a method of separation in which the compounds to be separated are in two phases, one of which is stationary (stationary phase) while the other (mobile phase) moves in a definite direction.

The method was first used to separate coloured pigments found in plants, hence the name (Greek, Chroma-colour).

Generally speaking, the different chromatographic techniques work on either of the two principles— the difference between adsorption affinities and solubilities of the various components of the mixture.

Based on this, we shall study the two categories of chromatography—adsorption chromatography and partition chromatography.

Adsorption chromatography

Chromatography in which separation is based mainly on the differences between the adsorption affinities of the components in a sample for the surface of an active solid is called adsorption chromatography.

A porous solid with adsorptive properties which help in chromatographic separations is known as an active solid.

Here the stationary phase is the adsorbent (active solid, e.g., alumina). Thus the principle involved is differential adsorption.

The two main types of chromatography based on the principle of differential adsorption are column chromatography and thin-layer chromatography. Column chromatography The stationary bed, in this technique, is within a tube.

The adsorbent or solid stationary phase may fill the inside of the tube or be concentrated along the inside tube wall leaving an unrestricted path for the mobile phase in the middle part of the tube. The most commonly used adsorbents are alumina and silica gel.

Once the adsorbent is packed in the glass tube, the sample is poured into the column and continuously washed with a solvent a process known as elution. The solvent is called an elu

Different components of the sample are adsorbed to different extents and move down the column at different rates. Thus the most readily adsorbed components are at the top of the column.

The solution is the mobile phase in this case. The usual method is to collect the solution as it passes out from the column in fractions.

Thin-layer chromatography (TLC) Chromatography is carried out on a layer of adsorbent spread on a glass plate.

The layer is thin (about 0.2 mm) and known as a thin-layer chromatography plate or chrome plate. A small spot of the solution of the mixture is put on the plate at a distance of about 2 cm from the base.

This is done with the help of a capillary tube. The plate is then dried and placed in a glass jar containing the eluent at the bottom. It is ascertained that the spot on the TLC plate does not touch or dip in the eluent. The jar is covered with a glass plate.

The eluent moves up the plate due to capillary action and meets the sample mixture. The components of the mixture get dissolved in the solvent (eluent) and are carried up the plate.

The components of the mixture get separated into a number of spots due to their different adsorption affinities. Each component corresponds to a component of the mixture.

The plate is taken out, and the solvent front is marked and dried. Each component is finally eluted with a suitable solvent to get the pure component.

The relative adsorption of each component of the mixture is denoted by its retention factor (Rÿ).

The Rj values of a spot can be determined by dividing the distance travelled by that spot (component) by the total distance travelled by the solvent (solvent front). The distances are measured from the baseline.

The spots of coloured compounds are visible on the TLC plate but analysing colourless compounds becomes difficult. There are several methods to make the colourless spots visible.

If a small amount of fluorescent dye is added to the adsorbent, ultraviolet radiation absorbing, colourless spots can be seen. Iodine vapours are also used as the colour reagent.

Specific colour reagents are also sprayed on the TLC plate. For instance, ninhydrin gives a yellow colour when it reacts with the amino add proline and a blue colour with other amino acids.

Partition Chromatography

In this type of chromatography, the separation of the components of the mixture is based mainly on the differences between their solubilities in the stationary and mobile phases.

Paper chromatography is a type of partition chromatography. In this case, a strip of chromatographic paper acts as the adsorbent. The molecules of water trapped in the chromatographic paper serve as the stationary phase. The mobile phase is the suitable solvent or a mixture of solvents.

A spot of the mixture to be separated is placed near one edge of the paper and the sheet is suspended vertically in a solvent, which rises through the paper by capillary action, carrying the components with it. The components of the mixture move at different rates and separate.

The adsorption of components to different extents on the paper and the partition between the solvent and the moisture in the paper are the two factors responsible for the separation of the components of the mixture.

The paper is removed, the solvent front is marked, and the paper is dried. The dried chromatographic paper with a line of spots of different components of the mixture is called a chromatogram.

The components can be identified by the distance they move in a given time. Colourless substances are detected by using ultraviolet radiations or by spraying with a substance which reacts to give a coloured spot (substance).

Rf can be calculated for each component. If for a given system at a known temperature is a characteristic of the component and can be used to identify compounds.

Qualitative Analysis

Once the compound has been purified, its structure can be determined. To do so, it is necessary to identify the elements constituting the compound. This is known as qualitative analysis.

You already know that organic compounds invariably contain carbon and hydrogen. Besides, they may also contain nitrogen, sulphur, a halogen and phosphorus. The presence or the absence of these elements is ascertained as follows.

Detection Of Carbon And Hydrogen

The presence of carbon and hydrogen is detected by strongly heating the compound with cupric oxide.

The carbon in the compound is oxidised to carbon dioxide (tested by passing the gas through limewater) and hydrogen is converted into water (tested by using anhydrous copper sulphate, which turns blue).

⇒ \(\begin{aligned}
& \mathrm{C}+2 \mathrm{CuO} \longrightarrow \mathrm{CO}_2+2 \mathrm{Cu} \\
& 2 \mathrm{H}+\mathrm{CuO} \longrightarrow \mathrm{H}_2 \mathrm{O}+\mathrm{Cu}
\end{aligned}\)

⇒ \(\mathrm{CO}_2+\mathrm{Ca}(\mathrm{OH})_2 \longrightarrow \mathrm{CaCO}_3 \downarrow+\mathrm{H}_2 \mathrm{O}\)

⇒ \(
\begin{aligned}
& \mathrm{C}+2 \mathrm{CuO} \longrightarrow \mathrm{CO}_2+2 \mathrm{Cu} \\
& 2 \mathrm{H}+\mathrm{CuO} \longrightarrow \mathrm{H}_2 \mathrm{O}+\mathrm{Cu} \\
& \mathrm{CO}_2+\mathrm{Ca}(\mathrm{OH})_2 \longrightarrow \mathrm{CaCO}_3 \downarrow+\mathrm{H}_2 \mathrm{O} \\
& \mathrm{H}_2 \mathrm{O}+\underset{\text { (White) }}{\mathrm{CuSO}_4} \longrightarrow \underset{\text { (Blue) }}{\mathrm{CuSO}_2 \cdot 5 \mathrm{H}_2 \mathrm{O}}
\end{aligned}
\)

Detection Of Other Elements

Apart from carbon and hydrogen, the other elements generally present are detected by Lassaigne’s test.

The compound to be analysed is fused with sodium metal. The elements covalently bonded to the carbon or the hydrogen atoms in the molecule of the compound get converted into water-soluble, ionic salts. The conversion to ionic forms makes the detection of elements easier.

⇒ \(Organic compound +\mathrm{Na} \longrightarrow \mathrm{NaCN}+\mathrm{Na}_2 \mathrm{~S}+\mathrm{NaX}
(C, H, O, N, S, X)\)

In case both nitrogen and sulphur are present in the same molecule, sodium thiocyanate (NaSCN) is obtained on fusion with sodium. The ionic salts arc extracted from the fused mass by boiling it with distilled water.

The solution obtained is the sodium extract or Lassaignc’s extract, which is then used to detect the elements.

Test for nitrogen

The sodium extract is heated to boiling with a few crystals of ferrous sulphate and then acidified with dilute sulphuric acid, and 2-3 drops of ferric chloride solution are added.

If nitrogen is present, a Prussian blue precipitate of ferric ferrocyanide is obtained. The blue colour is due to the cyanide ions.

Hydrazine (H2N—NH2) cannot be detected by Lassaigne’s test due to the presence of the N—N bond.

⇒ \(2 \mathrm{NaCN}+\mathrm{FeSO}_4 \longrightarrow \mathrm{Fe}(\mathrm{CN})_2+\mathrm{Na}_2 \mathrm{SO}_4\)

⇒ \(
\begin{gathered}
\mathrm{Fe}(\mathrm{CN})_2+4 \mathrm{NaCN} \longrightarrow \underset{\text { Sodium hexacyanoferrate(II) }}{\mathrm{Na}_4\left[\mathrm{Fe}(\mathrm{CN})_6\right]} \\
3 \mathrm{Na}_4\left[\mathrm{Fe}(\mathrm{CN})_6\right]+4 \mathrm{FeCl}_3 \longrightarrow \underset{\text { Ferriferrocyanide }}{\mathrm{Fe}_4\left[\mathrm{Fe}(\mathrm{CN})_6\right]_3+12 \mathrm{NaCl}}
\end{gathered}\)

The presence of nitrogen in a compound can also be detected by the soda lime test. The compound is heated with soda lime —the evolution of ammonia confirms the presence of nitrogen.

⇒ \(\underset{\text { Actamide }}{\mathrm{CH}_3 \mathrm{CONH}_2+\mathrm{NaOH}} \underset{\text { theat }}{\stackrel{\mathrm{CnO}}{\longrightarrow}} \mathrm{CH}_3 \mathrm{COONa}+\mathrm{NH}_3\)

The evolved ammonia can be tested by bringing a glass rod dipped in concentrated HC1 to the mouth of the test tube. White fumes of NH4C1 are seen.

Test for sulphur

Acetic acid followed by a lead acetate solution is added to the sodium extract. A black precipitate indicates the presence of sulphur.

⇒ \(\left(\mathrm{CH}_3 \mathrm{COO}\right)_2 \mathrm{~Pb}+\mathrm{Na}_2 \mathrm{~S} \stackrel{\mathrm{H}^{+}}{\longrightarrow} \underset{\text { (black) }}{\mathrm{PbS} \downarrow}+2 \mathrm{CH}_3 \mathrm{COONa}\)

Alternatively, when sodium nitroprusside solution is added to the sodium extract, a violet colour indicates the presence of sulphur.

⇒ \(\underset{\text { Sodium nitroprusside }}{\mathrm{Na}_2 \mathrm{~S}}+\underset{\mathrm{Na}_2\left[\mathrm{Fe}(\mathrm{CN})_5 \mathrm{NO}\right]}{\longrightarrow} \underset{\text { violet }}{\mathrm{Na}_4\left[\mathrm{Fe}(\mathrm{CN})_5 \mathrm{NOS}\right]}\)

In case sulphur is present along with nitrogen, then the sodium extract will contain sodium thiocyanate, which instead of Prussian blue gives a blood red colour with ferric chloride due to the presence of the thiocyanate.

⇒ \(3 \mathrm{NaSCN}+\mathrm{FeCl}_3 \longrightarrow \underset{\substack{\text { Ferrithiocyanate } \\ \text { (blood red) }}}{\mathrm{Fe}(\mathrm{SCN})_3}+3 \mathrm{NaCl}\)

However, with excess sodium, during sodium fusion, the thiocyanate decomposes to yield cyanide and sulphide, which respond positively to their usual tests.

⇒ \(\mathrm{NaSCN}+2 \mathrm{Na} \longrightarrow \mathrm{NaCN}+\mathrm{Na}_2 \mathrm{~S}\)

Test for halogens

The sodium extract is boiled with dilute nitric acid to convert sodium cyanide or sodium sulphide (if present) to hydrogen cyanide and hydrogen sulphide respectively.

The cyanide or sulphide ions otherwise interfere with further tests. The cooled solution is treated with silver nitrate.

A white precipitate soluble in ammonium hydroxide confirms the presence of chlorine.

A yellowish precipitate sparingly soluble in ammonium hydroxide indicates bromine while a yellow precipitate insoluble in ammonium hydroxide confirms the presence of iodine.

The presence of bromine and iodine can also be detected by using carbon disulphide or carbon tetrachloride.

The sodium extract is boiled with dilute H2S04, cooled, and chlorine water followed by CS2 or CC14 is added.

The solution is shaken and allowed to stand. The layer of CS2 or CC14 (organic layer) turns yellow or orange in the presence of bromine and violet in case iodine is present.

Test for phosphorus

To detect phosphorus, the organic compound is fused with sodium peroxide, which is an oxidising agent.

The phosphorus present is oxidised to phosphate (Na3P04). The aqueous extract containing the phosphate is boiled with concentrated HN03 and a few drops of ammonium molybdate solution are added to it.

A yellow solution or precipitate shows the presence of phosphorus. This yellow precipitate is due to the formation of ammonium phosphomolybdate.

⇒ \(\mathrm{Na}_3 \mathrm{PO}_4+3 \mathrm{HNO}_3 \longrightarrow \mathrm{H}_3 \mathrm{PO}_4+3 \mathrm{NaNO}_3\)

⇒ \(\mathrm{H}_3 \mathrm{PO}_4+12\left(\mathrm{NH}_4\right)_2 \mathrm{MoO}_4+21 \mathrm{HNO}_3 \longrightarrow\left(\mathrm{NH}_4\right)_3 \mathrm{PO}_4 \cdot 12 \mathrm{MoO}_3+21 \mathrm{NH}_4 \mathrm{NO}_3+12 \mathrm{H}_2 \mathrm{O}\)

There is no direct test for the detection of oxygen in an organic compound. Its presence can, however, be inferred by testing for the presence of an oxygen-containing functional group like —OH, —CHO, —COOH and NO₂.

Quantitative Analysis

Once the various elements present in an organic compound are detected by qualitative analysis, in order to derive its empirical formula, it is necessary to determine quantitatively the percentages of these elements in the compound.

Estimation Of Carbon And Hydrogen

Liebig’s method In this method, a known mass of the organic compound is heated in a current of pure dry oxygen in the presence of cupric oxide till all the carbon and hydrogen are oxidised to carbon dioxide and water respectively.

⇒ \(\text { Organic compound }+\mathrm{O}_2+\underset{\text { excess }}{\mathrm{CuO}} \stackrel{\text { heat }}{\longrightarrow} \mathrm{CO}_2+\mathrm{H}_2 \mathrm{O}+\mathrm{Cu}\)

After combustion, the gases are passed first through a U-tube containing anhydrous calcium chloride, which absorbs water and then through a U-tube containing potassium hydroxide solution, which absorbs carbon dioxide.

Both the U-tubes are weighed before and after the combustion so that the amount of HzO and CO₂ evolved from a known amount of the sample can be calculated.

Let the mass of the organic compound be m g.

• Mass of water formed = m1 g.
• Mass of carbon dioxide formed = m2 g.
• Since 44 g of CO₂ =12 g of carbon,
• m2 g of CO₂ \(\equiv \frac{12}{44} \times m_2\) ni2 g of carbon.

This is the mass of carbon present in m g of the organic compound.

∴ Percentage of C in the compound \(=\frac{12}{44} \times m_2 \frac{100}{m} \text {. }\)

Similarly, the percentage of H in the compound \(=\frac{2}{18} \times m_1 \times \frac{100}{m}.\)

Estimation Of Nitrogen

Nitrogen can be estimated either by the Dumas method or by the Kjeldahl method. Dumas method In this method, a weighed sample of the organic compound is heated with cupric oxide in an atmosphere of carbon dioxide.

On heating, the carbon and hydrogen are oxidised to CO₂ and H₂O respectively, while N2 is set free.

Any oxides of nitrogen produced during combustion are reduced back to nitrogen by passing the sample over a heated copper gauze. The gaseous mixture is collected in a nitrometer, which contains a solution of potassium hydroxide.

The mercury at the bottom of the nitrometer does not allow the potassium hydroxide solution to move from the nitrometer.

All gases except nitrogen are absorbed in the KOH solution. The volume of nitrogen gas collected at the top of the tube is measured.

The percentage of N in the given organic compound is calculated as follows.

• Let the mass of the organic compound = mg.
• The volume of nitrogen collected in the nitrometer = V mL.
• Room temperature = TK
• Pressure of dry nitrogen = (atmospheric pressure- aqueous tension at t° C)
  = p bar.

From the relation \(\frac{p_1 V_1}{t_1}=\frac{p_2 V_2}{t_2}\) We can find the volume of N2 gas at stp.

Experimental values

p₁ =pbar
V₁= VmL
t₁ =TK

At stp
p₂ = 1bar
V₂=?
T₂ = 273 K

Thus, \(V_2=\frac{p_1 \times V_1 \times 273}{T \times 1}\)

We know that 22,700 mL of N2 at stp weighs 28 g.

∴ \(V_2 \mathrm{~mL} \text { of } \mathrm{N}_2 \text { at stp will weigh } \frac{28 \times V_2}{22,700} \mathrm{~g} \text {. }\)

Percentage of N = \(\frac{\text { mass of nitrogen }}{\text { mass of organic compound }} \times 100\)

⇒ \(=\frac{28 \times V_2}{22700} \times \frac{100}{m} .\)

Kjeldahl method In this method a known mass of the organic compound is heated with concentrated sulphuric acid in the presence of copper sulphate, which acts as a catalyst.

The nitrogen of the organic compound gets converted into ammonium sulphate. The solution is then heated with an excess of sodium hydroxide.

⇒ \(\text { Organic compound }+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow\left(\mathrm{NH}_4\right)_2 \mathrm{SO}_4\)

⇒ \(\left(\mathrm{NH}_4\right)_2 \mathrm{SO}_4+2 \mathrm{NaOH} \longrightarrow \mathrm{Na}_2 \mathrm{SO}_4+2 \mathrm{NH}_3+2 \mathrm{H}_2 \mathrm{O}\)

The liberated ammonia gas is absorbed in a known volume (taken in excess) of a standard solution of sulphuric add.

⇒ \(2 \mathrm{NH}_3+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow\left(\mathrm{NH}_4\right)_2 \mathrm{SO}_4\)

The add that remains unused is estimated by titrating the solution with a standard solution of alkali.

The percentage of nitrogen in the organic compound can be calculated as follows.

• Let the mass of the organic compound = m g.
• Let the volume of the standard solution of added taking molarity M=V mL.
• Let the volume of unreacted acid (with ammonia) = V1 mL.

Let the volume of the standard solution of alkali of molarity M used for neutralising the unreacted acid = V₂ mL.

The chemical reaction involved in the titration is

⇒ \(2 \mathrm{NaOH}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{Na}_2 \mathrm{SO}_4+2 \mathrm{H}_2 \mathrm{O}\)

Thus at the endpoint,

⇒ \(n_1 M_1 V_1=n_2 M_2 V_2 \text {, }\)

where n1, M₁ and V₁ are the basicity, molarity and volume respectively of the acid used and;n2, M₂ and V₂ are the acidity, molarity and volume respectively of the base used. All these quantities are relevant only to the titration.

‍∴ \(\quad V_1=\frac{n_2 M_2 V_2}{n_1 M_1}=\frac{1 \times M \times V_2}{2 \times M}=\frac{V_2}{2}\)

or the volume of unreacted acid (with ammonia) \((V)=\frac{V_2}{2},\)

∴ The volume of acid reacted with NH₃ = (V- V₂/2) mL.

∴ Millimoles of NH3 that react with add- 2(V- V₂/2)M

or moles of NH3 \(=\frac{2\left(V-V_2 / 2\right) M}{1000} .\)

Now moles of N in NH3 =1 x mole of NH3 \(=\frac{1 \times 2\left(V-V_2 / 2\right)}{1000} .\)

Mass of N \(=\frac{2\left(V-V_2 / 2\right)}{1000} \times 14 \mathrm{~g}\)

∴ Percentage of N in the organic compound

⇒ \(\begin{aligned}
& =\frac{2\left(V-V_2 / 2\right) M \times 14 \times 100}{1000 \times m} \\
& =\frac{14 \times M \times 2\left(V-V_2 / 2\right)}{m} .
\end{aligned}\)

Estimation Of Halogen

The quantity of a halogen in an organic compound is estimated by the Carius method. In this method, a known mass of the organic compound is taken in a hard glass-sealed tube (Carius tube) with fuming nitric acid in the presence of silver nitrate.

The Carius tube is then heated in a furnace. On heating carbon and hydrogen are oxidised to CO₂ and H₂O respectively while halogens form a precipitate of silver halide (AgX). The silver halide precipitate is filtered and washed with water and alcohol. It is then dried and weighed.

The percentage of the halogen is calculated as follows.

• Let the mass of the organic compound = m g.
• Mass of silver halide (AgX) obtained = m2 g.

108 + x parts by mass of AgX contains x parts by mass of halogen (x is the atomic mass of the halogen atom and 108 is the atomic mass of Ag).

(108 + x) g of AgX contains x g of X.

Therefore, mt g of AgX contains \(\frac{x}{108+x} \times m_1 g \text { of } \mathrm{X} .\)

Percentage of halogen X \(\mathrm{X}=\frac{x \times m_1}{(108+x)} \times \frac{100}{m} .\)

Estimation Of Sulphur

Sulphur is also estimated by the Carius method. A known mass of the organic compound is heated with fuming nitric acid in the Carius tube.

Sulphur is converted to sulphuric acid, which is precipitated by barium chloride as barium sulphate.

The precipitate of barium sulphate is filtered, washed, dried and weighed. From the mass of barium sulphate obtained, the percentage of sulphur can be calculated.

⇒ \(\begin{aligned}
& \mathrm{S}+\mathrm{H}_2 \mathrm{O}+3 \mathrm{O} \stackrel{\mathrm{HNO}_3}{\longrightarrow} \mathrm{H}_2 \mathrm{SO}_4 \\
& \mathrm{H}_2 \mathrm{SO}_4+\mathrm{BaCl}_2 \longrightarrow \mathrm{BaSO}_4 \downarrow+2 \mathrm{HCl}
\end{aligned}\)

Let the mass of the organic compound = m g.

Let the mass of the precipitate = m1 g.

233 g of BaS04 contains 32 g of S.

Therefore, m1 g of BaSQ4 contains \(\frac{32}{233} \times m_1 g \text { of } S\)

Percentage of S \(=\frac{32}{233} \times m_1 \times \frac{100}{m} .\)

Estimation Of Phosphorus

A known mass of the organic compound is heated with fuming nitric acid. The phosphorus in the organic compound is oxidised to phosphoric acid.

It is then treated with magnesia mixture (a solution containing magnesium chloride, ammonium chloride and a little ammonia).

A precipitate of magnesium ammonium phosphate (MgNH4P04) is obtained. It is filtered, washed, dried and then ignited to give magnesium pyrophosphate (Mg2P₂O7), which is then weighed.

⇒ \(\mathrm{H}_3 \mathrm{PO}_4+\left(\mathrm{MgCl}_2+\mathrm{NH}_4 \mathrm{Cl}\right) \longrightarrow \mathrm{MgNH}_4 \mathrm{PO}_4
Magnesia mixture\)

Therefore, m1 g of Mg₂P₂O₇ \(\frac{62}{222} \times m_1\) contains of phosphorus

Percentage of phosphorus \(=\frac{62}{222} \times \frac{m_1}{m} \times 100\)

Alternatively, phosphoric acid may be precipitated as ammonium phosphomolybdate, (NH4)3P04 -12Mo03, by adding ammonia and ammonium molybdate.

⇒ \(\mathrm{H}_3 \mathrm{PO}_4+\underset{\substack{\text { Ammonium } \\ \text { molybdate }}}{12\left(\mathrm{NH}_4\right)_2 \mathrm{MoO}_4}+21 \mathrm{HNO}_3 \longrightarrow \underset{\substack{\text { Ammonium } \\ \text { phosphomolybdate }}}{\left(\mathrm{NH}_4\right)_3 \mathrm{PO}_4 \cdot 12 \mathrm{MoO}_3 \downarrow}+21 \mathrm{NH}_4 \mathrm{NO}_3+12 \mathrm{H}_2 \mathrm{O}\)

Then the percentage of phosphorus will be \(=\frac{31 \times m_1 \times 100}{1877 \times m},\) where m mass 0f ammonium phosphomolybdate.

Estimation Of Oxygen

The percentage of oxygen is generally determined by subtracting the sum of percentages of all other elements from 100. However, it can be estimated directly by the following method.

A known amount of the organic compound is decomposed by heating in nitrogen gas.

The mixture of the gaseous product formed is passed over red hot coke when all the oxygen (present in the mixture) is converted into carbon monoxide.

The mixture is then passed through warm iodine pentoxide (I₂O₅) when carbon monoxide is oxidised to carbon dioxide and iodine is reduced.

⇒ \(\begin{gathered}
2 \mathrm{C}+\mathrm{O}_2 \stackrel{1373 \mathrm{~K}}{\longrightarrow} 2 \mathrm{CO} \\
\mathrm{I}_2 \mathrm{O}_5+5 \mathrm{CO} \longrightarrow 5 \mathrm{CO}_2+\mathrm{I}_2
\end{gathered}\)

The percentage of oxygen can be calculated from the amount of carbon dioxide or iodine produced.

Let the mass of the organic compound = mg.

Let the mass of carbon dioxide produced = m g.

44 g of CO₂ contains 32 g of O.

Therefore, m1 g of CO₂ contains \(\frac{32}{44} \times m_1 g \text { of } \mathrm{O}\)

Percentage of O \(=\frac{32 \times m_2 \times 100}{44 \times m} .\)

Earlier, for quantitative analysis large amounts of the pure compound (about 1 g) were required.

However, with the advances in the recent past, it is now possible to carry out the analysis with 3-4 mg of the substance. The accuracy in these estimations is ±0.03%. Automatic CHN elemental analysers are also available, which give results in a few minutes.

Example 1. Calculate the percentage of carbon, hydrogen and oxygen, if 02722g of an organic compound on complete combustion gives 05545g of carbon dioxide and 02227 g of water.
Solution: Percentage of C =

⇒ \(\begin{aligned} & =\frac{12}{44} \times \frac{\text { mass of } \mathrm{CO}_2}{\text { mass of compound }} \times 100 \\
& =\frac{12}{44} \times \frac{0.5545}{0.2722} \times 100=54.5 .
\end{aligned}\)

Percentage of H=

⇒ \(\begin{aligned} & =\frac{2}{18} \times \frac{\text { mass of } \mathrm{H}_2 \mathrm{O}}{\text { mass of compound }} \times 100 \\ & =\frac{2}{18} \times \frac{0.2227}{0.2722} \times 100=9 \end{aligned}\)

Thus, the percentage ofO =100- (54.4 + 9) = 36.6.

Example 2. During the estimation of nitrogen by the Dumas method, 0.45 g of an organic compound gave 75mL of nitrogen, which was collected at 300 K and at 715 mmHg pressure. Calculate the percentage of nitrogen in the compound. (The vapour pressure of water at 300K is 15mmHg.)
Solution: Vapour pressure of gas = (715- 15) mmHg = 700 mmHg.

Using the gas equation \(\frac{p_1 V_1}{t_1}=\frac{p_2 V_2}{t_2}\) the volume of nitrogen at 760 mmHg pressure and 0°C can be calculated as

⇒ \(V_2=\frac{700 \times 75 \times 273}{760 \times 300} \mathrm{~mL} .\)

22,400 mL of nitrogen at 760 mmHg pressure and (PC weighs 28 g.

Therefore, \(\frac{700 \times 75 \times 273}{760 \times 300}\)
mL of nitrogen at the same pressure and temperature weighs

⇒ \(\frac{28}{22,400} \times \frac{760 \times 300}{700 \times 75 \times 273}=0.0786 \mathrm{~g} .\)

Percentage of nitrogen \(=\frac{0.786}{0.45} \times 100=17.46\)

Example 3. During the estimation of nitrogen by the Kjeldahl method 0.5 g of an organic compound evolved ammonia, which was absorbed in 100 mL of \(\frac{M}{10} \mathrm{H}_2 \mathrm{SO}_4 \text {. }\)

The unused acid required 150 mL \(\frac{M}{10}\) NaOH solution. Calculate the percentage composition of nitrogen in the compound.

Solution: The chemical reaction taking place in the titration is

⇒ \(2 \mathrm{NaOH}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{Na}_2 \mathrm{SO}_4+2 \mathrm{H}_2 \mathrm{O}\)

i.e., 2 moles of NaOH react with 1 mole of H₂SO₄.

M₁V₁=M₂V₂.

If the volume of the unused H2S04 is V1 then,

⇒ \(\begin{array}{rlrl}
& & V_1 \times \frac{1}{10} & =150 \times \frac{1}{10} \times \frac{1}{2} \\
\text { or } & V_1 & =75 \mathrm{~mL} .
\end{array}\)

Therefore, the volume of \(\frac{1}{10} \mathrm{MH}_2 \mathrm{SO}_4\) used by NH3 = 100- 75 = 25 mL.

Millimoles of H2S04 used by NH3 \(=25 \times \frac{1}{10}=2.5 .\)

Since \(2 \mathrm{NH}_3+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow\left(\mathrm{NH}_4\right)_2 \mathrm{SO}_4,\)

millimoles of NH3 = 2 x millimoles of H2S04

\(=2 \times 2.5=5.0 \text {. }\)

Mass of NH3 formed = moles x molar mass

\(=5.0 \times 10^{-3} \times 17 \text {. }\)

Mass of N \(=\frac{5.0 \times 10^{-3} \times 17 \times 14}{17} \mathrm{~g}\)

\(=5.0 \times 10^{-10} \times 14 \mathrm{~g}\) \(\text { Percentage of } \mathrm{N}=\frac{1 .}{1000} \times 5.0 \times \frac{100}{0.5}=14 .\)

Example 4. During bromine estimation by the Carius method, 0.165 g of a compound gave 0.132 g of AgBr. Find the percentage of bromine in the compound.
Solution: Molecular mass of AgBr = 188

188 g of AgBr contains 80 g of bromine.

0.132 g of AgBr contains \(\frac{80}{188} \times 0.132 \mathrm{~g} \text { of bromine. }\)

Percentage of bromine in the compound \(=\frac{80 \times 0.132}{188} \times \frac{100}{0.165}=34 .\)

Example 5. During sulphur estimation by the Carius method, 0.434 g of an organic compound gave 0640 g of BaSO, Calculate the percentage of sulphur in the compound.
Solution: 233 g of BaS04 contains 32 g of sulphur.

0.640 g of BaS04 contains \(\frac{32}{233} \times 0.640 \mathrm{~g}\) of sulphur.

Percentage of S \(=\frac{32}{233} \times \frac{0.640 \times 100}{0.434}=20.27\)

Organic Chemistry—Some Basic Principles And Techniques Multiple Choice Questions

Question 1. Which of the following has the least C—C bond length?

1. Ethane
2. Ethene
3. Ethyne
4. All are equal

Answer: 3. Ethyne

Question 2. How many tertiary hydrogen atoms are present in

1. One
2. Two
3. Three
4. Four

Answer: 1. One

Question 3. The compounds butene-1 and isobutene exhibit

1. Chain isomerism
2. Position isomerism
3. Functional isomerism
4. Metamerism

Answer: 1. Chain isomerism

Question 4. Which of the following has maximum -I effect?

1. OH
2. COOH
3. Br
4. NQ₂

Answer: 4. NQ₂

Question 5. Which of the carbon atoms numbered will have a maximum 6+ charge in the given compound?

⇒ \(\stackrel{3}{\mathrm{C}} \mathrm{H}_3-\stackrel{2}{\mathrm{C}} \mathrm{H}_2-\stackrel{1}{\mathrm{C}} \mathrm{H}_2-\mathrm{Cl}\)

1. Carbon 1
2. Carbon 2
3. Carbon 3
4. All will have equal 5+ charges.

Answer: 1. Carbon 1

Question 6. Which of the following carbocations is the most stable?

1. \(\mathrm{CH}_3 \mathrm{CH}_2 \stackrel{+}{\mathrm{C}} \mathrm{H}_2\)
2. \(\mathrm{CH}_2=\mathrm{CH}-\stackrel{+}{\mathrm{C}} \mathrm{H}_2\)
3. \(\mathrm{C}_6 \mathrm{H}_5 \stackrel{+}{\mathrm{C}} \mathrm{H}_2\)
4. All are Equally Stable

Answer: 3. \(\mathrm{C}_6 \mathrm{H}_5 \stackrel{+}{\mathrm{C}} \mathrm{H}_2\)

Question 7. Which of the following free radicals is the most stable?

1. Methyl
2. Ethyl
3. Isopropyl
4. Tertiary butyl

Answer: 4. Tertiary butyl

Question 8. Which of the following is/are electrophilic?

1. NO_2⁺
2. 
3. C₂H₅Cl
4. All the above

Answer: 4. All the above

Question 9. In which of the following reactions has the hybridised state of a carbon atom changed?

Answer: 3 and 4

Question 10. The IUPAC name of

1. Butanal
2. Butan-l-al
3. Butane-l-carboxaldehyde
4. Pentan-l-al

Answer: 4. Pentan-l-al

Question 11. The IUPAC name of CH₃CH=CH—C=CH is

1. 4-Pentyn-2-ene
2. l-Pentyn-3-ene
3. 3-Penten-l-yne
4. 2-Penten-4-yne

Answer: 3. 3-Penten-l-yne

Question 12. Identify the molecule/ion in which the inductive, resonance and hyperconjugative effects are operative.

1. (CH₃)3C
2. CH₂=CH—CH=0
3. (CH₃)3C—CH₂
4. CH₃CH=CH—CH=0

Answer: 4. CH₃CH=CH—CH=0

Qualitative 13. The smallest alkane with a 3° carbon is

1. Neopentane
2. Isopentane
3. Isohexane
4. Isobutane

Answer: 4. Isobutane

Question 14. Sublimation can be used for the purification of

1. Glucose
2. Acetamide
3. Naphthalene
4. Formic acid

Answer: 3. Naphthalene

Question 15. Glycerol boils at 536 K and decomposes at its bp. It can be purified by

1. Fractional distillation
2. Steam distillation
3. Sublimation
4. Distillation under reduced pressure

Answer: 4. Distillation under reduced pressure

Question 16. A mixture of benzene and toluene can be separated by

1. Steam distillation
2. Fractional distillation
3. Vacuum distillation
4. Simple distillation

Answer: 2. Fractional distillation

Question 17. Which of the following will respond positively to Lassaigne’s test for nitrogen?

1. Nitrobenzene
2. Acetamide
3. Urea
4. All the Above

Answer: 4. All the Above

Question 18. In Lassaigne’s test, when both N and S are present, a blood red colour is obtained. This is due to the formation of

1. Ferriferrocyanide
2. Ferrithionate
3. Sodium thiocyanate
4. Ferricyanide

Answer: 2. Ferrithionate

Question 19. A mixture of acetone (b.p. 329 K) and methyl alcohol (b.p. 338 K) can be separated by

1. Simple distillation
2. Distillation under reduced pressure
3. Steam distillation
4. Fractional distillation

Answer: 4. Fractional distillation

Question 20. In column chromatography, the separation of a mixture of two substances depends on their

1. Different solubilities
2. Different melting points
3. Different specific gravities
4. Differential adsorption

Answer: 4. Differential adsorption

Question 21. A substance which is insoluble in water and possesses a vapour pressure of 10-15 mmHg at 373 K can be purified by

1. Crystallisation
2. Distillation
3. Steam distillation
4. Sublimation

Answer: 3. Steam distillation

Question 22. In steam distillation, the total pressure of the organic substance and water vapour becomes

1. Equal to the atmospheric pressure
2. More than the atmospheric pressure
3. Less than the atmospheric pressure
4. There is no fixed relationship

Answer: 1. Equal to the atmospheric pressure

Question 23. 0.4 g of an organic compound on complete combustion gives 0.18 g of water. What will be the percentage of hydrogen in the compound?

1. 10
2. 15
3. 5
4. 2.5

Answer: 3. 5

Question 24. Which of the following compounds will give a blood-red colouration when nitrogen is present?

1. M-nitrobenzoic add
2. P-toluidine
3. Urea
4. M-nitrobenzene sulphonic add

Answer: 4. M-nitrobenzene sulphonic add

Question 25. In the Kjeldahl method, the nitrogen present in an organic compound is estimated by measuring the amount of

1. N₂
2. NO₂
3. NH₃
4. (NH₄)2SO₄

Answer: 3. NH₃

Question 26. Which of the following reagents is added to the sodium extract of an organic compound to detect die presence of sulphur in the compound?

1. Sodium nitroprusside
2. Ammonium molybdate
3. Ammonium phosphomolybdate
4. Sodium hexacyanoferrate

Answer: 1. Sodium nitroprusside

Question 27. In the sodium fusion test of organic compounds, the nitrogen of an organic compound is converted to

1. Sodium nitrate
2. Sodium nitrite
3. Sodium amide
4. Sodium cyanide

Answer: 4. Sodium cyanide

Question 28. Carbon and hydrogen present in an organic compound are estimated by

1. The dumas method
2. The various method
3. The Liebig method
4. None of these

Answer: 3. The lie big method

Thermodynamics

This chapter deals with energy changes that take place during a chemical reaction. In any chemical reaction, the atoms of the reactants are rearranged to form the products. This involves the breaking and forming of bonds. You know that energy is required to break bonds and that it is released when bonds are formed. It should then be easy to understand that a chemical reaction involving the dissociation and formation of bonds must be accompanied by energy changes.

The energy change accompanying a reaction may appear in different forms. When fuels are burnt, for instance, energy appears as heat and light. The chemical reaction in a battery produces electrical energy. When a grenade explodes, the chemical reaction produces heat, light, sound and kinetic energy. Consider the following reactions.

⇒ \(\mathrm{C}+\mathrm{O}_2\longrightarrow \mathrm{CO}_2 \text { + heat }\)

⇒ \(2 \mathrm{Mg}+\mathrm{O}_2\longrightarrow 2 \mathrm{MgO}+\text { heat }+ \text { light }\)

⇒ \(\mathrm{Zn}+\mathrm{CuSO}_4\longrightarrow \mathrm{ZnSO}_4+\mathrm{Cu}+\text { electrical energy }\)

In these reactions there is a net release of energy. There are other reactions in which energy is absorbed. Take the case of electrolysis, for example. Here electrical energy is absorbed and the electrolyte splits into its components. Photosynthesis, on which almost all living organisms depend directly or indirectly, is another example of a reaction in which energy is absorbed.

Thermodynamics Some Definitions

Before we start a systematic study of the energy changes associated with chemical reactions, let us define a few basic terms used in any discussion of energetics or chemical thermodynamics.

System: A system is that part of the universe which we are interested in investigating. For example, if we are studying a particular reaction in a vessel, then the vessel, the reactants, and the products constitute the system.

Surroundings: Everything other than the system or the part of the universe other than the system is called the surroundings. In the example we have just considered, everything other than the vessel in which the reaction is taking place is called the surroundings. A system is separated from the surroundings by boundaries which may be real or imaginary. Further, boundaries may be considered part of either the system or the surroundings, depending upon convenience.

There are three types of systems: open system, closed system, and isolated system.

Open system A system which can exchange matter and energy with the surroundings is called an open system. For example, an open test tube in which a reaction is taking place is an open system. It can exchange heat with the surroundings and gaseous products can escape into the surroundings.

Closed system A dosed system can exchange energy with the surroundings but not mass. If a reaction occurs in a sealed bulb, which can exchange heat with the surroundings but not matter, the bulb with the reactants and products constitutes a closed system.

Isolated system An isolated system can neither exchange matter nor energy with the surroundings. A thermos flask filled with hot tea is an isolated system.

Intensive and extensive properties: The properties of any substance can be classified as intensive or extensive. Intensive properties are those independent of the size of the substance. For example, by doubling the size of the given sample of a substance, the temperature and pressure of the substance do not double or do not change. These are called Intensive properties, other examples being viscosity, density, and all other molar properties.

If the value of the property depends on the size of the substance, it is called an extensive property. On doubling the size, internal energy doubles, and hence it is an extensive property. Other examples include mass, volume, heat capacity, enthalpy, entropy, and free energy.

State functions: State functions are those parameters or measurable macroscopic properties of a system that describe its state. The state of a system is defined by specifying the values of certain number of macroscopic properties. The number depends on the nature of the system.

• The values of state functions or state variables depend only on the state of the system and not on how that state is readied. Take a gaseous system, for example. Its state is described by the state functions: temperature (T), pressure (p), and volume (IQ. To take a more specific case, consider 1 mol of CO at stp. Its volume will be 22.7 L irrespective of the method by which it is obtained.
• All state functions or state variables are not independent because equations of state exist between different state functions. For example, consider the equation of state for an ideal gas, pV-nRT. Here out of the four variables (p. V. n and T), only three can be independently varied.
• Thus once the values of the minimum number of state functions are fixed, others have definite values. The equilibrium state of a system is characterised by the definite values of state functions which do not change with time. Internal energy, enthalpy, and entropy are the state functions you will learn about in this chapter.

The state of a system: As stated above, thermodynamic equilibrium exists in a system when the macroscopic properties or state functions do not change with time. If the equilibrium state is disturbed tire system again settles down to a new equilibrium state.

• If a particular state function does not have equal values in the system and its surroundings, exchange of matter or energy or both takes place between the thermodynamic system and its surroundings. After the interaction between system and its surroundings stops, the system attains a new equilibrium state with new values of state functions.
• The starting state of the system is referred to as the initial state and the state reached after interaction with the surroundings is the final state. When a thermodynamic system undergoes a change of state (from the initial to tire final), we say it has undergone a process. This implies that there will be a change in at least one of tire state functions of tire system during a process.
• A system can change from one state (initial state) to another (final state) through a number of paths. In other words, there can be a number of processes between an initial state and a final state. There are certain processes in which a particular state variable remains unchanged. Let us learn about these processes.

Isothermal If the temperature of the system remains constant during the change, the process is called isothermal.

Adiabatic If the system does not exchange heat with the surroundings, the process is called adiabatic.

Isobaric If the pressure of the system remains constant during the change, the process is called isobaric.

Isochoric If the volume of the system remains constant during the change, the process is called isochoric.

Reversible process In this process, the initial and the final states are connected through a succession of equilibrium states, i.e., at every state along the reversible path, there exists an equilibrium between the system and the surroundings. Such states are called quasi-equilibrium states.

Irreversible process The processes occurring in nature are generally irreversible. Their only difference from a reversible process is that equilibrium is not maintained during the transformation process.

Cyclic process The process that brings back a system to its original state after a series of changes is called a cyclic process.

Transference Of Energy

While describing open, closed, and isolated systems, we touched upon the idea of a system exchanging energy with the surroundings. There are two forms in which energy is exchanged between a system and the surroundings.

We often talk about heat flowing from a body at a higher temperature to one at a lower temperature. What we mean is that energy is exchanged between the two bodies because of a difference in temperature.

• So, one of the forms in which a system can exchange energy with the surroundings is heat. Energy is exchanged between a system and the surroundings in the form of heat when they are at different temperatures.
• The other mode of energy exchange between a system and the surroundings is energy. One example where energy is exchanged in this form is when the system and surroundings are at different pressures.
• Consider a gas enclosed in a cylinder that is fitted with a weightless, frictionless moving piston. If the gaseous system is at a higher pressure than the surroundings, the piston will move upwards (increasing the volume of the gas) until the pressure of the system and that of the surroundings become equal.

During the expansion of the gas, work is done by the system on the surroundings due to the pressure difference between the two. Here energy is transferred from the system to the surroundings as work.

• If, on the other hand, the pressure of the system is lower than that of the surroundings, the piston is pushed down until the pressures become the same. In this case the volume of the gas decreases and work is done by the surroundings on the system.
• Once again there is figure, when the gas enclosed in a cylinder transference of energy in the form of work, but from the fitted with a piston is at a higher pressure than the surroundings to the system. By convention, work done on the surroundings, the piston moves until the pressures system is positive, while work done by the system is negative. equalize.

Remember that neither heat, nor work is a property of a system. They are path functions as they depend on how a change is brought about. A system does not possess a particular amount of work or heat. It does, however, have a particular amount of energy under a particular set of conditions. The SI unit of heat is the same as that of work, i.e., the joule. However, heat is sometimes expressed in calories or kilocalories.

1 calorie = 4.184 J.

1 J = 10⁷ ergs.

Work

There are several kinds of work, such as mechanical work, electrical work, and chemical work. Work is said to be done if an object is moved by a force F through a distance d. The work done is given by

W = Fxd…….Equation 1

Some types of work encountered in chemistry are:

1. Expansion work (which we shall study in detail) in the case of expansion or compression of a gas against a force surface expansion in case of liquids—these are examples of mechanical work
2. When larger molecules are synthesized from smaller ones within living organisms—chemical work
3. An ion moving in the presence of an electric field—electrical work.

The most common form of mechanical work encountered in chemistry is the expansion work associated with the expansion of a gas against pressure. It is also called p-V or pressure-volume work.

To understand the concept further, let us once again consider a Figure but with a weight attached to the piston. When the gas expands, the piston moves up and the weight is lifted up. We say that work is done by the system.

Let us now calculate the work done in terms of pressure and volume. If an external pressure p_ex is applied on the piston and the piston moves inwards by a distance dl, then the change in volume of the gas is given by

dV=A • dl …….(1)

where A is the area of the cross-section of the piston. The force on the piston is given as

F = p_ex • A …..(2)

Now, the work done in moving the piston by a distance dl against an opposing force of magnitude F is given by

dW = -Fdl …….(3)

(the negative sign is due to the opposing nature of the force).

Substituting (2)  in (3)

dW = -p_ex • Adl

or dW = -p_ex dV

or simply W = -p Δ V …..Equation 2

• By the help of this equation, we can calculate the work done (or pressure/volume) during the expansion or compression of a gas. When expansion occurs ΔV in Equation 2 is positive, thereby resulting in a negative value for W.
• Similarly, when compression occurs, weight is lowered in the surroundings and we say that work is done on the system. Since AV is negative now, W is positive.
• Thus we can say that work is done when there is a change in height of a weight in the surroundings.

If due to a change in state of a system, a weight is lifted in the surroundings, work is done by the system and if a weight is lowered in the surroundings, work is done on the system. Now W can also be given as W = mgh,

where m is the mass lifted, g is the acceleration due to gravity and h is the height through which the mass is lifted.

Thus, during a change in state of the system, we can learn about any work done by measuring the relevant quantities only in the surroundings.

Reversible expansion or compression of a gas: Suppose a gas confined in a cylinder with a movable piston is in equilibrium. This means that there is no change in state of the system. This is possible when the external pressure p_ex (pressure that is applied) is equal to the internal pressure, p, of the gas. A small change in p_ex can disturb the equilibrium and the gas may expand or compress, resulting in a change in the volume and hence the state of the system.

• When p_ex is increased infinitesimally (infinitesimal means negligibly small) then compression occurs and the volume of the gas decreases. Equilibrium with the surroundings is also established almost immediately. The system can also be restored to its original state by reducing the external pressure to the original value.
• By continuously increasing the external pressure, infinitesimally, the gas can be made to undergo a finite amount of compression. This is achieved by keeping different weights on the piston one after the other.
• In each step, however, the change is infinitesimal and can be reversed by an infinitesimal change in external pressure. Again, in each step equilibrium is immediately established.
• Thus we have a process which is carried out in several infinitesimally small steps and throughout the process the system is in equilibrium with its surroundings. This is a reversible process.

If the difference between the internal pressure and the external pressure is large then there is a considerable disturbance of equilibrium and an infinitesimal change in p_ex in the opposite direction will not bring back the system to its original state. Such a process is termed an irreversible process.

Calculation of work done in various cases

1. Work done in free expansion When the external pressure is zero (p_ex = 0), there is no opposing force on the piston and the gas can expand freely. This is called free expansion. This occurs when a gas expands in vacuum. Both the work done on the system and by the system are zero in this case.

2. Work done in expansion against constant pressure If a constant external pressure is applied, the gas expands or compresses until the internal pressure becomes equal to the external pressure. The work done at every displacement dV is given by Equation 2. The total work done in the expansion from V₁ to V₂ is the sum of all such contributions. It is obtained by finding the area under the p-V plot, i.e., by integrating Equation.

∴ \(W=-\int_{V_1}^{V_2} p_{e x} d V\) ….. (1)

= \(-p_{e x} \int_{V_1}^{V_2} d V=-p_{e x}\left(V_2-V_1\right)\)

∴ \(W=-p_{e x} \Delta V\)

In case of expansion, ΔV is positive and W turns out to be negative. Therefore, work is done by the system.

If ΔV is negative as in case of compression, W is positive, i.e., work is done on the system.

3. Work done in reversible expansion In reversible expansion, the difference between external and internal pressure is infinitesimally small. With very small changes in pressure, the process of expansion and compression may be reversed. If the expansion occurs in several stages, at each stage, it is ensured that the external pressure is only infinitesimally different (less in case of expansion and more in case of compression) from the internal pressure of the gas.

Since \(p_{e x}=p_{\text {in }}\) we may replace p_ex in Equation 2 by p_in

dW = -p_in dV.

This is the work done at every stage of the expansion. The total work is obtained by summing up all such infinitesimal contributions (again) given by the area under the p-V plot.

⇒ \(\int d W=-\int p_{\mathrm{ma}} d V\)

∴ \(W_{\mathrm{rev}}=-\int p_{\mathrm{in}} d V\)

The subscript ‘rev’ indicates the reversible nature of the process.

If it is assumed that the gas behaves ideally then p_in be replaced by nRT/v using the ideal gas equation.

Therefore \(W_{\mathrm{rev}}=-\int_{V_1}^{V_2} \frac{n R T}{V} d V\)

If the process is carried out at a constant temperature (isothermally), T may be taken out of the integral sign.

⇒ \(W_{r e v}=-n R T \int_{V_1}^{V_1} \frac{d V}{V}\)

= \(-n R T|\ln V|_{V_1}^{V_2}\)

or, \(W_{n e v}=-n R T \ln \left(\frac{V_2}{V_1}\right)=-2303 n R T \log \frac{V_2}{V_1}\),

where V₁ and V₂ are the initial and final volumes respectively.

Internal Energy

The energy stored within a system (say chemical system) is its internal energy or intrinsic energy. Under a particular set of conditions, a thermodynamic system has a definite amount of internal energy.

• In other words, the internal energy of a system, generally represented as U, depends on the nature, amount, temperature, and pressure of the system. This energy possessed by a system is due to the different types of energy that its atoms or molecules have.
• It is, in fact, the sum of the energies of the elementary particles of the system, i.e., the sum of their potential and kinetic energies and the bond energy between constituting atoms.
• Instead of saying that a particular system under a particular set of conditions possesses a definite amount of internal energy, we could have said that internal energy is a state function, which means that it depends only on the initial and final state of the system and is independent of the way (path) the change takes place.

However, unlike other state functions, like pressure and temperature, it is not possible to determine the value of internal energy. This is because it is not possible to determine with exactness the values of the components of internal energy. Note that this matters little, because in the study of chemical processes, what we are really interested in knowing is the clumge in internal energy, ΔU (delta U).

ΔU = U₂-U₁

where U₂ is the internal energy of the system at the end of the process being studied and is the internal energy of the system at the start of the process. For a chemical reaction

ΔU = U_p-U_r,

where U₂ is the internal energy of the products and U_r is that of the reactants. Obviously, All is a state function since U_p and U_r are state functions.

So, how do we measure ΔU or the change in internal energy associated with a chemical process? Suppose we carry out a chemical reaction in such a way that the system remains at the same temperature, there is no work done on the system and it does no work on the surroundings.

• Whatever the change in the internal energy of the system in the course of the reaction must be equal to the energy exchanged by the system with the surroundings in the form of heat.
• Why? This in fact follows from the law of conservation of energy, which we will discuss subsequently, for the moment, imagine that the change in internal energy of the system is negative, i.e., U_p < U_r.
• What happens to this energy which the system has apparently lost? It cannot just vanish because that is against the law of conservation of energy. We have assumed that the system does not work and nor is any work done on it (i.e., volume remains constant), so the energy cannot be exchanged with the surroundings in the form of work.
• Since the temperature is constant, the energy must be exchanged with the surroundings in the form of heat.
• The change in the internal energy associated with a chemical reaction is, thus, determined by letting the reaction occur at constant temperature and constant volume and measuring the heat exchanged with the surroundings.

Law Of Conservation Of Energy

This is one of those common-sense laws which seem very obvious but have far-reaching implications. It states that energy can neither be created nor destroyed, though it may change from one form to another.

In the context of the system and the surroundings that we have been discussing, this means that the total energy of the system and the surroundings (i.e., the universe) remains constant.

• More specifically, it means that during a chemical reaction, energy may be absorbed or released, but the total energy of the reaction system and the surroundings remains constant.
• The law of conservation of energy is also known as the first law of thermodynamics. It is of relevance not only to chemists but also to physicists, engineers, and others who deal with the conversion of energy from one form into another.

The first law of thermodynamics being identical to the law of conservation of energy can be stated as:

1. Energy can neither be created nor destroyed although it can be changed from one form to another.
2. The energy of an isolated system is constant.

Consider the universe, which is an isolated system. Tire energy of the universe is conserved. Inside the universe, energy can be transferred from one part to another or it can be converted from one form to another, but it can neither be created nor destroyed.

Let us see if we can express this law mathematically. If the internal energy of a particular system is U₁ and it absorbs a certain amount of heat q, then its internal energy will become U₁ + q. Now suppose W amount of work is done on the system, then U₂, the final energy of the system is

U₂ =U₁ +q + W

or ΔU = U₂ – U₁ = q + W….. Equation 3

(If W is the work done on the system, -W is the work done by the system.)

• This means the change in the internal energy of the system is equal to the sum of the heat absorbed by the system and the work done on it.
• One can generalise this to say the change in the internal energy of the system is the sum of the heat exchanged by the system (with the surroundings) and the work done on or by the system. Equation 3 is the mathematical statement of the first law of thermodynamics.

If we now substitute for W in Equation 3, the expression for change in internal energy (when only pressure-volume type of work is done) becomes

ΔU = q – pΔV …. Equation 4

Now, if there is no change in the volume of the system then W = 0, i.e., W = -∫pdV = 0.

We can easily see that if there is no change in volume during a reaction, Equation 4 becomes ΔU = q_v,

where q_v is the heat exchanged (evolved or absorbed) by the reaction system at constant volume. When heat is absorbed by the system, q is positive and when heat is evolved by the system, q is negative. This is exactly what we said in the previous section.

The change in the internal energy of a system during a chemical reaction is equal to the heat exchanged with the surroundings, provided the volume and temperature of the system remain constant.

For any isothermal expansion of an ideal gas the total energy remains the same, and q = -W. In other words, the internal energy remains constant (ΔU = 0) when an ideal gas expands isothermally.

Thus for an isothermal irreversible change, q = -W = p_ex ΔV

and for an isothermal reversible change, q = \(-W=n R T \ln \frac{V_2}{V_1}\)

= \(-2.303 n R T \log \frac{V_2}{V_1}\),

where V₁ and V₂ are the initial and final volumes respectively.

For an adiabatic change, q = 0,

∴ ΔU = W_adiabstic  (from Equation 3).

Enthalpy

So far we have considered reactions taking place at constant volume and temperature, and the energy changes associated with such reactions. But the reactions we carry out in the laboratory normally occur in open vessels (beakers or test tubes, say).

Obviously, the volume of such a reaction system does not remain constant. However, the pressure does, since such a system, open to the atmosphere, is at atmospheric pressure and this pressure is more or less constant.

• The heat exchanged with the surroundings by a reaction system in the course of a reaction is equal to the change in the internal energy of the system if the temperature and volume are constant.
• What about the heat exchanged with the surroundings by a reaction system at constant pressure and not maintained at constant volume? It should be different, but why and how?
• Let us consider a reaction in which the volume of the system increases. An increase in volume can occur when the system does some work against the atmospheric pressure and energy is required for this work.
• Thus, in this case, the heat exchanged with the surroundings would be lower than that for a system at constant volume and temperature.
• On the other hand, if the reaction involves a decrease in the volume of the system, work would have to be done on the system by tire surroundings. The heat exchanged would then be greater than that exchanged by a system at constant volume.
• Thus, when a reaction proceeds at constant pressure and temperature, the heat exchanged by the system with tire surroundings is not equal to the change in the internal energy of the system.

In other words, the change in the internal energy of the system is not the only contributing factor to the total energy change associated with the reaction. Tire total energy change includes change in energy due to the pressure-volume type of work done by or on tire system.

Enthalpy or heat content is a property or state function introduced to take care of the energy changes associated with tire kind of system we have just been discussing. It is denoted by H and expressed mathematically as follows.

H = U + pV, …… Equation 5

where U is the internal energy, p the pressure, and V the volume of the system. The enthalpy of a system (substance) can be defined as the total energy associated with it, i.e., its internal energy and the energy due to factors such as pressure-volume conditions. The enthalpy of a substance depends on its state (temperature, pressure, etc.).

• Enthalpy changes are normally expressed with the substances in their standard states. The standard state of a pure substance is the pure form at a pressure of 1 bar and a specified temperature, the conventional temperature being 298.15 K.
• Enthalpy change in the standard state is called the standard enthalpy change. It is denoted by \(\Delta H^ominus\), where the superscript \(\ominus\) denotes standard conditions.

The molar enthalpy of a substance H_m = H/n (where n is the number of moles) is an intensive property and H_m = U_m + pV_m. When enthalpy changes have to be compared, the states of the systems must be identical.

Enthalpy change: As in the case of internal energy, the absolute value of the enthalpy of a system cannot be determined. What we are interested in knowing is the enthalpy change associated with a process. The total change in the energy of a system during a reaction at constant pressure is the enthalpy change, denoted by ΔH.

∴ \(\Delta H=H_{\text {products }}-H_{\text {reactants }}\)

= \(\left(U_p+p V_p\right)-\left(U_r+p V_r\right)\)

= \(\Delta U+\Delta p V\),

where U_p = internal energy of products,

V_p =volume of products,

U_r = internal energy of reactants, and V_t = volume of reactants.

Since p is constant, ΔH = ΔU + pΔV…….. Equation 6

The enthalpy change during a process is the sum of the change in internal energy and the pressure-volume work done.

Suppose the heat exchanged by a system with the surroundings during a reaction at constant pressure and temperature is q_p. Suppose also that the change in internal energy of the system is ΔU and the work done on the system is W. Then

q_p = ΔU-W = ΔU – (-pΔV)

= ΔU + pΔV

= ΔH. (ΔU + pΔV = ΔH)

• The heat exchanged by a system with the surroundings during a reaction at constant pressure and temperature is the enthalpy change associated with the reaction. In practice, the enthalpy change associated with a reaction is determined by insulating the system and allowing the heat of the reaction to alter its temperature.
• The amount of heat required to be supplied to or taken away from the system to let its temperature go back to the original value is then calculated to obtain the enthalpy change.

Significance of ΔU and ΔH: It is understood that the amount of heat exchanged with the surroundings for a reaction at a constant pressure (ΔH) is different from that exchanged at constant volume and temperature (ΔU).

The difference is not significant for solid or liquid systems but it does matter when gases are involved. Let us consider a gaseous reaction, where V_r is the total volume of the gaseous reactants V_p is the total volume of gaseous products, n_r, is the number of moles of reactants and n_r is the number of moles of products, all at constant pressure and temperature.

By the ideal gas law,

∴ \(\quad p V_t=n_r R T\)

and \(p V_p=n_p R T\)

Thus, \(p V_p-p V_r=\left(n_p-n_r\right) R T\)

or \(\quad p\left(V_p-V_r\right)=\left(n_p-n_r\right) R T\)

or, \(\quad p \Delta V=\Delta n_g R T\).

Here, Δn_g is the difference between the number of moles of the gaseous products and that of the gaseous reactants.

From the definition of enthalpy, it follows that ΔH = ΔU + pΔV.

Therefore, ΔH = ΔU + Δn_gRT.

The above equation is useful in situations where one of the two quantities ΔH and ΔU is known and the other has to be calculated. ΔH and ΔU differ significantly for processes involving gases. For solids and liquids, pV_p is only slightly different from pV_x.

Source of enthalpy change: You may be wondering what exactly leads to enthalpy change during a reaction. Any reaction involves the breaking and forming of bonds.

• Energy is released when bonds are broken and required for the formation of bonds. Simply put, the net change in energy due to the breaking and forming of bonds is the enthalpy change of the reaction.
• Of course, for the net change in energy to be termed enthalpy change, the reaction must take place at constant pressure and temperature. The simplest case is that of a gaseous system in which gas A reacts with gas B to form gas C.

If the reaction involves solutions, the interactions (hence energy changes) between the solvents and the reactants and products have to be considered. For liquid or solid reactants, we have to also consider the interactions between the molecules.

Enthalpy change(for a gaseous system at constant pressure) = (energy required to break bonds) – (energy released in formation of bonds).

Let us consider the reaction between hydrogen gas and chlorine gas to form HCl gas. Energy is required to break tire H—H and Cl—Cl bonds and released when H—Cl bonds are formed.

∴ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{HCl}(\mathrm{g})\)

The energy required to break H—H bonds = 436 kJ mol^-1.

Energy required to break Cl—Cl bonds = 242 kJ mol^-1.

Energy released in the formation of two H—Cl bonds = 2 x 431 kj mol^-1.

Enthalpy change (ΔH) = 436 + 242 – 2 x 431 = -184 kJ.

The negative value of ΔH indicates a decrease in the enthalpy of the system.

The heat evolved in this reaction is 184 kJ mol^-1.

Exothermic And Endothermic Reactions

In our discussion of the energy changes associated with chemical reactions so far, we have only mentioned that energy is released in some reactions and absorbed in others. Reactions in which energy is released are called exothermic while those in which energy is absorbed are called endothermic.

Exothermic reactions: While writing an exothermic reaction, the heat evolved is indicated on the right side, after the products.

∴ \(\mathrm{N}_2+3 \mathrm{H}_2 \longrightarrow 2 \mathrm{NH}_3+93.7 \mathrm{~kJ}\)

• If an exothermic reaction is carried out at constant volume and temperature, the heat evolved (q_ν) is (numerically) equal to the change in internal energy (ΔU). In such a reaction the internal energy of the products (U_p) is less than the internal energy of the reactants (U_r) and ΔU is negative.
• If an exothermic reaction occurs at constant pressure and temperature, the heat evolved is (numerically) equal to the change in enthalpy (ΔH). The enthalpy of the products is less than the enthalpy of the reactants, i.e., ΔH is negative.

Endothermic reactions: In the case of an endothermic reaction, the heat absorbed can be indicated along with reactants or with the products. Obviously, if it is shown on the left side of the equation, it will have a positive sign, and if it is shown on the right side, it will carry a negative sign.

∴ \(\mathrm{N}_2+\mathrm{O}_2+180.5 \mathrm{~kJ} \longrightarrow 2 \mathrm{NO}\)

or, \(\mathrm{N}_2+\mathrm{O}_2 \longrightarrow 2 \mathrm{NO}-180.5 \mathrm{~kJ}\)

When an endothermic reaction occurs at constant temperature and constant volume, the heat absorbed is (numerically) equal to the change in the internal energy of the system. The internal energy of the products (U_p) is greater than the internal energy of the reactants (U_r) and ΔU is positive.

When an endothermic reaction proceeds at constant pressure and temperature, the heat absorbed is (numerically) equal to the change in enthalpy of the system. The enthalpy of the products (H_p) is greater than the enthalpy of the reactants (H_r) and ΔH is positive.

Thermochemical Equations

You already know how to write a chemical equation. When a chemical equation not only indicates the quantities and physical states of the reactants and products involved, but also the change in enthalpy during a reaction, it is called a thermochemical equation. Fractional coefficients may also be used in such an equation.

⇒ \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ; \quad \Delta H=572 \mathrm{~kJ}\)

Certain conventions must be followed while writing a thermochemical equation. These conventions are listed below.

1. The heat evolved or absorbed is indicated as in the equation above, in terms of ΔH. Remember that ΔH is negative for exothermic reactions and positive for endothermic reactions.

2. The numerical value of ΔH corresponds to the reaction as written. In the absence of any information, it is assumed that a certain value of ΔH is due to the number of moles of reactants that combine as indicated by the chemical equation. Thus ΔH is expressed in kJ mol^-1.

3. The value of standard enthalpy (\(\Delta H^{\ominus}\)) in a thermochemical equation corresponds to the standard state of the substances involved in the reaction. The term ‘standard state of a substance’ refers to the pure substance at exactly 1 bar pressure.

4. The coefficients of the various substances represent the number of moles of the substances involved in the reaction and the value of ΔH corresponds to these coefficients. It stands to reason, therefore, that if the coefficients are multiplied or divided by some factor, so must ΔH be. Consider the following example.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \quad \Delta H=-242 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

If the coefficients are multiplied by 2, ΔH must also be multiplied by 2.

⇒ \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \quad \Delta \mathrm{H}=-(242 \times 2) \mathrm{kJ} \mathrm{mol}^{-1}\)

When the reaction is reversed, the sign of AH is reversed but its magnitude remains the same.

\(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{HI}(\mathrm{g})\Delta H=+53.9 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(2 \mathrm{HI}(\mathrm{g}) \longrightarrow \mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \Delta H=-53.9 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

5. The physical states of the reactants and products have to be indicated because ΔH changes with the physical state. The following example will make this clear.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\Delta H=-242 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l})\Delta H=-286 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Enthalpy Of Reactions

The enthalpy change accompanying a reaction is called reaction enthalpy and is denoted by Δ_rH. The standard enthalpy of reaction (Δ_rH^Θ) is the change in enthalpy per unit amount of the reaction when the reactants in their standard states change to products in their standard states.

By standard states we mean reference state, i.e., the most stable state of aggregation. For example the reference state of H₂ is pure gas at 1 bar and that of CaCO₃ is pure solid at 1 bar. By convention the standard states are reported at 298 K. There are several factors that determine the value of enthalpy of a reaction.

Quantities of reactants The amount of heat absorbed or released as also the enthalpy of a reaction depends on the quantities of reactants involved. This should be pretty easy to understand. If you bum 1 kg of coal it will produce less heat than if you bum 10 kg of coal.

The standard enthalpy change for the reaction \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \quad \Delta_{\mathrm{r}} \mathrm{H}^{\ominus}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\) has the units of kJ mol^-1. Per mole refers to the reaction as written above.

Let us take another example.

⇒ \(2 \mathrm{CH}_3 \mathrm{OH}(\mathrm{l})+3 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}_2(\mathrm{~g})+4 \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

∴ \(\Delta_{\mathrm{r}} H^{\ominus}\) for this reaction is -1276.9 kj mol^-1.

However, if the reaction is written with different stoichiometric coefficients, i.e., \(\mathrm{CH}_3 \mathrm{OH}(\mathrm{l})+\frac{3}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

∴ \(\Delta_{\mathrm{r}} H^{\ominus}\) is -638.4 kJ mol^-1, ‘per mole’ referring to the reaction as written here.

Physical State of Reactants and products The change of state of a substance involves heat changes, so the enthalpy of a reaction depends on the physical states of the reactants and products. We have already discussed the case of the formation of liquid water and gaseous water vapour from gaseous hydrogen and oxygen.

Allotropic forms The enthalpy of a reaction also depends on the allotropic forms of the substances involved in the reaction.

⇒ \(\mathrm{C} \text { (diamond) }+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \Delta H^{\ominus}=-395.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(\mathrm{C} \text { (graphite) }+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \Delta H^{\ominus}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Temperature The enthalpy of a reaction depends on the temperature at which the reaction proceeds. The value of enthalpy indicated in a thermochemical equation is generally the value at 298 K.

Constant pressure or volume As we have discussed already, the enthalpy of a reaction at a particular temperature depends on whether the reaction occurs at constant pressure or constant volume. From our discussion so far

ΔH = ΔU + pΔV.

But ΔH = q_p and ΔU = q_v.

∴ q_p = q_v + pΔV

Hess’s Law

The enthalpy of a substance is a stale function, independent of the method by which the substance is made. The enthalpy change in a reaction is the difference between the enthalpies of the products and the reactants.

• Both of these are consequences of the law of conservation of energy. Another consequence of the law is what is known as
  Hess’s law of constant heat summation, which states that the enthalpy change in a chemical or physical process is independent of the path taken or the manner in which the change is brought about.
• In the context of a chemical reaction, the law can be stated as follows. “The amount of heat absorbed or released during a reaction is the same whether the reaction proceeds in a single step or through several steps.”

Though G H Hess (a Russian chemist) came up with this law as a result of experimental observations, if you think a little you will realise that it follows from, or is a corollary of, the law of conservation of energy. How? Suppose a reactant A is converted into a product D and the heat evolved in the process is q.

• Now suppose the same reactant A changes first to B, then B is converted to C and finally, C changes to D and the heat evolved in the three steps is q₁, q₂, and q₃. Let q₁ + q₂ + q₃ = q′.  According to Hess’s law q = q’. If Hess’s law were not true, either q> q’ or q < q’. Let us consider the possibility that q >q’.
• Then the heat evolved in converting A to D in a single step would be greater than the heat absorbed when D is converted to A in three steps. This would lead to a situation in which (q – q‘) of heat would be ‘created’ after the completion of the cyclic process and the law of conservation of energy would be violated.

Hess’s law can be stated as follows: The enthalpy change for a reaction that is the sum of two or more other reactions is equal to the sum of the enthalpy changes of the constituent reactions.

Let us consider two ways in which carbon dioxide may be produced from carbon and oxygen. Either carbon dioxide can be produced directly by the combustion of carbon, or carbon can first be converted to carbon monoxide, which can then be converted to carbon dioxide.

⇒ \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \Delta_{\mathrm{r}} H^{\ominus}=-394 \mathrm{~kJ}\) …. (1)

⇒ \(\mathrm{C}(\mathrm{s})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}(\mathrm{g}) \Delta_{\mathrm{r}} H_1^{\ominus}=-110.5 \mathrm{~kJ}\) …. (2)

⇒ \(\mathrm{CO}(\mathrm{g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \Delta_{\mathrm{r}} H_2^{\ominus}=-283.5 \mathrm{~kJ}\) …..(3)

Adding the enthalpy changes in (2) and (3) you will get -394 kJ mol^-1, which is the same as the enthalpy change in (1). Do you see now why the law is called Hess’s law of constant heat summation?

Application of Hess’s law: Hess’s law is very useful in determining enthalpy changes in reactions for which it is not possible to experimentally determine enthalpy changes. It follows from Hess’s law that thermochemical equations can be added, subtracted, multiplied, or divided like algebraic equations.

Let us again consider the reaction between carbon and oxygen. The principal product of this reaction is CO₂ but CO may also be produced due to insufficient oxygen and this may then form CO₂. It is difficult to measure directly the enthalpy of combustion of carbon to carbon monoxide, CO. Let us assume it is unknown and determine its values by applying Hess’s law.

Reaction for which enthalpy is to be found: \(2 \mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}(\mathrm{g})\) …(1)

Reactions for which data is available: \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g})\) \(\Delta_{\mathrm{r}} H^\ominus=-393.5 \mathrm{~kJ}\) …. (2)

⇒ \(2 \mathrm{CO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}_2(\mathrm{~g})\) \(\Delta_{\mathrm{r}} H^{\ominus}=-566.0 \mathrm{~kJ}\) ….. (3)

How do we use these equations (with data) to get equation (1)? We need C and O₂, on the LHS and CO on the RHS. In Equation (2) C and O₂ are already on the LHS but the coefficient of C is 1 while we require 2 (from Equation (1)).

Hence, by multiplying Equation (2) by 2, we get

⇒ \(2 \mathrm{C}(\mathrm{s})+2 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}_2(\mathrm{~g}) \quad \Delta_{\mathrm{r}} H^{\ominus}=2 \times(-393.5) \mathrm{kJ}\) ….(4)

[If the equation is multiplied by 2, \(\Delta_r H^{\ominus}\)must also be multiplied by 2.]

Next CO must appear on the RHS. Reversing Equation (3) to get CO on RHS, we get

⇒ \(2 \mathrm{CO}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \quad \Delta_{\mathrm{r}} H^{\ominus}=-(-566)=+566 \mathrm{~kJ}\) …. (5)

[If the reaction is reversed, the sign of ΔH must also be reversed.]

Now adding reactions (4) and (5)

∴ \(2 \mathrm{C}(\mathrm{s})+2 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}_2(\mathrm{~g}) \quad \Delta_{\mathrm{r}} H^{\ominus}=-787.0 \mathrm{~kJ} \\
\begin{array}{lll}
2 \mathrm{CO}_2(\mathrm{~g}) & \longrightarrow 2 \mathrm{CO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g})  \Delta_{\mathrm{r}} H^{\ominus}=566 \mathrm{~kJ} \\
\hline 2 \mathrm{C}+\mathrm{O}_2 \longrightarrow 2 \mathrm{CO} & \Delta H^{\ominus}=-787+566=-221 \mathrm{~kJ}
\end{array}\)

Enthalpy Of Formation

The enthalpy or heat of the formation of a substance is the heat change accompanying the formation of 1 mol of the substance from its constituent elements and is usually written as Δ_tH. If all the substances involved in the reaction are in the standard state, the heat change is referred to as the standard heat of formation and is denoted by \(\quad \Delta_{\mathrm{f}} H^{\ominus}\) Consider the following equations.

∴ \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \quad \Delta_{\mathrm{f}} H^{\ominus}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

This means the heat liberated in the formation of 1 mol of gaseous carbon dioxide from its constituent elements is 393.5 kJ or that the enthalpy of formation of carbon dioxide is 393.5 kJ mol^-1.

∴ \(6 \mathrm{C}(\mathrm{s})+6 \mathrm{H}_2(\mathrm{~g})+3 \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{~s}) \quad \Delta_{\mathrm{f}} H^{\ominus}=-1169 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

When 1 mol of glucose is formed from its constituent elements in their standard states, the heat liberated is 1169 kJ, or the standard molar enthalpy of formation of glucose is 1169 kJ mol^-1 (‘molar’ referring to the formation of one mole of the substance).

By convention, the standard enthalpy of formation of elements is zero at all temperatures. However, when an element changes its state, the standard enthalpy of formation is not zero.

Usefulness of \(\Delta_{\mathrm{f}} H^{\ominus}\).

If you know the standard enthalpies of formation of the reactants and products of a chemical reaction, you can easily calculate the standard enthalpy change for that reaction. The difference between the sum of the enthalpies of formation of the products and the sum of the enthalpies of formation of the reactants is the enthalpy change associated with the reaction.

Standard enthalpy = \(\left(\begin{array}{c}
\text { sum of standard heats of } \\
\text { formation of products }
\end{array}\right)-\left(\begin{array}{c}
\text { sum of standard heats of } \\
\text { formation of reactants }
\end{array}\right)\)

∴ \(\Delta_r H^{\ominus}=\Sigma \Delta_f H^{\ominus} \text { (products) }-\Sigma \Delta_f H^{\ominus} \text { (reactants) }\)

Example 1. Calculate the enthalpy change for the following reaction. \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

Given that \(\Delta_t H^{\ominus}\) for CO₂(g), CO(g) and H₂O(g) are -393.5 kJ mol^-1, -111.3 kJ mol^-1, and -241.8 kJ mol^-1 respectively.

Solution:

⇒ \(\Delta_{\mathrm{r}} H^{\ominus}=\Sigma \Delta_{\mathrm{f}} H^{\ominus} \text { (products) }-\Delta_{\mathrm{f}} H^{\ominus} \text { (reactants) }\)

= \(\left[\Delta_f H^\ominus(\mathrm{CO})+\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{H}_2 \mathrm{O}\right)\right]-\left[\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{CO}_2\right)+\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{H}_2\right)\right]\)

=[(-1113) + (-2418)]-[(-393.5) + (0)] =- 353.1 + 393.5 = 40.4 kJ mol^-1.

Example 2. Calculate the enthalpy change for the following reaction.
\(\mathrm{CCl}_4(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g})+4 \mathrm{HCl}(\mathrm{g})_{;} \Delta_{\mathrm{r}} H^{\ominus}=-41.4 \mathrm{kcal}\)

Given that,

⇒ \(\Delta_{\mathrm{f}} \mathrm{H}^{\ominus} \text { for } \mathrm{CCl}_4(\mathrm{~g}), \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \text { and } \mathrm{CO}_2(\mathrm{~g}) \text { are }\) -25.5 k cal mol^-1,-57.8 k cal mol^-1 and -94.1k cal mol^-1 respectively.

Solution:

⇒ \(\Delta_{\mathrm{r}} H^{\ominus} =\left[\Sigma \Delta_{\mathrm{f}} H^{\ominus}(\text { products })\right]-\left[\Sigma \Delta_{\mathrm{f}} H^{\ominus}(\text { reactants })\right]\)

= \(\left[\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{CO}_2\right)+4 \times \Delta_{\mathrm{f}} H^{\ominus}(\mathrm{HCl})\right]-\left[\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{CCl}_4\right)+2 \times \Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{H}_2 \mathrm{O}\right)\right]\)

-41.4 = \(\left[(-94.1)+4 \Delta_{\mathrm{f}} H^{\ominus}(\mathrm{HCl})\right]-[(-25.5)+(2 \times-57.8)]\)

or -41.4 = \(-94.1+4 \Delta_{\mathrm{f}} H^{\ominus}(\mathrm{HCl})+141.1\)

∴ \(4 \times \Delta_{\mathrm{f}} H^{\ominus}(\mathrm{HCl})=-41.4-141.1+94.1=-88.4\).

∴ \(\Delta_f H^{\ominus}(\mathrm{HCl})=\frac{-88.4}{4}=-22.1 \mathrm{kcal} \mathrm{mol}^{-1}\).

In our discussion so far, we have not really distinguished between various types of reactions or processes such as combustion, neutralization, and change of state. When we have used the term enthalpy of a reaction, we have used it to refer to any chemical process or reaction. The enthalpies associated with different types of reactions or processes actually go by different names.

Enthalpy of combustion: The enthalpy or heat of combustion of a substance is the heat change accompanying the complete combustion of 1 mol of the substance in (excess) oxygen or air. The heat of combustion of carbon, for instance, is -393.5 kJ mol^-1.

⇒ \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) ; \quad \Delta_{\mathrm{c}} H^{\ominus}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Standard enthalpy of combustion is defined as the enthalpy per mol of a substance, when all the reactants and products are in their standard states at the specified temperature.

Remember that the heat of combustion of a substance is the heat evolved when 1 mol of the substance is completely burnt or oxidised. Carbon is converted to carbon monoxide according to the following reaction.

⇒ \(\mathrm{C}(\mathrm{s})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}(\mathrm{g}) ; \quad \Delta_c H^{\ominus}=-110.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

But -110.5 kJ mol^-1 is not the heat of combustion of carbon.

Remember also that combustion reactions are always accompanied by the evolution of heat, so the heat of combustion is always negative.

Calorific value Combustion reactions are very important for us. We bum fuels to meet our energy requirements. We use the energy released by the oxidation of food to survive. The calorific value of a fuel or food is the amount of heat (in calories) released when 1 mol of the fuel or food is burnt or oxidised completely.

Example 1. A cylinder of cooking gas contains 11 kg of butane. The thermochemical equation for the combustion of butane is \(\mathrm{C}_4 \mathrm{H}_{10}(\mathrm{~g})+\frac{13}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow 4 \mathrm{CO}_2(\mathrm{~g})+5 \mathrm{H}_2 \mathrm{O}(\mathrm{l}); \quad \Delta_{\mathrm{c}} \mathrm{H}=-2658 \mathrm{~kJ}\)

If a family’s energy requirement per day for cooking is 12000 kJ, how long would a cylinder last?
Solution:

Molar mass of butane = 58 g.

58 g of butane produces = 2658 of heat.

Daily requirement of energy = 12000 kJ.

∴ a cyclinder would last = \(\frac{2658 \times 11 \times 10^3}{58 \times 12,000}=\) = 42 days.

Example 2. Calculate the heat of combustion of glucose from the following data.

1. \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}); \Delta_{\mathrm{r}} \mathrm{H}_1^{\ominus}=-395.0 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
2. \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ; \Delta_{\mathrm{r}} \mathrm{H}_2^{\ominus}=-269.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
3. \(6 \mathrm{C}(\mathrm{s})+6 \mathrm{H}_2(\mathrm{~g})+3 \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{~s}) ; \Delta_{\mathrm{r}} H_3^{\ominus}=-1169.8 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Solution: The required equation for the heat of combustion of glucose is

∴ \(\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6+6 \mathrm{O}_2 \longrightarrow 6 \mathrm{CO}_2+6 \mathrm{H}_2 \mathrm{O} \quad \Delta_{\mathrm{r}} \mathrm{H}^{\ominus}=?\)

Applying Hess’s law, the required equation can be obtained by multiplying (1) by 6 and (2) by 6, adding the products and subtracting (3) from the sum.

∴ \(\begin{aligned}
& 6 \mathrm{C}(\mathrm{s})+6 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 6 \mathrm{CO}_2(\mathrm{~g}) \\
& \frac{6 \mathrm{H}_2(\mathrm{~g})+3\mathrm{O}_2(\mathrm{~g})}{} \longrightarrow 6 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \\
& \hline 6 \mathrm{H}_2(\mathrm{~g})+6 \mathrm{C}(\mathrm{s})+9 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 6 \mathrm{CO}_2(\mathrm{~g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \\
&-\left[6 \mathrm{H}_2(\mathrm{~g})+6 \mathrm{C}(\mathrm{s})+3 \mathrm{O}_2(\mathrm{~g})\right.\left.\longrightarrow \mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{~s})\right] \\
& \hline \mathrm{C}_6 \mathrm{H}_1 \mathrm{O}_6(\mathrm{~s})+6 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 6 \mathrm{CO}_2(\mathrm{~g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
\end{aligned}\)

Then \(\Delta_{\mathrm{r}} H^{\ominus}\) = \(\Delta_{\mathrm{r}} H^{\ominus}=6 \Delta_{\mathrm{r}} H_1^{\ominus}+6 \Delta_{\mathrm{r}} H_2^{\ominus}-\Delta_{\mathrm{r}} H_3^{\ominus}\)

= 6(-395) + 6(-269.4)-(-1169.8)=-2816.6 kJ.

Enthalpy of neutralisation: The enthalpy change associated with the neutralisation of one gram equivalent of an acid by a base (or vice versa) in a dilute aqueous solution is called the enthalpy of neutralisation. For instance, the enthalpy of neutralisation of NaOH by HCl or HCl by NaOH is -57.1 kJ mol^-1. In other words, the enthalpy change associated with the neutralisation of one gram equivalent of HCl by NaOH (or vice versa) is -57.1 kJ mol^-1.

∴ \(\mathrm{HCl}(\mathrm{aq})+\mathrm{NaOH}(\mathrm{aq}) \longrightarrow \mathrm{NaCl}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O} ; \quad \Delta_{\mathrm{n}} H^{\ominus}=-57.1 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

The enthalpy of neutralisation of any strong acid by a strong base (or vice versa) is always -57.1 kJ mol^-1. This is because neutralisation is actually a reaction between the H⁺ ions produced by an acid and the OH^– ions produced by a base. Let us see how this is so in the case of HCl and NaOH.

∴ \(\mathrm{Na}^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})+\mathrm{H}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{Na}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

or \(\mathrm{H}^{+}+\mathrm{OH}^{-} \longrightarrow \mathrm{H}_2 \mathrm{O}\)

• When 1 mol of OH^– ions combines with 1 mol of H⁺ ions to produce 1 mol of water, the heat liberated is 57.1 kJ mol^-1. Strong acids and bases are completely ionised in dilute aqueous solutions and the amount of H⁺ ions or OH^– ions produced by one gram equivalent of an acid or a base is always the same, i.e., 1 mol.
• If either the acid or the base, or both, are weak, the enthalpy of neutralisation is usually less than 57.1 kJ mol^-1 in magnitude. This is because weak acids and weak bases do not dissociate completely in an aqueous solution and a part of tire energy liberated during the combination of H⁺ ions and OH^– ions is utilised to ionise the weak acid or weak base.
• The heat used for ionising the weak acid (or base) is called the heat of ionisation or dissociation and the net heat of neutralisation is the difference between 57.1 kJ mol^-1 and the heat of dissociation.

∴ \(\underset{\text { Weak acdd }}{\mathrm{CH}_3 \mathrm{COOH}}+\underset{\text { Strong base }}{\mathrm{NaOH}} leftrightharpoons \mathrm{CH}_3 \mathrm{COONa}+\mathrm{H}_2 \mathrm{O} ; \quad \Delta \mathrm{H}=-55.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

To calculate the enthalpy of ionisation, let us write down the ionisation reaction and the neutralisation reaction separately.

Ionisation \(\mathrm{CH}_3 \mathrm{COOH} \longrightarrow \mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{H}^{+} ; \quad \Delta_{\text {ion }} H^{\ominus}=?\)

Neutralisation \(\mathrm{H}^{+}+\mathrm{OH}^{-} \longrightarrow \mathrm{H}_2 \mathrm{O} ; \quad \Delta_{\mathrm{n}} H^{\ominus}=-57.1 \mathrm{~kJ}\)

On adding the two equations, we get, \(\mathrm{CH}_3 \mathrm{COOH}+\mathrm{OH}^{-} \longrightarrow \mathrm{CH}_3 \mathrm{COO}^{-}+\mathrm{H}_2 \mathrm{O}; \Delta_{\text {net }} H^{\ominus}=-55.4 \mathrm{~kJ}\)

The net result is that \(\quad \Delta_{\text {net }} H^{\ominus}=\Delta_{\text {ion }} H^{\ominus}+\Delta_{\mathrm{n}} H^{\ominus} \text { (strong acid-strong base) }\)

or \(\quad-55.4=\Delta_{\text {ion }} H^{\ominus}-57.1 \)

∴\(\quad \Delta_{\text {ion }} H^{\ominus}=-55.4+57.1=2.1 \mathrm{~kJ}\)

In general \(\Delta_{\text {ion }} H^{\ominus}=\left(\Delta_{\text {net }} H^{\ominus}+57.1\right) \mathrm{kJ}\) .

Example: What would be the enthalpy change when

1. 0.25 mol of HCl in solution is neutralised by 0.25 mol of a NaOH solution?
2. 0.5 mol of nitric acid in solution is mixed with a solution containing 0.2 mol of a potassium hydroxide solution?
3. 200 cm³ of a 0.2-M HCl solution is mixed with 300 cm3 of a 0.1-M NaOH solution?

Solution:

1. 0.25 mol of HC1 s 0.25 mol of H⁺.

0. 25 mol of NaOH = 0.25 mol of OH^–.

⇒ \(\mathrm{H}^{+}+\mathrm{OH}^{-} \longrightarrow \mathrm{H}_2 \mathrm{O} \quad \Delta_n H^{\ominus}=-57.1 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Enthalpy change during the formation of 1 mol of H₂O = 57.1 kJ.

∴ enthalpy change when 0.25 mol of water is formed = 57.1 x 0.25 = 14.27 kJ.

2. 0.5 mol of HNO₃ = 0.5 mol of H⁺

0. 2 mol of KOH = 0.2 mol of OH^–

0. 5 mol of H⁺ ions will react with 0.2 mol of OH^– ions to produce 0.2 mol of H₂O.

Enthalpy change = 0.2 x 57.1 = 1142 kj.

3. 200 cm³ of 0.2-M HCl = 0.04 mol of H⁺.

300 cm³ of 0.1-M NaOH = 0.03 mol of OH^–.

0.03 moles of OH^– will react with 0.04 mol of H⁺ to produce 0.03 mol of H₂O.

Enthalpy change = 57.1 x 0.03 = 1.71 kj.

Enthalpies of phase change: A phase of a system is a homogeneous part of it throughout which all physical and chemical properties are the same. You will study phases and phase changes in detail later. A couple of examples will give you a basic idea.

• If you have a beaker full of water, the system you are considering consists only of liquid water, so it has one phase. If you drop a few cubes of ice in the water, your system now contains water and ice, so it is a two-phase system.
• When a system changes from one phase to another the process is referred to as a phase change or phase transition. Thus, the conversion of a solid into a liquid (fusion) is a phase change, as also the conversion of a liquid into a gas (vaporisation).
• There are other kinds of phase changes, but we are not concerned with those here. You already know that energy is needed to change a solid to a liquid and a liquid to a gas. The enthalpy changes associated with phase transitions go by different names. Remember, during a phase change, the temperature remains constant.

Enthalpy of fusion The enthalpy of fusion of a substance is the enthalpy change accompanying the conversion of 1 mol of the substance in its solid state into its liquid state at its melting point. For example, the standard enthalpy of fusion of ice is 6.0 kJ mol^-1.

∴ \(\mathrm{H}_2 \mathrm{O}(\mathrm{s}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l}) ; \quad \Delta_{\text {fus }} H^{\ominus}=+6.0 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

∴ \(\Delta_{\text {fus }} H^{\ominus}\) is the enthalpy of fusion in the standard state. Freezing is the reverse process of fusion, in that case an equal amount of heat is given off to the surroundings.

∴ \(\Delta_{\text {freex }} H^{\ominus}=-\Delta_{\text {fus }} H^{\ominus}\)

Enthalpy of vaporisation The enthalpy of vaporisation of a substance is the enthalpy change accompanying the conversion of 1 mol of the substance in its liquid state into its vapour state at the boiling point of the liquid. The standard enthalpy of vaporisation of water is 40.7 kj mol-1.

∴ \(\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g}) ; \quad \Delta_{\text {vap }} H^{\ominus}=40.7 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Enthalpy of sublimation The enthalpy of sublimation of a substance is the heat change associated with the conversion of 1 mol of it directly from its solid to its gaseous state at a temperature below its melting point. For instance, the standard enthalpy of sublimation of iodine is 62.39 kJ mol^-1.

∴ \(\mathrm{I}_2(\mathrm{~s}) \longrightarrow \mathrm{I}_2(\mathrm{~g}) ; \quad \Delta_{\mathrm{sub}} H^{\ominus}=61.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

The enthalpy change of n reverse transition is the negative of the enthalpy change of the forward transition (under the same conditions). This further proves enthalpy to be a state property. Therefore, the change in enthalpy would be same in both the cases when a solid is directly or indirectly converted to vapour. Thus, the enthalpy of sublimation can be expressed as:

⇒ \(\Delta_{\text {sub }} H^{\ominus}=\Delta_{\text {fus }} H^\ominus+\Delta_{\text {vap }} H^{\ominus}\)

• The striking differences in the magnitude of the enthalpy change for various substances is attributed to the intermolecular interaction in the substances. The enthalpy of vaporisation of water at its boiling point is 40.79 kJ mol^-1.
• This signifies that water molecules are held together more tightly than any other liquid with low enthalpy of vaporisation, for instance, acetone. The high enthalpy of vaporisation of water is partly responsible for low humidity in the atmosphere.

Enthalpy of atomisation: The enthalpy change on breaking a molecule completely into its gaseous atoms is called enthalpy of atomisation \(\Delta_{\mathrm{a}} H\). In case of a metal, the enthalpy of atomisation is tine same as the enthalpy of sublimation.

⇒ \(\mathrm{C}(\mathrm{s}) \longrightarrow \mathrm{C}(\mathrm{g}) \Delta_{\mathrm{a}} H^{\ominus}=716.7 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(\mathrm{Na}(\mathrm{s}) \longrightarrow \mathrm{Na}(\mathrm{g}) \Delta_{\mathrm{a}} H^{\ominus}=108.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

The enthalpy of atomisation of diatomic gases is half the bond dissociation enthalpy. For example, the standard bond dissociation enthalpy of O₂ is 497 kJ mol^-1 and the standard enthalpy of atomisation pertaining to the reaction is 249.2 kJ mol^-1.

⇒ \(\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{O}(\mathrm{g})\)

Enthalpy of allotropic transformation: You know that elements like carbon, sulfur, and phosphorus can exist in different allotropic forms and that such elements can change from one allotropic form into another. Allotropic transformations involve enthalpy changes.

• The enthalpy of the allotropic transformation of one allotropic form of a substance into another is the heat change accompanying the transformation per mole of the substance. The standard enthalpy of transformation of rhombic sulphur to monoclinic sulfur, for example, is 1.3 kJ mol^-1.
• It is not easy to determine enthalpy changes for allotropic transformations experimentally because such processes are rather slow and the enthalpy changes associated with them are small. Hess’s law can be used conveniently to determine the enthalpy changes accompanying allotropic transformations.

Example: Calculate the enthalpy of the allotropic transformation of rhombic sulphur to monoclinic sulphur from the following thermochemical equations.

1. \(
   \mathrm{S}\left(\text { rhombic) }+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{SO}_2(\mathrm{~g})\right. \Delta_{\mathrm{c}} H_1^{\ominus}=-295.1 \mathrm{~kJ} \mathrm{~mol}^{-1}\) …(1)
2. \(\mathrm{~S}(\text { monoclinic })+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{SO}_2(\mathrm{~g}) \Delta_{\mathrm{c}} H_2^{\ominus}=-296.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)……(2)

Solution:

The required equation is S(rhombic) → S(monoclinic) ΔH =?

Applying Hess’s law and subtracting equation (2) from (1)

∴ \(\begin{array}{rc}
\mathrm{S}(\mathrm{r})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{SO}_2(\mathrm{~g}) & \Delta_{\mathrm{c}} H_1=-295.1 \mathrm{~kJ} \\
\mathrm{~S}(\mathrm{~m}) \pm \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{SO}_2(\mathrm{~g}) & \Delta_{\mathrm{c}} H_2=-296.4 \mathrm{~kJ} \\
\hline \mathrm{S}(\mathrm{r}) \longrightarrow \mathrm{S}(\mathrm{m}) & \Delta H=13 \mathrm{~kJ}
\end{array}\)

Therefore, the enthalpy of the allotropic transformation of rhombic sulphur to monoclinic sulphur is 1.3 kJ mol^-1.

Enthalpy of solution: The enthalpy of reaction for dissolving one mole of a solute in n moles of a solvent is known as the integral enthalpy of the solution or the integral heat of the solution. Let us look at some such values for a solution of HNO₃ in water at 298 K.

1. \(\left.\mathrm{HNO}_3(\mathrm{l})+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{HNO}_3 \text { (in } 1 \mathrm{H}_2 \mathrm{O}\right) \Delta_{\text {sol }} H^{\ominus}=-187.6 \mathrm{~kJ} \mathrm{~mol}^{-1}\) ….(1)

2. \(\left.\mathrm{HNO}_3(\mathrm{l})+10 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{HNO}_3 \text { (in } 10 \mathrm{H}_2 \mathrm{O}\right) \Delta_{\text {sol }} H^{\ominus}=-205.8 \mathrm{~kJ} \mathrm{~mol}^{-1}\) …. (2)

3. \(\mathrm{HNO}_3(\mathrm{l})+100 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{HNO}_3 \text { (in } 100 \mathrm{H}_2 \mathrm{O} \text { ) } \Delta_{\text {sol }} H^{\ominus}=-206.8 \mathrm{~kJ} \mathrm{~mol}^{-1}\)…. (3)

4. \(\mathrm{HNO}_3(\mathrm{l})+500 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{HNO}_3 \text { (in } 500 \mathrm{H}_2 \mathrm{O} \text { ) } \Delta_{\text {sol }} H^{\ominus}=-206.9 \mathrm{~kJ} \mathrm{~mol}^{-1}\)…..(4)

5. \(\left.\mathrm{HNO}_3(\mathrm{l})+1000 \mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{HNO}_3 \text { (in } 1000 \mathrm{H}_2 \mathrm{O}\right) \Delta_{\text {sol }} H^{\ominus}=-206.9 \mathrm{~kJ} \mathrm{~mol}^{-1}\)….(5)

6. \(\mathrm{HNO}_3(\mathrm{l})+\mathrm{aq} \longrightarrow \mathrm{HNO}_3 \text { (aq) } \Delta_{\text {sol }} H^{\ominus}=-207.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\) …..(6)

As you can see from Equations (1)-(6), the heat of solution varies with concentration or decreases with increase in the amount of the solvent and finally stabilises at infinite dilution.

The enthalpy of solution at infinite dilution is the enthalpy change when 1 mol of the substance dissolves in such a large amount of solvent that the interaction between the solute molecules is negligible. In case of water as a solvent, infinite dilution is denoted by ‘aq’ (aqueous).

For HNO₃, the enthalpy of solution at infinite dilution refers to Equation (6) and is -207.36 kJ mol^-1.

Some more values of enthalpy of solution at infinite dilution are given below.

⇒ \(\mathrm{KCl}(\mathrm{s})+\mathrm{aq} \longrightarrow \mathrm{KCl}(\mathrm{aq}) ; \Delta_{\mathrm{sol}} H^{\ominus}=+18.6 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(\mathrm{CuSO}_4(\mathrm{~s})+\mathrm{aq} \longrightarrow \mathrm{CuSO}_4(\mathrm{aq}) ;  \Delta_{\mathrm{sol}} H^{\ominus}=-66.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(\mathrm{CuSO}_4 \cdot 5 \mathrm{H}_2 \mathrm{O}+\mathrm{aq} \longrightarrow \mathrm{CuSO}_4(\mathrm{aq}) ; \Delta_{\text {sol}} H^{\ominus}=+11.7 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

• In the first and third cases \(\Delta_{\text {sol}}\) is positive (endothermic), while in the second, it is negative (exothermic). In general, salts which do not form hydrates dissolve in water with the absorption of heat. Hydrated salts also dissolve in water with the absorption of heat. The process is exothermic only in the case of anhydrous salts which form hydrates.
• When a substance dissolves in water, it either absorbs (positive enthalpy) or releases energy (negative enthalpy). Ammonium nitrate has a positive enthalpy of solution. Tire cold pack used for minor injuries to sportsmen contains NH₄NO₃ and water in separate compartments.
• It is activated on punching the partition between the two upon which the salt dissolves and the temperature of water falls. Calcium chloride, on the other hand, has a negative enthalpy of solution, and this phenomenon is used to dissolve ice on sidewalks in winters.
• Let us see what happens when NaCl dissolves in water. First, the three-dimensional network of Na⁺ and Cl^– breaks into individual ions. For this purpose the lattice energy which is responsible for holding the ions together must be overcome. The separated Na⁺ and Cl^– ions get stabilised in tire solution by their interaction with the water molecules.

This process involves breaking some of the hydrogen bonds between the water molecules. The ions are then said to be hydrated. The process of dissolution of an ionic compound in a solvent (water) involves a complex interaction between the solute and the solvent species. However, it can be broadly taken to be happening in two steps:

1. First the ionic lattice breaks: \(\mathrm{NaCl}(\mathrm{s}) \longrightarrow \mathrm{Na}^{+}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g})\)

Energy is required for this process and therefore the reaction is endothermic. The enthalpy change associated with it is called lattice enthalpy it may be defined as the heat change when one mole of an ionic solid separates into its constituent gaseous atoms.

2. Next the gaseous Na⁺ and Cl^– ions interact with water molecules and become hydrated:

⇒ \(\mathrm{Na}^{+}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g}) \stackrel{\mathrm{H}_2 \mathrm{O}}{\longrightarrow} \mathrm{Na}^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

The enthalpy change associated with this process is called the enthalpy of solvation or more precisely the enthalpy of hydration as water is the solvent.

∴ \(\Delta_{\text {sol }} H=\Delta_{\text {lattlee }} H+\Delta_{\text {hyd }} H\)

Lattice enthalpy: It is not possible to determine lattice energy directly by experiments. Hence, it is determined on the basis of the Born-Haber cycle. The Bom-Haber cycle is a closed sequence of different processes which are involved in the breaking and finally in the making of an ionic crystal. To understand the cycle, let us take the example of NaCl(s). The steps involved in the formation of NaCl(s) are as follows:

1. Sublimation of Na(s) to Na(g): \(\mathrm{Na}(\mathrm{s}) \longrightarrow \mathrm{Na}(\mathrm{g}) \quad \Delta H=\Delta_{\mathrm{a}} H^{\ominus}[\mathrm{Na}(\mathrm{s})]=108.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

2. Dissociation of Cl₂(g) to give Cl(g): \(\frac{1}{2} \mathrm{Cl}_2(\mathrm{~g}) \longrightarrow \mathrm{Cl}(\mathrm{g}) \quad \Delta H=\frac{1}{2} \Delta_{\mathrm{Cl}-\mathrm{C}} H^{\ominus}=\frac{1}{2} \times 242 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

3. Ionisation of Na(g): \(\mathrm{Na}(\mathrm{g}) \longrightarrow \mathrm{Na}^{+}(\mathrm{g})+\mathrm{e}^{-} \quad \Delta H=\Delta_{\text {ien }} H^{\ominus}=495.8 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Ionisation enthalpy of sodium = 495.8 kJ mol^-1. Since sodium is in the gaseous state, the enthalpy change is given by

∴ \(\Delta_{\text {ion }} H=\Delta_{\text {ion }} U+\Delta n_g R T\)

∴ \(\Delta_{\text {ion }} H=495.8+(1) \times R T\)

(It may be observed subsequently that RT cancels out with -RT in the next step.)

4. The electron released by the sodium atom is gained by chlorine to give Cl^–.

⇒ \(\mathrm{Cl}(\mathrm{g})+\mathrm{e}^{-} \longrightarrow \mathrm{Cl}^{-}(\mathrm{g})\)

The electron affinity (E_A) of Cl is 348.6 kJ mol^-1. Since electron affinity is defined as the energy released in the above process, from thermodynamic considerations we must take a negative value.

Hence energy involved (-E_A) =-348.6 kJ mol^-1. Here again, we need the electron gain enthalpy (\(\Delta_{\mathrm{eg}} H)\), which is -E_A – RT (since Δn_g = -1)

∴ \(\Delta_{\mathrm{eg}} H)\) = -348.6 + (-1)RT = -348.6 – RT.

5. Na⁺(g) and Cl^– (g) (steps 3 and 4) combine to give NaCl(s).

⇒ \(\mathrm{Na}^{+}(\mathrm{g})+\mathrm{Cl}^{-}(\mathrm{g}) \longrightarrow \mathrm{NaCl}(\mathrm{s})\)

Enthalpy change for this process = –\(\Delta_{\text {Laltice }} H\)(The process involves the formation of the lattice.) These steps are depicted as the sequence of steps in the Bom-Haber cycle.

The basis of calculations using the above cycle is that enthalpy being a state function, the sum of enthalpy changes around the cycle (clockwise direction) is zero.

∴ \(-\Delta_{\mathrm{f}} H[\mathrm{NaCl}(\mathrm{s})]+\Delta_{\text {sub }} H[\mathrm{Na}(\mathrm{s})]\)+\(\frac{1}{2} \Delta_{\text {diss }} H\left[\mathrm{Cl}_2(\mathrm{~g})\right]+I \cdot E .+R T-E . A-R T-\Delta_{\text {lattice }}\) H =0

or \(\Delta_{\text {lattice }} H=-\Delta_{\mathrm{f}} H+\Delta_{\text {sub }} H+\frac{1}{2} \Delta_{\text {diss }} H+I \cdot E .-E . A .\)

The \(\Delta_{\mathrm{f}}H\) of NaCl(s) is -411.2 kJ.

Substituting the appropriate values on the RHS, we get

∴ \(\Delta_{\text {Lattice }} H =411.2+108.4+\frac{1}{2} \times 242+495.8-348.6\) =1136.4-348.6

∴ \(\Delta_{\text {Lattice }} H =787.8 \mathrm{~kJ}\).

Bond energy: By now you know what enthalpies of formation of compounds are. You also know that compounds are formed by the breaking and making of bonds. To have a precise knowledge of the enthalpy change for a process, the bond dissociation enthalpy or the bond dissociation energy [ΔH(A-B)] is considered.

For example, when the dissociation, or breaking, of a chemical bond occurs as in the following process,the corresponding molar enthalpy change is called the bond dissociation enthalpy. Thus, the bond dissociation enthalpy is tire enthalpy associated with the breaking of 1 mol of a substance in the gaseous state completely into its gaseous atoms.

∴ AB(g) → A(g) + B(g)

The values of bond enthalpies depend on the bonding present between two atoms in the molecule. Even in the same molecule, the values may differ. For example, to break the first O—H bond in water, the enthalpy change \(\Delta H^{\ominus}(\mathrm{HO}-\mathrm{H})\)= 492 kJ mol^-1 while for breaking the second bond, \(\Delta H^{\ominus}(\mathrm{O}-\mathrm{H})\) is 428 kJ mol^-1.

• In methane four hydrogen atoms are attached to a carbon atom and the four C—H bonds are equal in energy and bond length. In this case the total enthalpy is expected to be four times the C—H bond enthalpy.
• However, this is not the case, the reason being different dissociation steps. The first step involves the breaking of a C—H bond in the CH₄ molecule but in the next step the C—H bond is broken in a CH₃ radical, and so on.

The energies required to break the individual C—H bonds in different dissociation steps are as follows.

∴ \(\mathrm{CH}_4(\mathrm{~g}) \longrightarrow \mathrm{CH}_3(\mathrm{~g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {bond }} H^{\ominus}=427 \mathrm{~kJ} \mathrm{~mol}^{-1},\)

∴ \(\mathrm{CH}_3(\mathrm{~g}) \longrightarrow \mathrm{CH}_2(\mathrm{~g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {bond }} H^{\ominus}=439 \mathrm{~kJ} \mathrm{~mol}^{-1},\)

∴ \(\mathrm{CH}_2(\mathrm{~g}) \longrightarrow \mathrm{CH}(\mathrm{g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {bond }} H^{\ominus}=452 \mathrm{~kJ} \mathrm{~mol}^{-1},\)

∴ \(\mathrm{CH}(\mathrm{g}) \longrightarrow \mathrm{C}(\mathrm{g})+\mathrm{H}(\mathrm{g}) ; \Delta_{\text {bond }} H^{\ominus}=347 \mathrm{~kJ} \mathrm{~mol}^{-1}\).

The total enthalpy change for the atomisation of methane \(\left[\mathrm{CH}_4(\mathrm{~g}) \longrightarrow \mathrm{C}(\mathrm{g})+4 \mathrm{H}(\mathrm{g})\right] \text { is } \Delta_{\mathrm{a}} H^{\ominus}\) = 166 x 103 kJ mol^-1.

In case of reactions for which experimental data are not available for successive steps, mean bond enthalpy is used. It is the value of bond dissociation energy of a bond A—B averaged over a series of related compounds. For example, the bond energy for the O—H bond, \(\Delta H^{\ominus}\)(O—H) (averaged between H₂O and alcohols) is 463 kJ mol^-1.

Similarly, in case of CH₄, all the bond enthalpies added together come to 1665 kJ mol^-1. The mean bond enthalpy of C—H bond in CH₄ is

⇒ \(\frac{1}{4} \Delta_a H^{\ominus}=\frac{1}{4} \times 1665=416 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Now consider the atomisation of a diatomic molecule: \(\mathrm{H}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{H}(\mathrm{g}) ; \quad \Delta_a H^{\ominus}=435 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Since two atoms are formed, the energy value is the enthalpy of atomisation of H₂ at 298 K.

The corresponding bond energy \(\Delta_a U^{\ominus}\) for the same reaction (with a little difference from the enthalpy) is 430.8 kJ mol^-1. That is why the two quantities are often used interchangeably. But the correct way would be to convert from ΔU to ΔH.

We know that ΔH = ΔU + pΔV

Some important bond enthalpies (kJ mol^-1) of multiple bonds are as follows.

C—C = 612 N=N = 418 O=O= 497

C≡C = 837 N≡N = 946

C=O = 741 C=N = 615

• For gases, pΔV (at constant pressure) may be replaced by RT. In case of a diatomic molecule, the bond energy is equal to the bond dissociation energy.
• The dissociation energy may here be defined as the enthalpy change involved in breaking the bond between atoms of a gaseous diatomic molecule. Also, it can be seen that bond enthalpy in homonuclear diatomic molecules is twice the enthalpy of formation for the atom in the gaseous state.

Bond energies can be used to calculate the enthalpy of a reaction. The standard reaction enthalpy, \(\Delta_r H^{\ominus}\) is the difference between the sum of the standard enthalpies of the reactants and products.

∴ \(\Delta_r H^{\ominus}=\Sigma \text { bond enthalpies }{ }_{\text {reactants }}-\Sigma \text { bond enthalpies products }\)

This relationship is valid when all the substances in a chemical reaction are in the gaseous state.

Example 1. Calculate the enthalpy change for the following reaction. \(2 \mathrm{C}_2 \mathrm{H}_2(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 4 \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

The average bond energies of the C—H, C≡C, O=O, C—O, and O—H bonds are 414, Hit), 499, 724, and 460 kJ mol^-1 respectively.
Solution:

ΔH = sum of bond energies of reactants – sum of bond energies of products.

The given reaction can be written as 2H—C≡C—H(g) + 5O=O(g) → 4O=C=)(g) + 2H—O—H(g)

∴ \(\Delta H=\left[2 \Delta H_{\mathrm{C} \equiv \mathrm{C}}+4 \Delta H_{\mathrm{C}-\mathrm{H}}+5 \Delta H_{\mathrm{O}=\mathrm{O}}\right]-\left[8 \Delta H_{\mathrm{C}=\mathrm{O}}+4 \Delta H_{O-H}\right]\)

= (2 x 810 + 4 x 414 + 5 x 499) – (8 x 724 + 4 x 460)

= 5771 – 7632 = -1861 kJ mol^-1.

Example 2. Calculate the bond energy of the C—H bond in CH₄ front the following data.

1. \(\mathrm{C}(\mathrm{s})+2 \mathrm{H}_2(\mathrm{~g}) \longrightarrow \mathrm{CH}_4(\mathrm{~g}) \quad \Delta H_1^{\ominus}=-74.8 \mathrm{~kJ} \mathrm{~mol}^{-1}\) ….(1)
2. \(\mathrm{H}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{H}(\mathrm{g}) \quad \Delta \mathrm{H}_2^{\ominus}=435.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\) …..(2)
3. \(\mathrm{C}(\mathrm{s}) \longrightarrow \mathrm{C}(\mathrm{g}) \quad \Delta H_3^{\ominus}=718.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)….(3)

Solution:

To find the bond energy of the C—H bond in CH₄, let us first write the equation for the dissociation of CH₄ into C and H, The enthalpy change for this reaction would be four times the bond energy of the C—H bond since the dissociation of the CH₄ molecule involves the breaking of four C—H bonds.

CH₄ (g) → C(g) + 4H(g) ΔH = ?

The enthalpy change for this reaction can be calculated from the given data by applying Hess’s law. The equation for this reaction can be obtained by multiplying Equation (2) by 2, adding the product to Equation (3), and then subtracting Equation (1) from the sum.

∴ \(\begin{aligned}
\mathrm{C}(\mathrm{s})+2 \mathrm{H}_2(\mathrm{~g}) & \longrightarrow 4 \mathrm{H}(\mathrm{g})+\mathrm{C}(\mathrm{g}) \\
\mathrm{C}(\mathrm{s})+2 \mathrm{H}_2(\mathrm{~g}) & \longrightarrow \mathrm{CH}_4(\mathrm{~g}) \\
\hline \mathrm{CH}_4(\mathrm{~g}) & \longrightarrow 4 \mathrm{H}(\mathrm{g})+\mathrm{C}(\mathrm{g})
\end{aligned}\)

∴ ΔH = 2 x ΔH₂ + ΔH₃ – ΔH₁

= 2 x 435.4 + 718.4-(-748)

= 870.8 + 718.4 + 748 = 16640 kJ mol^-1.

Thus, the energy required to break four C—H bonds = 1664.0 kJ mol^-1.

Therefore, the bond energy of the C—H bond = 1664/4 = 416 kJ mol^-1.

Alternatively, the enthalpy of the formation of the reactants and products can also be used to find the enthalpy change for the required reaction.

ΔH = ∑ΔH_f (products) -∑ΔH_f (reactants)

ΔH = [ΔH₃ +2ΔH₂]-ΔH₁

= [718.4 + 2 x 435.4] – [-748]

= 718.4 + 870.4 + 74.8 = 1664.0 kJ mol^-1,

∴bond energy of C—H bond = 1664/4 = 416 kJ mol^-1.

The Measurement Of Heat

In the laboratory, heat changes in physical and chemical processes are measured with a calorimeter. Calorimetry is the measurement of heat changes associated with a process. The study of calorimetry involves the concept of specific heat and heat capacity. So let us define these first

The heal capacity (C) of a substance is the amount of heat required to raise the temperature of a given quantity of it by 1°C Heat capacity is an extensive property. It is more convenient to use an intensive property. Therefore, the molar heat capacity, C_m (C_m = C/n in JK^-1 mol^-1 where n is the amount of the substance), is used. The specific heat capacity C_s (C_s = C/m in JK^-1 g^-1, where m is the mass of the substance) is also an intensive property.

For water, the specific heat is \(1 \mathrm{cal} \mathrm{g}^{-1} \mathrm{C}^{-1} \text { or } 4.18 \mathrm{~J} \mathrm{~g}^{-10} \mathrm{C}^{-1}\)

The molar heat capacity of a substance is the heat required to raise the temperature of 1 mol of the substance by one degree.

The heat capacity at constant volume (C_v) is given by \(C_v=\frac{q_v}{\Delta T} .\)

From the first law of thermodynamics, we have q = ΔU ÷ pΔV.

At constant volume, ΔV = 0. q_v = AU.

∴ heat capacity at constant volume is given by \(C_V=\left(\frac{\Delta U}{\Delta T}\right)_V\)

Thus, the heat capacity at constant volume is defined as the rate of change of internal energy with temperature.

The heat capacity at constant pressure is given by \(C_p=\frac{q_p}{\Delta T}.\)

We have already learned that, at constant pressure, ΔH = q_p.

Therefore, heat capacity at constant pressure is given by \(C_p=\left(\frac{\Delta H}{\Delta T}\right)_p\)

Thus, the heat capacity at constant pressure is defined as the rate of change of enthalpy with temperature. Relationship between C_p and C_v We know that, at constant pressure (Equation 6),

ΔH = ΔU + pΔV.

For 1 mole of an ideal gas, pΔV = RΔT (ideal gas equation).

Thus, Equation 6 can be written as ΔH = ΔU + RΔT

On dividing the equation by ΔT, we get \(\frac{\Delta H}{\Delta T}=\frac{\Delta U}{\Delta T}+R\)

or C_p = C_v + R

or C_p – C_v = R

C_p is always greater than C_v for any gas, since in a constant-pressure process a system has to do work against the surroundings.

Coming back to the measurement of energy changes associated with chemical or physical processes, measurements are made under two different conditions:

1. at constant volume, ΔU -q_v, and
2. at constant pressure, ΔH = q_p.

Constant-volume calorimetry: The reactions that can be most easily studied under constant- volume conditions are combustion reactions. The apparatus used for this purpose is called the bomb calorimeter or adiabatic bomb calorimeter. It consists of a sealed constant-volume steel container (known as a bomb) in which the reaction occurs. The bomb can withstand high pressures.

• A known mass of a combustible substance is placed in the bomb, which is filled with oxygen at 30 atm pressure. The sealed bomb is then immersed in a known amount of water contained in an insulated container. The whole set-up is called the calorimeter. Since the outer covering is insulated, there is no heat exchange with the surroundings and hence the reaction process is adiabatic.
• The sample is ignited electrically and the heat produced by the combustion reaction is absorbed by the water surrounding the bomb and the bomb itself. The temperature of the water is monitored and the heat produced is calculated using the equation

∴ \(q=C_{\text {cal }} \Delta T,\) ….(1)

where C_cal is the heat capacity of the calorimeter. C_cal is determined separately by igniting a known amount of a substance whose heat of combustion is already known, in the same calorimeter.

• Thus the heat produced in the reaction may be determined. We already know that at constant volume q_v = ΔU. In constant- volume calorimetry, the heat change observed is simply the change in internal energy.
• This value may be modified to get the enthalpy, but the pressure changes are usually small and may be neglected. The heat changes may be simply assumed to correspond to enthalpy changes.

Constant-pressure calorimetry: To measure the heat changes at constant pressure, a device comparable to a thermos flask is used. The calorimeter is just a vessel with a stirrer and a thermometer.

The system is insulated from the surroundings and hence acts as an isolated system. The heat changes within the vessel are measured in terms of the change in temperature of the system. Constant monitoring of the temperature before and after the reaction helps in finding q and hence AH, as we know that, ΔH = q_p

The amount of heat exchanged (q_v or q_p) in any process is given by, q_p =msΔT……(2)

where m is the mass of the substance, s is its specific heat and ΔT is the change in the temperature.

You already know that q = CΔT =C_p ΔT (at constant pressure),

where C = ms, the heat capacity of the system.

• Thus to determine q, C and ΔT have to be known first. The experimental technique—calorimetry—actually involves two steps, the first being the determination of the heat capacity of the calorimeter.
• The second step involves the determination of the change in temperature during the completion of the reaction. Since it is an insulated system, no heat is lost to the surroundings as in the case of constant-volume calorimetry.

As you already know, the enthalpy of the reaction is simply the heat change at constant pressure,  ΔH = q_p (at constant pressure).

Enthalpy changes are commonly tabulated at 25°C and it is often required to know their values at other temperatures. They can be calculated from the heat capacities of the reactants and products.

You know that ΔH = H(products) – H(reactants).

At constant pressure ΔH /ΔT = C_p.

Therefore, for small changes in temperature, \(\frac{\Delta(\Delta H)}{\Delta T}=C_p \text { (products) }-C_p \text { (reactants) }=\Delta C_p \Delta T\)

∴ \(\Delta(\Delta H)=\Delta C_p\left(T_2-T_1\right)\)

or \(\Delta H_2-\Delta H_1=\Delta C_p\left(T_2-T_1\right)\),

where ΔH₂ is the enthalpy of the reaction at T₂ and ΔH₁ is that at T₁.

Example 1. Calculate the enthalpy change on the freezing of 1 mol of zoater at -5°C to ice at -5°C. Given that

⇒ \(\Delta_{\text {tom }} H^{\oplus}\left(\mathrm{H}_2 \mathrm{O}\right)=6.03 \mathrm{~kJ} \mathrm{~mol}^{-1} \text { at } 0^{\circ} \mathrm{C} \text { and } C_p\left[\mathrm{H}_2 \mathrm{O}(\mathrm{l})\right]\)

= \(75.3 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}, C_{,},\left[\mathrm{H}_2 \mathrm{O}(\mathrm{s})\right]=36.8 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \text {. }\)

Solution:

To find the enthalpy change at -5°C, we use the equation: \(\Delta H_2-\Delta H_1=\Delta C_p\left(T_2-T_1\right) .\)

First, we will find Δ_fus H at -5°C and then convert it to ΔH (freezing) by prefixing a (-) sign to Δ_fusH.

Also, ΔH is in kJ and C_p in J. Converting, Δ_fusH = 6.03 kJ mol^-1 = 6.03 x 1000 J mol^-1.

∴ \(\Delta H_2-6.03 \times 1000= (75.3-36.8)\times(-5-0) \)

= \(C_p(1)-C_p(\mathrm{~s})=-192.5\)

∴ \(\Delta H_2=-192.5+6030=5837.5\)

Thus \(\Delta_{\text {fus }} H at -5^{\circ} \mathrm{C}=5837.5 \mathrm{~J} \mathrm{~mol}^{-1}=5.84 \mathrm{~kJ} \mathrm{~mol}^{-1} and \Delta H (freezing) at -5^{\circ} \mathrm{C}\)

= \(-5.84 \mathrm{~kJ} \mathrm{~mol}^{-1}\).

Example 2. Find the heat required to raise the temperature of 27.9 g of Fe from 30 to 40°C. The molar heat capacity of Fe(s) =25.10 J K^-1mol^-1.
Solution:

The molar heat capacity is the heat required to raise the heat of 1 mol of the substance, i.e., 55.8 g (molar mass of Fe) by 1°C.

The heat required to raise the temperature of 55.8 g of Fe by 1°C = 25.1 J.

The heat required to raise the temperature of 27.9 g of Fe by 1°C = \(\frac{25.1}{55.8}\) x 27.9 J.

∴ the heat required to raise the temperature of 27.9 g of Fe by 10°C = \(\frac{25.1}{55.1}\)x 27.9 x 10 = 125.5 J.

Example 3. 1.922 g of methanol (CH₃OH) was burnt in a constant-volume bomb calorimeter. The temperature of water rose by 4.2°C. If the heat capacity of the calorimeter and its contents is 10.4 kJ °C^-1, calculate the molar heat of combustion of methanol.
Solution:

If qcal is the quantity of heat involved in the reaction and C„ is the heat capacity of the calorimeter, then

∴ \(q_{\text {eat }}=C_V \Delta T\)

But \(q_{\text {cal }}=-q_r\)

∴ \(\quad q_r=-C_v \Delta T\)

= \(-10.4 \times 4.2\left[because \text { the temperature rose by } 4.2^{\circ} \mathrm{C}, \Delta T \text { is positive }\right]\) = \(-43.68 \mathrm{~kJ}\).

The minus sign indicates exothermic nature of the reaction.

Since the pressure changes are small and can be neglected, q_r = ΔH_r.

Tim ΔH for burning 1.922 g of methanol is -43.68 kJ.

The ΔH for burning 1 mol or 32 g of methanol is obtained as

∴ \(\Delta H=\frac{-43.68 \mathrm{~kJ}}{1.922 \mathrm{~g}} \times 32 \mathrm{~g} \mathrm{~mol}^{-1}\) = -727.24 kJ mol^-1.

The molar enthalpy or molar heat of combustion is therefore -727.24 kJ mol^-1.

Spontaneous Processes

Generally speaking, when we say something has happened spontaneously, we mean that it has happened of its own accord. In chemistry, the meaning is a little different. It would be easy enough for you to associate the word spontaneous with a process like the dissolving of sugar in water, or the evaporation of water from an open vessel.

1. But the burning of coal in air, or the burning of ethane to produce carbon dioxide and water are also spontaneous processes, even though these processes have to be initiated by ignition.
2. Any process which can occur under a given set of conditions is called a spontaneous process, irrespective of whether it occurs on its own, or needs to be initiated. In other words, a spontaneous process occurs on its own or has a tendency to occur. A simple way of saying this is that a spontaneous process is a process which is possible.
3. It is not possible, for example, to dissolve sand in water, so this is not a spontaneous process. Water cannot flow uphill, so this is not a spontaneous process either. Some nonspontaneous processes can, however, be made to occur by providing energy from an external source.
4. For instance, water can be made to flow uphill by using a pump. Similarly, though the electrolysis of water is not a spontaneous process, it can be made to occur by supplying electrical energy.

You may wonder about the difference between a nonspontaneous process which can be made to occur by supplying energy and a spontaneous process which requires initiation. The combination of gaseous hydrogen and oxygen to form water is a spontaneous reaction which has to be initiated by an electric spark.

∴ \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

• The electrolysis of water is a nonspontaneous process which requires electrical energy. The difference is that once a spontaneous reaction has been initiated, it proceeds on its own, while a nonspontaneous process stops as soon as the supply of external energy stops.
• Once the electric spark starts the reaction between hydrogen and oxygen, the process continues on its own. But if the supply of electric current is stopped during the electrolysis of water, the process stops.

Criterion for spontaneity: What makes certain processes possible or spontaneous, and certain others not possible or nonspontaneous? What is the driving force behind the occurrence of different processes? If we know this we can predict whether a certain process would be possible.

• You have already read in several contexts that every system seeks to have the minimum possible energy in order to acquire the maximum stability. Water flows down a hill to have the minimum possible potential energy. A wound spring unwinds itself to minimise energy. Atoms form bonds with each other in order to have less energy.
• This may lead you to the conclusion that the criterion for a process is the reduction of energy, or that a process is possible if it causes a reduction in the energy of the system. Let us consider some chemical reactions and see if this is right. In exothermic reactions, the energy of the products is less than the energy of the reactants and the reaction is accompanied by the evolution of heat.

⇒ \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \Delta H =-394 \mathrm{~kJ}\)

⇒ \(\mathrm{~N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{NH}_3(\mathrm{~g}) \Delta H =-92 \mathrm{~kJ}\)

In such cases at least we may be right in saying that the tendency to attain a state of minimum energy (i.e., negative enthalpy change) is the driving force behind the occurrence of a reaction. But what about endothermic reactions which are spontaneous?

⇒ \(\mathrm{H}_2 \mathrm{O}(\mathrm{s}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \Delta H=5.86 \mathrm{~kJ}\)

⇒ \(\mathrm{NH}_4 \mathrm{Cl}(\mathrm{s})+\mathrm{aq} \longrightarrow \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq}) \Delta H=177.8 \mathrm{~kJ}\)

⇒ \(\mathrm{CaCO}_3(\mathrm{~s}) \longrightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_3(\mathrm{~g}) \Delta H=15.1 \mathrm{~kJ}\)

• These three reactions involve the absorption of heat, which means that the reactions lead to an increase in the energy of the system, so reduction of energy cannot be the only criterion determining the spontaneity of a reaction.
• Reversible reactions also prove that decrease in energy or negative enthalpy change cannot be the only determining factor for the feasibility of a reaction. Suppose the forward reaction is exothermic then the backward reaction has to be endothermic and it would not occur if the only criterion for spontaneity were reduction of energy.

The tendency towards maximum disorder: To investigate what other factors could possibly determine the spontaneity of a process, let us consider a process for which ΔH = 0, since for such a process the energy factor could not be the driving force. The mixing of air and bromine vapour is just such a process.

• Suppose vessel A contains bromine vapour and vessel B contains air and there is a movable partition between the two. Now suppose that the partition is removed. The two gases will mix completely. What makes this possible? When the samples of air and bromine vapour are in two separate vessels, there is more order and when they diffuse into each other, there is more disorder.
• This tendency of a system to move towards greater disorder or to maximise randomness is the other driving force which makes reactions possible. It explains why endothermic reactions are possible despite the fact that ΔH is positive for such reactions. Take the case of the dissolution of ammonium chloride in water.

⇒ \(\mathrm{NH}_4 \mathrm{Cl}(\mathrm{s})+\mathrm{aq} \longrightarrow \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{Cl}^{-}(\mathrm{aq})\)

• This is an endothermic process, but it is possible because the randomness of the system increases. How? When the ions are held together in the crystal lattice there is more order and when they go into the aqueous solution, they are more free to move about, hence there is more disorder.
• Just as the energy factor (minimising energy) cannot be the only criterion which determines the spontaneity of a process, nor can maximising randomness be the sole determining factor. If this were the case, the liquefaction of a gas (which increases order or decreases randomness) would not have been possible. But we will come to that later.

Entropy: The randomness or disorder of a system is measured in terms of a function called entropy. It is a state function, represented by S and measured in J K^-1.

Change in entropy (ΔS) = S_{final state} – Sintial state

or ∑ S_products – ∑ S_reatants

When ΔS for a process is positive, the process leads to an increase in randomness or disorder.

In the examples discussed earlier, the processes are accompanied by an increase in entropy. We may again tend to conclude that for spontaneous processes there must be an increase in entropy. However, there are cases where entropy decreases. For example, the spontaneous condensation of steam to liquid water.

⇒ \(\underset{s^{\ominus}=188.7 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}}{\mathrm{H}_2 \mathrm{O}(\mathrm{g})} \longrightarrow \underset{s^{\ominus}=70.0 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}}{\mathrm{H}_2 \mathrm{O}(\mathrm{l})}\)

• The standard molar entropy values for liquid water and water vapour are given and show that there is a decrease in entropy. Standard entropy may be defined in a manner similar to standard enthalpy.
• The standard molar entropy of a substance is the entropy of one mole of the pure substance at 1 bar pressure and a specified temperature, usually 298 K. Let us not be in a hurry to make conclusions. When steam condenses, energy is given out, \(\Delta H^\ominus\) being -44.1 kJ mol^-1 for the reaction.
• Where does this energy go? If the water condenses on a window, the energy is passed on to the window and when it condenses in the air, energy is taken up by the air molecules. Therefore, the entropy of the surroundings increases.
• The tendency towards disorder is summed up in the second law of thermodynamics, which states that spontaneous reactions are accompanied by a net increase in the entropy of the universe. Here the universe means the system and surroundings taken together,

⇒ \(\Delta S_{\text {univ }}>0 \) (2nd law thermodynamics).

⇒ \(\Delta S_{\text {uriv }}=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\)

In the case of condensation of water, \(\Delta S_{\text {univ }}=\Delta S_{\text {water }}+\Delta S_{\text {surr }}\)

• The positive ΔS_surr outweighs the negative ΔS_water and the total entropy increases.
• For all spontaneous processes, a stage is reached when the system attains equilibrium. A glass of hot water cools till it attains room temperature. It does not cool below room temperature. At this point, it is said to have attained equilibrium or, to be more precise, thermal equilibrium.

A gas expands till it fills the whole of the available space uniformly. Then no further expansion occurs. Again this is a state of equilibrium. At the point of equilibrium,

ΔS_univ = 0 (at equilibrium).

Having understood that entropy is a measure of disorder or randomness of a system, it may be easy to imagine that at absolute zero, the entropy of a perfectly crystalline substance would be zero. At any temperature above this, the entropy is positive and it increases with an increase in temperature.

For any substance S_solid < S_liquid < S_gas

For any system the heat changes are reflected in the entropy of that system. Hence, let us find an expression relating entropy and heat. Consider an exothermic reaction. The heat released in an exothermic reaction flows to the surroundings and the heat lost by the system is equal to the heat gained by the surroundings.

q_surr = -q_sys

This equation is valid even for an endothermic reaction. In the case of an exothermic reaction, the flow of heat into the surroundings increases its entropy, i.e.,

ΔS_surr>0.

The actual magnitude of ΔS_surr however, depends on the amount of heat released as well as the temperature. In fact, the effect of q on entropy is related to temperature. The addition of heat to colder surroundings has a greater effect on the entropy as compared to the effect produced on addition of heat to hotter surroundings. The effect of q is greater if the temperature is lower. This can be mathematically expressed as

⇒ \(\Delta S_{\text {surt }}=\frac{q_{\text {surr }}}{T}=-\frac{q_{\text {sys }}}{T} .\)….(1)

We know that at equilibrium \(\Delta S_{\text {undv }}=0=\Delta S_{\text {sys }}+\Delta S_{\text {surr }} \text {. }\)….. (2)

Therefore, form equations (1) and (2) we get \(\Delta S_{s y s}=\frac{+q_{s y s}}{T}\)

If the process is reversible, the change in entropy of the system is given by \(\Delta S_{r v}=\frac{q_{r v v}}{T}.\)

• You may wonder that if no real processes take place reversibly, what is the use of the above equation. Although transfer of heat between system and surroundings is almost impossible to achieve in a reversible manner, this idealised path is important for the definition of ΔS.
• Entropy is a state function and the value of ΔS is the same for a change from say any state A to any other state B, irrespective of the path taken. Whether the change is carried out in a reversible or an irreversible manner, ΔS is the same.
• Thus whatever may be the actual path taken, ΔS is calculated using q_rev only. q_rev is the heat associated with the process had it traversed a reversible path.

The overall criterion for spontaneity: To get back to what we were discussing earlier, the overall criterion for the spontaneity of a process is the resultant of two tendencies—

1. The tendency towards minimum energy and
2. The tendency towards maximum entropy. These two tendencies act independently of each other and may work in the same or opposite directions.

The resultant of the two tendencies is expressed by another thermodynamic function called Gibbs free energy (G). The free energy of a system is a measure of its capacity to do useful work. The enthalpy (H), entropy (S), and free energy (G) of a system are related by the following expression.

G = H-TS (here T is the absolute temperature).

At constant temperature and pressure, the change in free energy (AG) during a process can be obtained by the following equation.

ΔG = ΔH -TΔS…… Equation 7

1. The change in free energy takes into account both the change in enthalpy and the change in entropy, and is the factor which determines the spontaneity of a process. You know that a process is possible if it is accompanied by a decrease in energy (ΔH negative) and an increase in entropy (ΔS positive).
2. Some processes for which ΔH is positive are possible because they are accompanied by an increase in entropy (ΔS positive). Some processes for which ΔS is negative are possible because they are accompanied by a decrease in energy (ΔH negative).
3. Obviously, the conditions that are most favourable for the occurrence of a process are a decrease in energy and an increase in entropy, i.e., when ΔH is negative and ΔS is positive.

This makes ΔG negative. Basically, the criterion for a spontaneous reaction or feasibility of a reaction is that ΔG should be negative. A spontaneous reaction is always accompanied by a decrease in free energy, i.e.,

ΔG < 0 for a spontaneous process.

The tendency of the system to undergo a change in the direction of decreasing free energy makes it reach a state when ΔG = 0 at some point. This is the equilibrium state.

Thus, ΔG > 0 for a nonspontaneous process.

• However, the reverse of a nonspontaneous process (for which ΔG is positive) is spontaneous.
• In order to understand the meaning of free energy for a process being zero, let us consider the simple case of water. Water freezes spontaneously at T<0°C and icc melts spontaneously at T>0°C. At T = 0°C and 1 atm pressure, the ΔG for melting of ice and freezing of water is zero.
• At this temperature, theoretically, ice should not melt and water should not freeze. This means the two phases, liquid and solid, may coexist in equilibrium with each other.
• We may also have chemical reactions for which ΔG = 0. As a spontaneous chemical reaction proceeds (ΔG < 0), reactants turn into products and ΔG becomes less negative. At a point ΔG becomes zero—no more products are formed nor are any reactants consumed. This is a state of equilibrium or in fact chemical equilibrium.
• Reactions with negative ΔG are called exergonic and those with positive ΔG are called endergonic reactions.

When is ΔG negative? It is worth finding an answer to this question because it will help us determine which processes are feasible and under what conditions. The figure represents graphically the relation between ΔH, ΔS, and ΔG.

1. Obviously, when ΔH is negative and ΔS is positive, ΔG will be negative (line ‘a’)
2. When ΔH is negative and ΔS, too, is negative, ΔG will be negative if the magnitude of ΔH is greater than that of TΔS (line ‘b’), i.e., below temperature T_b.
3. When both ΔH and ΔS are positive, AG will be negative if the magnitude of TΔS is greater than that of ΔH (line ‘c’, i.e., above temperature T_c).
4. When ΔH is positive, while ΔS is negative, ΔG will be positive and the reaction will not be spontaneous.

Effect of temperature on spontaneity If you think about the last two conditions for ΔG to be negative, it will strike you that temperature must be an important factor in determining the spontaneity of a reaction. Say, both ΔH and ΔS are negative for a process. If tire magnitude of ΔH is greater than that of TΔS, ΔG will be negative and the process will be feasible.

• It could be possible that this is true up to a certain value of T, beyond which TΔS becomes greater in magnitude than ΔH. Similarly, if both ΔH and ΔS are positive for a particular process, there could be a temperature below which the magnitude of TΔS is less than that of ΔH, and the process is not feasible.
• For an endothermic process, ΔH is positive, i.e., the energy factor opposes the process. For such a process to occur, TΔS must be positive and its magnitude must be greater than that of ΔH.

• For such a process, a higher temperature is more favorable as tills increases the magnitude of TΔS. In fact, there may be a temperature below which the magnitude of TΔS becomes less than that of ΔH and the process becomes unfeasible.
• For an exothermic process, ΔH is negative and ΔG is negative at all temperatures if ΔS is positive. However, if ΔS is negative, the process is feasible only if the magnitude of TΔS is less than that of ΔH.
• Obviously, such a reaction would be more feasible at a low temperature and may even become nonspontaneous above a particular temperature.

If ΔH is the major factor contributing to negative ΔG value, the reaction is called ‘enthalpy driven’ and if entropy is the factor behind it, it is called an ‘entropy driven’ reaction. A few values of \(\Delta H^{\ominus}, \Delta G^{\ominus} \text { and } \Delta S^\ominus\) are given in Table. Let us now summarise whatever we have discussed so far pertaining to the feasibility of a reaction in Table.

Units of \(\Delta G^{\ominus}\): cal mol^-1 in the CGS system and J mol^-1 or kJ mol^-1 in the SI system.

Standard free energy change: The standard free energy change of a reaction is defined as the free energy change at a specified temperature when the reactants in their standard states are converted to products in their standard states. It is denoted by \(\Delta G^{\ominus}\).

Calculation of \(\Delta G^{\ominus}\)° of a reaction Free energy is a state function. Hence, similar to \(\Delta H^{\ominus}\), \(\Delta G^{\ominus}\) for a reaction can be calculated from the free energy of formation of reactants and products.

The standard free energy of formation of an element in its standard state is taken as zero. Table lists values of standard enthalpy of formation, the standard free energy of formation, and absolute standard entropies of some compounds.

Tire standard free energy change of a reaction is obtained by subtracting the sum of the standard free energy of formation of the reactants from that of the products.

∴ \(\Delta_r G^{\ominus}=\Sigma v \Delta_f G^{\ominus} \text { (products) }-\Sigma v \Delta_f G^{\ominus} \text { (reactants) }\)

where v’s are the stoichiometric coefficients of the products and reactants respectively.

∴ \(\Delta G^{\ominus}\) may also be calculated from \(\Delta H^{\ominus}\) and \(\Delta S^{\ominus}\) of the reaction using an equation similar to Equation 7.

∴ \(\Delta_f G^{\ominus}\) = \(\Delta_f G^{\ominus}\) at a particular temperature.

We have seen how to calculate \(\Delta G^{\ominus}\) for a reaction. However, all chemical reactions do not occur with the reactants and products in their standard states. We can determine AG for a reaction of this kind using \(\Delta G^{\ominus}\) of the same reaction at standard conditions and the reaction quotient of the reaction. Consider the reaction

αA + βB → γC + δD

A, B, C, and D are the reactants and products while α,β,γ, and δ represent the respective stoichiometries.

The reaction quotient, Q_c, of this reaction is given by \(Q_c=\frac{[C]^\gamma[D]^8}{[A]^\alpha[B]^\beta}\)

The square brackets indicate the concentrations of the reactant/product. Note that the products appear in the numerator and reactants appear in the denominator. The concentration terms of the species are raised to their respective stoichiometric coefficients.

ΔG at any temperature T is related to \(\Delta G^{\ominus}\) as follows:

ΔG = \(\Delta G^{\ominus}\) + RT In Q_c ……. Equation 8

where R is the gas constant.

If the species involved in the reaction are gaseous in nature, concentration is replaced by partial pressure, and the reaction quotient is represented as Q_p.

At equilibrium, Q = K, the equilibrium constant. (Q_c = K_c or Q_p = K_p, as the case may be.)

The Equilibrium constant K of the reaction αA + βB → γC + δD  is given by

K = \(\frac{[\mathrm{C}]_e^r[\mathrm{D}]_e^5}{[\mathrm{~A}]_e^\alpha[\mathrm{B}]_e^\beta}\)

where the subscripts e denote equilibrium concentrations. Also, at equilibrium, ΔG = 0.

Hence, \(\Delta G^{\ominus}\) = -RT In K = -2.303 RT log K.

This gives yet another method of determining \(\Delta G^{\ominus}\) of a reaction. The pressure should be expressed in bar and the concentration in mol L^-1 while determining K_p and K_c respectively.

Example 1. Calculate the entropy change AS per mole for the following reactions.

1. Combustion of hydrogen at 298 K \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

⇒ \(\Delta H=-241.6 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(\Delta G=-228.4 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

2. Vaporisation of methanol at its normal boiling point

Methanol (l) → Methanol (g), Δ_vap H = 23.9 kJ mol^-1, Boiling point = 338 K
Solution:

1. ΔG = ΔH – TΔS.

∴ \(\Delta S=\frac{\Delta H-\Delta G}{T}=\frac{-2416-(-228.4)}{298}=-0.044 \mathrm{~kJ} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} .\)

2. ΔG = ΔH -TΔS.

ΔG = 0.

∴ \(\Delta S=\frac{\Delta_{\mathrm{vap}} H}{T}=\frac{23.9}{338}=0.071 \mathrm{~kJ} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \text {. }\)

Example 2. Calculate the free energy change per mole for the following reactions and predict the feasibility of the reactions.

1. \(\mathrm{CaCO}_3(\mathrm{~s}) \longrightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g}) \quad \text { at } 298 \mathrm{~K}\)

⇒ \(\Delta H=177.9 \mathrm{~kJ} \mathrm{~mol}^{-1} \quad \Delta S=160.4 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\)

2. \(2 \mathrm{NO}_2(\mathrm{~g}) \longrightarrow \mathrm{N}_2 \mathrm{O}_4(\mathrm{~g}) \quad \text { at } 298 \mathrm{~K}\)

⇒ \(\Delta \mathrm{S}=175.6 \mathrm{JK}^{-1} \mathrm{~mol}^{-1} \quad \Delta H=-57.2 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Solution:

1. ΔG =ΔH – TΔS.

∴ ΔG = 177.9 x 10³ – 298 x 160.4 = 130100.8 J mol^-1 = 130.1 kJ mol^-1.

ΔG is positive. Therefore, the reaction is nonspontaneous at this temperature.

2. ΔG = -57.2×10³ – (298 x 175.6) =-109528.8 J mol-1 =-109.5 kj mol”1.

ΔG is negative. Therefore, this reaction is spontaneous at 298 K.

Why Should There Be An Energy Crisis

While reading about the law of conservation of energy, it may have struck you as strange that there should be an energy crisis in the world when energy is not really lost in any process, it is merely converted from one form into another. It is true that energy is merely converted from one form into another, but it is useful to us only in certain forms.

• In most processes that we encounter, a portion of energy is converted into forms we cannot use. Let us look at it in another way. Most of our energy requirements are met by the burning of fossil fuels. The combustion of fuels produces energy which we use. But it also produces carbon dioxide and water, which escape into the air.
• The combustion of fuels is a spontaneous process, but the reverse is not a spontaneous process. So, the combustion of fuels is a one-sided process, which increases disorder. It is this tendency of most processes to increase disorder that wastes energy in our terms.
• Even the energy released during the combustion of fuels cannot be utilised fully to perform useful work. A part of it goes to increase disorder or is wasted according to us. This is why the efficiency of an engine is always less than 1.

∴ \(\frac{\text { work done by engine }}{\text { energy fed into engine }}<1\)

This follows from the equation

ΔG = ΔH-TΔS

or ΔH = ΔG + TΔS.

• If ΔH is the total energy fed into an engine then some of it, i.e., TΔS, will be used to increase disorder and only a part of it (ΔG) will be available for useful work. This is why, though the total energy of the world remains constant, every living process converts a part of it into a form that cannot be used.
• This is the part that goes to increase disorder in the universe. Since AG is the useful part of energy that can be harnessed, it is a measure of the maximum amount of energy that is ‘free’ to do useful work. Hence its name.

Example 1. Calculate the standard enthalpy of formation of ethyl alcohol from the following data.

1. \(\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{l})+3 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}_2(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \Delta_{\mathrm{f}} \mathrm{H}_1^{\ominus}=-1368 \mathrm{~kJ} \mathrm{~mol}^{-1}\) ….. (1)
2. \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \Delta_{\mathrm{f}} H_2^{\ominus}=-393.5 \mathrm{~kJ} \mathrm{~mol}^{-1}\) …..(2)
3. \(\mathrm{H}_2(\mathrm{~g})+\mathrm{S}_2 \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \Delta_{\mathrm{f}} H_3^{\ominus}=-286.0 \mathrm{~kJ} \mathrm{~mol}^{-1}\)…..(3)

Solution: The required equation is

∴ \(2 \mathrm{C}(\mathrm{s})+3 \mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{l}) \quad \Delta_{\mathrm{f}} \mathrm{H}^{\ominus}=\)

To obtain this equation, first multiply Equation (2) by 2 and Equation (3) by 3 and add the products to get Equation (4). Then subtract Equation (1) from Equation (4),

∴ \(\Delta_{\mathrm{f}} H^{\ominus}=\left[2 \times \Delta_f H_2^{\ominus}+3 \times \Delta_{\mathrm{f}} H_3^{\ominus}\right]-\Delta_{\mathrm{f}} H_1^{\ominus}\)

= [(2 x – 393.5) + (3 x – 286.0)] – [-1368] = -1645 +1368 = -277 kJ mol^-1.

Example 2. Calculate the heat of formation of methane, given that the heats of combustion of methane, graphite and hydrogen are – 890, – 394, – 286 kJ mol^-1 respectively.
Solution:

The required equation is \(\mathrm{C}(\mathrm{s})+2 \mathrm{H}_2(\mathrm{~g}) \longrightarrow \mathrm{CH}_4(\mathrm{~g}) \quad \Delta_{\mathrm{f}} \mathrm{H}=\text { ? }\)

The equation for the combustion of methane is \(\mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \quad \Delta_{\mathrm{c}} \mathrm{H}_1=-890 \mathrm{~kJ} \mathrm{~mol}^{-1}\) ….(1)

The equation for the combustion of graphite is \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \quad \Delta_{\mathrm{c}} \mathrm{H}_2=-394 \mathrm{~kJ} \mathrm{~mol}^{-1}\) …..(2)

The equation for the combustion of hydrogen is \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2 \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \quad \Delta_{\mathrm{c}} \mathrm{H}_3=-286 \mathrm{~kJ} \mathrm{~mol}^{-1}\)…. (3)

Multiply Equation (3) by 2 and add the product to Equation (2).

This is the required equation.

Then Δ_fH =[Δ_cH₂ + (2 X Δ_cH₃)]-[Δ_cH₁]

= ((-394) + (2 x – 286)] – [-890] = -394-572 + 890 = -76 kJ mol^-1.

Example 3. Calculate the heat of reaction of \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

Given that

1. \(\mathrm{C}(\mathrm{s})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}(\mathrm{g}) \Delta_f H_2=-110.35 \mathrm{~kJ}\)
2. \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CO}_2(\mathrm{~g}) \Delta_f H_2=-393.35 \mathrm{~kJ}\)
3. \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \Delta_f H_3=-241.6 \mathrm{~kJ}\)

Solution:

This problem can be solved by two methods.

1. Applying Hess’s law:

Add Equation (1) and Equation (3) and then subtract Equation (2) from the resultant equation.

⇒ \(\begin{aligned}
\mathrm{C}(\mathrm{s})+\mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) & \longrightarrow \mathrm{CO}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \\
-\mathrm{C}\left(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g})\right. & \left.\longrightarrow \mathrm{CO}_2(\mathrm{~g})\right) \\
\hline \mathrm{H}_2(\mathrm{~g})+\mathrm{CO}_2(\mathrm{~g}) \longrightarrow & \longrightarrow \mathrm{CO}(\mathrm{g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})
\end{aligned}\)

This is the required equation.

∴ Δ_rH = Δ_fH₁ – Δ_fH₃ – Δ_fH₂ =(-110.35) + (- 2416)- (-39335) = + 414 kj.

2. Δ_fH = ∑Δ_fH(products) – ∑Δ_fH(reactants)

= [Δ_fH(CO) + Δ_fH(H₂O)]- Δ_fH(CO₂)

= -110.35 + (- 2416)- (-39335) = + 414 kj.

Example 4. Just before an athletic event, a participant is given 100 g of glucose (C₆H₁₂O₆), whose energy equivalent is 1560 kj. He utilises 50% of this gained energy in the event. Calculate the weight of water he would need to perspire in order to avoid storing extra energy in the body, ifthe enthalpy ofevaporation ofwater is 44 kj mol^-1.
Solution:

Energy from 100 g of glucose = 1560 kJ.

Energy utilised = 50% of1560 = 780 kJ.

Energy not used = 1560- 780 = 780 kJ.

Enthalpy of evaporation of water = 44 kJ mol^-1.

44 kJ of energy evaporates1 mol of water.

780 kJ of energy would evaporate \(\frac{1 \times 780}{44}\) =17.73 mol of water.

17.73 mol of water = 17.73 x18 g = 319.14 g of water.

Example 5. Calculate the bond energy of the Cl—Cl bondfrom the equation \(\mathrm{CH}_4(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \longrightarrow \mathrm{CH}_3 \mathrm{Cl}(\mathrm{g})+\mathrm{HCl}(\mathrm{g}) \Delta \mathrm{H}=-100.3 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

given that the bond energies ofC—H, C—Cl, H—Cl bonds are 413, 326 and 431 kJ mol^-1 respectively.

Solution: The given equation can be written as

∴ \(\Delta H=\left[4 \Delta H_{\mathrm{C}-\mathrm{H}}+\Delta H_{\mathrm{C}-\mathrm{a}}\right]-\left[3 \Delta H_{\mathrm{C}-\mathrm{H}}+\Delta H_{\mathrm{C}-\mathrm{a}}+\Delta H_{\mathrm{H}-\mathrm{a}}\right]\)

or \(-100.3=\left[(4 \times 413)+\Delta H_{\mathrm{a}-\mathrm{a}}\right]-[(3 \times 413)+326+431]\)

∴ \(\quad \Delta H_{\mathrm{a}-\mathrm{C}}=243.7 \mathrm{~kJ} \mathrm{~mol}^{-1}\).

Example 6. Calculate the enthalpy change for the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Br}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{HBr}(\mathrm{g})\) given that the bond enthalpies of H—H, Br—Br and H—Br are 435,192 and 364 kj mol^-1 respectively.
Solution:

ΔH =∑ bond enthalpies of reactants – ∑ bond enthalpies of products

= [ΔH_H-H + ΔH_Br-Br] – [2 x ΔH_H-Br]

= 435 + 192-(364 x 2)

= 627-728 =-101 kj mol^-1.

Example 7. Calculate the Gibbs energy change for the reaction \(4 \mathrm{Fe}(\mathrm{s})+3 \mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{Fe}_2 \mathrm{O}_3(\mathrm{~s})\) at 25°C when O₂ is at a partial pressure of 1.5 bar. \(\Delta_r G^e\) =-1484.4 kJ mol^-1

Solution:

The reaction quotient Q = \(\frac{\left[\mathrm{Fe}_2 \mathrm{O}_3(\mathrm{~s})\right]^2}{[\mathrm{Fe}(\mathrm{s})]^4\left[p_{\mathrm{O}_2}\right]^3}\).

Since the concentrations of pure solids and liquids are constant,

Q = \(\frac{1}{\left(p_{\mathrm{O}_2}\right)^3}=\frac{1}{(1.5)^3}=0.2963\)

Now, \(\Delta_r G=\Delta_r G^\ominus\) + RT ln Q

= -1484.4 x 10³ + 8.314 x 298 x ln (0.2963) (R = 8.314 JK^-1 mol^-1)

= – 1,484,400-3013.7 =-1,487,413.7 J mol^-1 = -1487.4 kJ mol^-1.

Example 8. Arrange the following systems in order of increasing entropy (compare one mole of each).

1. \(\mathrm{H}_2 \mathrm{O}$ (l), \mathrm{H}_2 \mathrm{O} (s), \mathrm{H}_2 \mathrm{O} (g)\)

2. \(\mathrm{H}_2(\mathrm{~g}), \mathrm{HBrO}_4(\mathrm{~g}), \mathrm{HBr}(\mathrm{g})\)

Solution:

Entropy varies as

1. \(\mathrm{H}_2 \mathrm{O}(\mathrm{s})<\mathrm{H}_2 \mathrm{O}(\mathrm{l})<\mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

2. \(\mathrm{H}_2(\mathrm{~g})<\mathrm{HBr}(\mathrm{g})<\mathrm{HBrO}_4(\mathrm{~g})\)

If the physical state is the same, the more complicated the molecule, the more is the entropy.

Example 9. For the reaction \(2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{SO}_3(\mathrm{~g})\) find ΔG at 25°C. The partial pressures of SO₂, O₂ and SO₃ are 1.0 bar, 0.5 bar and 0.1 bar respectively. \(\Delta G^{\ominus}\) = -141.8kj mol^-1.
Solution:

⇒ \(\Delta G=\Delta G^{\ominus}\) + RT In Qf; where Qf, is the reaction quotient.

⇒ \(Q_p=\frac{\left(p_{\mathrm{SO}_3}\right)^2}{\left(p_{\mathrm{SO}_2}\right)^2\left(p_{\mathrm{O}_2}\right)}=\frac{(0.1)^2}{(1)^2(0.5)}=0.02\)

∴ \(\Delta G=\Delta G^{\ominus}+R T \ln Q\)

= -1418 x 10³ + 8314 x 298 x In 0.02

=-151,4923 J mol^-1

=-151.5 kj mol^-1

Example 10. The \(\Delta S_{\text {system }} \text { and } \Delta_t H^{\ominus}\) for the following reaction at 25 C are 220.5 J k^-1 mol^-1 and 90.7 kJ mol^-1. Find S and say in which direction the reaction is not spontaneous.

⇒ \(\mathrm{CH}_3 \mathrm{OH}(\mathrm{g}) \rightleftharpoons \mathrm{CO}(\mathrm{g})+2 \mathrm{H}_2(\mathrm{~g})\)

Solution:

⇒ \(\Delta S_{\text {total }}=\Delta S_{\text {sys }}+\Delta S_{\text {surr }} \text {. }\)

⇒ \(\Delta S_{\text {sys }}=220.8 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \text {. }\)

⇒ \(\Delta S_{\text {surr }}=\frac{-\Delta H^{\ominus}}{T}\)

= \(-\frac{\left(90.7 \times 10^3\right)}{298} \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\)

= \(-304.4 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \text {. }\)

\(\Delta S_{\text {total }}=220.8-304.4=-83.6 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\)

As the entropy decreases (ΔS = -ve) the reaction is not spontaneous in the forward direction but the reverse reaction is spontaneous.

Example 11. Considering only entropy,find whether thefollowing reaction is spontaneous or not at 25°C

⇒ \(\mathrm{N}_2(\mathrm{~g})+2 \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons \mathrm{N}_2 \mathrm{H}_4(\mathrm{l})\)

⇒ \(\mathrm{N}_2(\mathrm{~g}) \quad \mathrm{H}_2(\mathrm{~g}) \quad \mathrm{N}_2 \mathrm{H}_4(\mathrm{l})\)

Given \(\begin{array}{lccc}
\Delta H^{\ominus}\left(\mathrm{kJ} \mathrm{mol}^{-1}\right) & 0 & 0 & 50.6 \\
\Delta S^{\ominus}\left(\mathrm{J} \mathrm{K}^{-1} \mathrm{~mol}^{-1}\right) & 191.5 & 130.6 & 121.2
\end{array}\)

Solution: To predict whether or not a reaction is spontaneous, we must find the sign of \(\Delta S_{\text {total }}=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\)

The entropy change of the system is equal to the standard entropy of the reaction and

⇒ \(\Delta S_{\text {surr }}=-\Delta_r H^{\ominus} / T \text {. }\)

⇒ \(\Delta S_{\mathrm{sys}}=S^{\ominus}\left(\mathrm{N}_2 \mathrm{H}_4(\mathrm{l})\right)-S^{\ominus}\left(\mathrm{N}_2(\mathrm{~g})\right)-2 S^{\ominus}\left(\mathrm{H}_2(\mathrm{~g})\right)\)

= \(121.2-191.5-(2 \times 130.6)\)

= \(-3315 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \text {. }\)

⇒ \(\Delta_{\mathrm{r}} H^{\ominus}=\Delta_f H^{\ominus}\left(\mathrm{N}_2 \mathrm{H}_4(\mathrm{l})\right)-\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{N}_2(\mathrm{~g})\right)-2 \Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{H}_2(\mathrm{~g})\right)\)

= \(50.6-0-0=50.6 \mathrm{~kJ}^{-1} \mathrm{~mol}^{-1} \text {. }\)

⇒ \(\Delta S_{\text {surr }}=-\frac{\Delta_r H^{\ominus}}{T}=\frac{-50.6}{25+273}=-0.1698 \mathrm{~kJ} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}=-169.8 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \text {. }\)

⇒ \(\Delta S_{\text {total }}=\Delta S_{\text {sys }}+\Delta S_{\text {surt }}\)

= \(-331.5+(-169.8)\)

= \(-5013 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \text {. }\)

As \(\Delta S_{\text {total }}\) is negative, the reaction is not spontaneous.

Example 12. The values of equilibrium constant for the following reaction at two different temperatures are 168 x 10^-5 and 0.0123 respectively. If the first temperature is 1000°C, find the second temperature.

⇒ \(\mathrm{H}_2 \mathrm{O}(\mathrm{g})+\mathrm{C}(\mathrm{s}) \longrightarrow \mathrm{H}_2(\mathrm{~g})+\mathrm{CO}(\mathrm{g})\)

Solution:

⇒ \(\Delta G^{\ominus}=-R T_1 \ln K_{p_1}\) …. (1)

⇒ \(\Delta G^{\ominus}=-R T_2 \ln K_{p_2}\)…. (2)

where T₁ and T₂ are the two different temperatures with the corresponding equilibrium constants \(K_{p_1}\) and \(K_{p_2}\) . Equating RHS of (1) and (2),

∴ \(R T_1 \ln K_{p_1}=R T_2 \ln K_{p_2}\)

or \(T_1 \ln K_{p_1}=T_2 \ln K_{p_2}\)

or \(T_2=T_1 \cdot \frac{\ln K_{p_1}}{\ln K_{p_2}}=(1273) \times \frac{\ln \left(168 \times 10^{-5}\right)}{\ln (0.0123)}=3182 \mathrm{~K}\) .

Example 13. Calculate Kp for thefollowing reactions at 298 K

1. \(2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{SO}_2(\mathrm{~g}) \Delta G^{\ominus}=-142 \mathrm{~kJ} \mathrm{~mol}^{-1}\)
2. \(\mathrm{SO}_3(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \mathrm{H}_2 \mathrm{SO}_4(\mathrm{l}) \Delta G^{\ominus}=-81.7 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Solution:

1. \(\Delta G^{\ominus}=-R^{\prime} T \ln K_r \) =\(-2.303 R T \log K_p\)

⇒ \(\log K_p=-\frac{\Delta G^{\ominus}}{2.303 R T}\)

⇒  \(\log K_p=-\frac{\Delta G^{\ominus}}{2.303 R T}\)

or \(K_p=\operatorname{Antilog}\left(\frac{-\Delta G^{\ominus}}{2.303 R T}\right)\)

= \(\text { Antilog }\left(\frac{142,000}{2.303 \times 8.314 \times 2.98}\right)=7.7 \times 10^{24}\).

2. \(K_p= Antilog \left(\frac{81,700}{2.303 \times 8.314 \times 298}\right)=2.08 \times 10^4\).

Example 14. Calculate \(\Delta G^{\ominus}\) for thefollowing reactions

1. \(\mathrm{CaCO},(\mathrm{s}) \longrightarrow \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})\)

⇒  \(K_p=1.06 \text { at } 500^{\circ} \mathrm{C}\)

2. \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\)

⇒  \(\mathrm{K}_p=98.9 \text { at } 300^{\circ} \mathrm{C}\).

3. \(\mathrm{CoO}(\mathrm{s})+\mathrm{CO}(\mathrm{g}) \rightleftharpoons \mathrm{Co}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})\)

⇒  \(K_p=1.09 \times 10^4 \text { at } 277^{\circ} \mathrm{C}\) .

Solution: Since \(\Delta G^{\ominus}\), substituting the values of R, T and Kp we get \(\Delta G^{\ominus}\) for each reaction.

1. \(\Delta G^{\ominus}\) = -8.314 x (500 + 273) x ln(1.06) = -374.4 J mol^-1.

2. \(\Delta G^{\ominus}\) = -8.314 x (300 + 273) x ln(98.9) = -21,885.9 J mol^-1 = -21.88 kj mol^-1.

3. \(\Delta G^{\ominus}\) = -8.314 x (277 + 273) x ln(1.09 x 10⁴ )\(\Delta G^{\ominus}\)= -42310.2 J mol^-1 = -42.51 kJ mol^-1.

Example 15. Calculate \(\Delta G^{\ominus}\) for the following reactions which are carried out under standard state conditions.

1. \(2 \mathrm{LiOH}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g}) \longrightarrow \mathrm{Li}_2 \mathrm{CO}_3(\mathrm{~s})+\mathrm{H}_2 \mathrm{O}(\mathrm{g})\)
2. \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Br}_2(\mathrm{I}) \longrightarrow 2 \mathrm{HBr}(\mathrm{g})\)
3. \(\mathrm{CaO}(\mathrm{s})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{Ca}(\mathrm{OH})_2(\mathrm{~s})\)
4. \(2 \mathrm{HgO}(\mathrm{s}, \text { red }) \rightarrow 2 \mathrm{Hg}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g})\)

The standardfree energies of the compounds are given below.

⇒ \(\Delta_i G\left(\mathrm{~kJ} \mathrm{~mol}^{-1}\right)\)

⇒  \(\mathrm{LiOH}(\mathrm{s}) -443.9 \)

⇒  \(\mathrm{CO}_2(\mathrm{~g}) -394.4\)

⇒ \(\mathrm{Li}_2 \mathrm{CO}_3(\mathrm{~s}) -1132.4\)

⇒ \(\mathrm{H}_2 \mathrm{O}(\mathrm{g}) -228.6\)

⇒  \(\mathrm{H}_2(\mathrm{~g}) 0\)

⇒ \(\mathrm{Br}_2(\mathrm{l}) 0\)

⇒ \(\mathrm{HBr}(\mathrm{g}) -53.43\)

⇒ \(\mathrm{CaO}(\mathrm{s}) -604.2\)

⇒ \(\mathrm{H}_2 \mathrm{O}(\mathrm{l}) -237.2\)

⇒ \(\mathrm{Ca}(\mathrm{OH})_2(\mathrm{~s}) -896.8\)

⇒ \(\mathrm{HgO}(\mathrm{s}, \text { red) } -58.55\)

⇒ \(\mathrm{Hg}(\mathrm{l}) 0\)

⇒ \(\mathrm{O}_2(\mathrm{~g}) 0\)

⇒ \(\Delta_1 \mathrm{H}(\mathrm{Hg}(\mathrm{s}, \text { red }))=-90.83 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

⇒ \(\text { Substance } \mathrm{S}^{\ominus}\left(\mathrm{JK}^{-1} \mathrm{~mol}^{-1}\right)\)

⇒ \(\mathrm{Hg}_{\mathrm{g}} 38.01\)

⇒ \(\mathrm{O}_2(\mathrm{~g}) 205.04\)

⇒ \(\mathrm{HgO}(\mathrm{s}, \text { red) } 70.29\)

Which of these reactions islare spontaneous? For those reactions that are not spontaneous,find the temperature at which they will become spontaneous assuming ΔH and εS to be independent of temperature.

Solution:

1. \(\Delta G^{\ominus}=\Delta_f G^{\ominus}\left(\mathrm{Li}_2 \mathrm{CO}_3(\mathrm{~s})\right)+\Delta_{\mathrm{f}} G^{\ominus}\left(\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right)-2 \times \Delta_f G^{\ominus}(\mathrm{LiOH}(\mathrm{s}))-\Delta_f G^{\ominus}\left(\mathrm{CO}_2(\mathrm{~g})\right)\)

= -1132.4 + (-228.6)- 2 x (-443.9)- (-3944)

= -78.8 kj Spontaneous reaction

2. \(\Delta G^{\ominus}=2 \times \Delta_f G^{\ominus}(\operatorname{HBr}(\mathrm{g}))-\Delta_f G^{\ominus}\left(\mathrm{H}_2(\mathrm{~g})\right)-\Delta_f G^{\ominus}\left(\mathrm{Br}_2(\mathrm{l})\right)\)

= 2 x -53.43- 0- 0

= -106.86 kj Spontaneous reaction

3. \(\Delta G^{\ominus}=\Delta_f G^{\ominus}\left(\mathrm{Ca}(\mathrm{OH})_2(\mathrm{~s})\right)-\Delta_{\mathrm{f}} G^{\ominus}(\mathrm{CaO}(\mathrm{s}))-\Delta_f G^{\ominus}\left(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\right)\)

-896.8- (-6042)- (-237.2)

= -55.4 kjSpontaneous reaction

4. \(\Delta G^{\ominus}=2 \times \Delta_f G^{\ominus}(\mathrm{Hg}(\mathrm{l}))+\Delta_f G^{\ominus}\left(\mathrm{O}_2(\mathrm{~g})\right)-2 \times \Delta_f \mathrm{G}^{\ominus}(\mathrm{HgO}(\mathrm{s} ; \text { red }))\)

= 0 + 0 -(-585) = +58.5 kj.

As \(\Delta G^{\ominus}\) is positive, this reaction is not spontaneous. Now let us find \(\Delta H^{\ominus}\) and \(\Delta S^{\ominus}\).

⇒ \(\Delta H^{\ominus}=2 \times \Delta_{\mathrm{f}} H^{\ominus}(\mathrm{Hg}(\mathrm{l}))+\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{O}_2(\mathrm{~g})\right)-2 \times \Delta_{\mathrm{f}} H^{\ominus}(\mathrm{HgO}(\mathrm{s}, \mathrm{red}))\)

= 0 + 0- (-90.83) = 90.83 kj.

⇒ \(\Delta S^{\ominus}=2 \times S^{\ominus}(\mathrm{Hg}(\mathrm{l}))+S^{\ominus}\left(\mathrm{O}_2(\mathrm{~g})\right)-2 \times S^{\ominus}(\mathrm{HgO}(\mathrm{s}, \text { red }))\)

= (2 x 38.01) + 205.04- 2 x 70.29 = 140.47 JK^-1

For the reaction to be spontaneous T\(\Delta S^{\ominus}\) should exceed \(\Delta H^{\ominus}\). Let us find the temperature at which T\(\Delta S^{\ominus}\) is equal to \(\Delta H^{\ominus}\). Assuming that \(\Delta H^{\ominus}\) and \(\Delta S^{\ominus}\) are independent of temperature.

⇒ T\(\Delta S^{\ominus}\) = \(\Delta H^{\ominus}\)

or T = \(\frac{\Delta H^{\ominus}}{\Delta S^{\ominus}}=\frac{90.83 \times 10^3}{140.47}\) = 646.6 K

Above 646.6 K, the reaction will be spontaneous because then T\(\Delta S^{\ominus}\) > \(\Delta H^{\ominus}\) and \(\Delta G^{\ominus}\) will be negative.

Example 16. Calculate \(\Delta S_295^{\ominus}\) for thefollowing phase changes.

1. \(\mathrm{C}_6 \mathrm{H}_6(\mathrm{l}) \longrightarrow \mathrm{C}_6 \mathrm{H}_6(\mathrm{~g})\)
2. \(\mathrm{Cu}(\mathrm{s}) \longrightarrow \mathrm{Cu}(\mathrm{g})\)
3. \(\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

The standard entropies of C₆H₆(l), C₆H₆(g), Cu(s), Cu(g), H₂O(l) and H₂O(g) are 172.8, 269.2, 33.15, 1663, 69.91 and 188.71 JK^-1 mol^-1 respectively.

Solution:

1. \(\Delta S_{\text {vap }}^{\ominus} =S^{\ominus}\left(\mathrm{C}_6 \mathrm{H}_6(\mathrm{~g})\right)-S^{\ominus}\left(\mathrm{C}_6 \mathrm{H}_6(\mathrm{l})\right)\)

=269.2-172.8

∴ \(\Delta S_{\text {vap }}^{\ominus} =96.4 \mathrm{JK}^{-1}\)

2. \(\Delta S_{\text {sub }}^{\ominus} =S^{\ominus}(\mathrm{Cu}(\mathrm{g}))-S^{\ominus}(\mathrm{Cu}(\mathrm{s}))\)

=166.3-33.15

∴ \(\Delta S_{\text {sub }}^{\ominus} =133.15 \mathrm{JK}^{-1}\)

3. \(\Delta S_{\text {vap }}^{\ominus} \left.=S^{\ominus}\left(\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right)-\mathrm{S}^{\ominus} \mathrm{H}_2 \mathrm{O}(\mathrm{l})\right)\)

=188.71-69.91

∴ \(\Delta S_{\text {vap }}^{\ominus} =118.8 \mathrm{JK}^{-1}\) .

Example 17. Calculate the standaril entropy changefor the combustion ofliquid ethanol, C₂H₅OH to gaseous CO₂ and liquid water. The standard entropies of CO₂(g), H₂O(l), C₂H₅OH(l) and O₂(g) are 213.6 K^-1 mol^-1, 161JK^-1 mol^-1 and 205.03 JK^-1 mol^-1 respectively.
Solution:

⇒ \(\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{l})+3 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{CO}_2(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

⇒  \(\Delta S^{\ominus}=2 \times S^{\ominus}\left(\mathrm{CO}_2(\mathrm{~g})\right)+3 \times S^{\ominus}\left(\mathrm{H}_2 \mathrm{O}(\mathrm{l})\right)-S^{\ominus}\left(\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}\right)-3 \times\left(S^{\ominus}\left(\mathrm{O}_2(\mathrm{~g})\right)\right.\)

= 2 x 213.4 +3 x 69.91- 161-3 x 205.3 = -139.97 J K^-1mol^-1.

Example 18. Find the equilibrium constant of the reaction \(\mathrm{CH}_4(\mathrm{~g})+4 \mathrm{Cl}_2(\mathrm{~g}) \rightleftharpoons \mathrm{Cl}_4(\mathrm{~g})+4 \mathrm{HCl}(\mathrm{g})\)

The standard heats offormation of CH₄ (g), CCl₄ (g) and HCl(g) are -74.81 kJ mol^-1,-102.9 kJ mol^-1 and -92.31 kJ mol⁷ respectively. The standard molar entropies of CH₄ (g), C₂(g), CCl₄(g), and HCl(g) are 186.26, 223.07, 309.7 and 186.91 J K^-1 mol^-1 respectively at 298 K.

Solution:

⇒ \(\Delta_{\mathrm{r}} H^{ominus}=\underset{\text { Products }}{\Sigma \Delta_{\mathrm{f}} H^{ominus}}-\underset{\text { Reactants }}{\Sigma \Delta_f H^{ominus}}\)

= \(\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{CCl}_4(\mathrm{~g})\right)+4 \Delta_{\mathrm{f}} H^{\ominus}(\mathrm{HCl}(\mathrm{g}))-\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{CH}_4(\mathrm{~g})\right)-4 \Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{Cl}_2(\mathrm{~g})\right)\)

= -102. 9 + (4 x -92.31)- (-74.81)

Since the standard enthalpies of formation of elements in their reference states are zero by definition

⇒ \(\Delta_{\mathrm{f}} H^{\ominus}\left(\mathrm{Cl}_2(\mathrm{~g})\right) \text { is } 0\)

⇒ \(\Delta_{\mathrm{r}} H^{\ominus} =-397.33 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

∴ \(\Delta_{\mathrm{r} S^{\ominus}} =\underset{\text { Reaction }}{\Sigma S^{\ominus}}-\underset{\text { Products }}{\Sigma S^{\ominus}}\)

= \(S^{\ominus}\left(\mathrm{CCl}_4(\mathrm{~g})\right)+4 S^{\ominus}(\mathrm{HCl}(\mathrm{g}))-S^{\ominus}\left(\mathrm{CH}_4(\mathrm{~g})\right)-4 S^{\ominus}\left(\mathrm{Cl}_2(\mathrm{~g})\right)\)

= 309.7 + (4 x186.91)- 186.26- (4 x 223.07) = -21.2 JK^-1 mol^-1

Substituting this value of \(\Delta_{\mathrm{r}} S \text { in } \Delta G^{\ominus}=\Delta H^{\ominus}-T \Delta S^{\ominus}\)

⇒ \(\Delta G^{\ominus}\) = -39733 x 10³ -298(-21.2) = -391.01 kJ mol^-1 = -391.01 kJ mol^-1

⇒ \(\Delta G^{\ominus}\) = -RT In K = -2.303 RT log K.

log K = \(-\frac{\Delta G^{\ominus}}{2303 R T}\)

∴ K = \({antilog}\left(\frac{-\Delta G^{\ominus}}{2.303 R T}\right)\)

= \({antilog}\left(\frac{391.01 \times 10^3}{2.303 \times 8.314 \times 298}\right)\)

= antilog (68.53) = 3.37×10⁶⁸.

Example 19. The standard enthalpy changefor the reaction \(\mathrm{NH}_3(\mathrm{aq})+\mathrm{HCl}(\mathrm{aq}) \longrightarrow \mathrm{NH}_4 \mathrm{Cl}(\mathrm{aq})\) at 298 K is -52.22 kJ. The standard Gibbs energy change is -52.81 kJ. Find the standard molar entropy of NH₃(aq) if that of HCl(aq) and NH₄Cl(aq) are 56.5 JK^-1 mol^-1 and 169.9 J K^-1 mol^-1 respectively.

Solution:

⇒ \(\Delta G^{\ominus}\)=\(\Delta H^{\ominus}-T \Delta S^{\ominus}\)

∴ \(T \Delta S^\ominus=\Delta H^\ominus-\Delta G^\ominus\)

or, \(\Delta S^{\ominus}=\frac{\Delta H^{\ominus}-\Delta G^{\ominus}}{T}\)

= \(\frac{-52220 \mathrm{~J}-(-52810 \mathrm{~J})}{298}=\frac{590}{298}=1.98 \mathrm{~J} \mathrm{~K}^{-1} \text {. }\)

Now \(\Delta S^{\ominus}=S_{\mathrm{NH}_4 \mathrm{Cl}(\mathrm{aq})}^{\ominus}-\left(S_{\mathrm{NH}_3(\mathrm{aq})}^{\ominus}+S_{\mathrm{HCl}(\mathrm{aq})}^{\ominus}\right)\).

Substituting the values, we get

1.098= \(169.9-\left(S_{\mathrm{NH}_3(q)}^{\ominus}+56.5\right)\)

∴ \(S_{\mathrm{NH}_3}^{\ominus}=169.9-56.5-198\)

= \(111.42 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\).

Example 20. The \(\Delta_{\text {fus }} H^\ominus \text { and } \Delta_{\text {fus }} S^\ominus \text { of } \mathrm{CCl}_4 \text { are } 2.5 \mathrm{~kJ} \mathrm{~mol}^{-1} \text { and } 9.99 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\) respectively at 298 K. Find the temperature at which solid CCl₄ and its liquid are in equilibrium at 1 atm.

Solution:

⇒ \(\Delta G^{\ominus}=\Delta H^{\ominus}-T \Delta S^{\ominus}\).

But at equilibrium, \(\Delta G^{\ominus}\) = 0.

∴ \(\Delta H^{\ominus}\) = T\(\Delta S^{\ominus}\)

or T = \(\frac{\Delta H^{\ominus}}{\Delta S^{\ominus}}\)=\(\frac{2.5 \times 10^3}{9.99}=250.2 \mathrm{~K}\)

Example 21. Consider the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{HCl}(\mathrm{g}).\)

The standard enthalpy change at 298 K is -186.62 kj. The standard molar entropies of H₂(g), Cl₂(g) and HCl(g) are respectively 130.684, 223.07 and 186.91 J K^-1 mol^-1 respectively. Calculate the standard Gibbs energy change at 298 Kfor the reaction.

Solution:

⇒ \(\Delta G^{\ominus}\) = \(\Delta H^{\ominus}\) – T \(\Delta S^{\ominus}\)

Given \(\Delta H^{\ominus}\) = -186.62 k] and T = 298 K

∴ \(\Delta S^{\ominus}\) = \(\Delta S^{\ominus}\)(products) – \(\Delta S^{\ominus}\)(reactants)

= \(2 \times S^{\ominus}(\mathrm{HCl}(\mathrm{g}))-S^{\ominus}\left(\mathrm{H}_2(\mathrm{~g})\right)-S^{\ominus}\left(\mathrm{Cl}_2(\mathrm{~g})\right)\)

= 2 x 186.91- 130.684- 223.07 = 20.07 JK^-1.

Substituting this value of \(\Delta S^{\ominus}\), we get

⇒ \(\Delta G^{\ominus}\) = -186.62 x 10³ – 298 x 20.07

= -186,620-5980.86 = -192,600.86 J.

The standard free energy change for the reaction is -192.6 kj.

Example 22. Predict whether the entropy of the following reactions wll increase or decrease when the reaction occurs.

1. \(\mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O}(\mathrm{s}) \longrightarrow \mathrm{CaSO}_4(\mathrm{~s})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)
2. \(\mathrm{CH}_4(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{C}(\mathrm{s})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)
3. \(\mathrm{Cu}(\mathrm{s})+\mathrm{S}(\mathrm{g}) \longrightarrow \mathrm{CuS}(\mathrm{s})\)
4. \(\mathrm{N}_2(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 2 \mathrm{NO}(\mathrm{g})\) .

Solution:

Verify your predictions by calculating \(\Delta S^{\ominus}\) using \(S^{\ominus}\) values.

1. In the reactant side we have only a solid whereas in the product side, we also have a gas apart from a solid. Since gases have large entropy, the entropy of system increases.

∴ \(\Delta S^{\ominus}=S^{\ominus}\left(\mathrm{CaSO}_4(\mathrm{~s})+2 \times S^{\ominus}\left(\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right)-S^{\ominus}\left(\mathrm{CaSO}_4 \cdot 2 \mathrm{H}_2 \mathrm{O}\right)\right.\)

= 106.5 + 2 x 188.71-194.0 = 289.92 JK^-1

2. The number of gas molecules (two) is the same on both the reactant and the product side.

Depending on the actual entropies of the substances, \(\Delta S^{\ominus}\) may increase or decrease but only slightly.

∴ \(\Delta S^{\ominus}=S^{\ominus}(\mathrm{C}(\mathrm{s}))+2 \times S^{\ominus}\left(\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right)-S^{\ominus}\left(\mathrm{CH}_4(\mathrm{~g})\right)-S^{\ominus}\left(\mathrm{O}_2(\mathrm{~g})\right)\)

= 5.74 + 2 x188.71- 186.15- 205.03 = -8.02JK^-1

3. One of the reactants is in the gaseous state but the only product is a solid. Hence, the entropy will decrease.

∴ \(\Delta S^{\ominus}=S^{\ominus}(\mathrm{CuS}(\mathrm{s}))-S^{\ominus}(\mathrm{Cu}(\mathrm{s}))-S^{\ominus}(\mathrm{S}(\mathrm{g}))\)

= 66.5- 33.15-167.75 =1344 J K^-1.

4. The total number of gas molecules decreases from three to two as the reaction proceeds from left to right. This results in a decrease in entropy.

∴ \(\Delta S^{\ominus}=2 \times S^{\ominus}(\mathrm{NO}(\mathrm{g}))-S^{\ominus}\left(\mathrm{N}_2(\mathrm{~g})\right)-2 \times S^{\ominus}\left(\mathrm{O}_2(\mathrm{~g})\right)\)

= 2 x 210.65-1915- 2 x 205.03 = -180.26 JK^-1

Thermodynamics Multiple Choice Questions

Question 1. A well-stoppered thermos flask containing some ice cubes is an example of a

1. Closed system
2. Open system
3. Isolated system
4. Nonthermodynamic system

Answer: 3. Isolated system

Question 2. Which of the following is correct in the context of an adiabatic process?

1. pΔV = 0
2. q = +W
3. ΔU=q
4. q = 0

Answer: 4. q = 0

Question 3. The enthalpy change for the reaction \(\mathrm{C}(\mathrm{s})+\mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})\) is

1. Positive
2. Negative
3. Zero
4. None of these

Answer: 2. Negative

Question 4. The enthalpy of formation of ammonia is – 46.0 kJ mol^-1 What is the enthalpy change for the following reaction?

⇒ \(2 \mathrm{NH}_3(\mathrm{~g}) \longrightarrow \mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g})\)

1. + 46.0 kj mol^-1
2. – 23.0 kj mol^-1
3. – 92.0 kj mol^-1
4. + 92.0 kj mol^-1

Answer: 4. + 92.0 kj mol^-1

Question 5. The heat released when 0.6 mol of HNO₃ solution is mixed with 0.2 mol of NaOH is

1. 57.0 kj
2. 11.4 kj
3. 28.5kj
4. 34.9 kj

Answer: 2. 11.4 kj

Question 6. When NaCl dissolves in water, the entropy

1. Increases
2. Decreases
3. Remains the same
4. None of these

Answer: 1. Increases

Question 7. The enthalpy change for the reaction \(\mathrm{H}_2(\mathrm{~g})+\mathrm{1/2}\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\) is called

1. Enthalpy of formation of water
2. Enthalpy of combustion of hydrogen
3. Enthalpy of vaporisation of water
4. None of these

Answer: 1. Enthalpy of formation of water and 2. Enthalpy of combustion of hydrogen

Question 8. The energy required to dissociate 4 g of gaseous hydrogen into free gaseous atoms is 208 kcal at 25°C. The bond energy of the H—H bond is

1. 104 kcal mol^-1
2. 10.4 kcal mol^-1
3. 208 kcal mol^-1
4. 416 kcal mol^-1

Answer: 1. 104 kcal mol^-1

Question 9. In which of the following does entropy decrease?

1. Crystallisation of sugar from a solution
2. Rusting of iron
3. Melting of ice
4. Vaporisation of camphor

Answer: 1. Crystallisation of sugar from a solution

Question 10. For the reaction X→y Y, ΔH and ΔS are negative at a certain temperature. This reaction will be spontaneous at

1. Low temperature
2. High temperature
3. The same temperature
4. Very high temperature

Answer: 1. Low temperature

Question 11. A spontaneous reaction is impossible if

1. Both ΔH and ΔS are positive
2. ΔH and ΔS are negative
3. ΔH is positive and ΔS is negative
4. ΔH is negative and ΔS is positive

Answer: 3. ΔH is positive and ΔS is negative

Question 12. When a solid melts, there is

1. An increase in entropy
2. An increase in enthalpy
3. A decrease in internal energy
4. Decrease in enthalpy

Answer: 1. An increase in entropy and 2. An increase in enthalpy

Question 13. Which of the following conditions are favourable for a spontaneous process?

1. ΔH=-ve TΔS = + ve
2. ΔH = -ve TΔS = -ve TΔS<ΔH
3. ΔH=+ve TΔS = + ve TΔS<ΔH
4. ΔH = +ve TΔS = + ve TΔS>ΔH

Answer: 1. ΔH=-ve TΔS = + ve,

2. ΔH = -ve TΔS = -ve TΔS<ΔH and

4. ΔH = +ve 7ΔS = + ve TΔS>ΔH

Question 14. The enthalpies of elements in their standard states are taken as zero. Thus, the enthalpy of formation of a compound

1. Will always be positive
2. Will always be negative
3. Will always be zero
4. May be negative or positive

Answer: 4. May be negative or positive

Question 15. The enthalpy of combustion of a substance

1. Is always positive
2. Is always negative
3. Is numerically equal to the enthalpy of formation
4. Cannot be predicted

Answer: 2. Is always negative

Question 16. When ammonium chloride is dissolved in water, the solution becomes cold. The change is

1. Exothermic
2. Endothermic
3. Super cooling
4. None of these

Answer: 2. Endothermic