Chapter 18 Area Of Circle Exercise 18
Formulae:
1. Area of a circle = πr2 sq.units
2. Area of a semi-circle = \(\frac{1}{2}\) πr2 sq.units
3. If the length of the radius of a circle is units r and a sector of the circle makes an angle of degrees then:
1. Length of the arc = \(\frac{\theta}{360}\) x Circumference of the circle
= \(\frac{\theta}{360}\) x 2πr
2. Area of the (sector) = \(\frac{\theta}{360}\) x Area of the circle
= \(\frac{\theta}{360}\) x πr2 sq.units
Read and Learn More WBBSE Solutions For Class 9 Maths
Class 9 Math solutions WBBSE Chapter 18
WBBSE Class 9 Math Chapter 18
Question 1.Today the cow of Aminabibi is fastened to a post with a rope of length 2.1 meters in the vacant field. Let us see by calculating how much maximum area the cow can graze.
Solution:
Given
Today the cow of Aminabibi is fastened to a post with a rope of length 2.1 meters in the vacant field.
∵ Here radius (r) = 2.1 m
∴ Area = πr2 sq. cm
\(=\frac{22}{7} \times(2.1)^2 \text { sq. } \mathrm{cm}\)
\(=\frac{22}{7} \times \frac{21}{10} \times \frac{21}{10} . \text { sq. cm }\)
= 13.86 sq. cm.
Wbbse Class 9 Maths Chapter 18 Area Of Circle Solutions
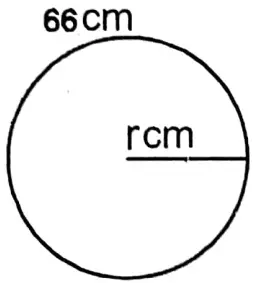
Question 2. Suhana will draw a circle whose perimeter will be 35.2 cm. Let us see by calculating what length of radius Suhana takes to draw a circle and what will be the area of that circular field.
Solution:
Given
Suhana will draw a circle whose perimeter will be 35.2 cm.
Let the radius = r cm
∴ Circumference of the circle is = 2πr cm
= \(2 \times \frac{22}{7} \mathrm{r} \mathrm{cm}=\frac{44 \mathrm{r}}{7} \mathrm{~cm}\)
By the problem, \(\frac{44 r}{7}=35.2\)
or, \(r=\frac{352 \times 7}{10 \times 44}\)
or, r = 5.6
∴ Radius of the circle drawn by Suhana is 5.6 cm.
Area of the circle = πr2
= \(\frac{22}{7}\) x (5.6)2 sq. cm
= \(\frac{22}{7} \times \frac{56}{10} \times \frac{56}{10}\) sq. cm
= 98.56 sq. cm
∴ 5.6 cm, 98.56 sq. cm

Wbbse Class 9 Area Of Circle Exercise Solutions
Question 3. Grandmother of Rekha has made a circular table cover whose area is 5544 sq. cm. She wants to paste coloring tape surrounding this circular cover of the table, let us see by calculating how much long coloring tape she will buy.
Solution:
Given
Grandmother of Rekha has made a circular table cover whose area is 5544 sq. cm. She wants to paste coloring tape surrounding this circular cover of the table,
Let the radius = r cm
∴ Area = πr2 sq. cm = \(\frac{22}{7} r^2\) sq.cm
By the problem, \(\frac{22}{7} r^2\) = 5544
= \(\mathrm{r}^2=\frac{5544 \times 7}{22}\)
or, r2 = 252 x 7
or, r2= 1764
or, r = √1764 = 42
∴ Radius of the table = 42 cm
∴ Circumference of the table = 2πr cm
= 2 x \(\frac{22}{7}\) x 42 cm = 264 cm
∴ Length of the tape = 264 cm.
WBBSE Class 9 Math Chapter 18
Question 4 The cost of fencing of our village playground with railing is Rs. 924 at the rate of Rs. 21 per meter. Let us write by calculating how much sq. meter canvas will be bought for covering the field.
Solution:
Given
The cost of fencing of our village playground with railing is Rs. 924 at the rate of Rs. 21 per meter.
∴ Circumference of the field = 924 = 21 m = 44 m.
Let the radius of the field = r m.
∴ Circumference of the field = 2πr m
= \(2 \times \frac{22}{7} \times r m\)
= \(\frac{44 r}{7}\)
By the problem, \(\frac{44 r}{7}\) = 44
or, \(r=\frac{44 \times 7}{44}=7\)
∴ Radius of the field = 7 m
∴ Area of the ground = r2 sq. cm
=\(\frac{22}{7} \times 7 \times 7\) sq.cm
= 154 sq. cm
Class 9 Wbbse Maths Area Of Circle Solved Problems
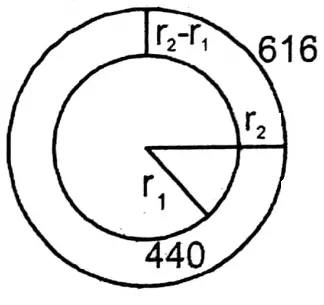
Question 5. Faruk will draw a circle whose area will be 616 sq. meters. Let us see by calculating what length of radius Faruk will take to draw a circle and what perimeter he will get.
Solution:
Given
Faruk will draw a circle whose area will be 616 sq. meters.
Let the radius = rm.
∴ Area of the circle = πr2 sq. cm = \(\frac{22}{7} r^2\) sq.cm
By the problem, \(\frac{22}{7} r^2\) = 616
or, sq. cm \(r^2=\frac{616 \times 7}{22}\)
or, r2 = 196
or, r = √196
or, r = 14
∴ Length of the radius of the circle drawn by Farukh = 14 cm.
Circumference of the circle = 2πr
= \(2 \times \frac{22}{7} \times 14 \mathrm{~cm}\) = 88 cm
∴ 14 cm, 88 cm
Question 6. Palash and Piyali have drawn two circles, the ratio of whose lengths of radii is 4 5. Let us write by calculating the ratio of areas of the two circular fields drawn by them.
Solution:
Given
Palash and Piyali have drawn two circles, the ratio of whose lengths of radii is 4 5.
Let the radii of two circles are 4r & 5r units respectively.
∴ Ratio of areas of the two circles
= π(4г)2: (5г)2
= 16r2: 25r2
= 16:25
Ratio of areas of the two circles = 16:25
Wbbse Class 9 Maths Chapter 18 Area Of Circle Notes
Question 7. Sumit and Reba have taken two copper wires of having the same length. Sumit bent the wire in the form of a rectangular shape whose length and breadth are 48 cm and 40 cm. But Reba bent the copper wire with the same length in the form of a circle. Let us see by calculating which will cover the maximum place between the rectangle drawn by Sumit and the circle drawn by Reba.
Solution:
Given
Sumit and Reba have taken two copper wires of having the same length. Sumit bent the wire in the form of a rectangular shape whose length and breadth are 48 cm and 40 cm. But Reba bent the copper wire with the same length in the form of a circle.
Area of the rectangle made by Sumit = 48 x 40 sq. cm = 1920 sq. cm
∴ Perimeter of the rectangle = 2(L + B)
= 2(48 +40) cm
= 2=88 cm
= 176 cm
∴ Circumference of the circle drawn by Reba is 176 cm.
Let the radius of the circle drawn by Reba is r cm.
∴ Circumference of the circle = 2πr cm
\(\begin{aligned}
& =2 \times \frac{22}{7} \times r \mathrm{~cm} \\
& =\frac{44 r}{7} \mathrm{~cm}
\end{aligned}\)
By the problem, \(\frac{44 r}{7}=176\)
or, \(r=\frac{176 \times 7}{44}=28 \mathrm{~cm}\) = 28 cm
∴ Area of the circle =πr2 sq. cm
\(\begin{aligned}
& =\frac{22}{7}(28)^2 \text { vsq. cm } \\
& =\frac{22}{7} \times 28 \times 28 \text { sq. } \mathrm{cm}
\end{aligned}\)
= 2464 sq. cm
Area of Circle Class 9 wbbse Question 8.
At the center of the rectangular field of Pioneer athletic club, there is a circular pool whose length of the radius is 14 meters. The length and breadth of the rectangular field are 60 meters and 42 meters respectively. Let us see by calculating how much cost it will take for planting grass of the remaining place of rectangular field except the pool at the rate of Rs. 75 per square meter.
Solution:
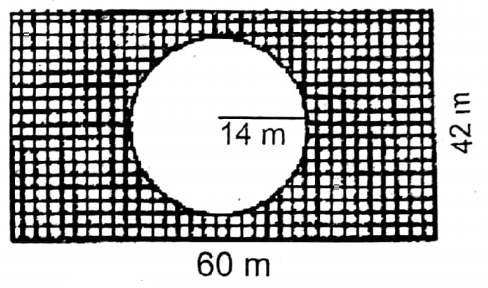
Area of the rectangular field = 60 x 42 sq. cm = 2520 sq. cm
Area of the circular pool = πr2 sq. cm
\(\begin{aligned}
& =\frac{22}{7} \times(14)^2 \text { sq. cm } \\
& =\frac{22}{7} \times 14 \times 14 \text { sq. cm }
\end{aligned}\) = 616 sq. cm
The remaining area of the field = (2520-616) sq. cm = 1904 sq. cm
∴ Cost for planting grass at the rate of Rs. 75 per sq. cm
= Rs. 1904 x 75
= Rs. 142800
West Bengal Board Class 9 Area Of Circle Chapter Solutions
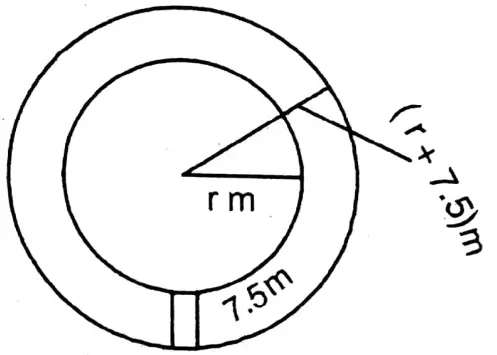
Question 9. A 7 meter wide path runs outside a circular park of Etalgacha Friends association club along its perimeter. Let us write by calculating the area of the path if the perimeter of the circular park is 352 meters; let us write by calculating how much the cost for concreting the path at the rate of Rs. 20 per square meter.
Solution:
Given
A 7 meter wide path runs outside a circular park of Etalgacha Friends association club along its perimeter. Let us write by calculating the area of the path if the perimeter of the circular park is 352 meters
Let the radius of the park = r m
∴ Perimeter of the park = 2πr m
\(\begin{aligned}
& =2 \times \frac{22}{7} \times r \mathrm{~m} \\
& =\frac{44 r}{7} \mathrm{~m}
\end{aligned}\)
By the problem, \(\frac{44 r}{7}=352\)
or, \(r=\frac{352 \times 7}{44}\)
or, r = 8 x7 = 56 m
∴ Now radius of park with the path of width 7 m = (56+7) m = 63 m
∴ Area of the path = π {(63)2-(56)2} sq. cm
= \(\frac{22}{7}\) (63+56) (63-56) sq. cm
= \(\frac{22}{7}\) x 119 x 7 sq. cm
= 2618 sq. cm
Now cost for concreting the path at the rate of Rs.20 per sq. cm
= Rs. 2618 x 20
= Rs. 52360
Question 10. Anwarbibi has spent Rs. 2664 at the rate of Rs. 18.50 per meter for fencing of her semi-circular land. Let us write by calculating how much cost it will take if she makes the semi-circular land plow at the rate of Rs. 32 per sq. meter.
Solution:
Given
Anwarbibi has spent Rs. 2664 at the rate of Rs. 18.50 per meter for fencing of her semi-circular land.
∴ Perimeter of the land = \(\frac{2664}{18.50} \mathrm{~m}\) = 144m
Let the radius of the land = r m.
∴ Perimeter of the land = (πr +2r) m
= г(π+2) m
= \(r\left(\frac{22}{7}+2\right) m\)
= \(r\left(\frac{22+14}{7}\right) m\)
= \(\frac{36 r}{7} \cdot m\)
By the problem, \(\frac{36 r}{7}=144\)
or, \(r=\frac{144 \times 7}{36}=28\)
∴ Radius of the land = 28 m
Area of the land \(\frac{1}{2} \pi r^2\)
= \(\frac{1}{2} \times \frac{22}{7} \times 28 \times 28 \text { sq. cm }\)
= 1232 sq. cm
∴ Cost of plowing at 32 Rs. per sq.m = Rs. 1232 x 32
= Rs. 39424
Ganit Prakash Class 9 Solutions
Question 11. The time my friend Rajat took today running with uniform speed to round one of a circular field of school is 30 seconds less than that when he ran diametrically with same speed. Let us write by calculating the area of the field of the school if his speed is 90 meters/second.
Solution:
Given
The time my friend Rajat took today running with uniform speed to round one of a circular field of school is 30 seconds less than that when he ran diametrically with same speed.
Let the radius of the circular field = r m.
∴ Diameter of the field = 2r m.
∴ Perimeter of the field = 2πr m.
∵ Rajat covers up 90 m distance in 60 sec.
∴ Rajat covers up 1 m distance in \(\frac{60}{90}\) sec.
∴ Rajat covers up 2πr m distance in \(\frac{2}{3} \times 2 \pi r\) sec.
∴ Rajat covers up 2r m distance in \(\frac{2}{3} \times 2 r \mathrm{sec}\)
By the problem,
\(\frac{2}{3} \times 2 \pi r-\frac{2}{3} \times 2 r=30\)
or, \(\)
or, \(\frac{2}{3} \times 2 r(\pi-1)=30\)
or, \(\frac{4 r}{3}\left(\frac{22}{7}-1\right)=30\)
or, \(\frac{4 r}{3}\left(\frac{22-7}{7}\right)=30\)
or, \(\frac{4 r}{3} \times \frac{15}{7}=30\)
or, \(4 r \times \frac{5}{7}=30\)
or, \(r=\frac{30 \times 7}{5 \times 4}=\frac{21}{2}\)
∴ Area of school’s field= π r2 sq. cm
= \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2} \text { sq. cm }\)
= \(\frac{693}{2} \text { sq. cm }\)
= 346.5 sq. cm
Wbbse Class 9 Area Of Circle Important Questions
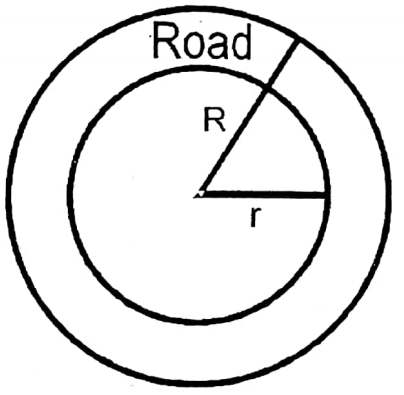
Question 12. An equally wide path runs outside the circular field of Bakultala. The length of the outer circumference exceeds the inner circumference by 132 meters. If the area of the path is 14190 sq. meters, let us write by calculating the area of the circular path.
Solution:
Given
An equally wide path runs outside the circular field of Bakultala. The length of the outer circumference exceeds the inner circumference by 132 meters. If the area of the path is 14190 sq. meters,
Let the inner radius = r m
& the outer radius = Rm
∴ Circumference of the small circle = 2πr m
& circumference of the big circle = 2πR m
2πR – 2πг = 132
or, 2π(R-r) 132
or, \(2 \times \frac{22}{7}(R-r)=132\)
or, R-r= \(\frac{132 \times 7}{2 \times 22}\)
or, R-r=21 ….()
According to the second condition,
πR2 – πr2 = 14190
or, π(R2 -r2) = 14190
or,\(\frac{22}{7}\) (R+r)(R-r) =14190
or, \(\frac{22}{7}\) (R+r).21 = 14190 [∵R-r=21]
or, R+r= \(\frac{14190}{22 \times 3}=215\)
or, R+r=215……… (2)
Subtracting, eq (2)-(1)
R+r=215
R-r=21
(-) (+) (-)
∵ 2r = 194
or, \(r=\frac{194}{2}\)
or, r = 97
∴ Radius of the field = 97 m
∴ Area of the field = πr2 sq. cm
= \(\frac{22}{7} \times(97)^2 \text { sq. cm }\)
= \(\frac{22}{7} \times 97 \times 97 \text { sq. cm }\)
= \(29571 \frac{1}{7} \text { sq. cm }\)
Ganit Prakash Class 9 Solutions Question 13.
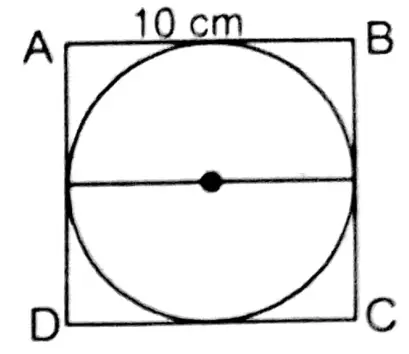
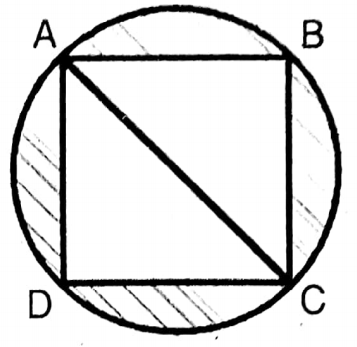
Let us write by calculating the area of the shaded regions in the pictures below:
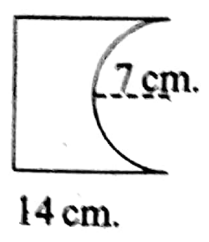
1. ABCD is a square. The length of the radius of the circle is 7 cm.
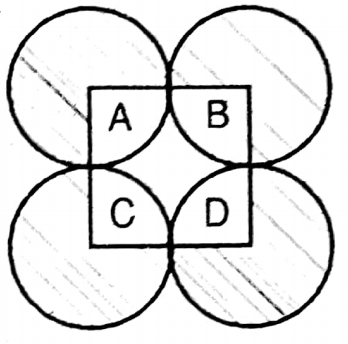
2. The length of the radius of each circle is 3.5 cm. The centers of the four circles are A, B, and D respectively.
Solution: Length of the radius (r) = 7 cm
∴ Area of the circle = πr2 sq. cm
= \(\begin{aligned}
& =\frac{22}{7} \times(7)^2 \text { sq. } \mathrm{cm} \\
& =\frac{22}{7} \times 7 \times 7 \text { sq. } \mathrm{cm}
\end{aligned}\)
= 154 sq. cm
Length of the diagonal = 2r
= 2 x 7 cm
= 14 cm
∴ Area of square = \(\frac{1}{2}(diagonal)2\) Χ (diagonal)2
\(\begin{aligned}
& =\frac{1}{2} \times(14)^2 \text { sq. cm } \\
& =\frac{1}{2} \times 196 \text { sq. cm }
\end{aligned}\)
= 98 sq. cm
∴ Area of shaded region (154-98) sq. cm
= 56 sq. cm
2. Radius of each circle = 3.5 cm
∴ Área of each circle = \(\frac{22}{7} \times(3.5)^2\) sq. cm
= \(\frac{22}{7} \times \frac{35}{10} \times \frac{35}{10} \text { sq. } \mathrm{cm}\)
= 38.5 sq. cm
∴ Total area of 4 circles = 4 x 38.5 sq. cm = 154 sq. cm
White portion of the pictures in the 4 circles
= \(4 \times \frac{90}{360} \times \frac{22}{7} \times(3.5)^2 \text { sq. cm }\)
= \(4 \times \frac{1}{4} \times \frac{22}{7} \times 3.5 \times 3.5 \text { sq. cm }\)
= 38.5 sq. cm
∴ Area of shaded region picture = (154-38.5) sq. cm
= 115.5 sq. cm
Wbbse Class 9 Maths Area Of Circle Chapter 18
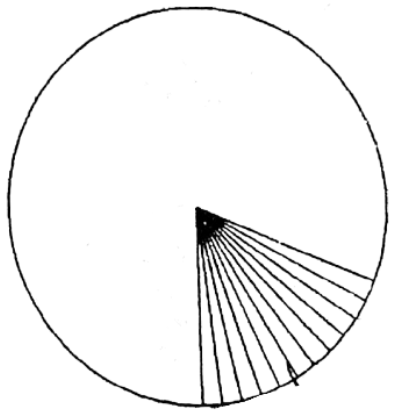
Question 14. Dinesh has made a pie chart of the students of their class who want to play some games. He has taken the length of the radius of the circle of 3.5 cm, let us write by calculating the perimeter and area of each sector of circles.
Solution: Let in Dinesh’s class there are 100 students where 50 play cricket, 30 play football and 20 play badminton.
| Name of Game |
Percentage |
Fraction |
Angle (part of 360°) |
| Cricket |
50 |
\(\frac{50}{100}=\frac{1}{2}\) |
\(\frac{1}{2} \times 360^{\circ}=180^{\circ}\) |
| Football |
30 |
\(\frac{30}{100}=\frac{3}{10}\) |
\(\frac{3}{10} \times 360^{\circ}=108^{\circ}\) |
| Badminton |
20 |
\(\frac{20}{100}=\frac{1}{5}\) |
\(\frac{1}{5} \times 360^{\circ}=72^{\circ}\) |
Dinesh made a pie chart of the list.
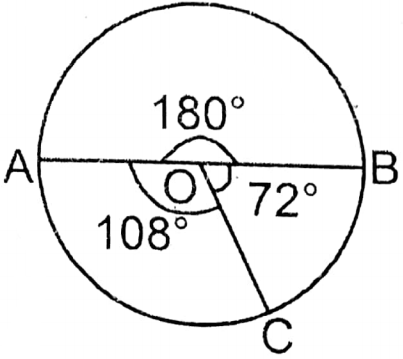
1. Length of the chord = \(\overline{\mathrm{AB}}=\frac{180}{360} \times 2 \pi r\)
=\(\frac{1}{2} \times 2 \times \frac{22}{7} \times 3.5 \mathrm{~cm}\)
= 11 cm
The perimeter of AOB (Sector)
= \(\overline{\mathrm{AB}}\) Length of + 2 x radius
= (11 + 2 x 3.5) cm = 18 cm
Area of sector AOB = \(\frac{180}{360} \times \pi r^2\)
= \(\frac{1}{2} \times \frac{22}{7} \times(3.5)^2 \text { sq.cm }\) = 19.25 sq.cm
2. Length of the chord \(\overline{\mathrm{AC}}=\frac{108}{360} \times 2 \times \frac{22}{7} \times 3.5 \mathrm{~cm}\)
= \(\frac{3}{10} \times 2 \times \frac{22}{7} \times \frac{35}{10} \mathrm{~cm}\)
= 6.6 cm
Perimeter of the sector AOC = \(\overline{\mathrm{AC}}\) length of 2 x length of radius
= (6.6+2 x 3.5) cm
= 13.6 cm
Area of the sector AOC = \(\frac{108}{360} \times \frac{22}{7} \times(3.5)^2 \text { sq.cm }\)
= \(\frac{3}{10} \times \frac{22}{7} \times \frac{35}{10} \times \frac{35}{10} \text { sq.cm }\)
= 11.55 sq. cm
3. Length of the sector \(\overline{\mathrm{BC}}=\frac{72}{360} \times 2 \times \frac{22}{7} \times 3.5 \mathrm{~cm}\)
= \(\frac{1}{5} \times 2 \times \frac{22}{7} \times \frac{35}{10} \mathrm{~cm}\)
= 4.4 cm
The perimeter of the sector BOC = \(\overline{\mathrm{BC}}\) length of + 2 x length of the radius
= (4.4+7) cm
= 11.4 cm
Area of the sector BOC = \(\frac{72}{360} \times \pi r^2\)
\(\begin{aligned}
& =\frac{1}{5} \times \frac{22}{7} \times(3.5)^2 \text { sq. cm } \\
& =\frac{1}{5} \times \frac{22}{7} \times \frac{35}{10} \times \frac{35}{10} \text { sq. cm }
\end{aligned}\)
= 7.7 sq. cm
Wbbse Maths Solution Class 9
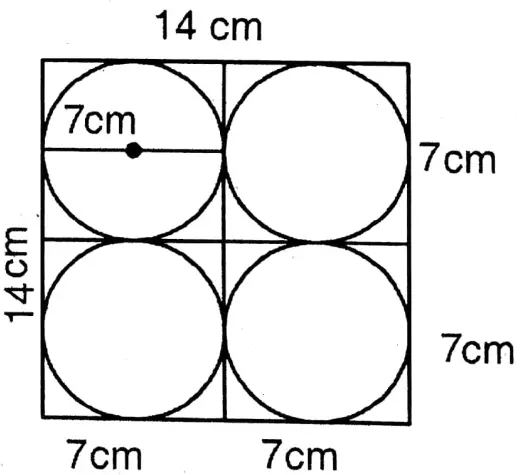
Question 15. Nitu has drawn a square ABCD whose length of each side is 12 cm. My sister has drawn four circular arcs with a length of radius 6 cm centering A, B, and D like pictures beside and she has designed some portions. Let us write by calculating the area of the shaded region.
Solution:
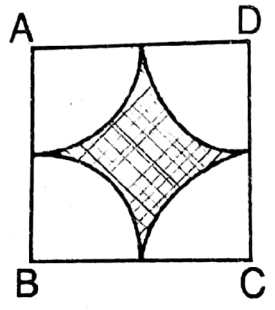
Given
Nitu has drawn a square ABCD whose length of each side is 12 cm. My sister has drawn four circular arcs with a length of radius 6 cm centering A, B, and D like pictures beside and she has designed some portions.
Length of each side of the square = 12 cm.
∴ Area of square ABCD = (12)2 sq. cm
= 144 sq. cm
Length of the arc of radius 6 cm
= \(\frac{90}{360} \times \text { Circumference of the circle }\)
\(\begin{aligned}
& =\frac{1}{4} \times 2 \times \frac{22}{7} \times 6 \mathrm{~cm} \\
& =\frac{66}{7} \mathrm{~cm}
\end{aligned}\)
Area of the sector of radius 6 cm = \(\frac{90}{360} \times \pi r^2\)
= \(\frac{1}{4} \times \frac{22}{7} \times(6)^2 \text { sq. cm }\)
∴ Area of the 4 sectors
= \(\begin{aligned}
& =4 \times \frac{1}{4} \times \frac{2}{7} \times 36 \text { sq. cm } \\
& =\frac{792}{7} \text { sq. cm }
\end{aligned}\)
Area of the 4 sectors = \(4 \times \frac{66}{7} \mathrm{~cm}\)
\(\begin{aligned}
& =\frac{264}{7} \mathrm{~cm} \\
& =37 \frac{5}{7} \mathrm{~cm}
\end{aligned}\)
Area of shaded region= \(\left(144-\frac{792}{7}\right) \text { sq. cm }\)
= \(\left(\frac{1008=792}{7}\right) \text { sq. } \mathrm{cm}\)
\(\begin{aligned}
& =\frac{216}{7} \text { sq. } \mathrm{cm} \\
& =30 \frac{6}{7} \text { sq. } \mathrm{cm}
\end{aligned}\)
∴ \(37 \frac{5}{7} \cdot \mathrm{cm} ; 30 \frac{6}{7} \mathrm{sq} . \mathrm{cm}\)
Wbbse 9th Class Maths Area Of Circle Step By Step Solutions
Question 16. The area of a circular field is 154 sq cm. Let us write by calculating the perimeter and area of circumfering the circular field with a square.
Solution:
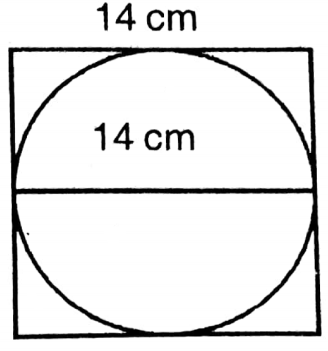
Let the radius of the circular field = r cm
∴ Area of the field = r2 sq. cm
= \(\frac{22}{7} r^2 \text { sq. } \mathrm{cm}\)
By the problem,
\(\frac{22}{7} r^2=154\)
or, \(r^2=\frac{154 \times 7}{22}\)
or, r2 = 49
or, r = √49
or, r = 7
∴ Diameter of the field = 2 x 7 cm
= 14 cm
∴ Length of one side of the square outside the circle = 14 cm.
∴ Perimeter of the square = 4 x 14 cm = 56 cm
∴ And the area of the square = (14)2 sq. cm = 196 sq. cm
Length of the diagonal of the internal square = 14 cm
= Diameter of the circle
∴ Length of one side of the inner square= \(\frac{14}{\sqrt{2}}\)
= \(\begin{aligned}
& =\frac{14 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \mathrm{~cm} \\
& =\frac{14 \sqrt{2}}{2} \mathrm{~cm}
\end{aligned}\)
= 7√2 cm
Perimeter of the inner square = 4×7√2 cm = 28√2 cm
Area of the internal square = \(\frac{1}{2}\) x (Diagonal)2
= \(\frac{1}{2}\) Χ (14)2
= \(\frac{1}{2}\) x 196 cm = 98 cm
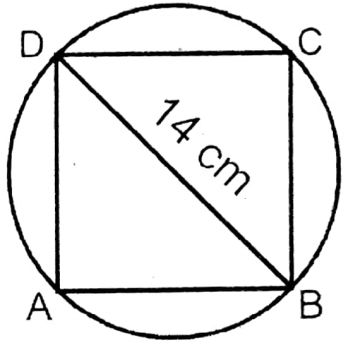
Question 17. Let us write the perimeter and area of the circular region shaded sector below.
Solution:
1.
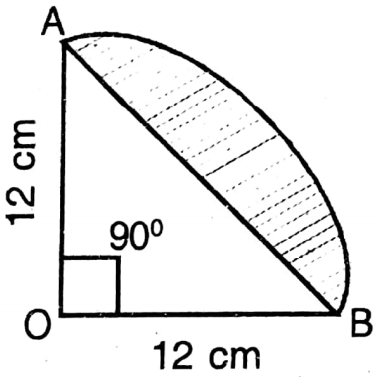
length of AB = \(\sqrt{(12)^2+(12)^2} \mathrm{~cm}\)
= \(\begin{aligned}
& =\sqrt{144+144} \mathrm{~cm} \\
& =\sqrt{288} \mathrm{~cm} \\
& =\sqrt{2 \times 12 \times 12} \mathrm{~cm} \\
& =12 \sqrt{2} \mathrm{~cm}
\end{aligned}\)
= 12 x 1.414 cm
= 16.97 cm (approx).
Length of the arc \(\widehat{\mathrm{AB}}=\frac{90}{360}\) x Circumference of the circle
\(\begin{aligned}
& =\frac{1}{4} \times 2 \times \frac{22}{7} \times 12 \mathrm{~cm} \\
& =\frac{132}{7} \mathrm{~cm}
\end{aligned}\)
= 18.86 cm (approx).
∴ Perimeter of the shaded region = (16.97 +18.86) cm
= 35.83 cm (approx).
Area of AOB (Sector) = \(\frac{90}{360} \times \pi r^2 \text { sq. cm }\)
\(\begin{aligned}
& =\frac{1}{4} \times \frac{22}{7} \times(12)^2 \text { sq. cm } \\
& =\frac{1}{4} \times \frac{22}{7} \times 12 \times 12 \text { sq. cm } \\
& =\frac{792}{7} \text { sq. } \mathrm{cm}
\end{aligned}\)
Area of the right-angled ΔAOB = \(\frac{1}{2}\) x 12 x 12 sq. cm = 72 sq. cm
∴ Area of the shaded region = \(\left(\frac{792}{7}-72\right) \text { sq. cm }\)
\(\begin{aligned}
& =\frac{792-504}{7} \text { sq. cm } \\
& =\frac{288}{7} \text { sq. cm } \\
& =41 \frac{1}{7} \text { sq. } \mathrm{cm}
\end{aligned}\)
2.
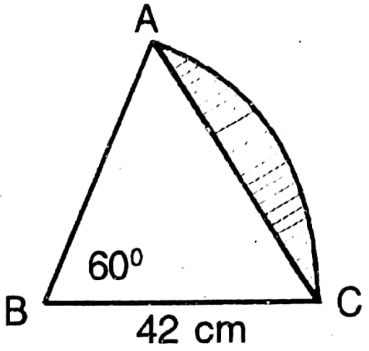
Length of AC = 42 cm ( ∵ ABC is an equilateral triangle
Length of arc \(\widehat{\mathrm{AB}}=\frac{60}{360}\) x Circumference of the circle
\(\begin{aligned}
& =\frac{1}{6} \times 2 \pi r \\
& =\frac{1}{6} \times 2 \times \frac{22}{7} \times 42 \mathrm{~cm} \\
& =44 \mathrm{~cm}
\end{aligned}\)
∴ Perimeter of the shaded region = (42 + 44) cm = 86 cm
Area of sector ABC = \(\frac{60}{360} \times \pi r^2\)
= \(\frac{1}{6} \times \frac{22}{7} \times 42 \times 42 \text { sq. } \mathrm{cm}\)
= 924 sq. cm
Area of equilateral triangle ABC = \(\frac{\sqrt{3}}{4} \times(\text { side })^2\)
\(\begin{aligned}
& =\frac{\sqrt{3}}{4} \times(42)^2 \text { sq. cin } \\
& =\frac{\sqrt{3}}{4} \times 42 \times 42 \text { sq. cm }
\end{aligned}\)
= 441√3 sq. cm
= 441 x 1.732 sq. cm
= 763.812 sq. cm
∴ Area of shaded region = (924-763.812) sq. cm
= 160.188 sq. cm
= 160.19 sq. cm (approx)
Wbbse Maths Solution Class 9
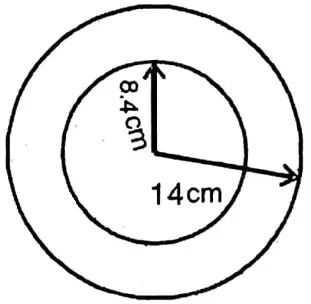
Question 18. Buying a bangle from the fair Nila wears in her hand. The bangle contains 269.5 sq. cm. metal. If the length of the outer diameter of the bangle is 28 cm, let us write by calculating the length of the inner diameter.
Solution:
Given
Buying a bangle from the fair Nila wears in her hand. The bangle contains 269.5 sq. cm. metal. If the length of the outer diameter of the bangle is 28 cm,
Length of the radius (R) = \(\frac{28}{2}\) = 14cm
& let the radius of the inner r cm.
∴ Area of the metal of the bangle = \(\pi\left(R^2-r^2\right)\)
= \(\frac{22}{7}\left\{(14)^2-r^2\right\} \text { sq. cm }\)
= \(=\frac{22}{7}\left(196-r^2\right) \text { sq. cm }\)
According to the problem,
\(\frac{22}{7}\left(196-r^2\right)=269.5\)
or, \(196-r^2=\frac{2695 \times 7}{10 \times 22}\)
or, 196-r2 = 85.75
or, -r2 = 85.75 -196
or, -r2 = -110.25
or, r2 = 110.25
or, r= √110.25 = 10.5
∴ Length of the inner diamter
= 2 x 10.5 cm 21 cm.
Question 19. Protul has drawn an equilateral triangle ABC (picture is given beside), whose length of each side is 10 cm. Sumita has drawn three circular arcs centering A, B,C with a length of radius 5 cm and has colored some portion at the middle. Let us write by calculating the area of the colored portion.
Solution:
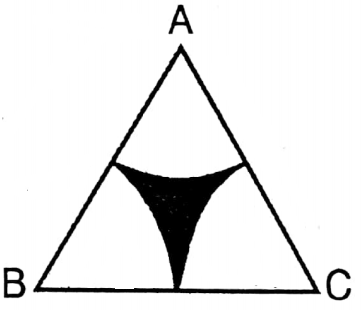
Given
Protul has drawn an equilateral triangle ABC (picture is given beside), whose length of each side is 10 cm. Sumita has drawn three circular arcs centering A, B,C with a length of radius 5 cm and has colored some portion at the middle.
Area of the equilateral triangle ABC = \(A B C=\frac{\sqrt{3}}{4} \times(\text { side })^2\)
= \(\frac{\sqrt{3}}{4} \times(10)^2 \text { sq. cm }\)
= \(\frac{\sqrt{3}}{4} \times 100 \text { sq. cm }\)
= 25√3 sq. cm
= 25 x 1.732 sq. cm
= 43.3 sq. cm
Area of each sector = \(\frac{60}{360} \times \pi r^2\)
= \(\frac{1}{6} \times \frac{22}{7} \times(5)^2 \text { sq. cm }\)
∴ Total area of the three sectors = \(3 \times \frac{1}{6} \times \frac{22}{7} \times 25 \text { sq. cm }\)
=\(\frac{11 \times 25}{7} \text {.sq. cm }\)
= 39.28 sq. cm
∴ Area of the coloured portion = (43.3-39.28) sq. cm = 4.02 sq. cm
Wbbse Class 9 Maths Area And Circumference Of Circle Formulas With Examples
Question 20. Rabeya drew an equilateral triangle with side of 21 cm on a big piece of paper. Drawing a circle inscribing that triangle the colored circular region, I write by calculating the area of the colored region.
Solution:
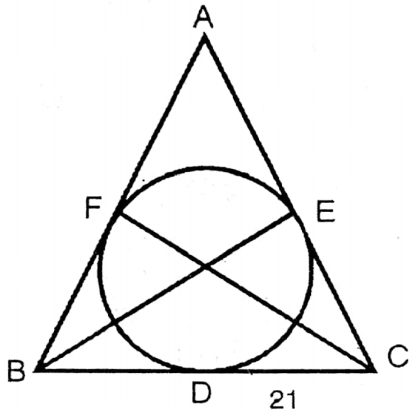
Given
Rabeya drew an equilateral triangle with side of 21 cm on a big piece of paper.
Length of each side of the equilateral triangle = 21 cm.
Length of the radius of the incircle = \(\frac{1}{3}\) Χ height of the equilateral triangle
= \(\begin{aligned}
& =\frac{1}{3} \times \frac{\sqrt{3}}{2} \times 21 \mathrm{~cm} \\
& =\frac{7 \sqrt{3}}{2} \mathrm{~cm}
\end{aligned}\)
Area of incircle = πr2
= \(\frac{22}{7}\left(\frac{7 \sqrt{3}}{2}\right)^2 \text { sq. cm }\)
= \(\frac{22}{7} \times \frac{7 \sqrt{3} \times 7 \sqrt{3}}{2 \times 2} \text { sq. } \mathrm{cm}\)
= 115.5 sq. cm
Question 21. The area of circumscribing an equilateral triangle is 462 sq. cm. Let us write by calculating the length of each side of this triangle.
Solution:
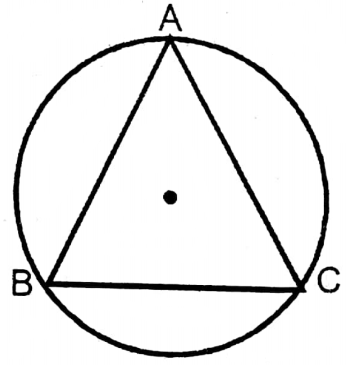
Area of the circumcircle of the equilateral triangle = 462 sq. cm
Let the radius of the circumcircle = r cm
∴ Area of the circumcircle = πr2 sq. cm
By the problem, \(\frac{22}{7} r^2=462\)
or, \(r^2=\frac{462 \times 7}{22}\)
or, r2 = 21 x 7
or, r = \(\sqrt{21 \times 7}\) = 7√3
∴ Radius of the circumcircle = \(\frac{2}{3}\) x height of the triangle
or, 7√3 = \(\frac{2}{3} \times \frac{\sqrt{3}}{2}\) x length of the triangle
∴ Length of each side of the triangle = \(\frac{7 \sqrt{3} \times 3}{\sqrt{3}} \mathrm{~cm}\) = 21 cm
∴ Length of each side of the equilateral triangle = 21 cm.
Wbbse Maths Solution Class 9
Question 22. The perimeter of a triangle is 32 cm and the area of its inscribing circle is 38.5 sq. cm. Let us write by calculating the area of this triangle.
Solution:
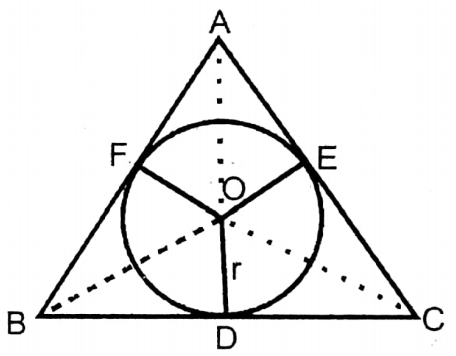
Let the radius of the incircle of the equilateral triangle = r cm.
∴ Area of the circle = πr2 sq. cm = \(\frac{22}{7} r^2 \text { sq. cm }\)
According to the problem,
\(\frac{22}{7} r^2\) = 38.5
or, \(r^2=\frac{385 \times 7}{10 \times 22}\)
or, \(r^2=\frac{49}{4}\)
or, \(r=\sqrt{\frac{49}{4}}=\frac{7}{2}\)
Area of ΔABC = Area of (ΔAOB + area of ΔBOC+ Area of ΔCOA)
\(\begin{aligned}
& =\frac{1}{2} \cdot A B \cdot r+\frac{1}{2} \cdot B C \cdot r \cdot+\frac{1}{2} C A \cdot r \\
& =\frac{1}{2} r(A B+B C+C A) \\
& =\frac{1}{2} \times \frac{7}{2} \times 32 \text { sq. cm }
\end{aligned}\)
= 56 sq. cm.
Question 23. Let us write by calculating the length of the radius of the incircle and circumcircle of a triangle, whose sides are 20 cm, 15 cm, and 25 cm. Let us calculate the area of the incircle and the circumcircle.
Solution:
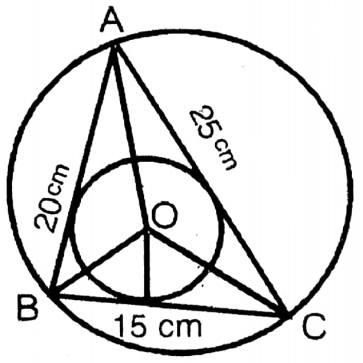
Let ABC is a triangle whose sides AB = 15 cm, BC = 25 cm, and AC = 20 cm, and the incentre is O and in radius is r cm.
∵ (15)2+(20)2 =(25)2
∴ Area of ΔABC = \(\frac{1}{2}\) x 15 x 20 sq. cm
= 150 sq. cm
∵ ΔABC = ΔAOB + ΔBOC+ΔCOA
\(\text { or, } 150=\frac{1}{2} \cdot 15 \cdot r+\frac{1}{2} \cdot 25 \cdot r+\frac{1}{2} \cdot 20 \cdot r\)
\(\text { or, } 150=\frac{1}{2} r(15+25+20)\)
\(\text { or, } r=\frac{150 \times 2}{60}\)
or, r = 5
∴ Radius of the incirle = 5 cm
Area of the incircle = πr2
\(\begin{aligned}
& =\frac{22}{7} \times(5)^2 \text { sq. cm } \\
& =\frac{22}{7} \times 25 \text { sq. cm } \\
& =\frac{550}{7} \text { sq. } \mathrm{cm} \\
& =78 \frac{4}{7} \text { sq. } \mathrm{cm}
\end{aligned}\)
∵ The hypotenuse of a right-angled triangle is the diameter of its circumcircle.
∴ Radius of the circumcircle = \(\frac{25}{2} \mathrm{~cm}\) = 12.5 cm
∴ Area of circumcircle = \(\frac{22}{7} \times \frac{25}{2} \times \frac{25}{2} \text { sq. cm }\)
\(\begin{aligned}
& =\frac{6875}{14} \text { sq. cm } \\
& =491 \frac{1}{14} \text { sq. } \mathrm{cm}
\end{aligned}\)
∴ The inradius and circumradius of the triangle are respectively, 5 cm and 12.5 cm and the areas of incircle and circumcircle are respectively \(78 \frac{4}{7}\) sq. cm and \(491 \frac{1}{14} \text { sq. cm. }\)
Class 9 Wbbse Area Of Circle Chapter 18 Solved Exercises
Question 24. Jaya drew an incircle of a square. That circle is also circumscribed an equilateral triangle, of which the length of each side is 4√3 cm. Let us write by calculating the length of the diagonal of the square.
Solution:
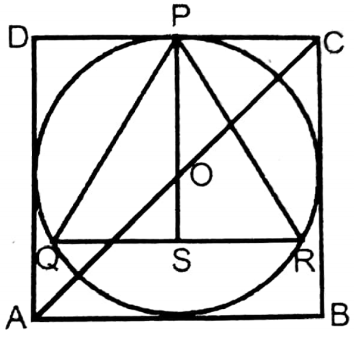
Given
Jaya drew an incircle of a square. That circle is also circumscribed an equilateral triangle, of which the length of each side is 4√3 cm.
Length of each side of the equilateral triangle = 4√3 cm.
∴ Height of the triangle = \(\frac{\sqrt{3}}{2}\) x side
= \(\frac{\sqrt{3}}{2} \times 4 \sqrt{3} \mathrm{~cm}\) = 6 cm
∴ The radius of the circumcircle = \(\frac{2}{3}\) x height of the triangle
= \(\frac{2}{3} \times 6 \mathrm{~cm}\)
= 4 cm
∴ Diameter of the circumcircle
= 2 x 4 cm
= 8 cm
∴ Length of the diagonal of the square = √2 × side
= √2×8 cm
= 8√2 cm.
Question 25. Sumit cut a wire into two equal parts. One part he bent in the form of a square and another part he bent in the form of a circle. If the area of the circle exceeds that of the square by 33 sq. cm, let us write by calculating the original length of the wire.
Solution:
Given
Sumit cut a wire into two equal parts. One part he bent in the form of a square and another part he bent in the form of a circle. If the area of the circle exceeds that of the square by 33 sq. cm
Let the length of the wire = x cm
∴ Each part of the wire = \(\frac{x}{2}\)
∴ Perimeter of square= \(\frac{x}{2}\)
∴ Length of each side of the square= \(\frac{x}{8}\)
∴ Area of the square =\(\left(\frac{x}{8}\right)^2 \text { sq. cm }\)
= \(\frac{x^2}{64} \text { sq. cm }\)
Again, the perimeter of the circle = \(\frac{x}{2}\)
oг, 2πr = \(\frac{x}{2} \mathrm{~cm}\)
or, \(r=\frac{x}{4 \pi}\)
Area of the circle = πr2
\(\begin{aligned}
& =\pi\left(\frac{x}{4 \pi}\right)^2 \text { sq. cm } \\
& =\pi \cdot \frac{x^2}{16 \pi^2} \text { sq. } \mathrm{cm} \\
& =\frac{x^2}{16 \pi} \text { sq. cm }
\end{aligned}\)
According to the problem, \(\frac{x^2}{16 \pi}-\frac{x^2}{64}=33\)
or, \(\frac{x^2}{16}\left(\frac{1}{\pi}-\frac{1}{4}\right)=33\)
or, \(\frac{x^2}{16}\left(\frac{1}{\frac{22}{7}}-\frac{1}{4}\right)=33\)
or, \(\frac{x^2}{16}\left(\frac{7}{22}-\frac{1}{4}\right)=33\)
or, \(\frac{x^2}{16}\left(\frac{14-11}{44}\right)=33\)
or, \(\frac{x^2}{16} \times \frac{3}{44}=33\)
or, \(x^2=\frac{33 \times 44 \times 16}{3}\)
or, x2 = 11 x 44 x 16
or, x = \(\sqrt{11 \times 11 \times 4 \times 16}\)
or, x = 11 x 2 x 4 = 88
∴ Length of the wire = 88 cm.
Chapter 18 Area Of Circle Multiple choice questions
1. If the area of a circular field is x sq unit, the perimeter is y unit, and the length of diameter is z unit then the value of \(\frac{x}{y z}\) is
1. \(\frac{1}{2}\)
2. \(\frac{1}{4}\)
3. 1
4. \(\frac{1}{8}\)
Solution: Let the radius = r unit
∴ \(\frac{x}{y z}=\frac{\pi r^2}{2 \pi r \cdot 2 r}=\frac{1}{4}\)
∴ 2. \(\frac{1}{4}\)
2. The ratio of areas of two squares circumscribed and inscribed by a circle is
1. 4: 1
2. 1:4
3. 2:1
4. 1:2
Solution: Let the radius = r unit
∴ Diameter = 2r unit
∴ Length of one side of the outer square = 2r unit
& diagonal of the inner square = 2r unit
∴ One side of the inner square= \(\frac{2 r}{\sqrt{2}} \text { unit }\)
∴ The ratio of areas of the two squares = \((2 r)^2:\left(\frac{2 r}{\sqrt{2}}\right)^2\)
\(\begin{aligned}
& =4 r^2: \frac{4 r^2}{2} \\
& =1: \frac{1}{2}
\end{aligned}\)
= 2:1
∴ 3. 2:1
Wbbse class 9 Maths Question 3.
The numerical value of the perimeter of a square and area of a circular field is equal. The length of the diagonal of the square circumscribed by a circle is
1. 4 unit
2. 2 unit
3. 4√2 unit
4. 2√2 unit
Solution: Let the radius = r unit
∴ Perimeter = 2πr unit
∴ & Area = πr2 unit
According to the problem,
πr2 = 2πr
or, r = 2
∴ Length of one side of the outer square Diameter of the circle
= 2r unit
∴ Length of the diagonal of the square = √2 × side
= √2x2r
=√2x2x2 unit
= 4√2 unit
3. 4√√2 unit
Question 4. The ratio of the areas of an equilateral triangle and its inscribing circle is
1. 4: 1
2. 1:4
3. 2:1
4. 1:2
∴ 1. 4:1
Question 5. The inner diameter and external diameter of an iron ring plate are 20 cm and 22 cm. The quantity of iron plates in the ring is
1. 22 sq. cm
2. 44 sq. cm
3. 66 sq. cm
4. 88 sq. cm
Solution: Area of iron ring = π(R2 – r2)
= \(\frac{22}{7}\left\{(11)^2-(10)^2\right\} \text { sq. cm }\)
= \(\frac{22}{7}(11+10)(11-10) \text { sq. cm }\)
= \(\frac{22}{7} \times 21 \times 1 \text { sq. cm }\)
= 66 sq. cm
∴ 3. 66 sq. cm
Class 9 Maths Chapter 18 Area Of Circle Short Question and Answers
Question 1. If the length of the radius of a circular field was increased by 10%, let us write by calculating what percent it increased the area of a circular field.
Solution: Let the radius of the circular field = r unit.
∴ Its area = r2 sq unit
Now, radius after increasing 10 %= \(\frac{110 r}{100} \text { unit }=\frac{11 r}{10} \text { sq unit }\)
∴ New area = \(=\pi\left(\frac{11 r}{10}\right)^2 \text { sq unit }\)
= \(\pi \cdot \frac{121 r^2}{100} \text { sq unit }\)
∴ Increase in area
\(\begin{aligned}
& =\pi \cdot \frac{121 r^2}{100}-\pi r^2 \text { sq unit } \\
& =\pi r^2\left(\frac{121}{100}-1\right) \text { sq unit } \\
& =\pi r^2\left(\frac{121-100}{100}\right) \text { sq unit } \\
& =\frac{21 \pi r^2}{100} \text { sq unit }
\end{aligned}\)
∴ Percentage increase in area
= \(\frac{21 \pi r^2}{\frac{100}{\pi r^2}} \times 100\)
= 21%
Wbbse class 9 Maths Question 2.
If the perimeter of a circular field was decreased by 50%, let us write by calculating what percent it decreases the area of the circular field.
Solution: Let the radius of the circular field = r unit.
∴ Permeter = 2πr unit
& Area = πr2 sq. unit
Now, new radius after decreasing 50%= \(\frac{50}{100} \times 2 \pi r=\pi r \text { unit }\)
∴ Perimeter = \(=\frac{r}{2} \text { unit }\)
New area = \(\pi\left(\frac{r}{2}\right)^2 \text { sq. unit } \frac{\pi r^2}{4} \text { sq. unit }\)
Decrease in the area = \(\left(\pi r^2-\frac{\pi r^2}{4}\right) \text { sq. unit }\)
\(\begin{aligned}
& =\frac{4 \pi r^2-\pi r^2}{4} \text { sq. unit } \\
& =\frac{3 \pi r^2}{4} \text { sq. unit }
\end{aligned}\)
Percentage decrease in area = \(\frac{3 \pi r^2}{4 \times \pi r^2} \times 100=75 \%\)
3. The length of radius of a circular field is r meter. If the area of the other circle is x times of the first circle, let us see by calculating how much length is of the radius of the other circle.
Solution: Radius first circular field = r m
∴ Let the radius of the other circular field = πr2 sq.m
Let the radius of the second circle be R m.
∴ Area of the second circle = πR2 sq.m
By the problem,
πR2 = x.πr2
or, R2 = xr2
or, R= \(R=\sqrt{x r^2}\)
or, R = r√x
∴ Radius of the other circle = r√x m
Wbbse class 9 Maths Question 4. Let us calculate the area of a circle which circumscribes a triangle, of which sides are 3 cm, 4 cm, and 5 cm.
Solution: ∵ (3)2 + (4)2 = (5)2
∴ The triangle whose sides are 3 cm, 4 cm & 5 cm is a right-angled triangle.
∴ The hypotenuse of a right-angled triangle is the diameter of its circumcircle.
∴ Length of the diameter of the circumcircle = 5 cm.
∴ Radius of the circle = \(\frac{5}{2} \mathrm{~cm}\)
∴ Area of the circumcircle = \(\pi\left(\frac{5}{2}\right)^2 \text { sq. cm }\)
\(\begin{aligned}
& =\frac{22}{7} \times \frac{25}{4} \text { sq. cm } \\
& =\frac{275}{14} \text { sq. } \mathrm{cm}
\end{aligned}\)
= \(19 \frac{9}{14} \text { sq. cm }\)
5. Three circular plates were cut off from a tin plate with equal width. If the ratio of lengths of the diameter of three circles is 3:5: 7, let us see by calculating the ratio of their weights.
Solution:
Given
Three circular plates were cut off from a tin plate with equal width. If the ratio of lengths of the diameter of three circles is 3:5: 7
Let the diameters of the 3 circles = 3r, 5r & 7r unit.
∴ Radius of 3 circles = \(\frac{3 r}{2} \text { unit } \frac{5 r}{2} \text { unit, and } \frac{7 r}{2} \text { unit }\)
∴ Ratio of areas of 3 circles = \(\pi\left(\frac{3 r}{2}\right)^2: \pi\left(\frac{5 r}{2}\right)^2: \pi\left(\frac{7 r}{2}\right)^2\)
\(=\frac{9 r^2}{4}: \frac{25 r^2}{4}: \frac{49 r^2}{4}\)
=9:25:49
∴ Ratio of weights of three circular rings is equal to the ratio of their areas.
∴ Ratio of weights of three circular rings 9:25:49