Motion In A Plane
Projectile Motion
A body that is in flight through the atmosphere, but if it is moving only under the influence of gravity, then it is a projectile.
Types of Projectile Motion
- Oblique projectile
- Horizontal projectile
Oblique Projectile
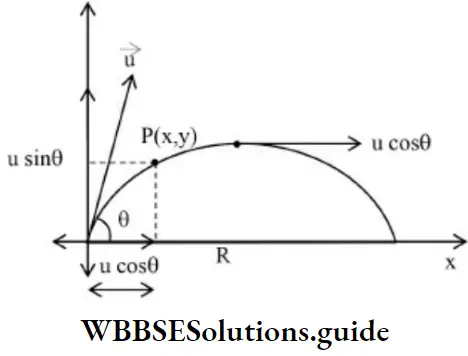
NEET Physics Motion in a Plane Important Formulas
1. The equation of the trajectory of the projectile is given by:
⇒ \(y=(\tan \theta) x-\left(\frac{g}{2 u^2 \cos ^2 \theta}\right) x^2\)
The above equation is similar to the equation of a parabola.
y= ax- bx2
i.e trajectroy of a projectile is a parabola
Read And Learn More: NEET Physics Notes
The equation of oblique projectile can also be written as,
⇒ \(y=x \tan \theta\left[1-\frac{x}{R}\right]\)
Whereas, R= \(\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}\)
Best Short Notes for Motion in a Plane NEET
2. Velocity of the projectile at any point on its trajectory is given by:
⇒ \(\vec{v}=v_x \hat{i}+v_y \hat{j}\)
⇒\(\mathrm{V}=\sqrt{\mathrm{V}_{\mathrm{x}}^2+\mathrm{V}_{\mathrm{y}}^2}\)
⇒ \(\mathrm{v}_{\mathrm{x}}=\mathrm{u} \cos \theta\)
⇒ \(\mathrm{v}_{\mathrm{y}}=\mathrm{u} \sin \theta-\mathrm{gt}\)
v= \(\sqrt{\left(u^2 \cos ^2 \theta\right)+(u \sin \theta-g t)^2}\)
v= \(\sqrt{u^2+g^2 t^2-2 u g t \sin \theta}\)
The direction of instantaneous velocity is given by, \(\tan \alpha=\frac{v_y}{v_x}\)

Motion in a Plane NEET Important Questions and Answers
3. Change in velocity of the projectile between the point of projection and the highest point is given by:
⇒ \(\Delta \overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{v}}_{\mathrm{f}}-\overrightarrow{\mathrm{v}}_{\mathrm{i}}=-\mathrm{u} \sin \theta \hat{\mathrm{j}}\)
Change in velocity during complete oblique projectile motion is given by
⇒ \(\Delta \overrightarrow{\mathrm{v}}=-2 \mathrm{u} \sin \theta \hat{\mathrm{i}}\)
4. The change in momentum of the projectile between the point of projection and the highest point is:
⇒ \(\Delta \overrightarrow{\mathrm{P}}=\overrightarrow{\mathrm{P}}_{\mathrm{f}}-\overrightarrow{\mathrm{P}}_{\mathrm{i}}=-\mathrm{mu} \sin \theta \hat{\mathrm{j}}\)
The change in momentum of the projectile during complete oblique projectile motion is given by,
⇒ \(\Delta \overrightarrow{\mathrm{P}}=-2 m u \sin \theta \hat{\mathrm{i}}\)
5. Angular momentum of the projectile at the highest point of trajectory about the point of projection is given by:
L = \(m v r\left(r=H=\frac{u^2 \sin ^2 \theta}{2 g}\right)\)
∴ L= \(\mathrm{m}(\mathrm{u} \cos \theta)\left(\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}}\right)\)
∴ L= \(=\frac{m u^3 \cos \theta \sin ^2 \theta}{2 \mathrm{~g}}\)
NEET Physics Motion in a Plane MCQs with Solutions
6. Time of maximum height:
⇒ \(\mathrm{t}_{\max }=\frac{\mathrm{u} \sin \theta}{\mathrm{g}}\)
7. Time of flight:
⇒ \(\mathrm{T}=2 \mathrm{t}_{\max }=\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\) Or \(\mathrm{T}=\frac{2 \mathrm{u}_{\mathrm{y}}}{\mathrm{g}}\)
8. Horizontal range:
It is the horizontal distance traveled by the projectile during its flight.
R = (ux) (T)
R= \((\mathrm{u} \cos \theta) \frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\)
r = \(\mathrm{R}\frac{\mathrm{u}^2}{\mathrm{~g}} \sin 2 \theta\)
R= \(\frac{2}{\mathrm{~g}}\left(\mathrm{u}_{\mathrm{x}}\right)\left(\mathrm{u}_{\mathrm{y}}\right)\)
Where ux = u cos θ: u = uy sin θ
For complementary angles of projection θ and 90 – θ range is the same.
Or
For angles of projection θ1 =(45 – α) and θ2 = (45 + α)) range will be the same.
If the angle of projection is 450, the range is maximum.
⇒ \(\mathrm{R}_{\max }=\frac{\mathrm{u}^2}{\mathrm{~g}}\)
9. Maximum height of a projectile is given by:
⇒ \(\mathrm{H}=\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}}\)
Or \(\mathrm{H}=\frac{\mathrm{u}_{\mathrm{y}}^2}{2 \mathrm{~g}}\)
⇒ \(\mathrm{H}_{\max }=\frac{\mathrm{u}^2}{2 \mathrm{~g}}\)
Or
⇒ \(\frac{\mathrm{H}}{\mathrm{T}^2}=\frac{\mathrm{g}}{8}\)
Energy of Projectile
When a projectile moves upwards through its trajectory its kinetic energy will decrease and potential energy will increase, but the total energy always remains constant.
Say a body of mass ‘m’ is projected obliquely with the angle of projection ‘0’.
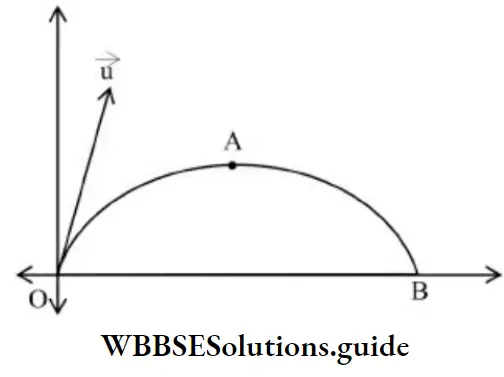
At’O’:
⇒ \(\mathrm{K} \cdot \mathrm{E}=\frac{1}{2} \mathrm{mu}^2\)
P.E = 0
Total energy E = ½ mu2
At’A’:
⇒ \(\mathrm{K} \cdot \mathrm{E} .=\frac{1}{2} \mathrm{mu}^2 \cos ^2 \theta\)
P.E = mgh
P.E = \(m g \frac{u^2 \sin ^2 \theta}{2 g}\)
P.E= \(\frac{1}{2} m u^2 \sin ^2 \theta\)
Total energy
E= K.E + P.E = \(=\frac{1}{2} m u^2 \cos ^2 \theta+\frac{1}{2} m u^2 \sin ^2 \theta\)
⇒ \(\mathrm{E}=\frac{1}{2} \mathrm{mu}^2\)
Similarly, at B,
⇒ \(\mathrm{E}=\frac{1}{2} \mathrm{mu}^2\)
Horizontal Projectile
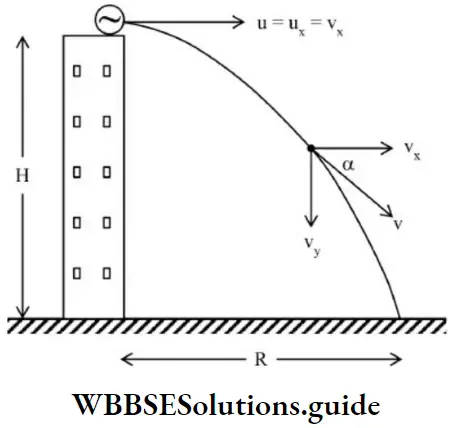
Suppose a body of mass ‘m’ is thrown horizontally with speed ‘u’ from the top of a tower.
The magnitude of velocity at any point on the trajectory is given by,
v= \(\sqrt{v_x^2+v_y^2}\)
Where, vx = u and vy = gt, tan \(\frac{v_y}{v_x}=\frac{g t}{u}\)
The time taken by the ball to reach the ground is given by,
⇒ \(t=\sqrt{\frac{2 H}{g}}\)
Projectile Motion and Relative Velocity NEET Notes
Range:
ux × t
⇒ \(\mathrm{R}=\mathrm{u} \sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}\)
Riverboat problem
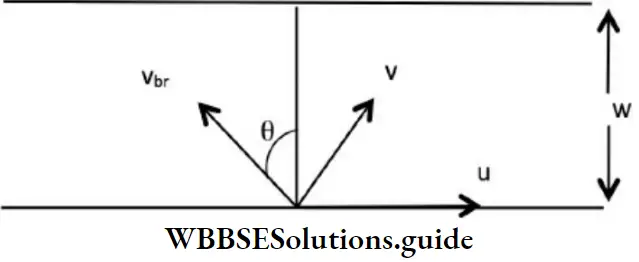
Vbr velocity of the boat w.r.to river
V is the velocity of the boat w.r.to ground
u is the velocity of the river
1. To cross the river straight, we should row the boat by making an angle with the upstream where 0 is the angle made by with the shortest distance (which is the width of the river)
⇒ \(\sin \theta=\frac{u}{v_{b r}}\)
The time taken to cross the river is given by
2. To cross the river in the shortest time, we should row the boat perpendicular to the bank. The time taken in this case is,
⇒ \(t_{\min }=\frac{w}{v_{b r}}\)
3. The horizontal distance traveled by the boat w.r.to starting point is,
⇒ \(xu \times t_{\min }\)
NEET Study Material for Motion in a Plane Chapter
Uniform Circular Motion
If a body is moving in a circular path with constant speed then the body is said to be in uniform circular motion.
Expression for centripetal acceleration is given by,
⇒\(a_c=\frac{v^2}{r}\)
Or, \(a_c=\omega^2 r\) (because ω = rω) where co is the angular velocity.
Expression for centripetal force is
⇒ \(F_c=\frac{m v^2}{r}=m \omega^2 r\)
