Ameerun

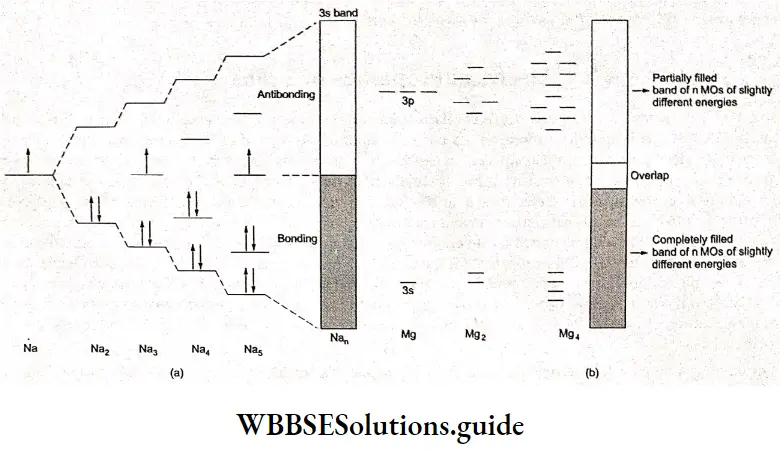
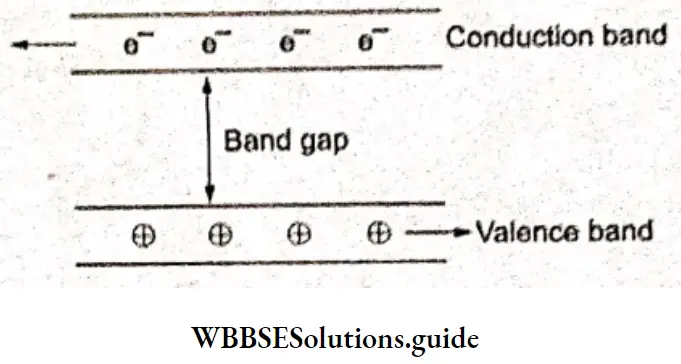
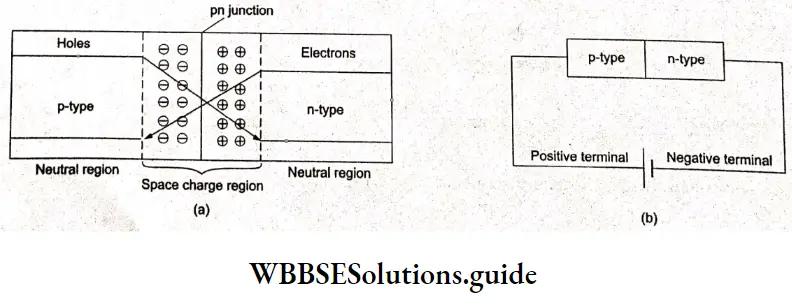
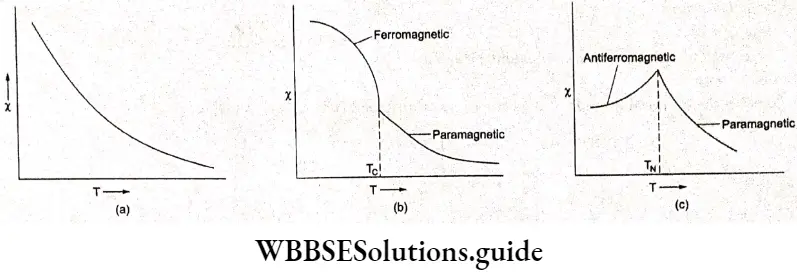
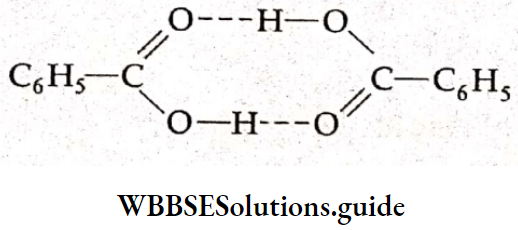
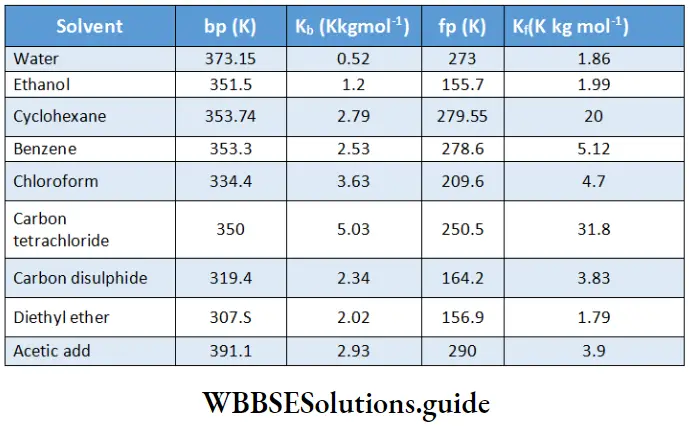
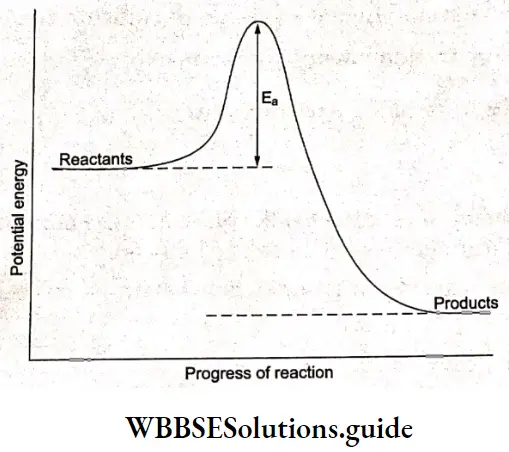
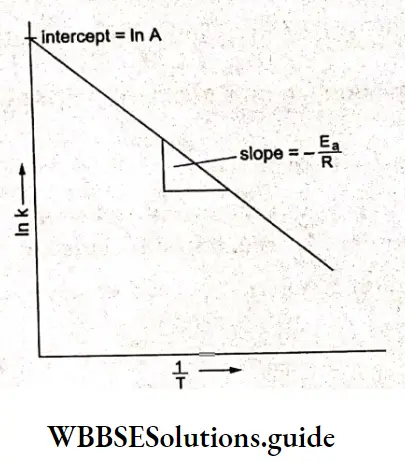
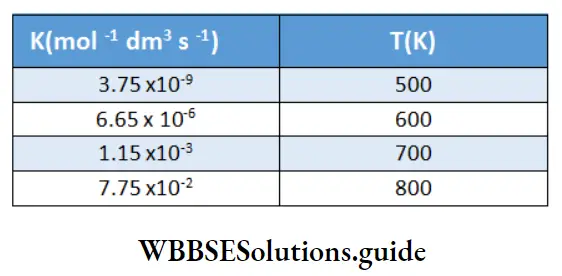
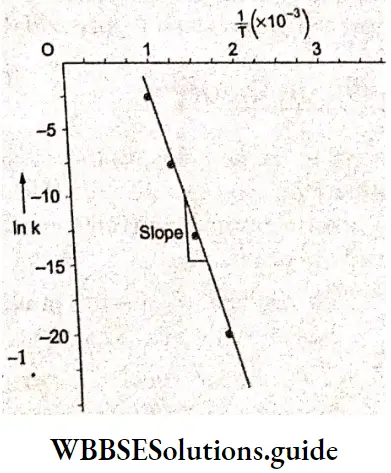
Electrochemistry

Electrochemistry:

Electrochemistry deals with the relationship between electrical energy and chemical energy and the interconversion of these two forms of energy. Chemical reactions can produce electrical energy. Also, certain nonspontaneous chemical reactions can be driven in the forward direction by applying an electric current.

Both these processes involve electrochemical reactions, i.e., chemical reactions using or generating electricity. The batteries we use in cars, toys, mobile phones, etc., are all examples of electrochemical cells. Methods like electroplating, employed to prevent corrosion, and electrorefining of metals involve electrochemical reactions.

Metallic and Electrolytic Conductance

Substances that allow the passage of electric current are called conductors. Metals are good conductors of electricity. Examples include copper, aluminum, and silver.

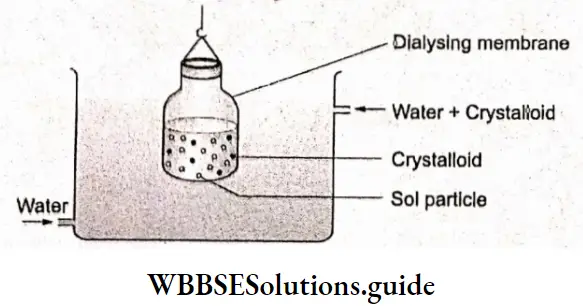
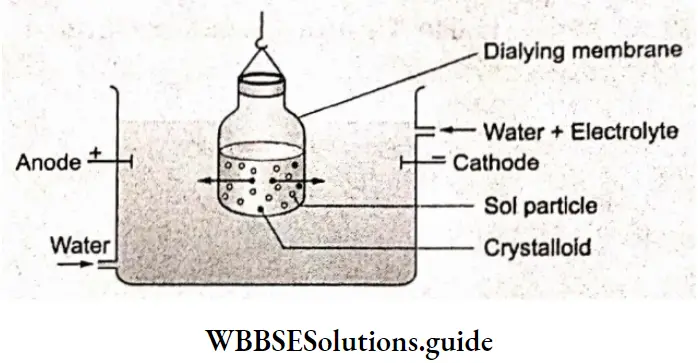
Apart from metals, there are other substances that allow the passage of electric current through them when they are in the molten state or in an aqueous solution. These substances are called electrolytes and the species responsible for the flow of current in electrolytes are the ions produced by the dissociation of these substances. This is in contrast to metallic conduction, in which the flow of current is due to the movement of free electrons.

The conduction of electricity by ions in solution is called ionic conduction. The conductivity of a solution depends upon various factors the

1. Nature of the electrolyte
2. The size of the ions in the solution,
3. The nature of the solvent and its viscosity
4. The temperature and concentration of the electrolyte.

On the other hand, metallic conduction occurs through electrons and is therefore also known as electronic conduction.

It depends on:

1. The nature (density) and structure of the metal
2. The number of valence electrons per atom
3. Temperature.

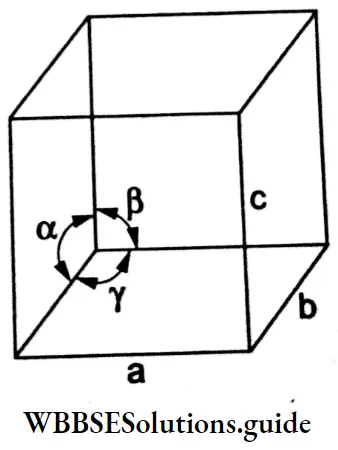
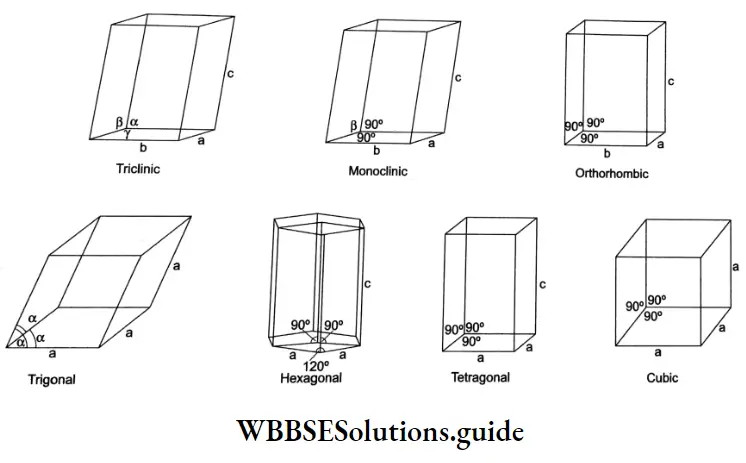
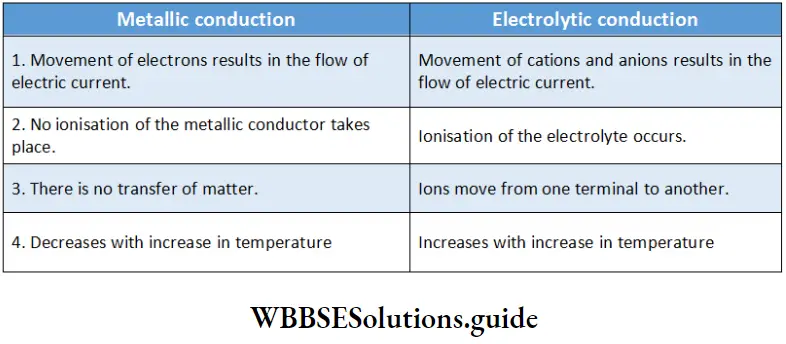
Summarises the important characteristics of metallic and electrolytic conduction.

A comparison of metallic and electrolytic conduction:

Substances like sucrose, which do not conduct electricity either in their molten state or in their aqueous solutions, are called nonelectrolytes.

Conductance and Conductivity

Electrolytic conduction can be studied by applying a potential difference between two electrodes dipped in the solution of a sample. The ions of the sample which is an electrolyte move across the electrodes and result in the flow of electric current through the solution.

Under this condition, the electrolyte obeys Ohm’s law, according to which the potential difference between the electrodes, V, is equal to the product of the current I flowing through the solution and the resistance offered, R.

V=IR.

The reciprocal of resistance is called conductance, G, of the electrolytic solution.

\(G=\frac{1}{R}\)

As resistance is expressed in Ω, conductance can be expressed in Ω. The SI unit of conductance is Siemens, S.

\(1 S=1 \Omega^{-1}\)

Specific resistance and specific conductance

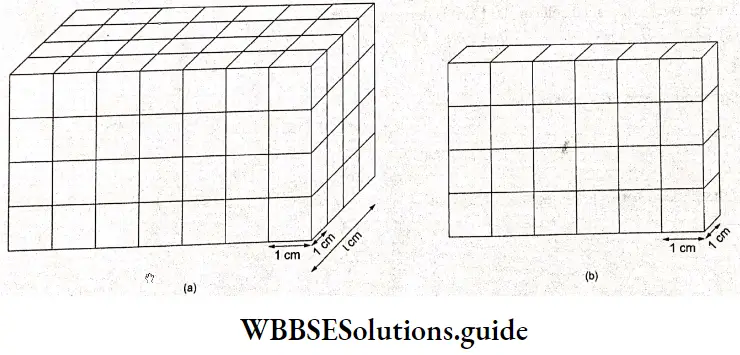
Consider a uniform bar of a conductor of length 1 cm and cross-sectional area A cm². Imagine that the cross-section is rectangular and that the bar is divided into cubes of side 1 cm.

The resistance of the bar is then equal to that of the I layers, in series with one another. Each layer is equivalent to A cubes, each cube of length 1 cm, whose resistances are in parallel. If p is the specific resistance (resistance of 1 cm cube) of the conductor, the resistance of one layer may be worked out from

\(\frac{1}{r}=\frac{1}{\rho}+\frac{1}{\rho}+\) ………. (A times)

Or \(\frac{1}{r}=A\left(\frac{1}{\rho}\right)\)

Or \(r=\frac{\rho}{A}\)

If R is the resistance of the whole bar, equivalent to the resistance of I layers, then

\(R=l r=l \cdot \frac{\rho}{A}=\rho \cdot \frac{l}{A} \Omega\)

This equation is valid for all types of conductors including electrolytic solutions. In this equation, p is called resistivity (or specific resistance).

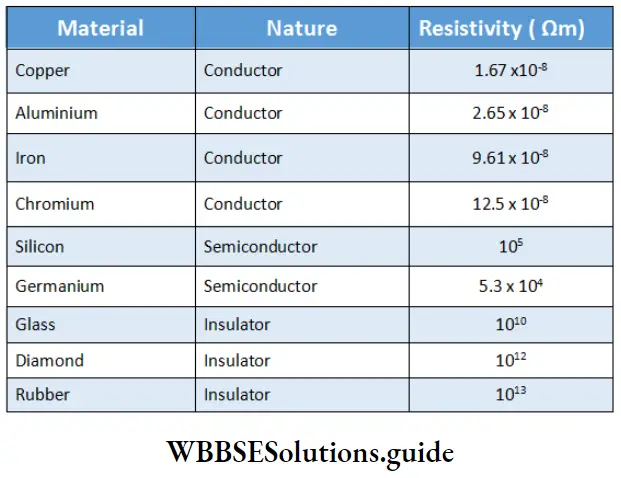
Substances can be classified as conductors, semiconductors, or insulators based on their resistivities. If I is expressed in cm and A in cm², the unit of p will be 2 cm. The SI unit is ohm m (22 m). The reciprocal of p is called specific conductance, or conductivity, denoted by K.

\(\kappa=\frac{1}{\rho}\)

Resistivities of some materials:

Equation 3.2 can now be written as

\(R=\frac{1}{\kappa} \cdot \frac{l}{A}\)

The quantity \(\frac{l}{A}\) is called cell constant and is denoted by G*.

\(G^*=\frac{l}{A}\)

Equation 3.3 can now be written as

\(R=\frac{G^*}{\kappa}\)

or, \(G^*=R \kappa\)

Taking the reciprocal of Equation 3.2, we get

\(\frac{1}{R}=\frac{1}{\rho} \cdot \frac{A}{l}\)

or, \(G=\kappa \cdot \frac{A}{l}\)

From Equation 3.4 it may be seen that the conductance G of a solution decreases with 1 and increases with A.

The SI unit of K may be obtained as follows.

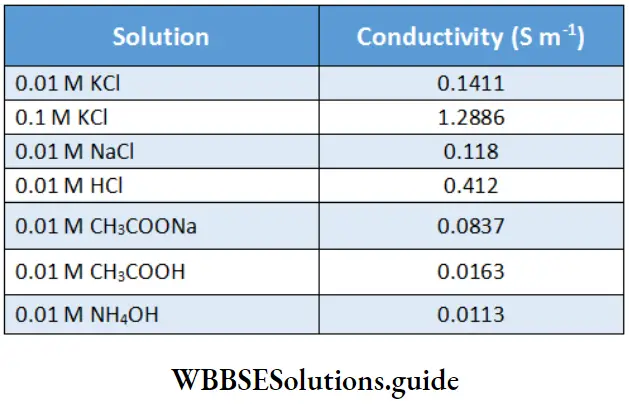
\(\mathrm{\kappa}=G \cdot \frac{l}{A}=\frac{1}{R} \cdot \frac{l}{A}=\frac{1}{\Omega} \cdot \frac{\mathrm{m}}{\mathrm{m}^2}=\Omega^{-1} \mathrm{~m}^{-1}=\mathrm{S} \mathrm{m}^{-1}\)

Lists the conductivity values of some electrolytes:

Conductivity may be defined as the conductance of a solution held between electrodes of a unit area of cross-section (1 cm² or 1 m²) and unit distance apart (1 cm or 1 m). It may be noted that

\(1 \mathrm{~S} \mathrm{~cm}^{-1}=1 \frac{\mathrm{S}}{\mathrm{cm}}=1 \frac{\mathrm{S}}{10^{-2} \mathrm{~m}}=100 \mathrm{~S} \mathrm{~m}^{-1}\)

Measurement Of The Conductivity Of Ionic Solutions

You must have studied in your physics lessons that the unknown resistance of a solid conductor can be measured using a Wheatstone bridge. However the resistance of an ionic solution cannot be measured by using a Wheatstone bridge because a solution cannot be connected to the bridge like a metallic wire.

Therefore, a specially designed conductivity cell is used to measure the electrical resistance of a solution of known concentration. Unlike in the Wheatstone bridge, where d.c. is used, in a conductivity cell, alternating current is used to minimize redox reactions.

Electrode reactions are prevented in an a.c. field since the electrodes change polarities very fast under the operating frequency. The reaction which occurs in the first half of the cycle is reversed in the second half.

The conductivity cell (in which the electrolyte is taken) consists of two platinum electrodes coated with platinum black. The electrodes have a cross-sectional area A and are a distance / apart.

In the conductivity cell, two known fixed resistances (R_x and R₂) and a variable resistance R₃ are arranged.

Tire current may flow along ABC and ADC as long as the potentials at B and D are different. The galvanometer will show a deflection. Once the two are balanced, no current flows and the galvanometer shows no deflection (null deflection). The resistance is adjusted to obtain null deflection on AB and at this point,

\(I_1 X=I_2 R_1 \text { and } I_1 R_3=I_2 R_2\)

where X is the resistance of the electrolyte solution in the conductivity cell.

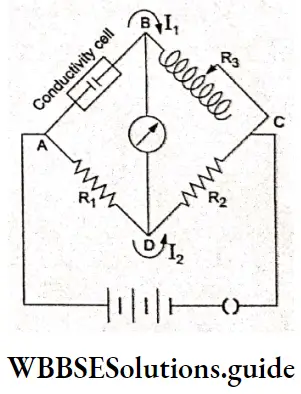
Hence \(\frac{R_3}{X}=\frac{R_2}{R_1}\)

\(X=R_3 \cdot \frac{R_1}{R_2}\)

Instruments based on the above setup are called conductivity bridges. Nowadays instruments which directly give the conductivity value are also available.

They are called conductometers. There are many types of conductivity cells, varying in size and shape, but they can broadly be divided into two categories the solution is poured into the cell, which acts as a vessel, and another dip-type cell in which the cell is dipped inside a beaker containing the electrolyte solution.

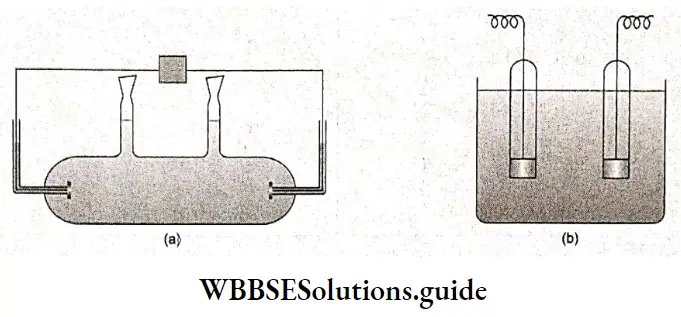
It is customary to determine the cell constant of the cell being used before measuring the conductance of the solution under study. For this purpose, the conductance of a solution of a known concentration of potassium chloride is measured.

For example, let us say the conductance of a 0.1 M KCl solution is observed to be 0.023 S. The specific conductance of this solution is noted from the literature and the cell constant is then calculated using the equation.

\(\frac{l}{A}=\frac{\kappa}{G}\)

The cell constant for the cell in the above example, therefore, is found to be

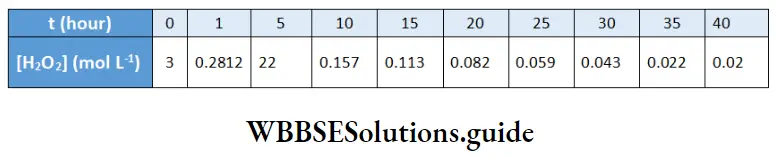
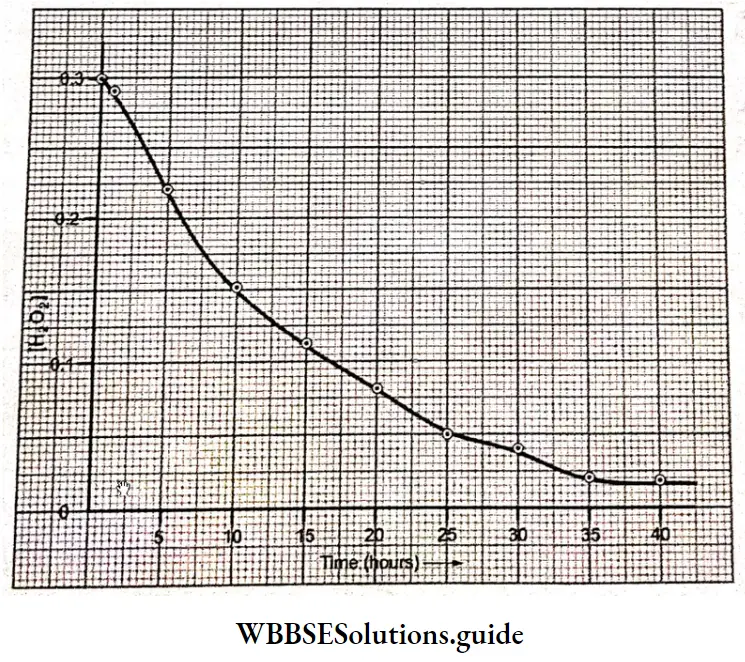
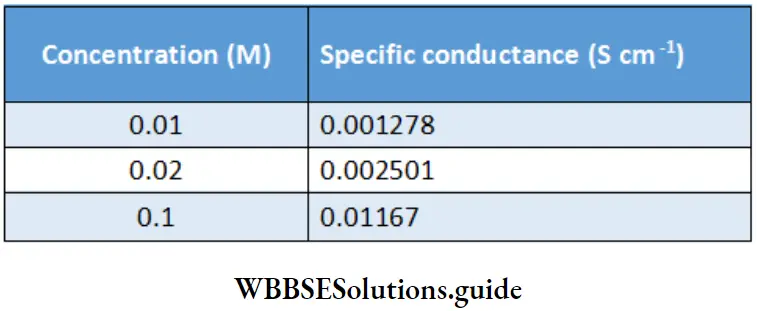
\(\frac{l}{A}=\frac{\kappa}{G}=\frac{0.01167}{0.023}=0.5 \mathrm{~cm}^{-1}\)

Gives the conductivity values of some standard solutions of potassium chloride.

Specific conductance (conductivity) of KCl solutions at 20°C for various concentrations:

Molar conductivity

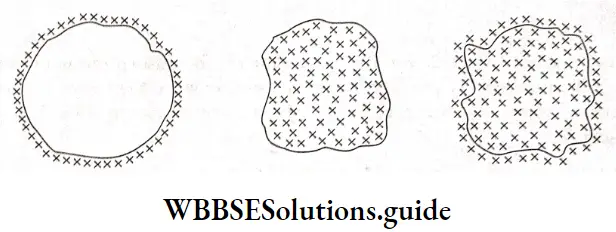
If the solution of one electrolyte is more concentrated than that of another, for a fixed volume of a solution held between the electrodes of a conductivity cell, the former will have more ions, and hence its conductivity may be higher.

To compare the conductances of different electrolytes, it was necessary to define another quantity, namely molar conductivity A. It is defined as the electrolytic conductivity к divided by concentration c.

Molar conductivity,

\(\Lambda_m=\frac{\kappa}{c}\)

If the cell constant is known, the conductivity of any solution can be measured by filling the conductivity cell with the solution and measuring the resistance. Conductivity depends on the nature of the material.

The SI unit of A is S m² mol-1. If x is expressed in S m1, concentration should be expressed in mol m3. If c is expressed in mol L-1 (M), the formula becomes

\(\Lambda_m=\frac{\kappa\left(\mathrm{S} \mathrm{m}^{-1}\right)}{c\left(\mathrm{~mol} \mathrm{~L}^{-1}\right)}\) \(\frac{\kappa}{c} \cdot \frac{\left(\mathrm{S} \mathrm{m}^{-1}\right)(\mathrm{L})}{(\mathrm{mol})}\)

\(\frac{\kappa\left(\mathrm{S} \mathrm{m}^{-1}\right)\left(\mathrm{dm}^3\right)}{c(\mathrm{~mol})}\)  [… 1L = 1 dm3]

\(\Lambda_m=\frac{10^{-3} \kappa}{c} \mathrm{~S} \mathrm{~m}^2 \mathrm{~mol}^{-1}\)

The CGS unit of A is S cm2 mol1. The two types of units are related to each other as

\(1 \mathrm{~S} \mathrm{~m}^2 \mathrm{~mol}^{-1}=10^4 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}\)

And \(1 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}=10^{-4} \mathrm{~S} \mathrm{~m}^2 \mathrm{~mol}^{-1}\)

Example 1. The conductance of a solution of acid as read from a conductometer is 5×10 S. If the conductance of a 0.1 M KCl solution using the same cell and conductometer is found to be 1.07 x 10³ S, calculate the conductivity of the acid solution. The conductivity of a 0.1 M KCl solution is 0.001289 S cm¹.
Solution:

Given

The conductance of a solution of acid as read from a conductometer is 5×10 S. If the conductance of a 0.1 M KCl solution using the same cell and conductometer is found to be 1.07 x 10³ S

Whenever conductance has to be measured, first the conductance of a standard solution of KCl is determined and the cell constant is calculated. Then the conductance of the sample solution is determined and multiplied by the cell constant to obtain its conductivity.

\(\text { Cell constant } G^*=\frac{\text { conductivity } \mathrm{\kappa}}{\text { conductance } G}=\frac{0.001289}{1.07 \times 10^{-3}}=1.2 \mathrm{~cm}^{-1}\)

Now conductivity of acid solution = K=5×10 -3 x 1.2=6×10 -3 S cm -1.

Example 2. The conductance of a 0.10 mol L-1 solution of NaCl was found to be 6.13×1032^-1. Calculate its molar conductivity if the cell constant is 1.5 cm¹.
Solution:

Given

The conductance of a 0.10 mol L-1 solution of NaCl was found to be 6.13×1032^-1.

For calculating molar conductivity, the conductivity has to be calculated.

K = \(G \cdot G^*=4 \times 0.005=0.02 \mathrm{~S} \mathrm{~m}^{-1}\)

\(9.195 \times 10^{-3} \Omega^{-1} \mathrm{~cm}^{-1} \text { or } \mathrm{Scm}^{-1}\)

Molar conductivity,

\(\Lambda_m=\frac{\kappa \times 1000}{c(\text { in M })}=\frac{9.195 \times 10^{-3}}{0.1} \times 1000=0.0919 \times 10^3 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}\)

Example The conductance of a 0.1 M solution of an electrolyte of formula AX2 is 4@@@-1. Calculate the molar conductivity of this solution if the cell constant is 0.005 m -1.

Solution Conductivity K = \(G \cdot G^*=4 \times 0.005=0.02 \mathrm{~S} \mathrm{~m}^{-1}\)

Molar conductivity \(\)

But 10 dm = 1 m ⇒ 1dm = 0.1 m

∴ \(\Lambda_m=\frac{\kappa}{c}=\frac{0.02 \mathrm{~S} \mathrm{~m}^{-1}}{0.1 \mathrm{~mol} \mathrm{dm}^{-3}}\)

\(\frac{0.02 \times(0.1)^3}{0.1} \mathrm{~S} \mathrm{~m}^2 \mathrm{~mol}^{-1}=0.002 \mathrm{~S} \mathrm{~m}^2 \mathrm{~mol}^{-1}\)

Example The conductance of 0.01 M HCl was found to be 3.296×103 using a cell in which the distance between the electrodes was 1 cm and the area of the cross-section of electrodes was 0.80 cm2. Calculate its molar conductivity.

Solution Cell constant \(\mathrm{G}^*=\frac{1}{0.80} \mathrm{~cm}^{-1}=1.25 \mathrm{~cm}^{-1}=1.25 \times \frac{1}{\mathrm{~cm}}=\frac{1.25}{10^{-2} \mathrm{~m}}\)

= 125 m^-1

Conductivity K=G x G* = \(3.296 \times 10^{-3} \times 125 \mathrm{~S} \mathrm{~m}^{-1}=0.412 \mathrm{~S} \mathrm{~m}^{-1}\)

Molar conductivity = \(\frac{10^{-3} \times \kappa}{c\left(\mathrm{~mol} \mathrm{~L}^{-1}\right)}=0.0412 \mathrm{~S} \mathrm{~m}^2 \mathrm{~mol}^{-1}\)

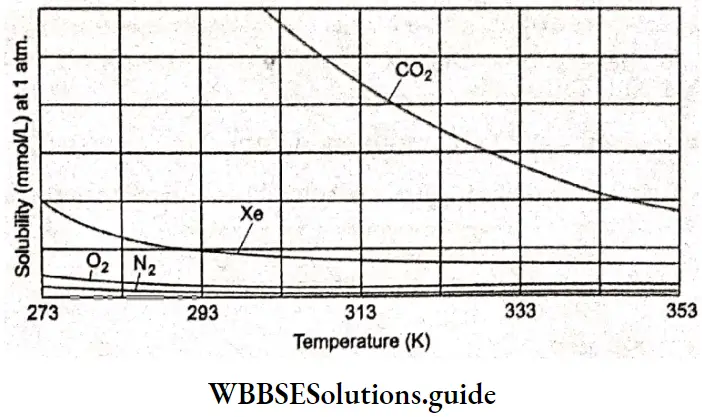
Variation Of Conductivity And Molar Conductivity With Concentration

Conductivity always decreases with a decrease in concentration for all kinds of electrolytes (both strong and weak). This can be understood from the relation between conductance and conductivity.

When both the distance I and the area of cross-section a are unity, the conductance measured is the specific conductance or conductivity. We are basically measuring the conductance of one unit volume of solution to obtain the specific conductance.

When the concentration decreases, i.e., the solution becomes dilute, the same unit volume of solution contains fewer ions and hence the conductivity decreases. In contrast to conductivity, molar conductivity increases on dilution. We can relate the molar conductivity to the volume of the solution as follows.

\(\Lambda_m=\frac{\kappa}{c}\)

If c is expressed in mol m^-3

\(\Lambda_m=\kappa \times\left(\frac{1}{c}\right)=\kappa V\)

where V is the volume of a solution containing 1 mol of the electrolyte (c moles contained in 1 m³; 1 mol contained in = \(\frac{1}{c} \mathrm{~m}^3\))

Am is directly related to the volume containing 1 mol of the substance. In a dilute solution, the volume containing 1 mol of the electrolyte will be larger and hence from Equation 3.6, A will be larger. As the concentration increases, the molar conductivity decreases.

We can therefore define molar conductivity as the conductance of a volume of a solution containing 1 mol of a dissolved substance when placed between two parallel electrodes which are a unit distance apart and are large enough to contain between them the whole solution.

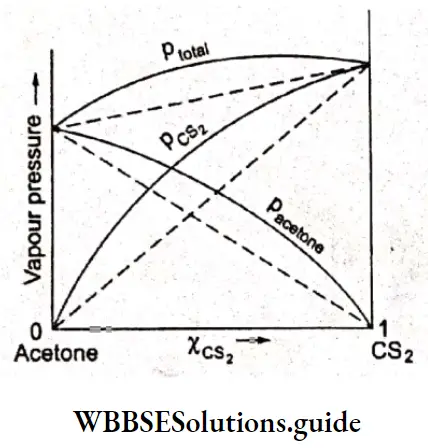
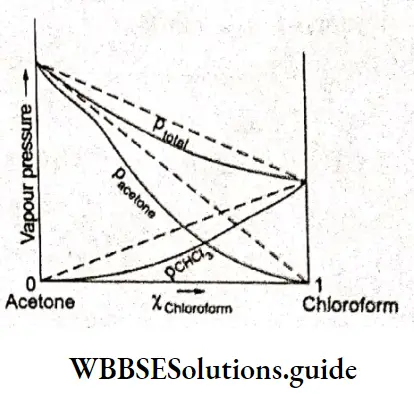
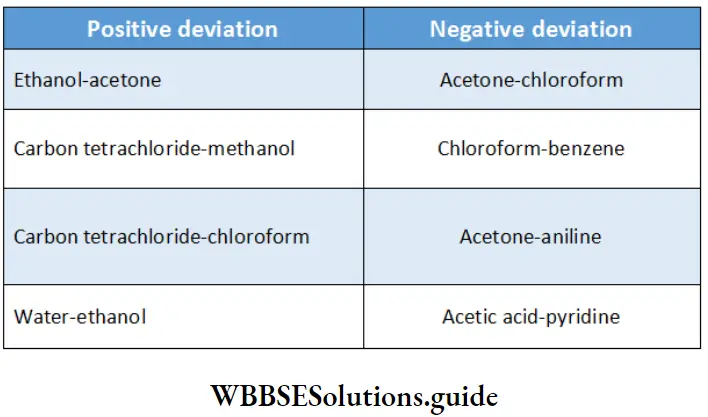
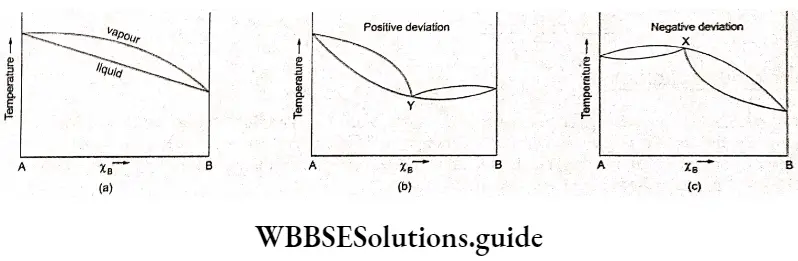
Strong And Weak Electrolytes

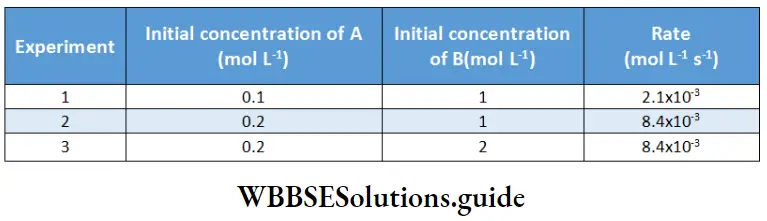
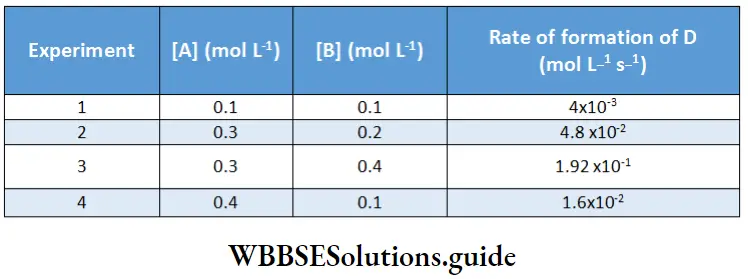
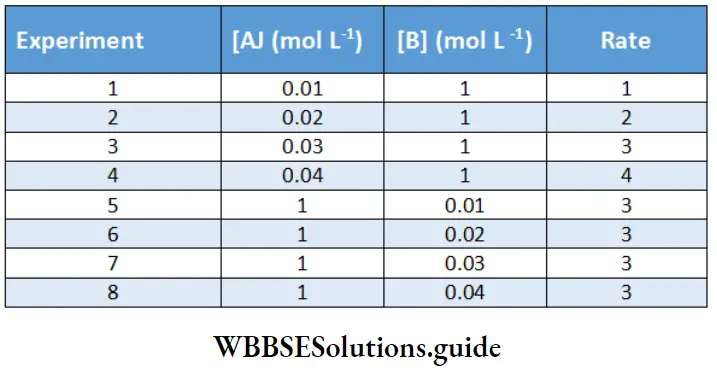
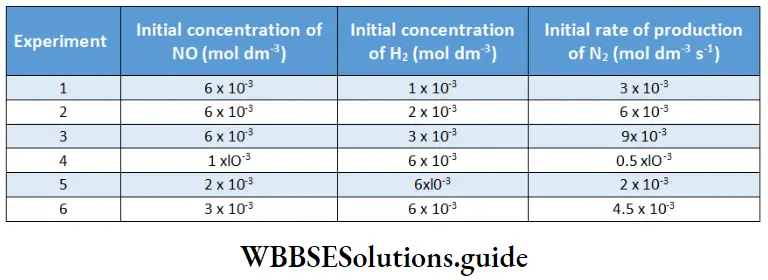
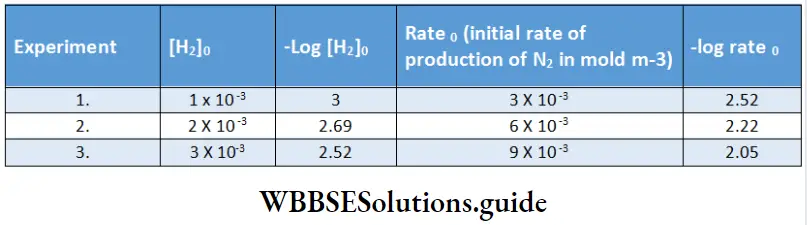
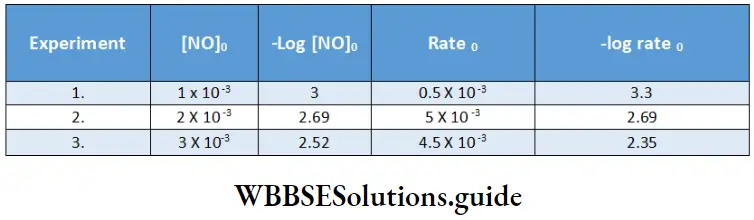
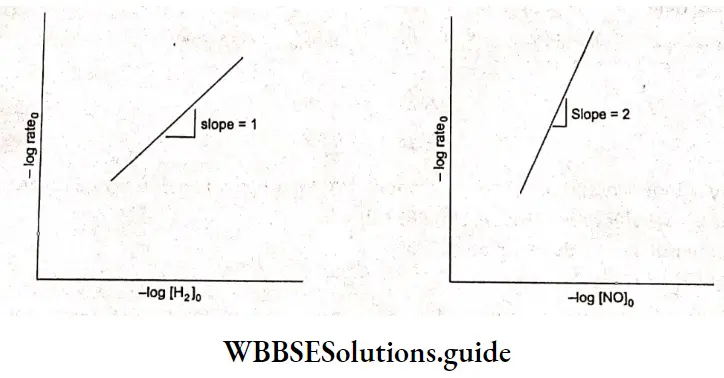
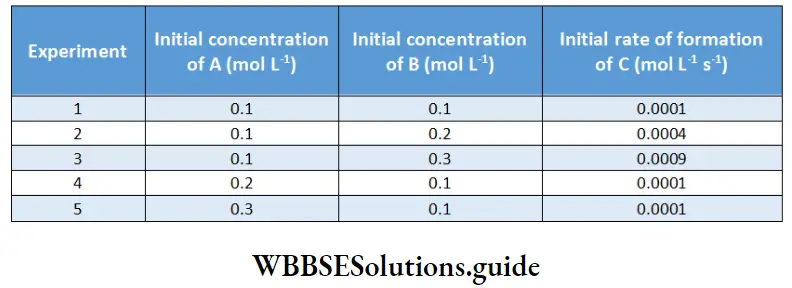
Between 1860 and 1880, Friedrich Kohlrausch and his coworkers performed a series of measurements of molar conductivities of aqueous solutions with varying concentrations of electrolytes. The molar conductivity was found to vary with the concentration of the electrolyte.

This variation is due to the fact that the number of ions per unit volume of the solution is not proportional to the molar concentration of the electrolyte. For example, in case of a weak acid, doubling the concentration of the acid does not double the number of ions. In addition, since ions interact with each other, the conductivity of a solution is not proportional to the number of ions present.

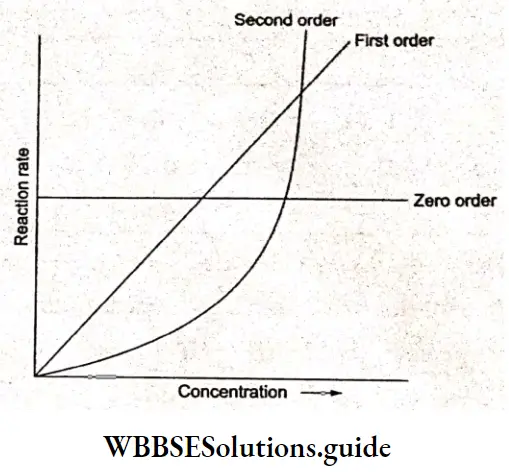
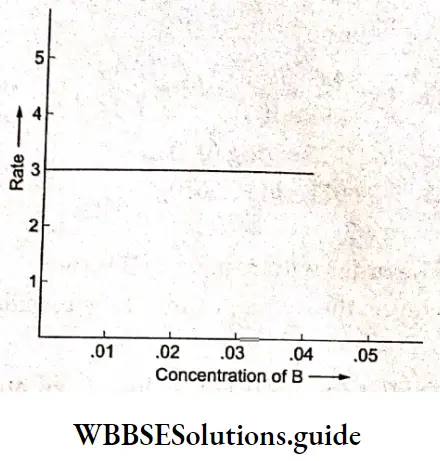
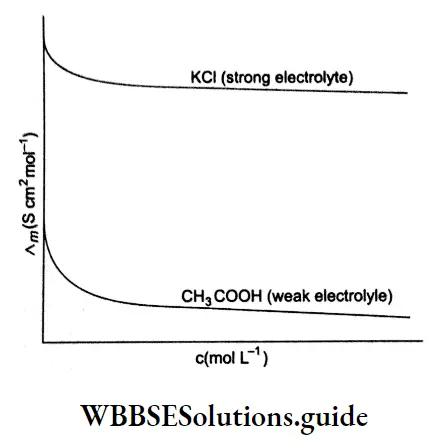
Based on the dependence of molar conductivity on concentration, electrolytes are divided into two classes-strong and weak. The characteristic of a strong electrolyte is that its molar conductivity decreases only slightly as its concentration is increased.

On the other hand, the molar conductivity of a weak electrolyte is appreciable at concentrations close to zero but falls sharply as the concentration increases. The classification of electrolytes also depends on the solvent employed. For example, lithium chloride is a strong electrolyte in water but a weak electrolyte in propanone.

Strong Electrolytes

Strong electrolytes are completely ionized in solution. Examples include ionic solids such as NaCl and KCl, and strong acids. The number of ions in a solution of a strong electrolyte is proportional to the concentration of the electrolyte added.

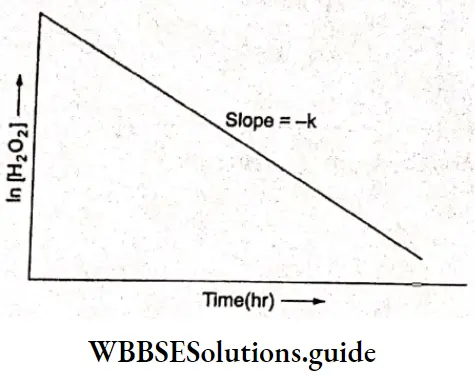
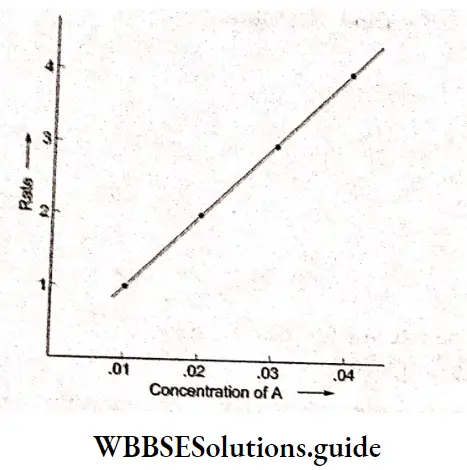
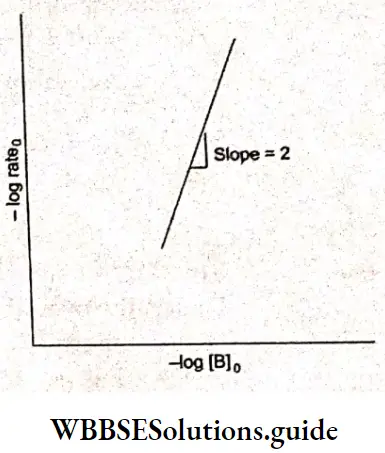
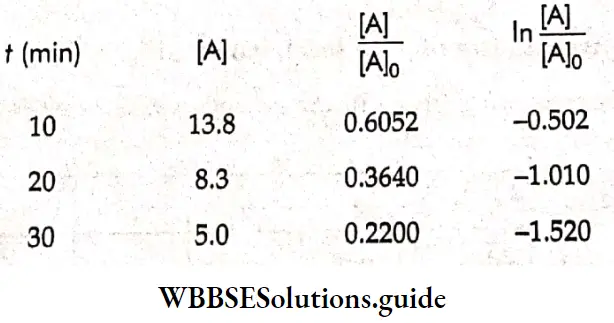
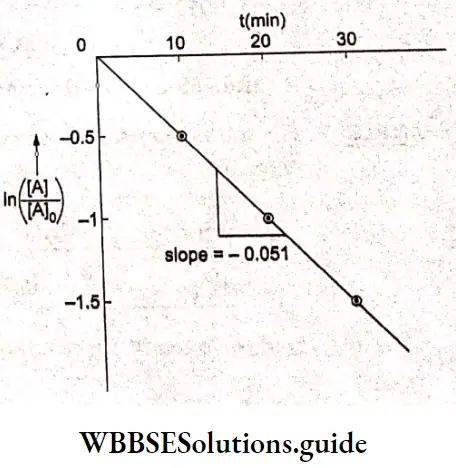
Kohlrausch, from a series of experiments, showed that at low concentrations the molar conductivities of strong electrolytes vary linearly with the square roots of their concentrations.

\(\Lambda_m=\Lambda_m^0-A \sqrt{c}\)

This is called Kohlrauseh’s law. The constant \(\Lambda_m^0\), is the limiting molar conductivity, the molar conductivity in the limit of zero concentration. This means that it is the molar conductivity of the solution when its concentration approaches zero. In other words, it refers to a solution that is so dilute that there are very few ions and they are far apart and do not interact with one another.

\(\Lambda=\Lambda_m^0 \text { as } c \rightarrow 0\)

Factor A is a constant and depends more on the stoichiometry of the electrolyte (i.e., whether it is M_A, M_2A, etc.) than on its specific identity. For example, NaCl and KCl are a particular type of electrolytes, i.e., 1-1, having the same value for A. Similarly CaCl₂ and MgSO₄ are respectively of types 2-1 and 2-2 respectively.

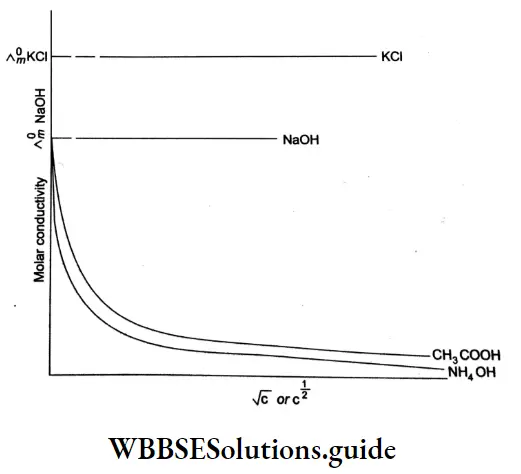
The value of \(\Lambda_m^0\), can be obtained by plotting \(\Lambda_m \operatorname{vs} \sqrt{c}\) and then extrapolating the graph to √c = 0. It can be seen that the plot of \(\Lambda_m \operatorname{vs} \sqrt{c}\) is nearly linear for KCl, a strong electrolyte, but \(\Lambda_m\) decreases slightly as the concentration increases.

The number of ions per unit volume of the solution increases as the concentration increases and an increase in Am is expected. However, there is a considerable change in interionic interaction (between K⁺ and Cl^–) as the concentration changes. The attraction between the ions increases with an increase in concentration.

The ability of the ions to move independently decreases, as a result of which the conductivity decreases (but only slightly) as the concentration increases. As the solution is diluted, the concentration decreases, the ions are far apart, the attraction decreases, and the conductivity increases.

When the concentration becomes very low, the interionic interactions are the least and the molar conductivity approaches the maximum limiting value A°m, a constant. In other words, the limiting molar conductivity is the molar conductivity in the limit of such low concentration that ions are no longer able to interact with one another.

The tin value is characteristic of every strong electrolyte. It is also called the molar conductivity at infinite dilution. The ions are very well separated at infinite dilution or in the limit of zero concentration and therefore behave independently of one another.

Kohlrausch gave the law of independent migration of ions. The law states that the limiting molar conductivity of an electrolyte can be expressed as the sum of the individual contributions of the anion and cation of the electrolyte.

If the limiting molar conductivity of cations is denoted by X°+ and that of anions by λ°_, then according to Kohlrausch’s law of independent migration of ions,

\(\Lambda_m^0=v_{+} \lambda_{+}^0+v_{-} \lambda_{-}^0\)

where v+ and v_ are tire numbers of cations and anions respectively per formula unit of the electrolyte. For example, for KC1 and \(v_{+}=v_{-}=1 ; \text { for } \mathrm{MgCl}_2, v_{+}=1, v_{-}=2\)

Weak Electrolytes

Weak electrolytes are not fully ionized in the solution. They include weak Bronsted acids and bases such as CH₃COOH and NH₃. The following equilibrium exists in solutions of weak electrolytes.

\(\mathrm{HA}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{A}^{-}(\mathrm{aq})\)

At low concentrations, the equilibrium shifts towards the right, thus increasing the number of ions in solution due to which the conductivity increases. Therefore, it is obvious that the conductivity depends on the degree of ionization, a, of the weak electrolyte. Therefore, if the molar concentration of the acid HA is c then the concentrations of HA, H₂O+, and A- at equilibrium will be

\([\mathrm{HA}]=(1-\alpha) c,\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\alpha c \text { and }\left[\mathrm{A}^{-}\right]=\alpha c \text {. }\)

The acidity constant or the acid dissociation constant is given by

\(k_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)

or, \(k_a=\frac{\alpha^2 c}{1-\alpha}\)

At infinite dilution (c→0), the electrolyte is fully ionized and the molar conductivity is A°nr According to Arrhenius, at infinite dilution, only a fraction a is actually present as ions in the solution, and the measured molar conductivity is given by

\(\Lambda_m=\alpha \Lambda_m^0\)

or, \(\alpha=\frac{\Lambda_m}{\Lambda_m^0}\)

Substituting this value of an in Equation (3.8), we get

\(k_a=\frac{\left(\frac{\Lambda_m}{\Lambda_m^0}\right)^2 c}{1-\left(\frac{\Lambda_m}{\Lambda_m^0}\right)}=\frac{c \Lambda_m^2}{\Lambda_m^0\left(\Lambda_m^0-\Lambda_m\right)}\)

Using Kohlrausch’s law of independent migration of ions \(\ Lambda_m^0te] for any electrolyte can be calculated from the X° of individual ions (Equation 3.7). Both the degree of ionization and dissociation constant for a weak electrolyte can be determined if [latex]\Lambda_m \text { and } \Lambda_m^0\) are known at a given concentration c.

Example Calculate the molar conductivity at infinite dilution (\(\Lambda_m^0\)) of acetic acid given that \(\Lambda_m^0\) of HC1, NaCl, and CH₃COONa are 426,126 and 91 Ω^-1 cm² mol^-1respectively.

Solution \(\Lambda_{m, \mathrm{HAC}}^0=\Lambda_{m, \mathrm{NaAc}}^0+\Lambda_{m, \mathrm{HCl}}^0-\Lambda_{m, \mathrm{NaCl}}^0\left(\text { Ac stands for acetate, } \mathrm{CH}_3 \mathrm{COO}^{-}\right)\)

∴ \(\Lambda_{m, \mathrm{HAc}}^0=91+426-126=391 \mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}\)

If the units are to be converted to S m² mol^-1, since 1 cm = 10-2 m, 1 cm2 = 10^-2 x 10^-2 m², multiply by 10-4 m²

∴ \(\Lambda_{m, \mathrm{HAc}}^0=391 \times 10^{-4} \mathrm{~S} \mathrm{~m}^2 \mathrm{~mol}^{-1}\)

= 0.0391 Sm² mol^-1

Example If the molar conductivity of 0.001 M acetic acid is 0.00492 S m² mol^-1, and its\(\Lambda_m^0\) is 0.03907 S m² mol⁴, calculate the degree of dissociation, &&&. Also, find the equilibrium constant for the dissociation of this acid.

Solution \(\alpha=\frac{\Lambda_m}{\Lambda_m^0}=\frac{0.00492}{0.03907}=0.1259\)

\(\mathrm{HAc} \rightleftharpoons \mathrm{H}^{+}+\mathrm{Ac}^{-}\) \(k=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{Ac}^{-}\right]}{[\mathrm{HAc}]}=\frac{(c \alpha)^2}{c(1-\alpha)}=\frac{c \alpha^2}{1-\alpha}\)

Thus the dissociation constant of acetic acid (HAc) is

\(k=\frac{0.001 \times(0.1259)^2}{1-0.13}=1.94 \times 10^{-5}\)

Electrochemical Cells

An electrochemical cell is a setup in which a spontaneous chemical reaction occurs to produce electrical energy or, a nonspontaneous chemical reaction is carried out by using an external source of are called galvanic cells or voltaic cells, and the latter, electrolytic cells All electrochem electrodes dipping into either one or two electrolyte solutions.

Current can pass. It may be made of a metal such as copper, silver zinc, etc. or electric Electrodes come in a variety of shapes-they may be wireSPplates or rodsd.

AnddectrolyteTs In The electrode and its surrounding electrolyte solution are contained in electrodes may or may not share the same compartment.

Compartment The two are made of zinc and copper. These electrodes are dipped in zinc sulfate and copper sulfate The electrodes are respectively, taken in different compartments. To complete the electrical circuit the solution (electrolytes) salt bridge. The following redox reaction occurs in the cell.

\(\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+\mathrm{Cu}(\mathrm{s})\)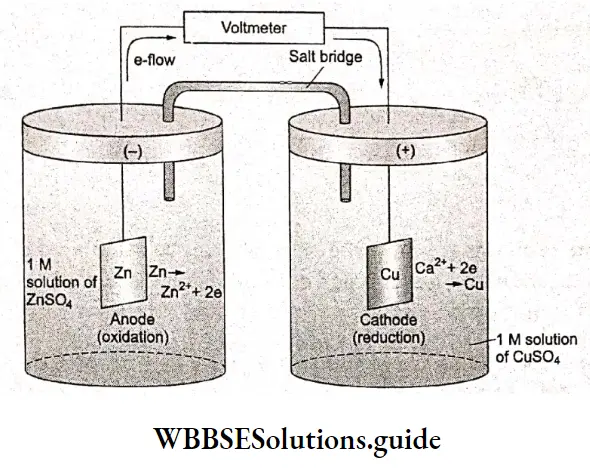

The chemical energy of this reaction is converted to electrical energy, which can be used to light a bulb, rim a motor, and so on.

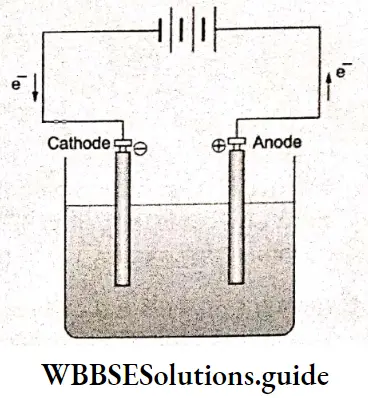
An electrolytic cell. A battery supplies electrical energy to carry out a nonspontaneous reaction.

Cell diagram

Any electrochemical cell can be represented by a cell diagram that shows the oxidized as well as the reduced forms of the electroactive substance and any other species that may be involved in the chemical reaction.

The electrodes, denoted by their atomic symbols, are indicated at the two ends of the diagram. Any insoluble substances or gases are denoted inside, next only to the electrodes.

The soluble species are represented in the middle of the diagram. The states of aggregation (solid, liquid, or gas) are also specified within brackets. In an abbreviated diagram, some of the above information is ignored and only the main components are given.

In a cell diagram, a phase boundary is indicated by a solid vertical bar; a junction between two miscible liquid phases is represented by a single dashed vertical bar.

A double dashed vertical bar indicates a junction between two miscible liquid phases at which the junction potential has been eliminated using a salt bridge. Commas separate different soluble species in the same phase. It is assumed that the right-hand electrode is the cathode and the left-hand electrode is the anode.

Some examples of cell diagrams are given below.

1. \(\mathrm{Zn}(\mathrm{s})\left|\mathrm{Zn}^{2+}(a=0.35): \mathrm{Cu}^{2+}(a=0.49)\right| \mathrm{Cu}(\mathrm{s})\) (complete diagram)(a denotes the activity of the ions)

\(\mathrm{Zn}\left|\mathrm{Zn}^{2+}: \mathrm{Cu}^{2+}\right| \mathrm{Cu} \text { (abbreviated diagram) }\)

This cell is called the Daniell cell.

2. \(\mathrm{Pt}\left|\mathrm{H}_2(\mathrm{~g})\right| \mathrm{HCl}(m)|\mathrm{AgCl}(S)| \mathrm{Ag}(\mathrm{s}) \mid \mathrm{Pt}\)

3. \(\mathrm{Pt}\left|\mathrm{H}_2(\mathrm{~g}), \mathrm{H}^{+}: \mathrm{Fe}^{3+}, \mathrm{Fe}^{2+}\right| \mathrm{Pt}\)

4. \(\mathrm{Zn}\left|\mathrm{Zn}^{2+}\left(c_1\right) \vdots \mathrm{Zn}^{2+}\left(c_2\right)\right| \mathrm{Zn}\)

(m denotes molality, c₁ and c₂ denotes the cons=centrations.)

Galvanic (Voltaic) Cell

A galvanic cell is an electrochemical cell that produces electricity from the spontaneous chemical reactions occurring inside it. Consider a cell made up of a zinc rod dipped in ZnSO₄ solution and a copper rod dipped in

CuSO₄ solution. This is a Daniell cell—a type of galvanic cell. To avoid direct mixing of the electrolyte solutions, these are taken in separate compartments, and connection between them is established through a salt bridge.

A salt bridge is made of a glass tube containing an inert electrolyte solution (whose ions do not react with the ions of the main electrolytes or the electrodes) such as KCl, KNOa, or NH₄NO₃, kept in agar-agar, a geL The two portions of the cell are called half-cells or redox couples.

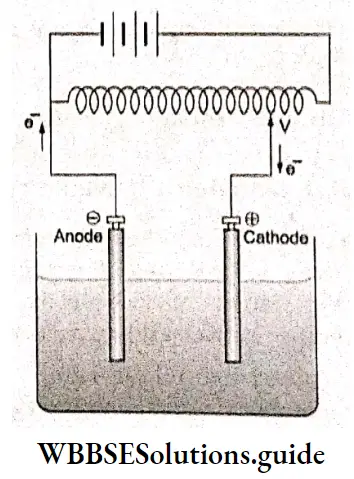
In one half-cell, the metal from an electrode dissolves in the solution leaving behind electrons, making the electrode negatively charged and simultaneously, in the other half-cell, the metal ions from the solution deposit on the other metal electrode, making this electrode positively charged. The actual reactions occurring at the two electrodes (half-cell reactions) are as follows.

Zn electrode (anode) Oxidation occurs at this electrode.

\(\mathrm{Zn}(\mathrm{s}) \rightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-}\)

Cu electrode (cathode) Reduction occurs at this electrode.

\(\mathrm{Cu}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}(\mathrm{s})\)

The overall reaction is obtained by adding the above two equations.

\(\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+\mathrm{Cu}(\mathrm{s})\)

We can see that Zn undergoes oxidation while the Cu²⁺ ions undergo reduction. Thus the Zn electrode is negatively charged and the copper electrode is positively charged. The electrode which is negatively charged is called the anode and that which is positively charged is called the cathode. In the solution, the cations Zn^2- and Cu²⁺ move towards the cathode while the anions SO⁴⁺ move towards the anode.

Since the two electrodes are oppositely charged, a potential difference occurs between them and electrons flow from the anode to the cathode. The direction of current is opposite to that of electron flow.

The conventional method is to write the reduction reactions for both electrodes (even though in reality oxidation may be occurring at one electrode) and obtain the overall reaction by subtracting the reduction reaction at the anode (left-hand electrode) from that occurring at the cathode (right-hand electrode). The half-reactions for the reduction of copper by zinc are as follows.

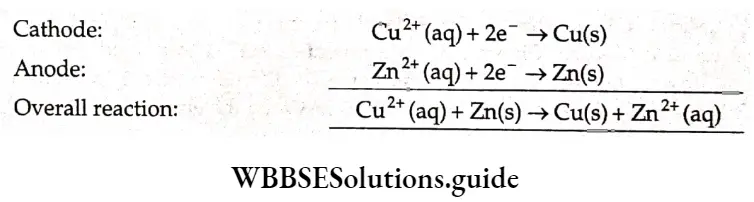
If the two solutions are not separated from each other, the Cu²⁺ ions react directly with the zinc bar.

\(\mathrm{Cu}^{2+}(\mathrm{aq})+\mathrm{Zn}(\mathrm{s}) \rightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}(\mathrm{aq})\)

In such a situation, no useful electrical work is obtained.

The cell potential of a galvanic cell:

A galvanic cell converts the chemical energy liberated during a chemical reaction to electrical energy. It produces a driving force through the chemical reaction that pushes electrons through an external circuit. The work done by a given transfer of electrons depends on the cell potential.

The cell potential or emf of the cell is the potential difference between the two electrodes. It may also be called cell voltage. The unit of cell potential is the volt (V).

Under balanced reversible conditions, a cell reaction can proceed in either direction. Here eversibility refers to the change in direction of the movement of ions by reversing the polarity of the electrodes. In a cell diagram, the cell reaction is written in such a manner that electrons are shown to be accepted from the external circuit by the electrode on the right and given up by the electrode on the left.

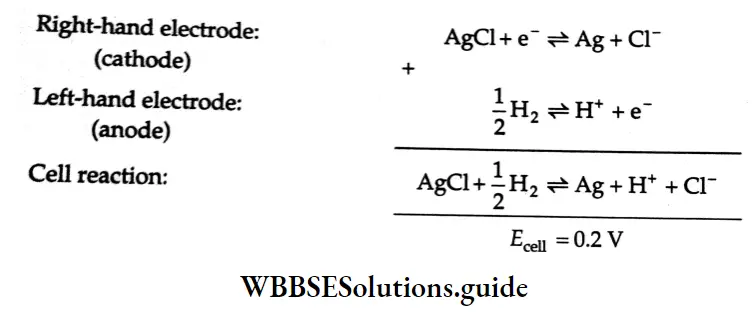
Consider the following example In which ft cell In represents an

\(\mathrm{Pt}\left|\mathrm{H}_2(1 \mathrm{bar}) \& \mathrm{HCl}(1 \mathrm{M})\right| \mathrm{AgCl} \mid \mathrm{Ag}\)

The reactions that occur in the electrodes of the cell are as follows,

Conversely, if the above cell diagram is shown as ns

\(\left.\mathrm{Ag}|\mathrm{AgCl}| \mathrm{HCl}(1 \mathrm{M}) \mid \mathrm{H}_2 \text { (1 bar }\right) \mid \mathrm{Pt}\)

then the reactions that occur at the two electrodes get reversed,

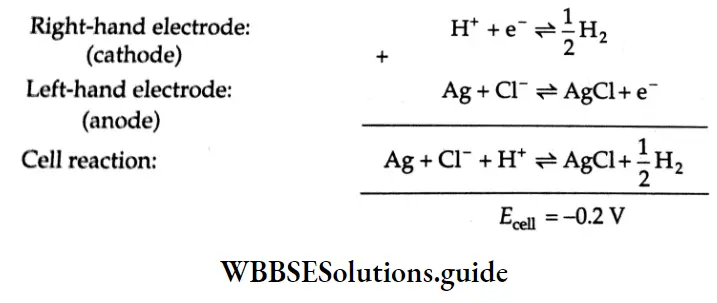
As you can see the emf of the reaction represented by Equation 3,9 Is positive and hence, by convention, the reaction will proceed from left to right. However, the emf of the reaction shown in Equation 3,10 is negative, indicating that the reverse of this reaction is spontaneous,

Measurement of the cell potential of a galvanic cell and that of a Daniell cell To measure the cell potential of a galvanic ceil, a potentiometer is placed in the circuit. In a potentiometer, a steady current from a battery flows through a resistor, A sliding contact is used to vary the potential difference across the slide wire connected to an electrochemical cell, If the applied potential difference (V) is less than the emf of the galvanic cell (Ecell) the cell discharges electricity spontaneously. When the two are exactly the same (V = Ea4l), then no current flows through the cell and this is the equilibrium potential difference (emf or Ece]|) we are interested in.

In practice, the two substances (electrodes and electrolytes) forming the cell are kept in their standard states (all the solutes are at 1 M and the gases are at 1 atm).

The cell potential measured under the standard state conditions is called the standard cell potential, Efcn. The superscript is used to indicate that all reactants and products are in their standard states.

When 1 M solutions of ZnSC)₄ and CuSO₄ are used for the redox reaction in the Daniell cell, the is found to be 1.1 V at 25°C. A galvanic cell has a positive emf if the cell reaction is spontaneous, i.e„ electrons are accepted by the right-hand electrode (cathode) and released by the left-hand electrode (anode). Therefore, Zn reduces copper ions to Cti(s) according to Equation 3.11 for which EceU is positive.

\(\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}(\mathrm{aq})\)

But, for the reverse reaction

\(\mathrm{Cu}(\mathrm{s})+\mathrm{Zn}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Cu}^{2+}(\mathrm{aq})+\mathrm{Zn}(\mathrm{s})\)

the emf is negative, i.e., \(E_{\text {cell }}^\theta=-1.1 \mathrm{~V}\) Tire reverse reaction is made possible by applying an external opposite potential to the galvanic cell. As long as the external voltage is less than 1.1V (\(E_{\text {cell }}\), of the Daniell cell) the exception proceeds spontaneously; zinc gets oxidized and Cu²⁺ ions get reduced deporting copper at the cathode.

Current flows from copper to zinc. When the external potential becomes equal to Ewll, neither do electrons flow through the cell nor does any reaction take place. When EwU is exceeded, the reaction proceeds in the reverse direction# electrons flow from copper to zinc as copper gets oxidized and Zn²⁺ ions get reduced, deputing zinc at the zinc electrode, which now acts as the cathode. The cell now functions as an electrolytic cell

Half-Cell Potential Of A Daniell Cell

Each compartment consisting of an electrode dipped in the corresponding electrolyte solution is called a half-veil As you already know, the electrode may be positively or negatively charged with respect to the solution, Hence, a potential difference develops between the electrode and the electrolyte, called electrode potential bach half-cell in a cell can therefore be assigned a half-cell potential which is nothing hut the electrode potential The ha I heel I potential could be either oxidation potential when oxidation occurs or reduction potential when reduction occurs, The sum of half-cell potentials gives the cell potential For the Daniel! cell formed of copper and zinc electrodes operating under standard state conditions, the anode or oxidation potential is 0.763 V and the cathode or reduction potential is 0.337 V at 25°C. Therefore, the cell potential \(\left(E_{\mathrm{cell}}^{\Theta}\right) \text { is } 1.1 \mathrm{~V}\)

It is, however, important to note that by convention, the half-reactions are written as reduction actions and the corresponding half-cell potentials, which are both reduction potentials, are considered fir calculating E-cell

When the species are in their standard states, the half-cell reduction potential is called standard electrode potential. The overall emf of the cell, is then obtained by subtracting the electrode potential of the anode (left-hand electrode) from that of the cathode (right-hand electrode) or simply by the relation

\(E_{\text {cell }}^{\ominus}=E_{\text {right }}^{\ominus}-E_{\text {left }}^{\ominus} \quad \text { (both } E_{\text {right }}^{\ominus} \text { and } E_{\text {left }}^{\ominus} \text { are reduction potentials) }\)

For the above Daniell cell,

\(E_{\text {cell }}^{\Theta}=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\Theta}-E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^\theta\)

\(E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{\Theta} \text { (for the reaction } \mathrm{Zn}^{2+}+2 \mathrm{e}^{-} \rightarrow \mathrm{Zn} \text { ) }\) is equal to the negative of that of the reverse reation,

i.e., \(\mathrm{Zn} \rightarrow \mathrm{Zn}^{2+}+2 \mathrm{e}^{-}[/lattex] whose potential is represented as [latex]E_{\mathrm{Zn} / \mathrm{Zn}^{2+}}^\theta(0.763 \mathrm{~V})\)

Hence \(E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{\Theta}=-0.763 \mathrm{~V}\)

Therefore,

\(E_{\mathrm{cell}}^{\Theta}=0.337-(-0.763) \mathrm{V}\)

or, \(E_{\text {cell }}^{\Theta}=1.1 \mathrm{~V}\)

The standard electrode potential of a galvanic cell

Although we can measure the overall cell potential of a galvanic cell, there In no satisfactory method to measure the individual actual potentials of the two electrodes. However, a standard potential can be assigned to one electrode and the other electrode can be assigned a relative value of potentials based on this.

The most commonly used reference electrode is the standard hydrogen electrode (SHE), which is assigned a potential of zero volts at all temperatures. The potentials of all other electrodes are reported relative to that of the SHE.

The standard hydrogen electrode is a gas-ion electrode. In a hydrogen electrode, hydrogen gas is bubbled through a solution of hydrogen ions in which a platinum foil coaled with very finely divided platinum black is dipping partially. Here platinum metal acts as an inert electrode; it does not participate in the reaction—it only provides its surface for the redox reaction. The net ionic equation for reduction in the electrode is

\(2 \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_2(\mathrm{~g}) \div 2 \mathrm{H}_2 \mathrm{O}(\mathrm{I})\)

The potential of a gas electrode changes with the pressure of die gas and with the concentration of the other components. If a hydrogen electrode operates at 298 K with hydrogen gas at a pressure of 1 bar bubbling around a platinum foil immersed in a 1M solution of hydronium ions, it is called a standard hydrogen electrode.

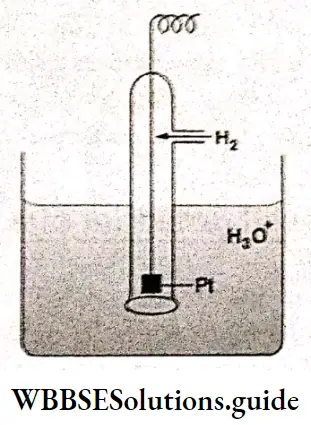
Measurement of the standard electrode potential of a galvanic cell:

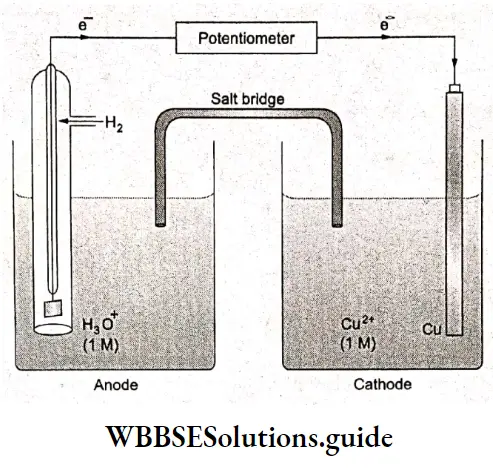
In order to measure the potential of an electrode relative to the SHE, a galvanic cell is constructed with the standard hydrogen electrode and electrode of interest. The cell potential is the potential of the other half-cell, i.e., the electrode whose potential is to be measured.

For example, the potential of a copper electrode can be determined by coupling it with a SHE. The cell diagram is \(\mathrm{Pt}(\mathrm{s})\left|\mathrm{H}_2(1 \mathrm{~atm})\right| \mathrm{H}^{+}(1 \mathrm{M}) \| \mathrm{Cu}^{2+}(1 \mathrm{M}) \mid \mathrm{Cu}(\mathrm{s}) .\). The SHE acts as the anode and the copper electrode as the cathode. The overall redox reaction and the two half-reactions in the cell are

\(\mathrm{Cu}^{2+}(\mathrm{aq})+\mathrm{H}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{Cu}(\mathrm{s})+2 \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})\)

Cathode: \(\mathrm{Cu}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}(\mathrm{s})\)

Anode: \(\mathrm{H}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow 2 \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+2 \mathrm{e}^{-}\)

The observed potential for the cell is 0.337 V at 25°C.

\(E_{\text {cell }}^{\Theta}=E_{\text {cathode }}^{\Theta}-E_{\text {anode }}^{\Theta}\) \(0.337=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\Theta}-E_{\mathrm{H}^{+} / \mathrm{H}_2}^{\Theta}\) \(E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\Theta}-0\)

Thus, \(E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\ominus}=0.337 \mathrm{~V}\)

The standard electrode potential of copper, \(E_{\mathrm{Cu}^{2+} / \mathrm{Cu}^{\prime}} \text {, is } 0.337 \mathrm{~V}\) the subscript Cu²⁺/Cu indicating the reaction \(\mathrm{Cu}^{2+}+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}\) If we wish to determine the standard electrode potential (the reduction potential) of a zinc electrode, the SHE acts as the cathode and the zinc electrode acts as the anode.

The cell diagram is

\(\mathrm{Zn}(\mathrm{s})\left|\mathrm{Zn}^{2+}(1 \mathrm{M}) \| \mathrm{H}^{+}(1 \mathrm{M})\right| \mathrm{H}_2(1 \mathrm{~atm}) \mid \mathrm{Pt}(\mathrm{s})\)

The two half-reactions and the overall reaction are as follows.

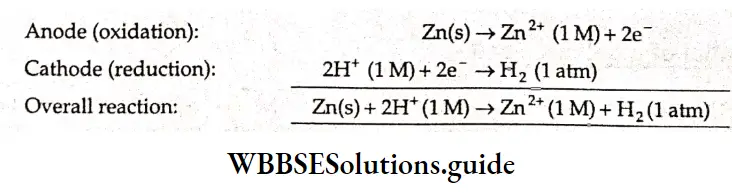
The \(E_{\text {cell }}^{\ominus}\) was found to be 0.76 V.

\(E_{\text {cell }}^{\Theta}=E_{\text {cathode }}^{\Theta}-E_{\text {anode }}^{\Theta}\) \(0.76=E_{\mathrm{H}^{+} / \mathrm{H}_2}^{\Theta}-E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{\Theta}\) \(0.76=0-E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{\ominus} \Rightarrow E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{\Theta}=-0.76 \mathrm{~V}\)

Thus tire standard reduction potential of zinc, \(E_{\mathrm{Zn}^{2+} / \mathrm{Zn}^{\prime}} \text { is }-0.76 \mathrm{~V}\)

Lists the values of standard electrode potentials (reduction potentials) for some half-cells.

The positive value of standard electrode potential in the example of copper indicates that Cu²⁺ ions get reduced more easily than the H⁺ ions. The negative value of standard electrode potential in case of zinc indicates that hydrogen ions can oxidize zinc easily.

The standard electrode potentials are useful in finding out the £Te’ for a combination of different half-cells. It is important to know the following facts about the standard electrode potential values,

1. The \(E^{\Theta}\) values are applicable to the half-cell reactions as read in the forward direction.

2. The half-cell reactions are reversible. A particular electrode can act as anode or cathode, depending on the electrode that is coupled to it,

3. The values of reduction potentials also indicate the tendency of a reaction to occur. The higher the value, the greater is the tendency for reduction, Those electrodes which have a positive electrode potential can be more easily reduced than those having a negative electrode potential. A positive electrode potential indicates a greater tendency to reduce than hydrogen ions.

4. The more positive the value of \(E^{\Theta}\), the greater is the tendency for the substance to be reduced. A look at Table 3.5 shows that P2 has the greatest tendency to get reduced or, in other words, it is the strongest oxidizing agent, Lithium figures at the bottom of the table, indicating that it has the lowest ability to get reduced or the greatest tendency to get oxidized—thus, it is the strongest reducing agent. Thus we see that the relative tendency of metals to get oxidized can be judged from the values of the standard electrode potentials of the corresponding half-cells. The electrochemical series is an arrangement of metal/metal ion electrode potentials in order to decrease the tendency to lose electrons.

5. If any two electrodes are chosen to form a cell, then the electrode that figures first in the table as we move from top to bottom acts ns the cathode and reduction occurs at this electrode. Conversely, the electrode that figures Inter in the table acts as the anode and oxidation occurs at that electrode.

6. Changing the stoichiometric coefficients of a half-cell reaction does not affect the value of \(E^{\Theta}\) as electrode potential is an intensive property.

7. The sign of \(E^{\Theta}\) changes when the reaction is reversed.

Example Calculate the emf of a cell consisting of two half-cells \(\mathrm{Ni}^{2+} / \mathrm{Ni} \text { and } \mathrm{Cd}^{2+} / \mathrm{Cd}\). Given \(E_{\mathrm{Ni}^{2+} / \mathrm{Ni}}^\theta=-0.25 \mathrm{~V}\) concentrations of Nl2+ and Cd2+ are 0.2 M and 0.3 M respectively.

Solution As the reduction potential of the cell Cd₂l/Cd is more negative, it has a tendency to undergo oxidation, the two electrode reactions are

\(E_{\mathrm{cell}}^{\mathrm{O}}=E_{\mathrm{kH}}^0-E_{\mathrm{l}, \mathrm{HI}}^{\mathrm{H}}=-0.25+0.4=0.15 \mathrm{~V}\) \(E_{\text {cell }}=E_{\text {cell }}^{\Theta}+\frac{R T}{n F} \ln \frac{\left[\mathrm{Cd}^{2+}\right]}{\left[\mathrm{Ni}^{2+}\right]}=0.15+\frac{8.314 \times 298}{2 \times 96500} \ln \left[\frac{(0.2)}{(0.3)}\right]\)

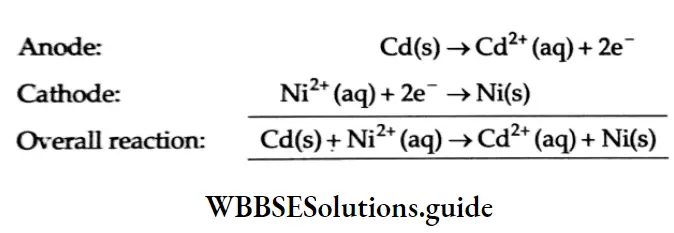
=0.145 V

Types Of Electrodes

The term ‘electrode’ is used in two different ways—one to refer to n wire or some conductor that delivers electrons through the external circuit and the other to refer to a complete half-cell. Let us touch upon the following types of electrodes to illustrate this point.

Gas-ion electrodes A gas-ion electrode consists of an inert collector of electrons such as platinum or graphite in contact with a gas ami a soluble ion, The hydrogen electrode is one example,

\(\mathrm{Pt}^{\mathrm{t}}\left|\mathrm{H}_2(\mathrm{~g})\right| \mathrm{H}^{+}\)

We can also have a chlorine electrode, represented by

\(\mathrm{Cl}_2\left|\mathrm{Cl}^{-}\right| \text {graphite }\)

Metal-metal ion electrodes A metal strip or rod dipped in a solution containing the metal ions constitutes a metal-metal ion electrode. The Zn²⁺ /Zn and Cu²⁺ /Cu electrodes of the Daniell cell are examples. Metal-insoluble salt-anion electrode Such an electrode consists of a bar of metal immersed in a solution containing a solid insoluble salt of the metal and anions of the salt.

The silver-silver chloride electrode, \(\mathrm{Cl}^{-}|\mathrm{AgCl}(\mathrm{s})| \mathrm{Ag}(\mathrm{s})\), and the calomel electrode, \(\mathrm{Cl}^{-}\left|\mathrm{Hg}_2 \mathrm{Cl}_2\right| \mathrm{Hg}\) are two examples.

Oxidation-reduction electrodes Although electrodes generally involve either oxidation or reduction in their operation, there are certain electrodes called oxidation-reduction electrodes. Such electrodes have an inert metal collector, usually platinum dipping in a solution that contains two soluble species in different states of oxidation. An example is the ferric-ferrous ion electrode.

Electrical Work And Free Energy

The chemical reaction in a galvanic cell proceeds spontaneously in the forward direction obeying laws of chemical equilibrium. Electrical work can be obtained using the galvanic cell and the total amount of energy available from a particular cell depends on the cell’s potential and the number of electrons involved. Let us now see how E^u and AGe are related. The unit of potential difference is the volt.

The work done to move a charge across a potential difference is given by the product of the charge and the potential difference. The unit of electrical work is the joule. Thus, one volt (V) is the potential difference required to impart one joule 0) of energy to a charge of one coulomb (C). In other words, one joule of energy is available when a charge of one coulomb passes between electrodes having a unit potential difference.

1J = 1V x 1C

In this context, it is important to recall that in a galvanic cell, the electrons flow in the direction determined by the potential difference between the two electrodes. When the two electrodes acquire the same potential, there is no passage of current. More work is available when more charge is moved between the electrodes.

The quantity of charge flowing through an electrical circuit connected to a galvanic cell equals the product of the number of moles of electrons (n) flowing through the circuit and the Faraday constant. The Faraday constant is the electrical charge contained in 1 mol of electrons. Experiments have shown that 1 faraday is equivalent to 96,487 coulombs.

Thus,

\(1 F=96,487 \frac{\mathrm{C}}{\mathrm{mol} \mathrm{e}^{-}} \text {or } 96,487 \frac{\mathrm{J}}{\mathrm{V} \mathrm{mol} \mathrm{e}^{-}} \text {and } C=n F\)

The electrical work (Wcle) done on the circuit is equal to the product of this charge and the electromotive force pushing it. When the work is expressed as the work done by the cell, a negative sign is introduced.

\(W_{\text {ele }}=-C E_{\text {cell }}=-n F E_{\text {cell }}\)

where n is the number of electrons transferred, F is the Faraday constant and Ecell is the cell potential. A negative cell potential means that energy is consumed while a positive potential means that work is done by the cell. The maximum amount of electrical work that can be done by the system is equal to the maximum amount of useful work. Hence,

\(W_{\max }=W_{\text {ele }}=-n F E_{\text {cell }}\)

A cell can do no work when the potential is zero (or the reaction is at equilibrium).

When the current produced by the cell is used to do work, the energy of the system (the cell) is reduced and the sign of work done is negative but the cell potential is positive. Thus the magnitude of the cell potential and the maximum amount of work Wmax available from the cell have opposite signs.

As you already know, the Gibbs free energy for a system (AG) is equal to the maximum possible useful work done by the system, Equation 3.12 can be further modified as

\(\Delta G=W_{\max }=-n F E_{\text {cell }}\)

where ΔG is the Gibbs energy change for the reaction,

The free energy of the system (here cell), therefore, decreases (i.e., has a net negative value) when the system does some useful work. The actual amount of work that a cell can do is, in fact, less than the calculated maximum amount of work because some energy is converted into heat owing to the resistance in the circuit.

When the concentrations of the reacting species are unity, the corresponding free energy change, and cell potential values are standard state values.

\(\Delta G^{\ominus}=-n F E_{\text {cell }}^{\ominus}\)

Thus, cell potential can be used to calculate \(\Delta G \text { or } \Delta G^{\ominus}\) for a process.

Example 1. Calculate the standard free energy change for the reaction occurring in the following cell.

\(\mathrm{Zn}(\mathrm{s})\left|\mathrm{Zn}^{2+}(\mathbf{1} \mathrm{M}) \| \mathrm{Cu}^{2+}(\mathbf{1} \mathrm{M})\right| \mathrm{Cu}(\mathrm{s})\)

\(\text { Given } E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^\theta=-0.76 \mathrm{~V} ; E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^\theta=0.34 \mathrm{~V} ; F=96500 \mathrm{C} \mathrm{mol}^{-1}\)
Solution:

Since \(\Delta G^{\ominus}=n F E_{\text {cell }}^{\Theta}\)

the number of electrons involved in the reaction (n) = \(2 \text { and } E_{\text {cell }}^{\Theta}=\underset{\substack{\text { cathode } \\(\mathrm{RHE})}}{E_{\text {and }}^{\Theta}}-\underset{\text { (LHE) }}{E_{\text {anode }}}=0.34-(-0.76)\)

\(E_{\text {cell }}^{\ominus}=0.34+0.76=1.10 \mathrm{~V}\)

∴\(\Delta G^{\ominus}=-2 \times 96500 \times 1.1=-212300 \mathrm{~J}=-212.3 \mathrm{~kJ} \quad(1000 \mathrm{~J}=1 \mathrm{~kJ})\)

Example 2. Calculate the maximum possible electrical work that can be obtained from the following cell under standard conditions of temperature and pressure.

\(\mathrm{Zn} / \mathrm{Zn}^{2+}(\mathrm{aq}) \| \mathrm{Sn}^{2+}(\mathrm{aq}) \mid \mathrm{Sn}\)

Given \(E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{\Theta}=-0.76 \mathrm{~V} \text { and } E_{\mathrm{Sn}^{2+} / \mathrm{Sn}}^{\Theta}=-0.14 \mathrm{~V}\)
Solution:

Electrical work done, \(W_{\text {ele }}=\Delta G^\theta\) under standard conditions and \(\Delta G^{\Theta}=-n F E_{\text {cell }}^{\Theta}\)

Also \(E_{\mathrm{cell}}^{\Theta}=E_{\mathrm{Sn}^{2+} / \mathrm{Sn}}^{\Theta}-E_{\mathrm{Zn}^{2+} / \mathrm{Zn}}^{\Theta}=-0.14-(-0.76)\)

\(E_{\text {cell }}^{\ominus}=0.62 \mathrm{~V} ; n=2\) (two electrons are involved in the cell reaction).

∴ \(\Delta G^{\ominus}=W_{\text {ele }}=-2 \times 96500 \times 0.62=-1,19,660 \mathrm{~J}\)

Thus, 119.7 kJ of work can be obtained from this cell.

It is important to note that since ΔG is an extensive thermodynamic property and the value depends on n, it changes with the change of stoichiometric coefficients. For example, the values of ΔG for the reactions

\(\mathrm{Zn}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Zn}^{2+}(\mathrm{aq})+\mathrm{Cu}(\mathrm{s})\)

and \(2 \mathrm{Zn}(\mathrm{s})+2 \mathrm{Cu}^{2+}(\mathrm{aq}) \rightarrow 2 \mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{Cu}(\mathrm{s})\)

\(\text { are }-2 F E_{\text {cell }} \text { and }-4 F E_{\text {cell }} \text { respectively. }\)

Effect Of Concentration On Cell Potential (Nernst Equation)

We may not always measure the potential of a cell under standard conditions. What happens when the concentrations of the species involved are not unity? The cell potential of the cell changes with the change in concentrations of the species

Let us consider a galvanic cell reaction of the general type

\(a \mathrm{~A}+b \mathrm{~B} \rightleftharpoons c \mathrm{C}+d \mathrm{D}\)

The reaction quotient Q is given by

\(Q=\frac{[\mathrm{C}]^c[\mathrm{D}]^d}{[\mathrm{~A}]^a[\mathrm{~B}]^b}\)

where the square brackets indicate the concentrations of the corresponding species and all quantities are raised to the power of the respective stoichiometric coefficients. Note that products appear in the numerator and reactants in the denominator.

The free energy change AG for the reaction is given by

\(\Delta G=\Delta G^{\Theta}+R T \ln \left[\frac{[\mathrm{C}]^c[\mathrm{D}]^d}{[\mathrm{~A}]^a[\mathrm{~B}]^b}\right]\)

Substituting \(\Delta G \text { and } \Delta G^{\ominus} \text { in terms of } E_{\text {cell }} \text { and } E_{\text {cell, }}^{\ominus} \text { we get }\)

\(-n F E_{\text {cell }}=-n F E_{\text {cell }}^\theta+R T \ln Q\).

\(E_{\text {cell }}=E_{\text {cell }}^{\Theta}-\frac{R T}{n F} \ln Q\).

Here n is the number of moles of electrons exchanged in the cell reaction. Equation (3-13) is known as the Nemst equation after the German chemist and physicist W H Nemst, who was awarded the Nobel Prize in Chemistry in 1920.

By converting the natural logarithm to the base 10 and at a temperature of 298 K, and substituting for the values of R and F, the above equation can be written as

\(E_{\text {cell }}=E_{\text {cell }}^{\ominus}-\frac{0.05916}{n} \log Q\)

For a half-cell reaction

\(\mathrm{M}^{n+}(\mathrm{aq})+n \mathrm{e}^{-} \rightarrow \mathrm{M}(\mathrm{s})\)

the electrode potential at any concentration measured by connecting it to an SHE can be represented by

\(E_{\mathrm{M}^{n+} / \mathrm{M}}=E_{\mathrm{M}^{n+} / \mathrm{M}}^{\Theta}-\frac{R T}{n F} \ln \frac{[\mathrm{M}]}{\left[\mathrm{M}^{n+}\right]}\)

Since M is a solid, its concentration is taken as unity and the above equation then becomes

\(E_{\mathrm{M}^{n+} / \mathrm{M}}=E_{\mathrm{M}^{n+} / \mathrm{M}}^{\Theta}-\frac{R T}{n F} \ln \frac{1}{\left[\mathrm{M}^{n+}\right]}\)

Consider the example of the Daniell cell; the cell potential is given by

\(E_{\text {cell }}=E_{\text {cell }}^{\Theta}-\frac{0.05916}{2} \log \frac{\left[\mathrm{Zn}^{2+}\right][\mathrm{Cu}]}{[\mathrm{Zn}]\left[\mathrm{Cu}^{2+}\right]}\)

Since the activities of solid copper and zinc are unity,

\(E_{\text {cell }}=E_{\text {cell }}^\theta-\frac{0.05916}{2} \log \frac{\left[\mathrm{Zn}^{2+}\right]}{\left[\mathrm{Cu}^{2+}\right]}\)

or \(E_{\text {cell }}=E_{\text {cell }}^{\Theta}+\frac{0.05916}{2} \log \frac{\left[\mathrm{Cu}^{2+}\right]}{\left[\mathrm{Zn}^{2+}\right]}\)

As you can see, the value of the cell potential depends on the concentrations of both Cu²⁺ and Zn²⁺. It increases with an increase in the concentration of Cu²⁺ and decreases with an increase in the concentration of Zn²⁺.

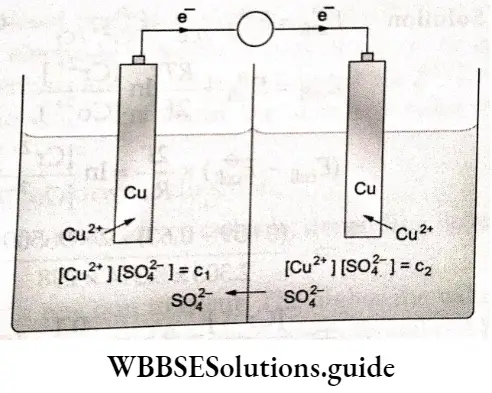
In case of cells with electrodes of some type dipping in same type of elect roly tie solutions hut wllli different concentrations (known as consent ml ion cells), (lie standard potentials of the electrodes cancel each other and the cell potential is given in terms of the concentration of electrolytic solutions, for example, In the concentration cell,
\(\mathrm{Cu}\left|\mathrm{CuSO}_4\left(c_1\right) \| \mathrm{CuSO}_4\left(c_2\right)\right| \mathrm{Cu}\) the cell potential is given by where q and c2 are the concentrations of the two solutions.

\(E_{\text {cell }}=\left(\frac{R T}{2 F}\right) \ln \left(\frac{c_2}{\epsilon_1}\right)\)

where c₁ and c₂ are the concentrations of the two solutions.

Cell Potential And Equilibrium Constant

The \(\Delta G^\theta\) of a reaction is related to the equilibrium constant K as

\(\Delta G^\theta=-R T \ln K\)

but \(\Delta G^\theta=-n F E_{\text {cell }}^\theta\)

Hence,

\(-n F E_{\mathrm{cell}}^{\Theta} \equiv-R T \ln K\) \(E_{\text {cell }}^\theta=\frac{R T}{n F} \ln K\)

If the standard potential of a cell is known then the equilibrium constant of a reaction taking place in that ceil can be obtained from Equation (3.15). On substituting the values of R and P and conversion to common logarithm at 298 K, we get

\(E_{\text {oell }}^{\Theta}=\frac{0.05916}{n} \log K\)

In an electrochemical cell, the voltage as read on a voltmeter drops gradually and becomes zero at some point of time. This is because as the reaction in the cell proceeds, the concentrations of reactants keep decreasing and those of products increase till equilibrium is attained, when there is no change in the concentrations of either. At that time, cell potential is zero.

Example 1. Calculate the end of a cell consisting of two half-cells \(\mathrm{Al}^{3+} / \mathrm{Al} \text { and } \mathrm{Ag}^{+} / \mathrm{Ag}\). Given that \(E_{\mathrm{Al}^{3 *} / \mathrm{Al}}^6=-1.66 \mathrm{~V}\) and \(E_{\mathrm{Ag}^{+} / \mathrm{Ag}^{\Theta}}^{\Theta}=0.8 \mathrm{~V} \text { at } 298 \mathrm{~K}\)
Solution:

The standard reduction potential of the half-cell reactions are

\(E_{\text {cell }}^{\Theta}=E_{\mathrm{RHE}}^{\Theta}-E_{\mathrm{LHE}}^{\Theta}=0.8-(-1.66)=0.8+1.66=2.46 \mathrm{~V}\) \(E_{\text {cell }}=E_{\text {cell }}^{\Theta}+\frac{R T}{n F} \ln \left[\frac{\left[\mathrm{Al}^{3+}\right]}{\left[\mathrm{Ag}^{+}\right]^3}\right]=2.46+\frac{8.314 \times 298}{3 \times 96500} \ln \frac{0.2}{(0.01)^3}\)

= 2.46 + 0.104

= 2.564 V.

Example 2. A cell is made up of two electrodes \(\mathrm{Cr}^{2+} / \mathrm{Cr} \text { and } \mathrm{Co}^{2+} / \mathrm{Co}\). The standard reduction potentials are \(E_{\mathrm{Cr}^{2+} / \mathrm{Cr}}^{\Theta}=-0.91 \mathrm{~V} ; E_{\mathrm{Cu}^{2+} / \mathrm{Co}}^{\Theta}=-0.28\) at 298 K. If the cell is 0.659 V and the concentration of Cr²⁺ 0.1 M, find the concentration of CO²⁺.
Solution:

\(E_{\mathrm{cell}}^{\Theta}=E_{\mathrm{Co}^{2+} / \mathrm{Co}_0}^{\Theta}-E_{\mathrm{Cr}^{2+} / \mathrm{Cr}}^{\Theta}=-0.28+0.91=0.63 \mathrm{~V}\) \(E_{\text {cell }}=E_{\text {cell }}^{\Theta}+\frac{R T}{2 F} \ln \frac{\left[\mathrm{Cr}^{2+}\right]}{\left[\mathrm{Co}^{2+}\right]}\) \(\left(E_{\text {cell }}-E_{\text {cell }}^{\Theta}\right) \times \frac{2 F}{R T}=\ln \frac{\left[\mathrm{Cr}^{2+}\right]}{\left[\mathrm{Co}^{2+}\right]}\) \(\frac{(0.659-0.63) \times 2 \times 96500}{2.303 \times 8.314 \times 298}=\log \frac{\left[\mathrm{Cr}^{2+}\right]}{\left[\mathrm{Co}^{2+}\right]}\) \(\frac{\left[\mathrm{Cr}^{2+}\right]}{\left[\mathrm{Co}^{2+}\right]}=9.6 \Rightarrow \frac{0.1}{9.6}=\left[\mathrm{Co}^{2+}\right] \Rightarrow\left[\mathrm{Co}^{2+}\right]\)

= 0.01 M.

Example 3. For a reaction, K = 1.8x 10 7 at 300 K. What is the value of \(\Delta G^{\ominus}\) at this temperature?
Solution:

\(\Delta G^\theta=-R T \ln K=-8.314 \times 300 \times \ln 1.8 \times 10^7\) \(-41667.8 \mathrm{~J} \mathrm{~mol}^{-1}=-41.7 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Example 4. Calculate the equilibrium constant of the reaction

\(\mathrm{Ni}(\mathrm{s})+\mathrm{Cu}^{2+}(\mathrm{aq}) \rightarrow \mathrm{Cu}(\mathrm{s})+\mathrm{Ni}^{2+}(\mathrm{aq})\)

\(E_{\mathrm{Ni}^{2+} / \mathrm{Ni}}^{\Theta}=-0.25 \mathrm{~V}, E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\Theta}=0.34 \mathrm{~V}\);

\(R=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}, F=96,500 \mathrm{C} \mathrm{mol}^{-1}\)
Solution:

\(\Delta G^\theta=-R T \ln K\) \(\text { Also } \Delta G^{\ominus}=-n F E_{\text {cell }}^{\ominus}\)

and \(E_{\mathrm{cell}}^{\ominus}=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\Theta}-E_{\mathrm{Ni}^{2+} / \mathrm{Ni}}^{\ominus}=0.34-(-0.25)=0.59 \mathrm{~V} \text { and } n=2\)

∴ \(\Delta G^{\ominus}=-2 \times 96500 \times 0.59=-113,870 \mathrm{~J} \mathrm{~mol}^{-1}\)

\(\ln K=-\frac{\Delta G^\theta}{R T}=\frac{113,870}{8.314 \times 298}=45.96\)

2.303 log K = 45.96

log K = 19.96

K = antilog (19.96)

= 9.12 x 10 19.

Electrolysis and electrolytic cells

When electrodes (metallic conductors) are dipped in a solution of an electrolyte and a sufficient potential difference, of the order of several volts, is applied across the electrodes, chemical reactions are observed at the electrodes. This process is known as electrolysis.

Electrolysis is observed in an electrolytic cell (or an electrochemical cell) in which a nonspontaneous reaction is driven by an external source of current. When electrolysis occurs in an electrolytic cell the electrode that is charged positively by the applied potential resulting in a deficit of electrons is called the anode and that chareed negatively with an excess of electrons is called the cathode.

In this context, it is also important to distinguish between inert electrodes and reacting electrodes. Inert electrodes, usually platinum wires, serve only to transfer electrons to and from the solution. Reacting electrodes chemically enter into an electrode reaction. Metals except platinum are examples of reacting electrodes and contribute metal ions to the solution.

The two major electrode reactions that occur in electrolysis are oxidation and reduction. At the anode, loss of electrons (oxidation) occurs whereas at the cathode electrons are introduced (by the external circuit) and reduction occurs.

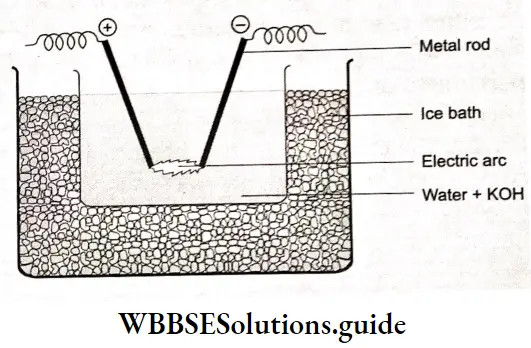
Electrolysis was studied extensively by Michael Faraday in 1820. He observed that the amount of charge passed through an electrolyte was quantitatively related to the amount of products formed at the electrodes.

These quantities axe conveniently related by introducing the faradav unit of charge with the symbol Fr defined as the charge of 3 mol, or an Avogadro number, of electrons. We have

1F = NA x (electronic charge)

= \(6.023 \times 10^{23} \times 1.602 \times 10^{-19}=96,485 \mathrm{C} \mathrm{mol}^{-1}\)

Based on his experimental findings, Faraday gave two laws of electrolysis, which are as follows.

First law:

The amount of a chemical substance liberated at an electrode during electrolysis is directly proportional to the quantity of electricity passed through the cell.

Second law:

The amounts of different substances produced by a given quantity of electricity (passing through the cell) are proportional to the molar masses of the substances.

The laws are applicable to molten electrolytes as well as to solutions of electrolytes and are independent of temperature, pressure or nature of the solvent. One important application of electrolysis is in the extraction of metals such as lithium, sodium, magnesium, aluminum and calcium.

Electrolysis of molten sodium chloride:

The commercial electrolysis of molten sodium chloride is carried out in a Down’s cell. This cell consists of an airtight vessel containing molten sodium chloride, two inert electrodes and a porous separator screen that permits diffusion of ions through the cell but prevents intermixing of the reactants and products. At the cathode, sodium ions get reduced to sodium metal At the anode the chloride ions get oxidized to chlorine gas. The two half-reactions are as follows.

Cathode: \(\mathrm{Na}^{+}(\mathrm{l})+\mathrm{e}^{-} \rightarrow \mathrm{Na}(\mathrm{s})\)

Anode: \(2 \mathrm{Cl}^{-}(\mathrm{l}) \rightarrow \mathrm{Cl}_2(\mathrm{~g})+2 \mathrm{e}^{-}\)

To balance the electrons, by multiplying Equation 3.17 by 2, we get

\(2 \mathrm{Na}^{+}(\mathrm{l})+2 \mathrm{e}^{-} \rightarrow 2 \mathrm{Na}(\mathrm{s})\)

The net reaction is obtained by adding Equations 3.18 and 3.19.

\(2 \mathrm{Na}^{+}(\mathrm{l})+2 \mathrm{Cl}^{-}(\mathrm{l}) \rightarrow 2 \mathrm{Na}(\mathrm{s})+\mathrm{Cl}_2(\mathrm{~g})\)

For this process, a voltage of about 5 V is applied with a current of thousands of amperes. Li, Mg, and Ca are obtained by the electrolysis of their respective chlorides—they are produced at the cathode.

Quantitative aspects To reduce one sodium ion, one electron is required. Therefore, to reduce one mole of sodium ions (Na~), one mole of electrons is required, and one mole of sodium ions gives rise to one gram atom, i.e., 23 of sodium metal. Thus, on passing one mole of electrons (one faraday of electricity), 23 g of sodium metal is produced. At the same time, if one faraday of electricity is removed from the anode, 35.4 g of chloride ions (CT) is discharged, Le., 0.5 mol of Cl2 gas is produced according to the reaction

\(\mathrm{Cl}^{-}(\mathrm{l}) \rightarrow \frac{1}{2} \mathrm{Cl}_2(\mathrm{~g})+\mathrm{e}^{-}\)

The charge carried by n moles of electrons is

Q = nF.

If the oxidation reaction is

\(2 \mathrm{Cl}^{-}(\mathrm{l}) \rightarrow \mathrm{Cl}_2(\mathrm{~g})+2 \mathrm{e}^{-}\)

then the total charge carried by the electrons is Q = 2F. Therefore, on passing two faradays of electricity, one mole of Cl₂(g) is produced. The charge passed through the cell during electrolysis is equal to the product of current (1) in amperes and time (t) in seconds.

Q = It.

Example 1. Calculate the amount of product formed at the two electrodes when a current of 0334 A is passed through a cell constructed for the electrolysis of calcium chloride for 2 h.
Given: Atomic mass of Ca = 40.08 and that of Cl = 35.4.
Solution:

The only species that we get from CaCl₂ are Ca²⁺ and Cl ions. Hence it is easy to guess that Cl ions will get oxidised while Ca²⁺ ions will get reduced.

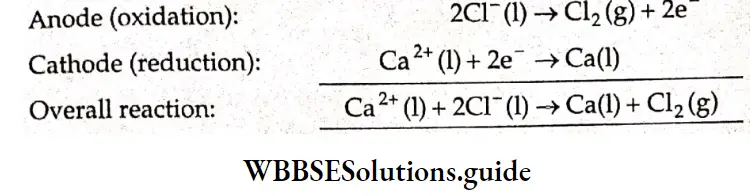
Amount of charge passed through the cell,

\(Q=I t=0.334 \mathrm{~A} \times 2 \mathrm{~h} \times \frac{3600 \mathrm{~s}}{1 \mathrm{~h}} \times \frac{1 \mathrm{C}}{1 \mathrm{~A} \cdot \mathrm{s}}=2404.8 \mathrm{C}\)

Since 1 mol of e- = 96,487 C and 2 mol of electrons is required to reduce 1 mol of Ca²⁺ ions, the mass of Ca formed at the cathode is calculated as follows.

Amount of Ca = \(2404.8 \mathrm{C} \times \frac{1 \mathrm{~mol} \mathrm{e}^{-}}{96,487 \mathrm{C}} \times \frac{1 \mathrm{~mol} \mathrm{Ca}}{2 \mathrm{~mol} \mathrm{e}^{-}} \times \frac{40.08 \mathrm{~g} \mathrm{Ca}}{1 \mathrm{~mol} \mathrm{Ca}}=0.5 \mathrm{~g}\)

For the anodic reaction, 2 mol of electrons is required to oxidize Cl ions or to produce 1 mol of Cl₂ gas.

Amount of Cl₂ (in grams) = \(2404.8 \mathrm{C} \times \frac{1 \mathrm{~mol} \mathrm{e}^{-}}{96,487 \mathrm{C}} \times \frac{1 \mathrm{~mol} \mathrm{Cl}_2}{2 \mathrm{~mol} \mathrm{e}^{-}} \times \frac{2 \times 35.4}{1 \mathrm{~mol} \mathrm{Cl}_2}=\mathbf{0 . 8 8 2}\)

Example 2. How much charge is required to be passed through a cell containing a Cd²⁺/ Cd electrode so that 0.5 mol of Cd is deposited at the electrode?
Solution:

The reaction occurring in the cell is

\(\mathrm{Cd}_{(\mathrm{aq})}^{2+}+2 \mathrm{e}^{-} \rightarrow \mathrm{Cd}(\mathrm{s})\)

1 mol of Cd (s) requires 2 mol of electrons.

∴ 0.5 mol Cd (s) requires 1 mol of electrons.

Charge on 1 mol of electrons = \(1.6023 \times 10^{-19} \mathrm{C} \times 6.023 \times 10^{23} \text { electron } \mathrm{mol}^{-1}=96,485 \mathrm{C}\)

Hence 96,485 C of charge should be passed for the deposition of 0.5 mol of Cd.

Example 3. How much charge is required to be passed through a cell containing a Cu²⁺/Cu electrode so that 25 g of Cu (atomic weight = 63.5) gets deposited at the electrode?
Solution:

\(\mathrm{Cu}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}(\mathrm{s})\)

1 mol of Cu²⁺ requires 2 mol of electrons (v charge of 1 mol of electrons = 96,485 C)

= 2x 96485 C ≅ 2 x 96500 C

= 193, 000 C.

For 63.5 g (1 mol) 193,000 C of charge is required.

∴ For 25 g of Cu \(\) of charge is required.

= 75,984 C of charge is required.

Example 4. Find the mass of Al deposited according to the reaction \(\mathrm{Al}^{3+}+3 \mathrm{e}^{-} \rightarrow \mathrm{Al}\), given that a current of 4 A is passed for 50 min. Atomic mass of AI = 27.
Solution:

Since \(\frac{193,000}{63.5} \times 25 \mathrm{C}\) = y, total charge passed = 4x50x60As = 12,000 C.

3 mol of electrons or 3 x 96,500 C of charge deposits 1 mol of Al.

∴12,000 C of charge will deposit \(\frac{12,000}{3 \times 96,500}\) = 0.0414 mol of  AI = 0.0414 x 27 g of AI = 1.117 g of AI.

Example 5. Find the amount of Na deposited at an electrode due to the reaction \(\mathrm{Na}^{+}+\mathrm{e}^{-} \rightarrow \mathrm{Na}\) when passed through molten NaCl for 80 min (atomic mass of Na = 23).
Solution:

According to the reaction, 1 mol of electrons is required for depositing 1 mol of Na.

Charge on 1 mol of electrons = 96,500 C.

Charge passed = 2 x 80 x 60 = 9600 C.

∴ amount of Na deposited = \(\frac{9600}{96,500} \times 1 \approx 0.1 \mathrm{~mol}\) = 0.1 x 23 = 2.3 g.

Example 6. How much time is required for the deposition of 15.875 g of Cu according to the electrode reaction \(\mathrm{Cu}^{2+}+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}\) when 4 A of current is passed through the cell? The atomic mass of Cu = 63.5.
Solution:

According to the electrode reaction, for 1 mol of Cu, 2 mol of electrons is required, i.e., for 63.5 g of Cu, 2 x 96,500 C of charge is required.

For 15.875 g of Cu, \(\frac{2 \times 96,500}{63.5}\) x 15.875 = 48,250 C of charge is required.

Charge = current x time.

∴ time required for the deposition of 15.875 g of Cu

\(=\frac{48,250}{4}=12,062.5 \mathrm{~s}=\frac{12,062.5}{3600} \text { hours }\)

= 3.35 hours.

Products Of Electrolysis

As the amount of the substance or products liberated at the electrode depends on the amount of electricity passed [ through the cell, the products of electrolysis depend on the state of the substance (i.e., molten or aqueous) and the nature of the electrodes being used in the electrolysis. For instance, the electrolysis of molten sodium chloride yields sodium metal and chlorine gas. But what will happen if an aqueous solution of sodium chloride is used? f Let us discuss this case along with some more examples.

Electrolysis of aqueous sodium chloride:

In tire electrolysis of an aqueous solution of sodium chloride, more than one reaction is possible at each electrode. At the cathode, the sodium ion as well as water can be reduced.

\(\mathrm{Na}^{+}+\mathrm{e}^{-} \rightarrow \mathrm{Na} \quad E_{\text {red }}^{\Theta}=-2.714 \mathrm{~V}\) \(2 \mathrm{H}_2 \mathrm{O}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_2+2 \mathrm{OH}^{-} \quad E_{\mathrm{red}}^{\ominus}=-0.828 \mathrm{~V}\)

Tire species with a higher reduction potential can get more easily reduced. Between sodium ions and water, water has a larger reduction potential and hence the reaction involving water is the one favored at the cathode.

At the anode, the chloride ion as well as water can be oxidised. In order to optimise the production of chlorine, n concentrated solution of sodium chloride is used.

The reactions occurring at the two electrodes and the overall reaction are as follows.

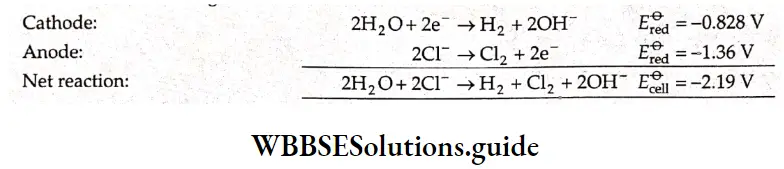
Because the sodium ions remain unchanged, more and more sodium hydroxide is formed in the solution as electrolysis proceeds. Hence the electrolysis of an aqueous solution of sodium chloride can be used for the commercial production of H₂ gas, Cl₂ gas and NaOH. This is possible by using currents of 10,000 – 60,000 A at about 3.8 V.

Electrolysis of aqueous HCI:

When an aqueous solution of hydrochloric acid is electrolyzed, hydronium ions are reduced to hydrogen gas at the cathode.

\(2 \mathrm{H}_3 \mathrm{O}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_2+2 \mathrm{H}_2 \mathrm{O}\)

At the anode, two oxidation reactions are possible.

\(2 \mathrm{Cl}^{-} \rightarrow \mathrm{Cl}_2+2 \mathrm{e}^{-} \quad E_{\mathrm{ov}}^{\Theta}=-1.36 \mathrm{~V}\) \(6 \mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{O}_2+4 \mathrm{H}_3 \mathrm{O}^{+}+4 \mathrm{e}^{-} \quad E_{\mathrm{ox}}^{\Theta}=-1.23 \mathrm{~V}\)

The oxidation potentials of these two reactions are comparable and both can occur with equal ease. However, which one of them occurs or whether both of them occur depends upon the concentration of chloride ions in the solution.

In a very dilute solution of HCl, H₂O is electrolysed and oxygen is released at the anode.

In concentrated solutions of HCl, chloride ions are reduced to form chlorine gas at the anode (Equation 3.20). The reactions are as follows.

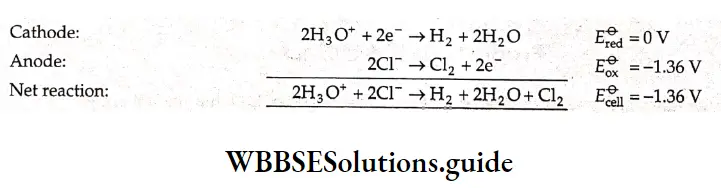
A voltage of 1.36 V (or more) has to be applied for the above reaction to occur at standard state conditions. At moderate concentrations of HCl, both the reactions—the electrolysis of water and the oxidation of chloride ions—occur.

Electrolytic deposition of metals:

Chrome plating, bronzing, and refining of copper, all employ electrolysis.

In bronzing, a metallic strip of copper is used as the anode. Copper is oxidized to form copper ions.

\(\mathrm{Cu} \rightarrow \mathrm{Cu}^{2+}+2 \mathrm{e}^{-}\)

The cathode may be any conducting material or a nonconducting material dusted with graphite powder to make it conduct. The copper ions formed are reduced at the cathode and copper is deposited there.

\(\mathrm{Cu}^{2+}+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}\)

Thus, the material used as the cathode is bronzed.

If copper is used as the cathode, refined copper is obtained. Copper is purified electrochemically to improve its conductivity. The process is called electrorefining. Impure copper is made of the anode whereas the cathode is pure copper. During electrolysis, the less active metals such as gold and silver, which do not get as easily oxidized as copper settle down as ‘anode mud’, at the bottom of the cell. Impurities

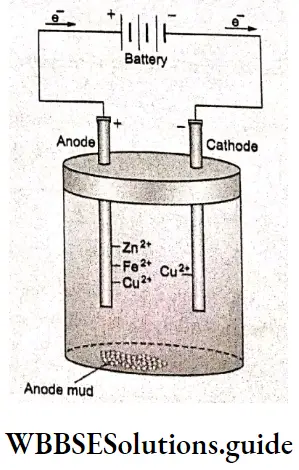
such as iron and zinc, which are more easily oxidized than copper, get oxidized at the anode and go into the solution as ions. When the potential difference between the electrodes is carefully controlled, copper is oxidized to copper ions at the anode and Fe²⁺ and Zn²⁺ are not reduced at the cathode. Only Cu²⁺ ions are reduced to form metallic copper, and deposit at the cathode (which can also be a metal other than copper). Thus pure copper is obtained at the cathode.

Corrosion

On exposure to air and water, the surfaces of many metallic objects, in particular those made of iron, rust. Rusting is nothing but corrosion. The presence of an electrolyte accelerates corrosion, which is an electrochemical process. When iron is in contact with even a droplet of water, it is oxidized and releases electrons. These electrons, on coming into contact with air, reduce oxygen forming the hydroxide ion. Thus two half-cells, whose reactions are given below, are created.

Anode: \(\mathrm{Fe} \rightarrow \mathrm{Fe}^{2+}+2 \mathrm{e}^{-}\)

Cathode: \(\mathrm{O}_2+2 \mathrm{H}_2 \mathrm{U}+4 \mathrm{e}^{-} \rightarrow 4 \mathrm{OH}^{-}\)

The Fe2+ and OH- ions thus formed diffuse together to form insoluble iron (2) hydroxide.

\(\mathrm{Fe}^{2+}(\mathrm{aq})+2\left(\mathrm{OH}^{-}\right)(\mathrm{aq}) \rightarrow \mathrm{Fe}(\mathrm{OH})_2(\mathrm{~s})\)

Ferrous hydroxide is rapidly oxidized by oxygen to rust with an approximate composition of Fe₂O₃. H₂O.

Corrosion may cause severe damage to buildings, ships, bridges and all objects made of metals, especially iron. Therefore prevention of corrosion is very important to avoid accidents such as the collapse of a bridge or the nonfunctioning of a part in an engine. The simplest of the methods is to prevent the metallic surface from coming in contact with air by coating the surface with paint or other chemicals.

Corrosion can also be prevented by coating iron with grease or asphalt or with ceramic enamel as used in sinks, refrigerators, etc. A tough coating of Fe₃O₄ is obtained by exposing iron to superheated steam. We can use alloys of iron such as stainless steel, which is corrosion-resistant.

Metals such as chromium, tin or zinc afford a more durable surface coating for iron than paint. The steel used in automobiles, for example, is coated with zinc by dipping it into a bath of molten zinc. This process is known as galvanization. Zinc is more easily oxidized than iron and whenever oxidation occurs, zinc is oxidized rather than iron.

\(\mathrm{Fe}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Fe}(\mathrm{s}) \quad E^{\Theta}=0.45 \mathrm{~V}\) \(\mathrm{Zn}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Zn}(\mathrm{s}) \quad E^{\ominus}=-0.76 \mathrm{~V}\)

Any oxidation, if at all, of iron is reversed immediately as Zn can reduce Fe₂ to Fe^2-.

Instead of covering the entire surface of a metal with another metal, a simple electrical contact with a second metal can save the first one from corroding. This is called cathodic protection.

Cathodic protection is an important application of electrochemistry used for protecting iron or steel. It is used in underground pipelines that are in contact with soil. The iron present as a component is connected by a wire to a more active metal such as zinc, aluminum, or magnesium. It then becomes a cathode where oxygen is reduced rather than an anode where iron is oxidized. The other metal acts as a sacrificial anode, which corrodes instead of iron.

An electric current flows between the two metals because of the difference in their activities; this results in the corrosion of the more active metal and thus iron remains protected. Taking the example of magnesium as the more active metal, the reactions are as follows.

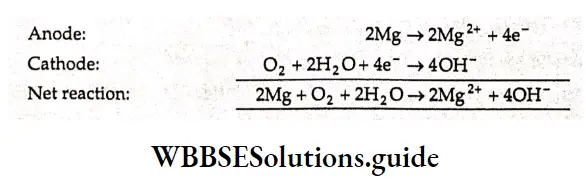
The active metal is slowly consumed and must be replaced periodically. This method of protection is used for large steel structures such as pipelines, storage tanks, bridges, and ships.

Batteries

Batteries are cells connected together so as to make maximum use of the reaction occurring in the cell and hence deliver a large current. Cells are of two types—primary and secondary.

Primary cells

Cells or batteries that cannot be recharged or become dead after use over a period of time are called primary cells or batteries. Examples include the Daniell cell and batteries used for torches, toys, etc.

A dry cell is a commonly used primary cell. Dry-cell batteries are used to power flashlights, radios, and other portable electronic devices. These are called ‘dry’ cells as the electrolyte inside them is a solid, in fact a paste. Since this type of cell was invented by the French engineer Georges Leclanche, it is also called a Leclanche cell.

The cell consists of a zinc container serving as an anode mid a graphite rod as the cathode. The graphite rod is surrounded by a moist mixture of ammonium chloride, manganese dioxide, zinc chloride and carbon. A porous paper liner serves as a separator of the two compartments and also as a salt bridge. When the cell is put to use, the zinc anode is oxidised forming zinc ions and electrons which flow through the external circuit to the cathode and reduce manganese dioxide at the cathode.

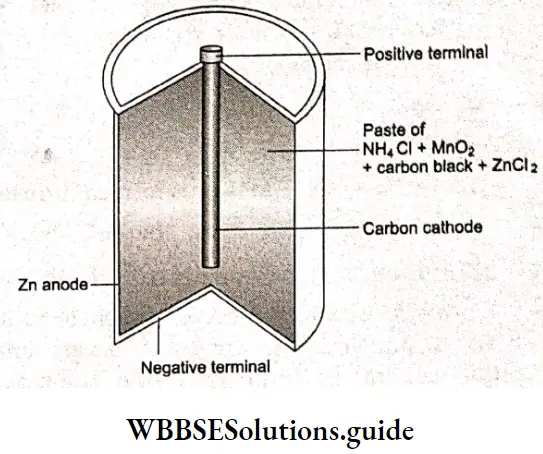
The reactions are:

anode: \(\mathrm{Zn}+2 \mathrm{NH}_4 \mathrm{Cl} \rightarrow 2 \mathrm{Zn}\left(\mathrm{NH}_3\right)_2 \mathrm{Cl}_2+2 \mathrm{H}^{+}+2 \mathrm{e}^{-} \text {or } \mathrm{Zn}(\mathrm{s}) \rightarrow \mathrm{Zn}^{2+}+2 \mathrm{e}^{-}\)

cathode: \(2 \mathrm{MnO}_2+2 \mathrm{e}^{-}+2 \mathrm{H}^{+} \rightarrow \mathrm{Mn}_2 \mathrm{O}_3+\mathrm{H}_2 \mathrm{O}\)

A cell commonly used in watches and also in pacemakers is the mercury cell. It consists of a zinc anode and a cathode made of steel in contact with mercury(II) oxide (HgO) in an alkaline medium of KOH and Zn(OH)^–,. Zinc is oxidized at the anode and HgO is reduced at the cathode. The anodic and cathodic reactions are as follows.

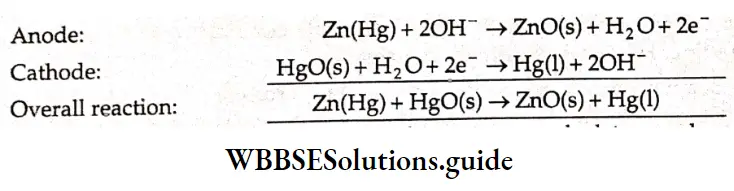
The small buttom-shaped batteries used in camars, calculators and watches are alkaline cells. Apart from these, dry cells have been replaced by longer lasting alkaline cells. An alkaline cell also consists of zinc and manages dioxide but the electrolyte contains potassium hydroxide instead of ammonium cloride. Under alkaline conditions, the anodic half reaction is

\(\mathrm{Zn}(\mathrm{s})+2 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{Zn}(\mathrm{OH})_2(\mathrm{~s})+2 \mathrm{e}^{-}\)

while at the cathode MnOz is reduced to solid Mn₂O₃

\(2 \mathrm{MnO}_2(\mathrm{~s})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})+2 \mathrm{e}^{-} \rightarrow \mathrm{Mn}_2 \mathrm{O}_3(\mathrm{~s})+2 \mathrm{OH}^{-}(\mathrm{aq})\)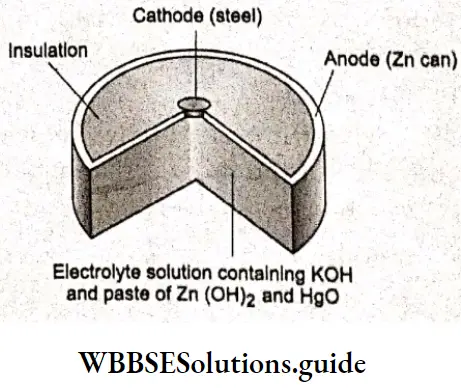

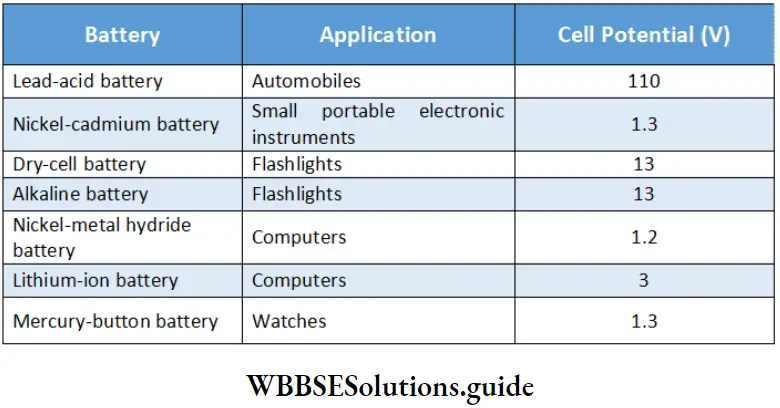
Alkaline cells have a greater shelf life (as Zn in the cell oxidizes slowly) and also last longer than dry cells as they have greater quantities of reactants than dry cells. Lists some commonly used batteries.

Some commonly used batteries and their applications:

Secondary cells

Secondary cells are galvanic cells whose reactions can be reversed by the application of an external electric potential in a direction opposite to that of the discharge. This recharges the cell. The lead storage battery and nickel-cadmium (NICAD) cells are secondary cells.

The lead-storage or lead-acid battery is a dead one used in an automobile. The electrodes consist of lead-alloy grids; one set of grids is filled with lead(TV) oxide and the other with spongy lead metal The electrolyte used is dilute sulphuric add. When the battery delivers current, lead is oxidized to lead ions, these combine with the sulfate ions of sulphuric add and coat the lead electrode with insoluble lead sulfate.

The electrons released by the anode reaction flow through the external circuit to the cathode and reduce lead(IV) oxide to lead(II) ions, also forming water. These lead(2) ions also combine with sulfate ions forming lead sulfate and coating the cathode. The two half-reactions are

Anode: \(\mathrm{Pb}(\mathrm{s})+\mathrm{SO}_4^{2-}(\mathrm{aq}) \rightarrow \mathrm{PbSO}_4(\mathrm{~s})+2 \mathrm{e}^{-}[/laetx]

Cathode:

[latex]\mathrm{PbO}_2(\mathrm{~s})+4 \mathrm{H}_3 \mathrm{O}^{+}(\mathrm{aq})+\mathrm{SO}_4^{2-}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{PbSO}_4(\mathrm{~s})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l})\)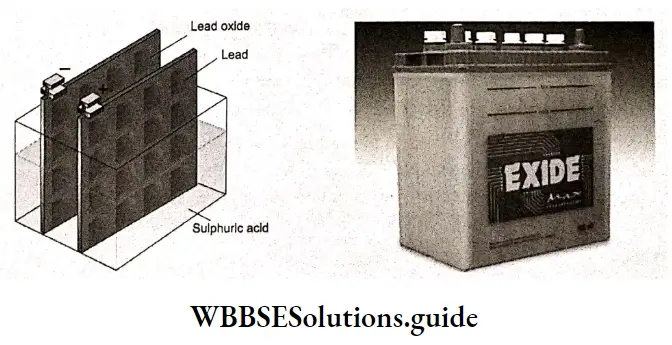

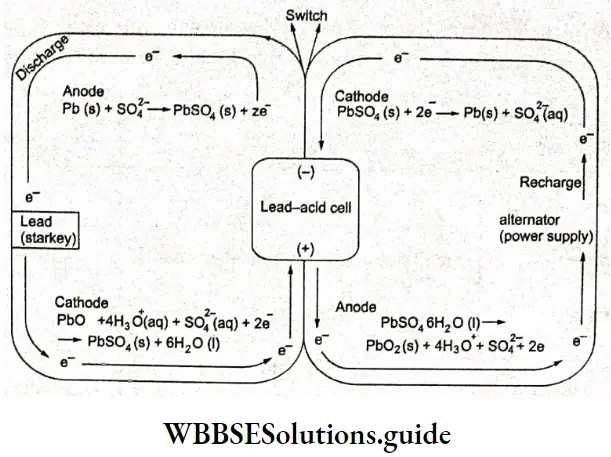
When used in a car, an alternator (power supply) recharges the battery by producing an external potential that pushes electrons in the reverse direction through the cell. The cell becomes an electrolytic cell during recharging. During recharging, the reactions at the cathode and anode are as follows.

Anode:

\(\mathrm{PbSO}_4(\mathrm{~s})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightarrow \mathrm{PbO}_2(\mathrm{~s})+4 \mathrm{H}_3 \mathrm{O}^{+}+\mathrm{SO}_4^{2-}(\mathrm{aq})+2 \mathrm{e}^{-}\)

Cathode:

\(\mathrm{PbSO}_4(\mathrm{~s})+2 \mathrm{e}^{-} \rightarrow \mathrm{Pb}(\mathrm{s})+\mathrm{SO}_4^{2-}(\mathrm{aq})\)

The net reversible cell reaction in the lead storage battery is

\(\mathrm{Pb}+\mathrm{PbO}_2+4 \mathrm{H}_3 \mathrm{O}^{+}+2 \mathrm{SO}_4^{2-} \underset{\text { recharge }}{\stackrel{\text { discharge }}{\rightleftharpoons}} 2 \mathrm{PbSO}_4+6 \mathrm{H}_2 \mathrm{O}\)

NICAD batteries contain nickel and cadmium electrodes. Cadmium acts as the anode and a hydroxide solution forms the electrolyte. NiO2 is reduced at the cathode.

The two half-reactions are:

anode:

\(\mathrm{Cd}(\mathrm{s})+2 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow \mathrm{Cd}(\mathrm{OH})_2(\mathrm{~s})+2 \mathrm{e}^{-}[/laetx]

cathode:

[latex]\mathrm{NiO}_2(\mathrm{~s})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+2 \mathrm{e}^{-} \rightarrow \mathrm{Ni}(\mathrm{OH})_2(\mathrm{~s})+2 \mathrm{OH}^{-}\)

The net reaction is

\(\mathrm{Cd}+\mathrm{NiO}_2+2 \mathrm{H}_2 \mathrm{O} \underset{\text { recharge }}{\stackrel{\text { discharge }}{\rightleftharpoons}} \mathrm{Ni}(\mathrm{OH})_2+\mathrm{Cd}(\mathrm{OH})_2\)

A solid coating of Cd(OH)₂ forms around the anode and a solid coating of Ni(OH)₂ forms around the cathode when the battery is discharged; these are converted back to the starting materials on recharging.

Earlier, Ni-Cd batteries were used in laptops but improvements were made and Ni-metal hydride (NiMH) batteries were developed. Here the cathode is NiO(OH) as in Ni-Cd batteries but the anode is made of a transition metal alloy such as LaNi₅. The two electrodes are separated by a porous spacer containing an aqueous solution of KOH.

The reactions are

Cathode:

\(\mathrm{NiO}(\mathrm{OH})(\mathrm{s})+\mathrm{H}_2 \mathrm{O}(\mathrm{I})+\mathrm{e}^{-} \rightarrow \mathrm{Ni}(\mathrm{OH})_2(\mathrm{~s})+\mathrm{OH}^{-}(\mathrm{aq})\)

Anode:

\(\mathrm{MH}(\mathrm{s})+\mathrm{OH}^{-} \rightarrow \mathrm{M}(\mathrm{s})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{e}^{-}\)

Lithium-Ion Batteries

High power demands by the late 1990s in high-speed processors, large video displays, and modem laptop computers led to the manufacture of lithium-ion batteries. These are based not on redox chemistry but on the concentration-driven migration of lithium ions. The anode is made of pure graphite and lithium ions are stored in it. The cathode is highly porous, made of transition-metal oxides such as MnOz, and forms a stable complex with lithium ions.

There is a high concentration of Li+ at the anode and a low concentration at the cathode. The migration of Li+ from the anode to the cathode (during discharge) is accompanied by that of electrons in an external circuit from the cathode to the anode. The electrolytes used in these batteries are solutions of lithium salts in non-aqueous solvents such as tetrahydrofuran, ethylene carbonate or propylene carbonate. Aqueous solutions cannot be used as electrolytes, because electrodes, particularly anodes, react with oxygen and water.

The electrode reactions are

Anode: \(\mathrm{Li}(\mathrm{s}) \rightarrow \mathrm{Li}^{+}+\mathrm{e}^{-}\)

Cathode: \(\mathrm{MnO}_2(\mathrm{~s})+\mathrm{Li}^{+}+\mathrm{e}^{-} \rightarrow \mathrm{LiMnO}_2(\mathrm{~s})\)

Fuel cells

In fuel cells, which are again galvanic cells, the electrode materials in the form of gases are supplied continuously to produce electricity. Such cells are used in space shuttles. The anode is a porous electrode with a catalyst such as finely divided platinum or palladium on its surface. Hydrogen gas is diffused through the anode.

The cathode is a porous electrode impregnated with cobalt oxide, platinum or silver as a catalyst. Oxygen gas is diffused through this electrode. The two electrodes are separated by a concentrated solution of sodium hydroxides or potassium hydroxide acting as an electrolyte. The two half-reactions are

Anode: \(2 \mathrm{H}_2+4 \mathrm{OH}^{-} \rightarrow 4 \mathrm{H}_2 \mathrm{O}+4 \mathrm{e}^{-} \quad E^{\ominus}=-0.828 \mathrm{~V}\)

Cathode: \(\mathrm{O}_2+2 \mathrm{H}_2 \mathrm{O}+4 \mathrm{e}^{-} \rightarrow 4 \mathrm{OH}^{-} \quad E^{\ominus}=0.401 \mathrm{~V}\)

The net cell reaction therefore leads to the formation of water as steam.

\(2 \mathrm{H}_2+\mathrm{O}_2 \rightarrow 2 \mathrm{H}_2 \mathrm{O}\)

Methane or other hydrocarbons can also be used instead of hydrogen. Hydroxide ions formed at the cathode migrate through the electrolyte to the anode where they combine with hydrogen to form water.

When acidic electrolytes have used the reactions at the anode and cathode are anode:

Anode: \(\mathrm{H}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}^{+}+2 \mathrm{e}^{-} \quad E^\theta=0.00 \mathrm{~V}\)

Cathode: \(\mathrm{O}_2(\mathrm{~g})+4 \mathrm{H}^{+}(\mathrm{aq})+4 \mathrm{e}^{-} \rightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \quad E^{\Theta}=1.229 \mathrm{~V}\)

Fuel cells are promising alternative energy sources for automobiles.

Most of the fuel cells used in vehicles have a proton exchange membrane (PEM) between the two halves of the cell. Gas diffusers bring H₂ and O₂ to opposite sides of the membrane. At the anode side, H₂ is oxidized to H+ ions. These ions migrate through die membrane to the cathodic side where they react with oxygen to produce water.

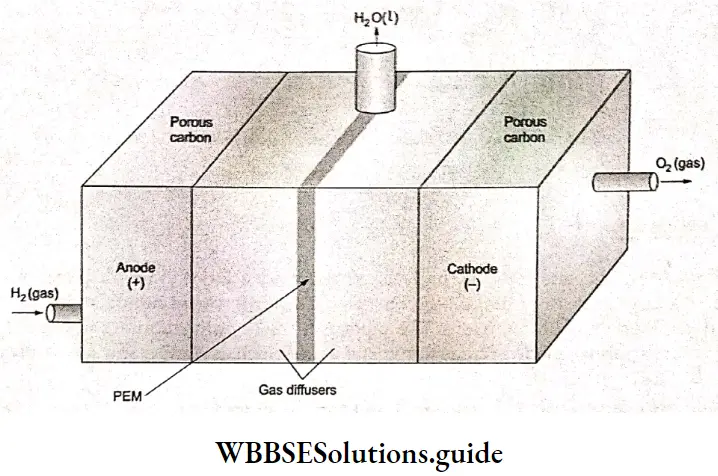
Another large-scale application of fuel cells is in power generation. Such cells have a lot of advantages over conventional thermal plants generating electricity. Their efficiency is 60 per cent more than that of thermal plants. In a thermal plant the liberated free energy of a chemical fuel (on burning) is used to first convert water into steam which is then used to drive a turbine. The turbine coupled with a generator produces electricity. A thermal plant causes pollution due to the burning of fossil fuels. On the other hand, fuel cells emit only water vapour—they do not pollute the air.

Electrochemistry Multiple-Choice Questions

Question 1. The flow of current in an electrolyte is due to the movement of

1. Electrons
2. Protons
3. Ions
4. None Of These

Answer: 3. Ions

Question 2. Metallic conductors conduct electricity through the movement of

1. Ions
2. Metal Atoms
3. Free Electrons
4. None Of These

Answer: 3. Free Electrons

Question 3. Which of the following substances does not conduct

1. Crystalline NaCl
2. Graphite
3. CuSO, solution
4. NaCl crystals with a defect

Answer: 1. Crystalline NaCl

Question 4. Conductance (G) is the reciprocal of electricity.

1. Specific Resistance
2. Current
3. Resistance
4. Concentration

Answer: 3. Resistance

Question 5. The specific conductance (K) or conductivity of any conducting material is defined as the

1. Reciprocal Of Current
2. Reciprocal Of Specific Resistance
3. Reciprocal Of Resistance
4. Product Of Specific Resistance And Current

Answer: 2. Reciprocal Of Specific Resistance

Question 6. The unit of specific conductance (x) is

1. Ωcm
2. Ω^-1 cm
3. -1 cm^-1
4. Ω cm^-1

Answer: 3. -1 cm^-1

Question 7. The cell constant of an electrochemical cell is given by

1. \(\frac{k}{R}\)
2. RK
3. R2k
4. \(\frac{R}{k}\)

Answer: 2. RK

Question 8. Calculate the molar conductivity of a 0.1 M H2SO, solution in S m2 mol^-1 given that its specific conductance is 26 x 102 cm^-1.

1. 26×10^-1
2. 26×10^-4
3. 52×10^-4
4. 52×10-1

Answer: 2. 26×10^-4

Question 9. On increasing the dilution, the specific conductance

1. Increases
2. Decreases
3. Remains Constant
4. None Of These

Answer: 2. Decreases

Question 10. Strong electrolytes are those which

1. Dissolve Readily In Water
2. Conduct Electricity
3. Dissociate Into Ions Even At High Concentration
4. Dissociate Into Ions At High Dilution

Answer: 3. Dissociate Into Ions Even At High Concentration

Question 11. Substances whose aqueous solutions are good conductors of electricity are called

1. Strong Electrolytes
2. Weak Electrolytes
3. Nonelectrolytes
4. Catalysts

Answer: 1. Strong Electrolytes

Question 12. The conductivity of an electrolyte depends on the

1. Molecular Mass Of The Electrolyte
2. The Boiling Point Of The Solvent
3. Volume Of The Solvent
4. Degree Of Ionization

Answer: 4. Degree Of Ionization

Question 13. In a galvanic cell

1. Chemical Energy Is Converted Into Electrical Energy
2. Electrical Energy Is Converted Into Chemical Energy
3. The Cathode Is The Negative Terminal And The Anode Is The Positive Terminal
4. None Of The Above

Answer: 1. Chemical Energy Is Converted Into Electrical Energy

Question 14. A salt bridge may contain

1. A Saturated Solution Of Kcl And Agar-Agar
2. A Saturated Solution Of Kno3 And Agar-Agar
3. A Saturated Solution Of Nh4no3 And Agar-Agar
4. All Of These

Answer: 4. All Of These

Question 15. The emf of a Daniell cell (given below) at 298 K is E.

\(\mathrm{Zn}\left|\mathrm{ZnSO}_4(0.01 \mathrm{M}) \| \mathrm{CuSO}_4(1.0 \mathrm{M})\right| \mathrm{Cu}\)

When the concentration of ZnSO, is 1.0 M and that of CuSO4 is 0.01 M, the emf changes to E2. What is the relationship between E and E2?

1. E₁ >E₂
2. E₁ < E₂
3. E₁ =E₂
4. E₂ = 0 ≠ E

Answer: 1. E₁ >E₂

Question 16. The Nearest equation

\(E_{\text {cell }}=E_{\text {cell }}^{\ominus}-\frac{R T}{n F} \ln Q\)

indicates that the equilibrium constant kc will be equal to Q when

1. \(E=E^{\ominus}\)
2. \(\frac{R T}{n F}=1\)
3. E=0
4. \(E^{\Theta}=1\)

Answer: 3. E=0

Question 17. The value of the reaction quotient Q for the cell

\(\mathrm{Zn}(\mathrm{s})\left|\mathrm{Zn}^{2+}(0.01 \mathrm{M}) \| \mathrm{Ag}^{+}(1.25 \mathrm{M})\right| \mathrm{Ag}(\mathrm{s})\) is

1. 156
2. 125
3. 1.25×10^-2
4. 6.4 x 10^-3

Answer: 4. 6.4×10^-3

Question 18. For the cell reaction

\(\mathrm{Cu}^{2+}\left(c_1, \mathrm{aq}\right)+\mathrm{Zn}(\mathrm{s}) \rightleftharpoons \mathrm{Zn}^{2+}\left(c_2, \mathrm{aq}\right)+\mathrm{Cu}(\mathrm{s})\)

the change in free energy, AG, at a given temperature is a function of

1. In c1
2. \(\ln \left(\frac{c_2}{c_1}\right)\)
3. In c2
4. In (c1+c2)

Answer: 2. \(\ln \left(\frac{c_2}{c_1}\right)\)

Question 19. The standard reduction potentials of three metals A, B and C are +0.5 V, -3.0 V and -1.2 V respectively. Th arrangement of the metals, in order of their reducing power, is

1. B>C>A
2. A > B >C
3. C>B>A
4. A>C>B

Answer: 1. B>C>A

Question 20. For a cell reaction involving a two-electron change, the standard emf of the cell is found to be 0.295 V at 25°C. The equilibrium constant of the reaction at 25°C will be

1. 1.0×10^-10
2. 29.5×10^-2
3. 10.0
4. 1.0 x 10¹⁰

Answer: 4. 1.0×10¹⁰

Question 21. Given \(E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\ominus}=0.337 \mathrm{~V} \text { and } E_{\mathrm{Cu}^{2+} / \mathrm{Cu}^{+}}^{\Theta}=0.153 \mathrm{~V} \text {, calculate } E_{\mathrm{Cu}^{+} / \mathrm{Cu}^{\circ}}^{\Theta}\)

1. 0.184 V
2. 0.827 V
3. 0.521 V
4. 0.490 V

Answer: 1. 0.184 V

Question 22. A cell reaction is spontaneous when

1. \(E_{\text {red }}^{\ominus} \text { is negative }\)
2. \(E_{\text {red }}^{\ominus} \text { is positive }\)
3. \(\Delta G^{\ominus} \text { is negative }\)
4. \(\Delta G^{\ominus} \text { is positive }\)

Answer: 3. \(\Delta G^{\ominus} \text { is negative }\)

Question 23. The electrode potential for the following half-cell reactions are

\(\mathrm{Zn} \rightleftharpoons \mathrm{Zn}^{2+}+2 \mathrm{e} ; \quad E^{\ominus}=+0.76 \mathrm{~V}\) \(\mathrm{Fe} \rightleftharpoons \mathrm{Fe}^{2+}+2 \mathrm{e} ; \quad E^{\ominus}=+0.44 \mathrm{~V}\)

The emf for the cell reaction

\(\mathrm{Fe}^{2+}+\mathrm{Zn} \longrightarrow \mathrm{Zn}^{2+}+\mathrm{Fe}\)

1. +0.32 V
2. +1.20 V
3. -0.32 V
4. -1.20 V

Answer: 1. +0.32 V

Question 24. 9650 C of charge is passed through a solution of AgNO₃. The mass of silver deposited on the cathode is (Atomic mass of Ag is 108)

1. 1.08 g
2. 10.8 g
3. 21.6 g
4. 100.0 g

Answer: 2. 10.8 g

Question 25. Three faradays of electricity are passed through molten Al₂O₃, an aqueous solution of CuSO, and molten NaCl taken in a separated electrolytic cell. The amount of Al, Cu, and Na deposited at the cathodes will be in the molar ratio of

1. 1:2:3
2. 3:2:1
3. 1:15:3
4. 1.5: 2:3

Answer: 3. 1:15:3

Question 26. Which of the following aqueous solutions remains neutral after electrolysis?

1. CuSO₄
2. AgNO₃
3. K2SO₄
4. NaCl

Answer: 3. K₂SO₄

Question 27. How many faradays are required to reduce one mole of \(\mathrm{MnO}_4^{-} \text {to } \mathrm{Mn}^{2+}\)

1. 1
2. 2
3. 3
4. 5

Answer: 4. 5

Question 28. Aluminum oxide may be electrolyzed at 1000°C to = 96,500 coulombs). The cathode reaction is Al³⁺+ 3e and would require furnished aluminum metal (at. mass = 27 amu, 1 faraday → AL To prepare 5.12 kg of aluminum metal by this method

1. 5.49 × 10 C of electricity
2. 5.49 x 10 C of electricity
3. 1.83×10⁷ C of electricity
4. 5.49×10¹ C of electricity

Answer: 1. 5.49 × 10⁷ C of electricity

Question 29. Copper containing zinc as an impurity is refined by electrolysis. The cathode and anode used are

Answer: 3.

Cathode: Pure copper

Anode: Impure copper

Question 30. Galvanized iron is

1. Iron Coated With Tin
2. Tin Coated With Iron
3. Zinc Coated With Iron
4. Iron Coated With Zinc

Answer: 4. Iron Coated With Zinc

Question 31. Rusting of iron is

1. A Decomposition Process
2. A Photochemical Process
3. An Electrochemical Process
4. A Reduction Process

Answer: 3. An Electrochemical Process

Question 32. In the rusting of iron, which of the following cell reactions occurs at the cathode?

1. Fe²⁺/Fe
2. O₂/H₂O
3. Fe³⁺/Fe²⁺
4. Fe/Fe3+

Answer: 3. Fe³⁺/Fe²⁺

Question 33. In a lead storage battery

1. Pb is oxidized to PbSO, at the anode
2. PbO₂ is reduced to PbSO, at the cathode
3. both electrodes are immersed in the same aqueous solution of H₂SO₄
4. All The Above Are True

Answer: 4. All The Above Are True

Question 34. Which of the following statements is correct in the context of a battery?

1. It is an electrochemical cell.
2. It is used as a source of energy.
3. The stored energy is released during the redox reaction.
4. All of these

Answer: 4. All of these

Question 35. Which of the following reactions is used to make a fuel cell?

1. Cd(s) + 2Ni(OH)₃(s) → CdO(S) + 2Ni(OH)₂(s) + H₂O(1)
2. Pb(s) + PbO2(s) + 2H₂SO₄(aq) → 2PbSO₄ + 2H₂O(1)
3. 2H₂(g) + O₂(g) → 2H₂O(1)
4. 2Fe(s) + O₂(g) + 4H₂(aq) → 2Fe²⁺(aq) + 2H₂O(1)

Answer: 3. 2H₂(g) + O₂(g) → 2H₂O(1)

The Solid State

You know from your previous classes that all three states Of matter are made of postludes, wSScfc osar be the molecules or ions. However, the arrangement of particles differs in each <m fe a gas, this precedes ece apart whereas in a liquid they are closer.

But in both gases and liquids, the oatstoenipszixSes-haver? arrangement and they are in motion. In contrast, in a solid, the particles are tightly packed and; are net free he move due to the strong forces of interaction, between them—they only oscillate about their fared pcasSkaas.

Therefore, solids are rigid and have a definite volume. As you know, liquids too have a despite voters. But they do not have a fixed shape, which solids do.

Crystalline And Amorphous Solids

Based on the order of arrangement of particles, solids can be categorised as crystalline or amorphous. Cryste-fre solids are those in which the particles (atoms, molecules or ions) are arranged in a pattern, that repeats itself over a long range.

Examples are sugar, ice, salt and metals. The particles of amorphous solids, on the other hand, are arranged in a pattern that repeats itself over a very short range. Examples are wax, butter, skin powder, glass and plastics.

Let us now look at a few properties of crystalline and amorphous solids. The differences in their presences arise due to the difference in the arrangement of their constituent particles.

Crystalline solids are anisotropic, meaning that their physical properties, such as electrical resistance, thermal expansion and refractive index, differ when measured along different directions in the same crystal This is because the arrangement of particles differs in different directions.

However, amorphous solids are isotropic, meaning that their physical properties are the same when measured along am. directions. lids are because their constituent particles are more or less randomly arranged.

A crystalline solid has a sharp melting point. In contrast, an amorphous solid liquefies over a range of temperatures. For example, glass and plastics soften over a range of temperatures and can be moulded or Hewn into various shapes, which they retain on cooling. Like liquids, amorphous solids have a tendency to Sow, although very slowly.

Therefore, they are called pseudo solids or supercooled liquids. Glass panes of old buildings are thicker at the bottom than at the top because of this tendency of amorphous solids to Bow.

When you cut a crystalline solid with a sharp object, it breaks into pieces which have smooth and regular surfaces. In other words, you can cut a crystalline solid clearly. If you were to cut an amorphous solid with a sharp 1 object, it would break into pieces with irregular surfaces.

Another important difference between crystalline and amorphous solids is that the former have definite heats of fusion whereas the latter do not.

Types Of Crystalline Solids

Crystalline solids are grouped into different types depending on the nature of the constituent particles and the bond formed between them. Such solids can be classified as ionic, covalent, metallic and molecular.

Ionic solids:

They are composed of anions and cations that are held together by electrostatic forces. For example, common salt, NaCl contains NaT and Cl- ions. Some other examples of ionic solids are CsCl, CaF₂ and ZnS.

Ionic solids have high melting points; they are hard and brittle, and conduct electricity when molten or in solution. Many compounds formed by the reaction of a metallic element with a nonmetallic element are ionic.

Covalent solids:

They are made up of atoms of the same or different elements held together by a network of covalent bonds.

Diamond is the most common example of a covalent solid. Silicon and silicon dioxide are also covalent solids.

These solids are very hard, and strong and have high melting points due to the presence of strong covalent bonds.

Diamond melts above 3500. The oxide of silicon, SiO₂ (commonly called silica), exists in several forms with different crystal structures. Such different forms of the same compound are called polymorphs and the phenomenon, of polymorphism.

SiO₂ does not contain discrete SiO₂ molecules. The large size of Si, together with the decreased tendency of Si to form multiple bonds, leads to the formation of Si—O single bonds in Si04 tetrahedral units. The tetrahedra are linked together in a three-dimensional network by the sharing of each O between two Si.

In a single crystal of quartz, SiO₂, all SiO₄ units are cross-linked into a single unit resulting in a giant molecule or covalent crystal. The strong covalent bonds account for the hardness, very high melting point, and electrical and thermal insulating properties of silica (the localisation of electrons in the covalent bonds prevents their moving freely under an applied electric field).

Metallic solids:

They comprise a network of positive ions whose positions are fixed. The valence electrons are free to move. The force of attraction between the valence electrons and the positive ions is called a metallic bond. Iron, copper and aluminium are examples of metallic solids.

Most metallic solids are very hard and strong, and all of them exhibit high thermal and electrical conductivity; they are malleable and ductile. The melting points of metallic solids vary depending on the strength of metallic bonding. Alkali metals melt below 473 K, most transition metals melt at temperatures above 1273 K. Mercury is a liquid at room temperature.

Molecular solids:

They consist of molecules held together by intermolecular forces. They are classified as polar or nonpolar on the basis of tire type of tire intermolecular force. The physical properties of molecular solids depend on the strength of the intermolecular forces.

In polar molecular solids, the intermolecular forces are dipole-dipole forces. Examples are solid NH₃ and solid HCl. They are soft and do not conduct electricity. Although gases or liquids at room temperature, they melt at higher temperatures than nonpolar molecular solids do. Some polar molecular solids are hydrogen-bonded. Examples are ice and solid ammonia.

Nonpolar molecular solids are bound by van der Waals forces (or dispersion forces), which are very weak. They may comprise small symmetric molecules such as H₂, N₂, O and F₂. Because of the weak intermolecular forces, their melting points are very low (below -73 K). They are soft and do not conduct electricity.

Crystal And Space Lattice

Now let us study the structure of crystalline solids, in which the particles making up the crystal have a basic, periodic arrangement.

A crystal may be defined as a three-dimensional pattern in which a structural motif is repeated in such a way that the environment of every motif is the same throughout the crystal. In other words, the crystal appears exactly the same at one point as it does at a series of other equivalent points. The motif or the repeat unit may be an atom, a molecule or a group of such entities.

To understand the arrangement of atoms/molecules in a crystal, first let us consider a set of parallel motifs separated by a distance say a (the structural motif is represented by a point)

This is a one-dimensional pattern. Now, if we consider the placement of such motifs at a distance b in the second direction, i.e., the y-direction, we can build a two-dimensional pattern by simply arranging the motifs in such a way that in the x-direction, they are separated by a distance a and in the y-direction, by a distance.

If the z-direction is also considered, we get a three-dimensional pattern. If we arrange the points in space so as to represent the actual disposition of the motifs in the crystal, we get what is called a space lattice.

A space lattice is thus a pattern formed by points representing the structural disposition of particles—atoms, of these. Each particle occupies a latte point in the array, Vie npm? the lattice of a crystal into identical parallelepiped by joining the lattice paints with straight Each such pM&fktepip&h with h ’Sat Bask repealing mat of the arrangement of atoms, form or molecule called a unit edh of a nail -cdi in three dimensions generates the entire pattern of a crystal.

Shows the possible unit cells- in a particular two-dimensional array, This arrangement can be extended in a parallel way to a lattice. The choice of a unit cell for a particular crystal depends on various factors such as symmetry and volume since there can be more than one way of placing atoms in a volume. At the present level of learning, we do not go into further details.

Primitive Unit Cell

A space lattice can be divided into unit cells in different ways. The lattice points In a unit cell could be placed only si the comers, or at the comers and inside the body of the cell. The former kind of unit cell Is called a primitive ve trust .cell (Hgnre 1.6).

Wherever the arrangement of particles an a crystal, in each case the lattice contains a volume represented by a unit cell which is regularly repeated throughout the crystal.

In order to describe the geometry of a unit cell for a frre^dimensional lattice, and we must specify the lengths F and c along the three axes, x, y and z, and also the three angles a,p and yin a three-dimensional parallelepiped.

There are 7 types of primitive unit cells and based on these we have seven crystal systems. The simplest unit cell is a cubic unit cell, where all sides are equal and all angles are 901

Cubic Unit Cell

There are three types of cubic unit cells—primitive, body-centred and face-centred. In the primitive unit cell (or a simple cubic unit cell), the atoms are located at the corners of the cell. In the body-centred unit cell, apart from the comers, the atoms are placed at the centre of the cell also. In the face-centred cubic (fee) structure, the atoms are placed at the centre of each face apart from the corners of the cube.

The number of atoms per unit cell varies according to the type of the cell. Assume a three-dimensional arrangement of cubes in space. Imagine four cubes arranged in such a manner that their faces form a square and four cubes arranged similarly above them.

Consider an atom that is at the centre of this arrangement. It is in fact an atom in the comer of a cube. It is being shared by eight cubes. Only 1/8 of the atom belongs to one cube. The same is the case with the other 7 atoms situated at the comers.

Hence, the number of atoms in a primitive cubic unit cell is \(8 \times \frac{1}{8}=1\).

In the case of the body-centred cubic (bcc) structure, the central atom belongs only to one cube. One atom from the comers and one at the centre of the body amount to two atoms per body-centred cubic unit cell. In the face-centred cubic (fee) arrangement, there are four atoms per unit cell. One atom is obtained from the comers as in the case of a primitive cubic unit cell.

Each atom at the face is shared by two cubes; there are six faces and hence \(6 \times \frac{1}{2}=3\) atoms are obtained from the faces.

We have seen that three types of cubic unit cells are possible. Regular stacking of each one of these unit cells results in a particular type of space lattice. Taking into account symmetry considerations (which we will not go into here), it is seen that for the tetragonal crystal system, there are two types of unit cells possible—primitive and body-centred.

In the other crystal systems, one or more than one type of unit cell is possible, amounting to a total of 14 types of unit cells. In 1848, Auguste Bravais showed that the arrangement of these 14 types results in 14 different lattices. They are therefore known as Bravais lattices.

Close Packing In Metallic Crystals

Particles of the same type, like atoms in a metal or anions of an ionic solid, can pack closely resulting in a stable structure of crystals. The particles of a crystal pack in a manner that gives the maximum possible density. Let us consider the various possibilities of this arrangement in a crystal, where the constituent particles are assumed to be spheres and of the same size.

First of all, let us consider the formation of one edge of a crystal. The closest packing in a row of spheres will be one where the spheres are simply touching each other.

In this type of arrangement, each sphere is in contact with two of its neighbours. The coordination number of a particle is the number of its nearest neighbours. In Fluence, in a one-dimensional arrangement of spheres, the coordination number is two.

Now, another row can be aligned below this in any one of the following two ways in order to obtain one face or plane of the crystal. One possibility is that the second row is placed in such a way that each sphere lies exactly above the sphere in the first row; this gives rise to an arrangement of spheres in a square. Hence this arrangement is called square packing.

The coordination number in square close packing in two dimensions is four since each sphere is in contact with the four nearest neighbours. In another type of arrangement, the spheres of the second row can lie in the depressions between the spheres in the first row. The same thing can be repeated for the third row to obtain a hexagonal packing arrangement where one sphere is surrounded by six other spheres in a plane.

The coordination number in the hexagonal close packing in two dimensions is six. Among these arrangements, we find that hexagonal packing results in a close-packed structure leaving less space between the particles of the crystal. If such planes of spheres are stacked one over the other we obtain the complete three-dimensional structure of the crystal.

Let us see how such a structure can be formed. Consider the hexagonal packing of spheres to form the first layer. In this case, a sphere can be surrounded at the maximum by six other spheres of the same size.

Then each of these spheres can again be surrounded by six such other spheres. This arrangement called closest packing can extend indefinitely in a single layer, say layer A.

Now a second layer, B, can be formed above the first layer A still maintaining close packing. If you look at, you will find that there are two types of holes, one type which lies on the same straight horizontal line and the other type which is diagonally opposite to the first ones.

It is not possible to keep spheres of the second layer together on both types of holes. The spheres of the second layer are kept on top of the holes in the first layer so that each particle in layer B is in contact with three particles in layer A.

The third layer can now be stacked above layer B in two ways. In the first arrangement, the spheres are placed exactly as in layer A, so that the third layer resembles layer A and the fourth layer resembles layer B. Thus, the stacking continues as ABABAB …

This arrangement is called the hexagonal closest packing (hep). Examples include Cd, Co, Li, Mg, Na and Zn from the metallic solids. A noncubic unit cell is formed from this arrangement.

In the second type of arrangement, which is called cubic closest packing, the third layer is formed by placing the spheres in the voids or interstices between tire spheres in layer B such that the newly formed layer C does not resemble either layer A or layer B.

Then, the fourth layer is formed by keeping spheres in the voids of layer C and exactly above the spheres in layer A. This is followed by a pattern which is the same as in layer B and then by one which is the same as in layer C.

This type of packing is therefore of the ABCABC … type and is called cubic closest packing or face-centred cubic arrangement (fee) (the smallest unit cell that can describe this arrangement is the face-centred cubic). Examples include Ag, Al, Ca, Cu, Ni and Pb.

Coordination number:

The coordination number of an atom or ion in a crystal is the number of neighbouring atoms or ions it touches. In both the hexagonal closest packed and cubic closest packed structures each particle touches 12 nearest neighbours. This can be understood if we consider three layers at a time and consider a sphere at the centre of a layer.

In the middle layer, there are six nearest neighbours for both hep and cup structures. In the layers above and below, three spheres from each layer touch this central sphere. Thus, in all, there are 12 spheres in close proximity, touching the central sphere. Hence, the coordination number is 12 in both cases.

Packing efficiency in CCP and hep arrangements:

In the help arrangement, there are six atoms belonging to a hexagonal prism, Let us see how. Assume a three-dimensional arrangement of such prisms. There are three spheres in layer B belonging exclusively to this prism. The central sphere at the top of the prism is shared by two prisms (one prism placed exactly above the one shown in the figure). Hence, only half of this sphere belongs to this prism.

There is another sphere of the same kind at the bottom; it also contributes only 1/2 to this prism. Then, the third type of sphere we must consider is placed at the corners. Each sphere in a corner is shared by 6 prisms; 3 in the same plane and 3 above it. There are 12 (6 on top, 6 at bottom) such spheres.

Hence, the spheres from corners contribute to the extent of \(12 \times \frac{1}{6}=2\) for the prism under consideration.

Therefore, the total number of spheres per prism = \(3+\frac{1}{2}+\frac{1}{2}+2=6\)

As you know, the unit cell in a ccp structure is face-centred cubic. You also know that there are four atoms per fee unit cell.

Even when the spheres are closely packed, there is a gap between them due to their shape. Packing efficiency or packing fraction is the fraction of the total space of a unit cell which is occupied by the spheres. To determine packing efficiency, we must first find the total volume of the cell and then the total volume of the spheres. The volume of spheres divided by the volume of the unit cell gives the packing fraction. For a cup structure, the unit cell is the volume of a cube where 7 is the edge length of the cube.

= a³

As there are four atoms per unit cell, the volume occupied by 4 atoms

⇒ \(4 \times \frac{4}{3} \pi r^3\)

where r is the radius of each sphere. Now, we have to relate r and a. As the spheres are in close contact along the face diagonal in a ccp structure, the face diagonal = 4r = √2 a

⇒ \(r=\frac{\sqrt{2}}{4} a\)

Substituting the expression for r from Equation (3) in Equation (2), we get

volume occupied by atoms ⇒ \(4 \times \frac{4}{3} \times \frac{22}{7} \times\left(\frac{\sqrt{2}}{4} a\right)=0.74 a^3\)

Hence, packing fraction ⇒ \(0.74 \frac{a^3}{a^3}=0.74 \text { or } 74 \%\)

Only 74% of the space in a cube is occupied by spheres/atoms in a ccp structure.

Even in a hep structure, the packing efficiency is 74%.

Other structures:

Most metals, other than those cited as forming a hep or a fee structure, crystallise in a bcc structure, where there is one particle in the centre of a cube and one in each corner of the cube. Those particles which are in the same plane do not touch each other.

Here the central particle touches four particles in the upper layer and four in the lower layer, resulting in a coordination number of 8. The crystal structure consists of such repeating units. The particles are not closely packed. Examples of elements with a bcc structure are Cr, Ba, Mo, W and Fe.

There is yet another arrangement possible though again it is not close-packed. It is called the simple cubic structure and is exhibited by polonium.

Here each sphere in a plane touches four of its nearest neighbours and the next layer is stacked in such a manner that each sphere in the second layer is exactly above a sphere in the first layer. This results in an arrangement where the spheres occupy all the comers of a cube and none is at the centre.

The coordination number can be determined by considering three layers at a time. In the middle layer, the central sphere is surrounded by four other spheres and by one sphere each in the upper and lower layers. Thus, the total number of nearest neighbours is 6. In the simple cubic structure, the coordination number of each atom is thus 6.

Packing efficiency In other cubic structures:

In a simple cubic unit cell, the atoms touch each other along the side of the tire cube. If the radius of the atom is jR, the volume of the cell is (2R)³.

The volume of each atom is = \(\frac{4}{3} \pi R^3\)

Therefore, packing efficiency = \(=\frac{\frac{4}{3} \pi R^3}{(2 R)^3}=\frac{\pi}{6}=0.52\)

Only 52% of the total space of the cube is occupied.

In a body-centred cubic unit cell, the atoms on the main body diagonal, and not at the sides, touch each other.

As can be seen, the length of the main body diagonal in terms of the radius of the sphere is 4R. Let us now find the side of the cube.

Let the side of the cube be s. Hence, AB =BC = s.

Consider A ABC. AB and BC are sides of the cube and AC is the face diagonal. ∠B = 90º.

We know that,

⇒ \((A B)^2+(B C)^2=(A-C)^2\)

or, \(s^2+s^2=(A C)^2\)

or, \((A C)^2=2 s^2\)

or, \(A C=\sqrt{2} s,\)

Since BD is also a face diagonal, AC = BD = √2s.

Now, consider A ABD. Again ZB = 90º

⇒ \((A B)^2+(B D)^2=(A D)^2\)

or, \(s^2+(\sqrt{2} s)^2=(A D)^2\)

or, \((A D)^2=s^2+2 s^2=3 s^2 .\)

But AD = 4R.

Hence, \(16 R^2=3 s^2 \text { or } s^2=\frac{16}{3} R^2\)

or, \(s=\frac{4}{\sqrt{3}} R\)

Hence, one side of the cube is \(\left(\frac{4}{\sqrt{3}}\right)^R\)

Volume of the cube = \(\left(\frac{4}{\sqrt{3}} R\right)^3=\frac{64 R^3}{3 \sqrt{3}}\)

Volume of one atom = \(\frac{4}{3} \pi R^3\)

Packing efficiency \(\frac{2 \times \frac{4}{3} \pi R^3}{\frac{64 R^3}{3 \sqrt{3}}}=0.68=68 \%.\)

Voids Or Holes In Close-Packed Structures

In the closest packed arrangement of spheres, the depressions formed by placing the spheres are called voids or holes. We find two types of holes or voids, the octahedral hole and the tetrahedral hole.

An octahedral hole is created when six spheres are in contact while a tetrahedral hole is one formed by four spheres in contact, When the spheres of layer B are placed in such a manner that they occupy the holes in the first layer A, there is a void below every sphere of layer B and above every sphere of layer A.

There are three spheres forming a triangle in one layer and one sphere in another layer, resulting in a total of four spheres around this void. Hence, it is called a tetrahedral void. When the triangles formed in the two layers are placed with their vertices in opposite directions, an octahedral void is obtained. This is obtained when the arrangement in the two layers A and B is such that there is a void in layer B above a void in layer A.

Both the hep and ccp structures have tetrahedral as well as octahedral holes. There are two tetrahedral holes for each atom in both structures. And for each atom, there is only one octahedral hole in the two structures. Shows the octahedral and tetrahedral holes in a ccp unit cell. Such units when repeated give rise to the three-dimensional structure of the crystal.

Location of voids:

Tetrahedral void Consider the fee unit cell. There are spheres at the corners of the cell and also at the centre of each face. Imagine this cube to be divided into eight smaller cubes of equal dimensions.

A close look at each of these smaller cubes shows that all the corners do not contain spheres; in fact, oriy alternate corners do Neither the resulting faces nor the centre contain any sphere.

Out of the eight corners of the smaller cubes, only four are occupied. On joining these four comers containing spheres a regular tetrahedron is obtained It is a Vacant space and the spheres surrounding it form a tetrahedron.

Hence, the void is called a tetrahedral void or tetrahedral hole Since one unit cell can be divided into eight cubes, each of which contains a tetrahedral hole, there are eight such holes per fee unit cell. We know that there are four atoms per fee unit cell and so the number of tetrahedral holes per atom in a fee unit cell is 8 holes/4 atoms = 2 holes per atom.

Octahedral void Again consider a face-centred cubic unit cell. It does not contain a sphere at the centre However, there are six faces, each of which contains a sphere. If the spheres at these faces are connected an octahedron is formed. Hence, we have an octahedral hole at the centre of a fee unit cell. There is an octahedral hole at the edge of the cube also.

In order to locate the hole, consider four cubes of fee unit cells arranged in the form of a rectangular parallelepiped. At the centre of this structure, there is an edge which is shared by all four cubes The spheres at the end of this edge, and those at the faces surrounding this edge, can be connected to form an octahedron. Since there is no sphere at the centre of this octahedron, it is an octahedral hole or octahedral void.

This hole, as can be, is shared by four fee unit cells. So only one-fourth of it belongs to a unit cell. There are twelve edges in a fee unit cell and each of these contains an octahedral hole.

So there are in all \(12 \times \frac{1}{4}=3\) holes per unit cell which are present at the edges.

Apart from this, there is one octahedral hole at the 4 centre which belongs completely to one fee unit cell. In all, there are 3 + 1 = 4 octahedral holes per fee unit cell. Since there are four atoms in a ccp structure, the number of octahedral holes per atom is one.

Ionic Compounds

By now you know that in a crystalline solid, the atoms, ions or molecules are arranged in a definite repeating pattern. The particles behave as though they are spheres and arrange themselves as closely as possible.

The type of packing depends upon of the interaction between the different kinds of spheres. This type of packing of the particles is the basis of the definite structure of crystalline solids.

In the case of ionic compounds, crystals consist of two different kinds of ions that usually have different sizes. The packing of these ions into a crystal structure: therefore depends on the geometry of the ions.

Any ion formed of a single atom behaves as a charged sphere and is surrounded by oppositely charged ions in all directions. Anions tend to be surrounded by cations and vice versa.

The force of attraction between the ions is the same in all directions. Stable ionic crystals result if each ion is surrounded by as many ions as possible of opposite charge and the oppositely charged ions (cations and anions) are in contact with each other. The final structure and the extent of packing is decided by the relative sizes of anions and cations and their relative numbers.

In simple ionic structures, anions, which are generally large, are arranged in a close-packed manner, touching each other with the smallest possible space between them. And cations are found to occupy the voids or holes (the space between the anions).

The holes can be either octahedral or tetrahedral. If the anions that surround the hole are arranged in a tetrahedral manner then the hole is called a tetrahedral hole and the anions are hence four in number. If the anions that surround the hole are arranged in an octahedral manner, an octahedral hole is obtained and we have six anions.

If the cations are small, they tend to occupy tetrahedral holes and those that are relatively bigger occupy octahedral holes. Sometimes the cations may be too large to be able to occupy either of these holes. In such a case, the anions assume a simple cubic structure occupying all the comers of a cube and the cations occupy the cubic holes thus formed, resulting in a body-centred cubic structure.

Let us consider the case where the anions occupy the comers of a cube and the cations occupy all the tetrahedral holes. As the number of one type of atoms/ions per unit cell in a ccp structure is four, the number of anions per unit cell is four. As the tetrahedral holes are eight in number, the number of cations per unit cell is eight.

Hence, the ratio of cations to anions is 8: 4, i.e., 2:1. The formula of the compound is then M₂X, where M is the cation and X is the anion. Similarly, if the cations occupy octahedral holes, the ratio is 1:1 and the formula of the compound will be MX.

Structures Of Ionic Compounds

The relative number of cations and anions varies in different ionic compounds. For the sake of convenience, ionic compounds are divided into four types—MX, MX₂, MX₃ and M₂X.

Ionic compounds of the formula MX generally possess any one of the following structures NaCl or rocksalt structure, caesium chloride or CsCl structure and zinc sulphide, ZnS structure. All these are cubic structures.

Shows the NaCl structure, where both Na+ and Cl^– ions form a fee (face-centred cubic) structure. You can imagine two separate fee lattices formed by Na⁺ and Cl^– ions, which then interpenetrate each other. The coordination number of the cations as well as the anions is 6.

In the structure, the Cs⁺ ion is bigger than the Na⁺ ion. Therefore, the C^– ions occupy the corners of the cube and the Cs⁺ ion is positioned at the centre, resulting in a body-centred cubic structure.

The ionic radius of Cs⁺ is 169 pm and that of Cl^– is 181 pm. When we place Cl^– ions at the comers, each of them touching the adjacent one, a cubic hole is formed and Cs⁺ can occupy this hole, resulting in a bcc structure. The CsCI unit cell can also be drawn with Cs⁺ at the comers and CP at the centre. The bee structure is a result of two interpenetrating simple cubic structures. As against the 6-6 coordination in NaCl, in the CsCI structure, there is an 8-8 coordination.

In the zinc sulphide (ZnS) structure, the large sulphide ions form a face-centred cubic structure that is almost close-packed. The zinc ions occupy alternate tetrahedral holes. Out of the eight tetrahedral sites available, only four sites are occupied.

Only half the tetrahedral sites are occupied as the compound has 1; 1 stoichiometry and for each sulphide ion there are 2 tetrahedral holes.

Both zinc and sulphur have a coordination number of four. ZnS is also known to form a hexagonal structure called the wurtzite structure. Here the sulphide ions form an hep array and zinc ions occupy half of the tetrahedral holes.

Compounds of formula MX₂, which have a 1: 2 stoichiometry (i.e., two anions for every cation), crystallise in the fluorite (CaF₂) structure and the tetragonal rutile (TiO₂) structure. The Ca²⁺ ions in fluorite are in a face-centred cubic arrangement and the fluoride (F^–) ions occupy the tetrahedral holes.

There are, thus, four cations per unit cell and eight anions (equal to the number of tetrahedral holes) resulting in an 8-4 coordination or 1-2 valence type of compound. The coordination of the cation is eight and that of the anion is four.

In the rutile (TiOz) structure, each Ti⁴⁺ ion is attached to 6O^2- ions and each O^2- ion is in turn attached to three Ti⁴⁺ ions. Hence, Ti⁴⁺ ions have a coordination number of 6 and the O^2- ions have a coordination number of 3.

Radius Ratio

The structure of an ionic compound depends largely on the relative sizes of the cation(s) and anion(s) constituting it. Let us see how the sizes of the ions determine the coordination number. Since cations are smaller than anions, let us consider the size requirements for a cation to fit into the interstitial space between anions.

In Δ ABC, cos BCA = cos (30°) = \(\frac{\sqrt{3}}{2}\)

But \(\cos \theta=\frac{\text { base }}{\text { hypotenuse }}=\frac{r^{-}}{r^{+}+r^{-}},\)

where r+ and r- are the radii of the cation and anion respectively.

From Equations 1 and 2, we get

⇒ \(\frac{r^{-}}{r^{+}+r^{-}}=\frac{\sqrt{3}}{2}\)

or, \(\frac{r^{+}+r^{-}}{r^{-}}=\frac{2}{\sqrt{3}}\)

⇒ \(\frac{r^{+}}{r^{-}}+1=\frac{2}{\sqrt{3}}\)

⇒ \(\frac{r^{+}}{r^{-}}=\frac{2}{\sqrt{3}}-1=0.155\)

The radii must satisfy the condition

⇒ \(r^{+}=0.155 r^{-}\)

Based on such calculations, Pauling laid down some rules as criteria for close packing in ionic crystals. These are known as radius ratio rules.

The radius ratio of any ionic compound is given by p = \(=\frac{r_s}{r_1}\), the ratio of the radius h of the smaller ion to the radius of the larger ion. In general, since cations are smaller than anions, the radius ratio is \(\frac{r^{+}}{r^{-}}\).

The cations and anions get as close to each other as possible as determined by their ratio. The larger the radius ratio, the larger is the coordination number of the cation. When the radius ratio is larger, the size of the cation is large and more anions can surround the cation.

Hence, the coordination number is also larger. According to Pauling’s radius ratio rules, if p is between 0.225 and 0.414, then a 4-4 coordination (zinc blende or wurtzite, tetrahedral coordination) is possible, where a cation touches 4 anions], if it is between 1,414 and 0.732 then the compound adepts a 6-6 coordination structure (NaCl, octahedral coordination) and If coordination structure is formed (CsCb cubic holes occupied),

Ionic Radii

X-ray studies of ionic crystals give us information about the dimensions of unit cells from which a of ionic radii can be obtained, assuming that the ions are spheres. Table 1,4 gives some of the Ionic radius values,

Note: pm denotes picometre, which is 1 x 10 ¯¹² metre.

Example 1. On the basis of data given in Tables 1.3 and 1.4, predict the structures of NaCl, KCl and
Solution:

NaCl: From Table 1.4, r_Na+ = 102 pm and r_cl- = 181 pm.

∴ \(\frac{r^{+}}{r^{-}}=\frac{102}{181}=0.564\)

As you can see in Table 1.3, the structure is octahedral. Therefore, there is 6-6 coordination, KCl:  rK = r+ = 138 pm, ra. = r¯ =181 pm,

∴ \(\frac{r^{+}}{r^{-}}=\frac{102}{181}=0.564\)

Li₂S: From Table 1.4, r+ =59 pm and r- =184 pm

∴ \(\frac{r^{+}}{r^{-}}=0.32\) the structure is tetrahedral.

Example 2. The edge length of the unit cell of NaCl is 5,66 A., Assuming close contact of ts a’ and ^– ions, calculate the ionic radius of the Cl Ion given that the ionic radius of the NaT ion is 10² pm.
Solution:

Given

The edge length of the unit cell of NaCl is 5,66 A., Assuming close contact of ts a’ and ^– ions

Along the edge, two Na+ ions and one Cl¯ ion are in close contact. While the two Na+ ions are centred at the corners, each one contributing only a length equal to its radius to the edge length, the Cl ion is in the middle and 2r¯ is its contribution to edge length. If the edge length is a, then

⇒ \(a=2 r^{+}+2 r^{-}\)

= 5.66Å

= 566 pm

r⁺ =102 pm  (given)

∴ \(2 r^{-}=566-2 r^{+}\)

2r¯ = 566 – (2×102)

⇒ \(r^{-}=\frac{(566-204)}{2}=\frac{362}{2}\)

r¯ = 181 pm.

The ionic radius of the Cl” ion is 181 pm.

Calculations Involving Unit Cell Dimensions

Knowledge of the edge length of the unit cell helps us to calculate the density of the crystals and also the mass of atoms in a unit cell. Let us see how density can be calculated.

If a is the edge length of a unit cell of the crystal, the volume is given by the cube of the edge length,

i.e., the volume of the unit cell = a³.

If the mass and volume are known, the density of a unit cell can be determined, which is the same as the density of the substance.

Mass of unit cell = sum of masses of all atoms present per unit cell since in a crystal of a single element all the atoms are of the same type.

Mass of unit cell = number of atoms per unit cell x mass of a single atom = \(n \times \frac{M}{N_{\mathrm{A}}}\)

where M is the atomic mass of the element and NA is the Avogadro constant.

Now,

density of until cell, d= \(n \times \frac{M}{\left(a^3 N_{\mathrm{A}}\right)}\)

If M is in grams and a is in centimetres, then the unit of density is g/cm³.

In the case of molecules, n is the number of molecules per unit cell and M is the molar mass.

Example 1. The density of sodium chloride (NaCl) is 2,163 g cm¯³. Find the edge length of a unit cell of NaCl.
Solution:

Given

The density of sodium chloride (NaCl) is 2,163 g cm¯³.

The molar mass of NaCl = 23 + 35.5 = 58.5 g mol¯¹

Molar volume of NaCl = \(\frac{58.5}{2.163}=27 \mathrm{~cm}^3 \mathrm{~mol}^{-1}\)

Volume of a molecule of NaCl = \(\frac{27}{6.023 \times 10^{23}}=4.48 \times 10^{-23} \mathrm{~cm}^3\) (∵ one mole contains 6.0^-23 x 10^-23 number of molecules).

One unit cell of a fee structure contains 4 molecules.

Hence, volume of unit cell = 4 x 4.48 x 10^-23 = 17.9 x 10^-23 cm³.

The volume of the unit cell in terms of edge length a = a3.

⇒ \(a^3=17.9 \times 10^{-23}\)

∴ \(a=\sqrt[3]{17.9 \times 10^{-23}}=\left(17.9 \times 10^{-23}\right)^{1 / 3} \mathrm{~cm}\)

Example 2. Compound CsCl crystallises in a bcc lattice with a unit cell edge length of 405 pm. Calculate the radius of Ca+ if that of Cr^– is 181 pm.
Solution:

Given

Compound CsCl crystallises in a bcc lattice with a unit cell edge length of 405 pm.

In a body-centred cubic structure, the ions are in close contact along the main body diagonal. In the figure given below the dotted line BC represents the main body diagonal.

Consider the triangle ADB.

If the edge length is a, by Pythagoras’ theorem, a² + a² = square of face diagonal = AB².

∴ AB = √2a.

The face diagonal, one edge and the main body diagonal form a right-angled triangle with the main diagonal as a hypotenuse Face diagonal (AG4B).

Hence, a² + {AB)² -(BC)²

⇒ a² +2a² – (BC)²

⇒ BC = √3a.

But along the main diagonal, we have two anions and one cation in contact; its length is \(2 r^{+}+2 r^{-}\)

⇒ \(\sqrt{3} a=2 r^{+}+2 r^{-}\)

⇒ \(\sqrt{3} \times 405 \mathrm{pm}=2 \times r^{+}+2 \times 181\)

⇒ \(\frac{(\sqrt{3} \times 405)-(2 \times 181)}{2}=r^{+}\)

r⁺=169.7 pm

The ionic radius of the Cs+ ion ≈ 170 pm.

Example 3. NaCl forms a fee structure. If the ionic radii of Na⁺ and Cl^– are 10² pm and 180 pm respectively, find the edge length and hence the volume of a unit cell. Also, calculate the density (the atomic masses of Na and Cl are 23 and 35.5 respectively).
Solution:

Given

NaCl forms a fee structure. If the ionic radii of Na⁺ and Cl^– are 10² pm and 180 pm respectively

Since the ions are closely packed and touching each other, edge length

a = 2r⁺ +2r^– =2×102 + 2×180 = 204+ 360

a =564 pm = 564 x 10^-10 cm.

Volume of unit cell = \(a^3=(564)^3 \times\left(10^{-10}\right)^3=1.79 \times 10^{-28} \mathrm{~cm}^3\)

Molar mass of NaCl = 23 + 35.5 = 58.5 g.

Mass of one molecule of NaCl = \(\frac{58.5}{N_{\mathrm{A}}}\)

There are 4 molecules of NaCl per unit cell.

Hence total mass of unit cell = \(\frac{4 \times 58.5}{6.023 \times 10^{23}} \mathrm{~g}=3.885 \times 10^{-22} \mathrm{~g}\)

Density = \(\frac{\text { mass }}{\text { volume }}=2.16 \mathrm{~g} \mathrm{~cm}^{-3}\)

Example 4. Europium (Eu) is the block element present in the lanthanide series with atomic mass 152. It crystallises in a body-centred cubic structure. Its density is 5.26 g cm¯³. Calculate the radius of an Eu atom.
Solution:

Given

Europium (Eu) is the block element present in the lanthanide series with atomic mass 152. It crystallises in a body-centred cubic structure. Its density is 5.26 g cm¯³.

The body diagonal of the cube = √3 a.

There are three atoms of Eu along this diagonal (one full and 2 half)

Hence, 4K = √3a

⇒ \(R=\frac{\sqrt{3} a}{4}\) (R = radius of atom).

There are 2 atoms in a unit cell of a bcc structure.

∴ \(\rho=\frac{2 \times M}{a^3 \times N_A}\)

⇒ \(5.26=\frac{2 \times 152}{a^3 \times 6.023 \times 10^{23}},\)

⇒ \(a=\sqrt[3]{\frac{2 \times 152}{5.26 \times 6.023 \times 10^{23}}} \mathrm{~cm}=4.58 \times 10^{-8} \mathrm{~cm}\)

= 485 pm.

∴ \(R=\frac{\sqrt{3} \times 458}{4}=198.3 \mathrm{pm}\)

This problem can be tackled in another way.

Alternative method:

Molar volume (volume occupied by 1 mole) = \(\frac{1}{5.26} \times 152=28.9 \mathrm{~cm}^3\)

Volume actually occupied by the Eu atoms without the empty space between them = 28.9 x 0.68 = 19.7 cm³ mol¯¹,

where 0.68 is the packing efficiency.

Volume of one atom = \(\frac{19.7}{6.023 \times 10^{23}}=3.26 \times 10^{-23} \mathrm{~cm}^3=\frac{4}{3} \pi R^3\)

Radius \(\left(\frac{3 V}{4 \pi}\right)^{1 / 3}=1.98 \times 10^{-8} \mathrm{~cm}=198 \mathrm{pm}\)

Example 5. KCI forms a fee structure. Its density is 1.984 g cm³. If the edge length of its unit cell is 629 pm, find the molar mass of KCI.
Solution:

Given

KCI forms a fee structure. Its density is 1.984 g cm³. If the edge length of its unit cell is 629 pm

Edge length = 629 pm = 629 x 10^-12 m = 629 x 10^-10cm.

Density = \(\frac{\text { mass }}{\text { volume }}\)

⇒ \(1.984=\frac{n \times M}{a^3 N_{\mathrm{A}}}\)

⇒ \(1.984=\frac{4 \times M}{\left(629 \times 10^{-10}\right)^3 \times 6.023 \times 10^{23}}\)

∴ M = 74.3.

the molar mass of KCI = 74.3 g mol-1

Example 6. The compound CuCl has a structure similar to that of ZnS. The edge length of the unit cell is 500 pm. Calculate the density (atomic masses: Cu = 63, Cl = 35.5).
Solution:

Given

The compound CuCl has a structure similar to that of ZnS. The edge length of the unit cell is 500 pm.

As you already know p = \(\frac{n M}{a^3 N_{\mathrm{A}}}\)

where p is the density, n is the number of atoms per unit cell, M is the molar mass, a is the edge length and NA is the Avogadro constant.

Therefore, p = \(\frac{4 \times 98.5}{125 \times 10^{-24} \times 6.02 \times 10^{23}}=5.22 \mathrm{~g} \mathrm{~cm}^{-3}\)

(In case of an fcc lattice, n=4).

Example 7. Chromium has a monatomic body-centred cubic structure. The edge length of its unit cell is 300 pm. What is i density (atomic mass of Cr = 52)?
Solution:

Given

Chromium has a monatomic body-centred cubic structure. The edge length of its unit cell is 300 pm.

a = 300 pm = 300 x 10^-10 cm.

⇒ \(\rho=\frac{n M}{a^3 N_A}=\frac{2 \times 52}{\left(300 \times 10^{-10}\right)^3 \times 6.023 \times 10^{23}}=6.39 \mathrm{~g} \mathrm{~cm}^{-3}\)

Example 8. An element has a ccp lattice with a cell edge length of 500 pm. The density of the element is 10 g/cm³. How many atoms are present in 270 g of the element?
Solution:

Given

An element has a ccp lattice with a cell edge length of 500 pm. The density of the element is 10 g/cm³.

Volume of one unit cell = \(=(300 \mathrm{pm})^3=\left(300 \times 10^{-10} \mathrm{~cm}\right)^3\)

⇒ \(=27 \times 10^6 \times 10^{-30} \mathrm{~cm}^3=27 \times 10^{-24} \mathrm{~cm}^3\)

⇒ \(2.7 \times 10^{-23} \mathrm{~cm}^3\)

Volume of 270 g of element = \(\frac{\text { mass }}{\text { density }}=\frac{270 \mathrm{~g}}{10 \mathrm{~g} / \mathrm{cm}^3}=27 \mathrm{~cm}^3 \text {. }\)

Number of unit cells in this volume = \(\frac{27}{2.7 \times 10^{-23}}=10^{24}\)

Since there are 4 atoms in one unit cell of a ccp structure, in 10²⁴ unit cells there will be 4 x 10²⁴ atoms.

Example 9. An element crystallises in a cubic lattice and is found to have a density of 705 g/cm³. The edge length of a unit cell is 250 pm and there are 4 x 10²⁴  atmos in 234 g of the element. Find the number of atoms in a unit cell.
Solution:

Given

An element crystallises in a cubic lattice and is found to have a density of 705 g/cm³. The edge length of a unit cell is 250 pm and there are 4 x 10²⁴  atmos in 234 g of the element

Proceeding as in the previous example, the volume of one unit cell=\(\left(250 \times 10^{-10} \mathrm{~cm}\right)^3=15625 \times 10^{-2} \mathrm{~cm}^3.\)

Number of unit cell in this volume = \(\frac{\text { mass }}{\text { density }}=\frac{234}{7.5}=31.2 \mathrm{~cm}^3\)

Given that the number of atoms in 234 g of the elements is 4 x 10²⁴, the number of atoms in one unit cell = \(\frac{4 \times 10^{24}}{2 \times 10^{24}}=2\).

Hence, there are 2 atmos per unit cell.

Imperfections In Solids

We have studied different types of lattices and you may think that all crystalline solids are perfect in that all unit cells consist of a perfect arrangement of atoms/ions/molecules and the unit cells line up sequentially to form a three-dimensional space lattice with no distortion.

However, only a few crystals have a complete and perfect arrangement of their entities. There may be fewer or more entities placed randomly in a unit cell.

Most crystals suffer from such types of imperfections, which are called defects. Crystal defects occur in points, along lines or along planes. Based on the number of dimensions to which they extend they may be classified as point defects (0 dimension, 0 D defect) involving one or two lattice sites, line defects (1 D defect, involving a row of a lattice), plane defects (2 D defect, when a plane of sites is imperfect) or bulk or volume defects extending in all the three dimensions.

These defects have an important effect on the mechanical, electrical, magnetic and optical properties of solids. Here we will confine ourselves to point defects. Point defects arise due to imperfections at one or more points in a lattice.

Point Defect

A point defect in a crystal may result from any of the following:

1. The creation of the vacancy
2. The presence of an atom/ion of the parent compound in the interstice
3. Substitution of an atom/ion by another atom/ion (the presence of an impurity)
4. The presence of interstitial impurities

The first two are called stoichiometric defects since the}- do not disturb the stoichiometry of the compound, the number of positive and negative ions are in the same ratio as indicated by their chemical formula.

The third one is classified as an impurity defect while the fourth one results in a nonstoichiometric defect due to deviation from the ideal stoichiometric composition of the compound.

Stoichiometric defect:

1. Vacancy defect f creation of vacancy) An atom may be missing from the place where it ought to be present, resulting in the creation of vacancy. Such a defect is called a vacancy defect- The density of the substance decreases due to this defect

2. Interstitial defect When an atom (or ion or molecule) occupies an interstitial site (space between atom/ Ions in the crystal), It results in an interstitial defect in the crystal. There is an increase in the density of the crystal in this case.

In the case of ionic solids, one or a combination of both of the above two defects may be observed. The imperfections in such solids are mainly classified as Schottky defects and Frenkel defects.

Schottky defect In an ionic solid, when a vacancy at an anionic site is compensated for by a vacancy at a cationic site, thus maintaining electrical neutrality, the defect is termed a Schottky defect.

The greater the number of Schottky pairs, the lower the density of the solid. This is the principal defect in alkali halides. Such defects are responsible for the optical and electrical properties of Nad 1 in KT pairs are vacant in Nad at room temperature.

Frenkel defect When an ion occupies an interstitial site (in between the ions) causing a vacancy at the original place, the defect is called a Frenkel defect A vacancy defect occurs at the original site resulting in an interstitial defect at the new site.

Here the density and the electrical neutrality of the solid are the same as that of the normal solid. Such defects occur when the anion and cation differ greatly in size so that the smaller ion can fit into the interstitial sites. A Frenkel defect in AgCl (which also has a Nad structure).

CaF₂ also has predominantly Frenkel defects but here it is the anion which occupies the interstitial site. SrF₂, PbF₂, ThO₂, UO₂ and ZrO, are other compounds shouting Frenkel defects similar to those in CaF¯.

Impurity defects (presence of substitutional impurity):

In ionic compounds, a cation may be replaced by another cation of similar size. Hus is what is called a substitutional impurity. For example, during the precipitation of BaSO₄ from a solution, if some Sr²⁺ ions are also present, then the Sr^2- ions occupy the lattice of BaS04 crystals. Similarly, some of the sites of Na⁺ ions in NaCl may be occupied by Sr²⁺ ions if molten Nad is crystallised in the presence of SrCl₂.

Nonstoichiometric defects:

When there is a change in the stoichiometry of the solid due to imperfections, the defect is called a nonstoichiometric defect There are two types of such defects—the metal-excess defect and the metal-deficiency defect.

Metal-excess defect This defect may arise due to the creation of anionic vacancies or dun-to (ho presence of extra cations at the interstitial sites, An example of the former type Is shown when Mt in cut rifle of Na vapour, This results in the formation of a colour centre, which imparls yellow Colour to Mat I crystals, 1 his is discussed in the section on colour centres.

The second type of metal-excess defect is observed in nQ, Here (the extra %w’ cations occupy the jMfefsHlidi sites and electrons occupy other interstitial sites to maintain electrical neutrality.

This defers is observed in chrysalis exhibiting Frenkel defect, When nO is healed, it loses oxygen and electrons to form it 31 and turns yellow in colour. These excess cations are trapped in interstitial sites with the electrons occupying the nearly interstitial sites.

Effects Of Imperfections In Solids

ionic conductivity in solids:

The most important aspect of point defects is that they make 11 possible for atoms or ions to move through the structure. If there were no defects it would be difficult to imagine the movement of ions in the la I life, Two mechanisms are possible—the vacancy mechanism (which may lie described as the movement of Him vacancy rather than the ion) and the interstitial mechanism, These form what is called Die hopping model.

Colour centres:

Sodium chloride is colourless when pure at room temperature, It is interesting to note that when it is healed in sodium vapour (for that matter any alkali halide in the alkali metal vapour) it allows a greenish-yellow colour.

In this process, NnCl becomes slightly nonstoichiometric to give \(\mathrm{Na}_{1+\delta} \mathrm{Cl} \text { with } \delta \ll 1\) What happens Is that,

When alkali metal halides are heated in Hie alkali metal vapour, the anions migrate to the surface of the crystal to combine with Hie neutral metal atoms. The metal atoms ionise by losing an electron and then combine with the anions to form the salt, As a result, anion vacancies are produced and the electrons released by the metal occupy the anionic vacancies.

The anionic sites occupied by electrons are called N’enlies, (F stands for Farbenzentre, which means colour centre in Herman.) A series of energy levels are available for Hie alec! runs in the colour centres and the energy required to transfer from one level to another falls hi the visible range of electromagnetism radiation.

When visible light falls on the crystal, the excitation of the electrons imparts a characteristic colour (yellow in ease of NaCl) to the crystal. Similarly, KCl heated in potassium vapour exhibits a violet colour and LiCl heated in Li vapour shows a pink colour.

Electrical Properties Of Solids

Solids can be conductors, semiconductors or insulators depending upon whether and to what extent they conduct electricity. Electrical conductivity is determined by the ease of movement of electrons past the atoms under the influence of an electric field.

It is the reciprocal of electrical resistivity and is measured in Sm^– (siemens per metre). Metals are good conductors of electricity with conductivity in the order of 106 to 108 Sm~ The conductivity in metals depends on the number of electrons available for conduction.

Semiconductors have conductivity in the range of 1Q^– to 10′ Sm^-1 while insulators have a conductivity of 10^-13 Sm^-1. A semiconductor is a substance with a conductivity which can be varied by several orders of magnitude by altering its chemical composition or by increasing electrical potential.

One important characteristic of metals is their ability to conduct electricity which increases as the temperature decreases. In contrast, insulators and semiconductors show a decrease in v conductivity as the temperature is decreased.

Ionic compounds are ordinarily nonconductors in the solid state at room temperature. However, there is a significant increase in conductivity on increasing the temperature or if an impurity is present.

Sometimes, a nonstoichiometric defect can make an insulator a semiconductor. For example, NiO is known to have variable stoichiometry. When prepared at a low temperature (1100 K), it is an insulator, pale green and its stoichiometry is 1: 1.

If nickel is oxidised in the presence of an excess of oxygen at 1500 K, the stoichiometry of the compound changes and is obtained. In this process, oxygen molecules are absorbed onto the surface, dissociate and undergo a redox reaction with some Ni2+ ions to form Ni3+ and O2- ions.

To restore electrical neutrality, some Ni2+ ions diffuse out to the surface and leave cation vacancies inside tire crystals. The colour of the compound so formed is black and it is a moderately good electrical conductor.

NiO can be represented as \(\mathrm{Ni}_{1-3 x}^{2+} \mathrm{Ni}_{2 x}^{3+} \mathrm{v}_x \mathrm{O}\), where v denotes vacancies and x is the number of vacancies. Accordingly, the number of Ni²⁺ and Ni³⁺ ions are indicated in NiO. In this case, there can be movement of electrons from Ni²⁺ to Ni³⁺; the Ni³⁺ ion is thus converted to Ni²⁺.

This leads to the formation of Ni³⁺ at another ‘ point. This ion (Ni³⁺) can again be converted into Ni²⁺ by the movement of an electron. This phenomenon involving the movement of electrons is responsible for the conduction of electricity. NiO is also called a hopping semiconductor.

The tire difference between the conductance of a conductor, that of a semiconductor and that of an insulator is explained based on the band theory of solids. According to the molecular orbital theory (MO theory), when atomic orbitals (AOs) on two atoms combine or mix, they form sets of higher-energy (called antibonding) and lower-energy (called bonding) molecular orbitals (MOs).

The total number of MOs obtained is equal to the number of AOs that combine. As the number of atoms in a molecule increases, so does that of MOs. With the rise in the number of MOs, their energy differences become small and we obtain a continuous band of MOs or energy levels.

Consequently, the MO theory for metals is called band theory. Let us take the example of sodium metal. The valence orbital in sodium is 3s. In diatomic sodium, the 3s orbitals of the two Na atoms combine to form one bonding and one antibonding molecular orbital.

When it is triatomic, three 3s orbitals will combine and when it is Na, n orbitals will combine. The difference in energy between successive MOs in a Na molecule decreases with the increase in the number of sodium atoms forming a continuous band.

The lower band is made of bonding MOs while the upper one is made of antibonding MOs. The rules for filling the MOs are the same as for AOs, with each MO accommodating 2 electrons and the lower-energy MO being filled first followed by the higher-energy MOs. Hence, the lower band is filled with electrons but the upper band is empty. This may be seen from the arrangement of electrons.

In the presence of electrical potential, the electrons can be shifted from one set of energy levels to the other or more precisely from the lower band to the upper band. If the upper band is filled, no such shifting can

In the case of magnesium (electronic configuration [Ar] 3s²) the 3s and 3p orbitals form bands, which overlap in energy, and the resulting composite band is only partially filled. Magnesium is thus a conductor of electricity.

As the valence shells of many metal atoms are only partly filled, all MOs will not be filled; some of the higher MOs will therefore be only partly filled or even empty. The filled band is generally referred to as the tire valence band, and the higher energy band is called the conduction band, In hi case of metals, the two bands overlap and easy electron transfer from the valence to the conduction band can occur, facilitating the conduction of electricity.

Metals are thus good conductors of electricity. However, the electrical conductivity of a metal decreases with increasing temperature. This is because the particles undergo increased vibrational motion about their lattice sites and this vibration disrupts the flow of electrons through the crystal.

In the case of semiconductors, the gap between the valence and tire conduction bands is small. Thus, some thermally excited electrons can move into their conduction band and tire substances can conduct electricity. An insulator, however, has a filled valence band and an appreciable gap between tire valence and the conduction bands

Semiconductors

Silicon and germanium are the most common examples of semiconductors; the width of the forbidden band (band gap which contains no allowed energy states) in them is very small and hence the electrons can easily move from the valence to the conduction band.

These are called intrinsic semiconductors. Their conductivity increases with an increase in temperature because electrons gain thermal energy with the rise in temperature and jump from the valence band to the conduction hand. However, their conductivity is too low for practical purposes.

If small amounts of impurities are incorporated into the lattice of these elements their conductivity increases. Crystal defects arising due to the incorporation of impurities can facilitate the movement of electrons through the solid under the influence of an electric field.

The impurity is called a dopant and the process is called doping- Such materials whose conductivity is controlled by the addition of dopants are called extrinsic semiconductors. Doping alters the number of charge carriers and increases conductivity to a large degree.

Two types of conduction mechanisms may be observed in semiconductors. Any electron that is promoted to the conduction band is a negative charge carrier and moves towards the positive electrode under an applied potential.

The valence electron levels that are left behind in the valence band may be regarded as positive holes. Positive holes move when electrons enter them leaving their own positions. Effectively, therefore, positive holes move in a direction opposite to that of electrons.

If doping increases tire conduction-band electron population, an n-type (negative charge carrier) semiconductor is produced. If doping removes electrons from the valence band, the semiconductor is of the p-type (positive charge carrier). These defects increase with temperature rise and hence the conductivity also increases with temperature.

In order to understand tire concepts better, let us take the example of Si, which is a Group 14 element. Alloys formed from the elements of Group 14 (say Si) and Group 15 are n-type semiconductors. Each atom of the element from Group 15 adds one extra valence electron to the alloy.

Let us see how this happens. Pure, crystalline silicon has four valence electrons at room temperature, forming four covalent bonds with the adjacent silicon atoms in a tetrahedral arrangement. If this crystal is now doped with a Group 15 element, say P, the added P atoms occupy normal Si positions in the structure.

But each P atom has five valence electrons. Of the five valence electrons, four are used to form covalent bonds (as if the dopant were a silicon atom) and one is extra not needed for bonding. According to the band theory, this extra electron occupies a discrete level which is slightly below the bottom of the conduction band.

This level acts as a donor level, meaning that the electrons here have sufficient thermal energy to move into the conduction band, where they are free to move. Since the number of electrons in the conduction band of silicon doped with phosphorus is greater than that in pure silicon, the conductivity of silicon doped in this manner is greater than that of pure silicon.

This type of semiconductor in which atoms with more valence electrons occupy sites in a crystal structure, adding extra electrons (negatively charged particles) to the structure, is called an n-type semiconductor. Germanium doped with arsenic also produces an n-type semiconductor.

If a p-type semiconductor has to be formed from Si, elements of Group 13 (for example Ga) are added to a silicon crystal. (We say that Si is doped with Ga.) Group 13 elements have one valence electron less than the elements of Group 14. Thus, in the case of Si-doped with Ga, the dopant atom has only three valence electrons when it is expected to form four covalent bonds.

Thus, one of the Ga-Si bonds must be deficient by one electron and as per the band theory, the energy level associated with this Ga-Si bond does not form part of the valence band but forms a discrete level just above the valence band. This level is known as the acceptor level since it is capable of accepting an electron.

The gap between the acceptor level and the top of the valence band is small. Consequently, electrons from the valence band have sufficient thermal energy to move to the acceptor level. This leaves behind positive holes in the valence band. These holes can move about in the crystal, contributing to electrical conduction. Shows a comparison of the bands in the three types of semiconductors.

Applications of semiconductors:

Semiconductors find use in transistors, silicon chips, photocells, etc. Doped semiconductors are essential components in the modem solid-state electronic devices, found in radios, televisions, calculators and computers.

The simplest example is the pn junction. In this, silicon is doped in such a way that half is n-type and the other half is p-type. The p-type region has positive charge carriers (holes) while the n-type region has negative charge carriers (electrons).

The electrons in this case can flow spontaneously from the n-type to the p-type region across the junction (band gap) combining with the holes in the p-type region to form negative ions. As electrons diffuse, they leave positively charged ions (donors) in the n region.

Similarly, holes near the pn interface begin to diffuse into the n-type region leaving localised ions (acceptors) with a negative charge. The regions near the pn interface lose their neutrality and become charged forming the space charge region, or depletion layer. The space charge then acts as a barrier to further electron flow.

If an external potential difference is applied to the sample such that the p-type end is positive and the n-type end is negative, current flows through the circuit. Electrons enter the sample from the right-hand electrode, flow through the conduction band of the n-type region, drop into the valence band of the p-type region at the pn junction and then flow through the valence band via the positive holes to leave at the left-hand electrode. A continuous current cannot flow in the opposite direction. The pn junction is a rectifier in the sense that

Gallium arsenide, GaAs, is a semiconductor used in solar cells, LEOs, etc, On applying an external difference, the electrons flow through the pn junction arid and finally fall ink) the holes of the p-type context, During this process they emit energy which is in the form of light (in case of silicon semiconductors tuggy fa released in the form of heat).

Thus, these act as light-emitting diodes (LEDs) in electronic displays, The red light in red laser pointers, bar code readers and CD players is all due to the presence of this semi/x/ruictetor, Partially sub stituting gallium with aluminium or arsenic with phosphorus changes the band gap energy faulting in diodes exhibiting various colours such as yellow, orange and green.

The general formula for such semiconductors is Transistors are typically single crystals of silicon doped to give three zones, They may contain pop or npn junctions and act as voltage amplifiers and oscillators in radios, televisions, hi-fi circuits and in amputees.

There are also controlled-valency semiconductors (in which the valency of the combining atoms is modified m per the need) which find application as thermisters—temperature-sensitive sensors. An example is Li_0.05 Ni_0.05O, It is a hopping semiconductor and its conductivity depends on

Some semiconductors are photoconductive, Le, their conductivity increases greatly on irradiation with light, Amorphous selenium is an example and forms an essential component of the photocopying process.

Superconductivity

In 1911 Kamerlingh Onnes discovered that mercury offers no resistance to the flow of electric current at the very low temperature of 4 K, This phenomenon of offering no resistance to the flow of electricity is called superconductivity. Most metals exhibit superconductivity between 2 K and 5 K,

Since 5 K is a temperature at which one cannot work normally, attempts were made to discover materials offering superconductivity at higher temperatures. Examples of such materials are Tl₂Ca₂ha₂Cu₃O₁₀; (125 K); Bi₂Ca₂Sr₂Cu₃O₁₀ (105 K) and YBa₂Cu₂O₇ (90 K). (The values in brackets indicate the temperatures at which time substances become superconducting,)

Magnetic Properties Of Solids

Before studying the magnetic properties of solids Let us see how a substance behaves under the influence of a magnetic field. A magnetic field produces lines of force that penetrate the medium in which it is applied.

The density of these lines of force is called magnetic flux density, B. The magnetic field H and the magnetic flux density are related as B~p0H in a vacuum, where p() is the permeability of free space.

If a magnetic material is placed in the field, it can change the magnetic flux density. The field of the sample in the applied field is known as its magnetisation, M., Now, the magnetic flux density is given by

⇒ \(B=\mu_0 H\)

There is another parameter, magnetic susceptibility, y (% ~ Magnetisation is usually discussed in terms of χ (chi).

Solids can be broadly classified into two types—(1) those materials which when placed in a magnetic field are drawn away from it and (2) those materials which are drawn towards a magnetic field.

The first type of materials are called diamagnetic materials, In such materials, all the electrons are paired and the magnetic moment of one of a pair is compensated by the equal and opposite moment of the other. When such a material is kept in a magnetic field, the number of lines of force emanating from the magnet is reduced, and the magnetic flux density is reduced.

They are weakly repelled by a magnetic field. Examples of diamagnetic substances are H₂O and C₆H₆, ‘Flic magnetism in the second type of materials is a clue to the presence of Urns, terms or molecules containing unpaired electrons. Magnetic behaviour is mainly exhibited by compounds of transition metals and lanthanides/ many of which possess unpaired d and f electrons respectively.

The unpaired electrons may be oriented M random on the different atoms, when the material is called paramagnetic f, both substances have permanent dipoles and are weakly attracted to a magnetic field. Examples are O₂ and CuO,

Substances which are strongly attracted to a magnetic field are said to be ferromagnetic. They can be permanently magnetised. Examples are iron, cobalt and nickel.

The metal ions of such substances, In the solid state, cluster together in small areas called domains. Each domain behaves like a small magnet. When the sample is demagnetised, the domains are oriented at random and their magnetic moments get cancelled. In the presence of a magnetic field, the domains are permanently aligned in one direction, that of the field, and the sample becomes permanently magnetised.

The orientation of domains in opposite directions leads to antiferromagnetism. The magnetic moments cancel each other out. Examples of antiferromagnetic substances are MnO and NiO, When the magnetic dipoles of the domains are aligned in parallel and antiparallel directions in unequal numbers, a net magnetic moment results and the substance is ferrimagnetic. Examples are ferrites (AFe₂O), where A is a divalent metal) and Fe₃O₄. Ferrimagnetic materials are not so strongly attracted to a magnetic field as ferromagnetic substances.

The magnetic properties are the outcome of the magnetic moments associated with the electrons. The magnetic moment of an unpaired electron arises from two causes, one due to orbital motion around the nucleus and the other due to the spin of the electron. The spin component is of more importance. If the electron is visualised as a bundle of negative charge spinning on its axis, the magnitude of the resulting spin moment pB is 1.73 Bohr magnetons. The Bohr magneton is the fundamental unit of magnetic moment.

It is defined as \(1 \mathrm{BM}=\frac{e h}{(4 \pi m c)}\), where e is the electronic charge, h is the Planck constant, m is the electronic mass and c is the velocity of light. It is equal to 9.27 x 10^-24 A m²,

The spin magnetic moment of an electron is ±ps. The orbital magnetic moment is given by the product of the magnetic quantum number and the Bohr magneton.

The effect of temperature on magnetic behaviour

The temperature dependence of the magnetic susceptibility of a paramagnetic substance is given by Curie’s law.

⇒ \(\chi=\frac{\dot{C}}{T},\)

where C is a constant called Curie constant and T is the temperature in kelvin. Curie’s law takes different forms in the case of ferromagnetic and antiferromagnetic substances as the variation of χ is observed to be different

Two temperatures called the Curie temperature and the N6el temperature, are significant. Ferromagnetic materials change to paramagnetic substances above a temperature called the Curie temperature (Tc). Materials which are antiferromagnetic at low temperatures become paramagnetic above a certain temperature called the Neel temperature (TN).

Metals and alloys:

Iron, cobalt and nickel are ferromagnetic while chromium and manganese are antiferromagnetic at low temperatures. The oxides MnO, FeO, CoO and NiO are all antiferromagnetic at low temperatures and change to paramagnetic above the Neel temperature.

Spinels owe their name to the mineral spinel, MgAl₂O₄.

They have the general formula AB₂O₄, A being a divalent ion and B being a trivalent ion. The commercially important spinels known as ferrites are of the type MFe204; where M is a divalent ion such as Fe²⁺, Ni²⁺, Cu²⁺ and Mg²⁺. They are all either antiferromagnetic or ferrimagnetic. Some garnets [M₃M₂ (SiO₄)₃; where M₁₁ = Ca²⁺, Mg²⁺ or Fe³⁺ and Mm = Al³⁺, Ca³⁺ or Fe³⁺ ] are important ferrimagnetic materials. For example, pyrope (Mg₃Al₂Si₃O₁₂) and andradite (Cr₃Fe₂Si₃O₁₂) are ferrimagnetic.

A major application of ferro- and ferrimagnetic materials is in transformers and motor cores. Magnetic bubble memory devices for storing information use thin films of garnets deposited on nonmagnetic substances.

The Solid State Multiple Choice Questions

Question 1. Bonding in diamonds is

1. Covalent
2. Ionic
3. Dipole
4. Metallic

Answer: 1. Covalent

Question 2. During the formation of a solid,

1. Some Energy Is Lost
2. Some Energy Is Gained
3. Energy Remains Constant
4. Some Energy May Be Gained Or Lost Depending On The System

Answer: 1. Some Energy Is Lost

Question 3. Tetrahedral bonding is characteristic of

1. Ionic Bonds
2. Molecular Bonds
3. Metallic Bonds
4. Covalent Bonds

Answer: 4. Covalent Bonds

Question 4. Ionic solids have

1. A Low Melting Point
2. A High Melting Point
3. A Moderate Melting Point
4. None Of These

Answer: 3. A Moderate Melting Point

Question 5. The bond between ice molecules is

1. Ionic
2. Covalent
3. A Hydrogen
4. Metallic

Answer: 3. A Hydrogen

Question 6. Among the following, the strongest bond is the

1. Ionic Bond
2. Hydrogen Bond
3. Metallic Bond
4. Covalent Bond

Answer: 1. Ionic Bond

Question 7. Ionic bonds are mainly formed in

1. Inorganic Compounds
2. Metals
3. Organic Compounds
4. None Of These

Answer: 1. Inorganic Compounds

Question 8. Molecular solids have

1. Very Low Melting Points
2. Fairly Low Melting Points
3. Very High Melting Points
4. None Of These

Answer: 3. Very High Melting Points

Question 9. Metallic solids are generally

1. Hard And Brittle
2. Soft And Plastically Deformable
3. Malleable And Ductile
4. None Of These

Answer: 2. Soft And Plastically Deformable

Question 10. Among the following, the element which has a covalently bonded crystal structure is

1. Al
2. Pb
3. Ge
4. Bi

Answer: 3. Ge

Question 11. Materials having different properties along different directions are called

1. Isotropic
2. Anisotropic
3. Amorphous
4. None Of These

Answer: 2. Anisotropic

Question 12. The tiny fundamental block which, when repeated in space indefinitely, generates a crystal is called

1. A Primitive Cell
2. A Lattice
3. A Unit Cell
4. None Of These

Answer: 3. A Unit Cell

Question 13. How many basic crystal systems are possible?

1. Four
2. Five
3. Six
4. Seven

Answer: 4. Seven

Question 14. How many types of Bravais lattices are possible in crystals?

1. 7
2. 14
3. 8
4. 5

Answer: 2. 14

Question 15. The number of lattice points in a primitive cell is

1. 4
2. 2
3. 8
4. 1

Answer: 4. 1

Question 16. A unit cell with crystallographic dimensions abc, a \(a \neq b \neq c, \alpha=\gamma=90^{\circ}, \beta \neq 90^{\circ}\), B 90° corresponds to

1. Calcite
2. Graphite
3. Rhombic Sulphur
4. Monoclinic Sulphur

Answer: 4. Monoclinic Sulphur

Question 17. Which of the following structures does a crystal, with a b c and interfacial angles a = B = y = 90°, have?

1. Cubic
2. Tetragonal
3. Trigonal
4. Orthorhombic

Answer: 4. Orthorhombic

Question 18. Cubic close packing of equal-sized spheres is described by

1. AB AB AB AB…
2. AB AC AC AB…
3. ABC ACB ABC ACB…
4. ABC ABC ABC…

Answer: 4. ABC ABC ABC…

Question 19. Which of the following metals has an FCC structure?

1. Al
2. Cu
3. Pb
4. All Of These

Answer: 4. All Of These

Question 20. The percentage of total volume occupied by the particles in a bcc structure is

1. 32
2. 68
3. 50
4. 74

Answer: 2. 68

Question 21. The FCC structure is often called

1. Cubic Close Packed
2. Hexagonal close-packed
3. The Graphite Structure
4. The diamond structure

Answer: 1. Cubic Close Packed

Question 22. The correct order of sizes of voids (holes) is

1. Trigonal > Tetrahedral > Octahedral
2. Hexagonal Close Packed
3. Octahedral > Tetrahedral > Trigonal
4. The Diamond Structure

Answer: 1. Trigonal > Tetrahedral > Octahedral

Question 23. The tetrahedral void has a coordination number of

1. Two
2. Three
3. Four
4. Eight

Answer: 3. Four

Question 24. The octahedral void has a coordination number of

1. Two
2. Six
3. Eight
4. Four

Answer: 2. Six

Question 25. In close-packed (hcp, ccp) arrangements of lattices comprising n atoms of a kind, the number of tetrahedral and octahedral voids present respectively are

1. 2n and n
2. n and 2n
3. n and n
4. 2n and 2n

Answer: 1. 2n and n

Question 26. The coordination number of the simple cubic structure is

1. 6
2. 8
3. 12
4. 4

Answer: 1. 6

Question 27. The effective number of atoms belonging to the unit cell of a simple cubic structure is

1. 8
2. 1
3. 4
4. 6

Answer: 2. 1

Question 28. The atomic packing efficiency of a simple cubic structure is

1. 0.68
2. 0.74
3. 1.00
4. 0.52

Answer: 4. 0.52

Question 29. The only element with a simple cubic structure is

1. Silver
2. Polonium
3. Zinc
4. Iron

Answer: 2. Polonium

Question 30. In the crystal structure of NaCl, the arrangement of Clions is

1. Fcc
2. Bcc
3. Both Fcc And Bcc
4. None Of These

Answer: 1. Fcc

Question 31. Interstitial impurities are a

1. Surface Defect
2. Point Defect
3. Line Defect
4. Volume Defect

Answer: 2. Point Defect

Question 32. In ionic crystals, an ion displaced from a regular site to an interstitial site results in what is called a/an

1. Electronic Defect
2. Schottky Defect
3. Frenkel Defect
4. None Of These

Answer: 3. Frenkel Defect

Question 33. In ionic crystals, the missing of a cation-anion pair results in a/an

1. Electronic Defect
2. Schottky Defect
3. Frenkel Defect
4. None Of These

Answer: 2. Schottky Defect

Question 34. In a solid-crystal lattice, a cation leaves its original site and moves to an interstitial position. The lattice defect is called a/an

1. Interstitial Defect
2. Vacancy Defect
3. Frenkel Defect
4. Schottky Defect

Answer: 3. Frenkel Defect

Question 35. An ionic solid with the Schottky defect contained in its structure

1. An Equal Number Of Cation And Anion Vacancies
2. Anion Vacancies And Interstitial Anions
3. Cation Vacancies
4. Cation Vacancies And Interstitial Cations

Answer: 1. An Equal Number Of Cation And Anion Vacancies

Question 36. For \(\mathrm{NaCl}, r_{\mathrm{Na}^{\prime}} / r_{\mathrm{Cl}}=0.325\) The ratio of the coordination numbers of the ions is

1. 6:6
2. 4:4
3. 8:4
4. 6:12

Answer: 1. 6:6

Question 37. Which of these is found in AgCI?

1. Frenkel defect involving cations
2. Frenkel defect involving anions
3. Schottky defect
4. Interstitial defect

Answer: 1. Frenkel defect involving cations

Question 38. The point defect found in Call Is called

1. Frenkel Defect Involving Cations
2. Schottky Defect
3. Frenkel Defect Involving Anions
4. Edge Dislocation Defect

Answer: 3. Frenkel Defect Involving Anions

Question 39. To prepare an n-type semiconductor, the element to be added to Si is

1. Germanium
2. Arsenic
3. Aluminum
4. Indium

Answer: 2. Arsenic

Question 40. To prepare a p-type semiconductor, the element to be added to Ge is

1. Silicon
2. Arsenic
3. Aluminum
4. Antimony

Answer: 3. Aluminum

Question 41. Which type of atoms are added to Ge to prepare an n-type semiconductor?

1. Trivalent
2. Pentavalent
3. Tetravalent
4. Divalent

Answer: 2. Pentavalent

Question 42. Which type of atoms are added to Si to prepare a p-type semiconductor?

1. Trivalent
2. Pentavalent
3. Tetravalent
4. None of these

Answer: 1. Trivalent

Question 43. An example of a superconductor Is

1. Cu
2. Si
3. Ge
4. Hg

Answer: 4. Hg

Question 44. A superconductor exhibits…… resistance.

1. Small
2. Large
3. Zero
4. Infinite

Answer: 3. Zero

Question 45. One Bohr magneton equals

1. 9.27 × 10^-24 Am²
2. 9.1 x 10^-31 Am²
3. 9.27 x 10^-16 Am²
4. 9.1 x 10^-24 Am²

Answer: 1. 9.27 × 10^-24 Am²

Question 46. The temperature at which an antiferromagnetic substance changes to a paramagnetic substance is called the

1. Curie-Weiss temperature
2. Curie temperature
3. Debye temperature
4. Néel temperature

Answer: 4. Néel temperature

Question 47. The transition from the ferromagnetic to the paramagnetic state takes place at the

1. Curie temperature
2. Curie-Weiss temperature
3. Néel temperature
4. Debye temperature

Answer: 1. Curie temperature

Surface Chemistry

Surface Chemistry Definition: 

Surface chemistry deals with phenomena that occur at surfaces, or interfaces. A surface is an interface where one phase ends and another begins. It is a region in which the properties vary from one phase to another.

The interface is represented by putting a hyphen or a slash between the two bulk phases. For example, the interface between a solid and a gas may be represented as solid gas or solid/gas. An interface may be liquid/vapor, solid/liquid, or solid/gas, among others. No interface exists between gases as they are completely miscible.

The study of surface chemistry is important since many chemical reactions in industry and in biological systems take place at interfaces. Important phenomena that take place at interfaces are corrosion, heterogeneous catalysis, electrode processes, dissolution and crystallization, and so on.

For a proper study of this important branch of chemistry, an extremely clean surface is required. For example, if a metal is involved, a very clean sample stored in a vacuum (at a pressure of 10-8 -10-9 pascal) is required. Otherwise, the surface of the metal will be covered by atmospheric nitrogen and oxygen.

The topics we will cover in this chapter are the adsorption of gases and solutes on solid surfaces, and colloids and catalysis.

Adsorption

The molecules of a gas or a solute are attracted to and retained by the surface of the solid with which they come in contact. For example, if a piece of charcoal is introduced into a closed vessel containing ammonia gas, an appreciable quantity of ammonia is quickly taken up by the charcoal and the pressure of the gas in the enclosed vessel decreases. Not only ammonia but almost all gases (such as H₂, O₂, CO, Cl₂, NH₃, and SO₂) are taken up by charcoal to a greater or lesser degree.

The gas that is thus taken up remains on the surface of the charcoal and does not pass into the interior. The simplest proof of this is that if the same sample of charcoal is more finely divided to produce a greater surface area per unit mass, it can take up more gas. The process of accumulation of any substance on the surface of another is called adsorption.

It is a fairly rapid process, as contrasted with absorption, which is a slow process as it involves diffusion into the interior of the material. The substance on the surface of which the concentration occurs is called the adsorbent and that taken up on the surface is called the adsorbate.

For example, in the example of charcoal adsorbing ammonia, ammonia is the adsorbate, and charcoal is the adsorbent.

How adsorption is different from absorption:

As you know, adsorption is purely a surface phenomenon. However, in absorption, the substance passes through the surface and is distributed throughout the bulk of the solid. For example, when a piece of chalk is dipped in ink, the surface of the chalk retains the color of the ink while the solvent of the ink goes into the bulk due to absorption.

On breaking the chalk, it is found to be white from the inside. Also, anhydrous CaCl₂ absorbs water to form a hydrate while acetic acid is adsorbed from its solution by charcoal. Sometimes the word sorption is used to describe the phenomenon of adsorption and absorption taking place simultaneously.

Examples of adsorption:

1. When a hot crucible is allowed to cool in the open, a film of moisture is formed on the die surface. This is an example of the adsorption of water vapor on the surface of the crucible.
2. Acetic add is adsorbed from its solution by charcoal.
3. When animal charcoal is stirred in a dilute solution of methylene blue, die color of the latter decreases in intensity because the charcoal adsorbs the coloured material and thus decolourises the solution.
4. Water vapor gets adsorbed on the surface of silica gel. Hence, silica gel is used to keep the air in a confined space dry.
5. When a raw sugar solution (yellowish brown) is stirred with animal charcoal, the solution becomes colorless as the coloring matter is adsorbed by the charcoal.

Mechanism Of Adsorption

All particles in the bulk of the adsorbent are surrounded by atoms or molecules of their own kind. Thus, the forces acting between the particles are balanced. However, on the surface, the particles are not surrounded by atoms or molecules of their own kind on all sides.

Therefore, these particles have imbalanced attractive forces. As a result of these forces, the surface of the adsorbent has a tendency to attract and retain the adsorbate molecules. Therefore, the magnitude of adsorption increases with an increase in the surface area of the adsorbent.

When adsorption takes place, there is always a reduction in the attractive forces on the surface. As a result, there is a decrease in surface energy, which appears in the form of heat. This proves that adsorption is an exothermic process.

In other words, adsorption is always accompanied by a decrease in the enthalpy of the system, i.e., is negative whenever a gas is adsorbed; the freedom of movement of its molecules is reduced. As a result, there is a decrease in the entropy of the gas, i.e., AS is negative.

Thus, adsorption results in a decrease in both enthalpy and entropy of the system.

The free energy change (AG) for the process of adsorption is given by

ΔG = ΔH -TΔS

The thermodynamic requirement for a spontaneous (or feasible) process is that, at constant temperature and pressure, there has to be a decrease in Gibbs energy, i.e., AG has to be negative. In the equation AG = AH- TAS, it is possible for AG to be negative only when AH has a sufficiently high negative value since -TAS is positive.

As the process of adsorption continues, AH becomes less and less negative and finally equals TAS. At this point, AG becomes zero and equilibrium is attained. This is called adsorption equilibrium.

Types Of Adsorption

Adsorption is of two types—physisorption (physical adsorption) and chemisorption (chemical adsorption).

Physisorption:

If a gas is held on a solid surface by weak van der Waals forces, the adsorption is termed physisorption or physical adsorption. It is also known as van der Waals adsorption since the forces involved are of the van der Waals type. Absorption of gases by charcoal is an example of physisorption. Let us now discuss some characteristics of physisorption.

Lack of specificity:

Physical adsorption is caused by nonspecific van der Waals forces which act universally between any two molecules. The solid surface (adsorbent) does not show a stronger attraction for permanent gases like H₂, O₂, and N₂.

Nature of adsorbate:

The nature of the gas determines the quantity adsorbed by a solid. It has been found that H₂, O₂, N₂, etc., are adsorbed to a lesser extent and less readily than the more easily liquefiable gases such as NH₃, HCl, and CO₂. The more easily a gas is liquefied (i.e., the higher the critical temperature), the more is physical adsorption. This is because van der Waals forces are stronger near the critical temperature.

Volumes of various gases adsorbed by 1 g of activated charcoal:

A look at Table 5.1 shows that 1 g of activated charcoal adsorbs more SO₂ (critical temperature 630 K) than methane (critical temperature 190 K) and more methane than hydrogen (critical temperature 33 K).

Reversible nature The physical adsorption of a gas by a solid is reversible.

⇒ \(\text { Solid + gas } \rightleftharpoons \text { gas } / \text { solid + heat }\)

According to Le Chatelier’s principle, physical adsorption increases at low temperatures and high pressure and decreases with an increase in temperature and decrease in pressure.

Le Chatelier’s Principle:

Definition:

When a system at equilibrium is subjected to a change, the equilibrium shifts in such a direction as to annul the effect of the change.

Effect of temperature:

Let us consider the reaction

⇒ \(\text { gas }+ \text { solid } \rightleftharpoons \text { gas } / \text { solid }+ \text { heat }\)

Here, the gas is adsorbed on the solid with evolution of heat (exothermic reaction) and desorption takes place1 by absorption of heat (endothermic reaction).

If the temperature of the reaction is increased, the system will absorb heat, and therefore desorption will take! place. Hence in order to effect more adsorption, the temperature of the system will have to be reduced.

Therefore, if a reaction is exothermic then a low temperature will shift the equilibrium in the forward direction. A high temperature favors an endothermic reaction.

An increase in temperature favors endothermic reactions.

A decrease in temperature favors exothermic reactions.

Effect of pressure:

The adsorption of a gas leads to a decrease in pressure. Therefore, according to Le Chatelier’s principle, the magnitude of adsorption will increase with the increase in pressure and vice versa.

Surface area of adsorbent The magnitude of adsorption is directly proportional to the surface area of the adsorbent. So, finely divided metals and porous substances, which have a large surface area for a given mass, are good adsorbents.

Enthalpy of adsorption Since the attraction between gas molecules and a solid surface is only due to weak van der Waals forces, the enthalpy of adsorption is low (20-40 kJ mol^-1 ).

Chemisorption:

When gas molecules or atoms are attracted to and retained by a solid surface through chemical bonds (ionic or covalent), the adsorption is known as chemical adsorption or chemisorption. Many chemisorption processes involve high activation energy.

Chemisorption is, therefore, often referred to as activated adsorption. Sometimes physisorption and chemisorption occur simultaneously. In such cases, it is very difficult to determine the exact kind of adsorption taking place. The physical adsorption of a gas at a low temperature may change to chemisorption at a high temperature.

We shall now discuss some characteristics of chemisorption. High specificity Just like chemical bond formation, chemisorption is highly specific and is caused by the same type of forces that help atoms combine chemically, i.e., by valency forces. Gases that can form compounds with the adsorbent are adsorbed chemically.

Examples are the adsorption of oxygen on a metal surface leading to the formation of an oxide, that of hydrogen on a transition element (such as Ni, Pt, or Pd) with unpaired d-orbitals, leading to the formation of a hydride, and the adsorption of oxygen on activated charcoal, resulting in the production of oxides of carbon.

Irreversibility Chemisorption is usually irreversible as it involves compound formation. Though exothermic, the process is very slow at low temperatures. The energy of activation being high, the rate of adsorption falls off rapidly, making chemisorption too slow to be observed at low temperatures.

So chemical adsorption generally takes place at comparatively high temperatures. As is also true for a chemical combination, an increase in pressure increases chemisorption. This is one of the reasons why high pressure is often used in industrial catalysis.

Surface area Chemical adsorption, too, increases with the increase of the surface area of Jae adsorbent.

Enthalpy of adsorption The enthalpy of chemisorption ranges from 80-240 kJ mol^-1. The high values can be attributed to the fact that chemisorption involves chemical bond formation.

Comparison of physisorption and chemisorption:

Adsorption Isotherm

The amount of gas adsorbed on the surface of the adsorbent depends on pressure and temperature. In other words, the amount of gas adsorbed is a function of temperature and pressure only. Mathematically, this can be represented as

⇒ \(\frac{x}{m}=f(p, T)\)

where x = amount of gas adsorbed on mass m of adsorbent at pressure p and temperature T.

If T is kept constant, then Equation 5.2 becomes

⇒ \(\frac{x}{m}=f(p)\)

Equation (5.3) gives the variation of \(\frac{x}{m}\) with pressure at constant temperature. When \(\frac{x}{m}\) is plotted against p at a constant temperature, the curve obtained is called an adsorption isotherm. Thus, an adsorption isotherm is a mathematical expression or a graphical curve, which represents the variation of adsorption with pressure, at constant temperature.

An increased pressure of a gas causes increased adsorption. The increase of adsorption with increased pressure is experimentally found not to be proportional to pressure but somewhat less. So, Freundlich put the adsorption proportional to a fractional power of pressure. The resulting equation which gives the relationship between the amount adsorbed and the pressure is known as the Freundlich adsorption isotherm.

⇒ \(\frac{x}{m}=k p^{1 / n} \quad \text { or } \quad\left(\frac{x}{m}\right)^n=k p\)

where x is the amount adsorbed by m grams of adsorbent at a pressure p and k and n are constants that depend on the nature of the adsorbent and the gas at a particular temperature.

The relationship is generally represented in the form of a curve the mass of the gas adsorbed per gram of the adsorbent is plotted against pressure. A study of these curves reveals that, at a fixed pressure, there is a decrease in physical adsorption with an increase in temperature.

These curves tend to approach a saturation or limiting value at high pressure. This shows that the Freundlich equation (or Freundlich adsorption isotherm) fails at high pressure.

On taking the logarithms of both sides of Equation 5.4, we have

⇒ \(\log \frac{x}{m}=\log k p^{1 / n}\)

or, \(\log \frac{x}{m}=\log k+\frac{1}{n} \log p\)

This is the equation of a straight line.

The validity of the Freundlich isotherm can be tested by plotting log \(\frac{x}{m}\) along the y-axis (ordinate) and log p along the x-axis (abscissa). If the plot is a straight line, then the Freundlich isotherm is valid. The slope of the straight line = \(\tan \theta=\frac{b}{a}=\frac{1}{n}\) The intercept on the y-axis \(\) gives the value of log k. E

The Freundlich isotherm only gives an approximation of the behavior of adsorption. The values of \(\frac{1}{n}\) lie between 0 and 1 (the probable range being 0.1-0.5).

Thus Equation 5.4 holds good over a limited range of pressure.

When \(\frac{1}{n}\) = 0

⇒ \(\frac{x}{m}=k=\text { constant }\)

Equation 5.6 shows that the magnitude of adsorption is independent of pressure when

⇒ \(\frac{1}{n}\) = 0

When, \(\frac{1}{n}=1\)

⇒ \(\frac{x}{m}=k p\)

or \(\frac{x}{m} \propto p\)

Equation 5.7 shows that the magnitude of adsorption is directly proportional to pressure when \(\frac{1}{n}\) = 1. Both the equations (Equations 5.6 and 5.7) are supported by experimental results.

Adsorption From The Solution Phase

Solid surfaces can also adsorb solutes from solutions. For example, when an aqueous solution of acetic acid is agitated with charcoal, a part of the acetic acid is adsorbed on the charcoal, resulting in a decrease in the concentration of acetic acid.

Also, when a litmus solution is shaken with charcoal, it turns colorless because its coloring matter is adsorbed by the charcoal. To take another example, Mg(OH)₂ becomes blue when it is precipitated in the presence of magnesium reagent (a blue dye). The color so obtained is due to the adsorption of the dye on the precipitate of Mg(OH)₂.

However, adsorption from solutions is much less understood than that of gases by solids.

Adsorption of solutes has the following features:

1. The magnitude of adsorption comes down with the increase in temperature.
2. It rises with an increase in the surface area of the adsorbent.
3. The magnitude of adsorption depends on the concentration of the solute.
4. It also depends on the nature of the adsorbent and the solute.

Hie Freundlich equation approximately describes the behavior of adsorption from solutions. In such cases instead of pressure p we have to use concentration C. Thus the relevant equation becomes

⇒ \(\frac{x}{m}=k C^{1 / n}\)

Taking the logarithm of both sides, we get,

⇒ \(\log \frac{x}{m}=\log k+\frac{1}{n} \log C\)

It has been experimentally shown that the plot of log \(\frac{x}{m}\) against log C is a straight line, which shows the validity of the Freundlich isotherm.

Experimental verification:

Equal volumes of solutions of different concentrations of acetic acid are added to equal amounts of charcoal in four different flasks. The final concentration is determined in each flask after adsorption. The difference in the initial and final concentrations gives the values of x. log \(\frac{x}{m}\) values for the different bottles can be plotted against log C.

Applications of adsorption:

Adsorption finds innumerable applications both in the laboratory and in the industry. We shall now discuss some of the important applications of adsorption.

Creation of high vacuum A partially evacuated vessel is connected to another vessel containing activated charcoal cooled in liquid air. The charcoal adsorbs all the gas molecules from the first vessel, thus creating an almost total vacuum.

Gas masks are used for breathing in areas that contain toxic gases. Such areas include coal mines and places where a major fire has broken out. A gas mask consists of activated charcoal or a mixture of adsorbents which adsorbs all toxic gases and vapours and allows only pure air to pass through the pores.

Removal of colouring matter from solutions Animal charcoal can remove colouring matter from solutions. This property is used for decolorizing sugar solutions.

Heterogeneous catalysis A number of industrial processes involve heterogeneously catalyzed reactions. Most of these reactions take place through the adsorption of reactants on the surface of solid catalysts (adsorbents). Examples include the manufacture of ammonia using an iron catalyst, that of sulphuric acid by the contact process using V₂O₅ as a catalyst, and the hydrogenation of oils employing finely divided nickel.

Separation of inert gases Charcoal adsorbs different gases in varying degrees. This property is used to separate a mixture of inert gases on coconut charcoal at different temperatures.

Curing diseases Many drugs used to kill germs are adsorbed on the surface of such organisms.

Froth floatation In froth floatation, the ore is mixed with pine oil and agitated with water. Air is passed through this solution. The ore particles are adsorbed on the air-oil interface while the impurities remain in water. The adsorbed ore particles come to the surface in the form of foam.

Adsorption indicators Surfaces of silver halide precipitate have the property of adsorbing dyes like eosin and fluorescein. In the case of precipitation titrations (AgNO₃ vs NaCl) the indicator is adsorbed at the endpoint producing a characteristic colour on the precipitate.

Chromatographic analysis based on adsorption is used for the separation, isolation, purification, and identification of the components of a mixture. This is achieved by passing the mixture (dissolved in petroleum ether, benzene, ethyl acetate, or some other solvent) through a column of a suitable adsorbent (alumina or silica gel).

Example 1. What is activated charcoal? How is the extent of absorption by charcoal increased?
Solution:

Activated charcoal:

The extent of absorption by charcoal can be increased by subjecting charcoal to a process of activation. This involves the heating of wood charcoal between 625 K and 1275 K in a vacuum.

During activation, hydrocarbons and other impurities are removed from charcoal and render it more porous, making available a very large surface area for adsorption. The resulting porous charcoal is called activated charcoal.

Example 2. What are the factors on which the amount of gas adsorbed by a solid depends?
Solution:

The factors on which the amount of gas adsorbed by a solid depends

1. The amount of a gas adsorbed by a solid depends upon the
2. Nature of the gas and the adsorbent, the surface area of the adsorbent
3. Temperature and pressure of the adsorbent-adsorbate system.

Example 3. What is desorption?
Solution:

Desorption

Desorption is the process of release of the adsorbed molecules. Desorption may also be called the evaporation of the adsorbed molecules.

Example 4. Why are powdered substances more effective adsorbents than their crystalline forms?
Solution:

Powdered substances have greater surface area than their crystalline forms. The greater the surface area, the greater the adsorption.

Catalysis

For a given temperature and pressure, every chemical reaction occurs at a characteristic rate. If the rate is rapid, the products are formed in a short period of time. If the rate is slow, it takes a long time for the products to be formed. Scientists are interested in discovering ways to increase the rates of slow reactions, particularly when they are important to industrial processes.

In 1835, Berzelius observed that the speed of a number of reactions was enhanced by the mere presence of a foreign substance, which did not apparently take part in the chemical reaction. Let us consider the example of potassium chlorate decomposing to potassium chloride and oxygen when heated to 653-873 K.

2KClO₃ → 2KCl+ 3O₂

The decomposition happens at a lower temperature (473-633 K) if the potassium chlorate is mixed with manganese dioxide at a much-accelerated rate. The amount of manganese dioxide remains unchanged at the end of the reaction and the compound may be used again and again. A substance that can be used to alter the speed of a reaction (usually to speed it up) but itself remains unchanged chemically is called a catalyst and the phenomenon of the speeding up of a reaction using a catalyst is called catalysis.

The speed of a reaction is very important in the chemical industry. (The greater the speed, the more is the productivity.) Catalysts play a major role in this context.

In the manufacture of ammonia, iron is used as a catalyst in the presence of molybdenum to increase the speed of the reaction between nitrogen and hydrogen. Molybdenum acts as a promoter for the iron catalyst. Promoters increase the activity of a catalyst while poisons bring it down.

In the petroleum industry, methods have been found to break up the less useful larger molecules into the smaller, more useful ones. The process is known as cracking. Cracking was first done simply by heating the heavy fractions to a very high temperature (thermal cracking).

More recently it has been found that by using a catalyst, a mixture of aluminum oxide and silicon oxide, cracking can be achieved at a temperature of only 773 K. This is known as catalytic cracking.

Catalysts are also very important in life processes. Photosynthesis is a chemical change that Is carried out in all green plants because of the catalyst chlorophyll which green plants contain.

Countless other chemical changes are carried out in living cells of all kinds. They all depend on biological catalysts called enzymes. Enzymes in our saliva, stomach, and intestines control the digestion of our food.

Though most catalysts help speed up reactions, some slow reactions down. For example, in the decomposition of ammonia on a platinum surface, hydrogen (a product) is strongly adsorbed and inhibits the reaction. Such a condition is called inhibition of the catalyst.

One of the reactants or the products that gets strongly adsorbed on the surface of the catalyst and thereby decreases the reaction rate is called the inhibitor. It is also possible for a reaction to be inhibited by a foreign molecule that does not take part in the reaction.

This type of inhibition is called catalytic poisoning. For example, in the manufacture of sulphuric acid by the contact process, arsenic compounds act as poison for the platinum catalyst in the conversion of SO₂ into SO₃.

Types Of Catalysis

Catalysis may be either homogeneous or heterogeneous.

Homogeneous catalysis:

In homogeneous catalysis, the catalyst and the reactants are present in one single phase (gaseous or liquid). The following are some classical examples of homogeneous catalysis.

1. The oxidation of sulphur dioxide to sulphur trioxide in the presence of nitric oxide as the catalyst in the lead-chamber process for the manufacture of sulphuric acid

⇒ \(2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \stackrel{\mathrm{NO}(\mathrm{g})}{\longrightarrow} 2 \mathrm{SO}_3(\mathrm{~g})\)

All the reactants (SO₂ and O₂) and the catalyst (NO) are in the same phase (gaseous).

2. In the stratosphere, the decomposition of ozone occurs in the presence of Cl atoms as a catalyst

⇒ \(\mathrm{O}_3+\mathrm{O} \stackrel{\mathrm{Cl}}{\longrightarrow} 2 \mathrm{O}_2\)

Cl atoms are formed upon the decomposition of CFCl₃ when the latter is exposed to UV radiation from sunlight.

3. The hydrolysis of ethyl acetate is catalyzed by hydrochloric acid.

⇒ \(\mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5(\mathrm{l})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\mathrm{H}_3 \mathrm{O}(\mathrm{aq})}{\longrightarrow} \mathrm{CH}_3 \mathrm{COOH}(\mathrm{l})+\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{l})\)

The reactants and the catalyst are in the same phase (liquid).

4. The process of esterification is catalyzed by concentrated

⇒ \(\mathrm{CH}_3 \mathrm{COOH}(\mathrm{l})+\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{l}) \underset{\mathrm{H}_2 \mathrm{SO}_4(\mathrm{l})}{\stackrel{\text { conc. }}{\longrightarrow}} \mathrm{CH}_3 \mathrm{COOC}_2 \mathrm{H}_5(\mathrm{l})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

The reactants and the catalyst are in the same phase (liquid).

5. The hydrolysis of cane sugar into glucose and fructose is catalyzed by a mineral acid (H₂SO₄)

⇒ \(\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\mathrm{H}_2 \mathrm{SO}_4(\mathrm{l})}{\longrightarrow} \underbrace{\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{aq})+\mathrm{Clucose}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{aq})}_{\text {in solution }}\)

The reactants and the catalyst in this reaction are in the same phase (liquid).

Heterogeneous catalysis:

In heterogeneous catalysis, the catalyst and the reactants are present in different phases.

The following are some classical examples of heterogeneous catalysis:

1. The oxidation of sulfur dioxide into sulfur trioxide in the presence of platinum

⇒ \(2 \mathrm{SO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \stackrel{\mathrm{Pr}(\mathrm{s})}{\longrightarrow} 2 \mathrm{SO}_3(\mathrm{~g})\)

Both the reactants are in a gaseous state while the catalyst is in a solid state.

2. The combination of nitrogen and hydrogen to form ammonia in the presence of iron in the Haber process

⇒ \(\mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g}) \stackrel{\mathrm{Fe}(\mathrm{s})}{\longrightarrow} 2 \mathrm{NH}_3(\mathrm{~g})\)

The reactants are in the gaseous state while the catalyst is in the solid state.

3. The hydrogenation of vegetable oils (unsaturated fatty acids) in the presence of finely divided nickel as a catalyst

⇒ \(\text { vegetable oil }(\mathrm{l})+\mathrm{H}_2(\mathrm{~g}) \stackrel{\mathrm{Ni}(\mathrm{s})}{\longrightarrow} \text { vegetable ghee (dalda) }\)

The two reactants are in different states (liquid and gaseous). The catalyst is in the solid state.

4. The dehydration of formic acid in the presence of Al₂O₃ as a catalyst

⇒ \(\mathrm{HCOOH}(\mathrm{g}) \stackrel{\mathrm{Al}_2 \mathrm{O}_3(\mathrm{~s})}{\longrightarrow} \mathrm{H}_2 \mathrm{O}(\mathrm{g})+\mathrm{CO}(\mathrm{g})\)

The reactant is in the gaseous state while the catalyst is in the solid state.

5. The oxidation of ammonia into nitric oxide in the presence of platinum gauze (catalyst) in Ostwald’s process.

⇒ \(4 \mathrm{NH}_3(\mathrm{~g})+5 \mathrm{O}_2(\mathrm{~g}) \stackrel{\mathrm{Pt}(\mathrm{s})}{\longrightarrow} 4 \mathrm{NO}(\mathrm{g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

Here, the reactants are in the gaseous state, and the catalyst is in the solid state.

Theories of heterogeneous catalysis:

The two old theories that explain the mechanism of heterogeneous catalysis are the intermediate compound theory and the adsorption theory.

Intermediate compound theory According to this theory, catalysis occurs due to the formation of a reaction intermediate between the reactant and the product. The catalyst is supposed to provide an alternate pathway b) reducing the activation energy between the reactants and products and hence lowering the potential energy barrier as shown in the figure given below.

In view of Arrhenius’s equation

⇒ \(k=A e^{-E_a / R T}\)

it is clear that the lower the value of activation energy (E_a), the greater will be the rate of the reaction.

Adsorption theory The adsorption theory applies only to heterogeneous catalysis. According to this theory, the solid catalyst adsorbs the reactants, which are either in the gaseous state or in solution.

The rise in concentration of the reacting molecules on the surface of the catalyst increases the rate of the reaction. As you know, adsorption is an exothermic process. The heat evolved due to adsorption is used in increasing the rate of the reaction.

The modem adsorption theory is a combination of the intermediate compound theory and the old adsorption theory. According to it, catalytic activity is localized on the surface of the solid catalyst, which has certain active spots at which there are free valencies. The mechanism of catalysis involves the following five steps.

1. The reactants diffuse to the surface of the catalyst.
2. They are adsorbed on the surface of the catalyst.
3. A chemical reaction occurs on the surface of the catalyst through the formation of an intermediate.
4. The products leave the surface of the catalyst to make room for fresh reactant molecules.
5. The reaction products diffuse away from the surface of the catalyst.

When a gas comes in contact with the catalyst’s surface (adsorbent), its molecules form loose chemical bonds with the latter. If different molecules form loose chemical bonds with the catalyst’s surface side by side, they may react with each other, resulting in the formation of new molecules. These new molecules leave the catalyst’s surface to make the surface available for more reactant molecules.

The modem theory explains why the catalyst remains unchanged in mass and chemical composition at the end of the reaction.

Important features of solid catalysts:

Activity The ability of a catalyst to accelerate a chemical reaction is called its activity. The activity of a catalyst largely depends upon the strength of chemical adsorption (chemisorption).

The reactant molecules must get chemically absorbed fairly strongly onto the catalyst. However, they must not be adsorbed so strongly that they stick to surface of the catalyst, leaving no room for other reactant molecules to take their place.

Selectivity Catalysts are highly selective—each of them catalyzes only a particular reaction. Carbon monoxide, on treatment with hydrogen, yields different products with different catalysts.

⇒ \(\mathrm{CO}(\mathrm{g})+3 \mathrm{H}_2(\mathrm{~g}) \stackrel{\mathrm{Ni}}{\longrightarrow} \mathrm{CH}_4(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{g})\)

⇒ \(\mathrm{CO}(\mathrm{g})+2 \mathrm{H}_2(\mathrm{~g}) \stackrel{\mathrm{Cu} / \mathrm{ZnO}-\mathrm{Cr}_2 \mathrm{O}_3}{\longrightarrow} \mathrm{CH}_3 \mathrm{OH}(\mathrm{g})\)

⇒ \(\mathrm{CO}(\mathrm{g})+\mathrm{H}_2(\mathrm{~g}) \stackrel{\mathrm{Cu}}{\longrightarrow} \mathrm{HCHO}(\mathrm{g})\)

Shape-selective catalysis by zeolites:

A catalytic reaction that depends upon the size of the pores and the cavities of the catalyst and the size of the molecules of the reactants and products is called shape-selective catalysis.

On account of their honeycomb-like structures, zeolites are good shape-selective catalysts. They are microporous aluminosilicates which have a three-dimensional network of silicates in which aluminum atoms replace some silicon atoms, resulting In an Al-O-Si framework.

Zeolites (natural or synthetic) are healed in a vacuum so that the water trapped in the pores boils off. As a result, the zeolites become porous. The size of the pores ranges from 260 pm to 740 pm. Only those molecules which are small enough can be adsorbed in these pores.

In the petrochemical industry, zeolites are widely used as catalysts for the cracking of hydrocarbons and isomerization. An important zeolite catalyst used in the petroleum industry is ZSM-5 (zeolite sieve of molecular porosity 5). It converts alcohols directly into petrol (a mixture of hydrocarbons) by the process of dehydration.

Enzyme Catalysis

Living plants and animals produce complex nitrogenous organic compounds called enzymes. Enzymes are proteins with molecular weights ranging from 13000 to several million. They form colloidal solutions in water.

Enzymes are effective catalysts that are involved in a wide variety of biological processes. For example, enzymes in the saliva begin the process of breaking starch in food. Some enzymes catalyze the formation of blood clots when necessary; others dissolve the clots after a wound has healed.

Certain enzymes act to enable the body to fight infection or disease. Enzymes can disrupt the cell walls of certain bacteria. Fruits ripen because of the action of enzymes. Enzymes catalyze several reactions that occur in animals and plants. So they are termed biochemical catalysts.

Many enzymes are isolated in pure crystalline forms from living cells. The structures of some of them, e.g., insulin, have been determined and a few enzymes have recently been synthesized. The first enzyme was synthesized in the laboratory in 1969.

Let us now touch upon a few enzyme-catalyzed reactions:

1. Inversion of cane sugar The enzyme invertase converts sucrose (cane sugar) into glucose and fructose.

⇒ \(\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\text { invertase }}{\longrightarrow} \underset{\text { glucose }}{\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6}+\underset{\text { fructose }}{\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6^{-}}\)

2. Conversion of glucose into ethyl alcohol The enzyme zymase converts glucose into ethyl alcohol and

⇒ \(\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{aq}) \stackrel{\text { zymase }}{\longrightarrow} \underset{\text { ethyl alcohol }}{2 \mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}(\mathrm{aq})}+2 \mathrm{CO}_2(\mathrm{~g})\)

This process is used in making wine (which contains alcohol) from grapes.

3. Conversion of starch into maltose The enzyme diastase catalyses starch into maltose by partial enzymatic hydrolysis.

⇒ \(\underset{\text { starch }}{2\left(\mathrm{C}_6 \mathrm{H}_{10} \mathrm{O}_5\right)_n(\mathrm{aq})+n \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\text { diastase }}{\longrightarrow}} \underset{\text { maltose }}{n \mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{aq})}\)

4. Conversion of maltose into glucose The enzyme maltase catalyses the formation of glucose from maltose and water.

⇒ \(\underset{\text { maltose }}{\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{aq})}+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\text { maltase }}{\longrightarrow} \underset{\text { glucose }}{2 \mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{aq})}\)

5. Decomposition of urea into ammonia and carbon dioxide The enzyme urease catalyzes the formation of ammonia and carbon dioxide from urea and water.

⇒ \(\mathrm{NH}_2 \mathrm{CONH}_2(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\text { urease }}{\longrightarrow} 2 \mathrm{NH}_3(\mathrm{~g})+\mathrm{CO}_2(\mathrm{~g})\)

6. Digestive enzymes (such as pepsin and trypsin) hydrolyze large protein molecules into smaller groups of proteins. In the stomach, pepsin hydrolyses proteins into peptides while in the intestine, trypsin hydrolyses proteins into amino acids.

7. Conversion of milk into curd Lactobacilli enzymes present in curd convert milk into curd

8. Mycoderma acetic enzymes convert ethyl alcohol into acetic acid.

⇒ \(\mathrm{CH}_3 \mathrm{CH}_2 \mathrm{OH}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g}) \longrightarrow \mathrm{CH}_3 \mathrm{COOH}(\mathrm{l})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

9. At 310 K (body temperature), sucrose can be hydrolyzed using an enzyme, suocharase.

⇒ \(\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \stackrel{\text { saccharase }}{\longrightarrow} \underset{6}{\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6}+\underset{\text { glucose }}{\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6} \text { fractose }\)

10. An enzyme found in the mouth converts sucrose into dextran (a polysaccharide made of glucose units). About 10% of dental plaque is composed of dextran. That is why your dentist tells you not to eat candy.

Summary of some important enzymatic reactions:

Characteristics of enzyme catalysis:

Efficiency Enzymes are extremely efficient. Some operate on as many as 25000 molecules in one second.

Highly specific An enzyme, like any other catalyst, is highly specific—it catalyzes only a certain reaction and not any other. The enzyme urease, for instance, catalyzes the hydrolysis of urea only. The hydrolysis of other amides is not catalyzed by urease.

The enzyme decomposing cane sugar does not decompose malt sugar. Lactic dehydrogenase oxidizes 1-lactic add but not d-lactic add.

Highly active at 298-310 K Enzymes are highly active at 298-310 K. At temperatures above 310 K, enzyme activity is reduced and extreme temperatures can even stop enzyme activity. Below 298 K too, enzyme activity decreases.

Enzymes in the body exhibit the greatest activity at normal body temperature (310 K). At much higher body temperatures, all physiological reactions cease due to loss of enzymatic activity. This is one reason why a high fever is dangerous.

Highly active under optimum pH Each enzyme exhibits maximum activity at its own optimum pH. The optimum pH for most enzymes is in the pH range 5-7.

On either side of that particular pH (or range), the activity of an enzyme is markedly decreased. Amylase in the saliva is the most active at a neutral pH and becomes inactive in the stomach where the pH is 1.6.

Activity increases in the presence of activators and coenzymes Some enzymes are initially in an inactive form. These are called proenzymes. They become active in the presence of another substance called an activatory Activators are generally inorganic ions (such as Ca²⁺, Zn²⁺, Mn²⁺, Mg²⁺, Na⁺ or K⁺, CO²⁺, Cu²⁺).

The catalytic activity of an enzyme is increased when these metal ions are weakly bonded to the enzyme molecule. For example, calcium activates prothrombin. Amylase in the presence of Na^– ions catalyzes normal blood clotting.

A coenzyme is a nonprotein that increases the catalytic activity of the enzyme. Vitamins frequently form part of coenzyme molecules.

Inhibitors, poisons, and promotors Inhibitors reduce enzyme activity. They may be either organic or inorganic molecules. They react either directly with the enzyme or with the activator to prevent the activation of the enzyme. Many poisons are fatal because they inhibit vital enzyme activity

There are two types of inhibitors—competitive and noncompetitive. Since they resemble the substrate in their chemical nature, competitive inhibitors compete directly with the substrate. After linking with such an inhibitor, the enzyme is no longer able to perform its normal function.

Noncompetitive inhibitors react with certain nonspecific functional groups of the enzyme, altering the shape of the active site so that the substrate is not able to fit in.

An example is the cyanide ion. It combines with iron to form a very stable complex, interfering with cytochrome oxidase, which is essential for respiration. Respiration ceases and the person dies.

Mechanism of enzyme catalysis:

The catalytic activity of an enzyme is due to the presence of a specific site on its surface, called the active site. This site is characterized by the presence of functional groups (such as —NH₂, —COOH, —SH, and —OH) which form weak bonds such as ionic bonds, hydrogen bonds, or van der Waals bonds with the molecules of the reactant (substrate).

A substrate that has a complementary shape fits into the active site like a key fits into a lock forming an enzyme-substrate complex. This complex intermediate then breaks apart into the products of the reaction, liberating the original enzyme.

As the enzyme surface has no affinity for the product molecules, the latter leaves the enzyme surface quickly to make room for fresh molecules of substrates to be bound at the active site. Because of this recycling, only small amounts of enzymes are needed.

Example 1. What is the root of desorption in catalysis?
Solution:

The root of desorption in catalysis

Desorption makes room on the surface of the solid catalyst for fresh molecules of reactants to be adsorbed.

Example 2. Why is it necessary to remove carbon monoxide when ammonia is manufactured by the Haber process?
Solution:

Carbon monoxide acts as a poison for the iron catalyst used in the manufacture of ammonia by the Haber process. Carbon monoxide forms pentacarbonyl iron [Fe(CO)₅] with iron at the reaction temperature.

Example 3. Why is a heterogeneous catalyst used in the form of a finely divided powder rather than as something with a smooth surface?
Solution:

For a heterogeneous catalyst to be effective, a large surface area is required. Since a finely divided powder has a large surface area per unit mass, a heterogeneous catalyst is employed in this form.

Example 4. Why is the hydrolysis of an ester slow in the beginning? Why does it become faster after some time?
Solution:

The acid hydrolysis of an ester may be expressed as

The add produced in the reaction acts as a catalyst (autocatalyst). The concentration of H⁺ ions increases due to the formation of the add.

Colloids

Fine particles of sand in water form what is known as a suspension. These particles settle down after a while. In a true solution, such as that of salt in water, the particles do not settle down.

In between the true solution and the suspension, there is a type of system that normally never separates; it is called a colloidal dispersion or sometimes just a colloid. A colloidal solution is also termed a sol in short.

A colloid can be defined as a stable two-phase (heterogeneous) system consisting of finely divided particles (usually a solid) dispersed in a continuous medium (often a liquid).

The finely divided particles form what is called the dispersed phase and the medium is called the dispersion medium. For example, in colloidal gold (also called gold sol), gold is the dispersed phase and water is the dispersion medium.

The basic difference between a true solution and a colloid involves particle size. In a true solution, the particles are ions or small molecules and in a colloid, the dispersed phase may comprise particles of very large individual molecules (e.g., a protein or a synthetic polymer) or an aggregate of many atoms, ions or small molecules.

The size of the dispersed particles in a colloidal system is more than that of the solute particles in a true solution and smaller than that of the particles in a suspension.

The particle size of the dispersed phase in a colloid lies in the range of 1 to 1000 nm (10^-9 to 10^-6 m). In a suspension, the size of the suspended particles is always larger than 1000 nm. In a true solution, the size of the solute molecules is less than 1 nm.

Colloids have a very large surface area per unit mass because they consist of many extremely small particles. Consider a cube of side 1 cm. The total surface area of the cube = 6a² = 6 cm². If the cube is divided into cubes of equal size, then

Volume of each small cube = \(\frac{1}{10^{12}} \mathrm{~cm}^3=10^{-12} \mathrm{~cm}^3\)

The side of each small cube = 10^-4 cm [since volume is (side)³].

surface area of each small cube = \(6 a^2=6 \times\left(10^{-4}\right)^2=6 \times 10^{-8} \mathrm{~cm}^2\).

Total surface area of all the 1012 cubes = \(\left(6 \times 10^{-8}\right) \times 10^{12} \mathrm{~cm}^2=60,000 \mathrm{~cm}^2\)

This large surface area provides them with the property of adsorption, one of their most important properties

Classification Of Colloids

Colloids are classified based on the following criteria:

1. The physical condition of the dispersed phase and the dispersion medium
2. The affinity between the tine dispersed phase and dispersion medium
3. The type of particles of the dispersed phase

One the basic physical condition of the dispersed phase and dispersion medium:

The following eight types of colloidal systems are possible, depending upon whether the dispersed phase and the dispersion medium are solids, liquids, or gases.

Types of colloidal systems:

Many commercial products such as whipped cream and fire-fighting foam are colloids. Whipped cream is a foam (a gas dispersed in a liquid). Most biological fluids are aqueous solids (solids dispersed in water). In a cell, for example, proteins and nucleic acids are particles of colloidal size dispersed in an aqueous solution of ions and small molecules.

Of the eight colloids mentioned in the Table, the most common are sols (solids in liquids), emulsions (liquids in liquids), and gels (liquids in solids). In this chapter, we shall discuss only sols and emulsions.

If water is the dispersion medium, such systems are called hydrosols or simply sols, e.g., ferric hydroxide sol. If alcohol is the dispersion medium, the system is called an alcohol.

On the basis of affinity between the dispersed phase and dispersion medium:

Based on the affinity between colloidal particles and the medium, solid-liquid sols can be classified as lyophilic and lyophobic.

Lyophilic colloids Lyophilic literally means ‘solvent-loving’. Lyophilic colloids include gelatin, gum-arabic, soaps, and starch, all of which have a marked affinity for water. These are simply prepared by mixing the solid (the dispersed phase) with the solvent (the dispersion medium) at a suitable temperature.

If the dispersion medium is separated from the dispersed phase by evaporation, the sol can be made again by simply remixing the dispersed phase with the dispersion medium. That is why these sols are sometimes called reversible sols. These are stable and cannot be easily coagulated.

Lyophobic colloids The word lyophobic means ‘solvent-hating’. When there Is little or no affinity between the dispersed phase and the dispersion medium, the colloid is called a lyophobic colloid.

Examples are gold sols, silver sols, and arsenic sulfide sols. Lyophobic sols cannot be prepared by simply mixing the solid (the dispersed phase) with the solvent (the dispersion medium) at a suitable temperature.

They are made by employing some special methods (as described later). These sols are relatively unstable and can be very easily coagulated by the addition of traces of electrolyte, on evaporation or by shaking.

Sometimes, they are called irreversible sols, because once the dispersed phase is precipitated out, it is not generally easy to get it back in the colloidal state on the addition of the dispersion medium. Lyophobic sols require stabilizing agents for their preservation.

Based on the types of particles of the dispersed phase:

Based on the nature of the particles of the dispersed phase, colloids may be classified as multimolecular, macromolecular, and associated.

Multimolecular colloids When a large number of atoms or molecules are dissolved in a solvent, they tend to form molecular aggregates of colloidal dimensions (diameter < 1 nm). The species formed in this fashion are called multimolecular colloids.

For example, a gold sol may have particles of various sizes possessing several atoms of gold. Similarly, a sulphur sol consists of particles which are aggregates of thousands of S8 molecules held by van der Waals forces. A silver sol (argyle) may contain particles of various sizes, each having several atoms of silver.

Macromolecular colloids True solutions of macromolecules in suitable solvents are called macromolecular colloids because the molecules themselves are large enough to be of colloidal dimensions.

Some naturally occurring macromolecules are starch, cellulose, proteins, and enzymes. Man-made macromolecules such as polyethylene, nylon, polystyrene, and synthetic rubber also belong to this class. These colloids are quite stable.

Associated colloids At low concentrations, some solutions behave as electrolytes. However, at higher concentrations, their solute particles aggregate, and colloids are formed.

Such species are called associated colloids. The molecules of associated colloids have both lyophobic and lyophilic groups. The molecular aggregates are called micelles and usually contain 20-100 molecules. The colloidal properties are due to these micelles.

Micelles are formed above a certain temperature called Kraft temperature (Tfc) and above a particular concentration called critical micelle concentration (CMC). Dyes, soaps, detergents, and many surface-active agents fall into this class. For soaps, the CMC is I ^-4 to 10^-3 mol L^-1.

Mechanism of micelle formation Soaps are sodium or potassium salts of fatty acids and may be represented by a general formula, where R is a straight chain of 10-20 carbon atoms and M⁺ is Na^– or K^–. When a soap, say sodium stearate, is dissolved in water, it dissociates into Na⁺ and RCOCT (carboxylate ion).

The carboxylate ion is composed of a large hydrocarbon group (the hydrophobic (water-repelling) group) called, the tail’ and a polar group (tire hydrophilic (water-loving) group] called the ‘head’.

The \(\mathrm{C}_{17} \mathrm{H}_{35} \mathrm{COO}^{-}\)ions are, therefore, present on the surface with their —COO^– groups in water and the hydrocarbon group away from water and remaining at the surface.

Long-chain carboxylate ions do not exist as individual ions in aqueous solutions, and at critical micelle concentration, the carboxylate ions are pulled into the bulk of the solution where they arrange themselves in a spherical cluster called a micelle.

Each micelle contains 50-100 long chain carboxylate ions. A micelle resembles a large ball. The polar carboxylate ions are on the outside of the ball because of their affinity for water, and the nonpolar tails are buried in the interior of the ball to minimize their contact with water.

The mechanism of micelle formation in the case of detergents is the same as that in the case of soaps. Detergents, like soaps, have a polar group and a long-chain nonpolar hydrocarbon group that causes the molecules to form micelles in solution.

Cleansing action of soaps and detergents:

Soaps and detergents are composed of molecules containing large hydrocarbon groups [the hydrophobic (water-repelling) group] and one or more polar groups [hydrophilic (water-loving groups). The dirt particles that stick to textile fibers are generally covered by a layer of oil molecules called grease. The dies are and, so, repel water.

Therefore, water cannot wash away such dirt particles from doth by Or* the soap, grease molecules get attached to the nonpolar hydrocarbon tail of the stearate ion, and poor head of stearate ion is directed towards the water.

Since the polar heads of the stearate tons can interact with the wafer., surrounded by the stearate ions is gradually lifted off and pulled in water, The grease finally floats off completely surrounded by detergent (or soap) molecules.

The negatively charged sheath around them prevents them from coming together and forming aggregates. Because of this cleansing action of soap, grease and hence dirt is washed away from doth

Preparation Of Colloids

Preparing lyophilic colloids is fairly simple. Generally, vigorously shaking the dispersed phase in the dispersion medium results in the formation of lyophilic solids. For example, gelatine, starch, and soaps form colloidal solutions by simply dissolving in water.

Due to their low stability, lyophobic colloids present greater difficulty In their preparation. Such colloidal solutions are usually made by the following methods.

Chemical methods:

Many molecules produced in chemical reactions (such as oxidation, reduction, hydrolysis, and double decomposition) aggregate to give particles of colloidal dimensions. For example, sulfur solids can be prepared by the oxidation of hydrogen sulfide.

⇒ \(2 \mathrm{H}_2 \mathrm{~S}+\mathrm{SO}_2 \stackrel{\text { oxidation }}{\longrightarrow} 3 \mathrm{~S}(\mathrm{sol})+2 \mathrm{H}_2 \mathrm{O}\)

The gold sol can be prepared by the reduction of \(\mathrm{AuCl}_4\left(\mathrm{AuCl}_3+\mathrm{HCl}\right)\) using reducing agents like formaldehyde or hydrazine.

⇒ \(2 \mathrm{AuCl}_3+3 \mathrm{HCHO}+3 \mathrm{H}_2 \mathrm{O} \stackrel{\text { reduction }}{\longrightarrow} 2 \mathrm{Au}(\mathrm{sol})+3 \mathrm{HCOOH}+6 \mathrm{HCl}\)

Ferric hydroxide sol is prepared when freshly prepared ferric chloride solution is poured slowly into boiling water.

⇒ \(\mathrm{FeCl}_3+3 \mathrm{H}_2 \mathrm{O} \stackrel{\text { hydrolysis }}{\longrightarrow} \mathrm{Fe}(\mathrm{OH})_3(\mathrm{sol})+3 \mathrm{HCl}\)

Areunions sulfide sol may be prepared by passing H₂S gas through an aqueous solution of arsenic oxide. double

⇒ \(\mathrm{As}_2 \mathrm{O}_3+3 \mathrm{H}_2 \mathrm{O} \underset{\text { decomposition }}{\stackrel{\text { double }}{\longrightarrow}} \mathrm{As}_2 \mathrm{~S}_3(\mathrm{sol})+3 \mathrm{H}_2 \mathrm{O}\)

Electrical disintegration or Bredig’s Arc method:

This method is particularly suitable for tire preparation of colloidal sols of metals such as gold, silver, and platinum. Two wires of the same metal (say, gold or platinum) used as electrodes are placed in a suitable dispersion medium containing a small amount of alkali.

An electric arc is struck between them. The heat produced by the arc converts the tire’s solid metal into a light vapor state. These vapours condense into liquid form to give lire required colloidal sol.

Peptization:

The conversion of a freshly formed precipitate into a colloidal solution by the addition of a small amount of electrolyte to tire dispersion medium is called peptization.

The electrolyte used is called the peptizing agent. In the tire peptization process, the tire’s freshly formed precipitate adsorbs one of the ions of the electrolyte on its surface.

This causes the development of either positive or negative charged particles on the precipitate, which repel each other and ultimately break up into particles of colloidal size.

For example, a freshly prepared precipitate of Fe(OH)₃ can be changed into a tire colloidal state when the precipitate is treated with water and a small amount of FeCl₃ solution (peptizing agent).

The ferric ions (Fe³⁺) resulting from the ionization of ferric chloride are preferentially adsorbed on the surface of the Fe(OH)₃ particles resulting in [Fe(OH)₃]Fe³⁺.

These positively charged particles of ferric hydroxide repel each other and ultimately break up into particles of colloidal size and are dispersed throughout the medium as a colloidal sol of Fe(OH)₃.

Purification Of Colloidal Solutions

Most lyophobic colloidal solutions prepared by the methods we have discussed contain massive amounts of electrolytes and other soluble impurities.

While the presence of a small amount of electrolytes is essential for the colloidal solution to be stable, larger quantities lead to coagulation. Therefore, the concentration of these soluble impurities must be minimized in order to make the colloidal solution stable. The following methods are generally used for the purification of colloidal solutions.

Ultrafiltration:

Colloidal particles cannot be filtered using ordinary filter papers because the pores are too large. However, the pore size in ordinary filter papers can be reduced by impregnating the filter paper with a solution of gelatin (an animal protein that can form gels) or collodion (a 4% solution of nitrocellulose in a mixture of alcohol and ether) to stop the flow of colloidal particles.

Colloidal particles can be filtered through specially prepared filter papers called ultrafilters. An ultrafilter can be made by dipping ordinary filter paper in a collodion solution, hardening it using formaldehyde, and then drying it.

The process of separating colloidal particles from the solvent and soluble solute present in the colloidal solution by ultrafilters is known as ultrafiltration.

This process is very slow. Sometimes, suction is applied to increase the rate of filtration. The colloidal particles left on the ultrafilter paper are then stirred in a fresh dispersion medium to get a pure colloidal solution.

Dialysis:

When a dissolved substance is separated from a colloidal solution by diffusion through a suitable membrane, the process is called dialysis. Colloidal particles cannot pass through animal membranes (bladder), parchment paper or cellophane sheets while Ions or small molecules can. In dialysis, we use such a membrane to separate ions and small molecules from the colloidal solution.

The apparatus used in dialysis is called a dialyzer. It consists of a parchment or collodion bag containing the colloidal solution which is suspended in a vessel through which water is continuously flowing.

The ions and small molecules (crystalloids) inside the bag migrate out leaving the colloidal solution behind. The process of diffusion can be made faster by using hot water instead of cold water. Remember, excessive dialysis may lead to destabilization of the colloidal solution, and a precipitate may result.

Electrodialysis:

Electrodialysis is especially used when the impurities are ionic. A parchment bag containing the colloidal solution Is suspended in a vessel containing water. Two electrodes are fitted in water. When an electric field is applied across the electrodes, the positive ions move towards the anode through the membrane in water.

By the application of an electric field, the rate of diffusion is increased. This method is utilized in producing pure water from seawater on a large scale.

Artificial kidney (Haemodiaiyser):

The kidney is the filter of the body for waste products; its membrane allows the dissolved waste products to pass through but at the same time, prevents the passage of very large protein molecules. The artificial kidney machine uses tubular coiled cellophane as the dialyzing membrane to purify the blood of patients with renal excretion problems. This process is called hemodialysis.

When the patient’s blood is pumped through the coils, dialysis takes place and the soluble waste products and toxic products in the blood pass through the dialyzing membrane into the dialyzing solutions, the dialyzer thus functioning more or less as a real kidney

Properties Of Colloidal Solutions

Colloidal solutions show characteristic properties which are different from those of true solutions. We shall now discuss some important properties of colloidal solutions.

Colligative properties:

Like true solutions, colloidal solutions also show colligative properties. The four colligative properties, namely lowering of vapor pressure, depression in freezing point, the elevation of boiling point and osmotic pressure depend on the number of particles present in the solution.

In ordinary colloidal solutions, the number of colloidal particles is very small in comparison to the number of molecules or ions of a solute present in a true solution as colloids are aggregates of particles. Hence, the values of colligative properties of colloidal solutions are markedly smaller than those shown by true solutions at the same concentration.

Tyndall effect:

When a beam of light is passed through a clear solution and viewed from a direction at right angles to the direction of the beam of light, it appears completely dark. However, in the case of a colloidal solution, we observe bluish light against this dark background.

This is due to the scattered light from the colloidal particles. The individual particles, which were otherwise invisible, can thus be observed. The above phenomenon was studied in detail by Tyndall and is known as the Tyndall effect.

The apparatus for viewing the colloidal particles is called an ultramicroscope, first constructed and used by Zsigmondy (1903). Using the ultramicroscope, we can distinguish between the different colloidal particles on the basis of light scattered by them.

A common example of the Tyndall effect can be observed in a cinema. You can observe the projection beam all the way from the projector to the screen due to the scattering of light by dust particles.

For the Tyndall effect to be observed, the following conditions must be satisfied.

1. The refractive index of the dispersed phase and that of the dispersion medium must differ appreciably
   in magnitude.
2. The size of the dispersed particles should be comparable to the wavelength of light used

Colour:

The color of a colloidal solution depends upon the wavelength of the light scattered by the dispersed particles, which in turn depends upon the size and nature of the particles. For example, the finest gold sol is red in color but as the size of the particles increases, it becomes purple, then blue, and ultimately golden.

The color also depends upon the manner in which the light is observed. For example, sulfur sols may be colorless, faint yellow, or deep yellow in reflected light and reddish in transmitted light. To cite another example, a mixture of milk and water appears blue when viewed through reflected light and red through transmitted light.

Brownian movement:

When viewed under a powerful ultramicroscope, colloidal particles appear to be in a state of continuous random motion. This ceaseless zigzag motion of the colloidal particles is called Brownian motion after the English botanist Robert Brown who for the first time observed such a movement in the case of the grains of pollen, suspended in water, with the help of a microscope.

Brownian motion is executed by all colloidal particles irrespective of their nature. Colloidal particles suspended in gaseous mediums also exhibit such motion. Brownian motion depends on the size of the colloidal particles and the viscosity of the dispersion medium. Smaller particles, and those in a less viscous medium, move faster.

Brownian motion occurs due to the unbalanced Impacts of the molecules of the dispersion medium colloidal particles. The colloidal units are constantly hit from all sides by the surrounding molecules and are tossed up and down just like a ship in a stormy sea.

Charge on colloidal particles:

Colloidal particles (both lyophobic and lyophilic) are electrically charged, in a given colloidal solution, the nature of the charge is always the same on all the particles of the dispersed phase.

The particles move in an electrical field either towards the cathode or the anode depending on whether they are positively or negatively charged. The following is a list of colloidal solutions along with the nature of charge on their particles.

Some examples of positively charged sols and negatively charged sols:

Sol particles require charge on account of one reason or more, One is electron capture by them during the electrodispersion of metals. Another is the formation of an electrical double layer.

A third, and most important, reason is the preferential adsorption of ions from the solution. Let us discuss the third process. On account of the large surface exposed by the colloidal particles, they preferentially adsorb either positively or negatively charged ions from their dispersion mediums.

When the dispersion medium has two ions or more, the ion is common to the dispersed phase, and the dispersion medium is preferentially adsorbed by the particles of the dispersed phase.

For example, when silver nitrate solution is added to a potassium iodide solution, the precipitated silver iodide sol particles adsorb the iodide ions from the solution and acquire a negative charge. However, when a KI solution is added to an AgNO₃ solution, the precipitated silver iodideol particles adsorb the Ag⁺ ions from the solution and carry a positive charge.

⇒ \(\begin{array}{cc}
\mathrm{AgI} / \mathrm{I}^{-} & \mathrm{AgI} / \mathrm{Ag}^{+} \\
\text {Negatively charged } & \text { Positively charged }
\end{array}\)

Similarly, if FeCl₃ is added to an excess of hot water, a positively charged sol of ferric hydroxide is formed due to the adsorption of Fe²⁺ ions. However, when ferric chloride is added to a NaOH solution, a negatively charged sol is obtained with the adsorption of OH^– ions.

⇒ \(\begin{array}{ll}
\mathrm{Fe}(\mathrm{OH})_3 / \mathrm{Fe}^{3+} & \mathrm{Fe}(\mathrm{OH})_3 / \mathrm{OH}^{-} \\
\text {Positively charged } & \text { Negatively charged }
\end{array}\)

The charged colloidal particles repel one another and save themselves from agglomeration and subsequent precipitation. Electrical charge is thus the cause of their stability.

However, the charged colloidal particles affect the charge distribution In the dispersion medium. The particles attract ions of opposite charge (counter ions) and repel ions having similar charge (coions) present in the medium, forming a second layer ns shown below,

⇒ \(\mathrm{Agl} / \mathrm{I}^{-} / \mathrm{K}^{+} \quad \mathrm{AgI} / \mathrm{Ag}^{+} / \mathrm{I}^{-}\)

This electrical double layer formed at the interface between the dispersed phase and the dispersion medium is called the Helmholtz electrical double layer. According to the modem concept, the first layer of ions is firmly held and is termed the fixed layer while the second layer is mobile and is termed the diffused layer.

The charges of opposite signs on the fixed and diffused parts of the double layer result in a difference in potential between these layers. This potential difference is called the electrokinetic potential or zeta potential.

Electrophoresis or cataphoresis:

The existence of electrical charges on the colloidal particles is shown by the migration of the particles towards either the positive or the negative electrode when they are placed between two charged electrodes.

This migration of colloidal particles towards either the cathode or anode under the influence of an electrical field is known as electrophoresis or cataphoresis. The phenomenon of electrophoresis can be demonstrated by the following experiment.

Two platinum electrodes are fitted, one in each limb of a U-tube. The U-tube is partially filled with water (solvent). A requisite quantity of colloidal solution is placed in the reservoir. The stopcock is opened slightly and the tire reservoir is raised to introduce the colloidal solution into the tire U-tube.

The water is displaced upward. The platinum electrodes must be dipped in the water layer and a direct current voltage in the range of 50 V to 250 V is applied across the electrodes.

If the colloidal particles have a positive charge on their surface, they will move towards the cathode and the level in the cathodic limb will rise whereas the level in the anodic limb will correspondingly move downwards.

On the other hand, if the particles are negatively charged, movement will take place in the opposite direction in the two limbs. Electrophoresis has been used for tire separation of various types of colloidal particles from a mixture. Since different particles move at different velocities, their separation becomes easy.

If the colloidal particles are not allowed to move under the influence of an electric field by some suitable means, then the dispersion medium itself moves. This phenomenon is known as electro-osmosis.

Coagulation or precipitation:

Tire electrical charge on colloidal particles is the cause of the stability of lyophobic sols. The charged colloidal particles repel one another and save themselves from agglomeration and subsequent precipitation.

If, by any means, the charge is removed, the particles will come closer to each other to form aggregates (or coagulate) and settle down under the force of gravity. The settling of particles of the dispersed phase is called coagulation or precipitation of the sol.

Lyophobic sols can be coagulated in the following ways. By electrophoresis, The colloidal particles move towards oppositely charged electrodes where they lose their charge and get coagulated.

By mixing oppositely charged sols Two sols having colloidal particles carrying opposite charges on mixing together in equal proportions get neutralized and precipitated.

For example, the mixing of ferric hydroxide sol with arsenious sulfide sol results in the neutralization of the charge on both sols, and both of them are coagulated. Such coagulation is known as mutual coagulation.

By boiling On boiling a sol, the adsorbed layer is disturbed on account of increased collisions with the particles of the dispersion medium. This reduces the charge on the particles of the dispersed phase and ultimately they settle down as a precipitate.

By excessive dialysis On excessive dialysis, traces of the electrolyte present in the sol are almost totally removed, causing destabilization of the sol, which ultimately gets coagulated.

By the addition of electrolyte When an electrolyte is added to a sol, the colloidal particles are precipitated. In the process, the ions of the electrolyte are taken up by the colloidal particles. This results in the neutralisation of the charge on the particles leading to their coagulation.

The ion that causes the charge on the particles of the dispersed phase to be neutralized is called the coagulating ion or flocculating ion. A positive ion causes the precipitation of a negatively charged sol and a negative ion causes the precipitation of a positively charged sol.

The quantity of the electrolyte required to coagulate a definite amount of sol depends upon the valency of the coagulating ion. The higher the valency of the coagulating ion, the smaller the amount of the electrolyte required to bring about coagulation. The smaller the quantity needed, the higher will be the coagulating power of the ion. This is called the Hardy-Schulze rule.

Thus, for the coagulation of the negatively charged arsenious sulfide sol, trivalent cations (Al³⁺ ) are far more effective than the divalent Ba²⁺ ions, which in turn are more effective than the monovalent Na⁺ ions. In the coagulation of the positively charged ferric hydroxide sol, the trivalent PO₃ ions are more effective than the divalent SO₂ ions which in turn are more effective than the monovalent Cl^– anions. The minimum concentration of an electrolyte in millimoles per liter required to cause coagulation in two hours is called the coagulation value.

Coagulation of lyophilic sols:

Lyophilic sols are more stable than lyophobic sols. Two factors that are responsible for the stability of lyophilic sols are the charges and solvation of the particles of the dispersed phase. Lyophilic sols can be coagulated by taking care of these two factors.

This is done by:

1. Using a suitable second solvent or by
2. Adding an electrolyte.

Introduction of a suitable solvent If a second solvent, which interacts strongly with the dispersion medium, is added to a lyophilic sol, coagulation takes place.

Thus, a hydrophilic sol (e.g., protein in water) can be coagulated by the introduction of alcohol. The water molecules interact strongly with the alcohol molecules, after which the protein molecules are desolvated. This brings about coagulation.

Introduction of an electrolyte When electrolytes are added to lyophilic solids, the ions of the electrolyte compete for the solvent molecules. If a sufficient amount of the electrolyte is added, the sol coagulates. This is called salting out of the sol.

Protection Of Colloids

Lyophobic sols, in contrast to lyophilic sols, are easily coagulated with the addition of a small amount of electrolyte. The relatively higher stability of lyophilic sols is due to the fact that lyophilic colloids are solvated, i.e., the particles of the dispersed phase are covered by a sheath of the liquid (dispersion medium).

The presence of a very small amount of a lyophilic colloid inhibits the precipitating action of an electrolyte on a lyophobic colloid. This is due to its formation of a very thin shell surrounding each particle of the lyophobic colloid through which the oppositely charged ions cannot easily penetrate to neutralize the charge on the particles of the lyophobic colloid.

Lyophilic colloids used for this purpose are called protective colloids. The photographic plate is a good example of protective action, where the lyophobic silver bromide is protected by the lyophilic gelatine.

Emulsions

An emulsion is simply a colloidal suspension of one liquid in another. It may be formed by shaking two immiscible liquids vigorously. Generally, one of the two liquids used is water.

Emulsions are of the following two types:

1. Oil-in-water type (o/w type), e.g., milk and vanishing
2. Water-in-oil type (w/o type), e.g., butter and cold cream

The oil-in-water emulsion has tiny droplets of an oily or waxy substance dispersed throughout a water solution (e.g., milk). In this system, water acts as the dispersion medium.

The water-in-oil emulsion has tiny droplets of water dispersed throughout an oil (e.g., natural petroleum, butter). In this system, oil acts as the dispersion medium. An oil-in-water emulsion can be washed off one’s hands with tap water, while a water-in-oil emulsion gives the hand a greasy water-repellent surface.

Emulsions are generally unstable and separate out into two distinct layers on standing. Thus, to get a stable emulsion, it is necessary to add a stabilizing agent.

This is called an emulsifier or emulsifying agent. Soap, gum, gelatine, and protein are some common emulsifying agents for o/w emulsions and heavy metal salts of fatty acids, long-chain alcohols, and lampblack are some common emulsifying agents for w/o emulsions.

Emulsions can be diluted by adding any amount of the liquid forming the dispersion medium. When an additional amount of the dispersed liquid is mixed with the emulsion, a separate layer is formed. Often, the liquid forming the dispersed phase has particles carrying a negative charge. These partides can be coagulated using a suitable electrolyte.

The stability of an emulsion can be reduced by adding a substance that negates the effect of the emulsifier. Sometimes centrifuging or freezing may also help in destabilizing an emulsion. The colloidal particles of an emulsion exhibit Brownian motion. The Tyndall effect is also observed.

Colloids Around Us

We come across many things which are colloidal in nature. Let us now briefly discuss a few of them.

Why the sky is blue:

The sky looks blue because dust particles, along with those of water suspended in air, scatter blue light, which reaches our eyes.

Fog, mist, and rain:

Air contains dust and moisture. When air is cooled below its dew point, the moisture condenses on the surface of dust particles forming tiny droplets that float in air, forming mist and fog.

Clouds are also a colloidal system in which tiny droplets of water are suspended in the air. As they reach the upper atmosphere (a cool region), the tiny colloidal droplets of water grow bigger and come down as rain. Sometimes, it rains when two oppositely charged clouds meet.

Artificial rain may be caused by spraying a sol carrying a charge opposite to the one on a cloud.

Food:

Much of the food we eat is colloidal in nature. Examples are milk, butter, ice cream, and fruit juices.

Ordinary milk is an emulsion of fat in water, the emulsifier being casein. Artificial beverages are either emulsions or colloidal solutions. Cocoa and coffee are emulsions but tea is a colloidal solution.

Blood:

Blood is a colloidal solution of negatively charged particles (albuminoid substance) in a liquid (blood plasma). The styptic action of alum and ferric chloride solution can be explained on the basis of coagulation. The Al³⁺ (from alum) or Fe³⁺ (from FeCl₃) ions cause the coagulation of the negatively charged albuminoid particles forming a clot, and preventing bleeding.

Soil:

Fertile soil is colloidal. Humus acts as a protective colloid and imparts stability to the soil. Due to the presence of humus, the soil adsorbs moisture and nutrients.

Formation of a delta:

River water is a sol of clay. Sea water contains several electrolytes. When water from the river comes in contact with seawater, the electrolytes present in seawater coagulate the sol of clay. This causes the deposition of clay, forming a delta.

Applications Of Colloids

Colloids find many applications in the industry. We shall now briefly discuss some important ones.

Removal of smoke:

Smoke is a sol of solid particles (carbon, arsenic compounds, dust, etc.) in the air. Air pollution is considerably reduced by fitting what is known as a Cottrell apparatus in the chimneys of factories.

Before it emerges from the chimney, the smoke is made to pass through the Cottrel apparatus, which contains plates that have a charge opposite to that carried by the smoke particles.

On coming in contact with these plates, the smoke particles lose their charge, get precipitated, and settle down on the floor of the chamber, from where they are removed

Purification of drinking water:

Water obtained from natural sources (rivers, lakes, etc.) contains suspended impurities. Impure water is usually purified by the addition of alum, which coagulates the suspended impurities and makes water fit for drinking

Tanning:

Changing hide (the skin removed from a dead animal) into leather by chemical treatment is known as tanning. Hide contains protein in the colloidal state. These colloidal particles in hides are positively charged.

On soaking the hides in tannin, which is a negatively charged sol, mutual coagulation takes place. This results in the hardening of leather. In chrome-tanning, chromium compounds are used in place of tannin.

Medicines:

Many medicines in use are colloidal. For example, colloidal silver (argyrol) is used as an eye lotion. Colloidal antimony is effective in curing kala-azar. Colloidal gold is used for intramuscular injections. Milk of magnesia, an emulsion, is used for stomach disorders. Colloidal medicines are more effective because of their large surface area.

Photographic plates and films: An emulsion of the light-sensitive silver bromide in gelatin is coated over glass plates or celluloid films for preparing photographic plates or films.

Rubber industry: Latex is a colloidal suspension of negatively charged rubber particles in water. To obtain rubber, latex is coagulated.

Industrial products: Many industrial products like paints, varnishes, printing inks, gums, adhesives, and resins are colloidal in nature.

Example 1. Why do lyophobic sols containing gelatin not coagulate with the addition of an electrolyte?
Solution:

Gelatin forms a thin protective layer around particles of the dispersed phase and prevents the neutralization of charge by electrolytes.

Example 2. Why is it essential to wash a precipitate with water before estimating it quantitatively?
Solution:

Colloidal particles are precipitated by the addition of an electrolyte. However, some electrolytes remain adsorbed on the surface of the particles of the precipitate. Therefore, it is necessary to wash the precipitate with water repeatedly to remove any electrolytes from the precipitate before estimating it quantitatively.

Surface Chemistry Multiple-Choice Questions

Question 1. The rate of physisorption increases with

1. Decrease in temperature
2. Increase in temperature
3. Decrease in pressure
4. Decrease in surface area

Answer: 1. Decrease in temperature

Question 2. Which one of the following statements is incorrect?

1. Chemical adsorption is reversible in nature.
2. Physical adsorption is due to van der Waals forces.
3. Physical adsorption is reversible in nature.
4. Activation energy plays an important role in chemical adsorption.

Answer: 1. Chemical adsorption is reversible in nature.

Question 3. Which of the following equations represent (s) Freundlich’s adsorption isotherm?

1. \(\frac{x}{m}=\left(\frac{1}{a}\right)+\left(\frac{b p}{a}\right)\)
2. \(\frac{x}{m}=k C^{1 / n}\)
3. \(\log \frac{x}{m}=\log k+n \log p\)
4. \(\log \frac{x}{m}=\log k+\frac{1}{n} \log C\)

Answer:

2. \(\frac{x}{m}=k C^{1 / n}\)

4. \(\log \frac{x}{m}=\log k+\frac{1}{n} \log C\)

Question 4. Which of the following gases will be adsorbed most easily?

1. N₂
2. H₂
3. O₂
4. CO₂

Answer: 4. CO₂

Question 5. According to the adsorption theory of catalysis, the speed of the reaction increases because

1. The Concentration of the reactant molecules at the active centers of the catalyst becomes high due to adsorption
2. In The Process of adsorption, the activation of like molecules becomes high
3. Adsorption produces heat, which increases the speed of the reactions
4. Adsorption lowers the activation energy of the reaction

Answer: 4. Adsorption lowers the activation energy of the reaction

Question 6. The function of an enzyme in an enzyme-catalyzed reaction is to

1. Transport oxygen
2. Conduct catalytic biochemical reactions
3. Provide immunity
4. Provide energy

Answer: 2. Conduct catalytic biochemical reactions

Question 7. Zeolites are

1. Enzyme catalysts
2. Shape-selective catalysts
3. Liquid catalysts
4. Nonspecific catalysts

Answer: 3. Liquid catalysts

Question 8. Which of the following is a true solution?

1. Cement
2. Muddy water
3. CuSO₄ solution
4. Milk

Answer: 3. CuSO₄ solution

Question 9. Which of the following is not a colloid?

1. Chlorophyll
2. Smoke
3. Protein
4. Blood

Answer: 1. Chlorophyll

Question 10. Substances that diffuse rapidly through water and certain membranes arc called

1. Colloids
2. Crystalloids
3. Gels
4. Emulsions

Answer: 2. Crystalloids

Question 11. The size of a particle in a colloidal solution is

1. Greater Than 1000 Nm
2. Within The Range of 1 Nm-1000 Nm
3. Less Than 1 Nm
4. None of these

Answer: 2. Within The Range of 1 Nm-1000 Nm

Question 12. A colloidal system consists of

1. NaCl and water
2. A Dispersion Medium Only
3. A Dispersed Phase Only
4. A Dispersed phase and a dispersion medium

Answer: 4. A Dispersed phase and a dispersion medium

Question 13. Sol is a general term usually applied to

1. A Solid dispersed in a liquid
2. A Solid dispersed in a solid
3. A Solid dispersed in a gas
4. All of these

Answer: 4. All of these

Question 14. Depending upon the types of the particles of the dispersed phase, colloids are classified as

1. Multimolecular colloids
2. Associated colloids
3. Macromolecular colloids
4. All of these

Answer: 4. All of these

Question 15. Fog is an example of a colloidal system of a

1. Solid dispersed in a gas
2. Gas dispersed in a gas
3. Gas dispersed in a liquid
4. Liquid dispersed in a gas

Answer: 4. Liquid dispersed in a gas

Question 16. Which of the following is/are lyophilic colloid(s)?

1. Starch
2. Gum arabic
3. Gelatin
4. Gold

Answer:

1. Starch

2. Gum arabic

3. Gelatin

Question 17. Lyophilic sols are more stable than lyophobic sols because

1. The Colloidal particles have a positive charge
2. The Colloidal particles have a negative charge
3. The Colloidal particles are solvated
4. There is strong electrostatic repulsion between the negatively charged colloidal particles

Answer: 3. The Colloidal particles are solvated

Question 18. The extra stability of lyophilic colloids is due to

1. The charge on the particles
2. A Protective film of the dispersion medium on the particles
3. The smaller size of the particles
4. The larger size of the particles

Answer: 2. A Protective film of the dispersion medium on the particles

Question 19. Lyophilic sols are

1. Irreversible
2. Coagulated by adding an electrolyte
3. Prepared from inorganic compounds
4. Self-stabilizing

Answer: 4. Self-stabilizing

Question 20. Which of the following statements is correct in the context of sodium stearate, \(\mathrm{CH}_3\left(\mathrm{CH}_{12}\right)_{16} \mathrm{COO}^{-} \mathrm{Na}^{+}\)?

1. It is a major component of many bar soaps.
2. The R-group is the nonpolar tail and is hydrophobic.
3. The —COO group is the polar ionic head and is hydrophilic.
4. All of these

Answer: 4. All of these

Question 21. When soap water interacts with grease, the grease

1. Forms micelles, which are removed
2. Forms macromolecular colloids, which are removed
3. Forms colloids of low molecular mass, which are removed
4. Forms multimolecular colloids, which are removed

Answer: 1. Forms micelles, which are removed

Question 22. Which of the following statements is correct?

1. Micelles are formal above critical micelle concentration.
2. Micelles are not associated with colloids.
3. Micelles are formed below critical micelle concentration.
4. Micelles are true solutions.

Answer: 1. Micelles are formal above critical micelle concentration.

Question 23. Micelles are also called

1. Associated colloids
2. Macromolecular colloids
3. Macromolecular colloids
4. Peptizing agents

Answer: 1. Associated colloids

Question 24. The cleansing action of soaps and detergents is due to

1. Their dissociation into ions in water
2. Their emulsifying nature in water
3. Their decrease in viscosity in water
4. The presence of bulky R-groups in them

Answer: 3. Their decrease in viscosity in water

Question 25. Which of the following method(s) is/are used in the preparation of colloidal solutions?

1. Peptization
2. Bredig’s arc method
3. Chemical methods
4. Electrophoresis

Answer:

1. Peptization

2. Bredig’s arc method

3. Chemical methods

Question 26. Peptization is a process

1. Of precipitation of colloidal particles
2. Of purification of colloids
3. Of dispersing precipitates into colloidal solutions
4. In which colloidal particles move in an electric field

Answer: 3. Of dispersing precipitates into colloidal solutions

Question 27. Adding a few drops of dilute HCl to freshly precipitated ferric hydroxide produces a red colloidal solution. This phenomenon is known as

1. Protective action
2. Peptization
3. Dialysis
4. Dissociation

Answer: 2. Peptization

Question 28. Colloidal solutions are purified by

1. Dialysis
2. Peptization
3. Coagulation
4. Flocculation

Answer: 1. Dialysis

Question 29. Tyndall effect can be observed in a

1. True solution
2. Solvent
3. Colloidal solution
4. Precipitate

Answer: 3. Colloidal solution

Question 30. Brownian motion is caused by

1. Heat change in the liquid state
2. Convection currents
3. The collision of the molecules of the dispersion medium with the colloidal particles
4. The attractive force between the colloidal particles and the molecules of the dispersion medium

Answer: 3. The collision of the molecules of the dispersion medium with the colloidal particles

Question 31. AS₂S₃ and Fe(OH)₃ colloidal solutions are

1. Respectively, positively and negatively charged
2. Respectively, negatively and positively charged
3. Both positively charged
4. Both negatively charged

Answer: 2. Respectively, negatively and positively charged

Question 32. The movement of colloidal particles under an applied electric field is known as

1. Dialysis
2. Electrophoresis
3. Electrodialysis
4. None of these

Answer: 2. Electrophoresis

Question 33. The AS₂S₃ sol has a negative charge. Which of the following has the maximum power to precipitate it?

1. H₂SO₄
2. Na₃PO₄
3. CaCl₂
4. AlCl₃

Answer: 4. AlCl₃

Question 34. Which of the following is arranged in order of decreasing coagulating power?

1. NaCl > BaCl₂ > AlCl₃
2. BaC₂2 > AlCl₃ > NaCl
3. AlCl₃ > BaCl₂ > NaCl
4. BaCl₂ > NaCl > AlCl₃

Answer: 3. AlCl₃ > BaCl₂ > NaCl

Question 35. In the context of an AS₂S₃ sol, which of the following has minimum coagulating value?

1. NaCl
2. KCl
3. BaCl₂
4. AlCl₃

Answer: 1. NaCl

Question 36. The method usually employed for the precipitation of a colloidal solution is

1. Dialysis
2. Addition of an electrolyte
3. Diffusion through an animal membrane
4. Condensation

Answer: 2. Addition of an electrolyte

Question 37. In making ice cream, gelatine is used mainly to

1. Prevent the formation of a colloidal sol
2. Enrich fragrance
3. Prevent crystallization and stabilize the mixture
4. Modify the taste

Answer: 3. Prevent crystallization and stabilize the mixture

Question 38. Which of the following is/are correct?

1. An Emulsion is a colloidal solution of a liquid in a liquid.
2. A Gel is a colloidal solution of a solid in a liquid.
3. An Aerosol is a colloidal solution of a liquid in a gas.
4. Foam is a colloidal solution of a gas in a liquid.

Answer:

1. An Emulsion is a colloidal solution of a liquid in a liquid.

3. An Aerosol is a colloidal solution of a liquid in a gas.

4. Foam is a colloidal solution of a gas in a liquid.

Question 39. Which of the following is used to treat diseases of the eye?

1. Colloidal gold
2. Colloidal silver
3. Colloidal antimony
4. None of these

Answer: 3. Colloidal antimony

Solutions

Solutions Definition:

A solution is a homogeneous mixture of two or more substances. Homogeneity implies uniformity of appearance throughout the mixture. Even though the substances (also called components) forming the solution can be in any state (solid, liquid or gas), the solutions, i.e., two-component solutions.

However, a solution may contain more than two components. Three-component solutions are known as tertiary solutions, four-component solutions as quaternary solutions, and so on.

In a solution, the component which is present in smaller quantities is called the solute and the one present in larger amounts is called the solvent. The state of the solvent determines the physical state in which the solution exists. Different types of binary solutions and their examples are given in the table.

Solid solutions of two more metals are called alloys.

Out of all the categories listed in the table, the most common binary solutions are solid-liquid and liquid-liquid solutions. A solid-liquid solution in which the solvent is water is called an aqueous solution. There is usually some interaction between the solvent and the solute molecules.

Two liquids that can mix at the molecular level are said to be miscible, e.g., water and alcohol. In this case, the molecules interact with each other strongly. In contrast, water and oil molecules are very weak and are, therefore, immiscible.

There is also a third category which is that partially describes liquid; in such cases, the two liquids are miscible at certain ratios and at others, they are immiscible, e.g., a phenol-water system.

Composition Of A Solutions

When we talk about the composition of a solution, we refer to the respective amounts of solute and solvent mixed together to form a certain amount of the solution. The concentration of a solution is the ratio of the solute to either the volume or the mass of the solution or the solvent in which the solute is dissolved.

A homogeneous solution has the same concentration throughout. Concentration can be expressed in several ways in terms of mass percentage, volume percentage, parts per million, and morality. The composition of a solution may also be expressed in mole fractions.

Mass percentage:

The mass percentage of a component of a solution is the mass of that component in grams per 100 grams of the solution. For example, a 10 per cent solution of sodium chloride in water by mass is indicated as 10% (w/w) and implies that 10 g of sodium chloride is dissolved in 90 g of water to make 100 g of solution. Commercially available concentrated aqueous reagents like acids and bases are usually labelled in terms of mass percentage.

Volume Percentage:

In the case of liquid-liquid solutions, concentration is generally expressed as volume percentage. The volume percentage of a component of a solution is the volume of that component in mL per 100 mL of the solution.

For example, a 10% solution of alcohol in water by volume implies that 10 mL of alcohol has been added to the requisite amount of water so as to obtain 100 mL of the solution. A 35% (v/v) solution of ethylene glycol is marked as permanent antifreeze. It lowers the freezing point of water to a great extent.

Mass by volume percentage:

We may also express the concentration of a solution in mass by volume percentage, i.e., the mass of the solute dissolved in 100 mL of the solution. For example, a 5% (w/v) solution of sodium chloride in water means 5g of solute (NaCl) has been dissolved in the requisite quantity of water to make 100 mL of the solution. Concentrations are often expressed this way in medicine and pharmacy.

Parts per million:

When a solute is present in trace quantities, the concentration is expressed in parts per million, abbreviated as ppm. It is the number of parts of a solute per million parts of the solution. The term parts could mean either mass or volume. concentration in ppm can thus be expressed in mass, volume to volume to volume or mass to volume grams of the solute in 10 6 mL of the solution or micrograms per mL of the solution (m g.mL^-1 ).

You know that 10% NaCl solution means 10 g of NaCl in 100 g of the solution. Therefore, in 10⁶ g of the solution, 10 x 10 g of NaCl will be present. Hence the concentration of the solution will be 10⁵ ppm.

Example 1. 5 g of NH4Cl is dissolved in water to obtain 500 mL of a solution. Express the concentration in ppm.
Solution:

Given

5 g of NH4Cl is dissolved in water to obtain 500 mL of a solution.

Since ppm denotes one unit of a substance for 999,999 units of the other substance we must find out the number of grams of NH4Cl dissolved in 10 6 mL of the solution. The concentration is derived in terms of mass by volume.

500 mL of solution contains 5 g of solute.

Therefore, 10⁶ mL of solution will contain \(\frac{5}{500} \times 10^6=10^4\) of solute.

Hence, the concentration of ammonium chloride in the solution is 10⁴ ppm

Example 2. Express the concentration in ppm of a 10% solution of ethanol in water by volume.
Solution:

Ten per cent by volume means 10 mL of ethanol has been mixed with enough water to obtain 100 mL of the solution.

100 mL of solution contains 10 mL ethanol.

∴ 106 mL of solution would contain \(\frac{10}{100} \times 10^6=10^5\) of ethanol.

Hence, the concentration is 10⁵ ppm.

Mole fraction (γ):

The mole fraction of a particular component is the number of moles of that component divided by the total number of moles of all the components present in a solution

⇒ \(x_i=\frac{n_i}{\sum_i n_i}\)

where n, is the number of moles of the ith component and Σn, indicates the summation of the number of moles of all the components. For a binary solution made up of components A and B,

v \(\chi_{\mathrm{A}}=\frac{n_{\mathrm{A}}}{n_{\mathrm{A}}+n_{\mathrm{B}}} \text { and } \chi_{\mathrm{B}}=\frac{n_{\mathrm{B}}}{n_{\mathrm{A}}+n_{\mathrm{B}}}\)

where χ and % are the mole fractions of components A and B respectively, and n and ng are the numbers of moles of the two components.

It may also be noted that in a given solution, the sum of the mole fractions of all the components is equal to one, i.e.,

Example 3. Calculate the mole fractions of the two components in a 10% by-mass solution of common salt in water.
Solution:

A 10% solution of common salt will contain 10 g of NaCl and 90 g of water.

The molar mass of NaCl = 23+35=58 g.

∴ number of moles of NaCl = \(\frac{10}{58}=0.1724\)

Molar mass of H₂O=2×1+16 = 18g.

∴ number of moles of H2O = \(\frac{90}{18}=5\)

Total number of moles of NaCl + H₂O=5+0.1724-5.1724.

⇒ \(\chi_{\mathrm{NaCC}}=\frac{0.1724}{5.1724}=0.0333\)

⇒ \(\chi_{\mathrm{H}, \mathrm{O}}=1-\chi_{\mathrm{NaCl}}=1-0.0333\)

= 0.9667.

Molarity The molarity (M) of a solution is defined as the number of moles of the solute per litre of the solution.

If n is the number of moles of solute in V litres of solution, then M = n/V. The unit for molarity is mol L^-1 or M.

Example 4. The molar concentration of glacial acetic acid is 17 M. Find the number of grams of acetic acid in half a litre of this solution.
Solution:

Given

The molar concentration of glacial acetic acid is 17 M.

17 M of a solution implies that 17 mol of the solute (glacial acetic acid) is present in 1 litre of the solution.

1 litre of the solution contains 17 mol of acetic acid.

∴ \(\frac{1}{2}\) litre of solution will contain \(\frac{17}{2}\) mol of acetic acid.

The molar mass of acetic acid (C₂H₄O₂) = 60 g.

∴ number of grams of acetic acid in half a litre of 17 M glacial acetic acid = \(\frac{17}{2} \times 60\)

= 510.

Molality (m):

The molality of a solution is defined as the number of moles of the solute dissolved in 1 kg of the solvent. To calculate the molality of a solution the individual weights of the solution and the solvent should be known. If ng moles of solute are dissolved in WA kilograms of solvent then mB = ng/WA. The unit of molality is mol kg -1.

Example 5. If 27 g of ammonium chloride is dissolved in 500 g of water, calculate the molality of the solution. One mole of NH4Cl weighs 54 g.
Solution:

Given

If 27 g of ammonium chloride is dissolved in 500 g of water

Number of moles of \(\mathrm{NH}_4 \mathrm{Cl}, n_{\mathrm{NH}_4 \mathrm{Cl}}=\frac{27}{54}=0.5\)

Amount of water, \(w_{\mathrm{H}_2 \mathrm{O}}=500 \mathrm{~g}\)

∴ \(m_{\mathrm{NH}_4 \mathrm{Cl}}=\frac{0.5}{500} \times 1000=1\)

The concentration of the given ammonium chloride solution is 1 m (read as a molal solution).

Nature of Solutions

When sugar is added to water in a beaker, it dissolves to give a solution. If we keep adding sugar to water, a stage will be reached when the sugar will stop dissolving. Such a solution in which no more of the solute can be dissolved is called a saturated solution.

If crystals of sugar are added to a saturated sugar solution, they settle at the bottom of the beaker, showing that dissolution has stopped. Actually what happens is that molecules of sugar from the crystals continue to leave the surface of the crystal and dissolve in water.

At the same time, molecules of sugar from the solution collide with the crystals and occupy positions in the crystal (crystallisation). In a given period of time, the number of molecules that return to the crystals is roughly equal to the number of molecules that dissolve in water.

Thus, a state of dynamic equilibrium exists between the solid sugar and the solution. The concentration of the solute in the solution remains constant at a particular temperature and pressure and is called its solubility.

Thus the solubility of a solute is the quantity that will dissolve in a given amount of solvent to produce a saturated solution. An unsaturated solution is one in which more of the solute will dissolve.

Factors Affecting The Formation Of A Solution

Generally, the solubility of a solute in a solvent depends on the nature of the solute and the solvent (like dissolves like), particle size of the solute (the smaller the size, the faster is the dissolution), temperature and pressure.

Solubility of a solid in a liquid:

The solubility of solutes with a positive enthalpy of solution (Asol H>0, endothermic process) increases as the temperature is increases. If we prepare a saturated solution and then cool it, some solute usually crystallises out so that the solution remains saturated as the temperature decreases.

However, if we prepare a saturated solution at a higher temperature and remove all the undissolved solutes, we can sometimes cool the solution without crystallisation of the solute. When the cooled solution contains more solute than it would have contained if the dissolved solute were in equilibrium with the undissolved solute, it is said to be supersaturated.

In the case of solutes with a negative enthalpy of solution (AH<0, exothermic process), an increase in temperature reduces solubility. Polar substances dissolve in polar solvents whereas nonpolar substances dissolve in nonpolar solvents. Some solvents in increasing order of their polarity are CCI₄, <CHCI₃, <C₂H₅OH < H₂O.

Inorganic salts such as NaCl are polar. They are therefore soluble in water, which is also polar. The solubility of an ionic solid in water depends on its lattice energy and ion-dipole interactions. The ion from the solute interacts with the dipole from the water molecule.

When an ionic solid dissolves, the ion-dipole interactions pull out the ions from the solid into the solution. The ion thus separated from its neighbours is surrounded by water molecules, forming a sphere of hydration.

These ions are said to be hydrated (if the solvent is water) or in general, solvated. The ionic solid dissolves when the ion-dipole interactions are stronger than ion-ion interactions in the solid.

The large covalent molecules may also be soluble in water provided they contain sufficiently strong polar bonds. Sucrose (sugar) contains eight polar \(8-\mathrm{O}-\mathrm{H}^{8+}\) groups per molecule and can therefore easily form hydrogen bonds with water. It is thus soluble in water.

However, within a series of organic compounds, solubility in water decreases as the number of carbon atoms in the chain increases. For example, while ethanoic acid is completely miscible with water, in all proportions, hexanoic acid is nearly insoluble in water.

In spite of possessing the highly polar >CO and O-H groups, the latter is insoluble because of large-scale London dispersion forces acting between the hydrocarbon chains of the solute molecules.

As you have already studied in class XI, London forces or dispersion forces are the intermolecular forces caused by temporary dipoles induced by neighbouring atoms or molecules in nonpolar substances. These forces are weaker than ion-ion and ion-dipole forces.

Solubility of a gas in a liquid:

You know that gases dissolve in liquids; for instance, oxygen dissolves in water. Another common example is soda water, which contains carbon dioxide dissolved in water under high pressure. The dissolved gas can be removed from the solution by heating the solution or releasing the pressure.

In such cases (H₂, O₂, N₂ and CH,) the equilibrium can be represented as

⇒ \(\text { gas molecules } \stackrel{\text { water }}{\rightleftharpoons} \text { dissolved molecules }\)

Gases such as NH₃, HCl and NO₂ chemically react with water. As a result, their solubility in water is more than that of gases which do not react with water. Here the equilibrium at dissolution may be expressed as

⇒ \(\text { gas molecules } \stackrel{\text { Water }}{\rightleftharpoons} \text { dissolved molecules } \stackrel{\text { water }}{\rightleftharpoons} \text { product }\)

⇒ \(\mathrm{NH}_3(\mathrm{~g}) \stackrel{\text { water }}{\rightleftharpoons} \mathrm{NH}_3(\mathrm{aq})\)

⇒ \(\mathrm{NH}_3(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{NH}_4^{+}(\mathrm{aq})+\mathrm{OH}^{-}(\mathrm{aq})\)

A gas can dissolve in a solid too, e.g., hydrogen dissolves in palladium.

Variation of solubility of gases with partial pressure At high altitudes, atmospheric pressure and temperature is low. A person climbing a mountain feels weak when he reaches the top because of the low concentration of oxygen in his blood at higher altitudes.

This is because of the lower partial pressure of oxygen at such heights. Thus, the solubility of a gas in a liquid depends not only on its nature but also on the temperature and pressure of the system.

A quantitative relation between the solubility of a gas in a liquid and its partial pressure was established by Henry and is known as Henry’s law. It states that the solubility of a gas in a liquid is proportional to the partial pressure of the gas.

Dalton, a contemporary of Henry, also independently reached the same conclusion. If the mole fraction of the gas is taken as a measure of its solubility then

⇒ \(p=K_{\mathrm{H}} \chi\),

where p is the partial pressure of the gas, K is Henry’s law constant for the gas in a particular solvent and X is the mole fraction of the gas. According to this equation, the partial pressure of a gas in the vapour phase is directly proportional to the mole fraction of the gas.

A plot of partial pressure of the gas versus mole fraction is a straight line. The slope of the line is Henry’s law constant K. Different gases have different K values at the same temperature.

It is interesting to note that in order to compensate for the decreased solubility of oxygen for people living at high altitudes, their body adapts to the prevailing environmental conditions by producing more haemoglobin, the iron-containing protein which binds oxygen.

Deep underwater, the solubility of oxygen is very high. Scuba divers experience a change in pressure of about 1 atm for every 33-foot increase in depth; this results in increased pressure in the lungs as compared to that at the surface and the divers should not come to the surface quickly after being underwater for 20 minutes.

Doing so may cause the formation of bubbles of nitrogen in the blood as the decrease in pressure will cause gases dissolved in the blood to rapidly revert to the gaseous state. Nitrogen gas in the blood blocks capillaries and creates a medical condition called “bends”, which is life-threatening.

Henry’s law constants for the solubility of gases in water at 298 K:

Variation of solubility of gases with temperature The values given in Table show that solubility decreases with an increase in temperature though the extent varies from one gas to another. The solubility decreases since heat is generally evolved during dissolution. There are exceptions, however, especially with solvents like liquid ammonia and many organic liquids. A plot of the solubility of some gases as a function of temperature.

One application of this decreased solubility at higher temperatures is in the case of carbonated drinks; these bubble continuously as they warm up to room temperature after being refrigerated for some time and consequently become “flat”. The heating of lakes and rivers can harm aquatic animals due to the decrease in dissolved oxygen.

Solubilities of some gases at different temperatures (solubilities are expressed as weights of gases in grams dissolved in 100 g of water when the pressure of the gas plus that of water vapour is 1 atm):

Example 1. The volume of blood in a normal human being is 5 L. Henry’s law constant for the solubility of N₂ in water is 9.04×10 bar at 298 K. Assume Henry’s law constant for N_f in blood to be the same as that in water. Also assume the density of blood to be the same as that of water, i.e., 1 kg L^-1. Calculate the number of moles of nitrogen absorbed in this amount of blood in air containing 80% N₂ at sea level, where the pressure is 1 bar, and also at a pressure of 50 bar deep under the sea.
Solution:

Given

The volume of blood in a normal human being is 5 L. Henry’s law constant for the solubility of N₂ in water is 9.04×10 bar at 298 K. Assume Henry’s law constant for N_f in blood to be the same as that in water. Also assume the density of blood to be the same as that of water, i.e., 1 kg L^-1.

⇒ \(p_{\mathrm{N}_2}=\chi_{\mathrm{N}_2} \cdot K_{\mathrm{H}}\)

⇒ \(\frac{n_{\mathrm{N}_2}}{n_{\mathrm{N}_2}+n_{\mathrm{H}_2 \mathrm{O}}} \cdot K_{\mathrm{H}}\)

The denominator may be approximated as nH2o since N2 is sparingly soluble in water.

Therefore, \(p_{\mathrm{N}_2}=\frac{n_{\mathrm{N}_2}}{n_{\mathrm{H}_2 \mathrm{O}}} \cdot K_{\mathrm{H}}\)

Or \(n_{\mathrm{N}_2}=n_{\mathrm{H}_2 \mathrm{O}} \cdot \frac{p_{\mathrm{N}_2}}{K_{\mathrm{H}}}=\frac{5 \times 10^3 \mathrm{~g} \times 0.8 \mathrm{bar}}{18 \mathrm{~g} \mathrm{~mol}^{-1} \times 9.04 \times 10^4 \mathrm{bar}}\)

Or \(n_{\mathrm{N}_2}=2.5 \times 10^{-3} \mathrm{~mol}\)

At 50 bar, PN₂ = 0.8 x 50 = 40 bar.

But \(p_{\mathrm{N}_2}=\frac{n_{\mathrm{N}_2}}{n_{\mathrm{H}_2 \mathrm{O}}} \times K_{\mathrm{H}}=\frac{n_{\mathrm{N}_2}}{5000 / 18} \times 9.04 \times 10^4\)

⇒ \(p_{\mathrm{N}_2}=\frac{n_{\mathrm{N}_2}}{n_{\mathrm{H}_2 \mathrm{O}}} \times K_{\mathrm{H}}=\frac{n_{\mathrm{N}_2}}{5000 / 18} \times 9.04 \times 10^4\)

⇒ \(40=\frac{n_{\mathrm{N}_2}}{500} \times 18 \times 9.04 \times 10^4\)

or, \(n_{\mathrm{N}_2}=\frac{40 \times 5000}{18 \times 9.04 \times 10^4}=0.12 \mathrm{~mol}\)

The solubility at 50 bar is 48 times more than that at 1 bar.

Example 2. Calculate the amount of oxygen dissolved in 5 L of the blood of a mountaineer at a pressure of 0.5 bar at 18000 feet. Assume that K for oxygen in the blood is 4.95 x 10 bar and that the density of blood is 1000 kg m3. Compare the value obtained with the amount of O₂ dissolved in blood at 1 bar at sea level. The mole fraction of O₂ in air is 0.21.
Solution:

⇒ \(p_{\mathrm{O}_2}=\chi_{\mathrm{O}_2} \cdot K_{\mathrm{H}}\)

Given \(\chi_{\mathrm{O}_2}^{\prime}=0.21 \text { (in air), } K_{\mathrm{H}}=4.95 \times 10^4 \text { bar, } \rho_{\text {blood }}=1000 \mathrm{~kg} \mathrm{~m}^{-3} \text {. }\)

⇒ \(p_{\mathrm{O}_2}=\chi_{\mathrm{O}_2}^{\prime} \cdot p_{\text {total }}=0.21 \times 0.5\)

⇒ \(p_{\mathrm{O}_2}=0.105 \text { bar. }\)

∴ \(p_{\mathrm{O}_2}=\chi_{\mathrm{O}_2} \cdot K_{\mathrm{H}}\)

Or \(0.105=\frac{n_{\mathrm{O}_2}}{n_{\mathrm{O}_2}+n_{\mathrm{H}_2 \mathrm{O}}} \times 4.95 \times 10^4\)

Neglecting no, in comparison to nн2o, we have

⇒ \(0.105=\frac{n_{\mathrm{O}_2}}{n_{\mathrm{H}_2 \mathrm{O}}} \times 4.95 \times 10^4\)

⇒ \(\frac{n_{\mathrm{O}_2}}{5000 / 18} \times 4.95 \times 10^4\) [… 5L = 5kg and p = 1000 kg dm^-3=1 kg L^-1]

Or \(n_{\mathrm{O}_2}=\frac{0.105 \times 5000}{18 \times 4.95 \times 10^4}=5 \times 10^{-4} \mathrm{~mol}\)

At 0.5 bar, 5 x 10 -4 mol of O2 is dissolved in 5 L of blood.

At sea level,

⇒ \(p_{\mathrm{O}_2}=\chi_{\mathrm{O}_2}^{\prime} \cdot p_{\text {total }}\)

= 0.21 x 1

= 0.21har.

But \(p_{\mathrm{O}_2}=\chi_{\mathrm{O}_2} \cdot K_{\mathrm{H}}=\frac{n_{\mathrm{O}_2}}{n_{\mathrm{H}_2 \mathrm{O}}} \cdot K_{\mathrm{H}}\)

Or \(n_{\mathrm{O}_2}=\frac{p_{\mathrm{O}_2} \cdot n_{\mathrm{H}_2 \mathrm{O}}}{K_{\mathrm{H}}}\)

⇒ \(\frac{0.21 \times 5000}{4.95 \times 10^4 \times 18}\)

Оr \(n_{\mathrm{O}_2}=0.0012=1.2 \times 10^{-3} \mathrm{~mol}\)

At sea level 1.2 × 10^-3 mol of oxygen is dissolved in 5 L of blood, which is 2.4 times (1.2x 10^-3/5×10⁴) that at 0.5 bar.

Example 3. Henry’s law constant for the solubility of methane (CH) in water is 4.19 x 10° Pa at 25°C. Estimate its molar solubility at 25°C and a partial pressure of 3.4 kPa.
Solution:

Given

Henry’s law constant for the solubility of methane (CH) in water is 4.19 x 10° Pa at 25°C.

According to Henry’s law,

⇒ \(p=K_{\mathrm{H}} \cdot \chi\)

Or \(\chi=\frac{p}{K_{\mathrm{H}}}\)

Given that p = 3.4 kPa = 3.4 x 10³ Pa

and KH = 4.19× 10⁹ Pa.

⇒ \(\chi_{\mathrm{CH}_4}=\frac{3.4 \times 10^3}{4.19 \times 10^9}=8.114 \times 10^{-7}\)

⇒ \(\chi_{\mathrm{CH}_4}\) may be approximated as follows,

⇒ \(\chi_{\mathrm{CH}_4}=\frac{n_{\mathrm{CH}_4}}{n_{\mathrm{CH}_4}+n_{\mathrm{H}_2 \mathrm{O}}} \approx \frac{n_{\mathrm{CH}_4}}{n_{\mathrm{H}_2 \mathrm{O}}}\)

Or \(n_{\mathrm{CH}_4}=\chi_{\mathrm{CH}_4} \cdot n_{\mathrm{H}_2 \mathrm{O}}\)

In 1 L of solution, the volume of water = 1 L.

If the density of water is assumed to be 1 kg/L, then the mass of 1 L of water = 1 kg.

Therefore, \(n_{\mathrm{H}_2 \mathrm{O}}=\frac{1000 \mathrm{~g}}{18 \mathrm{~g} / \mathrm{mol}}=55.6 \mathrm{~mol}\)

⇒ \(n_{\mathrm{CH}_4}=\gamma_{\mathrm{CH}_4} \cdot n_{\mathrm{H}_2 \mathrm{O}}\)

= 8.114 x 10^-7 x 55.6

= 4.511 x 10^-5 mol.

The concentration of methane in water is 4.51 x 10⁵ mol L^-1.

Example 4. Find the concentration of CO₂ in a 1-litre can of soda under 2.5 bar of vapour pressure of CO₂ at 25°C. Henry’s law constant for the dissolution of CO₂ in water is 1.65 x 10³ bar. Assume the density of the solution to be 10³ kg/m³. What will be the concentration when the can is opened and exposed to the atmosphere at 25°C, the partial pressure of CO₂ in air being 4×10 atm?
Solution: 

According to Henry’s law,

⇒ \(p=K_{\mathrm{H}} \chi\)

Given \(p=2.5 \text { bar }, K_H=1.65 \times 10^3 \text { bar. }\)

Therefore, \(2.5=1.63 \times 10^3 \cdot x_{\mathrm{CO}_2}\)

Or \(x_{\mathrm{CO}_2}=\frac{2.5}{1.63 \times 10^3}=1.515 \times 10^{-3}\)

⇒ \(\χ \mathrm{CO}_2\) may be approximated as follows.

⇒ \(x_{\mathrm{CO}_2}=\frac{n_{\mathrm{CO}_2}}{n_{\mathrm{CO}_2}+n_{\mathrm{H}_2 \mathrm{O}}} \approx \frac{n_{\mathrm{CO}_2}}{n_{\mathrm{H}_2 \mathrm{O}}}\)

Or \(n_{\mathrm{CO}_2}=\chi_{\mathrm{CO}_2} \cdot n_{\mathrm{H}_2 \mathrm{O}}\)

The density of the solution = \(=\frac{10^3 \mathrm{~kg}}{\mathrm{~m}^3}=\frac{10^3 \mathrm{~kg}}{(10)^3 \mathrm{dm}^3}\) (∵ 10 dm = 1m)

⇒ \(1 \mathrm{~kg} / \mathrm{dm}^3 \text { or } 1 \mathrm{~kg} / \mathrm{L}\)

Mass of 1 litre of solution = 1 kg.

Since water is the solvent used, the mass of water in 1 L of solution = 1 kg.

Number of moles of water = \(\frac{1 \mathrm{~kg}}{18 \mathrm{~g} \mathrm{~mol}^{-1}}\)

⇒ \(\frac{1000}{18} \mathrm{~mol}\)

= 55.6 mol.

Substituting from Equations (1) and (3) in Equation (2),

⇒ \(n_{\mathrm{CO}_2}=1.515 \times 10^{-3} \times 55.6\)

= 0.084 mol.

Therefore, the solution contains 0.084 mol of CO₂ in 1 L of water, or the concentration is 0.084 mol L^-1. When the can is exposed to the atmosphere, the partial pressure of CO₂ in the air

= 4 x 10^-4 atm (given)

Or \(p_{\mathrm{CO}_2}=4 \times 10^{-4} \times 1.03125 \mathrm{bar}\)

⇒ \(4.05 \times 10^{-4} \text { bar }\)

Using Henry’s law and proceeding as before, we get

⇒ \(n_{\mathrm{CO}_2}=\frac{p_{\mathrm{CO}_2}}{K_{\mathrm{H}}} \times 55.6=\frac{4.05 \times 10^{-3} \times 55.6}{1.65 \times 10^3}\)

⇒ \(1.36 \times 10^{-5} \mathrm{~mol}\)

or concentration = 1.36 x 10^-5 mol L^-1, which is much less than that when the bottle was closed.

Solid solutions are formed by mixing up solid substances. The solution so formed is also a solid. A mixture of lithium chloride and sodium chloride when melted and cooled forms a solid solution.

It contains an array of chloride ions with a random distribution of lithium and sodium ions. This solution is homogeneous and neither LiCl nor NaCl separates out on standing.

Some ionic substances appear to be nonstoichiometric; their chemical formulae deviate from the ideal ratios. In other respects, they resemble pure compounds. They are in fact solid solutions.

There are two types of solid solutions-substitutional and interstitial. In a substitutional solid solution, atoms, molecules or ions of one substance substitute the species in the lattice of the other substance.

Steel, brass and bronze are examples of substitutional solid solutions. When Al₂O₃ and Cr₂O, are mixed together at high temperatures they form a solid solution. The ions that replace the original ions must have the same charge and must be fairly similar in size.

Interstitial solid solutions, as the name suggests, involve the placing of the atom of one substance in the interstices or holes in the crystal of the other substance. Tungsten carbide is an example of such a solid solution. It is a hard substance and has many industrial uses, e.g., it is used to make grinding and cutting tools.

Liquid Solutions

Solutions of a solid, liquid or gas in a liquid are called liquid solutions as the solvent is a liquid. We will consider the case of a liquid in a liquid and a solid in a liquid in the following sections.

Solution of a liquid in a liquid:

If a liquid is placed in a closed container, after some time a dynamic equilibrium between the liquid and its vapour will be established. The pressure exerted by the vapour also reaches a constant value, which, as you already know, is called the vapour pressure of the liquid.

Now let us see what happens in a binary solution (a solution containing two components) made up of two volatile liquids. As both the liquids are volatile, both of them contribute to the vapour pressure. The pressure exerted by the vapour of each component is called the partial vapour pressure of that component.

If the two volatile components are denoted by A and B, the mole fractions and the partial pressures of the two components will be % and %, and PA and PB respectively. The French chemist Francois Raoult performed a series of experiments on structurally related liquids and from the results obtained concluded that the ratio of the partial vapour pressure of each component to its vapour pressure as a pure liquid is approximately equal to the mole fraction of that component in the liquid.

Thus, \(\frac{p_{\mathrm{A}}}{p_{\mathrm{A}}^{\circ}}=\chi_{\mathrm{A}} \text { and } \frac{p_{\mathrm{B}}}{p_{\mathrm{B}}^{\circ}}=\chi_{\mathrm{B}}\)

where p is the partial vapour pressure of a component in the solution and p° is its vapour pressure as a pure liquid. X is the mole fraction of a component.

This relationship can also be expressed as

⇒ \(p_{\mathrm{A}}=p_{\mathrm{A}}^{\circ} \chi_{\mathrm{A}}\).

This is called Raoult’s law.

Thus Raoult’s law states that, in a solution of volatile components, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction (applicable only when a homogeneous solution is obtained).

When pA or pB is plotted against the mole fraction of any one component A or B of a solution, then a straight line is obtained that meets the y-axis at pf and p°.

A line passes through the point pf, which corresponds to the partial vapour pressure of pure component A, and the other passes through y B, the partial vapour pressure of pure component B. The total vapour pressure varies between p ° and p it is given by the line joining p ° and p °. Thus, the total vapour pressure of the solution is given as

⇒ \(p_{\text {total }}=p_{\mathrm{A}}+p_{\mathrm{B}}\)

Note that the y-axis is drawn on both sides in the figure. This is to show that the value of the variable in the x-axis cannot exceed the value corresponding to the point where the right-hand side y-axis meets the x-axis.

The mole fraction is the x-variable and it can have a maximum value of 1. In a two-component system of A and B x B = zero refers to the component A being pure; the LHS y-axis corresponds to pure A. When xB is 1, it means only B is present and the RHS y-axis corresponds to pure B. In between these two extremes, both A and B are present.

The partial vapour pressures of the two components benzene and methylbenzene are proportional to their respective mole fractions, the total vapour pressure of the solution is the sum of the two partial vapour pressures.

Benzene and methylbenzene were found to obey Raoult’s law under all conditions of temperature and concentration. Such solutions are called ideal solutions and their vapour pressures are intermediate between the partial vapour pressures of the two components. We can define an ideal solution as one in which each component obeys Raoult’s law over a large range of concentrations.

This behaviour is observed when the components are structurally similar. In a solution formed by say A and B, if the nature of the intermolecular forces and their extent between A and B molecules (A-B interaction) is the same as that between A-A or B-B molecules, then the solution behaves ideally. Strictly speaking, no solution is ideal.

However, there are several nearly ideal solutions; for example, benzene and methylbenzene, chlorobenzene and bromobenzene, hexane and heptane and ethylene bromide and propylene bromide. Generally, all solutions show nearly ideal behaviour when progressively diluted. For an ideal solution, there is no change in enthalpy and volume on mixing the two components.

For an ideal solution \(\Delta_{\text {mix }} H=0\)

and \(\Delta_{\text {mix }} V=0\)

It is also possible to calculate the composition of the vapour phase. If yA and yB are the mole fractions of A and B in the vapour phase then according to Dalton’s law of partial pressures,

⇒ \(p_{\mathrm{A}}=y_{\mathrm{A}} p_{\text {total }}\)

and \(p_{\mathrm{B}}=y_{\mathrm{B}} p_{\text {total }}\)

Example 1. When equal masses of two liquid components A and B are mixed, their partial pressures are equal. If the total vapour pressure of the solution is 0.32 bar, the vapour pressures of pure A and pure B are 0.24 bar and 0.48 bar respectively, and the molar mass of A is 100, what is the molar mass of B?
Solution:

Given,

When equal masses of two liquid components A and B are mixed, their partial pressures are equal. If the total vapour pressure of the solution is 0.32 bar, the vapour pressures of pure A and pure B are 0.24 bar and 0.48 bar respectively, and the molar mass of A is 100,

P_A = P_B and P_A + P_B = 0.32

Or, \(2 p_A=0.32\)

⇒ \(p_A=\frac{0.32}{2}=0.16 \mathrm{bar}\)

We know that P = \(p_A^{\circ} x_A\)

On substituting for PA and \(p_A^0\), we get

⇒ \(0.16=0.24 \times \chi_{\mathrm{A}}\)

Or, \(\chi_A=\frac{0.16}{0.24}=0.67\)

Since

⇒ \(χ_A+χ_B=1\)

⇒ \(\chi_B=1-\chi_A=1-0.67=0.33\)

⇒ \(\chi_A=\frac{\frac{w_A}{M_A}}{\frac{w_A}{M_A}+\frac{w_B}{M_B}}\)

and \(\chi_{\mathrm{B}}=\frac{\frac{w_{\mathrm{B}}}{M_{\mathrm{B}}}}{\frac{w_{\mathrm{A}}}{M_{\mathrm{A}}}+\frac{w_{\mathrm{B}}}{M_{\mathrm{B}}}}\)

Or, \(\frac{x_A}{\psi_B}=\frac{w_A}{M_A} \cdot \frac{M_B}{w_B}\)

Given that w_A=w, and M_A =100.

∴ \(\frac{\chi_{\mathrm{A}}}{\chi_{\mathrm{B}}}=\frac{M_{\mathrm{B}}}{M_{\mathrm{A}}}\)

⇒ \(\frac{0.67}{0.33}=\frac{M_{\mathrm{B}}}{100}\)

⇒ \(M_B=\frac{100 \times 0.67}{0.33}=203\)

Thus, the molar mass of B is 203 g mol^-1.

Example 2. What will be the vapour pressure of a solution of 5 mol of sucrose in 1 kg of water if the vapour pressure of pure water is 4.57 mmHg?
Solution:

⇒ \(\frac{p_{\text {water }}^\sigma-p_{\text {solution }}}{p_{\text {water }}^\sigma}=\chi_{\text {sucrose }}\)

Given, n=5 moles, W = 1000 g and \(p_{\text {water }}^{\circ}=4.57 \mathrm{mmHg}\)

⇒ \(\chi_{\text {sucrose }}=\frac{n}{n+N}=\frac{n}{n+\frac{W}{M_{\text {water }}}}=\frac{5}{5+\frac{1000}{18}}=\frac{5}{60.5}=0.083\)

Now \(\frac{p^0-p}{p^0}=0.083\)

Or, \(p^{\circ}-p=0.083 \times p^{\circ}\)

= 0.083 x 4.57

= 0.38

∴ \(p=p^0-0.38\)

= 4.57 -0.38

= 4.19.

The vapour pressure of the solution is 4.19 mmHg.

Vapour pressure of a solution of a solid in a liquid

You have already seen that a pure solvent has a characteristic vapour pressure at any given temperature and if a volatile liquid is added to it, the partial vapour pressure is proportional to the mole fraction. The vapour pressure of many solid solutes is negligible at temperatures at which they are present in solutions. Such solids are called nonvolatile solutes.

If a nonvolatile solute is added to a solvent to make a solution, the vapour pressure of the solution is only due to the solvent and is also less than that of the pure solvent.

This is because, in such a solution, the surface is covered with molecules of the solute as well as the solvent as compared to the pure solvent where only solvent molecules are present on the surface. As a result, the number of solvent molecules escaping into the vapour phase is lower in the solution than in the pure solvent.

According to Raoult’s law, if p, denotes the vapour pressure of the solvent in solution (which is also simply the vapour pressure of the solution, as the solute is nonvolatile), then

⇒ \(p_{\text {solution }}=p_{\mathrm{A}}=p_{\mathrm{A}}^0 \chi_{\mathrm{A}}\)

A plot of P_A versus χ_A will be a straight line with slope po A.

Nonideal solutions

Solutions that obey Raoult’s law at all concentrations are called ideal solutions while those that do not obey Raoult’s law are called nonideal solutions. Both enthalpy and volume change on mixing the components of a nonideal solution. Some solutions deviate significantly from Raoult’s law.

The deviation from Raoult’s law can be of two types-positive and negative. When the vapour pressure curves of the two components as well as that of the solution lie above the ones predicted by Raoult’s law, the system is said to exhibit positive deviation from Raoult’s law (e.g., acetone and carbon disulphide).

Other examples are ethanol-acetone and carbon tetrachloride-methanol. On the other hand, if the vapour pressure curves lie below (i.e., measured vapour pressure is lower) the ones predicted by Raoult’s law, the negative deviation is exhibited; for example, in an acetone-chloroform system.

The solutions that exhibit positive deviation from Raoult’s law usually consist of one component whose molecules are associated such as water and alcohols (hydrogen bonding) and another component which is more or less inert, i.e., the structures of the two components are dissimilar.

The mixing of components tends to break some of the association between molecules and hence the enthalpy of mixing (Amix H) is positive. If the system is composed of components A and B, then the intermolecular forces between A and B in the solution are weaker than those between A and A, and B and B, as a consequence of which the molecules of A or B can escape more

easily from the solution than from the respective pure liquids. This causes an increase in the vapour pressure resulting in a positive deviation. The change in volume on mixing (Amix V) is positive. In a mixture of ethanol and acetone, which shows positive deviation, ethanol is hydrogen bonded and some of these bonds are broken on the mixing of ethanol with acetone, thus resulting in nonideal behaviour.

In the case of an acetone-chloroform system, the solution exhibits negative deviation from Raoult’s law, i.e., the vapour pressure curves lie below those suggested by Raoult’s law. Here the A-B interactions (ie., intermolecular interactions between acetone and chloroform) are much stronger than A-A or B-B interactions. Acetone and chloroform are held together by hydrogen bonding.

The result is that the escaping tendency of acetone or chloroform is less than that from the pure liquids and hence the vapour pressures are lower. On mixing the two components, the changes in enthalpy and volume are negative.

Some solutions show positive deviation and some show negative deviation from Raoult’s law:

Ideal Dilute Solutions

Many solutions do not show ideal behaviour. However, it must be noted that even in such cases Raoult’s law is obeyed by the solvent when the solution is dilute. This is because when the solution is dilute, the solvent molecules are far more in number, much like that in the pure solvent, as there are very few solute molecules. For dilute solutions, the solute obeys Henry’s law.

⇒ \(p=\chi K_{\mathrm{H}}\)

Such solutions are therefore called ideal dilute solutions; the solvent obeys Raoult’s law and the solute obeys Henry’s law.

Raoult’s law is a special case of Henry’s law:

According to Raoult’s law, the vapour pressure of a volatile component is proportional to its mole fraction in solution. Similarly, if one of the components is a gas as seen in the case of Henry’s law, the vapour pressure is again proportional to the mole fraction of the gas in the solution.

The only difference in the two cases is the proportionality constant, being på in the former and Henry’s law constant in the latter. Thus Raoult’s law may be considered as a special case of Henry’s law.

Boiling Of Liquid Solutions

A pure liquid boils at a temperature at which its vapour pressure becomes equal to the atmospheric pressure and the composition of the liquid phase and that of the vapour phase are the same. However, the boiling of a liquid solution differs from the boiling of a pure liquid; the composition of the vapour is different from the composition of the boiling solution.

The components of a solution can be separated by fractional distillation. In a simple distillation process, the vapour of the volatile component is collected and condensed, helping to separate it from the nonvolatile component, say a solid from a volatile liquid.

In fractional distillation, the process of boiling and condensation is repeated till the two components are completely separated.

After every step of boiling and condensation, the remaining liquid becomes richer in the less volatile component while the vapour becomes richer in more volatile component. After the distillation is complete, we get the less volatile component as the residue and the more volatile component as the vapour which is then condensed to get the liquid.

Such liquid mixtures which distil with a change in composition are called zeotropic mixtures. We are thus able to separate the two components completely from their solution at all compositions.

However, this is not possible in some nonideal solutions as they have the same composition in the liquid and vapour phases and boil at a constant temperature. In such solutions, the two components cannot be separated completely by fractional distillation. These mixtures are called azeotropic mixtures or simply azeotropes.

They are of two types-minimum-boiling and maximum-boiling. A solution showing negative deviation from Raoult’s law, on repeated distillation, leaves a residue with the highest boiling point instead of a pure liquid.

This residue has a boiling point higher than that of all other compositions and even the pure liquid. This liquid mixture boils at a constant temperature without further change in composition. Therefore, further distillation is not useful in separating the components. It is called a maximum boiling point azeotrope.

On the fractional distillation of solutions showing positive deviation from Raoult’s law, liquid residues with increasing boiling points are obtained and finally one of the components is obtained in the pure form. Which component is obtained depends upon the composition of the starting liquid solution.

The vapours collected, on fractionation, give rise to a constant-boiling mixture of composition Y, which is the azeotrope and has the minimum boiling point. As before, further distillation is futile and separation of the azeotrope mixture into its components is impossible.

Thus, a minimum in the vapour-pressure composition curve corresponds to a maximum in the boiling-point composition curve and vice versa.

Colligative Properties

In a dilute solution, there are certain properties which depend only on the number of solute particles present in it and not on their nature or identity.

Such properties are called colligative properties (derived from the Latin word co meaning ‘together’ and ligare meaning ‘to bind’). The relative lowering of the vapour pressure of the solvent, the elevation of the boiling point of the solvent, the depression of the freezing point of the solvent and the osmotic pressure of the solution are examples of colligative properties.

Relative Lowering Of Vapour Pressure

As you have already studied, the vapour pressure of a solvent decreases with the addition of a nonvolatile solute to it. The vapour pressure of the solution is solely due to the solvent and is given by

⇒ \(p_{\text {solution }}=p_{\mathrm{A}}=p_{\mathrm{A}}^{\circ} \psi_{\mathrm{A}}\)

where the subscript A refers to the volatile solvent.

If the nonvolatile solute is denoted by B, then in a binary solution of A and B,

⇒ \(χ_A+χ_B=1\)

Or \(\chi_A=1-\chi_B\)

Substituting Equation 2.2 in Equation 2.1, we have

⇒ \(p_A=p_A^g\left(1-\chi_{1 \beta}\right)\)

Or \(\frac{p_A}{p_A^5}=1-\chi_B \text { or } 1-\frac{p_A}{p_A^0}=χ_B\)

Or \(\frac{p_A^0-p_A}{p_A^0}=\chi_B\)

Here \(p_A^0-p_A\) is the lowering of vapour pressure and \(\left(p_A^0-p_A\right) / p_A^0\) is called the relative lowering of vapour pressure. Thus, we arrive at a relation according to which the relative lowering of the vapour pressure of a solvent in a solution containing a nonvolatile solute is equal to the mole fraction of the solute in the solution. This is the extension of Raoult’s law to solutions containing nonvolatile solutes.

The mole fraction of the solute B can be written as

⇒ \(x_B=\frac{n}{n+N^{\prime}}\)

where n is the number of moles of the solute and N is that of the solvent.

For dilute solutions, n<< N. Therefore, neglecting n in the denominator, we get

⇒ \(\chi_B=\frac{n}{N}=\frac{\frac{w}{M_B}}{\frac{W}{M_A}}\)

On equating Equations (2.3) and (2.4),

⇒ \(\frac{p_{\Lambda}^0-p_{\Lambda}}{p_{\Lambda}^0}=\frac{w}{M_B} \times \frac{M_{\Lambda}}{W}\)

where W and w are the amounts of the solvent and solute respectively in grams in the solution, and MA and M are the molar masses of the solvent and solute respectively. Thus Equation 2.5 can be employed to determine the molar mass of the solute.

Elevation Of Boiling Point

When a liquid is heated, its temperature rises and the vapour. pressure increases gradually. Finally, a temperature is reached when the vapour pressure of the liquid becomes equal to the external pressure above the liquid.

This temperature is called the boiling point of the liquid. As you know, the vapour pressure of a solution is always less than the vapour pressure of a pure solvent. Consequently, the presence of a nonvolatile solute makes the boiling point of a solution higher than that of the pure solvent in which it is prepared.

For example, the boiling point of water is 373 K and the vapour pressure of water at this temperature is 1.013 bar, which is equal to one atmospheric pressure.

But on adding sucrose, the vapour pressure of the water (or sucrose solution) lowers, i.e., it becomes less than 1.013 bar. Now, in order to make the solution boil, it has to be heated to a greater extent so that its vapour pressure equals the atmospheric pressure.

This means that the boiling point of the solution is greater than that of the pure solvent. The greater the concentration of the solute, the higher the boiling point of the solution.

plot of vapour pressure of the pure solvent, the dilute solution and the concentrated solution against temperature. As you can see from the graph T₁<T₂ <T₃ and ΔTb is the elevation in boiling point.

Experimental findings have proved that for a dilute solution the boiling point elevation AT, of a solvent is directly proportional to the number of moles of the nonvolatile, nondissociated solute dissolved in 1000 g of solvent.

⇒ \(\Delta T_b \propto m\)

Or \(\Delta T_{\mathrm{b}}=K_{\mathrm{b}} m\)

where m is the molality of the solution and K, is a constant, characteristic of the solvent, called the molal boiling point elevation constant.

If a known weight of a solute (w) is dissolved in a known quantity of a solvent (W), the elevation in boiling point can be determined and thus molality can be calculated.

Molality can also be written as

⇒ \(m=\frac{\frac{w}{M_{\mathrm{B}}}}{\frac{W}{1000}}=\frac{1000 \times w}{M_{\mathrm{B}} \times W}\)

where w is the weight of the solute in grams dissolved in W grams of solvent and M, is the molar mass of the solute. Thus, the molar mass of a solute can be determined if a known mass of it is taken in a known mass of a solvent and AT, is determined experimentally for a known solvent.

Substituting for the molality of the solution in the equation to determine the elevation of boiling point, we get

⇒ \(\Delta T_{\mathrm{b}}=K_{\mathrm{b}} \cdot\left(\frac{1000 \times w}{M_{\mathrm{B}} \times W}\right)\)

Or \(M_{\mathrm{B}}\left(M_{\text {solute }}\right)=K_{\mathrm{b}} \cdot \frac{1000 \times w}{\Delta T_{\mathrm{b}} \times W}\)

The elevation in boiling point is always positive since the boiling point of a solution is always greater than the boiling point of the pure solvent.

The constant K, which is the characteristic of a particular solvent, can be expressed in terms of its heat of vaporization, \(\Delta_{\text {vap }} H\).

⇒ \(K_{\mathrm{b}}=\frac{R T_0^2 M_{\text {solvent }}}{1000 \Delta_{\text {vap }} H} \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\)

Note that the molar mass of the solvent is given in units of g mol^-1; on dividing by 1000, we get it in kg mol^-1. Thus, the SI unit of K is K kg mol^-1. R is the gas constant (8.314 JK1 mol^-1), To is the boiling point of the pure solvent and Msolvent is its molar mass.

Example 1. A solution containing 29 g of a nonvolatile solute in 250 g of water boils at 373.52 K. The boiling point of pure water is 373 K. Find the molar mass of the solute. Given, K1 = 0.52 K kg mol1.
Solution:

Given

A solution containing 29 g of a nonvolatile solute in 250 g of water boils at 373.52 K. The boiling point of pure water is 373 K.

Elevation of boiling point, Δ Tb = 373.52-373= 0.52 K.

⇒ \(\Delta T_b=K_{\mathrm{b}} \cdot m\)

0.52 = 0.52 x m

Or \(m=\frac{0.52}{0.52}=1\)

But, \(m=\frac{w}{M_{\text {solute }}} \times \frac{1000}{W}\)

⇒ \(1=\frac{29}{M_{\text {solute }}} \times \frac{1000}{250}\) [∵ w= 29g, W= 250g]

Or \(M_{\text {solute }}=\frac{29 \times 1000}{250}=116 \mathrm{~g} \mathrm{~mol}^{-1}\)

Example 2. When 54 g of glucose (CH12O6, molar mass = 180) is dissolved in 100 g of water, it results in an elevation of the boiling point of water by 1.56 K. How many grams of another nonelectrolyte of molar mass 90 is required to be added to 100 g of water to elevate the boiling point by 1 K?
Solution:

Given

When 54 g of glucose (CH12O6, molar mass = 180) is dissolved in 100 g of water, it results in an elevation of the boiling point of water by 1.56 K.

The elevation in the boiling point of water on dissolving glucose, Δ Tb = 1.56 K.

Molality of glucose = \(\frac{\frac{54}{180}}{100} \times 1000=3 \mathrm{~m}\)

Since \(\Delta T_{\mathrm{b}}=K_{\mathrm{b}} \cdot m,\)

⇒ \(1.56 \mathrm{~K}=K_{\mathrm{b}} \times 3\)

Or \(K_{\mathrm{b}}=\frac{1.56}{3}=0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\)

Thus, the boiling point elevation constant K of water is 0.52 K kg mol^-1. The elevation in boiling point on dissolving another solute is 1.

∴ \(\Delta T_{\mathrm{b}}=1=K_{\mathrm{b}} \cdot m\)

Or 1 = 0.52 x m

⇒ \(m=\frac{1}{0.52}=1.92\)

But molality m = \(\frac{w}{\frac{w}{M_{\text {solute }}}} \times 1000\)

∴ \(m=\frac{w}{90 \times 100} \times 1000=1.92\)

w = 1.92 x 9

= 17.28 g

Therefore, 17.28 g of the other nonelectrolyte has to be added to 100 g of water to elevate its boiling point by 1 K.

Depression Of Freezing Point

While the addition of a nonvolatile solute or a solvent enhances the boiling point of the solvent, its freezing point is reduced. Solutions, in general, freeze at lower temperatures than pure liquids do.

Solutions of antifreeze compounds like ethylene glycol have been used in automobile radiators to avoid freezing. Sea water, due to its salt content, freezes at a lower temperature than does fresh water.

Like the elevation of the boiling point of a solvent, the depression of its freezing point is also a consequence of the lowering of its vapour pressure upon adding a nonvolatile solute. The temperature at which the solid and liquid phases of the solvent are in equilibrium and have the same vapour pressure is called the freezing point of the solvent.

For example, the freezing point of water is 273 K, the temperature at which both water and ice have the same vapour pressure. However, water in a solution has a lower vapour pressure than that of ice (pure solid solvent) at 273 K. Therefore, when ice and an aqueous solution of a compound are kept in contact, ice melts.

If the temperature is allowed to fall, the vapour pressure of the ice decreases more rapidly than that of the water in the solution and at a specific temperature below 273 K ice and water have the same vapour pressure. This is the point at which ice and solution are in equilibrium or the freezing point of the solution.

In general, 1 mol of a nonelectrolyte such as sucrose, glycerine or alcohol when dissolved in 1 kg of water gives a solution that freezes at -1.86°C. The difference AT, between the freezing point of a pure solvent and the freezing point in the presence of a solute is directly proportional to the molality of the solution, the proportionality constant being K, the molal freezing point depression constant.

Thus, \(\Delta T_f \propto m\)

Or, \(\Delta T_f=K_i m\)

With the help of the following relationship, the molar mass of the solute can be determined, if the quantities \(\Delta T_f, K_f\) are known and w grams of solute is present in W grams of solvent.

⇒ \(M_{\mathrm{B}}=M_{\text {solute }}=K_{\mathrm{f}} \cdot \frac{1000 \cdot w}{\Delta T_{\mathrm{f}} \cdot W} .\)

Like Kb, Kf can also be expressed in terms of thermodynamic quantities.

⇒ \(K_{\mathrm{f}}=\frac{R T_0^2 M_{\text {solvent }}}{1000 \Delta_{\text {fus }} H} \mathrm{Kkg} \mathrm{mol}^{-1}\)

where R is the gas constant and Msolvent is the molar mass of the solvent. A fuH is the change in enthalpy for the fusion of the pure solid solvent and To is its freezing point in the pure state.

Values of K, and K, for some solvents:

Example 1. 27.5 g of a nonelectrolyte of molar mass 100 g mol is dissolved in 500 g of water. What is the freezing point of this solution if Kf of water is 1.86 K kg mol and the freezing point of water is 0°C?

Solution:

Given

27.5 g of a nonelectrolyte of molar mass 100 g mol is dissolved in 500 g of water.

Molality m of the solution = \(\frac{\frac{27.5}{100}}{500} \times 1000=0.55 \mathrm{~m}\)

Given, Kf of water = 1.86.

⇒ \(\Delta T_{\mathrm{f}}=K_{\mathrm{f}} \cdot m=1.86 \times 0.55\)

= 1.02 k

i.e., Tf-T=1.02 (T_f and T are the freezing points of the solvent and the solution respectively)

273.15-T=1.02

Or T=272.13 K.

Therefore, the freezing point of the solution is 272.13 K.

Osmosis And Osmotic Pressure

When a solution and the solvent are separated by a semipermeable membrane, the spontaneous passage of the solvent through the membrane to the solution side is called osmosis. A semipermeable membrane is one which allows the passage of solvent molecules and prevents the passage of molecules of dissolved substances, i.e., solutes.

Cell membranes in plants and animals, certain parchment papers and some gelatinous inorganic compounds are a few examples of semipermeable membranes. The transportation of water in a tree from the roots to the leaves takes place by the process of osmosis, the cell membranes being the semipermeable membranes.

The swelling of dried vegetables when kept in water and the shrinking of vegetables due to loss of water, when kept in concentrated salt solutions, are some other examples. The functioning of the kidney is also based on this process. This process is also made use of to concentrate fruit juices, and to purify water.

Osmosis occurs when two solutions of different concentrations in the same solvent are separated by a semipermeable membrane. The solvent in this case flows spontaneously from the solution of lower concentration to the solution of higher concentration till the concentrations of both the solutions on either side of the membrane become the same.

Osmotic pressure:

Let us consider the following example to understand what osmotic pressure is. Two long-necked vessels are connected at the bottom through a semipermeable membrane. The two vessels contain an equal quantity of pure water in one and sugar solution in the other so that their levels in the vessels are the same.

Due to the difference in concentration of the solute on the two sides, osmosis takes place and after some time the level of the solution rises and that of the water lowers. The process continues on its own till the concentrations on the two sides become equal.

But if the membrane is strong enough to withstand the pressure and if the tube is long enough, the solution will rise until its hydrostatic pressure (due to the weight of the column of the solution in the tube) is great enough to prevent further osmosis of the pure solvent into the solution.

The pressure required to stop the passage of solvent molecules into the solution, i.e., to prevent osmosis, is called the osmotic pressure, II, of the solution. Osmotic pressure has the same units as those of pressure. The osmotic pressure of a dilute solution can be calculated from the following expression based on experimental findings.

π=CRT,

where C is the molarity of the solution, R is the gas constant and T is the temperature.

But \(\Pi=C R T\)

where n is the number of moles of the solute and V is the total volume of the solution.

But \(C=\frac{n}{V}\)

Therefore, ΠV = nRT. This equation is called the Van’t Hoff equation and corresponds to the ideal gas equation. If w grams of solute (of molar mass M) is present in the solution then

⇒ \(n=\frac{w}{M_{\text {solute }}}\)

Thus, \(\Pi V=\left(\frac{w}{M_{\text {solute }}}\right) R T\)

Or \(M_{\text {solute }}=\frac{w}{\Pi V} R T\)

Two solutions having the same osmotic pressure at a given temperature are called isotonic solutions. When such solutions are separated by a semipermeable membrane, osmosis does not occur across the membrane.

The fluids present in the human body have a certain osmotic pressure. And therefore the fluids that are injected into the body must be isotonic with the body fluids. A hypotonic solution (less concentrated) results in the swelling of blood cells and causes rupture. A hypertonic solution (of higher concentration) may lead to the death of blood cells due to loss of water.

Example 2. A 5% solution of cane sugar (molar mass 342 g mol^-1) is isotonic with a 0.877% solution of a substance X. Find the molar mass of X at 300 K.
Solution:

Given

A 5% solution of cane sugar (molar mass 342 g mol^-1) is isotonic with a 0.877% solution of a substance X.

The osmotic pressure of cane sugar solution,

⇒ \(\Pi_1=\frac{n_1 R T}{V_1}=\frac{5 \times 0.082 \times 300}{342 \times 100}\)

The osmotic pressure of a solution containing X,

⇒ \(\Pi_2=\frac{n_2 R T}{V_2}=\frac{\frac{0.877}{M_\chi}}{100} \times 0.082 \times 300\)

But П₁ =П₂.

Therefore, \(\frac{5}{342 \times 100} \times 0.082 \times 300=\frac{0.877}{M_X \times 100} \times 0.082 \times 300\)

Or \(\frac{5}{342}=\frac{0.877}{M_X}\)

Or \(M_{\mathrm{X}}=\frac{0.877}{5} \times 342\)

Or \(M_X=60\)

The molar mass of X is 60 g.

Reverse osmosis:

If a pressure greater than the osmotic pressure is applied on the solution side, then the process of osmosis gets reversed, i.e., the solvent from the solution passes to the solvent side, thereby increasing its volume. This is called reverse osmosis.

High pressures are required for reverse osmosis to occur. The process has many applications, such as in desalinating sea water. The semipermeable porous membrane used in the desalination of seawater is cellulose acetate, which is permeable to water but not to the ions and other impurities present in seawater.

The drinking-water purifying systems based on reverse osmosis include a thin film composite membrane made of polyamide or cellulose triacetate.

The other uses of reverse osmosis include the purification of rainwater collected from storm drains for use in irrigation, the purification of boiler water in power plants, and in dialysis.

Measurement of osmotic pressure:

The apparatus used for measuring osmotic pressure is called an osmometer. Shows a schematic diagram of the Berkeley and Hartley osmometer. The central or the inner compartment contains water and the two outer compartments contain solutions.

The compartments are connected to each other on the sides by a semipermeable membrane, which allows the passage of water only. The capillary tube attached to the central compartment indicates any flow of water from the central to the outer compartments.

If the water level in the capillary decreases, it means water has flowed out of the inner compartment to the solution side. On one of the solution sides, there is a pump to exert pressure and a pressure gauge to measure the pressure applied.

To stop osmosis, pressure is applied to the solution to keep the water level constant in the capillary. The applied pressure is read directly from the pressure gauge. This is the osmotic pressure.

Abnormal Molar Mass

As stated earlier, the colligative properties of a solution depend on the number of solute particles present in it. If the solute is a nonelectrolyte, which does not undergo dissociation, the number of particles is the same as the number of molecules.

However, when electrolytes (i.e., almost all acids, bases and salts) are dissolved in water, dissociation takes place and two or more ions are produced.

Each ion then acts as an independent particle and depending on the extent of dissociation, the observed values of colligative properties are higher than the theoretically expected values.

Since the molar mass of the solute is inversely proportional to the colligative property of the solution, the experimentally determined value of the colligative property is far less than the actual value in dissociation cases.

For example, one molal aqueous solution of sodium chloride, an electrolyte, freezes at -3.37°C as compared to one molal aqueous solution of a nonelectrolyte such as sugar, in which case the freezing point is -1.86°C.

The calculation of the molar mass of the electrolyte (here NaCl) gives a value which is nearly twice that of the normal molar mass of 58.5. This is because NaCl ionises to a large extent in water to give Na* and CI ions and the number of particles is two instead of one in one molecular formula of the solute. Hence, the number of particles (and therefore the depression in freezing point) is twice that obtained from a nonelectrolyte.

In 1886, the Dutch scientist Can’t Hoff introduced a factor, known as the Van’t Hoff factor, to account for abnormal molar masses.

⇒ \(\text { van’t Hoff factor, } i=\frac{\text { actual molar mass based on formula of compound }}{\text { observed molar mass }}\)

For such solutions, the respective equations for the colligative properties become

⇒ \(\frac{p_{\text {solvent }}^{\circ}-p_{\text {solution }}^{\circ}}{p_{\text {solvent }}^{\circ}}=i\left(\frac{n}{N+n}\right)\) (relative lowering of vapour pressure)

⇒ \(\Delta T_{\mathrm{b}}=i K_{\mathrm{b}} \cdot m\) (elevation of boiling point)

⇒ \(\Delta T_{\mathrm{f}}=i K_{\mathrm{f}} m\) (depression of freezing point)

⇒ \(\Pi V=i n R T\) (osmotic pressure of solution)

The value of I gives the number of particles obtained from one formula unit of the compound. When dissociation of the solute occurs in solution, i is greater than 1. If a solute is associated with a liquid solvent, then the observed molar mass is more than the theoretical molar mass.

If two molecules associate to form a single particle then the molar mass is nearly double that of the normal molar mass. For example, benzoic acid is found to dimerise in benzene.

In the case of an association, the can’t Hoff factor is less than unity. The modified equations for the colligative properties are the same as given in the case of the dissociation of solutes.

The can’t Hoff factor may be defined as the ratio of the observed value of a colligative properly to the theoretically calculated value of the property.

Values of can’t Hoff Factor I, at various concentrations, for NoCI, KCI, MgSO, and K₂SO₄

Example 1. A₂m solution of NaCl in water causes an elevation in the boiling point of water by 1.88 K. What is the value of the can’t Hoff factor I? What does it suggest? Normal molar mass of NaCl = 58.5 & K = 0.52 K kg mol -1.
Solution:

Given

A₂m solution of NaCl in water causes an elevation in the boiling point of water by 1.88 K.

Expected elevation in boiling point,

⇒ \(\Delta T_{\mathrm{b}}(\text { expected })=0.52 \times 2\)

= 1.04 K.

Observed elevation = 1.88 K.

⇒ \(\text { van’t Hoff factor } i=\frac{\text { observed elevation }}{\text { expected elevation }}\)

⇒ \(\frac{1.88}{1.04} \approx 2\)

A value of 2 for the can’t Hoff factor suggests that 1 molecule of NaCl dissociates into two particles- Na⁺ and CI^–.

Example 2. Calculate the amount of NaCl that must be added to 100 g of water so that the freezing point of water is depressed by 2 K. Given that K, for water, is 1.86 K kg mol^-1, can’t Hoff factor, i, is 2 for NaCl and the molar mass of NaCl is 58.5.
Solution:

Since \(\Delta T_f=i K_f m\)

2=2 x 1.86 x m,

⇒ \(m=\frac{2 \times 1.86}{2}=1.86\)

But \(m=\frac{\frac{w_{\mathrm{NaCl}}}{M_{\mathrm{NaCl}}}}{100} \times 1000\)

Where \(w_{\mathrm{NaCl}}\) is the amount of NaCl to be added and \(M_{\mathrm{NaCl}}\) is its molar mass.

Therefore, \(m=\frac{w_{\mathrm{NaCl}}}{58.5 \times 100} \times 1000\)

Ог \(1.86=\frac{w_{\mathrm{NaCl}}}{58.5 \times 100} \times 1000\)

⇒ \(w_{\mathrm{NaCl}}=\frac{1.86 \times 58.5 \times 100}{1000}\)

⇒ \(w_{\mathrm{NaCl}}=10.08\)

Therefore, 10.08 g of NaCl must be added to 100 g of water to cause a depression in the freezing point of 2 K

Solutions Multiple Choice Questions

Question 1. An amalgam of mercury with sodium is an example of a solution whose solvent is a

1. Solid
2. Liquid
3. Gas
4. None Of The Above

Answer: 1. Solid

Question 2. One litre of a sample of water contains 0.001 g of sodium ions. Its concentration in ppm is

1. 1×10^-6
2. 0.001
3. 1000
4. 1

Answer: 4. 1

Question 3. The sum of the mole fractions of all the components

1. Less Than One
2. Greater Than One
3. Equal To One
4. Either (1) Or (2)

Answer: 3. Equal To One

Question 4. What is the molality of 4 g of NaOH in 2000 g of water?

1. 0.002
2. 5×10^-5
3. 2
4. 0.05

Answer: 4. 0.05

Question 5. The dissolution of a particular solid in a liquid is endothermic. Its solubility

1. Increases With Temperature
2. Decreases With Temperature
3. Does Not Depend On The Temperature
4. Either (1) Or (2)

Answer: 1. Increases With Temperature

Question 6. What happens to the solubility of gases in liquids with an increase in temperature?

1. Increases
2. Does not change
3. Decreases
4. May increase or decrease depending on the gas

Answer: 3. Decreases

Question 7. Henry’s law gives the relation between

1. The Solubility Of A Gas In A Solvent And The Pressure
2. The Solubility Of The Gas And Concentration Of The Solution
3. The Solubility Of The Gas And The Temperature
4. None Of The Above

Answer: 1. The Solubility Of A Gas In A Solvent And The Pressure

Question 8. The vapour pressure of a solvent is…… by the addition of a nonvolatile solute.

1. Increased
2. Decreased
3. Not Affected
4. Any Of The Above

Answer: 2. Decreased

Question 9. An ideal solution is one

1. Which Obeys Raoult’s Law
2. For Which [Latex]\Delta_{\operatorname{mix}} H=0[/Latex]
3. For Which [Latex]\Delta_{\operatorname{mix}} V=0[/Latex]
4. All Of The Above

Answer: 4. All Of The Above

Question 10. A solution is said to show a positive deviation from Raoult’s law if

1. It Shows A Minimum In The Plot Of Vapour Pressure As A Function Of Mole Fraction
2. It Shows A Maximum In The Plot Of Vapour Pressure As A Function Of Mole Fraction
3. It Shows A Minimum In The Plot Of Temperature As A Function Of Mole Fraction
4. It Shows A Maximum In The Plot Of Temperature As A Function Of Mole Fraction

Answer: 2. It Shows A Maximum In The Plot Of Vapour Pressure As A Function Of Mole Fraction

Question 11. A solution that is formed by mixing two liquids has the same composition in the liquid and the vapour phase and boils at a constant temperature is called a/an

1. Zeotropic Mixture
2. Equilibrium Mixture
3. Azeotropic Mixture
4. Nonequilibrium Mixture

Answer: 3. Azeotropic Mixture

Question 12. Mixtures with azeotropic composition

1. Cannot Be Separated By Fractional Distillation
2. Can Be Separated By Fractional Distillation
3. Can Be Separated By Simple Distillation
4. Either (2) Or (3)

Answer: 1. Cannot Be Separated By Fractional Distillation

Question 13. Solutions which show positive deviation from Raoult’s law form

1. Maximum Boiling Azeotropes
2. Maximum Boiling Zeotropes
3. Minimum Boiling Zeotropes
4. Minimum Boiling Azeotropes

Answer: 4. Minimum Boiling Azeotropes

Question 14. Colligative properties are those properties that depend on the

1. Nature Of The Solute
2. Size Of The Solute Particles
3. Nature Of The Solvent
4. Number Of Solute Particles

Answer: 4. Number Of Solute Particles

Question 15. A nonvolatile solute is added to a volatile solvent. Its boiling point

1. Remains The Same As That Of The Pure Solvent
2. Increases
3. Decreases
4. None Of These Happens.

Answer: 3. Decreases

Question 16. A nonvolatile solute is added to a solvent. Its freezing point

1. Remains The Same As That Of The Pure Solvent
2. Decreases
3. Increases
4. None Of These Happens.

Answer: 2. Decreases

Question 17. The freezing point of a substance is defined as the temperature at which the

1. Vapour Pressure Of The Substance In The Liquid Phase Is Equal To That In The Solid Phase
2. Vapour Pressure Of The Liquid Is Equal To The Atmospheric Pressure
3. Vapour Pressure Of The Solid Is Equal To The Atmospheric Pressure
4. None Of These

Answer: 1. Vapour Pressure Of The Substance In The Liquid Phase Is Equal To That In The Solid Phase

Question 18. The decrease in the freezing point of a solvent in the presence of a nonvolatile solute is a consequence of

1. Zero Vapour Pressure Of The Solute
2. The Elevation Of The Vapour Pressure Of The Solvent Because Of The Presence Of The Solute
3. The Lowering Of The Vapour Pressure Of The Solvent Because Of The Presence Of The Solute
4. None Of These

Answer: 3. The Lowering Of The Vapour Pressure Of The Solvent Because Of The Presence Of The Solute

Question 19. A semipermeable membrane is one which

1. Allows The Passage Of Only Solute Molecules
2. Does Not Allow The Passage Of Matter Through It
3. Allows A Small Amount Of Solute And Solvent Molecules To Move Through It
4. Allows the passage of only solvent molecules through it

Answer: 4. Allows the passage of only solvent molecules through it

Question 20. In osmosis, the flow of solvent molecules takes place from

1. Concentrated To Dilute Solution
2. Dilute To The Concentrated Solution.
3. Solvent To The Solution Side
4. Either (2) Or (3)

Answer: 2. Dilute To The Concentrated Solution.

Question 21. Osmotic pressure depends on

1. The Molarity Of The Solution
2. Temperature
3. Both (1) And (2)
4. The Molar Mass Of The Solvent

Answer: 3. Both (1) And (2)

Question 22. Two solutions that have the same osmotic pressure at

1. Hypertonic Solutions
2. Isotonic Solutions
3. Hypotonic Solutions
4. None Of These

Answer: 2. Isotonic Solutions

Question 23. The shrinking of vegetables kept in salt water is due to

1. The Depression In The Vapour Pressure Of Water
2. The Elevation In The Boiling Point Of Water
3. The Depression In The Freezing Point Of Water
4. Osmosis

Answer: 4. Osmosis

Question 24. In reverse osmosis,

1. A Pressure Larger Than The Osmotic Pressure Is Applied On The Solution Side
2. A Pressure Larger Than The Osmotic Pressure Is Applied On The Solvent Side
3. A Pressure Smaller Than The Osmotic Pressure Is Applied On The Solution Side
4. A Pressure Smaller Than The Osmotic Pressure Is Applied On The Solvent Side

Answer: 1. A Pressure Larger Than The Osmotic Pressure Is Applied On The Solution Side

Question 25. When a solute associates with a solution the value of the can’t Hoff factor is

1. Equal To One
2. Less Than One
3. Greater Than One
4. Either (2) Or (3)

Answer: 2. Less Than One

Question 26. When a solute dissociates in solution, the observed molar mass is…… the actual molar mass

1. Greater Than
2. Less Than
3. Equal To
4. May Be (1) Or (2)

Answer: 1. Greater Than

Chemical Kinetics

A knowledge of the kinetics of the reaction employed in an industrial process helps to maintain optimum conditions for the reaction so that the process becomes economically viable. Generally, chemical reactions that are fast with a high yield of products at reasonable costs are used in industrial processes.

The study of rates of reactions helps in understanding the mechanisms of reactions. An understanding of the mechanism of a biochemical reaction helps in analyzing how an enzyme works.

Reaction Rate

The rate of a reaction may be expressed in terms of the amount of reactants consumed or the amount of products formed in n given time. In other words, it is the change in concentration of the reactant or product with respect to the change in time after the reaction has been initiated.

Since the rate of a reaction is influenced by temperature, the temperature of the reaction mixture should be held constant during the course of the reaction. If it is not possible to measure the concentration directly, then a change that is directly proportional to the concentration can be measured.

For example, the change in the number of moles per cubic meter or a change in the pressure of a gas, if a gas is involved in the reaction, can be measured.

Thus, the rate of a reaction can be defined as

⇒ \(\frac{change in the concentration of the product}{time taken}\)

or, \(\frac{change in the concentration of the reactant}{time taken}\)

Units of rate of reaction If the concentration is expressed in mol L^-1 then the unit of the rate of a reaction is mol Vs. In a gaseous reaction, when the concentration of gases is expressed in terms of their partial p then the unit of the rate is atm s^-1 or bar s^-1.

Let us consider the thermal decomposition of nitrogen pentoxide N₂O₅, which gives the brown gas nitrogen dioxide and molecular oxygen.

\(\underset{\text { colourless }}{2 \mathrm{~N}_2 \mathrm{O}_5(\mathrm{~g})} → \underset{\substack{\text { brown } \\(4 \text { moles })}}{4 \mathrm{NO}_2(\mathrm{~g})}+\underset{\text { colourless }}{\mathrm{O}_2(\mathrm{~g} \text { mole })}/latex]

The rate of the reaction is the rate at which N₂O₅ decomposes or the rate at which O₂ and NO₂ are formed.

Here we assume that there is no change in the volume of the reaction system. In other words, there is no removal from or addition to the reaction system. As you can see, the number of moles of gases increases from 2 to 5, which means there is an increase in the pressure of the reaction system during the course of the reaction.

The change in concentration of the reactant or the products can also be measured by measuring the increase in pressure.

Let us first study the formation of the product O₂.

⇒ [latex]\text { Reaction rate }=\frac{\text { change in concentration of oxygen }}{\text { time interval }}\)

⇒ \(\frac{\Delta\left[\mathrm{O}_2\right]}{\Delta t}=\frac{\text { concentration of } \mathrm{O}_2 \text { at time } t_2-\text { concentration of } \mathrm{O}_2 \text { at time } t_1}{t_2-t_1}\)

Here square brackets indicate molar concentration. Shows the concentration as a function of time at 55°C for the reaction

⇒ \(2 \mathrm{~N}_2 \mathrm{O}_5(\mathrm{~g}) \rightarrow 4 \mathrm{NO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g})\)

Refer to Table During the time period 400 s to 500 s, for example, the average rate of formation of O₂ will be 8 x 10^-6 mol L _1 s _1 because the rate of formation of

O₂ = \(\frac{0.0057-0.0049}{500-400}=8 \times 10^{-6} \mathrm{~mol}^{-1} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

Now let us express the rate of the reaction in terms of the change in the concentration of NO₂. During till same time period 400 seconds to 500 s, the rate of formation of NO₂ will be

⇒\(\frac{0.0229-0.0197}{500-400}=3.2 \times 10^{-5} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

The rate of formation of NO₂ is 4 times that of O₂ because for 2 mol of N₂O₅,1 mol of O₂ and 4 mol of NC are formed. In other words, the rate is in accordance with the 4: 1 stoichiometric coefficient ratio of NO₂ and C in the chemical equation.

Similarly, we can expect the rate of disappearance of N₂O₅ to be twice that of the formation of O₂ As the products form, the reactant disappears. Hence, the value of A[N₂O₂ ]/Af turns out to be negative.

B all rates of reactions are reported as positive quantities. Thus, to maintain the reaction rate as a positive quantity the rate of a reaction is defined as the rate of formation of products or rate of disappearance of reactants divided by the corresponding stoichiometric coefficient in the balanced chemical equation, the coefficient being taken as positive for products and negative for reactants.

Thus, rate of disappearance of

⇒\(-\frac{[0.0086-0.0101]}{[500-400]}=1.5 \times 10^{-5} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1} \approx 2 \times 8 \times 10^{-6} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

Thus, the rate of formation of O₂

⇒ \(\text { rate of formation of } \mathrm{NO}_2=\frac{1}{2} \text { the rate of decomposition of } \mathrm{N}_2 \mathrm{O}_5\)

or, \(\frac{\Delta\left[\mathrm{O}_2\right]}{\Delta t}=\frac{1}{4} \frac{\Delta\left[\mathrm{NO}_2\right]}{\Delta t}=-\frac{1}{2} \frac{\Delta\left[\mathrm{N}_2 \mathrm{O}_5\right]}{\Delta t}\)

Therefore, for the reaction

⇒ \(2 \mathrm{~N}_2 \mathrm{O}_5(\mathrm{~g}) \rightarrow 4 \mathrm{NO}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g})\)

Rate of reaction = \(\frac{1}{2} \frac{\Delta\left[\mathrm{N}_2 \mathrm{O}_5\right]}{\Delta t}=\frac{1}{4} \frac{\Delta\left[\mathrm{NO}_2\right]}{\Delta t}=\frac{\Delta\left[\mathrm{O}_2\right]}{\Delta t}=8 \times 10^{-6} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

A plot of concentration versus time for the three gases NO₂, N₂O_2, and O₂ using the data from Table. As you can see, there are no straight lines, which means the rate (as determined by the slope of the curve) is different for different time intervals. The steeper the slope, the faster the rate. For example, the rate between 600 s and 700 s turns out to be 5.5 x 10^-6 mol L^-1s^-1 while that between 300 s and 400 s is 9 x 10⁶ mol L^-1s^-1.

The slope of the curve can be determined by finding the coordinates of any two points on the curve. If we choose the x coordinates of the points to be 600 s and 700 s, the respective y coordinates will be 0.0072 mol L^-1 and 0.0061 mol L^-1 (concentration of N₂O₂).

⇒ \(\text { Slope }=\frac{\text { change in } y}{\text { change in } x}=\frac{\Delta y}{\Delta x}=\frac{\Delta\left[\mathrm{N}_2 \mathrm{O}_5\right]}{\Delta t}\)

⇒ \(\frac{0.0061-0.0072}{700-600}=-1.1 \times 10^{-5} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

Rate = \(-\frac{1}{2} \cdot \frac{\Delta\left[\mathrm{N}_2 \mathrm{O}_5\right]}{\Delta t}=-\frac{1}{2} \times\left(-1.1 \times 10^{-5}\right)=5.5 \times 10^{-6} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

The rote of a reaction is not uniform during the course of the reaction, Initially, It la more but decreases with the decrease in the concentration of the reactant, Therefore, we may conclude Ilia! the mill rate (tetmnlHrit during n time internal to the accrue mission rule during that lime, Thus fin 10 A mol ¹, 1 s ¹the average reaction rate during the time interval 400 to 500 s, instantaneous rate If the change In concentration of the reactant and the product la determined consecutively at gradually decreasing time-intervals, a lime-interval which Is almost zero will be readied, The reaction rate determined at such an instant is called Instantaneous rale, l! is represented as (considering decomposition of nitrogen pentoxide)

⇒ \(r_{\text {lint }}=-\underset{\Delta t \rightarrow 0}{2} \frac{1}{\Delta t} \frac{\Delta\left[\mathrm{N}_2 \mathrm{O}_5\right]}{\Delta t}=-\frac{1}{2} \frac{d\left[\mathrm{~N}_2 \mathrm{O}_5\right]}{d t}=\frac{1}{4} \times \frac{d\left|\mathrm{NO}_2\right|}{d t}=\frac{d\left[\mathrm{O}_2\right]}{d t}\)

(note that the denominator contains the respective stoichiometric coefficients)

The instantaneous rate of the consumption of a reactant or formation of a product at some time / can be calculated by finding the slope of a graph of cells (reactant’s or product’s) molar concentrations plotted against the time, and the slope evaluated at the instant of interest.

The plot of the molar concentration of NO₂ versus time. In order to find the Instantaneous rate of reaction at 400 s, a tangent Is drawn at this time and Its slope 11 is calculated as \(\left(\frac{\Delta y}{\Delta x}\right)\) as shown.

The instantaneous rate is then given by

⇒\(r_{\text {inst }}=\frac{1}{4} \text { slope }=\frac{1}{4} \times\left(\frac{0.011}{3.15}\right)=8.7 \times 10^{-6} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

We can also find the initial rate of the reaction, the rate when no products are formed, from the slope of the tangent at zero time

Initial rate = \(\frac{1}{4} \times\left(\frac{0.0038}{50}\right)=1.9 \times 10^{-5} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}\)

It may be clearly seen that the instantaneous rate and initial rate are different.

Example 1. Express the relationship between the rate of production of iodine and the rate of consumption of hydrogen iodide in the following reaction.

⇒ \(2 \mathrm{HI} \rightarrow \mathrm{H}_2+\mathrm{I}_2\)
Solution:

The stoichiometries of I₂ and HI in the reaction are 1 and 2 respectively.

Hence, the rate = \(-\frac{1}{2} \cdot \frac{\Delta[\mathrm{HI}]}{\Delta t}=\frac{\Delta\left[\mathrm{I}_2\right]}{\Delta t}\)

Now you know that the rate of a reaction is determined by measuring the change in concentration of any of the reactants or the products. But how is the concentration or a change in it during the course of the reaction measured? As you know, whether or not a reaction has occurred can be determined by observing changes in any of the reactants or products, such as changes in state, temperature, and color. Thus, by observing any such change in the property of either a reactant or a product, the change in its concentration can be determined.

Titration, colorimetry (a technique in which the absorption of light by a substance is measured), conductimetry (measuring the conductance of a solution) and pressure measurements are some of the techniques used to follow the concentration change of reactants or products.

Factors Affecting The Rate Of A Reaction

As you can see the rate of a reaction decreases with an increase in time. The rates tend to decrease as the reaction proceeds forward and reactants are consumed. You know that reactions take place as a result of collisions between molecules of reactants.

According to the kinetic molecular theory, the pressure exerted by a gas is proportional to the frequency with which molecules of the gas collide with tire walls of the container. The more the number of molecules present in a given volume, the greater is the number of collisions.

And if the number of collisions between the reacting molecules is larger (at the beginning of the reaction), the higher will be the rate.of the reaction. As the concentration of reactants decreases, the rate decreases.

Apart from the concentration of the reactants, there are several factors which influence the rate of a reaction. These are the surface area and concentration of the reactants, temperature and pressure conditions of the reaction, and the presence of catalysts and light. Electric and magnetic fields also affect the rate of a reaction.

A larger surface area helps in better contact between the reactants and hence leads to an increased number of collisions between the reactant molecules resulting in a faster rate of reaction. Increasing the concentration of a reactant does not always increase the rate of a reaction.

In general, increasing the temperature increases the rate of chemical reactions. This is why food, if not refrigerated, spoils faster in summer than in winter.

Influence Of Concentration Rate Law

You know that the rate of a reaction at a given temperature depends on the concentration of one or more reactants and products.

Let us consider the reaction between bromine and formic acid in an aqueous solution catalyzed by acid.

⇒ \(\mathrm{Br}_2(\mathrm{aq})+\mathrm{HCOOH}(\mathrm{aq}) \stackrel{\mathrm{H}^*}{\longrightarrow} 2 \mathrm{Br}^{-}(\mathrm{aq})+2 \mathrm{H}^{+}(\mathrm{aq})+\mathrm{CO}_2(\mathrm{~g})\)

When the concentration of bromine during the course of the reaction is plotted against time, we obtain a curve as shown. The rate of this reaction can thus be expressed as

⇒ \(\text { rate }=-\frac{d\left[\mathrm{Br}_2\right]}{d t}\)

A plot of the reaction rate against the concentration of bromine is shown. It is a straig] line, indicating that the reaction rate is directly proportional to the concentration of bromine, i.e.„

reaction rate ac [Br₂ ]

or, reaction rate = k[Br₂].

Here k is called the rate constant or velocity constant and is characteristic of the reaction being studied. The rate constant is independent of the concentrations of the reactants. However, it depends on the temperature. An equation of this kind which is experimentally determined for a reaction is called the rate equation or rate law of that equation. The rate law of a reaction gives the dependence of the reaction rate on the concentration of each reactant.

Experimental findings reveal that the rate of a reaction is usually proportional to the molar concentrations of the reactants raised to a simple power.

⇒ \(\text { Rate }=k[R]^n\)

In the given equation, [R] is the molar concentration of the reactant raised to a simple power n, which may or may not be the same as the stoichiometric coefficient of the reactants in the balanced chemical equation.

Similarly, for a general reaction

mA + nB → product

the rate law is of the form

⇒ \(\text { rate }=-\frac{d[\mathrm{~A}]}{d t}=k[\mathrm{~A}]^m[\mathrm{~B}]^n\)

This equation is called the differential rate equation or rate expression. The exponents m and n are usually positive integers. These exponents for a reaction are determined experimentally as also the rate constant k.

The rate law for the reaction between Br₂ and formic acid turns out to be

⇒ \(\text { rate }=k\left[\mathrm{Br}_2\right][\mathrm{HCOOH}]^0\)

or, \(\text { rate }=k\left[\mathrm{Br}_2\right]\)

In this case, the two exponents m and n are 1 and 0 respectively. The rate, therefore, depends only on the concentration of Br₂ and not on that of HCOOH. We could either have all the reactants appearing in the rate law or only some may appear; the exponents may or may not be the same as the stoichiometric coefficients.

Reaction order:

Let us now see how the rate is affected by the value of the exponent. In Equation 2, if m =1, it means that the rate of the reaction depends linearly on the concentration of one of the reactants, A. If the concentration of A is doubled so will be the rate. But if it is assumed that m = 2, then if the concentration of A is doubled, the rate quadruples, i.e., increases four times (∵ [2A] = 4[A]₂)

Similarly, the rate of the reaction is also affected by the value of n. If the concentration of A is kept constant and that of B is doubled, and the rate also doubles, it means the rate of the reaction depends linearly on the concentration of B. Now in the case of the reactant A, if we take the second assumption (m¯²) to be true then the rate equation for the reaction will be

rate = k [A]²[B]¹

=k[A]²[B].

Thus, exponents m and n in the rate law indicate how sensitive the rate is to changes in the concentration of A and B. The dependence of the reaction rate on concentration is expressed in terms of reaction order.

For the given chemical reaction the order of the reaction with respect to A is m (the exponent of A in the rate law) and the order with respect to B is n. The overall order of a reaction is the sum of the exponents in the rate law and is m + n for the above reaction.

A reaction whose overall order is 1 is called a first-order reaction, one with an order of 2 is called a second-order reaction, one with order 3 is called a third-order reaction, and so on.

For example, the reaction involving the decomposition of hydrogen peroxide is

⇒ \(2 \mathrm{H}_2 \mathrm{O}_2(\mathrm{aq}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g})\)

The rate law for this reaction is

rate = k[H₂O₂].

Its order with respect to H₂O2₂ is one and its overall order is also one. Hence it is a first-order reaction.

Let us consider the reaction between HCl and NaOH

⇒ \(\mathrm{Na}^{+}+\mathrm{Cl}^{-}+\mathrm{H}_3 \mathrm{O}^{+}+\mathrm{OH}^{-} \rightarrow \mathrm{H}_2 \mathrm{O}+\mathrm{Na}^{+}+\mathrm{Cl}^{-}\)

It is of the first order with respect to each of the reactants H₃O⁺ and OH^–.

⇒ \(\text { Rate }=k\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]\)

But the overall order is 2. Hence, it is a second-order reaction.

NO₂ (g) + CO(g) → NO(g) + CO₂ (g)

The rate law of the given reaction is

rate = k [NO₂]²[CO]O₂.

The order of this reaction is two with respect to NO₂ and zero with respect to CO. The overall order is two because [CO]⁰ =1, just as in algebra. It is called a second-order reaction. The concentration of carbon monoxide raised to power zero implies that the rate of the reaction is independent of the concentration of CO provided that some CO is present.

H₂(g) + 2NO(g) → N₂O(g) + H₂O(g)

The rate law for this reaction is

rate = k [NO]₂[H₂ ]

The order of the reaction is two with respect to NO and one with respect to H₂. The overall order of the reaction is three. Therefore it is a third-order reaction.

Note that the order of a reaction or the power of the concentration of the reactant in the rate expression of a reaction has no connection with the stoichiometric coefficient of the reactant.

It is also important to note that a rate law is established experimentally and cannot in general be inferred from the chemical equation for the reaction.

Unit of rate constant You know that

⇒ \(k=\frac{\text { rate }}{{\text { (concentration })^n}^{(}}\)

The SI unit of concentration is mol L^-1 and that of time is s.

Therefore,

⇒ \(k=\frac{\mathrm{mol} \mathrm{L}^{-1}}{\mathrm{~s}} \times \frac{1}{(\text { concentration })^n}\)

Thus, the units of k for different reaction orders will be as follows.

Integrated Rate Laws

As discussed earlier in the chapter, the rate law of a reaction gives the rate of a reaction at a given instant. In other words, it tells us the rate of a reaction at a certain composition of the reaction mixture. If we have to find out how the concentrations depend on time, we need to integrate the differential rate expressions.

An integrated rate law is an expression that gives the concentration of a species as a function of time. Another way of saying this is that the integrated rate law is used to predict the concentration of a species at any time after the start of the reaction.

Also, the law helps find the rate constant and thereby the order of the reaction. Let us derive and study the rate laws for zero- and first-order reactions.

Zero-order reactions:

Consider the reaction A → P, which obeys the zero-order rate law, i.e., the rate of the reaction is proportional to the concentration of the reactants, raised to the power zero.

⇒ \(\text { Rate }=-\frac{d[\mathrm{~A}]}{d t}=k[\mathrm{~A}]^0=k[1]=k\)

As the equation shows, the rate of such a reaction is independent of the concentration of the reactant throughout the course of the reaction. Integrating Equation 4.1 we get

⇒ \(\int_{[\hat{\mathrm{A}}]_0}^{[\mathrm{A}]} d \mathrm{~A}=-\int_0^t k d t\)

⇒ \([\mathrm{A}]-[\mathrm{A}]_0=-k t\)

or \([\mathrm{A}]=-k t+[\mathrm{A}]_0\)

where [A]⁰ is the initial concentration of A and [A] is its final concentration.

This equation is called the integrated rate law.

This is an equation of the form y = mx + c, which is the equation of a straight line. Hence a graph of [A] vs time is a straight line with a slope, -k. Zero-order reactions are uncommon but they can occur under special conditions. For example, the decomposition of gaseous ammonia on a hot platinum surface is a zero-order reaction.

⇒ \(2 \mathrm{NH}_3(\mathrm{~g}) \stackrel{\mathrm{Pt}, 1130 \mathrm{~K}}{\longrightarrow} \mathrm{N}_2(\mathrm{~g})+3 \mathrm{H}_2(\mathrm{~g})\)

⇒ \(\text { Rate }=k\left[\mathrm{NH}_3\right]^0=k\)

First-order reactions:

For a first-order reaction of the type

A → P

the differential rate law is

⇒ \(\text { rate }=-\frac{d[\mathrm{~A}]}{d t}=k[\mathrm{~A}]\)

⇒ \(-\frac{d[\mathrm{~A}]}{[\mathrm{A}]}=k d t .\)

On integrating from f = 0, when the concentration of A is [A]⁰, to the time t, when the molar concentration of A is [A], we obtain

⇒ \(|-\ln [\mathrm{A}]|_{[\mathrm{A}]_0}^{[\mathrm{A}]}=k|t|_0^t\)

⇒ \(-\ln [\mathrm{A}]+\ln [\mathrm{A}]_0=k t\)

or, \(\ln [\mathrm{A}]=\ln [\mathrm{A}]_0-k t\)

The exponential form of the equation can be given as

⇒ \(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=-k t\)

This suggests that for all first-order reactions the concentration of the reactant decays exponentially with time. [A] is the concentration of A at time f and [A]⁰ is its initial concentration. Thus, the integrated rate law equation can be written as

⇒ \(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=-k t\)

The above equation can also be written as

⇒ \(k=\frac{1}{t} \ln \frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\)

or, \(k=\frac{1}{\left(t_2-t_1\right)} \ln \frac{\left[\mathrm{A}_1\right]}{\left[\mathrm{A}_2\right]}\)

Here the concentrations [A x ] and [A 2 ] are at times fx and 12 respectively.

Integrated rate laws can be used to determine the order and rate constant of a reaction. For this we need experimental data of the concentration of the reactant as a function of time.

For a first-order reaction, the plot of In [A] vs f should be a straight line. This is clear from the equation

In [A] = In [A]⁰– kt

It is of the form Y-a~ bX. where Y is In [A], X is I. b, the slope, is(-) and the intercept is In[A]⁰.

For any reaction, we plot In [A] vs. f from the experimental data of that reaction, and if it does not give a straight line, the reaction is not of the first order.

Equation 43 may also be written as

⇒ \(2.303 \log \left\{\frac{[\mathrm{A}]}{[\mathrm{A}]_0}\right\}=-k t\)

or, \(-2.303 \log \left\{\frac{[\mathrm{A}]}{[\mathrm{A}]_0}\right\}=k t\)

or, \(2.303 \log \left\{\frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\right\}=k t\)

or, \(\log \left\{\frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\right\}=\frac{k t}{2.303}\)

A plot of log \(\left\{\frac{[\mathrm{A}]_0}{[\mathrm{~A}]}\right\}\) versus t gives a straight line with slope \(\frac{k}{2.303}\)

The thermal decomposition of N2 Og dealt with at the beginning of this chapter is a first-order reaction and its rate law is rate = k[N205].

The decomposition of hydrogen peroxide in a dilute sodium hydroxide solution is described by the equation

2H₂O₂(aq) → 2H₂O(1) + O₂ (g)

Let us find the order of this reaction. The concentration of H₂O₂ as a function of time was found to be as follows.

A plot of the concentration of H₂O₂ as a function of time. It may be seen from the graph the concentration of the reactant decays exponentially with time. On plotting In[H₂O₂] versus time, a fight line is obtained indicating that the reaction is of the first order

Whether a reaction is of zero, first, or second order can be found by a simple plot of the reaction rate concentration of the reactant.

Example 1. The reaction of N₂O₂ with water produces HNO₃.

⇒ \(\mathrm{N}_2 \mathrm{O}_5+\mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{HNO}_3\)

The reaction is of the first order with respect to each reactant. Write the rate law for the reaction.

When \(\left[\mathrm{N}_2 \mathrm{O}_5\right] \text { is } 0.13 \times 10^{-6} \mathrm{~mol} \mathrm{~L}^{-1}\) and \(\left[\mathrm{H}_2 \mathrm{O}\right]=2.3 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1}\)

the rate of the reaction is 4.55 x 10^-10 mol L^-1 min^-1. What is the rate constant for the reaction?
Solution:

Since the reaction is of the first order with respect to each reactant, the power of each reactant must be 1 in the rate law.

Therefore, rate = k[N₂O₅ ][H₂O].

Given that rate = \(4.55 \times 10^{-10} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1},\left[\mathrm{~N}_2 \mathrm{O}_5\right]=0.13 \times 10^{-6} \mathrm{~mol} \mathrm{~L}^{-1}\)

and \(\left[\mathrm{H}_2 \mathrm{O}\right]=2.3 \times 10^{-4} \mathrm{~mol} \mathrm{~L}^{-1}\)

Substituting these values in the rate law

⇒ \(4.55 \times 10^{-10}=k\left(0.13 \times 10^{-6}\right)\left(2.3 \times 10^{-4}\right)\)

or, \(k=\frac{4.55 \times 10^{-10}}{0.13 \times 10^{-6} \times 2.3 \times 10^{-4}}=15.05 \mathrm{~L} \mathrm{~mol}^{-1} \mathrm{~s}^{-1}\)

The rate constant is 15.05 L mol^-1 s^-1.

Example 2. The rate of formation of a dimer in a second-order dimerization reaction is 9.1 x 10^-6 mol L^-1 s^-1 at 0.05 M monomer concentration. Calculate the rate constant.
Solution:

Given

The rate of formation of a dimer in a second-order dimerization reaction is 9.1 x 10^-6 mol L^-1 s^-1 at 0.05 M monomer concentration.

For a second-order reaction

rate = k[A]²

or 9.1 x10⁶ =k(0.05)²

⇒ \(k=\frac{9.1 \times 10^{-6}}{(0.05)^2}=3.64 \times 10^{-3} \mathrm{~L} \mathrm{~mol}^{-1} \mathrm{~s}^{-1}\)

Example 3. Consider the following data the reaction.

A + B → product

Determine the order of reaction with respect to A and B, and the overall order of the reaction,
Solution:

In experiments 1 and 2, the concentration of B is constant. Hence,

⇒ \(\frac{\text { rate }_1}{\text { rate }_2}=\frac{k[\mathrm{~A}]_1^a[\mathrm{~B}]_1^b}{k[\mathrm{~A}]_2^a[\mathrm{~B}]_2^b}=\frac{k[\mathrm{~A}]_1^a}{k[\mathrm{~A}]_2^a}\)

⇒ \(\log \text { rate }_1-\log \text { rate }_2=a \log \frac{[\mathrm{A}]_1}{[\mathrm{~A}]_2}\)

On substituting the respective values, we get

⇒ \(\log 2.1 \times 10^{-3}-\log 8.4 \times 10^{-3}=a \log \left(\frac{0.1}{0.2}\right)=a \log (0.5)\)

or, \(-2.6778-(-2.0758)=a(-0.3010)\)

or, \(-0.6021=a(-0.3010)\)

or, \(\frac{0.6021}{0.3010}=a\)

⇒ a = 2.

The order with respect to A is 2.

Now consider experiments 2 and 3, where the concentration of A is the same. We get

⇒ \(\log \text { rate }_2-\log \text { rate }_3=b \log \left(\frac{[\mathrm{B}]_2}{[\mathrm{~B}]_3}\right)\)

or, \(\log 8.4 \times 10^{-3}-\log 8.4 \times 10^{-3}=b \log \left(\frac{1}{2}\right)\)

b log (0.5) = 0

⇒ b = 0 [as log (0.5) ≠ 0].

The order with respect to B is zero. Hence the overall order is a + b = 2.

Example 4. The following data was obtained at 300 K for the reaction 2A + B → C+ D.

Calculate the rate of formation of D when [A] = 0.7 mol L^-1 and[B] = 0.3 mol L^-1.
Solution:

In experiments 1 and 4, the concentration of B is the same.

Therefore, \(\log \frac{\text { rate }_1}{\text { rate }_4}=a \log \frac{[\mathrm{A}]_1}{[\mathrm{~A}]_4}\)

⇒ \(\log \frac{4 \times 10^{-3}}{1.6 \times 10^{-2}}=a \log \left(\frac{0.1}{0.4}\right)\)

log 0.25 = a log (0.25)

a = 1.

The order with respect to A is one.

In experiments 2 and 3, the concentration of A is the same. Therefore,

⇒ \(\log \frac{\text { rate }_2}{\text { rate }_3}=b \log \frac{[\mathrm{B}]_2}{[\mathrm{~B}]_3}\)

or, \(\log \frac{4.8 \times 10^{-2}}{1.92 \times 10^{-1}}=b \log \left(\frac{0.2}{0.4}\right)\)

or log 0.25 = blog (0.5)

⇒ -0.6021 = b(-0.3010)

⇒ b = 2.

The order with respect to B is two.

Hence, the overall order of the reaction is 3. The rate law for the reaction is

rate = k[A][B]².

Taking the observed values from any one of the experiments (say 1) and substituting the rate and concentration of A and B, we get

4 x 10¯³ = k(0.1)(0.1)²

⇒ \(k(0.1)(0.1)^2=4 \times 10^{-3} \Rightarrow k=\frac{4 \times 10^{-3}}{1 \times 10^{-3}}=4 \mathrm{~L}^2 \mathrm{~mol}^{-2} \mathrm{~min}\)

The value of the rate can now be determined with A = 0.7 mol L^-1 and B = 0.3 mol L^-1 by simply substituting the values of the concentrations and k in the rate law.

Rate = 4 x (0.7)(0.3)2 = (2.8)(0.09).

∴ rate = 0.252 mol L¯¹ min¯¹

Example 5. For a reaction A+B → C the following data was obtained.

By plotting a graph of reaction rate vs. concentration of the reactant, find the order of the reaction.
Solution:

In experiments 1 2,3 and 4 the concentration of B is much more than that of A. Hence, these data can tv used to determine order with respect to A,

⇒ \(\text { Rate }=K \mid A]^a[B]^b\)

⇒ \(\text { Nate }=K(A)^2\)

Since the plot of rate vs. concentration of A is a straight line, the reaction is of the first order with respect to A. In experiments 5, 6. 7, and 8 the concentration of A is in excess and hence these data can be used to determine the order with respect to B. A plot of rate vs. concentration of B is obtained as given below on the right.

Since we obtain a line parallel to the x-axis, the rate is independent of the concentration of B. The reaction is of zero order with respect to B. Even without plotting the graph, a close look at the data tells us that the rate is constant for all experiments 4-8 even though the concentration of B is varying. Hence the order is zero with respect to B. The overall order of the reaction is 1 + 0 =1.

Example 6. The reaction between NO and H₂ occurs as follows.

2H₂(g) + 2NO(g)₄ – 2H₂O(g) + N₂(g)

Several experiments were performed by keeping the concentration of one of the reactants constant and changing the concentration of the other. The initial rates obtained are tabulated below.

What is the order of the reaction with respect to NO and H₂? Write down the rate law. Calculate the rate constant k.
Solution:

In experiments 1, 2, and 3 the concentration of NO is constant; the data from these experiments give us the order of the reaction with respect to H₂. (The symbol 0 in the subscript denotes the initial conditions.)

The plot of -log rate 0 vs -log [H₂]₀ is a straight line with slope 1.

Hence, the order with respect to H₂ is one. Similarly, we can plot -log rate O vs -log[NO]₀ for experiments 4, 5, and 6.

The slope obtained from the plot gives a value of 2, which is the order with respect to NO.

Hence, the overall order = order (H₂) + order (NO)

=1 + 2

= 3.

Hence, the reaction is of the third order.

The rate law is rate = k[H₂][NO]₂.

Taking the observed values from any one of the experiments and substituting the concentration of H₂ and NO, we get (experiment 1)

⇒ \(3 \times 10^{-3}=k \cdot\left(1 \times 10^{-3}\right)\left(6 \times 10^{-3}\right)^2\)

⇒ \(k=\frac{3 \times 10^{-3}}{6 \times 10^{-9}}=0.5 \times 10^6=5 \times 10^5 \mathrm{dm}^6 \mathrm{~mol}^{-2} \mathrm{~s}^{-1}\)

Example 7. The reaction A+ B → C was studied by performing several experiments and the following information was obtained.

What is the order of the reaction with respect to A anti that with respect to B Write down the rate law.

Calculate the rate constant, k.

Solution:

In experiments 1, 2, and 3, the concentration of A is constant; hence these data can give us the order with respect to B.

In the initial rate method, \(-\log \text { rate }_0 \text { vs }-\log [\mathrm{B}]_0\) is plotted

The slope can be determined from the two corresponding values on the x- and y-axes.

For instance,

⇒ \(\frac{y_2-y_1}{x_2-x_1}=\frac{4-3.39}{1-0.7} \cong 2\).

Therefore the order with respect to B is two.

Using the values obtained from experiments 4 and 5, we get the following data.

The rate is independent of the concentration of A. Hence, the reaction is of zero order in A.

Therefore, the overall order of the reaction (2 + 0) = 2.

Hence, the rate law of the reaction,

rate = k[A]°[B]².

On substituting the values obtained from experiment 1 in the rate law equation, we calculate the
rate constant.

0.0001 = k[0.1][0.1]²

⇒ \(\frac{0.0001}{(0.1)^3}=k\)

k- 0.1 L mol^-1 s^-1

Example 8. A first-order reaction is 30% complete in one hour. Calculate the rate constant for the reaction. In how much time will the reaction proceed to 80% completion?
Solution:

Given

A first-order reaction is 30% complete in one hour. Calculate the rate constant for the reaction.

For a first-order reaction, the integrated rate law is

⇒ \(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=-k t\)

If the reaction proceeds to 30% completion, it means 30% of [A] has been consumed and 70% [A] remains.

Substituting 100 for [A]⁰ 70 for [A] and 60 min for t, we get

⇒ \(\ln \left(\frac{70}{100}\right)=-k \times 60\)

or, 2.303 log (0.7)= -k x 60

or, \(k=\frac{\log (0.7)}{60}=5.95 \times 10^{-3} \mathrm{~min}^{-1}\)

For the reaction to proceed to 80% completion, A must become 20.

In \(\ln \left(\frac{20}{100}\right)=-5.95 \times 10^{-3} \times t\)

or, \(t=\frac{-2.303 \log (0.2)}{1.12 \times 10^{-3}}=270.5 \mathrm{~min}\)

Example 9. A reaction that is of the first order with respect to reactant A has a rate constant of 5 min^-1. If we start with 5 mol L^-1 of A, would the concentration of A reach 0.05 mol L^-1?
Solution:

Given

A reaction that is of the first order with respect to reactant A has a rate constant of 5 min^-1. If we start with 5 mol L^-1 of A,

For a first-order reaction

⇒ \(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=-k t\),

where [A] is the concentration of A at time t and [A]⁰ is the initial concentration of A.

Substituting the values of [A] = 0.05 mol L^-1, [A]⁰ =5 mol L^-1and k =5 min^-1, we get

⇒ \(\ln \frac{0.05}{5}=-5 t\)

or, \(-\frac{1}{5} \ln \frac{0.05}{5}=t\)

⇒ \(-\frac{1}{5} \times 2.303 \log 0.01=t\)

⇒ \(-0.4606 \log \left(1 \times 10^{-2}\right)=t\)

⇒ -0.4606 x (-2) =t

⇒ 0.9212 = t

∴ t= 0.9212 min or 55.2 s.

It takes 55.2 seconds for the concentration of A to reach 0.05 mol L^-1.

Example 10. For the isomerization of cyclopropanone to propene in the gaseous phase at 433°C, the following data were obtained.

Find the order of the reaction and calculate the rate constant.
Solution:

If it is a first-order reaction, a plot of In \(\frac{[\mathrm{A}]}{[\mathrm{A}]_0}\) vs. t should be a straight line. Considering [A]⁰ =100 and the other values at various times as [A], we can calculate In \(\left(\frac{[\mathrm{A}]}{[\mathrm{A}]_0}\right)\)

A plot of In \(\frac{[\mathrm{A}]}{[\mathrm{A}]_0}\) vs f is a straight line with slope = -0.046

Hence it is n first-order reaction.

Since slope = -k,

k = 0.046 hours^-1

⇒ \(\frac{0.046}{3600}=1.277 \times 10^{-5} \mathrm{~s}^{-1}\)

Example 11. The rate of decomposition of hydrogen peroxide at a particular temperature was measured by titrating its solution acidic KMn04 solution. The following results were obtained

Show that it is a first-order reaction. Calculate the rate constant of the reaction.
Solution:

The titer value of KMnO₄ is proportionate to the amount of H₂O₂ left undecomposed.

For a first-order reaction,

In \(\frac{[\mathrm{A}]}{[\mathrm{A}]_0}\) = -kt and a plot of in \(\frac{[\mathrm{A}]}{[\mathrm{A}]_0}\) vs t is a straight line.

[A]₀ = 22.8 (at time = 0 min).

Since the plot is a straight line, the reaction is of the first order.

And slope = -0.051 = -k

=> k= 0.051 min^-1.

Example 12. Consider the decomposition of SO₂Cl₂ to SO₂ and Cl₂. It follows first-order kinetics at 675 K. If the rate constant is 2×10^-5 min^-1, find the percentage of SO₂Cl₂ that decomposes in 57.7 hours.
Solution:

Given

Consider the decomposition of SO₂Cl₂ to SO₂ and Cl₂. It follows first-order kinetics at 675 K. If the rate constant is 2×10^-5 min^-1,

For a first-order reaction

⇒ \(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=-k t ; \text { let } \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=\mathrm{X}\)

Then, In \((X)=-2 \times 10^{-5} \times 57.7 \times 60\)

⇒ \(\log X=-\frac{0.06924}{2.303}=-0.0300\)

X = 0.9332.

The ratio of SO₂Cl₂ remaining undissociated to the initial amount is 0.9332.

0.93 x 100= 93% of SO₂Cl₂ remains undissociated.

This means 100- 93 = 7% of SO₂Cl₂ would have dissociated in 57.7 hours.

Example 13. The dehydration of oxalic acid occurs according to the equation

H₂C₂O4 → CO + CO₂ + H₂O

The reaction is followed by titrating oxalic acid With KMnO₄. In one such experiment, the following data were obtained.

Find the order of the reaction and the rate constant.
Solution:

Here, we are titrating the oxalic acid that remains undissociated. Hence, the litre value at zero time gives the initial concentration of oxalic acid and other titer values indicate the amount of oxalic acid left behind.

For a first-order reaction a plot of In [A] vs. t must be a straight line.

In [A] = In [oxalic acid remaining undissociated].

Since we do not know the tire concentration of oxalic acid, the ratio of the titer values can give us the ratio of concentrations. At time 0 min, tire initial concentration, [A]₀ = 50.

The value of k can be determined from the equation

⇒ \(k=-\left(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}\right) \times \frac{1}{t}\)

Since the value of k is constant, the reaction is of the first order.

Half-life

The half-life of a reactant, denoted by f_1/2, is the time taken for the concentration of a reactant to fall to half of it initial amount.

For a first-order reaction, we can find the half-life of reactant A by substituting

⇒ \([\mathrm{A}]=\frac{1}{2}[\mathrm{~A}]_0 \text { and } t=t_{1 / 2}\)

Equation 4.3, so that

⇒ \(\ln \left(\frac{\frac{1}{2}[\mathrm{~A}]_0}{[\mathrm{~A}]_0}\right)=-k t_{1 / 2}\)

⇒ \(t_{1 / 2}=-\left[\ln \left(\frac{1}{2}\right)\right] \times\left(\frac{1}{k}\right)=\frac{\ln 2}{k}=\frac{0.693}{k}\)

It is interesting to note that the half-life of a first-order reaction does not depend on the initial concentration of the reactant. Natural and artificial radioactive decay takes place through first-order reactions.

The integrated rate law for a zero-order reaction is given by

[A] = -kt +[A]⁰.

Substituting \([\mathrm{A}] \text { by } \frac{1}{2}[\mathrm{~A}]_0 \text { and } t \text { by } t_{1 / 2} \text {, we get }\)

⇒ \(\frac{1}{2}[\mathrm{~A}]_0=-k t_{1 / 2}+[\mathrm{A}]_0\)

or, \(+k t_{1 / 2}=[\mathrm{A}]_0-\frac{1}{2}[\mathrm{~A}]_0\)

or, \(k=\frac{1}{2} \frac{[\mathrm{A}]_0}{t_{1 / 2}}\)

or, \(t_{1 / 2}=\frac{[\mathrm{A}]_0}{2 k}\)

where [A]⁰ is the initial concentration of the reactant and k, is the rate constant.

The half-life of a zero-order reaction is directly proportional to the initial concentration of the reactant.

Example 1. The following data were obtained for the decomposition of N₂O₂, which is a first-order reaction

Determine the value of the specific rate constant and the half-life of the reaction.
Solution:

For a first-order reaction,

⇒ \(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=-k t\)

If a graph is plotted between t and ln[N205], we obtain a straight line with slope = -k.

⇒ \(\text { Slope }=\frac{Y_2-Y_1}{X_2-X_1}=\frac{-0.35}{10}=-0.035=-k\)

⇒ k =0.035 min^-1.

⇒ \(\text { Half-life, } t_{1 / 2}=\frac{0.693}{k}=19.8 \mathrm{~min}\)

Example 2. The half-life for the reaction (first order)

⇒ \(\mathrm{N}_2 \mathrm{O}_5 \rightarrow 2 \mathrm{NO}_2+\frac{1}{2} \mathrm{O}_2\) is 2.4 hours at 30°C.

1. Starting with 100 g of N₂O₂, how many grams will remain after a period of 9.6 hours?
2. How much time should be required to reduce 5x 10⁵ molecules o/N₂O₂ to 10 molecules?

Solution:

Half-life means the time taken for half of the reactant to disappear. If we start with 100 g, after one half-life 50 g will remain. Now of this 50 g, half the amount = 25 g will remain after another half-life, and so on.

1. After 2.4 hours,\(\frac{1}{2}\) x 100 =50 g will remain.

After 4.8 hours, \(\frac{1}{2}\) (50) = 25 g will remain.

After 7.2 hours, \(\frac{1}{2}\)(25) =12.5 g will remain.

After 9.6 hours, \(\frac{1}{2}(12.5)=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times 100=6.25 g\) will remain,.

We can derive a general formula here.

After 4 half-lives, \(\left(\frac{1}{2}\right)^4\) (100) g will remain.

Therefore, after n half-lives, \(\left(\frac{1}{2}\right)^n\left(C_0\right)\) of the substance will remain, where CO is the initial amount present.

2. \(t_{1 / 2}=2.4 \text { hours }\)

For a first-order reaction,

⇒ \(k=\frac{0.693}{t_{1 / 2}}=\frac{0.693}{2.4}=0.288 \text { hour }^{-1}=\frac{0.288}{60 \times 60} \mathrm{~s}^{-1}\)

⇒ \(8.02 \times 10^{-5} \mathrm{~s}^{-1}\)

⇒ \(\ln \frac{[\mathrm{A}]}{[\mathrm{A}]_0}=-k t\)

⇒ \(2.303 \log \left(\frac{10^5}{5 \times 10^5}\right)=-8.02 \times 10^{-5} \times t\)

⇒ \(t=\frac{2.303 \log \left(\frac{1}{5}\right)}{-8.02 \times 10^{-5}}=\frac{-1.6097}{-8.02 \times 10^{-5}}=20071.42 \mathrm{~s}\)

⇒ \(\frac{20071.4}{3600} h=5.57\)

It will take 5.57 hours = 5 hours 34.2 min for reducing 5 x10⁵ molecules to 10⁵ molecules

Example 3. The thermal decomposition of N₂O₂ follows first-order reaction kinetics.

2N₂O₂(g) 4NO₂(g)+ O₂(g)

Rate= k[N₂O₂].

What will happen to the rate if the concentration of N₂Os is doubled and halved?
Solution:

Since the rate is directly proportional to [N₂O₅], increasing the concentration to double its value will double the value of the rate of the reaction (as k remains constant). Similarly, decreasing the concentration of N₂O₂ to half of its value will result in the rate being reduced to half.

Example 4. Consider the oxidation of nitric oxide

⇒ \(2 \mathrm{NO}(\mathrm{g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{NO}_2(\mathrm{~g})\)

The rate law is given as

rate= \(\text { rate }=[\mathrm{NO}]^2\left[\mathrm{O}_2\right]\)

How will the rate of the reaction be affected when the concentration of NO is doubled, NO is tripled and (c) O2 is doubled?
Solution:

The rate depends on the square of the concentration of NO.

On doubling the concentration, rate = k{2 x [NO]}₂[O₂ ] = k x 4[NO]₂[O₂]

The new rate will then be 4 times the earlier one. On tripling the concentration of NO, the rate will be 3 or 9 times the original rate. When the concentration of O₂ is doubled, the rate will be doubled as the rate depends directly on the first power of O₂

Determination of rate law

It is very important to note that a rate law is established experimentally and cannot in general be inferred from the chemical equation for the reaction. One of the methods for the determination of the rate law is called the Ostwald method in which the concentration of one of the reactants is much less than that of the others. Consider a reaction with two reactants A and B, If the reactant B is taken in excess, then even when the reaction reaches completion, the concentration of B is only marginally affected. It is a good approximation to take its concentration as a constant throughout the reaction. Even if the true rate law is

rate = k[A][B],

we say that rate =k[A] where k’ = k[B]0 where [B]0 is the initial concentration of the reactant B, which hardly changes. Since the true law has been forced into an effective first-order form, it is called a pseudo-first-order rate law and the reaction under such conditions is a pseudo-first-order reaction.

For example, consider the reaction between ozone and NO.

O₃ + NO → O₂ + NO₂

or that between O₃ and NO₂.

O₃+ 2NO_{2 →} 2N₃ + O₂

Both these reactions are of the second order overall and of the first order with respect to each reactant.

Rate = k[O₃][NO].

Rate = k[O₃][NO₂].

The integrated rate law for a reaction that is of the first order with respect to two reactants is complicated.

However, a simple rate law expression can be derived for such a reaction when the concentration of one of the reactants is much higher than that of the other. The concentration of O₃ is generally hundreds to thousands of times greater than the concentration of NO in polluted air. The concentration of ozone remains more or less constant during the course of the reaction.

The rate law can be simplified to

rate = k[NO],

where k = k[O₃]0 where [O₃]0 is the initial concentration of ozone.

The above rate law looks like the rate law of a first-order reaction; it appears to obey first-order kinetics. It is hence called a pseudo-first-order reaction and the rate constant is called the pseudo-first-order rate constant.

Temperature dependence of reaction rate

For many chemical reactions, the rate increases as the temperature is raised. You must have noticed that curd sets faster in summer than in winter. When the temperature is relatively high metabolic reactions are faster. It is said that fever is our friend because we fight infection with a fever.

The rise in the body temperature upsets the balance of mission rates in the foreign organism, thus preventing it from further invading the body. Also, an increase in the temperature of the body kills the invading organism. Reaction rates are found to increase exponentially with an increase in temperature. In general, for a 10 C rise in temperature, the reactions become two or three times faster. For example, the rate of hydrolysis of sucrose is 4.1 times more at 35’Cl than at 25cC.

Arrhenius’s equation:

In 1889 Arrhenius studied the data accumulated on reaction rates and found that the rate constant k of most chemical reactions increases exponentially as a function of temperature, T. The mathematical form of this relation is called Arrhenius’s equation, which is as follows.

⇒ \(k=A \exp \left(-\frac{E_a}{R T}\right)\)

Here, k is the rate constant, A is called the pre-exponential factor, frequency factor, or collision frequency. It is also simply called the Arrhenius constant. Ea is called the activation energy. The term exp \(\left(-\frac{E_a}{R T}\right)\) represents an activation state factor. Collectively these quantities (A and Ea) are called Arrhenius parameters.

Activation energy:

Activation energy is the minimum energy required for a chemical reaction to take place. It is the minimum kinetic energy required by reactant molecules to break bonds and form new ones (those of products).

To understand the concept of activation energy better, consider a boulder that has to be moved up a hill.

The boulder initially at position B loses some of its potential energy when it reaches position C. However, it should have sufficient kinetic energy to cross the barrier at A. As the boulder moves from position B to A, it gradually loses its kinetic energy and gains potential energy.

If the kinetic energy of the boulder is higher than its potential energy at A, it can cross and reach the other side of the hill. From here, it can simply slide down to reach C, The minimum energy required by the boulder to cross the barrier is the activation energy. It is the difference between the energy at B and that at A.

Let us now consider the following chemical reaction.

A + BC → AB + C

If the reaction occurs in a single step, the reactant molecules collide with each other, and the electron distribution about the three nuclei (A, B, and C) changes in the course of a collision such that a new bond between A and B is formed and at the same time the bond between B and C breaks.

Between the reactant stage and product stage, the nuclei pass through a stage in which all three species (A, B, and C) are weakly linked together. This has a higher potential energy than both reactants and products.

The reactants must gain enough energy to overcome this energy barrier. The energy actually comes from the ‘ kinetic energy of the molecules which is converted into potential energy. The height of the potential energy barrier is called activation energy.

Taking the natural logarithm of both sides of Arrhenius’s equation, we get

⇒ \(\ln k=\ln A-\frac{E_a}{R T}=\ln A-\left(\frac{E_a}{R}\right)\left(\frac{1}{T}\right)\)

A graph plotted between In k (In of rate constant) and \(\frac{1}{T}\) where T is the absolute temperature at which k is measured, is a straight line with a slope equal to \(-\frac{E_a}{R}\). The intercept is In A, from which A can be calculated.

Activation energy may also be calculated if the rates are available at only two temperatures. At temperature T1, the above equation becomes

⇒ \(\ln k_1=\ln A-\left(\frac{E_a}{R}\right) \cdot \frac{1}{T_1}\)

At temperature T2, it becomes

⇒ \(\ln k_2=\ln A-\left(\frac{E_a}{R}\right) \cdot \frac{1}{T_2}\)

Subtracting the first equation from the second,

⇒ \(\ln k_2-\ln k_1=-\frac{E_a}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right) \text { or } \ln \left(\frac{k_2}{k_1}\right)=-\frac{E_a}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)\)

This equation can be used to calculate Ea from the rate constants and k2 at temperatures Ta and T2.

Example 1. The rate constant first-order reaction becomes five times the original rate constant when the temperature rises from 350 K to 400 K. Calculate the activation energy for the reaction.
Solution:

Given

The rate constant first-order reaction becomes five times the original rate constant when the temperature rises from 350 K to 400 K.

⇒ \(\ln k=\ln A-\frac{E_a}{R T}\) (Arrhenius’s equation)

At T = 350 K, let the rate constant = k.

∴ at T = 400 K, the rate constant = 5k.

Substituting the values at 350 K and 400 K,

⇒ \(\ln k=\ln A-\frac{E_a}{8.314 \times 350}\)

and In (5k) = \(\ln A-\frac{E_a}{8.314 \times 400}\)

Subtracting Equation (1) from equation (2), we have

⇒ \(\ln (5 k)-\ln k=-\frac{E_a}{8.314 \times 400}+\frac{E_a}{8.314 \times 350}\)

⇒ \(\ln \left(\frac{5 k}{k}\right)=\frac{E_a}{8.314}\left(\frac{-1}{400}+\frac{1}{350}\right)\)

⇒ \(\ln 5=\frac{E_a}{8.314}\left(-2.5 \times 10^{-3}+2.857 \times 10^{-3}\right)\)

⇒ \(\frac{1.609 \times 8.314}{3.57 \times 10^{-4}}=E_a\)

⇒ \(E_a=37.47 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

Example 2. The rate constants for the decomposition of HI at different temperatures are as follows.

Find the value of the activation energy for this reaction.
Solution:

A plot of In k vs \(\frac{1}{T} \text { gives }\left(-\frac{E_a}{R}\right)\) as the slope.

⇒ \(\text { Slope }=-22727.2=-\frac{E_a}{R}\)

⇒ \(E_a=R \times 22727.2=8.314 \times 22727.2=188954.5 \mathrm{~J} \mathrm{~mol}^{-1}\)

or, \(E_a=188.9 \mathrm{~kJ} \mathrm{~mol}^{-1}\)

The activation energy for the decomposition of HI is 188.9 kJ mol^-1.

Effect of catalyst

Yet another very important factor determining the rate of a reaction is the presence of a catalyst. A catalyst is a substance that increases the rate of a reaction without itself undergoing any permanent chemical change. An example is manganese dioxide, which speeds up the thermal decomposition of potassium chlorate.

⇒ \(2 \mathrm{KClO}_3(\mathrm{~s}) \stackrel{\mathrm{MnO}_2 \text {, heat }}{\longrightarrow} 2 \mathrm{KCl}(\mathrm{s})+3 \mathrm{O}_2(\mathrm{~g})\)

In the absence of a catalyst, KClO₃ decomposes very slowly, even when heated, but when a small amount of MnO₂

is mixed with the KClO₃ before heating, the rapid evolution of oxygen takes place. The MnO₂ can be recovered unchanged after the reaction is complete.

Most industrial processes, such as the manufacture of ammonia, sulphuric add, nitric acid, and polymers, involve the use of catalysts. Biological catalysts or enzymes affect the rates of reactions taking place during metabolic activities.

How does a catalyst work? It increases the rate of a reaction by lowering the activation energy. The potential energy barrier between the reactants and products is reduced, thus facilitating a faster reaction (Figure 4.13). A catalyst participates in the chemical reaction by forming an intermediate complex with the reactants, which finally breaks down to form the products, and the catalyst is obtained back. The concentration of the catalyst does not appear in the rate law of any reaction because while it is consumed in one step, it is regenerated in another step. Let us consider the decomposition of H₂O₂

⇒ \(2 \mathrm{H}_2 \mathrm{O}_2(\mathrm{aq}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g})\)

This reaction has a high activation energy of 76 kJ mol^-1 at room temperature and hence this decomposition is very slow. In the presence of the iodide ion, the reaction is appreciably faster because it proceeds by a different, lower-energy, pathway.

\(\begin{gathered}
\mathrm{H}_2 \mathrm{O}_2(\mathrm{aq})+\mathrm{I}^{-}(\mathrm{aq}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{IO}^{-}(\mathrm{aq}) \\
\mathrm{H}_2 \mathrm{O}_2(\mathrm{aq})+\mathrm{IO}^{-}(\mathrm{aq}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g})+\mathrm{I}^{-}(\mathrm{aq}) \\
\hline 2 \mathrm{H}_2 \mathrm{O}_2(\mathrm{aq}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{O}_2(\mathrm{~g})
\end{gathered}\)

The H₂O₂ first oxidizes the catalyst I^– to the hypoiodite ion (IO^–) and then reduces the intermediate IO^– back to I^-1. The activation energy is, thus, lowered by 19 kJ mol^-1.

Collision Theory and Transition State Theory

Two theories have been put forward which explain the mechanistic and energetic aspects of chemical reactions. These are the collision theory and the transition state theory.

Collision theory:

According to the collision theory, an atom, ion or molecule can undergo a reaction only when it collides with another atom, ion or molecule. The reacting atoms, ions or molecules are assumed to be hard spheres. However, only a small number of collisions result in a chemical reaction. The following conditions must be fulfilled for a collision to be effective.

1. The transfer or sharing of electrons between the colliding species must give a structure that is capable of existence. In other words, stable bonds or new stable chemical species should be formed.

2. The collision must take place with sufficient energy—the outer electronic shells of the atoms should penetrate each other to some extent so that the bonding electrons can be rearranged.

3. The orientation of the molecules when they collide must that the atoms directly involved in the sharing or transfer of electrons come into contact with each other

Now, let us consider these three aspects in a rate equation of a bimolecular elementary reaction(see section or reaction mechanisms) A + B → P.

The rate of the reaction can be expressed as

Rate = f x P x Z [A][B]

where P and Z represent the three aspects of collision theory, [A] and [B] are the reactant concentrations. The rate constant k then takes the form.

k = f x P x Z

To understand what ‘f’ denotes, let us see the effect of temperature on the above reacting system Changing the temperature of a reacting system has two effects.

On raising the temperature, molecules tend to move faster and hence there are a larger number of collisions but calculations show that only a small percentage of the rate increase with temperature can be accounted for by the larger number of collisions. The more important factor is the kinetic energy of the molecules and it is found that the average kinetic energy of molecules increases with an increase in temperature.

In other words, the activation energy required for the reaction to take place is provided by the collisions of the reactant molecules with each other or with the walls of the reaction vessel. Only a few fast-moving molecules will have enough energy to react if the activation energy is larger than the average kinetic energy of the molecules. The kinetic energy is converted to the potential energy of the molecule.

If the activation energy is smaller than the kinetic energy, then the fraction of molecules having the required kinetic energy will be large and most collisions will result in the reaction. As a result, the reaction will be fast.

The fraction of molecules (f) that possesses kinetic energy equal to or greater than Ea is equal to \(e^{-E_f / k T}\) as in Arrhenius’s equation. As the temperature increases, the curve broadens resulting in an increase in the fraction of molecules having an energy Ea, As T increases, \(\frac{1}{T}\) decreases, and f increases exponentially, Z in Equation 4.7 is called the collision frequency and is defined as the number of collisions per second per unit volume of the reaction mixture.

For collisions between reactant molecules A and B, Z is represented as Though a large fraction of molecules may possess kinetic energy greater than the activation energy, all collisions between such molecules may not lead to products. This is the third aspect of collision theory.

The fraction of collisions that lead to products is restricted by the requirement of proper orientation of the colliding molecules. This is represented by the probability or steric factor P, which denotes the fraction of collisions in which the reacting molecules have the right orientation to form the product.

For example, in the reaction, between HCl and NH₃ to form NH₄Cl, the N end of NH3 must hit the H end of HCl. Such a collision which results in the formation of a product is called an effective collision. Collision of the N of NH₃ with Cl of HCl does not result in Hr formation of NH₄Cl and hence it is termed as ineffective collision. The following shows an effective and an ineffective collision for the reaction between HCl and NH-.,

The value of P is usually between 0 and 1. The rate constant can thus be written as

k = fPZ_AB = PZ_AB e^-2Ea/RT

It is interesting to note that tins resemble Arrhenius’s equation (Equation 4.6) and by a comparison of those two equations, we got

A = PZ_AB

where A is the Arrhenius factor.

Arrhenius’s equation reflects two aspects of the collision theory of reaction rates. The frequency factor A indicates the number of collisions that lead to a proper orientation of the reactant species to enable the formation of products, The exponential term \(e^{\left(-E_a / RT\right)}\) the fraction of collisions in which the energy of the reacting spades is greater than Ea

Limitation of collision theory:

The values of rate constants calculated using the collision theory are in agreement with the experimental values only for simple bimolecular reactions. This is because the molecules are considered to be hard spheres and the vibrations and rotations within them are ignored. There is no way of determining P. It can only be obtained by comparing the theoretically calculated A (Arrhenius factor) and the experimentally observed value. You will study more about this theory in higher classes,

Transition state theory

A different theory as to how reactions take place pictures the formation of a transition slate by the two (or more) reacting molecules instead of their collision. The molecules undergoing reactions are considered to be approaching each other and under each other’s influence, a transition state is formed.

The tire transition state or the activated complex is a combination of reacting molecules, intermediate between reactants and products. Some bonds begin to break while new ones begin to form.

For example, in the reaction between ammonia and methyl bromide, the N-C bond begins to form in the transition state, the C-Br bond begins to weaken, and partial charges develop on tire nitrogen and bromine atoms.

⇒ \(\mathrm{NH}_3+\mathrm{CH}_3 \mathrm{Br} \longrightarrow\left[\mathrm{CH}_3 \mathrm{NH}_3\right]^{+}+\mathrm{Br}^{-}\)

An activated complex cannot ordinarily be isolated. It breaks down to give either reactants or products depending on the conditions of the reaction.

The energy of the transition state is higher than that of the two reactants by an amount of Ea —the activation energy. For the reaction to take place, the sum of tire kinetic energies of A and B must be will least equal to or greater than E„.

After reaching the transition state, the molecules start losing energy and ultimately reach a state of energy even lower than that of the initial state. The energy thus lost is transferred to other molecules and they reach the transition state; the reaction proceeds in this the size of the activation energy barrier depends on the direction from which it is approached.

If the reaction is exothermic in the forward direction, Ea is smaller in the forward direction than in the reverse direction. It is easier to cross the smaller energy barrier in the case of the exothermic reaction than in the reverse endothermic reaction.

At the same temperature, some reactions have a high activation energy and some have a low activation energy. If we compare two reactions at the same temperature, the one with a lower activation energy will be fast and have a high rate constant whereas the one which has a higher activation energy will have lower k and lower rate.

Increasing the temperature increases the value of \(e^{\left(-E_a / R T\right)}\) and hence gives a larger k. A rise in temperature also increases A. Any change in the conditions of the reaction that increases the number of collisions with a favorable orientation of the molecules results in a high value of k.

Reaction mechanisms

Most chemical reactions occur in a series of elementary reaction steps, rather than in a single step.

The process or pathway by which a reaction occurs actually is called the reaction mechanism or reaction path.

A balanced chemical equation does not tell us anything about the actual pathway (steps in the reaction); it just tells us what molecules and how many of them react to form what kind of products. The mechanism of a reaction can be deduced from a knowledge of the rate law of that reaction.

As already discussed, the rate law and order of a reaction have to be experimentally determined, and once determined, a mechanism for the reaction can be suggested. Here, we shall look at the mechanisms of some simple reactions.

First, consider the example of the decomposition of ozone. The chemical equation for the overall reaction is

2O₃ → 3O₂

The reaction, however, appears to follow a mechanism involving two steps.

O₃ → O₂ + O

O+O₃ → 2O₂

Atomic oxygen is produced in the first step and is consumed in the second step. Hence it is not shown in the overall reaction. Such species which are produced in one step and consumed in another are called intermediates.

Most reactions proceed in several steps involving one or more reaction intermediates. These intermediates may be short-lived or may persist. The rate of such a multistep reaction is determined by the slowest step.

Now consider a reaction involving two consecutive steps of the first order. If in a chemical reaction, a reactant produces an intermediate (I) which decays to form the product (P), we can say that the reaction takes place in two steps.

A → I Rate of formation of I = k₁[A]

I → P Rate of formation of P = k₂[I]

Shows that the concentration of the intermediate (I) grows and reaches a maximum initially.

Meanwhile, the concentration of the product also rises. After the concentration of the intermediate reaches a maximum, it decays to zero and that of the product reaches its final value.

An example of such a reaction is the radioactive decay of uranium. The half-lives of uranium and neptunium are given.

⇒ \({ }^{239} \mathrm{U} \stackrel{23.5 \mathrm{~min}}{\longrightarrow}{ }^{239} \mathrm{~Np} \stackrel{2.35 \text { days }}{\longrightarrow}{ }^{239} \mathrm{Pu}\)

An intermediate may also be formed when we have two reactants; an example of such a reaction is the enzyme-catalyzed reaction in which a substrate S is converted to products. The proposed mechanism is

⇒ \(\mathrm{E}+\mathrm{S} \rightleftharpoons \mathrm{ES} \rightarrow \text { products }+\mathrm{E}\)

where E is the enzyme and ES is the intermediate, a state in which the enzyme is bound to the substrate.

The rate-determining step:

Reactions that take place in more than one step are called complex reactions. Each complex reaction is generally a combination of a sequence of elementary reactions, which we refer to as steps. The overall balanced equation for a reaction is the sum of its elementary steps.

Elementary reactions individually may involve one or more molecules. Those involving a single molecule are called unimolecular while those that involve two molecules are called bimolecular. Similarly, there may be tennolecular reactions (involving three molecules), and so on.

The molecularity of an elementary reaction refers to the number of reacting particles, viz., atoms, molecules, or ions, in that particular step. The order and molecularity of a reaction are two different aspects.

While the order is determined experimentally and may or may not be the same as the stoichiometry of the molecule under consideration, the molecularity of the reaction can be judged from the stoichiometry of a particular step of a reaction.

The order of a reaction is applicable to an elementary as well as a complex reaction while molecularity is applicable only to an elementary reaction. The order may be zero or fractional but molecularity can only be a positive integer. The order is determined by the slowest step in a complex reaction, i.e., the rate-determining step.

Generally, the molecularity of the rate-determining step is the same as the order of the overall reaction. To understand this better, let us consider the mechanism for the oxidation of the iodide ion by H₂O₂ in an acid medium and find the rate equation. For the reaction

⇒ \(\mathrm{H}_2 \mathrm{O}_2+2 \mathrm{H}^{+}+2 \mathrm{I}^{-} \rightarrow \mathrm{I}_2+2 \mathrm{H}_2 \mathrm{O}\)

the suggested mechanism is

⇒ \(\mathrm{H}_2 \mathrm{O}_2+\mathrm{I}^{-} \rightarrow \mathrm{OH}^{-}+\mathrm{HOI}\) (slow)

⇒ \(\mathrm{H}^{+}+\mathrm{OH}^{-} \rightarrow \mathrm{H}_2 \mathrm{O}\) (fast)

⇒ \(\mathrm{HOI}+\mathrm{H}^{+}+\mathrm{I}^{-} \rightarrow \mathrm{I}_2+\mathrm{H}_2 \mathrm{O}\) (fast)

Since the slowest step determines the rate, the rate equation for the reaction is

⇒ \(\text { rate }=-\frac{d\left[\mathrm{H}_2 \mathrm{O}_2\right]}{d t}=k\left[\mathrm{H}_2 \mathrm{O}_2\right]\left[\mathrm{I}^{-}\right]\)

Let us consider one more example and see how the rate law is In agreement with the rate-determining step.
Consider the decomposition of NO₂.

2NO₂(g) → 2NO(g) + O₂(g)

This reaction is of the second order with respect to NO₂. The two steps in which this reaction occurs are

2NO₂ → NO+NO₃

NO₃ → NO+O₂

In the first step, a collision between a pair of NO₂ molecules produces a short-lived activated complex in which the two molecules share an oxygen atom. Such activated complexes have a lifetime of ~ 10 ^-15 s and fall apart forming products or reactants.

To form products, the shared oxygen is transferred from one NO₂ molecule to another forming a molecule of NO and a molecule of NO₂. The NOa thus formed decomposes in the second step again by the formation of another activated complex.

NO₂ is called the intermediate in this mechanism as it is produced in one step and consumed in the next. Intermediates are neither considered as reactants nor as products and hence do not appear in the equation describing the reaction.

The lines between the atoms just show that a bond exists between the two—the nature of the bond is not shown.

The observed rate law which indicates an order of 2 with respect to NO₂ can be predicted for step 1 but not for step 2. This means that the rate of the overall reaction is controlled by step 1 rather than step 2. The first step is the controlling step which is also the slower of the two in this case and is called the rate-determining step.

The rate for the first step is

⇒ \(\text { rate }=-\frac{\Delta\left[\mathrm{NO}_2\right]}{\Delta t}=k_1\left[\mathrm{NO}_2\right]^2\)

If the rate constant k1 is much less than that for step 2, k2, then

⇒ \(\text { rate }=-\frac{\Delta\left[\mathrm{NU}_3\right]}{\Delta t}=k_2\left[\mathrm{NO}_3\right]\)

In fact, it has been found that

k₁ << k₂.

In an unimolecular reaction, a single molecule shakes itself apart or its atoms into a new arrangement as in the isomerization of cyclopropane to propene.

⇒ \(\underset{\text { Cyclopropane }}{\Delta} \rightarrow \mathrm{CH}_2=\underset{\text { Propene }}{\mathrm{CH}}-\mathrm{CH}_3\)

An unimolecular elementary reaction is of the first order. For example in a reaction A → B,

⇒ \(\frac{d[\mathrm{~A}]}{d t}=-k[\mathrm{~A}]\)

In a bimolecular elementary reaction, two molecules collide with each other and then react. Such a reaction is of second order; the rate is proportional to the concentrations of the two reactants.

For a reaction of the type A + B → product

⇒ \(\frac{d[\mathrm{~A}]}{d t}=-k[\mathrm{~A}][\mathrm{B}]\)

Chain reactions:

A chain reaction is a complex reaction comprising a sequence of reactions in which the intermediate formed in the first step generates a reactive intermediate in the subsequent step, and so on. The intermediates responsible for the propagation of a chain reaction are called chain carriers. They may be radicals ions, or neutrons in nuclear fission reactions.

The steps in a chain reaction are classified as the initiation step, propagation step, and termination step. There can be more than one propagation or termination step possible for a chain reaction. Many gas-phase reactions and liquid-phase polymerization reactions are chain reactions. The formation of HBr from H2 and Br2 is a chain reaction.

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Br}_2(\mathrm{~g}) \rightarrow 2 \mathrm{HBr}(\mathrm{g})\)

The rate law for the reaction is complicated.

⇒ \(\frac{d[\mathrm{HBr}]}{d t}=\frac{k\left[\mathrm{H}_2\right]\left[\mathrm{Br}_2\right]^{3 / 2}}{\left[\mathrm{Br}_2\right]+k^{\prime}[\mathrm{HBr}]}\)

where k and K are the rate constants for the forward and reverse reactions respectively.

The following mechanism has been proposed.

Initiation \(\mathrm{Br}_2+\mathrm{Br}_2 \rightarrow \mathrm{Br}+\mathrm{Br}+\mathrm{Br}_2\)

or \(\mathrm{Br}_2+\mathrm{H}_2 \rightarrow \dot{\mathrm{Br}}+\dot{\mathrm{Br}}+\mathrm{H}_2\)

Propagation \(\dot{\mathrm{Br}}+\mathrm{H}_2 \rightarrow \mathrm{HBr}+\dot{\mathrm{H}}\)

or \(\dot{\mathrm{H}}+\mathrm{Br}_2 \rightarrow \mathrm{HBr}+\dot{\mathrm{Br}}\)

Retardation \(\dot{\mathrm{H}}+\mathrm{HBr} \rightarrow \mathrm{H}_2+\dot{\mathrm{Br}}\)

Termination \(\dot{\mathrm{Br}}+\dot{\mathrm{Br}}+\mathrm{H}_2 \rightarrow \mathrm{Br}_2+\mathrm{H}_2^*\)

\(\dot{\mathrm{Br}}+\dot{\mathrm{Br}}+\mathrm{Br}_2 \rightarrow \mathrm{Br}_2+\mathrm{Br}_2^*\)

A dot indicates a free radical and a star indicates an activated molecule.

As you already know, free radicals are highly reactive. The chain reaction continues until the termination step occurs. In this step, either Br₂ or H₂ removes the excess energy of recombination and exists as an activated (high-energy) molecule.