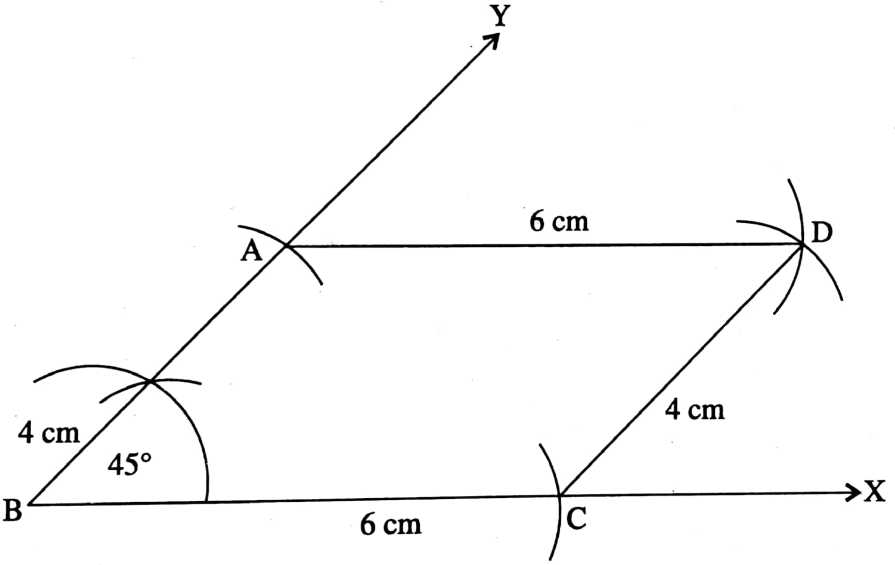
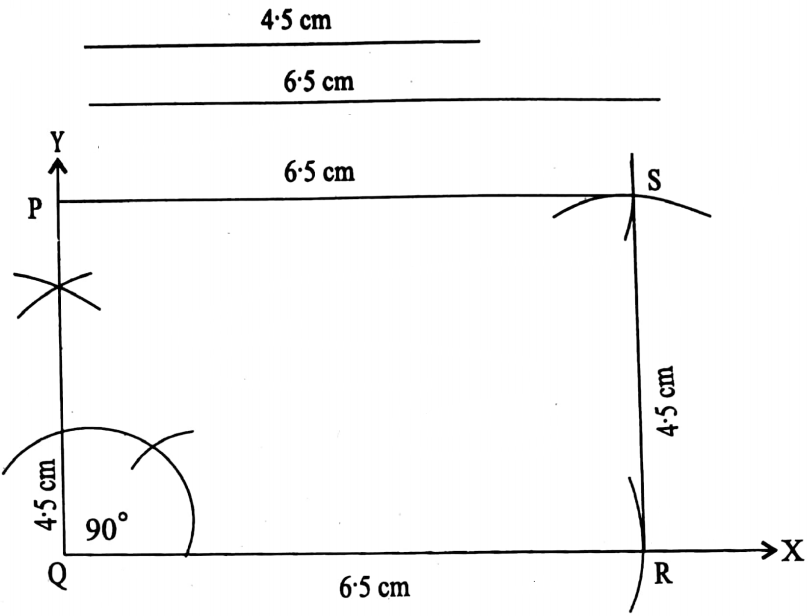
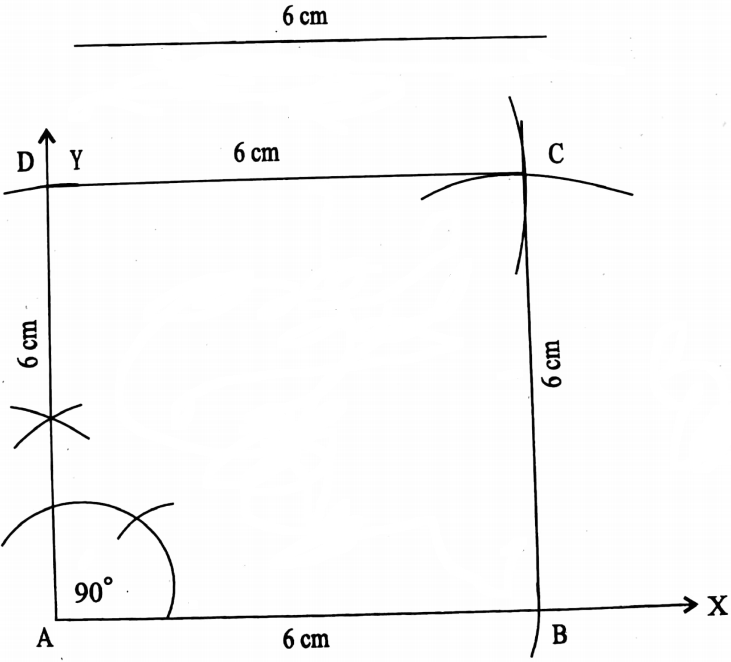
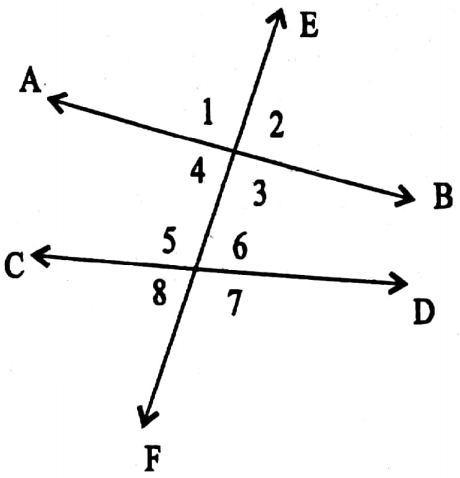
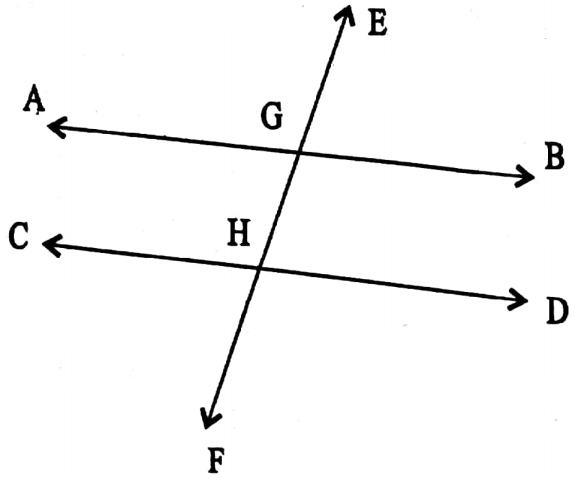
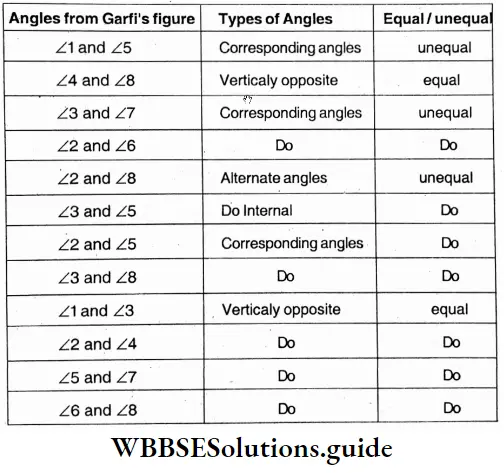
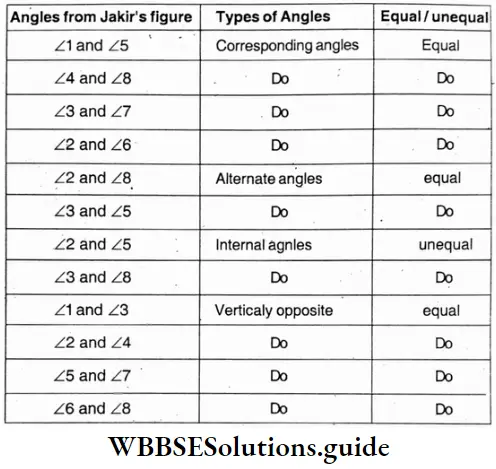
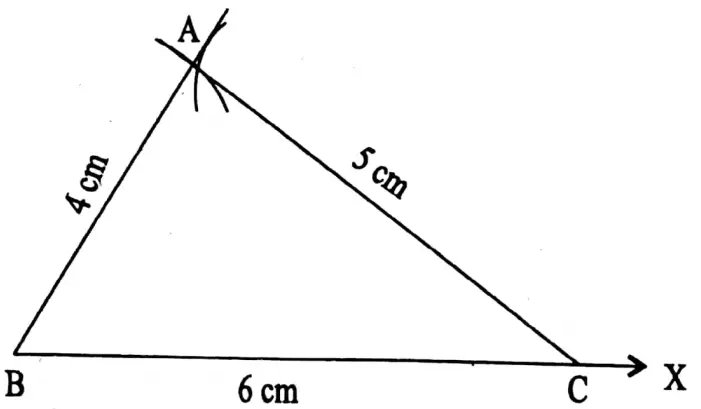
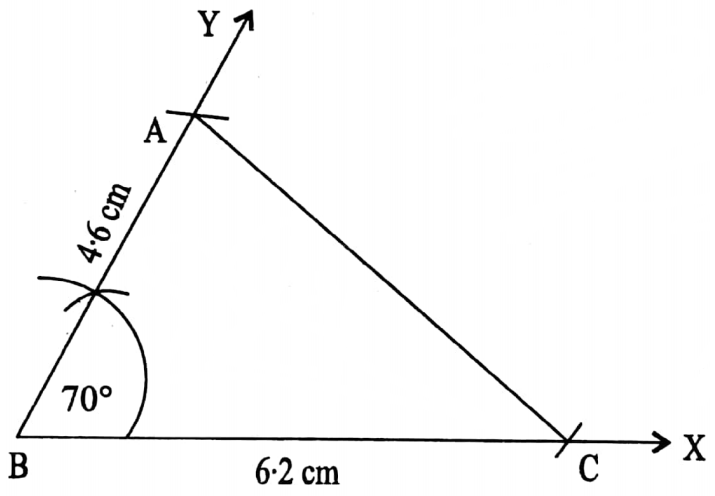
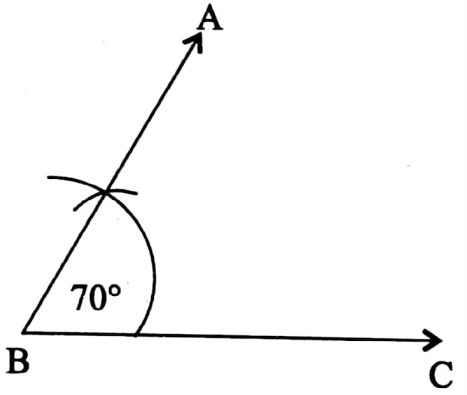
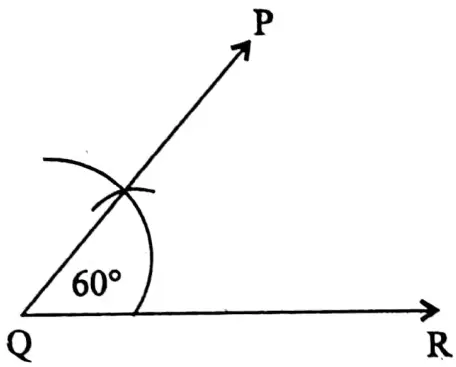
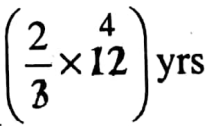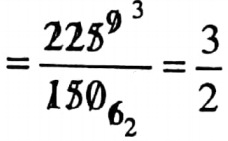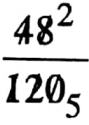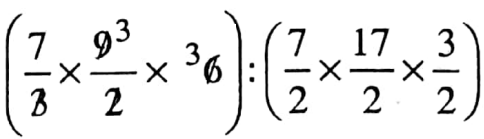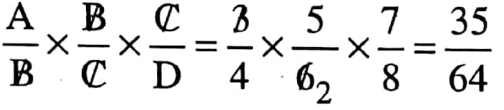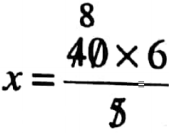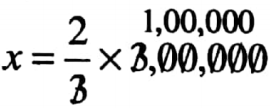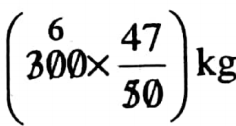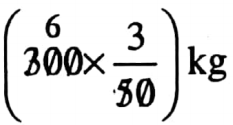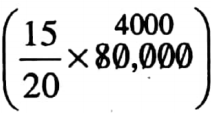Class 7 Maths

Class 7 Math Solution WBBSE Algebra Chapter 1 Revision Of Old Lesson Exercise 1 Solved Problems

Question 1. Choose the correct answer

1. The sum of 9 and (-y) is

1. y – 9
2. 9+ y
3. 9-y
4. None of these

Solution: Sum of 9 and (- y) is 9 + (− y) = 9-y

So the correct answer is 3. 9-y

2. What must be added to (-17) to get 12?

1. -5
2. 5
3. -29
4. 29

Solution: The number which is added to (-17) to get 12 is {12 – (-17)} = 12 + 17 = 29

So the correct answer is 4. 29

Read and Learn More WBBSE Solutions for Class 7 Maths

3. The value of (-2)² x (-3)² x (-5) is

1. 180
2. -180
3. 120
4. -120

Solution: (-2)² × (-3)²× (-5)
= (-2) x (-2) × (-3) x (-3) x (-5)
= 4 × 9 × (-5)
= 36 x (-5)
= – 180

So the correct answer is 2. -180

Wbbse Class 7 Maths Solutions

Question 2. Write ‘true’ or ‘false‘

1. Profit of -10 rupees mean that loss of 10 rupees.

Solution: The statement is true.

2. If the length and breadth of a rectangle are x and y respectively, its semi-perimeter is 2(x + y).

Solution: Semi-perimeter is (x + y),

So the statement is false.

3. The difference of the two numbers is x. If the greater number is y, then the least number is (x + y).

Solution: The least number is (y-x)

So the statement is false.

Question 3. Fill in the blanks

1. The value of (-5)² x (-7) x (-6) is

Solution: (-5)² × (-7) × (-6)
= 25 × 42
= 1050

2. If perimeter of a square is x cm, then its area is _____ Sq. cm.

Solution: The perimeter of the square is x cm; the length of each side is \(\frac{x}{4}\) cm

Area is \(\left(\frac{x}{4}\right)^2\) sq. cm

= \(\frac{x^2}{16}\)

3. The absolute value of (-3) is _____

Solution: 3

Wbbse Class 7 Maths Solutions

Question 4.  Write in language the following expressions

1. \(\frac{x}{4}-3\)

2.

3. 3p-2

Solution:

1. \(\frac{x}{4}-3\)

Three less than one fourth of x.

2.

a is not less than four.

3. 3p-2

2 is less three times of p

Question 5. Form the algebraic expression with signs and symbols

1. 5 is subtracted from 4 times y
2. 4 is not less than x
3. x is not equal to y
4. sum of five times y and 6.

Solution:

1. 4y-5
2.
3. x ≠ y
4. 5y + 6

Question 6. Subtract using concept of opposite number 

1. (-13) – (-16)
2. (+12) – (-15)
3. (-17) – (+18)
4. (+10) – (+15)

Solution:

1. (-13) – (-16)
= (-13) + (opposite number of -16)
= (-13) + (+16)
= +3

2. (+12) – (-15)
= (+12) + (opposite number -15)
= (+12) + (+15)
= + 27

3. (-17) – (+18)
= (-17) + (opposite number of +18)
= (-17) + (-18)
=-35

4. (+10) – (+15)
= (+10) + (opposite number of +15)
= (+10) + (-15)
= -5

Wbbse Class 7 Maths Solutions

Question 7. Simplify 10 -(opposite number of – 25) – (opposite number of +12) – (opposite number of -18) – (-6)

Solution: = 10 – (+25) – (-12) – (+18) – (-6)
= 10 – 25+ 12 – 18+ 6
= (10+ 12 + 6) – (25 +18)
= 28-43
= – 15

Question 8. Add the following on number line

1. (-7), (+2)
2. (+4), (-8)

Solution:

1.

 

(-7) + (-2) = -5

2.

 

(+4) + (-8) = -4

Wbbse Class 7 Maths Solutions

Question 9. Verify associative property of addition (-5), (3), (+2)

Solution: {(-5)+(-3)}+(+2)
= (-8) + (+2)
= (-6)

(-5)+ {(-3) + (+2)}
= (-5)+(-1)
=-6

So, {(-5)+(-3)} + (+2) = (-5) + {(-3) + (+2)}

Question 10. Find what must be added to the first to get the second 

1. (-15), (-10)
2. (+6), (-18)

Solution:

1. The number which added to the (-15) to get (-10) is
(-10) (-15) = (-10) + 15 +5

2. The required number is (-18) (+6)=-18 -6 =-24

 

Class 7 Math Solution WBBSE Algebraic Formula

Algebraic Formula Exercise 12.1

Question 1. To find the square of the algebraic expressions given below using (a + b)² = (a² + 2ab+ b²) let’s find what has to be substituted for a and b in each case, and hence find their squares 

Let’s substitute a = x and b = 3.

1.  x + 3
Solution :

(x + 3)² = (x)² +2.x.3+ (3)²

= x² +6x + 9

2. p + 9
Solution:

(p+ 9)²= (p)² +2.p.9+ (9)²

= p²+ 18p + 81

3. 6 – x
Solution :

(6-x)² = (6)² -2.6.x + (x)²

= 36-12x +x²

4. y-2
Solution :

(y-2)² = (y)² -2.y.2 + (2)²

= y² -4y + 4

5. mn + I²
Solution :

(mn+l²)² = (mn)²+2.mn.l²+(l²)²

= m²n²+ 2mnl²+ l⁴

6. 6x + 3
Solution :

(6x + 3)² = (6x)² + 2.6x.3 + (3)²

= 36x² + 36x + 9

7. 4x + 5y
Solution:

(4x + 5y)² = (4x)²+2.4x.5y + (5y)²

= 16x² + 40xy + 25y²

8. pqc + 2
Solution :

(pqc + 2)² = (pqc)² + 2.pqc.2 + (2)²

= p²c²q² + 4pqc + 4

9. \(\left(\frac{5}{k}+3\right)\)
Solution:

⇒ \(\left(\frac{5}{k}+3\right)^2\)

⇒ \(\left(\frac{5}{k}\right)^2+2 \cdot \frac{5}{k} \cdot 3+(3)^2\)

= \(\frac{25}{k^2}+\frac{30}{k}+9\)

10. \(\left(\frac{3}{r}+\frac{2}{p}\right)\)
Solution:

⇒ \(\left(\frac{3}{r}+\frac{2}{p}\right)^2\)

= \(\left(\frac{3}{r}\right)^2+2 \cdot \frac{3}{r} \cdot \frac{2}{p}+\left(\frac{2}{p}\right)^2\)

= \(\frac{9}{r^2}+\frac{12}{r p}+\frac{4}{p^2}\)

11. \(\frac{p}{q}+\frac{m}{n}\)
Solution:

⇒ \(\left(\frac{p}{q}+\frac{m}{n}\right)^2\)

= \(\left(\frac{p}{q}\right)^2+2 \cdot \frac{p}{q} \cdot \frac{m}{n}+\left(\frac{m}{n}\right)^2\)

= \(\frac{p^2}{q^2}+\frac{2 p m}{q n}+\frac{m^2}{n^2}\)

12. m² +n²
Solution :

= (m² +n²)² = (m² )²+ 2.m².n²+(n²)²

= m⁴+2m²n²+n⁴

13. 3xy + 4z
Solution:

= (3xy + 4z)² = (3xy)² +2.3xy.4z+ (4z)²

= 9x²y² +24 xyz+16z²

14. 2x + 3y + z
Solution :

= (2x + 3y + z)²

= (2x)² + (3y)²+ (z)² + 2.2x.3y+ 2.2x.z + 2.3y.z

= 4x² + 9y² + z² +12xy + 4xz + 6yz

15. 102
Solution:

= (102)² = (100 + 2)²

= (100) ²+ 2.1 00.2+(2)²

= 10000 + 400 + 4 = 10404

16. p + q + r + s
Solution :

= (p+ q+.r + s)²

= (p)² + (q)² +(r)² + (s)²+ 2pq+ 2pr + 2ps+ 2qr+ 2qs+ 2rs

Class 7 Math Solution WBBSE Algebraic Formula Exercise 12.2

To find the squares of the algebraic expressions given below, using (a- b)² = (a)² -2ab + b² what has to be substituted for a and b in, and hence let’s find the squares.

1. x-5
Solution:

(x-5)² = (x)-2.x.5+ (5)²

= x² -10x + 25

2. m – n
Solution :

(m – n)² = (m)² -2.m.n+ (n)²

= m² -2mn+ n²

3. 10- x
Solution:

(10-x)² = (10)^² -2.10.x + (x)^²

= 100-20x + x^²

4. x +y
Solution:

(x+y)² = (x)² +2.x.y +(y)

= x^² + 2xy + y^²

5. 3x – y
Solution :

(3x-y)^²  = (3x)^²  – 2.3x.y +(y)²

= 9x^²  – 6xy + y^²

6. 4m + 2
Solution:

(4m + 2)^²   = (4m)^²  +2.4m.2+ (2)²

= 16m^² + 16m + 4

7. 5y + x
Solution:

(5y + x)^² = (5y)^² +2.5y.x +(x)^²

= 25y^² +10xy + x^²

8. ce-fg
Solution:

(ce-fg)^² = (ce)^² -2.ce.fg+ (fg)^²

= c^² e^² -2cefg + f^² g^²

9.  \(p x-\frac{1}{2}\)
Solution:

⇒ \(p x-\frac{1}{2}\)

= (px)² – 2. px \(\frac{1}{2}\) + \(\left(\frac{1}{2}\right)^2\)

= p²x² – px + \(\frac{1}{4}\)

10. p + q – r
Solution :

(p +q-r)²

= (p+q)²- 2+(p+q). r +(r)²

= p² + 2pq+ q²+ 2pr- 2qr + r²

= p² +q² + r² – 2pq+ 2pr-2qr

11. p – q + r
Solution:

(p-q + r)² = (p-q)²+ 2.(p-q).r + (r)²

= p² – 2pq + q² + 2pr- 2qr + r²

= p² + q² + r² -2pq+ 2pr-2qr

12. \(\frac{2 x}{3}-\frac{3 y}{4}\)

⇒ \(\left(\frac{2 x}{3}-\frac{3 y}{4}\right)^2\)

= \(\left(\frac{2 x}{3}\right)^2-2 \cdot \frac{2 x}{3} \cdot \frac{3 y}{4}+\left(\frac{3 y}{4}\right)^2\)

= \(\frac{4 x^2}{9}-x y+\frac{9 y^2}{16}\)

13. 3m³ – 4n³
Solution :

(3m³-4n³)² = (3m³)² -2.3m³.4n³ +(4n³)²

= 9m⁶ -24m³n³ +16n⁶

14. 2x + y – z
Solution :

(2x + y-z)² = (2x + y)²- 2.(2x + y). z + (z)²

= 4x² +2.2x.y + y² -4xz-2yz + z²

= 4x² +y² +z² +4xy-4xz-2yz

15. 999
Solution :

(1000-1)² = (1000)² -2.1000.1 + (1)²

= 1000000-2000 + 1

= 998001

14. p + q – r – s
Solution :

(p + q-r-s)²

= {(p+q)-(r+ s)}²

= p+ q²-2.(p+ q).(r+ s)+(r+ s)²

= p² + 2pq + q² – 2pr- 2ps- 2qr + 2qs + r² + 2rs + s²

= p² + q² + r² + s² + 2pq- 2pr- 2ps- 2qr + 2qs + 2rs

WB Class 7 Math Solution Algebraic Formula Exercise 12.3

Question 1. Which one of the following is equal to the product of (a + b) x (a +b)

1. a² + b²
2. (a + b)²
3. 2(a + b)
4. 4ab

Solution: 2. (a + b)²

(a + b) (a + b) = a² + ab + ab + b² = a² + 2ab + b² = (a + b)²

Question 2. Let’s find, which of the following will be the value for k satisfying the identity (x + 7)² = x² + 14x + k.

1. 14
2. 49
3. 7
4. None of these

Solution: 2. 49

(x + 7)² = x²+2.x.7+ (7)² = x² +14x + 49

Question 3. Which one of the following algebraic expressions must be added to a² + b² so that the sum is a perfect square? Let’s find.

1. 4ab
2. – 4ab
3. 2ab or – 2ab
4. a²+b²+2ab = (a + b)²

Solution:  3. 2ab or – 2ab

a²+b²+2ab = (a + b)²

a² + b² – 2ab = (a – b)²

Question 4. If (a+ b)² = a² +6a + 9, let’s find, which of the following is the positive value for b.

1. 9
2. 6
3. 3
4. -3

Solution: 3. 3

(a + b)² = a² + 6a + 9

= a²+2.a.3 + (3)²

Question 5. Let’s find, which one of the following numbers when added to \(x^2+\frac{1}{4} x\) makes it a perfect square

1. \(\frac{1}{64}\)
2. – \(\frac{1}{64}\)
3. \(\frac{1}{8}\)
4. None of these

Solution: \(\frac{1}{64}\)

= \(x^2+\frac{1}{4} x\)

= \(x^2+2 \cdot x \frac{1}{8}+\left(\frac{1}{8}\right)^2-\frac{1}{64}\)

= \(\frac{1}{64}\)

Question 6.

1. Let’s find, for which values of k, will the expression c² + kc + \(\frac{1}{9}\) be a perfect square.
Solution:

c²  + kc + \(\frac{1}{9}\)

= \((c)^2 \pm 2 \cdot c \cdot \frac{1}{3}+\left(\frac{1}{3}\right)^2\)

= \(c^2 \pm \frac{2}{3} c+\left(\frac{1}{3}\right)^2\)

K = ± \(\frac{2}{3}\)

2. Let’s find what must be added or subtracted from \(9 p^2+\frac{1}{9 p^2}\) make it a perfect square.
Solution:

⇒ \(9 p^2+\frac{1}{9 p^2}\)

⇒ \((3 p)^2+\left(\frac{1}{3 p}\right)^2 \pm 2.3 p \cdot \frac{1}{3 p}\)

⇒ \((3 p)^2+\left(\frac{1}{3 p}\right)^2 \pm 2\)

⇒ \(\left(3 p \pm \frac{1}{3 p}\right)^2\)

= (2) or (-2)

3. If (x-y) = 4-4y + y² then let’s find the value of x.
Solution :

(x- y) = 4- 4y + y²

= (x- y)² = (x)² – 2xy + (y)

∴ x²= 4

∴  x = 2

4. If (c-3) = c² + kc + 9 , let’s find the value of k.
Solution :

(c-3) = c²+kc + 9 = (c)²-2.c.3+ (3)² .

∴ K = – 6

Question 7. Let’s simplify by using a formula.

1. (2q- 3z)²- 2 (2q- 3z)(q- 3z)+ (q- 3z)²
Solution:

= (2q- 3z)² – 2 (2q- 3z)(q- 3z)+ (q- 3z)²

= {(2q- 3z)-(q- 3z)}²

= (2q- 3z- q + 3z)²

= q²

2. (3p+ 2q- 4r)² + 2(3p + 2q- 4r)(4r- 2p- q) + (4r- 2p- q)²
Solution :

= (3p+ 2q-4r)² +2(3p+ 2q-4r)(4r-2p-q)+(4r-2p-q)²

= {(3p + 2q- 4r) + (4r- 2p- q))²

= (3p+ 2q- 4r + 4r- 2p- q)²

= (p+ q)²

= p² + 2pq + q²

Question 8. Let’s express the following as a perfect square.

1.  16a ² -40ac+ 25c²
Solution :

16a ² – 40ac + 25c².

= (4a)² – 2. 4a .5c +(5c)²

= (4a -5c)²

2. 4p²- 2p + \(\frac{1}{4}\)
Solution:

4p²- 2p +  \(\frac{1}{4}\)

= (2p)² – 2. 2p. \(\frac{1}{2}+\left(\frac{1}{2}\right)^2\)

= \(\left(2 p-\frac{1}{2}\right)^2\)

3. \(1+\frac{4}{a}+\frac{4}{a^2}\)
Solution:

⇒ \(1+\frac{4}{a}+\frac{4}{a^2}\)

⇒  \((1)^2+2 \cdot 1 \cdot \frac{2}{a}+\left(\frac{2}{a}\right)^2\)

⇒  \(\left(1+\frac{2}{a}\right)^2\)

4. 9a²+ 24ab + I6b²
Solution:

9a² +24ab+ I6b²

= (3a)² +2.3a.4b + (4b)²

= (3a + 4b)²

Question 9. Let’s express the following as a perfect square and hence find the values.

1.  64a² +16a +1 When 3 = 1
Solution:

= 64a²+ 16a +1

= (8a)² + 2.8a.1 + (1)²

= (8a + 1)²

= (8a + 1+ 1)²

Putting a = 1

= (8+ 1)²

= (9)²

= 81

2. 25a² -30ab + 9b² When a = 3&b = 2
Solution :

= 25a² -30ab + 9b²

= (5a)² – 2. 5a. 3b + (3b)²

= (5a- 3b)²

= (5 × 3-3 × 2)² Putting a = 3, b = 2

= (15-6)² = (9)² =81

3. \(64-\frac{16}{p}+\frac{1}{p^2}\) When p = -1
Solution:

⇒ \(64-\frac{16}{p}+\frac{1}{p^2}\)

= \((8)^2-2 \cdot 8 \cdot \frac{1}{p}+\left(\frac{1}{p}\right)^2\)

= \(\left(8-\frac{1}{p}\right)^2\)

= \(\left(8-\frac{1}{-1}\right)^2\)

Putting p = -1

= (8+1)²

= (9)²= 81

4. p²q² + 10pqr + 25r² When p = 2, q =-1 and r= 3
Solution:

= p²q² +I0pqr + 25r²

= (pq)² +2.pq.r+ (5r)²

= (pq + 5r)²

= {2.(-1)+ 5.3}²

= (-2+ 15)²

= (13)² =169

Question 10. Let’s apply, (a + b)² +(a-b)² = 2(a²+b²) Or,  (a + b)² – (a- b)² = 4ab Or, ab = \(\left(\frac{a+b}{2}\right)^2-\left(\frac{a-b}{2}\right)^2\) to find the following

1. Let’s find st and (s² + t² ) when s + 1 = 12 and s – 1 = 8
Solution:

st = \(\left(\frac{s+t}{2}\right)^2-\left(\frac{s-t}{2}\right)^2\)

= \(\left(\frac{12}{2}\right)^2-\left(\frac{8}{2}\right)^2\)

= (6)²- (4)²

= 36-16= 20

(s² + t²) = (s+t)²+(s-t)²

= (12)² +(8)

= 144 + 64

= 208

s²+t² = \(\frac{208}{2}\)

= 104

2. Let’s find 8xy(x² + y²) when (x + y) = 5 and (x – y) = 5
Solution :

8xy(x² + y²)

= 4xy × 2(x² +y²)

= {(x+ y)² -(x-y)²}× {(x-y)²+ (x-y)²}

= {(5)²- (1)² } × (5)²- (1)² }

= (25-1) (25 + 1)

=(25)²-(1)²

= 625 – 1 = 624

3. Let’s find when \(\frac{x^2+y^2}{2 x v}\) = 9 and (x – y) = 5
Solution:

⇒\(\frac{x^2+y^2}{2 x v}\)

= \(\frac{(x+y)^2+(x-y)^2}{2} \times \frac{1 \times 2}{4 x y}\)

= \(\frac{(x+y)^2+(x-y)^2}{(x+y)^2-(x-y)^2}\)

= \(\frac{(9)^2+(5)^2}{(9)^2-(5)^2}\)‘

= \(\frac{81+25}{81-25}\)

= \(\frac{106}{56}\)

= \(\frac{53}{28}\)

4. Let’s express 36 as the difference of two squares[ Hints, 36= 4 × 9  \(\left(\frac{4+9}{2}\right)^2-\left(\frac{4-9}{2}\right)\)
Solution:

36 = 4 × 9

= \(\left(\frac{4+9}{2}\right)^2-\left(\frac{4-9}{2}\right)^2\)

5. Let’s express 44 as the difference of two squares.
Solution :

44 = 11 × 4

⇒ \(\left(\frac{11+4}{2}\right)^2-\left(\frac{11-4}{2}\right)^2\)

= \(\frac{(15)^2}{4}-\frac{(7)^2}{4}\)

= \(\frac{225}{4}-\frac{49}{4}\)

= \(\frac{225-49}{4}\)

6. Let’s express 8x² + 50y² as the sum of two squares.
Solution:

8x² + 50y²

= 2 × (4x² + 25y²) = 4x² + l0xy+ 25y²+ 4x² – 10xy + 25y²

= (2x +5y)² + (2x- 5y)²

7. Let’s express x as the difference of.two squares.
Solution :

= x = x . 1

⇒ \(\left(\frac{x+1}{2}\right)^2-\left(\frac{x-1}{2}\right)^2\)

WB Class 7 Math Solution Algebraic Formula Exercise12.4

Question 1. Using the identity (x+ a) (x + b) = x² + (a + b) x + ab, let’s find the product of the following algebraic expressions.

1. (x + 7) (x + 1)
Solution :

(x + 7) (x + 1)

= x² +(7 +1)x + 7

= x² + 8x + 7

2. (x – 8) (x – 2)
Solution :

(x – 8) (x – 2)

= x² +(-8- 2)x + (-8)(-2)

= x²-10x + 16

3. (x + 9) (x – 6)
Solution :

(x + 9) (x – 6)

= x² + (9- 6)x+ (9)(-6)

= x²+ 3x – 54

4.(2x+1)(2x-1)
Solution :

(2x +1 ) (2x – 1 )

= (2x)² + (1- 1)2x + (1)(-1)

= 4x²- 1

5. (xy – 4) (xy + 2)
Solution :

(xy – 4) (xy + 2)

= (xy)²+(-4 + 1)xy + (-4)(+2)

= x²y²- 2xy-8

6. (a² + 5) (a²- 4)
Solution :

(a² +5) (a² -4)

= (a²)² + (5- 4)a²+ + (5)(-4)

= a⁴+a^²-20

Question  2. Using the formula, let’s show that 

1. (2x + 3y)² – (2x- 3y)² = 24xy
Solution :

(2x + 3y)²- (2x- 3y)²

= (2x + 3y + 2x- 3y) (2x + 3y- 2x + 3y)

= 4x × 6y

= 24xy RHS.

2. (a+ 2b)² +(a- 2b)²=2 (a² + 4b²)
Solution :

(a + 2b)² +(a- 2b)²

= a² + 4ab + 4b²+ a²- 4ab + 4b²

= 2a² + 8b²

= 2(a² + 4b²) = RHS.

3. (l +m)²= (l-m)²+4lm
Solution :

LHS = (l+ m)² = l²+2 lm + m²

= I² – 2lm + m² + 4lm

= (l- m)² + 4lm = RHS.

4. (2p- q)² = (2p + q)²- 8pq
Solution:

= (2p-q)² = (2p)² -2.2p.q + (q)²

= (2p) -2.2p.q + (q)²- 8pq

= (2p-q)² – 8pq

5. (3m + 4n)² = (3m- 4n)² + 48mn
Solution:

(3m + 4n)²

= (3m)² + 2.3m. 4n + (4n)²

= (3m)² -2.3m.4n +(4n)²+ 48mn

=  (3m- 4n)² + 48mn = R.H.S.

6. (6x + 7y)²- 84xy = 36x² + 49.y²
Solution :

(6x+ 7y)² – 84xy

84xy = 36x² + 2.6x.7y + 49 y² – 84xy

= 36x² -2.6x.7y + 9y² -84xy

= 36x² + 49y² = R.H.S.

7. (3a + 4b)² + 24 ab = 9a² +16b²
Solution:

= (3 – 4b)² +24ab

= (3a –  4b)²+ 24ab = 9a²- 2.3a.4b+(4b)² + 24ab

= 9a²- 24ab + 16b² + 24ab

= 9a² + 16 b²

8. \(\left(2 a+\frac{1}{a}\right)^2=\left(2 a-\frac{1}{a}\right)^2+8\)
Solution:

⇒  \(\left(2 a+\frac{1}{a}\right)^2\)

= \((2 a)^2+2 \cdot 2 a \cdot \frac{1}{a}+\left(\frac{1}{a}\right)^2\)

= \((2 a)^2-2 \cdot 2 a \cdot \frac{1}{a}+\left(\frac{1}{a}\right)^2+8 a \cdot \frac{1}{a}\)

= \(\left(2 a-\frac{1}{a}\right)^2+8\)

= R.H.S

Question  3. Using formula, let’s solve each of the following problems 

1. Let’s find the value of x² + y² when x – y = 3, xy = 28
Solution:

x² +y²

– x² + y² =(x- y)² + 2xy

= (3)² +2.2.8

= 9 + 56

= 65

2. Let’s find the value of ab when a² + b² = 52, a – b = 2
Solution:

ab = \(\frac{-\left(a^2+b^2\right)-(a-b)^2}{2}\)

= \(\frac{52-(2)^2}{2}\)

= \(\frac{52-4}{2}\)

= \(\frac{+48}{2}\)

= + 24

3. Let’s find the value of Im when l² + m² = 13, l + m = 5
Solution:

lm = \(\frac{(l+m)^2-\left(l^2+m^2\right)}{2}\)

= \(\frac{(5)^2-13}{2}\)

= \(\frac{25-13}{2}\)

= \(\frac{12}{2}\)

= 6

4. Let’s find the value of \(a^2+\frac{1}{a^2}\) when \(a+\frac{1}{a}\)= 4
Solution :

⇒ \(a^2+\frac{1}{a^2}\)

\(a^2+\frac{1}{a^2}=\left(a+\frac{1}{a}\right)^2-2 \cdot a \cdot \frac{1}{a}\) – 2

= (4)² – 2

= 16-2 = 14

5. Let’s find the value of \(a^2+\frac{1}{a^2}\) when = \(a-\frac{1}{a}\)= 4
Solution :

⇒ \(a^2+\frac{1}{a^2}\)

= \(a^2+\frac{1}{a^2}=\left(a-\frac{1}{a}\right)^2+2 \cdot a \cdot \frac{1}{a}\)

= (4)²+4

= 16 +2 = 18

6. If \(5 x+\frac{1}{x}\) = 6 lets show 25x²+ \(\frac{1}{x^2}\) = 26
Solution:

⇒ \(5 x+\frac{1}{x}\)= 6

= \(\left(5 x+\frac{1}{x}\right)^2\)

= (6)²= 36

L.H.S = \(25 x^2+\frac{1}{x^2}+2.5 x \cdot \frac{1}{x}\) = 36

L.H.S = \(25 x^2+\frac{1}{x^2}\) = 36 – 10

= 26 R.H.S

7. If \(2 x+\frac{1}{x}=5\) 1 let’s find the value of \(4 x^2+\frac{1}{x^2}\)
Solution:

= \(4 x^2+\frac{1}{x^2}\)

= \(4 x^2+\frac{1}{x^2}=\left(2 x+\frac{1}{x}\right)^2-2 \cdot 2 x \cdot \frac{1}{x}\)

= (5)²- 4

= 25-4

= 21

8. \(\frac{x}{y}+\frac{y}{x}\)= 3 , let find the value of \(\frac{x^2}{y^2}+\frac{y^2}{x^2}\) ,
Solution:

⇒ \(\frac{x^2}{y^2}+\frac{y^2}{x^2}\)

⇒  \(\frac{x^2}{y^2}+\frac{y^2}{x^2}\)= \(\left(\frac{x}{y}+\frac{y}{x}\right)^2-2 \cdot \frac{x}{y} \cdot \frac{y}{x}\)

= (3)²- 2

= 9-2= 7

9. If x² +y² = 4xy ,  let’s prove that .x⁴+ y⁴ = 14x²y²
Solution :

x² + y² = 4xy

Or, (x²+y²)= (4xy)²

Or, x⁴ + y⁴ + 2x²y²= 16x²y²

Or,  x⁴ +y⁴ =16x²y²=14x²y²

10. If \(2 a+\frac{1}{3 a}\)= 6, then let’s find the value of \(4 a^2+\frac{1}{9 a^2}\)
Solution:

⇒ \(4 a^2+\frac{1}{9 a^2}\)

= (2a)²+ \(\left(\frac{1}{3 a}\right)^2+2 \cdot 2 a \cdot \frac{1}{3 a}-\frac{4}{3}\)

= \(\left(2 a+\frac{1}{3 a}\right)^2-\frac{4}{3}\)

= (6)² – \(\frac{4}{3}\)

= 36 – \(\frac{4}{3}\)

= \(\frac{108-4}{3}\)

= \(\frac{104}{3^{-}}\)

= 34 \(\frac{2}{3}\)

11. If \(\) = 5, Then let’s find the value of \(25 a^2+\frac{1}{49 a^2}\)
Solution:

⇒ \(25 a^2+\frac{1}{49 a^2}\)

= \(\left(5 a+\frac{1}{7 a}\right)^2-2 \cdot 5 a \cdot \frac{1}{7 a}\)

= \((5)^2-\frac{10}{7}\)

= \(25-\frac{10}{7}\)

= \(\frac{175-10}{7}\)

= \(\frac{165}{7}\)

= \(23 \frac{4}{7}\)

12. If \(2 x-\frac{1}{x}=4\) , lets show that \(x^2-\frac{1}{4 x^2}\)
Solution:

⇒ \(2 x-\frac{1}{x}=4\)

Or, \(x-\frac{1}{2 x}=2\)

Or, \(\left(x-\frac{1}{2 x}\right)^2\) = (2)

Or, \(x^2+\frac{1}{4 x^2}-2 \cdot x \cdot \frac{1}{2 x}=4\)

Or, \(x^2+\frac{1}{4 x^2}\)

= 4+1

= 5

13. lf m + \(\frac{1}{m}\) = -p, let’s show that \(m^2+\frac{1}{m^2}\) p²- 2
Solution :

m + \(\frac{1}{m}\) = -p

or,\(\left(m+\frac{1}{m}\right)^2\) =(- p)²

Or, \(m^2+\frac{1}{m^2}+2 \cdot m \cdot \frac{1}{m}\) = p²

Or,\(m^2+\frac{1}{m^2}\) = p² – 2

14. lf a² + b² = 5ab, let’s show that \(\frac{a^2}{b^2}+\frac{b^2}{a^2}\) – 23.
Solution :

= a² + b² = 5ab

Or, \(\frac{a^2}{a b}+\frac{b}{a b}=\frac{5 a b}{a b}\)

Or, \(\frac{a}{b}+\frac{b}{a}\) = 5

Or, \(\left(\frac{a}{b}+\frac{b}{a}\right)^2\) = (5)²

= 25

Or, \(\frac{a^2}{b^2}+\frac{b^2}{a^2}+2 \cdot \frac{a}{b} \cdot \frac{b}{a}\) = 25

Or, \(\frac{a^2}{b^2}+\frac{b^2}{a^2}\) = 25 -2

= 23

15. If 6x² +1 = 4x> let’s show \(36 x^2+\frac{1}{x^2}\) = 28
Solution:

= 6x² +1 = 4x

Or, \(\frac{6 x^2}{x}-\frac{1}{x}\)

Or, 6x  \(\frac{1}{x}\) = 4

Squaring both sides

⇒ \(\left(6 x-\frac{1}{x}\right)^2=(4)^2\)

Or, \(36 x^2+\frac{1}{x^2}\)

= 16 +12

= 28

16. If \(m+\frac{1}{m}\)= p-2, then let’s show  \(m^2+\frac{1}{m^2}\) = p² – 4p + 6
Solution :

⇒ \(m+\frac{1}{m}\) = p-2

Or, \(\left(m+\frac{1}{m}\right)^2\)  + = (p-2)²

Or, \(m^2+\frac{1}{m^2}\) + 2m.\(\frac{1}{m}\) = p² -4p + 4

Or, \(m^2+\frac{1}{m^2}\) = p²-4p+ 4-2.

= P² – 4p + 2

18. If m= \(m-\frac{1}{m-2}\) = 6, then lats find the value of \((m-2)^2+\frac{1}{(m-2)^2}\)
Solution:

= m- \(\frac{1}{m-2}\) = 6

Or, m-2-\(\frac{1}{m-2}\)

= 6 – 2 = 4

Squaring both sides

⇒ \((m-2)^2-2 \cdot(m-2) \times\left(\frac{1}{m-2}\right)+\left(\frac{1}{m-2}\right)^2\) = (4)2

Or, \((m-2)^2-2+\frac{1}{(m-2)^2}\) = 16

Or, \((m-2)^2+\frac{1}{(m-2)^2}\) = 16+2

Or, \((m-2)^2+\frac{1}{(m-2)^2}\) = 18

WB Class 7 Math Solution Algebraic Formula Exercise 12.5

Question 1. In the identity No. (4) if x = a and a = b, then let’s find if it becomes identity No. (1).
Solution :

In the identity No. (4) ie.

(x + a) (x + b) = x² + (a + b)x + ab

When x = a & a = b

(a + b) (a + b) = a² + 2ab + b²

or, (a + b)² = a² + 2ab + b² . It is identified as No. (1)

Question 2. In the identity No. (4), let’s substitute x = a and a = – b, and verify if it becomes identity No. (3).
Solution:

In the identity No. (4) ie.

(x + a) (x + b) = x² + (a + b)x+ ab

(a-b) (a + b) = a² +(a-a)0 + (-b)(b)

= a²- b² It is identify No. (3)

Question 3. In identity (4), let’s substitute x = a and a = – b, and try to identify which identity it changes to.
Solution :

In identity No (4) ie.

(x + a) (x + b) = x²+ (a + b)x + ab

(a- b)(a +b) = a² + -ab + ab- b²

= a² – b²

Question 4. Using the formula (a² – b²) = (a + b) (a – b) let’s find the values 

1. (37)² – (13)²
Solution :

(37)² – (13)²

= (37+13) (37-13)

= 50 × 24 = 1200

(2.06)² – (0.94)²
Solution :

(2.06)² – (0.94)²

= (2.06 + 0.94) (2.06 – 0.94)

= (3.00) (1.12) = 3. 36

3. (78) × (82)
Solution :

(78) × (82)

= (80 – 2) (80 + 2)

= (80)² – (2)²

= 6400 – 4 = 6396

4. 1.15 × 0.85
Solution :

1.15 × 0.85

= (1.00 + .15) (1.00 – .15)

= (1)2-(.15)² = 1 – .0225

= 0.9775

5.(65)²- (35)²
Solution :

(65)²- (35)²

= (65 + 35) (65 – 35)

= 100 × 30 = 3000

Question 2.

 1. If k – p² = (9 + p) (9 – p) let’s find the value of k.
Solution :

k – p²= (9 + p) (9 – p)

= (9 + p)(9-p) =81 -p²

k = 81.

2. If (25 – 4x²) = (5 + ax) (5 – ax) let’s find the positive value of a.
Solution:

25 -4x² = (5 + ax) (5 – ax)

= 25 – a²x²

∴ a² = 4

∴ a = \(\sqrt{4}\) =2

3. Let us fill in the box, so that the identity (4 – x) x = (16 – x²) is satisfied.
Solution :

(4 – x) x = (1 6 – x²)

= (4)² – (x)²

= (4 – x) (4 + x)

= 4 + x

Question 3. Let’s express the following in the product form using a formula.

1. 25I² – 16m²
Solution:

25l²-16m²

= (5l)²-(43)²

= (5I + 4m) (5I – 4m)

2. 49x⁴ – 36y⁴
Solution :

49x⁴ – 36y⁴

= (7x²)² – (6y²)²

= (7x² + 6y²) (7x² – 6y²)

3. (2a + b)² – (a + b)²
Solution :

(2a + b)² – (a + b)²

‘= (2a + b + a + b) (2a + b – a – b)

= (3a + 2b) (a) = a(3a + 2b)

4. (x + y)² – (a + b)²
Solution :

(x + y)² – (a + b)²

= (x + y + a + b) (x + y – a – b)

5. (x + y – z)² – (x – y + z)²
Solution :

(x + y – z)² – (x – y + z)²

= (x + y – z + x – y + z) (x + y – z – x + y – z)

= 2x (2y – 2z) = 4x (y – z)

6. (m + p + q)² – (m – p – q)²
Solution :

(m + p> + q)² – (m – p – q)²

= (m + p + q + m – p – q) (m + p + q – m + p + q)

= 2m (2p + 2q) = 4m (p + q)

Question 4. Using the formula, let’s find the continued product of the following

1. (c + d) (c-d) (c² + d²)
Soluion :

(c + d) (c – d) (c² + d²)

= {(c)² -(d)²} (c² + d²)

= (c² – d²) (c² + d²)

= (c²)² – (d²)² = c⁴ – d⁴

2. (1 + 3x²) (1 + 3x²) (1 + 9x⁴)
Solution :

(1 + 3x²) (1 + 3x²) (1 + 9x⁴)

= {(1 )² – (3x²)²} (1 +9x⁴)

= (1 – 9x⁴) (1 + 9x⁴)

= (1² ) (9x⁴)²

= 1 – 81 x⁸

3. (a² + b²) (a² – b²) (a⁴ + b⁴) (a⁸ + b⁸)
Solution :

(a² + b²) (a² – b²) (a⁴ + b⁴) (a⁸ + b⁸)

= {(a²)² – (b²)^²} (a⁴ + b⁴) (a⁸ + b⁸)

= (a⁴ – b⁴) (a⁴ + b⁴) (a⁸ + b⁸)

= {(a⁴)² – (b⁴)²} (a⁸ + b⁸)

= (a⁸ – b⁸) (a⁸ + b⁸)

= (a⁸)² – (b⁸)²

= a¹⁶ – b¹⁶

Question 5. Let’s express the following in the product form.

1. 16c⁴ – 81 d⁴
Solution :

16c⁴ – 81

= (4c²)° – (9d²)²

= (4c² – 9d²) (4c² + 9d²)

= {(2c)² – (3d)²} (4c² + 9d²)

= (2c + 3d) (2c – 3d) (4c ²+ 9d²)

2. p⁴q⁴ – r⁴s⁴
Solution :

p⁴q⁴ – r⁴s⁴

= (p²q²)² (r²s²)²

= (p²q² + r²s²) (p²q² – r²s²)

= (P²q² + r²s²) {(pq)²- (rs)²}

= (p²q²+r²s²) (pq + rs) (pq – rs)

3. 81 – x⁴
Solution :

81 – x⁴

= (9)² – (x²)²

= (9 – x²) (9 + x²)

= {(3)² – (x)²} (9 + x²)

= (3 + x) (3 – x) (9 + x²)

4. 625 -a⁴b⁴
Solution :

625 -a⁴b⁴

= (25)²- (a²b²)²

= (25 – a²b²)(25 + a²b²)

= {(5)²-(ab)²} (25 + a²b²)

= (5 + ab) (5 – ab) (25 + ab)

Question 6. Let’s prove (p + q)⁴– (p – q)⁴ = 8pq (p² + q²)
Solution :

(p + q)⁴– (p – q)⁴ = 8pq (p² + q²)

LHS = {(P + q)² + (p – q)²} {(p + q)² – (P – q)²}

= (P² + 2pq + q² + p² – 2pq + q²) (p² + 2pq – q²)

= (2p² + 2q²) × 4pq

= 2 (p²q²) × 4pq

= 8pq (p² + q²) = RHS

Question 7. Using formula let’s multiply: (a + b + c) (b + c – a) (c + a – b) (a + b – c)
Solution :

(a + b + c) (b + c – a) (c + a – b) (a + b – c)

= (a + b + c) (a + b – c) (b + c – a) (c + a – b)

= {(a + b)² – c²} {c – (a – b)} {c + (a – b)}

= {(a + b)² – c²} {c² – (a -b)²}

= c² (a + b)² – c⁴ – (a – b)² (a + b)² + c² (a – b)²

= c² {(a + b)² + (a – b)²} – c⁴ – (a2 – b²)² .

=.c² (2a² + 2b²) – c⁴ – (a⁴ – 2a²b² + b⁴)

= 2a²c²+ 2b²c² + 2a²b² – a⁴ -b⁴ – c⁴

Question 8. If x = \(\frac{a}{b}+\frac{b}{a}\) and Y = \(\frac{a}{b}-\frac{b}{a}\) then ,et’s show that x⁴ + y⁴ – 2x²y² =16
Solution:

LHS= x⁴+y⁴-2x^²y^²= (x²)²+(y²)²-2x²y²

= (x² – y²)² = {(x + y) (x – y)}²

= \(\left(\frac{a}{b}+\frac{b}{a}+\frac{a}{b}-\frac{b}{a}\right)^2\left(\frac{a}{b}+\frac{b}{a}-\frac{a}{b}+\frac{b}{a}\right)^2\)

= \(\left(2 \frac{a}{b}\right)^2 \times\left(2 \frac{b}{a}\right)^2\)

= \(4 \frac{a^2}{b^2} \times 4 \frac{b^2}{a^2}\)

= 16 = RHS

Question 9. Using formula let’s multiply : (a² + a + 1) (a² – a + 1) (a⁴ – a² + 1)²
Solution :

(a² + a + 1) (a² – a + 1) (a⁴ – a² + 1)

= (a² +1 + a) (a² + 1- a) (a⁴ – a² + 1)

= { (a² + 1- a² }(a⁴ +1- a²)

= (a⁴+2a² +1-a²)(a⁴ +1-a²)

= (a⁴ +1 + a²)(a ⁴ +1-a²)

= (a⁴ )+ 2a⁴ +1- a⁴

= a⁸ +2a⁴ +1-a⁴

= a⁸+ a⁴+1

Question 10. If x = \(\left(a+\frac{1}{a}\right)\) and y= \(\left(a-\frac{1}{a}\right)\) , then lets find the value of x⁴ + y⁴-2x²y².

x⁴ + y⁴ -2x²y² .

= \(\left(x^2-y^2\right)^2\)

= \((x+y)^2(x-y)^2\)

= \(\left(a+\frac{1}{a}+a-\frac{1}{b}\right)^2\left(a+\frac{1}{a}-a+\frac{1}{a}\right)^2\)

= \((2 a)^2 \times\left(\frac{2}{a}\right)^2\)

= \(4 a^2 \times \frac{4}{a^2}\)

= 16

Question 11. Let’s express (4x² + 4x + 1- a² + 8a-16) as the difference of two squares, using the formula, (in the form a² – b² )

= (4x² + 4x +1)- (a² – 8a +1 6)

= (2x +1)²-(a-4)²

Question 12. Let’s express \(a^2+\frac{1}{a^2}-3\) as the difference of two squares (in the form a² – b²)
Solution:

⇒ \(a^2+\frac{1}{a^2}-3\)

= \(a^2+\frac{1}{a^2}-2-1\)

= a²- 2a \(\frac{1}{a}\)+ \(\frac{1}{a^2}\) – (1)²

= (a- \(\frac{1}{a}\))² – (1)²

 

Class 7 Math Solution WBBSE Arithmetic Chapter 2 Ratio Exercise 2 Solved Problems

Ratio: A ratio is a method to compare two quantities of the same kind having same unit, obtained by dividing the first quantity by the second quantity.

Hence, the ratio is an abstract number, it has no units.
The ratio of a to b is written as a: b and is read as ‘a is to b’.

Terms of the ratio:

The two number which forms the ratio are called the “Terms of the ratio”.

Read and Learn More WBBSE Solutions for Class 7 Maths

The first term of the ratio is called ‘Antecedent’ and the second one is called the ‘Consequent”.

In the ratio 37, 3 is called the antecedent of the ratio, whereas 7 is called ‘Consequent’.

The ratio can be expressed in fractional form. The antecedent becomes the numerator and the consequent becomes the denominator of the fraction.

The ratio are mainly of two types:

1.  Simple ratio
2. Mixed or Compound ratio

1. Simple ratio: The ratio between two quantities of the same kind is known as the simple ratio.

Example: 34, 8: 12.

2. Mixed or Compound ratio: The ratio whose antecedent is the product of the antecedents of two or more simple ratios and whose consequent is the product of the consequents of those ratios is termed as a mixed or compound ratio.

Example: The compound ratio of 2: 3, 5: 4, and 6: 8 is (2 x 5 x 6): (3 x 4 x 8) = 60: 96 = 5:8 [dividing each term by 12]

The simple ratio are of three types:

1. Ratio of greater equality (or Major Ratio): In this type of ratio, the antecedent is greater than the consequent.

Example: 5: 3.

2.  Ratio of lesser inequality (or Minor Ratio): In this type of ratio, the antecedent is less than the consequent.

Example: 3: 7.

3.  Ratio of Equality (or Equal Ratio): In this type of ratio, the antecedent is exactly equal to the consequent.

Example: 4: 4 or 1: 1.

Inverse Ratio: Of two ratios, if the antecedent and consequent of one are respectively the consequent and antecedent of the other, they are said to be inverse ratio or reciprocal to one another.

Example: the inverse ratio of 4:5 is 5: 4

The reciprocal fraction of \(\frac{7}{9} \text { is } \frac{9}{7}\)

Proportional part: To divide a given quantity into proportional parts is to divide it into parts that will be proportional to certain numbers.

Class 7 Math Solution WBBSE

Example: suppose divide ₹ 640 among A, B, and C in such a way that the money each gets will be in a ratio of 5: 3: 2. Find, how much money each of them gets.

A’s money B’s money: C’s money = 5:3:2

∴ Proportional part of A’s money = \(=\frac{5}{5+3+2}=\frac{5}{10}\)

Proportional part of B’s money = \(=\frac{3}{5+3+2}=\frac{3}{10}\)

Proportional part of C’s money=\(=\frac{2}{5+3+2}=\frac{2}{10}\)

Total money= ₹640

∴ A gets = ₹ \(\left(640 \times \frac{5}{10}\right)\) = ₹ 320

B gets = ₹ \(\left(640 \times \frac{3}{10}\right)\) = ₹ 192

C gets = ₹ \(\left(640 \times \frac{2}{10}\right)\) = ₹128

 

Question 1: The ratio of the ages of Samir and Aloke is 2: 3. If the age of Aloke is 12 yrs, then find the age of Samir.

Solution:

\(\frac{\text { Age of Samir }}{\text { Age of Aloke }}=\frac{2}{3}\) \(\frac{\text { Age of Samir }}{12 \mathrm{yrs}}=\frac{2}{3}\)

 

∴ Age of Samir =

= 8 yrs.

Wbbse Class 7 Maths Solutions

Question 2. The ratio of two numbers is 3: 4 and their H. C. F. is 15. Find the numbers and their L. C. M.

Solution: The ratio of two number is 3: 4.

Let the numbers are 3x and 4x [where x is common multiple and x > 0]

The H. C. F. of 3x and 4x is x and L. C. M. is (3 x 4 x x) or 12x.

According to question, x = 15

∴ The numbers are 3 x 15 or 45 and 4 x 15 or 60

Their LCM is 12 x 15 = 180.

Class 7 Math Solution WBBSE

Question 3. Reduce the following ratios into their lowest form and find their inverse ratios.

1. 225: 150
2. 20 ab: 25 ab [a ≠ 0, b ≠ 0]

Solution :
1. 225: 150

= 3 : 2

The inverse ratio of 3: 2 is 2: 3.

2. 20 ab: 25 ab

= 4 5 [dividing each term by 5ab]

The inverse ratio of 4 5 is 5:4

Wbbse Class 7 Maths Solutions

Question 4: Reduce the following into the ratio of the whole number and find their inverse ratio.

1. \(\frac{3}{8}: \frac{5}{16}\)

2. 0-125: 2.5

Solution: \(\frac{3}{8}: \frac{5}{16}\)

[L.C.M of 8  and 16 is 16]

[Multiplying both terms by 16]

The inverse ratio of 6: 5 is 5: 6.

2. 0.125: 2.5

= \(\frac{0 \cdot 125}{2 \cdot 5}\)

= 1:20

The inverse ratio of 1: 20 is 20: 1.

Class 7 Math Solution WBBSE

Question 5. Find the mixed ratio of the following ratios and identify the mixed ratio and find if these are ratios of greater or lesser inequality or ratio of equality.

1. 2 : 3, 4 : 5, and 6: 8

2. \(2 \frac{1}{3}: 3 \frac{1}{2}, 4 \frac{1}{2}: 5 \frac{2}{3} \text { and } 6: 1 \frac{1}{2}\)

3. 5:6, 3:2 and 4:5

Solution:

1. The mixed ratio of 2: 3, 4: 5, and 6: 8 is (2 x 4 x 6): (3 x 5 x 8) =48:120=

=2:5 [ratio of lesser in equality]

2. \(2 \frac{1}{3}: 3 \frac{1}{2}=\frac{7}{3}: \frac{7}{2}\)

\(4 \frac{1}{2}: 5 \frac{2}{3}=\frac{9}{2}: \frac{17}{2}\)

 

\(6: 1 \frac{1}{2}=6: \frac{3}{2}\)

The mixed ratio of \(\frac{7}{3}: \frac{7}{2}, \frac{9}{2}: \frac{17}{2} \text { and } 6: \frac{3}{2}\) is

= 63 : \(\frac{357}{8}\)

= 36 x 8 : [Multiplying each term by 8]

= 504:357

= 168:119

[ratio of greater inequality]

3. The mixed ratio of 5: 6, 3: 2, and 4: 5 is (5 x 3 x 4): (6 x 2 x 5)

= 60: 60
= 1:1 [ratio of equality]

Wbbse Class 7 Maths Solutions

Question 6: If A B = 2: 3 and B C 4 5. then find A: B: C.

Solution: A: B = 2:3= (2 x 4) : (3 x 4) = 8: 12

B: C 4:5 (4 x 3):(5 x 3) = 12 15

∴ A B C = 8: 12: 15

Question 7: If A: B=3: 4, B: C = 5:6, and C: D = 7: 8. then find

1. A: D and 2. A: B: C: D

Solution:

1.

⇒ A:D= 35: 64

2. A:B = 3: 4 = (3 x 5): (4 x 5) = 15: 20

B:C = 5:6 (5 x 4): (6 x 4) = 20:24

A:B:C = 15 20 24

= (15 x 7):(20 x 7): (24 x 7)

= 105:140:168

Again, C:D = 7:8 = (7 x 24) (8 x 24)

= 168: 192

A:B: C:D = 105: 140: 168: 192

Wbbse Class 7 Maths Solutions

Question 8: The ratio between the speeds of two trains is 5: 6. If the first train runs 200 km in 5 hours find the speed of the second train.

Solution: The first train in 5 hours runs 200 km

The first train in 1-hour runs \(\frac{200}{5}\) km = 40 km

∴ The speed of the 1st train is 40 km/hr

Let the speed of the second train is x km/hr.

According to question, 40: x = 5: 6

⇒ \(\frac{40}{x}=\frac{5}{6}\)

⇒ 5x = 40 x 6

⇒

= 48

∴ The speed of the 2nd train is 48 km/hr.

Question 9: The ratio of the costs of two cars is 2 : 3 and the cost of the second car is 3,00,000. Find the cost of the first car. If the cost of the first car was 50,000 more, then find the ratio of their costs.

Solution: Let the cost of 1st car is ₹ x

According to question, x: 3,00,000 = 2:3

⇒ \(\)

⇒ x= 2,00,000

∴ The cost of the first car is 2,00,000

If the cost of 1st car was 50,000 more, then the ratio of their cost is
(2,00,000+ 50,000): 3,00,000

= 2,50,000 3,00,000
= 5:6

Question 10. Out of 100 sums, Arpita got 70 sums correct. Out of 80 of those sums, Kabita got 60 sums correct. Express them in ratio to find, who got more sums correct.

Solution: Of Arpita the ratio of correct sums and the total sum is

70:100 = 7:10 = 7 x 2 : 10 x 2
= 14: 20

Of Kabita, the ratio of correct sums of the total sum is 60: 80 3:4 = 3 x 5:4×5 = 15:20

As 15 > 14,

∴ \(\frac{15}{20}>\frac{14}{20}\)

i.e 15:20:14:20

So Kabita got more sums correct.

Wbbse Class 7 Maths Solutions

Question 11: In a particular type of steel, the ratio of iron and carbon is 47: 3. Calculate to find in 300 kg of such steel how much iron is there.

Solution: The proportional parts of iron is

\(\frac{47}{47+3}=\frac{47}{50}\)

The proportional parts of carbon is

\(\frac{3}{47+3}=\frac{3}{50}\)

The quantity of steel in 300 kg of such steel is

and the quantity of carbon is

= 18 kg

Question 12: In a certain year, Vivekananda Youth Library received a Govt. grant of 74,350 and collected a subscription of 4350. Also, they got 1300 by selling old paper etc. If the entire money is spent on buying new books, for binding of old books, and paying salaries to employees in the ratio of 15: 3:2. Calculate for how much money new books were bought.

Solution: Total income is ₹(74,350 + 4350+ 1300) = ₹80,000.

The entire money is spent of buying new books, for binding of old books, and paying salaries to employees in the ratio of 15:3:2.

Proportional parts of money on buying new books is \(\frac{15}{15+3+2}=\frac{15}{20}\)

The cost for buying new books is

= ₹ 60,000

Wbbse Class 7 Maths Solutions

Question 13. The ratio between the average temperatures of Kolkata and Mumbai is 8: 7 and that between Kolkata and Delhi is 4: 5. Find the ratio of the average temperature of Mumbai and Delhi.

Solution:

\(\frac{\text { Temperature of Kolkata }}{\text { Temperature of Mumbai }}=\frac{8}{7}\)

 

⇒ \(\frac{\text { Temperature of Mumbai }}{\text { Temperature of Kolkata }}=\frac{7}{8}\)

again, ⇒ \(\frac{\text { Temperature of Kolkata }}{\text { Temperature of Delhi }}=\frac{4}{5}\)

 

∴ Temperature of Mumbai = Temperature of Delhi = 7: 10

Class 7 Math Solution WBBSE

Question 14. Divide 23,001 between A and B in the \(\frac{2}{3}: \frac{3}{4}\)

Solution:

\(\frac{2}{3}: \frac{3}{4}:\left(\frac{2}{3} \times 12\right):\left(\frac{3}{4} \times 12\right)=8: 9\)

Proportional part of A’s money = \(\frac{8}{8+9}=\frac{8}{17}\)

Proportional part of B’s money = \(\frac{9}{8+9}=\frac{9}{17}\)

 

 

Class VII Math Solution WBBSE Ratio

Ratio Exercise 2

Question 1.1 kg of rice costs Rs. 40 and 1 kg of pulse costs Rs. 100. Let’s find the ratio of the prices of rice and pulse.
Solution:

⇒ \(\frac{\text { Price of } 1 \mathrm{~kg} \text { rice }}{\text { Price of } 1 \mathrm{~kg} \text { pulse }}=\frac{\text { Rs. } 40}{\mathrm{RS} .100}\)

⇒ \(\frac{40}{100}\)

⇒  \(\frac{2}{5}\)

2:5

∴ The ratio of the prices of rice and pulse =2:5

Question 2. ∠BAC: ∠ABC: ∠ACB = What?
Solution :

∠BAC : ∠ABC: ∠ACB = 60= : 50° : 703 =6:5:7

Question 3. The price of a pencil is Rs. 3 and the cost of a toffee is 50 paise. Let’s write the ratio of the prices of a pencil and a toffee.
Solution :

The price of a pencil = Rs. 3 = 300 p.

The price of a toffee = 50p

⇒ \(\frac{\text { The price of a pencil }}{\text { The price of a toffee }}=\frac{300 p}{50 p}\)

⇒ \(\frac{6}{1}\)

6:1

∴ The ratio of the price of a pencil and a’toffeee is 6 : 1.

Question 4. Let’s find the ratio of the values of a 50 p coin, a rupee coin, and a two rupee coin.
Solution :

The value of a 50 p. coin; a rupee coin ; a two rupee coin

= 50 : 100 : 200 = 1 : 2 : 4

Class VII Math Solution WBBSE

Question 5. Lima’s age is 12 yrs 6 m, Ratul’s age is 12 yrs 4 m and Noorjahan’s age is 12 yrs. Let’s write the ratio of their ages.
Solution :

Lima’s age = 12 yrs 6 m = (12 × 12 + 6) m = 150 m

Rahul’s age = 12 yrs 4 m = (12 × 12 + 4) m = 148 m.

Noorjahan’s age = 12 yrs = (12 × 12) m = 144 m.

∴ The ratio of their ages

= 150 m : 148 m : 144 m = 150 : 148 : 144 = 75 : 74 : 72

Question 6. Let’s write the ratio of the angles of a right-angled isosceles triangle.
Solution:

The angles of right angles isosceles triangle are 90°, 45° & 45°

∴ The ratio of the angles = 90° : 45° : 45° =2:1:1

Question 7. Let’s write the ratio of the angles of an equilateral triangle.
Solution :

Each angle of an equilateral triangle = 60°

∴ The ratio of the 3 angles of an equilateral triangle

= 60° : 60° : 60° =1:1:1

Question 8. The ratio of the ages of Pulakbabu and Manikbabu is 7: 9. If the age of Manikbabu is 72 years, let’s find the age of Pulakbabu.
Solution:

⇒ \(\frac{\text { Age of Pulakbabu }}{\text { Age of Manikbabu }}=\frac{7}{9}\)

Or , \(\frac{\text { Age of Pulakbabu }}{72 \mathrm{yrs}}=\frac{7}{9}\)

Or, 9 Age of Pulkbabu= 7 × 72 yars

∴ Age of Pulakbabu = \(\frac{7 \times 72}{9}\) = 56 yrs

Class VII Math Solution WBBSE

Question 9. The ratio of the prices of two books is 2 : 5. If the price of the first book is Rs. 32.20, let’s find the price of the other book.
Solution :

⇒ \(\frac{\text { The price of the } 1 \text { st book }}{\text { The price of the } 2 \text { nd book }}=\frac{2}{5}\)

Or , \(\frac{\text { Rs. } 32.20}{\text { The price of the } 2 \text { nd book }}=\frac{2}{5}\)

Or, 2 x The price of the 2nd book = 5 × Rs. 32.20

The price of the 2nd book = \(\frac{5 \times \text { Rs. } 32.20}{2}\)

=5 × Rs.  16.10 = Rs. 80.50

Question 10. The ratio of the circumference and diameter of a circle is 22: 7. If the length of the diameter of the circle is 2m Idem., let’s calculate its circumference.
Solution:

⇒ \(\frac{\text { Circumference }}{\text { Diameter }}=\frac{22}{7}\)

Or, \(\frac{\text { Circumference }}{2 \mathrm{~m} \mathrm{1dcm}}=\frac{22}{7}\)

Or, 7 x circumference = 22 × 2m 1 dcm

Circumference= \(\frac{22 \times 21 \mathrm{dcm}}{7}\)

= 66 dcm

= 6m 6dcm.

Question 11. From our class seven, out of 150 students, 90 students and from 140 students of class six, 80 students participated in a sit-in-draw competition. Let’s express in ratio to find which of the two class has a greater participation.
Solution :

In Class 7:

The ratio of participent = \(\frac{90}{150}=\frac{3}{5}\)

= \(\frac{3 \times 7}{5 \times 7}=\frac{21}{35}\)

In Class 6:

The ratio of participant

= \(\frac{80}{140}=\frac{4}{7}\)

= \(\frac{4 \times 5}{7 \times 5}=\frac{20}{35}\)

∴ Class 7 has a greater participation.

Question 12. The ratio of two numbers is 5: 7 and their H.C.F is 13. Let us find the numbers.
Solution:

Let the numbers be 5x & 7x

Their H C F x = 13 (given)

1st number is 5x = 5 × 13 = 65

The 2nd number is 7x = 7 × 13 = 91

⇒ 65 and 91.

Class VII Math Solution WBBSE Ratio Exercise 2.1

Question 1. I shall prepare tea by mixing liqueur tea and milk in the same ratio. Let’s find how many cups of liqueur tea and how many cups of milk will be needed for preparing tea.

1. 24 Cups of tea, let’s find the ratio of liqueur tea and milk.
Solution:

In 24 Cups of tea, the ratio of liqueur tea and milk = 1 6 cups: 8 cups=2:1.

2. 15 Cups of tea, let’s find how many cups of milk are required.
Solution:

In 15 cups of tea, milk requires 5 cups.

Question 2. In the table given below, let’s fill up the blank squares

Let’s find the mixed ratio of the following :

1. 5 :3 , 8 : 12 & 7: 3
Solution:

A mixed ratio of 5: 9, 8: 12 & 7 : 3 is

⇒ \(\frac{5}{9} \times \frac{8}{12} \times \frac{7}{3}=\frac{5 \times 2 \times 7}{9 \times 3 \times 3}\)

⇒  \(\frac{70}{81}\)

70: 81

2. 1.2: 5, 3.5: 7 and 6: 4
Solution :

Mixed ratio of 1 .2 : 5, 3.5 : 7 & 6 : 4 is

⇒  \(\frac{12}{10 \times 5} \times \frac{35}{10 \times 7} \times \frac{6}{4}\)

⇒  \(\frac{9}{50}\)

= 9:50

Class VII Math Solution WBBSE

3. \(\frac{3}{5}: 2, \frac{5}{6}: 3\) and 4:5
Solution :

Mixed ratio of\(\frac{3}{5}: 2, \frac{5}{6}: 3\) and 4:5

⇒ \(\frac{3}{5} \times \frac{1}{2} \times \frac{5}{6} \times \frac{1}{3} \times \frac{4}{5}\)

⇒  \(\frac{1}{15}\)

= 1:15

Class VII Math Solution WBBSE Ratio Exercise 2.2

Question 1. Reduce the following ratios to their lowest form and let’s
find their inverse ratio.

1. 12: 15
Solution :

12 : 15 = 4 : 5

Its inverse ratio = 5:4

2. 36: 54
Solutions :

36 : 54 = 2 : 3

Its inverse ratio = 3:2

3. 75: 120
Solution :

75 : 120 = 5 : 8

Its inverse ratio = 8:5

4. 169: 221
Solution :

169 : 221 = 13 : 17

Its inverse ratio

= 17: 13

5. 9xy : 12xy
Solution :

9xy : 12xy = 3 : 4

Its inverse ratio = 4:3

6. 429: 663
Solution :

429 : 663 = 11 : 17

Its inverse ratio = 17:11

7. 3b: 12c
Solution :

3b : 12c = b : 4c

Its inverse ratio = 4c : b

8. 25xyz : 625xyz (Where a, b, x, y, z are not zero).
Solution :

25xyz : 625xyz =1 : 25

Its inverse ratio = 25 : 1

Question 2. Reduce the following into the ratio of whole numbers and let’s find their inverse ratio.

1. 2.5: 12.5
Solution : 2.5 : 12.5 = 1 : 5

Its inverse ratio = 5:1

2. \(\frac{5}{8}: \frac{7}{16}\)

⇒  \(\frac{5}{8}: \frac{7}{16}=\left(\frac{5}{8} x^{16}\right):\left(\frac{7}{16} x^{16}\right)\)

10: 7 and its inverse

Ratio= 7: 10

3. 0.7: 0.49
Solution:

0.70 : 0.49 = 10 : 7 = & its inverse ratio = 7:10

4. \(\frac{2}{5}: \frac{3}{4}\)
Solution:

⇒ \(\frac{2}{5}: \frac{3}{4}=\left(\frac{2}{5} x^{20}\right):\left(\frac{3}{4} x^{20}\right)\)

= 8: 15

Its inverse ratio = 15: 8

5. \(22: 4 \frac{5}{7}\)
Solution :

⇒ \(22: \frac{32}{7}=2: \frac{3}{7}\)

= 14 : 3 & its inverse ratio

= 3:14

6. \(\frac{7}{15}: \frac{3}{20}\)
Solution :

⇒ \(\frac{7}{15}: \frac{3}{20}\)

⇒ \(\left(\frac{7}{15} x^{60}\right):\left(\frac{3}{20} x^{60}\right)\)

= 28 : 9 & its inverse

Ratio = 9: 28

Class VII Math Solution WBBSE

7. \(1 \frac{2}{5}: \frac{7}{10}\)
Solution : \(1 \frac{2}{5}: \frac{7}{10}=\left(\frac{7}{5} x^{10}\right):\left(\frac{7}{10} x^{10}\right)\)

Inverse ratio = 1: 2

8. 4. 4: 5.61
Solution : 4. 4 : 5.61 = 4.40 : 5.61 = 440 : 561

= (440 ÷11): (561÷11) = 40: 51 & its inverse ratio

Question 3. Let’s find the mixed ratio of the following ratios and let’s identify the mixed ratio and find if these are ratios of greater or lesser inequality or ratio of equality.

1. 8: 6, 3: 6 and 26: 13
Solution :

A mixed ratio of 8: 6, 3: 6 & 26: 13 is

⇒ \(\frac{8}{6} \times \frac{3}{6} \times \frac{26}{13}=4: 3\)

The mixed ratio is of greater inequality.

2. \(\frac{7}{5} \times \frac{1}{3} \times \frac{5}{7} \times \frac{16}{17} \times \frac{3}{16}\)
Solution :

Mixed ratio of \(\frac{7}{5}: 3, \frac{5}{7}: 1 \frac{1}{16} \& 3: 16\) is

⇒  \(\frac{7}{5} \times \frac{1}{3} \times \frac{5}{7} \times \frac{16}{17} \times \frac{3}{16}\)

⇒  \(\frac{1}{17}\)

The mixed ratio is of lesser inequality.

= 1:17

The mixed ratio is of lesser inequality.

3. 8: 5, 7: 12 and 22: 13,
Solution :

Mixed ratio of 8: 5, 7: 12 and 22: 13 is

⇒  \(\frac{8}{5} \times \frac{7}{12} \times \frac{22}{13}\)

= \(\frac{308}{195}\)

= 308:195

The mixed ratio is of greater inequality.

4. \(\frac{2}{3}: 5, \frac{7}{8}:\)
Solution :

Mixed ratio of \(\frac{2}{3}: 5, \frac{7}{8}:\) is

⇒ \(\frac{2}{3} \times \frac{1}{5} \times \frac{7}{8} \times \frac{1}{2}=\frac{7}{120}\)

= 7:20

Question 4. Out of 100 sums, Rita got 60 sums correct. Out of 80 of those sums, Binoy got 50 sums correct. Let’s express them in ratio to find, who got more sums correct.
Solution:

Out of 100 sums, Rita got 60 sums correct.

∴ Rita’s ratio = \(\frac{60}{100}=\frac{3}{5}\) = 3:5

Out of 80 sums Binoy got 50 sums correct

∴  Bjnoy’s ratio = \(\frac{50}{80}=\frac{5}{8}\)

= 5: 8

Now , \(\frac{3}{5}=\frac{3 \times 8}{5 \times 8}\)

= \(\frac{24}{40}\)

∴  Binoy got more sums correct.

Question 5. In this year’s Madhymik examination out of 150 examinees of our school, 100 examinees passed with a grade – A. In another nearby school out of 100 examinees, 80 examinees passed with a grade – Of a. Let’s find which school has got a better result getting a grade – Of a, in this year’s Madhyamik examination.
Solution :

In our school, out of 150 examinees, 100 examinees got

∴  Ratio of getting grade A = \(\frac{100}{150}\)

= \(\frac{2}{3}\)

= 2:3

Percentage of getting grade A

= \(\frac{2}{3} \times 100 \%\)

= \(\frac{200}{3} \%\)

= \(66 \frac{2}{3} \%\)

In another school out of 100 examinees, 80 examinees got a grade A.

Ratio of getting grade A = \(\frac{80}{100}\)

= \(\frac{4}{5}\)

= 4: 5 and the percentage of getting grade A = \(\frac{4}{5}\) 100%

= 80 %

∴  The neighbouring school got a better result getting a grade of A.

Question 6. The ratio of the costs of two houses is 4 : 3 and the cost of the second house is Rs. 4,20,000. Let’s find the cost of the first house. If the cost of the first house was Rs. 70,000 more, then let’s find the ratio of their costs.
Solution:

⇒ \(\frac{\text { Cost of 1st house }}{\text { Cost of 2nd house }}=\frac{4}{3}\)

⇒ \(\frac{\text { Cost of 1st house }}{\text { Rs. } 4,20,000}=\frac{4}{3}\)

∴  3 ×  cost of 1st house = 4 × Rs. 4,20,000

Cost of 2nd house = \(\frac{4 \times 4,20,000}{3}\)

= Rs. 4 x 1 ,40,000 = Rs, 5,60,000

Question 7. From a bamboo, a piece of bamboo is cut off. It is found that the ratio of the two pieces is 3: 1. From the table below, let’s find the possible lengths of the two pieces and the length of the bamboo.
Solution:

∴  Ratio of the length of the bamboos = 40 dcm: 60 dcm = 2:3 (Ans.)

Class 7 Math Solution WBBSE Ratio Exercise 2.3

Question 1. Last year, the ratio of literate and illiterate people of Rashkundu Village was 4: 1. If the population of the village is 6550, let’s find the numbers of literate and illiterate people
Solution :

Ratio of literate & illiterate people = 4:1

Total population of the village = 6550

∴  Proportional part of literate people = \(\frac{4}{4+1}=\frac{4}{5}\)

And proportional part of illiterate people = \(\frac{4}{4+1}=\frac{4}{5}\)

∴ No. of literate people = \(\frac{4}{5} \times 6550\) = 4 × 1310

= 5240

No. of illiterate people = \(\frac{4}{5} \times 6550\)= 1 × 1310 = 1310

Question 2. If Rs. 640 is divided between Bishu and Aparna in the ratio of 5 : 3, let’s find how much each would get.
Solution :

The ratio of Bishu’s amount = 5:3

∴ Proportional part of Bishu’s amount = \(\frac{5}{5+3}=\frac{5}{8}\)

And Proportional part of Aparna’s amount = \(\frac{3}{5+3}=\frac{3}{8}\)

Total amount = Rs. 640

∴  Bishu’s share = Rs. \(640 \times \frac{5}{8}\) = Rs. 80 × 5= Rs. 400

Aparna’s share = Rs. \(640 \times \frac{5}{8}\) = Rs. 80 × 3 = Rs. 240

Question 3. In a particular type of steel, the ratio of iron and carbon is 49: 1. Let’s calculate to find, in 250 quintals of such steel how much iron is there.
Solution :

Ratio of Iron & Carbon = 49: 1

And Proportional part of Iron = \(\frac{49}{49+1}=\frac{49}{50}\)

And proportional part of Carbon =\(\frac{1}{49+1}=\frac{1}{50}\)

The total quantity of steel = 250 quintals

‎∴ Quality Of Iron = \(\frac{49}{50} \times 250\) quintal

49 5 quintal = 245 quintal

Question 4. Out of 143 girls in a school, the ratio of the number of girls who can only sing and those who can dance is 9: 2. If 3 more girls were found to sing, then let’s find the new ratio of girls who can sing and those who can dance.
Solution :

Ratio of number of girls who can sing & number of. girls

Who can dance = 9:2

∴  Proportional part of girls who can sing = \(\frac{9}{9+2}=\frac{9}{11}\)

And proportional part of girls who can dance = \(\frac{2}{9+2}=\frac{2}{11}\)

Total number of girls = 143

∴  No. of girls who can sing = \(\frac{9}{11} \times 143\) = 9×13 = 117

No. of girls who can dance = \(\frac{2}{11} \times 143\)

If 3 more girls are found to sing, the total number of girls who can sing

= 117 + 3 =120.

= 2 × 13 = 26

∴  A new ratio of girls who can sing and those who can dance

= 120 : 26 = 60 : 13.

Class 7 Math Solution WBBSE Question 5. In 240 ml of Dettol-water, the ratio of the volumes of water and Dettol is 1 : 3. If 60 ml of water is added to it, let’s find the ratio of the volume. water and Dettol in the new mixture.
Solution :

Ratio of volume water and Dettol = 1:3

∴  Proportional volume of water = \(\frac{1}{1+3}=\frac{1}{4}\)

And proportional volume of Dettol = \(\frac{3}{1+3}=\frac{3}{4}\)

Total volume of Dettol water mixture = 240 ml.

∴  Volume of water in this mixture = \(\frac{1}{4} \times 240 \mathrm{ml}\)  = 60 ml.

And Volume of Dettol in the mixture = \(\frac{3}{4} \times 240 \mathrm{ml}\) = 180 ml

Question 6. The monthly income of a man is Rs. 24,750. He pays house rent of Rs. 750 and the remaining money is spent on household expenses and the education of children in the ratio of 3:1. Let’s find how much money is spent on household expenses.
Solution :

Total monthly income = Rs. 24,750.

He pays for House rent = Rs. 750

Remaining money = Rs. 24000.

Now the ratio of expenses for household & educational experiences = 3:1

Proportional part of household expenses = \(\frac{3}{3+1}=\frac{3}{4}\)

And proportional part of educational expenses = \(\frac{1}{3+1}=\frac{1}{4}\)

∴  Expenses for household = \(\frac{3}{4}\) × Rs.2400

= 3 × Rs. 6,000 = Rs. 18,000.

Question 7. In a certain year, Vivekananda Youth Library received a Govt. grant of Rs. 74,350 and collected a subscription of Rs. 4,350. Also, they got Rs. 1,300 by selling old papers, etc. If the entire money is spent on buying new books, for binding old books and paying salaries to employees in the ratio of 15 : 3: 2. Now let’s calculate how much money new books were bought.
Solution :

Total income of Vivekananda Youth Library

= Rs (74350 + 4350 + 1300) = Rs. 80,000

Now, the ratio of expenses for buying newÿooks, for binding old books

And paying salary to employees = 15 : 3 : 2

∴  Proportional part for expenditure on buying new books

= \(\frac{15}{15+3+2}\frac{15}{20}=\frac{3}{4}\)

∴  Expenditure for buying new books

= Rs. 80,000 x \(\frac{3}{4}\)

= Rs. 20,000 × 3

= Rs. 60,000

Class 7 Math Solution WBBSE Question 8. 1050 people have come for training at a training center. They were asked to sit in three big halls in the ratio of Let’s find how many people will sit in each room.
Solution :

Ratio of sitting in three big rooms = 11:3:3\(\frac{1}{2}\)

= 11:3: = 22: 6: 7

∴  Proportional part of sitting in the 1st room = \(\frac{22}{22+6+7}\) = \(\frac{22}{35}\)

Propotional part of sitting in the 2nd room = \(\frac{6}{22+6+7}\) = \(\frac{6}{35}\)

The proportional part of sitting in the 3rd room = \(\frac{7}{22+6+7}\) = \(\frac{7}{35}\)

Total number of people = 1050

∴ No. of people will sit in 1st room = \(\frac{22}{35} \times 1050\) = 66o

No. of people will sit in 2nd room =\(\frac{6}{35} \times 1050\) =  180

No. of people will sit in 3rd room = \(\frac{7}{35} \times 1050\) = 210

Question 9. Rs. 12,000 is divided among Madhu, Manas, Kuntal, and Indra 2, let’s calculate how much each will get.
Solution :

Ratio of amount of Madhu, Manas, Kuntal & Indra = 2 : 3 : 4 : 2

Proportional part of Madhu’s money = \(\frac{2}{2+3+4+2}=\frac{2}{11}\)

Proportional part of Manas’s money = \(\frac{3}{2+3+4+2}=\frac{3}{11}\)

Proportional part of Kuntal’s money = \(\frac{4}{2+3+4+2}=\frac{4}{11}\)

Proportional part of Indra’s money = \(\frac{2}{2+3+4+2}=\frac{3}{11}\)

Total Amount = Rs. 12100

∴ Madhu will get = \(\frac{2}{11} \times \text { Rs. } 12100\) = 2 x 1100 = Rs. 2200

Manas will get = \(\frac{3}{11} \times \text { Rs. } 12100\) = 3 x 1100 = Rs. 3300

Kuntal will get = \(\frac{4}{11} \times \text { Rs. } 12100\) = 4 x 1100 = Rs. 4400

Indra will get = \(\frac{2}{11} \times \text { Rs. } 12100\) = 2 x 1100 = Rs. 2200

Question 10. The sum of the three angles of a triangle ABC is -180° The ratio of ∠BAC, ∠ABC, and ∠ACB is 3: 5: 10. If the value of ∠BAC is decreased by 10° ar|d value of an ∠ABC is increased by io°- Let’s calculate the new ratio of the three angles. 
Solution :

Ratio of the. 3 angles of a triangle = 3 : 5 : 10

Proportional part of the 1st angle ( ∠BAC) = \(\frac{3}{3+5+10}=\frac{3}{18}\)

Proportional part of the 2nd angle ( ∠ABC ) = \(\frac{5}{3+5+10}=\frac{5}{18}\)

And proportional part of the 3rd angle ( ∠ACB)=\(\frac{10}{3+5+10}=\frac{10}{18}\)

The sum of the three angles of a triangle = 180°

Measure of 1st angle ( ∠BAC ) = \(\frac{3}{8} \times 180^{\circ}\) = 3 ×10° = 30°

Measure of 2nd angle ( ∠ABC ) = \(\frac{5}{18} \times 180^{\circ}\)= 5 × 10° = 50°

Measure of 3rd angle ( ∠ACB ) = \(\frac{10}{18} \times 180^{\circ}\)= 10 × 10° = 100°

After decreasing – 10° , the value fo 1st angle ( ∠BAC ) = 30°-105 -20°

After increasing 10° > the value of 2nd angle ( ∠ABC ) = 50° +10° =60°

The new ratio of the three angel = 20° : 60° : 100° =2:6:10

= 1:3:5

Question 11. Let’s divide Rs. 9,000 among three friends in such a way that the second friend gets twice the amount the first friend gets. and the third friend gets half of the total sum of money the two friends have got. Let’s calculate how much amount of money each friend will get. [if the first friend gets Re.1, the second friend will get Rs.2, and the third friend will get Rs. \(\frac{1+2}{2}\)= Rs \(\frac{3}{2}\). The ratio of the amount of money that three friends get is = 1:2:1 = 2:4:3
Solution:

Let the 1st friend get Re. 1

2nd friend gets = 2 x Re. 1 = Rs. 2

The 3rd friend gets = Rs. \(\frac{1+2}{2}\) = \(\frac{3}{2}\)

∴ The ratio of the amount of money that three friends get

= 1:2:\(\frac{3}{2}\) = 2:4:3

Total amount of money = Rs. 9,000

Proportional part of money of 1st friend =\(\frac{2}{2+4+3}=\frac{2}{9}\)

Proportional part of moeny of 2nd friend = \(\frac{4}{2+4+3}=\frac{4}{9}\)

Proportional part of money of 3rd friend = \(\frac{3}{2+4+3}=\frac{2}{9}\)

∴  1 st friend will get = Rs. \(9000 \times \frac{2}{9}\) = Rs. 1000 × 2 = Rs. 2000

2nd friend will get = Rs. \(9000 \times \frac{4}{9}\) = Rs. 1000 × 4 = Rs. 4000

3rd friend will get =Rs. \(9000 \times \frac{3}{9}\) = Rs. 1000 × 3 = Rs. 3000.

Question 12. For constructing a road in our village, the ratio of the money spent for the last four,r years is 2: 4 : 3: 2. If the total money spent in those four years is Rs. 132 lac, then let’s find how much money was spent on the second year and total money spent on first and third year.
Solution :

The ratio of the amount of money spent for the last four year = 2:4:3:2

∴ Proportional amount of money spent on 1 st year = \(\frac{2}{2+4+3+2}=\frac{2}{11}\)

Proportional amount of money spent on 2nd year = \(\frac{4}{2+4+3+2}=\frac{4}{11}\)

Proportional amount of money spent on 3rd year = \(\frac{3}{2+4+3+2}=\frac{3}{11}\)

And the Proportional amount of money spent on 4th year = \(\frac{2}{2+4+3+2}=\frac{2}{11}\)

Total money spent in those four years = Rs. 132 lac.

Amount of money spent on the second year

= \(\frac{4}{11}\) × 132 lac = 4×12 lac = 48 lac.

Amount of money was spent on the third year

= \(\frac{2}{11}\) × Rs. 132 lac = 2 x 12 lac = 24 lac.

Amount of money spent on the first year

= \(\frac{3}{11}\) × Rs. 132 lac = 3 x 12 lac = 36 lac.

Total Amount of money spent on the 1st and 3rd year

= 24 lac + 36 lac = 60 lac.

Another was :

Let the amount of money spent on the 1st year = Rs. 2x lac.

Amount of money spent on the 2nd year = Rs. 4x lac.

Amount of money spent on the 3rd year = Rs. 3x lac.

Amount of money spent on the 4th year = Rs. 2x lac.

Total amount of money spent on four years = Rs. 132 lac.

2x + 4x + 3x + 2x = 132

11x = 132

x = \(\frac{132}{11}\)

x = 12

Amount of money spent on the 2nd year

= Rs. 4x lac = Rs 4 × 12 lac = Rs. 48 lac

Amount of money spent last year and 3rd year

Rs. (2x + 3x) = 5x = Rs. 5 × 12 lac = 60lac

Class 7 Math Solution WBBSE Question 13. During retirement, Binoybabu gets Rs. 1,96,150. He donated Rs. 20,000 to the school library and the remaining amount he divided among his wife, son, and daughter in the ratio of 5: 4: 4. Let’s find out how much money he gave each of them.
Solution :

The total amount of money Binoybabu gets = Rs. 1,96,150

He gives a donation for the school library = Rs. 20,000

Remaining among = Rs. 1,76,150

The ratio of the amount of money he divided among his wife, son daughter = \(\frac{5}{5+4+4}=\frac{5}{13}\)

Proportional amount of money for his wife = \(\frac{5}{5+4+4}=\frac{5}{13}\)

Proportional amount of money for his son = \(\frac{4}{5+4+4}=\frac{4}{13}\)

Proportional amount of money for his daughter = \(\frac{4}{5+4+4}=\frac{4}{13}\)

Amount of money he gave to his wife = \(\frac{15}{4}\) Rs. 176150

= Rs. 5 × 13550= Rs. 67750.

Amount of money the gave to his son = \(\frac{4}{13}\)

Rs. 4 ×13550 = Rs. 54200

Amount of money the gave to his daughter = \(\frac{4}{13}\) × Rs. 176150

= Rs. 54200

Question 14. Aminoor uncle cultivated brinjal and potato in a ratio of 4 : 3 is his 35 katha land. He made a profit of Rs. 150 per katha for brinjal and Rs. 125 per katha for potato. Let’s calculate the total amount of profit of Aminoor’s uncle from his cultivation of brinjal and potato in his total land.
Solution :

Ratio of area land for cultivation brinjal and potato = 4:3

The total area of land of Aminoor uncle = 35 Katha

Area of land for cultivation of brinjal = \(\frac{4}{7}\) x Rs. 35 Katha

= 4 × 5 katha = 20 Katha.

Area of land for cultivation potato = (35 – 20) Katha = 15 Katha

Now profit for cultivation of brinjal = Rs. 150 per Katha& profit for cultivation potato = Rs. 125 per Katha

Profit for cultivation of brinjal in 20 Katha = Rs. 150 × 20 = Rs. 3000

Profit for cultivation of potato in 15 Katha = Rs. 125× 15 = Rs. 1875

The total amount of profit of Aminoor’s uncle for the cultivation of brinjal & potato

= Rs. 3000+ Rs. 1875

= Rs. 4875

Ratio of profit for cultivation of brinjal & potato

= Rs. 3000: Rs. 1875

= 200: 125 (dividing both by 15)

= 8:5 (dividing both by 2)

 

WBBSE class 7 maths solutions Arithmetic

• WBBSE Class 7 Maths Chapter 1 Simple Problems
• WBBSE Class 7 Maths Chapter 2 Ratio
• WBBSE Class 7 Maths Chapter 3 Proportion
• WBBSE Class 7 Maths Chapter 4 Approximation Of Values
• WBBSE Class 7 Maths Chapter 5 Square Root Of Fractions
• WBBSE Class 7 Maths Chapter 6 Time and Distance
• WBBSE Class 7 Maths Chapter 7 Areas Of Rectangles and Square

 

WBBSE class 7 maths solutions Algegbra

• WBBSE Class 7 Maths Chapter 1 Revision of Old Lesson
• WBBSE Class 7 Maths Chapter 2 Addition, Subtraction, Multiplication and Division Of Integers
• WBBSE Class 7 Maths Chapter 3 Concept Of Index
• WBBSE Class 7 Maths Chapter 4 Algebraic Operations
• WBBSE Class 7 Maths Chapter 5 Algebraic Formula
• WBBSE Class 7 Maths Chapter 6 Factorisation
• WBBSE Class 7 Maths Chapter 7 Formation Of Equation And Solutions
• WBBSE Class 7 Maths Chapter 8 Double Bar Graph

 

WBBSE class 7 maths solutions Geometry

• WBBSE Class 7 Maths Chapter 1 Revision of Old Lesson
• WBBSE Class 7 Maths Chapter 2 Drawing Angles With Compass
• WBBSE Class 7 Maths Chapter 3 Properties Of Triangle
• WBBSE Class 7 Maths Chapter 4 Construction Of Triagles
• WBBSE Class 7 Maths Chapter 5 Concept of Congruency
• WBBSE Class 7 Maths Chapter 6 Parallel Lines And Transversal
• WBBSE Class 7 Maths Chapter 7 Type Of Quadrilateral
• WBBSE Class 7 Maths Chapter 8 Construction Of Quadrilateral
• WBBSE Class 7 Maths Chapter 9 Symmetry

WB Class 7 Math Solution Geometry Chapter 9 Symmetry Exercise 9 Solved Problems

Symmetry means an exact similarity in shape and size between parts of an object.

Classification of Symmetry:

There are three types of symmetry-
1. Linear symmetry
2. Point symmetry and
3. Rotational symmetry.

Linear symmetry:

An Image is said to be a line of symmetry or linear symmetry if there exists a straight line which divides the figure into two identical halves that completely coincide with each other when folded about that line.

Read and Learn More WBBSE Solutions for Class 7 Maths

The straight line is called the line of symmetry or line of reflection.

 

 

 

 

In the above images, the line PQ is called the line of symmetry or axis of symmetry.

Regular Polygon:

The polygon having all sides and all angles equal are called a regular polygon.

Wbbse Class 7 Maths Solutions

Axially Symmetric Images

 

 

Rotational symmetry:

If an image coincides with its image when it is rotated about a point through an angle less than 360°, the image is said to be rotational symmetry.

The point across which the figure rotates is called the centre of rotation.

The angle of rotational symmetry is the minimum angle through which a geometrical image is rotated about a point to get the first symmetrical image.

The number of times an object coincides with its image in the process of a complete rotation of 360° about a point is called the order of the rotational symmetry.

If the smallest angle of rotational symmetry of an image is x° then the order of rotational 360° symmetry is \(\frac{360°}{x°}\)

If 45° is the smallest angle of rotational symmetry. So the order of rotational symmetry = \(\frac{360°}{45°}\) = 8

Wbbse Class 7 Maths Solutions

Rotationally Symmetric Images

 

 

Question 1. Choose the correct answer 

1. The number of lines of symmetry of an equilateral triangle is

1. 1
2. 2
3. 3
4. 4

 

Solution: The number of line of symmetry of an equilateral triangle is 3.

So the correct answer is 3. 3

2. The number of line of symmetry of an isosceles trapezium is

1. 1
2. 2
3. 3
4. 4

 

Solution: The correct answer is 1. 1

3. If the period of rotational symmetry of an equilateral triangle be three then its angle of rotational symmetry is

1. 90°
2. 120°
3. 100°
4. 60°

Solution: The angle of rotational symmetry is \(\frac{360°}{3}\) or 120°

So the correct answer is 2. 120°

Wbbse Class 7 Maths Solutions

4. The number of axis of symmetry of a kite is

1. 0
2. 1
3. 2
4. 3

 

Solution: The number of line of symmetry of a kite is 1

So the correct answer is 2.1

5. If the angle of rotational symmetry of a regular polygon is 60°, then the number of sides is

1. 2
2. 4
3. 6
4. 7

 

Solution: The required number of sides = \(\frac{360°}{60°}\) = 6

So the correct answer is 3. 6

Question 2. Write true or false 

1. A scalene triangle has no line symmetry.

 

Solution: The statement is true.

2. The butterfly is not a symmetrical object.

 

Solution: The butterfly has one line of symmetry.

So the statement is false.

3. The order of rotational symmetry of an equilateral triangle is 2.

Solution: The angle of rotational symmetry of an equilateral triangle is 120°

So the order of rotational symmetry = \(\frac{360°}{120°}\)

So the statement is false.

4. The number of line of symmetry of a circle is infinite

 

 

Solution: As the axis of symmetry of a circle is its diameter. So there are infinite numbers of symmetry.

So the statement is true.

5. Isosceles trapezium has line and rotational symmetry.

 

Solution: Isosceles trapezium has only line of symmetry.

So the statement is false.

Question 3. Fill in the blanks 

1. If the angle of rotational symmetry of any figure is 180°, then its number of rotational symmetry will be _______

Solution: The required number of rotational symmetries is \(\frac{360°}{180°}\)

2. The angle of rotational symmetry of a square is ____ degree.

Solution: The angle of rotational symmetry of a square is\(\frac{360°}{4°}\) = 90°

3. The circle is linear and symmetric about its _____

Solution: diameter.

4. The centre of rotational symmetry of a rectangle is the point of intersection of the ______

Solution:

5. ______ has no line of symmetry but has two degrees of rotational symmetry.

 

 

Solution: parallelogram.

The center of rotational symmetry of a rectangle is the point of intersection of the diagonals.

Wbbse Class 7 Maths Solutions

Question 4. Which of the following images have line of symmetry

 

Solution:

Semicircle has one line of symmetry

 

Hexagonal has a sox line of symmetry

 

Scalene triangle has no line of summetry

Question 5. 1. Find the order of rotational symmetry.

1. Rhombus
2. Regular pentagon.

Solution:

1. The order of rotational symmetry of rhombus is \(\frac{360°}{180°}\)

2. The angle of rotation of regular pentagon is 72°

So degree of rotation = \(\frac{360°}{72°}\)= 5

2. Find the angle of rotation of a parallelogram.

Solution: The angle of rotation of a parallelogram is 180°

3.  Find the number of lines of symmetry of the butterfly. 

Solution:

The number of lines of symmetry of the butterfly is one.

WB Class 7 Math Solution Symmetry

Symmetry Exercise 9.1

Question 1. Let’s place a mirror along the line of symmetry and complete the following figure.
Solution:

Question 2. Let’s draw the reflections of A, B, C, and D in a mirror.
Solution:

Question 3. In the plane figures given below, which figures have line symmetry and which figures do not have line symmetry, let’s write and verify by cutting off the figures and folding them.
Solution:

 

Question4. Let us find a line of symmetry for
Solution:

1.  It is observed that the line of symmetry of A is Vertical
2. The line of symmetry of E is Horizontal

Question5. In the letter given below, identify which of them will have vertical which of them have horizontal, and which will have both, lines of symmetry
Solution:

E →  Horizontal lines of symmetry

H, O, X → Both horizontal & vertical of symmetry

M → Vertical line of symmetry

Question 6. Let us draw plane figures, then cut them off to find if they have rotational symmetry. Let’s write in the blank spaces given below and try to verify them.
Solution:

WBBSE Class 7 Math Solution Symmetry Exercise 9.2

Question 1. The isosceles triangle has only line symmetry.

• An equilateral triangle has line as well as rotational symmetry.
• The number of rotational symmetry of a square is 4.
• For a rectangle, the number of rotational symmetry is 2.
• There are 4 lines of symmetry for a square tut 2 lines of symmetry for a rectangle.
• Parallelogram has only rotational symmetry.
• If the angle of rotational symmetry of any figure is 1803> ‘ts number of rotational symmetry will be 2.
• A regular pentagon has line and rotational symmetry.
• For a regular hexagon, the angle of rotational symmetry is 60 degrees and its number is 6.
• Only Isosceles trapezium has line symmetry but no rotational symmetry.
• The centre of rotational symmetry of a parallelogram is 180°.
• The angle of rotational symmetry of an equilateral triangle is 120°
• The angle of rotational symmetry of a square is 90s.
• Parallelogram has no line symmetry but has two degrees of rotational symmetry.

Question 2. Which of the following geometric figures have line symmetry but don’t have rotational symmetry?

1.

1. Equilateral triangle,
2. Parallelogram,
3. Isosceles triangle,
4. Circle

Solution: Isosceles triangle

2. Which of the following geometric figures have a measure of rotational symmetry 2 but that figure has no line symmetry?

1. Rectangle
2. Parallelogram
3. Isosceles triangle
4. Circle

Solution: Parallelogram.

3. If the angle of rotational symmetry of a regular polygon be 60°, then its number of sides

1. 4
2. 4
3. 6
4. 7

Solution:  6.

4.  Which of the following figures have two lines of symmetry and the angles of rotational symmetry 180°
Solution:  Rectangle.

Question 3. Let’s observe the pictures and complete the chart given below
Solution:

WB Class 7 Math Solution Geometry Chapter 8 Construction Of Quadrilateral Exercise 8 Solved Problems

For the construction of a quadrilateral five of its parts must be known.

We can construct quadrilaterals in the following cases:

1. If the lengths of four sides and measure of one angle is given
2.  If the lengths of four sides and are diagonal is given
3. If the lengths of three sides and measures of two included angles is given
5.  If the lengths of two adjacent sides and measures of three angles is given
6. If the length of a side of a square is given
7. If two adjacent sides and their included angle of a parallelogram is given
8. If the length of a side of a rhombus and the measure of its angle is given.

Read and Learn More WBBSE Solutions for Class 7 Maths

Question 1. Construct a quadrilateral ABCD in which AB = 5 cm, BC= 5.8 cm, CD = 4.1 cm, AD = 6.7 cm and AC = 9.4 cm.

Solution:

 

 

Method:

1. We take a ray AX of any length.
2.  With centre A and radius 9-4 cm an arc is drawn at C on AX.
3. With A and C as centres and radii 5 cm and 5.8 cm respectively, two arcs are drawn, which intersect each other at point B.
4. Again, with A and C as centres and radii 6.7 cm and 4.1 cm respectively, two arcs are drawn on the other side of AC opposite to B, which intersect each other at point D.
5.  I join A, B; B, C; A, D and C, D.

Thus ABCD is the required quadrilateral whose AB = 5 cm, BC = 5.8 cm, CD = 4.1 cm, AD = 6.7 cm and AC = 9.4 cm.

Wbbse Class 7 Maths Solutions

Question 2. Construct a quadrilateral PQRS in which PQ = 6.5 cm, QR = 6 cm, RS = 5 cm, SP 4 cm and ∠PQR = 60°

Solution:

 

 

 

Method:

1. A ray PX is drawn and from it cut off a line segment PQ of length 6.5 cm.
2. Using pencil compass and scale an angle ∠PQY = 60° is drawn at Q.
3. From QY cut off a line segment QR of length 6 cm.
4. With P and R as centres and with radii equal to 4 cm and 5 cm respectively two arcs are drawn; to intersect each other at S. Then P, S and S, R are joined.

Thus PQRS is the required quadrilateral in which PQ = 6.5 cm, QR = 6 cm, RS = 5
cm, SP = 4 cm and ∠PQR = 60°

Wbbse Class 7 Maths Solutions

Question 3. Construct a parallelogram ABCD in which AB = 4 cm, BC = 6 cm, and ∠ABC = 45°

Solution:

 

 

 

Method :
1. A ray BX is drawn and from it cut off a line segment BC of length 6 cm.
2.At B on BX a ∠YBX = 45° is drawn.
3. From BY cut off a line segment AB of length 4 cm.
4. With centres A and C and radii equal to 6 cm and 4 cm respectively two arcs are drawn; to intersect each other at D. Then A, D and C, D are joined.

Thus ABCD is the required parallelogram in which AB = DC = 4 cm, AD = BC = 6 cm and ∠ABC = 45°.

Wbbse Class 7 Maths Solutions

Question 4. Construct a rectangle PQRS in which PQ = 4.5 cm and QR = 6.5 cm

Solution:

 

Method:
1. A ray QX is drawn and at Q on QX the angle ∠XQY = 90° is drawn.
2. The lengths QR = 6-5 cm and is cut down QX and the length QP = 4.5 cm is cut from QY.
3. With centres P and R and radii equal to 6.5 cm and 4.5 cm respectively two arcs are drawn to intersect each other at S. Then R, S and P, S are joined. Thus PQRS is the required rectangle.

Question 5. Construct a square ABCD on a side of length 6 cm.

Solution:

 

 

Method:

1. A ray AX is drawn and from it cut off a line segment AB of length 6 cm.
2. A perpendicular AY is drawn on AX at A and from it cut off a line segment AD of length 6 cm.
3.  With B and D as centres and radii equal to 6 cm two arcs are drawn, which intersect each other at C. Then D, C and B, C are joined.

Thus ABCD is a required square.

Question 6. Construct a rhombus ABCD in which AC = 4 cm and BD = 6 cm

Solution:

 

 

 

 

[The diagonals of a rhombus bisect each other perpendiculerly]

Method:
1. I take a line segment AC of length 4 cm and bisect it.
2. A ray BX is drawn and from it cut off a line segment BD of length 6 cm and bisect it by YZ at O.
3. With centre O and with a radius 2 cm (half of AC) draw an arc which cuts OY and OZ at A and C respectively. I join A, B; B, C; C, D and A, D.
Thus ABCD is the required rhombus.

 

WB Class 7 Math Solution Construction Of Quadrilateral

Construction Of Quadrilateral Exercise 8.1

Question 1. Let me draw a quadrilateral REST in which RE = 6 cm, ES = 4.5 cm, ST = 5 cm TR = 5.5 cm & ET = 7.5 cm
Solution :

1. From there ray RX, a line segment Re (= 6cm) is cut off.
2. With centre E two arcs of radius 4.5 cm & 7.5 cm is drawn.
3. Again with centre R, a arc of radius 5.5 cm is drawn.
4. By joining ES, TS, TR we get the required quadrilateral REST is obtained.

Question  2. Let me draw a parallelogram whose adjacent sides are 5 cm. & 8 cm and the length of the diagonal is 10 cm.
Solution :

1. From the ray GX, aline segment Gl (= 8 cm.) is taken, with centre I, two arcs of radius 5 cm. & radius 5 cm. is drawn which cuts the previous arc atL
2. By joining Gl, IR, RL & LG we get the required parallelo gram GIRL is obtained.

Question 3. Let me draw a rough sketch of a quadrilateral LAND & try to find it will be possible to draw a quadrilateral, in which LA = 4 cm, AN = 5 cm, ND = 4 cm, DL = 6.5 cm & AD = 1 0 cm.
Solution :

• From the ray LX, a line segment LA = 4 cm is taken.
• With centre A & OL, two arcs of radius 10 cm & 6.5 cm is drawn, they intersect at D.
• Now with centre A & D two arcs of radius 5 cm & 4 cm respectively arc drawn. Bu they do not intersect each other.
• So it is not possible to draw the quadrilateral LAND.

Question 4. 1 try to draw a rhombus whose one side is 3 cm and its diagonal is 5 cm.
Solution :

• From the ray KX, a line segment Kl (= 3 cm.) is cut off. Now with centre
• I two arcs of radius 3 cm & 5 cm. arc drawn.
• Now with centre K an arc of radius = 3 cm is drawn which cuts the previous arc at E.
• By joining IT, TE & EK, we get the required rhombus KITE is obtained.

WB Class 7 Math Solution Construction Of Quadrilateral Exercise 8.2

Question 1. Let us draw a quadrilateral GOLD, where two diagonals are GL = 8cm and DO = 10cm. and the other three sides are GO = 6cm, OL = 5 and DL = 5.6 cm. Let’s Measure the length GD and let’s write.
Solution :

1. Draw a ray GX, from this ray a line segment GO (6cm) is cut off.
2. Now with centre G & O two arcs of radius 8cm and 5cm is cut off. They meet at L, Join OL.
3. Now with O & L, two arcs of radius 10cm and 5 6cm is cut off. They meet at D, join GD.
4. Thus a quadrilateral GOLD is formed.

∴ GD = 95cm

Question 2. Let us draw a rhombus REST, whose two diagonals are, RS = 6.8cm and ET = 7.2cm. [Hints: The diagonals of a rhombas bisect each other at right angles. Hence let us draw a perpendicular bisector of diagonal ET with the mid point of the diagonal ET as centre side of the arcs are drawn with hold the length of the other diagonal RS, On either side of the perpendicular biscetor at R & S. Hence joining the points R, E, S and T, rhombus is formed.]
Solution :

1. Take a ray RS, from this ray a line segment RS. ( = 6.8cm) is cut off.
2. Now RS-. is bisected at O. At O, draw a perpendicular PQ. From OP &
3. OQ two parts OE & OT each equal 3.6cm (Total ET = 7.2cm.)
4. Join ER, RT, TS & SE.

∴ The rhombus REST is drawn.

Question 3. Let’s draw a quadrilateral LAND such that LA = 6.5cm AN = 5.4cm, ND = 4cm, DL = 3.5cm, LAN = 45°.
Solution :

Froim the ray AX, AN (=5.4cm) is cut off.

• Now at A draw an angle L AN (= 45° ) from the line sent LA (6.5cm is cut off.
• With centre N & L two arcs equal to 4cm & 3.5cm drawn they meet at D.
• Joining LD & ND, we get the required quadrilateral LAND is obtained.

Question 4. Let’s draw a parallelogram GATE whose adjacent sides are, GA = 7cm and AT – 5cm and ∠GAT = 45°
Solution :

Take a ray GX. From GX, take a line segment GA equal to 7cm.

• Now at A, draw an angle GAY equal to 45°. From AY, AT equal to 5cm is cut off.
• Now, at G & at T draw two arcs equal to radius 5cm and 7cm respectively.
• By joining GE & ET we get the required parallelogram GATE.

Question 5. Let me draw a rectangle RICH, So that Rl = 4cm and Cl = 7.5cm. [Hints : Opposite sides of a rectangle are equal and in each angle is degree.]
Solution :

To draw a rectangle RICH, take a ray RX, from RX, cut a line segment RH equal to 7.5cm.

Now, at R, draw perpendicular RY. From RY cut a line segment Rl equal to 4cm.

• Now, with centre H & I draw two arcs equal to radius 4cm & 7.5cm respectively.
• The two arcs intersects at C, join. Cl & CH, we get required rectangle RICH.

Question 6. Let’s construct a rhombus whose one angle is 60° and its equal sides are 6.5cm each.
Solution :

From the AX, a line segment AB (= 6.5) is cut off.

• At draw an angle YAX equal to 60° . From YA, a line segment DA = 6.5cm is cut off.
• Now with centre B & D two arcs of length 6.5cm is drawn. They meet at G. Joining BC & CD we get the required Rhombus ABCD.

Question 7. Let’s draw a square PATH whose sides are 8cm each.
Solution :

From the ray PX, PA = 8cm is cut off. Now, at P drawn angle 99° , YPA.

• From PY, PH = 8cm is taken,.Now with centre A & H two arcs equal to 8cm is drawn, let they meet at T.
• Join TA & TH. Thus, we get the required square

Question 8. Let us draw a quadrilateral PLAN is which PL = 4.6cm LA = 5.5cm, AN = 5cm, AN = 5cm & ∠PLA = 60° & ∠LAN = 90°
Solution :

• Draw 3 line segments PL (4.6cm), LA (5,5cm) & AN (5cm)
• Take a ray AX, from AX, AL (= 5.5cm) is cut off.
• At A & L dras two angles equal to 90° & 60° ie ∠LAY(=90°)& ∠ALK(= 60°) drawn.
• From AY, AN = 5cm & from LK, LP = 4.6cm is cut off.
• Join PN.

∴ Quadrilateral PLAN is obtained.

Question 9. Let us draw a quadrilateral HEAR, in which HE = 5cm RH = 6.8 cm, ∠EHR = 90°, ∠HEA = 1 20° and ∠HRA = 70°
Solution:

To construct a quardritateral HEAR

• Take a ray HP from HP cut off HF = 5cm. On HE at H & at E draw an angle = 90° and angle 120° respectively. From HY cut off HR = 6.8 cm. Now, at
• R, draw an angle = 70°  Which cut EQ at A. JoinÿR & we get the required quadrilateral HEAR.

Exercise

Question 1. Let’s think and write answers of the following: If four sides of a quardrilateral are given, is it possible to construct it. It we can’t draw, then what more data should be given so that the quardrilateral can be constructed, let’s find.

1. To draw specific parallelogram, what least data are required, let’s find.
Solution: 

Two adjacent side and an angle between two sides are required.

2. Let’s find, the least number of data required to construct a square.
Solution:   One side is required.

3. Let’s find if it is possible to construct a rhombus when the length of its two diagonals are given.
Solution: To construct a rhombus length of two diagrams is required.

4.  Let’s find the least number of data required to construct a rectangle.
Solution:  To the adjacent side’s length is required.

Question 2. Let’s construct a quadrilateral ABCD in which AB = 5.2cm, BC = 6cm, CD = 4.4cm, AD = 7cm and AC = 1 0cm. If in this quadrilateral, AC= 1 8cm, could it be possible to construct the quadrilateral, let’s find.
Solution :

To constract a quadrilateral ABCD, take a line AX, From AX, AB = 5.2cm is cut off.

• Now, with centre A & B two arcs of radius 10cm and 6cm are drawn, let they meet at C.
• Again with centre A & C two arcs 7cm and 4.4cm are drawn, they meet each other at D.
• By joining BC, Cd & DA we get the required quadrilateral ABCD.
• In AC = 1 2cm, it is not possible to draw the quadrilateral, as arcs AC & BC will never meet each other.

Question 3. Let construct a parallelogram JUMP in which JU = 5.2cm, UM = 4.8cm and JM = 7cm.
Solution :

From the ray JX, JU = 5.2cm is cut off.

• Now, with centres J & U two arcs of radius 7cm, 4.8cm are drawn, they meet at M.
• Again with centre J & M two arcs of radius 4.8cm & 5.2 cm are drawn.
• They meet at P. By joining JU, UM & MU we get the required parallelogram JUMP.

Question 4. Let’s contruct a rhombus PQRS in which PQ = 5.4cm and PR = 8cm.
Solution :

From the ray PX, take a line segment PQ equal to 7cm.

• Now at Q draw an angle YQP = 60°  From Qy, QR = 6.5cm taken, now with centre R and P two arcs of radius 5.2cm & 4.4 cm are dran, they meet at S by joining PS &
• RS we get the required quadrilateral PQRS.

Question 5. Let’s construct a quadrilateral PQRS in which PQ = 7cm, QR = 6.5cm, RS = 5.2cm, SP = 4.40cm, = 60°
Solution :

From the ray PX, PQ = 5.4cm is cut off.

• Now, with centre P &Q drawn two arcs of radius 8cm and 5.4cm are drawn.
• They meet at R. Now again with centre P & R two arcs are drawn with a radius 5.4cm, The meet at S, By joining SR & PS we get the required quadrilateral PQRS.

Question 6. Let’s construct a rhombus BEST in which BS = 6.8cm, and ET = 5.8cm.
Solution :

From the ray BL, BS = 6.8cm is taken, Now, we draw the perpendicular bisector PQ of BS, which cuts BS at O.

From OP & OQ, OE & OT equal to 2.9cm are taken, Now Joint BE, ES, ST & TB and we get the rhombus BEST.

Question 7. Let’s construct a square DEAR in which DE = 5.2cm.
Solution :

From the ray DX, De = 5.2cm is cut off.

• Now, at D draw an angle ZYDE = 90° From Dy, Dr = 5.2cm is taken. Now, with centres E and R two arcs equal to drawn.
• Let them meet at A. After joining AR & AE we getting square DEAR.

Question 8. Let’s draw a rectangle READ in which RE = 6cm & EA = 5cm.
Solution :

From the ray EX, ER = 6cm is cut off.

• Now at E draw a perpendicular EY, from EY cut-off.
• EA = 5cm. Now, with centre A & R draw two arcs equal to radius 6cm & 5cm respectively.
• They meet each other at DF joining DA & DR, we get the required rectangle READ.

Question 9. Let’s draw a quadrilateral SAND, such that SA = 5.6cm, AN = 4.5cm, ∠ASD = 75°, ∠SAN = 75° and ∠AND = 110°.
Solution :

From the ray SX, SA = 5.6cm is cut off.

• At A draw the angle ∠SAY = 75° > form AY cut off AN = 4.5. Then at N draw angle ∠PNA = 110°  at S draw ∠QSA = 75°
• They meet at D, by joining DA we get the required quadrilateral SAND.

Question 10. Let’s draw a parallelogram LAND such that LA = 6.6cm, AN = 4cm and ∠LAN = 45°
Solution :

• Draw two line segments LA (6.6 cm) & AN (5.4 cm).
• Now from the ray AX, AN = 5.4 cm is cut off.
• At A, ∠YAN = 45° is drawn, and from AY, AL = (6.6 cm) is cut off.
• Now at L & N draw two arcs with radius AN & AL arc drawn, There two arcs intersects at D. Join LD & DN.
• Thus the required parallelo gram LAND is obtained.

Question 11. Let’s construct a rhombus HOME such that ∠HOM 60 and HO = 6cm.
Solution :

From the ray HX, HO = 6cm is taken.

• Now at O draw an angle ∠YOH = 60° From OY , OM = 6cm is taken (As al1 the side of a rhombus are equal).
• Now, centre H & M two arcs equal to 8cm are drawn, then by joining EM & EH, we get the required rhombus HOME.

Question 12. Let’s construct a rhombus ROAD in which RA = 8cm and OD = 6cm.
Solution :

From the ray PX, take a line segment PQ equal to 7cm.

• Now, at Q draw an angle YQR = 60° From QY, QR = 6.5cm taken, now with centre R and P two arcs of radius 5.2cm & 4.4cm are drawn.
• They meet at S by joining PS & RS we get the required quadrilateral PQRS.

Question 13. Let’s draw a square TRAM such that TA = 6cm.
Solution :

A line segment TA = 6cm is drawn.

Now, draw the perpendicular bisector (PQ) of TA at O, from OP & OQ OM & OR each equal = 3cm is taken, by joining TM, MA, AR, RT we got the required square TRAM.

Question 14.  Let’s construct a rectangle ABCD such that AC = 5cm and ∠BAC = 30°.
Solution :

On the time AX at A draw an angle ∠YAX = 30°.

• From AY, ACT = 5cm is cut off. From C draw the perpendicular CB on AX.
• Now, with centres C & A draw two arcs equal to AB & BC respectively.
• They meet at D joining CD & AD, we get the required rectangle ABCD.

WB Class 7 Math Solution Geometry Chapter 7 Type Of Quadrilateral Exercise 7 Solved Problems

Quadrilateral: A closed plane figure bounded by four line segments is called a quadrilateral.

There are four sides and four vertices in a quadrilateral.

The line joining two opposite vertices is called a diagonal.

 

 

In the adjacent image, ABCD is a quadrilateral whose four sides are AB, BC, CD, and DA, four vertices are A, B, C, and D, two diagonals are AC and BD.

Wbbse Class 7 Maths Solutions

The sum of the measurement of four angles of a quadrilateral is 360°.

Read and Learn More WBBSE Solutions for Class 7 Maths

Convex Quadrilateral: A convex quadrilateral is a four-sided polygon that has interior angles that measure less than 180° each. The diagonals are contained entirely inside of these quadrilaterals. PQRS is a convex quadrilateral.

 

 

Concave Quadrilateral: If the quadrilateral has an interior angle greater than 180°, it is called a concave quadrilateral.

ABCD is a quadrilateral whose interior ∠BCD > 180°

 

 

Parallelogram: The quadrilateral whose opposite sides are parallel is called a parallelogram.

ABCD is a parallelogram whose AB || DC and AD || BC.

Wbbse Class 7 Maths Solutions

 

 

Trapezium: The quadrilateral whose one pair of opposite sides are parallel is called a trapezium.

The nonparallel sides of a trapezium are called oblique sides. ABCD is a trapezium whose AB || DC and AD BC

 

Isosceles trapezium: The trapezium whose oblique sides are equal is called isosceles trapezium.

ABCD is a isosceles trapezium whose AB || DC and AD BC.

Wbbse Class 7 Maths Solutions

 

 

Rectangle: If a parallelogram has its one angle a right angle (90°) is called a rectangle.

PQRS is a rectangle whose SR || PQ, SP || RQ, and ∠SPQ 90°.

 

 

Rhombus: A rhombus is a parallelogram whose one pairs of adjacent sides are equal in length.

Or, A rhombus is a quadrilateral whose four side are equal in length ABCD is a rhombus whose AB = BC = CD = DA.

 

 

Square: A square is a rectangle whose one pair of adjacent sides are equal in length.

ABCD is a square whose AB BC = CD = DA and ∠A = 90°

 

 

Kite: A kite is a quadrilateral whose one pairs of adjacent sides are equal and the other two sides are equal.

Wbbse Class 7 Maths Solutions

ABCD is a kite whose AB = BC and AD = CD

 

 

Properties of different quadrilaterals parallelogram:

1. Opposite sides are equal
2. Opposite angles are equal
3. Diagonals bisect each other
4. Opposite sides are parallel.

 

 

 

 

Rectangle: 

1. Opposite sides are parallel
2. Opposite sides are equal
3. Diagonals are equal
4. Diagonal bisect each other
5. Each angles is right angle.

Rhombus:

1. Opposite sides are parallel
2. Four sides are equal in length
3. Diagonals are not equal
4. Diagonals bisect each other perpendicularly.

Square:

1. Length of the four sides are equal
2. Length of the diagonals are same
3. Diagonals bisect each other perpendicularly
4. Each angle is a right angle.

 

WB Class 7 Math Solution Question 1. Choose the Correct Answer

1. The measurement of the sum of four angles of any quadrilateral is

1. 90°
2. 180°
3. 360°
4. None of these.

Solution: The measurement of sum of four angles of any quadrilateral is 360°

So the correct answer is 3. 360°

2. The quadrilateral whose one pairs of opposite side are parallel is

1. Trapezium
2. Rhombus
3. Rectangle
4. None of these

Solution: 1. Trapezium

3. In which quadrilateral, two diagonals are not equal?

1. Isosceles trapezium
2. Rhombus
3. Rectangle
4. Square

Solution: 2. Rhombus

Question 2. Write true or false 

1. Each interior angle of a square is a right angle.

Solution: The statement is true.

2. In a rhombus only one pair of the opposite side are equal.

Solution: The statement is false.

3.  In a parallelogram opposite sides are parallel.

Solution: The statement is true.

Wbbse Class 7 Maths Solutions

Question 3. Fill in the blanks

1. The length of the oblique sides of an isosceles trapezium is ______

Solution: Equal.

2. The lengths of opposite sides of a rectangle are _____

Solution: Equal.

3. Rhombus is one type of ____

Solution: parallelogram.

Question 4. Every rectangle are parallelogram. Explain.

Solution: The opposite sides of the rectangle are parallel. Also, the opposite side of a parallelogram are parallel. So each rectangle is a parallelogram.

Question 5. All parallelogram are trapezium-Explain.

Solution: The quadrilateral whose one pairs of opposite sides are parallel is called a trapezium. As two pairs of opposite sides of a parallelogram are parallel, so each parallelogram is a trapezium.

 

Type Of Quadrilateral

WB Class 7 Math Solution Type Of Quadrilateral Exercise 7.1

1. Hence, quadrilateral has __________ diagonals.
Solution: 2.

2. Pentagon has__________diagonals. But triangles do not have diagonals.
Solution: 5.

3. The number of sides of a triangle is 3 the number of its diagonals = \(\frac{3(3-3)}{2}\)= __________
Solution:

Number of its diagonal

= \(\frac{3(3-3)}{2}\)

= 0

4. The number of sides of a quadrilateral is 4. Number of diagonals \(\frac{4(4-3)}{2}\) = __________
Solution:

Number of its diagonal

= \(\frac{4(4-3)}{2}\)

5. The Pentagon has 5 Sides. It has \(\frac{5(5-3)}{2}\) = 5 Diagonals.
Solution:

The Pentagon has 5 Sides, Numbers is diagonal \(\frac{5(5-3)}{2}\) = 5

6. Hexagon has 6 sides. It has = \(\frac{6(6-3)}{2}\) = diagonals. 6(6-3)
Solution:

Hexagon has 6 sides, it has ___________ = 9 diagonals.

7. An n-sided polygon has n sides. Its number of diagonals ____________
Solution:

A n-sides polygon has n-sides

It’s number of diagonal = \(\frac{n(n-3)}{2}\)

WB Class 7 Math Solution Type Of Quadrilateral Exercise 7.2

Question 1. Let us identify the quadrilateral from the figures given below
Solution:

Solution: 2,3,4,5,6 →  Are quadrilateral

Question 2. Let us fill in the gaps 

1. Oblique sides of isosceles trapezium are [equal / unequal]
Solution: Equal.

2. If two pairs of opposite sides of a trapezium are equal it is a.
Solution: Isosceles trapezium.

3. Opposite sides of a parallelogram are mutually [parallel / not
parallel.
Solution: Parallel.

4. If one angle of a parallelogram is 90° then it will be, [Rectangle / Rhombus].
Solution: Rectangle.

5. Quadrilateral has_ diagonals.
Solution: Two.

6. Diagonals of a rhombus bisect each other at_.
Solution: Right angle.

7. The opposite sides of a rectangle are [equal/unequal]
Solution: Equal.

8. Rhombus is a special type of [square/parallel]
Solution: Parallelogram.

9. The diagonals of a parallelogram
Solution: Bisect.

Question 3. By cutting paper, let us verify
Solution:

• The diagonals of a square bisect each other at right angles.
• The diagonals of the rectangle bisect each other

Class 7 Math Solution WBBSE Geometry Chapter 6 Parallel Lines And Transversal Exercise 6 Solved Problems

Parallel lines: If two straight lines on the same plane do not intersect when produced in any direction, the two straight lines are said to be parallel to one another.

In the adjacent image, the straight lines AB, CD, and EF are parallel to each other i.e., AB || CD || EF

Transversal: If a straight line intersects two or more straight lines in different points then the straight line is called a transversal of the lines.

In the adjacent image, the straight line EF intersects the straight lines AB and CD at points G and H respectively. So EF is called the transversal of lines AB and CD.

Vertically opposite angles: If two straight lines intersect at a point, the angles formed on the opposite sides of the common point (vertex) are called vertically opposite angles.

 

In the adjacent image, two straight lines AB and CD intersect at O. ∠AOC and ∠BOD are two vertically opposite angles. Also, ∠AOD and ∠BOC are two vertically opposite angles.

Interior angles and exterior angles: In the adjacent image ∠3, ∠4, ∠5, and ∠6 are interior angles whereas ∠1, ∠2, ∠7, and ∠8 are exterior angles.”

Corresponding angles: Two angles lying on the same side of the transversal are known as corresponding angles if both lie either above are below the two given lines.

Alternate angles: The pair of interior angles on the opposite side of the transversal are called alternate angles.

In the adjacent image, there are four pairs of corresponding angles. (∠1, ∠5), (∠2, ∠6), (∠8, ∠4), and (∠7, ∠3). There are two pairs of alternate angles (∠4,∠6) and (∠3, ∠5).

If a straight line intersects two parallel lines then the measurement of each pair of corresponding angles are equal and the measurement of alternate angles are equal.

Hence, ∠AGE = ∠GHC, ∠CHF = ∠AGH, ∠DHF = ∠BGH and ∠EGB = ∠GHD

Again, ∠AGH = ∠GHD and ∠BGH = ∠GHC

 

 

[The sum of the measurement of two interior angles in the same side of the transversal is 180°]

 

WB Class 7 Math Solution Parallel Lines And Transversal

Parallel Lines And Transversal Exercise 6

When the lines not parallel

When the lines are parallel

Lines are not parallel:

Lines are parallel:

WBBSE Class 7 Math Solution Geometry Chapter 5 Concept Of Congruency Exercise 5 Solved Problems

If two geometrical figures are of the same shape and size, they are said to be congruent to each other.

Congruence is the property of two geometrical images if one of them can be made to coincide with the other by means of reflection, transformation, translation, rotation, or by their combination.

Read and Learn More WBBSE Solutions for Class 7 Maths

Congruence of the triangle:

Two triangles are said to be congruent if their respective sides, and angles are equal and when placed upon one another cover each other completely.

The congruence may be expressed by the symbol ‘≅’

 

 

 

In two triangles ABC and DEF, if AB = DE, BC = EF, CA = FD and ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

∴ ΔABC≅ ≅DEF

The followings are the conditions for the congruency of triangles

1. SSS (Side-Side – Side)
2. SAS (Side-Angle – Side)
3. AAS (Angle – Angle – Side)
4. RHS (Right Angle – Hypotenuse – Side)

Wbbse Class 7 Maths Solutions

1. SSS: If the lengths of three sides of a triangle are equal to the lengths of three sides of the other triangle then the triangles are congruent.

 

 

In ΔABC and ΔDEF,
AB = DE, BC= EF and AC = DF

∴ ΔABC=ΔDEF

2. SAS: Two triangles are congruent if the length of two sides and the measurement of the included angle of one triangle are equal to the length of two sides and the measurement of the included angle of the other triangle.

 

 

In ΔABC and ΔDEF,
AB = DE, ∠ABC = ∠DEF and BC= EF

∴ ΔABC ≅ ΔDEF

Wbbse Class 7 Maths Solutions

3. AAS: Two triangles are congruent if the measurement of any pair of angles and the length of one pair of corresponding sides are equal to the other triangle.

 

 

 

In ΔABC and ΔDEF,
∠B = ∠E, ∠C = ∠F and AB = DE

∴ ΔABC ≅ ΔDEF

4. RHS: If in two right-angled triangles, the length of the hypotenuse and the length of one triangle is equal to the length of the hypotenuse and the length of one side of the other triangle, then the two triangles are congruent.

 

 

 

In ΔABC and ΔDEF,
∠ABC = ∠DEF = 90°

hypotenuse AC = hypotenuse DF and AB = DE

∴ ΔABC ≅ ΔDEF

Wbbse Class 7 Maths Solutions

Similar triangle: If three angles of one triangle are equal to three angles of the other triangle then these two triangles are called similar triangles.

 

 

 

In ΔABC and ΔDEF,
∠A = ∠D, ∠B = ∠E and ∠C = ∠F

but AB ≠ DE, BC ≠ EF and AC ≠ DF

∴ ΔABC and ΔDEF are similar triangles.
Two congruent triangles are always similar triangles but two similar triangles may not always be congruent.

 

Class 7 Math Solution WBBSE Concept Of Congruency Exercise 9

1. Let us write does congruency means.
Solution:

Two shapes are said to be congruent if they have the exact same size and shape. One shape may be thought as of being an exact copy of a duplicate of the other.

Two triangles are congruent if all the angles and the sides in one triangle are exactly the same as the angles & sides of the other triangle.

2. Let’s write down the conditions of congruency of two triangles.
Solution:

There are four conditions of congruency of two triangles.

1. If the lengths of three sides of a triangle is equal to the lengths of three
   sides of the other triangle then the triangles are said to satisfy side – side – side or S – S – S condition.
2. If the measure of two sides and included angle of one triangle is equal to the measures of two sides and included angle of the two sides of that two side of the other, then the two triangles are said to satisfy side angle – side or S – A – S condition.
3. If the measure of two angles and the side included between them of one triangle are equal to two angles and the corresponding side included between them of the other than the two triangles are said to satisfy angle – side angle or A – S – A condition.
4. If the length of the hypotenuse and a side of a right-angled triangle is equal to the hypotenuse and a side of the other right-angled triangle, then the two right-angled triangles are said to satisfy Right angled – -hypotenuse – side ie. R – H – S condition or A – A – S condition.

3. Let’s explain with a figure whether angle-angle-angle can be a condition for the congruency of two triangles.
Solution :

ABC and DEF are two equilateral triangles In Δ ABC, all the angles equal to go’ and each side = 4cm.

In Δ DEF each angle is equal to 60° but each side = 6cm, But it is clear from the two figures above that if Δ ABC, is cut off and placed or Δ DEF, they will not be coined.

∴ The triangles are not Congruent.

These types of triangles are called similar triangles.

4. Let’s explain with conditions of congruency whether the following pair of triangles in all cases are congruent or not.
Solution :

Δ ABC & A PQR are two equilateral triangles each angle of both triangles is 60°

But each side of the 1st triangle is 4cm, whereas each side of the 2nd triangle is 5.5cm.

It is very clear from the figures above that if Δ ABC is cut off and placed on Δ PQR, they will not concede. That is the triangles are not congruent.

These triangles are called similar triangles.

5. Let’s explain with the condition of congruency whether the following pair of triangles in all cases are congruent or not.

1. Solution: These two triangles are congruent according to the S – S – S condition.

2. Solution: Δ PQR & Δ GHI are congruent according to the S – A – S condition.

3. Solution: Δ ABC & Δ DEF are congruent according to the S – A – S condition.

4. Solution: Δ ABC & Δ DEF are congruent according to the R – H – S condition.

5. Solution: Δ ABC & Δ DEF are not congruent.

6. Solution: Δ ABC & Δ DER. are congruent according to the A – S – A condition.

7. Solution: Δ ABC & Δ DEF are not congruent.

8. Solution: Δ ABC & Δ DEF are not congruent.

Class Vii Math Solution WBBSE Geometry Chapter 4 Construction Of Triangles Exercise 4 Solved Problems

Question 1. To construct an angle equal to the given angle.

Solution:

 

Given ABC is an angle of measure x°

 

 

Method:
1. I draw a straight line QR. With B as a centre and with any radius an arc is drawn to intersect the AB and BC at D and E respectively.
2. With Q as a centre and with the same radius another arc is drawn to cut the straight line QR at M.
3.  Now with M as a centre and with a radius equal to DE another arc is drawn to cut the previous arc at N. In joined Q, N and produced to P.

∠PQR is the required angle where ∠PQR = ∠ABC = x°

^{Wbbse Class 7 Maths Solutions}

Question 2. Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 5 cm

[ For any triangle the sum of lengths of its two smaller sides must be greater than the third side]

Solution:

Method:

 

 

1. At first, using scale and pencil we draw three line segments of length 4 cm, 5 cm and 6 cm.
2. I draw a ray BX with centre B and radius 6 cm an arc is drawn which cut BX at C.
3. With B and C as centres and with respective radius 4 cm and 5 cm two arcs are drawn on the same side of BC such that these two arcs intersect each other at A. A, B and A, C are joined.

Read and Learn More WBBSE Solutions for Class 7 Maths

∴ ABC is the required triangle whose AB = 4 cm, BC = 6 cm and AC = 5 cm.

Question 3. Construct a triangle ABC in which AB = 4.6 cm, BC= 6.2 cm and ∠ABC = 70°

 

 

 

Solution:

Method :

1. At first, I take two line segments of length 4.6 cm and 6.2 cm using scale and pencil and an angle of 70° with the protractor.
2. A rays BX is taken. At B on BX, ∠YBX = 70° is drawn. From BX, the portion BC = 6.2 cm is cut off and from BY, the portion BA = 4.6 cm is cut off. A, C is joined.

∴ ABC is required triangle whose AB = 4.6 cm, BC = 6.2 cm and ∠ABC = 70°

Wbbse Class 7 Maths Solutions

Question 4. Draw a triangle PQR whose QR

Solution:

 

 

 

Method:

1. I take a ray QX and cut off a line segment QR of length 7.5 cm
2. At Q and R two angles ∠YQX and ∠ZRQ are drawn where ∠YQX = 60° and ∠ZRQ = 45°. QY and RZ intersect at P.

So PQR is the required triangle whose QR = 7.5 cm, ∠PQR = 60° and ∠PRQ = 45°.

Wbbse Class 7 Maths Solutions

Question 5. Draw a right-angle triangle ABC such that ∠ABC = 90° and AC = 9.6 cm. 

Solution:

 

Method:

1. I draw line segment AB = 5 cm and AC = 9.6 cm
2.  A ray BX is drawn. At B on BX, ∠YBX = 90° is drawn.
3.  I take a line segment BA = 5 cm.
4. With A as a centre and with a radius equal to 9.6 cm an arc is drawn which intersects BX at C. I join A, C. So ΔABC is the required triangle.

Construction Of Triangles

Class Vii Math Solution WBBSE Construction Of Triangles Exercise 8.1

1. The length of the three sides of the triangles is given. Let’s identify the cases where, triangles can be constructed and construct those triangles, and give reasons for the cases where the triangle cannot be constructed.

1. 4cm, 5cm & 7cm.
2. 9cm, 4cm. And 4cm.
3. 6cm, 8cm and 10cm.

Solution :

For the construction of any triangle when the length of 3 sides is given, the sum of the length of two smaller sides must be greater than the third side.

In the 1st case. Here 4 cm + 5cm > 7cm

∴ It is possible to construct a triangle

In the 2nd case, here 4cm + 4cm < 9cm.

∴ It is not possible to construct a triangle

In the 3rd case, here 6cm + 8cm > 1 0 cm

∴ It is possible to construct a triangle

2. Let’s draw a triangle ABC in which AB = 5.5cm, BC = 5cm and CA= 6cm.
Solution :

1.  At first, using scale & pencil we draw three line segments of length 5cm, 6cm & 5.5cm.

2. Let’s draw a ray AX, with centre A & radius 6cm draw an arc on AX, such that AC = 6cm.

3. With centres A & C and with radius 5.5cm & 5cm respectively draw two arcs which cut each other’s B.

Points A, B and B, C are joined with scale to get the required triangle ABC, in which AB = 5,5cm, BC = 5cm & AC = 6cm.

3. Let’s draw an equilateral triangle having each side = 4.5cm. Let’s also measure its three angles with a protractor and write their measures.
Solution :

From the line BX, cut a line segment BC = 4.5cm

Now with centres B & C with a radius of 4.5cm, draw two arcs. Which cut each other at A. By joining AB & AC, we get the required equilateral triangle

ABC. By measuring the angles with the protector we get that each angle = 60°.

4. Let’s draw a triangle PQR, such that PQ = 6m, QR = 5cm, and PR = 6cm. Let’s measure each of its angles with a protractor and write them down.
Solution :

From the line QX, cut a line segment QR = 5cm with centre Q & R with radius 6cm two arcs are drawn which cut each other at P.

By joining PR & PQ, we get an isosceles triangle PQR, whose ∠ PQR = ∠ PRQ = 65° and∠ QPR = 50°

WBBSE Class 7 Math Solution Construction Of Triangles Exercise 8.2

1. Let’s construct a triangle ABC in which AB = 4cm, BC = 6cm and ∠ ABC = 45°
Solution :

First, take a ray BX. From BX cut BC = 6cm.

Now at B, draw an angle ∠ PBC = 45° with compass & scale. From BP cuts BA is equal to 4cm. Join AC.

∴ ABC is the required triangle whose AB = 4cm

BC = 6cm & included angle ABC = 45°

3. Let’s draw a triangle PQR, such that PQ = 4cm, QR = 3cm, and ∠ PQR = 90°  in Δ PQR, let’s also measure the side PR with scale and take down the measured value.
Solution :

Take a ray QX, from QX, cut QR = 3cm. Now draw ∠ YQR.= 90 from QY cut QP = 4cm, join PR.

∴ PQR is the required right-angled triangle whose PQ = 4cm, QR = 3cm & ∠ PQR = 90°

Now the length of PR = 5cm by measuring with scale.

4. Let’s draw an isosceles triangle whose two equal sides are 7.2 cm each and the angle included between them is – 100°
Solution :

From the ray BX, cut off BC = 7.2cm.

Now at B draw an angle YBC = 100° (given) with a compass.

From BY, cut BA = 7.2cm, and Join AC.

∴ ABC is the required isosceles triangle whose two equal sides BC

= AB = 7.2cm & the included angle ABC = 100°

WBBSE Class 7 Math Solution Construction Of Triangles Exercise 8.3

1. Let’s draw a triangle Δ XYZ, such that YZ – 6.5 cm. ∠ XYZ = 60 and ∠ XZY = 70°
Solution :

From the ray -YR cuts YZ = 6.5 cm

At Y draw an angle PYZ = 60° & at Z draw an angle QZY = 70°

Let YP & ZQ cut each other at X

∴ XYZ is the required triangle whose YZ = 6.5 XYZ = 603 & ∠ XZY = 70°

3. Let’s construct a Δ ABC, so that BC = 5.5 cm, ∠ ABC = 60° and ∠ ACB = 30
Solution :

From the ray BX, cut BC = 5.5cm. Now with the compass draw an angle at B,

MBC = 60° & at C draw an angle NCB = 30°.

MB & NC cut each other at A.

∴ ABC is the required triangle whose BC = 5.5cm &

∠ ABC = 60° ∠ ACB = 30°

4. Let’s try to draw a triangle whose one side QR = 7.2cm, ∠ PQR = 80° and ∠ PRQ = 115°. If a triangle can not be constructed, let’s try to find the reason for such a problem.
Solution :

In this case triangle cannot be constructed as here some of the two angles is 80° + 11 5° = 1 95°. More than 1 80°

We know that the sum of the 3 angles must be equal to 180°

5. Let’s draw an isosceles triangle Δ DEF in which the side EF is of length 6.2 cm and the two angles, adjacent to the side have their sum =  100°
Solution:

From the ray, EX cut EF = 6.2cm. Now at E & F draw two angles PEF & QFE, both equal to 50°

As here the sum of the two equal angles = 100° (given) as the triangle is an isosceles Δ PE & QF in interseptal  Δ DEF is the required isosceles triangle.

WBBSE Class 7 Math Solution Construction Of Triangles Exercise 8.4

1. Let’s construct a right-angled triangle in Δ PQR such that ∠ PQR = 90°, PQ = 6cm. And QR = 4cm.
Solution :

From the ray QX, QR = 4cm is cut off

At Q, Z YQX = 90° is drawn from YQ cut off PQ = 6cm. Joined PR

Hence, A PQR is the required right-angled triangle.

2. Let’s draw a right-angled isosceles triangle Δ ABC, such that ∠ ABC = 90° & AB = 7cm.
Solution:

To draw an isosceles right-angled triangle ABC

Here Δ ABC is the required isosceles triangle as AB = BC = 7cm & ∠ ABC = 90°.

3. Let’s draw a right-angled triangle Δ XYZ such that  ∠ XYZ = 90, XZ = 10cm and XY = 6cm.
Solution:

To draw a right-angled triangle Δ XYZ, such that ∠ XYZ = 90°, XZ = 1 0 cm & XY = 6cm.

XYZ is the required right angle triangle whose ∠ XYZ = 90° & XZ = 10 cm, XY = 6cm

∴ YZ = 8cm.

4. Let’s draw a right-angled triangle Δ ABC. Such that ∠ BAC = 90°, 6cm BC = 8cm and ∠ ACB = 45°.
Solution :

1. Draw a ray CX. Now, at C on CX an angle XCD = 90° is drawn.

2. ∠ XCD is bisected, we get ∠ XCY = 45°

3. From CY, CB = 8cm is cut off. From B, a perpendicular BA is drawn which cuts CX at A.

4. Δ ABC is the required triangle.

Where BC = 8cm, ∠ BAC = 90° & ∠ BCA = 45°

Class 7 Math Solution WBBSE Geometry Chapter 3 Properties Of Triangle Exercise 3 Solved Problems

Triangle: A plane figure bounded by three line segments is called a triangle.

 

 

In triangle ABC, three vertices are A, B and C. There are three sides AB, BC, and CA.

The side opposite to a vertex of a triangle is its base.
The sum of the measurement of three angles is 180°.

Read and Learn More WBBSE Solutions for Class 7 Maths

Classification of Triangles:

According to their sides, three triangles are
1. Equilateral triangle
2. Isosceles triangle
3. Scalene triangle

According to their angles, three triangles are
1.  Acute angled triangle
2. Right-angled triangle
3. Obtuse angled triangle

Equilateral triangle:

A triangle whose length of each side are equal is called an equilateral triangle.

 

 

In the equilateral triangle ABC,
AB = BC = CA and ∠A = ∠B = ∠C = 60°

Isosceles triangle: An isosceles triangle is a triangle that has two sides are equal in length.

 

 

In isosceles triangle ABC, AB = AC

Wbbse Class 7 Maths Solutions

Scalene triangle:

A scalene triangle is a triangle whose all sides are unequal in lengths.

 

 

In ΔABC, AB ≠ BC ≠ CA

Acute angled triangle: A triangle in which all three angles are acute (i.e. less than 90°) is called an acute angled triangle.

 

 

PQR is an acute-angled triangle in which all angles are acute.

Wbbse Class 7 Maths Solutions

Right-angled triangle: A triangle whose one angle is a right angle (i.e., 90°) is Q called a right-angled triangle.

 

 

The side opposite to the right angle is called the hypotenuse.
ΔABC is a right-angled triangle whose ∠ABC= 90° and AB² + BC² = AC² [Pythagorus theorem]

Obtuse angled triangle: A triangle in which one angle is obtuse (i.e. more than 90°) is called an obtuse angled triangle.

 

 

ABC is an obtuse-angled triangle.

Right-angled isosceles triangle:

A triangle in which one angle is a right angle and the adjacent sides of a right angle are equal in length is called a right-angled isosceles triangle.
In isosceles right-angled triangle ABC, ∠ABC= 90° and AB = BC.

 

The altitude or the height of a triangle: The length of the perpendicular from the vertex to the opposite side of a triangle is called the altitude or the height of the triangle.

 

 

In the adjacent image, AD is the altitude of the ΔABC.

The median of the triangle:

The median of a triangle is the line segment drawn from any vertex to the midpoint of the opposite side.

 

 

In ΔABC, AD is a median.

Area of the triangle = \(/frac{1}{2}\) × base x height.

The sum of length of any two sides of any triangle is greater than the length of the third side.

Question 1. Choose the correct answer

1. The number of medians of a triangle is

1. 1
2. 2
3. 3
4. None of these

 

 

Solution: There are three medians of a triangle ABC
AD, BE, and CF.

So the correct answer is 3.3

2. If the measurement of one angle of a triangle is 105° the triangle is

1.  Acute angled triangle
2. Right-angled triangle
3. Obtuse angled triangle
4. None of these

Solution: 105° is an obtuse angle. The triangle is an obtuse-angled triangle.

So the correct answer is 3. Obtuse angled triangle

Wbbse Class 7 Maths Solutions

3. In which triangle the length of the median and height are same?

1. Equilateral triangle
2. Isosceles triangle
3. Scalene triangle
4. None of these

Solution: In an equilateral triangle height and median are the same.

So the correct answer is 1. Equilateral triangle

Question 2. Write true or false 

 

 

1. The position of medians of a triangle always inside the triangle.

Solution: The statement is true.

2. The hypotenuse of the right angled triangle is the smallest side.

Solution:  The statement is false.

3. These are three altitudes in a triangle.

Solution: The statement is true.

Question 3. Fill in the blanks

1. The sum of the measurement of three angles of a triangle is _____

Solution:180°

2. The number of vertices is _____

Solution: 3

3. Triangle has _____ diagonal.

Solution: No

Question 4. If the length of two adjacent side of right angle of a right angled triangle are 3 cm and 4 cm. Then find the length of its hypotenuse.

Solution:

 

 

ΔABC its, ∠ABC = 90°
AB = 3 cm, BC = 4 cm

AC² =AB²+ BC² [by applying Pythagorus theorem]
= 3² + 4²
= 9+16
= 25

AC = √25 cm = 5 cm

Wbbse Class 7 Maths Solutions

Question 5. If length of base and height of a triangle are 10 cm and 8 cm respectively then find the area of the triangle.

Solution Area of the triangle = \(\)\frac{1}{2}] base x height

= 40 sq.cm

Question 6. Whether the length of three sides of a triangle are 4 cm, 5 cm and 9 cm is possible?

Solution: The length of biggest side of any triangle is less than the sum of lengths of other two sides.
As 4+5=9
So, the given length of three sides of the triangle is not possible.

Question 7. Find the perimeter of the triangle of lengths of sides are 6 cm, 7 cm and 8 cm.

Solution: Perimeter = (6+ 7+ 8) cm = 21 cm.

Properties Of Triangle

Class 7 Math Solution WBBSE Properties Of Triangle Exercise 3.1

Question 1. Let us try to draw and find the number of heights (altitudes) for a triangle.
Solution :

In Δ ABC, AD, BE & CF are three*altitudes, They meet at O on the side of the triangle.

Question 2. Let us try to draw the heights of all the triangles in the same way according to sides and angles, with the help of a compass and scale.
Solution :

1. In case of Isosceles triangle:

Here PQR is an isosceles triangle PS, QT & RM are three heights of a triangle drawn from vertexes P, Q & R respectively. They meet at point O.

2. In case of Equilateral and Acute angled triangles:

Here ABC is an equilateral & acute angled triangle. AD, BE & CF are the three heights of the triangle, they meet at 6.

3. In case of the Scalene triangle:

ABC is a scalene triangle AD, BF & CF are the three heights of the triangle.

4. In the case of the obtuse-angled triangle:

Here ABC is an obtuse-dangled triangle perpendiculars are drawn from the three vertexes.

5. In case of a right-angled triangle:

ABC is a right-angled triangle ∠ ABC = 90°

Question 3. Which of these triangles has its height as one of its sides? Let’s draw and find.
Solution :

In the case of a right-angled triangle. AB is the height and also one side of the triangle.

Question 4. Which of these triangles have their heights and medians are the same line segment, let’s draw and find.
Solution :

ABC is an equilateral triangle whose each side is 6 cm.

Here AD, BE & CF are their height, also AD, BE & CF are the three medians of the triangle, as D, E & F are the midpoints of the side BC, CA & AB, respectively.

∴ Height & medians are the same line segment

Class 7 Math Solution WBBSE Properties Of Triangle Exercise 3.2

Question 1. Given 

1. Let’s write how many medians are there in a triangle.
Solution: 3 Medians are there in a triangle.

2. Let’s find how many do the three medians of a triangle meet.
Solution: Three medians of a triangle meet at a point.

3. Let’s write how many heights are there in a triangle.
Solution: There are 3 heights of a triangle.

4. Let’s find how many points the three heights (altitudes) of a triangle meet.
Solution: Three heights (altitudes) of a triangle meet at a point.

5. Let’s identify the triangles whose medians and heights (altitudes) are the same.
Solution:  Equilateral & Isosceles triangle.

Question 2. Let us draw all the types of triangles classified according to sides and angles and then draw 3 medians for each of these triangles using a scale and compass. From the figure drawn, let us try to find if the medians always remain inside the triangle.
Solution:

1. In the case of equilateral triangle:

In this case, medians meet at ‘O’ inside the triangle.

2. In the case of Isosceles + Acute angled triangle:

In this case, medians meet at ‘O’ inside the triangle.

3. In the case of scalene triangle:

In these medians meet at ‘O’ in the side of the triangle.

4. In the case of right-angled triangle:

In these medians meet at ‘O’ which is the mid-point of the hypotenuse

5. In the case of the obtuse-angled triangle:

In these medians meet at ‘O’ which is outside the triangle.

Question 3. Let us measure the height of each of the triangles given below with a scale and pencil.

Solution:

In the 1st figure, right of Δ ABC = 3.5cm, In the 2nd fig. height of

A DEF = 4cm & in the 3rd figure height of Δ PQR = 2.5 cm.

Class Vii Math Solution WBBSE Question 4. Let us draw the triangles classified according to the angles. Let us draw the height (altitudes) using a scale and compass and find if all the heights remain inside the triangle.
Solution :

1. In the 1st figure ABC is an acute-angled triangle Height AM = 4cm

2. In the 2nd figure, DEF is a right-angled triangle Height DE = 3cm.

3. In the 3rd figure PQR is an obtised angled triangle. Height PS = 5.2cm.

4. ln> The first two figure height is inside the triangle. But in 3rd figure oblused angled triangle height is outside the triangle)