Class 7 Maths

Class 7 Math Solution WBBSE Geometry Chapter 2 Drawing Angles With Compass Exercise 2 Solved Problems

Question 1. To construct an angle of 90°

Solution: Method of construction

 

 

1. BC is any straight line. With B as a centre and with any radius I draw an arc with a compass so that it cuts the line segment BC at D.
2. With centre D and with the same radius, I draw an arc which cuts the previous arc at E.
3. Again with centre E and with the same radius, I draw another arc, to cut the first arc at F.
4. With E and F as centres and with the same radius two more arcs are drawn to cut each other at A. Points A and B are joined.

Thus ∠ABC = 90°

Read and Learn More WBBSE Solutions for Class 7 Maths

Question 2. To construct an angle of 45°

Solution: Method of construction

 

1. At first ∠ABC is drawn where ∠ABC = 90°

2. Then bisect angle ∠ABC with compass, so that ∠ABD = ∠DBC = 45°

Wbbse Class 7 Maths Solutions

Question 3. To construct the angles of 60°, 30° and 15°

Solution: Method of construction

1. BC is any straight line with B as centre and with any radius, an arc is drawn which cut BC at P. P as a centre and with the same radius another arc is drawn to cut the previous arc at Q. I joined B and B produced to A. Thus ∠ABC 60°

 

 

2. I bisect the ∠ABC by BD I get 30° i.e., ∠DBC = 30°

 

 

3.  Again bisecting ∠DBC by BE I get ∠EBC= 15°

 

 

Wbbse Class 7 Maths Solutions

Question 4. To construct the angles of 120° and 75°

Solution: Method of construction

 

 

From the adjacent
∠CQR = 120°
∠PQR = 90° and ∠DQR = 60°

So∠PQD = ∠PQR – ∠DQR
= 90° – 60°
= 30°
∠PQD = 30°

Bisecting angle ∠PQD by QE we get ∠EQD, where∠EQD = 15°
So ∠EQR = ∠EQD +∠DQR
= 15° + 60°
= 75°
∠EQR = 75°

Drawing Angles With Compass

Drawing Angles With Compass Exercise 7

Question 1.  At point a on the line segment AB, let’s construct an angle of go with the help of scale, pencil and compass, let’s construct the angle; 120° 75° and 60°= angles at the same point,
Solution :

Given

At an AB, first, we draw an angle of 60°, 90° & 120°

Here ∠ BAC = 90°

∠ BAD = 120°

∠ BAE = 75°

∠ BAF = 60°

2. Using scale, pencil and compass, let’s construct the angles, 45 and 22\(\frac{1}{2}\)
Solution:

Take a line segment AO. Now with centre O, & with any radius draw an arc which cuts OA at P. Now with centre P, draw an arc which cuts the previous arc at Q.

Again with centre Q with the same radius an arc is drawn which cuts the previous arc at R. Now with centre Q and R, draw two arcs which cut each other at B. Join BO & AOB = 90° is formed.

Now by bisecting ∠ AOB, two angles ∠ AOC & ∠ COB are formed each equal to 45°.

Again by bisecting ∠ AOC, two angles ∠ AOD & ∠ COD two angles are formed, each equal to 22\(\frac{1}{2}\).

Question 3. Using scale, pencil and compass let’s draw the following angles –

1. 30°
2. 60°
3. 75°
4. 105°
5. 120°
6. 135°
7. 150°
8. 15°.

Solution:

Then, At O, draw an angle ∠ EOQ =.90°; ∠ GOQ = 60°& ∠ COQ = 120° (E).

⇒ Now by bisecting ∠ GOQ (= 60°) we get ∠ HOQ = 30s (A).

⇒  Again by bisecting ∠ HOQ (= 30°) we get ∠ KOQ = 15° (H)

⇒ Now by bisecting ∠ EOG, we get ∠ QOF = 75° (C)%

⇒ Again by bisecting ∠ COE we get ∠ DOQ =105° (D)

⇒ Now by bisecting ∠ POC (= 60°), we get Z AOQ = 150° (G)

⇒ Lastly by bisecting ∠AOC (= 30°), we get ∠ BOQ = 1 35° (F)

Class 7 Math Solution WBBSE Question 4. Using scale, pencil and compass let’s draw an angle ∠ PQR of 60°. Let the side of RQ is produced to any point S, opposite to R. Then ∠ PQS = 120° Let’s also bisect the ∠ PQS and let’s verify using a protractor if ∠ PQS is bisected.
Solution:

Given

First ∠ PQR = 60° is drawn at Q, then RQ is produced to S, opposite to R.

∠ PQS = 180° – 60° = 120° as, straight angle ∠RQS = 180°, Now

∠ PQS is bisected by MQ

∠MQP = ∠ MQS = 60°

Question 5. Using scale, pencil and compass let’s draw an angle ∠ ABC of measure 30°. Then let’s produce the side CB to a point D opposite to C. Now let’s draw a bisector BE of angle ∠ ABD. Measuring by protractor it is found ∠ DBE = 75° ∠ EBC = 105°
Solution :

Given

First ∠ ABC = 30° is drawn at B on the line segment BC.

Now CB is produced to a point D opposite to C.

Now BE is drawn as the bisector of ∠ ABD

Measuring by a protractor it is found ∠ DBE = 75° and ∠ EBC = 105°.

Class 7 Math Solution WBBSE Geometry Chapter 1 Revision Of Old Lesson Exercise 1 Solved Problems

Question 1. Draw a line segment AB of length 10 cm. Bisect the line segment AB with the help of a compass and measure each part.

Solution: Method of construction:

 

1. I draw a line segment AB of length 10 cm
2. With A as a centre and with a radius more than half the length of AB, two arcs are drawn on either side of the line segment AB.
3. Again with B as the centre and with the radius two arcs are drawn on either of the line segment AB such that these two arcs intersect previous arcs at P and Q respectively. P and Q are joined with a scale and a pencil to get the midpoint O’ of the line segment AB.

Thus AO = OB = 5 cm.

Wbbse Class 7 Maths Solutions

Read and Learn More WBBSE Solutions for Class 7 Maths

Question 2. Draw an angle of 75° with the help of a protractor, then bisect the angle with the help of a scale, pencil and compass.

Solution:

Steps for drawing the angle:

1. I draw an angle ∠ABC where ∠ABC = 75°
2. With centre B and with any radius, I draw an arc cutting the arms AB and BC of the ∠ABC at P and Q respectively.

3. With centre P and radius equal to more than half the length PQ, an arc is drawn.
4. Again with centre Q and with the same radius, an arc is drawn to the previous arc at R. Points B and R are joined and produced. The ray BR is the bisector of ∠ABC.

Thus ∠ABR=∠CBR = 37-5°

Wbbse Class 7 Maths Solutions

Question 3. With the help of a scale, pencil and compass, draw a line segment perpendicular to a line from a point outside it.

Solution:

 

1. A straight line PQ is drawn and a point A is taken outside the straight line
2. I take any point T on the side of the straight line PQ opposite to point A.
3. With centre A and a radius AT, I draw an arc which cuts the straight line PQ at R and S.

4. With centres R and S and a radius equal to more than half of the line segment RS, two arcs are drawn on the side of the line PQ opposite to A, where two arcs intersect at B.
5. points A and B are joined with a scale and pencil. The line segment AB; cuts the straight line PQ at O.

∴ AO ⊥   and ∠AOP =∠AOQ = 90°

Algebra Chapter 8 Double Bar Graph Exercise 8 Solved Problems

A bar graph is a graphical representation of the numerical data by a number of rectangular bars of uniform width erected horizontally or vertically with equal spacing between them.

Each rectangle or bar represents only one value of the numerical data. The height or length of a bar indicates on a suitable scale the corresponding value of the numerical data.

This method of representing or explaining the statistical data is called the Bar diagram or Bar graph.

In order to draw a bar graph we draw two mutually perpendicular lines in the plane paper. The horizontal line is called X-axis and the vertical line is known as the Y-axis.

If the bars are drawn vertically on a horizontal line, then the scale of heights of the bars is shown along Y-axis. If the bar are drawn horizontally on the vertical line, then the scale of the height of the bars is shown along X-axis. The bars can be shaded, hatched or colored.

Read and Learn More WBBSE Solutions for Class 7 Maths

Double Bar Graph: When two bar graphs are drawn side by side along the same reference lines for better comparison of data as has been done in the graph, this is called a Double Bar Graph.

Wbbse Class 7 Maths Solutions

Question 1. We prepared a single bar graph of the number of members from each 55 families in our locality

Scale: 1 unit = 1 family.

 

 

From the bar graph answers the following questions:

1. Out of 55 families, how many families have 4 members?
2. Out of 55 families, how many have a maximum number of family members?
3. From the bar graph find families have 5 members and members and families have 3 members.

Solution:

1. Out of 55 families, 15 families have 4 members.
2. Out of 55 families, the maximum number of family members is 5.
3.  From the graph we find 5 families have 5 members and 20 families have 3 members.

Question 2. Read the following double-bar graph and answer the following questions.

Scale: 1 unit = 1 ton.

 

 

1. What information is given by the bar graph?
2. Which state is the largest producer of rice?
3. Which state is the largest producer of wheat?
4. Which state has total production of rice and wheat as its maximum?
5. Which state has the total production of rice and wheat minimum.

Solution:

1. It gives information regarding rice and wheat production in various states.
2. W. B.
3. U. P.
4. U. P.
5. Maharashtra.

Wbbse Class 7 Maths Solutions

Question 3. Given below the date of the number of clay dolls and sola dolls a potter in Krishnanagar has made in 5 months. Express the data through double-bar graph.

Month	January	February	March	April	May
Number of clay dolls	600	550	450	750	900
Number of sola dolls	500	450	600	650	700

Solution:

Scale: 1 Unit = 100 dolls

 

 

Question 4. After first continuous assessment, 6 friends worked in a group to grasp the subjects learnt through practical applications and through different methods. A table of the percentage of marks obtained in two continuous assessments after the second assessment.

Friends	Sumit	Rumki	Jahir	Merry	Joseph	Nazeen
1st assessments	45%	60%	55%	38%	72%	62%
2nd assessments	65%	65%	68%	60%	80%	70%

preparing the double bar graph

Solution:

Scale: 1 Unit = 1%

 

 

Question 5. The number of Male and Female people of a village in the year 2015-2018 are given the following table 

Year	2015	2016	2017	2018
Male	1200	1350	1450	1600
Female	1150	1200	1300	1450

Express the above information by a bar graph

Solution:

The number of Male and Female people of a village in the year 2015-2018 are given the table

Scale: 1 unit = 100 persons

 

 

 

Double Bar Graph

Double Bar Graph Exercise 8.1

Question 1. We prepared a single bar graph of the number of members from each of the 55 families in our locality. Let us study the bar graph and try to find the answers to the following question Scale: 1 unit = 1 family

1. Out of 55 families, how many families have 4 members?
Solution: 15

2. Out of 55 families how many have the maximum number of family members 
Solution: 3

Question 2. From the bar graph, we find families have 5 members and families have 3 members.
Solution: 5, 2

Question 2. A list of mountain peaks and their corresponding heights are given in the chart. Let us prepare a bar graph on squared paper taking 1 unit = 1000 metres.

Solution:

Single Bar graph of the Height of different Mountain peaks.

Question 3. For 55 students of class VII and 60 students of class 8 a list of their choice of games has been made. Let us express the data through a double-bar graph.

Solution:

Double bar graph of the students of Class 7 & Class 8 on their choice of games.

Question 4. Given below the date of the number of clay dolls and sola dolls a potter in Krishnakumar has made in 5 months. Let us express the data through a double-bar graph

Solution:

Bar Graph of Clay Dolls-& Sola Dolls of Krishnakumar made is 1st 5 months in a year.

Question 5. I made a list 50 students from my class according to the choices of colours as white, red, green, blue and black and then to express these daias through bar graph. [Let me do it myself.
Solution:

Given

I made a list 50 students from my class according to the choices of colours as white, red, green, blue

Bar graph of so students on their choice of colours

Question 6. The number of boys and girls of Tarai Tarapada Higher secondary school, in the last 4 years and also this year has been listed below. Let us express these data as a double bar graph. We all know the literacy rate has increased with time but let us find it whether the literacy rate of girls are more than boys or they are still backward

Solutions:

Given

The number of boys and girls of Tarai Tarapada Higher secondary school, in the last 4 years and also this year has been listed

Double bar graph: For increase in literacy for boys & girls for the year 2009 to 201 3 (5 years)

Question 7. After our first continuous assessment, we 6 friends worked in a group to grasp the subjects learnt through practical applications and through different methods. We prepared a table of the percentage of marks obtained in two continuous assessments after the second assessment. Preparing the double bar graph, let us understand, how much the new method helped to improve and who improved most.

Solution:

Double Bar Graph of Mark obtained (in percentage) in 1st & 2nd assessment by my 6 friends.

Question 8. The yearly production of cotton saris is woven by Utpal and Aminabibi from Phulia is shown is the double bar graph. Let us try to answer the following questions from the graph 

Given

The yearly production of cotton saris is woven by Utpal and Aminabibi from Phulia is shown is the double bar graph.

1. In which year did Utpal weave a maximum number of saris, and what is the number of saris woven? Again, in which year did he wove a minimum number of saris and how many are those, let’s find.
Solution:

2.  In which year did Aminabibi weave a maximum number of saris and how many are those? Also in which year did she wove a minimum number of saris and what is that number, let’s find out.
Solution:

3.  In which years did Utpal weave more saris than Aminabibi and in which year he wove a maximum number of saris than Aminabibi, let’s find.
Solution:

Utpal- 2008 & 2009 – 2008

4. In which years did Aminabibi weave more saris than Utpal and in which year she wove a maximum number of saris than Utpal, let’s find.
Solution:

Aminabibi – 2010 & 201 0 – 2011

WBBSE Class 7 Math Solution Algebra Chapter 7 Formation Of Equation And Solutions Exercise 7 Solved Problems

1. Variable, constant, and ‘equal to’ signs are used to express the problem in the language of Mathematics. This method is called the framing of the equation.
2. The value of the variable used in the equation is called an unknown number.
3. The specific value of unknown number for which the two sides of the sign are equal is the root or the solution of the equation.
4. The method of finding the value of the unknown number is called solving of the equation.

Example: 3x – 5 = 7 [x is variable]
⇒ 3x = 5 +7
⇒ 3x = 12

⇒ \(x=\frac{12}{3}=4\)

Here 4 is the root of the equation 3x – 5 = 7.

Again, (x-2)² = x² – 4x + 4 is true for any value of the variable.

Let, x = 3, (x-2)² = (3-2)²= (1)² = 1

x² – 4x + 4 = (3)² – 4 x 3+4=1

It is true for x = 3

x=-5, (x-2)² = (-5-2)² = (-7)² = 49

x²-4x+4= (-5)²– 4 (-5)+ 4 = 25 +20 + 4 = 49

It is also true for x = – 5 so it is identified.

Read and Learn More WBBSE Solutions for Class 7 Maths

If both sides of the equation become equal for any value of the unknown quantity then this is called an identity.

An equation containing only one unknown quantity is known as a simple equation. Solving an equation is the process of finding its root.

Method of solving linear equations in one variable.

1. Simplify both sides of an equation and collect the like terms.
2. Multiply both sides by an appropriate factor (L. C. M of fractions) in order to remove fractions (if any).
3. Keep all the variable terms on LHS and the constant terms on the RHS following the rules of transposition.
[Any term may be brought one side of the equation to the other by simply changing its sign. This is called transposition.]
4. Simplify both sides.
5. Divide both side by the coefficient of the variable. The resulting coefficient of the variable becomes 1.
6. Thus the solution or root of the equation is obtained.

WBBSE Class 7 Math Solution

Question 1. Choose the correct answer 

1. If \(\frac{x}{2}-\frac{5}{6}=1 \frac{2}{3}\) then the root of the equation is

1. 2
2. 3
3. 5
4. 6

Solution:

Given

If \(\frac{x}{2}-\frac{5}{6}=1 \frac{2}{3}\)

Root of the equation is 5.
So the correct answer is 3. 5

2. If \(\frac{x}{2}-\frac{2}{5}=\frac{x}{3}+\frac{1}{4}\) then value of x is

1. \(1 \frac{9}{10}\)

2. \(2 \frac{9}{10}\)

3. \(3 \frac{9}{10}\)

4. \(4 \frac{9}{10}\)

Solution:

Given

If \(\frac{x}{2}-\frac{2}{5}=\frac{x}{3}+\frac{1}{4}\)

So the correct answer is 3. \(3 \frac{9}{10}\)

Wbbse Class 7 Maths Solutions

3. If sum of \(\frac{1}{5}\)th and \(\frac{1}{7}\) th of a number is 144, then the number is

1. 288
2. 420
3. 1008
4. 720

Solution:

Given

If sum of \(\frac{1}{5}\)th and \(\frac{1}{7}\) th of a number is 144

Let the required number be x.

According to question, \(\frac{x}{5}\) + \(\frac{x}{7}\)=144

The number is 420
So the correct answer is 2. 420

Question 2. Write ‘true’ or ‘false’ 

1. For x= \(\frac{2}{3}\) the expressions (3 + 2x) and (1-x) are equal.

Solution 3 + 2x = 1 − x
⇒ 2x + x = 1-3
⇒ 3x= -2

⇒x=\(-\frac{2}{3}\)

The statement is false.

2. The root of equation 6 (7-3x) + 12x = 0 is 7.

Solution:

The statement is true.

Wbbse Class 7 Maths Solutions

3. 2x-3= \(\frac{3}{10}\)(5x-2), then the value of x is \(\frac{24}{5}\)

Solution: 2x-3=\(\frac{3}{10}\) (5x-2)

⇒ 20x – 30=15x – 6
⇒ 20x – 5x = 30 -6
⇒ 5x = 24

⇒ x = \(\frac{24}{5}\)

The statement is true.

Question 3. Fill in the blanks

1. If \(\frac{2x}{3}\) = \(\frac{3x}{8}\) + \(\frac{7}{12}\) then the value of x = _____

Solution:

Given

If \(\frac{2x}{3}\) = \(\frac{3x}{8}\) + \(\frac{7}{12}\)

The value of x =2

2. When x = ____, then \(\frac{ax+b}{3}\) and \(\frac{cx+d}{2}\) are equal.

Solution: \(\frac{ax+b}{3}\) = \(\frac{cx+d}{2}\)

⇒ 2ax + 2b = 3cx + 3d
⇒ 2ax – 3cx =3d – 2b
⇒ x(2a – 3c) = 3d – 2b

⇒ x = \(\frac{3d-2b}{2a-3c}\)

Wbbse Class 7 Maths Solutions

3. If the measurement of three angles of a triangle are x°, 2x, and 3x°, then the triangle is a ________ triangle.

Solution:

Given

The measurement of three angles of a triangle are x°, 2x, and 3x°

The sum of the measurement of the angles of a triangle is 180°
So x°+ 2x° + 3x° = 180°

⇒ 6x° = 180°

⇒x° = \(\frac{180°}{6}\) = 30°

⇒ 3x° = 3 x 30° = 90°
=2x° = 2 x 30° 60°

The triangle is a right angled triangle.

Question 4. Solve the following equations

1. \(\frac{x}{6}\) + \(\frac{3x-1}{12}\) + \(\frac{x-5}{18}\) = 4

2. 0.5x + \(\frac{x}{3}\) = 0.25+7

3. \(\frac{ax}{b}\) – \(\frac{bx}{a}\) =a² -b²

4. \(\frac{1}{6}\) (x−6) + \(\frac{1}{3}\) (x – 3)= \(\frac{1}{4}\) (x-4) + \(\frac{1}{5}\)  (x-5)

5. \(\frac{3x+1}{16}\) + \(\frac{2x-1}{7}\) = \(\frac{x+3}{8}\) + \(\frac{3x-1}{14}\)

6. \(\frac{x-a}{b}\) + \(\frac{x-b}{4}\) + \(\frac{x-3a-3b}{a+b}\)=0

Solution:

1. \(\frac{x}{6}\) + \(\frac{3x-1}{12}\) + \(\frac{x-5}{18}\) = 4

⇒ \(\frac{6x+9x-3+2x-10}{36}\) =4

⇒ \(\frac{17x-13}{36}\) = 4

⇒ 17x-13= 144
⇒ 17x= 144 + 13
⇒ 17x = 157

⇒ x = \(\frac{157}{17}\) = 9 \(\frac{4}{17}\)

2. 0.5x + \(\frac{x}{3}\) = 0.25 + 7

 

3. \(\frac{ax}{b}\) – \(\frac{bx}{a}\) =a² -b²

Wbbse Class 7 Maths Solutions

 

 

4. \(\frac{1}{6}\) (x−6) + \(\frac{1}{3}\) (x – 3)= \(\frac{1}{4}\) (x-4) + \(\frac{1}{5}\)  (x-5)

 

5. \(\frac{3x+1}{16}\) + \(\frac{2x-1}{7}\) = \(\frac{x+3}{8}\) + \(\frac{3x-1}{14}\)

 

6. \(\frac{x-a}{b}\) + \(\frac{x-b}{4}\) + \(\frac{x-3a-3b}{a+b}\)=0

Wbbse Class 7 Maths Solutions

 

 

WBBSE Class 7 Math Solution Question 5. Frame and solve the equations

1. In the fruit shop there are \(\frac{1}{3}\) part apples, \(\frac{2}{7}\) part is oranges, and the remaining 160 are pears. Find out the total number of fruits.

Solution:

Given

In the fruit shop there are \(\frac{1}{3}\) part apples, \(\frac{2}{7}\) part is oranges, and the remaining 160 are pears.

Let the total number of fruits be x [x > 0]

∴ Number of apples is \(\frac{x}{3}\)

The number of oranges is \(\frac{2x}{7}\)

Remaining 160 are pears.

∴ Total number of fruits is 420.

Wbbse Class 7 Maths Solutions

2. The ratio of the length and breadth of a rectangle is 5: 2 and its perimeter is 140 cm. Find the area of the rectangle.

Solution:

Given

The ratio of the length and breadth of a rectangle is 5: 2 and its perimeter is 140 cm.

Let x be a common factor of the ratio where x > 0.

∴ Length of the rectangle is 5x cm and breadth is 2x cm.

The perimeter is 2(5x + 2x) cm = 14x cm.

According to given condition, 14x= 140

⇒ x= \(\frac{140}{14}\) = 10

∴ Length is (10 x 5) cm or 50 cm and breadth is (10 x 2) cm or 20 cm.

∴ Area of the rectangle is (50 x 20) sq. cm = 1000 sq. cm.

3. Arun babu borrows some money to build his house. He returned ₹ 2000 more than \(\frac{1}{3}\)rd of the money he borrowed. However, he still has to repay amount of money he borrowed. However he still has to repay ₹ 21000. Find the amount of money he borrowed

Solution:

Given

Arun babu borrows some money to build his house. He returned ₹ 2000 more than \(\frac{1}{3}\)rd of the money he borrowed.

Let the amount of money Arun babu borrowed be  ₹ x

He returned ₹ ( \(\frac{x}{3}\) + 2000)

However he still has to reply ₹ 21000.

According to given condition, x=( \(\frac{x}{3}\) + 2000 + 21000) + \(\frac{x}{3}\) + 2000

⇒ x- \(\frac{x}{3}\) – \(\frac{x}{3}\) = 25000

⇒ \(\frac{3x-x-x}{3}\) = 75000

∴ The amount of money he borrowed ₹ 75000.

4. The sum of the ages of A and B is 54 years. 2 years ago \(\frac{2}{3}\)rds A’s age was greater than \(\frac{3}{4}\)ths the present age of B by 12 years. What are their present ages?

Solution:

Given

The sum of the ages of A and B is 54 years. 2 years ago \(\frac{2}{3}\)rds A’s age was greater than \(\frac{3}{4}\)ths the present age of B by 12 years.

Let present age of A is x years.

∴ Present age of B is (54 – x) years.

2 years ago A’s age was (x – 2) years.

According to given condition, \(\frac{2}{3}\)(x-2) =\(\frac{3}{4}\)(54-x)+12

The present age of A is 38 years and that of B is (5438) years or 16 years.

Wbbse Class 7 Maths Solutions

5. In a two digit number the digit in the unit’s place is 2 more than the digit in ten’s place. If the sum of the digits is 12 then find the number.

Solution:

Given

In a two digit number the digit in the unit’s place is 2 more than the digit in ten’s place. If the sum of the digits is 12

Let the digit in ten’s place be x

∴ The digit in unit place is (x + 2)

∴ The number is (10x+x+2)= (11x+2)

According to question, x + x + 2 = 12

⇒ 2x= 12-2 = 10

⇒x=\(\frac{10}{2}\) =5

∴ The required number is 11 x 5 + 2 = 57

6. A train traveled over a certain distance in a certain time at the rate of 30 km/hr. If the speed had been 25 km/hr, he would have taken 36 minutes more to cover the same distance. Find the distance.

Solution:

Given

A train traveled over a certain distance in a certain time at the rate of 30 km/hr. If the speed had been 25 km/hr, he would have taken 36 minutes more to cover the same distance.

Let the required distance is x km.

The time taken to cover the distance x km at 30 km/hr is \(\frac{x}{30}\)

The time taken to cover the distance x km at 25 km/hr is \(\frac{x}{25}\)

According to condition \(\frac{x}{25}\) – \(\frac{x}{30}\) = \(\frac{36}{60}\)

The required distance is 90 km

Wbbse Class 7 Maths Solutions

7. The difference between the numerator and denominator of a fraction is 5. If 2 is added to both the numerator and denominator, the fraction would become  \(\frac{2}{3}\) Find 3′ the fraction.

Solution:

Given

The difference between the numerator and denominator of a fraction is 5. If 2 is added to both the numerator and denominator, the fraction would become  \(\frac{2}{3}\)

Let the numerator of the fraction is x.

∴ Denominator is (x + 5). So the fraction is \(\frac{x}{x+5}\)

According to question \(\frac{x+2}{x+5+2}\) = \(\frac{2}{3}\)

⇒ \(\frac{x+2}{x+7}\) = \(\frac{2}{3}\)

⇒ 3x+6= 2x + 14
⇒ 3x – 2x = 14-6
⇒x= 8

∴ The fraction is \(\frac{8}{8+5}\) = \(\frac{8}{13}\)

 

Class 7 Math Solution WBBSE Algebra Chapter 6 Factorisation Exercise 6 Solved Problems

1. Factorisation of an algebraic expression is the process of finding two or more expressions whose product is the given expression.

These two or more expressions are called factors.
Factors of 6 are 1, 2, 3 and 6 [6 = 1 x 6 = 2 x 3]

The prime factors of 6 are 2, 3

2. Every number or expression is a factor of itself and 1 is a factor of any number or expression.

3. Generally 1 and the number itself may not be written to mention the factors of a number. The factors of 3ab is 3, a, and b where 3, a, and b are prime factors.

As 6x²y= 2 x 3 x x x x x y

Read and Learn More WBBSE Solutions for Class 7 Maths

Common factor: An expression that can divide all the terms of a polynomial is called the common factor of the polynomial.

Example: 4x³– 12x + 16x
= 4x x x² – 4x x 3 + 4x x 4
= 4x (x² – 3 + 4)

Here 4x is the common factor.

Method of factorization:

1. Dividing all the terms of the expression by the largest common factor which is written outside a bracket and putting the resulting quotient inside the bracket.

2.As we arrange the terms of the given algebraic expression in groups such that each group has a common factor. Then we factorise each group separately we take out factors which is common to each group.

3. If any expression is the difference of the square of two expressions, its factors will be the sum of those two expressions and their difference.
i.e., an expression of the form a²– b² can be expressed as the product of (a + b) and (a – b).

4. Some expressions which are not in the form a² – b², can be expressed as the difference of two squares by adding or subtracting some quantity to or from those expressions.

Wbbse Class 7 Maths Solutions

Question 1. Choose the correct answer 

1. The number of prime factors of 9x²y is

1. 2
2. 3
3. 4
4. 5

Solution: 9x²y= 3 x 3 x x x x x y
The number of prime factors of 9x²y is 5

So the correct answer is 4. 5

2. The common factor of 14ab² and 21ab is

1. 7ab
2. 7a
3. 7b
4. 7ab²

Solution: 14ab² = 2 x 7 x a x b x b
21 ab = 3 x 7 x a x b

The common factor of 14ab² and 21ab is (7 x a x b) or 7ab

So the correct answer is 1. 7ab

3. The sum of factors of (2x – 6) is

1. 2x-5
2. x – 1
3. x – 3
4. x-8

Solution: 2x – 6
= 2(x-3)

Sum of factors is 2 + x – 3 = x – 1

So the correct answer is 2. x – 1

4. If two factors of a expression are (x + 1) and (x 1), then the expression is

1. 2x
2. 2
3. x²-1
4. None of these

Solution: The expression is (x + 1)(x − 1) = x²– 1

So the correct answer is 3. x²-1

Wbbse Class 7 Maths Solutions

Question 2. Write ‘true’ or ‘false’

1. The common factor of 10x²y and 15xy² is 5xy

Solution: 10x²y=2 x 5 x x x x x y
15xy² =3 x 5 x x x y x y

The common factor is (5 x x x y) or 5xy

So the statement is true.

2. The sum of factors of (a³-a²+ a) is (a² + 1)

Solution: a³ – a² + a = a (a² – a + 1)

The sum of factors = a2 +1 = a2 + 1

So the statement is true.

3. Sum of factors of (3a² – 12a) is (4a + 4).

Solution: 3a² – 12a = 3a(a – 4)

Sum of factors= 3+a+a-4 = 2a – 1

So the statement is false.

Wbbse Class 7 Maths Solutions

Question 3. Fill in the blanks 

1. The common factor of 18x², 27x³ and 45x is _____

Solution:
18x² = 2 x 3 x 3 x x x x
27x³ = 3 x 3 x 3 x x x x x x
45x = 3 x 3 x 5 x x

The common factor is (3 x 3 x x) or 9x.

2. The sum of factors of (ax + bx- ay- by) is

Solution: ax + bx – ay – by
= x (a + b) -y (a + b)
=(a+b) (x-y)

Sum of factors = a+b+x-y.

3. The factors of (ab – 5b + a – 5) are ____

Solution: ab – 5b + a – 5
= b(a – 5) + 1(a-5)
= (a – 5)(b + 1)

The factors are (a – 5) and (b + 1).

Question 4. Find the number of prime factors of a(x² – y²).

Solution: a(x²– y²) = a(x + y)(x − y)

The prime factors are a, (x + y), and (x − y).
∴ The number of prime factor is 3.

Question 5. Find the sum of factors of (a³ – a).

Solution: a³ – a
= a(a² – 1)
= a(a + 1)(a− 1)

Sum of factors = a + a + 1+ a -1 = 3a

Wbbse Class 7 Maths Solutions

Question 6. Resolve into factors

1. a² – 1 + 2b – b²

2. x²– 2x – y²+ 2y

3. 81x⁴+4y⁴

4. 3x⁴ + 2x²y²– y⁴

5. a⁴ + a²b² + b⁴

6. \(a^2+\frac{1}{a^2}+1\)

7. xy(1 + z²) +z (x² +y²)

8. a² – 5a+6

9. 2a²b²+2b²c² + 2c²a²-a⁴-b⁴-c⁴

10. x² + 2x – 899

Solution:

1. a² – 1 + 2b – b²

2. x²– 2x – y²+ 2y

3. 81x⁴+4y⁴

4. 3x⁴ + 2x²y²– y⁴

5. a⁴ + a²b² + b⁴

6. \(a^2+\frac{1}{a^2}+1\)

7. xy(1 + z²) +z (x² +y²)

8. a² – 5a+6

9. 2a²b²+2b²c² + 2c²a²-a⁴-b⁴-c⁴

10. x² + 2x – 899

Wbbse Class 7 Maths Solutions

Question 7. Factorise the following

1. (a + b)⁴+ 4

2. a²(b-c)²-b²(c – a)²

3. 64ap²– 49a (p- 2q)²

4. a² – b² -6ap + 2bp + 8p²

5. 4a⁴ + 11a² + 25

Solution:

1. (a + b)⁴+ 4

2. a²(b-c)²-b²(c – a)²

3. 64ap²– 49a (p- 2q)²

4. a² – b² -6ap + 2bp + 8p²

5. 4a⁴ + 11a² + 25

 

Factorisation

Factorisation Exercise 6.1

Let us factorize the following :

1. 25xy = 5 × 5 × x × y

2. 18 × y² = 2 × 3 × 3 × x × y × y

3. 15q²r²= 3 × 5 × q × q× r × r

4. 10 × yz = 2 × 5 × x × y × z

5. 12 × yz = 2 × 2 × 3× x × y × z

Factorisation Exercise 6.2

Let us factorize the following :

1. 12x²y (x + 2)= 2 × 2 × 3 × x × x × y × (x + 2)

2. 1 8yz² (2y + 3z) = 2 × 3 × 3 × y × z × z × (2y + 3z)

3. 1 6 × yz (x + y)= 2 × 2 × 2×2 × x × y × z × (× + y)

4. 15pq² (p + 3q) = 3 × 5 × p × q × q × (p + 3q)

5. 14mn² (2m – n) = 2 × 7 × m × n × n × (2m-n)

Question 1. Let us factorize:

1. 2+14x
Solution:

2+14x  = 2(1 +7x)

2. 5x – 20y
Solution:

5x – 20y = 5 ( x- 4y)

3. 6x – 3y
Solution:

6x – 3y = 3 (2x – y)

4. 3a² – 12a
Solution:

3a² – 12a = 3a (a -4)

Question 2. Let us find the common factors of the following algebraic expressions.

1. 6a, 2a²
Solution:

6a, 2a²= 2, a, 2a:

2. 5x, 6xy
Solution:

5x, 6xy = x

3. 4xyz, 12yz
Solution:

4xyz, 12yz = 2, 4, yz, yz, 2y, 2z, 4y, 4z, 4yz.

4. 7a²b, 14abc
Solution:

7a²b, 14abc =  7, a, b, 7a, 7b, ab, 7ab

Class 7 Math Solution WBBSE

Factorization Exercise 6.3

Question 1. Let us Factorise the following 

1. xy + y + 3x + 3
Solution:

Given

xy + y + 3x + 3

xy + y + 3x + 3= y (x +1 ) + 3 (× + 1 )

= (x + 1 )(y + 3)

xy + y + 3x + 3 = (x + 1 )(y + 3)

2. pq – q + 2q – 2
Solution:

Given

pq – q + 2q – 2

pq – q + 2q – 2 = q (P – 1 ) + 2 (p – 1 )

= (p – 1 ) (q + 2)

pq – q + 2q – 2 = (p – 1 ) (q + 2)

3. 6xy + 3y + 4× + 2
Solution:

Given

6xy + 3y + 4x + 2

6xy + 3y + 4x + 2 = 3y (2x + 1) + 2 (2x + 1)

= (2x +1) (3y + 2)

6xy + 3y + 4x + 2 = (2x +1) (3y + 2)

4. 10xy + 2y + 5x + 1
Solution:

Given

10xy + 2y + 5x + 1

10xy + 2y + 5x + 1 = 2y (5x + 1 ) + 1 (5x + 1 )

= (5x + 1 ) (2y + 1 )

10xy + 2y + 5x + 1 = (5x + 1 ) (2y + 1 )

Question 2. Let us find the factors of the following algebraic expressions :

1. 7xy 
Solution:

7xy = 7 × x × y

2. 9 x²y
Solution:

9 x²y= 3 × 3 × x × x ×y

3. 16ab²c 
Solution:

16ab²c = 2 × 2 × 2 × 2 × a × b × b × c

4. -25lmn = 5 × 5 × | × m × n
Solution:

-25lmn = 5 × 5 × | × m × n

5. 12x (2 + x) 
Solution:

12x (2 + x) = 2 × 2 × 3 × a × (2 + x )

6. – 5 pq (p² + 8)
Solution:

– 5 pq (p² + 8) = -5 × p × q × (p² +8)

7. 21 xy² (3x – 2)
Solution:

21 xy² (3x – 2) = 3 × 7 × x × y × y × (3x -2)

8. 121mn (m² – n)
Solution: 

121mn (m² – n) = 11 × 11 × m × n × (m² -n)

Question 3. Let us find the common factors of the following algebraic expressions :

1. 22xy, 33xz
Solution:

22xy, 33xz

Common factors = 11 , x, 11x

2. 14ab² , 21ab
Solution: 

14ab² , 21ab

Common factors = 7, a, b, 7a, 7b, 7ab

3. – 16mnl, – 39nl²
Solution:

– 16mnl, – 39nl²

Common factors = – 1, – n, – 1, nl, – nl, n, I

4. 12a²b, 18ab², 24abc
Solution:

12a²b, 18ab², 24abc

Common factors = 2, 3, 6, a, b, 2a, 2b, 3a, 3b, 6a, 6b, ab, 2ab, 3ab, 6ab

5. 2xy, 4yz, 6xz
Solution:

2xy, 4yz, 6xz

Common factors = 2.

6. 18x², 27x³, – 45x
Solution:

18x², 27x³, – 45x

Common factors = 3, 9, x, 3x, 9x

7. 5mn, 6n²l², 7l³m²
Solution:

5mn, 6n²l², 7l³m²

Common factors = 1.

Question 4. Let us write two such algebraic e×pressions which have the following as their Common Factors 

1. x²
Solution:

⇒ x² =   3x², 4x³3y

2. 2xy
Solution:

2xy = 4x²y²q, 6xyq

3. 4a²
Solution:

4a²= 12a³y, 16a²x

4. (mn + 2)
Solution:

(mn + 2) =  5(mn + 2), 7(mn + 2)²

5. x (y + 2)
Solution:

x (y + 2) = 7x²(y + 2), 9x(p + q)(y + 2)

Question 5. Let us factorize the following 

1. 5 + 10x
Solution:

5 + 10x = 5(1 +2x)

2. 2x – 6
Solution:

2x – 6 = 2(x – 3)

3. 7m – 14n 
Solution:

7m – 14n = 7(m – 2n)

4. 18xy + 21 xz 
Solution:

18xy + 21 xz = 3x(6y + 7z)

5. 4xy + 6yz 
Soution:

4xy + 6yz = 2y(2x + 3z)

6. 7xyz – 6xy
Solution:

7xyz – 6xy = xy(7z – 6)

7. 7a² + 14a
Solution:

7a² + 14a = 7a(a + 2)

8. – 15m + 20 
Solution:

– 15m + 20 = 5(- 3m + 4)

9. 6a²b + 8a²b
Solution:

6a²b + 8a²b = 2ab(3a + 4b)

10. 3a² – ab²
Solution:

3a² – ab² = a (3a – b²)

11. abc – bcd =
Solution:

abc – bcd = bc(a – d)

12. 60xy³ – 4xy – 8 
Solution: 

60xy³ – 4xy – 8 = 4(15xy³ – xy – 2)

13.  x²yz + xy²z + xyz²
Solution:

x²yz + xy²z + xyz² = xyz(x + y + z)

14.  a³ – a² + a 
Solution:

a³ – a² + a = a(a² – a + 1 )

15. x²y²z² + x²y² + x²y²q² 
Solution:

x²y²z² + x²y² + x²y²q² = x²y²(z² +1 + q²)

Question 6. Let’s Factorise the following algebraic e×pressions 

1. xy + 2x + y + 2
Solution :

Given

xy + 2x + y + 2

= x(y + 2) + 1(y + 2) = (y + 2)(× + 1)

xy + 2x + y + 2 = (y + 2)(× + 1)

2. ab – 5b + a – 5
Solution:

Given

ab – 5b + a – 5

= b(a – 5) + 1 (a – 5) = (a – 5)(b + 5)

ab – 5b + a – 5 = (a – 5)(b + 5)

3. 6xy – 9y + 4x – 6
Solution :

Given

6xy – 9y + 4× – 6

= 3y(2x – 3) + 2(2x – 3) = (2x – 3)(3y + 2)

6xy – 9y + 4× – 6 = (2x – 3)(3y + 2)

4. 15m + 9 – 35mn – 21 n
Solution :

Given

15m + 9 – 35mn – 21 n

= 3(5m + 3) – 7n(5m + 3) = (3 – 7n)(5m + 3)

15m + 9 – 35mn – 21 n = (3 – 7n) (5m + 3)

5. ax + bx – ay – by 
Solution :

Given

ax + bx – ay – by

= x(a + b) – y(a + b) = (a +b)(x – y)

ax + bx – ay – by = (a +b)(x – y)

6. c – 9 + 9ab – abc
Solution :

Given

c – 9 + 9ab – abc

= – 1 (9 – c) + ab(9 – c) = (9 – c)(ab – 1)

c – 9 + 9ab – ABC = (9 – c)(ab – 1)

Class VII Math Solution WBBSE Factorization Exercise 6.4

Question 1. Let us factorize the following 

1. x² + 14× + 49
Solution :

Given

ײ + 14x + 49

= (x)² + 2.x.7 + (7)2 = (x + 7)² = (x + 7)(x+ 7)

ײ + 14x + 49 = (x + 7)(x+ 7)

2. 4m² – 36m + 81
Solution :

Given

4m² – 36m + 81

= (2m)² – 2.2m.9 + (9)²

= (2m – 9)² = (2m – 9)(2m – 9)

4m² – 36m + 81=(2m – 9)(2m – 9)

3. 25 x² + 30x + 9
Solution :

Given

25x² + 30x + 9

= (5x)² + 2.5 x .3 + (9)² = (5x + 3)² = (5x + 3) (5x + 3)

25x² + 30x + 9 = (5x + 3) (5x + 3)

4. 121b²– 88bc + 16c²
Solution :

Given

121b² – 88bc + 16c²

= (11b)² – 2.11 b.4c + (4c)² = (11 b – 4c)²

. = (11 b – 4c)(11 b – 4c)

121b² – 88bc + 16c² = (11 b – 4c)(11 b – 4c)

WBBSE Class 7 Math Solution

5. (xy)2 – 4x²y²
Solution :

Given

(x²y)² – 4x²y²

= x²y² – 4x²y² = .x²y²(x² – 4) = x²y²{(x)² – (2)2}

= x²y²(x + 2)(x – 2) = x.x.y.y.(x + 2)(x – 2)

(x²y)² – 4x²y² = x.x.y.y.(x + 2)(x – 2)

6. a⁴ + 4a²b² + 4b⁴
Solution :

Given

a⁴ + 4a²b² + 4b⁴

= (a²)² + 2.a².2b² + (2b)²

= (a² + 2b²)

= (a² + 2b²)(a² + 2b²)

a⁴ + 4a²b² + 4b⁴ = (a² + 2b²)(a² + 2b²)

7. 4x² – 1 6
Solution:

Given

4x²-16

= 4(x²– 4) = 4{(x)² – (2)²} = 2 × 2 × (x + 2)(x – 2)

4x²-16 = 2 × 2 × (x + 2)(x – 2)

8. 121 – 36x²
Solution :

Given

121 – 36x²

= (11)² – (6x)² = (11 + 6x)(11 – 6x)

121 – 36x² = (11 + 6x)(11 – 6x)

9. x²y² – p²q²
Solution :

Given

x²y² – p²q²

= (xy)² – (pq)²= (xy + pq)(xy – pq)

x²y² – p²q² = (xy + pq)(xy – pq)

10. 80m² -125
Solution :

Given

80m² -125

= 5(16m² – 25) = 5{(4m)² – (5)2} = 5(4m + 5)(4m – 5)

80m² -125 = 5(4m + 5)(4m – 5)

11. ax² – y²
Solution:

Given

ax² – y²

= ax² – ay² = a{(x)² – (y)²} = a (x + y)(x – y)

ax² – y²  = a (x + y)(x – y)

12.  I – (m + n)²
Solution :

Given

I – (m + n)²

= (I)² – (m + n)² = {I + (m + n)} {I – (m + n)}

= (I + m + n)(l – m – n)

I – (m + n)² = (I + m + n)(l – m – n)

13.  (2a – b – c)² – (a – 2b – c)²
Solution :

Given

(2a – b – c)² – (a – 2b – c)²

= {{2a – b – c) + (a – 2b – c)} {(2a – b – c) – (a – 2b – c)}

= (2a – b – c + a – 2b – c)(2a – b – c – a + 2b + c)

= (3a – 3b – 2c)(a + b)

(2a – b – c)² – (a – 2b – c)² = (3a – 3b – 2c)(a + b)

14.  x² – 2xy – 3y²
Solution :

Given

x² – 2xy – 3y²

= x² – (3 – 1 )xy – 3y² = x² – 3xy + xy – 3y²

= x(x – 3y) + y(x – 3y) = (x – 3y)(x + y)(xv)

x² – 2xy – 3y² = (x – 3y)(x + y)(xv)

15. x²+ 9y² + 6xy – z²
Solution :

Given

x²+ 9y² + 6xy – z²

= x + 6xy + 9y² – z²

= (x)² + 2.x.3y + (3y)² – (z)²

= (x + 3y)² – (z)²

= (x + 3y + z)(x + 3y – z)

x²+ 9y² + 6xy – z²  = (x + 3y + z)(x + 3y – z)

16. a² – b² + 2bc – c²
Solution :

Given

a² – b² + 2bc – c²

= a² – (b² – 2bc + c²) = (a)² – (b – c)²

= {a + (b – c)} {a – (b – c)} = (a + b – c)(a – b + c)

a² – b² + 2bc – c² = (a + b – c)(a – b + c)

WBBSE Class 7 Math Solution

17. a²(b-c)²-b²(c-a)²
Solution :

Given

a²(b-c)²-b²(c-a)²

= {a (b – c)}² – {b(c – a)}² = (ab – ac)² – (bc – ab)²

= {(ab – ac) + (bc – ab)} {(ab – ac) – (bc – ab)}

= (ab – ac + bc – ab) (ab – ac – be + ab)

= (bc – ac) (2ab – ac – bc)

= c(b – a) (2ab – bc – ca)

a²(b-c)²-b²(c-a)² = c(b – a) (2ab – bc – ca)

18. x² – y² – 6yz – 9z²
Solution :

Given

x² – y² – 6yz – 9z²

= x² – (y ²+ 6yz + 9z²)

= (x)² – {(y)² + 2.y.3z + (3z)²}

= (x)² – (y + 3z)²

= (x + y + 3z) (x – y – 3z)

x² – y² – 6yz – 9z²  = (x + y + 3z) (x – y – 3z)

19. x² – y² + 4x – 4y
Solution :

Given

x² – y² + 4x – 4y

= {(x)² -(y)} ² + 4(x-y)

= (x + y)(x – y) + 4(x – y) = (x – y)(x + y + 4)

x² – y² + 4x – 4y = (x – y)(x + y + 4)

20.  a² -b² + c² – d² – 2(ac – bd)
Solution :

Given

a² -b² + c² – d² – 2(ac – bd)

= a² – b²+ c² – d² – 2ac + 2bd

= a² – 2ac + c² – b² + 2bd – d²

= {(a)² – 2,a.c + (c)²} – (b² – 2bd + d²)

= (a – c)² – (b – d)²

= {(a – c) + (b – d)} {(a – c) – (b – d)}

= (a – c + b – d) (a – c – b + d)

= (a + b – c – d) (a – b – c + d)

a² -b² + c² – d² – 2(ac – bd) = (a + b – c – d) (a – b – c + d)

21.  2ab – a² – b² + c²
Solution :

Given

2ab – a² – b² + c²

= c² – a² + 2ab – b²

= (c)² – (a² – 2ab + b²) = (c)² – (a – b)²

= (c + a – b)(c – a + b) = (a – b + c)(b + c – a)

2ab – a² – b² + c² = (a – b + c)(b + c – a)

22. 36x² – 16a² – 24ab – 9b²
Solution :

Given

36x² – 16a² – 24ab – 9b²

= 36x² – (16a² + 24ab + 9b²)

= 36x² – {(4a)² + 2.4a.3b + (3b)²}

= (6x²) – (4a + 3b)²

= {6x + (4a + 3b)} {6x – (4a + 3b)}

= (6x + 4a + 3b) (6x – 4a – 3b)

36x² – 16a² – 24ab – 9b² = (6x + 4a + 3b) (6x – 4a – 3b)

23. a² – 1 + 2b – b²
Solution :

Given

a² – 1 + 2b – b²

= a² – (1 – 2b + b)²

= (a)² – (1 – b) = (a +1 – b) {a (1 b)}

= (a – b + 1 )(a + b – 1 )

a² – 1 + 2b – b² = (a – b + 1 )(a + b – 1 )

WBBSE Class 7 Math Solution

24. a² – 2a – b² + 2b
Solution :

Given

a² – 2a – b² + 2b

= a² – b² + 2b – 2a

= (a + b) (a – b) – 2(a – b)

= (a b)(a + b – 2)

a² – 2a – b² + 2b = (a b)(a + b – 2)

25. (a² – b²)(c² – d²– 4abcd)
Solution :

Given

(a² – b²)(c² – d²– 4abcd

(a² – b²)(c² – d²) – 4abcd

= a²c² – b²c²– a²d² + b²d² – 4abcd

= a²c² + b²d² -.2abcd – a²d²– 2abcd – b²c²

= {(ac)² – 2abcd + (bd)²} – {a²d² + 2abcd + b²c²}

= (ac – bd)² – (ad + bc)²

= {(ac – bd) + (ad + bc)} {(ac – bd) – (ad + bc)}

= (ac – bd + ad + bc) (ac – bd – ad – bc)

(a² – b²)(c² – d²– 4abcd = (ac – bd + ad + bc) (ac – bd – ad – bc)

26. a² – b² – 4ac + 4bc
Solution :

Given

a² – b² – 4ac + 4bc

= {(a)² – (b)²} – 4c(a – b)

= (a + b) (a – b) – 4c(a – b) = (a – b)(a + b – 4c)

a² – b² – 4ac + 4bc = (a – b)(a + b – 4c)

27. a² – b² – c²+ d²)² – 4(ad – bc)²
 Solution:

Given

a² – b² – c²+ d²)² – 4(ad – bc)²

= (a² – b² – c²+ d2)² – {2(ad – bc)}²

= (a² – b² – c² + d² + 2ad – 2bc)

= {a² + 2ad + d²– b² – 2bc – c2}

= [{(a)² + 2.a.d + (d)²} – {(b)² + 2.b.c + (c)²}]

= {(a + d)² – (b + c)²}

= {(a + d) + (b + c)} {(a + d) – (b + c)}

= (a + b + c + d) (a + d – b – c)

= (a + b + c + d)(a – b – c + d)

a² – b² – c²+ d²)² – 4(ad – bc)² = (a + b + c + d)(a – b – c + d)

28. 3x² – y² + z² – 2xy – 4xz
Solution :

Given

3x² – y² + z² – 2xy – 4xz

= 4x² – x² – y² + z² – 2xy – 4xz

= 4x² – 4xz + z² – x² – 2xy – y²

= {(2x)² – 2.2x.z + (z)²} – (x² + 2xy + y²)

= (2x – z)² – (x + y)²

= {(2x – z) + (x + y)} {(2x – z) – (x + y)}

= ( 2x – z + x + y) (2x – z – x – y)

= (3x + y – z) (x – y – z)

3x² – y² + z² – 2xy – 4xz = (3x + y – z) (x – y – z)

WBBSE Class 7 Math Solution Question 2. Let us factorize the following

1. 81x⁴ + 4v⁴
Solution :

Given

81x⁴+ 4y⁴

(9x²)² + (2y²)² + 2.9x².2y² – 36x2y²

= (9x² + 2y²)2 – (6xy)²

. = (9x² + 2y² + 6xy) (9x² + 2y² – 6xy)

= (9x² + 6xy + 2y²) (9x² – 6xy + 2y²)

81x⁴+ 4y⁴ = (9x² + 6xy + 2y²) (9x² – 6xy + 2y²)

2. p⁴ – 13p²q² + 4q⁴
Solution :

Given

p⁴ – 13p²q² + 4q⁴

= (p²)² – 2.p².2q² + (2q²)² -9p²q²

= (p² – 2q²)² – (3pq)² = (p² – 2q² + 3pq) (p²– 2q² – 3pq)

= (p² + 3pq – 2q²) (q² – 3pq – 2q²)

p⁴ – 13p²q² + 4q⁴ = (p² + 3pq – 2q²) (q² – 3pq – 2q²)

3. x⁸ – 16y⁸
Solution :

Given

x⁸ – 16y⁸

= (x⁴)² – (4y⁴)²

= (x⁴ + 4y⁴) (x⁴ – 4y⁴)

= {(x²)² + 2.x².2y² + (2y²)² – 4x²y²} {(x²)² – (2y)²}

= {(x² + 2y²)² – (2xy)²} (x² + 2y²) (x² – 2y²)

= (x² + 2y² + 2xy) (x² + 2y² – 2xy) (x² + 2y²) (x² – 2y²)

= (x² + 2xy + 2y²) (x² 2xy + 2y²) (x² + 2y²) (x² – 2y²)

x⁸ – 16y⁸= (x² + 2xy + 2y²) (x² 2xy + 2y²) (x² + 2y²) (x² – 2y²)

4. x⁴ + x²y² + y⁴
Solution :

Given

x⁴ + x²y² + y⁴

= (x²)² + 2x²y² + (y²)² – x²y²

= (x²+ y²)² – (xy)²

= (x² + y² + xy) (x² + y² – xy)

= (x² + xy + y²) (x² – xy + y²)

x⁴ + x²y² + y⁴ = (x² + xy + y²) (x² – xy + y²)

5. 3x⁴ + 2x²y² – y⁴
Solution:

Given

3x⁴ + 2x²y²– y⁴

= 3x⁴ + 3x²y² – x²y² – y⁴

= 3x²(x² + y²) – y²(x² + y²)

= (x² + y²) (3x² – y²)

3x⁴ + 2x²y²– y⁴ = (x² + y²) (3x² – y²)

6. x⁴ + x² + 1
Solution :

Given

x⁴ + x² + 1

= (x²)² + 2.x².1 +(1)²-x²

= (x² + 1 )² – (x)² = (x² + 1 +x) (x² + 1 – x)

= (x² + x + 1 ) (x² – x + 1 )

x⁴ + x² + 1 = (x² + x + 1 ) (x² – x + 1 )

7. x⁴ + 6x²y² + 8y⁴
Solution:

Given

x⁴ + 6x²y² + 8y⁴

= x⁴ + 4x²y² + 2x²y² + 8y²

= x²(x² + 4y²) + 2y²(x² + 4y²)

= (x² + 4y²)(x² + 2y²)

x⁴ + 6x²y² + 8y⁴ = (x² + 4y²)(x² + 2y²)

WBBSE Class 7 Math Solution 8. 3x² – y² + z² – 2xy – 4xz
Solution :

Given

3x² – y² + z² – 2xy – 4xz

= 4x² – x² – y² + z² – 2xy – 4xz

= 4x² – x² – y² + z² – 2xy – 4xz

= 4x² – 4xz + z² – x² – 2xy – y²

= (4x² – 4xz + z²) – (x² + 2xy + y²)

= {(2x)² – 2. 2x.z + z)²} – {(x)² + 2.x.y + (y)²}

= (2x – z)² – (x + y)²

= {(2x – z) + (x + y)} {(2x – z) – (x + y)

= (2x – z + x + y) (2x – z – x – y)

= (3x + y – z) (x – y – z)

3x² – y² + z² – 2xy – 4xz = (3x + y – z) (x – y – z)

9. 3x⁴ – 4x²y² + y⁴
Solution :

Given

= 3x⁴ – 3x²y²– x²y² + y⁴

= 3x²(x² – y²) – y²(x² – y²)

= (x² – y²) (3x² – y²)

= {(x)² -(y)²} (3x² – y²)

= (x + y) (x – y) (3x² – y²)

3x⁴ – 3x²y²– x²y² + y⁴ = (x + y) (x – y) (3x² – y²)

10. p⁴ – 2p²q² – 15q²
Solution :

Given

p⁴ – 2p²q² – 15q²

= p⁴ – (5 – 3)p²q² – 15q⁵

= p⁴ – 5p² q² + 3p²q² – 15q²

= P²(P² 5q²) + 3q²(p² + 3q²)

= (p² – 5q²) (p² + 3q²)

p⁴ – 2p²q² – 15q² = (p² – 5q²) (p² + 3q²)

11. x⁸ + x⁴y⁴ + y⁸
Solution :

Given

x⁸ + x⁴y⁴ + y⁸

= x⁸ + 2x⁴y⁴ + y⁸ – x⁴y⁴

= {(x⁴)² + 2x⁴y⁴ + y⁴ + (y⁴)⁴} – (x⁴y⁴)⁴

= (x⁴ + y⁴)⁴ – (x⁴y⁴)⁴

= (x⁴ + y⁴ + x²y²) (x² + y⁴ – x²y²)

= {x⁴ + 2x²y² + y⁴ – x²y²} (x⁴ + y⁴ – x²y²)

= {(x²)² + 2x²y² + (y²)² – (xy)²} (x⁴ + y⁴ – x²y²)

= {(x² + y²) – (xy)²} (x⁴ + y⁴ – x²y²)

= (x² + y² + xy) (x² + y²– xy) (x⁴ + y⁴ – x²y²)

x⁸ + x⁴y⁴ + y⁸  = (x² + y² + xy) (x² + y²– xy) (x⁴ + y⁴ – x²y²)

Class 7 Math Solution WBBSE Algebra Chapter 5 Algebraic Formula Exercise 5 Solved Problems

Necessary Formula (Identities)

1. (a + b)² = a² + 2ab+ b²
= (a – b) ² + 4ab

2. (a – b) ² = a² – 2ab+b²
= (a + b) ² – 4ab

3. (a+b+c) ² = a² + b² + c² + 2ab+ 2bc + 2ca

4. a²+ b² = (a + b) ² – 2ab
= (a – b) ²+2ab

5. a²– b² = (a + b)(a − b)

6. 2(a² + b²) = (a + b) ² + (a – b) ²

7. 4ab = (a + b) ²– (a – b) ²

8. ab=(a+b) ² – (a=b) ²

Proof:

Read and Learn More WBBSE Solutions for Class 7 Maths

1. (a + b) ²= (a + b)(a + b).
= a(a + b) + b(a + b)
= a²+ ab + ab + b²
= a²+2ab+ b²
= (a² – 2ab+b²) + 4ab
= (a – b) ² + 4ab

2. (a – b) ² = (a – b)(a – b)
= a(a – b) – b(a – b)
= a² – ab – ab + b²
= a² – 2ab+b²
= (a²+2ab+ b²) – 4ab
= (a + b) ² – 4ab

3. (a + b + c) ² = {(a + b) + c)} ²
= (a + b) ² + 2(a + b)c + c²
= a ² + 2ab+ b ² + 2ac + 2bc + c2 a ²+ b  ² + c  ²+2ab+ 2bc + 2ca
= a² + b² = (a ²+2ab+b ²) – 2ab
= (a + b) ² – 2ab

4. a²+ b² = (a ²-2ab+b ²)+2ab
= (a – b)2 + 2ab

5. a² – b² = a² + ab – ab-b²
= a(a + b) – b(a + b)
= (a + b)(a – b)

6. 2(a ²+ b ²)= a² + b²+ a²+ b²
= (a ²+2ab+b ²) + (a ² – 2ab+b²)
= (a + b) ² + (a – b)²

7. 4ab = 2ab+2ab
= (a²+2ab+b²) – a²+2ab-b²
= (a²+2ab+b²) + (a²– 2ab+b²)
= (a + b) ² – (a – b)²

Class 7 Math Solution WBBSE

8. \(a b=\frac{4 a b}{4}=\frac{(a+b)^2-(a-b)^2}{4}\)

= \(\frac{(a+b)^2}{4}-\frac{(a-b)^2}{4}\)

= \(\left(\frac{a+b}{2}\right)^2-\left(\frac{a-b}{2}\right)^2\)

Question 1. Choose the correct answer

1. If (x+8)² = x² + 16x + K, then the value of K is

1. 16
2. 64
3. 8
4. None of these

Solution:

Given

(x+8)² = x² + 16x + K

⇒ x² + 2. x. 8+ (8)² = x² + 16x + K

⇒ 64 K

So the correct answer is 2. 64

2. For which value or values of K, will the expression p² + pk + \(\frac{1}{25}\) be a perfect square.

1. \(\frac{1}{5}\)

2. \(\frac{1}{25}\)

3. \(\pm \frac{2}{5}\)

4. \(\pm \frac{1}{5}\)

Solution:

Given

p² + pk + \(\frac{1}{25}\)

So the correct answer is 3. \(\pm \frac{2}{5}\)

3.  If a = \(\frac{1}{8}\) then the value of (64a²+ 16a+ 1) is

1. 8
2. 0
3.16
4. 4

Solution:

Given

a = \(\frac{1}{8}\)

64a² + 16a+ 1
= (8a)² + 2.8a.1 + (1)²
= (8a+ 1)²

= \(\left(8 \times \frac{1}{8}+1\right)^2\)

[Putting the value of a]
= (1 + 1)² = (2)²
= 4

So the correct answer is 4. 4

Wbbse Class 7 Maths Solutions

4. If 3x + \(\frac{1}{5 x}\) =6, then the value of \(25 x^2+\frac{1}{9 x^2}\)

1. 96

2. \(96 \frac{2}{3}\)

3. \(103 \frac{2}{3}\)

4. None of these

Solution:

Given

3x+ \(\frac{1}{5 x}\) = 6

 

So the correct answer is 2. \(96 \frac{2}{3}\)

Wbbse Class 7 Maths Solutions

5. If a + b = 7 and a b = 3, then the value of ab is

1. 21
2. 10
3. 58
4. 40

Solution:

Given

a + b = 7, a b = 3

ab = \(\left(\frac{a+b}{2}\right)^2-\left(\frac{a-b}{2}\right)^2\)

= \(\left(\frac{7}{2}\right)^2-\left(\frac{3}{2}\right)^2\)

= \(\begin{aligned}
& =\frac{49}{4}-\frac{9}{4} \\
& =\frac{40}{4}=10
\end{aligned}\)

So the correct answer is 2. 10

Question 2. Write ‘true’ or ‘false’

1. If (xy)²= (96y+ y)², then the value of x is 3.

Solution :

Given

(xy)² = 96y+ y²

⇒ (x-y)² = (3)²-2.3.y + y²

⇒ (x-y)²=(3-y)²

⇒ x – y = 3-y

⇒x=3-y+y

⇒ x = 3

So the statement is true.

2. The value of 1015 x 985 is 999085

Solution:

1015 x 985

= (1000+15) (1000-15)
= (1000)²– (15)²
= 1000000 – 225
= 999775

So the statement is false.

Wbbse Class 7 Maths Solutions

3. If (a-5)² + (b + 3)²= 0, then the value (a + b) is ²

Solution:

Given

If (a-5)² + (b + 3)²= 0

If the sum of two or more two square is zero then the value of each square will be zero.
(a-5)² = 0
⇒ a 5=0
⇒ a = 5

(b + 3)² = 0
⇒b+3=0
⇒ b = -3

a+b=5-3=2.

So the statement is true.

Question 3. Fill in the blanks

1. The value of (0.75 x 0.75+1.5 x 0.25 +0.25 x 0.25 is) _______

Solution: 0.75 x 0.75 + 1.5 x 0.25 + 0.25 × 0.25
= (0-75)² + 2 x 0.75 x 0.25 + (0.25)²
= (0·75 + 0.25)²
= (1.00)²
= 1

2. If a + b = 5 and ab= 6, then the value of (a – b) is _____

Solution:

Given

If a + b = 5 and ab= 6

(a – b)² = (a + b)² – 4ab
= (5)² – 4 x 6
= 25-24
= 1

⇒ a-b=±√l=±1

3. If a + b + c = 7 and ab+be+ca = -5, then the value of (a²+ b²+ c²) is _____

Solution:

Given

If a + b + c = 7 and ab+be+ca = -5

a² + b² + c² + 2 (ab + bc + ca) = (a + b + c)²
⇒ a² + b² + c² + 2 x (-5) = (7)²
⇒ a² + b² + c² = 49+ 10 = 59

Question 4. Find the square of the algebraic expression given below:

1. 4x+5y
2. 2a+3b-4c
3. a +2b3c4d
4. 999
5. 1005

Solution:

Given
1. (4x+5y)²
= (4x)² + 2.4x.5y + (5y)²
= 16x² + 40xy + 25y²
(4x+5y)² = 16x² + 40xy + 25y²

2. (2a+3b – 4c)²

= {(2a + 3b) – 4c)²

= (2a+3b)² – 2 x (2a + 3b) x 4c + (4c)²

= (2a)² + 2 x 2a x 3b + (3b)² – 8c(2a + 3b) + 16c²

= 4a² + 12ab+9b² -16ac – 24bc + 16c²

= 4a² + 9b² + 16c² + 12ab – 16ac – 24bc.

(2a + 3b) – 4c)² = 4a² + 9b² + 16c² + 12ab – 16ac – 24bc.

3. (a + 2b – 3c + 4d)²

= {(a + 2b) – (3c – 4d)}²

= (a + 2b)²– 2(a + 2b)(3c4d) + (3c-4d)²

= a²+2.a.2b + (2b)² – 2(3ac-4ad + 6bc-8bd) + (3c)² – 2.3c.4d + (4d)²

= a²+4ab + 4b² – 6ac + 8ad – 12bc + 16bd + 9c² – 24cd + 16d²

= a² + 4b² + 9c² + 16d² + 4ab – 6ac + 8ad -16bd – 24cd.

{(a + 2b) – (3c – 4d)}² = a² + 4b² + 9c² + 16d² + 4ab – 6ac + 8ad -16bd – 24cd.

4. (999)²

= (1000 – 1)²

= (1000)²-2 × 1000 × 1 + (1)²

= 1000000-2000 + 1

= 998001

(999)²= 998001

5. (1005)²
= (1000 + 5)²

= (1000)² + 2 x 1000 × 5 + (5)²

= 1000000 + 10000 + 25.

= 1010025

(1005)² = 1010025

Wbbse Class 7 Maths Solutions

Question 5. Express x as a difference of two square.

Solution: x = x.1

= \(\left(\frac{x+1}{2}\right)^2-\left(\frac{x-1}{2}\right)^2\)

Question 6. Express (8a²+ 50b²) as a sum of two square.

Solution:

Given

8a²+ 50b²

= 2 (4a² + 25b²)

= 2{(2a)² + (5b)²}

= (2a + 5b)² + (2a – 5b)²

Question 7. Find the square (3x+4y) with the help of (a – b)²= a² – 2ab+ b²

Solution:

(3x+4y)²

= {3x-(-4y)}²

= (3x)²– 2 x 3x(-4y) + (-4y)²

= 9x² + 24xy + 16y²

Question 8. For what values of p; will the expression (9x² + px + 16) be a perfect square.

Solution :

Given

9x² + px + 16

=(3x)²+2.3x.\(\frac{p}{6}\)+ \(\left(\frac{p}{6}\right)^2\) – \(\left(\frac{p}{6}\right)^2\) +16

= \(\left(3 x+\frac{p}{6}\right)^2-\frac{p^2}{36}+16\)

The given expression will be perfect square if

\(-\frac{p^2}{36}\)+16=0

\(-\frac{p^2}{36}\) = -16

⇒ p² = 16 x 36

⇒ p=±\(\sqrt{16 \times 36}\)

⇒p=14×6

⇒p±24.

Wbbse Class 7 Maths Solutions

Question 9. Express the following in the product form

1. 49x⁴ – 36y⁴
2. (m + p + q)² – (m-p-q)²

Solution:

Given

1. 49x⁴ – 36y⁴

= (7x²)²– (6y²)²

= (7x²+6y²)(7x² – 6y²)

49x⁴ – 36y⁴ = (7x²+6y²)(7x² – 6y²)

Given

2. (m + p + q)²– (m-p-q)²

= (2m)(2p+ 2q)
= 2m x 2(p + q)
= 4m (p + q)

(m + p + q)²– (m-p-q)²  = 4m (p + q)

Question 10. For what value of t, will the expression \(\left(x^2-t x+\frac{1}{4}\right)\) be a perfect square.

Solution: \(x^2-t x+\frac{1}{4}\)

= \(x^2-2 \cdot x \cdot \frac{t}{2}+\left(\frac{t}{2}\right)^2-\left(\frac{t}{2}\right)^2+\frac{1}{4}\)

= \(\left(x-\frac{t}{2}\right)^2-\frac{t^2}{4}+\frac{1}{4}\)

The given expression is a perfect square.

So, \(-\frac{t^2}{4}+\frac{1}{4}=0\)

⇒ \(-\frac{t^2}{4}=-\frac{1}{4}=0\)

⇒ t² = 1

= t = ± 1

Wbbse Class 7 Maths Solutions

Question 11. Express the following as a perfect square and hence find the values

1. 49a² – 42ab+9b² [when a = 1, b = 2]

2. \(\frac{144}{p^2}-\frac{120}{p}+25\) [when p = -3]

Solution: 1. 49a² – 42ab+9b²
= (7a)² – 2 x 7a x 3b + (3b)²

= (7a-3b)²

= (7 x 1-3 x 2)²

= (7-6)²

= (1)² = 1

2. \(\frac{144}{p^2}-\frac{120}{p}+25\)

= \(\left(\frac{12}{p}\right)^2-2 \times \frac{12}{p} \times 5+(5)^2\)

= \(\left(\frac{12}{p}-5\right)^2\)

= \(\left(\frac{12}{-3}-5\right)^2\) [Putting p = -3]

= (-4-9)²

= (-13)² = 16

Question 13. If \(m-\frac{1}{m-5}=12\) then find the value of \((m-5)^2+\frac{1}{(m-5)^2}\)

Solution:

Given

\(m-\frac{1}{m-5}=12\)

The value of \((m-5)^2+\frac{1}{(m-5)^2}\) = 51

Wbbse Class 7 Maths Solutions

Question 14. If 3x – \(\frac{1}{x}\)=6, then find the value of \(\left(x^2+\frac{1}{9 x^2}\right)\)

Solution:

Given

3x – \(\frac{1}{x}\)=6

 

Question 15. If a² + b²= 52 and a – b = 2, then find the value of ab.

Solution:

Given

a² + b² = 52
⇒ (a – b)²+2ab = 52

⇒ (2)²+2ab = 52

⇒ 2ab = 52 – 4 = 48

⇒ ab= \(\frac{48}{2}\) =24

Question 16. If a + b = √3 and a b= √2, then find the value of

1.8ab (a² + b²)

2. \(\frac{3\left(a^2+b^2\right)}{a b}\)

Solution:

1. 8ab (a² + b²)

= 4ab x 2(a² + b²)
= {(a + b)² – (a – b)²} {(a + b)² + (a – b)²}

= {(V3)²– (√2)²}{(√3)² + (√2)²} [ Putting a + b = √3 and a b= √2 ]

= (3-2)(3 + 2)
= 1 x 5
= 5

8ab (a² + b²) = 5

2. \(\frac{3\left(a^2+b^2\right)}{a b}\)

= \(6 \times \frac{2\left(a^2+b^2\right)}{4 a b}\)

= \(6 \times \frac{(a+b)^2+(a-b)^2}{(a+b)^2-(a-b)^2}\)

= \(6 \times \frac{3+2}{3-2}=6 \times \frac{5}{1}\) = 30

\(\frac{3\left(a^2+b^2\right)}{a b}\) = 30

Question 17. Express as the difference of two squares

1. 72
2. (a + 3b)(2a – 5b)

Solution:
1. 72 = 9 x 8

\(\left(\frac{9+8}{2}\right)^2-\left(\frac{9-8}{2}\right)^2=\left(\frac{17}{2}\right)^2-\left(\frac{1}{2}\right)^2\)

 

2. (a + 3b)(2a 5b)=

Wbbse Class 7 Maths Solutions

Question 18. If x² – 3x-1= 0, then find the value of \(\left(x^4+\frac{1}{x^4}\right)\)

Solution:

Given

x² – 3x-1= 0

The value of \(\left(x^4+\frac{1}{x^4}\right)\) is 119.

 

Question 19. If x = \(a+\frac{1}{a}\) and y = \(a-\frac{1}{a}\) then find the value of (x² + y² – 2x²y²).

Solution:

Given

If x = \(a+\frac{1}{a}\) and y = \(a-\frac{1}{a}\)

The value of (x² + y² – 2x²y²) is 16.

 

Question 20. If \(\frac{a}{b}+\frac{c}{d}=\frac{b}{a}+\frac{d}{c}\) then prove that \(\frac{a^2}{b^2}-\frac{c^2}{d^2}=\frac{d^2}{c^2}-\frac{b^2}{a^2}\)

Solution:

Given

\(\frac{a}{b}+\frac{c}{d}=\frac{b}{a}+\frac{d}{c}\)

Wbbse Class 7 Maths Solutions

Question 21. Show that (a+b) (a² + b²)(a⁴ +b⁴)(a³ +b⁸ + b⁸) = \(\frac{a^{16}-b^{16}}{a-b}\)

Solution:

Wbbse Class 7 Maths Solutions

Question 22. If a² + b² + c² = 2(a – b − 1), then find the value of (a + b + c).

Solution:

Given

a²+ b² + c² = 2(a – b-1)

⇒ a² + b² + c² = 2a-2b-2

⇒ a² – 2a + b² + 2b + c² + 2 = 0

⇒ (a² – 2a + 1) + (b² + 2b + 1) + c² = 0

⇒(a – 1)² + (b +1)² + c² = 0

If sum of square of two or more than two square is zero then each square will be zero.

(a -1)² = 0
⇒ a-1=0
⇒ a=1

(b + 1)2 = 0
⇒b+1=0
⇒ b = -1

c² = 0
⇒ c=0

a+b+c=1=1-1+0=0

The value of (a + b + c) is 0.

Class 7 Math Solution WBBSE

Question 23. Prove that (a + b)⁴ – (a – b)⁴= 8ab (a² + b²).

Solution:
Proof:

(a + b)⁴ – (a – b)⁴

= \(\left\{(a+b)^2\right\}^2-\left\{(a-b)^2\right\}^2\)

= \(\left\{(a+b)^2+(a-b)^2\right\}\)\(\left\{(a+b)^2-(a-b)^2\right\}\)

=2(a²+b²) x 4ab

= 8ab(a²+ b²) (Proved)

Question 24. Multiply (a+b+c) (a – b + c)(b + c – a)(a + b – c).

Solution:

Given

(a+b+c)(ab+c)(b + c a)(a + b – c)

= {(a + c) + b}{(a + c) – b}{b + (ca)} {b (c – a)}

= {(a + c)² – b²}{b²– (c – a)²}

= (a²+2ac + c²– b²) (b² – c² + 2ac – a²)

= {2ac + (a² – b² + c²)}{2ac – (a² – b² + c²)}

= (2ac)²– (a² – b² + c²)²

= 4a²c² – {(a² – b²)² + 2(a² – b²)c² + (c²)²}

= 4a²c² – {a⁴ – 2a²b² + b4 + 2a²c² – 2a²c² + c⁴) = 4a²c²-a⁴ + 2a²b² – b⁴ – 2a²c² + 2b²c² – c⁴

= 2a²b² + 2b²c² + 2a²c² – a⁴– b⁴ – c⁴

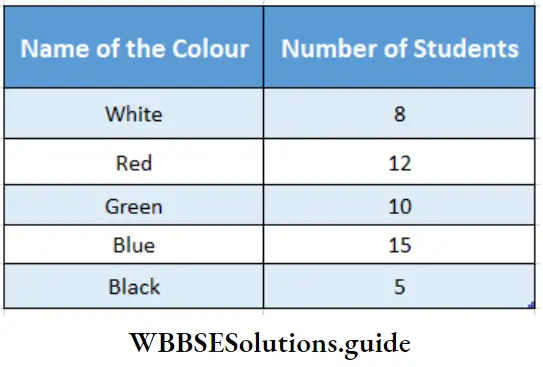
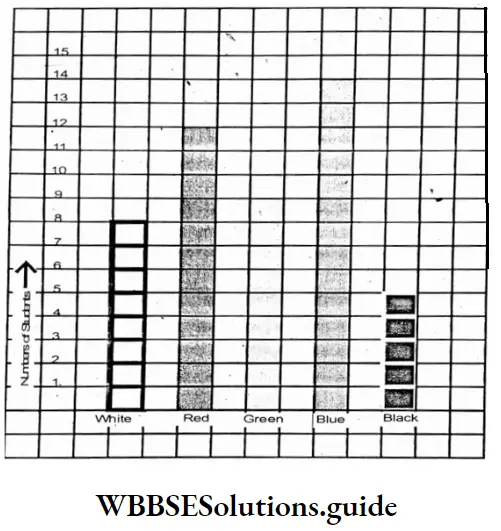
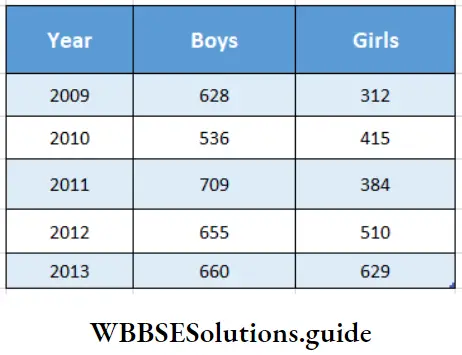
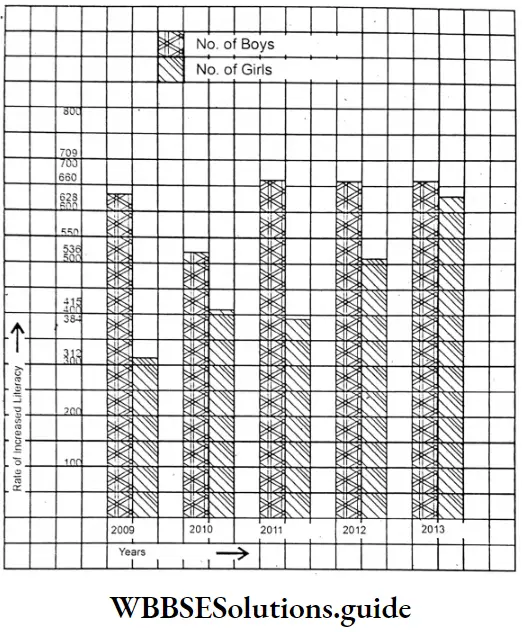
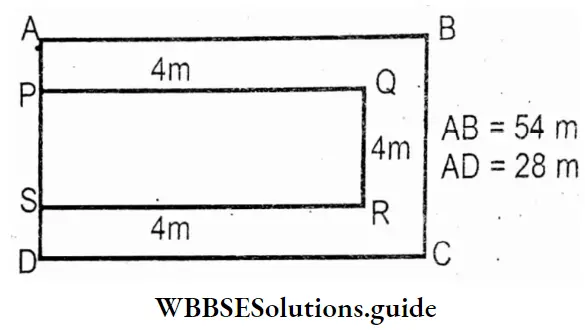
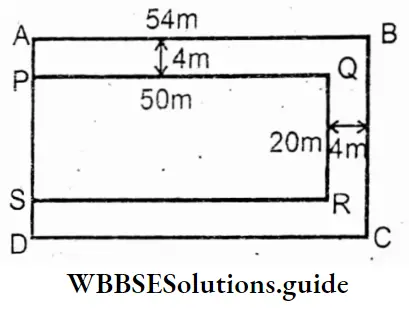
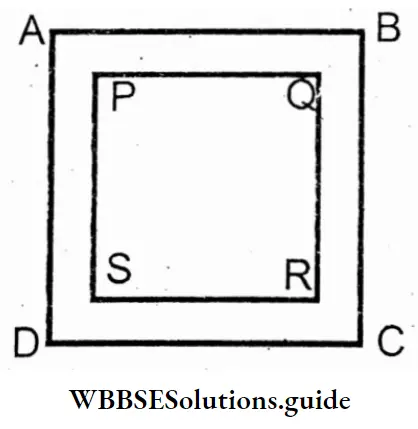
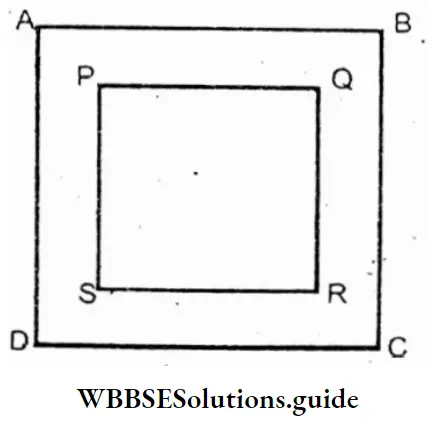
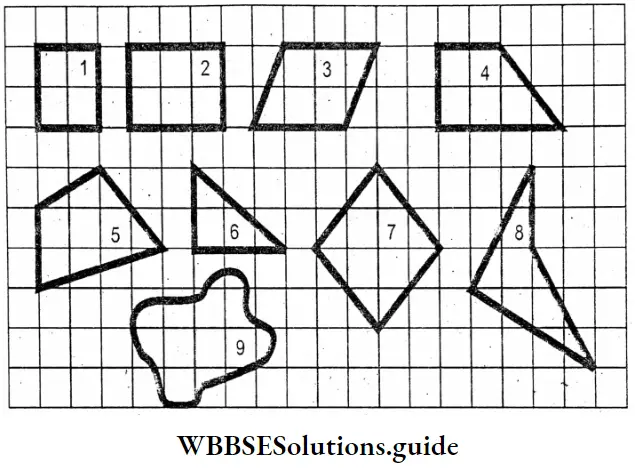
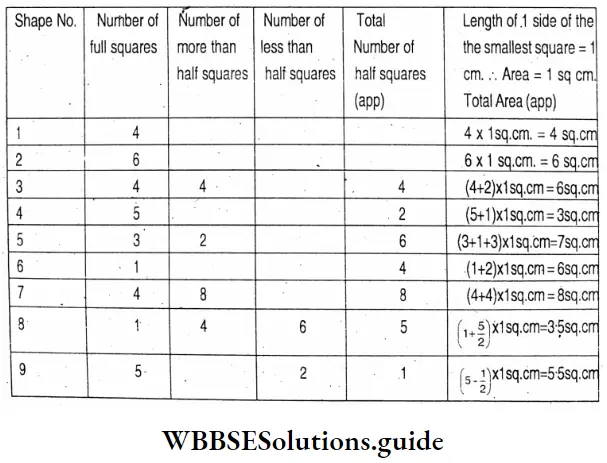
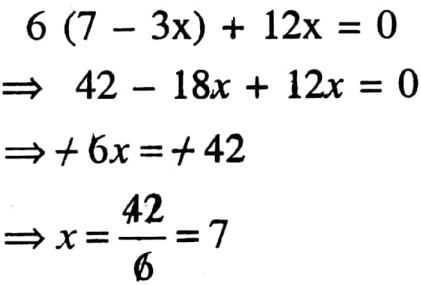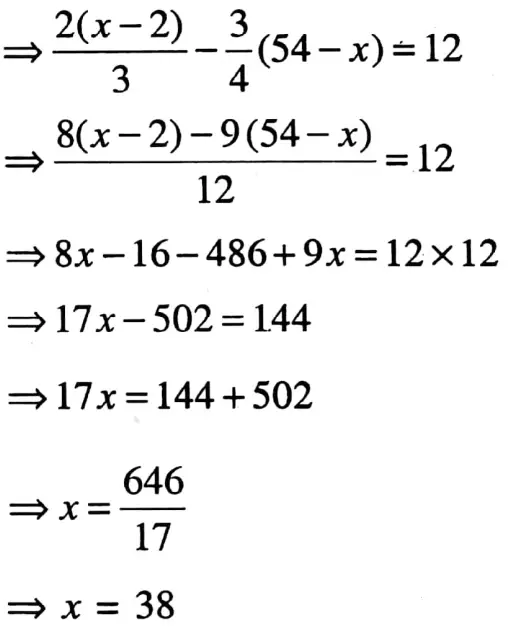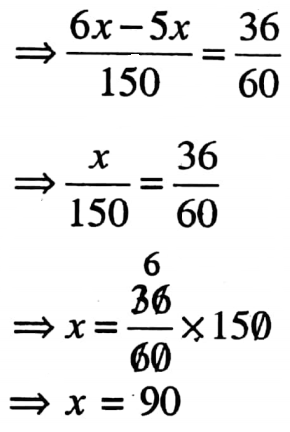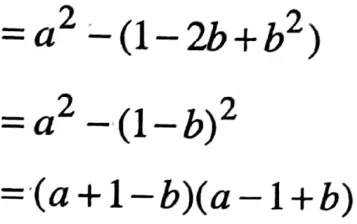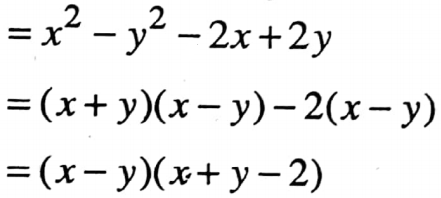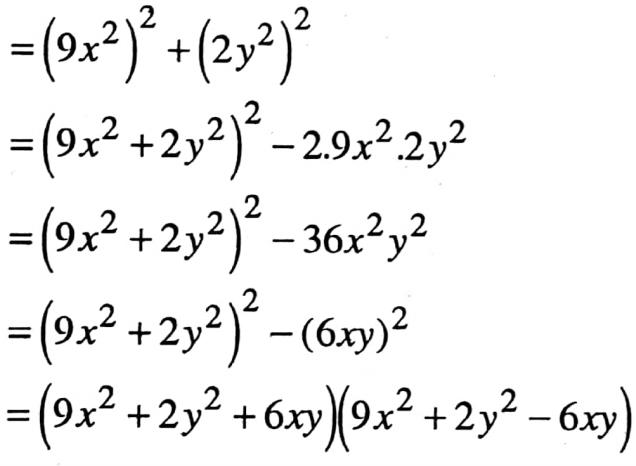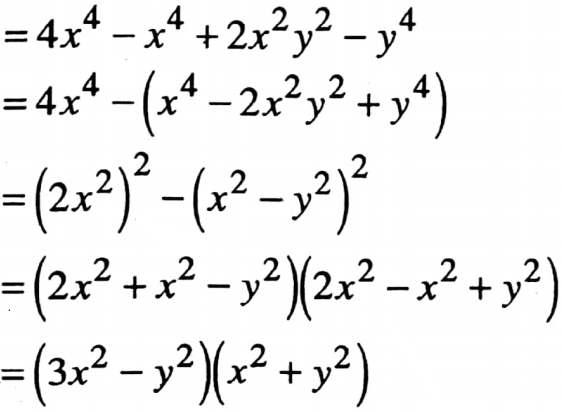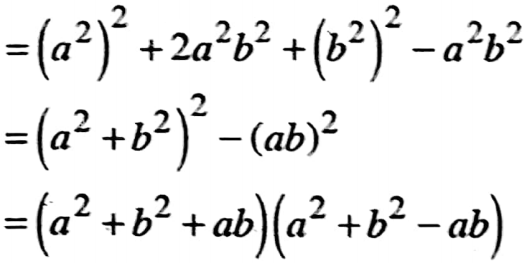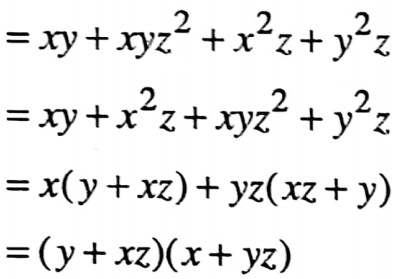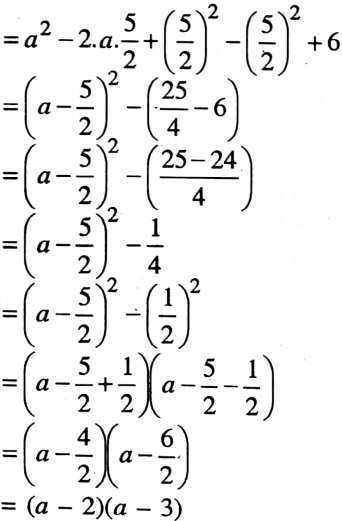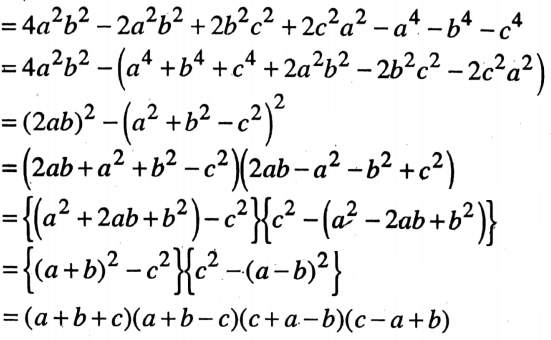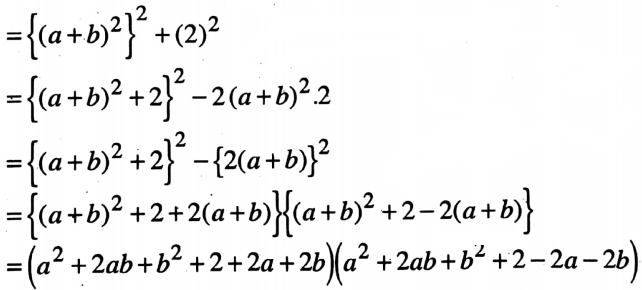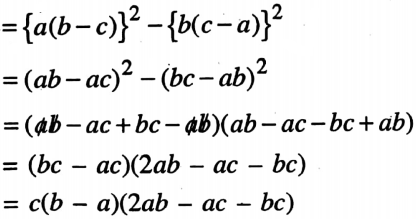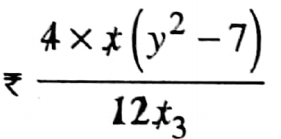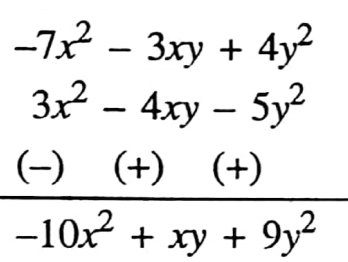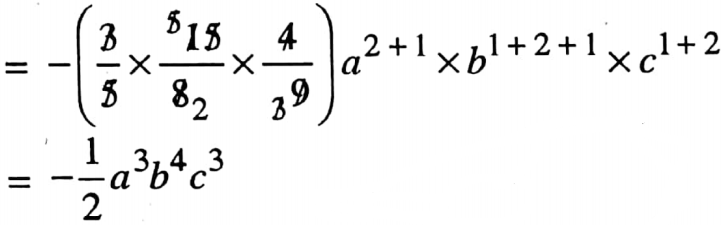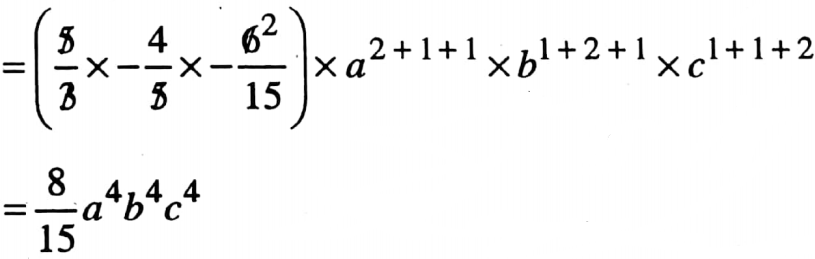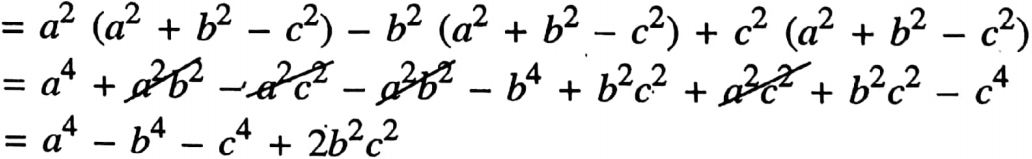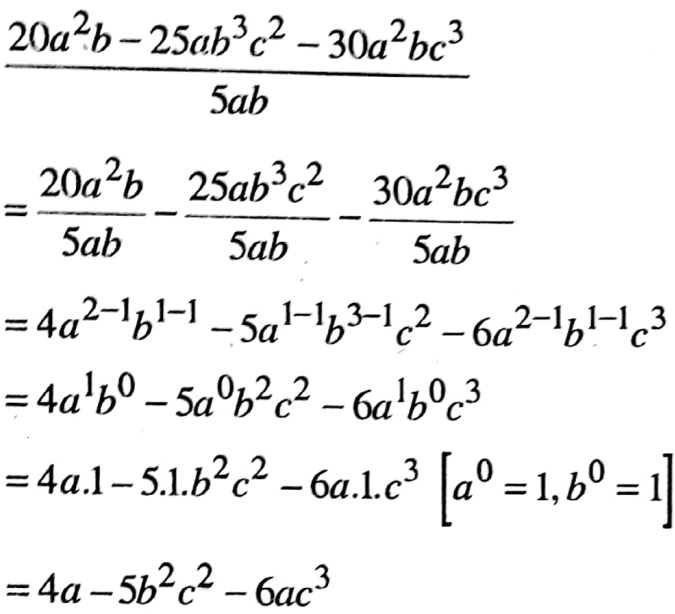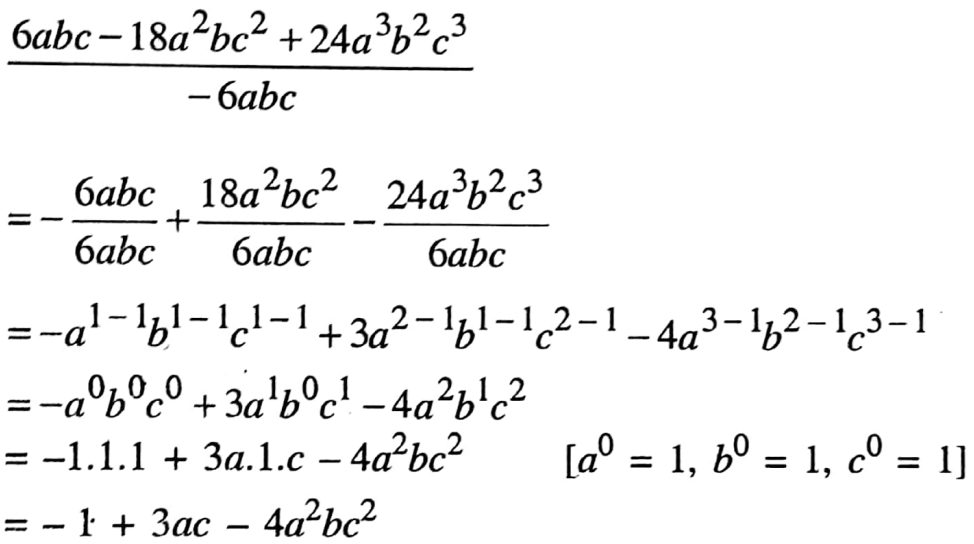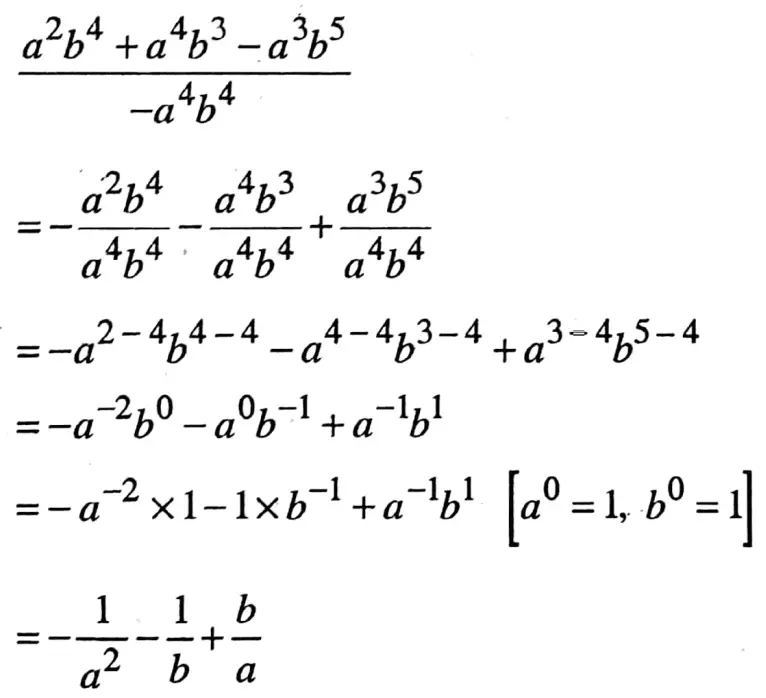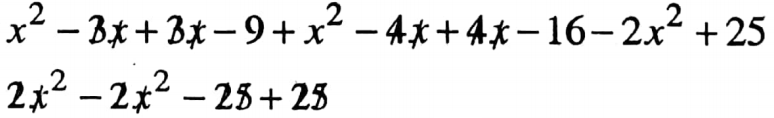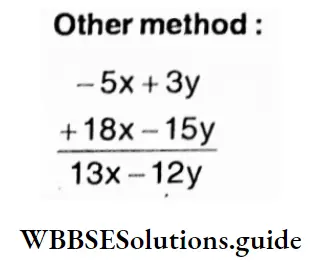WB Class 7 Math Solution Algebra Chapter 4 Algebraic Operations Exercise 4 Solved Problems

1. The term 5, 6, \(\frac{3}{4}\) etc are called constant term and are donated by a, b, c, etc. The term which is always changing are known as variable and are donated by x, y, z etc.

2. The term (7x – 2) and 9x are called algebraic expressing.

3. Relations formed by addition, subtraction, multiplication, and division of few variables and few constants are called an algebraic expression.

4. In expression (5p + 4), p is variable and 5 and 4 are constant.

5. In the algebraic expression 7y, the variable y is multiplied by the constant 7. The factors of 7y are 1, 7, y, and 7y.

6. 7y has only one term and is called a Monomial.
(5p+ 4) has two terms and it is called Binomials.

Read and Learn More WBBSE Solutions for Class 7 Maths

Like terms and Unlike terms:

If the terms of algebraic expression are alike. They are called like terms and if they are not alike, they are called, unlike terms.

3a²b and 4a²b  are like terms. But 3a²b and 4a²b are unlike terms.

Coefficients: A coefficient is a numerical factor present with any term.
In 5x², the coefficient of x² is 5 and the coefficient of 5x is x.

Wbbse Class 7 Maths Solutions

Question 1. Choose the correct answer 

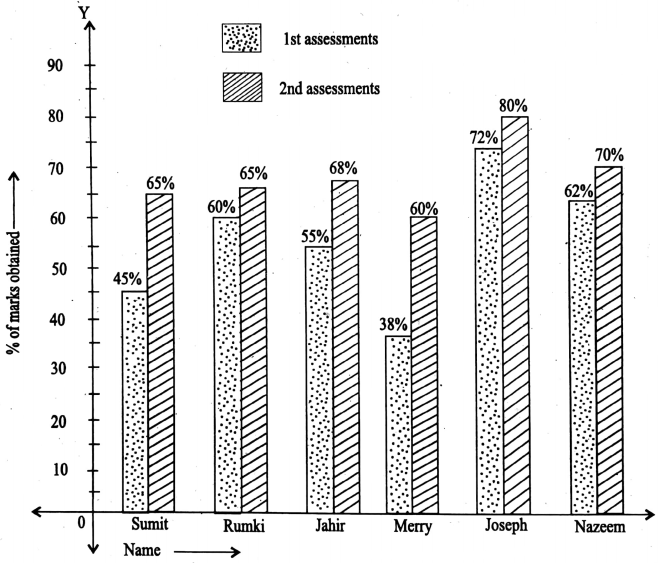
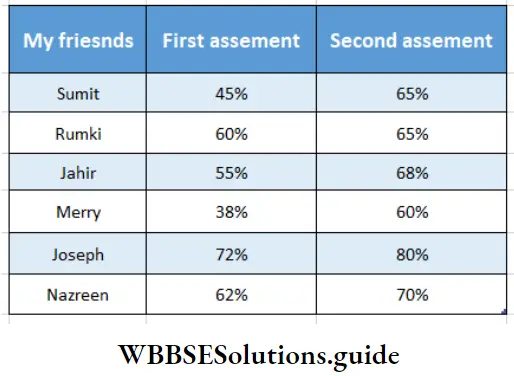
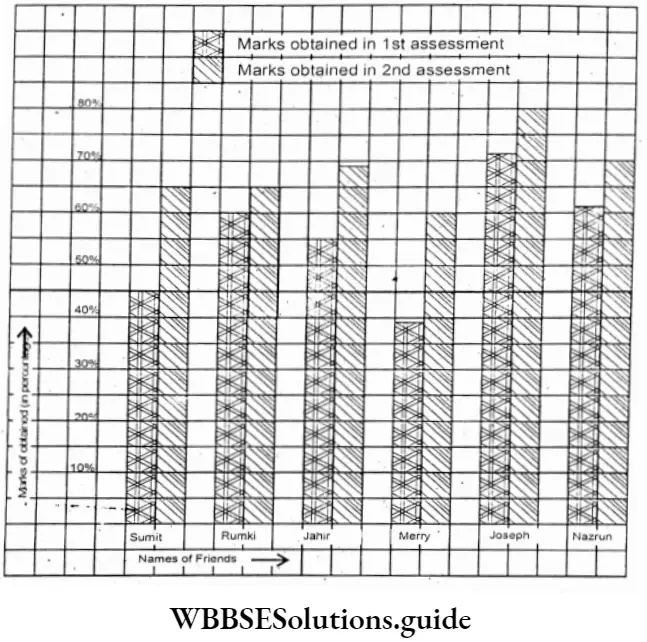
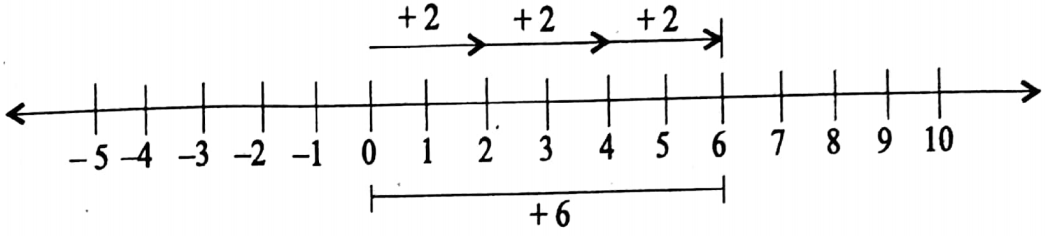
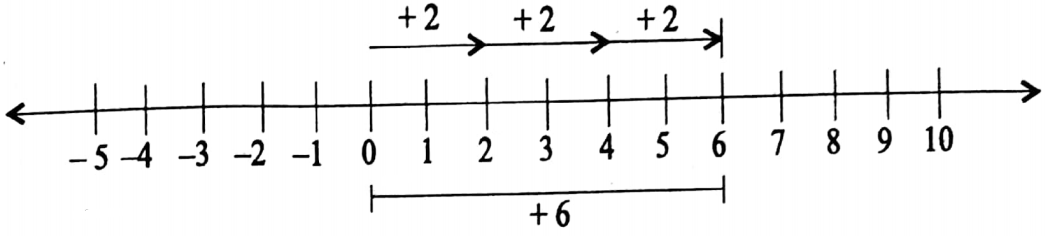
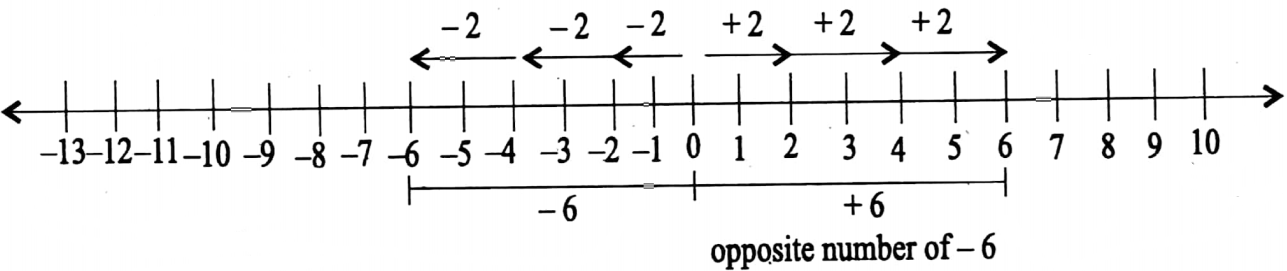
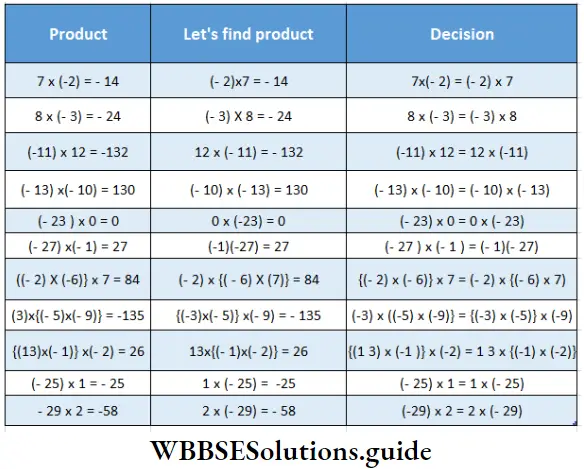
1. The sum of (-5x + 3y) and (18x – 15y) is

1. 23x 12y
2. 13x 12y
3. 13x 18y
4. None of these

Solution: -5x + 3y+ 18x-15y
=-5x+18x + 3y 15y
= 13x 12y

So the correct answer is

2. The value of (- 3m² + 2m+ 2) – (m² – 2) is

1. -2m² + 2m
2. -4m² + 2m + 4
3. -2m²+ 2m – 4
4. -2m² + 2m + 4

Solution: (- 3m² + 2m+ 2) – (m² – 2)

= -3m² + 2m + 2-m² + 2
= -3m² -m² + 2m + 2 + 2
=-4m² + 2m + 4

So the correct answer is 2. -4m² + 2m + 4

3. The value of (-3a²) x (4a²b) x (-2) is

1.  24a²b
2. 24a²b³
3. -24a⁴b
4. 24a⁴b

Solution: (-3a²) x (4a²b) x (-2)
=(-3) x (4) x (-2) x a²⁺² x b
= 24a⁴b

So the correct answer is 4. 24a⁴b

Question 2. Write ‘true’ or ‘false’

1. The number of factors of x²y is 6

Solution:

 

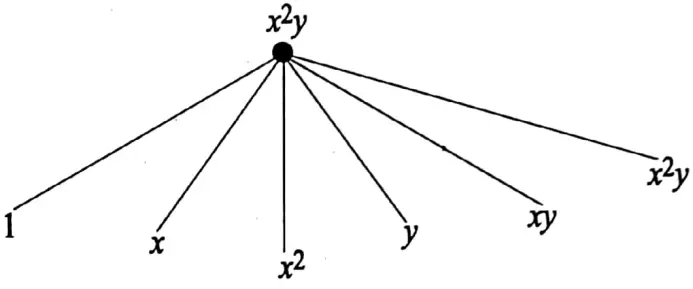
The factors of x²y is 1, x, x², y, xy, and i.e., the number of factors is 6.

So the statement is true.

2. The coefficient of x² in (5-6x²y² + 6xy) is 6y

Solution: In the expression (5-6x²y² + 6xy) the term with x is (-6x² y²) whose coefficient of x² is -6y²

So the statement is false.

Wbbse Class 7 Maths Solutions

3. The value of (-48x⁹ + 12x⁶) + 3x³ is (-16x⁶+ 4x³)

Solution: \(\frac{-48 \dot{x}^9+12 x^6}{3 x^3}\)

= \(-\frac{48 x^9}{3 x^3}+\frac{12 x^6}{3 x^3}\)

=-16x^9-3 +4x^6-3 =-16x⁶+4x³

So the statement is true.

Question 3. Fill in the blanks

1. 4x, (5x-2), (7x + 3) together are called _____

Solution: Algebrain expression

2. The product of a²b and (3a-4b) is _____

Solution: a²b (3a – 4b) = 3a³b – 4a²b²

3. If the price of x dozen of pen is ₹ (xy²-7x) then the price of 4 such pen is ₹ _____

Solution: x dozen = 12x

The price of the number of 12x pen is ₹ (xy² – 7x)

The price of 1 such pen is ₹ \(\frac{x y^2-7 x}{12 x}\)

The price of 4 such pen is ₹  \(\frac{4\left(x y^2-7 x\right)}{12 x}\)

=

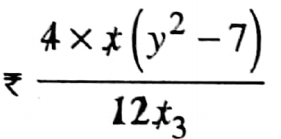
= ₹ \(\left(\frac{y^2-7}{3}\right)\)

Some important rules: a is non zero integers and also m and n are integers

1. a^m. aⁿ = a^{m + n}

2. a^m ÷ aⁿ = a^{m – n}

3. (a^m)ⁿ = a^mn

4. \(a^m=\frac{1}{a^{-m}}\)

5. a⁰ = 1

6. (ab)^m = a^m.bⁿ

7. \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

Proof: 

1. \(a^0=a^{m-m}=\frac{a^m}{a^m}=1\)

2. \(a^m=a^{0-(-m)}=\frac{a^0}{a^{-m}}=\frac{1}{a^{-m}}\)

Wbbse Class 7 Maths Solutions

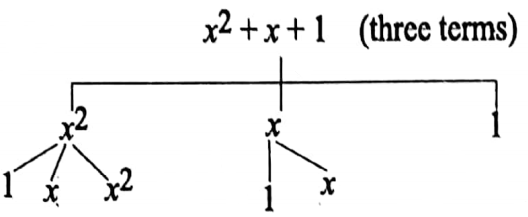
Question 4. Represent the following algebraic expressions into ‘factor free’ type of figure mentioning the prime factors of each term. Also mention the types these expressions with respect to their number of terms.

1. xy + yz + zx
2. x² + x + 1

Solution:

1.

 

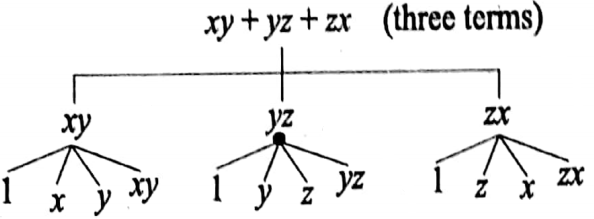
2.

 

Question 5. Find the numerical coefficients of the terms, other than the constant term.

1. x² + 6x + 5
2. x – 7xy + 9y

Solution: 1. x² + 6x + 5
The numerical co-efficient of x² is 1.
The numerical co-efficient of x is 6.

2. x – 7xy + 9y

The numerical co-efficient of x, xy, and y are 1, -7, and 9 respectively.

Question 6. Add

1. 7a²b+3ab²-9, 4a²b – 5ab² + 10, a²b + ab² – 15
2. xy-3yz.+4zx, 3xy+5yz-6zx, -2xy + 3yz-zx

Solution:

1. 7a²b+3ab²-9, 4a²b – 5ab² + 10, a²b + ab² – 15

= 7a²b+ 4a²b + a²b+3ab² – 5ab² +ab² – 9+ 10 – 15
= 12a²b – ab² – 14

Another method:

7a²b+3ab²-9
4a²b-5ab² + 10
+ a²b + ab² – 15

= 12a²b- ab² – 14

2. (xy 3yz+4zx) + (3xy + 5yz-6zx) + (-2xy + 3yz – zx)

=
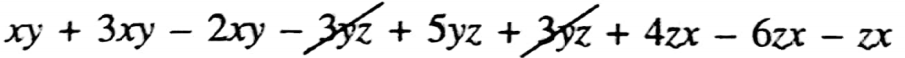
= xy + 3xy – 2xy – 3y + 5yz + 3yz + 4zx-6zxzx
= 2xy + 5yz-3zx.

Question 7. Subtract

1. (3x² – 4xy- 5y²) from (-7x²-3xy+4y²)
2. (m³ – 3m² + 4m – 5) from (m³+ 3m² – 6m + 2)

Solution:

1. (-7x² -3xy + 4y²) – (3x²-4xy – 5y²)

= -7x²-3xy+4y²-3x² + 4xy + 5y²
= -7x²-3x² – 3xy + 4xy+4y²+5y²
= -10x² + xy + 9y²

Alternative method

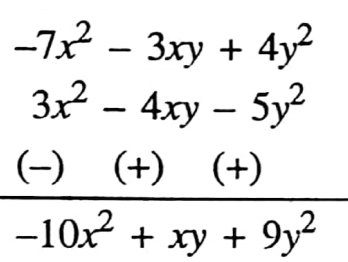
2. (m³+ 3m²– 6m+ 2) – (m³-3m² + 4m -5)
= m³+3m²-6m+2 -m³ + 3m² – 4m + 5

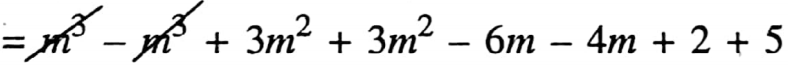
= 6m2 10m +7

Question 8. How much must be added to (6y² – 6y+ 1) to get (-15y²+ 7y – 7)

Solution:

The required expression is (-15y² + 7y – 7) (6y² – 6y+1)
=-15y²+ 7y-7-6y²+6y+ 1
=-15y²+ 13y-6

Question 9. What must be subtracted from (9x²-3x+7) to get (-3x²+6x-13)

Solution:

The required expression is (9x²-3x+7)-(-3x²+6x-13)
= 9x² – 3x + 7 + 3x²-6x + 13
= 12x² – 9x+20

Wbbse Class 7 Maths Solutions

Question 10. Subtract the sum of (-5y² + 3y -7) and (9y²-7y+ 12) from the sum of (y²+2y-6) and (12y – y² + 5)

Solution:

The required expression is
{(y²+2y-6)+(12y-y²+ 5)} – {(-5y2+ 3y 7) + (9y2-7y+ 12)}

=

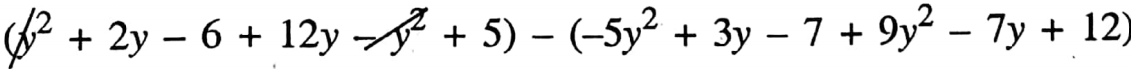
= (14y -1)- (2y²-4y+5)
=14y -1 – 2y² + 4y – 5
=-2y²+18y-6

Question 11. Multiply

1. \(\left(-\frac{3}{5} a^2 b\right) \times\left(\frac{15}{8} a b^2 c\right) \times\left(\frac{4}{9} b c^2\right)\)

2. \(\left(\frac{5}{3} a^2 b c\right) \times\left(-\frac{4}{5} a b^2 c\right) \times\left(-\frac{6}{15} a b c^2\right)\)

3. (3a-4b)(5a + 6b)

4. (a² – b² + c²)(a² + b² – c²)

Solution:

1. \(\left(-\frac{3}{5} a^2 b\right) \times\left(\frac{15}{8} a b^2 c\right) \times\left(\frac{4}{9} b c^2\right)\)

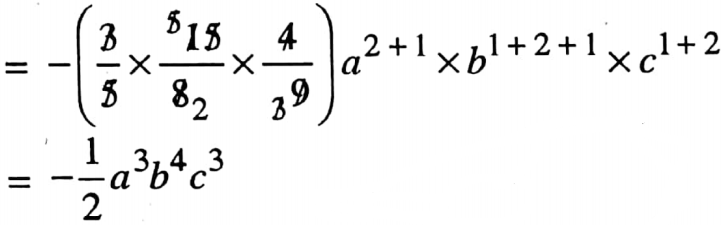
2. \(\left(\frac{5}{3} a^2 b c\right) \times\left(-\frac{4}{5} a b^2 c\right) \times\left(-\frac{6}{15} a b c^2\right)\)

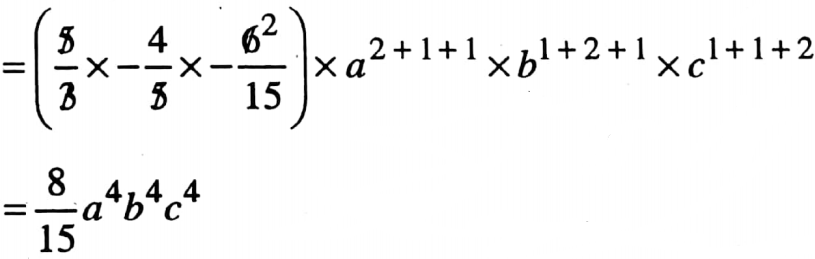
3. (3a-4b)(5a + 6b)

= 3a (5a + 6b) – 4b (5a + 6b)
= 15a² + 18ab – 20ab – 24b²
=15a²-2ab-24b²

4. (a²-b²+c²)(a²+b²-c²)

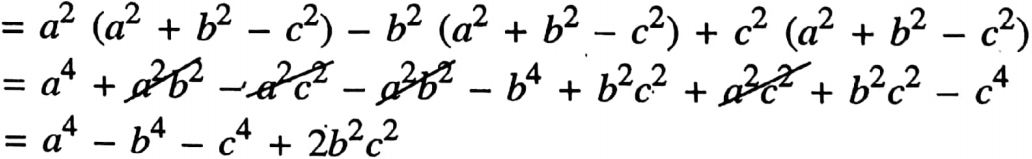
Wbbse Class 7 Maths Solutions

Question 13. Divide the first expression by the second.

1. 20a²b-25ab³c²-30a²bc³, 5ab
2. 6abc-18a²bc² + 24a³b²c³, -6abc
3. a²b⁴ + a4b³ – a³b⁵4, -a⁴b

Solution:

1.

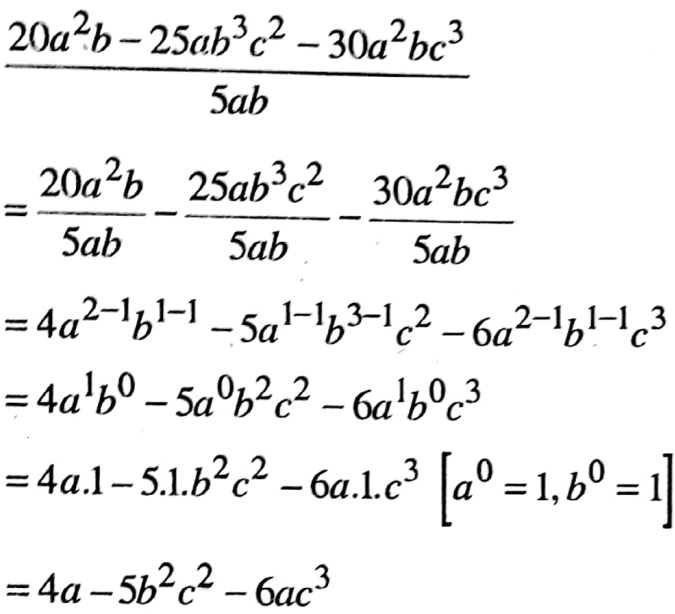
2.

 

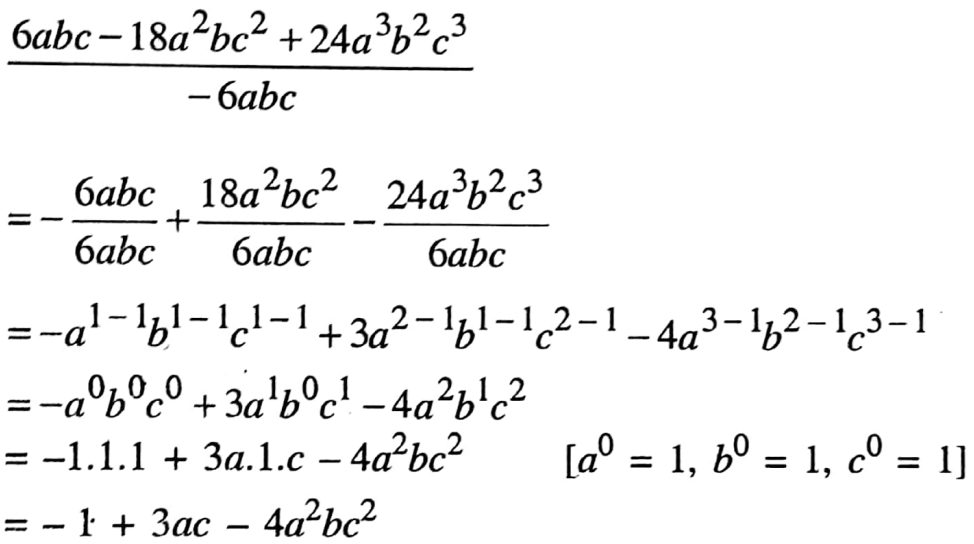
3.

 

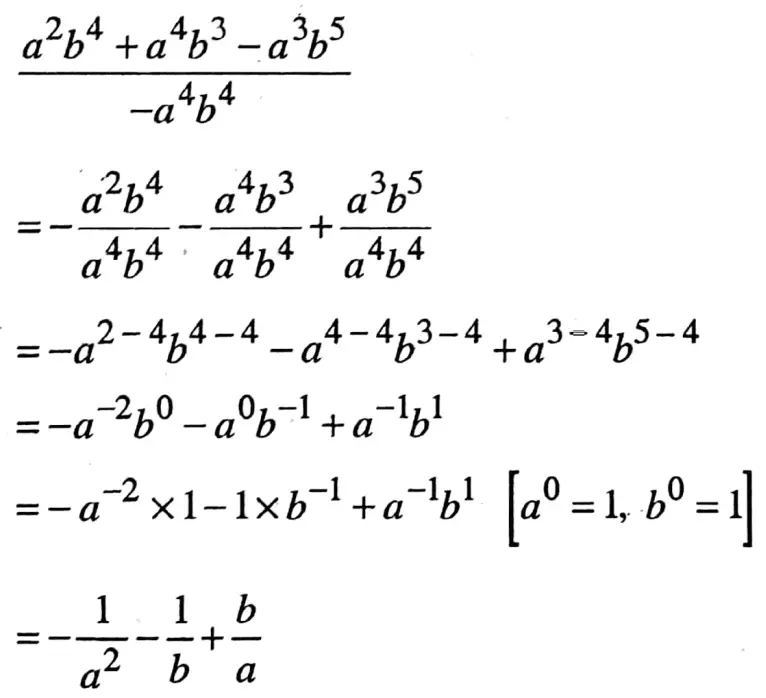
Question 14. If A = 2x + 3y – 4z, B= 2y+ 3z4x and C2z+3x4y. Find the sum of (A+B+C) and (A B+ C)

Solution:

Given

If A = 2x + 3y – 4z, B= 2y+ 3z4x and C2z+3x4y.

(A+B+ C) + (A- B+ C)
= 2A + 2C
= 2(2x + 3y 4z) + 2(2z+3x-4y)
=4x+6y8z+4z+6x-8y
= 10x 2y4z.

Question 15. If P = 3x² + 2xy + y², Q=-3x² – 2xy + y² and R = x² + y² and x = y – 2. Find the value of (P+Q + R).

Solution:

Given

If P = 3x² + 2xy + y², Q=-3x² – 2xy + y² and R = x² + y² and x = y – 2.

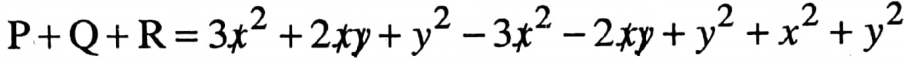
= x² + 3y²
=(-2)² + 3 (-2)² [Putting the value of x and y]
= 4+3×4
= 16.

Question 16. Simplify the following

1. 3x²+ 2x(x + 3) -4x (3x-5)
2. (a² + b²)(a² – b²) + (b² + c²)(b² – c²) + (c² + a²)(c² – a²)
3. (x²+5x)(x -1) – (x² + 2x)(x 1) – 5x (x + 1)
4. (x+3)(x-3)+(x+4)(x-4) – 2x² + 25
5. (x² + 2x – 1)(x − 1) + (x² – 2x + 1)(x + 1) − 2x(x − 1)

Solution:

1. 3x²+ 2x(x + 3) -4x (3x-5)

= 3x²+2x²+6x-12x² + 20x
= −7x² + 26x

2. (a² + b²)(a² – b²) + (b² + c²)(b² – c²) + (c² + a²)(c² – a²)

= a²(a²-b²) + b²(a² – b²) + b²(b² – c²) + c²(b² – c²) + c² (c² – a²) + a² (c² – a²)

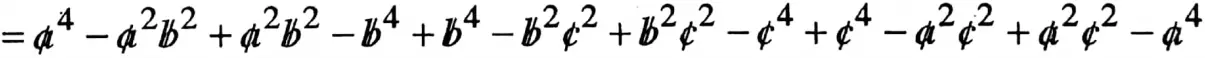
= 0

3. (x² + 5x)(x – 1) – (x² + 2x)(x – 1) – 5x (x + 1)

= x²(x -1) + 5x(x – 1) – x² (x – 1) – 2x(x – 1)- 5x(x + 1)

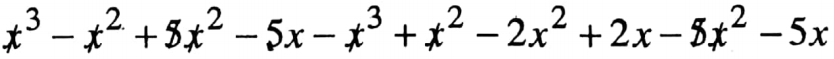
= -2x² – 8x

4. (x+3)(x-3)+(x+4)(x-4)- 2x² + 25.

= x(x-3)+3(x-3) + x(x-4)+4(x-4) – 2x² + 25

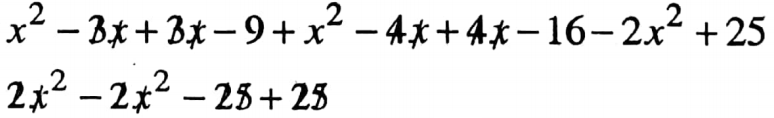
= 0

5. (x² + 2x-1)(x 1) + (x² – 2x + 1)(x + 1) 2x(x-1)

= x²(x-1) + 2x(x − 1) − 1(x − 1) + x² (x + 1) − 2x(x + 1) + 1(x + 1) − 2x(x-1)

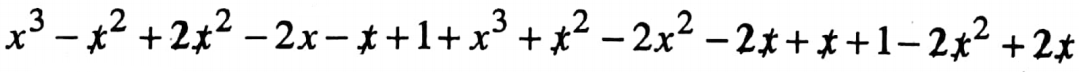
= 2x³ – 2x² – 2x + 2

 

WB Class 7 Math Solution Algebraic Operations

Algebraic Operations Exercise 6.1

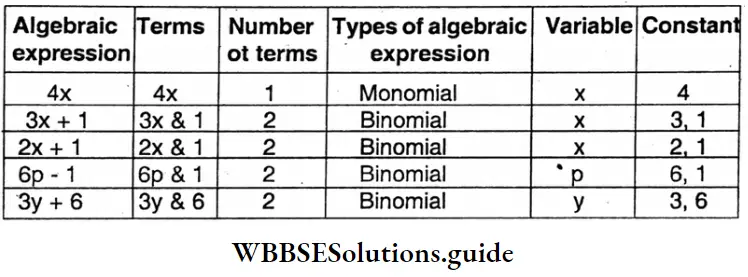
Let’s write the algebraic expression and find the number of terms.

4x, 3x + 1, 2x + 1, 6p – 1, 3y + 6

Class 7 Math Solution WBBSE Algebraic Operations Exercise 6.2

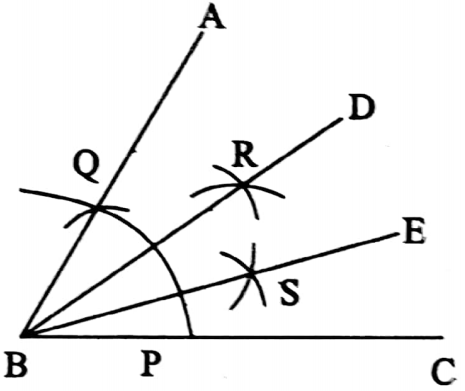
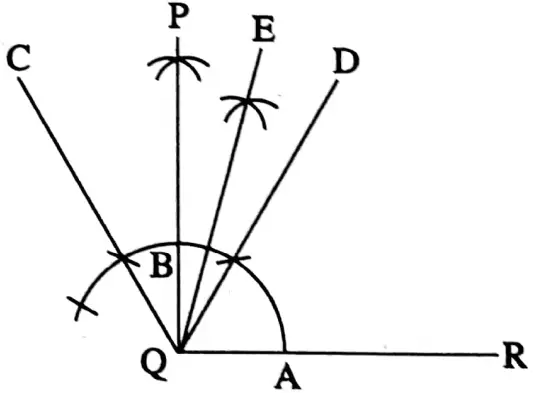
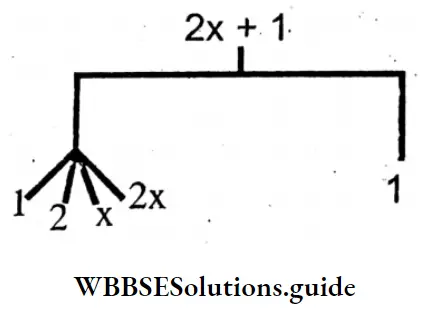
Question 1. Let’s draw ‘factor tree’ type figures and from there let’s find the number of terms and factors of the following algebraic expression :

1. 2x + 1
Solution:

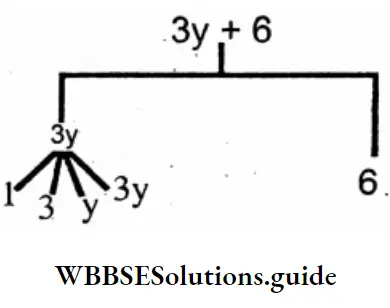
2. 3y+6
Solution:

Question 2.  Let’s study the algebraic expressions given below and fill in the gaps accordingly.

Class 7 Math Solution WBBSE Algebraic Operations Exercise 6.3

Question 1. Let’s form algebraic expressions from the statements given below-

1. y is added to x
Solution: x + y

2. x is subtracted from z
Solution: z – x

3. q is added to twice of p
Solution: 2p + q

4. Multiply x with a square of x.
Solution: x².x = x³

5. \(\frac{1}{4}\) th of the sum of x and y
Solution: \(\frac{x+y}{4}\)

6. 7 is added to 4 times the product of a & b
Solution:  4ab + 7

7. Half of y is added to twice of x
Solution: 2x +\(\frac{1}{2}\) y

8. The product of x and y is subtracted from sum of x and y.
Solution: (x + y) – xy.

Question 2. Let’s Let’s observe the patterns match and fill in the chart

1. 

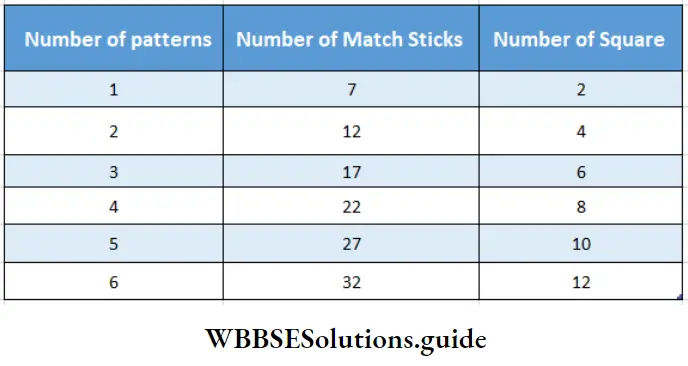
General Expression 5x + 2 = Number of Match Sticks.

2. Let’s form the general expression with a variable

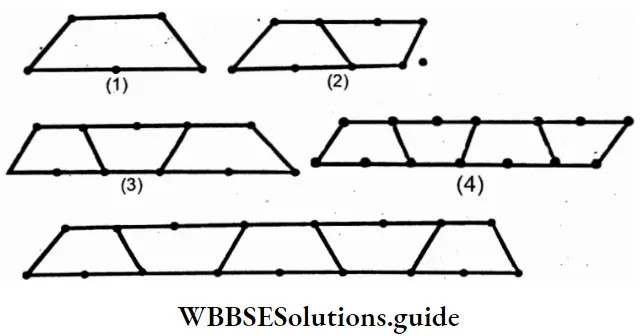
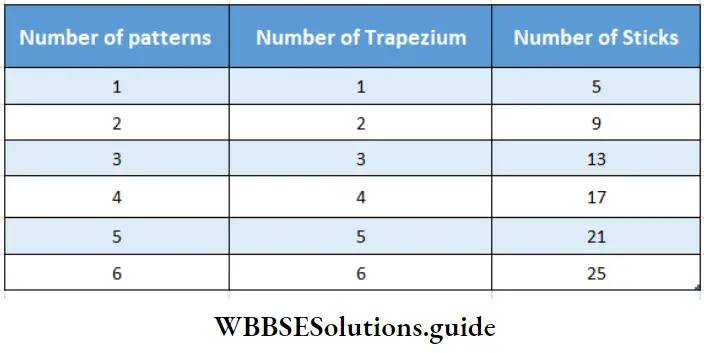
General Expression, Number of sticks = 4x + 1 where x = No. of trapezium

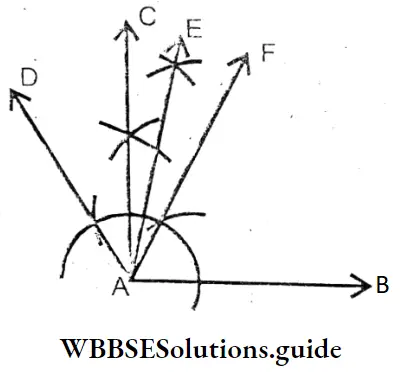
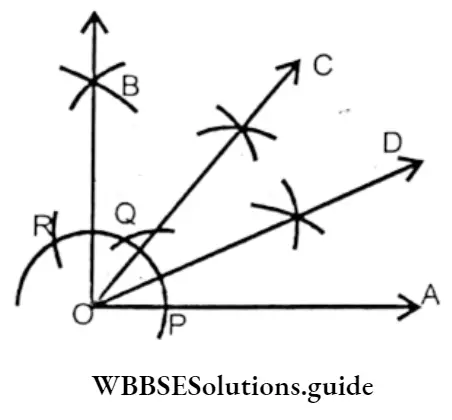
Question 3. Let us represent the following algebraic expressions into ‘factor tree’ type of figure mentioning the prime factor of each term. Also mention thetypes of these expressions with respect to their number to terms.

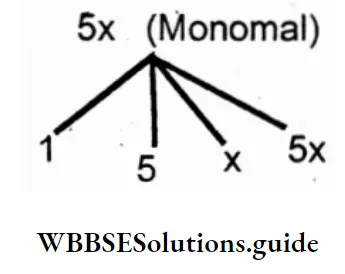
1. 5x (Monomial)
Solution:

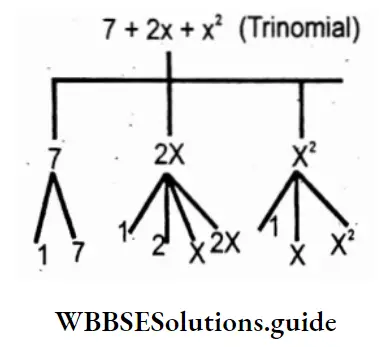
2. 7 + 2x + x² (Trinomial)
Solution:

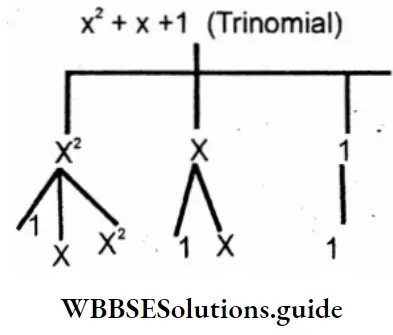
3. x² + x + 1 (Trinomial)
Solution:

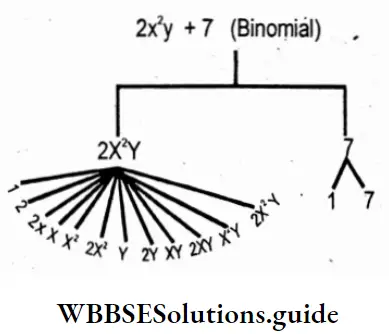
4. 2x²y + 7 (Binomial)
Solution:

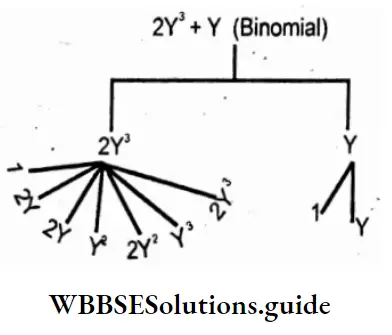
5. 2y³ + y (Binomial)
Solution:

6. x²y+xy²+xyz
Solution:

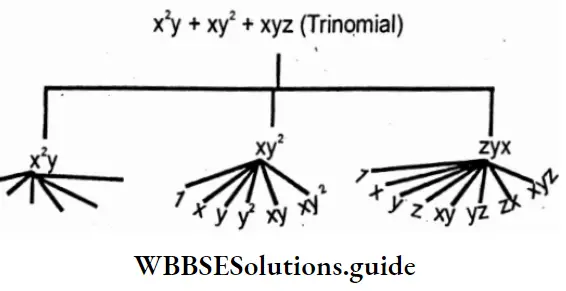
7. x²y + 2x²y² (Binomial)
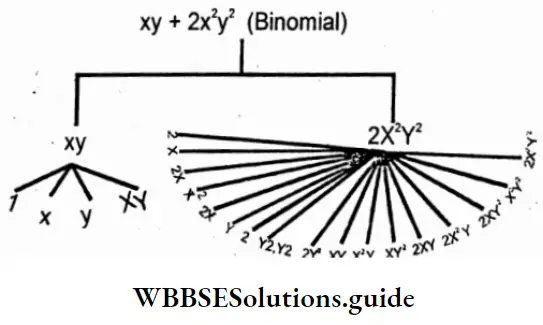
Solution:

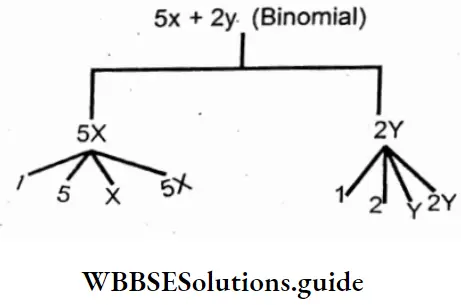
8. 5x + 2y (Binomial)
Solution:

Question 4. Let’s find the numerical coefficients of the terms, other than constant
term:

1. 2x + 3y
Solution: 2, 3.

2. x² + 2x + 5
Solution: 1, 2.

3. x + 5xy – 7y
Solution: 1, 5, – 7.

4. – 5 – z
Solution: – 1

5. x³ + x – y 
Solution: – 1,1, 1,

6. \(\frac{x}{2}+4\)
Solution: \(\frac{1}{2}\)

Question 5. In the following algebraic expression let’s find the coefficient of x in the terms or terms which have ‘x’ as their factor.

1. y³x + y²
Solution: y³x, y³

2. 5z² – 8zx
Solution: – 8zx, – 8z

3. – x – y + 2
Solution:– x, – 1

4. 4 + y +.yx
Solution: yx, y

5. 2 + x + xy²
Solution: x, 1 , xy2, y2

6.  5xy⁴-1 4
Solution: 15xy⁴, I5y⁴

Question 6. Let’s group the like terms from the algebraic expressions given below. 2x, y, 12xy, 13y², – 5x, 18y, – 4xy, – 2y², 21x²y, 3x, 3xy, – xy, – y, – 6x², -1 5x².
Solution:

2x, y, 12xy, 13y², – 5x, 18y, – 4xy, – 2y², 21x²y, 3x, 3xy, – xy, – y, – 6x², -1 5x²=

(2x, – 5x, 3x); (y, 18y, – y), (12xy, – 4xy, 3xy, – xy), (13y², – 2y²), (21x²y), (- 6x², – 15x²)

Question 7. Let’s identify the like and unlike pairs of terms with reasons from the pairs of terms given below.

1. 2x, 3y
2. 7x, 8x
3. 29x, 6Tx
4. 4xy, 6yz
5. 15 yx, 8xy
6. 5xy, 6x²y²

Solution:

Like term: 2,3,5

Unlike term: 1,4,5

Question 8. From the algebraic expressions given below, let’s write the terms which contain x². And also find the coefficient of x².

1. 5- xy²
Solution: No

2. – 6x² – 8y
Solution: -6

3. 3x² – 1 5xy² – 8y²
Solution: 3

4. 2 + 3k²y+4x
Solution: + 3y

5. 5 – 6x²y² + 6xy
Solution: – 6y²

Class Vii Math Solution WBBSE Algebraic Operations Exercise 6.4

Question 1. Let’s add the following

1. (- 5x + 3y) and (1 8x – 1 5y)
Solution :

Given

(- 5x + 3y) and (1 8x – 1 5y)

⇒ (- 5x + 3y) + (1 8x – 1 5y)

= – 5x + 1 8x + 3y – 1 5y

= 1 3x – 1 2y

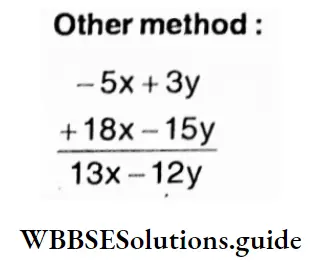
2. (7a – 8b + 2c) and (2a + 3b – d)
Solution :

Given

(7a – 8b + 2c) and (2a + 3b – d)

⇒ (7a – 8b + 2c) + (2a + 3b – d)

= 7a + 2a + (- 8b + 3b) + 2c – d

= 9a – 5b + 2c – d

Question 2. Let’s subtract:

1.  (-mn – m + n) from (4mn + m + n)
Solution :

Given

(-mn – m + n) and (4mn + m + n)

⇒ (-mn – m + n) – (4mn + m + n)= (4mn + m + n) – (-mn – m + n)

= 4mn + m + n + mn + m- n

= 4mn + mn + m + m + n- n

= 5mn + 2m

2. (2q² + 3P² – qp + pq²) from (p² + q² – pq + p²q)
Solution:

Given

(2q² + 3P² – qp + pq²) and (p² + q² – pq + p²q)

= (p² + q² – pq + p²q) – (2q² + 3p² – pq + pq²)

= p² + q² – pq + p²q – 2q² – 3p² + pq – pq²

= p² – 3r² + q² – 2q² – pq + pq + p²q – pq²

= – 2p² – q² + p²q – pq²

Class Vii Math Solution WBBSE Algebraic Operations Exercise 6.5

Question 1. Lefs add the algebraic expressions (2x² + x + 2) and (x² + 2x + 2) with the use of colored cards.
Solution:

Let’s add :

Given

(2x² + x + 2) and (x² + 2x + 2)

⇒ (2x² + x + 2) + (x² + 2x + 2)

= 2x² + x² x + 2x + 2 + 2

= 3x² + 3x + 4

Question 2. Let’s subtract the algebraic expressions (3x² + 3x – 2) from (5x² – 2x – 3)
Solution:

Given

(3x² + 3x – 2)and (5x² – 2x – 3)

Let’s subtract the algebraic expressions

(3x² + 3x – 2) from (5x² – 2x – 3)

= (5x² – 2x – 3) – (3x² + 3x – 2)

= 5x² – 2x – 3 – 3x² – 3x + 2

= 5x² – 3x² – 2x – 3x – 3 + 2

= 2x² – 5x 1

Algebraic Operations Exercise 6.6

Question 1. Let’s add the following :

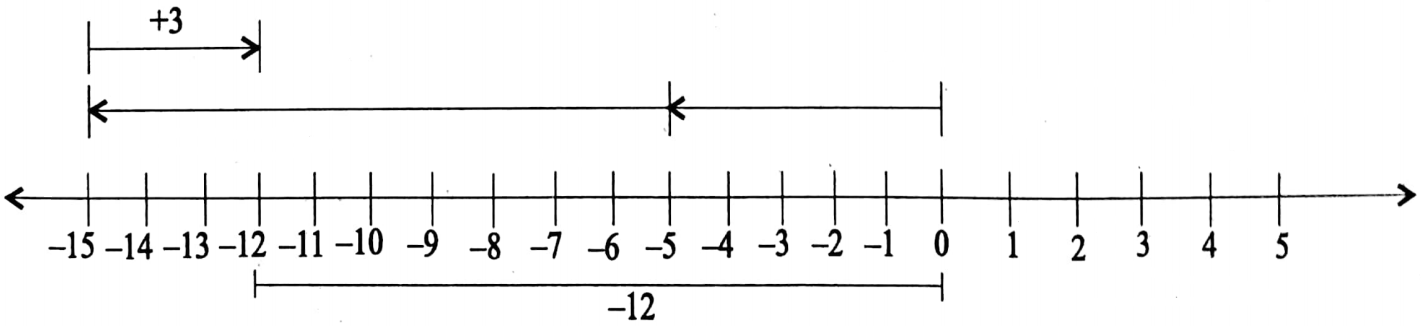
1. (- 5x + 3y) and (18x – 1 5y)
Solution:

Given

(- 5x + 3y) and (18x – 1 5y)

– 5x + 3y + 18x – 15y = – 5x + 18x + 3y – 15y

= 13x – 1 2y

2. (7a – 8b + 2c) and (2a + 3b – d)
Solution:

Given

(7a – 8b + 2c) and (2a + 3b – d)

7a – 8b + 2c + 2a + 3b – d = 7a + 2a – 8b + 3b + 2c – d

= 9a – 5b + 2c> d

Question 2. Let’s Let’s subtract.:

1. (- mn – m + n) from (4mn + m + n)
Solution:

Given

(- mn – m + n) and (4mn + m + n)

(4mn + m + n). – (- mn – m + n)

= 4mn + m + n + mn + m- n

= 4mn + mn + m + m + n- n

= 5mn + 2m

2. (2q² + 3p² – qp + pq²) from (p² + q² – pq + p2q)
Solution:

Given

(2q² + 3p² – qp + pq²) and (p² + q² – pq + p2q)

(p² + q² – pq + p²q) – (2q² + 3p²– qp + pq²)

p² + q² – pq + p²q – 2q² – 3p² + pq – pq²

= p² – 3p² + q² – 2q² – pq + pq + p²q – pq²

= – 2p² – q² + p²q – pq²

= p²q – 2p² – q² – pq²

Algebraic Operations Exercise 6.7

Question 1. Let’s calculate mentally 

1. 5x + 3x
Solution:

5x + 3x = 8x.

2. – 4y + 7y
Solution:

– 4y + 7y = 3y

3. 9y – 3y
Solution:

9y – 3y = 6y.

4. – 10x – 2x
Solution: –

10x-2x = – 12x

5. 3a + 4a – 2a
Solution:

3a + 4a – 2a = 3a – 2a

= 5a

6. – 7x-2x +5x
Solution:

– 7x-2x +5x = – 9x + 5x

= – 4x

7. 6p – 2p + 3p
Solution:

6p – 2p + 3p = 9p – 2p

= 7p

8. 4x² – 2x² – 3x² + x²
Solution:  

4x² – 2x² – 3x² + x²

= 5x² – 5x²

= 0

9. 5a²b – 2a²b – 3a²b + 8a²b
Solution:

5a²b – 2a²b – 3a²b + 8a²b = 13a²b – 5a²b

= 8a²b

10. 3x² – 6x² – 2x² – x² + 6x²
Solution: 

3x² – 6x² – 2x² – x² + 6x² = 9x² – 9x²

= 0

= 2.

Question 2. 

1. My age is ‘x’ years. Pallabi is 2 years older than me. Let’s find the sum of our ages.
Solution: 

Given

My age is ‘x’ years. Pallabi is 2 years older than me.

My age  = x years

Pallabi’s age = (x + 2) years

∴ Sum of our ages = (2x + 2) years

2. Today made ’x’ number of flower garlands. Mir made 6 more than twice the number of garlandsI made. In total, how many garlands we two have made.
Solution :

Given

Today made ’x’ number of flower garlands. Mir made 6 more than twice the number of garlandsI made.

I made = x  flower garlands

Mir made = 2x + 6 flower garlands

∴ Total number of flower

Garlands we made = 3x + 6

3. Today Ratul bought guava for Rs. x, apple for Rs. (x + 15) and cucumber for Rs. (2x + 3). Let’s find, how much money did Ratul spent today on fruits.
Solution:

Given

Today Ratul bought guava for Rs. x, apple for Rs. (x + 15) and cucumber for Rs. (2x + 3).

Ratul bought guava for = Rs. x

Apple for = Rs. (x + 15)

Cucumber for = Rs. (2x + 3)

∴ Ratul spent today on fruits = (x + x + 15 +2x + 3)

= Rs. (4x + 18)

4. Last year Firoza was present in school for x days. Firoza’s friend Mohini was present for (3x + 13) days, Let’s find, how much more days Mohini was present in school than Firoza last year.
Solution :

Given

Last year Firoza was present in school for x days. Firoza’s friend Mohini was present for (3x + 13) days

Mohini was present for = 3x + 13 days

Firoza was present for = x days

Mohini was present in school than Firoz = 3x + 13 = x

(3x + 13 –  x)  = 3x –  x+ 13

= (2x + 13) days

5. Today, Dipuda sold (2x + 19) newspapers. But yesterday he sold (5x – 8) newspapers. Let’s find, how many more newspapers did Dipuda sold today than yesterday.
Solution :

Given

Today, Dipuda sold (2x + 19) newspapers. But yesterday he sold (5x – 8) newspapers.

Yesterday he sold = (5x-8) newspaper

Today Dipuda sold = (2x+19) newspaper

∴ Dipuda sold more newspaper on yesterday  = (5x-8) = (2x+19)

(5x-8-2x-19) = 5x- 8- 2x -19

= 3x – 27

6. Pareshbabu earns Rs. 8x per month. But he spends Rs. (3x – 15) per month. Let’s find the amount of money he saves per month.
Solution :

Given

Pareshbabu earns Rs. 8x per month. But he spends Rs. (3x – 15) per month.

Monthly Incom of Pareshbabu = Rs. 8x

Monthly expenditure of Pareshbabu = Rs. 3x-15.

Monthly saving of Pareshbabu = 8x= 3x-15.

(8x – 3x +15 )=  8x – 3x+15 = 0

= 5x +15

Question 3. Let’s add:

1. 3a + b; 2a + 4b; 5a – b
Solution :

Given

3a + b; 2a + 4b; 5a – b

(3a +b) + (2a + 4b) + (5a – b)

= (3a + 2a + 5a) + (b + 4b-b)

= 1 0a + 4b

2. 5a – 4; 2a + 3; 2a – 4
Solution :

Given

5a – 4; 2a + 3; 2a – 4

(5a – 4) + (2a + 3) + (2a – 4)

= (5a + 2a+ 2a) + (- 4 + 3 – 4)

= 9a – 5

3. 6a + 7a +3; 9a² – 2a + 7; 4a² – 2a + 9
Solution :

Given

6a + 7a +3; 9a² – 2a + 7; 4a² – 2a + 9

(6a² + 7a + 3) + (9a² – 2a + 7) + (4a² – 2a + 9)

= (6a² + 9a² + 4a²) + (7a – 2a – 2a) + (3 + 7 + 9)

= 19a² + 3a + 19

4. 2a²b + 5b²a + 7; 3a²b – 2b²a + 6; 8a²b – b²a + 9
Solution:

Given

2a²b + 5b²a + 7; 3a²b – 2b²a + 6; 8a²b – b²a + 9

(2a²b + 5b²a + 7) + (3a²b – 2b²a + 6) + (8a²b – b²a + 9)

= (2a²b + 3a²b + 8a²b) + (5b²a – 2b²a – b²a) + (7 + 6 + 9)

= 13a²b + 2b²a + 22

5. 4xy + 5x + 7y; – 4xy – y – 3x; 3xy – 3y + 2x
Solution :

Given

4xy + 5x + 7y; – 4xy – y – 3x; 3xy – 3y + 2x

(4xy + 5x 7y) + (- 4xy y – 3x) + (3xy – 3y + 2x)

= (4xy – 4xy + 3xy) + (5x – 3x + 2x) + (7y – y – 3y)

= 3xy + 4x + 3y

Question 4. Let’s subtract:

1. (2x + 3y) from (8x + 6y)
Solution :

Given

(2x + 3y) and (8x + 6y)

(8x +6y) – (2x + 3y)

= 8x – 2x + 6y – 3y

= 6x + 3y

2. (m² – 2) from (- 3m² + 2m + 2)
Solution :

Given

(m² – 2) and (- 3m² + 2m + 2)

(- 3m² + 2m + 2) – (m² – 2)

= – 3m² – m² + 2m + 2 + 2

= – 4m² + 2m + 4

3. (8x + 4y + 7) from (2x + 3y)
Solution :

Given

(8x + 4y + 7) and (2x + 3y)

(2x + 3y) – (8x + 4y + 7)

= 2x – 8x + 3y – 4y – 7

= – 6x – y – 7

4.  (5a² + 2a – 1 ) from (- 9a² + 3a + 2)
Solution:

Given

(5a² + 2a – 1 ) and (- 9a² + 3a + 2)

(- 9a² + 3a + 2) – (5a² + 2a – 1 )

= -9a²-5a²+ 3a-2a + 2 + 1 .

= – 14a² + a + 3

5. (- 2x² + 3y² ) from x
Solution :

Given

(- 2x² + 3y² ) and x

x – (- 2x² + 3y²) = x + 2x² – 3y²

6. (2x² + xy + 3y²) from (3x² + 5xy)
Solution :

Given

(2x² + xy + 3y²) and (3x² + 5xy)

(3x² + 5xy) – (2x² + xy + 3y²)

= 3x² + 5xy – 2x² – xy – 3y²

= 3x² – 2x² + 5xy – xy – 3y²

= x² + 4xy – 3y²

Question 5. Let us Simplify the following :

1. 17x²y – 3xy² + 14x² y + 2xy²
Solution:

17x²y – 3xy² + 14x²y + 2xy²= 17x²y + 1 4 x²y – 3xy² + 2x²y

= 31x²y-xy²

2. – 5b + 18a + 6b – 2a
Solution :

– 5b + 1 8a + 6b – 2a = 1 8a – 2a + 6b – 5b

= 16a+b

3. 4m² + 3n² – (6m² + 7n²)
Solution :

4m² + 3n² – (6m² + 7n²)- 4m² – 6m² + 3n² – 7n²

= – 2m² – 4n²

4. a-b-(b-a)
Solution :

a – b – (b – a) = a – b – b + a

= a + a – b – b

= 2a – 2b

5.  (6p – 4q + 2r) + (2p + 3q – 4r)
Solution :

(6p – 4q + 2r) + (2p + 3q – 4r) = 6p + 2p – 4q + 3q + 2r – 4r

= 8p-q -2r

6.  – x + y + z – (2x – 3y + z)
Solution :

– x + y + z – (2x – 3y + z) = – x + y + z – 2x + 3y – z

= – x -2x + y + 3y + z – x

= – 3x + 4y (Ans )

7.  (x² + 2x – 5) + (3x² – 8x + 5)
Solution :

(x² + 2.x – 5) + (3×2 – 8x + 5) = x² + 2x – 5 + 3x² – 8x + 5

= x² + 3x² + 2x – 8x – 5 + 5

= 4x² – 6x

8. (7x² – 3x + 3) – (2x² – 13x – 7)
Solution :

(7x² – 3x + 3) – (2x² – 13x – 7) = 7x² – 3x + 3 – 2x² + 13x + 7

= 7x² – 2x² – 3x + 13x + 3 + 7

= 5x² + 1 0x + 1 0

9.  6a – 2a – ab – (3a + b – ab) + 2ab – b + a
Solution:

6a – 2a – ab – (3a + b – ab) + 2ab – b + a

= 6a – 2b – ab – 3a – b + ab + 2ab – b + a

= 6a – 3a + a – 2b – b – b – ab + ab + 2ab

= 4a – 4b + 2ab

Question 6. Ramu had Rs. (13x² + x – 3). He $pent Rs. (4x² – 3x – 12). Let’s find, how much money Ramu has got.
Solution :

Given

Ramu had Rs. (13x² + x – 3). He $pent Rs. (4x² – 3x – 12).

Ramu had =  Rs. 13x² + x – 3

He spent = Rs. 4x² – 3x -12

Remaining amount = Rs. (13x² + x – 3 – 4x² + 3x +12)

=   Rs. 9x² + 4x + 9

∴ Ramu has got Rs. 9x² + 4x + 9

Question 7. The lenght of three sides of a triangle are (x + 4) cm, (2x + 1) cm, and (4x – 8) cm, Let’s find the perimeter of the triangle.
Solution:

Given

The lenght of three sides of a triangle are (x + 4) cm, (2x + 1) cm, and (4x – 8) cm,

The perimeter of the triangle = Sum of the three side of the triangle.

= x + 4 + 2x + 1 +4x-8

= x + 2x + 4x + 4 + 1 – 8

= x + 2x + 4x + 5 – 8

= 7x – 3

Question 8. How much be added to – 8x² + 8x + 1 to get – 14x² + 11x – 3
Solution:

Required No. = (- 14x² + 1 1x – 3) – (- 8x² + 8x + 1)

= – 1 4x² + 11 x – 3 + 8x² – 8x – 1

= – 1 4x² + 8x² + 11 x – 8x – 3 – 1

= – 6x² + 3x – 4

Question 9. Let’s find, what must be subtracted from – 11 x – 7y – 9z to get – 7x +3y-5z.
Solution:

Required No. = (- 1 1x – 7y – 9z) -(- 7x + 3y – 5z)

= – 1 1 x – 7y – 9z + 7x – 3y + 5z

= – 1 1 x + 7x – 7y – 3y – 9z + 5z

= – 4x – 10y – 4z

Question 10. How much is the sum of (3x² + 4x) and (5x² – x) more than (3x – 5x²), let’s calculate.
Solution :

Required No. = (3x² + 4x) + (5x² – x) – (3x – 5x²)

= 3×2 + 4x + 5x² – x – 3x + 5x²

= 3x² + 5x² + 5x² + 4x – x – 3x

= 13x² + 4x – 4x

= 13x²

Question 11. Let’s subtract the sum (x² – 9x) and (- 2x² + 3x + 5) from the sum of (5 + 9x) and (6 – 7x + 4x²).
Solution : 

Required No. = {(5 + 9x) + (6 – 7x + 4x²)} – {(x² – 9x) + (- 2x² + 3x + 5)}

= (5 + 9x + 6 – 7x + 4x²) – (x² – 9x – 2x² + 3x + 5)

= (4x² + 9x – 7x + 5 + 6) – (x² – 9x – 2x² + 3x + 5)

= (4x² + 2x + 1 1 ) – (- x² – 6x + 5)

= 4x² + 2x + 1 1 + x² + 6x – 5

= 4x² + x² + 2x + 6x + 1 1 – 5

= 5x² + 8x + 6

WBBSE Class 7 Math Solution Algebraic Operations Exercise 6.8

Question 1. If x = 5 let’s find the values of the following algebraic expressions. When x = 5

1. 6x + 11
Solution:

6x+ 11 = 6 × 5 + 11 = 30 + 11 = 41.

2. \(\frac{x}{5}\) +2 
Solution:

⇒ \(\frac{x}{5}\)+2

= \(\frac{5}{5}\)+2

= 1+2 = 3

3. x² + 2x – 1
Solution :

x² + 2x – 1 = (5)²+ 2× 5-1

= 25 + 10-1

= 35- 1

= 34

4. x³> 8
Solution :

x³ + 8 = (5)³ + 8

= 125 + 8

= 133

5. 10 -x
Solution:

10 – x = 10 – 5

= 5

Question 2. If y= – 3, let’s find the values of the following algebraic expressions. \(\frac{y+5}{4}\)
Solution :

5-y = 5-(-3)

= 5 + 3

= 8

3. y + 8
Solution :

y + 8 = -3 + 8

= 5

4.  y² + 2y + 3
Solution :

y² + 2y + 3 = (- 3)² + 2 (- 3) + 3 =

9 – 6 + 3

= 12 – 6

= 6

5. y³ – 1
Solution :

= (-3)3 – 1

= – 27 – 1

= -28

Question 3. Let’s find the values of the following, when x = 2, y = – 1

1. 2x + 7y
Solution :

2x + 7y = 2 (2) + 7 (- 1)

= 4-7

= – 3

2. x² + y²
Solution:

x² + y²= (2)² + (- 1)²

= 4 + 1

= 5

3. x² + 7xy + y²
Solution :

x² + 7xy + y²= (2)² + 7. 2 (- 1) + (- 1)²

= 4 – 14 +1

= – 14 + 5

= – 9

4. x³ – 8y³
Solution:

x³ – 8y³ = (2)³ – 8(- 1)³ = 8 – 8 (- 1)

= 8 + 8

= 16

5. \(\frac{x}{9}+\frac{y}{4}\)
Solution:

⇒ \(\frac{x}{9}+\frac{y}{4}\)

= \(\frac{2}{9}+\frac{-1}{4}\)

= \(\frac{8-9}{36}\)

= \(\frac{1}{36}\)

WBBSE Class 7 Math Solution Algebraic Operations Exercise 6.9

Question 1. Let’s find the product of the following.

1. 7,2x
Solution:

7,2x = 7 × 2x = 14x (Ans.)

2. – 3x, 4x
Solution:

– 3x, 4x = (- 3x) × (4x)

= – 12 x²

3. – 2x, – 3x²
Solution:

– 2x, – 3x²= (- 2x) × (- 3x²)

= 6x³

4. 7x, 0
Solution :

7x, 0 = 7x  × 0 = 0

5. 3ab, 4ac
Solution :

3ab, 4ac= (3ab) × (4ac)

= 12a²bc (Ans.)

6. 8x², 2y²
Solution:

8x², 2y² = (8x²) × (2y²)

= 16x²y²

7. 2a²b, 3ab²
Solution :

2a²b, 3ab² = 2a²b × 3ab²

= 6a³b³

8.  (- 4xy), (- 4xy)
Solution:

(- 4xy), (- 4xy)  = (- 4xy) × (- 4xy) = 16x²y²

Question 2. Let’s muliply first monomial with second monomial and write the product in corresponding blanks spaces.
Solution :

Algebraic Operations Exercise 6.10

Question 1. In each of the following cases, let’s multiply and find their product.

1.  ab, (a² – b²)
Solution:

ab, (a² – b²) = ab x (a² – b²)

= ab³ – ab³

2. 4a, (a + b – c)
Solution :

4a, (a + b – c)= 4a × (a + b – c)

= 4a² + 4ab – 4ac

3. 6a²b², (2a + b)
Solution :

6a²b², (2a + b) = 6a²b² × (2a + b)

= 12a³b² + 6a²b³ (Ans.)

4. xyz, (x²y – y²x + z²y)
Solution :

xyz, (x²y – y²x + z²y) = xyz x (x²y – y²x + z²y)

= x³y²z – x²y³z + xy²z³

5. 0, (ab + bc – ca)
Solution :

0, (ab + bc – ca) = 0 x (ab + be + ca)

= 0

Question 2. Let’s simplify

1.  7x (2x + 3) – 5x (3x – 4)
Solution :

7x (2x + 3) – 5x (3x – 4) = 7x (2x + 3) – 5x (3x – 4)

= (14x² + 21 x) – (1 5x² – 20x)

= 1 4x² + 21 x – 1 5x² + 20xy

= 14x² – 15x² + 21 x + 20x

= – x² + 41x

2. x(x – y) + y (y – z) + z (z – x)
Solution :

x(x – y) + y (y – z) + z (z – x) = x² – xy +y² – yz + z² – zx

= x² + y² + z² – xy – yz – zx

3. 2x – 6x (5 – 8x – 3y)
Solution :

2x – 6x (5 – 8x – 3y) = 2x – 30x + 48x² + 18xy

= 48x² + 18xy – 28x

4. 7a – 2 (5a + 6b – 7)
Solution:

7a – 2 (5a + 6b – 7) = 7a – 10a – 12b + 14

= 14 -7a -12b.

WBBSE Class 7 Math Solution Algebraic Operations Exercise 6.11

Question 1. Let’s multiply :

1.  (10 – 3x) (7 + x)
Solution :

(10 – 3x) (7 + x) = 10 (7 + x) – 3x (7 + x)

= 70 + 10x – 21x – 3x²

= – 3x² – 1 1x + 70

2. (11 +2x) (8 – 2y)
Solution :

(11 + 2x) (8 – 2y) = (11+ 2x) × (8 – 2y)

= 11 (8 – 2y) + 2x (8 – 2y)

= 88 – 22y + 1 6x – 4xy

3. (a + by) (4a – 6y)
Solution :

(a + by) (4a – 6y) = (a + by) × (4a – 6y)

= a (4a – 6y) + by (4a – 6y)

= 4a² – 6ay + 4aby – 6by²

4. (2x² y – y² ) (3x-5y)
Solution :

(2x² y – y² ) (3x – 5y) = (2x² y – y² ) × (3 -5y)

= 2x² y (3x – 5y) – y² (3x – 5y)

= 6x³ y – 1 0x² y² – 3xy² + by³

5. \(\left(\frac{x}{2}-\frac{y}{3}\right)\left(\frac{2 x}{3}-\frac{3 y}{5}\right)\)
Solution:

⇒  \(\left(\frac{x}{2}-\frac{y}{3}\right)\left(\frac{2 x}{3}-\frac{3 y}{5}\right)=\left(\frac{x}{2}-\frac{y}{3}\right) \times\left(\frac{2 x}{3}-\frac{3 y}{5}\right)\)

= \(\frac{x}{2}\left(\frac{2 x}{3}-\frac{3 y}{5}\right)-\frac{y}{3}\left(\frac{2 x}{3}-\frac{3 y}{5}\right)\)

= \(\frac{x^2}{3}-\frac{3 x y}{10}-\frac{2 x y}{9}+\frac{y^2}{5}\)

= \(\frac{x^3}{3}-\frac{47 x y}{90}+\frac{y^2}{5}\)

6. \(\left(\frac{2 a^2}{7}-\frac{1}{5}\right)\left(\frac{3 a}{5}-\frac{2}{9}\right)\)
Solution:

⇒ \(\frac{2 a^2}{7}\left(\frac{3 a}{5}-\frac{2}{9}\right)-\frac{1}{5}\left(\frac{3 a}{5}-\frac{2}{9}\right)\)

=  \(\frac{6 a^3}{35}-\frac{4 a^2}{63}-\frac{3 a}{25}+\frac{2}{45}\)

Algebraic Operations Exercise 6.12

1. Let’s find values of the following mentally 

1. 3a × 4b 
Solution:

3a × 4b = 12ab

2. 12ab ÷ 3a 
Solution:

12ab ÷ 3a = 4b

3. 12ab ÷  3 
Solution:

12ab ÷  3 = 4ab or, 12ab ÷ 4ab = 3

4. (-x² ) × x 
Solution:

(-x² ) × x = – x³

5. 9x² – 3x² 
Solution:

9x² – 3x² = 3

6. x² × x² 
Solution:

x² × x² = x⁴

7. \(x^2 \times \frac{1}{x^2}\)
Solution:

\(x^2 \times \frac{1}{x^2}\)= 1

8.  0 ÷ ab = 0
Solution:

0 ÷ ab = 0

9. 4a²b²c² × 0
Solution:

4a²b²c² × 0 = 0

10. 3ab + 3b
Solution:

3ab + 3b = a or, = 3ab ÷ a = 3b.

11. x⁰ xy 
Solution:

x⁰ xy = 1 xy

= y

12. x÷ 0
Solution:

x÷ 0 =.undefined.

Question 2. Let’s multiply 

1. 2x² × (-3y) x 6z
Solution :

2x² × (-3y)× 6z = – 36x²yz

2. 7xy² × 8x²y × xy
Solution :

7xy² × 8x²y × xy= 56x⁴y⁴

3. (- 3a²) × (4a²b) × (-2)
Solution:

(- 3a²) × (4a²b) × (-2) = 24a⁴b

4. \((-2 m n) \times \frac{1}{6} m^2 n^2 \times 13 m^4 n^4\)
Solution: 

\((-2 m n) \times \frac{1}{6} m^2 n^2 \times 13 m^4 n^4\) = \((-2) \times \frac{1}{6} \times 13 m^{1+2+4} n^{1+2+4}\)

= \(\frac{13}{3} m^7 n^7\)

5. \(\frac{2}{3} x^2 y \times \frac{3}{5} x y^2\)
Solution: 

\(\frac{2}{3} x^2 y \times \frac{3}{5} x y^2\)

= \(\frac{2}{3} x \frac{3}{5} x^{2-1} y^{1+2}\)

= \(\frac{2}{5} x^3 y^3\)

6. \(\left(-\frac{18}{5} x^2 z\right) \times\left(-\frac{25}{6} x z^2 y\right)\)
Solution:

⇒ \(\left(-\frac{18}{5} x^2 z\right) \times\left(-\frac{25}{6} x z^2 y\right)\)

= \(\frac{18}{5} \times \frac{25}{6} x^{2+1} z^{1+2} y\)

= 15 x³z³y

7. \(\left(-\frac{3}{5} \mathrm{~s}^2 \mathrm{t}\right) \times\left(\frac{15}{7} \mathrm{st}^2 \mathrm{u}\right) \times\left(\frac{7}{9} \mathrm{su}^2\right)\)

⇒ \(\left(-\frac{3}{5} \mathrm{~s}^2 \mathrm{t}\right) \times\left(\frac{15}{7} \mathrm{st}^2 \mathrm{u}\right) \times\left(\frac{7}{9} \mathrm{su}^2\right)\)

= \(-\frac{3}{5} \times \frac{15}{7} \times \frac{7}{9} s^{2+1+1} t^{1+2} u^{1+2}\)

= – s⁴t³u³

8. \(\left(\frac{4}{3} x^2 y z\right) \times\left(\frac{1}{3} y^2 z x\right) \times\left(-6 x y z^2\right)\)
Solution:

⇒ \(\left(\frac{4}{3} x^2 y z\right) \times\left(\frac{1}{3} y^2 z x\right) \times\left(-6 x y z^2\right)\)

=  \(-\frac{4}{3} \times \frac{1}{3} \times 6 x^{2+1+1} y^{1+2+1} z^{1+1+2}\)

= – \(\frac{8}{3} x^4 y^4 z^4\)

9. 4a (3a + 7b)
Solution :

4a (3a + 7b) = 12a² + 28ab

10. 8a² × (2a + 5b)
Solution :

8a² × (2a + 5b)= 8a² × 2a+ 8a² x 5b

= 16 a³ + 40 a²b

11. – 1 7 x² × (3x – 4)
Solution :

– 1 7 x² × (3x – 4) = – 17x² × 3x – 17 x² (-4)

= – 51x³ + 68x²

12. \(\frac{2}{3} a b c\left(a^2+b^2-3 c^2\right)\)
Solution:

⇒ \(\frac{2}{3} a b c\left(a^2+b^2-3 c^2\right)\)

= \(\frac{2}{3} a b c \times a^2+\frac{2}{3} a b c \times b^2+\frac{2}{3} a b c\left(-3 c^2\right)\)

= \(\frac{2}{3} a^3 b c+\frac{2}{3} a b^3 c-2 a b c^3\)

13.  2 × 5x (10x²y – 100xy²)
Solution :

2 × 5x (10x²y – 100xy²) = 10x x (10x2y – 100xy2)

= 100x³y – 1000x²y²

14. (2x + 3y) (5x-y)
Solution :

(2x + 3y) (5x-y) = 2x (& – y) + 3y (5x – y)

= 10x²– 2xy + 15xy – 3y²

= 10 x² + 13xy – 3y²

15. (a² – b²) (2b – 6a)
Solution :

(a² – b²) (2b – 6a) = a² (2b²– 6a) – b² (2b – 6a)

= 2a²b – 6a³ – 2b³ + 6ab²

16. (x + 2.) (3x + 1 )
Solution :

(x + 2.) (3x + 1 ) = x (3x + 1 ) + 2 (3x + 1 )

= 3x² + x + 6x + 2

= 3x² + 7x + 2

Question 3.

1. Seema planted 3x saplings in a row, In 2x such rows let’s find how many saplings Seema can plant.
Solution :

In each row, Seema planted 3x saplings

∴ In 2x rows she will plant = 3x × 2x = 6x² saplings

2. The length of a rectangle is (4x + 1 ) m and its breadth is 3zm. Let’s calculate the area of the rectangle.
Solution :

Length & Breadth of the rectangle are (4x + 1 ) m & 3x m

∴ Area of the rectangle = (4x + 1) ×  3x sqm

= (12x²+3x) sqm.

3. Presently, the price of a dozen of bananas has increased by Rs. 6. If the previous price of a dozen of bananas was Rs. x, let’s find the cost of 2x dozen of bananas.
Solution :

Previously the price of one dozen banana was Rs. x.

Present price of one dozen banana is Rs. (x + 6)

Price of 2x dozen banana is Rs. (x + 6) × 2x

= Rs. (2x² + 12x).

4. Let’s find the area of a square whose each sode is 7x cm.
Solution :

Area of a square whose each side is 7x cm.

=  7x × 7x sqcm

= 49x² sqcm

5. The area of a rectangle is 8x² sq units. If its length is 4x units, let’s find its breadth.
Solution:

The area of rectangle = 8x² sq unit

And  its length = 4x unit

The breadth of the rectangle = (8x² ÷ 4x) unit

= 2x unit

6. Sushobhan sold 729y4 number of kites in 9y days. Let’s find the number of kites sold in average per day.
Solution:

Susobhan sold in 9y day 729 y⁴ kites

∴ He sold in 1 day = \(\frac{729 y^4}{9 y}\)  kites

= 81 y³ kites

4. Let’s divide the first algebraic expression by the second algebraic expression in the following pairs of algebraic numbers 

1. 8x³b, x²b
Solution :

= 8x³b ÷  x²b

= \(\frac{8 x^3 b}{x^2 b}\)

= 8x

2. 9xy³, xy
Solution:

9xy³, xy = – 9xy³ xy

= \(\frac{-9 x y^3}{x y}\)

= -9y²

3. -15xYz²,-x²yz²
Solution :

-15xyz²,-x²yz²= (- 1 5x²y⁴z²) -4- (- x²yz²)

= \(\frac{-15 x^2 y^4 z^2}{-x^2 y z^2}=15 y^3\)

4. 21 l³m³n³, – 4l⁴mn
Solution:

21 l³m³n³, – 4l⁴mn = (21 l³m³n³) ÷ (4l⁴mn)

= \(\frac{\left.21\right|^3 m^3 n^3}{-\left.4\right|^4 m n}\)

= \(-\frac{21}{4l} m^2 n^2\)

2. (5a² – 7ab²), a
Solution : = (5a² – 7ab²) ÷ a

= \(\frac{5 a^2}{a}-\frac{7 a b^2}{a}\)

= \(5 a-7 b^2\)

6. (- 48x⁹ + 12x⁶), 3x³
Solution :

(- 48x⁹ + 12x⁶), 3x³ = (- 48x⁹ + 1 2x⁶) ÷3x³

= \(\frac{-48 x^9}{3 x^3}+\frac{12 x^6}{3 x^3}\)

= – 16 x⁶ + 4x³

7. 15m²n + 20m²n², 5mn
Solution:

15m²n + 20m²n², 5mn = (15m²n + 20m²n²) ÷ (5mn)

= \(\frac{15 m^2 n}{5 m n}+\frac{20 m^2 n^2}{5 m n}\)

= 3m + 4mn

8. 36a⁵b² – 24a²b5, – 4a²b²
Solution:

36a⁵b² – 24a²b5, – 4a²b² = (36a⁵b² – 24a²b⁵) ÷ (-4a²b²)

= \(\frac{36 a^5 b^2}{-4 a^2 b^2}-\frac{24 a^2 b^5}{-4 a^2 b^2}\)

9. 3pqr + 6p²qr² – 9p³q²r³, – 3pqr
Solution :

3pqr + 6p²qr² – 9p³q²r³, – 3pqr = (3pqr + 6p²qr² – 9p³q²r³) ÷(- 3pqr)

= \(\frac{3 p q r}{-3 p q r}+\frac{6 p^2 q r^2}{-3 p q r}-\frac{9 p^3 q^2 r^3}{-3 p q r}\)

= – 1 – 2pr + 3²2qr²

10. m²n⁴ + m³n³ – m⁴n², – m⁴n⁴
Solution :

m²n⁴ + m³n³ – m⁴n², – m⁴n⁴ = (m²n⁴ + m³n³ – m⁴n²) ÷ (m⁴n⁴)

= \(\frac{m^2 n^4}{-m^4 n^4}+\frac{m^3 n^3}{-m^4 n^4}-\frac{m^4 n^4}{-m^4 n^4}\)

= \(-\frac{1}{m^2}-\frac{1}{m n}+\frac{1}{n^2}\)

5. Let us simplify the following –

1. a (b – c) + b (c – a) + c (a – b)
Solution :

a (b – c) + b (c – a) + c (a – b) a (b – c) + b (c – a) + c (a – b) = ab -ac +bc – ab + ac – bc

= 0

2. a (b – c) – b (c – a) – c (a – b)
Solution :

a (b – c) – b (c – a) – c (a – b) = ab – ac – bc + ab – ac + bc

= 2ab – 2ac .

3.  x (x + 4) + 2x (x – 3) – 3x²
Solution :

x (x + 4) + 2x (x – 3) – 3x² = x² + 4x + 2x² – 6x² – 3x

= x² – 2x – 3x² + 4x – 6x = – 2x

4. 3x² + x (x + 2) – 3x (2x + 1 )
Solution :

3x² + x (x + 2) – 3x (2x + 1 ) = 3x² + x² + 2x – 6x² – 3x

= 4x² – 6x² + 2x – 3x = – 2x² – x

5. (a + b) (a – b) + (b + c) (b – c) + (c + a) (c – a)
.Solution :

(a + b) (a – b) + (b + c) (b – c) + (c + a) (c a)

= a(a – b) + b(a – b) + b(b – c) + c(b – c) + c(c – a) + a (c – a)

= a² – ab + ab – b² + b² – bc + bc – c² + c² – ac + ac – a²

= 0

6. (a² + b²) (a² – b²) + (b² + c²) (b² – c²) + (c² + a²) (c² – a²)
Solution :

(a² + b²) (a² – b²) + (b² + c²) (b² – c²) + (c² + a²) (c² – a²)

= a² (a² – b²) + b² (a² – b²) + b² (b² – c²) + c² (b² – c²) + c² (c² – a²) + a² (c² – a²)

= a⁴ – a²b² + a²b² – b⁴ + b⁴ – b²c² + b²c² – c⁴ + c⁴ – a²c² + a²c² – a⁴

= 0

Class 7 Math Solution WBBSE Algebra Chapter 3 Concept Of Index Exercise 3 Solved Problems

Power or Index: The product obtained by multiplying a number several times by itself is called the power or Index of that number.

3 x 3 x 3 x 3 =3⁴ (Power or Index of 3 is 4)

a x a x a x a x a =a⁵ (Power or Index of a is 5)

Some important formulas on Index
[a is non zero integer and also m and n are integers]

1. a^m. aⁿ = a^{m + n}

2. a^m ÷ aⁿ = a^{m – n}

3. (a^m)ⁿ = a^mn

4. \(a^m=\frac{1}{a^{-m}}\)

5. a⁰ = 1

6. (ab)^m = a^m.bⁿ

7. \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

Wbbse Class 7 Maths Solutions

Question 1. Choose the correct answer 

Read and Learn More WBBSE Solutions for Class 7 Maths

1. If we express the number 35400000 in index of 10 we get

1. 354 x 10⁴
2. 354 x 10³
3. 354 x 10⁵
4. 354 x 10⁶

Solution: 35400000
= 354 x 100000
= 354 × 105

So the correct answer is 3. 354 x 10⁵

2. If we express the number 16489 in index form as power of 10 we get

1. 16.489 x 10²
2. 164.89 x 10²
3. 1.6489 x 10²
4. 1648.9 x 10²

Solution: 16489 = \(\frac{16489}{100}\) x 100

= 164.89 × 10²

So the correct answer is 2. 164.89 x 10²

3. The value of 7 x 10⁶ + 3 x 10⁴+ 4 x 10³ + 6 × 10² + 8 x 10 + 9 is

1. 734689
2. 7346089
3. 7340689
4. 7034689

Solution: 7 x 10⁶ + 3 x 10⁴+ 4 x 10³ + 6 × 10² + 8 x 10 + 9
= 7000000 + 30000 + 4000+ 600 + 80 +9
= 7034689

So the correct answer is 4. 7034689

Wbbse Class 7 Maths Solutions

Question 2. Write ‘true’ or ‘false’

1. The simplest form of (a⁷×a^-5)+(a^-3×a⁶) is \(\frac{1}{a}\)

Solution: (a⁷×a^-5)+(a^-3×a⁶)

= \(\frac{a^7 \times a^{-5}}{a^{-3} \times a^6}=\frac{a^{7-5}}{a^{-3+6}}=\frac{a^2}{a^3}=a^{2-3}=a^{-1}=\frac{1}{a}\)

So the statement is true.

2. (-5)⁴× (3)⁴= -50625

Solution: (-5)⁴× (3)⁴

= (-5) × (-5) × (-5) x (-5) × 3 × 3 × 3 × 3
= (+25) × (+25) x 81
= + 625 x 81
= 50625

So the statement is false.

3. The value of \(\frac{3 \times 7^2 \times 2^4}{21 \times 112}\) is 1

Solution: \(\frac{3 \times 7^2 \times 2^4}{21 \times 112}\)

= \(\frac{3 \times 7^2 \times 2^4}{3 \times 7 \times 2^4 \times 7}\)

= 3^1-1 x 7^2-1-1 x 2^4-4
= 3⁰ x 7⁰ x 2⁰
= 1 x 1 x 1
= 1

So the statement is true.

Question 3. Fill in the blanks

1. 20 x 18 x  = [2²×3×5]²

Solution: 20 x 18 x = 2⁴ x 3² x 5²

⇒ 2² × 5 ×3² x 2 x = 2⁴ x 3² x 5²

⇒ 2²⁺¹ x 5 x 3² x = 2⁴ x 3² x 5²

⇒   = \(\frac{2^4 \times 3^2 \times 5^2}{2^3 \times 5 \times 3^2}\)

=2^4-3 x 3^2-2 x 5^2-1
= 2¹x 3⁰ x 5¹

= 2 x 1 x 5
= 10

Wbbse Class 7 Maths Solutions

2. \(\left(x^2\right)^3 \times\left(y^{-3}\right)^2=\left(\frac{x}{y}\right)\)

Solution: \(\left(x^2\right)^3 \times\left(y^{-3}\right)^2\)

= x⁶ x y^-6

= \(\frac{x^6}{y^6}=\left(\frac{x}{y}\right)^6\)

So the answer is 6

3. 

Solution: (-7)² x 8²
= 49 x 8²
= 7² x 8²
= (7 x 8)²
= (56)²

⇔ (-7)² x 8²
= (-7 x 8)²= (-56)²

So the answer is 56 or -56.

Question 4. Express 49 x 49 x 49 x 49 as a power 7

Solution: 49 x 49 x 49 x 49
= 7 x 7 x 7 x 7 x 7 x 7 x 7 x 7
= 7⁸

Wbbse Class 7 Maths Solutions

Question 5. Express the following numbers in index form as the power of 10 (taking 1, 2, and 3 places of the decimal)

1. 4678
2. 526824

Solution: 1. 4678

= \(\frac{4678}{10}\) x 10 =467.8 x 10

4678 = \(\frac{4678}{100}\) x 100 = 46.78 x 10²

4678 = \(\frac{4678}{1000}\) x 1000 = 4.678 x 10³

2. 526824

526824 = \(\frac{526824}{10}\) x 10 = 52682.4 x 10

526824 = \(\frac{526824}{100}\) x 100 = 5268.24 x 10²

526824= \(\frac{526824}{1000}\)  x 1000 = 526.824 x 10³

Question 6. Form the numbers from their expanded form

1. 9 x 10⁴ + 3 x 10² + 7
2. 3 x 10⁷ + 4 x 10⁶ + 2 x 10⁴ +7 x 10² + 5

Solution:

1. 1. 9 x 10⁴ + 3 x 10² + 7

= 90000 + 300 + 7
= 90307

2. 3 x 10⁷ + 4 x 10⁶ + 2 x 10⁴ +7 x 10² + 5

= 30000000+4000000+ 20000 + 700 + 5
= 34020705

Question 7. Simplify and express each of them in powder form

1. \(\frac{10^3 \times 10^4}{2^5 \times 5^4}\)

2. \(\frac{4^8 \times a^{10} b^4}{4^3 \times a^4 b^2}\) [ a ≠ 0, b ≠ 0]

Solution:

1. \(\frac{10^3 \times 10^4}{2^5 \times 5^4}\)

= \(\frac{(2 \times 5)^3 \times(2 \times 5)^4}{2^5 \times 5^4}\)

= 2^3+4-5 x 5^3+4-4

= 2²x5³
= 4 × 125
= 500

2. \(\frac{4^8 \times a^{10} b^4}{4^3 \times a^4 b^2}\)

=4^8-3 x a^10-4 x b^4-2

= 4⁵ x a⁶ x b²

Question 8. So that \(a^m=\frac{1}{a^{-m}}\)

Solution: a^m = a^0-(-m)

= \(\frac{a^0}{a^{-m}}=\frac{1}{a^{-m}}\)

 

Class 7 Math Solution WBBSE Concept Of Index

Concept Of Index Exercise 5.1

Let’s expand the following in the index of 

Question 1. 8275
Solution:

8275 = 8 × 10³ + 2 × 10² +7 ×10 + 5

Question 2. 90925
Solution:

90925 = 9 × 10⁴ + 0 ×10³+9 ×10² +2 ×10 + 5

Question 3. 12578
Solution:

12578 = 1 × 10⁴ +2 × 10³ + 5 × 10² +7 ×10 + 8

Question  4. 7858
Solution:

7858 = 7 ×  10³ + 8 × 10² + 5×10 + 8

Class Vii Math Solution WBBSE Concept Of Index Exercise 5.2

Question 1. 100 = 10 ^____
Solution:

100  = 10 × 10

= 10²

Question 2. 27 = 3^____
Solution:

27 = 3 × 3 × 3

= 3³

Question 3.125 = 5^____
Solution:

125 = 5 × 5 × 5

= 5³

Question 4. 32 = 2^___
Solution:

32 =  2 × 2 × 2 × 2 × 2

= 2⁵

Question 5. 343 = 7____
Solution:

343 =  7 × 7 × 7

= 7³

Question 6.121 = 11______
Solution:

121=11

121= 11 × 11

=11²

Question 7. 625 = 5______
Solution: =

625 = 5 × 5 × 5 × 5

= 5⁴

Question 8. 2³  = ^____× ^_____×
Solution:

2³  = ^____× ^_____× = 2 × 2 ×2

= 2³

Question 9. 3⁴ = ^_____ ×^_____ ×^_____ ×
Solution: =

3⁴ = ^_____ ×^_____ ×^_____ × = 3 × 3 × 3 × 3=

= 3⁴

= 81

Question 10. 729 = 9^_____
Solution:

729 =  9 × 9 × 9

= 9³

Question 11. 2 × 2× 2 × 2 × 2 = ^_____
Solution:

2 × 2× 2 × 2 × 2 = 2⁵

Question 12. (- 2) × (- 2) × (- 2) = (- 2)_________
Solution:

2 × 2× 2 × 2 × 2 = (-2)³

Question 13. (- 2) ×(- 2) × (- 2) × (- 2) = (- 2) ________________
Solution:

(- 2) ×(- 2) × (- 2) × (- 2) = (- 2)

= (-2)⁴

Class Vii Math Solution WBBSE Concept Of Index Exercise 5.3

Let’s express the following numbers in the product of power from of their prime factors.

Question 1. 24.
Solution:

24= 2 × 2 × 2 × 3 = 2³ × 3

Question 2. 56.
Solution:

56 = 2× 2 × 2 ×7 = 2³ ×7

Question 3. 63.
Solution:

63. = 3 × 3 × 7 = 3² × 7

Question 4. 72
Solution:

72 = 2 × 2 × 2× 3 ×3 = 2³ × 3²

Question 5. 200
Solution:

200 = 2  ×2 × 2× 5× 5 = 2³ × 5²

Class Vii Math Solution WBBSE Concept Of Index Exercise 5.4

Let’s put > or < signs in the respective blank squares

Question 1. 5³ ____________ 3⁵
Solution:

5³ = 5× 5× 5

= 125

3⁵ = 3×3 × 3× 3×3

= 243

∴ 5³ < 3⁵

Question 2. 6²______________2⁶
Solution:

6² = 6 ×6

= 36

2⁶ = 2 × 2 × 2 × 2 × 2 × 2

= 64

∴ 6² < 2⁶

Question 3. 2⁴________4²
Solution:

2⁴ = 2 × 2 × 2 × 2

= 16

4²= 4 × 4 = 16

∴ 2⁴= 4²

Question 4. 7²______2⁷
Solution:

7² = 7x 7

= 49

2⁷ = 2×2 × 2 × 2 × 2 × 2 ×2

= 128

∴ 7²< 2⁷

Question 5. 3⁴_________4³
Solution:

3⁴ = 3 × 3 × 3 × 3

= 81

4³ = 4 × 4 × 4 = 64

∴ 3⁴> 4³

Question 6. 3⁵_______5³
Solution: 

3⁵ = 3 × 3 × 3 × 3 × 3

= 243

5³=5 × 5 × 5

= 125

∴ 3⁵>5³

WB Class 7 Math Solution Concept Of Index Exercise 5.5

Question 1. 2⁵ × 2⁷
Solution:

2⁵ × 2⁷ = 2⁵⁺⁷

= 2¹²

Question 2. (-3)¹⁸× (-3)¹²
Solution:

(-3)¹⁸× (-3)¹²= (3)¹⁸⁺¹²

= (-30)³⁰

Question 3. 10⁸ x 10²
Solution:

10⁸ x 10² = (10)⁸⁺²

= (10)¹⁰

Question 4. 2¹⁵ ÷ 2¹³ 
Solution:

2¹⁵ ÷ 2¹³ 

= (2)^15-13

= 2²

Question 5. 9¹⁵-9¹⁴
Solution:

9¹⁵-9¹⁴ = 9^15-14

= 9

Question 6. 11⁶÷ 11⁴
Solution:

11⁶÷ 11⁴ = 11^6-4

= 11²

Concept Of Index Exercise 5.6

Let’s fill the blank squares given below:

Question 1. 9²÷ 9² = ________________
Solution: =

9²÷ 9² = 9^2-2

= 9⁰

= 1

Question 2. 7³_______0 = 1
Solution:

7³_______0 = 1

7³ ÷7³ = 1

= 7⁰

Question 3. 11⁰= ______________
Solution:

11⁰ = 1

Question 4. 1 =13__________
Solution:

1 =13___

∴ 1= 13⁰= 1

∴ 1-1 = 0

Question 5. 1 =(- 13) _______________
Solution:

1 =(- 13)

= (-13)⁰

WB Class 7 Math Solution Concept Of Index Exercise – 5.7

Question 1. 6⁵÷2⁵ = ________________
Solution:

6⁵÷2⁵

= \(\frac{6^5}{2^5}\)

= \(\left(\frac{6}{2}\right)^5\)

= (3)⁵

Question 2. _____ =  7² ÷ 2²
Solution: 

= \(\frac{7^2}{2^2}\)

= \(\left(\frac{7}{2}\right)^5\)

Question 3. 10² = ______ × ________ 
Solution:

10² = 10 × 10

Question 4. (4)²  × 6² = ________²
Solution:

(4)²  × 6²

(-4² × 6²)  = (-24)²

Question 5. (5)⁰ = ______________
Solution:

(5)⁰ =  1

6.  \(\left(\frac{2}{3}\right)^3\)
Solution:

⇒ \(\left(\frac{2}{3}\right)^3\)

= \(\frac{2^3}{3^3}=\frac{8}{27}\)

Concept Of Index Exercise – 5.8

Question 1. Let us express 8 × 8 × 8 as power of 2.
Solution :

Given

8 × 8 × 8

= 2³ × 2³ × 2³⁺³⁺³

= (2)⁹

Question 2. 25 × 25 × 25 × 25 to be expessed as power of 5.
Solution :

Given

25 × 25 × 25 × 25

= 5² × 5² × 5²× 5²

= (5)^2+2+2+2

= (5)⁸

Question 3. Let’s express 36 × 36 × 36 as the power of 6.
Solution :

Given

36 × 36 ×  36

= (6)² × (6)² × (6)²

= (6)^{2+2 +2}  = 6⁶

Question 4. Let’s express 81 x 81 as power of 3.
Solution :

Given

81 x 81

= 3⁴ × 3⁴ = (3)⁴⁺⁴

= 3⁸

Question 5. Let us find the values of the following

1. \(\frac{2^6 \times 3^5}{(6)^5}\)
Solution:

Given

⇒ \(\frac{2^6 \times 3^5}{(6)^5}\)

= \(\frac{2^6 \times 3^5}{(2 \times 3)^5}\)

= \(\frac{2^6 \times 3^5}{2^5 \times 3^5}\)

= 2¹

= 2

2. \(\frac{10^3 \times 10^4}{2^5 \times 5^4}\)
Solution:

Given

⇒ \(\frac{10^3 \times 10^4}{2^5 \times 5^4}\)

= \(\frac{(2 \times 5)^3 \times(2 \times 5)^4}{2^5 \times 5^4}=\frac{2^3 \times 5^3 \times 2^4 \times 5^4}{2^5 \times 5^4}\)

= \(\frac{(2)^3 \times(2)^4 \times 5^3}{2^5}=2^{3+4-5} \times 5^3\)

2² × 5³ = 4 × 125

= 500

3. \(\frac{5^9 \times 5^6}{5^7}\)
Solution:

Given

⇒ \(\frac{5^9 \times 5^6}{5^7}\)

= \(5^{9+6-7}\)

= 5⁸

4. \(\frac{6^4 \times 3^8}{3^{12}}\)
Solution:

Given

⇒ \(\frac{6^4 \times 3^8}{3^{12}}\)

= \(\frac{(3 \times 2)^4 \times 3^8}{3^{12}}\)

= \(\frac{(3)^{4+8} \times 2^4}{3^{12}}\)

= 2 × 2 × 2 × 2

= 16

5. \(\frac{25^2 \times 25^5}{5^{10}}\)

Given

⇒ \(\frac{25^2 \times 25^5}{5^{10}}\)

= \(\frac{\left(5^2\right)^2 \times\left(5^2\right)^5}{5^{10}}\)

= \(\frac{5^4 \times 5^{10}}{5^{10}}\)

= 5⁴

5 × 5 × 5 × 5 = 625

6. \(\frac{2^3 \times 3^9}{3^6 \times 6^3}\)

Given

⇒ \(\frac{2^3 \times 3^9}{3^6 \times 6^3}\)

⇒  \(\frac{2^3 \times 3^9}{3^6 \times(2 \times 3)^3}\)

= \(\frac{2^3 \times 3^9}{3^6 \times 2^3 \times 3^3}\)

=\(\frac{3^9}{3^9}\)=1

7. \(\left(\frac{a^7}{a^5}\right) \times \begin{gathered}
a^2 \\
(a \neq 0)
\end{gathered}\)
Solution:

⇒ \(\left(\frac{a^7}{a^5}\right) \times \begin{gathered}
a^2 \\
(a \neq 0)
\end{gathered}\)

= \(\left(\frac{a^7}{a^5}\right) \times a^2\)

= \(\left(a^{7-5}\right) \times a^2\)

a² × a² = a⁴

8.\(\frac{3 \times 7^2 \times 2^4}{21 \times 112}\)
Solution:

Given

⇒ \(\frac{3 \times 7^2 \times 2^4}{21 \times 112}\)

= \(\frac{3 \times 2^4 \times 7^2}{3 \times 7 \times 7 \times 16}\)

= \(\frac{7^2 \times 2^4}{7^2 \times 2^4}\)

= 1

WB Class 7 Math Solution Concept Of Index Exercise 5.9

Question 1. Let’s express the distances given below in index of 10 and try to get a better idea of the distances Distance of Mercury from Sun is 57900000 km. Distances of Mars and Jupiter from Sun are 227900000 km. and 778300000 km respectively.
Solution :

Given

1. Distance of Mercury from Sun = 57900000 km.

= 579 × 10⁵ km.

2. Distance of Mars from Sun = 227900000 km

= 2279 ×10⁵ km.

3. Distance of Jupiter from Sun = 778300000 km.

= 7783 × 10⁵ km.

Question 2. Let’s fill in the gaps –

1. The distance between Earth and the Moon is 384,000,000 m. = 384 x____________ m.
Solution :

Distance between Earth and Moon

384,000,000 m = 384 x 10 ⁶

∴  10⁶

2. The speed of light in a vacuum is 3,00,000,000 m/sec. = 3 x_m/sec.
Solution:

The speed of light in a vacuum

= 3,00,000,000 m/sec. = 3 ×10⁸ m/sec

∴  10⁸

3. Let’s express the following number in index form as power of 10 (taking 1,2 and 3 places of decimal)

1. 978 =
Solution:

= 97. 8 × 10

= 9. 78 × 10²

= 0.978  × 10³

2. 1592170 =
Solution:

= 159217 × 10

= 15921 .7 × 10²

= 1592 .17 × 10²³

Question 4. Let’s form the numbers from their expanded form given below –

1. 3 ×10³ +2 ×10² +7 × 10+ 2
Solution:

3 ×10³ +2 ×10² +7 × 10+ 2 = 3000 + 200 + 70 + 2

= 3272

2. 2  × 10³+3 ×10+ 5
Solution:

2  × 10³+3 ×10+ 5 = 2000 + 30 + 5

= 2035

3. 8 ×10⁴ + 2 × 10³ + 3 × 10² + 6
Solution:

8 ×10⁴ + 2 × 10³ + 3 × 10² + 6

= 80000 + 2000 + 300 + 6

= 82306

4. 9 ×10⁴ +5 ×10³ +6 × 10² + 6 ×10
Solution:

9 ×10⁴ +5 ×10³ +6 × 10² + 6 ×10

= 90000 + 5000 + 600 + 70

= 95670

Question 5. Let’s simplify and express each of them in powder form

1. \(\frac{2^3 \times 3^5 \times 16}{3 \times 32}\)
Solution:

= \(\frac{2^3 \times 3^5 \times 2^4}{3 \times 2^5}=\frac{2^{3+4} \times 3^5}{2^5 \times 3}\)

= \(2^{7-5} \times 3^{5-1}\)

= \(2^2 \times 3^4\)‘

= 2² × 9²

= (18)²

= 18²

= 324

2. \(\left[\left(6^2\right)^3 \times 6^4\right] \div 6^7\)
Solution:

\(\left[\left(6^2\right)^3 \times 6^4\right] \div 6^7\) = 6⁶ × 6⁴÷ 6⁷

= 6^6+4-7

= 6³

3. \(\frac{3 \times \cdot 7^2 \times 11^0}{21 \times 7}\)
Solution:

⇒ \(\frac{3 \times 7^2 \times 1}{3 \times 7 \times 7}\)

= \(\frac{7^2}{7^2}\)

= 1

4. \(\left(3^0+2^0\right) \times 5^0\)
Solution:

(1+1) ×1

= 2 ×1 = 2

5. \(\frac{4^5 \times a^8 b^3}{4^5 \times a^5 b^2}(b \neq 0)\)
Solution:

6. \(\frac{2^8 x^7}{\left(2^2\right)^3 \times x^3}=\frac{2^8 \times x^7}{2^6 \times x^3}\)

⇒ \(\frac{2^8 x^7}{\left(2^2\right)^3 \times x^3}=\frac{2^8 \times x^7}{2^6 \times x^3}\)

= \(2^{8-6} \times x^{7-3}=2^2 \times x^4\)

= \((2)^2 \times\left(x^2\right)^2=\left(2 x^2\right)^2\)

 

WB Class 7 Math Solution Algebra Chapter 2 Addition Subtraction Multiplication And Division Of Integers Exercise 2 Solved Problems

Natural numbers: 1, 2, 3, 4, 5, …… are counting numbers or natural numbers such that 1 is the first natural number and there is no last natural number.

The natural numbers is denoted by N and is written as N = (1, 2, 3, 4, )

Whole numbers: The numbers 0, 1, 2, 3, . . . . . . . are called whole numbers.

The whole numbers is denoted by w and is written as w= (0, 1, 2, 3. . . . . .

Integers: The numbers……., -4, -3, -2, -1, 0, 1, 2, 3 ……. are called integers. The integers is denoted by z and is written as z = (…, -3, -2, -1, 0, 1, 2, 3 …)

The integers greater than 0, i.e 1, 2, 3,…. are called positive Integers and the integers less than 0, i.e. -1, -2, -3, . . . . are called Negative Integers.

0 (zero) is an integer that is neither positive nor negative.

Read and Learn More WBBSE Solutions for Class 7 Maths

Addition:

Question 1. Add with the help of a number line

1. {(+3) + (-5)} + (-10)
2. {(+3) + {(-5)+(-10)}

Solution:
1. {(+3)+(-5)) + (-10)

Wbbse Class 7 Maths Solutions

 

 

{(+3)+(-5)}+(-10)=-12

2. (+3)+ {(-5)+(-10)}

 

 

(+3)+{(-5)+(-10)}=-12

From (1) and (2), we can write,

{(+3)+(-5)}+(-10)= (+3) + {(-5)+(-10)}

These integers follow the associative law of addition.

WB Class 7 Math Solution Subtraction

Question 1. Subtraction by using the number line

1. {(+4) (-7)}-(-6)
2. (+4) {(-7)-(-6)}

Solution:

1. {(+4) (-7)} – (-6)= {(+4) + (+7)} + (+6)

Wbbse Class 7 Maths Solutions

 

 

= {(+4) – (-7)} – (-6)} = +17

2. (+4) – {(-7) – (-6)}

= (+4) – {(-7) + (+6)}
= (+40 + {(+7) + (-6)}

 

 

So (+4) – {(-7)-(-6)} = +5

Hence from (1) and (2), we can write
{(+4) (-7)}-(-6) ≠(+4) – {(-7) – (-6)}

Wbbse Class 7 Maths Solutions

Thus subtracting on the number line we found that for the subtraction of integers, the law of association does not hold.

Multiplication

Question 1. Multiply with the help of a number line

1. (+3) × (+2)
2. (+3) × (-2)
3. (-3) × (-2)

Solution:
1. (+3) x (+2) = (+3)+(+3)

 

 

(+3) x (+2) = +6

(+2) x (+3) = (+2) + (+2)

Wbbse Class 7 Maths Solutions

 

 

(+2) × (+3)= +6

So (+3) x (+2) = (+2) x (+3)

Hence two integers follow the commutative law of multiplication.

2. (+3) x (-2) = (-2)+(-2)+(-2)

 

 

(+3) x (-2) = -6

3. (-3) x (-2) = {(-2)+(-2)+(-2)}

Wbbse Class 7 Maths Solutions

 

 

(-3) x (-2) = +6

 

WB Class 7 Math Solution Divide

Question 1.(-24) ÷ {(-2)+8}
2. (-24)÷ (-2)+(-24) ÷ 8

Solution:

Given

1. (-24) ÷ {(-2) + 8}
= (-24)÷ 6
=-4

(-24) ÷ {(-2) + 8} =-4

2. (-24)÷ (-2)+(-24) ÷ 8
= (+12) + (-3)
= +9

(-24)÷ (-2)+(-24) ÷ 8 = +9

So (-24) ÷  {(-2)+8) ≠ (-24)÷ (-2) + (-24) ÷ 8
Thus distributive law does not hold for the division of numbers (excluding zero).

Such important points: For a nonzero integers a, b, c

1. a + (b + c) = (a + b) + c [Associative law of addition ]

2. a x (b x c) = (a x b) x c [Associative law of multiplication]

3. a x (b+c) = a x b+a x c [Distributive law of multiplication]

4. a – (b – c) ≠ (a – b) -c

5. a ÷ (b + c) ≠ a ÷ b + a ÷ c

6. a+b=b+ a [Commutative law of addition]

7. a – b ≠ b – a

Wbbse Class 7 Maths Solutions

8. a x b = b x a [Commutative law of multiplication]

9. a ÷ b ≠ b ÷ a

Question 1. Choose the correct answer

1. The value of (-3)+(-4)+(+10) is

1. – 17
2. +3
3. – 10
4. +9

Solution:

Given

(-3)+(-4)+(+10)
= (-7) + (+10)
= +3

So the correct answer is 2. +3

2. The value of (-15) – {(+3) + (-7)} is

1. -11
2. -19
3. +11
4. +19

Solution:

Given

(-15) – {(+3) + (-7)}
= (-15) – (-4)
= -15 + 4
= -11

So the correct answer is 1. -11

3. The value of (-24) ÷ (+4) × (-3) is

1. +2
2. -2
3. +18
4. -18

Solution:

Given

(-24) ÷ (+4) x (-3)
= (-6) × (-3)
= +18

So the correct answer is 3. +18

Wbbse Class 7 Maths Solutions

Question 2. Write ‘true’ or ‘false’ 

1. The value of (-6) x (-5) x (-7) x (+3) is -630

Solution:

Given

(-6) × (-5) × (-7) × (+3)
= (+30) × (-21)
=-630

So the statement is true.

2. The value of (-4) ÷ (-2) x (+2) – (+4) is 0

Solution:

Given

(-4) ÷ (-2) x (+2) – (+4)
= (+2) x (+2) – (+4)
= (+4) – (+4)
= 0

So the statement is true.

3. The value of (-15)+(-5) of (+3) x (-4) is 4

Solution:

Given

(-15)÷(-5) of (+3) x (-4)
= (-15)÷(-15) x (-4)
= (+1) × (-4)
=-4

So the statement is false.

Question 3. Fill in the blanks 

Wbbse Class 7 Maths Solutions

1. The value of (-18) + +3=-6

Solution: (-18)÷ +3=-6

⇒ (-18)÷ =-6 -3

⇒ (-18) ÷ = -9

⇒

⇒ = \(\frac{-18}{-9}\) = +2

2. x (-1) + 9 = 0

Solution: × (-1) + 9 = 0

⇒ × (-1) = -9

⇒ = \(\frac{-9}{-1}\) = 9

3. (-11) x (-9) x (-5) × (-6) × (-3) =

Solution: (-11) x (-9)-x (-5) x (-6) x (-3)
= (+99) x (+30) x (-3)
= (+2970) × (-3)
= – 8910.

Question 4. Verify, if the distributive law of multiplication holds for integers in the following cases.

1. (-3) x (8+ 4)
2. (-4) x {(-6) + (+3)}

Solution:

1. (-3) x (8 + 4)
= (-3) x (12)
=-36

(-3) x (8 + 4)
= (-3) x (8) + (-3) x (4)
= (-24) + (-12)
-36

∴ (-3) x (8+4)=(-3) x (8) + (-3) x (4)

2. (-4) x {(-6) + (+3)}
=(-4) (-3)
= + 12

(-4) x (-6) + (-4) x (+3)
= (+24) + (-12)
= + 12

∴ (-4) × {(-6) + (+3)} = (-4) x (-6) + (-4) x (+3)

Question 5. Divide

1. (-275) ÷ (-25)
2. (-150)÷(+15)

Solution:
1. (-275) ÷ (-25)= +11
2. (-150)÷(+15)=-10

 

WB Class 7 Math Solution Addition Subtraction Multiplication And Division Of Integers

Addition Subtraction Multiplication And Division Of Integers Exercise 4.1

Question 1. From the number line, let us write the predecessor (just before) and successor(just after) of the integers given below:

Solution:

• For the addition of 2 positive integers on the number line, from the position of the first integer one has to move further right.
• For the addition of 2 negative integers on a number line, from the position of the first integer one has to move further left.
• For subtraction of 2 positive integers on a number line, from the position of the first integer one has to move to the left.
• For subtraction of 2 negative integers on a number line, from the position of the first integer one has to move to the left.

Question 2. Let us complete the table given below:
Solution:

Question 3. Let’s fill up the chart below, with the steps followed by chhotu along the stairs.
Solution:

Question 4. Let us complete the chart below for Manai going up or down along the numbered steps of the stair
Solution:

Addition Subtraction Multiplication And Division Of Integers Exercise 4.2

Question 1. Let us match the two sides verifying the laws :
Solution:

(1) — (2) : (2)- (3) – (4)– (5)- (1)

Question 2. Let us write a negative integer which is the sum of two negative integers.
Solution:

(- 7) = (- 5) + (- 2)

Question 3. Let us write a negative integer which is the difference of two positive integers.
Solution:

(-15) = (+ 6) -(+21)

Question 4. Let us write such a negative integer which is the difference of two negative integers.
Solution:

(-12) = (- 32) – (- 20)

Class 7 Math Solution WBBSE Addition Subtraction Multiplication And Division Of Integers Exercise 4.3

Question 1. 6 x (-8)
Solution :

6 × (-8) = (- 8) + (- 8) + (- 8) + (- 8) + (- 8) + (- 8) = 48 = – (6 × 8)

Question 2. 7 × (-3)
Solution :

7 × (-3) = (- 3) + (- 3) + (- 3) + (- 3) + (- 3) + (- 3) + (- 3) = – 21

= -(7×3)

Question 3. 9 × (- 12)
Solution :

9 × (- 12) = (- 12) + (- 12) + (- 12) + (- 12) + (- 12) + (- 12) + (- 12) + (-12) + (-12)

= -108

= – (9 × 12)

Question 4. (- 4) x 3 
Solution :

(- 4) x 3 = 4 x (- 3)

= – 12

Question 5. 6 x (- 8)
Solution :

6 x (- 8) = 8 x (- 6) = – 48

Question 6. 7x(-3)
Solution:

7x(-3)= (- 7) x 3 = – 21

Class 7 Math Solution WBBSE Addition Subtraction Multiplication And Division Of Integers Exercise 4.4

Question 1. Let’s find the value of (- 5) × (- 2) starting from (- 5) × 2
Solution:

Given

(- 5) × 2 =-10

( -5) × 1 = 10-(-5) = -10 + 5 = – 5

(- 5) × 0 = -5-(-5) =-5 + 5 = 0

( 5) × (-1)= 0 – (-5) = 0 + 5 = 5

( 5) × (-2)= 5 – (-5) = 5 + 5 = 10

(- 5) × (-2)= 5 – (-5) = 5 + 5 = 10

Question 2. Let’s find the value of (- 7) × (- 3) starting from (- 7) × 3
Solution:

Given

(- 7) × 3 = – 21

(- 7) × 2= -21 -(-7)= – 1 4 – (- 7)= – 21 + 7= -14 =

(- 7) × 1 = – 1 4 – (- 7)= – 14 + 7= -7

(- 7) × 0 = – 7 – (- 7)= -7 + 7= 0

(- 7) × (- 1) = 0 – (- 7)= 0 + 7= 7

(- 7) × (- 2) = 7 – (- 7)= 7 + 7 = 14

(- 7) × 3 = 1 4 – (- 7)= 14 + 7 = 21

Question 3. Let s find the value of (- 6) × (- 4) starting from (- 6) × 2
Solution :

Given

(- 6) × 4 = – 24

(-6) × 3 = – 24 – (- 6)= – 24 + 6= – 18

(- 6) × 2 = -18 -(-6)= – 18 + 6= -12

(- 6) × 1 = -12-(- 6)= -12 + 6= – 6

(- 6) × 0 = (- 6) – (- 6)= – 6 + 6 = 0

(- 6) × (- 1 ) .= 0 – (- 6)= 0 + 6= 0= 6

(- 6) × (- 2)= 6 – (- 6)= 6 + 6= 12

We know if a and b are integers then (- a) × (- b) = ab.

4. (- 7)× (- 9) = 63

5.(- 2) × (- 33) = 66

6. 0 × (- 6) = 0

7.(- 12) × (- 3) = 36

8. (- 7) × 0 = 0

Addition Subtraction Multiplication And Division Of Integers Exercise 4.5

Question 1. Let’s complete the table given below:
Solution:

Question 2.  (- 7) × 7 + 12 x (- 8)
Solution:

(- 7) × 7 + 12 x (- 8) = – 49 – 96

= -145

(- 7) × 7 + 12 x (- 8) = -145

Question 3.(- 20) × 11 + (- 35) × 20
Solution:

(- 20) × 11 + (- 35) × 20 = – 220 – 700

= -920

(- 20) × 11 + (- 35) × 20 = -920

Question 4.(- 8) × 45 + (- 6) × 12
Solution:

(- 8) × 45 + (- 6) × 12 = -120 – 72

= -192

(- 8) × 45 + (- 6) × 12 = -192

Question 5. 4 × (- 4) + (- 5) × 5

Solution:

4 × (- 4) + (- 5) × 5 = – 1 6 – 25 =- 41

4 × (- 4) + (- 5) × 5  =- 41

Question 6.  (- 6) × (- 10) + (- 4) × 4
Solution:

(- 6) × (- 10) + (- 4) × 4 = + 60 – 16= 44

(- 6) × (- 10) + (- 4) × 4 = 44

Question 7. (- 9) × 3 + 7 x (- 4)
Solution:

(- 9) × 3 + 7 x (- 4) = – 27 – 28

= -55

(- 9) × 3 + 7 x (- 4) = -55

Addition Subtraction Multiplication And Division Of Integers Exercise 4.6

Question 1. (- 6) × (- 5) × (- 7) × (- 3) 
Solution:

(- 6) × (- 5) × (- 7) × (- 3) = 30 × (- 7) × (- 3) = -210 × (- 3) = 630.

(- 6) × (- 5) × (- 7) × (- 3) = 630.

Question 2. (- 5) × (- 2) × (- 10) x (- 8)  × (- 3) 
Solution:

(- 5) × (- 2) × (- 10) x (- 8)  × (- 3) = 10 x (- 10) × (- 8) x (- 3)

= 1 00 × (- 8) × (- 3) = 800 × (- 3) =-2400.

(- 5) × (- 2) × (- 10) x (- 8)  × (- 3) = -2400.

Question 3. (- 11) × (- 12) (- 2)
Solution:

(- 11) × (- 12) (- 2) = 1 32 × (- 2) = – 264.

(- 11) × (- 12) (- 2) = – 264.

Question  4. (- 11) × (- 9) × (- 5) × (- 6) × (- 3)
Solution:

(- 11) × (- 9) × (- 5) × (- 6) × (- 3) = 99 × (- 5) × (- 6) × (- 3)

= – 495 × (- 6) × (- 3) = 2970 × (- 3) = – 8910.

(- 11) × (- 9) × (- 5) × (- 6) × (- 3) = – 8910.

Question 5. Let’s complete the chart below and write our decision.
Solution:

Addition Subtraction Multiplication And Division Of Integers Exercise 4.7

Question 1. 9 × (8 + 3) ______ 19 × 8 + 9 × 3 [Let’s put = / ≠]
Solution :

9 × (8 + 3) = 9 × 8 + 9 x 3

Question 2. 6 × (5 +4)______ 6 × 5 + 6 × 4 [Let’s put = / ≠]
Solution:

6 × (5 + 4) = 6 × 5 + 6 × 4

Class 7 Math Solution WBBSE Addition Subtraction Multiplication And Division Of Integers Exercise 4.8

Question 1. Mizanoor, Tirtha and Nafura appeared for an examination, there were 1 0 Questions in the examination. In this examination, one will get 5 marks for each correct answer and – 2 marks for each incorrect answer.

1. Mizanoor has got 6 correct and the rest 4 incorrect answers.
Solution :

Mizanoor obtained = 6×5 + 4 ×(-2)

= 30 – 8 – 22 marks.

2. Tirtha has got 5 correct and the remaining 5 incorrect answers.
Solution:

Tirtha obtained = 5 × 5 + 5 (- 2)

= 25 – 10 = 15 marks.

3. Nafura has got 3 correct and the remaining 7 incorrect answers.
Solution :

Natura obtained = 3 × 5 + 7 (- 2)

= 15 – 14 = 1 marks.

Question 2. In a furniture shop, 15 wooden almirahs were sold in a month, from 10 almirahs, there was a profit of Rs. 300 per almirah, But for the remaining 5 almirahs there was a loss of Rs. 200 per almirah. What is the profit or loss of the shop owner for the month, let’s find out.
Solution :

Given

In a furniture shop, 15 wooden almirahs were sold in a month, from 10 almirahs, there was a profit of Rs. 300 per almirah, But for the remaining 5 almirahs there was a loss of Rs. 200 per almirah.

Total profit from 10 almirahs = 10 × Rs. 300 = Rs. 3000.

Total loss from 5 almirahs = 5 × Rs. 200 = Rs. 1 000.

Total profit in this month by 15 almirahs

= Rs. 3000 – Rs. 1000 = Rs. 2000.

Question 3. In another mine, the lift goes down 4 m in every one minute.

1. What will be the position of the lift after an hour, Let’s find.
Solution:

In 1 hour i.e in 60 minutes it goes down

= 4  60 = 240 m.

2. If the lift starts from 15m above the ground, let’s find the position
of the lift after 30 mins.
Solution:  In 30 min, the lift will go down = 4 × 30 = 120 m.

As the lift starts from 1 5 meters above the ground

∴ After 30 minutes the position of the lift will be

{(- 1 20 m) + 1 5 m} = -1 05 m i.e 1 05 m below

Addition Subtraction Multiplication And Division Of Integers Exercise 4.9

Question 1. 16 ÷ {(-4)4-2} ≠ 16 ÷ (-4) – 16 ÷ 2
Solution :

L H S = 1 6 -s- {(-4) 4- 2} = 1 6 + (- 2) = – 8

RHS = 16 ÷(-4)4-16÷2 = -4 + 8 = +4

∴ LHS ≠RHS

Question 2. (- 70)- {(7) – (- 5)} ≠ (- 70) + (7) + (- 70) ÷ (- 5)
Solution :

L H S = (- 70) ÷ {(7) > (- 5)} = – 70 ÷ 2 = – 35

R H S = (- 70) + 7 + (- 70) + (- 5) = – 10 + 14 =  4

= 14 = 4

∴ LHS ≠  RHS

Addition Subtraction Multiplication And Division Of Integers Exercise 4.10

Question 1. Let’s Calculate the values mentally :

1. (- 10) × 4 = ________
Solution:

(- 10) × 4 ________

= (- 10) × 4 =-40

2. ( – 15) × ________= -90
Solution:

( – 15) ×  ________= 90

= ( – 15) × 6= -90

3. 25 × ________= – 125
Solution:

25 × ________= – 125

= 25 ×(-5) = -125

4. (- 16) x ________= 96
Solution:

(- 16) x ________=96

(- 16) x 6 = 96

5. (-13)× ________ =-104
Solution:

(-13) × ________ =-104

(-13) x 8 =-104

6. ________21 =-126
Solution:

_______21 =-126

– 6 × 21 = -126

7. ________=-42
Solution:

________=-42

14 × -3 = -42

8.  ________ (- 30) = 330
Solution:

________ (- 30) = 330

-11 × (- 30) = 330

9. (-26) + ________=1
Solution:

-26 + ________=1

-26 ÷ -26 =1

10. ________ = – 29
Solution:

________ = – 29

29 ÷ 1 = – 29

11. ________+ (- 59) = – 1
Solution:

________+ (- 59) = – 1

59 ÷ (- 59)  = -1

12. 87  ________= – 87
Solution:

87  ________= – 87

87 ÷ -1= -87

Question 2. In an examination Joseph answered 15 questions, of which 9 answers were correct but the remaining 6 were incorrect- If he gets 5 marks for each correct answer and his total is 33, let’s find, the marks allotted for incorrect answers in the examinations.

Given

In an examination Joseph answered 15 questions, of which 9 answers were correct but the remaining 6 were incorrect- If he gets 5 marks for each correct answer and his total is 33

The total marks obtained by Joseph is 33

He got 5 marks for each of his 9 correct answers

Marks for his correct answer 9 × 5 45

For a wrong answer, his marks are reduced by

= (45 – 33) marks = 12 marks

For 6 incorrect answers, his marks were reduced by 12 marks

For 6 incorrect answers, he got = – 12

Marks for 1 incorrect answer is (- 12) + 6 = – 2. (Solution: )

Question 3. Rehana and Sayan both appeared for an examination & each of them will have to answer 12 questions

1. Rehana got 36 marks in total by answering 8 questions correctly and the remaining 4 questions incorrectly. If she got 6 marks for each correct answer, let’s find the total marks obtained by him.

2. Let’s find the total marks obtained by Sayan if he answered 6 questions correctly and 6 questions answered incorrectly.
Solution :

Rehana got for eight correct answer = 6 × 8 = 48 but she got less (48 – 36) = 1 2 for 4 wrong answer

Marks for each wrong answer = 12 ÷ 4 = 3.

 In the case of Sayan : 

For 6 correct answer, he got = 6 × 6 = 36 & marks deducted for 6 wrong answer = 6 × 3  = 18

∴ Sayan obtained = 36 – 1 8 = 18 marks.

Question 4. The temperature of a certain place is 12° C  The temperature reduces uniformly in every hour and reaches – 4°C after 8 hours. Let’s find the rate of reduction of temperature per hour.
Solution:

Given

The temperature of a certain place is 12° C  The temperature reduces uniformly in every hour and reaches – 4°C after 8 hours.

Total temperature reduced in 8 hours = 12°C -(-4°C)= 16°C
16°C

∴ Rate of reduction of temperature per hour = \(\frac{16^{\circ}}{8}\) = 2°C

Question 5. A lift in a mine moves down 24 m in 8 mins. If it moves in a uniform rate, let’s find at what distance below the surface, it will be after 6 mins. If the lift starts from a height of 10 m above the ground, let’s find how deep the lift will go from the surface after 70 mins.
Solution:

Given

A lift in a mine moves down 24 m in 8 mins. If it moves in a uniform rate, let’s find at what distance below the surface, it will be after 6 mins. If the lift starts from a height of 10 m above the ground

The lift moves down 24 meter in 8 min.

∴ In 6 minutes it moves down = \(\frac{24}{8}\)  × 6 m = 18 meters.

Again the lift moves down in 70 minutes = \(\frac{24}{8}\)  × 70 m = 21 0 meters.

As it is 10 m above the ground, so in 70 min. the lift will go down
from the surface = (21 0 – 1 0) m = 200 meter.

Question 6. Let us fill up the blank squares:

1. – 16 ÷ (-2) +________ = -1
Solution : or, = – 1 – 8 = – 9

∴ 8 + – 9 = – 1.

2. 20 – 50 + ___________ = – 1
Solution :

Or, ___________= – 1 + 30

= 29

∴ -30 + 29 = – 1.

3.  41 × (- 5) + = – 3
Solution:

Or. _______ = – 3 + 205 = 202

∴ 205 + 202 = – 3

4. (-9)×(-3)×_______= -81
Solution :

Or, ________ = (- 81 ) ÷ 27 = – 3

Or, 27 × _____________ = 81

∴ (- 9) × (- 3) × – 3 = – 81

5. (-15) ÷ (-5)- ______ = -1
Solution:

Or, 3 – = – 1

Or, 3 + 1 = ______ ie, ________= 4

∴ (-15) ÷ (- 5) -__________ = – 1

6. (-18) ÷ ___________+ 3 = -6
Solution:

Or, – 18 ÷ _______ = – 6 – 3 = – 9

Or, (-18) ÷ (-9) = 2

∴ (-18) – 2 + 3 = -6

7. ______ ÷  4 – 2 = – 7
Solution :

Or,  _________ 4 – 2 = – 7 + 2 = – 5

Or , ________= – 5 x 4 = – 20

∴ – 20 ÷ 4 – 2 = -7

8. ___________ ×(-1) + 9 = 0
Solution :

Or, × (- 1 ) = – 9

Or, = (- 9) ÷ (- 1) = 9

∴ 9 ×(- 1) + 9 = 0

Question 7. Let us take 2 examples to show that the cumulative law holds in case of multiplication but does not hold for the division of integers. Solution :

1. Commulative law holds for Multification:

Example: 

1.  32 x (- 4) = – 128 And  (- 4) × 32 = – 128

∴ 32 x (- 4) = (- 4) × 32

2. (- 20) x 5 = – 100 and 5 x (- 20) = – 100

∴ (-20) × 5 = 5 × (-20) = – 100 ‘

∴(- 20) × 5 = 5 × (- 20)

2.  Commutative law does not hold for Division.

Example: 

1. 32 ÷ (- 4) = – 8 and (- 4)÷ 32 = \(\frac{1}{8}\)

∴ 32 ÷ (- 4) ≠ (- 4) ÷ 32

2.  (- 20) ÷ 5 = – 4 & 5÷  (- 20) = – \(\frac{1}{4}\)

∴ (- 20) ÷-5 ≠ 5 (- 20)

Question 8. Let us take 2 examples to show that the commutative law holds in case of multiplication but does not always hold for the division of integers.
Solution:

1.  Distribution law holds for Multiplication

1. 40 x {(- 8) + 4} = 40 x (- 4) = – 160

And  40 x (- 8) + 40 x 4 = – 320 + 160 = – 160

∴ 40 x {(- 8) + 4} = 40 x (- 8) + 40 x 4

2. 25 x (7 + 3) = 25×10 =250

And  25 x 7+ 25 x 3 = 175 + 75 = 250

∴  25 x (7 + 3) = 25 x 7 + 25 x 3

2. Distribution law does not hold for Division:

1. For left distribution:

40 ÷ {(-8) + 4} = 40 ÷ (-8) + 40 – 4 = -5 + 10 = 5

& 40 ÷  {(- 8) + 4} = 40 + (- 4) = – 1 0

∴ 40 ÷  {(-8) + 4} * 40 -h (- 8) + 40 -r 4

2.  For Right distribution.

{(- 8) + 4} 40 = – 4 ÷ 40 = – \(\frac{1}{10}\)

And  {(-8) + 4} ÷ 40= \(\frac{-8}{40}+\frac{4}{40}=\frac{-1}{5}+\frac{1}{10}=\frac{-2+1}{10}=-\frac{1}{10}\)

Question 9. Let us find the values of the following

1. (- 125) ÷ 5
Solution:

(- 125) ÷ 5 = – 25

2. (-144) ÷6
Solution:

(-144) ÷6 = – 24

3. (- 49)÷ 7
Solution:

(- 49)÷ 7 = – 7

4. 225 ÷ (-3)
Solution:

225 ÷ (-3) = – 75

5. 169 ÷ (- 13)
Solution:

169 ÷ (- 13)= -13

6.100 ÷ (-5)
Solution:

100 ÷ (-5)= – 20

7. (-81) ÷ (-9)
Solution:

(-81) ÷ (-9) = 9

8. (- 150) ÷ (-5)
Solution:

(- 150) ÷ (-5) = (-81) + (-9)= 30

9. (-121) ÷ (-11)
Solution:

(-121) ÷ (-11)= 11

10.(- 275) ÷ (-25)
Solution:

(- 275) ÷ (-25) = 11