NEET Physics

Mechanical Properties Of Fluids

Pressure,  \(P=\frac{F}{A}\)

SI unit of pressure is Nm^-2 or Pascal

One atmospheric pressure, 1 atm = l.Olx 10⁵ Pa= 760toir

The atmospheric pressure is maximum at the surface of earth and goes on decreasing as we move up into earth’s atmosphere.

If P₀ is the atmospheric pressure then for a point at depth h below the surface of a liquid of density P, the hydrostatic pressure is given by,

P = P₀+hρg

The pressure difference between hydrostatic pressure P and atmospheric pressure P0 is called guage pressure.

Read And Learn More: NEET Physics Notes

P – P₀+hρg

Density, ρ = \(\frac{\text { mass }}{\text { volume }}=\frac{M}{V}\)

Relative density = specific gravity =\(\frac{\text { density of body }}{\text { density of water }}\)

Note

• The relative density of water is 1
• The relative density of mercury is 13.6

Pascal’s Law

According to Pascal’s law, if the gravity effect is neglected, the pressure at every point of liquid in the equilibrium of rest is the same.

This means, the increase in pressure at one point of the enclosed liquid in equilibrium of rest is transmitted equally to all other points of the liquid and also to the walls of the container, provided the effect of gravity is neglected.

NEET Physics Fluids Chapter Notes with Important Formulas

Hydraulic Lift

The working of hydraulic lift is based on pascal’s law.

It is used to lift heavy objects.

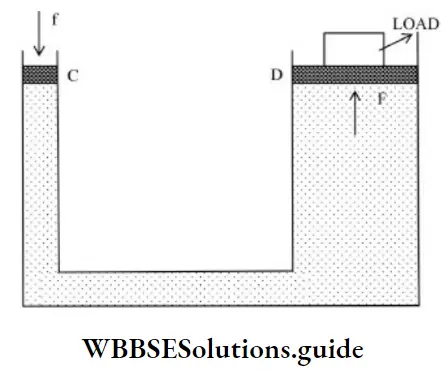
The pressure exerted on piston ‘C’ is given by

⇒ \(P=\frac{f}{a}\)

This pressure will be transmitted everywhere and even to piston D. Hence, force acting on piston D is given by,

⇒ \(F=P A=\frac{f}{a} A=f\left(\frac{A}{a}\right)\)

Since, A >> a, therefore, F >> f. Hence heavy objects placed on the larger piston are easily lifted upwards by applying a small force.

Best Short Notes for Mechanical Properties of Fluids NEET

Archimedes Principle

When a body is immersed party or wholly in a fluid, at rest, it is buoyed up with a force equal to the weight of the fluid displaced by the body.

Apparent weight of the body of density (ρ) when immersed in a liquid of density (σ) is given by

Apparent weight = Actual weight – Up thrust

⇒ \(W-F_{u p}\)

⇒ \(V \rho g-V \sigma g\)

⇒ \(W_{a p p}=V \rho g\left(1-\frac{\sigma}{\rho}\right)\)

If density of body is greater than that of liquid (ρ>σ), then weight will be more than up¬thrust so the body will sink.

If density of body is equal to that of liquid (ρ = σ), then weight will be equal to up-thrust so the body will float fully submerged.

If density of body is lesser than that of liquid (ρ <σ), then weight will be less than up-thrust so the body will, move upwards and in equilibrium will float and partially immersed, such that,

⇒ \(W_{a v p}=V_{i m} \sigma g\)

where Wapp is the apparent weight of the body and Vin is the volume of the body immersed in the liquid.

The velocity of liquid up to which its flow is streamline and above which it becomes turbulent is called critical velocity.

Reynold’s number determines the nature of flow of liquid

If N_R <1000 the flow of liquid is streamline or laminar.

If 1000 < N_R < 2000 the flow is unsteady.

If N_R > 2000 the flow is turbulent.

According to the equation of continuity,

av = constant

where a is area of cross section of pipe and v is velocity of fluid.

Bernoulli’s Theorem

For an incompressible non-viscous fluid flowing through a pipe, the sum of pressure energy, potential energy and kinetic energy per unit volume is a constant.

⇒ \(P+\rho g h+\frac{1}{2} \rho v^2\)= constant

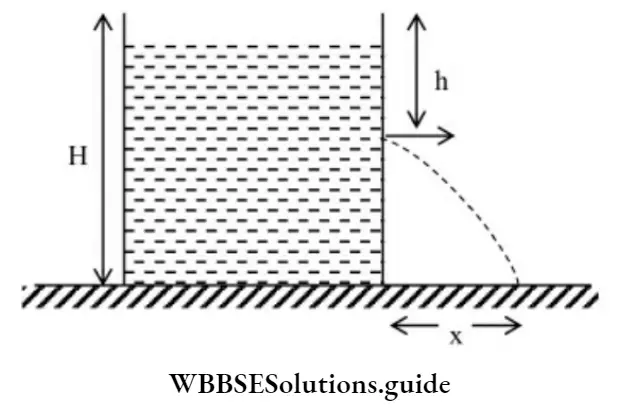
Velocity of efflux is given by

⇒ \(v=\sqrt{2 g h}\)

Mechanical Properties of Fluids NEET Important Questions

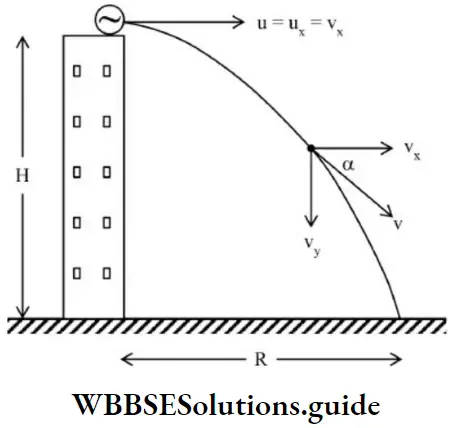
Where, h is the depth of the hole below the free surface of the liquid. The time required for the fluid to reach the ground is,

⇒ \(t=\sqrt{\frac{2(H-h)}{g}}\)

Range,

⇒ \(x=v_x t=\sqrt{2 g h} \sqrt{\frac{2(H-h)}{g}}\)

⇒ \(x=2 \sqrt{h(H-h)}\)

x is maximum when, \(\)

Maximum range is given by,

⇒ \(x=2 \sqrt{\frac{H}{2}\left(H-\frac{H}{2}\right)} \Rightarrow x_{\max }=H\)

Viscous force is given by

⇒ \(F=-\eta A \frac{d v}{d x}\)

If A = 1 and, \(\frac{d v}{d x}=1, \text { then } F=\eta\)

Where η is called co-efficient of viscosity.

Stoke’s law: According to this viscous force acting on a spherical object falling in a fluid medium is directly proportional to its velocity.

ie., \(F_{\text {viscows }} \propto v\)

or \(F=6 \pi \eta n v\)

Where, r is radius of the sphere, η is coefficient of viscosity.

The maximum velocity with which a spherical body moves in a viscous fluid when it is dropped is called terminal velocity.

Terminal velocity is given by,

⇒ \(v_t=\frac{2}{9} \frac{r^2(\rho-\sigma) g}{\eta}\)

where, ρ is the density of sphere and η is the density of fluid.

Bernoulli’s Theorem and Applications NEET Notes

Note

If ρ>σ, then, v_t is positive, sphere moves down

If ρ=σ, then v_t = 0

If ρ<σ, then sphere moves upwards ( v_t is negative)

Example: Air bubbles in water.

The force of attraction between molecules of same substance is called cohesive force.

The force of attraction between molecules of different substance is called adhesive force.

Surface tension: It is the property of the liquid due to which free surface of the liquid behaves like elastic stretched membrane.

Small liquid drops assume spherical shape due to surface tension.

Surface tension, T=\(\frac{f}{l}\)

Work done in blowing a liquid drop is,

W = T × inci ease in area

W =\(T \times 4 \pi\left[r_2^2-r_1^2\right] \Rightarrow W=4 \pi T\left[r_2^2-r_1^2\right]\)

Mechanical Properties of Fluids Previous Year Questions NEET

Work done in blowing a soap bubble is,

⇒ \(W=2\left[4 \pi T\left(r_2^2-r_1^2\right)\right]\)

(since the bubble has two free surfaces)

⇒ \(\Rightarrow W=8 \pi T\left[r_2^2-r_1^2\right]\)

Expression for capillary rise:

⇒ \(h=\frac{2 T \cos \theta}{r \rho g}\)

Where θ is the angle of contact, r is the radius of the capillary, p is the density of liquid and T is surface tension.

Excess pressure inside a drop is given by \(\Delta P=\frac{2 T}{r}\)

Excess pressure inside a soap bubble is given by, =\(\Delta P=\frac{4 T}{r}\)

NEET Physics Gravitation Notes

Kepler’s First Law Class 11

All planets revolve around the sun in an elliptical orbit, with the sun at one of the foci

A → perihelion; B → aphelion

Kepler’s Second Law

The imaginary line which connects the planet and the sun sweeps equal areas in equal intervals of time.

⇒i.e., area of velocity = \(\frac{\Delta \mathrm{A}}{\Delta \mathrm{t}}=\frac{\mathrm{L}}{2 \mathrm{~m}}=\text { constant }\)

Read And Learn More: NEET Physics Notes

Note:

In the case of central force L is constant. (Gravitational force is a central force).

Kepler’s Third Law (Law Of Periods)

The period of revolution of a planet around the sun is directly proportional to the cube of its semimajor axis.

⇒ \(\mathrm{T}^2 \propto \mathrm{a}^3\)

Note:

If the average radius is given, then

⇒ \(\mathrm{T}^2 \propto \mathrm{r}^3\)

NEET Physics Gravitation Notes PDF Download

Universal Law of Gravitation

The force of attraction between two masses mx and m2 separated by a distance ‘r’ is given by

⇒ \(\mathrm{F}=\mathrm{G} \frac{\mathrm{m}_1 \mathrm{~m}_2}{\mathrm{r}^2}\)

Where G is known as the universal gravitational constant. G= 6.67×10^-11Nm²kg^-2

The law of gravitation is strictly valid for point masses.

Shell Theorems

1. A uniformly dense spherical shell exerts a force on a body situated outside the shell as if the entire mass of the shell is concentrated at its center.
2. The force of attraction due to a uniformly dense spherical shell of uniform density, on a point mass situated inside it is zero.

Acceleration due to gravity/Gravitational field intensity/Gravitational field

Gravitational force at a point is the force experienced by a unit mass when placed at that point.

⇒ \(g=\frac{F}{m}\)

Acceleration due to gravity on the surface of the earth:

⇒ \(\mathrm{g}=\frac{\mathrm{GM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}^2}\)

Acceleration due to gravity due to a uniform solid sphere:

Gravitation NEET Important Questions with Solutions

⇒ \(\mathrm{g}_{\mathrm{p}}=\frac{\mathrm{GM}}{\mathrm{r}^2} ; \text { if } \mathrm{r} \geq \mathrm{R}\)

⇒ \(\mathrm{g}_{\mathrm{p}}=\frac{\mathrm{GM}}{\mathrm{R}^3} \mathrm{r} ; \text { if } \mathrm{r}<\mathrm{R}\)

Variation of ‘g’ with distance from the center of the sphere:

Best Notes for Gravitation NEET Preparation

Variation of acceleration due to gravity with height:

⇒ \(g(h)=\frac{G M}{(R+h)^2}=\frac{g^2}{(R+h)^2}\)

When h<<R,then

⇒ \(g(h)=g\left(1-\frac{2 h}{R}\right)\)

Where ‘g’ is acceleration due to gravity on the surface of earth.

Variation of acceleration due to gravity with depth:

⇒ \(g(d)=g\left(1-\frac{d}{R}\right)\)

Variation of ‘g’ with latitude due to rotation of earth:

NEET Previous Year Questions on Gravitation

Consider a body of mass ‘m’ at point P.

w.k.t.,

⇒ \(g=\frac{F_{\text {bet }}}{m}\)

⇒ \(g_\lambda=\frac{m g-m \omega^2 R \cos ^2 \lambda}{m}\)

⇒ \(g_\lambda=g-\omega^2 R \cos ^2 \lambda\)

Case 1:

At equator, λ = 0

⇒ \(g_\lambda=g-\omega^2 R\)

If ‘ ω’ of earth increases there is a possibility of ‘g’ at equator becoming zero.

i.e., 0 = g – ω²R ⇒ g=ω²R

⇒ \(\omega=\sqrt{\frac{g}{R}}\)

,i.e., when ω=\(\sqrt{\frac{g}{R}}\) g at equator will become zero.

Tricks to Solve Gravitation Problems for NEET

Case 2:

At pole,  λ = 90°,

∴ g_λ = 0

i.e., ‘g’ at poles is independent of rotation of earth.

Gravitational potential energy at a point is the work done in bringing a mass from infinity to that point against the gravitational force of the field.

⇒ \(\mathrm{U}=-\frac{\mathrm{Gm}_1 \mathrm{~m}_2}{\mathrm{r}}\)

Where ‘r’ is the distance from the centre of earth. For system of ‘3’ particles,

⇒ \(\mathrm{U}=-\mathrm{G}\left(\frac{\mathrm{m}_1 \mathrm{~m}_2}{\mathrm{r}_{12}}+\frac{\mathrm{m}_2 \mathrm{~m}_3}{\mathrm{r}_{23}}+\frac{\mathrm{m}_3 \mathrm{~m}_1}{\mathrm{r}_{31}}\right)\)

For ‘n’ particles,

⇒ \(\mathrm{U}=-\mathrm{G}\left(\frac{\mathrm{m}_1 \mathrm{~m}_2}{\mathrm{r}_{12}}+\frac{\mathrm{m}_1 \mathrm{~m}_3}{\mathrm{r}_{13}}+\ldots . .+\frac{\mathrm{m}_1 \mathrm{~m}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{ln}}}+\frac{\mathrm{m}_2 \mathrm{~m}_3}{\mathrm{r}_{23}}+\ldots . .\right)\)

Note:

For‘n’particle system, there are \({ }^{\mathrm{n}} \mathrm{C}_2=\frac{\mathrm{n}(\mathrm{n}-1)}{2}\) pairs.

Potential energy is calculated for each pair and then added to obtain the potential energy for the system.

⇒ \(F=-\frac{d U}{d x}\)

∴ \(U=-\int_{\infty}^r \vec{F} \cdot d \vec{x}\)

Gravitational potential at a point is the work done in bringing a unit mass from infinity to the given point against the gravitational force of the field.

⇒ \(\mathrm{V}=-\frac{\mathrm{GM}}{\mathrm{r}}\)

Newton’s Law of Gravitation NEET MCQs with Answers

Relation between gravitational field and gravitational potential

⇒ \(\mathrm{g}=-\frac{\mathrm{dV}}{\mathrm{dr}}\)

⇒ \(\mathrm{V}=-\int_{\infty}^{\mathrm{r}} \overrightarrow{\mathrm{g}} \cdot \mathrm{d} \overrightarrow{\mathrm{r}}\)

Potential due to solid sphere (if r > R )

⇒ \(V_p=-\int_{\infty}^r-\frac{G M}{r^2} \cdot d r\)

⇒ \(\mathrm{V}_{\mathrm{p}}=+\mathrm{GM}\left[\frac{\mathrm{r}^{-2+1}}{-2+1}\right]_{\infty}^{\mathrm{r}}=-\frac{\mathrm{GM}}{\mathrm{r}}\)

Potential due to solid sphere (if r < R)

NCERT Summary of Gravitation for NEET Physics

⇒ \(V_P=-\int_{\infty}^R-\frac{G M}{r^2} \cdot d r-\int_R^r-\frac{G M}{R^3} r d r\)

⇒ \(\mathrm{V}_{\mathrm{P}}=\mathrm{GM}\left[\frac{\mathrm{r}^{-1}}{-1}\right]_{\infty}^{\mathbb{R}}+\frac{\mathrm{GM}}{\mathrm{R}^3}\left[\frac{\mathrm{r}^{+2}}{+2}\right]_{\mathbb{R}}^{\mathrm{r}}\)

⇒ \(V_p=-\frac{G M}{R}+\frac{G M}{2 R^3}\left(r^2-R^2\right)\)

⇒ \(V_p=\frac{G M}{2 R^3}\left(r^2-R^2\right)-\frac{G M}{R}\)

⇒ \(V_P=\frac{G M}{2 R^3}\left[\left(r^2-R^2\right)-2 R^2\right]\)

⇒ \(V_P=-\frac{G M}{2 R^3}\left[3 R^2-r^2\right]\)

Orbital Speed of a Satellite

When gravitational force and centrifugal force on the satellite are same, then

⇒ \(\frac{\mathrm{GMm}}{\mathrm{r}^2}=\frac{\mathrm{mv}_0^2}{\mathrm{r}}\)

⇒ \(\mathrm{v}_0^2=\frac{\mathrm{GM}}{\mathrm{r}}\)

⇒ \(v_0=\sqrt{\frac{G M}{r}}=\sqrt{\frac{G M}{R+h}}\)

Where ‘h’ is the height of the satellite from earth’s surface. If h < < R, then,

⇒ \(\mathrm{v}_0=\sqrt{\frac{\mathrm{gR}^2}{\mathrm{R}}} \Rightarrow \mathrm{v}_0=\sqrt{\mathrm{gR}}\)

Step-by-Step Solutions for Gravitation NEET Problems

Expression for escape speed

⇒ \(v_e=\sqrt{\frac{2 G M}{r}}=\sqrt{\frac{2 G M}{R+h}}\)

If h < < R, then

⇒ \(\mathrm{v}_{\mathrm{e}}=\sqrt{\frac{2 \mathrm{gR}^2}{\mathrm{R}}} \Rightarrow \mathrm{V}_{\mathrm{e}}=\sqrt{2 \mathrm{gR}}\)

Note:

If a satellite is very close to the earth’s surface, then,

⇒ \(\mathrm{v}_{\mathrm{e}}=\sqrt{2} \mathrm{v}_0\)

Gravitational Potential Energy and Escape Velocity NEET Notes

Total Energy of a Satellite

The kinetic energy of a satellite is given by,

⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{mv}_0^2=\frac{1}{2} \mathrm{~m} \frac{\mathrm{GM}}{\mathrm{r}}=\frac{\mathrm{GMm}}{2 \mathrm{r}}\)

Potential energy of a satellite is given by,

⇒ \(\mathrm{U}=-\frac{\mathrm{GMm}}{\mathrm{r}}\)

∴ Total energy,

⇒ \(\mathrm{E}=\mathrm{K}+\mathrm{U}=\frac{\mathrm{GMm}}{2 \mathrm{r}}-\frac{\mathrm{GMm}}{\mathrm{r}}\)

⇒ \(\mathrm{E}=-\frac{\mathrm{GMm}}{2 \mathrm{r}}\)

System Of Particles And Rotational Motion

Angular displacement is given by

⇒ \(\theta=\frac{\text { length of the arc }}{\text { radius }}=\frac{s}{r} \text { radian }\)

Average angular velocity

⇒ \(\bar{\omega}=\frac{\theta_2-\theta_1}{t_2-t_1}=\frac{\Delta \theta}{\Delta t} \mathrm{rads}^{-1}\)

Instantaneous angular velocity

⇒ \(\omega=\frac{d \theta}{d t} \mathrm{rads}^{-1}\)

⇒ \(\omega=2 \pi f=\left(\frac{2 \pi}{T}\right)\)

Angular acceleration

Average angular acceleration

⇒ \(\bar{\alpha}=\frac{\omega_2-\omega_1}{t_2-t_1}=\frac{\Delta \omega}{\Delta t} \mathrm{rads}^{-2}\)

Read And Learn More: NEET Physics Notes

Instantaneous Angular Acceleration

⇒ \(\alpha=\frac{d \omega}{d t}=\frac{d^2 \theta}{d t^2} \mathrm{rads}^{-2}\)

NEET Physics System of Particles and Rotational Motion Notes

Relation between linear velocity and angular velocity

⇒ \(v=\omega r=2 \pi f r=\frac{2 \pi r}{T}\)

⇒ \(\vec{v}=\vec{\omega} \times \vec{r}\)

Relation between linear acceleration and angular acceleration

⇒ \(a=\frac{d v}{d t}=r \frac{d \omega}{d t}=r \alpha\)

Tangential acceleration

⇒ \(\vec{a}_i=\vec{\alpha} \times \vec{r}\)

Radial acceleration

⇒ \(\vec{a}_r=\vec{\omega} \times \vec{v}\)

Resultant acceleration

⇒ \(\vec{a}=\vec{a}_t+\vec{a}_r\)

NEET Physics Rotational Motion Important Formulas

The center of mass of a body is an imaginary point at which the entire mass of the body is considered to be concentrated.

If m₁ and m₂ are situated at a distance of x₁ and x₂ w.r.to origin then their center of mass is given by,

⇒ \(\mathrm{x}=\frac{\mathrm{m}_1 \mathrm{x}_1+\mathrm{m}_2 \mathrm{x}_2}{\mathrm{~m}_1+\mathrm{m}_2}\)

if m₁=m₂=m, then

⇒ \(\mathrm{X}=\frac{\mathrm{x}_1+\mathrm{x}_2}{2}\)

Suppose we have three particles, then

Best Short Notes for System of Particles and Rotational Motion NEET

⇒ \(\mathrm{X}=\frac{\mathrm{m}_1 \mathrm{x}_1+\mathrm{m}_2 \mathrm{x}_2+\mathrm{m}_3 \mathrm{x}_3}{\mathrm{~m}_1+\mathrm{m}_2+\mathrm{m}_3}\)

⇒ \(\mathrm{Y}=\frac{\mathrm{m}_1 \mathrm{y}_1+\mathrm{m}_2 \mathrm{y}_2+\mathrm{m}_3 \mathrm{y}_3}{\mathrm{~m}_1+\mathrm{m}_2+\mathrm{m}_3}\)

If m₁ = m₂ = m₃= m, then

⇒\(\mathrm{X}=\frac{\mathrm{x}_1+\mathrm{x}_2+\mathrm{x}_3}{3} \text { and } \mathrm{Y}=\frac{\mathrm{y}_1+\mathrm{y}_2+\mathrm{y}_3}{3}\)

Then, for three particles of equal mass center of mass coincides with the centroid of the triangle formed by the particles.

Conservation Of Momentum For System Of Particles

The total momentum of a system of particles is equal to the product of the total mass of the system and the velocity of its center of mass.

Note: External force is required to change the position of the center of mass.

The moment of force is called torque.

If a force F acts on a particle at a point P whose position for the origin ‘O’ is defined as the vector product,

⇒ \(\vec{\tau}=\vec{r} \times \vec{F}\)

⇒ \(\tau=\mathrm{rF} \sin \theta\)

Torque is a measure of the turning effect of a force.

System of Particles and Rotational Motion NEET Important Questions and Answers

Moment of linear momentum is called angular momentum.

The angular momentum \(\vec{\ell}\) of the particle w.r.to the origin ‘O’ is,

⇒ \(\vec{\ell}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{p}}\)

⇒ \(\mathrm{rp} \sin \theta\)

The rate of change of angular momentum is equal to torque.

⇒ \(\text { i.e., } \frac{\mathrm{d} \vec{\ell}}{\mathrm{dt}}=\overrightarrow{\boldsymbol{\tau}}\)

This is the rotational analog of the equation,

⇒ \(\frac{\mathrm{d} \overrightarrow{\mathrm{p}}}{\mathrm{dt}}=\overrightarrow{\mathrm{F}}\)

NEET Physics Rotational Motion MCQs with Solutions

Conditions for Mechanical Equilibrium of a Rigid Body

The vector sum of all the forces acting on a rigid body should be zero. i.e.,

⇒ \(\text { i.e., } \overrightarrow{\mathrm{F}}_1+\overrightarrow{\mathrm{F}}_2+\ldots .+\overrightarrow{\mathrm{F}}_{\mathrm{n}}=0\)

(This is the condition for translation equilibrium)

The vector sum of all the torques acting on a rigid body is zero. i.e.,

⇒ \(\text { i.e., } \vec{\tau}_1+\vec{\tau}_2+\ldots+\vec{\tau}_n=0\)

(This is the condition for rotational equilibrium)

Principle of Moments

For translational equilibrium of lever

⇒ \(\mathrm{R}-\mathrm{F}_1-\mathrm{F}_2=0 \text {, }\)

where R is the reaction of the support at the fulcrum. For rotational equilibrium

d₁F₁ – d₂F₂ = 0

or, d₁F₁= d₂F₂

System Of Particles

Where F₁ is the load, d₁ is the load arm, F₂ is effort and d₂ is effort arm.
The ratio \(\frac{F_1}{F_2}\) is called mechanical advantage (M.A.)

⇒ \(\text { M.A. }=\frac{F_1}{F_2}=\frac{d_2}{d_1}\)

NEET Study Material for Rotational Motion Chapter

The moment of inertia of a rigid body is given by,

⇒\(\mathrm{I}=\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{m}_{\mathrm{i}} \cdot \mathrm{r}_{\mathrm{i}}^2\)

Moment of inertia of is also  given by,

I = MK²

Where k is called the radius of gyration.

The radius of gyration is the distance from the axis of a mass point whose mass is equal to the mass of the whole body and whose moment of inertia is equal to the moment of inertia of the body about its axis.

Theorem of Perpendicular Axes

The moment of inertia of a planar body about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.

Theorem of Parallel Axes

The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its center of mass and the product of its mass (M) and the square of the distance (a) between two parallel axes.

Kinematic equations for rotational motion

⇒ \(\omega=\omega_0+\alpha t\)

⇒ \(\theta=\omega_0 t+\frac{1}{2} \alpha t^2\)

⇒ \(\omega^2=\omega_0^2+2 \alpha \theta\)

Where Q0 is the initial angular velocity, Q is the final angular velocity, a is the angular acceleration, 0 is the angular displacement, and ‘t’ is time.

Rotational Motion Class 11 NCERT NEET

According to the law of conservation of angular momentum

\(\mathrm{L}=\mathrm{I} \omega=\text { constant }\)

“If the net external torque on the system is zero, the angular momentum is conserved”. The kinetic energy of rolling motion is given by,

⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{I} \omega^2+\frac{1}{2} \mathrm{mv}_{\mathrm{cm}}^2\)

⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{~m} v_{\mathrm{cm}}^2\left(1+\frac{\mathrm{K}^2}{\mathrm{R}^2}\right)\)

where v_cm is the velocity of the center of mass.

The moment of inertia of some objects

Ring: I = MR² (about axis)

I = MR²/2 (about diameter)

I = 2 MR² (tangential to ring, parallel to the axis)

Where R is the radius and M is the mass of the ring.

Disc: \(I=\frac{1}{2} M R^2 \text { (axis) }\)

I = 1/4 MR² (diameter)

I = 3/2 MR² (tangential to the rim, parallel to the axis)

Cylinder:

About axis I = 1/2 MR²

Center of Mass and Torque NEET Notes

Perpendicular the length and passing through C.M.

⇒ \(I=\frac{M L^2}{12}+\frac{M R^2}{4}\)

Thin rod:

⇒ \(I_{\text {dia }}=\frac{2}{3} M R^2\)

⇒ \(I=\frac{1}{3} M \amalg^2 \text { (aboutoneend) }\)

Hollow sphere:

⇒ \(I_{\text {dia }}=\frac{2}{3} M R^2\)

⇒ \(I_{\text {tarmgential }}=\frac{5}{3} M R^2\)

Solid sphere:

⇒ \(I_{\text {dia }}=\frac{2}{5} M R^2\)

⇒ \(I_{\text {tangential }}=\frac{7}{5} M R^2\)

Rectangular plate:

⇒ \(I_c=\frac{M\left(L^2+B^2\right)}{12}\)

Where L and B are the length and breadth of the plate respectively.

Motion on An Inclined Plane

1. For translational motion (without rotation)

⇒ \(\frac{1}{2} m v^2=m g h, \text { velocity } v=\sqrt{2 g h}=\sqrt{2 g s \sin \theta}\)

⇒ \(\text { Acceleration } a=g \sin \theta \text {, time } t=\left(\frac{2 s}{g \sin \theta}\right)^{1 / 2}\)

2. For rolling motion (translational + rotational)

⇒ \(\frac{1}{2} m v^2\left(1+\frac{K^2}{R^2}\right)=m g h\)

⇒ \(\text { velocity } v=\left[\frac{2 g s \sin \theta}{\left(1+\frac{K^2}{R^2}\right)}\right]^{1 / 2}=\left[\frac{2 g h}{\left(1+\frac{K^2}{R^2}\right)}\right]^{7^2}\)

⇒ \(\text { Acceleration } f=\frac{g \sin \theta}{\left(1+\frac{K^2}{R^2}\right)}\)

⇒ \(\text { Time } t=\sqrt{\frac{2 s}{a}}=\left[\frac{2 s\left(1+\frac{K^2}{R^2}\right)}{g \sin \theta}\right]^{1 / 2}\)

Work Energy And Power

Work is said to be done if there is a displacement in the direction of applied force.

Work done is the dot product of force and displacement.

W = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{x}}\)

W = Fx cosθ

Work is zero, if F = 0, x = 0 or cosθ = 0 (θ= 90°)

NEET Physics Work Energy and Power notes

Example: 

• Work done by gravitational force of earth on its satellite is zero. (Since angle between gravitational force and instantaneous displacement is 900)
• Work done by force of tension of string on the bob of simple pendulum is zero. (Since angle between tension in the string and instantaneous displacement of the bob is 900)
• When a charged particle is moving in a uniform magnetic field in a circular path, work done by magnetic field is zero. (Since angle between magnetic force and instantaneous displacement of the charged particle is 900)

Read And Learn More: NEET Physics Notes

Potential Energy

Energy possessed by a body due to its position or configuration.

Example:

1. If a body is raised to a height ‘h’ from the ground, then its potential energy is given by,

U = mgh

2. P.E. of a spring is given by,

U= \(\frac{1}{2} \mathrm{kx}^2\)

Where k is spring constant and x is elongation/extension.

F=\(-\frac{\mathrm{dU}}{\mathrm{dx}}\)

Where U is potential energy.

Important formulas of Work Energy and Power for NEET

When the system is in equilibrium

\(\frac{\mathrm{dU}}{\mathrm{dx}}\)=0

Relation between kinetic energy and linear momentum

The kinetic energy of a body of mass ‘m’ and moving with velocity ‘v’ is given by

⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{mv}^2\)

⇒ \(\mathrm{K}=\frac{1}{2} \mathrm{mv}^2 \times \frac{\mathrm{m}}{\mathrm{m}}=\frac{\mathrm{m}^2 \mathrm{v}^2}{2 \mathrm{~m}}=\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)

⇒ \(\mathrm{K}=\frac{\mathrm{P}^2}{2 \mathrm{~m}}\)

⇒ \(\mathrm{P}=\sqrt{2 \mathrm{mK}}\)

Conservation of mechanical energy NEET questions

Conservative Force

A force is said to be conservative if work done by the force is independent of path. Or A force is said to be conservative if work done by the force depends only on initial and final position. Or A force is said to be conservative if work done by the force in a cyclic process is zero.

Work-Energy Theorem

If the forces acting on a body are conservative then change in kinetic energy of the body is equal to work done by the net force.

ΔK = W

K_f – K_i = W

Work Energy theorem NEET questions

Work Done By Variable Force

Constant force is rare in nature.

When there is variable force area under force versus displacement graph has to be calculated by the method of calculus.

⇒ \(\mathrm{W}=\int_{\mathrm{x}_1}^{\mathrm{x}} \overrightarrow{\mathrm{F}} \cdot \overline{\mathrm{dx}}\)

(Work done is the definite integral of force over displacement).

Area under F versus x graph gives work done.

Power

The rate at which work is done is called power.

⇒ \(P=\frac{W}{t}\)

⇒ \(P=\frac{\vec{F} \cdot \vec{x}}{t}\)

⇒ \(\mathrm{P}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}}\)

(i.e., power is the dot product of force and velocity)

Motion Of A Body In A Vertical Circle

Power and efficiency NEET Physics notes

If the body moving in a vertical plane has to complete a vertical circle, at the highest point,

⇒ \(\frac{m v_H^2}{r}=m g\)

So the minimum condition is

⇒ \(\frac{m v_H^2}{r}=m g\)

⇒ \(\mathrm{T}_{\mathrm{H}}=\frac{\mathrm{mv_{ \textrm {H } } ^ { 2 }}}{\mathrm{r}}-\mathrm{mg}\) ____________ (1)

⇒ \(\mathrm{T}_{\mathrm{A}}=\mathrm{T}_{\mathrm{B}}=\frac{\mathrm{mv_{ \textrm {A } } ^ { 2 }}}{\mathrm{r}}=\frac{\mathrm{mv_{B } ^ { 2 }}}{\mathrm{r}}\) (∵V_A=V_B)________________(2)

⇒ \(\mathrm{T}_{\mathrm{L}}=\frac{\mathrm{mv_{ \textrm {L } } ^ { 2 }}}{\mathrm{r}}+\mathrm{mg}\)____________(3)

In general, the tension at any point P is given by,

⇒ \(\mathrm{T}_{\mathrm{P}}=\frac{\mathrm{mv_{ \textrm {p } } ^ { 2 }}}{\mathrm{r}}+\mathrm{mg} \cos \theta\)

w.k.t., (T_H)_min= 0

⇒ (∵ at minimum condition \(\frac{\mathrm{mv}_{\mathrm{H}}^2}{\mathrm{r}}=\mathrm{mg}\))

∴(1) ⇒ \(0=\frac{m v_H^2}{r}-m g\)

⇒ \(\frac{m v_{\mathrm{H}}^2}{\mathrm{r}}=\mathrm{mg}\)

⇒ \(\mathrm{v}_{\mathrm{H}}=\sqrt{\mathrm{gr}}\)

Therefore the minimum velocity to be given at H so that the body completes a vertical circle is \(\sqrt{\mathrm{gr}}\)

Now, using law of conservation of mechanical energy we will calculate the minimum velocity to be given at L in order to complete a vertical circle.

KH + UH = KL + UL

⇒ \(\frac{1}{2} m v_{\mathrm{H}}^2+m g(2 r)=\frac{1}{2} m v_{\mathrm{L}}^2+0\)

⇒ \(\frac{1}{2}(\mathrm{gr})+2 \mathrm{gr}=\frac{1}{2} \mathrm{v}_{\mathrm{L}}^2\)

⇒ ∵ \(\mathrm{v}_{\mathrm{H}}=\sqrt{\mathrm{gr}}\)

⇒ \(g r+4 g r=v_L^2\)

⇒ \(\mathrm{v}_{\mathrm{L}}=\sqrt{5 \mathrm{gr}}\)

Similarly, it can be shown that,

⇒ \(\mathrm{v}_{\mathrm{A}}=\sqrt{3 \mathrm{gr}}\)

∴ \(T_A=\frac{m v_A^2}{r}=\frac{m(3 g r)}{r}\)

⇒ \(\mathrm{T}_{\mathrm{A}}=3 \mathrm{mg}\)

⇒ \(\mathrm{T}_{\mathrm{L}}=\frac{\mathrm{mv_{ \textrm {L } } ^ { 2 }}}{\mathrm{r}}+\mathrm{mg}=\frac{\mathrm{m}}{\mathrm{r}} 5 \mathrm{gr}+\mathrm{mg}\)

⇒ \(\mathrm{T}_{\mathrm{L}}=6 \mathrm{mg} .\)

⇒ \(\left(T_H\right)_{\min }=0\)

⇒ \(\left(T_A\right)_{\min }=\left(T_B\right)_{\min }=3 \mathrm{mg}\)

⇒ \(\left(\mathrm{T}_{\mathrm{L}}\right)_{\mathrm{mg}}=6 \mathrm{mg}\)

⇒ \(\left(\mathrm{V}_{\mathrm{H}}\right)_{\min }=\sqrt{\mathrm{gr}}\)

⇒ \(\left(\mathrm{V}_{\mathrm{A}}\right)_{\min }=\left(\mathrm{V}_{\mathrm{B}}\right)_{\min }=\sqrt{3 \mathrm{gr}}\)

⇒ \(\left(\mathrm{V}_{\mathrm{L}}\right)_{\min }=\sqrt{5 \mathrm{gr}}\)

⇒ \(T_L-T_H=6 m g\)

Always,

Workdone in pulling a uniform chain on a frictionless table

Let mass of chain be M and length L.

Workdone in pulling the hanging portion is given by,

⇒ \(\mathrm{W}=\left(\frac{\mathrm{M}}{\mathrm{n}}\right) \mathrm{g}\left(\frac{\mathrm{L}}{2 \mathrm{n}}\right)^2\)

⇒ \(\mathrm{W}=\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)

( centre of mass of hanging portion is a point A it is a distance of from the top).

Velocity of the chain when it just leaves the frictionless table

Kinetic and potential energy NEET problems

P.E. when \(\frac{\mathrm{L}}{\mathrm{n}}\) portion is hanging is given by,

⇒ \(\mathrm{U}_{\mathrm{i}}=-\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)

P.E. when the chain just leaves the table surface is,

⇒ \(\mathrm{U}_{\mathrm{f}}=-\frac{\mathrm{MgL}}{2}\)

w.k.t., K.E. gain = P.E. loss

⇒ \(\frac{1}{2} \mathrm{mv}^2=-\frac{\mathrm{MgL}}{2 \mathrm{n}^2}-\left[-\frac{\mathrm{MgL}}{2}\right]\)

⇒ \(\frac{1}{2} \mathrm{mv}^2=\frac{\mathrm{MgL}}{2}-\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)

⇒ \(\mathrm{v}^2=\mathrm{gL}-\frac{\mathrm{gL}}{\mathrm{n}^2}\)

⇒ \(\mathrm{v}^2=\mathrm{gL}\left(1-\frac{1}{\mathrm{n}^2}\right)\)

⇒ \(\mathrm{v}=\sqrt{\mathrm{gL}\left(1-\frac{1}{\mathrm{n}^2}\right)}\)

Collison

A body is said to undergo collision if there is an abrupt change in its velocity.

The collision is said to be perfectly elastic if there is no kinetic energy loss.

The collision is said to be inelastic if there is a kinetic energy loss during collision.

The collision is said to be perfectly inelastic if bodies undergoing collision move together with common velocity after collision.

Expression of K.E. loss in the case of perfectly inelastic collision in 1-D:

ΔK=\(\frac{1}{2} \frac{m_1 m_2}{m_1+m_2} u_1^2\)

Expression for final velocities when two bodies undergoing elastic collision in 1-D

Work done by variable force NEET questions

⇒ \(v_1=\left(\frac{m_1-m_2}{m_1+m_2}\right) u_1+\frac{2 m_2 u_2}{m_1+m_2}\)

⇒ \(v_2=\left(\frac{m_2-m_1}{m_1+m_2}\right) u_2+\frac{2 m_1 u_1}{m_1+m_2}\)

If u₂ = 0, then

⇒ \(v_1=\frac{\left(m_1-m_2\right)}{m_1+m_2} u_1\)

⇒ \(v_2=\frac{2 m_1 u_1}{m_1+m_2}\)

Case 1. If mx = m2, then vx = 0 & V2 = %

Case 2. If mx >> m2, then vx = ux & V2 = 2ux

Case3. If mx << m2, then vx = -ux & V2 = 0

Coefficient of Restitution (e)

⇒ \(\mathrm{e}=\frac{\mathrm{v}_2-\mathrm{v}_1}{\mathrm{u}_1-\mathrm{u}_2}=\frac{\text { Relative velocity of separation }}{\text { Relative velocity of appraoch }}\)

For perfectly elastic collision, e = 1

For perfectly inelastic collision, e = 0

For all other collisions, 0 < e < 1

If a ball is dropped from a height ‘h’,

Maximum height attained by the ball decreases progressively due to K.E. loss. After 1 collision the height attained is h1

∴ e = \(=\frac{\sqrt{2 g h_1}}{\sqrt{2 g h}}=\sqrt{\frac{h_1}{h}}\)

⇒ \(\mathrm{e}^2=\frac{\mathrm{h}_1}{\mathrm{~h}}\)

⇒ \(\mathbf{h}_{\mathrm{l}}=\mathrm{he}^{2 \times 1}\)

After 2 collisions,

⇒ \(\mathrm{e}=\frac{\sqrt{2 \mathrm{gh}_2}}{\sqrt{2 \mathrm{gh}_1}}=\sqrt{\frac{\mathrm{h}_2}{\mathrm{~h}_1}}\)

⇒ \(\mathrm{e}^2=\frac{\mathrm{h}_2}{\mathrm{~h}_1}=\frac{\mathrm{h}_2}{\mathrm{he}^2}\)

∴ \(h_2=h^4 \Rightarrow h_2=h e^{2 \times 2}\)

∴ After ‘n’ collisions.

⇒ \(h_n=h e^{2 n}\)

Collision in 2D

According to the law of conservation of linear momentum,

m₁u₁=m₁v₁cosθ+m₂v₂cosΦ

• Vectors Notes
• Units and Measurements Notes
• Motion in a Straight Line Notes Notes
• Motion in a Plane Notes
• Laws of Motion Notes
• Work, Energy and Power Notes
• System of Particles and Rotational Motion Notes
• Gravitation Notes
• Mechanical Properties of Solids Notes
• Mechanical Properties of Fluids Notes
• Thermal Properties of Matter Notes
• Thermodynamics and Kinetic Theory of Gases Notes

• Oscillation Notes
• Waves Notes
• Electric Charges and Fields Notes
• Electrostatic Potential and Capacitance Notes
• Current Electricity Notes
• Moving Charges and Magnetism Notes
• Magnetism and Matter Notes
• Electromagnetic Induction Notes
• Alternating Current Notes
• Electromagnetic Waves Notes
• Ray Optics and Optical Instruments Notes
• Wave Optics Notes
• Dual Nature of Radiation and Matter Notes
• Atoms Notes
• Nuclei Notes
• Semiconductor Electronics Notes
• Communication Systems Notes

Motion In A Straight Line

Distance: The actual length of the path travelled by the particle.

Displacement: Change in position in a particular direction (or the minimum distance between 2 points).

Speed = \(\frac{\text { distance }}{\text { time }}\)

Velocity = \(\frac{\text { displacement }}{\text { time }}\)

Avg. velocity = \(\frac{\text { total displacement }}{\text { total time }}\)

⇒ \(=\frac{x_f-x_i}{t_f-t_i}=\frac{\Delta x}{\Delta t}\)

Where xf is the final position, xi is the initial position, f is the final time and h is the initial time.

Read And Learn More: NEET Physics Notes

Instantaneous Velocity

Limiting value of average velocity is called instantaneous velocity.

⇒ \(\mathrm{v}=\lim _{\Delta \mathrm{t} \rightarrow 0} \frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}=\frac{\mathrm{dv}}{\mathrm{dt}}\)

The slope of the x – t graph is the average velocity.

The slope of the v – t graph is the acceleration

The area under the v – t graph is displacement.

Kinematic equations of motion for a body moving with uniform acceleration

NEET Physics Motion in a Straight Line Important Formulas

v= u +at

x= ut + ½ at²

v² = u² + 2ax

x= \(\left(\frac{\mathrm{u}+\mathrm{v}}{2}\right) \mathrm{t}\)

Sn = \(\mathrm{u}+\frac{\mathrm{a}}{2}(2 \mathrm{n}-1)\)

a= v \(v \frac{d v}{d x}\)

Where, u = initial velocity, v = final velocity, a = acceleration, t = time, x Sn= distance travelled in nth= displacement and second

Calculation of distance travelled in n^th second:

Sn = Distance travelled in ‘n’ seconds – distance travelled in ‘n – 1’ seconds

Sn = Xn- Xn-1

= \(\mathrm{un}+\frac{1}{2} \mathrm{an}^2-\left[\mathrm{u}(\mathrm{n}-1)+\frac{1}{2} \mathrm{a}(\mathrm{n}-1)^2\right]\)

= \(\mathrm{un}+\frac{1}{2} a n^2-\left[\mathrm{un}-\mathrm{u}+\frac{1}{2} a\left(\mathrm{n}^2+1-2 \mathrm{n}\right)\right]\)

= \(\mathrm{un}+\frac{1}{2} \mathrm{an}^2-\left[\mathrm{un}-\mathrm{u}+\frac{1}{2} \mathrm{an}^2+\frac{\mathrm{a}}{2}-\mathrm{an}\right]\)

= \(\mathrm{un}+\frac{1}{2} \mathrm{an}^2-\mathrm{un}+\mathrm{u}-\frac{1}{2} \mathrm{an}^2-\frac{\mathrm{a}}{2}+\text { an }\)

= \(\mathrm{u}+\frac{\mathrm{a}}{2}(2 \mathrm{n}-1)\)

Best Short Notes for Motion in a Straight Line NEET

Note:

x =  \(\mathrm{ut}+\frac{1}{2} \mathrm{at}^2\)

x= \((\mathrm{v}-\mathrm{at}) \mathrm{t}+\frac{1}{2} \mathrm{at}^2\)

x= \(\mathrm{vt}-\mathrm{at}^2+\frac{1}{2} \mathrm{at}^2\)

x= \(\mathrm{vt}-\frac{1}{2} a \mathrm{t}^2\)

[ v= u +at, u= v-at]

(This equation can be used to find displacement (x) if final velocity (v) is known).

If a particle travels half the distance with velocity v₁ and the remaining velocity with v₂, then the average velocity is given by

⇒ \(\bar{v}=\frac{2 v_1 v_2}{v_1+v_2}\)

If a particle travels with the velocity with vx for the first half-time, and the remaining half-time with v2, then the average velocity is given by

⇒ \(\overline{\mathrm{v}}=\frac{\mathrm{v}_1+\mathrm{v}_2}{2}\)

Basci Formulae Of Diffrrentiiation

Motion in a Straight Line NEET Important Questions and Answers

Where ‘a’ is a constant and ‘u’ is a function of ‘x’

Basic Formulae of Integration:

NEET Physics Motion in a Straight Line MCQs with Solutions

Definite integration

⇒ \(\int_a^b f(x) d x=\left.g(x)\right|_a ^b=g(b)-g(a)\)

Illustration:

Suppose f(x) = x2. Determine the value of the definite integral from x = 1 to x = 2.

⇒ \(\int_1^2 x^2 d x=\left[\frac{x^3}{3}\right]_1^2=\frac{8}{3}-\frac{1}{3}=\frac{7}{3}\)

Example:

Example:

The position of an object moving along the x-axis is given by x = a + bt² where a = 8.5 m, b = 2.5 ms^-2 and t is measured in seconds. What is its velocity at t = 0s and t = 2s. What is the average velocity between t = 2s and t = 4s?

Solution: 

Given

The position of an object moving along the x-axis is given by x = a + bt² where a = 8.5 m, b = 2.5 ms^-2 and t is measured in seconds.

Equations of motion for constant acceleration using the method of calculus

Consider a body starts with initial velocity ‘u’ (at t=0) and moves with a constant acceleration ‘a’ and attains a speed v in time ‘t’.w.k.t.,

Sign Convention

“Upward Direction Is Taken + Y–axis”

Graphs of Motion in a Straight Line NEET Notes

Free Fall:

Consider a body dropped from the top of the building at t = 0s (i.e ., u= 0 m/s^-2) and g= – 10 ms^-2)

The ratio of the distance travelled in 1 second, 2 seconds, 3 seconds and so on are in the ratio, x_1s: x_2s: x_3s= 1 : 4 : 9 := 1² : 2² : 3²:

The ratio of the distance travelled in 1^st second, 2^nd second, 3^rd second and so on are in the ratio, x_1n: x_2nd: x_3RD …………= 1:3:9:………(Galileo’s law of odd numbers)

x-t, v-t and a-t graphs in the case of free fall are given below

A car starts from rest and acquires a speed v with uniform acceleration a. Then it comes to stop with uniform retardation β.

NEET Study Material for Motion in a Straight Line Chapter

Distance Travelled in time ‘t’

x= \(x=\frac{1}{2}\left(\frac{\alpha \beta}{\alpha+\beta}\right) t^2\)

If a body is dropped from a height ‘h

The time required for the body to reach the ground is

t= \(\sqrt{\frac{2 \mathrm{~h}}{\mathrm{~g}}}\)

The velocity acquired by the body on reaching the ground is given by

v=  \(\sqrt{2 \mathrm{gh}}\)

Note:

Time of ascent (ta) = Time of descent (t_d)

Time of flight T = t_a + t_d

T= \(\frac{\mathrm{u}}{\mathrm{g}}+\frac{\mathrm{u}}{\mathrm{g}}\)

T= \(\frac{2 \mathrm{u}}{\mathrm{g}}\)

The stopping distance of vehicles moving with constant retardation is given by

⇒ \(D_s=\frac{u^2}{2 a}\)

i.e., the stopping distance is directly proportional to the square of the initial speed.

Laws Of Motion

Aristotle’s Fallacy

An external force is required to keep a body in motion.

Newton’s First Law of Motion

Everybody continues to be in its state of rest or of uniform motion unless compelled by an external force.
Or
If the net external force on a body is zero, its acceleration is zero.

Linear momentum is the product of mass and velocity.

⇒ \(\overrightarrow{\mathrm{p}}=\mathrm{m} \overrightarrow{\mathrm{v}}\)

Newton’s Second Law of Motion

The rate of change of linear momentum of a body is directly proportional to the applied force and takes place in the direction of the applied force.

i.e, \(\overrightarrow{\mathrm{F}} \propto \frac{\mathrm{d} \overrightarrow{\mathrm{p}}}{\mathrm{dt}}\)

⇒ \(\overrightarrow{\mathrm{F}}=\mathrm{k} \frac{\mathrm{d} \overrightarrow{\mathrm{p}}}{\mathrm{dt}}\)

In SI, k = 1

∴ \(\overrightarrow{\mathrm{F}}=\frac{\mathrm{d} \overrightarrow{\mathrm{p}}}{\mathrm{dt}}=\frac{\mathrm{d}}{\mathrm{dt}} \mathrm{m} \overrightarrow{\mathrm{v}}\)

Read And Learn More: NEET Physics Notes

For a body of fixed mass,

⇒ \(\overrightarrow{\mathrm{F}}=\mathrm{m} \frac{\mathrm{d} \overrightarrow{\mathrm{v}}}{\mathrm{dt}}\)

⇒ \(\overrightarrow{\mathrm{F}}\)= m\(\overrightarrow{\mathrm{a}}\)

⇒ ∵ \(\frac{\mathrm{d} \overrightarrow{\mathrm{v}}}{\mathrm{dt}}=\overrightarrow{\mathrm{a}}\)

SI unit of force is Newton (N).

1 newton(1 N) is that force which produces an acceleration of 1ms^-2 in a body of mass 1kg.

Laws of Motion NEET Important Questions with Solutions

Note:

In the equation \(\overrightarrow{\mathrm{F}}\) = \(m \vec{a}\) we see that, if \(\overrightarrow{\mathrm{F}}\) = 0, then \(\overrightarrow{\mathrm{a}}\) = 0,

Newton’s 1st law is a special case of Newton’s 2nd law:

Impulse = Force x time duration

Impulse = change in momentum

Impulse= P_f – P_i= mv – mu (where P_f is the final momentum and P_i is the initial momentum)

Impulse= m(v – u)

Impulse= m(at)

(∴ v = u + at)

Impulse = Ft

Newton’s Third Law

To every action, there is an equal and opposite reaction.

Note:

1. Forces always occur in pairs. Force on a body A by B is equal and opposite to the force on the body B by A.

2. Action and reaction forces act on different bodies, not on the same body According to Newton’s third law

⇒ \(\overrightarrow{\mathrm{F}}_{\mathrm{AB}}=-\overrightarrow{\mathrm{F}}_{\mathrm{BA}}\)

Where,  \(\overrightarrow{\mathrm{F}}_{\mathrm{AB}}\) is the force on A by B and \(\overrightarrow{\mathrm{F}}_{\mathrm{BA}}\) is the force on B by A.

According to law of conservation of momentum,

“The total momentum of an isolated system of interacting particles is conserved.”

A particle is said to be in equilibrium if net external force on a body is zero.

Static friction is directly proportional to normal reaction.

f_s α N

Best Notes for Laws of Motion NEET Preparation

The maximum value of static friction is given by,

(f_s )_max = μ_s N

It is also known as limiting friction.

Where μ_s is called the coefficient of kinetic friction.

Kinetic friction is given by,

(f_k) = μ_k N

Where μ_k called the coefficient of static friction.

The maximum permissible speed of a car rounding on a horizontal circular road is,

⇒ \(\mathrm{v}_{\max }=\sqrt{\mu_{\mathrm{s}} \mathrm{rg}}\)

Maximum permissible speed of a car rounding on a banked road is given by

⇒ \(\mathrm{v}_{\max }=\left[\mathrm{Rg} \frac{\mu_{\mathrm{s}}+\tan \theta}{1-\mu_{\mathrm{s}} \tan \theta}\right]^{\frac{1}{2}}\)

If μ_s = 0 (in the absence of friction)

v_o = \((\mathrm{Rg} \tan \theta)^{\frac{1}{2}}\)

At this optimum speed frictional force is not required to provide centripetal force. If the car moves in this speed wear and tear of the tyres will be less.

Acceleration of a block on a smooth inclined plane:

Normal reaction is given by,

N = mg cos θ

The force responsible for the acceleration of the block is mg sin θ.

i.e F = ma = mg sin θ

Acceleration of a block down a rough inclined plane

Tricks to Solve Laws of Motion Problems for NEET

The force responsible for the acceleration of the block is,

ma =mg sin θ —f

ma = mg sin θ – μ_s N

mg = mg sin θ – μ_smg cos θ

∴ a = g[sin θ  — μ cos θ ]

The motion of blocks in contact

Due to the applied force F the system moves with an acceleration a FBD of A

Where RAB is the reaction force between A & B

(F- R_AB) = m₁a ________________ (1)

FBD of B

Newton’s Laws of Motion NEET MCQs with Answers

R_AB = m₂ a ________________(2)

Substituting in (1) we get

F – m₂a = m₁ a

F= (m₁+m₂)a

a= \(\frac{F}{m_1+m_2}\)

(2) ⇒ R_AB = \(=\frac{\mathrm{m}_2 \mathrm{~F}}{\mathrm{~m}_1+\mathrm{m}_2}\)

If Three masses m_{1 ,} m₂ and m₃ are in contact

a= \(\frac{\mathrm{F}}{\mathrm{m}_1+\mathrm{m}_2+\mathrm{m}_3}\)

R_AB  \(=\frac{\left(\mathrm{m}_2+\mathrm{m}_3\right) \mathrm{F}}{\mathrm{m}_1+\mathrm{m}_2+\mathrm{m}_3}\)

R_BC = \(\frac{m_3 F}{m_1+m_2+m_3}\)

Motion of blocks connected by massless strings:

a= \(\frac{F}{m_1+m_2+m_3}\)

NCERT Summary of Laws of Motion for NEET Physics

⇒ \(\mathrm{a}=\frac{\mathrm{F}}{\mathrm{m}_1+\mathrm{m}_2+\mathrm{m}_2}\)

T₁ = (m₁+m₂)

T₂ = m₁a

Motion of connected blocks over a pulley:

m₁ >m₂

Say m₁ >m₂

Step-by-Step Solutions for Laws of Motion NEET Problems

(1)+(2) ⇒

m₁g – m₂g = (m₁ +m₂)a

⇒ \(\mathrm{a}=\frac{\left(\mathrm{m}_1-\mathrm{m}_2\right) \mathrm{g}}{\mathrm{m}_1+\mathrm{m}_2}\)

Substituting the value of an in (2) we get

Real-Life Applications of Newton’s Laws for NEET

Note: Angle of repose is defined as the angle of the inclined plane with horizontal such that a body placed on it just begins to slide.

μ = tan θ

Where θ  is the angle of repose.

Motion In A Plane

Projectile Motion

A body that is in flight through the atmosphere, but if it is moving only under the influence of gravity, then it is a projectile.

Types of Projectile Motion

1. Oblique projectile
2. Horizontal projectile

Oblique Projectile

NEET Physics Motion in a Plane Important Formulas

1. The equation of the trajectory of the projectile is given by:

⇒ \(y=(\tan \theta) x-\left(\frac{g}{2 u^2 \cos ^2 \theta}\right) x^2\)

The above equation is similar to the equation of a parabola.

y= ax- bx²

i.e trajectroy of a projectile is a parabola

Read And Learn More: NEET Physics Notes

The equation of oblique projectile can also be written as,

⇒ \(y=x \tan \theta\left[1-\frac{x}{R}\right]\)

Whereas, R= \(\frac{\mathrm{u}^2 \sin 2 \theta}{\mathrm{g}}\)

Best Short Notes for Motion in a Plane NEET

2. Velocity of the projectile at any point on its trajectory is given by:

⇒ \(\vec{v}=v_x \hat{i}+v_y \hat{j}\)

⇒\(\mathrm{V}=\sqrt{\mathrm{V}_{\mathrm{x}}^2+\mathrm{V}_{\mathrm{y}}^2}\)

⇒ \(\mathrm{v}_{\mathrm{x}}=\mathrm{u} \cos \theta\)

⇒  \(\mathrm{v}_{\mathrm{y}}=\mathrm{u} \sin \theta-\mathrm{gt}\)

v= \(\sqrt{\left(u^2 \cos ^2 \theta\right)+(u \sin \theta-g t)^2}\)

v= \(\sqrt{u^2+g^2 t^2-2 u g t \sin \theta}\)

The direction of instantaneous velocity is given by, \(\tan \alpha=\frac{v_y}{v_x}\)

Motion in a Plane NEET Important Questions and Answers

3. Change in velocity of the projectile between the point of projection and the highest point is given by:

⇒ \(\Delta \overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{v}}_{\mathrm{f}}-\overrightarrow{\mathrm{v}}_{\mathrm{i}}=-\mathrm{u} \sin \theta \hat{\mathrm{j}}\)

Change in velocity during complete oblique projectile motion is given by

⇒ \(\Delta \overrightarrow{\mathrm{v}}=-2 \mathrm{u} \sin \theta \hat{\mathrm{i}}\)

4. The change in momentum of the projectile between the point of projection and the highest point is:

⇒ \(\Delta \overrightarrow{\mathrm{P}}=\overrightarrow{\mathrm{P}}_{\mathrm{f}}-\overrightarrow{\mathrm{P}}_{\mathrm{i}}=-\mathrm{mu} \sin \theta \hat{\mathrm{j}}\)

The change in momentum of the projectile during complete oblique projectile motion is given by,

⇒ \(\Delta \overrightarrow{\mathrm{P}}=-2 m u \sin \theta \hat{\mathrm{i}}\)

5. Angular momentum of the projectile at the highest point of trajectory about the point of projection is given by:

L = \(m v r\left(r=H=\frac{u^2 \sin ^2 \theta}{2 g}\right)\)

∴  L= \(\mathrm{m}(\mathrm{u} \cos \theta)\left(\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}}\right)\)

∴ L= \(=\frac{m u^3 \cos \theta \sin ^2 \theta}{2 \mathrm{~g}}\)

NEET Physics Motion in a Plane MCQs with Solutions

6.  Time of maximum height:

⇒ \(\mathrm{t}_{\max }=\frac{\mathrm{u} \sin \theta}{\mathrm{g}}\)

7. Time of flight:

⇒ \(\mathrm{T}=2 \mathrm{t}_{\max }=\frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\) Or \(\mathrm{T}=\frac{2 \mathrm{u}_{\mathrm{y}}}{\mathrm{g}}\)

8. Horizontal range:

It is the horizontal distance traveled by the projectile during its flight.

R = (u_x) (T)

R= \((\mathrm{u} \cos \theta) \frac{2 \mathrm{u} \sin \theta}{\mathrm{g}}\)

r = \(\mathrm{R}\frac{\mathrm{u}^2}{\mathrm{~g}} \sin 2 \theta\)

R= \(\frac{2}{\mathrm{~g}}\left(\mathrm{u}_{\mathrm{x}}\right)\left(\mathrm{u}_{\mathrm{y}}\right)\)

Where u_x = u cos θ: u = u_y sin θ

For complementary angles of projection θ and 90 – θ range is the same.
Or
For angles of projection θ₁ =(45 – α) and θ₂ = (45 + α)) range will be the same.

If the angle of projection is 450, the range is maximum.

⇒ \(\mathrm{R}_{\max }=\frac{\mathrm{u}^2}{\mathrm{~g}}\)

9. Maximum height of a projectile is given by:

⇒ \(\mathrm{H}=\frac{\mathrm{u}^2 \sin ^2 \theta}{2 \mathrm{~g}}\)

Or \(\mathrm{H}=\frac{\mathrm{u}_{\mathrm{y}}^2}{2 \mathrm{~g}}\)

⇒ \(\mathrm{H}_{\max }=\frac{\mathrm{u}^2}{2 \mathrm{~g}}\)

Or

⇒  \(\frac{\mathrm{H}}{\mathrm{T}^2}=\frac{\mathrm{g}}{8}\)

Energy of Projectile

When a projectile moves upwards through its trajectory its kinetic energy will decrease and potential energy will increase, but the total energy always remains constant.

Say a body of mass ‘m’ is projected obliquely with the angle of projection ‘0’.

 

At’O’:

⇒ \(\mathrm{K} \cdot \mathrm{E}=\frac{1}{2} \mathrm{mu}^2\)

P.E = 0

Total energy E = ½ mu²

At’A’:

⇒ \(\mathrm{K} \cdot \mathrm{E} .=\frac{1}{2} \mathrm{mu}^2 \cos ^2 \theta\)

P.E = mgh

P.E = \(m g \frac{u^2 \sin ^2 \theta}{2 g}\)

P.E= \(\frac{1}{2} m u^2 \sin ^2 \theta\)

Total energy

E= K.E + P.E = \(=\frac{1}{2} m u^2 \cos ^2 \theta+\frac{1}{2} m u^2 \sin ^2 \theta\)

⇒ \(\mathrm{E}=\frac{1}{2} \mathrm{mu}^2\)

Similarly, at B,

⇒ \(\mathrm{E}=\frac{1}{2} \mathrm{mu}^2\)

Horizontal Projectile

Suppose a body of mass ‘m’ is thrown horizontally with speed ‘u’ from the top of a tower.

The magnitude of velocity at any point on the trajectory is given by,

v= \(\sqrt{v_x^2+v_y^2}\)

Where, v_x = u and v_y = gt, tan \(\frac{v_y}{v_x}=\frac{g t}{u}\)

The time taken by the ball to reach the ground is given by,

⇒ \(t=\sqrt{\frac{2 H}{g}}\)

Projectile Motion and Relative Velocity NEET Notes

Range:

u_x × t

⇒ \(\mathrm{R}=\mathrm{u} \sqrt{\frac{2 \mathrm{H}}{\mathrm{g}}}\)

Riverboat problem

V_br velocity of the boat w.r.to river

V is the velocity of the boat w.r.to ground

u is the velocity of the river

1. To cross the river straight, we should row the boat by making an angle with the upstream where 0 is the angle made by with the shortest distance (which is the width of the river)

⇒ \(\sin \theta=\frac{u}{v_{b r}}\)

The time taken to cross the river is given by

2. To cross the river in the shortest time, we should row the boat perpendicular to the bank. The time taken in this case is,

⇒ \(t_{\min }=\frac{w}{v_{b r}}\)

3. The horizontal distance traveled by the boat w.r.to starting point is,

⇒  \(xu \times t_{\min }\)

NEET Study Material for Motion in a Plane Chapter

Uniform Circular Motion

If a body is moving in a circular path with constant speed then the body is said to be in uniform circular motion.

Expression for centripetal acceleration is given by,

⇒\(a_c=\frac{v^2}{r}\)

Or, \(a_c=\omega^2 r\) (because ω = rω) where co is the angular velocity.

Expression for centripetal force is

⇒ \(F_c=\frac{m v^2}{r}=m \omega^2 r\)

Units And Measurements

A physical quantity can be completely represented by its magnitude and unit.

Physical quantity= magnitude (n) x unit (u)

The magnitude of a physical quantity and units are inversely proportional to each other.

The larger the unit, the smaller will be its magnitude.

i.e., nu = constant, or = n₁u₁ = n₂u₂ = constant

SI units and fundamental quantities NEET

SI System

NEET Physics Units and Measurements notes

Supplementary units

• Radian (rad), is used to measure plane angle.
• Steradian (Sr), used to measure solid angle.

Read And Learn More: NEET Physics Notes

Measurement of Large Distances

Larger distances such as the distance of a planet or a star from the Earth can be calculated using the parallax method

⇒ \(\mathrm{D}=\frac{\mathrm{b}}{\theta}\)

Where, b is the basis and 0 is a parallax angle.

The angular size of the planet can be calculated using the formula.

⇒ \(\alpha=\frac{d}{D}\)

Where ‘d’ is the diameter of the planet and ‘D’ is the distance between the planet and Earth.

Accuracy, precision, and errors in measurement NEET

Absolute error, Relative error, and Percentage error

Suppose a₁, a₂, a₃,….a_n, are the different-measured values of a physical quantity, then mean value or true value is given by,

⇒ \(a_{\text {mean }}=\frac{\left(a_1+a_2+\ldots .+a_n\right)}{n}\)

The magnitude of the difference between the true value and the individual measurement value is called the absolute error of the measurement. Absolute error |Δa| is denoted by meaning

⇒ \(\left|\Delta a_1\right|=a_{\text {mean }}-a_1\)

⇒ \(\left|\Delta a_2\right|=a_{\text {mean }}-a_2\)

⇒ \(\left|\Delta a_n\right|=a_{\text {mean }}-a_n\)

Absolute error |Δa | is always positive.

Significant figures and error analysis NEET

Important formulas in Units and Measurements for NEET

Units And Dimensions

The arithmetic mean of all absolute errors is called the mean absolute error.

Read And Learn More: NEET Physics Notes

⇒ \(\text { i.e., } \Delta a_{\text {mean }}=\frac{\left|\Delta a_1\right|+\left|\Delta a_2\right|+\ldots \ldots+\left|\Delta a_n\right|}{n}\)

Relative Error

The relative error is the ratio of the mean absolute error (Aa^^ )to the mean value (mean) of the quantity.

Relative error \(=\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}}\)

Percentage error = Relative error x 100

⇒ \(\frac{\Delta \mathrm{a}_{\text {mean }}}{\mathrm{a}_{\text {mean }}} \times 100\)

Error of a sum or difference:

Let the physical quantity Z is given by,

⇒ Z = A + B

⇒ Then, ± ΔZ = ± ΔA ± ΔB

When two physical quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.

Error of a product or quotient:

Let the physical quantity Z is given by,

Z = AB Then the maximum relative error is given by,

⇒ \(\frac{\Delta \mathrm{Z}}{\mathrm{Z}}=\frac{\Delta \mathrm{A}}{\mathrm{A}}+\frac{\Delta \mathrm{B}}{\mathrm{B}}\)

When two quantities are multiplied or divided, the relative error in the result is the sum of the relative errors in the multipliers.

Units and Measurements tricks for NEET

Error in case of a measured quantity raised to a power:

Let the physical quantity Z is given by,

⇒ Z= Aⁿ

Then maximum relative error is given by

⇒ \(\frac{\Delta \mathrm{Z}}{\mathrm{Z}}=2 \frac{\Delta \mathrm{A}}{\mathrm{A}}\)

In general if Z = \(\frac{A^x B^Y}{C^Z}\) then,

⇒ \(\frac{\Delta \mathrm{Z}}{\mathrm{Z}}=2 \frac{\Delta \mathrm{A}}{\mathrm{A}}\)

The relative error in a physical quantity raised to the power ‘n’ is n times the relative error in the individual quantity.

Units And Measurement Formula

Significant Figures

• All non-zero digits are significant.
• All the zeros between two non-zero digits are significant, no matter where the decimal point is.
• If the number is less than 1, the zeros on the right of decimal point but to the left of the first non-zero digit are not significant.
• The trailing zeros in a number without a decimal point are not significant.
• The trailing zeros in a number with a decimal point are significant.

Arithmetic operations with significant figures

• In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.
• In addition or subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.

Rounding off the digits

The preceding digit is raised by 1 if the digit to be dropped is more than 5, and is left unchanged if it is less than 5.

Note:

If the digit to be dropped is 5, and if the preceding digit is even, the digit is simply dropped, and if it is odd the preceding digit is raised by 1.

The nature of a physical quantity is represented by its dimensions:

Dimensional analysis NEET questions

• The dimensions of a physical quantity are the powers (or exponents) to which the base quantities are raised to represent that quantity.
• An equation obtained by equating a physical quantity with its dimensional formula is called dimensional equation.

Unit And Dimensions Notes Pdf

Applications Of Dimensional Analysis

• Checking the dimensional consistency of equations.
  • (If an equation is dimensionally wrong, then it is wrong, but it may not be right also. Thus a dimensionally correct equation need not be an exact equation)
• Deducing relation among physical quantities.

Vector

1. A scalar is a physical quantity that has only magnitude but no direction.
   • Example: Distance, Speed, Temperature, energy, Mass, etc.
2. A vector is a physical quantity that has both magnitude and direction.
   • Examples: displacement, velocity, acceleration, weight, force, electric field, etc.

Vectors Classification

(1) Null vector: A vector with zero magnitude and an arbitrary direction is called a null vector.

i.e.  \(\vec{A}+(-\vec{A})=\overrightarrow{0}\)

⇒ \(\vec{A}-\vec{A}=\overrightarrow{0} \text { and }|\overrightarrow{0}|\)

= 0

Since the magnitude of a null vector is zero, its direction cannot be specified.

Read And Learn More: NEET Physics Notes

Properties Of Null Vector

1. \(\vec{A} \times 0=\overrightarrow{0}\)

2. \(\vec{A}+\overrightarrow{0}=\vec{A}\)

3. \(\lambda \overrightarrow{0}=\overrightarrow{0}\)

1. Negative of a vector: A vector is said to be the negative of another vector if their magnitudes are equal but directions are opposite.
2. Equal vectors: Two vectors are considered equal if they have the same magnitude and direction.
3. Unequal vectors: Two vectors are said to be unequal if they have different magnitudes different directions or both.
4. Parallel vectors: Two vectors are said to be parallel if they have the same direction. Their magnitude may or may not be equal. “All equal vectors are parallel but the converse may not be true. ”
5. Antiparallel vectors: Two vectors are said to be anti-parallel if they point in opposite directions. Their magnitudes may or may not be equal.
6. Collinear vectors: Two or more vectors, which are in the same line are known as collinear vectors. A real-life example of collinear vectors is seen in a tug-of-war game. the individual forces applied by the players on the rope represent collinear vectors.
7. Coplanar vectors: Those vectors, that lie in the same plane, are called coplanar vectors.
8. Orthogonal vectors: If two or three vectors are perpendicular to each other, they are known as orthogonal vectors. The best example for orthogonal vectors is the Cartesian coordinate axes.
9. Unit vector: A vector having a magnitude equal to unity but having a specific direction is called a unit vector. To convert any vector into a unit vector, we divide the vector by its magnitude. Generally, a unit vector is represented by an alphabet in lowercase with a cap on it.
10. Co-initial vectors: Vectors that have a common initial point are known as co-initial vectors.

NEET Physics Vector notes

If a is \(\vec{a}\) vector then its unit vector in the direction of \(\vec{a}\) is written as, a (read as a cap’ or ‘a hat’)

∴ \(\hat{a}=\frac{\vec{a}}{|\vec{a}|}\)

Unit vector  \(\hat{a}=\frac{a}{|\vec{a}|}\)

It is a dimensionless quantity.

Multiplication Of A Vector By A Real Number

Multiplying a vector with a positive number X gives a vector whose magnitude is changed by the factor λ but the direction is the same as that of \(\vec{A}\).

For example, if A is multiplied by 2, the resultant vector 2\(\vec{A}\)  is in the same direction as \(\vec{A}\).

Triangle law of vector addition

If two vectors \(\vec{a}\)  and \(\vec{b}\)  are represented by two sides of a triangle in head-to-tail form, the closing side of the triangle taken from the tail of the first to the head of the second represents their vector sum.

From the figure, \(\vec{OA}\)  + \(\vec{AB}= \)  – \(\vec{OB}\)

\(\vec{OB}\)= \(\vec{a}\) +\(\vec{b}\)

Vector addition and subtraction NEET questions

Note:

1. Vector addition is commutative

i.e.,  \(\vec{A}+\vec{B}=\vec{B}+\vec{A}\)

2. Vector addition is associative

⇒ \((\vec{A}+\vec{B})+\vec{C}=\vec{A}+(\vec{B}+\vec{C})\)

Subtraction of vectors can be defined in terms of the addition of vectors:

We can define the difference between two vectors A and B as follows

⇒ \(\vec{A}-\vec{B}=\vec{A}+(-\vec{B})\)

Parallelogram Law Of Vector Addition

If two vectors are represented by two adjacent sides of a parallelogram, then the diagonal of the parallelogram drawn from the common initial point represents their vector sum.

In the below  \(\vec{a} \text { and } \vec{b}\) is drawn with a common initial point and a parallelogram is constructed using these two vectors as adjacent sides of a parallelogram. The diagonal \(\overrightarrow{O C}\) originating from the common initial point is the vector sum \(\vec{a}+\vec{b}\)

Important vector formulas for NEET Physics

Resolution of a vector

The process of splitting a vector into two or more vectors in such a way that their combined effect is the same as that of the given vector.

“The components of a vector in two or three mutually perpendicular directions are called rectangular components”.

Unit vectors along the X, Y, and Z axes of a rectangular coordinate system are denoted by \(\hat{i}, \hat{j}\) and \(\hat{k}\) respectively. Since these are unit vectors we have,

⇒ \(|\hat{i}|=|\hat{j}|=|\hat{k}|\)

= 1

These unit vectors are perpendicular to each other.

Consider a vector \(\vec{A}\) in the XY plane.

Scalar and vector quantities NEET

We draw lines from the head of \(\vec{A}\)  perpendicular to the coordinate axes and we get \(\vec{A}_1 \& \vec{A}_2\)  such that,

⇒ \(\overrightarrow{A_1}+\overrightarrow{A_2}=\vec{A}\)

⇒ \(\vec{A}=A_x \hat{i}+A_y \hat{j}\)

If A and θ are known A_x and A_y can be obtained using

A_x = A cos θ and A_y = A sin θ

If A_x and  A_y are given A and θ can be obtained as follows:

⇒ \(A_x^2+A_y^2=A^2 \cos ^2 \theta+A^2 \sin ^2 \theta\)

⇒ \(A_x^2+A_y^2=A^2\left(\cos ^2 \theta+\sin ^2 \theta\right)\)

A= \(\sqrt{A_x^2+A_y^2}\)

Because Cos² θ + Sin²θ =1  and

tan θ  \(=\frac{A_y}{A_x}\)

θ = tan-1\(\frac{A_y}{A_x}\)

The same procedure can be used to resolve a general vector A into three components along the X, Y, and Z axes in 3-D.

A_x = Acos α. A_y = A cos β & Az = A cos δ

⇒ \(A_x^2+A_y^2+A_z^2A^2=A^2 \cos ^2 \alpha+A^2 \cos ^2 \beta+A^2 \cos ^2 \delta\)

= \(A^2\left(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \delta\right)\)

⇒ \(A_x^2+A_y^2+A_z^2=A^2\)

i.e. A= \(\sqrt{A_x^2+A_y^2+A_z^2}\)

Tricks to solve vector problems for NEET

Vector Addition Analytical Method

⇒ If \(\vec{A}=A_x \hat{i}+A_y \hat{j}\) and \(\vec{B}=B_x \hat{i}+B_y \hat{j}\) are given vectors. Let R be their resultant.

⇒ \(\vec{R}=\vec{A}+\vec{B}=\left(A_x \hat{i}+A_y \hat{j}\right)+\left(B_x \hat{i}+B_y \hat{j}\right)\)

⇒ \(\vec{R}=\left(A_x+B_x\right) \hat{i}+\left(A_y+B_y\right) \hat{j}\)

⇒ \(\vec{R}=R_x \hat{i}+R_y \hat{j}\) where,

⇒ \(R_x=A_x+B_x\) and \(R_y=A_y+B_y\)

In 3-D:

Vector resolution and components NEET

⇒ \(\vec{A}=A_x \hat{i}+A_y \hat{j}+A_z \hat{k}, \vec{B}=B_x \hat{i}+B_y \hat{j}+B_z \hat{k}\)

⇒ \(\vec{R}=\vec{A}+\vec{B}=R_x \hat{i}+R_y \hat{j}+R_z \hat{k}\)

Where, \(R_x=A_x+B_x, R_y=A_y+B_y, R_z=A_z+B_z\)

Magnitude and direction of the resultant of two vectors A and B in terms of their magnitudes and the angle 9 between them.

Dot product and cross product NEET questions

Let OP and OQ represent the two vectors A and B making an angle θ

Using the parallelogram law of vector addition,

⇒ \(\vec{R}=\vec{A}+\vec{B}\)

⇒ \(R^2=A^2+B^2+2 A B \cos \theta\)  (Law of cosines)

⇒ \(R=\sqrt{A^2+B^2+2 A B \cos \theta}\) (This equation gives the magnitude of resultant)

⇒ \(\frac{R}{\sin \theta}=\frac{A}{\sin \beta}=\frac{B}{\sin \alpha}\) (Law of sines )

⇒ \(\tan \alpha=\frac{B \sin \theta}{A+B \cos \theta}\) (This equation gives the direction)

Dot Product (scalar product) of Two Vectors

⇒ \(\vec{a} \cdot \vec{b}=a b \cos \theta\)

Where, \(a=|\vec{a}|, b=|\vec{b}|\) and θ is the angle between \(\vec{a}\) and \(\vec{b}\)

If \(\vec{a} \cdot \vec{b}\)   = 0 then \(\vec{a}\) and \(\vec{b}\) are perpendicular to each other

If θ = 0. then  \(\vec{a} \cdot \vec{b}\)  = ab

⇒ \(\vec{a} \cdot \vec{a}=a^2\)

⇒  \(\hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1 \text { and } \hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0\)

The angle between two vectors \(\vec{a}\) and \(\vec{a}\)  is given by,

\(\cos \theta=\frac{\vec{a} \cdot \vec{b}}{a b}\)= Or

θ = \(\cos ^{-1}\left(\frac{\vec{a} \cdot \vec{b}}{a b}\right)\)

Scalar product is commutative i.e.,\(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)

Projection of a vector a on the other vector \(\vec{a}\) on the vector \(\vec{a}\)  is given by, \(\frac{\vec{a} \cdot \vec{b}}{b}\)

If α,β, and γ are the direction angles of the vector  \(\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}\) then its direction cosines are given by,

⇒  \(\cos \alpha=\frac{a_1}{a}, \cos \beta=\frac{a_2}{a} \text { and } \cos \gamma=\frac{a_3}{a}\)

Cross Product (vector product) Of Two Vectors

\(\vec{a} \times b=a b \sin \theta \hat{n}\) = ab sin \(\hat{n}\)

Where \(\hat{n}\) is a unit vector perpendicular to both \(\vec{a} and \vec{b}\) and  \(\hat{n}\)\(\vec{a} and \vec{b}\)    such that and h form a right-handed system.

⇒ If \(\vec{a} \times \vec{b}\) = 0 then \(\vec{a}\) and \(\vec{a}\)are parallel to each other.

⇒  If \(\theta=\frac{\pi}{2}\) , then \(\vec{a} \times \vec{b}=a b\)

Vector and projectile motion NEET

⇒  \(\hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{0}\)

⇒  \(\hat{i} \times \hat{j}=\hat{k}, \quad \hat{j} \times \hat{k}=\hat{i}, \quad \hat{k} \times \hat{i}=\hat{j}\)

⇒  \(\hat{j} \times \hat{i}=-\hat{k}, \quad \hat{k} \times \hat{j}=-\hat{i}, \quad \hat{i} \times \hat{k}=-\hat{j}\)

Vector Product Is Not Commutative

i.e., \(\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\)

But, \(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)

⇒ If \(\) and b represent the adjacent sides of a triangle then its area is given by

Area = \(\frac{1}{2}|\vec{a} \times \vec{b}|\)

⇒ If  \(\vec{a}\) and \(\vec{b}\) represent the adjacent sides of a parallelogram, then its area is given by

Area = \(|\vec{a} \times \vec{b}|\)

⇒  If \(\vec{a}=a_x \hat{i}+a_y \hat{j}+a_z \hat{k}\)  and \(\vec{b}=b_x \hat{i}+b_y \hat{j}+b_z \hat{k}\) then,

\(\vec{a} \times \vec{b}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\a_1 & a_2 & a_3 \\b_1 & b_2 & b_3\end{array}\right|\)